Annuités. Administration Économique et Sociale. Mathématiques XA100M
|
|
|
- Virginie Monette
- il y a 8 ans
- Total affichages :
Transcription
1 Annuités Administration Économique et Sociale Mathématiques XA100M
2 En général, un prêt n est pas remboursé en une seule fois. Les remboursements sont étalés sur plusieurs périodes. De même, un capital est rarement constitué en un seul versement, mais plus souvent en une succession de versements. Il faut alors savoir calculer les intérêts dans ces cas.
3 Définition 1. On appelle suite d annuités une succession de versements, pour créer ou rembourser un capital.
4 1. CARACTÉRISTIUES D UNE SUITE D ANNUITÉS Une suite d annuités est caractérisée par quatre élements : Sa périodicité ; Le nombre de versements ; Le montant de chaque versement ; La date de chaque versement.
5 1.1. ériodicité d une suite d annuités. La période d une suite d annuités est l intervalle de temps qui sépare deux versements consécutifs. La suite d annuités est certaine si la période est constante, c est-à-dire si le temps qui sépare deux versements est toujours le même. Dans le cas contraire, la suite d annuités est aléatoire.
6 Exemple 1. Vous placez 20 e tous les mois sur un compte-épargne : la suite d annuités est certaine de période mensuelle. Exemple 2. Vous faites un prêt sur un an, vous remboursez une partie après un mois, une partie après trois mois et le reste après un an. La période est de un mois avant le premier versement, de deux mois entre le premier et le deuxième versement et de neuf mois entre le deuxième et le dernier versement. La suite d annuités est aléatoire.
7 1.2. Nombre de versements d une suite d annuités. Le nombre de versements d une suite d annuités peut-être : Fini à échéance connue d avance : la suite d annuités est alors temporaire ; Fini à échéance non connue d avance : la suite d annuités est alors viagière ; Infini : la suite d annuités est alors perpétuelle.
8 1.3. Montant des versements d une suite d annuités. Le montant de chaque versement s appelle le terme. Si les termes sont égaux, c est-à-dire si tous les versements sont de même montant, la suite d annuités est dite constante. Une suite d annuités qui n est pas constante est dite variable.
9 Exemple 3. Vous placez 20 e tous les mois sur un compte-épargne : la suite d annuités est constante de terme 20 e. Exemple 4. Vous placez 10 e le 1 er janvier, 20 e le 1 er février et 30 e le 1 er mars : la suite d annuités est variable. Le premier terme est 10 e, le deuxième terme est 20 e et le dernier terme est 30 e.
10 1.4. Dates des versements d une suite d annuités. Si les versements débutent après la date d origine, la suite d annuités est dite différée. Si les versements débutent dès la première période, la suite d annuités est dite non différée.
11 Exemple 5. Vous empruntez 200 e le 1 er janvier mais vous ne commencez les remboursements qu à partir du 31 mars : la suite d annuités est différée. Exemple 6. Vous empruntez 200 e le 1 er janvier et commencez les remboursements le 31 janvier : la suite d annuités est non différée.
12 Si les versements sont effectués en début de période, la suite d annuités est dite de début de période ou à terme à échoir. Si les versements sont effectués en fin de période, la suite d annuités est dite de fin de période ou à terme échu.
13 Exemple 7. Lorsque vous placez de l argent à la banque, celle-ci ne vous verse les intérêts qu à la fin de l année : la suite d annuités est donc de fin de période.
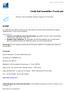
14 2. VALEUR ACUISE D UNE SUITE D ANNUITÉ CERTAINE TEMORAIRE 2.1. Méthode de calcul. endant n périodes, on place en début de période au taux d intérêt i par période les termes suivants A 0 au début de la 1 re période ; A 1 au début de la 2 e période ;. A n au début de la n + 1 e période. période 2 période 1 période 3 période n n 1 n A 0 placé A 1 placé A 2 placé A 3 placé A n placé A n 1 placé
15 La première somme placée, A 0, produit des intérêts pendant n périodes. Elle devient donc (1 + i) n A 0. La deuxième somme placée, A 1, produit des intérêts pendant n 1 périodes. Elle devient donc (1 + i) n 1 A 1. La troisième somme placée, A 2, produit des intérêts pendant n 2 périodes. Elle devient donc (1 + i) n 2 A 2.. La k 1 e somme placée, A k, produit des intérêts pendant n k périodes. Elle devient donc (1 + i) n k A k.. L avant dernière somme placée, A n 1, produit des intérêts pendant 1 période. Elle devient donc (1 + i)a n 1. La dernière somme placée, A n, ne produit pas d intérêt et demeure A n.
16 0 1 2 k 1 k n 1 n A 0 A 1 A 2 A k 1 A k A n 1 A n Valeurs acquises A n (1 + i)a n 1 (1 + i) n k A k (1 + i) n k+1 A k 1 (1 + i) n 2 A 2 (1 + i) n 1 A 1 (1 + i) n A 0
17 La valeur acquise totale est la somme de toutes les valeurs acquises des placements A 0, A 1,..., A n. La valeur acquise totale est donc V n = (1 + i) n A 0 + (1 + i) n 1 A (1 + i) n k A k + + (1 + i)a n 1 + A n. On écrit V n = n (1 + i) n k A k. k=0 our toutes les valeurs de k entre 0 et n, on calcule (1 + i) n k A k puis on fait la somme de toutes les valeurs ainsi obtenues.
18 Exemple 8. Sur trois périodes, on place au taux d intérêt 2% par période 15 e en début de 1 re période ; 20 e en début de 2 e période ; 25 e en début de 3 e période ; 30 e en début de 4 e période. On a alors i = 0,02, n = 3 et A 0 = 15, A 1 = 20, A 2 = 25, A 3 = 30. Le capital, en euros, dont on dispose en début de 4 e période est alors 1, , , =15, , , =92, 23. L intérêt total est 2,23 e.
19 Exemple 9. Sur trois périodes, on place au taux d intérêt 2% par période 30 e en début de 1 re période ; 25 e en début de 2 e période ; 20 e en début de 3 e période ; 15 e en début de 4 e période. On a alors i = 0,02, n = 3 et A 0 = 30, A 1 = 25, A 2 = 20, A 3 = 15. Le capital, en euros, dont on dispose en début de 4 e période est alors 1, , , =31, , , =93, 25. L intérêt total est 3,25 e.
20 On considère une suite d annuités temporaires certaines au taux i par période pendant n périodes. On place A 0 en début de 1 re période, A 1 en début de 2 e période, etc, A n en début de n + 1 e période. La valeur acquise est alors n V n = (1 + i) n k A k. k=0
21 2.2. Cas particulier des suites d annuités constantes Annuités de début de période. Les annuités sont supposées constantes, de terme égal à a. Le versement se fait en début de période et on veut calculer la valeur acquise en fin de n e période. Le versement de début de n + 1 e période n est donc pas pris en compte : A 0 = A 1 = = A n 1 = a et A n = 0.
22 On a alors V n = (1 + i) n k a + 0 n 1 k=0 = a(1 + i) n + a(1 + i) n a(1 + i). On reconnaît la somme des n premiers termes d une suite géométrique de premier terme a(1 + i) et de raison 1 + i. Ainsi V n = a(1 + i) (1 + i)n 1 (1 + i) 1.
23 Les annuités sont supposées constantes, de terme égal à a. Le versement se fait en début de période et on veut calculer la valeur acquise en fin de n e période : V n = a(1 + i) (1 + i)n 1. i
24 Toujours se poser la question :! «Cherche-t on la valeur acquise avant ou après le dernier versement?»
25 Annuités de fin de période. Les annuités sont supposées constantes, de terme égal à a. Le versement se fait en fin de période et on veut calculer la valeur acquise en début de n + 1 e période. Il n y a pas de versement au début de la première période donc A 0 = 0. Tous les autres versements ont pour montant a. A 0 = 0 et A 1 = = A n = a.
26 On a alors n V n = 0 + (1 + i) n k a k=1 = a(1 + i) n 1 + a(1 + i) n a(1 + i) + a. On reconnaît la somme des n premiers termes d une suite géométrique de premier terme a et de raison 1 + i. Ainsi V n = a (1 + i)n 1 (1 + i) 1.
27 Les annuités sont supposées constantes, de terme égal à a. Le versement se fait en fin de période et on veut calculer la valeur acquise en début de n + 1 e période : V n = a (1 + i)n 1. i
28 3. VALEUR ACTUELLE D UNE SUITE D ANNUITÉS CERTAINES TEMORAIRES On rappelle que la valeur actuelle d une somme A k est la somme placée qui, après intérêt, produit A k. La valeur actuelle d une suite d annuités A 0, A 1,...,A n est la somme V 0 qu on peut emprunter pour que la suite d annuités A 0, A 1,...,A n finance l emprunt, intérêt compris. La valeur actuelle d une suite d annuités A 0, A 1,...,A n est la somme V 0 répondant à la question : «uelle somme V 0 puis-je emprunter lors d un emprunt que je rembourse en versant A 0 au début de la 1 re période, A 1 en début de 2 e période, etc, A n en début de n + 1 e période?»
29 3.1. Méthode de calcul. On emprunte V 0 et on rembourse immédiatement A 0. Il reste donc à rembourser V 0 A 0. Cette somme produit un intérêt : si on remboursait juste avant le versement de A 1, il faudrait donc rembourser (V 0 A 0 )(1 + i) = V 0 (1 + i) A 0 (1 + i). Après le versement de A 1, il reste donc à rembourser V 0 (1 + i) A 0 (1 + i) A 1. Cette somme produit un intérêt : si on remboursait juste avant le versement de A 2, il faudrait donc rembourser [V 0 (1 + i) A 0 (1 + i) A 1 ](1 + i) = V 0 (1 + i) 2 A 0 (1 + i) 2 A 1 (1 + i). Après le versement de A 2, il reste donc à rembourser V 0 (1 + i) 2 A 0 (1 + i) 2 A 1 (1 + i) A 2.
30 De façon générale, après le versement de A k 1, il reste à rembourser V 0 (1 + i) k 1 A 0 (1 + i) k 1 A 1 (1 + i) k 2 A k 1. Cette somme produit un intérêt : si on remboursait juste avant le versement de A k, il faudrait donc rembourser [V 0 (1 + i) k 1 A 0 (1 + i) k 1 A 1 (1 + i) k 2 A k 1 ] (1 + i) = V 0 (1 + i) k A 0 (1 + i) k A 1 (1 + i) k 1 A k 1 (1 + i). Après le versement de A k, il reste donc à rembourser V 0 (1 + i) k A 0 (1 + i) k A 1 (1 + i) k 1 A k 1 (1 + i) A k. En particulier, après le versement de A n, il reste à rembourser V 0 (1 + i) n A 0 (1 + i) n A 1 (1 + i) n 1 A n 1 (1 + i) A n.
31 uisque A n est le dernier versement, on veut que la somme qui reste à rembourser après ce versement soit nulle. On veut donc c est-à-dire V 0 (1 + i) n A 0 (1 + i) n A 1 (1 + i) n 1 A n 1 (1 + i) A n = 0 V 0 (1 + i) n = A 0 (1 + i) n + A 1 (1 + i) n A n 1 (1 + i) + A n ou encore V 0 = A 0 + A 1 (1 + i) A n 1 (1 + i) (n 1) + A n (1 + i) n. On écrit V 0 = n (1 + i) k A k. k=0 our toutes les valeurs de k entre 0 et n, on calcule (1 + i) k A k puis on fait la somme de toutes les valeurs ainsi obtenues.
32 Exemple 10. On souhaite emprunter au taux d intérêt 2% par période. On peut rembourser sur trois périodes, 15 e en début de 1 re période ; 20 e en début de 2 e période ; 25 e en début de 3 e période ; 30 e en début de 4 e période. On a alors i = 0,02, n = 3 et A 0 = 15, A 1 = 20, A 2 = 25, A 3 = 30. La somme, en euros, empruntable grâce à ces remboursements est , , , = , , ,2697 =86.91.
33 On considère une suite d annuités temporaires certaines au taux i par période pendant n périodes. On rembourse A 0 en début de 1 re période, A 1 en début de 2 e période, etc, A n en début de n + 1 e période. La somme empruntable (valeur actuelle) est alors V 0 = n (1 + i) k A k. k=0 On se souvient que A 0 est la valeur actuelle de A 0 A 1 (1 + i) 1 est la valeur actuelle de A 1. A k (1 + i) k est la valeur actuelle de A k. A n (1 + i) n est la valeur actuelle de A n. La valeur actuelle est donc la somme des valeurs actuelles de chaque remboursements.
34 Valeurs actuelles A 0 A 1 (1 + i) 1 A 2 (1 + i) k 1 k n 1 n A 0 A 1 A 2 A k 1 A k A n 1 A n A k 1 (1 + i) (k 1) A k (1 + i) k A n 1 (1 + i) (n 1) A n (1 + i) n
35 3.2. Cas particulier des suites d annuités constantes Annuités de début de période. Comme au 2.2.1, on a A 0 = = A n 1 = a et A n = 0. On a alors V 0 = (1 + i) k a + 0 n 1 k=0 = a + a(1 + i) a(1 + i) (n 1). On reconnaît la somme des n premiers termes d une suite géométrique de premier terme a et de raison (1 + i) 1. Ainsi On simplifie en utilisant V 0 = a (1 + i) n 1 (1 + i) 1 1. (1 + i) n 1 (1 + i) 1 1 (1 + i) n = (1 + i)1. i
36 Les annuités sont supposées constantes, de terme égal à a. Le versement se fait en début de période et on veut calculer la valeur actuelle en fin de n e période : La valeur actuelle est alors 1 (1 + i) n V 0 = a(1 + i). i
37 Annuités de fin de période. Comme au 2.2.2, on a On a alors V 0 = 0 + A 0 = 0 et A 1 = = A n = a. n (1 + i) k a k=1 = a(1 + i) 1 + a(1 + i) a(1 + i) (n 1) + a(1 + i) n. On reconnaît la somme des n premiers termes d une suite géométrique de premier terme a(1 + i) 1 et de raison (1 + i) 1. Ainsi On simplifie en utilisant V 0 = a(1 + i) 1(1 + i) n 1 (1 + i) 1 1. (1 + i) n 1 (1 + i) 1 1 (1 + i) n = (1 + i)1. i
38 Les annuités sont supposées constantes, de terme égal à a. Le versement se fait en fin de période et on veut calculer la valeur actuelle en début de n + 1 e période : 1 (1 + i) n V 0 = a. i
Les emprunts indivis. Administration Économique et Sociale. Mathématiques XA100M
 Les emprunts indivis Administration Économique et Sociale Mathématiques XA100M Les emprunts indivis sont les emprunts faits auprès d un seul prêteur. On va étudier le cas où le prêteur met à disposition
Les emprunts indivis Administration Économique et Sociale Mathématiques XA100M Les emprunts indivis sont les emprunts faits auprès d un seul prêteur. On va étudier le cas où le prêteur met à disposition
Mathématiques financières
 Mathématique financière à court terme I) Les Intérêts : Intérêts simples Mathématiques financières - Intérêts terme échu et terme à échoir - Taux terme échu i u équivalent à un taux terme à échoir i r
Mathématique financière à court terme I) Les Intérêts : Intérêts simples Mathématiques financières - Intérêts terme échu et terme à échoir - Taux terme échu i u équivalent à un taux terme à échoir i r
Intérêts. Administration Économique et Sociale. Mathématiques XA100M
 Intérêts Administration Économique et Sociale Mathématiques XA100M 1. LA NOTION D INTÉRÊT 1.1. Définition. Définition 1. L intérêt est la rémunération d un prêt d argent effectué par un agent économique
Intérêts Administration Économique et Sociale Mathématiques XA100M 1. LA NOTION D INTÉRÊT 1.1. Définition. Définition 1. L intérêt est la rémunération d un prêt d argent effectué par un agent économique
15/02/2009. Le calcul des intérêts. Le calcul des intérêts. Le calcul des intérêts Les intérêts simples. Le calcul des intérêts Les intérêts simples
 Le taux d intérêt Comparer ce qui est comparable 2 Chapitre 1 La valeur du temps Aide-mémoire - 2009 1 Deux sommes de même montant ne sont équivalentes que si elles sont considérées à une même date. Un
Le taux d intérêt Comparer ce qui est comparable 2 Chapitre 1 La valeur du temps Aide-mémoire - 2009 1 Deux sommes de même montant ne sont équivalentes que si elles sont considérées à une même date. Un
MATHÉMATIQUES FINANCIÈRES
 MATHÉMATIQUES FINANCIÈRES Table des matières Version 2012 Lang Fred 1 Intérêts et taux 2 1.1 Définitions et notations................................ 2 1.2 Intérêt simple......................................
MATHÉMATIQUES FINANCIÈRES Table des matières Version 2012 Lang Fred 1 Intérêts et taux 2 1.1 Définitions et notations................................ 2 1.2 Intérêt simple......................................
Chapitre 5. Calculs financiers. 5.1 Introduction - notations
 Chapitre 5 Calculs financiers 5.1 Introduction - notations Sur un marché économique, des acteurs peuvent prêter ou emprunter un capital (une somme d argent) en contrepartie de quoi ils perçoivent ou respectivement
Chapitre 5 Calculs financiers 5.1 Introduction - notations Sur un marché économique, des acteurs peuvent prêter ou emprunter un capital (une somme d argent) en contrepartie de quoi ils perçoivent ou respectivement
Plan. 5 Actualisation. 7 Investissement. 2 Calcul du taux d intérêt 3 Taux équivalent 4 Placement à versements fixes.
 Plan Intérêts 1 Intérêts 2 3 4 5 6 7 Retour au menu général Intérêts On place un capital C 0 à intérêts simples de t% par an : chaque année une somme fixe s ajoute au capital ; cette somme est calculée
Plan Intérêts 1 Intérêts 2 3 4 5 6 7 Retour au menu général Intérêts On place un capital C 0 à intérêts simples de t% par an : chaque année une somme fixe s ajoute au capital ; cette somme est calculée
MATHÉMATIQUES FINANCIÈRES I
 MATHÉMATIQUES FINANCIÈRES I Quinzième cours Détermination des valeurs actuelle et accumulée d une annuité de début de période pour laquelle la période de paiement est plus courte que la période de capitalisation
MATHÉMATIQUES FINANCIÈRES I Quinzième cours Détermination des valeurs actuelle et accumulée d une annuité de début de période pour laquelle la période de paiement est plus courte que la période de capitalisation
LISTE D EXERCICES 2 (à la maison)
 Université de Lorraine Faculté des Sciences et Technologies MASTER 2 IMOI, parcours AD et MF Année 2013/2014 Ecole des Mines de Nancy LISTE D EXERCICES 2 (à la maison) 2.1 Un particulier place 500 euros
Université de Lorraine Faculté des Sciences et Technologies MASTER 2 IMOI, parcours AD et MF Année 2013/2014 Ecole des Mines de Nancy LISTE D EXERCICES 2 (à la maison) 2.1 Un particulier place 500 euros
GUIDE PRATIQUE déplacements professionnels temporaires en France et à l étranger
 GUIDE PRATIQUE déplacements professionnels temporaires en France et à l étranger SOMMAIRE GUIDE PRATIQUE déplacements professionnels temporaires en France et à l étranger o o o o o o o o o o o o
GUIDE PRATIQUE déplacements professionnels temporaires en France et à l étranger SOMMAIRE GUIDE PRATIQUE déplacements professionnels temporaires en France et à l étranger o o o o o o o o o o o o
Fiche mathématiques financières
 Fiche mathématiques financières Thème 1 : Les taux d'intérêts simples et composés Taux d'intérêts simples : Les taux d'intérêts simples sont appliqués dans le cas d'emprunts dont la durée est inférieure
Fiche mathématiques financières Thème 1 : Les taux d'intérêts simples et composés Taux d'intérêts simples : Les taux d'intérêts simples sont appliqués dans le cas d'emprunts dont la durée est inférieure
ANNUITES. Les annuités définissent une suite de versements identiques ou non effectués à intervalles de temps égaux. -annuités non constantes
 ANNUITES I Notions d annuités a.définition Les annuités définissent une suite de versements identiques ou non effectués à intervalles de temps égaux. Le processus de versements dépend du montant de l annuité,
ANNUITES I Notions d annuités a.définition Les annuités définissent une suite de versements identiques ou non effectués à intervalles de temps égaux. Le processus de versements dépend du montant de l annuité,
Chapitre 4 - La valeur de l argent dans le temps et l'actualisation des cash-flows
 Chapitre 4 - La valeur de l argent dans le temps et l'actualisation des cash-flows Plan Actualisation et capitalisation Calculs sur le taux d intérêt et la période Modalités de calcul des taux d intérêts
Chapitre 4 - La valeur de l argent dans le temps et l'actualisation des cash-flows Plan Actualisation et capitalisation Calculs sur le taux d intérêt et la période Modalités de calcul des taux d intérêts
L'INTÉRÊT COMPOSÉ. 2.1 Généralités. 2.2 Taux
 L'INTÉRÊT COMPOSÉ 2.1 Généralités Un capital est placé à intérêts composés lorsque les produits pendant la période sont ajoutés au capital pour constituer un nouveau capital qui, à son tour, portera intérêt.
L'INTÉRÊT COMPOSÉ 2.1 Généralités Un capital est placé à intérêts composés lorsque les produits pendant la période sont ajoutés au capital pour constituer un nouveau capital qui, à son tour, portera intérêt.
EMPRUNT INDIVIS. alors : a = III. Comment établir un tableau de remboursement d emprunt à amortissements constants?
 EMPRUNT INDIVIS Objectifs : - Savoir calculer une annuité de remboursement constante ; - Dresser un tableau d amortissement d emprunt par annuités constantes ou par amortissements constants ; - Calculer
EMPRUNT INDIVIS Objectifs : - Savoir calculer une annuité de remboursement constante ; - Dresser un tableau d amortissement d emprunt par annuités constantes ou par amortissements constants ; - Calculer
TAUX FIXE, TAUX INDEXE
 Catégories d emprunts Mobiliser un emprunt, c est essentiellement choisir un taux, une durée, un profil d amortissement et une périodicité. Nous décrivons ci-dessous les différentes modalités qui s offrent
Catégories d emprunts Mobiliser un emprunt, c est essentiellement choisir un taux, une durée, un profil d amortissement et une périodicité. Nous décrivons ci-dessous les différentes modalités qui s offrent
Apllication au calcul financier
 Apllication au calcul financier Hervé Hocquard Université de Bordeaux, France 1 er novembre 2011 Intérêts Généralités L intérêt est la rémunération du placement d argent. Il dépend : du taux d intérêts
Apllication au calcul financier Hervé Hocquard Université de Bordeaux, France 1 er novembre 2011 Intérêts Généralités L intérêt est la rémunération du placement d argent. Il dépend : du taux d intérêts
Emprunts indivis (amortissement)
 1. Amortissement constant : a) Activité : Une entreprise souhaite renouveler son parc informatique. Elle estime qu elle doit dépenser 5 000 ; elle emprunte cette somme au taux de 5 % annuel le 1 er janvier
1. Amortissement constant : a) Activité : Une entreprise souhaite renouveler son parc informatique. Elle estime qu elle doit dépenser 5 000 ; elle emprunte cette somme au taux de 5 % annuel le 1 er janvier
Mathématiques financières
 Mathématiques financières Table des matières 1 Intérêt simple 1 1.1 Exercices........................................ 1 2 Intérêt composé 2 2.1 Taux nominal, taux périodique, taux réel.......................
Mathématiques financières Table des matières 1 Intérêt simple 1 1.1 Exercices........................................ 1 2 Intérêt composé 2 2.1 Taux nominal, taux périodique, taux réel.......................
Amortissement annuité 1 180 000 14 400 12 425,31 26 825,31 2. 2) Indiquer ce que sera la deuxième ligne du tableau en justifiant chacun des résultats.
 EXERCICES SUR LES EMPRUNTS INDIVIS Exercice 1 Pour financer l extension de son magasin, un responsable a contracté un emprunt remboursable, intérêts compris, sur 10 ans par annuités constantes. Voici le
EXERCICES SUR LES EMPRUNTS INDIVIS Exercice 1 Pour financer l extension de son magasin, un responsable a contracté un emprunt remboursable, intérêts compris, sur 10 ans par annuités constantes. Voici le
Taux d intérêts simples
 Taux d intérêts simples Les caractéristiques : - < à 1 ans - Rémunération calculée uniquement sur investissement initial. Période de préférence = période sur laquelle on définit le taux de l opération
Taux d intérêts simples Les caractéristiques : - < à 1 ans - Rémunération calculée uniquement sur investissement initial. Période de préférence = période sur laquelle on définit le taux de l opération
Table des matières. Avant-propos. Chapitre 2 L actualisation... 21. Chapitre 1 L intérêt... 1. Chapitre 3 Les annuités... 33 III. Entraînement...
 III Table des matières Avant-propos Remerciements................................. Les auteurs..................................... Chapitre 1 L intérêt............................. 1 1. Mise en situation...........................
III Table des matières Avant-propos Remerciements................................. Les auteurs..................................... Chapitre 1 L intérêt............................. 1 1. Mise en situation...........................
Table des matières. I Mise à niveau 11. Préface
 Table des matières Préface v I Mise à niveau 11 1 Bases du calcul commercial 13 1.1 Alphabet grec...................................... 13 1.2 Symboles mathématiques............................... 14 1.3
Table des matières Préface v I Mise à niveau 11 1 Bases du calcul commercial 13 1.1 Alphabet grec...................................... 13 1.2 Symboles mathématiques............................... 14 1.3
GEOSI. Les intérêts et les Emprunts
 GEOSI Les intérêts et les Emprunts 1.Définition Lorsque qu une personne (prêteur) prête une somme à une autre personne (emprunteur) il est généralement convenu de rembourser, à l échéance, cet emprunt
GEOSI Les intérêts et les Emprunts 1.Définition Lorsque qu une personne (prêteur) prête une somme à une autre personne (emprunteur) il est généralement convenu de rembourser, à l échéance, cet emprunt
Compte bancaire ou assurance vie? 5. Amortissement direct ou indirect?
 92 LE GUIDE FINANCIER DU PROPRIÉTAIRE Compte bancaire ou assurance vie? La décision de prendre un compte bancaire dépendra du profil du client et de ses besoins. Par exemple, si l emprunteur est célibataire
92 LE GUIDE FINANCIER DU PROPRIÉTAIRE Compte bancaire ou assurance vie? La décision de prendre un compte bancaire dépendra du profil du client et de ses besoins. Par exemple, si l emprunteur est célibataire
La maison Ecole d ' Amortissement d un emprunt Classe de terminale ES. Ce qui est demandé. Les étapes du travail
 La maison Ecole d ' Amortissement d un emprunt Classe de terminale ES Suites géométriques, fonction exponentielle Copyright c 2004 J.- M. Boucart GNU Free Documentation Licence L objectif de cet exercice
La maison Ecole d ' Amortissement d un emprunt Classe de terminale ES Suites géométriques, fonction exponentielle Copyright c 2004 J.- M. Boucart GNU Free Documentation Licence L objectif de cet exercice
Mathématiques financières
 Ecole Nationale de Commerce et de Gestion de Kénitra Mathématiques financières Enseignant: Mr. Bouasabah Mohammed ) بوعصابة محمد ( ECOLE NATIONALE DE COMMERCE ET DE GESTION -KENITRA- Année universitaire:
Ecole Nationale de Commerce et de Gestion de Kénitra Mathématiques financières Enseignant: Mr. Bouasabah Mohammed ) بوعصابة محمد ( ECOLE NATIONALE DE COMMERCE ET DE GESTION -KENITRA- Année universitaire:
LES INFORMATIONS GÉNÉRALES
 GUIDE D UTILISATION Calculatrice Texas Instrument BA II Plus Avril 2007 LES INFORMATIONS GÉNÉRALES La calculatrice financière Texas Instrument BA II Plus a été conçue pour satisfaire aux diverses applications
GUIDE D UTILISATION Calculatrice Texas Instrument BA II Plus Avril 2007 LES INFORMATIONS GÉNÉRALES La calculatrice financière Texas Instrument BA II Plus a été conçue pour satisfaire aux diverses applications
0DWKpPDWLTXHVGHO DUJHQW. édité par Mr. G.Moumoulidis (OTE)
 3/$,78'RF) 0DWKpPDWTXHVGHO DUJHQW HW OHVpWXGHVWHFKQTXHVpFRQRPTXHV édité par Mr. G.Moumoulidis (OTE) 8,2,7(5$7,2$/('(67(/(&2008,&$7,26,7(5$7,2$/7(/(&2008,&$7,28,2 8,2,7(5$&,2$/'(7(/(&208,&$&,2(6 - - 0DWKpPDWTXHVGHO
3/$,78'RF) 0DWKpPDWTXHVGHO DUJHQW HW OHVpWXGHVWHFKQTXHVpFRQRPTXHV édité par Mr. G.Moumoulidis (OTE) 8,2,7(5$7,2$/('(67(/(&2008,&$7,26,7(5$7,2$/7(/(&2008,&$7,28,2 8,2,7(5$&,2$/'(7(/(&208,&$&,2(6 - - 0DWKpPDWTXHVGHO
L emprunt indivis - généralités
 L emprunt indivis - généralités Les modalités de calcul d un échéancier de remboursement d un emprunt indivis forment un thème d étude des outils de gestion en BTS HR (partie mathématiques financières)
L emprunt indivis - généralités Les modalités de calcul d un échéancier de remboursement d un emprunt indivis forment un thème d étude des outils de gestion en BTS HR (partie mathématiques financières)
TP1 Méthodes de Monte Carlo et techniques de réduction de variance, application au pricing d options
 Université de Lorraine Modélisation Stochastique Master 2 IMOI 2014-2015 TP1 Méthodes de Monte Carlo et techniques de réduction de variance, application au pricing d options 1 Les options Le but de ce
Université de Lorraine Modélisation Stochastique Master 2 IMOI 2014-2015 TP1 Méthodes de Monte Carlo et techniques de réduction de variance, application au pricing d options 1 Les options Le but de ce
3 Financement et emprunts
 C. Terrier 1 / 6 12/12/2013 Cours Mathématiques financières Auteur : C. Terrier ; mailto:webmaster@cterrier.com ; http://www.cterrier.com Utilisation : Reproduction libre pour des formateurs dans un cadre
C. Terrier 1 / 6 12/12/2013 Cours Mathématiques financières Auteur : C. Terrier ; mailto:webmaster@cterrier.com ; http://www.cterrier.com Utilisation : Reproduction libre pour des formateurs dans un cadre
Prêt hypothécaire. Programme de financement intégré Caméléon. Financez vos projets à la valeur de votre propriété
 Prêt hypothécaire Programme de financement intégré Caméléon Financez vos projets à la valeur de votre propriété 2 Programme de financement intégré Caméléon Profiter de la valeur nette accumulée de votre
Prêt hypothécaire Programme de financement intégré Caméléon Financez vos projets à la valeur de votre propriété 2 Programme de financement intégré Caméléon Profiter de la valeur nette accumulée de votre
Chapitre 4 : cas Transversaux. Cas d Emprunts
 Chapitre 4 : cas Transversaux Cas d Emprunts Échéanciers, capital restant dû, renégociation d un emprunt - Cas E1 Afin de financer l achat de son appartement, un particulier souscrit un prêt auprès de
Chapitre 4 : cas Transversaux Cas d Emprunts Échéanciers, capital restant dû, renégociation d un emprunt - Cas E1 Afin de financer l achat de son appartement, un particulier souscrit un prêt auprès de
CHAPITRE 1. Suites arithmetiques et géometriques. Rappel 1. On appelle suite réelle une application de
 HAPITRE 1 Suites arithmetiques et géometriques Rappel 1 On appelle suite réelle une application de dans, soit est-à-dire pour une valeur de la variable appartenant à la suite prend la valeur, ie : On notera
HAPITRE 1 Suites arithmetiques et géometriques Rappel 1 On appelle suite réelle une application de dans, soit est-à-dire pour une valeur de la variable appartenant à la suite prend la valeur, ie : On notera
Compte bancaire ou assurance vie?
 92 LE GUIDE FINANCIER DU PROPRIÉTAIRE Compte bancaire ou assurance vie? La décision de prendre un compte bancaire ou une assurance vie mixte dépendra du profil du client et de ses besoins en couverture
92 LE GUIDE FINANCIER DU PROPRIÉTAIRE Compte bancaire ou assurance vie? La décision de prendre un compte bancaire ou une assurance vie mixte dépendra du profil du client et de ses besoins en couverture
Utilisation des fonctions financières d Excel
 Utilisation des fonctions financières d Excel TABLE DES MATIÈRES Page 1. Calcul de la valeur acquise par la formule des intérêts simples... 4 2. Calcul de la valeur actuelle par la formule des intérêts
Utilisation des fonctions financières d Excel TABLE DES MATIÈRES Page 1. Calcul de la valeur acquise par la formule des intérêts simples... 4 2. Calcul de la valeur actuelle par la formule des intérêts
Les mathématiques financières
 Chapitre 13 Les mathématiques financières Gérer ses finances personnelles ou jouer le rôle de conseiller dans ce domaine demande que l on ait une bonne connaissance des produits financiers et des marchés
Chapitre 13 Les mathématiques financières Gérer ses finances personnelles ou jouer le rôle de conseiller dans ce domaine demande que l on ait une bonne connaissance des produits financiers et des marchés
REGLEMENT MUTUALISTE N 7 Branche n 20 Art L 221-2-II du code de la mutualité
 REGLEMENT MUTUALISTE N 7 Branche n 20 Art L 221-2-II du code de la mutualité Garantie EPARGNE (fiscalité assurance-vie ou P.E.P. sur option) à souscription individuelle Article 1 Objet La présente garantie
REGLEMENT MUTUALISTE N 7 Branche n 20 Art L 221-2-II du code de la mutualité Garantie EPARGNE (fiscalité assurance-vie ou P.E.P. sur option) à souscription individuelle Article 1 Objet La présente garantie
Options de 10, 15 et 20 ans
 Options de 10, 15 et 20 ans Simplifiez-vous la vie. Planifiez votre avenir avec des garanties. A s s u r a n c e V i e u n i v e r s e l l e d e l a G r e at- W e s t Coût de l assurance à versements déter
Options de 10, 15 et 20 ans Simplifiez-vous la vie. Planifiez votre avenir avec des garanties. A s s u r a n c e V i e u n i v e r s e l l e d e l a G r e at- W e s t Coût de l assurance à versements déter
Éléments de calcul actuariel
 Éléments de calcul actuariel Master Gestion de Portefeuille ESA Paris XII Jacques Printems printems@univ-paris2.fr 3 novembre 27 Valeur-temps de l argent Deux types de décisions duales l une de l autre
Éléments de calcul actuariel Master Gestion de Portefeuille ESA Paris XII Jacques Printems printems@univ-paris2.fr 3 novembre 27 Valeur-temps de l argent Deux types de décisions duales l une de l autre
Propriétés des options sur actions
 Propriétés des options sur actions Bornes supérieure et inférieure du premium / Parité call put 1 / 1 Taux d intérêt, capitalisation, actualisation Taux d intéret composés Du point de vue de l investisseur,
Propriétés des options sur actions Bornes supérieure et inférieure du premium / Parité call put 1 / 1 Taux d intérêt, capitalisation, actualisation Taux d intéret composés Du point de vue de l investisseur,
SOMMAIRE OPÉRATIONS COURANTES OPÉRATIONS D INVENTAIRE
 SOMMAIRE OPÉRATIONS COURANTES OPÉRATIONS D INVENTAIRE 1 Factures de doit p. 9 Processus 1 2 Réductions sur factures de doit p. 11 Processus 1 3 Frais accessoires sur factures p. 13 Processus 1 4 Comptabilisation
SOMMAIRE OPÉRATIONS COURANTES OPÉRATIONS D INVENTAIRE 1 Factures de doit p. 9 Processus 1 2 Réductions sur factures de doit p. 11 Processus 1 3 Frais accessoires sur factures p. 13 Processus 1 4 Comptabilisation
Licence 2 Mathématiques- Semestre 3 Introduction aux mathématiques
 Licence 2 Mathématiques- Semestre 3 Introduction aux mathématiques financières Année universitaire 2010-11 1 Version Septembre 2010 1 Responsable du cours: Marie-Amélie Morlais 2 0.1 Plan sommaire du cours
Licence 2 Mathématiques- Semestre 3 Introduction aux mathématiques financières Année universitaire 2010-11 1 Version Septembre 2010 1 Responsable du cours: Marie-Amélie Morlais 2 0.1 Plan sommaire du cours
Principe d optimisation. Optimisation technico-économique. Coût. Isolation thermique. Isolation optimale
 Optimisation technico-économique Objectif : obtenir une certaine prestation à moindre coût Dans le domaine du bâtiment, cette optimisation peut s appliquer à trois niveaux différents : choix des composants
Optimisation technico-économique Objectif : obtenir une certaine prestation à moindre coût Dans le domaine du bâtiment, cette optimisation peut s appliquer à trois niveaux différents : choix des composants
EVALUER LE JUSTE PRIX D UN CABINET
 EVALUER LE JUSTE PRIX D UN CABINET La notion de «fonds libéral», instituée par la Cour de Cassation il y a quelques années simplifie juridiquement la cession des cabinets libéraux. Auparavant, les juristes
EVALUER LE JUSTE PRIX D UN CABINET La notion de «fonds libéral», instituée par la Cour de Cassation il y a quelques années simplifie juridiquement la cession des cabinets libéraux. Auparavant, les juristes
Chapitre 1. L intérêt. 2. Concept d intérêt. 1. Mise en situation. Au terme de ce chapitre, vous serez en mesure de :
 Chapitre 1 L intérêt Au terme de ce chapitre, vous serez en mesure de : 1. Comprendre la notion générale d intérêt. 2. Distinguer la capitalisation à intérêt simple et à intérêt composé. 3. Calculer la
Chapitre 1 L intérêt Au terme de ce chapitre, vous serez en mesure de : 1. Comprendre la notion générale d intérêt. 2. Distinguer la capitalisation à intérêt simple et à intérêt composé. 3. Calculer la
BACCALAURÉAT PROFESSIONNEL SUJET
 SESSION 203 Métropole - Réunion - Mayotte BACCALAURÉAT PROFESSIONNEL ÉPREUVE E4 CULTURE SCIENTIFIQUE ET TECHNOLOGIQUE : MATHÉMATIQUES Toutes options Durée : 2 heures Matériel(s) et document(s) autorisé(s)
SESSION 203 Métropole - Réunion - Mayotte BACCALAURÉAT PROFESSIONNEL ÉPREUVE E4 CULTURE SCIENTIFIQUE ET TECHNOLOGIQUE : MATHÉMATIQUES Toutes options Durée : 2 heures Matériel(s) et document(s) autorisé(s)
Chapitre 2. Valeur temps de l argent : arbitrage, actualisation et capitalisation
 Fondements de Finance Chapitre 2. Valeur temps de l argent : arbitrage, actualisation et capitalisation Cours proposé par Fahmi Ben Abdelkader Version étudiants Février 2012 1 Préambule «Time is money»
Fondements de Finance Chapitre 2. Valeur temps de l argent : arbitrage, actualisation et capitalisation Cours proposé par Fahmi Ben Abdelkader Version étudiants Février 2012 1 Préambule «Time is money»
Bloc 1 Sens des nombres et des opérations (+- 6 cours)
 Bloc 1 Sens des nombres et des opérations (+- 6 cours) 1 Démontrer une compréhension du concept du nombre et l utiliser pour décrire des quantités du monde réel. (~6 cours) RÉSULTATS D APPRENTISSAGE SPÉCIFIQUES
Bloc 1 Sens des nombres et des opérations (+- 6 cours) 1 Démontrer une compréhension du concept du nombre et l utiliser pour décrire des quantités du monde réel. (~6 cours) RÉSULTATS D APPRENTISSAGE SPÉCIFIQUES
COURS GESTION FINANCIERE A COURT TERME SEANCE 4 LE VOCABULAIRE BANCAIRE ET FINANCIER
 COURS GESTION FINANCIERE A COURT TERME SEANCE 4 LE VOCABULAIRE BANCAIRE ET FINANCIER SEANCE 4 LE VOCABULAIRE BANCAIRE ET FINANCIER Objet de la séance 4: définir les termes techniques utilisés par le trésorier
COURS GESTION FINANCIERE A COURT TERME SEANCE 4 LE VOCABULAIRE BANCAIRE ET FINANCIER SEANCE 4 LE VOCABULAIRE BANCAIRE ET FINANCIER Objet de la séance 4: définir les termes techniques utilisés par le trésorier
EMPRUNTS OBLIGATAIRES EMIS PAR LES SOCIETES. Conséquences du financement par emprunt obligataire dans le tableau de financement de l'entreprise.
 EMPRUNTS OBLIGATAIRES EMIS PAR LES SOCIETES Objectif(s) : o Pré-requis : Conséquences du financement par emprunt obligataire dans le tableau de financement de l'entreprise. o Outils de mathématiques financières
EMPRUNTS OBLIGATAIRES EMIS PAR LES SOCIETES Objectif(s) : o Pré-requis : Conséquences du financement par emprunt obligataire dans le tableau de financement de l'entreprise. o Outils de mathématiques financières
Suites numériques 4. 1 Autres recettes pour calculer les limites
 Suites numériques 4 1 Autres recettes pour calculer les limites La propriété suivante permet de calculer certaines limites comme on verra dans les exemples qui suivent. Propriété 1. Si u n l et fx) est
Suites numériques 4 1 Autres recettes pour calculer les limites La propriété suivante permet de calculer certaines limites comme on verra dans les exemples qui suivent. Propriété 1. Si u n l et fx) est
ECGE1314 - Finance d entrepise Scéance 2 : évaluation d actifs Professor : Philippe Grégoire Assistant : J.Clarinval
 ECGE1314 - Finance d entrepise Scéance 2 : évaluation d actifs Professor : Philippe Grégoire Assistant : J.Clarinval Exercice 1 : Vous achetez une voiture 30.000 euros et vous empruntez ce montant sur
ECGE1314 - Finance d entrepise Scéance 2 : évaluation d actifs Professor : Philippe Grégoire Assistant : J.Clarinval Exercice 1 : Vous achetez une voiture 30.000 euros et vous empruntez ce montant sur
CORRIGES DES CAS TRANSVERSAUX. Corrigés des cas : Emprunts
 CORRIGES DES CAS TRANSVERSAUX Corrigés des cas : Emprunts Remboursement par versements périodiques constants - Cas E1 Objectifs : Construire un échéancier et en changer la périodicité, Renégocier un emprunt.
CORRIGES DES CAS TRANSVERSAUX Corrigés des cas : Emprunts Remboursement par versements périodiques constants - Cas E1 Objectifs : Construire un échéancier et en changer la périodicité, Renégocier un emprunt.
EXERCICES - ANALYSE GÉNÉRALE
 EXERCICES - ANALYSE GÉNÉRALE OLIVIER COLLIER Exercice 1 (2012) Une entreprise veut faire un prêt de S euros auprès d une banque au taux annuel composé r. Le remboursement sera effectué en n années par
EXERCICES - ANALYSE GÉNÉRALE OLIVIER COLLIER Exercice 1 (2012) Une entreprise veut faire un prêt de S euros auprès d une banque au taux annuel composé r. Le remboursement sera effectué en n années par
COURS CALCULS FINANCIERS STATISTIQUE
 UNIVERSITÉ JOSEPH FOURIER M1 MIAGE UFR IMA COURS DE CALCULS FINANCIERS ET STATISTIQUE Serge Dégerine 4 octobre 2007 INTRODUCTION Ce document comporte trois parties consacrées à deux thèmes très indépendants
UNIVERSITÉ JOSEPH FOURIER M1 MIAGE UFR IMA COURS DE CALCULS FINANCIERS ET STATISTIQUE Serge Dégerine 4 octobre 2007 INTRODUCTION Ce document comporte trois parties consacrées à deux thèmes très indépendants
SOLUTIONS DE FINANCEMENT. À chaque projet son financement!
 À chaque projet son financement! NOS SOLUTIONS POUR FINANCER VOS PROJETS Les solutions de financement de Groupama Banque sont conçues pour répondre à vos attentes. S S ADAPTÉS À VOS BESOINS Quel que soit
À chaque projet son financement! NOS SOLUTIONS POUR FINANCER VOS PROJETS Les solutions de financement de Groupama Banque sont conçues pour répondre à vos attentes. S S ADAPTÉS À VOS BESOINS Quel que soit
DUT Techniques de commercialisation Mathématiques et statistiques appliquées
 DUT Techniques de commercialisation Mathématiques et statistiques appliquées Francois.Kauffmann@unicaen.fr Université de Caen Basse-Normandie 3 novembre 2014 Francois.Kauffmann@unicaen.fr UCBN MathStat
DUT Techniques de commercialisation Mathématiques et statistiques appliquées Francois.Kauffmann@unicaen.fr Université de Caen Basse-Normandie 3 novembre 2014 Francois.Kauffmann@unicaen.fr UCBN MathStat
Exprimer ce coefficient de proportionnalité sous forme de pourcentage : 3,5 %
 23 CALCUL DE L INTÉRÊT Tau d intérêt Paul et Rémi ont reçu pour Noël, respectivement, 20 et 80. Ils placent cet argent dans une banque, au même tau. Au bout d une année, ce placement leur rapportera une
23 CALCUL DE L INTÉRÊT Tau d intérêt Paul et Rémi ont reçu pour Noël, respectivement, 20 et 80. Ils placent cet argent dans une banque, au même tau. Au bout d une année, ce placement leur rapportera une
FORMATION INDIVIDUALISEE A LA GESTION. Classe de terminale technologique hôtellerie IMMOBILISATIONS. 1/3 l amortissement linéaire
 FORMATION INDIVIDUALISEE A LA GESTION Classe de terminale technologique hôtellerie L AMORTISSEMENT DES IMMOBILISATIONS 1/3 l amortissement linéaire OBJECTIF DU DOSSIER : «ETRE CAPABLE D ETABLIR LE PLAN
FORMATION INDIVIDUALISEE A LA GESTION Classe de terminale technologique hôtellerie L AMORTISSEMENT DES IMMOBILISATIONS 1/3 l amortissement linéaire OBJECTIF DU DOSSIER : «ETRE CAPABLE D ETABLIR LE PLAN
1 À noter... 3. 2 Demande de prêt REER... 3. 3 But du produit... 4. 4 Le produit en bref... 5. 5 Les principaux avantages... 6
 Table des matières 1 À noter... 3 2 Demande de prêt REER... 3 3 But du produit... 4 4 Le produit en bref... 5 5 Les principaux avantages... 6 6 Utilisation du prêt REER... 6 6.1 Taux d intérêt... 6 7 Modalités
Table des matières 1 À noter... 3 2 Demande de prêt REER... 3 3 But du produit... 4 4 Le produit en bref... 5 5 Les principaux avantages... 6 6 Utilisation du prêt REER... 6 6.1 Taux d intérêt... 6 7 Modalités
Crédit Bail immobilier Fructicomi
 Crédit Bail immobilier Financez votre immobilier de façon souple avec. EN BREF Le crédit-bail immobilier est une solution de financement performante dédiée intégralement à votre actif immobilier. Points
Crédit Bail immobilier Financez votre immobilier de façon souple avec. EN BREF Le crédit-bail immobilier est une solution de financement performante dédiée intégralement à votre actif immobilier. Points
CREDIT D IMPOT SUR LES INTERETS DES PRETS CONCLUS POUR L ACHAT OU LA CONSTRUCTION DE LA RESIDENCE PRINCIPALE
 CREDIT D IMPOT SUR LES INTERETS DES PRETS CONCLUS POUR L ACHAT OU LA CONSTRUCTION DE LA RESIDENCE PRINCIPALE Un est institué au titre des des prêts contractés pour l acquisition ou la construction d un
CREDIT D IMPOT SUR LES INTERETS DES PRETS CONCLUS POUR L ACHAT OU LA CONSTRUCTION DE LA RESIDENCE PRINCIPALE Un est institué au titre des des prêts contractés pour l acquisition ou la construction d un
LE PROBLEME DU PLUS COURT CHEMIN
 LE PROBLEME DU PLUS COURT CHEMIN Dans cette leçon nous définissons le modèle de plus court chemin, présentons des exemples d'application et proposons un algorithme de résolution dans le cas où les longueurs
LE PROBLEME DU PLUS COURT CHEMIN Dans cette leçon nous définissons le modèle de plus court chemin, présentons des exemples d'application et proposons un algorithme de résolution dans le cas où les longueurs
Leçon 5. Systèmes de gestion à recomplétement périodique et stock de sécurité
 CANEGE Leçon 5 Systèmes de gestion à recomplétement périodique et stock Objectif : A l'issue de la leçon l'étudiant doit être capable : dans le cadre des calendriers d approvisionnement à recomplètement
CANEGE Leçon 5 Systèmes de gestion à recomplétement périodique et stock Objectif : A l'issue de la leçon l'étudiant doit être capable : dans le cadre des calendriers d approvisionnement à recomplètement
M2 IAD UE MODE Notes de cours (3)
 M2 IAD UE MODE Notes de cours (3) Jean-Yves Jaffray Patrice Perny 16 mars 2006 ATTITUDE PAR RAPPORT AU RISQUE 1 Attitude par rapport au risque Nousn avons pas encore fait d hypothèse sur la structure de
M2 IAD UE MODE Notes de cours (3) Jean-Yves Jaffray Patrice Perny 16 mars 2006 ATTITUDE PAR RAPPORT AU RISQUE 1 Attitude par rapport au risque Nousn avons pas encore fait d hypothèse sur la structure de
FISCALITÉ DES REVENUS DE PLACEMENT
 FISCALITÉ DES REVENUS DE PLACEMENT LA LECTURE DE CE DOCUMENT VOUS PERMETTRA : De connaître les différentes sources de revenus de placement et leur imposition; De connaître des stratégies afin de réduire
FISCALITÉ DES REVENUS DE PLACEMENT LA LECTURE DE CE DOCUMENT VOUS PERMETTRA : De connaître les différentes sources de revenus de placement et leur imposition; De connaître des stratégies afin de réduire
Un gain de temps et d argent pour vous
 i00 Un gain de temps et d argent pour vous Description de la fonctionnalité Chaque année, lors de la vérification des états financiers de l entreprise, le comptable agréé a besoin d une confirmation bancaire
i00 Un gain de temps et d argent pour vous Description de la fonctionnalité Chaque année, lors de la vérification des états financiers de l entreprise, le comptable agréé a besoin d une confirmation bancaire
A propos de l Audit des finances communales
 A propos de l Audit des finances communales (évoqué lors du Conseil municipal de septembre 2014) A la demande de la majorité municipale, un audit a été commandité auprès du cabinet FCL. Les conclusions
A propos de l Audit des finances communales (évoqué lors du Conseil municipal de septembre 2014) A la demande de la majorité municipale, un audit a été commandité auprès du cabinet FCL. Les conclusions
Plan du cours : électricité 1
 Semestre : S2 Module Physique II 1 Electricité 1 2 Optique géométrique Plan du cours : électricité 1 Partie A : Electrostatique (discipline de l étude des phénomènes liés aux distributions de charges stationnaires)
Semestre : S2 Module Physique II 1 Electricité 1 2 Optique géométrique Plan du cours : électricité 1 Partie A : Electrostatique (discipline de l étude des phénomènes liés aux distributions de charges stationnaires)
CREDIT D IMPOT SUR LES INTERETS D EMPRUNT SUPPORTES A RAISON DE L ACQUISITION OU DE LA CONSTRUCTION DE LA RESIDENCE PRINCIPALE. Questions / Réponses
 CREDIT D IMPOT SUR LES INTERETS D EMPRUNT SUPPORTES A RAISON DE L ACQUISITION OU DE LA CONSTRUCTION DE LA RESIDENCE PRINCIPALE Questions / Réponses Qui peut bénéficier du crédit d impôt? Faut-il remplir
CREDIT D IMPOT SUR LES INTERETS D EMPRUNT SUPPORTES A RAISON DE L ACQUISITION OU DE LA CONSTRUCTION DE LA RESIDENCE PRINCIPALE Questions / Réponses Qui peut bénéficier du crédit d impôt? Faut-il remplir
CH X Intérêts composés - Amortissements
 CH X Intérêts composés - Amortissements I) Les intérêts composés : 1) Situation : Un capital de 20 000,00 est placé à un taux d intérêts de 4 % l an pendant 5 ans. Chaque année les intérêts produits viennent
CH X Intérêts composés - Amortissements I) Les intérêts composés : 1) Situation : Un capital de 20 000,00 est placé à un taux d intérêts de 4 % l an pendant 5 ans. Chaque année les intérêts produits viennent
DCG 6. Finance d entreprise. L essentiel en fiches
 DCG 6 Finance d entreprise L essentiel en fiches DCG DSCG Collection «Express Expertise comptable» J.-F. Bocquillon, M. Mariage, Introduction au droit DCG 1 L. Siné, Droit des sociétés DCG 2 V. Roy, Droit
DCG 6 Finance d entreprise L essentiel en fiches DCG DSCG Collection «Express Expertise comptable» J.-F. Bocquillon, M. Mariage, Introduction au droit DCG 1 L. Siné, Droit des sociétés DCG 2 V. Roy, Droit
Probabilités III Introduction à l évaluation d options
 Probabilités III Introduction à l évaluation d options Jacques Printems Promotion 2012 2013 1 Modèle à temps discret 2 Introduction aux modèles en temps continu Limite du modèle binomial lorsque N + Un
Probabilités III Introduction à l évaluation d options Jacques Printems Promotion 2012 2013 1 Modèle à temps discret 2 Introduction aux modèles en temps continu Limite du modèle binomial lorsque N + Un
BTS OPTICIEN LUNETIER Economie et Gestion de l Entreprise SESSION 2012
 BTS OPTICIEN LUNETIER Economie et Gestion de l Entreprise SESSION 2012 Note : ce corrigé n a pas de valeur officielle et n est donné qu à titre informatif sous la responsabilité de son auteur par Acuité.
BTS OPTICIEN LUNETIER Economie et Gestion de l Entreprise SESSION 2012 Note : ce corrigé n a pas de valeur officielle et n est donné qu à titre informatif sous la responsabilité de son auteur par Acuité.
Cet ouvrage couvre totalement le programme de l UE 6 Finance
 Cet ouvrage couvre totalement le programme de l UE 6 Finance d entreprise du Diplôme de Comptabilité et de Gestion (DCG) des études de l expertise comptable. Il s inscrit également dans le cadre des programmes
Cet ouvrage couvre totalement le programme de l UE 6 Finance d entreprise du Diplôme de Comptabilité et de Gestion (DCG) des études de l expertise comptable. Il s inscrit également dans le cadre des programmes
LES RACHATS DE SERVICE. Commission administrative des régimes de retraite et d assurances
 LES RACHATS DE SERVICE Commission administrative des régimes de retraite et d assurances Table des matières Qu est-ce qu un rachat de service? 3 Quelles sont les périodes que je peux racheter? 4 Quels
LES RACHATS DE SERVICE Commission administrative des régimes de retraite et d assurances Table des matières Qu est-ce qu un rachat de service? 3 Quelles sont les périodes que je peux racheter? 4 Quels
FINANCE Mathématiques Financières
 INSTITUT D ETUDES POLITIQUES 4ème Année, Economie et Entepises 2005/2006 C.M. : M. Godlewski Intéêts Simples Définitions et concepts FINANCE Mathématiques Financièes L intéêt est la émunéation d un pêt.
INSTITUT D ETUDES POLITIQUES 4ème Année, Economie et Entepises 2005/2006 C.M. : M. Godlewski Intéêts Simples Définitions et concepts FINANCE Mathématiques Financièes L intéêt est la émunéation d un pêt.
Emprunt n 710 Budget Ville : 95,43 % + ancien piscine : 0,98 % Budget Eaux : 3,47 % Budget OIC : 0500 : 0,12 %
 [201876] Ville de MACON/Contrat N:8ORef: Type: Inconnue 110001201876-80 Emprunt n 710 Budget Ville : 95,43 % + ancien piscine : 0,98 % Budget Eaux : 3,47 % Budget OIC : 0500 : 0,12 % N de dossier : MPH199235EUR
[201876] Ville de MACON/Contrat N:8ORef: Type: Inconnue 110001201876-80 Emprunt n 710 Budget Ville : 95,43 % + ancien piscine : 0,98 % Budget Eaux : 3,47 % Budget OIC : 0500 : 0,12 % N de dossier : MPH199235EUR
Solutions d assurance hypothécaire
 Solutions d assurance hypothécaire Votre résidence est votre bien le plus précieux. Protégez-la grâce à une police d assurance contre la maladie grave! Solutions d assurance hypothécaire Protégez votre
Solutions d assurance hypothécaire Votre résidence est votre bien le plus précieux. Protégez-la grâce à une police d assurance contre la maladie grave! Solutions d assurance hypothécaire Protégez votre
FINANCER VOS EQUIPEMENTS OU VOTRE VEHICULE
 FINANCER VOS EQUIPEMENTS OU VOTRE VEHICULE Un professionnel libéral se doit d investir dans des équipements ou de faire des travaux d aménagement professionnels à plusieurs reprises au cours de sa carrière.
FINANCER VOS EQUIPEMENTS OU VOTRE VEHICULE Un professionnel libéral se doit d investir dans des équipements ou de faire des travaux d aménagement professionnels à plusieurs reprises au cours de sa carrière.
٥١٢ كورنيش النهر. ص.ب.: ٥٨٧٠-١٦.بيروت.لبنان.تلفون: ٠١-٤٢٥١٤٧/٩.فاكس: ٤٢٦٨٦٠-٠١ 512, Corniche al-naher. B.P. 16-5870. Beyrouth. Liban.
 البرنامج التحضيري لمباراة مجلس الخدمة المدنية للوظاي ف الشاغرة في وزارة المالية مراقب ضراي ب ري يسي ومراقب تحقق وري يس محاسبة في الفي ة الثالثة في ملاك مديرية المالية العامة فرنسي مادة الرياضيات المالية
البرنامج التحضيري لمباراة مجلس الخدمة المدنية للوظاي ف الشاغرة في وزارة المالية مراقب ضراي ب ري يسي ومراقب تحقق وري يس محاسبة في الفي ة الثالثة في ملاك مديرية المالية العامة فرنسي مادة الرياضيات المالية
LES PRINCIPALES AIDES AUX CREATEURS D ENTREPRISE AVRIL 2015
 LES PRINCIPALES AIDES AUX CREATEURS D ENTREPRISE AVRIL 2015 LES PRINCIPALES AIDES AUX CREATEURS Sommaire 2 SOMMAIRE : DISPOSITIF ACCRE 3 à 6 L ARE ou l ARCE 7 à 9 DISPOSITIF NACRE 10 à 13 FINANCEMENTS
LES PRINCIPALES AIDES AUX CREATEURS D ENTREPRISE AVRIL 2015 LES PRINCIPALES AIDES AUX CREATEURS Sommaire 2 SOMMAIRE : DISPOSITIF ACCRE 3 à 6 L ARE ou l ARCE 7 à 9 DISPOSITIF NACRE 10 à 13 FINANCEMENTS
Suites numériques. Exercice 1 Pour chacune des suites suivantes, calculer u 1, u 2, u 3, u 10 et u 100 : Introduction : Intérêts simpleset composés.
 Suites numériques 1ère STG Introduction : Intérêts simpleset composés. On dispose d un capital de 1 000 euros que l on peut placer de deux façons différentes : à intérêts simples au taux annuel de 10%.
Suites numériques 1ère STG Introduction : Intérêts simpleset composés. On dispose d un capital de 1 000 euros que l on peut placer de deux façons différentes : à intérêts simples au taux annuel de 10%.
PLAN DE LEÇON TITRE : Qu est-ce que le crédit? Résultats d apprentissage de la littératie financière. Attentes et contenus d apprentissage
 70 minutes Résultats d apprentissage de la littératie financière À la fin de la leçon, les élèves pourront : expliquer l objectif du crédit; analyser le rôle et l importance du crédit en ce qui concerne
70 minutes Résultats d apprentissage de la littératie financière À la fin de la leçon, les élèves pourront : expliquer l objectif du crédit; analyser le rôle et l importance du crédit en ce qui concerne
JUSQU AU 31 DéCEMBRE 2014 PRêT étudiant DES MéTIERS : UNE OFFRE à NE MANQUER SOUS AUCUN PRETEXTE
 Nos offres réservées aux Etudiants des Métiers * pour mieux vivre leur apprentissage * Nouvelle appellation d Apprenti 0,90 % (1) TAEG FIXE JUSQU AU 31 DéCEMBRE 2014 PRêT étudiant DES MéTIERS : UNE OFFRE
Nos offres réservées aux Etudiants des Métiers * pour mieux vivre leur apprentissage * Nouvelle appellation d Apprenti 0,90 % (1) TAEG FIXE JUSQU AU 31 DéCEMBRE 2014 PRêT étudiant DES MéTIERS : UNE OFFRE
Le modèle de Black et Scholes
 Le modèle de Black et Scholes Alexandre Popier février 21 1 Introduction : exemple très simple de modèle financier On considère un marché avec une seule action cotée, sur une période donnée T. Dans un
Le modèle de Black et Scholes Alexandre Popier février 21 1 Introduction : exemple très simple de modèle financier On considère un marché avec une seule action cotée, sur une période donnée T. Dans un
Les primes d assurances-maladie et accidents non obligatoires. La déduction est limitée au double de la prime moyenne cantonale, par tranche d âge;
 Déductions de primes Les montants versés pour le 1 er pilier sont entièrement déductibles du revenu. Les montants versés pour le 2 ème pilier sont entièrement déductibles du revenu. Sont déduits du revenu:
Déductions de primes Les montants versés pour le 1 er pilier sont entièrement déductibles du revenu. Les montants versés pour le 2 ème pilier sont entièrement déductibles du revenu. Sont déduits du revenu:
Conseil de Surveillance du 23 février 2012
 AIDES AUX MENAGES EN DIFFICULTE ARTICLE R. 313-19-3 V DU CCH ---- En application de l article R. 313-12 du code de la construction et de l habitation, l UESL peut déterminer par recommandation les modalités
AIDES AUX MENAGES EN DIFFICULTE ARTICLE R. 313-19-3 V DU CCH ---- En application de l article R. 313-12 du code de la construction et de l habitation, l UESL peut déterminer par recommandation les modalités
Logistique, Transports
 Baccalauréat Professionnel Logistique, Transports 1. France, juin 2006 1 2. Transport, France, juin 2005 2 3. Transport, France, juin 2004 4 4. Transport eploitation, France, juin 2003 6 5. Transport,
Baccalauréat Professionnel Logistique, Transports 1. France, juin 2006 1 2. Transport, France, juin 2005 2 3. Transport, France, juin 2004 4 4. Transport eploitation, France, juin 2003 6 5. Transport,
Financer. Quels que soient vos projets et vos réalisations, votre banque vous offre une solution sur mesure
 Quels que soient vos projets et vos réalisations, votre banque vous offre une solution sur mesure Financer Vous avez une dépense inattendue? Un achat important? Un projet qui vous tient à cœur? Vous voudriez
Quels que soient vos projets et vos réalisations, votre banque vous offre une solution sur mesure Financer Vous avez une dépense inattendue? Un achat important? Un projet qui vous tient à cœur? Vous voudriez
SECRÉTARIAT D ETAT CHARGE DU BUDGET. publique. Le Ministre de l Intérieur,
 MINISTÈRE DE L ÉCONOMIE, DES FINANCES ET DE L INDUSTRIE SECRÉTARIAT D ETAT CHARGE DU BUDGET MINISTÈRE DE L INTÉRIEUR Direction du Trésor Direction de la Comptabilité publique Direction générale des collectivités
MINISTÈRE DE L ÉCONOMIE, DES FINANCES ET DE L INDUSTRIE SECRÉTARIAT D ETAT CHARGE DU BUDGET MINISTÈRE DE L INTÉRIEUR Direction du Trésor Direction de la Comptabilité publique Direction générale des collectivités
Comment rembourser votre hypothèque plus rapidement
 Série L ABC des prêts hypothécaires Comment rembourser votre hypothèque plus rapidement Comment prendre de bonnes décisions en matière d hypothèques Table des matières Aperçu 1 Faire la distinction entre
Série L ABC des prêts hypothécaires Comment rembourser votre hypothèque plus rapidement Comment prendre de bonnes décisions en matière d hypothèques Table des matières Aperçu 1 Faire la distinction entre
Qu est-ce que le crédit?
 Qu est-ce que le crédit? NIVEAU 9 11 Dans cette leçon, les élèves examineront les différents types de cartes de crédit offertes ainsi que les avantages et les inconvénients d acheter à crédit. Cours Initiation
Qu est-ce que le crédit? NIVEAU 9 11 Dans cette leçon, les élèves examineront les différents types de cartes de crédit offertes ainsi que les avantages et les inconvénients d acheter à crédit. Cours Initiation
LOI LAGARDE DU 1ER JUILLET 2010
 LOI LAGARDE DU 1ER JUILLET 2010 PORTANT REFORME DU CREDIT A LA CONSOMMATION DOSSIER DE PRESSE FICHE 1 Les principales mesures de la loi LAGARDE FICHE 2 Le point sur l entrée en vigueur des principales
LOI LAGARDE DU 1ER JUILLET 2010 PORTANT REFORME DU CREDIT A LA CONSOMMATION DOSSIER DE PRESSE FICHE 1 Les principales mesures de la loi LAGARDE FICHE 2 Le point sur l entrée en vigueur des principales
Simulation d une économie monétaire (programmation impérative, sujet 3)
 Simulation d une économie monétaire (programmation impérative, sujet 3) http://sfc-abm.org/students/mief/ 10 février 2014 Table des matières 1 Sujet 2 2 Description plus détaillée de la simulation 3 2.1
Simulation d une économie monétaire (programmation impérative, sujet 3) http://sfc-abm.org/students/mief/ 10 février 2014 Table des matières 1 Sujet 2 2 Description plus détaillée de la simulation 3 2.1
EXPLOITATIONS PEDAGOGIQUES DU TABLEUR EN STG
 Exploitations pédagogiques du tableur en STG Académie de Créteil 2006 1 EXPLOITATIONS PEDAGOGIQUES DU TABLEUR EN STG Commission inter-irem lycées techniques contact : dutarte@club-internet.fr La maquette
Exploitations pédagogiques du tableur en STG Académie de Créteil 2006 1 EXPLOITATIONS PEDAGOGIQUES DU TABLEUR EN STG Commission inter-irem lycées techniques contact : dutarte@club-internet.fr La maquette
Auto-Entreprise : Activités : Eric SOTY - Siret n 47868353500023. Formation Bureautique, continue d'adultes. Tél : 0953020032 - Fax : 0958020032
 Auto-Entreprise : Activités : Eric SOTY - Siret n 47868353500023 Formation Bureautique, APE : 8559A formation continue d'adultes. identité visuelle, charte T.V.A. non applicable, article 293 B du CGI.
Auto-Entreprise : Activités : Eric SOTY - Siret n 47868353500023 Formation Bureautique, APE : 8559A formation continue d'adultes. identité visuelle, charte T.V.A. non applicable, article 293 B du CGI.
