Chapitre 3 Bilans d énergie : le premier principe de lathermodynamique
|
|
|
- Bernadette Bélanger
- il y a 8 ans
- Total affichages :
Transcription
1 Chapitre 3 Bilans d énergie : le premier principe de lathermodynamique Les di érentes formes d énergie; la notion d énergie interne Les énergies Exemple 1 ressort air masse enceinte calorifugée et fermée Fig.3.1. Considérons une masse accrochée au bout d un ressort, le tout placé dansuneenceinte remplie d air (voir schéma 3.1). L enceinte est fermée (pas d échange de matière avec l extérieur) et isolée (pas d échange d énergie avec l extérieur; la paroi de l enceinte est donc parfaitement calorifugée). Le système étudié est l ensemble (ressort + masse M + air). Un mouvement initial est donné à la masse M. Son énergie cinétique au départ est Ec 0, et son énergie potentielle est Ep 0. L énergie mécanique de M est dé nie comme étant Em = Ec+ Ep. Or, du fait de la présence de l air, il y a une force de frottement lors du mouvement de la masse qui aura donc un mouvement amorti, jusqu à s immobiliser dans sa position d équilibre. L énergie mécanique de la masse a diminuéau coursdu tempsà cause dela force de frottement qui est une force non conservative. Mais qu est devenue l énergie mécanique perdue? A-t-elle disparue ou s est-elle seulement transformée? Une fois l expérience terminée, la température de l air est mesurée précisément : on remarque qu elle a augmenté. L énergie mécanique perdue par M a donc été récupérée par le gaz sous forme d énergie interne. Le premier principe est tout simplement un principe de conservation de l énergie : celle-cine peut pas disparaître, mais seulement se transmettre sous L. Menguy, Lycée Montesquieu Le Mans. 18 avril 2004
2 30 Chapitre 3 Bilans d énergie : le premier principe de la thermodynamique diverses formes. Dans le cas présent, ce sont les chocs entre la masse en mouvement et les particules constituant l air qui ont transféré l énergie cinétique d ensemble de la masse M en énergie cinétique microscopique (énergie d agitation thermique) des particules. Bilan des énergies intervenant ici : -Ec macro de la masse -Ep macro énergie potentielle des forces extérieures (de pesanteur de la masse); -Ec micro = P ec somme de l énergie cinétique de chaque particule de l air ; -Ep micro énergie potentielle d interaction entre les particules (si l air est remplacé par un gaz non parfait). L énergie mécanique (macroscopique) est : Em = Ec macro + Ep macro L énergie dite interne (microscopique) est : U = Ec micro + Ep micro : Remarque 3.1 Les énergies cinétiques dites macroscopiques font référence à des mouvements d ensemble : toutes les particules (atomes) constituant la masse M ont un même mouvement; ils se déplacent en bloc. Les énergies cinétiques dites microscopiques font référence à des mouvements désordonnés : les particules vont dans tous les sens, mais en gardant une position moyenne constante. En réalité, la masse M aussi voit sa température augmenter; cela est lié au fait que les particules constituant la masse M, bienque xées proche d une position d équilibre, peuvent vibrer autour de cette dernière. L énergie cinétique microscopique d agitation thermique est cette énergie de vibration autour de la position d équilibre Exemple 2 Soit une masse m de gaz s écoulant dans un tuyau. Le but est d e ectuer un bilan de l énergie totale du gaz. Le centre de gravité de l ensemble des particules du gaz est noté G. D un point macroscopique, l ensemble du gaz s écoule à la vitesse! v G. Une observation microscopique d une seule particule permet constater qu en réalité le mouvement de celle-ci n est pas uniforme et égal à! v G, mais tout à fait désordonné. C est seulement la moyenne de la vitesse de toutes les particules qui donne l écoulement d ensemble! v G. Di érentes formes d énergie sont alors dé nies : -Ec macro = 1 2 mv2 G énergie cinétique de l écoulement -Ep macro énergie potentielle des forces extérieures (pesanteur); -Ec micro = P ec somme de l énergie cinétique de chaque particule du gaz dans le référentiel barycentrique; -Ep micro énergie potentielle d interaction entre les particules (si le gaz n est pas parfait) Conclusion En conclusion, quel que soit le système étudié, 4 formes d énergie sont distinguées : -Ec macro = 1 2 mv2 G énergie cinétique macroscopique (d ensemble); avec m masse totale et G centre de gravité -Ep macro énergie potentielle des forces extérieures; -Ec micro = P ec somme de l énergie cinétique de chaque particule dans le référentiel barycentrique; -Ep micro énergie potentielle d interaction entre les particules. L énergie mécanique (ou macroscopique) est : Em = Ec macro + Ep macro 18 avril 2004 L. Menguy, Lycée Montesquieu Le Mans.
3 Section 3.2 Le travail des forces de pression 31 L énergie interne (ou microscopique) est : U = Ec micro + Ep micro : La somme de l énergie mécanique et del énergie interne d un système est son énergie totale. Remarque 3.2 Il faudrait également ajouter dans l énergie interne U toutes les autres formes d énergie microscopique, comme les énergies de liaison au sein d une molécule, ou les énergies d interaction nucléaire dans un noyau. Ce chapitre exclue l étude de réactions chimiques et de réactions nucléaires; ces énergies précédemment citées restent donc constantes et ne participent à aucun échange. Ils ne seront pas pris en compte dans le cours de thermodynamique physique de math sup Les échanges d énergie L énergie peut s échanger par divers moyens que nous allons ici résumer : le travail des forces et le transfert calori que Transfert par le travail W d une force En mécanique, nous avons vu que le travail d une force (noté W) était à l origine d une variation d énergie cinétique (théorème de l énergie cinétique) : Z Z!F! W = ±W = : dl: Transfert calori que Le transfert calori que est appelé aussi transfert thermique ou chaleur, ce dernier terme étant à éviter. La mise en contact de deux gaz de températures di érentes modi e ces dernières jusqu à ce qu elles deviennent égales l une à l autre. Il y a donc eu un transfert calori que du plus chaud vers le plus froid que l on va noter Q par la suite. Le transfert calori que élémentaire, c est à dire ayant eu lieu pendant un court instant dt, est noté ±Q. Remarque 3.3 Il est important de distinguer les notions de chaleur, transfert calori que et température. Le terme chaleur enparticulier est très ambiguë et doit être évité. Ene et, la notion de chaleur est généralement reliée à la notion de température dans le langage courant. Ne dit-on pas quelle chaleur! quand la température est élevée? Alors que le terme chaleur, en physique, représenteraitplutôtuntransfertcalori que, c està dire untransfertd énergie d un système vers un autre pendant la durée de l expérience. Dire que la chaleur d un système vaut telle valeur n a aucun sens, contrairement à la température. On dit plutôt que la chaleur échangée (c est à dire le transfert calori que) lors d une expérience entre un système 1 et un système 2 vaut tant. En résumé, le transfert calori que et la chaleur sont deux termes équivalents en thermodynamique, mais l utilisation du mot chaleur doit être évitée. En n, les notions de transfert calori que et températures sont tout à fait di érentes. On peut chau er un système, c est à dire lui apporter de l énergie sous forme calori que sans pourautant que la température du système augmente. Par exemple, le chau age d eau enébullition n augmente pas la température, mais transforme tout simplement le liquide en vapeur Le travail des forces de pression L. Menguy, Lycée Montesquieu Le Mans. 18 avril 2004
4 32 Chapitre 3 Bilans d énergie : le premier principe de la thermodynamique Pression extérieure et pression dans un uide Exemple 1 Pext piston coulissant cales air (GP) Pi<Pext à t=0, les cales sont enlevées Fig.3.2. Soit un système (S 0 ) constitué d air enfermé dans un récipient (voir schéma 3.2), dont la partie supérieure est fermée par un piston de section S et coulissant. Au départ, la pression extérieure est P ext et la pression à l intérieur du récipient P i < P ext. Le piston est bloqué par deux cales. A début de l expérience, les cales sont enlevées. La pression extérieure pousse donc sur le piston qui descend jusqu à l équilibre. Ce dernier est atteint quand la pression du système (l air à l intérieur) est P f = P ext. Entre les deux états d équilibre, l air extérieur reste toujours à P ext, tandis que le système (air intérieur) varie progressivement de P i à P f. A un instant quelconque intermédiaire, la pression à l intérieur n a aucune raison d être égale à la pression à l extérieur Exemple 2 piston libre de coulisser P0 air (GP) à t=0, une masse M est placée sur le piston P0 M g Pi=P0 Pf état initial (t<0) état final Fig.3.3. Une expérience quasi similaire est ici réalisée. Le piston est laissé libre de coulisser (voir schéma 3.3). La pression du système au départ est donc P i = P 0. A t = 0, on place une 18 avril 2004 L. Menguy, Lycée Montesquieu Le Mans.
5 Section 3.2 Le travail des forces de pression 33 masse M sur le piston : ce dernier descend et s immobilise quand les forces appliquées sur ce piston s égalisent : P f = P 0 + Mg=S. Pendant toute la transformation, la pression s exerçant à l extérieur du piston est P ext = P f, alors que la pression à l intérieur varie de P 0 au départ à P f à la n. A un instant t intermédiaire quelconque, la pression du système est inconnue et en tout casdi érente de la pression à l extérieur, et n est d ailleurs même pas nécessairement homogène dans tout le système! En conclusion de ces deux exemples, il parait nécessaire de bien distinguer pression du système et pression extérieure, cette dernière étant la pression de ce qui entoure le système et poussant sur celui-ci Le travail élémentaire des forces de pression (transformation élémentaire) L exemple2 du paragraphe précédent est ici repris. Le système étudié est l air intérieur au récipient. Le but est de calculer le travail des forces extérieures de pression. Ces forces s appliquent sur toutes les parois délimitant le système choisi. Seule le piston bouge, donc seules les forces de pression s appliquant sur le piston travaillent. Entre des instants t et t + dt intermédiaires au cours de l expérience, le travail élémentaire de la force de pression extérieure s appliquant sur le système est : ±W =! F ext :! dl = ( P ext S! u z )! dl = P ext Sdx dx étant le déplacement élémentaire du piston. Le travail de la force de pression est donc : ±W = P ext dv: Il est important de remarquer que c est la pression extérieure qui applique une force sur le système; c est donc P ext qui doit être prise en compte dans le calcul du travail de la force de pression, et non la pression du système qui, comme nous l avons vu, peut être di érente. dv représente la variation de volume du système (de l air enfermé dans le récipient) Le travail au cours d une transformation non élémentaire Lors d une expérience, le travail élémentairedes forces depression entre deux instants très proches t et t +dt est ±W = P ext dv: Lors de l expérience complète, il su t de sommer tous les travaux élémentaires du début de l expérience à la n de l expérience : W = Z fin d ebut Z ±W = P ext dv: Le cas des transformations quasi-statiques réversibles Nous avons vu que lors de l expérience 2, la pression extérieure à un instant quelconque est di érente de la pression du système. En prenant certaines précautions, il est possible de réaliser des évolutions dites quasi-statiques au cours desquelles la pression extérieure reste toujours égale à la pression interne. Exemple 3 L. Menguy, Lycée Montesquieu Le Mans. 18 avril 2004
6 34 Chapitre 3 Bilans d énergie : le premier principe de la thermodynamique Réalisons l expérience 2 de manière quasi-statique réversible, c est à dire qu au lieu de mettreunemassemsur lepiston et lelâcher subitement, nousallonsmettreprogressivement et délicatement sur le piston deminuscules masses dm lesunes après les autres, en attendant entre chaque masse que l équilibre soit établi entre l extérieur et le système. L expérience est arrêtée quand la somme de toutes les petitesmasses dm est égale à la masse m de l expérience2. Pour chaque instant intermédiaire de l expérience, il y a équilibre entre l extérieur et l intérieur : P = P ext en notant P la pression du système. On a alors pour une transformation élémentaire : et pour la transformation globale Z W = ±W = PdV Z ±W = PdV P étant la pression du système (car cette dernière est égale à la pression extérieure) Exemples de calculs de travail de force de pression Evolution isochore (V = cte) Pour une évolution in nitésimale : ±W = P est dv = 0 car dv = 0. Lors d une évolution isochore, les forces de pression ne travaillent pas Evolution avec P ext = cte C est le cas des exemples 1 et 2. Pour l exemple 1 : P ext = P f ; pour l exemple 2 : P ext = P 0 + mg=s = P f. Le système est le gaz intérieur au récipient. Son état initial est noté : P i, V i, T i ; son état nal est : P f = P ext, V f, T f. Le travail est, compte tenu que P ext est constante : Z Z W = P est dv = P ext dv = P f (V f V i ): Evolution quasi-statique isotherme d un gaz parfait Quasi-statique signi e que l expérience est e ectuée su samment lentement pour qu il y ait toujours équilibre, à tout instant intermédiaire de l expérience : donc P ext = P. De plus s il s agit d un gaz parfait : PV = nrt. En n, la transformation est isotherme : T = cte. On peut donc écrire : avec soit qui s intègre en : ±W = P ext dv = PdV W = nrt ln P = nrt V ; ±W = nrt dv V µ Vf car P f V f = P i V i (la température est constante). V i µ Pf = nrt ln P i 18 avril 2004 L. Menguy, Lycée Montesquieu Le Mans.
7 Section 3.3 Le premier principe de la thermodynamique Le diagramme de Clapeyron Rédaction ultérieure 3.3. Le premier principe de la thermodynamique Le premier principe de la thermodynamique est tout simplement un principe de conservation de l énergie : cette dernière ne peut pas disparaître ou se créer mais seulement s échanger. Comme tout principe, il ne sedémontrepas mais reste posé tant qu aucune expérience nel a mise en défaut Enoncé La variation de l énergie totale (énergie mécanique et énergieinterne) d un systèmethermodynamique fermé est la somme destransferts calori ques Q et du travail des forces extérieures W de pression : (E m + U) = W + Q: En d autre termes, la variation de l énergie d un système ne peut être que le résultat d un échange avecl extérieur, soit par transfert calori que, soit par l intermédiaire du travaild une force. Remarque 3.4 E m = Em macro + Ec macro, avec Ec macro = 1=2mvG 2, G étant le centre de gravité du système. L énergie cinétique macroscopique est celle du mouvement d ensemble du uide. La vitesse d écoulement est généralement très lente devant la vitesse individuelle des particules; l énergie cinétique macroscopique est donc tout à fait négligeable devant l énergie cinétique microscopique. Si l on peut négliger également les variations d énergie potentielle macroscopique, ce qui est souvent le cas, le premier principe de la thermodynamique peut se simpli er sous la forme suivante : U = W + Q: (1) Par la suite, la relation simpli ée (1) sera utilisée, mais il faut bien garder à l esprit que (1) est une égalité qui n est valable que quand l énergie mécanique reste constante. Remarque 3.5 Un système recevant de l énergie de l extérieur voit évidemment sonénergie U augmenter. Les conventions de signe sont donc les suivantes : W et Q sont positifs si le système reçoit de l extérieur, et négatifs si le système donne de l énergie à l extérieur. Remarque 3.6 Dans le cas d un système fermé et isolé, il n y a ni force (donc pas de travail), ni transfert calori que : W = 0, Q = 0, et donc U = 0. Remarque 3.7 Pour une évolution isochore : V = cte donc W = 0, soit U = Q. Remarque 3.8 Si le système n est pas fermé, il faut ajouter l énergie des particules entrantes dans le système, et enlever l énergie des particules sortantes du système. Mais ce cas L. Menguy, Lycée Montesquieu Le Mans. 18 avril 2004
8 36 Chapitre 3 Bilans d énergie : le premier principe de la thermodynamique de gure n est pas au programme : on s arrangera alors toujours pour se ramener à des systèmes fermés, quitte à suivre le uide s il est en mouvement. Le premier principe (1) peut s écrire également pour une évolution élementaire (entre 2 états très proches) : du = ±W + ±Q: (2) Exemple de la détente de Joule-Gay Lussac Position du problème paroi retirable robinet V1 gaz V2 vide ou parois calorifugées V1 gaz V2 vide Fig.3.4. Représentation des deux con gurations possibles dans l expérience de Joule (états initiaux des compartiments) L expérience qui suit, que l on appelle détente de Joule-Gay Lussac (ou simplement détente de Joule), a été réalisée au XIXième siècle par Joule, Gay Lussac et Hirn. Elle consiste à séparer une enceinte calorifugée en deux compartiments (1) de volume V 1 et (2) de volume V 2 soit par une paroi amovible, soit par un robinet (voir gure 3.4). Le compartiment (1) est rempli de gaz à la pression P i alors que le compartiment (2) est initialement vide. La séparation entre les deux compartiments est ensuite enlevée (ou le robinet ouvert) : la di usion du gaz s e ectue dans tout le volume (V 1 + V 2 ) jusqu à l équilibre Résolution du problème Le système considéré est le gaz. La pression extérieure s appliquant sur ce gaz étant nul, il vient : W = 0 (l extérieur est vide). Les parois sont adiabatiques (calorifugées) : le transfert calori que est donc nul : Q = 0. En n U = W + Q = 0 : l énergie interne du gaz reste constante lors d une détente de Joule-Gay Lussac Détente de Joule d un gaz parfait Si le gaz est parfait, comme l énergie interne reste constante, alors la température reste également constante (1ière loi de Joule : U ne dépend que de T). La détente de Joule-Gay Lussac d un gaz parfait est isotherme. Remarque 3.9 L expérience de la détente de Joule permet de véri er la première de Joule : 18 avril 2004 L. Menguy, Lycée Montesquieu Le Mans.
9 Section 3.4 L enthalpie ; les capacités thermiques (ou calori ques) 37 si la température du gaz varie lors de cette expérience, la première loi de Joule n est pas véri ée : le gaz n est donc pas un gaz parfait Détente de Joule d un gaz de Van-der-Waals L énergie interne d un gaz de Van-der-Waals est U = nc V m T n2 a V : (3) Lors d une détente de Joule, l énergie interne reste constante. Notant T i et T f les températures initiales et nales, et V i, V f les volumes correspondants, l équation (3) donne : µ 1 nc V m (T f T i ) = n 2 a 1 : V f V i V f > V i, donc T f < T i : lors de la détente d un gaz de Van-der-Waals, la température baisse. La mesure de ces températures permet d estimer expérimentalement le coe cient a. L interprétation physique de ce phénomène s explique comme suit : le gaz occupe un volume plus important à la n de la détente : la distance inter-particulaire moyenne augmente donc. L énergie d interaction entre les molécules (négative pour un gaz de Van-der-Waals) se rapproche donc un peu plus de 0. Or l énergie interne reste constante : l énergie cinétique microscopique (et donc la température) baisse (U = cte = Ec micro + Ep int ) Calculs de transfert thermique Nousne disposonsencore d aucuneformulequipermettrait de calculer directement Q. Ce calcul peut toutefois s e ectuer de manière indirecte sachant que Q = U W. Exemple 1 : la transformation réversible isotherme d un gaz parfait. U = 0 (car T = cte) donc Q = W = nrt ln(v f =V i ). Exemple 2 : l évolution isochore. Comme le volume est constant, le travail des forces de pression est nul : W = 0, donc Q = U = nc V m (T f T i ): Exemple 3 : la compression à pression extérieure P ext constante. Pour un gaz parfait : du = nc V m dt soit U = nc V m (T f T i ). de plus W = R P est dv = P ext (V f V i ). Finalement Q = U W = nc V m (T f T i )+P ext (V f V i ). Cette dernière écriture peut être simpli ée : cela constitue l objet de la partie qui suit L enthalpie; les capacités thermiques (ou calori ques) Introduction de l enthalpie De très nombreuses réaction thermodynamiques s e ectuent en contact avec l atmosphère, donc à pression constante. Par exemple la réalisation de réaction chimique (qui est une transformation thermodynamique) par mélange de deux réactifs (état initial) dont résulte un ou des produit(s) (état nal) est fréquemment réalisé à l air libre, c est à dire que la pression reste constante et égale à la pression atmosphérique. Le volume par contre peut varier. L. Menguy, Lycée Montesquieu Le Mans. 18 avril 2004
10 38 Chapitre 3 Bilans d énergie : le premier principe de la thermodynamique On peut alors écrire P ext = P 0 de l atmosphère, donc ±W = P ext dv soit W = P 0 (V f V i ): Le transfert calori que avec l extérieur lors de l évolution est donc : Q = U W = U f U i + P 0 V f P 0 V i = (U f + P 0 V f ) (U i + P 0 V i ) = (U + PV ): Le transfert calori que Q est la variation de (U + PV ) entre l état initial et l état nal. Une nouvelle fonction H appelée enthalpie est introduite avec H = U + PV: On a donc, lors d une évolution à pression constante : Q = H; et pour une évolution in nitésimale : ±Q = dh: Rappel : à volume constant, W = 0 donc : Q = U; et pour une évolution in nitésimale : ±Q = du: Remarque 3.10 U est une fonctiond état (dépendant des paramètres d état); P et V sont des paramètres d état, donc l enthalpie H = U + PV est également une fonction d état Les capacités thermiques La capacité thermique à pression constante Dans un premier temps, un système est chau é à pression constante. La capacité thermique à pression constante notée C P est l énergie Q à apporter sous forme thermique pour augmenter la température du système de 1K : C P = µ ±Q dt P P car ±Q = dh à pression constante. C P est donc facile à déterminer expérimentalement : le système est chau é sous pression constante; c est l énergie de chau age apportée pour obtenir une élévation de température de 1K. 18 avril 2004 L. Menguy, Lycée Montesquieu Le Mans.
11 Section 3.4 L enthalpie ; les capacités thermiques (ou calori ques) La capacité thermique à volume constant Dans un second temps, le système est chau é à volume constant. La capacité thermique à volume constant notée C V est l énergie Q à apporter sous forme thermique pour augmenter la température du système de 1K : C V = µ ±Q dt V car ±Q = du à pression constante. C V est donc facile à déterminer expérimentalement : le système est chau é dans un récipient fermé de parois rigides de manière à ce que le volume reste constant (par exemple autocuiseur); c est l énergie de chau age apportée pour obtenir une élévation de température de 1K Les capacités molaires et massiques On peut dé nir également : -la capacité thermique massique à pression constante : c p = C P =m (m masse du système); -la capacité thermique massique à volume constant : c v = C V =m; ou encore : -la capacité thermique molaire à pression constante : C pm = C P =n (m quantité de matière); -la capacité thermique molaire à volume constant : C vm = C V =n. soit Exemple du gaz parfait : la relation de Mayer U ne dépend que de la température, donc du GP V U GP = C V T: V dt = C V dt La constante d intégration est nulle, car U ne contient que l énergie cinétique pour un gaz parfait (Ep micro = 0, pas d interaction inter-moléculaire), donc quand il n y a pas d agitation thermique (T = 0) : U = 0. D autre part : Or donc, pour un gaz parfait H = U + PV = C V T + nrt = (C V + nr)t: C P P C P = C V + nr; qui s écrit également en fonction des capacités molaires : C est la relation de Mayer. C pm = C vm + R L. Menguy, Lycée Montesquieu Le Mans. 18 avril 2004
12 40 Chapitre 3 Bilans d énergie : le premier principe de la thermodynamique D autre part, le coe cient est dé ni par : = C P C V : En résumé, pour un gaz parfait U GP = C V T et H GP = C P T, avec : C V C P GP monoatomique (3=2) nr (5=2) nr 5=3 GP diatomique (5=2) nr (7=2) nr 7=5 ' 1; Les autres gaz Si le gaz n est pas un gaz parfait : -à volume constant U = Q reste valable; -à pression constante H = Q reste valable. Par contre U = C V T et H = C P T ne restent pas valables! D ailleurs, l énergie et l enthalpie ne dépendent à priori plus uniquement de la température! Phase condensée Si le système est une phase condensée (liquide ou solide),on peut considérer en première approximation que le volume reste constant (systèmesincompressibles). Un chau ageà pression constante se fera donc également à volume constant : les deux capacités thermiques sont donc quasiment identiques : C V ' C P et sont souvent notées tout simplement C Exemple de la détente de Joule Thomson Position du problème écoulement P1 P2 écoulement P1 P2 T1 T2 ou T1 T2 paroi poreuse goulot d étranglement parois calorifugées Fig.3.5. Détente de Joule-Thomson (ou Joule-Kelvin) : un uide s écoule dansun conduitauxparois calorifugées; la pression et la température se trouvent modi ées par la présence d une paroi poreuse entravant l écoulement ( gure de gauche), ou par la présence d un étranglement ( gure de droite). Un uide s écoule dans un conduit dont les parois sont calorifugées (voir gure 3.5). Les propriétés du uide (pression et température) sont modi ées par la présence d une paroi 18 avril 2004 L. Menguy, Lycée Montesquieu Le Mans.
13 Section 3.4 L enthalpie ; les capacités thermiques (ou calori ques) 41 poreuse ou d un goulot d étranglement qui vient entraver l écoulement. La pression (notée P 1 ) en entrée est alors plus importante que la pression P 2 en sortie Résolution du problème A n de simpli er leraisonnement, nousallons considérer ledispositifde gauchede la gure 3.5, et supposer que la pression P 1 et la température T 1 sont à peu près uniforme à gauche de la paroi poreuse d une part, et que P 2 et T 2 sont également à peu près uniformes du coté droit de la paroi poreuse d autre part. Le premier principe tel qu il a été posé en équation (2) n est valable que pour un système fermé. Il faut donc choisir ici un système fermé. Prenons une partie du uide ABCD à l instant t et suivons le : à t + dt il se trouve en A0B0C0D0 (voir gure 3.6). A A paroi poreuse D D P1 P2 T1 T2 B B C C parois calorifugées Fig.3.6. Appliquons le premier principe dela thermodynamiqueau système dé ni précédemment : du = ±W + ±Q U A 0 B 0 C 0 D 0 U ABCD = ±W + ±Q: (4) Or l énergie interne est une grandeur extensive (donc additive) : U A 0 B 0 C 0 D 0 = U A 0 B 0 CD + U CC 0 D 0 D (5) U ABCD = U ABB 0 A 0 + U A 0 B 0 CD: (6) Deplus±Q =0 car les paroissont adiabatiques. Resteà exprimer ±W. C est letravaildes forces de pression s exerçant sur le gauche à gauche (pression P 1 ) et à droite (P 2 ) : ±W = P 1 dv 1 P 2 dv 2 ; (7) avec dv 1 = V ABB0 A 0 (signe négatif car le volume diminue à gauche) et dv 2 = V CC 0 D 0 D. En injectant les relations (5), (6) et (7) dans le premier principe (4), il vient : soit U CC0 D 0 D U ABB0 A 0 = P 1V ABB0 A 0 P 2V CC0 D 0 D U CC 0 D 0 D + P 2 V CC 0 D 0 D = U ABB 0 A 0 + P 1V ABB 0 A 0 H CC 0 D 0 D = H ABB 0 A0: (8) L enthalpie de ABB0A0 est la même que l enthalpie de CC0D0D. L. Menguy, Lycée Montesquieu Le Mans. 18 avril 2004
14 42 Chapitre 3 Bilans d énergie : le premier principe de la thermodynamique Or, par principe de conservation de la matière, la matière qui a été perdue à gauche (ABB0A0) est égale à la matière qui a été gagnée à droite (CC0D0D) : m ABB0 A 0 = m CC 0 D 0 D. En divisant la relation (8) par cette masse, il vient : soit H CC 0 D 0 D m CC0 D 0 D = H ABB 0 A 0 m ABB0 A 0 ; h 2 = h 1 : L enthalpie massique lors d une détente de Joule-Thomson est conservée Détente de Joule-Thomson pour un gaz parfait Pour un gaz parfait, l enthalpie ne dépend que de la température (Rappel : H = C P T). L enthalpie étant constante, la température reste constante lors de la détente de Joule- Thomson d un gaz parfait : T 1 = T 2. Cette expérience permet de véri er la deuxième loi de Joule. Remarque 3.11 Si le gaz n est pas parfait, par exemple pour un gaz de Van-der-Walls, alors la détente de Joule-Thomson est toujours isenthalpique, mais par contre la température est susceptible de varier Conclusion sur les détentes de Joule Le gaz parfait a été dé ni dans le premier chapitre de thermodynamique comme un gaz dont les particules sont ponctuelles, et sans interaction interne. C est une dé nition cinétique du gaz parfait. Le gaz parfait peut être également dé ni de la manière suivante par les thermodynamiciens : c est un gaz qui véri e les deux lois de Joule : U ne dépend que de la température, et H ne dépend que de la température. Les deux détentes de Joule-Gay Lussac et de Joule-Thomson permettent de véri er si un gazest parfait. Sila températureresteconstantelorsd unedétente dejoule-gay Lussac, alors cela signi e que ce gaz véri e la premier loi de Joule. Si la température reste constante lors d une détente de Joule-Thomson, alors cela signi e que la deuxième loi de Joule est véri ée. Si le gaz véri e les deux lois de Joule, c est qu il est parfait. Inversement, il su t que la température varie lors d une seule de ces deux expériences pour conclure que le gaz n est pas parfait. 18 avril 2004 L. Menguy, Lycée Montesquieu Le Mans.
Premier principe : bilans d énergie
 MPSI - Thermodynamique - Premier principe : bilans d énergie page 1/5 Premier principe : bilans d énergie Table des matières 1 De la mécanique à la thermodynamique : formes d énergie et échanges d énergie
MPSI - Thermodynamique - Premier principe : bilans d énergie page 1/5 Premier principe : bilans d énergie Table des matières 1 De la mécanique à la thermodynamique : formes d énergie et échanges d énergie
Chapitre 4 Le deuxième principe de la thermodynamique
 Chapitre 4 Le deuxième principe de la thermodynamique 43 4.1. Evolutions réversibles et irréversibles 4.1.1. Exemples 4.1.1.1. Exemple 1 Reprenons l exemple 1 du chapitre précédent. Une masse est placée
Chapitre 4 Le deuxième principe de la thermodynamique 43 4.1. Evolutions réversibles et irréversibles 4.1.1. Exemples 4.1.1.1. Exemple 1 Reprenons l exemple 1 du chapitre précédent. Une masse est placée
Premier principe de la thermodynamique - conservation de l énergie
 Chapitre 5 Premier principe de la thermodynamique - conservation de l énergie 5.1 Bilan d énergie 5.1.1 Énergie totale d un système fermé L énergie totale E T d un système thermodynamique fermé de masse
Chapitre 5 Premier principe de la thermodynamique - conservation de l énergie 5.1 Bilan d énergie 5.1.1 Énergie totale d un système fermé L énergie totale E T d un système thermodynamique fermé de masse
Chapitre 1 Cinématique du point matériel
 Chapitre 1 Cinématique du point matériel 7 1.1. Introduction 1.1.1. Domaine d étude Le programme de mécanique de math sup se limite à l étude de la mécanique classique. Sont exclus : la relativité et la
Chapitre 1 Cinématique du point matériel 7 1.1. Introduction 1.1.1. Domaine d étude Le programme de mécanique de math sup se limite à l étude de la mécanique classique. Sont exclus : la relativité et la
Chapitre 3 Les régimes de fonctionnement de quelques circuits linéaires
 Chapitre 3 Les régimes de fonctionnement de quelques circuits linéaires 25 Lechapitreprécédent avait pour objet l étude decircuitsrésistifsalimentéspar dessourcesde tension ou de courant continues. Par
Chapitre 3 Les régimes de fonctionnement de quelques circuits linéaires 25 Lechapitreprécédent avait pour objet l étude decircuitsrésistifsalimentéspar dessourcesde tension ou de courant continues. Par
Chapitre 5. Le ressort. F ext. F ressort
 Chapitre 5 Le ressort Le ressort est un élément fondamental de plusieurs mécanismes. Il existe plusieurs types de ressorts (à boudin, à lame, spiral etc.) Que l on comprime ou étire un ressort, tel que
Chapitre 5 Le ressort Le ressort est un élément fondamental de plusieurs mécanismes. Il existe plusieurs types de ressorts (à boudin, à lame, spiral etc.) Que l on comprime ou étire un ressort, tel que
Système formé de deux points
 MPSI - 2005/2006 - Mécanique II - Système formé de deux points matériels page /5 Système formé de deux points matériels Table des matières Éléments cinétiques. Éléments cinétiques dans R.......................2
MPSI - 2005/2006 - Mécanique II - Système formé de deux points matériels page /5 Système formé de deux points matériels Table des matières Éléments cinétiques. Éléments cinétiques dans R.......................2
Exercice 1. Exercice n 1 : Déséquilibre mécanique
 Exercice 1 1. a) Un mobile peut-il avoir une accélération non nulle à un instant où sa vitesse est nulle? donner un exemple illustrant la réponse. b) Un mobile peut-il avoir une accélération de direction
Exercice 1 1. a) Un mobile peut-il avoir une accélération non nulle à un instant où sa vitesse est nulle? donner un exemple illustrant la réponse. b) Un mobile peut-il avoir une accélération de direction
Chapitre 3 LES GAZ PARFAITS : EXEMPLES DE CALCULS DE GRANDEURS THERMODYNAMIQUES
 Chapitre 3 LES GAZ PARFAITS : EXEMPLES DE CALCULS DE GRANDEURS THERMODYNAMIQUES Entropie de mélange. - Evolution adiabatique. - Autres évolutions réversibles et irréversibles. L ensemble de ce chapitre
Chapitre 3 LES GAZ PARFAITS : EXEMPLES DE CALCULS DE GRANDEURS THERMODYNAMIQUES Entropie de mélange. - Evolution adiabatique. - Autres évolutions réversibles et irréversibles. L ensemble de ce chapitre
Physique : Thermodynamique
 Correction du Devoir urveillé n o 8 Physique : hermodynamique I Cycle moteur [Véto 200] Cf Cours : C P m C V m R relation de Mayer, pour un GP. C P m γr γ 29, 0 J.K.mol et C V m R γ 20, 78 J.K.mol. 2 Une
Correction du Devoir urveillé n o 8 Physique : hermodynamique I Cycle moteur [Véto 200] Cf Cours : C P m C V m R relation de Mayer, pour un GP. C P m γr γ 29, 0 J.K.mol et C V m R γ 20, 78 J.K.mol. 2 Une
Chapitre 11 Bilans thermiques
 DERNIÈRE IMPRESSION LE 30 août 2013 à 15:40 Chapitre 11 Bilans thermiques Table des matières 1 L état macroscopique et microcospique de la matière 2 2 Énergie interne d un système 2 2.1 Définition.................................
DERNIÈRE IMPRESSION LE 30 août 2013 à 15:40 Chapitre 11 Bilans thermiques Table des matières 1 L état macroscopique et microcospique de la matière 2 2 Énergie interne d un système 2 2.1 Définition.................................
AIDE-MÉMOIRE LA THERMOCHIMIE TABLE DES MATIERES
 Collège Voltaire, 2014-2015 AIDE-MÉMOIRE LA THERMOCHIMIE http://dcpe.net/poii/sites/default/files/cours%20et%20ex/cours-ch2-thermo.pdf TABLE DES MATIERES 3.A. Introduction...2 3.B. Chaleur...3 3.C. Variation
Collège Voltaire, 2014-2015 AIDE-MÉMOIRE LA THERMOCHIMIE http://dcpe.net/poii/sites/default/files/cours%20et%20ex/cours-ch2-thermo.pdf TABLE DES MATIERES 3.A. Introduction...2 3.B. Chaleur...3 3.C. Variation
1 Thermodynamique: première loi
 1 hermodynamique: première loi 1.1 Énoncé L énergie d un système isolé est constante, L énergie de l univers est constante, de univers = de syst + de env. = 0 1 L énergie d un système est une fonction
1 hermodynamique: première loi 1.1 Énoncé L énergie d un système isolé est constante, L énergie de l univers est constante, de univers = de syst + de env. = 0 1 L énergie d un système est une fonction
Optimisation des systèmes énergétiques Master 1 : GSI Génie Energétique et Thermique
 Optimisation des systèmes énergétiques Master 1 : GSI Génie Energétique et Thermique Année 2009-2010 2008-09 Stéphane LE PERSON Maître de Conférences Université Joseph Fourier Jean-Paul THIBAULT LEGI UMR
Optimisation des systèmes énergétiques Master 1 : GSI Génie Energétique et Thermique Année 2009-2010 2008-09 Stéphane LE PERSON Maître de Conférences Université Joseph Fourier Jean-Paul THIBAULT LEGI UMR
DYNAMIQUE DE FORMATION DES ÉTOILES
 A 99 PHYS. II ÉCOLE NATIONALE DES PONTS ET CHAUSSÉES, ÉCOLES NATIONALES SUPÉRIEURES DE L'AÉRONAUTIQUE ET DE L'ESPACE, DE TECHNIQUES AVANCÉES, DES TÉLÉCOMMUNICATIONS, DES MINES DE PARIS, DES MINES DE SAINT-ÉTIENNE,
A 99 PHYS. II ÉCOLE NATIONALE DES PONTS ET CHAUSSÉES, ÉCOLES NATIONALES SUPÉRIEURES DE L'AÉRONAUTIQUE ET DE L'ESPACE, DE TECHNIQUES AVANCÉES, DES TÉLÉCOMMUNICATIONS, DES MINES DE PARIS, DES MINES DE SAINT-ÉTIENNE,
Module d Electricité. 2 ème partie : Electrostatique. Fabrice Sincère (version 3.0.1) http://pagesperso-orange.fr/fabrice.sincere
 Module d Electricité 2 ème partie : Electrostatique Fabrice Sincère (version 3.0.1) http://pagesperso-orange.fr/fabrice.sincere 1 Introduction Principaux constituants de la matière : - protons : charge
Module d Electricité 2 ème partie : Electrostatique Fabrice Sincère (version 3.0.1) http://pagesperso-orange.fr/fabrice.sincere 1 Introduction Principaux constituants de la matière : - protons : charge
1 Mise en application
 Université Paris 7 - Denis Diderot 2013-2014 TD : Corrigé TD1 - partie 2 1 Mise en application Exercice 1 corrigé Exercice 2 corrigé - Vibration d une goutte La fréquence de vibration d une goutte d eau
Université Paris 7 - Denis Diderot 2013-2014 TD : Corrigé TD1 - partie 2 1 Mise en application Exercice 1 corrigé Exercice 2 corrigé - Vibration d une goutte La fréquence de vibration d une goutte d eau
CHAÎNES ÉNERGÉTIQUES I CHAÎNES ÉNERGÉTIQUES. II PUISSANCE ET ÉNERGIE
 CHAÎNES ÉNERGÉTIQUES I CHAÎNES ÉNERGÉTIQUES. II PUISSANCE ET ÉNERGIE I Chaine énergétique a- Les différentes formes d énergie L énergie se mesure en Joules, elle peut prendre différentes formes : chimique,
CHAÎNES ÉNERGÉTIQUES I CHAÎNES ÉNERGÉTIQUES. II PUISSANCE ET ÉNERGIE I Chaine énergétique a- Les différentes formes d énergie L énergie se mesure en Joules, elle peut prendre différentes formes : chimique,
À propos d ITER. 1- Principe de la fusion thermonucléaire
 À propos d ITER Le projet ITER est un projet international destiné à montrer la faisabilité scientifique et technique de la fusion thermonucléaire contrôlée. Le 8 juin 005, les pays engagés dans le projet
À propos d ITER Le projet ITER est un projet international destiné à montrer la faisabilité scientifique et technique de la fusion thermonucléaire contrôlée. Le 8 juin 005, les pays engagés dans le projet
La fonction exponentielle
 DERNIÈRE IMPRESSION LE 2 novembre 204 à :07 La fonction exponentielle Table des matières La fonction exponentielle 2. Définition et théorèmes.......................... 2.2 Approche graphique de la fonction
DERNIÈRE IMPRESSION LE 2 novembre 204 à :07 La fonction exponentielle Table des matières La fonction exponentielle 2. Définition et théorèmes.......................... 2.2 Approche graphique de la fonction
TD 9 Problème à deux corps
 PH1ME2-C Université Paris 7 - Denis Diderot 2012-2013 TD 9 Problème à deux corps 1. Systèmes de deux particules : centre de masse et particule relative. Application à l étude des étoiles doubles Une étoile
PH1ME2-C Université Paris 7 - Denis Diderot 2012-2013 TD 9 Problème à deux corps 1. Systèmes de deux particules : centre de masse et particule relative. Application à l étude des étoiles doubles Une étoile
Chapitre 5 : Noyaux, masse et énergie
 Chapitre 5 : Noyaux, masse et énergie Connaissances et savoir-faire exigibles : () () (3) () (5) (6) (7) (8) Définir et calculer un défaut de masse et une énergie de liaison. Définir et calculer l énergie
Chapitre 5 : Noyaux, masse et énergie Connaissances et savoir-faire exigibles : () () (3) () (5) (6) (7) (8) Définir et calculer un défaut de masse et une énergie de liaison. Définir et calculer l énergie
COURS DE THERMODYNAMIQUE
 I.U.T. de Saint-Omer Dunkerque Département Génie Thermique et énergie COURS DE THERMODYNAMIQUE eme Semestre Olivier PERROT 010-011 1 Avertissement : Ce cours de thermodynamique présente quelques applications
I.U.T. de Saint-Omer Dunkerque Département Génie Thermique et énergie COURS DE THERMODYNAMIQUE eme Semestre Olivier PERROT 010-011 1 Avertissement : Ce cours de thermodynamique présente quelques applications
Quantité de mouvement et moment cinétique
 6 Quantité de mouvement et moment cinétique v7 p = mv L = r p 1 Impulsion et quantité de mouvement Une force F agit sur un corps de masse m, pendant un temps Δt. La vitesse du corps varie de Δv = v f -
6 Quantité de mouvement et moment cinétique v7 p = mv L = r p 1 Impulsion et quantité de mouvement Une force F agit sur un corps de masse m, pendant un temps Δt. La vitesse du corps varie de Δv = v f -
Etudier le diagramme température-pression, en particulier le point triple de l azote.
 K4. Point triple de l azote I. BUT DE LA MANIPULATION Etudier le diagramme température-pression, en particulier le point triple de l azote. II. BASES THEORIQUES Etats de la matière La matière est constituée
K4. Point triple de l azote I. BUT DE LA MANIPULATION Etudier le diagramme température-pression, en particulier le point triple de l azote. II. BASES THEORIQUES Etats de la matière La matière est constituée
CONCOURS COMMUN 2010 PHYSIQUE
 CONCOUS COMMUN SUJET A DES ÉCOLES DES MINES D ALBI, ALÈS, DOUAI, NANTES Épreuve de Physique-Chimie (toutes filières) Corrigé Barème total points : Physique points - Chimie 68 points PHYSIQUE Partie A :
CONCOUS COMMUN SUJET A DES ÉCOLES DES MINES D ALBI, ALÈS, DOUAI, NANTES Épreuve de Physique-Chimie (toutes filières) Corrigé Barème total points : Physique points - Chimie 68 points PHYSIQUE Partie A :
Cours de mécanique des fluides. Olivier LOUISNARD
 Cours de mécanique des fluides Olivier LOUISNARD 25 septembre 2012 Cette création est mise à disposition selon le Contrat Paternité-Pas d Utilisation Commerciale-Pas de Modification 2.0 France disponible
Cours de mécanique des fluides Olivier LOUISNARD 25 septembre 2012 Cette création est mise à disposition selon le Contrat Paternité-Pas d Utilisation Commerciale-Pas de Modification 2.0 France disponible
Variations du modèle de base
 1 Variations du modèle de base Dans ce chapitre nous allons utiliser le modèle de base du chapitre précédent pour illustrer certaines questions économiques simples. Ainsi, le modèle précédent nous permettra
1 Variations du modèle de base Dans ce chapitre nous allons utiliser le modèle de base du chapitre précédent pour illustrer certaines questions économiques simples. Ainsi, le modèle précédent nous permettra
Erratum de MÉCANIQUE, 6ème édition. Introduction Page xxi (milieu de page) G = 6, 672 59 10 11 m 3 kg 1 s 2
 Introduction Page xxi (milieu de page) G = 6, 672 59 1 11 m 3 kg 1 s 2 Erratum de MÉCANIQUE, 6ème édition Page xxv (dernier tiers de page) le terme de Coriolis est supérieur à 1% du poids) Chapitre 1 Page
Introduction Page xxi (milieu de page) G = 6, 672 59 1 11 m 3 kg 1 s 2 Erratum de MÉCANIQUE, 6ème édition Page xxv (dernier tiers de page) le terme de Coriolis est supérieur à 1% du poids) Chapitre 1 Page
A retenir : A Z m n. m noyau MASSE ET ÉNERGIE RÉACTIONS NUCLÉAIRES I) EQUIVALENCE MASSE-ÉNERGIE
 CP7 MASSE ET ÉNERGIE RÉACTIONS NUCLÉAIRES I) EQUIVALENCE MASSE-ÉNERGIE 1 ) Relation d'équivalence entre la masse et l'énergie -énergie de liaison 2 ) Une unité d énergie mieux adaptée 3 ) application 4
CP7 MASSE ET ÉNERGIE RÉACTIONS NUCLÉAIRES I) EQUIVALENCE MASSE-ÉNERGIE 1 ) Relation d'équivalence entre la masse et l'énergie -énergie de liaison 2 ) Une unité d énergie mieux adaptée 3 ) application 4
Mesures du coefficient adiabatique γ de l air
 Mesures du oeffiient adiabatique γ de l air Introdution : γ est le rapport des apaités alorifiques massiques d un gaz : γ = p v Le gaz étudié est l air. La mesure de la haleur massique à pression onstante
Mesures du oeffiient adiabatique γ de l air Introdution : γ est le rapport des apaités alorifiques massiques d un gaz : γ = p v Le gaz étudié est l air. La mesure de la haleur massique à pression onstante
Les puissances 4. 4.1. La notion de puissance. 4.1.1. La puissance c est l énergie pendant une seconde CHAPITRE
 4. LES PUISSANCES LA NOTION DE PUISSANCE 88 CHAPITRE 4 Rien ne se perd, rien ne se crée. Mais alors que consomme un appareil électrique si ce n est les électrons? La puissance pardi. Objectifs de ce chapitre
4. LES PUISSANCES LA NOTION DE PUISSANCE 88 CHAPITRE 4 Rien ne se perd, rien ne se crée. Mais alors que consomme un appareil électrique si ce n est les électrons? La puissance pardi. Objectifs de ce chapitre
PHYSIQUE-CHIMIE. Partie I - Propriétés de l atome
 PHYSIQUE-CHIMIE Ce sujet traite de quelques propriétés de l aluminium et de leurs applications. Certaines données fondamentales sont regroupées à la fin du texte. Partie I - Propriétés de l atome I.A -
PHYSIQUE-CHIMIE Ce sujet traite de quelques propriétés de l aluminium et de leurs applications. Certaines données fondamentales sont regroupées à la fin du texte. Partie I - Propriétés de l atome I.A -
Stockage de chaleur solaire par sorption : Analyse et contrôle du système à partir de sa simulation dynamique
 Stockage de chaleur solaire par sorption : Analyse et contrôle du système à partir de sa simulation dynamique Kokouvi Edem N TSOUKPOE 1, Nolwenn LE PIERRÈS 1*, Lingai LUO 1 1 LOCIE, CNRS FRE3220-Université
Stockage de chaleur solaire par sorption : Analyse et contrôle du système à partir de sa simulation dynamique Kokouvi Edem N TSOUKPOE 1, Nolwenn LE PIERRÈS 1*, Lingai LUO 1 1 LOCIE, CNRS FRE3220-Université
THERMODYNAMIQUE: LIQUEFACTION D UN GAZ
 THERMODYNAMIQUE: LIQUEFACTION D UN GAZ B. AMANA et J.-L. LEMAIRE 2 LIQUEFACTION D'UN GAZ Cette expérience permet d'étudier la compressibilité et la liquéfaction d'un fluide en fonction des variables P,
THERMODYNAMIQUE: LIQUEFACTION D UN GAZ B. AMANA et J.-L. LEMAIRE 2 LIQUEFACTION D'UN GAZ Cette expérience permet d'étudier la compressibilité et la liquéfaction d'un fluide en fonction des variables P,
Plan du chapitre «Milieux diélectriques»
 Plan du chapitre «Milieux diélectriques» 1. Sources microscopiques de la polarisation en régime statique 2. Etude macroscopique de la polarisation en régime statique 3. Susceptibilité diélectrique 4. Polarisation
Plan du chapitre «Milieux diélectriques» 1. Sources microscopiques de la polarisation en régime statique 2. Etude macroscopique de la polarisation en régime statique 3. Susceptibilité diélectrique 4. Polarisation
TS Physique Satellite à la recherche de sa planète Exercice résolu
 P a g e 1 Phsique atellite à la recherche de sa planète Exercice résolu Enoncé Le centre spatial de Kourou a lancé le 1 décembre 005, avec une fusée Ariane 5, un satellite de météorologie de seconde génération
P a g e 1 Phsique atellite à la recherche de sa planète Exercice résolu Enoncé Le centre spatial de Kourou a lancé le 1 décembre 005, avec une fusée Ariane 5, un satellite de météorologie de seconde génération
Energie nucléaire. Quelques éléments de physique
 Energie nucléaire Quelques éléments de physique Comment produire 1 GW électrique Nucléaire (rendement 33%) Thermique (38%) Hydraulique (85%) Solaire (10%) Vent : 27t d uranium par an : 170 t de fuel par
Energie nucléaire Quelques éléments de physique Comment produire 1 GW électrique Nucléaire (rendement 33%) Thermique (38%) Hydraulique (85%) Solaire (10%) Vent : 27t d uranium par an : 170 t de fuel par
Initiation à la Mécanique des Fluides. Mr. Zoubir HAMIDI
 Initiation à la Mécanique des Fluides Mr. Zoubir HAMIDI Chapitre I : Introduction à la mécanique des fluides 1 Introduction La mécanique des fluides(mdf) a pour objet l étude du comportement des fluides
Initiation à la Mécanique des Fluides Mr. Zoubir HAMIDI Chapitre I : Introduction à la mécanique des fluides 1 Introduction La mécanique des fluides(mdf) a pour objet l étude du comportement des fluides
8 Ensemble grand-canonique
 Physique Statistique I, 007-008 8 Ensemble grand-canonique 8.1 Calcul de la densité de probabilité On adopte la même approche par laquelle on a établi la densité de probabilité de l ensemble canonique,
Physique Statistique I, 007-008 8 Ensemble grand-canonique 8.1 Calcul de la densité de probabilité On adopte la même approche par laquelle on a établi la densité de probabilité de l ensemble canonique,
Précis de thermodynamique
 M. Hubert N. Vandewalle Précis de thermodynamique Année académique 2013-2014 PHYS2010-1 Thermodynamique 2 Ce précis a été créé dans le but d offrir à l étudiant une base solide pour l apprentissage de
M. Hubert N. Vandewalle Précis de thermodynamique Année académique 2013-2014 PHYS2010-1 Thermodynamique 2 Ce précis a été créé dans le but d offrir à l étudiant une base solide pour l apprentissage de
Mesure de la dépense énergétique
 Mesure de la dépense énergétique Bioénergétique L énergie existe sous différentes formes : calorifique, mécanique, électrique, chimique, rayonnante, nucléaire. La bioénergétique est la branche de la biologie
Mesure de la dépense énergétique Bioénergétique L énergie existe sous différentes formes : calorifique, mécanique, électrique, chimique, rayonnante, nucléaire. La bioénergétique est la branche de la biologie
Économie d énergie dans les centrales frigorifiques : La haute pression flottante
 Économie d énergie dans les centrales frigorifiques : La haute pression flottante Juillet 2011/White paper par Christophe Borlein membre de l AFF et de l IIF-IIR Make the most of your energy Sommaire Avant-propos
Économie d énergie dans les centrales frigorifiques : La haute pression flottante Juillet 2011/White paper par Christophe Borlein membre de l AFF et de l IIF-IIR Make the most of your energy Sommaire Avant-propos
PHYSIQUE Discipline fondamentale
 Examen suisse de maturité Directives 2003-2006 DS.11 Physique DF PHYSIQUE Discipline fondamentale Par l'étude de la physique en discipline fondamentale, le candidat comprend des phénomènes naturels et
Examen suisse de maturité Directives 2003-2006 DS.11 Physique DF PHYSIQUE Discipline fondamentale Par l'étude de la physique en discipline fondamentale, le candidat comprend des phénomènes naturels et
U-31 CHIMIE-PHYSIQUE INDUSTRIELLES
 Session 200 BREVET de TECHNICIEN SUPÉRIEUR CONTRÔLE INDUSTRIEL et RÉGULATION AUTOMATIQUE E-3 SCIENCES PHYSIQUES U-3 CHIMIE-PHYSIQUE INDUSTRIELLES Durée : 2 heures Coefficient : 2,5 Durée conseillée Chimie
Session 200 BREVET de TECHNICIEN SUPÉRIEUR CONTRÔLE INDUSTRIEL et RÉGULATION AUTOMATIQUE E-3 SCIENCES PHYSIQUES U-3 CHIMIE-PHYSIQUE INDUSTRIELLES Durée : 2 heures Coefficient : 2,5 Durée conseillée Chimie
Transformations nucléaires
 I Introduction Activité p286 du livre Transformations nucléaires II Les transformations nucléaires II.a Définition La désintégration radioactive d un noyau est une transformation nucléaire particulière
I Introduction Activité p286 du livre Transformations nucléaires II Les transformations nucléaires II.a Définition La désintégration radioactive d un noyau est une transformation nucléaire particulière
Contenu pédagogique des unités d enseignement Semestre 1(1 ère année) Domaine : Sciences et techniques et Sciences de la matière
 Contenu pédagogique des unités d enseignement Semestre 1(1 ère année) Domaine : Sciences et techniques et Sciences de la matière Algèbre 1 : (Volume horaire total : 63 heures) UE1 : Analyse et algèbre
Contenu pédagogique des unités d enseignement Semestre 1(1 ère année) Domaine : Sciences et techniques et Sciences de la matière Algèbre 1 : (Volume horaire total : 63 heures) UE1 : Analyse et algèbre
T.P. FLUENT. Cours Mécanique des Fluides. 24 février 2006 NAZIH MARZOUQY
 T.P. FLUENT Cours Mécanique des Fluides 24 février 2006 NAZIH MARZOUQY 2 Table des matières 1 Choc stationnaire dans un tube à choc 7 1.1 Introduction....................................... 7 1.2 Description.......................................
T.P. FLUENT Cours Mécanique des Fluides 24 février 2006 NAZIH MARZOUQY 2 Table des matières 1 Choc stationnaire dans un tube à choc 7 1.1 Introduction....................................... 7 1.2 Description.......................................
L énergie sous toutes ses formes : définitions
 L énergie sous toutes ses formes : définitions primaire, énergie secondaire, utile ou finale. Quelles sont les formes et les déclinaisons de l énergie? D après le dictionnaire de l Académie française,
L énergie sous toutes ses formes : définitions primaire, énergie secondaire, utile ou finale. Quelles sont les formes et les déclinaisons de l énergie? D après le dictionnaire de l Académie française,
10 leçon 2. Leçon n 2 : Contact entre deux solides. Frottement de glissement. Exemples. (PC ou 1 er CU)
 0 leçon 2 Leçon n 2 : Contact entre deu solides Frottement de glissement Eemples (PC ou er CU) Introduction Contact entre deu solides Liaisons de contact 2 Contact ponctuel 2 Frottement de glissement 2
0 leçon 2 Leçon n 2 : Contact entre deu solides Frottement de glissement Eemples (PC ou er CU) Introduction Contact entre deu solides Liaisons de contact 2 Contact ponctuel 2 Frottement de glissement 2
Cours d électricité. Circuits électriques en courant constant. Mathieu Bardoux. 1 re année
 Cours d électricité Circuits électriques en courant constant Mathieu Bardoux mathieu.bardoux@univ-littoral.fr IUT Saint-Omer / Dunkerque Département Génie Thermique et Énergie 1 re année Objectifs du chapitre
Cours d électricité Circuits électriques en courant constant Mathieu Bardoux mathieu.bardoux@univ-littoral.fr IUT Saint-Omer / Dunkerque Département Génie Thermique et Énergie 1 re année Objectifs du chapitre
Systèmes de récupération de chaleur des eaux de drainage
 Systèmes de récupération de chaleur des eaux de drainage Les objectifs d'apprentissage: Cet exposé vous informera au sujet des systèmes de récupération de chaleur des eaux de drainage (SRCED) et: Comment
Systèmes de récupération de chaleur des eaux de drainage Les objectifs d'apprentissage: Cet exposé vous informera au sujet des systèmes de récupération de chaleur des eaux de drainage (SRCED) et: Comment
Chapitre 1: Facteurs d'échelle
 Chapitre 1: Facteurs d'échelle Des considérations générales sur la taille des objets ou des êtres vivants et leur influence sur différents paramètres, permettent d'établir simplement quelques lois ou tendances,
Chapitre 1: Facteurs d'échelle Des considérations générales sur la taille des objets ou des êtres vivants et leur influence sur différents paramètres, permettent d'établir simplement quelques lois ou tendances,
A QUOI SERT LE NIVEAU DE CUVE?
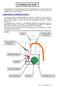 LE NIVEAU DE CUVE Les explications et les schémas qui suivent correspondent à ce que j ai compris du fonctionnement du carburateur MIKUNI qui équipe les BETA trial. Elles sont aussi valables pour les autres
LE NIVEAU DE CUVE Les explications et les schémas qui suivent correspondent à ce que j ai compris du fonctionnement du carburateur MIKUNI qui équipe les BETA trial. Elles sont aussi valables pour les autres
Circuits RL et RC. Chapitre 5. 5.1 Inductance
 Chapitre 5 Circuits RL et RC Ce chapitre présente les deux autres éléments linéaires des circuits électriques : l inductance et la capacitance. On verra le comportement de ces deux éléments, et ensuite
Chapitre 5 Circuits RL et RC Ce chapitre présente les deux autres éléments linéaires des circuits électriques : l inductance et la capacitance. On verra le comportement de ces deux éléments, et ensuite
Que nous enseigne la base de données PAE?
 Que nous enseigne la base de données PAE? Séminaire auditeurs PAE 8 juin 2009 Nicolas Heijmans, ir Division Energie et Climat CSTC - Centre Scientifique et Technique de la Construction 00/00/2006 Contenu
Que nous enseigne la base de données PAE? Séminaire auditeurs PAE 8 juin 2009 Nicolas Heijmans, ir Division Energie et Climat CSTC - Centre Scientifique et Technique de la Construction 00/00/2006 Contenu
Cours 1. Bases physiques de l électronique
 Cours 1. Bases physiques de l électronique Par Dimitri galayko Unité d enseignement Élec-info pour master ACSI à l UPMC Octobre-décembre 2005 1 Champ électrique et ses propriétés Ce premier cours introduit
Cours 1. Bases physiques de l électronique Par Dimitri galayko Unité d enseignement Élec-info pour master ACSI à l UPMC Octobre-décembre 2005 1 Champ électrique et ses propriétés Ce premier cours introduit
M6 MOMENT CINÉTIQUE D UN POINT MATÉRIEL
 M6 MOMENT CINÉTIQUE D UN POINT MATÉRIEL OBJECTIFS Jusqu à présent, nous avons rencontré deux méthodes pour obtenir l équation du mouvement d un point matériel : - l utilisation du P.F.D. - et celle du
M6 MOMENT CINÉTIQUE D UN POINT MATÉRIEL OBJECTIFS Jusqu à présent, nous avons rencontré deux méthodes pour obtenir l équation du mouvement d un point matériel : - l utilisation du P.F.D. - et celle du
BREVET DE TECHNICIEN SUPÉRIEUR AGRICOLE SUJET
 SESSION 2010 France métropolitaine BREVET DE TECHNICIEN SUPÉRIEUR AGRICOLE ÉPREUVE N 2 DU PREMIER GROUPE ÉPREUVE SCIENTIFIQUE ET TECHNIQUE Option : Génie des équipements agricoles Durée : 3 heures 30 Matériel
SESSION 2010 France métropolitaine BREVET DE TECHNICIEN SUPÉRIEUR AGRICOLE ÉPREUVE N 2 DU PREMIER GROUPE ÉPREUVE SCIENTIFIQUE ET TECHNIQUE Option : Génie des équipements agricoles Durée : 3 heures 30 Matériel
STI2D : Enseignements Technologiques Transversaux
 STI2D : Enseignements Technologiques Transversaux Activité : Etude des transfert énergétiques dans la cafetière Nespresso Problématique : On calcule la puissance électrique consommée, on détermine l énergie
STI2D : Enseignements Technologiques Transversaux Activité : Etude des transfert énergétiques dans la cafetière Nespresso Problématique : On calcule la puissance électrique consommée, on détermine l énergie
ÉNERGIE : DÉFINITIONS ET PRINCIPES
 DÉFINITION DE L ÉNERGIE FORMES D ÉNERGIE LES GRANDS PRINCIPES DE L ÉNERGIE DÉCLINAISONS DE L ÉNERGIE RENDEMENT ET EFFICACITÉ DÉFINITION DE L ÉNERGIE L énergie (du grec : force en action) est ce qui permet
DÉFINITION DE L ÉNERGIE FORMES D ÉNERGIE LES GRANDS PRINCIPES DE L ÉNERGIE DÉCLINAISONS DE L ÉNERGIE RENDEMENT ET EFFICACITÉ DÉFINITION DE L ÉNERGIE L énergie (du grec : force en action) est ce qui permet
IV- Comment fonctionne un ordinateur?
 1 IV- Comment fonctionne un ordinateur? L ordinateur est une alliance du hardware (le matériel) et du software (les logiciels). Jusqu à présent, nous avons surtout vu l aspect «matériel», avec les interactions
1 IV- Comment fonctionne un ordinateur? L ordinateur est une alliance du hardware (le matériel) et du software (les logiciels). Jusqu à présent, nous avons surtout vu l aspect «matériel», avec les interactions
Atelier : L énergie nucléaire en Astrophysique
 Atelier : L énergie nucléaire en Astrophysique Elisabeth Vangioni Institut d Astrophysique de Paris Fleurance, 8 Août 2005 Une calculatrice, une règle et du papier quadrillé sont nécessaires au bon fonctionnement
Atelier : L énergie nucléaire en Astrophysique Elisabeth Vangioni Institut d Astrophysique de Paris Fleurance, 8 Août 2005 Une calculatrice, une règle et du papier quadrillé sont nécessaires au bon fonctionnement
Chapitre 1 Régime transitoire dans les systèmes physiques
 Chapitre 1 Régime transitoire dans les systèmes physiques Savoir-faire théoriques (T) : Écrire l équation différentielle associée à un système physique ; Faire apparaître la constante de temps ; Tracer
Chapitre 1 Régime transitoire dans les systèmes physiques Savoir-faire théoriques (T) : Écrire l équation différentielle associée à un système physique ; Faire apparaître la constante de temps ; Tracer
Interactions des rayonnements avec la matière
 UE3-1 : Biophysique Chapitre 2 : Interactions des rayonnements avec la matière Professeur Jean-Philippe VUILLEZ Année universitaire 2011/2012 Université Joseph Fourier de Grenoble - Tous droits réservés.
UE3-1 : Biophysique Chapitre 2 : Interactions des rayonnements avec la matière Professeur Jean-Philippe VUILLEZ Année universitaire 2011/2012 Université Joseph Fourier de Grenoble - Tous droits réservés.
TSTI 2D CH X : Exemples de lois à densité 1
 TSTI 2D CH X : Exemples de lois à densité I Loi uniforme sur ab ; ) Introduction Dans cette activité, on s intéresse à la modélisation du tirage au hasard d un nombre réel de l intervalle [0 ;], chacun
TSTI 2D CH X : Exemples de lois à densité I Loi uniforme sur ab ; ) Introduction Dans cette activité, on s intéresse à la modélisation du tirage au hasard d un nombre réel de l intervalle [0 ;], chacun
Concours EPITA 2009 Epreuve de Sciences Industrielles pour l ingénieur La suspension anti-plongée de la motocyclette BMW K1200S
 Concours EPIT 2009 Epreuve de Sciences Industrielles pour l ingénieur La suspension anti-plongée de la motocyclette MW K1200S Durée : 2h. Calculatrices autorisées. Présentation du problème Le problème
Concours EPIT 2009 Epreuve de Sciences Industrielles pour l ingénieur La suspension anti-plongée de la motocyclette MW K1200S Durée : 2h. Calculatrices autorisées. Présentation du problème Le problème
Mario Geiger octobre 08 ÉVAPORATION SOUS VIDE
 ÉVAPORATION SOUS VIDE 1 I SOMMAIRE I Sommaire... 2 II Évaporation sous vide... 3 III Description de l installation... 5 IV Travail pratique... 6 But du travail... 6 Principe... 6 Matériel... 6 Méthodes...
ÉVAPORATION SOUS VIDE 1 I SOMMAIRE I Sommaire... 2 II Évaporation sous vide... 3 III Description de l installation... 5 IV Travail pratique... 6 But du travail... 6 Principe... 6 Matériel... 6 Méthodes...
Physique - Résumés de cours PCSI. Harold Erbin
 Physique - Résumés de cours PCSI Harold Erbin Ce texte est publié sous la licence libre Licence Art Libre : http://artlibre.org/licence/lal/ Contact : harold.erbin@gmail.com Version : 8 avril 2009 Table
Physique - Résumés de cours PCSI Harold Erbin Ce texte est publié sous la licence libre Licence Art Libre : http://artlibre.org/licence/lal/ Contact : harold.erbin@gmail.com Version : 8 avril 2009 Table
SYSTEME DE PARTICULES. DYNAMIQUE DU SOLIDE (suite) Table des matières
 Physique Générale SYSTEME DE PARTICULES DYNAMIQUE DU SOLIDE (suite) TRAN Minh Tâm Table des matières Applications de la loi de Newton pour la rotation 93 Le gyroscope........................ 93 L orbite
Physique Générale SYSTEME DE PARTICULES DYNAMIQUE DU SOLIDE (suite) TRAN Minh Tâm Table des matières Applications de la loi de Newton pour la rotation 93 Le gyroscope........................ 93 L orbite
Physique 1 TEMPÉRATURE, CHALEUR
 hysique EMÉRAURE, CHALEUR rof. André errenoud Edition mai 8 Andre.errenoud (at) heig-vd.ch HEIG-D / AD A B L E D E S M A I E R E S AGE. INRODUCION.... NOIONS DE EMÉRAURE E DE CHALEUR.... LES ÉCHANGES
hysique EMÉRAURE, CHALEUR rof. André errenoud Edition mai 8 Andre.errenoud (at) heig-vd.ch HEIG-D / AD A B L E D E S M A I E R E S AGE. INRODUCION.... NOIONS DE EMÉRAURE E DE CHALEUR.... LES ÉCHANGES
L ÉNERGIE C EST QUOI?
 L ÉNERGIE C EST QUOI? L énergie c est la vie! Pourquoi à chaque fois qu on fait quelque chose on dit qu on a besoin d énergie? Parce que l énergie est à l origine de tout! Rien ne peut se faire sans elle.
L ÉNERGIE C EST QUOI? L énergie c est la vie! Pourquoi à chaque fois qu on fait quelque chose on dit qu on a besoin d énergie? Parce que l énergie est à l origine de tout! Rien ne peut se faire sans elle.
DM 10 : La fusion nucléaire, l énergie de l avenir? CORRECTION
 Physique Chapitre 4 Masse, énergie, et transformations nucléaires DM 10 : La fusion nucléaire, l énergie de l avenir? CORRECTION Date :. Le 28 juin 2005, le site de Cadarache (dans les bouches du Rhône)
Physique Chapitre 4 Masse, énergie, et transformations nucléaires DM 10 : La fusion nucléaire, l énergie de l avenir? CORRECTION Date :. Le 28 juin 2005, le site de Cadarache (dans les bouches du Rhône)
Équivalence masse-énergie
 CHPITRE 5 NOYUX, MSSE ET ÉNERGIE Équivalence masse-énergie. Équivalence masse-énergie Einstein a montré que la masse constitue une forme d énergie appelée énergie de masse. La relation entre la masse (en
CHPITRE 5 NOYUX, MSSE ET ÉNERGIE Équivalence masse-énergie. Équivalence masse-énergie Einstein a montré que la masse constitue une forme d énergie appelée énergie de masse. La relation entre la masse (en
La conversion de données : Convertisseur Analogique Numérique (CAN) Convertisseur Numérique Analogique (CNA)
 La conversion de données : Convertisseur Analogique Numérique (CAN) Convertisseur Numérique Analogique (CNA) I. L'intérêt de la conversion de données, problèmes et définitions associés. I.1. Définitions:
La conversion de données : Convertisseur Analogique Numérique (CAN) Convertisseur Numérique Analogique (CNA) I. L'intérêt de la conversion de données, problèmes et définitions associés. I.1. Définitions:
Fiche de lecture du projet de fin d étude
 GENIE CLIMATIQUE ET ENERGETIQUE Fiche de lecture du projet de fin d étude Analyse du phénomène de condensation sur l aluminium Par Marine SIRE Tuteurs : J.C. SICK Manager du Kawneer Innovation Center &
GENIE CLIMATIQUE ET ENERGETIQUE Fiche de lecture du projet de fin d étude Analyse du phénomène de condensation sur l aluminium Par Marine SIRE Tuteurs : J.C. SICK Manager du Kawneer Innovation Center &
Chap 1: Toujours plus vite... Introduction: Comment déterminer la vitesse d une voiture?
 Thème 2 La sécurité Chap 1: Toujours plus vite... Introduction: Comment déterminer la vitesse d une voiture?! Il faut deux informations Le temps écoulé La distance parcourue Vitesse= distance temps > Activité
Thème 2 La sécurité Chap 1: Toujours plus vite... Introduction: Comment déterminer la vitesse d une voiture?! Il faut deux informations Le temps écoulé La distance parcourue Vitesse= distance temps > Activité
Examen d informatique première session 2004
 Examen d informatique première session 2004 Le chiffre à côté du titre de la question indique le nombre de points sur 40. I) Lentille électrostatique à fente (14) Le problème étudié est à deux dimensions.
Examen d informatique première session 2004 Le chiffre à côté du titre de la question indique le nombre de points sur 40. I) Lentille électrostatique à fente (14) Le problème étudié est à deux dimensions.
MESURE DE LA TEMPERATURE
 145 T2 MESURE DE LA TEMPERATURE I. INTRODUCTION Dans la majorité des phénomènes physiques, la température joue un rôle prépondérant. Pour la mesurer, les moyens les plus couramment utilisés sont : les
145 T2 MESURE DE LA TEMPERATURE I. INTRODUCTION Dans la majorité des phénomènes physiques, la température joue un rôle prépondérant. Pour la mesurer, les moyens les plus couramment utilisés sont : les
3 Charges électriques
 3 Charges électriques 3.1 Electrisation par frottement Expérience : Frottons un bâton d ébonite avec un morceau de peau de chat. Approchonsle de petits bouts de papier. On observe que les bouts de papier
3 Charges électriques 3.1 Electrisation par frottement Expérience : Frottons un bâton d ébonite avec un morceau de peau de chat. Approchonsle de petits bouts de papier. On observe que les bouts de papier
CAC, DAX ou DJ : lequel choisir?
 CAC, DAX ou DJ : lequel choisir? 1. Pourquoi cette question Tout trader «travaillant 1» sur les indices s est, à un moment ou un autre, posé cette question : «je sais que la tendance est bien haussière
CAC, DAX ou DJ : lequel choisir? 1. Pourquoi cette question Tout trader «travaillant 1» sur les indices s est, à un moment ou un autre, posé cette question : «je sais que la tendance est bien haussière
DM n o 8 TS1 2012 Physique 10 (satellites) + Chimie 12 (catalyse) Exercice 1 Lancement d un satellite météorologique
 DM n o 8 TS1 2012 Physique 10 (satellites) + Chimie 12 (catalyse) Exercice 1 Lancement d un satellite météorologique Le centre spatial de Kourou a lancé le 21 décembre 200, avec une fusée Ariane, un satellite
DM n o 8 TS1 2012 Physique 10 (satellites) + Chimie 12 (catalyse) Exercice 1 Lancement d un satellite météorologique Le centre spatial de Kourou a lancé le 21 décembre 200, avec une fusée Ariane, un satellite
Les rayons X. Olivier Ernst
 Les rayons X Olivier Ernst Lille La physique pour les nuls 1 Une onde est caractérisée par : Sa fréquence F en Hertz (Hz) : nombre de cycle par seconde Sa longueur λ : distance entre 2 maximum Sa vitesse
Les rayons X Olivier Ernst Lille La physique pour les nuls 1 Une onde est caractérisée par : Sa fréquence F en Hertz (Hz) : nombre de cycle par seconde Sa longueur λ : distance entre 2 maximum Sa vitesse
Chapitre 7: Dynamique des fluides
 Chapitre 7: Dynamique des fluides But du chapitre: comprendre les principes qui permettent de décrire la circulation sanguine. Ceci revient à étudier la manière dont les fluides circulent dans les tuyaux.
Chapitre 7: Dynamique des fluides But du chapitre: comprendre les principes qui permettent de décrire la circulation sanguine. Ceci revient à étudier la manière dont les fluides circulent dans les tuyaux.
Réduction de la pollution d un moteur diesel
 AUBERT Maxime SUP B Professeur accompagnateur : DELOFFRE Maximilien SUP B Mr Françcois BOIS PAGES Simon SUP E Groupe n Réduction de la pollution d un moteur diesel Introduction L Allemand Rudolf Diesel
AUBERT Maxime SUP B Professeur accompagnateur : DELOFFRE Maximilien SUP B Mr Françcois BOIS PAGES Simon SUP E Groupe n Réduction de la pollution d un moteur diesel Introduction L Allemand Rudolf Diesel
La physique nucléaire et ses applications
 La physique nucléaire et ses applications I. Rappels et compléments sur les noyaux. Sa constitution La représentation symbolique d'un noyau est, dans laquelle : o X est le symbole du noyau et par extension
La physique nucléaire et ses applications I. Rappels et compléments sur les noyaux. Sa constitution La représentation symbolique d'un noyau est, dans laquelle : o X est le symbole du noyau et par extension
Chap 8 - TEMPS & RELATIVITE RESTREINTE
 Chap 8 - TEMPS & RELATIVITE RESTREINTE Exercice 0 page 9 On considère deux évènements E et E Référentiel propre, R : la Terre. Dans ce référentiel, les deux évènements ont lieu au même endroit. La durée
Chap 8 - TEMPS & RELATIVITE RESTREINTE Exercice 0 page 9 On considère deux évènements E et E Référentiel propre, R : la Terre. Dans ce référentiel, les deux évènements ont lieu au même endroit. La durée
L énergie de l air extérieur pour une eau chaude sanitaire naturellement moins chère
 LE CHAUFFE-EAU THERMODYNAMIQUE L énergie de l air extérieur pour une eau chaude sanitaire naturellement moins chère LES PERFORMANCES DE TANÉO C EST L ASSURANCE : > DE 75 % D ÉNERGIE GRATUITE > D UN FONCTIONNEMENT
LE CHAUFFE-EAU THERMODYNAMIQUE L énergie de l air extérieur pour une eau chaude sanitaire naturellement moins chère LES PERFORMANCES DE TANÉO C EST L ASSURANCE : > DE 75 % D ÉNERGIE GRATUITE > D UN FONCTIONNEMENT
Technologie des contacteurs gaz liquide : cas des colonnes à plateaux et à garnissage. M. Prévost
 Technologie des contacteurs gaz liquide : cas des colonnes à plateaux et à garnissage M. Prévost Version V2/ nov 2006 Structure du cours Partie 1 : Introduction Partie 2 : Mise en contact de Gaz et de
Technologie des contacteurs gaz liquide : cas des colonnes à plateaux et à garnissage M. Prévost Version V2/ nov 2006 Structure du cours Partie 1 : Introduction Partie 2 : Mise en contact de Gaz et de
Cours de Physique Statistique. Éric Brunet, Jérôme Beugnon
 Cours de Physique Statistique Éric Brunet, Jérôme Beugnon 7 octobre 2014 On sait en quoi consiste ce mouvement brownien. Quand on observe au microscope une particule inanimée quelconque au sein d un fluide
Cours de Physique Statistique Éric Brunet, Jérôme Beugnon 7 octobre 2014 On sait en quoi consiste ce mouvement brownien. Quand on observe au microscope une particule inanimée quelconque au sein d un fluide
NOTIONS FONDAMENTALES SUR LES ENERGIES
 CHAPITRE 1 NOTIONS FONDAMENTALES SUR LES ENERGIES 1 suite Chapitre 1 : NOTIONS FONDAMENTALES SUR LES ENERGIES 1.1 Généralités 1.2 L'énergie dans le monde 1.2.1 Qu'est-ce que l'énergie? 1.2.2 Aperçu sur
CHAPITRE 1 NOTIONS FONDAMENTALES SUR LES ENERGIES 1 suite Chapitre 1 : NOTIONS FONDAMENTALES SUR LES ENERGIES 1.1 Généralités 1.2 L'énergie dans le monde 1.2.1 Qu'est-ce que l'énergie? 1.2.2 Aperçu sur
Mesures et incertitudes
 En physique et en chimie, toute grandeur, mesurée ou calculée, est entachée d erreur, ce qui ne l empêche pas d être exploitée pour prendre des décisions. Aujourd hui, la notion d erreur a son vocabulaire
En physique et en chimie, toute grandeur, mesurée ou calculée, est entachée d erreur, ce qui ne l empêche pas d être exploitée pour prendre des décisions. Aujourd hui, la notion d erreur a son vocabulaire
POLY-PREPAS Centre de Préparation aux Concours Paramédicaux. - Section Orthoptiste / stage i-prépa intensif -
 POLY-PREPAS Centre de Préparation aux Concours Paramédicaux - Section Orthoptiste / stage i-prépa intensif - 1 Suite énoncé des exos du Chapitre 14 : Noyaux-masse-énergie I. Fission nucléaire induite (provoquée)
POLY-PREPAS Centre de Préparation aux Concours Paramédicaux - Section Orthoptiste / stage i-prépa intensif - 1 Suite énoncé des exos du Chapitre 14 : Noyaux-masse-énergie I. Fission nucléaire induite (provoquée)
Les effets de température
 Les effets de température 1. Introduction La chaleur issue du combustible est transférée au caloporteur (eau) grâce au gradient de température qui existe entre ces deux milieux. Combustible Gaine Eau Profil
Les effets de température 1. Introduction La chaleur issue du combustible est transférée au caloporteur (eau) grâce au gradient de température qui existe entre ces deux milieux. Combustible Gaine Eau Profil
Chapitre 11: Réactions nucléaires, radioactivité et fission
 1re B et C 11 Réactions nucléaires, radioactivité et fission 129 Chapitre 11: Réactions nucléaires, radioactivité et fission 1. Définitions a) Nucléides (= noyaux atomiques) Les nucléides renferment les
1re B et C 11 Réactions nucléaires, radioactivité et fission 129 Chapitre 11: Réactions nucléaires, radioactivité et fission 1. Définitions a) Nucléides (= noyaux atomiques) Les nucléides renferment les
Capacité Métal-Isolant-Semiconducteur (MIS)
 apacité Métal-solant-Semiconducteur (MS) 1-onstitution Une structure Métal-solant-Semiconducteur (MS) est constituée d'un empilement de trois couches : un substrat semiconducteur sur lequel on a déposé
apacité Métal-solant-Semiconducteur (MS) 1-onstitution Une structure Métal-solant-Semiconducteur (MS) est constituée d'un empilement de trois couches : un substrat semiconducteur sur lequel on a déposé
Probabilités sur un univers fini
 [http://mp.cpgedupuydelome.fr] édité le 7 août 204 Enoncés Probabilités sur un univers fini Evènements et langage ensembliste A quelle condition sur (a, b, c, d) ]0, [ 4 existe-t-il une probabilité P sur
[http://mp.cpgedupuydelome.fr] édité le 7 août 204 Enoncés Probabilités sur un univers fini Evènements et langage ensembliste A quelle condition sur (a, b, c, d) ]0, [ 4 existe-t-il une probabilité P sur
Chapitre 2 Le problème de l unicité des solutions
 Université Joseph Fourier UE MAT 127 Mathématiques année 2011-2012 Chapitre 2 Le problème de l unicité des solutions Ce que nous verrons dans ce chapitre : un exemple d équation différentielle y = f(y)
Université Joseph Fourier UE MAT 127 Mathématiques année 2011-2012 Chapitre 2 Le problème de l unicité des solutions Ce que nous verrons dans ce chapitre : un exemple d équation différentielle y = f(y)
document proposé sur le site «Sciences Physiques en BTS» : http://nicole.cortial.net BTS AVA 2015
 BT V 2015 (envoyé par Frédéric COTTI - Professeur d Electrotechnique au Lycée Régional La Floride Marseille) Document 1 - Etiquette énergie Partie 1 : Voiture à faible consommation - Une étiquette pour
BT V 2015 (envoyé par Frédéric COTTI - Professeur d Electrotechnique au Lycée Régional La Floride Marseille) Document 1 - Etiquette énergie Partie 1 : Voiture à faible consommation - Une étiquette pour
Sommaire. Séquence 2. La pression des gaz. Séance 1. Séance 2. Séance 3 Peut-on comprimer de l eau? Séance 4 Je fais le point sur la séquence 2
 Sommaire La pression des gaz Séance 1 Comprimer de l air Séance 2 Mesurer la pression d un gaz Séance 3 Peut-on comprimer de l eau? Séance 4 Je fais le point sur la séquence 2 24 Cned, Physique - Chimie
Sommaire La pression des gaz Séance 1 Comprimer de l air Séance 2 Mesurer la pression d un gaz Séance 3 Peut-on comprimer de l eau? Séance 4 Je fais le point sur la séquence 2 24 Cned, Physique - Chimie
