CALCUL INTÉGRAL. 1. Définition de l'intégrale dans le cas d'une fonction continue positive sur un segment [a, b] Aire(rectangle OIKJ) = 1 u.a.
|
|
|
- Claudette Damours
- il y a 7 ans
- Total affichages :
Transcription
1 CALCUL INTÉGRAL. Défiiio de l'iégrle ds le cs d'ue focio coiue posiive sur u segme [, ].. Défiiio L'uié d'ire Soi P u pl mui d'u repère orhogol (O ; i, j ). Soie I, J e K les pois défiis pr : OI = i, OJ = j e OK = i + j O ppelle uié d'ire (oée e régé u..) l'uié de mesure des ires elle que : J j O u.. i I K Aire(recgle OIKJ) = u.. Remrques : OIKJ peu êre u crré lorsque le repère (O ; i, j ) es orhoormé. Si l'o, pr eemple, OI = 3 cm e OJ = cm, lors ue uié d'ire correspod à 6 cm... Défiiio Noio d'iégrle d'ue focio coiue posiive e qu'ire Soi P u pl mui d'u repère orhogol (O ; i, j ). Soie : e deu réels vec. ƒ ue focio coiue (ou coiue pr morceu () ) e posiive sur le segme () [, ]. O ppelle iégrle de ƒ de à l'ire, eprimée e u.., du domie D suiv : D = {M(, ) P els que e } (D es le domie délimié pr l coure de ƒ, l'e des scisses e les deu droies vericles d'équios = e = ) O oe cee quié : Les réels e s'ppelle les ores de l'iégrle. Illusrio : d ou ƒ( )d u.. = ue uié d'ire L'ire de D es de mesure C ƒ FINIE. E effe, ƒ es coiue sur le segme [, ] doc D mjorée. Il eise doc u recgle coe D. O Remrques : L vrile (ou ou ure) figur ds l'iégrle es "muee" ; elle peu êre oée pr oue ure lere. Le smole d (ou d) e joue ucu rôle pour le mome, si ce 'es de préciser quelle es l vrile. () Cee hpohèse es idispesle pour défiir l'iégrle d'ue focio e esclier. () U segme es u iervlle fermé oré. Clcul iégrl. Pge G. COSTANTINI hp://cmhs.e/
2 Premiers eemples : Rpporos le pl à u repère orhoormé (O ; i, j ) vec i = j = cm. (Aisi u.. correspod à cm ) Cs d'ue focio ƒ égle à ue cose posiive (oée k + ) sur [, ] lors : d = k d= ( )k u.. (O simpleme ppliqué l formule logueur lrgeur pour clculer l'ire d'u recgle!) k C ƒ J u.. D O I E priculier, si ƒ es ulle sur [, ] lors : d = Cs d'ue focio ƒ ffie (oos = m + p) supposée posiive sur [, ] lors : d = Aire du rpèze ABB'A' = (peie se + grde se) hueur m + p C ƒ B' m + p J u.. O I A' A D B d = ( AA + BB ) AB = ( m+ p+ m+ p )( ) = m( ) + p( ) L formule ci-core 'es ps à coîre pr cœur. Cs de l prole. Soi ƒ l focio défiie sur pr : = O vu (voir le DM sur l qudrure de l prole) qu'lors : d= 3 Cs d'ue focio e esclier (oujours supposée posiive) sur [, ] : Il s'gi des focios pour lesquelles il eise des réels,,..., vérifi : = < <... < = els que ƒ soi cose sur chcu des iervlles ouvers ] i, i+ [ ( i ) L'esemle { ; ;... ; } es ppelé ue sudivisio dpée à ƒ. Clcul iégrl. Pge G. COSTANTINI hp://cmhs.e/
3 E o λ i l vleur cose de ƒ sur ] i, i+ [, o lors : d = ( + ) λ i= i i i (Ps de pique, cee formule 'es qu'ue somme d'ires de recgles!) Illusrio vec = 4. λ Remrque : ƒ peu predre des vleurs quelcoques e les pois de l sudivisio, cel 'ur ps d'icidece sur l'ire. des recgles. λ λ 4 λ 3 O = 3 4 = Remrques : ƒ peu predre 'impore quelle vleur e chcu des pois i ; cel e modifie ps l'ire. L formule doée ci-dessus pour les focios e escliers e fodmele. C'es cee formule (géérlisée à des λ i réels quelcoques) qui ser prise e défiiio plus rd (clsses pos-c). E effe, d'ue pr, il es fcile de prouver les propriéés (elle que l liérié) des iégrles pour les focios e escliers. D'ure pr, il u résul rès for qui es que "oue focio coiue sur u segme peu êre pprochée pr des focios e escliers" ce qui perme d'éedre les propriéés oeues sur les focios e escliers u focios coiues. C'es isi que l'o cosrui, pr eemple, l'iégrle die de Riem. Eemple fodmel : qudrure de l'hperole Noos, pour ou [, + [, S() l'iégrle : S() = D'près l défiiio.., S() es l'ire du domie : d D() = {M(, ) P els que e } (D() es le domie délimié pr l coure de l focio iverse, l'e des scisses e les droies vericles d'équios = e = ) Soi u réel fié de l'iervlle [, + [. Soi u réel de l'iervlle [, + [. Disiguos deu cs : Clcul iégrl. Pge 3 G. COSTANTINI hp://cmhs.e/
4 O Cs :. Alors S() S( ) es l'ire du domie délimié pr l coure de l focio iverse, l'e des scisses e les deu droies vericles d'équios = e =. Or, pr décroissce de l focio iverse, o : S() S( ) es ecdrée pr l'ire de deu recgles, de lrgeur ( ) e de hueurs respecives O doc : S() S( ) S () S ( ) e : E pss à l limie lorsque ed vers, le héorème des gedrmes perme d'ffirmer que l'ccroisseme S () S ( ) moe dme ue limie e égl à, l focio S es doc dérivle à droie e. Cs :. U risoeme logue à ci-dessus more que S es dérivle à guche e. Bil : o doc : S'( ) = Ce risoeme é vlle pour ou réel de [, + [, o doc pour ou de [, + [ : S'() = Cosidéros mie l focio ƒ défiie sur [, + [ pr : = S() l L focio ƒ es dérivle sur [, + [ (cr l focio S e le logrihme épérie le so) e o : E coséquece, ƒ es cose sur [, + [ : ƒ'() = S'() (l )' = = = k Or, = S() l = D'où k = e ƒ es ulle sur [, + [, o coclu : S = l O moré que pour ou réel de [, + [ : d = l O more, de même, ce résul pour ] ; [. Clcul iégrl. Pge 4 G. COSTANTINI hp://cmhs.e/
5 Eercice : Soi ƒ l focio défiie sur [ ; ] pr : =. Vérifier que l coure C ƒ représe ƒ es le demi-cercle de cere O e de ro qui es siué ds le demi-pl des ordoées posiives.. E déduire : Soluio : d= 4. Soi M(, ) u poi de C ƒ. O lors : = Doc M es siué ds le demi-pl des ordoées posiives. De plus : OM = + E comme OM (c'es ue disce) : OM = = + = Doc M es siué sur le demi-cercle de cere O e de ro correspod u ordoées posiives. Réciproqueme, soi N(, ) u poi de ce demi-cercle. O lors : e ON = e + = e = E comme [, ], o, d'où : = = N C ƒ O moré que l coure C ƒ coïcide vec le demi-cercle de cere O e de ro qui es siué ds le demi-pl des ordoées posiives.. L quié dreprésee l'ire du domie délimié pr C ƒ, l'e des scisses e les droies vericles d'équios respecives = e =. Ce domie es u qur de disque de ro. So ire es doc égle à : 4 d= u.. 4 C ƒ O Clcul iégrl. Pge 5 G. COSTANTINI hp://cmhs.e/
6 .3. Propriéé Clcul de l'ire siuée ere deu coures Soie ƒ e g deu focios coiues e défiies sur u segme [, ]. O suppose que : g ƒ sur [, ] Alors, l'ire du domie D défii pr D = {M(, ) P els que e g() } es doée, e u.., pr : d g ()d Démosrio : Noos, pour oue focio coiue ƒ sur [, ] : D(ƒ) = {M(, ) P els que e compris ere e } Aisi, o l priio : D(g) D = D(ƒ) ( : uio disjoie) E pss u ires : Aire(D(g)) + Aire(D) = Aire(D(ƒ)) g ()d + Aire(D) = d D'où le résul. Eemple : Avec ƒ e g défiies sur [ ; ] pr : = e g() = C g C ƒ L'ire D hchurée ci-core es doée pr : Aire(D) = d d= 3 = 6 Eercice : Démorer que : d= 3 (O pourr se plcer ds u repère orhoormé e uiliser l fi que les coures représeives des focios défiies sur + pr e so smériques pr rppor à l droie d'équio = ).4. Défiiio Permuio des ores Soi P u pl mui d'u repère (O ; i, j ). Soie e deu réels vec e ƒ ue focio coiue sur [, ]. O covie lors que : = Aureme di, permuer les ores de l'iégrle chge le sige de celle-ci. Clcul iégrl. Pge 6 G. COSTANTINI hp://cmhs.e/
7 . Eesio u focios de sige quelcoque sur u segme [, ].. Défiiio Cs d'ue focio égive Soi P u pl mui d'u repère (O ; i, j ). Soie e deu réels vec. Soi ƒ ue focio coiue (ou coiue pr morceu) e égive sur le segme [, ]. O ppelle iégrle de ƒ de à l'opposé de l'ire, eprimée e u.., du domie D suiv : D = {M(, ) P els que e } Cee quié es ecore oée. Aureme di, lorsque ƒ es égive sur [, ], o : = Eemple : Clculer l'iégrle : ( )d O vérifie que l'pplicio ( ) es ie égive sur [ ; ]. Le domie D = {M(, ) P els que e } es ici u rpèze d'ire 3 u.. (eercice) Comme l focio iégrée es égive sur [ ; ], o e dédui : ( )d= 3.. Défiiio Cs d'ue focio de sige quelcoque Soi P u pl mui d'u repère (O ; i, j ). Soie e deu réels vec. Soi ƒ ue focio coiue (ou coiue pr morceu) sur le segme [, ]. O défii deu ouvelles focios coiues () (ou coiues pr morceu) ƒ + e ƒ pr : ƒ + ƒ( )si () = e ƒ () = sio O ppelle lors iégrle de ƒ de à l quié (Évidemme ƒ + es posiive e ƒ es égive) ƒ( )si sio + = ƒ ()d + ƒ ()d Cee derière iégrle es égive (cr ƒ l'es). E d'ures ermes, se clcule e comp posiiveme l'ire des domies où ƒ es posiive e égiveme l'ire des domies où ƒ es égive. () Le leceur cosciecieu pourr vérifier que ƒ + + ƒ = ƒ e ƒ + ƒ = ƒ. Il e déduir les relios ƒ + = ƒ+ƒ e ƒ = ƒ ƒ. Esuie, comme ƒ es supposée coiue (ou coiue pr morceu), l'pplicio ƒ l'es égleme (pr composiio) ; e comme l somme (e l différece) de focios coiues (ou coiues pr morceu) l'es ecore, o e dédui que les pplicios ƒ + = ƒ+ƒ e ƒ = ƒ ƒ so ie coiues (ou coiues pr morceu). Clcul iégrl. Pge 7 G. COSTANTINI hp://cmhs.e/
8 Illusrio e représeio des focios ƒ + e ƒ : C ƒ O + + C ƒ+ O O C ƒ Eemple : Clculer : I = 5 ( 3)d C ƒ + Après u clcul élémeire, o oie : I = + = 3 O Clculer l'ire A du domie hchuré. Cee fois-ci : A = + = 5 3 Clcul iégrl. Pge 8 G. COSTANTINI hp://cmhs.e/
9 Remrques : L'iégrle (d'ue focio coiue sur u segme) es doc ue ire lgérique. O verr, plus loi, ue méhode plus rpide de clcul des iégrles à l'ide des focios primiives. 3. Premières propriéés de l'iégrle d'ue focio ƒ sur u segme [, ] 3.. Propriéé Posiivié de l'iégrle Si ƒ es coiue e posiive sur le segme [, ] vec, lors : d Démosrio : C'es immédi puisque ue ire es posiive. Remrques : Évidemme, si ƒ es égive sur [, ] lors so iégrle es égive. Pr core, o e peu rie dire, priori, du sige de l'iégrle d'ue focio chge de sige sur [, ]. 3.. Propriéé Compiilié vec l'ordre (iégrio d'ue iéglié) Si ƒ e g so coiues sur le segme [, ] vec lors : ƒ g sur [, ] d g ()d Démosrio : Éudios d'ord le cs où ƒ e g so posiives (o doc ƒ g sur [, ]) : Noos pour oue focio coiue ƒ sur [, ] : D(ƒ) = {M(, ) P els que e } e D = {M(, ) P els que e g()} D C g C ƒ D(ƒ) O Vu les hpohèses, o l priio suive : D(g) = D(ƒ) D D'où : g ()d = + Aire(D) Clcul iégrl. Pge 9 G. COSTANTINI hp://cmhs.e/
10 E comme Aire(D), ous oeos : g ()d Éudios mie le cs où ƒ e g so de siges quelcoques sur [, ]. O suppose oujours que : ƒ g sur [, ] Comme ƒ es coiue sur [, ], elle es orée (e ei ses ores). Noos m le miimum de ƒ sur [, ]. Aisi les focios ƒ m e g m so posiives sur [, ]. Il es clir que l'ire du domie D compris ere les coures de ƒ e de g es égle à celle du domie compris ere les coures rslées de ƒ m e g m : Aire(D) = g ()d = ( g () m)d ( m)d O e dédui, là ecore que : g ()d Eemple :. Démorer que pour ou réel + :. E déduire que pour ou + : + l( + ) Soluio :. Comme +, o peu écrire : E e divis pr + > : + ( )( + ) + +. Soi +. E iégr, ere e, l'ecdreme ci-dessus, o oie : ( )d d + d Or, l'ire sous l coure représe l focio ere les pois d'scisses e es l même + (vi ue rslio) que celle sous l coure de l focio iverse ere les pois d'scisses e +. D'près le résul oeu lors de l qudrure de l'hperole, o : Pr illeurs, o clcule fcileme : d = + ( )d = + d = l( + ) e d = Nurelleme, ous verros plus loi des echiques plus priques pour clculer ces iégrles à l'ide des focios primiives. D'où : l( + ) Clcul iégrl. Pge G. COSTANTINI hp://cmhs.e/
11 3.3. Propriéé Iéglié rigulire Soi ƒ ue focio coiue sur u segme [, ] ( ). Alors : d d Démosrio : O oujours : ƒ ƒ ƒ sur [, ] E iégr les iégliés ere e ( ), o oie : d d d D'où : d d 3.4. Propriéé Relio de Chsles Soi ƒ ue focio coiue sur u segme I. Soie, e c ds I. Alors : = + c c Démosrio : Noos P le pl mui d'u repère orhogol (O ; i, j ). Pour ous réels e de I, o oe : D(, ) = {M(, ) P, e compris ere e } (D(, ) es le domie délimié pr l coure de ƒ, l'e des scisses e les deu droies vericles d'équios respecives = e = ) Disiguos plusieurs cs : Cs c : Ds ce cs, o : D(, ) = D(, c) D(c, ) ( : uio disjoie) E pss u ires, o oie : Aire(D(, )) = Aire(D(, c)) + Aire(D(c, )) D'où : = + c c Aures cs : ils se déduise du précéde à l'ide de l relio =. Pour mémoire, démoros l'u de ces ures cs, pr eemple c. D'près l relio de Chsles (cs précéde), o peu écrire : c = + c D'où : = = + c c c c Clcul iégrl. Pge G. COSTANTINI hp://cmhs.e/
12 Remrques : Cee relio de Chsles ser uilisée ds les deu ses (comme s cousie pour les veceurs), soi pour décomposer ue iégrle e deu (ou plus) soi pour regrouper plusieurs iégrles e ue seule. L relio de Chsles dme ue géérlisio pr récurrece : Pour ou,,..., ds I : = i= i+ i Eemple d'uilisio de l relio de Chsles : divergece de l série hrmoique. O pose, pour ou : u = k k = Soi. Comme l'pplicio es décroisse sur ] ; + [, o, pour ou k : k + k d k E somm, pour k ll de à, l relio de Chsles doe : Or, + d k k = l( + ) k k = lim l( + ) = +, doc, pr compriso, l suie (u ) diverge. + L méhode ci-core es ue des plus efficce pour prouver l divergece vers + de l série hrmoique Propriéé Compiilié vec l'ddiio Soie ƒ e g deu focios coiues sur u segme [, ]. Alors : ( ƒ () + g ()) d= + g ()d Démosrio (Hors progrmme) C'es u cs priculier de l liérié de l'iégrle e c'es rès délic à prouver. Nous uros esoi de deu lemmes impors sur les focios e esclier. Lemme Propriéé de compiilié vec l'ddiio pour les focios e escliers Soie ϕ e ψ deu focios e escliers sur u segme [, ]. Alors : ( ϕ () +ψ() ) d = ϕ()d + ψ()d Démosrio (Hors progrmme) Il eise doc u eier m * e des réels,..., m vérifi : = < <... < m = e els que : k, m, ϕ es cose sur ] k, k+ [ Clcul iégrl. Pge G. COSTANTINI hp://cmhs.e/
13 De même, il eise u eier * e des réels,..., vérifi : = < <... < = e els que : k,, ψ es cose sur ] k, k+ [ Noos s = { ;... ; m }, s = { ;... ; } e s = s s. L sudivisio s coie u mimum m + + scisses disices e u miimum. Noos c,..., c r les élémes ordoés de cee sudivisio s ( r m + + ). Aisi ϕ e ψ so des coses (oées λ k e µ k respeciveme) sur chque iervlle ]c k, c k+ [ ( k r ). O lors : ( ϕ () +ψ() ) d = ( λ k +µ k) ( ck+ ck) = λk ( ck+ ck) + µ k ( ck+ ck) = ϕ()d + ψ()d r k= r k= (O uilisé l propriéé suive : l'iégrle d'ue focio e esclier e es idépede de l sudivisio dpée à e) r k= Lemme Soi ƒ ue focio coiue sur u segme [, ]. Soi ε +. Il eise des focios e escliers ϕ e ψ elles que : ϕ ƒ ψ sur I e ψ ϕ ε sur I Démosrio (Hors progrmme) Pour ou *, o défii ue sudivisio régulière {,,..., } du segme [, ] pr : k,, k = + k Comme ƒ es coiue sur [, ], elle l'es ussi sur chcu des segmes [ k, k+ ] ( k ), doc es orée, ce qui perme de défiir : M k = sup ƒ () e m k = [ k, k+ ] if [ k, k+ ] O défii lors des pplicios e esclier ϕ e ψ sur [, ] pr : e : k,, [ k, k+ ], ϕ() = m k e ψ() = M k ϕ() = m e ψ() = M Aisi, o ie : ϕ ƒ ψ sur [, ] Pr illeurs, ƒ é coiue sur le segme [, ], elle es uiforméme coiue (héorème de Heie) : ε +, η +, (, ) [, ], ( η ƒ() ε) Soi η le réel oeu pour le réel ε fié ds les hpohèses. O si que le ps de l sudivisio es : Soi k, e (, ) [ k, k+ ]. O doc : k+ k Choisissos u ps plus fi que η, oeu pour les eiers qui vérifie : Clcul iégrl. Pge 3 G. COSTANTINI hp://cmhs.e/
14 E η + Aisi : De l coiuié uiforme de ƒ, o dédui : η ƒ() ε Cee derière iéglié é vlle pour ous e de [ k, k+ ]. E priculier pour u el que = M k e u el que ƒ() = m k (eise ie cr ƒ ei ses ores) : M k m k ε D'où ψ ϕ ε sur chque [ k, k+ ] e doc sur [, ] Fi de l démosrio du lemme. Prouvos mie l propriéé de compiilié vec l'ddiio : Soi ε +. D'près le lemme, il eise ϕ, ϕ, ψ e ψ e escliers sur [, ] elles que : ε ε ϕ ƒ ψ, ϕ g ψ, ψ ϕ e ψ ϕ sur [, ] Posos : ϕ = ϕ + ϕ e ψ = ψ + ψ ϕ e ψ so lors des focios e esclier (ce 'es ps rès difficile à prouver e cosidér ue sudivisio dpée à l fois à ϕ e ϕ (pour ϕ) ou ψ e ψ (pour ψ) ; il suffi pour cel de cosidérer l réuio des pois de chcue des deu sudivisios) Aisi o évidemme : ϕ ƒ + g ψ e ψ ϕ ε De plus, d'près l propriéé d'iégrio d'ue iéglié : ( ƒ () + g ()) d Ψ()d ϕ () +εd E comme l'iégrle des focios e escliers es compile vec l'ddiio : ϕ () +εd= ϕ()d + ε( ) D'près le lemme, comme ϕ es l somme des focios e esclier ϕ e ϕ : ϕ()d = ϕ ()d + ϕ ()d D'où : ( ƒ () + g ()) d ϕ ()d + ϕ ()d + ε( ) E d'près l propriéé d'iégrio d'ue iéglié, il vie fileme : Pr des rgumes du même gere : ( ƒ () + g ()) d + g ()d + ε( ) + g ()d ()d ψ + ()d ψ ψ()d ϕ()d + ε( ) ( ƒ () + g ()) d+ ε( ) E fis edre ε vers ds les deu iégliés, o oie fileme : ( ƒ () + g ()) d= + g ()d D'ures propriéés sero évoquées plus loi près le prgrphe 4 sur les primiives. Clcul iégrl. Pge 4 G. COSTANTINI hp://cmhs.e/
15 4. Noio de primiive d'ue focio sur u iervlle 4.. Défiiio Soi ƒ ue focio défiie sur u iervlle I. O ppelle primiive de ƒ sur I oue focio F dérivle sur I elle que F' = ƒ sur I. Eemple : O cosidère l focio ƒ défiie sur pr : = 3 + cos Trouver (meleme) ue primiive F de ƒ sur. L focio F défiie ci-près covie : F() = 3 + si E effe, pour ou, l focio F es dérivle (comme somme de focios qui le so) e o : F'() = 3 + cos = Remrquos que si l'o vi choisi pour F l focio défiie pr F() = 3 + si + 4, ous urios ecore eu ue cdide sisfise. Doc si ue focio ƒ dme ue primiive, lors elle e dme ue ifiié. Remrque : l défiiio rese vlle si I es ue prie (o vide) de. 4.. Théorème Soi ƒ ue focio dme des primiives sur u iervlle I. Soie F e G deu primiives d'ue focio ƒ sur u iervlle I. Alors F e G diffère d'ue cose : F() = G() + c (c ) pour ou I Démosrio : Puisque F e G so des primiives de ƒ sur I, o : F' = G' = ƒ sur I Pr coséque : F' G' = sur I Or, F' G' = (F G)' (c'es l liérié de l dérivio). Doc : (F G)' = sur I Or, les seules focios qui o ue dérivée ulle so les focios coses (), doc o, sur I, : F G = c où c es ue cose. C F Grphiqueme, ds u repère orhoorml (O ; i, j ) les représeios grphiques C F c C G e C G se correspode pr ue rslio de veceur c j. j O i () Ce résul (qui éé dmis e clsse de première) se démore à l'ide du héorème des ccroissemes fiis. Clcul iégrl. Pge 5 G. COSTANTINI hp://cmhs.e/
16 4.3. Tleu des primiives usuelles Les résuls de ces leu s'élisse e vérifi que l'o ie F' = ƒ sur l'iervlle cosidéré. Focio ƒ Focio primiive F (c = cose) Iervlle I = k (cose) F() = k + c = F() = + c = + F() = + + c = ( * e ) F() = + si > ; + + c ] ; [ ou ] ; + [ si = F() = + c ] ; + [ = F() = + c ] ; [ ou ] ; + [ = cos F() = si + c = si F() = cos + c = + = cos F() = + c + k ; + ( k+ ) (k ) = cos(ω + ϕ) (ω ) F() = si(ω + ϕ) + c ω = si(ω + ϕ) (ω ) F() = cos(ω + ϕ) + c ω = e F() = e + c = F() = l + c ] ; + [ Eemples : rouver ue primiive : Focio g défiie sur I = ; g() = représee (()). Posos : h() = g() + = + Ue primiive H de h sur I es défiie pr : H() = = + G() où G es ue primiive de g sur I D'où : G() = H() = Focio ƒ défiie sur J = ; Clcul iégrl. Pge 6 G. COSTANTINI hp://cmhs.e/
17 Ue primiive F de ƒ sur J es défiie pr : = si(3) 3cos() F() = 3 cos(3) 3 si() (+ c) 4.4. Opérios sur les primiives OPÉRATIONS SUR LES PRIMITIVES lorsque u e v so des focios dérivles sur u iervlle I Focio Ue primiive Codiios u' + v' ku' (k : cose) u' u ( e ) u + v ku + u + u sur I si u u u u > sur I v v v v sur I u' u e u e u l u u l( u) si u > sur I si u < sur I u' (v' o u) v o u Eemple : Trouver ue primiive F de l focio ƒ défiie sur ] ; + [ pr : = l L focio ƒ es de l forme u' u. Doc F es de l forme u : F() = (l ) (+ c) Eercice : Soi F l focio défiie sur ] ; + [ pr : F() = 3 Clculer F'(). Qu'--o démoré? Clcul iégrl. Pge 7 G. COSTANTINI hp://cmhs.e/
18 4.5. Théorème Primiive défiie pr ue codiio iiile Soi ƒ ue focio défiie sur u iervlle I dme des primiives sur I. Soie I e. Il eise ue uique primiive F de ƒ sur I sisfis l codiio iiile F( ) =. Démosrio : Soi G ue primiive de ƒ sur I (eise pr hpohèse). D'près le héorème 4.., oues les primiives F de ƒ sur I so de l forme F = G + c (où c es ue cose) L codiio F( ) = impose c = G( ). L cose c es déermiée de mière uique, ce qui démore le héorème. Eemple : Soi ƒ l focio défiie sur pr : = + Trouver l'uique primiive F de ƒ sur elle que F() =. Remrquos que peu s'écrire : = + O recoî l'epressio dérivée de +. Les primiives F de ƒ sur I so de l forme : F() = + + c L codiio iiile F() = s'ierprèe pr + + c = d'où c =. Coclusio : l primiive cherchée es l focio F défiie pr F() = + +. Remrque : ue quesio légiime qui se pose ds ce prgrphe es l suive : ue focio dme-elle oujours des primiives? L répose es o e géérl. Ceped si ore focio es coiue... Eh ie c'es ce que ous llos voir ds le prgrphe suiv. 5. Théorème fodmel du clcul iégrl. Formule de Newo-Leiiz Nous llos voir mie le héorème fodmel du clcul iégrl qui ur pour coséquece que oue focio coiue dme des primiives. 5.. Théorème Soi ƒ ue focio coiue sur u iervlle I. Soi I. L focio F défiie sur I pr F() = es l'uique primiive de ƒ sur I s'ul e. Aureme di : F( ) =, F es dérivle sur I e pour ou réel I : F'() = Démosrio (Hors progrmme) Le fi que F( ) soi ul es ue lié. Clcul iégrl. Pge 8 G. COSTANTINI hp://cmhs.e/
19 F( ) F( ) Soi I. Nous llos morer que l'ccroisseme moe dme ue limie lorsque ed vers e que cee limie es préciséme ƒ( ). Évluos : F ( ) F( ) ƒ( ) = ( ) ƒ( ) E uilis l relio de Chsles e l formule d'iégrio pour ue focio cose, o peu écrire : F ( ) F( ) ƒ( ) = ƒ( )d Mis d'près l propriéé de compiilié vec l'ddiio : ( )d ƒ = ( ) ƒ ƒ () ( ) d F ( ) F( ) D'où : ƒ( ) = ( ƒ( )) d E d'près l'iéglié rigulire : F ( ) F( ) ƒ( ) ƒ( )d Or, ƒ es coiue e doc dme ue limie fiie e. Cel sigifie que ou iervlle ouver e ceré e ƒ( ) coie oues les vleurs de pour ssez proche de : Soi ε + e I = ]ƒ( ) ε, ƒ( ) + ε[. Alors, il eise u réel η el que pour ou ] η, + η[, o i : ]ƒ( ) ε, ƒ( ) + ε[ C'es-à-dire : ƒ( ) < ε F ( ) F( ) D'où : ƒ( ) ε Comme ε peu êre choisi ussi pei que voulu, o ie : lim F( ) F( ) = ƒ( ) Doc, F es dérivle e e : F'( ) = ƒ( ) E comme ce risoeme es vlle pour ou I, F es ie ue primiive de ƒ sur I. Remrque : ds le cs où ƒ es ue focio croisse sur I, il eise ue démosrio plus simple (cee démosrio es u progrmme e fi prie des coissces eigiles) : F( ) F( ) Soi I fié. Nous llos morer que l'ccroisseme moe dme ue limie lorsque ed vers e que cee limie es préciséme ƒ( ). Cs : soi I vec >. Pour ou I el que, l croissce de l focio ƒ ous perme d'écrire : ƒ( ) E iégr ce ecdreme ere e, ous oeos : Clcul iégrl. Pge 9 G. COSTANTINI hp://cmhs.e/
20 ƒ( )( ) ( ) Or, d'près l relio de Chsles : = + = = F() F( ) Puisque >, o peu doc écrire : Comme ƒ es coiue e : F( ) F( ) ƒ( ) lim > = ƒ( ) D'où, pr le héorème des gedrmes : Cs : soi I vec <. lim > F( ) F( ) = ƒ( ) Pour ou I el que, l croissce de l focio ƒ ous perme d'écrire : ƒ( ) E iégr ce ecdreme ere e, ous oeos : ( ) ƒ( )( ) Or, d'près l relio de Chsles : = + = = F( ) F() Puisque >, o peu doc écrire : Comme ƒ es coiue e : F( ) F( ) ƒ( ) lim < = ƒ( ) D'où, pr le héorème des gedrmes : Bil : o ie : lim < lim F( ) F( ) = ƒ( ) F( ) F( ) = ƒ( ) Ceci é vlle pour ou I. Doc l focio F es dérivle sur I e pour ou I : F'() = Clcul iégrl. Pge G. COSTANTINI hp://cmhs.e/
21 Ce héorème dme les corollires fodmeu suivs : 5.. Corollire Eisece de primiives pour les focios coiues Toue focio coiue sur u iervlle I dme des primiives sur I. Démosrio C'es immédi cr si ƒ désige ue focio coiue sur I, ue primiive F de ƒ sur I es doée pr : F() = ( I) Quesio : ue focio o coiue ƒ peu-elle dmere des primiives sur ses iervlles de coiuié? Répose : oui si ƒ es coiue pr morceu : si Pr eemple : = sio Sur [ ; + [, ƒ dme des primiives F + de l forme : F + () = + c +. Sur ], [, ƒ dme des primiives F de l forme : F () = + c. Noos que l'o peu rès ie choisir c + c. O peu lors cosruire ue focio F sur qui es coiue pr morceu : F() = + c+ si + c sio C F+ C F c + c O peu même s'rrger pour que F soi coiue, il suffi de recoller les morceu e choisiss c + = c. Ceped, F 'es ps ue primiive de ƒ sur cr o dérivle e. Répose : o si ƒ dme ue ifiié de discoiuiés : Pr eemple : = si si \ 5.3. Corollire Formule de Newo-Leiiz Soi ƒ ue focio coiue sur u iervlle I e F ue primiive de ƒ sur I. Alors pour ous e ds I : Démosrio = F() F() Soi I e G l primiive de ƒ défiie pr : G() = O si que deu primiives F e G diffère d'ue cose. Doc il eise u réel k el que pour ou de I : F() = G() + k O lors : F() F() = G() G() = Noio : l quié F() F() se oe rès souve[ F ] () (c'es commode ds l prique). Clcul iégrl. Pge G. COSTANTINI hp://cmhs.e/
22 Eemples : d = = + = cosd = [ si ] = si si = e d = e d = e = e e = e e d = [ ] l = l l = l d = + = + + d = d = = e d l e = d l = [ l(l ) ] e = l(l ) Commeires : Le choi de l primiive F choisie 'iflue ps le résul de l'iégrle. E effe, si F e G so deu primiives d'ue même focio ƒ sur I, lors elles différe d'ue cose. Les quiés F() F() e G() G() so doc égles. Applicio de l formule de Newo-Leiiz : ue démosrio de l'iéglié des ccroissemes fiis : Soi ƒ ue focio dérivle sur u iervlle I elle que ƒ' soi coiue sur I. S'il eise u réel M el que ƒ' M sur I lors : pour ous réels e de I, o : M Pour <, o : Pour >, o : = ƒ ( ) d ƒ ( ) d M( ) M = ƒ ( ) d ƒ ( ) d M( ) M Remrque : l démosrio rdiioelle de l'iéglié des ccroissemes fiis (e éudi les vriios des focios M e + M) perme de se psser de l codiio "ƒ' coiue sur I ". Clcul iégrl. Pge G. COSTANTINI hp://cmhs.e/
23 5.4. Propriéé Liérié de l'iégrle Soie ƒ e g deu focios coiues sur u segme [, ] e k u réel. Alors : ( ƒ () + g ()) d = d + g ()d e k ƒ ()d = k d Démosrio : L première églié déjà éé démorée (compiilié vec l'ddiio) L deuième, qui ' ecore jmis éé uilisée ds les démosrios précédees se prouve fcileme vec l formule de Newo-Leiiz. Soi F ue primiive de ƒ sur [, ]. Alors, ue primiive de kƒ es kf d'où : Eemple : k ƒ ()d = kf() kf() = k[f() F()] = k d Clculer : I = Il suffi d'écrire, pr liérié : I = 3 3 e d 3 3e d Comme ue primiive de 3 3 e sur [, ] es 3 e, ous vos : I = 3 3 e = 3 e 3 Eercice simple : O cosidère l focio ƒ défiie sur ] ; + [ pr : = + 5 l. O oe C ƒ so grphe.. Démorer que C ƒ dme ue smpoe olique e + do o préciser so équio isi que s posiio pr rppor à C ƒ.. Éudier les vriios de ƒ. (O éudier le sige de g : + l ) 3. Clculer ue primiive F de ƒ e déermier l'ire A (e u..) du domie : [ ] l {( ; ) els que e e + 5} (Répose : ( ) e = ) 6. Prié e périodicié 6.. Théorème (Prié) Soi ƒ ue focio coiue sur u iervlle smérique [, ]. Si ƒ es pire lors : Si ƒ es impire lors : d = d d = Clcul iégrl. Pge 3 G. COSTANTINI hp://cmhs.e/
24 6.. Théorème (Périodicié) Soi ƒ ue focio coiue sur e T-périodique. Alors, pour ou réel : + T d = T d Démosrios : Relio de Chsles puis chgeme de vrile ( = ) pour l prié. Périodicié : ecore d'près l relio de Chsles : + T d = d+ d+ d T + T T E pos u = T, ds l roisième iégrle, o oie (du = d) : + T d = ƒ ( u+ T) du T E comme ƒ es T-périodique : ƒ(u + T) = ƒ(u) pour ou u, d'où ƒ ( u + T) du = ƒ( u) du E fileme : Eemple : + T d = d+ d+ ƒ( u) du= d T ( cos ) 9 7 si d = 8 ( + ) T 7. Vleur moee d'ue focio ƒ sur u segme [, ] Iroducio : supposos que l'o veuille iveler u erri do le profil 'es ps horizol (de sore que les remlis compese eceme les délis). Comme procéder? C ƒ µ Noos ƒ l focio représe le profil. O cherche do ue cose µ vérifi : µ( ) = d O doc : µ = d Clcul iégrl. Pge 4 G. COSTANTINI hp://cmhs.e/
25 7.. Défiiio Soi ƒ ue focio coiue sur u segme I = [, ]. O ppelle vleur moee de ƒ sur l'iervlle I le omre réel µ défii pr : µ = ƒ () d O oe souve ƒ u lieu de µ. Eemple : Soi ƒ le sigl siusoïdl -périodique défii pr : = si. Clculer l moee ƒ sur [, ] isi que l moee qudrique ƒ = si d = 4 ƒ = si d = cos( )d= 4 [ ] ƒ sur [, ]. = d'où ƒ = Lie vec l'élecricié : O ppelle iesié efficce I eff d'u cour lerif, l'iesié d'u cour coiu (o devri pluô dire "cos") qui produiri, à rvers l même résisce R, le même effe clorifique ped l durée d'ue période T. Ds le cs d'u cour de pe siusoïdl : si I() = I m si(ω) es l'iesié du cour à l'is du cour lerif, l loi de Joule doe : E(T) = R I eff T = RI ()d T D'où : I eff = T T Im si ( ω) d = I m T T cos( ω)d = I m T T = I m [] D'où l relio : I m = I eff 7.. Théorème (iéglié de l moee) Soi ƒ ue focio coiue sur u iervlle I = [, ]. Soi m e M des réels els que : m ƒ M sur I Alors : m( ) d M( ) Ue focio coiue sur u iervlle [, ] es oujours orée (e de plus ei ses ores). Les réels m e M cicore eise doc oujours. Le om de ce héorème es légiime, e effe, o peu le reformuler isi : si m ƒ M lors m µ M. Démosrio : il suffi d'iégrer l'iéglié m ƒ M sur [, ]. Eemple : à l'ide de l'iéglié de l moee, o peu rerouver l'iéglié : + e pour ou Soi +. Comme l focio epoeielle es croisse sur [ ; ], o pour ou [ ; ] : e e E d'près l'iéglié de l moee ppliquée à l focio ƒ : e sur l'iervlle [ ; ] : e d e e e Clcul iégrl. Pge 5 G. COSTANTINI hp://cmhs.e/
26 D'où, pour ou + : + e Si mie es u réel égif, o pour ou [ ; ] : e e E d'près l'iéglié de l moee : e e d e D'où, pour ou : Bil : o ie, pour ou réel : + e + e Comme le héorème de l'iéglié des ccroissemes fiis, o ue versio vec vleurs solues : 7.. is. Théorème (iéglié de l moee) Soi ƒ ue focio coiue sur u iervlle I = [, ]. Si ƒ M sur I lors d M Démosrio : D'près l première versio, o : M( ) d M( ) L disce ere de es doc iférieure à celle ere M( ) e d'où : d M Noos que ce héorème peu se démorer ussi vec l'iéglié des ccroissemes fiis ppliquée à l focio F défiie pr : F() = d Eemple : démorer que pour ous réels e : si si O pplique l'iéglié de l moee à l focio cos sur l'iervlle [ ; ] (si ) ou [ ; ] sio. Comme o pour ou réel : cos O oie lorsque : cos d si si E lorsque : cos d si si Ce qui es l même iéglié que celle oeue pour. Clcul iégrl. Pge 6 G. COSTANTINI hp://cmhs.e/
27 Eercice : démorer l "première formule de l moee" Soie ƒ e g deu focios coiues défiies sur u iervlle [, ] vec g posiive. Alors Il eise c ds [, ] el que ƒ( g ) ( )d= ƒ(c) g ( )d Comme ƒ es coiue sur le segme [, ], il eise des coses m e M elles que : m ƒ M sur [, ] Comme g es posiive : m g ƒ g M g sur [, ] E iégr ce ecdreme ere e ( < ) : m g ( )d ƒ( g ) ( )d M g ( )d Si g ( )d=, lors l formule de l moee es évidee (ou c de [, ] covie) Si g ( )d, lors o pose : λ = ƒ( g ) ( )d g ( )d Comme g ( )d> (puisque g l'es), o : m λ M E d'près le héorème des vleurs iermédiires, il eise c ds [, ] el que ƒ(c) = λ. D'où le résul. 8. Iégrio pr pries O di qu'ue focio ƒ es de clsse C sur u iervlle I si elle es dérivle sur I e si s dérivée ƒ' es coiue sur I. 8.. Théorème Soie u e v deu focios de clsse C sur [, ], lors : Démosrio : o si que pour ou [, ] : E iégr de à : E d'près l liérié de l'iégrle : uv () ()d = [ uv () ()] u ()()d v (uv)'() = u'()v() + u()v'() ( uv ()()) d= u ()() v + uv () ()d ( uv ()()) d= u ()()d v + uv () ()d D'où le héorème. () () = u ()()d v + uv () ()d [ uv] Clcul iégrl. Pge 7 G. COSTANTINI hp://cmhs.e/
28 Eemples : clculer I = e d e J() = l d O pose : u() = v'() = e u'() = D'où : I = [ e ] e v() = e (à ue cose près) d = e (e ) = O pose : u() = l v'() = u'() = v() = (à ue cose près) D'où : J() = [ ] l d = l ( ) = l + O déermié ici ue primiive de l focio logrihme. 9. Clcul de volumes Ds l'espce mui d'u repère orhogol (O ; i, jk, ), o cosidère u solide délimié pr des pls prllèles d'équio z = e z =. Si l focio S qui, à oue coe z ssocie l'ire de l secio coeue ds le pl perpediculire à l'e (O, k ) es coiue sur [ ; ] lors le volume V du solide es doé pr l formule : z z Secio d'ire S(z) V = Sz ()d zu.v. O (L'uié de volume es le volume du prllélépipède uié) Eemples : Volume d'ue sphère de ro R : O r = R z, d'où S(z) = (R z ) z R z r R V = R z d z = R V = R 3 3 R 3 = 4 3 R3 u.v. R R z d z 3 z = Rz 3 R z O Volume d'u côe de hueur h e de ro de se R : S(z) = r. h R D'près le héorème de Thlès : r R = z h z r Doc S(z) = R h V = R h z z d = Rh h 3 z. u.v. O Clcul iégrl. Pge 8 G. COSTANTINI hp://cmhs.e/
29 . Vri ou fu? ƒ e g désige des focios coiues sur les iervlles cosidérés. Si d g ()d lors ƒ g sur [, ] (Fu : d 3 d e pour sur [ ; ]!) Si d = g ()d lors ƒ = g sur [, ] (Fu : predre = e g() = sur [ ; ]) e l( + ) d (Vri : posiivié) 4 ( + ). Quelques eercices cos () d = 4 (Liériser : cos = + cos( ) ) 3 cos () d= 3 (Liériser : cos3 = 4 cos(3) cos()) 3 3 si d = (Uiliser Chsles : = + ce qui perme de supprimer les vleurs solues) I = e si d = e (Iégrer deu fois pr pries de fço à reomer sur l'iégrle I) d e J = ( ) d (iégrles de Wllis, voir compléme 3) I = ( si ) Clculer I e I. Élir ue relio de récurrece ere I + e I. Clculer J. Élir ue relio de récurrece ere J + e J. 3 (O rouve I =, I =. Iégrer I + pr pries, e écriv que si + = si + si. O peu lors eprimer I + e focio de I. O rouve : I + = + + I. O rouve J =. Puis o iègre J + pr pries, e écriv ( ) + rouve : J + = J ) = ( ) ( ) Trouver u réel α el que α d =. 4 Trouver u réel β el que β d =. (α = 3 e β = 3 5 ) Éudier l limie suive : lim ε ε d. (O rouve l e o...) ε. O peu lors eprimer J + e focio de J. O e Soi. O cosidère l focio I défiie pour > pr : I () = d (O dmer que cee limie es réelle) À l'ide d'ue iégrio pr pries, morer que I + = ( + )I. Clculer I e e déduire, pr récurrece, que I =!. O oe I = lim I (). + Clcul iégrl. Pge 9 G. COSTANTINI hp://cmhs.e/
30 Compléme : iégrles de Riem Soi α u omre réel quelcoque. Soi ε > e A >. O cosidère les iégrles suives : Le u du prolème es de déermier : I α (ε) = α d e J α (A) = ε A α d les vleurs de α pour lesquelles I α dme ue limie fiie lorsque ε ed vers. les vleurs de α pour lesquelles J α dme ue limie fiie lorsque A ed vers +. Éude de I α. Éude du cs α = ) Démorer que I (ε) = l ε. ) E déduire lim ε. Éude du cs α I (ε). ) Démorer que : I α (ε) = α ε α ) E écriv ε α = e (, déermier les vleurs du réel α pour lesquelles ε dme ue limie fiie lorsque ε ed vers. c) Coclure : I α dme ue limie fiie lorsque ε ed vers si e seuleme si... Remrque : o oe ds ce cs α α d cee limie e o doc α d = α Éude de J α. Éude du cs α = ) Démorer que J (A) = l A. ) E déduire lim A +. Éude du cs α J (A). α ) Démorer que : J α (A) = A α α ) E écriv A α ( )l = e α A, déermier les vleurs du réel α pour lesquelles A α dme ue limie fiie lorsque A ed vers +. c) Coclure : I α dme ue limie fiie lorsque A ed vers + si e seuleme si... Remrque : o oe ds ce cs RÉSUMÉ + α d + cee limie e o doc α d = α α d eise si e seuleme si α <. (O di lors que l'iégrle α d coverge) + α d + eise si e seuleme si α >. (O di lors que l'iégrle α d coverge) Clcul iégrl. Pge 3 G. COSTANTINI hp://cmhs.e/
31 Compléme : focio Γ O cosidère l focio Γ défiie pour ou réel de ], + [ pr : + Γ() = e d Ds ou ce qui sui es u réel sriceme posiif fié. +. Jusificio de l'écriure e d ) Éude e. O cosidère l focio I défiie pour ou ε de + pr : I (ε) = e d i) Démorer que pour ou réel de [ε ; ], o : e ε ii) E déduire (e uilis les résuls sur les iégrles de Riem) que I dme ue limie fiie lorsque ε ed vers. O oe e d cee limie. ) Éude u voisige de +. O cosidère l focio J défiie pour ou réel X de ], + [ pr : J (X) = X e d i) Démorer qu'il eise u réel A posiif el que pour ou réel de [A, + [ : + e (O pourr uiliser le fi que lim + E déduire que pour ou réel de [A, + [ : + e = ) e ii) O suppose ici que X A. E écriv J (X) = J (A) + X e d, démorer (e uilis les A résuls sur les iégrles de Riem) que J dme ue limie fiie lorsque X ed vers +. + O oe e d cee limie. Comme les iégrles e d e e d o oues les deu u ses, l focio Γ es doc + + ie défiie e l'écriure e d ie u ses.. Propriéés de l focio Γ ) Clculer Γ(). ) À l'ide d'ue iégrio pr pries, démorer que : pour ou > : Γ( + ) = Γ() c) Démorer, pr récurrece, que pour ou * : Γ() = ( )! Clcul iégrl. Pge 3 G. COSTANTINI hp://cmhs.e/
32 Compléme 3 : iégrles de Wllis Il s'gi, pour, des iégrles suives : I = (cos ) d J = (si ) d K = ( ) d L = ( ) d Clcul de I pr IPP O immédieme : I = e I = cos d =. Pour ou, o pr IPP : (u() = (cos ) + e v'() = cos ) I + = + + (cos ) cosd= (cos ) si + ( + ) I + = ( + )(I I + ) I + = + + (Vrie : I = I pour ou ) O e dédui immédieme : I = I = 4 ; I 3 = 3 I = 3 ; I 4 = 3 4 I 3 = 6 I (cos ) (si ) d Formule géérle : Si pir ( = p) I p = p p 3... I p p I p = (p)! p+ ( p!) = p p p + Si impir ( = p + ) I p+ = p p... I p + p 3 I p+ = p ( p!) ( p + )! Clcul de J e se rme à I E pos u =, o oie : J = (si ) d = (si( )) u ( d u ) = (cos u) du = I Clcul de K e se rme à I + E pos u = Arcsi. (Bijecio de [ ; ] ds, ). O doc : = si u. K = ( ) d= (cos u) cosudu= I + = + (!) ( + )! Clcul de L e se rme à K L = ( ) d= ( ) K = + ( ) (!) ( + )! Clcul iégrl. Pge 3 G. COSTANTINI hp://cmhs.e/
33 Équivle des iégrles de Wllis lorsque ed + O risoe vec l suie (I ). O, pour ou e ou ; : cos+ cos E iégr pour ll de à : I + I E coséquece, l suie (I ) es décroisse. O doc : I + I + I E comme I + > : I I + + I I + Or, o vu que : I I + = + + () D'où : I I Pr ecdreme, o e dédui que I I + + dme ue limie égle à e +. Aureme di : I ~ I + () + Moros efi que l suie (u ) défiie pr u = ( + )I I + es cose : L suie (u ) es doc ie cose. u + = ( + ) I + I + () = ( + ) I I + = u E comme u = I I =, o, pour ou eier : u = E mulipli l'équivle () pr ( + )I : ( + ) I ~ u + ~ + D'où : I ~ + ( + ) ~ + O reiedr ce résul rès uile : (cos ) d ~ + Clcul iégrl. Pge 33 G. COSTANTINI hp://cmhs.e/
Intégrales généralisées
 3 Iégrles géérlisées Pour ce chpire, les focios cosidérées so priori défiies sur u iervlle réel I o rédui à u poi, à vleurs réelles ou complees e coiues pr morceu. L défiiio e les propriéés de l iégrle
3 Iégrles géérlisées Pour ce chpire, les focios cosidérées so priori défiies sur u iervlle réel I o rédui à u poi, à vleurs réelles ou complees e coiues pr morceu. L défiiio e les propriéés de l iégrle
Calculer comment se constituer un capitale ; Calculer comment rembourser une dette en effectuant des versements réguliers.
 CHAP: 8 Objecifs de ce chpire : Clculer comme se cosiuer u cpile ; Clculer comme rembourser ue dee e effecu des versemes réguliers. RAPPELS : Qu'es-ce qu'ue vleur cquise? Qu'es-ce qu'ue vleur cuelle? Le
CHAP: 8 Objecifs de ce chpire : Clculer comme se cosiuer u cpile ; Clculer comme rembourser ue dee e effecu des versemes réguliers. RAPPELS : Qu'es-ce qu'ue vleur cquise? Qu'es-ce qu'ue vleur cuelle? Le
S euls les flux de fonds (dépenses et recettes) définis s ent l investissement.
 Choix d ives i s s eme e cer iude 1 Chapire 1 Choix d ivesissemes e ceriude. Défiiio L es décisios d ivesissemes fo parie des décisios sraégiques de l erepris e. Le choix ere différes projes d ivesisseme
Choix d ives i s s eme e cer iude 1 Chapire 1 Choix d ivesissemes e ceriude. Défiiio L es décisios d ivesissemes fo parie des décisios sraégiques de l erepris e. Le choix ere différes projes d ivesisseme
Exercices de révision
 Exercices de révisio Exercice U ivesisseur souscri à l émissio d u bille de résorerie do les caracérisiques so les suivaes : - Nomial : 5 M - Taux facial : 3,2% - Durée de vie : 9 mois L ivesisseur doi
Exercices de révisio Exercice U ivesisseur souscri à l émissio d u bille de résorerie do les caracérisiques so les suivaes : - Nomial : 5 M - Taux facial : 3,2% - Durée de vie : 9 mois L ivesisseur doi
Intégrales dépendant d un paramètre
 [hp://mp.cpgedupuydelome.fr] édié le 3 avril 5 Eocés Iégrales dépeda d u paramère Covergece domiée Exercice [ 9 ] [correcio] Calculer les limies des suies do les ermes gééraux so les suivas : a) u = π/4
[hp://mp.cpgedupuydelome.fr] édié le 3 avril 5 Eocés Iégrales dépeda d u paramère Covergece domiée Exercice [ 9 ] [correcio] Calculer les limies des suies do les ermes gééraux so les suivas : a) u = π/4
n 1 LES GRANDS THÈMES DE L ITB > 2009 Les intérêts simples et les intérêts composés ( ) C T D ( en mois)
 LES GRANDS THÈMES DE L ITB Les iérês simples e les iérês composés RAPPELS THÉORIQUES Les iérês simples : l'iérê «I» es focio de la durée «D» (jour, quizaie, mois, rimesre, semesre, aée) de l'opéraio (placeme
LES GRANDS THÈMES DE L ITB Les iérês simples e les iérês composés RAPPELS THÉORIQUES Les iérês simples : l'iérê «I» es focio de la durée «D» (jour, quizaie, mois, rimesre, semesre, aée) de l'opéraio (placeme
Baccalauréat S Asie 19 juin 2014 Corrigé
 Bcclurét S Asie 9 jui 24 Corrigé A. P. M. E. P. Exercice Commu à tous les cdidts 4 poits Questio - c. O peut élimier rpidemet les réposes. et d. cr les vecteurs directeurs des droites proposées e sot ps
Bcclurét S Asie 9 jui 24 Corrigé A. P. M. E. P. Exercice Commu à tous les cdidts 4 poits Questio - c. O peut élimier rpidemet les réposes. et d. cr les vecteurs directeurs des droites proposées e sot ps
Développement en Série de Fourier
 F-IRIS-5.ex Développeme e Série de Fourier Développer e série de Fourier les focios de période T défiies aisi : a b { f impaire T = f = si ] ; { f paire T = f = si ; ] Faire das chaque cas ue représeaio
F-IRIS-5.ex Développeme e Série de Fourier Développer e série de Fourier les focios de période T défiies aisi : a b { f impaire T = f = si ] ; { f paire T = f = si ; ] Faire das chaque cas ue représeaio
Synthèse de cours (Terminale S) Calcul intégral
 Synthèse de cours (Terminle S) Clcul intégrl Intégrle d une onction continue positive sur un intervlle [;] Dns cette première prtie, on considère une onction continue positive sur un intervlle [ ; ] (
Synthèse de cours (Terminle S) Clcul intégrl Intégrle d une onction continue positive sur un intervlle [;] Dns cette première prtie, on considère une onction continue positive sur un intervlle [ ; ] (
16.1 Convergence simple et convergence uniforme. une suite de fonctions de I dans R ou C.
 16 Suites de foctios Suf précisio cotrire, I est u itervlle réel o réduit à u poit et les foctios cosidérées sot défiies sur I à vleurs réelles ou complexes. 16.1 Covergece simple et covergece uiforme
16 Suites de foctios Suf précisio cotrire, I est u itervlle réel o réduit à u poit et les foctios cosidérées sot défiies sur I à vleurs réelles ou complexes. 16.1 Covergece simple et covergece uiforme
1 Mesure et intégrale
 1 Mesure et itégrale 1.1 Tribu boréliee et foctios mesurables Soit =[a, b] u itervalle (le cas où b = ou a = est pas exclu) et F ue famille de sous-esembles de. OditqueF est ue tribu sur si les coditios
1 Mesure et itégrale 1.1 Tribu boréliee et foctios mesurables Soit =[a, b] u itervalle (le cas où b = ou a = est pas exclu) et F ue famille de sous-esembles de. OditqueF est ue tribu sur si les coditios
x +1 + ln. Donner la valeur exacte affichée par cet algorithme lorsque l utilisateur entre la valeur n =3.
 EXERCICE 3 (6 poits ) (Commu à tous les cadidats) Il est possible de traiter la partie C sas avoir traité la partie B Partie A O désige par f la foctio défiie sur l itervalle [, + [ par Détermier la limite
EXERCICE 3 (6 poits ) (Commu à tous les cadidats) Il est possible de traiter la partie C sas avoir traité la partie B Partie A O désige par f la foctio défiie sur l itervalle [, + [ par Détermier la limite
Chapitre 3 : Fonctions d une variable réelle (1)
 Uiversités Paris 6 et Paris 7 M1 MEEF Aalyse (UE 3) 2013-2014 Chapitre 3 : Foctios d ue variable réelle (1) 1 Lagage topologique das R Défiitio 1 Soit a u poit de R. U esemble V R est u voisiage de a s
Uiversités Paris 6 et Paris 7 M1 MEEF Aalyse (UE 3) 2013-2014 Chapitre 3 : Foctios d ue variable réelle (1) 1 Lagage topologique das R Défiitio 1 Soit a u poit de R. U esemble V R est u voisiage de a s
MTH 2301 Méthodes statistiques en ingénierie. MTH 2301 Méthodes statistiques en ingénierie
 VARIABLES ALÉATOIRES déo oco de réro vrble léore dscrèe moyee - vrce - écr ye esérce mhémque vrble léore coue oco d ue vrble léore : rsormo combso lére de vrbles léores Déo E : eérece léore S : esce échllol
VARIABLES ALÉATOIRES déo oco de réro vrble léore dscrèe moyee - vrce - écr ye esérce mhémque vrble léore coue oco d ue vrble léore : rsormo combso lére de vrbles léores Déo E : eérece léore S : esce échllol
[http://mp.cpgedupuydelome.fr] édité le 10 juillet 2014 Enoncés 1. Exercice 6 [ 02475 ] [correction] Si n est un entier 2, le rationnel H n =
![[http://mp.cpgedupuydelome.fr] édité le 10 juillet 2014 Enoncés 1. Exercice 6 [ 02475 ] [correction] Si n est un entier 2, le rationnel H n = [http://mp.cpgedupuydelome.fr] édité le 10 juillet 2014 Enoncés 1. Exercice 6 [ 02475 ] [correction] Si n est un entier 2, le rationnel H n =](/thumbs/19/318291.jpg) [http://mp.cpgedupuydelome.fr] édité le 1 juillet 14 Eocés 1 Nombres réels Ratioels et irratioels Exercice 1 [ 9 ] [correctio] Motrer que la somme d u ombre ratioel et d u ombre irratioel est u ombre irratioel.
[http://mp.cpgedupuydelome.fr] édité le 1 juillet 14 Eocés 1 Nombres réels Ratioels et irratioels Exercice 1 [ 9 ] [correctio] Motrer que la somme d u ombre ratioel et d u ombre irratioel est u ombre irratioel.
Séries réelles ou complexes
 6 Séries réelles ou complexes Comme pour le chapitre 3, les suites cosidérées sot a priori complexes et les résultats classiques sur les foctios cotiues ou dérivables d ue variable réelle sot supposés
6 Séries réelles ou complexes Comme pour le chapitre 3, les suites cosidérées sot a priori complexes et les résultats classiques sur les foctios cotiues ou dérivables d ue variable réelle sot supposés
Chapitre 2 Le problème de l unicité des solutions
 Université Joseph Fourier UE MAT 127 Mthémtiques nnée 2009-2010 Chpitre 2 Le prolème de l unicité des solutions 1 Le prolème et quelques réponses : 1.1 Un exemple Montrer que l éqution différentielle :
Université Joseph Fourier UE MAT 127 Mthémtiques nnée 2009-2010 Chpitre 2 Le prolème de l unicité des solutions 1 Le prolème et quelques réponses : 1.1 Un exemple Montrer que l éqution différentielle :
Limites des Suites numériques
 Chapitre 2 Limites des Suites umériques Termiale S Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES Limite fiie ou ifiie d ue suite. Limites et comparaiso. Opératios sur les ites. Comportemet
Chapitre 2 Limites des Suites umériques Termiale S Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES Limite fiie ou ifiie d ue suite. Limites et comparaiso. Opératios sur les ites. Comportemet
Exercice I ( non spé ) 1/ u 1 = 3 4. 2 3 u 2 4 + 3 9. 19 4 2/ Soit P la propriété : u n + 4. > 0 pour n 1. P est vraie au rang 1 car u 1
 Bac blac TS Correctio Exercice I ( Spé ) / émotros par récurrece que 5x y = pour tout etier aturel 5x y = 5 8 = La propriété est doc vraie au rag = Supposos que la propriété est vraie jusqu au rag, o a
Bac blac TS Correctio Exercice I ( Spé ) / émotros par récurrece que 5x y = pour tout etier aturel 5x y = 5 8 = La propriété est doc vraie au rag = Supposos que la propriété est vraie jusqu au rag, o a
CHAPITRE 2 SÉRIES ENTIÈRES
 CHAPITRE 2 SÉRIES ENTIÈRES 2. Séries etières Défiitio 2.. O appelle série etière toute série de foctios ( ) f dot le terme gééral est de la forme f ()=a, où (a ) désige ue suite réelle ou complee et R.
CHAPITRE 2 SÉRIES ENTIÈRES 2. Séries etières Défiitio 2.. O appelle série etière toute série de foctios ( ) f dot le terme gééral est de la forme f ()=a, où (a ) désige ue suite réelle ou complee et R.
Intégration et probabilités ENS Paris, 2012-2013. TD (20)13 Lois des grands nombres, théorème central limite. Corrigé :
 Itégratio et probabilités EN Paris, 202-203 TD 203 Lois des grads ombres, théorème cetral limite. Corrigé Lois des grads ombres Exercice. Calculer e cet leços Détermier les limites suivates : x +... +
Itégratio et probabilités EN Paris, 202-203 TD 203 Lois des grads ombres, théorème cetral limite. Corrigé Lois des grads ombres Exercice. Calculer e cet leços Détermier les limites suivates : x +... +
. (b) Si (u n ) est une suite géométrique de raison q, q 1, on obtient : N N, S N = 1 qn+1. n+1 1 S N = 1 1
 Premières propriétés des ombres réels 2 Suites umériques 3 Suites mootoes : à faire 4 Séries umériques 4. Notio de série. Défiitio 4.. Soit (u ) ue suite de ombres réels ou complexes. Pour N N, o ote S
Premières propriétés des ombres réels 2 Suites umériques 3 Suites mootoes : à faire 4 Séries umériques 4. Notio de série. Défiitio 4.. Soit (u ) ue suite de ombres réels ou complexes. Pour N N, o ote S
Correction de l épreuve CCP 2001 PSI Maths 2 PREMIÈRE PARTIE ) (
 Correction de l épreuve CCP PSI Mths PREMIÈRE PARTIE I- Soit t u voisinge de, t Alors ϕt t s = ϕt ρt s ρs Pr hypothèse, l fonction ϕt ϕt est lorsque t, il en est donc de même de ρt s ρt s ρs cr ρ s est
Correction de l épreuve CCP PSI Mths PREMIÈRE PARTIE I- Soit t u voisinge de, t Alors ϕt t s = ϕt ρt s ρs Pr hypothèse, l fonction ϕt ϕt est lorsque t, il en est donc de même de ρt s ρt s ρs cr ρ s est
Etude de la fonction ζ de Riemann
 Etude de la foctio ζ de Riema ) Défiitio Pour x réel doé, la série de terme gééral,, coverge si et seulemet si x >. x La foctio zeta de Riema est la foctio défiie sur ], [ par : ( x > ), = x. Remarque.
Etude de la foctio ζ de Riema ) Défiitio Pour x réel doé, la série de terme gééral,, coverge si et seulemet si x >. x La foctio zeta de Riema est la foctio défiie sur ], [ par : ( x > ), = x. Remarque.
Séquence 5. La fonction logarithme népérien. Sommaire
 Séquece 5 La foctio logarithme épérie Objectifs de la séquece Itroduire ue ouvelle foctio : la foctio logarithme épérie. Coaître les propriétés de cette foctio : sa dérivée, ses variatios, sa courbe, sa
Séquece 5 La foctio logarithme épérie Objectifs de la séquece Itroduire ue ouvelle foctio : la foctio logarithme épérie. Coaître les propriétés de cette foctio : sa dérivée, ses variatios, sa courbe, sa
Chapitre 3: TESTS DE SPECIFICATION
 Chapitre 3: TESTS DE SPECIFICATION Rappel d u c h api t r e pr é c é d en t : l i de n t i f i c a t i o n e t l e s t i m a t i o n de s y s t è m e s d é q u a t i o n s s i m u lt a n é e s r e p o
Chapitre 3: TESTS DE SPECIFICATION Rappel d u c h api t r e pr é c é d en t : l i de n t i f i c a t i o n e t l e s t i m a t i o n de s y s t è m e s d é q u a t i o n s s i m u lt a n é e s r e p o
A11 : La représentation chaînée (1ère partie)
 A11 : L représettio chîée (1ère prtie) - Défiitio et schéms de cosulttio - Schéms de mise à jour (isertio, suppressio) - Exemples J-P. Peyri - L représettio chîée (première prtie) 0 Pricipe de l représettio
A11 : L représettio chîée (1ère prtie) - Défiitio et schéms de cosulttio - Schéms de mise à jour (isertio, suppressio) - Exemples J-P. Peyri - L représettio chîée (première prtie) 0 Pricipe de l représettio
Liens entre fonction de transfert et représentations d'état d'un système (formes canoniques de la représentation d'état)
 oqe V oqe Cor e ere foco de rfer e repréeo dé d èe fore coqe de l repréeo dé SI Coe oqe! Irodco! e ere le dfféree decrpo d èe! Pge odèle dé " foco de rfer # C d èe oovrle # C d èe lvrle! Pge foco de rfer
oqe V oqe Cor e ere foco de rfer e repréeo dé d èe fore coqe de l repréeo dé SI Coe oqe! Irodco! e ere le dfféree decrpo d èe! Pge odèle dé " foco de rfer # C d èe oovrle # C d èe lvrle! Pge foco de rfer
La spirale de Théodore bis, et la suite «somme=produit».
 Etde d e vrite de l spirle de Théodore, dot issce à e site dot les sommes prtielles sot égles x prodits prtiels. Mots clés : spirle de Théodore, théorème de Pythgore, site, série, polyôme. L spirle de
Etde d e vrite de l spirle de Théodore, dot issce à e site dot les sommes prtielles sot égles x prodits prtiels. Mots clés : spirle de Théodore, théorème de Pythgore, site, série, polyôme. L spirle de
LES ESCALIERS. Du niveau du rez-de-chaussée à celui de l'étage ou à celui du sous-sol.
 LES ESCALIERS I. DÉF I NIT I O N Un escalier est un ouvrage constitué d'une suite de marches et de paliers permettant de passer à pied d'un niveau à un autre. Ses caractéristiques dimensionnelles sont
LES ESCALIERS I. DÉF I NIT I O N Un escalier est un ouvrage constitué d'une suite de marches et de paliers permettant de passer à pied d'un niveau à un autre. Ses caractéristiques dimensionnelles sont
Théorème de Poincaré - Formule de Green-Riemann
 Chpitre 11 Théorème de Poincré - Formule de Green-Riemnn Ce chpitre s inscrit dns l continuité du précédent. On vu à l proposition 1.16 que les formes différentielles sont bien plus grébles à mnipuler
Chpitre 11 Théorème de Poincré - Formule de Green-Riemnn Ce chpitre s inscrit dns l continuité du précédent. On vu à l proposition 1.16 que les formes différentielles sont bien plus grébles à mnipuler
DÉRIVÉES. I Nombre dérivé - Tangente. Exercice 01 (voir réponses et correction) ( voir animation )
 DÉRIVÉES I Nombre dérivé - Tangente Eercice 0 ( voir animation ) On considère la fonction f définie par f() = - 2 + 6 pour [-4 ; 4]. ) Tracer la représentation graphique (C) de f dans un repère d'unité
DÉRIVÉES I Nombre dérivé - Tangente Eercice 0 ( voir animation ) On considère la fonction f définie par f() = - 2 + 6 pour [-4 ; 4]. ) Tracer la représentation graphique (C) de f dans un repère d'unité
* très facile ** facile *** difficulté moyenne **** difficile ***** très difficile I : Incontournable
 Exo7 Topologie Exercices de Jea-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-fracefr * très facile ** facile *** difficulté moyee **** difficile ***** très difficile I : Icotourable Exercice **
Exo7 Topologie Exercices de Jea-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-fracefr * très facile ** facile *** difficulté moyee **** difficile ***** très difficile I : Icotourable Exercice **
Trading de Volatilité
 M émoire moire d Eude d Approfodisseme Tradig de Volailié Chrisia DIDION & Thomas JANNAUD Valdo DURRLEMAN Ecole Polyechique Sommaire Iroducio. Modèle de Blac-Scholes. Iroducio 44. Modèle de Blac & Scholes..5
M émoire moire d Eude d Approfodisseme Tradig de Volailié Chrisia DIDION & Thomas JANNAUD Valdo DURRLEMAN Ecole Polyechique Sommaire Iroducio. Modèle de Blac-Scholes. Iroducio 44. Modèle de Blac & Scholes..5
Continuité et dérivabilité d une fonction
 DERNIÈRE IMPRESSIN LE 7 novembre 014 à 10:3 Continuité et dérivabilité d une fonction Table des matières 1 Continuité d une fonction 1.1 Limite finie en un point.......................... 1. Continuité
DERNIÈRE IMPRESSIN LE 7 novembre 014 à 10:3 Continuité et dérivabilité d une fonction Table des matières 1 Continuité d une fonction 1.1 Limite finie en un point.......................... 1. Continuité
Déroulement de l épreuve de mathématiques
 Dérouleet de l épreuve de thétiques MATHÉMATIQUES Extrit de l ote de service 2012-029 du 24 février 2012 (BOEN 13 du 29-3-2012) Durée de l épreuve : 2 heures Nture de l épreuve : écrite pr le socle cou
Dérouleet de l épreuve de thétiques MATHÉMATIQUES Extrit de l ote de service 2012-029 du 24 février 2012 (BOEN 13 du 29-3-2012) Durée de l épreuve : 2 heures Nture de l épreuve : écrite pr le socle cou
* très facile ** facile *** difficulté moyenne **** difficile ***** très difficile I : Incontournable
 Eo7 Séries etières Eercices de Jea-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-fracefr * très facile ** facile *** difficulté moyee **** difficile ***** très difficile I : Icotourable Eercice
Eo7 Séries etières Eercices de Jea-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-fracefr * très facile ** facile *** difficulté moyee **** difficile ***** très difficile I : Icotourable Eercice
L'algèbre de BOOLE ou algèbre logique est l'algèbre définie pour des variables ne pouvant prendre que deux états.
 ciences Industrielles ystèmes comintoires Ppnicol Roert Lycée Jcques Amyot I - YTEME COMBINATOIRE A. Algère de Boole. Vriles logiques: Un signl réel est une grndeur physique en générl continue, on ssocie
ciences Industrielles ystèmes comintoires Ppnicol Roert Lycée Jcques Amyot I - YTEME COMBINATOIRE A. Algère de Boole. Vriles logiques: Un signl réel est une grndeur physique en générl continue, on ssocie
Groupe orthogonal d'un espace vectoriel euclidien de dimension 2, de dimension 3
 1 Groupe orthogoal d'u espace vectoriel euclidie de dimesio, de dimesio Voir le chapitre 19 pour l'étude des espaces euclidies et des isométries. État doé u espace euclidie E de dimesio 1, o rappelle que
1 Groupe orthogoal d'u espace vectoriel euclidie de dimesio, de dimesio Voir le chapitre 19 pour l'étude des espaces euclidies et des isométries. État doé u espace euclidie E de dimesio 1, o rappelle que
O, i, ) ln x. (ln x)2
 EXERCICE 5 points Commun à tous les candidats Le plan complee est muni d un repère orthonormal O, i, j Étude d une fonction f On considère la fonction f définie sur l intervalle ]0; + [ par : f = ln On
EXERCICE 5 points Commun à tous les candidats Le plan complee est muni d un repère orthonormal O, i, j Étude d une fonction f On considère la fonction f définie sur l intervalle ]0; + [ par : f = ln On
Lot 4: Validation industrielle. Youness LEMRABET Pascal YIM, 19/11/2010
 Lot 4: Validation industrielle Youness LEMRABET Pascal YIM, 19/11/2010 Partenaires Lot 1 Modèle du processus métier L4.1 Modèles PSM Lot 2 Guide d implantation L4.2 Développement & Recette prototype Lot
Lot 4: Validation industrielle Youness LEMRABET Pascal YIM, 19/11/2010 Partenaires Lot 1 Modèle du processus métier L4.1 Modèles PSM Lot 2 Guide d implantation L4.2 Développement & Recette prototype Lot
ANNEXES...16 Notation...16 Rente financière certaine...16. Mémo d Actuariat - Sophie Terrier @ 2004 1/16
 ÉO TUIT FOULS TUILLS SU TT Probbé ouo 3 dfféré4 ee gère be à ere échu 5 ee gère be à ere échu ueur fo d ée 6 ee gère à ere be d ce7 ee gère à ere be d ce ueur fo d ée8 urce décè 9 urce décè à c rbe cro
ÉO TUIT FOULS TUILLS SU TT Probbé ouo 3 dfféré4 ee gère be à ere échu 5 ee gère be à ere échu ueur fo d ée 6 ee gère à ere be d ce7 ee gère à ere be d ce ueur fo d ée8 urce décè 9 urce décè à c rbe cro
LICENCE DE MATHÉMATIQUES DEUXIÈME ANNÉE. Unité d enseignement LCMA 4U11 ANALYSE 3. Françoise GEANDIER
 LICENCE DE MATHÉMATIQUES DEUXIÈME ANNÉE Unité d enseignement LCMA 4U ANALYSE 3 Frnçoise GEANDIER Université Henri Poincré Nncy I Déprtement de Mthémtiques . Tble des mtières I Séries numériques. Séries
LICENCE DE MATHÉMATIQUES DEUXIÈME ANNÉE Unité d enseignement LCMA 4U ANALYSE 3 Frnçoise GEANDIER Université Henri Poincré Nncy I Déprtement de Mthémtiques . Tble des mtières I Séries numériques. Séries
COURS D ANALYSE. Licence d Informatique, première. Laurent Michel
 COURS D ANALYSE Licence d Informtique, première nnée Lurent Michel Printemps 2010 2 Tble des mtières 1 Éléments de logique 5 1.1 Fbriquer des énoncés........................ 5 1.1.1 Enoncés élémentires.....................
COURS D ANALYSE Licence d Informtique, première nnée Lurent Michel Printemps 2010 2 Tble des mtières 1 Éléments de logique 5 1.1 Fbriquer des énoncés........................ 5 1.1.1 Enoncés élémentires.....................
Chapitre IV Les oscillations couplées «Les oscillations libres d un système à plusieurs degrés de liberté»
 Chre IV, cours de vbrons, ondes _Phs, Pr. Bds Bennecer MD 8-9 Chre IV es oscllons coulées «es oscllons lbres d un ssèe à luseurs degrés de lberé» Dns ce chre, nous llons coencer r éuder les oscllons lbres
Chre IV, cours de vbrons, ondes _Phs, Pr. Bds Bennecer MD 8-9 Chre IV es oscllons coulées «es oscllons lbres d un ssèe à luseurs degrés de lberé» Dns ce chre, nous llons coencer r éuder les oscllons lbres
3 ème 2 DÉVELOPPEMENT FACTORISATIONS ET IDENTITÉS REMARQUABLES 1/5 1 - Développements
 3 ème 2 DÉVELOPPEMENT FACTORISATIONS ET IDENTITÉS REMARQUABLES 1/5 1 - Développements Développer une expression consiste à transformer un produit en une somme Qu est-ce qu une somme? Qu est-ce qu un produit?
3 ème 2 DÉVELOPPEMENT FACTORISATIONS ET IDENTITÉS REMARQUABLES 1/5 1 - Développements Développer une expression consiste à transformer un produit en une somme Qu est-ce qu une somme? Qu est-ce qu un produit?
Processus et martingales en temps continu
 Chapitre 3 Processus et martigales e temps cotiu 1 Quelques rappels sur les martigales e temps discret (voir [4]) O cosidère u espace filtré (Ω, F, (F ) 0, IP). O ote F = 0 F. Défiitio 1.1 Ue suite de
Chapitre 3 Processus et martigales e temps cotiu 1 Quelques rappels sur les martigales e temps discret (voir [4]) O cosidère u espace filtré (Ω, F, (F ) 0, IP). O ote F = 0 F. Défiitio 1.1 Ue suite de
Compression Compression par dictionnaires
 Compression Compression par dictionnaires E. Jeandel Emmanuel.Jeandel at lif.univ-mrs.fr E. Jeandel, Lif CompressionCompression par dictionnaires 1/25 Compression par dictionnaire Principe : Avoir une
Compression Compression par dictionnaires E. Jeandel Emmanuel.Jeandel at lif.univ-mrs.fr E. Jeandel, Lif CompressionCompression par dictionnaires 1/25 Compression par dictionnaire Principe : Avoir une
Chafa Azzedine - Faculté de Physique U.S.T.H.B 1
 Chafa Azzedine - Faculté de Physique U.S.T.H.B 1 Définition: La cinématique est une branche de la mécanique qui étudie les mouements des corps dans l espace en fonction du temps indépendamment des causes
Chafa Azzedine - Faculté de Physique U.S.T.H.B 1 Définition: La cinématique est une branche de la mécanique qui étudie les mouements des corps dans l espace en fonction du temps indépendamment des causes
Module 2 : Déterminant d une matrice
 L Mth Stt Module les déterminnts M Module : Déterminnt d une mtrice Unité : Déterminnt d une mtrice x Soit une mtrice lignes et colonnes (,) c b d Pr définition, son déterminnt est le nombre réel noté
L Mth Stt Module les déterminnts M Module : Déterminnt d une mtrice Unité : Déterminnt d une mtrice x Soit une mtrice lignes et colonnes (,) c b d Pr définition, son déterminnt est le nombre réel noté
Suites et séries de fonctions
 [http://mp.cpgedupuydelome.fr] édité le 3 avril 5 Eocés Suites et séries de foctios Propriétés de la limite d ue suite de foctios Eercice [ 868 ] [correctio] Etablir que la limite simple d ue suite de
[http://mp.cpgedupuydelome.fr] édité le 3 avril 5 Eocés Suites et séries de foctios Propriétés de la limite d ue suite de foctios Eercice [ 868 ] [correctio] Etablir que la limite simple d ue suite de
Cours d Analyse. Fonctions de plusieurs variables
 Cours d Analyse Fonctions de plusieurs variables Licence 1ère année 2007/2008 Nicolas Prioux Université de Marne-la-Vallée Table des matières 1 Notions de géométrie dans l espace et fonctions à deux variables........
Cours d Analyse Fonctions de plusieurs variables Licence 1ère année 2007/2008 Nicolas Prioux Université de Marne-la-Vallée Table des matières 1 Notions de géométrie dans l espace et fonctions à deux variables........
Séquence 8. Probabilité : lois à densité. Sommaire
 Séquence 8 Proilité : lois à densité Sommire. Prérequis 2. Lois de proilité à densité sur un intervlle 3. Lois uniformes 4. Lois exponentielles 5. Synthèse de l séquence Dns cette séquence, on introduit
Séquence 8 Proilité : lois à densité Sommire. Prérequis 2. Lois de proilité à densité sur un intervlle 3. Lois uniformes 4. Lois exponentielles 5. Synthèse de l séquence Dns cette séquence, on introduit
Un exemple d étude de cas
 Un exemple d'étude de cas 1 Un exemple d étude de cas INTRODUCTION Le cas de la Boulangerie Lépine ltée nous permet d exposer ici un type d étude de cas. Le processus utilisé est identique à celui qui
Un exemple d'étude de cas 1 Un exemple d étude de cas INTRODUCTION Le cas de la Boulangerie Lépine ltée nous permet d exposer ici un type d étude de cas. Le processus utilisé est identique à celui qui
Dérivation : cours. Dérivation dans R
 TS Dérivation dans R Dans tout le capitre, f désigne une fonction définie sur un intervalle I de R (non vide et non réduit à un élément) et à valeurs dans R. Petits rappels de première Téorème-définition
TS Dérivation dans R Dans tout le capitre, f désigne une fonction définie sur un intervalle I de R (non vide et non réduit à un élément) et à valeurs dans R. Petits rappels de première Téorème-définition
STI2D Logique binaire SIN. L' Algèbre de BOOLE
 L' Algère de BOOLE L'lgère de Boole est l prtie des mthémtiques, de l logique et de l'électronique qui s'intéresse ux opértions et ux fonctions sur les vriles logiques. Le nom provient de George Boole.
L' Algère de BOOLE L'lgère de Boole est l prtie des mthémtiques, de l logique et de l'électronique qui s'intéresse ux opértions et ux fonctions sur les vriles logiques. Le nom provient de George Boole.
14 Chapitre 14. Théorème du point fixe
 Chapitre 14 Chapitre 14. Théorème du poit fixe Si l o examie de plus près les méthodes de Lagrage et de Newto, étudiées au chapitre précédet, elles revieet das leur pricipe à remplacer la résolutio de
Chapitre 14 Chapitre 14. Théorème du poit fixe Si l o examie de plus près les méthodes de Lagrage et de Newto, étudiées au chapitre précédet, elles revieet das leur pricipe à remplacer la résolutio de
Deuxième partie : LES CONTRATS D ASSURANCE VIE CLASSIQUES
 DEUXIEME PARTIE Deuième partie : LES CONTRATS D ASSURANCE VIE CLASSIQUES Chapitre. L assurace de capital différé Chapitre 2. Les opératios de retes Chapitre 3. Les assuraces décès Chapitre 4. Les assuraces
DEUXIEME PARTIE Deuième partie : LES CONTRATS D ASSURANCE VIE CLASSIQUES Chapitre. L assurace de capital différé Chapitre 2. Les opératios de retes Chapitre 3. Les assuraces décès Chapitre 4. Les assuraces
L ANALYSE EN COMPOSANTES PRINCIPALES (A.C.P.) Pierre-Louis GONZALEZ
 L ANALYSE EN COMPOSANTES PRINCIPALES (A.C.P.) Pierre-Louis GONZALEZ INTRODUCTION Données : n individus observés sur p variables quantitatives. L A.C.P. permet d eplorer les liaisons entre variables et
L ANALYSE EN COMPOSANTES PRINCIPALES (A.C.P.) Pierre-Louis GONZALEZ INTRODUCTION Données : n individus observés sur p variables quantitatives. L A.C.P. permet d eplorer les liaisons entre variables et
LES ÉCLIPSES. Éclipser signifie «cacher». Vus depuis la Terre, deux corps célestes peuvent être éclipsés : la Lune et le Soleil.
 Qu appelle-t-o éclipse? Éclipser sigifie «cacher». Vus depuis la Terre, deu corps célestes peuvet être éclipsés : la Lue et le Soleil. LES ÉCLIPSES Pour qu il ait éclipse, les cetres de la Terre, de la
Qu appelle-t-o éclipse? Éclipser sigifie «cacher». Vus depuis la Terre, deu corps célestes peuvet être éclipsés : la Lue et le Soleil. LES ÉCLIPSES Pour qu il ait éclipse, les cetres de la Terre, de la
Commun à tous les candidats
 EXERCICE 3 (9 points ) Commun à tous les candidats On s intéresse à des courbes servant de modèle à la distribution de la masse salariale d une entreprise. Les fonctions f associées définies sur l intervalle
EXERCICE 3 (9 points ) Commun à tous les candidats On s intéresse à des courbes servant de modèle à la distribution de la masse salariale d une entreprise. Les fonctions f associées définies sur l intervalle
Accueil Events, l accueil personnalisé des touristes d affaires Informations, bonnes adresses, réservations et découvertes!
 Lyon City Card 1 jour 2 jours 3 jours Ta xis et M inibus - Tarifs forfaitaires Jour : 7h - 19h Nuit : 19h - 7h Lyon/ Villeurbanne - Aéroport St Exupéry 59 81 Lyon 5ème et 9ème excentrés - Aéroport St Exupéry
Lyon City Card 1 jour 2 jours 3 jours Ta xis et M inibus - Tarifs forfaitaires Jour : 7h - 19h Nuit : 19h - 7h Lyon/ Villeurbanne - Aéroport St Exupéry 59 81 Lyon 5ème et 9ème excentrés - Aéroport St Exupéry
Corrigé du baccalauréat S Pondichéry 12 avril 2007
 Corrigé du baccalauréat S Pondichéry 1 avril 7 EXERCICE 1 Commun à tous les candidats 4 points 1 a Les vecteurs AB et AC ont pour coordonnées AB ; ; ) et AC 1 ; 4 ; 1) Ils ne sont manifestement pas colinéaires
Corrigé du baccalauréat S Pondichéry 1 avril 7 EXERCICE 1 Commun à tous les candidats 4 points 1 a Les vecteurs AB et AC ont pour coordonnées AB ; ; ) et AC 1 ; 4 ; 1) Ils ne sont manifestement pas colinéaires
TD/TP : Taux d un emprunt (méthode de Newton)
 TD/TP : Taux d un emprun (méhode de Newon) 1 On s inéresse à des calculs relaifs à des remboursemens d empruns 1. On noera C 0 la somme emprunée, M la somme remboursée chaque mois (mensualié), le aux mensuel
TD/TP : Taux d un emprun (méhode de Newon) 1 On s inéresse à des calculs relaifs à des remboursemens d empruns 1. On noera C 0 la somme emprunée, M la somme remboursée chaque mois (mensualié), le aux mensuel
Angles orientés et trigonométrie
 Chapitre Angles orientés et trigonométrie Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES Trigonométrie Cercle trigonométrique. Radian. Mesure d un angle orienté, mesure principale.
Chapitre Angles orientés et trigonométrie Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES Trigonométrie Cercle trigonométrique. Radian. Mesure d un angle orienté, mesure principale.
Limites finies en un point
 8 Limites finies en un point Pour ce chapitre, sauf précision contraire, I désigne une partie non vide de R et f une fonction définie sur I et à valeurs réelles ou complees. Là encore, les fonctions usuelles,
8 Limites finies en un point Pour ce chapitre, sauf précision contraire, I désigne une partie non vide de R et f une fonction définie sur I et à valeurs réelles ou complees. Là encore, les fonctions usuelles,
Chapitre 1 Cinématique du point matériel
 Chapitre 1 Cinématique du point matériel 7 1.1. Introduction 1.1.1. Domaine d étude Le programme de mécanique de math sup se limite à l étude de la mécanique classique. Sont exclus : la relativité et la
Chapitre 1 Cinématique du point matériel 7 1.1. Introduction 1.1.1. Domaine d étude Le programme de mécanique de math sup se limite à l étude de la mécanique classique. Sont exclus : la relativité et la
Calcul intégral élémentaire en plusieurs variables
 Calcul intégral élémentaire en plusieurs variables PC*2 2 septembre 2009 Avant-propos À part le théorème de Fubini qui sera démontré dans le cours sur les intégrales à paramètres et qui ne semble pas explicitement
Calcul intégral élémentaire en plusieurs variables PC*2 2 septembre 2009 Avant-propos À part le théorème de Fubini qui sera démontré dans le cours sur les intégrales à paramètres et qui ne semble pas explicitement
8.1 Généralités sur les fonctions de plusieurs variables réelles. f : R 2 R (x, y) 1 x 2 y 2
 Chapitre 8 Fonctions de plusieurs variables 8.1 Généralités sur les fonctions de plusieurs variables réelles Définition. Une fonction réelle de n variables réelles est une application d une partie de R
Chapitre 8 Fonctions de plusieurs variables 8.1 Généralités sur les fonctions de plusieurs variables réelles Définition. Une fonction réelle de n variables réelles est une application d une partie de R
SÉRIES STATISTIQUES À DEUX VARIABLES
 1 ) POSITION DU PROBLÈME - VOCABULAIRE A ) DÉFINITION SÉRIES STATISTIQUES À DEUX VARIABLES O cosidère deux variables statistiques umériques x et y observées sur ue même populatio de idividus. O ote x 1
1 ) POSITION DU PROBLÈME - VOCABULAIRE A ) DÉFINITION SÉRIES STATISTIQUES À DEUX VARIABLES O cosidère deux variables statistiques umériques x et y observées sur ue même populatio de idividus. O ote x 1
Activités numériques [13 Points]
![Activités numériques [13 Points] Activités numériques [13 Points]](/thumbs/21/1117704.jpg) N du candidat L emploi de la calculatrice est autorisé. Le soin, la qualité de la présentation entrent pour 2 points dans l appréciation des copies. Les résultats seront soulignés. La correction est disponible
N du candidat L emploi de la calculatrice est autorisé. Le soin, la qualité de la présentation entrent pour 2 points dans l appréciation des copies. Les résultats seront soulignés. La correction est disponible
AC AB. A B C x 1. x + 1. d où. Avec un calcul vu au lycée, on démontre que cette solution admet deux solutions dont une seule nous intéresse : x =
 LE NOMBRE D OR Présentation et calcul du nombre d or Euclide avait trouvé un moyen de partager en deu un segment selon en «etrême et moyenne raison» Soit un segment [AB]. Le partage d Euclide consiste
LE NOMBRE D OR Présentation et calcul du nombre d or Euclide avait trouvé un moyen de partager en deu un segment selon en «etrême et moyenne raison» Soit un segment [AB]. Le partage d Euclide consiste
Convergences 2/2 - le théorème du point fixe - Page 1 sur 9
 Au sommaire : Suites extraites Le théorème de Bolzao-Weierstrass La preuve du théorème de Bolzao-Weierstrass3 Foctio K-cotractate4 Le théorème du poit fixe5 La preuve du théorème du poit fixe6 Utilisatios
Au sommaire : Suites extraites Le théorème de Bolzao-Weierstrass La preuve du théorème de Bolzao-Weierstrass3 Foctio K-cotractate4 Le théorème du poit fixe5 La preuve du théorème du poit fixe6 Utilisatios
Chapitre 2 Le problème de l unicité des solutions
 Université Joseph Fourier UE MAT 127 Mathématiques année 2011-2012 Chapitre 2 Le problème de l unicité des solutions Ce que nous verrons dans ce chapitre : un exemple d équation différentielle y = f(y)
Université Joseph Fourier UE MAT 127 Mathématiques année 2011-2012 Chapitre 2 Le problème de l unicité des solutions Ce que nous verrons dans ce chapitre : un exemple d équation différentielle y = f(y)
Exercices - Fonctions de plusieurs variables : corrigé. Pour commencer
 Pour commencer Exercice 1 - Ensembles de définition - Première année - 1. Le logarithme est défini si x + y > 0. On trouve donc le demi-plan supérieur délimité par la droite d équation x + y = 0.. 1 xy
Pour commencer Exercice 1 - Ensembles de définition - Première année - 1. Le logarithme est défini si x + y > 0. On trouve donc le demi-plan supérieur délimité par la droite d équation x + y = 0.. 1 xy
Comportement d'une suite
 Comportemet d'ue suite I) Approche de "ses de variatio et de ite d'ue suite" : 7 Soit la suite ( ) telle que = 5 ( + ) 2 Représetos graphiquemet la suite das u pla mui d' u repère. Il suffit de placer
Comportemet d'ue suite I) Approche de "ses de variatio et de ite d'ue suite" : 7 Soit la suite ( ) telle que = 5 ( + ) 2 Représetos graphiquemet la suite das u pla mui d' u repère. Il suffit de placer
Chapitre 2 : Vecteurs
 1 Chapitre 2 : Vecteurs Nous allons définir ce qu'est un vecteur grâce à une figure (le parallélogramme), mais au préalable nous allons aussi définir une nouvelle transformation (la translation). Nous
1 Chapitre 2 : Vecteurs Nous allons définir ce qu'est un vecteur grâce à une figure (le parallélogramme), mais au préalable nous allons aussi définir une nouvelle transformation (la translation). Nous
Exo7. Limites de fonctions. 1 Théorie. 2 Calculs
 Eo7 Limites de fonctions Théorie Eercice Montrer que toute fonction périodique et non constante n admet pas de ite en + Montrer que toute fonction croissante et majorée admet une ite finie en + Indication
Eo7 Limites de fonctions Théorie Eercice Montrer que toute fonction périodique et non constante n admet pas de ite en + Montrer que toute fonction croissante et majorée admet une ite finie en + Indication
M e t h o d o l o g i e s & W o r k i n g p a p e r s. Manuel des indices des prix de l immobilier résidentiel
 M e h o d o l o g i e s & W o r k i g p a p e r s Mauel des idices des prix de l immobilier résideiel Édiio 23 M e h o d o l o g i e s & W o r k i g p a p e r s Mauel des idices des prix de l immobilier
M e h o d o l o g i e s & W o r k i g p a p e r s Mauel des idices des prix de l immobilier résideiel Édiio 23 M e h o d o l o g i e s & W o r k i g p a p e r s Mauel des idices des prix de l immobilier
EXERCICES : DÉNOMBREMENT
 Chapitre 7 ECE 1 - Grad Nouméa - 015 EXERCICES : DÉNOMBREMENT LISTES / ARRANGEMENTS Exercice 1 : Le code ativol Pour so vélo, Toto possède u ativol a code. Le code est ue successio de trois chiffres compris
Chapitre 7 ECE 1 - Grad Nouméa - 015 EXERCICES : DÉNOMBREMENT LISTES / ARRANGEMENTS Exercice 1 : Le code ativol Pour so vélo, Toto possède u ativol a code. Le code est ue successio de trois chiffres compris
Développements limités. Notion de développement limité
 MT12 - ch2 Page 1/8 Développements limités Dans tout ce chapitre, I désigne un intervalle de R non vide et non réduit à un point. I Notion de développement limité Dans tout ce paragraphe, a désigne un
MT12 - ch2 Page 1/8 Développements limités Dans tout ce chapitre, I désigne un intervalle de R non vide et non réduit à un point. I Notion de développement limité Dans tout ce paragraphe, a désigne un
L'important C'est la rose
 L'important 'est la rose Gilbert ecaud rr: M. de Leon opista: Felix Vela 200 Xiulit c / m F m m 7 9. /. m...... J 1 F m.... m7 ro - se. rois - ro - se. rois - ro - se. rois - ro - se. rois - oi qui oi
L'important 'est la rose Gilbert ecaud rr: M. de Leon opista: Felix Vela 200 Xiulit c / m F m m 7 9. /. m...... J 1 F m.... m7 ro - se. rois - ro - se. rois - ro - se. rois - ro - se. rois - oi qui oi
La santé de votre entreprise mérite notre protection.
 mutuelle mclr La santé de votre entreprise mérite notre protection. www.mclr.fr Qui sommes-nous? En tant que mutuelle régionale, nous partageons avec vous un certain nombre de valeurs liées à la taille
mutuelle mclr La santé de votre entreprise mérite notre protection. www.mclr.fr Qui sommes-nous? En tant que mutuelle régionale, nous partageons avec vous un certain nombre de valeurs liées à la taille
Les Nombres Parfaits.
 Les Nombres Parfaits. Agathe CAGE, Matthieu CABAUSSEL, David LABROUSSE (2 de Lycée MONTAIGNE BORDEAUX) et Alexadre DEVERT, Pierre Damie DESSARPS (TS Lycée SUD MEDOC LETAILLAN MEDOC) La première partie
Les Nombres Parfaits. Agathe CAGE, Matthieu CABAUSSEL, David LABROUSSE (2 de Lycée MONTAIGNE BORDEAUX) et Alexadre DEVERT, Pierre Damie DESSARPS (TS Lycée SUD MEDOC LETAILLAN MEDOC) La première partie
Estimation des incertitudes sur les erreurs de mesure.
 Estmto des certtdes sr les errers de mesre. I. Itrodcto : E sceces epérmetles, l este ps de mesres ectes. Celle-c e pevet être q etchées d errers pls o mos mporttes selo le protocole chos, l qlté des strmets
Estmto des certtdes sr les errers de mesre. I. Itrodcto : E sceces epérmetles, l este ps de mesres ectes. Celle-c e pevet être q etchées d errers pls o mos mporttes selo le protocole chos, l qlté des strmets
Planche n o 22. Fonctions de plusieurs variables. Corrigé
 Planche n o Fonctions de plusieurs variables Corrigé n o : f est définie sur R \ {, } Pour, f, = Quand tend vers, le couple, tend vers le couple, et f, tend vers Donc, si f a une limite réelle en, cette
Planche n o Fonctions de plusieurs variables Corrigé n o : f est définie sur R \ {, } Pour, f, = Quand tend vers, le couple, tend vers le couple, et f, tend vers Donc, si f a une limite réelle en, cette
Exercices - Polynômes : corrigé. Opérations sur les polynômes
 Opérations sur les polynômes Exercice 1 - Carré - L1/Math Sup - Si P = Q est le carré d un polynôme, alors Q est nécessairement de degré, et son coefficient dominant est égal à 1. On peut donc écrire Q(X)
Opérations sur les polynômes Exercice 1 - Carré - L1/Math Sup - Si P = Q est le carré d un polynôme, alors Q est nécessairement de degré, et son coefficient dominant est égal à 1. On peut donc écrire Q(X)
Dualité dans les espaces de Lebesgue et mesures de Radon finies
 Chapitre 6 Dualité dans les espaces de Lebesgue et mesures de Radon finies Nous allons maintenant revenir sur les espaces L p du Chapitre 4, à la lumière de certains résultats du Chapitre 5. Sauf mention
Chapitre 6 Dualité dans les espaces de Lebesgue et mesures de Radon finies Nous allons maintenant revenir sur les espaces L p du Chapitre 4, à la lumière de certains résultats du Chapitre 5. Sauf mention
F 2 = - T p K 0. ... F T = - T p K 0 - K 0
 Correcion de l exercice 2 de l assisana pré-quiz final du cours Gesion financière : «chéancier e aux de renabilié inerne d empruns à long erme» Quesion : rappeler la formule donnan les flux à chaque échéance
Correcion de l exercice 2 de l assisana pré-quiz final du cours Gesion financière : «chéancier e aux de renabilié inerne d empruns à long erme» Quesion : rappeler la formule donnan les flux à chaque échéance
LASTO Appuis élastomère
 LASTO Appuis élsomère LASTO BLOCK F Appuis de déformion non-rmés Swizerlnd www.mgeb.ch Chmps d pplicion e specs imporns Chmps d pplicion LASTO BLOCK F es un ppui de déformion non-rmé en élsomère qui es
LASTO Appuis élsomère LASTO BLOCK F Appuis de déformion non-rmés Swizerlnd www.mgeb.ch Chmps d pplicion e specs imporns Chmps d pplicion LASTO BLOCK F es un ppui de déformion non-rmé en élsomère qui es
Fonctions de plusieurs variables, intégrales multiples, et intégrales dépendant d un paramètre
 IUFM du Limousin 2009-10 PLC1 Mathématiques S. Vinatier Rappels de cours Fonctions de plusieurs variables, intégrales multiples, et intégrales dépendant d un paramètre 1 Fonctions de plusieurs variables
IUFM du Limousin 2009-10 PLC1 Mathématiques S. Vinatier Rappels de cours Fonctions de plusieurs variables, intégrales multiples, et intégrales dépendant d un paramètre 1 Fonctions de plusieurs variables
* très facile ** facile *** difficulté moyenne **** difficile ***** très difficile I : Incontournable T : pour travailler et mémoriser le cours.
 Eo7 Fonctions de plusieurs variables Eercices de Jean-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-francefr * très facile ** facile *** difficulté moenne **** difficile ***** très difficile I
Eo7 Fonctions de plusieurs variables Eercices de Jean-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-francefr * très facile ** facile *** difficulté moenne **** difficile ***** très difficile I
PROBLEME(12) Première partie : Peinture des murs et du plafond.
 PROBLEME(12) Une entreprise doit rénover un local. Ce local a la forme d'un parallélépipède rectangle. La longueur est 6,40m, la largeur est 5,20m et la hauteur est 2,80m. Il comporte une porte de 2m de
PROBLEME(12) Une entreprise doit rénover un local. Ce local a la forme d'un parallélépipède rectangle. La longueur est 6,40m, la largeur est 5,20m et la hauteur est 2,80m. Il comporte une porte de 2m de
Commande par calculateur Introduction à la représentation d état
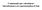 Commd r clclr Irodcio à l rrésio d é SIRE Chir I CNDUIE DE PRCESSUS PR CCUEUR. Prici d commd.. Schém d rici.. Echillog, qificio rolio d'ordr.3. Schéms fociols. scs mérils.. Covrissr mériq logiq.. Covrissr
Commd r clclr Irodcio à l rrésio d é SIRE Chir I CNDUIE DE PRCESSUS PR CCUEUR. Prici d commd.. Schém d rici.. Echillog, qificio rolio d'ordr.3. Schéms fociols. scs mérils.. Covrissr mériq logiq.. Covrissr
20. Algorithmique & Mathématiques
 L'éditeur L'éditeur permet à l'utilisateur de saisir les liges de codes d'u programme ou de défiir des foctios. Remarque : O peut saisir directemet des istructios das la cosole Scilab, mais il est plus
L'éditeur L'éditeur permet à l'utilisateur de saisir les liges de codes d'u programme ou de défiir des foctios. Remarque : O peut saisir directemet des istructios das la cosole Scilab, mais il est plus
Exercice 6 Associer chaque expression de gauche à sa forme réduite (à droite) :
 Eercice a Développer les epressions suivantes : A-(-) - + B-0(3 ²+3-0) -0 3²+-0 3+00 B -30²-30+00 C-3(-) -3 + 3-3²+6 D-(-) + ² Eerciceb Parmi les epressions suivantes, lesquelles sont sous forme réduite?
Eercice a Développer les epressions suivantes : A-(-) - + B-0(3 ²+3-0) -0 3²+-0 3+00 B -30²-30+00 C-3(-) -3 + 3-3²+6 D-(-) + ² Eerciceb Parmi les epressions suivantes, lesquelles sont sous forme réduite?
Fonctions de plusieurs variables : dérivés partielles, diérentielle. Fonctions composées. Fonctions de classe C 1. Exemples
 45 Fonctions de plusieurs variables : dérivés partielles, diérentielle. Fonctions composées. Fonctions de classe C 1. Exemples Les espaces vectoriels considérés sont réels, non réduits au vecteur nul et
45 Fonctions de plusieurs variables : dérivés partielles, diérentielle. Fonctions composées. Fonctions de classe C 1. Exemples Les espaces vectoriels considérés sont réels, non réduits au vecteur nul et
Ce document a été mis en ligne par le Canopé de l académie de Montpellier pour la Base Nationale des Sujets d Examens de l enseignement professionnel.
 Ce document a été mis en ligne par le Canopé de l académie de Montpellier pour la Base Nationale des Sujets d Examens de l enseignement professionnel. Ce fichier numérique ne peut être reproduit, représenté,
Ce document a été mis en ligne par le Canopé de l académie de Montpellier pour la Base Nationale des Sujets d Examens de l enseignement professionnel. Ce fichier numérique ne peut être reproduit, représenté,
Séries numériques. Chap. 02 : cours complet.
 Séris méris Cha : cors comlt Séris d réls t d comlxs Défiitio : séri d réls o d comlxs Défiitio : séri corgt o dirgt Rmar : iflc ds rmirs trms d séri sr la corgc Théorèm : coditio écssair d corgc Théorèm
Séris méris Cha : cors comlt Séris d réls t d comlxs Défiitio : séri d réls o d comlxs Défiitio : séri corgt o dirgt Rmar : iflc ds rmirs trms d séri sr la corgc Théorèm : coditio écssair d corgc Théorèm
Exercices - Nombres complexes : corrigé. Formes algébriques et trigonométriques, module et argument
 Formes algébriques et trigonométriques, module et argument Exercice - - L/Math Sup - On multiplie le dénominateur par sa quantité conjuguée, et on obtient : Z = 4 i 3 + i 3 i 3 = 4 i 3 + 3 = + i 3. Pour
Formes algébriques et trigonométriques, module et argument Exercice - - L/Math Sup - On multiplie le dénominateur par sa quantité conjuguée, et on obtient : Z = 4 i 3 + i 3 i 3 = 4 i 3 + 3 = + i 3. Pour
