Géométrie en sixième avec GéoSpace
|
|
|
- Albert Fontaine
- il y a 6 ans
- Total affichages :
Transcription
1 Géométrie en sixième avec GéoSpace Parallélépipède rectangle : perspective cavalière et patron Sommaire 1. Cube : perspective cavalière 2. Parallélépipède rectangle 3. Patron d'un parallélépipède rectangle Technique GéoSpace : patron d'un polyèdre Faire des maths avec GéoPlan-GéoSpace : Ce document PDF : Page HTML : Document n 84, réalisé le 27/6/2005 modifié le 10/1/ Cube : perspective cavalière Exemples de dessins qui évoquent un cube. D'après : Herrera Ruben Rodriguez et Salles-Le Gac Danielle - Du dessin perçu à la figure construite - ellipses Il est possible de faire tourner la figure GéoSpace cube.g3w à la souris ou au clavier : À la souris : clic droit maintenu Au clavier : touche majuscule maintenue Axe vertical Gauche - droite Flèches gauche - droite Axe horizontal de l'écran Bas - haut Flèches basse - haute Axe horizontal perpendiculaire à l'écran Choisir l'option du menu «Vues» : «plan de face maintenu» (avant-dernier bouton de la version PC) Touches page up/down Faire des mathématiques avec GéoSpace Page 1/5 L espace en sixième
2 Les paramètres de position se trouvent au début du texte de la figure : verticale: -20 horizontale: 25 frontale: 0 Projection oblique verticale: -10 horizontale: 8 verticale: -40 horizontale: 5 Dans ces dessins, le contour extérieur a une forme d'hexagone avec deux bords verticaux (Rotations de Rxyz: frontale: 0). Les 12 arêtes sont bien distinguées. La représentation sur l'écran pour GéoSpace est obtenue par projection orthogonale sur le plan de l'écran, il n'est donc pas possible d'obtenir la perspective cavalière où les deux faces perpendiculaires au champ de vision sont représentées par des carrés aux côtés parallèles aux bords de la feuille (avec des faces horizontales visibles). Avec l'option projection oblique, on obtient les deux carrés, mais les faces horizontales et latérales ne sont plus des parallélogrammes. Les paramètres de position se trouvent au début du texte de la figure cube1 : verticale: 0 horizontale: 0 frontale: 0 Projection oblique Exemples de dessins qui n'évoquent pas bien un cube. verticale: -1 horizontale: 2 verticale: -43 horizontale: 2 verticale: -45 horizontale: 4 Dans ces dessins, le contour extérieur évoque plus un rectangle qu'un hexagone et on distingue mal certaines arêtes. Faire des mathématiques avec GéoSpace Page 2/5 L espace en sixième
3 2. Parallélépipède rectangle Parallélépipède : polyèdre à six faces qui sont toutes des parallélogrammes. Les faces opposées sont égales et parallèles. C'est un prisme dont la base est un parallélogramme. Parallélépipède rectangle : polyèdre à six faces qui sont toutes des rectangles. C'est un prisme droit dont la base est un rectangle. À l'école, le terme parallélépipède rectangle n'est pas exigible au cycle 2, on lui préfèrera celui de pavé droit. Commandes GéoSpace Faire varier la taille du parallélépipède avec les flèches du clavier. Taper A pour modifier la longueur a, B pour modifier la largeur b et H pour modifier la hauteur h. Taper D pour visualiser les diagonales. Les diagonales sont concourantes en leur milieu Par exemple, les diagonales [AG] et [EC] sont les diagonales du rectangle ACGE. Elles se coupent en leur milieu I. Faire des mathématiques avec GéoSpace Page 3/5 L espace en sixième
4 2. Patron d'un parallélépipède rectangle Commandes GéoSpace Le patron est pilotable au clavier : appuyez sur les flèches de déplacement pour fermer le patron en faisant varier le coefficient d'ouverture m de 1 vers 0. La touche F permet d'obtenir une vue de face et la touche W permet de revenir à la vue initiale. Faire des mathématiques avec GéoSpace Page 4/5 L espace en sixième
5 Technique GéoSpace : patron d'un polyèdre (menu Créer) On obtient, parmi tous les patrons possibles, un patron choisi par le logiciel en fonction de l'ordre dans lequel ont été donnés les sommets du polyèdre lors de sa création. Les trois premiers sommets appartenant à une même face du polyèdre définissent la face principale du patron et le plan dans lequel sera situé le patron lorsqu'il sera complètement ouvert ; les autres faces s'articulent autour de cette face. En pratique si le polyèdre est un cube ABCDEFGH ou une pyramide ABCDS, donner (lors de la création) en premier la liste des sommets de la future base principale ABCD dans cet ordre, - pour un prisme, commencer par les sommets d'une face latérale pour obtenir un patron habituel. Le prisme ABCDEF de base triangulaire ABC sera nommé ABEDCF en commençant par la face ABED, sommets écrits dans cet ordre. Classe de sixième Patron de cube Classe de cinquième Patron de prisme droit à base triangulaire Classe de quatrième Patron de pyramide Le coefficient d'ouverture du patron est une variable réelle libre, m dans mes exemples, comprise entre 0 et 1 ; si elle est égale à 1 le patron est plan, si elle est égale à 0 le patron coïncide avec le polyèdre. Pour ouvrir un patron par étapes, il suffit de piloter cette variable au clavier. Faire des mathématiques avec GéoSpace Page 5/5 L espace en sixième
Créer une trace, obtenir son fichier gpx et sa carte Ou Afficher un fichier trace GPX
 Créer une trace, obtenir son fichier gpx et sa carte Ou Afficher un fichier trace GPX Logiciels nécessaires : - - - Google Chrome comme navigateur internet FireShot qui est un add-on qui se greffe sur
Créer une trace, obtenir son fichier gpx et sa carte Ou Afficher un fichier trace GPX Logiciels nécessaires : - - - Google Chrome comme navigateur internet FireShot qui est un add-on qui se greffe sur
EXCEL PERFECTIONNEMENT SERVICE INFORMATIQUE. Version 1.0 30/11/05
 EXCEL PERFECTIONNEMENT Version 1.0 30/11/05 SERVICE INFORMATIQUE TABLE DES MATIERES 1RAPPELS...3 1.1RACCOURCIS CLAVIER & SOURIS... 3 1.2NAVIGUER DANS UNE FEUILLE ET UN CLASSEUR... 3 1.3PERSONNALISER LA
EXCEL PERFECTIONNEMENT Version 1.0 30/11/05 SERVICE INFORMATIQUE TABLE DES MATIERES 1RAPPELS...3 1.1RACCOURCIS CLAVIER & SOURIS... 3 1.2NAVIGUER DANS UNE FEUILLE ET UN CLASSEUR... 3 1.3PERSONNALISER LA
LibreOffice Calc : introduction aux tableaux croisés dynamiques
 Fiche logiciel LibreOffice Calc 3.x Tableur Niveau LibreOffice Calc : introduction aux tableaux croisés dynamiques Un tableau croisé dynamique (appelé Pilote de données dans LibreOffice) est un tableau
Fiche logiciel LibreOffice Calc 3.x Tableur Niveau LibreOffice Calc : introduction aux tableaux croisés dynamiques Un tableau croisé dynamique (appelé Pilote de données dans LibreOffice) est un tableau
Si un quadrilatère a. Si un quadrilatère a. Si un quadrilatère a. Si un quadrilatère a. ses côtés opposés. ses côtés opposés de. deux côtés opposés
 P1 P2 P3 P4 a a a a ses côtés opposés ses côtés opposés de deux côtés opposés ses diagonales qui se parallèles, alors c est même longueur alors parallèles et de même coupent en leur un c est un longueur
P1 P2 P3 P4 a a a a ses côtés opposés ses côtés opposés de deux côtés opposés ses diagonales qui se parallèles, alors c est même longueur alors parallèles et de même coupent en leur un c est un longueur
AC AB. A B C x 1. x + 1. d où. Avec un calcul vu au lycée, on démontre que cette solution admet deux solutions dont une seule nous intéresse : x =
 LE NOMBRE D OR Présentation et calcul du nombre d or Euclide avait trouvé un moyen de partager en deu un segment selon en «etrême et moyenne raison» Soit un segment [AB]. Le partage d Euclide consiste
LE NOMBRE D OR Présentation et calcul du nombre d or Euclide avait trouvé un moyen de partager en deu un segment selon en «etrême et moyenne raison» Soit un segment [AB]. Le partage d Euclide consiste
CREER ET ANIMER SON ESPACE DE TRAVAIL COLLABORATIF
 CREER ET ANIMER SON ESPACE DE TRAVAIL COLLABORATIF SOMMAIRE Sommaire... 2 Un espace de travail collaboratif, pourquoi faire?... 3 Créer votre espace collaboratif... 4 Ajouter des membres... 6 Utiliser
CREER ET ANIMER SON ESPACE DE TRAVAIL COLLABORATIF SOMMAIRE Sommaire... 2 Un espace de travail collaboratif, pourquoi faire?... 3 Créer votre espace collaboratif... 4 Ajouter des membres... 6 Utiliser
Dans l idéal, ceci devrait être fait en amont pour chaque image envoyée sur l espace de stockage de votre site internet.
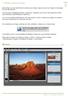 1- Optimiser le poids de votre image : Dans l idéal, ceci devrait être fait en amont pour chaque image envoyée sur l espace de stockage de votre site internet. Tous les types d utilisateurs (auteur, publicateur,
1- Optimiser le poids de votre image : Dans l idéal, ceci devrait être fait en amont pour chaque image envoyée sur l espace de stockage de votre site internet. Tous les types d utilisateurs (auteur, publicateur,
Maîtriser les fonctionnalités d un traitement de texte (Word OpenOffice)
 Utilisation de l'ordinateur et apport des TIC en enseignement (1NP) Module 03 Maîtriser les fonctionnalités d un traitement de texte. Sens du Module De nombreux documents remis aux enfants sont réalisés
Utilisation de l'ordinateur et apport des TIC en enseignement (1NP) Module 03 Maîtriser les fonctionnalités d un traitement de texte. Sens du Module De nombreux documents remis aux enfants sont réalisés
Deux disques dans un carré
 Deux disques dans un carré Table des matières 1 Fiche résumé 2 2 Fiche élève Seconde - version 1 3 2.1 Le problème............................................... 3 2.2 Construction de la figure avec geogebra...............................
Deux disques dans un carré Table des matières 1 Fiche résumé 2 2 Fiche élève Seconde - version 1 3 2.1 Le problème............................................... 3 2.2 Construction de la figure avec geogebra...............................
point On obtient ainsi le ou les points d inter- entre deux objets».
 Déplacer un objet Cliquer sur le bouton «Déplacer». On peut ainsi rendre la figure dynamique. Attraper l objet à déplacer avec la souris. Ici, on veut déplacer le point A du triangle point ABC. A du triangle
Déplacer un objet Cliquer sur le bouton «Déplacer». On peut ainsi rendre la figure dynamique. Attraper l objet à déplacer avec la souris. Ici, on veut déplacer le point A du triangle point ABC. A du triangle
L.T.Mohammedia CHAINE D ENERGIE - DESSIN TECHNIQUE S.CHARI
 I. Introduction Pourquoi le dessin technique? Le Dessin Technique est une façon de représenter des pièces réelles (donc en 3 dimensions) sur une feuille de papier (donc en 2 dimensions) que l on appelle
I. Introduction Pourquoi le dessin technique? Le Dessin Technique est une façon de représenter des pièces réelles (donc en 3 dimensions) sur une feuille de papier (donc en 2 dimensions) que l on appelle
iil est désormais courant de trouver sur Internet un document
 Matériels et systèmes L Acrobat qui cherche dans les PDF Michel NARCY - Formateur TICE et Médialog Bulletin officiel, programmes d enseignement, articles de quotidiens ou de revues scientifiques... De
Matériels et systèmes L Acrobat qui cherche dans les PDF Michel NARCY - Formateur TICE et Médialog Bulletin officiel, programmes d enseignement, articles de quotidiens ou de revues scientifiques... De
Utilisation de l éditeur.
 Utilisation de l éditeur. Préambule...2 Configuration du navigateur...3 Débloquez les pop-up...5 Mise en évidence du texte...6 Mise en évidence du texte...6 Mise en page du texte...7 Utilisation de tableaux....7
Utilisation de l éditeur. Préambule...2 Configuration du navigateur...3 Débloquez les pop-up...5 Mise en évidence du texte...6 Mise en évidence du texte...6 Mise en page du texte...7 Utilisation de tableaux....7
Silhouette Studio Leçon N 2
 Silhouette Studio Leçon N 2 Apprendre comment utiliser Ma Bibliothèque et la Boutique en Ligne Silhouette pour importer des nouveaux modèles. Matériels nécessaires Silhouette SD Feuille de transport colle
Silhouette Studio Leçon N 2 Apprendre comment utiliser Ma Bibliothèque et la Boutique en Ligne Silhouette pour importer des nouveaux modèles. Matériels nécessaires Silhouette SD Feuille de transport colle
Note de cours. Introduction à Excel 2007
 Note de cours Introduction à Excel 2007 par Armande Pinette Cégep du Vieux Montréal Excel 2007 Page: 2 de 47 Table des matières Comment aller chercher un document sur CVMVirtuel?... 8 Souris... 8 Clavier
Note de cours Introduction à Excel 2007 par Armande Pinette Cégep du Vieux Montréal Excel 2007 Page: 2 de 47 Table des matières Comment aller chercher un document sur CVMVirtuel?... 8 Souris... 8 Clavier
Les droites (d 1 ) et (d 2 ) sont sécantes en A Le point A est le point d intersection des 2 droites
 I Droites perpendiculaires Lorsque deux droites se coupent, on dit qu elles sont sécantes Les droites (d 1 ) et (d 2 ) sont sécantes en A Le point A est le point d intersection des 2 droites Lorsque deux
I Droites perpendiculaires Lorsque deux droites se coupent, on dit qu elles sont sécantes Les droites (d 1 ) et (d 2 ) sont sécantes en A Le point A est le point d intersection des 2 droites Lorsque deux
Priorités de calcul :
 EXERCICES DE REVISION POUR LE PASSAGE EN QUATRIEME : Priorités de calcul : Exercice 1 : Calcule en détaillant : A = 4 + 5 6 + 7 B = 6 3 + 5 C = 35 5 3 D = 6 7 + 8 E = 38 6 3 + 7 Exercice : Calcule en détaillant
EXERCICES DE REVISION POUR LE PASSAGE EN QUATRIEME : Priorités de calcul : Exercice 1 : Calcule en détaillant : A = 4 + 5 6 + 7 B = 6 3 + 5 C = 35 5 3 D = 6 7 + 8 E = 38 6 3 + 7 Exercice : Calcule en détaillant
Ceci est un Chromebook, ton ordinateur!
 Ceci est un Chromebook, ton ordinateur! CHROMEBOOK - Dans le royaume des ordinateurs personnels, il n'y a pas beaucoup de choix. Pour schématiser, soit vous avez un PC, soit vous avez un Mac. Et ce depuis
Ceci est un Chromebook, ton ordinateur! CHROMEBOOK - Dans le royaume des ordinateurs personnels, il n'y a pas beaucoup de choix. Pour schématiser, soit vous avez un PC, soit vous avez un Mac. Et ce depuis
CA 3000 CA 3000 PROGRAMMATION PAR MINITEL
 CA 3000 CA 3000 PROGRAMMATION PAR MINITEL UTILISATION A - CONFIGURATION CA 3000 B - DATE ET HEURE C - ENREGISTRE R RES IDENT D - MODIFIER RESIDENT E - LISTE REPERTOIRE F - GROUPES LECTEURS G - GROUPES
CA 3000 CA 3000 PROGRAMMATION PAR MINITEL UTILISATION A - CONFIGURATION CA 3000 B - DATE ET HEURE C - ENREGISTRE R RES IDENT D - MODIFIER RESIDENT E - LISTE REPERTOIRE F - GROUPES LECTEURS G - GROUPES
Un exemple avec WORKSPACE d'interwrite
 S'approprier un utilitaire de TNI Un exemple avec WORKSPACE d'interwrite Objectifs : S'approprier un utilitaire de TNI («soft»)afin de percevoir la plus-value pédagogique de l'outil. Pour cela utiliser
S'approprier un utilitaire de TNI Un exemple avec WORKSPACE d'interwrite Objectifs : S'approprier un utilitaire de TNI («soft»)afin de percevoir la plus-value pédagogique de l'outil. Pour cela utiliser
Tout savoir sur le clavier
 Tout savoir sur le clavier Niveau débutant Niveau intermédiaire Niveau confirmé Le clavier est un périphérique d entrée (interface homme / machine), composé de touches envoyant des instructions à la machine.
Tout savoir sur le clavier Niveau débutant Niveau intermédiaire Niveau confirmé Le clavier est un périphérique d entrée (interface homme / machine), composé de touches envoyant des instructions à la machine.
- Université Paris V - UFR de Psychologie ASDP4 Info Introduction à Windows
 Introduction à Windows 1. Démarrer Allumer l ordinateur On se trouve face au bureau, avec ses icônes, sa barre de tâches. Icônes Barre des tâches 2. La souris a. Cliquer Amener le pointeur de la souris
Introduction à Windows 1. Démarrer Allumer l ordinateur On se trouve face au bureau, avec ses icônes, sa barre de tâches. Icônes Barre des tâches 2. La souris a. Cliquer Amener le pointeur de la souris
Utilisation du logiciel Epson Easy Interactive Tools
 Utilisation du logiciel Epson Easy Interactive Tools Ce logiciel permet d'utiliser le stylo electronique comme souris pour contrôler l'ordinateur depuis l'écran et comme feutre électronique pour écrire
Utilisation du logiciel Epson Easy Interactive Tools Ce logiciel permet d'utiliser le stylo electronique comme souris pour contrôler l'ordinateur depuis l'écran et comme feutre électronique pour écrire
LES TABLETTES : GÉNÉRALITÉS
 LES TABLETTES : GÉNÉRALITÉS Fonctionnement Qu est-ce qu une tablette tactile? Une tablette tactile est un appareil doté d'un écran qui permet d'interagir simplement en touchant l'écran ou à l'aide d'un
LES TABLETTES : GÉNÉRALITÉS Fonctionnement Qu est-ce qu une tablette tactile? Une tablette tactile est un appareil doté d'un écran qui permet d'interagir simplement en touchant l'écran ou à l'aide d'un
Répertorier vos mots de passe avec Passbox : 1) Télécharger le fichier d'installation :
 Amicale laïque de Poisat 18-19 février 2013 Répertorier vos mots de passe avec Passbox : 1) Télécharger le fichier d'installation : a) Taper "Passbox" dans le moteur de recherche de votre navigateur. b)
Amicale laïque de Poisat 18-19 février 2013 Répertorier vos mots de passe avec Passbox : 1) Télécharger le fichier d'installation : a) Taper "Passbox" dans le moteur de recherche de votre navigateur. b)
Comment sélectionner des sommets, des arêtes et des faces avec Blender?
 Comment sélectionner des sommets, des arêtes et des faces avec Blender? VVPix v 1.00 Table des matières 1 Introduction 1 2 Préparation d une scène test 2 2.1 Ajout d objets dans la scène.........................................
Comment sélectionner des sommets, des arêtes et des faces avec Blender? VVPix v 1.00 Table des matières 1 Introduction 1 2 Préparation d une scène test 2 2.1 Ajout d objets dans la scène.........................................
Publication Assistée par Ordinateur
 Présentation OpenOffice Draw est l'outil de dessin vectoriel de la suite bureautique OpenOffice. De fait, Draw permet de réaliser certains documents comparables à ceux de Publisher, le logiciel de P.A.O.
Présentation OpenOffice Draw est l'outil de dessin vectoriel de la suite bureautique OpenOffice. De fait, Draw permet de réaliser certains documents comparables à ceux de Publisher, le logiciel de P.A.O.
Scénario de prise en main DataCar CRM v2.3 Gamme SFA
 Scénario de prise en main DataCar CRM v2.3 Gamme SFA 1 - Présentation et Restriction Vous venez d obtenir vos accès à l application DataCar CRM. Vous trouverez dans ce document un scénario de prise en
Scénario de prise en main DataCar CRM v2.3 Gamme SFA 1 - Présentation et Restriction Vous venez d obtenir vos accès à l application DataCar CRM. Vous trouverez dans ce document un scénario de prise en
Celestia. 1. Introduction à Celestia (2/7) 1. Introduction à Celestia (1/7) Université du Temps Libre - 08 avril 2008
 GMPI*EZVI0EFSVEXSMVIH%WXVSTL]WMUYIHI&SVHIEY\ 1. Introduction à Celestia Celestia 1.1 Généralités 1.2 Ecran d Ouverture 2. Commandes Principales du Menu 3. Exemples d Applications 3.1 Effet de l atmosphère
GMPI*EZVI0EFSVEXSMVIH%WXVSTL]WMUYIHI&SVHIEY\ 1. Introduction à Celestia Celestia 1.1 Généralités 1.2 Ecran d Ouverture 2. Commandes Principales du Menu 3. Exemples d Applications 3.1 Effet de l atmosphère
DOSSIER D'ACTIVITES SUR TUXPAINT Dessiner avec Tuxpaint. Objectifs :
 DOSSIER D'ACTIVITES SUR TUXPAINT Dessiner avec Tuxpaint Objectifs : Apprendre à l apprenant à connaître l'ordinateur Apprendre à l'apprenant à allumer l'ordinateur Faire découvrir à l'apprenant Linux Faire
DOSSIER D'ACTIVITES SUR TUXPAINT Dessiner avec Tuxpaint Objectifs : Apprendre à l apprenant à connaître l'ordinateur Apprendre à l'apprenant à allumer l'ordinateur Faire découvrir à l'apprenant Linux Faire
Guide de démarrage rapide Centre de copies et d'impression Bureau en Gros en ligne
 Guide de démarrage rapide Centre de copies et d'impression Bureau en Gros en ligne Aperçu du Centre de copies et d'impression Bureau en Gros en ligne Pour accéder à «copies et impression Bureau en Gros
Guide de démarrage rapide Centre de copies et d'impression Bureau en Gros en ligne Aperçu du Centre de copies et d'impression Bureau en Gros en ligne Pour accéder à «copies et impression Bureau en Gros
Initiation à Excel. Frédéric Gava (MCF) gava@univ-paris12.fr
 Initiation à Excel Frédéric Gava (MCF) gava@univ-paris12.fr LACL, bâtiment P2 du CMC, bureau 221 Université de Paris XII Val-de-Marne 61 avenue du Général de Gaulle 94010 Créteil cedex Plan de cette année
Initiation à Excel Frédéric Gava (MCF) gava@univ-paris12.fr LACL, bâtiment P2 du CMC, bureau 221 Université de Paris XII Val-de-Marne 61 avenue du Général de Gaulle 94010 Créteil cedex Plan de cette année
La C.A.O (Conception Assistée par Ordinateur). Le logiciel de C.A.O.
 CAO1 La C.A.O (Conception Assistée par Ordinateur). Aujourd'hui, lorsque des ingénieurs décident de concevoir un nouveau produit, ils n'utilisent plus de stylo. Les plans sont réalisés sur ordinateur.
CAO1 La C.A.O (Conception Assistée par Ordinateur). Aujourd'hui, lorsque des ingénieurs décident de concevoir un nouveau produit, ils n'utilisent plus de stylo. Les plans sont réalisés sur ordinateur.
Support de formation Notebook
 Support de formation Notebook Guide de l utilisateur du tableau interactif SMART Board Table des matières Le Tableau Blanc Interactif... 1 Comprendre le fonctionnement du TBI... 1 Utiliser le plumier
Support de formation Notebook Guide de l utilisateur du tableau interactif SMART Board Table des matières Le Tableau Blanc Interactif... 1 Comprendre le fonctionnement du TBI... 1 Utiliser le plumier
Débuter avec Excel. Excel 2007-2010
 Débuter avec Excel Excel 2007-2010 Fabienne ROUX Conseils & Formation 10/04/2010 TABLE DES MATIÈRES LE RUBAN 4 LE CLASSEUR 4 RENOMMER LES FEUILLES DU CLASSEUR 4 SUPPRIMER DES FEUILLES D UN CLASSEUR 4 AJOUTER
Débuter avec Excel Excel 2007-2010 Fabienne ROUX Conseils & Formation 10/04/2010 TABLE DES MATIÈRES LE RUBAN 4 LE CLASSEUR 4 RENOMMER LES FEUILLES DU CLASSEUR 4 SUPPRIMER DES FEUILLES D UN CLASSEUR 4 AJOUTER
Prénom : MATHÉMATIQUES. 120 minutes Compas, règle métrique, rapporteur, équerre, calculatrice non programmable
 Admission en 8 VSG 8 VSB cocher la voie visée MATHÉMATIQUES Durée Matériel à disposition 120 minutes Compas, règle métrique, rapporteur, équerre, calculatrice non programmable Rappel des objectifs fondamentaux
Admission en 8 VSG 8 VSB cocher la voie visée MATHÉMATIQUES Durée Matériel à disposition 120 minutes Compas, règle métrique, rapporteur, équerre, calculatrice non programmable Rappel des objectifs fondamentaux
Manuel d utilisation email NETexcom
 Manuel d utilisation email NETexcom Table des matières Vos emails avec NETexcom... 3 Présentation... 3 GroupWare... 3 WebMail emails sur internet... 4 Se connecter au Webmail... 4 Menu principal... 5 La
Manuel d utilisation email NETexcom Table des matières Vos emails avec NETexcom... 3 Présentation... 3 GroupWare... 3 WebMail emails sur internet... 4 Se connecter au Webmail... 4 Menu principal... 5 La
La perspective conique
 La perspective conique Définitions et principes. Deux cas de la perspective conique : la perspective conique oblique et la perspective conique centrale. Principe de la perspective conique : . La perspective
La perspective conique Définitions et principes. Deux cas de la perspective conique : la perspective conique oblique et la perspective conique centrale. Principe de la perspective conique : . La perspective
F.A.Q 1.0 Designer 3D Atex System
 -Sommaire- 1-Comment installer le logiciel?...2 2-Comment créer un projet?...3 3-Comment ouvrir un projet?...4 4-Comment se déplacer en 2D & 3D?...5 5-Comment ajouter des composants?...6 1-Comment installer
-Sommaire- 1-Comment installer le logiciel?...2 2-Comment créer un projet?...3 3-Comment ouvrir un projet?...4 4-Comment se déplacer en 2D & 3D?...5 5-Comment ajouter des composants?...6 1-Comment installer
à l édition de textes
 Introduction à l édition de textes Introduction Le traitement de texte consiste en la création et la modification de textes (appelés aussi documents) à l'aide d'un ordinateur. Les premiers logiciels de
Introduction à l édition de textes Introduction Le traitement de texte consiste en la création et la modification de textes (appelés aussi documents) à l'aide d'un ordinateur. Les premiers logiciels de
Guide d utilisation 2012
 Guide d utilisation 2012 Tout ce dont vous avez besoin pour bien démarrer REACOM La performance marketing SOMMAIRE Démarrez avec reagiciel Accédez à votre console d administration 4 Gestion internet Aperçu
Guide d utilisation 2012 Tout ce dont vous avez besoin pour bien démarrer REACOM La performance marketing SOMMAIRE Démarrez avec reagiciel Accédez à votre console d administration 4 Gestion internet Aperçu
WINDOWS 8. Windows 8 se distingue par la présence de 2 interfaces complémentaires :
 WINDOWS 8 Windows 8 : généralités Windows 8 est la dernière version du système d'exploitation de Windows, sortie en octobre 2012. Si vous possédez un ordinateur récent, il y a de fortes chances que votre
WINDOWS 8 Windows 8 : généralités Windows 8 est la dernière version du système d'exploitation de Windows, sortie en octobre 2012. Si vous possédez un ordinateur récent, il y a de fortes chances que votre
MÉDICLICK! STUDIO 3 GESTION DES IMAGES ET PIÈCES JOINTES SOMMAIRE
 MÉDICLICK! STUDIO 3 GESTION DES IMAGES ET PIÈCES JOINTES SOMMAIRE COMMENT AJOUTER DES IMAGES OU DES PIECES JOINTES? COMMENT SUPPRIMER DES IMAGES OU DES PIECES JOINTES? COMMENT CHANGER L APPARENCE DE LA
MÉDICLICK! STUDIO 3 GESTION DES IMAGES ET PIÈCES JOINTES SOMMAIRE COMMENT AJOUTER DES IMAGES OU DES PIECES JOINTES? COMMENT SUPPRIMER DES IMAGES OU DES PIECES JOINTES? COMMENT CHANGER L APPARENCE DE LA
Si deux droites sont parallèles à une même troisième. alors les deux droites sont parallèles entre elles. alors
 N I) Pour démontrer que deux droites (ou segments) sont parallèles (d) // (d ) (d) // (d ) deux droites sont parallèles à une même troisième les deux droites sont parallèles entre elles (d) // (d) deux
N I) Pour démontrer que deux droites (ou segments) sont parallèles (d) // (d ) (d) // (d ) deux droites sont parallèles à une même troisième les deux droites sont parallèles entre elles (d) // (d) deux
COURS AUTOCAD. Création et utilisation des blocs. b leclerc. ERP Jean Moulin METZ
 COURS AUTOCAD Création et utilisation des blocs QU EST-CE QU UN BLOC? C est un élément de dessin, auquel peut être associé du texte (des attributs ). Un bloc constitue un élément de bibliothèque. Il peut
COURS AUTOCAD Création et utilisation des blocs QU EST-CE QU UN BLOC? C est un élément de dessin, auquel peut être associé du texte (des attributs ). Un bloc constitue un élément de bibliothèque. Il peut
Les Enseignants de l Ere Technologique - Tunisie. Niveau 1
 Les Enseignants De l Ere Technologique - Tunisie - LE CLOUD COMPUTING TAT Tunisie 2014 Le Cloud Computing 1. Définition Les Enseignants de l Ere Technologique - Tunisie Le cloud computing (en français
Les Enseignants De l Ere Technologique - Tunisie - LE CLOUD COMPUTING TAT Tunisie 2014 Le Cloud Computing 1. Définition Les Enseignants de l Ere Technologique - Tunisie Le cloud computing (en français
FICHIERS ET DOSSIERS
 La différence entre fichier et dossier FICHIERS ET DOSSIERS La première notion à acquérir est la différence entre un dossier et un fichier Un dossier est une sorte de classeur dans lequel on range divers
La différence entre fichier et dossier FICHIERS ET DOSSIERS La première notion à acquérir est la différence entre un dossier et un fichier Un dossier est une sorte de classeur dans lequel on range divers
Mini_guide_Isis_v6.doc le 10/02/2005 Page 1/15
 1 Démarrer... 2 1.1 L écran Isis... 2 1.2 Les barres d outils... 3 1.2.1 Les outils d édition... 3 1.2.2 Les outils de sélection de mode... 4 1.2.3 Les outils d orientation... 4 2 Quelques actions... 5
1 Démarrer... 2 1.1 L écran Isis... 2 1.2 Les barres d outils... 3 1.2.1 Les outils d édition... 3 1.2.2 Les outils de sélection de mode... 4 1.2.3 Les outils d orientation... 4 2 Quelques actions... 5
TBI-DIRECT. Bridgit. Pour le partage de votre bureau. Écrit par : TBI Direct. http://www.tbi-direct.fr
 TBI-DIRECT Bridgit Pour le partage de votre bureau Écrit par : TBI Direct http://www.tbi-direct.fr Contenu Vue d'ensemble...4 Nom du serveur...5 Lancement du Bridgit...5 Installation du logiciel Bridgit
TBI-DIRECT Bridgit Pour le partage de votre bureau Écrit par : TBI Direct http://www.tbi-direct.fr Contenu Vue d'ensemble...4 Nom du serveur...5 Lancement du Bridgit...5 Installation du logiciel Bridgit
Le Dessin Technique.
 Jardin-Nicolas Hervé cours 1 / 9. Modélisation et représentation d un objet technique. La modélisation et la représentation d un objet sont deux formes de langage permettant de définir complètement la
Jardin-Nicolas Hervé cours 1 / 9. Modélisation et représentation d un objet technique. La modélisation et la représentation d un objet sont deux formes de langage permettant de définir complètement la
Avec PICASA. Partager ses photos. Avant de commencer. Picasa sur son ordinateur. Premier démarrage
 Avant de commencer Picasa est avant un logiciel que l'on peut installer sur son ordinateur et qui permet de transférer ses photos dans un espace pouvant être partagé sur Internet. Picasa sur son ordinateur.
Avant de commencer Picasa est avant un logiciel que l'on peut installer sur son ordinateur et qui permet de transférer ses photos dans un espace pouvant être partagé sur Internet. Picasa sur son ordinateur.
Guide d'utilisation. OpenOffice Calc. AUTEUR INITIAL : VINCENT MEUNIER Publié sous licence Creative Commons
 Guide d'utilisation OpenOffice Calc AUTEUR INITIAL : VINCENT MEUNIER Publié sous licence Creative Commons 1 Table des matières Fiche 1 : Présentation de l'interface...3 Fiche 2 : Créer un nouveau classeur...4
Guide d'utilisation OpenOffice Calc AUTEUR INITIAL : VINCENT MEUNIER Publié sous licence Creative Commons 1 Table des matières Fiche 1 : Présentation de l'interface...3 Fiche 2 : Créer un nouveau classeur...4
Nom : Groupe : Date : 1. Quels sont les deux types de dessins les plus utilisés en technologie?
 Nom : Groupe : Date : Verdict Chapitre 11 1 La communication graphique Pages 336 et 337 1. Quels sont les deux types de dessins les plus utilisés en technologie? Les dessins de fabrication. Les schémas.
Nom : Groupe : Date : Verdict Chapitre 11 1 La communication graphique Pages 336 et 337 1. Quels sont les deux types de dessins les plus utilisés en technologie? Les dessins de fabrication. Les schémas.
Mini_guide_Isis.pdf le 23/09/2001 Page 1/14
 1 Démarrer...2 1.1 L écran Isis...2 1.2 La boite à outils...2 1.2.1 Mode principal...3 1.2.2 Mode gadgets...3 1.2.3 Mode graphique...3 2 Quelques actions...4 2.1 Ouvrir un document existant...4 2.2 Sélectionner
1 Démarrer...2 1.1 L écran Isis...2 1.2 La boite à outils...2 1.2.1 Mode principal...3 1.2.2 Mode gadgets...3 1.2.3 Mode graphique...3 2 Quelques actions...4 2.1 Ouvrir un document existant...4 2.2 Sélectionner
Correction des Travaux Pratiques Organiser son espace de travail
 Module 01 Correction des Travaux Pratiques Organiser son espace de travail Correction de l exercice N 1 Organiser son espace de travail Objectif de l exercice : 1. Comprendre le dock 2. Afficher les règles
Module 01 Correction des Travaux Pratiques Organiser son espace de travail Correction de l exercice N 1 Organiser son espace de travail Objectif de l exercice : 1. Comprendre le dock 2. Afficher les règles
La saisie d un texte
 La saisie d un texte On utilise le clavier pour la saisie des textes. C est une partie importante du travail. Il est indispensable de respecter un certain nombre de règles pour que le travail soit plus
La saisie d un texte On utilise le clavier pour la saisie des textes. C est une partie importante du travail. Il est indispensable de respecter un certain nombre de règles pour que le travail soit plus
Manuel utilisateur Netviewer one2one
 Manuel utilisateur Netviewer one2one INDEX 1. Etablissement de la connexion...2 1.1. Client... 2 2. Travailler avec Netviewer en mode Show...3 2.1. Vue écran... 3 2.2. Le panneau Netviewer... 3 2.3. Caractéristiques...
Manuel utilisateur Netviewer one2one INDEX 1. Etablissement de la connexion...2 1.1. Client... 2 2. Travailler avec Netviewer en mode Show...3 2.1. Vue écran... 3 2.2. Le panneau Netviewer... 3 2.3. Caractéristiques...
Cette fonctionnalité est paramétrable et accessible dans le module administration via le menu "Dossier / Administration".
 Gestion du multilingues Cette nouveauté est disponible en édition Entreprise L'extension WaveSoft Customisation vous permet sur l'édition Entreprise de rendre les modules Gestion Commerciale, GRC, Comptabilité,
Gestion du multilingues Cette nouveauté est disponible en édition Entreprise L'extension WaveSoft Customisation vous permet sur l'édition Entreprise de rendre les modules Gestion Commerciale, GRC, Comptabilité,
Saisissez le login et le mot de passe (attention aux minuscules et majuscules) qui vous ont
 I Open Boutique Sommaire : I Open Boutique... 1 Onglet «Saisie des Produits»... 3 Création d'une nouvelle fiche boutique :... 3 Création d'une nouvelle fiche lieux de retraits :... 10 Création d'une nouvelle
I Open Boutique Sommaire : I Open Boutique... 1 Onglet «Saisie des Produits»... 3 Création d'une nouvelle fiche boutique :... 3 Création d'une nouvelle fiche lieux de retraits :... 10 Création d'une nouvelle
1 CRÉER UN TABLEAU. IADE Outils et Méthodes de gestion de l information
 TP Numéro 2 CRÉER ET MANIPULER DES TABLEAUX (Mise en forme, insertion, suppression, tri...) 1 CRÉER UN TABLEAU 1.1 Présentation Pour organiser et présenter des données sous forme d un tableau, Word propose
TP Numéro 2 CRÉER ET MANIPULER DES TABLEAUX (Mise en forme, insertion, suppression, tri...) 1 CRÉER UN TABLEAU 1.1 Présentation Pour organiser et présenter des données sous forme d un tableau, Word propose
POSTE INFORMATIQUE. Mr DUJARDIN a acheté du matériel informatique sur une boutique en ligne afin de se monter un PC. N'y
 NOM : Prénom : Classe : POSTE INFORMATIQUE Date : CI4 : TRANSPORT & TRANSMISSION DES SIGNAUX SUPPORT DE L INFORMATION AVM11 : Assemblage d un poste informatique Problématique Mr DUJARDIN a acheté du matériel
NOM : Prénom : Classe : POSTE INFORMATIQUE Date : CI4 : TRANSPORT & TRANSMISSION DES SIGNAUX SUPPORT DE L INFORMATION AVM11 : Assemblage d un poste informatique Problématique Mr DUJARDIN a acheté du matériel
Logiciel SCRATCH FICHE 02
 1. Reprise de la fiche 1: 1.1. Programme Figure : Logiciel SCRATCH FICHE 02 SANS ORDINATEUR : Dessiner à droite le dessin que donnera l'exécution de ce programme : Unité : 50 pas : Remarque : vous devez
1. Reprise de la fiche 1: 1.1. Programme Figure : Logiciel SCRATCH FICHE 02 SANS ORDINATEUR : Dessiner à droite le dessin que donnera l'exécution de ce programme : Unité : 50 pas : Remarque : vous devez
Prise en main du logiciel. Smart BOARD Notebook 10
 Prise en main du logiciel Smart BOARD Notebook 10 1. Introduction : Le logiciel Smart BOARD est utilisable avec les tableaux blancs interactifs de la gamme SMART. Toutefois, il n'est pas nécessaire d'avoir
Prise en main du logiciel Smart BOARD Notebook 10 1. Introduction : Le logiciel Smart BOARD est utilisable avec les tableaux blancs interactifs de la gamme SMART. Toutefois, il n'est pas nécessaire d'avoir
MESUREZ L'IMPACT DE VOS CAMPAGNES!
 MESUREZ L'IMPACT DE VOS CAMPAGNES! Concrètement, qu est-ce que mesurer l'impact de vos campagnes? L'utilisateur, après avoir envoyé une campagne e-mailing, peut mesurer son impact en consultant les résultats
MESUREZ L'IMPACT DE VOS CAMPAGNES! Concrètement, qu est-ce que mesurer l'impact de vos campagnes? L'utilisateur, après avoir envoyé une campagne e-mailing, peut mesurer son impact en consultant les résultats
WHS ProRealTime. édition 2008 1.52
 WHS ProRealTime édition 2008 1.52 Ce tutoriel est dédié aux fonctions de passage d'ordres sur ProRealTime avec WHSelfinvest. Pour obtenir une aide sur les autres fonctions de ProRealTime, veuillez consulter
WHS ProRealTime édition 2008 1.52 Ce tutoriel est dédié aux fonctions de passage d'ordres sur ProRealTime avec WHSelfinvest. Pour obtenir une aide sur les autres fonctions de ProRealTime, veuillez consulter
Bac Blanc Terminale ES - Février 2011 Épreuve de Mathématiques (durée 3 heures)
 Bac Blanc Terminale ES - Février 2011 Épreuve de Mathématiques (durée 3 heures) Eercice 1 (5 points) pour les candidats n ayant pas choisi la spécialité MATH Le tableau suivant donne l évolution du chiffre
Bac Blanc Terminale ES - Février 2011 Épreuve de Mathématiques (durée 3 heures) Eercice 1 (5 points) pour les candidats n ayant pas choisi la spécialité MATH Le tableau suivant donne l évolution du chiffre
«Cimetières de France en ligne»
 AIDE UTILISATEURS Logiciel de gestion de cimetière sur internet «Cimetières de France en ligne» INFORMATIONS ET MISES A JOUR DU DOCUMENT : www.cimetieres-de-france.fr ASSISTANCE TECHNIQUE - HOTLINE : 03.80.50.81.95
AIDE UTILISATEURS Logiciel de gestion de cimetière sur internet «Cimetières de France en ligne» INFORMATIONS ET MISES A JOUR DU DOCUMENT : www.cimetieres-de-france.fr ASSISTANCE TECHNIQUE - HOTLINE : 03.80.50.81.95
Présentation du tableau blanc interactif Interwrite
 Présentation du tableau blanc interactif Interwrite Joël Leporcq CDDP des Ardennes Le logiciel Interwrite propose 3 modes de fonctionnement : Interactif (ou «mode leçon») En mode souris, permet de travailler
Présentation du tableau blanc interactif Interwrite Joël Leporcq CDDP des Ardennes Le logiciel Interwrite propose 3 modes de fonctionnement : Interactif (ou «mode leçon») En mode souris, permet de travailler
Utilisation du logiciel GALAAD
 1 Sommaire: Présentation du logiciel GALAAD 1. Démarrer le programme........ 2. Présentation de l écran du logiciel....... Les barres d'outils, sauvegarder... 3. Créer un nouveau fichier........ 4. Préparer
1 Sommaire: Présentation du logiciel GALAAD 1. Démarrer le programme........ 2. Présentation de l écran du logiciel....... Les barres d'outils, sauvegarder... 3. Créer un nouveau fichier........ 4. Préparer
Exo7. Calculs de déterminants. Fiche corrigée par Arnaud Bodin. Exercice 1 Calculer les déterminants des matrices suivantes : Exercice 2.
 Eo7 Calculs de déterminants Fiche corrigée par Arnaud Bodin Eercice Calculer les déterminants des matrices suivantes : Correction Vidéo ( ) 0 6 7 3 4 5 8 4 5 6 0 3 4 5 5 6 7 0 3 5 4 3 0 3 0 0 3 0 0 0 3
Eo7 Calculs de déterminants Fiche corrigée par Arnaud Bodin Eercice Calculer les déterminants des matrices suivantes : Correction Vidéo ( ) 0 6 7 3 4 5 8 4 5 6 0 3 4 5 5 6 7 0 3 5 4 3 0 3 0 0 3 0 0 0 3
Modes Opératoires WinTrans Mai 13 ~ 1 ~
 Modes Opératoires WinTrans Mai 13 ~ 1 ~ Table des matières Facturation... 2 Tri Filtre... 2 Procédures facturation... 3 Transfert Compta... 8 Création d un profil utilisateur... Erreur! Signet non défini.
Modes Opératoires WinTrans Mai 13 ~ 1 ~ Table des matières Facturation... 2 Tri Filtre... 2 Procédures facturation... 3 Transfert Compta... 8 Création d un profil utilisateur... Erreur! Signet non défini.
Introduction au maillage pour le calcul scientifique
 Introduction au maillage pour le calcul scientifique CEA DAM Île-de-France, Bruyères-le-Châtel franck.ledoux@cea.fr Présentation adaptée du tutorial de Steve Owen, Sandia National Laboratories, Albuquerque,
Introduction au maillage pour le calcul scientifique CEA DAM Île-de-France, Bruyères-le-Châtel franck.ledoux@cea.fr Présentation adaptée du tutorial de Steve Owen, Sandia National Laboratories, Albuquerque,
SFEA. Ce document peut être imprimé au format livret. Guide utilisateurs du site "Se Former en Alsace"
 SFEA Ce document peut être imprimé au format livret Guide utilisateurs du site "Se Former en Alsace" Version 1.2-28/11/2012 SOMMAIRE 1 INTRODUCTION... 9 2 FONCTIONNALITES...10 3 CONNEXION A L APPLICATION...11
SFEA Ce document peut être imprimé au format livret Guide utilisateurs du site "Se Former en Alsace" Version 1.2-28/11/2012 SOMMAIRE 1 INTRODUCTION... 9 2 FONCTIONNALITES...10 3 CONNEXION A L APPLICATION...11
Guide d utilisation du ipad
 Guide d utilisation du ipad IMPORTANT AVANT MÊME D UTILISER LE IPAD Bien vous familiariser avec l emplacement des boutons «Marche-Veille» et «Accueil» sur l ipad. Vous familiariser avec la gestuelle ipad.
Guide d utilisation du ipad IMPORTANT AVANT MÊME D UTILISER LE IPAD Bien vous familiariser avec l emplacement des boutons «Marche-Veille» et «Accueil» sur l ipad. Vous familiariser avec la gestuelle ipad.
C.F.A.O. : Conception et Fabrication Assistées par Ordinateur.
 C.F.A.O. : Conception et Fabrication Assistées par Ordinateur. La CFAO réunit dans une même démarche informatique les actions de conception et de fabrication d un objet. La technique utilisée permet à
C.F.A.O. : Conception et Fabrication Assistées par Ordinateur. La CFAO réunit dans une même démarche informatique les actions de conception et de fabrication d un objet. La technique utilisée permet à
Manuel d utilisation 26 juin 2011. 1 Tâche à effectuer : écrire un algorithme 2
 éducalgo Manuel d utilisation 26 juin 2011 Table des matières 1 Tâche à effectuer : écrire un algorithme 2 2 Comment écrire un algorithme? 3 2.1 Avec quoi écrit-on? Avec les boutons d écriture........
éducalgo Manuel d utilisation 26 juin 2011 Table des matières 1 Tâche à effectuer : écrire un algorithme 2 2 Comment écrire un algorithme? 3 2.1 Avec quoi écrit-on? Avec les boutons d écriture........
Baccalauréat L spécialité, Métropole et Réunion, 19 juin 2009 Corrigé.
 Baccalauréat L spécialité, Métropole et Réunion, 19 juin 2009 Corrigé. L usage d une calculatrice est autorisé Durée : 3heures Deux annexes sont à rendre avec la copie. Exercice 1 5 points 1_ Soit f la
Baccalauréat L spécialité, Métropole et Réunion, 19 juin 2009 Corrigé. L usage d une calculatrice est autorisé Durée : 3heures Deux annexes sont à rendre avec la copie. Exercice 1 5 points 1_ Soit f la
Volet de visualisation
 Mode emploi pour ajouter une adresse email (compte de messagerie) et envoyer un message avec Windows Live Mail Dans ce mode d emploi nous allons ajouter une adresse email (compte de messagerie) et aussi
Mode emploi pour ajouter une adresse email (compte de messagerie) et envoyer un message avec Windows Live Mail Dans ce mode d emploi nous allons ajouter une adresse email (compte de messagerie) et aussi
Centre de formation: Collège IBN BASSAM - TEMARA. Ce cours est proposé par le professeur d informatique:
 Centre de formation: Collège IBN BASSAM - TEMARA Ce cours est proposé par le professeur d informatique: ABDALLAH RAKKANE Chapitre Page Initiation au système d exploitation: Windows. 2 Initiation au Traitement
Centre de formation: Collège IBN BASSAM - TEMARA Ce cours est proposé par le professeur d informatique: ABDALLAH RAKKANE Chapitre Page Initiation au système d exploitation: Windows. 2 Initiation au Traitement
Sommaire de la séquence 12
 Sommaire de la séquence 12 Séance 1................................................................................................... 367 Je redécouvre le parallélépipède rectangle..........................................................
Sommaire de la séquence 12 Séance 1................................................................................................... 367 Je redécouvre le parallélépipède rectangle..........................................................
À propos de Kobo Desktop... 4. Télécharger et installer Kobo Desktop... 6
 Kobo Desktop Manuel d utilisation Table des matières À propos de Kobo Desktop... 4 Télécharger et installer Kobo Desktop... 6 Installer Kobo Desktop pour Windows... 6 Installer Kobo Desktop pour Mac...
Kobo Desktop Manuel d utilisation Table des matières À propos de Kobo Desktop... 4 Télécharger et installer Kobo Desktop... 6 Installer Kobo Desktop pour Windows... 6 Installer Kobo Desktop pour Mac...
Bien travailler sur plusieurs écrans
 Bien travailler sur plusieurs écrans Pour améliorer votre confort sur votre ordinateur et travailler plus efficacement, vous pouvez lui ajouter un second voire un troisième écran. En étendant la surface
Bien travailler sur plusieurs écrans Pour améliorer votre confort sur votre ordinateur et travailler plus efficacement, vous pouvez lui ajouter un second voire un troisième écran. En étendant la surface
1 Presentation du bandeau. 2 Principe de création d un projet : C2 industrialisation Apprendre Gantt project Ver 2.6 planifier
 1 Presentation du bandeau Créer une tâche Supprimer une tâche Affiche les propriétés d une tâche Onglet Gantt ou Ressources Calendrier Liste des tâches (ID ; Nom ; Date début et Date de Fin) 2 Principe
1 Presentation du bandeau Créer une tâche Supprimer une tâche Affiche les propriétés d une tâche Onglet Gantt ou Ressources Calendrier Liste des tâches (ID ; Nom ; Date début et Date de Fin) 2 Principe
AGASC / BUREAU INFORMATION JEUNESSE 06700 Saint Laurent du Var Tel : 04.93.07.00.66 bij@agasc.fr www.agasc.fr. Word: Les tableaux.
 Word: Les tableaux Introduction 6 ième partie Il est préférable par moments de présenter de l'information sous forme de tableau. Les instructions qui suivent démontrent comment créer un tableau et comment
Word: Les tableaux Introduction 6 ième partie Il est préférable par moments de présenter de l'information sous forme de tableau. Les instructions qui suivent démontrent comment créer un tableau et comment
Initiation au dessin Bitmap
 Sébastien Stasse Initiation au dessin Bitmap Guide d apprentissage et notions de base 2e édition Nom : Classe : Produit par l École Alex Manoogian AW version 6 Initiation au dessin bitmap Initiation au
Sébastien Stasse Initiation au dessin Bitmap Guide d apprentissage et notions de base 2e édition Nom : Classe : Produit par l École Alex Manoogian AW version 6 Initiation au dessin bitmap Initiation au
Réaliser un PUBLIPOSTAGE
 Réaliser un PUBLIPOSTAGE avec le traitement de texte Writer ( OpenOffice ou LibreOffice ) Guide et captures d'écran réalisés avec la version 3.2 d'openoffice. Janvier 2011 - Jean-Claude EYRAUD Création
Réaliser un PUBLIPOSTAGE avec le traitement de texte Writer ( OpenOffice ou LibreOffice ) Guide et captures d'écran réalisés avec la version 3.2 d'openoffice. Janvier 2011 - Jean-Claude EYRAUD Création
ARCHIVES DEPARTEMENTALES DE L'EURE ALEXANDRIE 7-2013 -
 ARCHIVES DEPARTEMENTALES DE L'EURE ALEXANDRIE 7 BIBLIOTHEQUES DES ARCHIVES PORTAIL D'ACCES AU CATALOGUE - 03 - SOMMAIRE SOMMAIRE ICONES 3 MODE CONSULTATION 4 NOUVEAUTES DU MOIS 4 MENU CONSULTATION 4 SELECTIONS
ARCHIVES DEPARTEMENTALES DE L'EURE ALEXANDRIE 7 BIBLIOTHEQUES DES ARCHIVES PORTAIL D'ACCES AU CATALOGUE - 03 - SOMMAIRE SOMMAIRE ICONES 3 MODE CONSULTATION 4 NOUVEAUTES DU MOIS 4 MENU CONSULTATION 4 SELECTIONS
Table des matières : 16 ASTUCES OUTLOOK
 Table des matières : 16 ASTUCES OUTLOOK Accéder rapidement à votre boîte de réception Ajouter directement les caractéristiques dans le carnet d'adresses Classez vos emails par couleurs Créez des Post-It
Table des matières : 16 ASTUCES OUTLOOK Accéder rapidement à votre boîte de réception Ajouter directement les caractéristiques dans le carnet d'adresses Classez vos emails par couleurs Créez des Post-It
TP01: Installation de Windows Server 2012
 TP0: Installation de Windows Server 202 Rappel : nous utiliserons le terme «WS202» pour désigner Windows Server 202et le terme «VM» pour Machine Virtuelle. - Installation d une VM Windows Server 202 de
TP0: Installation de Windows Server 202 Rappel : nous utiliserons le terme «WS202» pour désigner Windows Server 202et le terme «VM» pour Machine Virtuelle. - Installation d une VM Windows Server 202 de
31. OOo Draw Réglages propres à Draw
 31. OOo Draw Réglages propres à Draw Thèmes de l'exercice Effectuer les réglages de bases spécifiques à OOo Draw. Tâches à effectuer Indications 1 Lancement de OOo Draw On démarre OOo Draw avec Démarrer
31. OOo Draw Réglages propres à Draw Thèmes de l'exercice Effectuer les réglages de bases spécifiques à OOo Draw. Tâches à effectuer Indications 1 Lancement de OOo Draw On démarre OOo Draw avec Démarrer
Interface PC Vivago Ultra. Pro. Guide d'utilisation
 Interface PC Vivago Ultra Pro Guide d'utilisation Version 1.03 Configuration de l'interface PC Vivago Ultra Configuration requise Avant d'installer Vivago Ultra sur votre ordinateur assurez-vous que celui-ci
Interface PC Vivago Ultra Pro Guide d'utilisation Version 1.03 Configuration de l'interface PC Vivago Ultra Configuration requise Avant d'installer Vivago Ultra sur votre ordinateur assurez-vous que celui-ci
MEDIAplus elearning. version 6.6
 MEDIAplus elearning version 6.6 L'interface d administration MEDIAplus Sommaire 1. L'interface d administration MEDIAplus... 5 2. Principes de l administration MEDIAplus... 8 2.1. Organisations et administrateurs...
MEDIAplus elearning version 6.6 L'interface d administration MEDIAplus Sommaire 1. L'interface d administration MEDIAplus... 5 2. Principes de l administration MEDIAplus... 8 2.1. Organisations et administrateurs...
COURS BARDON - EXCEL 2010
 COURS BARDON - EXCEL 2010 Sommaire EXCEL 2010 - INTRODUCTION 3 FONDAMENTAUX OFFICE 2010 3 EXCEL 3 1. L ECRAN 3 2. BARRE D ETAT : CALCULS ET MODES D AFFICHAGE 7 3. PARAMETRAGE DU LOGICIEL 7 Chapitre 1 GESTION
COURS BARDON - EXCEL 2010 Sommaire EXCEL 2010 - INTRODUCTION 3 FONDAMENTAUX OFFICE 2010 3 EXCEL 3 1. L ECRAN 3 2. BARRE D ETAT : CALCULS ET MODES D AFFICHAGE 7 3. PARAMETRAGE DU LOGICIEL 7 Chapitre 1 GESTION
LA COMPTABILITÉ ENGAGEMENT
 Finances LA COMPTABILITÉ ENGAGEMENT Objectif : établir un bon de commande par le logiciel Civil finances Personnel concerné : Personnes chargées de faire les bons de commande. I. Rappel des règles juridiques
Finances LA COMPTABILITÉ ENGAGEMENT Objectif : établir un bon de commande par le logiciel Civil finances Personnel concerné : Personnes chargées de faire les bons de commande. I. Rappel des règles juridiques
REPUBLIQUE ALGERIENNE DEMOCRATIQUE ET POPULAIRE MINISTERE DE LA FORMATION PROFESSIONNELLE. Microsoft. Excel XP
 IFP Birkhadem Alger Rue des trois frères Djillali 1 REPUBLIQUE ALGERIENNE DEMOCRATIQUE ET POPULAIRE MINISTERE DE LA FORMATION PROFESSIONNELLE INSTITUT DE LA FORMATION PROFESSIONNELLE DE BIRKHADEM Initiation
IFP Birkhadem Alger Rue des trois frères Djillali 1 REPUBLIQUE ALGERIENNE DEMOCRATIQUE ET POPULAIRE MINISTERE DE LA FORMATION PROFESSIONNELLE INSTITUT DE LA FORMATION PROFESSIONNELLE DE BIRKHADEM Initiation
Créer un diaporama avec Open Office. Sommaire
 Créer un diaporama avec Open Office I. Création I.1. Paramétrer le diaporama I.2. Valider et enregistrer l'album II. Le traitement des données II.1. Saisir les données II.2. Agir sur les pages III. Améliorez
Créer un diaporama avec Open Office I. Création I.1. Paramétrer le diaporama I.2. Valider et enregistrer l'album II. Le traitement des données II.1. Saisir les données II.2. Agir sur les pages III. Améliorez
Prise en main du logiciel Smart BOARD
 Prise en main du logiciel Smart BOARD 1. Introduction : Le logiciel Smart BOARD est utilisable avec les tableaux blancs interactifs de la gamme SMART. Toutefois, il n'est pas nécessaire d'avoir un tbi
Prise en main du logiciel Smart BOARD 1. Introduction : Le logiciel Smart BOARD est utilisable avec les tableaux blancs interactifs de la gamme SMART. Toutefois, il n'est pas nécessaire d'avoir un tbi
TBI et mathématique. Pour vous soutenir dans votre enseignement des mathématiques. Les outils du logiciel Notebook. les ressources internet
 TBI et mathématique Pour vous soutenir dans votre enseignement des mathématiques Dessin tiré du site www.recitus.qc.ca Les outils du logiciel Notebook et les ressources internet Document préparé par France
TBI et mathématique Pour vous soutenir dans votre enseignement des mathématiques Dessin tiré du site www.recitus.qc.ca Les outils du logiciel Notebook et les ressources internet Document préparé par France
Affichage de la date d'exigibilité sur les documents FAQ INV 011
 ADAPTATION DANS LA FACTURATION BOB50 Affichage de la date d'exigibilité sur les documents FAQ INV 011 Comment afficher la date d'exigibilité de la TVA sur les factures et notes de crédit? Lorsque le Report
ADAPTATION DANS LA FACTURATION BOB50 Affichage de la date d'exigibilité sur les documents FAQ INV 011 Comment afficher la date d'exigibilité de la TVA sur les factures et notes de crédit? Lorsque le Report
