Séquence MS-Word 2010 La numérotation hiérarchique appliquée aux styles "Titre"
|
|
|
- Mathieu Thierry Marion
- il y a 6 ans
- Total affichages :
Transcription
![Séqun MS-Wor 2010 L numérottion iérriqu ppliqué ux styls "Titr" Convntion 'éritur O[Auil] = Cliquz sur Onlt [Auil] G[Poli] = ns l Group 'outils [Poli] G[Poli ] = Bouton 'option u Group [Poli] 1.](/docs-images/66/55536647/images/1-0.jpg "Ojtis tt mnipultion. L'ojti prinipl s mnipultions proposés i-près st 'joutr un numérottion iérriqu ux prrps typ \"Titr\" 'un lon oumnt t n prtnt zéro.. Ouvrz l oumnt \"ExStyl_8_(Bs).ox\". Rm.")
1 Séqun MS-Wor 2010 L numérottion iérriqu ppliqué ux styls "Titr" Convntion 'éritur O[Auil] = Cliquz sur Onlt [Auil] G[Poli] = ns l Group 'outils [Poli] G[Poli ] = Bouton 'option u Group [Poli] 1. Ojtis tt mnipultion. L'ojti prinipl s mnipultions proposés i-près st 'joutr un numérottion iérriqu ux prrps typ "Titr" 'un lon oumnt t n prtnt zéro.. Ouvrz l oumnt "ExStyl_8_(Bs).ox". Rm.: n vous oupz ps l'xtnsion.ox r ll s mt tout sul.. C'st un lon oumnt plusiurs ps utilisnt s "Titrs" uxquls nous llons joutr un numérottion typ iérriqu (x.: t).. Ls iérnts nristrmnts intrméiirs qu vous rélisrz ns l éroulmnt tt séqun vous prmttront 'vnr étp pr étp t 'intrrompr tmporirmnt l suit s opértions ou rommnr à prtir 'un étp étrminé. 2. Déouvrt l'outil "List à plusiurs nivux". Sns rmr l oumnt ouvrt préémmnt ("ExStyl_8_(Bs).ox"), ouvrz n plus l oumnt "ExStyl_8_(Num).ox". C oumnt st l résultt touts ls mnipultions proposés i-près: il ontint s "Titrs" numérotés iérriqumnt.. Cliquz sur un titr qulonqu (pr x.: "1. Introution") Dns l roup "Prrp" ( l'onlt "Auil"), osrvz qu l'outil "Numérottion" 1 st ti ontrirmnt à l'outils "List à plusiurs nivux" 2.. Cliquz sur l'outil "List à plusiurs nivux" 2. Un mnu rpiqu pprît onstitué trois zons (voir poto érn p suivnt): List tull C'st l styl numérottion ppliqué u prrp tullmnt "montré" pr l ursur txt (liqué u point 2..). Biliotèqu lists L iliotèqu lists ontint ls "lists pr éut" isponils ou qu'un utilistur rn isponils n nristrnt un list à lui I.E.P.S.F.W.B. Fléron Cêné 1 N. Lst - Novmr 2012
2 5 L iliotèqu lists st mémorisé ns l iir : "Wor.ListGl.t" situé ns l ossir : "C:\Usrs\utilistur\AppDt\Romin\Mirosot ". L'option "Déinir un nouvll list à plusiurs nivux " prmt à trm 'joutr un list prsonnll ns l "Biliotèqu lists". Pr moyn, l list réé rst isponil 'un nouvu oumnt à l'utr. Styls list Dns tt zon s trouvnt ls styls list qu l'utilistur ré lui-mêm. L'option "Déinir un nouvu styl list " 7 prmt rér un nouvu styl (totlmnt orinté list t numérottion). A trm, styl st stoké ns l oumnt-mêm (ox) ou ns son moèl oumnt (otx). Pr moyn, l list réé n'st isponil qu si on ré un nouvu oumnt u éprt u oumnt qui l ontint. D'où l'intérêt rér un moèl oumnt L styl numérottion typ TFE l iliotèqu st "étuux" L styl numérottion simpl (sns notion "Cpitr") s titrs 'un TFE (Trvil Fin 'Étus) oit êtr smll à un styl isponil ns l "Biliotèqu lists". Cpnnt, il mnqu un point à roit u numéro l plus à roit! Styl inomplt isponil ns l "Biliotèqu lists" ( i-ssus) Styl prsonnl "omplt" réé pr l'utilistur vi un "Styl list" ( 5 i-ssus) Comm il st impossil moiir un styl l "Biliotèqu list", il ut rér un numérottion prsonnll. Dux métos sont possils: 1) pr l'option "Déinir un nouvll list à plusiurs nivux " ( i-ssus); (=> qui sr plutôt jouté à Wor) 2) pr l'option "Déinir un nouvu styl list " ( 7 i-ssus). (=> qui sr nristré ns l iir u oumnt ou son moèl) C'st tt uxièm méto ("Déinir un nouvu styl list ") qui sr érit i-près. I.E.P.S.F.W.B. Fléron Cêné 2 N. Lst - Novmr 2012
![. Rmplz l nom pr éut "Styl1" 5 pr un nom plus équt pr xmpl: "ListTFE". 5. Cliquz sur l outon [Formt ].](/docs-images/66/55536647/images/3-4.jpg ". Dns l ptit mnu éroulnt qui st ppru, 8 liquz sur \"Numérottion \" 7. 7 L nêtr \"Moiir l list à plusiurs nivux\" pprit 8.")
3 . Prmièr étp - Crér un styl numérottion. Cliquz sur l'outil "List à plusiurs nivux" 1. L list rpiqu s styls numérottion s'ouvr Cliquz sur "Déinir un nouvu styl list ". L nêtr "Déinir un nouvu styl list" s'ouvr.. Rmplz l nom pr éut "Styl1" 5 pr un nom plus équt pr xmpl: "ListTFE". 5. Cliquz sur l outon [Formt ].. Dns l ptit mnu éroulnt qui st ppru, 8 liquz sur "Numérottion " 7. 7 L nêtr "Moiir l list à plusiurs nivux" pprit 8.. Cliquz (évntullmnt) sur [Plus >>] 9 pour voir touts ls options tt nêtr. 9 I.E.P.S.F.W.B. Fléron Cêné N. Lst - Novmr 2012
4 D nouvux élémnts sont pprus sur l nêtr. Ell s'st 'illurs rni n lrur.. Cliquz sur nivu 1 Ez l ontnu "Mis n orm l Coisissz "1, 2,..." ns "Styl numérottion pour nivu" numérottion :". Vériiz "Alinmnt :" à 0 m Ajustz l "Rtrit u txt à :" sur 1 m Coisissz "Titr 1" pour l "Styl à ppliqur à nivu :". Au prmir nivu, l'outil "Inlur l numéro nivu à prtir :" n'st ps ti ; 'st norml. NE PAS CLIQUER SUR [OK]. En t, ls utrs nivux s prmètrnt imméitmnt ns l mêm nêtr. Voyz l suit! Si vous vz it [OK], vous pouvz y rvnir: [Formt]-[Numérottion ] ( t 7 i-ssus). I.E.P.S.F.W.B. Fléron Cêné N. Lst - Novmr 2012
5 . Cliquz sur nivu 2. Ez l ontnu "Mis n orm l Coisissz "Nivu 1" ns "Inlur l numéro nivu à prtir :". Coisissz "1, 2,..." ns "Styl numérottion pour nivu :". Vériiz "Alinmnt :" à 0 m Ajustz l "Rtrit u txt à :" sur 1,5 m Coisissz "Titr 2" pour l "Styl à ppliqur à nivu :". i. Cliquz sur nivu. Ez l ontnu "Mis n orm l Coisissz "Nivu 1" ns "Inlur l numéro nivu à prtir :". Coisissz "Nivu 2" ns "Inlur l numéro nivu à prtir :". Coisissz "1, 2,..." ns "Styl numérottion pour nivu :". Vériiz "Alinmnt :" à 0 m I.E.P.S.F.W.B. Fléron Cêné 5 N. Lst - Novmr 2012
![Vériiz "Alinmnt :" à 0 m Ajustz l "Rtrit u txt à :" sur 2 m Coisissz "Titr " pour l "Styl à ppliqur à nivu :". Si vous n vouliz éinir qu ls qutr prmirs nivux, vous vz ini ; vous pouvz liqur sur [OK].](/docs-images/66/55536647/images/6-1.jpg "Dns s ussi, votr styl list st ussi trminé, liquz sur [OK] ns l nêtr \"Déinir un nouvu styl list \" (.i-ssus). Normlmnt l nouvll numérottion sr 'oi ppliqué à tous ls styls \"Titr\".")
6 Ajustz l "Rtrit u txt à :" sur 2 m Coisissz "Titr " pour l "Styl à ppliqur à nivu :". Cliquz sur nivu. Ez l ontnu "Mis n orm l Coisissz "Nivu 1" ns "Inlur l numéro nivu à prtir :". Coisissz "Nivu 2" ns "Inlur l numéro nivu à prtir :". Coisissz "Nivu " ns "Inlur l numéro nivu à prtir :". Coisissz "1, 2,..." ns "Styl numérottion pour nivu :". Vériiz "Alinmnt :" à 0 m Ajustz l "Rtrit u txt à :" sur 2 m Coisissz "Titr " pour l "Styl à ppliqur à nivu :". Si vous n vouliz éinir qu ls qutr prmirs nivux, vous vz ini ; vous pouvz liqur sur [OK]. Dns s ussi, votr styl list st ussi trminé, liquz sur [OK] ns l nêtr "Déinir un nouvu styl list " (.i-ssus). Normlmnt l nouvll numérottion sr 'oi ppliqué à tous ls styls "Titr". Si n'st ps l s, il ur pssr pr l'étp 5 i-près. Cl rriv qun on ipot un pu trop pnnt l onstrution l list. I.E.P.S.F.W.B. Fléron Cêné N. Lst - Novmr 2012
![5. Duxièm étp Appliqur l nouvll numérottion. Vériiz qu l list rpiqu l'outil "List à plusiurs nivux" 1 s'st in étoé votr nouvll numérottion 2 ns l zon "Styls list". 1. Ouvrz l volt s styls Cliquz sur G[Styl ].](/docs-images/66/55536647/images/7-3.jpg "L volt \"Styls\" s'ouvr.. Plz l souris à utur u styl \"Titr 1\", liquz-roit (PAS CLIC GAUCHE!!!) Si vous vz liqué (sur l outon u), vous vz imposé l styl \"Titr 1\" à un prrp qulonqu.")
7 5. Duxièm étp Appliqur l nouvll numérottion. Vériiz qu l list rpiqu l'outil "List à plusiurs nivux" 1 s'st in étoé votr nouvll numérottion 2 ns l zon "Styls list". 1. Ouvrz l volt s styls Cliquz sur G[Styl ]. L volt "Styls" s'ouvr.. Plz l souris à utur u styl "Titr 1", liquz-roit (PAS CLIC GAUCHE!!!) Si vous vz liqué (sur l outon u), vous vz imposé l styl "Titr 1" à un prrp qulonqu. Il suir l orrir plus tr Dns l mnu ontxtul qui s'st ouvrt, liquz sur "Séltionnr tout : (Auun onné)". Wor i "(Auun onné)" qun il n' ps nor omptilisé l nomr 'ourrns (sinon il i l nomr).. Cliquz sur l'outil "List à plusiurs nivux" ( 1 i-ssus) Cliquz sur l loo votr nouvll numérottion ( 2 i-ssus) ns l zon "Styls list".. Rommnz ls opértions, t pour ls styls "Titr 2" t "Titr " (t "Titr " évntullmnt).. Enristrr ls moiitions Pssr à l suit (Insrtion 'un tl s mtièrs). Vi l ommn [Fiir]-[Enristrr sous ], nristrz sous l nom "ExStyl_8_(Num).ox".. Grz iir "ExStyl_8_(Num).ox" ouvrt t ouvrz l oumnt "ExStyl_8_(InsrtionTM).ox" (TM=Tl s Mtièrs). o o o o o o o o o o o o I.E.P.S.F.W.B. Fléron Cêné 7 N. Lst - Novmr 2012
NOTICE DE MONTAGE VERSION 72
L â pour port oulnt motl NOTIE E MONTGE VERSION â pour port oulnt motl NOMENLTURE: â, rl t qunllr m l Montnt vrtux ntérur Entrto ( u) Fullr (0 u) l n polytyrèn ( u) Montnt vrtl potérur Smll Prt or upérur
Uniformiser la mise en forme du document. Accélère les mises à jour. Permets de générer des tables de matières automatiquement.
Les styles Table des matières Les styles... 1 1. Tutoriels... 1 2. Pourquoi utiliser les styles?... 1 3. Qu'est-ce qu'un style?... 1 4. Utiliser les styles existants... 2 Afficher les styles... 2 Appliquer
Chapitre 6: Graphes eulériens et hamiltoniens
CHAPITRE 6 GRAPHES EULERIENS ET HAMILTONIENS 36 Cpitr 6: Grps ulérins t miltonins 6.1 Introution t ls prmièrs éinitions Introution L t nissn l téori s rps put êtr ixé à l'nné 1736. L'istoir ront qu ls
Matériau pour greffe MIS Corporation. Al Rights Reserved.
Matériau pour grff MIS Corporation. All Rights Rsrvd. : nal édicaux, ISO 9001 : 2008 atio itifs m rn pos méd int i dis c a u x 9 positifs 3/42 té ls s dis /CE ur r l E. po ou u x U SA t s t appr o p a
Réseau des bibliothèques du Pays de Pamiers Guide du Numérique
Réau d bibliothèqu du Pay d Pamir Guid du Numériqu Sit Intrnt du réau d lctur http://www.pamir.raubibli.fr C qu vou pouvz fair dpui notr it Intrnt : EXPLORER LE CATALOGUE : Plu d 80 000 documnt ont à votr
Avec PICASA. Partager ses photos. Avant de commencer. Picasa sur son ordinateur. Premier démarrage
Avant de commencer Picasa est avant un logiciel que l'on peut installer sur son ordinateur et qui permet de transférer ses photos dans un espace pouvant être partagé sur Internet. Picasa sur son ordinateur.
Répertorier vos mots de passe avec Passbox : 1) Télécharger le fichier d'installation :
Amicale laïque de Poisat 18-19 février 2013 Répertorier vos mots de passe avec Passbox : 1) Télécharger le fichier d'installation : a) Taper "Passbox" dans le moteur de recherche de votre navigateur. b)
Chapitre 3: TESTS DE SPECIFICATION
Chapitre 3: TESTS DE SPECIFICATION Rappel d u c h api t r e pr é c é d en t : l i de n t i f i c a t i o n e t l e s t i m a t i o n de s y s t è m e s d é q u a t i o n s s i m u lt a n é e s r e p o
STI2D Logique binaire SIN. L' Algèbre de BOOLE
L' Algère de BOOLE L'lgère de Boole est l prtie des mthémtiques, de l logique et de l'électronique qui s'intéresse ux opértions et ux fonctions sur les vriles logiques. Le nom provient de George Boole.
Impôts 2012. PLUS ou moins-values
Impôt 2012 PLUS ou moin-values SUR VALEURS MOBILIÈRES ET DROITS SOCIAUX V v ti t à d f co o OP m à l Et L no di (o 20 o C c tit po Po c c or o o ou c l ou d 2 < Vou avz réalié d cion d valur mobilièr t
Comment se connecter au VPN ECE sous vista
Comment se connecter au VPN ECE sous vista Pour commencer, aller dans le Centre de Réseau et partage (qui est aussi accessible via le panneau de configuration onglet internet et réseau), en faisant clic
Observatoires du Bruit. Import des données du Classement sonore : Utilisation de l'outil VSMAP
Observatoires du Bruit Import des données du Classement sonore : Utilisation de l'outil VSMAP SOMMAIRE SOMMAIRE... 2 1. INTÉRÊT DE L'UTILISATION DE L'OUTIL VSMAP POUR LA MISE EN FORME DES DONNÉES DE CLASSEMENT
Guide de correction TD 6
Guid d corrction TD 6 JL Monin nov 2004 Choix du point d polarisation 1- On décrit un montag mttur commun à résistanc d mttur découplé, c st à dir avc un condnsatur n parallèl sur R. La condition d un
Techniques d analyse de circuits
Chpitre 3 Tehniques d nlyse de iruits Ce hpitre présente différentes méthodes d nlyse de iruits. Ces méthodes permettent de simplifier l nlyse de iruits ontennt plusieurs éléments. Bien qu on peut résoudre
Exporter des écritures. Importer des écritures. Depuis EBP Comptabilité. www.ebp.com
Coala Comptabilité (Ecritures) Depuis EBP Comptabilité Accédez à l option du Sélectionnez Transmettre des données à votre expert comptable (ou à votre client). Cochez la case Dossier complet si vous souhaitez
Sciences Industrielles Précision des systèmes asservis Papanicola Robert Lycée Jacques Amyot
Scence Indutrelle Précon de ytème erv Pncol Robert Lycée Jcque Amyot I - PRECISION DES SYSTEMES ASSERVIS A. Poton du roblème 1. Préentton On vu que le rôle d un ytème erv et de fre uvre à l orte (t) une
TABLE DES MATIERES...
Comment désinstaller un produit concurrent lorsque le script n'est pas inclus dans le paquet Table des matières d'installation du client Kaspersky TABLE DES MATIERES... 1 1. PROJET... ERREUR! SIGNET NON
a g c d n d e s e s m b
PPrrooppoossiittiioo 22001111JJPP 22770055 000011 uu 0088 fféévvrriirr 22001111 VVlliiiittéé jjuussqquu uu 3300//0044//22001111 tim c ir tv é p g c h u i rè s G A Z iv lu s IC.G R é c lo y m ip s 9 r7
UNE AVENTVRE DE AGILE & CMMI POTION MAGIQUE OU GRAND FOSSÉ? AGILE TOVLOVSE 2011 I.VI VERSION
UN AVNTVR D AGIL & CMMI POTION MAGIQU OU GRAND FOÉ? AGIL TOVLOV 2011 VRION I.VI @YAINZ AKARIA HT T P: / / W WW.MA RTVIW.F HT T P: / / W R WW.KIND OFMAG K.COM OT @ PAB L OP R N W.FR MARTVI. W W W / :/ P
Le guide du parraina
AGREMENT DU g L guid du parraina nsillr co t r g ra u co n r, Partag rs ls mini-ntrprnu alsac.ntrprndr-pour-apprndr.fr Crér nsmbl Ls 7 étaps d création d la Mini Entrpris-EPA La Mini Entrpris-EPA st un
Corrigé du baccalauréat S Pondichéry 13 avril 2011
Corrigé du baccalauréat S Pondichéry avril EXERCICE Commun à tous ls candidats Parti I points. L ax ds ordonnés st asymptot à C au voisinag d ; la fonction étant décroissant sur ] ; + [, la limit quand
EXCEL 2007. Les tableaux croisés dynamiques
EXCEL 2007 Les tableaux croisés dynamiques 1 La Fonction VPM... 3 La Valeur Cible... 4 Les Tableaux Croisés Dynamiques (T.C.D.)... 6 2 Fonction VPM Cette fonction d EXCEL permet de calculer le remboursement
Un exemple d étude de cas
Un exemple d'étude de cas 1 Un exemple d étude de cas INTRODUCTION Le cas de la Boulangerie Lépine ltée nous permet d exposer ici un type d étude de cas. Le processus utilisé est identique à celui qui
Manuel d'utilisation: Gestion commerciale - CRM
Manuel d'utilisation: Gestion commerciale - CRM Partie: Plan de vente Version : 1.1 Structure du document 1 Introduction...2 2 Glossaire...2 3 Plan de vente...3 3.1 Plan de vente...4 3.1.1 Gestion...4
Latitude 49.37 N Longitude 06.13 E Altitude 376 m RÉSUMÉ MENSUEL DU TEMPS DE JANVIER 2014
RÉSUMÉ MENSUEL DU TEMPS DE JANVIER 2014 Valeurs moyennes: Valeur Jour Valeur (en C) (en C) (en C) gazon (en C) 11,4 7 13,9 1975 3,6 0,8 4,9 2007-6,3 1963-3,0 29-17,8 1979-2,8 12-24,6 1985 37,1 50,3 95,5
Télécharger et Installer OpenOffice.org sous Windows
Télécharger et Installer OpenOffice.org sous Windows Version Date Auteur Commentaires 1.00 15/11/2008 Denis Bourdillon Création du document. Mise en forme de texte 1/15 Saison 2008-2009 Table des matières
Vu la loi n 17-99 portant code des assurances prom ulguée par le dahir n 1-02-238 du 25 rejeb 1423 (3 octobre 2002), telle qu'elle a été complétée ;
Arrêté du ministr s financs t la privatisation n 2241-04 du 14 kaada 1425 rlatif à la présntation s opérations d'assurancs (B.O. n 5292 du 17 févrir 2005). Vu la loi n 17-99 portant co s assurancs prom
Publication Assistée par Ordinateur
Présentation OpenOffice Draw est l'outil de dessin vectoriel de la suite bureautique OpenOffice. De fait, Draw permet de réaliser certains documents comparables à ceux de Publisher, le logiciel de P.A.O.
Espace pro. Installation des composants avec Firefox. Pour. Windows XP Vista en 32 et 64 bits Windows 7 en 32 et 64 bits
Espace pro Installation des composants avec Firefox Pour Windows XP Vista en 32 et 64 bits Windows 7 en 32 et 64 bits Version 2.0.3 1 Sommaire 1. Installation du composant de lecture de la carte Vitale
ActoPalm 1.0 b. Logiciel d'aide au relevé d'observation in situ sur Organiseurs PalmOS Compatibles. Alain Kerguelen, mai 2002
ActoPalm 1.0 b Logiciel d'aide au relevé d'observation in situ sur Organiseurs PalmOS Compatibles Alain Kerguelen, mai 2002 ActoPalm permet le relevé d'observations chronologiques par désignation de zones
FICHE 17 : CREER UN SITE WEB
Publisher permet de créer des sites web. FICHE 17 : CREER UN SITE WEB Créez une nouvelle composition et choisissez Site web. Vous avez le choix entre utiliser le générateur rapide de site web, créer un
McAfee Firewall Enterprise Control Center
Guie e émrrge rpie Révision A MAfee Firewll Enterprise Control Center version 5.3.1 Ce guie e émrrge rpie fournit es instrutions générles sur l onfigurtion e MAfee Firewll Enterprise Control Center. 1
PARAMETRER LA MESSAGERIE SOUS THUNDERBIRD
PARAMETRER LA MESSAGERIE SOUS THUNDERBIRD Ref : FP. P763 V 5.0 Résumé Ce document vous indique comment paramétrer votre messagerie sous Thunderbird. Vous pourrez notamment, créer, modifier ou supprimer
Guide pour la réalisation d'un document avec Open Office Writer 2.2
Guide pour la réalisation d'un document avec Open Office Writer 2.2 1- Lancement de l'application : Le Traitement de textes de la Suite OpenOffice peut être lancé : soit depuis le menu «Démarrer / Programmes/OpenOffice2.2/Writer
LES ESCALIERS. Du niveau du rez-de-chaussée à celui de l'étage ou à celui du sous-sol.
LES ESCALIERS I. DÉF I NIT I O N Un escalier est un ouvrage constitué d'une suite de marches et de paliers permettant de passer à pied d'un niveau à un autre. Ses caractéristiques dimensionnelles sont
AGASC / BUREAU INFORMATION JEUNESSE 06700 Saint Laurent du Var - E mail : bij@agasc.fr / Tel : 04.93.07.00.66 CONSIGNE N 1 :
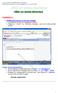CONSIGNE N 1 : Rédiger puis envoyer un nouveau message La fenêtre de la boîte de messagerie s affiche Cliquer sur «Ecrire» ou «Nouveau message» pour ouvrir cette nouvelle fenêtre. Ensuite, suivre cette
Choisir le mode d envoi souhaité. Option 1 : Envoyer un SMS à un nombre réduit de numéros (0 10 )
Ce service permet d effectuer des envois de SMS texte à partir d une source de numéros de GSM (Maroc Telecom, Meditel,INWI ou Etrangers) sous format texte ou sous format Excel. Il est nécessaire au préalable
DE MODIFICATION PROCEDURE ELYXBADGE APPLICATION. PI Électronique Restobadge
PROCEDURE DE MODIFICATION DE LA PROGRAMMATION DES T.V.A APPLICATION ELYXBADGE 1 Introduction Avant toute modification, veuillez procéder aux opérations suivantes : - Effectuer une fin de service - Effectuer
LES REGLEMENTS AVEC SOCIEL.NET DERNIERE MISE A JOUR : le 14 juin 2010
LES REGLEMENTS AVEC SOCIEL.NET DERNIERE MISE A JOUR : le 14 juin 2010 Guillaume Informatique 10 rue Jean-Pierre Blachier 42150 La Ricamarie Tél. : 04 77 36 20 60 - Fax : 04 77 36 20 69 - Email : info@guillaume-informatique.com
Tutoriel : Comment installer une compte email (une adresse email) sur un logiciel de messagerie (ou client messagerie)?
Tutoriel : Comment installer une compte email (une adresse email) sur un logiciel de messagerie (ou client messagerie)? Sur Thunderbird (V.3.0.5) Etape 1 - Introduction Lancez l'application Thunderbird
Styler un document sous OpenOffice 4.0
Mars 2014 Styler un document sous OpenOffice 4.0 Un style est un ensemble de caractéristiques de mise en forme (police, taille, espacement, etc.) qui sert à structurer un document en l organisant de manière
Licence de Biologie, 1ère année. Aide. [Aide 1] Comment utiliser l'explorateur Windows? Comment créer des dossiers?
![Licence de Biologie, 1ère année. Aide. [Aide 1] Comment utiliser l'explorateur Windows? Comment créer des dossiers?](/thumbs/18/825045.jpg "Licence de Biologie, 1ère année. Aide. [Aide 1] Comment utiliser l'explorateur Windows? Comment créer des dossiers?")
Aide [Aide 1] Comment utiliser l'explorateur Windows? Comment créer des dossiers? Au sein d'un ordinateur, les données et les fichiers sont stockés suivant une structure d'arbre appelée arborescence. Pour
Application de Gestion des Notes de Frais sous Lotus Notes via un navigateur avec WorkFlow 1
Gestion des Notes de Frais avec Workflow pour Lotus Notes R5 et R6 Application de type Navigateur CVM sas 8 rue Paul Cézanne 93360 Neuilly-Plaisance - Tél : 33 (0)1.43.67.09.03 - Fax : 33 (0)1 43.67.35.40
Gestion des Factures
Gestion des Factures Sommaire Comment enregistrer une facture client... 3 Sous 2DCaisse... 3 Création d une facture sur ticket validé... 3 Réglé une facture non soldée... 5 Valider un ticket sans règlement...
Créer et modifier un fichier d'importation SAU avec Excel
Créer et modifier un fichier d'importation SAU avec Excel Manuel d'utilisation Date : 26.03.2015 Version: 1.0 Collaborateur /-trice : Urs Matti Statut : en cours d élaboration validé Classification : public
Utiliser CHAMILO pour le travail collaboratif
1/5 TP utiliser CHAMILO pour le travail collaboratif Chamilo 1.8 Utiliser CHAMILO pour le travail collaboratif 1. Qu'est ce que CHAMILO? Chamilo est une plate-forme d apprentissage à distance offrant une
Helpdesk : Traitement d'un incident
Helpdesk : Traitement d'un incident Réalisation Contrôle Approbation Nom Visa Date Informatique IPSL \\admin.intra\data\dossier_permanent_ipsl\exploitation\ Page 1/12 HISTORIQUE DES VERSIONS Version V1.0
Mode Opératoire Ciel Gestion commerciale V 12 et s (2006)
1/6 09/05/2006-18:44:31 Mode Opératoire Ciel Gestion commerciale V 12 et s (2006) C. Terrier Reproduction autorisée pour des formateurs dans un cadre pédagogique et non commercial après autorisation de
CSMA 2013 11e Colloque National en Calcul des Structures 13-17 Mai 2013
Enrichissmnt modal du Slctiv Mass Scaling Sylvain GAVOILLE 1 * CSMA 2013 11 Colloqu National n Calcul ds Structurs 13-17 Mai 2013 1 ESI, sylvain.gavoill@si-group.com * Autur corrspondant Résumé En raison
Guide d installation des licences Solid Edge-NB RB-18-09-2012
Ce document vous guide dans la gestion, l installation et la mise à jour des licences Solid Edge. Contenu Les types de licences...2 Le site GTAC : support.ugs.com...3 Création d un compte GTAC...3 Identifiant
Au préalable, nous nous plaçons dans l espace au sein duquel nous allons créer notre raccourci vers l ENTG.
Disque virtuel (Windows XP) et (MAC OS X) ENTG Disque virtuel (Windows XP) Objectif : Le disque virtuel va vous permettre d accéder à vos documents ENTG sans vous connecter systématiquement à celui-ci.
MO-Call pour les Ordinateurs. Guide de l utilisateur
MO-Call pour les Ordinateurs Guide de l utilisateur Sommaire MO-CALL POUR ORDINATEURS...1 GUIDE DE L UTILISATEUR...1 SOMMAIRE...2 BIENVENUE CHEZ MO-CALL...4 MISE EN ROUTE...5 CONNEXION...5 APPELS...7 COMPOSITION
Comment créer une facture
Comment créer une facture Nous sous-entendons que la «société», les véhicules et chauffeurs aient été créés dans le logiciel. Si ce n est pas le cas, veuillez lire le document «Démarrage rapide TéléTaxi».
Créer un sondage en ligne
Créer un sondage en ligne Par Clément JOATHON Dernière mise à jour : 02/04/2015 Que cela soit pour récolter l'avis des membres d'une association ou encore les idées de vos visiteurs, il est toujours intéressant
Mise à jour d avast! et de vos logiciels Ciel
Mise à jour d avast! et de vos logiciels Ciel Chère Cliente, Cher Client, Suite à une mise à jour de votre anti-virus avast!, celui-ci pourrait bloquer votre logiciel Ciel Paye Ciel Bâtiment ou Ciel Point
Guide de référence de l'installateur et de l'utilisateur
Gui référn l'instlltur t l'utilistur Climtisur systèm VRV IV REYQ8T7Y1B REYQ10T7Y1B REYQ12T7Y1B REYQ14T7Y1B REYQ16T7Y1B REYQ18T7Y1B REYQ20T7Y1B REMQ5T7Y1B Gui référn l'instlltur t l'utilistur Climtisur
Logiciels concernés. Situation. Ciel et le pont comptable. Note conçue et rédigée par Jalons sprl tous droits réservés - 27/06/2007.
Logiciels concernés Ciel Gestion Commerciale Premium, Evolution, et Réseau et Ciel Compta Premium, Evolution et Réseau. Situation Ciel Gescom et Ciel Compta ne sont pas des logiciels intégrés. C'est-à-dire
SAGE Financements Notice de mise à jour via internet
SAGE Financements Notice de mise à jour via internet Version 12.0 Février 2013 Préambule Ce document détaille la procédure de mise à jour du logiciel SAGE Financements version 12.0. Pré-requis Pour installer
nous votre service clients orange.fr > espace client 3970*
nous votr srvi lints orang.fr > spa lint 3970* vous souhaitz édr votr abonnmnt Orang Mobil Bonjour, Vous trouvrz i-joint l formulair d ssion d abonnmnt Orang Mobil à rtournr omplété t par vous-mêm t par
LibreOffice Calc : introduction aux tableaux croisés dynamiques
Fiche logiciel LibreOffice Calc 3.x Tableur Niveau LibreOffice Calc : introduction aux tableaux croisés dynamiques Un tableau croisé dynamique (appelé Pilote de données dans LibreOffice) est un tableau
Mouvement d'une particule chargée dans un champ magnétique indépendant du temps
Moueent d'une patiule hagée dans un hap agnétique indépendant du teps iblio: Pee elat Gaing Magnétise Into expéientale: Dispositif: On obsee une déiation du faseau d'életons losqu'il aie ae une itesse
Comment choisir ou modifier les options de facturation sans papier
Comment choisir ou modifier les options de facturation sans papier Présentation Par défaut, les partenaires et les clients Citrix reçoivent leurs factures au format papier par courrier postal. Il est simple
ECO ECO. Probablement le chauffe-eau solaire le plus évolué du monde. Eco 200 / Eco 250 / Eco 300 / Eco 450 ENERGIE CATALOGUE 13
co 00 / co 0 / co 00 / co 0 NR TOU O Probabement e chauffe-eau soaire e pus évoué du monde isponibe avec des capacités de 00 à 0 itres. Versions avec un ou deu panneau soaires, avec ou sans serpentin suppémentaire.
Bases de données. Table des matières. Introduction. (ReferencePlus.ca)
Bases de données (ReferencePlus.ca) Table des matières Introduction Ouvrir une nouvelle Base de données Ouvrir une Base de données déjà existante Retirer une base de données de la liste des bases dans
SPECIFICATIONS TECHNIQUES : Gestion des Médicaments et des commandes de médicaments
SPECIFICATIONS TECHNIQUES : Gestion des Médicaments et des commandes de médicaments Développement d une application en web/ client lourd en C# permettant la gestion des médicaments et des commandes de
PORTAIL INTERNET DECLARATIF. Configuration du client Mail de MICROSOFT VISTA
PORTAIL INTERNET DECLARATIF Configuration du client Mail de MICROSOFT VISTA Configuration du client messagerie MAIL de MICROSOFT VISTA Ce chapitre fourni les informations nécessaires à la configuration
SOS Info: Traitement de textes. 1. Structurer un document. 2. Enregistrer un document
De plus en plus de documents seront «lus» par des systèmes automatiques. Il est important que les textes soient parfaitement structurés pour qu'un ordinateur puisse repérer les éléments importants. On
ONe Key ID Compte InfoCentre pour les entreprises Compte auprès du ministère de l Environnement (MEO)
Pour avoir accès au Registre environnemental des activités et des secteurs (REAS), vous aurez besoin des éléments suivants : ONe Key ID Compte InfoCentre pour les entreprises Compte auprès du ministère
MICROINFORMATIQUE NOTE D APPLICATION 1 (REV. 2011) ARITHMETIQUE EN ASSEMBLEUR ET EN C
Haute Ecole d Ingénierie et de Gestion Du Canton du Vaud MICROINFORMATIQUE NOTE D APPLICATION 1 (REV. 2011) ARITHMETIQUE EN ASSEMBLEUR ET EN C Programmation en mode simulation 1. DOCUMENTS DE RÉFÉRENCE...
au Point Info Famille
Qustion / Répons au Point Info Famill Dossir Vivr un séparation La séparation du coupl st un épruv souvnt longu t difficil pour la famill. C guid vous présnt ls différnts démarchs n fonction d votr situation
(Fig. 1 :assistant connexion Internet)
MAIL > configuration de OUTLOOK EXPRESS > SOMMAIRE Qu'est ce que Outlook Express? Configuration Installation d'un compte POP Installation d'un compte IMAP Configuration du serveur SMTP En cas de problème
Comptabilité - USR. Logiciel : Comptabilité USR - Version 2,16 Documentation réalisée par JJ Gorge Trésorier Tir à l'arc le 04/04/2010 1 / 15
Logiciel : Comptabilité USR - Version 2,16 Documentation réalisée par JJ Gorge Trésorier Tir à l'arc le 04/04/2010 1 / 15 Table des matières Ecran principal de saisie...3 Ajouter une nouvelle opération
Module 2 : Déterminant d une matrice
L Mth Stt Module les déterminnts M Module : Déterminnt d une mtrice Unité : Déterminnt d une mtrice x Soit une mtrice lignes et colonnes (,) c b d Pr définition, son déterminnt est le nombre réel noté
CERES logiciel de gestion commerciale pour négociants en vin
CERES logicil gion commrcial pour négocian n vin. Gion complè acha vn : comman, rérvaion, gion courag commrciaux.. Moul campagn primur : piloag la campagn via un ablau bor prman viualir accér aux informaion
ODH. Mon Espace. Manuel d utilisation. MON ESPACE ODH Manuel d utilisation. Une question? Contactez le service client au 02 72 68 27 19
Mon Espace ODH Manuel d utilisation Réalisé par Vecteur Plus Janvier 2013 Sommaire Mon Espace ODH Présentation - Accueil - Livraisons ODH - Gestionnaire d information - Accompagnement ODH - Compte Mon
Photoshop Séquence 4 - Créer une image de taille personnalisée taille
cterrier.com 1/5 20/09/2006 Photoshop Séquence 4 - Créer une image de taille personnalisée taille Auteur : C. Terrier ; mailto:webmaster@cterrier.com ; http://www.cterrier.com Utilisation : Reproduction
8 rue Paul Cézanne 93360 Neuilly-Plaisance - Tél : 33 (0)1.43.67.09.03 - Fax : 33 (0)1 43.67.35.40 E-mail : cvm@cvm.
SMS-Manager Utilisation Version 3.0 Application navigateur 8 rue Paul Cézanne 93360 Neuilly-Plaisance - Tél : 33 (0)1.43.67.09.03 - Fax : 33 (0)1 43.67.35.40 E-mail : cvm@cvm.fr Serveur Web : http://www.cvm.fr
Installation de TeamLab sur un serveur local Ce guide est destiné aux utilisateurs ayant des connaissances de base en administration Windows
Information sur la version serveur TeamLab Serveur TeamLab est une version du portail destinée à ceux qui ont décidé d'installer et de configurer TeamLab sur leur propre serveur. A partir de la version
Programme GénieArts Î.-P.-É. 2009-2010. GénieArts
Programm GéniArts Î.-P.-É. 2009-2010 GéniArts Allum l nthousiasm ds juns à l égard d l acquisition ds matièrs d bas par l truchmnt ds arts. Inspir la collaboration ntr ls artists, ls nsignants, ls écols
Vous y trouverez notamment les dernières versions Windows, MAC OS X et Linux de Thunderbird.
MAIL > configuration de mozilla thunderbird > SOMMAIRE Qu'est ce que Thunderbird? Téléchargement du logiciel Thunderbird Configuration Installation d'un compte POP Installation d'un compte IMAP En cas
Volet de visualisation
Mode emploi pour ajouter une adresse email (compte de messagerie) et envoyer un message avec Windows Live Mail Dans ce mode d emploi nous allons ajouter une adresse email (compte de messagerie) et aussi
Export et import des RIB et IBAN avec les progiciels LD
Export et import des RIB et IBAN avec les progiciels LD Révision 3 Décembre 2013 Présentation générale Cet utilitaire permet d extraire les coordonnées bancaires (RIB) présentes dans les bases de données
Le pare-feu de Windows 7
Le pare-feu de Windows 7 Le pare-feu (firewall) intégré à Windows 7 vous permet d'empêcher les utilisateurs ou logiciels non autorisés (comme les vers) d'accéder à votre ordinateur depuis un réseau ou
Début de la procédure
Service informatique Introduction au VPN sous Windows 7 Ce document décrit comment configurer votre ordinateur personnel pour pouvoir accéder au serveur d archives médicales du collège. Il contient deux
Animation Shop PREAMBULE... 2 CONTRAINTE... 2 CREER UNE ANIMATION... 2 AJOUTER DES IMAGES... 3 ENREGISTRER UNE ANIMATION... 3
Jasc Software Animation Shop Sommaire : PREAMBULE... 2 CONTRAINTE... 2 CREER UNE ANIMATION... 2 AJOUTER DES IMAGES... 3 ENREGISTRER UNE ANIMATION... 3 AJOUTER DE L'EFFET... 5 TRANSISSIONS D'IMAGE... 5
Date de diffusion : Rédigé par : Version : Mars 2008 APEM 1.4. Sig-Artisanat : Guide de l'utilisateur 2 / 24
Guide Utilisateur Titre du projet : Sig-Artisanat Type de document : Guide utilisateur Cadre : Constat : Les Chambres de Métiers doivent avoir une vision prospective de l'artisanat sur leur territoire.
FONDATION CLEMENTINE ET MAURICE ANTILLE
FONDATION CLEMENTINE ET MAURICE ANTILLE Règlement d ttriution de ourses et de prêts d études et de formtion du déemre 006 Artile premier Ojet et hmp d pplition Le présent règlement est étli en pplition
Import d un fichier de contacts dans une campagne
Import d un fichier de contacts dans une campagne Objectif Importer des contacts dans une campagne de l'enquête à partir d un fichier CSV ou TXT. Cette procédure est à privilégier lorsque le fichier contact
Les tableaux croisés dynamiques
Les tableaux croisés dynamiques Table des matières Les tableaux croisés dynamiques... 1 1. Les tutoriels... 1. Quelle est l'utilité d'un tableau croisé dynamique... 3. Vérifier les données de départ...
Améliorations Sage Gestion Commerciale version 7.71 Sage Comptabilité version 7.72
Améliorations Sage i7 v7.71 et v7.72 et Nouveautés Sage i7 v7.72 Améliorations Sage Gestion Commerciale version 7.71 Sage Comptabilité version 7.72 Vous trouverez ci-dessous la liste des améliorations
Il semble toutefois que, faisant écho à. champ opératoire. évidemment. odontologie restauratrice. le champ opératoire
oontologi rsturtri l hmp opértoir L hmp opértoir évimmnt Guthir Wisrok, Jn-Louis Brouillt Alors qu nos prtnirs inustrils s ornt à situr utour 3 % l nomr ntists utilisnt l igu, l moitié un éhntillon signiiti
C est signé 11996 mars 2015 Mutuelle soumise au livre II du Code de la Mutualité - SIREN N 780 004 099 DOC 007 B-06-18/02/2015
st signé 11996 mars 2015 Mutull soumis au livr II du od d la Mutualité - SIREN N 780 004 099 DO 007 B-06-18/02/2015 Édition 2015 Madam, Monsiur, Vous vnz d crér ou d rprndr un ntrpris artisanal ou commrcial
1. Création d'un état... 2. 2. Création d'un état Instantané Colonnes... 3. 3. Création d'un état Instantané Tableau... 4
1. Création d'un état... 2 2. Création d'un état Instantané Colonnes... 3 3. Création d'un état Instantané Tableau... 4 4. Création d'un état avec plusieurs tables... 9 5. Modifier la structure d'un état...11
AFTEC SIO 2. Christophe BOUTHIER Page 1
Christophe BOUTHIER Page 1 Nous allons traiter ici quelques exemples de stratégies de groupe courantes. Sommaire : Stratégie de groupe pour déploiement logiciel... 3 1. Introduction... 3 2. Création du
Utiliser Internet Explorer 7
1 - Le navigateur WEB Utiliser Internet Explorer 7 Un navigateur est un logiciel qui nous permet de profiter et de se déplacer dans l océan d information qu est l Internet, il nous permet de, comme on
Importation des données dans Open Office Base
Importation des données dans Open Office Base Il est aujourd'hui assez rare dans les bureaux de créer un environnement de base de données de toutes pièces. Les données sont manipulées depuis longtemps
Compression Compression par dictionnaires
Compression Compression par dictionnaires E. Jeandel Emmanuel.Jeandel at lif.univ-mrs.fr E. Jeandel, Lif CompressionCompression par dictionnaires 1/25 Compression par dictionnaire Principe : Avoir une
1 sur 5 10/06/14 13:10
Time Machine est un outil proposé par Mac OS depuis sa version 10.5 (Leopard) et qui permet d'effectuer des sauvegardes de votre disque dur de manière régulière. Mais au-delà de la simple sauvegarde périodique,
Bientôt la rentrée!...personnaliser et configurer un ordinateur pour faciliter son utilisation en classe
Bientôt la rentrée!......personnaliser et configurer un ordinateur pour faciliter son utilisation en classe Tout comme l'achat des fournitures scolaires, la préparation de l'ordinateur s'effectue avant