EA MAP571 Enseignements d Approfondissement du PA de Mathématiques Appliquées Catalogue des sujets
|
|
|
- Patrice Laroche
- il y a 8 ans
- Total affichages :
Transcription
1 EA MAP571 Enseignements d Approfondissement du PA de Mathématiques Appliquées Catalogue des sujets 15 septembre 2014 La dernière version de ce document se trouve sur les ressources pédagogiques de MAP571: 1
2 Table des matières Introduction 3 Objectifs, rapport et soutenance, notation Simulations, calculs, informatique Thématiques proposées et cours correspondants Choix et attribution des sujets Déroulement du projet, encadrement Liste des sujets 8 1 Analyse numérique Imagerie élastique cardiovasculaire Microstructures, homogénéisation et métamatériaux Déformations d un réseau de poutres inextensibles Modèles stochastiques en finance 11 Techniques de valorisation d options Options sur taux d intérêt Options vanille sur actions et dividendes discrets Produits dérivés sur la volatilité et modèle de variance forward Erreurs de couverture Trading discret et erreur de spécification Méthodes numériques de discrétisation et de Monte-Carlo Méthodes asymptotiques pour les options sur panier Options américaines : l approche par conditions aux limites artificielles Options américaines et méthode duale Options barrière et techniques de correction de domaine Modèle à volatilité incertaine et méthode primale pour BSDEs Modèle à volatilité incertaine et méthode duale pour BSDEs Méthodes de différences finies généralisées pour les options avec volatilité stochastique Surface de volatilité et calibration de modèle Asymptotique du smile Prix de marché des Calls et absence d arbitrage statique Calibration d un triangle de taux de change Calibration d un modèle hybrique taux-action par une méthode particulaire Autour du modèle Sabr Risque de Contrepartie CVA sur CDS (ou risque de contrepartie sur un swap de défaut).. 21 Gestion de portefeuille et délit d initié Assurance de portefeuille Délit d initié : modélisation et détection Stratégies haute fréquence, microstructure des marchés
3 2.20 Exécution optimale haute fréquence : ordre limite versus ordre de marché Estimation du Market impact à partir de données haute fréquences Estimation haute fréquence de la volatilité, application au trading d options Corrélation haute fréquence, application au market impact Optimisation et recherche opérationnelle Preferential Bidding Systems pour les pilotes Construction de grilles horaires pour le personnel au sol Affectation optimale des numéros de vol Optimisation de l affectation temps réel des trafics dans un contexte de réseau d accès mobile multi-technologies (2G/3G/LTE) Modélisation de l optimisation de la qualité d expérience pour les services de vidéo streaming dans les réseaux mobiles Distribution de contenus vidéos Conception d un réseau de caches Feasibility Recovery Algorithms for The Unit Commitment Problem of Interconnected Hydro Plants Optimisation du processus de réception et de traitement des appels d urgence bornes pire des cas Optimisation du processus de réception et de traitement des appels d urgence étude probabiliste Des systèmes biologiques à la géométrie tropicale Bases de Graver pour l optimisation entière Falsifier formellement la conjecture de Hirsch Planification de tournées de techniciens Réseaux de communication Stochastic Models of Algorithms for Data Centers Equilibrium states of stochastic neural networks Stochastic Models of Protein Production of Bacteria Cells Capacité des réseaux mobiles Traitement du signal et de l image Synthèse additive : Analyse, resynthèse et transformation de signaux musicaux Segmentation : méthode déterministe ou aléatoire? Débruitage par non-local means Statistique, grandes données, systèmes en interaction On the influence of the seed graph in the preferential attachment model L 2 -Boosting et k-plus proches voisins Régression nonparamétrique lorsque n est grand
4 Introduction Objectifs, rapport et soutenance, notation Objectifs : Le but de ces enseignements d approfondissement (EA) est la réalisation par l élève d un projet, selon la démarche d un mathématicien appliqué, en résumé : comprendre l essence d un problème pertinent et en faire la modélisation ; effectuer une étude mathématique du modèle obtenu ; fournir des résultats qualitatifs et quantitatifs, en particulier grâce à des simulations et des méthodes numériques. Ce projet personnel est effectué en binôme et constitue un véritable travail d équipe. Il porte sur un problème spécifique issu du domaine des applications d un cours suivi par les deux élèves, et il leur permet d y approfondir leurs connaissances et bénéficier d une initiation à la recherche. Il constitue souvent une condition nécessaire pour obtenir un stage de recherche ou une 4 ème Année dans ce domaine, notamment en finance ou à l étranger. Rapport et soutenance : Ce travail se concluera par la remise d un rapport pour le mardi 25 novembre Ce rapport sera à transmettre sous forme de deux copies papier au secrétariat du département de MAP et à envoyer sous forme d un fichier pdf à tous les membres du jury. Il fera l objet d une soutenance orale sur slides le mardi 2 ou vendredi 5 décembre. Dans le rapport comme lors de la soutenance, vous devez considérer que le jury ne connaît rien au problème, et donc le présenter en montrant son importance, expliquer votre approche ainsi que vos résultats analytiques et numériques, et donner vos conclusions sur le sujet en faisant un bilan de votre travail. Une bonne ligne de conduite est de faire comme s il s agissait d une étude que l on vous aurait commandée, à présenter aux commanditaires. Le rapport, de préférence écrit en L A TEX, devra être rédigé et présenté très soigneusement, et comprendre une bibliographie des ouvrages et articles étudiés. Vous êtes fortement encouragés à aller chercher de la documentation sur votre sujet à la bibliothèque. La soutenance orale dure 40 minutes par binôme : un exposé de 30 minutes (partagées équitablement par les élèves) suivi de 10 minutes de questions. Il est extrêmement important de bien la préparer. Elle doit tenir dans le temps imparti. 4
5 Evaluation : Elle tient compte de la qualité du contenu et de la présentation du rapport et de la soutenance, ainsi que des interactions avec l enseignant. Elle prendra également en compte le sens critique sur les résultats obtenus ainsi que la précision de la bibliographie. Une seule note est généralement attribuée au deux membres du binôme. Simulations, calculs, informatique Tous les sujets proposés demanderont d effectuer des simulations et des calculs numériques. Une analyse critique des résultats ainsi obtenus devra être faite dans le rapport et la présentation orale. L informatique devra être utilisée comme outil de compréhension et d expérimentation, et non comme une fin en soi. Notez bien qu il ne s agit pas d un projet d informatique. Logiciels et langages utilisés : On utilisera le plus souvent Python ou le logiciel Scilab, pendant libre de Matlab, qui permet de faire des calculs avec un minimum de programmation. Certains sujets utilisent des logiciels de calcul plus avancés et spécialisés, tels que FreeFem++. Suivant les goûts et compétences, l utilisation de langages de programmation évolués, notamment C, C++, ou Java, est tout à fait envisageable. TP Python : Quatre séances de travaux dirigés Python avec une orientation numérique vous sont proposés. A noter que ces travaux dirigés auront lieu les mardi 23, 30 septembre et 7 et 14 octobre de 13h30 à 15h30 dans les salles informatique 35 et 36. La première séance consistera en une prise en main de Python. Les trois dernières seront consacrées à la réalisation complète d un micro-projet, l accent étant mis sur la programmation, l affichage des résultats et leur inclusion dans un rapport écrit en LaTeX. Ce projet constitue un très bon exercice pour découvrir les besoins (aussi bien en Python qu en LaTeX) que vous aurez au cours de votre EA et pour apprendre à y répondre. Ceux qui le souhaitent pourront effectuer leur projet en Scilab. Ces TP et l encadrement informatique tout au long de votre travail seront assurés par Raphaël Deswarte, Caroline Hillairet et Aldjia Mazari. Notez que vous pourrez joindre ces intervenants par courrier électronique à l adresse sos@cmap.polytechnique.fr 5
6 Soutien FreeFem++ : Les élèves qui doivent manipuler FreeFem++ dans le cadre de leur sujet d EA pourront obtenir un soutien en contactant Olivier Pantz olivier.pantz@polytechnique.org. Thématiques proposées Liste des thématiques et cours correspondants : La liste des sujets proposés est regroupés en six thèmes correspondant aux cours de période 1 du PA de MAP : 1. Analyse Numérique (MAP559, François Alouges et Bertrand Maury) 2. Modèles en finance et simulations (divisé en sept sous-thèmes) (MAP552, Nizar Touzi) 3. Optimisation et recherche opérationnelle (MAP557, Stéphane Gaubert) 4. Réseaux de communication (MAP554, Philippe Robert) 5. Traitement du signal et de l image (MAP555, Erwan Le Pennec) 6. Statistique, grandes données, systèmes en interaction (MAP553, Alexandre Tsybakov) Contrainte pour le choix des sujets : Pour demander un sujet il faut suivre le cours correspondant dans cette période 1 du PA. Cependant par exception : Modèles en finance et simulations en P2 : les élèves de MAP552 (Modèles stochastiques en finance) pourront effectuer un EA de Modèles en finance et simulations en période 2, sous condition d effectuer un EA sur un autre thème en période 1. Analyse numérique : la plupart des sujets sont accessibles aux élèves ayant suivi MAP431 Statistique, grandes données, systèmes en interaction : un des sujets est accessible aux élèves ayant suivi MAP433 Enseignants référents pour les différentes thématiques : Pour chacune des six thématiques, un enseignant référent est disponible pour répondre à vos questions. Ses coordonnées seront indiqués dans la suite de ce catalogue au début de chaque thématique. Vous pouvez les contacter pour vous aider 6
7 à faire votre choix. Vous pouvez également leur proposer un sujet qui vous intéresse particulièrement, afin d en discuter avec eux, pour voir si votre proposition est raisonnable et convenir d un encadrement. Choix et attribution des sujets Séance de présentation : L EA MAP571 est présenté le mardi 16 septembre 2014 de 14h à 17h30 en amphithéâtre Becquerel avec : une présentation générale sur ses principes, son organisation, et ce que l on attend des élèves la présentation de chaque thème par son responsable durant 15 à 30 minutes enfin, les élèves intéressés pourront discuter plus à fond avec les enseignants responsables de sujet présents. Procédure de choix : Il vous faudra communiquer avant le jeudi 18 septembre 2014 à 17h00 une liste de 3 choix de sujets ordonnés par préférence (en indiquant les numéros des sujets) appartenant à au moins 2 sous-thèmes pour Modèles en finance et simulation par courrier électronique ayant pour sujet «choix sujet EA» adressé à Nathalie Hurel departement@cmap.polytechnique.fr (Secrétariat du Département de Mathématiques Appliquées). Attribution des sujets : Elle sera faite au plus vite, en essayant de respecter au mieux les choix des élèves à l heure et respectant les règles de choix. Ceux-ci seront tous traités de façon égalitaire. Les autres seront traités ensuite, et par ordre d arrivée. Déroulement du projet, encadrement Démarrage du projet : Dès que votre sujet vous aura été attribué, vous devrez prendre immédiatement contact avec l enseignant qui en est responsable afin de fixer la date d un premier rendez-vous. Cet enseignant vous précisera les modalités de travail particulières pour votre sujet, puis vous encadrera. 7
8 Déroulement du projet : Ce projet constitue un travail personnel dont l intérêt et la richesse dépendront principalement de votre investissement. L enseignant qui vous encadre vous guidera dans votre démarche. Surtout n hésitez pas à le contacter. C est à vous de le solliciter et à lui de déterminer les modalités de vos rencontres, et non l inverse. Ces rencontres n auront pas nécessairement lieu le mardi, mais vous devez utiliser les créneaux libres ce jour-là à bon escient. Il vous faudra commencer votre travail immédiatement, car vous pouvez vous attendre à être très occupé lors des dernières semaines, par la finition des calculs numériques, la rédaction du rapport, la préparation de votre présentation, les examens des autres cours et les dossiers pour la quatrième année. Lettre de recommandation : Si vous avez besoin d une lettre de recommandation pour des dossiers d admission, notamment pour les universités étrangères, vous pourrez la demander à votre encadrant après la soutenance. 8
9 Liste des sujets 1 Analyse numérique Enseignant référent : Aline Lefebvre-Lepot aline.lefebvre@polytechnique.edu 1.1 Imagerie élastique cardiovasculaire Habib Ammari ammari@ens.fr De nombreuses pathologies cardiaques se caractérisent par un changement des paramètres mécaniques du coeur. L objet de ce sujet est de développer un cadre mathématique et numérique à l imagerie visco-élastique du coeur à l aide d une sonde optique. Il aboutirait à la reconstruction en temps réel du module d Young et de la viscosité locale du coeur et des artères. Il s agit là d un enjeu majeur en imagerie cardiaque. [1] H. Ammari, E. Bretin, J. Garnier, H. Kang, H. Lee et A. Wahab, Mathematical Methods in Elasticity Imaging, Princeton Series in Applied Mathematics, Princeton University, [2] H. Ammari, E. Bretin, P. Millien, L. Seppecher et J.K. Seo, Mathematical modeling in full-field optical coherence elastography, arxiv : Microstructures, homogénéisation et métamatériaux Antonin Chambolle antonin.chambolle@cmap.polytechnique.fr L homogénéisation consiste à déterminer les propriétés macroscopiques d un matériau dont la structure microscopique varie très rapidement. Cette technique permet à la fois de pouvoir faire des calculs numériques macroscopiques plus efficaces que s il fallait résoudre en même temps les échelles microscopiques, mais aussi de concevoir des matériaux inexistants dans la nature (ou métamatériaux ) : composites (le plus souvent, des matériaux légers renforcés par des fibres elastiques très solides), matériaux aux propriétés originales qui se dilatent lorsqu on tire dessus (coefficient de Poisson négatif)... L objet de cette étude sera d implémenter (a priori, en 2D) des calculs de propriétés effectives de matériaux à microstructures périodiques (ou aléatoires si le temps le permet), d abord pour des problèmes de diffusion (scalaire) puis en élasticité linéarisée. On pourra par exemple essayer le motif calculé dans [2] qui donne théoriquement un matériau à coefficient de Poisson négatif (voir Figure 1). [1] Antoine Gloria. Numerical Homogenization : Survey, New Results, And Perspectives. ESAIM : PROCEEDINGS, September 2012, Vol. 37,
10 Figure 1 Matériau à coefficient de Poisson négatif calculé dans [2]. [2] G. Allaire, F. De Gournay, F. Jouve. Méthodes de synthèse et d optimisation de mécanismes compliants, Actes des 5eme journées nationales de recherche en robotique (JNRR 05), Guidel, Octobre 2005, Déformations d un réseau de poutres inextensibles Alexandre Ern ern@cermics.enpc.fr Les Grid Shells constituent une technique de construction récente et innovante permettant de réaliser des structures coques discrètes aux formes variables et aux propriétés mécaniques particulièrement favorables (grande rigidité notamment et faible densité) ; voir par exemple [1]. Le principe est de déployer un réseau de poutres initialement plan puis de solliciter ce réseau en lui appliquant des efforts ponctuels afin qu il se déforme en une hypersurface de l espace. Les poutres sont élastiques et inextensibles et sont reliées entre elles par des mécanismes permettant le glissement et la rotation, et on s intéresse ici au problème statique. Afin d appréhender la simulation de tels systèmes, on commencera par se concentrer sur les déformations d une unique poutre. On formulera le problème comme la minimisation d une fonctionnelle quadratique (la poutre est élastique) sous des contraintes ponctuelles non-linéaires (la poutre est inextensible). La méthode numérique sera basée sur une formulation par décomposition-coordination et lagrangien augmenté [2] (on pourra également consulter [3] pour la même approche sur un problème différent). On réalisera des simulations sous Scilab en considérant divers types de sollicitations (par exemple, déplacements ou efforts imposés aux extrémités de la poutre). Dans un deuxième temps, on étudiera une extension de la formulation par Lagrangien augmenté au réseau de poutres et, si le temps le permet, on réalisera quelques simulations (toujours sous Scilab) afin d appréhender la réponse statique du réseau à des sollicitations extérieures. 10
11 [1] C. Douthe, O. Baverel, J.-F. Caron, Form-finding of a grid shell in composite materials, J. Int. Assoc. Shell and Spatial Struct., 47(150), [2] R. Glowinski and P. Le Tallec, Augmented Lagrangian and Operator-Splitting Methods in Nonlinear Mechanics, SIAM, [3] D. Doyen, A. Ern et S. Piperno, A three-field augmented Lagrangian formulation of unilateral contact problems with cohesive forces, ESAIM Math. Mod. Numer. Anal., 44(2), (2010). 11
12 2 Modèles stochastiques en finance Enseignant référent : Caroline Hillairet caroline.hillairet@polytechnique.edu Sujets proposés par : Emmanuel Bacry - CMAP-École Polytechnique emmanuel.bacry@polytechnique.fr Frédéric Bonnans - INRIA Saclay Frederic.Bonnans@inria.fr Stefano De Marco - CMAP-École Polytechnique demarco@cmap.polytechnique.fr Laurent Denis - Université du Mans laurent.denis@univ-lemans.fr Caroline Hillairet - CMAP-École Polytechnique caroline.hillairet@polytechnique.edu Pierre Henry-Labordère - Société Générale pierre.henry-labordere@sgcib.com Benjamin Jourdain - CERMICS, École des Ponts ParisTech jourdain@cermics.enpc.fr Anis Matoussi - Université du Mans Anis.Matoussi@univ-lemans.fr Mathieu Rosenbaum - LPMA-Université Pierre et Marie Curie mathieu.rosenbaum@polytechnique.edu Peter Tankov - LPMA-Université Paris Diderot peter.tankov@polytechnique.org Techniques de valorisation d options 2.1 Options sur taux d intérêt On commencera par étudier en détail le modèle de Vasicek. On s intéressera au problème d évaluation et de couverture dans ce cadre. On montrera que le formalisme de réplication parfaite est vérifié et conduit à des formules relativement simples pour le prix des zéro-coupons (cf. cours) et des options «vanilles». On vérifiera par simulation l existence d un panier de couverture (diverses stratégies seront envisagées et implémentées). On abordera par la suite les modèles de marché (BGM, Libor Market Model). Ils ont pour avantage d être compatibles avec les formules de valorisation de caps, floors et swaptions. On étudiera la valorisation de ces options dans les modèles de marché par des méthodes analytiques et de simulation Monte Carlo. On cherchera à comprendre les différences avec l approche de type «Heath, Jarrow, Morton». 12
13 [1] D. Brigo, F. Mercurio, Interest rate models - theory and practice, Springer, [2] N. El Karoui, J.C. Rochet, A pricing formula for options on coupon bonds, [3] A. Brace, D. Gatarek, M. Musiela, The market model of interest rate dynamics, Mathematical Finance, 7(2), , [4] A. Kawai, Analytical and Monte Carlo swaption pricing under the forward swap measure, Journal of Computational Finance, 6(1), [5] D. Heath, R. Jarrow, A. Morton, Contingent claim valuation with a random evolution of interest rate, Rev. Future Markets, 9, 54-76, [6] D. Heath, R. Jarrow, A. Morton, Bond pricing and the term structure of interest rates : A new methodology for contingent claim valuation, Econometrica, 6, , Options vanille sur actions et dividendes discrets Lorsque l actif sous-jacent ne verse pas de dividende, il est possible de donner une formule explicite d une option d achat écrite sur ce sous-jacent, c est la célèbre formule de Black-Scholes. En revanche, si des dividendes sont versées à des dates discrètes (ce qui est le cas pratique pour les actions), il n existe plus de formule exacte possible et il devient nécessaire d avoir recours à des procédures numériques (arbre ou Monte-Carlo) ou des procédures d approximation pour évaluer le prix d options vanille. Dans ce sujet, nous étudions et comparons les différentes approches théoriques et numériques à ce problème. [1] R. Bos, A. Gairat, D. Shepeleva, Dealing with discrete dividends, Risk Magazine, 16, p , [2] H. Buehler, Volatility and dividends - Volatility modeling with cash dividends and simple credit risk, SSRN working paper, TU Berlin, 2009, http ://papers.ssrn.com/sol3/papers.cfm?abstract id= [3] P. Etore, E. Gobet, Stochastic expansion for the pricing of call options with discrete dividends, Applied Mathematical Finance, [4] C. Veiga, U. Wystup, Closed formula for options with discrete dividends and its derivatives, Applied Mathematical Finance, 16, , [5] M. Vellekoop, J. Nieuwenhuis, Efficient Pricing of Derivatives on Assets with Discrete Dividends, Applied Mathematical Finance, 13, , Produits dérivés sur la volatilité et modèle de variance forward Les années récentes ont vu l émergence de produits dérivés d un nouveau type, dont le pay-off dépend de la volatilité réalisée par un actif de référence sur une 13
14 période à venir. Ces «swaps de variance» ou «swaps de volatilité» permettent à un investisseur de faire un pari sur le niveau futur de la volatilité sans avoir à émettre de vues sur le niveau des prix eux-mêmes. L objectif de ce travail sera d étudier ces instruments et les méthodes proposées pour les évaluer. [1] P. Carr, D. Madan, Towards a theory of volatility trading, in : Volatility, ed. R.A. Jarrow, Risk Publications, [2] K. Demeterfi, E. Derman, M. Kamal, J. Zou, More than you ever wanted to know about volatility swaps, Journal of Derivatives, Summer [3] B. Bühler, Consistent Variance Curve Models, Finance and Stochastics, , Erreurs de couverture 2.4 Trading discret et erreur de spécification La propriété de réplication exacte dans le modèle de Black-Scholes repose sur les hypothèses de rebalancement continu du portefeuille et de connaissance parfaite des paramètres du modèle. Dans les conditions réelles du marché, le trading continu est impossible à cause par exemple des coûts de transaction, ce qui conduit à une erreur de couverture non-négligeable. Par ailleurs, des stratégies mal spécifiées peuvent conduire à des pertes arbitrairement grandes. À partir d exemples, on étudiera mathématiquement et numériquement le comportement de ces différents types d erreurs de couverture. Si le temps le permet l effet de microstructure de marché sera également abordé. [1] D. Bertsimas, L. Kogan, A. W. Lo, When is time continuous?, Journal of Financial Economics, 55, , [2] C. Gallus, Exploding hedging errors for digital options, Finance and Stochastics, 3, , [3] E. Gobet, A. Makhlouf, The tracking error rate of the Delta-Gamma hedging strategy,mathematical Finance, Vol. 22, No. 2 (April 2012), Méthodes numériques de discrétisation et de Monte- Carlo 2.5 Méthodes asymptotiques pour les options sur panier La valorisation des options sur un panier d actifs présente des difficultés à la fois du point de vue de modélisation de la dynamique des actifs et du point de vue de la 14
15 mise en oeuvre de l algorithme de pricing en grande dimension. Du fait de la malédiction de la dimension, les méthodes déterministes (différences finies / éléments finis) ne peuvent pas être utilisées et on est obligé de choisir entre la méthode de Monte Carlo, lente, mais dont la complexité n explose pas avec la dimension, et les méthodes d approximation asymptotique, rapides mais de précision variable. Le but de cet EA est de comparer la performance de ces deux méthodes, dans le cadre d une option sur un panier d actifs. On supposera dans un premier temps que les actifs suivent le modèle de Black-Scholes multidimensionnel. En fonction de l évolution du projet, on s intéressera dans un deuxième temps aux modèles à volatilité locale multidimensionnels. [1] M. Avellaneda, D. Boyer-Olson, J. Busca, and P. Friz, Reconstruction of volatility : Pricing index options using the steepest-descent approximation, RISK Magazine, 15 (2002). [2] C. Bayer and P. Laurence, Asymptotics beats Monte Carlo : The case of correlated local vol baskets, Commun. Pure Appl. Math., 67 (2014), pp Options américaines : l approche par conditions aux limites artificielles La résolution numérique d un problème d évaluation d une option américaine conduit à résoudre une équation aux dérivées partielles (EDP) à frontière libre (la limite de la zone d exercice de l option). En dimension 1 on peut éviter l essentiel des calculs dans la zone où le sousjacent a un prix plus petit que le prix d exercice. Pour cela on utilise la technique de conditions aux limites artificielles décrite dans [2]. L étude commencera par l implémentation de l algorithme standard de différences finies, puis analysera l approche par conditions aux limites artificielles de manière à chercher une implémentation rapide et stable. [1] M. Ehrhardt : Finite difference schemes on unbounded domains. In Advances in the applications of nonstandard finite difference schemes, World Sci. Publ., Hackensack, NJ, , [2] M. Ehrhardt, R. E. Mickens : A fast, stable and accurate numerical method for the Black-Scholes equation of American options. Int. J. Theor. Appl. Finance, 11(5), , Options américaines et méthode duale Une option américaine peut être exercée à tout instant entre la date de son acquisition et son échéance. Pour comprendre si l option doit être exercée à la date t, il faut comparer le montant récupéré à l exercice avec la valeur de l option condi- 15
16 tionnelle au fait que l acheteur décide de ne pas exercer en t. La nécessitée de calculer les espérances conditionnelles rend l utilisation de la méthode de Monte Carlo particulièrement délicate. Les objectifs de cet EA sont : Comprendre la théorie classique des options américaines et l algorithme de Longstaff- Schwartz. Comparer les méthodes duales. [1] F. A. Longstaff, E. S. Schwartz, Valuing American options by simulation : A simple least-squares approach, Review of Financial Studies, 14, , [2] Rogers, C. : Monte-Carlo valuation of American options, Mathematical finance 12 N03, [3] Broadie, M, Cao, M. : Improved lower and upper bound algorithms for pricing American options by simulation. [4] P. Glasserman, Monte Carlo methods in financial engineering, Chap 8, Springer. 2.8 Options barrière et techniques de correction de domaine Les options barrière sont des options classiques assorties d une clause du type : l option ne peut être exercée que si le sous-jacent a franchi (ou n a pas dépassé) un niveau fixé dans le contrat. Elles représentent actuellement 25% des options de change. Une raison de ce succès est leur prix, moins élevé que celui d une option standard. Dans le cas particulier du modèle log-normal, il existe des formules explicites. Pour une large classe de modèles, la valorisation d une option à barrière avec observations discrètes peut être reliée à celle à observation continue modulo une modification appropriée du domaine associé à l option. Dans le cadre du modèle de Black et Scholes, des arguments de renouvellement ont permis à Broadie et al. [1] de précisément caractériser la modification nécessaire dans le cas où la valeur initiale du sous-jacent est suffisamment loin du bord du domaine par rapport à la fréquence d observation. Dans le cas contraire Howison et Steinberg [2] ont mis en évidence d autres types de corrections. Cette approche a été étendue par Howison [3] au cas des options bermudéennes (i.e. options américaines à observations discrète). Le propos de l EA est dans un premier temps d étudier le cas log-normal puis dans un deuxième temps de comprendre précisément les techniques proposées et de les implémenter de façon efficace. [1] M. Broadie, P. Glasserman, S. Kou, A continuity correction for discrete barrier options, Mathematical Finance, 7, , [2] S. Howison, M. Steinberg, A matched asymptotic expansions approach to continuity corrections for discretely sampled options. Part 1 : Barrier options, Applied 16
17 Mathematical Finance, 14, 63-89, [3] S. Howison, M. Steinberg, A matched asymptotic expansions approach to continuity corrections for discretely sampled options. Part 2 : Bermudan options, Applied Mathematical Finance, 14, , [4] P. Glasserman, Monte Carlo Methods in Financial Engineering, Stochastic Modelling and Applied Probability, 53, Chapitre 6, Springer. [5] E. Gobet, Advanced Monte Carlo methods for barrier and related exotic options, Handbook of Numerical Analysis, Vol. XV. Elsevier. Special Volume : Mathematical Modeling and Numerical Methods in Finance, , Modèle à volatilité incertaine et méthode primale pour BSDEs Dans le cas où l on suppose que la volatilité n est pas connue, l EDP linéaire de Black-Scholes est remplacée par une EDP non-linéaire. La résolution de cette EDP en grande dimension nécessite des méthodes probabilistes comme les équations stochastiques rétrogrades (BSDEs). Les objectifs de cet EA sont : Comprendre la représentation probabiliste des equations Hamilton-Jacobi-Bellman par des BSDEs. Implémenter un schéma numérique primale pour un modèle à volatilité incertaine. [1] J. Guyon, P. Henry-Labordère : Uncertain volatility model : A Monte-Carlo approach, Journal of computational Finance, [2] A. Fahim, N. Touzi, X. Warin : A probabilistic numerical method for fully nonlinear parabolic PDEs, Ann. Appl. Probab. 21, , [3] E. Gobet, Lemor, X. Warin : A regression-based Monte Carlo method to solve backward stochastic differential equations, Ann. Appl. Probab. 15,3(2005), Modèle à volatilité incertaine et méthode duale pour BSDEs Dans le cas où l on suppose que la volatilité n est pas connue, l EDP linéaire de Black-Scholes est remplacée par une EDP non-linéaire. La résolution de cette EDP en grande dimension nécessite des méthodes probabilistes comme les équations stochastiques rétrogrades (BSDEs). Les objectifs de cet EA sont : Comprendre la représentation probabiliste des equations Hamilton-Jacobi-Bellman par des BSDEs. Implementer un schéma numerique duale pour un modèle à volatilité incertaine. 17
18 [1] C. Bender, N. Schweizer, J. Zhuo : A primal-dual algorithm for BSDEs, arxiv : v1, preprint (2013) Méthodes de différences finies généralisées pour les options avec volatilité stochastique L évaluation d options pour des modèles avec volatilité stochastique [3] peut se faire en résolvant une équation aux dérivées partielles. Comme celle-ci ne satisfait pas les conditions de la méthode classique de différences finies [4], on est amené à utiliser la méthodes de différences finies généralisées DFG [1] et son implémentation rapide en dimension 2 [2]. On comparera l approche de [2] aux approches classiques par Monte-Carlo. Enfin on étudiera l extension de cette approche au cas d options américaines. [1] J. F. Bonnans, H. Zidani, Consistency of generalized finite difference schemes for the stochastic HJB equation. SIAM J. Numerical Analysis, 41, , [2] J. F. Bonnans, E. Ottenwaelter, H. Zidani, Numerical schemes for the two dimensional second-order HJB equation. ESAIM : M2AN, 38, , [3] S. Heston, A closed-form solution for options with stochastic volatility with application to mathematical finance, Rev. Fin. Studies, 6, , [4] P.-L. Lions, B. Mercier, Approximation numérique des équations de Hamilton- Jacobi-Bellman. RAIRO Analyse numérique, 14, , Surface de volatilité et calibration de modèle 2.12 Asymptotique du smile Dans le modèle de Black-Scholes, le prix d une option est déterminé de manière unique à partir d un seul paramètre inobservable : la volatilité. Si on connaît le prix de marché d une option de type Call ou Put, on peut inverser la formule de Black-Scholes et extraire sa volatilité, appelée volatilité implicite de l option. La volatilité implicite devient ainsi une fonction non constante du prix d exercice, phénomène connu sous le nom de «smile de volatilité». Il est alors intéressant d étudier quelques propriétés universelles du smile généré par un modèle stochastique (autre que Black-Scholes), pour le comparer avec le smile de marché. Une certaine attention a été portée au comportement asymptotique : dans une série de travaux récents, on montre que le carré de la volatilité implicite est asymptotiquement linéaire en fonction du logarithme du prix d exercice, la pente asymptotique étant liée au nombre de moments finis de la loi de l actif sous-jacent, voir [1] et [2]. Le but de ce projet est de tester ce résultat dans un modèle paramètrique : étude du modèle de Heston [1] ; 18
19 évaluation théorique de la forme asymptotique de volatilité implicite dans ce modèle [3], [4] ; calcul numérique des prix d options et de la volatilité implicite et comparaison avec le résultat théorique [5]. [1] R. Lee, The moment formula for implied volatility at extreme strike, Mathematical Finance, 14, p , [2] A. Gulisashvili, Asymptotic formulas with error estimates for call pricing functions and the implied volatility at extreme strikes, SIAM Journal on Financial Mathematics, 1, p , [3] S. Heston, A closed-form solution for options with stochastic volatility with applications to bond and currency options, Rev. Fin. Studies, 6, , [4] M. Keller-Ressel. Moment explosions and long-term behavior of affine stochastic volatility models. Mathematical Finance, 21, p , [5] H. Albrecher, P. Mayer, W. Schoutens, and J. Tistaert. The little Heston trap. Wilmott Magazine, January issue :83 92, Prix de marché des Calls et absence d arbitrage statique On s intéresse à la surface des prix des Calls portant sur un sous-jacent donné, vus comme une fonction du couple maturité/strike. Les conditions qui assurent l absence d opportunité d arbitrage sur un ensemble de prix correspondant à un nombre fini de couples maturité/strike sont bien connues [1], [2]. Sous ces conditions, on peut construire un modèle stochastique qui permet de reproduire ces prix [1]. En faisant de plus l hypothèse que les prix soient générés par un processus de diffusion (pas forcément Markovien), on peut construire une diffusion unidimensionnelle (ou modèle à volatilité locale) qui permet de reproduire l intégralité de la surface des prix [3]. Cette construction requiert néanmoins de connaitre les prix (et leur dérivées) pour un continuum de strikes et maturités : puisqu en pratique seul un nombre fini de Calls sont cotés sur le marché, une étape d interpolation des données de marché est typiquement nécessaire. En pratique, cette étape est souvent réalisée par la calibration d une forme paramétrique à la surface des prix (ou plutôt à la surface de volatilité implicite) ; il est donc crucial à ce niveau que la paramétrisation choisie respecte les contraintes d absence d arbitrage. L objectif de cet EA est donc d étudier et implémenter à partir de [1] et [2] : les conditions qui assurent qu un ensemble fini de prix de Calls est bien compatible avec l absence d opportunité d arbitrage ; la construction d un modèle stochastique permettant de reproduire ces prix ; et si le temps le permet, à partir de [3], [4] : la construction d un modèle de diffusion à volatilité locale permettant de reproduire les prix. 19
20 [1] H. Buehler, Expensive martingales, Quantitative Finance, 6(3), p , [2] M. Davis, D. Hobson, The range of traded option prices, Mathematical Finance, 17(1), p. 1-14, [3] B. Dupire, Pricing with a smile, RISK, January [4] J. Gatheral, A. Jacquier, Arbitrage-Free SVI Volatility Surfaces, preprint, Calibration d un triangle de taux de change Le modèle simple de Garman-Kohlhagen permet de comprendre le pricing des options portant sur un taux de change. Il est alors facile de généraliser la formule de Dupire [1] pour construire un modèle à volatilité locale qui reproduise les prix de marché des options liquides portant sur ce taux. Lorsque l on considère maintenant deux taux de change impliquant deux fois la même devise, par exemple DOL/EUR et GBP/EUR, le problème de la calibration devient beaucoup plus complexe : en effet le quotient du premier taux par le second est lui-même le taux de change GBP/DOL. Il s agit alors de construire un modèle compatible avec les prix d options liquides portant sur les deux taux de départ DOL/EUR et GBP/EUR mais aussi sur leur rapport GBP/DOL. Le but de cet EA est de comprendre la calibration d un seul taux de change avant d étudier l approche proposée dans [2] pour calibrer deux taux de change. [1] B. Dupire, Pricing with a smile, Risk, January [2] J. Guyon, A new class of local correlation models, preprint SSRN, Calibration d un modèle hybrique taux-action par une méthode particulaire La calibration de modèles diffusifs sur des smiles de marché se formalise comme la résolution numérique d une équation de Fokker-Planck non-linéaire. La résolution de cette EDP en grande dimension nécessite des méthodes probabilistes comme les méthodes particulaires pour les EDS non-linéaires de MCKean. Les objectifs de cet EA sont : Comprendre la théorie classique des EDS non-linéaires de MCKean et l algorithme particulaire. Implémenter un schéma numérique pour la calibration d un modèle hybrique tauxaction. [1] J. Guyon, P. Henry-Labordère : The Smile Calibration Problem Solved, Risk magazine (2012). 20
21 2.16 Autour du modèle Sabr Le modèle diffusif SABR a connu un grand succès dès sa naissance en 2002 [1] en particulier grâce à l existence d une formule explicite pour son smile de volatilité, qui permet une calibration rapide des paramètres aux données de marché. Le SABR est devenu depuis un des modèles de référence pour les marchés de taux d intérêt et de taux d échange. La formule analytique proposée par les fondateurs du modèle n étant qu une formule approchée valide dans certaines conditions, son usage peut conduire à des problèmes de génération d arbitrage. C est pourquoi nombreux travaux récents se sont concentrés sur (i) la recherche de corrections à la formule originaire et (ii) des aspects plus fondamentaux tels la simulation du modèle, à laquelle on fait finalement recours pour obtenir des valeurs fiables, et qui sort du cadre classique de simulation d équations stochastiques à cause de la nature des coefficients (non-lipschitz) du modèle. Les objectifs de cet EA sont : Comprendre et implémenter le schéma numérique présenté dans [2]. Etudier des alternatives à ce modèle qui ne sont pas soumises au même problème de génération d arbitrage, comme celle proposé par [3]. [1] P. Hagan, D. Kumar, A. Lesniewski and D. Woodward, Managing smile risk, Wilmott Magazine, , [2] B. Chen, C. Oosterlee and H. van der Weide. Efficient unbiased simulation scheme for the SABR stochastic volatility model. preprint, [1] P. Balland and Q. Tran, SABR goes normal, Risk Magazine, May Risque de Contrepartie Les crises financières récentes ont mis l accent sur l importance d une bonne gestion par les banques de leur risque de contrepartie, ou risque de pertes liées au défaut d une contrepartie dans des transactions de gré à gré de produits dérivés. De manière générale, les ajustements de crédit ou CVA (Credit Value Adjustment) matérialisent la valeur de marché du risque de crédit. Plus précisément, les CVAs mesurent la différence entre la valeur d un portefeuille de crédit sans risque et la valeur risqué de ce même portefeuille (c est-à-dire la valeur du portefeuille intégrant la probabilité de défaut des contreparties). Le montant de CVA sert à compenser les pertes de marché liées au défaut de la contrepartie. A ce titre, la CVA peut être considérée comme une «provision prospective» du risque de contrepartie. 21
22 2.17 CVA sur CDS (ou risque de contrepartie sur un swap de défaut) On étudiera dans ce sujet le cas de Credit Default Swap (CDS) avec risque de contrepartie, plus précisement le prix et la couverture dynamique de la CVA dans le cadre d un modèle Markovien. Des simulations numériques permettront d étudier l impact de différents facteurs (comme la corrélation entre la contrepartie et la firme sous jacente au CDS, ou bien la qualité de crédit de la contrepartie...) sur l exposition au risque de contrepartie. [1] T. Bielecki, S. Crépey, M. Jeanblanc and B. Zargari. Valuation and Hedging of CDS Counterparty Exposure in a Markov Copula Model. IJTAF, Vol 15, Num 1, [2] T. Bielecki, M. Jeanblanc and M. Rutkowski. Pricing and Trading Credit Default Swaps in a hazard process model, Annals of Applied Probability, Vol. 18, No. 6, pp , [3] S. Crépey, M. Jeanblanc and B. Zargari. Counterparty Risk on a CDS in a Markov Chain Copula Model with Joint Defaults. Forthcoming in Recent Advances in Financial Engineering 2009, M. Kijima, C. Hara, Y. Muromachi and K. Tanaka eds, World Scientific Publishing Co. Pte., Gestion de portefeuille et délit d initié 2.18 Assurance de portefeuille Afin de rassurer leur clientèle, les gestionnaires de portefeuille proposent des fonds avec garantie de capital. Du point de vue du gestionnaire, il s agit d implémenter le meilleure allocation de portefeuille, selon un critère donné, sous la contrainte que la valeur du portefeuille soit supérieure à la garantie à laquelle il s est engagé avec son client. L objectif de cet EA est de comprendre et de comparer différentes stratégies de gestion qui assurent une telle garantie. En particulier, on étudiera : La stratégie qui consiste à acheter une action et une option de vente (Put) portant sur cette action, La stratégie du coussin. [1] P. Bertrand, J.-L. Prigent, Portfolio insurance strategies : A comparison of standard methods when the volatility of the stock is stochastic, International Journal of Business, 8(4), , [2] R. Cont, P. Tankov. Constant Proportion Portfolio Insurance in presence of jumps in asset prices, Mathematical Finance, 19(3), ,
23 [3] N. El Karoui, M. Jeanblanc, V. Lacoste, Optimal portfolio management with American capital guarantee, Journal of Economic Dynamics and Control, 29, , [4] R. C. Merton, Optimum consumption and portfolio rules in a continuous-time model, Journal of Economic Theory, 3, , Délit d initié : modélisation et détection En France, l AMF (Autorité des Marchés Financiers) est chargée de surveiller les opérations boursières. Depuis une dizaine d années, ces autorités de surveillance ont fait beaucoup de progrès dans la détection de comportement initié grâce notamment à de meilleures techniques de surveillance. Un exemple de grande envergure a eu lieu entre novembre 2005 et mars 2006, période durant laquelle 10 millions de titres EADS ont éte vendus, pour une plus value de près de 90 millions d euros. Ces mouvements anormaux ont été décelés par l AMF, et ont conduit à des enquêtes sur 21 hauts dirigeants d EADS. L objectif des deux sujets suivants est d étudier une modélisation d un délit d initié et de mettre en place un test de détection. On se placera dans le cadre d un marché financier dont les prix des actifs sont dirigés par un mouvement brownien. L information minimale dont disposent les agents pour résoudre leur problème d optimisation est celle obtenue par l observation du processus des prix. Cependant, il semble que les agents sont informés de manière hétérogène et reçoivent un flux d information qui leur est propre. Pour de tels initiés, on étudiera : - Les problèmes d arbitrage et de réplication d actifs risqués, - Le gain de l initié (par rapport à un non-initié), - La mise en oeuvre de tests de détection. On peut considérer plusieurs modélisations de l information privée. Nous étudierons le cas où l investisseur possède une information initiale, i.e. il connait, dès l instant t = 0, une fonctionnelle des trajectoires du processus des prix. La clé de cette modélisation est la théorie du grossissement initial de filtration par une variable aléatoire. On étudiera par exemple le cas où l initié connait le ratio du prix terminal de deux actifs, ou bien encore le cas où l initié sait si le prix terminal d un actif sera dans une fourchette donnée ou non. [1] A. Grorud, M. Pontier, Comment détecter le délit d initié, C.R. Acad. Sci. Paris, t. 324, p , [2] A. Grorud, M. Pontier, Insider trading in a continuous time market model, International Journal of Theoretical and Applied Finance, 1, p , [3] M. Pontier, Modélisation et détection du délit d initié, Matapli 77,
24 Stratégies haute fréquence, microstructure des marchés La disponibilité de données haute fréquence, la multiplication des places de marchés, ainsi qu une compréhension de plus en plus fine des phénomènes de microstructure, ont ouvert de nouvelles perspectives en finance de marché. En particulier, le trading haute fréquence est né de la volonté d optimiser les transactions en profitant de ce nouveau contexte. Son essor récent a nécessité le développement de méthodes originales de mathématiques financières et de statistique des processus. Un nombre grandissant d équipes de trading propriétaires, de salles de marchés et de hedge funds y ont aujourd hui constamment recours Exécution optimale haute fréquence : ordre limite versus ordre de marché De façon générale, lorsque qu un acteur désire acheter ou vendre un certains nombres de contrats sur un marché financier, il envoie à ce marché des ordres d exécution qui peuvent être soit des ordres marchés (market orders) qui sont automatiquement exécutés au meilleur prix disponible, soit des ordres limites (limit orders) qui restent dans le carnet d ordre jusqu au moment où ils sont mis en correspondance avec un ordre de marché. Ce choix (ordre de marché ou limite) implique un choix entre le risque de non exécution (et donc certainement une exécution plus coûteuse plus tard) et un coût à payer pour une exécution immédiate (typiquement de l ordre du bid-ask spread [1]). Dans ce projet, on vise à caractériser le choix optimal, tout d abord dans le cadre d un modèle spécifique pour la dynamique microstructurelle du carnet d ordre [2] puis dans le cadre de généralisations de ce modèle (notamment en modélisant les flux d ordres par des processus de Hawkes [3]). L essentiel du travail sera réalisé sur des données réelles sur lesquelles les paramètres des modèles seront estimés. [1] Madhavan, A, Market microstructure : A survey, Journal of Financial Markets Vol. 3, No 3, [2] Cont, R. and De Larrard, A., Price dynamics in a Markovian limit order market SIAM Journal on Financial Mathematics, Vol. 4, No 1, 2013 [3] Hawkes, A.G., Point spectra of some mutually exciting point processes, J. R. Statist. Soc. B, Vol. 33,
25 2.21 Estimation du Market impact à partir de données haute fréquences L estimation de la courbe de market impact d un meta-ordre (ordre composé de plusieurs petits ordres) est essentielle dans la problématique d exécution optimale. Il s agit de quantifier, la variation moyenne du prix à partir du début de l exécution de ce meta-ordre. Cette courbe présente généralement deux phases : une phase ascendante où le prix monte (dans le cas d un ordre d achat) et, dès que l exécution du meta-ordre est fini, une phase de relaxation. L estimation, généralement obtenue à l aide de données clients (pour identifier le meta-ordre), est excessivement difficile et bruitée. Des modèles (processus ponctuels) de prix et flux d ordres haute fréquence sur des données de marché (anonymes) peuvent être utilisées pour stabiliser grandement cette estimation. Dans le cadre de ce projet, les modèles à base de processus ponctuels auto-excitants seront étudiés. [1] A.G. Hawkes, Point spectra of some mutually exciting point processes, Biometrika, 58 (1971), pp [2] Bershova, N. and Rakhlin, D., The Non-Linear Market Impact of Large Trades : Evidence from Buy-Side Order Flow., Social Science Research Network Working Paper Series [3] E. Bacry, J.F. Muzy, Hawkes model for price and trades high-frequency dynamics Quantitative Finance Vol. 14, Iss. 7, Estimation haute fréquence de la volatilité, application au trading d options Dans cet EA, on se placera dans la situation d un trader haute fréquence souhaitant faire de l arbitrage sur options. L idée est de détecter les anomalies de valorisation en comparant prix d options et mesures de volatilité. On montrera dans un premier temps que le cadre usuel d une modélisation brownienne est insuffisant dans ce contexte de données haute fréquence. On s appuiera ensuite sur différentes extensions de ce cadre pour modéliser la microstructure des marchés et construire des stratégies de trading. [1] Y. Aït-Sahalia, P. A. Mykland, L. Zhang, A tale of two time scales : Determining integrated volatility with noisy high frequency data, JASA 77, 100(472), , [2] F. G. Bandi, J. R. Russell, C. Yang, Realized volatility forecasting and option pricing, Journal of Econometrics, 147(1), 34-46, [3] O. E. Barndorff-Nielsen, P. Hansen, A. Lunde, N. Shephard, Designing realised kernels to measure the ex-post variation of equity prices in the presence of noise, Econometrica,
26 2.23 Corrélation haute fréquence, application au market impact Bien que la présence de corrélations haute fréquence soit un consensus de marché et que de nombreuses stratégies en place (comme le pair trading) optimisent un critère multi-titres, la mesure et l exploitation des dépendances entre les variations des prix de deux titres ont été peu explorées. On montrera tout d abord que, même dans le cadre brownien, la simple asynchronicité des prix (les transactions n ont pas lieu aux mêmes instants pour deux actifs différents) explique en partie l effet Epps, c est à dire une estimation haute fréquence des corrélations systématiquement proche de zéro. On montrera comment corriger cet effet puis on tentera de résoudre le problème dans un cadre plus réaliste, permettant de reproduire les effets de microstructure des marchés. On appliquera les résultats obtenus à l optimisation de la vente d un portefeuille d actifs. [1] R. Almgren, N. Chriss, Optimal execution of portfolio transactions, J. Risk 3, 5-39, [2] T. Hayashi, N. Yoshida, On covariance estimation of non-synchronously observed diffusion processes, Bernoulli 11(2), , [3] L. Zhang, Estimating covariation : Epps effect, microstructure noise, Journal of Econometrics, 160(1), 33-47,
27 3 Optimisation et recherche opérationnelle Enseignant référent : Xavier Allamigeon xavier.allamigeon@inria.fr 3.1 Preferential Bidding Systems pour les pilotes Rémi Pacqueau (repacqueau@airfrance.fr), Air France Benoit Robillard, Air France Dans le cadre de la construction des plannings des pilotes, la plupart des compagnies aériennes se sont dotées de systèmes permettant aux pilotes d exprimer des souhaits ou préférences sur leurs plannings (destination, période de repos, type d activités, etc.). L un des plus utilisés se nomme PBS (Preferential Bidding System), dont l objectif est de satisfaire au mieux les pilotes ordonnés par priorité, sous contrainte de pouvoir opérer tous les vols et de respecter la réglementation. L objectif de l EA sera d étudier les différentes techniques permettant de résoudre le problème du PBS et d en implémenter une ou plusieurs sur un cas simplifié. 3.2 Construction de grilles horaires pour le personnel au sol Marine Le Touze (maletouze@airfrance.fr), Air France Au sein d Air France, la plupart des agents de piste (bagagistes) et de passage (embarquement / enregistrement) ont leurs horaires de travail régis par un système de grilles horaires. Celles-ci consistent en des patterns réguliers de prise et de fin de service, reproduits de manière cyclique tout au long de l année. La problématique de construction des grilles horaires est un enjeu majeur pour les gestionnaires de ressources, puisqu ils doivent couvrir au mieux une charge non lissée (plus d activité aux horaires de pointe) avec un coût pour l entreprise minimum. L objectif de l EA sera d étudier les différentes techniques permettant de résoudre le problème de la construction de grille horaire et d en implémenter une ou plusieurs sur un cas simplifié. 3.3 Affectation optimale des numéros de vol Mathieu Sanchez (masanchez@airfrance.fr), Air France Yousra Tourki, Air France Dans un contexte de développement des partenariats avec d autres compagnies et de croissance de l offre, il est nécessaire pour Air France d optimiser l utilisation des numéros de vol disponibles pour ses vols en propre et pour les partages de code avec ses partenaires. Ces numéros de vols sont définis par quatre chiffres et leur utilisation est limitée par IATA afin d éviter par exemple toute confusion dans la communication entre le contrôleur aérien et le commandant de bord. Ainsi les 27
28 numéros de vol sont soumis à des règles du type «tous les numéros sont différents à une permutation près sur une plage horaire donnée». L objectif de l EA est de proposer une solution pour optimiser les plages de numéros de vol, d en libérer pour des partages de code tout en considérant les règles IATA et des critères de stabilité par rapport à leur utilisation actuelle. 3.4 Optimisation de l affectation temps réel des trafics dans un contexte de réseau d accès mobile multi-technologies (2G/3G/LTE) Mustapha Bouhtou (mustapha.bouhtou@orange.com), Orange Labs Recherche Les terminaux mobiles actuels (smartphones) sont équipés d interfaces leurs permettant d accéder à plusieurs types de réseaux d accès disponibles (2G, 3G, LTE, WIFI,...). Les usagers peuvent donc se connecter au réseau d accès leur offrant la meilleure connectivité dans la limite de leurs contrats. Cela pourrait à certains endroits et certaines périodes induire des surcharges importantes sur un réseau d accès particulier avec une dégradation de la qualité de service pour les clients. Dans ce contexte, se pose alors la question de comment bien répartir de façon dynamique le trafic des clients d un opérateur entre ces différents réseaux d accès disponible. L objectif étant de permettre à chaque terminal de pouvoir automatiquement se connecter au bon réseau au bon moment et au bon endroit. Les préférences à la fois des utilisateurs et de l opérateur sont à considérer. Dans cet EA on essaiera de modéliser et simuler la dynamique d affectation des flux de trafic en temps réel aux différents réseaux d accès, d étudier l optimisation du système global et de proposer des algorithmes pour le résoudre. Le cas de plusieurs services, avec plusieurs profils de clients sera abordé. Les contraintes sur la mobilité des clients devra aussi être traitée. 3.5 Modélisation de l optimisation de la qualité d expérience pour les services de vidéo streaming dans les réseaux mobiles Mustapha Bouhtou (mustapha.bouhtou@orange.com), Orange Labs Recherche Aujourd hui les terminaux mobiles sont de plus performants en termes de puissance de calcul, de mémoire, de taille et de la qualité de l écran. Ces performances ont aussi fortement stimulé la demande de services multimédias notamment le service de vidéo streaming. Les clients sont aussi de plus en plus exigeants quant à la qualité rendue et perçue sur ce type de service. Optimiser la qualité d expérience (QoE) des clients sur les services de vidéo streaming est pour cela un enjeu important pour les opérateurs. Le problème de la modélisation de la QoE a déjà été abordé dans la littérature. Dans ce projet on s intéressera particulièrement à une modélisation basée sur des processus stochastiques (chaines de Markov) pour 28
29 prendre en compte la dynamique des arrivées des clients sur le réseau mais aussi celle des flux de trafics que génèrent leurs demandes en services de streaming. On étudiera comment introduire un critère d optimisation dans cette modélisation et on traitera ensuite comment le résoudre. Des tests numériques seront à effectuer et les résultats devront être comparés à ceux de la simulation. 3.6 Distribution de contenus vidéos Eric Gourdin (eric.gourdin@orange.com), Orange Labs OMN/NMP/TRM Contexte Télécom. Le développement considérable d applications multimédias (réseaux sociaux, virtualisation des données et des applications, jeux en lignes,...) conduit les principaux acteurs de l Internet à optimiser de plus en plus les infrastructures pour la diffusion de contenus vidéos, que ce soit les vidéos visionnées en «streaming» délinéarisé ou en live. Pour les contenus live, un très grand nombre de clients souhaitant visionner simultanément le contenu, l infrastructure réseau doit être soigneusement optimisée de manière à éviter de repliquer inutilement des flux ou à mal utiliser les ressources en bande passante. Problématique de distribution de contenus vidéos. On s intéresse au problème qui consiste à définir une architecture permettant de diffuser simultannément un flux vidéo, depuis un serveur origine (source) vers un ensemble de clients (terminaux). On modélise le réseau par un graphe orienté G = (V, A) où V est l ensemble des noeuds et A l ensemble des arcs. On note C a la capacité (débit maximum) de l arc a A. On suppose qu un ensemble C V de clients souhaitent accéder simultanément au même contenu vidéo (vidéo live). Pour cela, on utilise un protocole multicast [1] qui permet à un noeud intermédiaire de répliquer un flux vidéo entrant vers plusieurs arcs en sortie. Le flux vidéo s écoule donc, depuis la source vers les clients, sur un arbre (ou plutôt une arborescence) multicast. Une première question qui se pose est de définir le «meilleur» arbre possible. Une façon de qualifier l arbre multicast est de mesurer le débit maximum qu il permet d écouler, entre la source et les clients : si on suppose qu on écoule un débit d sur l arbre T A, alors le débit maximum est donné par max T T (s,c) min a T C a, où T (s, C) désigne l ensemble des arbres de racine s et couvrant les clients C. Ce problème (P1) consiste à chercher un arbre bottleneck et il peut être calculé en temps polynomial [2]. Pour améliorer le débit offert, on peut choisir d utiliser plusieurs arbres en parallèle, le débit total entrant d étant fractionner sur les différents arbres. La contrainte de capacité sur les arcs impose alors que la somme des débits des différents arbres passant par a soit inférieur à C a. Le problème (P2) consistant à calculer ce débit maximum est un Fractional Steiner Tree Packing problem [3] qui est difficile, la plupart du temps. En pratique, l opérateur réseau préfère ne pas avoir à gérer trop d arbres multicast en parallèle (pour la complexité de gestion et les limitations des équipements). On peut donc s intéresser au même problème, mais en limitant le nombre d arbres 29
30 multicast (P3). On peut aussi envisager une solution où l on utilise des arbres multicast «partiels», c est-à-dire ne couvrant qu un sous-ensemble de terminaux. L objectif est alors d utiliser plusieurs arbres partiels, de manière à ce que chaque client recoive le même débit et que ce débit soit maximal (P4). Enfin, comme tous les noeuds du réseaux ne sont pas nécéssairement pourvus de la fonctionalité de réplication multicast, on peut ne considérer, dans les problèmes ci-dessus, que les arbres où les noeuds de degré sortant supérieur (ou égal) à 2 sont des noeuds multicast (P5). Travail attendu et extensions possibles. Le travail de cet EA consistera à s inspirer des modèles existants dans la litérature pour les problèmes (P1) et (P2) pour proposer des modélisations pour les extentions (P3), (P4) et (P5). On s intéressera également, pour chaque problème considéré, à sa complexité et au liens éventuels entre les modèles. Finalement, on proposera au moins une méthode de résolution pour l un des problèmes étendus que l on testera numériquement sur quelques instances de réseaux typiques (par ex. [1] L. Sahasrabuddhe and B. Mukherjee. Multicast routing algorithms and protocols : A tutorial. IEEE Networks, 14 :90 102, [2] L. Georgiadis. Bottleneck multicast trees in linear time. IEEE Commun. Lett., 7, no. 1 : , Sep [3] K. Jain, M. Mahdian, and M. R. Salavatipour. Packing steiner trees. In In Proc. SODA 03 Proceedings of the fourteenth annual ACM-SIAM symposium on Discrete algorithms, Conception d un réseau de caches Eric Gourdin (eric.gourdin@orange.com), Orange Labs OMN/NMP/TRM Contexte Télécom. La demande toujours plus importante en contenus vidéos délinéarisés (UGC, Web TV, replay,...) oblige les acteurs de l Internet á optimiser le placement et la réplication des contenus dans le réseau de distribution. L un des équipements les plus utilisés dans la conception d architectures de distributions de contenus (CDN pour Content Delivery Network) est le cache. Un cache est un serveur déployé dans le réseau et équipé d un espace de stockage qui stocke de manière temporaire les contenus qui font l objet d une requète par un ou plusieurs clients. Plus précisément, une requète pour un contenu d un client «proche» est aiguillée vers le cache par un proxy. Si le contenu est déjà stocké par le cache, celui-ci le renvoie directement au client. Si le contenu n est pas présent dans le cache, celui-ci va le récupérer depuis un serveur central distant qui stocke tous les contenu. Au passage, le cache en stocke une copie dans son espace de stockage. Le principal paramètre qui va jouer sur l efficacité du cache est sa politique de remplacement : il s agit de l algorithme qui va permettre au cache de décider quel contenu supprimer lorsque son espace de stockage est plein et qu il a un nouveau 30
31 contenu a stocker. Parmi les politiques de remplacement les plus utilisées, on peut citer LRU (Least Recently Used) qui supprime le contenu ayant la plus ancienne requète de lecture, FIFO ou même random (choix aléatoire du contenu). La performance d un cache se mesure par son hit ratio qui est la proportion de requètes auxquelles il peut répondre à partir d un contenu stocké dans sa mémoire. Le hit ratio pour un cache donné va dépendre de la loi de distibution des arrivées de requètes, de la taille de son espace de stockage et de sa politique de remplacement. Il y a eu de nombreux travaux autour des caches et, en particulier, pour analyser la performance de caches utilisant telle ou telle politique de remplacement [1, 2]. Ces travaux sont fortement basés sur les hypothèse faites concernant la distribution des arrivées de requêtes. Pour les contenus vidéos dans l Internet, il est communément admis que les requêtes suivent une distribution en loi de puissance (l essentiel des requêtes est concentré sur un très petit nombre de vidéos), de type Zipf ou I-Weibull (p i = η exp( αi β )). Problématique de localisation de caches. On s intéresse au problème qui consiste à définir une architecture permettant de diffuser de manière optimale des contenus vidéos, depuis un serveur origine (source) vers un ensemble de clients (terminaux). On modélise le réseau par un graphe orienté G = (V, A) où V est l ensemble des noeuds et A l ensemble des arcs. On suppose qu on connait la loi de distribution des requêtes moyennes des clients pour les différents contenus et on note C V l ensemble des clients. On suppose que tous les contenus sont stockés sur un serveur central S V. Le problème consiste à décider sur quels noeuds du réseau on va installer un cache de manière à servir au mieux les clients tout en minimisant un budget B. Dans le budget, on comptera le coût individuel c i de chaque cache installé en i mais aussi le bénéfice obtenu en terme d utilisation de la bande passante (le contenu caché en i ne nécéssite pas d être envoyé depuis le serveur central). Le problème peut s assimiler en partie à un problème de localisation avec des constraintes additionnelles spécifiques au contexte réseau [3, 4, 5]. Ce dernier modèle fait l hypothèse que le hit ratio h [0, 1] est connu à l avance et détermine donc la quantité de trafic qui sera servie par chaque cache. Cette hypothèse n est malheureusement pas très réaliste dans la mesure où le hit ratio qui sera effectivement observé au niveau de chaque cache dépend de sa localisation et de l ensemble des requêtes qui lui seront affectées (donc du résultats du problème d optimisation). Travail attendu et extensions possibles. Le travail de cet EA consistera à analyser les modèles étudiés dans la litérature et proposer des extensions ou des variantes pour mieux prendre en compte l aspect dynamique du hit ratio. On testera le modèle proposé sur quelques instances de réseaux typiques (par ex. de). [1] Dan Asit and Don Towsley. An approximate analysis of the lru and fifo buffer replacement schemes. SIGMETRICS Perform. Eval. Rev., 18(1) : , [2] Erol Gelenbe. A unified approach to the evaluation of a class of replacement 31
32 algorithms. IEEE Trans. Comput., 22(6) : , [3] S. L. Hakimi. Optimum locations of switching centers and the absolute centers and medians of a graph. Operations Research, 12 : , [4] S.L. Hakimi and E.F. Schmeichel. Locating replicas of a database on a network. Networks, 30(1) :31 36, [5] P. Krishnan, Danny Raz, and Yuval Shavitt. The cache location problem. IEEE/ACM Transactions on Networking, 8(5) : , Feasibility Recovery Algorithms for The Unit Commitment Problem of Interconnected Hydro Plants Claudia D Ambrosio (dambrosio@lix.polytechnique.fr), CNRS & LIX, École Polytechnique Raouia Taktak (taktak@lix.polytechnique.fr), LIX, École Polytechnique We aim at investigating the computational complexity of the optimization problem that identifies the best unit commitment (UC) of interconnected hydro plants by minimizing the production cost. The UC is a crucial problem in energy management, see [1], and the presence of combinatorial elements leads to hard hydro valley problems. This is especially true for some of the larger French Hydro valleys. Typical approaches like relaxing the combinatorial aspects and rounding the fractional value don t work and lead to infeasible solutions. A feasibility recovery algorithm is needed so as to find a good quality solution starting from an infeasible solution of the problem. Moreover, this type of algorithm can be useful also in the context of decomposition methods. In [2], the authors propose a genetic algorithm with a recovery phase to deal with infeasibility for the thermal UC problem. Interest of this project is survey the state-of-the-art of UC of feasibility recovery algorithm, develop, and compare them with new ideas to find good quality solutions for hard hydro valleys problems in the context of rounding techniques or decomposition methods. [1] G. Hechme-Doukopoulos, S. Charousset-Brignol, J. Malik, C. Lemarechal. The short-term electricity production management problem at EDF, OPTIMA 84, pp. 2-6, [2] J.M. Arroyo and A.J. Conejo. A parallel repair genetic algorithm to solve the unit commitment problem, IEEE Transactions on Power Systems, 17(4), pp , Optimisation du processus de réception et de traitement des appels d urgence bornes pire des cas Stéphane Gaubert (Stephane.Gaubert@inria.fr), INRIA École Polytechnique 32
33 Le but de cet EA est d étudier un problème d évaluation de performance, posé par la brigade des Sapeurs Pompiers de Paris et sa tutelle (la Préfecture de Police), concernant la nouvelle organisation du centre d appel situé à l État Major de la BSPP (Porte de Champeret). Il est prévu d intégrer au sein d un même centre d appels le traitement des urgences relevant des pompiers (18) et celles relevant de la police (17), dans Paris et sa petite couronne. L une des motivations est le remplacement progressif des numéros d appels historiques spécialisés par un seul numéro identique pour les différents pays (112). La BSPP a bien évidemment défini un ensemble de mécanismes de traitement des appels basés sur des règles éprouvées. Elle souhaiterait une étude théorique des mécanismes possibles, en complément des études qu elle a déjà réalisées. Il s agit notamment de mieux prédire le comportement de la chaîne de réponse dans des situations anormales ou critiques, et le cas écheant de faire des propositions d amélioration de cette chaîne. Par exemple, une première difficulté à prendre en compte est le nombre d appels injustifiés ou redondants au 112 (qui a augmenté à cause de la facilité d alerte au moyen de téléphone portable). Ceci amène typiquement à avoir un traitement à deux étages, avec un premier filtrage, puis un traitement par un expert. Il s agit par exemple de savoir comment un tel système se comporterait dans une situation de violent orage urbain, avec une superposition de multiples appels sérieux mais peu critiques (innondations simples) et de vraies urgences plus rares, et de voir s il serait possible de quantifier le seuil de criticité au dela duquel une reconfiguration du système (pré-filtrage par automate associé à la mise en place d un numéro vert) deviendrait pertinent. Dans cet EA, on se propose de partir du modèle de logigrammes de la BSPP, de le décliner en réseau de Petri (par exemple), de l affiner si nécessaire, et d obtenir si possible des bornes rigoureuses sur la qualité de service, en s attachant particulièrement à un modélisation «pire des cas». Une piste de modélisation envisagée est le «calcul d enveloppe» dans les réseaux, ou «network calculus». Il s agit d une collection d outils analytiques, qui, supposant des bornes déterministes sur les arrivées, permettent de calculer des bornes sur les temps de service où les débits. On pourra aussi utiliser des outils de programmation linéaire ou des modèles de jeux à somme nulle. La masse de données statistiques dont dispose la BSPP sera accessible pour cette étude. Des contacts pour ce sujet seront le Cdt Stéphane Raclot (BSPP) ainsi que Régis Reboul (Préfecture de Police de Paris). Vu l importance du sujet et ses prolongements potentiels, outre le responsable d EA, d autres chercheurs du CMAP impliqués dans la collaboration avec la BSPP (M. Akian, X. Allamigeon), ainsi qu un doctorant, Vianney Boeuf (ENPC, CMAP et INRIA), pourront être associés à l encadrement. Ce sujet demandera des déplacements à la BSPP. On se propose de traiter ce thème par 2 binômes d EA au lieu d un (soit 4 élèves en tout). Un binôme traitera particulièrement l analyse du comportement pire des cas, par des méthodes déterministes, c est ce travail qui est décrit dans la présente section («pire des cas»). L autre binôme s attachera à développer un modèle 33
34 stochastique, comme décrit dans la section suivante («étude probabiliste»). Nota bene. Cet EA sera couvert par une convention entre la Préfecture de Police/BSPP et l École Polytechnique. Vu la nature du travail projeté, cette convention ne peut concerner que des élèves de nationalité française. [1] C.-S. Chang : Performance Guarantees in Communications Networks, Springer, [2] J.-Y. Le Boudec and P. Thiran : Network Calculus : A Theory of Deterministic Queuing Systems for the Internet, Springer, LNCS, [3] A. Bouillard, Algorithms and efficiency of network calculus, habilitation thesis, Optimisation du processus de réception et de traitement des appels d urgence étude probabiliste Stéphane Gaubert (Stephane.Gaubert@inria.fr), INRIA École Polytechnique Philippe Robert (Philippe.Robert@inria.fr), INRIA École Polytechnique Cet EA porte sur le même thème général que l EA précédent auquel on renvoie, et s effectuera dans des conditions semblables. À la différence de l EA précédent (analyse pire des cas), celui-ci portera sur la modélisation probabiliste de la chaîne de réponse, et fera donc appel à la fois aux outils du cours «Recherche Opérationnelle» et à ceux du cours «Réseaux de communication». On cherchera ici à effectuer une étude probabiliste, en modélisant la chaîne de réponse aux appels par un réseau de files d attentes, afin d évaluer des paramètres de performance tels que les temps d attente ou le débit maximal de la chaîne de traitement. Nota bene. Cet EA sera couvert par une convention entre la Préfecture de Police/BSPP et l École Polytechnique. Vu la nature du travail projeté, cette convention ne peut concerner que des élèves de nationalité française Des systèmes biologiques à la géométrie tropicale Xavier Allamigeon (Xavier.Allamigeon@inria.fr), INRIA École Polytechnique Stéphane Gaubert (Stephane.Gaubert@inria.fr), INRIA École Polytechnique L étude des systèmes biologiques amène à considérer de grands réseaux de réactions biochimiques, gouvernés par des équations différentielles ordinaires dont le second membre est un terme polynomial dans lequel apparaissent les concentrations des différentes espèces. On cherche à étudier ces systèmes d un point de vue structurel : les coefficients de ces systèmes sont en général mal connus, et l on s intéresse plutôt à des propriétés de nature plus qualitatives, robustes par perturbation des paramètres, telles que l existence d un point fixe, la convergence des 34
35 orbites vers une sous-variété, etc. Ceci amène à résoudre des problèmes de nature algébrique portant sur de gros systèmes d équations polynomiales sur les réels. Ces derniers ont été très recemment abordés via la géométrie tropicale. Celle-ci regarde l ensemble des solutions d un système d équations polynômiales avec des «lunettes logarithmiques». L image d un tel ensemble par ces lunettes est appelé amibe archimédienne, on sait, au moins dans de bons cas, qu il est «proche» d un complexe polyédral (variété tropicale) qui peut être déterminé directement de manière combinatoire (sans avoir à résoudre les équations polynômiales, mais de manière parfois coûteuse). Intuitivement, cette méthode formalise la démarche consistant à effectuer des hypothèses sur les ordres de grandeur des concentrations, et à les vérifier à posteriori. Ceci motive l étude des variétés tropicales réelles et plus généralement des ensembles semi-algébriques tropicaux, qui sont définis par des système d inégalités sur le vecteur x R n de la forme : max α S (c α + α x) max β T (c β + β x) où S, T N n sont des ensembles disjoints, et c α, c β R { }. Dans cet EA, on s intéresse à la conception de techniques permettant de déterminer si un tel système admet une solution ou non. On propose d aborder ce problème par l introduction de variables de relèvement associées à chaque terme α x, et d exprimer l ensemble des solutions du système comme une intersection de polyèdres convexes au sens usuel et au sens tropical. Plusieurs algorithmes existent pour manipuler ces deux types de polyèdres. L objectif de l EA est d étudier comment les combiner afin d obtenir des méthodes effectives sur les semi-algébriques tropicaux. On peut penser pour cela à des stratégies de pivotage dans des complexes polyédraux, ou bien à des algorithmes à base de projection cyclique. [1] Martin Avendano, Roman Kogan, Mounir Nisse, and J. Maurice Rojas. Metric estimates and membership complexity for archimedean amoebae and tropical hypersurfaces, arxiv: [2] O. Radulescu, A. N. Gorban, A. Zinovyev, and V. Noël. Reduction of dynamical biochemical reaction networks in computational biology. Frontiers in Genetics. To appear, available from [3] H. Attouch, J. Bolte, P. Redont, and A. Soubeyran. Proximal Alternating Minimization and Projection Methods for Nonconvex Problems : An Approach Based on the Kurdyka-Lojasiewicz Inequality, Mathematics of Operations Research, vol. 35, n 2, mai 2010, p doi : /moor Bases de Graver pour l optimisation entière Xavier Allamigeon (Xavier.Allamigeon@inria.fr), INRIA École Polytechnique De nombreux problèmes de recherche opérationnelle conduisent à optimiser une fonction, linéaire ou non, sur l ensemble des points entiers d un polytope. Ces 35
36 problèmes sont en général NP-difficiles. Pour les résoudre, on recourt souvent à des techniques qui consistent intuitivement à explorer de manière efficace l ensemble des points entiers (par exemple branch-and-bound). On s intéresse ici à une technique très différente, de nature algébrique, qui se fonde sur les bases de Graver [1, 2]. Etant donné un point entier d un polytope et une fonction objectif, la base de Graver associée fournit une direction d amélioration vers un autre point entier du polytope, ou certifie que le premier point est optimal. C est pourquoi les bases de Graver sont utilisées dans des algorithmes dits «d augmentation». Ceux-ci consistent en la répétition de plusieurs étapes d amélioration de la fonction objectif jusqu à atteindre un optimum. L intérêt des bases de Graver est que l on peut borner polynomialement le nombre d étapes d amélioration [3]. L inconvénient est que ces bases sont difficiles à calculer, car elles peuvent contenir beaucoup d éléments. On se propose dans cet EA d étendre ces algorithmes à des problèmes d optimisation avec un très grand nombre de contraintes. L objectif est en particulier de définir une méthode calculant de manière incrémentale les bases de Graver, par ajout successif de coupes. L idée sous-jacente est que seul un petit nombre de coupes peut suffire pour déterminer un optimum pour le problème d optimisation complet. L EA comprendra également une implémentation de cette technique, et des expérimentations sur des problèmes d optimisation en nombres entiers de grande taille. [1] Jesús A. De Loera, Raymond Hemmecke, Matthias Köppe, Algebraic and Geometric Ideas in the Theory of Discrete Optimization. MOS-SIAM Series on Optimization. [2] Shmuel Onn, Nonlinear Discrete Optimization. Zurich Lectures in Advanced Mathematics, European Mathematical Society. ~onn/book/ndo.pdf [3] Jesús A. De Loera, Raymond Hemmecke, Jon Lee, Augmentation Algorithms for Linear and Integer Linear Programming. arxiv: Falsifier formellement la conjecture de Hirsch Xavier Allamigeon (Xavier.Allamigeon@inria.fr), INRIA École Polytechnique Le diamètre d un polyèdre est défini comme la distance maximale entre deux sommets du polytope par des chemins ne passant que par des arêtes. Cette notion revêt une importance toute particulière en optimisation car elle est notamment reliée à la complexité de l algorithme du simplexe (question encore ouverte et très regardée dans le cadre du 9 ème problème de Smale). Hirsch avait conjecturé en 1957 que le diamètre d un polytope de dimension d avec n faces était borné par n d. En 2009, Francisco Santos a réussi la prouesse de trouver un contre-exemple à cette conjecture [1]. 36
37 L EA s inscrit dans un projet qui vise à prouver formellement que le polytope trouvé par Santos est bien un contre-exemple. La preuve formelle consiste à démontrer des résultats mathématiques à l aide d outils informatiques, les assistants de preuve. L intérêt est d élever très significativement le niveau de confiance en les preuves. Par exemple, l assistant de preuve Coq [2, 3] s est illustré dans la preuve du théorème des quatres couleurs, ou plus récemment du théorème de Feit et Thompson. Afin de falsifier formellement la conjecture de Hirsch, il est nécessaire de fabriquer une preuve différente de celle de Santos. Certains assistants de preuve comme Coq se fondent en effet sur des logiques dans lesquelles les résultats doivent être montrés de manière constructive. Cependant, on peut se permettre de construire une preuve très longue et calculatoire, impossible à vérifier par un humain en pratique, mais tout à fait abordable pour une machine. L objet de cet EA est en premier lieu d étudier comment écrire une telle preuve du contre-exemple de Santos, ce qui nécessite de bien comprendre la théorie des polytopes. En parallèle, l EA comprendra un développement des différents éléments de la preuve en Coq. [1] Francisco Santos, A counterexample to the Hirsch conjecture, Ann. Math., vol. 176, no 1, 2012, p [2] The Coq Proof Assistant, [3] Yves Bertot, Pierre Castéran. Coq Art : The Calculus of Inductive Constructions Planification de tournées de techniciens Bayram Kaddour (bayram.kaddour@edf.fr), EDF R&D La planification des tournées d interventions des techniciens du gestionnaire du réseau de distribution électrique représente chaque année un enjeu important en termes d agents et matériels mobilisés et de kilomètres parcourus. Cette planification est élaborée en plusieurs étapes coordonnées dans le temps et résumées ci-après (le projet se focalisera sur l axe 3) : 1. La planification stratégique est l optimisation du placement de sites. 2. La planification tactique est le découpage des zones d intervention des agents dans l optique d optimiser les tournées. 3. La planification opérationnelle est la détermination des tournées journalières d interventions des techniciens d une agence de conduite régionale. Cette planification vise à satisfaire les demandes d interventions reçues (changement de puissance souscrite, rétablissement des coupures,...) en fonction de plusieurs critères (distances à parcourir, matériel à prendre dans le véhicule de l agent en début de journée, qualifications de l agent pour effectuer les interventions,...). 4. La planification en temps réel est l ajustement du planning d interventions des techniciens en tournée suite à des aléas (annulation d un client, intempéries, embouteillages,...). 37
38 4 Réseaux de communication Enseignant référent : Philippe Robert philippe.robert@inria.fr 4.1 Stochastic Models of Algorithms for Data Centers Philippe Robert Philippe.Robert@inria.fr Some 96% of current Internet traffic is currently generated by users retrieving content of one form or another, according to Cisco Visual Networking Forecasts in 2011, it is decomposed as follows. UGC stands for User Generated Content (example Youtube videos), B is byte and VoD is Video on Demand. traffic share population mean object overall size size volume Web B B File sharing B B UGC B B VoD B B The data centers of the various operators of the Internet like Orange Labs, Google, Microsoft, Apple, Amazon,... have to be designed so that users can retrieve quickly the contents they propose. The easiest way of achieving this goal that is by installing in each country/region a memory with a copy of all possible contents so that users can access locally these contents. This solution is hardly possible for the moment. According to the numbers above, the architecture required should be composed of large number of memories whose size is of the order of the Peta-Byte (10 15 Bytes). Such a system is almost impossible for several reasons : the im plied costs and the complexity of managing multiple copies of a large number of contents. The solution which is used consists in using a local memory, a cache memory, for each region where the most popular contents are stored. When a requested content is not in the cache, it is retrieved in a distant server and, therefore, with some delay. In an architecture with a fixed cache memory, one has to define the policy to determine which contents are kept in the cache and to evaluate its performances : what is the miss ratio? i.e. the fraction of requested contents which are fetched in the distant server. It is assumed that the contents is a finite set of objects S = {1,..., N} and that contents are requested at random accoridng to some probability distribution (p i, 1 i N). This is the Independent Reference Model (IRM) which is used in most of the Markovian analyses. The recent evolutions of data centers (their increasing sizes of contents stored in particular) show that this architecture with one memory cache turns out to have limited performances. The work proposed here consists in designing and analyzing with stochastic models an architecture where several cache memories for a hierarchical network with multiple access points. A simple ring network will be analyzed in a first step. The key quantity to investigate is the global miss ratio of 38
39 such a system at equilibrium. A stochastic model of such a system will be used : the Markov chain describing the contents of the various cache memories of the network. [1] Christine Fricker, Philippe Robert, and James Roberts, A versatile and accurate approximation for cache performance, 24th International Teletraffic Congress (Kraków), IEEE Communications Society, September [2] Phillipa Gill, Martin Arlitt, Zongpeng Li, and Anirban Mahanti, Youtube traffic characterization : a view from the edge, Proceedings of the 7th ACM SIG- COMM conference on Internet measurement (New York, NY, USA), IMC 07, ACM, 2007, pp [3] P. R. Jelenkovic, Approximation of the move-to-front search cost distribution and least-recently-used caching fault probabilities, Annals of Applied Probability 9 (1999), no. 2, Equilibrium states of stochastic neural networks Philippe Robert Philippe.Robert@inria.fr In this proposal, one investigates the dynamics of networks of connected excitatory and inhibitory integrate-and-fire neurons. The integrate-and-fire neuron model describes the state of a neuron in terms of its membrane potential, which is determined by the synaptic inputs and the injected current that the neuron receives. When the membrane potential reaches a threshold, an action potential (spike) is generated. It is believed that a rich repertoire of states are possible : synchronous states in which neurons fire regularly ; asynchronous states with stationary global activity and very irregular individual cell activity ; and states in which the global activity oscillates but individual cells fire irregularly, typically at rates lower than the global oscillation frequency. We propose to analyze through simulations and analytical models simple models of such networks. The model will be the following : a neuron with potential state x > 0 will spike at rate b(x) where b( ) is some non-decreasing function, after the spike its potential is 0 and the potential of its neighbors is increased by some random quantity with the same distribution as some random variable W. In a first step the simple case of a completely connected network with a constant functon b is considered, and in a second step a function b with a thereshold a 0. In a final step, the equilibrium states of grid topologies will be considered. 39
40 [1] Nicolas Brunel and David Hansel, How noise affects the synchronization properties of recurrent networks of inhibitory neurons., Neural computation 18 (2006), no. 5, [2] Erwan Ledoux and Nicolas Brunel, Dynamics of networks of excitatory and inhibitory neurons in response to time-dependent inputs., Frontiers in computational neuroscience 5 (2011). 4.3 Stochastic Models of Protein Production of Bacteria Cells Philippe Robert Philippe.Robert@inria.fr The gene expression is the process by which the genetic information is synthesised into a functional product, the proteins. The production of proteins is the most important cellular activity, both for the functional role and the high associated cost in terms of resources (in prokaryotic cells it can reach up to 85% of the cellular resources). In a E. Coli bacterium for example there are about proteins of approximately 2000 different types with a large variability in concentration, depending on their types : from a few dozen up to The gene expression is a highly stochastic process and results from the realization of a very large number of elementary stochastic processes of different nature. For example, the thermal excitation affects many processes, since it implies for example the random diffusion in the cytoplasm of the various components of the cell. One of the important questions is of understanding the mechanisms by which the cell manages to produce different types of proteins with different, fixed, concentrations. Due to random nature of the production process, the variance of the number of proteins in the cell is a key indicator for the efficiency of a production strategy, since it gives a measure of the fluctuation of resources of the cell consumed by the production process. The work proposed here consists in the analysis of a simple stochastic model describing the evolution of the number of proteins of different types. One will be interested in particular in the equilibrium properties of the fraction of the number of proteins of given type. Mathematically, in a first step, it will consist in the analysis of a sequence of simple Markov processes indexed by a scaling parameter which converges to infinity. One will investigate the asymptotic properties (as N and time go to infinity) of these processes. The second step will consider similar problems but in a more general setting where the key components of the production process are taken into account. 40
41 [1] J. Paulsson, Models of stochastic gene expression, Physics of Life Reviews 2 (2005), no. 2, [2] Peccoud, J. and Ycart, B. Markovian modeling of gene-product synthesis, Theoretical Population Biology 48 (1995), no. 2, [3] D. Rigney and W. Schieve, Stochastic model of linear, continuous protein synthesis in bacterial populations, Journal of Theoretical Biology 69 (1977), no. 4, Capacité des réseaux mobiles Philippe Robert Philippe.Robert@inria.fr Un réseau mobile est vu ici comme un ensemble de ressources distribuées géographiquement auxquelles des utilisateurs peuvent accéder sous réserve de proximité. Les capacités de calcul d un nœud sont attribuées de façon égalitaire à tous les mobiles de la zone géographique concernée. Un mobile utilise ainsi les ressources qui sont à sa disposition sur son parcours. Il est important de pouvoir estimer la capacité de calcul globale d un tel système, la mobilité permettant d utiliser éventuellement des nœuds peu chargés. On se propose dans cette étude d estimer les caractéristiques suivantes : Délais de transmission d un message dans un tel réseau. Étude de la stabilité du réseau (débit maximal de sortie). Conception d algorithmes d allocation de bande passante dans un tel réseau. P.R. Jelenkovic and P. Momcilovic and M. S. Squillante. Scalability of wireless networks http ://comet.columbia.edu/ predrag/mypub/wirelessscaling2006.pdf M. Grossglauser and D. Tse Mobility increases the capacity of ad-hoc wireless networks. http ://citeseer.ist.psu.edu/article/grossglauser01mobility.html 41
42 5 Traitement du signal et de l image Enseignant référent : Stéphanie Allassonnière stephanie.allassonniere@polytechnique.edu 5.1 Synthèse additive : Analyse, resynthèse et transformation de signaux musicaux Emmanuel Bacry emmanuel.bacry@polytechnique.edu La synthèse additive" de signaux sonores consiste à modéliser un signal par un ensemble de générateurs sinusoïdaux (appelés partiels) dont l amplitude et la fréquence varient en fonction du temps. Afin d obtenir, à chaque instant, les paramètres de chacun des partiels, le signal est analysé à l aide d une transformation de Fourier à fenêtre glissante. On étudiera ce type d analyse/synthèse dans le cadre de signaux musicaux et l on s attachera plus particulièrement à l étude des algorithmes de suivi" des partiels en fonction du temps. On s intéressera aux transformations que permettent ce type de représentation : soustraction de la partie harmonique d un signal (utilisation ultérieure pour un instrument synthétique hybride), dilatation/contraction temporelle sans modification du timbre (recalage d une partie rythmique), ajustement de la hauteur d un son sans modification de timbre (correction d un chanteur qui chante faux, ou harmonisation d une ligne mélodique),... C est un modèle extrèmement populaire, il existe de très nombreuses extensions. [1] Speech Analysis/Synthesis based on a sinusoidal representation, R.J. McAulay et T.F. Quatieri, IEEE Trans. on Acoustics, Speech and Signal Proc. Vol. ASSP-34, No 4, [2] Musical signal processing in Studies on New Music Research, X. Serra, editors Swets and Zeitlinger, 1997 [3] Sinusoidal Modeling, Summer 2006 lecture on analysis, modeling and transformation of audio signals, A. Robel, 2006, available at ircam.fr/anasyn/roebel/amt_audiosignale/vl6.pdf 5.2 Segmentation : méthode déterministe ou aléatoire? Stéphanie Allassonnière stephanie.allassonniere@polytechnique.edu L idée de ce projet est de tester et comparer plusieurs méthodes de segmentation. La segmentation est l extraction d objets dans une image où cet objet n est pas seul (le plus simple des cas étant un objet sur un fond non informatif). Ces techniques sont très utilisée en imagerie médicale pour la détection d organe, et 42
43 l analyse de leur forme. Nous étudierons dans ce projet plusieurs méthodes de recalage : l une déterministe basée sur le gradient de l image et la seconde stochastique appelée le "Random walker". Figure 2 caption 5.3 Débruitage par non-local means Stéphanie Allassonnière stephanie.allassonniere@polytechnique.edu Le but de cet EA sera de comprendre les avantages de la méthode des Nonlocal means pour le débruitage d images. Lorque l on possède plusieurs fois la même image et que l on suppose que le bruit observé est additif gaussien, la loi des grands nombres nous assure que la moyenne empirique sera une image débruitée. Le problème est souvent qu il est impossible d avoir plusieurs copies de la même image. La méthode étudiée ici tient compte de la redondance de l information contenue dans une seule image pour débruiter toute la scène. Ceci pourra aussi être appliqué à des séquences de film pour sa restauration. Figure 3 caption 43
DIPLOME D'ETUDES APPROFONDIES EN ECONOMIE ET FINANCE THEORIE DES MARCHES FINANCIERS. Semestre d hiver 2001-2002
 Département d économie politique DIPLOME D'ETUDES APPROFONDIES EN ECONOMIE ET FINANCE THEORIE DES MARCHES FINANCIERS Semestre d hiver 2001-2002 Professeurs Marc Chesney et François Quittard-Pinon Séance
Département d économie politique DIPLOME D'ETUDES APPROFONDIES EN ECONOMIE ET FINANCE THEORIE DES MARCHES FINANCIERS Semestre d hiver 2001-2002 Professeurs Marc Chesney et François Quittard-Pinon Séance
Liste des notes techniques... xxi Liste des encadrés... xxiii Préface à l édition internationale... xxv Préface à l édition francophone...
 Liste des notes techniques.................... xxi Liste des encadrés....................... xxiii Préface à l édition internationale.................. xxv Préface à l édition francophone..................
Liste des notes techniques.................... xxi Liste des encadrés....................... xxiii Préface à l édition internationale.................. xxv Préface à l édition francophone..................
Hedging delta et gamma neutre d un option digitale
 Hedging delta et gamma neutre d un option digitale Daniel Herlemont 1 Introduction L objectif de ce projet est d examiner la couverture delta-gamma neutre d un portefeuille d options digitales Asset-Or-Nothing
Hedging delta et gamma neutre d un option digitale Daniel Herlemont 1 Introduction L objectif de ce projet est d examiner la couverture delta-gamma neutre d un portefeuille d options digitales Asset-Or-Nothing
 Les mathématiques de la finance Université d été de Sourdun Olivier Bardou olivier.bardou@gdfsuez.com 28 août 2012 De quoi allons nous parler? des principales hypothèses de modélisation des marchés, des
Les mathématiques de la finance Université d été de Sourdun Olivier Bardou olivier.bardou@gdfsuez.com 28 août 2012 De quoi allons nous parler? des principales hypothèses de modélisation des marchés, des
Probabilités III Introduction à l évaluation d options
 Probabilités III Introduction à l évaluation d options Jacques Printems Promotion 2012 2013 1 Modèle à temps discret 2 Introduction aux modèles en temps continu Limite du modèle binomial lorsque N + Un
Probabilités III Introduction à l évaluation d options Jacques Printems Promotion 2012 2013 1 Modèle à temps discret 2 Introduction aux modèles en temps continu Limite du modèle binomial lorsque N + Un
MATHS FINANCIERES. Mireille.Bossy@sophia.inria.fr. Projet OMEGA
 MATHS FINANCIERES Mireille.Bossy@sophia.inria.fr Projet OMEGA Sophia Antipolis, septembre 2004 1. Introduction : la valorisation de contrats optionnels Options d achat et de vente : Call et Put Une option
MATHS FINANCIERES Mireille.Bossy@sophia.inria.fr Projet OMEGA Sophia Antipolis, septembre 2004 1. Introduction : la valorisation de contrats optionnels Options d achat et de vente : Call et Put Une option
IdR Trading et Microstructure CA Cheuvreux. Charles-Albert Lehalle
 IdR Trading et Microstructure CA Cheuvreux Charles-Albert Lehalle 2010-2014 Crédit Agricole Cheuvreux Kepler Cheuvreux L objectif de cette IdR «trading et microstructure des marchés» est de stimuler la
IdR Trading et Microstructure CA Cheuvreux Charles-Albert Lehalle 2010-2014 Crédit Agricole Cheuvreux Kepler Cheuvreux L objectif de cette IdR «trading et microstructure des marchés» est de stimuler la
CURRICULUM VITAE. Directeur de thèse : Nizar Touzi, Ecole Polytechnique
 CURRICULUM VITAE Dylan Possamaï 26 ans 21, boulevard de Grenelle Célibataire 75015 Paris Nationalité française Mail : dylan.possamai@polytechnique.edu Tél : 06 33 87 38 88 FORMATION Doctorat de Mathématiques
CURRICULUM VITAE Dylan Possamaï 26 ans 21, boulevard de Grenelle Célibataire 75015 Paris Nationalité française Mail : dylan.possamai@polytechnique.edu Tél : 06 33 87 38 88 FORMATION Doctorat de Mathématiques
Finance, Navier-Stokes, et la calibration
 Finance, Navier-Stokes, et la calibration non linéarités en finance 1 1 www.crimere.com/blog Avril 2013 Lignes directrices Non-linéarités en Finance 1 Non-linéarités en Finance Les équations de Fokker-Planck
Finance, Navier-Stokes, et la calibration non linéarités en finance 1 1 www.crimere.com/blog Avril 2013 Lignes directrices Non-linéarités en Finance 1 Non-linéarités en Finance Les équations de Fokker-Planck
Mathématiques pour la finance Définition, Evaluation et Couverture des Options vanilles Version 2012
 Mathématiques pour la finance Définition, Evaluation et Couverture des Options vanilles Version 2012 Pierre Andreoletti pierre.andreoletti@univ-orleans.fr Bureau E15 1 / 20 Objectifs du cours Définition
Mathématiques pour la finance Définition, Evaluation et Couverture des Options vanilles Version 2012 Pierre Andreoletti pierre.andreoletti@univ-orleans.fr Bureau E15 1 / 20 Objectifs du cours Définition
Résumé des communications des Intervenants
 Enseignements de la 1ere semaine (du 01 au 07 décembre 2014) I. Titre du cours : Introduction au calcul stochastique pour la finance Intervenante : Prof. M hamed EDDAHBI Dans le calcul différentiel dit
Enseignements de la 1ere semaine (du 01 au 07 décembre 2014) I. Titre du cours : Introduction au calcul stochastique pour la finance Intervenante : Prof. M hamed EDDAHBI Dans le calcul différentiel dit
QUESTIONS D ENTRETIENS EN FINANCE DE MARCHE
 QUESTIONS D ENTRETIENS EN FINANCE DE MARCHE Le présent document est un recueil de questions, la plupart techniques, posées à des candidats généralement jeunes diplômés, issus d école d ingénieurs, de commerce
QUESTIONS D ENTRETIENS EN FINANCE DE MARCHE Le présent document est un recueil de questions, la plupart techniques, posées à des candidats généralement jeunes diplômés, issus d école d ingénieurs, de commerce
Options et Volatilité (introduction)
 SECONDE PARTIE Options et Volatilité (introduction) Avril 2013 Licence Paris Dauphine 2013 SECONDE PARTIE Philippe GIORDAN Head of Investment Consulting +377 92 16 55 65 philippe.giordan@kblmonaco.com
SECONDE PARTIE Options et Volatilité (introduction) Avril 2013 Licence Paris Dauphine 2013 SECONDE PARTIE Philippe GIORDAN Head of Investment Consulting +377 92 16 55 65 philippe.giordan@kblmonaco.com
PROJET MODELE DE TAUX
 MASTER 272 INGENIERIE ECONOMIQUE ET FINANCIERE PROJET MODELE DE TAUX Pricing du taux d intérêt des caplets avec le modèle de taux G2++ Professeur : Christophe LUNVEN 29 Fevrier 2012 Taylan KUNAL - Dinh
MASTER 272 INGENIERIE ECONOMIQUE ET FINANCIERE PROJET MODELE DE TAUX Pricing du taux d intérêt des caplets avec le modèle de taux G2++ Professeur : Christophe LUNVEN 29 Fevrier 2012 Taylan KUNAL - Dinh
Chaire FBF Marchés en Mutation
 Chaire FBF Marchés en Mutation Vers une refondation des risques en nance Ecole Polytechnique & Université d'evry Co-titulaires: N. El Karoui, M. Jeanblanc, N. Touzi Chaire présentée par Stéphane Crépey,
Chaire FBF Marchés en Mutation Vers une refondation des risques en nance Ecole Polytechnique & Université d'evry Co-titulaires: N. El Karoui, M. Jeanblanc, N. Touzi Chaire présentée par Stéphane Crépey,
TP1 Méthodes de Monte Carlo et techniques de réduction de variance, application au pricing d options
 Université de Lorraine Modélisation Stochastique Master 2 IMOI 2014-2015 TP1 Méthodes de Monte Carlo et techniques de réduction de variance, application au pricing d options 1 Les options Le but de ce
Université de Lorraine Modélisation Stochastique Master 2 IMOI 2014-2015 TP1 Méthodes de Monte Carlo et techniques de réduction de variance, application au pricing d options 1 Les options Le but de ce
Problèmes de crédit et coûts de financement
 Chapitre 9 Problèmes de crédit et coûts de financement Ce chapitre aborde un ensemble de préoccupations devenues essentielles sur les marchés dedérivésdecréditdepuislacriseducréditde2007.lapremièredecespréoccupations
Chapitre 9 Problèmes de crédit et coûts de financement Ce chapitre aborde un ensemble de préoccupations devenues essentielles sur les marchés dedérivésdecréditdepuislacriseducréditde2007.lapremièredecespréoccupations
Le modèle de Black et Scholes
 Le modèle de Black et Scholes Alexandre Popier février 21 1 Introduction : exemple très simple de modèle financier On considère un marché avec une seule action cotée, sur une période donnée T. Dans un
Le modèle de Black et Scholes Alexandre Popier février 21 1 Introduction : exemple très simple de modèle financier On considère un marché avec une seule action cotée, sur une période donnée T. Dans un
Théorie Financière 8 P. rod i u t its dé dérivés
 Théorie Financière 8P 8. Produits dit dérivés déié Objectifsdelasession session 1. Définir les produits dérivés (forward, futures et options (calls et puts) 2. Analyser les flux financiers terminaux 3.
Théorie Financière 8P 8. Produits dit dérivés déié Objectifsdelasession session 1. Définir les produits dérivés (forward, futures et options (calls et puts) 2. Analyser les flux financiers terminaux 3.
de calibration Master 2: Calibration de modèles: présentation et simulation d
 Master 2: Calibration de modèles: présentation et simulation de quelques problèmes de calibration Plan de la présentation 1. Présentation de quelques modèles à calibrer 1a. Reconstruction d une courbe
Master 2: Calibration de modèles: présentation et simulation de quelques problèmes de calibration Plan de la présentation 1. Présentation de quelques modèles à calibrer 1a. Reconstruction d une courbe
Modélisation aléatoire en fiabilité des logiciels
 collection Méthodes stochastiques appliquées dirigée par Nikolaos Limnios et Jacques Janssen La sûreté de fonctionnement des systèmes informatiques est aujourd hui un enjeu économique et sociétal majeur.
collection Méthodes stochastiques appliquées dirigée par Nikolaos Limnios et Jacques Janssen La sûreté de fonctionnement des systèmes informatiques est aujourd hui un enjeu économique et sociétal majeur.
Mesure et gestion des risques d assurance
 Mesure et gestion des risques d assurance Analyse critique des futurs référentiels prudentiel et d information financière Congrès annuel de l Institut des Actuaires 26 juin 2008 Pierre THEROND ptherond@winter-associes.fr
Mesure et gestion des risques d assurance Analyse critique des futurs référentiels prudentiel et d information financière Congrès annuel de l Institut des Actuaires 26 juin 2008 Pierre THEROND ptherond@winter-associes.fr
Les Obligations Convertibles (introduction)
 TROISIEME PARTIE Les Obligations Convertibles (introduction) Avril 2011 Licence Paris Dauphine 2011 Sommaire LES OBLIGATIONS CONVERTIBLES Sect 1 Présentation, définitions Sect 2 Eléments d analyse et typologie
TROISIEME PARTIE Les Obligations Convertibles (introduction) Avril 2011 Licence Paris Dauphine 2011 Sommaire LES OBLIGATIONS CONVERTIBLES Sect 1 Présentation, définitions Sect 2 Eléments d analyse et typologie
Méthodes de la gestion indicielle
 Méthodes de la gestion indicielle La gestion répliquante : Ce type de gestion indicielle peut être mis en œuvre par trois manières, soit par une réplication pure, une réplication synthétique, ou une réplication
Méthodes de la gestion indicielle La gestion répliquante : Ce type de gestion indicielle peut être mis en œuvre par trois manières, soit par une réplication pure, une réplication synthétique, ou une réplication
OPTIMISATION DE LA MAINTENANCE DES EQUIPEMENTS DE MANUTENTION DU TERMINAL A CONTENEURS DE BEJAIA (BMT)
 OPTIMISATION DE LA MAINTENANCE DES EQUIPEMENTS DE MANUTENTION DU TERMINAL A CONTENEURS DE BEJAIA (BMT) LAGGOUNE Radouane 1 et HADDAD Cherifa 2 1,2: Dépt. de G. Mécanique, université de Bejaia, Targa-Ouzemour
OPTIMISATION DE LA MAINTENANCE DES EQUIPEMENTS DE MANUTENTION DU TERMINAL A CONTENEURS DE BEJAIA (BMT) LAGGOUNE Radouane 1 et HADDAD Cherifa 2 1,2: Dépt. de G. Mécanique, université de Bejaia, Targa-Ouzemour
Filtrage stochastique non linéaire par la théorie de représentation des martingales
 Filtrage stochastique non linéaire par la théorie de représentation des martingales Adriana Climescu-Haulica Laboratoire de Modélisation et Calcul Institut d Informatique et Mathématiques Appliquées de
Filtrage stochastique non linéaire par la théorie de représentation des martingales Adriana Climescu-Haulica Laboratoire de Modélisation et Calcul Institut d Informatique et Mathématiques Appliquées de
De la mesure à l analyse des risques
 De la mesure à l analyse des risques Séminaire ISFA - B&W Deloitte Jean-Paul LAURENT Professeur à l'isfa, Université Claude Bernard Lyon 1 laurent.jeanpaul@free.fr http://laurent.jeanpaul.free.fr/ 0 De
De la mesure à l analyse des risques Séminaire ISFA - B&W Deloitte Jean-Paul LAURENT Professeur à l'isfa, Université Claude Bernard Lyon 1 laurent.jeanpaul@free.fr http://laurent.jeanpaul.free.fr/ 0 De
MATHÉMATIQUES ET APPLICATIONS
 MASTER 2 ème ANNÉE MATHÉMATIQUES ET APPLICATIONS Parcours Mathématiques du Risque et Actuariat ANNÉE UNIVERSITAIRE 2015 2016 1 PRESENTATION Le Master 2 Mathématiques du Risque et Actuariat a pour objectif
MASTER 2 ème ANNÉE MATHÉMATIQUES ET APPLICATIONS Parcours Mathématiques du Risque et Actuariat ANNÉE UNIVERSITAIRE 2015 2016 1 PRESENTATION Le Master 2 Mathématiques du Risque et Actuariat a pour objectif
Enseignements d Approfondissement de Mathématiques Appliquées
 Enseignements d Approfondissement de Mathématiques Appliquées Septembre 2009 http://www.enseignement.polytechnique.fr/mathematiques-appliquees/ enseignements/annee3_ea.php Ces enseignements sont l occasion
Enseignements d Approfondissement de Mathématiques Appliquées Septembre 2009 http://www.enseignement.polytechnique.fr/mathematiques-appliquees/ enseignements/annee3_ea.php Ces enseignements sont l occasion
Master Modélisation Aléatoire Paris VII, Cours Méthodes de Monte Carlo en nance et C++, TP n 2.
 Master Modélisation Aléatoire Paris VII, Cours Méthodes de Monte Carlo en nance et C++, TP n 2. Techniques de correction pour les options barrières 25 janvier 2007 Exercice à rendre individuellement lors
Master Modélisation Aléatoire Paris VII, Cours Méthodes de Monte Carlo en nance et C++, TP n 2. Techniques de correction pour les options barrières 25 janvier 2007 Exercice à rendre individuellement lors
Campus. Les formations Finance active
 Campus Les formations Finance active Gestion du risque de change 1. Négocier et traiter au mieux spots et termes S approprier les fondamentaux du risque de change - Déterminer sa position et son risque
Campus Les formations Finance active Gestion du risque de change 1. Négocier et traiter au mieux spots et termes S approprier les fondamentaux du risque de change - Déterminer sa position et son risque
FORMATIONS FINANCIÈRES RÉALISÉES
 FORMATIONS FINANCIÈRES RÉALISÉES l'ensemble de ces sujets de formations ont été construits sur mesure à la demande de nos clients SOMMAIRE LES MARCHÉS 3 LES MARCHÉS FINANCIERS NIVEAU 1 4 LES MARCHÉS FINANCIERS
FORMATIONS FINANCIÈRES RÉALISÉES l'ensemble de ces sujets de formations ont été construits sur mesure à la demande de nos clients SOMMAIRE LES MARCHÉS 3 LES MARCHÉS FINANCIERS NIVEAU 1 4 LES MARCHÉS FINANCIERS
Formation «Comptabilité bancaire : cycle long»
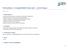 Formation «Comptabilité bancaire : cycle long» REFERENCE : 202 1. Objectif général Situer l'activité bancaire dans son environnement économique et réglementaire. Souligner les aspects techniques et économiques
Formation «Comptabilité bancaire : cycle long» REFERENCE : 202 1. Objectif général Situer l'activité bancaire dans son environnement économique et réglementaire. Souligner les aspects techniques et économiques
Gestion obligataire passive
 Finance 1 Université d Evry Séance 7 Gestion obligataire passive Philippe Priaulet L efficience des marchés Stratégies passives Qu est-ce qu un bon benchmark? Réplication simple Réplication par échantillonnage
Finance 1 Université d Evry Séance 7 Gestion obligataire passive Philippe Priaulet L efficience des marchés Stratégies passives Qu est-ce qu un bon benchmark? Réplication simple Réplication par échantillonnage
Capital économique en assurance vie : utilisation des «replicating portfolios»
 Capital économique en assurance vie : utilisation des «replicating portfolios» Anne LARPIN, CFO SL France Stéphane CAMON, CRO SL France 1 Executive summary Le bouleversement de la réglementation financière
Capital économique en assurance vie : utilisation des «replicating portfolios» Anne LARPIN, CFO SL France Stéphane CAMON, CRO SL France 1 Executive summary Le bouleversement de la réglementation financière
Optimisation et programmation mathématique. Professeur Michel de Mathelin. Cours intégré : 20 h
 Télécom Physique Strasbourg Master IRIV Optimisation et programmation mathématique Professeur Michel de Mathelin Cours intégré : 20 h Programme du cours d optimisation Introduction Chapitre I: Rappels
Télécom Physique Strasbourg Master IRIV Optimisation et programmation mathématique Professeur Michel de Mathelin Cours intégré : 20 h Programme du cours d optimisation Introduction Chapitre I: Rappels
un environnement économique et politique
 Vision d un économiste sur le risque agricole et sa gestion un sol un climat un environnement économique et politique Jean Cordier Professeur Agrocampus Ouest Séminaire GIS GC HP2E Prise en compte du risque
Vision d un économiste sur le risque agricole et sa gestion un sol un climat un environnement économique et politique Jean Cordier Professeur Agrocampus Ouest Séminaire GIS GC HP2E Prise en compte du risque
ANALYSE DU RISQUE DE CRÉDIT
 ANALYSE DU RISQUE DE CRÉDIT Banque & Marchés Cécile Kharoubi Professeur de Finance ESCP Europe Philippe Thomas Professeur de Finance ESCP Europe TABLE DES MATIÈRES Introduction... 15 Chapitre 1 Le risque
ANALYSE DU RISQUE DE CRÉDIT Banque & Marchés Cécile Kharoubi Professeur de Finance ESCP Europe Philippe Thomas Professeur de Finance ESCP Europe TABLE DES MATIÈRES Introduction... 15 Chapitre 1 Le risque
Scénarios économiques en assurance
 Motivation et plan du cours Galea & Associés ISFA - Université Lyon 1 ptherond@galea-associes.eu pierre@therond.fr 18 octobre 2013 Motivation Les nouveaux référentiels prudentiel et d'information nancière
Motivation et plan du cours Galea & Associés ISFA - Université Lyon 1 ptherond@galea-associes.eu pierre@therond.fr 18 octobre 2013 Motivation Les nouveaux référentiels prudentiel et d'information nancière
TRAVAIL D ETUDE ET DE RECHERCHE. Utilisation des arbres binomiaux pour le pricing des options américaines
 Ensimag - 2éme année Mai 2010 TRAVAIL D ETUDE ET DE RECHERCHE Utilisation des arbres binomiaux pour le pricing des options américaines Anne-Victoire AURIAULT 1/48 2/48 Cadre de l Étude Cette étude a été
Ensimag - 2éme année Mai 2010 TRAVAIL D ETUDE ET DE RECHERCHE Utilisation des arbres binomiaux pour le pricing des options américaines Anne-Victoire AURIAULT 1/48 2/48 Cadre de l Étude Cette étude a été
ERRATA ET AJOUTS. ( t) 2 s2 dt (4.7) Chapitre 2, p. 64, l équation se lit comme suit : Taux effectif = 1+
 ERRATA ET AJOUTS Chapitre, p. 64, l équation se lit comme suit : 008, Taux effectif = 1+ 0 0816 =, Chapitre 3, p. 84, l équation se lit comme suit : 0, 075 1 000 C = = 37, 50$ Chapitre 4, p. 108, note
ERRATA ET AJOUTS Chapitre, p. 64, l équation se lit comme suit : 008, Taux effectif = 1+ 0 0816 =, Chapitre 3, p. 84, l équation se lit comme suit : 0, 075 1 000 C = = 37, 50$ Chapitre 4, p. 108, note
Hedge funds: des faiblesses dans la gestion des risques
 Avec leurs rendements supérieurs aux actifs traditionnels et leur faible volatilité, les hedge funds attirent toujours de nombreux investisseurs. Néanmoins, ils restent risqués. Hedge funds: des faiblesses
Avec leurs rendements supérieurs aux actifs traditionnels et leur faible volatilité, les hedge funds attirent toujours de nombreux investisseurs. Néanmoins, ils restent risqués. Hedge funds: des faiblesses
L ÉVALUATION DES OPTIONS AVEC PRIME DE LIQUIDITÉ
 L ÉVALUATION DES OPTIONS AVEC PRIME DE LIQUIDITÉ L ÉVALUATION DES OPTIONS AVEC PRIME DE LIQUIDITÉ Mondher Bellalah (Université du Maine) et Jean-Luc Prigent (Université de Cergy-Pontoise) 1 Résumé. Les
L ÉVALUATION DES OPTIONS AVEC PRIME DE LIQUIDITÉ L ÉVALUATION DES OPTIONS AVEC PRIME DE LIQUIDITÉ Mondher Bellalah (Université du Maine) et Jean-Luc Prigent (Université de Cergy-Pontoise) 1 Résumé. Les
Théorie Financière 2. Valeur actuelle Evaluation d obligations
 Théorie Financière 2. Valeur actuelle Evaluation d obligations Objectifs de la session. Comprendre les calculs de Valeur Actuelle (VA, Present Value, PV) Formule générale, facteur d actualisation (discount
Théorie Financière 2. Valeur actuelle Evaluation d obligations Objectifs de la session. Comprendre les calculs de Valeur Actuelle (VA, Present Value, PV) Formule générale, facteur d actualisation (discount
4.2 Unités d enseignement du M1
 88 CHAPITRE 4. DESCRIPTION DES UNITÉS D ENSEIGNEMENT 4.2 Unités d enseignement du M1 Tous les cours sont de 6 ECTS. Modélisation, optimisation et complexité des algorithmes (code RCP106) Objectif : Présenter
88 CHAPITRE 4. DESCRIPTION DES UNITÉS D ENSEIGNEMENT 4.2 Unités d enseignement du M1 Tous les cours sont de 6 ECTS. Modélisation, optimisation et complexité des algorithmes (code RCP106) Objectif : Présenter
Examen Final. Indications
 DANS LE SECTEUR BANQUE-ASSURANCE NOM : MATRICULE : PRENOM : Examen Final Problèmes Indications Veuillez respecter les indications suivantes: 1. Vous avez 3 heures à disposition 2. Veuillez vérifier que
DANS LE SECTEUR BANQUE-ASSURANCE NOM : MATRICULE : PRENOM : Examen Final Problèmes Indications Veuillez respecter les indications suivantes: 1. Vous avez 3 heures à disposition 2. Veuillez vérifier que
Manuel d Utilisateur - Logiciel ModAFi. Jonathan ANJOU - Maud EYZAT - Kévin NAVARRO
 Manuel d Utilisateur - Logiciel ModAFi Jonathan ANJOU - Maud EYZAT - Kévin NAVARRO Grenoble, 12 juin 2012 Table des matières 1 Introduction 3 2 Modèles supportés 3 2.1 Les diérents modèles supportés pour
Manuel d Utilisateur - Logiciel ModAFi Jonathan ANJOU - Maud EYZAT - Kévin NAVARRO Grenoble, 12 juin 2012 Table des matières 1 Introduction 3 2 Modèles supportés 3 2.1 Les diérents modèles supportés pour
PRIME D UNE OPTION D ACHAT OU DE VENTE
 Université Paris VII - Agrégation de Mathématiques François Delarue) PRIME D UNE OPTION D ACHAT OU DE VENTE Ce texte vise à modéliser de façon simple l évolution d un actif financier à risque, et à introduire,
Université Paris VII - Agrégation de Mathématiques François Delarue) PRIME D UNE OPTION D ACHAT OU DE VENTE Ce texte vise à modéliser de façon simple l évolution d un actif financier à risque, et à introduire,
I Stabilité, Commandabilité et Observabilité 11. 1 Introduction 13 1.1 Un exemple emprunté à la robotique... 13 1.2 Le plan... 18 1.3 Problème...
 TABLE DES MATIÈRES 5 Table des matières I Stabilité, Commandabilité et Observabilité 11 1 Introduction 13 1.1 Un exemple emprunté à la robotique................... 13 1.2 Le plan...................................
TABLE DES MATIÈRES 5 Table des matières I Stabilité, Commandabilité et Observabilité 11 1 Introduction 13 1.1 Un exemple emprunté à la robotique................... 13 1.2 Le plan...................................
Chaire FBF - IDEI «Chaine de Valeur Marchés Financiers et Banque d Investissement» Mardi 29 avril 2014
 Chaire FBF - IDEI «Chaine de Valeur Marchés Financiers et Banque d Investissement» Mardi 29 avril 2014 Objectifs Contacts praticiens - chercheurs Recherche d excellence sur la banque d investissement et
Chaire FBF - IDEI «Chaine de Valeur Marchés Financiers et Banque d Investissement» Mardi 29 avril 2014 Objectifs Contacts praticiens - chercheurs Recherche d excellence sur la banque d investissement et
Projet SINF2275 «Data mining and decision making» Projet classification et credit scoring
 Projet SINF2275 «Data mining and decision making» Projet classification et credit scoring Année académique 2006-2007 Professeurs : Marco Saerens Adresse : Université catholique de Louvain Information Systems
Projet SINF2275 «Data mining and decision making» Projet classification et credit scoring Année académique 2006-2007 Professeurs : Marco Saerens Adresse : Université catholique de Louvain Information Systems
Contents. 1 Introduction Objectifs des systèmes bonus-malus Système bonus-malus à classes Système bonus-malus : Principes
 Université Claude Bernard Lyon 1 Institut de Science Financière et d Assurances Système Bonus-Malus Introduction & Applications SCILAB Julien Tomas Institut de Science Financière et d Assurances Laboratoire
Université Claude Bernard Lyon 1 Institut de Science Financière et d Assurances Système Bonus-Malus Introduction & Applications SCILAB Julien Tomas Institut de Science Financière et d Assurances Laboratoire
La tarification d options
 La tarification d options Proposition pour une approche déterministe Pierre Bernhard 1 Stéphane Thiery 2 Marc Deschamps 3 Nous proposons ici une théorie de la tarification d options sur la base d un modèle
La tarification d options Proposition pour une approche déterministe Pierre Bernhard 1 Stéphane Thiery 2 Marc Deschamps 3 Nous proposons ici une théorie de la tarification d options sur la base d un modèle
TURBOS WARRANTS CERTIFICATS. Les Turbos Produits à effet de levier avec barrière désactivante. Produits non garantis en capital.
 TURBOS WARRANTS CERTIFICATS Les Turbos Produits à effet de levier avec barrière désactivante. Produits non garantis en capital. 2 LES TURBOS 1. Introduction Que sont les Turbos? Les Turbos sont des produits
TURBOS WARRANTS CERTIFICATS Les Turbos Produits à effet de levier avec barrière désactivante. Produits non garantis en capital. 2 LES TURBOS 1. Introduction Que sont les Turbos? Les Turbos sont des produits
Valorisation d es des options Novembre 2007
 Valorisation des options Novembre 2007 Plan Rappels Relations de prix Le modèle binomial Le modèle de Black-Scholes Les grecques Page 2 Rappels (1) Définition Une option est un contrat financier qui confère
Valorisation des options Novembre 2007 Plan Rappels Relations de prix Le modèle binomial Le modèle de Black-Scholes Les grecques Page 2 Rappels (1) Définition Une option est un contrat financier qui confère
Pratique des options Grecs et stratégies de trading. F. Wellers
 Pratique des options Grecs et stratégies de trading F. Wellers Plan de la conférence 0 Philosophie et structure du cours 1 Définitions des grecs 2 Propriétés des grecs 3 Qu est ce que la volatilité? 4
Pratique des options Grecs et stratégies de trading F. Wellers Plan de la conférence 0 Philosophie et structure du cours 1 Définitions des grecs 2 Propriétés des grecs 3 Qu est ce que la volatilité? 4
Francisco José Silva Álvarez
 Francisco José Silva Álvarez Né le 22 Juillet 1982 Nationalité chilienne Célibataire. Coordonnées professionnelles Dipartimento di Matematica Guido Castelnuovo, Università La Sapienza Piazzale Aldo Moro,
Francisco José Silva Álvarez Né le 22 Juillet 1982 Nationalité chilienne Célibataire. Coordonnées professionnelles Dipartimento di Matematica Guido Castelnuovo, Università La Sapienza Piazzale Aldo Moro,
Le théorème des deux fonds et la gestion indicielle
 Le théorème des deux fonds et la gestion indicielle Philippe Bernard Ingénierie Economique& Financière Université Paris-Dauphine mars 2013 Les premiers fonds indiciels futent lancés aux Etats-Unis par
Le théorème des deux fonds et la gestion indicielle Philippe Bernard Ingénierie Economique& Financière Université Paris-Dauphine mars 2013 Les premiers fonds indiciels futent lancés aux Etats-Unis par
Options, Futures, Parité call put
 Département de Mathématiques TD Finance / Mathématiques Financières Options, Futures, Parité call put Exercice 1 Quelle est la différence entre (a) prendre une position longue sur un forward avec un prix
Département de Mathématiques TD Finance / Mathématiques Financières Options, Futures, Parité call put Exercice 1 Quelle est la différence entre (a) prendre une position longue sur un forward avec un prix
DERIVES SUR ACTIONS ET INDICES. Christophe Mianné, Luc François
 DERIVES SUR ACTIONS ET INDICES Christophe Mianné, Luc François Sommaire Notre activité Nos atouts La gestion du risque Conclusion 2 Notre activité 3 Les métiers Distribution de produits dérivés actions
DERIVES SUR ACTIONS ET INDICES Christophe Mianné, Luc François Sommaire Notre activité Nos atouts La gestion du risque Conclusion 2 Notre activité 3 Les métiers Distribution de produits dérivés actions
LES OPTIONS DE CHANGE DE SECONDE GÉNÉRATION : UN APERÇU
 LES OPTIONS DE CHANGE DE SECONDE GÉNÉRATION : UN APERÇU En forte croissance depuis le début des années quatre-vingt, le marché des options sur devises s est enrichi, au début des années quatre-vingt-dix,
LES OPTIONS DE CHANGE DE SECONDE GÉNÉRATION : UN APERÇU En forte croissance depuis le début des années quatre-vingt, le marché des options sur devises s est enrichi, au début des années quatre-vingt-dix,
WARRANTS TURBOS CERTIFICATS. Les Warrants. Découvrir et apprendre à maîtriser l effet de levier
 WARRANTS TURBOS CERTIFICATS Les Warrants Découvrir et apprendre à maîtriser l effet de levier 2 WARRANTS Qu est-ce qu un Warrant? Un warrant est une option cotée en Bourse. Emis par des établissements
WARRANTS TURBOS CERTIFICATS Les Warrants Découvrir et apprendre à maîtriser l effet de levier 2 WARRANTS Qu est-ce qu un Warrant? Un warrant est une option cotée en Bourse. Emis par des établissements
CURRICULUM VITAE. CHAMP DE SPÉCIALISATION Économie financière. Économétrie financière. Économétrie.
 CURRICULUM VITAE Nom: Bruno Feunou Citoyenneté: Canadien Langues: Bangam, Bandjoun, Français, Anglais Adresse: Duke University Department of Economics 213 Social Sciences Building Durham, NC 27708, US
CURRICULUM VITAE Nom: Bruno Feunou Citoyenneté: Canadien Langues: Bangam, Bandjoun, Français, Anglais Adresse: Duke University Department of Economics 213 Social Sciences Building Durham, NC 27708, US
Modèle de troncature gauche : Comparaison par simulation sur données indépendantes et dépendantes
 de troncature gauche : Comparaison par simulation sur données indépendantes et dépendantes Zohra Guessoum 1 & Farida Hamrani 2 1 Lab. MSTD, Faculté de mathématique, USTHB, BP n 32, El Alia, Alger, Algérie,zguessoum@usthb.dz
de troncature gauche : Comparaison par simulation sur données indépendantes et dépendantes Zohra Guessoum 1 & Farida Hamrani 2 1 Lab. MSTD, Faculté de mathématique, USTHB, BP n 32, El Alia, Alger, Algérie,zguessoum@usthb.dz
Table des matières. l a r c i e r
 Chapitre 1 Introduction... 1 1.1. Objectifs et structure du livre.... 1 1.2. Qu est-ce que la gestion de portefeuille?.... 2 1.3. Qu est-ce que «investir»?.... 3 1.4. Canalisation des flux d épargne et
Chapitre 1 Introduction... 1 1.1. Objectifs et structure du livre.... 1 1.2. Qu est-ce que la gestion de portefeuille?.... 2 1.3. Qu est-ce que «investir»?.... 3 1.4. Canalisation des flux d épargne et
Propriétés des options sur actions
 Propriétés des options sur actions Bornes supérieure et inférieure du premium / Parité call put 1 / 1 Taux d intérêt, capitalisation, actualisation Taux d intéret composés Du point de vue de l investisseur,
Propriétés des options sur actions Bornes supérieure et inférieure du premium / Parité call put 1 / 1 Taux d intérêt, capitalisation, actualisation Taux d intéret composés Du point de vue de l investisseur,
Contribution sur le thème relatif au point de vue et au rôle des actuaires vis-à-vis des nouvelles normes comptables
 Valorisation du risque IARD et nouvelles normes comptables Mathieu Gatumel et Guillaume Gorge Axa Group Risk Management 9 avenue de Messine 75008 Paris Tel. : +33 1 56 43 78 27 Fax : +33 1 56 43 78 70
Valorisation du risque IARD et nouvelles normes comptables Mathieu Gatumel et Guillaume Gorge Axa Group Risk Management 9 avenue de Messine 75008 Paris Tel. : +33 1 56 43 78 27 Fax : +33 1 56 43 78 70
Équation de Langevin avec petites perturbations browniennes ou
 Équation de Langevin avec petites perturbations browniennes ou alpha-stables Richard Eon sous la direction de Mihai Gradinaru Institut de Recherche Mathématique de Rennes Journées de probabilités 215,
Équation de Langevin avec petites perturbations browniennes ou alpha-stables Richard Eon sous la direction de Mihai Gradinaru Institut de Recherche Mathématique de Rennes Journées de probabilités 215,
D Expert en Finance et Investissements
 MODULES FINAL D Expert en Finance et Investissements Copyright 2014, AZEK AZEK, Feldstrasse 80, 8180 Bülach, T +41 44 872 35 35, F +41 44 872 35 32, info@azek.ch, www.azek.ch Table des matières 1. Modules
MODULES FINAL D Expert en Finance et Investissements Copyright 2014, AZEK AZEK, Feldstrasse 80, 8180 Bülach, T +41 44 872 35 35, F +41 44 872 35 32, info@azek.ch, www.azek.ch Table des matières 1. Modules
Qu est-ce-qu un Warrant?
 Qu est-ce-qu un Warrant? L epargne est investi dans une multitude d instruments financiers Comptes d epargne Titres Conditionnel= le detenteur à un droit Inconditionnel= le detenteur a une obligation Obligations
Qu est-ce-qu un Warrant? L epargne est investi dans une multitude d instruments financiers Comptes d epargne Titres Conditionnel= le detenteur à un droit Inconditionnel= le detenteur a une obligation Obligations
Value at Risk. CNAM GFN 206 Gestion d actifs et des risques. Grégory Taillard. 27 février & 13 mars 20061
 Value at Risk 27 février & 13 mars 20061 CNAM Gréory Taillard CNAM Master Finance de marché et estion de capitaux 2 Value at Risk Biblioraphie Jorion, Philippe, «Value at Risk: The New Benchmark for Manain
Value at Risk 27 février & 13 mars 20061 CNAM Gréory Taillard CNAM Master Finance de marché et estion de capitaux 2 Value at Risk Biblioraphie Jorion, Philippe, «Value at Risk: The New Benchmark for Manain
Le risque Idiosyncrasique
 Le risque Idiosyncrasique -Pierre CADESTIN -Magali DRIGHES -Raphael MINATO -Mathieu SELLES 1 Introduction Risque idiosyncrasique : risque non pris en compte dans le risque de marché (indépendant des phénomènes
Le risque Idiosyncrasique -Pierre CADESTIN -Magali DRIGHES -Raphael MINATO -Mathieu SELLES 1 Introduction Risque idiosyncrasique : risque non pris en compte dans le risque de marché (indépendant des phénomènes
Principe de symétrisation pour la construction d un test adaptatif
 Principe de symétrisation pour la construction d un test adaptatif Cécile Durot 1 & Yves Rozenholc 2 1 UFR SEGMI, Université Paris Ouest Nanterre La Défense, France, cecile.durot@gmail.com 2 Université
Principe de symétrisation pour la construction d un test adaptatif Cécile Durot 1 & Yves Rozenholc 2 1 UFR SEGMI, Université Paris Ouest Nanterre La Défense, France, cecile.durot@gmail.com 2 Université
L industrie financière sait elle décrire les produits qu elle traite?
 L industrie financière sait elle décrire les produits qu elle traite? De la nécessité d une représentation formelle des contrats financiers pour améliorer la gestion et la régulation des opérations de
L industrie financière sait elle décrire les produits qu elle traite? De la nécessité d une représentation formelle des contrats financiers pour améliorer la gestion et la régulation des opérations de
Résumé... 9... 10... 10... 10
 Bibliographie 1 Table des matières Table des matières.................................... 3 Résumé............................................ 9........................................ 10........................................
Bibliographie 1 Table des matières Table des matières.................................... 3 Résumé............................................ 9........................................ 10........................................
I. Introduction. 1. Objectifs. 2. Les options. a. Présentation du problème.
 I. Introduction. 1. Objectifs. Le but de ces quelques séances est d introduire les outils mathématiques, plus précisément ceux de nature probabiliste, qui interviennent dans les modèles financiers ; nous
I. Introduction. 1. Objectifs. Le but de ces quelques séances est d introduire les outils mathématiques, plus précisément ceux de nature probabiliste, qui interviennent dans les modèles financiers ; nous
Nathalie REY DIPLOMES UNIVERSITAIRES
 Nathalie REY Fonction (depuis septembre 1999) : Maître de Conférences en Sciences Economiques Université Paris 13, Sorbonne Paris Cité CEPN, UMR 7234 U.F.R. Sciences Économiques et de Gestion, Bureau J308
Nathalie REY Fonction (depuis septembre 1999) : Maître de Conférences en Sciences Economiques Université Paris 13, Sorbonne Paris Cité CEPN, UMR 7234 U.F.R. Sciences Économiques et de Gestion, Bureau J308
Sujet proposé par Yves M. LEROY. Cet examen se compose d un exercice et de deux problèmes. Ces trois parties sont indépendantes.
 Promotion X 004 COURS D ANALYSE DES STRUCTURES MÉCANIQUES PAR LA MÉTHODE DES ELEMENTS FINIS (MEC 568) contrôle non classant (7 mars 007, heures) Documents autorisés : polycopié ; documents et notes de
Promotion X 004 COURS D ANALYSE DES STRUCTURES MÉCANIQUES PAR LA MÉTHODE DES ELEMENTS FINIS (MEC 568) contrôle non classant (7 mars 007, heures) Documents autorisés : polycopié ; documents et notes de
Does it pay to improve Corporate Governance? An empirical analysis of European Equities
 Does it pay to improve Corporate Governance? An empirical analysis of European Equities Joseph GAWER NATIXIS Asset Management Université Paris Dauphine joseph.gawer@am.natixis.com Association Française
Does it pay to improve Corporate Governance? An empirical analysis of European Equities Joseph GAWER NATIXIS Asset Management Université Paris Dauphine joseph.gawer@am.natixis.com Association Française
Résumés des projets de GMM5-2014/2015
 Résumés des projets de GMM5-2014/2015 Option MMS Statistical analysis of Raman Spectra skin to evaluate the benefit of Pierre Fabre s acne treatment cream Classification appliquée à la biologie structurale
Résumés des projets de GMM5-2014/2015 Option MMS Statistical analysis of Raman Spectra skin to evaluate the benefit of Pierre Fabre s acne treatment cream Classification appliquée à la biologie structurale
I. Risques généraux s appliquant à l ensemble des instruments financiers
 I. Risques généraux s appliquant à l ensemble des instruments financiers 1. Risque de liquidité Le risque de liquidité est le risque de ne pas pouvoir acheter ou vendre son actif rapidement. La liquidité
I. Risques généraux s appliquant à l ensemble des instruments financiers 1. Risque de liquidité Le risque de liquidité est le risque de ne pas pouvoir acheter ou vendre son actif rapidement. La liquidité
Ask : Back office : Bar-chart : Bear : Bid : Blue chip : Bond/Junk Bond : Bull : Call : Call warrant/put warrant :
 Parlons Trading Ask : prix d offre ; c est le prix auquel un «market maker» vend un titre et le prix auquel l investisseur achète le titre. Le prix du marché correspond au prix le plus intéressant parmi
Parlons Trading Ask : prix d offre ; c est le prix auquel un «market maker» vend un titre et le prix auquel l investisseur achète le titre. Le prix du marché correspond au prix le plus intéressant parmi
$SSOLFDWLRQGXNULJHDJHSRXUOD FDOLEUDWLRQPRWHXU
 $SSOLFDWLRQGXNULJHDJHSRXUOD FDOLEUDWLRQPRWHXU Fabien FIGUERES fabien.figueres@mpsa.com 0RWVFOpV : Krigeage, plans d expériences space-filling, points de validations, calibration moteur. 5pVXPp Dans le
$SSOLFDWLRQGXNULJHDJHSRXUOD FDOLEUDWLRQPRWHXU Fabien FIGUERES fabien.figueres@mpsa.com 0RWVFOpV : Krigeage, plans d expériences space-filling, points de validations, calibration moteur. 5pVXPp Dans le
Le Fol Gaëlle. Current Position - Status. Former positions. Education and qualification. Full professor. gaelle.le_fol@dauphine.fr
 Le Fol Gaëlle Full professor gaelle.le_fol@dauphine.fr Current Position - Status Head of an education program : Master 203 - Financial Markets Department of attachment : MSO Centre of Research : Dauphine
Le Fol Gaëlle Full professor gaelle.le_fol@dauphine.fr Current Position - Status Head of an education program : Master 203 - Financial Markets Department of attachment : MSO Centre of Research : Dauphine
ESSEC. Cours «Management bancaire» Séance 3 Le risque de crédit
 ESSEC Cours «Management bancaire» Séance 3 Le risque de crédit Plan de la séance 3 : Le risque de crédit (1) Les opérations de crédit Définition d un crédit La décision de crédit Les crédits aux petites
ESSEC Cours «Management bancaire» Séance 3 Le risque de crédit Plan de la séance 3 : Le risque de crédit (1) Les opérations de crédit Définition d un crédit La décision de crédit Les crédits aux petites
SECTION 5 : OPERATIONS SUR PRODUITS DERIVES
 SECTION 5 : OPERATIONS SUR PRODUITS DERIVES 1 - DEFINITION DES PRODUITS DERIVES 2 - DEFINITIONS DES MARCHES 3 - USAGE DES CONTRATS 4 - COMPTABILISATION DES OPERATIONS SUR PRODUITS DERIVES 51 SECTION 5
SECTION 5 : OPERATIONS SUR PRODUITS DERIVES 1 - DEFINITION DES PRODUITS DERIVES 2 - DEFINITIONS DES MARCHES 3 - USAGE DES CONTRATS 4 - COMPTABILISATION DES OPERATIONS SUR PRODUITS DERIVES 51 SECTION 5
EXAMEN CRITIQUE D UN DOSSIER TECHNIQUE
 EXAMEN CRITIQUE D UN DOSSIER TECHNIQUE (Préparation : 5 heures -- Exposé et Questions : 1 heure) Rapport établi par : P.J. BARRE, E. JEAY, D. MARQUIS, P. RAY, A. THIMJO 1. PRESENTATION DE L EPREUVE 1.1.
EXAMEN CRITIQUE D UN DOSSIER TECHNIQUE (Préparation : 5 heures -- Exposé et Questions : 1 heure) Rapport établi par : P.J. BARRE, E. JEAY, D. MARQUIS, P. RAY, A. THIMJO 1. PRESENTATION DE L EPREUVE 1.1.
CURRICULUM VITAE Anne de Bouard
 CURRICULUM VITAE Anne de Bouard née le 1er mai 1965 à Caen (14) Mariée, 2 enfants Nationalité : Française http://www.cmap.polytechnique.fr/~debouard debouard@cmap.polytechnique.fr CMAP, Ecole Polytechnique
CURRICULUM VITAE Anne de Bouard née le 1er mai 1965 à Caen (14) Mariée, 2 enfants Nationalité : Française http://www.cmap.polytechnique.fr/~debouard debouard@cmap.polytechnique.fr CMAP, Ecole Polytechnique
L essentiel des marchés financiers
 Éric Chardoillet Marc Salvat Henri Tournyol du Clos L essentiel des marchés financiers Front office, post-marché et gestion des risques, 2010 ISBN : 978-2-212-54674-3 Table des matières Introduction...
Éric Chardoillet Marc Salvat Henri Tournyol du Clos L essentiel des marchés financiers Front office, post-marché et gestion des risques, 2010 ISBN : 978-2-212-54674-3 Table des matières Introduction...
1. Prolongements de la théorie des options i. Rappel de la théorie de la valorisation des actifs contingents
 1 Plan du cours de Théorie financière III 1. Prolongements de la théorie des options i. Rappel de la théorie de la valorisation des actifs contingents ii. Modèles de structure par terme des taux d intérêt
1 Plan du cours de Théorie financière III 1. Prolongements de la théorie des options i. Rappel de la théorie de la valorisation des actifs contingents ii. Modèles de structure par terme des taux d intérêt
MATHÉMATIQUES ET APPLICATIONS
 MASTER 2 ème ANNÉE MATHÉMATIQUES ET APPLICATIONS Parcours Finance Computationnelle ANNÉE UNIVERSITAIRE 2015 2016 1 PRESENTATION Le master Finance Computationnelle spécialise les étudiants sur l ingénierie
MASTER 2 ème ANNÉE MATHÉMATIQUES ET APPLICATIONS Parcours Finance Computationnelle ANNÉE UNIVERSITAIRE 2015 2016 1 PRESENTATION Le master Finance Computationnelle spécialise les étudiants sur l ingénierie
Best Styles ou comment capturer au mieux les primes de risque sur les marchés d actions
 Stratégie Best Styles ou comment capturer au mieux les primes de risque sur les marchés d actions La recherche des primes de risque constitue une stratégie relativement courante sur les marchés obligataires
Stratégie Best Styles ou comment capturer au mieux les primes de risque sur les marchés d actions La recherche des primes de risque constitue une stratégie relativement courante sur les marchés obligataires
Table des matières. Avant-propos. Chapitre 2 L actualisation... 21. Chapitre 1 L intérêt... 1. Chapitre 3 Les annuités... 33 III. Entraînement...
 III Table des matières Avant-propos Remerciements................................. Les auteurs..................................... Chapitre 1 L intérêt............................. 1 1. Mise en situation...........................
III Table des matières Avant-propos Remerciements................................. Les auteurs..................................... Chapitre 1 L intérêt............................. 1 1. Mise en situation...........................
Apprentissage Automatique
 Apprentissage Automatique Introduction-I jean-francois.bonastre@univ-avignon.fr www.lia.univ-avignon.fr Définition? (Wikipedia) L'apprentissage automatique (machine-learning en anglais) est un des champs
Apprentissage Automatique Introduction-I jean-francois.bonastre@univ-avignon.fr www.lia.univ-avignon.fr Définition? (Wikipedia) L'apprentissage automatique (machine-learning en anglais) est un des champs
EXPLOITATIONS PEDAGOGIQUES DU TABLEUR EN STG
 Exploitations pédagogiques du tableur en STG Académie de Créteil 2006 1 EXPLOITATIONS PEDAGOGIQUES DU TABLEUR EN STG Commission inter-irem lycées techniques contact : dutarte@club-internet.fr La maquette
Exploitations pédagogiques du tableur en STG Académie de Créteil 2006 1 EXPLOITATIONS PEDAGOGIQUES DU TABLEUR EN STG Commission inter-irem lycées techniques contact : dutarte@club-internet.fr La maquette
Génération de scénarios économiques
 Modélisation des taux d intérêt Pierre-E. Thérond ptherond@galea-associes.eu pierre@therond.fr Galea & Associés ISFA - Université Lyon 1 22 novembre 2013 Motivation La modélisation des taux d intérêt est
Modélisation des taux d intérêt Pierre-E. Thérond ptherond@galea-associes.eu pierre@therond.fr Galea & Associés ISFA - Université Lyon 1 22 novembre 2013 Motivation La modélisation des taux d intérêt est
Rapport de projet Risque de Crédit, Risque de Défaut : Étude de l influence du taux de recouvrement sur le prix de CDOs.
 Rapport de projet Risque de Crédit, Risque de Défaut : Étude de l influence du taux de recouvrement sur le prix de CDOs. Auteurs : Hecht Frédéric, Porzier Rémi, Font Guillaume Cours «Risque de Crédit,
Rapport de projet Risque de Crédit, Risque de Défaut : Étude de l influence du taux de recouvrement sur le prix de CDOs. Auteurs : Hecht Frédéric, Porzier Rémi, Font Guillaume Cours «Risque de Crédit,
Ce document synthétise les principaux aspects de DayTrader Live, le service le plus haut de gamme de DayByDay.
 Bienvenue chez DayByDay, Ce document synthétise les principaux aspects de DayTrader Live, le service le plus haut de gamme de DayByDay. Il est en deux parties : - Les idées de trading : quels sont les
Bienvenue chez DayByDay, Ce document synthétise les principaux aspects de DayTrader Live, le service le plus haut de gamme de DayByDay. Il est en deux parties : - Les idées de trading : quels sont les
Introduction au pricing d option en finance
 Introduction au pricing d option en finance Olivier Pironneau Cours d informatique Scientifique 1 Modélisation du prix d un actif financier Les actions, obligations et autres produits financiers cotés
Introduction au pricing d option en finance Olivier Pironneau Cours d informatique Scientifique 1 Modélisation du prix d un actif financier Les actions, obligations et autres produits financiers cotés
