TD 16 Loi de la quantité de mouvement
|
|
|
- Jean-René Cardinal
- il y a 6 ans
- Total affichages :
Transcription
1 Mécanique I TPC TD 6 Loi de la quantité de mouvement Eercice Mouvement sur un plan incliné Un solide de masse m=5kg glisse sans frottement sur un plan incliné d'angle α =5 par rapport à l'horiontale. Il est entraîné à vitesse constante par un câble faisant un angle β =0 avec la ligne de plus grande pente du plan incliné (g = 9,8 m.s - ).. Quelle relation vectorielle eiste-t-il entre les forces appliquées?. Déterminer par projection de la relation du. sur des aes bien choisis a. la tension du fil de traction. Application numérique. b. la réaction du plan incliné. Application numérique. Eercice la poussée d Archimède Un objet ancien en étain de volume V = L repose au fond d une épave. La poussée d Archimède est une force verticale ascendante dont la valeur est égale au poids du fluide déplacé. Données : Masse volumique de l eau : ρ0 =,0.0 3 kg. m -3 ; Masse volumique de l étain : ρ = 5, kg. m -3 ;. Faire l inventaire des forces qui s appliquent sur l objet.. Calculer le poids de l objet et la poussée d Archimède qui s appliquent sur l objet. 3. En déduire la réaction que l épave eerce sur l objet. 4. Pour faire remonter l objet, on accroche à l objet un ballon gonflé d air. A la profondeur où se situe l épave, on peut considérer que la masse volumique de l air emprisonné vaut kg. m -3. Quel doit être le volume du ballon pour que la remontée de l objet soit possible? Eercice 3 Feu d artifice On étudie le lancement de deu fusées d'un feu d'artifice. I. Un feu d'artifice non perturbé Deu fusées sont tirées simultanément du sol. La fusée A part du point O, origine du repère cartésien à l'instant t = 0, avec la vitesse initiale v0 faisant un angle α avec l'horiontale. La fusée B est lancée du point P (abscisse P) avec une vitesse verticale v. Les deu fusées ont la même masse m.
2 On néglige les frottements de l'air. Données : v0 = 45 m.s -, v = 50 m.s - ; g = 9,8 m.s - ; P = 5 m ; m = 300 g y 5 m 40m α v O P barrière de sécurité. Établir les équations horaires B(t), yb(t) et A(t), ya(t) du mouvement de chacune des fusées.. En déduire l'équation ya = f(a) de la trajectoire de la fusée A. Quelle est la nature de sa trajectoire? 3. Les deu fusées eplosent au bout de te = 4 secondes. Déterminer l'angle α 0 pour que l'eplosion de la fusée ait lieu à la verticale du point P. 4. La fusée A est lancée avec cet angle α 0, quelle distance d sépare les deu fusées au moment de l'eplosion? 5. Si la fusée A n'eplose pas, les spectateurs se trouvant juste derrière la barrière de sécurité sont-ils en sécurité? II. Un feu d'artifice perturbé par le vent Le soir du feu d'artifice, un vent perturbe le lancer des fusées. 5. On modélise la force du vent par un vecteur force horiontal, dirigé de la gauche vers la droite et de norme constante Fv = N.. La fusée A est lancée avec l'angle α 0 déterminé au I.3. et eplose toujours au bout de te = 4 secondes. Déterminer numériquement ses coordonnées lors de l'eplosion.. Les spectateurs sont-ils en danger? 6. III. En tenant compte des frottements de l air Aucun vent ne perturbe le lancement des fusées. Par contre, on tient compte de la force de frottement fluide, que l on modélise par une force de la forme f = -k v avec v la vitesse de la fusée. On prendra k = 0, S.I.. Faire une analyse dimensionnelle de k et donner ses unités S.I. (unités de base du système international). 7.. Etablir les équations horaires du mouvement de la fusée A. 3. Quelles sont ses coordonnées au moment te où elle eplose (elle est lancée avec l angle α déterminé au I.3.)? Application numérique. 0 Eercice 4 Chute d'un alpiniste urbain (Les Eperts, Manhattan) Au début d'un épisode des Eperts, Manhattan, on voit un alpiniste (désigné par la suite par système A, considéré comme un point matériel) escalader un gratte-ciel de plus de 00 étages. Malheureusement pour lui, arrivé au 34 ème étage, il tombe et atterrit lourdement sur la terrasse du 6 ème étage, où il meurt sur le coup. Les Eperts arrivent sur les lieu et leur chef, Mac Taylor dit : "il a pu tomber d'asse haut pour atteindre la vitesse maimale". A. Chute verticale sans frottements
3 On commence par étudier la chute verticale du système A, de masse m, sous la seule action de son poids. On négligera donc dans cette partie les frottements de l'air. On considère qu'à t = 0, le système A a une vitesse initiale v0 nulle et qu'il est au point O à une hauteur H au-dessus de la terrasse du 6 ème étage. On donne g = 9,8 m.s -. Un étage fait h = 3 m de haut. étage 34 O système A à t = 0 étage 6 O H terrasse Le schéma n est pas à l échelle. Déterminer numériquement la hauteur H.. Déterminer la vitesse v de A au point O en fonction de g et H. Application numérique. sol B. Chute verticale avec frottements L'étude précédente montrerait que plus le système A tombe de haut, plus sa vitesse d'impact est grande, sans tendre vers une limite, ce qui contredit l'affirmation de Mac Taylor de "vitesse maimale". Mais Mac Taylor sait (car c'est un Epert) qu'en fait le système A, en plus de son poids, va être soumis à des frottements de l'air, que l'on peut modéliser par une force =- (proportionnelle au carré de la vitesse). étage 34 O système A à t = 0 étage 6 O H terrasse sol Mac Taylor sait de plus que la vitesse maimale de chute d'un homme dans l'air (aussi appelée vitesse limite) est vlim = 50 m.s -. Les conditions initiales sont bien entendu les mêmes que dans la partie II-A. 3. Que vaut l'accélération de A quand A a atteint sa vitesse limite? En déduire, en écrivant le Principe Fondamental de la Dynamique, mais sans essayer de résoudre d'équation différentielle, l'epression de vlim en fonction de m, g et λ. 4. En déduire la valeur de λ (on donnera son unité en fonction des unités de base du Système International) pour le système A (dont la masse est m = 70 kg). 5. Pour résoudre l'équation différentielle donnée par le PFD, il faut faire quelques manipulations mathématiques. du λ On admettra qu'en posant u = v, u est solution de l'équation différentielle + u = g. d m H0 En déduire que u( ) = vlim e où on aura posé une hauteur caractéristique H0 en fonction de m et λ. 6. En déduire la valeur de la vitesse v de A au point O avec ce modèle. 7. Le sommet du bâtiment étant à 366 m au-dessus de la terrasse, quelle aurait été la valeur de la vitesse atteinte par A au point O si A était tombé du sommet du bâtiment sans vitesse initiale? On peut ainsi considérer (à moins de 3% près) que la vitesse limite a bien été atteinte et que Mac Taylor avait raison : si A était tombé de tout en haut, il aurait pu atteindre (enfin presque) la vitesse maimale. C. Mouvement parabolique (sans frottements) 3
4 Une fois arrivé en O, l'impact est tellement violent qu'une partie B de A (on considérera B comme un point matériel de masse mb) est epulsée et va suivre un mouvement parabolique (cf. ci-contre). On considérera que B part du point O avec une vitesse v = 0 m.s - et avec un angle α avec l'horiontale. B atterrira à D = 30 m plus loin et à H = 5m plus bas (le re-de-chaussée est l'étage ), où B sera trouvé par les Eperts. étage 6 v O terrasse α On négligera à nouveau dans cette partie les frottements de l'air. 8. Ecrire les équations différentielles en et en du mouvement de B (attention, l'ae des est à présent vers le haut). ur ur O, e, e. 9. En déduire l'équation de la trajectoire = f() dans le repère ( ) 0. Donner l'équation littérale dont α est solution, faisant intervenir H, D, g, v et bien sur α.. En se rappelant que tan α cos α = +, montrer que tanα est solution d'une équation du second degré de la forme a tan α + b tanα + c = 0. On donnera les valeurs numériques de a, b et c.. Résoudre l'équation précédente et donner la valeur de l'angle α. H D B sol Eercice 5 Un pendule simple non amorti (eercice clé : pendule simple) On considère un point matériel M de masse m accroché à un point fie O par l'intermédiaire d'un fil inetensible de O longueur l et de masse nulle. L'ensemble est situé dans le champ de pesanteur terrestre g = g. u (avec g = 9,8 m.s - ), u étant un vecteur unitaire de l'ae O. On note l'angle : θ = (O,OM ) = ( u,u) où u est un vecteur unitaire colinéaire à OM. On néglige les frottements. On lâche la masse d un angle θo sans vitesse initiale. θ(t) l M y. Quelle base de projection sera-t-il judicieu d utiliser? Justifier votre réponse et représenter les vecteurs unitaires sur le schéma.. Déterminer l équation du mouvement par projection du PFD dans la base choisie. 3. Ces oscillations sont-elles ce qu on appelle des oscillations harmoniques? Justifier. 4. Le pendule s arrête-t-il? Justifier. Eercice 6 Masse au bout d'un ressort vertical (eercice clé : système masse-ressort) Soit un solide matériel M (de masse m) qui se déplace verticalement. M est relié à un ressort de constante de raideur k et de longueur au repos l0. On notera la position de M sur cet ae. On considérera le référentiel lié au sol comme galiléen et on considérera qu'il n'y a aucun amortissement. Données: accélération de la pesanteur: g = 9,8m.s - ; k = 0N.m - ; l0 = 0cm; m = 00g. 4
5 O M. Déterminer la longueur du ressort à l'équilibre. Application numérique. A t = 0, le ressort a une longueur l0 et on lâche M sans vitesse initiale.. Déterminer l'équation différentielle qui régit les mouvements de M. 3. Déterminer alors (t) en prenant comme origine de l'ae des celle indiquée sur le schéma. 4. Avec ces conditions initiales, M peut-il remonter jusqu'en O? Justifier qualitativement votre réponse (on ne demande aucun calcul). Eercice 7 Glissement sans frottements sur une demi-jante circulaire (mouvement circulaire, utilisation des coordonnées polaires) Un point matériel de masse m, placé initialement en M0 et lâché sans vitesse (v0=0), glisse sans frottements sur un rail circulaire de rayon r. La position de M est repérée par l angle polaire ( u, ur ) y M0 =θ. M u θ u r θ O r On note R= Ru r la réaction eercée par le support sur le point matériel.. Eprimer R en fonction de m,g, θ et de la vitesse angulaire & θ. Etablir l équation θ & & = C cosθ, C étant une constante à préciser.. Résoudre cette équation en multipliant les deu membres par dθ=θ & dt. En déduire & θ en fonction de θ puis R en fonction de θ. 3. Le point M quitte le rail pour un angle limite l θ que l on calculera. Eercice 9 Lois de Kepler. Représenter sur un schéma la force eercée par la Terre sur la Lune 5 F T L, puis la force eercée par la Lune sur la terre F L. T mm. L epression de la force d attraction gravitationnelle est F = G u avec G = 6, S.I., m et d M masse des deu corps en interactions, d distance entre les centre de masse des deu corps. a. Donner l unité de G. b. Calculer la norme de la force d intéraction dans le cas considéré. Données : masse de la Lune : m = 7,35.0 kg ; masse de la terre : M = 5, kg ; distance Terre Lune d = kms 3. En utilisant les lois de Newton, et en supposant que la Lune a un mouvement de rotation circulaire et uniforme autour de la Terre
6 a. Donner l epression de la vitesse v de la Lune en fonction de G, M et d. T T b. Retrouver la troisième loi de Képler : = cte (le rapport 3 3 ne dépend que de l astre attracteur). d d Eercice 0 Portait de phase On étudie le mouvement d une balle, assimilable à un point matériel libre, dans le référentiel terrestre galiléen. Sa trajectoire est rectiligne, suivant la verticale du lieu O orientée vers le haut. On donne la trajectoire de phase ci-dessous : en fonction de. les graduations sont en mètre pour et en mètre par seconde pour. Décrire le plus précisément possible le mouvement de la balle et ce que l on peut en déduire sur les forces qu elle subit. 6
Chapitre 0 Introduction à la cinématique
 Chapitre 0 Introduction à la cinématique Plan Vitesse, accélération Coordonnées polaires Exercices corrigés Vitesse, Accélération La cinématique est l étude du mouvement Elle suppose donc l existence à
Chapitre 0 Introduction à la cinématique Plan Vitesse, accélération Coordonnées polaires Exercices corrigés Vitesse, Accélération La cinématique est l étude du mouvement Elle suppose donc l existence à
Repérage d un point - Vitesse et
 PSI - écanique I - Repérage d un point - Vitesse et accélération page 1/6 Repérage d un point - Vitesse et accélération Table des matières 1 Espace et temps - Référentiel d observation 1 2 Coordonnées
PSI - écanique I - Repérage d un point - Vitesse et accélération page 1/6 Repérage d un point - Vitesse et accélération Table des matières 1 Espace et temps - Référentiel d observation 1 2 Coordonnées
TS Physique Satellite à la recherche de sa planète Exercice résolu
 P a g e 1 Phsique atellite à la recherche de sa planète Exercice résolu Enoncé Le centre spatial de Kourou a lancé le 1 décembre 005, avec une fusée Ariane 5, un satellite de météorologie de seconde génération
P a g e 1 Phsique atellite à la recherche de sa planète Exercice résolu Enoncé Le centre spatial de Kourou a lancé le 1 décembre 005, avec une fusée Ariane 5, un satellite de météorologie de seconde génération
Chafa Azzedine - Faculté de Physique U.S.T.H.B 1
 Chafa Azzedine - Faculté de Physique U.S.T.H.B 1 Définition: La cinématique est une branche de la mécanique qui étudie les mouements des corps dans l espace en fonction du temps indépendamment des causes
Chafa Azzedine - Faculté de Physique U.S.T.H.B 1 Définition: La cinématique est une branche de la mécanique qui étudie les mouements des corps dans l espace en fonction du temps indépendamment des causes
Voyez la réponse à cette question dans ce chapitre. www.hometownroofingcontractors.com/blog/9-reasons-diy-rednecks-should-never-fix-their-own-roof
 Une échelle est appuyée sur un mur. S il n y a que la friction statique avec le sol, quel est l angle minimum possible entre le sol et l échelle pour que l échelle ne glisse pas et tombe au sol? www.hometownroofingcontractors.com/blog/9-reasons-diy-rednecks-should-never-fix-their-own-roof
Une échelle est appuyée sur un mur. S il n y a que la friction statique avec le sol, quel est l angle minimum possible entre le sol et l échelle pour que l échelle ne glisse pas et tombe au sol? www.hometownroofingcontractors.com/blog/9-reasons-diy-rednecks-should-never-fix-their-own-roof
POLY-PREPAS Centre de Préparation aux Concours Paramédicaux. - Section Audioprothésiste / stage i-prépa intensif -
 POLY-PREPAS Centre de Préparation aux Concours Paramédicaux - Section Audioprothésiste / stage i-prépa intensif - 70 Chapitre 8 : Champ de gravitation - Satellites I. Loi de gravitation universelle : (
POLY-PREPAS Centre de Préparation aux Concours Paramédicaux - Section Audioprothésiste / stage i-prépa intensif - 70 Chapitre 8 : Champ de gravitation - Satellites I. Loi de gravitation universelle : (
LES LOIS PHYSIQUES APPLIQUÉES AUX DEUX-ROUES : 1. LA FORCE DE GUIDAGE
 LES LOIS PHYSIQUES APPLIQUÉES AUX DEUX-ROUES : 1. LA FORCE DE GUIDAGE 2. L EFFET GYROSCOPIQUE Les lois physiques qui régissent le mouvement des véhicules terrestres sont des lois universelles qui s appliquent
LES LOIS PHYSIQUES APPLIQUÉES AUX DEUX-ROUES : 1. LA FORCE DE GUIDAGE 2. L EFFET GYROSCOPIQUE Les lois physiques qui régissent le mouvement des véhicules terrestres sont des lois universelles qui s appliquent
Chapitre 5: Oscillations d un pendule élastique horizontal
 1 re B et C 5 Oscillations d'un pendule élastique horizontal 40 Chapitre 5: Oscillations d un pendule élastique horizontal 1. Définitions a) Oscillateur écanique * Un systèe écanique qui effectue un ouveent
1 re B et C 5 Oscillations d'un pendule élastique horizontal 40 Chapitre 5: Oscillations d un pendule élastique horizontal 1. Définitions a) Oscillateur écanique * Un systèe écanique qui effectue un ouveent
1 Définition. 2 Systèmes matériels et solides. 3 Les actions mécaniques. Le système matériel : Il peut être un ensemble.un sous-ensemble..
 1 Définition GÉNÉRALITÉS Statique 1 2 Systèmes matériels et solides Le système matériel : Il peut être un ensemble.un sous-ensemble..une pièce mais aussi un liquide ou un gaz Le solide : Il est supposé
1 Définition GÉNÉRALITÉS Statique 1 2 Systèmes matériels et solides Le système matériel : Il peut être un ensemble.un sous-ensemble..une pièce mais aussi un liquide ou un gaz Le solide : Il est supposé
C est un mouvement plan dont la trajectoire est un cercle ou une portion de cercle. Le module du vecteur position OM est constant et il est égal au
 1 2 C est un mouvement plan dont la trajectoire est un cercle ou une portion de cercle. Le module du vecteur position est constant et il est égal au rayon du cercle. = 3 A- ouvement circulaire non uniforme
1 2 C est un mouvement plan dont la trajectoire est un cercle ou une portion de cercle. Le module du vecteur position est constant et il est égal au rayon du cercle. = 3 A- ouvement circulaire non uniforme
M6 MOMENT CINÉTIQUE D UN POINT MATÉRIEL
 M6 MOMENT CINÉTIQUE D UN POINT MATÉRIEL OBJECTIFS Jusqu à présent, nous avons rencontré deux méthodes pour obtenir l équation du mouvement d un point matériel : - l utilisation du P.F.D. - et celle du
M6 MOMENT CINÉTIQUE D UN POINT MATÉRIEL OBJECTIFS Jusqu à présent, nous avons rencontré deux méthodes pour obtenir l équation du mouvement d un point matériel : - l utilisation du P.F.D. - et celle du
Chapitre 5. Le ressort. F ext. F ressort
 Chapitre 5 Le ressort Le ressort est un élément fondamental de plusieurs mécanismes. Il existe plusieurs types de ressorts (à boudin, à lame, spiral etc.) Que l on comprime ou étire un ressort, tel que
Chapitre 5 Le ressort Le ressort est un élément fondamental de plusieurs mécanismes. Il existe plusieurs types de ressorts (à boudin, à lame, spiral etc.) Que l on comprime ou étire un ressort, tel que
Michel Henry Nicolas Delorme
 Michel Henry Nicolas Delorme Mécanique du point Cours + Exos Michel Henry Maître de conférences à l IUFM des Pays de Loire (Le Mans) Agrégé de physique Nicolas Delorme Maître de conférences à l université
Michel Henry Nicolas Delorme Mécanique du point Cours + Exos Michel Henry Maître de conférences à l IUFM des Pays de Loire (Le Mans) Agrégé de physique Nicolas Delorme Maître de conférences à l université
La gravitation universelle
 La gravitation universelle Pourquoi les planètes du système solaire restent-elles en orbite autour du Soleil? 1) Qu'est-ce que la gravitation universelle? activité : Attraction universelle La cohésion
La gravitation universelle Pourquoi les planètes du système solaire restent-elles en orbite autour du Soleil? 1) Qu'est-ce que la gravitation universelle? activité : Attraction universelle La cohésion
Trépier avec règle, ressort à boudin, chronomètre, 5 masses de 50 g.
 PHYSQ 130: Hooke 1 LOI DE HOOKE: CAS DU RESSORT 1 Introduction La loi de Hooke est fondamentale dans l étude du mouvement oscillatoire. Elle est utilisée, entre autres, dans les théories décrivant les
PHYSQ 130: Hooke 1 LOI DE HOOKE: CAS DU RESSORT 1 Introduction La loi de Hooke est fondamentale dans l étude du mouvement oscillatoire. Elle est utilisée, entre autres, dans les théories décrivant les
Cours et Exercices de Mécanique :
 Cours et Eercices de Mécanique : Mécanique du Point Ingénieur CESI Préparation au tests de sélection Version 40-1 - Programme de physique B Mécanique Chapitre 5 : Statique - Forces, moments de forces,
Cours et Eercices de Mécanique : Mécanique du Point Ingénieur CESI Préparation au tests de sélection Version 40-1 - Programme de physique B Mécanique Chapitre 5 : Statique - Forces, moments de forces,
DÉRIVÉES. I Nombre dérivé - Tangente. Exercice 01 (voir réponses et correction) ( voir animation )
 DÉRIVÉES I Nombre dérivé - Tangente Eercice 0 ( voir animation ) On considère la fonction f définie par f() = - 2 + 6 pour [-4 ; 4]. ) Tracer la représentation graphique (C) de f dans un repère d'unité
DÉRIVÉES I Nombre dérivé - Tangente Eercice 0 ( voir animation ) On considère la fonction f définie par f() = - 2 + 6 pour [-4 ; 4]. ) Tracer la représentation graphique (C) de f dans un repère d'unité
TD de Physique n o 1 : Mécanique du point
 E.N.S. de Cachan Département E.E.A. M FE 3 e année Phsique appliquée 011-01 TD de Phsique n o 1 : Mécanique du point Exercice n o 1 : Trajectoire d un ballon-sonde Un ballon-sonde M, lâché au niveau du
E.N.S. de Cachan Département E.E.A. M FE 3 e année Phsique appliquée 011-01 TD de Phsique n o 1 : Mécanique du point Exercice n o 1 : Trajectoire d un ballon-sonde Un ballon-sonde M, lâché au niveau du
Travaux dirigés de mécanique du point
 Travaux dirigés de mécanique du point Année 011-01 Arnaud LE PADELLEC Magali MOURGUES alepadellec@irap.omp.eu magali.mourgues@univ-tlse3.fr Travaux dirigés de mécanique du point 1/40 P r é s e n t a t
Travaux dirigés de mécanique du point Année 011-01 Arnaud LE PADELLEC Magali MOURGUES alepadellec@irap.omp.eu magali.mourgues@univ-tlse3.fr Travaux dirigés de mécanique du point 1/40 P r é s e n t a t
Chapitre 1 Cinématique du point matériel
 Chapitre 1 Cinématique du point matériel 7 1.1. Introduction 1.1.1. Domaine d étude Le programme de mécanique de math sup se limite à l étude de la mécanique classique. Sont exclus : la relativité et la
Chapitre 1 Cinématique du point matériel 7 1.1. Introduction 1.1.1. Domaine d étude Le programme de mécanique de math sup se limite à l étude de la mécanique classique. Sont exclus : la relativité et la
STATIQUE GRAPHIQUE ET STATIQUE ANALYTIQUE
 ÉCOLE D'INGÉNIEURS DE FRIBOURG (E.I.F.) SECTION DE MÉCANIQUE G.R. Nicolet, revu en 2006 STATIQUE GRAPHIQUE ET STATIQUE ANALYTIQUE Eléments de calcul vectoriel Opérations avec les forces Equilibre du point
ÉCOLE D'INGÉNIEURS DE FRIBOURG (E.I.F.) SECTION DE MÉCANIQUE G.R. Nicolet, revu en 2006 STATIQUE GRAPHIQUE ET STATIQUE ANALYTIQUE Eléments de calcul vectoriel Opérations avec les forces Equilibre du point
Angles orientés et fonctions circulaires ( En première S )
 Angles orientés et fonctions circulaires ( En première S ) Dernière mise à jour : Jeudi 01 Septembre 010 Vincent OBATON, Enseignant au lycée Stendhal de Grenoble (Année 006-007) Lycée Stendhal, Grenoble
Angles orientés et fonctions circulaires ( En première S ) Dernière mise à jour : Jeudi 01 Septembre 010 Vincent OBATON, Enseignant au lycée Stendhal de Grenoble (Année 006-007) Lycée Stendhal, Grenoble
Problèmes sur le chapitre 5
 Problèmes sur le chapitre 5 (Version du 13 janvier 2015 (10h38)) 501 Le calcul des réactions d appui dans les problèmes schématisés ci-dessous est-il possible par les équations de la statique Si oui, écrire
Problèmes sur le chapitre 5 (Version du 13 janvier 2015 (10h38)) 501 Le calcul des réactions d appui dans les problèmes schématisés ci-dessous est-il possible par les équations de la statique Si oui, écrire
Chapitre 9 : Applications des lois de Newton et Kepler à l'étude du mouvement des planètes et des satellites
 I- Les trois lois de Kepler : Chapitre 9 : Applications des lois de Newton et Kepler à l'étude du mouvement des planètes et des satellites Les lois de Kepler s'applique aussi bien pour une planète en mouvement
I- Les trois lois de Kepler : Chapitre 9 : Applications des lois de Newton et Kepler à l'étude du mouvement des planètes et des satellites Les lois de Kepler s'applique aussi bien pour une planète en mouvement
Chapitre 2 : Caractéristiques du mouvement d un solide
 Chapitre 2 : Caractéristiques du mouvement d un solide I Rappels : Référentiel : Le mouvement d un corps est décris par rapport à un corps de référence et dépend du choix de ce corps. Ce corps de référence
Chapitre 2 : Caractéristiques du mouvement d un solide I Rappels : Référentiel : Le mouvement d un corps est décris par rapport à un corps de référence et dépend du choix de ce corps. Ce corps de référence
MECANIQUE DU POINT. y e y. z e z. ] est le trièdre de référence. e z. où [O, e r. r est la distance à l'axe, θ l'angle polaire et z la côte
![MECANIQUE DU POINT. y e y. z e z. ] est le trièdre de référence. e z. où [O, e r. r est la distance à l'axe, θ l'angle polaire et z la côte MECANIQUE DU POINT. y e y. z e z. ] est le trièdre de référence. e z. où [O, e r. r est la distance à l'axe, θ l'angle polaire et z la côte](/thumbs/19/247967.jpg) I) Cinématique du point matériel: 1) Référentiel: MECANIQUE DU POINT L ensemble de tous les systèmes d axes de coordonnées liés à un même solide de référence S constitue un repère Soit une horloge permettant
I) Cinématique du point matériel: 1) Référentiel: MECANIQUE DU POINT L ensemble de tous les systèmes d axes de coordonnées liés à un même solide de référence S constitue un repère Soit une horloge permettant
10 leçon 2. Leçon n 2 : Contact entre deux solides. Frottement de glissement. Exemples. (PC ou 1 er CU)
 0 leçon 2 Leçon n 2 : Contact entre deu solides Frottement de glissement Eemples (PC ou er CU) Introduction Contact entre deu solides Liaisons de contact 2 Contact ponctuel 2 Frottement de glissement 2
0 leçon 2 Leçon n 2 : Contact entre deu solides Frottement de glissement Eemples (PC ou er CU) Introduction Contact entre deu solides Liaisons de contact 2 Contact ponctuel 2 Frottement de glissement 2
Bac Blanc Terminale ES - Février 2011 Épreuve de Mathématiques (durée 3 heures)
 Bac Blanc Terminale ES - Février 2011 Épreuve de Mathématiques (durée 3 heures) Eercice 1 (5 points) pour les candidats n ayant pas choisi la spécialité MATH Le tableau suivant donne l évolution du chiffre
Bac Blanc Terminale ES - Février 2011 Épreuve de Mathématiques (durée 3 heures) Eercice 1 (5 points) pour les candidats n ayant pas choisi la spécialité MATH Le tableau suivant donne l évolution du chiffre
Quantité de mouvement et moment cinétique
 6 Quantité de mouvement et moment cinétique v7 p = mv L = r p 1 Impulsion et quantité de mouvement Une force F agit sur un corps de masse m, pendant un temps Δt. La vitesse du corps varie de Δv = v f -
6 Quantité de mouvement et moment cinétique v7 p = mv L = r p 1 Impulsion et quantité de mouvement Une force F agit sur un corps de masse m, pendant un temps Δt. La vitesse du corps varie de Δv = v f -
PHYSIQUE Discipline fondamentale
 Examen suisse de maturité Directives 2003-2006 DS.11 Physique DF PHYSIQUE Discipline fondamentale Par l'étude de la physique en discipline fondamentale, le candidat comprend des phénomènes naturels et
Examen suisse de maturité Directives 2003-2006 DS.11 Physique DF PHYSIQUE Discipline fondamentale Par l'étude de la physique en discipline fondamentale, le candidat comprend des phénomènes naturels et
Mécanique. Chapitre 4. Mécanique en référentiel non galiléen
 Mécanique Chapitre 4 Mécanique en référentiel non galiléen I Référentiel en translation Mécanique en référentiel non galiléen Jusqu à présent, nous avons fait de la mécanique du point dans un référentiel
Mécanique Chapitre 4 Mécanique en référentiel non galiléen I Référentiel en translation Mécanique en référentiel non galiléen Jusqu à présent, nous avons fait de la mécanique du point dans un référentiel
PHYS-F-104_C) Physique I (mécanique, ondes et optiques) Solutions des questions d'examens (2004-2013)
 PRESSES UNIVERSITAIRES DE BRUXELLES UNIVERSITÉ LIBRE DE BRUXELLES Physique I (mécanique, ondes et optiques) Solutions des questions d'examens (004-013) Pascal VANLAER Titulaire Notes rédigées par Pierre
PRESSES UNIVERSITAIRES DE BRUXELLES UNIVERSITÉ LIBRE DE BRUXELLES Physique I (mécanique, ondes et optiques) Solutions des questions d'examens (004-013) Pascal VANLAER Titulaire Notes rédigées par Pierre
Sommaire Table des matières
 Notice de montage 1 Sommaire Table des matières I. Mise en garde... 3 II. Avant de commencer... 4 1. Préparer vos outils... 4 2. Pièces nécessaires pour le montage de votre porte Keritek... 5 III. Étape
Notice de montage 1 Sommaire Table des matières I. Mise en garde... 3 II. Avant de commencer... 4 1. Préparer vos outils... 4 2. Pièces nécessaires pour le montage de votre porte Keritek... 5 III. Étape
Q6 : Comment calcule t-on l intensité sonore à partir du niveau d intensité?
 EXERCICE 1 : QUESTION DE COURS Q1 : Qu est ce qu une onde progressive? Q2 : Qu est ce qu une onde mécanique? Q3 : Qu elle est la condition pour qu une onde soit diffractée? Q4 : Quelles sont les différentes
EXERCICE 1 : QUESTION DE COURS Q1 : Qu est ce qu une onde progressive? Q2 : Qu est ce qu une onde mécanique? Q3 : Qu elle est la condition pour qu une onde soit diffractée? Q4 : Quelles sont les différentes
Corrigé Exercice 1 : BRIDE HYDRAULIQUE AVEC HYPOTHÈSE PROBLÈME PLAN.
 TD 6 corrigé - PFS Résolution analytique (Loi entrée-sortie statique) Page 1/1 Corrigé Exercice 1 : BRIDE HYDRAULIQUE AVEC HYPOTHÈSE PROBLÈME PLAN. Question : Réaliser le graphe de structure, puis compléter
TD 6 corrigé - PFS Résolution analytique (Loi entrée-sortie statique) Page 1/1 Corrigé Exercice 1 : BRIDE HYDRAULIQUE AVEC HYPOTHÈSE PROBLÈME PLAN. Question : Réaliser le graphe de structure, puis compléter
Oscillations libres des systèmes à deux degrés de liberté
 Chapitre 4 Oscillations libres des systèmes à deux degrés de liberté 4.1 Introduction Les systèmes qui nécessitent deux coordonnées indépendantes pour spécifier leurs positions sont appelés systèmes à
Chapitre 4 Oscillations libres des systèmes à deux degrés de liberté 4.1 Introduction Les systèmes qui nécessitent deux coordonnées indépendantes pour spécifier leurs positions sont appelés systèmes à
La fonction exponentielle
 DERNIÈRE IMPRESSION LE 2 novembre 204 à :07 La fonction exponentielle Table des matières La fonction exponentielle 2. Définition et théorèmes.......................... 2.2 Approche graphique de la fonction
DERNIÈRE IMPRESSION LE 2 novembre 204 à :07 La fonction exponentielle Table des matières La fonction exponentielle 2. Définition et théorèmes.......................... 2.2 Approche graphique de la fonction
- MANIP 2 - APPLICATION À LA MESURE DE LA VITESSE DE LA LUMIÈRE
 - MANIP 2 - - COÏNCIDENCES ET MESURES DE TEMPS - APPLICATION À LA MESURE DE LA VITESSE DE LA LUMIÈRE L objectif de cette manipulation est d effectuer une mesure de la vitesse de la lumière sur une «base
- MANIP 2 - - COÏNCIDENCES ET MESURES DE TEMPS - APPLICATION À LA MESURE DE LA VITESSE DE LA LUMIÈRE L objectif de cette manipulation est d effectuer une mesure de la vitesse de la lumière sur une «base
Chapitre 7 - Relativité du mouvement
 Un bus roule lentement dans une ville. Alain (A) est assis dans le bus, Brigitte (B) marche dans l'allée vers l'arrière du bus pour faire des signes à Claude (C) qui est au bord de la route. Brigitte marche
Un bus roule lentement dans une ville. Alain (A) est assis dans le bus, Brigitte (B) marche dans l'allée vers l'arrière du bus pour faire des signes à Claude (C) qui est au bord de la route. Brigitte marche
F411 - Courbes Paramétrées, Polaires
 1/43 Courbes Paramétrées Courbes polaires Longueur d un arc, Courbure F411 - Courbes Paramétrées, Polaires Michel Fournié michel.fournie@iut-tlse3.fr http://www.math.univ-toulouse.fr/ fournie/ Année 2012/2013
1/43 Courbes Paramétrées Courbes polaires Longueur d un arc, Courbure F411 - Courbes Paramétrées, Polaires Michel Fournié michel.fournie@iut-tlse3.fr http://www.math.univ-toulouse.fr/ fournie/ Année 2012/2013
PRECISION - REJET DE PERTURBATIONS T.D. G.E.I.I.
 PRECISION - REJET DE PERTURBATIONS T.D. G.E.I.I.. Donner les erreurs en position, en vitesse et en accélération d un système de transfert F BO = N(p) D(p) (transfert en boucle ouverte) bouclé par retour
PRECISION - REJET DE PERTURBATIONS T.D. G.E.I.I.. Donner les erreurs en position, en vitesse et en accélération d un système de transfert F BO = N(p) D(p) (transfert en boucle ouverte) bouclé par retour
Mécanique : Cinématique du point. Chapitre 1 : Position. Vitesse. Accélération
 2 e B et C 1 Position. Vitesse. Accélération 1 Mécanique : Cinéatique du point La écanique est le doaine de tout ce qui produit ou transet un ouveent, une force, une déforation : achines, oteurs, véhicules,
2 e B et C 1 Position. Vitesse. Accélération 1 Mécanique : Cinéatique du point La écanique est le doaine de tout ce qui produit ou transet un ouveent, une force, une déforation : achines, oteurs, véhicules,
Fonctions de plusieurs variables
 Module : Analyse 03 Chapitre 00 : Fonctions de plusieurs variables Généralités et Rappels des notions topologiques dans : Qu est- ce que?: Mathématiquement, n étant un entier non nul, on définit comme
Module : Analyse 03 Chapitre 00 : Fonctions de plusieurs variables Généralités et Rappels des notions topologiques dans : Qu est- ce que?: Mathématiquement, n étant un entier non nul, on définit comme
DM n o 8 TS1 2012 Physique 10 (satellites) + Chimie 12 (catalyse) Exercice 1 Lancement d un satellite météorologique
 DM n o 8 TS1 2012 Physique 10 (satellites) + Chimie 12 (catalyse) Exercice 1 Lancement d un satellite météorologique Le centre spatial de Kourou a lancé le 21 décembre 200, avec une fusée Ariane, un satellite
DM n o 8 TS1 2012 Physique 10 (satellites) + Chimie 12 (catalyse) Exercice 1 Lancement d un satellite météorologique Le centre spatial de Kourou a lancé le 21 décembre 200, avec une fusée Ariane, un satellite
DURÉE DU JOUR EN FONCTION DE LA DATE ET DE LA LATITUDE
 DURÉE DU JUR E FCTI DE LA DATE ET DE LA LATITUDE ous allons nous intéresser à la durée du jour, prise ici dans le sens de période d éclairement par le Soleil dans une journée de 4 h, en un lieu donné de
DURÉE DU JUR E FCTI DE LA DATE ET DE LA LATITUDE ous allons nous intéresser à la durée du jour, prise ici dans le sens de période d éclairement par le Soleil dans une journée de 4 h, en un lieu donné de
VOITURE A REACTION. Kart à réaction réalisé par un bricoleur «fou» (Bruce Simpson)
 VOITURE A REACTION Kart à réaction réalisé par un bricoleur «fou» (Bruce Simpson) 1 Introduction BUT DE L ACTIVITE Fabriquer une voiture à réaction originale et sans danger Jouer avec et essayer plein
VOITURE A REACTION Kart à réaction réalisé par un bricoleur «fou» (Bruce Simpson) 1 Introduction BUT DE L ACTIVITE Fabriquer une voiture à réaction originale et sans danger Jouer avec et essayer plein
Système formé de deux points
 MPSI - 2005/2006 - Mécanique II - Système formé de deux points matériels page /5 Système formé de deux points matériels Table des matières Éléments cinétiques. Éléments cinétiques dans R.......................2
MPSI - 2005/2006 - Mécanique II - Système formé de deux points matériels page /5 Système formé de deux points matériels Table des matières Éléments cinétiques. Éléments cinétiques dans R.......................2
Dimensionnement d une roue autonome pour une implantation sur un fauteuil roulant
 Dimensionnement d une roue autonome pour une implantation sur un fauteuil roulant I Présentation I.1 La roue autonome Ez-Wheel SAS est une entreprise française de technologie innovante fondée en 2009.
Dimensionnement d une roue autonome pour une implantation sur un fauteuil roulant I Présentation I.1 La roue autonome Ez-Wheel SAS est une entreprise française de technologie innovante fondée en 2009.
Les correcteurs accorderont une importance particulière à la rigueur des raisonnements et aux représentations graphiques demandées.
 Les correcteurs accorderont une importance particulière à la rigueur des raisonnements et aux représentations graphiques demandées. 1 Ce sujet aborde le phénomène d instabilité dans des systèmes dynamiques
Les correcteurs accorderont une importance particulière à la rigueur des raisonnements et aux représentations graphiques demandées. 1 Ce sujet aborde le phénomène d instabilité dans des systèmes dynamiques
* très facile ** facile *** difficulté moyenne **** difficile ***** très difficile I : Incontournable T : pour travailler et mémoriser le cours.
 Eo7 Fonctions de plusieurs variables Eercices de Jean-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-francefr * très facile ** facile *** difficulté moenne **** difficile ***** très difficile I
Eo7 Fonctions de plusieurs variables Eercices de Jean-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-francefr * très facile ** facile *** difficulté moenne **** difficile ***** très difficile I
Jean-Marc Schaffner Ateliers SCHAFFNER. Laure Delaporte ConstruirAcier. Jérémy Trouart Union des Métalliers
 Jean-Marc Schaffner Ateliers SCHAFFNER Laure Delaporte ConstruirAcier Jérémy Trouart Union des Métalliers Jean-Marc SCHAFFNER des Ateliers SCHAFFNER chef de file du GT4 Jérémy TROUART de l Union des Métalliers
Jean-Marc Schaffner Ateliers SCHAFFNER Laure Delaporte ConstruirAcier Jérémy Trouart Union des Métalliers Jean-Marc SCHAFFNER des Ateliers SCHAFFNER chef de file du GT4 Jérémy TROUART de l Union des Métalliers
Test : principe fondamental de la dynamique et aspect énergétique
 Durée : 45 minutes Objectifs Test : principe fondamental de la dynamique et aspect énergétique Projection de forces. Calcul de durée d'accélération / décélération ou d'accélération / décélération ou de
Durée : 45 minutes Objectifs Test : principe fondamental de la dynamique et aspect énergétique Projection de forces. Calcul de durée d'accélération / décélération ou d'accélération / décélération ou de
CONCOURS COMMUN 2010 PHYSIQUE
 CONCOUS COMMUN SUJET A DES ÉCOLES DES MINES D ALBI, ALÈS, DOUAI, NANTES Épreuve de Physique-Chimie (toutes filières) Corrigé Barème total points : Physique points - Chimie 68 points PHYSIQUE Partie A :
CONCOUS COMMUN SUJET A DES ÉCOLES DES MINES D ALBI, ALÈS, DOUAI, NANTES Épreuve de Physique-Chimie (toutes filières) Corrigé Barème total points : Physique points - Chimie 68 points PHYSIQUE Partie A :
PROBLEME(12) Première partie : Peinture des murs et du plafond.
 PROBLEME(12) Une entreprise doit rénover un local. Ce local a la forme d'un parallélépipède rectangle. La longueur est 6,40m, la largeur est 5,20m et la hauteur est 2,80m. Il comporte une porte de 2m de
PROBLEME(12) Une entreprise doit rénover un local. Ce local a la forme d'un parallélépipède rectangle. La longueur est 6,40m, la largeur est 5,20m et la hauteur est 2,80m. Il comporte une porte de 2m de
MATIE RE DU COURS DE PHYSIQUE
 MATIE RE DU COURS DE PHYSIQUE Titulaire : A. Rauw 5h/semaine 1) MÉCANIQUE a) Cinématique ii) Référentiel Relativité des notions de repos et mouvement Relativité de la notion de trajectoire Référentiel
MATIE RE DU COURS DE PHYSIQUE Titulaire : A. Rauw 5h/semaine 1) MÉCANIQUE a) Cinématique ii) Référentiel Relativité des notions de repos et mouvement Relativité de la notion de trajectoire Référentiel
INVERSIO. N Azur 0 810 104 104. www.castorama.fr Service consommateur Castorama BP101-59175 Templemars. réf. R1-99879
 INVERSIO Réf. ALTERNA 0 7 FR www.castorama.fr Service consommateur Castorama BP0-97 Templemars N Azur 0 80 0 0 PRI D UN APPEL LOCAL DEPUIS UN POSTE FIE réf. R-99879 R 99880-0909 Notice_INVERSIO_LIVRET_A_EE.indd
INVERSIO Réf. ALTERNA 0 7 FR www.castorama.fr Service consommateur Castorama BP0-97 Templemars N Azur 0 80 0 0 PRI D UN APPEL LOCAL DEPUIS UN POSTE FIE réf. R-99879 R 99880-0909 Notice_INVERSIO_LIVRET_A_EE.indd
Savoir lire une carte, se situer et s orienter en randonnée
 Savoir lire une carte, se situer et s orienter en randonnée Le b.a.-ba du randonneur Fiche 2 Lire une carte topographique Mais c est où le nord? Quel Nord Le magnétisme terrestre attire systématiquement
Savoir lire une carte, se situer et s orienter en randonnée Le b.a.-ba du randonneur Fiche 2 Lire une carte topographique Mais c est où le nord? Quel Nord Le magnétisme terrestre attire systématiquement
DYNAMIQUE DE FORMATION DES ÉTOILES
 A 99 PHYS. II ÉCOLE NATIONALE DES PONTS ET CHAUSSÉES, ÉCOLES NATIONALES SUPÉRIEURES DE L'AÉRONAUTIQUE ET DE L'ESPACE, DE TECHNIQUES AVANCÉES, DES TÉLÉCOMMUNICATIONS, DES MINES DE PARIS, DES MINES DE SAINT-ÉTIENNE,
A 99 PHYS. II ÉCOLE NATIONALE DES PONTS ET CHAUSSÉES, ÉCOLES NATIONALES SUPÉRIEURES DE L'AÉRONAUTIQUE ET DE L'ESPACE, DE TECHNIQUES AVANCÉES, DES TÉLÉCOMMUNICATIONS, DES MINES DE PARIS, DES MINES DE SAINT-ÉTIENNE,
METEOROLOGIE CAEA 1990
 METEOROLOGIE CAEA 1990 1) Les météorologistes mesurent et prévoient le vent en attitude à des niveaux exprimés en pressions atmosphériques. Entre le niveau de la mer et 6000 m d'altitude, quels sont les
METEOROLOGIE CAEA 1990 1) Les météorologistes mesurent et prévoient le vent en attitude à des niveaux exprimés en pressions atmosphériques. Entre le niveau de la mer et 6000 m d'altitude, quels sont les
Salle de technologie
 Prénom : Nom : Classe : Date : Salle de technologie Séquence Le dessin technique Définition du dessin technique : Le dessin technique est un ensemble de règles pour représenter des objets ; ces règles
Prénom : Nom : Classe : Date : Salle de technologie Séquence Le dessin technique Définition du dessin technique : Le dessin technique est un ensemble de règles pour représenter des objets ; ces règles
I - Quelques propriétés des étoiles à neutrons
 Formation Interuniversitaire de Physique Option de L3 Ecole Normale Supérieure de Paris Astrophysique Patrick Hennebelle François Levrier Sixième TD 14 avril 2015 Les étoiles dont la masse initiale est
Formation Interuniversitaire de Physique Option de L3 Ecole Normale Supérieure de Paris Astrophysique Patrick Hennebelle François Levrier Sixième TD 14 avril 2015 Les étoiles dont la masse initiale est
Chap 8 - TEMPS & RELATIVITE RESTREINTE
 Chap 8 - TEMPS & RELATIVITE RESTREINTE Exercice 0 page 9 On considère deux évènements E et E Référentiel propre, R : la Terre. Dans ce référentiel, les deux évènements ont lieu au même endroit. La durée
Chap 8 - TEMPS & RELATIVITE RESTREINTE Exercice 0 page 9 On considère deux évènements E et E Référentiel propre, R : la Terre. Dans ce référentiel, les deux évènements ont lieu au même endroit. La durée
Etoiles doubles (et autres systèmes de deux points matériels)
 Projet de Physique P6-3 STPI/P6-3/009 35 Etoiles doubles (et autres systèmes de deux points matériels) Etudiants : Eve ARQUIN Anastacia BILICI Mylène CHAMPAIN Arnaud DELANDE Zineb LAMRANI Coralie PONSINET
Projet de Physique P6-3 STPI/P6-3/009 35 Etoiles doubles (et autres systèmes de deux points matériels) Etudiants : Eve ARQUIN Anastacia BILICI Mylène CHAMPAIN Arnaud DELANDE Zineb LAMRANI Coralie PONSINET
Représentation géométrique d un nombre complexe
 CHAPITRE 1 NOMBRES COMPLEXES 1 Représentation géométrique d un nombre complexe 1. Ensemble des nombres complexes Soit i le nombre tel que i = 1 L ensemble des nombres complexes est l ensemble des nombres
CHAPITRE 1 NOMBRES COMPLEXES 1 Représentation géométrique d un nombre complexe 1. Ensemble des nombres complexes Soit i le nombre tel que i = 1 L ensemble des nombres complexes est l ensemble des nombres
OM 1 Outils mathématiques : fonction de plusieurs variables
 Outils mathématiques : fonction de plusieurs variables PCSI 2013 2014 Certaines partie de ce chapitre ne seront utiles qu à partir de l année prochaine, mais une grande partie nous servira dès cette année.
Outils mathématiques : fonction de plusieurs variables PCSI 2013 2014 Certaines partie de ce chapitre ne seront utiles qu à partir de l année prochaine, mais une grande partie nous servira dès cette année.
Continuité et dérivabilité d une fonction
 DERNIÈRE IMPRESSIN LE 7 novembre 014 à 10:3 Continuité et dérivabilité d une fonction Table des matières 1 Continuité d une fonction 1.1 Limite finie en un point.......................... 1. Continuité
DERNIÈRE IMPRESSIN LE 7 novembre 014 à 10:3 Continuité et dérivabilité d une fonction Table des matières 1 Continuité d une fonction 1.1 Limite finie en un point.......................... 1. Continuité
TSTI 2D CH X : Exemples de lois à densité 1
 TSTI 2D CH X : Exemples de lois à densité I Loi uniforme sur ab ; ) Introduction Dans cette activité, on s intéresse à la modélisation du tirage au hasard d un nombre réel de l intervalle [0 ;], chacun
TSTI 2D CH X : Exemples de lois à densité I Loi uniforme sur ab ; ) Introduction Dans cette activité, on s intéresse à la modélisation du tirage au hasard d un nombre réel de l intervalle [0 ;], chacun
Planche n o 22. Fonctions de plusieurs variables. Corrigé
 Planche n o Fonctions de plusieurs variables Corrigé n o : f est définie sur R \ {, } Pour, f, = Quand tend vers, le couple, tend vers le couple, et f, tend vers Donc, si f a une limite réelle en, cette
Planche n o Fonctions de plusieurs variables Corrigé n o : f est définie sur R \ {, } Pour, f, = Quand tend vers, le couple, tend vers le couple, et f, tend vers Donc, si f a une limite réelle en, cette
Les calculatrices sont autorisées
 Les calculatrices sont autorisées Le sujet comporte quatre parties indépendantes. Les parties 1 et portent sur la mécanique (de la page à la page 7). Les parties 3 et 4 portent sur la thermodnamique (de
Les calculatrices sont autorisées Le sujet comporte quatre parties indépendantes. Les parties 1 et portent sur la mécanique (de la page à la page 7). Les parties 3 et 4 portent sur la thermodnamique (de
ÉVALUATION EN FIN DE CM1. Année scolaire 2014 2015 LIVRET DE L'ÉLÈVE MATHÉMATIQUES
 ÉVALUATION EN FIN DE CM1 Année scolaire 2014 2015 LIVRET DE L'ÉLÈVE MATHÉMATIQUES NOM :....... Prénom :....... Né le :./../ École :............ Classe : Domaine Score de réussite NOMBRES ET CALCUL GÉOMÉTRIE
ÉVALUATION EN FIN DE CM1 Année scolaire 2014 2015 LIVRET DE L'ÉLÈVE MATHÉMATIQUES NOM :....... Prénom :....... Né le :./../ École :............ Classe : Domaine Score de réussite NOMBRES ET CALCUL GÉOMÉTRIE
CABLECAM de HYMATOM. Figure 1 : Schéma du système câblecam et détail du moufle vu de dessus.
 CABLECAM de HYMATOM La société Hymatom conçoit et fabrique des systèmes de vidéosurveillance. Le système câblecam (figure 1) est composé d un chariot mobile sur quatre roues posé sur deux câbles porteurs
CABLECAM de HYMATOM La société Hymatom conçoit et fabrique des systèmes de vidéosurveillance. Le système câblecam (figure 1) est composé d un chariot mobile sur quatre roues posé sur deux câbles porteurs
Cours IV Mise en orbite
 Introduction au vol spatial Cours IV Mise en orbite If you don t know where you re going, you ll probably end up somewhere else. Yogi Berra, NY Yankees catcher v1.2.8 by-sa Olivier Cleynen Introduction
Introduction au vol spatial Cours IV Mise en orbite If you don t know where you re going, you ll probably end up somewhere else. Yogi Berra, NY Yankees catcher v1.2.8 by-sa Olivier Cleynen Introduction
Plan du cours : électricité 1
 Semestre : S2 Module Physique II 1 Electricité 1 2 Optique géométrique Plan du cours : électricité 1 Partie A : Electrostatique (discipline de l étude des phénomènes liés aux distributions de charges stationnaires)
Semestre : S2 Module Physique II 1 Electricité 1 2 Optique géométrique Plan du cours : électricité 1 Partie A : Electrostatique (discipline de l étude des phénomènes liés aux distributions de charges stationnaires)
LES ESCALIERS. Du niveau du rez-de-chaussée à celui de l'étage ou à celui du sous-sol.
 LES ESCALIERS I. DÉF I NIT I O N Un escalier est un ouvrage constitué d'une suite de marches et de paliers permettant de passer à pied d'un niveau à un autre. Ses caractéristiques dimensionnelles sont
LES ESCALIERS I. DÉF I NIT I O N Un escalier est un ouvrage constitué d'une suite de marches et de paliers permettant de passer à pied d'un niveau à un autre. Ses caractéristiques dimensionnelles sont
TP 7 : oscillateur de torsion
 TP 7 : oscillateur de torsion Objectif : étude des oscillations libres et forcées d un pendule de torsion 1 Principe général 1.1 Définition Un pendule de torsion est constitué par un fil large (métallique)
TP 7 : oscillateur de torsion Objectif : étude des oscillations libres et forcées d un pendule de torsion 1 Principe général 1.1 Définition Un pendule de torsion est constitué par un fil large (métallique)
* très facile ** facile *** difficulté moyenne **** difficile ***** très difficile I : Incontournable
 Eo7 Fonctions de plusieurs variables Eercices de Jean-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-francefr * très facile ** facile *** difficulté moenne **** difficile ***** très difficile I
Eo7 Fonctions de plusieurs variables Eercices de Jean-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-francefr * très facile ** facile *** difficulté moenne **** difficile ***** très difficile I
Calcul intégral élémentaire en plusieurs variables
 Calcul intégral élémentaire en plusieurs variables PC*2 2 septembre 2009 Avant-propos À part le théorème de Fubini qui sera démontré dans le cours sur les intégrales à paramètres et qui ne semble pas explicitement
Calcul intégral élémentaire en plusieurs variables PC*2 2 septembre 2009 Avant-propos À part le théorème de Fubini qui sera démontré dans le cours sur les intégrales à paramètres et qui ne semble pas explicitement
CHAPITRE 1. Suites arithmetiques et géometriques. Rappel 1. On appelle suite réelle une application de
 HAPITRE 1 Suites arithmetiques et géometriques Rappel 1 On appelle suite réelle une application de dans, soit est-à-dire pour une valeur de la variable appartenant à la suite prend la valeur, ie : On notera
HAPITRE 1 Suites arithmetiques et géometriques Rappel 1 On appelle suite réelle une application de dans, soit est-à-dire pour une valeur de la variable appartenant à la suite prend la valeur, ie : On notera
Exprimer ce coefficient de proportionnalité sous forme de pourcentage : 3,5 %
 23 CALCUL DE L INTÉRÊT Tau d intérêt Paul et Rémi ont reçu pour Noël, respectivement, 20 et 80. Ils placent cet argent dans une banque, au même tau. Au bout d une année, ce placement leur rapportera une
23 CALCUL DE L INTÉRÊT Tau d intérêt Paul et Rémi ont reçu pour Noël, respectivement, 20 et 80. Ils placent cet argent dans une banque, au même tau. Au bout d une année, ce placement leur rapportera une
Equations cartésiennes d une droite
 Equations cartésiennes d une droite I) Vecteur directeur d une droite : 1) Définition Soit (d) une droite du plan. Un vecteur directeur d une droite (d) est un vecteur non nul la même direction que la
Equations cartésiennes d une droite I) Vecteur directeur d une droite : 1) Définition Soit (d) une droite du plan. Un vecteur directeur d une droite (d) est un vecteur non nul la même direction que la
Exo7. Limites de fonctions. 1 Théorie. 2 Calculs
 Eo7 Limites de fonctions Théorie Eercice Montrer que toute fonction périodique et non constante n admet pas de ite en + Montrer que toute fonction croissante et majorée admet une ite finie en + Indication
Eo7 Limites de fonctions Théorie Eercice Montrer que toute fonction périodique et non constante n admet pas de ite en + Montrer que toute fonction croissante et majorée admet une ite finie en + Indication
Erratum de MÉCANIQUE, 6ème édition. Introduction Page xxi (milieu de page) G = 6, 672 59 10 11 m 3 kg 1 s 2
 Introduction Page xxi (milieu de page) G = 6, 672 59 1 11 m 3 kg 1 s 2 Erratum de MÉCANIQUE, 6ème édition Page xxv (dernier tiers de page) le terme de Coriolis est supérieur à 1% du poids) Chapitre 1 Page
Introduction Page xxi (milieu de page) G = 6, 672 59 1 11 m 3 kg 1 s 2 Erratum de MÉCANIQUE, 6ème édition Page xxv (dernier tiers de page) le terme de Coriolis est supérieur à 1% du poids) Chapitre 1 Page
Projet de parc éolien en mer au large de Courseulles-sur-Mer
 ÉOLIENNES OFFSHORE DU CALVADOS avril 2013 Projet de parc éolien en mer au large de Courseulles-sur-Mer Synthèse d étude relative à la protection des câbles Sommaire 1. CONTEXTE ET OBJECTIF DE L ETUDE...
ÉOLIENNES OFFSHORE DU CALVADOS avril 2013 Projet de parc éolien en mer au large de Courseulles-sur-Mer Synthèse d étude relative à la protection des câbles Sommaire 1. CONTEXTE ET OBJECTIF DE L ETUDE...
Cours de Mécanique du point matériel
 Cours de Mécanique du point matériel SMPC1 Module 1 : Mécanique 1 Session : Automne 2014 Prof. M. EL BAZ Cours de Mécanique du Point matériel Chapitre 1 : Complément Mathématique SMPC1 Chapitre 1: Rappels
Cours de Mécanique du point matériel SMPC1 Module 1 : Mécanique 1 Session : Automne 2014 Prof. M. EL BAZ Cours de Mécanique du Point matériel Chapitre 1 : Complément Mathématique SMPC1 Chapitre 1: Rappels
Cours de résistance des matériaux
 ENSM-SE RDM - CPMI 2011-2012 1 Cycle Préparatoire Médecin-Ingénieur 2011-2012 Cours de résistance des matériau Pierre Badel Ecole des Mines Saint Etienne Première notions de mécanique des solides déformables
ENSM-SE RDM - CPMI 2011-2012 1 Cycle Préparatoire Médecin-Ingénieur 2011-2012 Cours de résistance des matériau Pierre Badel Ecole des Mines Saint Etienne Première notions de mécanique des solides déformables
SINE QUA NON. Découverte et Prise en main du logiciel Utilisation de bases
 SINE QUA NON Découverte et Prise en main du logiciel Utilisation de bases Sine qua non est un logiciel «traceur de courbes planes» mais il possède aussi bien d autres fonctionnalités que nous verrons tout
SINE QUA NON Découverte et Prise en main du logiciel Utilisation de bases Sine qua non est un logiciel «traceur de courbes planes» mais il possède aussi bien d autres fonctionnalités que nous verrons tout
SEANCE 4 : MECANIQUE THEOREMES FONDAMENTAUX
 SEANCE 4 : MECANIQUE THEOREMES FONDAMENTAUX 1. EXPERIENCE 1 : APPLICATION DE LA LOI FONDAMENTALE DE LA DYNAMIQUE a) On incline d un angle α la table à digitaliser (deuxième ou troisième cran de la table).
SEANCE 4 : MECANIQUE THEOREMES FONDAMENTAUX 1. EXPERIENCE 1 : APPLICATION DE LA LOI FONDAMENTALE DE LA DYNAMIQUE a) On incline d un angle α la table à digitaliser (deuxième ou troisième cran de la table).
Manutention et Levage
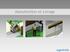 Manutention et Levage Manutentions Manuelles : la norme NF X35-109 La masse unitaire maximale acceptable est fixée à 15kg pour le soulever/ tirer Pour les hommes et les femmes. Et ce, dans des conditions
Manutention et Levage Manutentions Manuelles : la norme NF X35-109 La masse unitaire maximale acceptable est fixée à 15kg pour le soulever/ tirer Pour les hommes et les femmes. Et ce, dans des conditions
Equipe EPS 68 L athlétisme à l école primaire Page 56 sur 109
 Equipe EPS 68 L athlétisme à l école primaire Page 56 sur 109 LANCER EN ROTATION lancer d anneaux FONDAMENTAUX Tenir l engin en pronation (paume vers le bas) Lancer avec tout le corps Les lancers en rotation
Equipe EPS 68 L athlétisme à l école primaire Page 56 sur 109 LANCER EN ROTATION lancer d anneaux FONDAMENTAUX Tenir l engin en pronation (paume vers le bas) Lancer avec tout le corps Les lancers en rotation
Escalade durant l'e.p.s. à l'école primaire
 Escalade durant l'e.p.s. à l'école primaire Fabrice Paget B.E.E.S Escalade Tél : +336 88 31 14 72 fabrice.paget@orange.fr 1 Glossaire Effectifs Durée des séances Atelier escalade sans être encordée Traversées
Escalade durant l'e.p.s. à l'école primaire Fabrice Paget B.E.E.S Escalade Tél : +336 88 31 14 72 fabrice.paget@orange.fr 1 Glossaire Effectifs Durée des séances Atelier escalade sans être encordée Traversées
FctsAffines.nb 1. Mathématiques, 1-ère année Edition 2007-2008. Fonctions affines
 FctsAffines.nb 1 Mathématiques, 1-ère année Edition 2007-2008 Fonctions affines Supports de cours de mathématiques de degré secondaire II, lien hpertete vers la page mère http://www.deleze.name/marcel/sec2/inde.html
FctsAffines.nb 1 Mathématiques, 1-ère année Edition 2007-2008 Fonctions affines Supports de cours de mathématiques de degré secondaire II, lien hpertete vers la page mère http://www.deleze.name/marcel/sec2/inde.html
Nom : Groupe : Date : 1. Quels sont les deux types de dessins les plus utilisés en technologie?
 Nom : Groupe : Date : Verdict Chapitre 11 1 La communication graphique Pages 336 et 337 1. Quels sont les deux types de dessins les plus utilisés en technologie? Les dessins de fabrication. Les schémas.
Nom : Groupe : Date : Verdict Chapitre 11 1 La communication graphique Pages 336 et 337 1. Quels sont les deux types de dessins les plus utilisés en technologie? Les dessins de fabrication. Les schémas.
MESURE ET PRECISION. Il est clair que si le voltmètre mesure bien la tension U aux bornes de R, l ampèremètre, lui, mesure. R mes. mes. .
 MESURE ET PRECISIO La détermination de la valeur d une grandeur G à partir des mesures expérimentales de grandeurs a et b dont elle dépend n a vraiment de sens que si elle est accompagnée de la précision
MESURE ET PRECISIO La détermination de la valeur d une grandeur G à partir des mesures expérimentales de grandeurs a et b dont elle dépend n a vraiment de sens que si elle est accompagnée de la précision
SYSTEME DE PARTICULES. DYNAMIQUE DU SOLIDE (suite) Table des matières
 Physique Générale SYSTEME DE PARTICULES DYNAMIQUE DU SOLIDE (suite) TRAN Minh Tâm Table des matières Applications de la loi de Newton pour la rotation 93 Le gyroscope........................ 93 L orbite
Physique Générale SYSTEME DE PARTICULES DYNAMIQUE DU SOLIDE (suite) TRAN Minh Tâm Table des matières Applications de la loi de Newton pour la rotation 93 Le gyroscope........................ 93 L orbite
Mécanique. 1 Forces. 1.1 Rappel. 1.2 Mesurer des forces. 3BC - AL Mécanique 1
 3BC - AL Mécanique 1 Mécanique 1 Forces 1.1 Rappel Pour décrire les effets d une force, nous devons préciser toutes ses propriétés : son point d application ; sa droite d action, c est-à-dire sa direction
3BC - AL Mécanique 1 Mécanique 1 Forces 1.1 Rappel Pour décrire les effets d une force, nous devons préciser toutes ses propriétés : son point d application ; sa droite d action, c est-à-dire sa direction
Chapitre 7: Dynamique des fluides
 Chapitre 7: Dynamique des fluides But du chapitre: comprendre les principes qui permettent de décrire la circulation sanguine. Ceci revient à étudier la manière dont les fluides circulent dans les tuyaux.
Chapitre 7: Dynamique des fluides But du chapitre: comprendre les principes qui permettent de décrire la circulation sanguine. Ceci revient à étudier la manière dont les fluides circulent dans les tuyaux.
SAUVEGARDE DES PERSONNES ET LUTTE CONTRE L INCENDIE DANS LES BATIMENTS D HABITATION DE LA 3ème FAMILLE INC/HAB COL 3/1986-2
 1. CLASSEMENT ET GENERALITES : 1.1. Classement Sont classées dans la 3ème famille les habitations collectives dont le plancher bas du logement le plus haut est situé à 28 mètres au plus au-dessus du sol
1. CLASSEMENT ET GENERALITES : 1.1. Classement Sont classées dans la 3ème famille les habitations collectives dont le plancher bas du logement le plus haut est situé à 28 mètres au plus au-dessus du sol
Géométrie dans l espace Produit scalaire et équations
 Chapitre 11. 2ème partie Géométrie dans l espace Produit scalaire et équations Terminale S Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES 2ème partie Produit scalaire Produit scalaire
Chapitre 11. 2ème partie Géométrie dans l espace Produit scalaire et équations Terminale S Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES 2ème partie Produit scalaire Produit scalaire
TOUT CE QU IL FAUT SAVOIR POUR LE BREVET
 TOUT E QU IL FUT SVOIR POUR LE REVET NUMERIQUE / FONTIONS eci n est qu un rappel de tout ce qu il faut savoir en maths pour le brevet. I- Opérations sur les nombres et les fractions : Les priorités par
TOUT E QU IL FUT SVOIR POUR LE REVET NUMERIQUE / FONTIONS eci n est qu un rappel de tout ce qu il faut savoir en maths pour le brevet. I- Opérations sur les nombres et les fractions : Les priorités par
Exercice 1. Exercice n 1 : Déséquilibre mécanique
 Exercice 1 1. a) Un mobile peut-il avoir une accélération non nulle à un instant où sa vitesse est nulle? donner un exemple illustrant la réponse. b) Un mobile peut-il avoir une accélération de direction
Exercice 1 1. a) Un mobile peut-il avoir une accélération non nulle à un instant où sa vitesse est nulle? donner un exemple illustrant la réponse. b) Un mobile peut-il avoir une accélération de direction
