poursuit P a ris, 26 avril. M. L oucheur, ÿ t, -----verte à la suite de l assassin at de

SAV ET RÉPARATION. Savoir-faire. www.jarltech.fr

i & V : SA E b i i 1 3 2 0 1 Ai 0800 9 h P i iè P i i i i S j C i Si E ) i Ti (i ib i Q,. bq i, FA V k, Pi b h iè i Si b, D Z, P E q Si-i SAV ET RÉPARATION S hiq : E q SSII VAR, i hiq Jh i h 0800 910 231.

Condition inf-sup pour l Elément Fini de Taylor-Hood È ¾ -iso-è ½

Condition inf-sup pour l Elément Fini de Taylor-Hood È ¾ -iso-è ½ Patrick Ciarlet et Vivette Girault ciarlet@ensta.fr & girault@ann.jussieu.fr ENSTA & Laboratoire Jacques-Louis Lions, Paris 6 Condition

Bougez, protégez votre liberté!

> F a Bgz, pégz v bé! www.a-. CAT.ELB.a240215 - Cé ph : Fa Daz à v p aé N az p a v gâh a v! Aj h, p g évq v ; Pa, p 4 aça q, v, éq qaé v. Ca ax é ç, b pa évé ax p âgé a h a p j. E pè v, h pa épagé. Pa

[Le Canada a 10 ans pour changer ses politiques économiques et sociales Paul Martin

G G à É FÉ 0 ppç pp g Q [ 0 p g pq éq è gé g p éé q QÉB Qéb y qq p bé éé pp éà p pp g bé Qéb épé ég Qéb pé bé éé «é ppy épé x «p q ép âg 7 pq p 5 é q p 88 é épp b p égq pp b pp Fç pp g Q x b ég Qéb «Bp

! " #$ % $! & '(# ) (%%

" #$ % $ & '(# ) (%% "#$ %&' # ( ) #* +,#*+-),- ). * /. 0),12-3 45 #3 /45 ) 67 #*+ & ) 5 ) #*+ )5 #& #*+ 0 / )5 8 )0 ) 0)12 5+ )& ) )12) 7)0 5 ) 9/ 5 2 ) ) '12 ) /) 5" ) 7) 6 ): 05 2 5 80 7 ) 0,$#- ) &

ISAN System: 5 Œuvre à épisodes ou en plusieurs parties

sm: 5 Œ à épsds pss ps Wb f B Rs s: E b W B bs d mdè Vs j www.sb. B ss Psfh B 7 T. +4 5 Fx +4 7 EM: f@sb. www.sb. B ss Psfh B 7 T. +4 5 Fx +4 7 EM: f@sb. wzd 5 Œ à épsds pss ps mm: TRODUTO DEMRE. OEXO.

Pour l épreuve d algèbre, les calculatrices sont interdites.

Les pages qui suivent comportent, à titre d exemples, les questions d algèbre depuis juillet 003 jusqu à juillet 015, avec leurs solutions. Pour l épreuve d algèbre, les calculatrices sont interdites.

Chapitre 3 : Repères et positionnement 3D

Chapitre 3 : Repères et positionnement 3D Modélisation 3D et Synthèse Fabrice Aubert fabrice.aubert@lifl.fr Master Informatique 2014-2015 F. Aubert (MS2) M3DS/ 3 - Repères et positionnement 3D 2014-2015

3 : «L amitié éternelle» 4 : «L amour» 5 à 11 : Le Dossier 12 : Loisirs 13 : Fin d année en beauté

L c - 3 : «L mé é» 4 : «L m» 5 à 11 : L D 12 : L 13 : F é bé L J éèv Lycé L P, èm égé éèv, é f é c 2013-2014, D éc ccé à c ; x c ô, c éê vfé qq é. L - émé chz j? C mé év qq, é à c m q... B... c! LC, c.

Correction du Baccalauréat S Amérique du Nord mai 2007

Correction du Baccalauréat S Amérique du Nord mai 7 EXERCICE points. Le plan (P) a une pour équation cartésienne : x+y z+ =. Les coordonnées de H vérifient cette équation donc H appartient à (P) et A n

RDV E-commerce 2013 Mercredi 6 Mars, Technopark

RDV E-mm 2013 Md 6 M, Thpk Smm 1 P q E 2 Q x p? 3 Q v? 4 d é d 2 0 1 5 p 2 0 1 3 6 h g 7 d f é 1 Pq E-mm? Pq S E-Cmm? D d d Md IT XCOM gé dp 2009 phé E-mm.m F à mhé p, XCOM h d déd E-mm, Pm éq, E-Mkg Chff

ISAN System: 3 Création d un V-ISAN

sm: é d V Wb f B Rs s: E b W B bs d mdè Vs j www.sb. B ss Psfh B 7 T. +4 5 Fx +4 7 EM: f@sb. www.sb. B ss Psfh B 7 T. +4 5 Fx +4 7 EM: f@sb. wzd é d V mm: TRODUTO DEMRE. OEXO. RETO D U V 4 FORMTO UPPLEMETRE

Formes quadratiques. 1 Formes quadratiques et formes polaires associées. Imen BHOURI. 1.1 Définitions

Formes quadratiques Imen BHOURI 1 Ce cours s adresse aux étudiants de niveau deuxième année de Licence et à ceux qui préparent le capes. Il combine d une façon indissociable l étude des concepts bilinéaires

Polynômes à plusieurs variables. Résultant

Polynômes à plusieurs variables. Résultant Christophe Ritzenthaler 1 Relations coefficients-racines. Polynômes symétriques Issu de [MS] et de [Goz]. Soit A un anneau intègre. Définition 1.1. Soit a A \

Solutions particulières d une équation différentielle...

Solutios particulières d ue équatio différetielle......du premier ordre à coefficiets costats O cherche ue solutio particulière de y + ay = f, où a est ue costate réelle et f ue foctio, appelée le secod

FICHE DE RENSEIGNEMENTS SAISON 2013 2014

USC BASKET Salle S. Chénedé Rue Sainte Croix 35410 CHATEAUGIRON Tél. 02.99.37.89.89 Site : www.chateaugiron-basket.com FICHE DE RENSEIGNEMENTS SAISON 2013 2014 Mme M. Nom et prénom de l adhérent : Adresse

Les Angles. I) Angles complémentaires, angles supplémentaires. 1) Angles complémentaires. 2 Angles supplémentaires. a) Définition.

Les Angles I) Angles complémentaires, angles supplémentaires 1) Angles complémentaires Deux angles complémentaires sont deux angles dont la somme des mesures est égale à 90 41 et 49 41 49 90 donc Les angles

Intégrales doubles et triples - M

Intégrales s et - fournie@mip.ups-tlse.fr 1/27 - Intégrales (rappel) Rappels Approximation éfinition : Intégrale définie Soit f définie continue sur I = [a, b] telle que f (x) > 3 2.5 2 1.5 1.5.5 1 1.5

L AIDE AUX ATELIERS D ARTISTES :

RAPPORT DAVID LANGLOIS-MALLET SOUS LA COORDINATION DE CORINNE RUFET, CONSEILLERE REGIONALE D ILE DE FRANCE L AIDE AUX ATELIERS D ARTISTES : PROBLÉMATIQUES INDIVIDUELLES, SOLUTIONS COLLECTIVES? DE L ATELIER-LOGEMENT

ILT. Interfacultair Instituut voor Levende Talen. T@@lvaardig. Actes de communication. Serge Verlinde Evelyn Goris. Katholieke Universiteit Leuven

IL If I L S V Ey G Khk U L 13/02/02 pé? xp qé xp pz à pz p héhq pé p à q z p à p héhq fé à p à q pz xp q 'p (è) f, '-à- p. x. ' é ff. N xp à py qq' q z b ( f) P xp pô pp L p - pé pz ': z qq', q -? Bj,

Ê ÙÐ Ø ÓÒ Ö Ò Ð Ý Ø Ñ ØÖ Ù Ö Ø ØÙÖ Ø Ð ÓÖ Ø Ñ Ö Ö Ï ÙØ Ð Ø ÙÐØ ÆÓØÖ ¹ Ñ Ä È Ü Æ ÑÙÖ Ð ÕÙ Û ÙØ Ð Ò Óº ÙÒ Ôº º Ê ÙÑ º ij ÑÔÓÖØ Ò Ð ÓÖ Ø Ñ Ö Ô ÖØ Ø ÓÒ Ö Ò Ð Ý Ø Ñ ØÖ Ù Ò³ Ø ÔÐÙ ÑÓÒØÖ Öº Ò Ø Ð Ó Ü ³ÙÒ ØÝÔ

STATUTS DE L ASSOCIATION. Association régie par par la Loi du 1 er juillet 1901

STATUTS DE L ASSOCIATION Association régie par par la Loi du 1 er juillet 1901 Statuts adoptés par l Assemblée Générale Extraordinaire du dimanche 1 er avril 2007 ËØ ØÙØ Ð³ Ó Ø ÓÒ ÖØ Ð ÔÖ Ñ Ö¹ ÒÓÑ Ò Ø

Exemple 4.4. Continuons l exemple précédent. Maintenant on travaille sur les quaternions et on a alors les décompositions

Exemple 4.4. Continuons l exemple précédent. Maintenant on travaille sur les quaternions et on a alors les décompositions HQ = He 1 He 2 He 3 He 4 HQ e 5 comme anneaux (avec centre Re 1 Re 2 Re 3 Re 4

DELIBERATION N CP 13-639

CONSEIL REGIONAL D ILE DE FRANCE 1 CP 13-639 DELIBERATION N CP 13-639 DU 17 OCTOBRE 2013 La politique sociale régionale La politique régionale pour les personnes en situation de handicap Cinquième affectation

Premier réseau social rugby

Premier réseau social rugby Rugbygeneration.com est le premier site de la communauté autour de Rugby. Dédié à tous les fans de rugby et les amateurs de toutes générations. Rugby? Échanger, rester en contact,

TUBES ET ACCESSOIRES Serrurier A ailettes Construction Canalisation Spéciaux

TUBES ET ACCESSOIRES 47 Serrurier A ailettes Construction Canalisation Spéciaux Possibilité d autres sections sur demande. Les caractéristiques indiquées sont théoriques et non garanties. TUBES 48 TUBES

%$&$#' "!# $! ## BD0>@6,;2106>+1:+B2.6;;/>0.2106>9*27+2.1/+BB+:/@6>.106>>+;+>1:+>6;*,+/EA,6.+77/7A,6@+7706>>+B79 561,+76.08189:+;61,+8.6>6;0+976>1:+?+>/+7@6,1+;+>1:8A+>:2>1+7:+B21+.C>6B630+:+ 1+.C>6B630=/+FGD+7A06>>23+8.6>6;0=/++1A6B010=/+:2>7B+.)*+,+7A2.+;+1+>:2>3+,B+A61+>10+B

Votre succès notre spécialité!

V ccè pécé! C Cchg Fm Igé Rcm V ccè pécé! L p mbx mché. E MPS I C g démq p ff pé pf d chq c : p é. N Fc: EMPSI Cg éé céé 2010 P Bddd Bchb q pé p d 8 d md d p. I dévpp N cmp xgc d é d. N c pfm mé d q gg

Exercices de géométrie

Exercices de géométrie Stage olympique de Bois-le-Roi, avril 2006 Igor Kortchemski Exercices vus en cours Exercice 1. (IMO 2000) Soient Ω 1 et Ω 2 deux cercles qui se coupent en M et en N. Soit la tangente

Exo7. Matrice d une application linéaire. Corrections d Arnaud Bodin.

Exo7 Matrice d une application linéaire Corrections d Arnaud odin. Exercice Soit R muni de la base canonique = ( i, j). Soit f : R R la projection sur l axe des abscisses R i parallèlement à R( i + j).

3. Caractéristiques et fonctions d une v.a.

3. Caractéristiques et fonctions d une v.a. MTH2302D S. Le Digabel, École Polytechnique de Montréal H2015 (v2) MTH2302D: fonctions d une v.a. 1/32 Plan 1. Caractéristiques d une distribution 2. Fonctions

Onveutetudierl'equationdierentiellesuivante

Quelques resultats sur l'equation des ondes Onveutetudierl'equationdierentiellesuivante (Ondes) @tu xu=f surr Rd: C'est dratique une equation +jj designature(;d).cettenoteestorganiseedela hyperbolique

Intégrale et primitives

Chpitre 5 Intégrle et primitives 5. Ojetif On herhe dns e hpitre à onstruire l opérteur réiproue de l opérteur de dérivtion. Les deux uestions suivntes sont lors nturelles. Question : Soit f une pplition

L Econométrie des Données de Panel

Ecole Doctorale Edocif Séminaire Méthodologique L Econométrie des Données de Panel Modèles Linéaires Simples Christophe HURLIN L Econométrie des Données de Panel 2 Figure.: Présentation Le but de ce séminaire

Exposing a test of homogeneity of chronological series of annual rainfall in a climatic area. with using, if possible, the regional vector Hiez.

Test d homogéné$é Y. BRUNET-MORET Ingénieur hydrologue, Bureau Central Hydrologique Paris RÉSUMÉ Présentation d un test d homogénéi.té spécialement conçu pour vérijier Z homogénéité des suites chronologiques

OM 1 Outils mathématiques : fonction de plusieurs variables

Outils mathématiques : fonction de plusieurs variables PCSI 2013 2014 Certaines partie de ce chapitre ne seront utiles qu à partir de l année prochaine, mais une grande partie nous servira dès cette année.

ÍÒ Ú Ö Ø ÅÓÒØÖ Ð ÍÒ ÑÓ Ð ÙÒ ÓÖÑ ÔÓÙÖ Ð ÑÓ Ð Ø ÓÒ Ø Ð Ñ Ø ÑÓ Ð Ø ÓÒ ³ÙÒ Ñ ÑÓ Ö ³ ÒØÖ ÔÖ Ô Ö ÇÐ Ú Ö Ö Ô ÖØ Ñ ÒØ ³ Ò ÓÖÑ Ø ÕÙ Ø Ö Ö ÓÔ Ö Ø ÓÒÒ ÐÐ ÙÐØ ÖØ Ø Ò Ì ÔÖ ÒØ Ð ÙÐØ ØÙ ÙÔ Ö ÙÖ Ò ÚÙ Ð³Ó Ø ÒØ ÓÒ Ù Ö È

Sujet 4: Programmation stochastique propriétés de fonction de recours

Sujet 4: Programmation stochastique propriétés de fonction de recours MSE3313: Optimisation Stochastiqe Andrew J. Miller Dernière mise au jour: October 19, 2011 Dans ce sujet... 1 Propriétés de la fonction

Géométrie dans l espace Produit scalaire et équations

Chapitre 11. 2ème partie Géométrie dans l espace Produit scalaire et équations Terminale S Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES 2ème partie Produit scalaire Produit scalaire

Liste des variables du Fichier Activité professionnelle des individus (localisation à la zone d'emploi du lieu de travail)

Liste des variables du Fichier Activité professionnelle des individus (localisation à la zone d'emploi du lieu de travail) Nom de variable ZELT Libellé Zone d'emploi du lieu de travail Précisions sur modalités

NOMBRES COMPLEXES. Exercice 1 :

Exercice 1 : NOMBRES COMPLEXES On donne θ 0 un réel tel que : cos(θ 0 ) 5 et sin(θ 0 ) 1 5. Calculer le module et l'argument de chacun des nombres complexes suivants (en fonction de θ 0 ) : a i( )( )(1

Partie 1: Gestion de l interférence entre symboles

Partie 1: Gestion de l interférence entre symboles Philippe Ciblat Télécom ParisTech, France Algo de Viterbi Egalisation OFDM Section 11 : Algorithme de Viterbi Philippe Ciblat Gestion de l interférence

Loi d une variable discrète

MATHEMATIQUES TD N : VARIABLES DISCRETES - Corrigé. P[X = k] 0 k point de discontinuité de F et P[X = k] = F(k + ) F(k ) Ainsi, P[X = ] =, P[X = 0] =, P[X = ] = R&T Saint-Malo - nde année - 0/0 Loi d une

Les équations différentielles

Les équations différentielles Equations différentielles du premier ordre avec second membre Ce cours porte exclusivement sur la résolution des équations différentielles du premier ordre avec second membre

Nicolas Petit. Commande prédictive. Notes de cours Option Procédé Environnement. http ://cas.ensmp.fr/~petit/

Nicolas Petit Commande prédictive Notes de cours Option Procédé Environnement http ://cas.ensmp.fr/~petit/ École Centrale Paris Année scolaire 2005-2006 Table des matières 1 Théorie générale de la commande

MUTATIONS ÉCONOMIQUES DANS LE DOMAINE AUTOMOBILE. Démarche méthodologique et synthèse

MUTATIONS ÉCONOMIQUES DANS LE DOMAINE AUTOMOBILE Démarche méthodologique et synthèse AVRIL 2010 Démarche méthodologique et synthèse Premier ministre Ministère de l espace rural et de l aménagement du

Cylindre interrupteur

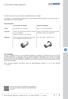Cylindres mis en œuvre pour actionner des éléments de verrouillage. Si nécessaire, votre partenaire professionnel ou nous-mêmes se fera/nous ferons un plaisir de vous assister dans le choix du bon produit.

Corrigé du baccalauréat S Asie 21 juin 2010

Corrigé du baccalauréat S Asie juin 00 EXERCICE Commun à tous les candidats 4 points. Question : Le triangle GBI est : Réponse a : isocèle. Réponse b : équilatéral. Réponse c : rectangle. On a GB = + =

Programme Prélavage vapeur. Nettoyage automatique du tambour Permet de nettoyer automatiquement le tambour.

Ó ² ¼ù ² «½ ±² ¼«Ô ª»óÔ ²¹» ÓßÒËÛÔ Üù ÒÍÌÎËÝÌ ÑÒÍ ÜÉÝóÔÝïîïïÍ ñ ÜÉÜóÔÜïìïÕÝÍ Verrouillage enfant Le système de verrouillage enfant empêche que les enfants appuient sur un bouton et modifient le programme

8.1 Généralités sur les fonctions de plusieurs variables réelles. f : R 2 R (x, y) 1 x 2 y 2

Chapitre 8 Fonctions de plusieurs variables 8.1 Généralités sur les fonctions de plusieurs variables réelles Définition. Une fonction réelle de n variables réelles est une application d une partie de R

Objet : Division, couverture desrisqueset suivi des engagements

(2Titnisîe DE Tunis, ie 6 décembre 12 Objet : Division, couverture desrisqueset suivi des engagements Le de la de Vu la loi n 58-90 du 19 septembre 1958 portant création et organisation de la Banque Centrale

Exercice 3 (5 points) A(x) = 1-e -0039' -0 156e- 0,039x A '() -'-,..--,-,--,------:-- X = (l_e-0,039x)2

Les parties A et B sont indépendantes. Partie A Exercice 3 (5 points) Commun à tous les candidats On considère la fonction A définie sur l'intervalle [1 ; + 00 [ par A(x) = 1-e -0039' ' x 1. Calculer la

sessions story 2014 Forum come a volunteer How to be mile an alumni ess Make BC S ED New application proc p for Forum Message from the New Friendshi

c. f. www i l y v 14 F c li 20 b w C Sil c H B i k M lic h ED w f f F N g hi M i w F N Th 2 014 i yh bg f h v c 300 x C ic O fif w, h C l liic l y c. T c hy ck b h, lci hi v ic wih cii y -k. Thi y w lgi

Corrigé Exercice 1 : BRIDE HYDRAULIQUE AVEC HYPOTHÈSE PROBLÈME PLAN.

TD 6 corrigé - PFS Résolution analytique (Loi entrée-sortie statique) Page 1/1 Corrigé Exercice 1 : BRIDE HYDRAULIQUE AVEC HYPOTHÈSE PROBLÈME PLAN. Question : Réaliser le graphe de structure, puis compléter

Al attention du praticien et des étudiants, nous avons développé

Chapitre 15 Applications informatiques Al attention du praticien et des étudiants, nous avons développé deux applications informatiques téléchargeables gratuitement sur le site www.digilex.ch. La première

Rupture et plasticité

Rupture et plasticité Département de Mécanique, Ecole Polytechnique, 2009 2010 Département de Mécanique, Ecole Polytechnique, 2009 2010 25 novembre 2009 1 / 44 Rupture et plasticité : plan du cours Comportements

Structures algébriques

Structures algébriques 1. Lois de composition s Soit E un ensemble. Une loi de composition interne sur E est une application de E E dans E. Soient E et F deux ensembles. Une loi de composition externe

Proposition. Si G est un groupe simple d ordre 60 alors G est isomorphe à A 5.

DÉVELOPPEMENT 32 A 5 EST LE SEUL GROUPE SIMPLE D ORDRE 60 Proposition. Si G est un groupe simple d ordre 60 alors G est isomorphe à A 5. Démonstration. On considère un groupe G d ordre 60 = 2 2 3 5 et

E-REPUTATION ET IDENTITE

E-REPUTATION ET IDENTITE NUMERIQUE DES ORGANISATION Typologie des menaces et identification des modes de traitement applicables La gestion de l'identité numérique, appelée également e-réputation, constitue

CHAPITRE 1. Suites arithmetiques et géometriques. Rappel 1. On appelle suite réelle une application de

HAPITRE 1 Suites arithmetiques et géometriques Rappel 1 On appelle suite réelle une application de dans, soit est-à-dire pour une valeur de la variable appartenant à la suite prend la valeur, ie : On notera

MECANIQUE DU POINT. y e y. z e z. ] est le trièdre de référence. e z. où [O, e r. r est la distance à l'axe, θ l'angle polaire et z la côte

I) Cinématique du point matériel: 1) Référentiel: MECANIQUE DU POINT L ensemble de tous les systèmes d axes de coordonnées liés à un même solide de référence S constitue un repère Soit une horloge permettant

FONCTIONS DE PLUSIEURS VARIABLES (Outils Mathématiques 4)

FONCTIONS DE PLUSIEURS VARIABLES (Outils Mathématiques 4) Bernard Le Stum Université de Rennes 1 Version du 13 mars 2009 Table des matières 1 Fonctions partielles, courbes de niveau 1 2 Limites et continuité

Exercices - Fonctions de plusieurs variables : corrigé. Pour commencer

Pour commencer Exercice 1 - Ensembles de définition - Première année - 1. Le logarithme est défini si x + y > 0. On trouve donc le demi-plan supérieur délimité par la droite d équation x + y = 0.. 1 xy

1 Systèmes triphasés symétriques

1 Systèmes triphasés symétriques 1.1 Introduction Un système triphasé est un ensemble de grandeurs (tensions ou courants) sinusoïdales de même fréquence, déphasées les unes par rapport aux autres. Le système

Exercices - Nombres complexes : corrigé. Formes algébriques et trigonométriques, module et argument

Formes algébriques et trigonométriques, module et argument Exercice - - L/Math Sup - On multiplie le dénominateur par sa quantité conjuguée, et on obtient : Z = 4 i 3 + i 3 i 3 = 4 i 3 + 3 = + i 3. Pour

ÍÒ Ú Ö Ø ËØÖ ÓÙÖ Á ÙÐØ Ë Ò ÓÒÓÑ ÕÙ Î ÄÍ ÌÁÇÆ ÅÈÁÊÁÉÍ Ë Å ÆÁËÅ Ë ÌÊ ÆËÅÁËËÁÇÆ Ë ÀÇ Ë ÇÆ Å ÆÌ Í Ì ÆÇÆ ÇÆ Å ÆÌ Í Î ÊË Ä Ë Å Ê À Ë ÇÍÊËÁ ÊË Ì ÔÖ ÒØ ÔÓÙÖ Ð³Ó Ø ÒØ ÓÒ Ù Ø ØÖ ÓØ ÙÖ Ä³ÍÒ Ú Ö Ø ËØÖ ÓÙÖ Á ÈÖ ÒØ

Prises et bornes de recharge de véhicules électriques pour bâtiments d habitation ou professionnels

Garage ou abris couvert destinés aux stationnements dans les bâtiments collectifs d'habitation Murale Type de charge Normale - 4kW Point de charge 1 Accès à la charge Libre Type de prise Prise EV Plug

ÇÆ ÈÌÁÇÆ Ì Ê ÄÁË ÌÁÇÆ ³ÍÆ ÈÈÄÁ ÌÁÇÆ ËÌÁÇÆ Ê Ë Í Ë ÇÅÈÇË ÆÌË Ê È ÊÌÁË Ô Ö ÅÓ Ñ Ö Þ Ñ ÑÓ Ö ÔÖ ÒØ Ù Ô ÖØ Ñ ÒØ Ñ Ø Ñ Ø ÕÙ Ø ³ Ò ÓÖÑ Ø ÕÙ Ò ÚÙ Ð³Ó Ø ÒØ ÓÒ Ù Ö Ñ ØÖ Ò ÅºËºµ ÍÄÌ Ë Ë Á Æ Ë ÍÆÁÎ ÊËÁÌ ËÀ Ê ÊÇÇÃ

Séquence 10. Géométrie dans l espace. Sommaire

Séquence 10 Géométrie dans l espace Sommaire 1. Prérequis 2. Calculs vectoriels dans l espace 3. Orthogonalité 4. Produit scalaire dans l espace 5. Droites et plans de l espace 6. Synthèse Dans cette séquence,

Variations du modèle de base

1 Variations du modèle de base Dans ce chapitre nous allons utiliser le modèle de base du chapitre précédent pour illustrer certaines questions économiques simples. Ainsi, le modèle précédent nous permettra

Modèles et Méthodes de Réservation

Modèles et Méthodes de Réservation Petit Cours donné à l Université de Strasbourg en Mai 2003 par Klaus D Schmidt Lehrstuhl für Versicherungsmathematik Technische Universität Dresden D 01062 Dresden E

MCMC et approximations en champ moyen pour les modèles de Markov

MCMC et approximations en champ moyen pour les modèles de Markov Gersende FORT LTCI CNRS - TELECOM ParisTech En collaboration avec Florence FORBES (Projet MISTIS, INRIA Rhône-Alpes). Basé sur l article:

Méthode de l équilibrage harmonique généralisé

Méthode de l équilibrage harmonique généralisé Application à l interaction modale rotor/stator Sébastien Roques * Mathias Legrand * Christophe Pierre ** Bernard Peseux * Patrice Cartraud * * GeM, Pôle

Corrigé du baccalauréat S Pondichéry 12 avril 2007

Corrigé du baccalauréat S Pondichéry 1 avril 7 EXERCICE 1 Commun à tous les candidats 4 points 1 a Les vecteurs AB et AC ont pour coordonnées AB ; ; ) et AC 1 ; 4 ; 1) Ils ne sont manifestement pas colinéaires

CNAM UE MVA 210 Ph. Durand Algèbre et analyse tensorielle Cours 4: Calcul dierentiel 2

CNAM UE MVA 210 Ph. Duran Algèbre et analyse tensorielle Cours 4: Calcul ierentiel 2 Jeui 26 octobre 2006 1 Formes iérentielles e egrés 1 Dès l'introuction es bases u calcul iérentiel, nous avons mis en

-2 -j: ;-. ^ S - R é d a ç t e i i r s 1 ^ 3 ^ 'TOM AtJXV. 'S E N i l S P i» é e ''a e = m éés Nte-Vrac^.11;^ S E N t l S

- ï -/ - U => ( >- K î --3>? - -- """" EO 8- * 0-2 - - - é ç 3 îh é Êh 5 0 X - /W O * zè v î b L bâ& b q â* ï O X E N é = éé N- E N y3 -HHh- ï ÊU - ~--y - L é é > X

YASHKA STEINER GRAPHIC DESIGN +41 079 340 19 41 +41 022 732 78 00. www.yashka.ch

YASHKA STEINER GRAPHIC DESIGN 53, Rue de Lausanne 1202 Genève-CH +41 079 340 19 41 +41 022 732 78 00 www.yashka.ch steiner@yashka.ch MULTIMEDIA QUICKMEUBLE.CH SITE INTERNET OKONOMI FILM PROMOTIONNEL OKONOMI

Virtualisation. du poste de travail Windows 7 et 8. avec Windows Server 2012

Virtualisation du poste de travail Windows 7 et 8 avec Windows Server 2012 Contraintes d architecture VDI et RDS App-V UE-V Citrix AppSense Norskale RES Software William Bories Abderrahmane Laachir Philippe

EXEMPLAIRE DESTINÉ AU DÉCLARANT

BILAN - ACTIF N 2050 203 Désignation de l entreprise : ASS VAL HOR Adresse de l entreprise Numéro SIRET ACTIF IMMOBILISÉ ACTIF CIRCULANT Comptes de régularisation IMMOBILISATIONS INCORPORELLES IMMOBILISATIONS

sommaire Introduction Fiches des 41 soldats disparus Le devoir de mémoire lettre à la mère de Maurice Quemin Glossaire / Sources

a I 4 F 41 a a L L é à a è Ma Q Ga / S 5 46 51 53 55 2 La Ga G a é a a XX è è, a, a aa. E a é a. D a, ï, aa. L a éé a a a a a. N a a é a a a a Ga G, a a aé a a a, a. é E a a, a ê aé a a é, a aé a. A, a-à

Centre d'etudes Nucléaires de Fontenay-aux-Roses Direction des Piles Atomiques Département des Etudes de Piles

CEA-N-1195 Note CEA-N-1195 Centre d'etudes Nucléaires de Fontenay-aux-Roses Direction des Piles Atomiques Département des Etudes de Piles Service d'etudes de Protections de Piles PROPAGATION DES NEUTRONS

Manuel d utilisation. ShareCenter Quattro DNS-345 VeRsion 1.0

Manuel d utilisation ShareCenter Quattro DNS-345 VeRsion 1.0 Table des matières Table des matières introduction...1 Pré-requis...2 Coniguration système requise...2 Présentation du produit...3 Contenu de

Un exemple d étude de cas

Un exemple d'étude de cas 1 Un exemple d étude de cas INTRODUCTION Le cas de la Boulangerie Lépine ltée nous permet d exposer ici un type d étude de cas. Le processus utilisé est identique à celui qui

la TV d Orange adsl avec satellite guide d utilisation Bord à poser sur le niveau à bulle : 3

0 ze plie ns tc an ui v e ett lign e pliez en suivant cette ligne France Télécom - SA au capital de 10 457 395 644 E - 6, place d Alleray - 75505 Paris Cedex 15 - RCS Paris 380 129 866 - WPS - Juin 2008

Modélisation intégrée des écoulements pour la gestion en temps réel d'un bassin versant anthropisé

1 TGR Modélisation intégrée des écoulements pour la gestion en temps réel d'un bassin versant anthropisé Simon Munier Institut des Sciences et Industries du Vivant et de l'environnement (AgroParisTech)

COMITÉ ADMINISTRATIF ET JURIDIQUE. Quarante-huitième session Genève, 20 et 21 octobre 2003

ORIGINAL : anglais DATE : 18 juillet 2003 F UNION INTERNATIONALE POUR LA PROTECTION DES OBTENTIONS VÉGÉTALES GENÈVE COMITÉ ADMINISTRATIF ET JURIDIQUE Quarante-huitième session Genève, 20 et 21 octobre

EI - EXERCICES DE PROBABILITES CORRIGES

EI 1 EI - EXERCICES DE PROBABILITES CORRIGES Notations 1 Les coefficients du binôme sont notés ( n p 2 Un arrangement de n objets pris p à p est noté A p n 3 Si A est un ensemble fini, on notera A ou card

Ä ÇÊ ÌÇÁÊ ÈÀ ËÁÉÍ ÌÀ ÇÊÁÉÍ ÍÆÁÎ ÊËÁÌ ÈÁ ÊÊ ÌÅ ÊÁ ÍÊÁ ij ÇÄ ÆÇÊÅ Ä ËÍÈ ÊÁ ÍÊ ÌÀ Ë Ç ÌÇÊ Ì Ä³ÍÆÁÎ ÊËÁÌ È ÊÁË ËÔ Ð Ø ÈÀ ËÁÉÍ ÌÀ ÇÊÁÉÍ Ë Ö ÄÇÊ ÆË ÔÖ ÒØ Ô Ö Ç Ì ÍÊ Ä³ÍÆÁÎ ÊËÁÌ È ÊÁË ÔÓÙÖÓ Ø Ò ÖÐ Ö ÇÀ Ê Æ ÌÄÇ

2012 écoles. International. Graines d artistes. les appelle

L x p j é y 2012 é D q é - pé jx 2011/2012? Déz- é, éx, w, b h, égg, pè, éé p CLEMI. I C? pp p p O., b I p. b p- q J. f R N L J T 15, j 2012, é Chp, P 3 (75) A : Réé P/J Pg é Chp (P 3), L J T pé é q éè

Actuariat I ACT2121. septième séance. Arthur Charpentier. Automne 2012. charpentier.arthur@uqam.ca. http ://freakonometrics.blog.free.

Actuariat I ACT2121 septième séance Arthur Charpentier charpentier.arthur@uqam.ca http ://freakonometrics.blog.free.fr/ Automne 2012 1 Exercice 1 En analysant le temps d attente X avant un certain événement

Equations différentielles linéaires à coefficients constants

Equations différentielles linéaires à coefficients constants Cas des équations d ordre 1 et 2 Cours de : Martine Arrou-Vignod Médiatisation : Johan Millaud Département RT de l IUT de Vélizy Mai 2007 I

Fiche technique GOSPEL UNITED (1 musicien 6 chanteurs)

Fiche technique GOSPEL UNITED ( musicien chanteurs) 0 0 0 0 Chœur Chœur Chœur Chœur Chant solo Chant solo 0V sur groupes / Régie facade : console /// (dans le cas de retours de scène depuis la console

CHAPITRE I : Cinématique du point matériel

I. 1 CHAPITRE I : Cinémaique du poin maériel I.1 : Inroducion La plupar des objes éudiés par les physiciens son en mouvemen : depuis les paricules élémenaires elles que les élecrons, les proons e les neurons

INFO DEFENSIE NOVEMBRE 2010

Nos craintes se confirment! 2 Le congé et le degré de parenté 4 Stop à l exode à la Défense! 5 Près de 60 % des militaires belges sont en surpoids 6 Notre sécurité sociale : une caisse sans fond? 7 Déblocage

Lot 4: Validation industrielle. Youness LEMRABET Pascal YIM, 19/11/2010

Lot 4: Validation industrielle Youness LEMRABET Pascal YIM, 19/11/2010 Partenaires Lot 1 Modèle du processus métier L4.1 Modèles PSM Lot 2 Guide d implantation L4.2 Développement & Recette prototype Lot

Charte de partenariat Risque Routier Professionnel

Charte de partenariat Risque Routier Professionnel Entre : La CRAM XXX représentée par et La Préfecture du département YY représentée d'une part, et L entreprise ZZ représentée par d autre part. Il est

à Rodilhan 3 résidences pour 3 styles de vie Faites le choix d un logement respectueux de l environnement

Les 3 Domaines à Rodilhan 3 résidences pour 3 styles de vie Faites le choix d un logement respectueux de l environnement Ville, Village et Verdure les 3 clés d une adresse 6AÝH EVgX CVijgZa YZh 8 kzcczh