Méthodes d analyse et d interprétation d images de télédétection multi-sources Extraction de caractéristiques du paysage
|
|
|
- Philippe Bastien
- il y a 10 ans
- Total affichages :
Transcription
1 Habilitation à diriger des recherches INP Toulouse Méthodes d anallyse et d iinterprétatiion d iimages de téllédétectiion mulltii-sources Extractiion x de caractéristiiques i du paysage Mémoire de recherches Danielle DUCROT Jury : Présidente Josiane Zerubia Directrice de recherche INRIA Rapporteurs Isabelle Bloch Professeur ENST Robert Jeansoulin Directeur de recherche CNRS Philippe Marthon Professeur ENSEEIHT INP Membres Jean Claude Menaut Directeur de recherche CNRS Michel Cattoen Professeur ENSEEIHT INP Eliane Cubero Ingénieur CNES 1 ier décembre 2005
2
3 Habilitation à diriger des recherches INP Toulouse Danielle Ducrot Méthodes d analyse et d interprétation d images de télédétection multi-sources Extraction de caractéristiques du paysage Résumé Un système d analyse et d interprétation sémantique d images de télédétection le plus automatique possible est présenté. Des classifications supervisées ou non supervisées multispectrales, multitemporelles, multitexturales, multisources de données optique et/ou radar sont développées, notamment à partir de méthodes globales telle que la méthode ICM (iterative conditional mode). La fusion, dans ce contexte de données multi-sources très hétérogènes est également abordée. La finalité étant, d une part la caractérisation des paysages avec l extraction d attributs (géométriques, morphologiques ou autres) afin de donner une approche quantitative aux écologues, d autre part le suivi pluri-annuel de l évolution des paysages, l étude des changements sur le long terme. Une méthode de reconnaissance automatique de thèmes paysagers à partir de bases de données et de classifications non supervisées, a été développée. Abstract Analysis and interpretation methods of remote sensing multi-source images Extraction of landscape features The purpose of this study is to present a system of analysis and semantic interpretation of remote sensing data that is the most automatic possible. Whether supervised or not, multi-spectral, multitemporal, multi-textural, multi-source classifications of optic and/or radar data are developed, in particular from global methods such as the ICM (Iterative Conditional Mode) method. In this context, fusion of very heterogeneous multi-source data is also explored. Our final aim is, on the one hand, to characterize landscapes with the extraction of attributes (whether geometrical, morphological or other) in order to give a quantitative approach to the ecologists ; on the other hand to follow up the long term evolution of landscapes, and the study of the changes in the long term. A method of automatic recognition of landscape topics from non supervised classification and databases has been developed.
4
5 Remerciements Je tiens d abord à remercier Josiane Zérubia présidente du jury, les rapporteurs Isabelle Bloch, Robert Jeansoulin, Philippe Marthon, qui malgré leurs charges importantes ont accepter d examiner ce travail, ainsi que les membres de jury Michel Cattoen, Eliane Cubero. Je remercie Monsieur Menaut directeur du CESBIO et membre du jury, pour m avoir permis de travailler dans de bonnes conditions. Je remercie Armand Lopes qui m a fait profiter de ses connaissances très étendues sur le radar. Je remercie Pierrette Gouaux qui m a initiée aux subtilités de l agriculture et des écosystèmes et surtout pour son soutien moral et matériel. Je remercie également Gérard Dedieu et les membres du projet Sud Ouest qui m ont permis de mieux comprendre les problèmes actuels des cycles de l eau et du carbone et la modélisation du transfert radiatif pour la simulation d images. Je n oublierai pas de remercier également : les membres du projet «Sud Med», les administrateurs du réseau du CESBIO pour leur gentillesse, qui m ont facilité les accès directs aux diverses stations par leurs montages réseaux automatiques, les membres du secrétariat pour leur disponibilité, les nombreux stagiaires sans qui tout ce travail n aurait pu être réalisé. Je dédie ce travail à mes enfants qui m ont encouragée.
6
7 SOMMAIRE Glossaire Chapitre 1 Introduction : présentation de la recherche 1 Chapitre 2 - LA CLASSIFICATION Introduction Classification non supervisée Classification supervisée ou dirigée Les images Les images optiques Propriétés de base des images Radar à haute résolution spatiale Principe de base du radar à visée latérale Discrimination en distance Discrimination parallèlement à l axe de vol (azimut) pour les RSO Valeur complexe d un pixel (image SLC) et corrélation avec les voisins Images monopolarisation multivues Chatoiement ou «speckle» Zone non homogène, texture et «bruit» multiplicatif Capteurs polarimétriques et interférométrie Perspectives de développement Les images filtrées - principe du filtre spatial et multitemporel du speckle VMMSE La détection des forts diffuseurs et des structures isolées Les images segmentées de contours ou de région Principe de la segmentation introduite dans les étapes de la classification Utilisation de la segmentation dans la classification Les algorithmes de classification développés Introduction Les modes opératoires des classifications Classification ponctuelle Méthodes locales ou contextuelles Loi de Gauss-Wischart réelle Système de Pearson Méthodes globales La méthode développée de type ICM...38 I
8 Chapitre 3 - APPRENTISSAGE AVEC ACQUISTION AUTOMATIQUE DES ECHANTILLONS - VERIFICATION 3.1- Apprentissage à partir d une méthode de saisie automatique des échantillons Description de la base de données cartographiques Agribase Principe de la méthode automatique d apprentissage Evaluation des classifications - Matrice de confusion Calcul de distance inter classe Logiciel d extraction systématique des mesures des combinaisons de canaux (procédure automatique) Application : Mesure de la qualité des données satellitales Résultats obtenus dans le cadre du Projet Sud-Ouest Analyse monodate Etude multi-temporelle Combinaisons en additions chronologiques Combinaisons en additions ciblées Quatre premières dates (cycle végétatif des cultures d hiver) et quatre dernières dates (cycle végétatif des cultures d été) Apport du canal PIR (XS3) Apport du canal MIR (XS4) Conclusion : choix de la meilleure combinaison pour la classification supervisée pour Classification d un parcellaire agricole à l aide de données temporelles ERS-1 (région de BOURGES) Introduction Classification ponctuelle Classification date à date non filtrée Série temporelle non filtrée Série temporelle filtrée Classification contextuelle (loi de Gauss-Wishart réelle) Étude pour le choix du meilleur voisinage Etude multitemporelle sur les données en amplitude non filtrées avec une classification contextuelle sur un voisinage 7* Images filtrées : classification contextuelle sur un voisinage 5* Conclusion Repérage de communautés côtières benthiques par télédétection aéroportée a très haute résolution Autres applications Conclusion sur l analyse multitemporelle...78 ANNEXE...79 II
9 Chapitre 4 LA FUSION, l incertain, le possible Introduction Définition de la fusion Modélisation de la fusion Modèles probabilistes et bayésiens : La fusion selon la théorie Bayésienne Modèles flous, le raisonnement, le plausible, le possible Modélisation avec la théorie des croyances de Dempster et Shafer Application à la classification : les différentes approches mises en place Etape A : fusion au niveau classification avant le calcul des probabilités Introduction Elimination de classes candidates Les canaux non discriminants Région Masque Etape B : fusion au niveau du calcul des probabilités Etape C : post-classification Régularisation Régularisation avec segmentation Régulation plus fine Applications Etude de cas de l île de Minorque Projet Sud ouest Classification optique Classification radar ERS Fusion des images SPOT et ERS Images SPOT Bassin du Grand Morin en Seine et Marne III
10 Chapitre 5 - ANALYSE DE PAYSAGE Concepts et définitions Concepts Définitions Les descripteurs du paysage Introduction Descripteurs surfaciques des classes Aire moyenne, coefficient de variation de l aire Aire de la plus grande UEP, rapport avec l aire de la classe, et avec l aire du paysage Etude de l hétérogénéité des classes Indice de morcellement : rapport du nombre d UEPs sur l aire de la classe Descripteur de fragmentation Les noyaux, la couronne Descripteur de circonvolution Composition des UEPs : pourcentage d UEPs à 0 noyau, 1 noyau, un nombre supérieur à 1 noyau Indice de régularité géométrique Descripteurs de forme Les périmètres et longueurs de contours inter-classes La forme Indices de formes La dimension fractale dans le paysage Combinaison des descripteurs surfaciques et de formes Mesure de l arrangement spatial Dispersion : Distance intra-classe, distance moyenne entre les UEPs d'une classe Connectivité : voisinage inter-classe Indice de juxtaposition : amalgame Étude des descripteurs sur l image découpée en régions Descriptif linguistique des classes La réalisation d'images dérivées Définition automatique des grandes régions Application Changement de l organisation paysagère du paysage de la région du Sud-Ouest toulousain Comportement et écologie du chevreuil Application pour l étude de la biodiversité Autre application IV
11 Chapitre 6 - INTERPRETATION SEMANTIQUE ET ETUDE DES CHANGEMENTS A LONG TERME 6.1 Analyses multitemporelles et scénarios du futur Corrections géométriques Le géoréférencement Correction radiométrique (cas des images optiques) Normalisation par bande spectrale Introduction La méthode Principe algorithmique Méthode d interprétation automatique de classification non supervisée Les distances : correspondance spectrale et temporelle Principe des possibilités Elimination spectrale et temporelle Intégration de la notion de variation temporelle Données exogènes Correspondance spatiale : VALIDATION Applications Classification non supervisée 2003 et son interprétation Résultat de classification non supervisée après interprétation sur une image Sud-Ouest Etude des changements de paysage Caractères et précision de la carte d occupation du sol Occupation du sol en Version simplifiée de l occupation du sol Mise en évidence des changements d occupation du sol Chapitre 7 CONCLUSIONS PROSPECTIVES 197 Références bibliographiques V
12 Glossaire GLOSSAIRE Analyse haut niveau : se dit d un traitement au départ d une image déjà traitée, par exemple lorsqu une image a été transformée par un filtrage, une classification, ce qui a permis déjà d extraire des informations «cachées» et que cette image est utilisée comme base de traitement. Les traitements haut niveau sont souvent appelés post traitements. La classification est considérée comme de haut niveau. Les traitements bas niveau sont appelés pré traitements. Canal : un canal fait référence à l'image obtenue à une date donnée dans un canal spectral donné, d un capteur donné, il peut également être un canal de «synthèse» (ou dérivé). Classe : numéro correspondant à un thème, affecté à un point ou à une région ou segment après classification, en classification non supervisée on confond étiquette et classe. Date : une date est une donnée comprenant un ou plusieurs canaux correspondant à des images prises à une date (ou plusieurs dates si elles ont un point commun temporel lié au stade phénologique des cultures, par exemple). Donnée : une donnée comprend une sélection de quelques images utiles à associer, par exemple les images d'une même date et/ou d'une même source (optique ou radar). Ecosystème : unité d organisation biologique composée de tous les organismes présents dans une aire donnée et présentant des interactions avec le milieu physique avec pour résultat l existence d un flux d énergie conduisant à une structure caractéristique et à des cycles de matière. Etiquette : numéro affecté à un point ou une région ou segment. Forts diffuseurs dans les images RSO, les forts diffuseurs sont en général des rétrodiffuseurs en forme de coin qui ont une très grande réponse. Ilots : un patch (ou UEP*) correspond à un îlot qui est un ensemble de parcelles adjacentes, agricoles ou autres. Ainsi, s il y a plusieurs parcelles de blé adjacentes, l ensemble de ces parcelles forme l îlot, ce qui correspond à un ensemble connexe de pixels dans l image classée. Image de synthèse ou dérivée : il s agit d image obtenue après un traitement de transformation locale (écart type local, dimension fractale ) calculée sur un voisinage de points et cette valeur est affectée au pixel central. Image radar «brute» c est une image non filtrée, telle qu elle est délivrée au départ. Le phénomène de chatoiement («speckle» en anglais) est parfaitement déterministe, dû à la cohérence de l illumination du capteur et à l interférence constructive et/ou destructive des champs rétrodiffusés par les objets à l intérieur de chaque cellule de résolution. Il se transforme en un aspect granuleux aléatoire sur les images. Lot : Un lot correspond à des dates ou à une manière de regrouper les dates et les données. En général, un lot contient une ou plusieurs données rassemblant chacune, les canaux d'une date précise. Plusieurs lots peuvent également être construits avec les données d'une seule date. VI
13 Glossaire Parcelle : équivalent au patch, doit être compris au sens agronomique du terme. Patch : UEP* Paysage : Un paysage est une portion de surface terrestre à étudier, en général ce que peut voir un observateur. Dans notre cas, ce sera la surface représentée par une image satellite classée, de plusieurs kilomètres carrés au sol. Le paysage est un niveau d organisation des systèmes écologiques, supérieur à l écosystème ; il se caractérise par son hétérogénéité et par sa dynamique gouvernée pour partie par les activités humaines. Région : 1) sens géographique du terme 2) régions issue d une segmentation (que nous appellerons segments pour être distingué de la 1 ière signification) chacune d'entre elles étant homogène au sens d'attributs préalablement définis. Scénario : Description du futur possible ou faisable selon les schémas d évolution souhaités. En matière d environnement rural, les scénarios comportent trois éléments : 1) une description de la situation présente, 2) un certain nombre de futurs alternatifs, 3) les voies possibles entre le présent et ces images du futur. Segment : employé pour éviter toute confusion avec la région au sens géographique du terme. Segmentation : c est une partition de l image en régions uniformes qui vérifient des propriétés d homogénéité sur des critères caractéristiques donnés, chacune d'entre elles étant homogène au sens d'attributs préalablement définis ; à chaque région est attribuée une étiquette différente. Speckle = chatoiement (voir image radar chapitre 2) Tache : UEP* * UEP : Unité Élémentaire du Paysage est un ensemble de points connexes appartenant à la même classe ou au même écosystème (pluriel, UEPs), synonyme patch. VII
14
15 Chapitre 1 INTRODUCTION
16
17 Chapitre 1 INTRODUCTION : présentation de la recherche Mes recherches effectuées au CESBIO sont axées sur un système d analyse et d interprétation sémantique des images le plus automatique possible, qui comprend la classification des données spatiales, l extraction géométrique et morphologique de descripteurs pour l analyse de paysage, l étude des changements sur le long terme. Ce mémoire présente un ensemble de travaux, parmi les plus récents, résultats de nombreuses évolutions. Ils concernent le développement de méthodes algorithmiques sur les axes cités. Ces méthodes relèvent de l informatique, plus particulièrement du traitement d images. L informatique n est pas une fin en soi : ce n est un outil puissant que s il peut avoir des répercussions pratiques. C est donc dans ce souci que je présente des applications relevant des méthodes développées. Elles sont conçues afin d être adaptées à des données hétérogènes. Sans avoir la prétention d être universel, le spectre des méthodes a voulu être le plus large possible. Ces recherches ont donné lieu à un système de classification et de caractérisation de paysage présenté figure 1.2. Ce mémoire se décompose en 7 chapitres : l introduction, la classification, l apprentissage et la vérification, la fusion, l analyse de paysage, l interprétation sémantique et l étude des changements, la conclusion et les prospectives. Des applications sont présentées dans certains de ces chapitres. La classification (chapitre 2) est le noyau essentiel, la plupart des méthodes développées s articulant autour de la classification des images. Le résultat de la classification, permet d obtenir le plan d occupation du sol. La classification est aussi utilisée comme mesure de la qualité discriminatoire des bandes spectrales et temporelles des images. Notons qu un effort particulier a été porté sur les classifications multidimensionnelles qui permettent de traiter tout type d image : multi-spectrales, multi-temporelles, multi-capteurs, et d intégrer des données exogènes (SIG, MNT, ), ainsi qu une segmentation. Plusieurs méthodes sont décrites en fonction du type d image, en particulier les images radar qui nécessitent des traitements spécifiques en raison du chatoiement (speckle) inhérent à ces images. Si l application première de la classification est d'établir une cartographie et une statistique de l'occupation du sol (figure 1.1). Elle permet aussi, éventuellement associée à d autres caractéristiques (hydrographie...) de suivre : les conditions de développement des cultures, d'évaluer les consommations d'eau, d induire des travaux sur la prévision des productions, la conservation des sols, la dégradation des terrains de parcours, la déforestation, l évaluation de l'érosion en amont des barrages et actions de prévention, l évolution de la qualité des sols en zones irriguées, le suivi de l'emprise urbaine sur les terres agricoles, pour ne citer qu un certain nombre d applications. 1
18 Présentation de la recherche Figure 1.1 : principe de combinaison des caractéristiques du milieu pour le zonage de l'espace en unités fonctionnelles L apprentissage et la vérification (chapitre 3) : une partie importante de mon travail a été de tester, valider, modifier les diverses méthodes développées au travers d un très grand nombre d applications. Mon objectif essentiel était que les méthodes de classification ou liées à la classification soient opérationnelles en toutes circonstances. La prise des échantillons déduits des vérité-terrains, première étape de l apprentissage, est très fastidieuse, de celle-ci dépend les résultats de la classification supervisée et de la fiabilité des tests. Une nouvelle méthode d acquisition automatique pour l apprentissage (prise d échantillons à partir de relevé terrain) a été mise au point à partir d une base de données géoréférencées, de données GPS et d une segmentation des images sur des données multi-spectrale, multi-date, multisource. La multi-dimensionnalité est un atout pour déterminer des parcelles d entraînement homogènes. Elles sont temporellement plus homogènes, ce qui permet une augmentation de la précision. Elle nous sert de mesure de la qualité des données satellitales. Divers algorithmes permettent d obtenir des mesures sur toutes les combinaisons possibles de données, d une part pour la vérification de la classification, d autre part pour choisir les meilleures combinaisons. Ces travaux sont validés par les données au sol, les méthodes classiques d interprétation des images photographiques et de données satellitales. Plusieurs applications sont proposées sur des études temporelles avec des images SPOT et radar. La fusion (chapitre 4) : les techniques d acquisition de données de télédétection offrent aujourd hui une grande quantité d informations. Mais elles sont pour la plupart imprécises, incomplètes, voire erronées. Malgré ce manque d exactitude, on est amené à prendre des décisions. Le but de la fusion est donc d'extraire l'information la plus fiable et exacte possible ; pour ce faire, on combine les informations issues des différents capteurs pour décider de l'appartenance d'une information à une classe d'objets. Plusieurs méthodes de fusion ont été intégrées dans la classification, au niveau pré ou post-classification, à partir de plusieurs concepts : logique floue, incertain, évidence, principe bayésien, markovien. La fusion est également utilisée au niveau de l interprétation automatique (chapitre 6). L analyse du paysage (chapitre 5) : l'ensemble des procédures réalisées pour l'analyse du paysage est composé de la caractérisation, de la modélisation de l'hétérogénéité et de l étude de l'évolution du paysage. Les changements écologiques déduits des données satellitales offrent pour chaque grand type d'écosystèmes des indicateurs écologiques potentiels tel que la fragmentation du couvert. Pourquoi étudier les paysages? L organisation de l espace est sous la double influence du milieu physique et de l activité humaine. En perpétuel mouvement l espace a vu depuis quelques décennies, accélérer ses transformations sous la pression de plus en plus forte du facteur humain dans un 2
19 Présentation de la recherche environnement socio-économique déterminant. Le paysage donne une illustration de cette «confrontation continue entre la société et son milieu» (Burel & Baudry, 1999), exprimant à un instant donné un état de ces relations qui impliquent des structures changeantes dans l espace et dans le temps. Abordée par la télédétection, l étude du paysage permet, à l échelle régionale, la caractérisation des divers systèmes qui le composent. En effet, une série multi temporelle d images satellitales donne une vision synoptique de l espace conduisant à la détermination de ses divers états multitemporels et la mise en évidence de ses changements. La méthode d analyse de paysage que nous proposons, permet de quantifier l organisation de la mosaïque paysagère comme assemblage d «unités élémentaires de paysage» (UEPs) qui correspondent à la parcelle ou l îlot caractéristique d une classe d occupation du sol. Chaque classe d occupation du sol est distinguée par un certain nombre de caractéristiques fondées sur des éléments de forme (dimension fractale par exemple), de taille, de voisinage et de proximité des différentes UEPs. Ce sont des indicateurs de mesure en relation avec l hétérogénéité, la fragmentation et la connectivité de la structure paysagère. Un des objectifs est de permettre l étude spatio-temporelle du paysage et son hétérogénéité. Par la suite, les unités de paysage susceptibles de se comporter comme des puits ou sources de carbone sont identifiées et localisées et leur fonctionnement sera modélisé. Les unités correspondent à différents stades de la dynamique de la végétation «naturelle», différents types d occupation et d utilisation du sol. Ainsi, les étapes pionnières de la dynamique végétale (jachères, friches, landes) doivent accroître leur stock de matière organique ; les forêts matures représentent un stade pour lequel le bilan des échanges de carbone est «équilibré». Interprétation sémantique et étude des changements sur le long terme par des données inter-annuelles (chapitre 6) : des images satellitales d'observation de la terre ont été rassemblées et archivées pendant des décennies. En combinant des données satellitales, des cartes, des systèmes d information géographiques et des mesures sur le terrain, il est possible d'améliorer la description des processus se déroulant à la surface de la Terre. A la différence des mesures in situ, les données satellitales peuvent être obtenues sur de grandes étendues et surtout peuvent prolonger l'analyse dans le passé, à des dates où aucune autre donnée n'était disponible. Mon objectif a été d exploiter ces longues séries temporelles, seules à même de faire ressortir du bruit de fond des tendances évolutives claires ou l impact d événements marquants plus ou moins périodiques. Pour utiliser conjointement les séries d images multi date et/ou d autres documents cartographiques, une image commune corrigée géométriquement et éventuellement radiométriquement, est élaborée. Elle servira de base aux classifications. Malgré ces corrections, des erreurs persistent. Pour les surmonter, nous avons mis au point une méthode de normalisation des valeurs radiométriques, à partir d invariants recherchés automatiquement, dans le but de rendre comparables les données multitemporelles à long terme. Puis, des classifications non supervisées sont réalisées. Le problème de ces classifications est leur interprétation. La classification attribue des étiquettes, mais on ne sait pas à quel type de surface cela correspond. Aucune légende n est donnée a priori. Il est donc nécessaire de faire suivre ce type de classification d une étape d interprétation afin d attribuer une sémantique aux classes trouvées. Une méthode de reconnaissance automatique a été développée pour effectuer cette interprétation. 3
20 Présentation de la recherche Les applications Les résultats de mes recherches sont utilisés dans le domaine de la surveillance écologique, et de l environnement. Les satellites constituent un des rares moyens disponibles d'obtenir des mesures cohérentes sur de larges superficies. Aux échelles du paysage et de la région, les caractéristiques particulières des observations spatiales sont utilisées pour l'évaluation et la gestion des ressources renouvelables, végétales et hydriques. Les études portent d une part sur une bonne compréhension des différents mécanismes déterminant les échanges d eau, de carbone et d'énergie entre la biosphère et l'atmosphère. Les dynamiques de la biosphère et de l atmosphère évoluent de façon couplée par l'intermédiaire des processus régissant les flux d'énergie, d'eau, et de carbone. Ainsi, un changement de mode d'occupation du sol affecte les interactions entre la biosphère et l'atmosphère. Par effet de rétroaction, les modifications de ces interactions peuvent donner lieu à une modification du fonctionnement et de la structure de la végétation, et par voie de conséquence à des modifications du cycle hydrologique. L interaction avec des processus représentés par des modèles hydrologiques et atmosphériques nécessite alors d intégrer une discrétisation de la structure des systèmes de surface, et donc les caractéristiques de paysage. Une des finalités est de concevoir et de développer une modélisation intégrée des surfaces continentales, représentant explicitement la structuration et les hétérogénéités de la surface et permettant de simuler les processus couplés impliqués dans le cycle de l eau, du carbone, de l'azote et de substances polluantes aux échelles de la parcelle, du paysage et de la région. En ce qui concerne le cycle de l eau et celui de la végétation, les processus de surface se produisent à différents pas de temps journalier et saisonnier. Les évolutions inter-annuelles marquent les changements climatiques et de mode d'occupation du sol. Les échelles pertinentes ici sont d'abord la parcelle ou l unité élémentaire de paysage avec une dimension régionale indissociable pour généraliser les résultats. Les espaces géographiques qui concernent le paysage, du bassin versant à la région sont l'objet de multiples enjeux socio-économiques et scientifiques. C'est à ces échelles que s'élaborent et s'évaluent les politiques d'aménagement du territoire et de gestion des ressources, que s'appliquent de nombreuses lois et réglementations : loi sur l eau, loi "littoral", contrat territorial d exploitation, politiques contractuelles diverses (ex : Parcs Naturels Régionaux). Ces échelles sont également le domaine d'intervention de nombreux organismes publics et professionnels liés à la gestion des ressources agricoles et des ressources en eau. Ainsi, il s agit de dresser l'état actuel des ressources : état des sols et de la couverture végétale, occupation du sol, réserves en eau. Dans ce cas l outil télédétection permet de pallier le manque d informations distribuées dans l espace et remises à jour régulièrement, et de restituer une vision cartographique actuelle de l activité agricole. En comparant avec des images de satellites acquises au cours des 30 dernières années, il est même possible de reconstituer l évolution de l'occupation des sols. Les données de télédétection sont également utilisées pour suivre le développement des principales cultures et grâce aux modèles simplifiés d en déduire des cartes de la consommation d eau par culture. En utilisant les cartes d occupation des sols, actuelles ou issues d évolutions possibles, le bilan régional de l utilisation de l eau par l agriculture pourra être établi pour différents scénarios. 4
21 Présentation de la recherche Pour résumer, les objectifs sont la compréhension et la modélisation du fonctionnement des surfaces continentales aux échelles de la parcelle, du paysage et de la région. Ceci conduit sur un plan pratique à : - la gestion «opérationnelle» des territoires ; - aux diagnostics, suivis : production végétale, ressources hydriques, substances polluantes, crues ; - l alerte phytosanitaire pour lesquels les services techniques ne disposent pas de moyens suffisants - aux scénarios : changement climatique, modifications de l'occupation des terres, politiques agricoles - l aménagement et ingénierie environnementale Ma contribution dans ces divers points se situe au niveau de l occupation des sols, afin d obtenir une carte d occupation des sols la plus correcte possible, ceci par le biais de classifications supervisées ou non. L autre axe important, est l extraction de descripteurs de paysage afin d intégrer des données quantitatives dans les modèles. L aboutissement est l étude des changements au niveau des écosystèmes et du paysage. La multiplicité des données, nous a conduit à une attention particulière à l automatisation des traitements informatiques, à la facilité et à la convivialité des interfaces logiciel-expert. De nombreuses applications (en quantité et en diversité) ont été réalisées. Certaines sont présentées pour montrer les résultats obtenus avec les méthodes développées, en particulier le projet Sud-ouest du CESBIO, «Bilans de Carbone et d Eau en région Midi-Pyrénées ; vers un observatoire Régional de l Environnement» (chapitre 3 et 4). Ces travaux interviennent ou vont intervenir dans d autres projets. Citons le projet Sud méditerranéen : «Fonctionnement et ressources hydro-écologiques de régions semi-arides : caractérisation, modélisation et prévision» (IRD), partenaires : au Maroc : faculté des sciences Semlalia de l'université Cadi Ayyad (Marrakech), service de la production à l'office Régional de Mise en Valeur Agricole du Haouz (ORMVAH), Direction de la Région Hydraulique (DRH) du Tensift, la Direction Provinciale de l'agriculture (DPA), Direction des Eaux et Forêts du Haut Atlas, en France LTHE (Laboratoire d Etude des Transferts en Hydrologie et Environnement) Grenoble, CEFE (Centre d Ecologie fonctionnelle et Evolutive) Montpellier, Etranger : SAI-JRC Université de Valence - Espagne, USDA Université d'arizona, EPA Université du Maryland, Centres nationaux de télédétection Algérie, Egypte, Israël, Jordanie, Syrie, Tunisie. Le projet APOGE : «Aide à la Planification de l'occupation des sols et à la Gestion de la ressource en Eau» et de la production agricole à l'échelle régionale. Les objectifs du projet sont le développement d'un démonstrateur d'outil d'aide à la décision. Partenaires : INRA, Météo France (CNRM) et des partenaires opérationnels industriels, Astrium et SCOT, et la Direction de la Production de Météo France (Division Agro-météorolgie). Le projet GICC «Gestion et Impacts du Changement Climatique» Bilans de carbone et d eau de la région Sud-Ouest : Historique récent, états actuels et scénarios du futur ; comparaison des pressions climatiques et anthropiques. Le projet ECCO : Fonctionnement intégré de l espace rural du paysage à la région en collaboration avec le LMTG UPS, LADYBIO UPS, CNRM Météo France, LTGT, ESAP, INRA Toulouse, ENSAT/DYNAFOR Toulouse, CSE INRA Avignon, INFOSOL INRA Orléans. Le projet CLIME/INRIA (Rocquencourt): Couplage de la donnée environnementale et des modèles de simulation numérique pour une intégration logicielle. 5
22 Présentation de la recherche Système de classification et caractérisation de paysage Images satellitales Pré-traitements (recalage, zone commune). Base de données Création d échantillons Saisie automatique d échantillons Travail par zones Masques Vérification calcul de la corrélation Etiquetage Classification non supervisée Classification supervisée Vérification, modification d échantillons Images échantillons normalisation Images Classées non supervisées Images Classées supervisées Interprétation Fusion d images classées Matrice de confusion Matrice de confusion Régularisation Réduction Regroupement des classes Image régularisée Analyse du paysage Extraction d indices Images synthétiques Statistiques et Informations Analyse de l homogénéité Figure 1.1 : schéma général du système de classification et d analyse d image présenté 6
23 Chapitre 2 LA CLASSIFICATION
24
25 Chapitre 2 LA CLASSIFICATION Introduction La classification est un processus de reconnaissance des formes. En télédétection, elle consiste à effectuer la correspondance entre les éléments d une scène de l image matérialisés généralement par leurs valeurs radiométriques, et des classes connues a priori ou non par un utilisateur. La correspondance est réalisée par des fonctions discriminantes sous forme de règle de décision telle que le maximum de vraisemblance des probabilités, ou des distances géométriques. Les méthodes qui sont décrites dans ce mémoire ont toutes été implantées. Je développe surtout la méthode ICM sous contraintes qui donne de très bons résultats, notamment pour les images RSO, dans un temps de calculs non prohibitif pour des images qui ont de très grandes tailles. En général, leur taille est de plus de 10 méga octets, qui, multiplié par le nombre de canaux spectraux et temporels, donne une taille de l ordre du giga octets. Quelques principes généraux sont expliqués afin de bien situer les conditions de cette étude. Certains points sont détaillés pour bien suivre les procédés et pour montrer pourquoi ils ont été choisis. L implémentation des méthodes présentées, qui sont plus ou moins connues, est originale, et doit s adapter à différents types d images. Je me suis attachée à développer certaines méthodes plus que d autres par rapport aux résultats obtenus. De très nombreux tests ont été réalisés sur des images, pratiquement toujours de très grandes tailles, très différentes, et le soucis a toujours était que ces méthodes soient opérationnelles dans des conditions très diverses qu il serait trop long de détailler ici. A la fin du chapitre 3 des exemples sont montrés. La classification peut être interprétée comme un problème de données incomplètes. En chaque site (pixel) s expriment des données de deux types différents : la donnée observée et l autre cachée, la classe que l on cherche à trouver. Ainsi, la classification vise à attribuer aux pixels des étiquettes dont l origine est thématique. Très généralement, soit un ensemble de points auxquels sont attribués M scalaires représentant des caractéristiques, pour une image multidimensionnelle elles correspondent aux différents canaux. En chaque site, ces caractéristiques sont présentées sous la forme d un vecteur appartenant à M l espace E = R (ou C M ) pour les données complexes. M correspond aux nombres de canaux. M=1 dans le cas des images monospectrales telle que les images RSO. Désignons par S l ensemble des sites spatialement organisés, indicés {1,, N}. Dans l image les éléments de S sont interprétés comme les pixels d une grille régulière à 2 dimensions. Au site s = (i,j) S, la valeur du pixel d indice s ou niveau de gris du canal m se note y ms. Et y s est un vecteur de M composantes dont la k ième composante représente la valeur de l image observée au pixel d indice s, y s Y. Ch 2 7
26 La classification Rappelons que Y est le résultat d un processus de dégradation d une image réelle Ỹ. Les images observées, sont une réalisation y d un champ aléatoire Y de configurations possibles (en se référant à des configuration des valeurs radiométriques des pixels dans l image). Sur la base des valeurs de chaque composante de y s, le but est de ranger chaque vecteur dans l une des N ω classes de l ensemble fini des étiquettes Ω= {ω1, ω 2,, ω k }, les ω i étant en général des entiers correspondants à des noms de classes par exemple {Classe 1 ; Classe 2 ; ; Classe N ω }. Ainsi, à partir d une image acquise y de N valeurs, (N nombre de pixels), on obtient une image classée x dont chaque pixel notés x s prend ses valeurs dans l ensemble fini discret Ω. A chaque pixel est attribué une étiquette (ou label) identifiant sa classe. Le champ des N ω classes est noté X. Les modèles du champ de classes et le champ de mesure dépendent de paramètres qu il convient d estimer pour procéder à la classification. Soit θ l ensemble des paramètres du couple (X, Y), la loi de ce couple est donnée par la loi du champ de classes X et par l ensemble des distributions des variables Y s /X. Soit α les paramètres de la loi du champ et β celle des lois conditionnelles (θ = (α,β)). Ainsi, α est composée des probabilité a priori des N ω classes si X est stationnaire et composé de variables aléatoires indépendantes. Si le processus de mesure est gaussien (Y s /ω κ ) N(µ κ,σ k )), β = (µ κ, Σ k ) k {1,..., N ω}. Deux types d approches peuvent être distinguées : les classifications non supervisées sans aucune connaissance a priori sur les données, et les classifications supervisées. Ces méthodes qu elles soient supervisées ou non, partagent des principes communs Classification non supervisée (ou non dirigée) La classification non supervisée ou non dirigée détermine automatiquement les classes. Les algorithmes des centres mobiles, (nuées dynamiques appliquées au centre de gravité) et des distances adaptatives sont des méthodes itératives qui, à chaque itération calculent respectivement les centres de gravité ou les distances associées aux classes. Les fonctions discriminantes dépendent, soit des paramètres des densités de probabilité, soit d un jeu de coefficients qui peuvent être évalués théoriquement par des études physiques, la classification est alors totalement non supervisée. Elle peut être semi-supervisée quand certains paramètres sont fixés par l utilisateur en fonction du type d image et de scène, ou que certains objets sont reconnus par l utilisateur qui peut ainsi initialiser le processus de recherche des classes pour certaines d entre elles. L estimation non dirigée de θ à partir de Y est approchée par des algorithmes basés sur le maximum de vraisemblance, la solution des équations de vraisemblance est approchée par des méthodes itératives Classification supervisée ou dirigée Les classes sont définies à partir des besoins de l utilisateur et correspondent à des unités sémantiques de l image, ce qui nécessite une étape d apprentissage préalable à la classification. La classification supervisée consiste à déterminer les classes par un apprentissage qui peut être effectué soit sur chaque scène traitée, soit pour chaque type d application (agriculture, forêt, littoral, géologie,...) ou encore à chaque type de capteur utilisé (optique : Landsat, Spot, Ikonos, Noaa, ou radar : ERS, JERS1, Radarsat ). Cette étape influence fortement les résultats de la classification. Ch 2 8
27 La classification Pour l estimation dirigée (avec apprentissage), on dispose pour chaque classe de l image des vecteurs caractéristiques de plusieurs pixels de l image (échantillons des classes) dont on connaît a priori la classe d appartenance. En supposant le processus ergodique, les paramètres sont estimés à l aide des méthodes classiques d estimation telles que la méthode du maximum de vraisemblance. Les échantillons sont sélectionnés sur des observations faites sur le terrain (vérités terrain) en repérant au sol des parcelles représentatives des différents éléments devant être présent dans la classification de la zone étudiée, si possible à une date idéalement identique à celle des prises de vues. A ces vérités terrain peuvent s ajouter des connaissances thématiques obtenues auprès d un expert. Les échantillons de classes stables temporellement (routes, urbain, etc...), peuvent être sélectionnés sur la base de cartes précises de la région. Les classifications supervisées sont nécessaires lorsque les besoins thématiques sont pointus. En effet les techniques non supervisées se limitent souvent à la reconnaissance de grandes classes thématiques (forêt, urbain, surface nue, végétation haute et basse et surface d eau) Les images Les images optiques Les systèmes de télédétection qui opèrent dans le domaine spectral du rayonnement solaire réfléchi (visible, proche infrarouge : PIR, moyen infrarouge : MIR), qualifié dans ce document de domaine optique, sont des systèmes incohérents passifs. Ils mesurent le rayonnement solaire qui est réfléchi par les surfaces terrestres et par l atmosphère. La grandeur physique mesurée est la luminance (W.m -2.sr -1 ). Tout rayonnement mesuré est affecté par un certain nombre d interactions (réflectance, absorption, transmittance, etc.) qui surviennent à la fois au niveau des surfaces terrestres et de l atmosphère. Compte tenu du fait que l objet observé est la surface terrestre, l atmosphère s avère être une des principales sources de «bruit» qui affecte les images optiques acquises depuis les satellites. L atmosphère est un milieu de gaz et aérosols dont l influence est plus ou moins forte selon les domaines spectraux considérés. Certains de ces aspects sont détaillés dans le chapitre 6. La valeur radiométrique (en général en compte numérique) des pixels dans les images optiques peut être approchées par une loi Gaussienne Propriétés de base des images Radar à haute résolution spatiale Principe de base du radar à visée latérale Le capteur radar est un système actif qui fournit sa propre illumination et qui utilise les microondes, dans un domaine de longueurs d onde très peu sensibles à l humidité de l air, qui traversent aisément l atmosphère, ainsi qu une couverture nuageuse ou des précipitations (fréquence < 14 GHz). L imagerie radar peut donc être utilisée à tout moment et indépendamment de l éclairement solaire. Le principe du radar consiste à émettre une onde électromagnétique cohérente et parfaitement polarisée qui est ensuite réfléchie en direction du radar par une ou plusieurs cibles. Le terme cible est d origine militaire mais désigne des diffuseurs de tout type. Dans notre cas, il s agira de toute surface terrestre ou d eau. L onde rétrodiffusée peut être partiellement dépolarisée, ce qui permet Ch 2 9
28 La classification l emploi de capteurs polarimétriques. La cohérence des ondes permet la formation d images à très haute résolution spatiale (THRS), ainsi que l interférométrie donnant accès à des paramètres de la géométrie des surfaces observées. Sur une polarisation donnée, le champ électrique reçu par l antenne du radar à un instant donné correspond à la somme vectorielle (addition cohérente) des champs ainsi rétrodiffusés par tous les diffuseurs situés à l intérieur d une surface ou plus généralement d un volume, délimité par la forme, la durée et les directions d émission de l onde émise. La grandeur mesurée est l amplitude complexe du champ électrique rétrodiffusé, c est-à-dire une amplitude et une phase. Dans le cas de radars imageurs, des impulsions de forme carrée et de courte durée τ sont émises latéralement (radar à visée latérale) dans la portion de l espace délimitée par le diagramme de rayonnement de l antenne dont l axe fait un angle θ avec la verticale. Chaque impulsion illumine les points d une bande de terrain perpendiculaire au vol (empreinte) dont la longueur utile représente la fauchée. La fréquence de répétition des impulsions (PRF), pour les RSO (Radar à Synthèses d Ouverture) qui présentent les meilleures performances parmi les radars à visée latérale, est déterminée par le critère d échantillonnage de Nyquist Shannon, soit en pratique celle applicable à la fréquence Doppler consécutive au déplacement du capteur. De façon abrégée, une impulsion doit être émise pour un déplacement azimutal de l ordre de la moitié de la dimension de l antenne réelle dans cette direction [Maître et al «Traitement des images de RSO», chapitres 2 et 3]. Les données brutes sont alors obtenues par enregistrements des lignes successives Discrimination en distance Une première discrimination des points imagés est obtenue par séparation en distance radiale r (Slant range). Plus la durée d impulsion τ sera courte, plus la résolution spatiale en distance r = cτ /2 sera fine. Cette distance, perpendiculaire à la direction de déplacement du radar et selon la direction de visée, ne doit pas être confondue avec la distance au sol (ground range) de résolution égale à r /sinθ. Pour les capteurs spatiaux basés sur des plateformes de puissance disponible maximale incompatible avec un bon bilan de liaison radar, on utilise la technique de compression d impulsion. Les impulsions émises sont de puissance moyenne, de plus longue durée T et modulées linéairement en fréquence (bande passante B f ) pour pallier le manque de puissance maxi instantanée tout en simulant un signal de grande bande passante équivalent à un signal plus bref de durée τ 1 / B f. La compression de l impulsion rétrodiffusée permet obtenir des résolutions métriques (cas des radars classiques type SeaSat, ERS, Radarsat, Envisat ), voire décimétriques pour les radars militaires. Elles sont généralement définies à 3 db ou 3,9 db par rapport au maximum, car l impulsion comprimée n est plus de forme carrée mais présente un lobe principal et des rebonds de moindres niveaux. Pour ERS les résolutions à 3,9 db en distance r et au sol r /sin θ sont de l ordre de 9,5 m et 25 m mais peuvent varier en fonction de divers filtres appliqués ou non [Maitre et al. Traitement des images de RSO, chapitres 2 et 3]. RSO Discrimination parallèlement à l axe de vol (azimut) pour les La réponse d un point au sol est inscrite dans plusieurs (centaines) d impulsions du fait des diagrammes d antenne usuels et de leur fréquence de répétition (PRF). Par conséquent dans la direction parallèle à l axe de vol, la résolution spatiale (dite azimutale) serait catastrophique si l on sous échantillonnait les données brutes des RSO comme pour les simples radars à visée latérale dont l usage est par conséquent restreint à de courtes distances. Pour séparer plus finement les objets dans la direction de l azimut, on utilise donc la technique de la Ch 2 10
29 La classification synthèse d ouverture, RSO (radar à synthèse d ouverture, ou SAR, synthetic aperture radar) permettant d obtenir des résolutions azimutales métriques, voire décimétriques pour les radars militaires. Le principe de base se fonde sur le fait que le pouvoir de résolution angulaire d une antenne est inversement proportionnel à sa dimension dans le plan considéré. La synthèse d ouverture consiste donc à simuler un très long réseau discret d antennes obtenu grâce aux différentes positions de l antenne réelle le long de la trajectoire du capteur. Un pixel final dans l image synthétisée, par opposition aux données brutes citées plus haut, est obtenu par des traitements informatiques sur ces données brutes basés sur les paramètres de vol, les caractéristiques de l antenne, de l onde émise et des conditions de propagation dans l atmosphère que l on suppose parfaitement connus (cas idéal). Ces traitements reviennent en pratique, après avoir effectué des corrections en distance radiale, à faire passer le signal temporel (Doppler) à travers un filtre adapté dont les paramètres sont calculés dans ces conditions idéales de prise de vue, pour un point situé au milieu d un pixel donné de la grille, où l on veut reconstituer la valeur du champ électrique rétrodiffusé Valeur complexe d un pixel (image SLC) et corrélation avec les voisins Il est utile de rappeler que l image ainsi synthétisée à la sortie d un processeur RSO est, à la base toujours une image complexe, dont la valeur du pixel est (amplitude A / phase φ), ou bien (partie réelle i / partie imaginaire q). La signification physique de z est qu elle est proportionnelle au champ électrique rétrodiffusé dont l amplitude complexe E d s écrit : = E Ch 2 11 E d i où E i représente le champ incident, r la distance et f la fonction de rétrodiffusion complexe dans la polarisation de mesure. C est la quantité, qui, après étalonnage du capteur/processeur représente la quantité physique caractéristique du pixel considéré. L amplitude complexe dans l image complexe monovue (SLC) est donnée par z = C f où C représente l étalonnage radiométrique de la chaîne capteur/processeur. Une constante additive peut être rajoutée, elle représente alors le bruit thermique moyen. Les données étalonnées ne sont utiles que lorsque l on est confronté à des comparaisons des données images avec des mesures de terrain ou à des modèles physique de rétrodiffusion, qui par ailleurs ne sont pas toujours aptes à représenter précisément la complexité des phénomènes de rétrodiffusion radar cohérente sur les surfaces aléatoires terrestres. L image complexe subit généralement une correction géométrique (interpolation linéaire) afin de positionner les pixels, sur les pas d une grille, qui doivent être égaux à environ la moitié des résolutions spatiales. Les pixels provenant du radar sont donc toujours fortement corrélés dans les deux directions, contrairement aux pixels «optiques» où la corrélation peut être nulle ou très faible perpendiculairement à l axe de vol, mais importante parallèlement du fait de l effet de «filé» pendant le temps d intégration de la luminance pour les satellite à défilement (en orbite basse). Par exemple, les données fournies par les satellites ERS 1 et 2 (Agence Spatiale Européenne ESA), peuvent être donnée au Format SLC (Single Look Complex). Ce sont des images SAR (Radar à Ouverture Synthétique) qui ont subit un prétraitement, mais aucune réduction du niveau du bruit. Ce sont des images «une vue» (nombre de vue : 1). Chaque pixel est codé par un nombre complexe dont la partie réelle (i) et la partie imaginaire (q) sont chacune codée sur 2 octets (16 Bits). La taille de l image est de l ordre 2500 valeurs par ligne sur lignes, ce qui fait un volume d environ 150 Mo. e jkr r f
30 La classification Images monopolarisation multivues En général, les images complexes des capteurs spatiaux ont des résolutions spatiales au sol moins bonnes d un facteur 3 à 4 en distance par rapport à la direction azimutale. On a donc préféré distribuer dans un premier temps des images détectées corrigeant l aspect d étirement prononcé qui est très désagréable. Pour cela, des images multivues (multilook) furent créées en dégradant la résolution azimutale, généralement de l ordre de 5-6 m, pour l amener aux environs des m typiques de la valeur de la résolution en distance au sol. Cette transformation revient à synthétiser l image en azimut sur des portions réduites de l ouverture synthétique. On divise la bande passante Doppler initiale B D par exemple en L = 3 ou 4 bandes moins larges permettant de synthétiser L images de résolution dégradée. Les L images obtenues correspondent effectivement bien à des prises de «vue» sous des angles très légèrement différents. L image multivue est obtenue en ne conservant que le module (amplitude) de chaque image complexe. La sommation multivue se fait soit en amplitude A, soit en intensité I = A 2 suivie d une racine carrée, sauf en polarimétrie et en interférométrie. Si les filtres sont disjoints et de type fonction «porte», on montre que la résolution spatiale est L fois moins bonne en azimut. Cependant les L filtres se recouvrent souvent fortement et la dégradation spatiale est alors moins forte, mais la réduction du speckle moindre. Ce fut le cas pour les radars cités plus hauts, où les images PRI (Precision Radar Image) distribuées en premier avaient un échantillonnage identique (pixel tous les 12,5 m pour ERS à comparer aux résolutions spatiales radiale et au sol de l ordre de 25 et 30 m). L image fournie est ici un nombre réel représentant l amplitude du champ électrique rétrodiffusé par la cellule de résolution centrée autour du pixel, la phase étant donc perdue. Taille : 8000 valeurs par ligne sur 8200 lignes, volume : environ 131 Mo, codage : 16 Bits. Cependant, les images PRI gagnent en résolution radiométrique ce qu'elles perdent en résolution spatiale. Ceci est lié au principal inconvénient de l interprétation visuelle ou automatique des images radar : le phénomène de chatoiement («speckle» en anglais) expliqué sommairement ciaprés. Depuis la mise en évidence pratique des potentiels de l interférométrie radar et de la polarimétrie, nécessitant toutes deux la conservation de la cohérence et de la différence de phase, les données complexes (SLC, Single Look Complex) sont devenues un produit disponible distribué par les grandes agences. Mais même en dehors de ces deux cas, l image complexe est la seule à conserver toute l information initiale, sur la surface observée et sur le capteur au sens large ayant produit cette image, ce qui permet d optimiser certains traitements ultérieurs (estimation optimale de la réflectivité radar, du contraste d un monocontour, etc ) Chatoiement ou «speckle» Ce phénomène physique parfaitement déterministe est dû à la cohérence de l illumination, du système capteur/processeur et à l interférence constructive et/ou destructive des champs rétrodiffusés par les objets à l intérieur de chaque cellule de résolution. Le résultat de ce phénomène est parfaitement reproductible si on observe le même pixel dans le temps et à condition que rien, ni lui ni les conditions de prise de vue n aient changé. Cela signifie aussi que le radar sera extrêmement sensible à tout changement intervenant dans chaque pixel ou dans les conditions de prise de vue et donc pour les géophysiciens une source d informations précieuses sur de grandes surfaces. Un exemple parfaitement parlant est l interférométrie radar et l interférométrie différentielle qui «comparent» deux ou plusieurs images prises simultanément ou dans le temps, sous des angles légèrement différents. Elles ont permis l établissement de MNE (Modèle Numérique d Elévation), Ch 2 12
31 La classification de changements dans le temps de ces MNE (glissement de terrain, subsidences, activité de volcans, mesure des déplacements lors de tremblements de terre...) malgré les changements spatiotemporels atmosphériques. Toutefois, si la surface ou le volume observé sont de nature désordonnée (la nature, la position ou l orientation d une partie des diffuseurs changent aléatoirement d un pixel à l autre), le phénomène d interférences, déterministe à l intérieur de chaque pixel, se transforme en un processus spatialement aléatoire. L image amplitude de telles surfaces prend un aspect aléatoire extrêmement granuleux sur les images de tels volumes et surfaces. L onde diffusée par une cellule de résolution est la somme des ondes diffusées par chaque diffuseur à l intérieur de cette cellule. Si une surface est formée de cellules de résolution ayant toutes le même nombre de diffuseurs appartenant tous à la même population, et si ce nombre est suffisamment grand, les fonctions de diffusion f mesurées sur les différentes cellules de résolution, vont fluctuer aléatoirement de façon gaussienne. Cette surface est appelée «surface homogène» car elle n est qu un échantillonnage de la même population caractérisée par un seul paramètre de puissance rétrodiffusée. Les changements d amplitude complexes ou d intensité rétrodiffusée I = A 2 d un pixel à l autre sont dus essentiellement à de petits changements de distance r des différents diffuseurs au radar, de l ordre ou supérieurs à λ/2 (rugosité d un sol, de la mer, de la végétation ) Ces fluctuations peuvent être modélisées, dans ce cas, par le phénomène de la marche aléatoire dans le plan complexe (amplitude/phase) du champ rétrodiffusé et conduit, dans le cas d un nombre élevé de diffuseurs (en pratique > 10) au modèle de «speckle gaussien pleinement développé» où les parties réelle i et imaginaire q de z sont 2 variables aléatoires gaussiennes indépendantes de moyenne nulle mais de même variance (processus complexe gaussien circulaire). La seule information, hormis les cas interférométrique ou polarimétrique, est contenue dans la variance, proportionnelle à la puissance moyenne rétrodiffusée, souvent appelée réflectivité radar R de la surface homogène. R est proportionnelle au coefficient de rétrodiffusion radar σ des physiciens. L intensité I est alors distribuée pour une image monovue, selon la loi de Laplace (exponentielle) de moyenne R : p I (I ) = (1/R) exp (- I /R) I 0 La phase est uniformément distribuée sur [-π,+π] : p ( φ ) = et l amplitude A est distribuée A 2A selon la loi de Rayleigh p ( A) = e R A 0 Ch 2 13 A R 2 Pour une image multivue, la loi exponentielle devient une loi Gamma si les vues sont décorrélées. Sinon, l approximation Gamma est acceptable à condition de remplacer le nombre de sous vues L par un nombre effectif L < L de vues. L amplitude A obéit à des changements analogues par l intermédiaire d une loi Chi [Maître et al «Traitement des images de RSO ]. Le qualificatif de «bruit» multiplicatif souvent attribué au speckle est justifié ici par le fait que l on peut, par exemple, écrire l intensité I des pixels comme I = N.R où N est une variable aléatoire de moyenne 1 distribuée selon la loi exponentielle (Gamma en multivue). En amplitude, elle serait distribuée selon une loi de Rayleigh (Chi en multivue) et de moyenne non unitaire Zone non homogène, texture et «bruit» multiplicatif Si le nombre moyen de diffuseurs par cellule varie aléatoirement tout en restant grand, on peut montrer la validité du speckle pleinement développé ayant les mêmes caractéristiques que celui d une surface homogène, mais pour un pixel donné caractérisé par sa réflectivité radar R. Autrement dit la loi exponentielle ne s écrit que conditionnellement : p I (I /R) = (1/R) exp (- I /R) φ 1 2π
32 La classification Par contre les fluctuations à l intérieur de la surface ne proviennent plus des effets du seul speckle mais des variations du nombre de diffuseurs induisant des changements de réflectivité radar R d un pixel à l autre. On parle ici de «zone texturée» ou de «zone hétérogène». La notion de «texture» est introduite pour caractériser les fluctuations du champ (A ou I) qui ne sont pas dues au seul speckle. A la différence du speckle, la texture va avoir des paramètres statistiques variables pour chaque surface hétérogène, celles de la distribution de la réflectivité radar R. La loi de l intensité est obtenue en intégrant la distribution conditionnelle p I (I /R) par rapport à la distribution de la réflectivité radar R. Un exemple bien connu est la loi K obtenue quand la réflectivité R suit une loi Gamma [Maître et al «Traitement des images de RSO ]. Le modèle multiplicatif I = N. R reste toujours valable, mais ici R est en plus considérée comme un processus aléatoire indépendant de N. Lorsque le nombre de diffuseurs est faible ou lorsqu un petit nombre de diffuseurs a une importance prépondérante par rapport aux autres, il n est plus possible de faire une approximation gaussienne et des paramètres supplémentaires doivent être introduits. Le speckle, qui peut être assimilé à un «bruit» pour les surfaces homogènes ou hétérogènes, est alors dit «speckle non développé» et devient une source d information spécifique de la surface. Les surfaces de ce type se caractérisent par la présence d objets anguleux de tailles importantes telles que des habitations dans une zone urbaine Capteurs polarimétriques et interférométrie Les capteurs polarimétriques émettent et reçoivent de façon cohérente et quasi simultanée dans deux polarisations orthogonales, généralement Vertical V et Horizontale H. Il y a donc 4 champs rétrodiffusés mesurés, en combinant 2 par 2 les polarisation de base : VV, HV, VH et HH. Dans ce cas la mesure, après étalonnage, est une matrice complexe de rétrodiffusion S donnée par exemple par f f vv vh S = f f hv hh Pour les données multivues, des informations entre la différence de phase entre canaux de polarisation mais aussi sur leurs degrés de cohérence mutuelles (corrélations complexes) sont aussi conservées par l intermédiaire d une sommation multivue sur les intensités I proportionnelles à f 2 et sur les produits f pq f rs *. Ceci revient à faire la sommation multivue sur la matrice de covariance 4x4 associée au vecteur de mesure à 4 composantes Z = t ( f vv f vh f hv f hh ). La donnée fournie est alors soit une matrice de covariance, soit un vecteur de Stokes, représentant chacun 16 variables réelles dans le cas général. Lorsqu il y a réciprocité du processus de rétrodiffusion ( f vh = f hv ), il y a 9 variables (matrice 3x3) au maximum. Le cas de deux canaux de polarisation revient à une matrice de covariance polarimétrique 2x2. C est aussi le cas d un couple interférométrique, mais ici la sommation multivue ne s effectue pas dans le domaine spectral mais dans le domaine spatial pour une meilleure estimation de la cohérence dont la phase constitue l interférogramme. Le module de la corrélation est un indice de la précision de l interférogramme. Cependant, il indique ainsi la stabilité du processus de rétrodiffusion lors de l acquisition et par là même, fournit une information dans une classification. Par exemple, en cas d acquisitions non simultanées, la cohérence est nulle sur des surfaces d eau, plus ou moins faible sur la végétation en fonction de sa croissance ou du vent, plutôt forte sur le minéral, le bâti. Ch 2 14
33 La classification Dans tous les cas, le vecteur speckle est une variable aléatoire complexe de dimension correspondant au nombre de canaux N. Plus précisément, c est un processus circulaire gaussien à N dimensions. Pour une image multivue, le speckle est distribué selon une loi de Wishart complexe à N dimensions et de paramètre L. Une zone homogène est caractérisée par une matrice de covariance (16 paramètres réels au maximum) représentant 4 réflectivités radar et 6 degrés de corrélation complexes entre les 4 canaux de polarisation mesurés VV, VH, HV et HH. Une région texturée peut être modélisée par des schémas plus ou moins simples. Par exemple, la texture peut être représentée par un simple scalaire positif t représentant la variation du nombre de diffuseurs et conduisant à une loi K polarimétrique si t est distribuée selon une loi Gamma [A. Lopès, F. Séry 1997, Maître et al «Traitement des images de RSO»]. Ce modèle doit cependant être fortement compliqué lorsque, par exemple, les 4 canaux de polarisation n observent pas la même population (pénétration plus ou moins forte dans la végétation, le sol, ) Perspectives de développement L idéal serait le lancement de capteurs à plusieurs fréquences comme en optique afin d obtenir des informations physiques très décorrélées, ce que ne permet pas la polarimétrie. Le coût en puissance embarqué est pour l heure prohibitif. Le mélange interférométrie polarimétrie partielle est actuellement exploré tout comme le multitemporel à haute fréquence de répétition (constellations de capteurs radar, en liaison ou non avec des capteurs optiques). Nous avons vu également que la présence du chatoiement réduit considérablement l intérêt de tels capteurs sur des surfaces de petite dimension (décamétrique) car il induit des estimations biaisées et imprécises des paramètres de surface, néfastes aussi bien en classification qu en physique. C est pourquoi le succès mérité des capteurs radar (diffusiomètre, altimètre, RSO pour la détection des icebergs et grands navires) est essentiellement obtenu sur des surfaces très larges, en océanographie surtout. La seule parade consiste à réduire dès le départ son niveau en permettant l obtention d images dont le nombre de vues dépasse la dizaine, tout en conservant une résolution spatiale de l ordre de quelques mètres, typiques de nombreux objets terrestres. Ceci revient en fait à améliorer la résolution spatiale de base (images SLC) pour la faire passer au niveau (ou en dessous) du mètre. Nous nous situons alors dans le domaine militaire qui permet sans aucun doute l obtention d informations très précieuses mais strictement réservées Les images filtrées - Principe du filtre spatial et multitemporel du speckle LVMMSE Le chatoiement implique la nécessité d un filtrage pour certains traitements. L idéal est d utiliser l image radar «brute», sans filtrage car les filtres font perdre des détails qui peuvent être importants, et surtout les structures. Pour pallier ce problème, le filtre LVMMSE (linear vectorial minimum mean square error) a été développé au CESBIO [Lopès et al 93]. Les filtres classiques du speckle dans les images RSO (un canal en amplitude ou en intensité) sont des filtres locaux : - non adaptatifs et ne tenant pas compte de la nature du speckle et des propriétés locales de la réflectivité radar R : médian, moyenne (convolution par un masque à coefficients constants positifs), morphologiques etc... Ch 2 15
34 La classification - adaptatifs car tenant compte de certaines propriétés du speckle et de la réflectivité radar: Frost (82), Lee (81) et Kuan (87)(estimations linéaires par moindres carrés), Gamma-MAP (non linéaire, maximisant la probabilité a posteriori en supposant que la réflectivité radar est distribuée selon une loi Gamma). L'estimation des paramètres étant faite localement, des améliorations nettes sont apportées par différents détecteurs qui permettent d'éliminer dans les calculs les pixels d'autres régions (détecteurs de contour, de lignes) ou les forts diffuseurs. La fenêtre d'estimation peut alors être agrandie, de forme variable et orientable pour s'adapter au mieux à la géométrie locale des régions. Une étape supplémentaire est franchie en utilisant une segmentation de l'image éventuellement couplée aux détections de lignes et forts diffuseurs, pour calculer les statistiques locales sur la totalité de chaque segment et non sur une partie limitée. Dans le cas polarimétrique (ou interférométrique, ou de données SLC avec pixels très corrélés) et compte tenu de la complexité (nombre élevé de variables corrélées, de surcroît parfois complexes, modélisation du speckle et de la variable multidimentionnelle représentant les propriétés d'un pixel), un filtre linéaire vectoriel complexe minimisant l'erreur quadratique moyenne (LVMMSE) généralisant l'estimateur de Kuan (1 variable réelle) semble une bonne base (compromis "modèlisation / estimation des paramètres"). Pour plus de détails, on pourra consulter les ouvrages cités : Séry F. (97), Maître et al «Traitement des images de RSO», (00). Le filtre LVMMSE est une généralisation, version multitemporelle, du filtre scalaire linéaire d écart quadratique moyen minimum vectoriel, filtre adaptatif pour images non stationnaires [Fjørtoft et al. 1997]. Il est basé sur la segmentation et sur la minimisation de l erreur quadratique moyenne minimale linéaire entre l'estimation de la valeur radiométrique du pixel et la valeur réelle, les statistiques sont calculées par régions définies par une segmentation de l image [Fjørtoft 1999]. On fait l hypothèse que le bruit, dû au chatoiement, est multiplicatif et non corrélé entre les plans. L avantage du filtre adaptatif LVMMSE est qu il effectue un filtrage pour chaque plan séparément mais pas indépendamment des autres plans. La corrélation entre les plans de l image est exploitée pour la réduction du chatoiement, grâce aux matrices de covariance. Ainsi la méthode tient également compte des similitudes et des différences entre les dates et donc la performance du filtre est plus grande par rapport à des filtres qui n utilisent pas ces similitudes. Avec ce filtre, les structures sont bien conservées grâce à l introduction de la segmentation. Des améliorations supplémentaires ont été apportées par : La détection des forts diffuseurs et des structures isolées. La détection des structures linéaires et filtrage indépendant des lignes. Le filtrage assisté suivant un coefficient d hétérogénéité pour chaque canal. Au niveau qualitatif, les transitions entre région deviennent plus nettes et mieux définies, les statistiques sont en général mieux préservées, au niveau visuel l image filtrée a un aspect plus net La détection des forts diffuseurs et des structures isolées Dans les images RSO, les forts diffuseurs sont en général des rétro-diffuseurs en forme de coin qui ont une très grande réponse. La valeur radiométrique détectée est très élevée car presque tous les rayonnements qui ont été émis par le système radar sont renvoyés par ce type de cibles vers le radar. Ils peuvent être de taille très variable. Ainsi, dans le cas des images ERS (résolution de 20m approximativement) on trouve des forts diffuseurs de quelques pixels qui correspondent à des cibles relativement petites, comme des maisons. Mais on peut trouver des forts diffuseurs de quelques centaines de pixels correspondant à des agglomérations d objets en forme de coin ou de réponse spéculaires comme un toit d usine. Ch 2 16
35 La classification Quand les cibles sont isolées, la réponse individuelle est en général en forme de croix et de l ordre de quelques pixels (5 à 10 pixels). Ces dimensions peuvent être facilement calculées à partir de la réponse impulsionnelle. Pour le cas d agglomérations, qui présentent des forts diffuseurs, la sommation des réponses implique une forme qui ne suit pas une géométrie déterministe, mais dépendant de la forme de l agglomération. Ce dernier type de forts diffuseurs est plus difficile à détecter, car ce n est pas possible par des méthodes géométriques, mais par des méthodes de type seuillage radiométrique. La présence du chatoiement complique la détection automatique de ces structures isolées. Les forts diffuseurs sont une partie de l information de l image très importante qui peut être utile pour détecter certains objets. Cependant, pour estimer les statistiques locales des pixels en filtrage, segmentation ou classification, ils ne doivent pas être pris en compte dans les calculs. En conséquence, il faut d abord les détecter, les localiser précisément puis les exclure de la procédure de calcul des statistiques. Ces points ne doivent pas être non plus filtrés. Deux méthodologies ont été implantées pour la détection des forts diffuseurs. par seuillage géométrique : ce type de détection est effectué, à partir des masques en forme de croix, par des méthodes géométriques, qui déterminent la position des forts diffuseurs, indépendamment des régions trouvées par la segmentation. Cette approche permet la détection des cibles de type croix de différentes dimensions, de cibles isolées et relativement petites, qui ne forment pas une agglomération (figure 2.1). Figure 2.1 : un fort diffuseur isolé par seuillage radiométrique : permet une détection plus fine de la forme des forts diffuseurs. En pratique le but est de distinguer les agglomérations des forts diffuseurs qui n ont pas pu être détectés dans la méthodologie précédente. (a) (b) (c) Figure 2.2 : compositions colorées de l image de la région Bourges (chapitre 3), (a) image ERS1 originale non filtrée, nombre de vues indépendantes L = 3 ; (b) image filtrée par VMMSE sans détection des forts diffuseurs image ; (c) nouveau filtrage avec détection des forts diffuseurs On peut observer qu au centre de l image (a) il existe quelques pixels avec une radiométrie beaucoup plus élevée qui correspondent à un fort diffuseur. Dans l image (b) il existe une région centrale qui a été fortement polluée par la présence du fort diffuseur et d autres régions plus petites qui ont été aussi polluées par d autres forts diffuseurs, plus petits. Dans la troisième image (c) le nouveau filtrage avec détection des forts diffuseurs a permis de mieux conserver les statistiques des Ch 2 17
36 La classification régions et surtout des valeurs radiométriques des pixels immédiatement autour du fort diffuseur. Les forts diffuseurs ont été isolés et non filtrés, ils sont mieux préservés. Une fois détecté, une image des forts diffuseurs peut être obtenue, qui peut être utilisée en tant qu image dérivée (comme les images SIG ou de contours) et introduite comme contrainte dans la classification (méthode ICM), pour améliorer la discrimination des classes, pour ne pas confondre les forts diffuseurs, avec d autres objets, par exemple. Figure 2.3 : extraction des forts diffuseurs ; à gauche image originale, à droite les forts diffuseurs Les images segmentées de contours ou de région La segmentation est une opération qui décompose l'image en un ensemble de régions uniformes, (que nous appellerons segments, suivant le contexte, pour ne pas confondre avec la région au sens géographique du terme) chacune d'entre elles étant homogène au sens d'attributs préalablement définis. Puis les régions (segments) sont étiquetées : à chaque segment est attribué une étiquette différente. C est donc une partition de l image en régions qui vérifient des propriétés d homogénéité sur des critères caractéristiques donnés, comme la réflectivité ou des attributs texturaux. En imagerie RSO ces critères peuvent être polarimétriques ou interférométriques. Au final, une segmentation (figure 2.4.) est une représentation de l image en terme de contours fermés et de régions [Coquerez 1995]. Comparaison avec la classification : Par opposition à la segmentation, la classification (figure 2.4) consiste à identifier la nature des régions trouvées. Les régions identifiées lors de la segmentation peuvent être reconnues ou interprétées sémantiquement. Les points ou les régions présentant des similitudes basées, elles aussi, sur le calcul de critères caractéristiques sont ainsi regroupées dans une même classe. Segmentation Classification Figure 2.4 : à droite : image segmentée, à gauche : des classes ont été affectées aux régions. Ch 2 18
37 La classification Principe de la segmentation introduite dans les étapes de la classification La méthode de segmentation a été développée à l ENSEEIHT (IRIT/LIMA) [Fjortoft, Marthon et al 95] pour son application aux images optiques et modifiée au CESBIO pour les images radar. L approche locale de détection de contours consiste à balayer l image avec une fenêtre définissant la zone d intérêt. Un opérateur est appliqué sur les pixels de la fenêtre afin d estimer s il y a une transition significative au niveau de l attribut choisi. L opérateur choisi est celui de Shen et Castan [Shen & Castan 1992] car, il est robuste au bruit, il permet une bonne localisation, pour les images optiques et le ROEWA (Ratio Of Exponentially Weighted Average) qui tient compte du speckle, pour les images radars [Fjortoft 99]. L opérateur de Shen et Castan est optimal pour un bruit additif blanc gaussien et une distribution de Poisson de contours. Il obtient de très bons résultats selon des critères de bonne détection de contours : robustesse au bruit, bonne localisation, et faible multiplicité des maxima dus au bruit. Cet opérateur consiste à calculer la différence entre les moyennes calculées de chaque côté du pixel central, en introduisant une pondération exponentielle négative au niveau des moyennes de support infinie. L opérateur ROEWA adapte l opérateur de Shen et Castan pour les données RSO à partir du rapport des moyennes. Une fois l image de puissance de contour créée, il faut en extraire des contours fermés et amincis pour établir une segmentation. L algorithme de ligne de partage des eaux [Vincent et Soille 1991], est une méthode issue de la morphologie mathématique, qui extrait directement des contours fermés et squelettisés à partir d une image de puissance de contour (image de module de gradient). L image de puissance est interprétée comme une surface, dont les lignes de crête, sont supposées correspondre aux contours de l image origine. Pour détecter les lignes de crête, on simule une inondation de la surface. Comme la méthode crée une région pour chaque minimum local dans l image de puissance de contour, elle a tendance à être sur-segmentée, d autant plus que l image est bruitée. Une méthode plus robuste au bruit est appliquée : le seuillage des dynamiques de bassin à partir d'une carte de puissance de contour, réalisant ainsi une représentation hiérarchique des différents niveaux de segmentation de l'image [Fjørtoft et al. 1998,1999, Lemaréchal et al. 1998]. Cette méthode est particulièrement intéressante pour réduire le nombre de faux contours. La dynamique du bassin associée à un minimum local est définie comme la différence d'altitude entre ce minimum, et le point de crête le plus bas qui doit être franchi pour arriver dans un bassin ayant un minimum plus bas que le premier. On définit la dynamique d'un arc de contour comme étant la valeur maximale du seuil pour lequel cet arc de contour subsiste, lorsqu'on supprime tous les bassins ayant une dynamique inférieure au seuil L'image de dynamique de contour n'est pas binaire. Chaque arc de contour a la valeur de sa dynamique de contour. Le concept de dynamique de contour permet de créer une représentation hiérarchique et compacte des segmentations obtenues en appliquant différents seuils aux dynamiques de bassin. Les limites sont fermées et ainsi définissent des régions (taches ou segments). Le logiciel crée une représentation hiérarchique de toutes les segmentations possibles, en attribuant à chaque pixel du contour la dynamique de contour de l'arc auquel il appartient. La méthode permet de créer plusieurs niveaux de segmentation plus ou moins fins, correspondant à un seuil donné. Au fur et à mesure que le niveau de segmentation grandit, les régions seront moins finement définies. Pour obtenir la segmentation correspondant à un seuillage des dynamiques de bassin, il suffit d'effectuer un simple seuillage sur l'image de dynamique de contour, en ne gardant que les pixels dont la dynamique de contour est supérieure ou égale au seuil. Au fur et à mesure que le niveau de segmentation grandit, les régions seront moins finement définies. Ch 2 19
38 La classification (a) (b) (c) (d) Figure 2.5 (a) extrait d une image TM d une zone forestière et agricole de Minorque (R : TM-4, V : TM- 3, B : TM-2), (b) image de puissance, (c) niveau de segmentation 10, (d) niveau de segmentation Utilisation de la segmentation dans la classification Le système de classification et d analyse du paysage que j ai développées utilise la segmentation à plusieurs niveaux : dans la classification, en post classification, dans l analyse du paysage, dans l apprentissage automatique. Le choix du seuil de segmentation est délicat, car il dépend des objectifs de la segmentation. Une part de décision est laissée à l'utilisateur, afin de le moduler en fonction des résultats souhaités. 1. Dans la classification : vers une classification par objet La classification peut être effectuée sur les régions déterminées par la segmentation, on ne s intéresse plus au pixel mais à un objet correspondant à un écosystème ou à une partie de cet écosystème. Il est préférable d utiliser une segmentation fine (sur-segmentée), car il vaut mieux de Ch 2 20
39 La classification petits segments, la classification permettant de corriger d'éventuelles erreurs de segmentation. Ainsi plusieurs petits segments seront affectés à la même classe, ces segments appartenant au même objet. Par contre il ne faut pas classer deux objets de nature différente dans une même classe. Ceci peut se produire en augmentant le seuil de segmentation : des parcelles proches au sens de l homogénéité, mais différentes sémantiquement, sont rassemblées, ce qui ne sera pas le cas en sur-segmentant. Pour les images RSO, les parcellaires agricoles, constituées de champs homogènes, sont généralement bien adaptées à une classification basée sur la segmentation. En général les structures apparaissent bien dans ce type d image. 2. Pour l'amélioration de classification a posteriori Nous avons développé diverses méthodes qui utilisent le contexte, dans le cas le plus simple, le principe correspond à éliminer des points isolés et effectuer un lissage. L'apport d'une image segmentée permet de conserver des contours nets et les structures donc il faut une segmentation plutôt moyenne s approchant de la parcelle. 3. Aide à l'extraction d'objets La segmentation est une aide intéressante pour l extraction d objets tels que les nuages, les villes, les rivières. Elle constitue une information supplémentaire (mais non suffisante) aux algorithmes d'extraction. 4. Pour l analyse du paysage : calcul de l hétérogénéité, L indice d hétérogénéité se calcule à partir de la segmentation (chapitre 5). Des combinaisons d'images sous segmentées et sur segmentées, permettent de détecter des sous classes, dans des parcelles hétérogènes Les algorithmes de classification développés Introduction Les méthodes de classification proposées intègrent un grand nombre de données et de concepts. L application autour de la classification est une chaîne assez conséquente et complexe. Je ne pourrai pas ici tout détailler, seul les points les plus importants sont décrits. Des procédures permettent d obtenir des images dérivées. L addition de ces images supplémentaires dans la procédure de classification (images provenant d une segmentation, image de contours, forts diffuseurs, images représentant des textures) a pour but son amélioration et peut être utilisée pour les contraintes de contexte spatial dans la méthode ICM, et ainsi renforcer les résultats de la classification. Dans certains cas, comme pour les images RSO des filtrages sont nécessaires. Les images filtrées grâce au filtre par région LVMMSE vectoriel et temporel ( 2.2.3) avec détection des forts diffuseurs améliorent la définition et la qualité des images filtrées. Les logiciels sont conçus pour être le plus automatique possible, mais comme pour la segmentation une part de décision est toujours laissée à l'utilisateur, s il souhaite interagir. Le fonctionnement général de l application de classification peut être résumé par la figure 2.6. Ch 2 21
40 La classification Images dérivées ou données exogènes Types de traitement Images S.I.G. Canaux texturaux Image des régions Images masques Image des contours Images filtrées Ponctuel ou Contextuel Canaux optiques ou radar Choix de la loi : Gauss Gauss-Wishart Gauss complexe Pearson K Gamma barycentrique Image classée CLASSIFICATION Matrice de Confusion (supervisée) Historique Fusion Classes englobantes Elimination de classes ou de canaux Figure 2.6 : représentation des méthodes de classification Les images dérivées introduites dans la classification sont les : Images texturales : obtenues 1) par le calcul d écart type ou de coefficient de variation sur les images sur un voisinage centré sur le pixel traité, 2) par les modules d analyse du paysage présentés dans le chapitre 5 Image des régions : pour introduire la connaissance de l expert par l emplacement de certaines classes dans certaine zone, afin de faciliter la détection des classes (figure 5.33 chapitre 5) Image des contours : résultant d une opération de segmentation ou tout autre opération permet : 1) d affiner la classification dans le cas d images texturales lorsque des régions ont un fort écart type. Si un pixel appartient à un contour, l information texturale ne sera pas considérée, car ce pixel peut appartenir à une classe homogène tout en ayant un écart type élevé dû au fait qu il est sur un contour. Par contre, si les pixels n appartiennent pas au contour, son écart type sera pris en compte pour la discrimination texturale. 2) d aiguiller la décision d affectation du pixel à une classe en analysant son voisinage, utilisée ici en tant que contrainte markovienne dans la méthode ICM. Image «masque» : permettent d établir des zones de l image à ne pas classer en raison du recalage des images, par exemple, ce qui permet de ne pas tenir compte des zones non commune de plusieurs dates. Image du MNT (Modèle Numérique de Terrain) SIG (Système d information géographiques) : permettent de discriminer directement certaines classes à partir d éléments contenus dans le SIG Image du réseau routier et/ou hydrographique Ch 2 22
41 La classification Images filtrées pour les images RSO afin de diminuer l effet du chatoiement (speckle) dans les images Les modes opératoires des classifications Trois modes opératoires de classification ont été implantés : le mode ponctuel, contextuel ou local et global. Rappelons que la plupart des méthodes présentées ont été réalisées de façon supervisée ou non. Les méthodes non supervisées sont itératives. Nous avons mis au point leur version supervisée qui est initialisée à partir d échantillons et exécutée avec peu d itération. Ce procédé d abord utilisé pour les images radar car chaque itération réduit le speckle, s est également révélé intéressant pour les images optiques car il diminue des confusions de classes, et fait disparaître les points isolés, et comme une image segmentée est introduite, les structures sont mieux dessinées. Ces méthodes supervisées ou non, partagent des principes communs Classification ponctuelle Les méthodes de classification bayésiennes ponctuelle (pixel à pixel), utilisent un jeu de probabilités a priori, constant sur toute l image, qui ne dépend pas du contexte du pixel. En pratique, les caractéristiques d un pixel dépendent, sinon de l ensemble des pixels de l image, tout au moins d un voisinage de celui-ci. Par la suite nous verrons que la modélisation du mécanisme de formation des régions de l image par un processus markovien permet de ramener la considération des pixels de l image entière à celle de ses plus proches voisins. La première étape consiste à déterminer les termes d observation (probabilité conditionnelle) et d a priori. Pour le terme d observation, on approche la distribution P(y s x s =k) par la distribution empirique de l image sur les échantillons correspondants à la classe k (pour le supervisé). Une autre solution consiste à choisir un système de distributions paramétriques et à ajuster les paramètres aux échantillons prélevés de manière à obtenir les mêmes moments. Dans le cas d images RSO, on approche la distribution P(y s x s =k) de chaque classe par des lois Gamma ayant la même moyenne et le même écart-type que les échantillons. Si les régions sont homogènes, la loi de Gauss peut être utilisée, sinon les lois K ou le système de Pearson seront préférés. Pour les images optiques, la loi de Gauss est appropriée. Une méthode a permis d introduire la notion de texture dans la cas ponctuel comme la méthode de la moyenne des classes sous hypothèse gaussienne et la texture sous hypothèse d une distribution gamma dans le modèle multiplicatif du speckle (gamma-texture) (Nezry et al (96)). Pour la deuxième étape, il suffit d affecter à chaque pixel la classe qui maximise sa probabilité d observation. Le problème d optimisation se limite ici à la comparaison directe de N ω probabilités. La qualité de la classification est liée au taux de recouvrement des classes. Dans le cas d images RSO brutes c est à dire non filtrées, la dynamique conduit à un fort recouvrement des classes. Les données radar, offrent des aspects très différents. Par exemple, une route peut apparaître très réfléchissante ou non selon son orientation (pente). En y ajoutant le chatoiement, le recouvrement des classes est alors trop important pour garantir des résultats fiables. Les résultats sont insuffisants, et donnent à la classification ponctuelle un aspect pointilliste. Le taux de classification pour un canal de type ERS/JERS/RADARSAT est de 15% à 25% de pixels bien classés en moyenne suivant ces capteurs. Pour avoir des résultats corrects avec ces méthodes, il vaut mieux, au préalable, filtrer les images ( 2.2.3, exemple chapitre 3). Il peut être préférable de transformer les images par le logarithme des amplitudes dans ce cas l approximation gaussienne est plus acceptable (voir chapitre Ch 2 23
42 La classification 3, exemple). Pour le cas multitemporel (à partir d au moins 3 dates) et si les images sont filtrées, les taux de bien classés sont de l ordre de 60 à 70%, ce taux augmentant avec le nombre de dates. Pour les images optiques la loi Normale multivariée est une approximation correcte de la distribution : p ( y ω ) i = ( 2π ) 1 d 2 C i 1 2 e 1 2 t 1 ( y µ ) C ( y µ ) où d : dimension de la variable aléatoire correspondant au nombre de canaux traités simultanément C i : la matrice de covariance et µ i le vecteur moyen de la classe ω i L avantage de cette méthode est la simplicité d application, la prise en compte des corrélations inter-dimensions, notamment temporelles, la possibilité d ajouter aux canaux de base, des canaux synthétiques tels que des textures locales ou autres s ils ont une distribution approchant une gaussienne. La loi K Pour les images radar, la loi K est plus précise que la distribution gaussienne, quand la réflectivité est distribuée selon une loi Gamma. Bien que la loi K soit une meilleure approximation, l estimation des paramètres nécessaires à ces fonctions discriminantes peut générer des erreurs annulant le gain de cet ajustement plus précis surtout quand le nombre de pixels des échantillons est faible. i i i Cas particulier des images polarimétriques Plusieurs approches du problème de la classification ponctuelle utilisant l ensemble des variables contenues dans des données polarimétriques radar ont été étudiées. Des tests ont été réalisés avec le capteur SIR-C, embarqué sur la navette spatiale américaine en 1993 et 1994, pour évaluer le potentiel de données polarimétriques. Ce capteur possède des bandes de fréquence L et C, et fourni des données polarimétriques complètes, mais symétrisées [Goze et al 92]. Les deux bandes spectrales des données SIR-C enrichissent nettement l information disponible. Nous avons utilisé des classifications filtrées ou non. Un filtre spatial polarimétrique plus élaboré peut également être appliqué avec succès afin d améliorer nettement les classifications à l intérieur des parcelles [Goze 92, 93]. Les inconvénients de cette méthode sont bien connus : perte de résolution spatiale et taux de bonne classification chutant au voisinage des contours et des forts diffuseurs. Une classification polarimétrique doit tenir compte des informations, sur le type de mécanisme de rétrodiffusion de la cellule de résolution, contenues par les données polarimétriques. La plupart des informations qui peuvent être extraites sont des informations sur les mécanismes du premier ordre. C est à dire que la modélisation des interactions s arrête généralement au couple (onde incidente, onde diffusée par un objet simple), les interactions multiples ne permettant pas d obtenir des modèles généraux. Les mécanismes de premier ordre sont, pour les plus simples, reliables à des surfaces génériques (surface plane ou légèrement rugueuse, couvert végétal dense, surface plane avec présence d objets anguleux, etc..). Des méthodes de classification non supervisées [Freeman et al 92, Cloude & Pottier 96] affectent automatiquement un pixel à l une de ces surfaces génériques. Dans le cadre d une application supervisée, cet apport d informations pourrait paraître mineur en regard des statistiques obtenues grâce aux échantillons. En fait, ces renseignements peuvent être directement utiles pour au moins trois étapes d une classification supervisée. Tout d abord, la Ch 2 24
43 La classification découpe automatique de la donnée en surfaces génériques permet de simplifier le premier contact visuel avec celle-ci et de faciliter ainsi le choix des classes et leur localisation. Dans un deuxième temps, elle permet d éliminer, dans les parcelles sélectionnées, certains pixels mal choisis. Finalement, en cours de traitement, le nombre de classes à tester peut être réduit grâce à l élimination directe de certaines d entre elles pour non-conformité au modèle de rétrodiffusion du pixel. Les méthodes effectuent une pré-classification de l image en mécanismes de rétrodiffusion simples dont les caractéristiques statistiques sont déterminées en absolu par la modélisation physique. Ici, on peut parler de classification puisque à chaque région de l image ainsi découpée correspond un type répertorié de rétrodiffusion : réflexion de Bragg (surfaces d eau et sols nus), réflexion dièdre pour les classes formées d objets anguleux (villes...), diffusion de volume (forêts...) [Sery 97 ]. Nous proposons des classifications maximum de vraisemblance notée MV utilisant le modèle gaussien classique et dans lesquelles nous introduisons des canaux d hétérogénéité locale, la classification supervisée, pouvant être dirigée par les résultats d une première classification de 1 ier niveau (I), non supervisée. Classifieur hiérarchique de Pierce et al. Pierce et al. (94) ont proposé une méthode de classification de type hiérarchique fonctionnant par seuillages successifs, les canaux sur lesquels sont effectués les seuillages sont choisis en fonction du mécanisme de rétrodiffusion de chaque classe. Le premier niveau décide si le pixel est un élément d une zone urbaine, d une zone de végétation haute, d une zone de végétation basse ou d une surface nue (rugueuse avec éventuellement de la végétation de hauteur inférieure à 15cm). Si le pixel est déterminé comme appartenant à une surface nue, une étude de la texture locale permet de distinguer si c est une surface d eau ou un sol nu. Si c est un sol nu, des algorithmes d inversion déterminent l humidité et la rugosité de ce sol. Un deuxième niveau de classification est prévu pour affiner les classes «végétation haute» et «végétation basse». Si la classe «végétation haute» est constituée de forêts, le deuxième niveau déterminera le type d arbres la constituant : «excurrent» (arbres ayant des branches épaisses dans leur couronne, ex : chêne), «decurrent» (arbre dont le tronc se rétrécit de bas en haut, et dont la couronne est formée de branches fines, ex : pins) ou «columnar» (arbres n ayant aucune branche, ex : palmiers). Le niveau 3 réalisera l extraction de paramètres biophysique tels que la biomasse ou la densité d arbres. Ce système expert est destiné à être utilisé sur les données SIR-C et n utilise que les bandes L et C. Certaines règles utilisent la texture d un canal, cette texture est caractérisée par le coefficient de variation de la scène sous-jacente (hétérogénéité) et se déduit du coefficient de variation local des intensités et du nombre équivalent de vues des images. Le niveau 1 du classifieur base ses critères de décision sur des propriétés physiques connues des quatre grandes classes. Ceci en fait un système automatique dans la mesure où il est appliqué sur des données bien étalonnées. Ces critères de décision se traduisent par des seuillages ou des partages de plans par des droites ou des zones rectangulaires. La simplicité des principes physiques à la base de ce classifieur permet de contrôler chacune des règles et d éventuellement les modifier si le besoin s en fait sentir. Des modifications du classifieur de Pierce et al (94) s imposaient. Les seuils nécessaires à ce système expert sont actuellement déterminés en visualisant les nuages de points des différentes classes, si bien que ce n est pas une méthode automatique. L étalonnage des données SIR-C est toutefois suffisamment précis pour que les seuils ne nécessitent que de légères modifications d une image à l autre. Bergen et al. (96) présentent une étude de classification multitemporelle (zones de forêts de pins dans le Michigan, pas de classes d urbain) à partir de données SIR-C acquises à deux dates. Les seuils obtenus pour les classifieurs de niveaux 1 sont identiques aux deux dates (σ est exprimé en db) : Ch 2 25
44 La classification Si (σ Lhv >(-0.91σ Lhh -25.0)) alors forêt Sinon, Si (σ Chv >-20.0) alors végétation basse Sinon, Si (σ Chv <-20.0 et σ Lhv <-20.0) alors surface nue Sinon, végétation basse. Un niveau 2 de classification est appliqué aux classes de forêts. C est un classifieur bayésien avec hypothèse gaussienne sur les coefficients de retrodiffusion σ des 6 intensités. Grâce à ce deuxième niveau, 3 classes de forêts (conifères de basse altitude, conifères de haute altitude et décidus) peuvent être distinguées avec des taux de classification de 95 ou 75% selon les dates. - la classe «urbain» regroupe des pixels des classes «urbain I», «urbain II», «marais» et «sable sec», - la classe «forêt jeune» est essentiellement constituée des peuplements d âge inférieur ou égal à 2 ans et d une partie des peuplements de 3 ans, - la classe «forêt ancienne ou dense», mis à part les peuplements d âge supérieur ou égal à 3ans, contient les parties les moins urbanisées de la classe «urbain I», - la classe «végétation basse» est la réunion des classes «culture I» et «sable humide», - la classe «sol nu» est constituée des classes «culture II», «piste aérodrome» et «chenal I», - la classe «surface d eau» rassemble les classes «étang» et «chenal II», - les classes de «route», «voie ferrée» et «parc à huîtres» se dispersent à l intérieur de plusieurs autres. Figure 2.7 : résultat de la classification hiérarchique de type Pierce et al. : en jaune la classe «urbain», en vert clair «forêt jeune», en vert foncé «forêt ancienne», en rouge «végétation basse», en blanc «sol nu» et en bleu «surface d eau». Cette méthode, basée sur des principes physiques simples donc robustes, donne un moyen rapide et sûr d obtenir une cartographie de niveau 1 à partir de données polarimétriques SIR-C. L étalonnage des données SIR-C semble même de qualité suffisante pour que les seuils ou coefficients utilisés n aient pas à être modifiés d une image à l autre. Cette quasi-automaticité et cette grande adaptabilité sont les atouts majeurs de cette technique. Appliquer un niveau 2 de type bayésien fait de la méthode complète une méthode rapide car le nombre de classes utilisé dans la procédure finale est réduit, mais l'amélioration en terme d erreur de classification est faible. Les classes discriminables par simple seuillage de canaux ne sont généralement pas celles qui posent problème lors d une classification maximum de vraisemblance. Mis à part les classes d urbain pour lesquelles la texture locale a été utilisée (canal non pris en compte dans une classification bayésienne simple), le résultat de la classification complète après application d un niveau 2 bayésien est semblable au Ch 2 26
45 La classification résultat d une classification MV simple (figure 2.7) Méthodes locales ou contextuelles Les caractéristiques d un pixel dépendent de l ensemble des pixels de l image ou tout au moins d un voisinage de celui ci. Les méthodes de classification contextuelles utilisent le contexte spatial du pixel (parfois temporel) dans leurs critères de décision. Ce principe implique alors la définition de probabilités des configurations de classification sur un voisinage. La qualité des résultats dépend de la taille du voisinage utilisé, qui varie suivant le type de capteur. La connaissance préalable des contours des objets de l image, obtenus grâce à la segmentation, ouvre une voie intéressante aux méthodes contextuelles qui consistent alors à tenir compte des pixels du segment contenant le pixel étudié à la place du voisinage. Car, ainsi la distribution est calculée sur une région homogène déterminée par la segmentation ; en effet, sur un voisinage, le point central peut être à la frontière de deux parcelles contenues dans le voisinage, les statistiques sont alors faussées Loi de Gauss-Wischart réelle Les meilleurs résultats obtenus en classification supervisée avec les images RSO, sont avec la distribution de Gauss-Wishart réelle [Fukunaga 72] sur un voisinage de 5*5 à 9*9, ou avec les régions de la segmentation, distribution jointe des moyennes et matrices de covariance empiriques d une série de données gaussiennes multidimensionnelles. Au chapitre 3 nous verrons que le voisinage pour les images brutes doit être 7*7, pour les images filtrées 5*5. Cette distribution a été choisie car elle permet d estimer directement p(m i, C i M vois, C vois, N vois ), pour chaque classe i, avec M i et C i, respectivement le vecteur moyen et la matrice de covariance de la classe i, M vois, C vois et N vois, le vecteur moyen empirique, la matrice de covariance empirique et le nombre de points du voisinage ou du segment utilisé. Soit Y une variable aléatoire gaussienne de dimension m, de vecteur moyen M et de matrice de covariance C. Si M e et C e sont respectivement le vecteur moyen et la matrice de covariance empiriques d un certain nombre N 0 de réalisations de Y, la distribution Gauss-Wishart réelle a posteriori conjointe de M et C, conditionnellement à M e, C e et N 0, définie comme suit : 1 P M, e e, 0 N C 0 0 e e 2 n / ( ) (2 ) 1/ t 1 C M,C N = π exp N (M M ) C (M M ) * ( N0 1) / ( N0 m 2) / 2 ( n, N 0 ) N 0Ce C c exp Tr( N CeC ) 2 2 nn ( 1) / 4 n avec cnn (, 0 ) = 1/ π Γ[( N0 i)/ 2] i= 1 Les classifications basées sur la méthode de Gauss-Wishart obtiennent, sur les images radar RSO brutes, des taux de pixels bien classés (voir chapitre 3) de l ordre de 70%, les résultats sont comparables à ceux obtenus par des images optiques, les structures sont mieux conservées. Le filtrage aussi performant soit-il, perd toujours en contour et en netteté. Toutefois l effet pointilliste n a pas totalement disparu. En introduisant la segmentation à la place des fenêtres glissantes pour les voisinages, les résultats sont légèrement améliorés, l image obtenue est visuellement meilleure et le temps de calcul est divisé par un facteur supérieur à 10. Ch 2 27
46 La classification Système de Pearson Dans le cas des images dont les distributions ont une forme non symétrique dépendant du type de l image ou de la texture analysée, afin de s affranchir du problème du choix d une distribution paramétrique, les densités f m,k (m étant le canal considéré et k la classe) sont modélisées dans un ensemble de distributions de formes variées appelé système de distributions de Pearson. Les méthodes d estimations des paramètres modélisant les distributions associées à ce système permettent d affecter à chacune des images spectrales ou texturales, une distribution paramétrique de forme spécifique. Pour k fixé, les distributions f m,k peuvent être de types différents, ce qui est le cas pour une scène imagée par deux procédés différents tels que le radar et l optique. Nous avons déjà vus que les distributions obtenues dans chacune des deux images sont différentes. La scène imagée par un capteur optique, admet, relativement à ses régions homogènes, des distributions gaussiennes. La même scène imagée par un radar possède des distributions non symétriques décrites par le système de Pearson [Marzouki A. 96]. Les distributions du système de Pearson sont solution de l équation différentielle suivante : df ( x) ( x + a) = f ( x) 2 dx c0 + c1x + c2x 2 Soient a 1 et a 2 les racines réelles ou complexes de l équation c0 + c1x + c 2x = 0 ( x+ a) a + a2 En posant p = q = c2( a2 a1) c2( a2 a1) forme : df ( x) dx Ch 2 28 = p x a l équation différentielle s écrit alors sous la q + x a 2 2 f ( x) La résolution de cette équation permet de distinguer huit distributions unimodales différentes réparties en trois grandes familles : Famille bêta de première espèce Si a 1 et a 2 sont toutes les deux réelles et si le produit (a 1 - µ 1 )(a 2 - µ 2 ) est négatif (µ i moment d ordre 1), la distribution correspondante du système de Pearson est la distribution bêta de première espèce définie par : Avec p> -1, q>-1, a1< µ 1 <a2 p q ( x a1) ( a2 x) f ( x) = p+ q+ 1 ( a2 a1) B( p+ 1, q+ 1) f ( x) = 0 si x sinon ] a1, a2[ La fonction bêta à deux variables p et q peut être donnée par B p q x p q (, ) = 1 1 ( 1 x) dx Famille bêta de seconde espèce Si les racines a 1 et a 2 sont toutes les deux réelles et si le produit (a 1 - µ 1 )(a 2 - µ 2 ) est positif, la 1 0
47 La classification distribution correspondante du système de Pearson est la distribution bêta de seconde espèce définie par : p q ( x a1) ( x a2) f ( x) = p+ q+ 1 ( a2 a1) B( q + 1, p q 1) f(x)= 0 sinon si q > 1 et a1< a2 < µ 1 et par : p q ( a1 x) ( a2 x) f ( x) = p+ q+ 1 ( a2 a1) B( p+ 1, p q 1) f ( x) = 0 si p > 1 et µ 1< a1< a2 [ a2, [ si x + si x sinon [, a1[ Famille bêta de type 4 Dans ce cas, les paramètres a1, a2, p et q sont complexes. Soient z r =Re(z) (respectivement z i = im(z)) la partie réelle (respectivement imaginaire) d un nombre complexe z quelconque. La solution de l équation différentielle est alors de la forme : pr ( pr ) B( p, q)( x ax r ar ai ) e f ( x) = pr+ 1 2Π( 2ai) parctg x a r 2 i ai Nous avons vu que le système de Pearson permet de définir huit distributions unimodales différentes caractérisées par deux paramètres exprimant la forme de la courbe : Le coefficient d asymétrie (skewness) de la distribution est donné par : Le coefficient d aplatissement (kurtosis) de la distribution est : Ch 2 29 $ β 2 $ 4 = m ( m2 $ ) 2 m2, m3 et m4 désignant respectivement les moments centrés d ordre 2, 3 et 4. Un moment centré d ordre r peut être approché en utilisant l estimateur : n 1 m$ r = ( xi µ) n i= 1 r ˆ ( mˆ 3) β 1= ( mˆ 2) Avec : n = Nombre d échantillons de la classe µ = Moyenne de la classe Rappelons que les distributions du système de Pearson sont solution de l équation différentielle : df ( x) ( x+ a) = dx c0+ c1x + c2x Les coefficients c 0, c 1, c 2 et a sont ainsi définis : cˆ 0 ) m2(4 ˆ β 2 3 ˆ β 1) = 10 ˆ β 2 12 ˆ β 1 18 c$ 1 2 f ( x) $ β $ ( $ 1m2 β 2+ 3) 2 ˆ β 2 3 ˆ β1 6 = c ˆ2 = 10 $ β $ 2 12β ˆ 2 12 ˆ a$ c$ β β1 18 où m$, m$ etm$ sont respectivement les moments centrés d ordre 2, 3 et = 1 2 3
48 La classification Ainsi, pour un échantillon donné, la sélection de la loi paramétrique parmi les distributions du système de Pearson est donnée par le couple ( $ β, $. Les estimateurs $ 1 β2 ) c$, $, $ 0 c1 c2 eta permettent de déduire des estimateurs de a1, a 2, p et q qui modélisent les principales distributions du système de Pearson Le choix de la loi est délicat. En effet, une loi sera plus au moins efficace suivant le type de données sur lequel elle est appliquée. Elle est donc choisie après avoir analysé la distribution des valeurs des pixels sur le canal traité (étude d'histogramme) et mis en œuvre une série de tests comparatifs. En pratique bien que le système de Pearson ajuste au mieux les images RSO ou texturale, les résultats obtenus sont inférieurs à ceux obtenus avec la distribution de Gauss-Wishart, (ou des lois gaussiennes multidimensionnelles), qui a l avantage d avoir une matrice de covariance qui introduit les relations inter-canaux Méthodes contextuelles spécifiques - cas particulier des images complexes et polarimètriques Des distributions différentes sont proposées pour les matrices de covariances mesurées, selon que la zone, à laquelle appartiennent ces matrices de covariance, est homogène ou hétérogène. Lorsque qu une surface est homogène, la distribution utilisée est la distribution de Wishart complexe, de paramètre de forme L, le nombre de vues, qui représente la distribution de la matrice de covariance d un vecteur gaussien complexe circulaire. Le classifieur bayésien proposé par Lee & Grunes (94) utilise le modèle Wishart (C i, L 0 ), i=1..n ω (N ω, nombre de classes). Chaque classe est caractérisée par sa matrice de covariance moyenne C i et le paramètre de forme L 0 qui est donc le même sauf, si les classes sont à des angles d incidence très différents et les données de type aéroportées avec projection des coordonnées au sol (le nombre d échantillons indépendants par pixel est alors variable). C est une généralisation au cas multidimensionnel du classifieur monocanal multivues de Frost & Yurowski (85). Pour tous ces classifieurs, les classes étant supposées représenter des surfaces homogènes de l image, la seule caractéristique discriminante est la matrice de covariance des classes. Concrètement, les règles de décision ne sont fonctions que des valeurs locales et moyennes des caractéristiques de rétrodiffusion des classes. Classifieur MV dans le cas 1 vue La distribution du vecteur des amplitudes complexes Z = (HH, HV, VV) t à l intérieur d une même zone homogène est une distribution gaussienne complexe multi-variables. Si C i, i=1...n ω, sont les matrices de covariance complexes des N ω classes, représentant des surfaces homogènes, la densité de probabilité conditionnelle d un vecteur Z par rapport à la classe ω i s écrit : 1 P( Z / ω i) = n π C i e Z C t *. 1 i. Cette distribution a été utilisée pour définir le classifieur de Bayes optimal [Kong 1987] (il minimise l erreur de classification), les fonctions discriminantes D i étant définies par : D ( Z) ln P( Z/ ) P( ) ln P( ) Z t* 1 = ω ω = ω.c.z lnc i i i i i Z i Ch 2 30
49 La classification Classifieurs MV dans le cas L vues utilisant la loi de Wishart complexe de paramètres Ci et L0 (Wishart(Ci,L0)) Pour une image L 0 vues et avec les mêmes conditions d homogénéité, les matrices de covariance empirique Σ Z sont distribuées selon la distribution Wishart (C zh,l 0 ). Cette distribution a été utilisée dans le critère de Bayes [Lee & Grunes 94]. Les fonctions discriminantes sont, pour la classe i : 1 [ i iσ ] D ( Σ ) = ln P( ω ) L0 ln C + Tr( C ) i Z i Z Ces classifieurs prennent en compte les propriétés radiométriques moyennes des classes ainsi que des caractéristiques temporelles ou polarimétriques (degré de cohérence). Cependant ils ne tiennent pas compte de la texture (hétérogénéité). Pour les résultats ce ces deux classifieurs voir les ouvrages cités [Lopes & Sery 96, Sery F. 97] Loi de Gauss complexe La distribution du vecteur des amplitudes complexes Z à l'intérieur d'une zone homogène est une distribution gaussienne complexe multi-variable. Si C i, i = 1 N, sont les matrices de covariance complexe des N classes, la densité de probabilité conditionnelle d'un vecteur Z par rapport à la classe i s'écrit : p( Z / i) 1 π n* 1 Z t* * Z = * e i C i Cette distribution a été utilisée pour définir le classifieur de Bayes optimal, les fonctions discriminantes D i étant définies par : D i (Z) = ln P(Z/i)P(i) = ln P(i) Z t*. C -1 i. Z ln Ci Les résultats obtenus avec cette loi, sont meilleurs qu avec une image non filtrées en intensité ou en amplitude, car ils sont beaucoup moins influencés par le speckle. Sans traitement particulier, c est à dire avec l application de cette loi seule, ils se rapprochent des images classées obtenues avec les images SPOT. Dans la figure 2.8, on peut voir que l effet du speckle est très réduit, il n y a plus l effet de pointillisme, la classification sans introduction de contraintes ou d image dérivée, est déjà très correcte, en comparaison avec l image en amplitude non filtrées obtenue (voir également chapitre 3 application région de Bourges), toutefois les classes Blé et Orge sont très confondues, ce qui est courant, ces deux cultures étant très proches. C Ch 2 31
50 La classification Figure 2.8 : en haut à gauche image classée à partir des données brutes ERS-1 multitemporelle (6 dates), en haut à droite même image classée, mais filtrée, en bas l image classée avec les même données mais complexes Ch 2 32
51 La classification EM (estimation-maximisation) des probabilités a priori des classes L algorithme Estimation-Maximisation (expectation-maximisation) (EM) [Marzouki 96, Sery 97] consiste à maximiser par rapport aux paramètres θ du modèle, la fonction de vraisemblance de l observation y, puis de ré-estimer les paramètres θ à partir de la classification ainsi obtenue. Ces deux étapes sont itérées jusqu'à convergence de la vraisemblance vers un maximum. A l étape courante, l algorithme EM consiste d abord à calculer les lois de X s conditionnelles à Y à l aide des paramètres obtenus à l itération précédente, puis à estimer les paramètres du processus de mesure et ceux du champ de classes par la méthode du maximum de vraisemblance. Une fois ces paramètres estimés, on retourne au calcul des lois de X s conditionnelles à l observation y. L algorithme EM est généralement utilisé de façon non supervisée. Nous avons implanté une version semi-supervisée, avec introduction d échantillons, mais principe itératif. Une approximation itérative des estimateurs MV des paramètres est effectuée. Cette méthode est déterministe et fournit un ensemble de paramètres déterminant le modèle noté θ comprenant une estimation des probabilités a priori de chaque classe. A partir d une valeur initiale θ 0, une suite θq est obtenue dont la fonction de vraisemblance est croissante et converge vers un maximum local. L estimation des poids et les paramètres statistiques des distributions de chacune des classes sont corrigés de manière récurrente, les paramètres sont affinés et les poids obtenus peuvent être utilisés comme probabilités a priori des classes à l itération suivante. Donc la classification des pixels du voisinage ou du segment est faite sur la base des paramètres calculés à l itération précédente. La méthode EM donne de bons résultats si l initialisation du processus n est pas très éloignée du maximum absolu de la vraisemblance, le risque principal étant la convergence vers un maximum local très différent du maximum absolu, en semi supervisée nous sommes proche de la solution. L initialisation influence également la rapidité de la convergence. Dans les images RSO, l estimation des statistiques à partir des échantillons n est pas toujours correcte. Il est souvent difficile d avoir des échantillons parfaitement représentatifs des classes. L utilisation de pixels dont la classe d appartenance est inconnue a été proposée pour stabiliser les statistiques de chaque classe (Shashahani & Landgrebe 94). P pixels d appartenances inconnues sont ajoutés à l ensemble S des pixels des échantillons de toutes les classes. Ce principe a tendance à favoriser les classes ayant le moins de points d échantillons. Les classes après chaque modification ne correspondent plus forcément à celles prédéfinies, et celles pour lesquelles on ne dispose que de peu de pixels d apprentissage vont ainsi voir leurs statistiques évoluer de manière importante. Il est à noter que ce schéma n est observé que lorsque le voisinage n est pas dominé par l une des classes prédéfinies. La solution consiste à ne faire que très peu d itérations. Dans la version non supervisée qui est d ailleurs la version initiale de cet algorithme, la modification qui introduit l étape stochastique précédente a pour avantage l élimination de classes peu ou pas probables (quelques pixels) d après le processus d estimation, ce qui la rend complètement non supervisée. Cet algorithme est la version stochastique du EM connue sous le nom de SEM (Stochastic Expectation Maximisation), il permet d éviter les maxima locaux de la vraisemblance. Entre l étape d estimation et celle de maximisation, l algorithme simule une réalisation de X suivant la loi de X conditionnelle à l image observée y. Les résultats obtenus sont très satisfaisants, et comparable à ceux de la classification ICM présentée plus bas. Ch 2 33
52 La classification Méthodes globales Les méthodes globales ont été introduites par Geman & Geman (84), pour les images bruitées additivement. Plus tard elles ont été appliquées à l'imagerie radar par M. Siegelle, X. Descombes et Hegarat-Mascle, mais également à d autres types d images [Kato & Zerubia & Berthod 92,99]. La caractéristique la plus importante de ces méthodes réside dans leur aspect global qui conduit à l'utilisation de champs markoviens. En effet l'imagerie radar est très complexe, et l'outil markovien y joue un rôle très important en montrant sa capacité à imposer la continuité car il s'agit de donner un sens à l'expression de la probabilité a priori d'une classe. Ce terme peut dépendre d'une paramétrisation simple et efficace grâce aux champs markoviens Champs aléatoires de Markov En traitement d'images l idée fondamentale des champs de Markov (CAM) [Coquerez 95, Pony et al 00] est d introduire des relations contextuelles sur un voisinage local. Grâce aux CAM les pixels ne sont plus considérés indépendamment mais dans leur globalité ; la modélisation du mécanisme de formation des régions de l image par un processus markovien permet de restreindre cette dépendance aux pixels voisins : en agissant localement sur les pixels de l image on agira sur la probabilité de l image entière. L'intérêt des champs de Markov est leur grande souplesse pour introduire plusieurs sortes de contraintes (contexte spatial, temporelle, etc). L ajout de ces contraintes dans le calcul de la probabilité a priori de la classe va permettre, à chaque itération, de pouvoir améliorer le résultat de la classification. De plus, les champs aléatoires de Markov sont un cadre méthodologique qui permet à des images prises par différents capteurs, à différentes dates, etc., d être traitées de manière conjointe. En effet une propriété puissante des CAM est que l information a priori et les données observées dans différentes dates ou différents capteurs peuvent être combinées facilement à partir de fonctions d énergie. } Soit une image { x s définie sur un réseau fini (ou treillis) S de sites s : valeur dans E. { s= ( i j) ;1 i j M} S=,, à E est l ensemble des «configurations» possibles des classes sur l image du champ de vecteurs. Un champ aléatoire X, défini sur un ensemble de sites S, est Markovien si la probabilité d'observer une valeur en un site s ne dépend que d'un nombre fini de sites voisins V s. L'ensemble des voisins est donné par un système de voisinage noté V. Considérons une famille arbitraire V de «voisinages locaux» de S : V { V () s s S} =, où s S, s V( s) A cette famille est associée une classe de distribution de probabilités, appelée champ de Markov et caractérisée par la propriété suivante : p ( ) > 0, pour toute configuration x s : p ( x x r S {} s ) = p( x x, r V ( s) { s} s r s r x s, ) probabilité d un pixel x s conditionnelle à tous les autres est égale à la probabilité de x s conditionnelle connaissant les pixels de son voisinage local V(s). La valeur des autres sites r est supposée connue, r S-{s}. Ch 2 34
53 La classification Champ de Markov et distribution de Gibbs A un système de voisinage donné correspond un ensemble de cliques, une clique étant un ensemble de points du treillis mutuellement voisins, l ordre d une clique étant le nombre de sites qui la compose (on s intéresse en général aux cliques d ordre 2). Soient respectivement, V s le voisinage d un pixel composé de ses plus proches voisins, C l ensemble des cliques et c une clique correspondant au voisinage choisi. Deux pixels appartiennent à une clique s ils sont mutuellement voisins ou s ils sont isolés. Cliques associées v h d1 d2 Ordre 1 Ordre 2 Ordre 3 Ordre 4 On appelle alors «énergie» toute fonction U(x) que l on peut décomposer sur l ensemble des cliques de l image, exprimée sous forme d une somme de potentiels associés à ces cliques : Ux ( ) = V( x) c C c où x appartient à l ensemble E des configurations, précédemment définie V c ( x) est une fonction «potentielle» permettant d exprimer les contraintes spatiales ou temporelles de l image. V c ( x) peut être, a priori, tout à fait quelconque, mais ne doit dépendre que d éléments x s appartenant à la clique c. En général, les champs sont stationnaires, c est à dire indépendant de la position du site s, et la fonction potentielle la clique. V c ( x) est une fonction indépendante de la position de Le théorème de Hammersley-Clifford [Besag 74, Guyon 92] permet de caractériser les CAM en termes globaux à partir de l expression de la probabilité a priori d une configuration des classes p ( X = x). Il permet d'établir une correspondance entre un champ de Markov et un champ de Gibbs lorsqu aucune réalisation de X n'est de probabilité nulle. Il montre qu un champ aléatoire défini sur un réseau est un champ de Markov si et seulement si sa distribution de probabilité a priori p(x) est une distribution de Gibbs, définie par : p U ( x) ( x) e = 1 (1) Z où Z est une constante de normalisation sur l ensemble des réalisations de Ω de cette fonction d énergie, elle est appelée fonction de partition et assure que l équation (1) définit une mesure de probabilité. La constante Z peut être exprimée par : Z = U e toutes _ configurations ( x) Cette fonction est calculée sur toutes les configurations x possibles, des contraintes associées aux fonctions potentielles de U ( x). La probabilité d une configuration dépend donc d un ensemble d interactions locales (au niveau des cliques). Plus l énergie totale U(x) est grande, moins la configuration est probable. Ch 2 35
54 La classification Suivant la définition de ces fonctions potentielles, c est à dire en fonction des contraintes considérées, plusieurs modèles existent. Nous avons implanté le «modèle de Potts» [Geman & Geman, 1984, Descombes 96]. Les potentiels associés à la fonction d énergie, ont les valeurs suivantes : Clique d ordre 2 : ( x) = β où le paramètre β est positif. V c si les pixels de la clique ont des valeurs différentes x s x r V c ( x) = β si les pixels de la clique ont la même valeur de la classe x s = x r L énergie sera faible si les étiquettes des pixels voisins (les 4 ou 8 voisins) tendent à avoir des étiquettes identiques, sinon plus les étiquettes voisines sont différentes plus l énergie sera élévée. p(x) est une fonction décroissante de sa fonction énergie : elle est élevée pour une image x dont les étiquettes voisines tendent à se ressembler (énergie petite). Les points isolés ont tendance à disparaître, mais également les lignes. Si l on cherche à préserver les lignes alors on peut utiliser le «chien-modèle» (Descombes 1995) qui considère des cliques plus complexes (donc des fonctions potentielles plus complexes) et toutes les configurations possibles. Il permet de contrôler la longueur des contours et des lignes dans l'image. Ainsi les structures fines sont préservées. Nous avons implanté un modèle différent du chien-modèle, il utilise la segmentation (carte de contours) pour la préservation des contours. Critères d estimation dans les champs aléatoires de Markov Il existe plusieurs critères d estimation des variables d intérêt, x, celui qui est appliqué dans la méthode développée est l estimateur MAP, maximisation de la probabilité a posteriori, pour que la meilleure estimation soit la plus probable étant donné la réalisation y et qui revient à minimiser l énergie U x. ( ) D autres critères tels que MPM (Maximum a Posteriori Marginal) ou les champs moyens de Markov diffèrent par la fonction de coût associé à ces critères. Chacun de ces critères d estimation a son algorithme de relaxation et de recherche de la solution associée. Dans le cas du MAP il existe plusieurs méthodes de recherche de sa solution, des algorithmes déterministes, comme méthode ICM, et des algorithmes stochastiques comme le recuit simulé. Les modèles de relaxation stochastiques ont de meilleures performances que les modèles déterministes pour l'optimisation de fonctions présentant de multiples extrema locaux. Avec les méthodes déterministes, on obtient des solutions optimales locales par rapport à des méthodes stochastiques qui obtiennent des solutions optimales globales. Cependant les méthodes déterministes s'avèrent être plus intéressantes en raison de la vitesse de convergence vers la solution ce qui les rend plus rapide que les méthodes stochastiques. Si les problèmes d initialisation de la méthode sont bien gérés, cette méthode donne de très bons résultats. Nous avons implantés les deux méthodes, nous ne nous étendrons pas trop sur le recuit simulé, car le but de mes recherches est de traiter des images de grandes tailles et cela n est pas raisonnable d utiliser le recuit. Toutefois nous le présentons, car une des innovations dans ces méthodes, porte sur une méthode de type ICM avec l introduction de la température comme dans le recuit, et de plus, celui-ci bénéficie des modifications apportées à cette méthode. Ch 2 36
55 La classification Méthodes stochastiques : implantation d un recuit simulé Le recuit simulé (simulated annealing) proposé par Kirkpatrick (83) est une métaheuristique 1 inspirée d'un processus utilisé en thermodynamique. Ce processus alterne des cycles de refroidissement lent et de réchauffage (recuit) qui tendent à minimiser l'énergie du matériau, dans notre cas, cela correspond à obtenir les extrema de la fonction d énergie. Le circuit simulé permet de sortir d un minimum local en acceptant avec une certaine probabilité une augmentation de la fonction. C est un algorithme de relaxation stochastique, qui recherche des configurations les plus probables dans l image des classes. Au départ le recuit simulé s'appuie sur l'algorithme de Metropolis (53) pour modéliser l'évolution d'un système thermodynamique. Par analogie avec le processus physique, la fonction à minimiser est devenue l'énergie E du système. On introduit également un paramètre fictif, la température T du système. En général, en traitement d image on utilise l échantillonneur de Gibbs proposé par Geman & Geman (84). Nous sommes amenés à minimiser l énergie, mais la fonction d'énergie présente en général un grand nombre de minima locaux, ce qui complique la tâche de trouver un minimum global. Si, pour un état initial donné, l'algorithme arrive après quelques itérations à un minimum local, et que l on ne peut plus diminuer l'énergie, l'algorithme se trouve alors piégé. L'idée de l'algorithme du recuit simulé est de donner la possibilité de sortir des minima locaux en autorisant l'algorithme à prendre des configurations éloignées de la solution avec une faible probabilité. Le recuit simulé génère un champ de Markov qui converge vers le minimum global. Le paramètre de température T est introduit au départ assez élevé, afin de franchir les minima locaux, puis il est régulièrement diminué, lentement de telle sorte que les transitions avec remontées d énergie soient de moins en moins présentes jusqu à stabilisation des résultats. La température initiale ne doit pas être trop élevée, sinon le temps de convergence est prohibitif. Nous avons besoin d'un échantillonneur, pour cela nous introduisons la distribution de Gibbs avec paramètre de température T, simulateur de Gibbs combiné à une décroissance de température, défini en (2). L expression (1) devient : P(x)= 1 Z T U( x) exp( ) (2) T où Z T, la constante normalisatrice, dépend de la température T qui gouverne les modes de la distribution P(x). Pour une température très élevée, les configurations sont pratiquement équiprobables, c'est-à-dire un grand nombre de configurations sont accessibles. Tandis qu une basse température augmente la probabilité des configurations d énergie minimale, les états à haute énergie deviennent peu probables par rapport à ceux de faible énergie. Le paramètre T contrôle les déplacements vers les points voisins les moins bons, pour échapper aux optima locaux, sans pour autant trop s'écarter du chemin vers le vrai minimum. L échantillonneur de Gibbs traite des images comme étant des champs de Markov et la probabilité conditionnelle locale d'un pixel ne dépend alors uniquement de la configuration du voisinage. La convergence de l'algorithme a été démontrée par Winkler (1995). Dans nos applications, nous 1 Les métaheuristiques sont généralement des algorithmes stochastiques, qui progressent vers un optimum par échantillonnage d'une fonction. Ch 2 37
56 La classification considérerons que l'on a convergé lorsque les changements sont petits (de l ordre de 1%). En pratique, l algorithme consiste à visiter aléatoirement tous les pixels de l image et tirer au sort leurs étiquettes suivant leurs lois conditionnelles (locales) par rapport à l état des voisins. Le changement de l étiquette du site est accepté si la variation énergétique entre la configuration x s et x s-1, U = U(x s-1 ) - U(x s ) < 0 (c'est-à-dire baisse d'énergie du système), sinon, en tirant selon la probabilité p = exp (-U), le changement peut être accepté ; s il est rejeté, on essaie une autre configuration. Les transformations qui accroissent l énergie sont acceptées, même si elles dégradent momentanément la solution, pour permettre de sortir d un minimum local. Plus la température est élevée, plus de configurations sont acceptées, puis avec sa décroissance, moins celles qui augmentent l énergie sont retenues. Au bout d un nombre infini d itérations, la convergence est assurée proche de la solution optimum, mais toutefois sans garantir le résultat. L image obtenue a été tirée au sort suivant la loi P(x). Il faut plus de 100 itérations pour le type d image qui nous concerne. Pour les images RSO qui sont très complexes, ce nombre est beaucoup plus important Minimisation de l énergie postérieure par la méthode ICM (iterative conditionnal mode) Proposée par Besag (74), la méthode ICM (Iterative Conditional Mode) est une méthode de recherche déterministe qui est une alternative à l algorithme du recuit simulé. Cette méthode itérative approche la solution du MAP (Maximum A Posteriori) en affectant à chaque site s la classe qui maximise la probabilité conditionnelle (d où le nom de la méthode) à l observation en s (et non, comme dans le recuit simulé, en simulant selon cette même distribution une réalisation de X s ) et minimise donc la fonction d énergie. Une manière simple de voir cette méthode est la suivante : en développant la probabilité a p X = xy = y = p x x, r s, y p x, r s y posteriori par rapport à un pixel s, on obtient : ( ) ( ) ( ) On choisit comme nouvelle valeur en s celle qui maximise la probabilité conditionnelle p ( X = xy = y). Le calcul du maximum de la probabilité conditionnelle au fil des itérations permet d obtenir un maximum local de la distribution. Ce maximum peut s avérer suffisant dans le cas où la distribution a posteriori présente une certaine régularité, c est à dire quand le contraste entre les classes est fort, ce qui n est pas souvent le cas. La méthode ICM, a une convergence rapide vers la solution, avec une solution optimale locale. s r r La méthode développée de type ICM La méthode a été développée suivant les modes : dirigé, semi dirigé, non dirigé, multi-temporel et multi-source. Elle peut fonctionner avec plusieurs types d images (optique, radar, ) en utilisant des lois différentes pour chaque type d image avec des poids pour donner plus ou moins d importance aux différentes lois lors de leur fusion. Les modèles sont statistiques (maximum de vraisemblance), gaussien, de Pearson, gaussien complexe, ou géométriques (barycentrique). Le champ des classes est stationnaire et markovien sous contraintes de continuité spatiale, temporelle et de contour. L initialisation est réalisée par un maximum de vraisemblance contextuel (RSO) ou ponctuel (optique) avec possibilité de pondération par une gaussienne. La méthode de minimisation de Ch 2 38
57 La classification l'énergie est le recuit simulé ou la méthode ICM, au choix, mais nous privilégions cette dernière. Dans les cas de la classification supervisée, on dispose des échantillons obtenus à partir des véritésterrain, le nombre des classes est fixé par l expert. Dans le cas de la classification non supervisée, le majorant du nombre de classes est choisie par l utilisateur ou calculé automatiquement, les échantillons sont crées automatiquement (aléatoirement ou régulièrement), ou semiautomatiquement. Cette partie a particulièrement été étudiée car de cette initialisation dépend la convergence plus ou moins rapide et, surtout, correcte de la solution de la classification. Initialement l ICM est une simulation de Gibbs à température constante et nulle et avec choix de la classe déterministe. L originalité de la version implémentée, est la variabilité de la température comme dans le recuit simulé. Au fil des itérations, l influence de certains paramètres et en particulier les paramètres de contexte, de segmentation et temporel vont augmenter. Cet algorithme affine la classification en ré-estimant les statistiques des classes en fonction de l itération précédente et en accordant de plus en plus d importance à l information contextuelle par le biais, du paramètre de température T. Cet algorithme est parfaitement déterministe dans la mesure où il n y a aucun tirage aléatoire, les seuls paramètres qui influent sur le résultat final sont : le nombre d itérations, la température initiale, l ordre de décroissance, et la configuration initiale des classes. Un critère d arrêt simple consiste à compter le nombre de modifications d état lors d une itération et à s arrêter si ce nombre est suffisamment petit Lot Donnée 1 Donnée 2 Canal 1 Canal 2 Canal 3 Figure 2.9 : exemple de regroupement simplifié d images La méthode telle qu elle a été développée nécessite la définition de quelques termes : Canal : Un canal fait référence à l'image obtenue à une date donnée dans un canal spectral donné, d un capteur donné, il peut également être un canal de «synthèse» (dérivé). Date : Une date est une donnée comprenant un ou plusieurs canaux correspondant à des images prises à une date (ou plusieurs dates si elles ont un point commun temporel dans le stade phénologique des cultures par exemple). Donnée : Une donnée comprend une sélection de quelques images utiles à associer, par exemple les images d'une même date et/ou d'une même source (optique ou radar). Ch 2 39
58 La classification Lot : Un lot correspond à des dates ou à une manière de regrouper les dates et les données. En général, un lot contient une ou plusieurs données rassemblant chacune, les canaux d'une date précise. Plusieurs lots peuvent également être construits avec les données d'une seule date. Par exemple : une scène sera traitée avec trois lots de deux, trois, cinq jeux de données, le premier lot : jeux de données (1) est constitué d une image SPOT à 3 canaux, XS1, XS2, XS3, (2) d images ERS1, le deuxième lot de 3 jeux de données : (1) 2 images SPOT (2 dates proches) avec XS1, XS2, XS3, XS4, (2) une image radar ERS1, (3) une image radar ERS1 en complexe, le troisième lot constitué de 5 jeux de données d images SPOT à des dates différentes. Premier lot : le premier jeu de données est classé par une approximation gaussienne et le deuxième par le système de Pearson, le deuxième lot est classé par une approximation gaussienne, le système de Pearson, une approximation Gaussienne Complexe et ainsi de suite. La notion de lot et de donnée a été introduite pour pouvoir associer avec une grande souplesse toute combinaison offrant un intérêt thématique pour l expert. Un système de poids peut être donné pour favoriser les données de façon différente. Par exemple les images SPOT peuvent intervenir à 100% dans l estimation et l image radar à 80%, c est une des raisons de ce découpage en lots et données. La classification offre donc les possibilités suivantes : Choix du type de loi qui va nous permettre de calculer la probabilité : radar bruitée, radar filtrée, optique, etc., et selon que l on utilise un classement contextuel ou bien ponctuel. Génération de toutes les combinaisons possibles des données multispectrales, multitemporelles, multitexturales. Choix de la loi de distribution pour chaque canal Choix du coefficient de pondération des images rassemblées par dates, par lots Fusion des données Sont pris en compte : Le contexte spatial sur l image multi-dates Le contexte temporel, chaque date influe sur le classement de la date suivante La segmentation Les probabilités d appartenances des classes dans toutes les dates La singularité des matrices de covariance : des classes sont éliminées Masque qui permet de classer certaines parties de l image. Tous ces traitements peuvent être faits avec un voisinage déterminé par la segmentation ou par des fenêtres variables Algorithme général de la classification Choisir une configuration initiale, aussi proche que possible d une configuration optimale : classification initiale par maximum de vraisemblance. Balayer l ensemble des sites s de Ω, et en chaque site, calculer l ensemble des probabilités conditionnelles déduites de p T ( x), et sélectionner l état qui correspond à la probabilité maximale. On donne à x l étiquette qui minimise E. Poursuivre les balayages jusqu`à convergence ou pour un nombre déterminé d itérations ou jusqu à la réalisation d un critère d arrêt. Ch 2 40
59 La classification Version détaillée 1. Apprentissage 1.1. Echantillonnage Dans le cas de la classification supervisée, cette étape consiste seulement à récupérer les vérités terrains fournies par l'utilisateur pour obtenir un jeu d échantillons pour l'estimation des statistiques initiales et un autre pour la vérification. Pour la classification non supervisée, les échantillons sont créés automatiquement de différentes façons suivant l utilisation : - espacés régulièrement de taille variable en fonction des dimensions de l image, l'écart entre les échantillons de forme carrée est variable afin d éviter le chevauchement. - tirés aléatoirement. Dans le cas semi supervisé il y a introduction de vérités-terrain, ou d échantillons interprétés visuellement sur l image auquel s ajoute des échantillons créés automatiquement, espacés régulièrement ou aléatoirement. Le nombre de classes est adapté à la distribution dans ces deux cas. 1.2 Estimation initiale des statistiques Cette partie correspond à la détermination des vecteurs statistiques des différents attributs (canaux, ) Poser T = T 0, la température initiale. 2. Classification initiale Chaque pixel est classé dans chaque lot selon la règle du maximum de vraisemblance et une loi de distribution au choix (gaussienne, Gauss-Wishart, Pearson ou gaussienne complexe) ou barycentrique. Puis il est affecté à la classe dont la moyenne des probabilités sur tous les lots est la plus élevée. Cette classification initiale est effectuée de manière ponctuelle pour les images optiques, ou de manière contextuelle pour les images radar. Si un lot rassemble plusieurs jeux de données, la fusion de ces données est réalisée lors de la classification globale. 3. Itérations extérieures : cette étape est composée de quatre étapes Calcul de la matrice transition inter dates : calcul des contraintes temporelles (éventuellement) Balayer l ensemble des sites s de Ω, et en chaque site : - Calculer l ensemble des probabilités conditionnelles déduites de p T ( x). - Le type de règle de classification peut être différent selon les données : modèle barycentrique, gaussien pour les images optiques (Spot, Landsat...). système Pearson pour les images radars (ERS, JERS...), distribution gaussienne complexe (SLC). - Le classement est effectué dans une certaine proportion fixée par un poids qui permet d accorder plus ou moins d importance à une donnée. Les images par dates (ou lots) peuvent être classée en parallèle, ou séparément puis une Ch 2 41
60 La classification image multi-lots (ou multi-dates) est faite. 3.1 Itérations intérieures Ces itérations consistent à classer les lots de façon séquentielle (séparément), selon la règle du maximum de vraisemblance. Chacune de ces classifications tient compte du contexte (voisinage proche), des contours (contrainte spatiale à partir de la segmentation), des paramètres de transition, contraintes temporelles, forts diffuseurs et de la température. 3.2 Classification par lot Il s'agit des mêmes calculs que ceux effectués dans les itérations intérieures, mais les lots sont traités de façon parallèle (chaque pixel est classé dans chacun des lots). 3.3 Fusion des lots : classification globale Cette étape consiste à combiner pour chaque pixel les classes trouvées dans les lots (fusion), et d'en produire une image classée finale (voir chapitre 4, union des meilleures classes des lots). 3.4 Ré-estimation des statistiques Il s'agit des mêmes calculs que ceux effectués lors de l'estimation initiale des statistiques. 4. Faire décroître la température : T k+1 = Tk où k est le numéro de l itération. 5. Poursuivre les balayages pour un nombre déterminé d itération ou jusqu à la réalisation d un critère d arrêt. Le nombre de classe peut être imposé par l utilisateur ou être donné automatiquement, c'està-dire déterminé par une formule dépendant du nombre de la taille de l image. Des itérations extérieures, sans contrainte sont d abord exécutées seules. Les itérations intérieures avec contraintes sont ensuite effectuées à température constante, puis la température est diminuée avec la nouvelle itération extérieure ainsi de suite jusqu à la convergence vers la solution. Ce procédé raccourci les traitements et permet d introduire les contraintes plus proches de la solution Introduction des contraintes Le formalisme des Champs Aléatoires Markoviens permet d introduire, de manière souple, les contraintes du contexte spatial grâce à leur modélisation par des fonctions potentielles. Nous avons introduit d autres contraintes que celle du modèle de Pott : contraintes de contour, temporelle, de fort diffuseur qui minimisent l énergie postérieure dans la classification. Le logiciel donne la possibilité de moduler l importance que l on veut donner à l une ou l autre de ces contraintes, ce qui permet d utiliser, par exemple, des cartes de contours imparfaites. Les fonctions potentielles décrivant les contraintes contextuelles et temporelles Ces contraintes introduites dans la classification sont des fonctions potentielles associées à des fonctions d énergie. En sachant que la probabilité a posteriori d une classe en présence de plusieurs données ou images provenant de différents capteurs, supposés indépendants est exprimé par : Ch 2 42
61 La classification p ( X Y,.., Y ) p( Y X ) p( Y X ) p( X ) donnee _ 1 donnee _ n donnee _1.. donnee _ n La fonction d énergie globale associée à un site est la sommation de deux termes d énergie. Le premier terme est lié à la fonction d énergie conditionnelle d une classe associée au type de donnée (radar, optique) et donc à la loi d estimation (Gauss, Pearson, etc.) du modèle d observation. Le deuxième terme est le terme d énergie associée aux contraintes définies par les fonctions potentielles. Ainsi l énergie globale associée à un site de l image des classes peut s exprimer de la suivante manière : U = β d U donnee + U contra int e (2) toutes _ donnees toutes _ contra int es La minimisation du premier terme de l équation est équivalent à maximiser la probabilité a posteriori (MAP) la fonction de vraisemblance ou modèle d observation (équivalent a réécrire la loi d estimation en terme d énergie) pour un capteur : ( = y X x) U donnee p Y = β d est un facteur pondérateur des données dans un même lot. Il s utilise pour donner plus d importance aux données optiques par rapport aux données radar, par exemple. La minimisation du dernier terme d énergie est équivalent à maximiser la probabilité a priori d une classe modélisée de façon markovienne à partir des contraintes spatiales et temporelles associées à U p X x des fonctions potentielles : ( ) contra int e = Une étude autour des contraintes de contexte spatial et temporel a été effectuée afin de maximiser l efficacité de ces contraintes. Cette étude a d abord été réalisée pour la classification supervisée afin d éviter les effets transitionnels associés aux premières itérations de la méthode non supervisée (apprentissage automatique de qualité moindre que celui effectué à partir des vérités terrain). Deux contraintes spatiales sont introduites au travers de la fonction d énergie : une contrainte de régularisation (lissage) et une contrainte de contours. Les contraintes spatiales : continuité spatiale Pour la contrainte de régularisation, la classe la plus présente dans le voisinage du pixel est favorisée. Ainsi, la fonction potentielle suivante sur le voisinage (8-connexes) est introduite : U liss s' V ( s) ( ( x( s)) = β liss δ sp x( s), x( s') ) énergie de lissage ou de contexte δ(.,.) symbole de Kronecker 1si x( s) = x( s') 0 si x( s) x( s') elle s exprime : δ [ ] sp x( s), x( s') = βliss est un paramètre qui permet de moduler l importance que l on veut donner à la contrainte. L énergie diminue lorsque la fréquence d apparition de la classe augmente. Lorsque cette contrainte est la seule a être utilisée, son effet sur le résultat de la classification sera un lissage plus ou moins fort selon la valeur du paramètre de contexte associé ( β liss ). Ch 2 43
62 La classification Contrainte de contour : modèle de régions markovien sous contrainte d une carte de contours Le lissage va être contrôlé par les contours de la segmentation. Pour ne pas imposer les contours comme des barrières infranchissables, ou comme les contours de la classification résultante, ceux ci sont aussi modélisés par un processus markovien dit processus des lignes [Geman & Geman 84]. Pour saisir la notion de lignes, il faut se représenter une image dédoublée. Entre chaque ligne de l image est introduite une ligne de contours horizontaux. Entre chaque colonne, une colonne de contours verticaux (on ne considère pas les contours obliques). Ces contours, l g (i,j), prennent des valeurs binaires : 0 si les deux pixels qu il sépare appartiennent à la même région, 1 s'ils appartiennent à des régions différentes. Schistad et al (96), qui se basent sur une carte de contours fiable, vont imposer des contraintes pour que la classification résultante ait des contours s approchant le plus possible de ceux de la carte. Pour cela, ils utilisent deux processus de ligne : l un, L g = {l g (x s )}, celui de la carte des contours, est fixe durant tout le traitement. Le deuxième, L c = {l c (x s )}, celui de la classification, est amené à varier pendant le traitement : l c (x s ) = 0 si les deux pixels qu il sépare appartiennent à la même classe, 1 sinon. Les auteurs définissent alors une mesure de similarité entre ces deux processus: W l [ (x ), l (x )] c s g s 0 si lc (x s ) = 1si lc (x s ) La fonction d énergie s exprime par : U lg[ lc( xs ), lg(xs] = β g W [ lc(x' s), lg(x' s) ] On voit que l énergie d une classe diminue lorsque l affectation du pixel à cette classe crée des contours de classes différents de ceux de la segmentation. Le paramètre β g permet de moduler le poids que l on veut donner à cette contrainte. Méthode implantée ( δ( )) { x's } V Ucont ( x()) s = βcont 1 lc ('), s lm(') s énergie de contour s' V ( s) c La régularisation est contrôlée par les contours de la segmentation. La probabilité d une classe diminue lorsque l affectation du pixel à cette classe crée des contours de classes différents de ceux de la segmentation. Si la carte de contours est fiable, les contraintes permettront d obtenir une classification qui ait des contours s approchant le plus possible de ceux de la carte. Les deux potentiels suivants sont introduits : V cont et V cont-connexes V cont tient compte des couples de points adjacents dans le voisinage du pixel traité, V cont-connexes tient compte des 4-connexes autour du pixel traite, dans les deux cas s il existe une cohérence entre les étiquettes et les classes (elles sont identiques), les potentiels augmentent. Ces contrainte de contour sont contrôlées par un paramètre pondérateur, β cont. g ij = l g l (x g s (x ) s ) Ch 2 44
63 La classification Matrice de transition Les contraintes temporelles Plusieurs solutions ont été réalisées, testées et comparées les unes aux autres, afin de déterminer celles s'approchant le mieux possible de la réalité. L objectif est de retrouver le stade phénologique des cultures, c est à dire l état de la végétation suivant la date. Le voisinage n est plus spatial, mais il est composé des x s,t où t correspond aux valeurs des classes à chaque date. La classification multi-temporelle (Schistad et al 96) se fait date à date, le traitement de la date t+1 utilisant les résultats obtenus à la date t par le biais d une matrice de transition. Cette méthode présuppose que la classification initiale, à la date t 0, est suffisamment acceptable pour ne pas fausser l ensemble du traitement. Or ce n est pas le cas puisque l initialisation dans le cas non supervisé est aléatoire, ainsi la matrice de transition n est calculée qu après un certains nombres d itérations, afin d être plus prés de la solution. Dans la méthode développée (chapitre 4) cette contrainte est sous forme d une matrice de transition qui est calculé à partir de la classification obtenue de l itération précédente, le traitement de la date t+1 utilisée. Les résultats de la obtenus à la date t. Ce terme qui exprime le pourcentage de points ayant la classe dans l image finale à l itération précédente et ayant été classés dans la classe k image k lot _ precedent dans le lot n lot-1 et dans la classe k lot _ courant dans le lot n lot, à la date i qui ont été classé en j à la classification résultante. L utilisation d'une matrice de transition dans le cas multitemporel permet d'utiliser successivement les informations des dates précédentes. Cette contrainte temporelle est contrôlée par un paramètre pondérateur, β t. Contraintes associées à une fonction d énergie sur un voisinage temporel Cette fois le voisinage de points est constitué des valeurs de ce point à chaque date. Le maximum de vraisemblance est calculé à chaque date séparément, pour chaque classe. La valeur de l énergie potentielle V x,t correspond à la somme des probabilités par classe pour chaque date dans chaque lot. canal 1. x1 canal 2 canal 3.. x 4 canal 4. x 5 canal 5 Pour chaque lot, une probabilité ou un degré de confiance est associée à chaque classe pour un pixel donné. Lors de la classification globale (ou fusion des lots), pour chaque classe, la somme des probabilités des lots devient une fonction potentielle supplémentaire (voir chapitre 4). Récapitulatif des contraintes L'expression finale de la fonction d'énergie, correspondant aux contraintes utilisées dans la modélisation markovienne de la probabilité a priori implantée dans notre application, est la suivante : U(x(s)) = Ucontrainte= ( β t U t+ βliss U liss+ βcontu cont) toutes_ contraintes Avec la température : U(x(s)) = U 1 contrainte= ( β t U t+ βliss U liss+ βcontu cont) T toutes_ contraintes où les β i sont des facteurs pondérateurs pour temporiser l'influence des différentes contraintes. Ch 2 45
64 La classification Cette fonction d'énergie est calculée pour chaque classe au niveau de chaque pixel, les contraintes U sont déterminées de la façon suivante : - U liss est le nombre de pixels du voisinage 8-connexe affectés à la classe en cours d'étude. Ce nombre est divisé par le nombre maximum de voisins possibles (dans notre cas, 8). - U cont est calculé lors de l'utilisation d'une segmentation : U cont = V cont + V cont--connexes. V cont est le nombre de voisins 4-connexes appartenant à la même région segmentée que le pixel traité, et étant affectés à la classe étudiée. V cont connexes est le nombre de voisins 4- connexes n'appartenant pas à la même région que le pixel courant, et ayant une classe différente de celle étudiée. - U temporel peut avoir plusieurs formulations (chapitre 4) Le paramètre de température : variation de la température Les paramètres (β et T) sont fixés de manière empirique. Avec le recuit simulé, pour une température importante, l équation sur la probabilité marginale des étiquettes admet une seule solution pour laquelle les étiquettes ont une probabilité égale. Les simulations de la loi P donnent alors lieu à des images aux étiquettes totalement désordonnées. La corrélation entre étiquettes d un même voisinage est faible. Quand la température diminue et atteint une valeur dite critique, l équation aux étiquettes admet plusieurs solutions, on rate le maximum de la probabilité a posteriori. Pour chacune de ces solutions, les étiquettes n ont pas la même probabilité. La longueur de corrélation augmente et les étiquettes commencent à se propager. Ce phénomène est analogue à l aimantation spontanée à basse température en physique statistique. En dessous de cette température, les interactions entre les pixels de l image sont fortes et les simulations montrent le début de formation d agrégats réguliers sur l image. Ainsi, il faut décroître à partir d une position haute température jusqu à une contrainte basse température. Une descente trop rapide de la température provoque une cristallisation dans des minima locaux d énergie. Le schéma de refroidissement exige donc un certain nombre d itérations. Cependant, pour les images RSO même avec un nombre important d itérations, on n est pas assuré d atteindre le maximum global de la probabilité a posteriori, étant donné l hétérogénéité de ces images. Pour la méthode présentée, le raisonnement est similaire à celui du recuit simulé. Toutes ces contraintes sont contrôlées à chaque itération par le paramètre de température. La température initiale est prise élevée, elle est régulièrement diminuée jusqu à stabilisation des résultats, ce qui lui permet de favoriser le voisinage du pixel. La diminution de température entre deux itérations doit suivre un schéma lent pour que la méthode soit efficace. Au fur et à mesure des itérations, on fait intervenir de plus en plus l effet des contraintes ce qui affine le résultat. Si l on diminue brusquement la température, on risque de se fixer sur un mauvais minimum local d énergie (maximum de probabilité). Il faut donc éviter les brusques changements de température entre deux itérations intérieures. Toutefois cet algorithme ne comporte pas la caractéristique essentielle du recuit simulé qui est de visiter plusieurs puits d énergie avant de se stabiliser dans l un d eux. Il ne peut être adapté qu à des énergies pour lesquelles on peut disposer d une configuration initiale convenable. Le nombre d itérations nécessaires pour un ICM est en général très nettement inférieur à celui nécessaire à un recuit simulé (de l ordre de un 1% à 10% du temps du recuit simulé). U Ch 2 46 = U contra int e toutes _ contra int es β d U donnee + (3) T toutes _ donnees
65 La classification D après l équation (3), lorsque la température est maximale, c est la probabilité estimée qui prédomine sur les prises en compte des contextes spatial et temporel, puis peu à peu (itérations après itérations), lors de la diminution de la température, les contextes spatial et temporel prennent de l importance pour définitivement classer les points encore en balance entre plusieurs classes. Si la température a atteint un seuil assez bas ou que le système devient figé, l'algorithme s'arrête. Inconvénients La principale difficulté réside dans le choix de la température initiale, du rythme de décroissance, éventuellement la durée de relaxation (le nombre d itérations de la transformation par palier de température), des critères d'arrêt. Ces paramètres sont en général choisis expérimentalement. La température initiale T = T 0 ne doit pas être choisie trop faible, pour assurer la convergence, mais pas non plus trop élevée, pour assurer un temps de calcul raisonnable. Tout au long de l'algorithme, on va donc faire décroître T, ni trop vite pour éviter de rester bloqué autour d'un minimum local, ni trop lentement si on veut avoir un résultat en un temps raisonnable. En théorie la décroissance logarithmique est utilisée de façon optimale par [Guyon 92] : T k T0 = log k T ou k Tk 1 = log k mais en pratique des décroissances géométriques donnent de bons résultats : Tk+1 = α Tk avec 0,8< α < 0,9 Dans nos tests la décroissance logarithmique a donné de meilleurs résultats, toutefois la décroissance géométrique donne des résultats assez proches. La température de passage du désordre à l ordre (appelé température critique) est très intéressante car à partir de cette température commencent à apparaître des regroupements de classes. Il serait utile de pouvoir calculer cette température critique pour permettre de mieux affiner le choix de la température initiale et finale. Le choix de la température initiale, dans le cas de la méthode présentée est plus basse que dans le recuit simulé Problème de la convergence de l ICM Avec peu d itérations on arrive déjà à une solution optimale mais l inconvénient est qu il faut une classification initiale correcte sinon on court le risque de ne pas avoir celle qui va donner le minimum global (figure 2.10). Plage d initialisation correcte Minimum local Minimum global Figure 2.10 : schéma des minima locaux et globaux Ch 2 47
66 La classification Un des premiers effets du manque de cohérence des algorithmes d échantillonnage dans la classification non supervisée, est un nombre d itérations important jusqu à ce que le système se stabilise. Plus l échantillonnage est cohérent dès le départ, plus la classification se stabilise rapidement. Des classes sont prises aléatoirement et sont parfois très proches statistiquement. Nous avons implantés des traitements qui permettent d améliorer la séparabilité des classes, de corriger ce manque de cohérence lors de la création automatique des échantillons, afin de commencer avec un échantillonnage plus représentatif, pour avoir une meilleure configuration initiale. L amélioration de l apprentissage consiste en : la fusion des classes similaires, la suppression des classes ayant trop peu d effectifs et la division des classes trop hétérogènes. Pour cela, nous avons cherché à optimiser : Le critère de différenciation : afin que les classes soient le plus hétérogènes possibles entre elles, par la maximisation de la variance inter classes, qui correspond aux fluctuations d une classe à l autre Le critère de similarité : afin que les signatures spectrales de chaque pixel appartenant à une classe soient le plus homogène possible, par la minimisation de la variance intra classe, qui correspond aux fluctuations des valeurs des pixels à l intérieur d une même classe. La distribution spatiale des classes (outils de caractérisation de paysage) ayant peu d effectifs, apporte une information pour déterminer si une classe est à conserver ou à éliminer. Les traitements sont également réalisés sous certaines conditions dans les itérations extérieures. Réunion des classes La réunion des classes, basée sur la distribution des statistiques, a pour but d unifier les classes qui sont statistiquement très proches, et font normalement partie d une même classe. Elle se fait selon un critère de minimisation de l erreur de décision entre classes, deux à deux par le calcul de la distance de Bhattacharyya (chapitre 3). Ch 2 48 Toutefois certaines classes peuvent être très proches statistiquement, et être des entités différentes. La prise de décision doit donc être faite très prudemment. Division des classes Ce traitement a pour objectif de diviser les classes qui contiennent et masquent deux classes différentes. Le critère de division des classes se fait selon un critère d hétérogénéité. Pour chacune des classes on calcule un coefficient d hétérogénéité qui doit être supérieur à une certaine borne, puis on décide de la division ou pas. L étude de ce coefficient d hétérogénéité est basée sur l analyse de la variance des classes qui consiste à tester l «hypothèse nulle», c est à dire : l hypothèse que les échantillons ou pixels appartiennent à une même classe. Ainsi si les pixels de la classe appartiennent à une même population, la différence de ces variances ne correspond qu aux fluctuations de l échantillonnage. Par contre si l écart est important les fluctuations ne sont plus fortuites, on peut diviser la classes en sous classes. Le coefficient d hétérogénéité est lié à la variance inter groupe et intra groupe, et est exprimé de la variance _ inter _ groupe manière suivante : C h = variance _ intra _ groupe
67 La classification L analyse de la variance est une étude sur des moyennes. Ce procédé est plus rapide qu une étude des moyennes deux à deux. Ceci permet également d éviter qu une classe ne devienne un point d accumulation des pixels, qui agit comme attracteur des pixels des autres classes. Nous supposons que les classes sont distribuées selon une loi gaussienne qui est une approche suffisante. La procédure est donc : chaque classe est divisée en deux sous groupes. Le test de la variance est effectué, le résultat est comparé avec un seuil de décision basé sur la loi de Snédécor. Si la valeur est plus grande que ce seuil, la classe est divisée, sinon la modification n est pas effectuée. Une fois la décision de la division de la classe prise, deux classes différentes sont créées à partir des statistiques suivantes qui vont représenter les deux nouvelles classes: moyenne moyenne = moyenne 0. 5 Cov Cov = Cov nouvelle _ clas1 originel ii ii _ nouvelle _ clas1 ii = moyenne Cov Cov = Cov nouvelle_ clas2 originel ii ii _ nouvelle _ clas2 ii où Cov est la matrice de covariance. La distribution est ainsi partagée en deux classes. Élimination des classes Des classes ont très peu d effectifs en fin de classification, elles peuvent être considérées peu représentatives car ce sont principalement des pixels parasites ou des bordures, elles peuvent être éliminées. L inconvénient de ce critère, est l élimination d une classe qui a très peu d effectifs, mais représente un objet dans l image qu il faut conserver, par exemple des classes de parcelles de petite taille, ou du type «fort diffuseur». Si les points d une classe avec peu d effectifs se trouvent éparpillés dans une image, les points de cette classe sont des points parasites, résidus de classes ne correspondant à aucun objet de la réalité et elle peut être éliminée. Si ces points sont regroupés, c est un objet et on n élimine pas la classe. La caractérisation de paysage offre des outils pour déterminer le degré de dispersion des classes (chapitre 5). Ce type de calcul est introduit à la fin des d itérations. Des classes sont également éliminées lorsqu elles présentent une singularité de la matrice de covariance. Le phénomène de singularité peut se produire: Si la classe est très homogène (valeurs radiométriques identiques), par exemple un banc de sable, une anomalie atmosphérique, un nuage, une surface d eau (dans les images optiques). Si la classe a très peu d effectifs. Il est nécessaire que la matrice de covariance soit inversible dans la formule de Gauss, donc non singulière. Si elle est singulière, plusieurs traitements sont réalisés : Dans le cas non supervisé : 1) lors de l'estimation initiale des statistiques : la taille de l échantillon de la classe concernée est augmentée, ce qui permet de varier la distribution. Lorsqu il s agit d échantillons représentés par un segment (issu de la segmentation), un autre segment est choisi. Ch 2 49
68 La classification 2) au cours de la classification : pour l'estimation des statistiques, on supprime les classes dont la matrice est singulière. Dans le cas d'une classification supervisée : Il est gênant de supprimer des classes ou de modifier leurs échantillons, sachant que ce sont des informations essentielles. De ce fait, on modifie la matrice de covariance en supprimant le canal cause de la singularité. Elle perd alors une dimension. Si trop de canaux sont défectueux pour une même classe, cela signifie que les échantillons de cette classe sont à revoir. Une fois que la classe qui doit disparaître est localisée, elle peut être supprimée. Ces points sont mis artificiellement «non classés», à la prochaine itération, ces points vont être assignés à la classe la plus proche statistiquement. Un procédé a été intégré pour contrôler ces réunions, divisions, éliminations des classes, pour que le nombre des classes ne soit pas trop réduit. Avec ce procédé l accumulation vers certaines classes est évitée. Le nombre de classes de départ dépend de la taille de l image, il est préférable qu il soit élevé et laisser le système supprimer très progressivement des classes en les regroupant. Ch 2 50
69 Chapitre 3 APPRENTISSAGE AVEC ACQUISITION AUTOMATIQUE DES ECHANTILLONS - VERIFICATION
70
71 Chapitre 3 APPRENTISSAGE AVEC ACQUISTION AUTOMATIQUE DES ECHANTILLONS - VERIFICATION La classification supervisée nécessite l intervention de l expert qui doit définir les thèmes qu il juge importants et caractéristiques du milieu étudié. L occupation du sol varie d une année à l autre du fait des rotations de cultures et de divers changements de gestion des parcelles agricoles ou forestière. Il est indispensable de se rendre sur le terrain pour le choix d échantillons d apprentissage et de vérification de l occupation du sol, ce qui donne lieu, souvent, à plusieurs sorties sur le terrain. Des polygones d entraînements sont définis sur l image. Une fois que les polygones références ont été placés, l algorithme calcule les statistiques sur les canaux spectraux, temporels, ou autres des N classes sur chaque polygone. Ces vecteurs de référence sont les échantillons, caractéristiques de chacune des classes. Une base de connaissances qui va servir à analyser l image est ainsi établie. Les échantillons doivent être représentatifs, il faut que des parcelles soient sélectionnées dans toutes les parties de l image ou la classe est présente. Dans le cas de données radars, l intensité va varier avec l angle d incidence, c est à dire que la réflectivité change dans la direction de prise de vue, selon la direction radiale, cela ajoute une difficulté supplémentaire au choix des échantillons sur une composition colorée temporelle. Deux échantillonnages indépendants sont nécessaires : (1) pour les calculs statistiques de la méthode de classification, les échantillons sont pris alors avec précaution, au centre des classes afin d éviter les pixels mixtes, (2) pour la validation de la classification, les échantillons ont une taille beaucoup plus large. Ces échantillons doivent être différents de ceux qui servent à l estimation des paramètres. Les techniques d apprentissage classiques reposent en général sur l utilisation des cartes topographiques, des photos aériennes et des logiciels de traitement d image comme ENVI, IDRISI ou Erdas Imagine pour localiser et créer les fichiers des échantillons (ROIs). La prise des échantillons est une tâche fastidieuse et contraignante ; de celle-ci dépend en grande partie les résultats de la classification supervisée. L inconvénient majeur de ces méthodes est que seul trois canaux sont utilisés pour la visualisation de la composition colorée indispensable pour le choix des échantillons Apprentissage à partir d une méthode de saisie automatique des échantillons Nous avons développé une nouvelle méthode d apprentissage. Elle présente l avantage de créer les échantillons d une manière automatique à partir d'une segmentation série d images (multi-spectrale, multi-date, multi-source), éventuellement d une base de données géoréférencée, de données GPS. Toute l information contenue dans la région d échantillonnage est collectée et donne lieu à plusieurs relevés de terrain. Chaque vérité terrain est repérée grâce à un GPS (Global Positioning System) qui permet de géoréférencer les échantillons relevés. Ils sont reliés à un Système d Information Ch 3 51
72 Apprentissage automatique, vérification Géographique (S.I.G), indiquant à l aide d un pointeur sa position sur une image satellite géoréférencée de la région. Ces informations sont regroupées dans une base de données «Agribase». La base de données est composée des coordonnées géographiques (longitude, latitude), des numéros de la mesure GPS et des numéros des classes. Les images satellites étant géoréférencées, les pixels sont reliés directement à la réalité du terrain, associé à une image segmentée (chapitre 2), les échantillons sont alors les segments correspondants à la coordonnée. L image segmentée assure l homogénéité des échantillons au sens de critères statistiques pré-définis. L apprentissage doit être d une taille et d une diversité suffisante pour rendre compte de la variabilité des réponses spectrales de chacune des classes d occupation du sol afin de fournir une image classée de bonne qualité. La précision de la caractérisation de l occupation du sol dépend de la résolution spatiale des images (20 mètres pour SPOT). Les avantages de l approche proposée sont : l automaticité, la localisation des échantillons grâce à la base de données (à partir de coordonnées GPS), la multi-dimensionnalité : utilisation de tous les canaux disponibles pour la segmentation de l image, l obtention de zone homogène comme parcelle d entraînement et donc d un échantillonnage temporellement plus homogène et une augmentation de la précision Base de données + Image segmentée Image des échantillons Une interface a été réalisée d abord en langage IDL (Interactive Data Language), puis sous JAVA afin de faciliter l utilisateur, pour visualiser et modifier les échantillons Description de la base de données cartographiques Agribase Agribase est une base de données créée sous ACCESS dont l objectif est de gérer les informations collectées sur le terrain en vue de constituer l échantillonnage de référence. Ces informations concernent essentiellement les classes de végétation ; les autres classes présentes dans le référentiel telles le Bâti/Minéral, l Eau ne font pas l objet de recensement systématique et ne figurent pas dans Agribase. L information collectée concerne : la localisation du point ou de la surface échantillonnée à l aide d un GPS qui délivre les coordonnées géographiques (Longitude (δ) et Latitude (ϕ)) du point ou du centre de la parcelle, identifié par le numéro GPS Le numéro de la mesure GPS qui nous permet de retrouver rapidement toutes les caractéristiques de ce point La nature de l occupation du sol, le numéro de classe associé, catégorie de la parcelle, stades de développement végétatifs, structure de la végétation (verticale et horizontale), hauteur et autres détails susceptibles d'améliorer leur description pour un meilleur lien avec les données de la télédétection Ch 3 52
73 Apprentissage automatique, vérification GPS Collecte de données de terrain géo-localisées PComputer AGRIBASE Référentiel d échantillonnage Figure 3.1 : réalisation du référentiel d échantillonnage pour la classification : Agribase, GPS, SIG MapInfo pour la cartographie des relevés (triangle rouge. L utilisation de la base de données consiste en : (1) Saisie des données sur le terrain par renseignement de la base à l aide d une fenêtre de saisie unique, le formulaire de relevé lié aux différentes tables et leur localisation grâce au GPS ; (2) Etablissement automatique du référentiel d échantillonnage. Il comporte les coordonnées géographiques, la nature et le numéro de la classe d occupation du sol ; (3) Cartographie des relevés de terrain grâce au lien (base de données ACCESS Information géographique MapInfo) Principe de la méthode automatique d apprentissage Une interrogation d Agribase sous la forme de requête permet d extraire ces informations qui constituent la trame du référentiel de terrain ; elle est affichée sous la forme d un tableau comportant quatre champs relatifs aux coordonnées de la mesure GPS, au numéro de la mesure GPS et au numéro de classe d occupation du sol de chaque échantillon. Le logiciel convertit les coordonnées géographiques (longitude, latitude) en coordonnées cartographiques (Lambert II étendu, système de projection choisi pour le géoréférencement des scènes SPOT) et en coordonnées pixels (colonne, ligne). Il positionne alors les points GPS sur l image segmentée de la zone d étude qui contient les contours de régions (segments), radiométriquement homogènes, pour un seuil défini. Il leur affecte un numéro de classe approprié. Les échantillons sont donc les régions qui entourent ces points (figure 3.5). Suivant la valeur du seuil, les régions adjacentes sont plus ou moins fusionnées et donc plus ou moins grandes (figure 3.2). La segmentation de la figure 3.5 a été effectuée sur une image à 14 canaux spectraux et temporels. Si l on ne dispose pas de points GPS, on peut toutefois utiliser le logiciel, en cliquant sur un segment (région) correspondant aux parcelles choisies par l utilisateur. Tout échantillonnage peut être repris à tout moment en ouvrant le fichier «échantillons», après avoir ouvert l image originale et celles des contours correspondants. L échantillonnage peut s effectuer à des seuils différents cela permet de faire une sélection Ch 3 53
74 Apprentissage automatique, vérification des segments d une façon extrêmement précise. La gestion des seuils permet de faire varier la taille des segments de l image de contours. Plus le seuil est élevé plus les segments sont grands (fugure 3.2). La sélection, désélection et information des segments se font par un click de la souris. Erosion : Une fois l échantillonnage effectué, l utilisateur peut éroder les contours des segments pour que celui-ci soit le plus homogène possible, surtout pour l échantillonnage d apprentissage. En effet, les bordures des parcelles sont des pixels mixtes non significatifs et doivent être éliminés. (a) Figure 3.2 : image sur-segmentées (a), (b) sous-segmentée (b) Image de télédétection multi-source (optique et/ou radar), Multi-spectrale ou multi -date Image géoréférencée géoréférencement Détecteur Superposition Image gradient Image de dynamique Extracteur Seuillage Base de données Image de contour Image segmentée et étiquetée Etiquetage (labelisation) Image des échantillons Figure 3.3 : méthodologie de la création automatique des fichiers des échantillons Ch 3 54
75 Apprentissage automatique, vérification Bordure Champs de maïs Champs de maïs Figure 3.4 : exemple d érosion d une parcelle Figure 3.5 : positionnement automatique d échantillons (segments blancs) sur l image segmentée Ch 3 55
76 Apprentissage automatique, vérification Figure 3.6 : classification supervisée Evaluation des classifications - Matrice de confusion La matrice de confusion des classes est un élément clé de mon travail pour l analyse «haut niveau» des images. Un procédé de mesure de la qualité des données satellitales a été développé. Cette partie est donc détaillée. Lorsque les échantillons sont jugés représentatifs des classes étudiées et en nombre suffisant, l estimation de leur qualité et de la qualité de la classification, se fait par le biais de deux matrices de confusion qui indiquent pour chaque classe, les confusions qui sont apparues lors du processus de classification : a priori sur les échantillons d estimation et a posteriori sur les échantillons de vérification. La matrice de confusion offre une mesure quantitative de la qualité de l échantillonnage et de la «séparabilité» des classes. Soit n le nombre de classes. La matrice de confusion Mc est une matrice n * n, ou n * (n+1) s'il y a des pixels non classés, calculée à partir des échantillons de référence ou de vérification. Les éléments diagonaux, de la matrice de confusion Mc(i, i) représentent le nombre de pixels de la classe i ayant effectivement été affecté à celle-ci, après classification. L'élément non diagonal Mc(i, j) est le nombre de pixels de la classe i ayant été affecté à la classe j. Les lignes de la matrice correspondent aux nombres (ou pourcentages) de pixels des classes du référentiel affectés dans l image classées. A partir de ces matrices, les mesures suivantes sont calculées : qualité "utilisateur" ou précision : le taux de pixels bien classés de la classe i, P uc (i, i) = Mc (i, i) / m i. où m i. est la somme des points de la classe i dans l'image (somme des colonnes sur la ligne i) L'erreur de "commission" (%) = qualité utilisateur (%) La précision ou qualité "producteur" de la classe i est donnée par : P pc = Mc (i, i)/m.i où m.i est le nombre de points de la classe i dans l'image classée (somme des lignes sur la colonne i). Ch 3 56
77 Apprentissage automatique, vérification Un taux élevé indique que la classe a été très peu affectée par les échantillons des autres classes; à l'inverse un taux faible indique que cette classe a souvent été choisie à la place d'autres classes. L'erreur d' "omission" (%) = qualité producteur (%) La précision globale de la classification est donnée par la moyenne des Pourcentages des Pixels Correctement Classés (MPCC) et par le Kappa (Congalton, 1991). La moyenne de pixels correctement classés (overall accuracy en anglais) : n n MPCC = 1/n Σ P uc (i, i) = 1/n Σ Mc(i, i)/m i. i =1 i =1 Le coefficient Kappa (noté K) est donné par : où N est le nombre total de points. n N Σ Mc( i, i) i= 1 K = 2 n N Σ m i= 1. i i= 1 m. i n n Σ m Ce coefficient a l'avantage de considérer tous les éléments de la matrice de confusion. i m. Un coefficient Kappa peut être également donné pour chaque classe : Nmii m. i mi. K i = = Nm. m. i m. i i i classification Feuillus Résineux Eucalyptus Blé Colza Orge Maïs référentiel Feuillus Résineux Eucalyptus Blé Colza Orge Maïs Tournesol Sorgho Soja Pois Jachère Prairie Eau Lac Bâti/Minéral MPCC Kappa Tournesol Sorgho Soja Pois Jachère Prairie Eau Lac Bâti/Minéral Tableau 3.1 : matrice de confusion. En gras les pourcentage des pixels bien classés. Le Kappa est un estimateur de la précision d une classification qui tient compte des erreurs en ligne et en colonne (Congalton, 1991). Il permet une évaluation globale mais aussi au niveau de chaque classe, le Kappa donne une estimation plus précise de la qualité de la classification. Le PCC moyen (MPCC) correspond plutôt à une mesure de la séparabilité des classes en fonction des divers canaux Ch 3 57
78 Apprentissage automatique, vérification Les statistiques obtenues à partir des matrices de confusion (MPCC et Kappa) servent de base de mesures de la qualité des différentes données. Elles permettent de faire des comparaisons de combinaisons de dates Calcul de distance inter classe Des distances entre classes peuvent être calculés, quand il est nécessaire d analyser précisément certaines confusions entre classes, ainsi la distance de Battacharya est calculée sur toutes les combinaisons de canaux et de classe 2 à 2. La distance de Bhattacharyya [Fukunaga K. 1972] est basée sur une analyse en fréquence des classes, avec le principe de Bayes (supposition a priori que les classes soient distribuées selon une loi gaussienne). L'atout des distances probabilistes quand on connaît les distributions a priori des classes, est qu elle tient compte de la relation entre les différents canaux par le biais de la matrice de covariance et elles sont donc plus performante que les autres distances basées sur des critères géométriques (calculs de moyenne et éventuellement d écart type). L avantage de cette distance est qu elle permet d avoir une expression qui donne l erreur associée à une décision selon la théorie bayesienne, à partir de la «borne de Chernoff» (qui calcule la borne supérieure de l erreur de décision). Elle est une particularité de l expression de µ(s), car on pose s=1/2 et on suppose les distributions normales, où µ(s) dépend du logarithme népérien de la fonction caractéristique des distribution des probabilités des classes analysés. La borne de Chernoff correspond 1 s s µ ( s ) à l erreur de décision maximale: ε p( C ) p( C ) e 1 2 En supposant que les distribution des classes sont normales, la distance de Bhattacharyya, définie comme suit : 1 1 µ = t 1 2 ( µ µ ) ( µ µ ) 2 1 C + C ln 2 ( C C ) C C µ, est 2 où µ 1 et µ 2 : sont les moyennes des deux classes, et C1 et C2 : la matrice de covariance des deux classes. Les distances sont calculées deux à deux Logiciel d extraction systématique des mesures des combinaisons de canaux (procédure automatique) Il est impossible d analyser manuellement chaque matrice de confusion les une après les autres, certaines combinaisons sont choisies, par la connaissance de l expert, mais avec beaucoup d incertitude, or si l on veut connaître les meilleurs canaux pour la classification, il est indispensable de pouvoir mesurer le pouvoir discriminateur de ces canaux, ce qui est donné par le MPCC. Pour favoriser l étude des données de télédétection, nous avons développé une procédure qui donne de façon automatique la série de matrices de confusion de toutes les combinaisons possibles des Ch 3 58
79 Apprentissage automatique, vérification différentes dates (éventuellement spectrales), ce qui est plus objectif. L algorithme permet d obtenir par ordre de décroissance les MPCC (de vérification ou d apprentissage), de toutes les combinaisons possibles de l ensemble des canaux étudiés. Pour la zone test du Sud Ouest toulousain nous avons sélectionné sept dates, soit 26 canaux ce qui donne i C 7 = 127 possibilités. i= 1,7 À partir de ces matrices de confusion un tableau récapitulatif est obtenu ; il est composé des éléments diagonaux des matrices de confusion dans l'ordre décroissant des valeurs du MPCC. Cette procédure permet une comparaison rapide de toutes les classifications effectuées dans toutes les conditions spectrales et temporelles. Ainsi nous pouvons extraire les meilleures combinaisons Application : Mesure de la qualité des données satellitales Une partie importante de mon travail a été de tester, valider, modifier les diverses méthodes développées grâce à un très grand nombre d applications, dans des conditions très différentes avec des images de télédétection de capteurs hétérogènes, mon objectif essentiel étant que le système de classification soit opérationnel dans toutes circonstances. Ainsi chaque méthode offre un grand nombre de possibilité d utilisation en fonction des images à traiter. Le résultat de la classification, permet d obtenir le plan d occupation du sol. Mais elle est aussi utilisée comme mesure de la qualité discriminatoire des bandes spectrales et temporelles des images. Je présente ici des résultats obtenus sur des études temporelles avec des images SPOT et radar. Le pouvoir discriminant des différentes combinaisons est mesuré par les matrices de confusion sur la base de l échantillonnage témoin. La précision globale de la classification est donnée par la Moyenne des Pourcentages des Pixels Correctement Classés (MPCC) et par le Kappa. Dans cette étude, nous nous intéressons surtout à la séparabilité des classes, ainsi, nous donnerons le MPCC. La méthodologie présentée au travers des exemples ci-après, est reproductible et a été appliquée dans un grand nombre de cas Résultats obtenus dans le cadre du Projet Sud-Ouest Projet «SUD OUEST» du CESBIO : Bilans de carbone et d eau en région Midi-Pyrénées. Vers un observatoire Régional de l Environnement : comprendre et prévoir l influence de l homme et du climat sur les ressources en eau et les écosystèmes. Les objectifs de ce projet sont : de contribuer à la compréhension et à la modélisation du fonctionnement des surfaces continentales aux échelles du paysage et de la petite région et de développer des connaissances et des méthodes utilisables de façon générique. de constituer les bases scientifiques et méthodologiques permettant de : - comprendre le fonctionnement d'un ensemble hétérogène d'écosystèmes; - diagnostiquer les évolutions ; Ch 3 59
80 Apprentissage automatique, vérification - modéliser ce fonctionnement et ces évolutions ; - parvenir à des scénarios potentiels d évolution du fonctionnement et de la structure des écosystèmes, de leurs bilans d'eau et de carbone, en réponse à des pressions climatiques ou anthropiques. Les applications concernent : - l obtention de bases scientifiques pour la gestion agri-environnementale des territoires - la fourniture d outils d aide à la décision pour les diagnostics et les scénarios - la mise en place d un observatoire régional de l environnement s appuyant sur les outils spatiaux Le projet Sud-Ouest contribue au volet régional du projet européen CarboEurope et participe aux projets suivants: projet APOGE (Division Agro-météorolgie: «Aide à la Planification de l'occupation des sols et à la Gestion de la ressource en Eau et de la production agricole à l'échelle régionale», projet GICC «Gestion et Impacts du Changement Climatique» Bilans de carbone et d eau de la région Sud-Ouest, projet ECCO : Fonctionnement intégré de l espace rural du paysage à la région. Dans le cadre de ce projet, certaines zones de la région disposent d archives assez complètes sur l évolution des modes de couverture des terres et sur certaines variables comme le niveau annuel de production ou le stock de matière organique du sol. Des cartes de végétation incluant le parcellaire existent, des photographies aériennes sont parfois disponibles depuis 40 ans ; des images LANDSAT existent depuis 1972, SPOT depuis 1986, ERS depuis Les états et les variations observées sur un parcellaire reconnu fournissent des données qui seront assemblées et mises en forme, puis traitées pour en faire ressortir les attributs fonctionnels et structuraux pertinents. L évolution de ces attributs et les résultats des modèles qui se fondent sur les séries temporelles devraient permettre de comprendre l évolution des états de surface opérés dans les dernières années. La connaissance des changements passés aidera à prévoir les modifications futures avec des hypothèses sur 1) la stabilité des pressions, 2) l'augmentation des pressions dues à l'homme, par exemple, l'application de la PAC (Politique Agricole Commune) en matière de jachères, les modifications d'assolement imposées par les consignes de l UE et aux événement naturels (feu, inondation, sécheresse, 3) la baisse des pressions (abandon des cultures dans le piémont Pyrénéen avec retour au processus naturel du couvert végétal). Dans l exemple présenté la matrice de confusion est calculée sur sept dates (mars à septembre) d image SPOT de 2002 et 2003 de la région du Sud-Ouest toulousain. Elle donne un MPCC égal à 98% en 2002, à 98.55% en 2003 pour l échantillonnage d apprentissage, 87.44% (2002), 81.26% (2003) pour celui de vérification, ce qui est comparable, toutefois inférieur pour la vérification en 2003, année climatique exceptionnelle (sécheresse). Les résultats de l évaluation sont donnés avec l échantillonnage d apprentissage et celui de vérification ; le premier a un résultat évidemment supérieur au deuxième Analyse monodate. L analyse monodate porte sur les mois de mars à décembre (figure 3.7). Les résultats MPCC et Kappa mettent en évidence les limites de discrimination de la totalité des classes dans le paysage régional, avec une seule image, les pourcentages de pixels bien classés ne sont donc pas très élevés. Les trois dates fournissant les meilleurs résultats (mai, mars et avril) sont des images SPOT4 (quatre canaux avec XS4 moyen infrarouge). Ch 3 60
81 Apprentissage automatique, vérification Pourcentage des pixels bien classés mars 05 avril 23 mai 14 juin 10 juillet 03 septembre 25 septembre 07 novembre Apprentissage avec MIR Vérification avec MIR Apprentissage sans MIR Vérification sans MIR Figure 3.7 : qualité de l information monodate, à partir des matrices de confusion pour chacune des dix dates de 2003, MPCC en ordonnée Mai et mars sont les mois qui apportent le plus d informations montrant les MPCC les plus élevés pour les deux échantillonnages et au niveau des classes ; pour ces deux dates on obtient le plus grand nombre de classes dont le PCC est le plus élevé. Il est à noter la bonne qualité de l information apportée par le mois de juin (trois canaux) délivrant un MPCC de 68.58% pour l échantillonnage d apprentissage et 54.57% avec celui de vérification ; il s agit du meilleur résultat à niveau égal d information (trois canaux) se plaçant même devant septembre qui possède quatre canaux. Parmi les mois d été, on note la supériorité du mois d août, fournissant des résultats corrects. D après les résultats obtenus par l analyse des monodates, il est possible de prévoir que les meilleures matrices de confusion seraient obtenues en utilisant les images des mois de mars, avril, juin, août et éventuellement septembre pour l année 2002 alors qu elles le seront en utilisant les images des mois de mai, mars, avril et août pour l année Importance du canal Moyen Infrarouge En supprimant le canal XS4 (moyen infrarouge) sur les cinq dates possédant ce canal (mars, avril, mai, août et septembre), on constate une baisse générale sauf pour l échantillonnage de vérification de septembre. La baisse des MPCC est de l ordre de 7 à 10% pour l échantillonnage d apprentissage et de 3 à 7% pour celui de vérification. Les diminutions les plus notables sont enregistrées pour les mois d août et de septembre, mois de la sécheresse estivale durant lesquels la demande climatique en eau est l une des plus fortes, principalement pour cette année 2003 particulièrement sèche. Ces résultats témoignent donc de l importance du canal MIR de SPOT4 dans le processus de discrimination des classes (figure 3.7). Ch 3 61
82 Apprentissage automatique, vérification Etude multi-temporelle Combinaisons en additions chronologiques Dans un premier temps, une série de combinaisons d images est réalisée en ajoutant par ordre chronologique, une nouvelle date à chaque combinaison de date antérieure, depuis le mois de mars jusqu au mois de septembre. L évolution des MPCC par classes va globalement de pair avec le nombre de dates considérées. Pourcentage des pixels bien classés mars mars-avril mars-avril-mai mars-avril-maijuin mars-avril-maijuin-juillet mars-avril-maijuin-juillet-août mars-avril-maijuin-juillet-aoûtseptembre Apprentissage avec MIR Apprentissage sans MIR Vérification avec MIR Vérification sans MIR Dates mars marsavril mars-avrilmai marsavrilmai-juin mars-avrilmai-juinjuillet mars-avrilmai-juin-juilaoût mars-avrilmai-juinjuil-aoûtsept. MPCC apprent % 88.79% 94.44% 96.84% 97.80% 98.18% 98.55% MPCC vérif % 60.69% 62.14% 66.70% 66.63% 68.20% 68.34% Kappa apprent % 87.76% 93.20% 96.09% 97.13% 97.47% 97.73% Kappa vérif % 69.37% 72.94% 77.40% 78.93% 79.91% 80.33% Figure 3.8 : combinaisons en additions chronologiques, qualité de l'information multitemporelle à partir des matrices de confusion, MPCC en ordonnée L information apportée à chaque ajout de dates fait croître de manière continue le MPCC. L augmentation est très élevée au départ, principalement avec l échantillonnage d apprentissage, puis décroît avec le nombre de dates ajoutées et finit par se stabiliser pour les deux échantillonnages avec août et septembre, ce qui correspond à deux courbes à tendance asymptotique (figure 3.8) Combinaisons en additions ciblées Toutes les combinaisons possibles de l ensemble des canaux étudiés (26 canaux, 127 possibilités), grâce à la procédure automatique ( 3.4), sont données par ordre de décroissance des MPCC (de vérification ou d apprentissage) (figure 3.9). Ainsi nous avons pu extraire les meilleures combinaisons pour l échantillonnage de vérification. Parmi les dix meilleures combinaisons retenues, le 1 er pourcentage correspond à l apprentissage, le 2 ième à la vérification: o une combinaison deux dates (avec le MIR) : «mai-août» 92.82%, 70.43%; o trois combinaisons ternaires : «mai-juin-août», 94,80% 70.66%, «mai-juin-septembre» 94,70% 69.76%, et «avril-juin-août» 94.91%, 69,64%; o quatre combinaisons de quatre dates : «avril-mai-juin-août», 96,25% 72.25%, «avril-mai- Ch 3 62
83 Apprentissage automatique, vérification o juin-septembre», 96,73%, 70.16%, «mars-mai-juin-août» 97.12%, 70,13% et «mai-juinjuillet-août» 96,09%, 70,10%; deux combinaisons de cinq dates : «avril-mai-juin-juillet-août» 97,36%, 70.99%. et «avril-mai-juin-août-septembre» 97.68% 69.30% ; Pourcentage de pixels bien classés mai-août avril-maijuin-août avril-maijuin-juilletaoût mai-juinaoût avril-mai- mars-maijuin-aoûjuinseptembre mai-juinjuillet-août mai-juinseptembre avril-juinaoût avril-maijuin-aoûtseptembre Apprentissage Vérification Figure 3.9 : qualité de l'information multitemporelle, meilleures combinaisons à l'aide des matrices de confusion ; MPCC en ordonnée Notons l importance de certaines dates : mai (avec Mir) et juin (sans Mir), dès que participant à une combinaison, assurent un meilleur score. Sur l ensemble des combinaisons 2003 vérifiées, ces deux dates apparaissent chacune dans neuf cas sur dix et sont associées dans huit combinaisons sur dix. les mois d avril et d août qui assurent une augmentation de la moyenne de pixels correctement classés. L ajout du mois d avril permet au MPCC de passer de 94.80% (mai-juin-août) à 96.53% pour la combinaison «avril-mai-juin-août» Quatre premières dates (cycle végétatif des cultures d hiver) et quatre dernières dates (cycle végétatif des cultures d été) Le référentiel d échantillonnage regroupe les représentants des principales classes d occupation du sol présentes dans la région. Or si certaines de ces classes occupent le territoire de manière continue (forêt, Bâti/Minéral, Eau), d autres ne sont présentes que sur des périodes limitées, les cultures annuelles par exemple. Les dates considérées dans la classification 2003 couvrent la période de mars à septembre. Les deux grandes catégories de cultures annuelles, les cultures d hiver (en place de mars jusqu à juin) et les cultures d été (en place de mai à septembre), se relaient dans le temps avec une courte période commune (mai-juin). Il est donc proposé de tester la qualité de l information apportée en matière de classification, par chacune des combinaisons de quatre dates calées sur les cycles culturaux des deux grandes catégories de cultures annuelles. Les combinaisons proposées en 2002, «mars-avril-mai-juin» et «juillet-août-septembre-octobre» ont 4 dates, (14 canaux, deux SPOT4). Les combinaisons de 2003 sont «mars-avril-mai-juin» (15 canaux) et «juin-juillet-aoûtseptembre» (14 canaux). Ch 3 63
84 Apprentissage automatique, vérification printemps mars-avril-mai-juin Apprentissage Vérification Apprentissage Vérification MPCC 92.10% 75.90% 96.84% 66.70% Kappa 91.70% 74.70% 96.09% 77.40% été juillet-août-septembre-octobre 2002 juin-juillet-août-septembre 2003 Apprentissage Vérification Apprentissage Vérification MPCC % 65.61% Kappa % 77.08% Tableau 3.2 : qualité de l'information multitemporelle, combinaisons quatre dates de printemps et d été 2002 et 2003, à l'aide des matrices de confusion Avec l échantillonnage d apprentissage (tableau 3.2), les résultats sont assez comparables pour les deux années car tous supérieurs à 90%. Pour l échantillonnage de vérification de 2003, les scores sont toujours plus faibles. Ceci peut être mis en relation avec la forte période de sécheresse présente lors de l année 2003 qui a agi sur le cycle des cultures d été en particulier sur la durée des cycles des cultures d été en sec. Les combinaisons des quatre dates calées sur les cycles culturaux apportent une quantité d information quasi identique. Toutefois elle est moins importante que celle apportée par la combinaison «avril-mai-juin-août» obtenue par le classement automatique des meilleures combinaisons de dates, et étalée sur l ensemble des cycles de la végétation Apport du canal PIR (XS3) La structure morphologique et l anatomie des végétaux influencent fortement leur réponse vis-à-vis du proche infrarouge (PIR, capteur SPOT XS3). Les végétaux dont les feuilles auront un parenchyme palissadique (tissu foliaire) développé ainsi qu un parenchyme lacuneux faible, absorbent plus dans le PIR que les végétaux dont les feuilles ont un parenchyme palissadique faible et un parenchyme lacuneux développé [Girard & Girard, 1999]. Dates Echantillon de vérification Différence de MPCC Avec et sans PIR mars avril mai août septembre SPOT4 SPOT4 SPOT4 SPOT4 SPOT4-5,84% -5,29% -1,19% -2,39% -3,03% Tableau 3.3 : pertes des MPCC sur les monodates après le retrait du canal XS3 (PIR). Le retrait du canal XS3, en mars ou bien en avril entraîne une baisse de la moyenne des pixels bien classés de 3 à 3.5% (échantillonnage de vérification). En août et septembre la diminution est de 6 à 7% (tableau 4.11). L information contenue dans le proche infrarouge est moins importante en mai, août et septembre (inférieure à 3.03%). Ch 3 64
85 Apprentissage automatique, vérification Apport du canal MIR (XS4) Une série de tests a été réalisée pour étudier l importance du MIR (canal XS4). Ces longueurs d ondes du moyen infrarouge sont en général absorbées par l eau et notamment par l eau contenue dans les plantes. Or cette teneur en eau varie selon les espèces et selon le stade de maturité des plantes. Donc observer les végétaux dans le moyen infrarouge est utile pour les différencier. Echantillons de vérification mars avril mai août septembre. Différence de MPCC avec et sans MIR -3,6% -3,18% -2,93% -6,04% -7,14% Tableau 3.4 : pertes des MPCC sur les monodates après le retrait du canal XS4 (MIR). Les tests consistent à calculer les matrices de confusion à partir des données avec ou sans le MIR avec les échantillons de vérification (tableau 4.6, 4.7, 4.10). La différence est plus importante pour août et septembre (supérieure à 6%), période où la demande climatique (évapotranspiration potentielle) est forte. A cette époque de l année, les cultures d été sénescentes (qui ont subi pour la plupart, un stress hydrique) se distinguent nettement sur les images satellites. L apport du MIR est important lorsqu il y a peu de dates, plus on ajoute de dates moins sa portée est visible. mars marsavril marsavril-mai marsavrilmai-juin mars-avrilmai-juinjuillet mars-avrilmai-juinjuil-août mars-avrilmai-juin-juilaoût-sept. Echantillons de vérification Différence MPCC sans PIR -5.84% 0.0% -0.64% -0.39% +0.32% +1.45% -0.58% Différence MPCC sans MIR -3.6% -1.11% 0.0% +2.24% +0.9% 0.0% -0.4% Tableau 3.5 : différences des MPCC sur les combinaisons de dates après le retrait du canal XS3 (PIR) ou du canal MIR. En résumé : le canal MIR apporte une information importante en matière de discrimination, surtout pendant la période estivale où l eau est un facteur déterminant pour la végétation. Ceci est particulièrement vérifié avec la sécheresse estivale 2003 et l importance de ce canal en août et septembre, son retrait engendrant des MPCC faibles. La baisse du MPCC est plus importante avec le retrait du PIR que celui du MIR. Plus le nombre de dates est important moins la différence est grande entre le MIR et le PIR. Ces résultats sont intéressants pour le choix des meilleures bandes spectrales pour les futurs capteurs et plateformes Conclusion : choix de la meilleure combinaison pour la classification supervisée pour 2003 L étude multitemporelle met en évidence la prédominance de certaines dates en Il s agit des mois printaniers, mars, mai et avril et des mois d août et juin. La combinaison trois dates «mars-juin-août» ou «avril-juin-août» délivre des résultats très satisfaisants de l ordre de 95 % (apprentissage) et de 67.57% et 69.94% (vérification) à peine Ch 3 65
86 Apprentissage automatique, vérification inférieurs aux combinaisons de quatre et cinq dates. Les classifications retenues sont sélectionnées à partir des résultats de la matrice de confusion calculée avec l échantillonnage de vérification (MPCC et Kappa les plus élevés). Il s agit des classifications réalisées à partir : de la combinaison de sept dates «mars-avril-mai-juin-juillet-août-septembre», possédant le kappa le plus élevé, le meilleur MPCC d apprentissage (98.55%) et un MPCC de vérification parmi les plus correct (68.34%), de la combinaison de quatre dates «avril-mai-juin-août». Le MPCC est le plus élevé : 72.25% et le Kappa est de 80.83%. combinaisons marsjuin-août avril-juinaoût avril-maijuin-août mars-avrilmai-juinjuillet-aoûtseptembre. MPCC apprent % 94.91% 96.53% 98.55% MPCC vérif % 69.94% 72.25% 68.34% Kappa apprent % 93.89% 95.55% 97.73% Kappa vérif % 78.25% 80.83% 80.33% Tableau 3.6 : récapitulatif des meilleures combinaisons de dates en 2003 (MPCC et kappa des matrices de confusion : apprentissage et vérification) Ainsi la combinaison des canaux spectraux des mois d avril, mai juin et août reste un bon compromis entre la qualité du résultat et l investissement financier nécessaire à l acquisition des images satellites, du moins au niveau de notre zone d étude couvrant une région majoritairement agricole Classification d un parcellaire agricole à l aide de données temporelles ERS-1 (région de BOURGES) Introduction En région au climat tempéré, les données optiques sont généralement bien adaptées pour l établissement de cartes de surfaces agricoles. Néanmoins, la précision des cartes obtenues par classification de données optiques est fortement dépendante des dates d acquisition de ces images. En effet, les stades phénologiques des cultures doivent pouvoir être repérés dans la série temporelle. La précision temporelle des prises de vue optiques étant dépendante de la clémence des conditions météorologiques, les possibilités offertes par les capteurs radar spatiaux intéressent les organismes chargés d effectuer ces suivis. Des tests ont été effectués sur beaucoup d applications et de capteurs ERS1, ERS2, ou Radarsat dans des paysages différents : agricole (Bourges, Sud-Ouest toulousain), forestier (fontainebleau, vallée de la Marne, Landes), tropical Indonésie Sumatra, et dernièrement ( ) le désert de Monegros prés de Saragosse pour détecter les zones humides correspondant à des salines [Ducrot et al 04]. Les tests ont été notamment réalisés pour trouver les meilleures conditions : pour le contexte (meilleure taille du voisinage), pour la segmentation, introduction de données texturales, principalement l hétérogénéité, utilisation de données filtrées, choix du meilleur filtre qui s est avéré être le LVMMSE présenté au chapitre 2, utilisation des données transformées en logarithme Ch 3 66
87 Apprentissage automatique, vérification L application présentée concerne la région de Bourges, elle a été réalisée dans le cadre d un contrat de recherche et de développement CNES en collaboration avec l ENSEEIHT (IRIT/LIMA), qui avait pour objet des méthodes de filtrage du speckle des images radar et le développement de méthodes spécifiques de segmentation/classification en tenant compte de la présence du speckle [Sery et al 96]. L étude présentée utilise la segmentation [Fjortoft et al. 96] pour améliorer la classification, en particulier dans le cas de cultures, grâce à une meilleure détection des contours. Nous verrons qu avec les méthodes proposées les taux de bien classés avec une série temporelle ERS-1 approchent ceux que l on pourrait obtenir avec des données optiques. La tendance des résultats présentés ici est constante et reproductible dans d autres applications ( 3.5.4). Les données disponibles sont : 6 images ERS-1, Single Look Complex (SLC), prises aux dates : 26 Mars 1993, 30 Avril 1993, 04 Juin 1993, 09 Juillet 1993, 13 août 1993, 17 Septembre données SPOT du 09 Juin et du 26 Août jeux de vérités terrain, effectuées, l une en Juillet et l autre fin Septembre, réalisées pour une campagne aéroportée. La zone sur laquelle nous avons travaillé est d une surface au sol d environ 36 km x14 km (le pixel correspond à une surface au sol de 12.5x12.5 m 2 ). Ces données ont donc été ramenées au format PRI par moyennage des intensités de 3 pixels en azimut. Les données SLC (Single Look Complex) permettent d utiliser les cohérences inter-dates. Les données SPOT ont été fournies pour établir des comparaisons et pour la fusion optique/radar. Les images SPOT ont été recalées sur les données ERS-1. Classes Apprentissage Vérification Classes Apprentissage Vérification Forêt Trèfle Vergers Prairie Blé Ray-grass Blé tendre Jachère Maïs Sol nu Tournesol Urbain Orge Route Colza Eau Pois Tableau 3.7 : nombre de points utilisés, par classe, pour l apprentissage des méthodes et pour la vérification des résultats. Les points utilisés pour l apprentissage sont inclus dans ceux utilisés pour la vérification Les données ont été transformées en logarithme afin d améliorer l ajustement des distributions à des distributions gaussiennes. Il est montré que la transformation en logarithme en rendant le speckle additif permet d utiliser des méthodes adaptées au bruit gaussien. Or le logarithme du speckle n est pas gaussien pour de faible nombre de vues, et surtout le niveau du speckle reste toujours aussi élevé, ce qui est le principal problème. Dans cette étude, les résultats ont toutefois était améliorés. Pour introduire une mesure d hétérogénéité locale dans certaines méthodes, les images transformées par le coefficient de variation sur une fenêtre 5x5, sur les données amplitudes brutes, sont utilisées. Ch 3 67
88 Apprentissage automatique, vérification Figure 3.7 : partie de l image ERS1 de Bourges, à gauche l image brute, à droite l image filtrée Classification ponctuelle Les méthodes de classification sont présentées au chapitre 2. Dans un premier temps des classifications sans prise en compte du contexte ont été effectuées Classification date à date non filtrée Le tableau 3.8 donne les taux moyens de MPCC ayant été obtenus avec chacune des 6 dates, séparément. On peut observer que ces taux sont extrêmement faibles, ce qui est normal puisque les données sont en mono-polarisation, mono-fréquence. L amélioration apportée par les coefficients de variations est en moyenne 2.5%. On remarque la légère augmentation de ces taux pour les dates correspondant aux périodes de maturité des cultures. Date d'acquisition 26-mars 30-avr 04-juin 09-juil 13-août 17-sept % Taux moyen bien classés MPCC 18,16 19,98 14,34 18,61 16,06 19,08 logarithmes des amplitudes % Taux moyen bien classés logarithmes des 24, ,73 21,5 18,03 24,33 amplitudes et coefficients de variation Tableau 3.8 : taux moyens de correctement classés par dates, avec logarithme des amplitudes et coefficients de variation Série temporelle non filtrée Le tableau 3.9 donne les taux de bien classés obtenus en ajoutant une à une chacune des dates chronologiquement. Comme dans la zone test du Sud Ouest toulousain, l apport du multitemporel est important. Toutefois avec 6 dates le taux reste trop faible (45.21%) pour ces images non filtrées. Dans Ch 3 68
89 Apprentissage automatique, vérification le tableau 3.10 sont ajoutées les images texturales obtenues par le calcul du coefficient de variation local sur un voisinage 7*7, les résultats avec les 6 dates atteignent, plus de 52%. 26-mars 26-mars 26-mars 26-mars 26-mars 26-mars 30-avr 30-avr 30-avr 30-avr 30-avr 04-juin 04-juin 04-juin 04-juin Taux de bien classés % 09-juil 09-juil 09-juil 13-août 13-août 17-sept forêt blé blé tendre mais tournesol orge colza pois trèfle prairie ray grass sol nu urbain eau MPCC Tableau 3.9 : taux de bien classés pour la suite temporelle des 6 données en logarithme 26-mars 26-mars 26-mars 26-mars 26-mars 26-mars % 30-avr 30-avr 30-avr 30-avr 30-avr Taux de bien classés PCC 04-juin 04-juin 04-juin 04-juin 09-juil 09-juil 09-juil logarithme 13-août 13-août et coefficients de variation 17-sept forêt blé blé tendre mais tournesol orge colza pois trèfle prairie ray grass sol nu urbain eau MPCC Tableau 3.10 : taux de PCC pour la suite temporelle des 6 données en logarithme, avec coefficients de variation, et éventuellement écarts type MPCC Ch 3 69
90 Apprentissage automatique, vérification Série temporelle filtrée Dés que les images sont filtrées par le LVMMSE (chapitre 2), Les résultats s approchent de ceux d une image SPOT pour atteindre avec les 6 dates 70,22% de MPCC. De plus ce filtre vectoriel avec segmentation préserve les contours 26-mars 26-mars 26-mars 26-mars 26-mars 26-mars 30-avr 30-avr 30-avr 30-avr 30-avr % 04-juin 04-juin 04-juin 04-juin Taux de bien classés 09-juil 09-juil 09-juil 13-août 13-août 17-sept forêt blé blé tendre mais tournesol orge colza pois trèfle prairie ray grass sol nu urbain eau Taux moyen de bien classés Tableau 3.11 : taux de PCC pour la suite temporelle des 6 données filtrée par le LVMMSE avec segmentation Classification contextuelle (loi de Gauss-Wishart réelle) Les méthodes contextuelles sont basées sur la distribution de Gauss-Wishart réelle. C est la distribution jointe des moyennes et matrices de covariance empiriques d une série de données gaussiennes multidimensionnelles. Cette distribution compare les statistiques calculées sur un voisinage du point avec les statistiques de chacune des classes Étude pour le choix du meilleur voisinage De nombreux tests ont été établis pour trouver la meilleure taille de la fenêtre contextuelle quand on n utilise pas la segmentation. Pour les images non filtrées le meilleur choix est 7*7, pour une taille plus grande trop de variation sont intégrée, plus de valeurs radiométriques appartiennent à des classes différentes (figure 3.12). Lorsque l image est filtrée, un voisinage 5*5 suffit, puisque le speckle est bien atténué (figure 3.13). Ch 3 70
91 Apprentissage automatique, vérification Comparaison contextuelle du % de pixels correctement classés: % de pixels correctement classés E+05 combinaison de dates (ordre chronologique) fen 1 fen 3 fen 5 fen 7 fen 9 fen 11 Figure 3.12 : variation des taux de MPCC pour la suite temporelle des 6 données en logarithme en fonction de la taille du voisinage et de l ajout des dates (1, 1+2, 1+2+3, ), fen i voisinage i*i Comparaison contextuelle du % de pixels correctement classés fen 1 % pixels correctement classés combinaisons de dates (ordre chronologique) fen 3 fen 5 fen 7 fen 9 Figure 3.13 : variation des taux de MPCC pour la suite temporelle des 6 données en filtrées (LVMMSE) en fonction de la taille du voisinage et de l ajout des dates (1, 1+2, 1+2+3, ), fen i voisinage i*i Etude multitemporelle sur les données en amplitude non filtrées avec une classification contextuelle sur un voisinage 7*7 Pour la classification (voisinage 7*7), avec des données non filtrées classées suivant les conditions d utilisation de ces données, le MPCCC varient de 70% à plus de 75% pour 6 dates. Ce qui est comparable à des données SPOT. L image est bien classée (tableau 3.14), mais le speckle est toujours présent dans la visualisation des images. L ajout de canaux texturaux (coefficient de variation) n est intéressant qu en complément lorsqu il y a peu de canaux. Pour 6 dates ils n apportent pas d élément discriminateur. Ch 3 71
92 Apprentissage automatique, vérification 26-mars 26-mars 26-mars 26-mars 26-mars 26-mars 30-avr 30-avr 30-avr 30-avr 30-avr % 04-juin 04-juin 04-juin 04-juin Taux de bien classés 09-juil 09-juil 09-juil 13-août 13-août 17-sept forêt blé blé tendre mais tournesol orge colza pois trèfle prairie ray grass sol nu urbain eau Données brutes en amplitude Données brutes en amplitude transformées en logarithme Données brutes en amplitude en logarithme + néo canal coefficient de variation Tableau 3.14 : taux de PCC pour la suite temporelle des 6 données non filtrée Le tableau 3.15 présente les taux de MPCC des combinaisons de 1, 2, 3, 4, 5, 6 dates. On peut observer des variations suivant le choix de la date liée au stade végétatif saisonnier des cultures. % de pixels correctement classés pour toutes les combinaisons de 6 dates possibles 1 date % bien classés 2 dates % bien classés 3 dates % bien classés 4 dates % bien classés 26 mars: 1 32, , , ,21 30 avril : 2 36, , , ,78 4 juin: 3 24, , , ,65 9 juillet: 4 24, , , ,47 13 août: 5 27, , , ,43 17 septem: 6 32, , , , , , ,39 5 dates % bien classés , , , , , , , , , , , , , , , , , , , , , , , , , , , , , ,07 6 dates % bien classés , , ,99 Tableau 3.15 : résumé des combinaisons des dates non filtrées en logarithme voisinage 7*7 Ch 3 72
93 Apprentissage automatique, vérification Images filtrées : classification contextuelle sur un voisinage 5*5 Différents filtres ont été testés ; le filtre LVMMSE avec la segmentation (voir chapitre 2), mis au point au CESBIO donne les meilleurs résultats. 26-mars 26-mars 26-mars 26-mars 26-mars 26-mars 30-avr 30-avr 30-avr 30-avr 30-avr % 04-juin 04-juin 04-juin 04-juin Taux de bien classés 09-juil 09-juil 09-juil 13-août 13-août 17-sept données filtrées avec smc_log données filtrées avec map données filtrées kuan données filtrées avec SMC_KUAN données filtrées avec SMC_MAP données filtrées avec LVMMSE avec segmentation données filtrées avec LVMMSE avec segmentation et transformées en logarithme Figure 3.14 : taux de PCC pour la suite temporelle des 6 données avec différents filtres La classification peut être menée par région entière (segment), les résultats sont montrés dans les figures la méthode par segments entiers est visuellement meilleure. Si l on considère le temps de calcul nécessaire pour l obtention de l image classée, la méthode par régions (segments) entiers présente un avantage certain. Un facteur supérieur à 10 existe entre le temps de calcul avec et sans segmentation. Cette dernière classification impose une segmentation plutôt fine Conclusion La présence du speckle rend nécessaire l utilisation de méthodes de filtrage, l inconvénient étant la perte de détails. Toutefois les logiciels développés permettent de garder les structures, mais des éléments très fin comme les routes à cette résolution (12,5 m* 12,5m) disparaissent. Des améliorations dans le sens détecteur de lignes, d objets sont toujours en cours. La dynamique des valeurs prises sur la végétation avec ERS1 ne permet la discrimination que de certaines classes. Toutefois, nous avons donc pu montrer que la dynamique des données ERS-1, si elles sont multitemporelles, pour une application agricole telle que celle présentée ici donne une discrimination de 13 classes de cultures ce qui est comparable aux données SPOT. La méthode la plus satisfaisante sur le plan des résultats et sur le plan de la facilité d utilisation, est celle qui utilise la loi de Gauss-Wishart réelle avec la segmentation appliquée aux segments entiers. Elle est un moyen extrêmement rapide d obtenir des résultats satisfaisants. Mais l EM (chapitre 2) donne aussi de très bons résultats (non présentés ici) Ch 3 73
94 Apprentissage automatique, vérification Figure 3.15 : classification supervisée sur la région de Bourges, en haut à gauche : classification sur les données non filtrées avec Gauss-Wishart avec une fenêtre 7*7, en haut à droite : classification des images filtrées avec Gauss-Wishart avec une fenêtre 5*5, en bas les images filtrées avec Gauss-Wishart et la segmentation Ch 3 74
95 Apprentissage automatique, vérification Repérage de communautés côtières benthiques par télédétection aéroportée a très haute résolution La Caulerpa taxifolia, algue d origine tropicale a été signalée pour la première fois dans la baie de Menton en Le Centre scientifique de Monaco, Observatoire Océanographique Européen nous a proposé d établir la cartographie de l évolution de l occupation de l'algue Caulerpa taxifolia dans la baie de Menton débouchant sur le application au suivi de l'algue Caulerpa taxifolia. Ce que nous avons fait à partir de données CASI, spectromètre imageur à très haute résolution et hyperspectral. Le projet était complexe en raison de la détection sous l eau, d où la recherche d une méthodologie spécifique. Pourquoi utiliser des méthodes de télédétection? Cela permet d avoir une image globale de la surface envahie par la Caulerpa, la surveillance des sites où Posidonia oceanica (autre plante) et C. taxifolia sont présentes en même temps, la création de cartes thématiques «objectives», l acquisition rapide de résultats. Le radiomètre canadien aéroporté CASI permet de choisir la résolution spectrale : jusqu à 288 bandes entre 403 et 914 nm (1.8 nm), et la résolution spatiale (de 0.4m à 5m sur nos images). Des classifications supervisées et non supervisées (ICM), ont permis de détecter les algues (figure 3.16). Ce qui a conduit aux questions : quels sont les canaux séparateurs? Les longueurs d ondes les plus adaptées à l étude? Particularités de l étude - Difficultés rencontrées : la taille des pixels (5 m, 2.5m,1 m et 0.5 m), la profondeur variable modifie les réponses spectrales ce qui a impliqué la nécessité d avoir beaucoup de sous-classes, de respecter la bathymétrie, les images sont très bruitées d où l utilisation de méthodes contextuelles. En conclusion : les méthodes de télédétection sont utilisables pour le suivi de l algue, la taille du pixel modifie largement les résultats de la classification, les canaux spectraux les plus adaptés à l étude sont ceux entre 400 et 550 nm Autres applications Toutes les méthodes présentées dans ce mémoire, ont été testées sur un grand nombre d images et différents capteurs tels que Landsat, Spot, Noaa, Végétation, Radar (ERS1, Radarsat) dans des zones thématiques tropicales ou tempérées (Inde, Indonésie, Thaïlande, Guyane, Nord de Toulouse, Landes, forêt de Fontaiebleau, San Francisco, Minorque, vallée de la Marne), dont voici des exemples donnés de façon non exhaustive : Classification multidimensionnelle (spectrale et texturale) des images satellite Application à la cartographie automatique de la végétation tropicale en Thaïlande, données LANDSAT Action thématique programmée (ATP) Inventaires des ressources naturelles renouvelables et de l occupation des sols. Evaluation des surfaces et des transformations forestières en cours au Sud de Sumatra, données LANDSAT Ch 3 75
96 Apprentissage automatique, vérification Figure 3.16 : détection de la Caulerpa taxifolia Ch 3 76
97 Apprentissage automatique, vérification Opération pilote Verfeil animée par le Service Statistique de la DRAF (Direction Régionale de l Agriculture et des forêts) qui a pour but l adéquation entre l occupation du sol et des terroirs (1987). Classification supervisée multispectrale, multitexturale, multitemporelle - région du Nord - Est de Toulouse, simulation du futur satellite SPOT (lancé en 1986), puis données SPOT. Mon intervention s est située au niveau de l implémentation d un nouveau logiciel et sa validation (contrat de recherche CNES : 85/CNES/5105/00/833 et contrat 833/CNES/86/4316/00) Projet de recherche n 95/CNES/0368 Evaluation des ressources végétales tropicales à partir du système SPOT 4/MIR de fin 1995 à 1998 (laboratoire d'écologie terrestre et Biotrop, Indonésie) [Trichon V., Ducrot D., Gastellu-Etchegorry J. P]. Mangrove et forêt dense en Guyane données ERS-1 [Sery, Ducrot et al 96] Programme de recherche ADRO (Application Developement and Research Opportinity) pour la promotion des données Radarsat, dont l objectif est de définir un indicateur d environnement pour évaluer la vulnérabilité du milieu naturel face à des pollutions engendrées par l activité humaine. Un indice de vulnérabilité des eaux superficielles par les produits phytosanitaires doit être déduit. Notre travail a consisté à établir des cartes de végétation par le biais de plusieurs méthodes de classification que nous avons développées, à partir des données : Radar (multitemporelles Radarsat en amplitude (non filtrées (brutes) et filtrées), optiques (multispectrales SPOT ), avec fusion Radar et optique de novembre 1997 à novembre Région du Grand Morin (vallée de la Marne) : série multitemporelle de 4 images RADARSAT de type Single Look Complex en collaboration avec Alcatel-Espace et la Sogreah de Grenoble pour la partie application [Ducrot D., Sassier H., et al]. Analyse spatiale des images satellitaires pour l'étude de la biodiversité à plusieurs échelles dans deux systèmes montagneux : les Pyrénées et insulaire : l île de Minorque, images SPOT, LANDSAT, ERS-1, ERS-2 [Chust G., Ducrot D. et al]. Etude du potentiel des données optique /radar pour la cartographie forestière au Gabon et des méthodes de classification appliquées à ces images, LANDSAT et ERS-1. Détection des changements par analyse multitemporelle d images satellites, application à une région du Danube, données LANDSAT et SPOT [Krystof D.]. Application sur des salines du désert de Monegros au sud de Sarragosse avec (CITA Centro de Invetigation y tecnologia del Gobierno de Aragon) données LANDSAT et ERS-1 [Ducrot D., Castañeda del Alamo C]. Paris : série multitemporelle de 7 images provenant du satellite ERS-1 de type Single Look Complex. Fontainebleau : série multitemporle de 6 images provenant du satellite ERS-1 de type Single Look Complex [Mougin E., Proisy C., Ducrot D., et al]. Forêt d Haguenau Alsace : afin d étudier le potentiel de l imagerie radar sur la forêt, image à très haute résolution spatiale, images émulées Pleïades, 1m en azimut, 1m en distance, bande X, fournies par le CNES (voir figure A.1 en annexe), divers traitements ont été réalisés sur des images de la forêt d Haguenau (Alsace). On pu discriminer deux classes agricoles et une classes de forêt, plus du bâti/minéral. Ces traitements sont une amorce pour les futurs traitements des images radar à très haute résolution. Voir communications et publications dans la bibliographie pour ces applications. Ch 3 77
98 Apprentissage automatique, vérification Conclusion sur l analyse multitemporelle Après un grand nombre d études chronologiques, on obtient toujours une asymptote temporelle (figure 3.16) où le pourcentage de pixels correctement classés en fonction du nombre de dates croit asymptotiquement quelque soit le type de capteur, pour atteindre un plateau à 6 dates, ceci se retrouve pour les images optique et radar. % de pixels correctement classés nb de dates Figure 3.17 : évolution du MPCC en fonction du nombre de dates croissantes. L exemple (figure 3.17) avec l ajout chronologique d image monotemporelle ERS1 résume bien cette courbe. Après 6 dates ont arrive sur un plateau, la croissance des biens classés est négligeable. Ce résultat est similaire avec les images SPOT de la région Sud Ouest toulousain, et les autres applications citées précédemment. 80 % pixels correctement classés min max moy combinaison min max moyenne 1 date 24,2 36,39 29,712 2 dates 35,62 49,29 45,546 3 dates 48,24 61,38 57,126 4 dates 54,39 67,54 64,213 5 dates 68,25 72,41 70,41 6 dates 74,78 74,78 74,78 nombres de dates (combinaisons) Figure 3.18 : les combinaisons (les traits verticaux représentent les valeurs minimum et maximum suivant les dates) Ch 3 78
99 Apprentissage automatique, vérification ANNEXE Figure A.1 : en haut, image très haute résolution spatiale, émulée Pleïades, 1m en azimut, 1m en distance, fournies par le CNES, de la forêt d Haguenau Alsace. En bas classification non supervisée de la zone ;en jaune et vert deux type de territoire agricole, en vert foncé la forêt, en rouge bâti/minéral, en mauve non identifié, en noir l ombre Ch 3 79
100 Apprentissage automatique, vérification Figure 3.A.2 : résultat de la classification avec les grandes routes et le réseau hydrographique Ch 3 80
101 Chapitre 4 LA FUSION, L INCERTAIN, LE POSSIBLE
102
103 Chapitre 4 LA FUSION, l incertain, le possible Introduction Grâce à l évolution des techniques d acquisition, les données de télédétection contiennent de plus en plus d informations. Pour bien comprendre l intérêt fondamental de la fusion de données, rappelons la diversité des données utilisées (chapitre 2) en traitement d images de télédétection : images optiques et radar, basse, haute, très haute résolution, hyperspectral, images dérivées (images texturales, images masques), données exogènes telles que M.N.T, S.I.G, données physiques. Ces dernières informations permettent d apporter des éléments discriminatoires supplémentaires. Les capteurs optiques et les capteurs radar ne sont pas sensibles aux mêmes informations. La figure 4.1 montre la différence entre l image SPOT (partie supérieure) et l image radar (RSO). Les parcelles se distinguent mieux sur SPOT contrairement à ERS 1 où l information radiométrique est très hétérogène. Toutefois l insensibilité de l acquisition radar aux conditions atmosphériques reste un avantage majeur. Nous pouvons exploiter la complémentarité de ces données afin d extraire une information plus complète, et permettre une meilleure distinction des différentes classes. Le traitement, l analyse et l intégration de ces données pose des problèmes particuliers, et exige l utilisation de méthodes spécifiques. Ces informations sont pour la plupart imparfaites c est à dire incertaines, imprécises, incomplètes, voire erronées. Les erreurs sont situées à toutes les étapes de la chaîne des traitements des images : du phénomène observé, du capteur, des traitements de corrections, géométriques, radiométriques, au niveau du géoréférencement (on observe un décalage selon les dates un décalage de 1 à 4 pixels, voir chapitre 6), les coordonnées planes des cartes (en Lambert pour la France) sont approximatives suivant les endroits (projection conique). On peut avoir des «mixels», pixels mixtes, principalement en bordure des frontières. Certaines classes ont des valeurs radiométriques identiques dans certains canaux, parfois dans tous les canaux (maïs et sorgho), donc indifférentiables. Ces caractéristiques de l information sont toujours présentes dans l image. Malgré le manque d exactitude on est amené à prendre des décisions : affecter les pixels à des classes. Pour que cette décision soit rationnelle et cohérente il faut prendre en compte ces imprécisions et incertitudes. Ch 4 81
104 La fusion, l incertain, le possible Définition de la fusion La fusion est l utilisation conjointe d images hétérogènes pour l aide à la prise de décision [Bloch & Maitre1994]. Le terme de fusion est employé lorsqu il n est pas possible de trouver une métrique permettant de traiter en parallèle toutes les images, quelque soit leur source, comme pour les classifications multispectrales. La fusion est particulièrement intéressante dans le cas de données imparfaites afin d obtenir une information plus fiable. Le but est de combiner les informations issues des différentes sources (capteurs, multitemporel,...) pour décider de l'appartenance d'une information à une classe d'objets et d'extraire l'information la plus fiable et exacte possible. C'est cette étape qui constitue à proprement parler la fusion des images. La fusion est utilisée dans ce document, dans le sens de combinaison d informations, ce qui nécessite dans un premier temps de quantifier la pertinence de l information issue des données fournies par les différents capteurs. Elle intervient dans plusieurs étapes du système d analyse des images. Plusieurs méthodes de fusion ont été développées suivant leur utilisation, ou introduites dans la classification, à partir des concepts : logique flou, théorie des possibilités, méthode bayésienne, champs markoviens, théorie de l évidence, et au niveau pré- ou postclassification. Dans ce dernier cas les classifications peuvent être réalisées indépendamment les unes des autres puis fusionnées. Ces techniques sont également utilisées au niveau de l interprétation automatique (chapitre 6). Figure 4.1 : images SPOT (partie supérieure) et Radar ERS1 sur une même zone (près de Bourges) Ch 4 82
105 La fusion, l incertain, le possible Modélisation de la fusion Soient p images représentant des données hétérogènes. Soit x l'élément sur lequel porte la décision. Il peut s'agir d'un pixel, ou de tout autre objet plus complexe extrait de l image. La décision consiste à lui affecter un élément C i de l'espace de décision θ= {C 1,.., C n } [Bloch 96, Le Hégarat-Mascle et al 97]. Les C i représente les décisions possibles, en l'occurrence l'appartenance à une classe ou non. La décision est prise par l'intermédiaire de "mesures" M j i (x) reliant des informations sur x extraites de l'image Ij à une décision potentielle C i. Ces mesures ont des interprétations différentes et prennent des formes mathématiques variées selon les cadres théoriques employés pour cette fusion (maximum de vraisemblance, distance, degré d appartenance...). C 1 M 1 1 C 2 M 2 1 I 1 I 2 I p M 1 2 M 2 2 M 1 p M 2 p C n 1 M n 2 M n 2 M n Tableau 4.1 : informations à fusionner - mesures des p images relatives aux n classes Les différents modèles : La décision est prise à partir des mesures M j complètes, mesures reliant i ( x) toutes les images à toutes les classes. Ce modèle ne néglige aucune information ce qui le rend complexe. La prise de décision est dans un premier temps locale dans le sens où elle s effectue sur chaque image séparément. Puis dans un second temps on fusionne les décisions locales en une décision globale. Ce modèle est idéal si les images ne sont pas disponibles simultanément, son principal inconvénient est qu il ne tient pas compte des relations entre capteur, des corrélations et/ou dépendance entre images et de plus peut conduire à des décisions locales contradictoires. La décision est prise après combinaison de toutes mesures, relative à la décision, issues de toutes les images. Ce modèle nécessite de disposer de toutes les images en même temps. Un modèle hybride, choisi les informations nécessaires pour un problème en fonction des spécificités des images. Copiant l expert humain il est utilisé dans les systèmes de fusion à base de règles. Notion d incertitude et de précision : ce sont deux notions qui doivent être intégrées dans le raisonnement qui conduira ensuite à la décision. Il ne faut pas confondre ces deux termes. L imprécision concerne le contenu de l information et porte sur un défaut quantitatif de connaissance tandis que l incertitude est relative à la réalité d une information. On dit qu'un événement est incertain si sa probabilité n'est ni égale à 1 ni à 0 (pour 0 il est certain de ne pas être) donc comprise entre 0 et 1 (avec 0 et 1 exclus). L imprécision concerne l erreur sur la mesure des M i j (x). Cependant, il peut y avoir une imprécision sur la mesure de sa probabilité, une mesure est imprécise si l'erreur sur sa valeur n'est pas nulle. M n p Ch 4 83
106 La fusion, l incertain, le possible Il conviendra donc que le système de décision liée à la fusion gère explicitement incertitude et imprécision pour éviter les incohérences d images [Bloch 93]. L'étape de modélisation concerne le passage d'informations extraites des images à une représentation mathématique liée à une théorie particulière. Les principales approches de la fusion de données sont les méthodes probabilistes de type bayésien (les plus anciennes), la théorie des ensembles flous, puis la théorie des possibilités introduites par Zadeh [Zadeh 65, 78, Dubois & Prades 88, 94] et la théorie des croyances de Dempster-Schafer (d abord Dempster (1960) puis reformalisée par Shafer (1976)) appelée également théorie de l évidence, utilisée récemment dans le domaine du traitement d'image Modèles probabilistes et bayésiens : La fusion selon la théorie Bayésienne Les méthodes probabilistes sont largement répandues. Elles caractérisent l incertitude et assez difficilement l imprécision, elles conduisent donc souvent à confondre ces deux notions. De plus, lors de l'apprentissage, des contraintes assez strictes doivent être vérifiées par les mesures, ce qui peut rendre leur mise en œuvre délicate. Les probabilités bayésiennes sont un outil puissant, trop pour pouvoir exprimer fidèlement des informations pauvres reflétant une ignorance partielle. La méthode bayésienne permet de faire la combinaison des informations de manière associative sur l'ensemble des logiques : conjonction, disjonction et moyennes. L'information y est modélisée par une probabilité conditionnelle, par exemple, la probabilité pour qu'un pixel appartienne à une classe particulière. Ainsi la mesure s'écrit : M j i ( x) = p( x C I ) Cette probabilité est calculée à partir des caractéristiques de l'information extraite des images. La fusion est effectuée grâce à la règle de Bayes. Il faut calculer p(x C i I 1,,I l ) : p ( x C I, L, I ) p i j ( I, L, I x C ) p( x C ) 1 l i i i 1 l =, p( I1, L, I l ) Ce qui nécessite l'estimation des probabilités. Les différents termes sont estimés par apprentissage (supervisé ou aléatoire) (voir chapitre 2). Probabilités conditionnelles des informations multicapteurs : dans le cas gaussien, les valeurs des covariances expriment la liaison entre les images. Modélisation par les champs de Markov : présentée dans le chapitre 2, elle permet d'intégrer l'hypothèse de dépendance spatiale et contextuelle propre aux images et aux bases de données. Elle régularise les informations contradictoires. Ch 4 84
107 La fusion, l incertain, le possible Modèles flous, le raisonnement, le plausible, le possible Les approches du raisonnement automatique utilisé en intelligence artificielle fournissent un cadre pour l utilisation de ces données imparfaites. L automatisation des processus devient essentielle pour modéliser la connaissance de l expert. La logique floue (Zadeh 1965) excelle dans la représentation de connaissances imprécises ou incomplètes. La logique floue a été introduite pour pallier certaines difficultés liées à l'utilisation d'interprétation binaire dans la logique des prédicats : son utilisation dans les systèmes experts a permis de dépasser la logique binaire du tout ou rien. Par ailleurs elle permet de s'affranchir en partie des incohérences ou inconsistance de l'expertise. Elle peut manipuler des propositions non claires, plusieurs interprétations des assertions peuvent exister simultanément et sont donc équivoques. La théorie des ensembles flous est non probabiliste et fournit un bon outil pour représenter des informations imprécises, sous la forme de fonction d'appartenances. La mesure prend la forme : M j ( x) ( x) =, j i µ i où µ ( x) désigne par exemple le degré d'appartenance de x à la classe Ci selon l'image I j. j i L'inconvénient des ensembles flous est qu'ils représentent essentiellement le caractère imprécis des informations, l'incertitude n'étant accessible que par déduction. On a également la notion d appartenance partielle. Elle constitue l interface commode pour la modélisation du langage naturel, comme les concepts linguistiques utilisés par les experts tels que : grand, moyen, petit, ainsi les ensembles flous peuvent être interprétés en termes linguistiques. Le système permet d assigner aux variables linguistiques un nom et de définir ses fonctions d'appartenance. Les fonctions d'appartenance possèdent également des noms. Par exemple, la variable "hétérogénéité" peut avoir des fonctions d'appartenance appelées "pas hétérogène", "peu hétérogène", "moyennement hétérogène", "hétérogène" ou "très hétérogène". Chaque fonction d'appartenance est tracée comme un graphique donnant le degré d'appartenance satisfaisant aux concepts de "pas", "peu", "moyennement", etc. La logique floue réalise des opérations logiques sur des degrés d'appartenance plutôt que sur des "0" et des "1". La base du raisonnement est l induction représentée dans sa plus simple expression par l expression logique «si prémisse alors conclusion». Les règles de type ET, OU peuvent être combinées. Elle permet d'exprimer des concepts du type : «si la température est très élevée, alors refroidir beaucoup». Une fois que les variables sont définies, il faut les combiner en règles logiques de la forme : «si l altitude est élevée et si la surface est verte alors pelouse». Les valeurs actuelles de l altitude élevée et de couleur de la surface (valeur radiométrique) déterminent la classe Prairie. Au chapitre 5 nous utiliserons ce concept pour l analyse de paysage, où les descripteurs doivent être combinés. Il existe aussi un choix de méthodes d'inférence incluant la méthode MIN-MAX (si des valeurs sont comprises dans un intervalle de valeurs minimum et maximum). Plusieurs facteurs peuvent être pris en compte dans la façon de réguler l appartenance d un pixel à une Ch 4 85
108 La fusion, l incertain, le possible classe. Parmi eux, citons les valeurs radiométriques dans les canaux spectraux, temporels, le relief, les régions (zones prédéterminées de l image). On peut introduire la notion le degré de confiance donné par chaque règle. Par exemple il peut être inférieur à 100 %. Une règle donne une valeur a = 50 avec un taux de "confiance" de 25% tandis que la seconde règle propose une valeur b = 90 avec un taux de 75 %. Cette dernière règle devra ainsi avoir plus d'influence dans la décision finale mais la première règle y contribuera également. La méthode moyenne les deux valeurs en les pondérant par les taux de confiance respectifs. On obtient la valeur finale grâce au calcul suivant : [(50 x 0,25) + (90 x 0,75)] / (0,25 + 0,75) = 80 La moyenne pondérée mesure un degré de préférence, mais elle est insuffisante pour obtenir la valeur vraie dans un ensemble de valeurs possibles. Le consensus par moyennes pondérées de probabilités (ou autre mesure) est un inconvénient quand il s agit d agréger des opinions conflictuelles : l une des sources affirme que le pixel x C1 et l autre que x C2 La théorie des possibilités dérive de celle des ensembles flous, elle permet de représenter à la fois l'imprécision et l'incertitude. Soit p x (s) le degré de possibilité pour que x vaille s, p x (s) = 0 si c est impossible que x vaille s, p x (s) =1, rien n empêche que x vaille s. La vraie valeur de x existe, mais n est pas connue. Une distribution des possibilités P est une fonction d appartenance à un certain ensemble flou. La possibilité P et la nécessité N (degré de nécessité (certitude)) sont des cas particuliers de la plausibilité et de la crédibilité (voir théorie de l évidence ci-après). P(A) = sup {p(s), s A} N (A) = inf { 1 - p(s), s A} = 1 P (A c ) où A c est le complémentaire de A N (A) = 1 P (A c ) c est à dire que x A est certain si et seulement si x A est impossible N (A B) = min [N(B)] Ce qui remplace p (A B) = p(a) + P(B) P(A B) Pour 2 sources fiables N (A) = 1. Pour plus de détails on pourra consulter [Dubois & Prades de 1988 à 1997] Une technique d analyse courante en théorie des possibilités est l utilisation d arbres de décisions. L arbre est un sous espaces des règles possibles, il sera utilisé au chapitre 5. La logique floue et la théorie des possibilités s'avère plus efficace que les méthodes traditionnelles : pour les systèmes complexes dans lesquels la modélisation est difficile, voire impossible, pour les systèmes contrôlés par des experts humains, de nombreuses entrées/sorties continues ou discontinues et des réponses non linéaires, quand l'observation humaine est à l'origine d'entrées ou de règles de contrôle du système, Ce qui est le cas pour certains traitements présentées dans ce mémoire. Ch 4 86
109 La fusion, l incertain, le possible Modélisation avec la théorie des croyances de Dempster et Shafer La théorie des croyances ("théorie de l'évidence" ou "théorie de Dempster Shafer") modélise l'ignorance et l information manquante, c'est-à-dire : à la fois "l'imprécision" et "l'incertitude" qui intervient lors de l'attribution d'un pixel à une classe, en fournissant des mesures explicites de l'imprécision et du conflit entre les informations des différentes sources qui peuvent conduire à des décisions contradictoires. La théorie de l évidence suppose d abord un ensemble de définitions ou d hypothèses, pour un problème traité (le cadre d intérêt ou de discernement), qui sont exhaustives et exclusives, l une d entre elle étant susceptible d être la solution du problème. Pour notre problématique les hypothèses seront l appartenance à une classe C i ou encore l appartenance des valeurs d une classe à un intervalle radiométrique ou textural. Soit l ensemble θ des N hypothèses simples (singletons) correspondant en classification d'images aux classes possibles. On pose θ le nombre de singleton de θ et on note 2 θ l'ensemble des sous-ensembles de θ, il est de cardinal 2 θ. Dans le cas général (N classes) { A A θ } = { H,.., H N, H,.., θ } θ H 2 = avec = {,.., } θ H1 H N les 2 N 1 sousensembles A de θ qui servent de référence pour l ensemble des grandeurs utilisées par la théorie de l évidence pour évaluer les propositions A (événement ou hypothèse A, appartenance à une classe C i ). Ces hypothèses ou propositions A peuvent être singulières (singletons) : correspondant à l hypothèse simple «d appartenir à une classe C i» (comme dans la théorie bayésienne), ou à l hypothèse double B avec B A (doubletons) correspondant à l hypothèse «d appartenir à une classe Ci ou C j», aux hypothèses généralement multiples. Ces dernières hypothèses sont l avantage majeur de cette théorie qui la différencie de la théorie bayésienne. Des fonctions de masses m j sur les singletons sont calculées à partir des mesures m j ( C ) M ( x) j i = i Les M i j (x) sont estimées comme une mesure d'un des autres principes exposés ci-dessus (probabilité, degré d'appartenance ou de possibilité). Il reste à répartir les masses sur les hypothèses composées. Cette théorie présente de nombreux avantages : une modélisation très souple de l'ambiguïté ou de l'hésitation entre classe, une mesure explicite de l'ignorance que l'on a sur un événement A et son complémentaire. Elle permet de fusionner les avis des différents experts en prenant compte les incertitudes et imprécisions si ces dernières ont été quantifiées par des fonctions d attributions de masse de croyances. Elle associe à chaque pixel ou objet - un degré de croyance vis à vis de son appartenance à l une des classes - un degré d ignorance quand à son affectation aux classes de θ Ch 4 87
110 La fusion, l incertain, le possible Exemple : On considère le cas de six classes (C 1 à C 6 ) et de deux capteurs S 1, S 2 : C 1, C 2, C 3, C 4, C 5, C 6 S 1 est capable de bien distinguer C 1, C 2, C 3, C 4, mais C 4 recouvre C 6 et C 1 recouvre C 5 S 2 est capable de distinguer C 3, C 4, C5, C 6, mais C 5 recouvre C 1 et C 2 recouvre C 3. Image issue de S 1 Image issue de S 2 Image finale possible obtenue après la fusion image 1 + image 2, en fonction des calculs des masses, ou des degrés de confiance. Ci-dessous nous présentons un autre exemple pouvant correspondre à des classifications non supervisées obtenus à deux dates différentes, où l on peut voir de nouvelles classes définies avec l intersection des deux images, avec peut être un degré d incertitude non négligeable. L'ensemble des singletons à considérer est l'ensemble des intersections non vides entre les classes des différentes images. Les mélanges de classes sont plus complexes. Image issue de S 1 Image issue de S 2 Fusion image 1 + image 2 Images finales possibles en fonction des règles choisies Ch 4 88
111 La fusion, l incertain, le possible Dans la première image deux nouvelles classes ont été reconnues, elles peuvent correspondre à des doubletons C 1 C4 ou C 4 C 5 et C 1 C 2 ou C 5 C 2 Dans l'exemple:θ = C 1 C 2 C 3 C 4 C 5 C 6 où C 1, C 2 C 3, C 4, C 5 et C 6 sont les hypothèses simples. 2 θ possède les 2 6 = 64 éléments suivant :, C 1, C 2, C 3, C 1 C 2, C 1 C 3, C 2 C 3..., C 1 C 2 C3..., ainsi de suite et θ = C 1 C 2 C 3 C 4 C 5 C 6 c'est-à-dire : l'ensemble vide, les hypothèses simples et les hypothèses composées. Définition des fonctions "masse", "plausibilité" et "croyance" Dans la théorie de l évidence trois grandeurs sont définies la "plausibilité" (Pl) et la "croyance" (Cr) qui dérivent toutes deux de la fonction "masse" (m).: La fonction "masse" m : la masse élémentaire de probabilité représente la partie du degré de croyance placée exactement sur la proposition A, est définie pour chaque élément A sur 2 θ dans [0;1] de manière à vérifier pour toute hypothèse A de 2 θ : m( )=0 et m( A) = 1 où est l ensemble vide. A θ Les masses correspondant aux hypothèses simples expriment la certitude d une classe par rapport aux autres et les masses correspondant aux hypothèses composées expriment la confusion associée au manque d information pour décider entre une classe ou une autre. L évaluation conjointe d ensembles (doubletons) quelconques de ces singletons confère une grande souplesse de représentation qui permet de modéliser rigoureusement l ignorance totale par le jeu de masses. La croyance (ou crédibilité) Cr mesure à quel point les informations données par une source soutiennent la proposition A, (la force avec laquelle on croit à la véracité de la proposition). Cr est définie de 2 θ dans [0;1] telle que pour toute hypothèse A de 2 θ : Cr (A) = m ( B) B A C'est la somme des masses des hypothèses incluses dans A. La plausibilité Pl mesure toute l intensité avec laquelle on ne doute pas de la proposition A, c est à dire avec laquelle on trouve A plausible, fonction duale de Cr. Pl est définie de 2 θ dans [0 ; 1] telle que pour toute hypothèse A de 2 θ : Pl (A) = m( B) = 1 - Cr ( A ) BI A Si l'on affecte des masses uniquement aux hypothèses simples (m(a)=0 pour card(a)>1), alors les trois fonctions m, Cr, Pl sont égales et sont une probabilité. L'incertitude sur A est représentée par l'ensemble des valeurs de l'intervalle [Cr(A),Pls(A)]. Cet intervalle est appelé l'intervalle de croyance et sa longueur représente l'imprécision sur la mesure de l'incertitude [Shaffer 76, Le Hegarat 97, Smets 93]. Dans le cadre de la théorie Bayésienne l'incertitude sur un événement est mesurée par une valeur unique : sa probabilité et l'imprécision sur cette mesure est supposée nulle. Ch 4 89
112 La fusion, l incertain, le possible Avec la théorie des croyances, la croyance (Cr) sur une hypothèse A peut être interprétée comme l'incertitude minimum sur A ou mesure de sa vraisemblance minimale, tandis que la plausibilité (Pl) de A peut être interprétée comme l'incertitude maximum sur A ou mesure de sa vraisemblance maximale. Sa différence donne l ignorance relative à cet événement. La théorie bayésienne est limitée puisqu elle ne prend pas en compte l'ignorance et l imprécision, de plus elle est contraignante puisqu'elle nécessite la connaissance de la distribution des classes et de leur probabilité a priori. Ainsi, elle peut être vue comme une limite de la théorie de l évidence s il n'y a pas d'imprécision, supposée nulle, et où seule l'incertitude sur un événement est considérée et mesurée par une valeur unique : sa probabilité qui représente la partie du degré de croyance placée exactement sur l hypothèse (avoir la classe Ci). Nous avons vu que la théorie de Dempster-Shafer ne porte pas uniquement sur les singletons (C i, "avoir la classe C i ") mais sur tous les sous-ensembles de l'espace de discernement θ. Règle de Dempster La combinaison des données dans la théorie de l évidence est faite selon la loi de combinaison orthogonale de Dempster [Shaffer 76]. Cette loi suppose que les observations soient indépendantes. Elle a pour effet de renforcer la croyance sur les événements pour lesquels les différentes sources, sont concordantes et au contraire de l atténuer en cas de conflit. Elle permet de redistribuer les différentes masses potentielles selon le consensus général. La sommation orthogonale est équivalente à faire une intersection des classes entre sources différentes et à déterminer, selon les masses élémentaires, si cette intersection est suffisamment importante pour supprimer la balance d une classe vers une classe. Il semble correct d'affecter une masse nulle aux hypothèses qui unissent des classes totalement séparables. En effet, cela signifie que l'ignorance sur ces deux classes est nulle, ce qui est parfaitement acceptable. En revanche, si deux classes C i, C j ne sont pas séparables pour une même source, la masse de leur union sera non nulle. Critère de décision Il est nécessaire de définir un critère de décision, afin de sélectionner l'hypothèse la plus réaliste. Généralement le choix de ce critère est dépendant de l'application, on utilise le plus souvent : - La maximisation de la plausibilité. - La maximisation de la croyance. - La maximisation de la croyance sous condition de non recouvrement des intervalles de croyance. - On peut aussi utiliser des compromis comme la maximisation de Cr(A) +Pls(A) Remarque: La règle de maximisation de la croyance est la plus utilisée et se fait souvent sur les hypothèses simples. Ch 4 90
113 La fusion, l incertain, le possible Application à la classification : les différentes approches mises en place La fusion s'impose pour regrouper les informations disponibles à partir des images de sources différentes qui peuvent être des données issues de capteurs différents, de bandes spectrales ou temporelles différentes, mais aussi des données exogènes, une base de donnée (SIG), des information données par l expert. Dans le chapitre 3, on montre que l on peut faire beaucoup de combinaisons de canaux qui apportent des informations différentes, pas forcément fausses, et donnent des résultats différents qui peuvent aboutir à des conclusions contradictoires. Des classifications peuvent être obtenues avec des lois différentes, les résultats obtenus ne sont plus comparables. Les modèles de fusion sont particulièrement appropriés pour gérer ces informations. En pratique la fusion n est pas un problème simple. Les sources apportent des informations souvent imprécises, contradictoires. Le problème du recalage se pose, sa qualité n étant pas toujours parfaite, il ajoute une imprécision. Il s agit alors de tenir compte du degré de fiabilité que l on accorde aux différentes sources. Dans les méthodes de classification classique, une classe est forcément attribuée au point en fonction d une décision qui suppose un certain coût d erreur sur cette décision, mais on peut choisir de ne pas décider : alors, un point peut appartenir à plusieurs classes. Le problème consiste à recouper des informations afin d obtenir des plages de consensus. Plus ces plages de consensus sont étendues, plus ces informations sont concordantes. Par contre lors d informations conflictuelles, on peut s accorder à dire qu une des sources est fausses, je préfère dire mal exploitée. Deux sources jugées concordantes et dépendantes ne doivent pas compter pour deux. Lorsqu une source est jugée plus fiable qu une autre elle doit être prioritaire dans le cas de conflit par rapport à l autre. Dans le cas d informations reçues en parallèle, on parlera de révision lorsque le changement de la source originel est minimal, on donne la priorité à un nouvel élément d information. On introduit des poids sur l appartenance possible du point à chaque classe. Par exemple, un point aura un poids de 0.6 d appartenir à la classe i et un poids 0.4 à la classe j. Les poids varient de 0 (n appartient pas à la classe) à 1 (appartenance totale). D autres règles de classification pourront éventuellement départager les classes. Dans la méthode implantée, la fusion de données peut se faire à différentes étapes qui concernent des types différents de données : Etape A : fusion au niveau classification (méthode présentée au chapitre 2) avant le calcul des probabilités, utilisation des données exogènes, ou images dérivées, les classes possibles sont recherchées. Le calcul des probabilités, étape B, ne se fera que sur les classes possibles. Etape B : fusion au niveau classification pour le calcul des probabilités : données multisources (lots), les classifications sont faite, indépendamment, puis fusion des lots, lois différentes. Etape C : fusion au niveau post-classification, concerne la fusion de classifications, peut se faire dans la classification après l obtention des classifications pour chaque lot ou après la classification finale, avec des classifications réalisées dans diverses conditions. Ch 4 91
114 La fusion, l incertain, le possible Etape A : fusion au niveau classification avant le calcul des probabilités Introduction Cette partie est basée sur les possibilités. A priori, toutes les classes sont possibles. On se propose de réduire le domaines des possibles, par l utilisation de valeurs minimales et maximales obtenues à partir d échantillons donnés par l expert par le biais des vérités terrain, ou d informations exogènes. Dans la méthode développée certains types d images permettent de ne garder que les classes possibles, de choisir les canaux à exclure lorsque le pixel présente des valeurs spécifiques données par l expert. Ceci peut conduire à éliminer les nuages des images optiques, l «ombre radar» des images RSO, de n utiliser que certaine canaux discriminant particulièrement bien certaines classes,. Dans le cas supervisé, il très souvent difficile de choisir les échantillons, pour qu ils soient représentatifs de la classe, les campagnes terrain sont souvent dans des conditions malaisées. Les objets contenus dans l image sont soumis à des variations, suivant les années, d ordre climatique, des habitudes culturales différentes pour une même espèce : on ne plante pas au même moment. Ainsi, dans une même classe il peut y avoir beaucoup de variations. La décision de l appartenance à une classe est toujours très incertaine. Il existe une «chance» plus ou moins forte que ce soit à une classe plutôt qu à une autre. Dépendance et fiabilité doivent être prise en compte. Si une source est jugée plus fiable qu une autre, elle doit être prioritaire Elimination de classes candidates Ce principe est utilisé surtout pour les canaux texturaux, des données SIG ou MNT, mais également pour les canaux spectraux. L élimination de classes s effectue sur l appartenance ou la non appartenance à un intervalle (bornes inf et sup) correspondants aux valeurs de la classe. Au cours de la classification si la classe trouvée pour x est C1 pour la source 1, C2 pour la source 2 et ainsi de suite, les classes possibles sont C1, C2, C3.. On ne peut pas dire qu une source est défaillante, car chaque source présente un aspect de l objet x. Aucune ne sont rejetée, il faut trouver la caractéristique qui va les départager, certaines sources peuvent être pondérées. La valeur du pixel est testée successivement dans tous les canaux afin de contrôler s il est contenu dans l intervalle donné et appartient donc à une classe ; sinon il est éliminé de cette classe. Ceci revient à éliminer pour chaque pixel, les classes candidates dont la valeur du pixel à classer n est pas contenue dans l intervalle [Minimum, Maximum]. Les valeurs minimales et maximales peuvent être données par l expert, par la base de connaissance, ou calculées. C est un fonctionnement tout ou rien : soit la classe peut être choisie soit non. On réduit ainsi le nombre de classes pour le calcul des probabilités mais si la réduction est trop forte, des pixels non classés risque d apparaître. L intervalle peut être calculé à partir des pixels répertoriés dans l image des échantillons, mais ils ne sont pas toujours tous représentatifs de la population d une classe, ce qui amène Ch 4 92
115 La fusion, l incertain, le possible une imprécision supplémentaire. C est alors que qu une fonction linéaire remplace l intervalle strict, afin d introduire un degré d appartenance dés que la condition devient imprécise. x min-ext min max max-ext Exemple : Figure 4.2 : application d une fonction linéaire, principe du degré d appartenance Dans la figure 4.2, le degré de d appartenance de x est une fonction µ(x) telle que : 0 µ(x) 1 Ainsi dans un canal, pour une classe, les valeurs minimales et maximales possibles sont : min = 120 et max = 150 (figure 4.2), pour les valeurs comprises entre ces bornes, le degré d appartenance est 1, mais au delà, il y a une incertitude, le degré d appartenance décroît plus on s éloigne de la borne Les canaux non discriminants Le principe précédent est également appliqué aux canaux eux même. Les canaux sont éliminés pour une classe quand ils ne sont pas discriminants pour celle-ci. Si un canal j n apporte pas d information pertinente pour une classe i, l information apportée par le canal j à la classe i est totalement incertaine, voire impossible. Si ce fait est connu d avance, le canal est alors éliminé pour la discrimination de cette classe, c est à dire qu il n est pas pris en compte pour cette classe. Ainsi lors de l apprentissage et de la classification, seuls les canaux souhaités seront utilisés. La connaissance de l existence d un canal non discriminant peut se faire à deux niveaux : Ceux connus de l utilisateur : utilisation d un canal d information tel qu un canal représentant des SIG, MNT, bathymétrie, ou un canal textural. Certaines classes dans certains canaux sont plus ou moins hétérogènes (tableau 4.2) : par exemple, l agglomération est très hétérogène, elle a un coefficient de variation en général très élevé. Coefficient de variation σ µ Agglomérations Forêts Champs Texture très hétérogène Texture hétérogène Texture homogène σ µ > 067 σ σ 055. < < 067. µ µ < 055 Tableau 4.2 : exemple de degré d hétérogénéité Ch 4 93
116 La fusion, l incertain, le possible Pour l étude sur l île de Minorque ( 4.7.2) un modèle numérique de terrain (MNT) qui représente l altitude, allant par palier du niveau de la mer (0) au point culminant de l île, a été pris en compte. Les résultats obtenus ont été satisfaisants, en moyenne la classification s améliore d environ 3% en terme de MPCC. Ceux détectés par le programme : dans certains cas la matrice de covariance nécessaire au calcul de probabilité peut être singulière, le canal qui pose problème pour la classe est éliminé (voir chapitre 2, ) Région Le principe est d introduire des connaissances a priori de l expert dans certaines parties de l image, ainsi dans la région k, la classe i est très présente, elle sera donc favorisée ; par contre la classe j est inexistante, elle sera au contraire défavorisée, elle pourra avoir un degré d appartenance nul. Ces informations sont données par classe, par l expert et associées aux régions introduites sous forme d image, les étiquettes représentant les régions (figure 6.5 chapitre 6). L introduction de renseignements dans la classification tel que, la distance à la côte (océan) permet d éliminer des confusions entre classes : à partir d une certaine distance à la côte il ne peut plus y avoir de mangrove, par exemple. Ceci est proche du raisonnement avec les MNT. La mangrove peut également être donnée dans une région Masque Quand on effectue une classification sur plusieurs canaux (qui se différentient de part leur provenance ou leur date d acquisition), il faut donc s assurer que chaque pixel est défini par une information significative sur chaque canal. Par exemple dans le cas où les images sont multitemporelles, après un recalage, les images ont des parties de l image qui ne contiennent aucune information radiométrique, ces parties peuvent être masquées (figure 4.3). L utilisateur détermine les zones dans lesquelles certains canaux ne doivent pas être pris en compte. Ce principe s apparente à celui des régions, mais il s applique aux canaux. L information apportée par un canal est significative d'une part si elle existe (cas cité cidessus), d autre part si elle est pertinente. Il se peut que dans une zone (exemple : mer) l'information contenue dans un canal nuise à l'analyse car elle n'est pas discriminante, elle sera donc masquée. Figure 4.3 : masque, rouge : absence d'information, vert : présence d'informations Ch 4 94
117 La fusion, l incertain, le possible Etape B : fusion au niveau du calcul des probabilités Nous pouvons exploiter la complémentarité des données optiques et radar afin d extraire une information plus riche, elle permet ainsi une meilleure distinction des différentes classes. Ce type de fusion nous permet de choisir la loi à appliquer aux différents lots d image. Niveau 1 : L approche la plus simple consiste à concaténer les données des capteurs différents comme si elles étaient issues du même capteur et donc traitées identiquement. La difficulté d une telle approche réside dans l établissement d un modèle pour ces données multi-source : la fusion par concaténation des vecteurs caractéristiques n est plus valable lorsque les différentes sources ne peuvent être décrites par un modèle commun. Niveau 2 : La fusion Bayésienne Les sources différentes induisent des traitements particuliers appropriés, par l'application d'une loi plus pertinente. Pour effectuer la combinaison des données selon la théorie de Bayes, la probabilité du modèle d observation est calculée en supposant les sources des données indépendantes et avec des lois différentes suivant le type de capteurs. En général, la loi de Gauss est choisie pour l image SPOT et la loi de Gauss-Wishart pour l image radar. Comme les lois sont différentes, les résultats obtenus ne sont plus comparables, ce qui implique des règles de fusion. La probabilité d appartenance de chaque pixel est calculée par la recherche du maximum de mesures ou de la somme des mesures (éventuellement normalisées, log vraisemblance) de chaque lot. A chaque lot est associé un poids qui donne plus d importance (crédibilité) aux résultats d un lot par rapport aux autres La probabilité (en log) ou la distance ainsi pondérée donne une mesure qui est attribuée à chaque classe. Pour tous les lots, la mesure maximale est recherchée et la classe qui correspond à cette mesure lui est associée. On peut également additionner les mesures de chaque lot. La classe choisie est celle dont la somme est la plus élevée. Niveau 3 : intersection des classes admissibles Ce procédé consiste à une prise de décision locale dans un premier temps, car elle s effectue sur chaque image séparément. Puis dans un second temps, on fusionne les décisions locales en une décision globale : à partir des classifications obtenues pour chaque source (ou lots), des mesures sur les intersections de classes entre sources sont effectuées. En fonction de ces mesures obtenues lors de la classification, on détermine la classe la plus représentative. Le degré d appartenance (ou la probabilité d appartenir) à une classe est similaire à d autres classes, la classe qui a le meilleur score est conservée, mais le 2 ième score est le plus souvent très poche. Etant donné l imprécision dans laquelle les données se trouvent, pourquoi garder une seule classe? La différence entre les n premières meilleures mesures est négligeable. Ainsi plusieurs classes sont admissibles pour un pixel, si leur mesure est acceptable (degré de confiance). Pour chaque loi, pour chaque lot, les mesures (les probabilités ou les distances suivant la méthode) sont calculées, les classes admissibles sont déterminées pour le lot, par la loi. Puis l intersection des ensembles de classes admissibles pour chaque loi, par lot est effectuée. Si l intersection est vide il faut relancer la recherche en étant moins restrictif et prendre plus de classes, ou prendre l union des classes. Ch 4 95
118 La fusion, l incertain, le possible Si l intersection ne contient qu une seule classe, c est la classe choisie. Si l intersection contient plusieurs classes, le principe du maximum de vraisemblance (log vraisemblance) sur les classes communes est appliqué avec la somme des mesures (éventuellement normalisées et pondérées) suivant la source. Comme dans le cas précédent, à chaque source peut être associée un poids qui donne plus de crédibilité à une source par rapport aux autres. Plusieurs stratégies ont été adoptées et testées. Veerrssi ioonn 11 : tri des probabilités avec pondération La méthode consiste à trier dans l'ordre des mesures, les classes obtenues pour chaque lot. Pour chaque pixel, les quatre meilleures classes de chacun des lots sont conservées. Un poids est affecté à chaque classe en fonction de son rang. Le nombre d'apparitions de chacune de ces classes est comptabilisé, et plus une classe sera bien placée dans chaque date, plus elle sera pondérée, plus elle sera privilégiée. Figure 4.4 : résultat obtenu par la méthode des poids, version 1 Exemple : le coefficient par ordre de classement est 4, 3, 2, 1 sur les 4 premières classes de chaque lot. D après le tableau 4.3, la classe 5 obtient le meilleur score, elle est donc associée au pixel étudié. Si des classes ont un même poids, la règle de décision (maximum de vraisemblance, log vraisemblance ou autre) est appliquée sur ces classes, globalement. Cette méthode permet d'accélérer la fusion des lots, mais le résultat n'est pas très satisfaisant. Des points isolés sont parsemés au niveau des contours des différentes parcelles, ce qui nous donne l'impression d'un manque de netteté (figure 4.4). Le maximum de vraisemblance est rarement exécuté, car une classe est très souvent choisie. Ce principe n est acceptable qu au cœur des zones homogènes. En revanche, beaucoup de classes «se disputent» les pixels au niveau des contours. Le choix des classes est trop rapidement et radicalement réalisé. Ch 4 96
119 La fusion, l incertain, le possible Lot 1 Lot 2 Lot 3 Meilleures classes 4, 5, 9, 3 5, 3, 9, 4 3, 5, 4, 10 Poids 4, 3, 2, 1 4, 3, 2, 1 4, 3, 2, 1 Classes présentes mesures = = = = Tableau 4.3 : mesure pour obtenir le degré d appartenance du pixel à une classe Veerrssi ioonn 22 : intersection des classes Une solution consiste à faire l intersection des classes. Au préalable, la mesure est calculée. Comme précédemment, les n (ici n = 4) meilleures classes sont choisies par sources, mais on choisit les classes communes aux sources. Source S1 S2 S3 S4 Classes possibles Tableau 4.4 : classes possibles pour un pixel (ordre croissant), dans les diverses sources (ou lots) Avec l exemple du tableau 4.4, pour les sources S1, S2, S3, S4, les classes communes sont les classes 7 et 5. La règle de décision globale se fera uniquement sur ces classes. Si une seule classe reste, c est cette classe qui sera choisie. Veerrssi ioonn 33 : intersection des classes, avec des masses Comme précédemment les n meilleures classes sont choisies par sources, mais la mesure qui leur est associée est conservée, ainsi des masses sont associées aux classes, ce sont elles qui vont déterminer la classe qui obtiendra le meilleur score (par exemple la meilleure probabilité). Source S1 S2 S3 S4 Classes possibles masse Tableau 4.5 : même exemple que 4.4 mais des masses sont associées aux classes Tableau 4.6 : préparation du cumul des probabilités de chaque classe Ch 4 97
120 La fusion, l incertain, le possible Dans le tableau 4.5 : les classes 1, 2, 3, 4, 5, 7, 8 sont possibles pour le pixel x, en faisant la somme des masses, la classe 7 obtient le meilleur score. C est cette classe qui est choisie. Veerrssi ioonn 44 : contraintes associées à une fonction d énergie sur un voisinage temporel (Markov) Au chapitre 2, les contraintes données par les fonctions potentielles au sens de Markov sont calculées par lots (dates), elles sont données pour chaque lot ou date. Pour chaque lot ou date, une masse est associée à chaque classe pour un pixel donné, puis ces masses sont additionnées comme précédemment (tableau 4.6), mais au lieu de servir d élimination des classes, la somme déduite devient la fonction potentielle appliquée dans la classification globale (fusion des lots). Le voisinage est ici temporel. Cette méthode donne de meilleurs résultats que la précédente. Veerrssi ioonn 55 : possibilités et fonctions potentielles Cet algorithme associe les deux principes : classes possibles et fonctions potentielles. La version précédente est appliquée sur l intersection des meilleures classes (celles qui ont le meilleur score) par lot. Chaque liste contient au départ la meilleure classe du lot correspondant. L'intersection des listes est calculée. Si l'intersection n'est pas vide, alors la règle de décision (maximum de vraisemblance, log vraisemblance ou autre) est appliquée pour les classes contenues dans la liste produite par l'intersection. Si l'intersection est vide, la deuxième meilleure classe est ajoutée dans chacune des listes par lot, pour lesquelles le même traitement est effectué. L'opération est répétée jusqu'à trouver une intersection non vide. Les résultats sont moins bons que ceux de la version précédente. L'intersection ne contient qu'une ou deux classes communes lorsque les dix premières classes (environ) par lot sont sélectionnées, ce n est pas suffisant. Les cultures agricoles n'ont pas la même signature spectrale toute l'année. Par exemple, le maïs est nettement reconnu en juillet. Mais au mois d'avril, comme il n'a pas encore poussé, il est identifié en tant que sol nu. Ainsi, la règle de décision n'est effectuée que pour une ou deux classes, ce qui revient au choix trop rapide de la version 1. Veerrssi ioonn 66 : union des meilleures classes à partir de l'intersection D'après les résultats des versions précédentes, il est préférable de calculer pour chaque pixel les masses (ou la probabilité) sur un nombre de classes assez grand. La quatrième version donne de bons résultats, mais il n'est pas nécessaire d'effectuer ce calcul pour toutes les classes. Le principe de l'intersection permet de déterminer pour chaque pixel le nombre minimum Nmin de classes nécessaires pour avoir au moins une classe commune parmi les meilleures. Toutes les Nmin premières classes des lots sont conservées et la règle de décision globale est exécutée pour cet ensemble de classes. Le résultat obtenu est similaire à celui de la Version 4. Le nombre de classes sélectionnées parmi les meilleures des lots est suffisant. Pour l exemple précédent, autour de 6 classes sont retenues par lot et par pixel, ce qui donne 16 classes au total. L'algorithme est plus rapide que la version 4 qui utilise toutes les classes pour la décision. Ch 4 98
121 La fusion, l incertain, le possible Veerrssi ioonn 77 : union des meilleures classes selon la distance des probabilités Cette méthode part du même principe que la version précédente, mais ici l idée est que la classe qui a le meilleur score, la plus part du temps, est très proche des suivantes du point de vue de sa mesure, et donc, dans le contexte d imprécision dans lequel se trouvent les applications, il n y a pas plus de raison de choisir la 1 ère que la 2 ième et ainsi de suite. Il est nécessaire de déterminer pour chaque pixel un nombre limite de classes à conserver parmi les meilleures afin d'avoir un résultat satisfaisant. Cette limite est cette fois calculée en fonction des mesures calculées pour chacun des lots. Par exemple, si la liste des mesures d'un lot pour un pixel donné est ordonnée dans l'ordre décroissant, on pourrait avoir par exemple [0.3865, , , , , 0.29,...]. Dans ce cas, les cinq premières classes de ce lot ont des mesures très proches, elles peuvent être sélectionnées. Le nombre limite de classes à sélectionner est déterminé grâce au seuil de distance entre la meilleure classe et les suivantes. Ce seuil est calculé de la façon suivante : µ max µmin nbclasses où µ max et µ min sont les mesures associées à chaque lot Dès que la mesure d'une classe est trop distante de la première, elle n'est pas sélectionnée dans les meilleures classes par lot. Ce traitement est effectué pour chacun des lots, puis la règle du maximum de vraisemblance est appliquée aux classes résultantes de l'union des meilleures classes de tous les lots. Exemple : Liste de probabilité ordonnée pour le lot i : [0.51, 0.5, 0.4,...] --> on garde les 2 premières classes Liste de probabilité ordonnée pour le lot j : [0.39, , , 0.388, 0.379, ] --> on garde les 5 premières classes Figure 4.5 : résultat obtenu par la méthode des poids, version 7 L'image obtenue avec cette méthode est similaire à celle de la version 4. Pour notre exemple, 13 classes en moyenne sont sélectionnées, les taux de la matrice de confusion sont semblables, plutôt supérieurs que ceux des Versions 4 et 6. Ch 4 99
122 La fusion, l incertain, le possible Matrice de transition Le but de cette méthode est d intégrer l évolution des stades phénologiques de la végétation, en utilisant ses variations saisonnières comme fonctions potentielles temporelles. Ce modèle n est valable que proche de la solution finale de la classification, car on suppose que la classification à l'itération précédente est correcte, et on en déduit le «chaînage» temporel des étiquettes. En d'autres termes, soit une classe obtenue à l itération précédente, il lui correspond à l itération courante, à chaque date, des étiquettes éventuellement différentes. Tableau 4.7 : colonne de gauche : classe affectée à l itération précédente, puis affectée à chaque date Une matrice de transitions des classes par date est calculée. C est un tableau à 3 dimensions d élément t(i,j,k) qui contient le nombre de pixel de la classe k à une date i de l itération courante et en j à la classification globale à l itération précédente. Par exemple (tableau 4.7) pour une classification de 7 dates, si un pixel a été affecté à la classe 4 «blé» à l'itération précédente, et à la classe 9 «tournesol» à la 7 ème date (septembre) on ajoutera 1 à la valeur transition [7] [4] [9]. La fonction potentielle U t est calculée de la façon suivante : Cette méthode a tendance à fusionner trop de classes (lissage trop important). Ch 4 100
123 La fusion, l incertain, le possible Etape C : post-classification De très nombreux tests ont montrés que la combinaison de tous les canaux ne donne pas forcément les meilleurs résultats. Parfois, trop d informations nuit à l information. Avec certaines combinaisons de canaux des classifications offrent de meilleurs résultats pour certaines classes, avec d autres combinaisons les résultats sont meilleurs pour d autres classes. Il est alors intéressant de combiner différentes classifications, ce qui revient à une fusion a posteriori. Ce principe est idéal si les images ne sont pas disponibles simultanément, son inconvénient majeur est qu il ne tient pas compte des relations entre capteur, des corrélations et/ou dépendance entre images. Pour améliorer les classifications d images une méthode de fusion dirigée ou automatique des images classées a été développée. Fusion dirigée Les fusions dirigées consistent à améliorer le résultat d une image classée en «combinant» des informations d une autre image classée, jugée meilleure par l expert, après observation de cette classification. Des critères de fusion donc sont imposés par l utilisateur. Des classes de la meilleure classification (Mpcc), qui ont un score insuffisant, sont remplacées par celle d une autre classification dont le score est correct. Fusion automatique La fusion automatique est réalisée à partir des matrices de confusions de chaque image classée [Chust, Ducrot 2004]. Des classifications indépendantes sont effectuées sur chacun des n lots d images, chaque lot étant choisi à une même date ou à une même saison. Une image est prise comme référence, en général c est celle dont le MPCC et le kappa sont les meilleurs. Donc cette classification est globalement la meilleure. Mais certaines classes sont mieux discriminées dans d autres classifications. Il y a conflit entre deux classes, lorsque pour un même pixel, pour deux classifications avec des combinaisons de canaux différentes, deux classes différentes lui sont attribuées. Pour lever l ambiguïté, le choix final est déterminé par la comparaison des matrices de confusion des deux images. Le principe est simple, s il y a conflit entre deux classes c est la classe qui a le meilleur MPCC dans l une des matrices de confusion qui est choisie. Soit la matrice de confusion M calculée à partir des échantillons de référence (chapitre 3). Les éléments diagonaux, mi,i représentent le pourcentage de pixels (nombre de pixels divisé par le nombre de pixels de la classe Ci) de la classe Ci ayant effectivement été affectés à celle ci, ce porcentage correspondra au degré de confiance que l on accorde à l affectation à la classe i. L'élément non diagonal mi,j est le pourcentage de pixels de la classe Ci (nombre de pixels divisé par le nombre de pixels de la classe Ci) ayant été affectés à la classe Cj. Ce sont ces éléments qui vont nous permettrent d obtenir les masses élémentaires (ou les degrés de confiance). Ainsi, si un terme diagonal mi,i correspondant à une classe Ci (hypothèse singleton) est poche de 1 cela veut dire que la classe est bien reconnue et qu il n y a donc pas d incertitude Ch 4 101
124 La fusion, l incertain, le possible (incertitude nulle), mais si mi,i a une valeur faible (inférieure à 0.5) et que la classe est confondue avec une autre classe Cj, alors le terme mi,j, différent de zéro, donne le taux de confusion entre les deux classes. Si mi,j = 0 alors les deux classes sont totalement séparables et il n y a donc pas d incertitude au sujet de ces deux classes. Figure 4.9 : Exemple simple de fusion (les masses sont en %) La somme de mi,i et mi,j est la proposition composée, on ne peut séparer ces deux classes (hypothèse doubleton), et ainsi de suite, avec d autres classes qui peuvent former des triplets, quadruplets. Alors on considère les sommes de mi,i, mi,j 1 et mi,j 2 ou mi,i, mi,j 1, mi,j 2 et mi,j 3, où j 1, j 2, j 3 sont les classes avec lesquelles i est confondue. Soit une partie de matrice de confusion obtenue à partir d une classification de la source S p i i m p ii m p ij j m p ji m p jj j Si i j =, dans S p source quelconque alors m p ij =0 et m p ji =0 (1) Cela signifie : pas de confusion entre les classes i et j, le degré de confiance est maximum sur i pour la source S p sinon x i j pixel x Sp si m p ij 0 alors il y a des confusions entre i et j, des pixels de la classe i sont affectés à la classe j si m p ji 0 alors il y a des confusions entre i et j, mais des pixels de la classe j sont affectés à la classe i L expression (1) est nécessaire et suffisante donc pour S p, i j =, m p ij =0 et m p ji =0 p quelconque Dans le cas de deux sources S k et S l, soient M Sk, M Sl les matrices de confusion correspondant aux résultats de classification de chaque source. Les sources pouvant être des Ch 4 102
125 La fusion, l incertain, le possible capteurs différents, des dates différentes ou plus généralement des combinaisons de canaux différents (spectraux, temporels, multi source). Une source, celle qui donne les meilleurs résultats globaux (donnés par le kappa et le MPCC), peut servir de référence. Soit une partie des deux matrices de confusion M Sk et M Sl, des sources S k et S l, en considérant les classes i et j. On notera les éléments de ces matrices M Sk ( i,j ) par m k ij et M Sl ( i,j ) par m l ij i j i j i m k ii m k ij i m l ii m l ij j m k ji m k jj j m l ji m l jj S il y a des confusions entre i et j dans la source S k, si l on veut séparer i et j, la source S l peut lever cette ambiguïté, si i j = dans S l. Soit un pixel x, classé en i avec la source S k et en j avec la source S l. - Si la classe i présente un mauvais score donné par la matrice de confusion dans l image S k, et qu elle est très confondue avec la classe j, lorsque le classifieur affecte un pixel à la classe j, j n est pas certain, x appartient peut être à la classe i. Si dans l image de S l, cette confusion est faible ou n existe pas, la fusion favorise la classe trouvée avec cette deuxième image, c'est-à-dire i. Soit S k la source de référence. - Si m k ii - m l i,i > seuil, alors la classe C i est mieux classée par la source S k, c est cette classe C i qui sera privilégiée dans la cas où il y a contradiction entre C i et une autre classe. Dans le cas contraire à partir des termes m k ij on cherche les classes qui présentent des confusions avec C i : par exemple C j, si dans la source S l la confusion entre C i et C j n existe pas, alors en cas de conflit entre ces deux classes, c est le résultat de classification de la source S l qui sera conservé. Le conflit est levé dans la source S l. Mais comme on l a vu précédemment cela est plus compliqué. Echantillon Classification 1 Classification 2 Classe a : classe a : classe b Résultat : classe c : classe d Figure 4.10 : schéma des confusions entre classes Dans la figure 4.10, soit l échantillon de la classe a, la classe a est mal reconnue dans la classification 1, (confusion avec les classes b, c, d), dans la classification 2, il n y a pas de Ch 4 103
126 La fusion, l incertain, le possible confusion avec la classe c et d, la fusion améliore cette confusion. On obtient une image de meilleure qualité que la précédente. Mais ceci est plus complexe car il peut y avoir des classes qui ont un bon score dans la matrice de confusion, mais qui peuvent être sur-représentées dans l image, car elles se substituent à d autres classes. Si un pixel est affecté à la classe i dans l image de référence S k, puis ré-affecté à la classe j après la fusion, la décision n est pas forcément correcte, il peut se produire une augmentation des confusions avec la classe j, si la classe j à tendance à être confondue avec la classe i dans la deuxième image S l, par la règle précédente. SPOT 5 10 Maquis Maquis littotal 5 Maquis Maquis littotal ERS 5 10 Maquis Maquis littotal 5 Maquis Maquis littotal Tableau 4.8 : extrait de matrices de confusion obtenues avec deux sources Exemple de substitution malencontreuse : dans des matrices de confusion obtenues à partir d images ERS et SPOT (tableau 4.8), soient les classes 5 et 10. Pour le Maquis (5), mal classé, dans la classification avec SPOT, 9.39% des pixels ont été classés en classe 10. Quand un pixel à la valeur 10 dans la classification de SPOT, il est possible que ce pixel soit de la classe 5. S il est affecté à la classe 5 dans la classification ERS, comme il n y a pas de confusion entre ces deux classes avec ERS, on peut a priori effectuer le changement de 10 en 5. Lorsque le pixel est affecté à la classe 10 pour SPOT et 5 pour ERS, il affectera la valeur 5 dans la classification résultante. Mais il existe beaucoup de confusions entre la classe 10 et la classe 5 dans ERS. Le changement précédent va donc induire des confusions dans la classification résultat alors que dans celle de SPOT, elles n existaient pas. SPOT ERS Résultat Classe 5 Classe 5 Classe Gain de 9.39 % dans la classe % 17 l 10 classe10 Classe % 10 5 Perte de 28 % dans la classe 10, remplacée en partie par 5 Figure 4.11 : exemple de substitution malencontreuse Ch 4 104
127 La fusion, l incertain, le possible Pour résumer : Pour un échantillon de la classe 5, la classification SPOT a affecté des pixels à la classe 10, par contre ils sont bien affectés avec ERS, si on fait la substitution le résultat est correct. Dans le cas de l échantillon de la classe 10 dont tous les pixels sont bien affectés dans la classification SPOT (gain 9,39%). Si on applique une règle générale de substitution les pixels de l image ERS du même échantillon, mais mal classé (classe 5), seront affectés à la classe 5 d où perte de 28%. Il faut donc combiner l ensemble des règles. En cas de conflit entre deux classes i et j attribuées à un même pixel respectivement par la classification de référence S k et la deuxième classification S l, il faut envisager plusieurs cas : Il y a des confusions dans l'image de référence entre les deux classes i et j, c est possible que la classe i soit mal affectée On considère donc la matrice de confusion S l, les deux termes m k ij et m l ij sont du même ordre de grandeur; il y a autant de confusion dans l'image de référence que dans S l Les erreurs ne sont pas forcément aux mêmes points Il n y a pas de confusion entre les classes i et j dans la deuxième image c est j qui sera affecté au pixel Il y a une augmentation des confusions dans cette classe : on ne peut ne pas faire de changement car on défavorise la classe j qui contient déjà beaucoup de confusions Si m l ji < seuil est faible et m k ji < seuil est faible, on ne change rien, si on ne veut pas prendre de risque, même s il y a moins de confusions avec la deuxième image Algorithme Notations : m ref (i, i) : pourcentage de pixels bien classés de la classe i dans l image de référence. m img2 (i, i) : pourcentage de pixels bien classés de la classe i dans la deuxième image. m ref (i, j) : confusions de la classe j avec la classe i de l image de référence. m img2 (i, j) : confusions de la classe j avec la classe i de la deuxième image. m ref (j, i) : pourcentage de pixels de la classe j reconnu comme appartenant à la classe i dans l'image de référence m img2 (j, i) : pourcentage de pixels de la classe j reconnu comme appartenant à la classe i dans l'image 2. conf_max : confusion maximum autorisée (à régler par l utilisateur suivant le type d image). Par défaut, conf_max = 0 diffmin : Différence minimum entre les pourcentages des matrices de confusion des deux images (ref et im2) au delà de laquelle on procède à un changement d'attribution de classe. diffpondmin gainmin pma différence pondérée minimale gain minimal perte maximum autorisé On introduit un facteur (diffpondmin) sur la différence entre m ref (i,j) et m img2 (i,j), car on suppose que si la différence est minime autant ne pas faire de changement, en sachant l imprécision contenue dans les données. Ch 4 105
128 La fusion, l incertain, le possible Sinon, on considère le fait qu un changement va améliorer la classe i, mais qu il peut introduire des erreurs dans la classe j. Ainsi, on introduit la notion de gain : on compare le gain de choisir la classe i avec la perte sur le choix de la classe j, si la perte est trop importante on ne fait rien si le gain est plus important que la perte alors on change la classe. Tous les paramètres ont des valeurs par défaut connues par apprentissage. Le principe algorithmique implanté est le suivant : Lorsque la classe j est affectée à l image img2 et la classe i à l image ref. Si le pourcentage de pixels de valeur j classés en i dans l'image référence est supérieur à conf_max (dans le cas contraire, aucun traitement n est effectué donc c'est la valeur du pixel dans l'image de référence qui sera choisie) Si m ref (j, i) > conf_max alors // confusion entre la classe i et j // Si le pourcentage de pixels de valeur i classés en j dans la seconde image est inférieur ou égal à // conf_max et s il y a plus de chance (de plus en plus strict si diffmin augmente) que j ait été mal // classé en i dans l'image ref plutôt que du i en j dans l'image 2 Si m ref (j, i) - m img2 (j, i) >= diffmin alors Si mimg2 (i,j) = 0 ou mimg2 (i,j) <= (m ref (j, i) + m img2 (j, i) )/ gainmin et m img2 (i,j) <= pma alors la classe j de img2 est affectée au point //C'est la valeur dans la seconde image qui sera résultat Fin Si Fin Si Fin Si Ce principe peut être appliqué pendant la classification ou après en post-classification Remarque : Lorsque les échantillons sont pris séparément, les confusions observées dans chaque image ne le sont pas sur les mêmes échantillons, ce qui ajoute une imprécision supplémentaire. Les résultats sont présentés dans les applications ( 4.6) Régularisation Les résultats des classifications sont affinés grâce aux traitements de post-classification tel que la fusion, mais aussi grâce à la régularisation (lissage). Celle-ci est, en général, plus importante que dans la classification ICM avec contraintes. Des méthodes ont été développées pour effectuer des régularisations adaptées aux types de résultats cherchés, qui diffèrent suivant l application de l image : plan d occupation du sol, analyse du paysage. Cette opération permet d ajuster la carte d occupation du sol à différents niveaux d observation (parcelle, paysage). Pour cela des images : segmentées, des images représentant des «bruits», des nuages, sont introduites dans le traitement de régularisation. Ch 4 106
129 La fusion, l incertain, le possible La régularisation des images classées peut être dirigée ou automatique. Le principe le plus simple est celui du filtre majoritaire sur un voisinage de points (la classe la plus représentée dans le voisinage remplace le point central). Mais ce filtre à tendance à éliminer les contours, nous lui préférons le suivant. Figure 4.12 : Exemple de Régularisation Régularisation avec segmentation La régularisation correspond à un ajustement de l image classée aux parcelles, ce qui permet d éliminer les pixels isolés en les affectant à la classe majoritaire l entourant. Le seuil de segmentation est choisi en fonction de l application. Le principe est toujours celui du filtre majoritaire, mais la fenêtre sur laquelle le filtre est appliqué est la région de l image segmentée, les pixels de la région sont remplacés par la classe majoritaire. Une variante permet d améliorer le contour des classes. Les points situés sur un contour sont comparés à leurs voisins. Ils sont réaffectés de la façon suivante : soit la majorité des points du contour appartiennent à une classe alors ils sont tous affectés à cette classe soit, ils sont affectés à une classe particulière qui correspond à des mixels, pouvant être des routes, des chemins, des haies, et qui sera analysée par la suite. L image est mieux contrastée, les points des frontières sont mieux affectés. Dans le même esprit des masques représentant des bruits peuvent être pris en compte pour éliminer ces bruits Les classes régularisées peuvent être ciblées, certaines peuvent être privilégiées, ou ne pas être modifiées, ce principe est donc dirigé. Ch 4 107
130 La fusion, l incertain, le possible Régulation plus fine Un algorithme a été implanté à partir des matrices de confusions locales, avec une méthode similaire à la fusion. Cette méthode est fondée sur une comparaison de deux résultats, d une part provenant de matrices de confusion calculées d après les échantillons et d autre part à partir des fréquences d apparition des classes dans le voisinage (ou segment). La décision de modification du point central est prise en fonction de la comparaison des différences entre les taux des matrices de confusion et les fréquences, qui ne devront pas dépasser un seuil donné, défini par l utilisateur (par défaut 0.2). Ce seuil correspond au pourcentage moyen d écart accordé entre chaque classe (le seuil 0.2 signifie que l on tolère une erreur moyenne de 20%). On affecte au pixel, la classe qui a le plus de similitude, entre la ligne de la matrice de confusion la concernant, et les taux obtenus sur les fréquences d apparition des classes dans le voisinage du pixel considéré. Ce qui correspond à prendre en compte le degré d appartenance du pixel dans son voisinage. Les seuils associés à chaque classe peuvent être variables et déduits de précédentes statistiques. Classe k Taux sur Fréquence sur le Différence (%) confusions l échantillonnage (%) voisinage (%) Classe Classe Classe Classe Classe Total 24.3 Tableau 4.9 : exemple du calcul des différences de taux pour une classe k Le principe revient à comparer les confusions dans le voisinage du point avec celles des échantillons. Echantillonnage (%) Fenêtre (%) Différence (%) Seuil (%) Classe Classe Classe Classe Tableau 4.10 : exemple du calcul des différences de taux pour une classe k avec un seuil d acceptation de chaque classe Dans le voisinage (ou le segment) du pixel affecté à la classe k (tableau 4.9) apparaît 17.6% de fois la classe 1, 68.4% la classe 3 et ainsi de suite. La colonne 2 du tableau correspond aux taux de la matrice de confusion pour la classe k, la colonne 3 représente la fréquence d apparition des classes dans le voisinage, la colonne 4 les différences, avec une moyenne de 24.3 / 5 = 4.86 %. Si le seuil par défaut est 0.2 (i.e 20%) la classe k pourra être choisie, sinon elle n est pas acceptée. Dans le tableau 4.10, le seuil est donné par classe. On remarque que la différence sur la classe 8 dépasse le seuil accordé (5%), donc la classe 8 ne peut pas être choisie pour remplacer la classe courante, les autres classes 1, 4, 11, 12 restent en compétition. Les classes très fines comme les routes ou les rivières ont un traitement particulier pour éviter leur disparition. Chaque classe peut être accompagnée d une liste de classes contradictoires, Ch 4 108
131 La fusion, l incertain, le possible par lesquelles elle ne pourra être remplacée. Une classe peut n être remplacée par aucune autre Applications En pratique, la fusion n est pas un problème simple, ne serait-ce qu à cause du recalage, dont la qualité pas toujours parfaite introduit une imprécision supplémentaire. Dans la complexité du problème de fusion, il faut savoir que pour chaque source, des échantillons spécifiques sont pris, par exemple les nuages pour une image optique et des effets de relief ou des forts diffuseur pour le radar. Ils doivent être traité de façon particulière dans la fusion Etude de cas de l île de Minorque Deux classifications de l île de Minorque ont été réalisées indépendamment : la première avec 4 dates d ERS (quatre canaux), la deuxième avec deux dates de SPOT, juillet et octobre (six canaux). Chaque classification a été menée avec ses propres échantillons. Ce cas présente toutes les difficultés, recalage très imparfait (erreur de 1 à 3 pixels suivants les endroits), les deux classifications ERS et SPOT ont été réalisées de façon séparée, l échantillonnage d apprentissage et de vérification ont été également réalisés séparément sur les deux sources, le jeu d échantillonnage est alors doublé. SPOT ERS Echantillons 1 Données images Echantillons 2 Données images Classification Classification Classification Fusion Figure 4.13 : schéma de la fusion L interpréteur est tributaire de la visualisation différente suivant les deux types de capteurs, de la scène. Il est souhaitable de prendre les échantillons avec les différentes sources d images pour mieux préciser leur emplacement et obtenir ainsi un échantillonnage utilisable pour les deux sources. Mais cela n est pas toujours possible surtout si les données ne sont pas obtenues en même temps. Ce qui a été notre cas. Dans la région étudiée les échantillons ont été très difficiles à prendre en raison de leur petitesse et l accessibilité du terrain. Pour la classification radar, 35 classes et sous-classes ont été distinguées, et 36 pour la Ch 4 109
132 La fusion, l incertain, le possible classification optique. La plupart de ces classes sont communes aux deux types d image, mais certaines sont spécifiques (meilleures discriminations de certains types de végétation, nuages, dans l image SPOT du mois d octobre, effet du relief dans les images radar). Les images classées sont fusionnées par la méthode automatique. ERS1 spot juillet spot octobre Spot Juillet Spot Octobre 4 dates + ERS1 + ERS1 Jachère Maquis 1 ouvert Maquis 2 ouvert 28f Maquis littoral Maquis littoral Maquis littoral Maquis et pins Foret Etang Mer Culture non irriguée Culture irriguée Zone humide Zone urbaine Rocher Moyenne Tableau 4.11: comparaison des taux PCC et MPCC avec ERS1, SPOT et leur fusion A partir des matrices de confusion calculées sur l échantillonnage de vérification, le tableau 4.11 présente le pourcentage des bien classés (PCC) correspondant à la diagonale de la matrice de confusion et le MPCC. La fusion a permis d améliorer les classifications SPOT des deux dates utilisées seules (de 69,6% à 76.09% pour juillet et de 68.9% à 72.1% pour octobre), mais ERS n ayant pas de meilleurs résultats que la classification avec les deux dates SPOT, la fusion dans ce cas n apporte rien. Il est intéressant d observer que la classe "Maquis littoral 2" qui présente des résultats médiocres dans chaque image (ERS : 48%, SPOT : 22.8%), offre une amélioration importante avec la fusion. Les confusions de cette classe se trouvent presque exclusivement avec une seule classe et elles sont différentes dans les deux classifications (ERS : 48.71% de confusion avec la classe "Cultures non irriguées"; SPOT : 62.87% de confusion avec la classe "Forêt"), ce qui a permis de jouer sur la balance entre ces classes par le principe suivant : si dans la classification SPOT nous sommes en présence de la classe "Forêt" et dans la classification ERS la classe "Maquis littoral 2" c est cette dernière qui sera privilégiée. D autres résultats ne sont pas améliorés, voire légèrement diminués, ceci s explique par le fait des deux échantillonnages différents, les mesures d erreur de classification ne sont pas faites avec le même échantillonnage de vérification pour ERS et pour la fusion, c est l apprentissage de SPOT qui a été utilisé pour ce cas. Ch 4 110
133 La fusion, l incertain, le possible Projet Sud ouest Le descriptif du projet est donné au chapitre 3 (applications). Données radar : ERS-2, SAR, du 13 mars 2000, 17 avril 2000, 22 mai 2000, 26 juin Données optiques : SPOT 13/05/2000, 22/07/2000 et SPOT 4 27/07/2000, les données sont géoréférencées en Lambert. Les deux classifications ERS et SPOT ont été faites de façon séparée puis fusionnée Classification optique Les classes qui sont confondues dans les deux dates sont souvent celles qui sont en sol nu (semis, chaume). En mai, le maïs, le sorgho, le soja et le tournesol, en juillet le blé, l orge et le colza se confondent (tableau 4.12). Ils sont en sol nu. En mai, les feuillus se confondent avec le stade végétatif printanier du blé, alors qu en juillet, cette similitude est supprimée. Avec les deux dates, le gain sur le pourcentage des correctement classés (PCC) est meilleur dans l échantillonnage d apprentissage, mais il est faible dans l échantillonnage de vérification. Ce dernier jeu d échantillonnage est influencé par des cultures souvent hétérogènes en raison de pratiques culturales différentes. spot 13/05/00 apprentissage spot13/05/00 vérification spot 22/07/00 apprentissage spot 22/07/00 vérification spot mai et juillet apprentissage spot mai et juillet 2000 vérification Maïs 78,7 63,5 94,9 95,9 96,3 94,4 Sorgho. 100,0 0,0 60,0 53,1 100,0 0,8 Soja. 64,3 0,0 46,4 59,0 94,6 31,3 Pois 96,2 73,3 96,2 47,7 100,0 82,6 Ble 72,9 83,1 76,4 88,7 99,5 99,2 Orge. 97,8 95,2 93,3 11,3 97,8 56,5 Tournesol 57,9 70,1 86,5 79,9 99,2 98,9 Colza. 100,0 95,4 79,1 51,2 100,0 65,1 Lin. 79,4 11,8 90,4 62,1 97,8 20,5 Jachere jeune. 87,2 36,2 19,2 19,2 91,5 25,5 Jachere ancienne 69,3 64,4 86,3 58,6 95,1 46,8 Prairie perm. 33,0 15,6 34,1 34,4 76,1 62,9 Feuillu. 90,8 57,6 87,7 87,7 99,9 88,1 Resineux. 99,5 97,7 93,3 98,4 100,0 97,6 Eau libre. 94,8 100,0 93,3 91,7 94,8 100,0 Batis lisse. 66,2 87,4 92,3 95,0 93,9 100,0 Batis lache. 93,6 76,8 52,6 96,2 98,3 87,4 Nuage. 100,0 100,0 100,0 100,0 Bord nuage. 100,0 43,7 100,0 54,5 PCC 81,3 60,5 78,0 67,0 96,4 69,9 Tableau 4.12 : comparaison des taux PCC et MPCC avec SPOT Classification radar ERS-2 Nous avons montré l apport graduel (adjonctions successives) de séries temporelles dans une classification d images radar jusqu à un nombre critique au delà duquel le pourcentage des correctement classés ne peut pas être significativement amélioré. Les images ERS-2 ont été filtrées avec le filtre vectoriel LVMMSE (chapitre 2). Après ce filtre, les structures sont bien conservées grâce à l introduction de la segmentation. Ch 4 111
134 La fusion, l incertain, le possible Amélioration du % de bien classé par addition de date PCC 80,0 70,0 60,0 50,0 40,0 30,0 Graphique montrant l amélioration du pourcentage de bien classé en fonction de l augmentation du nombre de dates utilisées 20,0 10,0 0,0 1 date 2 dates 3 dates 4 dates nombre de dates (ordre chronologique) Figure 4.14 : addition chronologique des dates Contrairement aux images de SPOT, les confusions se font souvent à cause d une similarité de structure entraînant une réponse quasi équivalente. D autres confusions sont dues à des échantillons qui présentent une grande hétérogénéité dans une même classe. On peut faire la même remarque au sujet des résultats obtenus avec l échantillonnage de vérification. ers 4 dates 2000 apprentissage ers 4 dates 2000 vérification Maïs 76,6 79,3 Sorgho. 60,0 0,0 Soja. 92,9 45,1 Pois 88,5 68,6 Ble 71,8 62,5 Orge. 73,3 38,7 Tournesol 94,6 59,2 Colza 89,3 36,7 Lin. 55,9 23,0 Jachere jeune. 48,9 42,6 Jachere ancienne 63,9 16,6 Prairie perm. 86,4 22,6 Feuillu. 86,2 84,4 Resineux. 73,2 9,8 Batis lisse. 47,7 40,3 Batis 67,8 38,7 Fort diff. 100,0 100,0 Ombre radar. 70,9 50,9 MOYENNE 74,9 45,5 Tableau 4.13 : comparaison des taux PCC et MPCC avec ERS Fusion des images SPOT et ERS La fusion est réalisée avec une date SPOT (3 canaux) et quatre dates ERS2 (4 canaux). Ce choix vient de ce qu en général une classification avec deux dates SPOT donne de très bons résultats alors que l apport ERS2 est plus limité. Par contre, si l on ne dispose que d une seule date SPOT, l aspect multitemporel de ERS2 apporte des éléments discriminateurs Ch 4 112
135 La fusion, l incertain, le possible surtout dans des régions de prédominance agricole. Dans le tableau 4.14 seules les classes communes ont été conservées (les classes «Fort diffuseur»... sont supprimées). En mai, l amélioration est importante pour les classes Soja, Pois, Prairie permanente, Feuillu, Bâtis. Cependant, certaines classes comme l Orge et le Tournesol sont moins bien discriminées. En juillet, l amélioration est importante pour les classes Soja, Pois, Orge, Tournesol, Jachère jeune et Prairie permanente. Certaines classes comme le Blé, la Jachère ancienne et les Bâtis sont moins bien discriminées. ERS2, 4dates vérification spot mai vérification fusion spot mai ERS2, 4 dates vérification spot juillet vérification fusion spot juillet ERS2, 4 dates vérification Maïs 79,3 63,5 64,6 95,9 96,0 Sorgho. 0,0 0,0 0,0 53,1 57,8 Soja. 45,1 0,0 35,4 59,0 79,9 Pois 68,6 73,3 93,0 47,7 86,1 Ble 62,5 83,1 87,5 88,7 80,2 Orge. 38,7 95,2 87,1 11,3 59,7 Tournesol 59,2 70,1 59,5 79,9 87,2 Colza 36,7 95,4 89,5 51,2 64,0 Lin. 23,0 11,8 14,3 62,1 67,1 Jachere jeune. 42,6 36,2 42,6 19,2 48,9 Jachere ancienne 16,6 64,4 66,4 58,6 33,2 Prairie perm. 22,6 15,6 36,6 34,4 48,4 Feuillu. 84,4 57,6 87,2 87,7 88,0 Resineux. 9,8 97,7 95,4 98,4 99,0 Eau libre. 100,0 96,8 91,7 90,4 Batis lisse. 40,3 87,4 93,3 95,0 97,5 Batis 38,7 76,8 82,1 96,2 65,2 MOYENNE 41,8 60,5 66,5 64,9 71,2 Tableau 4.14 : comparaison des taux PCC et MPCC avec ERS1, SPOT, fusion SPOT/ERS1 Un extrait de la zone d étude (figure 4.15) représentatif de la zone des coteaux du Gers où se pratique une polyculture caractérisée par l'alternance Blé / Tournesol est présenté ici. La carte a est obtenue par la classification des données optique et radar (méthode de fusion). Deux principales classes : le "Blé et autres céréales" et "Tournesol" se partagent le territoire, le "Lin" en culture secondaire et la "Jachère" complètent l'assolement. La distribution de la "Jachère", en dehors de la zone cultivée est intéressante ; on la trouve autour de la classe "Bâti", elle correspond alors à l'environnement non minéralisé des fermes, et sous forme linéaire (bandes enherbées) située le long des talwegs du bassin versant. Les limites du parcellaire cadastral superposé à l'image classée permet de juger visuellement de la pertinence de la classification obtenue, par comparaison avec la carte b, carte vraie de l'assolement réalisée à partir de la base de données agricoles constituée à partir des informations acquises au cours d'enquêtes de terrain. Ch 4 113
136 La fusion, l incertain, le possible Figure 4.15 : carte d'occupation des sols du bassin versant d'auradé en 2000 d'après l'imagerie spatiale (a) et la carte de l'assolement 2000 d'après la base de données Images SPOT 2003 Pour obtenir une classification qui soit la plus précise possible, la seule solution est de procéder à des fusions de quelques classifications réalisées avec ces diverses combinaisons choisies pour leur discrimination. Classification supervisée La classification des images SPOT 2003, s est avérée difficile (sécheresse). Par conséquent, un nombre important de fusions ont été réalisées, afin d améliorer au maximum les scores. Fusion 1 : L image de départ est la classification avec ensemble des sept dates, la deuxième classification est «avril-mai-juin-août». Ces deux classifications supervisées sont choisies, car considérées comme les plus performantes et complémentaires. La fusion de ces deux classifications est automatique selon des règles définies par le taux de pixels bien classés. Elle améliore globalement la classification et elle a permis d améliorer notablement le MPCC, passant de 68.34% (vérification) à 74.65%, (kappa : de 80.33% à 82.99%). Fusion 2 : le tracé des cours d eau ainsi que les lacs et gravières sont mal dessinés, malgré des PCC élevés. Visuellement ces classes se révèlent incomplètes et la matrice de confusion met en évidence des confusions avec notamment la classe Bâti. En revanche, les contours et tracés sont nets dans l image composée des sept dates, avec les seuls canaux PIR et MIR (canaux très importants dans la discrimination de l eau et dans sa différenciation avec le Bâti). La fusion de ces deux classifications a permis d obtenir les cours d eau bien tracés. Puis on a pu fusionner d autres combinaisons qui discriminent mieux certaines classes (Colza, Pois, Jachère et Friche) avec la classification comprenant uniquement le canal XS4 pour les sept dates. Une fusion avec la classification «mars-avril-juin-juillet-août-septembre» apporte une amélioration de la classe Prairie, une meilleure qualité visuelle de la classification, et corrige l excès de Colza. On est passé ainsi successivement pour le MPCC de : 68.34%, 74,65%, 74,82%, 76.22%, 78,10%, 81,26% et le kappa de 80.33%, 82,99%, 83,16%, 82.55%, 83,84%, 86,21% Ch 4 114
137 La fusion, l incertain, le possible Classification non supervisée Une classification non supervisée des données SPOT du projet Sud Ouest 2003 avec sept dates de mars à septembre a été effectuée, puis interprétée. Une partie du Bâti apparaît en eau. Les canaux PIR et MIR permettent très bien de différencier ces deux classes grâce à la connaissance des réponses spectrales de ces classes. Les plantations d Eucalyptus ont été classées en «Bâti dense», les Résineux sont mélangés avec les Feuillus. Or les eucalyptus se séparent bien du Bâti dans le MIR. Une classification est alors réalisée avec seulement les canaux PIR et MIR et les 7 dates. Echantillons 2002 Classification dates Reconnaissance Classification 2003 PIR/MIR 7 dates Fusion1 : amélioration de l eau, du bâti, de l eucalyptus Regroupement de classes Regroupement de classes Classification à 34 classes classe10 can Reconnaissance Classification décembre 2003 Fusion 2 Amélioration de feuillus/résineux et prairie Echantillons 2003 Classification finale 20 classes (19+1 non classé) Amélioration Matrices de confusion Figure 4.16 : Démarche suivie pour la classification non supervisée Ch 4 115
138 La fusion, l incertain, le possible Dans l image classée avec PIR et MIR, on distingue parfaitement trois classes de Bâtis (dense, suburbain, lâche) ainsi que la classe Eau. Une fusion des deux classifications est alors réalisée afin d importer ces classes dans la première classification, qui donne globalement de meilleurs résultats. Une image avec 48 étiquettes est obtenue. En décembre, les Résineux apparaissent bien, alors qu ils n étaient pas très bien différenciés avec les Feuillus : la classe mixte Feuillus/Résineux devient Résineux et Feuillus après la fusion de la classification de décembre. La fusion des deux classifications ajoute, ces trois nouvelles classes et sépare les Résineux des Feuillus. La classe Feuillus 2, nouvellement créée, est différente spectralement de la classe Feuillus 1, car elle correspond aux forêts situées à proximité des Petites Pyrénées. Elle est donc une sous classe de Feuillus. feuillus résineux eucalyptus blé colza maïs tournesol soja prairie/jachère/pelouse eau bâti rural bâti périurbain bâti dense prairie (blé) prairie (tournesol) Culture d été Culture (certitude 0.6) ripisylve-lisiere Tournesol2 (certitude 0.6) Tableau 7.6 : Classes définitives reconnues en 2003 à partir des données terrain 2002 (en partie automatiquement) Ces fusions sont dirigées, car l interprétation des classes est donnée par le logiciel de reconnaissance présenté au chapitre Bassin du Grand Morin en Seine et Marne Dans le cadre d un programme de recherche pour la promotion des données Radarsat (ADRO : Application Developement and Research Opportinity), l objectif était de définir un indicateur d environnement pour évaluer la vulnérabilité du milieu naturel face à des pollutions engendrées par l activité humaine. Pour cela on calcule un indice de vulnérabilité des eaux superficielles par les produits phytosanitaires. Un modèle hydrologique de différents paramètres (pente, proximité d une rivière, présence de culture, présence de produits phytosanitaires...), sera utilisé. L évaluation du paramètre «présence de culture» à l échelle du site étudié, dans lequel le ruissellement des eaux de pluies entraîne les particules des produits polluants tel que l atrazine, dans les eaux superficielles, passe par l établissement d une carte d occupation des sols. La localisation des cultures est un facteur incontournable pour l étude du risque de pollution par l atrazine. Ces cartes d occupation des sols ont été établies par le biais de plusieurs classifications à partir des données : radar (multitemporelles Radarsat en amplitude (non filtrées (brutes) et filtrées) ; optiques (multispectrales SPOT ) ; fusion radar et optique avec ou sans segmentation. Le site d étude La zone d étude se situe dans un bassin du Grand Morin (le Vannetin affluent du Grand Morin) en Seine et Marne (3 14 Est et Nord) qui fournit en eau potable une partie de la région parisienne. La zone comprend les villes : Ferté Gaucher et son aérodrome, Choisyen -Brie, Chevru, Leudon-en-Brie. Le site est essentiellement constitué de parcellaires agricoles, de bois et de forêts. Ch 4 116
139 La fusion, l incertain, le possible Les données Nous avions à notre disposition les données suivantes : 4 images Radarsat, Single Look Complexe (SLC) en mode F1, prises aux dates : 28 Juin Juillet Septembre Novembre image SPOT en mode XS (multispectral) du 13 Août 1997 Méthodes et données Gauss Spot GW Radarsat brutes gauss GW Spot + Radarsat brutes + Pearson Radarsat brutes Spot forêt 98,6 94,87 98,05 98,06 maïs 85,46 80,52 99,18 97,54 blé 1 49,55 59,89 88,87 87,79 blé 2 86,21 62,3 88,89 90,03 orge 59,62 45,56 59,91 60,35 colza 46,02 40,15 46,02 46,02 pois 1 54,65 60,21 55,43 55,81 pois 2 79,78 70,57 80,66 82,97 betterave 97,92 86,32 99,14 94,1 herbe 97,09 86,25 97,43 97,44 urbain 97,5 93, sol nu 99,56 87, ,84 moyenne 79,33 72,33 84,46 83,43 Tableau 4.15 : pourcentage de bien classés pour les classifications des données Spot, Radarsat et fusion Radar-Spot (GW = Gauss-Wishart) Le processus de fusion avec les images Radar non filtrées, classées avec la loi de Gauss Wishart (GW), améliore les résultats de l image SPOT (loi de Gauss) pour la majorité des classes : environ 5% en moyenne (tableau 6). La visualisation de cette classification (figure 4.17 à droite) montre les résultats améliorés pour la Forêt, le Maïs et le Pois. La fusion élimine des pixels d urbain (qui peuvent être des routes) disséminés un peu partout dans l image. La confusion des pixels de contours des champs de maïs avec l herbe est réduite, ce qui améliore les structures des champs. Ch 4 117
140 La fusion, l incertain, le possible 4,080 Km 3, K m N S Figure 4.17 : à gauche image classée avec SPOT, à droite image classée avec SPOT + Radarsat Ch 4 118
141 Chapitre 5 ANALYSE DE PAYSAGE
142
143 Chapitre 5 ANALYSE DE PAYSAGE Concepts et définitions Concepts L écologie du paysage, selon Risser et al. (1984), s intéresse principalement à l évolution et à la dynamique de l hétérogénéité spatiale sous l action de l Homme, c est à dire à des systèmes spatiaux et hétérogènes, aux interactions et aux échanges entre paysages (entre éléments de la mosaïque et des réseaux du paysage), à l influence de l hétérogénéité spatiale sur les processus biotiques (ce qui concerne le vivant) et abiotiques (le milieu physique). Cette discipline est ainsi fondée sur l étude des relations entre les processus écologiques et la structure spatiale du paysage [Burel et al. 1999]. D après plusieurs auteurs, le paysage possède des seuils critiques pour des variables environnementales comme la fragmentation de l habitat, le nombre ou la longueur des frontières ou encore la fréquence des perturbations, seuils au-delà desquels la réponse des processus écologiques peut s avérer drastique [Turner et al 1991]. Urban et al (1987) définissent le paysage comme un système formé par une mosaïque de parcelles. La parcelle, plus exactement la tache, «patch» en anglais est l unité élémentaire du paysage (UEP), qui est une aire homogène au sens écologique et constituée de pixels contigus, avec des frontières précises au sens physique ou biologique, cela est difficile à identifier dans la nature, car le passage d une unité à une autre se fait graduellement. Ce qui importe au niveau du paysage est la façon dont ces éléments sont connectés, on parlera de connectivité pour décrire leurs relations, en distinguant une connectivité structurale qui s'applique aux relations spatiales et une connectivité fonctionnelle pour tout ce qui a trait aux échanges entre éléments du paysage [King A.W. 1999]. Les recherches sur la mosaïque du paysage ont porté essentiellement sur les effets de taille et la forme des éléments (plus ils sont grands et compacts, moins ils sont soumis aux influences des éléments voisins). Un autre aspect concerne la mise en place des mosaïques paysagères, des facteurs qui régulent leurs évolutions ; il existe actuellement des méthodes permettant de mesurer la part de différents groupes de variables dans cette organisation. Parmi ces variables il y a celles qui ont trait aux milieux physiques, aux pratiques agricoles, qui sont elles-mêmes contraintes par les structures spatiales (distance à l'exploitation, taille des parcelles...). La prise en compte de l activité humaine devient inévitable dès que l'on pose le problème de l'organisation, il n'est plus possible de se réfugier dans des espaces "naturels" (du moins dans nos régions). Cette activité n'est plus vue comme une source de perturbation mais comme un ensemble Ch 5 119
144 Analyse de paysage de processus faisant partie du système paysager. Cette perspective est fondamentale car elle permet d'appréhender la façon dont on peut agir sur l'évolution du système, ce qui est essentiel pour les opérations d'aménagement et pour la compréhension de l'évolution de l'espace rural, préoccupation de l'inra par exemple. L'écologie du paysage n'a pas pour prétention de couvrir l'ensemble du champ de l'écologie ; elle conduit généralement à voir que plusieurs niveaux d'organisation agissent simultanément sur un processus (l'érosion dépend des caractéristiques des parcelles mais également des flux d'eau venant d'autres parcelles, qui, eux, sont régulés par des fossés, talus, bandes herbeuses hors de l'espace cultivé). Cette démarche disciplinaire apparaît comme étant le moyen d'approcher les processus écologiques aux niveaux micro et méso-régionaux (ceux des systèmes agraires) et donc de pouvoir discuter avec d'autres disciplines (économie, sociologie) qui sont presque seules à travailler à ces niveaux. Pour aborder l analyse de paysage à partir d une scène satellite, au sens écologique, il est nécessaire que ces taches soient des unités fonctionnelles c'est-à-dire des entités homogènes du point de vue écologique, donc chaque UEP est un écosystème. L observation visuelle d une scène satellite (SPOT, TM, radar ERS, Radarsat ) en composition colorée, ou sous forme d images classées, montre des régions se distinguant les unes des autres par leur contenu (distribution des couleurs, des classes) et par leur structure (forme, taille des UEPs). La scène satellite est donc une vision globale d une mosaïque de taches contiguës caractérisées par leurs valeurs radiométriques. L étude présentée, cherche à trouver des descripteurs qui permettent de quantifier au mieux les paysages, à dégager les plus intéressants, ainsi que des seuils de valeurs qui permettent de distinguer les différentes unités de paysage composant les images. L analyse est réalisée à partir d une image classée car chaque tache ou unité élémentaire de paysage est associée à une classe (occupation du sol) et peut être caractérisée par son fonctionnement écologique (cycle et bilan fonctionnels). Les résultats présentés dans ce chapitre sont obtenus principalement à partir des images satellites SPOT, et ont été effectués sur la région test (Sud Ouest de Toulouse) décrit au chapitre 3 et concernent les divers projets affiliés au projet Sud-Ouest du CESBIO Définitions Le paysage Un paysage est une portion de surface terrestre à étudier. En général, ce sera une partie ou la totalité de la surface que représente une image satellite, de plusieurs kilomètres carrés au sol, qui a été traitée afin de reconnaître à quelle classe chaque pixel appartient [Wiens et al. 1993]. Les classes La valeur d un pixel sera affectée à une classe qui correspond à la nature de la surface qu il représente, issue d une classification. Le thème de ces classes est, en général, choisi par l expert qui connaît la région, en fonction du sujet étudié. Les Unités Élémentaires du Paysage (UEP) ou patchs Un patch ou unité élémentaire de paysage (UEP) est un ensemble de points connexes appartenant à la même classe. La frontière d un patch avec ses voisins définit le contour du patch. Le périmètre du patch est établi à partir de sa frontière extérieure. Echelle des îlots Un patch (ou UEP) correspond à un îlot qui est un ensemble de parcelles, agricoles ou autres, adjacentes. Ainsi, s il y a plusieurs parcelles de blé adjacentes, l ensemble de ces parcelles forment un îlot, ce qui correspond à un ensemble connexe de pixels dans l image classée. Ch 5 120
145 Echelle du parcellaire Analyse de paysage Une segmentation (chapitre 2) de l image permet de diviser les îlots du paysage en segments ou sous-unités, qui identifient des objets à un seuil choisi. Le seuil de segmentation sélectionné dans un milieu agricole est celui qui se rapproche le plus du parcellaire. Les UEPs sont alors ces segments, correspondant aux parcelles, ou à des sous-zones de ces parcelles dans le cas où l on souhaite étudier l hétérogénéité. D une façon plus générale, il est choisi en fonction du niveau d observation souhaité (figure 5.1). Résineux non différenciés Résineux différenciés A Figure 5.1 : (A) classification et image de contour au seuil 16, proche du parcellaire agricole, (B) au seuil 9 qui permet de mieux identifier les résineux (projet Sud - Ouest) Le nombre d UEPs avec la segmentation est supérieur ou égal au nombre d UEPs des îlots. Cependant, dans certains cas, ce nombre est inférieur. La méthode d analyse utilisée attribue au segment, la classe qu il contient majoritairement. Ainsi, au seuil choisi, de très petites unités ne sont plus identifiées et disparaissent englobées dans un segment. Cela élimine, en général, les quelques UEPs, erreur de classification, issues de confusions de classes, qui ont quelques pixels. De même, si un segment est à cheval sur deux îlots, ce segment sera affecté à l îlot dont les points sont majoritaires. Ceci entraîne alors un léger agrandissement de l îlot au détriment de l îlot voisin. Toutefois, cela n a que peu d incidence sur l aire de la classe qui n est, en général, pratiquement pas modifiée. B Les descripteurs du paysage Introduction Le logiciel développé permet de quantifier l organisation structurale tributaire du paysage biologique (occupation du sol) par un grand nombre de descripteurs (caractéristiques et indices des UEPs du paysage). Ils participent à la description de la métrique du paysage, en perspective de son évolution. Certaines caractéristiques sont développées dans «FRAGSTATS» (Mac Garigal et al. 1994), logiciel libre développé au Forest Science Department de l'université d'état de l'oregon, Corvallis, Etats-Unis. D autres caractéristiques ont été créées pour répondre aux besoins spécifiques de l analyse d image. Les descripteurs sont également utilisés pour créer des images. Ch 5 121
146 Analyse de paysage Image 5.1: classification supervisée du Sud Ouest toulousain d après une série 2004 d images SPOT Cette analyse peut se faire à l échelle des îlots, dont certaines caractéristiques seront comparées avec l échelle du parcellaire et sur l image entière ou sur l image découpée en régions. Chaque classe d occupation du sol est caractérisée par N «patchs», unités élémentaires du paysage. Les descripteurs (calculs de forme, de taille, ) sont calculés sur les UEPs, les classes, la région totale (image entière), ou des sous régions. Les descripteurs du paysage peuvent être scindés en plusieurs groupes caractérisant : la dimension de la classe la forme des UEPs la distribution et/ou la répartition des classes : leur agencement Les caractéristiques du paysage sont combinées, pour parvenir à des résultats plus précis. Sans être expert, tout le monde peut observer une image et en donner une description linguistique, mais ceci reste très subjectif. La modélisation de ces observations doit tenir compte de la complexité, de la richesse et de l ambiguïté des représentations, ce qui les rend difficilement modélisable. L automatisation des processus du raisonnement est essentielle, pour modéliser la connaissance de l expert. Les approches du raisonnement automatique utilisé en intelligence artificielle fournissent un cadre pour la description du paysage, qui est si complexe. Nous avons vu (chapitre 4) que la logique floue constitue l interface commode pour la modélisation du langage naturel, en particulier des concepts linguistiques utilisés par les experts tels que : «grand», «moyen», «petit». Ainsi la logique floue permet d'exprimer des concepts du type : x Ch 5 122
147 Analyse de paysage est grand, où x est une variable à valeurs floues. Par ailleurs elle permet de s'affranchir en partie des incohérences ou inconsistances de l'expertise. Nous savons aussi que la base du raisonnement est l induction représentée par l expression logique : Si prémisse alors conclusion et que les règles de type ET, OU de l algèbre de Boole, peuvent être combinées, pour représenter des règles multicritères. Par exemple les valeurs de l aire et du périmètre déterminent la forme, ce qui donne, une fois que les variables sont définies, en les combinant en règles logiques : "si l aire est grande et le périmètre est petit alors l objet s approche de la forme carrée. Il est possible d utiliser des coefficients de confiance exprimés en pourcentage, ce qui correspond à la mesure de confiance que l on a dans une règle. Par exemple : si a alors b, cette proposition est vraie avec une probabilité de 0.6. La logique floue réalise des opérations logiques sur des degrés d'appartenance plutôt que sur des "0" et des "1". Le système permet ainsi d assigner aux variables linguistiques un nom et de définir ses fonctions d'appartenance. Les fonctions d'appartenance possèdent également des noms. Par exemple, la variable "taille" peut avoir des fonctions d'appartenance appelées "grande ", "petite", "moyenne". Chaque fonction d'appartenance donne le degré d'appartenance ou de «confiance» utilisé dans l'inférence floue, satisfaisant aux concepts "grand", "petit", "moyen". La variation du degré d appartenance est le plus souvent linéaire, pour simplifier. Dans la littérature des auteurs, utilisateurs des ces descripteurs, ont du mal a en déduire l information utile. Ainsi : Nous avons associé les descripteurs, car leur analyse séparée ne fournit, que des résultats incomplets : aire moyenne et coefficient de variation, indice de forme, rapport nombre de noyau/nombre d UEPs, UEPs à 0, à 1 ou à plusieurs noyaux. Ainsi nous pouvons arriver à traduire de façon quantitative les termes utilisés pour caractériser le paysage tels que : morcellement, fragmentation, fractionnement, répartition, distribution, partition, étalement ; uni, réuni, joint, régulier, uniforme, homogène, accolé, connecté, groupé, disséminé, éparpillé, dispersé, disjoint, sectionné, crénelé, séparé, déchiqueté, découpé, désagrégé, parcellé et convoluté. Convoluté : «Qui est roulé en cornet autour d'un corps ou sur lui-même» (Ac. 1932), dérivé du latin convolutus, participe passé de convolvere «s'enrouler autour». Les feuilles du bananier sont convolutées (Ac ). Un des objectifs est de trouver des seuils afin que les valeurs des caractéristiques correspondent à une description quantitative. Ainsi un coefficient de variation de l aire des UEPs peut être faible (<2,5) ou élevé (>2,5), l aire petite (<5 ha), moyenne (de 5 à 10 ha), grande (>10 ha). Ces seuils sont actuellement déduits d un système d échelle entre les valeurs minimales et maximales des indices, soit sur un graphique, soit par le calcul, et ils sont fonction du niveau d observation. Une technique d analyse courante en logique floue est l utilisation d arbres de décisions. L arbre est un sous espace des règles possibles Descripteurs surfaciques des classes Ces descripteurs sont basés sur les concepts d aire, de variabilité de l aire, du nombre d UEPs, de noyaux, d inclusions de classes. Le nombre d UEPs donne par exemple une information sur la dispersion ou le morcellement. Ainsi, une espèce vivant dans une classe répartie sur beaucoup d UEPs sera moins sensible aux Ch 5 123
148 perturbations (maladie, feu, ). Par contre cela peut limiter l extension d une espèce. Analyse de paysage Le descripteur de base, qui est le départ de toute analyse, est le pourcentage d occupation de la classe dans l'image totale, qui est sans ambiguïté et bien connu Aire moyenne, coefficient de variation de l aire L aire d une classe est une mesure de la composition du paysage, qui fournit une information dans beaucoup d applications écologiques. Par exemple, un certain nombre d espèces vertébrées, qui se sont spécialisées sur un habitat ne peuvent exister que si elles ont un minimum d espace pour vivre [Wiens et al. 1993]. Il existe une corrélation entre la taille d un patch, de la classe «zone boisée» par exemple, et la diversité des espèces d oiseaux, l abondance d espèces terrestres, [With et al. 1997]. La variation de l aire des patchs donne plus d informations que, la moyenne de l aire des patchs analysée seule. En effet si deux classes possèdent la même aire moyenne d UEP, mais que la première possède un coefficient de variation beaucoup plus faible que la seconde, cela indique que les caractéristiques écologiques de la première sont plus homogènes, alors que la seconde risque de posséder des patchs aux propriétés plus variables (nombre d espèces, ) Aire de la plus grande UEP, rapport avec l aire de la classe, et avec l aire du paysage Ces descripteurs peuvent servir à compléter l interprétation, et vont permettre d expliquer certains résultats précédents. Ils représentent le pourcentage qu'occupe la plus grande UEP dans sa classe. Ils sont utiles lorsque certaines UEPs sont très grandes, ce qui influence fortement la valeur des indices. Un seul patch peut occuper la majorité de la surface de la classe. Mais un patch peut être dominant dans une classe et ne représenter qu une faible surface dans le paysage. Le rapport de l aire de la plus grande UEP sur l aire du paysage permet de relativiser le rapport précédent. Si la plus grande UEP de la classe est très petite, alors le descripteur est proche de 0. Si la plus grande UEP de la classe est égale à 100, alors l'ensemble de la classe n'est constitué que d'une seule UEP. Cette notion n est intéressante que pour les classes contenant un nombre élevé d UEPs, car pour une classe contenant peu d UEPs, un seul de ses patchs peut facilement influencer ce pourcentage sans qu il n y ait pas vraiment de signification, ce qui est le cas dans la zone test (Sud Ouest toulousain) pour les Résineux, l Eucalyptus, le Sorgho, le Bâti dense et le Peuplier, qui ont peu de patchs et dont l aire de leur plus grand patch représente de 20 à plus de 50% de l aire de la classe alors qu il ne représente que moins de 0,2% de l aire totale du paysage. Deux classes sont intéressantes à considérer : la Prairie, dont la plus grande UEP représente 22% de l aire de la classe, soit 6% de l aire du paysage, et le Bâti lâche (53% de l aire de la classe, soit 4% de l aire du paysage). Ces deux classes sont bien représentées dans l image, donc ce chiffre indique qu elles possèdent un très grand îlot, qui a pour conséquence d influencer toutes les caractéristiques étudiées. Cet îlot rassemble un grand nombre de parcelles visibles à un niveau d observation plus fin. C est pourquoi, au niveau des îlots, ces classes sont peu morcelées, mais fragmentées. En effet, ce patch est très grand et contient beaucoup de trous Etude de l hétérogénéité des classes L étude de l hétérogénéité des classes présentes dans une image, constitue une information importante pour la caractérisation du paysage ; rappelons que l écologie du paysage s intéresse particulièrement à l influence de l hétérogénéité spatiale sur les processus biotiques et abiotiques. Les paysages sont par nature hétérogènes et soumis à une dépendance d'échelle. Il est possible de Ch 5 124
149 Analyse de paysage faire varier l'échelle de description du paysage par le biais de l image des contours issue de la segmentation dont les seuils varient, ce qui permet d observer le paysage à des niveaux différents. Une méthode de calcul de l hétérogénéité interne du paysage a été crée, grâce à des mesures avec divers rapports qui l'évalue à différents niveaux d observation suivant les variations des seuils de segmentation. Ils sont calculés relativement aux nombres de patchs correspondant aux îlots d une classe, ou à l aire de chaque classe, et aux nombres de segments, correspondant aux patchs de l image segmentée (les patchs de l image segmentée sont appelés segments pour les différencier des autres), ceci à différents seuils de segmentation. Un patch est dit hétérogène lorsque les éléments qui le composent ne sont pas radiométriquement proches, l'hétérogénéité d'une classe est dépendante de celle de ses patchs. Ainsi, une première façon de mesurer l'hétérogénéité des classes d'un paysage, consiste à étudier le nombre de segments qui la constitue en ayant superposé les contours d une segmentation, ce nombre variant en fonction du seuil de la segmentation. Plus la valeur obtenue est élevée, plus la classe est hétérogène. Mais, la notion d hétérogénéité dépend du niveau d observation ; des classes peuvent être hétérogènes pour un niveau d observation fin alors qu elles seront homogènes à un niveau plus élevé. Plusieurs rapports ont été calculés, mais celui qui représente le mieux l hétérogénéité est le suivant : la caractéristique h d hétérogénéité au seuil de segmentation i est le rapport du nombre de segments à ce seuil i sur le nombre de patchs de la classe. Lorsque le seuil de segmentation est petit, l observation est très détaillée. A ce niveau, l hétérogénéité est élevée, étant donné le nombre de détails perçus. Lorsque le seuil augmente, les critères d homogénéité sont moins stricts, les segments s agrandissent et l hétérogénéité diminue, en même temps que la perception des détails. Au seuil de segmentation le plus bas, certaines classes sont très hétérogènes (indice très élevé), alors que d autres ne le sont pas. Lorsque le seuil augmente, l indice d hétérogénéité diminue très rapidement pour certaines classes, alors qu il diminue plus lentement pour d autres. Ainsi la pente de la courbe est un élément important pour l étude de l hétérogénéité. Lorsque la pente de la courbe de variation de l indice en fonction du seuil de segmentation s affaiblit (tend vers zéro), cela signifie que l indice varie peu, on a atteint une stabilité dans le degré d hétérogénéité, quelque soit le niveau d observation. Si la valeur de cet indice est proche de 1, alors les segments correspondent aux îlots. S il est supérieur à 1 alors les îlots sont composés d un nombre plus ou moins important de segments et sont donc hétérogènes. Si l indice devient inférieur à 1 alors des îlots sont englobés dans un segment, ce qui est incorrect. En prenant l exemple des Résineux (figure 5.2), au seuil 16 les segments de feuillus englobent des îlots de résineux : l indice est inférieur à 1. Ils sont distingués au seuil 9. Choix du meilleur seuil de segmentation pour l apprentissage automatique Lorsque cet indice devient égal à 1, cela donne le seuil de segmentation maximum pour discriminer des unités de paysage homogènes. Ceci est notamment important pour le choix du seuil de segmentation pour l apprentissage automatique. Lorsque l indice d hétérogénéité est égal à 1, nous avons vu que les segments correspondent en moyenne aux îlots. Mais la variabilité de l indice d hétérogénéité sur les îlots implique le choix d un seuil de segmentation tenant compte de cette variabilité, donc l indice doit être choisi légèrement supérieur à 1, pour éviter que certains îlots soient englobés dans un segment plus grand qui contiendrait d autres classes (ce rapport est une Ch 5 125
150 Analyse de paysage moyenne). Le seuil de segmentation optimum est variable suivant les classes. Application Le niveau d observation est donné par l aire moyenne des segments dans l image. Par exemple, au seuil de segmentation 1, le niveau d observation correspond à un grain de 0,56 ha. Au seuil de segmentation 1, d après la figure 5.2, on distingue deux grands groupes : classes homogènes : ce groupe peut être divisé en trois sous groupes classes très homogènes (h 3) : Orge, Peuplier, classes homogènes (4 h 5) : Jachère, Lac, Gravière, Sorgho, Pois classes moyennement homogènes (6 h 8): Soja, Bâti dense, Colza, Bâti/minéral, Eucalyptus classes hétérogènes : ce groupe peut être divisé en deux sous groupes classes hétérogènes (h 11) : Feuillu, Résineux, Tournesol, Rivière, Blé, Maïs, classes très hétérogènes (h 15) Prairie, Bâti lâche seuil 1 seuil 2 seuil 3 seuil 4 seuil 5 seuil 6 seuil 7 seuil 8 seuil 9 seuil 10 seuil 11 seuil 12 seuil 13 seuil 14 seuil 15 seuil 16 seuil 17 seuil 18 seuil 19 seuil 20 Feuillu Résineux Eucalyptus Blé Colza Orge Maïs Tournesol Sorgho Soja Pois Jachère Prairie Rivière Lac Bâti dense Bâti/Minéral Gravière Peuplier Bâti lache/minéral Seuils de segmentation Figure 5. 2 : rapport du nombre de segments sur le nombre d îlots (seuils de 1 à 30) Au seuil de segmentation 4 (niveau d observation : grain de 1,12 ha), les classes apparaissent globalement un peu moins hétérogènes, mais on retrouve les deux groupes principaux. A partir de ce seuil, pour les classes Feuillu et Résineux, qui étaient hétérogènes au seuil de segmentation 1, la pente s affaiblit rapidement et rejoint les classes plus homogènes. De même, l Eucalyptus, moyennement homogène, rejoint les classes les plus homogènes. Au seuil de segmentation 16 (niveau d observation : grain de 3,36 ha), identifié comme le plus proche du parcellaire agricole, l indice devient faible et les classes encore hétérogènes ont tendance à s homogénéiser. Cependant des classes sont plus hétérogènes que d autres : classes hétérogènes (h 4) : Prairie, Bâti lâche, Rivière, Tournesol classes peu hétérogènes (h légèrement supérieur à 1) : Blé, Maïs et Bâti/minéral classes homogènes (h 1, mais par valeur inférieure) : toutes les autres classes Ch 5 126
151 Analyse de paysage La figure 5.2 confirme le bon choix du seuil 16 pour certaines classes, et le seuil 9 pour d autres classes telle que la classe Résineux Indice de morcellement : rapport du nombre d UEPs sur l aire de la classe Un nouvel indice : l indice du morcellement de la classe (noté Im) a été crée. Il est le rapport du nombre d UEP sur l aire de la classe. Il indique la façon dont les UEPS sont séparées. Ainsi, si une classe a beaucoup d UEPs par rapport à la surface de la classe celle-ci est très morcelée. Ce qui est différent de la dispersion car une classe peut être morcelée, mais située dans la même zone. On peut avoir une classe dispersée et morcelée. Une classe morcelée (indice de morcellement élevé) est constituée d un grand nombre de petites UEPs (beaucoup d UEPs par rapport à l aire de la classe). Pour une même surface, une classe non morcelée (indice de morcellement faible) a peu d UEPs, mais de grande taille, la classe est plus «unie» (figure 3). Exemple : Pour une aire de 100 ha, si une classe est composée de 6 UEPs, alors l indice est faible 6/100 = 0,06. Si elle est composée de 24 UEPs, alors l indice est plus élevé 24/100 = 0,24 Classes peu morcelées Classes morcelées Figure 5.3: représentation schématique de la notion de morcellement L indice de morcellement au niveau des îlots correspond au morcellement de la classe dans l image, ce qui caractérise une hétérogénéité inter UEPs. Au niveau parcellaire il indique plutôt une hétérogénéité au point de vue du stade végétatif et/ou des pratiques culturales et correspond à une hétérogénéité intra UEPs. Le rapport des indices de morcellement (Im îlots / Im parcellaire) équivaut à interpréter le rapport du nombre d îlots sur le nombre de segments (à l approximation près au niveau du calcul des aires des îlots et des segments), et correspond à l étude de l hétérogénéité (rapport inverse de celui présenté pour l étude de l hétérogénéité). Application (zone test Sud-Ouest toulousain) Echelle des îlots L Eucalyptus possède très peu d UEPs qui se trouvent pratiquement d un seul tenant. Cette classe est donc très peu morcelée (figure 5.4). On peut regrouper les classes en trois catégories : o Classes peu morcelées (0,046 Im 0,133) : Feuillu, Résineux, Eucalyptus, Blé, Maïs, Tournesol, Prairie, Rivière, Gravière, Bâti lâche/minéral Ch 5 127
152 Analyse de paysage o Classes moyennement morcelées (0,177 Im 0,294) : Colza, Sorgho, Soja, Bâti/Minéral o Classes morcelées (0,325 Im 0,459) : Orge, Pois, Jachère, Lac, Bâti dense, Peuplier L Orge présente une particularité : certaines parcelles sont très petites. Elles se trouvent souvent à l intérieur d autres parcelles, ce qui indique plutôt des erreurs de classification. Cette classe est confondue avec le Blé, leur morphologie et phénologie sont concordantes Feuillu Résineux Eucalyptus Blé Colza Orge Maïs Tournesol Sorgho Soja Pois Jachère Prairie Rivière Lac Bâti dense Bâti/Minéral Gravière Peuplier Bâti lache/minéral Echelle du parcellaire Figure 5.4 : indice de morcellement à l échelle de l îlot Les valeurs de cet indice au niveau parcellaire, comparées à celui des îlots donne une indication de «l hétérogénéité» de la classe Feuillu Résineux Eucalyptus Blé Colza Orge Maïs Tournesol Sorgho Soja Pois Jachère Prairie Rivière Lac Bâti dense Bâti/Minéral Gravière Peuplier Bâti lache/minéral Figure 5.5 : indice de morcellement (hétérogénéité) à l échelle du parcellaire Ch 5 128
153 Analyse de paysage Dans l exemple présenté le seuil de segmentation choisi est 16. Parmi les cultures, la classe la plus hétérogène est le Tournesol (figure 5.5). L indice de morcellement indique ainsi une grande variabilité de développement végétatif, en relation avec des itinéraires culturaux diversifiés. Les moins hétérogènes sont les cultures irriguées (Maïs, Sorgho, Soja), au développement plus homogène. Les autres cultures, qui sont des cultures d hiver, ont un indice de morcellement intermédiaire. Rappelons que les classes Prairie, Bâti lâche, Rivière et Tournesol étaient assez hétérogènes avec l indice d hétérogénéité à ce seuil, Blé, Maïs et Bâti/minéral peu hétérogènes, toutes les autres classes homogènes. Lien avec l hétérogénéité Le rapport Im îlot / Im parcellaire (correspond au rapport inverse de celui présenté pour l étude de l hétérogénéité, ) peut être inférieur à 1 pour les classes peu représentées et de petite taille : Orge, Sorgho, Soja, Pois, Jachère et Peuplier. Pour les classes Feuillu, Eucalyptus, Colza, Lac, Bâti dense Gravière, il est proche de 1 (de 1 à 1,5), les îlots sont alors homogènes et une parcelle correspond à un îlot de paysage Rapport (ind morcellement îlots / ind morcellement parcelles) Feuillu Résineux Eucalyptus Blé Colza Orge Maïs Tournesol Sorgho Soja Pois Jachère Prairie Rivière Lac Bâti dense Bâti/Minéral Gravière Peuplier Bâti lache/minéral Figure 5.6 : rapport de l indice de morcellement au niveau des îlots sur l indice de morcellement au niveau des parcelles Quatre classes ont un rapport supérieur à 1 (de 1,5 à 3), il s agit des Résineux, Blé, Maïs et Bâti/minéral. Cela signifie que les îlots de ces classes sont hétérogènes ; pour les Résineux, l hétérogénéité peut être due à des plantations d âges différents, pour le Bâti/minéral à des différences de densité et de type de bâtis. Pour le Blé, les causes peuvent être diverses, soit des différences de phénologie, soit la séparation de deux parcelles contiguës et de faible contact. Quatre autres classes sont, elles, très hétérogènes (rapport supérieur 3), le Tournesol, la Prairie, la Rivière et le Bâti lâche. La Prairie et le Bâti lâche possédent chacune un très grand îlot qui a été fortement divisé Descripteur de fragmentation Cette caractéristique est déduite des inclusions de classes («les trous»). Cet un nouveau concept qui a été introduit : les inclusions de classes dans d autres classes. Les inclusions sont représentées par des UEPs de classes différentes qui sont contenues à l intérieur d une UEP d une classe. Par exemple on peut avoir une forêt avec une clairière (figure 5.7-A). Ces inclusions sont indicatrices Ch 5 129
154 Analyse de paysage de la fragmentation. Au préalable il faut avoir éliminé certaines inclusions dues à des confusions entre les classes. A Figure 5.7: exemples : une forêt avec une clairière (A) ; un grand patch de prairie contenant des «trous» de bâti, bosquets, point d eau, parcelles en culture (B). Si la classe compte beaucoup d inclusions, et que celles-ci représentent une proportion non négligeable de l aire de la classe, alors la classe est fragmentée. Dans la figure 5.7-B la classe Prairie est fragmentée. L indice de fragmentation est égal au rapport du nombre d inclusions sur le nombre d UEPs, il est indépendant de l aire des UEPs. Mais seul, cet indice est insuffisant. L indice de fragmentation est complété par le rapport du nombre d UEPs sans inclusion sur le nombre d UEPs, ce qui permet de savoir si la classe est réellement fragmentée ou seulement dans certains endroits (pour certains patchs). En effet, on peut avoir un indice de fragmentation élevé, mais les inclusions se trouvent uniquement sur quelques patchs, plutôt grands. La proportion de l aire des inclusions par rapport à l aire de la classe renseigne aussi sur l importance de la fragmentation, une classe pouvant avoir peu d inclusions mais ceux-ci occupent un espace conséquent. C est un indice de taille des fragments ou taille du «tamis». Remarque : Les inclusions dépendent du niveau d observation choisi pour l image étudiée. La signification des «trous» est différente suivant que l image est sur-segmentée ou sous-segmentée. Donc pour étudier la fragmentation il faut faire attention au choix du seuil de segmentation, surtout si des régularisations sont faites. En résumé : le descripteur de la fragmentation est composé de plusieurs facteurs : du pourcentage ST (sans trou) du nombre d UEPs sans inclusion par rapport au nombre d UEPs de la classe, du pourcentage MT (trous multiples) de nombre d UEPs à inclusions multiples par rapport au nombre d UEPs de la classe, du pourcentage AT (aire trou/aire classe) d aire des inclusions par rapport à l aire de la classe (figure 5.8). Ainsi : Si ST est élevé et AT est faible alors la classe n est pas fragmentée Si ST est élevé et AT est élevé alors certaines UEPs sont fragmentées, et d autres pas Si ST est faible et MT est élevé alors la classe est fragmentée Si ST est faible et MT est faible et AT est élevé alors la classe est fragmentée, par de grandes surfaces Si ST est faible et MT est faible et AT est faible alors la classe est peu ou moyennement fragmentée Application B Dans l image correspondant à la région test, au niveau des îlots, les classes apparaissent globalement uniformes et non fragmentées car elles contiennent peu d inclusions. Dans ce cas, l aire des inclusions est faible. Les classes les plus fragmentées sont le Résineux, la Prairie Ch 5 130
155 Analyse de paysage (beaucoup de patchs contenant des inclusions et/ou de faible surface) et deux classes de bâtis, le Bâti dense et le Bâti lâche. Ces dernières présentent un nombre de patchs avec inclusions très faible (2%), mais avec une aire plus importante qui indique une concentration des inclusions dans quelques patchs de plus grande taille. ST faible élevé MT AT faible élevé faible élevé AT Classe Classe non Certaines UEPs faible élevé fragmentée fragmentée sont fragmentées Classe peu fragmentée Classe fragmentée par de grandes surfaces Figure 5.8 : graphe du descripteur de fragmentation La Prairie constitue le fond du paysage (appelée la matrice paysagère) car cette classe regroupe non seulement les parcelles agricoles de prairie, mais aussi les ensembles végétalisés telles que les diverses bandes enherbées constituant les bordures du parcellaire et autres lisières (pelouses autour des maisons, lisières de bois). Les inclusions sont donc plus nombreuses. Les Résineux sont souvent implantés à l intérieur des forêts de feuillus, ce qui donne un mélange souvent complexe de ces deux espèces, et qui entraîne un enchevêtrement d alvéoles composé de ces deux classes. Les inclusions peuvent être aussi bien dans les Feuillus que les Résineux. Cependant les Résineux présentent relativement plus d inclusions (1,12%), en général les classes Feuillus et Prairie, que les Feuillus (0,69%). Les classes incluses dans le Bâti dense (en général du Bâti lâche), peu nombreuses mais de surface non négligeable, correspondent souvent à des zones minéralisées (Bâti/minéral tel que les parkings) et à des espaces verts. Les classes incluses dans le Bâti Lâche, qui est caractéristique de zones rurales et périurbaines, correspondent à des pelouses, des jardins ou d autres types de Bâti Les noyaux, la couronne Les bords d une UEP ont un rôle important pour le règne animal et végétal. Par exemple, certaines espèces de conifères ne se développent pas de la même façon à la frontière, et à l intérieur d une forêt (problème de pénétration de la lumière). De la même façon, le territoire de certaines espèces animales, peut s arrêter bien avant les limites d un territoire forestier. Il paraît alors naturel, de définir le noyau («Core» en anglais) d une UEP comme l ensemble des points de celle ci, à l intérieur d une couronne (Figure 5.9) de taille «m» prédéfinie. Du point de vue morphologie mathématique, le noyau est la zone d un patch dont la distance au bord est supérieure à «m», ce qui correspond à l'érosion du patch par une boule centrée de diamètre «m», donné en fonction du type d étude. Ch 5 131
156 Analyse de paysage Figure 5.9 : noyau A d une UEP d aire A pour une couronne de largeur m L aire du noyau donne des informations à la fois sur la configuration et sur la composition du paysage. La plupart des indices, utilisant l aire des UEPs, ont leur équivalent avec le noyau ; ils sont calculés de la même manière après l élimination des points de la couronne. L objectif est de quantifier «ces effets de bord», liés à une combinaison de facteurs biotiques et abiotiques qui modifient les conditions environnementales entre les bords et l intérieur des UEPs. Ces effets diffèrent selon les organismes et les processus. Par exemple, certaines espèces d oiseaux sont affectées par la prédation, la compétition, la confrontation aux parasites, ainsi que d autres facteurs le long des contours forestiers. L aire du noyau est alors considérée, selon les spécialistes comme un bien meilleur indicateur de la qualité de l habitat (terme écologique signifiant l emplacement d une espèce) que l aire totale. A la différence de l aire totale (d une UEP), l aire du noyau est affectée par la forme de celle ci. Par conséquent, alors qu une UEP semblerait être assez grande pour supporter une certaine espèce, elle peut ne pas contenir assez d espace habitable nécessaire à son développement. Figure 5.10 : cas d apparition de noyaux disjoints, et de disparition de noyau Au niveau d une classe, il est intéressant de connaître l aire totale du noyau, ainsi que son rapport sur l aire totale de la classe, et celle du paysage. Ces descripteurs intègrent des notions de nature différente : aire totale, forme, et effets de bords. Bien qu ils quantifient la composition du paysage, ils sont affectés par sa configuration. Ainsi, au niveau de la classe, certains de ces descripteurs peuvent être efficaces dans l étude de la fragmentation de l habitat, car celle ci se traduit en même temps par l aire du milieu, et sa configuration. Lors de la création du noyau, plusieurs noyaux disjoints (figure 5.10) peuvent apparaîtrent à l intérieur d une UEP. L apparition de zones habitables disjointes pouvant profondément modifier un système écologique, le nombre de noyaux est un indicateur de la structure de l habitat. Ch 5 132
157 Analyse de paysage Descripteur de circonvolution Un descripteur de circonvolution a été introduit qui est le rapport du nombre de noyaux par UEPs sur le nombre d UEPs. Il donne une indication générale sur la taille et/ou la forme des patchs du point de vue des circonvolutions. Il est indépendant de l aire des UEPs, il est global et nécessite l utilisation d autres caractéristiques pour une description précise. Si ce rapport est proche de 1 (de 0,9 à 1,1), alors on ne peut pas conclure En effet, il peut y avoir une majorité d UEPs à forme simple et/ou de grande taille, un mélange d UEPs de petite taille (donc pas de noyau) et des UEPs convolutées, il est nécessaire de préciser avec d autres indices. Si ce rapport est inférieur à < 0,9 alors beaucoup d UEPs sont de taille trop petite pour posséder un noyau, ou bien ces UEPs sont très convolutées. Si ce rapport est supérieur à 1 (>1,1) alors beaucoup d UEPs sont convolutées (plusieurs noyaux) traduit une forme plutôt convolutée Composition des UEPs : pourcentage d UEPs à 0 noyau, 1 noyau, un nombre supérieur à 1 noyau Cette caractéristique complète l indice précédent, et permet de relativiser l interprétation d après les effectifs. En effet, il existe plusieurs types d UEPs : UEP à 1 noyau UEP convolutée à plusieurs noyaux UEP à 0 noyau, petite ou très convolutée Figure 5.11 : noyaux en fonction des forme d UEPs Si beaucoup d UEPs à 1 seul noyau alors les UEPs sont de taille suffisamment grande pour contenir un noyau et/ou sont de forme simple. Si beaucoup d UEPs à multiples noyaux alors les UEPs sont convolutées (de forme complexe). Si beaucoup d UEPs à 0 noyaux alors les UEPs sont de petite taille ou très convolutées Indice de régularité géométrique L indice de régularité géométrique Irg est le pourcentage d aire totale des noyaux par rapport à l aire de la classe (aire des noyaux / aire de la classe, ramené en pourcentage) varie de 0 à 100. Cet indice, seul, apporte peu d informations précises, mais il permet de confirmer les résultats obtenus par les descripteurs précédents, et ceux des indices de forme ( 5.2.4), si l information obtenue est incertaine. Cet indice est très dépendant de la taille des UEPs. Ch 5 133
158 Analyse de paysage Classe à UEPs de taille suffisante pour avoir un noyau (indice 0,6) Classe à plusieurs UEPs de tailles différentes, contenant des petites UEPs et des UEPs convolutées, (indice 0,3) Figure 5.12 : différents cas de présence de noyaux Si Irg est élevé alors la classe possède des UEPs de forme plutôt simple et/ou de grande taille. Si Irg est faible alors la classe possède des UEPs de petite taille et/ou de forme complexe Pourcentages Feuillu Résineux Eucalyptus Blé Colza Orge Maïs Tournesol Sorgho Soja Pois Jachère Prairie Rivière aire noyaux/aire classe(%)(régularité) Lac Bâti dense Bâti/Minéral Gravière Peuplier Bâti lache/minéral Figure 5.13 : courbe de variation l indice de régularité en fonction des différentes classes Pour l ensemble des classes (figure 5.13), cet indice reste proche d une valeur moyenne de 50% variant de 40% à 65%. Autour de 40% sont les classes Orge, Sorgho, Pois, Jachère, Rivière, Lac, Bâti dense, Bâti minéral et Peuplier (peu régulières). Autour de 50% se trouvent le Colza et le Soja, puis le Tournesol, la Prairie et la Gravière (classes moyennement régulières). Les autres classes sont au delà de 60% (plutôt régulières). On retrouve les résultats de l étude «taille, forme», mais moins détaillée. On peut noter que l allure de la courbe est très proche de celle des aires moyennes des UEPs. Rappelons que plus les UEPs sont grandes plus le rapport est grand même avec des formes complexes. Pour enlever les doutes et les imprécisions, les caractéristiques sont combinées : le nombre d UEPs sans noyau, le nombre d UEPs à noyaux multiples, le nombre d UEPs à un seul noyau, le plus grand nombre de noyaux dans un patch, le rapport du nombre de noyaux sur le nombre d UEPs qui est indépendant de l aire des UEPs, le résultat de cette combinaison est présenté Ch 5 134
159 Analyse de paysage Descripteurs de forme Ces descripteurs sont indicateurs de la forme, mais aussi de la dimension fractale, de la densité (non présentée ici) Le périmètre et la longueur des contours inter-classes Le périmètre ne donne pas d informations sur la composition spatiale du paysage. En revanche, associés à d autres indices il caractérise la conformation de celui-ci. Les longueurs des frontières inter-ueps (des contours inter-classes) fournissent des indices sur le côtoiement des classes entre elles qui aident à comprendre la configuration du paysage, mais ces indices ne donnent aucune information d ordre spatial. Il est reconnu que beaucoup de problèmes liés à la vie animale ou végétale sont dues aux effets de voisinages. Par exemple, deux parcelles peuvent posséder la même aire et avoir des formes très différentes : l'une permettra la coexistence de certaines espèces l autre pourra être plus propice à l habitat d'autres espèces, mais peut-être en moins grand nombre. La somme des contours des unités élémentaires est également liée à l hétérogénéité du paysage. En effet, plus un paysage est hétérogène, plus les contours deviennent prépondérants. Ainsi si l on ramène la somme des longueurs des contours à l aire il est possible de fournir des informations sur la complexité du paysage, et de permettre leur comparaison. La longueur du contour entre chacune des classes permet de connaître, par exemple leur juxtaposition ( 5.7.3), c est à dire le taux de contact qu une classe possède avec les autres. Périmètre moyen Il donne une indication du découpage de la classe, plus ce périmètre moyen est petit, plus la classe est découpée en UEPs (confirme l indice de morcellement) ou les UEPs ne sont pas convolutées. Mais, ces caractéristiques sont calculées par ailleurs. La somme des contours donne une indication sur l hétérogénéité du paysage. Des indices de contours (longueur totale du contour d une classe), la densité de contours peuvent être calculés. Les formules basées sur les périmètres les plus intéressantes sont présentées ici : indices de formes, dimension fractale. Elles sont appliquées aux classes ou au paysage, pondérés ou non La forme La forme est un élément difficile à quantifier, qui peut donner libre cours à de multiples interprétations. La forme influence la vie du règne animal (migration de certains mammifères). Comme pour les contours, elle est liée à l hétérogénéité du paysage : un ensemble complexe aura une forme convolutée. Elle est également liée à des degrés d artificialisation de la parcelle étudiée : les terres agricoles sont très souvent polygonales, rectangulaires, alors que les formations naturelles telles que les forêts sont souvent à contours complexes (sauf au niveau des zones de contact avec des parcelles agricoles). Le principe du calcul de la forme est basé sur un rapport entre le périmètre et l aire. Une méthode consiste à se ramener à une forme connue, en général à une forme standard, comme le carré ou le cercle (de préférence carré car il correspond à la forme du pixel, et se rapproche de celle du parcellaire agricole). Ch 5 135
160 Analyse de paysage Terre agraire : indice de Rivière : indice de forme forme proche de 1 élevé Figure 5.14 : exemple de formes La complexité spatiale d une classe est évaluée en moyennant les indices de formes des unités élémentaires de la classe. La complexité [Institute for complexity de Santa Fe] est équivalente : au degré de détails qu'un système montre à des échelles de plus en plus petites au degré de régularité (plutôt qu'au degré d'aléatoire) qui se manifeste dans un système à la diversité déployée par les différents niveaux d'un système structuré d'une façon hiérarchique. Figure 5.15 : exemple d UEPs de petites tailles influençant l indice de forme Il est possible de pondérer les indices par l aire de chaque UEP. Cette dernière méthode présente l avantage d atténuer l influence des petites UEPs car une image classée peut contenir beaucoup de petites UEPs de quelques pixels. La classe A (figure 5.15) possède une grande région agraire, et des petites régions qui peuvent provenir, par exemple, de défauts dus à la classification, mais souvent de surfaces restées enherbées, ou de petits bosquets. L évolution de l indice après pondération est donc un indicateur de la répartition des formes selon la taille. Si par exemple les grandes étendues agraires sont moins complexes que les petites, le rapport indice pondéré sur celui qui est non pondéré sera plus petit que 1. Appliqué à l image entière, l indice de forme moyen (moyenne, sur tous les UEPs de toutes les classes, pondérée ou non par l aire de UEP), devient une caractéristique de la complexité de l image. Ch 5 136
161 Analyse de paysage Indices de formes Indice de forme L indice de forme (IF), calculé d après le périmètre et l aire, indique si les UEPs, ont une configuration proche d un carré ou si au contraire ils s en éloignent [McGarigal K. & Marks B.J. 1994]. Le rapport entre le quart du périmètre et l aire d une UEP permet d obtenir un indice égal à 1 pour un carré, et supérieur dans les autres cas. si IF moyen est proche de 1 (jusqu à 1,2), alors la plupart des UEPs de la classe ont une forme qui se rapproche du carré (forme simple). Indice de forme par rapport à l aire L indice de forme par rapport à l aire, LSI, [McGarigal K. & Marks B.J. 1994] est la somme, sur l'ensemble des classes, des contours entre la classe i et la classe j sur la racine carrée de l aire totale de la classe i, fois un terme de normalisation 0.25 dû à la forme carrée de l'élément de base, le pixel:. LSI = 0.25* j j aij pij LSI >=1, LSI tend vers 1 lorsque la classe n'est constituée que d'ueps de forme simple se rapprochant du carré. LSI augmente lorsque la forme des UEPs de la classe s écarte en moyenne du carré, les formes des UEPs deviennent plus complexes. Indice de forme moyen d une UEP L indice de forme sur la totalité de la classe (périmètre total et aire totale) est moins précis que l indice de forme moyen qui tient compte du nombre d UEPs. MSI est la moyenne des indices de forme de chaque UEP pour la classe. pij j aij 0.25 MSI = MSI >=1 ni MSI tend vers 1 lorsque la majorité des UEPs de la classe se rapprochent du carré MSI augmente avec le nombre d'ueps dont la forme s'éloigne du carré Indice de forme moyen pondéré par l aire (classe) AWMSI est la moyenne pondérée par l aire a ij de l UEP, des indices de forme de chaque UEP, pour la classe. AWMSI majore les grandes UEPs. AWMSI= 0.25 pij j aij aij aij j AWMSI >=1 AWMSI =1 lorsque les UEPs de la classe ont toutes une forme carrée. Ch 5 137
162 L indice de forme moyen pondéré donne plus de poids aux UEPs de grande surface. Analyse de paysage si IF moyen pondéré > IF moyen alors les UEPs de plus grande taille sont de forme plus complexe. Souvent les petites UEPs ne contiennent que quelques pixels (d où une forme proche du carré) La dimension fractale dans le paysage A l'origine de la géométrie fractaliste se situe l'étude mathématique des formes infiniment irrégulières dans leurs moindres détails, brisées, rompues et morcelées en chacune de leurs parcelles, dont la morphologie est par conséquent discontinue. Les objets fractals incluaient l'abandon du concept mathématique traditionnel de symétrie spatiale, liée à la géométrie euclidienne, au profit d'un autre type «d'ordre» mathématique régissant les éléments d'une configuration spatiale irrégulière en toutes ses composantes. Ce nouvel «ordre fractal» était défini en terme strictement mathématique comme un indice algébrique d'irrégularité morphologique : la dimension fractale, qui est un nombre absolu ne désignant pas une mesure de grandeur, mais une mesure évaluative de la complexité formelle des configurations géométriques (en deux ou trois dimensions spatiales). C est le mathématicien Benoît Mandelbrot (1992) qui a introduit le concept des fractales. C'est luimême qui a introduit le néologisme «fractal», venant du mot latin fractus, qui signifie irrégulier, brisé, dans la première édition française de son célèbre livre : «Les Objets fractals -- Forme, hasard et dimension» (1975, Paris, éditions Flammarion). Il montra que les fractales peuvent être présentes autant en mathématique que dans la nature. La définition proposée dans le Larousse est la suivante : «Se dit d'objets mathématiques dont la création ou la forme ne trouve ses règles que dans l'irrégularité ou la fragmentation». Quelles formes peuvent être considérées comme infiniment irrégulières et discontinues? En théorie, toute forme existante ou mathématiquement imaginable relève de la mathématique du discontinu. Ce sont les échelles d'examen de l'objet, naturel ou géométrique, qui définissent les degrés variables de discontinuité de la forme. Les objets de la nature, observés à grande distance, peuvent apparaître globalement comme des formes simples, régulières, descriptibles au moyen des catégories de la traditionnelle géométrie euclidienne : des cercles, des triangles, des parallélépipèdes, des sphères, des cônes, des cylindres, des polyèdres, et toute combinaison de ces formes élémentaires primitives. Pourtant, observées de plus près, à la «loupe mathématique», ces formes naturelles deviennent plus compliquées, moins linéaires, moins «euclidiennes»; elles présentent des contours brisés et des structures surfaciques ramifiées, enchevêtrées. Si le niveau d'observation, toujours plus exigeant, continue de s'affiner, le moindre détail apparaît alors comme une myriade de détails plus fins et toujours plus riches de microformes, elles-mêmes saturées à l'infini de microformes gigognes hyper détaillées, aux apparences nouvelles. Le corollaire de l'affinement de l'échelle d'observation réside dans le fait qu'aucune symétrie euclidienne connue n'est détectable en chaque fragment étudié. Les exemples puisés dans la nature sont omniprésents. La structure des nuages en mouvement, la forme des montagnes, tout comme une simple feuille de châtaignier, un morceau de rocher, sont affectés d'innombrables zones d'irrégularité en fonction des niveaux d'observation auxquels on les soumet. Il existe évidemment des taux d'irrégularité plus différenciés, plus tranchés que d'autres, selon l'échelle adoptée, mais aucune reproduction structurale à l'identique, douée de symétrie absolue, n'existe à l'état naturel. Le mérite de la géométrie fractale est précisément d'avoir permis de caractériser ces degrés ou niveaux d'irrégularité relative qui signent l'hétérogénéité morphostructurale de la matière. Ch 5 138
163 Analyse de paysage En géométrie euclidienne, les figures ont une dimension entière : 0 pour un point, 1 pour une courbe (un segment), 2 pour une surface (un carré) et 3 pour un volume (un cube). On dit qu'une courbe est un espace à 1 dimension parce qu'on sait mesurer les longueurs le long de la courbe et qu'on peut repérer tout point de la courbe par un seul nombre, son abscisse, c est à dire sa distance depuis le point de la courbe pris comme origine. En revanche, la dimension d'une fractale peut prendre des valeurs qui ne sont pas des nombres entiers : ce sont des dimensions fractionnées. La dimension fractale constitue donc une généralisation de la notion de dimension en géométrie euclidienne. Une approche intuitive consiste à considérer qu'une fractale est la transformation récursive d'un objet par n copies de lui même à l'échelle r (avec r < 1). Cette propriété est appelée l'autosimilarité. Lorsque l'on prend les cartes côtières, quelle que soit l'échelle, elles représentent toutes une distribution semblable de baies et de caps, ceux-ci ayant eux-mêmes des baies et des caps plus petits et ainsi de suite. Ainsi, si l'on agrandit une côte, de nouvelles baies et de nouveaux caps apparaissent, et l'ensemble continue de ressembler à une côte réelle. Donc un minuscule morceau de côte, agrandi 10 fois, ressemble toujours à une côte. Ceci reprend le principe d'autosimilarité, même si dans le cas des côtes la similarité n'est que statistique, car les proportions moyennes des baies et caps restent inchangés quelque soit l'échelle, mais leur distribution peut changer. Un objet fractal est caractérisé par sa dimension fractale notée D, nombre réel. Mandelbrot définit la dimension fractale D comme liée au nombre d'éléments constituants N et au rapport d'homothétie S par la relation: N= (1/K) D, avec N : nombre d éléments, 1/K: rapport homothétique, D : dimension fractale. D'où : D = -log(n)/log(k) cette relation donne des dimensions fractionnaires ou fractales. La dimension du flocon de neige de Von Koch, bien connu est D =log(4)/log(3) 1,26 D est proche de 1 quand la fractale est "plutôt" lisse, augmente quand la fractale devient plus accidentée. Les fractales ont une dimension comprise entre 1 et 2 pour le plan ou entre 2 et 3 pour les volumes. Application aux images et à l étude du paysage Les objets naturels diffèrent des objets mathématiques par le fait que ces derniers possèdent un nombre d échelles infini [Mandelbrot 1992]. La dimension fractale sert à quantifier le degré d irrégularité et de fragmentation d un ensemble géométrique de ces objets. Son intérêt en analyse du paysage a été démontré par sa capacité de définir un espace quelle que soit l échelle d observation [Burel et al, 1999]. La dimension fractale calculée au niveau des îlots est suffisante pour définir l organisation structurale des paysages. La méthode du «périmètre-aire» mesure le degré de complexité des formes planes. Le degré de complexité d'un polygone est caractérisé par la dimension de fractale D, tel que le périmètre P d'une D 1 UEP est lié à l aire A par : P A ou log P D log A [Burrough 1986]. 2 Pour des formes euclidiennes simples (par exemple, cercles et rectangles), P A D = 1. Quand les polygones deviennent très complexes, le périmètre devient de plus en plus complexe P A avec D 2. Avec cette méthode de calcul, la mesure de la dimension fractale est dépendante de l unité utilisée (différence avec l indice de forme). Cela veut donc dire que deux formes homothétiques auront deux dimensions fractales différentes. En effet, ce rapport est calculé séparément pour la dimension de fractale de chaque patch. La dimension fractale calculée de cette manière dépend donc de la taille des patchs [Rogers 1993]. Ainsi, changer la taille des cellules de l'image affecte la dimension fractale du patch. Par conséquent, il faut être prudent quant à l interprétation de cet indice de dimension fractale pour mesurer la complexité de forme d un patch. Ch 5 139
164 Analyse de paysage En tout état de cause, la plus grande limite de la dimension fractale reste peut être la difficulté à la conceptualiser, mais elle est appelée à être de plus en plus utilisée dans le domaine de l écologie. Exemple : La dimension fractale DF illustre la complexité du contour des UEPs. 1,16 1,14 1,12 1,1 1,08 1,06 1,04 1,02 1 Feuillu Résineux Eucalyptus Blé Colza Orge Maïs Tournesol Sorgho Soja Pois Jachère Prairie Rivière Lac Bâti dense Bâti/Minéral Gravière Peuplier Bâti lache/minéral Figure 5.16 : indice de dimension fractale moyen si DF moyen est proche de 1 (jusqu à 1,1) alors les contours des UEPs sont réguliers, s il est proche de 2, alors les contours sont très irréguliers. Ce même indice pondéré par l aire donne plus de poids aux UEPs de grande taille si DF moyen pondéré > DF moyen alors les contours des grandes UEPs sont plus irréguliers. Sur la région test, pour la plupart des classes, les contours des UEPs des classes sont assez réguliers (figure 5.16) (cet indice est inférieur à 1,1). Toutefois, la classe Rivière se détache, les contours de ses UEPs apparaissant plus disséqués. Figure 5.17 : UEPs au contour régulier ou irrégulier Ch 5 140
165 Combinaison des descripteurs surfaciques et de formes Analyse de paysage Les descripteurs vus précédemment sont informatifs, mais souvent incomplets pour l analyse du paysage. Combinés on obtient une description des classes et du paysage. L arbre de décision de la figure 5.18 représente l interprétation obtenue avec ces associations. A : UEPs petites, de forme simple, dont la majorité n a qu un seul noyau. B : UEPs petites, de forme simple, le nombre d'ueps sans noyau n'est pas négligeable. C : UEPs petites, de forme complexe, les UEPs peuvent être convolutées, avec des UEPs sans noyau ou bien être de forme complexe mais n'avoir qu'un noyau. D : UEPs petites, de forme complexe, avec beaucoup de volutes. E : UEPs petites, de forme complexe, le nombre d'ueps sans noyau n'est pas négligeable. F : UEPs variables mais plutôt petites, de forme simple, dont la majorité n a qu un seul noyau. G : UEPs variables mais plutôt petites, de forme simple, le nombre d'ueps sans noyau n'est pas négligeable H : UEPs variables mais plutôt petites, de forme complexe, les UEPs peuvent être convolutées, avec des UEPs sans noyau ou bien être de forme complexe mais n'avoir qu'un noyau. I : UEPs variables mais plutôt petites, de forme complexe, avec beaucoup de volutes. J : UEPs variables mais plutôt petites, de forme complexe, le nombre d'ueps sans noyau n'est pas négligeable. K : UEPs grandes, de forme simple, dont la majorité n a qu un seul noyau. Les effectifs particuliers peuvent modifier ce rapport. L : UEPs grandes, de forme complexe, beaucoup d'ueps sont convolutées, mais la taille implique un seul noyau. M : UEPs grandes, de forme complexe, beaucoup d'ueps sont convolutées et ont plusieurs noyaux. N : UEPs variables mais plutôt grandes, de forme simple, dont la majorité n a qu un seul noyau. O : UEPs variables plutôt grandes, de forme simple, dont la majorité n'ont qu'un seul noyau, mais le nombre d'ueps sans noyau n'est pas négligeable. P : UEPs variables plutôt grandes, de forme complexe, beaucoup sont convolutées mais la taille implique un seul noyau ou bien elles sont petites ou convolutées. Q : UEPs variables mais plutôt grandes, de forme complexe, avec beaucoup de volutes avec plusieurs noyaux. R : UEPs variables mais plutôt grandes, de forme complexe, dont la majorité sont grandes et convolutées mais le nombre d'ueps sans noyau n'est pas négligeable. Ch 5 141
166 Analyse de paysage petite < 7,5 ha AIRE MOYENNE grande > 7,5 ha faible CV élevé faible CV élevé < 2,5 < 2,5 < 2,5 < 2,5 1 IF IF IF IF >> 1 1 >> 1 1 >> 1 1 >> 1 RC RC RC RC RC RC RC RC 1 < < 1 1 < > 1 1 < 1 1 < 1 > 1 > 1 > 1 A B C D E F G H I J K L M N O P Q R Figure 5.18 : arbre de description de certaines caractéristiques du paysage : tailles et formes des UEPs CV: coefficient de variation sur l aire moyenne des UEPs ; IF : indice de forme ; RC : rapport de convolution (nombre de noyaux / nombre d UEPs). Ch 5 142
167 Analyse de paysage Application : zone test Sud-Ouest toulousain Echelle des îlots A l échelle de l îlot paysager, un agencement de parcelles de forme simple pourra créer un îlot de forme complexe. L analyse simultanée de ces éléments permet de décrire précisément les nombreux cas de figure que présentent les UEPs de chaque classe, par leur taille et leur forme (figures 5.19 à 5.22). Ce sont des îlots de : très petite taille (autour de 2,5ha), de forme simple (indice proche de 1) rapport de convolution inférieur à 0,85, et un grand nombre d UEPs trop petites pour posséder un noyau, donc ne sont pas convolutées : Orge, Sorgho, Pois, Jachère, Lac, Bâti/Minéral, Peuplier. petite taille (autour de 5ha), de forme simple (indice proche de 1), rapport de convolution proche de 1, la majorité ont une taille suffisante pour posséder un noyau, donc ne sont pas convolutées : Colza, Soja. petite taille (autour de 7,5 ha), de forme complexe (indice supérieur à 1,2), rapport de convolution supérieur à 1,15 et de nombreux noyaux, donc le nombre d UEPs convolutés est important : Rivière. Remarque : les parties linéaires et fines de cette classe facilite l élimination ou, au contraire, la multiplication des noyaux. Ilots de taille variable (écart type élevé) en moyenne plutôt petite (autour de 5ha), de forme simple (indice proche de 1), rapport de convolution inférieur à 0,85, avec un grand nombre d UEPs trop petites pour posséder un noyau, donc non convolutées : Bâti dense, Bâti lâche. Ces classes de bâtis sont en effet dispersées de façon anarchique sur l image, le bâti dense se trouvant dans les zones concentrées des villes ou villages (donc souvent petits patchs) ainsi que bâti lâche représenté par beaucoup de groupes de maisons isolées (donc également petits). Ilots de grande taille (autour de 10 ha), de forme simple (indice proche de 1), rapport de convolution proche de 1, une très forte majorité d UEPs n ont qu un noyau donc non convolutées, ce qui confirme des formes très géométriques : Gravière. Ilots de grande taille (autour de 8 ha), de forme complexe (indice supérieur à 1,2), rapport de convolution proche de 1, la majorité ont un seul noyau (56%) donc peu convolutées : Tournesol. Pour cette classe, on observe aussi quelques UEPs convolutées (18%) et des UEPs sans noyau (26%) (figure 5.22). Ilots de taille variable à tendance plutôt grande (autour de 10 ha), de forme complexe (indice supérieur à 1,2), rapport de convolution supérieur à 1,15, la majorité (50%) n ont qu un noyau mais on trouve aussi des UEPs convolutés engendrant de nombreux noyaux ainsi que des UEPs sans noyau : Prairie. Pour cette classe, le nombre important de patchs sans noyau (30%) indique que les UEPs convolutées contiennent donc de très nombreux noyaux engendrant un rapport de convolution élevé. Ilots de taille variable plutôt grande (autour de 10 ha), de forme complexe (indice supérieur à 1,2), rapport de convolution proche de 1, avec à la fois des UEPs convolutés à plusieurs noyaux et un nombre de petites UEPs sans noyau non négligeable : Blé. Ilots de taille variable plutôt grande (autour de 12 ha), de forme complexe (indice supérieur à 1,2), rapport de convolution proche de 1, à un seul noyau donc peu convolutés : Feuillu, Résineux, Maïs. Ilots de grande taille (autour de 22 ha), de forme complexe (indice supérieur à 1,2), rapport de convolution supérieur à 1,15 avec beaucoup de volutes contenant plusieurs noyaux : Eucalyptus. Ce résultat est à relativiser par le nombre peu important de patchs de la classe, en effet, un seul patch est convoluté avec plusieurs noyaux. Ch 5 143
168 Analyse de paysage Feuillu Résineux Eucalyptus Blé Colza Orge Maïs Tournesol Sorgho Soja Pois aire moyenne des UEPs (ha) Jachère Prairie Rivière Lac CV aire des UEPs Bâti dense Bâti/Minéral Gravière Peuplier Bâti lache/minéral Figure 5.19 : aire moyenne des UEPs et coefficient de variation Feuillu Résineux Eucalyptus Blé Colza Orge Maïs Tournesol Sorgho Soja Pois Jachère Prairie Rivière Lac Bâti dense Bâti/Minéral Gravière Peuplier Bâti lache/minéral Figure 5.20 : indice de forme moyen (voir 5.2.4) Feuillu Résineux Eucalyptus Blé Colza Orge Maïs Tournesol Sorgho Soja Pois Jachère Prairie Rivière Lac Bâti dense Bâti/Minéral Gravière Peuplier Bâti lache/minéral Figure 5.21 : rapport du nombre de noyaux sur le nombre d UEPs. Ch 5 144
169 Analyse de paysage 10 0 % 90% 80% % 60% 50% 40% 30% 20% 10 % 0% Feuillu Résineux Eucalyptus Blé Colza Orge Maïs Tournesol Sorgho Soja Pois Jachère Prairie Rivière Lac Bâti dense Bâti/Minéral UEPs à 0 noyaux UEPs à 1 noyau UEPs à plusieurs noyaux Gravière Peuplier Bâti lache/minéral Conclusion : Figure 5.22 : composition, en nombre de noyaux, des UEPs des classes. Malgré une importante variabilité, possible, de la taille et de la forme des UEPs, on retrouve dans cette région des cas souvent similaires : Des cultures représentées par des îlots de petite taille et de forme simple, ce qui dénote le caractère anthropique de l exploitation des sols : Colza, Soja, Orge, Sorgho, Pois. Des cultures avec des îlots de grande taille qui sont les plus représentées dans l image : Blé, Maïs, Tournesol. Des boisements avec des UEPs de plus grande taille et de forme complexe, ce qui traduit une pression anthropique moindre, mis à part les boisements implantés sur d anciennes prairies ou cultures tels que les peupliers (UEPs inscrites dans le parcellaire agricole). Les classes d eau avec des caractéristiques différentes : petites UEPs convolutées pour la rivière (linéaire) ; petites et régulières pour les lacs ; grandes et de forme très géométrique pour les gravières creusées par l homme. Les classes de bâtis, aux UEPs généralement petites (voire très petites) et régulières reflètent les constructions à la géométrie simple (bloc de maisons, zones industrielles ). Echelle du parcellaire A cette échelle d étude, le niveau d observation est celui de la parcelle d exploitation. L observation des caractéristiques, formes et tailles des UEPs c'est-à-dire des parcelles, permettra de conclure sur le degré d artificialisation de la classe. La première constatation provient des coefficients de variation qui sont très bas, la taille des UEPs de chaque classe se situe donc globalement autour de la moyenne. Seules les classes de Feuillu et Rivière ont des variations plus importantes, comme à l échelle des îlots, dans ce Ch 5 145
170 Analyse de paysage cas, le niveau d observation ne change pas ces caractéristiques de classes Feuillu Résineux Eucalyptus Blé Colza Orge Maïs Tournesol Sorgho Soja aire moyenne de patchs (ha) Pois Jachère Prairie Rivière Lac Bâti dense CV aire patchs Bâti/Minéral Gravière Peuplier Bâti lache/minéral Les UEPs des classes boisées sont de grande taille. Les feuillus, plus variables, se trouvent dans des forêts, des bosquets ou des haies. Les UEPs d Eucalyptus sont très grandes mais seulement au nombre de quatre. De manière générale, les parcelles de toutes les autres classes sont petites, avec quelques cas particuliers : les UEPs de Sorgho plus grandes, mais il n y a que deux patchs, les UEPs de Maïs sont les plus grandes parmi les cultures, et celles de Tournesol les plus petites. Les Gravières sont aussi de taille plus importante Feuillu Résineux Eucalyptus Blé Colza Orge Maïs Tournesol Sorgho Soja Pois Jachère Prairie Rivière Lac Bâti dense Bâti/Minéral Gravière Peuplier Bâti lache IF moyen Figure 5.23 : taille moyenne et CV, indice de forme En ce qui concerne la forme de ces parcelles, elle est, dans tous les cas, assez simple, mais ce sont les UEPs des classes boisées qui ont les formes les plus complexes (sans tenir compte du Sorgho). En conclusion : Les cultures sont à un degré d artificialisation important, du fait de la géométrie des parcelles d assez petite taille. Les forêts, inscrites dans un parcellaire essentiellement cultivé, subissent moins cette simplification de forme et ont aspect plus naturel, plus complexe, cependant cette forme dépend aussi des pressions agricoles environnantes. Ch 5 146
171 Analyse de paysage Mesure de l arrangement spatial Dispersion : distance intra-classe, distance moyenne entre les UEPs d'une classe La répartition géographique de la classe dans l image est déterminée par la distance intra classe, c est à dire la distance de chaque UEPs entre elles, elle est indicatrice de la dispersion de la classe. Elle influence un nombre important de processus écologiques. Figure 5.24 : Exemple de deux configurations de paysages différentes. Les descripteurs calculés jusqu'à présent ne permettent pas d accéder à un aspect de la conformation du paysage : l éloignement des UEPs. Par exemple (figure 5.24), deux configurations ayant les mêmes statistiques de périmètre et d aire, auront les mêmes indices de forme, de morcellement Or la configuration B est plus éclatée que la configuration A. dans la configuration B, la distance entre UEPs est plus grande que dans la configuration A. Ainsi on peut avoir une classe morcelée, mais non dispersée et vive versa Distances (m) Feuillu Eucalyptus Soja Prairie dist moy + ECT dist moy - ECT distance moyenne Figure 5.25 : exemple d analyse de dispersion schématisée Une moyenne faible avec un écart type faible exprime une classe très regroupée (ex : Eucalyptus ). Une moyenne élevée et un écart type assez faible montre que les UEPs de la classe sont réparties sur toute l image de manière uniforme (ex : Feuillu et Soja ). Un écart type σ important et une moyenne faible indique que les UEPs se trouvent sur toute l image mais avec un caractère regroupé très prononcé (ex : Prairie ). Le logiciel permet de définir une répartition sur toute l image, sur une ou plusieurs zones. Ch 5 147
172 Analyse de paysage Cette distance, peut être calculée soit par la distance au plus proche voisin qui caractérise une UEP en indiquant la plus petite distance entre cette UEP et tous les autres patchs du paysage, de la même classe, soit par la distance moyenne au barycentre des UEPs de chaque classe. La dispersion est évaluée à l aide de la moyenne des distances entre les barycentres des UEPs de chaque de classe, et de leur écart type. Plus la distance moyenne est élevée, plus les patchs sont espacés dans l'image. A l échelle des îlots : les UEPs d une classe peuvent être réparties de différentes manières sur le territoire. Les distances calculées sont intra- classes, mais inter- îlots. D après la figure 5.26, on peut distinguer quatre catégories : Gravière o o type très regroupé (distance moyenne 8,9 km, σ faible) : Eucalyptus, type localisé (distance moyenne autour de 18,6 km, σ faible) : Sorgho, Rivière, o type dispersé dans toute l image mais regroupées par endroits (distance moyenne < 25 km, σ important) : Bâti dense, Prairie, Peuplier, Bâti/Minéral o type dispersé dans toute l image (distance moyenne autour de 27,1 km, σ faible) : Feuillu, Résineux, Blé, Colza, Orge, Maïs, Tournesol, Pois, Jachère, Bâti lâche, Lac, Soja Distances (m) Feuillu Résineux Eucalyptus Blé Colza Orge Maïs Tournesol Sorgho Soja Pois Jachère Prairie Rivière Lac Bâti dense dist moy + ECT dist moy - ECT distance moyenne Bâti/Minéral Gravière Peuplier Bâti lache/minéral Figure 5.26 : échelle des îlots ; graphique de dispersion des classes (distance barycentrique moyenne entre UEPs, et écart type) A l échelle du parcellaire : l étude permet de préciser la répartition des classes dans le paysage et affine la typologie précédente. La distance calculée est intra classe, intra et inter îlots. Les îlots sont partagés en segments qui correspondent approximativement aux parcelles, les distances sont calculées entre les segments. Si les îlots d une classe sont partagés en beaucoup de segments, alors les distances sont faibles. Mais, si elle est dispersée dans toute l image, ces distances sont élevées, ce qui donne une distance moyenne plus ou moins élevée suivant la dispersion et le nombre de segments partageant les îlots. En fonction de la variation des Ch 5 148
173 Analyse de paysage distances, l écart type est élevé. On obtient ainsi, des sous catégories en fonction des distances et de l écart type exprimant ces différences : o type très regroupé (distance moyenne 8,7km, σ très faible) : Eucalyptus o type localisé (distance moyenne 22,1km, σ faible) : Sorgho (deux patchs seulement) o type localisé, beaucoup de parcelles constituent les îlots : (distance moyenne autour de 15 km, σ moyen) : Rivière, Gravière o type localisé, les îlots sont très divisés : (distance moyenne autour de 15 km, σ élevé) Bâti/Minéral, Bâti dense, Bâti lâche o type dispersé dans toute l image, beaucoup de parcelles constituent les îlots (distance moyenne < 9 km, σ très élevé) : Prairie, Blé, Tournesol o type dispersé dans toute l image (distance moyenne autour de 25,8km, σ assez faible) : Feuillu, Résineux, Colza, Orge, Maïs, Soja, Pois, Jachère, Lac, Peuplier Distances (m) Feuillu Résineux Eucalyptus Blé Colza Orge Maïs Tournesol Sorgho Soja Pois Jachère Prairie Rivière Lac Bâti dense Bâti/Minéral Gravière Peuplier Bâti lache/minéral dist moy + ECT dist moy - ECT distance moyenne Figure 5.27 : Echelle du parcellaire ; graphique de dispersion des classes (distance barycentrique moyenne entre UEPs, et écart type) En conclusion : La plupart des classes ont des UEPs réparties sur tout le territoire : il s agit de la majorité des cultures, mais aussi des bois (forêts, buissons). Cependant certaines classes sont plus régionalisées : les bâtis (villes, villages ), les plantations artificielles telles que l Eucalyptus, ainsi que les classes liées à la plaine alluviale de la Garonne (Rivière et Gravière). De la même manière, les classes Prairie, Blé et Tournesol, bien que plus répandues dans l image, ont aussi des zones où elles sont plus représentées. Ch 5 149
174 Analyse de paysage Connectivité : voisinage inter-classe Connectivité : relation spatiale entre les classes (Burel F., Baudry P., 1999). Nous distinguons deux niveaux de connectivité : Au niveau du pixel : Une matrice de cooccurrence P est calculée sur l image classée. Elle donne l occurrence d avoir la classe i à côté de la classe j (dans toutes les directions autour du pixel), en effectifs et en pourcentage (fréquence d apparition du couple de points (i, j)). Pij donne le nombre de fois qu un pixel de la classe i est en contact avec un pixel de la classe j, ce qui permet de connaître les voisins des classes. Autrement la matrice rassemble les fréquences d apparition du couple de points (i, j). La diagonale (pourcentage de pixels immergés dans leur classe) renseigne sur le niveau de compacité de la classe, dépendant du périmètre et de la taille des l UEPs. Les autres éléments de la matrice sont dépendants de l importance de l occupation de la classe voisine (des classes sont plus souvent voisines que d autres) (tableau 5.1). Si le pourcentage de la classe i à côté d elle même est élevé alors cette classe est compacte, peu fragmentée et peu morcelée Par exemple, 44,5 % des pixels de feuillus sont voisins de pixels de feuillus, cette classe est en général compacte (tableau 5.1). Si le pourcentage de la classe i à côté d elle même est faible alors cette classe, peu compacte, est plutôt linéaire et/ou convolutée, ou plutôt morcelée. Feuillu Résineux Eucalyptus Blé Colza Orge Maïs Tournesol Sorgho Feuillu 44,5 1,2 0,0 11,5 0,5 0,2 2,4 7,0 0,0 0,4 0,2 6,7 20,4 0,2 0,2 0,2 0,1 0,0 0,1 2,9 Résineux 27,2 32,9 0,3 7,4 0,1 0,0 3,5 4,9 0,0 0,8 0,0 4,8 14,8 0,1 0,7 0,1 0,0 0,0 0,0 2,1 Eucalyptus 9,5 8,1 21,5 12,6 0,0 0,0 18,2 7,8 0,0 0,1 0,0 4,4 15,2 0,0 0,0 0,3 0,0 0,0 0,1 2,3 Blé 5,1 0,2 0,0 43,5 1,0 0,4 4,2 14,5 0,0 0,8 0,5 6,5 17,3 0,1 0,2 0,3 0,1 0,1 0,1 3,9 Colza 4,6 0,0 0,0 21,2 23,3 0,3 4,5 12,4 0,0 0,5 0,5 5,6 20,2 0,2 0,3 0,4 0,2 0,2 0,1 5,0 Orge 5,7 0,1 0,0 26,7 1,0 12,6 3,9 12,8 0,0 0,8 0,4 7,2 22,5 0,0 0,1 0,3 0,1 0,0 0,1 4,5 Maïs 3,9 0,3 0,1 15,6 0,8 0,2 38,6 9,5 0,0 1,6 0,4 5,8 16,5 0,4 0,3 0,3 0,2 0,4 0,2 4,3 Tournesol 4,9 0,2 0,0 23,1 0,9 0,3 4,1 36,9 0,0 0,8 0,5 6,3 16,3 0,1 0,2 0,3 0,1 0,0 0,1 3,6 Sorgho 2,3 0,3 0,0 6,1 0,6 0,2 37,3 10,3 15,9 2,5 0,1 8,5 14,5 0,0 0,0 0,1 0,0 0,0 0,0 1,5 Soja 4,3 0,4 0,0 19,8 0,6 0,2 9,9 12,3 0,0 23,8 0,6 6,3 17,9 0,1 0,2 0,2 0,0 0,0 0,2 3,2 Pois 3,1 0,0 0,0 22,8 1,1 0,3 5,3 15,3 0,0 1,2 21,7 6,2 16,9 0,2 0,3 0,3 0,1 0,2 0,0 3,3 Jachère 8,0 0,3 0,0 17,8 0,7 0,3 4,3 10,8 0,0 0,7 0,4 25,1 23,1 0,2 0,3 0,4 0,3 0,1 0,1 6,3 Prairie 8,3 0,3 0,0 15,9 0,9 0,3 4,1 9,4 0,0 0,7 0,3 7,7 44,3 0,2 0,2 0,3 0,2 0,1 0,1 5,4 Rivière 5,6 0,1 0,0 10,3 0,7 0,0 8,2 4,8 0,0 0,2 0,3 4,8 12,9 22,9 3,1 4,3 1,4 1,2 0,1 18,7 Lac 6,6 1,0 0,0 13,7 0,9 0,1 5,9 8,0 0,0 0,5 0,4 6,5 16,9 2,6 19,6 1,2 1,0 1,3 0,1 13,4 Bâti dense 2,3 0,1 0,0 8,0 0,5 0,1 2,6 5,1 0,0 0,3 0,2 3,9 10,4 1,6 0,5 28,2 3,5 0,2 0,1 31,2 Bâti/Minéral 2,6 0,0 0,0 4,7 0,4 0,0 2,8 2,2 0,0 0,1 0,2 4,3 11,5 0,8 0,7 5,5 25,8 0,8 0,1 36,6 Gravière 1,4 0,0 0,0 11,8 1,1 0,1 11,7 2,4 0,0 0,1 0,6 5,5 16,2 1,9 2,4 0,8 2,2 25,6 0,1 16,2 Peuplier 8,1 0,2 0,0 18,5 0,5 0,3 8,4 15,5 0,0 1,4 0,1 7,8 16,5 0,3 0,2 0,7 0,3 0,2 13,7 6,7 Bâti lache 3,3 0,1 0,0 10,1 0,6 0,2 3,0 5,8 0,0 0,4 0,2 5,9 15,3 0,6 0,5 2,8 2,1 0,3 0,1 47,8 Tableau 5.1 : tableau récapitulatif du voisinage des classes, en pourcentage de voisinage de pixels Au niveau de l objet (UEP) : Le nombre de patchs d une classe j en contact avec un patch d une classe i est calculé c'est-àdire le nombre de patchs de classe i ayant un voisin de la classe j, ce qui permet de connaître les classes qui sont le plus en contact. Soja Pois Jachère Prairie Rivière Lac Bâti dense Bâti/Minéral Gravière Peuplier Bâti lache/minéra l Ch 5 150
175 Analyse de paysage Pour un patch de la classe i, il peut y avoir un ou plusieurs patch(s) de la classe j qui sont en contact, mais on ne compte qu un contact avec la classe j. Les résultats sont donnés en effectifs et en pourcentages (les effectifs sont divisés par le nombre total de patchs de la classe i). Exemple : 3 patchs de Feuillu ont pour voisin la classe Eucalyptus, 2 patchs d Eucalyptus ont pour voisin la classe Feuillu. Le patch E1 n a qu un seul contact compté avec la classe Feuillu, bien qu il ait 2 patchs voisins (figure 5.28). F E1 E2 F classe i classe j Feuillu Eucalyptus Feuillu 0 3 Eucalyptus 2 0 F Figure 5.28 : exemple du voisinage de trois classes Cependant il faut relativiser ce voisinage en tenant compte du nombre de patchs des classes, c est pourquoi il est exprimé en pourcentages. Si on reprend l exemple précédent, 100% des patchs de Feuillus (3 sur 3) ont pour voisin la classe Eucalyptus et 100% des patchs d Eucalyptus (2 sur 2) ont pour voisin la classe Feuillu. Une classe peut être plus répandue sur la région (par exemple Feuillu) alors que l Eucalyptus reste exceptionnel, tous les patchs ne sont pas voisins entre eux et peuvent avoir plusieurs voisins, donc les pourcentages du nombre de patchs ayant pour voisin une classe sur le nombre de patchs de la classe considérée donnent plus d informations. Exemple : la figure 5.29 est composée, au niveau parcellaire, de 6 patchs de Feuillu, 2 patchs d Eucalyptus et 8 patchs de Prairie, les résultats en effectifs sont consignés dans le tableau suivant. classe j Feuillu Eucalyptus Prairie classe i Feuillus 0 3 soit 50% 6 soit 100% Eucalyptus 2 soit 100% 0 2 soit 100% Prairie 7 soit 87,5% 4 soit 50% 0 Figure 5.29 : calcul de voisinage 50% des patchs de Feuillu ont pour voisin la classe Eucalyptus, 100% des patchs de Feuillu ont pour voisin la Prairie. 100% des patchs d Eucalyptus ont pour voisin la classe Feuillu et de même avec la Prairie. La Prairie a 87,5% de ses patchs qui ont pour voisin la classe Feuillu et 50% la classe Eucalyptus ; de plus, tous les patchs de Prairie ont un autre patch de Prairie comme voisin. Ch 5 151
176 Analyse de paysage Exemple (région du Sud Ouest toulousain) Toutes les classes sont voisines des classes Blé, Maïs, Tournesol et Prairie, qui sont les plus répandues sur le territoire. Une mention particulière pour la Prairie qui montre les proportions de voisinage les plus fortes (par exemple 92,2% avec les Feuillus, 92,5% avec le Blé) car elle constitue, le ciment d une trame paysagère. Les autres classes sont les trois principales cultures de l assolement régional. Les classes ont aussi pour voisines, dans une moindre mesure, des classes Feuillu, Jachère et Bâti lâche, qui sont également bien présentes sur le territoire. Ceci illustre le fait que les feuillus se trouvent dispersés sur le territoire, sous forme de «résidus boisés» (bois, bosquets, haies), témoin d une exploitation agricole intense depuis au moins un millénaire. Le bâti lâche représentant aussi bien la ville que les villages ou les fermes, etc. se trouve donc éparpillé sur tout le territoire. La Jachère est dispersée dans toute l image, à relier avec la Politique Agricole Commune qui a rendu obligatoire le gel des terres. Les différentes classes de bâtis sont souvent voisines entre elles du fait de l imbrication des différents types d habitats (villages anciens, lotissements modernes). Les classes d eau sont aussi plus souvent voisines des classes de Bâti (les autres classes sont moins proches du Bâti), ce qui s explique par le fait que les villes et les villages sont construits près des rivières et que les berges sont souvent minérales (plages caillouteuses, rochers, etc. ). Une autre classe indique aussi un rapprochement : les Résineux sont en grande majorité voisin de la classe Feuillu, car l enrésinement est pratiqué majoritairement dans les forêts existantes. Enfin, on observe un voisinage plus important entre le Soja et le Maïs, qui sont toutes deux des cultures irriguées et sont donc dans les mêmes espaces. Feuillu Résineux Eucalyptus Blé Colza Orge Maïs Tournesol Sorgho Feuillu 0,0 4,5 0,1 60,8 3,8 0,7 13,8 48,7 0,0 2,6 2,4 50,2 92,2 3,1 3,6 0,9 0,7 0,2 0,7 21,2 Résineux 92,8 0,0 2,4 40,0 0,0 0,0 10,4 32,0 0,0 4,0 0,8 26,4 67,2 1,6 3,2 0,0 0,0 0,0 0,0 16,0 Eucalyptus 66,7 66,7 0,0 66,7 0,0 0,0 66,7 33,3 0,0 0,0 0,0 0,0 100,0 0,0 0,0 0,0 0,0 0,0 0,0 0,0 Blé 33,6 1,1 0,1 0,0 6,5 2,7 20,3 56,4 0,1 4,8 6,4 47,5 92,5 1,2 2,6 1,9 0,8 0,6 1,0 29,0 Colza 19,6 0,0 0,0 72,8 0,0 0,0 15,4 57,5 0,0 3,0 10,4 31,9 92,6 0,4 0,8 1,6 1,0 0,8 0,0 26,5 Orge 8,4 0,0 0,0 75,7 0,0 0,0 14,9 46,0 0,0 2,5 5,0 29,7 78,2 0,0 0,0 0,5 0,0 0,5 1,5 17,8 Maïs 23,2 1,1 0,1 67,6 4,9 2,0 0,0 87,1 0,2 17,2 5,2 37,6 82,0 1,5 3,4 1,5 1,1 0,8 1,0 23,8 Tournesol 27,1 0,8 0,0 66,5 6,0 1,7 34,2 0,0 0,0 8,1 6,8 42,8 86,9 1,1 2,2 2,8 1,9 0,3 0,3 30,5 Sorgho 0,0 0,0 0,0 66,7 0,0 0,0 100,0 66,7 0,0 0,0 0,0 33,3 66,7 0,0 0,0 0,0 0,0 0,0 0,0 66,7 Soja 15,1 1,3 0,0 55,9 2,9 1,1 57,6 80,7 0,0 0,0 4,0 24,8 70,4 0,2 0,6 1,1 0,0 0,4 0,8 15,3 Pois 11,5 0,2 0,0 74,1 9,6 1,5 15,6 68,5 0,0 3,9 0,0 27,4 77,2 0,4 2,2 1,3 0,2 0,0 0,0 17,0 Jachère 28,4 0,7 0,0 55,3 2,5 0,9 10,9 45,7 0,0 1,9 2,4 0,0 86,5 0,8 1,5 1,7 0,9 0,4 0,6 29,2 Prairie 34,9 1,4 0,1 70,7 6,0 1,7 20,4 59,6 0,0 4,2 4,8 48,3 0,0 2,0 3,0 3,1 2,0 0,8 0,8 39,0 Rivière 46,2 1,5 0,0 42,4 1,5 0,0 14,4 32,6 0,0 0,8 1,5 33,3 70,5 0,0 56,1 11,4 14,4 3,8 0,8 78,8 Lac 29,9 0,9 0,0 44,3 1,2 0,0 17,1 36,5 0,0 0,9 3,6 27,5 61,7 23,1 0,0 4,5 5,7 11,1 0,6 58,4 Bâti dense 3,4 0,0 0,0 17,2 1,1 0,1 3,7 22,0 0,0 0,7 1,0 16,9 37,3 2,5 1,9 0,0 22,6 1,1 1,0 85,0 Bâti/Minéral 5,3 0,0 0,0 14,5 1,0 0,0 4,1 22,8 0,0 0,0 0,2 15,3 36,6 4,4 3,6 35,8 0,0 3,4 0,0 93,2 Gravière 6,1 0,0 0,0 50,0 6,1 1,5 25,8 24,2 0,0 3,0 0,0 33,3 77,3 6,1 47,0 10,6 22,7 0,0 0,0 90,9 Peuplier 22,4 0,0 0,0 69,7 0,0 4,0 21,1 23,7 0,0 5,3 0,0 54,0 73,7 1,3 2,6 10,5 0,0 0,0 0,0 18,4 Bâti lâche 17,0 0,8 0,0 53,8 3,8 1,0 14,5 51,4 0,1 2,4 2,8 41,8 80,6 3,4 5,5 7,5 4,6 2,2 0,3 0,0 Tableau 5.2 : récapitulatif du voisinage des UEPs, en pourcentage d UEPs. Soja Pois Jachère Prairie Rivière Lac Bâti dense Bâti/Minéral Gravière Peuplier Bâti lache/minéral En conclusion : Les classes les plus représentées dans la région sont voisines des autres classes. Ceci indique qu il n y a en général pas de «préférence» et que le voisinage ne dépend que de la conjoncture économique, sauf pour les classes de bâtis, qui sont plus imbriquées entre elles, et l eau liée aux bâti, les résineux aux feuillus, le soja au maïs. Ch 5 152
177 Analyse de paysage Indice de juxtaposition : amalgame Les longueurs des frontières inter-ueps (des contours inter-classes) fournissent des indices sur le côtoiement des classes entre elles qui aident à comprendre la configuration du paysage, mais ils ne donnent aucune information d ordre spatial. La longueur du contour entre chacune des classes permet de connaître leur juxtaposition, c est à dire le taux de contact qu une classe possède avec les autres. Un taux de contact de 100 serait celui d une classe qui toucherait également toutes les autres. Figure 5.30 : exemple de cause de variation du taux de contact La figure 5.30 montre un exemple de variation de taux de contact. Les différentes classes de la zone forestière (résineux, ) ont peu de contacts avec celles de la zone agricole (colza, maïs, ). En effet, la plupart du temps les zones sont bien séparées. Le taux de contact des classes de ces deux zones va donc être limité aux classes de la même zone, l indice de juxtaposition est faible. En revanche, si une rivière traverse les deux zones, celle-ci va côtoyer presque toutes les classes, et elle aura donc un indice de juxtaposition élevé. L indice de juxtaposition comme la caractéristique précédente donne une mesure de voisinage d une classe par rapport aux autres classes, mais le taux de contact avec les autres classes, intervient dans le calcul. Ainsi une classe peut être voisine de trois autres classes mais la troisième à un taux de contact ou d adjacence beaucoup plus élevé que les autres, l indice de juxtaposition sera plus faible. L indice de juxtaposition est inversement proportionnel au taux de contact. IJI mesure la moyenne de l'adjacence des UEPs d'une classe vis-à-vis des UEPs de toutes les autres classes. IJI= k eik eik ln eik eik k k IJI 100 ln ( NC 1) Ch 5 153
178 Analyse de paysage eik périmètre en contact entre les classes i et k, NC nombre de classes présentes dans l'image. IJI=0 quand la classe est adjacente à seulement une autre classe IJI=100 quand la classe est adjacente identiquement à toutes les autres classes Feuillu Résineux Eucalyptus Blé Colza Orge Maïs Tournesol Sorgho Soja Pois Jachère Prairie ind juxtaposition (%) Rivière Lac Bâti dense Bâti/Minéral Gravière Peuplier Bâti lache/minéral Figure 5.31 : indice de juxtaposition La plupart des classes ont une adjacence équivalente, autour de 60%, ce qui confirme le caractère non préférentiel du voisinage évoqué dans le paragraphe précédent. Les Résineux, le Bâti dense et le Bâti/Minéral ont une valeur plus faible qui indique un voisinage plus ciblé, avec moins de classes. L indice de juxtaposition des Rrésineux confirme l implantation de la classe dans des forêts de feuillus. Celui des deux bâtis démontre leur association préférentielle avec la classe de Bâti lâche. Les classes d eau possèdent le plus fort taux d adjacence, qui illustre l utilité de l eau pour les cultures, les villes : retenues et plans d eau pour l irrigation, barrages hydroélectriques De même, la forte valeur pour le Bâti lâche exprime l aspect disséminé et de fonction variable de cette classe (maisons, fermes, etc ). On retrouve le peuplier dans cette gamme Étude des descripteurs sur l image découpée en régions Nous définirons ici une région de l'image comme une portion rectangulaire de l'image totale. L image peut être divisée en 4, 9 ou 16 régions 4 régions 9 régions 16 régions Les descripteurs du paysage sont alors calculés pour chacune des régions. Nous nous sommes intéressés à la localisation des classes dans l'image. C'est à dire au nombre de patchs de Ch 5 154
179 Analyse de paysage chaque classe présents dans chaque région de l'image. Les résultats sont donnés en effectif (en nombre de patchs) et en pourcentage (ramené au nombre total de patchs de la classe). L intérêt de cette étude est de faire émerger des entités paysagères caractérisées par un ensemble de descripteurs aux valeurs reconnues et de mettre en relation ces résultats avec une interprétation écologique. Par exemple, la répartition surfacique pour une image divisée en quatre régions (figure 5.32 ) montre que la région nord-ouest est majoritairement occupée par des feuillus, la région nordest par de la prairie, la région sud-ouest par du blé et la sud-est par du bâti. Il est ainsi possible, d après l ensemble des descripteurs d identifier des régions aux particularités différentes. Région NO Région NE Région SO Région SE Feuillu 60% 5% 15% 10% Blé 0% 15% 60% 0% Prairie 30% 80% 25% 25% Bâti 10% 0% 0% 65% Feuillu Blé Bâti Prairie Figure 5.32 : exemple d image découpée en 4 régions caractérisées par un seul descripteur (%land : pourcentage de la surface d occupation de la classe) Région Sud-Ouest toulousain Pour la majorité des cultures (Blé, Colza, Orge, Pois, Tournesol et Sorgho), la surface occupée se trouve essentiellement dans la région Nord-Ouest. C est donc une région dédiée à l agriculture. Les classes Peuplier, Sorgho (avec un seul patch), Rivière, Lac, Gravière, et pratiquement toute la surface couverte par le Bâti dense, Bâti/minéral, Bâti lâche sont surtout concentrées dans la région Nord-Est, c est donc un espace réservé à l habitat et aux activités tertiaires. Les classes Feuillu, Résineux, Eucalyptus et Prairie sont plutôt développées dans la région Sud-Ouest, où la pression agricole est moins forte et le milieu biophysique moins apte à une agriculture céréalière. Seules les classes d Eucalyptus, Rivière et Gravière sont plus représentées dans la région Sud-Est. Les autres classes, bien que présentes, ne sont pas majoritairement représentées dans cette zone. Les plantations d Eucalyptus sont venues occuper un espace libéré par l agriculture (déprise agricole), les gravières occupant un espace d exploitation des alluvions de la Garonne. Les caractéristiques de paysage sont relativement similaires dans les quatre régions. On note certaines différences : L indice de morcellement est plus faible, dans la région Nord-Est pour les classes de Bâti dense (0,39) et Bâti lâche (0,06), qui sont moins morcelées car ces classes sont plus Ch 5 155
180 Analyse de paysage présentes, donc les îlots sont plus grands. L indice de forme pour le Feuillu est le plus faible dans la région Nord-Ouest (1,15) traduisant une pression agricole qui simplifie la forme des bois, au contact des parcelles cultivées. Au contraire, pour le Blé et le Tournesol, il est plus élevé dans la région Nord-Ouest (respectivement 1,35 et 1,33) que dans les autres régions (autour de 1,2). Ces classes sont fortement représentées, donc les parcelles sont proches, et regroupées en îlots plus complexes. Pour la Prairie, les îlots ont une forme plus simple dans la partie Nord (indice d environ 1,3) que dans la partie Sud (indice d environ 1,22). En effet nous avons vu que dans le Sud de l image les prairies sont très représentées, donc très proches, et formant des îlots plus complexes. Les lacs, d origine anthropique ont une forme plus simple dans la région Nord-Ouest (indice 1,08) ; ce sont souvent des étendues d eau bordées par les cultures servant à l irrigation, et plus ou moins façonnées par l homme, par contre, dans la région Sud-Ouest, ils ont une forme plus complexe (indice 1,17) liée au relief plus accentué de la zone. Le Bâti dense et le Bâti lâche ont un indice plus faible dans la région Nord-Ouest (respectivement 1,04 et 1,09). La surface bâtie est minime dans cette zone, et représentée essentiellement par des villages et des fermes isolées qui apparaissent donc avec une forme plutôt géométrique, inscrits dans le parcellaire agricole. Par contre, dans la région Nord-Est, le Bâti lâche, qui représente la région toulousaine, a des formes plus complexes (indice de 1,23). La fragmentation est très faible, cependant elle se remarque un peu plus dans les régions Nord-Est et Sud-Ouest (la surface des inclusions représentant au maximum 0,015% de l aire des régions). Ici, la présence de très grands îlots, prédisposés à contenir plus d inclusions, influence la fragmentation. Il s agit d un îlot de Bâti lâche dans le Nord-Est (représentant 18% de l aire de la région), et de Prairie dans le Sud-Est (représentant 21,7% de l aire de la région) Figure 5.33 : exemple de région phytogéographique Ch 5 156
181 Analyse de paysage Pour aborder l étude paysagère de manière plus ciblée, nous avons réalisé une étude régionalisée adaptée au zonage «phytogéographique» de 8 régions (figure 5.33). Les descripteurs de paysage sont étudiés dans ces régions contrastées. Elle donne des résultats similaires, mais plus détaillés que l étude précédente Descriptif linguistique des classes A partir des descripteurs de l analyse précédente un récapitulatif de la description de chacune des classes a été traduit en terme linguistique. Feuillu Classe bien représentée dans la région (10%), de manière peu morcelée et non fragmentée. Elle est hétérogène pour des seuils de segmentation bas et devient rapidement homogène avec des seuils de segmentation plus élevés. Les îlots sont de taille variable (on trouve à la fois des petits bosquets, des haies, des bois plus étendus) mais souvent assez grands, aux contours réguliers et aux formes plutôt complexes mais ne contenant cependant qu un seul noyau. Ces feuillus sont répartis sur toute l image, le piémont pyrénéen et les hautes terrasses de la Garonne présentent les plus grandes surfaces. Ils ont pour principaux voisins les classes les plus répandues dans la région. Résineux Classe peu représentée dans le paysage (0,45%), peu morcelée mais un peu fragmentée. La classe est hétérogène pour des seuils de segmentation bas et devient rapidement homogène avec des seuils de segmentation plus élevés. Les îlots sont de taille variable mais plutôt grands, aux contours réguliers et aux formes plutôt complexes mais ne contenant cependant qu un seul noyau. Les résineux, répartis sur l image, sont le plus souvent localisés prés de la classe Feuillu (réimplantés dans les forêts). Eucalyptus Classe très peu représentée (0,02%), peu morcelée, homogène et non fragmentée. Elle ne compte que très peu de patchs, de grande taille aux formes complexes au niveau des îlots, et aux contours réguliers. Ces UEPs sont très regroupées et sont aussi proche des bois que des cultures ou des prairies, ce qui montre que ces plantations ne remplacent pas les bois (comme les résineux) mais ont été introduites dans des milieux déjà exploités. Peuplier Classe très peu représentée (0,06%), morcelée, homogène et non fragmentée. Les îlots sont de forme simple, aux contours réguliers, petits, souvent très petits ne contenant pas de noyau. Ils sont répartis dans l image, et sont proches essentiellement des classes les plus répandues et parfois du Bâti dense, ce qui indique leur présence dans les villes. Blé Classe très bien représentée (21,08% c est la culture principale), peu morcelée, moyennement hétérogène et non fragmentée. Les îlots sont de taille variable mais plutôt grands, aux contours réguliers et aux formes géométriques plutôt complexes, avec un mélange de volutes (plusieurs noyaux), de très petits patchs et/ou à un seul noyau. Le blé est réparti sur toute l image, mais plus particulièrement dans certaines zones, les coteaux de Gascogne (50% de la classe) et du Volvestre (15% de la classe)). Toutes les classes lui sont voisines, avec plus de contact avec les classes majoritaires dans l image. Ch 5 157
182 Analyse de paysage Colza Classe peu représentée (0,88%), moyennement morcelée, homogène et non fragmentée. Les îlots sont petits et de forme simple, la plupart possédant quand même un noyau, avec des contours réguliers. Ces UEPs sont réparties sur toute l image, et ont comme principales classes voisines les classes les plus répandues, avec un peu plus de proximité avec le pois. Orge Classe peu représentée (0,14%), très morcelée, homogène et non fragmentée. Les îlots sont petits de forme simple, aux contours réguliers, beaucoup étant très petits ne contenant pas de noyau. Mais ceci est à prendre avec précaution car beaucoup de parcelles très petites, correspondent à des erreurs de classification, réduisant parfois les parcelles au profit d autres classes spectralement proches (Blé ou Prairie). L orge est répartie partout dans l image, proche des principales classes, particulièrement du Blé et de la Prairie. Maïs Classe bien représentée dans la région (6,12%, c est la troisième culture), peu morcelée, moyennement hétérogène et non fragmentée. Les îlots sont de taille variable mais souvent assez grands, aux contours réguliers et aux formes plutôt complexes mais ne contenant cependant qu un seul noyau. Le Maïs est réparti sur toute l image, et a pour principales voisines, les classes les plus répandues dans la région, ainsi qu un rapprochement avec le Soja. C est la culture qui apparaît la moins morcelée, car même si on retrouve du maïs sur tout le territoire, il est dépendant de l irrigation, et on observe des grandes zones «réservée» au Maïs (et Soja, dans les vallées et les terrasses de la Garonne), c est pourquoi la taille des îlots est importante. Tournesol Classe très bien représentée (15,50%, c est la deuxième principale), peu morcelée, hétérogène et non fragmentée. Les îlots sont grands, aux contours réguliers, de forme complexe mais ne possédant pour la plupart qu un seul noyau. Le Tournesol est présent sur toute l image mais plus particulièrement dans certaines zones, les coteaux de Gascogne (52% de la classe) et du Volvestre (15% de la classe), et a pour principales voisines les classes les plus répandues dans la région. Sorgho Classe très peu représentée (0,003%), moyennement morcelée, homogène et non fragmentée. Les îlots sont de forme simple, aux contours réguliers, et petits, avec un nombre non négligeable de très petits patchs ne contenant pas de noyau. Ils sont regroupés et ne sont voisins que des six classes les plus répandues, sauf le Feuillu. Le Sorgho est une classe particulière car elle n est composée que de trois UEPs correspondants aux échantillons et ces résultats ne peuvent donc être significatifs car la classe est sous estimée. Certaines parcelles peuvent être confondues avec le Maïs. Soja Classe peu représentée (0,75%), moyennement morcelée, homogène et non fragmentée. Les îlots sont de forme simple, aux contours réguliers, et petits. Le Soja est réparti sur tout le territoire et a pour principales voisines les classes les plus répandues, avec un rapprochement important avec le Maïs, car, tout comme celui-ci, le Soja est une culture irriguée et on peut observer des zones (vallées) où il est présent. Pois Classe peu représentée (0,52%), morcelée, homogène mais non fragmentée. Les îlots sont de Ch 5 158
183 Analyse de paysage forme simple, aux contours réguliers, petits, souvent très petits ne contenant pas de noyau. Le pois est réparti dans tout le territoire ayant comme principales voisines les classes les plus répandues et un voisinage un peu plus marqué avec le Colza mais pour lequel nous avions noté une confusion. Jachère Classe bien représentée (6,48%), morcelée, homogène mais non fragmentée. Les îlots sont petits, de forme simple, aux contours réguliers, souvent très petits ne contenant pas de noyau. La Jachère se rencontre sur tout le paysage, voisine des principales classes, en particulier de la Prairie, très proche spectralement et avec qui elle peut souvent être confondue. Prairie Classe très bien représentée dans ce paysage (28,11%, la plus répandue), peu morcelée, hétérogène et un peu fragmentée. Les îlots sont de taille variable mais plutôt grands, de forme complexe, avec des patchs, à un seul noyau, ou très petits sans noyau, ou convolutés. La Prairie constitue le ciment de ce paysage, elle se retrouve donc dans toute l image mais particulièrement dans la moitié sud (60% de la classe), voisine à toutes les classes mais de manière plus importante avec les classes les plus répandues. Il faut noter qu à l échelle des îlots on recense un patch représentant plus de 20% de la surface de la classe, qui représente une surface de près de ha, ceci est donc caractéristique d une zone où la prairie est largement dominante. Rivière Classe peu représentée (0,31%), peu morcelée, hétérogène et non fragmentée. Les îlots sont de petite taille aux contours assez irréguliers, de forme complexe, comprenant aussi bien des patchs avec un seul noyau que de très petits sans noyau ou des patchs convolutés. La classe est localisée, correspond à la vallée de la Garonne (98% de la classe), au contact des classes les plus répandues avec un contact plus important avec les classes de bâtis (berges, bâti). Lac Classe peu représentée (0,26%), morcelée, homogène et non fragmentée. Les îlots sont de forme simple, aux contours réguliers, petits, et très petits ne contenant pas de noyau. Les lacs sont répartis sur tout le territoire, proches des classes principales. Gravière Classe peu représentée (0,18%), peu morcelée, homogène et non fragmentée. Les îlots sont de grande taille, de forme simple et aux contours réguliers. Les gravières sont localisées dans la partie Est de l image (94% de la classe), proches des lacs (confusions) et des classes de bâtis. Bâti dense Classe peu représentée (0,49%), morcelée, homogène et un peu fragmentée. Les îlots sont de forme simple, aux contours réguliers, de taille variable mais plutôt petits, et souvent très petits ne contenant pas de noyau. Ce type de bâti est assez localisé, dans le quart Nord-Est (82% de la classe), en contact principalement avec le Bâti lâche et le Bâti/Minéral, puis de façon moins importante avec les classes principales. Bâti/Minéral Classe peu représentée (0,44%), moyennement morcelée, moyennement hétérogène et non fragmentée. Les îlots sont de forme simple, aux contours réguliers, petits, souvent très petits ne contenant pas de noyau. Ces UEPs sont assez localisées, dans le quart Nord-Est (84% de la classe). Les contacts sont surtout avec le Bâti lâche et le Bâti dense, et de façon moins Ch 5 159
184 Analyse de paysage importante avec les classes principales. Bâti lâche/minéral Classe bien représentée (8,14%), morcelée, hétérogène et un peu fragmentée. Les îlots sont de forme simple, aux contours réguliers, de taille variable mais plutôt petits, souvent très petits ne contenant pas de noyau. Ce type de bâti est plutôt localisé dans le quart Nord-Est de l image (80% de la classe), principalement en contact avec les classes les plus répandues. Cette étude à l échelle des îlots a révélé un patch représentant plus de la moitié de la surface de la classe, soit environ ha correspondant à toute l agglomération toulousaine, qui présente le plus d inclusions (Prairie, les autres classes de bâti) et qui donne le caractère légèrement fragmenté de la classe. Remarque : classes de Bâti et Minéral : plusieurs classes pour cette occupation du sol sont identifiées. Ces classes possèdent une grande variété de réponses spectrales. Elles regroupent les pixels correspondant aux agglomérations, routes et autres structures bétonnées, ainsi que les surfaces minérales comme les carrières ou les berges des étendues d eau. Les réponses spectrales varient selon la densité des toits des constructions sur une surface donnée et selon leur nature : type de tuiles (minérales, synthétiques, noires, ocres ). Les sols nus sur les terres cultivées sont généralement absents de ces classes car il persiste souvent des résidus, une fine couche superficielle de végétation, de plus le stade sol nu n est que temporaire Réalisation d'images dérivées Des images dérivées peuvent être générées à partir des descripteurs du paysage, en affectant à chaque pixel la valeur de l'indice calculé sur les classes. Ces indices faisant toujours référence à un patch, la valeur du pixel sera donc celle du patch auquel il appartient. Ces images (figures 5.34, 5.35) permettent de déterminer les grandes zones ou régions du paysage. Ordre croissant des aires Figure 5.34 : exemple d objet obtenu avec l aire Les descripteurs suivants construisent une image dérivée : Aire, Périmètre, Contour (nombre de pixels pour le calcul du contour), Dimension fractale, Indice de forme, Distance barycentrique, Nombre de trous, Nombre de noyaux, Rapport aire de trou sur aire de patchs, Ch 5 160
185 Analyse de paysage Régularité : rapport aire de trou sur aire de patchs, Changement de direction (chaque valeur représente le rapport nombre changements de direction / aire patch). Avec l image dérivée construite à partir de l aire moyenne des UEPs (îlots) (figure 5.34). Les objets dont l aire est très grande se détachent des autres. Cela confirme les résultats obtenus dans les études précédentes : dans la partie Sud-Ouest, on trouve un très grand patch qui correspond à de la prairie ( ) et dans la partie Nord-Est, un autre correspond au bâti toulousain ( ). On identifie aussi, avec des aires moins importantes, deux autres patchs de prairie ( ), en partie sud de l image, ainsi que trois patchs de forêt (forêt de Bouconne et dans les Petites Pyrénées, ). Pour des valeurs plus basses (aires plus petites), les classes ont des aires similaires, il est donc difficile d identifier des objets pour ces valeurs. Pour la dimension fractale (figure 5.35), on observe des particularités différentes : pour les valeurs qui permettent d identifier précisément les objets, on retrouve comme pour les aires moyennes, les grands patchs de prairie (au Sud) et de Bâti (Nord-Est), auxquels s ajoutent quelques patchs de Prairie, qui n étaient pas identifiés précédemment car plus petits, mais ils apparaissent déchiquetés. Par contre, les îlots de forêts distingués par leur aire moyenne ne le sont plus, en raison de leur contour plus lisse. Figure 5.35 : exemple d objet obtenu avec la dimension fractale 5.6- Définition automatique des grandes régions Le but de cette partie est d obtenir les principales régions de la scène étudiée. Les classes sont regroupées afin d obtenir des thèmes généraux (grandes cultures, forêt, ). Un niveau d observation est choisi, il lui correspond un seuil de segmentation. Par exemple, pour la zone test, le niveau d observation choisi est de l ordre de 15 ha (le seuil de segmentation correspondant est 45), choisi en fonction des regroupements parcellaires. On ne se situe plus au niveau du pixel (niveau d observation 0,04 ha), mais au niveau des segments dont la surface moyenne est 15ha. A partir de la classification initiale, les classes ont été regroupées en 6 types d occupation du sol : Forêt, Cultures non irriguées, Cultures irriguées, Prairie, Eau et Bâti. Puis, une Ch 5 161
186 Analyse de paysage régularisation importante permet d éliminer des patchs isolés, la surface moyenne des UEPs est augmentée, ce qui donne un niveau d observation de l ordre de 20 ha. Toutefois l Eau n a pas été modifiée dans un souci de lecture plus aisée de l image. Région 1 : Forêts Région 2 : Cultures en sec Région 3 : Cultures irriguées Région 4 : Surfaces enherbées Région 5 : Eau Région 6 : Bâti Figure 5.36 : zonage automatique D après l observation visuelle, on constate une similitude avec le zonage phytogéographique précédent, effectué manuellement (figure 5.38). La zone de forêts correspond à la région 3, 7 et 8 (hautes terrasses et petites Pyrénées) du zonage phytogéographique, la région des cultures en sec correspond à la région 4 et 6 (coteaux), celle des cultures irriguées étant un mélange des régions 1 et 2 (basses et moyennes terrasses), de même que la zone bâtie. La région de surfaces enherbée représente en grande partie la région 5 mais empiète aussi sur les autres régions. La similitude de ces deux zonages entraîne une caractérisation du paysage similaire. Ainsi, on retrouve des résultats identiques dans l analyse du paysage : les classes sont moins morcelées dans les régions correspondant à leur type cultural (par exemple le Blé est moins morcelé dans la région des cultures en sec, les Feuillus dans la région des forêts, etc. ). De même, pour la forme des îlots, les classes typiques d une région considérée ont des îlots de forme plus complexes, par rapport aux autres régions. Ceci confirme la similitude de ces deux zonages. Ch 5 162
187 Analyse de paysage Application Changement de l organisation paysagère du paysage de la région du Sud-Ouest toulousain Organisation paysagère Objectif : Quantification des changements structuraux du paysage, modification de la structure paysagère (cartes d occupation du sol 1991 et 2002, chapitre 3) à partir des caractéristiques suivantes : taille moyenne des parcelles (ha) densité (nombre /ha) indice de forme (variable de 1 à l infini) dimension fractale indice de juxtaposition qui mesure la diversité du voisinage d une classe par rapport aux autres (variable de 0 à100) Au niveau global du paysage de l image Il apparaît une augmentation notable de la taille moyenne des parcelles de l ensemble des classes présentes sur les images, de 1.7ha en 1991 à 6.2 ha en A l inverse leur densité (nombre de parcelles par km², au niveau de l image entière) diminue de 59 parcelles par km² en 1991 à 16 au km² en L indice de juxtaposition baisse tout en restant important en 2002 ; il varie de 94 en 1991 à 76 en La dimension fractale, faible, indique seulement que le paysage est d origine anthropique, mais on ne peut retirer aucune tendance de la légère diminution entre les deux dates (1.12 en 1991 et 1.08 en 2002). L analyse de ces quelques éléments montre, au niveau du paysage de la zone étudiée une modification de la trame foncière caractérisée par un maillage plus lâche (parcelles plus grandes). La distribution des classes dans le paysage reste étalée (indice de juxtaposition fort). Au niveau du parcellaire cultural Les caractéristiques et indices de paysage calculés décrivent le parcellaire agricole aux deux dates (figure 5.39) mettant en lumière les changements opérés entre elles. Au niveau cultural, on note globalement le même constat qu au niveau global. L augmentation de l aire moyenne des parcelles est confirmée avec quelques nuances qui permettent de bien typer le parcellaire agricole par rapport à l ensemble du paysage. L aire moyenne des cultures d hiver augmente peu (3 ha en 1991 à 3.7 ha en 2002) alors que celle des autres cultures est multipliée par un facteur 3, passant de 1.7 ha à 5 ha pour les cultures irriguées, de 0.9 à 2.5 pour les cultures d été en sec et de 0.8 à 3 pour les prairies. Au delà de l augmentation de l aire moyenne des parcelles, le fait le plus significatif est le changement de hiérarchie opéré dans le parcellaire. Le parcellaire actuel est dominé par de grandes parcelles dédiées à la pratique de l irrigation, de taille nettement supérieure aux autres cultures en sec. En outre l augmentation significative de la taille moyenne des parcelles de cultures irriguées paraît liée avec l évolution de la conduite de l irrigation dans la zone. A l inverse de la taille, la densité des parcelles diminue dans le parcellaire agricole. En 10 ans l indice de Forme (IF) a nettement régressé et devient assez homogène sur Ch 5 163
188 Analyse de paysage l ensemble des classes. En 1991, il présente des valeurs étalées entre 2.0 et 2.6 liées à des formes de plus en plus complexes. Dans le parcellaire de 1991, les formes les plus régulières correspondent aux cultures d été en sec (IF=2.0), suivi des cultures d été irriguées (IF=2.3) puis des cultures d hiver et prairies avec un indice similaire de l ordre de 2.6. En 2002, l indice de forme a régressé notablement et prend une valeur similaire pour toutes les cultures de l ordre de 1.4. On peut dire que le parcellaire agricole 2002 est constitué de forme de géométrie régulière et homogène sur l ensemble des cultures. L analyse de la variation de la dimension fractale (DF) entre les deux dates va dans le même sens, la baisse générale est nette. En 1991, seule la classe Prairie a une valeur différente des trois autres classes montrant la sinuosité plus marquée des contours de ses parcelles. En 2002, cette classe retrouve une valeur comparable aux autres, ce qui peut témoigner d une évolution de la pratique d élevage 2,8 1,4 Aire moyenne ha Cultures d'hiver Cultures d'été irriguées Cultures d'été en sec Prairie/Jachere 1,4 1,2 1 0,8 0,6 0,4 0,2 0 Densité N/Aire Classe INDICE DE FORME 2,6 2,4 2,2 2 1,8 1,6 1,4 1,2 1 Cultures d'hiver Cultures d'été irriguées Cultures d'été en sec Prairie/Jachere IF 1991 IF 2002 DFDL 1991 DFDL ,2 1 0,8 0,6 0,4 0,2 DFDL Aire moyenne ha Aire moyenne UEPs 1991 Aire moyenne UEPs 2002 Densité moyenne UEPs 1991 Densité moyenne UEPs 2002 Cultures d'hiver Cultures d'été irriguées Cultures d'été en sec Prairie/Jachere ind juxtaposition (%) 1991 ind juxtaposition (%) 2002 Densité moyenne UEPs 1991 Densité moyenne UEPs ,4 1,2 1 0,8 0,6 0,4 0,2 0 Densité N/Aire Classe IF : Indice de forme = périmètre/aire* coeff-pond DF : Dimension fractale I. Juxtaposition adjacence classe/autres classes Quantification de : Augmentation de la taille des parcelles Baisse de la densité parcellaire Réduction de l adjacence des classes Simplification de la forme géométrique des parcelles. Figure 5.39 : divers indices de paysage et évaluation du changement de la trame paysagère En résumé : Sur une courte période (onze ans), l évolution a conduit à une augmentation des superficies des parcelles cultivées, en partie liée ces dernières années à la pratique de l irrigation, à une simplification et à une régularisation des formes du foncier de toutes les parcelles y compris celles des cultures permanentes en lien probable avec une évolution de la pratique d élevage. Les changements sont nettement perceptibles et permettent de dégager les faits et tendances d évolution du paysage régional influencés par les politiques de gestion du territoire : changements significatifs malgré la courte période examinée : 11 ans typologie des changements : temporaire (rotations des cultures), pérenne (modification de l affectation des terres) mise en évidence et caractérisation des rotations des assolements quantification des modifications de l organisation paysagère Ch 5 164
189 Analyse de paysage Comportement et écologie du chevreuil Une étude est menée avec l équipe «Comportement et Ecologie de la Faune Sauvage» UR35 de l INRA qui travaille sur le comportement et fonctionnement des populations et l écologie des populations, sur le rôle de l hétérogénéité de l espace, sur le fonctionnement et la structuration des populations d ongulés sauvages. Le fonctionnement et la structuration du Chevreuil sont étudiés dans le cadre de l'écologie comportementale. Les thèmes abordés concernent l'utilisation des ressources trophiques ou à valeur refuge (étude du comportement alimentaire, de l'occupation et de la sélection des habitats disponibles), la variabilité des traits d'histoire de vie (croissance, survie, âge à la reproduction, succès reproducteur), les capacités de dispersion, la structuration génétique et démographique des populations, en relation avec la structuration du paysage. Les applications concernent le déterminisme des dégâts et des collisions, ainsi que les problèmes de gestion, de suivi, ou de conservation. Nous intervenons pour l analyse du paysage avec ses descripteurs pour mesurer l influence du paysage sur les mouvements de dispersion du chevreuil en milieu fragmenté Application pour l étude de la biodiversité Des applications ont été réalisées, à partir d images SPOT, Landsat TM, et ERS, sur deux zones test : le massif de l Arize, zone montagneuse des Pyrénées françaises, et sur l île de Minorque (Espagne), choisies en raison de leur intérêt pour étudier le degré de conservation d espèces, et pour leur structure très morcelée. Les différences liées à leur environnement climatique et à leur relief, ont permis de tester les méthodes développées dans diverses conditions Les effets du morcellement de l habitat et de l hétérogénéité paysagère sur la composition en espèces et sur la diversité des insectes terrestres ont été étudiés. Deux approches basées sur la notion de grain d observation ont été proposées : approche à plusieurs échelles spatiales, afin de déterminer l aire d influence sur la faune locale, et une approche à plusieurs niveaux de contraste, afin d identifier le grain d observation du paysage pour lequel la faune est sensible. La détermination des échelles spatiales et des niveaux de contraste optimaux à l aide de modèles statistiques permet de générer des cartes de prévision de la biodiversité. Trois ordres d insectes terrestres ont été choisis en tant qu indicateurs de biodiversité liés à deux types de milieux : les Collemboles en tant que représentants de la faune du sol en forêt de feuillus du site de l Arize, les Diptères et les Hemiptères en tant que représentants de la faune qui habite la végétation méditerranéenne du site de Minorque. Des insectes ont été choisis car ce taxon représente 56% du total des espèces eucaryotes, vivantes et connues, soit 1,5 millions d espèces (mai 1995). Les résultats obtenus ont été des mesures des effets de la fragmentation de l habitat sur les espèces et cartographie de la biodiversité, résultats présentés dans diverses publications [Chust G., et al 2000, Chust, G., et al 2001]. Ch 5 165
190 Analyse de paysage Autre application Une application de l analyse du paysage sera réalisée avec le projet SEVE : projet soutenu par le programme/aci ECCO (INSU-Ministère de la Recherche), associant 14 laboratoires français et le projet APPOGE soutenu par le réseau Terre et Espace du Ministère de la Recherche : occupation des terres et besoins en eau des cultures. Partenariat ASTRIUM, CNRM, INRA, Météo-France, SCOT. L objectif de SEVE est de concevoir et de développer une modélisation intégrée des surfaces continentales, représentant explicitement la structuration et les hétérogénéités de la surface et permettant de simuler les processus couplés impliqués dans le cycle de l eau, du carbone, de l'azote et de substances polluantes aux échelles de la parcelle, du paysage et de la région Ch 5 166
191 Chapitre 6 INTERPRETATION SEMANTIQUE ET ETUDE DES CHANGEMENTS A LONG TERME
192
193 Chapitre 6 INTERPRETATION SEMANTIQUE ET ETUDE DES CHANGEMENTS A LONG TERME 6.1 Analyses multitemporelles et scénarios du futur L établissement de scénarios d évolution futur des surfaces (écosystème, paysage, région) ne peut se faire sur la seule connaissance des états actuels. Seules les longues séries temporelles permettent de : discerner les tendances à long terme des fluctuations annuelles ; distinguer les effets respectifs des modifications anthropiques et climatiques ; cerner les champs d évolution potentielle des caractéristiques fonctionnelles et structurales de la surface, hors perturbation drastique. En particulier, il est possible de replacer ces transformations dans les conditions de milieu qui en sont le siège. Ainsi, l étude des changements observés en fonction de ces conditions permettra de déterminer la part du climat et la part de la pression humaine dans l évolution observée. Des images satellites d'observation de la terre ont été rassemblées et archivées pendant des décennies. Comparées aux mesures in situ ponctuelles, ces données peuvent être obtenues sur de grandes étendues et sur des périodes assez importantes permettant l analyse d un espace régional actuel et passé. L archivage de ces données permet de prolonger l'analyse dans le passé, à des dates où les données disponibles (photographies aériennes par exemple) demanderaient un travail long et coûteux, et, souvent aucune donnée n'est disponible. Une série multi-temporelle d images de satellites donne une vision synoptique de l espace conduisant à la détermination de ses divers états multi-temporels et à la mise en évidence de ses changements. La constitution et l exploitation d une archive suppose l acquisition des données de satellite récentes et rétrospectives ainsi que l intégration de l ensemble des informations spatialisées dans un SIG, pour permettre l analyse des changements (Lowell, 1991). Une description actualisée de la végétation peut être obtenue en couplant les informations écologiques existantes avec les données sur la physionomie des paysages obtenue par observation spatiale. Par conséquent, on peut décrire les changements de l occupation du sol et la dynamique des écosystèmes pendant un demi-siècle et les techniques de géographie numérique permettent de quantifier ces transformations. La quantité et la qualité des données du passé (climatologie, couverture et sols) sont telles qu une reconstitution des états antérieurs semble pouvoir être tentée. Une paramétrisation Ch 6 167
194 Interprétation sémantique et étude des changements à long terme raisonnée des modèles écologiques devrait fournir des estimations (biomasse, MOS (matière organique du sol)) pouvant être confrontées aux données terrain. On peut, sur les quinze dernières années, utiliser des données de satellites pour l obtention d estimations de biomasse et de production. On devrait ainsi être capable de discerner sur les dernières décennies, et au pas de temps annuel, les tendances fortes des effets relatifs de la variabilité climatique et de changements d utilisation des terres sur les stocks de carbone (végétation, sol) Corrections géométriques En raison des conditions physiques et des particularités techniques de l acquisition, des distorsions radiométriques et géométriques apparaissent, les images de télédétection ne correspondent pas aux valeurs du monde réel. Certains effets peuvent être modélisés analytiquement, d autres sont représentés par des techniques d approximation, mais il est impossible d obtenir une correction géométrique parfaite. La géométrie des images est primordiale pour établir des liens entre les valeurs observées et les surfaces terrestres, entre des images de la même scène prises par des capteurs différents. Les principales sources de distorsions géométriques sont liées aux caractéristiques des capteurs, aux mouvements des porteurs, à la courbure et au relief de la Terre et à d autres conditions d acquisition. Une grande variété de méthodes de correction géométrique existe. Les méthodes «absolues» et analytiques sont basées sur la modélisation de la configuration géométrique d acquisition pour décrire le rapport mathématique entre le système des coordonnées de l image et celui de référence. Ces méthodes exigent la connaissance de nombreux paramètres comme la géométrie interne du capteur, la position du capteur, la topographie etc Presque toutes les méthodes d orthorectification sont basées sur les équations de colinéarité. Les corrections relatives utilisent les statistiques de points de repère pour approcher le rapport mathématique de deux systèmes de référence. Des fonctions polynomiales sont souvent utilisées, notamment celle d ordre deux. Comme les fonctions globales habituelles n incorporent que deux dimensions, les distorsions géométriques aléatoires, telles que celles causées par les effets topographiques, ne peuvent pas être corrigées. Pour résoudre ce problème, de nombreux concepts à partir de polynômes 3D ont été développés, comme celui proposé par Pala et Pons (1995). A part les fonctions globales, il existe également des modèles de déformations locales, comme celui proposé par Blanc (1999). De plus, il propose une méthode pour l identification automatique d un grand nombre de points de repère, basée sur des mesures de similarité. Des méthodes hybrides ont également été développées pour diminuer le nombre de paramètres requis par l orthorectification. Le procédé élaboré par Toutin et Cheng (2001) ne requiert pas la connaissance des paramètres exacts, mais utilise des approximations basées sur des connaissances a priori et des points de repère. Les méthodes alternatives reflètent une autre approche. Le passage du niveau des pixels au niveau des objets spectraux homogènes peut apporter des améliorations dans la détection des changements. Bruzzone et Prieto (2000) proposent une méthode dans laquelle des objets homogènes sont délimités sur deux images de la même scène, prises à dates différentes. La détection des changements est alors basée sur les statistiques spatiales des objets (régions). L effet des défauts géométriques résiduels a été minimisé, et la précision de la détection des changements a montré une amélioration nette. Ch 6 168
195 Interprétation sémantique et étude des changements à long terme 6.3- Le géoréférencement Cette opération associe à une image une transformation de coordonnées lignes/colonnes en coordonnées cartographiques ou géographiques. Le descripteur géographique ou cartographique contient un nom qui définit une projection cartographique donc un système de coordonnées cartographiques (métriques) telles que la projection Lambert II, la projection UTM, un système géodésique et donc des coordonnées géographiques, une unité différente suivant le système choisi, kilomètre ou mètre pour les coordonnées cartographiques, degré pour les coordonnées géodésiques. Figure 6.1 : composition colorée diachronique avec les canaux : R : XS3 avril 2004, G : XS2 mai 2004, B : XS1 juin Mais le géoréférencemet ne s effectue pas correctement, les coordonnées planes des cartes (en Lambert pour la France) sont approximatives suivant les endroits (projection conique). A partir de points remarquables facilement identifiables, répartis sur toute la surface de la scène : carrefours, confluences, passages à niveau, ponts ont peut constater les décalages (figure 6.1). Par exemple, le géoréférencement des images ne correspond pas exactement à celui du Scan25 (numérisation des cartes au 1/25000 fournies par l IGN). Bien que les deux systèmes de projection soient identiques, il existe des décalages. Sur l image du Sud Ouest toulousain : le pixel ciblé («viseur» rouge, (figure 6.2)) correspond à la position du point en avril. Sur l image de chaque mois, apparaît ce point avec une autre couleur qui donne son emplacement au mois précédent. La croix représente les coordonnées sur le Scan25. On observe alors un décalage selon les dates, par exemple le point en juin est décalé de 1 pixel en x et de 1 pixel en y par rapport à sa position au mois de mai. Ce décalage n est pas homogène dans l image, selon les zones de l image, le décalage est plus ou moins important et dirigé dans des directions différentes. On observe en moyenne un décalage d environ 1 pixel dans les deux directions, mais on peut avoir 1 pixel en x et jusqu à 3 pixels en y. Les causes possibles sont l angle d acquisition, la stabilité du satellite, le type du satellite (SPOT2, 4). Les problèmes de géoréférencement ont des conséquences à deux niveaux : - un échantillon relevé sur un autre support géoréférencé différent (carte IGN par exemple) pourra être mal attribué sur l image si un décalage existe entre leurs géoréférencements respectifs. - le décalage entre les images d une même série entraîne des erreurs pour la classification. Ch 6 169
196 Interprétation sémantique et étude des changements à long terme avril mai juin juillet août septembre Figure 6.2 : visualisation du décalage sur la série temporelle SPOT Correction radiométrique (cas des images optiques) Les relations entre les rayonnements provenant des surfaces terrestres et les valeurs radiométriques enregistrées dans les images sont complexes. Parmi les effets «naturels», les différences des angles d illumination et d acquisition, les effets atmosphériques et l anisotropie des surfaces terrestres sont les plus importants. Un autre type d effets est lié aux différentes caractéristiques spectrales et à la calibrations des capteurs, aux différences dues à la conversion analogique/numérique et à des distorsions dues à la procédure d acquisition. L «effet de bord» est également important : les pixels aux bordures des objets contiennent Ch 6 170
197 Interprétation sémantique et étude des changements à long terme des valeurs spectrales mixtes. Pour des images prises à des années différentes, les valeurs radiométriques obtenues pour une même zone, une même bande spectrale, à une même époque (phénologie des végétaux), sont différentes ; notamment en raison du rayonnement solaire et des perturbations atmosphériques dues principalement aux interactions entre gaz atmosphériques et particules en suspension : absorption, diffusion, réfraction entraînant une modification du signal reçu, constituant un filtre non stationnaire dans le temps. Similairement aux corrections géométriques, les méthodes de correction radiométrique peuvent être absolues, relatives et hybrides. Elles sont basées sur le calcul des quantités physiques du rayonnement émergeant des surfaces terrestres. La procédure est composée de plusieurs étapes. En premier, les luminances spectrales mesurées par le capteur doivent être calculées par l inversion de la fonction de calibration, à partir des comptes numériques. La relation étant linéaire dans la plupart des cas, la formule générale est décrite par la formule L λ =a λ + b λ *Q λ où L λ est la radiance spectrale, a λ et b λ sont des coefficients déterminés pour la bande spectrale du capteur, Q λ est le compte numérique de la bande spectrale. L effet des différentes calibrations des capteurs est éliminé par ce calcul. Dans une étape suivante, pour éliminer la plupart des effets liés aux différences d illumination, la réflectance apparente (mesurée au capteur) peut être calculée selon π L λ d 2 l équation ρ TOA =, ρ E s (λ) cos θ TOA est la réflectance apparente, L λ est la radiance s spectrale, d est la distance Terre-Soleil actuelle, E s (λ) et l irradiation solaire à la longueur d onde λ, θ s est l angle zénithale solaire. Il est important de noter que cette équation utilise une approche lambertienne. Parmi les distorsions radiométriques résiduelles, les effets atmosphériques (globaux et locaux) sont très importants. Les effets de l anisotropie des surfaces terrestres et les effets radiométriques de la topographie peuvent être également importants. Pour la correction des effets atmosphériques, de nombreux modèles atmosphériques (ou codes de transfert radiatif atmosphériques) existent. Néanmoins, ces modèles exigent la connaissance des paramètres atmosphériques et de la configuration d observation, faute desquels des modèles atmosphériques «standards» peuvent être utilisés. En utilisant ces modèles standards, on ne tient pas compte de la variation d importants paramètres atmosphériques (vapeur d eau, aérosols, ). Pour résoudre ce problème, des méthodes hybrides ont été conçues, basés sur le fait que certains paramètres atmosphériques peuvent être calculés en utilisant les valeurs de certains objets terrestres (lacs profonds, végétation dense). L autre solution est l utilisation des méthodes relatives, statistiques. Dans des applications où le calcul de réflectances terrestres n est pas nécessaire, ces méthodes, basées directement sur les valeurs radiométriques des images, peuvent s avérer très efficaces. Les études de changement, par exemple, sont les applications typiques qui peuvent être basées sur des méthodes relatives. Au cours des deux dernières décennies, de nombreuses méthodes ont été développées. En général, elles utilisent une transformation linéaire pour calculer les valeurs radiométriques à une échelle de référence. Yuan et Elvidge (1996) et Song et al. (2001) ont trouvé que les méthodes de régression linéaire, basée sur des invariants, donnent des résultats supérieurs à d autres méthodes testées. Dans ces méthodes, des points de repère radiométriques, caractérisés par une réflectance invariante, sont identifiés sur les images, et les coefficients de la transformation sont déterminés en utilisant les statistiques de ces points. L identification des points de repère est le plus souvent effectuée de façon visuelle sur un document ou un ordinateur. Du et al. (2002) proposent une méthode automatique pour l identification des Ch 6 171
198 Interprétation sémantique et étude des changements à long terme invariants des deux images de la même scène. Une analyse en composantes principales (ACP) bitemporelle est utilisée sur les bandes spectrales correspondantes des deux images pour une détermination objective des pixels caractérisés par une interdépendance linéaire forte Normalisation par bande spectrale Introduction Après les corrections géométriques et radiométriques, les images ne sont pas exemptes de défauts, elles contiennent toujours une variabilité temporelle importante non liée aux changements réels des surfaces terrestres. Cette variabilité est due principalement aux effets atmosphériques, mais l anisotropie des surfaces terrestres peut également être importante. Dans une étude de changement temporel, il est indispensable de minimiser ces effets, mais il n est pas indispensable d obtenir des réflectances réelles. Nous avons mis au point une méthode de normalisation (correction relative)[krystof D. thèse 2005], qui va permettre aux images, de dates analogues phénologiquement, mais éloignées dans le temps (année différente), d'être radiométriquement comparables. Elle comporte deux phases : La détermination des points invariants (ou variants peu) entre les deux images La transformation linéaire des valeurs radiométriques de l'image cible L'image de référence doit être choisie si possible sans nuage et défauts géométriques et radiométriques majeurs. Les dates ne doivent pas être trop éloignées, surtout dans les périodes à changement rapide. Plus la date est proche plus les résultats seront corrects. Un calcul du coefficient de corrélation pour toutes les paires d'images permet d avoir une mesure de la qualité de la normalisation. Lorsque les valeurs radiométriques sont trop éloignées, les résultats obtenus ne sont pas suffisants, et sont donc rejetés La méthode Nous avons alors décidé d utiliser une méthode relative (elle normalise les données entre elles deux à deux). La méthode décrite par Du et al. (2002), a été choisie mais des modifications importantes ont été effectuées. Les hypothèses de base de la méthode sont : l invariance de la réflectance des objets utilisés pour la transformation ; la linéarité et l homogénéité spatiale des effets causant des distorsions radiométriques ; l indépendance des effets de distorsion, et la linéarité du produit de ces effets ; la majorité des pixels n a pas changé entre deux dates consécutives. La formule de la transformation linéaire est : Q ref (i) = Q j (i) α j + β j j = 1, 2, 3,, m (1) où i est l indice de l invariant (appelés PIF (pseudo invariant feature)), j est l indice de la bande spectrale, m est le nombre de bandes spectrales, m est le nombre des images, Q ref est le niveau de référence radiométrique, Q est la valeur radiométrique du pixel, α et β sont les coefficients de la transformation linéaire. Pour l identification des invariants PIFs sur deux images de la même scène, prises à des dates Ch 6 172
199 Interprétation sémantique et étude des changements à long terme différentes, Du et al. (2002) proposent une méthode semi-automatique. D abord, les pixels caractérisés par des changements brusques doivent être éliminés : nuages, eaux superficielles, changements dans la couverture du sol. Puis, une ACP entre les bandes correspondantes des deux dates est effectuée. Les pixels les plus proches de l axe de la première composante sont identifiés en tant que candidats d invariants. Après plusieurs étapes de vérification de leur qualité, les statistiques des invariants sont utilisées pour calculer les coefficients de la transformation linéaire. Pour éliminer les eaux superficielles et les nuages, Du et al. (2002) utilisent des seuils absolus pour toutes les bandes, déterminés visuellement. Un seuil de différence est également utilisé pour éliminer les brusques changements. Néanmoins, cette méthode est laborieuse, et peut causer la perte des invariants si les distorsions radiométriques linéaires sont fortes. Pour résoudre ce problème, une autre méthode pour l élimination préliminaire des pixels aberrants est proposée [Krystof D. 05]. La différence multitemporelle normalisée (MNBD) peut être calculée conformément à l équation : MNBD xyi = B xyi A xyi B xyi + A xyi (2) où A et B sont deux images de la même scène acquises à deux dates différentes, i est l indice de la bande spectrale, x et y sont des coordonnées spatiales. La distribution des valeurs d une image MNBD est symétrique, et les valeurs sont comprises entre -1 et +1. Pour déterminer les seuils, nous proposons d utiliser les statistiques (moyenne et écart type) de l image MNBD : les pixels en dehors de l intervalle (µ MNBD n * σ MNBD ; µ MNBD + n * σ MNBD ) peuvent être éliminés. La variable n détermine le nombre des pixels retenus. Ainsi, la perte d invariants est évitée, et les pixels aberrants sont éliminés. Les candidats invariants sont alors identifiés. L étape suivante est l identification des vrais invariants. Conformément à la méthode de Du et al. (2002), une ACP (Analyse en Composante Principale) bitemporelle est utilisée pour déterminer les axes principaux. Les pixels caractérisés par une très forte interdépendance linéaire sont proches du premier axe principal, ils peuvent être donc identifiés en tant qu invariants. Pour déterminer la distance l autour de l axe principal, les auteurs emploient une méthode itérative basée sur le calcul des coefficients de corrélation. Nous proposons d utiliser les statistiques de la deuxième bande principale pour déterminer cette distance l. Les coefficients de corrélation (r) sont calculés pour vérification ; les invariants sont acceptés si r > 0,95. a) b) c) Figure 6.3 : nuage des points des images A et B à 2 dates d'acquisition, PC 1 est l'axe principal ; b)pc 1' est le nouvel axe principal après le masque, c) identification des invariants Ch 6 173
200 Interprétation sémantique et étude des changements à long terme La figure 6.3 illustre le fonctionnement de la méthode, A et B représentent deux dates d'acquisition différentes de l'image a) : à partir des valeurs originales, le schéma montre que de l'axe principal PC 1 est incorrectement déterminé en raison des effets de changement de nuage et de couverture de terre ; b) : les valeurs des pixels candidats invariants après le filtrage (masque) moyenne +/- écart type de MNBD (n = 1), PC 1' représente le nouvel axe principal ; c) : identification des invariants, les pixels les plus proches de l'axe principal sont identifiés comme invariants (critère de corrélation (r2 = 0.95)). Après la vérification de la qualité des invariants par des calculs de coefficients de corrélation, les équations gain BAi = σa i offset σb BAi = µa i - σa i µb i σb i sont utilisées pour calculer les i coefficients de la transformation linéaire. Puis, la transformation est effectuée conformément à l équation (1) avec α= gain BAI et β = offset BAI. Pour évaluer la qualité de la normalisation, une deuxième ACP post-normalisationest réalisée. Si la pente de l axe principal est proche de l unité, la normalisation est de bonne qualité. Cette méthode permet d évaluer la qualité uniquement pour des paires d images. Pour évaluer la qualité de la normalisation sur toutes les images de la série, nous proposons une autre méthode. Les invariants les plus stables sont identifiés : ce sont ceux qui ont été sélectionnés comme invariant sur toutes les images de la série. Si l écart type temporel est calculé pour ces pixels, on obtient une mesure d erreur, car la variation temporelle des valeurs de ces invariants doit être faible. Minimisation des effets des défauts géométriques Nous avons développé une autre méthode pour la minimisation de l effet des défauts géométriques résiduels. Cette méthode part du principe que les défauts géométriques ont un effet plus important aux bordures des objets. En effet, s il existe un décalage, à l intérieur d un objet il a moins d incidence puisque les pixels ont pratiquement les mêmes valeurs radiométriques, l incidence du décalage est amoindrie. Tandis qu à la frontière les valeurs correspondent à celles d un objet voisin autre que celui étudié, en raison du décalage, ces valeurs sont donc très différentes. Les défauts géométriques résiduels, mesurés sur les points de repère, n excèdent souvent pas 0,8 pixel, mais ils sont plus importants sur les pixels répartis dans l image. Dans une analyse multitemporelle, ces défauts géométriques apparaissent comme des faux changements. Lorsque les défauts géométriques n excédent pas un pixel, une segmentation multitemporelle détecte les bords des objets reconnus dans chaque date. En raison des défauts géométriques, les contours détectés contiennent des fausses variations temporelles (figure 6.1) ; l algorithme masque ces contours élargis, et ils ne sont pas utilisés dans les analyses de changements. Dans le cas où les erreurs résiduelles dépassent un pixel, des contours sont dilatés. Le choix d un seuil de segmentation donnant de plus grandes régions (segments) peut limiter ce problème. Une deuxième approche détecte les régions par la segmentation multitemporelle qui sont des groupes homogènes de pixels avec des tendances similaires. En général, la variabilité interne des segments n apporte pas d information supplémentaire utile. Dans ce cas, les statistiques spatiales (moyenne et écart type) peuvent être utilisées pour représenter chaque segment dans les analyses multitemporelles. Ces deux approches sont utilisées séparément et combinées. Ch 6 174
201 Interprétation sémantique et étude des changements à long terme Principe algorithmique L algorithme peut s'appuyer sur une image référence, ou calcule cette image référence sur les valeurs moyennes multitemporelles d'un canal. Cette méthode fait la moyenne des canaux correspondants, image à normaliser et référence, un pixel de l'image créée correspond donc à la valeur moyenne des pixels de même coordonnée sur les différentes dates. Il est nécessaire d avoir plusieurs dates. Les résultats ne sont satisfaisants qu à partir d au moins 7 dates. Dans les deux cas, l'objectif final est de dégager un certain nombre de pixels représentatifs (invariants), afin de pouvoir ensuite appliquer aux images une transformation radiométrique linéaire. L'image de référence X doit être de bonne qualité, choisie si possible sans nuage ou défaut radiométrique, X représente l'ensemble des canaux spectraux définissant cette image, Y est l'image cible (même nombre de canaux spectraux. Ce modèle va comparer deux à deux toutes les bandes spectrales équivalentes des images (deux images à des dates différentes, mais même bande spectrale). Le logiciel est prévu pour effectuer le traitement sur plusieurs images cibles, pour cela il suffit d'itérer le traitement décrit précédemment sur toutes les images. Le modèle utilisé définit les intervalles des pixels à exclure, de façon variable, l'utilisateur peut modifier la taille des intervalles. Dans le cas du calcul de l image de référence, l'écart est calculé sur toutes les images à normaliser afin de déterminer les pixels invariants. Les invariants les plus stables sont identifiés : ce sont ceux qui ont été sélectionnés comme invariant sur toutes les images de la série. Les coordonnées de ces N pixels sont conservées, pour avoir la position des points invariants. La valeur moyenne sur toutes les images leur est affectée. Les coefficients de linéarisation et l'image transformée sont calculés comme précédemment. Si l écart type temporel est calculé pour ces pixels, on obtient une «mesure d erreur», car la variation temporelle des valeurs de ces invariants doit avoir la valeur nulle. A la fin de la normalisation d'un canal la qualité de celle-ci est donnée. Les résultats sont en général satisfaisants. Le coefficient de corrélation est calculé pour toutes les paires d'images. L image des contours peut être introduite pour ne pas tenir compte des contours dans le calcul de la corrélation. Le calcul du coefficient de corrélation est donné sur l'image entière, sur l'image sans les pixels du contour, puis uniquement sur les points du contour. Algorithme : Tant que il y a des bandes spectrales faire 1. Lecture de l image de référence (X) et l image à normaliser (Y) : bande spectrale correspondante Création d une image masque représentant les points invariants, (ils auront la valeur 1). 2. masquer les pixels en dehors de la zone commune (intersection des 2 images) 3. Calcul de l image MNBD (pour les pixels hors masque) : MNBDij =(Yij Xij) \ (Yij + Xij) 4. Calcul des moyenne et écart type de l image MNBD µ = Σ n i = 1 Σ m j = 1 MNBD ij / (n * m) (σ = Σ n i = 1 Σ m j = 1 ΣΣ [MNBD(ij)- µ] 2 / (n * m) Ch 6 175
202 Interprétation sémantique et étude des changements à long terme 5. En utilisant les valeurs de l image MNBD, créer le masque des pixels en dehors de l intervalle [µ - σ; µ + σ], c est à dire [moyenne +/- N écart type] (par défaut N = 1) des deux bandes à mettre en intersection avec l autre masque (ajout de masque) Nous conserverons uniquement les pixels de l'image MNBD appartenant à l'intervalle. La technique visant à faire évoluer pas à pas le fichier masque, est la base de l'étape de détermination des pixels invariants. 6. ACP sur les pixels non-masqués des deux bandes, résultat : deux bandes dérivées L'ACP consiste à réduire les redondances d'informations entre les deux canaux. Cette méthode crée, à partir des deux bandes, deux composantes. La première contient les informations relatives à la variance maximale, la seconde, que nous utiliserons, les informations relatives à la variance minimale. 7. Calcul moyenne et écart type sur la 2 ième bande en composante principale (CP) transformée 8. En utilisant les valeurs de la 2 ième bande CP transformée, créer un 3 ième masque avec les pixels hors intervalle [moyenne +/- M écart type] (défaut M = 0,5) : les pixels n'appartenant pas à l'intervalle [µ - 0,5* σ; µ + 0,5 * σ] sont également masqués. 9. Les pixels des deux bandes originales sont masqués avec les 3 masques ceux qui sont non-masqués sont considérés comme candidats «invariants» ; 10. Vérification de la corrélation : calcul du coefficient de corrélation Pearson (r) sur les 2 bandes originales masquées Il faut ensuite vérifier que les pixels non-masqués soient suffisamment invariants, pour cela le coefficient de Pearson P = cov i,j / σ i *σ j est calculé sur les deux canaux masqués. Si la valeur obtenue est supérieure à 0,95 alors les invariants sont acceptés, sinon il faut recommencer le traitement depuis la première phase en diminuant les intervalles. 11. Si r >= Z (défaut Z=0,95) : corrélation suffisante, alors les invariants sont acceptés, aller en Sinon r < Z, diminuer N (par ex. N = N - 0,1) et/ou M (par ex. M = M-0,05) et répéter 5-10 jusqu à l obtention d une corrélation suffisante (d abord diminuer N et éventuellement M) mais en général ce n est pas nécessaire, retour à l étape 5 ATTENTION : si le pourcentage des pixels masqués devient supérieur à ~ 80%, ne plus diminuer N et M car il y a un risque d avoir des invariants non significatifs, une répartition non-homogène des erreurs de normalisation Diminuer plutôt Z. Mais si r > 0.9 ne peut pas être obtenu, ne pas continuer car il y a trop de différence entre les deux dates, donc la normalisation est impossible! 13. Invariants acceptés : calcul de moyenne et écart type des invariants (sur les 2 bandes et sur les non-masqués (3 masques)) 14. Afin d'effectuer la normalisation, il faut calculer les coefficients servant à la transformation linéaire : déterminer les moyennes et écarts-type des deux images sur les invariants, calcul des coefficients de transformation radiométrique linéaire a et b, en utilisant les statistiques des invariants : a = σx invar σy invar b = µx invar - σx invar σy invar µy invar où X est l image de référence, Y est l image à normaliser, Ch 6 176
203 Interprétation sémantique et étude des changements à long terme σx invar est l écart type des pixels invariants de l image X de référence, en considérant uniquement les pixels non masqués. De même, σy invar est l écart type des pixels invariants de l image Y à normaliser, µx invar et µy invar sont les moyennes des pixels invariants de l image de référence et de l image à normaliser. Si, après avoir déterminer les invariants, le coefficient de corrélation entre les deux bandes masquées est trop faible, les calculs sont recommencés avec des valeurs différentes. 15. Génération de l'image transformée, en appliquant à chaque pixel de l'image cible la transformation :Y i,j = a * Yi,j + b VERIFICATION refaire une partie des calculs avec la nouvelle bande 16. masquer les pixels en dehors de la zone commune (masque 1 précédent) 17. Calcul image MNBD (pour tous les pixels) : ( Y X ) / (Y + X ) 18. Calcul de moyenne et écart type de l image MNBD 19. En utilisant les valeurs de l image MNBD, masquer les pixels en dehors de l intervalle [moyenne +/- N écart type] (défaut N = 1) des deux bandes 20. ACP sur les pixels non-masqués des deux bandes 21. Calculde la pente de la première composante principale : matrice des vecteurs propres 22. Si la pente est proche de 1 : la transformation est de bonne qualité ; sinon, probablement trop de différences (phénologie, changements de couverture du sol, ), normalisation impossible. FinTantQue La méthode de normalisation des données dans le cas de l interprétation d image classée s est s avérée très efficace. Elle permet la portabilité des signatures spectrales, pour d autres applications Méthode d interprétation automatique de classification non supervisée Si les traitements des données spatiales sont réalisés durant l année d acquisition de la véritéterrain, la méthode de classification appliquée peut s appuyer sur un échantillonnage de référence établi sur le terrain (méthode supervisée). Il est impossible d'obtenir une classification supervisée sans réalité terrain. Or, sur des dates éloignées dans le temps, ces renseignements ne sont en général pas disponibles. En l absence d échantillonnage de référence adapté, la méthode de classification ne peut être que non supervisée. Le problème des classifications non supervisées est leur interprétation. La classification donne une partition de l image en N classes avec des numéros (les étiquettes), mais on ne sait pas à quel type de surface cela correspond. Aucune légende ou clé de lecture n est donnée a priori, pour indiquer la nature des classes obtenues, comme pour les méthodes supervisées. C est pour cela qu il est nécessaire de faire suivre ce type de classification par une étape d interprétation afin d attribuer une sémantique aux classes trouvées, c est-à-dire trouver à Ch 6 177
204 Interprétation sémantique et étude des changements à long terme quoi elles correspondent : eau, forêt, bâti, maïs, etc, C est le photo-interprète qui, par sa connaissance déduit l affectation des classes, en général, visuellement. Cela est aisé pour les classes qui changent peu comme la forêt, le bâti, les rivières. Mais pour les cultures c est pratiquement impossible, en raison de la rotation des cultures, suivant les années on ne retrouve pas les mêmes cultures aux mêmes endroits. Une méthode de reconnaissance automatique a été développée pour effectuer l'interprétation d'une classification non supervisée à partir des valeurs radiométriques des classes de référence issues de vérités terrain (échantillons) d autre(s) année(s) ou inscrites dans un catalogue (statistiques cataloguées). La méthode consiste à mettre en correspondance les valeurs radiométriques des classes (en compte numérique ou en réflectance) de l'image à interpréter avec les valeurs radiométriques des classes de référence, même stade phénologique (même mois, date la plus proche possible), grâce à des distances multi spectrales, -temporelles. On recherche, pour chaque étiquette de la classification non supervisée, la classe qui est la plus proche par des calculs de ressemblance avec la référence. Plusieurs méthodes de calcul de ressemblances entre les classes sont effectuées. Chacune des deux classifications est associées à une série d'images, de plusieurs dates composées de plusieurs canaux, et éventuellement de plusieurs sources. Au préalable l opération de normalisation de ces données doit être effectuée Les distances : correspondance spectrale et temporelle Plusieurs méthodes de calcul des ressemblances entre les classes sont possibles. Pour chaque classe à interpréter, le résultat est donné par l appartenance à un jeu de trois classes les plus semblables dans une ou plusieurs références (d après des données obtenues dans une ou plusieurs années), avec quatre calculs de ressemblance : distance de Bhattacharrya (voir chapitre 3), distance euclidienne, distance euclidienne avec élimination de classes, et le maximum de vraisemblance avec une loi gaussienne. Ces trois classes sont «possibles». A l issu des calculs, des classes sont «certaines», sans ambiguïté, d autres restent incertaines. Un calcul d incertitude est fait à partir des distances calculées et du maximum de vraisemblance, le degré de certitude étant compris entre 0 et 1, où 1 est la certitude totale. La classe avec un degré de certitude proche de 1 est choisie, sinon elle appartient à deux ou trois classes à l issue de l interprétation. La distance euclidienne, principe barycentrique, utilise la valeur moyenne des pixels de chaque classe pour tous les canaux. La distance d d une classe de la classification à interpréter avec la référence est calculée en faisant la somme des différences des moyennes µ i des classes C i dans tous les canaux. n d clas_a _interpréter cla_ref = Σ ( µ i clas_a _interpréter µ i cla_ref ) i avec n nombre de canaux (spectraux ou temporels) µ i clas_a _interpréter : valeur moyenne de la classe clas_a _interpréter pour le canal i, µ i cla_ref la moyenne de la classe de référence. Certaines de ces mesures peuvent être très différentes, une normalisation est alors nécessaire. Ch 6 178
205 Interprétation sémantique et étude des changements à long terme moyenne Année 2004 Année 2003 Année 2002 euclidienne élimine bhatta euclidienne élimine maxvrai bhatta euclidienne maxvrai bhatta euclidienne élimine maxvrai Classe 1 à interpréter Classe 2 à interpréter Classe 3 à interpréter Tableau 6.1 : distances calculées avec les 4 méthodes sur 3 années différentes et la moyenne sur ces années (Bhatta signifie bhattacharya, élimine : élimination, max vrai : maximum de vraisemblance), les nombres correspondent aux n de classe suivi de la mesure Un logiciel permet de générer des statistiques (avec les matrices de covariance sur toutes les années) pour chaque image classée à différentes années. La concordance entre les différentes dates et les différents canaux spectraux est gérée. Dans le tableau 6.1, les distances sont calculées pour les années 2004, 2003, La moyenne par classe des valeurs radiométriques est effectuée pour chaque année, puis comparée avec les valeurs de la classification non supervisée à interpréter. On peut constater qu il y a conflit entre plusieurs classes. La classe 1 appartient en priorité aux classes de référence 8, 21, 10, 7, 14, toutefois la classe 8 intervient plus souvent avec une distance plus proche. Elle sera donc privilégiée. Pour la classe 2, la classe de référence 17 sera privilégiée. Si la classe est choisie dans tous les cas, le degré de certitude est égal à 1. L'interprétation s'appuie sur les valeurs radiométriques, comme dans la classification, la mise en correspondance de certaines classes peut-être parfois délicate, surtout lorsqu elles sont radiométriquement proches. Des informations et traitements supplémentaires, présentés cidessous permettent d améliorer la reconnaissance Principe des possibilités Les différentes sources (dates ou capteurs) apportent des informations souvent imprécises, contradictoires. Il s agit alors de tenir compte du degré de fiabilité que l on accorde aux différentes sources. Le problème consiste à recouper ces informations afin d obtenir des plages de consensus. Plus ces plages de consensus sont étendues, plus ces informations sont concordantes. Ch 6 179
206 Interprétation sémantique et étude des changements à long terme Elimination spectrale et temporelle Les classes correspondantes possibles sont recherchées à partir des références pour chaque classe (étiquette) de la classification non supervisée. Si les valeurs radiométriques correspondant à l étiquette ne sont pas incluses dans un intervalle d appartenance à une classe de l image de référence pour un canal donné, cette classe de référence sera éliminée des classes possibles. Ceci est réalisé successivement canal après canal, date après date. Cette technique cherche à limiter le nombre de classes pouvant être affectées à une étiquette non supervisée, et suppriment certaines confusions. Les bornes sont des valeurs minimales et maximales possibles pour les classes (connues par les vérités terrain). L intervalle est donné, soit par [min ; max], correspondant aux bornes de chaque canal dans chaque classe de l'image de référence, soit calculé par [µ α σ; µ+α σ], avec : µ : moyenne des valeurs radiométriques des classes pour un canal spectral ou temporel. α : coefficient (proche de 2,5 ou 3, si on se rapproche d une distribution de Gauss) σ : l écart type. Les statistiques de 1 er et 2 nd ordre sont calculées sur les références, ou données par l expert, ou appartiennent à la base de connaissance. Les classes qui n ont pas leurs valeurs radiométriques comprises dans cet intervalle sont éliminées, successivement date par date. La distance euclidienne précédemment définie est appliquée sur les classes restantes. Ce principe évite un effet de «moyennage» des informations données par chaque classe dans chaque canal spectral, ce qui tend à diminuer les effets caractéristiques des classes, contenus uniquement dans certains canaux. En effet, un canal peut donner une information particulière qui va être «noyée» parmi les informations des autres canaux, plus «ordinaire». Oct Nov. Déc. Janv. Fév. Mars Avril Mai Juin Juill. Août Sept. Céréales d'hiver Blé /Orge Orge tardif Oléagineux Protéagineux Colza Tournesol Soja Pois Céréales d'été Maïs Sorgho semis / sol nu couvert veg faible couvert veg fort sénescence / récolte épiaison / floraison Figure 6.4 : Calendrier cultural dans le Sud ouest de la France L utilisateur peut contrôler les classes possibles dans certains canaux, pour pouvoir intégrer sa connaissance d expert. Il peut s aider par exemple du calendrier cultural (figure 6.4), pour donner une valeur aux bornes. Ch 6 180
207 Interprétation sémantique et étude des changements à long terme Intégration de la notion de variation temporelle Des variations mensuelles, saisonnières ont lieu, suivant le cycle végétatif et le calendrier cultural. Par exemple le Maïs est en sol nu en mars, en pleine végétation en août, alors que le Blé a déjà bien poussé en mars et est récolté en août Cette notion est intégrée dans la reconnaissance par le calcul des différences entre les moyennes temporelles de chaque classe. S il y a ambiguïté sur l affectation d une classe, on ajoute comme paramètre discriminatoire supplémentaire la variation entre deux dates. La différence des valeurs radiométriques est calculée, pour la classe testée avec celle de référence, cela dans tous les canaux. L idée part d un principe d ajustement à la courbe des variations de la classe de référence. La somme de ces variations sera effectuée sur tous les canaux, si elle est très faible cela signifie que la classe de l image de référence suit la même variation que la classe comparée. = Σ (δ ik - δ jk ) où δ ik est la différence entre la variation temporelle de la classe i k δik = a ik - a jk+1, a ik, a jk+1 sont les valeurs radiométriques d un pixel à deux dates différentes dans les mêmes canaux spectraux, δ jk de la classe j pour les dates k et k+1. Si est très petit, alors le degré de possibilité pour qu il appartienne à la classe j est élevée. Afin de pouvoir intégrer sa connaissance d expert, un contrôle sur le choix des classes est possible pour l utilisateur Données exogènes Nous avons donné la possibilité à l expert d introduire des données a priori pour guider l'interprétation. Les régions Le premier cas s'appuie sur la connaissance a priori par l'utilisateur de la composition des grandes régions de l'image dans laquelle il est possible d avoir certaines classes, et impossible certaines autres. Ainsi en introduisant une image des régions, (figure 6.5), l expert va pouvoir spécifier quelles classes peuvent se trouver (ou ne pas se trouver) dans les régions. Figure 6.5 : image des régions Ch 6 181
208 Interprétation sémantique et étude des changements à long terme L algorithme élimine certaines classes pour une étiquette à interpréter, sachant qu elle n est pas possible dans une région. Par exemple, pour l image de 1991 du Sud-Ouest toulousain, quinze régions sont définies (figure 6.5). Pour chaque pixel de ces zones, l'utilisateur pourra limiter le nombre de classes pouvant lui être affectées. Supposons que pour la région numéro j on ne peut avoir que les classes 4, 5, 6, 10, 16, alors, pour chaque pixel de cette région, la correspondance avec le calcul de distance n est fait que sur les classes présentes dans cette liste. Les informations imprécises peuvent être représentées explicitement sous forme de fonction d appartenance, on peut également donner des degrés d appartenance (chapitre 3) qui favorise des classes par rapport aux autres sans les rejeter. Ainsi des poids peuvent être affectés aux classes suivant les régions. Par exemple la région 8 est plus une région de culture que de prairie, alors que c est l inverse pour la région 9. La région 10 est très urbanisée, on ne doit pas trouver du tournesol dans cette région. Ce cas a permis d enlever les confusions entre le Bâti et le Tournesol. Système d Information Géographique, Modèle Numérique de Terrain Le deuxième cas s'appuie sur les valeurs provenant de données exogènes telles que SIG, MNT (Modèle Numérique de Terrain), où la valeur des pixels indique, par exemple l'altitude des pixels de l'image. Le raisonnement est similaire au précédent. La valeur minimum valmin et maximum valmax pour chaque classe, chaque canal est donnée par l expert (ou la base de connaissance). Pour un canal j pour la classe i, les classes possibles devront avoir des valeurs comprises entre valmin et valmax. Dans ce cas la classe i est admise, sinon elle est rejetée. Ainsi les classes qui ne correspondent pas aux critères sont éliminées. Ce modèle permet de s'assurer que la classe affectée à un pixel lui corresponde suffisamment, les classes possibles pour un pixel forment un ensemble plus restreint et évite des erreurs d affectation. Par exemple, un pixel situé à 1000 mètres d'altitude ne pourra pas être comparé à la classe Maïs, si celui ci est supposé ne pas être présent à cette altitude. Mais il faut connaître a priori l'intervalle de définition des valeurs de la classe. Comme dans le cas précédent des poids peuvent être associés et au lieu d un rejet de la classe cela peut être un degré d appartenance Correspondance spatiale : VALIDATION Dans le cas de la classification supervisée, il existe des méthodes concrètes et objectives d évaluation des résultats d une classification à partir des matrices de confusion calculées sur la deuxième série d échantillons, les «échantillons de vérification». Ces méthodes d évaluation sont intégrées dans la classification. Par contre, pour la classification non supervisée il n existe pas de possibilités d évaluation en dehors de la comparaison visuelle avec des cartes ou des images classées supervisées d années précédentes. Nous avons crée une application qui génère des matrices de confusion (ou de correspondance) des classes pour les classifications non supervisées à partir des échantillons de vérification d années différentes pour lesquelles on possède les vérités terrain. La classification non supervisée est comparée spatialement et non plus spectralement. Le procédé met en correspondance spatiale cette classification, soit à une classification Ch 6 182
209 Interprétation sémantique et étude des changements à long terme supervisée de référence (de bonne qualité et pour laquelle on connaît l erreur), soit à l image des échantillons acquis à une époque différente. Une normalisation, puis l interprétation, sont effectuées préalablement. Une nouvelle image est crée avec les classes interprétées. Pour chaque classe i de l image à interpréter, la classe j de l image de référence lui est associée spatialement, c'est-à-dire pixel à pixel, ou objet à objet lorsque une segmentation est intégrée. La correspondance donne la liste de toutes les classes possibles avec leur probabilité d appartenance (tableau 6.2). Cette procédure est un élément de la discrimination dans les cas où les classes sont stables comme les classes Bâti, Rivière Forêt, Prairie dont l emplacement n a pu changer. On peut s aider éventuellement avec l image des invariants obtenue après la normalisation. Par contre la correspondance pour les classes de cultures ne peut être considérée qu avec prudence car l occupation du sol par les surfaces agricoles n est pas forcément identique selon les années (rotation des cultures). Mais on peut s en servir pour le suivi des rotations des cultures. Ce procédé permet également de préciser l interprétation dans les cas ambigus, et de déterminer la séparation de classes en sous-classes, quand elle est appliquée à la correspondance entre deux classifications supervisées avec des combinaisons de canaux différentes. Dans le tableau 6.2, l étiquette 15 correspond pour 89% à la classe 20 (Bâti) des échantillons, on peut donc lui attribuer cette classe. Il est difficile parfois d affecter une classe, par exemple, l étiquette 28 est partagée en plusieurs classes (8, 9, 17), l étiquette 14 correspond à 72.97% de la classe 4 (Blé), mais également 25.68% à la classe 7 (Orge), ces deux classes sont très proches spectralement et souvent confondues. L étiquette 16 est partagée dans plusieurs classes, cette classe ne peut être alors qu une classe mixte. Ceci peut servir également à déterminer des sous classes, dans le cas ou deux étiquettes de la classification non supervisée appartiennent à une même classe i. Cette classe i peut être divisée en deux sous classes qui représentent des hétérogénéités différentes, ou des s les à des dates éloignées. Etiquettes (classification à interpréter) Classe des échantillons de référence, suivie des pourcentages d appartenance % % % % 17 11% % % % % % % % % % % % % % % % % % % % % 9 35% 17 15% 1 6% % 11 25% 3 2% Tableau 6.2 : Exemple de la correspondance spatiale des classes entre la classification à interpréter et les échantillons de références (Sud-Ouest 2004) Une fois les étiquettes de la classification non supervisée affectées aux classes, une matrice de confusion peut être donnée à titre indicatif avec un échantillonnage d une autre année, mais à prendre avec précaution pour les classes qui sont soumises à variation annuelles. Ch 6 183
210 Interprétation sémantique et étude des changements à long terme Applications Pour l étude sur le long terme toutes les images de 1989, 1991, 1994, 1995, 2000, 2002, 2003, 2004 du projet Sud Ouest (128 images spectrales avec 37 dates, données SPOT) ont été rendues superposables entre elles et des zones communes ont été choisies. La zone commune de 2002 et 2003 possède 68 canaux. Nous présentons, les états d occupation du sol à des dates différentes, 1991, 2002, 2003 et Pour chaque année, la composition et la distribution des classes d occupation du sol dans l espace régional ainsi que des caractéristiques spatiales de la trame paysagère (forme et taille des parcelles) sont analysées. Une mise en évidence des changements est réalisée par analyse croisée des deux états multi-temporels de l occupation du sol 1991 et 2002 et par comparaison numérique des éléments de la trame paysagère. Les résultats sont de deux types, ceux visant à valider le modèle et ceux destinés à l'étude de l'évolution du paysage entre 1991 et La classification supervisée de 2002 sert de référence dans les deux cas [Ducrot et al 02]. Pour valider le modèle d'interprétation d'une classification non supervisée de 2003 et 2004, l interprétation est effectuée avec les échantillons de 2002, les résultats sont vérifiés avec les échantillons 2003 et de Pour effectuer l'interprétation de 1991 nous utiliserons la partie commune avec 2002 réduite Classification non supervisée 2003 et son interprétation Il existe un décalage important entre les séries géoréférencées 2002 et 2003, malgré la superposition automatique possible avec le géoréférencement. Le décalage de 4 pixels (en moyenne) en X et de 1 pixel (en moyenne) en Y, il varie suivant les dates, il a pu être réduit. Les dates choisies pour la normalisation, les plus proches possibles, sont données dans le tableau Canaux spectraux Spot 10/03/03 21/03/02 XS3, XS2, XS1, XS4 05/04/03 23/04/02 XS3, XS2, XS1, XS4 23/05/03 15/05/02 XS3, XS2, XS1 14/06/03 14/06/02 XS3, XS2, XS1 10/07/03 20/07/02 XS3, XS2, XS1 04/08/03 14/08/02 XS3, XS2, XS1, XS4 03/09/03 14/09/02 XS3, XS2, XS1, XS4 25/09/03 06/10/02 XS3, XS2, XS1 07/11/03 22/11/02 XS3, XS2, XS1 5/12/03 22/11/02 XS3, XS2, XS1, XS4 Tableau 6.3 : dates mises en correspondance pour la normalisation Après la normalisation des données multi -spectrales et -temporelles, une interprétation est effectuée à partir des échantillons de 2002, (apprentissage et vérification confondus). Deux types de normalisation ont été calculées : 1) en compte numérique, 2) en réflectance. Les résultats obtenus sont très proches avec ces deux types de calcul, ce qui laisse supposer que la normalisation fonctionne plutôt bien, puisque pour transformer des images en réflectance, certaines corrections radiométriques sont effectuées. Sans ces corrections la normalisation rend les images très comparables. Ch 6 184
211 Interprétation sémantique et étude des changements à long terme Diverses classifications non supervisées ont été réalisées avec des combinaisons de dates et de canaux spectraux différents, d une cinquantaine d étiquettes chacune. Les classes de culture sont mieux distinguées avec la classification sept dates de mars à septembre. Mais une partie du Bâti apparaît en Eau. Les canaux PIR et MIR permettent très bien de différencier ces deux classes. Les plantations d Eucalyptus ont été classées en Bâti dense, les Résineux sont mélangés avec les Feuillus. Les Eucalyptus se séparent bien du Bâti dans le MIR. Une classification est alors réalisée avec les canaux PIR et MIR avec les 7 dates. Dans l image classée avec PIR et MIR, on distingue parfaitement trois classes de Bâtis (dense, suburbain, lâche) ainsi que la classe Eau. A partir de cette image, le logiciel d interprétation permet d identifier les classes. Des classes sont «certaines», sans ambiguïté, d autres restent incertaines. Un calcul d incertitude est fait à partir des distances calculées, (distances de Bhattacharrya, euclidienne) et du maximum de vraisemblance, le degré de certitude étant compris entre 0 et 1, où 1 est la certitude totale. Une fusion des deux classifications privilégiant ces classes est réalisée. Une image avec 48 étiquettes est obtenue. Les listes des classes sont répertoriées dans le tableau 6.4, avec un coefficient indiquant la mesure de la certitude d affectation à la classe. L interprétation automatique donne l affectation aux classes de façon certaine pour les classes Forêt, Bâti, Tournesol, Blé, Maïs, beaucoup de cas sont des classes mixtes Blé (Prairie), Blé/Orge, une interprétation visuelle est complémentaire pour séparer ces classes, mais parfois c est impossible. L interprétation visuelle n est fiable que pour les classes telles que la forêt, des lisières, villes, eau, dont on connaît les emplacements. blé (orge), 0.9, 0.6 blé (prairie, tournesol, blé, 0.9 blé tournesol, prairie, 1, 0.5 tournesol, 1 tournesol, 1 tournesol (soja, blé, mais), 1, eau bâti (pelouse), 1, bâti (prairie), 1, 0.9 blé, 1 blé, 1 blé, 1 blé (prairie), 2 prairie (jachère), 1 Prairie (jachère), 1 soja (mais) (tournesol), 1, 0.5 colza (blé), 1, 0.4 forêt, 1 forêt, 1 forêt de résineux, 1 blé, 0.8 blé (prairie), 0.7 (nuages) tournesol, (prairie), 1, 0.8 eucalyptus ripisylve, 1, 0.8 prairie (jachère), 1 jachère (prairie), 1 prairie, jachère, tournesol, blé, prairie (jachère) (blé), 0.8 eau, 1 Prairie, jachère (foret) prairie bâti bordure (blé), 0.8 Colza, soja, maïs, prairie (blé), 1, 0.6 foret (lisière) (prairie) bordure, prairie (blé), 0.8 blé (prairie) (bordure), 0.7 prairie (jachère) (blé), 1, 0.5 prairie (jachère) (blé), 1, mais, 1 mais (irrigué), 1 prairie jachère (blé), 1, 0.8 prairie (lisière foret) tournesol (bordure), blé bâti lâche /suburbain bâti dense, 1 prairie,1 bâti suburbain prairie blé (jachère), 1, Tableau 6.4 : liste des classes reconnues ; les classes entre parenthèses sont des classes possibles (confusions); les chiffres indiquent le degré de certitude de 0 à 1 (0 incertitude totale, 1 certitude maximum). S il y a 2 chiffres le 1 er correspond au degré de certitude toutes classes confondues, le 2 ième de degré de certitude de la classe la plus probable. 1 signifie 1 Toutes les étiquettes identifiées de façon quasi certaine à une même classe thématique, sont regroupées, ce qui réduit leur nombre à 34. Afin de lever au mieux les incertitudes, une matrice de correspondance de cette nouvelle Ch 6 185
212 Interprétation sémantique et étude des changements à long terme image avec les échantillons est effectuée (éventuellement avec la classification supervisée de 2002). Ainsi, avec cette mise en correspondance, grâce à nos connaissances du terrain et à l interprétation sur l image (bordures de champ, ), on arrive à préciser le type d occupation de certaines classes (hors cultures) qui restaient incertaines (et à valider les précédentes). Toutefois des classes restent non identifiables car elles sont un mélange de plusieurs couvertures végétales (par exemple : Blé/Prairie, Tournesol/Maïs/Blé/Sorgho, ). Suite à cela un deuxième regroupement de classes est effectué et une classification contenant 17 classes, dont cinq sont incertaines est obtenue (tableau 6.5). La classe Culture d été correspond aux classes possibles : Maïs, Tournesol, Soja, Sorgho. La classe «Ripisylve/Lisière» correspond à de la végétation de bord de rivière, et de bord de champs. feuillus feuillus+résineux eucalyptus blé colza maïs tournesol soja prairie/jachère/pelouse eau bâti rural/suburbain bâti périurbain bâti dense Culture d été blé/prairie ripisylve-lisière tournesol/prairie Tableau 6.5 : classes après le regroupement Deux de ces cinq classes sont des mélanges de cultures/prairies. Pour les discriminer une classification avec le mois de décembre 2003 est effectuée, car à cette date les cultures sont en sol nu. Une matrice de correspondance avec la classification non supervisée de décembre, a permis de mieux séparer les deux classes mixtes : Blé/Prairie et Tournesol/Prairie, sans éliminer totalement ce mélange. Des parcelles ont basculé vers le Blé, le Tournesol, la Prairie. Les classes mixtes ont diminué d importance. Mais il reste deux nouvelles classes incertaines que nous appelons : 1) Culture, qui correspondrait plutôt à du Blé, d après les calculs de distance avec la référence, 2) Tournesol2 avec un degré de certitude égal à 0.6, alors que la classe Tournesol est quasi certaine. Les Résineux apparaissent bien dans la classification de décembre, alors qu ils n étaient pas très bien différenciés avec les Feuillus : la classe mixte Feuillus/Résineux devient Résineux et Feuillus. feuillus résineux eucalyptus blé colza maïs tournesol soja prairie/jachère/pelouse eau bâti rural bâti périurbain bâti dense prairie (blé) prairie (tournesol) culture d été culture (certitude 0.6) ripisylve-lisiere Tournesol2 (certitude 0.6) Tableau 6.6 : classes définitives reconnues en 2003 à partir des données terrain 2002 (en partie automatiquement) La fusion des deux classifications ajoute, ces trois nouvelles classes et sépare les Résineux des Feuillus. La classe Feuillus 2, nouvellement crée, est différente spectralement de la classe Feuillus 1, car elle correspond aux forêts situées à proximité des petites Pyrénées. Elle est donc une sous classe de Feuillus. Toutefois cette distinction n ayant pas été faite en 2002, nous avons regroupée ces deux classes de Feuillus. On obtient une classification finale comprenant 20 classes. Puis, l image est légèrement régularisée pour supprimer quelques pixels isolés (figure 6.6). Ch 6 186
213 Interprétation sémantique et étude des changements à long terme Figure 6.6 : classification SPOT non supervisée 2003 (mars, avril, mai, juin, juillet, août, septembre, décembre) interprétée avec les échantillons de 2002 Validation de la classification Pour valider la classification, la matrice de confusion est calculée avec les échantillons 2003 (échantillons d apprentissage et de vérification confondus). Le MPCC est de 73,39%, le Kappa 81.75%. Si on regroupe les 3 types de bâti le MPCC est de 76,46% Les classes supplémentaires de la matrice de confusion (tableau 6.7) correspondent aux classes incertaines, qui sont des classes mixtes. En conclusion : Avec la classification non supervisée : 7 classes ont pu être discriminées avec certitude : Feuillu, Résineux, Eucalyptus, Blé/Orge, Maïs/Sorgho, Eau, Bâti, Trois types de Bâti apparaissent nettement. Les classes Soja, Prairies/Jachères sont moyennement bien classées. Le Colza n est pas bien reconnu (les dates disponibles ne facilitent pas sa discrimination), mais la classe Culture 2 que l on n a pu identifier avec certitude car elle correspondait à des mélanges de classes, s avère être du Colza ce qui ramène son pourcentage de reconnaissance à plus de 63,5%. Ch 6 187
214 Interprétation sémantique et étude des changements à long terme Echantillons 2003 Feuillu Resineux Eucalyp tus Blé /Orge Colza Mais /Sorgho Classification non supervisée 2003 Tournesol Soja Prairie/ Jachère Eau Bâti dense Bâti périurbain Bâti rural/ suburbain Feuillus 94,66 1,99 0,00 0,08 0,00 0,15 0,57 0,02 1,71 0,14 0,02 0,07 0,02 0,00 0,20 0,00 0,00 0,01 Resineux 0,51 92,70 0,66 2,74 0,00 0,61 0,96 0,00 1,17 0,05 0,25 0,00 0,00 0,00 0,20 0,00 0,00 0,00 Eucalyptus 0,00 8,50 81,09 0,13 0,00 2,79 0,00 0,63 1,52 0,00 0,76 0,51 0,00 0,00 0,00 0,00 0,00 0,00 Blé/Orge 0,00 0,00 0,00 83,13 0,78 1,91 3,31 0,36 3,50 0,34 0,15 0,49 1,04 3,88 0,38 0,32 0,06 0,00 Colza 0,00 0,00 0,00 20,63 38,79 0,45 0,45 0,00 3,36 0,00 1,35 0,00 0,00 0,00 0,00 34,75 0,00 0,00 Mais/Sorgho 0,00 0,00 0,00 0,51 0,03 70,16 8,68 4,67 1,09 0,10 0,00 0,00 0,08 0,00 14,36 0,00 0,30 0,03 Tournesol 0,00 0,00 0,00 1,87 0,15 2,62 63,35 2,77 8,60 0,07 0,52 0,67 1,65 0,30 1,12 0,07 8,60 6,28 Soja 0,00 0,00 0,00 6,09 0,00 12,18 2,54 64,47 1,52 1,02 0,00 0,00 2,03 0,00 8,63 0,00 0,00 0,00 Prairie/Jachère 0,00 0,03 0,00 6,53 0,36 2,03 1,90 0,03 58,81 0,00 0,82 1,84 8,89 8,83 0,62 0,00 6,99 1,94 Eau 0,02 0,00 0,00 0,00 0,02 0,08 0,05 0,00 0,17 99,48 0,11 0,08 0,00 0,00 0,00 0,00 0,00 0,00 Bâti dense 0,00 0,00 0,00 0,00 0,00 0,00 2,03 0,00 0,11 1,24 60,61 33,86 2,14 0,00 0,00 0,00 0,00 0,00 Prairie (blé) Culture 1 Tableau 6.7 : Matrice de confusion des classes de la classification non supervisée avec les échantillons 2003 Culture 2 Tourne sol 1 Prairie (tournesol) Résultat de classification non supervisée après interprétation sur une image Sud-Ouest 2004 La même opération a été faite avec les données de 2004, les résultats sont globalement meilleurs que ceux de 2003, en raison de la sécheresse, mais également des améliorations apportées à tous les niveaux du système de classification. Afin de valider la classification non supervisée, une matrice de confusion est calculée avec les échantillons 2004 (échantillons d apprentissage et de vérification confondus). Pour cela certains échantillons sont regroupés car la classification ne différentie pas les mêmes classes, c est le cas des échantillons de Résineux/Eucalyptus, Blé/Orge, Maïs/Sorgho, Prairie/Jachère, les classes d Eau et les classes de Bâtis. Le MPCC est de 81,37% et le Kappa 81%. Les échantillons ne possédant que deux classes de bâtis, les trois classes de bâtis de la classification non supervisée ont été regroupées. Le MPCC est alors de 85,56%. Feuillus Resineux/ Eucalyptus Ble/ Orge Colza Mais Tournesol Soja Prairie/ jachère Eau Bâti dense Bâti Bâti rural/ periurbain suburbain Prairie/ culture Prairie/ blé Prairie/ lisière Ripisylve/ lisière Feuillus 90,24 7,66 0,00 0,00 0,00 0,08 0,00 1,14 0,15 0,00 0,03 0,26 0,00 0,33 0,00 0,12 Resineux/ Eucalyptus 7,47 92,33 0,00 0,00 0,00 0,00 0,00 0,05 0,00 0,05 0,00 0,00 0,05 0,00 0,00 0,05 Ble/ Orge 2,65 0,53 77,23 3,18 0,86 0,38 0,04 5,58 0,01 0,02 0,01 0,20 0,02 9,04 0,00 0,24 Colza 0,00 0,00 2,05 92,18 0,00 2,00 0,00 3,22 0,00 0,00 0,00 0,00 0,00 0,55 0,00 0,00 Mais/Sorgho 0,00 0,00 0,30 0,20 79,31 3,42 11,21 0,13 0,00 0,13 0,00 0,02 4,50 0,15 0,03 0,59 Tournesol 0,30 0,00 1,12 0,00 1,39 84,26 7,73 0,88 0,00 0,03 1,37 1,78 0,07 0,49 0,00 0,59 Soja 0,00 0,00 0,46 0,00 1,52 12,71 75,82 0,00 0,00 0,00 0,00 0,00 6,86 0,97 0,00 1,66 Prairie/ jachère 2,85 0,15 13,41 2,45 0,00 0,38 0,15 67,21 0,05 0,24 0,49 4,75 1,34 6,50 0,00 0,04 Eau 0,25 0,00 0,00 0,00 0,00 0,00 0,00 0,04 98,18 1,48 0,03 0,00 0,00 0,02 0,00 0,00 Bâtis 0,00 0,00 0,68 0,00 0,00 0,43 0,00 0,00 0,00 56,97 32,70 9,14 0,00 0,09 0,00 0,00 bati regroupé 98,81 Tableau 6.8 : matrice de confusion des classes de la classification non supervisée avec les échantillons 2004 (en ligne les classes des échantillons, en colonne celles de la classification non supervisée) Ch 6 188
215 Interprétation sémantique et étude des changements à long terme De manière générale, les échantillons sont donc bien classés, on note cependant quelques scores plus faibles : - La classe Blé/Orge est légèrement confondue, avec la classe en PrairieJ ou la classe Prairie/Blé (mais cette dernière représente en partie la classe Blé). - La classe Prairie/Jachère est légèrement confondue, avec la classe Blé/orge ou la classe Prairie/Blé (mais cette dernière représente en partie la classe Prairie). Des confusions existent entre les cultures d été, et la classe Prairie/cultures qui englobe quelques échantillons de Maïs/Sorgho et de Soja Etude des changements de paysage Le changement est évalué sur une période de onze ans en comparant les occupations du sol et la trame paysagère de deux années 1991 et 2002, à partir des classifications sur les données SPOT. Pour 1991, en l absence d échantillonnage de vérité de terrain, l interprétation automatique de la classification non supervisée avec la classification supervisée Une image commune, corrigée géométriquement dans le système de projection Lambert 2 étendu, les deux séries d images multidates et éventuellement d autres documents cartographiques, servent de base aux deux classifications réalisées sur les données 1991 et Caractères et précision de la carte d occupation du sol La classification des données multidate de 2002 par la méthode supervisée produit une carte d occupation du sol comportant 16 classes [Ducrot D. & Gouaux P. 2003]. On y trouve trois classes de formations boisées (Feuillu, Résineux, Eucalyptus), 10 classes de cultures (Blé, Orge, Colza, Maïs, Tournesol, Sorgho, Soja, Pois, Prairie et Jachère), deux classes d eau (Eau libre, Lac/Gravière) et la classe de Bâti. La précision de la classification donnée par la matrice de confusion calculée avec l échantillonnage de vérification donne les pourcentages de pixels correctement classés (PCC). La précision globale de la classification est égale à 87.4% (MPCC) et le Kappa est de 88.7%. La classification 2002 présente un taux d erreur de 12 % environ. Ce résultat est nuancé par l observation détaillée de la matrice (PCC des classes, affectation erronée des pixels des classes et des échantillons) qui montre des classes très bien discriminées par exemple les trois classes de végétation arborée Feuillu, Résineux, Eucalyptus avec respectivement 96.7%, 98.7% et 93.8% de pixels bien classés, le Maïs avec un PCC de 94.3%, le Blé 90.3%. Les classes Eau et Lac sont aussi bien classées avec respectivement 97.0% et 89.8% de pixels bien classés. Les quelques confusions observées se font avec le Bâti/Minéral. Ceci s explique par le fait qu aucune classe de sol nu n était présente dans l échantillonnage. Ainsi les surfaces minérales le long des cours d eau et autour des lacs collinaires (niveau d eau fluctuant) sont affectées à la classe Bâti/Minéral. En revanche certaines classes sont moins bien classées, le Sorgho par exemple (PCC égal à 71.8%) présentant des confusions avec le Maïs. L analyse globale (figure 6.7) indique le caractère rural de la zone d étude avec une superficie importante occupée par les classes cultivées ( ha) couvrant 78.2% du territoire ; on y Ch 6 189
216 Interprétation sémantique et étude des changements à long terme trouve dans l ordre d importance de la classe, les classes de Blé (23.8%), de Prairie 23.3%, de Tournesol (17.6%), de Maïs (6.6%), de Sorgho (4.1%), de Soja (1.5%), d Orge (0.8%), de Colza (0.5%) et de Pois très faiblement représenté. La classe Jachère avec 9.6% reste conforme aux directives de la PAC (Politique Agricole Commune) et correspond à 10% de la SAU (Statistique Agricole annuelle). Ce paysage agricole est ponctué de boisements occupant 6.9% du territoire et l on trouve 5.3% de surfaces essentiellement dédiées à l urbanisation et localisées au nord-est du territoire étudié correspondant à la bordure ouest et sud de l agglomération toulousaine. OS 2002 Superficie ha Superficie % Feuillus % Résineux % Eucalyptus % Blé % Colza % Orge % Maïs % Tournesol % Sorgho % Soja % Pois % Jachères % Prairies % eau libre % Eau / lacs % Urbain / surfaces minérales % Figure 6.7 : occupation du sol 2002 en 16 classes dans le territoire de comparaison Occupation du sol en 1991 Trois scènes SPOT acquises à 3 dates (22 mai 1991, 3 août 1991, 24 septembre 1991) seules disponibles sur la zone d étude. En fonction des résultats précédents relatifs à la qualité de l information fournie par les divers jeux de données multitemporelles (chapitre 3), on peut espérer que la combinaison des trois dates étalées sur deux saisons est suffisamment performante pour la classification. La méthode de classification est non supervisée avec interprétation automatique des classes sur le référentiel des classes de 2002, appliquée sur des données normalisées, selon le schéma Ch 6 190
217 Interprétation sémantique et étude des changements à long terme décrit précédemment ( 6.2). Des traitements de post-classification sont réalisés afin d améliorer les résultats : fusion de classifications, régularisation Superficies ha Proportions Bois de Feuillus et de Résineu ,58% Cultures d'hiver ,13% Cultures d'été irriguées ,33% Cultures d'été non irriguées ,01% Prairies/Jachères ,75% Eau ,15% Urbain/ Surfaces minérales ,71% non classés ,35% Total ,00% Figure 6.8 : occupation du sol 1991 en 7 classes La carte d occupation du sol 1991 est obtenue entièrement automatiquement à partir du catalogue pré-établi des signatures spectrales des classes. Le nombre de classes identifiables est réduit car l information multitemporelle est pauvre et ne permet pas d atteindre un niveau de discrimination fin. On ne peut accéder qu à la reconnaissance des grandes catégories d occupation du sol. En effet une seule date, 22 mai 1991, pour l observation des cultures d hiver (récolte début juillet) n autorise pas à faire des distinctions au sein de cette catégorie. En revanche deux date, 3 août et 24 septembre 1991, pour les cultures d été, assurent leur différenciation grâce à des pratiques culturales différentes comme par exemple la conduite avec irrigation ou non. Trois dates sont suffisantes pour discriminer les autres éléments pérennes du territoire bois, prairie/jachère, bâti, eau. L interprétation de l image classée de 1991 fournit un état simplifié de l occupation du sol de huit classes. Elles correspondent à des grandes catégories d occupation du sol (Bois, Cultures d hiver, Cultures d été irriguées, Cultures d été non irriguées, Prairie/Jachère, Eau, Bâti), plus une classe particulière, de superficie non négligeable (7.4%), qui n a pu faire l objet d aucune affectation automatique à l une des sept autres classes étant donné sa variabilité radiométrique. Néanmoins, compte tenu de sa taille et de sa distribution très localisée, il a été décidé de la conserver et de l identifier visuellement grâce à son profil radiométrique moyen à une classe nommée «Friches urbaines» ; à titre d information dans le référentiel de terrain de 2002 certains éléments de cette classe apparaissent dans la classe «Jachère», elle a été affectée à cette classe. Il reste une classe de rejet regroupant tous les pixels non classés (3.4%). Ch 6 191
218 Interprétation sémantique et étude des changements à long terme La validation visuelle et statistique prouve que les grands ensembles sont extrêmement bien reconnus. Néanmoins, une légère confusion existe pour les cultures d'été, cela peut s'expliquer par le fait que les dates discriminantes pour ces cultures n'étaient pas disponibles (seulement trois dates pour 1991) Version simplifiée de l occupation du sol 2002 Une version simplifiée de l occupation du sol 2002 est nécessaire pour la comparaison avec la classification de 1991 qui est moins détaillée que celle de 2002, 8 classes au lieu de 16. Superficies ha Proportions Bois de Feuillus et de Résineu ,91% Cultures d'hiver ,08% Cultures d'été irriguées ,25% Cultures d'été non irriguées ,58% Prairies/Jachères ,89% Eau ,62% Urbain/ Surfaces minérales ,67% Total ,00% Figure 6.9 : occupation du sol 2002 en 7 classes dans le territoire de comparaison La classe des Bois regroupe toutes les formations arborées feuillues et résineuses. La classe Cultures d hiver est composée des cultures au cycle de développement étalé sur les périodes hivernale et printanière comme le blé, l orge et le colza. Les deux classes Cultures d été au cycle de développement estival isolent les Cultures irriguées, maïs, soja et sorgho, des Cultures non irriguées ou en sec, Tournesol et Pois.. La classe Prairie/Jachère est difficilement séparable avec l interprétation automatique des classes. Les autres classes sont la classe Eau, et la classe de Surfaces Minérales (bâti, route). La classe «Friches urbaines» est une classe interprétée visuellement, elle n existe pas en 2002, les friches urbaines étant englobées dans la classe Jachère/Friche. Ch 6 192
219 Interprétation sémantique et étude des changements à long terme Mise en évidence des changements d occupation du sol La mise en évidence des changements consiste à comparer les affectations de l occupation du sol de chaque point du territoire ce qui engage à uniformiser les classes d occupation du sol. Elle est évaluée à deux niveaux : Au niveau global : par comparaison des deux états d occupation du sol 1991 et 2002 ; mise en parallèle des superficies des différentes classes d occupation du sol aux deux dates. Au niveau spatial : par analyse croisée des deux états d occupation du sol appliquée pixel à pixel ; le résultat est exprimé sous la forme d un tableau croisé (matrice des changements) et de la carte des changements. Au niveau global L écart entre les superficies de chaque classe donne une indication globale du changement intervenu. On note une diminution significative des bois de l ordre de 10%, une augmentation des cultures de l ordre de 6.5%. L analyse plus détaillée des superficies des cultures indique que les cultures irriguées étaient déjà en place en 1991 et que l augmentation de la surface cultivée pourrait être attribuée aux cultures en sec rentrant en rotation majoritairement biennale sur ce territoire. La classe Prairie/Jachère est en progression importante de l ordre de 14.5%. Cette augmentation va de pair avec l obligation de gel de terre mise en place par la PAC en Il faut noter que l augmentation de cette classe resterait significative (7.5%), si la classe «Friche urbaine» avait été affectée à la classe Prairie/Jachère dans la classification La classe Bâti voit sa superficie croître de 2% environ. La classe Eau, correspondant principalement à la rivière, est sous-estimée en Les bords des rivières se retrouvent classés en minéral. En 1991 nous avons pallié ce problème en intégrant l Eau par fusion de classification, parfaitement discriminable avec les seuls canaux PIR et MIR. Les deux éléments les plus marquants sont : diminution des surfaces boisées augmentation des cultures en particulier des classes Cultures d été en sec et Prairie/Jachère Peut-on valider ces résultats avec les données connues? Plusieurs documents de référence on aidé à montrer la cohérence des résultats : Corine Land Cover (CLC) : base de données cartographiques établie entre 1988 et 1992, à partir de laquelle sont extraites les couvertures du sol rangées en cinq catégories dans la zone d étude : Territoires artificialisés (1.4%), Territoires agricoles (91.7%), Forêts et semi naturels (6.2%), Zones humides (0.0%), Surfaces en Eau (0.2%). Seules les surfaces > 25 ha sont prises en compte sur CLC, entraînant une sous représentation des classes très fragmentées à l avantage des catégories peu découpées ; c est la cas des classes «Forêts et semi naturels», des territoires artificialisés qui voient leur représentation diminuer à l avantage de la catégorie des Territoires agricoles représentant 91.7% alors que la SAU en 1991 (Source : AGRESTE Statistique Agricole annuelle) n atteint que 64% dans la Haute-Garonne et 76% dans le Gers. Renseignements généraux pour l Agriculture (RGA) : AGRESTE - statistique agricole annuelle : statistiques au niveau départemental (renseignements utilisés dans l analyse pour l année 1991). Ch 6 193
220 Interprétation sémantique et étude des changements à long terme Eléments du recensement 2002 pour les départements Haute-Garonne et Gers données par le Service Central des Enquêtes et Etudes Statistiques (SCEES) 2004 Chambre Régionale d Agriculture de Midi-Pyrénées - Statistiques départementales des Boisements : état de la couverture boisée de la totalité du département (%) pour l année de recensement forestier (année). Les surfaces boisées : les statistiques départementales donnent des valeurs comparables à celle de 1991 qui est de : 17.6% pouvant ainsi valider la valeur issue de la classification. D autre part l état CLC indique des surfaces boisées de l ordre de 6% à la même époque. Le mode de réalisation de la base CLC (prise en compte uniquement des superficies supérieures à 25 ha) laisse penser que la superficie boisée est très fragmentée et constituée de petites unités de superficie non cartographiable au sens du CLC, et sont ainsi englobées des territoires agricoles surévalués à 91.7% dans CLC. Ces territoires agricoles (ensemble des cultures) occupent 74.2% du territoire dans l état 1991 réalisé, ce qui est plus proche des valeurs des SAU départementales 63.8% et 76.2%. En revanche sur 10 ans ( ) les proportions des surfaces boisées varient très peu dans les deux départements (AGRESTE 1991, 1999). L état 2002 avec 6.9% paraît être trop restrictif. La diminution de 10% mise en lumière paraît ainsi surévaluée. L augmentation des cultures : l analyse comparée des classes indique que cette augmentation est due essentiellement aux cultures d été en sec et à la classe Prairie/Jachère ; les modifications des assolements intervenus ces dix dernières années sont caractérisées par la hausse des oléagineux et des superficies en jachères rendues obligatoires par la PAC de La difficulté de la discrimination, en 1991, des deux classes Prairie et Jachère n a pas permis de les traiter séparément. On ne peut donc mettre en évidence la diminution des surfaces consacrées à l élevage, seule l augmentation des jachères évaluée de 6 à 9% peut expliquer l écart entre les deux classes 1991 et 2002 ( 7% environ). Au niveau spatial : mise en évidence d une typologie générale du changement du mode de couverture des terres Le changement peut être identifié au niveau cartographique et analysé de manière plus fine classe à classe. Le résultat est exprimé sous la forme d un tableau croisé constituant la matrice des changements et de la carte des changements. L analyse des changements classe à classe apporte divers niveaux d information liés à la gestion du mode de couverture des terres. Le basculement d une culture 1 à une culture 2 n indique pas de changement particulier de l affectation des terres et ne relève que de la pratique agricole (rotation des cultures) ; Le passage d une culture à une Prairie/Jachère peut témoigner de l influence de la politique agricole ; le passage d une culture à un bois ou à un bâti indique un changement net d affectation du territoire indiquant une baisse de la SAU sous l influence de diverses pressions d ordre socio-économique. Le passage d un bois à une autre classe appartenant à une nouvelle catégorie d occupation du sol non boisé (culture ou bâti) indique un changement plus profond d affectation de l espace. Il faut donc en rechercher la cause pour en mesurer l impact en terme paysager et à terme écologique. Pour apprécier ces diverses évolutions et dégager une typologie du changement l analyse croisée est réalisée à deux niveaux, par grandes catégories d occupation du sol : Bois, Ch 6 194
221 Interprétation sémantique et étude des changements à long terme Cultures et autre, et par classes. Par catégories d occupation du sol : Bois, Cultures, autre (Urbain, Eau) Par analyse croisée des deux états d occupation du sol réduits à 3 classes d affectation du territoire très différente, Bois, Cultures, Autre, se dégage une image du changement du mode de couverture des terres survenu sur une période de 11 ans (figure 6.10). Bois 2002 Cultures 2002 Autre 2002 Total Classes 1991 Bois 1991 Cultures 1991 Autre 1991 non classés 5,95% 11,17% 0,46% 17,58% 0,78% 69,86% 3,57% 74,22% 0,15% 3,62% 1,09% 4,86% 0,03% 3,16% 0,16% 3,35% stable 76,90% Total Classes ,91% 87,81% 5,28% 100% Stabilité 76.9% Changement d affectation 19.8% Vers : agriculture 14.8% urbanisation 4.8% vers: forestier 0.9% Figure 6.10 : carte et matrice des changements pour les grandes catégories d occupation du sol entre 1991 et 2002 Le changement qui affecte la région Sud-Ouest toulousaine est : 76.9% des terres ne changent pas d affectation entre 1991 et Les 23% des terres qui ont subit un changement d affectation sont : la classe Bois en 1991 subit la plus grande modification : un tiers reste boisé, les deux autres tiers cèdent la place principalement aux cultures. la classe Cultures est la plus stable : le reste se substitue en eau et surfaces minérales (ou habitat). avec l évolution des surfaces minérales de 1991, on retrouve le problème relatif à une erreur de classification évoquée plus haut (classe Eau surdimensionnée en 1991). Par classes d occupation du sol Un traitement similaire appliqué aux deux cartes d occupation du sol en 8 classes permet d affiner l analyse précédente. Il permet de caractériser la nature des changements permanents et temporaires en particulier ceux relevant de la rotation des cultures dans l assolement. La proportion de territoire stable, sans changement d affectation de l usage des terres, est estimée de manière identique à 76.9% ; elle peut être typée en deux catégories : 32.5% est Ch 6 195
222 Interprétation sémantique et étude des changements à long terme réellement stable, conservant un usage des terres identique, le reste 44.4% montre un changement temporaire de l usage des terres sans changement d affectation global. Les derniers 23.1% ont subi un changement pérenne du mode d usage des terres (figure 6.11). Stabilité 35,9% Changement temporaire Assolement:rotation des cultures 40,6% entre Cultures annuelles en sec 10,4% Cultures annuelles en sec/ C.pérennes 16,0% Cultures annuelles en sec/irriguées 9,5% Cultures annuelles irriguées/c.pérennes 4,8% Changement pérenne Affectation différente Déforestation 11,6% vers agriculture 11,2% vers urbanisation 0,5% Mise en culture 3,6% Artificalisation croissante aux dépends de l'agriculture 4,2% Reboisement 0,9% Stabilité 35.9% Rotation 40.6 % changement d affectation 19.8% - vers: agriculture 14.8% ( %) - vers: urbanisation 4.8%( %) - vers: sylviculture 0.9% Figure 6.11 : carte et matrice des changements pour les classes d occupation du sol entre 1991 et 2002 Le changement temporaire de l usage des terres pour la classe des cultures assimilé pour l essentiel au mode de rotation pratiqué, montre les résultats suivants : ce sont les cultures d été irriguées les plus stables dans l assolement cultural (50% de la classe) ; elles alternent majoritairement avec les cultures d hiver (25%). Les cultures d été non irriguées sont les plus présentes dans les rotations d assolement (79%) alternant de préférence avec les cultures d hiver (41%). La classe Prairie associée à la classe des friches urbaines reste la classe la plus permanente dans le paysage (55%). La comparaison donne quelques éléments de changement au niveau du Bâti. L urbanisation en 2002 correspond à un noyau urbain peu développé en Les terres urbanisées ont colonisé les bois, les terres de cultures en sec principalement et fortement la classe identifiée sous le nom de friches urbaines en Ch 6 196
223 CONCLUSION PROSPECTIVES
224
225 7- CONCLUSIONS et PERSPECTIVES Les logiciels développés sont un premier pas vers l automatisation de l analyse d image de télédétection. D abord par l apprentissage avec acquisition automatique des échantillons grâce au GPS, à une base de donnée, à la segmentation. On obtient un gain de temps et une plus grande précision dans les résultats. La création des matrices de confusion de manière exhaustive et automatique permet de mesurer la qualité de l information apportée par chaque date et ainsi définir les combinaisons de dates les plus performantes, ajustées aux conditions saisonnières, pour obtenir un résultat de classification optimum. La méthode de classification de type ICM (Iterative Conditional Mode), basée sur un modèle de région markovien, non supervisée ou supervisée, a été implantée afin d offrir beaucoup de possibilités d application dans des conditions très diverses avec une grande souplesse d utilisation. Les résultats sont globalement satisfaisants, surtout pour les images radar, dans un temps de calcul non prohibitif pour des images de télédétection qui ont de très grandes tailles. L avantage des méthodes non supervisées est qu elles ne nécessitent aucune intervention de l expert et peuvent être complètement automatiques. Mais il reste le problème de l interprétation des classes. Ces classifications conjuguées à une méthode d interprétation automatique à partir de catalogues, permettent de traiter un grand nombre de données collectées depuis plusieurs décades. Toutefois nous avons dû mettre au point un système de normalisation de ces données entre elles, afin de neutraliser les différences radiométriques entre deux dates comparables (reliquat des corrections). Ainsi, nous pouvons réaliser l étude du changement du paysage, de façon pluriannuelle ou de façon saisonnière avec les acquisitions mensuelles. Grâce à la fusion de plusieurs classifications réalisées dans des conditions différentes les résultats donnent la carte de l occupation des sols précises. Après l obtention de cette carte, il est possible de l'intégrer aux modèles d'estimation des flux de carbone et d'eau, mais également de l'utiliser afin d'analyser le paysage. Deux niveaux d analyses peuvent être étudiés : niveau parcellaire (pour l image entière et pour l image découpée en sous-régions), niveau plus large, se rapprochant de l échelle régionale. L analyse de paysage s inscrit dans la démarche de recherche d une meilleure compréhension du fonctionnement des couverts végétaux. Les relations démontrées entre les processus écologiques et la structure spatiale du paysage montre l intérêt de donner une mesure quantitative à l arrangement spatial des diverses unités fonctionnelles. L analyse du paysage est complétée par la caractérisation des structures spatiales des couvertures du sol, grâce à leur hétérogénéité interne à plusieurs niveaux d observation. Les limites L automatisation des traitements autorise l intégration d informations plus nombreuses, et donc des résultats plus précis, tout en laissant à l expert la possibilité de modifier le système. Mais, il subsiste beaucoup de difficultés et de problèmes non résolus. L aspect multi-échelle, est simplement abordé par les niveaux d observation dans le paysage. Pour des images à différentes échelles, aucun traitement spécifique n est fait. Les images sont recalées et traitées 197
226 Conclusions et Perspectives en parallèle. Pour les images à très haute résolution (THRS), les méthodes fonctionnent bien pour des images de zone de végétation, toutefois cette partie devra être approfondie. Les méthodes développées s appliquent à la végétation sous toutes ses formes, ce qui est déjà positif, car les paysages naturels sont très complexes. Mais elles ne s appliquent pas à la reconnaissance d objets dans une ville, des routes, qui nécessite des opérateurs différents de ceux de la classification (de type détection de lignes). Les valeurs précises des paramètres tels que les seuils utilisés dans plusieurs méthodes, ne sont pas toujours connues. Certains de ces seuils sont calculés ou appris, tout en laissant à l utilisateur la possibilité du choix grâce à un guidage interactif. Parfois leur utilisation est compliquée, un effort doit être fait vers la simplification, au niveau des paramètres. Pour l étude des changements sur le long terme avec des données inter annuelle, la normalisation (chapitre 6) s applique aux données optiques, pour les données radar le problème est plus complexe et n est pas encore étudié. De plus cette étude, relativement nouvelle, nécessite une base de données, représentant les valeurs radiométriques, qui est en cours de construction. Mais, la base de donnée devra être adaptée aux types de paysage, au milieu géographique. Perspectives de recherches Analyse des changements, et base de données : pour améliorer les résultats de l interprétation, la base de donnée doit être enrichie et exprimer la diversité des thèmes et la variabilité de chacun d entre eux (sous thèmes) présents sur une image. Elle devra être intégrée à un SIG. L ensemble des informations spatialisées dans le SIG, permettra l analyse des changements. La description des paramètres sera organisée selon une approche par objets, formalisée par des tables de données. Les paramètres seront donc accessibles par les attributs qui présenteront deux types d information : i) les caractéristiques intrinsèques des objets, ii) les caractéristiques d organisation spatiale des objets. Cette approche s appuiera sur le traitement d image combiné à la modélisation. La notion d objet est importante car, le plus souvent, on ne dispose pas d information de référence au niveau de pixels individuels, mais seulement à l échelle des objets ; de plus, l objectif est l extraction d information sur des objets (les classes). Caractérisation de l occupation du sol : l amélioration des outils de classification est toujours actuelle, la classification étant le départ de toutes les applications. L introduction de données 3-D, des détecteurs de lignes dans les images optiques et radars devra apporter des éléments complémentaires pour la discrimination des classes. D'autre part, la contribution de données de type biophysique (hauteur du couvert, biomasse, rugosité, LAI calculée par modélisation.) sera étudiée. La notion de variation temporelle va être approfondie. La méthode de classification présentée, de type markovienne, est en fait une combinaison de plusieurs méthodes, une autre méthode sera ajoutée pour la fusion par date par un principe hiérarchique et un modèle de variation saisonnière. En partant d un nombre restreint de classes, pour chaque date : les cultures en sol nu, couverture végétale faible, floraison, récolte, sénescence. Le profil saisonnier sera affiné au fil des itérations grâce à l information donnée par date. 198
227 Conclusions et Perspectives Nous envisageons également des développements appliqués aux nouvelles sources de données spatiales avec un effort particulier concernant la très haute résolution, l'hyperspectral. Analyse du paysage : l analyse des relations entre pixels, base de l analyse du paysage, va devenir nécessaire avec l arrivée des images à très haute résolution, sur lesquelles certaines classes apparaissent décomposées en objets élémentaires. Cette décomposition ne doit pas être considérée comme un handicap mais au contraire comme un atout dans la mesure où cette connaissance fine par les composantes d un couvert apporte une information supplémentaire par rapport au pixel d image à haute résolution. Les méthodes devront, de façon encore plus importante, associer analyse spectrale et opérateurs spatiaux. A partir des descripteurs de l analyse du paysage, il faudra aboutir à des résultats traductibles en terme de fonctionnement des écosystèmes, introduit dans les modèles écologiques. A l échelle décennale, l évolution des paysages est probablement le facteur le plus important, avant le climat, affectant l évolution des stocks de carbone, les flux hydriques verticaux et latéraux et la biodiversité. Au niveau de l analyse du paysage, nous obtenons des images «synthétiques» à partir de certaines caractéristiques de paysage, qui devront conduire vers la définition des grandes régions du paysage. Les images radar RSO : les développements se poursuivent à divers niveaux. L analyse multitemporelle des images RSO doit intégrer des aspects multirésolution et interférométrique pour la détection des cibles et des changements de surface, la caractérisation des surfaces (rugosité verticale), l analyse de texture et la classification. D autre part la fusion des informations optique-radar bas niveau (pour la détection de réseau, de surfaces urbaines, d objets particuliers...) ou haut niveau (classification) en y intégrant des considérations physiques devra être développée. Pour atteindre ces objectifs et les prolonger, il est utile de fédérer la recherche entre disciplines (informatique, physique et écologie), entre les équipes et projets du laboratoire, avec des équipes extérieures. Nous projetons d intégrer nos méthodes au système de fouille d informations actuellement développé par le CNES, le DLR, l ENST et l ENSEEIHT, système dont l objectif est l interprétation et la recherche de phénomènes spatio-temporels. Nous débutons une collaboration avec le Laboratoire des Sciences de l Information et des Systèmes, LSIS/INCOD de l Université de Marseille, sur un projet de recherche (Accès Transparent à l Imagerie Satellitale), multi-thématique associé à l imagerie spatiale. L objectif de ce projet est de répondre aux besoins des applications qui nécessitent l exploitation simultanée de plusieurs sources d imagerie spatiale, en leur fournissant un ensemble de services intégrés dans une architecture de médiation garantissant l autonomie des sources et le suivi de leur évolution. Le but est d exploiter des systèmes de médiation en étendant leurs fonctionnalités génériques et en leur adjoignant des fonctions spécifiques à la gestion de l imagerie satellitaire. Les images, produites en masse par des satellites sont stockées dans des sources d informations volumineuses et hétérogènes auxquelles il est indispensable d améliorer l accès pour un usage rapide et efficace, ceci par : (i) un accès transparent aux sources à travers une description virtuelle unique (ontologie ou schéma de médiation), en masquant notamment leur localisation, 199
228 Conclusions et Perspectives (ii) (iii) (iv) le suivi de la dynamique des sources et adaptation à leur évolution sémantique, la mise en œuvre de métadonnées facilitant un accès sélectif et optimal, la mise à disposition de service d analyse et de recoupement des contenus des sources (aide à l interprétation) : ce qui correspond à des besoins génériques (tel le géoréférencement) ou au contraire spécifiques à certaines applications. La collaboration avec l équipe CLIME de l INRIA (Rocquencourt) devrait se poursuivre. Cette équipe s occupe du traitement de données satellite pour l environnement, avec prise en compte des processus physiques de la formation de l image et des phénomènes observés ; de l assimilation de données et notamment assimilation de données image dans des modèles géophysiques ; de l intégration de données et méthodes dans des systèmes d information distribués Un projet (PNTS) dont le titre est «Caractérisation de la dynamique spatio-temporelle de la végétation à l échelle régionale dans le Sud-Ouest de la France», démarre avec le laboratoire Ecologie fonctionnelle et Physique de l Environnement, de l INRA, Bordeaux, le CNRM (centre national de Recherche Météorologique METEO-France), au laboratoire de Biométrie et Intelligence artificielle Climat Sol et Environnement, INRA Toulouse, et le CNES. Le quart Sud-Ouest de la France est un lieu d'intenses activités de recherche visant à suivre et à comprendre le fonctionnement des écosystèmes terrestres et le bilan des flux (carbone, eau). Le volet «Regional Experiment» du projet CARBOEUROPE (projet intégré du 6 ième PCRD), les projets «Sud Ouest» du CESBIO, et COSMOS (campagne de mesure SMOS de l'esa en 2005) sont centrés sur cette région. Pour ces différents projets, il est important de disposer d'un suivi régulier de la dynamique de la végétation et de ses variations spatiales, d'une bonne caractérisation de la distribution spatiale des unités fonctionnelles constituant le paysage de cette région. Le travail proposé est essentiellement méthodologique. Son objectif est de comparer plusieurs méthodes de cartographie fonctionnelle des couverts végétaux prenant en compte la dynamique temporelle des signaux de télédétection. L'évaluation des méthodologies utilisées sera guidée par l obtention : (i) d une amélioration de la connaissance de la répartition spatiale des unités de paysages fonctionnelles sur l ensemble de la zone, par exemple, la discrimination entre cultures d hiver et d été, cartographie des pédopaysages en forêt landaise de pin maritime, (ii) d une évaluation des impacts d'évènements de type exceptionnel (tempêtes de 1999 ou sécheresse de 2003). Enfin, nous souhaitons développer une coopération avec l IRIT pour la mise à jour de cartes urbaines et péri-urbaines à partir d images satellitales optiques et radar THRS. 200
229 REFERENCES BIBLIOGRAPHIQUES
230
231 Références bibliographiques Aarts E.H.L. &. Korst J.H.M. (1989) Simulated Annealing & Boltzmann Machines. John Wiley & Sons. Bell E.J. (1974). «Markov analysis of land use change an application to remotely sensed data. Socio-Economic Planning Science 8: Bergen K.M., L.E. Pierce, M.C. Dobson & F.T. Ulaby, (1996) "A multi-temporal classifier for SIRC/X-SAR Imagery", Proc. of IGARSS96,vol III, , Lincoln, Nebraska, USA, May Besag, J. (1974). ``Spatial interaction and the statistical analysis of lattice systems'' (with discussions). Journal of the Royal Statistical Society, Series B, 36: Besag J. (1986). On the statistical analysis of dirty pictures, Journal of the Royal Statistic Society, serie B 48(3): Blanc, P. (1999), Développement de méthodes pour la détection de changement». PhD thesis, Ecole des Mines de Paris, France. Bloch.I, Maitre H. (1994). «Fusion de données en traitement d images : modèles d information et décisions». Traitement du Signal 11(6): Bloch I. (1996). Information Combination Operators for Data Fusion: A Comparative Review with Classification» IEEE Systems, Man and Cybernetics : jan 1996 vol. 26, n 1, pp Bloch I. (1996). «Incertitude, imprécision et additivité en fusion de données : point de vue historique» Traitement du Signal 1996 vol. 13, n 4, pp Bloch I. (2005). Fuzzy Spatial Relationships for Image Processing and Interpretation: A Review Image and Vision Computing 2005 vol. 23, n 2, pp Bloch I. & Maître H. (2002). «Fusion d'informations en traitement d'images : spécificités, modélisation et combinaison par des méthodes numériques» Techniques de l'ingénieur 2002 vol. TE 5 230, pp Bloch I. (1999). On Fuzzy Distances and their Use in Image Processing under Imprecision Pattern Recognition 1999 vol. 32, n 11, pp Brandt C. K. Tso & Paul M. Mather. (1999). «Classification of Multisource Remote Sensing Imagery using a genetic algorithm and Markov Random Fields», IEEE Trans. On Geo. And Rem. Sesing, vol. 37. no. 3. pp , Bruniquel J. & Lopès A. (1997). "Multivariate optimal speckle reduction in SAR imagery", Intern. Journal of Remote Sensing, Vol.18 n 3, pp Burel F. & Baudry J. (1999). Ecologie du paysage». Ed. Tec& Doc, Paris. 359 pp. Burrough P.A. (1981). Fractal dimensions of landscapes and other environmental data. Nature 294: Burrough P.A. (1986). Principles of geographical information systems for land resources assessment. Oxford: Oxford University Press. Bruzzone, L., & Cossu, R. (2003), An Adaptive Approach to Reducing Registration Noise Effects in Unsupervised Change Detection. IEEE Trans. Geosci. Remote Sensing, vol. 41, no. 11, pp Bruzzone, L., & Fernandez Prieto, D. (2000), An adaptive parcel-based technique for unsupervised change detection. Int. J. Remote Sensing, vol. 21, no. 4, pp Carlile D.W., Skalski J.R., Batker J.E., Thomas & Cullinan V.I. (1989). Determination of ecological scale. Landscape Ecology 2 (4):
232 Références bibliographiques Celeux G., Diebolt J. (1986). «L algorithme SEM : un algorithme d apprentissage probabiliste pour la reconnaissance de mélange de densités». Revue de Statistique Appliquée, 34, no2, pp30-33 Celeux G., Diebolt J. (1987). The EM and SEM algorithms for mixtures: statistical and numerical aspects. Rapport de l INRIA RR-0641 Celeux G., Chauveau, D. Diebolt J. (1995). On Stochastic Versions of the EM Algorithm. Rapport de l INRIA RR-2514 Chust, G., S. Lek, L. Deharveng, D. Ventura, D. Ducrot & J. Pretus (2000), The effects of the landscape pattern on arthropod assemblages: an analysis of scale-dependence using satellite data. Belgian Journal of Entomology 2 (1) : Chust G., Ducrot D., Pretus J. & Deharveng L. (2001). Extrapolating biodiversity values from landscape features. In Proceedings of the International Workshop of Mapping Subterranean Biodiversity. Moulis, France, March. pp Chust G., Ducrot D., J. LL. Riera, J.LL. Pretus Characterising human-modelled landscapes at a stationnary state: a case study of Minorca, Spain Environmental Conservation 26(4) p , 1999 Chust G.,. Pretus J. Ll,. Ducrot D, A. Bedòs & L. Deharveng, 2003 Soil fauna response to landscape heterogeneity, determining optimal scales for biodiversity modeling. Conservation Biology 17 (6): Chust G., Pretus J. Ll., Ducrot D., & D. Ventura «Scale dependency of insect assemblages in response to landscape pattern». Landscape Ecology pp Chust G., Ducrot D. & Pretus J. Ll.. Land cover discrimination potential of radar multitemporal series and optical multispectral images in a Mediterranean cultural landscape. International Journal of Remote Sensing vol 5 (2004), n 17, Chust G., Ducrot D. & Pretus J. Ll.. Land cover mapping with patch-derived landscape indices. Landscape and Urban Planning 69 (2004) pp Cloude S.R. & E. Pottier, (1996)."An entropy based classification scheme for land application of polarimetric SAR", Proc. of Retrival of bio and geophysical parameters from SAR data for land applications, Symposium, CNES/IEEE, , Oct Cloude S.R. & E. Pottier, (1996)."A review of target decomposition theorems in radar polarimetry", IEEE Trans. on GRS, Vol. 34 n 2, pp , March Cocquerez J.P. & Philipp S. (1995). «Analyse d images : filtrage et segmentation.» Masson, Paris. Congalton R.G. (1991). A review of assessing the accuracy of classification of remotely sensed data. Remote Sensing of Environment 37: Davies K.F., Melbourne B.A., & Margules C.R. (2001). Effects of within- and between-patch processes on community dynamics in a fragmentation experiment. Ecology 82 (7): Debinski D. M., Kindscher K., & Jakubauskas M. E. (1999). A remote sensing and GIS-based model of habitats and biodiversity in the Greater Yellowstone Ecosystem. International Journal of Remote Sensing 20 (17): Dempster A.P. (1967). Upper and lower probabilities induced by a multi-value mapping. Annals of mathematical statistics 38: Dempster A.P. (1968). A generalisation of bayesian inference. Journal of the Royal Statistical Society B 30: Dempster N. (1977), Laird N;, Rubin. Maximum likelihood fropm incomplete data via the EM algorithm Journal of the Royal Statistical Society B 9:1-38 Denoeux T. (1995) A k-nearest neighbor classification rule basesd on Dempster-shafer theory IEEE Trans. SMC: 25: Descombes X., Mangin J., Pechersky., E., & Sigelle M., (1995), Fine Structure Preserving Markov model for image processing, SCIA'95, Uppsala, Sweden, pp
233 Références bibliographiques Descombes X., (1996). Application of stochastic techniques in image processing for automatic tissue classification in MRI and blood vessel restoration in MRA, Rapp.KUL/ESAT/MI2/9603, Laboratory for Medical Imaging Research (ESAT-Radiology), K.U.Leuven, Belgium. Descombes X., Morris R., Zerubia J., Berthod M. (1996) Estimation of Markov Random Field prior parameters using Markov chain Marc Monte Carlo Maximum Likelihood rapport Inria Projet PASTIS October Descombes X., Morris R., Zerubia J. (1996) «Quelques améliorations à la segmentation d'images bayesienne» Sophia Antipolis, Projet PASTIS, Juin 1996 Du, Y., Teillet, P. M., & Cihlar, J. (2002), Radiometric normalization of multitemporal highresolutionsatellite images with quality control for land cover change detection. Remote Sens. Environ. 82: Dubois D. & Prade H. (1987) «Théorie des possibilités» Editions Masson, Paris. Dubois D. & Prade H. (1988). «Théorie des possibilités : applications à la reconnaissance en informatique», Editions Masson, Paris. Dubois D. & Prade H., Testemale C., (1988). Weighted fuzzy pattern matching, Fuzzy Sets and Systems, v.28 n.3, p , December 1988 Dubois D. & Prade H. (1988). Réprésentation and combination of uncertainty with belief functions and possibility measures Computatinal Intelligence, 4, Dubois D. & Prade H. (1992). «When upper probabilities are possibility measures Fuzzy sets abd systems, 49, Dubois D. & Prade H. (1992). Evidence, Knowledge, and belief functions, Int.J.of approximate Reasoing, 6, Dubois D. & Prades H., (1993). Combination of information in the framework of possibility theory data fusionin robotics and machine intelligence Academic Press. Dubois D. & Prade H. (1994). «La fusion d informations imprécises». Traitement du Signal 11(6): Dubois D., Prade H., Yager R.R. (1997). «Fuzzy Information Engineering: A Guided Tour of Applications, Wiley, New York, Ducrot D., Sassier H., Mombo J., Goze S. & Planes J.G. (1998). «Contextual methods for multisource land cover classification with application to RADARSAT and SPOT data. In Proceedings of European Symposium on Remote Sensing, Image and Signal Processing for Remote Sensing Vol. SPIE 3500, Barcelona, Spain, September Ducrot D., Sery F., Sassier H., Goze S., Planes J.G. (1998). Classification and fusion of optical and radar satellite data for land use extraction Fusion of Earth Data98, Sophia Antipolis, France, January (1) : Ducrot D., P.Gouaux, A.M. Barbier et B.Mora «Analyse des images SPOT 2002 du projet SUD-OUEST Occupation du sol et analyse de paysage» Rapport interne CESBIO, UMR UPS-CNRS-CNES-IRD, avril 2004 Ducrot D., Castañeda del Alamo C. (2004) Tratamiento de imagines de RADAR, Aplication al sur de Monegros (CITA) Rapport interne CITA Centro de Invetigation y tecnologia del Gobierno de Aragon & CESBIO, Septembre 2004 Ducrot D., Gouaux P., Barbier A.M., Raspeau L., (2005). «Analyse des images SPOT 2003 du projet SUD-OUEST et suivi temporel d une série d images depuis 1989» Rapport interne CESBIO, UMR 5126-UPS-CNRS-CNES-IRD, mars 2005 Ducrot. D., Kristóf, D., (2001) Using airborne remote sensing techniques in coastal plant population studies», Proc. IALE European Conference: «Development of European Landscapes, 30 juin 01 juillet 2001, Stockholm, Suède Ducrot. D., Kristóf, D., (2001) Development of European Landscapes, University of Tartu, Tartu, Estonie Conference Proceedings, Instituti Geographici Universitatis Tartuensis, vol. 92, p. 665 Tartu, Estonie 203
234 Références bibliographiques Dupias G, Rey P, (1985). «Documentation pour un zonage des régions phyto-écologiques», Centre d Ecologie des Ressources Renouvelables, CNRS. Fjortoft R., Marthon P., Lopes A. & Cubero-Castan E. (1995). "Edge detection in radar images using recursive filters", Proc. of 2d ACCV 95 Confr., Vol.3 pp.87-91, Singapore, 5-8 December 1995 Fjørtoft R., Sery F., Ducrot D., Lopes A., Lemaréchal C., Fortier C., Marthon P., & Cubero- Castan E. (1997). Segmentation, filtering and classification of SAR images In Proceedings of VII Latin American Symposium on Remote sensing (SELPER 97), Venezuela, November Fjortoft R., A. Lopès, P.Marthon, & E. Cubero-Castan, (1997). "An optimum Multi Edge detector for SAR image segmentation", IEEE GRS., January.. Fjørtoft R. (1999). Segmentation d images radar par détection de contours». Ph.D. thesis at the Institut National Polytechnique de Toulouse, France. Freeman A. & S. Durden, (1992). "A three component scattering model to describe polarimetric SAR data", Radar Polarimetry, Vol. SPIE 1748, , Frost V.S., J.A. Stiles, K.S. Shanmugan & J.C. Holtzman, (1982). "A model for radar images and its application to adaptive digital filtering of multiplicative noise", IEEE Trans. on PAMI, Vol.4 n 2, , March Frost V.S.& Yurovsky L.S., (1985) "Maximum likelihood classification of SAR imagery", CVGIP., n 32, , Foody G.M. (1992). On the compensation for chance agreement in image classification accuracy assessment. Photogrammetric Engineering and Remote Sensing 58: Forman, R.T.T., & Godron, M. (1986). Landscape Ecology, John Wiley & sons Press, New York. Fu K.S., (1976). Digital Pattern Recognition, Springer Verlag, pp Fukunaga K. (1972). Introduction to statistical pattern recognition. Electrical Sciences Series, Academic press, London (UK). Geman S. & Geman D., (1984), Stochastic Relaxation, Gibbs Distribution and the Bayesian Restoration of Images, IEEE Transactions on Pattern Analysis and Machine Intelligence vol PAMI- 6 (1984), no. 6, Geman D., Geman S., Graffigne C., Dong P., (1990), Boundary detection by constrained optimization, IEEE Transactions on Pattern Analysis and Machine Intelligence, 12 (1990), pp Girard & Girard, (1999), «Traitement des données en télédétection», DUNOD Gong P., Marceau D.J. & Howarth P.J. (1992). A Comparison of Spatial Feature Extraction Algorithms for Land-Use Classification with SPOT HRV Data. Remote Sensing of Environment 40: Goodman N.R., (1963) "Statistical analysis based on a certain multivariate complex gaussian distribution (An introduction)", Ann. Math. Statist., Vol. 34, pp , Goze S., (1992) "Observation de la Terre par radar polarimétriques: prétraitement et développement de discriminateurs", thèse UPS n 1208, Toulouse, 15 juin Goze S., A. Lopès, Nezry E., Ducrot D. (1992) "Speckle filtering and discriminators for polarimetric SAR data", Proc. of the 2nd JIPR 92 Symp. (Journées Internationales sur la Polarimétrie Radar), pp , IRESTE Nantes France, 8-10 Sept Goze S. & Lopès A. (1993) "A MMSE speckle filter for full resolution SAR polarimetric data", Journal of Electromagnetic Waves and Applications, Vol. 7 n 5, , Gustafson E.J. & Gardner R.H. (1996) The effects of landscape heterogeneity on the probability of patch colonization. Ecology 77: Gustafson E.J. & Parker G.R. (1992). Relationships between landcover proportion and indices of landscape spatial pattern. Landscape ecology 7 (2):
235 Références bibliographiques Guyon X., (1992) ``Champs aléatoires sur un réseau : modélisations, statistiques et applications'', Masson. Hanski I. (1994). Patch-occupancy dynamics in fragmented landscapes. Trends in Ecology and Evolution 9: Haralick R.M., Shanmugan K.S. & Dinstein I. (1973). Textural features for image classification. IEEE Transactions on Systems, Man, and Cybernetics SMC-3: Herr A.M. & Queen L.P. (1993). Crane habitat evaluation using GIS and remote sensing. Photogrammetric Engineering & Remote Sensing 59 (10): Hery P., D. Ducrot, A. Lopes, E. Mougin, G. Marty, F. Fromard, F. Blasco, J.P. Rudant, M. Lointier, M.T. Prost, (1993) "Cartographie de la végétation tropicale et suivi de la dynamique des mangroves de Guyane par SPOT et ERS-1", Proceedings of the Symposium «From optics to radar, SPOT and ERS applications», Paris, May 10-13, , Hiebeler D. (2000). Populations of fragmented landscapes with spatially structured heterogeneities: landscape generation and local dispersal. Ecology 81(6): Hill M.O. (1973). Diversity and eveness: a unifying notation and its consequences. Ecology 54: Hillion A. & J.M. Boucher, (1991) "Filtrage des images radar", Statistiques et Analyse des données, Vol.16 n 2, pp.35-57, Hsu S. (1978). Texture-tone analysis for automated land use mapping. Photogrammetric Engineering & Remote Sensing 44 (11): Jeansoulin R. (1990). " Basic Tools for Spatial Logic ", Proceedings of the third COGNITIVA symposium COGNITIVA'90, Madrid, Spain, nov pp Jennings M.D. (2000). Gap analysis: concepts, methods, and recent results. Landscape Ecology Karathanassi V., Iossifidis Ch. & Rokos D. (2000). A texture-based classification method for classifying built areas according to their density. International Journal of Remote Sensing 21(9): Kato Z., Zerubia J., Berthod M., (1992) Image Classification using Markov Random Fields with two new relaxation methods: deterministic pseudo annealing and modified Metropolis dynamics, Rappor tde l INRIA. 606, I-, Mars Kato Z., Zerubia J., Berthod M. (1999) Unsupervised parallel image classification using Markovian models. Pattern Recognition 32(4): King A.W. (1999). Hierarchy theory and the landscape level? Or: words do matter. In Issues in Landscape Ecology (ed. J.A. Weisn & M.R. Moss), pp Greeley (CO) USA: Pioneer Press of Greeley, Inc. Kendall M.G. & Stuart A., (1958) The advanced theory of statistics, VOL I 3rd Edn, Butler & Tanner Ltd. Kirkpatrick S., Gellatt C. D., Vecchi M. P., (1983), Optimization by Simulated Annealing, Science, no. 220, Kotliar N.B. & Wiens J.A. (1990). Multiple scales of patchiness and patch structure: a hierarchical framework for the study of heterogeneity. Oikos 59: Kong J.A., Swartz, Yueh H.A., Novak L.M. & Shin R.T. (1987), "Identification of terrain cover using the optimum polarimetric classifier", Journal of Electromagnetic Waves and Applications, Vol.2 n 2, , Krystof Dàniél (2005), «Détection des changements par analyse multitemporelle d images satellites» Thèse Université Szent István, Gödöllö (Budapest), Hongrie 30 septembre 2005 Kuan D.T., Sawchuck A.A., Strand T.C., Chavel P., (1987) "Adaptive restoration of images with speckle"; IEEE Trans. on ASSP, Vol.35 n 3, , March Laarhoven P.J.M. &. Aarts E.H.L, (1987). Simulated Annealing: Theories and Applications, Riedel, Dordrecht, Holland Laur H., (1989) "Analyse d images radar en télédétection: discriminateurs radiométriques et 205
236 Références bibliographiques texturaux", Thèse n 403 de l Université Paul Sabatier Toulouse III, 23 mars Lavorel S., Gardner R.H. & O Neill R.V. (1993). «Analysis of patterns in hierarchically structured landscapes. Oikos 67: Lee J.S., (1981) "Speckle analysis and smoothing of radar SAR images", Computer Graphics and Image Processing, n 17, 24-32, Lee J.S., (1981) "Refined filtering of image noise using local statistics", Computer Graphics and Image Processing, n 15, , 1981 Lee J.S., Grunes M.R., Mango S.A., (1991) "Speckle reduction in multipolarization multifrequency SAR imagery", IEEE Trans. on GRS, Vol.29 n 4, , July Lee J.S., Grunes M.R. & R. Kwok., (1994) "Classification of multilook polarimetric SAR imagery based on complex Wishart distribution", Int. Journal of Remote Sensing, Vol. 15 n 11, , Le Hégarat-Mascle (1996). «Classification non supervisée d images SAR polarimétriques» Thèse ENST septembre 1996 Le Hégarat-Mascle S., D. Vidal-Madjar & P. Olivier (1996), "Applications of simulated annealing to SAR image clustering and classification problems", Int. Journal of Remote Sensing, Vol. 17 n 9, , Le Hégarat-Mascle S., I. Bloch & D. Vidal-Madjar (1997), Application of Dempster-Shafer Evidence Theory to Unsupervised Classification in Multisource Remote Sensing IEEE Transactions on Geoscience and Remote Sensing jul 1997 vol. 35, n 4, pp Le Hégarat-Mascle S., Bloch I. Vidal-Madjar D. (1998). «Introduction of Neighborhood Information in Evidence Theory and Application to Data Fusion of Radar and Optical Images with Partial Cloud Cover Pattern Recognition 1998 vol. 31, n 11, pp Le Hégarat-Mascle S., Quesney A., Vidal-Madjar D., Taconet O. (2000), Land cover discrimination from multitemporal ERS images and multispectral Landsat images: a study case in an agricultural area in France. International Journal of Remote Sensing 21 (3): Lemaréchal C., Fjørtoft R., Marthon P. & Cubero-Castan E. (1998). Comments on Geodesic saliency of watershed contours and hierarchical segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence 20 (7): Lippe E., De Smidt J.T. & Glenn-Lewin D.C. (1985). Markov Models and Succession: a Test from a Heathland in the Netherlands. Journal of Ecology 73: Lopès A., Nezry E., Touzi R., Laur H. (1990) "Maximum A Posteriori Speckle Filtering and First Order Texture in SAR Images". Proc. of IGARSS'90, Washington D.C., USA, pp , Ref IEEE 90CH2825-8, May Lopès A. & al, (1992) "Phase difference statistics related to sensor and forest parameters", Proceedings of the IGARSS'92, Vol.1, pp , IEEE 92CH3041-1, Houston, May Lopès A., Goze S & Nezry E (1992). "Polarimetric speckle filters for SAR data", Proc. of IGARSS'92, IEEE 92CH3081-1, pp 80-82, Clear Lake USA, May Lopès A., Nezry E., Touzi E., Laur H. (1993) "Structure Detection and Statistical Adaptive Speckle Filtering in SAR Images", Int. Journal of Remote Sensing, Vol. 14 n 9, , Lopès A., Séry F., (1996). "Optimal speckle reduction for the product model in multilook polarimetric data and the complex Wishart distribution", IEEE Trans. on Geosciences and Remote Sensing. Lorette A., Descombes X., Zerubia J. (2000). Texture Analysis through a Markovian Modelling and Fuzzy Classification: Application to Urban Area Extraction from Satellite Images. International Journal of Computer Vision 36(3): Lowell, K. (1991). Utilizing discriminant function analysis with a geographical information system to model ecological sucession. International Journal of Geographical Information Systems, 5(2):
237 Références bibliographiques Mainguenaud P. & Jeansoulin R. (1994). " Texture Filtering as a Pre-Processing for Neural Network Learning and Classification of ERS1 Images ", Proceedings "Europto94", Roma, Italia, septembre Mainguenaud P., Jeansoulin R. (1994). " Multi-source SAR Image Texture Classification using an Artificial Neural Network Model ", 14th International Conference on Airborne Remote Sensing, ERIM'94, Strasbourg, sep Mandelbrot B. (1982). The fractal geometry of nature. W.H. Freeman & Co. New York. Masson P. & Pieczynski W., (1993) SEM algorithm and unsupervised statistical segmentation of satellite images, IEEE Trans. Geoscience and Remote Sensing, vol. 34, no. 3, pp Marthon P., B. Paci & E. Cubero-Castan, (1994). "Finding the structure of a sattelite image", Proc. EurOpto Image and Signal Processing for Remote Sensing, Vol. SPIE 2315, Rome, Italy, , Marzouki A., Delignon Y. & Quelle C., "Adaptative segmentation of SAR images" OCEAN 94/ OSATES, Brest Septembre, Marzouki A., (1996). "Segmentation statistique d images radar", Thèse de l Université de Lille I, 8 Novembre 1996.McGarigal, K. & Marks, B.J. (1994). «Fragstats: Spatial pattern analysis program for quantifying landscape structure». Version 2.0. McGarigal K, McComb WC. (1995). FRAGSTATS: spatial pattern analysis program for quantifying landscape structure. Portland (OR): USDA Forest Service, Pacific Northwest Research station; General Technical Report PNW-GTR-351. Mead R.A., Sharik T.L., Prisley S.P. & Heinen J.T. (1981). A computerized spatial analysis system for assessing wildlife habitat from vegetation maps. Canadian Journal of Remote Sensing 7: Metropolis, N., Rosenbluth, A.W., Rosenbluth, M.N., Teller, A.H. & Teller, E. (1953). Equations of state calculations by fast computing machines. Journal of Chemical Physics, 21: Musick H.B. & Grover H.D. (1991). Image Textural Measures as indices of Landscape Pattern. In Quantitative Methods in Landscape Ecology, : The Analysis and Interpretation of Landscape Heterogeneity. eds. Turner, M.G. & R.H. Gardner. Springer-Verlag, New York. Mougin E., Proisy C., Ducrot D., Lopes A., Rivalland V., Marty G., Dufrêne E., Le Dantec V., Sarti, Souyris J.C., Adragna F., «Radar Remote Sensing of a Mixed Deciduous F. Temperate Forest Results and Perspectives.» colloque de l'esa: «Retrieval of Bio- and Geo-physical parameters from SAR data for Land applications» à l ESTEC (Noordwijk - Hollande) 21-23octobre 1998 Nagendra H. & Gadgil M. (1999). Satellite imagery as a tool for monitoring species diversity: an assessment. Journal of Applied Ecology 36: Nezry E., A. Lopès, D. Ducrot, C. Nezry & J.S. Lee, (1996) "Probability of error in supervised classification of K-distributed terrains in SAR images", IEEE Trans. on GRS, Vol.34 n 5, pp , September Oliver C.J., (1993) "Optimal texture estimators for SAR clutter", J. Phys. D: Appl. Phys. Vol.26, pp , O'Neill R.V., Turner S.J., Cullinan V.I., Coffin D.P., Cook T., Conley W., Brunt J., Thomas J.M., Conley M.R. & Gosz J. (1991). Multiple landscape scales: An intersite comparison. Landscape Ecology 5 (3): Pala, V., & Pons, X. (1995), Incorporation of relief into geometric corrections based on polynomials. Photogrammetric. Engineering & Remote Sensing, vol. 61, no. 7, pp Pickett S.T.A. &White P. Eds. (1985). The ecology of natural disturbance and patch dynamics, Academic Press, New York. Pierce L.E., Ulaby F.T., K. Sarabandi & M.C. Dobson (1994) "Knowledge-based classification of polarimetric SAR images", IEEE Trans. on Geosciences and Remote Sensing, Vol.32 n 5, , Sept
238 Références bibliographiques Pierdicca N & al, (1995) "Classification of multifrequency radar polarimetric data: role and contribution of vectorial filters", Proceedings of the IGARSS'95, , Firenze, Italia. Pham, T.T., Jeansoulin R., Comber, A.J. (2004). " Land-cover Land cover change detection: a quality-aware and semantic-based aproach ". IPMU 2004 Conference, Special Session 4, Perugia, Italy, 4-9 July, pp Phan-Luong T., Pham T., R. Jeansoulin, (2004) ``Data Quality Based Fusion: Application to the Land Cover", in: 7th International Conference on Information Fusion, FUSION 2004, Stockholm, Sweden, June 28th- July 1st pp Pony O., Descombes X, Zérubia J. (2000) «Classification d imafges satellitaires hyperspectrales en zone rurale et périurbaine» projet Ariana rapport de recherché n 4008, sept 2000 Quattrochi D.A. & Pelleter R.E. (1991). «Remote sensing for analysis of landscape: an introduction. Quantitative Methods in Landscape Ecology. Edited by M.G. Turner & R.H. Gardner, Ecological Studies 82, New York, 307 pp. Quelle H.C., Delignon Y. & Marzouki A., "Unsupervised bayesian segmentation of SAR images using the Pearson system distributions," in proceedings IGARSS'93 symp, pp , Tokyo 18-21, August Rahman, H., & G. Dedieu, SMAC A (1994), Simplified Method for the Atmospheric Correction of Satellite Measurements in the Solar Spectrum, Int. J. Remote Sens., 15 (1), Richard J.F. (1975). «Paysages, écosystème, environnement : une approche géographique». L espace géographique 2: Richards J.F. (1990). Land transformation. The earth as transformed by human action. Ed. by B.L. Turner II, W.C. Clarck, R.W. Kates, J.F. Richards, J.T. Mathews & W; Meyer. Cambridge University Press, Cambridge, pp Risser P.G., Karr J.R. & Forman R.T.T. (1984). Landscape Ecology: Directions and Approaches. Special publication no. 2. Illinois Natural History Survey, Champaign. Rogers, C., 1993, Describing landscapes: indices of structure. M.S. Thesis, Simon Fraser University, Burnaby, British Columbia, 170 pp Saunders D.A., Hobbs R. & Margules C.R. (1991). Biological consequences of ecosystem fragmentation: a review. Conservation Biology 5: Schermznn N., Baudry J. (2002). «Analyse descriptive multi-èchelle de la structure d un paysage. Application à la mosaïque d occupation du sol d un territoire agricole dans un bocage breton». Revue internationale de géomatique, vol 12 (3-4) : H. Sassier, D. Ducrot, S.Goze, J.G. Planes, C.Liégé, C.Freissinet, M Vauclin. Radarsat data assimilation into a hydrological risk management system Canadian journal of remote sensing, 1999 Schistad Solberg Anne H, Taxt Torfinn,. Jain Anil K, (1996), Markov random fields models for Classification of multisource Satellite Imagery, IEEE Trans. On Geo. And Rem. Sesing, vol. 34. no. 1., , January 1996 Sery F., Ducrot D., Fjortoft R., Lebon F., Lopès A., Marthon P. (1996) "Segmentation et classification des images SAR de type ERS1" Rapport de contrat N 833/CNES/94/1022/00, janvier 1996 Sery Franck, (1997). «Filtrage du Speckle dans les images RSO polarimetriques et classification Multi-Sources», Thèse N 2636 CESBIO UPS, Toulouse. Shafer G. (1976). A mathematical theory of evidence. Princeton University Press. Princeton, NJ. Shahshahani B.M. & D. A. Landgrebe, (1994) "The effect of unlabeled samples in reducing the small sample size problem and mitigating the Hughes phenomenon", IEEE Trans on GRS, vol. 32 n 5, , September Shen J. & Castan S. (1992). An optimal linear operator for step edge detection. CVGIP, Graphics Models and Image Processing Vol.54 n 2, , March Slater J. & Brown R. (2000). Changing landscapes : monitoring environmental sensitivity areas 208
239 Références bibliographiques using satellite imagery. International Journal of Remote Sensing 21 (13&14):2753. Smets P. (1983) Information Content of an Evidence. International Journal of Man-Machine Studies 19(1): 33 Smets P., Magrez P. (1983). Implication in fuzzy logic. Int. J. Approx. Reasoning 1(4): (1987) -43 Smets P. (1988). Belief functions. In Non standard logics for automated reasoning, edited by Smets P., Mamdani A., Dubois D. & Prade H., Academic Press, London, pp Smets P. (1993) Probability of Deductibility and Belief Functions. ECSQARU 1993: Smets P, (1993), Belief function : the disjonctive rule of combination and the generalized bayesian theorem. International Journal of Approximate Reasoning vol.9, p1-35. Smets P. (1999) Imperfect Information: Imprecision, Uncertainity report IRIDIA July 27, 1999 Smets P. (1999) Numerical Representation of Uncertainty report IRIDIA July 27, 1999 Smets P. (2000) Practical Uses of Belief functions report IRIDIA 2000 Stehman S.V. (1997). Selecting and interpreting measures of thematic classification accuracy. Remote Sensing of Environment 62: Soltner D., (1972). «Les grandes productions végétales». Collection Sciences et techniques agricoles, 4ème ed., 349p, Imprimerie H.Siraudeau Angers. Song, C., Woodcock, C. E., Seto, K. C., Pax Lenney, M., & Macomber, S. A. (2001), «Classification andchange Detection Using Landsat TM Data: When and How to Correct Atmospheric Effects? Remote Sens.Environ. 75: Trichon V., Ducrot D., Gastellu-Etchegorry J. P., «Contribution for the monitoring of tropical vegetation : an assessment using Landsat TM data in Sumatra», International Journal of Remote Sensing (IJRS), January Toutin, T., & Cheng, P. (2000), «Demystification of IKONOS». Earth Observation Magazine, vol. 9, no. 7, pp Touzi R. & Lopès A. (1994). "The principle of speckle filtering in Polarimetric SAR imagery", IEEE Trans. on Geosciences and Remote Sensing, Vol.32 n 5, , Sept Tupin F., Sigelle M., ChkeifA., Véran J.P., (1997). Restoration of SAR Images Using Recovery of Discontinuities and Non-linear Optimization. EMMCVPR 1997: Turner M.G. (1987). Spatial Simulation of Landscapes Changes in Georgia: a Comparison of 3 Transition Models. Landscape Ecology 1: Turner M.G., O Neill R.V., Gardner R.H. & Milne B.T. (1989). Effects of changing spatial scale on the analysis of landscape pattern. Landscape Ecology 3 (3&4): Turner M.G. & Gardner R.H. (1991). Quantitative Methods in Landscape Ecology. Ecological Studies 82, New York, 307 pp. Turner W., Sterling E.J., & Janetos A.C. (2001). Introduction to the special section Contributions of remote sensing to biodiversity conservation: a NASA approach. Conservation Biology 15(4): Urban D.L., O Neill R.V. & Shugart Jr. H.H. (1987). Landscape ecology: A hierarchical perpective can help scientist understand spatial patterns. BioScience 37: Van Hulst R. (1979). On the dynamics of vegetation: Markov chains as a model of succession. Vegetation 40:3-14. Weska J.C., Dyer R. & Rosenfeld A. (1976). A comparative study of texture measures for terrain classification. IEEE Transactions on Systems, Man, and Cybernetics 6 (4): Wiens J. A. (1989). Spatial scaling in ecology. Functional Ecology 3: Wiens J.A., Stenseth N.C., Van Horne B. & Ims R.A. (1993). Ecological mechanisms and landscape ecology. Oikos 66: Winkler G., (2003) Image analysis, random fields and dynamic Monte Carlo methods : a mathematical introduction 2ème édition Springer-Verlag,. 209
240 Références bibliographiques With K.A. & Crist T.O. (1995). Critical thresholds in species responses to landscape structure. Ecology 76(8): With K.A., Gardner R.H. & Turner M.G. (1997). Landscape connectivity and population distributions in heterogeneous environments. Oikos 78: Wu Y & H. Maitre, (1992) Smoothing speckled SAR images by using maximum homogeneous regions filters, Optical Eng., Vol.31 n 8, , Yuan, D., & Elvidge, C. D. (1996) Comparison of relative radiometric normalization techniques. ISPRS Journal of Photogrammetry & Remote Sensing, 51: Zadeh L.A.(1965) Fuzzy sets, Inform.and Control 8, Zadeh L.A (1978) Fuzzy sets as a basis for a theory of possibility, Fuzzy Sets and Systems 1, 3-28 Zerubia J., Kato Z., Berthod M. (1994). Multi-Temperature Annealing: a new approach for the energy-minimization of hierarchical Markov Random Field models. ICPR-Computer Vision and Applications, Jerusalem, Oct
SPOT4 (Take 5) : Sentinel-2 avec deux ans d avance
 SPOT4 (Take 5) : Sentinel-2 avec deux ans d avance Olivier Hagolle Mercredi 6 février 2012 Sentinel-2 : révolution du suivi de la végétation par télédétection 13 bandes spectrales, résolution 10m à 20m,
SPOT4 (Take 5) : Sentinel-2 avec deux ans d avance Olivier Hagolle Mercredi 6 février 2012 Sentinel-2 : révolution du suivi de la végétation par télédétection 13 bandes spectrales, résolution 10m à 20m,
Projet de Traitement du Signal Segmentation d images SAR
 Projet de Traitement du Signal Segmentation d images SAR Introduction En analyse d images, la segmentation est une étape essentielle, préliminaire à des traitements de haut niveau tels que la classification,
Projet de Traitement du Signal Segmentation d images SAR Introduction En analyse d images, la segmentation est une étape essentielle, préliminaire à des traitements de haut niveau tels que la classification,
Cartes de l étendue des eaux libres liés aux inondations Guide des produits
 Cartes de l étendue des eaux libres liés aux inondations Guide des produits Contexte Les crues ont parfois des effets dévastateurs sur la vie humaine, les infrastructures, l économie, les espèces sauvages
Cartes de l étendue des eaux libres liés aux inondations Guide des produits Contexte Les crues ont parfois des effets dévastateurs sur la vie humaine, les infrastructures, l économie, les espèces sauvages
Perspectives d applications de la télédétection en grandes culture à court et moyen terme dans le Sud-Ouest
 Perspectives d applications de la télédétection en grandes culture à court et moyen terme dans le Sud-Ouest Jean-François DEJOUX CESBIO & Luc CHAMPOLIVIER CETIOM Télédétection en agriculture : nouveau
Perspectives d applications de la télédétection en grandes culture à court et moyen terme dans le Sud-Ouest Jean-François DEJOUX CESBIO & Luc CHAMPOLIVIER CETIOM Télédétection en agriculture : nouveau
CarrotAge, un logiciel pour la fouille de données agricoles
 CarrotAge, un logiciel pour la fouille de données agricoles F. Le Ber (engees & loria) J.-F. Mari (loria) M. Benoît, C. Mignolet et C. Schott (inra sad) Conférence STIC et Environnement, Rouen, 19-20 juin
CarrotAge, un logiciel pour la fouille de données agricoles F. Le Ber (engees & loria) J.-F. Mari (loria) M. Benoît, C. Mignolet et C. Schott (inra sad) Conférence STIC et Environnement, Rouen, 19-20 juin
AMTEC RESOURCES MANAGEMENT LTD. CREATION D UNE BANQUE DE DONNEES DONNEES GEOSPATIALES NATIONALE
 AMTEC RESOURCES MANAGEMENT LTD. CREATION D UNE BANQUE DE DONNEES GEOSPATIALE CREATION A D UNE L ECHELLE BANQUE NATIONAL DE DONNEES GEOSPATIALES NATIONALE 1 AMTEC RESOURCES MANAGEMENT LTD. P O Box 3463
AMTEC RESOURCES MANAGEMENT LTD. CREATION D UNE BANQUE DE DONNEES GEOSPATIALE CREATION A D UNE L ECHELLE BANQUE NATIONAL DE DONNEES GEOSPATIALES NATIONALE 1 AMTEC RESOURCES MANAGEMENT LTD. P O Box 3463
Franck VAUTIER, Jean-Pierre TOUMAZET, Erwan ROUSSEL, Marlène FAURE, Mohamed ABADI, Marta FLOREZ, Bertrand DOUSTEYSSIER
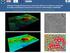 Utilisation d images dérivées d un jeu de données LIDAR pour la détection automatisée de vestiges archéologiques (programme de recherche méthodologique LiDARCHEO) Franck VAUTIER, Jean-Pierre TOUMAZET,
Utilisation d images dérivées d un jeu de données LIDAR pour la détection automatisée de vestiges archéologiques (programme de recherche méthodologique LiDARCHEO) Franck VAUTIER, Jean-Pierre TOUMAZET,
Introduction au datamining
 Introduction au datamining Patrick Naïm janvier 2005 Définition Définition Historique Mot utilisé au départ par les statisticiens Le mot indiquait une utilisation intensive des données conduisant à des
Introduction au datamining Patrick Naïm janvier 2005 Définition Définition Historique Mot utilisé au départ par les statisticiens Le mot indiquait une utilisation intensive des données conduisant à des
Analyse de la vidéo. Chapitre 4.1 - La modélisation pour le suivi d objet. 10 mars 2015. Chapitre 4.1 - La modélisation d objet 1 / 57
 Analyse de la vidéo Chapitre 4.1 - La modélisation pour le suivi d objet 10 mars 2015 Chapitre 4.1 - La modélisation d objet 1 / 57 La représentation d objets Plan de la présentation 1 La représentation
Analyse de la vidéo Chapitre 4.1 - La modélisation pour le suivi d objet 10 mars 2015 Chapitre 4.1 - La modélisation d objet 1 / 57 La représentation d objets Plan de la présentation 1 La représentation
Traitement bas-niveau
 Plan Introduction L approche contour (frontière) Introduction Objectifs Les traitements ont pour but d extraire l information utile et pertinente contenue dans l image en regard de l application considérée.
Plan Introduction L approche contour (frontière) Introduction Objectifs Les traitements ont pour but d extraire l information utile et pertinente contenue dans l image en regard de l application considérée.
Détection en environnement non-gaussien Cas du fouillis de mer et extension aux milieux
 Détection en environnement non-gaussien Cas du fouillis de mer et extension aux milieux hétérogènes Laurent Déjean Thales Airborne Systems/ENST-Bretagne Le 20 novembre 2006 Laurent Déjean Détection en
Détection en environnement non-gaussien Cas du fouillis de mer et extension aux milieux hétérogènes Laurent Déjean Thales Airborne Systems/ENST-Bretagne Le 20 novembre 2006 Laurent Déjean Détection en
Document d Appui n 3.3. : Repérage ou positionnement par Global Positionning System G.P.S (extrait et adapté de CAMELEO 2001)
 Document d Appui n 3.3. : Repérage ou positionnement par Global Positionning System G.P.S (extrait et adapté de CAMELEO 2001) 1. Présentation du GPS Le GPS (Global Positionning System=système de positionnement
Document d Appui n 3.3. : Repérage ou positionnement par Global Positionning System G.P.S (extrait et adapté de CAMELEO 2001) 1. Présentation du GPS Le GPS (Global Positionning System=système de positionnement
Projet de traitement d'image - SI 381 reconstitution 3D d'intérieur à partir de photographies
 Projet de traitement d'image - SI 381 reconstitution 3D d'intérieur à partir de photographies Régis Boulet Charlie Demené Alexis Guyot Balthazar Neveu Guillaume Tartavel Sommaire Sommaire... 1 Structure
Projet de traitement d'image - SI 381 reconstitution 3D d'intérieur à partir de photographies Régis Boulet Charlie Demené Alexis Guyot Balthazar Neveu Guillaume Tartavel Sommaire Sommaire... 1 Structure
LES CARACTERISTIQUES DES SUPPORTS DE TRANSMISSION
 LES CARACTERISTIQUES DES SUPPORTS DE TRANSMISSION LES CARACTERISTIQUES DES SUPPORTS DE TRANSMISSION ) Caractéristiques techniques des supports. L infrastructure d un réseau, la qualité de service offerte,
LES CARACTERISTIQUES DES SUPPORTS DE TRANSMISSION LES CARACTERISTIQUES DES SUPPORTS DE TRANSMISSION ) Caractéristiques techniques des supports. L infrastructure d un réseau, la qualité de service offerte,
RESERVOIR MONITORING A PARTIR D IMAGES SATELLITES APPLICATIONS POUR LES ACTIVITÉS AMONT DE SONATRACH EN ALGÉRIE
 RESERVOIR MONITORING A PARTIR D IMAGES SATELLITES APPLICATIONS POUR LES ACTIVITÉS AMONT DE SONATRACH EN ALGÉRIE Johanna GRANDA (1), Alain ARNAUD (1) et Azzédine BOUDIAF (2) (1) ALTAMIRA INFORMATION S.L.,
RESERVOIR MONITORING A PARTIR D IMAGES SATELLITES APPLICATIONS POUR LES ACTIVITÉS AMONT DE SONATRACH EN ALGÉRIE Johanna GRANDA (1), Alain ARNAUD (1) et Azzédine BOUDIAF (2) (1) ALTAMIRA INFORMATION S.L.,
Prédiction de couverture de champ radioélectrique pour les réseaux radiomobiles : L apport du Système d Information Géographique ArcInfo 8
 Prédiction de couverture de champ radioélectrique pour les réseaux radiomobiles : L apport du Système d Information Géographique ArcInfo 8 Christine TURCK 1 * et **, Christiane WEBER**, Dominique THOME*
Prédiction de couverture de champ radioélectrique pour les réseaux radiomobiles : L apport du Système d Information Géographique ArcInfo 8 Christine TURCK 1 * et **, Christiane WEBER**, Dominique THOME*
4. Résultats et discussion
 17 4. Résultats et discussion La signification statistique des gains et des pertes bruts annualisés pondérés de superficie forestière et du changement net de superficie forestière a été testée pour les
17 4. Résultats et discussion La signification statistique des gains et des pertes bruts annualisés pondérés de superficie forestière et du changement net de superficie forestière a été testée pour les
Les bases de données Les systèmes d informations
 2 Les bases de données Les systèmes d informations Surface annuelle moyenne brûlée (en ha) 250 000 200 000 150 000 100 000 50 000 0 Part de la surface forestière brûlée (en %) 3,5 3,0 2,5 2,0 1,5 1,0 0,5
2 Les bases de données Les systèmes d informations Surface annuelle moyenne brûlée (en ha) 250 000 200 000 150 000 100 000 50 000 0 Part de la surface forestière brûlée (en %) 3,5 3,0 2,5 2,0 1,5 1,0 0,5
Apprentissage Automatique
 Apprentissage Automatique Introduction-I [email protected] www.lia.univ-avignon.fr Définition? (Wikipedia) L'apprentissage automatique (machine-learning en anglais) est un des champs
Apprentissage Automatique Introduction-I [email protected] www.lia.univ-avignon.fr Définition? (Wikipedia) L'apprentissage automatique (machine-learning en anglais) est un des champs
LIDAR LAUSANNE 2012. Nouvelles données altimétriques sur l agglomération lausannoise par technologie laser aéroporté et ses produits dérivés
 LIDAR LAUSANNE 2012 Nouvelles données altimétriques sur l agglomération lausannoise par technologie laser aéroporté et ses produits dérivés LIDAR 2012, nouveaux modèles altimétriques 1 Affaire 94022 /
LIDAR LAUSANNE 2012 Nouvelles données altimétriques sur l agglomération lausannoise par technologie laser aéroporté et ses produits dérivés LIDAR 2012, nouveaux modèles altimétriques 1 Affaire 94022 /
Christophe SANNIER [email protected]
 Systèmes d Information à Référence Spatiale Utilisation d un Estimateur de Régression avec des Données Landsat pour l Estimation de l Etendu et des Changements du Couvert Forestier du Gabon de 1990 à 2010
Systèmes d Information à Référence Spatiale Utilisation d un Estimateur de Régression avec des Données Landsat pour l Estimation de l Etendu et des Changements du Couvert Forestier du Gabon de 1990 à 2010
Intérêt du découpage en sous-bandes pour l analyse spectrale
 Intérêt du découpage en sous-bandes pour l analyse spectrale David BONACCI Institut National Polytechnique de Toulouse (INP) École Nationale Supérieure d Électrotechnique, d Électronique, d Informatique,
Intérêt du découpage en sous-bandes pour l analyse spectrale David BONACCI Institut National Polytechnique de Toulouse (INP) École Nationale Supérieure d Électrotechnique, d Électronique, d Informatique,
Transmission de données. A) Principaux éléments intervenant dans la transmission
 Page 1 / 7 A) Principaux éléments intervenant dans la transmission A.1 Equipement voisins Ordinateur ou terminal Ordinateur ou terminal Canal de transmission ETTD ETTD ETTD : Equipement Terminal de Traitement
Page 1 / 7 A) Principaux éléments intervenant dans la transmission A.1 Equipement voisins Ordinateur ou terminal Ordinateur ou terminal Canal de transmission ETTD ETTD ETTD : Equipement Terminal de Traitement
La base de données régionale sur les sols. d Alsace. La base de données régionale sur les sols d Alsace
 3 outils complémentaires pour connaître les sols en Alsace La base de données régionale sur les sols d Alsace Le guide des sols d Alsace La base de données régionale sur les sols Le réseau de mesure de
3 outils complémentaires pour connaître les sols en Alsace La base de données régionale sur les sols d Alsace Le guide des sols d Alsace La base de données régionale sur les sols Le réseau de mesure de
Comprendre l Univers grâce aux messages de la lumière
 Seconde / P4 Comprendre l Univers grâce aux messages de la lumière 1/ EXPLORATION DE L UNIVERS Dans notre environnement quotidien, les dimensions, les distances sont à l échelle humaine : quelques mètres,
Seconde / P4 Comprendre l Univers grâce aux messages de la lumière 1/ EXPLORATION DE L UNIVERS Dans notre environnement quotidien, les dimensions, les distances sont à l échelle humaine : quelques mètres,
Géométrie discrète Chapitre V
 Géométrie discrète Chapitre V Introduction au traitement d'images Géométrie euclidienne : espace continu Géométrie discrète (GD) : espace discrétisé notamment en grille de pixels GD définition des objets
Géométrie discrète Chapitre V Introduction au traitement d'images Géométrie euclidienne : espace continu Géométrie discrète (GD) : espace discrétisé notamment en grille de pixels GD définition des objets
PHYSIQUE Discipline fondamentale
 Examen suisse de maturité Directives 2003-2006 DS.11 Physique DF PHYSIQUE Discipline fondamentale Par l'étude de la physique en discipline fondamentale, le candidat comprend des phénomènes naturels et
Examen suisse de maturité Directives 2003-2006 DS.11 Physique DF PHYSIQUE Discipline fondamentale Par l'étude de la physique en discipline fondamentale, le candidat comprend des phénomènes naturels et
Évolution du climat et désertification
 Évolution du climat et désertification FACTEURS HUMAINS ET NATURELS DE L ÉVOLUTION DU CLIMAT Les activités humaines essentiellement l exploitation de combustibles fossiles et la modification de la couverture
Évolution du climat et désertification FACTEURS HUMAINS ET NATURELS DE L ÉVOLUTION DU CLIMAT Les activités humaines essentiellement l exploitation de combustibles fossiles et la modification de la couverture
L analyse d images regroupe plusieurs disciplines que l on classe en deux catégories :
 La vision nous permet de percevoir et d interpreter le monde qui nous entoure. La vision artificielle a pour but de reproduire certaines fonctionnalités de la vision humaine au travers de l analyse d images.
La vision nous permet de percevoir et d interpreter le monde qui nous entoure. La vision artificielle a pour but de reproduire certaines fonctionnalités de la vision humaine au travers de l analyse d images.
Mesure agnostique de la qualité des images.
 Mesure agnostique de la qualité des images. Application en biométrie Christophe Charrier Université de Caen Basse-Normandie GREYC, UMR CNRS 6072 Caen, France 8 avril, 2013 C. Charrier NR-IQA 1 / 34 Sommaire
Mesure agnostique de la qualité des images. Application en biométrie Christophe Charrier Université de Caen Basse-Normandie GREYC, UMR CNRS 6072 Caen, France 8 avril, 2013 C. Charrier NR-IQA 1 / 34 Sommaire
L accès aux données spatiales au profit des applications satellitaires
 L accès aux données spatiales au profit des applications satellitaires Le projet Geosud Pierre Maurel, coordinateur du projet GEOSUD Journée du CINES Montpellier, 9 juin 2015 1 Projet GEOSUD Des financements
L accès aux données spatiales au profit des applications satellitaires Le projet Geosud Pierre Maurel, coordinateur du projet GEOSUD Journée du CINES Montpellier, 9 juin 2015 1 Projet GEOSUD Des financements
N. Paparoditis, Laboratoire MATIS
 N. Paparoditis, Laboratoire MATIS Contexte: Diffusion de données et services locaux STEREOPOLIS II Un véhicule de numérisation mobile terrestre Lasers Caméras Système de navigation/positionnement STEREOPOLIS
N. Paparoditis, Laboratoire MATIS Contexte: Diffusion de données et services locaux STEREOPOLIS II Un véhicule de numérisation mobile terrestre Lasers Caméras Système de navigation/positionnement STEREOPOLIS
Synthèse des réponses au questionnaire
 Etat des lieux sur les réseaux et programmes de Monitoring dans les pays partenaires méditerranéens Synthèse des réponses au questionnaire X. Detienne Aquapôle, Université de Liège Réalisé pour le compte
Etat des lieux sur les réseaux et programmes de Monitoring dans les pays partenaires méditerranéens Synthèse des réponses au questionnaire X. Detienne Aquapôle, Université de Liège Réalisé pour le compte
Le concept cellulaire
 Le concept cellulaire X. Lagrange Télécom Bretagne 21 Mars 2014 X. Lagrange (Télécom Bretagne) Le concept cellulaire 21/03/14 1 / 57 Introduction : Objectif du cours Soit un opérateur qui dispose d une
Le concept cellulaire X. Lagrange Télécom Bretagne 21 Mars 2014 X. Lagrange (Télécom Bretagne) Le concept cellulaire 21/03/14 1 / 57 Introduction : Objectif du cours Soit un opérateur qui dispose d une
Surveillance et Detection des Anomalies. Diagnostic d une digue: rappel méthodologique
 Surveillance et Detection des Anomalies Diagnostic d une digue: rappel méthodologique issu de l expérience d EDF Jean-Paul BLAIS Service Géologie - Géotechnique EDF 1 La méthodologie utilisée par EDF,
Surveillance et Detection des Anomalies Diagnostic d une digue: rappel méthodologique issu de l expérience d EDF Jean-Paul BLAIS Service Géologie - Géotechnique EDF 1 La méthodologie utilisée par EDF,
Sujet proposé par Yves M. LEROY. Cet examen se compose d un exercice et de deux problèmes. Ces trois parties sont indépendantes.
 Promotion X 004 COURS D ANALYSE DES STRUCTURES MÉCANIQUES PAR LA MÉTHODE DES ELEMENTS FINIS (MEC 568) contrôle non classant (7 mars 007, heures) Documents autorisés : polycopié ; documents et notes de
Promotion X 004 COURS D ANALYSE DES STRUCTURES MÉCANIQUES PAR LA MÉTHODE DES ELEMENTS FINIS (MEC 568) contrôle non classant (7 mars 007, heures) Documents autorisés : polycopié ; documents et notes de
Oscillations libres des systèmes à deux degrés de liberté
 Chapitre 4 Oscillations libres des systèmes à deux degrés de liberté 4.1 Introduction Les systèmes qui nécessitent deux coordonnées indépendantes pour spécifier leurs positions sont appelés systèmes à
Chapitre 4 Oscillations libres des systèmes à deux degrés de liberté 4.1 Introduction Les systèmes qui nécessitent deux coordonnées indépendantes pour spécifier leurs positions sont appelés systèmes à
«Bases de données géoréférencées pour la gestion agricole et environnementale en Roumanie»
 «Bases de données géoréférencées pour la gestion agricole et environnementale en Roumanie» Dr. Alexandru BADEA Directeur Applications Spatiales Agence Spatiale Roumaine Tél : +40(0)744506880 [email protected]
«Bases de données géoréférencées pour la gestion agricole et environnementale en Roumanie» Dr. Alexandru BADEA Directeur Applications Spatiales Agence Spatiale Roumaine Tél : +40(0)744506880 [email protected]
3 - Description et orbite d'un satellite d'observation
 Introduction à la télédétection 3 - Description et orbite d'un satellite d'observation OLIVIER DE JOINVILLE Table des matières I - Description d'un satellite d'observation 5 A. Schéma d'un satellite...5
Introduction à la télédétection 3 - Description et orbite d'un satellite d'observation OLIVIER DE JOINVILLE Table des matières I - Description d'un satellite d'observation 5 A. Schéma d'un satellite...5
Transmission d informations sur le réseau électrique
 Transmission d informations sur le réseau électrique Introduction Remarques Toutes les questions en italique devront être préparées par écrit avant la séance du TP. Les préparations seront ramassées en
Transmission d informations sur le réseau électrique Introduction Remarques Toutes les questions en italique devront être préparées par écrit avant la séance du TP. Les préparations seront ramassées en
La (les) mesure(s) GPS
 La (les) mesure(s) GPS I. Le principe de la mesure II. Equation de mesure GPS III. Combinaisons de mesures (ionosphère, horloges) IV. Doubles différences et corrélation des mesures V. Doubles différences
La (les) mesure(s) GPS I. Le principe de la mesure II. Equation de mesure GPS III. Combinaisons de mesures (ionosphère, horloges) IV. Doubles différences et corrélation des mesures V. Doubles différences
Chapitre 22 : (Cours) Numérisation, transmission, et stockage de l information
 Chapitre 22 : (Cours) Numérisation, transmission, et stockage de l information I. Nature du signal I.1. Définition Un signal est la représentation physique d une information (température, pression, absorbance,
Chapitre 22 : (Cours) Numérisation, transmission, et stockage de l information I. Nature du signal I.1. Définition Un signal est la représentation physique d une information (température, pression, absorbance,
CAPTEURS - CHAINES DE MESURES
 CAPTEURS - CHAINES DE MESURES Pierre BONNET Pierre Bonnet Master GSI - Capteurs Chaînes de Mesures 1 Plan du Cours Propriétés générales des capteurs Notion de mesure Notion de capteur: principes, classes,
CAPTEURS - CHAINES DE MESURES Pierre BONNET Pierre Bonnet Master GSI - Capteurs Chaînes de Mesures 1 Plan du Cours Propriétés générales des capteurs Notion de mesure Notion de capteur: principes, classes,
MASTER (LMD) GESTION DE DONNEES ET SPATIALISATION EN ENVIRONNEMENT (GSE)
 MASTER (LMD) GESTION DE DONNEES ET SPATIALISATION EN ENVIRONNEMENT (GSE) RÉSUMÉ DE LA FORMATION Type de diplôme : Master (LMD) Domaine ministériel : Sciences, Technologies, Santé Mention : STIC POUR L'ECOLOGIE
MASTER (LMD) GESTION DE DONNEES ET SPATIALISATION EN ENVIRONNEMENT (GSE) RÉSUMÉ DE LA FORMATION Type de diplôme : Master (LMD) Domaine ministériel : Sciences, Technologies, Santé Mention : STIC POUR L'ECOLOGIE
L image satellite : simple effet de mode ou. apport réel?
 Comment suivre les évolutions urbaines? L image satellite : simple effet de mode ou apport réel? Pierre ALBERT Scot Pierre ALBERT L image satellite : simple effet de mode ou apport réel? 29/10/04 1 Plan
Comment suivre les évolutions urbaines? L image satellite : simple effet de mode ou apport réel? Pierre ALBERT Scot Pierre ALBERT L image satellite : simple effet de mode ou apport réel? 29/10/04 1 Plan
SOCLE COMMUN - La Compétence 3 Les principaux éléments de mathématiques et la culture scientifique et technologique
 SOCLE COMMUN - La Compétence 3 Les principaux éléments de mathématiques et la culture scientifique et technologique DOMAINE P3.C3.D1. Pratiquer une démarche scientifique et technologique, résoudre des
SOCLE COMMUN - La Compétence 3 Les principaux éléments de mathématiques et la culture scientifique et technologique DOMAINE P3.C3.D1. Pratiquer une démarche scientifique et technologique, résoudre des
Le rôle des technologies de l imagerie dans le secteur de l environnement
 Le rôle des technologies de l imagerie dans le secteur de l environnement Présenté par Valérie Gouaillier Conseillère, Équipe Vision et imagerie CRIM Présenté à Montréal Le 20 novembre 2008 CRIM 2008 1
Le rôle des technologies de l imagerie dans le secteur de l environnement Présenté par Valérie Gouaillier Conseillère, Équipe Vision et imagerie CRIM Présenté à Montréal Le 20 novembre 2008 CRIM 2008 1
Equation LIDAR : exp 2 Equation RADAR :
 Contexte scientifique Systèmes LIDAR/RADAR Equation LIDAR : exp Equation RADAR : p (r) : puissance rétrodiffusée r : altitude ou profondeur. C : constante instrumentale. β : coefficient de rétrodiffusion
Contexte scientifique Systèmes LIDAR/RADAR Equation LIDAR : exp Equation RADAR : p (r) : puissance rétrodiffusée r : altitude ou profondeur. C : constante instrumentale. β : coefficient de rétrodiffusion
Vision industrielle et télédétection - Détection d ellipses. Guillaume Martinez 17 décembre 2007
 Vision industrielle et télédétection - Détection d ellipses Guillaume Martinez 17 décembre 2007 1 Table des matières 1 Le projet 3 1.1 Objectif................................ 3 1.2 Les choix techniques.........................
Vision industrielle et télédétection - Détection d ellipses Guillaume Martinez 17 décembre 2007 1 Table des matières 1 Le projet 3 1.1 Objectif................................ 3 1.2 Les choix techniques.........................
Environmental Research and Innovation ( ERIN )
 DÉpartEment RDI Environmental Research and Innovation ( ERIN ) Le département «Environmental Research and Innovation» (ERIN) du LIST élabore des stratégies, des technologies et des outils visant à mieux
DÉpartEment RDI Environmental Research and Innovation ( ERIN ) Le département «Environmental Research and Innovation» (ERIN) du LIST élabore des stratégies, des technologies et des outils visant à mieux
Rapport. Mesures de champ de très basses fréquences à proximité d antennes de stations de base GSM et UMTS
 Rapport Mesures de champ de très basses fréquences à proximité d antennes de stations de base GSM et UMTS A.AZOULAY T.LETERTRE R. DE LACERDA Convention AFSSET / Supélec 2009-1 - 1. Introduction Dans le
Rapport Mesures de champ de très basses fréquences à proximité d antennes de stations de base GSM et UMTS A.AZOULAY T.LETERTRE R. DE LACERDA Convention AFSSET / Supélec 2009-1 - 1. Introduction Dans le
Mobilité du trait de côte et cartographie historique
 Mobilité du trait de côte et cartographie historique 1 Frédéric POUGET Université de La Rochelle UMR 6250 LIENSS (Littoral Environnement et SociétéS) Colloque Les littoraux à l heure du changement climatique
Mobilité du trait de côte et cartographie historique 1 Frédéric POUGET Université de La Rochelle UMR 6250 LIENSS (Littoral Environnement et SociétéS) Colloque Les littoraux à l heure du changement climatique
Assemblée générale. Nations Unies A/AC.105/772
 Nations Unies A/AC.105/772 Assemblée générale Distr.: Générale 7 décembre 2001 Français Original: Anglais Comité des utilisations pacifiques de l espace extra-atmosphérique Rapport du deuxième Atelier
Nations Unies A/AC.105/772 Assemblée générale Distr.: Générale 7 décembre 2001 Français Original: Anglais Comité des utilisations pacifiques de l espace extra-atmosphérique Rapport du deuxième Atelier
TP SIN Traitement d image
 TP SIN Traitement d image Pré requis (l élève doit savoir): - Utiliser un ordinateur Objectif terminale : L élève doit être capable de reconnaître un format d image et d expliquer les différents types
TP SIN Traitement d image Pré requis (l élève doit savoir): - Utiliser un ordinateur Objectif terminale : L élève doit être capable de reconnaître un format d image et d expliquer les différents types
Approche expérimentale du rayonnement électromagnétique émis par un téléphone portable
 Approche expérimentale du rayonnement électromagnétique émis par un téléphone portable RÉSUMÉ U N I O N D E S P R O F E S S E U R S D E P H Y S I Q U E E T D E C H I M I E par Lycée Victor Hugo - 25000
Approche expérimentale du rayonnement électromagnétique émis par un téléphone portable RÉSUMÉ U N I O N D E S P R O F E S S E U R S D E P H Y S I Q U E E T D E C H I M I E par Lycée Victor Hugo - 25000
Anticiper la gestion d'un séisme dommageable Anticipare la gestione dei danni di un terremoto
 Atelier 1 groupe de travail sismique franco-italo-suisse du projet Interreg Alcotra RiskNET Atelier 1 gruppo di lavoro sismico franco-italo-svizzero del progetto Interreg Alcotra RiskNET Anticiper la gestion
Atelier 1 groupe de travail sismique franco-italo-suisse du projet Interreg Alcotra RiskNET Atelier 1 gruppo di lavoro sismico franco-italo-svizzero del progetto Interreg Alcotra RiskNET Anticiper la gestion
Echantillonnage Non uniforme
 Echantillonnage Non uniforme Marie CHABERT IRIT/INP-ENSEEIHT/ ENSEEIHT/TéSASA Patrice MICHEL et Bernard LACAZE TéSA 1 Plan Introduction Echantillonnage uniforme Echantillonnage irrégulier Comparaison Cas
Echantillonnage Non uniforme Marie CHABERT IRIT/INP-ENSEEIHT/ ENSEEIHT/TéSASA Patrice MICHEL et Bernard LACAZE TéSA 1 Plan Introduction Echantillonnage uniforme Echantillonnage irrégulier Comparaison Cas
Champ électromagnétique?
 Qu est-ce qu un Champ électromagnétique? Alain Azoulay Consultant, www.radiocem.com 3 décembre 2013. 1 Définition trouvée à l article 2 de la Directive «champs électromagnétiques» : des champs électriques
Qu est-ce qu un Champ électromagnétique? Alain Azoulay Consultant, www.radiocem.com 3 décembre 2013. 1 Définition trouvée à l article 2 de la Directive «champs électromagnétiques» : des champs électriques
Résonance Magnétique Nucléaire : RMN
 21 Résonance Magnétique Nucléaire : RMN Salle de TP de Génie Analytique Ce document résume les principaux aspects de la RMN nécessaires à la réalisation des TP de Génie Analytique de 2ème année d IUT de
21 Résonance Magnétique Nucléaire : RMN Salle de TP de Génie Analytique Ce document résume les principaux aspects de la RMN nécessaires à la réalisation des TP de Génie Analytique de 2ème année d IUT de
La classification automatique de données quantitatives
 La classification automatique de données quantitatives 1 Introduction Parmi les méthodes de statistique exploratoire multidimensionnelle, dont l objectif est d extraire d une masse de données des informations
La classification automatique de données quantitatives 1 Introduction Parmi les méthodes de statistique exploratoire multidimensionnelle, dont l objectif est d extraire d une masse de données des informations
$SSOLFDWLRQGXNULJHDJHSRXUOD FDOLEUDWLRQPRWHXU
 $SSOLFDWLRQGXNULJHDJHSRXUOD FDOLEUDWLRQPRWHXU Fabien FIGUERES [email protected] 0RWVFOpV : Krigeage, plans d expériences space-filling, points de validations, calibration moteur. 5pVXPp Dans le
$SSOLFDWLRQGXNULJHDJHSRXUOD FDOLEUDWLRQPRWHXU Fabien FIGUERES [email protected] 0RWVFOpV : Krigeage, plans d expériences space-filling, points de validations, calibration moteur. 5pVXPp Dans le
EVOLUTION SPATIO-TEMPORELLE DE L OCCUPATION DES ESPACES SUR LE TRIANGLE MARNAIS
 EVOLUTION SPATIO-TEMPORELLE DE L OCCUPATION DES ESPACES SUR LE TRIANGLE MARNAIS MARTIN S. *, DELAHAYE F. ** Bureau d études E3C 2 rue Léon Patoux CS 50001 51664 REIMS CEDEX * Mr Stéphane MARTIN, Directeur
EVOLUTION SPATIO-TEMPORELLE DE L OCCUPATION DES ESPACES SUR LE TRIANGLE MARNAIS MARTIN S. *, DELAHAYE F. ** Bureau d études E3C 2 rue Léon Patoux CS 50001 51664 REIMS CEDEX * Mr Stéphane MARTIN, Directeur
L apprentissage automatique
 L apprentissage automatique L apprentissage automatique L'apprentissage automatique fait référence au développement, à l analyse et à l implémentation de méthodes qui permettent à une machine d évoluer
L apprentissage automatique L apprentissage automatique L'apprentissage automatique fait référence au développement, à l analyse et à l implémentation de méthodes qui permettent à une machine d évoluer
LA TÉLÉDETECTION EN AGRICULTURE. par Bruno Tisseyre 1
 1 LA TÉLÉDETECTION EN AGRICULTURE par Bruno Tisseyre 1 RÉSUMÉ Avec la médiatisation des applications développées à partir des drones, la télédétection appliquée à l'agriculture fait aujourd hui beaucoup
1 LA TÉLÉDETECTION EN AGRICULTURE par Bruno Tisseyre 1 RÉSUMÉ Avec la médiatisation des applications développées à partir des drones, la télédétection appliquée à l'agriculture fait aujourd hui beaucoup
RESUMÉ NON TECHNIQUE ELABORATION DES CARTES DE BRUIT COMMUNAUTE D AGGLOMERATION DU HAUT VAL DE MARNE
 DIRECTION GENERALE ADJOINTE CHARGEE DE L AMENAGEMENT ET DU DEVELOPPEMENT Service études et prospective RESUMÉ NON TECHNIQUE ELABORATION DES CARTES DE BRUIT COMMUNAUTE D AGGLOMERATION DU HAUT VAL DE MARNE
DIRECTION GENERALE ADJOINTE CHARGEE DE L AMENAGEMENT ET DU DEVELOPPEMENT Service études et prospective RESUMÉ NON TECHNIQUE ELABORATION DES CARTES DE BRUIT COMMUNAUTE D AGGLOMERATION DU HAUT VAL DE MARNE
Modélisation aléatoire en fiabilité des logiciels
 collection Méthodes stochastiques appliquées dirigée par Nikolaos Limnios et Jacques Janssen La sûreté de fonctionnement des systèmes informatiques est aujourd hui un enjeu économique et sociétal majeur.
collection Méthodes stochastiques appliquées dirigée par Nikolaos Limnios et Jacques Janssen La sûreté de fonctionnement des systèmes informatiques est aujourd hui un enjeu économique et sociétal majeur.
Demande d examen au cas par cas préalable à la réalisation d une étude d impact
 Demande d examen au cas par cas préalable à la réalisation d une étude d impact Article R. 122-3 du code de l environnement N 14734*02 Ministère chargé de l'environnement Ce formulaire n est pas applicable
Demande d examen au cas par cas préalable à la réalisation d une étude d impact Article R. 122-3 du code de l environnement N 14734*02 Ministère chargé de l'environnement Ce formulaire n est pas applicable
Une fréquence peut-elle être instantanée?
 Fréquence? Variable? Instantané vs. local? Conclure? Une fréquence peut-elle être instantanée? Patrick Flandrin CNRS & École Normale Supérieure de Lyon, France Produire le temps, IRCAM, Paris, juin 2012
Fréquence? Variable? Instantané vs. local? Conclure? Une fréquence peut-elle être instantanée? Patrick Flandrin CNRS & École Normale Supérieure de Lyon, France Produire le temps, IRCAM, Paris, juin 2012
Joint AAL Information and Networking Day. 21 mars 2012
 Joint AAL Information and Networking Day 21 mars 2012 Présentation TéSA a pour objet : la mise en commun de moyens permettant de : rassembler et accueillir des doctorants ou post-doctorants dont les thèses
Joint AAL Information and Networking Day 21 mars 2012 Présentation TéSA a pour objet : la mise en commun de moyens permettant de : rassembler et accueillir des doctorants ou post-doctorants dont les thèses
Les indices à surplus constant
 Les indices à surplus constant Une tentative de généralisation des indices à utilité constante On cherche ici en s inspirant des indices à utilité constante à définir un indice de prix de référence adapté
Les indices à surplus constant Une tentative de généralisation des indices à utilité constante On cherche ici en s inspirant des indices à utilité constante à définir un indice de prix de référence adapté
TD1 Signaux, énergie et puissance, signaux aléatoires
 TD1 Signaux, énergie et puissance, signaux aléatoires I ) Ecrire l'expression analytique des signaux représentés sur les figures suivantes à l'aide de signaux particuliers. Dans le cas du signal y(t) trouver
TD1 Signaux, énergie et puissance, signaux aléatoires I ) Ecrire l'expression analytique des signaux représentés sur les figures suivantes à l'aide de signaux particuliers. Dans le cas du signal y(t) trouver
Introduction au Data-Mining
 Introduction au Data-Mining Alain Rakotomamonjy - Gilles Gasso. INSA Rouen -Département ASI Laboratoire PSI Introduction au Data-Mining p. 1/25 Data-Mining : Kèkecé? Traduction : Fouille de données. Terme
Introduction au Data-Mining Alain Rakotomamonjy - Gilles Gasso. INSA Rouen -Département ASI Laboratoire PSI Introduction au Data-Mining p. 1/25 Data-Mining : Kèkecé? Traduction : Fouille de données. Terme
Comme chaque ligne de cache a 1024 bits. Le nombre de lignes de cache contenu dans chaque ensemble est:
 Travaux Pratiques 3. IFT 1002/IFT 1005. Structure Interne des Ordinateurs. Département d'informatique et de génie logiciel. Université Laval. Hiver 2012. Prof : Bui Minh Duc. Tous les exercices sont indépendants.
Travaux Pratiques 3. IFT 1002/IFT 1005. Structure Interne des Ordinateurs. Département d'informatique et de génie logiciel. Université Laval. Hiver 2012. Prof : Bui Minh Duc. Tous les exercices sont indépendants.
Compression et Transmission des Signaux. Samson LASAULCE Laboratoire des Signaux et Systèmes, Gif/Yvette
 Compression et Transmission des Signaux Samson LASAULCE Laboratoire des Signaux et Systèmes, Gif/Yvette 1 De Shannon à Mac Donalds Mac Donalds 1955 Claude Elwood Shannon 1916 2001 Monsieur X 1951 2 Où
Compression et Transmission des Signaux Samson LASAULCE Laboratoire des Signaux et Systèmes, Gif/Yvette 1 De Shannon à Mac Donalds Mac Donalds 1955 Claude Elwood Shannon 1916 2001 Monsieur X 1951 2 Où
Comptes des changements de la biodiversité des systèmes et des espèces
 ATELIER INFRAREGIONAL POUR LA REGION DE L AFRIQUE DE L OUEST SUBSAHARIENNE SUR L ÉVALUATION ET LES MESURES INCITATIVES Ouagadougou, Burkina Faso, 14 17 Mai 2013 COMPTABILITÉ DE L ENVIRONNEMENT ET DES ÉCOSYSTÈMES
ATELIER INFRAREGIONAL POUR LA REGION DE L AFRIQUE DE L OUEST SUBSAHARIENNE SUR L ÉVALUATION ET LES MESURES INCITATIVES Ouagadougou, Burkina Faso, 14 17 Mai 2013 COMPTABILITÉ DE L ENVIRONNEMENT ET DES ÉCOSYSTÈMES
INF6304 Interfaces Intelligentes
 INF6304 Interfaces Intelligentes filtres collaboratifs 1/42 INF6304 Interfaces Intelligentes Systèmes de recommandations, Approches filtres collaboratifs Michel C. Desmarais Génie informatique et génie
INF6304 Interfaces Intelligentes filtres collaboratifs 1/42 INF6304 Interfaces Intelligentes Systèmes de recommandations, Approches filtres collaboratifs Michel C. Desmarais Génie informatique et génie
Développement et Evaluation PHYsiques des modèles atmosphériques
 Développement et Evaluation PHYsiques des modèles atmosphériques Motivations : Augmenter la confiance dans les prévision du changement climatique. 1. nécessite d'utiliser les modèles le plus "physiques"
Développement et Evaluation PHYsiques des modèles atmosphériques Motivations : Augmenter la confiance dans les prévision du changement climatique. 1. nécessite d'utiliser les modèles le plus "physiques"
La collecte et la gestion des données dans le cadre de la prospection d énergie solaire
 Conférence SIG 2012 - ESRIFRANCE La collecte et la gestion des données dans le cadre de la prospection d énergie solaire Serge MANG-JOUBERT GAIAGO Eric VIDALENC - ADEME 1 Auteurs : Rodrigo MARIONI, Serge
Conférence SIG 2012 - ESRIFRANCE La collecte et la gestion des données dans le cadre de la prospection d énergie solaire Serge MANG-JOUBERT GAIAGO Eric VIDALENC - ADEME 1 Auteurs : Rodrigo MARIONI, Serge
Cours IV Mise en orbite
 Introduction au vol spatial Cours IV Mise en orbite If you don t know where you re going, you ll probably end up somewhere else. Yogi Berra, NY Yankees catcher v1.2.8 by-sa Olivier Cleynen Introduction
Introduction au vol spatial Cours IV Mise en orbite If you don t know where you re going, you ll probably end up somewhere else. Yogi Berra, NY Yankees catcher v1.2.8 by-sa Olivier Cleynen Introduction
L ANALYSE DU «PARC SOCIAL DE FAIT» PARISIEN EN 2003 : UNE ANALYSE TERRITORIALISÉE DES PROFILS D OCCUPATION DES PARCS ET DES QUARTIERS
 ATELIER PARISIEN D URBANISME - 17, BD MORLAND 75004 PARIS TÉL : 01 42 71 28 14 FAX : 01 42 76 24 05 http://www.apur.org Observatoire de l'habitat de Paris L ANALYSE DU «PARC SOCIAL DE FAIT» PARISIEN EN
ATELIER PARISIEN D URBANISME - 17, BD MORLAND 75004 PARIS TÉL : 01 42 71 28 14 FAX : 01 42 76 24 05 http://www.apur.org Observatoire de l'habitat de Paris L ANALYSE DU «PARC SOCIAL DE FAIT» PARISIEN EN
Intelligence Artificielle et Systèmes Multi-Agents. Badr Benmammar [email protected]
 Intelligence Artificielle et Systèmes Multi-Agents Badr Benmammar [email protected] Plan La première partie : L intelligence artificielle (IA) Définition de l intelligence artificielle (IA) Domaines
Intelligence Artificielle et Systèmes Multi-Agents Badr Benmammar [email protected] Plan La première partie : L intelligence artificielle (IA) Définition de l intelligence artificielle (IA) Domaines
LA TÉLÉDÉTECTION AÉRO-SPATIALE : UNE INTRODUCTION
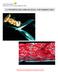 Claude Kergomard Professeur Ecole Normale Supérieure Paris LA TÉLÉDÉTECTION AÉRO-SPATIALE : UNE INTRODUCTION Cliquez sur les images pour entrer dans le cours Le cours est au format.pdf lisible avec Acrobat
Claude Kergomard Professeur Ecole Normale Supérieure Paris LA TÉLÉDÉTECTION AÉRO-SPATIALE : UNE INTRODUCTION Cliquez sur les images pour entrer dans le cours Le cours est au format.pdf lisible avec Acrobat
 Utilisation d informations visuelles dynamiques en asservissement visuel Armel Crétual IRISA, projet TEMIS puis VISTA L asservissement visuel géométrique Principe : Réalisation d une tâche robotique par
Utilisation d informations visuelles dynamiques en asservissement visuel Armel Crétual IRISA, projet TEMIS puis VISTA L asservissement visuel géométrique Principe : Réalisation d une tâche robotique par
Extraction et reconstruction de bâtiments en 3D à partir de relevés lidar aéroportés
 Thèse présentée pour obtenir le grade de Docteur de l Université Louis Pasteur Strasbourg I Discipline : Sciences pour l Ingénieur Spécialité : Topographie-Géomatique Par : Fayez TARSHA KURDI Extraction
Thèse présentée pour obtenir le grade de Docteur de l Université Louis Pasteur Strasbourg I Discipline : Sciences pour l Ingénieur Spécialité : Topographie-Géomatique Par : Fayez TARSHA KURDI Extraction
Document d accompagnement pour le référentiel national du C2i niveau 2 Métiers de l environnement et de l aménagement durables
 Document d accompagnement pour le référentiel national du C2i niveau 2 Métiers de l environnement et de l aménagement durables A - Compétences générales et transversales liées à l exercice des métiers
Document d accompagnement pour le référentiel national du C2i niveau 2 Métiers de l environnement et de l aménagement durables A - Compétences générales et transversales liées à l exercice des métiers
UE 4 Comptabilité et Audit. Le programme
 UE 4 Comptabilité et Audit Le programme Légende : Modifications de l arrêté du 8 mars 2010 Suppressions de l arrêté du 8 mars 2010 Partie inchangée par rapport au programme antérieur 1. Information comptable
UE 4 Comptabilité et Audit Le programme Légende : Modifications de l arrêté du 8 mars 2010 Suppressions de l arrêté du 8 mars 2010 Partie inchangée par rapport au programme antérieur 1. Information comptable
UE 503 L3 MIAGE. Initiation Réseau et Programmation Web La couche physique. A. Belaïd
 UE 503 L3 MIAGE Initiation Réseau et Programmation Web La couche physique A. Belaïd [email protected] http://www.loria.fr/~abelaid/ Année Universitaire 2011/2012 2 Le Modèle OSI La couche physique ou le
UE 503 L3 MIAGE Initiation Réseau et Programmation Web La couche physique A. Belaïd [email protected] http://www.loria.fr/~abelaid/ Année Universitaire 2011/2012 2 Le Modèle OSI La couche physique ou le
CAHIER DES CHARGES DE LA FORMATION OUVERTURE D ACTION. Certificat de Qualification Professionnelle des Services de l Automobile
 CAHIER DES CHARGES DE LA FORMATION OUVERTURE D ACTION Certificat de Qualification Professionnelle des Services de l Automobile A.N.F.A. Département Ingénierie et Compétences Mars 2013 SOMMAIRE INFORMATIONS
CAHIER DES CHARGES DE LA FORMATION OUVERTURE D ACTION Certificat de Qualification Professionnelle des Services de l Automobile A.N.F.A. Département Ingénierie et Compétences Mars 2013 SOMMAIRE INFORMATIONS
Chapitre 2 : Systèmes radio mobiles et concepts cellulaires
 Chapitre 2 : Systèmes radio mobiles et concepts cellulaires Systèmes cellulaires Réseaux cellulaires analogiques de 1ère génération : AMPS (USA), NMT(Scandinavie), TACS (RU)... Réseaux numériques de 2ème
Chapitre 2 : Systèmes radio mobiles et concepts cellulaires Systèmes cellulaires Réseaux cellulaires analogiques de 1ère génération : AMPS (USA), NMT(Scandinavie), TACS (RU)... Réseaux numériques de 2ème
Chapitre 2 : communications numériques.
 Chapitre 2 : communications numériques. 1) généralités sur les communications numériques. A) production d'un signal numérique : transformation d'un signal analogique en une suite d'éléments binaires notés
Chapitre 2 : communications numériques. 1) généralités sur les communications numériques. A) production d'un signal numérique : transformation d'un signal analogique en une suite d'éléments binaires notés
possibilités et limites des logiciels existants
 possibilités et limites des logiciels existants Dominique Groleau CERMA, UMR CNRS 1563, Ecole d Architecture de Nantes Journée thématique SFT- IBPSA, Outils de simulation thermo-aéraulique du bâtiment.
possibilités et limites des logiciels existants Dominique Groleau CERMA, UMR CNRS 1563, Ecole d Architecture de Nantes Journée thématique SFT- IBPSA, Outils de simulation thermo-aéraulique du bâtiment.
Projet CoDrive : utilisation des données de véhicules communicants, intégration avec un système de gestion de trafic (119)
 Projet CoDrive : utilisation des données de véhicules communicants, intégration avec un système de gestion de trafic (119) Résumé : La diffusion large des smartphones et des suivis dédiés de flottes de
Projet CoDrive : utilisation des données de véhicules communicants, intégration avec un système de gestion de trafic (119) Résumé : La diffusion large des smartphones et des suivis dédiés de flottes de
DIPLÔME INTERUNIVERSITAIRE D ECHOGRAPHIE. Examen du Tronc Commun sous forme de QCM. Janvier 2012 14 h à 16 h
 ANNEE UNIVERSITAIRE 2011-2012 DIPLÔME INTERUNIVERSITAIRE D ECHOGRAPHIE Examen du Tronc Commun sous forme de QCM Janvier 2012 14 h à 16 h Les modalités de contrôle se dérouleront cette année sous forme
ANNEE UNIVERSITAIRE 2011-2012 DIPLÔME INTERUNIVERSITAIRE D ECHOGRAPHIE Examen du Tronc Commun sous forme de QCM Janvier 2012 14 h à 16 h Les modalités de contrôle se dérouleront cette année sous forme
Fonctions de plusieurs variables
 Module : Analyse 03 Chapitre 00 : Fonctions de plusieurs variables Généralités et Rappels des notions topologiques dans : Qu est- ce que?: Mathématiquement, n étant un entier non nul, on définit comme
Module : Analyse 03 Chapitre 00 : Fonctions de plusieurs variables Généralités et Rappels des notions topologiques dans : Qu est- ce que?: Mathématiquement, n étant un entier non nul, on définit comme
Détection des points d intérêt et Segmentation des images RGB-D. Présentée par : Bilal Tawbe. Semaine de la recherche de l UQO
 Détection des points d intérêt et Segmentation des images RGB-D Présentée par : Bilal Tawbe Semaine de la recherche de l UQO 25 Mars 2015 1. Introduction Les méthodes de détection de points d intérêt ont
Détection des points d intérêt et Segmentation des images RGB-D Présentée par : Bilal Tawbe Semaine de la recherche de l UQO 25 Mars 2015 1. Introduction Les méthodes de détection de points d intérêt ont
Compte-rendu Réunion générale. Grenoble, le 29 juin 2011 URBASIS
 URBASIS Sismologie urbaine : évaluation de la vulnérabilité et des dommages sismiques par méthodes innovantes ANR09RISK009 URBASIS Compterendu Réunion générale Grenoble, le 29 juin 2011 Participants: J.
URBASIS Sismologie urbaine : évaluation de la vulnérabilité et des dommages sismiques par méthodes innovantes ANR09RISK009 URBASIS Compterendu Réunion générale Grenoble, le 29 juin 2011 Participants: J.
T.P. FLUENT. Cours Mécanique des Fluides. 24 février 2006 NAZIH MARZOUQY
 T.P. FLUENT Cours Mécanique des Fluides 24 février 2006 NAZIH MARZOUQY 2 Table des matières 1 Choc stationnaire dans un tube à choc 7 1.1 Introduction....................................... 7 1.2 Description.......................................
T.P. FLUENT Cours Mécanique des Fluides 24 février 2006 NAZIH MARZOUQY 2 Table des matières 1 Choc stationnaire dans un tube à choc 7 1.1 Introduction....................................... 7 1.2 Description.......................................
Partie Observer : Ondes et matière CHAP 04-ACT/DOC Analyse spectrale : Spectroscopies IR et RMN
 Partie Observer : Ondes et matière CHAP 04-ACT/DOC Analyse spectrale : Spectroscopies IR et RMN Objectifs : Exploiter un spectre infrarouge pour déterminer des groupes caractéristiques Relier un spectre
Partie Observer : Ondes et matière CHAP 04-ACT/DOC Analyse spectrale : Spectroscopies IR et RMN Objectifs : Exploiter un spectre infrarouge pour déterminer des groupes caractéristiques Relier un spectre
Chapitre 02. La lumière des étoiles. Exercices :
 Chapitre 02 La lumière des étoiles. I- Lumière monochromatique et lumière polychromatique. )- Expérience de Newton (642 727). 2)- Expérience avec la lumière émise par un Laser. 3)- Radiation et longueur
Chapitre 02 La lumière des étoiles. I- Lumière monochromatique et lumière polychromatique. )- Expérience de Newton (642 727). 2)- Expérience avec la lumière émise par un Laser. 3)- Radiation et longueur
