COO : Spécification du logiciel - OCL
|
|
|
- Véronique Beauchemin
- il y a 9 ans
- Total affichages :
Transcription
1 COO : Spécification du logiciel - OCL Philippe Collet Licence 3 parcours Informatique et MIAGE Septembre - Décembre 2012
2 Objectifs r Comprendre l activité de spécification logicielle r Apprendre la spécification par assertions r Comprendre la nécessité et la portée d OCL r Apprendre OCL et la manière de spécifier avec ce langage dans UML r Comprendre les techniques de vérification des assertions Ph. Collet 2
3 Plan r Introduction aux spécifications r Introduction à la spécification par assertions r OCL : première approche r Types et valeurs de base r Conception par contrats r Annexe OCL r Navigation dans les modèles r Autres éléments du langage r Collections Ph. Collet 3
4 Introduction aux spécifications r Spécification fonctionnelle : définition r Principaux formalismes de spécification r Notions autour de la spécification r Spécification en langage naturel r Tour rapide d autres techniques de spécifications «formelles» Ph. Collet 4
5 Spécification fonctionnelle r Définition : n définir ce que doit faire un logiciel... n avant d écrire ce logiciel! n => le quoi, sans le comment! r S oppose à implémentation, n comme le plan d un pont à sa construction. n Sauf... qu en informatique, plan et réalisation ne manipulent que de l écriture... Ph. Collet 5
6 Pourquoi spécifier? r Définir le travail de réalisation, avant de le faire... n la spécification est censée être moins coûteuse, plus rapide à obtenir r Comment vérifier la correction d un programme, n si l on ne sait pas ce qu il est censé faire... n la spécification est la référence pour toutes les activités de vérification et de validation (V&V) : u tests, preuves, mesures, inspections... r Obtenir une description stable, plus abstraite, moins dépendante des contingences du matériel, des systèmes, des fluctuations de l environnement. Ph. Collet 6
7 Qualités recherchées pour une spécification fonctionnelle r précision, non ambiguïté, non contradiction, r concision, abstraction, r complétude, r facilité d utilisation : écriture, lecture, vérification r réalisable avant l implémentation, r si possible à un coût réduit, r référence contractualisable, pour les litiges... Ph. Collet 7
8 Spécifications fonctionnelles vs extrafonctionnelles r En génie logiciel, on distingue : n spécification fonctionnelle : décrit le «fonctionnement» du logiciel, le quoi n spécification extrafonctionnelle (ou non fonctionnelle) : les conditions de fonctionnement, le comment r Dans le monde industriel, spécification sous-entend, spécifications techniques r En génie logiciel, par défaut spécification sous-entend spécification fonctionnelle r Les spécifications techniques du logiciel : coût, temps de réponse, performance, robustesse, capacité de charge, consommation de ressource, confort d utilisation, ergonomie... sont appelées : n qualités de service (QoS) n spécifications non fonctionnelles n spécifications extrafonctionnelles Ph. Collet 8
9 Principaux formalismes de spécification r Texte informel n En langage naturel (cahier des charges, commentaires) n éventuellement encadré par une méthode ou un formalisme graphique (contraintes UML) r Graphique n sauf exception (réseaux de Petri...) rarement très formel : (SADT, UML) n pas très précis, mais utile pour la synthèse et en complément r Semi-formel n Sans ambiguïté, leur expressivité est insuffisante pour établir une preuve, mais on peut souvent les tester : r Formel u techniques assertionnelles, spécification axiomatique n Sans ambiguïté, leur expressivité est suffisante pour tout décrire, donc pour établir des preuves, humaines («à la main») ou automatiques Ph. Collet 9
10 Spécification vs Implémentation r Spécification n décrit ce que doit faire le logiciel, si possible très tôt dans le processus logiciel, à un coût faible, indépendamment des «détails» : u type de machine, plate-forme, langage utilisé, conditions d utilisation, fréquences des primitives, représentation, formats... n Une spécification fonctionnelle doit se concentrer sur les fonctionnalités, sans considération de performance ou de qualités de services (spécifications extrafonctionnelles) r Implémentation n doit correspondre aux fonctionnalités décrites (idée de correction), n mais de manière efficace, performante, en tenant compte: u des conditions réelles ou prévues d utilisation : langage, spécificité du langage utilisé, fréquence d emploi des primitives fournies, volumes des données traitées... n des contraintes exprimées dans les spécifications extrafonctionnelles Ph. Collet 10
11 Spécification vs Implémentation (suite) r En simplifiant, r spécifier, c est définir n sans se soucier des contingences du monde réel... r implémenter, c est optimiser, réifier n c est tenir compte de la réalité... r Si l implémentation nécessite beaucoup de détails, l écart de niveaux d abstraction avec la spécification est grand, et cela nécessite des descriptions intermédiaires : n approches par raffinements successifs Ph. Collet 11
12 Spécification vs Implémentation (suite) r Relations d abstraction et de raffinement n Considérons une suite de n descriptions du même problème, à différents niveaux d abstraction, numérotées par niveau d abstraction décroissant : u desc1 desc2... descn n la desc1, de plus haut niveau d abstraction, u est la spécification, n la descn, de plus bas niveau d abstraction, u est l implémentation r Toutes les descriptions sont liées par deux relations : n abstraction : u desci = abstract(desci+1) desci desci+1 n raffinement : u desci = refine(desci 1) desci desci 1 r Il existe une théorie qui formalise ces relations : refinement calculus Ph. Collet 12
13 Spécification, Formalité et Exécutabilité r Deux sens au mot formel : 1. formel = non ambigu, précis, sans équivoque u syntaxe et sémantique précise, interprétable par une machine 2. formel = privilégie la forme au détriment du contenu u non ambigu et vérifiable, prouvable à la main ou automatiquement. r Exemple: (a + b)² = a² + 2ab + b² r formel n implique donc pas abstrait (sens 1), mais on confond souvent les deux mots (sens 2) r Exemple : n logique formelle, avec des formules, par opposition à logique philosophique, avec (beaucoup) de mots... (sens 2) n spécification (formelle) et implémentation sont formelles! (sens 1) u... puisque sans ambiguïté!!! Ph. Collet 13
14 Spécification, Formalité et Exécutabilité (suite) r Mais n un programme dans un langage de bas niveau se prête difficilement à des preuves, c est-à-dire à l établissement de propositions vraies pour toutes exécutions : n généralement, on teste un programme exécutable r Inversement, n une preuve théorique de spécification ne prouve pas que le logiciel décrit sera utilisable : n temps de réponse? ergonomie? adéquation aux besoins? r La frontière entre spécification et implémentation est assez floue et arbitraire et dépend des époques : n il y a quelques années, un texte en Prolog aurait été considéré comme une spécification abstraite exécutable Ph. Collet 14
15 Spécification fonctionnelle et correction r Qualité de correction n un logiciel est correct, si dans des conditions normales d utilisation, il se comporte comme cela est attendu par ses utilisateurs n Si la spécification traduit bien ce que veulent les utilisateurs, alors la correction revient à vérifier (prouver, tester) que l implémentation est conforme à sa spécification r Conséquences : n Pour vérifier la correction d une description, il faut une deuxième description : la redondance est indispensable à tout contrôle : preuve par neuf, contrôle de qualité, vérification des cartes perforées (autrefois)... n Comment vérifier la correction d une spécification? u l un des gros problèmes des spécifications formelles, lorsqu elles sont incompréhensibles aux commanditaires ou aux utilisateurs Ph. Collet 15
16 Utilisation des spécifications fonctionnelles r définition du travail d implémentation, n à un coût normalement inférieur : l équivalent des plans d un immeuble, d une machine, avant sa réalisation. n (sauf qu ici, spécification et implémentation, c est de l écriture!) r référence pour tout ce qui concerne les fonctionnalités du logiciel : n les documentations d utilisation, de maintenance, les tests externes, les preuves de correction... Ph. Collet 16
17 Spécification en langage naturel r Description en langage naturel (anglais, français...) : n de manière complètement libre, littéraire... n de manière très encadrée (structurée) par une méthode qui fournit un plan précis de ce qu il faut décrire n Exemples : normes de cahiers des charges (ISO 900x, IEEE 930), outils d aide à la documentation pour certains langages de programmation (Java, Eiffel) ou certains systèmes (Unix, Emacs...) r Utilisation d une syntaxe pour les aspects structurels, les signatures de méthodes... n importance de la phase de conception préalable r Utilisation de glossaires ou de dictionnaires de données (identificateurs...) n pour éviter d utiliser des mots voisins ou synonymes : utiliser au contraire un seul mot pour chaque concept r Règles de description et d abréviations n Exemple : un prédicat rend une valeur logique vraie ou faux, donc il suffit de décrire le cas vrai Ph. Collet 17
18 Exemple d une (mauvaise) spécification en langage naturel r Ce module gère une file d attente de transactions selon l ordre premier arrivé - premier servi (FIFO)... r La queue a au plus 500 transactions et est manipulée par les opérations suivantes : n déposer une transaction dans la file, à la fin, si c est possible, sinon envoyer le message d erreur déposer impossible. n retirer la première transaction de la file (la plus ancienne, en tête), si elle existe, sinon donner le message d erreur retirer impossible. n connaître à tout instant la longueur de la file. Ph. Collet 18
19 Avantages de la spécification en langage naturel r (en principe) utilisable et compréhensible par tous, en particulier le commanditaire r expressivité non limitée : tout concept peut se décrire en langage naturel, mathématique, philosophique, esthétique... r concision possible, par réutilisation de connaissances antérieures des lecteurs : il n est pas toujours nécessaire de tout dire! r toujours utile, doivent toujours accompagner les spécifications les plus formelles ou les textes des programmes (commentaire d en-tête, description résumée) Ph. Collet 19
20 Inconvénients de la spécification en langage naturel r non compréhensibles par des machines... n et parfois par des humains! r défauts fréquents : ambiguïté, silence, repentir, contradiction, sur-spécification, sous-spécification, changement de terminologie, description verbeuse, répétition, lourdeur de style, charabia, bruit, franglais,... r nécessité de relectures, qui peuvent être très coûteuses pour un résultat de qualité r utilité d une description formelle pour rectifier une description informelle Ph. Collet 20
21 Quelques défauts de l exemple de la file r Ce module gère une file d attente de transactions selon l ordre premier arrivé - premier servi (FIFO) r La queue a au plus 500 transactions et est manipulée par les opérations suivantes : n déposer une transaction dans la file, à la fin, si c est possible, sinon envoyer le message d erreur déposer impossible n retirer la première transaction de la file (la plus ancienne, en tête), si elle existe, sinon donner le message d erreur retirer impossible n permettre de connaître à tout instant la longueur de la file r Légende : n lourdeur de style, repentir, verbiage n sur-spécification n changement de terminologie Ph. Collet 21
22 Spécification structurée en langage naturel r La structure de l objet informatique (sa syntaxe) est donnée dans un formalisme précis (UML, langage de classe...). r La sémantique est donnée en langage naturel, mais avec des conventions d abréviations et en utilisant un dictionnaire de données (les identificateurs), r On évite des répétitions par les possibilités de factorisation de propriétés ou d opérations données : héritage multiple, généricité... r Les paramétrages (par généricité contrainte si possible) et les signatures précisent de manière claire les propriétés. r Le cadre syntaxique permet l usage d outils : hypertexte, présentation normalisée, dictionnaire / glossaire des identificateurs... Ph. Collet 22
23 Exemple en langage naturel structuré classe File < Element : Object > -- file bornée, protocole FIFO, deux extrémités tête et queue. héritage Conteneur < Element >, StructureBornée opérations File (n : Naturel) -- création d une file vide d au plus n éléments -- hérité de StructureBornée tête : Element -- prochain élément à retirer, si longueur > 0 queue : Element -- dernier élément déposé, si longueur > 0 déposer (e: Element) -- dépose e à la queue de self, si longueur < n retirer -- retire l élément situé en tête longueur : Naturel -- nb d éléments (hérité de Conteneur) vide : Booleen -- longueur > 0 (hérité de Conteneur) Ph. Collet 23
24 Autres techniques «formelles» r Techniques algébriques : n Clear, ASL, ACT1, Larch, OBj2, LPG, Pluss, Affirm, Reve, Asspegique... r Techniques orientées modèle abstrait : n opérationnelle : langages de haut niveau : CLU, Euclide, CAML, Prolog... n axiomatiques : Z, VDM, B n model-checking: logique temporelle, TLA, SMV, Spin, Kronos, etc r Techniques orientées lambda calcul : n théories des types r Techniques orientées logique ordre supérieur, treillis : n refinement calculus..., r Techniques orientées processus : n réseaux de Petri, CSP, CCS, arbres JSD... Ph. Collet 24
25 Exemple : spécification algébrique r Une technique très formelle et très abstraite, développée dans les années 1970 : chaque objet informatique est considéré comme une classe d algèbre. r La syntaxe des primitives est donnée par une signature, de manière fonctionnelle r La sémantique est donnée par des axiomes (équations ou prédicats) qui combinent les primitives de manière à obtenir des propositions vraies pour tout objet du type défini r Le temps est absent : les objets ne changent pas d état, mais toutes les primitives sont des fonctions qui rendent une valeur, éventuellement un nouvel état de l objet considéré r Une spécification algébrique est comme un dictionnaire, par exemple du chinois écrit en chinois : chaque mot est défini par une combinaison de signes, qui sont eux-même définis dans une entrée du dictionnaire. Ph. Collet 25
26 Spécification algébrique : primitives r On distingue trois sortes de primitives : n les générateurs qui permettent de construire tous les états possibles des objets du type n les accesseurs qui renseignent sur les objets du type, sans les modidier, n les modifieurs qui rendent un nouvel état de l objet r Les axiomes expriment toutes les propriétés pertinentes des accesseurs et des modifieurs pour tous les états possibles des objets n Ces états sont décrits par les générateurs, par induction structurale r Les cas d erreurs correspondent à des domaines de définition de fonctions partielles (équivalent des préconditions des langages d assertions) Ph. Collet 26
27 Spec. Algébrique d une file infinie type File <E> primitives -- générateurs créer : > File <E> déposer : File <E> E > File <E> -- accesseurs vide : File <E> > Booléen tête : File <E> / > E -- modifieurs retirer : File <E> / > File <E> préconditions f: File <E> (p1) retirer(f) requiert vide (f) (p2) tête(f) requiert vide (f) Ph. Collet 27
28 Spec. Algébrique d une file infinie (suite) axiomes e: E, f: File <E> (a1) vide(créer()) (a2) vide(déposer(f,e)) (a3) tête(déposer(créer(),e)) = e (a4) tête(déposer(f,e)) = tête(f) (a5) retirer(déposer(créer(),e)) = créer() (a6) retirer(déposer(f,e)) = déposer(retirer(f),e) Ph. Collet 28
29 Spécification algébrique : bilan de la spec. r Avantages n concise, précise, élégante, abstraite... n autonome, ne dépend d aucune autre spécification, n exhibe les primitives usuelles de manipulation r Inconvénients n n explicite pas deux propriétés cachées incontournables des files : nombre d éléments, accès à la valeur de chaque élément u mais on peut le faire... n ne fait pas apparaître de relation d héritage n pas de commentaires en langage naturel : u on doit le faire (absents sur transparents) n séparation des informations qui marchent ensemble : u syntaxe, sémantique, commentaire... Ph. Collet 29
30 Bilan global sur les spécifications algébriques r Comme en programmation, il y a plusieurs manières possibles de spécifier le même problème... r La spécification algébrique est une technique orientée programmation fonctionnelle, peu adaptée au monde objet n L héritage ne marche pas bien pour les axiomes r Possibilité de généricité et d importation d autres spécifications comme dans la programmation modulaire classique (Java 5) r Exigence de définition complète : forme un tout, pas de définition incrémentale de la conception d un logiciel r Outils d aide : vérification syntaxique, complétude, absence de contradiction, prouveurs de théorème n mais il faut les aider, et plutôt lents... r Conformité du code? preuves de théorèmes et une adaptation nécessaire aux différents langages r Accessibilité aux programmeurs? n difficulté de construction et de compréhension par la majorité des programmeurs, et en cas de logiciel nécessitant des milliers d axiomes Ph. Collet 30
31 Bilan : Avantages des techniques formelles r Formalité : n propriétés établies par raisonnement formel : argumentation stricte, non intuitive n contradictions et incomplétudes révélées avant l implémentation n outils de preuve calculent et vérifient (semi-) automatiquement, r Précision : n meilleure compréhension n définition de référence pour l implémenteur r Abstraction : n concision n description plus stable, indépendante des techniques d implémentation, plus réutilisable Ph. Collet 31
32 Bilan : inconvénients des techniques formelles r Difficultés : n manque de lisibilité n aptitudes mathématiques nécessaires n erreurs possibles, si preuves humaines r Manque de maturité : n nombreux formalismes, même si quelques standards existent n outils de preuves insuffisants et malaisés n manque de structuration, héritage absent, généricité difficile r Domaines d application restreints n généralement inadéquates pour d autres domaines r Les spécifications formelles sont quand même indispensables pour les logiciels où la fiabilité est critique Ph. Collet 32
33 Introduction à la spécification par assertions r Historique r Principes r Accesseurs et modifieurs r Illustration r Invariant Ph. Collet 33
34 Spécification par assertions r Introduites par Floyd (1967) et Hoare (1969), les assertions servaient au début pour annoter les programmes en vue d en établir la preuve de correction (preuve de programme) n C était donc des commentaires formels r Les assertions définissent le comportement d un programme par des formules logiques qui caractérisent, de manière pertinente et synthétique, les états successifs de toute exécution r Pouvant référencer des états, cette technique s oppose aux techniques formelles purement fonctionnelles, comme le lambda-calcul Ph. Collet 34
35 Principes de spécification r Comme pour toute spécification formelle, une assertion est utilement redondante avec : n les textes en langages naturels : résumé, commentaire, libellé... n le code exécutable : instructions d un programmes pour l exécuter, comprises par un compilateur, un interprète ou une machine. r Les assertions peuvent fournir une spécification complète ou partielle d un programme. n Elles peuvent être données de manière incrémentale, au cours d un processus logiciel. Ph. Collet 35
36 Eléments de syntaxe r Une assertion est placée à un endroit caractéristique du moment où elle doit être vraie, et introduite par un mot réservé: n pre:, post:, inv:, etc. r Elle est composée d une ou plusieurs clauses, chacune étant reliée aux autres par une conjonction implicite (and). r Chaque clause est une proposition logique r Chaque type d assertions a un rôle, afin de n Faciliter la conception des classes n Raisonner sous forme de contrats Ph. Collet 36
37 Termes d une assertion r Les termes des formules logiques ne sont pas nécessairement liés à des états des variables d un programme. r Elles peuvent donc exprimer une grande variété de propriétés... r Exemple d assertions intégrées au langage de programmation : class Account... deposit (sum: Integer ) -- deposit sum into the account pre: truedeposit: sum >= 0 post: balance = balance@pre + sum Ph. Collet 37
38 Termes d une assertion (suite) r Exemple de vue concrète (boîte blanche) : class Account... deposit (sum: Integer ) -- deposit sum into the account pre: truedeposit: sum >= 0 body: balance := balance + sum post: balance = balance@pre + sum Ph. Collet 38
39 Assertions dans les langages r Par nature, les assertions sont associées aux descriptions d un logiciel : n schémas de conception, textes des programmes r Elles peuvent être : n intégrées au langage et aux descriptions : u clause assert : C, C++, Ada; assertions d Eiffel u D où code autonome, autodocumenté, autovérifiable, autotestable n définies dans un langage compagnon, mais séparées des descriptions : u contraintes en langage OCL pour UML, assertions pour plates-formes de composants n proposées en extension d un langage, placées en commentaire : u assertions pour Java : JML, icontract... r NB: concilier expressivité, efficacité des techniques de vérification et performance de l évaluation des assertions est encore un problème de recherche Ph. Collet 39
40 Redondance des assertions r Comme pour toute spécification formelle, une assertion est utilement redondante avec : n les textes en langages naturels : résumé, commentaire, libellé... n le code exécutable : instructions d un programmes pour l exécuter, comprises par un compilateur, un interprète ou une machine. r Les assertions peuvent fournir une spécification complète ou partielle d un programme r Elles peuvent être données de manière incrémentale, au cours d un processus logiciel Ph. Collet 40
41 Vérification des assertions r Ces propriétés peuvent se vérifier par : n des relectures ou des inspections n des preuves «à la main» (avec sa tête) n des tests, lorsqu elles sont exécutables en un temps acceptable u plus il y a de quantifications universelles ou existentielles, de parcours de collections, plus cela est coûteux! r Des assertions exécutables n Les langages qui intègrent des assertions exécutables fournissent u des mécanismes d armement sélectifs (problème du ralentissement de l exécution) : quelles assertions évaluer, pour quels objets ou classes, en fonction de leur catégorie et du degré de confiance dans les composants d un logiciel u des moyens de traitement en cas de violation : déclenchement d une exception, par défaut un diagnostic, possibilité de «programmation défensive» Ph. Collet 41
42 Utilisation des assertions r Technique de spécification : n formelle, partielle, incrémentale r Conception et programmation par contrats : n établissement clair des responsabilités entre les clients et les programmeurs, utilisation dès la conception (OCL) r Aide à la fiabilité : n pour la correction vs exceptions pour la robustesse r Technique de preuve : n méthode axiomatique de Hoare, Dijkstra, Morgan, Gries, refinement calculus... r Plus précis que le typage classique : n héritage des invariants, règles de redéfinitions covariantes, contraintes d intégrité... r Aide à la maintenance et aux autotests : n non régression, diagnostic, localisation des erreurs... r Aide à la documentation, à la réutilisation : n Compléments lisibles des descriptions en langage naturel, documentation testable en accord avec la réalité du code Ph. Collet 42
43 Clause d une assertion (pas forcément OCL) r Chaque clause est une proposition logique formée : n de connecteurs logiques (not, and, or, xor, implies) n d opérateurs booléens (=, <>, <,, etc) n de valeurs littérales, de constantes symboliques, d attributs n et d appels de fonctions sans effet de bord r Exemple : x > 0 and premier(x) implies 0 <= result <= y r Chaque clause peut être introduite par un label (identificateur) n qui rappelle de manière brève l intention, la propriété énoncée par la clause n Cela sert aussi à identifier les formules dans les diagnostics en cas de violation n En l absence de label, les clauses sont numérotées Ph. Collet 43
44 Rôle des assertions r Préconditions n doivent être vraies juste avant chaque appel de la méthode. n expriment les conditions ou hypothèses à satisfaire pour que le développeur sache implémenter la méthode. r Postconditions n doivent être vraies juste après chaque sortie de la méthode. n définissent l essentiel : u du travail réalisé sur l instance ou un système : cas d un modifieur, générateur, initialiseur u ou du résultat retourné : cas d un accesseur secondaire n si elles sont assez précises, elles peuvent spécifier complétementou partiellement une primitive. Ph. Collet 44
45 Exemple : classe Account class Account feature balance: Integer -- attribut, accesseur primaire minbalance: Integer = constante, accesseur primaire creation initial (sum: Integer ) -- initialize account with balance sum pre: sufficientdeposit: sum >= minbalance post: balance = sum Ph. Collet 45
46 Accesseurs primaires et secondaires r Accesseur primaire n permet d accéder aux états ou aux constantes des objets, n n a pas de précondition, la plupart du temps n ne peut se définir explicitement, mais leur définition implicite apparaît dans leur utilisation dans les autres assertions, n est implémenté par des variables, attributs, constantes, fonctions. r Accesseur secondaire n définit des valeurs, à partir d autres valeurs ou états : u services de confort, prédicats... n peut être défini explicitement par une postcondition sur la valeur retournée Ph. Collet 46
47 Accesseur secondaire : classe Account -- toujours dans la classe Account maywithdraw (sum: Integer): Boolean -- is account supplied enough to withdraw sum? pre: truewithdraw: sum >= 0 body: Result := balance >= sum + minbalance post: Result = (balance >= sum + minbalance) Ph. Collet 47
48 Constructions spécifiques aux langages d assertions r Constructions sans effet de bord n l évaluation des assertions ne doit avoir aucun effet de bord n chaque accesseur secondaire (fonction) ne doit avoir aucun effet de bord sur l état abstrait d un objet, visible à ses clients publiques et décrit par les accesseurs primaires n chaque accesseur secondaire peut avoir un effet de bord sur l état concret, privé, pour améliorer les performances : accélérateurs de primitives d accès, caches r Accès aux valeurs antérieures n Distinguent l état d une variable/expression à l entrée et à la sortie d une méthode n Etat à la sortie : pas de notation particulière n Etat à l entrée : indiqué par un opérateur spécial en OCL i = i@pre +1 Ph. Collet 48
49 Utilisation : classe Account deposit (sum: Integer ) -- deposit sum into the account pre: truedeposit: sum >= 0 body: move ( sum ) post: balance = balance@pre + sum withdraw (sum: Integer ) -- withdraw sum from the account pre: truewithdraw: sum >= 0 suppliedenough: maywithdraw(sum) body: move ( -sum ) post: balance = balance@pre sum move (sum: Integer) -- private body: balance := balance + sum post: balance = balance@pre + sum Ph. Collet 49
50 Invariants r Chaque instance est susceptible de passer par un grand nombre d états observables, lors des périodes de stabilité de l instance : n pas d initialiseur ou de modifieur actif r Un invariant d instance exprime une propriété remarquable, vraie pour tous ses instants stables et observables. r Un invariant d instance doit donc être vrai juste après : n chaque primitives d initialisation, n chaque modifieur exporté r Donc, pour chaque initialiseur/constructeur ou modifieur : postcondition => invariant r Et chaque précondition, sauf pour les constructeurs, requiert l invariant. r Exemple: classe Account inv: balance >= minbalance Ph. Collet 50
51 OCL : 1 ère partie r Introduction n OCL et UML n Motivations n OCL : principes et forme du langage r OCL : première approche n Contraintes et contexte n Commentaires n Stéréotypes et mots-clés pour structurer les spécifications n Types de spécification r Types et valeurs de base n Types du modèle n Règles de précédence n Enumérations n Conformance de type Ph. Collet 51
52 OCL et UML r UML est un langage de modélisation essentiellement graphique. r Dans les diagrammes il est difficile, voire impossible dans certains cas, de préciser de manière complète toutes les subtilités d'un modèle. Ph. Collet 52
53 OCL et UML r Contourner le problème? n écrire des spécifications plus complètes en langue naturelle n inconvénient : des ambiguïtés restent possibles r l'utilisation d'un langage formel avec une sémantique connue s'impose! r OCL est une réponse à ces attentes n un langage formel n pour annoter les diagrammes UML n permettant notamment l'expression de contraintes Ph. Collet 53
54 OCL : objectifs r Accompagner les diagrammes UML de descriptions : n précises n non ambiguës r Eviter les désavantages des langages formels traditionnels n peu utilisables par les utilisateurs et les concepteurs non «matheux» r Rester facile à écrire n Tout en étant orienté objet r Et facile à lire Ph. Collet 54
55 Petit historique r OCL s'inspire de Syntropy n méthode basée sur une combinaison d'omt (Object Modeling Technique) et d'un sous-ensemble de Z. r Origine n OCL a été développé à partie de 95 par Jos Warmer (IBM) n sur les bases du langage IBEL (Integrated Business Engineering Language). r Première définition : IBM, 1997 r Formellement intégré à UML 1.1 en 1999 r OCL2.0 intégré dans la définition d UML2.0 en 2003 n conforme à UML 2 et au MOF 2.0 n fait partie du catalogue de spécifications de l'omg n chapitres 7 (OCL Language Description) et 11 (OCL Standard Library) Ph. Collet 55
56 Bibliographie r Steve Cook, John Daniels, Designing Object Systems: Object- Oriented Modelling with Syntropy, Prentice Hall, 1994 r Pierre-Alain Muller, Nathalie Gaertner, Modélisation objet avec UML, Eyrolles, 2000 r OMG (Object Management Group), "Uml 2.0 ocl specification. Technical report, Object Management Group, ptc/ «r OMG (Object Management Group), "Uml 2.0 superstructure specification. Technical report, Object Management Group, ptc/ " Ph. Collet 56
57 OCL : principes r La notion de contrainte n Définition : Une contrainte est une expression à valeur booléenne que l'on peut attacher à n'importe quel élément UML n Elle indique en général une restriction ou donne des informations complémentaires sur un modèle r OCL : Langage typé, basé sur n La théorie des ensembles n La logique des prédicats r OCL : Langage déclaratif n Les contraintes ne sont pas opérationnelles. u On ne peut pas invoquer de processus ni d'opérations autres que des requêtes u On ne décrit pas le comportement à adopter si une contrainte n'est pas respectée r OCL : Langage sans effet de bord n Les instances ne sont pas modifiées par les contraintes Ph. Collet 57
58 Utilisation des contraintes r Description d'invariants sur les classes et les types r Préconditions et postconditions sur les opérations r Contraintes sur la valeur retournée par une opération r Règles de dérivation des attributs r Description de cibles pour les messages et les actions r Expression des gardes n conditions dans les diagrammes dynamiques r Invariants de type pour les stéréotypes n Les contraintes servent en particulier à décrire la sémantique d'uml. Ph. Collet 58
59 Contraintes et contexte r Une contrainte OCL est liée à un contexte : n le type, n la méthode n ou l'attribut auquel la contrainte se rapporte r Exemple : context moncontexte <stéréotype> : Expression de la contrainte context Personne inv : (age <= 140) and (age >=0) -- l'âge ne peut dépasser 140 ans -- : commentaire en OCL (qui s'achève avec la fin de la ligne) Ph. Collet 59
60 Contexte et package r Si les contraintes sont placées sans ambiguïté, pas besoin de plus r Si elles sont dans un fichier global, il faut spécifier le package dans lequel les contraintes se placent package Package::SubPackage context X inv:... un invariant... context X::operationName(..) pre:... une precondition... endpackage Ph. Collet 60
61 Contraintes : les stéréotypes r Le stéréotype peut prendre les valeurs suivantes : n inv invariant de classe n Un invariant exprime une contrainte prédicative sur un objet, ou un groupe d objets, qui doit être respectée en permanence context Personne inv : (age <= 140) and (age >=0) n pre précondition n post postcondition n Une précondition (respectivement une postcondition) permet de spécifier une contrainte prédicative qui doit être vérifiée avant (respectivement après) l appel d une opération context Personne::setAge(a : integer) pre: (a <= 140) and (a >=0) and (a >= age) post: age = a Ph. Collet 61
62 Contraintes : les stéréotypes (suite) n body indique le résultat d'une opération query n Ce type de contrainte permet de définir directement le résultat d une opération context Personne::getAge() : integer body: age n init indique la valeur initiale d'un attribut context Personne::age : integer init: 0 n derive indique la valeur dérivée d'un attribut context Personne::majeur : boolean derive: age>=18 Ph. Collet 62
63 Contraintes : version visuelle r Une version alternative, graphique n un commentaire dans le diagramme UML. r Le contexte est l'élément UML auquel se rattache le commentaire contenant la contrainte r Les outils UML permettent aussi la saisie de contraintes dans les «propriétés» de l élément UML n Cela définit automatiquement le contexte Ph. Collet 63
64 Contrainte nommée / label r Une contrainte peut être nommée par un label r Utilité n Rappeler la contrainte dans une autre contrainte n Retrouver une contrainte en cas d évaluation dans un outil, de production de code de vérification, etc. r Exemple : n Reprise de la contrainte, nommée «ageborné» context Personne inv ageborné: (age <= 140) and (age >=0) -- l'âge ne peut depasser 140 ans Ph. Collet 64
65 Référence, nommage des objets r Le mot-clef «self» permet de désigner l'objet à partir duquel part l'évaluation n Exemple : context Personne inv: (self.age <= 140) and (self.age >=0) -- l'âge ne peut depasser 140 ans n Caractère «.» : accès à l attribut (cf. navigation) r Un nom formel peut être donné à l'objet à partir duquel part l'évaluation n Exemple : context p : Personne inv: (p.age <= 140) and (p.age >=0) -- l'age ne peut depasser 140 ans Ph. Collet 65
66 Exercice r Ajoutez un attribut mère de type Personne dans la classe Personne. r Ecrivez une contrainte précisant n que la mère d'une personne ne peut être cette personne elle-même n et que l'âge de la mère doit être supérieur à celui de la personne context Personne inv: self.mere <> self and self.mere.age > self.age Ph. Collet 66
67 Types : hiérarchie r Organisation des types dans une hiérarchie n Des types de base, des collections, des éléments réflexifs sur le typage et certains éléments du langage Ph. Collet 67
68 Types r Les types de base prédéfinis : n Entier n Réel n String n Booléen r Des types spéciaux s'y ajoutent : n OclModelElement (énumération des éléments du modèle) n OclType (énumération des types du modèle) n OclAny (tout type autre que Tuple et Collection) n OclState (pour les diagrammes d'états) n OclVoid sous-type de tous les types Ph. Collet 68
69 Types de base r Le type entier (Integer) n Les constantes littérales s'écrivent de manière ordinaire : u n Les opérateurs sont les suivants : u = <> + - * / abs div mod max min < > <= >= n L'opérateur - est unaire ou binaire r Le type réel (Real) n Les constantes s'écrivent de manière ordinaire : u n Les opérateurs sont les suivants : u = <> + - * / abs floor round max min < > <= >= n L'opérateur - est unaire ou binaire Ph. Collet 69
70 Types de base r Le type chaîne de caractères (String) n Les constantes s'écrivent entre simples quotes : u 'ceci est une chaîne OCL' n Les opérateurs sont (notamment) les suivants : u = u size u concat(string) u toupper u tolower u substring(entier, Entier) Ph. Collet 70
71 Types de base r Le type booléen (Boolean) n Les constantes s'écrivent u true u false n Les opérateurs sont les suivants : u = or xor and not u b1 implies b2 u if b then expression1 else expression2 endif Ph. Collet 71
72 Exercice r Avec la classe Personne «étendue» n Indiquez qu une personne mariée est forcément majeur context Personne inv: marié implies majeur n Trouvez une version plus compacte de l expression suivante context Personne inv majeurif: if age >=18 then majeur=vrai else majeur=faux endif context Personne inv: majeur = age >= 18 Ph. Collet 72
73 Précédence des opérateurs n. -> n not - unaire n * / n + - n if then else n < > <= >= n <> = n and or xor n implies Ph. Collet 73
74 Types énumérés r Leur syntaxe est la suivante n <nom_type_enuméré>::valeur r Le nom du type est déduit de l attribut de déclaration n catégorie => Catégorie r Exemple : context Personne inv: if age <=12 then categorie = Categorie::enfant else if age <=18 then categorie = Categorie::ado else categorie = Categorie::adulte endif endif Ph. Collet 74
75 Type des modèles r Les types des modèles utilisables en OCL sont n les classifieurs, donc n les classes, les interfaces et les associations r Manipulation de la relation de spécialisation n oclastype(t) (conversion ascendante ou descendante de type vers t) u la conversion ascendante sert pour l'accès à une propriété redéfinie n oclistypeof(t) (vrai si t est supertype direct) n ocliskindof(t) (vrai si t est supertype indirect) p = r p.oclastype(rectangle) r.oclistypeof(rectangle) (vrai) r.ocliskindof(polygone) (vrai) Ph. Collet 75
76 (mauvais) exercice r En supposant l'existence n d'un attribut hauteur dans la classe Rectangle n d'une méthode hauteur():réel dans Polygone r Ecrivez un invariant dans Polygone disant que le résultat de hauteur():réel vaut hauteur pour les polygones qui sont des rectangles, sinon 0 context p : Polygone::hauteur() inv: if p.ocliskindof(rectangle) then result=p.oclastype(rectangle).hauteur else result=0 endif r Ceci un exemple de très mauvaise conception objet! Ph. Collet 76
77 2 ème partie r Navigation dans les modèles n Accès aux attributs, opérations n Navigations sur les associations n Navigations sur les classes-association r Autres éléments du langage n Structures let et def n if n result n Types OCL avancés r Collections n Hiérarchie n Opérations spécifiques n Opérations collectives n Conformance de type r Exploitation d OCL Ph. Collet 77
78 Navigation : accès aux attributs r Pour faire référence à un attribut de l objet désigné par le contexte, il suffit d utiliser le nom de cet élément context Personne inv: age r L objet désigné par le contexte est également accessible par l expression self n On peut donc également utiliser la notation pointée context Personne inv: self.age Ph. Collet 78
79 Navigation : accès aux attributs r L'accès (navigation) vers un attribut s'effectue en mentionnant l'attribut derrière l'opérateur d'accès noté '.' context Voiture inv propriétairemajeur : self.propriétaire.age >= 18 context Voiture inv propriétairemajeur : propriétaire.age >= 18 context v : Voiture inv propriétairemajeur : v.propriétaire.age >= 18 Ph. Collet 79
80 Exercice r Ecrivez la contrainte qui caractérise l'attribut dérivé cartevermeil n Un voyageur a droit à la carte vermeil si c'est une femme de plus de 60 ans ou un homme de plus de 65 ans. context Voyageur inv : cartevermeil = ((age >= 65) or ((sexe = Sexe::féminin) and (age >= 60)) ) -- Cette contrainte peut également s'écrire avec derive. Ph. Collet 80
81 Accès aux opérations r notation identique à la notation utilisée pour l'accès aux attributs (utilisation du '.') context Voiture inv : self.propriétaire.getage() >= 18 context Personne inv : getage() Seules les opérations de type query peuvent apparaître dans les contraintes puisqu'elles ne modifient pas l'objet sur lequel porte la contrainte n Les contraintes n'ont pas d'effet de bord Ph. Collet 81
82 Naviguer via les associations r La navigation le long des associations se fait en utilisant : n soit les noms de rôles n soit les noms des classes extrémités en mettant leur première lettre en minuscule, à condition qu'il n'y ait pas ambiguïté context Voiture inv : self.propriétaire.age >= 18 context Voiture inv : self.personne.age >= 18 r Que faudrait-il pour qu il y ait ambiguïté sur cet exemple? Ph. Collet 82
83 Naviguer via les associations - typage r Le type du résultat dépend n de la multiplicité du côté de l objet référencé n du type de l objet référencé r Si on appelle X la classe de l objet référencé, dans le cas d une multiplicité de : n 1, le type du résultat est X n * ou 0..n,, le type du résultat est Set(X) n * ou 0..n,, et s il y a en plus une contrainte {ordered}, le type du résultat est OrderedSet(X) r On y reviendra Ph. Collet 83
84 Navigation - ambiguïtés context C1 inv : c2.attr2=c2.c3.attr3 context C2 inv : attr2=c3.attr3 r Les deux contraintes ci-dessus sont-elles équivalentes? NON : la première dit que pour des instances de C2 et C3 liées avec une instance de C1, les attributs attr2 et attr3 sont égaux, mais n'impose rien à des instances de C2 et C3 non liées à une instance de C1 (et il y en a à cause de la multiplicité). La deuxième dit que pour tout couple d'instances de C2 et C3 liées, ces deux attributs sont égaux. Ph. Collet 84
85 Navigation via une association qualifiée r Une association qualifiée utilise un ou plusieurs qualificatifs pour sélectionner des instances de la classe cible de l association. n En OCL : utilisation de [ ] r Dans le contexte de banque (context Banque) on fait référence au nom des clients dont le compte porte le numéro : self.client[ ].nom r Dans le cas où il y a plusieurs qualificatifs, il faut séparer chacune des valeurs par une virgule en respectant l ordre des qualificatifs du diagramme UML. r Il n est pas possible de ne préciser la valeur que de certains qualificatifs en en laissant d autres non définis. r Par contre, il est possible de ne préciser aucune valeur de qualificatif : self.client.nom r le résultat sera l ensemble des noms de tous les clients de la banque Attention à la cardinalité de la cible Ph. Collet 85
86 Navigation et classes association r Pour naviguer vers une classe association, on utilise le nom de la classe (en mettant le premier caractère en minuscule). context p : Personne inv : p.contrat.salaire >= 0 r Une autre manière de naviguer consiste à utiliser le nom de rôle opposé (c'est même obligatoire pour une association réflexive) context p : Personne inv : p.contrat[employeur].salaire >= 0 Ph. Collet 86
87 Exercice r Depuis une instance p de la classe Personne 1. Comment naviguer vers l objet Encadrement de son responsable? 2. Comment naviguer vers l objet Encadrement de son agentsecrétariat? context p : Personne p.encadrement[responsable] -- 1 p.encadrement[agentsecrétariat] -- 2 Ph. Collet 87
88 Navigation et classes association (suite) r Pour naviguer depuis une classe association, on utilise les noms des rôles n ou s'il n'y en a pas le nom de la classe concernée avec la première lettre en minuscule n La navigation depuis une classe association vers un rôle ne peut donner qu'un objet. context c:contrat inv : c.employé.age >= 16 Ph. Collet 88
89 Exercice r Le salaire d'un agent de secrétariat est inférieur à celui de son responsable? r Un agent de secrétariat a un type de contrat agentadministratif (String)? context e : encadrement inv : e.responsable.contrat.salaire >= e.agentsecrétariat.contrat.sal aire context e : encadrement inv : e.agentsecrétariat.contrat.typecontrat='agentadministratif' Ph. Collet 89
90 Exercice De l aide? Un diagramme d objets r Un agent de secrétariat a une date d'embauche antérieure à la date de début de l'encadrement (on suppose que les dates sont des entiers) context e : Encadrement inv : e.agentsecrétariat.contrat.dateembauche <= e.datedebut r Même chose dans le contexte de la classe Personne context p : Personne inv : p.agentsecrétariat.contrat.dateembauche <= p.encadrement[agentsecrétariat].datedebut Ph. Collet 90
91 Structure let r On peut définir des variables pour simplifier l'écriture de certaines expressions. On utilise pour cela la syntaxe suivante : let variable : type = expression1 in expression2 r Exemple : n en ajoutant l'attribut dérivé impot dans Personne, n on pourrait écrire la contrainte suivante pour définir cet attribut context Personne inv : let montantimposable : Real = contrat.salaire*0.8 in if (montantimposable >= ) then impot = montantimposable*45/100 else if (montantimposable >= 50000) then impot = montantimposable*30/100 else impot = montantimposable*10/100 endif endif n il serait plus correct de vérifier tout d'abord que contrat est valué Ph. Collet 91
92 Structure def r Si on veut définir une variable utilisable dans plusieurs contraintes de la classe, on peut utiliser la construction def : r Exemple : montant imposable context Personne def : montantimposable : Real = contrat.salaire*0.8 r Lorsqu'il est utile de définir de nouvelles opérations, on peut procéder avec la même construction def r Exemple : agecorrect context Personne def : agecorrect(a : Real ):Booléen = a>=0 and a<=140 Ph. Collet 92
93 Désignation de la valeur antérieure r Dans une post-condition, il est utile de pouvoir désigner la valeur d'une propriété avant l'exécution de l'opération n Nous faisons de la spécification par état n Nous décrivons donc les modifications d état en exprimant les différences avant et après (l appel d une opération) r Ceci se fait en suffixant le nom de la propriété n Exemple : context Personne :: feteanniversaire() pre : age < 140 post :age = + 1 Ph. Collet 93
94 Désignation du résultat d une opération r L'objet retourné par une opération est désigné par result r Exemple : n Une manière de décrire la post-condition de l'opération getage vous est indiquée ci-dessous. context Personne :: getage() : integer post : result = age r Lorsque la postcondition se résume à décrire la valeur du résultat, c'est équivalent à l'utilisation de la construction body Ph. Collet 94
95 Exercice r Imaginez une classe Etudiant, disposant de 3 notes et munie d'une opération mention qui retourne la mention de l'étudiant sous forme d'une chaîne de caractères. r Ecrivez les contraintes en utilisant let et result pour écrire la postcondition de mention context Etudiant :: mention() : String post: let moyenne : Real =(note1+note2+note3)/3 in if (moyenne >= 16) then result='très bien' else if (moyenne >= 14) then result='bien' else result='moins bien' endif endif Ph. Collet 95
96 Types OCL avancés r OclInvalid n Type conforme à tous les autres qui ne contient que la valeur invalid (ex : résultat d'une division par 0). r OclVoid n Type conforme à tous les autres qui ne contient que la valeur null (pas de référence). r Tout appel d'opération appliqué à null produit invalid. r null ou invalid = valeur indéfinie n en général, une expression dont une partie s'évalue à indéfini est elle-même indéfinie. n cas particuliers des booléens : true or indéfini = true r OclAny n Super-type de tous les types d'ocl, propose des opérations qui s'appliquent à tout objet Ph. Collet 96
97 Collections : hiérarchie r Cinq types de collections existant en OCL n Collection est un type abstrait n Set correspond à la notion mathématique d'ensemble n OrderedSet correspond à la notion mathématique d'ensemble ordonné n Bag correspond à la notion mathématique de famille (un élément peut y apparaître plusieurs fois) n Sequence correspond à la notion mathématique de famille, et les éléments sont, de plus, ordonnés Ph. Collet 97
98 Collections : litéraux r On peut définir des collections par des littéraux de la manière suivante. n Set { 2, 4, 6, 8 } n OrderedSet { 2, 4, 6, 8 } n Bag { 2, 4, 4, 6, 6, 8 } n Sequence { 'le', 'chat', 'boit', 'le', 'lait' } n Sequence { } spécification d'un intervalle d'entiers r Les collections peuvent avoir plusieurs niveaux, il est possible de définir des collections de collections, par exemple : n Set { 2, 4, Set {6, 8 }} Ph. Collet 98
99 Retour sur les navigations r On obtient naturellement un Set en naviguant le long d'une association ordinaire n ne mentionnant pas les contraintes bag ni seq à l'une de ses extrémités r Dans le contexte Texte n l'expression self.occurence est un Set n l'expression self.occurrence.mot est un Bag Ph. Collet 99
100 Retour sur les navigations r On peut obtenir un ensemble ordonné en naviguant vers une extrémité d'association munie de la contrainte ordered r Dans le contexte FileAttente n l expression personne est un OrderedSet r On peut obtenir une séquence en naviguant vers une extrémité d'association munie de la contrainte seq r Dans le contexte Texte n l'expression self.mot est une Sequence Ph. Collet 100
101 Opérations sur collection r Nous présentons les principales opérations applicables à toutes les collections n Pour une liste plus exhaustive, voir l annexe r Nous considérons des collections d'éléments de type T n Les opérations sur une collection sont mentionnées avec la flèche formée de deux caractères -> r Itérateurs n Les opérations qui prennent une expression comme paramètre peuvent déclarer optionnellement un itérateur n toute opération de la forme operation(expression) existe également sous deux formes plus complexes. u operation(v expression-contenant-v) u operation(v : Type expression-contenant-v) Ph. Collet 101
102 Opérations sur toutes types de collection r Deux opérations permettent de tester si la collection est vide ou non r Elles servent en particulier à tester l'existence d'un lien dans une association dont la multiplicité inclut 0 isempty() : Boolean notempty : Boolean r Exemple : n Retour sur la contrainte de cohérence de la date d embauche n nous pouvons à présent l'écrire de manière plus précise, en vérifiant que la personne a bien un agent de secrétariat context p : Personne inv : p.agentsecretariat->notempty() implies p.agentsecrétariat.contrat.dateembauche <= p.encadrement[agentsecrétariat].datedebut Ph. Collet 102
103 Opérations sur toutes types de collection r Taille d'une collection size() : integer r Nombre d'occurrences d'un objet dans une collection count(unobjet : T) : integer r Addition des éléments de la collection n Il faut que le type T supporte une opération + associative sum() : T r Appartenance d'un élément à la collection n Deux opérations retournent vrai (resp. faux) si et seulement si un certain objet est (resp. n'est pas) un élément de la collection includes(unobjet : T) : Boolean excludes(o : T) : Boolean Ph. Collet 103
104 Opérations sur toutes types de collection r Appartenance des éléments d'une collection à la collection n Deux opérations retournent vrai (resp. faux) si et seulement si la collection contient tous les (resp. ne contient aucun des) éléments d'une certaine collection passée en paramètre includesall(unecollection : Collection(T)) : Boolean excludesall(unecollection : Collection(T)) : Boolean r Vérification d'une propriété pour tous les éléments d'une collection n Une opération permet de vérifier qu'une certaine expression passée en paramètre est vraie pour tous les éléments de la collection forall(uneexpression : Boolean) : Boolean n Cette opération a une variante permettant d'itérer avec plusieurs itérateurs sur la même collection. On peut ainsi parcourir des ensembles produits de la même collection forall( t1,t2 : T uneexpression-contenant-t1-et-t2) : Boolean Ph. Collet 104
105 Opérations sur toutes types de collection r Existence d'un élément satisfaisant une expression n L'opération suivante vaut vrai si et seulement si au moins un élément de la collection satisfait une certaine expression passée en paramètre exists(uneexpression : Boolean) : Boolean r Itération n Cette opération, plus complexe que les autres, permet de les généraliser u i est un itérateur sur la collection u acc est un accumulateur initialisé avec uneexpression. u L'expression ExpressionAvecietacc est évaluée pour chaque i et son résultat est affecté dans acc. u Le résultat de iterate est acc. iterate(i : T ; acc : Type = uneexpression ExpressionAvec-i-etacc) : Type n Exemple : masse salariale de l entreprise context Entreprise :: massesalariale():real post : result = employé->iterate(p : Personne ; ms : Real=0 ms+p.contrat.salaire) Ph. Collet 105
106 Exercice r Ecrivez, dans le contexte de la classe Collection, l'opération size à l'aide de l'opération iterate context Collection :: size() post : result = self->iterate(elem; acc:integer=0 acc +1) r Ecrivez, dans le contexte de la classe Collection, l'opération forall à l'aide de l'opération iterate. context Collection :: forall(expr) : boolean post : result = self->iterate(elem; acc : Boolean=true acc and expr) Ph. Collet 106
107 Opérations sur toutes types de collection r Evaluation unique n L'opération suivante vaut vrai si et seulement si uneexpression s'évalue avec une valeur distincte pour chaque élément de la collection isunique(uneexpression : BooleanExpression) : Boolean r sortedby(uneexpression) : Sequence n L opération retourne une séquence contenant les éléments de la collection triés par ordre croissant suivant le critère décrit par une certaine expression. n Les valeurs résultant de l'évaluation de cette expression doivent donc supporter l'opération <. sortedby(uneexpression) : Sequence n Exemple: les salariés, ordonnés par leur salaire context Entreprise :: salariestries() : orderedset(personne) post : result = self.employe->sortedby(p p.contrat.salaire) Ph. Collet 107
108 Opérations communes mais spécifiques r L'opération select n est commune aux trois types de collection concrets, n'est pas définie dans Collection, mais seulement dans les types concrets avec des signatures spécifiques : select(expr:booleanexpression): Set(T) select(expr:booleanexpression): Bag(T) select(expr:booleanexpression): Sequence(T) n Pour simplifier select(expr:booleanexpression): Collection(T) Ph. Collet 108
109 Opérations communes mais spécifiques r Sélection et rejet d'éléments n Deux opérations retournent une collection du même type construite par sélection des éléments vérifiant (resp. ne vérifiant pas) une certaine expression. select(uneexpression : BooleanExpression) : Collection(T) reject(uneexpression : BooleanExpression) : Collection(T) r Exemple : expression représentant dans le contexte d'une entreprise les employés âgés de plus de 60 ans : context Entreprise self.employé->select(p : Personne p.age>=60) Ph. Collet 109
110 Opérations communes mais spécifiques r L'opération collect retourne une collection composée des résultats successifs de l'application d'une certaine expression à chaque élément de la collection. collect(expr:booleanexpression): Collection(T) r Exemple : n Les trois manières standards d'atteindre les mots d'un texte s'écrivent ainsi dans le contexte d'un texte self.occurrence->collect(mot) self.occurrence->collect(o o.mot) self.occurrence->collect(o : Occurrence o.mot) r cette notation admet un raccourci : n self.occurrence.mot Ph. Collet 110
111 Opérations communes mais spécifiques r Ajout/retrait d'éléments n Ces deux opérations retournent une collection résultant de l'ajout (resp. du retrait) d'un certain objet à la collection. including(unobjet : T) : Collection(T) excluding(unobjet : T) : Collection(T) r Union de deux collections union(c : Collection) : Collection Ph. Collet 111
112 Opérations de conversion r Chaque sorte de collection (set, orderedset, sequence ou bag) peut être transformée dans n'importe quelle autre sorte. r Par exemple un bag peut être transformé en : n séquence par l'opération assequence():sequence(t) u L'ordre résultant est indéterminé n ensemble par l'opération asset():set(t) u Les doublons sont éliminés n ensemble ordonné par l'opération asorderedset():orderedset(t) u Les doublons sont éliminés ; l'ordre résultant est indéterminé r Illustration : il y a plus de 2 occurrence d un certain mot : context Texte inv: self.occurrence->collect(mot)->asset()->size() >= 2 Ph. Collet 112
113 Opérations propres à Set et Bag r L'intersection est une opération commune aux sets et aux bags context Set :: intersection (s : Set(T)) : Set(T) post : result -> forall(elem self -> includes(elem) and s -> includes(elem) ) post : self -> forall(elem s -> includes(elem) = result -> includes(elem) ) post : s -> forall(elem self -> includes(elem) = result -> includes(elem) ) Ph. Collet 113
114 Opérations liées à l ordre (OrderedSet, Sequence) r Certaines opérations sont propres à la manipulation des collections dont les éléments sont ordonnés append(unobjet):sequence(t) ; ajout d'un objet à la fin prepend(unobjet):sequence(t) ; ajout d'un objet au début r partie d'une collection ordonnée délimitée par deux indices subsequence(inf:entier, sup:entier):sequence(t); spécifique des séquences suborderedset(inf:entier, sup:entier):orderedset(t); spécifique des ordered sets r D autres opérations du même genre at(inf:entier):t first():t last():t insertat(i:integer, o:t):sequence(t) indexof(o:t):integer Ph. Collet 114
115 Compléments r allinstances() n S'applique à une classe et non un objet. n Retourne l'ensemble de toutes les instances d'une classe et de ses soustypes. u allinstances() : Set(T) r Itérateur isunique(expr) n Retourne vrai si chaque évaluation du corps pour les éléments de la collection source produit un résultat différent, vrai sinon. c->isunique(expr: OclExpression): Boolean -- true if expr evaluates to a different value -- for each element in c. post: result = c->collect(expr)->forall(e1, e2 e1 <> e2) Ph. Collet 115
116 Exercice r Quelle est la signification de cette expression? context Personne inv: Personne.allInstances()->forAll(p1, p2 p.1 <> p2 implies p1.nom <> p2.nom ) r Comment l écrire avec isunique? context Personne inv: Personne.allInstances()->isUnique(nom) Ph. Collet 116
117 Conformance de type Transport r Sous-typage n Set(Bicycle) conforme à Set(Transport) n Set(Bicycle) conforme à Collection(Bicycle) n Set(Bicycle) conforme à Collection(Transport) n Set(Bicycle) non conforme à Bag(Bicycle) Bicycle Car Ph. Collet 117
118 Limites d expressivité d OCL r Limites de la logique des prédicats r Comment les contourner? r Check List 1. Manque-t-il une primitive à ma classe? r r Défaut de conception Ajouter la primitive (avec «def» si on ne peut toucher à la classe) 2. Manque-t-il un moyen d exprimer une propriété importante? r r r Défaut de d expressivité d OCL Ajouter une primitive qui représente tout ou partie de la propriété recherchée Spécifier cette primitive, même partiellement Ph. Collet 118
119 Exploitation d ocl : Garde r Utilisation d OCL pour exprimer des gardes dans les diagrammes d automates à états finis : n Diagrammes d états n Diagrammes d activités Ph. Collet 119
120 Actions r Utilisation dans la description des actions qui étiquettent les transitions n OCL est utilisé comme langage de navigation n On n écrit pas forcément une expression booléenne Ph. Collet 120
121 Redondance des informations r Une partie des informations du diagramme d états peut se retrouver dans le diagramme de classes n n n Etat comme un attribut Gardes : pré et postconditions Actions : postconditions Ph. Collet 121
122 V& V, et contrats r V&V : introduction r Approche par contrats Ph. Collet 122
123 V & V r Définitions n Validation : construisons-nous le bon produit? n Vérification : le construisons-nous bien? r Pour vérifier, il faut une spécification précise, si possible formelle, du fonctionnement du logiciel r Applications n Validation : recherche des défauts de conception u essentiellement un technique de tests dynamiques, fonctionnels (en boîte noire) n Vérification : des erreurs des développeurs u à partir cahier des charges (ou spécifications précises) u Ce qui permet plusieurs techniques : revues, inspections, preuves, analyses statiques et dynamiques, tests fonctionnels et structurels, en boîte noire ou blanche... Ph. Collet 123
124 Techniques statiques et dynamiques : complémentarité r Techniques statiques n Elles portent sur des documents (en particulier les programmes), sans exécuter le logiciel n Avantages : u contrôle systématique valable, pour toute exécution, applicable à tout document n Inconvénients : u ne portent pas forcément sur le code réel (qui peut évoluer) ni l environnement réel u Sauf pour les preuves, les vérifications statiques sont sommaires u Les preuves complètes sont difficiles et longues et nécessitent des spécifications formelles et complètes... également difficiles r Techniques dynamiques n Elles nécessitent une exécution du logiciel, une parmi des multitudes d autres possibles n Avantages : u contrôle qui porte sur des conditions proches de la réalité u plus à la portée du commun des programmeurs n Inconvénients : u il faut provoquer des expériences, donc écrire du code et construire des données d essais u un test qui réussit ne prouve pas qu il n y a pas d erreurs Ph. Collet 124
125 Approche par contrats r L idée de contrat a été introduite en 1988 par Bertrand Meyer, l auteur du langage Eiffel r L intérêt d un contrat est de bien préciser les responsabilités entre les acteurs d une conception, d un développement logiciel r Par abus de langage, on parle parfois de contrats entre classes ou composants : ce sont en fait des contrats entre les utilisateurs des classes, des composants r Un contrat définit explicitement les droits et les devoirs de chaque intervenant dans la conception et l utilisation d une unité n aucun contrôle ne manque n aucun contrôle n est superflu Ph. Collet 125
126 Types de contrats r Contrat de clientèle n entre les utilisateurs externes des services (primitives exportées, publiques) d une classe, les clients, et l auteur de cette classe fournisseur r Contrat d héritage n entre les (re)utilisateurs par adaptations n dans des classes héritières, descendantes et l auteur de la classe héritée, la classe ancêtre. Ph. Collet 126
127 Contrat de clientèle : exemple Context MathUtil:: sqrt (x, eps: Real): Real -- Square Root of x with precision eps pre: x >= 0 pre: eps >= 10^-6 post: abs(result^2 - x) <= 2*eps*result Devoirs Droits client fournisseur Appeler sqrt uniquement si la précondition est satisfaite Rendre le résultat correct avec la précision attendue, spécifiée dans la postcondition Obtenir le résultat correct avec la précision attendue, spécifiée dans la postcondition Refuser le calcul (dégager sa responsabilité) si la précondition n est pas satisfaite Ph. Collet 127
128 Assertions et héritage r Une classe héritière hérite de tous les invariants de ses classes parentes n Ils sont tous conjugués par des «and» r Lorsqu il y a redéfinition de méthodes lors de l héritage, on peut avoir nouvelles pré/post conditions n précondition moins exigeante, moins forte n postcondition plus précise, plus forte Les préconditions moins exigeantes, c est parfois contre intuitif! context NewMathUtil:: sqrt (x, eps: Real): Real pre: eps >= 10^-9 Ph. Collet 128
129 Contrats d héritage Devoirs Droits Classe parente Classe héritière Fournir aux héritiers des services fiables, performants et réutilisables Respecter les invariants Redéfinir en respectant les règles pre/post Les héritiers ne doivent pas déformer la pensée initiale Invariants = code génétique La classe parente doit fournir des services de qualité. Les assertions initiales doivent être cohérentes Ph. Collet 129
130 Annexe : Opérations de manipulation des collections r Les opérations de collection utilisent l opérateur -> n (tous les indices commencent à 1) : n = <> Collections identiques ou différentes n append(obj) Rend la valeur de la collection ordonnée avec obj ajouté à la fin n asset(), asorderedset(), assequence() Conversion de type entre collections n at(idx) Rend l objet à l indice idx dans une collection ordonnée n count(obj) Nombre d apparition de obj dans une collection n excludes(obj) Rend count(obj) = 0? n excludesall(coll) Est-ce que tous les éléments de coll satisfont count(obj) = 0? n excluding(obj) Rend la valeur de la collection sans l objet obj n first() Rend le premier élément d une collection ordonnée Ph. Collet 130
131 Annexe : Opérations de manipulation des collections n includes(obj) Rend count(obj) > 0? n includesall(coll) Est-ce que tous les éléments de coll satisfont count(obj) > 0? n including(obj) Rend la valeur de la collection avec l objet obj ajouté n indexof(obj) Rend l indice de la 1ère occurrence de obj dans une séquence n insertat(idx,obj) Rend la valeur de la collection avec obj ajouté à l indice idx n intersection(coll) Intersection des collections non ordonnées self et coll n isempty() Rend size() = 0? n last() Rend le dernier élément d une collection ordonnée n notempty() Rend size() > 0? n prepend(obj) Rend la valeur de la collection ordonnée avec obj ajouté en tête n size() Nombre d éléments dans la collection n suborderedset(start,end) Sous-partie d un ensemble ordonné entre les indices n subsequence(start,end) Sous partie d une séquence extraite entre les indices n sum() Somme des éléments d une collection (Integer ou Real) n union(coll) Union des collections self et c Ph. Collet 131
132 Annexe : opérations collectives n collect(expr) Rend un bag contenant la valeur de exp appliquée à chaque élément de la collection u macollection.valeur est équivalent à macollection->collect(valeur) n exists(expr) Est-ce l expression expr est satisfaite pour l un des éléments de la collection? n forall(expr) Est-ce l expression expr est satisfaite pour tous les éléments de la collection? n isunique(expr) Rend vrai si expr donne une valeur différente pour chaque élément de la collection n iterate(i : Type; a : Type expr) u Opération à partir de laquelle les autres sont définies. La variable «i» est l itérateur et «a» est l accumulateur, qui récupère la valeur de expr après chaque évaluation n one(expr) Rend l expression coll->select(expr)->size()=1 n reject(expr) Rend la sous-collection des éléments pour lesquelles expr n est pas satisfaite n select(expr) Rend la sous-collection des éléments pour lesquelles expr est satisfaite n sortedby(expr) Rend la séquence contenant tous les éléments de la collection, ordonnés par la valeur u expr (le type des éléments doit posséder un opérateur «<») Ph. Collet 132
Expression des contraintes. OCL : Object C o n t r a i n t L a n g u a g e
 P r o b l é m a t i q u e OCL : O b j e c t C o n s t r a i n t L a n g u a g e Le langage de contraintes d UML Les différents diagrammes d UML permettent d exprimer certaines contraintes graphiquement
P r o b l é m a t i q u e OCL : O b j e c t C o n s t r a i n t L a n g u a g e Le langage de contraintes d UML Les différents diagrammes d UML permettent d exprimer certaines contraintes graphiquement
OCL - Object Constraint Language
 OCL - Object Constraint Language Laëtitia Matignon [email protected] Département Informatique - Polytech Lyon Université Claude Bernard Lyon 1 2012-2013 Laëtitia Matignon SIMA - OCL - Object
OCL - Object Constraint Language Laëtitia Matignon [email protected] Département Informatique - Polytech Lyon Université Claude Bernard Lyon 1 2012-2013 Laëtitia Matignon SIMA - OCL - Object
Plan. Exemple: Application bancaire. Introduction. OCL Object Constraint Language Le langage de contraintes d'uml
 OCL Object Constraint Language Le langage de contraintes d'uml Plan 1. Introduction 2. Les principaux concepts d'ocl Object Constraint Language 1 Object Constraint Language 2 Exemple: une application bancaire
OCL Object Constraint Language Le langage de contraintes d'uml Plan 1. Introduction 2. Les principaux concepts d'ocl Object Constraint Language 1 Object Constraint Language 2 Exemple: une application bancaire
Object Constraint Language (OCL) Une introduction
 Object Constraint Language (OCL) Une introduction Master 2 IFPRU - Module Ingénierie des modèles - FMIN310 Marianne Huchard 7 novembre 2008 1 Présentation générale OCL est un langage formel, basé sur la
Object Constraint Language (OCL) Une introduction Master 2 IFPRU - Module Ingénierie des modèles - FMIN310 Marianne Huchard 7 novembre 2008 1 Présentation générale OCL est un langage formel, basé sur la
Object Constraint Language (OCL)
 Object Constraint Language (OCL) Eric Cariou Université de Pau et des Pays de l'adour UFR Sciences Pau Département Informatique [email protected] 1 Plan 1. Pourquoi OCL? Introduction par l'exemple
Object Constraint Language (OCL) Eric Cariou Université de Pau et des Pays de l'adour UFR Sciences Pau Département Informatique [email protected] 1 Plan 1. Pourquoi OCL? Introduction par l'exemple
Développement d un interpréteur OCL pour une machine virtuelle UML.
 ObjeXion Software Prototyping made easy SA au capital de 500 000 F Siret 421 565 565 00015 APE 722Z Téléphone : 03 89 35 70 75 Télécopie : 03 89 35 70 76 L embarcadère 5, rue Gutemberg 68 800 Vieux-Thann,
ObjeXion Software Prototyping made easy SA au capital de 500 000 F Siret 421 565 565 00015 APE 722Z Téléphone : 03 89 35 70 75 Télécopie : 03 89 35 70 76 L embarcadère 5, rue Gutemberg 68 800 Vieux-Thann,
TP n 2 Concepts de la programmation Objets Master 1 mention IL, semestre 2 Le type Abstrait Pile
 TP n 2 Concepts de la programmation Objets Master 1 mention IL, semestre 2 Le type Abstrait Pile Dans ce TP, vous apprendrez à définir le type abstrait Pile, à le programmer en Java à l aide d une interface
TP n 2 Concepts de la programmation Objets Master 1 mention IL, semestre 2 Le type Abstrait Pile Dans ce TP, vous apprendrez à définir le type abstrait Pile, à le programmer en Java à l aide d une interface
basée sur le cours de Bertrand Legal, maître de conférences à l ENSEIRB www.enseirb.fr/~legal Olivier Augereau Formation UML
 basée sur le cours de Bertrand Legal, maître de conférences à l ENSEIRB www.enseirb.fr/~legal Olivier Augereau Formation UML http://olivier-augereau.com Sommaire Introduction I) Les bases II) Les diagrammes
basée sur le cours de Bertrand Legal, maître de conférences à l ENSEIRB www.enseirb.fr/~legal Olivier Augereau Formation UML http://olivier-augereau.com Sommaire Introduction I) Les bases II) Les diagrammes
Ingénierie des Modèles. Méta-modélisation
 Ingénierie des Modèles Méta-modélisation Eric Cariou Master Technologies de l'internet 2 ème année Université de Pau et des Pays de l'adour UFR Sciences Pau Département Informatique [email protected]
Ingénierie des Modèles Méta-modélisation Eric Cariou Master Technologies de l'internet 2 ème année Université de Pau et des Pays de l'adour UFR Sciences Pau Département Informatique [email protected]
Chapitre VI- La validation de la composition.
 Chapitre VI- La validation de la composition. Objectifs du chapitre : Expliquer les conséquences de l utilisation de règles de typage souples dans SEP. Présenter le mécanisme de validation des connexions
Chapitre VI- La validation de la composition. Objectifs du chapitre : Expliquer les conséquences de l utilisation de règles de typage souples dans SEP. Présenter le mécanisme de validation des connexions
Classes et Objets en Ocaml.
 Classes et Objets en Ocaml. Didier Rémy 2001-2002 http://cristal.inria.fr/ remy/mot/2/ http://www.enseignement.polytechnique.fr/profs/informatique/didier.remy/mot/2/ Cours Exercices Slide 1 1. Objets 2.
Classes et Objets en Ocaml. Didier Rémy 2001-2002 http://cristal.inria.fr/ remy/mot/2/ http://www.enseignement.polytechnique.fr/profs/informatique/didier.remy/mot/2/ Cours Exercices Slide 1 1. Objets 2.
3. SPÉCIFICATIONS DU LOGICIEL. de l'expression des besoins à la conception. Spécifications fonctionnelles Analyse fonctionnelle et méthodes
 PLAN CYCLE DE VIE D'UN LOGICIEL EXPRESSION DES BESOINS SPÉCIFICATIONS DU LOGICIEL CONCEPTION DU LOGICIEL LA PROGRAMMATION TESTS ET MISE AU POINT DOCUMENTATION CONCLUSION C.Crochepeyre Génie Logiciel Diapason
PLAN CYCLE DE VIE D'UN LOGICIEL EXPRESSION DES BESOINS SPÉCIFICATIONS DU LOGICIEL CONCEPTION DU LOGICIEL LA PROGRAMMATION TESTS ET MISE AU POINT DOCUMENTATION CONCLUSION C.Crochepeyre Génie Logiciel Diapason
IFT2255 : Génie logiciel
 IFT2255 : Génie logiciel Chapitre 6 - Analyse orientée objets Section 1. Introduction à UML Julie Vachon et Houari Sahraoui 6.1. Introduction à UML 1. Vers une approche orientée objet 2. Introduction ti
IFT2255 : Génie logiciel Chapitre 6 - Analyse orientée objets Section 1. Introduction à UML Julie Vachon et Houari Sahraoui 6.1. Introduction à UML 1. Vers une approche orientée objet 2. Introduction ti
Pour signifier qu'une classe fille hérite d'une classe mère, on utilise le mot clé extends class fille extends mère
 L'héritage et le polymorphisme en Java Pour signifier qu'une classe fille hérite d'une classe mère, on utilise le mot clé extends class fille extends mère En java, toutes les classes sont dérivée de la
L'héritage et le polymorphisme en Java Pour signifier qu'une classe fille hérite d'une classe mère, on utilise le mot clé extends class fille extends mère En java, toutes les classes sont dérivée de la
Génie Logiciel avec Ada. 4 février 2013
 Génie Logiciel 4 février 2013 Plan I. Généralités II. Structures linéaires III. Exceptions IV. Structures arborescentes V. Dictionnaires I. Principes II. Notions propres à la POO I. Principes Chapitre
Génie Logiciel 4 février 2013 Plan I. Généralités II. Structures linéaires III. Exceptions IV. Structures arborescentes V. Dictionnaires I. Principes II. Notions propres à la POO I. Principes Chapitre
UML et les Bases de Données
 CNAM UML et les Bases de Données UML et les Bases de Données. Diagramme de classes / diagramme d objets (UML)...2.. Premier niveau de modélisation des données d une application...2.2. Les éléments de modélisation...2.2..
CNAM UML et les Bases de Données UML et les Bases de Données. Diagramme de classes / diagramme d objets (UML)...2.. Premier niveau de modélisation des données d une application...2.2. Les éléments de modélisation...2.2..
Langage SQL : créer et interroger une base
 Langage SQL : créer et interroger une base Dans ce chapitre, nous revenons sur les principales requêtes de création de table et d accès aux données. Nous verrons aussi quelques fonctions d agrégation (MAX,
Langage SQL : créer et interroger une base Dans ce chapitre, nous revenons sur les principales requêtes de création de table et d accès aux données. Nous verrons aussi quelques fonctions d agrégation (MAX,
LES TYPES DE DONNÉES DU LANGAGE PASCAL
 LES TYPES DE DONNÉES DU LANGAGE PASCAL 75 LES TYPES DE DONNÉES DU LANGAGE PASCAL CHAPITRE 4 OBJECTIFS PRÉSENTER LES NOTIONS D ÉTIQUETTE, DE CONS- TANTE ET DE IABLE DANS LE CONTEXTE DU LAN- GAGE PASCAL.
LES TYPES DE DONNÉES DU LANGAGE PASCAL 75 LES TYPES DE DONNÉES DU LANGAGE PASCAL CHAPITRE 4 OBJECTIFS PRÉSENTER LES NOTIONS D ÉTIQUETTE, DE CONS- TANTE ET DE IABLE DANS LE CONTEXTE DU LAN- GAGE PASCAL.
TP1 : Initiation à Java et Eclipse
 TP1 : Initiation à Java et Eclipse 1 TP1 : Initiation à Java et Eclipse Systèmes d Exploitation Avancés I. Objectifs du TP Ce TP est une introduction au langage Java. Il vous permettra de comprendre les
TP1 : Initiation à Java et Eclipse 1 TP1 : Initiation à Java et Eclipse Systèmes d Exploitation Avancés I. Objectifs du TP Ce TP est une introduction au langage Java. Il vous permettra de comprendre les
Bases de données. Chapitre 1. Introduction
 Références : Bases de données Pierre Wolper Email : [email protected] URL : http : //www.montefiore.ulg.ac.be/~pw/ http : //www.montefiore.ulg.ac.be/ ~pw/cours/bd.html Henry F. Korth, Abraham Silberschatz,
Références : Bases de données Pierre Wolper Email : [email protected] URL : http : //www.montefiore.ulg.ac.be/~pw/ http : //www.montefiore.ulg.ac.be/ ~pw/cours/bd.html Henry F. Korth, Abraham Silberschatz,
Évaluation et implémentation des langages
 Évaluation et implémentation des langages Les langages de programmation et le processus de programmation Critères de conception et d évaluation des langages de programmation Les fondations de l implémentation
Évaluation et implémentation des langages Les langages de programmation et le processus de programmation Critères de conception et d évaluation des langages de programmation Les fondations de l implémentation
Débuter avec EXPRESS. Alain Plantec. 1 Schema 2
 Débuter avec EXPRESS Alain Plantec Table des matières 1 Schema 2 2 Entité 2 2.1 Attributs simples................................................ 2 2.2 Attributs collection...............................................
Débuter avec EXPRESS Alain Plantec Table des matières 1 Schema 2 2 Entité 2 2.1 Attributs simples................................................ 2 2.2 Attributs collection...............................................
Langage et Concepts de ProgrammationOrientée-Objet 1 / 40
 Déroulement du cours Introduction Concepts Java Remarques Langage et Concepts de Programmation Orientée-Objet Gauthier Picard École Nationale Supérieure des Mines de Saint-Étienne [email protected]
Déroulement du cours Introduction Concepts Java Remarques Langage et Concepts de Programmation Orientée-Objet Gauthier Picard École Nationale Supérieure des Mines de Saint-Étienne [email protected]
16H Cours / 18H TD / 20H TP
 INTRODUCTION AUX BASES DE DONNEES 16H Cours / 18H TD / 20H TP 1. INTRODUCTION Des Fichiers aux Bases de Données 2. SYSTEME DE GESTION DE BASE DE DONNEES 2.1. INTRODUCTION AUX SYSTEMES DE GESTION DE BASES
INTRODUCTION AUX BASES DE DONNEES 16H Cours / 18H TD / 20H TP 1. INTRODUCTION Des Fichiers aux Bases de Données 2. SYSTEME DE GESTION DE BASE DE DONNEES 2.1. INTRODUCTION AUX SYSTEMES DE GESTION DE BASES
1. Qu'est-ce que SQL?... 2. 2. La maintenance des bases de données... 2. 3. Les manipulations des bases de données... 5
 1. Qu'est-ce que SQL?... 2 2. La maintenance des bases de données... 2 2.1 La commande CREATE TABLE... 3 2.2 La commande ALTER TABLE... 4 2.3 La commande CREATE INDEX... 4 3. Les manipulations des bases
1. Qu'est-ce que SQL?... 2 2. La maintenance des bases de données... 2 2.1 La commande CREATE TABLE... 3 2.2 La commande ALTER TABLE... 4 2.3 La commande CREATE INDEX... 4 3. Les manipulations des bases
UML Diagramme de communication (communication diagram) Emmanuel Pichon 2013
 UML Diagramme de communication (communication diagram) 2013 Diagramme de communication (communication diagram) Utilisation / objectifs Sens Ce diagramme présente des objets, des acteurs, des liens et des
UML Diagramme de communication (communication diagram) 2013 Diagramme de communication (communication diagram) Utilisation / objectifs Sens Ce diagramme présente des objets, des acteurs, des liens et des
Université de Bangui. Modélisons en UML
 Université de Bangui CRM Modélisons en UML Ce cours a été possible grâce à l initiative d Apollinaire MOLAYE qui m a contacté pour vous faire bénéficier de mes connaissances en nouvelles technologies et
Université de Bangui CRM Modélisons en UML Ce cours a été possible grâce à l initiative d Apollinaire MOLAYE qui m a contacté pour vous faire bénéficier de mes connaissances en nouvelles technologies et
Projet Active Object
 Projet Active Object TAO Livrable de conception et validation Romain GAIDIER Enseignant : M. Noël PLOUZEAU, ISTIC / IRISA Pierre-François LEFRANC Master 2 Informatique parcours MIAGE Méthodes Informatiques
Projet Active Object TAO Livrable de conception et validation Romain GAIDIER Enseignant : M. Noël PLOUZEAU, ISTIC / IRISA Pierre-François LEFRANC Master 2 Informatique parcours MIAGE Méthodes Informatiques
Premiers Pas en Programmation Objet : les Classes et les Objets
 Chapitre 2 Premiers Pas en Programmation Objet : les Classes et les Objets Dans la première partie de ce cours, nous avons appris à manipuler des objets de type simple : entiers, doubles, caractères, booléens.
Chapitre 2 Premiers Pas en Programmation Objet : les Classes et les Objets Dans la première partie de ce cours, nous avons appris à manipuler des objets de type simple : entiers, doubles, caractères, booléens.
UML (Diagramme de classes) Unified Modeling Language
 UML (Diagramme de classes) Unified Modeling Language Sommaire Introduction Objectifs Diagramme de classes Classe (Nom, attribut, opération) Visibilité et portée des constituants d une classe Association
UML (Diagramme de classes) Unified Modeling Language Sommaire Introduction Objectifs Diagramme de classes Classe (Nom, attribut, opération) Visibilité et portée des constituants d une classe Association
LMI 2. Programmation Orientée Objet POO - Cours 9. Said Jabbour. [email protected] www.cril.univ-artois.fr/~jabbour
 LMI 2 Programmation Orientée Objet POO - Cours 9 Said Jabbour [email protected] www.cril.univ-artois.fr/~jabbour CRIL UMR CNRS 8188 Faculté des Sciences - Univ. Artois Février 2011 Les collections
LMI 2 Programmation Orientée Objet POO - Cours 9 Said Jabbour [email protected] www.cril.univ-artois.fr/~jabbour CRIL UMR CNRS 8188 Faculté des Sciences - Univ. Artois Février 2011 Les collections
Cours Composant 2. Qualité logicielle et spécications algébriques
 UPMC Paris Universitas Master Informatique STL Cours Composant 2. Qualité logicielle et spécications algébriques c 2005-2008 Frédéric Peschanski UPMC Paris Universitas 24 février 2008 c 2005-2008 Frédéric
UPMC Paris Universitas Master Informatique STL Cours Composant 2. Qualité logicielle et spécications algébriques c 2005-2008 Frédéric Peschanski UPMC Paris Universitas 24 février 2008 c 2005-2008 Frédéric
Chapitre 2. Eléments pour comprendre un énoncé
 Chapitre 2 Eléments pour comprendre un énoncé Ce chapitre est consacré à la compréhension d un énoncé. Pour démontrer un énoncé donné, il faut se reporter au chapitre suivant. Les tables de vérité données
Chapitre 2 Eléments pour comprendre un énoncé Ce chapitre est consacré à la compréhension d un énoncé. Pour démontrer un énoncé donné, il faut se reporter au chapitre suivant. Les tables de vérité données
Chapitre I : le langage UML et le processus unifié
 I. Introduction Les méthodes d analyse orientées objet sont initialement issues des milieux industriels. La préoccupation dominante de leurs auteurs est le génie logiciel, c est-àdire les principes et
I. Introduction Les méthodes d analyse orientées objet sont initialement issues des milieux industriels. La préoccupation dominante de leurs auteurs est le génie logiciel, c est-àdire les principes et
Manuel d utilisation 26 juin 2011. 1 Tâche à effectuer : écrire un algorithme 2
 éducalgo Manuel d utilisation 26 juin 2011 Table des matières 1 Tâche à effectuer : écrire un algorithme 2 2 Comment écrire un algorithme? 3 2.1 Avec quoi écrit-on? Avec les boutons d écriture........
éducalgo Manuel d utilisation 26 juin 2011 Table des matières 1 Tâche à effectuer : écrire un algorithme 2 2 Comment écrire un algorithme? 3 2.1 Avec quoi écrit-on? Avec les boutons d écriture........
1 Introduction et installation
 TP d introduction aux bases de données 1 TP d introduction aux bases de données Le but de ce TP est d apprendre à manipuler des bases de données. Dans le cadre du programme d informatique pour tous, on
TP d introduction aux bases de données 1 TP d introduction aux bases de données Le but de ce TP est d apprendre à manipuler des bases de données. Dans le cadre du programme d informatique pour tous, on
UEO11 COURS/TD 1. nombres entiers et réels codés en mémoire centrale. Caractères alphabétiques et caractères spéciaux.
 UEO11 COURS/TD 1 Contenu du semestre Cours et TDs sont intégrés L objectif de ce cours équivalent a 6h de cours, 10h de TD et 8h de TP est le suivant : - initiation à l algorithmique - notions de bases
UEO11 COURS/TD 1 Contenu du semestre Cours et TDs sont intégrés L objectif de ce cours équivalent a 6h de cours, 10h de TD et 8h de TP est le suivant : - initiation à l algorithmique - notions de bases
Machines virtuelles Cours 1 : Introduction
 Machines virtuelles Cours 1 : Introduction Pierre Letouzey 1 [email protected] PPS - Université Denis Diderot Paris 7 janvier 2012 1. Merci à Y. Régis-Gianas pour les transparents Qu est-ce qu une
Machines virtuelles Cours 1 : Introduction Pierre Letouzey 1 [email protected] PPS - Université Denis Diderot Paris 7 janvier 2012 1. Merci à Y. Régis-Gianas pour les transparents Qu est-ce qu une
Nom de l application
 Ministère de l Enseignement Supérieur et de la Recherche Scientifique Direction Générale des Etudes Technologiques Institut Supérieur des Etudes Technologiques de Gafsa Département Technologies de l Informatique
Ministère de l Enseignement Supérieur et de la Recherche Scientifique Direction Générale des Etudes Technologiques Institut Supérieur des Etudes Technologiques de Gafsa Département Technologies de l Informatique
Langage et Concepts de Programmation Objet. 1 Attributs et Méthodes d instance ou de classe. Travaux Dirigés no2
 Langage et Concepts de Programmation Objet Travaux Dirigés no2 Pôle Informatique École Nationale Supérieure des Mines de St-Etienne Vous trouverez plus de détails sur les concepts abordés lors de ce TD
Langage et Concepts de Programmation Objet Travaux Dirigés no2 Pôle Informatique École Nationale Supérieure des Mines de St-Etienne Vous trouverez plus de détails sur les concepts abordés lors de ce TD
Généralités sur le Langage Java et éléments syntaxiques.
 Généralités sur le Langage Java et éléments syntaxiques. Généralités sur le Langage Java et éléments syntaxiques....1 Introduction...1 Genéralité sur le langage Java....1 Syntaxe de base du Langage...
Généralités sur le Langage Java et éléments syntaxiques. Généralités sur le Langage Java et éléments syntaxiques....1 Introduction...1 Genéralité sur le langage Java....1 Syntaxe de base du Langage...
Diagramme de classes
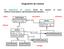 Diagramme de classes Un diagramme de classes décrit les classes et leurs relations (associations, généralisation/spécialisation, ). classe association méthodes attributs héritage Diagramme de classes :
Diagramme de classes Un diagramme de classes décrit les classes et leurs relations (associations, généralisation/spécialisation, ). classe association méthodes attributs héritage Diagramme de classes :
Recherche dans un tableau
 Chapitre 3 Recherche dans un tableau 3.1 Introduction 3.1.1 Tranche On appelle tranche de tableau, la donnée d'un tableau t et de deux indices a et b. On note cette tranche t.(a..b). Exemple 3.1 : 3 6
Chapitre 3 Recherche dans un tableau 3.1 Introduction 3.1.1 Tranche On appelle tranche de tableau, la donnée d'un tableau t et de deux indices a et b. On note cette tranche t.(a..b). Exemple 3.1 : 3 6
RTDS G3. Emmanuel Gaudin [email protected]
 RTDS G3 Emmanuel Gaudin [email protected] PragmaDev Dédiée au développement d un AGL pour le développement des applications temps réel et embarquées. Réseau de partenaires: Formations, Service,
RTDS G3 Emmanuel Gaudin [email protected] PragmaDev Dédiée au développement d un AGL pour le développement des applications temps réel et embarquées. Réseau de partenaires: Formations, Service,
C++ COURS N 2 : CLASSES, DONNÉES ET FONCTIONS MEMBRES Classes et objets en C++ Membres d'une classe Spécification d'une classe Codage du comportement
 C++ COURS N 2 : CLASSES, DONNÉES ET FONCTIONS MEMBRES Classes et objets en C++ Membres d'une classe Spécification d'une classe Codage du comportement des objets d'une classe Utilisation d'une classe Droit
C++ COURS N 2 : CLASSES, DONNÉES ET FONCTIONS MEMBRES Classes et objets en C++ Membres d'une classe Spécification d'une classe Codage du comportement des objets d'une classe Utilisation d'une classe Droit
Cours 1 : La compilation
 /38 Interprétation des programmes Cours 1 : La compilation Yann Régis-Gianas [email protected] PPS - Université Denis Diderot Paris 7 2/38 Qu est-ce que la compilation? Vous avez tous déjà
/38 Interprétation des programmes Cours 1 : La compilation Yann Régis-Gianas [email protected] PPS - Université Denis Diderot Paris 7 2/38 Qu est-ce que la compilation? Vous avez tous déjà
Les diagrammes de modélisation
 L approche Orientée Objet et UML 1 Plan du cours Introduction au Génie Logiciel L approche Orientée Objet et Notation UML Les diagrammes de modélisation Relations entre les différents diagrammes De l analyse
L approche Orientée Objet et UML 1 Plan du cours Introduction au Génie Logiciel L approche Orientée Objet et Notation UML Les diagrammes de modélisation Relations entre les différents diagrammes De l analyse
Système binaire. Algèbre booléenne
 Algèbre booléenne Système binaire Système digital qui emploie des signaux à deux valeurs uniques En général, les digits employés sont 0 et 1, qu'on appelle bits (binary digits) Avantages: on peut utiliser
Algèbre booléenne Système binaire Système digital qui emploie des signaux à deux valeurs uniques En général, les digits employés sont 0 et 1, qu'on appelle bits (binary digits) Avantages: on peut utiliser
Chapitre 2. Classes et objets
 Chapitre 2: Classes et Objets 1/10 Chapitre 2 Classes et objets Chapitre 2: Classes et Objets 2/10 Approche Orientée Objet Idée de base de A.O.O. repose sur l'observation de la façon dont nous procédons
Chapitre 2: Classes et Objets 1/10 Chapitre 2 Classes et objets Chapitre 2: Classes et Objets 2/10 Approche Orientée Objet Idée de base de A.O.O. repose sur l'observation de la façon dont nous procédons
Arithmétique binaire. Chapitre. 5.1 Notions. 5.1.1 Bit. 5.1.2 Mot
 Chapitre 5 Arithmétique binaire L es codes sont manipulés au quotidien sans qu on s en rende compte, et leur compréhension est quasi instinctive. Le seul fait de lire fait appel au codage alphabétique,
Chapitre 5 Arithmétique binaire L es codes sont manipulés au quotidien sans qu on s en rende compte, et leur compréhension est quasi instinctive. Le seul fait de lire fait appel au codage alphabétique,
Algorithmique et programmation : les bases (VBA) Corrigé
 PAD INPT ALGORITHMIQUE ET PROGRAMMATION 1 Cours VBA, Semaine 1 mai juin 2006 Corrigé Résumé Ce document décrit l écriture dans le langage VBA des éléments vus en algorithmique. Table des matières 1 Pourquoi
PAD INPT ALGORITHMIQUE ET PROGRAMMATION 1 Cours VBA, Semaine 1 mai juin 2006 Corrigé Résumé Ce document décrit l écriture dans le langage VBA des éléments vus en algorithmique. Table des matières 1 Pourquoi
Langage SQL (1) 4 septembre 2007. IUT Orléans. Introduction Le langage SQL : données Le langage SQL : requêtes
 Langage SQL (1) Sébastien Limet Denys Duchier IUT Orléans 4 septembre 2007 Notions de base qu est-ce qu une base de données? SGBD différents type de bases de données quelques systèmes existants Définition
Langage SQL (1) Sébastien Limet Denys Duchier IUT Orléans 4 septembre 2007 Notions de base qu est-ce qu une base de données? SGBD différents type de bases de données quelques systèmes existants Définition
Généralités. javadoc. Format des commentaires. Format des commentaires. Caractères spéciaux. Insérer du code
 Généralités javadoc Université de Nice - Sophia Antipolis Richard Grin Version 1.4.1 8/2/11 javadoc produit de la documentation en partant de commentaires particuliers insérés dans le code source des classes
Généralités javadoc Université de Nice - Sophia Antipolis Richard Grin Version 1.4.1 8/2/11 javadoc produit de la documentation en partant de commentaires particuliers insérés dans le code source des classes
Chapitre VIII. Les bases de données. Orientées Objet. Motivation
 Chapitre VIII Motivation Le modèle relationnel connaît un très grand succès et s avère très adéquat pour les applications traditionnelles des bases de données (gestion) Les bases de données Orientées Objet
Chapitre VIII Motivation Le modèle relationnel connaît un très grand succès et s avère très adéquat pour les applications traditionnelles des bases de données (gestion) Les bases de données Orientées Objet
Cours Informatique Master STEP
 Cours Informatique Master STEP Bases de la programmation: Compilateurs/logiciels Algorithmique et structure d'un programme Programmation en langage structuré (Fortran 90) Variables, expressions, instructions
Cours Informatique Master STEP Bases de la programmation: Compilateurs/logiciels Algorithmique et structure d'un programme Programmation en langage structuré (Fortran 90) Variables, expressions, instructions
Information utiles. [email protected]. webpage : Google+ : http://www.ibisc.univ-evry.fr/ digiusto/
 Systèmes de gestion de bases de données Introduction Université d Evry Val d Essonne, IBISC utiles email : [email protected] webpage : http://www.ibisc.univ-evry.fr/ digiusto/ Google+ : https://plus.google.com/u/0/b/103572780965897723237/
Systèmes de gestion de bases de données Introduction Université d Evry Val d Essonne, IBISC utiles email : [email protected] webpage : http://www.ibisc.univ-evry.fr/ digiusto/ Google+ : https://plus.google.com/u/0/b/103572780965897723237/
Pourquoi l apprentissage?
 Pourquoi l apprentissage? Les SE sont basés sur la possibilité d extraire la connaissance d un expert sous forme de règles. Dépend fortement de la capacité à extraire et formaliser ces connaissances. Apprentissage
Pourquoi l apprentissage? Les SE sont basés sur la possibilité d extraire la connaissance d un expert sous forme de règles. Dépend fortement de la capacité à extraire et formaliser ces connaissances. Apprentissage
Cours 1 : Introduction Ordinateurs - Langages de haut niveau - Application
 Université de Provence Licence Math-Info Première Année V. Phan Luong Algorithmique et Programmation en Python Cours 1 : Introduction Ordinateurs - Langages de haut niveau - Application 1 Ordinateur Un
Université de Provence Licence Math-Info Première Année V. Phan Luong Algorithmique et Programmation en Python Cours 1 : Introduction Ordinateurs - Langages de haut niveau - Application 1 Ordinateur Un
Présentation générale de la méthode orientée objet : O.M.T. (Rumbaugh & al.)
 Présentation générale de la méthode orientée objet : O.M.T. (Rumbaugh & al.) Bernard ESPINASSE Professeur à l'université d'aix-marseille Plan Introduction Les modèles d'omt Le Modèle Objet (MO) Le Modèle
Présentation générale de la méthode orientée objet : O.M.T. (Rumbaugh & al.) Bernard ESPINASSE Professeur à l'université d'aix-marseille Plan Introduction Les modèles d'omt Le Modèle Objet (MO) Le Modèle
INITIATION AU LANGAGE C SUR PIC DE MICROSHIP
 COURS PROGRAMMATION INITIATION AU LANGAGE C SUR MICROCONTROLEUR PIC page 1 / 7 INITIATION AU LANGAGE C SUR PIC DE MICROSHIP I. Historique du langage C 1972 : naissance du C dans les laboratoires BELL par
COURS PROGRAMMATION INITIATION AU LANGAGE C SUR MICROCONTROLEUR PIC page 1 / 7 INITIATION AU LANGAGE C SUR PIC DE MICROSHIP I. Historique du langage C 1972 : naissance du C dans les laboratoires BELL par
Image d un intervalle par une fonction continue
 DOCUMENT 27 Image d un intervalle par une fonction continue La continuité d une fonction en un point est une propriété locale : une fonction est continue en un point x 0 si et seulement si sa restriction
DOCUMENT 27 Image d un intervalle par une fonction continue La continuité d une fonction en un point est une propriété locale : une fonction est continue en un point x 0 si et seulement si sa restriction
Informatique Générale
 Informatique Générale Guillaume Hutzler Laboratoire IBISC (Informatique Biologie Intégrative et Systèmes Complexes) [email protected] Cours Dokeos 625 http://www.ens.univ-evry.fr/modx/dokeos.html
Informatique Générale Guillaume Hutzler Laboratoire IBISC (Informatique Biologie Intégrative et Systèmes Complexes) [email protected] Cours Dokeos 625 http://www.ens.univ-evry.fr/modx/dokeos.html
6. Les différents types de démonstrations
 LES DIFFÉRENTS TYPES DE DÉMONSTRATIONS 33 6. Les différents types de démonstrations 6.1. Un peu de logique En mathématiques, une démonstration est un raisonnement qui permet, à partir de certains axiomes,
LES DIFFÉRENTS TYPES DE DÉMONSTRATIONS 33 6. Les différents types de démonstrations 6.1. Un peu de logique En mathématiques, une démonstration est un raisonnement qui permet, à partir de certains axiomes,
UML. Diagrammes de classes (suite) Delphine Longuet. [email protected]
 Polytech Paris-Sud Formation initiale 3 e année Spécialité Informatique Année 2014-2015 UML Diagrammes de classes (suite) Delphine Longuet [email protected] Opérations Opérations Service qui peut
Polytech Paris-Sud Formation initiale 3 e année Spécialité Informatique Année 2014-2015 UML Diagrammes de classes (suite) Delphine Longuet [email protected] Opérations Opérations Service qui peut
Présentation du langage et premières fonctions
 1 Présentation de l interface logicielle Si les langages de haut niveau sont nombreux, nous allons travaillé cette année avec le langage Python, un langage de programmation très en vue sur internet en
1 Présentation de l interface logicielle Si les langages de haut niveau sont nombreux, nous allons travaillé cette année avec le langage Python, un langage de programmation très en vue sur internet en
1. LA GESTION DES BASES DE DONNEES RELATIONNELLES
 Dossier G11 - Interroger une base de données La base de données Facturation contient tout un ensemble d'informations concernant la facturation de la SAFPB (société anonyme de fabrication de produits de
Dossier G11 - Interroger une base de données La base de données Facturation contient tout un ensemble d'informations concernant la facturation de la SAFPB (société anonyme de fabrication de produits de
Java Licence Professionnelle CISII, 2009-10
 Java Licence Professionnelle CISII, 2009-10 Cours 4 : Programmation structurée (c) http://www.loria.fr/~tabbone/cours.html 1 Principe - Les méthodes sont structurées en blocs par les structures de la programmation
Java Licence Professionnelle CISII, 2009-10 Cours 4 : Programmation structurée (c) http://www.loria.fr/~tabbone/cours.html 1 Principe - Les méthodes sont structurées en blocs par les structures de la programmation
Langage propre à Oracle basé sur ADA. Offre une extension procédurale à SQL
 Cours PL/SQL Langage propre à Oracle basé sur ADA Offre une extension procédurale à SQL PL/SQL permet d utiliser un sous-ensemble du langage SQL des variables, des boucles, des alternatives, des gestions
Cours PL/SQL Langage propre à Oracle basé sur ADA Offre une extension procédurale à SQL PL/SQL permet d utiliser un sous-ensemble du langage SQL des variables, des boucles, des alternatives, des gestions
Proposition de sujet de thèse CIFRE EUROCOPTER / LGI2P
 EUROCOPTER SAS Groupe EADS Marignane Ecole des Mines d Alès Laboratoire de Génie Informatique et d Ingénierie de Production LGI2P Nîmes Proposition de sujet de thèse CIFRE EUROCOPTER / LGI2P Titre Domaine
EUROCOPTER SAS Groupe EADS Marignane Ecole des Mines d Alès Laboratoire de Génie Informatique et d Ingénierie de Production LGI2P Nîmes Proposition de sujet de thèse CIFRE EUROCOPTER / LGI2P Titre Domaine
Java Licence Professionnelle 2009-2010. Cours 7 : Classes et méthodes abstraites
 Java Licence Professionnelle 2009-2010 Cours 7 : Classes et méthodes abstraites 1 Java Classes et méthodes abstraites - Le mécanisme des classes abstraites permet de définir des comportements (méthodes)
Java Licence Professionnelle 2009-2010 Cours 7 : Classes et méthodes abstraites 1 Java Classes et méthodes abstraites - Le mécanisme des classes abstraites permet de définir des comportements (méthodes)
Cours Base de données relationnelles. M. Boughanem, IUP STRI
 Cours Base de données relationnelles 1 Plan 1. Notions de base 2. Modèle relationnel 3. SQL 2 Notions de base (1) Définition intuitive : une base de données est un ensemble d informations, (fichiers),
Cours Base de données relationnelles 1 Plan 1. Notions de base 2. Modèle relationnel 3. SQL 2 Notions de base (1) Définition intuitive : une base de données est un ensemble d informations, (fichiers),
Logiciel Libre Cours 3 Fondements: Génie Logiciel
 Logiciel Libre Cours 3 Fondements: Génie Logiciel Stefano Zacchiroli [email protected] Laboratoire PPS, Université Paris Diderot 2013 2014 URL http://upsilon.cc/zack/teaching/1314/freesoftware/
Logiciel Libre Cours 3 Fondements: Génie Logiciel Stefano Zacchiroli [email protected] Laboratoire PPS, Université Paris Diderot 2013 2014 URL http://upsilon.cc/zack/teaching/1314/freesoftware/
MODE OPERATOIRE OPENOFFICE BASE
 MODE OPERATOIRE OPENOFFICE BASE Openoffice Base est un SGBDR : Système de Gestion de Base de Données Relationnelle. L un des principaux atouts de ce logiciel est de pouvoir gérer de façon efficace et rapide
MODE OPERATOIRE OPENOFFICE BASE Openoffice Base est un SGBDR : Système de Gestion de Base de Données Relationnelle. L un des principaux atouts de ce logiciel est de pouvoir gérer de façon efficace et rapide
Fonctions de plusieurs variables
 Module : Analyse 03 Chapitre 00 : Fonctions de plusieurs variables Généralités et Rappels des notions topologiques dans : Qu est- ce que?: Mathématiquement, n étant un entier non nul, on définit comme
Module : Analyse 03 Chapitre 00 : Fonctions de plusieurs variables Généralités et Rappels des notions topologiques dans : Qu est- ce que?: Mathématiquement, n étant un entier non nul, on définit comme
Conventions d écriture et outils de mise au point
 Logiciel de base Première année par alternance Responsable : Christophe Rippert [email protected] Introduction Conventions d écriture et outils de mise au point On va utiliser dans cette
Logiciel de base Première année par alternance Responsable : Christophe Rippert [email protected] Introduction Conventions d écriture et outils de mise au point On va utiliser dans cette
SOCLE COMMUN - La Compétence 3 Les principaux éléments de mathématiques et la culture scientifique et technologique
 SOCLE COMMUN - La Compétence 3 Les principaux éléments de mathématiques et la culture scientifique et technologique DOMAINE P3.C3.D1. Pratiquer une démarche scientifique et technologique, résoudre des
SOCLE COMMUN - La Compétence 3 Les principaux éléments de mathématiques et la culture scientifique et technologique DOMAINE P3.C3.D1. Pratiquer une démarche scientifique et technologique, résoudre des
Cours de Programmation 2
 Cours de Programmation 2 Programmation à moyenne et large échelle 1. Programmation modulaire 2. Programmation orientée objet 3. Programmation concurrente, distribuée 4. Programmation monadique 5. Les programmes
Cours de Programmation 2 Programmation à moyenne et large échelle 1. Programmation modulaire 2. Programmation orientée objet 3. Programmation concurrente, distribuée 4. Programmation monadique 5. Les programmes
STAGE IREM 0- Premiers pas en Python
 Université de Bordeaux 16-18 Février 2014/2015 STAGE IREM 0- Premiers pas en Python IREM de Bordeaux Affectation et expressions Le langage python permet tout d abord de faire des calculs. On peut évaluer
Université de Bordeaux 16-18 Février 2014/2015 STAGE IREM 0- Premiers pas en Python IREM de Bordeaux Affectation et expressions Le langage python permet tout d abord de faire des calculs. On peut évaluer
ECR_DESCRIPTION CHAR(80), ECR_MONTANT NUMBER(10,2) NOT NULL, ECR_SENS CHAR(1) NOT NULL) ;
 RÈGLES A SUIVRE POUR OPTIMISER LES REQUÊTES SQL Le but de ce rapport est d énumérer quelques règles pratiques à appliquer dans l élaboration des requêtes. Il permettra de comprendre pourquoi certaines
RÈGLES A SUIVRE POUR OPTIMISER LES REQUÊTES SQL Le but de ce rapport est d énumérer quelques règles pratiques à appliquer dans l élaboration des requêtes. Il permettra de comprendre pourquoi certaines
Algèbre binaire et Circuits logiques (2007-2008)
 Université Mohammed V Faculté des Sciences Département de Mathématiques et Informatique Filière : SMI Algèbre binaire et Circuits logiques (27-28) Prof. Abdelhakim El Imrani Plan. Algèbre de Boole 2. Circuits
Université Mohammed V Faculté des Sciences Département de Mathématiques et Informatique Filière : SMI Algèbre binaire et Circuits logiques (27-28) Prof. Abdelhakim El Imrani Plan. Algèbre de Boole 2. Circuits
TP 1. Prise en main du langage Python
 TP. Prise en main du langage Python Cette année nous travaillerons avec le langage Python version 3. ; nous utiliserons l environnement de développement IDLE. Étape 0. Dans votre espace personnel, créer
TP. Prise en main du langage Python Cette année nous travaillerons avec le langage Python version 3. ; nous utiliserons l environnement de développement IDLE. Étape 0. Dans votre espace personnel, créer
Cours d introduction à l informatique. Partie 2 : Comment écrire un algorithme? Qu est-ce qu une variable? Expressions et instructions
 Cours d introduction à l informatique Partie 2 : Comment écrire un algorithme? Qu est-ce qu une variable? Expressions et instructions Qu est-ce qu un Une recette de cuisine algorithme? Protocole expérimental
Cours d introduction à l informatique Partie 2 : Comment écrire un algorithme? Qu est-ce qu une variable? Expressions et instructions Qu est-ce qu un Une recette de cuisine algorithme? Protocole expérimental
Cours d Algorithmique-Programmation 2 e partie (IAP2): programmation 24 octobre 2007impérative 1 / 44 et. structures de données simples
 Cours d Algorithmique-Programmation 2 e partie (IAP2): programmation impérative et structures de données simples Introduction au langage C Sandrine Blazy - 1ère année 24 octobre 2007 Cours d Algorithmique-Programmation
Cours d Algorithmique-Programmation 2 e partie (IAP2): programmation impérative et structures de données simples Introduction au langage C Sandrine Blazy - 1ère année 24 octobre 2007 Cours d Algorithmique-Programmation
Initiation à la Programmation en Logique avec SISCtus Prolog
 Initiation à la Programmation en Logique avec SISCtus Prolog Identificateurs Ils sont représentés par une suite de caractères alphanumériques commençant par une lettre minuscule (les lettres accentuées
Initiation à la Programmation en Logique avec SISCtus Prolog Identificateurs Ils sont représentés par une suite de caractères alphanumériques commençant par une lettre minuscule (les lettres accentuées
Cycle de vie du logiciel. Unified Modeling Language UML. UML: définition. Développement Logiciel. Salima Hassas. Unified Modeling Language
 Unified Modeling Language UML Salima Hassas Version Cycle de vie du logiciel Client Besoins Déploiement Analyse Test Conception Cours sur la base des transparents de : Gioavanna Di Marzo Serugendo et Frédéric
Unified Modeling Language UML Salima Hassas Version Cycle de vie du logiciel Client Besoins Déploiement Analyse Test Conception Cours sur la base des transparents de : Gioavanna Di Marzo Serugendo et Frédéric
Limites finies en un point
 8 Limites finies en un point Pour ce chapitre, sauf précision contraire, I désigne une partie non vide de R et f une fonction définie sur I et à valeurs réelles ou complees. Là encore, les fonctions usuelles,
8 Limites finies en un point Pour ce chapitre, sauf précision contraire, I désigne une partie non vide de R et f une fonction définie sur I et à valeurs réelles ou complees. Là encore, les fonctions usuelles,
Qualité du logiciel: Méthodes de test
 Qualité du logiciel: Méthodes de test Matthieu Amiguet 2004 2005 Analyse statique de code Analyse statique de code Étudier le programme source sans exécution Généralement réalisée avant les tests d exécution
Qualité du logiciel: Méthodes de test Matthieu Amiguet 2004 2005 Analyse statique de code Analyse statique de code Étudier le programme source sans exécution Généralement réalisée avant les tests d exécution
M1 : Ingénierie du Logiciel
 M1 : Ingénierie du Logiciel UNIVERSITE PIERRE & MARIE CURIE (PARIS VI) Examen Réparti 2eme partie 16 Mai 2013 (2 heures avec documents : tous SAUF ANNALES CORRIGEES). Barème indicatif sur 20,5 points (max
M1 : Ingénierie du Logiciel UNIVERSITE PIERRE & MARIE CURIE (PARIS VI) Examen Réparti 2eme partie 16 Mai 2013 (2 heures avec documents : tous SAUF ANNALES CORRIGEES). Barème indicatif sur 20,5 points (max
I4 : Bases de Données
 I4 : Bases de Données Passage de UML au modèle relationnel Georges LOUIS Département Réseaux et Télécommunications Université de La Rochelle Module I4 2008-2009 1 G.Louis Sommaire 1 Des classes aux tables
I4 : Bases de Données Passage de UML au modèle relationnel Georges LOUIS Département Réseaux et Télécommunications Université de La Rochelle Module I4 2008-2009 1 G.Louis Sommaire 1 Des classes aux tables
3. UML - Unified Modeling Language Diagrammes statiques
 3. UML - Unified Modeling Language Diagrammes statiques Laëtitia Matignon [email protected] Département Informatique - Polytech Lyon Université Claude Bernard Lyon 1 2012-2013 Laëtitia Matignon
3. UML - Unified Modeling Language Diagrammes statiques Laëtitia Matignon [email protected] Département Informatique - Polytech Lyon Université Claude Bernard Lyon 1 2012-2013 Laëtitia Matignon
Table des matières PRESENTATION DU LANGAGE DS2 ET DE SES APPLICATIONS. Introduction
 PRESENTATION DU LANGAGE DS2 ET DE SES APPLICATIONS Depuis SAS 9.2 TS2M3, SAS propose un nouveau langage de programmation permettant de créer et gérer des tables SAS : le DS2 («Data Step 2»). Ces nouveautés
PRESENTATION DU LANGAGE DS2 ET DE SES APPLICATIONS Depuis SAS 9.2 TS2M3, SAS propose un nouveau langage de programmation permettant de créer et gérer des tables SAS : le DS2 («Data Step 2»). Ces nouveautés
Raisonnement par récurrence Suites numériques
 Chapitre 1 Raisonnement par récurrence Suites numériques Terminale S Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES Raisonnement par récurrence. Limite finie ou infinie d une suite.
Chapitre 1 Raisonnement par récurrence Suites numériques Terminale S Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES Raisonnement par récurrence. Limite finie ou infinie d une suite.
Conception des bases de données : Modèle Entité-Association
 Conception des bases de données : Modèle Entité-Association La modélisation d un problème, c est-à-dire le passage du monde réel à sa représentation informatique, se définit en plusieurs étapes pour parvenir
Conception des bases de données : Modèle Entité-Association La modélisation d un problème, c est-à-dire le passage du monde réel à sa représentation informatique, se définit en plusieurs étapes pour parvenir
Créer le schéma relationnel d une base de données ACCESS
 Utilisation du SGBD ACCESS Polycopié réalisé par Chihab Hanachi et Jean-Marc Thévenin Créer le schéma relationnel d une base de données ACCESS GENERALITES SUR ACCESS... 1 A PROPOS DE L UTILISATION D ACCESS...
Utilisation du SGBD ACCESS Polycopié réalisé par Chihab Hanachi et Jean-Marc Thévenin Créer le schéma relationnel d une base de données ACCESS GENERALITES SUR ACCESS... 1 A PROPOS DE L UTILISATION D ACCESS...
Chap 4: Analyse syntaxique. Prof. M.D. RAHMANI Compilation SMI- S5 2013/14 1
 Chap 4: Analyse syntaxique 1 III- L'analyse syntaxique: 1- Le rôle d'un analyseur syntaxique 2- Grammaires non contextuelles 3- Ecriture d'une grammaire 4- Les méthodes d'analyse 5- L'analyse LL(1) 6-
Chap 4: Analyse syntaxique 1 III- L'analyse syntaxique: 1- Le rôle d'un analyseur syntaxique 2- Grammaires non contextuelles 3- Ecriture d'une grammaire 4- Les méthodes d'analyse 5- L'analyse LL(1) 6-
Modèle Entité/Association
 Base de données Modèle Entité/Association L3 Informatique Antoine Spicher [email protected] Contexte du cours Organisation du cours 1 ère partie (C. D.) Modèle et algèbre relationnel Langage SQL
Base de données Modèle Entité/Association L3 Informatique Antoine Spicher [email protected] Contexte du cours Organisation du cours 1 ère partie (C. D.) Modèle et algèbre relationnel Langage SQL
Reconstruction de bâtiments en 3D à partir de nuages de points LIDAR
 Reconstruction de bâtiments en 3D à partir de nuages de points LIDAR Mickaël Bergem 25 juin 2014 Maillages et applications 1 Table des matières Introduction 3 1 La modélisation numérique de milieux urbains
Reconstruction de bâtiments en 3D à partir de nuages de points LIDAR Mickaël Bergem 25 juin 2014 Maillages et applications 1 Table des matières Introduction 3 1 La modélisation numérique de milieux urbains
MEMOIRE. Présenté à. L École Nationale d Ingénieurs de Sfax. en vue de l obtention du MASTERE
 République Tunisienne Ministère de l Enseignement Supérieur, De la Recherche Scientifique et de la Technologie Université de Sfax École Nationale d Ingénieurs de Sfax Ecole Doctorale Sciences et Technologies
République Tunisienne Ministère de l Enseignement Supérieur, De la Recherche Scientifique et de la Technologie Université de Sfax École Nationale d Ingénieurs de Sfax Ecole Doctorale Sciences et Technologies
Objets et Programmation. origine des langages orientés-objet
 Objets et Programmation origine des langages orientés-objet modularité, encapsulation objets, classes, messages exemples en Java héritage, liaison dynamique G. Falquet, Th. Estier CUI Université de Genève
Objets et Programmation origine des langages orientés-objet modularité, encapsulation objets, classes, messages exemples en Java héritage, liaison dynamique G. Falquet, Th. Estier CUI Université de Genève
