UN POLYEDRE SYMBOLE DE L EAU
|
|
|
- Auguste Sergerie
- il y a 9 ans
- Total affichages :
Transcription
1 UN POLYEDRE SYMBOLE DE L EAU ATHENEE ROYAL GATTI DE GAMOND 65, rue du MARAIS 1000 Bruxelles Parrain du projet: JEAN DRABBE Professeur Emérite de l ULB Professeur: CHANTAL RANDOUR-GABRIEL
2 Lorsque l Opération Chercheurs d Eau fut lancée, les élèves de 6ème décidèrent de participer avec un sujet qu ils avaient développé lors d une exposition à Gatti de Gamond en avril Le sujet de cette exposition était POLYEDRES: ART OU MATHEMATIQUE? Après un travail de recherche en bibliothèque et sur le web, ces élèves avaient parcouru l histoire et découvert des polyèdres à travers leur représentation artistique et scientifique. Ils avaient représenté ces objets en perspective et étudié en même temps, certaines de leurs propriétés mathématiques. L utilisation de la géométrie descriptive alliée au logiciel Cabri-Géomètre TM permit de représenter notamment la famille des polyèdres réguliers convexes obtenus par symétrie dans des kaléidoscopes. Jean Drabbe était le conseiller scientifique. L exposition montrait divers artistes et mathématiciens qui ont représenté des polyèdres, du Néolithique à nos jours. Divers aspects philosophiques ainsi qu une recherche sur les pyramides à travers différentes civilisations accompagnaient ce voyage au pays des mathématiques. Une recherche des plans de ville de forme polygonale ainsi que l étude géométrique de pierres semi-précieuses complétaient cette exposition. Chaque élève s était consacré à un artiste ou à un mathématicien afin de réaliser des panneaux et un document écrit. Parmi les polyèdres, l icosaèdre, choisi par Platon comme symbole de l eau, devenait le sujet des jeunes chercheurs. Ils ont sélectionné, parmi leurs documents, quelques images, textes et constructions pour réaliser ce diaporama. C.Randour ATHENEE ROYAL GATTI DE GAMOND 65, rue du Marais Bruxelles POLYEDRES ART OU MATHEMATIQUE? Exposition du 22 au 26 avril 2002 de 14 à 16 heures ou sur rendez-vous du 29 avril au 3 mai 2002
3 Vernissage en présence de Monsieur le Ministre Hazette et quelques photos de l exposition en avril 2002
4 Quelques représentations de l icosaèdre au fil des siècles...
5 Des polyèdres au Néolithique Ces cinq solides platoniciens datent de plus de 1000 ans avant Platon. Ashmolean Museum Oxford J.Soares Source: Blackwell, Geometry in architecture, Key Curriculum Press, 1984
6 Platon né à Athènes vers 427 av.j.-c....le troisième est fait de l assemblage de cent vingt éléments; il est formé de douze angles solides, délimités chacun par cinq plans qui sont des triangles équilatéraux, et il a vingt bases qui sont des triangles équilatéraux..attribuons à l eau la forme la moins mobile...le corps le plus grand le troisième corps. Platon Extrait du Timée Platon, tenant le Timée Raphaël L Ecole d Athènes Vatican
7 Piero della Francesca 1410(?) artiste et mathématicien de la Renaissance Piero étudie la perspective et écrit De Prospectiva Pingendi, un véritable manuel de mathématique à l usage des peintres. Son oeuvre mathématique reste longtemps ignorée au profit de la réputation de Luca Pacioli qui publie la majorité des travaux de Piero, son maître, sans mentionner ses sources. Piero redécouvre les solides archimédiens obtenus par troncature des solides platoniciens, vraisemblablement connus d Archimède. Le manuscript de Piero qui remet à la mode la géométrie connue de Platon et d Euclide et fascine les artistes de la Renaissance est conservé à la bibliothèque du Vatican: c est le Libellus De Quinque Corporibus Regularibus. Auto-portrait Résurrection (detail) Museo Civico - San Sepulcro A.Andrino Dessin de Piero d un icosaèdre inscrit dans un cube. Euclide ne mentionne pas cette construction dans ses Eléments. Source: Piero Della Francesca, De la perspective en peinture, In Media Res, 1998
8 Leonardo da Vinci artiste et ingénieur de la Renaissance. Il illustre La Divine Proportion de Luca Pacioli. Source: Divine Proportion, Librairie du Compagnonnage, Paris, 1988
9 Pacioli offrant De Divina Proportione à Ludovic Le Maure Bibliothèque publique et universitaire de Genève Luca Pacioli Moine franciscain, né à Borgo San Sepolcro, ville natale de Piero della Francesca. Professeur de mathématiques, il se lie d amitié avec Alberti, son maître Piero et Vinci. En 1494, il publie la Summa di arithmetica, geometria, proportione et proportionalita qu il dédicace à Federico da Montefreltro, Duc d Urbino. Il devient professeur de Guidobaldo, fils du Duc. En 1509, De Divina proportione est imprimée à Venise. Pacioli avait offert le manuscrit à Ludovic le Maure, duc de Milan quelques années auparavant. Bal Leila, Tabich Hafsa Source:Haulotte et Stevelinck, Luca Pacioli, Ed Institut des Experts-Comptables,1994
10 Albrecht Dürer originaire de Nüremberg en Allemagne. Peintre et graveur de la renaissance allemande qui développe la gravure sur bois et sur cuivre. Il voyage à de nombreuses reprises aux Pays-Bas et en Italie où il est influencé par les artistes qu il y rencontre. Il réalise de nombreux autoportraits et se détache ainsi de l art médiéval. Dürer est un humaniste intéressé par les mathématiques. Il écrit en 1525 l Underweissung der messung à l usage des artistes et des artisans. Il y décrit les corpus redécouverts des écrits d Euclide et d Archimède. Son but est de donner aux artisans les moyens de construire avec du bois ou du papier les solides décrits par Pacioli et dessinés par Vinci. Autoportrait source : Dürer, Art-Poche Ed. de la Martinière 1999 Instruction sur la manière de mesurer, avec le compas et la règle, les lignes, les surfaces, les corps entiers/composée par Albrecht Dürer/ à l intention de tous les amateurs d art, accompagnée de figures/ portée à l impression en 1525.
11 La Mélancolie, gravure sur bois de Dürer, 1514 représente un cube dont le sommet supérieur est coupé. Remarquer que la projection verticale est erronnée: les 6 sommets ne peuvent être sur le cercle. Chellai Imane Source: Albrecht Dürer Géométrie, Présentation et traduction de Jeanne Peiffer, Sources du savoir - Seuil- Paris-1995
12 Icosaèdre représenté avec Cabri. Les constructions sont réalisées géométriquement. Cliquer sur cette image pour animer la construction Cabri Chellai I. et Tabich H.
13 Construction de l icosaèdre inscrit dans une sphère de plastique. Les dimensions sont calculées avec Cabri et le patron de l icosaèdre dessiné à l aide de ce logiciel. Source: Dalle 2000 théorèmes et problèmes de géométrie avec solutions la Procure, 1943
14 Wentzel Jamnitzer Orfèvre, graveur des poinçons de Nuremberg en 1543, nommé échevin de cette ville en 1573, il recherche le perfectionnement dans sa corporation. Il publie en 1568 le Perspectiva Corporum Regularium. Kayaalp T. Source: Wentzel Jamnitzer, Perspectiva Corporum Regularium, préface d André Flocon, Gutenberg reprints, Paris, 1981
15 Johannes Kepler Astronome allemand connu par ses trois lois sur le mouvement des planètes, c est aussi un mathématicien qui classe les polyèdres. Il décrit en 1619 dans l Harmonice Mundi, les solides de Platon et semble alors encore attaché aux symboles mystiques.
16 En 1596, dans son Mysterium Cosmographicum, Kepler propose un modèle dans lequel un solide de Platon se situe entre 2 sphères associées à chaque planète. Ce modèle est bien sûr faux. Mohammad Rachid N. Source: Kepler, Pour la Science
17 Source: Cromwell, Polyhedra, Cambridge University Press, 1964
18 Mohammad Rachid N. Cliquer sur cette image pour voir la construction Cabri
19 Source: Cromwell, Polyhedra, Cambridge University Press, 1964
20 Cliquer sur cette image pour animer la construction Cabri de l antiprisme.
21 Cliquer sur cette image pour animer la construction Cabri
22 Cliquer sur cette image pour voir la construction Cabri
23 Cliquer sur cette image pour animer la construction Cabri réalisée en classe. Budak G.
24 J.F.Niceron Erudit et mathématicien de l ordre des Minimes à Paris. Il édite en 1638, La Perspective Curieuse, un des premiers traités consacrés à l étude des anamorphoses.. Mutombo F.
25 Euler né à Bâle, élève de Jean Bernoulli, il reste à Berlin entre 1744 et 1766 près de Frédéric II de Prusse et y rencontre Voltaire. Il part en Russie en C est un des mathématiciens les plus productifs de l histoire qui a su utiliser tous les outils forgés par ses prédécesseurs pour établir des théories cohérentes. Timbre illustrant la célèbre formule d Euler liant le nombre de faces, de sommets et d arêtes d un polyèdre convexe. El Hafid B.
26 Un icosaèdre pour bébé!
27 Ernst Haeckel Biologiste allemand. Il pratiqua d abord la médecine. Il dessina entre 1899 et 1904, les planches de Kunstformen der Natur dont certaines représentent des radiolaires (protozoaires marins microscopiques ne possédant qu une seule cellule). Il formula une loi biogénétique controversée selon laquelle le développement de l individu (ontogénèse) reproduirait celui de l espèce (phylogénèse). Source: Ernst von Haeckel, Kunstformen der Natur, Prestel Verlag 1998 Dur A.
28 Maurits Cornelis Escher Né en Hollande, il entre à l Ecole d Architecture et des Arts décoratifs de Harlem. Il s intéresse aux polyèdres et partage cette fascination avec son frère géologue. Son oeuvre est principalement constituée de lithographies et de gravure sur bois. Il dessine pour la Compagnie Verblifa, en 1963 une boîte métallique en forme d icosaèdre décorée de coquillages et d étoiles de mer. Le projet peut se voir sur le site: Des polyèdres en carton décorent notre stand Escher à l Expo-Sciences 2002 Ils proviennet d un album de découpages, M.C.Caleidocycli D.Schattschneider et W.Walker Taco/Librero
29 Buckminster Fuller, est un architecte américain connu pour ses dômes géodésiques qu il inventa en La distorsion de la représentation de la terre sur un plan le préoccupe et en 1944, il propose une représentation du globe sur un cuboctaèdre. Il améliore cette forme de représentation en projetant la surface terrestre sur un icosaèdre (avec le centre de la terre, comme point fixe) Buckminster Fuller Chellai I. et Tabich H. Souce: Blackwell, Geometry in architecture, Key Curriculum Press, 1984
30 Modèle réalisé pour l exposition en utilisant une mappemonde gonflable vendue dans les magasins de jouets.
31 Source: La Recherche n 353 Un icosaèdre dans l espace!
32 Modèle realisé par J.J.Gabriel
33 Casse-tête en bois
34 Bibliographie Blackwell, Geometry in architecture, Key Curriculum Press, 1984 Cromwell, Polyhedra, Cambridge University Press, 1964 Dalle 2000 théorèmes et problèmes de géométrie avec solutions La Procure, 1943 Albrecht Dürer Géométrie, Présentation et traduction de Jeanne Peiffer, Sources du savoir - Seuil- Paris-1995 Dürer, Art-Poche Ed. de la Martinière 1999 Ernst von Haeckel, Kunstformen der Natur, Prestel Verlag 1998 Haulotte et Stevelinck, Luca Pacioli, Ed Institut des Experts-Comptables,1994 Wentzel Jamnitzer, Perspectiva Corporum Regularium, préface d André Flocon, Gutenberg reprints, Paris, 1981 Kepler, Pour la Science Pacioli, Divine Proportion, Librairie du Compagnonnage, Paris, 1988 Piero Della Francesca, De la perspective en peinture, In Media Res, von Haeckel
35 ULB Printemps des Sciences 2003 Expo-Sciences des Jeunesses Scientifiques 2003
Corps des nombres complexes, J Paul Tsasa
 Corps des nombres complexes, J Paul Tsasa One Pager Février 2013 Vol. 5 Num. 011 Copyright Laréq 2013 http://www.lareq.com Corps des Nombres Complexes Définitions, Règles de Calcul et Théorèmes «Les idiots
Corps des nombres complexes, J Paul Tsasa One Pager Février 2013 Vol. 5 Num. 011 Copyright Laréq 2013 http://www.lareq.com Corps des Nombres Complexes Définitions, Règles de Calcul et Théorèmes «Les idiots
Les Éditions du patrimoine présentent La tenture de l Apocalypse d Angers Collection «Sensitinéraires»
 é Les Éditions du patrimoine présentent La tenture de l Apocalypse d Angers Collection «Sensitinéraires» >Un ouvrage conçu en collaboration avec l IRAG (Institut pour la recherche d applications gravées),
é Les Éditions du patrimoine présentent La tenture de l Apocalypse d Angers Collection «Sensitinéraires» >Un ouvrage conçu en collaboration avec l IRAG (Institut pour la recherche d applications gravées),
Fermat Science www.voyage-mathematique.com [DOSSIER PEDAGOGIQUE] Dossier à destination des enseignants
![Fermat Science www.voyage-mathematique.com [DOSSIER PEDAGOGIQUE] Dossier à destination des enseignants Fermat Science www.voyage-mathematique.com [DOSSIER PEDAGOGIQUE] Dossier à destination des enseignants](/thumbs/18/822770.jpg) Exposition Voyage en Mathématique Fermat Science www.voyage-mathematique.com,,,, [DOSSIER PEDAGOGIQUE] Dossier à destination des enseignants SOMMAIRE SOMMAIRE... 1 PRESENTATION DE L EXPOSITION... 2 HISTORIQUE
Exposition Voyage en Mathématique Fermat Science www.voyage-mathematique.com,,,, [DOSSIER PEDAGOGIQUE] Dossier à destination des enseignants SOMMAIRE SOMMAIRE... 1 PRESENTATION DE L EXPOSITION... 2 HISTORIQUE
ALAIN-DOMINIQUE GALLIZIA
 ALAIN-DOMINIQUE GALLIZIA est un architecte français, mécène urbain et curateur-collectionneur œuvrant à la RECONNAISSANCE DE L ART DU GRAFFITI. L atelier de Boulogne Billancourt appelé «La Ruche du Tag»
ALAIN-DOMINIQUE GALLIZIA est un architecte français, mécène urbain et curateur-collectionneur œuvrant à la RECONNAISSANCE DE L ART DU GRAFFITI. L atelier de Boulogne Billancourt appelé «La Ruche du Tag»
L'ENTREPRISE À L'ŒUVRE
 L'ENTREPRISE À L'ŒUVRE Rapprocher la culture et le monde du travail en offrant aux salariés une rencontre au quotidien avec l art, tel est le but de L Entreprise à l œuvre, opération organisée sous l égide
L'ENTREPRISE À L'ŒUVRE Rapprocher la culture et le monde du travail en offrant aux salariés une rencontre au quotidien avec l art, tel est le but de L Entreprise à l œuvre, opération organisée sous l égide
Introduction au maillage pour le calcul scientifique
 Introduction au maillage pour le calcul scientifique CEA DAM Île-de-France, Bruyères-le-Châtel [email protected] Présentation adaptée du tutorial de Steve Owen, Sandia National Laboratories, Albuquerque,
Introduction au maillage pour le calcul scientifique CEA DAM Île-de-France, Bruyères-le-Châtel [email protected] Présentation adaptée du tutorial de Steve Owen, Sandia National Laboratories, Albuquerque,
Cabri et le programme de géométrie au secondaire au Québec
 Cabri et le programme de géométrie au secondaire au Québec Benoît Côté Département de mathématiques, UQAM, Québec [email protected] 1. Introduction - Exercice de didactique fiction Que signifie intégrer
Cabri et le programme de géométrie au secondaire au Québec Benoît Côté Département de mathématiques, UQAM, Québec [email protected] 1. Introduction - Exercice de didactique fiction Que signifie intégrer
COMPTE-RENDU «MATHS EN JEANS» LYCEE OZENNE Groupe 1 : Comment faire une carte juste de la Terre?
 Claire FORGACZ Marion GALLART Hasnia GOUDJILI COMPTERENDU «MATHS EN JEANS» LYCEE OZENNE Groupe 1 : Comment faire une carte juste de la Terre? Si l on se pose la question de savoir comment on peut faire
Claire FORGACZ Marion GALLART Hasnia GOUDJILI COMPTERENDU «MATHS EN JEANS» LYCEE OZENNE Groupe 1 : Comment faire une carte juste de la Terre? Si l on se pose la question de savoir comment on peut faire
Revue de presse MARS WWW.SERVICE4ETOILES.FR (14/03/14) NC. Meljac habille l hôtel Félicien. Lampe Opéra Ambre tissée - MELJAC
 Mars 2014 Revue de presse MARS WWW.SERVICE4ETOILES.FR (14/03/14) NC Meljac habille l hôtel Félicien WWW.ARCHIDESIGNCLUB.COM (10/03/14) 120.000 visiteurs Lampe Opéra Ambre tissée - MELJAC WWW.ARCHIDESIGNCLUB.COM
Mars 2014 Revue de presse MARS WWW.SERVICE4ETOILES.FR (14/03/14) NC Meljac habille l hôtel Félicien WWW.ARCHIDESIGNCLUB.COM (10/03/14) 120.000 visiteurs Lampe Opéra Ambre tissée - MELJAC WWW.ARCHIDESIGNCLUB.COM
Serrurier-Bovy Masterworks, d une collection
 mercredi 3 juin 2015 à 19h Serrurier-Bovy Masterworks, d une collection exposition Vendredi 29 mai de 10 à 19 heures Samedi 30 mai de 11 à 19 heures Lundi 1er juin de 10 à 19 heures Mardi 2 juin de 10
mercredi 3 juin 2015 à 19h Serrurier-Bovy Masterworks, d une collection exposition Vendredi 29 mai de 10 à 19 heures Samedi 30 mai de 11 à 19 heures Lundi 1er juin de 10 à 19 heures Mardi 2 juin de 10
PARTICIPER À UNE VENTE AUX ENCHÈRES D ŒUVRES D ART
 Activités éducatives pour les élèves de 10 à 11 ans PARTICIPER À UNE VENTE AUX ENCHÈRES D ŒUVRES D ART NIVEAU : PRIMAIRE GROUPE D ÂGE : ÉLÈVES DE 10 À 11 ANS SOMMAIRE DE L ACTIVITÉ Les élèves observent
Activités éducatives pour les élèves de 10 à 11 ans PARTICIPER À UNE VENTE AUX ENCHÈRES D ŒUVRES D ART NIVEAU : PRIMAIRE GROUPE D ÂGE : ÉLÈVES DE 10 À 11 ANS SOMMAIRE DE L ACTIVITÉ Les élèves observent
JUNGHANS DIE DEUTSCHE UHR
 JUNGHANS DIE DEUTSCHE UHR JUNGHANS THE GERMAN WATCH FRANÇ AIS félicitations pour l achat d une montre junghans. ce qui débuta en 1861 à schramberg avec la fondation de la société, s est rapidement transformé
JUNGHANS DIE DEUTSCHE UHR JUNGHANS THE GERMAN WATCH FRANÇ AIS félicitations pour l achat d une montre junghans. ce qui débuta en 1861 à schramberg avec la fondation de la société, s est rapidement transformé
Nouveau site Internet Roger Dubuis Découvrir et voyager dans l Incredible World of Roger Dubuis
 Information Presse L univers The Incredible Warrior, collection Excalibur Avec le lancement de son nouveau site Internet www.rogerdubuis.com, la Maison genevoise vous invite à découvrir et vivre l intense
Information Presse L univers The Incredible Warrior, collection Excalibur Avec le lancement de son nouveau site Internet www.rogerdubuis.com, la Maison genevoise vous invite à découvrir et vivre l intense
Les Foires et Salons vecteurs de communication efficace dans la prospection de nouveaux marchés
 Les Foires et Salons vecteurs de communication efficace dans la prospection de nouveaux marchés Quoi? Lequel? Comment? Jean Thomas Leplat Directeur général Artexis Expo Groupe basé à Bruxelles, 340 collaborateurs
Les Foires et Salons vecteurs de communication efficace dans la prospection de nouveaux marchés Quoi? Lequel? Comment? Jean Thomas Leplat Directeur général Artexis Expo Groupe basé à Bruxelles, 340 collaborateurs
Éditorial. Tangente ÉDUCATION. Scratch, AlgoBox, Python. Trimestriel - n 15 - janvier 2011 Numéro spécial 16 activités TICE pour le lycée
 Tangente ÉDUCATION Trimestriel - n 15 - janvier 2011 Numéro spécial 16 activités TICE pour le lycée et leurs programmes dans les trois langages les plus utilisés : Scratch, AlgoBox, Python Python Éditorial
Tangente ÉDUCATION Trimestriel - n 15 - janvier 2011 Numéro spécial 16 activités TICE pour le lycée et leurs programmes dans les trois langages les plus utilisés : Scratch, AlgoBox, Python Python Éditorial
Je fais le point 1. PrénoM :... Il y a... oiseaux. Guide de l enseignant p.64. Écris les nombres dictés. Écris les nombres effacés par Gribouille.
 1 Guide de l enseignant p.64 Écris les nombres dictés. Je fais le point 1 PrénoM :.... 2 Écris les nombres effacés par Gribouille. 2 20 1 4 11 10 1 16 1 3 Écris combien il y a d oiseaux. sur l image d
1 Guide de l enseignant p.64 Écris les nombres dictés. Je fais le point 1 PrénoM :.... 2 Écris les nombres effacés par Gribouille. 2 20 1 4 11 10 1 16 1 3 Écris combien il y a d oiseaux. sur l image d
Carré parfait et son côté
 LE NOMBRE Carré parfait et son côté Résultat d apprentissage Description 8 e année, Le nombre, n 1 Démontrer une compréhension des carrés parfaits et des racines carrées (se limitant aux nombres entiers
LE NOMBRE Carré parfait et son côté Résultat d apprentissage Description 8 e année, Le nombre, n 1 Démontrer une compréhension des carrés parfaits et des racines carrées (se limitant aux nombres entiers
Le château de Versailles Architecture et décors extérieurs
 Le château de Versailles Architecture et décors extérieurs Les rois de France viennent régulièrement chasser à Versailles à partir du XVI ème siècle. Henri IV y amène son fils, le futur Louis XIII. Devenu
Le château de Versailles Architecture et décors extérieurs Les rois de France viennent régulièrement chasser à Versailles à partir du XVI ème siècle. Henri IV y amène son fils, le futur Louis XIII. Devenu
El Tres de Mayo, GOYA
 Art du visuel / «Arts, ruptures, continuités» Problématique : «Comment l expression du sentiment surgit-elle dans l art au XIX è siècle?» El Tres de Mayo, GOYA Le Tres de Mayo, Francisco Goya, huile sur
Art du visuel / «Arts, ruptures, continuités» Problématique : «Comment l expression du sentiment surgit-elle dans l art au XIX è siècle?» El Tres de Mayo, GOYA Le Tres de Mayo, Francisco Goya, huile sur
LA BANQUE NATIONALE DE SERBIE EXPRIME SES REMERCIEMENTS À LA BANQUE DE FRANCE POUR LES COPIES DE DOCUMENTS D ARCHIVES
 Banque Nationale de Serbie BANQUE NATIONALE DE SERBIE BANQUE DE FRANCE Fabrication des billets serbes et yougoslaves à la Banque de France 1885 85 1930 LA BANQUE NATIONALE DE SERBIE EXPRIME SES REMERCIEMENTS
Banque Nationale de Serbie BANQUE NATIONALE DE SERBIE BANQUE DE FRANCE Fabrication des billets serbes et yougoslaves à la Banque de France 1885 85 1930 LA BANQUE NATIONALE DE SERBIE EXPRIME SES REMERCIEMENTS
Les propriétés esthétiques du nombre d or sur le visage humain : mythe ou réalité?
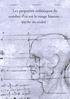 20 octobre 2011 Travail de Maturité Nina Dâmaso Les propriétés esthétiques du nombre d or sur le visage humain : mythe ou réalité? gsfgsg I Analyse du profil d un visage par Léonard de Vinci Table des
20 octobre 2011 Travail de Maturité Nina Dâmaso Les propriétés esthétiques du nombre d or sur le visage humain : mythe ou réalité? gsfgsg I Analyse du profil d un visage par Léonard de Vinci Table des
Notre nom est un gage de responsabilité. Wealth-Assurance AG
 Notre nom est un gage de responsabilité Wealth-Assurance AG Qualité suisse et service personnalisé c est notre emblème Aloyse Steichen Président directeur général Bienvenue Au nom de Wealth-Assurance AG
Notre nom est un gage de responsabilité Wealth-Assurance AG Qualité suisse et service personnalisé c est notre emblème Aloyse Steichen Président directeur général Bienvenue Au nom de Wealth-Assurance AG
Exercices Alternatifs. Quelqu un aurait-il vu passer un polynôme?
 Exercices Alternatifs Quelqu un aurait-il vu passer un polynôme? c 2004 Frédéric Le Roux, François Béguin (copyleft LDL : Licence pour Documents Libres). Sources et figures: polynome-lagrange/. Version
Exercices Alternatifs Quelqu un aurait-il vu passer un polynôme? c 2004 Frédéric Le Roux, François Béguin (copyleft LDL : Licence pour Documents Libres). Sources et figures: polynome-lagrange/. Version
Exercices Alternatifs. Quelqu un aurait-il vu passer un polynôme?
 Exercices Alternatifs Quelqu un aurait-il vu passer un polynôme? c 2004 Frédéric Le Roux, François Béguin (copyleft LDL : Licence pour Documents Libres). Sources et figures: polynome-lagrange/. Version
Exercices Alternatifs Quelqu un aurait-il vu passer un polynôme? c 2004 Frédéric Le Roux, François Béguin (copyleft LDL : Licence pour Documents Libres). Sources et figures: polynome-lagrange/. Version
Aide à l interrogation pour les catalogues bibliographiques de la documentation générale et du patrimoine culturel
 Aide à l interrogation pour les catalogues bibliographiques de la documentation générale et du patrimoine culturel Cette application Web vous donne accès aux bases bibliographiques de la Région Basse-
Aide à l interrogation pour les catalogues bibliographiques de la documentation générale et du patrimoine culturel Cette application Web vous donne accès aux bases bibliographiques de la Région Basse-
Optimisation et programmation mathématique. Professeur Michel de Mathelin. Cours intégré : 20 h
 Télécom Physique Strasbourg Master IRIV Optimisation et programmation mathématique Professeur Michel de Mathelin Cours intégré : 20 h Programme du cours d optimisation Introduction Chapitre I: Rappels
Télécom Physique Strasbourg Master IRIV Optimisation et programmation mathématique Professeur Michel de Mathelin Cours intégré : 20 h Programme du cours d optimisation Introduction Chapitre I: Rappels
Comité scientifique 7 décembre 2007. Observatoire de Paris
 Comité scientifique 7 décembre 2007. Observatoire de Paris Présents : C. Blin, I. Diu, J. Ducos, A. Gaillard, V. Giacomotto Excusés : L. Bobis, P. Duris, V. Fromentin, N. Ly, B. Mondrain, I. Pantin, I.
Comité scientifique 7 décembre 2007. Observatoire de Paris Présents : C. Blin, I. Diu, J. Ducos, A. Gaillard, V. Giacomotto Excusés : L. Bobis, P. Duris, V. Fromentin, N. Ly, B. Mondrain, I. Pantin, I.
De la fiche manuscrite à Internet : l informatisation des collections et de la documentation au musée du quai Branly
 Séminaire «Muséologie, Muséographie et nouvelles formes d adresse au public» Paris, 28 mars 2007 De la fiche manuscrite à Internet : l informatisation des collections et de la documentation au musée du
Séminaire «Muséologie, Muséographie et nouvelles formes d adresse au public» Paris, 28 mars 2007 De la fiche manuscrite à Internet : l informatisation des collections et de la documentation au musée du
Mario Botta (1943) Le Musée d'art moderne de San Francisco
 Mario Botta (1943) Architecte suisse. De 1961 à 1964, il étudie au Liceo Artistico à Milan puis, jusqu'en 1969 à l'istituto Universitario di Architettura à Venise où il est l élève de Carlo Scarpa. En
Mario Botta (1943) Architecte suisse. De 1961 à 1964, il étudie au Liceo Artistico à Milan puis, jusqu'en 1969 à l'istituto Universitario di Architettura à Venise où il est l élève de Carlo Scarpa. En
Trimble Geomatics Office
 Trimble Geomatics Office Notes de version Informations du produit F Version 1.61 Révision A Juin 2003 Bureau d entreprises Trimble Navigation Limited Geomatics & Engineering Division 5475 Kellenburger
Trimble Geomatics Office Notes de version Informations du produit F Version 1.61 Révision A Juin 2003 Bureau d entreprises Trimble Navigation Limited Geomatics & Engineering Division 5475 Kellenburger
Institut Universitaire Professionnalisé Génie Mathématiques et Informatique
 Institut Universitaire Professionnalisé Génie Mathématiques et Informatique Muriel Boutet Anthony Canto Emmanuel Roux Année 2003-2004 Avant Propos Sommaire Vous trouverez dans ce manuel des explications
Institut Universitaire Professionnalisé Génie Mathématiques et Informatique Muriel Boutet Anthony Canto Emmanuel Roux Année 2003-2004 Avant Propos Sommaire Vous trouverez dans ce manuel des explications
Organiser, plannifier
 Dossier HABITAT - Organiser, plannifier Organiser, plannifier 010-011 Les métiers et l organisation Situation de départ : Les travaux de la maison vont commencer, qui doit intervenir en premier, comment
Dossier HABITAT - Organiser, plannifier Organiser, plannifier 010-011 Les métiers et l organisation Situation de départ : Les travaux de la maison vont commencer, qui doit intervenir en premier, comment
INSTITUT INTERNATIONAL DES DROITS DE L HOMME INTERNATIONAL INSTITUTE OF HUMAN RIGHTS
 INSTITUT INTERNATIONAL DES DROITS DE L HOMME INTERNATIONAL INSTITUTE OF HUMAN RIGHTS Fondé par / Founded by René Cassin (1969) L ENFANT ET LE DROIT INTERNATIONAL DES DROITS DE L HOMME 46 ème Session annuelle
INSTITUT INTERNATIONAL DES DROITS DE L HOMME INTERNATIONAL INSTITUTE OF HUMAN RIGHTS Fondé par / Founded by René Cassin (1969) L ENFANT ET LE DROIT INTERNATIONAL DES DROITS DE L HOMME 46 ème Session annuelle
Facile à allier Antimicrobien Antifouling Facile à façonner Conducteur Durable Facile à assembler Coloré Essentiel Malléable et ductile Sûr
 Le cuivre est E s t h é t i q u e Facile à allier Antimicrobien Antifouling Facile à façonner Conducteur Durable Facile à assembler Coloré Essentiel Malléable et ductile Sûr Recyclable Solide Disponible
Le cuivre est E s t h é t i q u e Facile à allier Antimicrobien Antifouling Facile à façonner Conducteur Durable Facile à assembler Coloré Essentiel Malléable et ductile Sûr Recyclable Solide Disponible
TPG 12 - Spectrophotométrie
 TPG 12 - Spectrophotométrie Travail par binôme Objectif : découvrir les conditions de validité et les utilisations possibles de la loi de Beer-Lambert I- Tracé de la rosace des couleurs Choisir un des
TPG 12 - Spectrophotométrie Travail par binôme Objectif : découvrir les conditions de validité et les utilisations possibles de la loi de Beer-Lambert I- Tracé de la rosace des couleurs Choisir un des
CLASSE : : : ; : : : : LA LIBERTE GUIDANT LE PEUPLE EUGENE DELACROIX
 HISTOIRE DES ARTS CLASSE : 4 ème Période historique : XIXème siècle Moment choisi : le retour à la monarchie ; les Trois Glorieuses Thématique : Arts, Etats et pouvoir (œuvre engagée) Sujet : Comment un
HISTOIRE DES ARTS CLASSE : 4 ème Période historique : XIXème siècle Moment choisi : le retour à la monarchie ; les Trois Glorieuses Thématique : Arts, Etats et pouvoir (œuvre engagée) Sujet : Comment un
THEME : LES ENJEUX DE LA COMMUNICATION A LA GARDE DE SECURITE PENITENTIAIRE
 MINISTERE DE L ADMINISTRATION TERRITORIALE, BURKINA FASO DE LA DECENTRALISATION ET DE LA SECURITE ********* ************ Unité-Progrès-Justice SECRETARIAT GENERAL ************ DIRECTION DE L ECOLE NATIONALE
MINISTERE DE L ADMINISTRATION TERRITORIALE, BURKINA FASO DE LA DECENTRALISATION ET DE LA SECURITE ********* ************ Unité-Progrès-Justice SECRETARIAT GENERAL ************ DIRECTION DE L ECOLE NATIONALE
REPUBLIQUE ET FAIT RELIGIEUX DEPUIS 1880
 REPUBLIQUE ET FAIT RELIGIEUX DEPUIS 1880 «La grande idée, la notion fondamentale de l Etat laïque, c est-àdire la délimitation profonde entre le temporel et le spirituel, est entrée dans nos mœurs de manière
REPUBLIQUE ET FAIT RELIGIEUX DEPUIS 1880 «La grande idée, la notion fondamentale de l Etat laïque, c est-àdire la délimitation profonde entre le temporel et le spirituel, est entrée dans nos mœurs de manière
Musée temporaire. Le jeu
 Musée temporaire Le jeu Bienvenue à la Banque nationale de Belgique! La Banque nationale de Belgique n est pas une banque comme les autres Par exemple, tu ne peux pas y ouvrir de compte bancaire : seules
Musée temporaire Le jeu Bienvenue à la Banque nationale de Belgique! La Banque nationale de Belgique n est pas une banque comme les autres Par exemple, tu ne peux pas y ouvrir de compte bancaire : seules
Conclusion : -30- 41 Voir Annexe p.33
 Conclusion : Les trois collections universitaires qui viennent d être évoquées sont les seules des universités françaises que l on peut toujours visiter. Toutes les autres collections universitaires comme
Conclusion : Les trois collections universitaires qui viennent d être évoquées sont les seules des universités françaises que l on peut toujours visiter. Toutes les autres collections universitaires comme
FONDS CHARLES COURNAULT (1815-1904)
 ARCHIVES MUNICIPALES DE NANCY 3 Z FONDS CHARLES COURNAULT (1815-1904) REPERTOIRE NUMERIQUE DETAILLE THIBAUD PETER SOUS LA DIRECTION DE DANIEL PETER, CONSERVATEUR, NANCY 2008 2 FICHE DESCRIPTIVE CHAMP DESCRIPTION
ARCHIVES MUNICIPALES DE NANCY 3 Z FONDS CHARLES COURNAULT (1815-1904) REPERTOIRE NUMERIQUE DETAILLE THIBAUD PETER SOUS LA DIRECTION DE DANIEL PETER, CONSERVATEUR, NANCY 2008 2 FICHE DESCRIPTIVE CHAMP DESCRIPTION
Technique de la peinture
 Supports pédagogiques: Fiches de travail n 1, 2 et 4 (lycée), fiche de travail n 3 (école primaire et collège). ENSEIGNANT E : Michel Haider (retable de Hohenlandenberg), Triptyque de la Crucifixion, panneau
Supports pédagogiques: Fiches de travail n 1, 2 et 4 (lycée), fiche de travail n 3 (école primaire et collège). ENSEIGNANT E : Michel Haider (retable de Hohenlandenberg), Triptyque de la Crucifixion, panneau
AC AB. A B C x 1. x + 1. d où. Avec un calcul vu au lycée, on démontre que cette solution admet deux solutions dont une seule nous intéresse : x =
 LE NOMBRE D OR Présentation et calcul du nombre d or Euclide avait trouvé un moyen de partager en deu un segment selon en «etrême et moyenne raison» Soit un segment [AB]. Le partage d Euclide consiste
LE NOMBRE D OR Présentation et calcul du nombre d or Euclide avait trouvé un moyen de partager en deu un segment selon en «etrême et moyenne raison» Soit un segment [AB]. Le partage d Euclide consiste
ARTIS TRADING ALG a développé un réseau de partenaires dans toute l Algérie :
 Présentation : ARTIS TRADING ALG s est donné comme objectif de proposer à ses clients une large gamme de produits de décoration issue de l art et l artisanat Algérien. Ainsi il regroupe les compétences
Présentation : ARTIS TRADING ALG s est donné comme objectif de proposer à ses clients une large gamme de produits de décoration issue de l art et l artisanat Algérien. Ainsi il regroupe les compétences
En 1987, la signature par le gouvernement,
 Mise en espace des collections Une mise en scène de collections : LA MÉDIATHÈQUE DU VAL-D EUROPE «La bibliothèque devrait utiliser des méthodes de présentation la faisant apparaître comme un horizon infi
Mise en espace des collections Une mise en scène de collections : LA MÉDIATHÈQUE DU VAL-D EUROPE «La bibliothèque devrait utiliser des méthodes de présentation la faisant apparaître comme un horizon infi
LA DEFISCALISATION PAR L ART
 LA DEFISCALISATION PAR L ART LA DEFISCALISATION PAR L ART EXCO ECAF Novembre 2009 2 L AVANTAGE FISCAL OFFERT AUX ENTREPRISES EXCO ECAF Novembre 2009 3 ACQUISITION D ŒUVRES ORIGINALES D ARTISTES VIVANTS
LA DEFISCALISATION PAR L ART LA DEFISCALISATION PAR L ART EXCO ECAF Novembre 2009 2 L AVANTAGE FISCAL OFFERT AUX ENTREPRISES EXCO ECAF Novembre 2009 3 ACQUISITION D ŒUVRES ORIGINALES D ARTISTES VIVANTS
Extraits d'email reçus : Ce sont les utilisateurs qui savent le mieux parler du logiciel BatiFree Devis et du service d'assistance.
 Extraits d'email reçus : Ce sont les utilisateurs qui savent le mieux parler du logiciel BatiFree Devis et du service d'assistance. # Ce qu'ils disent Notre Commentaire Région 57 "Bonjour, je viens de
Extraits d'email reçus : Ce sont les utilisateurs qui savent le mieux parler du logiciel BatiFree Devis et du service d'assistance. # Ce qu'ils disent Notre Commentaire Région 57 "Bonjour, je viens de
Collections et dépôts techniques aux XVIIIe et XIXe siècles
 Collections et dépôts techniques aux XVIIIe et XIXe siècles INTRODUCTION * Soraya BOUDIA: tension chez les scientifiques : entre légitimation par le patrimoine / hantise de l obsolescence des représentations
Collections et dépôts techniques aux XVIIIe et XIXe siècles INTRODUCTION * Soraya BOUDIA: tension chez les scientifiques : entre légitimation par le patrimoine / hantise de l obsolescence des représentations
LA FRANC-MACONNERIE EXPLIQUÉE PAR L IMAGE
 Percy John Harvey LA FRANC-MACONNERIE EXPLIQUÉE PAR L IMAGE Échantillon des illustrations Presentation_FMEI.indd 1 20/09/13 14:54:55 La cérémonie d initiation n est pas une opération magique qui transformerait
Percy John Harvey LA FRANC-MACONNERIE EXPLIQUÉE PAR L IMAGE Échantillon des illustrations Presentation_FMEI.indd 1 20/09/13 14:54:55 La cérémonie d initiation n est pas une opération magique qui transformerait
Présentation de la session 2015 du Master de deuxième niveau
 Présentation de la session 2015 du Master de deuxième niveau MEDIATIONS INTERCULTURELLES LES SIGNES, LES MOTS, LES IMAGES POUR LA MISE EN ŒUVRE DE PROJETS PERSONNELS D UTILITE PUBLIQUE Directeur : prof.
Présentation de la session 2015 du Master de deuxième niveau MEDIATIONS INTERCULTURELLES LES SIGNES, LES MOTS, LES IMAGES POUR LA MISE EN ŒUVRE DE PROJETS PERSONNELS D UTILITE PUBLIQUE Directeur : prof.
Enjeux de l égalité au XXI siècle en Suisse
 Eidgenössisches Departement des Innern EDI Eidg. Büro für die Gleichstellung von Frau und Mann EBG Enjeux de l égalité au XXI siècle en Suisse Helvetia Latina Berne 25 novembre 2014 Points abordés 1. Rappel
Eidgenössisches Departement des Innern EDI Eidg. Büro für die Gleichstellung von Frau und Mann EBG Enjeux de l égalité au XXI siècle en Suisse Helvetia Latina Berne 25 novembre 2014 Points abordés 1. Rappel
GESTION D UNE BASE BIBLIOGRAPHIQUE
 GESTION D UNE BASE BIBLIOGRAPHIQUE BTS Bioanalyses et contrôles Gil Voge Lycée Louise Michel, Grenoble Base de données (BD ou DB, database) Ensemble de données relatif à un domaine particulier des connaissances
GESTION D UNE BASE BIBLIOGRAPHIQUE BTS Bioanalyses et contrôles Gil Voge Lycée Louise Michel, Grenoble Base de données (BD ou DB, database) Ensemble de données relatif à un domaine particulier des connaissances
Quelqu un de précieux
 Quelqu un de précieux Introduction Le Mandala O n désigne par ce nom des images organisées autour d un point central, généralement à l intérieur d un cercle mais qui peuvent contenir de multiples formes
Quelqu un de précieux Introduction Le Mandala O n désigne par ce nom des images organisées autour d un point central, généralement à l intérieur d un cercle mais qui peuvent contenir de multiples formes
Anne Cauquelin, L'invention du paysage.
 Anne Cauquelin, L'invention du paysage. Anne Cauquelin, L'invention du paysage, QUADRIGE, PUF, 2000, 2002 [1ère édition Libriarie Plon, 1989]. Analyse historique de la notion de paysage : - Qu'est ce qu'un
Anne Cauquelin, L'invention du paysage. Anne Cauquelin, L'invention du paysage, QUADRIGE, PUF, 2000, 2002 [1ère édition Libriarie Plon, 1989]. Analyse historique de la notion de paysage : - Qu'est ce qu'un
Prendre en main le TNI Ebeam
 Prendre en main le TNI Ebeam Comment récupérer le logiciel du TNI (Ebeam Interact)? Se rendre sur le site de la société Luidia (éditeur d Ebeam) et cliquer sur Downloads Choisir la version la plus récente
Prendre en main le TNI Ebeam Comment récupérer le logiciel du TNI (Ebeam Interact)? Se rendre sur le site de la société Luidia (éditeur d Ebeam) et cliquer sur Downloads Choisir la version la plus récente
Les éditions liégeoises de Don Quichotte de 1750 à 1795 1
 Les éditions liégeoises de Don Quichotte de 1750 à 1795 1 Pierre MOURIAU DE MEULENACKER L année 2005 est celle des anniversaires : les 175 ans de la Belgique, les 200 ans de la naissance d Andersen, le
Les éditions liégeoises de Don Quichotte de 1750 à 1795 1 Pierre MOURIAU DE MEULENACKER L année 2005 est celle des anniversaires : les 175 ans de la Belgique, les 200 ans de la naissance d Andersen, le
Agence de publicité BOOK 2015. www.lordibra.net
 Agence de publicité BOOK 2015 P O R T F O L I O www.lordibra.net Qui sommes-nous? Spécialiste en création graphique et multimédia, Lordibra est une agence de publicité constituée de jeunes talents spécialisés
Agence de publicité BOOK 2015 P O R T F O L I O www.lordibra.net Qui sommes-nous? Spécialiste en création graphique et multimédia, Lordibra est une agence de publicité constituée de jeunes talents spécialisés
ACTIVITES MATHEMATIQUES
 MINISTÈRE DE LA COMMUNAUTÉ FRANÇAISE ENSEIGNEMENT DE LA COMMUNAUTÉ FRANÇAISE Administration Générale de l'enseignement et de la Recherche Scientifique Service général des Affaires pédagogiques et du Pilotage
MINISTÈRE DE LA COMMUNAUTÉ FRANÇAISE ENSEIGNEMENT DE LA COMMUNAUTÉ FRANÇAISE Administration Générale de l'enseignement et de la Recherche Scientifique Service général des Affaires pédagogiques et du Pilotage
VENTE DE PRESTIGE D ART DECO. 28 mai 2013
 Communiqué VENTE DE PRESTIGE D ART DECO 28 mai 2013 La vente, qui se tiendra le 28 mai sous le marteau de François Tajan, propose un vaste panorama des Arts décoratifs, de l Art nouveau à la grande décoration
Communiqué VENTE DE PRESTIGE D ART DECO 28 mai 2013 La vente, qui se tiendra le 28 mai sous le marteau de François Tajan, propose un vaste panorama des Arts décoratifs, de l Art nouveau à la grande décoration
Situations d apprentissage. Mat-2101-3
 Situations d apprentissage Mat-2101-3 Un vendredi au chalet (Activités 1, 2 et 3) Le taxi (Activités 1 et 2) Un entrepôt «sans dessus dessous» (Activités 1, 2, 3 et 4) France Dugal Diane Garneau Commission
Situations d apprentissage Mat-2101-3 Un vendredi au chalet (Activités 1, 2 et 3) Le taxi (Activités 1 et 2) Un entrepôt «sans dessus dessous» (Activités 1, 2, 3 et 4) France Dugal Diane Garneau Commission
PRESENTATION DE L ASSOCIATION LETTRES ET IMAGES (ALI)
 PRESENTATION DE L ASSOCIATION LETTRES ET IMAGES (ALI) Association d intérêt public à but non lucratif, fondée en 1998 à l occasion des manifestations «150 ans de l Etat fédéral -150 ans de patrimoine industriel»
PRESENTATION DE L ASSOCIATION LETTRES ET IMAGES (ALI) Association d intérêt public à but non lucratif, fondée en 1998 à l occasion des manifestations «150 ans de l Etat fédéral -150 ans de patrimoine industriel»
6. Les différents types de démonstrations
 LES DIFFÉRENTS TYPES DE DÉMONSTRATIONS 33 6. Les différents types de démonstrations 6.1. Un peu de logique En mathématiques, une démonstration est un raisonnement qui permet, à partir de certains axiomes,
LES DIFFÉRENTS TYPES DE DÉMONSTRATIONS 33 6. Les différents types de démonstrations 6.1. Un peu de logique En mathématiques, une démonstration est un raisonnement qui permet, à partir de certains axiomes,
Agence Véronique Lopez Relations Presse - Conseils en Communication
 Agence Véronique Lopez Relations Presse - Conseils en Communication PRÉSENTATION DE L AGENCE VÉRONIQUE LOPEZ 2015 contact : [email protected] Sommaire Page 3 Une agence à taille humaine Page 6 Résultats
Agence Véronique Lopez Relations Presse - Conseils en Communication PRÉSENTATION DE L AGENCE VÉRONIQUE LOPEZ 2015 contact : [email protected] Sommaire Page 3 Une agence à taille humaine Page 6 Résultats
Planet AIXCAET. Edito par Marie Allantaz. Bienvenue à Sandra Carrette. Septembre 2013. Biographie. Mes plus beaux voyages
 Septembre 2013 Planet AIXCAET Edito par Marie Allantaz Une année 2013/2014 qui s annonce chargée de bonnes surprises et une rentrée sur les chapeaux de roue avec le traditionnel rendez-vous de l IFTM/TopRésa.
Septembre 2013 Planet AIXCAET Edito par Marie Allantaz Une année 2013/2014 qui s annonce chargée de bonnes surprises et une rentrée sur les chapeaux de roue avec le traditionnel rendez-vous de l IFTM/TopRésa.
Items étudiés dans le CHAPITRE N5. 7 et 9 p 129 D14 Déterminer par le calcul l'antécédent d'un nombre par une fonction linéaire
 CHAPITRE N5 FONCTIONS LINEAIRES NOTION DE FONCTION FONCTIONS LINEAIRES NOTION DE FONCTION FONCTIONS LINEAIRES NOTION DE FONCTION Code item D0 D2 N30[S] Items étudiés dans le CHAPITRE N5 Déterminer l'image
CHAPITRE N5 FONCTIONS LINEAIRES NOTION DE FONCTION FONCTIONS LINEAIRES NOTION DE FONCTION FONCTIONS LINEAIRES NOTION DE FONCTION Code item D0 D2 N30[S] Items étudiés dans le CHAPITRE N5 Déterminer l'image
MENER UNE RECHERCHE D INFORMATION
 MENER UNE RECHERCHE D INFORMATION Pourquoi ne pas chercher seulement ses informations dans Google? Crédits photo : Flickr On N importe qui publie n importe quoi sur le Web! Parce que... Les résultats sont
MENER UNE RECHERCHE D INFORMATION Pourquoi ne pas chercher seulement ses informations dans Google? Crédits photo : Flickr On N importe qui publie n importe quoi sur le Web! Parce que... Les résultats sont
Découvrez les Artisans d Art qui vous entourent
 Découvrez les Artisans d Art qui vous entourent Contact Roland Le Joliff-Service communication 06.69.22.44.92 [email protected] www.cma-var.fr Avril 2014 2 / 10 1 er avril 2014 En avant première
Découvrez les Artisans d Art qui vous entourent Contact Roland Le Joliff-Service communication 06.69.22.44.92 [email protected] www.cma-var.fr Avril 2014 2 / 10 1 er avril 2014 En avant première
Droits d auteurs : quelles opportunités fiscales?
 Droits d auteurs : quelles opportunités fiscales? Vincent Lamberts et Jean-Luc Wuidard Avocats au Barreau de Liège 26 novembre 2010 Petit déjeuner conférence Etudes et Expansion ASBL Plan des exposés -1.
Droits d auteurs : quelles opportunités fiscales? Vincent Lamberts et Jean-Luc Wuidard Avocats au Barreau de Liège 26 novembre 2010 Petit déjeuner conférence Etudes et Expansion ASBL Plan des exposés -1.
Environnement. Aménagement & Urbanisme. Énergie. Société d avocats au Barreau de Paris - 250, rue Saint Jacques - 75005 Paris - www.carlenckell.
 Environnement Aménagement & Urbanisme Énergie Société d avocats au Barreau de Paris - 250, rue Saint Jacques - 75005 Paris - www.carlenckell.com Nos domaines d expertise Environnement Urbanisme Énergie
Environnement Aménagement & Urbanisme Énergie Société d avocats au Barreau de Paris - 250, rue Saint Jacques - 75005 Paris - www.carlenckell.com Nos domaines d expertise Environnement Urbanisme Énergie
C ONGRESS INCENTIVE. 10 Raisons BERLIN. de (re)découvrir
 C ONGRESS INCENTIVE 10 Raisons de (re)découvrir BERLIN MR CONGRESS & INCENTIVE GMBH DESTINATION Meeting Incentive Congress Event Ses hôtels boutiques, design, de charme et de luxe Ses lieux de soirées
C ONGRESS INCENTIVE 10 Raisons de (re)découvrir BERLIN MR CONGRESS & INCENTIVE GMBH DESTINATION Meeting Incentive Congress Event Ses hôtels boutiques, design, de charme et de luxe Ses lieux de soirées
Nicolas VAN LABEKE LORIA/CNRS, Université Henri Poincaré - Nancy I, BP 239, F-54506 Vandoeuvre les Nancy Cedex,FRANCE vanlabek@loria.
 Développement d un logiciel pour l enseignement de la géométrie spatiale en partenariat Université/Second degré : démarche et présentation de Calques 3D Nicolas VAN LABEKE LORIA/CNRS, Université Henri
Développement d un logiciel pour l enseignement de la géométrie spatiale en partenariat Université/Second degré : démarche et présentation de Calques 3D Nicolas VAN LABEKE LORIA/CNRS, Université Henri
BnF Service d Action pédagogique de la Bibliothèque nationale de France
 PARTIE 3 les merveilles de la mer Éternelle source de rêve NIVEAU 2 De même qu on se prend à imaginer une vie dans les étoiles, n existe t-il pas un monde sous-marin peuplé d êtres aux allures humaines?
PARTIE 3 les merveilles de la mer Éternelle source de rêve NIVEAU 2 De même qu on se prend à imaginer une vie dans les étoiles, n existe t-il pas un monde sous-marin peuplé d êtres aux allures humaines?
Livret de visite. Collège À LA DÉCOUVERTE DES ARCHIVES DÉPARTEMENTALES DE LA DORDOGNE
 Livret de visite Collège À LA DÉCOUVERTE DES ARCHIVES DÉPARTEMENTALES DE LA Nom, Prénom : _ Classe : _ Le lieu L institution Les Archives départementales sont une institution ancienne. Elles ont été créées
Livret de visite Collège À LA DÉCOUVERTE DES ARCHIVES DÉPARTEMENTALES DE LA Nom, Prénom : _ Classe : _ Le lieu L institution Les Archives départementales sont une institution ancienne. Elles ont été créées
BIENVENUE A MARSEILLE
 BIENVENUE A MARSEILLE Congrès MATh.en.JEANS 2013 à Marseille Programme général Vendredi, 11:00-14:00 : Repas Vendredi, 12:00-13:30 : Installation des stands Vendredi, 13:30-15:00 : Exposés et animations
BIENVENUE A MARSEILLE Congrès MATh.en.JEANS 2013 à Marseille Programme général Vendredi, 11:00-14:00 : Repas Vendredi, 12:00-13:30 : Installation des stands Vendredi, 13:30-15:00 : Exposés et animations
5-9. L enveloppe. Objectif Ecrire une adresse sur une enveloppe. L enveloppe 5-9. Le dispositif de techniques de recherche d emploi 1
 Objectif Ecrire une adresse sur une enveloppe. Le dispositif de techniques de recherche d emploi 1 Sommaire Dispositif Toute diffusion est dûment conseillée conception et réalisation par sylvain Lesage
Objectif Ecrire une adresse sur une enveloppe. Le dispositif de techniques de recherche d emploi 1 Sommaire Dispositif Toute diffusion est dûment conseillée conception et réalisation par sylvain Lesage
GEORGES-HENRI LUQUET ET LA FRANC-MAÇONNERIE.
 GEORGES-HENRI LUQUET ET LA FRANC-MAÇONNERIE. Nous tenons à exprimer nos plus vifs remerciements à Irène Mainguy, Pierre Mollier et Georges Odo pour leur aide précieuse, et pour nous avoir autorisé à publier
GEORGES-HENRI LUQUET ET LA FRANC-MAÇONNERIE. Nous tenons à exprimer nos plus vifs remerciements à Irène Mainguy, Pierre Mollier et Georges Odo pour leur aide précieuse, et pour nous avoir autorisé à publier
Qui mange qui? Objectif : Prendre conscience des nombreuses relations qui existent entre les êtres vivants et notamment les relations alimentaires.
 Qui mange qui? Objectif : Prendre conscience des nombreuses relations qui existent entre les êtres vivants et notamment les relations alimentaires. Tous les êtres vivants ont besoin d énergie pour vivre,
Qui mange qui? Objectif : Prendre conscience des nombreuses relations qui existent entre les êtres vivants et notamment les relations alimentaires. Tous les êtres vivants ont besoin d énergie pour vivre,
Le point de vue du contrôleur technique
 Le point de vue du contrôleur technique mars 2010 P-E Thévenin Contrôle technique en zone sismique le contrôle technique missions et finalité contrôle technique obligatoire les attestations PS de contrôle
Le point de vue du contrôleur technique mars 2010 P-E Thévenin Contrôle technique en zone sismique le contrôle technique missions et finalité contrôle technique obligatoire les attestations PS de contrôle
huile sur bois 67 x 49 cm Origine : Renaissance
 L'autoportrait Un autoportrait est une représentation d'un artiste, dessinée, peinte, photographiée ou sculptée par l'artiste lui-même. Bien que l'exercice de l'autoportrait ait été pratiqué depuis les
L'autoportrait Un autoportrait est une représentation d'un artiste, dessinée, peinte, photographiée ou sculptée par l'artiste lui-même. Bien que l'exercice de l'autoportrait ait été pratiqué depuis les
Étienne-Martin. 25 juin 16 septembre 2014. www.mba-lyon.fr
 Étienne-Martin 25 juin 16 septembre 2014 www.mba-lyon.fr DOSSIER DE PRESSE En couverture Étienne-Martin (Loriol, 1913 Paris, 1919) Hommage à Brown, 1988-1990 Bois (frêne) peint Cet hommage monumental à
Étienne-Martin 25 juin 16 septembre 2014 www.mba-lyon.fr DOSSIER DE PRESSE En couverture Étienne-Martin (Loriol, 1913 Paris, 1919) Hommage à Brown, 1988-1990 Bois (frêne) peint Cet hommage monumental à
Sites web éducatifs et ressources en mathématiques
 Sites web éducatifs et ressources en mathématiques Exercices en ligne pour le primaire Calcul mental élémentaire : http://www.csaffluents.qc.ca/wlamen/tables-sous.html Problèmes de soustraction/addition
Sites web éducatifs et ressources en mathématiques Exercices en ligne pour le primaire Calcul mental élémentaire : http://www.csaffluents.qc.ca/wlamen/tables-sous.html Problèmes de soustraction/addition
le plancher intelligent
 DELTAfloor FICHE PRODUIT Bas, léger, amovible le plancher intelligent laisse le passage aux câbles! Le plancher surélevé idéal en LOCATION et RENOVATION Système EXCLUSIF breveté Plancher surélevé MOBILIER
DELTAfloor FICHE PRODUIT Bas, léger, amovible le plancher intelligent laisse le passage aux câbles! Le plancher surélevé idéal en LOCATION et RENOVATION Système EXCLUSIF breveté Plancher surélevé MOBILIER
HORLOGE ET MONTRE IN SITU : MÉCANIQUE 2
 IN SITU : MÉCANIQUE 2 HORLOGE ET MONTRE Réalisation : Toni Marin CNDP, le Département d Enseignement de la Generalitat de Catalunnya, 2000 Durée : 04 min 12 s Le film démarre par un historique chronologique
IN SITU : MÉCANIQUE 2 HORLOGE ET MONTRE Réalisation : Toni Marin CNDP, le Département d Enseignement de la Generalitat de Catalunnya, 2000 Durée : 04 min 12 s Le film démarre par un historique chronologique
FERMETURES VENTOISES 167, rue des frères Bernouilli Z.I. n 2 La Madeleine 27000 EVREUX
 FERMETURES VENTOISES 167, rue des frères Bernouilli Z.I. n 2 La Madeleine 27000 EVREUX 2013 Montant en Euros SAS SOGEPROM HABITAT Immeuble IDF 3, Place de la Pyramide 92067 PARIS LA DEFENSE CEDEX AMELLER-DUBOIS
FERMETURES VENTOISES 167, rue des frères Bernouilli Z.I. n 2 La Madeleine 27000 EVREUX 2013 Montant en Euros SAS SOGEPROM HABITAT Immeuble IDF 3, Place de la Pyramide 92067 PARIS LA DEFENSE CEDEX AMELLER-DUBOIS
Résolution d équations non linéaires
 Analyse Numérique Résolution d équations non linéaires Said EL HAJJI et Touria GHEMIRES Université Mohammed V - Agdal. Faculté des Sciences Département de Mathématiques. Laboratoire de Mathématiques, Informatique
Analyse Numérique Résolution d équations non linéaires Said EL HAJJI et Touria GHEMIRES Université Mohammed V - Agdal. Faculté des Sciences Département de Mathématiques. Laboratoire de Mathématiques, Informatique
Les Technologies de l Information et de la Communication et leurs impacts sur l environnement
 Les Technologies de l Information et de la Communication et leurs impacts sur l environnement Selon le rapport "Impacts of Information and Communication Technologies on EnergyEfficiency", réalisé par BIOIS
Les Technologies de l Information et de la Communication et leurs impacts sur l environnement Selon le rapport "Impacts of Information and Communication Technologies on EnergyEfficiency", réalisé par BIOIS
Parfums et saveurs du Sud-Ouest au Nailloux Outlet Village
 I COMMUNIQUE DE PRESSE I Nailloux, le 10 octobre 2014 Semaine du goût Parfums et saveurs du Sud-Ouest au Nailloux Outlet Village A l occasion de la semaine du goût, qui se tiendra du 13 au 19 octobre,
I COMMUNIQUE DE PRESSE I Nailloux, le 10 octobre 2014 Semaine du goût Parfums et saveurs du Sud-Ouest au Nailloux Outlet Village A l occasion de la semaine du goût, qui se tiendra du 13 au 19 octobre,
Comment sélectionner des sommets, des arêtes et des faces avec Blender?
 Comment sélectionner des sommets, des arêtes et des faces avec Blender? VVPix v 1.00 Table des matières 1 Introduction 1 2 Préparation d une scène test 2 2.1 Ajout d objets dans la scène.........................................
Comment sélectionner des sommets, des arêtes et des faces avec Blender? VVPix v 1.00 Table des matières 1 Introduction 1 2 Préparation d une scène test 2 2.1 Ajout d objets dans la scène.........................................
Annexe C : Codes de fonction
 Annexe C : Codes de fonction Les codes figurant dans cette liste peuvent être employés dans la sous-zone $4 des zones du bloc 7XX (Bloc des responsabilités). Lorsqu il est nécessaire d associer plusieurs
Annexe C : Codes de fonction Les codes figurant dans cette liste peuvent être employés dans la sous-zone $4 des zones du bloc 7XX (Bloc des responsabilités). Lorsqu il est nécessaire d associer plusieurs
La programmation linéaire : une introduction. Qu est-ce qu un programme linéaire? Terminologie. Écriture mathématique
 La programmation linéaire : une introduction Qu est-ce qu un programme linéaire? Qu est-ce qu un programme linéaire? Exemples : allocation de ressources problème de recouvrement Hypothèses de la programmation
La programmation linéaire : une introduction Qu est-ce qu un programme linéaire? Qu est-ce qu un programme linéaire? Exemples : allocation de ressources problème de recouvrement Hypothèses de la programmation
Tâche complexe produite par l académie de Clermont-Ferrand. Mai 2012 LE TIR A L ARC. (d après une idée du collège des Portes du Midi de Maurs)
 (d après une idée du collège des Portes du Midi de Maurs) Table des matières Fiche professeur... 2 Fiche élève... 5 1 Fiche professeur Niveaux et objectifs pédagogiques 5 e : introduction ou utilisation
(d après une idée du collège des Portes du Midi de Maurs) Table des matières Fiche professeur... 2 Fiche élève... 5 1 Fiche professeur Niveaux et objectifs pédagogiques 5 e : introduction ou utilisation
PARIS BRUXELLES DEUX SIECLES D AFFINITES ARCHITECTURALES
 PARIS BRUXELLES Après Vienne - Bruxelles en 2007, première d une série qui explore les allées et venues architecturales entre la capitale de la Belgique et ses voisins européens, l exposition Paris Bruxelles
PARIS BRUXELLES Après Vienne - Bruxelles en 2007, première d une série qui explore les allées et venues architecturales entre la capitale de la Belgique et ses voisins européens, l exposition Paris Bruxelles
GUIDE D UTILISATION DU PORTAIL FAMILLE S E J. Mairie/SEJE/CG 1 Guide d utilisation du portail famille
 GUIDE D UTILISATION DU PORTAIL FAMILLE S E J E Mairie/SEJE/CG 1 Guide d utilisation du portail famille Accueil Mon compte Mes enfants Relevé de compte Boite de réception Liste des demandes Deconnexion
GUIDE D UTILISATION DU PORTAIL FAMILLE S E J E Mairie/SEJE/CG 1 Guide d utilisation du portail famille Accueil Mon compte Mes enfants Relevé de compte Boite de réception Liste des demandes Deconnexion
Rhône-Alpes le Québec&
 Délégation générale Paris Rhône-Alpes le Québec& ensemble naturellement En 2008, la Région Rhône-Alpes est partenaire de la célébration du 400 e anniversaire de Québec Édito Rhône-Alpes partage avec le
Délégation générale Paris Rhône-Alpes le Québec& ensemble naturellement En 2008, la Région Rhône-Alpes est partenaire de la célébration du 400 e anniversaire de Québec Édito Rhône-Alpes partage avec le
«Quand le territoire devient source d inspiration et souffle d expression créative : Présentation du Festival Art-Pierre-Terre»
 «Quand le territoire devient source d inspiration et souffle d expression créative : Présentation du Festival Art-Pierre-Terre» Cet exposé vous est présenté par Liliane Gordos,Stéphanie Natalis, Bernadette
«Quand le territoire devient source d inspiration et souffle d expression créative : Présentation du Festival Art-Pierre-Terre» Cet exposé vous est présenté par Liliane Gordos,Stéphanie Natalis, Bernadette
EXTRAIT DU REGISTRE DES DELIBERATIONS DU CONSEIL MUNICIPAL
 EXTRAIT DU REGISTRE DES DELIBERATIONS DU CONSEIL MUNICIPAL Conseillers en exercice : 61 Date de Publicité : 21/12/2010 Reçu en Préfecture le : CERTIFIE EXACT, Séance du lundi 20 décembre 2010 D -20100712
EXTRAIT DU REGISTRE DES DELIBERATIONS DU CONSEIL MUNICIPAL Conseillers en exercice : 61 Date de Publicité : 21/12/2010 Reçu en Préfecture le : CERTIFIE EXACT, Séance du lundi 20 décembre 2010 D -20100712

