calcul Logique 1. Le dia ma nt aztèque d ' ordre n est l'empi lement de lig nes cent
|
|
|
- Jean-Noël Lecompte
- il y a 10 ans
- Total affichages :
Transcription
1 Logique calcul et Dominons les dominos Quels assem blages obtient- on avec des dom i nos? Au détour de ces ques tions pos é es par les a mateurs de diverti ssements géom é t r iques et qui int é r essent au jou rd hui les prof ess ion nel s, on ren contre les nom br es de Fi bonacci, d'éton na nts résu ltats et des ques tions non résol ues. out juste un peu plus compliqué que le carré, l'anodin double carré, ou domino, est une source inattendue de questions géom é t riques et combinatoires qui plaisent à t o u s, car les astuces utilisées dans les d é m o n s t rations sont remarquables d ingén i o s i t é. Ainsi lorsque l'on a devant soi un polygone orthogonal (polygone obtenu en accolant par les côtés des carrés égaux) et une pile de dominos, la question que l'on se pose est celle du pavage : le polygone orthogonal peut-il être pavé par des dominos sans recouvrement, ni espace vide? Nous emploierons l'adjectif d o m i n a bl e pour qualifier ces figures «pavables» avec des dominos. Bien sûr, pour qu'un polygone orthogonal soit dominabl e, il faut que le nombre de carrés qui le composent soit un nombre p a i r, car chaque domino recouvre deux carrés d un coup.c e t t e condition est-elle suffisante? Non. Un exemple du contra i r e est la figure en fo rme de T (une barre hori zontale et une barre ve rticale de même nombre de carrés). Un T composé de 6 carrés ( voir la lettrine du début du tex t e ), trois pour la barre h o ri zo n t a l e, trois pour le pied, n'est pas dominabl e. D é t e rminer quels sont les rectangles dominables est fa c i l e. Un rectangle n x m est dominable si et seulement si n ou m est pair : si n est pair, on pave chacune des m lignes de longueur n qui compose le rectangle en plaçant n/2 dominos ; s i m est pair, on procède de la même façon en décomposant la figure en lignes de longueur m ; si n et m sont tous les deux i m p a i r s, leur produit l est aussi et le pavage d un nombre impair de cases avec des dominos est impossibl e. L aide du coloriage en damier Des raisonnements très astucieux, fondés sur le coloriage en damier, permettent de déterminer la «d o m i n a b i l i t é» pour les figures obtenues en enlevant deux carrés à un rectangle n x m (voir la figure 2a où l on raisonne sur un carré n x n, mais la méthode est générale). Nous allons examiner trois autres résultats généraux obtenus avec cette technique du coloriage en damier que le physicien Georges Gamov présentait comme un «m i racle d ingéniosité mathématique». Le premier est le théorème des côtés pairs. Il affirme que si un polygone orthogonal n'a que des côtés de longueur paire, alors il est dominabl e.la démonstration est facile si on ajoute l ' hypothèse que la figure est sans trou, elle l'est un peu moins si on considère des figures avec trous ( voir la figure 3). L e second résultat dû à Philip Hall a été découve rt en I l indique que si un polygone orthogonal n'est pas dominabl e, alors un raisonnement simple par damier le prouve ra. La figure 5 donne les explications concernant ce beau résultat. En 1999, György Csizmadia, Jurek Czyzowicz, Leze k G a s i e n i e c, Evangeos Kranakis et Jorge Urrutia ont proposé un troisième résultat général : le théorème des côtés impairs (voir la figure 6). À l'inverse du théorème des côtés pairs, il donne un critère permettant de savoir qu'un polygone ort h o- gonal n'est pas dominable : si un polygone orthogonal sans trou n'a que des côtés de longueur impaire, alors il n'est pas d o m i n a bl e. N'est-il pas étonnant qu'il ait fallu attendre la fin du X X e siècle pour découvrir un théorème aussi simple? Ainsi, le T composé de 3 carrés pour la barre horizontale et ayant un pied de longueur 3 n'a que des côtés de longueur impaire : 1 ou 3. D'après le nouveau critère et sans aucun raisonnement supplémentaire, nous savons qu il n'est pas dominabl e. De même, un double escalier composé de lignes de 1, 3, 5, 7 carrés n'est pas dominable, car ses côtés ont pour longueur 1 ou 7. Le résultat est vrai plus généralement pour les doubles escaliers 1, 3, 5,..., 2n+1. L a d é m o n s t ration, assez longue et délicate, de ce nouve a u résultat se fonde sur la technique du damier et consiste à montrer que, dans le cas indiqué, le nombre de cases bl a n c h e s n'est pas égal au nombre de cases noires, ce qui bien sûr e n t raîne l'impossibilité d'un pavage par des dominos. Si une figure possède un ou plusieurs trous, le théorème des côtés impairs n'est plus vrai comme le montre l'anneau carré le plus simple ( voir la figure 6 ). Lorsqu'un polygone o rthogonal possède à la fois des côtés de longueur paire et des côtés de longueur impaire, on ne peut rien dire : p a r fois il est dominabl e, parfois non! 1. Le dia ma nt aztèque d ' ordre n est l'empi lement de lig nes cent r é es de carrés de long ueur 2, 4, 6,..., 2N 2, 2N, 2N, 2N 2,..., 6, 4, 2. La figure cent ra le dom i nable est étra nge : pr esque tous les pav ages par dom i nos d'un gra nd dia ma nt aztèque poss è dent une zone cent ra le ci r cu laire désordonnée à l int é r ieur d un cer cle «pola i r e», alors qu ' à l ' ext é r ieur de ce tte zone tout est gelé en réseaux de dom i nos pa ra l- l è les (voir le site htt p : / / w w w. math. w i sc. edu /~propp / ti l i ng / ). 90 POUR LA SCIENCE - N 345 JUILLET 2006
2 Jean-Paul Delahaye POUR LA SCIENCE Logique & calcul 91
3 2. Les miraculeux raisonnements par damier. ( a ) Si on en l è ve deux coi ns opposés à un carré (2n) x ( 2n) dom i nable, la f igure obtenue n'est pl us «dom i nable» (pl us recou v rable exactement par des dom i nos). Pour le mont r er, color ions les cases com me cel les d un da m ier. Tout dom i no, cons titué de deux cases, posé sur le da m ier, couvre tou jours une case bla n che et une case noi r e. Une figure dom i nable a donc au ta nt de cases noi r es que de bla n ches et la figure obtenue qua nd on en l è ve deux coi ns opposés d'un carré (2n) x ( 2n) poss è de deux cases bla n ches de pl us que de cases noi r es (ou l'inver se selon les coi ns que l on pr end ), car les coi ns en levés sont de la même cou leur : el le n'est don c pas dom i nable. ( b ) Si on en l è ve deux carrés de cou leurs diff é r entes à un carré colorié en da m ier, la figure obtenue est tou jours dom i- nable. Dess i nons un chemin passa nt par tous les carrés du recta ng le. Les deux cases en lev é es (ma r qu é es d u ne croi x) coupent ce chemin en deux pa r ties aya nt chacu ne une long ueur pa i r e ( car les cases en lev é es sont de cou leurs diff é r entes et que les cases du chemin alternent bla n che- noi r e- bla n che- noi r e-...). Chacun de ces deux mor ceaux de chemin est dom i nable, donc la fig u r e t rou é e ( c ) est dom i nable. ( d ) Si on en l è ve un carré de la cou leu r des coi ns (tous les quatre de la même cou leur) à un rec ta ng le non dom i nable (2n + 1 ) x ( 2m + 1) colorié en da m ier, la figure obtenue dev ient dom i nable : il su ff it de dess i ner un chemin en zig zag sur le da m ier et de ra i son ner com me pr é c é dem ment. 3. Le théorème des côtés pairs i nd ique que si un polygone orthogonal n'a que des côtés de long ueur pa i r e, alors il est dom i nable. Si la figure est sa ns trou, on peut la diviser en carrés de côté 2, chacu n pou v a nt alors être pavé par 2 dom i nos ( a ). Da ns ce cas, d'ailleu r s, tous les dom i nos peu vent être placés hor izonta lement( b ), ou tous vertica lement ( c ). Si la figure poss è de des trous ( a ) cela se compl ique. La m é tho de pour paver la figure se décompose en trois étapes. 1- On place la figure sur le plan de faç on que les co ordon n é es des poi nts du pou rtour soient tou tes pa i r es (poi nts verts) : on obtient un tel pos ition nement en plaç a nt l'un des coi ns ext é r ieurs de la figure au poi nt de co ordon n é es (0, 0). La diff icu lté prov ient de ce que les somme ts internes délimita nt les trous n'ont pas de ra i son d'avoir des co ordon n é es pa i r es, ce qui emp ê che de ra i son ner com me da ns le cas où il n'y a pas de trou. 2- On pave les bords de chaque trou (soit tous les bords, soit les bords hor izontaux, soit les bords verticaux) de faç on que la pa rtie res ta nt à paver n'ait pl us que des som me ts de co ordon n é es pa i r es ( b ). 3- Pour la pa rtie res ta nte, on est ra mené à une situation équ i v a- lente à celle de la configuration sans trou (une figure décomposable en carrés de côté 2), car ce tte pa r tie est délimitée par des som me ts ext é r ieurs et int é r ieu r s aya nt à chaque fois deu x coordonnées paires. 4. Pro blème invers e. Pour tout entier n, peu t- on trou ver une f igure poss é da nt exac tement n pav ages diff é r ents par dom i nos? Les rec ta ng les troués ci - dessus don nent la réponse : le rec ta ng le ayant n 1 trous possède exactement n pavages par dominos. 92 POUR LA SCIENCE N 345 JUILLET 2006
4 Pour beaucoup de figures particulières (comme les figures en fo rme de L, d'anneaux, de U, de croix, etc.), on sait déterminer si elles sont dominables ou pas et c'est une source inépuis a ble d'exercices géométriques simples et amu s a n t s. N o t o n s que le problème de savoir si un polygone orthogonal est domin a ble ou non appartient à la classe des problèmes polynomiaux : il peut être traité en un temps inférieur à C x n 3 / 2 (où C est une c o n s t a n t e, et n le nombre de carrés de la figure). Nombre de pava g es poss i bl es Très naturellement, lorsqu'un polygone est dominable se pose la question du nombre de façons différentes de le paver par des dominos (lors de ces décomptes, si un pavage se déduit d un autre par une symétrie ou une rotation, on le compte quand même). Pour les rectangles 1xN (N évidemment pair), la réponse est patente : il n'y a qu'une façon de paver le rectangle. Po u r les rectangles 2 x N, la réponse est intéressante puisqu'elle p e rmet de retrouver la plus célèbre des suites de nombres e n t i e r s : la suite de Fibonacci 1, 1, 2, 3, 5, 8, 13,... où chaque t e rme f (N ) est la somme des deux précédents. Voici le raisonnement par récurrence montrant que le nombre de façons différentes de paver un rectangle de taille 2 x N p a r des dominos est f (N + 1 ). Pour paver le rectangle 2 x 1, il n'y a évidemment qu'une façon, 1 = f ( 2 ). Pour le rectangle 2 x 2, il y en a 2, soit f (3) : deux dominos hori zontaux ou deux dominos ve rt i c a u x. Examinons la récurrence : supposons que pour paver par des dominos les rectangles de taille 2 x 1, 2 x 2,..., 2 x N, il y a respectivement f (2),..., f (N + 1) fa ç o n s de le faire et montrons que pour paver le rectangle 2 x (N + 1 ), il y en a f (N + 2 ). Il y a deux façons de placer les dominos remplissant l'extrémité droite du rectangle. ( a ) Soit nous plaçons un domino ve rticalement, et alors il reste un rectangle de taille 2 x N à couvri r, ce qui par hy p o- thèse peut se faire de f (N + 1) façons différentes. ( b ) Soit on place un domino hori zontalement, mais alors il faut en placer un autre hori zontalement sur le premier, et alors il reste un rectangle de taille 2 x (N 1) à recouvri r, ce qui, par hy p o t h è s e, peut se faire de f (N) façons différentes. Au total, le nombre de façons différentes de couvrir le rectangle de taille 2 x (N + 1) est donc bien f (N + 1) + f (N) = f (N + 2 ). Pour les rectangles de fo rme 3 x ( 2N), il existe un résultat a n a l o g u e.le nombre de façons différentes de paver le rectangle est donné par la suite : g(0) = 1, g(1) = 3, g(2) = 11, g(n +1 ) = 4 g(n) g(n 1 ). Les premiers termes de cette suite sont 3, 11, 41, 153, 571, 2131, 7953, 29681, , , , , , , Il s'agit de la suite numérotée A de l'encyclopédie des suites d'entiers du mathématicien Neil Sloane que vous trouverez en : h t t p : / / w w w. r e s e a r c h. a t t. c o m / ~ n j a s / s e q u e n c e s / Pour un rectangle quelconque (2n)x( 2m), une fo rmule générale donnant le nombre de façons de le paver par des dominos a été découve rte en 1961 simultanément et indépendamment par trois personnes, M.F i s h e r, H.Te m p e rl ey et P.K a s t e l ey n.n o u s l'indiquons car, bien que complexe et difficile à démontrer, elle est étrange et belle. Elle montre que la résolution d un problème simple oblige parfois à recourir à des outils inattendus, 5. Le théorème de Philip Ha l l. Qua nd une figure coloriée en da m ier a le même nom bre de cases de chaque cou leu r, il ex i s te un arg u- ment sta nda rd qui montre (si c'est le cas) que la figure n'est pas dom i- nable. La figure a trouée comporte 32 ca r r é s, 16 de chaque sorte, ma i s el le n est pas dom i nable. Cons id é rons sur la figure b les cases ma r qu é es par des ronds. Les cases avec lesquel les el les peu vent s'appa r ier (qua nd on y pose un dom i no) sont ma r qu é es par des étoi les. Il y a 6 ronds et seu lement 5 étoi les : il sera donc imposs i ble de poser des dom i nos su r les 6 ronds sa ns qu'ils se chev auchent : la figure n'est pas dom i nable. Le th é or è me de Philip Hall ind ique que si une figure n'est pas dom i nable, il est tou jours poss i ble de le démont r er avec ce ra i son nement. 6. Le théorème des côtés impairs, d é cou vert et démontré il y a six ans, ind ique que si un polygone orthogonal sa ns trou n'a que des côtés de long ueur impaire alors il n'est pas dom i nable. Le double esca l ier à 16 carrés ( a ) qui n'a que des côtés de long ueur 1 ou 7 n'es t donc pas dom i nable (colorié en da m ier, il comporte 15 cases noi r es et 10 cases bla n ches). Si la figure a des trous, le cr itère n est pl us valable, com me le montre la fig u r e ( b ) que l'on pave faci lement avec 4 dom i- nos. Lor squ ' u ne figure poss è de à la fois des côtés de long ueurs pa i r es et impa i r es, rien de général ne peut être aff i rmé : la figure c est dom i- nable, la figure d ne l est pas. 7. Roberto Toraso de l'université Tor Vergata de Rome a démontré en 2004 deux intéressants résultats. (a) Le nombre de pavages par des dominos d'un L dont l'axe central est composé de deux segments de longueurs n et m est donné par l'expression f(n + 1) f(m) + f(n) f(m + 1) où f(n) est la suite de Fibonacci. (b) Le nombre de pavages par des dominos d'un anneau carré de largeur 2 et dont le côté de l'axe cent ral a pour long ueur n est donné par l'ex pr ess ion 4(f(n + 1)f(n 1) + f(n) 2 ) 2. POUR LA SCIENCE Logique & calcul 93
5 8. Po rtra its de dominos. Pour les cons t ru i r e, Robert Bosch util i se des jeux comple ts de dom i nos (Dom i no A rt wor k. com). Ces port ra its uti l i sent 48 jeux comple ts de dom i nos jusqu au double neuf alor s que les dom i nos habituels ne vont que jusqu au double six. Pour trou- ici les fonctions tri g o n o m é t riques (bien sûr on ne sait pas simplifier cette fo rmu l e ). Le nombre de façons différentes de pave r un rectangle (2n) x ( 2m) par des dominos est exactement : Par exe m p l e, pour m = 2, n = 3 la fo rmule donne : 4 6 ( c o s c o s 2 25,71... ) (cos c o s 2 5 1, ) ( c o s c o s 2 77,14... ) (cos c o s 2 2 5, ) ( c o s c o s 2 51,43... ) (cos c o s 2 7 7, ) = 4 6 ( 1, ) ( 1, ) ( 0, ) ( 0, ) ( 0, ) ( 0, ) = 281. On obtient un nombre entier à l'issue du calcul, bien 9. Le théorème de Th u rsto n. En fa i sa nt tou rner de 90 un couple de dominos formant un carré, on transforme une paire horizontale en paire verticale et réciproquement (a). Considérons deux pav ages ( b ) e t (c) d i ff é r ents par dom i nos. En répéta nt l'op é ration de rotation de couples de dominos accolés (d), on passe du pavage (b) au pav age ( c ). D après le th é or è me de Thu r s ton, si le polygone orthogonal dont on part est sans trou, le passage d'un pavage à un autre par de telles rotations de couples de dominos accolés est toujours possible. L'anneau simple (e) montre que la condition «sans trou» est essentielle. que les facteurs soient tous des nombres réels non entiers! Vous pouvez véri f i e r, avec un programme d'ordinateur, qu'il y a bien 281 façons de paver un carré 4 x 6 par des dominos. Avec cette fo rmu l e, les problèmes de dominos quittent le domaine des récréations mathématiques élémentaires! Les dia ma nts aztèques Plus récemment, N.E l k i e s, G.Kuperberg, M. Larsen et J. P r o p p ont montré que le nombre de pavages par des dominos du diamant aztèque d'ordre N la figure symétrique composée de lignes de carrés ayant respectivement pour longueur 2, 4, 6,..., 2N, 2N,..., 6, 4, 2 ( voir la figure 1) est 2 N(N + 1)/2, ce qui est tout de même plus sympathique que la fo rmule pour le rectangle! On connaît aujourd'hui 12 démonst rations de ce résultat.malheureusement, aucune n'est simple. Le degré de liberté pour paver une figure est le nombre de façons de paver la figure par dominos. Le d e gré de liberté par carré est la racine n-ième de ce degré, où n est le nombre de carrés de la figure. Plus ce nombre est petit plus il est difficile de paver la figure. Un diamant aztèque d'ordre N possède 2N (N + 1) carrés et donc le degré de liberté par carré de cette figure est exactement : (2 N (N + 1)/2 ) 1/2N (N + 1) = 2 1/4 = 1, Pour un carré N x N, on évalue le degré de liberté par carré à partir de la fo rmule avec des cosinu s. On trouve que ce nombre est 1, ce qui est sensiblement plus que pour le diamant aztèque. Cela n'est pas surprenant puisqu'on sent bien, en tentant de remplir un diamant aztèque par des dominos, que les côtés en escalier créent de nombreuses contraintes qui limitent les choix possibl e s, alors qu'on a beaucoup plus de liberté quand on remplit un carré N x N. D autres propriétés fascinantes du diamant aztèque sont aujourd'hui étudiées par J. Propp et un groupe de chercheurs autour de lui. En particulier, ils ont démontré que lorsqu'on prend au hasard un pavage par dominos du diamant aztèque, il existe une zone circulaire centrale à l intérieur d un cercle d é n o m m é cercle polaire, où les dominos sont placés de fa ç o n assez désordonnée dans les deux sens, alors que les parties autour sont très bien rangées (dominos bien para l- 94 POUR LA SCIENCE N 345 JUILLET 2006
6 ) (b) (c) (d) ver les emplacements opti maux des dom i nos, R. Bosch divise l image ( a ) en carrés ( b ) et mesure de 0 à 9 les intens ités de gris ( c ) de chaque carré. Puis son prog ra m me ca lcu le quel arra ngement de dom i- nos (pris au complet) réalise au mieux ces intens ités ( d ). lèles). L'existence de ce cercle inattendu reste mystérieuse (voir la figure 1). Indiquons, d autre part, pour les pavages par dominos, deux résultats plus faciles démontrés par Robert o Toraso et décrits sur la figure 7. Un étra n g e, délicat et merveilleux théorème a été fo r- mulé et démontré par William Thurston de l'université de P ri n c e t o n. Que ce lauréat de la médaille Fields 1982 ( l ' é q u i valent pour les mathématiques du prix Nobel) ait trouvé bon de s'occuper de dominos montre que tous les sujets m a t h é m a t i q u e s, y compris ceux qu'on classe parfois ave c condescendance dans la catégorie des récréations mathém a t i q u e s, sont susceptibles d'intéresser les meilleurs mathématiciens qui y découvrent parfois de véri t a bles petits bijoux (voir la figure 9). Le décompte des pavages par dominos suggère une question simple : est-ce que pour tout entier N, il existe une figure d o m i n a ble possédant exactement N p avages différents par d o m i n o s? La réponse, positive, a été donnée par plusieurs amateurs dont B. H a r ri s, Brendam Owen, Alexandre Muniz, Tr evor Green et T i m o t hy Luffingham qui ont proposé des constru c- tions générales ( voir la figure 4). Une autre question est moins bien résolue : pour un N donné, quel est le nombre minimal D(N ) de carrés que doit posséder une figure pour qu'elle admette exactement N p avages différents par des dominos? Pour N = 7, par exe m p l e, on connaît une figure à 1 0 carrés possédant 7 pavages différents par dominos et on n'en connaît aucune ayant moins de 10 carrés. On pense donc que D(7) = 10. Pour N = 2000, la question a été étudiée avec un soin particulier par de nombreux amateurs de récréation mathématique, car en l'an 2000 année mondiale des mathématiques elle avait été soumise comme d é f i. De nombreuses solutions à 38 carrés furent proposées, mais finalement le Japonais Yoshiyuki Kotani en trouva une à 34 carrés par une méthode de recherche systémat i q u e. Nous ignorons si 34 est le minimum possibl e, voir : h t t p : / / w w w. s t e t s o n. e d u / ~ e f ri e d m a / m a t h m a g i c / h t m l. Les lecteurs de Pour la Science feront-ils progresser notre connaissance de ce problème de minimalité? Si vous trouvez ces questions de pavages trop abst ra i t e s, un jeu artistique vous réconciliera avec les dominos : le dessin avec des jeux complets de dominos. On se donne plusieurs jeux complets de dominos (avec des points allant de 0 à 6 ou de 0 à 9) ; on se donne aussi une image, par exemple la Joconde, et le but est de placer au mieux tous les dominos dont on dispose pour reproduire l'image choisie. Les portra its de Ro b e rt Bosch R o b e rt Bosch a ainsi réalisé des dizaines d'images assez étonnantes (voir d o m i n o a rt wo rk. c o m / ). La méthode qu'il utilise est expliquée sur la figure 8. Sauf hasard ex t ra o r d i- n a i r e, un recouvrement exact n'est pas possibl e, et donc il faut mener une recherche parmi tous les pavages utilisant les jeux complets de dominos pour trouver celui qui s'éloigne le moins de la grille de niveau de gri s. Pour ce fa i r e, R. Bosch utilise des algori t h m e s, nommés algorithmes d'optimisation en nombres entiers, développés depuis longtemps pour traiter des p r o blèmes d'emplois du temps ou de conception de circuits. Les innocents dominos occupent ainsi les artistes mathém a t i c i e n s, les amateurs de récréations géométriques et info r- m a t i q u e s, et les plus brillants des chercheurs, chacun fa i s a n t avancer notre maîtrise et notre compréhension du démoniaque petit rectangle. Notons enfin que les surp rises comme celle du «cercle polaire» montrent que les mathématiques sont d é c o u ve rtes et non inventées car, si elles l étaient, il n y aura i t pas de tels inattendus. Jean-Paul DELAHAYE est prof esseur d informatique à l Un i v. de Lille. E. FRIEDMAN, Le problème inverse et quelques autres questions de pavage par dominos. Math Magic 2005 : J. - P. DE LA H AY E, Les inattendus math é matiques, Bel i n / Pour la Scien ce, Fr eder ico AR DILA, Richa rd STA N LEY, Ti l i ngs 2004 : htt p : / / w w w. clay math. org/ fas / sen ior _ schola r s / Sta n ley / G. CSIZ M A DI A et al., Dom i no ti l i ngs of orth ogonal polygons, i n I nter nationa l Jou r nal of Pu re and Appl ied Mathematics, 13(4), pp , R. BOS C H, Constructi ng Dom i no Portra its, i n Tr i bu te to a Mathemag icia n ( Ed. B. Ci pra, E. Dema i ne, M. Dema i ne, T. Ro dgers), A.K. Pe ter s, Wel les ley, Massachuse tts, pages , POUR LA SCIENCE Logique & calcul 95
Date : 18.11.2013 Tangram en carré page
 Date : 18.11.2013 Tangram en carré page Titre : Tangram en carré Numéro de la dernière page : 14 Degrés : 1 e 4 e du Collège Durée : 90 minutes Résumé : Le jeu de Tangram (appelé en chinois les sept planches
Date : 18.11.2013 Tangram en carré page Titre : Tangram en carré Numéro de la dernière page : 14 Degrés : 1 e 4 e du Collège Durée : 90 minutes Résumé : Le jeu de Tangram (appelé en chinois les sept planches
LE PROBLEME DU PLUS COURT CHEMIN
 LE PROBLEME DU PLUS COURT CHEMIN Dans cette leçon nous définissons le modèle de plus court chemin, présentons des exemples d'application et proposons un algorithme de résolution dans le cas où les longueurs
LE PROBLEME DU PLUS COURT CHEMIN Dans cette leçon nous définissons le modèle de plus court chemin, présentons des exemples d'application et proposons un algorithme de résolution dans le cas où les longueurs
LES ESCALIERS. Du niveau du rez-de-chaussée à celui de l'étage ou à celui du sous-sol.
 LES ESCALIERS I. DÉF I NIT I O N Un escalier est un ouvrage constitué d'une suite de marches et de paliers permettant de passer à pied d'un niveau à un autre. Ses caractéristiques dimensionnelles sont
LES ESCALIERS I. DÉF I NIT I O N Un escalier est un ouvrage constitué d'une suite de marches et de paliers permettant de passer à pied d'un niveau à un autre. Ses caractéristiques dimensionnelles sont
6. Les différents types de démonstrations
 LES DIFFÉRENTS TYPES DE DÉMONSTRATIONS 33 6. Les différents types de démonstrations 6.1. Un peu de logique En mathématiques, une démonstration est un raisonnement qui permet, à partir de certains axiomes,
LES DIFFÉRENTS TYPES DE DÉMONSTRATIONS 33 6. Les différents types de démonstrations 6.1. Un peu de logique En mathématiques, une démonstration est un raisonnement qui permet, à partir de certains axiomes,
Carl-Louis-Ferdinand von Lindemann (1852-1939)
 Par Boris Gourévitch "L'univers de Pi" http://go.to/pi314 [email protected] Alors ça, c'est fort... Tranches de vie Autour de Carl-Louis-Ferdinand von Lindemann (1852-1939) est transcendant!!! Carl Louis
Par Boris Gourévitch "L'univers de Pi" http://go.to/pi314 [email protected] Alors ça, c'est fort... Tranches de vie Autour de Carl-Louis-Ferdinand von Lindemann (1852-1939) est transcendant!!! Carl Louis
Raisonnement par récurrence Suites numériques
 Chapitre 1 Raisonnement par récurrence Suites numériques Terminale S Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES Raisonnement par récurrence. Limite finie ou infinie d une suite.
Chapitre 1 Raisonnement par récurrence Suites numériques Terminale S Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES Raisonnement par récurrence. Limite finie ou infinie d une suite.
Université Paris-Dauphine DUMI2E 1ère année, 2009-2010. Applications
 Université Paris-Dauphine DUMI2E 1ère année, 2009-2010 Applications 1 Introduction Une fonction f (plus précisément, une fonction réelle d une variable réelle) est une règle qui associe à tout réel x au
Université Paris-Dauphine DUMI2E 1ère année, 2009-2010 Applications 1 Introduction Une fonction f (plus précisément, une fonction réelle d une variable réelle) est une règle qui associe à tout réel x au
Fonctions de plusieurs variables
 Module : Analyse 03 Chapitre 00 : Fonctions de plusieurs variables Généralités et Rappels des notions topologiques dans : Qu est- ce que?: Mathématiquement, n étant un entier non nul, on définit comme
Module : Analyse 03 Chapitre 00 : Fonctions de plusieurs variables Généralités et Rappels des notions topologiques dans : Qu est- ce que?: Mathématiquement, n étant un entier non nul, on définit comme
Un exemple d étude de cas
 Un exemple d'étude de cas 1 Un exemple d étude de cas INTRODUCTION Le cas de la Boulangerie Lépine ltée nous permet d exposer ici un type d étude de cas. Le processus utilisé est identique à celui qui
Un exemple d'étude de cas 1 Un exemple d étude de cas INTRODUCTION Le cas de la Boulangerie Lépine ltée nous permet d exposer ici un type d étude de cas. Le processus utilisé est identique à celui qui
III- Raisonnement par récurrence
 III- Raisonnement par récurrence Les raisonnements en mathématiques se font en général par une suite de déductions, du style : si alors, ou mieux encore si c est possible, par une suite d équivalences,
III- Raisonnement par récurrence Les raisonnements en mathématiques se font en général par une suite de déductions, du style : si alors, ou mieux encore si c est possible, par une suite d équivalences,
La persistance des nombres
 regards logique & calcul La persistance des nombres Quand on multiplie les chiffres d un nombre entier, on trouve un autre nombre entier, et l on peut recommencer. Combien de fois? Onze fois au plus...
regards logique & calcul La persistance des nombres Quand on multiplie les chiffres d un nombre entier, on trouve un autre nombre entier, et l on peut recommencer. Combien de fois? Onze fois au plus...
Durée de L épreuve : 2 heures. Barème : Exercice n 4 : 1 ) 1 point 2 ) 2 points 3 ) 1 point
 03 Mai 2013 Collège Oasis Durée de L épreuve : 2 heures. apple Le sujet comporte 4 pages et est présenté en livret ; apple La calculatrice est autorisée ; apple 4 points sont attribués à la qualité de
03 Mai 2013 Collège Oasis Durée de L épreuve : 2 heures. apple Le sujet comporte 4 pages et est présenté en livret ; apple La calculatrice est autorisée ; apple 4 points sont attribués à la qualité de
Exercices - Polynômes : corrigé. Opérations sur les polynômes
 Opérations sur les polynômes Exercice 1 - Carré - L1/Math Sup - Si P = Q est le carré d un polynôme, alors Q est nécessairement de degré, et son coefficient dominant est égal à 1. On peut donc écrire Q(X)
Opérations sur les polynômes Exercice 1 - Carré - L1/Math Sup - Si P = Q est le carré d un polynôme, alors Q est nécessairement de degré, et son coefficient dominant est égal à 1. On peut donc écrire Q(X)
TOUT CE QU IL FAUT SAVOIR POUR LE BREVET
 TOUT E QU IL FUT SVOIR POUR LE REVET NUMERIQUE / FONTIONS eci n est qu un rappel de tout ce qu il faut savoir en maths pour le brevet. I- Opérations sur les nombres et les fractions : Les priorités par
TOUT E QU IL FUT SVOIR POUR LE REVET NUMERIQUE / FONTIONS eci n est qu un rappel de tout ce qu il faut savoir en maths pour le brevet. I- Opérations sur les nombres et les fractions : Les priorités par
Soit la fonction affine qui, pour représentant le nombre de mois écoulés, renvoie la somme économisée.
 ANALYSE 5 points Exercice 1 : Léonie souhaite acheter un lecteur MP3. Le prix affiché (49 ) dépasse largement la somme dont elle dispose. Elle décide donc d économiser régulièrement. Elle a relevé qu elle
ANALYSE 5 points Exercice 1 : Léonie souhaite acheter un lecteur MP3. Le prix affiché (49 ) dépasse largement la somme dont elle dispose. Elle décide donc d économiser régulièrement. Elle a relevé qu elle
Baccalauréat L spécialité, Métropole et Réunion, 19 juin 2009 Corrigé.
 Baccalauréat L spécialité, Métropole et Réunion, 19 juin 2009 Corrigé. L usage d une calculatrice est autorisé Durée : 3heures Deux annexes sont à rendre avec la copie. Exercice 1 5 points 1_ Soit f la
Baccalauréat L spécialité, Métropole et Réunion, 19 juin 2009 Corrigé. L usage d une calculatrice est autorisé Durée : 3heures Deux annexes sont à rendre avec la copie. Exercice 1 5 points 1_ Soit f la
Exo7. Limites de fonctions. 1 Théorie. 2 Calculs
 Eo7 Limites de fonctions Théorie Eercice Montrer que toute fonction périodique et non constante n admet pas de ite en + Montrer que toute fonction croissante et majorée admet une ite finie en + Indication
Eo7 Limites de fonctions Théorie Eercice Montrer que toute fonction périodique et non constante n admet pas de ite en + Montrer que toute fonction croissante et majorée admet une ite finie en + Indication
Fonctions de plusieurs variables, intégrales multiples, et intégrales dépendant d un paramètre
 IUFM du Limousin 2009-10 PLC1 Mathématiques S. Vinatier Rappels de cours Fonctions de plusieurs variables, intégrales multiples, et intégrales dépendant d un paramètre 1 Fonctions de plusieurs variables
IUFM du Limousin 2009-10 PLC1 Mathématiques S. Vinatier Rappels de cours Fonctions de plusieurs variables, intégrales multiples, et intégrales dépendant d un paramètre 1 Fonctions de plusieurs variables
Chapitre 3. Quelques fonctions usuelles. 1 Fonctions logarithme et exponentielle. 1.1 La fonction logarithme
 Chapitre 3 Quelques fonctions usuelles 1 Fonctions logarithme et eponentielle 1.1 La fonction logarithme Définition 1.1 La fonction 7! 1/ est continue sur ]0, +1[. Elle admet donc des primitives sur cet
Chapitre 3 Quelques fonctions usuelles 1 Fonctions logarithme et eponentielle 1.1 La fonction logarithme Définition 1.1 La fonction 7! 1/ est continue sur ]0, +1[. Elle admet donc des primitives sur cet
La fonction exponentielle
 DERNIÈRE IMPRESSION LE 2 novembre 204 à :07 La fonction exponentielle Table des matières La fonction exponentielle 2. Définition et théorèmes.......................... 2.2 Approche graphique de la fonction
DERNIÈRE IMPRESSION LE 2 novembre 204 à :07 La fonction exponentielle Table des matières La fonction exponentielle 2. Définition et théorèmes.......................... 2.2 Approche graphique de la fonction
PROBLEME(12) Première partie : Peinture des murs et du plafond.
 PROBLEME(12) Une entreprise doit rénover un local. Ce local a la forme d'un parallélépipède rectangle. La longueur est 6,40m, la largeur est 5,20m et la hauteur est 2,80m. Il comporte une porte de 2m de
PROBLEME(12) Une entreprise doit rénover un local. Ce local a la forme d'un parallélépipède rectangle. La longueur est 6,40m, la largeur est 5,20m et la hauteur est 2,80m. Il comporte une porte de 2m de
Nombre de marches Nombre de facons de les monter 3 3 11 144 4 5 12 233 5 8 13 377 6 13 14 610 7 21 15 987 8 34 16 1597 9 55 17 2584 10 89
 Soit un escalier à n marches. On note u_n le nombre de façons de monter ces n marches. Par exemple d'après l'énoncé, u_3=3. Pour monter n marches, il faut d'abord monter la première. Soit on la monte seule,
Soit un escalier à n marches. On note u_n le nombre de façons de monter ces n marches. Par exemple d'après l'énoncé, u_3=3. Pour monter n marches, il faut d'abord monter la première. Soit on la monte seule,
Image d un intervalle par une fonction continue
 DOCUMENT 27 Image d un intervalle par une fonction continue La continuité d une fonction en un point est une propriété locale : une fonction est continue en un point x 0 si et seulement si sa restriction
DOCUMENT 27 Image d un intervalle par une fonction continue La continuité d une fonction en un point est une propriété locale : une fonction est continue en un point x 0 si et seulement si sa restriction
EXERCICES DE REVISIONS MATHEMATIQUES CM2
 EXERCICES DE REVISIONS MATHEMATIQUES CM2 NOMBRES ET CALCUL Exercices FRACTIONS Nommer les fractions simples et décimales en utilisant le vocabulaire : 3 R1 demi, tiers, quart, dixième, centième. Utiliser
EXERCICES DE REVISIONS MATHEMATIQUES CM2 NOMBRES ET CALCUL Exercices FRACTIONS Nommer les fractions simples et décimales en utilisant le vocabulaire : 3 R1 demi, tiers, quart, dixième, centième. Utiliser
Compression Compression par dictionnaires
 Compression Compression par dictionnaires E. Jeandel Emmanuel.Jeandel at lif.univ-mrs.fr E. Jeandel, Lif CompressionCompression par dictionnaires 1/25 Compression par dictionnaire Principe : Avoir une
Compression Compression par dictionnaires E. Jeandel Emmanuel.Jeandel at lif.univ-mrs.fr E. Jeandel, Lif CompressionCompression par dictionnaires 1/25 Compression par dictionnaire Principe : Avoir une
Structures algébriques
 Structures algébriques 1. Lois de composition s Soit E un ensemble. Une loi de composition interne sur E est une application de E E dans E. Soient E et F deux ensembles. Une loi de composition externe
Structures algébriques 1. Lois de composition s Soit E un ensemble. Une loi de composition interne sur E est une application de E E dans E. Soient E et F deux ensembles. Une loi de composition externe
Cours d algorithmique pour la classe de 2nde
 Cours d algorithmique pour la classe de 2nde F.Gaudon 10 août 2009 Table des matières 1 Avant la programmation 2 1.1 Qu est ce qu un algorithme?................................. 2 1.2 Qu est ce qu un langage
Cours d algorithmique pour la classe de 2nde F.Gaudon 10 août 2009 Table des matières 1 Avant la programmation 2 1.1 Qu est ce qu un algorithme?................................. 2 1.2 Qu est ce qu un langage
chapitre 4 Nombres de Catalan
 chapitre 4 Nombres de Catalan I Dénitions Dénition 1 La suite de Catalan (C n ) n est la suite dénie par C 0 = 1 et, pour tout n N, C n+1 = C k C n k. Exemple 2 On trouve rapidement C 0 = 1, C 1 = 1, C
chapitre 4 Nombres de Catalan I Dénitions Dénition 1 La suite de Catalan (C n ) n est la suite dénie par C 0 = 1 et, pour tout n N, C n+1 = C k C n k. Exemple 2 On trouve rapidement C 0 = 1, C 1 = 1, C
Projet de traitement d'image - SI 381 reconstitution 3D d'intérieur à partir de photographies
 Projet de traitement d'image - SI 381 reconstitution 3D d'intérieur à partir de photographies Régis Boulet Charlie Demené Alexis Guyot Balthazar Neveu Guillaume Tartavel Sommaire Sommaire... 1 Structure
Projet de traitement d'image - SI 381 reconstitution 3D d'intérieur à partir de photographies Régis Boulet Charlie Demené Alexis Guyot Balthazar Neveu Guillaume Tartavel Sommaire Sommaire... 1 Structure
Ch.G3 : Distances et tangentes
 4 e - programme 2011 mathématiques ch.g3 cahier élève Page 1 sur 14 1 DISTC D U PIT À U DRIT Ch.G3 : Distances et tangentes 1.1 Définition ex 1 DÉFIITI 1 : Soit une droite et un point n'appartenant pas
4 e - programme 2011 mathématiques ch.g3 cahier élève Page 1 sur 14 1 DISTC D U PIT À U DRIT Ch.G3 : Distances et tangentes 1.1 Définition ex 1 DÉFIITI 1 : Soit une droite et un point n'appartenant pas
Paris et New-York sont-ils les sommets d'un carré?
 page 95 Paris et New-York sont-ils les sommets d'un carré? par othi Mok (3 ), Michel Vongsavanh (3 ), Eric hin (3 ), iek-hor Lim ( ), Eric kbaraly ( ), élèves et anciens élèves du ollège Victor Hugo (2
page 95 Paris et New-York sont-ils les sommets d'un carré? par othi Mok (3 ), Michel Vongsavanh (3 ), Eric hin (3 ), iek-hor Lim ( ), Eric kbaraly ( ), élèves et anciens élèves du ollège Victor Hugo (2
Angles orientés et trigonométrie
 Chapitre Angles orientés et trigonométrie Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES Trigonométrie Cercle trigonométrique. Radian. Mesure d un angle orienté, mesure principale.
Chapitre Angles orientés et trigonométrie Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES Trigonométrie Cercle trigonométrique. Radian. Mesure d un angle orienté, mesure principale.
Chapitre 2 Le problème de l unicité des solutions
 Université Joseph Fourier UE MAT 127 Mathématiques année 2011-2012 Chapitre 2 Le problème de l unicité des solutions Ce que nous verrons dans ce chapitre : un exemple d équation différentielle y = f(y)
Université Joseph Fourier UE MAT 127 Mathématiques année 2011-2012 Chapitre 2 Le problème de l unicité des solutions Ce que nous verrons dans ce chapitre : un exemple d équation différentielle y = f(y)
I - PUISSANCE D UN POINT PAR RAPPORT A UN CERCLE CERCLES ORTHOGONAUX POLES ET POLAIRES
 I - PUISSANCE D UN POINT PAR RAPPORT A UN CERCLE CERCLES ORTHOGONAUX POLES ET POLAIRES Théorème - Définition Soit un cercle (O,R) et un point. Une droite passant par coupe le cercle en deux points A et
I - PUISSANCE D UN POINT PAR RAPPORT A UN CERCLE CERCLES ORTHOGONAUX POLES ET POLAIRES Théorème - Définition Soit un cercle (O,R) et un point. Une droite passant par coupe le cercle en deux points A et
Par combien de zéros se termine N!?
 La recherche à l'école page 79 Par combien de zéros se termine N!? par d es co llèg es An dré Do ucet de Nanterre et Victor Hugo de Noisy le Grand en seignants : Danielle Buteau, Martine Brunstein, Marie-Christine
La recherche à l'école page 79 Par combien de zéros se termine N!? par d es co llèg es An dré Do ucet de Nanterre et Victor Hugo de Noisy le Grand en seignants : Danielle Buteau, Martine Brunstein, Marie-Christine
AC AB. A B C x 1. x + 1. d où. Avec un calcul vu au lycée, on démontre que cette solution admet deux solutions dont une seule nous intéresse : x =
 LE NOMBRE D OR Présentation et calcul du nombre d or Euclide avait trouvé un moyen de partager en deu un segment selon en «etrême et moyenne raison» Soit un segment [AB]. Le partage d Euclide consiste
LE NOMBRE D OR Présentation et calcul du nombre d or Euclide avait trouvé un moyen de partager en deu un segment selon en «etrême et moyenne raison» Soit un segment [AB]. Le partage d Euclide consiste
DIFFRACTion des ondes
 DIFFRACTion des ondes I DIFFRACTION DES ONDES PAR LA CUVE À ONDES Lorsqu'une onde plane traverse un trou, elle se transforme en onde circulaire. On dit que l'onde plane est diffractée par le trou. Ce phénomène
DIFFRACTion des ondes I DIFFRACTION DES ONDES PAR LA CUVE À ONDES Lorsqu'une onde plane traverse un trou, elle se transforme en onde circulaire. On dit que l'onde plane est diffractée par le trou. Ce phénomène
Les probabilités. Chapitre 18. Tester ses connaissances
 Chapitre 18 Les probabilités OBJECTIFS DU CHAPITRE Calculer la probabilité d événements Tester ses connaissances 1. Expériences aléatoires Voici trois expériences : - Expérience (1) : on lance une pièce
Chapitre 18 Les probabilités OBJECTIFS DU CHAPITRE Calculer la probabilité d événements Tester ses connaissances 1. Expériences aléatoires Voici trois expériences : - Expérience (1) : on lance une pièce
5 ème Chapitre 4 Triangles
 5 ème Chapitre 4 Triangles 1) Médiatrices Définition : la médiatrice d'un segment est l'ensemble des points équidistants des extrémités du segment (cours de 6 ème ). Si M appartient à la médiatrice du
5 ème Chapitre 4 Triangles 1) Médiatrices Définition : la médiatrice d'un segment est l'ensemble des points équidistants des extrémités du segment (cours de 6 ème ). Si M appartient à la médiatrice du
Bac Blanc Terminale ES - Février 2011 Épreuve de Mathématiques (durée 3 heures)
 Bac Blanc Terminale ES - Février 2011 Épreuve de Mathématiques (durée 3 heures) Eercice 1 (5 points) pour les candidats n ayant pas choisi la spécialité MATH Le tableau suivant donne l évolution du chiffre
Bac Blanc Terminale ES - Février 2011 Épreuve de Mathématiques (durée 3 heures) Eercice 1 (5 points) pour les candidats n ayant pas choisi la spécialité MATH Le tableau suivant donne l évolution du chiffre
Logiciel SCRATCH FICHE 02
 1. Reprise de la fiche 1: 1.1. Programme Figure : Logiciel SCRATCH FICHE 02 SANS ORDINATEUR : Dessiner à droite le dessin que donnera l'exécution de ce programme : Unité : 50 pas : Remarque : vous devez
1. Reprise de la fiche 1: 1.1. Programme Figure : Logiciel SCRATCH FICHE 02 SANS ORDINATEUR : Dessiner à droite le dessin que donnera l'exécution de ce programme : Unité : 50 pas : Remarque : vous devez
Coefficients binomiaux
 Probabilités L2 Exercices Chapitre 2 Coefficients binomiaux 1 ( ) On appelle chemin une suite de segments de longueur 1, dirigés soit vers le haut, soit vers la droite 1 Dénombrer tous les chemins allant
Probabilités L2 Exercices Chapitre 2 Coefficients binomiaux 1 ( ) On appelle chemin une suite de segments de longueur 1, dirigés soit vers le haut, soit vers la droite 1 Dénombrer tous les chemins allant
Rappels et compléments, première partie : Nombres complexes et applications à la géométrie
 Rappels et compléments, première partie : Nombres complexes et applications à la géométrie 1 Définition des nombres complexes On définit sur les couples de réels une loi d addition comme suit : (x; y)
Rappels et compléments, première partie : Nombres complexes et applications à la géométrie 1 Définition des nombres complexes On définit sur les couples de réels une loi d addition comme suit : (x; y)
CONJUGUÉ D'UN POINT PAR RAPPORT À UN TRIANGLE
 CONJUGUÉ D'UN POINT PAR RAPPORT À UN TRIANGLE Jean Luc Bovet, Auvernier L'article de Monsieur Jean Piquerez (Bulletin de la SSPMP No 86), consacré aux symédianes me paraît appeler une généralisation. En
CONJUGUÉ D'UN POINT PAR RAPPORT À UN TRIANGLE Jean Luc Bovet, Auvernier L'article de Monsieur Jean Piquerez (Bulletin de la SSPMP No 86), consacré aux symédianes me paraît appeler une généralisation. En
Chapitre 7. Récurrences
 Chapitre 7 Récurrences 333 Plan 1. Introduction 2. Applications 3. Classification des récurrences 4. Résolution de récurrences 5. Résumé et comparaisons Lectures conseillées : I MCS, chapitre 20. I Rosen,
Chapitre 7 Récurrences 333 Plan 1. Introduction 2. Applications 3. Classification des récurrences 4. Résolution de récurrences 5. Résumé et comparaisons Lectures conseillées : I MCS, chapitre 20. I Rosen,
Probabilités sur un univers fini
 [http://mp.cpgedupuydelome.fr] édité le 7 août 204 Enoncés Probabilités sur un univers fini Evènements et langage ensembliste A quelle condition sur (a, b, c, d) ]0, [ 4 existe-t-il une probabilité P sur
[http://mp.cpgedupuydelome.fr] édité le 7 août 204 Enoncés Probabilités sur un univers fini Evènements et langage ensembliste A quelle condition sur (a, b, c, d) ]0, [ 4 existe-t-il une probabilité P sur
Axiomatique de N, construction de Z
 Axiomatique de N, construction de Z Table des matières 1 Axiomatique de N 2 1.1 Axiomatique ordinale.................................. 2 1.2 Propriété fondamentale : Le principe de récurrence.................
Axiomatique de N, construction de Z Table des matières 1 Axiomatique de N 2 1.1 Axiomatique ordinale.................................. 2 1.2 Propriété fondamentale : Le principe de récurrence.................
EVALUATIONS MI-PARCOURS CM2
 Les enseignants de CM2 de la circonscription de METZ-SUD proposent EVALUATIONS MI-PARCOURS CM2 Mathématiques Livret enseignant NOMBRES ET CALCUL Circonscription de METZ-SUD Page 1 Séquence 1 : Exercice
Les enseignants de CM2 de la circonscription de METZ-SUD proposent EVALUATIONS MI-PARCOURS CM2 Mathématiques Livret enseignant NOMBRES ET CALCUL Circonscription de METZ-SUD Page 1 Séquence 1 : Exercice
Exercices de dénombrement
 Exercices de dénombrement Exercice En turbo Pascal, un entier relatif (type integer) est codé sur 6 bits. Cela signifie que l'on réserve 6 cases mémoires contenant des "0" ou des "" pour écrire un entier.
Exercices de dénombrement Exercice En turbo Pascal, un entier relatif (type integer) est codé sur 6 bits. Cela signifie que l'on réserve 6 cases mémoires contenant des "0" ou des "" pour écrire un entier.
* très facile ** facile *** difficulté moyenne **** difficile ***** très difficile I : Incontournable T : pour travailler et mémoriser le cours
 Exo7 Continuité (étude globale). Diverses fonctions Exercices de Jean-Louis Rouget. Retrouver aussi cette fiche sur www.maths-france.fr * très facile ** facile *** difficulté moyenne **** difficile *****
Exo7 Continuité (étude globale). Diverses fonctions Exercices de Jean-Louis Rouget. Retrouver aussi cette fiche sur www.maths-france.fr * très facile ** facile *** difficulté moyenne **** difficile *****
PARTIE NUMERIQUE (18 points)
 4 ème DEVOIR COMMUN N 1 DE MATHÉMATIQUES 14/12/09 L'échange de matériel entre élèves et l'usage de la calculatrice sont interdits. Il sera tenu compte du soin et de la présentation ( 4 points ). Le barème
4 ème DEVOIR COMMUN N 1 DE MATHÉMATIQUES 14/12/09 L'échange de matériel entre élèves et l'usage de la calculatrice sont interdits. Il sera tenu compte du soin et de la présentation ( 4 points ). Le barème
PROBLEMES D'ORDONNANCEMENT AVEC RESSOURCES
 Leçon 11 PROBLEMES D'ORDONNANCEMENT AVEC RESSOURCES Dans cette leçon, nous retrouvons le problème d ordonnancement déjà vu mais en ajoutant la prise en compte de contraintes portant sur les ressources.
Leçon 11 PROBLEMES D'ORDONNANCEMENT AVEC RESSOURCES Dans cette leçon, nous retrouvons le problème d ordonnancement déjà vu mais en ajoutant la prise en compte de contraintes portant sur les ressources.
Inscription en ligne FQSC. Guide d utilisation
 Inscription en ligne FQSC Guide d utilisation Ce Guide est rédigé comme aide-mémoire pour l achat de votre licence sur le site internet de la FQSC. Dans un prem ier temps, vous devrez vous rendre sur le
Inscription en ligne FQSC Guide d utilisation Ce Guide est rédigé comme aide-mémoire pour l achat de votre licence sur le site internet de la FQSC. Dans un prem ier temps, vous devrez vous rendre sur le
Retour d expérience sur le management des processus
 GSI Gestion des systèmes d information Retour d expérience sur le management des processus Université d été 8-31 août 00 Dijon Guy Rivoire Consultant ELNOR Guy RIVOIRE 30/08/00 / 1 Présentation ELNOR Cabinet
GSI Gestion des systèmes d information Retour d expérience sur le management des processus Université d été 8-31 août 00 Dijon Guy Rivoire Consultant ELNOR Guy RIVOIRE 30/08/00 / 1 Présentation ELNOR Cabinet
De même, le périmètre P d un cercle de rayon 1 vaut P = 2π (par définition de π). Mais, on peut démontrer (difficilement!) que
 Introduction. On suppose connus les ensembles N (des entiers naturels), Z des entiers relatifs et Q (des nombres rationnels). On s est rendu compte, depuis l antiquité, que l on ne peut pas tout mesurer
Introduction. On suppose connus les ensembles N (des entiers naturels), Z des entiers relatifs et Q (des nombres rationnels). On s est rendu compte, depuis l antiquité, que l on ne peut pas tout mesurer
Prêt(e) pour le CE1. Tu es maintenant au CE1. Avant de commencer les leçons, nous allons réviser avec toi!
 Jour Prêt(e) pour le CE Tu es maintenant au CE. vant de commencer les leçons, nous allons réviser avec toi! Géométrie Retrouver un itinéraire en tenant compte des informations. Lis les explications de
Jour Prêt(e) pour le CE Tu es maintenant au CE. vant de commencer les leçons, nous allons réviser avec toi! Géométrie Retrouver un itinéraire en tenant compte des informations. Lis les explications de
Continuité et dérivabilité d une fonction
 DERNIÈRE IMPRESSIN LE 7 novembre 014 à 10:3 Continuité et dérivabilité d une fonction Table des matières 1 Continuité d une fonction 1.1 Limite finie en un point.......................... 1. Continuité
DERNIÈRE IMPRESSIN LE 7 novembre 014 à 10:3 Continuité et dérivabilité d une fonction Table des matières 1 Continuité d une fonction 1.1 Limite finie en un point.......................... 1. Continuité
I. Ensemble de définition d'une fonction
 Chapitre 2 Généralités sur les fonctions Fonctions de références et fonctions associées Ce que dit le programme : Étude de fonctions Fonctions de référence x x et x x Connaître les variations de ces deux
Chapitre 2 Généralités sur les fonctions Fonctions de références et fonctions associées Ce que dit le programme : Étude de fonctions Fonctions de référence x x et x x Connaître les variations de ces deux
Calcul intégral élémentaire en plusieurs variables
 Calcul intégral élémentaire en plusieurs variables PC*2 2 septembre 2009 Avant-propos À part le théorème de Fubini qui sera démontré dans le cours sur les intégrales à paramètres et qui ne semble pas explicitement
Calcul intégral élémentaire en plusieurs variables PC*2 2 septembre 2009 Avant-propos À part le théorème de Fubini qui sera démontré dans le cours sur les intégrales à paramètres et qui ne semble pas explicitement
3 Approximation de solutions d équations
 3 Approximation de solutions d équations Une équation scalaire a la forme générale f(x) =0où f est une fonction de IR dans IR. Un système de n équations à n inconnues peut aussi se mettre sous une telle
3 Approximation de solutions d équations Une équation scalaire a la forme générale f(x) =0où f est une fonction de IR dans IR. Un système de n équations à n inconnues peut aussi se mettre sous une telle
Introduction à l étude des Corps Finis
 Introduction à l étude des Corps Finis Robert Rolland (Résumé) 1 Introduction La structure de corps fini intervient dans divers domaines des mathématiques, en particulier dans la théorie de Galois sur
Introduction à l étude des Corps Finis Robert Rolland (Résumé) 1 Introduction La structure de corps fini intervient dans divers domaines des mathématiques, en particulier dans la théorie de Galois sur
Mathématiques et petites voitures
 Mathématiques et petites voitures Thomas Lefebvre 10 avril 2015 Résumé Ce document présente diérentes applications des mathématiques dans le domaine du slot-racing. Table des matières 1 Périmètre et circuit
Mathématiques et petites voitures Thomas Lefebvre 10 avril 2015 Résumé Ce document présente diérentes applications des mathématiques dans le domaine du slot-racing. Table des matières 1 Périmètre et circuit
D'UN THÉORÈME NOUVEAU
 DÉMONSTRATION D'UN THÉORÈME NOUVEAU CONCERNANT LES NOMBRES PREMIERS 1. (Nouveaux Mémoires de l'académie royale des Sciences et Belles-Lettres de Berlin, année 1771.) 1. Je viens de trouver, dans un excellent
DÉMONSTRATION D'UN THÉORÈME NOUVEAU CONCERNANT LES NOMBRES PREMIERS 1. (Nouveaux Mémoires de l'académie royale des Sciences et Belles-Lettres de Berlin, année 1771.) 1. Je viens de trouver, dans un excellent
Quels polygones sont formés par les milieux des côtés d un autre polygone?
 La recherche à l'école page 13 Quels polygones sont formés par les milieux des côtés d un autre polygone? par d es co llèg es n dré o ucet de Nanterre et Victor ugo de Noisy-le-rand enseignants : Martine
La recherche à l'école page 13 Quels polygones sont formés par les milieux des côtés d un autre polygone? par d es co llèg es n dré o ucet de Nanterre et Victor ugo de Noisy-le-rand enseignants : Martine
Chapitre 1 : Évolution COURS
 Chapitre 1 : Évolution COURS OBJECTIFS DU CHAPITRE Savoir déterminer le taux d évolution, le coefficient multiplicateur et l indice en base d une évolution. Connaître les liens entre ces notions et savoir
Chapitre 1 : Évolution COURS OBJECTIFS DU CHAPITRE Savoir déterminer le taux d évolution, le coefficient multiplicateur et l indice en base d une évolution. Connaître les liens entre ces notions et savoir
Comment gérer sans stress
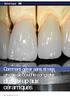 E s t h é t i q u e Comment gérer sans stress Comment gérer sans stress un cas de bouche complète du wax-up aux c é r a m i q u e s 28 Tech. Dent. N 311-11/12 «Par Christophe H U E P rothésiste Dentaire
E s t h é t i q u e Comment gérer sans stress Comment gérer sans stress un cas de bouche complète du wax-up aux c é r a m i q u e s 28 Tech. Dent. N 311-11/12 «Par Christophe H U E P rothésiste Dentaire
Proposition de programmes de calculs en mise en train
 Proposition de programmes de calculs en mise en train Programme 1 : Je choisis un nombre, je lui ajoute 1, je calcule le carré du résultat, je retranche le carré du nombre de départ. Essai-conjecture-preuve.
Proposition de programmes de calculs en mise en train Programme 1 : Je choisis un nombre, je lui ajoute 1, je calcule le carré du résultat, je retranche le carré du nombre de départ. Essai-conjecture-preuve.
avec des nombres entiers
 Calculer avec des nombres entiers Effectuez les calculs suivants.. + 9 + 9. Calculez. 9 9 Calculez le quotient et le rest. : : : : 0 :. : : 9 : : 9 0 : 0. 9 9 0 9. Calculez. 9 0 9. : : 0 : 9 : :. : : 0
Calculer avec des nombres entiers Effectuez les calculs suivants.. + 9 + 9. Calculez. 9 9 Calculez le quotient et le rest. : : : : 0 :. : : 9 : : 9 0 : 0. 9 9 0 9. Calculez. 9 0 9. : : 0 : 9 : :. : : 0
TBI et mathématique. Pour vous soutenir dans votre enseignement des mathématiques. Les outils du logiciel Notebook. les ressources internet
 TBI et mathématique Pour vous soutenir dans votre enseignement des mathématiques Dessin tiré du site www.recitus.qc.ca Les outils du logiciel Notebook et les ressources internet Document préparé par France
TBI et mathématique Pour vous soutenir dans votre enseignement des mathématiques Dessin tiré du site www.recitus.qc.ca Les outils du logiciel Notebook et les ressources internet Document préparé par France
DOCM 2013 http://docm.math.ca/ Solutions officielles. 1 2 10 + 1 2 9 + 1 2 8 = n 2 10.
 A1 Trouvez l entier positif n qui satisfait l équation suivante: Solution 1 2 10 + 1 2 9 + 1 2 8 = n 2 10. En additionnant les termes du côté gauche de l équation en les mettant sur le même dénominateur
A1 Trouvez l entier positif n qui satisfait l équation suivante: Solution 1 2 10 + 1 2 9 + 1 2 8 = n 2 10. En additionnant les termes du côté gauche de l équation en les mettant sur le même dénominateur
I. Polynômes de Tchebychev
 Première épreuve CCP filière MP I. Polynômes de Tchebychev ( ) 1.a) Tout réel θ vérifie cos(nθ) = Re ((cos θ + i sin θ) n ) = Re Cn k (cos θ) n k i k (sin θ) k Or i k est réel quand k est pair et imaginaire
Première épreuve CCP filière MP I. Polynômes de Tchebychev ( ) 1.a) Tout réel θ vérifie cos(nθ) = Re ((cos θ + i sin θ) n ) = Re Cn k (cos θ) n k i k (sin θ) k Or i k est réel quand k est pair et imaginaire
Objectifs du cours d aujourd hui. Informatique II : Cours d introduction à l informatique et à la programmation objet. Complexité d un problème (2)
 Objectifs du cours d aujourd hui Informatique II : Cours d introduction à l informatique et à la programmation objet Complexité des problèmes Introduire la notion de complexité d un problème Présenter
Objectifs du cours d aujourd hui Informatique II : Cours d introduction à l informatique et à la programmation objet Complexité des problèmes Introduire la notion de complexité d un problème Présenter
CORRIGE LES NOMBRES DECIMAUX RELATIFS. «Réfléchir avant d agir!»
 Corrigé Cours de Mr JULES v3.3 Classe de Quatrième Contrat 1 Page 1 sur 13 CORRIGE LES NOMBRES DECIMAUX RELATIFS. «Réfléchir avant d agir!» «Correction en rouge et italique.» I. Les nombres décimaux relatifs.
Corrigé Cours de Mr JULES v3.3 Classe de Quatrième Contrat 1 Page 1 sur 13 CORRIGE LES NOMBRES DECIMAUX RELATIFS. «Réfléchir avant d agir!» «Correction en rouge et italique.» I. Les nombres décimaux relatifs.
Eteindre. les. lumières MATH EN JEAN 2013-2014. Mme BACHOC. Elèves de seconde, première et terminale scientifiques :
 MTH EN JEN 2013-2014 Elèves de seconde, première et terminale scientifiques : Lycée Michel Montaigne : HERITEL ôme T S POLLOZE Hélène 1 S SOK Sophie 1 S Eteindre Lycée Sud Médoc : ROSIO Gauthier 2 nd PELGE
MTH EN JEN 2013-2014 Elèves de seconde, première et terminale scientifiques : Lycée Michel Montaigne : HERITEL ôme T S POLLOZE Hélène 1 S SOK Sophie 1 S Eteindre Lycée Sud Médoc : ROSIO Gauthier 2 nd PELGE
Tutoriel Infuse Learning. Créer des quizzes multimédias sur ordinateur ou tablette
 Tutoriel Infuse Learning Créer des quizzes multimédias sur ordinateur ou tablette 1- Présentation Infuselearning.com est un service web (en ligne) gratuit qui permet aux enseignants de créer des exercices
Tutoriel Infuse Learning Créer des quizzes multimédias sur ordinateur ou tablette 1- Présentation Infuselearning.com est un service web (en ligne) gratuit qui permet aux enseignants de créer des exercices
Chapitre 2 : Vecteurs
 1 Chapitre 2 : Vecteurs Nous allons définir ce qu'est un vecteur grâce à une figure (le parallélogramme), mais au préalable nous allons aussi définir une nouvelle transformation (la translation). Nous
1 Chapitre 2 : Vecteurs Nous allons définir ce qu'est un vecteur grâce à une figure (le parallélogramme), mais au préalable nous allons aussi définir une nouvelle transformation (la translation). Nous
Correction du Baccalauréat S Amérique du Nord mai 2007
 Correction du Baccalauréat S Amérique du Nord mai 7 EXERCICE points. Le plan (P) a une pour équation cartésienne : x+y z+ =. Les coordonnées de H vérifient cette équation donc H appartient à (P) et A n
Correction du Baccalauréat S Amérique du Nord mai 7 EXERCICE points. Le plan (P) a une pour équation cartésienne : x+y z+ =. Les coordonnées de H vérifient cette équation donc H appartient à (P) et A n
Arithmétique binaire. Chapitre. 5.1 Notions. 5.1.1 Bit. 5.1.2 Mot
 Chapitre 5 Arithmétique binaire L es codes sont manipulés au quotidien sans qu on s en rende compte, et leur compréhension est quasi instinctive. Le seul fait de lire fait appel au codage alphabétique,
Chapitre 5 Arithmétique binaire L es codes sont manipulés au quotidien sans qu on s en rende compte, et leur compréhension est quasi instinctive. Le seul fait de lire fait appel au codage alphabétique,
Cours 02 : Problème général de la programmation linéaire
 Cours 02 : Problème général de la programmation linéaire Cours 02 : Problème général de la Programmation Linéaire. 5 . Introduction Un programme linéaire s'écrit sous la forme suivante. MinZ(ou maxw) =
Cours 02 : Problème général de la programmation linéaire Cours 02 : Problème général de la Programmation Linéaire. 5 . Introduction Un programme linéaire s'écrit sous la forme suivante. MinZ(ou maxw) =
Probabilités. I Petits rappels sur le vocabulaire des ensembles 2 I.1 Définitions... 2 I.2 Propriétés... 2
 Probabilités Table des matières I Petits rappels sur le vocabulaire des ensembles 2 I.1 s................................................... 2 I.2 Propriétés...................................................
Probabilités Table des matières I Petits rappels sur le vocabulaire des ensembles 2 I.1 s................................................... 2 I.2 Propriétés...................................................
Sur certaines séries entières particulières
 ACTA ARITHMETICA XCII. 2) Sur certaines séries entières particulières par Hubert Delange Orsay). Introduction. Dans un exposé à la Conférence Internationale de Théorie des Nombres organisée à Zakopane
ACTA ARITHMETICA XCII. 2) Sur certaines séries entières particulières par Hubert Delange Orsay). Introduction. Dans un exposé à la Conférence Internationale de Théorie des Nombres organisée à Zakopane
C f tracée ci- contre est la représentation graphique d une
 TLES1 DEVOIR A LA MAISON N 7 La courbe C f tracée ci- contre est la représentation graphique d une fonction f définie et dérivable sur R. On note f ' la fonction dérivée de f. La tangente T à la courbe
TLES1 DEVOIR A LA MAISON N 7 La courbe C f tracée ci- contre est la représentation graphique d une fonction f définie et dérivable sur R. On note f ' la fonction dérivée de f. La tangente T à la courbe
PR OC E D U RE S D E B A S E
 Photofiltre Préparé par Philipe Lampron, auxiliaire du cours FPE 7650 en 2004-2005. *** Pour optimiser une image : enregistrer sous et augmenter la compression PR OC E D U RE S D E B A S E PhotoFiltre
Photofiltre Préparé par Philipe Lampron, auxiliaire du cours FPE 7650 en 2004-2005. *** Pour optimiser une image : enregistrer sous et augmenter la compression PR OC E D U RE S D E B A S E PhotoFiltre
Calcul matriciel. Définition 1 Une matrice de format (m,n) est un tableau rectangulaire de mn éléments, rangés en m lignes et n colonnes.
 1 Définitions, notations Calcul matriciel Définition 1 Une matrice de format (m,n) est un tableau rectangulaire de mn éléments, rangés en m lignes et n colonnes. On utilise aussi la notation m n pour le
1 Définitions, notations Calcul matriciel Définition 1 Une matrice de format (m,n) est un tableau rectangulaire de mn éléments, rangés en m lignes et n colonnes. On utilise aussi la notation m n pour le
1 radian. De même, la longueur d un arc de cercle de rayon R et dont l angle au centre a pour mesure α radians est α R. R AB =R.
 Angles orientés Trigonométrie I. Préliminaires. Le radian Définition B R AB =R C O radian R A Soit C un cercle de centre O. Dire que l angle géométrique AOB a pour mesure radian signifie que la longueur
Angles orientés Trigonométrie I. Préliminaires. Le radian Définition B R AB =R C O radian R A Soit C un cercle de centre O. Dire que l angle géométrique AOB a pour mesure radian signifie que la longueur
Exercices - Nombres complexes : corrigé. Formes algébriques et trigonométriques, module et argument
 Formes algébriques et trigonométriques, module et argument Exercice - - L/Math Sup - On multiplie le dénominateur par sa quantité conjuguée, et on obtient : Z = 4 i 3 + i 3 i 3 = 4 i 3 + 3 = + i 3. Pour
Formes algébriques et trigonométriques, module et argument Exercice - - L/Math Sup - On multiplie le dénominateur par sa quantité conjuguée, et on obtient : Z = 4 i 3 + i 3 i 3 = 4 i 3 + 3 = + i 3. Pour
PROBABILITÉS CONDITIONNELLES
 PROBABILITÉS CONDITIONNELLES A.FORMONS DES COUPLES Pour la fête de l école, les élèves de CE 2 ont préparé une danse qui s exécute par couples : un garçon, une fille. La maîtresse doit faire des essais
PROBABILITÉS CONDITIONNELLES A.FORMONS DES COUPLES Pour la fête de l école, les élèves de CE 2 ont préparé une danse qui s exécute par couples : un garçon, une fille. La maîtresse doit faire des essais
Géométrie dans l espace Produit scalaire et équations
 Chapitre 11. 2ème partie Géométrie dans l espace Produit scalaire et équations Terminale S Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES 2ème partie Produit scalaire Produit scalaire
Chapitre 11. 2ème partie Géométrie dans l espace Produit scalaire et équations Terminale S Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES 2ème partie Produit scalaire Produit scalaire
Chapitre 1 Cinématique du point matériel
 Chapitre 1 Cinématique du point matériel 7 1.1. Introduction 1.1.1. Domaine d étude Le programme de mécanique de math sup se limite à l étude de la mécanique classique. Sont exclus : la relativité et la
Chapitre 1 Cinématique du point matériel 7 1.1. Introduction 1.1.1. Domaine d étude Le programme de mécanique de math sup se limite à l étude de la mécanique classique. Sont exclus : la relativité et la
Probabilités sur un univers fini
 [http://mp.cpgedupuydelome.fr] édité le 10 août 2015 Enoncés 1 Proailités sur un univers fini Evènements et langage ensemliste A quelle condition sur (a,, c, d) ]0, 1[ 4 existe-t-il une proailité P sur
[http://mp.cpgedupuydelome.fr] édité le 10 août 2015 Enoncés 1 Proailités sur un univers fini Evènements et langage ensemliste A quelle condition sur (a,, c, d) ]0, 1[ 4 existe-t-il une proailité P sur
Recherche dans un tableau
 Chapitre 3 Recherche dans un tableau 3.1 Introduction 3.1.1 Tranche On appelle tranche de tableau, la donnée d'un tableau t et de deux indices a et b. On note cette tranche t.(a..b). Exemple 3.1 : 3 6
Chapitre 3 Recherche dans un tableau 3.1 Introduction 3.1.1 Tranche On appelle tranche de tableau, la donnée d'un tableau t et de deux indices a et b. On note cette tranche t.(a..b). Exemple 3.1 : 3 6
Logique binaire. Aujourd'hui, l'algèbre de Boole trouve de nombreuses applications en informatique et dans la conception des circuits électroniques.
 Logique binaire I. L'algèbre de Boole L'algèbre de Boole est la partie des mathématiques, de la logique et de l'électronique qui s'intéresse aux opérations et aux fonctions sur les variables logiques.
Logique binaire I. L'algèbre de Boole L'algèbre de Boole est la partie des mathématiques, de la logique et de l'électronique qui s'intéresse aux opérations et aux fonctions sur les variables logiques.
Compter à Babylone. L écriture des nombres
 Compter à Babylone d après l article de Christine Proust «Le calcul sexagésimal en Mésopotamie : enseignement dans les écoles de scribes» disponible sur http://www.dma.ens.fr/culturemath/ Les mathématiciens
Compter à Babylone d après l article de Christine Proust «Le calcul sexagésimal en Mésopotamie : enseignement dans les écoles de scribes» disponible sur http://www.dma.ens.fr/culturemath/ Les mathématiciens
Définition : On obtient les nombres entiers en ajoutant ou retranchant des unités à zéro.
 Chapitre : Les nombres rationnels Programme officiel BO du 8/08/08 Connaissances : Diviseurs communs à deux entiers, PGCD. Fractions irréductibles. Opérations sur les nombres relatifs en écriture fractionnaire.
Chapitre : Les nombres rationnels Programme officiel BO du 8/08/08 Connaissances : Diviseurs communs à deux entiers, PGCD. Fractions irréductibles. Opérations sur les nombres relatifs en écriture fractionnaire.
Les algorithmes de base du graphisme
 Les algorithmes de base du graphisme Table des matières 1 Traçage 2 1.1 Segments de droites......................... 2 1.1.1 Algorithmes simples.................... 3 1.1.2 Algorithmes de Bresenham (1965).............
Les algorithmes de base du graphisme Table des matières 1 Traçage 2 1.1 Segments de droites......................... 2 1.1.1 Algorithmes simples.................... 3 1.1.2 Algorithmes de Bresenham (1965).............
SOCLE COMMUN - La Compétence 3 Les principaux éléments de mathématiques et la culture scientifique et technologique
 SOCLE COMMUN - La Compétence 3 Les principaux éléments de mathématiques et la culture scientifique et technologique DOMAINE P3.C3.D1. Pratiquer une démarche scientifique et technologique, résoudre des
SOCLE COMMUN - La Compétence 3 Les principaux éléments de mathématiques et la culture scientifique et technologique DOMAINE P3.C3.D1. Pratiquer une démarche scientifique et technologique, résoudre des
Groupe symétrique. Chapitre II. 1 Définitions et généralités
 Chapitre II Groupe symétrique 1 Définitions et généralités Définition. Soient n et X l ensemble 1,..., n. On appelle permutation de X toute application bijective f : X X. On note S n l ensemble des permutations
Chapitre II Groupe symétrique 1 Définitions et généralités Définition. Soient n et X l ensemble 1,..., n. On appelle permutation de X toute application bijective f : X X. On note S n l ensemble des permutations
Chapitre 2. Eléments pour comprendre un énoncé
 Chapitre 2 Eléments pour comprendre un énoncé Ce chapitre est consacré à la compréhension d un énoncé. Pour démontrer un énoncé donné, il faut se reporter au chapitre suivant. Les tables de vérité données
Chapitre 2 Eléments pour comprendre un énoncé Ce chapitre est consacré à la compréhension d un énoncé. Pour démontrer un énoncé donné, il faut se reporter au chapitre suivant. Les tables de vérité données
Probabilités et Statistiques. Feuille 2 : variables aléatoires discrètes
 IUT HSE Probabilités et Statistiques Feuille : variables aléatoires discrètes 1 Exercices Dénombrements Exercice 1. On souhaite ranger sur une étagère 4 livres de mathématiques (distincts), 6 livres de
IUT HSE Probabilités et Statistiques Feuille : variables aléatoires discrètes 1 Exercices Dénombrements Exercice 1. On souhaite ranger sur une étagère 4 livres de mathématiques (distincts), 6 livres de
