POSITIONING AND CONTROL OF MOBILE ROBOTS
|
|
|
- Jean-Michel Roberge
- il y a 9 ans
- Total affichages :
Transcription
1 Laboratoire d Automatique POSITIONING AND CONTROL OF MOBILE ROBOTS Projet de Semestre / Eté Année académique 2004 / 2005 Jean Martial Miamo Nguekam Etudiant en 4 ième année Electricité Dr. Denis Gillet Levente Bodizs EPFL - LA
2 TABLE DES MATIERES 1 INTRODUCTION MODÉLISATION DU ROBOT KHEPERA LE SYSTÈME DE MESURE LE TRAITEMENT D IMAGE Matrice de pixels couleur et matrice de pixels noirs et blancs Détermination du centre de gravité des deux robots Séparation de l image Calcul des positions de chaque robot dans le repère associé à chaque image Cas de la coupe verticale Cas de la coupe horizontale Test du programme de traitement d image LE FILTRE DE KALMAN ETENDU La prédiction La correction des mesures Simulation du filtre de Kalman sous Matlab et Labview Implantation du filtre de Kalman en temps réel LA COMMANDE PRÉDICTIVE Schéma de commande Génération de la trajectoire de référence Les paramètres de la commande prédictive implantée TESTS EXPÉRIMENTAUX Test de convergence du filtre de Kalman Etendu Expérience Expérience Effet du filtre de Kalman suite aux perturbations Expérience 1 : 4 perturbations Expérience 2 : 3 perturbations Trajectoire du maître et de l esclave Maître immobile
3 Expérience Expérience Maître mobile Expérience Expérience Expérience CONCLUSION...34 ANNEXE A...35 ANNEXE B
4 1 Introduction Le robot Khepera est un véhicule autonome muni de deux roues qui a été développé par le Laboratoire des systèmes autonomes de l EPFL. Il a fait l objet de plusieurs projets menés au sein du Laboratoire d automatique de l EPFL. Contrairement aux études précédentes, notre étude porte sur deux robots. L objectif était d implémenter en temps réel sur un Robot «esclave ou prédateur» une technique de contrôle commande qui lui permet de rattraper un deuxième robot «maître» qui se déplace selon une trajectoire aléatoire sur une plate-forme. Le système de mesure que nous utilisons est celui proposé par Herrera [1]. Il s agit principalement d une camera digitale. L image qu elle fournit est traitée par un programme de traitement d image développé sous LabView. Le résultat dudit traitement est l obtention en temps réel de la position du robot mobile sur la plate-forme. Les positions mesurées sont entachées d erreurs. C est la raison pour laquelle nous avons choisi de les filtrer avant de les utiliser dans l algorithme de commande : pour cela, le filtre de Kalman est utilisé. Les raisons de ce choix seront exposées dans les paragraphes suivants. Pour commander le robot «esclave», la commande Prédictive a été utilisée. Dans la suite, nous consacrerons un bref paragraphe à la modélisation du robot Khepera. Le système de mesure et le programme de traitement d image pour deux robots mobiles feront l objet d un autre paragraphe détaillé. Ensuite, il sera question du Filtre de Kalman Etendu puis l implémentation de la commande prédictive. 4
5 2 Modélisation du robot Khepera La modélisation d un système dynamique est une étape très importante pour la conception d une commande telle que la commande prédictive. La qualité d un régulateur dépend fortement de celle du modèle du système dynamique qu on veut commander. Herrera [1] et Niederberger [2] ont proposé deux modèles pour le robot Khepera. Seul celui basé sur une trajectoire rectiligne et qui considère le robot comme un point a été retenu. Il est causal et non linéaire : x y θ h 2 h 2 h L ( k + 1) = x( k) + ( V ( k) + V ( k) ) cosθ ( k) ( k + 1) = y( k) + ( V ( k) + V ( k) ) sinθ ( k) ( k + 1) = θ ( k) + ( V ( k) V ( k) ) r r r l l l Ce set d équations montre qu il s agit d un système multivariable qui possède deux entrées V r ( k) et V l ( k) qui sont respectivement les signaux qui permettent d alimenter les roues droite et gauche du robot. Il y a trois sorties qui sont x ( k), y ( k), θ ( k) qui sont respectivement l abscisse, l ordonnée et la position angulaire du robot dans le repère définit comme sur la figure ci-dessous : 5
6 h est la période d échantillonnage et L est la distance entre les deux roues du robots. Le modèle d état du robot est donné ci-dessous : Le programme et les résultats de simulation dans Matlab et Labview du modèle se trouvent en annexe A. Le programme Labview qui permet de simuler le modèle doit être utilisé avec la version 6.1 de Matlab. Avant de l exécuter, il faut au préalable ouvrir Matlab 6.1 6
7 3 Le système de mesure : camera digitale 2 : plate-forme 3 : robot Khepera Sur la plate-forme de couleur noire, on peut voir deux robots : l esclave et le maître. Vu de dessus, le maître est de couleur blanche alors que l esclave l est aussi mais avec deux cercles remplis en noire qui permettent au programme de traitement d image de calculer sa position angulaire. La camera digitale fournit une image en couleur qui sera ensuite traitée par le programme de traitement d image afin de déterminer les trois états de chaque robot. 7
8 4 Le Traitement d image Nous nous sommes largement inspirés du programme de traitement d image développé par Herrera [1] qui permet de calculer les trois états x, y, θ d un seul robot. Le programme que nous avons développé tient compte de la présence de deux robots sur la plate forme. La procédure de traitement est divisée en plusieurs étapes. 4 1 Matrice de pixels couleur et matrice de pixels noirs et blancs Tout d abord, l image en couleur acquise est transformée en une matrice de pixels dont chacun est codé sur 24 bits. Cette matrice est ensuite transformée en une autre matrice toujours codée sur 24 bits mais dont les couleurs sont noires ou blanches. Cette matrice donne une image qui a l apparence suivante : Robot «esclave» Robot «maître» 4 2 Détermination du centre de gravité des deux robots Dans l optique de diviser l image ci-dessus en deux images distinctes, l abscisse et l ordonnée du centre de gravité des deux robots sont calculées. 8
9 4 3 Séparation de l image Selon le résultat d un critère qui porte sur la position d un robot par rapport à l autre, une coupe verticale ou horizontale de l image est effectuée. Si les deux robots ont par exemple la position suivante, alors une coupe verticale est faite : Une coupe horizontale est faite dans le cas suivant : 9
10 4 4 Calcul des positions de chaque robot dans le repère associé à chaque image Après avoir effectué les coupes, chaque robot se trouve dans un système d axe dans lequel on déterminera sa position. Pour le robot «esclave», les trois états seront calculés alors seuls l abscisse et l ordonnée du robot «maître»seront estimées Cas de la coupe verticale Calcul de x 1, y1, θ1 10
11 Calcul de x, y Cas de la coupe horizontale Calcul de x 1, y1, θ1 11
12 Calcul de x, y Test du programme de traitement d image L acquisition d image et son traitement prennent un temps relativement grand. En ce qui concerne les résultats fournis par le programme, ils sont «noyés» dans du bruit. C est la raison pour laquelle nous devons les filtrer. Le filtre de Kalman set bien adapté pour ce type d expérience. 12
13 5 Le filtre de Kalman Etendu Le filtre de Kalman a été développé dans les années 1960 par R.E Kalman. Il est constitué d un set d équations discrètes qui permettent d estimer les états d un système par rapport aux données mesurées. Etant donné que le modèle du système est non linéaire, nous avons choisi le filtre de Kalman Etendu. L exécution du filtre de Kalman Etendu se fait en deux étapes et d une façon cyclique. 5 1 La prédiction Connaissant le modèle d état du système, on estime l état a priori du système. 13
14 Il faut initialiser l exécution avec le vecteur d état nul c'est-à-dire x = 0 x = y = 0. 0 θ = 0 Le vecteur déplace. k 1 v r u = k 1 est fourni en temps réel par le robot «esclave» qui se k 1 vl Pour calculer dimension 3. P, il faut initialiser P 1 par K k 1,0, 0 P 0 = 0,1, 0 la matrice identité de 0,0,1 f X h h x + cosθ * v r + * cosθ * v l 2 2 h h = y + * sinθ * v r + * sinθ * v 2 2 h h θ + * v r - * v l L L x = y θ l v u = v r l A k 1,0, -1/2 * h * sin( θ (k)) * v r (k) -1/2 * h * sin( θ (k)) * v l (k) = 0,1, 1/2 * h * cos( θ (k)) * v r (k) +1/2 * h * cos( θ (k)) * v l (k) = 0,0,1 jacobien ( f, X ) W k 1,0, 0 = 0,1, 0 0,0,1 14
15 15 = ,0, 0, 0, 0,0, σ σ σ k Q Matrice constante obtenue par tuning qui modélise le bruit du système. 5 2 La correction des mesures On calcule le gain de Kalman k K par l expression suivante : = 0,0,1 0 0,1, 0 1,0, k H = 0,0,1 0 0,1, 0 1,0, k V = 2 2 y 2 x 0,0, 0, 0, 0,0, σ θ σ σ k R Matrice constante qui modélise le bruit sur les mesures. Mise à jour de l état du système sur la base des mesures = mesurée mesurée mesurée k y x z θ : Mise à jour de l erreur de covariance : = 0,0,1 0 0,1, 0 1,0, I
16 5 3 Simulation du filtre de Kalman sous Matlab et Labview Nous avons simulé le modèle avec un bruit blanc ce qui caractérise les mesures. Ensuite l algorithme du filtre de Kalman Etendu a été utilisé pour filtrer ces mesures. Le programme et les résultats de la simulation se trouvent en annexe B. Avant d exécuter le programme sous Labview, il faut ouvrir Matlab
17 Face avant 5 4 Implantation du filtre de Kalman en temps réel Après avoir obtenu des bons résultats lors de la simulation, nous avons implanté filtre de Kalman Etendu afin qu il puisse marché en temps réel. Nous avons remarqué deux problèmes : L algorithme utilise comme état initial le vecteur x = 0 = y = 0. Avant la 0 θ = 0 mise en marche du robot, il occupe une position qui différente de celle du vecteur initial. Il faut donc attendre un certain temps pour que le résultat converge vers la vraie position du robot sur la plate-forme avant de mettre le robot en marche. Sinon les résultats seront faussés. La période d échantillonnage utilisée pour la simulation n est identique à celle de Labview. Nous l avons d abord estimée. Elle est environ 140ms. x 17
18 Pour vérifier la qualité du filtre implanté, nous avons réalisé deux expériences : le robot «esclave» décrivant une trajectoire rectiligne le robot «esclave» décrivant une trajectoire circulaire Les résultats de ces deux expériences se trouvent en annexe B. 18
19 6 La commande prédictive Pour que le robot «esclave» puisse rattraper le robot «maître», nous avons opté d utiliser la commande prédictive. Ce choix a été motivé par les études précédemment faites par Niederberger [2] et Herrera [1]. En fait, la commande prédictive consiste à trouver sur un horizon donné, la commande à appliquer sur un système et qui minimiserait une fonction de coût. Cette dernière dépend de la trajectoire de référence r ( k), de l état du système x ( k) et de la grandeur de réglage ( k) u. La fonction de coût que nous avons choisie est de la forme suivante : Connaissant le modèle du système, le prédicteur est : 19
20 La commande qui minimise la fonction de coût est la suivante : Avec : 6 1 Schéma de commande Choix de la trajectoire du «Maître» Position des deux robots Camera -Traitement d image -Implantation du filtre de Kalman -Commande prédictive Commande du robot «Maître» Commande du robot «Esclave» Le PC1 permet de commander le robot «maître» afin qu il puisse se déplacer sur la plate-forme en décrivant une trajectoire aléatoire. La camera est relié au PC2.Sur ce dernier, est installé le programme de traitement d image qui fournit en temps réel les positions des deux robots mobiles. Le filtre de Kalman Etendu y est aussi utilisé pour filtrer les mesures de position du robot «esclave». Enfin la commande prédictive y est aussi implantée pour le robot «esclave». 20
21 6 2 Génération de la trajectoire de référence Pour utiliser la commande prédictive, il faut connaître la trajectoire de référence. Etant donné que les deux robots sont mobiles, cette trajectoire doit être générée après chaque période d échantillonnage. A cause de cette trajectoire variable d une période d échantillonnage à l autre, on pourrait dire qu il ne s agit plus de la commande prédictive classique. La génération de cette trajectoire se fait en plusieurs étapes : Grâce à la camera digitale et au programme de traitement d image, les positions des deux robots sont utilisées pour estimer en temps réel la distance qui les sépare. Ensuite on choisit la vitesse à laquelle le robot «esclave» doit se déplacer pour rattraper le robot «maître». Connaissant la distance entre les deux robots et la vitesse de déplacement, on peut estimer le temps de parcours nécessaire au robot «esclave» pour rattraper le robot «maître». Ce temps de parcours est ensuite converti en nombre d échantillons. Par interpolation linéaire, on génère une trajectoire partant de la position de l esclave à celle du maître. θ Esclave 21
22 6 3 Les paramètres de la commande prédictive implantée Nous avons choisi un horizon de control N = 5 et un horizon de prédiction N = 6. Les matrices Q et Λ sont des matrices identité. p c 22
23 7 Tests expérimentaux L esclave doit rattraper le maître quelques soit la trajectoire que ce dernier décrit. L esclave ne doit pas percuter le maître. Le robot «esclave» s arrête lorsque la distance qui sépare les centres de gravité des deux robots est égale à 5 fois L (distance qui sépare les deux roues d un robot). 7 1 Test de convergence du filtre de Kalman Etendu L algorithme du filtre de Kalman Etendu que nous avons implanté a été initialisé avec le vecteur ( x = 0, y = 0, θ = 0). Expérimentalement, le robot «esclave» peut être initialement positionné en n importe quel point sur la plate-forme. C est la raison pour laquelle avant de démarrer l expérience, on laisse d abord quelques secondes afin que le filtre de Kalman converge vers la vraie position initiale du robot Expérience 1 Trajectoire d un robot 23
24 Angle θ Expérience 2 Trajectoire d un robot 24
25 Angle θ 7 2 Effet du filtre de Kalman suite aux perturbations Expérience 1 : 4 perturbations Trajectoire d un robot 25
26 Angle θ Expérience 2 : 3 perturbations Trajectoire d un robot 26
27 Angle θ L expérience 2 a été réalisée avec les valeurs des matrices de covariance différentes de celles de l expérience 1: Pour la seconde expérience, les éléments diagonaux de la matrice Q sont 10 fois inférieures à celle de la première expérience. Le filtre de Kalman de la première expérience est moins robuste aux perturbations. Alors qu il atténue quasiment bien les perturbations lors de la seconde expérience. 27
28 7 3 Trajectoire du maître et de l esclave Maître immobile Expérience 1 Trajectoire 28
29 Angle θ Expérience 2 Trajectoire 29
30 Angle θ Maître mobile Expérience 1 Trajectoire 30
31 Angle θ Lorsqu on observe la variation de l angle θ tout au long de cette expérience, on se rend compte que lorsque l esclave est proche du maître, il varie brusquement. Ceci est dû au programme de traitement d image. 31
32 Expérience 2 Trajectoire Angle θ 32
33 Expérience 3 Trajectoire Angle θ 33
34 Pour les deux expériences précédentes, l esclave percute le maître lorsqu il le rattrape. La représentation dans Matlab des trajectoires et de la position finale des deux robots montre le contraire. Nous pensons que ceci est à la camera qui filme les deux robots sous un angle. 8 Conclusion Malgré plusieurs difficultés rencontrées lors de la phase d implantation du filtre de Kalman et de la commande prédictive non classique, on peut dire que le cahier de charge a été quasiment respecté. Il reste encore des quelques améliorations à apportées, notamment sur l'amélioration du temps de traitement des différents algorithmes qui est encore relativement élevé et le programme de traitement d image. Nous avons aussi bénéficié d une solide base théorique réalisée par Niederberger et Herrera. 34
35 ANNEXE A A1 : Programme Matlab de calcul du Jacobien A2 : Programme Matlab pour le modèle A3 : Programme de simulation du modèle 35
36 A4 : résultat de la simulation A5 : résultat simulation dans Labview 36
37 ANNEXE B B1 : Programme qui simule le modèle bruité B2 : Simulation du filtre de Kalman Etendu 37
38 B3 : Résultat de la simulation du modèle bruité 38
39 B4 : Résultat de la simulation du filtre de Kalman Etendu B5 : Résultat sous Labview : modèle bruité 39
40 B6 : Résultat sous Labview : sortie filtrée B7 : Simulation en temps réel : trajectoire rectiligne 40
41 B8 : Simulation en temps réel : angle θ pour trajectoire rectiligne B9 : Simulation en temps réel : trajectoire circulaire 41
42 B10 : Simulation en temps réel : angle θ pour trajectoire circulaire 42
43 BIBLIOGRAPHIE: [1] Trajectory tracking trough predictive control: application to the Khepera robot, Juan Herrera, Diploma thesis, 1999 [2] Predictive control Design for a Khepera robot: Principles, Simulations and Real-time Implementation, André S.P Niederberger, Diploma thesis, February 2002 [3] Position estimation and control of an autonomous vehicle, Joana Maria Comas Marti, Diploma thesis, June 2005 [4] An introduction to the Kalman filter, Greg Welch and Gary Bishop, University of North California at Chapel Hill, April
I Stabilité, Commandabilité et Observabilité 11. 1 Introduction 13 1.1 Un exemple emprunté à la robotique... 13 1.2 Le plan... 18 1.3 Problème...
 TABLE DES MATIÈRES 5 Table des matières I Stabilité, Commandabilité et Observabilité 11 1 Introduction 13 1.1 Un exemple emprunté à la robotique................... 13 1.2 Le plan...................................
TABLE DES MATIÈRES 5 Table des matières I Stabilité, Commandabilité et Observabilité 11 1 Introduction 13 1.1 Un exemple emprunté à la robotique................... 13 1.2 Le plan...................................
Traitement bas-niveau
 Plan Introduction L approche contour (frontière) Introduction Objectifs Les traitements ont pour but d extraire l information utile et pertinente contenue dans l image en regard de l application considérée.
Plan Introduction L approche contour (frontière) Introduction Objectifs Les traitements ont pour but d extraire l information utile et pertinente contenue dans l image en regard de l application considérée.
MOTORISATION DIRECTDRIVE POUR NOS TELESCOPES. Par C.CAVADORE ALCOR-SYSTEM WETAL 2013 10 Nov
 1 MOTORISATION DIRECTDRIVE POUR NOS TELESCOPES Par C.CAVADORE ALCOR-SYSTEM WETAL 2013 10 Nov Pourquoi motoriser un télescope? 2 Pour compenser le mouvement de la terre (15 /h) Observation visuelle Les
1 MOTORISATION DIRECTDRIVE POUR NOS TELESCOPES Par C.CAVADORE ALCOR-SYSTEM WETAL 2013 10 Nov Pourquoi motoriser un télescope? 2 Pour compenser le mouvement de la terre (15 /h) Observation visuelle Les
 Utilisation d informations visuelles dynamiques en asservissement visuel Armel Crétual IRISA, projet TEMIS puis VISTA L asservissement visuel géométrique Principe : Réalisation d une tâche robotique par
Utilisation d informations visuelles dynamiques en asservissement visuel Armel Crétual IRISA, projet TEMIS puis VISTA L asservissement visuel géométrique Principe : Réalisation d une tâche robotique par
C est un mouvement plan dont la trajectoire est un cercle ou une portion de cercle. Le module du vecteur position OM est constant et il est égal au
 1 2 C est un mouvement plan dont la trajectoire est un cercle ou une portion de cercle. Le module du vecteur position est constant et il est égal au rayon du cercle. = 3 A- ouvement circulaire non uniforme
1 2 C est un mouvement plan dont la trajectoire est un cercle ou une portion de cercle. Le module du vecteur position est constant et il est égal au rayon du cercle. = 3 A- ouvement circulaire non uniforme
Opérations de base sur ImageJ
 Opérations de base sur ImageJ TPs d hydrodynamique de l ESPCI, J. Bico, M. Reyssat, M. Fermigier ImageJ est un logiciel libre, qui fonctionne aussi bien sous plate-forme Windows, Mac ou Linux. Initialement
Opérations de base sur ImageJ TPs d hydrodynamique de l ESPCI, J. Bico, M. Reyssat, M. Fermigier ImageJ est un logiciel libre, qui fonctionne aussi bien sous plate-forme Windows, Mac ou Linux. Initialement
Formation des enseignants. Le tensiomètre. Objet technique modélisable issu de l environnement des élèves
 Le tensiomètre Objet technique modélisable issu de l environnement des élèves Un peu d'histoire C'est en 1628 que W. Harvey découvrit la circulation du sang. C'est pourtant seulement en 1730 que la pression
Le tensiomètre Objet technique modélisable issu de l environnement des élèves Un peu d'histoire C'est en 1628 que W. Harvey découvrit la circulation du sang. C'est pourtant seulement en 1730 que la pression
Voyez la réponse à cette question dans ce chapitre. www.hometownroofingcontractors.com/blog/9-reasons-diy-rednecks-should-never-fix-their-own-roof
 Une échelle est appuyée sur un mur. S il n y a que la friction statique avec le sol, quel est l angle minimum possible entre le sol et l échelle pour que l échelle ne glisse pas et tombe au sol? www.hometownroofingcontractors.com/blog/9-reasons-diy-rednecks-should-never-fix-their-own-roof
Une échelle est appuyée sur un mur. S il n y a que la friction statique avec le sol, quel est l angle minimum possible entre le sol et l échelle pour que l échelle ne glisse pas et tombe au sol? www.hometownroofingcontractors.com/blog/9-reasons-diy-rednecks-should-never-fix-their-own-roof
PRECAUTIONS DESCRIPTION DU PRODUIT
 Vous venez d acquérir un produit de la marque Essentiel b et nous vous en remercions. Nous apportons un soin particulier au design, à l'ergonomie et à la simplicité d'usage de nos produits. Nous espérons
Vous venez d acquérir un produit de la marque Essentiel b et nous vous en remercions. Nous apportons un soin particulier au design, à l'ergonomie et à la simplicité d'usage de nos produits. Nous espérons
Mathématique et Automatique : de la boucle ouverte à la boucle fermée. Maïtine bergounioux Laboratoire MAPMO - UMR 6628 Université d'orléans
 Mathématique et Automatique : de la boucle ouverte à la boucle fermée Maïtine bergounioux Laboratoire MAPMO - UMR 6628 Université d'orléans [email protected] Plan 1. Un peu de
Mathématique et Automatique : de la boucle ouverte à la boucle fermée Maïtine bergounioux Laboratoire MAPMO - UMR 6628 Université d'orléans [email protected] Plan 1. Un peu de
Projet de traitement d'image - SI 381 reconstitution 3D d'intérieur à partir de photographies
 Projet de traitement d'image - SI 381 reconstitution 3D d'intérieur à partir de photographies Régis Boulet Charlie Demené Alexis Guyot Balthazar Neveu Guillaume Tartavel Sommaire Sommaire... 1 Structure
Projet de traitement d'image - SI 381 reconstitution 3D d'intérieur à partir de photographies Régis Boulet Charlie Demené Alexis Guyot Balthazar Neveu Guillaume Tartavel Sommaire Sommaire... 1 Structure
Continuité et dérivabilité d une fonction
 DERNIÈRE IMPRESSIN LE 7 novembre 014 à 10:3 Continuité et dérivabilité d une fonction Table des matières 1 Continuité d une fonction 1.1 Limite finie en un point.......................... 1. Continuité
DERNIÈRE IMPRESSIN LE 7 novembre 014 à 10:3 Continuité et dérivabilité d une fonction Table des matières 1 Continuité d une fonction 1.1 Limite finie en un point.......................... 1. Continuité
Projet Matlab : un logiciel de cryptage
 Projet Matlab : un logiciel de cryptage La stéganographie (du grec steganos : couvert et graphein : écriture) consiste à dissimuler une information au sein d'une autre à caractère anodin, de sorte que
Projet Matlab : un logiciel de cryptage La stéganographie (du grec steganos : couvert et graphein : écriture) consiste à dissimuler une information au sein d'une autre à caractère anodin, de sorte que
Intérêt du découpage en sous-bandes pour l analyse spectrale
 Intérêt du découpage en sous-bandes pour l analyse spectrale David BONACCI Institut National Polytechnique de Toulouse (INP) École Nationale Supérieure d Électrotechnique, d Électronique, d Informatique,
Intérêt du découpage en sous-bandes pour l analyse spectrale David BONACCI Institut National Polytechnique de Toulouse (INP) École Nationale Supérieure d Électrotechnique, d Électronique, d Informatique,
Vision industrielle et télédétection - Détection d ellipses. Guillaume Martinez 17 décembre 2007
 Vision industrielle et télédétection - Détection d ellipses Guillaume Martinez 17 décembre 2007 1 Table des matières 1 Le projet 3 1.1 Objectif................................ 3 1.2 Les choix techniques.........................
Vision industrielle et télédétection - Détection d ellipses Guillaume Martinez 17 décembre 2007 1 Table des matières 1 Le projet 3 1.1 Objectif................................ 3 1.2 Les choix techniques.........................
BeSpoon et l homme Connecté
 BeSpoon et l homme Connecté Paris 25 et 26 Mars BeSpoon est une société «Fabless» qui a développé en collaboration avec le CEA-Leti un composant IR-UWB (Impulse Radio Ultra Wide Band) dédié à la localisation
BeSpoon et l homme Connecté Paris 25 et 26 Mars BeSpoon est une société «Fabless» qui a développé en collaboration avec le CEA-Leti un composant IR-UWB (Impulse Radio Ultra Wide Band) dédié à la localisation
Algorithmes pour la planification de mouvements en robotique non-holonome
 Algorithmes pour la planification de mouvements en robotique non-holonome Frédéric Jean Unité de Mathématiques Appliquées ENSTA Le 02 février 2006 Outline 1 2 3 Modélisation Géométrique d un Robot Robot
Algorithmes pour la planification de mouvements en robotique non-holonome Frédéric Jean Unité de Mathématiques Appliquées ENSTA Le 02 février 2006 Outline 1 2 3 Modélisation Géométrique d un Robot Robot
Ensemble léger de prise de photo sous UV-A Tam Photo Kit n 1 pour appareil photo compact
 Ensemble léger de prise de photo sous UV-A Tam Photo Kit n 1 pour appareil photo compact Phone +33 (0)130 808 182 - Fax. +33 (0)130 808 199 /15 rue des Frères Lumière - ZI des Ebisoires BP136-78374 PLAISIR
Ensemble léger de prise de photo sous UV-A Tam Photo Kit n 1 pour appareil photo compact Phone +33 (0)130 808 182 - Fax. +33 (0)130 808 199 /15 rue des Frères Lumière - ZI des Ebisoires BP136-78374 PLAISIR
Repérage d un point - Vitesse et
 PSI - écanique I - Repérage d un point - Vitesse et accélération page 1/6 Repérage d un point - Vitesse et accélération Table des matières 1 Espace et temps - Référentiel d observation 1 2 Coordonnées
PSI - écanique I - Repérage d un point - Vitesse et accélération page 1/6 Repérage d un point - Vitesse et accélération Table des matières 1 Espace et temps - Référentiel d observation 1 2 Coordonnées
Création d articles sur le site web du GSP
 Création d articles sur le site web du GSP Mode d emploi pour les membres du groupe spéléo Porrentruy. www.speleoporrentruy.ch 1 Article avec photo et document pdf sur le site du groupe spéléo Porrentruy
Création d articles sur le site web du GSP Mode d emploi pour les membres du groupe spéléo Porrentruy. www.speleoporrentruy.ch 1 Article avec photo et document pdf sur le site du groupe spéléo Porrentruy
Cours IV Mise en orbite
 Introduction au vol spatial Cours IV Mise en orbite If you don t know where you re going, you ll probably end up somewhere else. Yogi Berra, NY Yankees catcher v1.2.8 by-sa Olivier Cleynen Introduction
Introduction au vol spatial Cours IV Mise en orbite If you don t know where you re going, you ll probably end up somewhere else. Yogi Berra, NY Yankees catcher v1.2.8 by-sa Olivier Cleynen Introduction
Vidéosurveillance. Collection 2012 (m-à-j 06/2012) Gamme IP - Sans fil - Filaires - Caméras factices - Accessoires
 Vidéosurveillance Collection 2012 (m-à-j 06/2012) Gamme IP - Sans fil - Filaires - Caméras factices - Accessoires Gamme IP : Surveillance à distance via Internet KIT IP 4 CAMÉRAS AVEC DISQUE DUR INTÉGRÉ
Vidéosurveillance Collection 2012 (m-à-j 06/2012) Gamme IP - Sans fil - Filaires - Caméras factices - Accessoires Gamme IP : Surveillance à distance via Internet KIT IP 4 CAMÉRAS AVEC DISQUE DUR INTÉGRÉ
Sujet proposé par Yves M. LEROY. Cet examen se compose d un exercice et de deux problèmes. Ces trois parties sont indépendantes.
 Promotion X 004 COURS D ANALYSE DES STRUCTURES MÉCANIQUES PAR LA MÉTHODE DES ELEMENTS FINIS (MEC 568) contrôle non classant (7 mars 007, heures) Documents autorisés : polycopié ; documents et notes de
Promotion X 004 COURS D ANALYSE DES STRUCTURES MÉCANIQUES PAR LA MÉTHODE DES ELEMENTS FINIS (MEC 568) contrôle non classant (7 mars 007, heures) Documents autorisés : polycopié ; documents et notes de
Limites finies en un point
 8 Limites finies en un point Pour ce chapitre, sauf précision contraire, I désigne une partie non vide de R et f une fonction définie sur I et à valeurs réelles ou complees. Là encore, les fonctions usuelles,
8 Limites finies en un point Pour ce chapitre, sauf précision contraire, I désigne une partie non vide de R et f une fonction définie sur I et à valeurs réelles ou complees. Là encore, les fonctions usuelles,
Scanner laser HDS7000 Ultra rapide, à portée étendue
 > 1 million de points / sec Scanner laser HDS7000 Ultra rapide, à portée étendue > 180 m de portée HDS7000 Scanner laser ultra rapide pour les professionnels exigeants Les scanners à mesure de phase sont
> 1 million de points / sec Scanner laser HDS7000 Ultra rapide, à portée étendue > 180 m de portée HDS7000 Scanner laser ultra rapide pour les professionnels exigeants Les scanners à mesure de phase sont
Projet Robot Centaure
 Projet Robot Centaure Année 2013-2014 IMA4 S8 Étudiants : Clément TACHÉ Liying WANG Enseignants : Robert Litwak Xiavier Redon Table des matières : Remerciements Introduction Présentation et état des lieux
Projet Robot Centaure Année 2013-2014 IMA4 S8 Étudiants : Clément TACHÉ Liying WANG Enseignants : Robert Litwak Xiavier Redon Table des matières : Remerciements Introduction Présentation et état des lieux
Expérience 3 Formats de signalisation binaire
 Expérience 3 Formats de signalisation binaire Introduction Procédures Effectuez les commandes suivantes: >> xhost nat >> rlogin nat >> setenv DISPLAY machine:0 >> setenv MATLABPATH /gel/usr/telecom/comm_tbx
Expérience 3 Formats de signalisation binaire Introduction Procédures Effectuez les commandes suivantes: >> xhost nat >> rlogin nat >> setenv DISPLAY machine:0 >> setenv MATLABPATH /gel/usr/telecom/comm_tbx
Baccalauréat L spécialité, Métropole et Réunion, 19 juin 2009 Corrigé.
 Baccalauréat L spécialité, Métropole et Réunion, 19 juin 2009 Corrigé. L usage d une calculatrice est autorisé Durée : 3heures Deux annexes sont à rendre avec la copie. Exercice 1 5 points 1_ Soit f la
Baccalauréat L spécialité, Métropole et Réunion, 19 juin 2009 Corrigé. L usage d une calculatrice est autorisé Durée : 3heures Deux annexes sont à rendre avec la copie. Exercice 1 5 points 1_ Soit f la
intelligence artificielle et cognitique"
 Dialogue on Education, 11h-11h10 Course overview on "Automatisation avancée, intelligence artificielle et cognitique" Prof. Dr. Jean-Daniel Dessimoz, MBA, HES-SO / HEIG-VD 11:00-11:10, 18 November 2014
Dialogue on Education, 11h-11h10 Course overview on "Automatisation avancée, intelligence artificielle et cognitique" Prof. Dr. Jean-Daniel Dessimoz, MBA, HES-SO / HEIG-VD 11:00-11:10, 18 November 2014
Station Totale Geomax Série Zoom30
 Station Totale Geomax Série Zoom30 GeoMax Profil de l entreprise GeoMax est une entreprise fort de solides positions sur L étroite collaboration qui présente à l international et le marché des technologies
Station Totale Geomax Série Zoom30 GeoMax Profil de l entreprise GeoMax est une entreprise fort de solides positions sur L étroite collaboration qui présente à l international et le marché des technologies
Master IMA - UMPC Paris 6 RDMM - Année 2009-2010 Fiche de TP
 Master IMA - UMPC Paris 6 RDMM - Année 2009-200 Fiche de TP Préliminaires. Récupérez l archive du logiciel de TP à partir du lien suivant : http://www.ensta.fr/~manzaner/cours/ima/tp2009.tar 2. Développez
Master IMA - UMPC Paris 6 RDMM - Année 2009-200 Fiche de TP Préliminaires. Récupérez l archive du logiciel de TP à partir du lien suivant : http://www.ensta.fr/~manzaner/cours/ima/tp2009.tar 2. Développez
G.P. DNS02 Septembre 2012. Réfraction...1 I.Préliminaires...1 II.Première partie...1 III.Deuxième partie...3. Réfraction
 DNS Sujet Réfraction...1 I.Préliminaires...1 II.Première partie...1 III.Deuxième partie...3 Réfraction I. Préliminaires 1. Rappeler la valeur et l'unité de la perméabilité magnétique du vide µ 0. Donner
DNS Sujet Réfraction...1 I.Préliminaires...1 II.Première partie...1 III.Deuxième partie...3 Réfraction I. Préliminaires 1. Rappeler la valeur et l'unité de la perméabilité magnétique du vide µ 0. Donner
Système à enseigner : Robot M.I.M.I. MultipodeIntelligent à Mobilité Interactive. Version 1.0
 Système à enseigner : Robot M.I.M.I. MultipodeIntelligent à Mobilité Interactive Sommaire - Le Robot M.I.M.I. (Multipode Intelligent à Mobilité Interactive) - Présentation du Système à Enseigner. - Composition
Système à enseigner : Robot M.I.M.I. MultipodeIntelligent à Mobilité Interactive Sommaire - Le Robot M.I.M.I. (Multipode Intelligent à Mobilité Interactive) - Présentation du Système à Enseigner. - Composition
FONTANOT CREE UNE GAMME D ESCALIERS IMAGINÉE POUR CEUX QUI AIMENT LE BRICOLAGE.
 STYLE FONTANOT CREE UNE GAMME D ESCALIERS IMAGINÉE POUR CEUX QUI AIMENT LE BRICOLAGE. DVD v i d e o ARKÈ: Créez votre escalier en une demi-journée! votre style Trouvez l escalier qui convient à votre
STYLE FONTANOT CREE UNE GAMME D ESCALIERS IMAGINÉE POUR CEUX QUI AIMENT LE BRICOLAGE. DVD v i d e o ARKÈ: Créez votre escalier en une demi-journée! votre style Trouvez l escalier qui convient à votre
Q6 : Comment calcule t-on l intensité sonore à partir du niveau d intensité?
 EXERCICE 1 : QUESTION DE COURS Q1 : Qu est ce qu une onde progressive? Q2 : Qu est ce qu une onde mécanique? Q3 : Qu elle est la condition pour qu une onde soit diffractée? Q4 : Quelles sont les différentes
EXERCICE 1 : QUESTION DE COURS Q1 : Qu est ce qu une onde progressive? Q2 : Qu est ce qu une onde mécanique? Q3 : Qu elle est la condition pour qu une onde soit diffractée? Q4 : Quelles sont les différentes
Intelligence artificielle et les défis en robotique mobile et autonome
 Intelligence artificielle et les défis en robotique mobile et autonome Éric Beaudry http://planiart.usherbrooke.ca/~eric/ Étudiant au doctorat en informatique Laboratoires Planiart et Laborius 13 février
Intelligence artificielle et les défis en robotique mobile et autonome Éric Beaudry http://planiart.usherbrooke.ca/~eric/ Étudiant au doctorat en informatique Laboratoires Planiart et Laborius 13 février
TP SIN Traitement d image
 TP SIN Traitement d image Pré requis (l élève doit savoir): - Utiliser un ordinateur Objectif terminale : L élève doit être capable de reconnaître un format d image et d expliquer les différents types
TP SIN Traitement d image Pré requis (l élève doit savoir): - Utiliser un ordinateur Objectif terminale : L élève doit être capable de reconnaître un format d image et d expliquer les différents types
2013 Pearson France Photoshop Elements 12 pour les photographes du numérique Loïc Olive
 améliorer les PhOtOs L amélioration d une photo passe quasiment toujours par les mêmes étapes. On commence par la redresser, puis on s attelle à corriger ses dominantes de couleurs et sa tonalité. Vient
améliorer les PhOtOs L amélioration d une photo passe quasiment toujours par les mêmes étapes. On commence par la redresser, puis on s attelle à corriger ses dominantes de couleurs et sa tonalité. Vient
SYSTÈME DE SURVEILLANCE VIDÉO À DISTANCE
 SYSTÈME DE SURVEILLANCE VIDÉO À DISTANCE 1 CATALOGUE 2015 SOMMAIRE en bref... 3 Les services gratuits de la version standard Family... 4 Les différentes versions : les services supplémentaires par version...
SYSTÈME DE SURVEILLANCE VIDÉO À DISTANCE 1 CATALOGUE 2015 SOMMAIRE en bref... 3 Les services gratuits de la version standard Family... 4 Les différentes versions : les services supplémentaires par version...
Structure du format BMP, sa lecture, sa construction et son écriture
 Structure du format BMP, sa lecture, sa construction et son écriture Claude Parisel Mars 2003 Table des matières : 1. Le choix du format 2. Commentaires sur les autres formats 3. Format BMP pour noir&blanc,
Structure du format BMP, sa lecture, sa construction et son écriture Claude Parisel Mars 2003 Table des matières : 1. Le choix du format 2. Commentaires sur les autres formats 3. Format BMP pour noir&blanc,
Conception Electronique (CEL) Prof. Maurizio Tognolini
 Conception Electronique (CEL) Prof. Maurizio Tognolini iai institut d Automatisation industrielle MTI/CEL 19/09/2010 v2.0 1 CEL semestre «automne» 2010-2011 Enseignement: cours et labo: (Chaque semaine)
Conception Electronique (CEL) Prof. Maurizio Tognolini iai institut d Automatisation industrielle MTI/CEL 19/09/2010 v2.0 1 CEL semestre «automne» 2010-2011 Enseignement: cours et labo: (Chaque semaine)
Commande Prédictive. J. P. Corriou. LSGC-ENSIC-CNRS, Nancy. e-mail : [email protected]
 Commande Prédictive J P Corriou LSGC-ENSIC-CNRS, Nancy e-mail : corriou@ensicinpl-nancyfr Ý Consigne Trajectoire de référence Ý Ö Réponse Ý Horizon de prédiction À Ô ¹ Ù ¹ Temps Entrée Ù Horizon de commande
Commande Prédictive J P Corriou LSGC-ENSIC-CNRS, Nancy e-mail : corriou@ensicinpl-nancyfr Ý Consigne Trajectoire de référence Ý Ö Réponse Ý Horizon de prédiction À Ô ¹ Ù ¹ Temps Entrée Ù Horizon de commande
Chapitre 2 : Caractéristiques du mouvement d un solide
 Chapitre 2 : Caractéristiques du mouvement d un solide I Rappels : Référentiel : Le mouvement d un corps est décris par rapport à un corps de référence et dépend du choix de ce corps. Ce corps de référence
Chapitre 2 : Caractéristiques du mouvement d un solide I Rappels : Référentiel : Le mouvement d un corps est décris par rapport à un corps de référence et dépend du choix de ce corps. Ce corps de référence
Bologne à l EPFL. Réforme de Bologne Implications pour l EPFL. Prof. Dominique Bonvin, Doyen Bachelor-Master
 Bologne à l EPFL Réforme de Bologne Implications pour l EPFL Prof. Dominique Bonvin, Doyen Bachelor-Master EPFL Quelques chiffres 6 600 Etudiants, 23% femmes, 38% étrangers, 109 nationalités 1 400 Doctorants
Bologne à l EPFL Réforme de Bologne Implications pour l EPFL Prof. Dominique Bonvin, Doyen Bachelor-Master EPFL Quelques chiffres 6 600 Etudiants, 23% femmes, 38% étrangers, 109 nationalités 1 400 Doctorants
BTS Groupement A. Mathématiques Session 2011. Spécialités CIRA, IRIS, Systèmes électroniques, TPIL
 BTS Groupement A Mathématiques Session 11 Exercice 1 : 1 points Spécialités CIRA, IRIS, Systèmes électroniques, TPIL On considère un circuit composé d une résistance et d un condensateur représenté par
BTS Groupement A Mathématiques Session 11 Exercice 1 : 1 points Spécialités CIRA, IRIS, Systèmes électroniques, TPIL On considère un circuit composé d une résistance et d un condensateur représenté par
Optimisation, traitement d image et éclipse de Soleil
 Kléber, PCSI1&3 014-015 I. Introduction 1/8 Optimisation, traitement d image et éclipse de Soleil Partie I Introduction Le 0 mars 015 a eu lieu en France une éclipse partielle de Soleil qu il était particulièrement
Kléber, PCSI1&3 014-015 I. Introduction 1/8 Optimisation, traitement d image et éclipse de Soleil Partie I Introduction Le 0 mars 015 a eu lieu en France une éclipse partielle de Soleil qu il était particulièrement
Projet de Traitement du Signal Segmentation d images SAR
 Projet de Traitement du Signal Segmentation d images SAR Introduction En analyse d images, la segmentation est une étape essentielle, préliminaire à des traitements de haut niveau tels que la classification,
Projet de Traitement du Signal Segmentation d images SAR Introduction En analyse d images, la segmentation est une étape essentielle, préliminaire à des traitements de haut niveau tels que la classification,
Salle de technologie
 Prénom : Nom : Classe : Date : Salle de technologie Séquence Le dessin technique Définition du dessin technique : Le dessin technique est un ensemble de règles pour représenter des objets ; ces règles
Prénom : Nom : Classe : Date : Salle de technologie Séquence Le dessin technique Définition du dessin technique : Le dessin technique est un ensemble de règles pour représenter des objets ; ces règles
Lightroom. Chambre noire numérique. Organisation. Lightroom Catalog.lrcat. Lightroom Catalog Previews.lrdata 2005, 2006, 2007
 N O E Lightroom S Organisation Lightroom permet d organiser nos photos, de «développer» nos négatifs numériques, aussi bien en RAW qu en format JPEG, de les imprimer, et d en faire des diaporamas ou des
N O E Lightroom S Organisation Lightroom permet d organiser nos photos, de «développer» nos négatifs numériques, aussi bien en RAW qu en format JPEG, de les imprimer, et d en faire des diaporamas ou des
FONCTIONS DE PLUSIEURS VARIABLES (Outils Mathématiques 4)
 FONCTIONS DE PLUSIEURS VARIABLES (Outils Mathématiques 4) Bernard Le Stum Université de Rennes 1 Version du 13 mars 2009 Table des matières 1 Fonctions partielles, courbes de niveau 1 2 Limites et continuité
FONCTIONS DE PLUSIEURS VARIABLES (Outils Mathématiques 4) Bernard Le Stum Université de Rennes 1 Version du 13 mars 2009 Table des matières 1 Fonctions partielles, courbes de niveau 1 2 Limites et continuité
Equipement. électronique
 MASTER ISIC Les générateurs de fonctions 1 1. Avant-propos C est avec l oscilloscope, le multimètre et l alimentation stabilisée, l appareil le plus répandu en laboratoire. BUT: Fournir des signau électriques
MASTER ISIC Les générateurs de fonctions 1 1. Avant-propos C est avec l oscilloscope, le multimètre et l alimentation stabilisée, l appareil le plus répandu en laboratoire. BUT: Fournir des signau électriques
Comment expliquer ce qu est la NANOTECHNOLOGIE
 Comment expliquer ce qu est la NANOTECHNOLOGIE Vous vous souvenez que tout est constitué d atomes, non? Une pierre, un stylo, un jeu vidéo, une télévision, un chien et vous également; tout est fait d atomes.
Comment expliquer ce qu est la NANOTECHNOLOGIE Vous vous souvenez que tout est constitué d atomes, non? Une pierre, un stylo, un jeu vidéo, une télévision, un chien et vous également; tout est fait d atomes.
NON-LINEARITE ET RESEAUX NEURONAUX
 NON-LINEARITE ET RESEAUX NEURONAUX Vêlayoudom MARIMOUTOU Laboratoire d Analyse et de Recherche Economiques Université de Bordeaux IV Avenue. Leon Duguit, 33608 PESSAC, France tel. 05 56 84 85 77 e-mail
NON-LINEARITE ET RESEAUX NEURONAUX Vêlayoudom MARIMOUTOU Laboratoire d Analyse et de Recherche Economiques Université de Bordeaux IV Avenue. Leon Duguit, 33608 PESSAC, France tel. 05 56 84 85 77 e-mail
Résolution d équations non linéaires
 Analyse Numérique Résolution d équations non linéaires Said EL HAJJI et Touria GHEMIRES Université Mohammed V - Agdal. Faculté des Sciences Département de Mathématiques. Laboratoire de Mathématiques, Informatique
Analyse Numérique Résolution d équations non linéaires Said EL HAJJI et Touria GHEMIRES Université Mohammed V - Agdal. Faculté des Sciences Département de Mathématiques. Laboratoire de Mathématiques, Informatique
Fonctions de deux variables. Mai 2011
 Fonctions de deux variables Dédou Mai 2011 D une à deux variables Les fonctions modèlisent de l information dépendant d un paramètre. On a aussi besoin de modéliser de l information dépendant de plusieurs
Fonctions de deux variables Dédou Mai 2011 D une à deux variables Les fonctions modèlisent de l information dépendant d un paramètre. On a aussi besoin de modéliser de l information dépendant de plusieurs
Concours de création
 Concours de création du visuel de la 6 e édition du Master U BNP PARIBAS DEMANDE INITIALE Le Comité Régional du Sport Universitaire de Haute-Normandie souhaite communiquer sur cet événement international
Concours de création du visuel de la 6 e édition du Master U BNP PARIBAS DEMANDE INITIALE Le Comité Régional du Sport Universitaire de Haute-Normandie souhaite communiquer sur cet événement international
Netbook Asus 1000H / Samsung NC10 et Ecran 3D ZALMAN
 Netbook Asus 1000H / Samsung NC10 et Ecran 3D ZALMAN Les Netbooks par Daniel Chailloux et Jacques Claverie Récemment de nouveaux ordinateurs portables ont vu le jour. Ils font partie de la famille des
Netbook Asus 1000H / Samsung NC10 et Ecran 3D ZALMAN Les Netbooks par Daniel Chailloux et Jacques Claverie Récemment de nouveaux ordinateurs portables ont vu le jour. Ils font partie de la famille des
BAMOSONIC IT. - Mesure de niveau -
 - Mesure de niveau - Le capteur de niveau F est destiné à la mesure de niveau de liquide sur des cuves de forme cylindrique ou rectangulaire avec possibilité d'un affichage en niveau, distance, volume
- Mesure de niveau - Le capteur de niveau F est destiné à la mesure de niveau de liquide sur des cuves de forme cylindrique ou rectangulaire avec possibilité d'un affichage en niveau, distance, volume
uc : Cas d utilisation Top-Chair [Utilisation normale] Fauteuil Top-Chair Déplacer le fauteuil sur tous chemins «include» «include» «extend»
![uc : Cas d utilisation Top-Chair [Utilisation normale] Fauteuil Top-Chair Déplacer le fauteuil sur tous chemins «include» «include» «extend» uc : Cas d utilisation Top-Chair [Utilisation normale] Fauteuil Top-Chair Déplacer le fauteuil sur tous chemins «include» «include» «extend»](/thumbs/18/800414.jpg) TopChair S c Première partie Présentation du système Plus d autonomie pour plus de liberté! TopChair S c offre aux personnes à mobilité réduite une nouvelle possibilité de se déplacer sans assistance à
TopChair S c Première partie Présentation du système Plus d autonomie pour plus de liberté! TopChair S c offre aux personnes à mobilité réduite une nouvelle possibilité de se déplacer sans assistance à
Programmes Prioritaires Nationaux : Fumées de soudage. Y. CAROMEL - Contrôleur de sécurité
 Programmes Prioritaires Nationaux : Fumées de soudage Y. CAROMEL - Contrôleur de sécurité Règles essentielles de ventilation appliquées aux activités de soudage Y. CAROMEL - Contrôleur de sécurité Règles
Programmes Prioritaires Nationaux : Fumées de soudage Y. CAROMEL - Contrôleur de sécurité Règles essentielles de ventilation appliquées aux activités de soudage Y. CAROMEL - Contrôleur de sécurité Règles
Exemple d application en CFD : Coefficient de traînée d un cylindre
 Exemple d application en CFD : Coefficient de traînée d un cylindre 1 Démarche générale Avec Gambit Création d une géométrie Maillage Définition des conditions aux limites Avec Fluent 3D Choix des équations
Exemple d application en CFD : Coefficient de traînée d un cylindre 1 Démarche générale Avec Gambit Création d une géométrie Maillage Définition des conditions aux limites Avec Fluent 3D Choix des équations
Mini_guide_Isis_v6.doc le 10/02/2005 Page 1/15
 1 Démarrer... 2 1.1 L écran Isis... 2 1.2 Les barres d outils... 3 1.2.1 Les outils d édition... 3 1.2.2 Les outils de sélection de mode... 4 1.2.3 Les outils d orientation... 4 2 Quelques actions... 5
1 Démarrer... 2 1.1 L écran Isis... 2 1.2 Les barres d outils... 3 1.2.1 Les outils d édition... 3 1.2.2 Les outils de sélection de mode... 4 1.2.3 Les outils d orientation... 4 2 Quelques actions... 5
ÉCOLE POLYTECHNIQUE DE MONTRÉAL. Département de Génie Électrique. La technologie de TEXAS INSTRUMENTS DSP pour le cours Analyse des Signaux ELE2700
 ÉCOLE POLYTECHNIQUE DE MONTRÉAL Département de Génie Électrique La technologie de TEXAS INSTRUMENTS DSP pour le cours Analyse des Signaux ELE2700 M. Corinthios et Zaher Dannawi 29 août 2007 2 Tables des
ÉCOLE POLYTECHNIQUE DE MONTRÉAL Département de Génie Électrique La technologie de TEXAS INSTRUMENTS DSP pour le cours Analyse des Signaux ELE2700 M. Corinthios et Zaher Dannawi 29 août 2007 2 Tables des
Avira Version 2012 (Windows)
 Informations Release 1. Fiabilité et stabilité améliorées Tous les composants sont désormais sensiblement plus résistants aux attaques par les logiciels malveillants qui deviennent de plus en plus agressifs.
Informations Release 1. Fiabilité et stabilité améliorées Tous les composants sont désormais sensiblement plus résistants aux attaques par les logiciels malveillants qui deviennent de plus en plus agressifs.
30.avr.10 Présentation miniprojet. 9.mars.10 Cours 3 4.mai.10 Cours C++ 1. 16.mars.10 Cours 4 11.mai.10 Cours C++ 2
 2ème partie de cours: 23.fév.10 Cours 1 20.avr.10 TEST 24.fév.10 TP1 21.avr.10 miniprojet 26.fév.10 TP réserve 23.avr.10 miniprojet 2.mars.10 Cours 2 27.avr.10 Présentation miniprojet 3.mars.10 TP2 28.avr.10
2ème partie de cours: 23.fév.10 Cours 1 20.avr.10 TEST 24.fév.10 TP1 21.avr.10 miniprojet 26.fév.10 TP réserve 23.avr.10 miniprojet 2.mars.10 Cours 2 27.avr.10 Présentation miniprojet 3.mars.10 TP2 28.avr.10
Codage d information. Codage d information : -Définition-
 Introduction Plan Systèmes de numération et Représentation des nombres Systèmes de numération Système de numération décimale Représentation dans une base b Représentation binaire, Octale et Hexadécimale
Introduction Plan Systèmes de numération et Représentation des nombres Systèmes de numération Système de numération décimale Représentation dans une base b Représentation binaire, Octale et Hexadécimale
Equation LIDAR : exp 2 Equation RADAR :
 Contexte scientifique Systèmes LIDAR/RADAR Equation LIDAR : exp Equation RADAR : p (r) : puissance rétrodiffusée r : altitude ou profondeur. C : constante instrumentale. β : coefficient de rétrodiffusion
Contexte scientifique Systèmes LIDAR/RADAR Equation LIDAR : exp Equation RADAR : p (r) : puissance rétrodiffusée r : altitude ou profondeur. C : constante instrumentale. β : coefficient de rétrodiffusion
Tp_chemins..doc. Dans la barre "arche 2" couleur claire 1/5 21/01/13
 TP de création : utilisation des chemins vectoriels Finis les mauvais rêves : vous aurez enfin votre dreamcatcher (Indienss des Grands Lacs) 1 ) Créez une nouvelle image de 300 pixels sur 600 pixels en
TP de création : utilisation des chemins vectoriels Finis les mauvais rêves : vous aurez enfin votre dreamcatcher (Indienss des Grands Lacs) 1 ) Créez une nouvelle image de 300 pixels sur 600 pixels en
TD : Codage des images
 TD : Codage des images Les navigateurs Web (Netscape, IE, Mozilla ) prennent en charge les contenus textuels (au format HTML) ainsi que les images fixes (GIF, JPG, PNG) ou animée (GIF animée). Comment
TD : Codage des images Les navigateurs Web (Netscape, IE, Mozilla ) prennent en charge les contenus textuels (au format HTML) ainsi que les images fixes (GIF, JPG, PNG) ou animée (GIF animée). Comment
Projet audio. Analyse des Signaux ELE2700
 ÉCOLE POLYTECHNIQUE DE MONTRÉAL Département de Génie Électrique Projet audio Analyse des Signaux ELE2700 Saad Chidami - 2014 Table des matières Objectif du laboratoire... 4 Caractérisation du bruit...
ÉCOLE POLYTECHNIQUE DE MONTRÉAL Département de Génie Électrique Projet audio Analyse des Signaux ELE2700 Saad Chidami - 2014 Table des matières Objectif du laboratoire... 4 Caractérisation du bruit...
Contrôle par commande prédictive d un procédé de cuisson sous infrarouge de peintures en poudre.
 Contrôle par commande prédictive d un procédé de cuisson sous infrarouge de peintures en poudre. Isabelle Bombard, Bruno da Silva, Pascal Dufour *, Pierre Laurent, Joseph Lieto. Laboratoire d Automatique
Contrôle par commande prédictive d un procédé de cuisson sous infrarouge de peintures en poudre. Isabelle Bombard, Bruno da Silva, Pascal Dufour *, Pierre Laurent, Joseph Lieto. Laboratoire d Automatique
C.F.A.O. : Conception et Fabrication Assistées par Ordinateur.
 C.F.A.O. : Conception et Fabrication Assistées par Ordinateur. La CFAO réunit dans une même démarche informatique les actions de conception et de fabrication d un objet. La technique utilisée permet à
C.F.A.O. : Conception et Fabrication Assistées par Ordinateur. La CFAO réunit dans une même démarche informatique les actions de conception et de fabrication d un objet. La technique utilisée permet à
Sommaire. Introduction. Nouveautés d Adobe InDesign CS3. Visite guidée d Adobe InDesign
 Sommaire Introduction À propos de ce manuel................................ 1 Contexte d utilisation.................................. 2 Installation d Adobe InDesign.......................... 2 Installation
Sommaire Introduction À propos de ce manuel................................ 1 Contexte d utilisation.................................. 2 Installation d Adobe InDesign.......................... 2 Installation
«Diplomatie»: le portail interministériel de la correspondance diplomatique
 «Diplomatie»: le portail interministériel de la correspondance diplomatique Présentation au Congrès Qualita, Compiègne, 20 mars 2013 24/04/2013 1 1. Diplomatie numérique (digital diplomacy) 2. Trois impératifs
«Diplomatie»: le portail interministériel de la correspondance diplomatique Présentation au Congrès Qualita, Compiègne, 20 mars 2013 24/04/2013 1 1. Diplomatie numérique (digital diplomacy) 2. Trois impératifs
BACCALAURÉAT GÉNÉRAL SÉRIE SCIENTIFIQUE
 BACCALAURÉAT GÉNÉRAL SÉRIE SCIENTIFIQUE ÉPREUVE DE SCIENCES DE L INGÉNIEUR ÉPREUVE DU VENDREDI 20 JUIN 2014 Session 2014 Durée de l épreuve : 4 heures Coefficient 4,5 pour les candidats ayant choisi un
BACCALAURÉAT GÉNÉRAL SÉRIE SCIENTIFIQUE ÉPREUVE DE SCIENCES DE L INGÉNIEUR ÉPREUVE DU VENDREDI 20 JUIN 2014 Session 2014 Durée de l épreuve : 4 heures Coefficient 4,5 pour les candidats ayant choisi un
Chapitre 5: Oscillations d un pendule élastique horizontal
 1 re B et C 5 Oscillations d'un pendule élastique horizontal 40 Chapitre 5: Oscillations d un pendule élastique horizontal 1. Définitions a) Oscillateur écanique * Un systèe écanique qui effectue un ouveent
1 re B et C 5 Oscillations d'un pendule élastique horizontal 40 Chapitre 5: Oscillations d un pendule élastique horizontal 1. Définitions a) Oscillateur écanique * Un systèe écanique qui effectue un ouveent
UEO11 COURS/TD 1. nombres entiers et réels codés en mémoire centrale. Caractères alphabétiques et caractères spéciaux.
 UEO11 COURS/TD 1 Contenu du semestre Cours et TDs sont intégrés L objectif de ce cours équivalent a 6h de cours, 10h de TD et 8h de TP est le suivant : - initiation à l algorithmique - notions de bases
UEO11 COURS/TD 1 Contenu du semestre Cours et TDs sont intégrés L objectif de ce cours équivalent a 6h de cours, 10h de TD et 8h de TP est le suivant : - initiation à l algorithmique - notions de bases
Mathématiques I Section Architecture, EPFL
 Examen, semestre d hiver 2011 2012 Mathématiques I Section Architecture, EPFL Chargé de cours: Gavin Seal Instructions: Mettez votre nom et votre numéro Sciper sur chaque page de l examen. Faites de même
Examen, semestre d hiver 2011 2012 Mathématiques I Section Architecture, EPFL Chargé de cours: Gavin Seal Instructions: Mettez votre nom et votre numéro Sciper sur chaque page de l examen. Faites de même
PRESS RELEASE. La première Demand Side Platform française est une DSP mobile netadge, la performance RTB, au service des stratégies media mobile
 PRESS RELEASE La première Demand Side Platform française est une DSP mobile netadge, la performance RTB, au service des stratégies media mobile www.netadge.com Janvier 2014 S ommaire LDMServices lance
PRESS RELEASE La première Demand Side Platform française est une DSP mobile netadge, la performance RTB, au service des stratégies media mobile www.netadge.com Janvier 2014 S ommaire LDMServices lance
ITIL Gestion de la capacité
 ITIL Sommaire 1 GENERALITES 3 2 PERIMETRE DE LA GESTION DES CAPACITES 3 3 ACTIVITES ET LIVRABLES DE LA GESTION DES CAPACITES 4 3.1 ACTIVITES ITERATIVES OU GESTION DE PERFORMANCES : 4 3.2 GESTION DE LA
ITIL Sommaire 1 GENERALITES 3 2 PERIMETRE DE LA GESTION DES CAPACITES 3 3 ACTIVITES ET LIVRABLES DE LA GESTION DES CAPACITES 4 3.1 ACTIVITES ITERATIVES OU GESTION DE PERFORMANCES : 4 3.2 GESTION DE LA
Transmission d informations sur le réseau électrique
 Transmission d informations sur le réseau électrique Introduction Remarques Toutes les questions en italique devront être préparées par écrit avant la séance du TP. Les préparations seront ramassées en
Transmission d informations sur le réseau électrique Introduction Remarques Toutes les questions en italique devront être préparées par écrit avant la séance du TP. Les préparations seront ramassées en
Recherche De Coalescences Binaires Étalonnage Du Détecteur
 Recherche De Coalescences Binaires Étalonnage Du Détecteur Fabrice Beauville Journées Jeunes Chercheurs 18/12/2003 Les Coalescences Binaires & VIRGO Système binaire d objets compacts (étoiles à neutrons,
Recherche De Coalescences Binaires Étalonnage Du Détecteur Fabrice Beauville Journées Jeunes Chercheurs 18/12/2003 Les Coalescences Binaires & VIRGO Système binaire d objets compacts (étoiles à neutrons,
$SSOLFDWLRQGXNULJHDJHSRXUOD FDOLEUDWLRQPRWHXU
 $SSOLFDWLRQGXNULJHDJHSRXUOD FDOLEUDWLRQPRWHXU Fabien FIGUERES [email protected] 0RWVFOpV : Krigeage, plans d expériences space-filling, points de validations, calibration moteur. 5pVXPp Dans le
$SSOLFDWLRQGXNULJHDJHSRXUOD FDOLEUDWLRQPRWHXU Fabien FIGUERES [email protected] 0RWVFOpV : Krigeage, plans d expériences space-filling, points de validations, calibration moteur. 5pVXPp Dans le
SYSTÈME DE SURVEILLANCE VIDÉO À DISTANCE
 SYSTÈME DE SURVEILLANCE VIDÉO À DISTANCE 1 CATALOGUE 2014 SOMMAIRE en bref... 3 Les services gratuits de la version standard Family... 4 Les différentes versions : les services supplémentaires par version...
SYSTÈME DE SURVEILLANCE VIDÉO À DISTANCE 1 CATALOGUE 2014 SOMMAIRE en bref... 3 Les services gratuits de la version standard Family... 4 Les différentes versions : les services supplémentaires par version...
ÉdIteur officiel et fournisseur de ServIceS professionnels du LogIcIeL open Source ScILab
 ÉdIteur officiel et fournisseur de ServIceS professionnels du LogIcIeL open Source ScILab notre compétence d'éditeur à votre service créée en juin 2010, Scilab enterprises propose services et support autour
ÉdIteur officiel et fournisseur de ServIceS professionnels du LogIcIeL open Source ScILab notre compétence d'éditeur à votre service créée en juin 2010, Scilab enterprises propose services et support autour
Manuel d utilisation email NETexcom
 Manuel d utilisation email NETexcom Table des matières Vos emails avec NETexcom... 3 Présentation... 3 GroupWare... 3 WebMail emails sur internet... 4 Se connecter au Webmail... 4 Menu principal... 5 La
Manuel d utilisation email NETexcom Table des matières Vos emails avec NETexcom... 3 Présentation... 3 GroupWare... 3 WebMail emails sur internet... 4 Se connecter au Webmail... 4 Menu principal... 5 La
Contrôle Non Destructif : Implantation d'algorithmes sur GPU et multi-coeurs. Gilles Rougeron CEA/LIST Département Imagerie Simulation et Contrôle
 Contrôle Non Destructif : Implantation d'algorithmes sur GPU et multi-coeurs Gilles Rougeron CEA/LIST Département Imagerie Simulation et Contrôle 1 CEA R & D for Nuclear Energy 5 000 people Nuclear systems
Contrôle Non Destructif : Implantation d'algorithmes sur GPU et multi-coeurs Gilles Rougeron CEA/LIST Département Imagerie Simulation et Contrôle 1 CEA R & D for Nuclear Energy 5 000 people Nuclear systems
SINE QUA NON. Découverte et Prise en main du logiciel Utilisation de bases
 SINE QUA NON Découverte et Prise en main du logiciel Utilisation de bases Sine qua non est un logiciel «traceur de courbes planes» mais il possède aussi bien d autres fonctionnalités que nous verrons tout
SINE QUA NON Découverte et Prise en main du logiciel Utilisation de bases Sine qua non est un logiciel «traceur de courbes planes» mais il possède aussi bien d autres fonctionnalités que nous verrons tout
Création d une application Android (APPInventor)
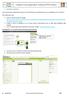 1. Matériel et logiciel Vous pouvez avec le logiciel App Inventor créer très facilement une application pour votre téléphone sous «Android». Vous devez pour cela : 1. Créer un compte Gmail sous Google
1. Matériel et logiciel Vous pouvez avec le logiciel App Inventor créer très facilement une application pour votre téléphone sous «Android». Vous devez pour cela : 1. Créer un compte Gmail sous Google
Ecoles Européennes DECISION
 Ecoles Européennes Bureau du Secrétaire général Unité de développement pédagogique Bruxelles, le 30 Juin 2015 MEMORANDUM : A To An 2015-06-M-6-FR Directeurs des Ecoles Européennes De From Von Giancarlo
Ecoles Européennes Bureau du Secrétaire général Unité de développement pédagogique Bruxelles, le 30 Juin 2015 MEMORANDUM : A To An 2015-06-M-6-FR Directeurs des Ecoles Européennes De From Von Giancarlo
Utiliser le logiciel Photofiltre Sommaire
 Utiliser le logiciel Photofiltre Sommaire 1. Quelques mots sur l image 2. Obtenir des images numériques 3. Le tableau de bord de logiciel PhotoFiltre 4. Acquérir une image 5. Enregistrer une image 6. Redimensionner
Utiliser le logiciel Photofiltre Sommaire 1. Quelques mots sur l image 2. Obtenir des images numériques 3. Le tableau de bord de logiciel PhotoFiltre 4. Acquérir une image 5. Enregistrer une image 6. Redimensionner
Introduction à MATLAB R
 Introduction à MATLAB R Romain Tavenard 10 septembre 2009 MATLAB R est un environnement de calcul numérique propriétaire orienté vers le calcul matriciel. Il se compose d un langage de programmation, d
Introduction à MATLAB R Romain Tavenard 10 septembre 2009 MATLAB R est un environnement de calcul numérique propriétaire orienté vers le calcul matriciel. Il se compose d un langage de programmation, d
************************ Système de reconstruction cinématique corps entier : fusion et exploitation de données issues de MEMS
 pour l obtention du Grade de DOCTEUR DE L UNIVERSITE DE POITIERS (Faculté des Sciences Fondamentales et Appliquées) (Diplôme National - Arrêté du 7 août 2006) Ecole Doctorale : Science et Ingénierie en
pour l obtention du Grade de DOCTEUR DE L UNIVERSITE DE POITIERS (Faculté des Sciences Fondamentales et Appliquées) (Diplôme National - Arrêté du 7 août 2006) Ecole Doctorale : Science et Ingénierie en
Fermettes + tuiles terre cuite = totale fiabilité en cas de séisme
 * Fermettes + tuiles terre cuite = totale fiabilité en cas de séisme Le programme, lancé en 2009** et coordonné par FCBA, a pour objet d affiner les connaissances sur le comportement au séisme des habitats
* Fermettes + tuiles terre cuite = totale fiabilité en cas de séisme Le programme, lancé en 2009** et coordonné par FCBA, a pour objet d affiner les connaissances sur le comportement au séisme des habitats
IMAGES NUMÉRIQUES MATRICIELLES EN SCILAB
 IMAGES NUMÉRIQUES MATRICIELLES EN SCILAB Ce document, écrit par des animateurs de l IREM de Besançon, a pour objectif de présenter quelques unes des fonctions du logiciel Scilab, celles qui sont spécifiques
IMAGES NUMÉRIQUES MATRICIELLES EN SCILAB Ce document, écrit par des animateurs de l IREM de Besançon, a pour objectif de présenter quelques unes des fonctions du logiciel Scilab, celles qui sont spécifiques
SFERA. NoUveLLES. platines 2 FILS. audio vidéo
 SFERA NoUveLLES platines audio vidéo 2 FILS audio vidéo 2 fils SFERA Deux PERSONNALITÉS un CŒUR ÉLECTRONIQUE unique Le design 2 La flexibilité 4 Combinaisons illimitées 6 Technologie, qualité et robustesse
SFERA NoUveLLES platines audio vidéo 2 FILS audio vidéo 2 fils SFERA Deux PERSONNALITÉS un CŒUR ÉLECTRONIQUE unique Le design 2 La flexibilité 4 Combinaisons illimitées 6 Technologie, qualité et robustesse
F210. Automate de vision hautes fonctionnalités. Caractèristiques. Algorithmes vectoriels
 Automate de vision hautes fonctionnalités Caractèristiques Algorithmes vectoriels Les algorithmes permettent de sélectionner les éléments de traitement requis dans la bibliothèque, puis les combinent et
Automate de vision hautes fonctionnalités Caractèristiques Algorithmes vectoriels Les algorithmes permettent de sélectionner les éléments de traitement requis dans la bibliothèque, puis les combinent et
TER Licence 3 Electronique des Télécoms Transmission GSM
 Université de Savoie Module TER (Travaux d études et réalisation) TER Licence 3 Electronique des Télécoms Transmission GSM Note : L ensemble des documents du projet se trouve sur l espace étudiant du site
Université de Savoie Module TER (Travaux d études et réalisation) TER Licence 3 Electronique des Télécoms Transmission GSM Note : L ensemble des documents du projet se trouve sur l espace étudiant du site
