INEX. Informatique en Nuage : Expérimentations et Vérification. Livrable n M1 PARALLÉLISME ET ÉVALUATION
|
|
|
- Antonin Gamache
- il y a 8 ans
- Total affichages :
Transcription
1 INEX Informatique en Nuage : Expérimentations et Vérification Livrable n M1 PARALLÉLISME ET ÉVALUATION DE PERFORMANCES DES JOINTURES ET SEMI-JOINTURES SUR DES ARCHITECTURES CLOUD Abdeljallil Abajjane Septembre 2012
2 ii INEX
3 PARALLÉLISME ET ÉVALUATION DE PERFORMANCES DES JOINTURES ET SEMI- JOINTURE SUR DES ARCHITECTURES CLOUD ÉTAT DE L'ART Abdeljalil ABAJJANE Master 2 IRAD/Recherche Université d Orléans Avril 2012 Référant : Mostafa BAMHA Université d'orléans Page 1/26 A. Abajjane
4 Table des matières La jointure...3 Les bases de la jointure...3 La jointure par boucles imbriquées...4 La jointure par tri-fusion...6 La jointure par fonction de hachage...6 Jointure Parallèles...9 Jointure parallèle par boucles imbriquées...9 Jointure parallèle tri-fusion...10 Jointure parallèle par fonction de hachage...11 Synthèse...12 Équilibre de charge et distributivité des données...13 Gestion parallèle des tâches...13 Génération des tâches...13 Découpage des relations...13 Choix du nombre de tâches...14 Placement des tâches...14 Collecte des statistiques...15 Affectation des tâches...15 Mesures de charge...16 Stratégie d'affectation...16 Exécution des tâches...16 Équilibrage de charge...17 Équilibrage de charge statique...17 Équilibrage dynamique...18 Synthèse...19 Mise en œuvre du parallélisme en architecture de type «Shared-nothing»...21 Problématique...21 Map-Reduce...21 Map-Reduce-Merge...22 Portée du modèle Map-Reduce-Merge...23 Synthèse...23 Conclusion...24 Bibliographie...25 Université d'orléans Page 2/26 A. Abajjane
5 La jointure La jointure est l'opération incontournable dans le domaine des bases de données relationnelles. Elle est ce qui permet le lien entre données de plusieurs sources au sein d'une seule ou plusieurs bases de données. La difficulté particulière de la jointure est son coût en terme de ressources machines : stockage, mémoire et CPU. Ces trois ressources pouvant être différemment sollicitées selon l'algorithme mis en œuvre. De ce fait, le domaine foisonne d'approches algorithmiques plus ou moins orientées. Toutefois, on peut quasiment tous les ramener à 3 méthodes principales : la jointure par boucle imbriquées (nested-loop), la jointure par tri-fusion (sort-merge) et la jointure par fonction de hachage (hash-join). Au delà des difficultés intrinsèques à la jointure, l'évolution constante des environnements techniques ouvrent d'autres voies visant à utiliser de façon optimale les capacités des machines (mémoire, multiprocessing...). Nous verrons comment chacune des trois méthodes citées s'apprête à ces évolutions. Ainsi que les variantes résultantes qui donnent les meilleurs résultat soit de façon particulière, soit pour des cas de figures plus généraux. En plus des évolutions des architectures des ordinateurs, la jointure est également indirectement impactée par des évolutions plus «culturelles» en matière d'utilisation des données et de leur répartition. De fait, l'extension des réseaux informatiques, et l inter-connectivité entre une multitude de sites, implique une dissémination des données au sein d'un vaste réseau, et donc une distribution «subie» des données exigeant toujours des traitements de type jointure ; dans ce contexte, la jointure prend une autre dimension et la remise en cause des idées acquises en la matière est souvent nécessaire : impossibilité d'indexation des données, données pauvrement structurées... Comme nous le verrons plus loin, le pragmatisme et les approches naïves sont souvent les meilleures pour ce type de problématique. Dans un premier temps, nous rappelons les différentes approches de jointure, et leur implantation indépendamment de l'environnement d'exécution. Nous exposerons ensuite leur adaptabilité aux architecture parallèles, en essayant de dégager parmi les trois méthodes de base celles qui sont les mieux appropriées à une situations donnée. Nous étendons ensuite cette parallélisation de la jointure aux architectures plus vastes notamment les architectures dites «sharing-nothing», et de façon plus particulière aux architectures de type «Cloud Computing». Nous exposons ensuite une méthode technique de mise en œuvre de la jointure au sein de tels réseau. Notre exposé se base sur le plan et les synthèses élaborées dans le livre «Query processing in parallel relational database systems» [1]. Quand c'est nécessaire, nous apportons des précisons émanant d'autres sources. Nous adaptons également autant que possible les solutions développées dans les différentes étude, mais, comme nous le mettons en évidence plus loin, les techniques d'implémentation classiques sont loin d'être adaptable dans l'état à un environnement Cloud et à ses contraintes. Par ailleurs, nous taisons volontairement les orientations qui ne nous semblent pas pertinentes ou porteuses d'enseignement pour notre contexte. Les bases de la jointure La jointure entre deux relations R et S sur les attributs R.A et S.B consiste à coupler les tuples de R et S ayant les attributs R.A et S.B égaux. De façon générale, un tuple de R (i.e S) peut être couplés à un nombre quelconque de tuples de S (i.e R). Dans le cas particulier où les attributs R.A et S.B sont tous les deux des clés uniques de leur relation respectives, un tuple de R (i.e S) ne peut être couplé qu'au plus avec un tuple de S (i.e R). Il y a une multitude technique de mise en œuvre de cette opération et, des nombreuses études portant sur le sujet, trois méthodes se sont dégagées comme regroupant l'ensemble des approches qui peuvent être proposées. Ces trois principales méthodes visant à réaliser ces opérations sont la jointure par boucles imbriquées qui consiste pour deux relations R et S, d'une part à parcourir une des ces relations de façon séquentielle et d'autre part, à comparer chaque tuple de R lu avec l'ensemble des tuples de S afin d'extraire les tuples pour Université d'orléans Page 3/26 A. Abajjane
6 lesquels A = B. La première relation parcourue (ici R) est désignée sous le nom de «inner» et la seconde (ici S) est désignée sous le nom «outer». La deuxième méthode repose sur un tri préalable des deux relations R et S, suivi d'une mise en œuvre équivalente aux boucles imbriquées avec toutefois une économie du nombre de lecture de la seconde relation comme nous l'exposons plus loin. Enfin, la troisième méthode, quant à elle, est basée sur une fonction de hachage des deux relations visant à permettre l'accès directes aux tuples de S ayant une relation avec les tuples de R, sans nécessité la recherche séquentielle par parcours de la relation S. La jointure par boucles imbriquées Cette jointure est la plus naturelles des trois. Longtemps négligée elle a été remis au goût du jour du fait de la puissance des données et de l'apparition de variantes beaucoup plus efficaces [2]. Comme on peut le voir dans l'algorithme ci-dessous, elle est composée de 2 boucles, la première nommée outer parcours une fois la première relation, et, pour chaque tuple de la relation parcourue, également nommée la relation outer, la seconde boucle désignée par inner parcours la seconde relation également désignée inner afin de trouver les tuples ayant une égalité des attributs de jointure des deux relations. Algorithme BoucleImbriquéeBasique pour chaque tuple r de R faire pour chaque tuple s de S faire si r.a = s.b alors émettre(r,s) Bien que cet algorithme soit robuste de par sa nature et sa simplicité, il présente néanmoins un défaut majeur et quasi rédhibitoire. La seconde relation nommée inner est parcourue un nombre important de fois, en fait R (nombre de tuples de R) fois. Par ailleurs, la concurrence de lecture des deux relations entraîne fatalement un nombre important de défaut de pages et donc d'accès disques répétés aux mêmes données. Afin de limiter l'inconvénient de cette méthode, une évolution consiste à bufferiser les données en mémoire pour limiter le nombre de défaut de pages. Ce qui donne l'algorithme à accès par blocs suivant, avec M le nombre de pages mémoire disponibles pour le traitement : Algorithme BoucleImbriquéeBasiqueBlocs faire Copier (M-1) pages de R vers mémoire faire Copier 1 page de S vers mémoire pour chaque tuple r de R en mémoire faire pour chaque tuple s de S en mémoire faire si r.a = s.b alors émettre(r,s) jusqu'à lecture de toutes les pages de S jusqu'à traitement de toutes les pages de R Avec cette évolution nous passons d'une situation où le nombre de lectures en disque est incertain et pouvant être extrêmement important du fait de la concurrence des deux relations en tampon disque, à une situation plus contrôlée ou le nombre de lecture en disque est de l'ordre de : R + R (M 1) S où R et S sont le nombre de pages de pages de de R et S. Université d'orléans Page 4/26 A. Abajjane
7 Toutefois, nous parcourrons toujours la relation S R fois, que cela soit en mémoire ou en disque, ce qui implique une complexité des deux algorithme de O( R * S ), avec R et S le nombre de tuples respectivement de R et S. En effet, dans tous les cas S est parcourue pour chaque tuple de R, et, chaque tuple de R peut ne pas avoir de tuples correspondants du point de vue de la jointure dans S ou très peu. Une méthode visant à repousser cette limite est l'utilisation d'index sur les attributs de jointure, et plus particulièrement sur l'attribut de jointure de la relation S. En effet, le principe d'un index d'une relation sur un attribut, consiste à associer à chaque valeur d'attribut une position «physique» (numéro de page...) sur disque du tuple associé. Ainsi, il n'est plus utile de parcourir à chaque itération outer entièrement la relation S puisque il suffit d'accéder sur disque au tuple associé à la relation R directement à travers cet index. Cette évolution nous amène à l'algorithme suivant : Algorithme BoucleImbriquéeIndexée faire Copier 1 page de R vers mémoire pour chaque tuple r de R en mémoire faire Calculer l'index sur S.B pour la valeur r.a pour chaque valeur trouvée faire extraire les valeurs de la page émettre(r,s) jusqu'à traitement de toutes les pages de R On constate alors qu'il n'est plus utile de lire un nombre important de pages de R puisque le parcours de S ne dépend plus du nombre de pages de R en mémoire mais est accédée directement à travers l'index. La zone mémoire ainsi libérée pouvant alors contenir l'index et éviter qu'il ne devienne un goulet d'étranglement. La complexité algorithmique est théoriquement en O( R + S ). Le nombre d'accès disque est quant à lui proportionnel à la sélectivité de la jointure qui est définie par le rapport entre le nombre de tuples résultant de la jointure et le produit du nombre de tuple de R par le nombre de tuples de S : R S / R * S. On remarquera que l'efficacité de cet algorithme dépend également beaucoup de l'organisation de l'index sur S. En effet selon que les tuples de S ayant la même valeur d'attribut de jointure sont regroupées ou pas au sein d'une même page ou d'un ensemble de pages contiguës, le bénéfice de cet algorithme peut être plus ou moins important. Dans le cas d'une bonne organisation des tuples de S sur l'attribut B de jointure, pour un tuple r de R donnée le nombre de pages de S lues est au plus égal au nombre de pages dans lesquelles les tuples s de S ayant pour valeur s.b =r.a sont stockés ; ce nombre est minimal de façon inductive de par la contiguïté imposée ci-dessus. De plus, si la relation R est préalablement triée, les pages de S sont lues au plus une fois, selon le taux de sélectivité de la jointure définie ci-dessus. L'un des enseignements structurant que l'on peut tirer de cette méthode est l'apport significatif du tri préalable des relations. Au delà du coût de celui-ci, le tri permet d'éviter de répéter plusieurs fois le parcours d'une relation, ou tout du moins le limiter significativement. C'est ce constat qui nous amène à une autre famille d'algorithme de jointure basées sur le tri-fusion. Université d'orléans Page 5/26 A. Abajjane
8 La jointure par tri-fusion La méthode de jointure par tri-fusion nécessite un tri préalable, selon les attributs de jointure des deux relations. Théoriquement un seul parcours des relations est nécessaire afin d'extraire les tuples ayant une égalité sur les attributs de jointure. Il est toutefois nécessaire de procéder par moment à des retours arrière sur l'une des relation dans le cas de non unicité de son attribut de jointure. L'impact de ce retour arrière est néanmoins limité car il est la plupart du temps réalisé en mémoire, mais des ré-lectures sur disque suite à un défaut de page restent possibles mais néanmoins très rares. L'algorithme résultant est le suivant : Algorthme TriFusionSimple trier R sur R.A et S sur S.B selon l'ordre ascendant initialiser r et rp avec le premier tuple de R initialiser s et sp avec le premier tuple de S tantque non (eof(r) ou eof(s)) faire tantque non (eof(r) ou eof(s) or r.a = s.b) faire si (r.a < s.b) initialiser r et rp avec le tuple suivant de R sinon initialiser s et sp avec le tuple suivant de S fintantque si non (eof(r) ou eof(s)) tantque r.a = rp.a et non eof(r) faire tantque s.b = r.a et non eof(s) faire émettre(rp,s) initialiser s avec le tuple suivant de S fintantque initialiser r avec le tuple suivant de R si r.a = sp.b alors initialiser s à sp //retour arrière fintantque Cet algorithme est une approche générale de la jointure par tri-fusion. Il fonctionne que les attributs de jointure A et B soient une clé unique de leurs relation respectives ou pas. Dans le cas de clés unique, il n'est pas nécessaire de vérifier la nécessité du retour arrière et l'algorithme s'en trouve alors simplifié. L'algorithme est cependant simple et robuste, le principal défaut étant la nécessité d'un tri préalable ; mais, si les relations sont déjà maintenues triées, son intérêt devient plus grand. L'enseignement tiré de cette méthode, mais également dans une certaine mesure de la précédente, est la problématique d'accès directe aux données évitant ainsi de devoir accéder à une multitude de tuples inutiles pour un tuple r donné avant d'atteindre le tuple s pertinent. Nous avons vu que l'une des façon d'atteindre cet objectif était le tri, nous allons maintenant voir une autre méthode basée elle sur une fonction de hachage visant à segmenter les données d'une part, et en accélérer l'accès d'autre part. La jointure par fonction de hachage Nous avons mis en évidence que le principal problème de la jointure est la nécessité de parcourir un certain nombre de fois l'une des deux relations, alors même que la plupart des valeurs parcourues ne participent nullement au résultat. Un tri préalable pouvant être coûteux ou la disponibilité d'un index précisément sur les attributs de jointure n'étant pas toujours garantie, il nous faut trouver un autre moyen d accéder directement aux données pertinentes pour un tuple courant donnée avec un surplus de coût borné. Une méthode allant dans ce sens est le découpage des relations R et S en partitions R1, R2,...,Rn et S1,S2,...,Sn tel que pour tout tuple r et s avec r Ri et s Sj, si i j alors r.a s.b. Dans ce cas, la jointure Université d'orléans Page 6/26 A. Abajjane
9 globale de R et S peut être ramenée à l'union des jointure Ri et Si. On remarquera que cette condition dans l'état est purement théorique et que dans les faits il est difficile d'arriver immédiatement à cette situation. Nous verrons par la suite les évolutions possible afin de satisfaire cette condition. On notera également que les différentes partition d'une même relation peuvent êtres de tailles différentes, et il en est de même pour les partitions Ri et Si. L'algorithme de base peut être directemet amélioré dès lors que l'on dispe de suffisamment de mémoire pour stocker plusieurs partitions et limiter ainsi les accès disque répétés. Cet algorithme simple a été implémenté pour la première fois au sein du système de base de données GRACE [3]. Il se décline de la façon suivante : Algorithme BasicHashJoin découper R en n partitions avec une fonction de hachage sur R.A découper S en n partitions avec la même fonction de hachage sur S.B pour chaque partition i faire pour chaque tuple r de R i faire hachage sur r.a et insertion dans la table de hachage pour chaque tuple s de S i faire hachage sur s.b et sonder la table de hachage si r.a = s.b alors émettre(r,s) On identifie deux fonctions de hachage. La première est utilisée lors de la première phase du traitement pour la partition des relations. Cette phase est nommée phase de construction (built). Et, celle utilisée pour générer la table de hachage lors de la seconde phase qui est nommée phase de sondage (probe). Les deux fonctions peuvent être identiques, mais l'utilisation de deux fonctions distinctes évite les problèmes de collision liées aux fonctions de hachage. Par ailleurs, l'objectif de l'une et l'autre des fonctions n'est pas le même. L'une a pour but de distribuer les tuples vers un ensemble de partition de la façon la plus équitable et éviter ainsi une forte disparité des tailles des partitions. L'autre a pour but l'accès efficace aux tuples de la première relation. Ceci peut contraindre selon les cas à utiliser deux fonctions distinctes adaptées chacune à chaque étape La complexité de cette première version, en ne comptant que les lectures de R et S, est : O( R + S +n ( R i + S i )) et i, j si i j alors R i + S i Un axe d'amélioration possible de cette version d'algorithme est le nombre d'i/o. En effet dans le cas de «la boucle imbriquée», la mise en concurrence des deux relations (i.e. Boucles) induit un nombre de défaut de pages pouvant être conséquent et donc extrêmement pénalisant en fonction de la taille des relations en rapport avec la quantité mémoire disponible. Une évolution naturelle consiste donc à veiller à ce qu'une partition de la relation outer puisse tenir dans une quantité mémoire fixée, donnant ainsi une seconde contrainte qui est : R i M 2, pour 1 i n et M étant le nombre de pages mémoire disponibles. Les pages restantes (2) sont utilisées pour le stockage de la partition S i pour la première page et, comme tampon du résultat pour la seconde page. Toutefois, les partitions étant générées à l'aide d'une fonction de hachage, elle même prenant comme critère de calcul l'attribut de jointure, il est extrêmement difficile de prédire la taille de toutes les partitions. De ce fait, il n'est pas exclu qu'une partition soit supérieur en pages au nombre maximum de pages disponibles (M-2). Dans ce cas, si on souhaite éviter ce cas de figure, une solution consiste à diviser à nouveau la ou les partitions posant problème jusqu'à atteindre une taille inférieure à M-2. On rappelle également que le mode opératoire des algorithmes basés sur une fonction de hachage se déroule en deux étapes : la construction des partitions, suivie de la jointure des partitions sur la base d'une Université d'orléans Page 7/26 A. Abajjane
10 table de hachage de la première relation. La première étape lit puis réécrit sous forme de partions la relation outer. Une optimisation consiste donc à mettre à profit la lecture des relations R et S dès la phase de construction afin de réaliser la jointure d'une partie de la relation outer. C'est dans cet objectif qu'un algorithme hybride a été proposé [4]. Celui-ci se décline de la façon suivante : i) Construction des partitions R i et mise en mémoire des tuples relatifs à R 0 ii) Construction des partitions S i et jointure des tuples relatifs à S 0 avec R 0 iii) jointure des des R i /S i, pour i > 0. Durant l'étape ii, on construit les partitions S i et on réalise également la jointure avec R 0 dès qu'un tuple appartenant à S 0 est «identifié» à la volée par la fonction de hachage. L'économie est moindre mais peut être significative dans le cas où le nombre de partitions est petit. Les algorithmes vus jusqu'à maintenant ont pour effet de favoriser les accès aléatoires au disque. On rappellera qu'un accès disque aléatoire est beaucoup moins efficace qu'un accès disque séquentiel. L'algorithme suivant se propose donc de favoriser les accès séquentiels. Il est connue sous le nom de SimpleHashJoin et, sous sa forme générale, se présente de la façon suivante : Algorithme SimpleHashJoin pour chaque partition i faire pour chaque tuple r de R non traité faire hachage sur r.a pour déterminer le numéro de partition j de r si i = j alors insérer r dans la table de hachage sinon écrire r sur disque // ou ne rien faire pour chaque tuple s de S non traité faire hachage sur s.b pour déterminer le numéro de partition j de s si i j alors écrire s sur disque // ou ne rien faire sinon hachage sur s.b et sonder la table de hachage si s.b = r.a alors émettre (r,s) Cet algorithme procède par itération sur le numéro de partition. Ainsi, à chacune de ces itérations itération, soit un tuple fait partie de la partition courante et dans ce cas il est traité (mis en table de hachage ou jointure selon qu'il s'agit de R ou S), soit il n'en fait pas partie et alors il est enregistré sur disque. Si on souhaite éliminer les écritures aléatoires et donc favoriser les écritures séquentielles, il suffit, dans le cas ou un tuple n'est pas concerné lors de l'itération courante, de le rejeter sans écriture sur disque. Certes, cela multipliera les lectures sur disque, mais ces lectures restent séquentielles et donc beaucoup plus performantes que des lectures aléatoire et qui plus est concurrentes [4]. Nous avons exposé trois familles d'algorithmes de jointure. Beaucoup d'autres algorithme, visant à apporter des amélioration particulières ou à répondre à des jointures particulières, ont été également proposés. Nous nous sommes contenté d'exposer les principaux dont le pivot intrinsèque relatif à chacun est : I) Les boucles imbriquées II) Le tri des relations (suivi de boucles imbriquées) III) Le partitionnement et le hachage des relations Université d'orléans Page 8/26 A. Abajjane
11 On constatera aisément que le premier et le deuxième sont malgré tout assez proches. La ressemblance entre le premier et le troisième est moins évidente mains non moins réelle. En effet, une fonction de hachage peut tout à fait se baser sur le numéro de page. Ainsi le numéro de partition serait calculé par : i= numpage(r) où, M 2 numpage est le numéro de page du tuple r de R, compris entre 0 et R -1 M est la quantité mémoire en pages disponible Dans cette configuration, il ne s'agit ni plus ni moins que de l'algorithme BoucleImbriquéeBasiqueBlocs vu précédemment. L'un est l'autre de ces algorithmes trouvent leur justification dans divers configurations. L'un va être plus performant en cas de présence d'index sur l'une des relations ; L'autre sera favorisé dans le cas de relations triées. Mais d'autres critères de choix, plus techniques, peuvent également entrer en ligne de compte tels par exemple la taille mémoire disponible eu égard à la talle des relations, ou plus fonctionnelles, tels que la distributivité des valeurs des attributs de jointure. Toutes ces évolutions visent à augmenter l'efficacité des algorithmes de base afin de, soit exploiter les ressources internes, soit s'y adapter. Un autre axe d'évolution souhaité ou subit est la parallélisation des traitements de jointure. Dans cet autre environnement, tous les algorithmes cités ne sont pas équivalents face la parallélisation comme nous l'exposons dans le chapitre suivant. Jointure Parallèles La jointure parallèle est parfois subie, dans le cas de relations distribuées à travers un vaste réseau, et, parfois souhaitée dans le cas de machines à architecture parallèle. Dans le second cas, la jointure parallèle est utilisée afin de réduire les temps de traitement en exploitant au mieux les ressources machine. Beaucoup d'extensions des algorithmes vu auparavant vers le parallélisme ont été proposées. Et, comme tout traitement parallèle, ceux-ci se déclinent en 3 étapes qui sont : i) Décomposition de la jointure en n tâches ii) Assignation des n tâches à p processeurs iii) Assemblage des résultats locaux Bien entendu, l'étape iii est fortement dépendante de la façon dont l'étape i est réalisée. Cette étape iii peut également être optionnelle. Par ailleurs, on peut distinguer deux familles d'architectures parallèles qui sont les architecture partagées et les architecture distribuées. Dans la première architecture des ressources telles que la mémoire ou l'espace de stockage disque sont partagés et donc accessibles de façon concurrentiel par l'ensemble des processeurs en jeu. Dans la seconde, ces ressources sont distribuées sur différentes machines interconnectées par un réseau de communication. Notre problématique, à savoir la jointure parallèle en environnement Cloud, étant plutôt concernée par la seconde architecture nous mettrons essentiellement l'accent sur les algorithmes adaptée à celle-ci. Nous adapterons les principes généraux à notre besoin, et nous mettons de côté les principes trop inhérents aux architectures partagées ou alors nous signalons cette forte adhérence s'il nous faut tirer un enseignement du principe en question. Jointure parallèle par boucles imbriquées La jointure par boucles imbriquées est l'un des algorithmes qui se prête le mieux à la parallélisation. En effet, une parallélisation naturelle du traitement consiste à distribuer la relation outer (R) vers les p processeurs (i.e machines) concernées. Chaque processeur réalisant localement la jointure de sa partition avec l'ensemble de la relation inner (S). Cela implique, en préalable à la jointure, la réplication (i.e. copie) de Université d'orléans Page 9/26 A. Abajjane
12 la relation inner vers l'ensemble des processeurs (i.e. Nœuds) concernés. L'algorithme résultant est le suivant : Algorithme BouclesImbriqueesParalleles Chaque nœud qui dispose d'un fragment de S le dispatche aux autres nœuds distribution de R vers l'ensemble des nœuds concernés chaque nœud i joint la partition R i avec l'ensemble de la relation S La jointure locale des partition R i avec S peut être réalisée selon n'importe lequel des algorithmes exposés. Si le nœud i en charge de la partition R i dispose d'un index sur celle-ci alors l'algorithme boucles imbriquées indexé exposé en première partie peut être utilisé. En effet, la relation S peut être déjà distribuée, sur un ensemble de machine pour des besoins techniques (ex. stockage) ou fonctionnels, et donc disposer d'index permanents. Cette distribution préexistante nous permet également d'envisager une autre optimisation : seul les nœuds disposant d'une partition de la relation S sont utilisés pour la jointure parallèle. Nonobstant, cette optimisation peut être antinomique avec la nécessité de distribuer le traitement sur un large ensemble de nœuds afin de garantir le meilleur équilibre de charge. De façon générale, une relation est distribuée, pour raison de contrainte technique ou fonctionnelle, selon la valeur d'un attribut de cette même relation. Cet attribut peut être choisi pour raison de sa bonne distribution : lorsqu'il s'agit de contrainte technique visant notamment à faire supporter le stockage d'une relation par plusieurs nœuds. Dans ce cas, on souhaite que le partage soit équitable entre les différents nœuds. L'attribut de distribution peut également être choisi sur des bases fonctionnelle : les traitements produisant la relation en question sont distribués sur un ensemble de nœuds, comme par exemple la prise en charge d'un intervalle de numéros de clients par chaque nœuds. En conséquence, l'attribut de distribution de la relation n'est pas nécessairement l'attribut sur lequel porte la jointure. Une solution d'abstraction de cette problématique est proposée dans l'article [1]. Elle s'appuie sur une table de translation MapS dont le schéma est (P,B). Sur la base de cette table, chaque nœud disposant d'une partition de R peut identifier les nœuds disposant d'une partition de S vers lesquels il doit envoyer sa partition R. Ainsi, pour chaque tuple s de S, il existe un tuple m dans MapS tel que m.b = s.b et m.p est l'attribut de distribution de la relation S sur différents nœuds. Et donc, pour un tuple r, le tuple m de MapS tel que m.b = r.a nous permet d'extraire l'attribut m.p correspondant et donc identifier le site sur lequel la partition de S est localisée. Une extension à cette méthode consiste à distribuer également MapS selon l'attribut m.b, ce qui produit l'algorithme suivant prenant comme hypothèse structurante le fait que S est distribuée selon l'attribut S.P : Algorithme BouclesImbriqueesParalleleSousEnsemble pour chaque tuple s de S faire maintenir un tuple m de MapS avec m.p = s.p et m.b = s.b Partition de MapS selon MapS.B et stockage de MapSi sur le nœud n i pour chaque tuple r de R faire trouver N i contenant MapS i avec m.b = r.a trouver N j contenant S i avec s.p = m.p envoyer r à toules nœuds N j réaliser la jointure sur chaque nœud N i Bien entendu, si l'attribut de jointure est également l'attribut de distribution de la relation S, alors il devient inutile de maintenir la table MapS puisque le nœud i contenant la partition S i est directement obtenu avec l'attribut S.B. Comme le montre les algorithmes décris ci-dessus, la jointure par boucles imbriquées se prête naturellement à la parallélisation. Toutefois, on constate également que le placement initial des données est Université d'orléans Page 10/26 A. Abajjane
13 essentiel. En effet, à défaut, de très nombreuses communications sont nécessaires ce qui peut être extrêmement pénalisant. Nous verrons par la suite que ce placement est un enjeu majeur qu'il nous faudra favoriser en amont de la jointure et/ou exploiter au mieux au moment de la jointure. Jointure parallèle tri-fusion Contrairement à la jointure précédente, la méthode par tri fusion s'apprête moyennement à la parallélisation. Si la phase de tri des relations peut être naturellement parallélisée sur chacun des nœuds disposant d'une partition R ou S, la phase de jointure exige quant à elle un traitement préalable et complexe pouvant conduire à des performances équivalentes à un traitement séquentiel. C'est pour cette raison que, dans un premier temps, cette seconde phase a souvent été réalisée de façon séquentielle. Il est possible d'envisager la parallélisation de cette seconde phase selon deux modes opératoires distincts qui sont : I) Jointure des différentes partitions triées une à une (R i et S i ). Ce qui implique une combinaison de l'ensemble des partitions Si et Ri par chaque nœud détenant l'une ou l'autre des partition. Ainsi, pour m partitions R i et n partitions S i, m*n jointures sont nécessaires. II) Assemblage de la petite relation en une seule partition R, réplication de cette partition vers les différents nœud détenant une partition Si, puis jointure de chaque partition Si avec la totalité de la jointure R. On constate que dans l'un et l'autre cas on se ramène à une jointure par boucles imbriquées sans aucun apport de la phase de tri préalable particulière à la jointure par tri-fusion. Pour tirer profit de la propriété du tri, il est nécessaire de maintenir cette propriété au sein des différentes partitions i traitées par les différents nœuds. Ainsi, les relations S et R sont découpés en k partitions chacune, ces partitions devant respecter les propriétés suivantes : i) i [1,k], R i. A<R i+1. A S i.b<s i+1. B ii) i [1,k], R i + S i R i+1 + S i+1 Afin d'obtenir cette configuration sur chacun les k nœuds devant procéder à la jointure des paires de partitions Ri et Si respectant la propriété ci-dessus, une étape intermédiaire est nécessaire. Chaque nœud disposant d'une partition Ri et/ou Si triée doit procéder au découpage selon la contraintes ci-dessus, ce qui produit un ensemble de sous partitions. Chaque sous partition est ensuite fusionnée afin de produire une partition globale triée également respectant les mêmes contraintes. Il existe de nombreuses solutions de tri parallèle pouvant être adaptées aux jointures, dès lors qu'elles prenne en compte la distributivité des attributs et assure une répartition équilibrée des données (contrainte ii) [5]. Pour atteindre des performances compatibles avec le gain attendu par un traitement parallèle de la jointure, sur une quantité de données très importantes distribuées une étude fait état d'un comparatif entre un algorithme de tri parallèle avec découpage exact et l'autre utilisant une méthode stochastique[6]. Le seconde algorithme présente ue efficacité beaucoup plus grande dès lors la distributivité des données est maîtrisé et que l échantillonnage choisi est représentatif. On note bien que cette étape intermédiaire, nécessaire, annule le bénéfice attendu par la parallélisation, ou dans le meilleur des cas présente un gain incertain. Jointure parallèle par fonction de hachage Plus encore que la jointure par boucle imbriquée, ce type de jointure est totalement compatible avec la parallélisation. En effet, le principe de la jointure par fonction de hachage est le partitionnement des relations. En réalité, dans le cas d'architecture parallèle à mémoire et disques partagées, les algorithme monoprocesseur fonctionnent dans l'état au sein d'une architecture parallèle, puisque chaque processeur peut Université d'orléans Page 11/26 A. Abajjane
14 accéder de façon concurrentielle aux différentes partions [7]. Dans le cas d'architecture distribuée, qui nous intéresse particulièrement, il est nécessaire de procéder à quelques échanges entre les différents nœuds afin de mener la jointure sur plusieurs nœuds en parallèle. La distribution des tuples associés à un nœud est aisément réalisable à l'aide de la fonction de hachage, utilisée pour découper les relations en partitions, et associée à une table de routage prédéfinie. À l'issue de cette distribution, chaque nœud dispose alors de deux partions Si et Ri sur lesquelles il peut appliquer la jointure par fonction de hachage. La principale difficulté, comme dans le cas de l'algorithme monoprocesseur, réside dans la bonne distribution des relations. En effet, il est difficile de prévoir la taille de chaque partition résultant de la fonction de hachage, puisque cela dépend de la fonction elle même mais également de la distribution inhérente aux valeurs de l'attribut sur lequel porte la jointure. Une mauvaise distribution des données implique fatalement un dépassement de la capacité mémoire des nœuds de traitement dégradant ainsi fortement l'efficacité de l'algorithme parallèle. D'un autre côté, un découpage trop fin des relations entraîne une sous utilisation des capacités des nœuds de traitement. L'approche générale consiste à découper les relation en un nombre de partitions suffisamment important afin d'éviter un dépassement mémoire et, durant la phase de construction, si des partitions sont jugées trop petites, alors on procède à leur assemblage en une partition assez grande afin d'optimiser l'usage de la mémoire. On constate à nouveau que la bonne ou mauvaise distribution des données ainsi que celle de l'attribut de jointure joue un rôle primordial dans le cas d'environnement monoprocesseur et encore plus dans la cadre d'un environnement parallèle. Cet aspect fait l'objet d'une étude particulière au chapitre «La jointure par fonction de hachage» Synthèse Parmi l'ensemble des algorithmes exposés, il est difficile d'en désigner un comme plus performant que tous les autres. La quasi-totalité des études réalisées à ce jour partent d'hypothèse restrictive sur la distribution des données. En réalité, l'un et l'autre des algorithmes exposés trouve son intérêt dans des configurations particulières telles que la bonne distribution des attributs de jointure, la différence de la taille des deux relations ou encore la présence d'index. La jointure basée sur une fonction de hachage (H dans figure ci-dessous) semble selon les études réalisées assez généraliste et globalement efficace. Toutefois, celle-ci est fortement sensible à la distribution de l'attribut de jointure ainsi qu'à la taille des relations versus la quantité de mémoire disponible. La jointure par boucles imbriquées (NL) est quant à elle complètement insensible à la distribution de l'attribut de jointure et gagne en efficacité dans un environnement parallèle. Enfin la jointure par tri-fusion (SM) n'est réellement efficace que lorsque les relations de jointure sont déjà triées, et, dans ce cas cette méthode est de loin la plus performante même dans une configuration monoprocesseur [8]. Université d'orléans Page 12/26 A. Abajjane
15 Temps en secondes Processeurs SM H NL Figure 1 : performances comparées : source [8] Équilibre de charge et distributivité des données Il ressort du précédent chapitre qu'une bonne distribution des données assure une efficacité optimale du traitement de jointure parallèle. Un bon partage des données entre les différents nœuds assure un bon équilibre de charge des traitements. Or le facteur majeur qui conditionne la possibilité de procéder à une telle répartition est la distributivité des données à joindre, mais également de la distribution des valeurs de l'attribut de jointure [9]. En effet, malgré une bonne distribution des données sur un attribut quelconque des relations en jeu, il peut s'avérer qu'un nœud se voit affecté une paire de partitions Si et Ri telle que la distributivité des valeurs de l'attribut implique un traitement lourd pour un ensemble de nœud et un traitement quasi-nul pour un autre ensemble. Ceci produit un déséquilibre qui annule l'efficacité attendue d'un traitement parallèle en introduisant des goulets d'étranglement. Il existe une multitude d'approches pour appréhender ce type cette problématique. Une méthode pragmatique consiste à envisager plusieurs cas de figure (i.e. Algorithme) qui sont ensuite mis en œuvre durant l'exécution selon une estimation de la distributivité des données [10]. D'autres plus formelle s'appuient sur des histogrammes visant à équilibrer la charge selon la fréquence des valeurs de l'attribut de jointure[11,12]. Cette étape est un élément clé du traitement parallèle d'une jointure entre deux relations. Sur la base d'un algorithme de découpage des données, la méthodologie généralement suivie afin de générer un ensemble de tâches devant exécuter chacune une partie de la jointure se décline en trois étapes qui sont : la génération des tâches, l'allocation des tâches aux nœuds et enfin l'exécution des tâches. Bien entendu ces tâches peuvent être entrelacées dans le cas où une allocation dynamique des tâches est nécessaire : il Université d'orléans Page 13/26 A. Abajjane
16 s'agit alors de mécanismes d'équilibre de charge. Nous exposons ici dans un premier temps la méthodologie de gestion parallèle des tâches puis nous donnons quelques axes d'évolution vers une gestion plus dynamique basée sur des relevés de statistiques et de ré-allocation de tâches. Gestion parallèle des tâches Comme indiqué plus haut, la gestion des tâches parallèle est généralement décomposée en trois phases : la génération des tâches, l'allocation suivie de l'exécution des tâches. Chacune de ces étapes peut être également découpée en plusieurs étapes. Génération des tâches C'est une phase clé du traitement parallèle d'une jointure. Elle a pour but de découper la jointure en un ensemble de jointures sur des sous ensemble des relations. L'union de de ces jointures devant impérativement produire le même résultat qu'une jointure directe sur la totalité des relations initiales sans découpage. Cette phase est généralement déclinée en quatre étapes qui sont : i) le découpage des relations en partitions (sous relations), ii) l'évaluation du nombre de tâches à générer, iii) le placement des tâches, iv) la collecte des statistiques. Découpage des relations Le but étant de découper les relations de jointure en sous relations de telle sorte que l'union du résultat de leurs jointures respectives produise le même résultat que la jointure des relations initiales sans découpage. Trois combinaisons de découpage des relations sont possibles : Découpage total : consiste à découper les deux relations en partitions avec l'objectif que tout tuple de l'une ou l'autre relation participe à une et une seule tâche de jointure, en d'autres termes qu'aucune réplication de tuple n'est réalisée. Cela implique que les tuples en relation doivent être regroupés au sein des mêmes partitions. Ceci est réalisable soit par découpage des relations en partitions selon des intervalles de valeurs de l'attribut de jointure. Soit par utilisation d'une fonction de hachage. Ce découpage est le plus recherché et le plus communément utilisée quand cela est possible. Découpage et réplication : ici une relation est découpée tandis que l'autre est répliquée. Généralement, c'est la relation la plus volumineuse qui est découpée tandis que la plus petite est répliquée. Ainsi chaque tâche se voit affecté d'une part une partition de la plus grande relation et, d'autre, la totalité de la plus petite relation. Cette méthode est particulièrement pertinente quand la relation répliquée est suffisamment petite pour tenir en mémoire, et dans ce cas l'usage de la jointure par boucles imbriquée avec blocs est la plus appropriée. Réplication totale : dans ce cas les deux relation sont répliquées. Les m partitions de la première et les n partitions de la seconde relation sont jointes une à une donnant lieu à n*m tâches différentes. Cette méthode peu efficace n'est utilisée que dans des situations particulières au sein d'architectures à ressources partagées. Choix du nombre de tâches L'objectif de cette étape est l'estimation du nombre optimal de tâches nécessaires au traitement des Université d'orléans Page 14/26 A. Abajjane
17 différentes partitions générées à l'étape précédente. Le but recherché est l'utilisation optimale des N nœuds élus pour le traitement, notamment en terme d'occupation mémoire. Il y a donc une corrélation directe entre le nombre optimal recherché et la taille des données à traiter. Ainsi, un nombre trop important de tâches induit un découpage extrêmement fin des données à traiter et donc une inadéquation entre le traitement effectifs et le traitement de préparation des tâches. Par ailleurs, ce découpage trop fin engendre une fragmentation des données traitées et donc un accès aléatoire au stockage avec les dégradations de performances mises en évidence plus haut. A contrario, un découpage trop grossier risque de générer des partitions dépassant les capacités mémoire des nœuds avec une efficacité moindre des jointures locales à chaque nœud. Cela limite également les possibilités d'allocation aux différents nœuds du fait du faible nombre de partitions eut égard au nombre potentiel de nœuds. En résumé, les quatre alternatives ou orientations généralement adoptées sont : a) Génération d'un nombre de tâches égal au nombre de nœuds disponibles. b) Génération d'un nombre de tâches supérieur au nombre de nœuds disponibles. Cette orientation ouvre notamment la possibilité de pouvoir allouer les tâches en fonction de critères d'optimisation. Un nœud pouvant se voir affecté plus de tâches qu'un autre. c) Génération d'un nombre de tâches supérieur au nombre de nœuds, et ajustement de nouveau de ce nombre en l augmentant au moment de l'affectation d'une tâche à un nœud. Ce choix permet un découpage plus fin d'une partition de relation avant de l'affecter à un nœud notamment pour des raisons d'occupation mémoire. d) Génération d'un nombre de tâches supérieur au nombre de nœuds, et réduction de ce nombre juste avant l'allocation au nœud. Ce choix est le complément du précédent puisqu'il permet l'augmentation des tailles de partition (par regroupement de partitions) afin d'optimiser l'utilisation des ressources mémoire d'un nœud donné. Placement des tâches Cette étape répond à un besoin purement structurel. Il s'agit en effet de savoir s'il est nécessaire de placer chaque paire de partition des deux relations au sein du nœud élu pour leur traitement ou pas. Dans la négative, les données associées à un nœud i, et donc localisées sur d'autres nœuds, devront être regroupés au préalable vers ce nœud i avant leur traitement. L'abstraction de la localisation physique des données permet une allocation dynamique des tâches aux différents nœuds disponible. Le placement de départ peut être à l'opposé de celui souhaité pour les besoins de la jointure. En effet, le placement initial répond souvent à des besoins fonctionnelles ou technique, tandis que le placement ponctuelle pour la jointure a plutôt un caractère opportuniste lié à la disponibilité des ressources (i.e. Des nœuds) à un instant t. Cette problématique se prête assez aisément à des modélisations de type graphe ou bien encore de type CSP. Une étude intéressante sur le sujet est exposée dans l'article [13] essentiellement basée sur la fréquence d'accès aux données et sur la notion de température d'un objet (i.e partition) estimée à partir de la taille de cet objet et de la fréquence d'accès. Une autre étude plutôt orientée contraintes propose un algorithme de pilotage continue du placement des données pour un traitement parallèle : elle part d'un état optimal de placement et maintiens cet état tout au long de l'exécution[14]. Collecte des statistiques La collecte de données statistiques est particulièrement nécessaire dans le cas d'allocation dynamique. Ces informations sont utiles afin de permettre l'ajustement dynamique des affectations de tâches aux nœuds. Si pour diverses raisons aucune statistique n'est collectée, alors les tâches sont affectées de Université d'orléans Page 15/26 A. Abajjane
18 manière arbitraire. Pour un pilotage optimal des affectations de tâches, les deux valeurs essentielles sont la taille des différentes partitions et la taille du résultat de jointure attendues pour une paire de partitions donnée. Cependant, seul le premier indicateur est disponible tandis que le second ne peut qu'être approximé. Une approche proposée dans l'étude [X6] exprime la taille du résultat global de la jointure par la formule : e i=1 s i d i où, e est le nombre de classes d'équivalence des attributs de jointure, r i et s i le nombre de tuples des relations R et S appartenant à la classe, d i le nombre d'attributs distincts au sein de la classe d'équivalence. On remarquera que cette approximation est exacte pour le cas théorique où d i = 1, et dans ce cas le nombre e de classes est égale au nombre d'attributs distincts des deux relations. Sur la base de cette approximation et de la taille des partitions, il est alors possible d'estimer le temps d'exécution d'une jointure. Affectation des tâches Une fois les relations de jointure découpées, on dispose d'un ensemble de tâches à affecter aux différents nœuds pour un traitement parallèle. Deux modes d'affectations peuvent êtres mis en œuvre, à savoir l'allocation statique ou bien dynamique (i.e. avec équilibre de charge). Chacune de ces méthodes est mise en œuvre dans des situations appropriées : Mesures de charge allocation statique : elle exige une gestion minimale de l'affectation puisque les tâches sont affectées une fois pour toute aux nœuds élus pour le traitement. Cette approche peut s'avérer efficace si d'une part l'ensemble des nœuds ont la même capacité de traitement et, d'autre part, les données sont équitablement distribuées. Dans le cas contraire, les temps de calcul globaux peuvent s'avérer incertains voir désastreux [9]. Allocation dynamique avec équilibre de charge : sur la base d'un découpage adapté des relations de jointure, et donc d'un nombre suffisamment important de tâches à affecter, il est possible de piloter l'allocation en veillant à ce que les temps d'exécution soient approximativement les mêmes à travers tous les nœuds qui participent au traitement. L'une des stratégies les plus utilisées afin de maintenir cet équilibre de charge est celle dite best-fitlike qui consiste à : trier les tâches de manière décroissante selon un critère donné puis, selon un algorithme glouton, affecter la tâche suivante au nœud qui est sur le point de terminer sa tâche courante. Cette méthode se décline selon deux axes qui sont les mesures utilisées et la stratégie d'allocation choisie. Une étude dans un contexte d'architecture de type Sharednothing a fait usage d'une telle méthode, mais en ramenant cette architecture un architecture de type mémoire virtuelle partagée[15] Il s'agit là de mesures prédictives visant à évaluer la charge associée à chaque tâche. Ces mesures sont essentiellement celles exposées dans le chapitre «Collecte des statistiques» où une approximation est développée. Taille des partitions : sur la base de cette mesure, le but est de garantir que l'ensemble des nœuds traitent le même nombre de tuples. Pour un bon équilibre de charge, cela suppose que les relations de jointure sont bien distribuée sur l'attribut de jointure, et donc que le temps d'exécution est proportionnel au nombre de tuples traités. Université d'orléans Page 16/26 A. Abajjane
19 Temps d'exécution estimé : sur la base d'un temps d'exécution estimé les tâches sont distribuées de tel sorte que l'ensemble des nœuds se voient affecté la même durée totale de traitement. Dès lors qu'il est possible d'estimer correctement à moindre coût le temps élémentaire d'exécution, cette mesure devient la plus pertinente. Stratégie d'affectation Sur la base des mesures de charge, deux stratégies sont possibles : statique ou dynamique. La première consiste à affecter une fois pour toutes les tâches de façon équitable aux différents nœuds et sur la base des critères de charge susmentionnés. Si ces mesures sont justes, alors cette approche donne d'excellents résultats. La seconde stratégie nécessite un pilotage tout au long des traitements afin que chaque nœud se voit affecté une tâche dès lors qu'il a terminé sa tâche courante, et pas avant. Il semblerait que cette approche n'ait pas donné lieu à des études approfondies dans le cadre des architectures distribuées. En effet, le placement des données est très coûteux dans ce cas, car il s'avère souvent primordial qu'un nœud connaisse à l'avance les tâches qui lui sont affectées afin d'anticiper leur transfert vers ses ressources locales et leur fusion si nécessaire. Exécution des tâches A ce stade, chaque nœud dispose d'une ou plusieurs tâches à traiter localement. Et les seules interrogation qui subsistent est de savoir si une gestion de la charge de travail est possible et quel algorithme est le plus approprié pour exécuter la jointure des partitions locales. La gestion de la charge se décline selon deux possibilités : Aucune redistribution à posteriori : dans ce cas une fois les tâches affectées au nœud, elles devront être menées à bien par ce nœud quelque soit l'issue en terme de charge. Cela est notamment le cas lorsqu'on considère que l'essentiel du travail d'équilibre a été correctement réalisé en amont. Redistribution de charge : dans cette configuration tout ou partie d'une tâche peut être réaffectée par le nœud à qui elle a été initialement assignée en cas de surcharge de celui-ci. Plusieurs méthodes de redistribution de tâche peuvent êtres mises en œuvre. Celles-ci sont soit initiées par le nœud surchargé à destination d'un nœud libre, soit initiées par le nœud libre qui récupère une ou plusieurs tâches à un nœud surchargé, comme dans l'approche par «vol de tâches». Quant au choix du meilleur algorithme de jointure locale, il est orienté selon les principes exposés dans le précédent chapitre. On retiendra les situations suivantes : L'algorithme par boucles imbriquées est appropriée quand l'une des partitions est suffisamment petite pour tenir en mémoire ou quand on dispose d'un index sur la partition inner. L'algorithme par tri-fusion est le plus approprié si les partitions sont déjà triées. L'algorithme basé sur une fonction de hachage s'avère le plus pertinent dès lors que le nœud dispose de suffisamment de mémoire et que les valeurs de l'attribut de jointure sont uniformément distribuées. Équilibrage de charge Nous avons jusqu'à maintenant exposé les mécanisme de création et répartition des tâches entre différents nœuds, en mettant en évidence des leviers permettant de procéder à un équilibre de charge soit Université d'orléans Page 17/26 A. Abajjane
20 statique, c'est à dire évaluer une fois pour toute lors de la première affectation des tâches, ou bien dynamique, et donc ajusté au fil du temps en fonction du déroulement des traitements au sein de chaque nœud et de leur niveau de charge effectif. Nous allons maintenant apporter plus de précisions à ce sujet qui nous intéresse au plus haut lieu. Ces deux type d'équilibrage de charge est utilisé dans des cas biens précis : dan le cas d'une bonne distribution des valeurs d'attribut de jointure pour le premier, et, dans le cas où cette donnée n'étant pas maîtrisée, il subsiste un risque majeur de dégradation des performances et donc d'augmentation importante de la durée nécessaire au traitement global. Équilibrage de charge statique Une estimation du temps global ainsi que du temps nécessaire à chaque tâche est effectuée juste avant l'affectation des tâches aux nœuds. Sur cette base, les tâches sont ensuite affectées de façon à minimiser le temps total nécessaire à la jointure des deux relations R et S. Un tel mécanisme peut être implémenté selon l'algorithme suivant : i) Dans un premier temps, un nombre de tâches, généralement supérieur au nombre de nœuds disponibles, est produit. Selon que l'on s'oriente vers l'une ou l'autre méthode de découpage des relations, à savoir le «découpage total» ou le «découpage et réplication» exposés plus haut, chaque tâche est soit une jointure entre deux partitions de R et de S dans le premier cas soit, dans le second cas, la jointure entre une partition de la plus grande des deux relation et la totalité de la plus petite. Ainsi, chaque nœud qui détient déjà des partitions (fonctionnelles) procède au découpage de celles-ci en partitions technique (à des fins de jointure) en les chargeant en mémoire à hauteur de ce qui lui a été assigné en terme de tâches. Une fois la limite de ses tâches atteinte, le reste des partitions est envoyé vers les nœuds auxquels ces les tâches correspondant à ces partitions ont été affectées. ii) Une fois les partitions produites, chaque nœud collecte les informations relatives à ces partitions sur la base des partitions fonctionnelles qu'il détenait. Et, une fois le découpage et les collectes statiques réalisées, chaque nœud estime le temps nécessaire au traitement de chaque tâche qui lui a été assignée. Un nœud coordinateur récolte alors l'ensemble de ces statistiques et calcul le temps moyen nécessaire pour la réalisation de la jointure globale qui est le temps nécessaire pour que tous les nœuds aient effectué leurs tâches respectives. iii) Sur la base de ces estimations, chaque nœud identifie le nombre minimum parmi les tâches préaffectées de tel sorte que : k j=1 k+1 Coût j Coût moy Coût j >Coût moy j=1 Coût j le temps nécessaire pour réaliser la tâche j et, Coût moy le temps moyen nécessaire pour réaliser l'ensemble des tâches Toutes les tâches supérieures à la k ème tâche d'un nœud sont alors considérées comme un surplus de travail pour ce nœud et sont affectées à un autre nœud. Dans le cas contraire, si k est inférieur au nombre de tâches pré-affectées à ce nœud alors ce nœud est considéré comme potentiellement capable de prendre en charge d'autres tâches, et se voit, le cas échéant affecté des tâches de nœuds surchargés de façon à ramener la durée de traitement de chaque nœud sous la durée moyenne de traitement globale (Coût moy ). avec, iv) Chaque nœud procède alors à la réalisation de ses jointures locales, sans ré-affectation possible même en cas de surcharge avérée. Université d'orléans Page 18/26 A. Abajjane
21 Équilibrage dynamique Ce mode d'équilibrage de charge autorise le transfert de tâches d'un nœud à l'autre durant la phase d'exécution. A cette fin, il est nécessaire d'une part, au sein de chaque nœud, de maintenir les informations relatives au traitement en cours, à savoir la quantité de données traitées et la quantité de données générées en résultat. D'autre part, il appartient à chaque nœud qui a terminé l'ensemble de ses tâches ou en phase finale de ses traitements de signaler cet état. Ainsi, s'il existe un nœud n'ayant pas encore terminé ses tâches, alors une estimation de la quantité à transférer est réalisée puis transmise au nœud demandeur. Bien entendu, un ensemble de surplus de tâches d'un nœud peut également être partagé entre plusieurs nœuds demandeurs. On notera que l'identification du demandeur est aisée puisque c'est lui même qui initie la demande dès lors qu'il a terminé l'ensemble de ses tâches. A contrario, il n'est pas toujours aisé d'identifier le donneur (le nœud en surcharge) et a fortiori la quantité de données que celui-ci peut transférer compte tenu d'un ensemble de critères d'optimisation. Cette démarche suit une stratégie qui peut être déroulée selon l'algorithme suivant : i) Le nœud libre émet une demande de tâches à un coordinateur ii) Le nœud coordinateur met en attente le nœud demandeur selon le principe FIFO, puis émet une demande à l'ensemble des nœuds afin de connaître leur état de charge. iii) Dès réception de la demande, chaque nœud élabore sa charge courante puis la transmet au coordinateur. iv) Le coordinateur effectue les estimations nécessaires, détermine le donneur approprié à qui il transmet la requête du demandeur (le nœud libre), puis passe à la demande suivante. S'il y un nombre important de demandes et d'offres, le coordinateur peut réaliser des réponses groupées en mettant en relation les k premiers donneurs avec les k premiers demandeurs en attente. v) Le donneur reçoit l'identité du demandeur à qui il transmet la quantité de données qu'il aura déterminé au préalable. Le processus est poursuivi jusqu'à la fin des traitements, l'objectif étant que la durée globale des traitements soit aussi minimale que possible. Pour une implémentation correcte de tout algorithme d'équilibre de charge, beaucoup de questions doivent auparavant être soulevées : Quelles sont les informations les plus pertinentes que chaque nœud doit collecter, en évitant de générer un surplus de travail de collecte d'informations inexploitables. Qui doit initier la demande d'équilibre de charge : le nœud libre ou le nœud surchargé. Quels sont les critères de choix du donneur. Quelle est la quantité optimale de donnée à transférer pour répondre à une demande. En fait, les principaux indicateurs sont basés sur le nombre de pages déjà traitées ainsi que le nombre de pages générées comme résultat par un nœud. Ce qui implique que l'initiateur de la demande de transfert de charge est le le nœud ayant terminé (ou sur le point de terminer) ses tâches. Cette facette de l'équilibrage est très peu dépendante des caractéristiques propres au nœud ainsi que de la méthode de jointure utilisée. De l'autre côté, l'estimation de la quantité exacte de données à transférer d'un nœud donneur vers le nœud demandeur est fortement liée au système hôte et à la méthode de jointure. Ainsi, si le temps de fin de traitement (qu'on nommera ECT) est l'indicateur de charge d'un nœud, alors le processeur dont le ECT est le plus grand sera systématiquement désigné comme donneur en réponse à une demande. Et ainsi, si i est le nœud donneur et p le nombre de nœuds participant au traitement, alors i doit vérifier la relation suivante : Université d'orléans Page 19/26 A. Abajjane
22 i= Argmax(ECT i ), j [1, p] et, k ECT i = EET ij +EFT i où k est le nombre de tâches de i non encore traitées. j=1 Le terme k ECT i = EET ij est le temps d'exécution totale nécessaire pour achever les k tâches j=1 restantes. Il est estimé à partir des statistiques collectées au sein du nœud, qui sont dépendant du type de jointure utilisé, ainsi que de la taille des relations de jointure. Sur la base de ces éléments EET est donnée par : EET=CoûtJointure( R, S, Résultat ) avec Résultat est la taille estimée en nombre de pages du résultat de la jointure. R et S étant, en nombre de pages, les tailles respectives des partitions R et S. Et la quantité EFT est le temps nécessaire pour terminer la tâche courante incluant les pages en cours des partitions de la tâches. Il est exprimé par la formule : EFT=CoûtJointure(absR, S, Résultat ) CoûtJointure( r, s, res ), avec res le résultat en nombre de page déjà produit et, r et s les quantités de pages des partitions R et S déjà traitées. Ces données sont facilement estimables sur la base des logs de traitement. Et, en conclusion, l'estimation de la quantité de données efficacement transférable d'un donneur vers le demandeur peut être réalisée selon les heuristiques pertinente suivantes : I) Priorité aux tâches non consommées : s'il existe une tâche qui n'est pas en cours de traitement par le donneur, alors celle-ci sera transférée. En effet, transférer une partie d'une tâche en cours de traitement peut s'avérer extrêmement compliqué et pénalisant, puisque fatalement une partie du travail réalisée devra être réalisée à nouveau sur le nœud demandeur. C'est notamment le cas pour les algorithme utilisant une table de hachage. Toutefois, cette méthode bien que fortement déconseillée, est tout à fait envisageable. II) La quantité de données transférée doit être suffisamment grande afin de garantir un gain significatif pour le temps d'exécution globale : la gestion des transferts entraîne nécessairement une surcharge de travail qui doit être compensée par une quantité de données suffisante. III) La quantité de données transférée ne doit pas être excessivement importante au point que le temps de fin de traitement du demandeur dépasse celui du donneur : cette heuristique envisage le transfert d'une tâche vers plusieurs demandeur si cela s'avère nécessaire, plutôt qu'uniquement vers un seul nœud demandeur. Université d'orléans Page 20/26 A. Abajjane
23 Synthèse La gestion du parallélisme, comme nous l'avons exposé, est faiblement liée aux algorithmes utilisés pour la jointure. Toutefois certaines méthodes de jointure peuvent mieux s'apprêter à ce contexte. On évitera ainsi l'utilisation de la jointure par fonction de hachage quand on souhaite mettre en œuvre un équilibre de charge dynamique «poussé». On favorisera celle ci dès qu'on envisage un équilibre de charge statique. Par ailleurs, ce qui fonctionne pour des environnements parallèle de type SMP mais également NUMA ne fonctionne pas nécessairement pour des architecture totalement distribuées ne partageant aucune ressource physique ou logique (sharing-nothing). En effet, dans le premier cas, une stratégie d'affectation ne transférant les données d'un nœud à l'autre qu'au début effectif du traitement de ces données par ces nœuds est tout à fait envisageable. Le nœud donneur s'il ne partage pas de la mémoire ou du disque avec le demandeur partage au moins un bus interne permettant des transfert rapides et peu coûteux. Dans le cas des architecture distribuées, le placement des données est un enjeu majeur. On veillera autant que possible à positionner les données d'une tâche avant le début du traitement de celle-ci afin d'absorber les latences nécessaires à leur transfert. On veillera également à favoriser le traitement par le nœud qui détient déjà des partitions des relations de jointure, en le soulageant du surplus de travail, selon les méthodologies exposées, en adéquation avec la durée fixée (ou estimée) pour le traitement global. Par ailleurs, la philosophie de la parallélisation dans l'une et l'autre architecture peut être diamétralement opposé. En effet, si dans le cas d'architecture partagées on recherche à tirer profit d'un certain nombre de processeurs appartenant à un même système, dans le cas des architectures de type sharing-nothing on est amenés à réaliser des opérations ne pouvant raisonnablement êtres menées à bien que par le parallélisme imposé par la dissémination des données à travers un vaste réseau. La quasi-totalité des études menées dans ce sens sont exclusivement tournées vers le premier type d'architecture. Pour notre problématique, une difficulté supplémentaire consiste à choisir parmi toutes les méthodologies étudiées celles compatibles avec notre contexte. Enfin, on note également que les architectures qui nous intéressent ici ne partagent également aucune ressource système. Il s'agit de machines distribuées à travers un vaste réseau, pouvant dans certains cas exécuter des systèmes assez différents les uns des autres. Et donc, il n'est pas envisageable de baser les traitements sur un mécanisme supposant une quelconque cohérence à travers les nœuds utilisés. Il s'avère de facto nécessaire d'utiliser une surcouche logiciel visant à homogénéiser la relation entre les différents nœuds. Nous exposons dans le chapitre suivant ce que devrait être un tel FrameWork en nous basant sur celui proposé par Google, nommé Map-Reduce [16], et son extension Map-Reduce-Merge[17]. Université d'orléans Page 21/26 A. Abajjane
24 Mise en œuvre du parallélisme en architecture de type «Shared-nothing» Problématique Les jointures dans des environnements shared-nothing en vaste réseau présentent des difficultés particulière et des obstacles techniques pour lesquelles les SGBDR traditionnels n'offrent pas de solution efficace. L'un de ses obstacles est la pauvreté de la structure des fichers matérialisant les relations à joindre. Un autre obstacle est la dissémination des partions des relations de jointure à travers ce vaste réseau. Un autre obstacle majeur est l'hétérogénéité des machines (à moindre coût) qui hénérgent les partions et qui peuvent êtres intégrées aux traitements. Le modèle de programmation «Map-Reduce» [16] répond à cette nécessité de traiter des quantités importantes de données, au sein de vastes réseaux de machines, tout en offrant une transparence quasi complète des aspects parallélisation de ce traitement et du système hôte du traitement. Dans son utilisation initiale, il est destiné au traitement de données homogènes et n'offre pas de mécanismes de traitement direct d'une jointure. En effet, une jointure est une opération entre deux tables (i.e fichiers) distincts n'ayant pas nécessairement le même schéma et partageant au minimum un attribut dit de jointure. Pour couvrir directement le domaine des jointures, une extension nommée «Map-Reduce-Merge» [17] est proposée : l'adjonction d'une troisième étape ayant pour fonction la combinaison des données issues des deux premières étapes : Map et Reduce. Nous décrivons dans un premier temps le fonctionnement du modèle Map-Reduce afin d'exposer le champ d'application du mécanisme et, inductivement, explorer ses limites. Nous décrivons ensuite l extension basée sur l'adjonction de la fonction merge, nous énumérons son apport puis nous exposons quelques cas d'utilisation. Map-Reduce Map-Reduce est un modèle de programmation dont les principales motivations sont le traitement ( data processing ), à moindre coût, de données importantes au sein d importants réseaux de machines tout en offrant des temps d'exécution satisfaisants. Comme indiqué précédemment, Map-Reduce travaille sur des données homogènes. Le concept est basé sur deux fonctions standards map et reduce. Dans un premier temps, la fonction map, instanciée autant de fois que nécessaire, prend en entrée les données initiales faisant l'objet du traitement et les restitue sous forme d'une liste de tuples du type <Clé, Valeur>. Dans un second temps, la fonction reduce, également instanciée, fusionne les valeurs ayant la même clé pour produire une nouvelle liste de valeurs uniquement. La sémantique de ce mécanisme est indiquée par la description «formelle» suivante : map : (k 1, v 1 ) [(k 2, v 2 )] reduce : (k 2, [v 2 ]) [v 3 ] La structure et le contenu des champs Clé et Valeur ainsi que la nature des traitements sont laissés à la discrétion du développeur. De l'autre côté, la parallélisation, l'optimisation des traitements et la tolérance aux pannes sont totalement gérés par le mécanisme Map-Reduce. Le développeur ne se souciant alors à aucun moment de ces aspects purement techniques. Pour ce faire, et afin de faciliter la mise en œuvre de ces mécanismes inhérents aux systèmes parallèles, Map-Reduce s'appuie sur «Google File System» [18] qui est un système de fichier distribué. Map prend sa source dans des fichiers GFS et reduce produit ses sorties également vers un fichier GFS. Le Goole File System assure la gestion de ces fichiers, plus ou moins volumineux, sous forme de partitions (Chunks) distribuées et partagées à travers un vaste réseau informatique. Ce service offre une abstraction complète quant à la localisation des fichiers faisant l'objet du traitement, ainsi que de la nature de leur système hôte, et assure également leur redondance et leur sécurité. Néanmoins, le mécanisme Map-Reduce peut être amené, pour des raisons d'optimisation, à tenir compte de l'affinité d'un nœud élu pour un traitement map avec une ou plusieurs partitions (i.e. chunks) d'un fichier. Les structures des fichier des fichiers d'entrée et de sortie sont laissés à l'entière discrétion de l'utilisateur. Contrairement à l'application BigTable [19] qui propose un modèle de donnée simple et une Université d'orléans Page 22/26 A. Abajjane
25 structure des fichiers en matrice, Map-Reduce permet manipule des fichiers bruts que l'utilisateur manipule selon ses besoins, extrait éventuellement une partie des informations disponibles et produit des fichiers bruts en sortie. Contrairement au concept «Data Aggregation Acces» [20] qui propose le paramétrage d'un niveau de qualité, Map-Reduce ne propose pas de tel mécanisme et donc, dans la forme, une exécution est complète ou abandonnée. Bien qu'initialement conçu pour la mise en œuvre de moteur de recherche, Map-Reduce a depuis fait ses preuves en servant de base de développement à de multiples autres applications. Ces applications manipulent des données de l'ordre de plusieurs Téraoctets et s'appuient sur des milliers de «serveurs» ; ce qui démontre l'adaptation à grande échelle de ce mécanisme. La nature de ces traitements est essentiellement la recherche de documents à travers un vaste réseau ou encore l'analyse de logs de recherche Web. Ainsi l'utilisation première pour laquelle Map-Reduce a été conçue est largement couverte, bien au delà de l'objectif premier. Ce qui est la garantie d'une bonne robustesse. Mais l'extension des Systèmes d'information et de leur besoin fait apparaître d'autres obstacles pour lesquelles Map-Reduce n'offre pas une solution directe et satisfaisante. Ainsi, la nécessité de composer avec divers sources d'informations met en évidence les limites de ce mécanisme. En effet, il est extrêmement difficile sur la base du mécanisme initiale, de recouper par exemple les données d'une compagnie A avec celle d'une autre compagnie B afin d'en tirer un certain nombre d'enseignements. De façon plus précise, la notion de jointure n'est en l'état pas couverte sans utiliser un mécanisme basé sur deux phases Map-Reduce qui nécessite une manipulation (coloration) des données intermédiaires. Map-Reduce-Merge Map-Reduce-Merge se positionne comme une continuité du mécanisme initial Map-Reduce avant de fournir des solutions aux à des problématique apparemment non couvertes par le modèle de base. Cette nécessité de continuité ne concerne pas seulement les aspects fonctionnels mais elle est également étendue aux aspects ergonomiques, à savoir une utilisation aisée et une transparences totale de la gestion des mécanismes de parallélisation, d'optimisation et de tolérance aux pannes. Toutefois, une sensible complexification du Workflow, linéaire dans le premier cas, peut ne pas être évitable suite à l'ajout de la troisième primitive Merge. Grâce à cette extension, Map-Reduce-Merge est en mesure de couvrir la plupart des types de jointure parallèles incluant le hash-join, le netsted-loop ou encore le sort_merge. La sémantique de cette extension étant alors décrite par les règles suivantes : map : (k 1, v 1 ) α [(k 2, v 2 )] α Ici α et β sont les deux chaînes de traitement Map-Reduce reduce : (k 2, [v 2 ]) α (k 2,[v 3 ]) α portant sur deux fichiers distincts, chacune de ces deux merge : ((k 2,[v 3 ]) α, (k 3,[v 4 ]) β ) ([k 2,v 5 ]) γ chaînes produit une entrée pour Merge, qui produit à son tour γ. Les étapes Map et Reduce initiales restent identiques à celles du mécanisme de base, à la différence près que la sortie produite par la fonction merge inclut la clé pour chaque valeurs associées à cette même clé (ici k 2 et [v 3 ]). Le maintien de cette clé, ainsi que le tri selon cette clé, est absolument nécessaire à la fonction merge afin de fusionner correctement (i.e. traiter selon la méthode requise) les données issues des lignes de traitement α et β, ayant la même valeur de clé. Un exemple concret de mise en œuvre de cette méthode : le calcul des primes annuels d employer rattachés à différents départements. Deux structures de données hétérogènes sont ici manipulées. La première est le fichier des différentes primes octroyés à chaque employer, un employer pouvant être bénéficiaire de plusieurs type de primes (assiduité, efficacité, etc...), dont la structure est : <id-employer, id-département, description_bonus>. La seconde est le fichier des département référençant les coefficients globaux appliqués aux primes des employer d'un département donné, dont la structure est : <id-département, coefficient_bonus>. L'un et l'autre fichiers sont traités par deux chaînes Map-Reduce distincts. La première chaîne produit une table agrégée des primes par employer (avec un unique enregistrement par employer) triée selon la clé «id-dep» puis «id-emp», la seconde produit l'ajustement des bonus par département qui est ensuite triée par la fonction merge selon la clé «id-dep». Enfin la fonction merge élabore la prime finale en réalisant les opérations de jointure puis de produit, pour chaque employer, des primes et du coefficient d'ajustement associé à chaque département. L'implantation du mécanisme Map-Reduce-Merge s'appuie sur la librairie initiale de Map-Reduce Université d'orléans Page 23/26 A. Abajjane
26 avec toutefois quelques modification sur les signatures des fonctions. Cette librairie est ensuite augmentée par la fonction merge ainsi que d'autres fonctions utiles : processor, partition selector et configurable interator. La fonction merge met en œuvre le même mode opératoire que les fonctions map et reduce. A savoir, la possibilité offerte au développeur de définir la suite d'actions à appliquer aux deux paires <Clé, valeurs> issues des deux chaînes de traitement. Dans cette phase de merge, le développeur peut également s'appuyer sur la fonction processor afin d'appliquer des traitements particuliers aux données sources. Le partition selector quant à lui, en se basant sur le numéro du merger, affecté par le coordinateur global, identifie les données sources à traiter. Enfin un «itérateur configurable» (ou iterator manager) est utilisé afin de synchroniser les deux sources de données du merger. Car contrairement au reducer, qui utilise également un iterator mais basé sur une source unique de données, le merger offre à l'utilisateur la possibilité de manipuler l'une ou l'autre source de données, selon un mode opératoire particulier en fonction du type de jointure à mettre en œuvre. Par ailleurs, l'iterator est la technique qui couvre, dans les deux cas (Map-Reduce et Map-Reduce-Merge), la lecture à la volée de l'entrée, évitant ainsi le stockage sur disque local des données intermédiaire. Portée du modèle Map-Reduce-Merge L'une des principales ambitions de Map-Reduce-Merge est de doter les mécanismes de traitement parallèle d'une dimension relationnelle à l échelle des moteurs de recherche. En effet, Map-Reduce-Merge se présente en SGBD relationnel, comme nous l'illustrons ci-après, tout en apportant des fonctionnalités d'optimisations relatives aux contraintes de parallélisme. Si on Considère une relation R structurée selon un schéma A. Le développeur Map-Reduce-Merge peut alors décomposer, selon ses besoins, ce schéma en deux parties K et V. Ici K représente le schéma de la clé k et V celui de la valeur v, un tuple t de R est alors représenté par la concaténation des champs k et v, correspondant ni plus ni qu'aux clés et valeurs manipulées par Mep-Reduce-Merge. Ceci posé, il est possible de réaliser l'ensemble des opérations attendues d'un SGBD relationnel, il suffit pour ce faire d'élaborer le worklow adéquat afin d'appliquer les traitements successifs aux tuples initiaux. De cette façon les réalisations suivantes et bien d'autres sont aisément envisageables : la projection apparaît dans ce contexte triviale, seules les étapes map et reduce sont mises en jeu et produisent en sortie un tuple t' = (k', v') dont les schémas respectifs K' et V' sont une sous partie du schéma A. La jointure est quant à elle décrite dans l'exemple exposé dans ce document. Elle est réalisable selon l'ensemble des variantes standards. L'intersection se fait selon le même mode opératoire que la jointure aux étapes map et reduce, le merger n'ayant alors plus qu'à itérer sur l'une et l'autre entrée des deux reducer afin de restituer les tuples t partagés par l'une et l'autre relation. Le produit cartésien est également facilement réalisable par lecture des sorties des deux reducer et composition par le merger des combinaisons des tuples de l'une et l'autre entrée. Une composition simple ou complexe,selon les cas, de ces fonctions rend possible la réalisation de tout type de traitement nécessitant le recoupement entre deux sources de données ou plus. Ceci est notamment possible grâce à une imbrication, assez naturelle, de plusieurs processus Map-Reduce-Merge. Synthèse Le concept Map-Reduce augmenté par le Merge semble être un outils extrêmement efficace pour la réalisation de programmes parallèles mettant en œuvre une foultitude de machine plus ou moins hétéroclites en terme de configuration, de puissance de calcul ou encore de fiabilité. C'est en fait, le principal challenge que se sont fixé l'outil Map-Reduce et son extension Merge. A savoir, l'exploitation de serveurs (i.e. Machines) disponibles à travers un vaste réseau (Internet), mettant en œuvre des traitements pouvant s'avérer lourd, coûteux et peu efficaces s'ils devaient être réalisés sur des serveurs dédiés et conçus pour cet usage. L'autre challenge est de proposer un modèle de programmation générique masquant autant que possible les fonctionnalités inhérentes au parallélisme telles que la tolérance aux pannes ou encore l'équilibrage de la charge des machines ; ceci est notamment facilité par l'utilisation de GFS. Par ailleurs, contrairement au concept «Data Aggregation Call» orienté service et qui admet des solutions partielles (niveau de qualité de service paramétrable), Map-Reduce-Merge se fixe des objectifs de résultats déterministes et complets en terme de restitution des traitements. Université d'orléans Page 24/26 A. Abajjane
27 Si la fonction Merge étend de façon favorable les possibilités de Map-Reduce et en fait un concept extrêmement puissant, elle présente néanmoins un certain nombre de limitations techniques mises en évidence de façon explicite dans l'implémentation du Hash-Join. Ailleurs, cette limitation est moins explicite mais non moins vraie : c'est le cas de l'implémentation du produit cartésien. De façon générale, dès lors que les données à traiter par le merger nécessitent plusieurs passes, il s'avère inévitable de stocker les données intermédiaires en local marquant ainsi une rupture avec le concept Map-Reduce favorisant quant à lui le traitement des données au fil de l'eau afin d'éviter ce type de désagrément. Par ailleurs, les mises en œuvre de jointures passent sous silence le déséquilibre des données traitées. Une autre alternative visant plutôt à doter le concept initial d outils plus puissants, lui ouvrant d autres perspectives, au lieu de l augmenter par une troisième primitive est également envisageable. Dans l un et l autre cas, repenser la dynamique de Map- Reduce, notamment la coordination (et instantiation) des processus map et reduce aujourd hui brutale, semble nécessaire pour garantir une plus grande souplesse du concept, et une réelle scalabilité. Toutefois, le FrameWork Map-Reduce ayant à ce jour fait ses preuves, il est aujourd'hui implémenté par divers organismes : Google, Yahoo ou encore Apache. Il semble donc incontournable dans le cadre d'expérimentations techniques d'exécution de requêtes de jointure au travers un vaste réseau. Le FrameWork Map-Reduce-Merge n'est à ce jour pas finalisé puisqu'il ajoute un nombre assez important de primitive en plus de la primitive Merge. Et, à ce titre sauf pour des travaux spécifiques à cette extension, il est préférable de s'appuyer sur le FrameWork initial Map-Reduce. Conclusion Le traitement de jointure en environnement totalement distribué présente de multiple facette. Des difficultés sont rencontrées à chaque étape, et à chaque une multitude de solutions sont possibles. Toutefois, les études menées à ce jour dans ce domaine se limitent souvent soit à des architecture partageant une ressource efficace en matière d'échange de données : disques, bus, réseau dédié..., soit elles s'appuient sur des hypothèses simplificatrices sur la bonne distribution des données. Malgré tout, comme tenu des différents méthodes exposées ici, il est possible de mettre l'accent sur certaines orientations qui sont les suivantes : a) Le placement des données est essentiel, car de lui dépend la minimisation du transfert des données à traiter. b) On veillera à suffisamment découper les relations de jointure afin de limiter les temps de transfert d'une tâche, tout en n'ayant pas besoin de recourir à un second découpage de ces tâches afin d'en distribuer la charge entre deux nœuds. Cela est d'autant plus aisé que le nombre de nœuds dans ce contexte peut être très important. Toutefois cette démarche est à mener de façon cohérente avec le premier point. c) On favorisera autant que possible la recherche de mesures pertinentes visant à nous donner les moyens de procéder à une distribution initiale des traitements la plus efficace possible. Ainsi, dans le meilleur des cas on pourra se cantonner à l'équilibre de charge statique. Dans le pire des cas, si on doit envisager un équilibrage de charge dynamique, celui-ci pourra être utilisé comme levier d'appoint afin d'ajuster légèrement la distribution initiale. d) Sauf dans le cas où les données sont déjà triées, et dans ce cas la jointure par tri-fusion est fatalement la plus performante, on s'orientera systématiquement vers la jointure par boucles imbriquées avec blocs ne nécessitant aucun pré-traitement et dont la durée d'exécution est aisément prévisible. e) Nous veillerons, autant que possible, à utiliser les mêmes algorithmes de jointure au sein de tous les nœuds qui participent au traitement. Ainsi, les mesures collectées et les prévisions réalisées sur la base de ces mesures sont aisées et globalement cohérentes étant donné le nombre important de nœuds qui peuvent êtres mis en jeu. f) Compte tenu du faible coût d'utilisation d'un nœud, au cas où la fin du traitement d'un nœud semble fortement compromise, plutôt que de l'interrompre ou lui retirer un certaine quantité de tâches, on Université d'orléans Page 25/26 A. Abajjane
28 préférera initier la redistribution des tâches qui lui sont affectées et non encore traitées vers un ou plusieurs nœuds disponibles. Si celui-ci venait à finalement terminer ses tâches dans le temps imparti son résultat pourra être intégré au traitement global et les autres traitements abandonnés. g) Tant que cela est possible, on maintiendra les partitions du résultat d'une jointure au sein des nœuds les ayant élaborés. Aucune consolidation de ces partitions n'est à priori envisagée. Bibliographie [1] H. Lu, B.C. Ooi, K.L. Tan. Query Processing in Parallel Relational Database Systems. IEE Computer Society Press [2] D.J. DeWitt, J.F. Naughton, J. Burger.Nested Loops Revisited [3] M. Kitsuregawa, H. Tanaka, T. Moto-oka. Applications of Hash to Data Base Machine and its Architecture [4] D. J. DeWitt, R. Gerber. Multiprocessor Hash-Based Join Algorithms [5] B.R. Iyer, G.R. Ricard, P. J. Varman. Percentile Finding algorithm for Multiple Sorted Runs [6] D. J. DeWitt, J. F. Naughton, D. A. Schneidery. Parallel Sorting on a Shared-Nothing Architecture using Probabilistic Splitting [7] D. J. DeWitt, R. Gerbe. Multiprocessor Hash-Based Join Algorithms [8] D. A. Schneider, D. J. DeWitt. A Performance Evaluation of Four Parallel Join Algorithms in a Shared-Nothing Multiprocessor Environment [9] M.S. Lakshmi, P.S. Yu. Effectiveness of Parallel Joins [10] D. J. DeWitt, J. F. Naughton, D. A. Schneidery, S. Seshadri. Practical Skew Handling in Parallel Joins [11] M. Bamha. An Optimal Skew-insensitive Join and Multi-join Algorithm for Distributed Architectures [12] M. Bahma, G. Hans. A skew-insensitive algorithm for join and multi-join operations on Shared Nothing machines [13] G. Copeland, W. Alexander, E. Boughter, T. Keller. Data Placement In Bubba [14] D. K. Lowenthal, G. R. Andrews. An Adaptive Approach to Data Placement [15] A. Shatdal, J.F. Naughton. Using Shared Virtual Memory for Parallel Join Processing [16] J. Dean and S. Ghemawat. MapReduce: Simplified data processing on Large Clusters. In OSDI, pages , [17] H. Yang, A. Dasdan, R.L. Hsiao, D. Stott Parker. Map-Reduce-Merge: Simplified Relational Data Processing on Large Clusters [18] S. Ghemawat, H. Gobioff and S.-T. Leung. The Google sile system [19] F. Chang et al. Bigtable: A Distributed Storage System for Structured Data [20] L. Chu et al. Optimiing Data Aggregation for Cluster-based Internet Services Université d'orléans Page 26/26 A. Abajjane
29 PARALLÉLISME ET ÉVALUATION DE PERFORMANCES DES JOINTURES ET SEMI- JOINTURE SUR DES ARCHITECTURES CLOUD MÉMOIRE DE RECHERCHE MASTER 2 RECHERCHE INFORMATIQUE Abdeljalil ABAJJANE Université d Orléans Septembre 2012 Référant : Mostafa BAMHA (LIFO) Tuteur : Frédéric LOULERGUE (LIFO) Rapporteur : Nikolai KOSMATOV (CEA)
30 Table des matières PREMIÈRE PARTIE : ETAT DE L'ART DE LA JOINTURE PARRALLÈLE1 1 LA JOINTURE LES BASES DE LA JOINTURE La jointure par boucles imbriquées La jointure par tri-fusion La jointure par fonction de hachage JOINTURE PARALLÈLES Jointure parallèle par boucles imbriquées Jointure parallèle tri-fusion Jointure parallèle par fonction de hachage SYNTHÈSE ÉQUILIBRE DE CHARGE ET DISTRIBUTIVITÉ DES DONNÉES GESTION PARALLÈLE DES TÂCHES Génération des tâches Découpage des relations Choix du nombre de tâches Placement des tâches Collecte des statistiques Affectation des tâches Mesures de charge Stratégie d'affectation EXÉCUTION DES TÂCHES ÉQUILIBRAGE DE CHARGE Équilibrage de charge statique Équilibrage dynamique SYNTHÈSE MISE EN ŒUVRE DU PARALLÉLISME EN ARCHITECTURE DE TYPE «SHARED-NOTHING» PROBLÉMATIQUE MAP-REDUCE MAP-REDUCE-MERGE PORTÉE DU MODÈLE MAP-REDUCE-MERGE SYNTHÈSE CONCLUSION...25 SECONDE PARTIE : ÉTUDE DE LA JOINTURE EN ENVIRONNEMENT CLOUD PROBLEMATIQUE DE LA JOINTURE PARALLELE DÉSÉQUILIBRE DES DONNÉES ALGORITHMES À HISTOGRAMME SIMULATION DU DÉSÉQUILIBRE Fonction de simulation de distribution des clés Jeux de données avec déséquilibre contrôlé...34 ii
31 7 LE CADRE LE PRINCIPE LIMITATIONS ENVIRONNEMENT TECHNIQUE LA JOINTURE PARALLELE EN ENVIRONNEMENT CLOUD AVANT PROPOS LA JOINTURE BASIQUE SOUS MAPREDUCE Algorithme de marquage Principe du marquage Phase map du marquage Analyse de la complexité de map Phase reduce du marquage Analyse de la complexité de reduce Algorithme de jointure basique La phase map de la jointure basique La phase reduce de la jointure basique Analyse de la complexité LA JOINTURE À BASE D'HISTOGRAMME Jointure histogramme de premier niveau Calcul parallèle d'histogramme Phase map du calcul d'histogramme Phase Reduce du calcul d'histogramme Exemple de calcul parallèle d'histogramme La jointure à histogramme Jointure à histogramme simplifiée La phase Map de l'algo simplifié HistoJoinV La phase reduce de l'algo simplifié HistoJoinV Analyse de la complexité Jointure de second niveau ou évoluée Élaboration du plan d'exécution Choix du type de partitionnement Jointure avec partitionnement Phase Map de la jointure Phase reduce de la jointure ETUDE COMPARATIVE ÉTUDE D'IMPACT DE LA VOLUMÉTRIE Méthodologie de l'évaluation de l'impact de la volumétrie Impact de la volumétrie ÉTUDE COMPARATIVE DES ALGORITHMES DE JOINTURE Comparaison analytique Comparaison expérimentale ÉVALUATION DE L'IMPACT DU PARTITIONNEMENT Évaluation théorique Évaluation expérimentale Méthode pour le choix du partitionnement Seuil arbitraire de partitionnement Seuil formel de partitionnement PERSPECTIVES ET EVOLUTIONS ALGORITHME DE JOINTURE À CHAÎNES DE TRAITEMENT PARALLÈLES INDÉPENDANTES ALGORITHME DE JOINTURE À CHAÎNE DE TRAITEMENT PARALLÈLES À BOUCLE FERMÉE Approche à pseudo boucle fermée...78 iii
32 Approche à boucle fermée Implémentation de k-means avec MapReduce en boucle fermée CONCLUSION BIBLIOGRAPHIE ANNEXES...84 iv
33 Liste des Figures Figure 1: performances comparées : source [8]...12 Figure 2: représentation de la fonction zipf pour F=100, N=100 et s entre 0 et Figure 3: effet de l'affectation aléatoire (mixage) des fréquences...34 Figure 4: workflow d'évaluation de la volumétrie sur les durées de traitement...63 Figure 5: comparaison des durées de traitement pour différents déséquilibres...68 Figure 6: chaînes de traitements parallèles et indépedantes...76 Figure 7: MapReduce en pseudo boucle fermée...78 Figure 8: Mapreduce en boucle fermée...79 Figure 9: MapReduce BF avec impulsion R+S...80 Figure 10: MapReduce BF avec échelon R+S...80 Figure 11: K-means avec MapReduce BF...81 Liste des Tableaux Tableau 1: exemple de génération de base de données...34 Tableau 2: caractéristiques des modèles de relations de jointure utilisés...35 Tableau 3: exemple de marquage et calcul d'histogramme...48 Tableau 4: processus MapReduce de marquage et calcul d'histogramme...49 Tableau 5: caractéristiques base bd Tableau 6: durée de traitement en fonction de la volumétrie...63 Tableau 7: durée de traitement à 32Mo en fonction du nb de mappers et reducers..65 Tableau 8: durée de traitement à 64Mo en fonction du nb de mappers et reducers..65 Tableau 9: durée de traitement à 240Mo en fonction du nb de mappers et reducers 65 Tableau 10: durée de traitement à 480Mo en fonction du nb de mappers et reducers...65 Tableau 11: durée de traitement à 960Mo en fonction du nb de mappers et reducers...65 Tableau 12: durée de traitement de chaque algorithme en fonction du déséquilibre..67 Tableau 13: part de durée de traitement de chaque algorithme...67 Tableau 14: durée de traitement en fonction de HSw/HRw et de la taille de partitionnement pour nb_reducers= Tableau 15: coût en ms d'un tuple de jointure...73 Tableau 16: exemple de décision naïve de partitionnement...74 Annexes Annexe A : Code Java algorithme BasicPreJoin...84 Annexe B : Code Java algorithme BasicJoin...86 Annexe C : Code Java algorithme HistoPreJoin...88 Annexe D : Code Java algorithme HistoPlan...91 Annexe E : Code Java algorithme HistoJoinV Annexe F : Code Java algorithme HistoJoinV v
34 Liste des Abbreviations et Symboles F s Fréquence seuil de partitionnement f p Fréquence primaire (f p > f s) f s Fréquence secondaire (f s < f p) NR Nombe de reducers M Nombre de mappers (sauf indication contraire) R La relation R S La relation S T Nombre de tuples de la relation T T Nombre de pages mémoire de la relation T R.A ou A Attribut de jointure de la relation R S.B ou B Attribut de jointure de la relation S T i Hist(T) Hist(T i) Hist i(t) Hist(T)(w) ou F w Mappers V(T.A) Partition de T détenue par le noeud (i.e processus) i Histogramme global de la relation T Histogramme de la partition T i Histogramme de la relation T détenu par le noeud i Fréquence de la valeur w dans la relation T Ensemble des mappers Ensemble des valeurs distinctes de l'attribut A de la relation T vi
35 REMERCIEMENTS Je souhaite remercier dans un premier temps J.M. Couvreur pour avoir compris mes aspirations et m'avoir en conséquence orienté vers ce domaine très passionnant. Je remercie également F. Loulergue pour avoir ensuite pris le relais et guidé vers le sujet du Cloud et du concept MapReduce qui m'ont particulièrement inspiré. Enfin je remercie M. Bamha pour m'avoir accompagné tout au long de mes recherches et m'avoir prodigué les meilleurs conseils, d'avoir tempéré mon zèle et fait preuve en l'occurrence de la plus grande patience envers mon obstination. Je félicite et remercie également l'ensemble du personnel du département Informatique de l'université d'orléans ainsi que du LIFO pour leur professionnalisme, leur proximité et leur enthousiasme dans tout ce qu'ils réalisent. vii
36 . PREMIÈRE PARTIE : ETAT DE L'ART DE LA JOINTURE PARRALLÈLE 1
37 1. La jointure 1 La jointure La jointure est l'opération incontournable dans le domaine des bases de données relationnelles. Elle est ce qui permet le lien entre données de plusieurs sources au sein d'une seule ou plusieurs bases de données. La difficulté particulière de la jointure est son coût en terme de ressources machines : stockage, mémoire et CPU. Ces trois ressources pouvant être différemment sollicitées selon l'algorithme mis en œuvre. De ce fait, le domaine foisonne d'approches algorithmiques plus ou moins orientées. Toutefois, on peut quasiment tous les ramener à 3 méthodes principales : la jointure par boucle imbriquées (nested-loop), la jointure par tri-fusion (sort-merge) et la jointure par fonction de hachage (hash-join). Au delà des difficultés intrinsèques à la jointure, l'évolution constante des environnements techniques ouvrent d'autres voies visant à utiliser de façon optimale les capacités des machines (mémoire, multiprocessing...). Nous verrons comment chacune des trois méthodes citées s'apprête à ces évolutions. Ainsi que les variantes résultantes qui donnent les meilleurs résultat soit de façon particulière, soit pour des cas de figures plus généraux. En plus des évolutions des architectures des ordinateurs, la jointure est également indirectement impactée par des évolutions plus «culturelles» en matière d'utilisation des données et de leur répartition. De fait, l'extension des réseaux informatiques, et l inter-connectivité entre une multitude de sites, implique une dissémination des données au sein d'un vaste réseau, et donc une distribution «subie» des données exigeant toujours des traitements de type jointure ; dans ce contexte, la jointure prend une autre dimension et la remise en cause des idées acquises en la matière est souvent nécessaire : impossibilité d'indexation des données, données pauvrement structurées... Comme nous le verrons plus loin, le pragmatisme et les approches naïves sont souvent les meilleures pour ce type de problématique. Dans un premier temps, nous rappelons les différentes approches de jointure, et leur implantation indépendamment de l'environnement d'exécution. Nous exposerons ensuite leur adaptabilité aux architecture parallèles, en essayant de dégager parmi les trois méthodes de base celles qui sont les mieux appropriées à une situations donnée. Nous étendons ensuite cette parallélisation de la jointure aux architectures plus vastes notamment les architectures dites «sharing-nothing», et de façon plus particulière aux architectures de type «Cloud Computing». Nous exposons ensuite une méthode technique de mise en œuvre de la jointure au sein de tels réseau. Notre exposé se base sur le plan et les synthèses élaborées dans le livre «Query processing in parallel relational database systems» [1]. Quand c'est nécessaire, nous apportons des précisons émanant d'autres sources. Nous adaptons également autant que possible les solutions développées dans les différentes étude, mais, comme nous le mettons en évidence plus loin, les techniques d'implémentation classiques sont loin d'être adaptable dans l'état à un environnement Cloud et à ses contraintes. Par ailleurs, nous taisons volontairement les orientations qui ne nous semblent pas pertinentes ou porteuses d'enseignement pour notre contexte. 1.1 Les bases de la jointure La jointure entre deux relations R et S sur les attributs R.A et S.B consiste à coupler les tuples de R et S ayant les attributs R.A et S.B égaux. De façon générale, un tuple de R (i.e S) peut être couplés à un nombre quelconque de tuples de S (i.e R). Dans le cas particulier où les attributs R.A et S.B sont tous les deux des clés uniques de leur relation respectives, un tuple de R (i.e S) ne peut être couplé qu'au plus avec un tuple de S (i.e R). Il y a une multitude technique de mise en œuvre de cette opération et, des nombreuses études portant sur le sujet, trois méthodes se sont dégagées comme regroupant l'ensemble des approches qui peuvent être proposées. 2
38 1. La jointure Ces trois principales méthodes visant à réaliser ces opérations sont la jointure par boucles imbriquées qui consiste pour deux relations R et S, d'une part à parcourir une des ces relations de façon séquentielle et d'autre part, à comparer chaque tuple de R lu avec l'ensemble des tuples de S afin d'extraire les tuples pour lesquels A = B. La première relation parcourue (ici R) est désignée sous le nom de «inner» et la seconde (ici S) est désignée sous le nom «outer». La deuxième méthode repose sur un tri préalable des deux relations R et S, suivi d'une mise en œuvre équivalente aux boucles imbriquées avec toutefois une économie du nombre de lecture de la seconde relation comme nous l'exposons plus loin. Enfin, la troisième méthode, quant à elle, est basée sur une fonction de hachage des deux relations visant à permettre l'accès directes aux tuples de S ayant une relation avec les tuples de R, sans nécessité la recherche séquentielle par parcours de la relation S La jointure par boucles imbriquées Cette jointure est la plus naturelles des trois. Longtemps négligée elle a été remis au goût du jour du fait de la puissance des données et de l'apparition de variantes beaucoup plus efficaces [2]. Comme on peut le voir dans l'algorithme ci-dessous, elle est composée de 2 boucles, la première nommée outer parcours une fois la première relation, et, pour chaque tuple de la relation parcourue, également nommée la relation outer, la seconde boucle désignée par inner parcours la seconde relation également désignée inner afin de trouver les tuples ayant une égalité des attributs de jointure des deux relations. Algorithme BoucleImbriquéeBasique pour chaque tuple r de R faire pour chaque tuple s de S faire si r.a = s.b alors émettre(r,s) Bien que cet algorithme soit robuste de par sa nature et sa simplicité, il présente néanmoins un défaut majeur et quasi rédhibitoire. La seconde relation nommée inner est parcourue un nombre important de fois, en fait R (nombre de tuples de R) fois. Par ailleurs, la concurrence de lecture des deux relations entraîne fatalement un nombre important de défaut de pages et donc d'accès disques répétés aux mêmes données. Afin de limiter l'inconvénient de cette méthode, une évolution consiste à bufferiser les données en mémoire pour limiter le nombre de défaut de pages. Ce qui donne l'algorithme à accès par blocs suivant, avec M le nombre de pages mémoire disponibles pour le traitement : Algorithme BoucleImbriquéeBasiqueBlocs faire Copier (M-1) pages de R vers mémoire faire Copier 1 page de S vers mémoire pour chaque tuple r de R en mémoire faire pour chaque tuple s de S en mémoire faire si r.a = s.b alors émettre(r,s) jusqu'à lecture de toutes les pages de S jusqu'à traitement de toutes les pages de R 3
39 1. La jointure Avec cette évolution nous passons d'une situation où le nombre de lectures en disque est incertain et pouvant être extrêmement important du fait de la concurrence des deux relations en tampon disque, à une situation plus contrôlée ou le nombre de lecture en disque est de l'ordre de : R R+ (M 1) S où R et S sont le nombre de pages de pages de de R et S. Toutefois, nous parcourrons toujours la relation S R fois, que cela soit en mémoire ou en disque, ce qui implique une complexité des deux algorithme de O( R * S ), avec R et S le nombre de tuples respectivement de R et S. En effet, dans tous les cas S est parcourue pour chaque tuple de R, et, chaque tuple de R peut ne pas avoir de tuples correspondants du point de vue de la jointure dans S ou très peu. Une méthode visant à repousser cette limite est l'utilisation d'index sur les attributs de jointure, et plus particulièrement sur l'attribut de jointure de la relation S. En effet, le principe d'un index d'une relation sur un attribut, consiste à associer à chaque valeur d'attribut une position «physique» (numéro de page...) sur disque du tuple associé. Ainsi, il n'est plus utile de parcourir à chaque itération outer entièrement la relation S puisque il suffit d'accéder sur disque au tuple associé à la relation R directement à travers cet index. Cette évolution nous amène à l'algorithme suivant : Algorithme BoucleImbriquéeIndexée Faire Copier 1 page de R vers mémoire pour chaque tuple r de R en mémoire faire Calculer l'index sur S.B pour la valeur r.a pour chaque valeur trouvée faire extraire les valeurs de la page émettre(r,s) jusqu'à traitement de toutes les pages de R On constate alors qu'il n'est plus utile de lire un nombre important de pages de R puisque le parcours de S ne dépend plus du nombre de pages de R en mémoire mais est accédée directement à travers l'index. La zone mémoire ainsi libérée pouvant alors contenir l'index et éviter qu'il ne devienne un goulet d'étranglement. La complexité algorithmique est théoriquement en O( R + S ). Le nombre d'accès disque est quant à lui proportionnel à la sélectivité de la jointure qui est définie par le rapport entre le nombre de tuples résultant de la jointure et le produit du nombre de tuple de R par le nombre de tuples de S : RS / R * S. On remarquera que l'efficacité de cet algorithme dépend également beaucoup de l'organisation de l'index sur S. En effet selon que les tuples de S ayant la même valeur d'attribut de jointure sont regroupées ou pas au sein d'une même page ou d'un ensemble de pages contiguës, le bénéfice de cet algorithme peut être plus ou moins important. Dans le cas d'une bonne organisation des tuples de S sur l'attribut B de jointure, pour un tuple r de R donnée le nombre de pages de S lues est au plus égal au nombre de pages dans lesquelles les tuples s de S ayant pour valeur s.b =r.a sont stockés ; ce nombre est minimal de façon inductive de par la contiguïté imposée ci-dessus. De plus, si la relation R est préalablement triée, les pages de S sont lues au plus une fois, selon le taux de sélectivité de la jointure définie ci-dessus. 4
40 1. La jointure L'un des enseignements structurant que l'on peut tirer de cette méthode est l'apport significatif du tri préalable des relations. Au delà du coût de celui-ci, le tri permet d'éviter de répéter plusieurs fois le parcours d'une relation, ou tout du moins le limiter significativement. C'est ce constat qui nous amène à une autre famille d'algorithme de jointure basées sur le tri-fusion La jointure par tri-fusion La méthode de jointure par tri-fusion nécessite un tri préalable, selon les attributs de jointure des deux relations. Théoriquement un seul parcours des relations est nécessaire afin d'extraire les tuples ayant une égalité sur les attributs de jointure. Il est toutefois nécessaire de procéder par moment à des retours arrière sur l'une des relation dans le cas de non unicité de son attribut de jointure. L'impact de ce retour arrière est néanmoins limité car il est la plupart du temps réalisé en mémoire, mais des ré-lectures sur disque suite à un défaut de page restent possibles mais néanmoins très rares. L'algorithme résultant est le suivant : Algorthme TriFusionSimple trier R sur R.A et S sur S.B selon l'ordre ascendant initialiser r et rp avec le premier tuple de R initialiser s et sp avec le premier tuple de S tantque non (eof(r) ou eof(s)) faire tantque non (eof(r) ou eof(s) or r.a = s.b) faire si (r.a < s.b) initialiser r et rp avec le tuple suivant de R sinon initialiser s et sp avec le tuple suivant de S fintantque si non (eof(r) ou eof(s)) tantque r.a = rp.a et non eof(r) faire tantque s.b = r.a et non eof(s) faire émettre(rp,s) initialiser s avec le tuple suivant de S fintantque initialiser r avec le tuple suivant de R si r.a = sp.b alors initialiser s à sp //retour arrière fintantque Cet algorithme est une approche générale de la jointure par tri-fusion. Il fonctionne que les attributs de jointure A et B soient une clé unique de leurs relation respectives ou pas. Dans le cas de clés unique, il n'est pas nécessaire de vérifier la nécessité du retour arrière et l'algorithme s'en trouve alors simplifié. L'algorithme est cependant simple et robuste, le principal défaut étant la nécessité d'un tri préalable ; mais, si les relations sont déjà maintenues triées, son intérêt devient plus grand. L'enseignement tiré de cette méthode, mais également dans une certaine mesure de la précédente, est la problématique d'accès directe aux données évitant ainsi de devoir accéder à une multitude de tuples inutiles pour un tuple r donné avant d'atteindre le tuple s pertinent. Nous avons vu que l'une des façon d'atteindre cet objectif était le tri, nous allons maintenant voir une autre méthode basée elle sur une fonction de hachage visant à segmenter les données d'une part, et en accélérer l'accès d'autre part. 5
41 1.1.3 La jointure par fonction de hachage 1. La jointure Nous avons mis en évidence que le principal problème de la jointure est la nécessité de parcourir un certain nombre de fois l'une des deux relations, alors même que la plupart des valeurs parcourues ne participent nullement au résultat. Un tri préalable pouvant être coûteux ou la disponibilité d'un index précisément sur les attributs de jointure n'étant pas toujours garantie, il nous faut trouver un autre moyen d accéder directement aux données pertinentes pour un tuple courant donnée avec un surplus de coût borné. Une méthode allant dans ce sens est le découpage des relations R et S en partitions R1, R2,...,Rn et S1,S2,...,Sn tel que pour tout tuple r et s avec r Ri et s Sj, si ij alors r.a s.b. Dans ce cas, la jointure globale de R et S peut être ramenée à l'union des jointure Ri et Si. On remarquera que cette condition dans l'état est purement théorique et que dans les faits il est difficile d'arriver immédiatement à cette situation. Nous verrons par la suite les évolutions possible afin de satisfaire cette condition. On notera également que les différentes partition d'une même relation peuvent êtres de tailles différentes, et il en est de même pour les partitions Ri et Si. L'algorithme de base peut être directemet amélioré dès lors que l'on dispe de suffisamment de mémoire pour stocker plusieurs partitions et limiter ainsi les accès disque répétés. Cet algorithme simple a été implémenté pour la première fois au sein du système de base de données GRACE [3]. Il se décline de la façon suivante : Algorithme BasicHashJoin découper R en n partitions avec une fonction de hachage sur R.A découper S en n partitions avec la même fonction de hachage sur S.B pour chaque partition i faire pour chaque tuple r de R i faire hachage sur r.a et insertion dans la table de hachage pour chaque tuple s de S i faire hachage sur s.b et sonder la table de hachage si r.a = s.b alors émettre(r,s) On identifie deux fonctions de hachage. La première est utilisée lors de la première phase du traitement pour la partition des relations. Cette phase est nommée phase de construction (built). Et, celle utilisée pour générer la table de hachage lors de la seconde phase qui est nommée phase de sondage (probe). Les deux fonctions peuvent être identiques, mais l'utilisation de deux fonctions distinctes évite les problèmes de collision liées aux fonctions de hachage. Par ailleurs, l'objectif de l'une et l'autre des fonctions n'est pas le même. L'une a pour but de distribuer les tuples vers un ensemble de partition de la façon la plus équitable et éviter ainsi une forte disparité des tailles des partitions. L'autre a pour but l'accès efficace aux tuples de la première relation. Ceci peut contraindre selon les cas à utiliser deux fonctions distinctes adaptées chacune à chaque étape La complexité de cette première version, en ne comptant que les lectures de R et S, est : O(R+S+n(R i +S i )) et i, j si i j alors R i +S i Un axe d'amélioration possible de cette version d'algorithme est le nombre d'i/o. En effet dans le cas de «la boucle imbriquée», la mise en concurrence des deux relations (i.e. Boucles) induit un nombre de défaut de pages pouvant être conséquent et donc extrêmement pénalisant en fonction de la taille des relations en rapport avec la quantité mémoire disponible. Une évolution naturelle consiste donc à veiller à ce qu'une partition de la relation outer puisse tenir dans une quantité mémoire fixée, donnant ainsi une seconde contrainte qui est : R i M2, pour 1 i n et M étant le nombre de pages mémoire disponibles. 6
42 1. La jointure Les pages restantes (2) sont utilisées pour le stockage de la partition S i pour la première page et, comme tampon du résultat pour la seconde page. Toutefois, les partitions étant générées à l'aide d'une fonction de hachage, elle même prenant comme critère de calcul l'attribut de jointure, il est extrêmement difficile de prédire la taille de toutes les partitions. De ce fait, il n'est pas exclu qu'une partition soit supérieur en pages au nombre maximum de pages disponibles (M-2). Dans ce cas, si on souhaite éviter ce cas de figure, une solution consiste à diviser à nouveau la ou les partitions posant problème jusqu'à atteindre une taille inférieure à M-2. On rappelle également que le mode opératoire des algorithmes basés sur une fonction de hachage se déroule en deux étapes : la construction des partitions, suivie de la jointure des partitions sur la base d'une table de hachage de la première relation. La première étape lit puis réécrit sous forme de partions la relation outer. Une optimisation consiste donc à mettre à profit la lecture des relations R et S dès la phase de construction afin de réaliser la jointure d'une partie de la relation outer. C'est dans cet objectif qu'un algorithme hybride a été proposé [4]. Celui-ci se décline de la façon suivante : i) Construction des partitions R i et mise en mémoire des tuples relatifs à R 0 ii) Construction des partitions S i et jointure des tuples relatifs à S 0 avec R 0 iii) jointure des des R i /S i, pour i > 0. Durant l'étape ii, on construit les partitions S i et on réalise également la jointure avec R 0 dès qu'un tuple appartenant à S 0 est «identifié» à la volée par la fonction de hachage. L'économie est moindre mais peut être significative dans le cas où le nombre de partitions est petit. Les algorithmes vus jusqu'à maintenant ont pour effet de favoriser les accès aléatoires au disque. On rappellera qu'un accès disque aléatoire est beaucoup moins efficace qu'un accès disque séquentiel. L'algorithme suivant se propose donc de favoriser les accès séquentiels. Il est connue sous le nom de SimpleHashJoin et, sous sa forme générale, se présente de la façon suivante : Algorithme SimpleHashJoin pour chaque partition i faire pour chaque tuple r de R non traité faire hachage sur r.a pour déterminer le numéro de partition j de r si i = j alors insérer r dans la table de hachage sinon écrire r sur disque // ou ne rien faire pour chaque tuple s de S non traité faire hachage sur s.b pour déterminer le numéro de partition j de s si i j alors écrire s sur disque // ou ne rien faire sinon hachage sur s.b et sonder la table de hachage si s.b = r.a alors émettre (r,s) Cet algorithme procède par itération sur le numéro de partition. Ainsi, à chacune de ces itérations itération, soit un tuple fait partie de la partition courante et dans ce cas il est traité (mis en table de hachage ou jointure selon qu'il s'agit de R ou S), soit il n'en fait pas partie et alors il est enregistré sur disque. Si on souhaite éliminer les écritures aléatoires et donc favoriser les écritures séquentielles, il suffit, dans le cas ou un tuple n'est pas concerné lors de l'itération courante, de le rejeter sans écriture sur disque. Certes, cela multipliera les lectures sur disque, mais ces lectures 7
43 1. La jointure restent séquentielles et donc beaucoup plus performantes que des lectures aléatoire et qui plus est concurrentes [4]. Nous avons exposé trois familles d'algorithmes de jointure. Beaucoup d'autres algorithme, visant à apporter des amélioration particulières ou à répondre à des jointures particulières, ont été également proposés. Nous nous sommes contenté d'exposer les principaux dont le pivot intrinsèque relatif à chacun est : I) Les boucles imbriquées II) Le tri des relations (suivi de boucles imbriquées) III) Le partitionnement et le hachage des relations On constatera aisément que le premier et le deuxième sont malgré tout assez proches. La ressemblance entre le premier et le troisième est moins évidente mains non moins réelle. En effet, une fonction de hachage peut tout à fait se baser sur le numéro de page. Ainsi le numéro de partition serait calculé par : i= numpage(r) où, M2 numpage est le numéro de page du tuple r de R, compris entre 0 et R -1 M est la quantité mémoire en pages disponible Dans cette configuration, il ne s'agit ni plus ni moins que de l'algorithme BoucleImbriquéeBasiqueBlocs vu précédemment. L'un est l'autre de ces algorithmes trouvent leur justification dans divers configurations. L'un va être plus performant en cas de présence d'index sur l'une des relations ; L'autre sera favorisé dans le cas de relations triées. Mais d'autres critères de choix, plus techniques, peuvent également entrer en ligne de compte tels par exemple la taille mémoire disponible eu égard à la talle des relations, ou plus fonctionnelles, tels que la distributivité des valeurs des attributs de jointure. Toutes ces évolutions visent à augmenter l'efficacité des algorithmes de base afin de, soit exploiter les ressources internes, soit s'y adapter. Un autre axe d'évolution souhaité ou subit est la parallélisation des traitements de jointure. Dans cet autre environnement, tous les algorithmes cités ne sont pas équivalents face la parallélisation comme nous l'exposons dans le chapitre suivant. 1.2 Jointure Parallèles La jointure parallèle est parfois subie, dans le cas de relations distribuées à travers un vaste réseau, et, parfois souhaitée dans le cas de machines à architecture parallèle. Dans le second cas, la jointure parallèle est utilisée afin de réduire les temps de traitement en exploitant au mieux les ressources machine. Beaucoup d'extensions des algorithmes vu auparavant vers le parallélisme ont été proposées. Et, comme tout traitement parallèle, ceux-ci se déclinent en 3 étapes qui sont : i) Décomposition de la jointure en n tâches ii) Assignation des n tâches à p processeurs iii) Assemblage des résultats locaux Bien entendu, l'étape iii est fortement dépendante de la façon dont l'étape i est réalisée. Cette étape iii peut également être optionnelle. Par ailleurs, on peut distinguer deux familles d'architectures parallèles qui sont les architecture partagées et les architecture distribuées. Dans la première architecture des ressources telles que la mémoire ou l'espace de stockage disque sont partagés et donc accessibles de façon concurrentiel par l'ensemble des processeurs en jeu. Dans la seconde, ces ressources sont distribuées sur différentes machines interconnectées par un réseau de communication. Notre problématique, à savoir la jointure parallèle en environnement Cloud, étant plutôt concernée par la seconde architecture nous mettrons essentiellement l'accent sur les 8
44 1. La jointure algorithmes adaptée à celle-ci. Nous adapterons les principes généraux à notre besoin, et nous mettons de côté les principes trop inhérents aux architectures partagées ou alors nous signalons cette forte adhérence s'il nous faut tirer un enseignement du principe en question Jointure parallèle par boucles imbriquées La jointure par boucles imbriquées est l'un des algorithmes qui se prête le mieux à la parallélisation. En effet, une parallélisation naturelle du traitement consiste à distribuer la relation outer (R) vers les p processeurs (i.e machines) concernées. Chaque processeur réalisant localement la jointure de sa partition avec l'ensemble de la relation inner (S). Cela implique, en préalable à la jointure, la réplication (i.e. copie) de la relation inner vers l'ensemble des processeurs (i.e. Nœuds) concernés. L'algorithme résultant est le suivant : Algorithme BouclesImbriqueesParalleles Chaque nœud qui dispose d'un fragment de S le dispatche aux autres nœuds distribution de R vers l'ensemble des nœuds concernés chaque nœud i joint la partition R i avec l'ensemble de la relation S La jointure locale des partition R i avec S peut être réalisée selon n'importe lequel des algorithmes exposés. Si le nœud i en charge de la partition R i dispose d'un index sur celle-ci alors l'algorithme boucles imbriquées indexé exposé en première partie peut être utilisé. En effet, la relation S peut être déjà distribuée, sur un ensemble de machine pour des besoins techniques (ex. stockage) ou fonctionnels, et donc disposer d'index permanents. Cette distribution préexistante nous permet également d'envisager une autre optimisation : seul les nœuds disposant d'une partition de la relation S sont utilisés pour la jointure parallèle. Nonobstant, cette optimisation peut être antinomique avec la nécessité de distribuer le traitement sur un large ensemble de nœuds afin de garantir le meilleur équilibre de charge. De façon générale, une relation est distribuée, pour raison de contrainte technique ou fonctionnelle, selon la valeur d'un attribut de cette même relation. Cet attribut peut être choisi pour raison de sa bonne distribution : lorsqu'il s'agit de contrainte technique visant notamment à faire supporter le stockage d'une relation par plusieurs nœuds. Dans ce cas, on souhaite que le partage soit équitable entre les différents nœuds. L'attribut de distribution peut également être choisi sur des bases fonctionnelle : les traitements produisant la relation en question sont distribués sur un ensemble de nœuds, comme par exemple la prise en charge d'un intervalle de numéros de clients par chaque nœuds. En conséquence, l'attribut de distribution de la relation n'est pas nécessairement l'attribut sur lequel porte la jointure. Une solution d'abstraction de cette problématique est proposée dans l'article [1]. Elle s'appuie sur une table de translation MapS dont le schéma est (P,B). Sur la base de cette table, chaque nœud disposant d'une partition de R peut identifier les nœuds disposant d'une partition de S vers lesquels il doit envoyer sa partition R. Ainsi, pour chaque tuple s de S, il existe un tuple m dans MapS tel que m.b = s.b et m.p est l'attribut de distribution de la relation S sur différents nœuds. Et donc, pour un tuple r, le tuple m de MapS tel que m.b = r.a nous permet d'extraire l'attribut m.p correspondant et donc identifier le site sur lequel la partition de S est localisée. Une extension à cette méthode consiste à distribuer également MapS selon l'attribut m.b, ce qui produit l'algorithme suivant prenant comme hypothèse structurante le fait que S est distribuée selon l'attribut S.P : 9
45 1. La jointure Algorithme BouclesImbriqueesParalleleSousEnsemble pour chaque tuple s de S faire maintenir un tuple m de MapS avec m.p = s.p et m.b = s.b Partition de MapS selon MapS.B et stockage de MapSi sur le nœud n i pour chaque tuple r de R faire trouver N i contenant MapS i avec m.b = r.a trouver N j contenant S i avec s.p = m.p envoyer r à toules nœuds N j réaliser la jointure sur chaque nœud N i Bien entendu, si l'attribut de jointure est également l'attribut de distribution de la relation S, alors il devient inutile de maintenir la table MapS puisque le nœud i contenant la partition S i est directement obtenu avec l'attribut S.B. Comme le montre les algorithmes décris ci-dessus, la jointure par boucles imbriquées se prête naturellement à la parallélisation. Toutefois, on constate également que le placement initial des données est essentiel. En effet, à défaut, de très nombreuses communications sont nécessaires ce qui peut être extrêmement pénalisant. Nous verrons par la suite que ce placement est un enjeu majeur qu'il nous faudra favoriser en amont de la jointure et/ou exploiter au mieux au moment de la jointure Jointure parallèle tri-fusion Contrairement à la jointure précédente, la méthode par tri fusion s'apprête moyennement à la parallélisation. Si la phase de tri des relations peut être naturellement parallélisée sur chacun des nœuds disposant d'une partition R ou S, la phase de jointure exige quant à elle un traitement préalable et complexe pouvant conduire à des performances équivalentes à un traitement séquentiel. C'est pour cette raison que, dans un premier temps, cette seconde phase a souvent été réalisée de façon séquentielle. Il est possible d'envisager la parallélisation de cette seconde phase selon deux modes opératoires distincts qui sont : I) Jointure des différentes partitions triées une à une (R i et S i ). Ce qui implique une combinaison de l'ensemble des partitions Si et Ri par chaque nœud détenant l'une ou l'autre des partition. Ainsi, pour m partitions R i et n partitions S i, m*n jointures sont nécessaires. II) Assemblage de la petite relation en une seule partition R, réplication de cette partition vers les différents nœud détenant une partition Si, puis jointure de chaque partition Si avec la totalité de la jointure R. On constate que dans l'un et l'autre cas on se ramène à une jointure par boucles imbriquées sans aucun apport de la phase de tri préalable particulière à la jointure par tri-fusion. Pour tirer profit de la propriété du tri, il est nécessaire de maintenir cette propriété au sein des différentes partitions i traitées par les différents nœuds. Ainsi, les relations S et R sont découpés en k partitions chacune, ces partitions devant respecter les propriétés suivantes : i) i[1, k], R i. A<R i+1. AS i. B<S i+1. B ii) i[1, k], R i +S i R i+1 +S i+1 10
46 1. La jointure Afin d'obtenir cette configuration sur chacun les k nœuds devant procéder à la jointure des paires de partitions Ri et Si respectant la propriété ci-dessus, une étape intermédiaire est nécessaire. Chaque nœud disposant d'une partition Ri et/ou Si triée doit procéder au découpage selon la contraintes ci-dessus, ce qui produit un ensemble de sous partitions. Chaque sous partition est ensuite fusionnée afin de produire une partition globale triée également respectant les mêmes contraintes. Il existe de nombreuses solutions de tri parallèle pouvant être adaptées aux jointures, dès lors qu'elles prenne en compte la distributivité des attributs et assure une répartition équilibrée des données (contrainte ii) [5]. Pour atteindre des performances compatibles avec le gain attendu par un traitement parallèle de la jointure, sur une quantité de données très importantes distribuées une étude fait état d'un comparatif entre un algorithme de tri parallèle avec découpage exact et l'autre utilisant une méthode stochastique[6]. Le seconde algorithme présente ue efficacité beaucoup plus grande dès lors la distributivité des données est maîtrisé et que l échantillonnage choisi est représentatif. On note bien que cette étape intermédiaire, nécessaire, annule le bénéfice attendu par la parallélisation, ou dans le meilleur des cas présente un gain incertain Jointure parallèle par fonction de hachage Plus encore que la jointure par boucle imbriquée, ce type de jointure est totalement compatible avec la parallélisation. En effet, le principe de la jointure par fonction de hachage est le partitionnement des relations. En réalité, dans le cas d'architecture parallèle à mémoire et disques partagées, les algorithme monoprocesseur fonctionnent dans l'état au sein d'une architecture parallèle, puisque chaque processeur peut accéder de façon concurrentielle aux différentes partions [7]. Dans le cas d'architecture distribuée, qui nous intéresse particulièrement, il est nécessaire de procéder à quelques échanges entre les différents nœuds afin de mener la jointure sur plusieurs nœuds en parallèle. La distribution des tuples associés à un nœud est aisément réalisable à l'aide de la fonction de hachage, utilisée pour découper les relations en partitions, et associée à une table de routage prédéfinie. À l'issue de cette distribution, chaque nœud dispose alors de deux partions Si et Ri sur lesquelles il peut appliquer la jointure par fonction de hachage. La principale difficulté, comme dans le cas de l'algorithme monoprocesseur, réside dans la bonne distribution des relations. En effet, il est difficile de prévoir la taille de chaque partition résultant de la fonction de hachage, puisque cela dépend de la fonction elle même mais également de la distribution inhérente aux valeurs de l'attribut sur lequel porte la jointure. Une mauvaise distribution des données implique fatalement un dépassement de la capacité mémoire des nœuds de traitement dégradant ainsi fortement l'efficacité de l'algorithme parallèle. D'un autre côté, un découpage trop fin des relations entraîne une sous utilisation des capacités des nœuds de traitement. L'approche générale consiste à découper les relation en un nombre de partitions suffisamment important afin d'éviter un dépassement mémoire et, durant la phase de construction, si des partitions sont jugées trop petites, alors on procède à leur assemblage en une partition assez grande afin d'optimiser l'usage de la mémoire. On constate à nouveau que la bonne ou mauvaise distribution des données ainsi que celle de l'attribut de jointure joue un rôle primordial dans le cas d'environnement monoprocesseur et encore plus dans la cadre d'un environnement parallèle. Cet aspect fait l'objet d'une étude particulière au chapitre «La jointure par fonction de hachage» 1.3 Synthèse Parmi l'ensemble des algorithmes exposés, il est difficile d'en désigner un comme plus performant que tous les autres. La quasi-totalité des études réalisées à ce jour partent d'hypothèse 11
47 1. La jointure restrictive sur la distribution des données. En réalité, l'un et l'autre des algorithmes exposés trouve son intérêt dans des configurations particulières telles que la bonne distribution des attributs de jointure, la différence de la taille des deux relations ou encore la présence d'index. La jointure basée sur une fonction de hachage (H dans figure ci-dessous) semble selon les études réalisées assez généraliste et globalement efficace. Toutefois, celle-ci est fortement sensible à la distribution de l'attribut de jointure ainsi qu'à la taille des relations versus la quantité de mémoire disponible. La jointure par boucles imbriquées (NL) est quant à elle complètement insensible à la distribution de l'attribut de jointure et gagne en efficacité dans un environnement parallèle. Enfin la jointure par tri-fusion (SM) n'est réellement efficace que lorsque les relations de jointure sont déjà triées, et, dans ce cas cette méthode est de loin la plus performante même dans une configuration monoprocesseur [8]. Temps en secondes SM H NL Processeurs Figure 1: performances comparées : source [8] 2 Équilibre de charge et distributivité des données Il ressort du précédent chapitre qu'une bonne distribution des données assure une efficacité optimale du traitement de jointure parallèle. Un bon partage des données entre les différents nœuds assure un bon équilibre de charge des traitements. Or le facteur majeur qui conditionne la possibilité de procéder à une telle répartition est la distributivité des données à joindre, mais également de la distribution des valeurs de l'attribut de jointure [9]. 12
48 2. Équilibre de charge et distributivité des données En effet, malgré une bonne distribution des données sur un attribut quelconque des relations en jeu, il peut s'avérer qu'un nœud se voit affecté une paire de partitions Si et Ri telle que la distributivité des valeurs de l'attribut implique un traitement lourd pour un ensemble de nœud et un traitement quasi-nul pour un autre ensemble. Ceci produit un déséquilibre qui annule l'efficacité attendue d'un traitement parallèle en introduisant des goulets d'étranglement. Il existe une multitude d'approches pour appréhender ce type cette problématique. Une méthode pragmatique consiste à envisager plusieurs cas de figure (i.e. Algorithme) qui sont ensuite mis en œuvre durant l'exécution selon une estimation de la distributivité des données [10]. D'autres plus formelle s'appuient sur des histogrammes visant à équilibrer la charge selon la fréquence des valeurs de l'attribut de jointure[11,12]. Cette étape est un élément clé du traitement parallèle d'une jointure entre deux relations. Sur la base d'un algorithme de découpage des données, la méthodologie généralement suivie afin de générer un ensemble de tâches devant exécuter chacune une partie de la jointure se décline en trois étapes qui sont : la génération des tâches, l'allocation des tâches aux nœuds et enfin l'exécution des tâches. Bien entendu ces tâches peuvent être entrelacées dans le cas où une allocation dynamique des tâches est nécessaire : il s'agit alors de mécanismes d'équilibre de charge. Nous exposons ici dans un premier temps la méthodologie de gestion parallèle des tâches puis nous donnons quelques axes d'évolution vers une gestion plus dynamique basée sur des relevés de statistiques et de ré-allocation de tâches. 2.1 Gestion parallèle des tâches Comme indiqué plus haut, la gestion des tâches parallèle est généralement décomposée en trois phases : la génération des tâches, l'allocation suivie de l'exécution des tâches. Chacune de ces étapes peut être également découpée en plusieurs étapes Génération des tâches C'est une phase clé du traitement parallèle d'une jointure. Elle a pour but de découper la jointure en un ensemble de jointures sur des sous ensemble des relations. L'union de de ces jointures devant impérativement produire le même résultat qu'une jointure directe sur la totalité des relations initiales sans découpage. Cette phase est généralement déclinée en quatre étapes qui sont : i) le découpage des relations en partitions (sous relations), ii) l'évaluation du nombre de tâches à générer, iii) le placement des tâches, iv) la collecte des statistiques Découpage des relations Le but étant de découper les relations de jointure en sous relations de telle sorte que l'union du résultat de leurs jointures respectives produise le même résultat que la jointure des relations initiales sans découpage. Trois combinaisons de découpage des relations sont possibles : Découpage total : consiste à découper les deux relations en partitions avec l'objectif que tout tuple de l'une ou l'autre relation participe à une et une seule tâche de jointure, en d'autres termes qu'aucune réplication de tuple n'est réalisée. Cela implique que les tuples en relation doivent être regroupés au sein des mêmes partitions. Ceci est réalisable soit par découpage des relations en partitions selon des intervalles de valeurs de l'attribut de 13
49 2. Équilibre de charge et distributivité des données jointure. Soit par utilisation d'une fonction de hachage. Ce découpage est le plus recherché et le plus communément utilisée quand cela est possible. Découpage et réplication : ici une relation est découpée tandis que l'autre est répliquée. Généralement, c'est la relation la plus volumineuse qui est découpée tandis que la plus petite est répliquée. Ainsi chaque tâche se voit affecté d'une part une partition de la plus grande relation et, d'autre, la totalité de la plus petite relation. Cette méthode est particulièrement pertinente quand la relation répliquée est suffisamment petite pour tenir en mémoire, et dans ce cas l'usage de la jointure par boucles imbriquée avec blocs est la plus appropriée. Réplication totale : dans ce cas les deux relation sont répliquées. Les m partitions de la première et les n partitions de la seconde relation sont jointes une à une donnant lieu à n*m tâches différentes. Cette méthode peu efficace n'est utilisée que dans des situations particulières au sein d'architectures à ressources partagées Choix du nombre de tâches L'objectif de cette étape est l'estimation du nombre optimal de tâches nécessaires au traitement des différentes partitions générées à l'étape précédente. Le but recherché est l'utilisation optimale des N nœuds élus pour le traitement, notamment en terme d'occupation mémoire. Il y a donc une corrélation directe entre le nombre optimal recherché et la taille des données à traiter. Ainsi, un nombre trop important de tâches induit un découpage extrêmement fin des données à traiter et donc une inadéquation entre le traitement effectifs et le traitement de préparation des tâches. Par ailleurs, ce découpage trop fin engendre une fragmentation des données traitées et donc un accès aléatoire au stockage avec les dégradations de performances mises en évidence plus haut. A contrario, un découpage trop grossier risque de générer des partitions dépassant les capacités mémoire des nœuds avec une efficacité moindre des jointures locales à chaque nœud. Cela limite également les possibilités d'allocation aux différents nœuds du fait du faible nombre de partitions eut égard au nombre potentiel de nœuds. En résumé, les quatre alternatives ou orientations généralement adoptées sont : a) Génération d'un nombre de tâches égal au nombre de nœuds disponibles. b) Génération d'un nombre de tâches supérieur au nombre de nœuds disponibles. Cette orientation ouvre notamment la possibilité de pouvoir allouer les tâches en fonction de critères d'optimisation. Un nœud pouvant se voir affecté plus de tâches qu'un autre. c) Génération d'un nombre de tâches supérieur au nombre de nœuds, et ajustement de nouveau de ce nombre en l augmentant au moment de l'affectation d'une tâche à un nœud. Ce choix permet un découpage plus fin d'une partition de relation avant de l'affecter à un nœud notamment pour des raisons d'occupation mémoire. d) Génération d'un nombre de tâches supérieur au nombre de nœuds, et réduction de ce nombre juste avant l'allocation au nœud. Ce choix est le complément du précédent puisqu'il permet l'augmentation des tailles de partition (par regroupement de partitions) afin d'optimiser l'utilisation des ressources mémoire d'un nœud donné Placement des tâches Cette étape répond à un besoin purement structurel. Il s'agit en effet de savoir s'il est nécessaire de placer chaque paire de partition des deux relations au sein du nœud élu pour leur 14
50 2. Équilibre de charge et distributivité des données traitement ou pas. Dans la négative, les données associées à un nœud i, et donc localisées sur d'autres nœuds, devront être regroupés au préalable vers ce nœud i avant leur traitement. L'abstraction de la localisation physique des données permet une allocation dynamique des tâches aux différents nœuds disponible. Le placement de départ peut être à l'opposé de celui souhaité pour les besoins de la jointure. En effet, le placement initial répond souvent à des besoins fonctionnelles ou technique, tandis que le placement ponctuelle pour la jointure a plutôt un caractère opportuniste lié à la disponibilité des ressources (i.e. Des nœuds) à un instant t. Cette problématique se prête assez aisément à des modélisations de type graphe ou bien encore de type CSP. Une étude intéressante sur le sujet est exposée dans l'article [13] essentiellement basée sur la fréquence d'accès aux données et sur la notion de température d'un objet (i.e partition) estimée à partir de la taille de cet objet et de la fréquence d'accès. Une autre étude plutôt orientée contraintes propose un algorithme de pilotage continue du placement des données pour un traitement parallèle : elle part d'un état optimal de placement et maintiens cet état tout au long de l'exécution[14] Collecte des statistiques La collecte de données statistiques est particulièrement nécessaire dans le cas d'allocation dynamique. Ces informations sont utiles afin de permettre l'ajustement dynamique des affectations de tâches aux nœuds. Si pour diverses raisons aucune statistique n'est collectée, alors les tâches sont affectées de manière arbitraire. Pour un pilotage optimal des affectations de tâches, les deux valeurs essentielles sont la taille des différentes partitions et la taille du résultat de jointure attendues pour une paire de partitions donnée. Cependant, seul le premier indicateur est disponible tandis que le second ne peut qu'être approximé. Une approche proposée dans l'étude [X6] exprime la taille du résultat global de la jointure par la formule : e i=1 s i d i où, e est le nombre de classes d'équivalence des attributs de jointure, r i et s i le nombre de tuples des relations R et S appartenant à la classe, d i le nombre d'attributs distincts au sein de la classe d'équivalence. On remarquera que cette approximation est exacte pour le cas théorique où d i = 1, et dans ce cas le nombre e de classes est égale au nombre d'attributs distincts des deux relations. Sur la base de cette approximation et de la taille des partitions, il est alors possible d'estimer le temps d'exécution d'une jointure Affectation des tâches Une fois les relations de jointure découpées, on dispose d'un ensemble de tâches à affecter aux différents nœuds pour un traitement parallèle. Deux modes d'affectations peuvent êtres mis en œuvre, à savoir l'allocation statique ou bien dynamique (i.e. avec équilibre de charge). Chacune de ces méthodes est mise en œuvre dans des situations appropriées : allocation statique : elle exige une gestion minimale de l'affectation puisque les tâches sont affectées une fois pour toute aux nœuds élus pour le traitement. Cette approche peut s'avérer efficace si d'une part l'ensemble des nœuds ont la même capacité de traitement et, d'autre part, les données sont équitablement distribuées. 15
51 2. Équilibre de charge et distributivité des données Dans le cas contraire, les temps de calcul globaux peuvent s'avérer incertains voir désastreux [9]. Allocation dynamique avec équilibre de charge : sur la base d'un découpage adapté des relations de jointure, et donc d'un nombre suffisamment important de tâches à affecter, il est possible de piloter l'allocation en veillant à ce que les temps d'exécution soient approximativement les mêmes à travers tous les nœuds qui participent au traitement. L'une des stratégies les plus utilisées afin de maintenir cet équilibre de charge est celle dite best-fit-like qui consiste à : trier les tâches de manière décroissante selon un critère donné puis, selon un algorithme glouton, affecter la tâche suivante au nœud qui est sur le point de terminer sa tâche courante. Cette méthode se décline selon deux axes qui sont les mesures utilisées et la stratégie d'allocation choisie. Une étude dans un contexte d'architecture de type Sharednothing a fait usage d'une telle méthode, mais en ramenant cette architecture un architecture de type mémoire virtuelle partagée[15] Mesures de charge Il s'agit là de mesures prédictives visant à évaluer la charge associée à chaque tâche. Ces mesures sont essentiellement celles exposées dans le chapitre «Collecte des statistiques» où une approximation est développée. Taille des partitions : sur la base de cette mesure, le but est de garantir que l'ensemble des nœuds traitent le même nombre de tuples. Pour un bon équilibre de charge, cela suppose que les relations de jointure sont bien distribuée sur l'attribut de jointure, et donc que le temps d'exécution est proportionnel au nombre de tuples traités. Temps d'exécution estimé : sur la base d'un temps d'exécution estimé les tâches sont distribuées de tel sorte que l'ensemble des nœuds se voient affecté la même durée totale de traitement. Dès lors qu'il est possible d'estimer correctement à moindre coût le temps élémentaire d'exécution, cette mesure devient la plus pertinente Stratégie d'affectation Sur la base des mesures de charge, deux stratégies sont possibles : statique ou dynamique. La première consiste à affecter une fois pour toutes les tâches de façon équitable aux différents nœuds et sur la base des critères de charge susmentionnés. Si ces mesures sont justes, alors cette approche donne d'excellents résultats. La seconde stratégie nécessite un pilotage tout au long des traitements afin que chaque nœud se voit affecté une tâche dès lors qu'il a terminé sa tâche courante, et pas avant. Il semblerait que cette approche n'ait pas donné lieu à des études approfondies dans le cadre des architectures distribuées. En effet, le placement des données est très coûteux dans ce cas, car il s'avère souvent primordial qu'un nœud connaisse à l'avance les tâches qui lui sont affectées afin d'anticiper leur transfert vers ses ressources locales et leur fusion si nécessaire. 2.2 Exécution des tâches A ce stade, chaque nœud dispose d'une ou plusieurs tâches à traiter localement. Et les seules interrogation qui subsistent est de savoir si une gestion de la charge de travail est possible et quel algorithme est le plus approprié pour exécuter la jointure des partitions locales. La gestion de la charge se décline selon deux possibilités : 16
52 2. Équilibre de charge et distributivité des données Aucune redistribution à posteriori : dans ce cas une fois les tâches affectées au nœud, elles devront être menées à bien par ce nœud quelque soit l'issue en terme de charge. Cela est notamment le cas lorsqu'on considère que l'essentiel du travail d'équilibre a été correctement réalisé en amont. Redistribution de charge : dans cette configuration tout ou partie d'une tâche peut être réaffectée par le nœud à qui elle a été initialement assignée en cas de surcharge de celuici. Plusieurs méthodes de redistribution de tâche peuvent êtres mises en œuvre. Celles-ci sont soit initiées par le nœud surchargé à destination d'un nœud libre, soit initiées par le nœud libre qui récupère une ou plusieurs tâches à un nœud surchargé, comme dans l'approche par «vol de tâches». Quant au choix du meilleur algorithme de jointure locale, il est orienté selon les principes exposés dans le précédent chapitre. On retiendra les situations suivantes : L'algorithme par boucles imbriquées est appropriée quand l'une des partitions est suffisamment petite pour tenir en mémoire ou quand on dispose d'un index sur la partition inner. L'algorithme par tri-fusion est le plus approprié si les partitions sont déjà triées. L'algorithme basé sur une fonction de hachage s'avère le plus pertinent dès lors que le nœud dispose de suffisamment de mémoire et que les valeurs de l'attribut de jointure sont uniformément distribuées. 2.3 Équilibrage de charge Nous avons jusqu'à maintenant exposé les mécanisme de création et répartition des tâches entre différents nœuds, en mettant en évidence des leviers permettant de procéder à un équilibre de charge soit statique, c'est à dire évaluer une fois pour toute lors de la première affectation des tâches, ou bien dynamique, et donc ajusté au fil du temps en fonction du déroulement des traitements au sein de chaque nœud et de leur niveau de charge effectif. Nous allons maintenant apporter plus de précisions à ce sujet qui nous intéresse au plus haut lieu. Ces deux type d'équilibrage de charge est utilisé dans des cas biens précis : dan le cas d'une bonne distribution des valeurs d'attribut de jointure pour le premier, et, dans le cas où cette donnée n'étant pas maîtrisée, il subsiste un risque majeur de dégradation des performances et donc d'augmentation importante de la durée nécessaire au traitement global Équilibrage de charge statique Une estimation du temps global ainsi que du temps nécessaire à chaque tâche est effectuée juste avant l'affectation des tâches aux nœuds. Sur cette base, les tâches sont ensuite affectées de façon à minimiser le temps total nécessaire à la jointure des deux relations R et S. Un tel mécanisme peut être implémenté selon l'algorithme suivant : i) Dans un premier temps, un nombre de tâches, généralement supérieur au nombre de nœuds disponibles, est produit. Selon que l'on s'oriente vers l'une ou l'autre méthode de découpage des relations, à savoir le «découpage total» ou le «découpage et réplication» exposés plus haut, chaque tâche est soit une jointure entre deux partitions de R et de S dans le premier cas soit, dans le second cas, la jointure entre une partition de la plus grande des deux relation et la totalité de la plus petite. Ainsi, chaque nœud qui détient déjà des partitions (fonctionnelles) procède au découpage de celles-ci en partitions technique (à des fins de jointure) en les chargeant en mémoire à hauteur de ce qui lui a été assigné en terme de 17
53 2. Équilibre de charge et distributivité des données tâches. Une fois la limite de ses tâches atteinte, le reste des partitions est envoyé vers les nœuds auxquels ces les tâches correspondant à ces partitions ont été affectées. ii) Une fois les partitions produites, chaque nœud collecte les informations relatives à ces partitions sur la base des partitions fonctionnelles qu'il détenait. Et, une fois le découpage et les collectes statiques réalisées, chaque nœud estime le temps nécessaire au traitement de chaque tâche qui lui a été assignée. Un nœud coordinateur récolte alors l'ensemble de ces statistiques et calcul le temps moyen nécessaire pour la réalisation de la jointure globale qui est le temps nécessaire pour que tous les nœuds aient effectué leurs tâches respectives. iii) Sur la base de ces estimations, chaque nœud identifie le nombre minimum parmi les tâches pré-affectées de tel sorte que : k j=1 k+1 Coût j Coût moy Coût j >Coût moy j=1 avec, Coût j le temps nécessaire pour réaliser la tâche j et, Coût moy le temps moyen nécessaire pour réaliser l'ensemble des tâches Toutes les tâches supérieures à la k ème tâche d'un nœud sont alors considérées comme un surplus de travail pour ce nœud et sont affectées à un autre nœud. Dans le cas contraire, si k est inférieur au nombre de tâches pré-affectées à ce nœud alors ce nœud est considéré comme potentiellement capable de prendre en charge d'autres tâches, et se voit, le cas échéant affecté des tâches de nœuds surchargés de façon à ramener la durée de traitement de chaque nœud sous la durée moyenne de traitement globale (Coût moy ). iv) Chaque nœud procède alors à la réalisation de ses jointures locales, sans ré-affectation possible même en cas de surcharge avérée Équilibrage dynamique Ce mode d'équilibrage de charge autorise le transfert de tâches d'un nœud à l'autre durant la phase d'exécution. A cette fin, il est nécessaire d'une part, au sein de chaque nœud, de maintenir les informations relatives au traitement en cours, à savoir la quantité de données traitées et la quantité de données générées en résultat. D'autre part, il appartient à chaque nœud qui a terminé l'ensemble de ses tâches ou en phase finale de ses traitements de signaler cet état. Ainsi, s'il existe un nœud n'ayant pas encore terminé ses tâches, alors une estimation de la quantité à transférer est réalisée puis transmise au nœud demandeur. Bien entendu, un ensemble de surplus de tâches d'un nœud peut également être partagé entre plusieurs nœuds demandeurs. On notera que l'identification du demandeur est aisée puisque c'est lui même qui initie la demande dès lors qu'il a terminé l'ensemble de ses tâches. A contrario, il n'est pas toujours aisé d'identifier le donneur (le nœud en surcharge) et a fortiori la quantité de données que celui-ci peut transférer compte tenu d'un ensemble de critères d'optimisation. Cette démarche suit une stratégie qui peut être déroulée selon l'algorithme suivant : i) Le nœud libre émet une demande de tâches à un coordinateur ii) Le nœud coordinateur met en attente le nœud demandeur selon le principe FIFO, puis émet une demande à l'ensemble des nœuds afin de connaître leur état de charge. iii) Dès réception de la demande, chaque nœud élabore sa charge courante puis la transmet au coordinateur. 18
54 2. Équilibre de charge et distributivité des données iv) Le coordinateur effectue les estimations nécessaires, détermine le donneur approprié à qui il transmet la requête du demandeur (le nœud libre), puis passe à la demande suivante. S'il y un nombre important de demandes et d'offres, le coordinateur peut réaliser des réponses groupées en mettant en relation les k premiers donneurs avec les k premiers demandeurs en attente. v) Le donneur reçoit l'identité du demandeur à qui il transmet la quantité de données qu'il aura déterminé au préalable. Le processus est poursuivi jusqu'à la fin des traitements, l'objectif étant que la durée globale des traitements soit aussi minimale que possible. Pour une implémentation correcte de tout algorithme d'équilibre de charge, beaucoup de questions doivent auparavant être soulevées : Quelles sont les informations les plus pertinentes que chaque nœud doit collecter, en évitant de générer un surplus de travail de collecte d'informations inexploitables. Qui doit initier la demande d'équilibre de charge : le nœud libre ou le nœud surchargé. Quels sont les critères de choix du donneur. Quelle est la quantité optimale de donnée à transférer pour répondre à une demande. En fait, les principaux indicateurs sont basés sur le nombre de pages déjà traitées ainsi que le nombre de pages générées comme résultat par un nœud. Ce qui implique que l'initiateur de la demande de transfert de charge est le le nœud ayant terminé (ou sur le point de terminer) ses tâches. Cette facette de l'équilibrage est très peu dépendante des caractéristiques propres au nœud ainsi que de la méthode de jointure utilisée. De l'autre côté, l'estimation de la quantité exacte de données à transférer d'un nœud donneur vers le nœud demandeur est fortement liée au système hôte et à la méthode de jointure. Ainsi, si le temps de fin de traitement (qu'on nommera ECT) est l'indicateur de charge d'un nœud, alors le processeur dont le ECT est le plus grand sera systématiquement désigné comme donneur en réponse à une demande. Et ainsi, si i est le nœud donneur et p le nombre de nœuds participant au traitement, alors i doit vérifier la relation suivante : i= Argmax(ECT i ), j[1, p] et, k ECT i = EET ij +EFT i où k est le nombre de tâches de i non encore traitées. j=1 k Le terme ECT i = EET ij est le temps d'exécution totale nécessaire pour achever les k j=1 tâches restantes. Il est estimé à partir des statistiques collectées au sein du nœud, qui sont dépendant du type de jointure utilisé, ainsi que de la taille des relations de jointure. Sur la base de ces éléments EET est donnée par : EET=CoûtJointure(R,S,Résultat) avec Résultat est la taille estimée en nombre de pages du résultat de la jointure. R et S étant, en nombre de pages, les tailles respectives des partitions R et S. Et la quantité EFT est le temps nécessaire pour terminer la tâche courante incluant les pages en cours des partitions de la tâches. Il est exprimé par la formule : EFT=CoûtJointure(absR,S,Résultat)CoûtJointure(r,s,res), avec res le résultat en nombre de page déjà produit et, r et s les quantités de pages des partitions R et S déjà traitées. Ces données sont facilement estimables sur la base des logs de traitement. 19
55 2. Équilibre de charge et distributivité des données Et, en conclusion, l'estimation de la quantité de données efficacement transférable d'un donneur vers le demandeur peut être réalisée selon les heuristiques pertinente suivantes : I) Priorité aux tâches non consommées : s'il existe une tâche qui n'est pas en cours de traitement par le donneur, alors celle-ci sera transférée. En effet, transférer une partie d'une tâche en cours de traitement peut s'avérer extrêmement compliqué et pénalisant, puisque fatalement une partie du travail réalisée devra être réalisée à nouveau sur le nœud demandeur. C'est notamment le cas pour les algorithme utilisant une table de hachage. Toutefois, cette méthode bien que fortement déconseillée, est tout à fait envisageable. II) La quantité de données transférée doit être suffisamment grande afin de garantir un gain significatif pour le temps d'exécution globale : la gestion des transferts entraîne nécessairement une surcharge de travail qui doit être compensée par une quantité de données suffisante. III) La quantité de données transférée ne doit pas être excessivement importante au point que le temps de fin de traitement du demandeur dépasse celui du donneur : cette heuristique envisage le transfert d'une tâche vers plusieurs demandeur si cela s'avère nécessaire, plutôt qu'uniquement vers un seul nœud demandeur. 2.4 Synthèse La gestion du parallélisme, comme nous l'avons exposé, est faiblement liée aux algorithmes utilisés pour la jointure. Toutefois certaines méthodes de jointure peuvent mieux s'apprêter à ce contexte. On évitera ainsi l'utilisation de la jointure par fonction de hachage quand on souhaite mettre en œuvre un équilibre de charge dynamique «poussé». On favorisera celle ci dès qu'on envisage un équilibre de charge statique. Par ailleurs, ce qui fonctionne pour des environnements parallèle de type SMP mais également NUMA ne fonctionne pas nécessairement pour des architecture totalement distribuées ne partageant aucune ressource physique ou logique (sharing-nothing). En effet, dans le premier cas, une stratégie d'affectation ne transférant les données d'un nœud à l'autre qu'au début effectif du traitement de ces données par ces nœuds est tout à fait envisageable. Le nœud donneur s'il ne partage pas de la mémoire ou du disque avec le demandeur partage au moins un bus interne permettant des transfert rapides et peu coûteux. Dans le cas des architecture distribuées, le placement des données est un enjeu majeur. On veillera autant que possible à positionner les données d'une tâche avant le début du traitement de celle-ci afin d'absorber les latences nécessaires à leur transfert. On veillera également à favoriser le traitement par le nœud qui détient déjà des partitions des relations de jointure, en le soulageant du surplus de travail, selon les méthodologies exposées, en adéquation avec la durée fixée (ou estimée) pour le traitement global. Par ailleurs, la philosophie de la parallélisation dans l'une et l'autre architecture peut être diamétralement opposé. En effet, si dans le cas d'architecture partagées on recherche à tirer profit d'un certain nombre de processeurs appartenant à un même système, dans le cas des architectures de type sharing-nothing on est amenés à réaliser des opérations ne pouvant raisonnablement êtres menées à bien que par le parallélisme imposé par la dissémination des données à travers un vaste réseau. La quasi-totalité des études menées dans ce sens sont exclusivement tournées vers le premier type d'architecture. Pour notre problématique, une difficulté supplémentaire consiste à choisir parmi toutes les méthodologies étudiées celles compatibles avec notre contexte. 20
56 2. Équilibre de charge et distributivité des données Enfin, on note également que les architectures qui nous intéressent ici ne partagent également aucune ressource système. Il s'agit de machines distribuées à travers un vaste réseau, pouvant dans certains cas exécuter des systèmes assez différents les uns des autres. Et donc, il n'est pas envisageable de baser les traitements sur un mécanisme supposant une quelconque cohérence à travers les nœuds utilisés. Il s'avère de facto nécessaire d'utiliser une surcouche logiciel visant à homogénéiser la relation entre les différents nœuds. Nous exposons dans le chapitre suivant ce que devrait être un tel FrameWork en nous basant sur celui proposé par Google, nommé Map-Reduce [16], et son extension Map-Reduce-Merge[17]. 21
57 3. Mise en œuvre du parallélisme en architecture de type «Shared-nothing» 3 Mise en œuvre du parallélisme en architecture de type «Sharednothing» 3.1 Problématique Les jointures dans des environnements shared-nothing en vaste réseau présentent des difficultés particulière et des obstacles techniques pour lesquelles les SGBDR traditionnels n'offrent pas de solution efficace. L'un de ses obstacles est la pauvreté de la structure des fichers matérialisant les relations à joindre. Un autre obstacle est la dissémination des partions des relations de jointure à travers ce vaste réseau. Un autre obstacle majeur est l'hétérogénéité des machines (à moindre coût) qui hénérgent les partions et qui peuvent êtres intégrées aux traitements. Le modèle de programmation «Map-Reduce» [16] répond à cette nécessité de traiter des quantités importantes de données, au sein de vastes réseaux de machines, tout en offrant une transparence quasi complète des aspects parallélisation de ce traitement et du système hôte du traitement. Dans son utilisation initiale, il est destiné au traitement de données homogènes et n'offre pas de mécanismes de traitement direct d'une jointure. En effet, une jointure est une opération entre deux tables (i.e fichiers) distincts n'ayant pas nécessairement le même schéma et partageant au minimum un attribut dit de jointure. Pour couvrir directement le domaine des jointures, une extension nommée «Map-Reduce-Merge» [17] est proposée : l'adjonction d'une troisième étape ayant pour fonction la combinaison des données issues des deux premières étapes : Map et Reduce. Nous décrivons dans un premier temps le fonctionnement du modèle Map-Reduce afin d'exposer le champ d'application du mécanisme et, inductivement, explorer ses limites. Nous décrivons ensuite l extension basée sur l'adjonction de la fonction merge, nous énumérons son apport puis nous exposons quelques cas d'utilisation. 3.2 Map-Reduce Map-Reduce est un modèle de programmation dont les principales motivations sont le traitement ( data processing ), à moindre coût, de données importantes au sein d importants réseaux de machines tout en offrant des temps d'exécution satisfaisants. Comme indiqué précédemment, Map-Reduce travaille sur des données homogènes. Le concept est basé sur deux fonctions standards map et reduce. Dans un premier temps, la fonction map, instanciée autant de fois que nécessaire, prend en entrée les données initiales faisant l'objet du traitement et les restitue sous forme d'une liste de tuples du type <Clé, Valeur>. Dans un second temps, la fonction reduce, également instanciée, fusionne les valeurs ayant la même clé pour produire une nouvelle liste de valeurs uniquement. La sémantique de ce mécanisme est indiquée par la description «formelle» suivante : map : (k 1, v 1) [(k 2, v 2)] reduce : (k 2, [v 2]) [v 3] La structure et le contenu des champs Clé et Valeur ainsi que la nature des traitements sont laissés à la discrétion du développeur. De l'autre côté, la parallélisation, l'optimisation des traitements et la tolérance aux pannes sont totalement gérés par le mécanisme Map-Reduce. Le développeur ne se souciant alors à aucun moment de ces aspects purement techniques. Pour ce faire, et afin de faciliter la mise en œuvre de ces mécanismes inhérents aux systèmes parallèles, Map-Reduce s'appuie sur «Google File System» [18] qui est un système de fichier distribué. Map prend sa source dans des fichiers GFS et reduce produit ses sorties également vers un fichier GFS. Le Goole File System assure la gestion de ces fichiers, plus ou moins volumineux, sous forme de partitions (Chunks) distribuées et partagées à travers un vaste réseau informatique. Ce service offre une abstraction complète quant à la localisation des fichiers faisant l'objet du traitement, ainsi que de la nature de leur système hôte, et assure également leur redondance et leur sécurité. Néanmoins, le mécanisme Map-Reduce peut être amené, pour des raisons d'optimisation, à tenir compte de l'affinité d'un nœud élu pour un traitement map avec une ou plusieurs partitions (i.e. chunks) d'un fichier. Les structures des fichier des fichiers d'entrée et de sortie sont laissés à l'entière discrétion de l'utilisateur. Contrairement à l'application BigTable [19] qui propose un modèle de donnée simple et une 22
58 3. Mise en œuvre du parallélisme en architecture de type «Shared-nothing» structure des fichiers en matrice, Map-Reduce permet manipule des fichiers bruts que l'utilisateur manipule selon ses besoins, extrait éventuellement une partie des informations disponibles et produit des fichiers bruts en sortie. Contrairement au concept «Data Aggregation Acces» [20] qui propose le paramétrage d'un niveau de qualité, Map-Reduce ne propose pas de tel mécanisme et donc, dans la forme, une exécution est complète ou abandonnée. Bien qu'initialement conçu pour la mise en œuvre de moteur de recherche, Map-Reduce a depuis fait ses preuves en servant de base de développement à de multiples autres applications. Ces applications manipulent des données de l'ordre de plusieurs Téraoctets et s'appuient sur des milliers de «serveurs» ; ce qui démontre l'adaptation à grande échelle de ce mécanisme. La nature de ces traitements est essentiellement la recherche de documents à travers un vaste réseau ou encore l'analyse de logs de recherche Web. Ainsi l'utilisation première pour laquelle Map-Reduce a été conçue est largement couverte, bien au delà de l'objectif premier. Ce qui est la garantie d'une bonne robustesse. Mais l'extension des Systèmes d'information et de leur besoin fait apparaître d'autres obstacles pour lesquelles Map-Reduce n'offre pas une solution directe et satisfaisante. Ainsi, la nécessité de composer avec divers sources d'informations met en évidence les limites de ce mécanisme. En effet, il est extrêmement difficile sur la base du mécanisme initiale, de recouper par exemple les données d'une compagnie A avec celle d'une autre compagnie B afin d'en tirer un certain nombre d'enseignements. De façon plus précise, la notion de jointure n'est en l'état pas couverte sans utiliser un mécanisme basé sur deux phases Map-Reduce qui nécessite une manipulation (coloration) des données intermédiaires. 3.3 Map-Reduce-Merge Map-Reduce-Merge se positionne comme une continuité du mécanisme initial Map-Reduce avant de fournir des solutions aux à des problématique apparemment non couvertes par le modèle de base. Cette nécessité de continuité ne concerne pas seulement les aspects fonctionnels mais elle est également étendue aux aspects ergonomiques, à savoir une utilisation aisée et une transparences totale de la gestion des mécanismes de parallélisation, d'optimisation et de tolérance aux pannes. Toutefois, une sensible complexification du Workflow, linéaire dans le premier cas, peut ne pas être évitable suite à l'ajout de la troisième primitive Merge. Grâce à cette extension, Map-Reduce-Merge est en mesure de couvrir la plupart des types de jointure parallèles incluant le hash-join, le netsted-loop ou encore le sort_merge. La sémantique de cette extension étant alors décrite par les règles suivantes : map : (k 1, v 1) [(k 2, v 2)] Ici et sont les deux chaînes de traitement Map-Reduce reduce : (k 2, [v 2]) (k 2,[v 3]) portant sur deux fichiers distincts, chacune produit merge : ((k 2,[v 3]), (k 3,[v 4]) ) ([k 2,v 5]) une entrée pour Merge, qui produit à son tour. Les étapes Map et Reduce initiales restent identiques à celles du mécanisme de base, à la différence près que la sortie produite par la fonction merge inclut la clé pour chaque valeurs associées à cette même clé (ici k 2 et [v 3]). Le maintien de cette clé, ainsi que le tri selon cette clé, est absolument nécessaire à la fonction merge afin de fusionner correctement (i.e. traiter selon la méthode requise) les données issues des lignes de traitement et, ayant la même valeur de clé. Un exemple concret de mise en œuvre de cette méthode : le calcul des primes annuels d employer rattachés à différents départements. Deux structures de données hétérogènes sont ici manipulées. La première est le fichier des différentes primes octroyés à chaque employer, un employer pouvant être bénéficiaire de plusieurs type de primes (assiduité, efficacité, etc...), dont la structure est : <id-employer, iddépartement, description_bonus>. La seconde est le fichier des département référençant les coefficients globaux appliqués aux primes des employer d'un département donné, dont la structure est : <id-département, coefficient_bonus>. L'un et l'autre fichiers sont traités par deux chaînes Map-Reduce distincts. La première chaîne produit une table agrégée des primes par employer (avec un unique enregistrement par employer) triée selon la clé «id-dep» puis «id-emp», la seconde produit l'ajustement des bonus par département qui est ensuite triée par la fonction merge selon la clé «id-dep». Enfin la fonction merge élabore la prime finale en réalisant les opérations de jointure puis de produit, pour chaque employer, des primes et du coefficient d'ajustement associé à chaque département. L'implantation du mécanisme Map-Reduce-Merge s'appuie sur la librairie initiale de Map-Reduce avec toutefois quelques modification sur les signatures des fonctions. Cette librairie est ensuite augmentée par la fonction merge ainsi que d'autres fonctions utiles : processor, partition selector et configurable 23
59 3. Mise en œuvre du parallélisme en architecture de type «Shared-nothing» interator. La fonction merge met en œuvre le même mode opératoire que les fonctions map et reduce. A savoir, la possibilité offerte au développeur de définir la suite d'actions à appliquer aux deux paires <Clé, valeurs> issues des deux chaînes de traitement. Dans cette phase de merge, le développeur peut également s'appuyer sur la fonction processor afin d'appliquer des traitements particuliers aux données sources. Le partition selector quant à lui, en se basant sur le numéro du merger, affecté par le coordinateur global, identifie les données sources à traiter. Enfin un «itérateur configurable» (ou iterator manager) est utilisé afin de synchroniser les deux sources de données du merger. Car contrairement au reducer, qui utilise également un iterator mais basé sur une source unique de données, le merger offre à l'utilisateur la possibilité de manipuler l'une ou l'autre source de données, selon un mode opératoire particulier en fonction du type de jointure à mettre en œuvre. Par ailleurs, l'iterator est la technique qui couvre, dans les deux cas (Map-Reduce et Map-Reduce-Merge), la lecture à la volée de l'entrée, évitant ainsi le stockage sur disque local des données intermédiaire. 3.4 Portée du modèle Map-Reduce-Merge L'une des principales ambitions de Map-Reduce-Merge est de doter les mécanismes de traitement parallèle d'une dimension relationnelle à l échelle des moteurs de recherche. En effet, Map-Reduce-Merge se présente en SGBD relationnel, comme nous l'illustrons ci-après, tout en apportant des fonctionnalités d'optimisations relatives aux contraintes de parallélisme. Si on Considère une relation R structurée selon un schéma A. Le développeur Map-Reduce-Merge peut alors décomposer, selon ses besoins, ce schéma en deux parties K et V. Ici K représente le schéma de la clé k et V celui de la valeur v, un tuple t de R est alors représenté par la concaténation des champs k et v, correspondant ni plus ni qu'aux clés et valeurs manipulées par Mep-Reduce-Merge. Ceci posé, il est possible de réaliser l'ensemble des opérations attendues d'un SGBD relationnel, il suffit pour ce faire d'élaborer le worklow adéquat afin d'appliquer les traitements successifs aux tuples initiaux. De cette façon les réalisations suivantes et bien d'autres sont aisément envisageables : la projection apparaît dans ce contexte triviale, seules les étapes map et reduce sont mises en jeu et produisent en sortie un tuple t' = (k', v') dont les schémas respectifs K' et V' sont une sous partie du schéma A. La jointure est quant à elle décrite dans l'exemple exposé dans ce document. Elle est réalisable selon l'ensemble des variantes standards. L'intersection se fait selon le même mode opératoire que la jointure aux étapes map et reduce, le merger n'ayant alors plus qu'à itérer sur l'une et l'autre entrée des deux reducer afin de restituer les tuples t partagés par l'une et l'autre relation. Le produit cartésien est également facilement réalisable par lecture des sorties des deux reducer et composition par le merger des combinaisons des tuples de l'une et l'autre entrée. Une composition simple ou complexe,selon les cas, de ces fonctions rend possible la réalisation de tout type de traitement nécessitant le recoupement entre deux sources de données ou plus. Ceci est notamment possible grâce à une imbrication, assez naturelle, de plusieurs processus Map-Reduce-Merge. 3.5 Synthèse Le concept Map-Reduce augmenté par le Merge semble être un outils extrêmement efficace pour la réalisation de programmes parallèles mettant en œuvre une foultitude de machine plus ou moins hétéroclites en terme de configuration, de puissance de calcul ou encore de fiabilité. C'est en fait, le principal challenge que se sont fixé l'outil Map-Reduce et son extension Merge. A savoir, l'exploitation de serveurs (i.e. Machines) disponibles à travers un vaste réseau (Internet), mettant en œuvre des traitements pouvant s'avérer lourd, coûteux et peu efficaces s'ils devaient être réalisés sur des serveurs dédiés et conçus pour cet usage. L'autre challenge est de proposer un modèle de programmation générique masquant autant que possible les fonctionnalités inhérentes au parallélisme telles que la tolérance aux pannes ou encore l'équilibrage de la charge des machines ; ceci est notamment facilité par l'utilisation de GFS. Par ailleurs, contrairement au concept «Data Aggregation Call» orienté service et qui admet des solutions partielles (niveau de qualité de service paramétrable), Map-Reduce-Merge se fixe des objectifs de résultats déterministes et complets en terme de restitution des traitements. Si la fonction Merge étend de façon favorable les possibilités de Map-Reduce et en fait un concept extrêmement puissant, elle présente néanmoins un certain nombre de limitations techniques mises en évidence de façon explicite dans l'implémentation du Hash-Join. Ailleurs, cette limitation est moins explicite mais non moins vraie : c'est le cas de l'implémentation du produit cartésien. De façon générale, dès 24
60 3. Mise en œuvre du parallélisme en architecture de type «Shared-nothing» lors que les données à traiter par le merger nécessitent plusieurs passes, il s'avère inévitable de stocker les données intermédiaires en local marquant ainsi une rupture avec le concept Map-Reduce favorisant quant à lui le traitement des données au fil de l'eau afin d'éviter ce type de désagrément. Par ailleurs, les mises en œuvre de jointures passent sous silence le déséquilibre des données traitées. Une autre alternative visant plutôt à doter le concept initial d outils plus puissants, lui ouvrant d autres perspectives, au lieu de l augmenter par une troisième primitive est également envisageable. Dans l un et l autre cas, repenser la dynamique de Map-Reduce, notamment la coordination (et instantiation) des processus map et reduce aujourd hui brutale, semble nécessaire pour garantir une plus grande souplesse du concept, et une réelle scalabilité. Toutefois, le FrameWork Map-Reduce ayant à ce jour fait ses preuves, il est aujourd'hui implémenté par divers organismes : Google, Yahoo ou encore Apache. Il semble donc incontournable dans le cadre d'expérimentations techniques d'exécution de requêtes de jointure au travers un vaste réseau. Le FrameWork Map-Reduce-Merge n'est à ce jour pas finalisé puisqu'il ajoute un nombre assez important de primitive en plus de la primitive Merge. Et, à ce titre sauf pour des travaux spécifiques à cette extension, il est préférable de s'appuyer sur le FrameWork initial Map-Reduce. 4 Conclusion Le traitement de jointure en environnement totalement distribué présente de multiple facette. Des difficultés sont rencontrées à chaque étape, et à chaque une multitude de solutions sont possibles. Toutefois, les études menées à ce jour dans ce domaine se limitent souvent soit à des architecture partageant une ressource efficace en matière d'échange de données : disques, bus, réseau dédié..., soit elles s'appuient sur des hypothèses simplificatrices sur la bonne distribution des données. Malgré tout, comme tenu des différents méthodes exposées ici, il est possible de mettre l'accent sur certaines orientations qui sont les suivantes : a) Le placement des données est essentiel, car de lui dépend la minimisation du transfert des données à traiter. b) On veillera à suffisamment découper les relations de jointure afin de limiter les temps de transfert d'une tâche, tout en n'ayant pas besoin de recourir à un second découpage de ces tâches afin d'en distribuer la charge entre deux nœuds. Cela est d'autant plus aisé que le nombre de nœuds dans ce contexte peut être très important. Toutefois cette démarche est à mener de façon cohérente avec le premier point. c) On favorisera autant que possible la recherche de mesures pertinentes visant à nous donner les moyens de procéder à une distribution initiale des traitements la plus efficace possible. Ainsi, dans le meilleur des cas on pourra se cantonner à l'équilibre de charge statique. Dans le pire des cas, si on doit envisager un équilibrage de charge dynamique, celui-ci pourra être utilisé comme levier d'appoint afin d'ajuster légèrement la distribution initiale. d) Sauf dans le cas où les données sont déjà triées, et dans ce cas la jointure par tri-fusion est fatalement la plus performante, on s'orientera systématiquement vers la jointure par boucles imbriquées avec blocs ne nécessitant aucun pré-traitement et dont la durée d'exécution est aisément prévisible. e) Nous veillerons, autant que possible, à utiliser les mêmes algorithmes de jointure au sein de tous les nœuds qui participent au traitement. Ainsi, les mesures collectées et les prévisions réalisées sur la base de ces mesures sont aisées et globalement cohérentes étant donné le nombre important de nœuds qui peuvent êtres mis en jeu. f) Compte tenu du faible coût d'utilisation d'un nœud, au cas où la fin du traitement d'un nœud semble fortement compromise, plutôt que de l'interrompre ou lui retirer un certaine quantité de tâches, on préférera initier la redistribution des tâches qui lui sont affectées et non encore 25
61 4. Conclusion traitées vers un ou plusieurs nœuds disponibles. Si celui-ci venait à finalement terminer ses tâches dans le temps imparti son résultat pourra être intégré au traitement global et les autres traitements abandonnés. g) Tant que cela est possible, on maintiendra les partitions du résultat d'une jointure au sein des nœuds les ayant élaborés. Aucune consolidation de ces partitions n'est à priori envisagée. 26
62 . SECONDE PARTIE : ÉTUDE DE LA JOINTURE EN ENVIRONNEMENT CLOUD 27
63 5. PROBLEMATIQUE DE LA JOINTURE PARALLELE 5 PROBLEMATIQUE DE LA JOINTURE PARALLELE La problématique récurrente de la jointure parallèle est essentiellement due à la nature des données jointes quant à leur distribution. En effet, si on considère la fréquence d'apparition d'une valeur d'un attribut de jointure donné, celui-ci, dans l'une et l'autre relation en jeu, peut être soit équilibré, à savoir l'ensemble des valeurs distinctes d'un attribut d'une relation apparaissent de façon équilibrée, c'est à dire à peu près le même nombre de fois, ou bien, au contraire ces valeurs distinctes apparaissent de façon déséquilibrée au sein de ces relations ; autrement dit une valeur ou un groupe de valeurs apparaissent de façon disproportionnée par rapport au reste des valeurs. De manière combinatoire, cette particularité peut être présente indépendamment dans l'une ou l'autre relation de jointure. Étant donné un algorithme de jointure parallèle, chaque cas de figure de distribution des données induit un comportement différent. Dans le cadre d'une première approche de traitement parallèle, comme mentionné dans la première partie, il est nécessaire de distribuer les données à joindre selon l'attribut de jointure des deux relations ; de telle sorte que les même valeurs de l'attribut de jointure, des deux relations, soient localisées in fine sur le même nœud. Cette distribution, ou répartition des données, est la, plupart du temps réalisée à l'aide d'une fonction de hachage associée à une fonction modulo, sans que le principe soit limité à ces méthodes ; toute méthode susceptible de produire une meilleure distribution ou bien imposée par la nature des données pouvant être envisagée.toutefois, dès lors qu'il n'est pas possible de tabler sur une distribution naturelle, répartissant correctement les données à joindre vers les différents nœuds de traitement, des méthodes basées sur le partitionnement de données homogènes s'imposent ; en veillant à ce que l'union des jointures locales soit toujours strictement égale à la jointure globale. La difficulté de la jointure parallèle est encore plus prononcée dans le cadre d'un environnement CLOUD ou dit Shared-notyhing. En effet, l'échange de données n'est pas à moindre coup, et la synchronisation bilatérale entre nœuds n'est pas chose envisageable. Et ceci est encore plus vrai lorsqu'il s'agit de réseau de machines à très grande échelle, ce qui est notre cas d'étude. Ne pouvant être synchronisés et coordonnés en temps continu, ces multiples nœuds doivent fatalement s'appuyer sur des mécanismes implicites, nécessitant un minimum de communications de contrôle. Les seuls flux d'échange, avec restriction, sont les données traitées. Dans ces conditions, les caractéristiques des données de jointure influent énormément sur l'efficacité effective des algorithmes mis en jeu. Notre démarche consiste dans un premier temps à évaluer, dans le cadre du CLOUD et à l'aide du FrameWork MapReduce, décrit dans la première partie de ce document, des algorithmes de jointure de données massives. Nous proposons l'étude comparative d'un algorithme basé sur des méthodes naïves avec un autre plus sophistiqué mettant en œuvre le partitionnement en s'appuyant sur la fréquences des valeurs d'attributs de jointure. Dans un deuxième temps nous dotons cet algorithme évolué d'outils formels pour son paramétrage. Nous utilisons ensuite les résultats obtenus afin d'explorer d'autre voies d'évolution de la jointure propres au contexte CLOUD. Nous terminons par une proposition d'évolution du concept MapReduce permettant une implémentation plus naturelle de la jointure ainsi que d'autres usages. Auparavant, nous exposons une vision plus précise du déséquilibre de données et le contexte dans lequel nous menons nos travaux. 28
64 6. DÉSÉQUILIBRE DES DONNÉES 6 DÉSÉQUILIBRE DES DONNÉES Afin d'illustrer le comportement induit par une distribution des valeurs des attributs de jointure, prenant le cas où les attributs A et B de jointure, de deux relations R et S, sont de type entier, compris entre 1 et N, et la méthode de distribution des données sur les différents nœuds est la fonction modulo. On peut identifier dans ce contexte plusieurs cas de figue qui sont : 1 vers 1 : Les attributs A et B prennent chacun, pour chaque valeur possible entre 1 et N, une et une seule fois cette valeur. Ainsi A et B prennent une seule fois la valeurs 1, une seule fois la valeur 2, une seule fois la valeur N. C'est notamment le cas quand ces deux attributs sont une clé dite primaire, dont la valeur est générée de façon incrémentale. C'est une situation réaliste et assez fréquente en SGBDR. M vers M : Les attributs A et B prennent chacun, pour chaque valeur possible entre 1 et N, n fois cette valeur. La valeur 1 apparaissant donc M fois, la valeur 2 également M fois... Ce cas de figure bien qu'étant très particulier peut être généralisé si on admet une légère variation de M d'une valeur à l'autre et d'un attribut à l'autre. n vers m : les attributs A et B prennent chacun respectivement, pour chaque valeur possible entre 1 et N, n fois et m fois cette valeur. Dans ce cas de figure, la valeur 1 apparaît n 1 fois pour l'attribut A et m 1 fois pour l'attribut B, 2 apparaît n 2 fois pour A et m 2 fois pour B, n i et m i étant quelconques supérieures ou égales à 0. Si on applique la fonction de répartition des données, ici modulo, au premier cas, on aura une distribution des données équilibrée. Dans le deuxième cas, l'équilibre est également prévisible dès lors que N est grand. Le troisième cas de figure présente plus de difficultés car il ne nous est pas possible de prévoir la distribution des données résultant de l application de la fonction choisie modulo. Ainsi si la situation est proche des cas 1 et 2, on retrouve une bonne distribution, dans le cas contraire le doute est permis. Prenons comme exemple le cas où les valeurs de A et B sont elles mêmes, de par leur nature, restreintes à un sous ensemble de valeurs dont le modulo conduit à un autre sous ensemble de valeurs : donc si A et B prennent les valeurs paires uniquement, l application de la fonction modulo 10 par exemple conduit immanquablement au sous ensemble 0, 2, 4, 6 et 8. Par conséquence, si on souhaite procéder au traitement de la jointure sur 10 nœuds, dans ce cas, on n'exploitera que la moitié des nœuds à savoir les nœuds 0, 2, 4, 6 et 8 ; ce qui conduit à une durée de traitement théoriquement deux fois plus longue que celle escomptée avec 10 nœuds. Cette première cause de déséquilibre, c'est à dire la prédisposition des données à se distribuer de façon déséquilibrée sous l'application d'une fonction de répartition de ces données, n'est pas la seule à poser problème. En effet, on peut décomposer la méthodologie de jointure parallèle en au moins 2 phases qui sont : Répartition des données sur N nœuds Jointure des données locales à chaque nœud Nous l'avons vu, la première phase peut poser problème dès lors que les quantités de données présentes sur chaque nœud sont déséquilibrées. Une autre source de difficulté réside dans la maîtrise du nombre de tuples, sur chaque nœud, résultants de la jointure locale durant la seconde phase. En effet, malgré une bonne distribution de la quantité de données sur chacun des nœuds, les quantités de tuples résultants de la jointure produites sur chaque nœud peuvent, même dans ce cas, être extrêmement déséquilibrées comme l'exemple suivant peut l'illustrer : i. On considère deux nœuds de traitements sur lesquels 16 tuples sont distribués, 8 de chaque relation. 29
65 6. DÉSÉQUILIBRE DES DONNÉES ii. Sur le premier nœud, on identifie 4 valeurs distincts pour chaque relation, dont la fréquence est de 2 pour chacune de ces valeurs. iii. Sur le second nœud, on dispose aussi de 16 tuples, 8 pour chaque relation, avec deux valeurs distinctes des attributs de jointure et donc ayant chacune une fréquence de 4. iv. Sur le premier nœud, on produit 2x2+2x2+2x2+2x2 = 16 tuples de jointure. v. Sur le second nœud, on produit 4x4 + 4x4 = 32 tuples de jointure. On constate ici que malgré un très bon équilibre de la quantité de données sur l'un et l'autre nœud, le second nœud produit 2 fois plus de tuples de jointure que le premier nœud. L'impact d'un tel déséquilibre est double. Dans un premier temps, nous avons besoin d'un effort de traitement deux fois supérieur d'un nœud à l'autre, mais nous produisons également 2 fois plus de données d'un nœud à l'autre. L'effet immédiat est la génération de 2 fois plus d'i/o ; ce qui a un impact encore plus important sur les durées de traitement. En conclusion, bien au delà de la quantité de données, il est essentiel d'équilibrer non seulement celle-ci mais également la quantité de données produites par chaque jointure locale. Si n 1, n 2... n N sont les fréquences des valeurs de l'attribut A de la première relation et m 1, m 2,..., m N les fréquences de l'attribut B de la seconde relation, si K est le nombre de nœuds disponible, il nous faut donc équilibrer : ip i (n i +m i )avec P j ={tout i[1, N]tq j=i %K et ip i (n i m i )avec P j ={touti[1, N]tq j=i%k Par ailleurs, les motivations et donc l'impact de l'une et l'autre des ces deux recherches d équilibre ne sont pas nécessairement les mêmes. Dans le premier cas, il peut s'agir d'équilibrer les communications ou bien encore la quantité de mémoire occupée par les données de jointure, dans le second cas c'est principalement la motivation portant sur la quantité d'i/o générée qui peut être mise en avant. Pour traiter cette problématique, deux approches sont possibles. La première consiste à adopter une méthode visant à se détacher le plus possible de la distribution des données. Celle-ci minimise l'impact d'un déséquilibre mais ne peut en aucun cas le supprimer complètement. La deuxième méthode consiste à analyser au préalable les données à joindre avant de procéder à leur répartition puis leur jointure. La première méthode peut s'appuyer soit sur des algorithmes naïfs (exemple modulo) pour distribuer les données si les caractéristiques de celles-ci sont bornées, soit mettre en œuvre des algorithmes plus complexe. La seconde méthode, s appuie sur une analyse préliminaire portant soit sur la totalité des données soit sur un échantillon représentatif. Dans cette étude nous nous attardons principalement sur la seconde méthode avec analyse complète des données. Il s'agit des algorithmes basés sur le calcul des histogrammes des relations à joindre visant à catégoriser les différentes valeurs des attributs de jointure selon leurs fréquences respectives. Nous nous appuierons également sur la première méthode et notamment sur la variante naïve dès lors que cela est jugée opportun en conjugaison avec les algorithmes basés sur les histogrammes. Pour des raisons de simplification de l'implantation des algorithmes, nous nous restreignons, pour les attributs de jointure, à des entiers naturels strictement supérieurs à 0. Cette limitation ne retire rien à la généralité de nos propos, à l'inverse elle facilite grandement la production de jeux de données ainsi que le parsing des attributs. Par ailleurs, sauf indication contraire, nous considérons que les nœuds du Cloud sont tous de même puissance. 30
66 6. DÉSÉQUILIBRE DES DONNÉES 6.1 Algorithmes à histogramme Une méthode de jointure parallèle développée au sein du LIFO est basée sur l'analyse exhaustive des fréquences des valeurs des attributs de jointure. Elle vise d'une part à procéder à un comptage systématique et totale des occurrences de chaque valeur des attributs de jointure et, d'autre part selon différents algorithme redistribuer les données en veillant à équilibrer à la fois les données à joindre et et le résultat de jointure. Ces algorithmes prennent également en compte les localités initiales des données afin d'optimiser les flux de redistribution. Plusieurs variantes de cet algorithme ont été développées, toutefois, la plupart sont destinées soit à des systèmes parallèles, multiprocesseurs et Clusters multi-nœuds disposant d'un réseau de communication homogène. Parmi ces variantes, l'algorithme partiellement mais aisément adaptable à notre environnement CLOUD est le SFA_JOIN. Le principe de cet algorithme se résume en 5 phases qui sont les suivantes : i. Chaque nœud qui détient une partition fonctionnelle d'une relation, c'est à dire une partition basée sur un autre attribut que l'attribut de jointure, évalue l'histogramme local de cette partie de relation. On notera cet histogramme local Hist(R i ) ou Hist(S i ) selon qu'il s'agit de la première ou seconde relation, où i est le nœud qui détient la partition. ii. Selon une fonction de hachage prédéfinie chaque nœud émet l'histogramme locale associé à une valeur v de l'attribut de jointure A ou B. iii. L'ensemble des histogrammes locaux associés à une valeur v d'attribut de jointure se trouve maintenant sur un même nœud. Celui-ci peut alors agréger ces histogrammes locaux en un histogramme global pour chaque valeur qu'il détient. On notera cet histogramme global d'un sous ensemble de valeurs associé au nœud i : Hist i (R) (resp. Hist i (S)). Sur la base de ces histogrammes globaux associés à chaque valeur, le nœud j selon différents méthodes, décrite plus loin, peut décider s'il est nécessaire ou pas de distribuer les tuples associé à la valeur v de R (resp. S) pour un traitement parallèle. iv. En recevant les histogramme locaux des nœuds j, le nœud i a mémorisé le nombre d occurrences présentes sur chaque nœud j. Ainsi, le plan d'exécution et le schéma de communication associé peut être élaboré selon cette connaissance, et sur la base du partitionnement décidé durant la phase précédente. Et donc, afin de minimiser le flux d'échange de données, pour une taille de partition P pour d'une valeur v de l'attribut A (resp. B), le nœud i estime la quantité de tuple soit à ajouter soit à retirer à chaque nœud j. Ainsi, chaque nœud j : - si (P-Hist(Rj)(v)) > 0 le nœud j reçoit (P - Hist(Rj)(v)) tuples - si (P-Hist(Rj)(v)) < 0 le nœud j perd (Hist(Rj)(v) - P ) tuples v. Le nœud i émet alors ce plan de communication à chaque nœud j concerné afin qu'ils procèdent aux échanges nécessaires à l'équilibre de données. Un nœud qui doit perdre n tuples doit les répartir de façon équitable vers l'ensemble des nœud qui doivent recevoir des tuples de compensation pour équilibrer les données. Dès lors que chaque nœud détient l'ensemble des valeurs, associées aux attributs de jointure A et B, qui lui ont été attribuées, le traitement de la jointure parallèle peut être réalisé. Dans ce phasing, nous remarquerons que cet algorithme utilise de façon systématique la communication de données entre nœuds. 6.2 Simulation du déséquilibre Dans le cadre de nos expérimentations, il nous est nécessaire de disposer d'un outil capable de fournir à la demande un ensemble de données (relations) présentant les caractéristiques voulues, à savoir : nombre d'item : clés distinctes 31
67 6. DÉSÉQUILIBRE DES DONNÉES la fréquence maximale : pour une valeur de clé donnée le nombre maximal de fois qu'elle peut apparaître. Le déséquilibre : l'accélération de la baisse de fréquence entre l'item le plus fréquent et le deuxième plus fréquent, entre le deuxième plus fréquent et le troisième plus fréquent... Ce premier outil nous fourni une distribution quelconque des valeurs de clé de la relation, ou des valeurs de l'attribut de jointure. Il nous faut maintenant associer à ces clé des valeurs pour constituer un tuple (k, v). De plus, la taille de v détermine la quantité de données (en octets) que pèse la relation concernée Fonction de simulation de distribution des clés En ce qui concerne le premier outil, notre choix s'est porté sur la fonction de distribution Zipf. Celle-ci présente l intérêt d'être aisément implantable et de répondre aux exigences posées cidessus. Cette fonction a été élaborée dans le cadre d'études de la distribution de mots dans un texte. Au début empirique, l'idée fut développée pour en faire un modèle mathématique dont la formule est : f (k)= 1 1 N ( 1 n s) k s n=1 Où : N est un entier naturel, qui représente le nombre de clés (mots) distinctes. k est un entier naturel non nul, qui représente le rang en terme de fréquence. s est un réel non nul représentant le coefficient de déséquilibre. La forme précédente est une forme générale non exploitable pour nos tests. Afin de pouvoir maîtriser aisément les fréquences maximales nous remplaçons le premier terme de l'équation par F qui est la fréquence maximale, soit : f (k)=f 1 k s On remarquera que pour un nombre d'items (valeurs de clé distinctes) donné et une fréquence maximale donnée, la densité de cette loi baisse énormément selon s. Ainsi pour F=100, N=100 et s=0 le nombre de tuples correspondant est de Pour F=100, N=100 et s=2.0 le nombre de tuples chute à 153, cela s'explique par le fait que le terme k s croit rapidement pour s > 0. Ce constat peut être observé sur le graphique ci-après qui est une représentation de la fonction f(k) avec N=100, F=100 pour s compris entre 0 et 2 avec un pas de 0.1. On observe l'augmentation rapide du déséquilibre entre l'item le plus fréquent (ici 1) est les suivants. Ainsi, pour la suite de nos travaux, nous nous limitons pour s aux seules valeurs 0, 0.25, 0.5 et Pour un déséquilibre maximal, on génère artificiellement un jeu de données pour lequel seul le premier item apparaît avec une fréquence maximale. Pour des raisons pratiques, le graphique ci-dessous illuste les courbes de distribution en fonction de s pour une fréquence maximale normalisée à
68 6. DÉSÉQUILIBRE DES DONNÉES S=0 S=0.1 S=0.2 S=0.3 S=0.4 S=0.5 S=0.6 S=0.7 S=0.8 S=0.9 S=1.0 S=2.0 Figure 2: représentation de la fonction zipf pour F=100, N=100 et s entre 0 et 2 La sortie produite notre outil de génération d'une distribution de type zipf est deux fichiers textes. Le premier contient la liste des fréquences pour chaque clé. Le second contient la liste des clés qui est une sorte d'extension de la liste des fréquences. Ainsi dans ce second fichier, une clé k dont la fréquence est f apparaît f fois ce qui matérialise une relation dépouillée de ses champs valeurs. De plus le fichier des fréquences peut être mixé ou pas : la clé la plus fréquente peut être 1 et la moins fréquente N si le mixage n'est pas désiré, à l'inverse la clé la plus fréquente peut être tiré aléatoirement afin de produire une relation au contenu réaliste comme l'illustre la figure ci-après pour s=0.5, la courbe M montrant cette même distribution dont les fréquences entre 1 et 100 sont affectées aléatoirement à chaque clé. 33
69 6. DÉSÉQUILIBRE DES DONNÉES S=0.5 M Figure 3: effet de l'affectation aléatoire (mixage) des fréquences Jeux de données avec déséquilibre contrôlé Une relation est caractérisée par une clé k à laquelle on associe une valeur v. La volumétrie totale des occurrences de chaque clé associées à leurs valeurs respectives est également un élément important dans l'analyse et l'estimation des temps de traitement d'une jointure. Un second outil nous est donc nécessaire afin de générer les jeux de données selon des critères de volumétrie. Étant donné un fichier contenant la liste étendue des clés en jeux, où chaque clé apparaît le nombre de fois correspondant à sa fréquence, et une volumétrie souhaitée, l'outil génère une relation à laquelle est associée à chaque clé une valeur v d'une taille suffisante pour atteindre la volumétrie globale comme l'illustre l'exemple suivant : Clé (valeurs de clés) valeurs associées ( R =70 octets) valeurs associées ( R 200 octets) 3 acpi addu acpi adduser.conf alternat 2 acpi addu acpi adduser.conf alternat 3 acpi addu acpi adduser.conf alternat 1 acpi addu acpi adduser.conf alternat 1 acpi addu acpi adduser.conf alternat 2 acpi addu acpi adduser.conf alternat 3 acpi addu acpi adduser.conf alternat Tableau 1: exemple de génération de base de données 34
70 6. DÉSÉQUILIBRE DES DONNÉES On remarquera que le contenu du champ valeur associé à une clé n'a pas une grande importance dans nos traitement de jointure. Celle-ci peut donc être quelconque voir comme dans notre cas égale pour toute clé k. Cependant lorsqu'il a été nécessaire de vérifier la complétude d'un résultat de jointure, nous ajoutons dans le champ valeur une information du type «donnée de la n ème occurrence de la clé k». Ce second outil produit donc un fichier contenant l'ensemble des (clés, valeurs) dans l'ordre d'apparition des clés dans le fichier fourni en entrée et pesant la taille désirée. Chaque relation R et S est générée selon ces principes en fonction des caractéristiques qui lui sont associées selon la modélisation recherchée. Pour nos travaux, nous avons opté pour les caractéristiques suivantes, où bdnnn désigne la base de données contenant les relations R et S et dont le coefficient de déséquilibre est n.nn. Bd111 représente une base de donnée pour laquelle la relations S contient une seule valeur de clé avec une très grande fréquence, ceci pour modéliser un déséquilibre extrême. Ce jeux de données est désigné dans la suite du document par l'identifiant «BDD». Relation Coef. N Fmax R ou S Mixage Tendance Bd000/R oui Décroissante Bd000/S oui Décroissante bd025/r oui Décroissante bd025/s oui Décroissante bd050/r oui Décroissante bd050/s oui Décroissante bd075/r oui Décroissante bd075/s oui Décroissante bd111/r - 1M 1M 1M non - bd111/s non - Tableau 2: caractéristiques des modèles de relations de jointure utilisés. 7 LE CADRE Pour la mise en œuvre de la jointure en environnement CLOUD, notre choix s'est porté sur le FrameWork MapReduce décrit plus haut, et plus particulièrement sur une de ses implémentations Apache/Hadoop. C'est à ce jour le concept le plus abouti et sur lequel un nombre assez important d'études ont déjà été menées. On notera toutefois, comme mise en garde, que ce concept n'a pas pour vocation de produire des requêtes avec des performances optimales telles qu'on peut les exiger sur des environnements Multiprocesseurs ou bien encore sur des environnement Clusters. Il vise avant tout à rendre possible ce qui était impossible auparavant. En réalité son principal but est de faciliter le traitement de données extrêmement massives disséminées sur un ensemble important de nœuds hétérogènes. 35
71 7. LE CADRE 7.1 Le principe Selon le concept de base de MapReduce le traitement des données s'appuie sur les deux phases map et reduce suivantes : Durant la phase Map, un premier ensemble de processus nommés mappers prennent en entrée chacun une fraction des données à traiter (split), pouvant êtres locales ou distantes. Ces données sont pré-formatées si nécessaire pour être ensuite orientées vers la seconde étape nommée reduce composée d'un certain nombre de processus nommés reducers. Les reducers reçoivent chacun un sous ensemble de données issues des mappers. Les données reçues par un reducer dépendent de la fonction de partitionnement choisie en phase map, cette fonction étant généralement appliquée au champ identifié comme étant la clé. Ainsi un partitionnement basé sur la fonction modulo sur une clé de type entier non nul, verra les clés être affectées cycliquement aux reducers : si on dispose de NR reducers, la clé 0 est affecté au reducer 0, la clé 1 au reducer 1,..., la clé (NR-1) au reducer (NR-1), la clé NR au reducer 0... Le reducer traite alors ses données selon le besoin de l'utilisateur et produit à son tour des données vers un fichier. Ces deux phases sont modélisées par les règles de réécriture suivantes : map : (k 1, v 1 ) [(k 2, v 2 )] reduce : (k 2, [v 2 ]) [v 3 ] Dans notre cas, les données en entrée sont stockées sur un système de fichiers distribués (DFS) visible de tous les nœuds. Les fichiers en sortie sont également de type DFS. Seuls les fichiers produits par les mappers sont des fichiers, structurés en buckets, locaux à chaque noeud hébergeant le dit processus mapper. Dans tous les cas, ces derniers sont des fichiers temporaires amenés à disparaître à la fin du traitement MapReduce. 7.2 Limitations Le traitement de données massives au sein d'un vaste réseau entraîne pour des raisons d'efficacité et de réalisme technique un certain nombre de contraintes. Parmi les contraintes notoires et inhérentes au concept MapReduce, on peut relever les trois suivantes : Un mapper ne peut communiquer avec un autre mapper, et il en est de même entre reducers. Un mapper fournit des données au reducer, mais n'en reçoit jamais Par ailleurs, aucune communication de type contrôle n'est possible entre les différents processus mappers et reducers dans quelques sens que cela soit. En réalité, le Framework prend en charge, à partir d'un nœud master, la totalité des mécanismes de contrôle et de synchronisation des processus, ainsi que les mécanismes de suivi des traitement et de tolérance aux pannes. Seul est laissé à l'utilisateur le choix des algorithmes de traitement de données et, s'il est nécessaire de communiquer une information quelconque du mapper vers les reducers, l'utilisateur insère les informations souhaitées dans le flux de données. Par ailleurs, on peut noter qu'un mapper n'a aucune idée de la localisation des données qui lui sont affectées en entrée. Le concept rend inutile ce type d'information pour le mapper. En effet, ce choix est majeur pour une meilleure abstraction des sources de données, celles-ci pouvant émaner d'un environnement quelconque tels qu'un DFS, une base de données ou bien d'autres types de flux abstraits. De plus, le mapper est une entité non rémanente, et donc un même traitement exécuté 36
72 7. LE CADRE consécutivement deux fois sur les mêmes données peut se voir affecté une association données/mappers différente. Le fonctionnement naturel de MapReduce, et principalement de la phase Map, est de traiter ligne (ou tuples) par ligne le fragment (ou l'ensemble de fragments dits Splits) des fichiers en entrée. Ainsi comme indiqué plus haut, une ligne est lue puis découpée en une structure de type (k,v) avant d'être émise au reducer. Le mapper traite son entrée comme un flux pour lequel il n'a aucune information directe ou indirecte de fin de flux. Cet état de fait ne permet donc pas de procéder naturellement à un traitement global de la totalité des données en entrée avant leur émission vers les reducers. Cela est néanmoins réalisable dans l'implémentation Hadoop en détournant l'usage de certaines méthodes à cette fin. Toutefois, nous considérons un tel détournement comme une régression, du concept MapReduce, pouvant compromettre la portabilité (i.e. la portée) des algorithmes développés sur la base de tels contournements. Nous verrons par la suite qu'en phase reduce, dans le cadre de la jointure notamment, un traitement groupé de plusieurs tuples est possible et réalisable de façon assez naturelle, avec néanmoins certaines restrictions. 7.3 Environnement technique Notre environnement technique sur lequel est exécuté Hadoop (implémentation Apache de MapReduce) est constitué de 17 serveurs multi-coeurs reliés par un réseau Gigabit pour certains et 100Mb/s pour d'autres. Ces serveurs sont dotés de 2 ou 4 processeurs double coeurs cadencés aux environs de 2.2MHz et une mémoire supérieure à 8Go. La version Hadoop utilisée est la Bien que d'autres versions plus récentes soient disponibles, celle-ci nous a semblé la plus stable et celle pour laquelle la quasi totalité des dysfonctionnements observés trouvent réponse sur les forums de discussion Hadoop. Nous verrons par la suite que, bien que répondant à toutes nos exigences, cette version reste toutefois désuète, les nouvelles versions incluant de nouvelles fonctionnalités pouvant néanmoins présenter quelques régressions du concept MapReduce. Nous reviendrons plus en détail en fin de notre étude sur cet aspect. Nous avons choisi de dédier un serveur à la fonction Master à la fois de MapReduce et de HDFS (implémentation Apache de DFS). Cette configuration est celle préconisée par la plupart des acteurs sur le sujet comme étant la plus stable. Nous avons nous même observé quelques dysfonctionnements lorsque le Master est également utilisé en tant que Slave, notamment durant des traitements massifs. Nous avons développé des scripts de collecte de données système afin de suivre les consommations de ressources des différents noeuds. Ces données sont injectées en base de données Mysql afin de vérifier automatiquement les tendances et différentes valeurs seuils. Nous avons également développé des outils d'extraction et d'injection des logs Hadoop, ainsi que des logs de nos scripts d'ordonnancement de traitements, en base de données. Cela nous a permis, pour la dernière vague d'expérimentation d'où sont issues nos résultats, après validation des paramètres et protocoles de test, plus de 5 millions de mesures de plusieurs indicateurs système, 2992 traitements (jobs) MapReduce, environ points informations détaillées de chaque job et quelques informations sur les tâches produites par ces jobs. Cela a constitué pour nous un riche entrepot de données utilisé pour vérifier nos hypothèses et produire des résultats synthétiques exposés dans cette étude. 37
73 8. LA JOINTURE PARALLELE EN ENVIRONNEMENT CLOUD 8 LA JOINTURE PARALLELE EN ENVIRONNEMENT CLOUD La jointure en environnement CLOUD est un domaine ouvert pour lequel subsiste encore beaucoup de zones à explorer. En effet, sur des environnements multiprocesseurs ou bien encore Cluster, la mise en œuvre d'algorithmes de jointure a atteint sa pleine maturité avec comme seul obstacle l'échelle non infini de la quantité de données à traiter. Nous avons vu ces dernières décennies périodiquement apparaître des systèmes de plus en plus performants visant à répondre aux masse de données présentes, pour voir l'instant d'après ces données croître et dépasser les capacités de traitement de ces gros systèmes. Ce cycle a mis en exergue l'évidence de la limitation physique qui ne permet pas de paralléliser à l'infini des processeurs, pas plus que des nœuds de Cluster proprement dits. A cela s'est ajouté la démocratisation des réseaux étendus que cela soit Internet ou des réseaux inter-sites au sein d'un même groupe (Société, administration...) pouvant êtres étendus au delà des frontières d'un pays. Cela a fatalement entraîné une dissémination de données, dans un premier temps «dormantes», qu'il a fallu plus tard agréger afin d'en tirer des informations pertinentes. Dans ce genre d'environnement, les méthodes classiques de traitement (i.e jointure) parallèle sont inopérantes. Cet état de fait a donc entraîné l'apparition du concept MapReduce proposant la simplification de la mise en œuvre de traitement parallèles sur de telles quantité de données éparpillées sur un vaste réseau. Par la suite, l'émergence du CLOUD a propulsé la nécessité de généraliser un tel concept. Concernant la jointure, de multiples études se sont penchées sur sa mise en œuvre dans un premier temps avec des visées d'opérabilité et dans un second temps avec des objectifs d'optimisation. A notre connaissance, la totalité de ces études ou bien se restreignent à une configuration particulière ou bien à optimiser les traitements et notamment les communications pour des configurations assez générales tout en s'appuyant sur les algorithmes standards de jointure exposés auparavant. Nous nous proposons ici d'envisager l'exploration, voir la découverte, d'autres formes d'algorithmes susceptibles de trouver un terrain fertile au sein du concept MapReduce et du CLOUD en général. Dans un premier nous revenons sur les algorithmes standards (ou naïfs) de la jointure basés sur MapReduce en apportant une analyse, dans notre contexte, du comportement de Hadoop lors des exécutions de ces algorithmes. Nous proposons ensuite des algorithmes basés sur le principe d'histogramme pour lesquels nous réalisons une étude comparative avec les algorithmes standard ainsi qu'une exploration des leviers susceptibles de les rendre plus performants. Enfin, à titre d'ouverture, nous proposons une autre méthode de mise en œuvre de la jointure présentant une forme de «régression» du concept MapReduce ; régression dont nous étendons le concept afin d'en faire une évolution majeure de MapReduce. 8.1 Avant propos Durant nos expérimentations, pour des raisons de simplification, nous avons opté pour des fichiers de type texte. Chaque tuple est matérialisé par une ligne de texte du fichier d'entrée. Par ailleurs, la clé, comme indiqué dans le jeu de données fourni en exemple plus haut, est un entier non nul et positionné en début de ligne. De façon générale, une clé peut être extraite de n'importe quelle position dans la ligne d'entrée, ou bien à l'aide d'une expression régulière quelconque. Toutefois, notre limitation si elle simplifie l'implémentation de la jointure n'introduit aucune régression ou limitation dans le comportement global du traitement de celle-ci. Ainsi, chaque ligne d'entrée est de la forme : <k> <v> où k est un entier non nul, et v une chaîne de caractères quelconque séparés par un espace ou une tabulation. 38
74 8. LA JOINTURE PARALLELE EN ENVIRONNEMENT CLOUD 8.2 La jointure basique sous MapReduce La mise en œuvre de la jointure basique ne présente en réalité aucune difficulté particulière au sein du FrameWork MapReduce. Seul subsiste la problématique inhérente aux limitations des mappers pour lesquels il est impossible d'identifier la source (i.e localisation) des données en entrée, et donc distinguer l'une et l'autre des deux relations de jointure. Comme palliatif, il existe une méthode communément utilisée qui consiste à procéder à une première étape MapReduce visant à marquer chacune des deux sources de données : les relations R et S. Ainsi, une jointure se déroule en trois étapes, donnat lieu chacune à un workflow MapReduce, qui sont : Le marquage de la première relation (R) Le marquage de la seconde relation (S) La jointure des deux relations On notera que les deux première étapes étant indépendantes peuvent être exécutées en parallèle en fonction de la disponibilité des ressources du CLOUD Algorithme de marquage Principe du marquage Le principe de cette première étape, que nous nommons ici, pré-jointure, consiste à insérer dans chaque tuple en entrée un identifiant de la relation concernée. Dans notre cas nous insérons la lettre 'r' pour la relation R et la lettre 's' pour la relation S. Ainsi, à cette fin, l'expression du modèle de traitement MapReduce devient : map : (k 1, v 1 ) reduce : ((k 2,t), [v 2 ]) [((k 2,t), v 2 )] [(k 2,t), v 2 ] <t> désigne le marquage de la relation concernée, soit 'r' ou 's', (k,t) devenant la nouvelle clé. Pour cela, nous avons besoin de développer deux méthodes : map et reduce. Nous omettons ici d'autres méthodes ayant pour objet le paramétrage de nos traitements, et n'apportant rien à notre problématique, le détail de ces méthodes se trouvant en annexe. Quand nous avons besoin d'un paramètre de configuration, nous indiquons sa source et les valeurs attendues sans plus de détails Phase map du marquage Le code java suivant est une implantation du mapper. Il utilise comme paramètre de configuration la variable globale tag contenant le marquage 'r' ou 's'. Algorithme BasicPreJoin : mapper de marquage public void map(longwritable key, Text value, OutputCollector<Text, Text> output, \ Reporter reporter) throws IOException { String line = value.tostring(); String v = ""; StringTokenizer tokenizer = new StringTokenizer(line); if (tokenizer.hasmoretokens()) k.set(tokenizer.nexttoken()); while (tokenizer.hasmoretokens()) { 39
75 8. LA JOINTURE PARALLELE EN ENVIRONNEMENT CLOUD v=v+" "+tokenizer.nexttoken(); output.collect(new Text(k.toString()+" "+tag), new Text(v)); Les tuples, ou lignes de fichiers, étant structurés sous la forme (k,v), il n'est pas utile de modifier le «parsing» standard Hadoop. Chaque ligne est donc transformée en objet JAVA de type Token, la clé en est extraite ainsi que le reste pour être envoyée sous la forme désirée. En général, l'étape suivante de la phase mapper est l'étape combiner visant à agréger l'ensemble des valeur ayant la même valeur de clé k en une seule structure à des fins d'optimisation. Nous avons volontairement désactivé cette étape car elle nous paraît inutile. L'étape suivant le combiner est l'étape qui consiste à répartir ces données (tuples) entre différents reducers. Nous avons modifié la méthode (partitionner) utilisée à cette étape afin de la spécifier à un modulo sur des types entiers. En effet, la méthode standard Hadoop procède au modulo d'un objet Text auquel on applique préalablement une fonction de hachage. L'inconvénient de cette méthode standard est que le partitionnement, bien qu'équivalent au notre, devient imprévisible, ce qui compliquerait nos tâches de modélisation du déséquilibre des données. On veillera bien entendu, au sein de cette méthode partitionner, à distinguer la partie k de la partie tag de la clé du tuple à émettre aux reducers afin d'aiguiller les tuples uniquement en fonction du champ k Analyse de la complexité de map Complexité algorithmique Le traitement d'une ligne peut se faire selon différentes façons plus ou moins efficaces en fonction de la structure spécifique de la ligne et du traitement particulier qui y est appliqué. Ceci introduit une multitudes de variantes quant à la complexité de traitement d'une ligne élémentaire. Notre objectif étant la comparaison, nous considérons, sauf cas particulier qui sera signalé, le traitement d'une ligne comme une exécution élémentaire de notre algorithme. Ainsi, la complexité de la phase mapper devient proportionnelle à la taille en nombre de lignes des données en entrées. MapReduce en général et Hadoop en particulier veille à fournir en entrée une quantité de données équivalentes en terme de poids en octets. En ce qui nous concerne, on pose une seconde hypothèse qui est : r 1, r 2 R,r 1 r 2, où r i est la taille en octets du tuple r i, et R la relation concernée. On en déduit que, i, j[0, NR1],R i R j U R i =R, où NR est le nombre de reducers du traitement MapReduce en cours, R i est une partition physique de la relation R. Et donc la complexité globale de la phase map est de l'ordre de : O( R ), M étant le M nombre de mappers. Communications Nous entendons par complexité de communication le nombre de paires de communication établies entre les mappers cible des données et les nœuds sources du Cloud. Celle-ci dépend essentiellement de la localisation de ces données. En effet, le principe du DFS étant de distribuer un fichier volumineux sous forme de fragments nommés Chunks vers l'ensemble des nœuds identifiés 40
76 8. LA JOINTURE PARALLELE EN ENVIRONNEMENT CLOUD comme Slave par le Master DFS. Sachant qu'un nœud peut être à la fois slave (i.e. candidat) DFS et slave MapReduce, une donnée (i.e un split) par rapport à un mapper peut être dans 3 situations : (1) locale : c'est à dire que l'ensemble des fragments (splits) affectés par le traitement MapReduce au mapper est contenu en totalité dans un ou plusieurs Chunks détenus par ce mapper. Ce mapper n'établit aucune communication et traite la donnée de façon autonome. (2) partiellement locale : les fragments affectés au mapper sont partiellement contenus dans un ou plusieurs chunks locaux. Dans ce cas, le mapper établit les communications nécessaires vers un ou plusieurs noeuds distants afin de récupérer le reste des données nécessaires au traitement. Quelque soit la quantité de données restant à transférer vers ce mapper, nous considérons cette situation comme étant équivalente à la troisième. (3) Distante : le mapper ne détient aucune donnée relative aux fragments qui lui ont été affectés, et dans ce cas ce mapper établit à coup sûr autant de communication que nécessaire afin de disposer des données à traiter. Le FrameWork MapReduce veille en général à favoriser la situation de premier type. Toutefois, l'objectif de performance étant global, un mapper, malgré le fait qu'il détient une partie des données peut, se voir affecté une autre partie de deuxième ou de troisième type. Le soucis majeur étant d'une part d'équilibrer les communications entre les différents nœuds et, d'autre part de saturer ces liens de communication afin de tirer le maximum de la quintessence du réseau. On notera que, indépendamment des contraintes d'optimisation globale, les chances qu'un fragment quelconque soit local à un nœud peut s'exprimer sous forme probabiliste. En effet, dans un premier temps nous pouvons exprimer la probabilité que le nœud i d'un CLOUD de taille N détienne un chunk quelconque de la relation R par : R chunk P(c i)= N = R N chunk Où : c est un chunk quelconque, chunk est la taille en pages de la partition élémentaire DFS, R est la taille en nombre de pages de la relation R, et R la nombre de chunks nécessaires au stockage DFS de la relation R chunk De plus, étant donné M le nombre de nœuds élus pour la phase map, et Mappers l'ensemble des identifiants de ces nœuds avec M= Mappers (en restreingant la création d'un seul mapper par nœud), la probabilité qu'un nœud m soit élu est : P(mMappers)= M N Et, sous hypothèse d'indépendance, la probabilité qu'un nœud détienne un chunk de R en étant élu au sein des Mappers est : R P(c mm Mappers)=P(c m) P(c Mappers)= N chunk M N = R M N 2 chunk En posant l'hypothèse que le fragment de données affecté est un split, ou un ensemble de splits contiguës, la taille en nombre de pages d'un fragment affecté à chaque mapper est : split= R, avecmmappers et doncr=split M., cela nous permet d'exprimer la M probabilité ci-dessus en fonction de split et de voir que cette probabilité est fortement dépendante split du rapport. Et donc constater que cette probabilité est fortement liée à la taille chunk 41
77 8. LA JOINTURE PARALLELE EN ENVIRONNEMENT CLOUD élémentaire d'un chunk. La taille d'un chunck est toutefois limitée par des considérations techniques d'importance supérieure tant sur ses limites inférieures que supérieures. Enfin, un mapper peut se voir affecté un nombre de fragments (splits) supérieur à 1. Dans ce cas, la probabilité qu'un mapper ne génère aucune communication est une conjonction de la probabilité ci-dessus autant de fois qu'il y a de splits localisés sur des chunks différents. Un autre élément à prendre en compte est le facteur de redondance des chunk au sein du DFS. En effet, pour des besoins de tolérance aux pannes et de sécurité des données, DFS duplique systématiquement chaque chunk sur p nœuds différents. Généralement, p=3 mais d'autres valeurs sont également possible sachant que pour p trop petit le risque de perte de données augmente, et, pour p trop grand, la gestion de la redondance devient coûteuse et inefficace. Dans notre cadre, une valeur 3 pour p est un bon compromis largement partagé. La forme de la probabilité finale devenant alors P(cmmMappers)=P m com = p R M N 2, ce qui améliore la probabilité de détention chunk d'un chunk par un mapper. Cette expression est la probabilité qu'un nœud n'établisse pas de communication. A l'inverse, la probabilité qu'un nœud m établisse une communication est : P m com =1P m com. Est donc, la quantité moyenne de communications établies au sein des M mappers est exprimée par m l'espérance de : P com E(P M com )= (1P m com )=MM p split M 2 m Mappers N 2 chunk Nous constatons que la quantité de communications établies par les différents mappers de la phase map dépend de plusieurs paramètres fixés ou conjoncturels. De ce fait, il est extrêmement difficile d'évaluer cette quantité de communications de façon précise. En conclusion, tablant sur le fait que le Framework prend en charge les affectations des splits de façon à optimiser globalement les communications entre nœuds élus pour la phase map, sauf cas particulier, nous ne prendrons pas en considération dans nos estimations futures les communications à ce niveau et nous nous contenterons d'étudier le contexte technique ponctuel et sa propension à fournir des leviers pour de meilleures performances Phase reduce du marquage La phase map émet chaque ligne du fichier d'entrée sous la forme ((k,tag), v)). Ce tuple est ensuite transmis à un reducer selon un modulo de la sous clé k, (k, tag) étant la clé complète au sens de MapReduce. L'algorithme suivant indique la façon dont ces tuples sont traités au sein de la phase reduce sur chaque reducer. Algorithme BasiPreJoin : reducer de marquage de relation public void reduce(text key, Iterator<Text> values, OutputCollector<Text, Text> output, \ Reporter reporter) throws IOException { while (values.hasnext()) output.collect(key, values.next()); Comme nous le constatons la phase reduce se contente de passer d'une forme groupée ((k,tag), [v]) des tuples en entrée vers la forme initiale ((k,tag), v) avant de les émettre vers le fichier de sortie DFS. Il est essentiel de veiller à cette mise en forme sous peine de perdre la structure initiale de la relation traitée une fois stockée en fichier texte. 42
78 Analyse de la complexité de reduce 8. LA JOINTURE PARALLELE EN ENVIRONNEMENT CLOUD Complexité algorithme Pour les mêmes raisons qu'en phase map, la complexité est inversement proportionnelle aux nombre de reducers soit de l'ordre de : O( R ), NR étant le nombre de reducers. La complexité NR globale est de de l'ordre de O( R NR +R M ). Si MNR, alors on peut approximer cette complexité globale (map+reduce) à O( R NR )carr NR R. Nous verrons en phase M expérimentation que cette approximation est la plupart du temps vérifiée même pour M et NR 2 R proches, de plus NR n'étant jamais supérieur à M, la complexité est au plus égale à. NR Communications En ce qui concerne le nombre de communications en terme de nombre de couples (mapper,reducer) ayant établis une communication en vue du transfert des données pré-traitées en phase mapper, celle-ci est égale à NR M, avec NR le nombre de reducers et M le nombre de mappers. Cette égalité est sous hypothèse que les tuples d'un mapper sont équitablement répartis entre les différents reducers. Chaque mapper communique alors une quantité de données équivalente à : R pages vers chaque reducer. Cette hypothèse est très réaliste en phase marquage puisque NR M les tuples sont marqués indépendament les uns des autres et peuvent donc être equitablement distribués vers l'ensemble des reducers. Dans le cadre de notre étude, aucun axe majeure d'optimisation de cette quantité n'est possible. Nous verrons toutefois que compte tenu des différents mécanismes mis en œuvre par le framework afin d'optimiser les communications, et étant donné que la phase d'écriture sur fichier DFS est largement plus pénalisante, le processus MapReduce est passablement insensible à la volumétrie des données échangées. Un autre aspect des communications établies en phase reduce est celui des communications nécessaires au moment de l'écriture des données de sorties vers un fichier DFS. Nous avons vu que chaque fichier est découpé en chunks et chaque chunk est répliqué p fois. Ceci nous permet d'écrire la quantité de chunks nécessaire qui est : NbChunks=p R chunk. On rappellera que le Master DFS ne s'occupant que des flux de contrôle et de synchronisation des nœuds Slaves, le nœud initiant une écriture vers le DFS prend en charge la communication de la totalité des données vers les nœuds élus pour héberger un ou plusieurs chunks de cette nouvelle écriture. Ainsi, chaque reducer devrait théoriquement écrire en DFS une quantité R de chunks égale p NR chunk. En réalité, GFS (Google) et HDFS (Apache) mettent en œuvre un protocole d'écriture basé sur un mécanisme de relais de transfert des données vers l'ensemble des nœuds de stockage. Ainsi, pour chaque chunck, le nœud écrivain n'aura à procéder qu'à un seul transfert, chacun des autres nœuds s'occupant du transfert vers les autres nœuds hebergeant le chunk. L'écriture n'est toutefois validée qu'une fois qu'un chunk a atteint l'ensemble des nœuds de stockage qui lui ont été assignés. Cette optimisation visant à limiter la charge de communication sur le client (i.e. Écrivain) a comme inconvénient majeur de complexifier un peu plus le bilan des 43
79 8. LA JOINTURE PARALLELE EN ENVIRONNEMENT CLOUD R communications traitées par un nœud. Et, en définitif, la quantité présente un NR chunk intérêt limité puisqu'elle ne prend pas en considération les écritures relayées pour le compte d'autres nœuds. Cette deuxième quantité pouvant être importante notamment dans le cas d'un CLOUD avec un nombre de nœuds restreint et tous affectés au traitement Reduce. On identifie donc deux bornes qui sont : R p NR chunk et R selon respectivement que NR N ou NRN. NR chunk En conclusion on constate qu'autant en phase map le master peut affecter les splits en modélisant, sous forme de contraintes, l'efficacité de ces affectations, avec un objectif assez proche du résultat réel, sous hypothèse de non activité préalable des mappers, autant les nœuds hébergeant les chunks sont dans une certaine mesure affectés indépendamment les uns des autres, et donc sans aucune garantie de compatibilité des activités système, disque et réseau des uns et des autres. Cette situation entraîne une efficacité très fluctuante de l'écriture du résultat vers le DFS et, comme nous le constatons durant nos expérimentations, un reducer ayant une certaine capacité de traitement et une certaine quantité de données à traiter peut produire une durée de traitement extrêmement différente d'un autre nœud ayant les mêmes caractéristiques, ceci étant généralisable à tous les nœuds Algorithme de jointure basique La phase de marquage nous permet de distinguer la relation R de la relation S, afin de procéder à la jointure consistant à coupler les tuples r et s ayant la même valeurs de leur attribut de jointure respectif A et B. Nous produisons donc de nouveaux tuples (r,s) pour touts tuples r et s ayant r.a=s.b. On rappelle que, techniquement, la phase reduce du marquage produit NR fichiers différents, chaque fichier est une partition de R (resp. S) ayant la caractéristique suivante : i et j[0, NR1],si i j alors R i R j =, avecsur lavaleur des sous clés k. De plus, bien que chaque partition soit triée selon la valeur de la clé (k,tag), il ne nous est pas possible d'exploiter cette caractéristique en phase map de jointure car le découpage des deux relations en splits est uniquement basée sur des considérations techniques, et aucun découpage sur des bases fonctionnelles (i.e contenu des fichiers) n'est possible. Toutefois, cette caractéristique de tri et de disjonction est également vérifiée sur les données transmises par les mappers vers les reducers, chaque reducer disposant à nouveau de partition respectant cette contrainte pour les deux relations R et S. Le tri étant réalisé selon la clé (k,tag), apparaissent, pour une clé donnée, en premier les tuples relatifs à la relation R, soit les clés de la forme (k, r) suivi des tuples de la relation S pour cette même clé La phase map de la jointure basique Cette phase ne présente aucune difficulté, chaque mapper se contente de rediriger les tuples inclus dans les splits traités vers le bon reducer selon la méthode choisie La phase reduce de la jointure basique Il y a essentiellement deux façons de procéder à cette jointure. Une méthode que nous avons expérimenté, mais que nous ne traiterons pas ici, consiste à stocker l'ensemble des tuples de la sous 44
80 8. LA JOINTURE PARALLELE EN ENVIRONNEMENT CLOUD relation R i dans une table de hachage avant de la joindre avec les tuples de S i. Pour cela, une petite modification consiste à faire présenter les tuples par le mapper sous la forme ((tag,k) v), ainsi la totalité des tuples de R i seront présentés avant ceux de la partition S i permettant ainsi la mise en table de hachage de R i. Les expérimentations réalisées n'ont pas montré une supériorité flagrante de cette méthode sur la seconde méthode, pour laquelle nous avons opté, consistant à traiter les tuples de R i et S i pour chaque valeur de clé. Cette seconde méthode présente l'intérêt de nécessiter une quantité de mémoire de travail bien moindre que la première. Ainsi, dans la méthode choisie, chaque reducer i reçoit donc deux partitions R i et S i, avec les caractéristiques citées ci-dessus. Le reducer pour chaque tuple R i et de S i de la forme ((k 1,'r'),v 1 ) et ((k 2,'s'),v 2 ) si k 1 =k 2 alors un tuple de la forme (k 1,v 1,v 2 ) est produit. L'algorithme résultant est le suivant que nous avons nommé BasicJoinV1 : Algorithme BasicJoinV1 : reducer de la jointure basique public static class Reduce extends MapReduceBase implements Reducer<Text, Text, Text, Text> { public String rtag = null; public String stag = null; public void configure(jobconf job) { rtag = job.get("outerrelation"); stag = job.get("innerrelation"); private Text reste = new Text(); ArrayList RBuf = new ArrayList(); String lastkey = ""; String Vide = ""; public void reduce(text key, Iterator<Text> values, OutputCollector<Text, Text> output, \ Reporter reporter) throws IOException { String subkey = getkey(key); String tag = gettag(key); String tup = ""; // Lecture des tuples de R si tag='r' if (tag.equals(rtag)) { RBuf.clear(); lastkey=getkey(key); while (values.hasnext()) { tup=values.next().tostring(); RBuf.add(tup);//values.next()); // Lecture des tuples de S et jointure si tag='s' et qu'il existe des tuples r joignable if (tag.equals(stag) && RBuf.size() > 0 && lastkey.equals(getkey(key))) { while (values.hasnext()) { tup=values.next().tostring(); 45
81 8. LA JOINTURE PARALLELE EN ENVIRONNEMENT CLOUD for (int i = 0; i < RBuf.size(); i++) Vide=RBuf.get(i).toString(); La première phase de cet algorithme consiste à lire tous les tuples de R i pour une valeur de clé donnée, chacun de ces tuples est stocké dans une structure indexée pas nécessairement triée. Ensuite lorsque, dans un second temps, les tuples de S i pour la même valeur de clé sont présentés, ils sont lus un par un et joint en vol un par un avec l'ensemble des tuples stockés dans la structure indexée. Cette séquence est celle attendue et produisant une jointure. Pour une valeur v d'attribut de jointure, deux autres séquences sont possibles, à savoir : soit vv (R i. A)vV (S i. B)alors vv (J i. A) ou soit vv (S i. B)vV (R i. A)alors vv (J i. A) Où T.A est la projection de la relation T sur l'attribut A, V(T.A) est l'ensemble de valeurs prises par l'attribut A de la relation T et J i =R i S i. En terme d'histogramme, on peut exprimer ces deux cas de façon générale par : si Hist(R i )(v)=0hist(s i )(v)=0 alorshist(j i )(v)=hist(r i )(v) Hist(S i )(v)= Analyse de la complexité Complexité algorithme Cela se traduit dans l'algorithme par l'abandon des tuples de S i n'ayant pas de tuples correspondant dans R i, et inversement. Dans ces deux cas, la structure indexée est vidée et les tuples suivants de R i (ou S i ) correspondants à une nouvelle valeurs de clé sont lus et traités. La complexité de cet algorithme s'exprime par : R i +S i + vv Hist(R i )(v) Hist(S i )(v). Avec V l'union des valeurs distinctes possibles dans R i et S i pour k. Cette quantité peut être bornée du côté minimum par O(R i +S i +min(r i,s i )) si vv Hist i (R)(v) Hist i (S)(v) 1 et du côté maximum par O(R i +S i +R i S i ) siv=1v (R i. A)V (S i. B) autrement dit les attributs A et B des relations R i et S i ont une unique et même valeur. Nous ne prendrons pas en considération ici la situation dans laquelle les relations R et S n'auraient aucune valeur d'attribut de jointure commune. Ce cas ne nous paraît que très peu réaliste, car lorsqu'on réalise une jointure on est la plupart du temps certain d'obtenir un résultat non nul. La borne minimale pour laquelle nous avons opté est beaucoup plus réaliste et se rencontre fréquemment notamment dans le cas où une des deux relations de jointure est une table de référence. Et, dans ce cas, l'ensemble des valeurs de l'attribut de jointure de cette table sont la plupart du temps strictement inclus dans la seconde table. Communications Faute de pouvoir faire un bilan formel des communications établies compte tenu du nombre important de cas de figure, on se contente d'analyser la quantité de données produite. En effet, la quantité de données écrite est proportionnelle aux complexités d'exécution ci-dessus, ce qui fournit 46
82 8. LA JOINTURE PARALLELE EN ENVIRONNEMENT CLOUD un ordre de grandeur de communications DFS établies. Et, si le cas de figure rencontré est la borne maximale, alors la durée de traitement peut devenir rédhibitoire. De plus, nous avons auparavant dit que cette phase d'écriture est extrêmement pénalisante en impactant directement et fortement les durées de traitement ; principalement si ce cas de figure est rencontré uniquement sur un sous ensemble des reducers possibles. Ceci met en évidence la nécessité absolue de détecter ces cas de figure et de partitionner le cas échéant par d'autres méthodes que le modulo de base les valeurs de clé ayant une fréquence trop élevée. Nous allons donc étudier une méthode de partitionnement basée sur l'analyse des histogrammes des attributs de jointure des relations R et S. 8.3 La jointure à base d'histogramme Pour mettre en œuvre une telle méthode, deux opérations supplémentaires au marquage sont nécessaires. La première consiste à calculer pour chaque relation l'histogramme de son attribut de jointure, prenant en entrée le fichier de la relation concernée. La seconde, consiste à rapprocher les histogrammes des deux relations R et S afin de produire le plan d'exécution et de communication adéquat, et prenant donc en entrée les deux relations R et S. Le calcul d'histogramme peut facilement être inséré dans la phase de marquage, évitant ainsi la nécessité d'une deuxième tâche MapReduce. L'étape d'élaboration du plan d'exécution est quant à elle absolument distincte car elle nécessite au préalable le calcul des histogrammes des deux relations. Nous avons dans nos expérimentations exploré la possibilité de procéder par approximation lors de la phase de marquage, et nous avons conclu à une mauvaise efficience de telles méthodes qui rendent le résultat attendu très hypothétique. Nous nous cantonnerons donc à procéder par calcul exacte, le but étant, entre autres, d'explorer les méthodes basées sur les histogrammes. L'exploitation de l'histogramme durant la jointure peut se faire de différentes manières à différents niveaux. Dans notre étude, nous allons procéder selon deux niveaux d'exploitation de cet histogramme qui sont : (1) On exploite l'histogramme comme prévision de la présence ou pas de tuples de R et S pour une même valeur d'attribut de jointure afin d'éviter de stocker en mémoire (structure indexée) inutilement les tuples de R. Cette méthode a l'avantage de ne pas nécessiter l'étape de calcul du plan d'exécution, les histogrammes exploités étant calculés en phase de marquage. (2) On exploite l'histogramme à la fois pour l'optimisation ci-dessus mais également pour élaborer un plan d'exécution limitant l'effet des attributs à hautes fréquences et du déséquilibre des données Jointure histogramme de premier niveau Calcul parallèle d'histogramme Cela consiste à compter pour chaque valeur v de l'attribut de jointure A (resp. B) de la relation R (resp. S) le nombre de fois qu'elle apparaît. Un tel calcul au sein du Framework MapReduce consiste à émettre pour chaque tuple un couple (k, 1), k étant l'attribut de jointure. La règle de transformation pour cette opération est alors : map : (k 1, v 1 ) [((k 2,t), v 2 ), ((k2,'h'.t), 1)] reduce : ((k 2,t), [v 2 ]) [(k 2,t), v 2 ] ((k 2,'h'.t), [1]) [(k 2,'h'.t), sum([1])] <t> désigne le marquage de la relation concernée, soit 'r' ou 's', (k,t) devenant la nouvelle clé. Et 'h' est le caractère h qui concaténé à <t> désigne l'histogramme de la clé k pour la relation t. 47
83 8. LA JOINTURE PARALLELE EN ENVIRONNEMENT CLOUD A titre d'exemple, une relation R contenant les tuples : 1 aaa bbb ccc 1 hr 3 2 ddd eee fff 1 r aaa bbb ccc 1 ggg hhh iii 1 r ggg hhh iii devient 1 jjj kkk lll 1 r jjj kkk lll 2 hr 1 2 r ddd eee fff Tableau 3: exemple de marquage et calcul d'histogramme Avec donc Hist(R)(1)=3 et Hist(R)(2)= Phase map du calcul d'histogramme HistoPreJoinV1 : mapper calcul histogramme public void map(longwritable key, Text value, OutputCollector<Text, Text> output, \ Reporter reporter) throws IOException { String line = value.tostring(); String reste = ""; StringTokenizer tokenizer = new StringTokenizer(line); if (tokenizer.hasmoretokens()) word.set(tokenizer.nexttoken()); while (tokenizer.hasmoretokens()) { reste=reste.trim()+" "+tokenizer.nexttoken(); output.collect(new Text(word.toString()+" "+tag), new Text(reste)); output.collect(new Text(word.toString()+" "+Htag+tag), new Text("1")); La seule différence avec l'algorithme de marquage décrit plus haut réside dans l'ajout, de la ligne surlignée en gras, qui consiste à émettre au reducer un '1' pour chaque clé de tuple lu. Htag est ici par convention le caractère 'h' d'histogramme qui distingue un tuple de donnée d'un tuple d'histogramme. De plus, la même analyse de complexité peut être appliquée pour cet algorithme et, bien que la quantité de tuples émis soit doublée, la quantité de données reste approximativement la même compte tenu du faible poids d'un tuple d'histogramme qui est dépouillé de la partie données des tuples initiaux. Par ailleurs, l'agrégation des tuples histogramme avant envois aux reducers peut réduire le surplus de données de façon importante Phase Reduce du calcul d'histogramme HistoPreJoinV1 : reducer de caclul d'histogramme public void reduce(text key, Iterator<Text> values, OutputCollector<Text, Text> output, Reporter reporter) throws IOException { long sumhis=0; String reste = ""; if (gethtag(key).equals(htag)) { while (values.hasnext()) sumhis+=integer.parseint(values.next().tostring()); 48
84 8. LA JOINTURE PARALLELE EN ENVIRONNEMENT CLOUD output.collect(key, new Text(String.valueOf(sumhis))); else while (values.hasnext()) output.collect(key, values.next()); L'algorithme consiste à agréger les valeurs d'histogramme issues des différents mappers pour une même clé et, dégrouper les tuples de données afin de les émettre en fichier DFS sous le format ((k,tag), v) et ne pas perdre la structure de donnée initiale du fichier matérialisant la relation R Exemple de calcul parallèle d'histogramme Si on reprend notre exemple précédent un traitement parallèle avec 2 mappers et deux reducers de la relation R se déroule selon le processus suivant, avec «modulo 2» comme méthode de partitionnement : Relation R Map Reduce Résultat 1 aaa bbb ccc 2 ddd eee fff 1 ggg hhh iii 1 jjj kkk lll Mapper 0 Reducer 0 Fichier 0 Reçoit (R 0 ) Émet Reçoit Émet 1 aaa bbb ccc 2 ddd eee fff 1 r aaa bbb ccc 1 hr 1 2 r ddd eee fff 2 hr 1 2 hr <1> 2 r <ddd eee fff> 2 hr 1 2 r ddd eee fff 2 hr 1 2 r ddd eee fff Mapper 1 Reducer 1 Fichier 1 Reçoit (R 1 ) Émet Reçoit Émet 1 ggg hhh iii 1 jjj kkk lll 1 hr 1 1 r ggg hhh iii 1 hr 1 1 r jjj kkk lll 1 hr <1> <2> 1 r <aaa bbb ccc> <ggg hhh iii> <jjj kkk lll> 1 hr 3 1 r aaa bbb ccc 1 r ggg hhh iii 1 r jjj kkk lll Tableau 4: processus MapReduce de marquage et calcul d'histogramme 1 hr 3 1 r aaa bbb ccc 1 r ggg hhh iii 1 r jjj kkk lll On remarquera particulièrement la forme groupée sous laquelle les reducers reçoivent les tuples de données ayant la même valeur de clé. Les valeurs entières du tuple d'histogramme sont elles pré-agrégées par la méthode Combiner des mappers d'où ils sont issues, si cette phase a été préalablement activée. En réalité, la méthode Combiner correspond la plupart du temps à la méthode reducer exécutée en phase mapper et donc sur les données locales au mapper. De ce fait, l'agrégation des histogrammes au sein d'un mapper correspond à la grandeur qu'on notera : Hist(R i ), R i étant la partie de R contenue dans les splits affectés au mapper i. On notera que cette grandeur n'est qu'une partie de l'histogramme des valeurs de clé, celles-ci étant encore réparties au sein des différents mappers comme on peut le remarquer sur notre exemple pour la clé de valeur '1' dont une partie se trouve détenue par le mapper 0 et l'autre partie par le mapper 1. Le résultat du traitement de marquage et calcul d'histogramme permet de réaliser une jointure selon la méthode basique ou selon la méthode histogramme de premier niveau sans nécessiter aucun traitement supplémentaire. 49
85 8. LA JOINTURE PARALLELE EN ENVIRONNEMENT CLOUD La jointure à histogramme Pour raison de méthodologie, nous décomposons la jointure à base d'histogramme en deux niveaux ou catégories. Le premier niveau, ou jointure simplifiée, utilise l'histogramme uniquement pour optimiser le code d'exécution, avec l'avantage de nécessité aucun traitement préalable. Le second niveau vise à utiliser pleinement l'histogramme afin d'élaborer un plan d'exécution optimal Jointure à histogramme simplifiée A ce niveau, l'histogramme est utilisé en tant qu'heuristique visant à élaguer des branches d'exploration des relations quand aucun résultat de jointure n 'est possible pour une valeur de clé donnée. Cette méthode exploite le fait que les tuples sont présentés triés aux reducers selon le couple (k, tag). Sous cette condition, les tuples, lorsqu'il existe un résultat de jointure pour une valeur de clé k 1, sont présentés dans l'ordre suivant : k 1 hr <n> k 1 hs <m> k 1 r <data 0 >... k 1 r <data n-1 > k 1 s <data 0 >... k 1 s <data m-1 > k 2 h Et ainsi, si pour une valeur de clé Hist i (R) Hist i (S)>0 alors il existe un résultat et la suite des données est lue puis jointe. Dans le cas contraire, les données sont ignorées jusqu'à la présentation d'une nouvelle clé pour laquelle ce test est à nouveau réalisé, comme on peut le voir dans l'algorithme HistoJoinV1: La phase Map de l'algo simplifié HistoJoinV1 HistoJoinV1 : mapper de jointure simplifiée à histogramme public void map(longwritable key, Text value, OutputCollector<Text, Text> output, Reporter reporter) throws IOException { String line = value.tostring(); String reste = "";//rtag.gettag(); String tag = ""; String tkey = ""; StringTokenizer tokenizer = new StringTokenizer(line); if (tokenizer.hasmoretokens()) tkey = tokenizer.nexttoken(); //word.set(tokenizer.nexttoken()); if (tokenizer.hasmoretokens()) tag = tokenizer.nexttoken(); //tag.text(tokenizer.nexttoken()); while (tokenizer.hasmoretokens()) { reste=reste.trim()+" "+tokenizer.nexttoken(); 50
86 8. LA JOINTURE PARALLELE EN ENVIRONNEMENT CLOUD output.collect(new Text(tkey+" "+tag), new Text(reste)); Le principal rôle de la phase map est de reformuler les tuples lus du fichier plat en tuples de la forme ((k, tag), v). Ainsi ils seront présentés triés selon la valeur de clé et de tag comme décrit cidessus La phase reduce de l'algo simplifié HistoJoinV1 HistoJoinV1 : reducer de jointure simplifiée à histogramme public void reduce(text key, Iterator<Text> values, OutputCollector<Text, Text> output, \ Reporter reporter) throws IOException { String subkey = getkey(key); String tag = gethtag(key); String tup = ""; if (tag.equals(htag)) { String hv=values.next().tostring().trim(); if (gettag(key).equals(rtag)) hr=integer.parseint(hv); else hs=integer.parseint(hv); if (tag.equals(rtag) && hr*hs > 0) { RBuf.clear(); lastkey=getkey(key); while (values.hasnext()) { tup=values.next().tostring(); Rbuf.add(tup); if (tag.equals(stag) && (RBuf.size() > 0) && lastkey.equals(getkey(key)) && hs*hr > 0) { while (values.hasnext()) { tup=values.next().tostring(); for (int i = 0; i < RBuf.size(); i++) Vide=RBuf.get(i).toString(); if ( tag.equals(stag) (tag.equals(rtag) && hr*hs == 0)) { hr=0; hs=0; 51
87 8. LA JOINTURE PARALLELE EN ENVIRONNEMENT CLOUD Les variables rtag et stag contiennent les étiquettes de marquage choisies pour les relations R et S. Les routines getkey(key) et gethtag(key) ont pour objectif d'extraire la valeur de clé pour la première et l'étiquette de relation ou d'histogramme pour la seconde. Initialement ou en cas de changement de clé, les valeurs courantes d'histogramme des deux relations sont à 0. Quand des données de R ou S relatives à une valeur de clé sont présentées, aucune fréquence (histogramme) de R ou S n'a été préalablement présenté pour cette même valeur de clé, dès lors toute la suite des données présentées est abandonnée sans traitement. Dans le cas contraire, les données de R sont mis en buffer, puis joints avec les données de S dans un second temps. Cette utilisation de l'histogramme ne présente un intérêt que la sous la condition : V (R i. A)V (S i.b)v (R i. A)V (S i. B), i unreducer et V (T i. X)l ' ensemble des valeursdistinctes de l' attribut X delarelation T i. L efficacité de cette heuristique est plus prononcée quand cette différence est importante. Dans le cas contraire, la gestion de l'optimisation par histogramme introduit un surplus de code qui peut pénaliser d'une façon assez sensible les performances. Nous verrons par la suite que cela est vérifiée par les tests réalisés, pour lesquels d'ailleurs la différence ci-dessus est nulle. L'intérêt majeur de cette version de jointure est de mettre en évidence ce surplus de traitements induit par la gestion d histogramme qui, s'il n'est pas compensé, augmente la durée de la jointure Analyse de la complexité Complexité algorithmique La complexité du traitement est donc fortement dépendante de la condition d'efficacité de cet algorithme. En remarquant qu'il existe un et un seul tuple d'histogramme pour chaque valeur distincte de A et B, la complexité maximale pour chaque phase est de l'ordre de : Map : O(R i +S i +V (R i. A)+V (S i. B)) si les valeurs de A et B présentent tous des fréquences autour de 1 (0 inclu), et O(R i +S i ) s'ils présentent des hautes fréquences (>>1). Reduce : O(R i +S i +R i S i ) si les attributs A et B des partitions R i et S i prennent une et une seule valeur, ce qui peut être approximé à O(R i S i ). Communications Le quantité de communication en phase map est similaire à celle étudiée pour l'algorithme basique. Toutefois, la quantité de données traitée est ici plus importante puisqu'on prend en entrée les deux relations à joindre ainsi que leurs histogrammes respectifs. Cette augmentation est généralement compensée par l'augmentation du nombre de mappers ramenant les communication au même niveau. En phase reduce, cette quantité est beaucoup plus importante, notamment dans le cas extrême présenté ci-dessus où la complexité est de l'ordre de O(R i S i ). Dans ce cas, les données enregistrées sur le DFS sont très volumineuses, générant de multiples communications et impactant fortement les performances de la jointure de chaque reducer. La quantité de chunks nécessaire et donc le nombre de communications établies est par conséquent : NbCom R i S i., car on ne prend pas en compte les communications établies pour chunck le compte des autres nœuds dans le cadre du protocole d'écriture DFS. 52
88 8. LA JOINTURE PARALLELE EN ENVIRONNEMENT CLOUD Jointure de second niveau ou évoluée Nous avons vu que l'efficacité de l'algorithme de premier niveau (i.e. simplifié) est assez hypothétique et dépend très fortement de la topologie des données. D'autant que, la majeure partie du temps, les jointures sont réalisées essentiellement sur des données joignables, et donc ne présentant pas d'intérêt pour l'algorithme HistoJoinV1. En réalité cet algorithme n'a d'intérêt qu'en tant que témoin ou référentiel pour l'algorithme évolué durant la phase d'expérimentation. Afin d'exploiter pleinement le calcul d'histogramme, il est nécessaire de pousser la démarche pour permettre un partitionnement sensible aux fréquences des données, et inversement pour rendre le traitement insensible au déséquilibre des données. A cette fin, une autre étape de préparation des relations est nécessaire. En effet, dans les pré-traitements réalisés jusqu'à maintenant, chaque relation a été présentée seule aux processus de traitement MapReduce. Pour établir un plan d'exécution sur des informations exactes et complètes, il est absolument nécessaire de présenter les deux relations à un processus MapReduce afin de pouvoir traiter de manière similaires les tuples de ces deux relations ayant la même valeur d'attribut de jointure Élaboration du plan d'exécution L'élaboration du plan d'exécution consiste à établir les cas de figure suivants pour chaque valeur de clé : Aucun partitionnement Partition de R et réplication de S Partition de S et réplication de R Outre cette décision, durant ce pré-traitement, il nous faut, dans le cas d'un partitionnement, identifier les différents nœuds susceptibles d'accueillir une partition de la première relation et une copie de la seconde. De façon générale, il existe de notre point de vue deux façons d'adresser un tel nœud. La première technique est basée sur un adressage absolu, la seconde sur un adressage relatif. Adressage absolu Le partitionnement consiste à découper la totalité des tuples d'une relation ayant la même valeur d'attribut de jointure en n partitions destinées chacune à un nœud distinct. En réalité, l'adressage se faisant au niveau du tuple, l'ensemble des tuples d'une même partition est adressé au même nœud. L'adressage absolu consiste donc à affecter un nœud à chaque tuple. Le choix du nœud peut se faire de différentes façon, la méthode la plus appropriée étant le choix aléatoire. Afin d'éviter de choisir deux fois le même nœud, on tire un nœud aléatoirement à partir duquel on peut déduire les nœuds suivants par itération ou par ajout du numéro de partition de la façon suivante : n 0 =random(nr), avec NR lenombre dereducers. Noeud( p)=n 0 + p,avec p un numéro de partition. Cet adressage doit se faire simultanément sur les deux partitions afin de garantir sa cohérence. Ainsi, l'adressage d'une copie de la totalité des tuples de la relation à répliquer se fait de la façon suivante : Noeud(c)=n 0 +c,avec cunnumérode copie. Adressage relatif L'adressage relatif exploite l'information déjà contenue dans chaque tuple, et plus précisément dans la valeur de son attribut de jointure. En effet, initialement un tuple est orienté vers un reducer par la méthode partitionner sur la base d'une fonction d'aiguillage telle que modulo. Cette information inhérente au tuple peut donc être utilisée comme base d'adressage. Il devient alors 53
89 8. LA JOINTURE PARALLELE EN ENVIRONNEMENT CLOUD suffisant d'indiquer le nombre de partitions en lieu et place de l'adresse exacte du nœud de destination. Sur la base de ces deux informations, le traitement lors de la phase map de la jointure peut diriger efficacement chaque tuple vers le reducer concerné. Dans l'élaboration de nos algorithmes, nous avons opté pour cette solution présentant une plus grande simplicité. Mais nous reviendrons sur la première méthode qui est plus efficace dans certains cas extrêmes. Plan d'exécution La façon la plus efficace d'enregistrer un plan d'exécution dans notre contexte est de le faire donc porter directement par les données traitées. Ainsi, pour ce faire, il nous faut à nouveau modifier les tuples des deux relations selon le modèle suivant, prenant comme hypothèse simplificatrice pour une valeur w donnée d'attribut de jointure : Hist i (R)(w) > Hist i (S)(w). Ce qui donne les transformations suivantes : map : (k 1, v 1 ) reduce : ((k 2,'r'), [v 2 ]) [((k 2,t), v 2 )] ((k 2,'s'), [v 2 ]) [(k 2,'r'), p, v 2 ] [(k 2,'s'), '*'.P, v 2 ] ((k 2,'hr'), [v3]) set(p,cell(v3/mp)) <t> désigne le marquage de la relation ou de l'histogramme concerné, soit 'r', 's', 'hr' ou 'hs' ; (k,t) devenant la nouvelle clé. p désigne la p ème partition courante et P le nombre total de partitions pour la valeur de clé courante. P est calculé à partir de la valeur de Hist i (R)(w) et des critères de partitions choisis sur lesquels nous revenons plus loin dans ce document, notamment sur la base de mp qui est la taille élémentaire de partition. Les tuples d'histogramme de R et S sont soit également émis, avec un tuple de R pour chaque partition et un seul tuple pour tous les tuples de S ayant comme valeur d'attribut w, soit ignorés après leur exploitation pour le calcul des partitions. Dans notre cas, nous avons choisi de les émettre sans les exploiter dans nos expérimentations, mais ils peuvent être nécessaires dans certains cas de figure. Nous avons exposé ici le cas où la fréquence de w dans R est supérieure ou égale à la fréquence de w dans S, le traitement du cas opposé se fait de la même façon en substituant 'r' à 's' et inversement. Suite à ce traitement, les tuples des données contiennent de nouvelles informations permettant l'aiguillage des différents tuples vers les reducers en garantissant une bonne répartition des données sur l'ensemble de ces reducers, contournant ainsi un éventuel déséquilibre de ces données. En rappelant que nous avons opté pour l'adressage relatif, au moment de la jointure, cet aiguillage se fait selon les règles suivantes compte tenu de l'information portée par le tuple courant : (1) Le tuple est de la forme ((k,t), p, v) : il est émis au reducer ((k mod NR) + p), p étant un entier naturel compris entre 0 et P-1.. (2) Le tuple est de la forme ((k,t), '*'.P, v) : il est émis aux reducers ((k mod NR) + i) pour i=0 à P-1, P étant un entier naturel éagal au nombre de partitions (i.r réplications) nécessaire. La phase Map du plan d'exécution La phase map de l'algorithme HistoPlan ne présente pas d'intérêt particulier. Elle se contente d'émettre les tuples formatés correctement. L'analyse de sa complexité algorithmique conduit aux mêmes résultats que celle de l'algorithme BasicJoin. 54
90 8. LA JOINTURE PARALLELE EN ENVIRONNEMENT CLOUD La phase Reduce du plan d'exécution Sur cet algorithme, on remarquera tout d'abord que s'il n'existe pas de tuples de S ou de R pour une valeur d'attribut de jointure w, alors les tuples de S ou de R pour lesquels cette valeur existe sont abandonnés. Ceci revient à procéder au test de nullité de Histi(R)(w)xHisti(S)(w). Les fonctions need_partition() et need_replication() sont les méthodes d'abstraction de la gestion des choix de partitionnement que nous commentons dans le paragraphe suivant. Elles retournent un entier qui correspond, en cas de nécessité de partitionnement, au nombre de partitions. Lorsqu'un jeu de tuples de R et de S, c'est à dire l'ensemble des tuples de R et S ayant comme même valeur d'attribut w, ne nécessite pas de partitionnement, alors ces tuples sont adressés au numéro relatif de reducer 0. Ainsi,dans ce cas, la méthode de partitionnement classique est utilisée. HistoPlan : reducer de jointure évoluée à histogramme public void reduce(text key, Iterator<Text> values, OutputCollector<Text, Text> output, \ Reporter reporter) throws IOException { long sumhis=0; long nbi=0; if (gethtag(key).equals(htag)) { if (values.hasnext()) sumhis+=integer.parseint(values.next().tostring().trim()); if (gettag(key).equals(rtag)) hr=sumhis; else if (hr > 0) hs=sumhis; else hs=0; return; if (hr*hs == 0) return; int np = need_partition(key,hr,hs); int nr = need_replication(key,hr,hs); if (np == 0) { if (nr > 0) adr = StarTag+String.valueOf(nr); else adr="0"; while (values.hasnext()) output.collect(new Text(key.toString()+" "+adr), values.next()); else { while (values.hasnext()) { output.collect(new Text(key.toString()+" "+String.valueOf(nbi/max_partition)), values.next()); nbi+=1; if (gethtag(key).equals(stag)) { hr=0; hs=0; 55
91 8. LA JOINTURE PARALLELE EN ENVIRONNEMENT CLOUD Choix du type de partitionnement Il existe de nombreuses façons de procéder au partitionnement des données d'une relation. Dans le cadre de partitionnement statique, qui nous intéresse ici, nous pouvons classer ces méthodes en deux catégories. Nous désignons pour notre part, dans un premier temps, ces deux méthodes de participative pour la première et de directive pour la seconde. Nous entendons par participative, les méthodes qui consistent à apporter un complément de traitement visant à éliminer autant que possible le déséquilibre des données sans pour autant viser à l'élimination totale de ce déséquilibre. La méthode directive quant à elle vise à réaliser l'équilibre parfait en contrôlant la volumétrie allouée à la totalité des nœuds de jointure. Nous pouvons résumer ces deux méthodes par le fait que i, j[0, NR1], la méthode participative cherche à approximer le terme wv ( R.AS.B) hist i (R)(w) hist i (S)(w) wv (R.AS.B) hist j (R)(w) hist j (S)(w) tandis que la méthode directive recherche l'égalité parfaite. Si l'équilibre parfait a un intérêt indéniable, il nécessite un traitement plus lourd et plus complexe avec stockage en mémoire locale d'une quantité de données proportionnelle aux données traitées, ce qui réduit la scalabilité notamment sur des nœuds à faible ressources. Par ailleurs, l'équilibre parfait des données ne signifie pas l'équilibre parfait des traitements. En effet, d'autres paramètres peuvent impacter significativement la durée des traitements comme notamment la charge du nœud, ses capacités ainsi que les contentions réseau. De plus, cette méthode selon la façon dont elle est réalisée, locale ou globale, peut générer un nombre important de partitions et donc plus de réplication de données, augmentant ainsi la volumétrie qui transite sur le réseau. On verra par la suite durant nos expérimentations que cette assertion est particulièrement vérifiée même pour des données initialement parfaitement équilibrées( zipf à coefficient nul). Nous l'avons dit, la méthode directive nécessite un développement assez pointu, puisqu'elle s'apparente aux problématiques de «sac à dos» ou bien encore d'ordonnancement de tâches. Par ailleurs, nous démontrons dans nos expériences que, compte tenu du déséquilibre par nature des nœuds dû aux contentions conjoncturelles de leurs ressources, un équilibre parfait n'est pas exploitable dans un contexte où le développeur ne maîtrise par chaque action relative à la gestion du parallélisme. Dans le cadre du framework MapReduce et du DFS, une méthode de type participative est hautement plus compatible tant du point de vue du contexte technique que de l'esprit : cette méthode ne nécessitant que de faibles rétentions de données en mémoire. Enfin, un autre avantage de la méthode participative est qu'elle se contente de traiter l'histogramme fréquence par fréquence, voir tuple par tuple. Cette approche est beaucoup plus compatible avec le concept MapReduce. On peut conclure que la méthode participative opère un équilibre des fréquences, là où une méthode directive opère un équilibre des histogrammes. Sous cet angle, il apparaît clairement que cette dernière méthode est quelque peu incompatible avec le concept MapReduce et que, par la suite, bien que nous continuons à parler d'algorithmes à histogramme il s'agit d'un abus de langage ; en réalité il serait plus correct de les qualifier d'algorithmes à équilibre de fréquences. Méthode participative Cette méthode vise donc à essentiellement éliminer les situations pouvant apporter un déséquilibre important du traitement. Étant communément admis que le facteur le plus important de déséquilibre sont les fréquences élevées des attributs de jointure, dans un premier temps notre méthode s'appuie sur ce constat. En effet, réduire les hautes fréquences de valeurs d'attributs présentées sur chaque nœud, et leur distribution vers d'autres nœuds, élimine un nombre très important de situation de déséquilibre. 56
92 8. LA JOINTURE PARALLELE EN ENVIRONNEMENT CLOUD Notre problématique se ramène donc à définir ce qu'est une haute fréquence et de quoi elle dépend. Par ailleurs, on admettra la règle qui dit que pour une valeur d'attribut w donnée : Si HIST i (R)(w)HIST i (S)(w)alors on partitionne R et onréplique S. et Si HIST i (R)(w)<HIST i (S)(w)alorson partitionne Set onréplique R. En ce qui concerne la taille des partitions, dans un premier temps nous paramétrons nos algorithme pour cette valeur. Dans un second temps, grâce à des expérience appropriées nous mettons en évidence les dépendances de cette quantité avec d'autres paramètres de nos relations et de notre environnement technique. Compte tenu d'une valeur de partition fixe, nous définissons deux méthodes JAVA need_partition et need_replication. Elles prennent en entrée la valeur de l'attribut de jointure courant, ainsi que les valeurs d'histogramme des deux relations pour cette valeur d'attribut. La première retourne le nombre de partition s'il y a partitionnement et 0 sinon. La seconde retourne le nombre de partition s'il y a réplication et 0 sinon. Décision de partitionnement Cette méthode extrait la relation concernée de la clé, du tuple traité, fournie en entrée ainsi que la valeur d'attribut. Si la fréquence de cette valeur d'attribut est supérieure à la seconde fréquence (de l'autre relation) fournie en entrée, et que la fréquence de l'attribut courant est supérieure à la taille élémentaire de partitionnement alors il y a nécessité de partition et donc le nombre de partitions est calculé puis retourné. Sous hypothèses que la relation courante est R, ce nombre est exprimé par : np(w)= HIST i ( R)(w) mp Le code résultant est le suivant :, avec mpla taillede partition. public int need_partition(text key, long vhr, long vhs) { long vhc = Math.max(hr,hs); if (vhc <= max_partition) return 0; if ((gethtag(key).equals(rtag) && vhr >= vhs) (gethtag(key).equals(stag) && vhr < vhs)) return (int) Math.ceil(1.0*vhc/max_partition); else return 0; Décision de réplication A l'inverse de la méthode précédente celle-ci près avoir extrait la relation concernée de la clé, du tuple traité, fournie en entrée ainsi que la valeur d'attribut, si la fréquence de cette valeur d'attribut est inférieur à la seconde fréquence (de l'autre relation) fournie en entrée, et que la fréquence de l'autre l'attribut est supérieure à la taille élémentaire de partitionnement alors il y a nécessité de répliquer le tuple courant autant de fois que le nombre de partitions qui est calculé de la même façon que précédemment, c'est à dire sous hypothèses que la relation courante est R, le nombre de répliques est exprimé par : nr(w)= HIST i (S)(w) mp, avec mpla taille de partition. 57
93 Le code résultant est le suivant : public int need_replication(text key, long vhr, long vhs) { long vhc = Math.max(hr,hs); if (vhc <= max_partition) return 0; if ((gethtag(key).equals(rtag) && vhr < vhs) (gethtag(key).equals(stag) && vhr >= vhs)) return (int) Math.ceil(1.0*vhc/max_partition); else return 0; 8. LA JOINTURE PARALLELE EN ENVIRONNEMENT CLOUD Jointure avec partitionnement Après le marquage et l'élaboration du plan d'exécution rendant la jointure insensible aux déséquilibres des données, nous sommes maintenant en mesure de réaliser la jointure proprement dite. Nous adoptons la méthode jointure de type NestedLoop avec présentation triée des tuples de jointure selon leur clé et leur nom de relation. Ainsi pour une même valeur de clé w, sont présentés d'abord les tuples de la relation R puis les tuples de la relation S. Les premiers sont stockés en structure indexée, puis dans un deuxième temps joints avec les seconds au fil de leur présentation. Une variante consisterait à trier les tuples selon leur clé puis selon la fréquence de leur valeur de clé ; ainsi seront d'abord présentés les tuples ayant la plus petite fréquence suivis de ceux ayant une plus grande fréquence pour une même valeur de clé. Un troisième critère de tri basé sur l'étiquette de relation évitera le mélange des tuples des deux relations en cas d'égalité de leurs fréquences. Nous n'avons pas jugé utile de mettre en œuvre cette optimisation qui a pour principal avantage de réduire la quantité de mémoire utilisée notamment dans le cas de présence de très hautes fréquences dans les relations jointes ; cela n'est pas notre cas car ces hautes fréquences ont été préalablement distribuées sur plusieurs nœud Phase Map de la jointure La phase Map est essentielle pour la mise en œuvre du plan d'exécution. En effet, c'est à cet instant que les informations portées par les tuple sur leur destination sont décodées et appliquées. Ainsi,comme indiqué plus haut, il existe 3 cas de figure pouvant se ramener à deux : (1) Le tuple est de la forme ((k,t), p, v) : le tuple est émis au reducer ((k mod NR) + p), p étant un entier naturel entre 0 et P-1 et P le nombre de partitions. (2) Le tuple est de la forme ((k,t), '*'.P, v) : le tuple est émis aux reducers ((k mod NR) + i) pour i=0 à P-1, P étant un entier naturel égal au nombre de répliques nécessaire. Les tuples ne nécessitant ni réplication ni partition sont portés par le cas de figure (1) avec p=0. Le numéro du reducer courant est quant à lui, compte tenu de notre méthode modulo, égal à (k mod NR), où NR est le nombre de reducers utilisés. Et donc l'adressage se fait relativement au reducer courant. Et ainsi un déséquilibre sur le reducer courant se verra lissé sur les P reducers suivants. La méthode d'aiguillage utilisée est indépendante du nombre de reducers. En effet, si P>NR il y a risque de dépassement du champ d'adressage. Pour prendre en compte ce cas, le calcul de l'adressage devient : ((k mod NR) + p) mod NR. Ainsi l'affectation des partitions se fait de manière cyclique autant de fois que nécessaire, un nœud pouvant alors se voir affecté une ou plusieurs partitions d'une même valeur de clé. De la même façon, et pour les mêmes raisons, afin d'éviter qu'un tuple se voit dupliqué plusieurs fois sur le même nœud, le calcul des adresses de réplication devient : (((k mod NR) + i) pour i=0 à min(p-1,nr-1)) mod NR. 58
94 8. LA JOINTURE PARALLELE EN ENVIRONNEMENT CLOUD On notera que ce traitement d'aiguillage est réalisé par la méthode partitionner. La méthode map ne faisant qu'extraire les informations requises afin de les rendre intelligible pour la méthode partitionner, ce qui garantie une meilleure adaptabilité du code. HistoJoinV4 : mapper jointure à histogramme public void map(longwritable key, Text value, OutputCollector<Text, Text> output, Reporter reporter) throws IOException { String line = value.tostring(); String reste = "" String tag = ""; String tkey = ""; String off_part="0"; StringTokenizer tokenizer = new StringTokenizer(line); if (tokenizer.hasmoretokens()) tkey = tokenizer.nexttoken(); if (tokenizer.hasmoretokens()) tag = tokenizer.nexttoken(); if (tokenizer.hasmoretokens()) off_part = tokenizer.nexttoken().trim(); while (tokenizer.hasmoretokens()) { reste=reste.trim()+" "+tokenizer.nexttoken(); if (off_part.substring(0,1).equals(startag)) for (int p=0;p<math.min(numred,integer.parseint(off_part.substring(1,off_part.length())));p++) { output.collect(new Text(tkey+" "+tag+" "+String.valueOf(p)), new Text(reste)); else { output.collect(new Text(tkey+" "+tag+" "+off_part), new Text(reste)); Complexité algorithmique Au traitement des tuples initiaux s'ajoute le traitement des tuples à répliquer. La quantité des tuples répliqués dépend fortement de la taille de partition élémentaire (mp) ainsi que du déséquilibre des données. De façon analytique ce surplus peut s'exprimer par la somme des grandeurs : et vv( R.A S.B) vv( R.A S.B) HIST i (R)(v) mp HIST i (S)(v) mp pour tout v avec HIST i (R)(v)HIST i (S)(v)HIST i (R)(v)>mp. pour tout v avec HIST i (S)(v)>HIST i (R)(v)HIST i (S)(v)>mp. Une hypothèse simplificatrice, pour ce calcul, consiste à poser la contrainte: vv (R.AS.B), HIST i (R)HIST i (S). Cette contrainte n'impacte pas notre résultat même si ce n'est pas la réalité. Car en effet, si un cas de figure où cette contrainte n'est pas vérifiée est rencontré, il suffit alors de déplacer les tuples 59
95 8. LA JOINTURE PARALLELE EN ENVIRONNEMENT CLOUD concernés de S vers R et inversement. Sous cette condition, on peut borner le surplus de tuples dû à la réplication par : TR mp v V( R.A S.B) ( HIST i(r)(v) mp 1), oùmp est la taillemax de partition. La complexité pouvant alors être bornée par : O(R+S+TR) Communications La quantité des communications établies sont également identiques à celle décrite plus haut, c'est à dire proportionnelle au surplus TR près. Par ailleurs, le partitionnement assure un lissage des communications vers un nombre de nœuds plus important, ce qui participe à la qualité des transferts entre les différents nœuds de traitement. Le surplus de communication dépend également de la taille moyenne d'un tuple. Sous l'hypothèse précédente et d'une seconde hypothèse stipulant que les tuples de R et S ont de tailles moyennes approximativement égales, la quantité de données supplémentaires communiquée due à la réplication s'exprime par : CR=tm mp ( HIST i(r)(v) vv (R.AS.B) mp 1),où tmest lataille moyenned ' untuple. Cette quantité supplémentaire est, par la nature même du partitionnement, distribuée équitablement entre l'ensemble des nœuds reducers. En réalité, notre méthode favorisant les nœuds voisins du nœud détenant initialement la donnée, la distribution de ce surplus est réalisée au sein d'un groupe clos, sauf pour les très hautes fréquences. Cette dernière exception n'est pas un inconvénient car elle auto-régule l'effet de la localisation de la distribution. La limitation à un groupe clos de la distribution des hautes fréquences présente l'avantage de ne pas générer une granularité trop fine des données émises par les mappers vers les reducers qui aurait pour effet d'établir des communications pour de très faibles volumes, ce qui est peu efficace car l'impact de la latence réseau se trouverait amplifiée Phase reduce de la jointure La phase reduce réalise la jointure de la même façon que l'algorithme de jointure HistoJoinV1, à ceci près que la structure des tuples est différente puisqu'elle porte également l'adressage de reducer pour les partitions, à savoir de la forme ((k,t), rr, v) où rr est le numéro relatif du reducer cible. Les histogrammes ne sont pas exploités car devenant inutiles. En effet, d'une part le plan d'exécution est porté par les tuples et, d'autre part l'optimisation consistant à abandonner les tuples ne donnant pas lieu à une jointure est obsolète car ceux-ci ont déjà été supprimés lors de l'élaboration du plan d'exécution. Le code JAVA résultant est alors : HistoJoinV4 : reducer de jointure à histogramme public void reduce(text key, Iterator<Text> values, OutputCollector<Text, Text> output, \ Reporter reporter) throws IOException { String subkey = getkey(key); String tag = gethtag(key); String tup = ""; int nbi = 0; 60
96 8. LA JOINTURE PARALLELE EN ENVIRONNEMENT CLOUD if (tag.equals(rtag)) { if (! lastkey.equals(getkey(key))) RBuf.clear(); lastkey=getkey(key); while (values.hasnext()) { tup=values.next().tostring(); RBuf.add(tup); nbi+=1; if (tag.equals(stag) && (RBuf.size() > 0) && lastkey.equals(getkey(key))) { while (values.hasnext()) { tup=values.next().tostring(); for (int i = 0; i < RBuf.size(); i++) output.collect(new Text(lastkey), new Text(RBuf.get(i).toString() +" >< "+tup)); nbi+=1; Complexité algorithmique Elle est du même ordre de grandeur que la complexité de l algorithme HistoJoinV1, à la différence près qu'ici le déséquilibre des données est moindre. En effet, la borne maximale O(R i S i ). mise en évidence sur le précédent algorithmique est beaucoup moins probable avec l'algorithme HistoJoinV4 du fait de la distribution des hautes fréquences vers plusieurs nœuds. R Cette borne maximale devenant alors sous cette hypothèses : i k S i, avec k1. On suppose k ici pour simplification du raisonnement que les valeurs d'attribut A de R sont toujours plus fréquentes que pour l'attribut B de S. Communications La communication est également fortement liée à la complexité algorithmique car celle-ci dépend du nombre de tuples traités et donc générés en sortie. Limiter le cas extrême ci-dessus revient donc à limiter les quantité de communications de la même façon. 61
97 9. ETUDE COMPARATIVE 9 ETUDE COMPARATIVE Nous avons présenté un ensemble de méthodes visant à réaliser la jointure en environnement CLOUD sur la base du framework MapReduce. Le but de chacune des méthodes étant soit de réaliser la jointure de la façon la plus basique (naïve) possible, en comptant sur le bon ordonnancement naturel des données, soit de façon plus optimale en espérant gommer le déséquilibre des données. Nous n'avons pas cependant exploré des méthodes, que nous avons nommé directives, contrôlant totalement la distribution de données mais nous avons exposé plusieurs inconvénients majeur à ce type de méthode dans notre contexte CLOUD de type «Shared Nothing». Nous nous proposons donc dans ce chapitre de procéder à la comparaison des ces algorithmes sur la base de leur efficacité mais également de leur consommation de ressource afin de vérifier leur extension à des échelles de données et réseaux plus importants. Nous réalisons également une étude comparative de l'algorithme le plus abouti HistoJoinV4 selon plusieurs paramétrages notamment en ce qui concerne les choix relatifs au partitionnement : taille de partition, nœuds cibles... Auparavant, nous souhaitons répondre par une série d'expérimentations et d'analyse à une interrogation qui a été présente tout au long du précédent chapitre, à savoir : quel est l'impact sur les performances de l'augmentation de la volumétrie traitée. En effet, le partitionnement génère une augmentation significative de données, puisqu'elle consiste à dupliquer les tuples de l'une des deux relations, avec un impact certain sur les transferts entre mappers et reducers lors de la jointure. Le résultat de cette phase d'expérimentation nous donne l'assise nécessaire pour aborder rationnellement la problématique de l'efficacité du partitionnement et de l'impact de la volumétrie en général. 9.1 Étude d'impact de la volumétrie Cette expérience consiste à appliquer aux algorithmes de prétraitement HistoPreJoin et HistoPlan une volumétrie croissante et d'observer l'impact de cette croissance sur les durées de traitement. Nous avons lancé une série de tests pour lesquels nous avons fait une moyenne pour chaque algorithme, le second prenant en entrée les deux relations marquées et avec histogramme. Il ressort de cette étude que l'impact de la volumétrie, bien que certain, est beaucoup plus faible que ce que nous étions en droit de penser. Nous verrons dans notre analyse les raisons de ce faible impact Méthodologie de l'évaluation de l'impact de la volumétrie Les algorithmes sollicités sont les prétraitements HistoPreJoin et HistoPlan, auxquels nous avons soumis la base de données Bd050 décrite plus haut et dont nous rappelons ici les caractéristiques initiales : Relation Coef. N Fmax R ou S Mixage bd050/r oui bd050/s oui Tableau 5: caractéristiques base bd050 62
98 9. ETUDE COMPARATIVE Nous avons ensuite décliné cette base en différentes volumétries des deux relations R et S, en augmentant la taille du champ valeur v des tuples. Ces tailles sont à peu près doublées à chaque itération, soit : 32Mo, 64Mo, 240Mo, 480Mo, puis 960Mo. Ce qui donne 5 nouvelles bases de données nommées respectivement : bd032, bd064, bd240, bd480 et bd960. Le schéma du workflow des traitements MapReduce exécutés est le suivant : DFS HistoPreJoin DFS DFS R bdnnn S HistoPlan HistoPreJoin Figure 4: workflow d'évaluation de la volumétrie sur les durées de traitement Impact de la volumétrie Le traitement des relations R et S par HistoPreJoin ne sont pas, comme peut l'indiquer le schéma, lancés en parallèle. Nous l'avons présenté ainsi pour des raisons de commodité et pour montrer le potentiel de ce traitement en matière de parallélisme. Ces traitements sont lancés de manière séquentielle sur chaque relation afin d'éviter les effets de bord des uns sur les autres. Et, de la même façon les différentes bases bdnnn sont utilisées les unes après les autres. Ces traitements sont exécutés selon plusieurs paramétrages de MapReduce. Nous avons fait progresser le nombre de mapper de 8 à 64 et les reducers également de 8 à 64 et appliqué ces deux paramètres de façon combinatoire. Les durées moyennes relevées par base de données sont : Tableau 6: durée de traitement en fonction de la volumétrie La fonction de progression des durées de traitement s'exprime comme suit : T i =T 0 + i kt T 0, avec T 0 la durée initiale pour la volumétrie initialev 0, T i ladurée pourla volumétriev i, i, i= V i V 0 V 0 et kt le coefficient de progression. On constate de prime abord une faible progression des durées de traitement. Si on rapporte la différence de durée avec la plus petite base bd32m au rapport de volumétrie entre chaque base et cette base bd32m, on constate que le taux de progression des durées est de l'ordre de seulement 4% par unité de rapport quelque soit la volumétrie mise en jeu. Là où la volumétrie a augmenté de 63
99 9. ETUDE COMPARATIVE 100%, la durée de traitement n'a augmenté que d'environ 3%, et quand la volumétrie augmente de 6500%, la durée n'augmente à nouveau que d'environ 24%. Bien entendu, d'une architecture à l'autre, cette progression et les échelles des données peuvent varier. Toutefois, les différentes expériences menées montre que le modèle MapReduce entre en jeu de façon importante dans le modèle global. Nous dirions que l'architecture technique influe sur les valeurs quantitatives, tandis que le modèle MapReduce influ sur les aspects qualitatifs en l'ocurrence la nature de la progression d'une échelle de données à l'autre, à savoir la linéarité. Il est possible de pousser la modélisation jusqu'à une quantité de données égale à 0. Par corrélation on peut mettre en évidence une durée théorique incompressible qui est ici de l'ordre de 35.5 secondes, en ramenant l'équation ci-dessus par translation à cette durée de référence en lieu et place de T 0. En réalité, vu le faible écart entre T 0 et cette durée incompressible, prendre l'une ou l'autre dans nos calculs n'aurait qu'un très faible impact. A l'inverse, il faut veiller à prendre en compte cette durée (ou latence MapReduce) afin d'en exploiter le comportement dans les modélisations futures. Par ailleurs, si on regarde l'évolution des durées de traitement base par base, en fonction des différents paramétrage du nombre de reducers et de mappers, on constate, pour la plus petite base, une relative insensibilité des durées de traitement au nombre de mappers mais une assez grande sensibilité à un nombre de reducers trop important. A l'inverse la base la plus volumineuse est plutôt sensible au rapport nb m /nb r (respectivementnb demapperset nbdereducers) avec une durée de traitement qui se dégrade proportionnellement à ce rapport, mais une amélioration de performances lorsque le nombre de reducers augmente. Il semble donc que l'ajustement du rapport nb m /nb r soit plus sensible pour les fortes volumétries et beaucoup moins pour les faibles volumétries. Pour les bases intermédiaires, on constate un glissement des meilleurs temps vers des configurations du nombre de reducers et de mapper intermédiaires. On notera que ces relevés ne sont pas universels et sont avant tout applicables à notre infrastructure. Nous pouvons néanmoins extrapoler ces résultats sans grand risque vers des environnement CLOUD à plus grande échelle mais également pour des volumétries de la même échelle. Ainsi on peut relever les règles générales suivantes : i. Le nombre de mappers doit être supérieur au nombre de reducers ii. Le rapport nb m /nb r doit augmenter avec la volumétrie iii. Le nombre de reducers doit augmenter proportionnellement à la volumétrie pour maintenir des durées de traitement équivalentes. Par la suite, lorsque nous souhaitons réaliser des évaluations de performances, nous opterons pour des configurations du nombre de mappers de 32 et de reducers de 8 ou 16 selon les cas. 64
100 9. ETUDE COMPARATIVE Tableau 7: durée de traitement à 32Mo en fonction du nb de mappers et reducers Tableau 8: durée de traitement à 64Mo en fonction du nb de mappers et reducers Tableau 9: durée de traitement à 240Mo en fonction du nb de mappers et reducers Tableau 10: durée de traitement à 480Mo en fonction du nb de mappers et reducers Tableau 11: durée de traitement à 960Mo en fonction du nb de mappers et reducers 65
101 9. ETUDE COMPARATIVE 9.2 Étude comparative des algorithmes de jointure Dans le chapitre précédent, nous avons identifié trois algorithmes de jointure, du plus naïf au plus évolué. Nous avons donné quelques indications analytiques sur le comportement de chacun de ces algorithmes qui laisse entrevoir une efficacité acceptable dans un cadre général pour le premier mais une meilleure prise en charge de certains cas extrêmes pour le dernier. L'algorithme intermédiaire étant là principalement pour évaluer l'impact des traitements des structures d'histogramme, puisqu'il ne les exploite que très partiellement. Ce constat est encore plus remarquable à la lumière des résultats de l'étude d'impact de la volumétrie qui nous montre que, somme toutes, la volumétrie n'a qu'une faible incidence sur les performances finales. Nous allons donc dans un premier temps présenter une comparaison analytique entre ces différents algorithmes. Dans un deuxième temps, nous mettons en œuvre les expérimentations nécessaire à la comparaison pratique et nous en tirons le constat que notre prévision est juste, à savoir un réel apport de l'algorithme le plus évolué HistoJoinV4 principalement pour des cas extrêmes, mais un apport néanmoins très net. Enfin, en vue de l'optimisation des techniques de partitionnement de l'algorithme HistoJoinV4, nous proposons une étude pratique et analytique visant à doter de tels algorithmes d'un outil de décision sur la taille des partitions qui est un élément extrêmement important comme nous le montrons dans nos évaluations Comparaison analytique L étude des trois algorithme BasicJoin, HistoJoinV1 et HistoJoinV4 a mis en évidence quelques bornes supérieurs quant à la complexité algorithmique et quantité de données communiquées ou nombre de communications établies. Nous disposons donc de base visant à évaluer l'apport de chacun de ces algorithmes en fonction de différentes situations. En effet, nous avons établis dans nos bilans analytiques une propension de l'algorithme HistoJoinV4 à augmenter la quantité de données qui transite entre les mappers et les reducers. D'un autre côté ce surplus est supposé être compensé par une réduction notoire des durées de traitement. En effet, sous cette hypothèse, la borne supérieure de la complexité de la phase reducer se trouve divisé par un coefficient non négligeable ce qui suppose de meilleures performances que l'algorithme naïf BasicJoinV1, soit : O(R i +S i +R i S i ) pourla jointure naïve,et O(R i +S i + R i k S i ) pour la jointure à histograme. k Il n'est guère possible de pousser plus en avant une telle analyse dans le contexte MapReduce. Celui-ci utilise des mécanismes qui lui sont propres et qui prennent en compte un nombre important de paramètres, implicite et explicites, comme nous l'avons exposé plus haut dans l'analyse des communication DFS vers les mappers de l'algorithme HistoPreJoinV1. Nous avons établi que le seul recours pour le développeur dans ce contexte est de veiller à borner les différentes grandeurs participant à de meilleures performances. A l'inverse, le concept MapReduce de par son formalisme et son déterminisme, dû à la simplicité relative des algorithmes mis en œuvre, présente un très bon terrain d'expérimentation dès lors que nous veillons à rester d'une part dans des zones linéaires en termes de temps de réponse et, d'autres part à mettre en œuvre des algorithmes dans le respect du concept MapReduce. 66
102 9. ETUDE COMPARATIVE Comparaison expérimentale En s'appuyant sur la collection de bases de données BDD décrite plus haut nous avons mené une série de tests, de durée de traitement, pour lesquels nous avons retenu la moyenne des durées. Le paramétrage utilisé est : 32 mappers, 8 reducers et un partitionnement pour HistoJoinV4 de 200 qui correspond à 10% de la fréquence max du déséquilibre médian (base bd050). Afin de garantir l'exactitude de nos relevés, nous avons prélevé puis contrôlé les sollicitations système des différents nœuds (cpu, mémoire, I/O, réseau...), afin de nous assurer que ces nœuds n'atteignent pas les seuils de saturation de leurs ressources. Nous avons également contrôlé les parts de temps consommées par les différentes étapes de MapReduce (shuffle, sort...) et veillé à ce que chacune reste dans des proportions standards. Sans ces précautions, le comportement des nos traitements aurait été aléatoire et nous n'aurions pas pu en tirer des conclusions cohérentes. Une synthèse des relevés de traitements est produite dans le premier tableau qui donne les durées moyennes pour chaque algorithme et base de données (i.e. déséquilibre). Le second tableau met en forme le premier tableau en affichant la part en pour-cent de la durée de chaque algorithme par rapport à la durée globale pour chaque base. Il s'agit de faciliter la lecture comparative des relevés. Enfin, le graphique donne une vue comparative des performances des trois algorithmes. Tableau 12: durée de traitement de chaque algorithme en fonction du déséquilibre Tableau 13: part de durée de traitement de chaque algorithme 67
103 9. ETUDE COMPARATIVE Figure 5: comparaison des durées de traitement pour différents déséquilibres La première observation remarquable sur le graphique ci-dessus est le comportement équivalent des deux algorithmes HistoJoinV1 et HistoJoinV4 pour les bases bd000, bd025 et bd075. Dans le premier et le second cas, cela indique que le partitionnement ne fait ici aucun effet, car pour bd000 il n'y a pas de déséquilibre des données et pour bd025 d'une part le déséquilibre est limité et d'autre part le nombre de valeurs d'attribut ayant une fréquence supérieure à 200 est très faibles. S'il n'y avait pas le référentiel matérialisé par HistoJoinV1, on aurait pu imaginer que pour cette base bd025 la sensible efficacité d'histojoinv4 par rapport à BasicJoinV1 était due au partitionnement ; grâce au témoin HistoJoinV1 on peut affirmer qu'il n'en est rien. Par ailleurs, on constate également la non efficacité d'histojoinv4 pour un déséquilibre de 0.75 qui est explicable, comme nous le verrons plus loin, par un mauvais choix de taille de partitionnement (soit 200). On constate une sensible efficacité du partitionnement pour un déséquilibre de 0.50 corroborée par le témoin HistoJoinV1 qui se détache nettement des durées d'histojoinv4 en restant collé à l'algorithme naïf BasiCJoinV1. On verra par la suite que cette efficacité est confirmée par des tests plus pointus sur l'effet du partitionnement dans le paragraphe suivante. Enfin, dès que le déséquilibre est flagrant ou extrême comme modélisé par la base bds111, le partitionnement est très nettement efficace puisque la performance de l'algorithme HistoJoinV4 est sans équivoque en étant ici plus de 4 fois supérieure aux deux autres algorithmes. Ce cas de figure montre également l'effet de bord du traitement d'histogrammes qui, lorsqu'il n'est pas compensé par une amélioration des performances par le partitionnement, induit une nette dégradation des durées de traitements. En conclusion, on retiendra, que malgré un faible intérêt de l'algorithme HistoJoinV4 dans certains cas de figure, notamment si on y ajoute le temps nécessaire à l'élaboration du plan d'exécution qui peut représenter de 50% à 5% du temps de traitement de la jointure, il offre un réel potentiel pour des déséquilibres importants. Toutefois, comme nous l'avons constaté, le choix de la taille de partitionnement n'est pas optimale compte tenu qu'elle a été choisie de façon assez arbitraire faute de règle formelle. Faute d'avoir pu trouver au début, dns les différentes études, une méthode formelle, nous nous sommes donc proposé d'explorer dans le cadre particulier du CLOUD s'il est possible de formaliser ce choix, analyser dans quelle mesure cela est possible et corroborer nos choix par des données expérimentales. 68
104 9. ETUDE COMPARATIVE 9.3 Évaluation de l'impact du partitionnement Le pivot de tout algorithme de partitionnement de relations en vue de réaliser une jointure parallèle et distribuée se trouve être le choix de la taille du partitionnement de données nécessitant un découpage. Le principe étant de découper une relation ou sous relation qu'on nommera partition physique et de répliquer la seconde relation (ou sous relation). Ces sous relations devant nécessairement, dans un premier temps, contenir l'ensemble des attributs de même valeur de sorte que : i, j[0, NR1] et vv (R.AS.B), si i jvv (R i. AS i.b) alors vv (R j. AS j. B) En général, la partition la plus grande est découpée tandis que la plus petite est répliquée sur les nœuds recevant une partition de la première. De cette façon, l'union des jointures sur chacun de ces nœud est strictement égale à la jointure globale. De façon plus précise, et notamment dans le cadre des algorithmes basés sur histogramme, le partitionnement se fait non pas au niveau de la partition physique, mais au niveau des valeurs d'attribut de jointure. L'ensemble des tuples ayant la même valeur d'attribut dans R et S étant alors considérés comme deux sous partitions ; ceci revenant à découper les histogrammes des attributs de jointure des relations en question. La difficulté dans tous les cas est de trouver la taille optimale de partition car celle-ci conditionne fortement la quantité de données supplémentaire, à faire transiter sur le réseau, dans le cadre de la réplication de la seconde partition, et ce supplément de données est d'autant plus important que les deux sous relations sont de taille équivalente. En revanche, si l'une des deux sous relations est beaucoup plus petite que l'autre, alors le problème se pose dans une moindre mesure. Ainsi, nous identifions trois paramètres majeurs qui entrent en jeu dans le cadre du partitionnement de données qui sont : (a) Le coût élémentaire du traitement d'une jointure, qu'on nommera dt (b) Le surcoût temporelle élémentaire dû à l'augmentation des données, qu'on nommera k (c) Et la différence entre la taille de la première et la seconde relation. Les deux premiers sont des constantes et inhérents à l'infrastructure utilisée. Le paramètre dt dépend fortement des ressources machines englobant le coût de calcul de la jointure de deux tuples ainsi que le coût d'enregistrement. Le paramètre k quant à lui, dans le cadre du concept MapReduce, dépend fortement des ressources réseau et dans une moindre mesure des ressource machine pour le traitement des tuples répliqués. Le paramètre k a été approché dans l'étude d'impact précédente, il est exprimé en seconde et relativement aux taux d'augmentation des données par rapport à une volumétrie initiale V 0 et une durée de traitement T 0. Les tailles des données partitionnées ne portent aucune information pertinente lorsqu'elles sont considérées isolément, c'est donc dans un premier temps leur différence qui nous paraît la plus pertinente. Nous allons tout d'abord évaluer théoriquement le partitionnement optimal et, dans un second temps, recouper cette évaluation avec une expérimentation mettant en évidence la nature de l'évolution des performances en fonction de l'évolution du partitionnement. Puis nous proposons une approche permettant de faire le choix le plus judicieux du seuil de partitionnement. 69
105 9. ETUDE COMPARATIVE Évaluation théorique Soit w une valeur des attributs A et B des relations R et S, tel que Hist(R)(w)Hist(S)(w). En supposant que les tuples de R et S ont une taille moyenne équivalente, le bilan volumétrique et temporelle pour w est le suivant : Volumétrie initiale : V 0 =Hist(S)(w)+Hist(R)(w). Durée de traitement de jointure : T 0 =Hist(S)(w) Hist(R)(w) dt, où dt estla duréeélémentaire pour traiteruntuple de jointure, soit lecouplage de deux tuples de R et S. Volumétrie supplémentaire due à la réplication : V s =Hist(S)(w) ( p1), avec p= Hist(R)(w) et mp est lataille max de partition(taille élémentaire). mp La nouvelle durée théorique de traitement T th due au partitionnement et le coût en durée de traitement T p due au supplément de volumétrie sont: T th = T 0 p et T p=k V s, où V 0 k est l ' impact en durée par taux d' augmentation de lavolumétrie. Le temps T 0 subit une accélération qui suit 1/p, le point d'équilibre est atteint quand la durée T th est annulée par le supplément de durée de T p dû au supplément de volumétrie, soit : T 0 T th T p =0 et donc p k V s =0 V 0 En supposant que p1, ce qui est vrai dans notre cas puisque le partitionnement suppose des fréquences élevées et, l'optimisation de ce partitionnement suppose des fréquences plus élevés induisant une fragmentation plus importante qu'on souhaite borner afin de limiter l'impact de l'augmentation de la volumétrie. Sous cette hypothèse, on peut poser que : V s =Hist(S)(w) ( p1) p Hist(S)(w)= Hist(R)(w) Hist(S)(w)= T o mp mp dt. Et en posant pour simplification d'écriture : H R w =Hist(R)(w) et H S w =Hist(S)(w) On obtient : T 0 p k V s = H R w H S w mp dt k H R S w H w R V 0 H w mp (H R w +H S w ) =mp H S w mp dt mp k H R S w H w mp (H R w + H S w ) =0 et donc mp 2 H S w dt k H R S w H w k H R S H R S =0 mp 2 = w H w w +H w H S w dt ( H R w +H S w ) = H R w H R w +H k S w dt Et donc : mp=k MR R H w avec K H R S MR= k une constante MapReduce w +H w dt S On constate que pour H w petit, le second terme tend vers1, la taille de partition ne S dépendant alors plus que de la constante MapReduce K MR. A l'inverse, pour H w proche de H w R le second terme tend vers 1 2. La taille de partition varie donc entre 70
106 9. ETUDE COMPARATIVE K MR 1 2 et K MR. On notera par ailleurs que kdt puisque le premier terme donne le surcoût pour un doublement de volumétrie et est donc de l'ordre de quelques centièmes, tandis que le second est de l'ordre de quelques microsecondes comme nous le verrons en phase d'expérimentation. Par ailleurs on attirera l'attention sur le paradoxe qui fait que la taille de partition diminue (et donc l'effet de la réplication augmente) avec la taille de la partition répliquée. De plus, celle-ci n'est pas conditionnée par la taille des deux relations, mais par le rapport beaucoup plus H w R subtile. H R S En réalité ceci est compatible avec notre première intuition puisque la partition w +H w répliquée se comporte dans ce rapport comme un atténuateur de la taille de partitionnement sans l'inhiber fortement. Et, quand la taille de cette partition devient petite, elle s'efface pour laisser le pilotage de la taille de partitionnement à la seule constante MapReduce. R On remarquera enfin, que le terme H w n'entre pas dans le calcul et n'influe pas directement sur la taille de partitionnement. Cela s'explique par le fait que le facteur majeur qui détermine s'il faut ou pas partitionner est le taux de déséquilibre des données. Cette notion est bien R S plus relative et ne dépend donc elle même que relativement des fréquences H w ou H w. Une méthode simple est de fixer un seuil (i.e. fréquence) à partir duquel le partitionnement est appliqué. Une méthode naïve consiste à choisir un seuil minimal, puisque l'équation ci dessus de mp procédera à l'ajustement de celui-ci afin qu'il ne soit pas trop pénalisant pour les performances. Une méthode complémentaire consisterait également à remplacer la constante K MR par une taille de partition maximale qui sera ensuite ajustée automatiquement dans l'intervalle indiqué plus haut. Ainsi une taille max de mp de 500 fera évoluer mp entre environ 350 et 500. Nous proposons plus loin une approche beaucoup plus formelle de choix du seuil d'activation du partitionnement. Si la problématique ne se pose que modérément pour des environnements multiprocesseurs voir pour des environnements Clusers restreints à un super réseau privé, le problème est entier dans un environnement CLOUD pour lequel le réseau est avant tout un média de communication entre nœud avant d'être un canal de transfert de données massives dédié Évaluation expérimentale Afin d'étayer les résultats précédents, nous avons procédé à une série de tests visant dans un premier temps à mettre en évidence l'impact de la taille de partitionnement sur les performances, et de déterminer dans quelle mesure dans un second temps. Le protocole de tests part du constat que la différence entre la taille de la partition découpée (que nous nommerons fréquence principale) et la taille de la partition répliquée (que nous nommerons fréquence secondaire) joue un rôle important. Ainsi nous faisons évoluer nos tests selon les deux axes qui sont la taille de partition et cette différence. Pour ce faire, nous avons généré un jeu de test, s'appuyant initialement sur la base bd050 décrite plus haute. Afin d'introduire un déséquilibre dans le déséquilibre initial, nous avons affecté artificiellement les fréquences les plus hautes de R au reducer ayant un numéro modulo 4, à savoir le 0 et le 4 pour 8 reducers. Les fréquences les plus basses ont quant à elles été distribuées aléatoirement entre les autres reducers. Ensuite, pour chaque valeur affectée au reducer modulo 4, nous avons affecté à S la même fréquence de cette valeur multipliée par un coefficient allant de 0.1 à 1 pour chaque base. Ce qui produit 7 bases de données bdp01, bdp02, bdp04 bdp05, bdp06, bdp08, bdp10 avec les coefficients respectifs 0.1, 0.2, 0.4, 0.5, 0.6, 0.8, Ainsi pour la base bdp01 on a : vv (R.A)si HIST (R)(v)>fmax alors HIST(S)(v)=0.1 HIST (R)(v). Et, pour bdp02 on a : v V (R.A)si HIST ( R)(v)>fmax alors HIST( S)(v)=0.2 HIST ( R)(v) etc... 71
107 9. ETUDE COMPARATIVE Les premiers tests sont réalisés avec un nombre de reducers de 8. On peut constater dans les tableaux ci dessous les résultats obtenus qui montrent que lorsque les fréquences de la partition répliquée sont très basses (bdp01), une trop petite valeur de mp est très pénalisante. On remarque alors que la meilleure performance (en vert) est obtenue pour mp=5000 qui est la fréquence max des deux relations, ce qui signifie donc qu'il n'y a pas de partitionnement pour cette valeur de mp. Cela met en évidence que lorsque le partitionnement est réalisé sur des données peu déséquilibrées, il y a une incidence directe et négative sur les performances. Le reste du temps, on constate que le partitionnement est nécessaire puisque les durées de traitement pour mp=5000 (en rouge) sont très médiocres. On constate également une augmentation de la taille de partition et donc une diminution du nombre de partitions avec l'augmentation du déséquilibre pour se replier en milieu de tableau et stagner enfin autour de mp=100. Cela corrobore notre théorie puisque pour les faibles déséquilibres, la valeur des fréquences de la partition découpée étant faible, tout en présentant un déséquilibre sensible (bases > bdp01), le coût du partitionnement étant faible une valeur faible de mp est privilégiée. Celle-ci est ensuite atténuée par l'augmentation de la fréquence secondaire. Lorsque la fréquence secondaire croit de façon plus importante (base > bdp05) la nécessité de découper cette fréquence devient grande ce qui a tendance à diminuer mp vers la valeur pour laquelle le traitement est optimal. Une autre exploitation de ces résultats consiste à estimer la valeur moyenne en ms du coût de traitement de la jointure élémentaire de deux tuples de R et S. Il s'agit de la grandeur que nous avons nommé dt dans le paragraphe précédent et qui participe au calcul de la constante K MR. Ainsi la durée de jointure élémentaire calculée en fonction des tailles de jointure est dt=1000 Tableau 14: durée de traitement en fonction de H S w/h R w et de la taille de partitionnement pour nb_reducers=8. v V (R. A S.B) T [bd, mp] HIST (R)(v) HIST (S)(v) avec T le tableau des durées de traitement, et bd la base de donnée concernée. Le résultat pour chaque configuration, en fonction de la taille de partitionnement pour nb_reducers=8, est alors : H w S H w R et de 72
108 9. ETUDE COMPARATIVE La valeur moyenne globale est de 3.6 µs, tandis que la meilleure valeur moyenne est de 3.2µs et la moins bonne est de 4.7µs. Logiquement, nous retiendrons la meilleure moyenne qui est celle dépouillée d'autres surcoûts liés notamment à une sur-gestion de tout ce qui entoure la jointure proprement dite, on peut également penser que tout traitement dans sa configuration optimale, que nous recherchons, tend vers cette valeur. Ainsi, grâce à la formule précédente, on obtient une taille de partitionnement seuil (I.e constante MapReduce) : K MR= k dt = et donc mp= H R S H R S 110 et fluctue dans[55,110] w +H w On notera une légère différence entre la valeur théorique qui donne 110 et la valeur 150 (entre 100 et 200) observée durant notre expérience. Nous en précisons les raisons dans le paragraphe suivant. En réalité le facteur k ici n'est pas tout à fait le même facteur kt évalué durant l'étude d'impact de la volumétrie. Toutefois, nous estimons qu'il s'agit de la même grandeur. Nous avons poussé l'analyse pour établir ceci formellement, sur la base notamment d'équation différentielle afin d'isoler la partie dynamique de la partie plus statique due à la latence MapReduce, sans toutefois y parvenir. Néanmoins, nos recoupements nous laissent croire que cela est possible. En réalité, plus précisément, nous soupçonnons que la latence MapReduce soulevée au chapitre entre en jeu à la fois dans le calcul du coût de jointure élémentaire dt pour une part et dans le calcul de k pour une autre part, cette part de latence s'annulant dans le rapport k/dt. Enfin, les différents analyses et recoupements des données expérimentale font plus que conforté cette intuition, puisque nous collons analytiquement, à peu de chose près, aux résultats expérimentaux Méthode pour le choix du partitionnement Nous avons proposé une méthode théorique de calcul de la taille de partitionnement optimal, méthode que nous avons validé dans une certaine mesure par notre expérience avec modulation du rapport H w S H w R Tableau 15: coût en ms d'un tuple de jointure. Il nous reste à préciser les modalités de choix de partitionnement, à savoir le seuil de fréquence à partir duquel le partitionnement est nécessaire ou tout du moins pouvant présenter un intérêt pour les performances sans risque de les détériorer Seuil arbitraire de partitionnement La méthode généralement utilisée, faute de mieux, s'appuie sur le postulat que les fréquences hautes participent le plus probablement au déséquilibre des données. Ce qui trouve ses limites dans le fait que des données ayant des fréquences hautes pour chaque valeur d'attribut ne peuvent pas 73
Chapitre V : La gestion de la mémoire. Hiérarchie de mémoires Objectifs Méthodes d'allocation Simulation de mémoire virtuelle Le mapping
 Chapitre V : La gestion de la mémoire Hiérarchie de mémoires Objectifs Méthodes d'allocation Simulation de mémoire virtuelle Le mapping Introduction Plusieurs dizaines de processus doivent se partager
Chapitre V : La gestion de la mémoire Hiérarchie de mémoires Objectifs Méthodes d'allocation Simulation de mémoire virtuelle Le mapping Introduction Plusieurs dizaines de processus doivent se partager
Partie 7 : Gestion de la mémoire
 INF3600+INF2610 Automne 2006 Partie 7 : Gestion de la mémoire Exercice 1 : Considérez un système disposant de 16 MO de mémoire physique réservée aux processus utilisateur. La mémoire est composée de cases
INF3600+INF2610 Automne 2006 Partie 7 : Gestion de la mémoire Exercice 1 : Considérez un système disposant de 16 MO de mémoire physique réservée aux processus utilisateur. La mémoire est composée de cases
Chapitre 1 : Introduction aux bases de données
 Chapitre 1 : Introduction aux bases de données Les Bases de Données occupent aujourd'hui une place de plus en plus importante dans les systèmes informatiques. Les Systèmes de Gestion de Bases de Données
Chapitre 1 : Introduction aux bases de données Les Bases de Données occupent aujourd'hui une place de plus en plus importante dans les systèmes informatiques. Les Systèmes de Gestion de Bases de Données
ORACLE TUNING PACK 11G
 ORACLE TUNING PACK 11G PRINCIPALES CARACTÉRISTIQUES : Conseiller d'optimisation SQL (SQL Tuning Advisor) Mode automatique du conseiller d'optimisation SQL Profils SQL Conseiller d'accès SQL (SQL Access
ORACLE TUNING PACK 11G PRINCIPALES CARACTÉRISTIQUES : Conseiller d'optimisation SQL (SQL Tuning Advisor) Mode automatique du conseiller d'optimisation SQL Profils SQL Conseiller d'accès SQL (SQL Access
Ebauche Rapport finale
 Ebauche Rapport finale Sommaire : 1 - Introduction au C.D.N. 2 - Définition de la problématique 3 - Etat de l'art : Présentatio de 3 Topologies streaming p2p 1) INTRODUCTION au C.D.N. La croissance rapide
Ebauche Rapport finale Sommaire : 1 - Introduction au C.D.N. 2 - Définition de la problématique 3 - Etat de l'art : Présentatio de 3 Topologies streaming p2p 1) INTRODUCTION au C.D.N. La croissance rapide
Systèmes de transport public guidés urbains de personnes
 service technique des Remontées mécaniques et des Transports guidés Systèmes de transport public guidés urbains de personnes Principe «GAME» (Globalement Au Moins Équivalent) Méthodologie de démonstration
service technique des Remontées mécaniques et des Transports guidés Systèmes de transport public guidés urbains de personnes Principe «GAME» (Globalement Au Moins Équivalent) Méthodologie de démonstration
SEP 2B juin 20. Guide méthodologique de calcul du coût d une prestation
 SEP 2B juin 20 12 Guide méthodologique de calcul du coût d une Sommaire Préambule 3 Objectif et démarche 3 1 Les objectifs de la connaissance des coûts 4 2 Définir et identifier une 5 Calculer le coût
SEP 2B juin 20 12 Guide méthodologique de calcul du coût d une Sommaire Préambule 3 Objectif et démarche 3 1 Les objectifs de la connaissance des coûts 4 2 Définir et identifier une 5 Calculer le coût
DÉVELOPPEMENT INFONUAGIQUE - meilleures pratiques
 livre blanc DÉVELOPPEMENT INFONUAGIQUE MEILLEURES PRATIQUES ET APPLICATIONS DE SOUTIEN DÉVELOPPEMENT INFONUAGIQUE - MEILLEURES PRATIQUES 1 Les solutions infonuagiques sont de plus en plus présentes sur
livre blanc DÉVELOPPEMENT INFONUAGIQUE MEILLEURES PRATIQUES ET APPLICATIONS DE SOUTIEN DÉVELOPPEMENT INFONUAGIQUE - MEILLEURES PRATIQUES 1 Les solutions infonuagiques sont de plus en plus présentes sur
Nom-Projet MODELE PLAN DE MANAGEMENT DE PROJET
 Nom-Projet MODELE PLAN DE MANAGEMENT DE PROJET Glossaire La terminologie propre au projet, ainsi que les abréviations et sigles utilisés sont définis dans le Glossaire. Approbation Décision formelle, donnée
Nom-Projet MODELE PLAN DE MANAGEMENT DE PROJET Glossaire La terminologie propre au projet, ainsi que les abréviations et sigles utilisés sont définis dans le Glossaire. Approbation Décision formelle, donnée
Compte-rendu de projet de Système de gestion de base de données
 Compte-rendu de projet de Système de gestion de base de données Création et utilisation d'un index de jointure LAMBERT VELLER Sylvain M1 STIC Université de Bourgogne 2010-2011 Reponsable : Mr Thierry Grison
Compte-rendu de projet de Système de gestion de base de données Création et utilisation d'un index de jointure LAMBERT VELLER Sylvain M1 STIC Université de Bourgogne 2010-2011 Reponsable : Mr Thierry Grison
PROBLEMES D'ORDONNANCEMENT AVEC RESSOURCES
 Leçon 11 PROBLEMES D'ORDONNANCEMENT AVEC RESSOURCES Dans cette leçon, nous retrouvons le problème d ordonnancement déjà vu mais en ajoutant la prise en compte de contraintes portant sur les ressources.
Leçon 11 PROBLEMES D'ORDONNANCEMENT AVEC RESSOURCES Dans cette leçon, nous retrouvons le problème d ordonnancement déjà vu mais en ajoutant la prise en compte de contraintes portant sur les ressources.
Complexité. Licence Informatique - Semestre 2 - Algorithmique et Programmation
 Complexité Objectifs des calculs de complexité : - pouvoir prévoir le temps d'exécution d'un algorithme - pouvoir comparer deux algorithmes réalisant le même traitement Exemples : - si on lance le calcul
Complexité Objectifs des calculs de complexité : - pouvoir prévoir le temps d'exécution d'un algorithme - pouvoir comparer deux algorithmes réalisant le même traitement Exemples : - si on lance le calcul
Technologie SDS (Software-Defined Storage) de DataCore
 Technologie SDS (Software-Defined Storage) de DataCore SANsymphony -V est notre solution phare de virtualisation du stockage, dans sa 10e génération. Déployée sur plus de 10000 sites clients, elle optimise
Technologie SDS (Software-Defined Storage) de DataCore SANsymphony -V est notre solution phare de virtualisation du stockage, dans sa 10e génération. Déployée sur plus de 10000 sites clients, elle optimise
Les réseaux cellulaires
 Les réseaux cellulaires Introduction Master 2 Professionnel STIC-Informatique Module RMHD 1 Introduction Les réseaux cellulaires sont les réseaux dont l'évolution a probablement été la plus spectaculaire
Les réseaux cellulaires Introduction Master 2 Professionnel STIC-Informatique Module RMHD 1 Introduction Les réseaux cellulaires sont les réseaux dont l'évolution a probablement été la plus spectaculaire
Modèle de maturité en analyse client et en analyse marketing
 E-BOOK Modèle de maturité en analyse client et en analyse marketing JOE DALTON, SMARTFOCUS $ INTRODUCTION Présentation Les consommateurs interagissent avec les marques via un nombre croissant de points
E-BOOK Modèle de maturité en analyse client et en analyse marketing JOE DALTON, SMARTFOCUS $ INTRODUCTION Présentation Les consommateurs interagissent avec les marques via un nombre croissant de points
LE PROBLEME DU PLUS COURT CHEMIN
 LE PROBLEME DU PLUS COURT CHEMIN Dans cette leçon nous définissons le modèle de plus court chemin, présentons des exemples d'application et proposons un algorithme de résolution dans le cas où les longueurs
LE PROBLEME DU PLUS COURT CHEMIN Dans cette leçon nous définissons le modèle de plus court chemin, présentons des exemples d'application et proposons un algorithme de résolution dans le cas où les longueurs
Programmation parallèle et distribuée
 Programmation parallèle et distribuée (GIF-4104/7104) 5a - (hiver 2015) Marc Parizeau, Département de génie électrique et de génie informatique Plan Données massives («big data») Architecture Hadoop distribution
Programmation parallèle et distribuée (GIF-4104/7104) 5a - (hiver 2015) Marc Parizeau, Département de génie électrique et de génie informatique Plan Données massives («big data») Architecture Hadoop distribution
Évaluation et optimisation de requêtes
 Évaluation et optimisation de requêtes Serge Abiteboul à partir de tranparents de Philippe Rigaux, Dauphine INRIA Saclay April 3, 2008 Serge (INRIA Saclay) Évaluation et optimisation de requêtes April
Évaluation et optimisation de requêtes Serge Abiteboul à partir de tranparents de Philippe Rigaux, Dauphine INRIA Saclay April 3, 2008 Serge (INRIA Saclay) Évaluation et optimisation de requêtes April
Systemes d'exploitation des ordinateurs
 ! " #$ % $ &' ( $ plan_ch6_m1 Systemes d'exploitation des ordinateurs Conception de Systèmes de Gestion de la Mémoire Centrale Objectifs 1. Conception de systèmes paginés 2. Conception des systèmes segmentés
! " #$ % $ &' ( $ plan_ch6_m1 Systemes d'exploitation des ordinateurs Conception de Systèmes de Gestion de la Mémoire Centrale Objectifs 1. Conception de systèmes paginés 2. Conception des systèmes segmentés
Programmation Objet - Cours II
 Programmation Objet - Cours II - Exercices - Page 1 Programmation Objet - Cours II Exercices Auteur : E.Thirion - Dernière mise à jour : 05/07/2015 Les exercices suivants sont en majorité des projets à
Programmation Objet - Cours II - Exercices - Page 1 Programmation Objet - Cours II Exercices Auteur : E.Thirion - Dernière mise à jour : 05/07/2015 Les exercices suivants sont en majorité des projets à
COMMUNICATEUR BLISS COMMANDE PAR UN SENSEUR DE POSITION DE L'OEIL
 COMMUNICATEUR BLISS COMMANDE PAR UN SENSEUR DE POSITION DE L'OEIL J. TICHON(1) (2), J.-M. TOULOTTE(1), G. TREHOU (1), H. DE ROP (2) 1. INTRODUCTION Notre objectif est de réaliser des systèmes de communication
COMMUNICATEUR BLISS COMMANDE PAR UN SENSEUR DE POSITION DE L'OEIL J. TICHON(1) (2), J.-M. TOULOTTE(1), G. TREHOU (1), H. DE ROP (2) 1. INTRODUCTION Notre objectif est de réaliser des systèmes de communication
TP Bases de données réparties
 page 1 TP Bases de données réparties requêtes réparties Version corrigée Auteur : Hubert Naacke, révision 5 mars 2003 Mots-clés: bases de données réparties, fragmentation, schéma de placement, lien, jointure
page 1 TP Bases de données réparties requêtes réparties Version corrigée Auteur : Hubert Naacke, révision 5 mars 2003 Mots-clés: bases de données réparties, fragmentation, schéma de placement, lien, jointure
GESTION DE LA MEMOIRE
 GESTION DE LA MEMOIRE MEMOIRE CENTRALE (MC) MEMOIRE SECONDAIRE (MS) 1. HIÉRARCHIE ET DIFFÉRENTS TYPES DE MÉMOIRE... 2 2. MÉMOIRE CACHE... 3 3. MODÈLE D'ALLOCATION CONTIGUË (MC OU MS)... 5 3.1. STRATÉGIE
GESTION DE LA MEMOIRE MEMOIRE CENTRALE (MC) MEMOIRE SECONDAIRE (MS) 1. HIÉRARCHIE ET DIFFÉRENTS TYPES DE MÉMOIRE... 2 2. MÉMOIRE CACHE... 3 3. MODÈLE D'ALLOCATION CONTIGUË (MC OU MS)... 5 3.1. STRATÉGIE
a) La technique de l analyse discriminante linéaire : une brève présentation. 3 étapes de la méthode doivent être distinguées :
 a) La technique de l analyse discriminante linéaire : une brève présentation. Nous nous limiterons ici à l'analyse discriminante linéaire et à deux groupes : - linéaire, la variante utilisée par ALTMAN
a) La technique de l analyse discriminante linéaire : une brève présentation. Nous nous limiterons ici à l'analyse discriminante linéaire et à deux groupes : - linéaire, la variante utilisée par ALTMAN
Logiciel SCRATCH FICHE 02
 1. Reprise de la fiche 1: 1.1. Programme Figure : Logiciel SCRATCH FICHE 02 SANS ORDINATEUR : Dessiner à droite le dessin que donnera l'exécution de ce programme : Unité : 50 pas : Remarque : vous devez
1. Reprise de la fiche 1: 1.1. Programme Figure : Logiciel SCRATCH FICHE 02 SANS ORDINATEUR : Dessiner à droite le dessin que donnera l'exécution de ce programme : Unité : 50 pas : Remarque : vous devez
Bases de Données. Plan
 Université Mohammed V- Agdal Ecole Mohammadia d'ingénieurs Rabat Bases de Données Mr N.EL FADDOULI 2014-2015 Plan Généralités: Définition de Bases de Données Le modèle relationnel Algèbre relationnelle
Université Mohammed V- Agdal Ecole Mohammadia d'ingénieurs Rabat Bases de Données Mr N.EL FADDOULI 2014-2015 Plan Généralités: Définition de Bases de Données Le modèle relationnel Algèbre relationnelle
PRODIGE V3. Manuel utilisateurs. Consultation des métadonnées
 PRODIGE V3 Manuel utilisateurs Consultation des métadonnées Pour plus d'information sur le dispositif : à remplir par chaque site éventuellement 2 PRODIGE V3 : Consultation des métadonnées SOMMAIRE 1.
PRODIGE V3 Manuel utilisateurs Consultation des métadonnées Pour plus d'information sur le dispositif : à remplir par chaque site éventuellement 2 PRODIGE V3 : Consultation des métadonnées SOMMAIRE 1.
Virtualisation des postes de travail
 Virtualisation des postes de travail Relever les défis de sécurité posés à votre infrastructure de postes de travail virtuels Un livre blanc de Trend Micro Trend Micro est distribué par: I. INTRODUCTION
Virtualisation des postes de travail Relever les défis de sécurité posés à votre infrastructure de postes de travail virtuels Un livre blanc de Trend Micro Trend Micro est distribué par: I. INTRODUCTION
Julien MATHEVET Alexandre BOISSY GSID 4. Rapport RE09. Load Balancing et migration
 Julien MATHEVET Alexandre BOISSY GSID 4 Rapport Load Balancing et migration Printemps 2001 SOMMAIRE INTRODUCTION... 3 SYNTHESE CONCERNANT LE LOAD BALANCING ET LA MIGRATION... 4 POURQUOI FAIRE DU LOAD BALANCING?...
Julien MATHEVET Alexandre BOISSY GSID 4 Rapport Load Balancing et migration Printemps 2001 SOMMAIRE INTRODUCTION... 3 SYNTHESE CONCERNANT LE LOAD BALANCING ET LA MIGRATION... 4 POURQUOI FAIRE DU LOAD BALANCING?...
Introduction. I Étude rapide du réseau - Apprentissage. II Application à la reconnaissance des notes.
 Introduction L'objectif de mon TIPE est la reconnaissance de sons ou de notes de musique à l'aide d'un réseau de neurones. Ce réseau doit être capable d'apprendre à distinguer les exemples présentés puis
Introduction L'objectif de mon TIPE est la reconnaissance de sons ou de notes de musique à l'aide d'un réseau de neurones. Ce réseau doit être capable d'apprendre à distinguer les exemples présentés puis
Le Raid c est quoi? Comment ca marche? Les différents modes RAID :
 Le Raid c est quoi? Redundant Array of Inexpensive Disks: ensemble redondant de disques peu chers. Le RAID est une technologie qui a été dévellopée en 1988 pour améliorer les performances des unités de
Le Raid c est quoi? Redundant Array of Inexpensive Disks: ensemble redondant de disques peu chers. Le RAID est une technologie qui a été dévellopée en 1988 pour améliorer les performances des unités de
LIVRE BLANC Pratiques recommandées pour l utilisation de Diskeeper sur les réseaux SAN (Storage Area Networks)
 LIVRE BLANC Pratiques recommandées pour l utilisation de Diskeeper sur les réseaux SAN (Storage Area Networks) Think Faster. [Pensez plus vite] Visitez Condusiv.com RECOMMANDATIONS D UTILISATION DE DISKEEPER
LIVRE BLANC Pratiques recommandées pour l utilisation de Diskeeper sur les réseaux SAN (Storage Area Networks) Think Faster. [Pensez plus vite] Visitez Condusiv.com RECOMMANDATIONS D UTILISATION DE DISKEEPER
SYNTHÈSE DOSSIER 1 Introduction à la prospection
 SYNTHÈSE DOSSIER 1 Introduction à la prospection La prospection est une activité indispensable pour développer le nombre de clients, mais aussi pour contrecarrer la perte de clients actuels. Elle coûte
SYNTHÈSE DOSSIER 1 Introduction à la prospection La prospection est une activité indispensable pour développer le nombre de clients, mais aussi pour contrecarrer la perte de clients actuels. Elle coûte
3 Les premiers résultats des plans d'actions
 3 Les premiers résultats des plans d'actions Les résultats que nous avons obtenus en ce qui concerne les plans d'action, résultent de l'analyse de 48 entreprises seulement. Revenons sur notre échantillon.
3 Les premiers résultats des plans d'actions Les résultats que nous avons obtenus en ce qui concerne les plans d'action, résultent de l'analyse de 48 entreprises seulement. Revenons sur notre échantillon.
Démontage d'un ordinateur
 Espaces multimédias Communauté de Communes Moyenne Vilaine et Semnon : Démontage d'un ordinateur 1- A quoi sert-il de démonter son ordinateur? A) Par simple curiosité B) Pour nettoyer C) Pour remplacer
Espaces multimédias Communauté de Communes Moyenne Vilaine et Semnon : Démontage d'un ordinateur 1- A quoi sert-il de démonter son ordinateur? A) Par simple curiosité B) Pour nettoyer C) Pour remplacer
Méthodologie de conceptualisation BI
 Méthodologie de conceptualisation BI Business Intelligence (BI) La Business intelligence est un outil décisionnel incontournable à la gestion stratégique et quotidienne des entités. Il fournit de l information
Méthodologie de conceptualisation BI Business Intelligence (BI) La Business intelligence est un outil décisionnel incontournable à la gestion stratégique et quotidienne des entités. Il fournit de l information
Pourquoi l apprentissage?
 Pourquoi l apprentissage? Les SE sont basés sur la possibilité d extraire la connaissance d un expert sous forme de règles. Dépend fortement de la capacité à extraire et formaliser ces connaissances. Apprentissage
Pourquoi l apprentissage? Les SE sont basés sur la possibilité d extraire la connaissance d un expert sous forme de règles. Dépend fortement de la capacité à extraire et formaliser ces connaissances. Apprentissage
Guide de configuration de SQL Server pour BusinessObjects Planning
 Guide de configuration de SQL Server pour BusinessObjects Planning BusinessObjects Planning XI Release 2 Copyright 2007 Business Objects. Tous droits réservés. Business Objects est propriétaire des brevets
Guide de configuration de SQL Server pour BusinessObjects Planning BusinessObjects Planning XI Release 2 Copyright 2007 Business Objects. Tous droits réservés. Business Objects est propriétaire des brevets
Conclusions du Conseil sur l'innovation dans l'intérêt des patients
 Conseil de l'union Européenne PRESSE FR CONCLUSIONS DU CONSEIL Bruxelles, le 1 décembre 2014 Conclusions du Conseil sur l'innovation dans l'intérêt des patients Session du Conseil Emploi, politique sociale,
Conseil de l'union Européenne PRESSE FR CONCLUSIONS DU CONSEIL Bruxelles, le 1 décembre 2014 Conclusions du Conseil sur l'innovation dans l'intérêt des patients Session du Conseil Emploi, politique sociale,
Observation des modalités et performances d'accès à Internet
 Observation des modalités et performances d'accès à Internet Avant-propos La base de cette étude est constituée par les informations collectées par l'outil Cloud Observer d'iplabel (chargement des différents
Observation des modalités et performances d'accès à Internet Avant-propos La base de cette étude est constituée par les informations collectées par l'outil Cloud Observer d'iplabel (chargement des différents
Du 10 Fév. au 14 Mars 2014
 Interconnexion des Sites - Design et Implémentation des Réseaux informatiques - Sécurité et Audit des systèmes - IT CATALOGUE DE FORMATION SIS 2014 1 FORMATION ORACLE 10G 11G 10 FEV 2014 DOUALA CAMEROUN
Interconnexion des Sites - Design et Implémentation des Réseaux informatiques - Sécurité et Audit des systèmes - IT CATALOGUE DE FORMATION SIS 2014 1 FORMATION ORACLE 10G 11G 10 FEV 2014 DOUALA CAMEROUN
Programmation parallèle et distribuée
 Programmation parallèle et distribuée (GIF-4104/7104) 5a - (hiver 2014) Marc Parizeau, Département de génie électrique et de génie informatique Plan Mégadonnées («big data») Architecture Hadoop distribution
Programmation parallèle et distribuée (GIF-4104/7104) 5a - (hiver 2014) Marc Parizeau, Département de génie électrique et de génie informatique Plan Mégadonnées («big data») Architecture Hadoop distribution
SYSTÈME DE GESTION DE FICHIERS
 SYSTÈME DE GESTION DE FICHIERS - DISQUE 1 Les couches logiciels réponse requête Requêtes E/S Système E/S Pilote E/S Interruptions utilisateur traitement S.E. commandes S.E. S.E. matériel Contrôleur E/S
SYSTÈME DE GESTION DE FICHIERS - DISQUE 1 Les couches logiciels réponse requête Requêtes E/S Système E/S Pilote E/S Interruptions utilisateur traitement S.E. commandes S.E. S.E. matériel Contrôleur E/S
Projet de traitement d'image - SI 381 reconstitution 3D d'intérieur à partir de photographies
 Projet de traitement d'image - SI 381 reconstitution 3D d'intérieur à partir de photographies Régis Boulet Charlie Demené Alexis Guyot Balthazar Neveu Guillaume Tartavel Sommaire Sommaire... 1 Structure
Projet de traitement d'image - SI 381 reconstitution 3D d'intérieur à partir de photographies Régis Boulet Charlie Demené Alexis Guyot Balthazar Neveu Guillaume Tartavel Sommaire Sommaire... 1 Structure
Algorithmes d'apprentissage
 Algorithmes d'apprentissage 1 Agents qui apprennent à partir d'exemples La problématique : prise de décision automatisée à partir d'un ensemble d'exemples Diagnostic médical Réponse à une demande de prêt
Algorithmes d'apprentissage 1 Agents qui apprennent à partir d'exemples La problématique : prise de décision automatisée à partir d'un ensemble d'exemples Diagnostic médical Réponse à une demande de prêt
I. Introduction aux fonctions : les fonctions standards
 Chapitre 3 : Les fonctions en C++ I. Introduction aux fonctions : les fonctions standards A. Notion de Fonction Imaginons que dans un programme, vous ayez besoin de calculer une racine carrée. Rappelons
Chapitre 3 : Les fonctions en C++ I. Introduction aux fonctions : les fonctions standards A. Notion de Fonction Imaginons que dans un programme, vous ayez besoin de calculer une racine carrée. Rappelons
2. Activités et Modèles de développement en Génie Logiciel
 2. Activités et Modèles de développement en Génie Logiciel Bernard ESPINASSE Professeur à l'université d'aix-marseille Plan Les Activités du GL Analyse des besoins Spécification globale Conceptions architecturale
2. Activités et Modèles de développement en Génie Logiciel Bernard ESPINASSE Professeur à l'université d'aix-marseille Plan Les Activités du GL Analyse des besoins Spécification globale Conceptions architecturale
Optimisations des SGBDR. Étude de cas : MySQL
 Optimisations des SGBDR Étude de cas : MySQL Introduction Pourquoi optimiser son application? Introduction Pourquoi optimiser son application? 1. Gestion de gros volumes de données 2. Application critique
Optimisations des SGBDR Étude de cas : MySQL Introduction Pourquoi optimiser son application? Introduction Pourquoi optimiser son application? 1. Gestion de gros volumes de données 2. Application critique
IBM CloudBurst. Créer rapidement et gérer un environnement de Cloud privé
 IBM CloudBurst Créer rapidement et gérer un environnement de Cloud privé Points clés Accélérez le déploiement d'un Cloud privé à l'aide d'un système préinstallé et préintégré avec des logiciels, des serveurs
IBM CloudBurst Créer rapidement et gérer un environnement de Cloud privé Points clés Accélérez le déploiement d'un Cloud privé à l'aide d'un système préinstallé et préintégré avec des logiciels, des serveurs
SYSTÈME DE GESTION DE FICHIERS SGF - DISQUE
 SYSTÈME DE GESTION DE FICHIERS SGF - DISQUE C.Crochepeyre MPS_SGF 2000-20001 Diapason 1 Les couches logiciels réponse SGF requête matériel matériel Requêtes E/S Système E/S Pilote E/S Interruptions Contrôleur
SYSTÈME DE GESTION DE FICHIERS SGF - DISQUE C.Crochepeyre MPS_SGF 2000-20001 Diapason 1 Les couches logiciels réponse SGF requête matériel matériel Requêtes E/S Système E/S Pilote E/S Interruptions Contrôleur
Programmation parallèle et distribuée (Master 1 Info 2015-2016)
 Programmation parallèle et distribuée (Master 1 Info 2015-2016) Hadoop MapReduce et HDFS Note bibliographique : ce cours est largement inspiré par le cours de Benjamin Renaut (Tokidev SAS) Introduction
Programmation parallèle et distribuée (Master 1 Info 2015-2016) Hadoop MapReduce et HDFS Note bibliographique : ce cours est largement inspiré par le cours de Benjamin Renaut (Tokidev SAS) Introduction
Déduplication des données : un élément essentiel de votre stratégie de protection des données
 LIVRE BLANC : ÉVOLUTION DE LA DÉDUPLICATION DES DONNÉES Déduplication des données : un élément essentiel de votre stratégie de protection des données JUILLET 2010 Andy Brewerton CA TECHNOLOGIES RECOVERY
LIVRE BLANC : ÉVOLUTION DE LA DÉDUPLICATION DES DONNÉES Déduplication des données : un élément essentiel de votre stratégie de protection des données JUILLET 2010 Andy Brewerton CA TECHNOLOGIES RECOVERY
Symantec Backup Exec.cloud
 Protection automatique, continue et sécurisée qui sauvegarde les données vers le cloud ou via une approche hybride combinant la sauvegarde sur site et dans le cloud. Fiche technique : Symantec.cloud Seulement
Protection automatique, continue et sécurisée qui sauvegarde les données vers le cloud ou via une approche hybride combinant la sauvegarde sur site et dans le cloud. Fiche technique : Symantec.cloud Seulement
GESTION DE PROJET SÉANCE 2 : LES CYCLE DE VIE D'UN PROJET
 GESTION DE PROJET SÉANCE 2 : LES CYCLE DE VIE D'UN PROJET 1 Tianxiao LIU Licence Professionnelle Réseaux & Sécurité Université de Cergy-Pontoise http://depinfo.u-cergy.fr/~tliu/lpg.php PLAN Objectif et
GESTION DE PROJET SÉANCE 2 : LES CYCLE DE VIE D'UN PROJET 1 Tianxiao LIU Licence Professionnelle Réseaux & Sécurité Université de Cergy-Pontoise http://depinfo.u-cergy.fr/~tliu/lpg.php PLAN Objectif et
Introduire un nouveau type de maille ou un nouvel élément de référence
 Titre : Introduire un nouveau type de maille ou un nouvel [...] Date : 05/10/2012 Page : 1/11 Introduire un nouveau type de maille ou un nouvel élément de référence Résumé : Ce document décrit ce qu il
Titre : Introduire un nouveau type de maille ou un nouvel [...] Date : 05/10/2012 Page : 1/11 Introduire un nouveau type de maille ou un nouvel élément de référence Résumé : Ce document décrit ce qu il
données en connaissance et en actions?
 1 Partie 2 : Présentation de la plateforme SPSS Modeler : Comment transformer vos données en connaissance et en actions? SPSS Modeler : l atelier de data mining Large gamme de techniques d analyse (algorithmes)
1 Partie 2 : Présentation de la plateforme SPSS Modeler : Comment transformer vos données en connaissance et en actions? SPSS Modeler : l atelier de data mining Large gamme de techniques d analyse (algorithmes)
Baccalauréat technologique
 Baccalauréat technologique Épreuve relative aux enseignements technologiques transversaux, épreuve de projet en enseignement spécifique à la spécialité et épreuve d'enseignement technologique en langue
Baccalauréat technologique Épreuve relative aux enseignements technologiques transversaux, épreuve de projet en enseignement spécifique à la spécialité et épreuve d'enseignement technologique en langue
GOL-502 Industrie de services. Travaux Pratique / Devoir #7
 GOL-502 Industrie de services Travaux Pratique / Devoir #7 Version 2012 Modélisation à l'aide du langage UML 1) Diagramme de cas d'utilisation 2) Diagramme de classes 3) Diagramme de séquence 4) Diagramme
GOL-502 Industrie de services Travaux Pratique / Devoir #7 Version 2012 Modélisation à l'aide du langage UML 1) Diagramme de cas d'utilisation 2) Diagramme de classes 3) Diagramme de séquence 4) Diagramme
Stratégie de rémunération
 CONSULTING Offre Conseil RH Stratégie de rémunération La stratégie de rémunération est un facteur de stabilité et de performance de l'entreprise. GFI Consulting vous accompagne en mettant en cohérence
CONSULTING Offre Conseil RH Stratégie de rémunération La stratégie de rémunération est un facteur de stabilité et de performance de l'entreprise. GFI Consulting vous accompagne en mettant en cohérence
la virtualisation pour quoi faire?
 J. F. DAVID Ingénieur Commercial Agence Paris Industrie de Base et de Transformation 24 Mai 1975 la virtualisation pour quoi faire? "Etre transparent, c'est exister et ne pas se voir. Etre virtuel, c'est
J. F. DAVID Ingénieur Commercial Agence Paris Industrie de Base et de Transformation 24 Mai 1975 la virtualisation pour quoi faire? "Etre transparent, c'est exister et ne pas se voir. Etre virtuel, c'est
RapidMiner. Data Mining. 1 Introduction. 2 Prise en main. Master Maths Finances 2010/2011. 1.1 Présentation. 1.2 Ressources
 Master Maths Finances 2010/2011 Data Mining janvier 2011 RapidMiner 1 Introduction 1.1 Présentation RapidMiner est un logiciel open source et gratuit dédié au data mining. Il contient de nombreux outils
Master Maths Finances 2010/2011 Data Mining janvier 2011 RapidMiner 1 Introduction 1.1 Présentation RapidMiner est un logiciel open source et gratuit dédié au data mining. Il contient de nombreux outils
Chapitre 10. Architectures des systèmes de gestion de bases de données
 Chapitre 10 Architectures des systèmes de gestion de bases de données Introduction Les technologies des dernières années ont amené la notion d environnement distribué (dispersions des données). Pour reliér
Chapitre 10 Architectures des systèmes de gestion de bases de données Introduction Les technologies des dernières années ont amené la notion d environnement distribué (dispersions des données). Pour reliér
Encryptions, compression et partitionnement des données
 Encryptions, compression et partitionnement des données Version 1.0 Grégory CASANOVA 2 Compression, encryption et partitionnement des données Sommaire 1 Introduction... 3 2 Encryption transparente des
Encryptions, compression et partitionnement des données Version 1.0 Grégory CASANOVA 2 Compression, encryption et partitionnement des données Sommaire 1 Introduction... 3 2 Encryption transparente des
Annexe sur la maîtrise de la qualité
 Version du 09/07/08 Annexe sur la maîtrise de la qualité La présente annexe précise les modalités d'application, en matière de maîtrise de la qualité, de la circulaire du 7 janvier 2008 fixant les modalités
Version du 09/07/08 Annexe sur la maîtrise de la qualité La présente annexe précise les modalités d'application, en matière de maîtrise de la qualité, de la circulaire du 7 janvier 2008 fixant les modalités
PARAGON SYSTEM BACKUP 2010
 PARAGON SYSTEM BACKUP 2010 Paragon System Backup 2010 2 Manuel d'utilisation SOMMAIRE 1 Introduction...3 1.1 Comment System Backup protège mon ordinateur?...3 1.1.1 Emplacement du stockage des clichés...
PARAGON SYSTEM BACKUP 2010 Paragon System Backup 2010 2 Manuel d'utilisation SOMMAIRE 1 Introduction...3 1.1 Comment System Backup protège mon ordinateur?...3 1.1.1 Emplacement du stockage des clichés...
GLOBAL SUPPLY CHAIN MANAGEMENT & STRATEGIE LOGISTIQUE
 GLOBAL SUPPLY CHAIN MANAGEMENT & STRATEGIE LOGISTIQUE La logistique représentait traditionnellement l activité allant de la mise à disposition des produits finis par l usine ou le négociant jusqu à la
GLOBAL SUPPLY CHAIN MANAGEMENT & STRATEGIE LOGISTIQUE La logistique représentait traditionnellement l activité allant de la mise à disposition des produits finis par l usine ou le négociant jusqu à la
Nouveau Web Client marquant, Cumulus Video Cloud, optimisations de la base de données, et plus..
 INFORMATION PRODUIT : Quoi de Neuf dans Cumulus 9.0? Nouveau Web Client marquant, Cumulus Video Cloud, optimisations de la base de données, et plus.. Les nouveautés marquantes et les améliorations disponibles
INFORMATION PRODUIT : Quoi de Neuf dans Cumulus 9.0? Nouveau Web Client marquant, Cumulus Video Cloud, optimisations de la base de données, et plus.. Les nouveautés marquantes et les améliorations disponibles
L apprentissage automatique
 L apprentissage automatique L apprentissage automatique L'apprentissage automatique fait référence au développement, à l analyse et à l implémentation de méthodes qui permettent à une machine d évoluer
L apprentissage automatique L apprentissage automatique L'apprentissage automatique fait référence au développement, à l analyse et à l implémentation de méthodes qui permettent à une machine d évoluer
Réseau : Interconnexion de réseaux, routage et application de règles de filtrage.
 TD réseau - Réseau : interconnexion de réseau Réseau : Interconnexion de réseaux, routage et application de règles de filtrage. Un réseau de grande importance ne peut pas seulement reposer sur du matériel
TD réseau - Réseau : interconnexion de réseau Réseau : Interconnexion de réseaux, routage et application de règles de filtrage. Un réseau de grande importance ne peut pas seulement reposer sur du matériel
Installation et Réinstallation de Windows XP
 Installation et Réinstallation de Windows XP Vous trouvez que votre PC n'est plus très stable ou n'est plus aussi rapide qu'avant? Un virus a tellement mis la pagaille dans votre système d'exploitation
Installation et Réinstallation de Windows XP Vous trouvez que votre PC n'est plus très stable ou n'est plus aussi rapide qu'avant? Un virus a tellement mis la pagaille dans votre système d'exploitation
Méthodes de développement
 1 / 9 Méthodes de développement Méthodes agiles 1 - Introduction... 2 2 -Le manifeste agile et les méthodes agiles... 2 2.1 Le manifeste agile... 2 2.2 Les méthodes agiles... 3 3 - Caractéristiques communes
1 / 9 Méthodes de développement Méthodes agiles 1 - Introduction... 2 2 -Le manifeste agile et les méthodes agiles... 2 2.1 Le manifeste agile... 2 2.2 Les méthodes agiles... 3 3 - Caractéristiques communes
Maxpho Web Services. Maxpho Cloud Services. Date: 20 Septembre 2013 Version: 1.2 Auteur: Maxpho Ltd
 Maxpho Web Services Maxpho Cloud Services Date: 20 Septembre 2013 Version: 1.2 Auteur: Maxpho Ltd Sommaire général 1 - Introduction... 3 2 - Service Cloud Base... 4 2.1 - Comment ça marche... 4 2.2 - Sécurité...
Maxpho Web Services Maxpho Cloud Services Date: 20 Septembre 2013 Version: 1.2 Auteur: Maxpho Ltd Sommaire général 1 - Introduction... 3 2 - Service Cloud Base... 4 2.1 - Comment ça marche... 4 2.2 - Sécurité...
Ne laissez pas le stockage cloud pénaliser votre retour sur investissement
 Ne laissez pas le stockage cloud pénaliser votre retour sur investissement Préparé par : George Crump, analyste senior Préparé le : 03/10/2012 L investissement qu une entreprise fait dans le domaine de
Ne laissez pas le stockage cloud pénaliser votre retour sur investissement Préparé par : George Crump, analyste senior Préparé le : 03/10/2012 L investissement qu une entreprise fait dans le domaine de
Installation d un serveur DHCP sous Gnu/Linux
 ROYAUME DU MAROC Office de la Formation Professionnelle et de la Promotion du Travail Installation d un serveur DHCP sous Gnu/Linux DIRECTION RECHERCHE ET INGENIERIE DE FORMATION SECTEUR NTIC Installation
ROYAUME DU MAROC Office de la Formation Professionnelle et de la Promotion du Travail Installation d un serveur DHCP sous Gnu/Linux DIRECTION RECHERCHE ET INGENIERIE DE FORMATION SECTEUR NTIC Installation
Le tableau comparatif suivant reprend les principaux articles concernant le monde de l édition.
 Rapport Reda, tableau comparatif Le tableau comparatif suivant reprend les principaux articles concernant le monde de l édition. Alors que Julia Reda appelait à une harmonisation hâtive et à un élargissement
Rapport Reda, tableau comparatif Le tableau comparatif suivant reprend les principaux articles concernant le monde de l édition. Alors que Julia Reda appelait à une harmonisation hâtive et à un élargissement
Module BDR Master d Informatique (SAR)
 Module BDR Master d Informatique (SAR) Cours 6- Bases de données réparties Anne Doucet Anne.Doucet@lip6.fr 1 Bases de Données Réparties Définition Conception Décomposition Fragmentation horizontale et
Module BDR Master d Informatique (SAR) Cours 6- Bases de données réparties Anne Doucet Anne.Doucet@lip6.fr 1 Bases de Données Réparties Définition Conception Décomposition Fragmentation horizontale et
Journal officiel de l'union européenne
 20.5.2014 L 148/29 RÈGLEMENT DÉLÉGUÉ (UE) N o 528/2014 DE LA COMMISSION du 12 mars 2014 complétant le règlement (UE) n o 575/2013 du Parlement européen et du Conseil en ce qui concerne les normes techniques
20.5.2014 L 148/29 RÈGLEMENT DÉLÉGUÉ (UE) N o 528/2014 DE LA COMMISSION du 12 mars 2014 complétant le règlement (UE) n o 575/2013 du Parlement européen et du Conseil en ce qui concerne les normes techniques
Licences Windows Server 2012 R2 dans le cadre de la virtualisation
 Résumé des licences en volume Licences Windows Server 2012 R2 dans le cadre de la virtualisation Ce résumé s'applique à tous les programmes de licences en volume Microsoft. Sommaire Synthèse... 2 Nouveautés
Résumé des licences en volume Licences Windows Server 2012 R2 dans le cadre de la virtualisation Ce résumé s'applique à tous les programmes de licences en volume Microsoft. Sommaire Synthèse... 2 Nouveautés
ORACLE DIAGNOSTIC PACK 11G
 ORACLE DIAGNOSTIC PACK 11G PRINCIPALES CARACTÉRISTIQUES : Surveillance automatique des diagnostics (ADDM Automatic Database Diagnostic Monitor) Référentiel automatique de la charge (AWR Automatic Workload
ORACLE DIAGNOSTIC PACK 11G PRINCIPALES CARACTÉRISTIQUES : Surveillance automatique des diagnostics (ADDM Automatic Database Diagnostic Monitor) Référentiel automatique de la charge (AWR Automatic Workload
Le Langage De Description De Données(LDD)
 Base de données Le Langage De Description De Données(LDD) Créer des tables Décrire les différents types de données utilisables pour les définitions de colonne Modifier la définition des tables Supprimer,
Base de données Le Langage De Description De Données(LDD) Créer des tables Décrire les différents types de données utilisables pour les définitions de colonne Modifier la définition des tables Supprimer,
Rapport d'analyse des besoins
 Projet ANR 2011 - BR4CP (Business Recommendation for Configurable products) Rapport d'analyse des besoins Janvier 2013 Rapport IRIT/RR--2013-17 FR Redacteur : 0. Lhomme Introduction...4 La configuration
Projet ANR 2011 - BR4CP (Business Recommendation for Configurable products) Rapport d'analyse des besoins Janvier 2013 Rapport IRIT/RR--2013-17 FR Redacteur : 0. Lhomme Introduction...4 La configuration
La méthode des cas et le plan marketing : énoncé seul
 La méthode des cas et le plan marketing : énoncé seul 12_07_2011 Table des matières Table des matières 3 I - 1. Point méthodologique 7 A. 1.1. Définitions...7 B. 1.2. Plan d'analyse type...8 C. 1.3. Synthèse...13
La méthode des cas et le plan marketing : énoncé seul 12_07_2011 Table des matières Table des matières 3 I - 1. Point méthodologique 7 A. 1.1. Définitions...7 B. 1.2. Plan d'analyse type...8 C. 1.3. Synthèse...13
Diagramme de classes
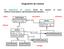 Diagramme de classes Un diagramme de classes décrit les classes et leurs relations (associations, généralisation/spécialisation, ). classe association méthodes attributs héritage Diagramme de classes :
Diagramme de classes Un diagramme de classes décrit les classes et leurs relations (associations, généralisation/spécialisation, ). classe association méthodes attributs héritage Diagramme de classes :
Didacticiel du service cartographique en cache
 Didacticiel du service cartographique en cache Copyright 1995-2012 Esri All rights reserved. Table of Contents Didacticiel : Création d'un service de carte mis en cache................... 3 Copyright 1995-2012
Didacticiel du service cartographique en cache Copyright 1995-2012 Esri All rights reserved. Table of Contents Didacticiel : Création d'un service de carte mis en cache................... 3 Copyright 1995-2012
1. LA GESTION DES BASES DE DONNEES RELATIONNELLES
 Dossier G11 - Interroger une base de données La base de données Facturation contient tout un ensemble d'informations concernant la facturation de la SAFPB (société anonyme de fabrication de produits de
Dossier G11 - Interroger une base de données La base de données Facturation contient tout un ensemble d'informations concernant la facturation de la SAFPB (société anonyme de fabrication de produits de
L'évolution de VISUAL MESSAGE CENTER Architecture et intégration
 L'évolution de VISUAL MESSAGE CENTER Architecture et intégration Sommaire Résumé exécutif Base technologique : VISUAL Message Center 2 3 VISUAL Message Center Core Engine VISUAL Message Center Extended
L'évolution de VISUAL MESSAGE CENTER Architecture et intégration Sommaire Résumé exécutif Base technologique : VISUAL Message Center 2 3 VISUAL Message Center Core Engine VISUAL Message Center Extended
Artica. La déduplication. Révision Du 08 Février 2011 version 1.5.020818
 Artica La déduplication Révision Du 08 Février 2011 version 1.5.020818 Table des matières Introduction :...2 Historique du projet :...2 A qui s'adresse Artica?...2 Licence et support...2 Que fait Artica?...
Artica La déduplication Révision Du 08 Février 2011 version 1.5.020818 Table des matières Introduction :...2 Historique du projet :...2 A qui s'adresse Artica?...2 Licence et support...2 Que fait Artica?...
Université de Bangui. Modélisons en UML
 Université de Bangui CRM Modélisons en UML Ce cours a été possible grâce à l initiative d Apollinaire MOLAYE qui m a contacté pour vous faire bénéficier de mes connaissances en nouvelles technologies et
Université de Bangui CRM Modélisons en UML Ce cours a été possible grâce à l initiative d Apollinaire MOLAYE qui m a contacté pour vous faire bénéficier de mes connaissances en nouvelles technologies et
Conditions : stage indemnisé, aide au logement possible, transport CEA en Ile-de-France gratuit.
 Proposition de stage de BAC+4 ou BAC+5 Pro ou Recherche Etude comparative des outils de vérification d'algorithmes parallèles Logiciels (LSL), localisé à Palaiseau (Essonne), développe les outils d'aide
Proposition de stage de BAC+4 ou BAC+5 Pro ou Recherche Etude comparative des outils de vérification d'algorithmes parallèles Logiciels (LSL), localisé à Palaiseau (Essonne), développe les outils d'aide
Introduction à l approche bootstrap
 Introduction à l approche bootstrap Irène Buvat U494 INSERM buvat@imedjussieufr 25 septembre 2000 Introduction à l approche bootstrap - Irène Buvat - 21/9/00-1 Plan du cours Qu est-ce que le bootstrap?
Introduction à l approche bootstrap Irène Buvat U494 INSERM buvat@imedjussieufr 25 septembre 2000 Introduction à l approche bootstrap - Irène Buvat - 21/9/00-1 Plan du cours Qu est-ce que le bootstrap?
Série TD 3. Exercice 4.1. Exercice 4.2 Cet algorithme est destiné à prédire l'avenir, et il doit être infaillible! Exercice 4.3. Exercice 4.
 Série TD 3 Exercice 4.1 Formulez un algorithme équivalent à l algorithme suivant : Si Tutu > Toto + 4 OU Tata = OK Alors Tutu Tutu + 1 Tutu Tutu 1 ; Exercice 4.2 Cet algorithme est destiné à prédire l'avenir,
Série TD 3 Exercice 4.1 Formulez un algorithme équivalent à l algorithme suivant : Si Tutu > Toto + 4 OU Tata = OK Alors Tutu Tutu + 1 Tutu Tutu 1 ; Exercice 4.2 Cet algorithme est destiné à prédire l'avenir,
Préparer la synchronisation d'annuaires
 1 sur 6 16/02/2015 14:24 En utilisant ce site, vous autorisez les cookies à des fins d'analyse, de pertinence et de publicité En savoir plus France (Français) Se connecter Rechercher sur TechNet avec Bing
1 sur 6 16/02/2015 14:24 En utilisant ce site, vous autorisez les cookies à des fins d'analyse, de pertinence et de publicité En savoir plus France (Français) Se connecter Rechercher sur TechNet avec Bing
La nouvelle planification de l échantillonnage
 La nouvelle planification de l échantillonnage Pierre-Arnaud Pendoli Division Sondages Plan de la présentation Rappel sur le Recensement de la population (RP) en continu Description de la base de sondage
La nouvelle planification de l échantillonnage Pierre-Arnaud Pendoli Division Sondages Plan de la présentation Rappel sur le Recensement de la population (RP) en continu Description de la base de sondage
Cloud Computing : forces et faiblesses
 Chapitre 7 Cloud Computing : forces et faiblesses 1. Présentation Cloud Computing : forces et faiblesses Le monde informatique a connu une véritable révolution ces dernières années avec l'apparition d'un
Chapitre 7 Cloud Computing : forces et faiblesses 1. Présentation Cloud Computing : forces et faiblesses Le monde informatique a connu une véritable révolution ces dernières années avec l'apparition d'un
DOSSIER SOLUTION : CA RECOVERY MANAGEMENT
 DOSSIER SOLUTION : CA RECOVERY MANAGEMENT Comment la solution CA Recovery Management peut-elle nous aider à protéger et garantir la disponibilité des informations essentielles au fonctionnement de notre
DOSSIER SOLUTION : CA RECOVERY MANAGEMENT Comment la solution CA Recovery Management peut-elle nous aider à protéger et garantir la disponibilité des informations essentielles au fonctionnement de notre
Hyper-V et SC Virtual Machine Manager sous Windows Server 2008 R2
 186 Hyper-V et SC Virtual Machine Manager sous Windows Server 2008 R2 L'utilisation des fonctionnalités de haute disponibilité intégrées aux applications, L'ajout de solutions tierces. 1.1 Windows Server
186 Hyper-V et SC Virtual Machine Manager sous Windows Server 2008 R2 L'utilisation des fonctionnalités de haute disponibilité intégrées aux applications, L'ajout de solutions tierces. 1.1 Windows Server
Séance 4. Gestion de la capacité. Gestion des opérations et de la logistique 4-530-03
 Gestion des opérations et de la logistique Séance 4 4-530-03 Gestion de la capacité Points importants présentés au dernier cours Les principaux types d aménagement Étude du travail et l amélioration des
Gestion des opérations et de la logistique Séance 4 4-530-03 Gestion de la capacité Points importants présentés au dernier cours Les principaux types d aménagement Étude du travail et l amélioration des
Bénéficiez d'un large choix d'applications novatrices et éprouvées basées sur les systèmes d'exploitation i5/os, Linux, AIX 5L et Microsoft Windows.
 1. Le nouveau eserver i5 en bref Gérez plusieurs systèmes d'exploitation et environnements d'applications sur un seul serveur pour simplifier votre infrastructure et réduire les frais de gestion Simplifiez
1. Le nouveau eserver i5 en bref Gérez plusieurs systèmes d'exploitation et environnements d'applications sur un seul serveur pour simplifier votre infrastructure et réduire les frais de gestion Simplifiez
Article 2 : Conseils et meilleures pratiques pour gérer un cloud privé
 Article 2 : Conseils et meilleures pratiques pour gérer un cloud privé Sponsored by Mentions relatives aux droits d'auteur 2011 Realtime Publishers. Tous droits réservés. Ce site contient des supports
Article 2 : Conseils et meilleures pratiques pour gérer un cloud privé Sponsored by Mentions relatives aux droits d'auteur 2011 Realtime Publishers. Tous droits réservés. Ce site contient des supports
LA QUALITE DU LOGICIEL
 LA QUALITE DU LOGICIEL I INTRODUCTION L'information est aujourd'hui une ressource stratégique pour la plupart des entreprises, dans lesquelles de très nombreuses activités reposent sur l'exploitation d'applications
LA QUALITE DU LOGICIEL I INTRODUCTION L'information est aujourd'hui une ressource stratégique pour la plupart des entreprises, dans lesquelles de très nombreuses activités reposent sur l'exploitation d'applications
