paw s Le temps qu il fera On ne sig n a le q u un vio len t in ciden t mais entre Allemands henleinistes et démocrates

SAV ET RÉPARATION. Savoir-faire. www.jarltech.fr

i & V : SA E b i i 1 3 2 0 1 Ai 0800 9 h P i iè P i i i i S j C i Si E ) i Ti (i ib i Q,. bq i, FA V k, Pi b h iè i Si b, D Z, P E q Si-i SAV ET RÉPARATION S hiq : E q SSII VAR, i hiq Jh i h 0800 910 231.

CHAPITRE V SYSTEMES DIFFERENTIELS LINEAIRES A COEFFICIENTS CONSTANTS DU PREMIER ORDRE. EQUATIONS DIFFERENTIELLES.

CHAPITRE V SYSTEMES DIFFERENTIELS LINEAIRES A COEFFICIENTS CONSTANTS DU PREMIER ORDRE EQUATIONS DIFFERENTIELLES Le but de ce chapitre est la résolution des deux types de systèmes différentiels linéaires

Condition inf-sup pour l Elément Fini de Taylor-Hood È ¾ -iso-è ½

Condition inf-sup pour l Elément Fini de Taylor-Hood È ¾ -iso-è ½ Patrick Ciarlet et Vivette Girault ciarlet@ensta.fr & girault@ann.jussieu.fr ENSTA & Laboratoire Jacques-Louis Lions, Paris 6 Condition

W i r e l e s s B o d y S c a l e - i B F 5 T h a n k y o u f o r p u r c h a s i n g t h e W i r e l e s s B o d y S c a l e i B F 5. B e f o r e u s i n g t h i s u n i t f o r t h e f i r s t t i m

DELIBERATION N CP 13-639

CONSEIL REGIONAL D ILE DE FRANCE 1 CP 13-639 DELIBERATION N CP 13-639 DU 17 OCTOBRE 2013 La politique sociale régionale La politique régionale pour les personnes en situation de handicap Cinquième affectation

l u N D I 15 M D I D I 3 17 J u D I N D D I I M N C h COuPE Du PrEsIDENT OPEN 104 FEuChErOllEs EAuBONNE s1 20h15 COuPE Du OPEN 104 EAuBONNE s2 20h15

6-boc caendie 220415_6 agenda 2006 p218-237 23/04/2015 15:36 Page 1 1 6-boc caendie 220415_6 agenda 2006 p218-237 23/04/2015 15:36 Page 2 36 31 août PTB 2015 37 38 7 14 1 8 15 OP 104 1 2015 OP PT Té BO

%$&$#' "!# $! ## BD0>@6,;2106>+1:+B2.6;;/>0.2106>9*27+2.1/+BB+:/@6>.106>>+;+>1:+>6;*,+/EA,6.+77/7A,6@+7706>>+B79 561,+76.08189:+;61,+8.6>6;0+976>1:+?+>/+7@6,1+;+>1:8A+>:2>1+7:+B21+.C>6B630+:+ 1+.C>6B630=/+FGD+7A06>>23+8.6>6;0=/++1A6B010=/+:2>7B+.)*+,+7A2.+;+1+>:2>3+,B+A61+>10+B

FICHE DE RENSEIGNEMENTS SAISON 2013 2014

USC BASKET Salle S. Chénedé Rue Sainte Croix 35410 CHATEAUGIRON Tél. 02.99.37.89.89 Site : www.chateaugiron-basket.com FICHE DE RENSEIGNEMENTS SAISON 2013 2014 Mme M. Nom et prénom de l adhérent : Adresse

rf( 1 f(x)x dx = O. ) U concours externe de recrutement de professeurs agreg6s composition d analyse

page 8 AGREGATIN de MATHEMATIQUES: 1991 1/5 externeanalyse concours externe de recrutement de professeurs agreg6s composition d analyse NTATINS ET DGFINITINS Dans tout le problème, R+ désigne l intervalle

POUR ATTEINDRE VOS OBJECTIFS D AFFAIRES

LE RÔLE DU MARKETING STRATÉGIQUE SIX ÉTAPES POUR ATTEINDRE VOS OBJECTIFS D AFFAIRES POUR QU UNE ENTREPRISE ATTEIGNE SES OBJECTIFS D AFFAIRES, ELLE DOIT ÉQUILIBRER SA STRATÉGIE MARKETING. Une saveur unique

Un exemple d étude de cas

Un exemple d'étude de cas 1 Un exemple d étude de cas INTRODUCTION Le cas de la Boulangerie Lépine ltée nous permet d exposer ici un type d étude de cas. Le processus utilisé est identique à celui qui

TD1 Signaux, énergie et puissance, signaux aléatoires

TD1 Signaux, énergie et puissance, signaux aléatoires I ) Ecrire l'expression analytique des signaux représentés sur les figures suivantes à l'aide de signaux particuliers. Dans le cas du signal y(t) trouver

Chafa Azzedine - Faculté de Physique U.S.T.H.B 1

Chafa Azzedine - Faculté de Physique U.S.T.H.B 1 Définition: La cinématique est une branche de la mécanique qui étudie les mouements des corps dans l espace en fonction du temps indépendamment des causes

Ê ÙÐ Ø ÓÒ Ö Ò Ð Ý Ø Ñ ØÖ Ù Ö Ø ØÙÖ Ø Ð ÓÖ Ø Ñ Ö Ö Ï ÙØ Ð Ø ÙÐØ ÆÓØÖ ¹ Ñ Ä È Ü Æ ÑÙÖ Ð ÕÙ Û ÙØ Ð Ò Óº ÙÒ Ôº º Ê ÙÑ º ij ÑÔÓÖØ Ò Ð ÓÖ Ø Ñ Ö Ô ÖØ Ø ÓÒ Ö Ò Ð Ý Ø Ñ ØÖ Ù Ò³ Ø ÔÐÙ ÑÓÒØÖ Öº Ò Ø Ð Ó Ü ³ÙÒ ØÝÔ

ce n est pas un livre auto-suffisant (il est loin d être exhaustif )!

L MASS 1/13 Aide-mémoire et exercices corrigés. USTV MS41 Optimisation I Table des matières 1 Fonctions de plusieurs variables 3 Limites et continuité 13 3 Dérivabilité et différentiabilité, fonctions

Bougez, protégez votre liberté!

> F a Bgz, pégz v bé! www.a-. CAT.ELB.a240215 - Cé ph : Fa Daz à v p aé N az p a v gâh a v! Aj h, p g évq v ; Pa, p 4 aça q, v, éq qaé v. Ca ax é ç, b pa évé ax p âgé a h a p j. E pè v, h pa épagé. Pa

Centre d'etudes Nucléaires de Fontenay-aux-Roses Direction des Piles Atomiques Département des Etudes de Piles

CEA-N-1195 Note CEA-N-1195 Centre d'etudes Nucléaires de Fontenay-aux-Roses Direction des Piles Atomiques Département des Etudes de Piles Service d'etudes de Protections de Piles PROPAGATION DES NEUTRONS

Premier réseau social rugby

Premier réseau social rugby Rugbygeneration.com est le premier site de la communauté autour de Rugby. Dédié à tous les fans de rugby et les amateurs de toutes générations. Rugby? Échanger, rester en contact,

!" #$# % *(!( % (+#$#, ) ( 5- % % 2! $!!!!87777777777!!!!8777777 -% %. / 0 1 ' 2% %. (3 4 562( % 4 5

Bulletin d adhésion au contrat groupe Responsabilité Civile Professionnelle n B1302525PNPI souscrit par AMAVIE pour le compte exclusif des écoles accréditées.!" #$# % &%!'(" "()' ( *(!( % (+#$#, ) -% %.

!" #$#% #"& ' ( &)(*"% * $*' )#""*(+#%(' $#),")- '(*+.%#"'#/* "'") $'

!" #$#% #"& ' ( &)(*"% * $*' )#""*(+#%(' $#),")- '(*+.%#"'#/* "'") $' &!*#$)'#*&)"$#().*0$#1' '#'((#)"*$$# ' /("("2"(' 3'"1#* "# ),," "*(+$#1' /&"()"2$)'#,, '#' $)'#2)"#2%#"!*&# )' )&&2) -)#( / 2) /$$*%$)'#*+)

Exercices - Fonctions de plusieurs variables : corrigé. Pour commencer

Pour commencer Exercice 1 - Ensembles de définition - Première année - 1. Le logarithme est défini si x + y > 0. On trouve donc le demi-plan supérieur délimité par la droite d équation x + y = 0.. 1 xy

Le transistor bipolaire. Page N 6 Tranlin

V. Etude d'un montage à 1 transtor. (montage charge répart ac découplage d'émetteur Pour toute la suite, on utilera comme exemple le schéma suivant appelé montage charge répart ac découplage d'émetteur

STATUTS DE L ASSOCIATION. Association régie par par la Loi du 1 er juillet 1901

STATUTS DE L ASSOCIATION Association régie par par la Loi du 1 er juillet 1901 Statuts adoptés par l Assemblée Générale Extraordinaire du dimanche 1 er avril 2007 ËØ ØÙØ Ð³ Ó Ø ÓÒ ÖØ Ð ÔÖ Ñ Ö¹ ÒÓÑ Ò Ø

Géométrie dans l espace Produit scalaire et équations

Chapitre 11. 2ème partie Géométrie dans l espace Produit scalaire et équations Terminale S Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES 2ème partie Produit scalaire Produit scalaire

Modélisation intégrée des écoulements pour la gestion en temps réel d'un bassin versant anthropisé

1 TGR Modélisation intégrée des écoulements pour la gestion en temps réel d'un bassin versant anthropisé Simon Munier Institut des Sciences et Industries du Vivant et de l'environnement (AgroParisTech)

L AIDE AUX ATELIERS D ARTISTES :

RAPPORT DAVID LANGLOIS-MALLET SOUS LA COORDINATION DE CORINNE RUFET, CONSEILLERE REGIONALE D ILE DE FRANCE L AIDE AUX ATELIERS D ARTISTES : PROBLÉMATIQUES INDIVIDUELLES, SOLUTIONS COLLECTIVES? DE L ATELIER-LOGEMENT

ANNEX 1 ANNEXE RÈGLEMENT DÉLÉGUÉ (UE) N /.. DE LA COMMISSION

COMMISSION EUROPÉENNE Bruxelles, le 26.11.2014 C(2014) 8734 final ANNEX 1 ANNEXE au RÈGLEMENT DÉLÉGUÉ (UE) N /.. DE LA COMMISSION remplaçant les annexes I et II du règlement (UE) n 1215/2012 du Parlement

Circuits RL et RC. Chapitre 5. 5.1 Inductance

Chapitre 5 Circuits RL et RC Ce chapitre présente les deux autres éléments linéaires des circuits électriques : l inductance et la capacitance. On verra le comportement de ces deux éléments, et ensuite

Géomètres-Experts, simplifiez-vous la vie!

Géomètres-xperts, simplifiez-vous la vie! Septembre 2012 Pour découvrir les services de votre syndicat, cliquez sur les applications. CO FO TIO MA C U C CO M MU TIO ICA O -B UT IQ U S I S FA AF CIAL SO

F411 - Courbes Paramétrées, Polaires

1/43 Courbes Paramétrées Courbes polaires Longueur d un arc, Courbure F411 - Courbes Paramétrées, Polaires Michel Fournié michel.fournie@iut-tlse3.fr http://www.math.univ-toulouse.fr/ fournie/ Année 2012/2013

Chapitre 3: TESTS DE SPECIFICATION

Chapitre 3: TESTS DE SPECIFICATION Rappel d u c h api t r e pr é c é d en t : l i de n t i f i c a t i o n e t l e s t i m a t i o n de s y s t è m e s d é q u a t i o n s s i m u lt a n é e s r e p o

COMMENT PAYEZ-VOUS? COMMENT VOUDRIEZ-VOUS PAYER?

COMMENT PAYEZ-VOUS? COMMENT VOUDRIEZ-VOUS PAYER? 2/09/2008-22/10/2008 329 réponses PARTICIPATION Pays DE - Allemagne 55 (16.7%) PL - Pologne 41 (12.5%) DK - Danemark 20 (6.1%) NL - Pays-Bas 18 (5.5%) BE

CNAM UE MVA 210 Ph. Durand Algèbre et analyse tensorielle Cours 4: Calcul dierentiel 2

CNAM UE MVA 210 Ph. Duran Algèbre et analyse tensorielle Cours 4: Calcul ierentiel 2 Jeui 26 octobre 2006 1 Formes iérentielles e egrés 1 Dès l'introuction es bases u calcul iérentiel, nous avons mis en

Diane-Gabrielle Tremblay (Dir.) Maryse Larivière

Travailler plus longtemps!? L aménagement des fins de carrière en Belgique et au Québec Note de recherche no 2009-1 De l ARUC (Alliances de recherche universités-communautés) Sur la gestion des âges et

LES ESCALIERS. Du niveau du rez-de-chaussée à celui de l'étage ou à celui du sous-sol.

LES ESCALIERS I. DÉF I NIT I O N Un escalier est un ouvrage constitué d'une suite de marches et de paliers permettant de passer à pied d'un niveau à un autre. Ses caractéristiques dimensionnelles sont

J ai demandé l asile dans l Union européenne quel pays sera responsable de l analyse de ma demande?

FR J ai demandé l asile dans l Union européenne quel pays sera responsable de l analyse de ma demande? A Informations sur le règlement de Dublin pour les demandeurs d une protection internationale en vertu

CHAPITRE 1. Suites arithmetiques et géometriques. Rappel 1. On appelle suite réelle une application de

HAPITRE 1 Suites arithmetiques et géometriques Rappel 1 On appelle suite réelle une application de dans, soit est-à-dire pour une valeur de la variable appartenant à la suite prend la valeur, ie : On notera

Théorèmes du Point Fixe et Applications aux Equations Diérentielles

Université de Nice-Sophia Antipolis Mémoire de Master 1 de Mathématiques Année 2006-2007 Théorèmes du Point Fixe et Applications aux Equations Diérentielles Auteurs : Clémence MINAZZO - Kelsey RIDER Responsable

Informations techniques et questions

Journée Erasmus Appel à propositions 2015 Informations techniques et questions Catherine Carron et Amanda Crameri Coordinatrices de projet Erasmus Contenu Call solution transitoire 2015 : remarques générales

MASTER DROIT-ECONOMIE-GESTION Co-diplômation Mentions «Droit Public» et «Science politique»

Mai 0 U.F.R. Droit et Science Politique MASTER DROIT-EONOMIE-GESTION o-diplômation Mentions «Droit Public» et «Science politique» Spécialité recherche et professionnelle (M) Métiers de l administration

OutilsMathematiques-L1-2004/2005-D.Brito.&G.Legaut.

OutilsMathematiques-L1-2004/2005-DBrito&GLegaut lapremiereseancedutp,soitlasemainedu22novembre2004 Lesreponsesauxquestions1a7sontarendresurpapierlorsde TPinformatiquen5 d'uneequationdierentielle: Resolutionnumerique

Je suis sous procédure Dublin qu est-ce que cela signifie?

FR Je suis sous procédure Dublin qu est-ce que cela signifie? B Informations pour les demandeurs d une protection internationale dans le cadre d une procédure de Dublin en vertu de l article 4 du Règlement

ISAN System: 5 Œuvre à épisodes ou en plusieurs parties

sm: 5 Œ à épsds pss ps Wb f B Rs s: E b W B bs d mdè Vs j www.sb. B ss Psfh B 7 T. +4 5 Fx +4 7 EM: f@sb. www.sb. B ss Psfh B 7 T. +4 5 Fx +4 7 EM: f@sb. wzd 5 Œ à épsds pss ps mm: TRODUTO DEMRE. OEXO.

La réglementation Mardi de la DGPR. sur les produits biocides 05/04/2011

La réglementation r Mardi de la DGPR 05/04/2011 sur les produits biocides Direction générale de la prévention des risques Service de la prévention des nuisances et de la qualité de l environnement Département

Calendrier des collectes 2015

N j t t hgé? O! g! Tz, t f! C t 2015 O mégè, mbg, mbt, éht t, t txt, éhtt D pt ptq Ctt bh t p m m tmt à, m pté q j pét tt q m jt hgé mt t. L tâh q m t fé t mpt mx hbtt t pépt mj t pmt é. E t ff à m té

3 Approximation de solutions d équations

3 Approximation de solutions d équations Une équation scalaire a la forme générale f(x) =0où f est une fonction de IR dans IR. Un système de n équations à n inconnues peut aussi se mettre sous une telle

l Agence Qui sommes nous?

l Agence Qui soes nous? Co Justine est une agence counication globale dont la ission est prendre en charge l enseble vos besoins et probléatiques counication. Créée en 2011, Co Justine a rapient investi

Chapitre 2 Le problème de l unicité des solutions

Université Joseph Fourier UE MAT 127 Mathématiques année 2011-2012 Chapitre 2 Le problème de l unicité des solutions Ce que nous verrons dans ce chapitre : un exemple d équation différentielle y = f(y)

Chapitre 1 Régime transitoire dans les systèmes physiques

Chapitre 1 Régime transitoire dans les systèmes physiques Savoir-faire théoriques (T) : Écrire l équation différentielle associée à un système physique ; Faire apparaître la constante de temps ; Tracer

3 : «L amitié éternelle» 4 : «L amour» 5 à 11 : Le Dossier 12 : Loisirs 13 : Fin d année en beauté

L c - 3 : «L mé é» 4 : «L m» 5 à 11 : L D 12 : L 13 : F é bé L J éèv Lycé L P, èm égé éèv, é f é c 2013-2014, D éc ccé à c ; x c ô, c éê vfé qq é. L - émé chz j? C mé év qq, é à c m q... B... c! LC, c.

Les enfants ayant besoin d une protection internationale

FR Les enfants ayant besoin d une protection internationale Informations destinées aux enfants non accompagnés qui introduisent une demande de protection internationale conformément à l article 4 du Règlement

8.1 Généralités sur les fonctions de plusieurs variables réelles. f : R 2 R (x, y) 1 x 2 y 2

Chapitre 8 Fonctions de plusieurs variables 8.1 Généralités sur les fonctions de plusieurs variables réelles Définition. Une fonction réelle de n variables réelles est une application d une partie de R

Chapitre 3 Les régimes de fonctionnement de quelques circuits linéaires

Chapitre 3 Les régimes de fonctionnement de quelques circuits linéaires 25 Lechapitreprécédent avait pour objet l étude decircuitsrésistifsalimentéspar dessourcesde tension ou de courant continues. Par

M2 20.00% 6.09 UN 20.00% 13.40 M 20.00% 10.11 M 20.00% 31.69 M 20.00% 21.79 M2 20.00% 95.51 UN 20.00% 222.62 UN 20.00% 292.91 UN 20.00% 444.

ou n identification fiscal pays hors CEE Aménagement de stand l Décoration DS01 Fourniture et pose de moquette type tapis aiguilleté (norme M3) M2 20.00% 6.09 DS02 Pose de tenture murale norme M1 M2 20.00%

Exercices - Nombres complexes : corrigé. Formes algébriques et trigonométriques, module et argument

Formes algébriques et trigonométriques, module et argument Exercice - - L/Math Sup - On multiplie le dénominateur par sa quantité conjuguée, et on obtient : Z = 4 i 3 + i 3 i 3 = 4 i 3 + 3 = + i 3. Pour

Tests non-paramétriques de non-effet et d adéquation pour des covariables fonctionnelles

Tests non-paramétriques de non-effet et d adéquation pour des covariables fonctionnelles Valentin Patilea 1 Cesar Sanchez-sellero 2 Matthieu Saumard 3 1 CREST-ENSAI et IRMAR 2 USC Espagne 3 IRMAR-INSA

ALGORITHMIQUE II NOTION DE COMPLEXITE. SMI AlgoII

ALGORITHMIQUE II NOTION DE COMPLEXITE 1 2 Comment choisir entre différents algorithmes pour résoudre un même problème? Plusieurs critères de choix : Exactitude Simplicité Efficacité (but de ce chapitre)

É í í Ö í í í Í ÍÍ Á Á ó Á Í ü í Ü Ü É É í í É ü TXUOGNAGE Courir ]Tst D u s p o r t a u t o m o b i ldea n s1 e s p a y sd e ' E s t i... D a n sn o t r e e n t o u r a g eq, u a n dn o u s e n p a r

Corrigé du baccalauréat S Pondichéry 12 avril 2007

Corrigé du baccalauréat S Pondichéry 1 avril 7 EXERCICE 1 Commun à tous les candidats 4 points 1 a Les vecteurs AB et AC ont pour coordonnées AB ; ; ) et AC 1 ; 4 ; 1) Ils ne sont manifestement pas colinéaires

Equations différentielles linéaires à coefficients constants

Equations différentielles linéaires à coefficients constants Cas des équations d ordre 1 et 2 Cours de : Martine Arrou-Vignod Médiatisation : Johan Millaud Département RT de l IUT de Vélizy Mai 2007 I

[Le Canada a 10 ans pour changer ses politiques économiques et sociales Paul Martin

G G à É FÉ 0 ppç pp g Q [ 0 p g pq éq è gé g p éé q QÉB Qéb y qq p bé éé pp éà p pp g bé Qéb épé ég Qéb pé bé éé «é ppy épé x «p q ép âg 7 pq p 5 é q p 88 é épp b p égq pp b pp Fç pp g Q x b ég Qéb «Bp

Les deux points les plus proches

MPSI Option Informatique Année 2001, Deuxième TP Caml Vcent Simonet (http://cristal.ria.fr/~simonet/) Les eux pots les plus proches Lors e cette séance, nous allons nous téresser au problème suivant :

VARIABLES LATENTES ET MODÉLISATION STATISTIQUE EN ASSURANCE

VARIABLES LATENTES ET MODÉLISATION STATISTIQUE EN ASSURANCE A. MONFORT CNAM et CREST-INSEE 1 1. INTRODUCTION. Les variables latentes, ou inobservables, jouent un rôle de plus en plus important dans la

Les Réunions d information aux associations

REUNION D INFORMATION AUX ASSOCIATIONS Les Réunions d information aux associations du 1 er au 16 octobre 2014 Direction Générale Adjointe du Cadre de Vie 1 Programme Les nouveautés Le projet associatif

SYSTEMES LINEAIRES DU PREMIER ORDRE

SYSTEMES LINEIRES DU PREMIER ORDRE 1. DEFINITION e(t) SYSTEME s(t) Un système est dit linéaire invariant du premier ordre si la réponse s(t) est liée à l excitation e(t) par une équation différentielle

COMITÉ ADMINISTRATIF ET JURIDIQUE. Quarante-huitième session Genève, 20 et 21 octobre 2003

ORIGINAL : anglais DATE : 18 juillet 2003 F UNION INTERNATIONALE POUR LA PROTECTION DES OBTENTIONS VÉGÉTALES GENÈVE COMITÉ ADMINISTRATIF ET JURIDIQUE Quarante-huitième session Genève, 20 et 21 octobre

B o u r s e d e m o b i l i t é B E E p o u r l e s d é p a r t s e n 2 0 1 2 1

1 B o u r s e d e m o b i l i t é B E E p o u r l e s d é p a r t s e n 2 0 1 2 1 Objectif : Acquérir une expérience professionnelle en réalisant un stage en entreprise de 3 mois à temps plein à l étranger

Le commerce de détail en Europe : la diversité des tissus commerciaux

Le commerce de détail en Europe : la diversité des tissus commerciaux Claire de Kermadec* Les habitudes culturelles, la taille et la dynamique des marchés modèlent le paysage du commerce de détail en Europe.

Loi d une variable discrète

MATHEMATIQUES TD N : VARIABLES DISCRETES - Corrigé. P[X = k] 0 k point de discontinuité de F et P[X = k] = F(k + ) F(k ) Ainsi, P[X = ] =, P[X = 0] =, P[X = ] = R&T Saint-Malo - nde année - 0/0 Loi d une

ILT. Interfacultair Instituut voor Levende Talen. T@@lvaardig. Actes de communication. Serge Verlinde Evelyn Goris. Katholieke Universiteit Leuven

IL If I L S V Ey G Khk U L 13/02/02 pé? xp qé xp pz à pz p héhq pé p à q z p à p héhq fé à p à q pz xp q 'p (è) f, '-à- p. x. ' é ff. N xp à py qq' q z b ( f) P xp pô pp L p - pé pz ': z qq', q -? Bj,

«Trop de chats en refuge : Aidons-les!»

q io iific bo ch Mlic g f! l o h c To i? co cio collboio vc Pl 5899 ch 7398 ch y éé boé C l ob félié qi, chq jo, o cibl joi fg Blgiq! 4641 ch l o l chc ov i à l g l fg fill i foy ê à l hx! C qlq chiff

NOMBRES COMPLEXES. Exercice 1 :

Exercice 1 : NOMBRES COMPLEXES On donne θ 0 un réel tel que : cos(θ 0 ) 5 et sin(θ 0 ) 1 5. Calculer le module et l'argument de chacun des nombres complexes suivants (en fonction de θ 0 ) : a i( )( )(1

Solutions de Verrouillage Électronique et Monnayeurs

Soltions de Verroillage Électroniqe et Monnayers MONNAYEURS OMEGA 100 Boîtier en acrylonitrile btadiène styrène (ABS) Utilisation en environnement sec Fonction retor de pièce 2 clés nickelées Jsq à 3000

SPECIFICATION DES ECHANGES DE DONNEES INFORMATISES (E.D.I.)

SPECIFICATION DES ECHANGES DE DONNEES INFORMATISES (E.D.I.) Dernière mise à jour : octobre 2013 Ce document a pour objectif de décrire ce que l OPCA (OPCA 3+) attend du fichier à transmettre par l adhérent.

#$ %! # & ( & # % % * +!, %! & & &!. $&/ 1 2!0 3$&& &

" #$ # & ' " ( ) ( & # * (( +, & - #&, & & # (#-./. $&/.(#((/ 0#/ 1 20 3$&& & ( (456789 PREAMBULE... 1. A QUI CE GUIDE EST-IL DESTINE? COMMENT EST-IL ORGANISE? COMMENT LIRE CE GUIDE?... 8 2. VIDEOSURVEILLANCE

Union générale des étudiants de Tunisie Bureau de l institut Préparatoire Aux Etudes D'ingénieurs De Tunis. Modèle de compte-rendu de TP.

Union générale des étudiants de Tunisie Modèle de compte-rendu de TP Dipôle RC Ce document a été publié pour l unique but d aider les étudiants, il est donc strictement interdit de l utiliser intégralement

Sur la Commande des Systèmes (max,+) Linéaires.

Sur la Commande des Systèmes (max,+) Linéaires. DEA Automatique et Informatique Appliquée - Angers Laurent Hardouin Septembre 2008 2 Table des matières 1 Introduction 7 2 Préliminaires algébriques 9 2.1

Prix de l énergie dans l Union européenne en 2010

COMMISSARIAT GÉNÉRAL AU DÉVELOPPEMENT DURABLE n 249 Septembre 2011 Prix de l énergie dans l Union européenne en 2010 OBRVATION ET STATISTIQU ÉNERG En 2010, le prix du gaz a diminué dans l Union européenne

Lot 4: Validation industrielle. Youness LEMRABET Pascal YIM, 19/11/2010

Lot 4: Validation industrielle Youness LEMRABET Pascal YIM, 19/11/2010 Partenaires Lot 1 Modèle du processus métier L4.1 Modèles PSM Lot 2 Guide d implantation L4.2 Développement & Recette prototype Lot

Innover à l'ère du numérique : ramener l'europe sur la bonne voie Présentation de J.M. Barroso,

Innover à l'ère du numérique : ramener l'europe sur la bonne voie Présentation de J.M. Barroso, Président de la Commission européenne, au Conseil européen des 24 et 25 octobre 213 Indice de compétitivité

Problème 1 : applications du plan affine

Problème 1 : applications du plan affine Notations On désigne par GL 2 (R) l ensemble des matrices 2 2 inversibles à coefficients réels. Soit un plan affine P muni d un repère (O, I, J). Les coordonnées

Exemple 4.4. Continuons l exemple précédent. Maintenant on travaille sur les quaternions et on a alors les décompositions

Exemple 4.4. Continuons l exemple précédent. Maintenant on travaille sur les quaternions et on a alors les décompositions HQ = He 1 He 2 He 3 He 4 HQ e 5 comme anneaux (avec centre Re 1 Re 2 Re 3 Re 4

GUIDE GÉNÉRAL SUR LE CCSP ET LA PRÉSENTATION DE L I N F O R M ATION FINANCIÈRE DES CONSEILS SCOLAIRES

GUIDE GÉNÉRAL SUR LE CCSP ET LA PRÉSENTATION DE L I N F O R M ATION FINANCIÈRE DES CONSEILS SCOLAIRES Ministère de l Éducation TA B L E D E S M AT I È R E S 2 I N T RO D UC TI ON E T C O N T EX T E Q

RO04/TI07 - Optimisation non-linéaire

RO04/TI07 - Optimisation non-linéaire Stéphane Mottelet Université de Technologie de Compiègne Printemps 2003 I Motivations et notions fondamentales 4 I1 Motivations 5 I2 Formes quadratiques 13 I3 Rappels

! " # $%& '( ) # %* +, -

! " # $%& '( ) # %* +, - 1.! "# $ % &%%'( #)*+,)#-. "/%)0123* 4%5%&!$!% 6)"7 '%%% 48-0 9::!%%% % 79;< "# 8 Ploc la lettre du haïku n 40 page 1 Décembre 2010, Association pour la promotion du haïku =%%)>

ARRANGEMENT ET PROTOCOLE DE MADRID CONCERNANT L ENREGISTREMENT INTERNATIONAL DES MARQUES DEMANDE D ENREGISTREMENT INTERNATIONAL RELEVANT

MM1(F) ARRANGEMENT ET PROTOCOLE DE MADRID CONCERNANT L ENREGISTREMENT INTERNATIONAL DES MARQUES DEMANDE D ENREGISTREMENT INTERNATIONAL RELEVANT EXCLUSIVEMENT DE L ARRANGEMENT DE MADRID (Règle 9 du règlement

Chapitre VI Fonctions de plusieurs variables

Chapitre VI Fonctions de plusieurs variables 6. 1 Fonctions différentiables de R 2 dans R. 6. 1. 1 Définition de la différentiabilité Nous introduisons la différentiabilité sous l angle des développements

Cylindre interrupteur

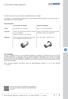Cylindres mis en œuvre pour actionner des éléments de verrouillage. Si nécessaire, votre partenaire professionnel ou nous-mêmes se fera/nous ferons un plaisir de vous assister dans le choix du bon produit.

Introduction. aux équations différentielles. et aux dérivées partielles

Université Claude Bernard, Lyon I Licence Sciences, Technologies & Santé 43, boulevard 11 novembre 1918 Spécialité Mathématiques 69622 Villeurbanne cedex, France L. Pujo-Menjouet pujo@math.univ-lyon1.fr

Capacité d un canal Second Théorème de Shannon. Théorie de l information 1/34

Capacité d un canal Second Théorème de Shannon Théorie de l information 1/34 Plan du cours 1. Canaux discrets sans mémoire, exemples ; 2. Capacité ; 3. Canaux symétriques ; 4. Codage de canal ; 5. Second

Exercices de géométrie

Exercices de géométrie Stage olympique de Bois-le-Roi, avril 2006 Igor Kortchemski Exercices vus en cours Exercice 1. (IMO 2000) Soient Ω 1 et Ω 2 deux cercles qui se coupent en M et en N. Soit la tangente

CHEMINS DANS LE QUART DE PLAN : PREMIÈRE PARTIE

CHEMINS DANS LE QUART DE PLAN : PREMIÈRE PARTIE MIREILLE BOUSQUET-MÉLOU. Introduction On considère des chemins dans Z 2, issus de (0,0), et prenant leurs pas dans un ensemble S Z 2 fini, par exemple S

>> TECHNIQUES DE COMPTABILITÉ ET DE GESTION 410.B0

Pondération : le 1 er chiffre représente le nombre d heures de théorie, le 2 e chiffre représente le nombre d heures de laboratoire et le 3 e chiffre représente le nombre d heures de travail personnel.

Cours d analyse numérique SMI-S4

ours d analyse numérique SMI-S4 Introduction L objet de l analyse numérique est de concevoir et d étudier des méthodes de résolution de certains problèmes mathématiques, en général issus de problèmes réels,

ÍÒ Ú Ö Ø ÅÓÒØÖ Ð ÍÒ ÑÓ Ð ÙÒ ÓÖÑ ÔÓÙÖ Ð ÑÓ Ð Ø ÓÒ Ø Ð Ñ Ø ÑÓ Ð Ø ÓÒ ³ÙÒ Ñ ÑÓ Ö ³ ÒØÖ ÔÖ Ô Ö ÇÐ Ú Ö Ö Ô ÖØ Ñ ÒØ ³ Ò ÓÖÑ Ø ÕÙ Ø Ö Ö ÓÔ Ö Ø ÓÒÒ ÐÐ ÙÐØ ÖØ Ø Ò Ì ÔÖ ÒØ Ð ÙÐØ ØÙ ÙÔ Ö ÙÖ Ò ÚÙ Ð³Ó Ø ÒØ ÓÒ Ù Ö È

(51) Int Cl.: B23P 19/00 (2006.01) B23P 19/04 (2006.01) F01L 1/053 (2006.01)

(19) (12) DEMANDE DE BREVET EUROPEEN (11) EP 1 886 760 A1 (43) Date de publication: 13.02.2008 Bulletin 2008/07 (21) Numéro de dépôt: 0711197.6 (1) Int Cl.: B23P 19/00 (2006.01) B23P 19/04 (2006.01) F01L

Cours C6 : Vibrations non linéaires

Vibrations non linéaires Bruno COCHELIN Laboratoire de Mécanique et d Acoustique, CNRS UPR 751 Ecole Centrale Marseille Acoustique non linéaire et milieux complexes -6 Juin 14 - Oléron Acoustique non linéaire

Christian JUTTEN Théorie du signal

Christian UTTEN Théorie du signal Cours de deuxième année (3i4) du département 3i Université oseph Fourier - Polytech Grenoble novembre 2009 1 Table des matières 1 Introduction à la théorie du signal 6