Le nombre d'or, clé de la beauté?
|
|
|
- Antoine Charbonneau
- il y a 9 ans
- Total affichages :
Transcription
1 On le nomme aussi «divine proportion». Le nombre d'or, clé de la beauté? Il serait la clé de la beauté en peinture, en sculpture ou encore en architecture. Mais la réputation du fameux nombre d'or est-elle justifiée? J ai fait le choix de vous laisser faire votre propre opinion : c est d ailleurs là que débute votre argumentation Vous avez ci-dessous de nombreux liens, beaucoup de documents : ceux qui valident la thèse du nombre d or comme «divine proportion», mais aussi ceux qui la contestent. Je remercie toutes les personnes qui ont déposé des documents si riches sur l Internet, sur un sujet si passionnant. Depuis l'antiquité, artistes et philosophes croient à l'existence d'une proportion privilégiée permettant d'obtenir harmonie et beauté. Il vaut 1 + 5, soit environ 1,6. A l'époque, il s'appelle Phi*. Phi revient à la mode à la 2 Renaissance sous le nom de divine proportion, puis section dorée, et finalement nombre d'or. Pourquoi nombre d'or? Il serait la clé de la beauté et de l'harmonie, et nombreux artistes se sont appuyés sur lui pour construire leurs œuvres. Certes, le nombre d'or semble être très présent dans la nature, c'est aussi un précieux élément en mathématiques, mais qu'a-t-il à voir avec l'esthétique? C'est à Euclide que l'on doit les premières traces écrites du fameux nombre d'or.
2 Le nombre d or chez les grecs Ce sont les grecs qui ont découverts les propriétés étranges de ce nombre. Vers 1930, le Roumain Matila Ghyka voit du nombre d'or partout, dans la nature comme dans l'architecture et la peinture. Il popularise la notion selon laquelle les rectangles construits à partir du nombre d'or sont attrayants visuellement. Ghyka trouve en effet des approximations de Phi dans des tableaux comme la Joconde ou des monuments comme le Parthénon. Le grand public retiendra que le nombre d'or est sans nul doute à la source de la beauté. On l'a bien sûr aussitôt utilisé dans l'architecture pour ses qualités harmonieuses. Par exemple, Phidias, a construit le Parthénon d'athènes (447 av. J.C) dans les proportions du nombre d'or. Ici le rapport, entre la largeur de l'édifice et sa hauteur vaut le nombre d'or. C'est surtout grâce aux travaux du mathématicien grec Euclide, aux alentours de 285 av. J.C que l'on a découvert le nombre d'or au détour du problème de géométrie suivant: Sur un segment [AC], comment placer B, de sorte que le rapport entre le tout et le grand côté soit le même que le rapport entre le grand et le petit côté? Et bien le point B partage le segment selon la proportion du nombre d'or. On dit même que le point B forme la section dorée.
3 Cette section dorée se retrouve dans beaucoup de situations, mais il est remarquable de voir que l'on peut la remarquer dans le partage du bras. L'homme serait-il construit selon de divines proportions? Essayez. On retrouve approximativement le même rapport entre la taille et la hauteur du nombril. Le nombre d'or et la géométrie On sait que les grecs furent de grands géomètres et certains d'entre eux, les pythagoriciens, furent tellement séduits par la beauté des nombres en particulier celle du nombre d'or, qu'ils décidèrent de faire du pentagone leur emblème. Et oui, dans le pentagone on retrouve le nombre d'or. Ainsi la nature exprime elle aussi les propriétés du nombre d'or, admirez ce squelette d'oursin pentagonal.
4 Le nombre d'or dans la nature La fleur de tournesol s'arrange en spirales. Des spirales qui partent du centre et qui vont vers l'extérieur en tournant vers la gauche et d'autres qui tournent vers la droite. Si l on compte le nombre de spirales dans les deux sens, le rapport 34/21 vaut ce qui est très proche du nombre d'or. Le nombre d'or en peinture Les peintres de la renaissance surtout en Italie ont cédé à l'appel quasi mystique du nombre d'or pour construire leurs tableaux. Par exemple dans l'annonciation de Léonard de Vinci (galerie des Offices, Florence), si l'on découpe les côtés du tableau selon les proportions du nombre d'or, on obtient des lignes qui délimitent l'emplacement des personnages (lignes verticales) ou qui définissent la ligne des épaules, des mains ou des genoux (lignes horizontales).
5 Le nombre d or en architecture Dans toute l œuvre de Le Corbusier, on retrouve le nombre d'or : dans les dimensions de ses bâtiments (rectangle d'or), mais aussi dans l'intérieur de ceux ci, comme dans la chapelle de Ronchamps, où tous les vitraux sont placés de manière harmonique, en fonction des proportions données par le nombre d'or, de manière à avoir une illumination constante. L'esthétique du rectangle d'or Pour en avoir le cœur net, Fechner un philosophe allemand ( ) soumet à quelques centaines de personnes plusieurs rectangles, chaque personne devant designer le rectangle le plus "attrayant". Les résultats mettent en avant une nette préférence pour le rectangle de Or il se trouve que 34/21 1,619 : il s'agit donc d'une forme extrêmement proche de celle du rectangle d'or. Le public aurait donc une préférence instinctive pour ce rectangle? Quel rectangle vous parait le plus harmonieux? A, B, C... Le C bien sûr. Voyons un peu en quoi ce rectangle est particulier
6 Et bien, ce rectangle a des dimensions telles que le rapport de sa hauteur sur sa largeur vaut le "nombre d'or", noté phi, en l'honneur de l'architecte grec Phidias. Ce nombre vaut approximativement , c'est un nombre irrationnel, c'est à dire ne s'écrivant pas sous la forme d'une fraction (comme pi). Au cours des siècles et surtout au moment de la renaissance, on lui a donné le nom de "divine proportion" (Luca Pacioli) Seulement plusieurs points viennent mettre en doute ces résultats. D'une part le public n'a pas dessiné les rectangles, mais s'est contenté de les choisir. D'autre part, ce format de tableau "le plus esthétique" est très peu utilisé par les peintres à la recherche de l'esthétique parfaite. Etrange que le rectangle "parfait" soit si peu utilisé par ceux qui en font le plus l'usage. De surcroît, les mesures du Roumain Matila Ghyka sont contestables, approximatives. Ses résultats sont complexes, parfois tirés par les cheveux. Bref, il n'y aurait de nombre d'or qu'en s'arrangeant avec les mesures! Par la suite, de nombreux scientifiques ont essayé de valider ou non, cette théorie du nombre d'or. Par exemple le professeur Singh (Texas) affirme lui que notre cerveau, grâce à l'hémisphère droit, perçoit le nombre d'or et nous le fait ressentir à travers le plaisir esthétique. De son côté, George Markowsky propose un test avec 48 rectangles de proportions différentes (entre 0.4 et 2.5), à hauteur fixe, et à largeur variable. Lorsque les rectangles sont organisés de manière aléatoire, la plupart des gens sont incapables de trouver le rectangle d'or. Lorsque les figures sont ensuite ordonnées selon leur largeur dans l'ordre croissant, le rectangle le plus souvent nominé est celui dont le rapport est de Or, rappelons-le, le nombre d'or vaut environ 1,6 Les secrets du "beau" Impossible donc d'affirmer que le rectangle d'or est le rectangle le plus esthétique. D'ailleurs, les critères de beauté ne peuvent se résumer à quelques proportions. Un tableau ou un monument sont des couleurs, des matières, des agencements soit bien plus que des constructions géométriques.
7 L'attrait des spectateurs pour une œuvre a probablement d'autres explications que l'existence prouvée ou non de rapports géométriques. Certains pensent même que le nombre d'or n'a jamais été utilisé dans l'art. Bref, l'utilisation consciente ou inconsciente dans l'art du nombre d'or reste un sujet hautement polémique. "Il n'y aurait de nombre d'or qu'en s'arrangeant avec les mesures! "
AC AB. A B C x 1. x + 1. d où. Avec un calcul vu au lycée, on démontre que cette solution admet deux solutions dont une seule nous intéresse : x =
 LE NOMBRE D OR Présentation et calcul du nombre d or Euclide avait trouvé un moyen de partager en deu un segment selon en «etrême et moyenne raison» Soit un segment [AB]. Le partage d Euclide consiste
LE NOMBRE D OR Présentation et calcul du nombre d or Euclide avait trouvé un moyen de partager en deu un segment selon en «etrême et moyenne raison» Soit un segment [AB]. Le partage d Euclide consiste
«Aucune investigation humaine ne peut être qualifiée de science véritable si elle ne peut être démontrée mathématiquement.
 «Aucune investigation humaine ne peut être qualifiée de science véritable si elle ne peut être démontrée mathématiquement.» Léonard de Vinci MATHEMATIQUES Les mathématiques revêtaient un caractère particulier
«Aucune investigation humaine ne peut être qualifiée de science véritable si elle ne peut être démontrée mathématiquement.» Léonard de Vinci MATHEMATIQUES Les mathématiques revêtaient un caractère particulier
Maths et nombre d'or
 Maths et nombre d'or Sommaire 1) 2) 3) 4) Définition du nombre d'or Origine de la lettre φ Histoire du nombre d'or Architecture et phi 5) Le nombre d'or et la peinture 6) Le nombre d'or et la musique 7)
Maths et nombre d'or Sommaire 1) 2) 3) 4) Définition du nombre d'or Origine de la lettre φ Histoire du nombre d'or Architecture et phi 5) Le nombre d'or et la peinture 6) Le nombre d'or et la musique 7)
Le nombre d or. Carte d identité. Dans les constructions de l homme. Celui des proportions harmonieuses
 1 Celui des proportions harmonieuses Carte d identité Son nom : On le désigne par la lettre grecque ( phi ) en hommage au sculpteur grec Phidias (né vers 490 et mort vers 430 avant J.C) qui décora le Parthénon
1 Celui des proportions harmonieuses Carte d identité Son nom : On le désigne par la lettre grecque ( phi ) en hommage au sculpteur grec Phidias (né vers 490 et mort vers 430 avant J.C) qui décora le Parthénon
Les propriétés esthétiques du nombre d or sur le visage humain : mythe ou réalité?
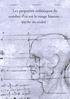 20 octobre 2011 Travail de Maturité Nina Dâmaso Les propriétés esthétiques du nombre d or sur le visage humain : mythe ou réalité? gsfgsg I Analyse du profil d un visage par Léonard de Vinci Table des
20 octobre 2011 Travail de Maturité Nina Dâmaso Les propriétés esthétiques du nombre d or sur le visage humain : mythe ou réalité? gsfgsg I Analyse du profil d un visage par Léonard de Vinci Table des
Bac Blanc Terminale ES - Février 2011 Épreuve de Mathématiques (durée 3 heures)
 Bac Blanc Terminale ES - Février 2011 Épreuve de Mathématiques (durée 3 heures) Eercice 1 (5 points) pour les candidats n ayant pas choisi la spécialité MATH Le tableau suivant donne l évolution du chiffre
Bac Blanc Terminale ES - Février 2011 Épreuve de Mathématiques (durée 3 heures) Eercice 1 (5 points) pour les candidats n ayant pas choisi la spécialité MATH Le tableau suivant donne l évolution du chiffre
Exercices Alternatifs. Une fonction continue mais dérivable nulle part
 Eercices Alternatifs Une fonction continue mais dérivable nulle part c 22 Frédéric Le Rou (copleft LDL : Licence pour Documents Libres). Sources et figures: applications-continues-non-derivables/. Version
Eercices Alternatifs Une fonction continue mais dérivable nulle part c 22 Frédéric Le Rou (copleft LDL : Licence pour Documents Libres). Sources et figures: applications-continues-non-derivables/. Version
Exercices Alternatifs. Une fonction continue mais dérivable nulle part
 Eercices Alternatifs Une fonction continue mais dérivable nulle part c 22 Frédéric Le Rou (copyleft LDL : Licence pour Documents Libres). Sources et figures: applications-continues-non-derivables/. Version
Eercices Alternatifs Une fonction continue mais dérivable nulle part c 22 Frédéric Le Rou (copyleft LDL : Licence pour Documents Libres). Sources et figures: applications-continues-non-derivables/. Version
enquête pour les fautes sur le fond, ce qui est graves pour une encyclopédie.
 4.0 Contrôles /4 4 e enquête pour les fautes sur le fond, ce qui est graves pour une encyclopédie. RPPEL de 0. Wikipédia 2/2 Dans le chapitre : XX e siècle : ( 4.0 mythe paroxysme ) sous la photo d un
4.0 Contrôles /4 4 e enquête pour les fautes sur le fond, ce qui est graves pour une encyclopédie. RPPEL de 0. Wikipédia 2/2 Dans le chapitre : XX e siècle : ( 4.0 mythe paroxysme ) sous la photo d un
TOUT CE QU IL FAUT SAVOIR POUR LE BREVET
 TOUT E QU IL FUT SVOIR POUR LE REVET NUMERIQUE / FONTIONS eci n est qu un rappel de tout ce qu il faut savoir en maths pour le brevet. I- Opérations sur les nombres et les fractions : Les priorités par
TOUT E QU IL FUT SVOIR POUR LE REVET NUMERIQUE / FONTIONS eci n est qu un rappel de tout ce qu il faut savoir en maths pour le brevet. I- Opérations sur les nombres et les fractions : Les priorités par
Date : 18.11.2013 Tangram en carré page
 Date : 18.11.2013 Tangram en carré page Titre : Tangram en carré Numéro de la dernière page : 14 Degrés : 1 e 4 e du Collège Durée : 90 minutes Résumé : Le jeu de Tangram (appelé en chinois les sept planches
Date : 18.11.2013 Tangram en carré page Titre : Tangram en carré Numéro de la dernière page : 14 Degrés : 1 e 4 e du Collège Durée : 90 minutes Résumé : Le jeu de Tangram (appelé en chinois les sept planches
Petit lexique de calcul à l usage des élèves de sixième et de cinquième par M. PARCABE, professeur au collège Alain FOURNIER de BORDEAUX, mars 2007
 Petit lexique de calcul à l usage des élèves de sixième et de cinquième par M. PARCABE, professeur au collège Alain FOURNIER de BORDEAUX, mars 2007 page 1 / 10 abscisse addition additionner ajouter appliquer
Petit lexique de calcul à l usage des élèves de sixième et de cinquième par M. PARCABE, professeur au collège Alain FOURNIER de BORDEAUX, mars 2007 page 1 / 10 abscisse addition additionner ajouter appliquer
Carl-Louis-Ferdinand von Lindemann (1852-1939)
 Par Boris Gourévitch "L'univers de Pi" http://go.to/pi314 [email protected] Alors ça, c'est fort... Tranches de vie Autour de Carl-Louis-Ferdinand von Lindemann (1852-1939) est transcendant!!! Carl Louis
Par Boris Gourévitch "L'univers de Pi" http://go.to/pi314 [email protected] Alors ça, c'est fort... Tranches de vie Autour de Carl-Louis-Ferdinand von Lindemann (1852-1939) est transcendant!!! Carl Louis
Définition : On obtient les nombres entiers en ajoutant ou retranchant des unités à zéro.
 Chapitre : Les nombres rationnels Programme officiel BO du 8/08/08 Connaissances : Diviseurs communs à deux entiers, PGCD. Fractions irréductibles. Opérations sur les nombres relatifs en écriture fractionnaire.
Chapitre : Les nombres rationnels Programme officiel BO du 8/08/08 Connaissances : Diviseurs communs à deux entiers, PGCD. Fractions irréductibles. Opérations sur les nombres relatifs en écriture fractionnaire.
Soit la fonction affine qui, pour représentant le nombre de mois écoulés, renvoie la somme économisée.
 ANALYSE 5 points Exercice 1 : Léonie souhaite acheter un lecteur MP3. Le prix affiché (49 ) dépasse largement la somme dont elle dispose. Elle décide donc d économiser régulièrement. Elle a relevé qu elle
ANALYSE 5 points Exercice 1 : Léonie souhaite acheter un lecteur MP3. Le prix affiché (49 ) dépasse largement la somme dont elle dispose. Elle décide donc d économiser régulièrement. Elle a relevé qu elle
Frédéric Laroche 2009
 Frédéric Laroche 2009 Les Entiers Caractériser les nombres : peut-être avec des figures géométriques? En triangle * * * * * * * * * * --------------- Une formule 1 3 6 10 --- En carré * * * * * * * * *
Frédéric Laroche 2009 Les Entiers Caractériser les nombres : peut-être avec des figures géométriques? En triangle * * * * * * * * * * --------------- Une formule 1 3 6 10 --- En carré * * * * * * * * *
Nombre de marches Nombre de facons de les monter 3 3 11 144 4 5 12 233 5 8 13 377 6 13 14 610 7 21 15 987 8 34 16 1597 9 55 17 2584 10 89
 Soit un escalier à n marches. On note u_n le nombre de façons de monter ces n marches. Par exemple d'après l'énoncé, u_3=3. Pour monter n marches, il faut d'abord monter la première. Soit on la monte seule,
Soit un escalier à n marches. On note u_n le nombre de façons de monter ces n marches. Par exemple d'après l'énoncé, u_3=3. Pour monter n marches, il faut d'abord monter la première. Soit on la monte seule,
TRUCTURES TUBULAIRES EN ARCHITECTURE
 TRUCTURES TUBULAIRES EN ARCHITECTURE Mick Eekhout _,k?~i -~P'i. TU Delft Delft University of Technology STRUCTURES TUBULAIRES EN ARCHITECTURE Prof.dr. Mick Eekhout a /'initiative du CIDECT (Comite International
TRUCTURES TUBULAIRES EN ARCHITECTURE Mick Eekhout _,k?~i -~P'i. TU Delft Delft University of Technology STRUCTURES TUBULAIRES EN ARCHITECTURE Prof.dr. Mick Eekhout a /'initiative du CIDECT (Comite International
«la mouche» : 1958 / 1987, l'adaptation au travers des affiches.
 Oui, mais c'est l œuvre de quelqu'un d'autre 1 «On parle souvent des cinéastes qui, à Hollywood, déforment l œuvre originale. Mon intention est de ne jamais faire cela»¹ «la mouche» : 1958 / 1987, l'adaptation
Oui, mais c'est l œuvre de quelqu'un d'autre 1 «On parle souvent des cinéastes qui, à Hollywood, déforment l œuvre originale. Mon intention est de ne jamais faire cela»¹ «la mouche» : 1958 / 1987, l'adaptation
Vision industrielle et télédétection - Détection d ellipses. Guillaume Martinez 17 décembre 2007
 Vision industrielle et télédétection - Détection d ellipses Guillaume Martinez 17 décembre 2007 1 Table des matières 1 Le projet 3 1.1 Objectif................................ 3 1.2 Les choix techniques.........................
Vision industrielle et télédétection - Détection d ellipses Guillaume Martinez 17 décembre 2007 1 Table des matières 1 Le projet 3 1.1 Objectif................................ 3 1.2 Les choix techniques.........................
Fonctions linéaires et affines. 1 Fonctions linéaires. 1.1 Vocabulaire. 1.2 Représentation graphique. 3eme
 Fonctions linéaires et affines 3eme 1 Fonctions linéaires 1.1 Vocabulaire Définition 1 Soit a un nombre quelconque «fixe». Une fonction linéaire associe à un nombre x quelconque le nombre a x. a s appelle
Fonctions linéaires et affines 3eme 1 Fonctions linéaires 1.1 Vocabulaire Définition 1 Soit a un nombre quelconque «fixe». Une fonction linéaire associe à un nombre x quelconque le nombre a x. a s appelle
CORRIGE LES NOMBRES DECIMAUX RELATIFS. «Réfléchir avant d agir!»
 Corrigé Cours de Mr JULES v3.3 Classe de Quatrième Contrat 1 Page 1 sur 13 CORRIGE LES NOMBRES DECIMAUX RELATIFS. «Réfléchir avant d agir!» «Correction en rouge et italique.» I. Les nombres décimaux relatifs.
Corrigé Cours de Mr JULES v3.3 Classe de Quatrième Contrat 1 Page 1 sur 13 CORRIGE LES NOMBRES DECIMAUX RELATIFS. «Réfléchir avant d agir!» «Correction en rouge et italique.» I. Les nombres décimaux relatifs.
COMPTE-RENDU «MATHS EN JEANS» LYCEE OZENNE Groupe 1 : Comment faire une carte juste de la Terre?
 Claire FORGACZ Marion GALLART Hasnia GOUDJILI COMPTERENDU «MATHS EN JEANS» LYCEE OZENNE Groupe 1 : Comment faire une carte juste de la Terre? Si l on se pose la question de savoir comment on peut faire
Claire FORGACZ Marion GALLART Hasnia GOUDJILI COMPTERENDU «MATHS EN JEANS» LYCEE OZENNE Groupe 1 : Comment faire une carte juste de la Terre? Si l on se pose la question de savoir comment on peut faire
SOCLE COMMUN - La Compétence 3 Les principaux éléments de mathématiques et la culture scientifique et technologique
 SOCLE COMMUN - La Compétence 3 Les principaux éléments de mathématiques et la culture scientifique et technologique DOMAINE P3.C3.D1. Pratiquer une démarche scientifique et technologique, résoudre des
SOCLE COMMUN - La Compétence 3 Les principaux éléments de mathématiques et la culture scientifique et technologique DOMAINE P3.C3.D1. Pratiquer une démarche scientifique et technologique, résoudre des
1. Utilisation du logiciel Keepass
 Utilisation du logiciel Keepass L'usage de mots de passe est nécessaire pour de nombreux accès ou pour la protection de données personnelles. Il convient d'en utiliser plusieurs, suivant le type d'accès
Utilisation du logiciel Keepass L'usage de mots de passe est nécessaire pour de nombreux accès ou pour la protection de données personnelles. Il convient d'en utiliser plusieurs, suivant le type d'accès
LA BANQUE NATIONALE DE SERBIE EXPRIME SES REMERCIEMENTS À LA BANQUE DE FRANCE POUR LES COPIES DE DOCUMENTS D ARCHIVES
 Banque Nationale de Serbie BANQUE NATIONALE DE SERBIE BANQUE DE FRANCE Fabrication des billets serbes et yougoslaves à la Banque de France 1885 85 1930 LA BANQUE NATIONALE DE SERBIE EXPRIME SES REMERCIEMENTS
Banque Nationale de Serbie BANQUE NATIONALE DE SERBIE BANQUE DE FRANCE Fabrication des billets serbes et yougoslaves à la Banque de France 1885 85 1930 LA BANQUE NATIONALE DE SERBIE EXPRIME SES REMERCIEMENTS
Baccalauréat L spécialité, Métropole et Réunion, 19 juin 2009 Corrigé.
 Baccalauréat L spécialité, Métropole et Réunion, 19 juin 2009 Corrigé. L usage d une calculatrice est autorisé Durée : 3heures Deux annexes sont à rendre avec la copie. Exercice 1 5 points 1_ Soit f la
Baccalauréat L spécialité, Métropole et Réunion, 19 juin 2009 Corrigé. L usage d une calculatrice est autorisé Durée : 3heures Deux annexes sont à rendre avec la copie. Exercice 1 5 points 1_ Soit f la
LA PHYLLOTAXIE SPIRALE
 ALBERTIN Thierry - CAVALLARO Jean-Sébastien - MARCHESE Emilie 1 ère S 3 LA PHYLLOTAXIE SPIRALE Lycée Thierry MAULNIER Année Scolaire : 2004-2005 Professeurs : M. Gouy (S.V.T.) M. Martinez (Mathématiques)
ALBERTIN Thierry - CAVALLARO Jean-Sébastien - MARCHESE Emilie 1 ère S 3 LA PHYLLOTAXIE SPIRALE Lycée Thierry MAULNIER Année Scolaire : 2004-2005 Professeurs : M. Gouy (S.V.T.) M. Martinez (Mathématiques)
PARTIE NUMERIQUE (18 points)
 4 ème DEVOIR COMMUN N 1 DE MATHÉMATIQUES 14/12/09 L'échange de matériel entre élèves et l'usage de la calculatrice sont interdits. Il sera tenu compte du soin et de la présentation ( 4 points ). Le barème
4 ème DEVOIR COMMUN N 1 DE MATHÉMATIQUES 14/12/09 L'échange de matériel entre élèves et l'usage de la calculatrice sont interdits. Il sera tenu compte du soin et de la présentation ( 4 points ). Le barème
SINE QUA NON. Découverte et Prise en main du logiciel Utilisation de bases
 SINE QUA NON Découverte et Prise en main du logiciel Utilisation de bases Sine qua non est un logiciel «traceur de courbes planes» mais il possède aussi bien d autres fonctionnalités que nous verrons tout
SINE QUA NON Découverte et Prise en main du logiciel Utilisation de bases Sine qua non est un logiciel «traceur de courbes planes» mais il possède aussi bien d autres fonctionnalités que nous verrons tout
LES DÉTERMINANTS DE MATRICES
 LES DÉTERMINANTS DE MATRICES Sommaire Utilité... 1 1 Rappel Définition et composantes d'une matrice... 1 2 Le déterminant d'une matrice... 2 3 Calcul du déterminant pour une matrice... 2 4 Exercice...
LES DÉTERMINANTS DE MATRICES Sommaire Utilité... 1 1 Rappel Définition et composantes d'une matrice... 1 2 Le déterminant d'une matrice... 2 3 Calcul du déterminant pour une matrice... 2 4 Exercice...
6 ème. Rallye mathématique de la Sarthe 2013/2014. 1 ère épreuve de qualification : Problèmes Jeudi 21 novembre 2013
 Retrouver tous les sujets, les corrigés, les annales, les finales sur le site du rallye : http://sarthe.cijm.org I Stéphane, Eric et Christophe sont 3 garçons avec des chevelures différentes. Stéphane
Retrouver tous les sujets, les corrigés, les annales, les finales sur le site du rallye : http://sarthe.cijm.org I Stéphane, Eric et Christophe sont 3 garçons avec des chevelures différentes. Stéphane
Introduction à l étude des Corps Finis
 Introduction à l étude des Corps Finis Robert Rolland (Résumé) 1 Introduction La structure de corps fini intervient dans divers domaines des mathématiques, en particulier dans la théorie de Galois sur
Introduction à l étude des Corps Finis Robert Rolland (Résumé) 1 Introduction La structure de corps fini intervient dans divers domaines des mathématiques, en particulier dans la théorie de Galois sur
NOM : Prénom : Date de naissance : Ecole : CM2 Palier 2
 NOM : Prénom : Date de naissance : Ecole : CM2 Palier 2 Résultats aux évaluations nationales CM2 Annexe 1 Résultats de l élève Compétence validée Lire / Ecrire / Vocabulaire / Grammaire / Orthographe /
NOM : Prénom : Date de naissance : Ecole : CM2 Palier 2 Résultats aux évaluations nationales CM2 Annexe 1 Résultats de l élève Compétence validée Lire / Ecrire / Vocabulaire / Grammaire / Orthographe /
OLYMPIADES ACADEMIQUES DE MATHEMATIQUES. 15 mars 2006 CLASSE DE PREMIERE ES, GMF
 OLYMPIADES ACADEMIQUES DE MATHEMATIQUES 15 mars 2006 CLASSE DE PREMIERE ES, GMF Durée : 4 heures Les quatre exercices sont indépendants Les calculatrices sont autorisées L énoncé comporte trois pages Exercice
OLYMPIADES ACADEMIQUES DE MATHEMATIQUES 15 mars 2006 CLASSE DE PREMIERE ES, GMF Durée : 4 heures Les quatre exercices sont indépendants Les calculatrices sont autorisées L énoncé comporte trois pages Exercice
Priorités de calcul :
 EXERCICES DE REVISION POUR LE PASSAGE EN QUATRIEME : Priorités de calcul : Exercice 1 : Calcule en détaillant : A = 4 + 5 6 + 7 B = 6 3 + 5 C = 35 5 3 D = 6 7 + 8 E = 38 6 3 + 7 Exercice : Calcule en détaillant
EXERCICES DE REVISION POUR LE PASSAGE EN QUATRIEME : Priorités de calcul : Exercice 1 : Calcule en détaillant : A = 4 + 5 6 + 7 B = 6 3 + 5 C = 35 5 3 D = 6 7 + 8 E = 38 6 3 + 7 Exercice : Calcule en détaillant
Attestation de maîtrise des connaissances et compétences au cours moyen deuxième année
 Attestation de maîtrise des connaissances et compétences au cours moyen deuxième année PALIER 2 CM2 La maîtrise de la langue française DIRE S'exprimer à l'oral comme à l'écrit dans un vocabulaire approprié
Attestation de maîtrise des connaissances et compétences au cours moyen deuxième année PALIER 2 CM2 La maîtrise de la langue française DIRE S'exprimer à l'oral comme à l'écrit dans un vocabulaire approprié
3 thèses : Problématique :
 LA CONSCIENCE Problématique : 3 thèses : Thèse 1 : L âme est une substance. A. L âme est une substance individuelle. B. La conscience comme substance pensante une et indivisible. Thèse 2 : La conscience
LA CONSCIENCE Problématique : 3 thèses : Thèse 1 : L âme est une substance. A. L âme est une substance individuelle. B. La conscience comme substance pensante une et indivisible. Thèse 2 : La conscience
PROBLEME(12) Première partie : Peinture des murs et du plafond.
 PROBLEME(12) Une entreprise doit rénover un local. Ce local a la forme d'un parallélépipède rectangle. La longueur est 6,40m, la largeur est 5,20m et la hauteur est 2,80m. Il comporte une porte de 2m de
PROBLEME(12) Une entreprise doit rénover un local. Ce local a la forme d'un parallélépipède rectangle. La longueur est 6,40m, la largeur est 5,20m et la hauteur est 2,80m. Il comporte une porte de 2m de
La fonction exponentielle
 DERNIÈRE IMPRESSION LE 2 novembre 204 à :07 La fonction exponentielle Table des matières La fonction exponentielle 2. Définition et théorèmes.......................... 2.2 Approche graphique de la fonction
DERNIÈRE IMPRESSION LE 2 novembre 204 à :07 La fonction exponentielle Table des matières La fonction exponentielle 2. Définition et théorèmes.......................... 2.2 Approche graphique de la fonction
EVALUATIONS FIN CM1. Mathématiques. Livret élève
 Les enseignants de CM1 de la circonscription de METZ-SUD proposent EVALUATIONS FIN CM1 Mathématiques Livret élève Circonscription de METZ-SUD page 1 NOMBRES ET CALCUL Exercice 1 : Écris en chiffres les
Les enseignants de CM1 de la circonscription de METZ-SUD proposent EVALUATIONS FIN CM1 Mathématiques Livret élève Circonscription de METZ-SUD page 1 NOMBRES ET CALCUL Exercice 1 : Écris en chiffres les
Exercice numéro 1 - L'escalier
 Exercice numéro 1 - L'escalier On peut monter un escalier une ou deux marches à la fois. La figure de droite montre un exemple. 1. De combien de façons différentes peut-on monter un escalier de une marche?
Exercice numéro 1 - L'escalier On peut monter un escalier une ou deux marches à la fois. La figure de droite montre un exemple. 1. De combien de façons différentes peut-on monter un escalier de une marche?
Le contexte. Le questionnement du P.E.R. :
 Le contexte Ce travail a débuté en janvier. Le P.E.R. engagé depuis fin septembre a permis de faire émerger ou de réactiver : Des raisons d être de la géométrie : Calculer des grandeurs inaccessibles et
Le contexte Ce travail a débuté en janvier. Le P.E.R. engagé depuis fin septembre a permis de faire émerger ou de réactiver : Des raisons d être de la géométrie : Calculer des grandeurs inaccessibles et
PROBLEMES D'ORDONNANCEMENT AVEC RESSOURCES
 Leçon 11 PROBLEMES D'ORDONNANCEMENT AVEC RESSOURCES Dans cette leçon, nous retrouvons le problème d ordonnancement déjà vu mais en ajoutant la prise en compte de contraintes portant sur les ressources.
Leçon 11 PROBLEMES D'ORDONNANCEMENT AVEC RESSOURCES Dans cette leçon, nous retrouvons le problème d ordonnancement déjà vu mais en ajoutant la prise en compte de contraintes portant sur les ressources.
Magnitudes des étoiles
 Magnitudes des étoiles 24/03/15 Observatoire de Lyon 24/03/15 () Magnitudes des étoiles Observatoire de Lyon 1 / 14 Magnitude apparente d une étoile Avant la physique... Hipparque, mathématicien et astronome
Magnitudes des étoiles 24/03/15 Observatoire de Lyon 24/03/15 () Magnitudes des étoiles Observatoire de Lyon 1 / 14 Magnitude apparente d une étoile Avant la physique... Hipparque, mathématicien et astronome
FctsAffines.nb 1. Mathématiques, 1-ère année Edition 2007-2008. Fonctions affines
 FctsAffines.nb 1 Mathématiques, 1-ère année Edition 2007-2008 Fonctions affines Supports de cours de mathématiques de degré secondaire II, lien hpertete vers la page mère http://www.deleze.name/marcel/sec2/inde.html
FctsAffines.nb 1 Mathématiques, 1-ère année Edition 2007-2008 Fonctions affines Supports de cours de mathématiques de degré secondaire II, lien hpertete vers la page mère http://www.deleze.name/marcel/sec2/inde.html
La Joconde. (1503-1506, 0,77x 0,53 m) de Léonard de Vinci TEMPS MODERNES
 La Joconde (1503-1506, 0,77x 0,53 m) de Léonard de Vinci TEMPS MODERNES La Joconde de Léonard de Vinci est incontestablement le tableau le plus célèbre. Il est conservé au musée du Louvre à Paris et a
La Joconde (1503-1506, 0,77x 0,53 m) de Léonard de Vinci TEMPS MODERNES La Joconde de Léonard de Vinci est incontestablement le tableau le plus célèbre. Il est conservé au musée du Louvre à Paris et a
RÉALISATION DE GRAPHIQUES AVEC OPENOFFICE.ORG 2.3
 RÉALISATION DE GRAPHIQUES AVEC OPENOFFICE.ORG 2.3 Pour construire un graphique : On lance l assistant graphique à l aide du menu Insérer è Diagramme en ayant sélectionné au préalable une cellule vide dans
RÉALISATION DE GRAPHIQUES AVEC OPENOFFICE.ORG 2.3 Pour construire un graphique : On lance l assistant graphique à l aide du menu Insérer è Diagramme en ayant sélectionné au préalable une cellule vide dans
Vous revisiterez tous les nombres rencontrés au collège, en commençant par les nombres entiers pour finir par les nombres réels.
 Cette partie est consacrée aux nombres. Vous revisiterez tous les nombres rencontrés au collège, en commençant par les nombres entiers pour finir par les nombres réels. L aperçu historique vous permettra
Cette partie est consacrée aux nombres. Vous revisiterez tous les nombres rencontrés au collège, en commençant par les nombres entiers pour finir par les nombres réels. L aperçu historique vous permettra
Le seul ami de Batman
 Le seul ami de Batman Avant de devenir un héros de cinéma en 1989, Batman est depuis plus de 50 ans un fameux personnage de bandes dessinées aux États-Unis. Il fut créé en mai 1939 dans les pages de Détective
Le seul ami de Batman Avant de devenir un héros de cinéma en 1989, Batman est depuis plus de 50 ans un fameux personnage de bandes dessinées aux États-Unis. Il fut créé en mai 1939 dans les pages de Détective
C f tracée ci- contre est la représentation graphique d une
 TLES1 DEVOIR A LA MAISON N 7 La courbe C f tracée ci- contre est la représentation graphique d une fonction f définie et dérivable sur R. On note f ' la fonction dérivée de f. La tangente T à la courbe
TLES1 DEVOIR A LA MAISON N 7 La courbe C f tracée ci- contre est la représentation graphique d une fonction f définie et dérivable sur R. On note f ' la fonction dérivée de f. La tangente T à la courbe
Manuel d utilisation 26 juin 2011. 1 Tâche à effectuer : écrire un algorithme 2
 éducalgo Manuel d utilisation 26 juin 2011 Table des matières 1 Tâche à effectuer : écrire un algorithme 2 2 Comment écrire un algorithme? 3 2.1 Avec quoi écrit-on? Avec les boutons d écriture........
éducalgo Manuel d utilisation 26 juin 2011 Table des matières 1 Tâche à effectuer : écrire un algorithme 2 2 Comment écrire un algorithme? 3 2.1 Avec quoi écrit-on? Avec les boutons d écriture........
Chapitre 14. La diagonale du carré
 Chapitre 4 La diagonale du carré Préambule Examinons un puzzle tout simple : on se donne deux carrés de même aire et on demande, au moyen de quelques découpages, de construire un nouveau carré qui aurait
Chapitre 4 La diagonale du carré Préambule Examinons un puzzle tout simple : on se donne deux carrés de même aire et on demande, au moyen de quelques découpages, de construire un nouveau carré qui aurait
Exo7. Calculs de déterminants. Fiche corrigée par Arnaud Bodin. Exercice 1 Calculer les déterminants des matrices suivantes : Exercice 2.
 Eo7 Calculs de déterminants Fiche corrigée par Arnaud Bodin Eercice Calculer les déterminants des matrices suivantes : Correction Vidéo ( ) 0 6 7 3 4 5 8 4 5 6 0 3 4 5 5 6 7 0 3 5 4 3 0 3 0 0 3 0 0 0 3
Eo7 Calculs de déterminants Fiche corrigée par Arnaud Bodin Eercice Calculer les déterminants des matrices suivantes : Correction Vidéo ( ) 0 6 7 3 4 5 8 4 5 6 0 3 4 5 5 6 7 0 3 5 4 3 0 3 0 0 3 0 0 0 3
D'UN THÉORÈME NOUVEAU
 DÉMONSTRATION D'UN THÉORÈME NOUVEAU CONCERNANT LES NOMBRES PREMIERS 1. (Nouveaux Mémoires de l'académie royale des Sciences et Belles-Lettres de Berlin, année 1771.) 1. Je viens de trouver, dans un excellent
DÉMONSTRATION D'UN THÉORÈME NOUVEAU CONCERNANT LES NOMBRES PREMIERS 1. (Nouveaux Mémoires de l'académie royale des Sciences et Belles-Lettres de Berlin, année 1771.) 1. Je viens de trouver, dans un excellent
Cours Fonctions de deux variables
 Cours Fonctions de deux variables par Pierre Veuillez 1 Support théorique 1.1 Représentation Plan et espace : Grâce à un repère cartésien ( ) O, i, j du plan, les couples (x, y) de R 2 peuvent être représenté
Cours Fonctions de deux variables par Pierre Veuillez 1 Support théorique 1.1 Représentation Plan et espace : Grâce à un repère cartésien ( ) O, i, j du plan, les couples (x, y) de R 2 peuvent être représenté
Enoncé et corrigé du brevet des collèges dans les académies d Aix- Marseille, Montpellier, Nice Corse et Toulouse en 2000. Énoncé.
 Enoncé et corrigé du brevet des collèges dans les académies d Aix- Marseille, Montpellier, Nice Corse et Toulouse en 2000. Énoncé. I- ACTIVITES NUMERIQUES (12 points) Exercice 1 (3 points) On considère
Enoncé et corrigé du brevet des collèges dans les académies d Aix- Marseille, Montpellier, Nice Corse et Toulouse en 2000. Énoncé. I- ACTIVITES NUMERIQUES (12 points) Exercice 1 (3 points) On considère
RapidMiner. Data Mining. 1 Introduction. 2 Prise en main. Master Maths Finances 2010/2011. 1.1 Présentation. 1.2 Ressources
 Master Maths Finances 2010/2011 Data Mining janvier 2011 RapidMiner 1 Introduction 1.1 Présentation RapidMiner est un logiciel open source et gratuit dédié au data mining. Il contient de nombreux outils
Master Maths Finances 2010/2011 Data Mining janvier 2011 RapidMiner 1 Introduction 1.1 Présentation RapidMiner est un logiciel open source et gratuit dédié au data mining. Il contient de nombreux outils
Lisez ATTENTIVEMENT ce qui suit, votre avenir financier en dépend grandement...
 Bonjour, Maintenant que vous avez compris que le principe d'unkube était de pouvoir vous créer le réseau virtuel le plus gros possible avant que la phase d'incubation ne soit terminée, voyons COMMENT ce
Bonjour, Maintenant que vous avez compris que le principe d'unkube était de pouvoir vous créer le réseau virtuel le plus gros possible avant que la phase d'incubation ne soit terminée, voyons COMMENT ce
Baccalauréat ES/L Métropole La Réunion 13 septembre 2013 Corrigé
 Baccalauréat S/L Métropole La Réunion 13 septembre 2013 Corrigé A. P. M.. P. XRCIC 1 Commun à tous les candidats Partie A 1. L arbre de probabilité correspondant aux données du problème est : 0,3 0,6 H
Baccalauréat S/L Métropole La Réunion 13 septembre 2013 Corrigé A. P. M.. P. XRCIC 1 Commun à tous les candidats Partie A 1. L arbre de probabilité correspondant aux données du problème est : 0,3 0,6 H
Trois personnes mangent dans un restaurant. Le serveur
 29=30 Trois personnes mangent dans un restaurant. Le serveur leur amène une addition de 30 francs. Les trois personnes décident de partager la facture en trois, soit 10 francs chacun. Le serveur rapporte
29=30 Trois personnes mangent dans un restaurant. Le serveur leur amène une addition de 30 francs. Les trois personnes décident de partager la facture en trois, soit 10 francs chacun. Le serveur rapporte
Education, visions d'un monde
 Education, visions d'un monde 29th August 2012 La Fondation s inte_resse de pre_s a_ l e_conomie et a_ son fonctionnement sur le long terme. Nous nous attachons a_ analyser et comprendre la transition
Education, visions d'un monde 29th August 2012 La Fondation s inte_resse de pre_s a_ l e_conomie et a_ son fonctionnement sur le long terme. Nous nous attachons a_ analyser et comprendre la transition
La lettre de l IMSEPP
 La lettre de l IMSEPP N 22 05 décembre 2013 La trésorerie des entreprises en novembre : Les difficultés d accès au financement s atténuent. Novembre 2013 : ce document présente l analyse détaillée des
La lettre de l IMSEPP N 22 05 décembre 2013 La trésorerie des entreprises en novembre : Les difficultés d accès au financement s atténuent. Novembre 2013 : ce document présente l analyse détaillée des
BANQUES DE DONNÉES PÉDAGOGIQUES
 223 Daniel BURET, Jean-Claude BLANCHARD. HISTORIQUE L'EPI a entrepris en 1989 de créer des bases d'énoncés mathématiques destinées aux enseignants pour la production de documents et accompagnées d'un outil
223 Daniel BURET, Jean-Claude BLANCHARD. HISTORIQUE L'EPI a entrepris en 1989 de créer des bases d'énoncés mathématiques destinées aux enseignants pour la production de documents et accompagnées d'un outil
T.P.E. LA PHYLLOTAXIE: ASSOCIATION DES SPIRALES DANS LA CROISSANCE DES PLANTES. Juan Carlos Marroquin, T le S.
 T.P.E. LA PHYLLOTAXIE: ASSOCIATION DES SPIRALES DANS LA CROISSANCE DES PLANTES. Juan Carlos Marroquin, T le S. SOMMAIRE Introduction I Quelques spirales et leurs propriétés A. La spirale logarithmique
T.P.E. LA PHYLLOTAXIE: ASSOCIATION DES SPIRALES DANS LA CROISSANCE DES PLANTES. Juan Carlos Marroquin, T le S. SOMMAIRE Introduction I Quelques spirales et leurs propriétés A. La spirale logarithmique
N 39 Du 3 déc au 7 déc 2012
 N 39 Du 3 déc au 7 déc 2012 LA SÉANCE D ACTU DE LA SEMAINE L article choisi de la semaine : 5 décembre 2012 par Pauline Martineau Où peut-on voir ce célèbre tableau? FICHE ÉLÈVE LES MOTS DE LA SEMAINE
N 39 Du 3 déc au 7 déc 2012 LA SÉANCE D ACTU DE LA SEMAINE L article choisi de la semaine : 5 décembre 2012 par Pauline Martineau Où peut-on voir ce célèbre tableau? FICHE ÉLÈVE LES MOTS DE LA SEMAINE
Extracto de la entrevista del Señor Louis Schweitzer a propósito del proceso de
 Anexo 2 Extracto de la entrevista del Señor Louis Schweitzer a propósito del proceso de alianza con Nissan. Fuente: http://www.medefparis.fr/itw_schweitzer.html Louis SCHWEITZER Président de Renault Renault
Anexo 2 Extracto de la entrevista del Señor Louis Schweitzer a propósito del proceso de alianza con Nissan. Fuente: http://www.medefparis.fr/itw_schweitzer.html Louis SCHWEITZER Président de Renault Renault
Notre nom est un gage de responsabilité. Wealth-Assurance AG
 Notre nom est un gage de responsabilité Wealth-Assurance AG Qualité suisse et service personnalisé c est notre emblème Aloyse Steichen Président directeur général Bienvenue Au nom de Wealth-Assurance AG
Notre nom est un gage de responsabilité Wealth-Assurance AG Qualité suisse et service personnalisé c est notre emblème Aloyse Steichen Président directeur général Bienvenue Au nom de Wealth-Assurance AG
Le chiffre est le signe, le nombre est la valeur.
 Extrait de cours de maths de 6e Chapitre 1 : Les nombres et les opérations I) Chiffre et nombre 1.1 La numération décimale En mathématique, un chiffre est un signe utilisé pour l'écriture des nombres.
Extrait de cours de maths de 6e Chapitre 1 : Les nombres et les opérations I) Chiffre et nombre 1.1 La numération décimale En mathématique, un chiffre est un signe utilisé pour l'écriture des nombres.
Guide de configuration d'une classe
 Guide de configuration d'une clae Viion ME Guide de configuration d'une clae Contenu 1. Introduction...2 2. Ajouter de cour...4 3. Ajouter de reource à une leçon...5 4. Meilleure pratique...7 4.1. Organier
Guide de configuration d'une clae Viion ME Guide de configuration d'une clae Contenu 1. Introduction...2 2. Ajouter de cour...4 3. Ajouter de reource à une leçon...5 4. Meilleure pratique...7 4.1. Organier
UEO11 COURS/TD 1. nombres entiers et réels codés en mémoire centrale. Caractères alphabétiques et caractères spéciaux.
 UEO11 COURS/TD 1 Contenu du semestre Cours et TDs sont intégrés L objectif de ce cours équivalent a 6h de cours, 10h de TD et 8h de TP est le suivant : - initiation à l algorithmique - notions de bases
UEO11 COURS/TD 1 Contenu du semestre Cours et TDs sont intégrés L objectif de ce cours équivalent a 6h de cours, 10h de TD et 8h de TP est le suivant : - initiation à l algorithmique - notions de bases
Mario Botta (1943) Le Musée d'art moderne de San Francisco
 Mario Botta (1943) Architecte suisse. De 1961 à 1964, il étudie au Liceo Artistico à Milan puis, jusqu'en 1969 à l'istituto Universitario di Architettura à Venise où il est l élève de Carlo Scarpa. En
Mario Botta (1943) Architecte suisse. De 1961 à 1964, il étudie au Liceo Artistico à Milan puis, jusqu'en 1969 à l'istituto Universitario di Architettura à Venise où il est l élève de Carlo Scarpa. En
Autoconsommation en photovoltaïque Principe et intérêt
 Autoconsommation en photovoltaïque Principe et intérêt Par AD44, LR83, Looping, Ramses, Valtrede. Le principe de l'injection d'électricité dans le réseau est bien connu des personnes qui sont équipées
Autoconsommation en photovoltaïque Principe et intérêt Par AD44, LR83, Looping, Ramses, Valtrede. Le principe de l'injection d'électricité dans le réseau est bien connu des personnes qui sont équipées
Algèbre binaire et Circuits logiques (2007-2008)
 Université Mohammed V Faculté des Sciences Département de Mathématiques et Informatique Filière : SMI Algèbre binaire et Circuits logiques (27-28) Prof. Abdelhakim El Imrani Plan. Algèbre de Boole 2. Circuits
Université Mohammed V Faculté des Sciences Département de Mathématiques et Informatique Filière : SMI Algèbre binaire et Circuits logiques (27-28) Prof. Abdelhakim El Imrani Plan. Algèbre de Boole 2. Circuits
CODE CIVIL FRANÇAIS (ANTERIEUR A 1960)
 CODE CIVIL FRANÇAIS (ANTERIEUR A 1960) ARTICLES 1874 À 1914 DU PRÊT Téléchargé sur Le premier portail consacré au droit des affaires à Madagascar TITRE DIXIEME Du prêt Art. 1874 - Il y a deux sortes de
CODE CIVIL FRANÇAIS (ANTERIEUR A 1960) ARTICLES 1874 À 1914 DU PRÊT Téléchargé sur Le premier portail consacré au droit des affaires à Madagascar TITRE DIXIEME Du prêt Art. 1874 - Il y a deux sortes de
Durée de L épreuve : 2 heures. Barème : Exercice n 4 : 1 ) 1 point 2 ) 2 points 3 ) 1 point
 03 Mai 2013 Collège Oasis Durée de L épreuve : 2 heures. apple Le sujet comporte 4 pages et est présenté en livret ; apple La calculatrice est autorisée ; apple 4 points sont attribués à la qualité de
03 Mai 2013 Collège Oasis Durée de L épreuve : 2 heures. apple Le sujet comporte 4 pages et est présenté en livret ; apple La calculatrice est autorisée ; apple 4 points sont attribués à la qualité de
Le jugement de Pâris et la pomme Par A. Labarrière 2 2
 Le jugement de Pâris et la pomme Par A. Labarrière 2 2 I. Origine et Protagonistes Cette légende fut narrée pour la première fois par Homère, un poète grec du 9 e siècle avant J.-C. ayant écrit l Iliade
Le jugement de Pâris et la pomme Par A. Labarrière 2 2 I. Origine et Protagonistes Cette légende fut narrée pour la première fois par Homère, un poète grec du 9 e siècle avant J.-C. ayant écrit l Iliade
Chapitre 2 : Vecteurs
 1 Chapitre 2 : Vecteurs Nous allons définir ce qu'est un vecteur grâce à une figure (le parallélogramme), mais au préalable nous allons aussi définir une nouvelle transformation (la translation). Nous
1 Chapitre 2 : Vecteurs Nous allons définir ce qu'est un vecteur grâce à une figure (le parallélogramme), mais au préalable nous allons aussi définir une nouvelle transformation (la translation). Nous
La micro be. Image Sébastien PLASSARD, Baigneuse 2014
 h c a La micro be DROITE Image Sébastien PLASSARD, Baigneuse 2014 PAR L I G N E 26 JUIN - 31 JUILLET 2015 La micro beach Achetez de l art les pieds dans le sable! Pour fêter sa première année d existence
h c a La micro be DROITE Image Sébastien PLASSARD, Baigneuse 2014 PAR L I G N E 26 JUIN - 31 JUILLET 2015 La micro beach Achetez de l art les pieds dans le sable! Pour fêter sa première année d existence
Photoshop Séquence 4 - Créer une image de taille personnalisée taille
 cterrier.com 1/5 20/09/2006 Photoshop Séquence 4 - Créer une image de taille personnalisée taille Auteur : C. Terrier ; mailto:[email protected] ; http://www.cterrier.com Utilisation : Reproduction
cterrier.com 1/5 20/09/2006 Photoshop Séquence 4 - Créer une image de taille personnalisée taille Auteur : C. Terrier ; mailto:[email protected] ; http://www.cterrier.com Utilisation : Reproduction
Notion de fonction. Résolution graphique. Fonction affine.
 TABLE DES MATIÈRES 1 Notion de fonction. Résolution graphique. Fonction affine. Paul Milan LMA Seconde le 12 décembre 2011 Table des matières 1 Fonction numérique 2 1.1 Introduction.................................
TABLE DES MATIÈRES 1 Notion de fonction. Résolution graphique. Fonction affine. Paul Milan LMA Seconde le 12 décembre 2011 Table des matières 1 Fonction numérique 2 1.1 Introduction.................................
Logiciel SCRATCH FICHE 02
 1. Reprise de la fiche 1: 1.1. Programme Figure : Logiciel SCRATCH FICHE 02 SANS ORDINATEUR : Dessiner à droite le dessin que donnera l'exécution de ce programme : Unité : 50 pas : Remarque : vous devez
1. Reprise de la fiche 1: 1.1. Programme Figure : Logiciel SCRATCH FICHE 02 SANS ORDINATEUR : Dessiner à droite le dessin que donnera l'exécution de ce programme : Unité : 50 pas : Remarque : vous devez
Publication Assistée par Ordinateur
 Présentation OpenOffice Draw est l'outil de dessin vectoriel de la suite bureautique OpenOffice. De fait, Draw permet de réaliser certains documents comparables à ceux de Publisher, le logiciel de P.A.O.
Présentation OpenOffice Draw est l'outil de dessin vectoriel de la suite bureautique OpenOffice. De fait, Draw permet de réaliser certains documents comparables à ceux de Publisher, le logiciel de P.A.O.
Lecture graphique. Table des matières
 Lecture graphique Table des matières 1 Lecture d une courbe 2 1.1 Définition d une fonction.......................... 2 1.2 Exemple d une courbe........................... 2 1.3 Coût, recette et bénéfice...........................
Lecture graphique Table des matières 1 Lecture d une courbe 2 1.1 Définition d une fonction.......................... 2 1.2 Exemple d une courbe........................... 2 1.3 Coût, recette et bénéfice...........................
Raisonnement par récurrence Suites numériques
 Chapitre 1 Raisonnement par récurrence Suites numériques Terminale S Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES Raisonnement par récurrence. Limite finie ou infinie d une suite.
Chapitre 1 Raisonnement par récurrence Suites numériques Terminale S Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES Raisonnement par récurrence. Limite finie ou infinie d une suite.
La méthode des cas et le plan marketing : énoncé seul
 La méthode des cas et le plan marketing : énoncé seul 12_07_2011 Table des matières Table des matières 3 I - 1. Point méthodologique 7 A. 1.1. Définitions...7 B. 1.2. Plan d'analyse type...8 C. 1.3. Synthèse...13
La méthode des cas et le plan marketing : énoncé seul 12_07_2011 Table des matières Table des matières 3 I - 1. Point méthodologique 7 A. 1.1. Définitions...7 B. 1.2. Plan d'analyse type...8 C. 1.3. Synthèse...13
SAINT-PETERSBOURG EN PETIT GROUPE MEILLEUR TARIF GARANTI 2015/2016
 SAINT-PETERSBOURG EN PETIT GROUPE MEILLEUR TARIF GARANTI 2015/2016 Vous n'aimez pas les voyages en groupe? Le voyage sur mesure vous paraît trop cher? Vous n êtes pas rassurés à l idée de voyager seul?
SAINT-PETERSBOURG EN PETIT GROUPE MEILLEUR TARIF GARANTI 2015/2016 Vous n'aimez pas les voyages en groupe? Le voyage sur mesure vous paraît trop cher? Vous n êtes pas rassurés à l idée de voyager seul?
METEOROLOGIE CAEA 1990
 METEOROLOGIE CAEA 1990 1) Les météorologistes mesurent et prévoient le vent en attitude à des niveaux exprimés en pressions atmosphériques. Entre le niveau de la mer et 6000 m d'altitude, quels sont les
METEOROLOGIE CAEA 1990 1) Les météorologistes mesurent et prévoient le vent en attitude à des niveaux exprimés en pressions atmosphériques. Entre le niveau de la mer et 6000 m d'altitude, quels sont les
Module 16 : Les fonctions de recherche et de référence
 Module 16 : Les fonctions de recherche et de référence 16.0 Introduction L une des fonctions les plus importantes d Excel, c est la possibilité de chercher une valeur spécifique dans un grand nombre de
Module 16 : Les fonctions de recherche et de référence 16.0 Introduction L une des fonctions les plus importantes d Excel, c est la possibilité de chercher une valeur spécifique dans un grand nombre de
CHAPITRE IX : Les appareils de mesures électriques
 CHAPITRE IX : Les appareils de mesures électriques IX. 1 L'appareil de mesure qui permet de mesurer la différence de potentiel entre deux points d'un circuit est un voltmètre, celui qui mesure le courant
CHAPITRE IX : Les appareils de mesures électriques IX. 1 L'appareil de mesure qui permet de mesurer la différence de potentiel entre deux points d'un circuit est un voltmètre, celui qui mesure le courant
MAT2027 Activités sur Geogebra
 MAT2027 Activités sur Geogebra NOTE: Il n est pas interdit d utiliser du papier et un crayon!! En particulier, quand vous demandez des informations sur les différentes mesures dans une construction, il
MAT2027 Activités sur Geogebra NOTE: Il n est pas interdit d utiliser du papier et un crayon!! En particulier, quand vous demandez des informations sur les différentes mesures dans une construction, il
Navigation dans Windows
 Cours 03 Navigation dans Windows Comme je le disais en introduction, notre souris se révèle plus maligne qu'elle n'en a l'air. À tel point qu'il faut apprendre à la dompter (mais c'est très simple, ce
Cours 03 Navigation dans Windows Comme je le disais en introduction, notre souris se révèle plus maligne qu'elle n'en a l'air. À tel point qu'il faut apprendre à la dompter (mais c'est très simple, ce
ALAIN-DOMINIQUE GALLIZIA
 ALAIN-DOMINIQUE GALLIZIA est un architecte français, mécène urbain et curateur-collectionneur œuvrant à la RECONNAISSANCE DE L ART DU GRAFFITI. L atelier de Boulogne Billancourt appelé «La Ruche du Tag»
ALAIN-DOMINIQUE GALLIZIA est un architecte français, mécène urbain et curateur-collectionneur œuvrant à la RECONNAISSANCE DE L ART DU GRAFFITI. L atelier de Boulogne Billancourt appelé «La Ruche du Tag»
NOTE D INTENTION EXTRAIT DE PRESSE
 NOTE D INTENTION L'idée de ce spectacle hors du commun, par sa forme de pseudo- conférence d'abord, par son sujet ensuite, est né de la rencontre entre Peggy D'Argenson, galeriste, critique d'art, qui
NOTE D INTENTION L'idée de ce spectacle hors du commun, par sa forme de pseudo- conférence d'abord, par son sujet ensuite, est né de la rencontre entre Peggy D'Argenson, galeriste, critique d'art, qui
Activités numériques [13 Points]
![Activités numériques [13 Points] Activités numériques [13 Points]](/thumbs/21/1117704.jpg) N du candidat L emploi de la calculatrice est autorisé. Le soin, la qualité de la présentation entrent pour 2 points dans l appréciation des copies. Les résultats seront soulignés. La correction est disponible
N du candidat L emploi de la calculatrice est autorisé. Le soin, la qualité de la présentation entrent pour 2 points dans l appréciation des copies. Les résultats seront soulignés. La correction est disponible
OLYMPIADES ACADÉMIQUES DE MATHÉMATIQUES
 OLYMPIADES ACADÉMIQUES DE MATHÉMATIQUES ACADÉMIE DE RENNES SESSION 2006 CLASSE DE PREMIERE DURÉE : 4 heures Ce sujet s adresse à tous les élèves de première quelle que soit leur série. Il comporte cinq
OLYMPIADES ACADÉMIQUES DE MATHÉMATIQUES ACADÉMIE DE RENNES SESSION 2006 CLASSE DE PREMIERE DURÉE : 4 heures Ce sujet s adresse à tous les élèves de première quelle que soit leur série. Il comporte cinq
Cryptologie à clé publique
 Cryptologie à clé publique La cryptologie est partout Chacun utilise de la crypto tous les jours sans forcément sans rendre compte en : - téléphonant avec un portable - payant avec sa carte bancaire -
Cryptologie à clé publique La cryptologie est partout Chacun utilise de la crypto tous les jours sans forcément sans rendre compte en : - téléphonant avec un portable - payant avec sa carte bancaire -
Le nombre d or et Fibonacci
 Août 2004, Bordeaux Pentagone et nombre d or Irrationalité Séries géométriques Equation Remarques et exercice Le pentagramme magique se retrouve partout dans la nature et hors de la nature est le symbole
Août 2004, Bordeaux Pentagone et nombre d or Irrationalité Séries géométriques Equation Remarques et exercice Le pentagramme magique se retrouve partout dans la nature et hors de la nature est le symbole
REPRESENTER LA TERRE Cartographie et navigation
 REPRESENTER LA TERRE Seconde Page 1 TRAVAUX DIRIGES REPRESENTER LA TERRE Cartographie et navigation Casterman TINTIN "Le trésor de Rackham Le Rouge" 1 TRIGONOMETRIE : Calcul du chemin le plus court. 1)
REPRESENTER LA TERRE Seconde Page 1 TRAVAUX DIRIGES REPRESENTER LA TERRE Cartographie et navigation Casterman TINTIN "Le trésor de Rackham Le Rouge" 1 TRIGONOMETRIE : Calcul du chemin le plus court. 1)
