PERSPECTIVE DES ARCHITECTES - TOITS DE
|
|
|
- Géraldine Mercier
- il y a 10 ans
- Total affichages :
Transcription
1 Chapitre 2 - PA PERSPECTIVE DES ARCHITECTES - TOITS DE MAISONS PA_01 PA_02 PA_03 PA_04 PA_05 Perspective des architectes : construction de l image d'un cube Projection parallèle d un cube sur un plan variable Maison à toit gauche Maison à toit convexe ou concave Maison à toit variable
2 PA_01 Perspective des architectes : construction de l image d'un cube et une animation en boucle Description de la fenêtre à l ouverture La fenêtre présente deux dessins associés : - en haut, en perspective parallèle, un cube noir posé sur un plan horizontal gris - en bas, en vraie grandeur, le carré représentant la face du cube située dans le plan horizontal gris. PA_01 Perspective des architectes : construdtion de l image d un cube et une animation en boucle Le pivotement du cube se fait autour d un axe supposé vertical. La direction des projetantes est fixe. Commande «direction des projetantes» Cette commande permet de choisir la direction des projetantes.notons que ces projetantes restent inclinées à 45. Déroulement de l animation Les deux dessins (dans l espace et dans le plan) sont synchronisés. Première étape En haut : dessin dans l espace L animation montre la construction de l image du cube sur le plan horizontal gris dans une projection parallèle selon une direction faisant un angle de 45 avec la verticale. Simultanément : - un point décrit l arête verticale, située à gauche dans la position initiale du cube - la projetante en bleu de ce point se déplace, tandis que le projeté dessine en rouge l image de l arête. En bas : dessin dans le plan en perspective des architectes Le contenu de la face située dans le plan gris se dessine en vraie grandeur. Le segment rouge est un segment vertical, conformément à la perspective choisie pour ce dessin. Deuxième étape Le tracé d un quart de cercle, simultanément sur les deux dessins, met en évidence l égalité des longueurs du segment rouge, projeté de l arête verticale choisie, et de l arête du cube. En effet, la projetante de l extrémité supérieure de cette arête fait un angle de 45 avec l arête verticale ; ainsi l arête verticale et la projetée de cette arête sur le plan horizontal sont les deux côtés d un triangle rectangle isocèle dont l hypoténuse est la projetante. Troisième étape Sur les deux dessins synchronisés, les images des trois autres arêtes verticales se dessinent simultanément suivant le procédé décrit dans la deuxième étape. Quatrième étape L image du cube est complétée par le tracé de l image de sa face supérieure. Remarques - Sur le dessin du haut, quand le basculement est maximum (curseur à droite), on obtient en vraie grandeur l image du cube en perspective des architectes. - En manipulant la commande «pivotement», on peut placer le dessin du haut - en perspective des architectes - dans la même orientation que le dessin du bas.
3 PA_02 Projection parallèle d un cube sur un plan variable Projetantes de direction fixe Description de la fenêtre La fenêtre contient deux dessins. - À gauche, le dessin - obtenu par projection orthogonale sur le plan frontal - présente : un cube bleu un plan représenté en traits fins noirs sur ce plan, le projeté noir du cube obtenu par une projection parallèle les projetantes - en bleu clair - inclinées à 45. Le plan de projection coupe le plan de la face inférieure du cube selon la droite rouge. - À droite, le dessin donne en vraie grandeur le projeté du cube sur le plan de projection. Commande «inclinaison du plan de projection» Cette commande permet de choisir l inclinaison du plan de projection. Lorsque le plan de projection est perpendiculaire à la direction des projetantes, le projeté du cube correspond sensiblement à la photographie obtenue quand l axe de l appareil est incliné à 45.
4 PA_03 Maison à toit gauche Description de la fenêtre La fenêtre présente une maison schématisée : le toit est formé de deux pans, l un contient des solives rouges et l autre des solives bleues. À l ouverture, la hauteur du pignon avant est inférieure à celle du pignon arrière ; la faîtière est alors inclinée vers l avant. Commande «flèche» La hauteur de l un des murs pignon avant à l ouverture est réglable par cette commande. Quand le curseur est à gauche, la hauteur du pignon avant est la même que celle du pignon arrière ; la faîtière est alors horizontale et les deux pans du toit sont des rectangles. Dans les autres cas, les deux pans du toit sont des quadrilatères gauches.
5 PA_04 Maison à toit convexe ou concave En 04a comme en 04b, la fenêtre présente une maison schématisée : les deux pans du toit - deux quadrilatères gauches, composés de deux triangles chacun - l un à solives bleues, l autre à solives rouges, ont la faîtière pour côté commun. 04a Maison à toit convexe Description de la fenêtre à l ouverture La hauteur du pignon situé en avant à l ouverture - pignon A - est inférieure à la hauteur du pignon arrière ; la faîtière est alors inclinée vers l avant. Chacun des deux pans du toit est composé de deux triangles. Les quatre triangles ont un point commun, le sommet du pignon arrière. Le toit est donc composé de quatre surfaces planes. Commande «flèche» La hauteur du pignon A est réglable par cette commande. Les deux triangles du toit qui ont un côté sur le pignon A varient avec la la hauteur de ce pignon. Les deux autres triangles du toit sont fixes. Quand le curseur est à gauche, la hauteur du pignon A est la même que celle du pignon opposé ; la faîtière est horizontale et le toit est alors composé de deux pans qui sont des quadrilatères plans rectangles. Quand le curseur est à droite, le pignon A est un rectangle, et les deux triangles ayant un côté commun avec ce pignon sont coplanaires et forment un seul triangle ; le toit comporte alors trois pans triangulaires. Dans les cas intermédiaires - c est le cas à l ouverture - le toit est composé de deux quadrilatères gauches ; le toit comporte alors quatre pans triangulaires. 04b Maison à toit concave Description de la fenêtre à l'ouverture La hauteur du pignon situé en avant à l'ouverture - pignon A - est inférieure à la hauteur du pignon arrière ; la faîtière est alors inclinée vers l avant. Chacun des deux pans du toit est composé de deux triangles. Les quatre triangles ont un point commun, le sommet du pignon avant. Le toit est donc composé de quatre surfaces planes. Commande «flèche» La hauteur du pignon A est réglable par cette commande. Les quatre triangles du toit varient avec la hauteur du pignon A. Quand le curseur est à gauche, la hauteur du pignon A est la même que celle du mur opposé ; la faîtière est horizontale et le toit est alors composé de deux pans qui sont des quadrilatères plans rectangles. Dans les autres cas - c est le cas à l ouverture - le toit est formé de quatre triangles.
6 PA_05 Maison à toit variable Description de la fenêtre La fenêtre présente une maison schématisée. Le mur avant est un rectangle, le toit est formé de quatre quadrilatères gauches, constituant quatre pans. Deux poutres noires ayant un point commun sur la faîtière supportent respectivement les solives rouges et les solives bleues. Chacun des quatre quadrilatères a un côté porté par l une des deux poutres noires et un autre côté porté par la faîtière. Commande «poutres noires» Cette commande permet de passer du toit convexe à trois pans triangulaires curseur à gauche, au toit concave à quatre pans triangulaires curseur à droite (voir PA_04). A l'ouverture, lorsque le curseur coïncide avec le trait rouge, les deux poutres noires sont en position médiane. Dans ce cas, les solives sont placées deux par deux dans le prolongement l une de l autre, et le toit est alors réduit à deux pans qui sont des quadrilatères gauches. Dans les autres cas, le toit comporte quatre pans qui sont des quadrilatères gauches.
Le contexte. Le questionnement du P.E.R. :
 Le contexte Ce travail a débuté en janvier. Le P.E.R. engagé depuis fin septembre a permis de faire émerger ou de réactiver : Des raisons d être de la géométrie : Calculer des grandeurs inaccessibles et
Le contexte Ce travail a débuté en janvier. Le P.E.R. engagé depuis fin septembre a permis de faire émerger ou de réactiver : Des raisons d être de la géométrie : Calculer des grandeurs inaccessibles et
Designer d escalier GUIDE DE L UTILISATEUR. Stair Designer-1
 Designer d escalier GUIDE DE L UTILISATEUR Stair Designer-1 Stair Designer-2 Designer d escalier Le Designer d escalier rend facile la réalisation et la mise en place d escaliers sur mesure dans votre
Designer d escalier GUIDE DE L UTILISATEUR Stair Designer-1 Stair Designer-2 Designer d escalier Le Designer d escalier rend facile la réalisation et la mise en place d escaliers sur mesure dans votre
EXERCICES DE REVISIONS MATHEMATIQUES CM2
 EXERCICES DE REVISIONS MATHEMATIQUES CM2 NOMBRES ET CALCUL Exercices FRACTIONS Nommer les fractions simples et décimales en utilisant le vocabulaire : 3 R1 demi, tiers, quart, dixième, centième. Utiliser
EXERCICES DE REVISIONS MATHEMATIQUES CM2 NOMBRES ET CALCUL Exercices FRACTIONS Nommer les fractions simples et décimales en utilisant le vocabulaire : 3 R1 demi, tiers, quart, dixième, centième. Utiliser
Cours de tracés de Charpente, Le TRAIT
 Page 1/5 Cours de tracés de Charpente, Le TRAIT Recherches de vraies grandeurs, angles de coupes, surfaces. Les Méthodes : Le tracé et les calculs Chaque chapitre ou fichier comportent une explication
Page 1/5 Cours de tracés de Charpente, Le TRAIT Recherches de vraies grandeurs, angles de coupes, surfaces. Les Méthodes : Le tracé et les calculs Chaque chapitre ou fichier comportent une explication
Problèmes sur le chapitre 5
 Problèmes sur le chapitre 5 (Version du 13 janvier 2015 (10h38)) 501 Le calcul des réactions d appui dans les problèmes schématisés ci-dessous est-il possible par les équations de la statique Si oui, écrire
Problèmes sur le chapitre 5 (Version du 13 janvier 2015 (10h38)) 501 Le calcul des réactions d appui dans les problèmes schématisés ci-dessous est-il possible par les équations de la statique Si oui, écrire
Problèmes de dénombrement.
 Problèmes de dénombrement. 1. On se déplace dans le tableau suivant, pour aller de la case D (départ) à la case (arrivée). Les déplacements utilisés sont exclusivement les suivants : ller d une case vers
Problèmes de dénombrement. 1. On se déplace dans le tableau suivant, pour aller de la case D (départ) à la case (arrivée). Les déplacements utilisés sont exclusivement les suivants : ller d une case vers
Le Dessin Technique.
 Jardin-Nicolas Hervé cours 1 / 9. Modélisation et représentation d un objet technique. La modélisation et la représentation d un objet sont deux formes de langage permettant de définir complètement la
Jardin-Nicolas Hervé cours 1 / 9. Modélisation et représentation d un objet technique. La modélisation et la représentation d un objet sont deux formes de langage permettant de définir complètement la
Le seul ami de Batman
 Le seul ami de Batman Avant de devenir un héros de cinéma en 1989, Batman est depuis plus de 50 ans un fameux personnage de bandes dessinées aux États-Unis. Il fut créé en mai 1939 dans les pages de Détective
Le seul ami de Batman Avant de devenir un héros de cinéma en 1989, Batman est depuis plus de 50 ans un fameux personnage de bandes dessinées aux États-Unis. Il fut créé en mai 1939 dans les pages de Détective
AC AB. A B C x 1. x + 1. d où. Avec un calcul vu au lycée, on démontre que cette solution admet deux solutions dont une seule nous intéresse : x =
 LE NOMBRE D OR Présentation et calcul du nombre d or Euclide avait trouvé un moyen de partager en deu un segment selon en «etrême et moyenne raison» Soit un segment [AB]. Le partage d Euclide consiste
LE NOMBRE D OR Présentation et calcul du nombre d or Euclide avait trouvé un moyen de partager en deu un segment selon en «etrême et moyenne raison» Soit un segment [AB]. Le partage d Euclide consiste
Voyez la réponse à cette question dans ce chapitre. www.hometownroofingcontractors.com/blog/9-reasons-diy-rednecks-should-never-fix-their-own-roof
 Une échelle est appuyée sur un mur. S il n y a que la friction statique avec le sol, quel est l angle minimum possible entre le sol et l échelle pour que l échelle ne glisse pas et tombe au sol? www.hometownroofingcontractors.com/blog/9-reasons-diy-rednecks-should-never-fix-their-own-roof
Une échelle est appuyée sur un mur. S il n y a que la friction statique avec le sol, quel est l angle minimum possible entre le sol et l échelle pour que l échelle ne glisse pas et tombe au sol? www.hometownroofingcontractors.com/blog/9-reasons-diy-rednecks-should-never-fix-their-own-roof
PROGRAMME D HABILETÉS EN FAUTEUIL ROULANT (WSP-F)
 PROGRAMME D HABILETÉS EN FAUTEUIL ROULANT (WSP-F) LIGNES DIRECTRICES POUR LE PARCOURS À OBSTACLES VERSION 4.1 CANADIENNE-FRANÇAISE Les activités d entraînement et d évaluation du WSP-F 4.1 peuvent se dérouler
PROGRAMME D HABILETÉS EN FAUTEUIL ROULANT (WSP-F) LIGNES DIRECTRICES POUR LE PARCOURS À OBSTACLES VERSION 4.1 CANADIENNE-FRANÇAISE Les activités d entraînement et d évaluation du WSP-F 4.1 peuvent se dérouler
MAT2027 Activités sur Geogebra
 MAT2027 Activités sur Geogebra NOTE: Il n est pas interdit d utiliser du papier et un crayon!! En particulier, quand vous demandez des informations sur les différentes mesures dans une construction, il
MAT2027 Activités sur Geogebra NOTE: Il n est pas interdit d utiliser du papier et un crayon!! En particulier, quand vous demandez des informations sur les différentes mesures dans une construction, il
Comment sélectionner des sommets, des arêtes et des faces avec Blender?
 Comment sélectionner des sommets, des arêtes et des faces avec Blender? VVPix v 1.00 Table des matières 1 Introduction 1 2 Préparation d une scène test 2 2.1 Ajout d objets dans la scène.........................................
Comment sélectionner des sommets, des arêtes et des faces avec Blender? VVPix v 1.00 Table des matières 1 Introduction 1 2 Préparation d une scène test 2 2.1 Ajout d objets dans la scène.........................................
point On obtient ainsi le ou les points d inter- entre deux objets».
 Déplacer un objet Cliquer sur le bouton «Déplacer». On peut ainsi rendre la figure dynamique. Attraper l objet à déplacer avec la souris. Ici, on veut déplacer le point A du triangle point ABC. A du triangle
Déplacer un objet Cliquer sur le bouton «Déplacer». On peut ainsi rendre la figure dynamique. Attraper l objet à déplacer avec la souris. Ici, on veut déplacer le point A du triangle point ABC. A du triangle
Correction : E = Soit E = -1,6. F = 12 Soit F = -6 3 + 45. y = 11. et G = -2z + 4y G = 2 6 = 3 G = G = -2 5 + 4 11
 Correction : EXERCICE : Calculer en indiquant les étapes: (-6 +9) ( ) ( ) B = -4 (-) (-8) B = - 8 (+ 6) B = - 8 6 B = - 44 EXERCICE : La visite médicale Calcul de la part des élèves rencontrés lundi et
Correction : EXERCICE : Calculer en indiquant les étapes: (-6 +9) ( ) ( ) B = -4 (-) (-8) B = - 8 (+ 6) B = - 8 6 B = - 44 EXERCICE : La visite médicale Calcul de la part des élèves rencontrés lundi et
Adobe Illustrator Logiciel de dessin vectoriel et de Cartographie Assistée par Ordinateur
 Adobe Illustrator Logiciel de dessin vectoriel et de Cartographie Assistée par Ordinateur I- Ouverture d une nouvelle feuille de travail Fichier / Nouveau (ou ctrl + N) Indiquer dans la fenêtre qui s ouvre
Adobe Illustrator Logiciel de dessin vectoriel et de Cartographie Assistée par Ordinateur I- Ouverture d une nouvelle feuille de travail Fichier / Nouveau (ou ctrl + N) Indiquer dans la fenêtre qui s ouvre
Guide des autorisations d urbanisme
 Guide des autorisations d urbanisme de Service Urbanisme Villenoy 2014 TABLE DES MATIERES QUEL DOSSIER DEPOSER POUR MON PROJET?... 2 QUELQUES NOTIONS POUR BIEN DEMARRER.... 2 MON PROJET EST-IL SOUMIS A
Guide des autorisations d urbanisme de Service Urbanisme Villenoy 2014 TABLE DES MATIERES QUEL DOSSIER DEPOSER POUR MON PROJET?... 2 QUELQUES NOTIONS POUR BIEN DEMARRER.... 2 MON PROJET EST-IL SOUMIS A
Manuel Utilisateur Logiciel PEB Partie modeleur version 2.5
 Manuel Utilisateur Logiciel PEB Partie modeleur version 2.5 Table des matières Table des matières... 3 Introduction... 7 Objectifs du modeleur... 7 Coup d oeil... 9 Principes sous-tendant l utilisation
Manuel Utilisateur Logiciel PEB Partie modeleur version 2.5 Table des matières Table des matières... 3 Introduction... 7 Objectifs du modeleur... 7 Coup d oeil... 9 Principes sous-tendant l utilisation
COMFORTLIFT ONE VOTRE MONTE-ESCALIER DISCRET. www.comfortlift.be
 0800 20 950 www.comfortlift.be COMFORTLIFT ONE VOTRE MONTE-ESCALIER DISCRET www.comfortlift.be COMFORTLIFT ONE Le monte-escalier monorail Vous voulez un monte-escalier se fondant dans votre intérieur?
0800 20 950 www.comfortlift.be COMFORTLIFT ONE VOTRE MONTE-ESCALIER DISCRET www.comfortlift.be COMFORTLIFT ONE Le monte-escalier monorail Vous voulez un monte-escalier se fondant dans votre intérieur?
Baccalauréat L spécialité, Métropole et Réunion, 19 juin 2009 Corrigé.
 Baccalauréat L spécialité, Métropole et Réunion, 19 juin 2009 Corrigé. L usage d une calculatrice est autorisé Durée : 3heures Deux annexes sont à rendre avec la copie. Exercice 1 5 points 1_ Soit f la
Baccalauréat L spécialité, Métropole et Réunion, 19 juin 2009 Corrigé. L usage d une calculatrice est autorisé Durée : 3heures Deux annexes sont à rendre avec la copie. Exercice 1 5 points 1_ Soit f la
Vision industrielle et télédétection - Détection d ellipses. Guillaume Martinez 17 décembre 2007
 Vision industrielle et télédétection - Détection d ellipses Guillaume Martinez 17 décembre 2007 1 Table des matières 1 Le projet 3 1.1 Objectif................................ 3 1.2 Les choix techniques.........................
Vision industrielle et télédétection - Détection d ellipses Guillaume Martinez 17 décembre 2007 1 Table des matières 1 Le projet 3 1.1 Objectif................................ 3 1.2 Les choix techniques.........................
Tp_chemins..doc. Dans la barre "arche 2" couleur claire 1/5 21/01/13
 TP de création : utilisation des chemins vectoriels Finis les mauvais rêves : vous aurez enfin votre dreamcatcher (Indienss des Grands Lacs) 1 ) Créez une nouvelle image de 300 pixels sur 600 pixels en
TP de création : utilisation des chemins vectoriels Finis les mauvais rêves : vous aurez enfin votre dreamcatcher (Indienss des Grands Lacs) 1 ) Créez une nouvelle image de 300 pixels sur 600 pixels en
DOSSIER D'ACTIVITES SUR TUXPAINT Dessiner avec Tuxpaint. Objectifs :
 DOSSIER D'ACTIVITES SUR TUXPAINT Dessiner avec Tuxpaint Objectifs : Apprendre à l apprenant à connaître l'ordinateur Apprendre à l'apprenant à allumer l'ordinateur Faire découvrir à l'apprenant Linux Faire
DOSSIER D'ACTIVITES SUR TUXPAINT Dessiner avec Tuxpaint Objectifs : Apprendre à l apprenant à connaître l'ordinateur Apprendre à l'apprenant à allumer l'ordinateur Faire découvrir à l'apprenant Linux Faire
Si deux droites sont parallèles à une même troisième. alors les deux droites sont parallèles entre elles. alors
 N I) Pour démontrer que deux droites (ou segments) sont parallèles (d) // (d ) (d) // (d ) deux droites sont parallèles à une même troisième les deux droites sont parallèles entre elles (d) // (d) deux
N I) Pour démontrer que deux droites (ou segments) sont parallèles (d) // (d ) (d) // (d ) deux droites sont parallèles à une même troisième les deux droites sont parallèles entre elles (d) // (d) deux
DURÉE DU JOUR EN FONCTION DE LA DATE ET DE LA LATITUDE
 DURÉE DU JUR E FCTI DE LA DATE ET DE LA LATITUDE ous allons nous intéresser à la durée du jour, prise ici dans le sens de période d éclairement par le Soleil dans une journée de 4 h, en un lieu donné de
DURÉE DU JUR E FCTI DE LA DATE ET DE LA LATITUDE ous allons nous intéresser à la durée du jour, prise ici dans le sens de période d éclairement par le Soleil dans une journée de 4 h, en un lieu donné de
Pop-Art façon Roy Liechtenstein
 1 sur 6 22/01/2010 22:35 Pop-Art façon Roy Liechtenstein Ce tutoriel peut paraître loin de la photographie, mais il contient des techniques très utiles, voire indispensables en matière de retouche. 1 -
1 sur 6 22/01/2010 22:35 Pop-Art façon Roy Liechtenstein Ce tutoriel peut paraître loin de la photographie, mais il contient des techniques très utiles, voire indispensables en matière de retouche. 1 -
Comment démontrer que deux droites sont perpendiculaires?
 omment démontrer que deux droites sont perpendiculaires? Utilisons On sait que (hypothèses) or...(propriété, définition) donc...(conclusion) Réciproque de Pythagore,5 1,5 = + Si dans un triangle le carré
omment démontrer que deux droites sont perpendiculaires? Utilisons On sait que (hypothèses) or...(propriété, définition) donc...(conclusion) Réciproque de Pythagore,5 1,5 = + Si dans un triangle le carré
C0nstruire une mais0n. Sommaire
 Sommaire Page 2 : Le terrain Page 3 : Les raccordements Page 4 : Les fondations Page 5 : La chape Page 6 : Les murs Page 8 : Les planchers Page 9 : Le toit Page 10 : La charpente Page 12 : Les tuiles C0nstruire
Sommaire Page 2 : Le terrain Page 3 : Les raccordements Page 4 : Les fondations Page 5 : La chape Page 6 : Les murs Page 8 : Les planchers Page 9 : Le toit Page 10 : La charpente Page 12 : Les tuiles C0nstruire
Priorités de calcul :
 EXERCICES DE REVISION POUR LE PASSAGE EN QUATRIEME : Priorités de calcul : Exercice 1 : Calcule en détaillant : A = 4 + 5 6 + 7 B = 6 3 + 5 C = 35 5 3 D = 6 7 + 8 E = 38 6 3 + 7 Exercice : Calcule en détaillant
EXERCICES DE REVISION POUR LE PASSAGE EN QUATRIEME : Priorités de calcul : Exercice 1 : Calcule en détaillant : A = 4 + 5 6 + 7 B = 6 3 + 5 C = 35 5 3 D = 6 7 + 8 E = 38 6 3 + 7 Exercice : Calcule en détaillant
Nom : Groupe : Date : 1. Quels sont les deux types de dessins les plus utilisés en technologie?
 Nom : Groupe : Date : Verdict Chapitre 11 1 La communication graphique Pages 336 et 337 1. Quels sont les deux types de dessins les plus utilisés en technologie? Les dessins de fabrication. Les schémas.
Nom : Groupe : Date : Verdict Chapitre 11 1 La communication graphique Pages 336 et 337 1. Quels sont les deux types de dessins les plus utilisés en technologie? Les dessins de fabrication. Les schémas.
1 Création d une pièce. 2 Travail complémentaire. 1-1 Réglage des barres d outils. 1-2 Exemples de réalisation de pièces à l aide d un modeleur 3D
 SolidWorks Logiciel de DAO (Dessin Assisté par Ordinateur) Palonnier Servomoteur SOMMAIRE : 1 Création d une pièce 1-1 Réglage des barres d outils 1-2 Exemples de réalisation de pièces à l aide d un modeleur
SolidWorks Logiciel de DAO (Dessin Assisté par Ordinateur) Palonnier Servomoteur SOMMAIRE : 1 Création d une pièce 1-1 Réglage des barres d outils 1-2 Exemples de réalisation de pièces à l aide d un modeleur
Si un quadrilatère a. Si un quadrilatère a. Si un quadrilatère a. Si un quadrilatère a. ses côtés opposés. ses côtés opposés de. deux côtés opposés
 P1 P2 P3 P4 a a a a ses côtés opposés ses côtés opposés de deux côtés opposés ses diagonales qui se parallèles, alors c est même longueur alors parallèles et de même coupent en leur un c est un longueur
P1 P2 P3 P4 a a a a ses côtés opposés ses côtés opposés de deux côtés opposés ses diagonales qui se parallèles, alors c est même longueur alors parallèles et de même coupent en leur un c est un longueur
Mathématiques et petites voitures
 Mathématiques et petites voitures Thomas Lefebvre 10 avril 2015 Résumé Ce document présente diérentes applications des mathématiques dans le domaine du slot-racing. Table des matières 1 Périmètre et circuit
Mathématiques et petites voitures Thomas Lefebvre 10 avril 2015 Résumé Ce document présente diérentes applications des mathématiques dans le domaine du slot-racing. Table des matières 1 Périmètre et circuit
TBI et mathématique. Pour vous soutenir dans votre enseignement des mathématiques. Les outils du logiciel Notebook. les ressources internet
 TBI et mathématique Pour vous soutenir dans votre enseignement des mathématiques Dessin tiré du site www.recitus.qc.ca Les outils du logiciel Notebook et les ressources internet Document préparé par France
TBI et mathématique Pour vous soutenir dans votre enseignement des mathématiques Dessin tiré du site www.recitus.qc.ca Les outils du logiciel Notebook et les ressources internet Document préparé par France
Construire. Statique. Styled by Smou. SEMA France SARL: 50, avenue d Alsace F-68027 Colmar Tél. +49-8304-939-0 Fax +49-8304-939-240
 Construire Statique Styled by Smou SEMA France SARL: 50, avenue d Alsace F-68027 Colmar Tél. +49-8304-939-0 Fax +49-8304-939-240 Manuel d'application - Calcul statique -- Ferme et pannes à devers Page
Construire Statique Styled by Smou SEMA France SARL: 50, avenue d Alsace F-68027 Colmar Tél. +49-8304-939-0 Fax +49-8304-939-240 Manuel d'application - Calcul statique -- Ferme et pannes à devers Page
Ch.G3 : Distances et tangentes
 4 e - programme 2011 mathématiques ch.g3 cahier élève Page 1 sur 14 1 DISTC D U PIT À U DRIT Ch.G3 : Distances et tangentes 1.1 Définition ex 1 DÉFIITI 1 : Soit une droite et un point n'appartenant pas
4 e - programme 2011 mathématiques ch.g3 cahier élève Page 1 sur 14 1 DISTC D U PIT À U DRIT Ch.G3 : Distances et tangentes 1.1 Définition ex 1 DÉFIITI 1 : Soit une droite et un point n'appartenant pas
EVALUATIONS MI-PARCOURS CM2
 Les enseignants de CM2 de la circonscription de METZ-SUD proposent EVALUATIONS MI-PARCOURS CM2 Mathématiques Livret enseignant NOMBRES ET CALCUL Circonscription de METZ-SUD Page 1 Séquence 1 : Exercice
Les enseignants de CM2 de la circonscription de METZ-SUD proposent EVALUATIONS MI-PARCOURS CM2 Mathématiques Livret enseignant NOMBRES ET CALCUL Circonscription de METZ-SUD Page 1 Séquence 1 : Exercice
Deux disques dans un carré
 Deux disques dans un carré Table des matières 1 Fiche résumé 2 2 Fiche élève Seconde - version 1 3 2.1 Le problème............................................... 3 2.2 Construction de la figure avec geogebra...............................
Deux disques dans un carré Table des matières 1 Fiche résumé 2 2 Fiche élève Seconde - version 1 3 2.1 Le problème............................................... 3 2.2 Construction de la figure avec geogebra...............................
Savoir lire une carte, se situer et s orienter en randonnée
 Savoir lire une carte, se situer et s orienter en randonnée Le b.a.-ba du randonneur Fiche 2 Lire une carte topographique Mais c est où le nord? Quel Nord Le magnétisme terrestre attire systématiquement
Savoir lire une carte, se situer et s orienter en randonnée Le b.a.-ba du randonneur Fiche 2 Lire une carte topographique Mais c est où le nord? Quel Nord Le magnétisme terrestre attire systématiquement
Prêt(e) pour le CE1. Tu es maintenant au CE1. Avant de commencer les leçons, nous allons réviser avec toi!
 Jour Prêt(e) pour le CE Tu es maintenant au CE. vant de commencer les leçons, nous allons réviser avec toi! Géométrie Retrouver un itinéraire en tenant compte des informations. Lis les explications de
Jour Prêt(e) pour le CE Tu es maintenant au CE. vant de commencer les leçons, nous allons réviser avec toi! Géométrie Retrouver un itinéraire en tenant compte des informations. Lis les explications de
5 ème Chapitre 4 Triangles
 5 ème Chapitre 4 Triangles 1) Médiatrices Définition : la médiatrice d'un segment est l'ensemble des points équidistants des extrémités du segment (cours de 6 ème ). Si M appartient à la médiatrice du
5 ème Chapitre 4 Triangles 1) Médiatrices Définition : la médiatrice d'un segment est l'ensemble des points équidistants des extrémités du segment (cours de 6 ème ). Si M appartient à la médiatrice du
Muret Laurentien MC. Classique et Versatile
 Muret Laurentien MC Classique et Versatile Le muret Laurentien par son look classique s agence à toutes nos gammes de pavé. Qualités et caractéristiques Intégration particulièrement harmonieuse du muret
Muret Laurentien MC Classique et Versatile Le muret Laurentien par son look classique s agence à toutes nos gammes de pavé. Qualités et caractéristiques Intégration particulièrement harmonieuse du muret
COMPTE-RENDU «MATHS EN JEANS» LYCEE OZENNE Groupe 1 : Comment faire une carte juste de la Terre?
 Claire FORGACZ Marion GALLART Hasnia GOUDJILI COMPTERENDU «MATHS EN JEANS» LYCEE OZENNE Groupe 1 : Comment faire une carte juste de la Terre? Si l on se pose la question de savoir comment on peut faire
Claire FORGACZ Marion GALLART Hasnia GOUDJILI COMPTERENDU «MATHS EN JEANS» LYCEE OZENNE Groupe 1 : Comment faire une carte juste de la Terre? Si l on se pose la question de savoir comment on peut faire
Championnat de France de Grilles Logiques Finale 7 juin 2014. Livret d'instructions
 Championnat de France de Grilles Logiques Finale 7 juin 0 Livret d'instructions Épreuve Thème Horaires Durée Points Déjà vu? h h minutes 0 Medley international h h 0 minutes 00 Futur proche? h h0 minutes
Championnat de France de Grilles Logiques Finale 7 juin 0 Livret d'instructions Épreuve Thème Horaires Durée Points Déjà vu? h h minutes 0 Medley international h h 0 minutes 00 Futur proche? h h0 minutes
Ecran : Processeur : OS : Caméra : Communication : Mémoire : Connectique : Audio : Batterie : Autonomie : Dimensions : Poids : DAS :
 SMARTPHONE - DUAL-CORE - NOIR 3483072425242 SMARTPHONE - DUAL-CORE - BLEU XXXX SMARTPHONE - DUAL-CORE - BLANC 3483072485246 SMARTPHONE - DUAL-CORE - ROSE 3483073704131 SMARTPHONE - DUAL-CORE - ROUGE XXXX
SMARTPHONE - DUAL-CORE - NOIR 3483072425242 SMARTPHONE - DUAL-CORE - BLEU XXXX SMARTPHONE - DUAL-CORE - BLANC 3483072485246 SMARTPHONE - DUAL-CORE - ROSE 3483073704131 SMARTPHONE - DUAL-CORE - ROUGE XXXX
AGASC / BUREAU INFORMATION JEUNESSE 06700 Saint Laurent du Var Tel : 04.93.07.00.66 [email protected] www.agasc.fr. Word: Les tableaux.
 Word: Les tableaux Introduction 6 ième partie Il est préférable par moments de présenter de l'information sous forme de tableau. Les instructions qui suivent démontrent comment créer un tableau et comment
Word: Les tableaux Introduction 6 ième partie Il est préférable par moments de présenter de l'information sous forme de tableau. Les instructions qui suivent démontrent comment créer un tableau et comment
LA CHARPENTE. Les principales pièces des charpentes traditionnelles
 Les principales pièces des charpentes traditionnelles La charpente (fig. 5.1 et 5.2) : ensemble de pièces en bois qui portent la couverture. Les charpentes présentent diverses formes et différentes pentes
Les principales pièces des charpentes traditionnelles La charpente (fig. 5.1 et 5.2) : ensemble de pièces en bois qui portent la couverture. Les charpentes présentent diverses formes et différentes pentes
PARTIE NUMERIQUE (18 points)
 4 ème DEVOIR COMMUN N 1 DE MATHÉMATIQUES 14/12/09 L'échange de matériel entre élèves et l'usage de la calculatrice sont interdits. Il sera tenu compte du soin et de la présentation ( 4 points ). Le barème
4 ème DEVOIR COMMUN N 1 DE MATHÉMATIQUES 14/12/09 L'échange de matériel entre élèves et l'usage de la calculatrice sont interdits. Il sera tenu compte du soin et de la présentation ( 4 points ). Le barème
Opérations de base sur ImageJ
 Opérations de base sur ImageJ TPs d hydrodynamique de l ESPCI, J. Bico, M. Reyssat, M. Fermigier ImageJ est un logiciel libre, qui fonctionne aussi bien sous plate-forme Windows, Mac ou Linux. Initialement
Opérations de base sur ImageJ TPs d hydrodynamique de l ESPCI, J. Bico, M. Reyssat, M. Fermigier ImageJ est un logiciel libre, qui fonctionne aussi bien sous plate-forme Windows, Mac ou Linux. Initialement
Sommaire. Aide Page 1
 Aide Page 1 Sommaire Objectif du logiciel............ 2 Présentation................ 2 Créer un nouveau quadrillage... 3 Démarrer un nouveau plan..... 3 Sélectionner une ligne......... 3 Insérer une nouvelle
Aide Page 1 Sommaire Objectif du logiciel............ 2 Présentation................ 2 Créer un nouveau quadrillage... 3 Démarrer un nouveau plan..... 3 Sélectionner une ligne......... 3 Insérer une nouvelle
PROTECTIONS COLLECTIVES
 PROTECTIONS COLLECTIVES SOMMAIRE PROTECTIONS COLLECTIVES DE RIVES ET TOITURES presse rapide et ses consoles, protections avec poteaux, protection de rive par traversée de mur 3 CONSOLES POUR PLANCHERS
PROTECTIONS COLLECTIVES SOMMAIRE PROTECTIONS COLLECTIVES DE RIVES ET TOITURES presse rapide et ses consoles, protections avec poteaux, protection de rive par traversée de mur 3 CONSOLES POUR PLANCHERS
Comment réaliser une capture d écran dans Word. Alors comment ouvrir une page Word?
 Comment réaliser une capture d écran dans Word Pour réaliser une capture d écran dans Word, l idéal est d ouvrir d abord la page Word. Mais on peut bien l ouvrir après la capture d écran. Alors comment
Comment réaliser une capture d écran dans Word Pour réaliser une capture d écran dans Word, l idéal est d ouvrir d abord la page Word. Mais on peut bien l ouvrir après la capture d écran. Alors comment
GLOSSAIRE DU BÉTON ARMÉ
 GLOSSAIRE DU BÉTON ARMÉ Accessoires Articles, à l'exception des barres d'armature; par exemple, les supports de barre. Adhérence Force de liaison entre l'acier d'armature et le béton. Armature en cisaillement
GLOSSAIRE DU BÉTON ARMÉ Accessoires Articles, à l'exception des barres d'armature; par exemple, les supports de barre. Adhérence Force de liaison entre l'acier d'armature et le béton. Armature en cisaillement
AGORA 2014 Appel à idées Habiter les toits à Bordeaux Et pour compléter
 AGORA 2014 Appel à idées Habiter les toits à Bordeaux Et pour compléter 1 SOMMAIRE Vues générales des toits 3 Type de charpentes, de la plus simple à la plus sophistiquée quelques coupes transversales
AGORA 2014 Appel à idées Habiter les toits à Bordeaux Et pour compléter 1 SOMMAIRE Vues générales des toits 3 Type de charpentes, de la plus simple à la plus sophistiquée quelques coupes transversales
1 Définition. 2 Systèmes matériels et solides. 3 Les actions mécaniques. Le système matériel : Il peut être un ensemble.un sous-ensemble..
 1 Définition GÉNÉRALITÉS Statique 1 2 Systèmes matériels et solides Le système matériel : Il peut être un ensemble.un sous-ensemble..une pièce mais aussi un liquide ou un gaz Le solide : Il est supposé
1 Définition GÉNÉRALITÉS Statique 1 2 Systèmes matériels et solides Le système matériel : Il peut être un ensemble.un sous-ensemble..une pièce mais aussi un liquide ou un gaz Le solide : Il est supposé
Mise en scène d un modèle dans l espace 3D
 CHAPITRE 3 Mise en scène d un modèle dans l espace 3D Blender permet de construire des espaces à la manière d une scène de théâtre. Pour cela, il présente dès l ouverture tout ce dont on a besoin : un
CHAPITRE 3 Mise en scène d un modèle dans l espace 3D Blender permet de construire des espaces à la manière d une scène de théâtre. Pour cela, il présente dès l ouverture tout ce dont on a besoin : un
Catalogue de location
 Catalogue de location 514-523-2211 1-877-677-2211 2600, William-Tremblay, suite 128 Montréal (QC) H1Y 3J2 location Nous disposons de près d un millier de pièces en location pour vos projets temporaires
Catalogue de location 514-523-2211 1-877-677-2211 2600, William-Tremblay, suite 128 Montréal (QC) H1Y 3J2 location Nous disposons de près d un millier de pièces en location pour vos projets temporaires
Dans l idéal, ceci devrait être fait en amont pour chaque image envoyée sur l espace de stockage de votre site internet.
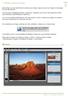 1- Optimiser le poids de votre image : Dans l idéal, ceci devrait être fait en amont pour chaque image envoyée sur l espace de stockage de votre site internet. Tous les types d utilisateurs (auteur, publicateur,
1- Optimiser le poids de votre image : Dans l idéal, ceci devrait être fait en amont pour chaque image envoyée sur l espace de stockage de votre site internet. Tous les types d utilisateurs (auteur, publicateur,
Utilisation du logiciel GALAAD
 1 Sommaire: Présentation du logiciel GALAAD 1. Démarrer le programme........ 2. Présentation de l écran du logiciel....... Les barres d'outils, sauvegarder... 3. Créer un nouveau fichier........ 4. Préparer
1 Sommaire: Présentation du logiciel GALAAD 1. Démarrer le programme........ 2. Présentation de l écran du logiciel....... Les barres d'outils, sauvegarder... 3. Créer un nouveau fichier........ 4. Préparer
COMFORTLIFT TWO LE PLUS COMPACT ET LE PLUS FACILE D'UTILISATION
 0800 20 950 www.comfortlift.be COMFORTLIFT TWO LE PLUS COMPACT ET LE PLUS FACILE D'UTILISATION www.comfortlift.be COMFORTLIFT TWO Le monte-escalier double rail Ce que vous remarquez en premier est que
0800 20 950 www.comfortlift.be COMFORTLIFT TWO LE PLUS COMPACT ET LE PLUS FACILE D'UTILISATION www.comfortlift.be COMFORTLIFT TWO Le monte-escalier double rail Ce que vous remarquez en premier est que
6 ème. Rallye mathématique de la Sarthe 2013/2014. 1 ère épreuve de qualification : Problèmes Jeudi 21 novembre 2013
 Retrouver tous les sujets, les corrigés, les annales, les finales sur le site du rallye : http://sarthe.cijm.org I Stéphane, Eric et Christophe sont 3 garçons avec des chevelures différentes. Stéphane
Retrouver tous les sujets, les corrigés, les annales, les finales sur le site du rallye : http://sarthe.cijm.org I Stéphane, Eric et Christophe sont 3 garçons avec des chevelures différentes. Stéphane
Maîtriser les fonctionnalités d un traitement de texte (Word OpenOffice)
 Utilisation de l'ordinateur et apport des TIC en enseignement (1NP) Module 03 Maîtriser les fonctionnalités d un traitement de texte. Sens du Module De nombreux documents remis aux enfants sont réalisés
Utilisation de l'ordinateur et apport des TIC en enseignement (1NP) Module 03 Maîtriser les fonctionnalités d un traitement de texte. Sens du Module De nombreux documents remis aux enfants sont réalisés
Prénom : MATHÉMATIQUES. 120 minutes Compas, règle métrique, rapporteur, équerre, calculatrice non programmable
 Admission en 8 VSG 8 VSB cocher la voie visée MATHÉMATIQUES Durée Matériel à disposition 120 minutes Compas, règle métrique, rapporteur, équerre, calculatrice non programmable Rappel des objectifs fondamentaux
Admission en 8 VSG 8 VSB cocher la voie visée MATHÉMATIQUES Durée Matériel à disposition 120 minutes Compas, règle métrique, rapporteur, équerre, calculatrice non programmable Rappel des objectifs fondamentaux
Fiche Technique d Évaluation sismique : Construction basse en Maçonnerie Non-armée, Chaînée, ou de Remplissage en Haïti
 .0 RISQUES GEOLOGIQUES DU SITE NOTES. LIQUÉFACTION : On ne doit pas trouver de sols granulaires liquéfiables, lâches, saturés, ou qui pourraient compromettre la performance sismique du bâtiment, dans des
.0 RISQUES GEOLOGIQUES DU SITE NOTES. LIQUÉFACTION : On ne doit pas trouver de sols granulaires liquéfiables, lâches, saturés, ou qui pourraient compromettre la performance sismique du bâtiment, dans des
Plus petit, plus grand, ranger et comparer
 Unité 11 Plus petit, plus grand, ranger et comparer Combien y a-t-il de boules sur la tige A? Sur la tige B? A B Le nombre de boules sur la tige A est plus grand que sur la tige B. On écrit : > 2 On lit
Unité 11 Plus petit, plus grand, ranger et comparer Combien y a-t-il de boules sur la tige A? Sur la tige B? A B Le nombre de boules sur la tige A est plus grand que sur la tige B. On écrit : > 2 On lit
TUTORIEL IMPRESS. Ouvrir Impress cocher «présentation vierge», «suivant» cocher «écran», «suivant» cocher «standard», «créer»
 TUTORIEL IMPRESS Ouvrir Impress cocher «présentation vierge», «suivant» cocher «écran», «suivant» cocher «standard», «créer» Une page impress s'ouvre : Le volet gauche contiendra toutes les diapositives
TUTORIEL IMPRESS Ouvrir Impress cocher «présentation vierge», «suivant» cocher «écran», «suivant» cocher «standard», «créer» Une page impress s'ouvre : Le volet gauche contiendra toutes les diapositives
2013 Pearson France Photoshop Elements 12 pour les photographes du numérique Loïc Olive
 améliorer les PhOtOs L amélioration d une photo passe quasiment toujours par les mêmes étapes. On commence par la redresser, puis on s attelle à corriger ses dominantes de couleurs et sa tonalité. Vient
améliorer les PhOtOs L amélioration d une photo passe quasiment toujours par les mêmes étapes. On commence par la redresser, puis on s attelle à corriger ses dominantes de couleurs et sa tonalité. Vient
Les Angles. I) Angles complémentaires, angles supplémentaires. 1) Angles complémentaires. 2 Angles supplémentaires. a) Définition.
 Les Angles I) Angles complémentaires, angles supplémentaires 1) Angles complémentaires Deux angles complémentaires sont deux angles dont la somme des mesures est égale à 90 41 et 49 41 49 90 donc Les angles
Les Angles I) Angles complémentaires, angles supplémentaires 1) Angles complémentaires Deux angles complémentaires sont deux angles dont la somme des mesures est égale à 90 41 et 49 41 49 90 donc Les angles
Une brique dans le cartable. Du Plan à l Ouvrage
 Une brique dans le cartable Du Plan à l Ouvrage Une brique dans le cartable Du plan à l ouvrage Visites et rencontres possibles - Rencontre avec un architecte o Voir la création des plans (orientation
Une brique dans le cartable Du Plan à l Ouvrage Une brique dans le cartable Du plan à l ouvrage Visites et rencontres possibles - Rencontre avec un architecte o Voir la création des plans (orientation
La médiatrice d un segment
 EXTRT DE CURS DE THS DE 4E 1 La médiatrice d un segment, la bissectrice d un angle La médiatrice d un segment Définition : La médiatrice d un segment est l ae de smétrie de ce segment ; c'est-à-dire que
EXTRT DE CURS DE THS DE 4E 1 La médiatrice d un segment, la bissectrice d un angle La médiatrice d un segment Définition : La médiatrice d un segment est l ae de smétrie de ce segment ; c'est-à-dire que
Les calques : techniques avancées
 Les calques : techniques avancées 9 Au cours de cette leçon, vous apprendrez à : importer un calque d un autre fichier ; créer un masque d écrêtage ; créer et modifier un calque de réglage ; employer les
Les calques : techniques avancées 9 Au cours de cette leçon, vous apprendrez à : importer un calque d un autre fichier ; créer un masque d écrêtage ; créer et modifier un calque de réglage ; employer les
TABLE DES MATIÈRES. 1- Historique... 1. 2- Types de ventilateurs et leurs différents usages... 1
 LA VENTILATION DES COUVERTURES 01-01-1998 TABLE DES MATIÈRES Page 1- Historique... 1 2- Types de ventilateurs et leurs différents usages... 1 3- Recommandations et investigations avant réfection... 3 4-
LA VENTILATION DES COUVERTURES 01-01-1998 TABLE DES MATIÈRES Page 1- Historique... 1 2- Types de ventilateurs et leurs différents usages... 1 3- Recommandations et investigations avant réfection... 3 4-
FÊTE DE LA SCIENCE 2005 (Village des Sciences)
 FÊTE DE LA SCIENCE 2005 (Village des Sciences) Présentation des applications de réalité virtuelle et augmentée présentées par le Laboratoire LISA les samedi 15 et dimanche 16 octobre 2005 à l Ecole Supérieure
FÊTE DE LA SCIENCE 2005 (Village des Sciences) Présentation des applications de réalité virtuelle et augmentée présentées par le Laboratoire LISA les samedi 15 et dimanche 16 octobre 2005 à l Ecole Supérieure
PROGRAMME CARÉA. Guide d utilisation : pages 4 et 5 Index technique (sur demande)
 Structures plaquées hêtre naturel verni satiné de 44 mm d'épaisseur, montées sur vérins. Un double face s'obtient par l'assemblage dos à dos de 2 simples faces. La pièce en métal qui les relie sert aussi
Structures plaquées hêtre naturel verni satiné de 44 mm d'épaisseur, montées sur vérins. Un double face s'obtient par l'assemblage dos à dos de 2 simples faces. La pièce en métal qui les relie sert aussi
Structure du format BMP, sa lecture, sa construction et son écriture
 Structure du format BMP, sa lecture, sa construction et son écriture Claude Parisel Mars 2003 Table des matières : 1. Le choix du format 2. Commentaires sur les autres formats 3. Format BMP pour noir&blanc,
Structure du format BMP, sa lecture, sa construction et son écriture Claude Parisel Mars 2003 Table des matières : 1. Le choix du format 2. Commentaires sur les autres formats 3. Format BMP pour noir&blanc,
Sommaire Table des matières
 Notice de montage 1 Sommaire Table des matières I. Mise en garde... 3 II. Avant de commencer... 4 1. Préparer vos outils... 4 2. Pièces nécessaires pour le montage de votre porte Keritek... 5 III. Étape
Notice de montage 1 Sommaire Table des matières I. Mise en garde... 3 II. Avant de commencer... 4 1. Préparer vos outils... 4 2. Pièces nécessaires pour le montage de votre porte Keritek... 5 III. Étape
SEMA France S.A.R.L. 50 Avenue d'alsace F-68027 COLMAR Tél.: 0033-243-091-092 Fax : 0033-243-091-093
 Planifier Construire Styled by Smou SEMA France S.A.R.L. 50 Avenue d'alsace F-68027 COLMAR Tél.: 0033-243-091-092 Fax : 0033-243-091-093 SEMA GmbH Allemagne Dorfmühlstraße 7-11 87499 Wildpoldsried Telefon
Planifier Construire Styled by Smou SEMA France S.A.R.L. 50 Avenue d'alsace F-68027 COLMAR Tél.: 0033-243-091-092 Fax : 0033-243-091-093 SEMA GmbH Allemagne Dorfmühlstraße 7-11 87499 Wildpoldsried Telefon
TP Blender n 2 : Importation d un modèle SketchUp et animation
 TP Blender n 2 : Importation d un modèle SketchUp et animation Service de Conception Géométrique Université de Liège Aérospatiale et Mécanique Conçu avec Blender 2.66 et SketchUp 8 De SketchUp à Blender
TP Blender n 2 : Importation d un modèle SketchUp et animation Service de Conception Géométrique Université de Liège Aérospatiale et Mécanique Conçu avec Blender 2.66 et SketchUp 8 De SketchUp à Blender
FONTANOT CREE UNE LIGNE D ESCALIERS IMAGINÉE POUR CEUX QUI AIMENT LE BRICOLAGE.
 STILE FONTANOT CREE UNE LIGNE D ESCALIERS IMAGINÉE POUR CEUX QUI AIMENT LE BRICOLAGE. 2 3 Magia. Une gamme de produits qui facilitera le choix de votre escalier idéal. 4 06 Guide pour la sélection. 16
STILE FONTANOT CREE UNE LIGNE D ESCALIERS IMAGINÉE POUR CEUX QUI AIMENT LE BRICOLAGE. 2 3 Magia. Une gamme de produits qui facilitera le choix de votre escalier idéal. 4 06 Guide pour la sélection. 16
ÉVALUATION EN FIN DE CM1. Année scolaire 2014 2015 LIVRET DE L'ÉLÈVE MATHÉMATIQUES
 ÉVALUATION EN FIN DE CM1 Année scolaire 2014 2015 LIVRET DE L'ÉLÈVE MATHÉMATIQUES NOM :....... Prénom :....... Né le :./../ École :............ Classe : Domaine Score de réussite NOMBRES ET CALCUL GÉOMÉTRIE
ÉVALUATION EN FIN DE CM1 Année scolaire 2014 2015 LIVRET DE L'ÉLÈVE MATHÉMATIQUES NOM :....... Prénom :....... Né le :./../ École :............ Classe : Domaine Score de réussite NOMBRES ET CALCUL GÉOMÉTRIE
KompoZer. Composition du site : _ une page d'accueil : index.html. _ une page pour la théorie : theorie.html. _ une page pour les photos : photos.
 KompoZer Créer un site «simple» Composition du site : _ une page d'accueil : index.html _ une page pour la théorie : theorie.html _ une page pour les photos : photos.html _ une page avec la galerie : galerie.html
KompoZer Créer un site «simple» Composition du site : _ une page d'accueil : index.html _ une page pour la théorie : theorie.html _ une page pour les photos : photos.html _ une page avec la galerie : galerie.html
Les droites (d 1 ) et (d 2 ) sont sécantes en A Le point A est le point d intersection des 2 droites
 I Droites perpendiculaires Lorsque deux droites se coupent, on dit qu elles sont sécantes Les droites (d 1 ) et (d 2 ) sont sécantes en A Le point A est le point d intersection des 2 droites Lorsque deux
I Droites perpendiculaires Lorsque deux droites se coupent, on dit qu elles sont sécantes Les droites (d 1 ) et (d 2 ) sont sécantes en A Le point A est le point d intersection des 2 droites Lorsque deux
Corrigé du baccalauréat S Pondichéry 12 avril 2007
 Corrigé du baccalauréat S Pondichéry 1 avril 7 EXERCICE 1 Commun à tous les candidats 4 points 1 a Les vecteurs AB et AC ont pour coordonnées AB ; ; ) et AC 1 ; 4 ; 1) Ils ne sont manifestement pas colinéaires
Corrigé du baccalauréat S Pondichéry 1 avril 7 EXERCICE 1 Commun à tous les candidats 4 points 1 a Les vecteurs AB et AC ont pour coordonnées AB ; ; ) et AC 1 ; 4 ; 1) Ils ne sont manifestement pas colinéaires
Initiation au dessin Bitmap
 Sébastien Stasse Initiation au dessin Bitmap Guide d apprentissage et notions de base 2e édition Nom : Classe : Produit par l École Alex Manoogian AW version 6 Initiation au dessin bitmap Initiation au
Sébastien Stasse Initiation au dessin Bitmap Guide d apprentissage et notions de base 2e édition Nom : Classe : Produit par l École Alex Manoogian AW version 6 Initiation au dessin bitmap Initiation au
2013 Pearson France Adobe Illustrator CC Adobe Press
 Au cours de cette démonstration d Adobe Illustrator CC, vous découvrirez les nouvelles fonctionnalités du logiciel, comme les outils de retouche et la sélection du texte, ainsi que d autres aspects fondamentaux
Au cours de cette démonstration d Adobe Illustrator CC, vous découvrirez les nouvelles fonctionnalités du logiciel, comme les outils de retouche et la sélection du texte, ainsi que d autres aspects fondamentaux
EVALUATIONS FIN CM1. Mathématiques. Livret élève
 Les enseignants de CM1 de la circonscription de METZ-SUD proposent EVALUATIONS FIN CM1 Mathématiques Livret élève Circonscription de METZ-SUD page 1 NOMBRES ET CALCUL Exercice 1 : Écris en chiffres les
Les enseignants de CM1 de la circonscription de METZ-SUD proposent EVALUATIONS FIN CM1 Mathématiques Livret élève Circonscription de METZ-SUD page 1 NOMBRES ET CALCUL Exercice 1 : Écris en chiffres les
Trois personnes mangent dans un restaurant. Le serveur
 29=30 Trois personnes mangent dans un restaurant. Le serveur leur amène une addition de 30 francs. Les trois personnes décident de partager la facture en trois, soit 10 francs chacun. Le serveur rapporte
29=30 Trois personnes mangent dans un restaurant. Le serveur leur amène une addition de 30 francs. Les trois personnes décident de partager la facture en trois, soit 10 francs chacun. Le serveur rapporte
DIFFRACTion des ondes
 DIFFRACTion des ondes I DIFFRACTION DES ONDES PAR LA CUVE À ONDES Lorsqu'une onde plane traverse un trou, elle se transforme en onde circulaire. On dit que l'onde plane est diffractée par le trou. Ce phénomène
DIFFRACTion des ondes I DIFFRACTION DES ONDES PAR LA CUVE À ONDES Lorsqu'une onde plane traverse un trou, elle se transforme en onde circulaire. On dit que l'onde plane est diffractée par le trou. Ce phénomène
4. Exercices et corrigés
 4. Exercices et corrigés. N 28p.304 Dans une classe de 3 élèves, le club théâtre (T) compte 0 élèves et la chorale (C) 2 élèves. Dix-huit élèves ne participent à aucune de ces activités. On interroge au
4. Exercices et corrigés. N 28p.304 Dans une classe de 3 élèves, le club théâtre (T) compte 0 élèves et la chorale (C) 2 élèves. Dix-huit élèves ne participent à aucune de ces activités. On interroge au
My Custom Design ver.1.0
 My Custom Design ver.1.0 Logiciel de création de données de broderie Mode d emploi Avant d utiliser ce logiciel, veuillez lire attentivement ce mode d emploi pour bien l utiliser correctement. Conservez
My Custom Design ver.1.0 Logiciel de création de données de broderie Mode d emploi Avant d utiliser ce logiciel, veuillez lire attentivement ce mode d emploi pour bien l utiliser correctement. Conservez
315 et 495 sont dans la table de 5. 5 est un diviseur commun. Leur PGCD n est pas 1. Il ne sont pas premiers entre eux
 Exercice 1 : (3 points) Un sac contient 10 boules rouges, 6 boules noires et 4 boules jaunes. Chacune des boules a la même probabilité d'être tirée. On tire une boule au hasard. 1. Calculer la probabilité
Exercice 1 : (3 points) Un sac contient 10 boules rouges, 6 boules noires et 4 boules jaunes. Chacune des boules a la même probabilité d'être tirée. On tire une boule au hasard. 1. Calculer la probabilité
Enoncé et corrigé du brevet des collèges dans les académies d Aix- Marseille, Montpellier, Nice Corse et Toulouse en 2000. Énoncé.
 Enoncé et corrigé du brevet des collèges dans les académies d Aix- Marseille, Montpellier, Nice Corse et Toulouse en 2000. Énoncé. I- ACTIVITES NUMERIQUES (12 points) Exercice 1 (3 points) On considère
Enoncé et corrigé du brevet des collèges dans les académies d Aix- Marseille, Montpellier, Nice Corse et Toulouse en 2000. Énoncé. I- ACTIVITES NUMERIQUES (12 points) Exercice 1 (3 points) On considère
C.F.A.O. : Conception et Fabrication Assistées par Ordinateur.
 C.F.A.O. : Conception et Fabrication Assistées par Ordinateur. La CFAO réunit dans une même démarche informatique les actions de conception et de fabrication d un objet. La technique utilisée permet à
C.F.A.O. : Conception et Fabrication Assistées par Ordinateur. La CFAO réunit dans une même démarche informatique les actions de conception et de fabrication d un objet. La technique utilisée permet à
Charte Graphique Caisse d Epargne Rhône Alpes
 Charte Graphique Caisse d Epargne Rhône Alpes 1. Les éléments de base du logotype Groupe Caisse d Epargne A. LE LOGOTYPE - VERSION HORIZONTALE La version quadrichromie Les couleurs La version monochrome
Charte Graphique Caisse d Epargne Rhône Alpes 1. Les éléments de base du logotype Groupe Caisse d Epargne A. LE LOGOTYPE - VERSION HORIZONTALE La version quadrichromie Les couleurs La version monochrome
Indications pour une progression au CM1 et au CM2
 Indications pour une progression au CM1 et au CM2 Objectif 1 Construire et utiliser de nouveaux nombres, plus précis que les entiers naturels pour mesurer les grandeurs continues. Introduction : Découvrir
Indications pour une progression au CM1 et au CM2 Objectif 1 Construire et utiliser de nouveaux nombres, plus précis que les entiers naturels pour mesurer les grandeurs continues. Introduction : Découvrir
OFPPT ROYAUME DU MAROC RESUME THEORIQUE & GUIDE DE TRAVAUX PRATIQUES APPLICATIONS DE DESSIN ASSISTE PAR ORDINATEUR MODULE N 9: :BTP SECTEUR
 OFPPT ROYAUME DU MAROC Office de la Formation Professionnelle et de la Promotion du Travail DIRECTION RECHERCHE ET INGENIERIE DE FORMATION RESUME THEORIQUE & GUIDE DE TRAVAUX PRATIQUES MODULE N 9: SECTEUR
OFPPT ROYAUME DU MAROC Office de la Formation Professionnelle et de la Promotion du Travail DIRECTION RECHERCHE ET INGENIERIE DE FORMATION RESUME THEORIQUE & GUIDE DE TRAVAUX PRATIQUES MODULE N 9: SECTEUR
CHARPENTE - COUVERTURE
 CHARPENTE - COUVERTURE TERMINOLOGIE GÉNÉRALE TERMINOLOGIE GÉNÉRALE CHARPENTE COUVERTURE CHARPENTE - COUVERTURE TERMINOLOGIE : LES TOITURES... 1.Rampant (ou versant, ou long pan) 2.Longueur ou rampant 3.Projection
CHARPENTE - COUVERTURE TERMINOLOGIE GÉNÉRALE TERMINOLOGIE GÉNÉRALE CHARPENTE COUVERTURE CHARPENTE - COUVERTURE TERMINOLOGIE : LES TOITURES... 1.Rampant (ou versant, ou long pan) 2.Longueur ou rampant 3.Projection
Du Premier au Second Degré
 Du Premier au Second Degré Première Bac Pro 3 ans November 26, 2011 Première Bac Pro 3 ans Du Premier au Second Degré Sommaire 1 Fonction Polynôme du second degré 2 Fonction Polynôme du Second Degré: Synthèse
Du Premier au Second Degré Première Bac Pro 3 ans November 26, 2011 Première Bac Pro 3 ans Du Premier au Second Degré Sommaire 1 Fonction Polynôme du second degré 2 Fonction Polynôme du Second Degré: Synthèse
PR OC E D U RE S D E B A S E
 Photofiltre Préparé par Philipe Lampron, auxiliaire du cours FPE 7650 en 2004-2005. *** Pour optimiser une image : enregistrer sous et augmenter la compression PR OC E D U RE S D E B A S E PhotoFiltre
Photofiltre Préparé par Philipe Lampron, auxiliaire du cours FPE 7650 en 2004-2005. *** Pour optimiser une image : enregistrer sous et augmenter la compression PR OC E D U RE S D E B A S E PhotoFiltre
Jean Dubuffet AUTOPORTRAIT II - 1966
 Jean Dubuffet AUTOPORTRAIT II - 1966 MON VISAGE A LA MANIERE DE JEAN DUBUFFET OBJECTIFS - utiliser son expérience sensorielle visuelle pour produire une œuvre picturale. - réaliser une œuvre s'inspirant
Jean Dubuffet AUTOPORTRAIT II - 1966 MON VISAGE A LA MANIERE DE JEAN DUBUFFET OBJECTIFS - utiliser son expérience sensorielle visuelle pour produire une œuvre picturale. - réaliser une œuvre s'inspirant
