1 Premiers pas avec Xcas
|
|
|
- Nicole Bibeau
- il y a 10 ans
- Total affichages :
Transcription
1 L2- mat231 TP de maths 2009/10 Ce document propose un petit guide de référence de Xcas, puis des énoncés de TP pour 6 séances de 1h30 : 1. TP1 : apprentissage de xcas 2. TP2 : écriture sous forme matricielle des problemes d algebre lineaire) 3. TP3,4 : programmation du pivot de Gauss et applications : inverse, base du noyau/de l image, 4. TP5 : polynome minimal et recherche des espaces propres 5. TP6 : codes correcteurs (peut etre donné sous forme de mini-projets?) 1 Premiers pas avec Xcas Pour télécharger Xcas, allez sur le site Pour traiter les exemples, il est conseillé d ouvrir Xcas : Sous Windows en installation locale, on clique sur l icone xcasfr du bureau. Sous Linux avec Gnome, on clique sur Xcas du menu Education. Sinon, ouvrir un terminal et taper xcas &. sur Mac, cliquez sur Xcas dans le menu Applications du Finder. Lors de la première utilisation, choisissez Xcas lorsqu on vous demande de choisir une syntaxe (sauf si vous connaissez le langage Maple). Nous donnons ici seulement le minimum de l interface à connaitre pour commencer à programmer. On consultera plutot le manuel Débuter en calcul formel ou les autres manuels (menu Aide) pour apprendre à utiliser les fonctionnalités de Xcas en calcul formel, géométrie, tableur, etc.. L interface apparaît comme suit au lancement de Xcas. Aide Numero du niveau Ligne de commande Nom de session Menu general Interrompre Fich Edit Cfg Aide CAS Tableur Graphe Geo Prg Expression Cmds Phys Scolaire Tortue Unnamed? Save Config : exact real RAD 12 xcas M STOP Kbd X 1 Mettre/enlever clavier Fermer session Configuration Clavier scientifique x y " [] {} ; π z t := (, ) i factor D I a sin a cos a tan simplify convert L Σ ln exp log10 10^ inv neg ^ % + - * / E esc b7 ctrl coller X cmds msg abc Effacer 1
2 Vous pouvez la redimensionner. De haut en bas cette interface fait apparaître : un barre de menu gris cliquable : Fich, Edit, Cfg, Aide, CAS, Tableur, Graphe, Geo,... un onglet indiquant le nom de la session, ou Unnamed si la session n a pas encore été sauvegardée, une zone de gestion de la session avec un bouton? pour ouvrir l index de l aide un bouton Save pour sauvegarder la session, un bouton Config: exact real... affichant la configuration et permettant de la modifier, un bouton STOP permettant d interrompre un calcul trop long, un bouton Kbd pour faire apparaitre un clavier ressemblant à celui d une calculatrice, qui peut faciliter vos saisies, et un bouton x pour fermer la session une zone rectangulaire blanche numérotée 1 (première ligne de commande) dans laquelle vous pouvez taper votre première commande (cliquez si nécessaire pour faire apparaitre le curseur dans cette ligne de commande) : 1+1, suivi de la touche "Entrée" ("Enter" ou "Return" selon les claviers). Le résultat apparaît au-dessous, et une nouvelle ligne de commande s ouvre, numérotée 2. Vous pouvez modifier l aspect de l interface et sauvegarder vos modifications pour les utilisations futures (menu Cfg). Vous n avez pour l instant qu à entrer des commandes dans les lignes de commandes successives. Si vous utilisez la version html de ce cours, vous pouvez copier-coller les commandes proposées depuis votre navigateur. Chaque ligne de commande saisie est exécutée par la touche "Entrée". Essayez par exemple d exécuter les commandes suivantes. 1/3+1/4 sqrt(2)^5 resoudre(x+3=1,x) 50! Toutes les commandes sont gardées en mémoire. Vous pouvez donc remonter dans l historique de votre session pour modifier des commandes antérieures. Essayez par exemple de changer les commandes précédentes en : 1/3+3/4 sqrt(5)^2 resoudre(2*x+3=0) 500! Notez que pour effacer une ligne de commande, on clique dans le numéro de niveau à gauche de la ligne de commande, qui apparait alors en surbrillance. On appuie ensuite sur la touche d effacement. On peut aussi déplacer une ligne de commande avec la souris. Le menu Edit vous permet de préparer des sessions plus élaborées qu une simple succession de commandes. Vous pouvez créer des groupes de lignes de commandes (sections), ajouter des commentaires ou fusionner des niveaux en un seul niveau. Le menu Prg contient la plupart des instructions utiles pour programmer. 2
3 2 Les objets du calcul formel 2.1 Les nombres Les nombres peuvent être exacts ou approchés. Les nombres exacts sont les constantes prédéfinies, les entiers, les fractions d entiers et plus généralement toute expression ne contenant que des entiers et des constantes, comme sqrt(2)*e^(i*pi/3). Les nombres approchés sont notés avec la notation scientifique standard : partie entière suivie du point de séparation et partie fractionnaire (éventuellement suivie de e et d un exposant). Par exemple, 2 est un entier exact, 2.0 est la version approchée du même entier ; 1/2 est un rationnel, 0.5 est la version approchée du même rationnel. Xcas peut gérer des nombres entiers en précision arbitraire : essayez de taper 500! et comptez le nombre de chiffres de la réponse. On passe d une valeur exacte à une valeur approchée par evalf, on transforme une valeur approchée en un rationnel exact par exact Les calculs sont effectués en mode exact si tous les nombres qui interviennent sont exacts. Ils sont effectués en mode approché si un des nombres est approché. Ainsi renvoie un nombre approché alors que 3/2+1 renvoie un nombre exact. sqrt(2) evalf(sqrt(2)) sqrt(2)-evalf(sqrt(2)) exact(evalf(sqrt(2)))*10^9 exact(evalf(sqrt(2)*10^9)) Pour les nombres réels approchés, la précision par défaut est proche de 14 chiffres significatifs (la précision relative est de 53 ou 45 bits pour les réels flottants normalisés selon les versions de Xcas). Elle peut être augmentée, en donnant le nombre de décimales désiré comme second argument de evalf. evalf(sqrt(2),50) evalf(pi,100) On peut aussi changer la précision par défaut pour tous les calculs en modifiant la variable Digits. Digits:=50 evalf(pi) evalf(exp(pi*sqrt(163))) La lettre i est réservée à 1 et ne peut être réaffectée ; en particulier on ne peut pas l utiliser comme indice de boucle. (1+2*i)^2 (1+2*i)/(1-2*i) e^(i*pi/3) Xcas distingue l infini non signé infinity ( ), de +infinity (+ ) et de -infinity ( ). 3
4 1/0; (1/0)^2; -(1/0)^2 2.2 Les caractères et les chaînes Constantes prédéfinies pi π e e i i = 1 infinity +infinity + -infinity Une chaîne est parenthésée par des guillemets ("). Un caractère est une chaîne ayant un seul élément. s:="azertyuiop" size(s) s[0]+s[3]+s[size(s)-1] concat(s[0],concat(s[3],s[size(s)-1])) head(s) tail(s) mid(s,3,2) l:=asc(s) ss:=char(l) string(123) expr(123) expr(0123) asc char size concat ou + mid head tail string expr Chaînes chaîne->liste des codes ASCII liste des codes ASCII->chaîne nombre de caractères concaténation morceau de chaîne premier caractère chaîne sans le 1ier caractère nombre ou expression->chaîne chaîne->nombre (base 10 ou 8) ou expression 2.3 Les variables On dit qu une variable est formelle si elle ne contient aucune valeur : toutes les variables sont formelles tant qu elles n ont pas été affectées (à une valeur). L affectation est notée :=. Au début de la session a est formelle, elle devient affectée après l instruction a:=3, a sera alors remplacé par 3 dans tous les calculs qui suivent, et 4
5 a+1 renverra 4. Xcas conserve tout le contenu de votre session. Si vous voulez que la variable a après l avoir affectée, soit à nouveau une variable formelle, il faut la "vider" par purge(a). Dans les exemples qui suivent, les variables utilisées sont supposées avoir été purgées avant chaque suite de commandes. Il ne faut pas confondre le signe := qui désigne l affectation le signe == qui désigne une égalité booléenne : c est une opération binaire qui retourne 1 ou 0 (1 pour true qui veut dire Vrai et 0 pour false qui veut dire Faux) le signe = utilisé pour définir une équation. a==b a:=b a==b solve(a=b,a) solve(2*a=b+1,a) On peut faire certains types d hypothèses sur une variable avec la commande assume, par exemple assume(a>2). Une hypothèse est une forme spéciale d affectation, elle efface une éventuelle valeur précédemment affectée à la variable. Lors d un calcul, la variable n est pas remplacée mais l hypothèse sera utilisée dans la mesure du possible, par exemple abs(a) renverra a si on fait l hypothèse a>2. sqrt(a^2) assume(a<0) sqrt(a^2) assume(n,integer) sin(n*pi) La fonction subst permet de remplacer une variable dans une expression par un nombre ou une autre expression, sans affecter cette variable. subst(a^2+1,a=1) subst(a^2+1,a=sqrt(b-1)) a^2+1 Remarque : pour stocker une valeur dans une variable par référence, par exemple pour modifier une valeur dans une liste (un vecteur, une matrice), sans recréer une nouvelle liste mais en modifiant en place la liste existante, on utilise l instruction =< au lieu de :=. Cette instruction est plus rapide que l instruction :=, car elle économise le temps de copie de la liste. 2.4 Les expressions Définition Une expression est une combinaison de nombres et de variables reliés entre eux par des opérations : par exemple x^2+2*x+c. Lorsqu on valide une commande, Xcas remplace les variables par leur valeur si elles en ont une, et exécute les opérations. 5
6 (a-2)*x^2+a*x+1 a:=2 (a-2)*x^2+a*x+1 Certaines opérations de simplification sont exécutées automatiquement lors d une évaluation : les opérations sur les entiers et sur les fractions, y compris la mise sous forme irréductible les simplifications triviales comme x + 0 = x, x x = 0, x 1 = x... quelques formes trigonométriques : cos( x) = cos(x), cos(π/4) = 2/2, tan(π/4) = 1... Nous verrons dans la section comment obtenir plus de simplifications Développer et simplifier une expression En-dehors des règles de la section précédente, il n y a pas de simplification systématique. Il y a deux raisons à cela. La première est que les simplifications non triviales sont parfois coûteuses en temps, et le choix d en faire ou non est laissé à l utilisateur ; la deuxième est qu il y a en général plusieurs manières de simplifier une même expression, selon l usage que l on veut en faire. Les principales commandes pour transformer une expression sont les suivantes : expand : développe une expression en tenant compte uniquement de la distributivité de la multiplication sur l addition et du développement des puissances entières. normal et ratnormal : d un bon rapport temps d exécution-simplification, elles écrivent une fraction rationnelle (rapport de deux polynômes) sous forme de fraction irréductible développée ; normal tient compte des nombres algébriques (par exemple comme sqrt(2)) mais pas ratnormal. Les deux ne tiennent pas compte des relations entre fonctions transcendantes (par exemple comme sin et cos). factor : un peu plus lente que les précédentes, elle écrit une fraction sous forme irréductible factorisée. simplify : elle essaie de se ramener à des variables algébriquement indépendantes avant d appliquer normal. Ceci est plus coûteux en temps et "aveugle" (on ne contrôle pas les réécritures intermédiaires). Les simplifications faisant intervenir des extensions algébriques (par exemple des racines carrées) nécessitent parfois deux appels et/ou des hypothèses (assume) pour enlever des valeurs absolues avant d obtenir la simplification souhaitée. tsimplify essaie de se ramener à des variables algébriquement indépendantes mais sans appliquer normal ensuite. Dans le menu Math du bandeau supérieur, les 4 sous-menus de réécriture contiennent d autres fonctions, pour des transformations plus ou moins spécialisées. b:=sqrt(1-a^2)/sqrt(1-a) ratnormal(b) normal(b) tsimplify(b) 6
7 simplify(b) simplify(simplify(b)) assume(a<1) simplify(b) simplify(simplify(b)) La fonction convert permet de passer d une expression à une autre équivalente, sous un format qui est spécifié par le deuxième argument. convert(exp(i*x),sincos) convert(1/(x^4-1),partfrac) convert(series(sin(x),x=0,6),polynom) simplify tsimplify normal ratnormal expand factor assume convert Transformations simplifier simplifier (moins puissant) forme normale forme normale (moins puissant) développer factoriser rajout d hypothèses transformer en un format spécifié 2.5 Les fonctions Fonctions usuelles De nombreuses fonctions sont déjà définies dans Xcas, en particulier les fonctions classiques. Les plus courantes figurent dans le tableau ci-après ; pour les autres, voir le menu Math. 7
8 Fonctions classiques abs valeur absolue round arrondi floor partie entière (plus grand entier ) ceil plus petit entier abs module arg argument conj conjugué sqrt racine carrée exp exponentielle log logarithme naturel ln logarithme naturel log10 logarithme en base 10 sin sinus cos cosinus tan tangente asin arc sinus acos arc cosinus atan arc tangente sinh sinus hyperbolique cosh cosinus hyperbolique tanh tangente hyperbolique asinh argument sinus hyperbolique acosh argument cosinus hyperbolique atanh argument tangente hyperbolique Fonctions algébriques définies par l utilisateur Pour créer une nouvelle fonction, il faut la déclarer à l aide d une expression contenant la variable. Par exemple l expression x 2 1 est définie par x^2-1. Pour la transformer en la fonction f qui à x associe x 2 1, trois possibilités existent : f(x):= x^2-1 f:=x->x^2-1 f:=unapply(x^2-1,x) f(2); f(a^2) On peut définir des fonctions de plusieurs variables à valeurs dans R comme f(x,y):=x+2*y et des fonctions de plusieurs variables à valeurs dans R p par exemple f(x,y):=(x+2*y,x-y) Distinguer expression et fonction Si f est une fonction d une variable et E est une expression, f(e) est une autre expression. Il est essentiel de ne pas confondre fonction et expression. Si on définit : E:=x^2-1, alors la variable E contient l expression x 2 1. Pour avoir la valeur de cette expression en x = 2 il faut écrire subst(e,x=2) et non E(2) car E n est pas une fonction. Lorsqu on définit une fonction, le membre de droite de l affectation n est 8
9 pas évalué. Ainsi l écriture E:=x^2-1; f(x):=e définit la fonction f : x E car E n est pas évalué. Par contre E:= x^2-1; f:=unapply(e,x) définit bien la fonction f : x x 2 1 car E est évalué. La fonction diff permet de calculer la dérivée d une expression par rapport à une ou plusieurs de ses variables. Pour dériver une fonction f, on peut appliquer diff à l expression f(x), mais alors le résultat est une expression. Si on souhaite définir la fonction dérivée, il faut utiliser function_diff. E:=x^2-1 diff(e) f:=unapply(e,x) diff(f(x)) f1:=function_diff(f) Il ne faut pas définir la fonction dérivée par f1(x):=diff(f(x)), car x aurait dans cette définition deux sens incompatibles : c est d une part la variable formelle de dérivation et d autre part l argument de la fonction f1. D autre part, cette définition évaluerait diff à chaque appel de la fonction (car le membre de droite d une affectation n est jamais évalué), ce qui serait inefficace. Il faut donc soit utiliser f1:=function_diff(f), soit f1:=unapply(diff(f(x)),x) Opérations sur les fonctions On peut ajouter et multiplier des fonctions, par exemple f:=sin*exp. Pour composer des fonctions, on utilise l et pour composer plusieurs fois une fonction avec elle-même, on utilise l f:=x->x^2-1 f1:=f@sin f2:=f@f f3:=f@@3 f1(a) f2(a) f3(a) 2.6 Listes, séquences, ensembles Xcas distingue plusieurs sortes de collections d objets, séparés par des virgules : les listes (entre crochets) les séquences (entre parenthèses) les ensembles (entre pourcentage-accolades) liste:=[1,2,4,2] sequence:=(1,2,4,2) ensemble:=%{1,2,4,2%} 9
10 Les listes peuvent contenir des listes (c est le cas des matrices), alors que les séquences sont plates (un élément d une séquence ne peut pas être une séquence). Dans un ensemble, l ordre n a pas d importance et chaque objet est unique. Il existe une autre structure, appelée table, dont nous reparlerons plus loin. Il suffit de mettre une séquence entre crochets pour en faire une liste ou entre accolades précédées de % pour en faire un ensemble. On passe d une liste à sa séquence associée par op, d une séquence à sa liste associée en la mettant entre crochets ou avec la fonction nop. Le nombre d éléments d une liste est donné par size (ou nops). se:=(1,2,4,2) li:=[se] op(li) nop(se) nops(se) %{se%} size([se]) size(%{se%}) Pour fabriquer une liste ou une séquence, on utilise des commandes d itération comme $ ou seq (qui itèrent une expression) ou makelist (qui définit une liste à l aide d une fonction). 1$5 k^2 $ (k=-2..2) seq(k^2,k=-2..2) seq(k^2,k,-2..2) [k^2$(k=-2..2)] seq(k^2,k,-2,2) seq(k^2,k,-2,2,2) makelist(x->x^2,-2,2) seq(k^2,k,-2,2,2) makelist(x->x^2,-2,2,2) La séquence vide est notée NULL, la liste vide []. Pour ajouter un élément à une séquence il suffit d écrire la séquence et élément séparés par une virgule. Pour ajouter un élément à une liste on utilise append. On accède à un élément d une liste ou d une séquence grâce à son indice mis entre crochets, le premier élément étant d indice 0. se:=null; se:=se,k^2$(k=-2..2); se:=se,1 li:=[1,2]; (li:=append(li,k^2))$(k=-2..2) li[0],li[1],li[2] Les polynômes sont souvent définis par une expression, mais ils peuvent aussi être représentés par la liste de leurs coefficients par ordre de degré décroissant, avec comme délimiteurs poly1[ et ]. Il existe aussi une représentation pour les polynômes à plusieurs variables. Les fonctions symb2poly et poly2symb permettent de passer de la représentation expression à la représentation par liste et inversement, le deuxième argument détermine s il s agit de polynômes en une variable (on met le nom de la variable) ou de polynômes à plusieurs variables (on met la liste des variables). 10
11 Séquences et listes E$(k=n..m) créer une séquence seq(e,k=n..m) créer une séquence [E$(k=n..m)] créer une liste makelist(f,k,n,m,p) créer une liste op(li) passer de liste à séquence nop(se) passer de séquence à liste nops(li) nombre d éléments size(li) nombre d éléments sum somme des éléments product produit des éléments cumsum sommes cumulées des éléments apply(f,li) appliquer une fonction à une liste map(li,f) appliquer une fonction à une liste poly2symb polynôme associé à une liste symb2poly coefficients d un polynôme 2.7 Instructions graphiques Toutes les instructions du menu Geo ont un résultat graphique, par exemple point(1,2) affiche le point de coordonnées 1 et 2, droite(a,b) la droite passant par deux points A et B définis auparavant. On peut donner des attributs graphiques aux objets graphiques en ajoutant à la fin de l instruction graphique l argument affichage=... dont la saisie est facilitée par le menu Graphic->Attributs. Lorsqu une ligne de commande contient une instruction graphique, le résultat est affiché dans un repère 2-d ou 3-d selon la nature de l objet généré. On peut controler le repère avec les boutons situés à droite du graphique, par exemple orthonormaliser avec le bouton _ _. Si une ligne de commande contient des instructions graphique et non graphiques, c est la nature de la dernière instruction qui décide du type d affichage. L instruction A:=click() permet de définir une variable contenant l affixe d un point du plan que l on clique avec la souris. 2.8 Aide en ligne Les commandes de Xcas sont regroupées par thèmes dans les menus du bandeau gris supérieur : CAS, Graphic, Geo, Cmds, Phys,... Lorsqu on sélectionne une commande dans un menu, soit l index de l aide s ouvre à la commande sélectionnée (par exemple pour les commandes du menu CAS). Cliquez sur le bouton Details pour afficher la page du manuel correspondant à la commande dans votre navigateur. soit une boite de dialogue s ouvre vous permettant de spécifier les arguments de la commande (par exemple pour tracer une courbe depuis le menu Graphic) soit la commande est recopiée dans la ligne de commande. Pour connaitre la syntaxe de cette commande, appuyez sur le bouton? en haut à gauche, ou faites afficher la zone de Messages (en utilisant le menu Cfg,). Vous pouvez aussi configurer Xcas (menu Cfg puis Configuration generale puis 11
12 cocher la case Aide HTML automatique) pour que la page correspondante du manuel s ouvre automatiquement dans votre navigateur. Le menu Aide contient les différentes formes d aide possible : un guide de l utilisateur (interface), un guide de référence (Manuels->Calcul formel, aide detaillée sur chaque commande), un Index (liste des commandes classées par ordre alphabétique avec une ligne d entrée permettant de se déplacer facilement) et une recherche par mots clefs. Si vous connaissez déjà le nom d une commande et que vous désirez vérifier sa syntaxe (par exemple factor), vous pouvez saisir le début du nom de commande (disons fact) puis taper sur la touche de tabulation (située à gauche de la touche A sur un clavier français) ou cliquer sur le bouton? en haut à gauche. L index des commandes apparaît alors dans une fenêtre, positionné à la première complétion possible, avec une aide succinte sur chaque commande. Par exemple, vous voulez factoriser un polynôme, vous supposez que le nom de commande commence par fact, vous tapez donc fact puis la touche de tabulation, vous sélectionnez à la souris factor (ou un des exemples) puis vous cliquez sur OK. Vous pouvez aussi saisir?factor pour avoir l aide succinte en réponse. Si le nom que vous avez saisi n est pas reconnu, des commandes proches vous sont suggérées. 2.9 Temps de calcul, place mémoire Le principal problème du calcul formel est la complexité des calculs intermédiaires. Elle se traduit à la fois par le temps nécessaire à l exécution des commandes et par la place mémoire requise. Les algorithmes implémentés dans les fonctions de Xcas sont performants, mais ils ne peuvent pas être optimaux dans tous les cas. La fonction time permet de connaître le temps d exécution d une commande (si ce temps est très court, Xcas exécute plusieurs fois la commande pour afficher un résultat plus précis). La mémoire utilisée apparaît dans les versions Unix dans la ligne d état (en rouge à bas à gauche). Si le temps d exécution d une commande dépasse quelques secondes, il est possible que vous ayez commis une erreur de saisie. N hésitez pas à interrompre l exécution (bouton orange stop en bas à droite, il est conseillé de faire une sauvegarde de votre session auparavant). 3 Programmation Comme le texte définissant un programme ne tient en général pas sur une ou deux lignes, il est commode d utiliser un éditeur de programmes. Pour cela, on utilise le menu Prg->Nouveau programme de Xcas. Le menu Prg->Ajouter facilite aussi la saisie des principales structures de controle de programmation. 3.1 Tests On peut tester l égalité de 2 expressions en utilisant l instruction ==, alors que!= teste si 2 expressions ne sont pas égales. On peut aussi tester l ordre entre 2 expressions 12
13 avec <, <=, >, >=, il s agit de l ordre habituel sur les réels pour des données numériques ou de l ordre lexicographique pour les chaines de caractères. Un test renvoie 1 s il est vrai, 0 s il est faux. On peut combiner le résultat de deux tests au moyen des opérateurs logiques && (et logique), (ou logique) et on peut calculer la négation logique d un résultat de test! (négation logique). On utilise ensuite souvent la valeur du test pour exécuter une instruction conditionnelle si... alors... sinon... fsi. N.B. : Xcas admet aussi une syntaxe compatible avec le langage C if (condition) { bloc_vrai } else { bloc_faux }. Par exemple, on pourrait stocker la valeur absolue d un réel x dans y par : si x>0 alors y:=x; sinon y:=-x; fsi; (on peut bien sur utiliser directement y:=abs(x)). Exemples : Tester si un triangle dont on fait cliquer les 3 sommets à l utilisateur est rectangle. 3.2 Boucles On peut exécuter des instructions plusieurs fois de suite en utilisant une boucle définie (le nombre d exécutions est fixé au début) ou indéfinie (le nombre d exécutions n est pas connu). On utilise en général une variable de controle (indice de boucle ou variable de terminaison). Boucle définie for(init;condition;incrementation){ instructions } for... from... to... do... od Exemple, calcul de 10! f:=1; for (j:=1;j<=10;j++){ f:=f*j; } f:=1; for j from 1 to 10 do f:=f*j; od; Attention, vous ne pouvez pas utiliser i comme indice de boucle, car i est prédéfini (comme 1) Boucle indéfinie while (...) {... } Exemple, algorithme d Euclide while (b!=0){ r:=irem(a,b); a:=b; b:=r;} Xcas accepte aussi l arrêt de boucle en cours d exécution (if (...) break;) dont l usage peut éviter l utilisation de variables de controle compliquées. 3.3 Fonctions (non algébriques) La plupart des fonctions ne peuvent avoir une définition par une formule algébrique. On doit souvent calculer des données intermédiaires, faire des tests et des boucles. Il faut alors définir la fonction par une suite d instructions, délimitées par {... }. La valeur calculée par la fonction est alors la valeur calculée par la dernière instruction ou peut être explicitée en utilisant le mot-clef return suivi de la valeur à renvoyer (N.B. : l exécution de return met un terme à la fonction même s il y a encore des instructions après). 13
14 Pour éviter que les données intermédiaires n interfèrent avec les variables de la session principale, on utilise un type spécial de variables, les variables locales, dont la valeur ne peut être modifiée ou accédée qu à l intérieur de la fonction. On utilise à cet effet le mot-clef local suivi par les noms des variables locales séparés par des virgules. Si une fonction calcule plusieurs données on peut les renvoyer dans une liste. Exemple : le PGCD pgcd(a,b):={ local r; while (b!=0){ r:=irem(a,b); a:=b; b:=r; } return a; } On clique ensuite sur le bouton OK, si tout va bien, le programme pgcd est défini et on peut le tester dans une ligne de commande par exemple par pgcd(25,15). Dans la section suivante, on va voir comment exécuter en mode pas à pas un programme, ce qui peut servir à comprendre le déroulement d un algorithme, mais aussi à corriger un programme erroné. 3.4 Exécuter en pas à pas et mettre au point La commande debug permet de lancer un programme en mode d exécution pas à pas. Elle ouvre une fenêtre permettant de diriger l exécution du programme passé en argument. Par exemple, on entre le programme : carres(n):={ local j,k; k:=0; for (j:=1;j<n+1;j++) { k:=k+j^2; } return k; }:; On tape pour debugger le programme carres ci-dessus : debug(carres(5)) cela ouvre la fenêtre du debugger. En cliquant sur le bouton sst on peut exécuter pas à pas le programme en visualisant l évolution des valeurs des variables locales et des paramètres du programme. Cela permet de détecter la grande majorité des erreurs qui font qu un programme ne fait pas ce que l on souhaite. Pour des programmes plus longs, le debugger permet de controler assez finement l exécution du programme en placant par exemple des points d arrêt. Exercice : exécuter en mode pas à pas le programme pgcd pour quelques valeurs des arguments. 14
15 4 TP1 prise en main 1. Écrire le polynôme (x + 3) 7 (x 5) 6 selon les puissances décroissantes de x. 2. Simplifier les expressions suivantes : 3. Factoriser : , , eiπ/6, 4atan( 1 5 ) atan( ) x 8 3x 7 25x x x 4 756x x 2 960x x 6 2x 3 + 1, ( y + x)z 2 xy 2 + x 2 y 4. Calculez les intégrales et simplifiez le résultat : 1 e x 1 dx, 1 xln(x) ln(ln(x))dx, Vérifiez en dérivant les expressions obtenues. 5. Déterminer la valeur de : 2 1 (1 + x 2 ) 3, 6. Calculer les sommes suivantes N k, 1 k=1 2 1 N k 2, k=1 e x2 dx, 1 x dx k=1 1 k 2 xsin(x)e x dx 7. Développer sin(3x), linéariser l expression obtenue et vérifier qu on retrouve l expression initiale. 8. Calculer le développement de Taylor en x = 0 à l ordre 4 de : ln(1 + x + x 2 ), exp(sin(x)) 1 x + x 2, 1 + ex, ln(1 + x) exp(x) sin(x) 9. Trouver les entiers n tels que le reste de la division euclidienne de 123n par 256 soit Déterminer la liste des diviseurs de Factoriser 100! 11. Résoudre le système linéaire : 12. Déterminer l inverse de la matrice : x + y + az = 1 x + ay + z = 2 ax + y + z = 3 A = a 1 1 a 1 1 a 1 1 a
16 5 TP 2 : ramener un problème d algèbre linéaire à un pivot de Gauss Les instructions de Xcas correspondantes sont dans le menu Cmds->Alglin->Gauss. Exercice 1 Écrire le système linéaire sous forme matricielle : x + y + az = 1 x + ay + z = 2 ax + y + z = 3 puis le résoudre avec l instruction de réduction sous forme échelonnée rref. Exercice 2 Calcul de la somme de deux sous-espaces vectoriels. On donne deux sous-espaces vectoriels E 1 et E 2 de R n par deux familles géneratrices (c est-à-dire une liste de vecteurs), il s agit d écrire un algorithme permettant de trouver une base de E 1 + E 2 de trouver une écriture d un élément de E 1 + E 2 comme somme d un élément de E 1 et d un élément de E 2 On pourra utiliser les fonctions rref ou/et ker de Xcas. Tester avec deux sousespaces de dimension 2 de R 5. N oubliez pas de rédiger une justification mathématique de la méthode mise en oeuvre. Exercice 3 Calcul de l intersection de deux sous-espaces vectoriels. On donne deux sous-espaces vectoriels E 1 et E 2 de R n par deux familles géneratrices (c est-à-dire une liste de vecteurs), il s agit d écrire un algorithme permettant de trouver une base de E 1 E 2. On pourra utiliser les fonctions rref ou/et ker de Xcas. Tester avec 2 sous-espace de dimension 3 de R 4. N oubliez pas de rédiger une justification mathématique de la méthode mise en oeuvre. Exercice 4 Mise en oeuvre du théorème de la base incomplète. On donne une famille de vecteurs de R n (liste de vecteurs), il s agit d écrire un algorithme permettant d extraire une base du sous-espace engendré, puis de compléter par des vecteurs afin de former une base de R n tout entier, et enfin d écrire un vecteur de R n comme combinaison linéaire des vecteurs de la base complétée. On pourra utiliser les fonctions rref ou/et ker de Xcas. Tester avec une famille de 3 vecteurs de R 5. N oubliez pas de rédiger une justification mathématique de la méthode mise en oeuvre. 16
17 6 TP3,4 : pivot de Gauss et applications 6.1 Programmation On rappelle qu en mode Xcas, les indices commencent à 0 (en mode maple les indices commencent à 1). Etant donné une matrice M ayant L lignes et C colonnes, on demande de programmer l algorithme du pivot de Gauss que l on rappelle : 1. Initialiser la ligne courante l et la colonne courante c à 0 2. Tant que l < L et c < C faire 3. Chercher dans la colonne c à partir de la ligne l un coefficient non nul (appelé pivot) 4. S il n y en a pas, incrémenter c et revenir à l étape 2 5. S il y en a un, échanger la ligne l avec la ligne du pivot (rowswap(matrice,l1,l2)) 6. Pour les lignes j variant de l+1 à L 1 ou de 0 à L 1 à l exclusion de la ligne l (selon que l on effectue une réduction sous-diagonale ou complète), remplacer la ligne L j par L j αl l où α est calculé pour annuler le coefficient de la colonne c de L j (mrowadd(coeff,matrice,l1,l2)) 7. Incrémenter l et c et revenir à l étape Normaliser à 1 le premier coefficient non nul de chaque ligne (en divisant la ligne par ce coefficient) 6.2 Inverse d une matrice Pour calculer l inverse d une matrice M carrée de taille n, on peut résoudre simultanément n systèmes linéaires du type Mx k = y k où y k représente (en colonne) les coordonnées du k-ième vecteur de la base canonique pour k variant de 1 à n. On écrit donc la matrice M puis les colonnes des coordonnées de ces n vecteurs, donc la matrice identité de taille n. On réduit complètement la matrice par l algorithme du pivot de Gauss. Si M est inversible, les n premières colonnes après réduction doivent être la matrice identité de taille n, alors que les n colonnes qui suivent sont les coordonnées des x k donc ces n colonnes constituent M 1. Écrire un programme de calcul d inverse de matrice par cet algorithme. 6.3 Noyau d une application linéaire Soit M la matrice d une application linéaire dont on veut calculer une base du noyau. On réduit complètement M par le pivot de Gauss. On enlève les lignes de 0 finales de M. Puis on insère des lignes de 0 pour placer les pivots (premier coefficient non nul de chaque ligne) sur la diagonale principale. On obtient ainsi une matrice carrée M r de taille le nombre de colonnes de M. On parcourt la diagonale de M r, et chaque fois qu on rencontre un 0, on ajoute un vecteur à la base du noyau, ce vecteur ayant pour coordonnées la colonne actuelle où on a remplacé le 0 de la diagonale par
18 6.4 Algorithme de Gauss-Bareiss Lorsque les coefficients de la matrice M = (m j,k ) 0 j<l,0 k<c sont entiers, on peut souhaiter éviter de faire des calculs dans les rationnels, et préférer utiliser une combinaison linéaire de lignes ne faisant intervenir que des coefficients entiers. On peut par exemple effectuer l opération (où l,c désignent la ligne et colonne du pivot) L j m l,c L j m j,c L l Tester la taille des coefficients obtenus pour une matrice carrée aléatoire de taille 5 puis 10. L idée est-elle bonne? On peut montrer qu on peut toujours diviser par le pivot utilisé pour réduire la colonne précédente (initialisé à 1 lors de la réduction de la première colonne) L j 1 p prec (m l,c L j m j,c L l ) Tester à nouveau sur des matrices carrées de taille 5, 10, vérifier que les calculs sont bien effectués dans Z. Comparer le dernier coefficient en bas à droite avec le déterminant de la matrice (si vous avez vu les propriétés des déterminants, démontrez ce résultat. Plus difficile : en déduire qu on peut bien diviser par le pivot de la colonne précédente en considérant des déterminants de matrices extraites) 7 TP5 : polynome minimal et caractéristique. On propose ici quelques algorithmes de calcul du polynôme minimal M et/ou caractéristique P d une matrice carrée A de taille n. On peut bien sur calculer le polynôme caractéristique en calculant directement le déterminant (par exemple avec l algorithme de Gauss-Bareiss pour éviter les fractions de polynômes), mais c est souvent plus couteux que d utiliser un des deux algorithmes ci-dessous. 7.1 Interpolation de Lagrange On sait que le degré de P est n, il suffit donc de connaitre la valeur de P en n + 1 points distincts pour connaitre P. Par exemple, on calcule P(k) pour k = 0,...,n, et en utilisant l instruction lagrange de Xcas, on en déduit le polynôme caractéristique. Programmer cet algorithme et testez votre programme en comparant le résultat de votre programme et de l instruction charpoly de Xcas sur quelques matrices. 7.2 Algorithme probabiliste. Cet algorithme permet de calculer le polynôme caractéristique C dans presque tous les cas, en recherchant le polynôme minimal M de A (on note m le degré de M). Cf. le DM 3 pour un exemple de mise en oeuvre. On sait que M(A) = 0, donc pour tout vecteur v, M(A)v = 0. Si M(x) = m k=0 M kx k, alors m 0 = M(A)v = M k A k v 18 k=0
19 On va donc rechercher les relations linéaires qui existent entre les n + 1 vecteurs v,...,a n v. Cela revient à déterminer le noyau K de l application linéaire dont la matrice a pour colonnes v,...,a n v. On sait que le vecteur (M 0,...,M m,0,...,0) R n+1 des coefficients de M (complété par des 0 si m < n) appartient à ce noyau K. Si le noyau K est de dimension 1, alors m = n, et les coefficients de M sont proportionnels aux coefficients du vecteur de la base du noyau calculé. On en déduit alors le polynôme minimal M et comme m = n, et aussi le polynôme caractéristique C = M. Programmer cet algorithme en prenant un vecteur v aléatoire. Attention, pour calculer A k v on formera la suite récurrente v k = Av k 1, pourquoi? Si on n a pas de chances dans le choix de v, on trouvera un noyau de dimension plus grande que 1 bien que le polynome minimal soit de degré n. On peut alors recommencer avec un autre vecteur. On peut aussi chercher la relation de degré minimal pour un v donné (elle apparait automatiquement comme premier vecteur de la base dans l algorithme de calcul du noyau donné au TP2), prendre le PPCM P des polynomes pour 2 ou 3 vecteurs aléatoires et conclure s il est de degré n. Programmer cette variante. Si le polynome minimal est de degré m < n, on peut tester si le PPCM P est le polynome minimal en calculant P(A) mais ce calcul est couteux. On peut aussi faire confiance au hasard, supposer que le polynome minimal est bien M = P et essayer de déterminer C/M par d autres moyens, par exemple la trace si n = m + 1. On dispose alors d un moyen de vérification en calculant l espace caractéristique correspondant à la valeur propre double. Programmer cette variante. 8 TP6 : codes correcteurs linéaires. La transmission (ou la lecture) d information de manière fiable a pris une importance grandissante avec le développement des réseaux informatiques, la numérisation des données (y compris audio et vidéo) mais aussi la communication à grande distance (par exemple sonde spatiale sur Mars). Il a fallu trouver des moyens économiques : de détecter des erreurs de lecture ou de transmission de corriger une erreur de lecture ou de transmission sans avoir besoin de la relire ou de la réémettre (pour éviter une coupure dans la lecture d un flux audio ou vidéo, ou un délai trop long par exemple pour communiquer avec une sonde spatiale) On présente dans ce TP quelques méthodes de détection et correction d erreurs qui utilisent de l algèbre linéaire et des polynômes dont les coefficients au lieu d être des réels ou des complexes sont des entiers modulo un nombre premier, en général 2, qui forment un corps. Dans Xcas, on représente les nombres ou les vecteurs ou les polynômes modulo 2 en ajoutant mod 2 ou %2, par exemple 1%2, [1,2] %2, (x^3+3x+1)%2 On appellera symbole d information l unité de base transmise, qu on supposera appartenir à un corps fini K, par exemple pour un bit un élément de K = Z/2Z (pour un octet on pourrait utiliser un élément du corps à 256 éléments K = GF(2,8) mais l étude de ce corps est hors programme). On veut coder un message de longueur k avec des possibilités de détection et de correction d erreurs, pour cela on rajoute des symboles calculés à partir des précédents, 19
20 et on envoie un mot ayant n symboles (avec n > k). 8.1 Le bit de parité. On prend k = 7 bits et n = 8 bits. On compte le nombre de 1 parmi les 7 bits envoyés, si ce nombre est pair, on envoie 0 comme 8ième bit, sinon 1. Au final le nombre de bits à 1 de l octet (1 octet=8 bits) est pair. On peut ainsi détecter une erreur de transmission si à la réception le nombre de bits d un octet est impair, mais on ne peut pas corriger d erreurs. On peut aussi dire que l octet représente un polynôme à coefficients dans Z/2Z divisible par X + 1. Exercice : Écrire un programme Xcas permettant de rajouter un bit de parité à une liste composée de 7 bits. Puis un programme de vérification qui accepte ou non un octet selon sa parité. On peut convertir un entier en une liste de bits par convert(j,base,2) (le bit de poids fort est à droite) puis en un polynome avec symb2poly. On peut effectuer la vérification de deux manières, en comptant le nombre de 1 ou avec l instruction rem. 8.2 Codes linéaires Définition : On multiplie le vecteur v des k symboles à transmettre par une matrice M à coefficients dans K de taille n k et on transmet l image Mv. Pour assurer qu on peut identifier un antécédent unique à partir d une image, il faut que M corresponde à une application linéaire injective (ce qui entraine n k). On dit qu un vecteur de n symboles est un mot du code s il est dans l image de l application linéaire. Pour assurer l injectivité tout en facilitant le décodage, on utilise souvent une matrice identité k,k comme sous-bloc de la matrice n,k, par exemple on prend l identité pour les k premières lignes de M, on ajoute ensuite n k lignes. Pour savoir si un vecteur w est un mot de code, il faut vérifier qu il est dans l image de M. On peut par exemple vérifier qu en ajoutant la colonne de ses coordonnées à M, on ne change pas le rang de M (qui doit être k) ou, lorsque M a comme premier sous-bloc une matrice identité, on teste si w est bien l image de l antécédent calculé à partir des k premières coordonnées de w. Exercice : créez une matrice M de taille 7,4 injective. Puis un programme qui teste si un vecteur w est un mot de code et en extrait alors la partie avant codage, c est-àdire le vecteur v tel que Mv = w. Vérifiez votre programme : si on prend un vecteur v K k et w = Mv, on doit retrouver v à partir de w. Instructions utiles : idn (matrice identité) ker (noyau d une application linéaire), rank (rang), tran (tranposée),... Pour créer une matrice, on peut coller les lignes de 2 matrices A et B par [op(a),op(b)] ou avec blockmatrix. 8.3 Codes polynomiaux Définition : Il s agit d un cas particulier de codes linéaires. On se donne un polynôme g(x) de degré n k, On représente le message de longueur k à coder par un polynôme P de degré k 1 dont les coefficients sont les symboles du message. On multiplie P par x n k, on calcule le reste R de la division euclidiennt de Px n k par g. On émet 20
21 alors Px n k R qui est divisible par g. Un des intérêts des codes polynomiaux est que la vérification d appartenance au code est très simple : les mots de code correspondent à des polynômes divisibles par g. Exercice : écrire de cette facon le codage du bit de parité. Puis une procédure Xcas de codage utilisant g = X 7 + X (ce polynôme était utilisé par le Minitel). 8.4 Détection et correction d erreur Si le mot recu n est pas dans l image de l application linéaire il y a eu erreur de transmission. Sinon, il n y a pas eu d erreur détectable (il pourrait y avoir eu plusieurs erreurs qui se compensent ). Plutôt que de demander la réémission du mot mal transmis (ce qui serait par exemple impossible en temps réel depuis un robot en orbite autour de Mars), on essaie d ajouter suffisamment d information pour pouvoir corriger des erreurs en supposant que leur nombre est majoré par un entier N. Remarque : Si les erreurs de transmissions sont indépendantes, la probabilité d avoir au moins N + 1 erreurs dans un message de longueur p est p k=n+1 (p k ) ǫk (1 ǫ) p k, où ǫ est la probabilité d une erreur de transmission. Par exemple, pour un message de 10 3 caractères, chacun ayant une probabilité d erreur de transmission de 10 3, si on prend N = 3, alors la probabilité d avoir au moins 4 erreurs est de (arrondi par excès) : P(N,eps,p):=sum(comb(p,k)*eps^k*(1-eps)^(p-k),k,N+1,p):; P(3,1e-3,10^3) Selon la nature du message, on acceptera une probabilité d avoir au moins N +1 erreurs plus ou moins petite. Exemple : On ne peut pas corriger d erreur avec le bit de parité. 8.5 Distances La distance de Hamming de 2 mots est le nombre de symboles qui diffèrent. (il s agit bien d une distance au sens mathématique, elle vérifie l inégalité triangulaire). Exercice : écrire une procédure de calcul de la distance de Hamming de 2 mots (la fonction Xcas correspondante s appelle hamdist). La distance d un code est la distance de Hamming minimale de 2 mots différents du code. Pour un code linéaire, la distance est aussi le nombre minimal de coefficients non nuls d un vecteur non nul de l image. Pour un code polynomial, la distance du code est le nombre minimal de coefficients non nuls d un multiple de g de degré inférieur à n. Exercice : quelle est la distance du code linéaire que vous avez créé plus haut? Majoration de la distance du code : La distance minimale d un code linéaire est inférieure ou égale à n k + 1 : en effet on écrit en ligne les coordonnées des images de la base canonique (ce qui revient à transposer la matrice) et on réduit par le pivot de Gauss, comme l application linéaire est injective, le rang de la matrice est k, donc la réduction de Gauss crée k 1 zéros dans chaque ligne, donc le nombre de coefficients non nuls de ces k lignes (qui sont toujours des mots de code) est au plus de n k
22 Exercice : si votre code linéaire n est pas de distance 3, modifiez les 3 dernières lignes pour réaliser un code de distance 3. On ne peut pas obtenir une distance n k + 1 = 4 avec n = 7 et k = 4 dans Z/2Z, essayez! Essayez sur Z/3Z et Z/5Z. N.B. : Pour les codes non polynomiaux, par exemple convolutifs, la distance n est pas forcément le paramètre le mieux adapté à la correction d erreurs. 8.6 Correction au mot le plus proche Une stratégie de correction basée sur la distance consiste à trouver le mot de code le plus proche d un mot donné. Si la distance d un code est supérieure ou égale à 2t+1, et s il existe un mot de code de distance inférieure ou égale à t au mot donné, alors ce mot de code est unique. On corrige alors le mot transmis en le remplacant par le mot de code le plus proche. Exercice : écrivez un programme permettant de corriger une erreur dans un mot dans votre code linéaire. On dit qu un code t-correcteur est parfait si la réunion des boules de centre un mot de code et de rayon t (pour la distance de Hamming) est disjointe et recouvre l ensemble des mots (K n ). Exercice : votre code linéaire sur Z/2Z (celui de distance 3) est-il un code 1- correcteur parfait? Remarque : Pour avoir un système de codage efficace, la correction d une erreur au mot le plus proche doit pouvoir être effectuée plus rapidement que par recherche d un mot de code parmi les mots ayant 1, 2,..., t symboles différents du mot recu. Certains codes polynomiaux le permettent. Il en est ainsi pour les codes de Reed-Solomon, utilisés par exemple pour corriger des erreurs de lecture sur les CD audio, l algorithme de recherche du mot de code est une version modifiée de l algorithme de Bézout pour les polynômes (avec des coefficients dans le corps fini à 256 éléments). 22
Maple: premiers calculs et premières applications
 TP Maple: premiers calculs et premières applications Maple: un logiciel de calcul formel Le logiciel Maple est un système de calcul formel. Alors que la plupart des logiciels de mathématiques utilisent
TP Maple: premiers calculs et premières applications Maple: un logiciel de calcul formel Le logiciel Maple est un système de calcul formel. Alors que la plupart des logiciels de mathématiques utilisent
MATLAB : COMMANDES DE BASE. Note : lorsqu applicable, l équivalent en langage C est indiqué entre les délimiteurs /* */.
 Page 1 de 9 MATLAB : COMMANDES DE BASE Note : lorsqu applicable, l équivalent en langage C est indiqué entre les délimiteurs /* */. Aide help, help nom_de_commande Fenêtre de travail (Command Window) Ligne
Page 1 de 9 MATLAB : COMMANDES DE BASE Note : lorsqu applicable, l équivalent en langage C est indiqué entre les délimiteurs /* */. Aide help, help nom_de_commande Fenêtre de travail (Command Window) Ligne
Exercices - Polynômes : corrigé. Opérations sur les polynômes
 Opérations sur les polynômes Exercice 1 - Carré - L1/Math Sup - Si P = Q est le carré d un polynôme, alors Q est nécessairement de degré, et son coefficient dominant est égal à 1. On peut donc écrire Q(X)
Opérations sur les polynômes Exercice 1 - Carré - L1/Math Sup - Si P = Q est le carré d un polynôme, alors Q est nécessairement de degré, et son coefficient dominant est égal à 1. On peut donc écrire Q(X)
F7n COUP DE BOURSE, NOMBRE DÉRIVÉ
 Auteur : S.& S. Etienne F7n COUP DE BOURSE, NOMBRE DÉRIVÉ TI-Nspire CAS Mots-clés : représentation graphique, fonction dérivée, nombre dérivé, pente, tableau de valeurs, maximum, minimum. Fichiers associés
Auteur : S.& S. Etienne F7n COUP DE BOURSE, NOMBRE DÉRIVÉ TI-Nspire CAS Mots-clés : représentation graphique, fonction dérivée, nombre dérivé, pente, tableau de valeurs, maximum, minimum. Fichiers associés
Découverte du logiciel ordinateur TI-n spire / TI-n spire CAS
 Découverte du logiciel ordinateur TI-n spire / TI-n spire CAS Mémento Ouvrir TI-Nspire CAS. Voici la barre d outils : L insertion d une page, d une activité, d une page où l application est choisie, pourra
Découverte du logiciel ordinateur TI-n spire / TI-n spire CAS Mémento Ouvrir TI-Nspire CAS. Voici la barre d outils : L insertion d une page, d une activité, d une page où l application est choisie, pourra
Introduction à MATLAB R
 Introduction à MATLAB R Romain Tavenard 10 septembre 2009 MATLAB R est un environnement de calcul numérique propriétaire orienté vers le calcul matriciel. Il se compose d un langage de programmation, d
Introduction à MATLAB R Romain Tavenard 10 septembre 2009 MATLAB R est un environnement de calcul numérique propriétaire orienté vers le calcul matriciel. Il se compose d un langage de programmation, d
Premiers pas avec Mathematica
 Premiers pas avec Mathematica LP206 : Mathématiques pour physiciens I Année 2010/2011 1 Introduction Mathematica est un logiciel de calcul formel qui permet de manipuler des expressions mathématiques symboliques.
Premiers pas avec Mathematica LP206 : Mathématiques pour physiciens I Année 2010/2011 1 Introduction Mathematica est un logiciel de calcul formel qui permet de manipuler des expressions mathématiques symboliques.
Correction de l examen de la première session
 de l examen de la première session Julian Tugaut, Franck Licini, Didier Vincent Si vous trouvez des erreurs de Français ou de mathématiques ou bien si vous avez des questions et/ou des suggestions, envoyez-moi
de l examen de la première session Julian Tugaut, Franck Licini, Didier Vincent Si vous trouvez des erreurs de Français ou de mathématiques ou bien si vous avez des questions et/ou des suggestions, envoyez-moi
LES TYPES DE DONNÉES DU LANGAGE PASCAL
 LES TYPES DE DONNÉES DU LANGAGE PASCAL 75 LES TYPES DE DONNÉES DU LANGAGE PASCAL CHAPITRE 4 OBJECTIFS PRÉSENTER LES NOTIONS D ÉTIQUETTE, DE CONS- TANTE ET DE IABLE DANS LE CONTEXTE DU LAN- GAGE PASCAL.
LES TYPES DE DONNÉES DU LANGAGE PASCAL 75 LES TYPES DE DONNÉES DU LANGAGE PASCAL CHAPITRE 4 OBJECTIFS PRÉSENTER LES NOTIONS D ÉTIQUETTE, DE CONS- TANTE ET DE IABLE DANS LE CONTEXTE DU LAN- GAGE PASCAL.
Exercices - Nombres complexes : corrigé. Formes algébriques et trigonométriques, module et argument
 Formes algébriques et trigonométriques, module et argument Exercice - - L/Math Sup - On multiplie le dénominateur par sa quantité conjuguée, et on obtient : Z = 4 i 3 + i 3 i 3 = 4 i 3 + 3 = + i 3. Pour
Formes algébriques et trigonométriques, module et argument Exercice - - L/Math Sup - On multiplie le dénominateur par sa quantité conjuguée, et on obtient : Z = 4 i 3 + i 3 i 3 = 4 i 3 + 3 = + i 3. Pour
Présentation du langage et premières fonctions
 1 Présentation de l interface logicielle Si les langages de haut niveau sont nombreux, nous allons travaillé cette année avec le langage Python, un langage de programmation très en vue sur internet en
1 Présentation de l interface logicielle Si les langages de haut niveau sont nombreux, nous allons travaillé cette année avec le langage Python, un langage de programmation très en vue sur internet en
Calcul matriciel. Définition 1 Une matrice de format (m,n) est un tableau rectangulaire de mn éléments, rangés en m lignes et n colonnes.
 1 Définitions, notations Calcul matriciel Définition 1 Une matrice de format (m,n) est un tableau rectangulaire de mn éléments, rangés en m lignes et n colonnes. On utilise aussi la notation m n pour le
1 Définitions, notations Calcul matriciel Définition 1 Une matrice de format (m,n) est un tableau rectangulaire de mn éléments, rangés en m lignes et n colonnes. On utilise aussi la notation m n pour le
Manuel d utilisation 26 juin 2011. 1 Tâche à effectuer : écrire un algorithme 2
 éducalgo Manuel d utilisation 26 juin 2011 Table des matières 1 Tâche à effectuer : écrire un algorithme 2 2 Comment écrire un algorithme? 3 2.1 Avec quoi écrit-on? Avec les boutons d écriture........
éducalgo Manuel d utilisation 26 juin 2011 Table des matières 1 Tâche à effectuer : écrire un algorithme 2 2 Comment écrire un algorithme? 3 2.1 Avec quoi écrit-on? Avec les boutons d écriture........
Initiation à LabView : Les exemples d applications :
 Initiation à LabView : Les exemples d applications : c) Type de variables : Créer un programme : Exemple 1 : Calcul de c= 2(a+b)(a-3b) ou a, b et c seront des réels. «Exemple1» nom du programme : «Exemple
Initiation à LabView : Les exemples d applications : c) Type de variables : Créer un programme : Exemple 1 : Calcul de c= 2(a+b)(a-3b) ou a, b et c seront des réels. «Exemple1» nom du programme : «Exemple
Algorithme. Table des matières
 1 Algorithme Table des matières 1 Codage 2 1.1 Système binaire.............................. 2 1.2 La numérotation de position en base décimale............ 2 1.3 La numérotation de position en base binaire..............
1 Algorithme Table des matières 1 Codage 2 1.1 Système binaire.............................. 2 1.2 La numérotation de position en base décimale............ 2 1.3 La numérotation de position en base binaire..............
Licence Sciences et Technologies Examen janvier 2010
 Université de Provence Introduction à l Informatique Licence Sciences et Technologies Examen janvier 2010 Année 2009-10 Aucun document n est autorisé Les exercices peuvent être traités dans le désordre.
Université de Provence Introduction à l Informatique Licence Sciences et Technologies Examen janvier 2010 Année 2009-10 Aucun document n est autorisé Les exercices peuvent être traités dans le désordre.
3 Approximation de solutions d équations
 3 Approximation de solutions d équations Une équation scalaire a la forme générale f(x) =0où f est une fonction de IR dans IR. Un système de n équations à n inconnues peut aussi se mettre sous une telle
3 Approximation de solutions d équations Une équation scalaire a la forme générale f(x) =0où f est une fonction de IR dans IR. Un système de n équations à n inconnues peut aussi se mettre sous une telle
Exercices - Fonctions de plusieurs variables : corrigé. Pour commencer
 Pour commencer Exercice 1 - Ensembles de définition - Première année - 1. Le logarithme est défini si x + y > 0. On trouve donc le demi-plan supérieur délimité par la droite d équation x + y = 0.. 1 xy
Pour commencer Exercice 1 - Ensembles de définition - Première année - 1. Le logarithme est défini si x + y > 0. On trouve donc le demi-plan supérieur délimité par la droite d équation x + y = 0.. 1 xy
Représentation des Nombres
 Chapitre 5 Représentation des Nombres 5. Representation des entiers 5.. Principe des représentations en base b Base L entier écrit 344 correspond a 3 mille + 4 cent + dix + 4. Plus généralement a n a n...
Chapitre 5 Représentation des Nombres 5. Representation des entiers 5.. Principe des représentations en base b Base L entier écrit 344 correspond a 3 mille + 4 cent + dix + 4. Plus généralement a n a n...
Calcul Formel et Numérique, Partie I
 Calcul Formel et Numérique N.Vandenberghe [email protected] Table des matières 1 Introduction à Matlab 2 1.1 Quelques généralités.......................... 2 2 Où trouver des informations 2 3 Opérations
Calcul Formel et Numérique N.Vandenberghe [email protected] Table des matières 1 Introduction à Matlab 2 1.1 Quelques généralités.......................... 2 2 Où trouver des informations 2 3 Opérations
Baccalauréat S Antilles-Guyane 11 septembre 2014 Corrigé
 Baccalauréat S ntilles-guyane 11 septembre 14 Corrigé EXERCICE 1 6 points Commun à tous les candidats Une entreprise de jouets en peluche souhaite commercialiser un nouveau produit et à cette fin, effectue
Baccalauréat S ntilles-guyane 11 septembre 14 Corrigé EXERCICE 1 6 points Commun à tous les candidats Une entreprise de jouets en peluche souhaite commercialiser un nouveau produit et à cette fin, effectue
TOUT CE QU IL FAUT SAVOIR POUR LE BREVET
 TOUT E QU IL FUT SVOIR POUR LE REVET NUMERIQUE / FONTIONS eci n est qu un rappel de tout ce qu il faut savoir en maths pour le brevet. I- Opérations sur les nombres et les fractions : Les priorités par
TOUT E QU IL FUT SVOIR POUR LE REVET NUMERIQUE / FONTIONS eci n est qu un rappel de tout ce qu il faut savoir en maths pour le brevet. I- Opérations sur les nombres et les fractions : Les priorités par
Introduction à l étude des Corps Finis
 Introduction à l étude des Corps Finis Robert Rolland (Résumé) 1 Introduction La structure de corps fini intervient dans divers domaines des mathématiques, en particulier dans la théorie de Galois sur
Introduction à l étude des Corps Finis Robert Rolland (Résumé) 1 Introduction La structure de corps fini intervient dans divers domaines des mathématiques, en particulier dans la théorie de Galois sur
TP 1. Prise en main du langage Python
 TP. Prise en main du langage Python Cette année nous travaillerons avec le langage Python version 3. ; nous utiliserons l environnement de développement IDLE. Étape 0. Dans votre espace personnel, créer
TP. Prise en main du langage Python Cette année nous travaillerons avec le langage Python version 3. ; nous utiliserons l environnement de développement IDLE. Étape 0. Dans votre espace personnel, créer
Fonctions de plusieurs variables
 Module : Analyse 03 Chapitre 00 : Fonctions de plusieurs variables Généralités et Rappels des notions topologiques dans : Qu est- ce que?: Mathématiquement, n étant un entier non nul, on définit comme
Module : Analyse 03 Chapitre 00 : Fonctions de plusieurs variables Généralités et Rappels des notions topologiques dans : Qu est- ce que?: Mathématiquement, n étant un entier non nul, on définit comme
Conversion d un entier. Méthode par soustraction
 Conversion entre bases Pour passer d un nombre en base b à un nombre en base 10, on utilise l écriture polynomiale décrite précédemment. Pour passer d un nombre en base 10 à un nombre en base b, on peut
Conversion entre bases Pour passer d un nombre en base b à un nombre en base 10, on utilise l écriture polynomiale décrite précédemment. Pour passer d un nombre en base 10 à un nombre en base b, on peut
L informatique en BCPST
 L informatique en BCPST Présentation générale Sylvain Pelletier Septembre 2014 Sylvain Pelletier L informatique en BCPST Septembre 2014 1 / 20 Informatique, algorithmique, programmation Utiliser la rapidité
L informatique en BCPST Présentation générale Sylvain Pelletier Septembre 2014 Sylvain Pelletier L informatique en BCPST Septembre 2014 1 / 20 Informatique, algorithmique, programmation Utiliser la rapidité
1 radian. De même, la longueur d un arc de cercle de rayon R et dont l angle au centre a pour mesure α radians est α R. R AB =R.
 Angles orientés Trigonométrie I. Préliminaires. Le radian Définition B R AB =R C O radian R A Soit C un cercle de centre O. Dire que l angle géométrique AOB a pour mesure radian signifie que la longueur
Angles orientés Trigonométrie I. Préliminaires. Le radian Définition B R AB =R C O radian R A Soit C un cercle de centre O. Dire que l angle géométrique AOB a pour mesure radian signifie que la longueur
Rappels sur les suites - Algorithme
 DERNIÈRE IMPRESSION LE 14 septembre 2015 à 12:36 Rappels sur les suites - Algorithme Table des matières 1 Suite : généralités 2 1.1 Déition................................. 2 1.2 Exemples de suites............................
DERNIÈRE IMPRESSION LE 14 septembre 2015 à 12:36 Rappels sur les suites - Algorithme Table des matières 1 Suite : généralités 2 1.1 Déition................................. 2 1.2 Exemples de suites............................
Algorithmique et Programmation, IMA
 Algorithmique et Programmation, IMA Cours 2 : C Premier Niveau / Algorithmique Université Lille 1 - Polytech Lille Notations, identificateurs Variables et Types de base Expressions Constantes Instructions
Algorithmique et Programmation, IMA Cours 2 : C Premier Niveau / Algorithmique Université Lille 1 - Polytech Lille Notations, identificateurs Variables et Types de base Expressions Constantes Instructions
STAGE IREM 0- Premiers pas en Python
 Université de Bordeaux 16-18 Février 2014/2015 STAGE IREM 0- Premiers pas en Python IREM de Bordeaux Affectation et expressions Le langage python permet tout d abord de faire des calculs. On peut évaluer
Université de Bordeaux 16-18 Février 2014/2015 STAGE IREM 0- Premiers pas en Python IREM de Bordeaux Affectation et expressions Le langage python permet tout d abord de faire des calculs. On peut évaluer
Info0101 Intro. à l'algorithmique et à la programmation. Cours 3. Le langage Java
 Info0101 Intro. à l'algorithmique et à la programmation Cours 3 Le langage Java Pierre Delisle, Cyril Rabat et Christophe Jaillet Université de Reims Champagne-Ardenne Département de Mathématiques et Informatique
Info0101 Intro. à l'algorithmique et à la programmation Cours 3 Le langage Java Pierre Delisle, Cyril Rabat et Christophe Jaillet Université de Reims Champagne-Ardenne Département de Mathématiques et Informatique
Nathalie Barbary SANSTABOO. Excel 2010. expert. Fonctions, simulations, Groupe Eyrolles, 2011, ISBN : 978-2-212-12761-4
 Nathalie Barbary Nathalie Barbary SANSTABOO Excel 2010 Fonctions, simulations, bases bases de de données expert Groupe Eyrolles, 2011, ISBN : 978-2-212-12761-4 Du côté des mathématiciens 14 Il n est pas
Nathalie Barbary Nathalie Barbary SANSTABOO Excel 2010 Fonctions, simulations, bases bases de de données expert Groupe Eyrolles, 2011, ISBN : 978-2-212-12761-4 Du côté des mathématiciens 14 Il n est pas
Représentation géométrique d un nombre complexe
 CHAPITRE 1 NOMBRES COMPLEXES 1 Représentation géométrique d un nombre complexe 1. Ensemble des nombres complexes Soit i le nombre tel que i = 1 L ensemble des nombres complexes est l ensemble des nombres
CHAPITRE 1 NOMBRES COMPLEXES 1 Représentation géométrique d un nombre complexe 1. Ensemble des nombres complexes Soit i le nombre tel que i = 1 L ensemble des nombres complexes est l ensemble des nombres
Calcul Formel et Numérique, Partie I
 Calcul Formel et Numérique NicolasVandenberghe [email protected] Table des matières 1 Introduction à Matlab 2 1.1 Quelques généralités.......................... 2 1.2 Où trouver des informations......................
Calcul Formel et Numérique NicolasVandenberghe [email protected] Table des matières 1 Introduction à Matlab 2 1.1 Quelques généralités.......................... 2 1.2 Où trouver des informations......................
Correction du Baccalauréat S Amérique du Nord mai 2007
 Correction du Baccalauréat S Amérique du Nord mai 7 EXERCICE points. Le plan (P) a une pour équation cartésienne : x+y z+ =. Les coordonnées de H vérifient cette équation donc H appartient à (P) et A n
Correction du Baccalauréat S Amérique du Nord mai 7 EXERCICE points. Le plan (P) a une pour équation cartésienne : x+y z+ =. Les coordonnées de H vérifient cette équation donc H appartient à (P) et A n
Logiciel. Table de matières I Environnement requis...2
 1 Table de matières I Environnement requis...2 I 1 - Configuration minimum conseillée...2 I 2 - Désinstallation de l application...2 I 3 - Lancement de l application...2 II Installation du logiciel...2
1 Table de matières I Environnement requis...2 I 1 - Configuration minimum conseillée...2 I 2 - Désinstallation de l application...2 I 3 - Lancement de l application...2 II Installation du logiciel...2
TP1 - Prise en main de l environnement Unix.
 Mise à niveau UNIX Licence Bio-informatique TP1 - Prise en main de l environnement Unix. Les sujets de TP sont disponibles à l adresse http://www.pps.jussieu.fr/~tasson/enseignement/bioinfo/ Les documents
Mise à niveau UNIX Licence Bio-informatique TP1 - Prise en main de l environnement Unix. Les sujets de TP sont disponibles à l adresse http://www.pps.jussieu.fr/~tasson/enseignement/bioinfo/ Les documents
Exo7. Matrice d une application linéaire. Corrections d Arnaud Bodin.
 Exo7 Matrice d une application linéaire Corrections d Arnaud odin. Exercice Soit R muni de la base canonique = ( i, j). Soit f : R R la projection sur l axe des abscisses R i parallèlement à R( i + j).
Exo7 Matrice d une application linéaire Corrections d Arnaud odin. Exercice Soit R muni de la base canonique = ( i, j). Soit f : R R la projection sur l axe des abscisses R i parallèlement à R( i + j).
EXCEL TUTORIEL 2012/2013
 EXCEL TUTORIEL 2012/2013 Excel est un tableur, c est-à-dire un logiciel de gestion de tableaux. Il permet de réaliser des calculs avec des valeurs numériques, mais aussi avec des dates et des textes. Ainsi
EXCEL TUTORIEL 2012/2013 Excel est un tableur, c est-à-dire un logiciel de gestion de tableaux. Il permet de réaliser des calculs avec des valeurs numériques, mais aussi avec des dates et des textes. Ainsi
1) Installation de Dev-C++ Téléchargez le fichier devcpp4990setup.exe dans un répertoire de votre PC, puis double-cliquez dessus :
 1) Installation de Dev-C++ Téléchargez le fichier devcpp4990setup.exe dans un répertoire de votre PC, puis double-cliquez dessus : La procédure d installation démarre. La fenêtre suivante vous indique
1) Installation de Dev-C++ Téléchargez le fichier devcpp4990setup.exe dans un répertoire de votre PC, puis double-cliquez dessus : La procédure d installation démarre. La fenêtre suivante vous indique
www.h-k.fr/publications/objectif-agregation
 «Sur C, tout est connexe!» www.h-k.fr/publications/objectif-agregation L idée de cette note est de montrer que, contrairement à ce qui se passe sur R, «sur C, tout est connexe». Cet abus de langage se
«Sur C, tout est connexe!» www.h-k.fr/publications/objectif-agregation L idée de cette note est de montrer que, contrairement à ce qui se passe sur R, «sur C, tout est connexe». Cet abus de langage se
Cours 7 : Utilisation de modules sous python
 Cours 7 : Utilisation de modules sous python 2013/2014 Utilisation d un module Importer un module Exemple : le module random Importer un module Exemple : le module random Importer un module Un module est
Cours 7 : Utilisation de modules sous python 2013/2014 Utilisation d un module Importer un module Exemple : le module random Importer un module Exemple : le module random Importer un module Un module est
Développement décimal d un réel
 4 Développement décimal d un réel On rappelle que le corps R des nombres réels est archimédien, ce qui permet d y définir la fonction partie entière. En utilisant cette partie entière on verra dans ce
4 Développement décimal d un réel On rappelle que le corps R des nombres réels est archimédien, ce qui permet d y définir la fonction partie entière. En utilisant cette partie entière on verra dans ce
UEO11 COURS/TD 1. nombres entiers et réels codés en mémoire centrale. Caractères alphabétiques et caractères spéciaux.
 UEO11 COURS/TD 1 Contenu du semestre Cours et TDs sont intégrés L objectif de ce cours équivalent a 6h de cours, 10h de TD et 8h de TP est le suivant : - initiation à l algorithmique - notions de bases
UEO11 COURS/TD 1 Contenu du semestre Cours et TDs sont intégrés L objectif de ce cours équivalent a 6h de cours, 10h de TD et 8h de TP est le suivant : - initiation à l algorithmique - notions de bases
De même, le périmètre P d un cercle de rayon 1 vaut P = 2π (par définition de π). Mais, on peut démontrer (difficilement!) que
 Introduction. On suppose connus les ensembles N (des entiers naturels), Z des entiers relatifs et Q (des nombres rationnels). On s est rendu compte, depuis l antiquité, que l on ne peut pas tout mesurer
Introduction. On suppose connus les ensembles N (des entiers naturels), Z des entiers relatifs et Q (des nombres rationnels). On s est rendu compte, depuis l antiquité, que l on ne peut pas tout mesurer
Première partie. Préliminaires : noyaux itérés. MPSI B 6 juin 2015
 Énoncé Soit V un espace vectoriel réel. L espace vectoriel des endomorphismes de V est désigné par L(V ). Lorsque f L(V ) et k N, on désigne par f 0 = Id V, f k = f k f la composée de f avec lui même k
Énoncé Soit V un espace vectoriel réel. L espace vectoriel des endomorphismes de V est désigné par L(V ). Lorsque f L(V ) et k N, on désigne par f 0 = Id V, f k = f k f la composée de f avec lui même k
1/24. I passer d un problème exprimé en français à la réalisation d un. I expressions arithmétiques. I structures de contrôle (tests, boucles)
 1/4 Objectif de ce cours /4 Objectifs de ce cours Introduction au langage C - Cours Girardot/Roelens Septembre 013 Du problème au programme I passer d un problème exprimé en français à la réalisation d
1/4 Objectif de ce cours /4 Objectifs de ce cours Introduction au langage C - Cours Girardot/Roelens Septembre 013 Du problème au programme I passer d un problème exprimé en français à la réalisation d
Pour l épreuve d algèbre, les calculatrices sont interdites.
 Les pages qui suivent comportent, à titre d exemples, les questions d algèbre depuis juillet 003 jusqu à juillet 015, avec leurs solutions. Pour l épreuve d algèbre, les calculatrices sont interdites.
Les pages qui suivent comportent, à titre d exemples, les questions d algèbre depuis juillet 003 jusqu à juillet 015, avec leurs solutions. Pour l épreuve d algèbre, les calculatrices sont interdites.
Angles orientés et trigonométrie
 Chapitre Angles orientés et trigonométrie Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES Trigonométrie Cercle trigonométrique. Radian. Mesure d un angle orienté, mesure principale.
Chapitre Angles orientés et trigonométrie Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES Trigonométrie Cercle trigonométrique. Radian. Mesure d un angle orienté, mesure principale.
IN 102 - Cours 1. 1 Informatique, calculateurs. 2 Un premier programme en C
 IN 102 - Cours 1 Qu on le veuille ou non, les systèmes informatisés sont désormais omniprésents. Même si ne vous destinez pas à l informatique, vous avez de très grandes chances d y être confrontés en
IN 102 - Cours 1 Qu on le veuille ou non, les systèmes informatisés sont désormais omniprésents. Même si ne vous destinez pas à l informatique, vous avez de très grandes chances d y être confrontés en
Python - introduction à la programmation et calcul scientifique
 Université de Strasbourg Environnements Informatique Python - introduction à la programmation et calcul scientifique Feuille de TP 1 Avant de commencer Le but de ce TP est de vous montrer les bases de
Université de Strasbourg Environnements Informatique Python - introduction à la programmation et calcul scientifique Feuille de TP 1 Avant de commencer Le but de ce TP est de vous montrer les bases de
EXCEL PERFECTIONNEMENT SERVICE INFORMATIQUE. Version 1.0 30/11/05
 EXCEL PERFECTIONNEMENT Version 1.0 30/11/05 SERVICE INFORMATIQUE TABLE DES MATIERES 1RAPPELS...3 1.1RACCOURCIS CLAVIER & SOURIS... 3 1.2NAVIGUER DANS UNE FEUILLE ET UN CLASSEUR... 3 1.3PERSONNALISER LA
EXCEL PERFECTIONNEMENT Version 1.0 30/11/05 SERVICE INFORMATIQUE TABLE DES MATIERES 1RAPPELS...3 1.1RACCOURCIS CLAVIER & SOURIS... 3 1.2NAVIGUER DANS UNE FEUILLE ET UN CLASSEUR... 3 1.3PERSONNALISER LA
Cours d algorithmique pour la classe de 2nde
 Cours d algorithmique pour la classe de 2nde F.Gaudon 10 août 2009 Table des matières 1 Avant la programmation 2 1.1 Qu est ce qu un algorithme?................................. 2 1.2 Qu est ce qu un langage
Cours d algorithmique pour la classe de 2nde F.Gaudon 10 août 2009 Table des matières 1 Avant la programmation 2 1.1 Qu est ce qu un algorithme?................................. 2 1.2 Qu est ce qu un langage
avec des nombres entiers
 Calculer avec des nombres entiers Effectuez les calculs suivants.. + 9 + 9. Calculez. 9 9 Calculez le quotient et le rest. : : : : 0 :. : : 9 : : 9 0 : 0. 9 9 0 9. Calculez. 9 0 9. : : 0 : 9 : :. : : 0
Calculer avec des nombres entiers Effectuez les calculs suivants.. + 9 + 9. Calculez. 9 9 Calculez le quotient et le rest. : : : : 0 :. : : 9 : : 9 0 : 0. 9 9 0 9. Calculez. 9 0 9. : : 0 : 9 : :. : : 0
Représentation d un entier en base b
 Représentation d un entier en base b 13 octobre 2012 1 Prérequis Les bases de la programmation en langage sont supposées avoir été travaillées L écriture en base b d un entier est ainsi défini à partir
Représentation d un entier en base b 13 octobre 2012 1 Prérequis Les bases de la programmation en langage sont supposées avoir été travaillées L écriture en base b d un entier est ainsi défini à partir
Complément d information concernant la fiche de concordance
 Sommaire SAMEDI 0 DÉCEMBRE 20 Vous trouverez dans ce dossier les documents correspondants à ce que nous allons travailler aujourd hui : La fiche de concordance pour le DAEU ; Page 2 Un rappel de cours
Sommaire SAMEDI 0 DÉCEMBRE 20 Vous trouverez dans ce dossier les documents correspondants à ce que nous allons travailler aujourd hui : La fiche de concordance pour le DAEU ; Page 2 Un rappel de cours
La fonction exponentielle
 DERNIÈRE IMPRESSION LE 2 novembre 204 à :07 La fonction exponentielle Table des matières La fonction exponentielle 2. Définition et théorèmes.......................... 2.2 Approche graphique de la fonction
DERNIÈRE IMPRESSION LE 2 novembre 204 à :07 La fonction exponentielle Table des matières La fonction exponentielle 2. Définition et théorèmes.......................... 2.2 Approche graphique de la fonction
IV- Equations, inéquations dans R, Systèmes d équations
 IV- Equations, inéquations dans R, Systèmes d équations 1- Equation à une inconnue Une équation est une égalité contenant un nombre inconnu noté en général x et qui est appelé l inconnue. Résoudre l équation
IV- Equations, inéquations dans R, Systèmes d équations 1- Equation à une inconnue Une équation est une égalité contenant un nombre inconnu noté en général x et qui est appelé l inconnue. Résoudre l équation
IMAGES NUMÉRIQUES MATRICIELLES EN SCILAB
 IMAGES NUMÉRIQUES MATRICIELLES EN SCILAB Ce document, écrit par des animateurs de l IREM de Besançon, a pour objectif de présenter quelques unes des fonctions du logiciel Scilab, celles qui sont spécifiques
IMAGES NUMÉRIQUES MATRICIELLES EN SCILAB Ce document, écrit par des animateurs de l IREM de Besançon, a pour objectif de présenter quelques unes des fonctions du logiciel Scilab, celles qui sont spécifiques
Chapitre 2 Le problème de l unicité des solutions
 Université Joseph Fourier UE MAT 127 Mathématiques année 2011-2012 Chapitre 2 Le problème de l unicité des solutions Ce que nous verrons dans ce chapitre : un exemple d équation différentielle y = f(y)
Université Joseph Fourier UE MAT 127 Mathématiques année 2011-2012 Chapitre 2 Le problème de l unicité des solutions Ce que nous verrons dans ce chapitre : un exemple d équation différentielle y = f(y)
Introduction. Mathématiques Quantiques Discrètes
 Mathématiques Quantiques Discrètes Didier Robert Facultés des Sciences et Techniques Laboratoire de Mathématiques Jean Leray, Université de Nantes email: v-nantes.fr Commençons par expliquer le titre.
Mathématiques Quantiques Discrètes Didier Robert Facultés des Sciences et Techniques Laboratoire de Mathématiques Jean Leray, Université de Nantes email: v-nantes.fr Commençons par expliquer le titre.
BACCALAURÉAT GÉNÉRAL SESSION 2012 OBLIGATOIRE MATHÉMATIQUES. Série S. Durée de l épreuve : 4 heures Coefficient : 7 ENSEIGNEMENT OBLIGATOIRE
 BACCALAURÉAT GÉNÉRAL SESSION 2012 MATHÉMATIQUES Série S Durée de l épreuve : 4 heures Coefficient : 7 ENSEIGNEMENT OBLIGATOIRE Les calculatrices électroniques de poche sont autorisées, conformément à la
BACCALAURÉAT GÉNÉRAL SESSION 2012 MATHÉMATIQUES Série S Durée de l épreuve : 4 heures Coefficient : 7 ENSEIGNEMENT OBLIGATOIRE Les calculatrices électroniques de poche sont autorisées, conformément à la
Baccalauréat ES Pondichéry 7 avril 2014 Corrigé
 Baccalauréat ES Pondichéry 7 avril 204 Corrigé EXERCICE 4 points Commun à tous les candidats. Proposition fausse. La tangente T, passant par les points A et B d abscisses distinctes, a pour coefficient
Baccalauréat ES Pondichéry 7 avril 204 Corrigé EXERCICE 4 points Commun à tous les candidats. Proposition fausse. La tangente T, passant par les points A et B d abscisses distinctes, a pour coefficient
Items étudiés dans le CHAPITRE N5. 7 et 9 p 129 D14 Déterminer par le calcul l'antécédent d'un nombre par une fonction linéaire
 CHAPITRE N5 FONCTIONS LINEAIRES NOTION DE FONCTION FONCTIONS LINEAIRES NOTION DE FONCTION FONCTIONS LINEAIRES NOTION DE FONCTION Code item D0 D2 N30[S] Items étudiés dans le CHAPITRE N5 Déterminer l'image
CHAPITRE N5 FONCTIONS LINEAIRES NOTION DE FONCTION FONCTIONS LINEAIRES NOTION DE FONCTION FONCTIONS LINEAIRES NOTION DE FONCTION Code item D0 D2 N30[S] Items étudiés dans le CHAPITRE N5 Déterminer l'image
Théorème du point fixe - Théorème de l inversion locale
 Chapitre 7 Théorème du point fixe - Théorème de l inversion locale Dans ce chapitre et le suivant, on montre deux applications importantes de la notion de différentiabilité : le théorème de l inversion
Chapitre 7 Théorème du point fixe - Théorème de l inversion locale Dans ce chapitre et le suivant, on montre deux applications importantes de la notion de différentiabilité : le théorème de l inversion
Simulation de variables aléatoires
 Chapter 1 Simulation de variables aléatoires Références: [F] Fishman, A first course in Monte Carlo, chap 3. [B] Bouleau, Probabilités de l ingénieur, chap 4. [R] Rubinstein, Simulation and Monte Carlo
Chapter 1 Simulation de variables aléatoires Références: [F] Fishman, A first course in Monte Carlo, chap 3. [B] Bouleau, Probabilités de l ingénieur, chap 4. [R] Rubinstein, Simulation and Monte Carlo
http://cermics.enpc.fr/scilab
 scilab à l École des Ponts ParisTech http://cermics.enpc.fr/scilab Introduction à Scilab Graphiques, fonctions Scilab, programmation, saisie de données Jean-Philippe Chancelier & Michel De Lara cermics,
scilab à l École des Ponts ParisTech http://cermics.enpc.fr/scilab Introduction à Scilab Graphiques, fonctions Scilab, programmation, saisie de données Jean-Philippe Chancelier & Michel De Lara cermics,
Fonctions de plusieurs variables
 Maths MP Exercices Fonctions de plusieurs variables Les indications ne sont ici que pour être consultées après le T (pour les exercices non traités). Avant et pendant le T, tenez bon et n allez pas les
Maths MP Exercices Fonctions de plusieurs variables Les indications ne sont ici que pour être consultées après le T (pour les exercices non traités). Avant et pendant le T, tenez bon et n allez pas les
Enoncé et corrigé du brevet des collèges dans les académies d Aix- Marseille, Montpellier, Nice Corse et Toulouse en 2000. Énoncé.
 Enoncé et corrigé du brevet des collèges dans les académies d Aix- Marseille, Montpellier, Nice Corse et Toulouse en 2000. Énoncé. I- ACTIVITES NUMERIQUES (12 points) Exercice 1 (3 points) On considère
Enoncé et corrigé du brevet des collèges dans les académies d Aix- Marseille, Montpellier, Nice Corse et Toulouse en 2000. Énoncé. I- ACTIVITES NUMERIQUES (12 points) Exercice 1 (3 points) On considère
Date M.P Libellé Catégorie S.Catégorie Crédit Débit Solde S.B
 Excel : Réalisation d un classeur Compta Saisir les étiquettes Renommer la première feuille Compta Laisser la première ligne vide et sur la deuxième ligne saisir les étiquettes Se placer sur A2 et saisir
Excel : Réalisation d un classeur Compta Saisir les étiquettes Renommer la première feuille Compta Laisser la première ligne vide et sur la deuxième ligne saisir les étiquettes Se placer sur A2 et saisir
SOCLE COMMUN - La Compétence 3 Les principaux éléments de mathématiques et la culture scientifique et technologique
 SOCLE COMMUN - La Compétence 3 Les principaux éléments de mathématiques et la culture scientifique et technologique DOMAINE P3.C3.D1. Pratiquer une démarche scientifique et technologique, résoudre des
SOCLE COMMUN - La Compétence 3 Les principaux éléments de mathématiques et la culture scientifique et technologique DOMAINE P3.C3.D1. Pratiquer une démarche scientifique et technologique, résoudre des
Développements limités, équivalents et calculs de limites
 Développements ités, équivalents et calculs de ites Eercice. Déterminer le développement ité en 0 à l ordre n des fonctions suivantes :. f() e (+) 3 n. g() sin() +ln(+) n 3 3. h() e sh() n 4. i() sin(
Développements ités, équivalents et calculs de ites Eercice. Déterminer le développement ité en 0 à l ordre n des fonctions suivantes :. f() e (+) 3 n. g() sin() +ln(+) n 3 3. h() e sh() n 4. i() sin(
Projet Matlab : un logiciel de cryptage
 Projet Matlab : un logiciel de cryptage La stéganographie (du grec steganos : couvert et graphein : écriture) consiste à dissimuler une information au sein d'une autre à caractère anodin, de sorte que
Projet Matlab : un logiciel de cryptage La stéganographie (du grec steganos : couvert et graphein : écriture) consiste à dissimuler une information au sein d'une autre à caractère anodin, de sorte que
Programmation linéaire
 1 Programmation linéaire 1. Le problème, un exemple. 2. Le cas b = 0 3. Théorème de dualité 4. L algorithme du simplexe 5. Problèmes équivalents 6. Complexité de l Algorithme 2 Position du problème Soit
1 Programmation linéaire 1. Le problème, un exemple. 2. Le cas b = 0 3. Théorème de dualité 4. L algorithme du simplexe 5. Problèmes équivalents 6. Complexité de l Algorithme 2 Position du problème Soit
Cours d introduction à l informatique. Partie 2 : Comment écrire un algorithme? Qu est-ce qu une variable? Expressions et instructions
 Cours d introduction à l informatique Partie 2 : Comment écrire un algorithme? Qu est-ce qu une variable? Expressions et instructions Qu est-ce qu un Une recette de cuisine algorithme? Protocole expérimental
Cours d introduction à l informatique Partie 2 : Comment écrire un algorithme? Qu est-ce qu une variable? Expressions et instructions Qu est-ce qu un Une recette de cuisine algorithme? Protocole expérimental
Guide de l utilisateur Mikogo Version Windows
 Guide de l utilisateur Mikogo Version Windows Table des matières Création d un compte utilisateur 3 Téléchargement et installation 4 Démarrer une session 4 Joindre une session 5 Fonctionnalités 6 Liste
Guide de l utilisateur Mikogo Version Windows Table des matières Création d un compte utilisateur 3 Téléchargement et installation 4 Démarrer une session 4 Joindre une session 5 Fonctionnalités 6 Liste
Résolution de systèmes linéaires par des méthodes directes
 Résolution de systèmes linéaires par des méthodes directes J. Erhel Janvier 2014 1 Inverse d une matrice carrée et systèmes linéaires Ce paragraphe a pour objet les matrices carrées et les systèmes linéaires.
Résolution de systèmes linéaires par des méthodes directes J. Erhel Janvier 2014 1 Inverse d une matrice carrée et systèmes linéaires Ce paragraphe a pour objet les matrices carrées et les systèmes linéaires.
Initiation à la programmation en Python
 I-Conventions Initiation à la programmation en Python Nom : Prénom : Une commande Python sera écrite en caractère gras. Exemples : print 'Bonjour' max=input("nombre maximum autorisé :") Le résultat de
I-Conventions Initiation à la programmation en Python Nom : Prénom : Une commande Python sera écrite en caractère gras. Exemples : print 'Bonjour' max=input("nombre maximum autorisé :") Le résultat de
Groupe Eyrolles, 2006, pour la présente édition, ISBN : 2-212-11782-5
 Groupe Eyrolles, 2006, pour la présente édition, ISBN : 2-212-11782-5 Table des matières Chapitre A : Principes de base des scripts... 1 Élaboration de votre premier script... 1 Importance du modèle...
Groupe Eyrolles, 2006, pour la présente édition, ISBN : 2-212-11782-5 Table des matières Chapitre A : Principes de base des scripts... 1 Élaboration de votre premier script... 1 Importance du modèle...
DOCM 2013 http://docm.math.ca/ Solutions officielles. 1 2 10 + 1 2 9 + 1 2 8 = n 2 10.
 A1 Trouvez l entier positif n qui satisfait l équation suivante: Solution 1 2 10 + 1 2 9 + 1 2 8 = n 2 10. En additionnant les termes du côté gauche de l équation en les mettant sur le même dénominateur
A1 Trouvez l entier positif n qui satisfait l équation suivante: Solution 1 2 10 + 1 2 9 + 1 2 8 = n 2 10. En additionnant les termes du côté gauche de l équation en les mettant sur le même dénominateur
Algorithmique et programmation : les bases (VBA) Corrigé
 PAD INPT ALGORITHMIQUE ET PROGRAMMATION 1 Cours VBA, Semaine 1 mai juin 2006 Corrigé Résumé Ce document décrit l écriture dans le langage VBA des éléments vus en algorithmique. Table des matières 1 Pourquoi
PAD INPT ALGORITHMIQUE ET PROGRAMMATION 1 Cours VBA, Semaine 1 mai juin 2006 Corrigé Résumé Ce document décrit l écriture dans le langage VBA des éléments vus en algorithmique. Table des matières 1 Pourquoi
Logique. Plan du chapitre
 Logique Ce chapitre est assez abstrait en première lecture, mais est (avec le chapitre suivant «Ensembles») probablement le plus important de l année car il est à la base de tous les raisonnements usuels
Logique Ce chapitre est assez abstrait en première lecture, mais est (avec le chapitre suivant «Ensembles») probablement le plus important de l année car il est à la base de tous les raisonnements usuels
Solutions du chapitre 4
 Solutions du chapitre 4 Structures de contrôle: première partie 4.9 Identifiez et corrigez les erreurs (il peut y en avoir plus d une par segment de code) de chacune des proposition suivantes: a) if (
Solutions du chapitre 4 Structures de contrôle: première partie 4.9 Identifiez et corrigez les erreurs (il peut y en avoir plus d une par segment de code) de chacune des proposition suivantes: a) if (
SOMMAIRE. 1. Préambule...2. 2. Le calendrier...2. 3. Trajectoire d un objet lancé...6. 4. Régression linéaire...9
 SOMMAIRE 1. Préambule...2 2. Le calendrier...2 3. Trajectoire d un objet lancé...6 4. Régression linéaire...9 5. Calcul de commissions par tranches...12 6. Base de données...16 7. Valeur cible...19 ATTENTION
SOMMAIRE 1. Préambule...2 2. Le calendrier...2 3. Trajectoire d un objet lancé...6 4. Régression linéaire...9 5. Calcul de commissions par tranches...12 6. Base de données...16 7. Valeur cible...19 ATTENTION
CORRIGE LES NOMBRES DECIMAUX RELATIFS. «Réfléchir avant d agir!»
 Corrigé Cours de Mr JULES v3.3 Classe de Quatrième Contrat 1 Page 1 sur 13 CORRIGE LES NOMBRES DECIMAUX RELATIFS. «Réfléchir avant d agir!» «Correction en rouge et italique.» I. Les nombres décimaux relatifs.
Corrigé Cours de Mr JULES v3.3 Classe de Quatrième Contrat 1 Page 1 sur 13 CORRIGE LES NOMBRES DECIMAUX RELATIFS. «Réfléchir avant d agir!» «Correction en rouge et italique.» I. Les nombres décimaux relatifs.
NOMBRES COMPLEXES. Exercice 1 :
 Exercice 1 : NOMBRES COMPLEXES On donne θ 0 un réel tel que : cos(θ 0 ) 5 et sin(θ 0 ) 1 5. Calculer le module et l'argument de chacun des nombres complexes suivants (en fonction de θ 0 ) : a i( )( )(1
Exercice 1 : NOMBRES COMPLEXES On donne θ 0 un réel tel que : cos(θ 0 ) 5 et sin(θ 0 ) 1 5. Calculer le module et l'argument de chacun des nombres complexes suivants (en fonction de θ 0 ) : a i( )( )(1
Probabilités sur un univers fini
 [http://mp.cpgedupuydelome.fr] édité le 7 août 204 Enoncés Probabilités sur un univers fini Evènements et langage ensembliste A quelle condition sur (a, b, c, d) ]0, [ 4 existe-t-il une probabilité P sur
[http://mp.cpgedupuydelome.fr] édité le 7 août 204 Enoncés Probabilités sur un univers fini Evènements et langage ensembliste A quelle condition sur (a, b, c, d) ]0, [ 4 existe-t-il une probabilité P sur
Chapitre VI - Méthodes de factorisation
 Université Pierre et Marie Curie Cours de cryptographie MM067-2012/13 Alain Kraus Chapitre VI - Méthodes de factorisation Le problème de la factorisation des grands entiers est a priori très difficile.
Université Pierre et Marie Curie Cours de cryptographie MM067-2012/13 Alain Kraus Chapitre VI - Méthodes de factorisation Le problème de la factorisation des grands entiers est a priori très difficile.
C f tracée ci- contre est la représentation graphique d une
 TLES1 DEVOIR A LA MAISON N 7 La courbe C f tracée ci- contre est la représentation graphique d une fonction f définie et dérivable sur R. On note f ' la fonction dérivée de f. La tangente T à la courbe
TLES1 DEVOIR A LA MAISON N 7 La courbe C f tracée ci- contre est la représentation graphique d une fonction f définie et dérivable sur R. On note f ' la fonction dérivée de f. La tangente T à la courbe
URECA Initiation Matlab 2 Laurent Ott. Initiation Matlab 2
 Initiation Matlab 2 1 Chaînes de caractères (string) Une chaîne de caractères (string en anglais) est une suite ordonnée de caractères (du texte, par exemple). Sous matlab, les chaînes de caractères sont
Initiation Matlab 2 1 Chaînes de caractères (string) Une chaîne de caractères (string en anglais) est une suite ordonnée de caractères (du texte, par exemple). Sous matlab, les chaînes de caractères sont
COURS EULER: PROGRAMME DE LA PREMIÈRE ANNÉE
 COURS EULER: PROGRAMME DE LA PREMIÈRE ANNÉE Le cours de la première année concerne les sujets de 9ème et 10ème années scolaires. Il y a bien sûr des différences puisque nous commençons par exemple par
COURS EULER: PROGRAMME DE LA PREMIÈRE ANNÉE Le cours de la première année concerne les sujets de 9ème et 10ème années scolaires. Il y a bien sûr des différences puisque nous commençons par exemple par
Access et Org.Base : mêmes objectifs? Description du thème : Création de grilles d écran pour une école de conduite.
 Access et Org.Base : mêmes objectifs? Description du thème : Création de grilles d écran pour une école de conduite. Mots-clés : Niveau : Bases de données relationnelles, Open Office, champs, relations,
Access et Org.Base : mêmes objectifs? Description du thème : Création de grilles d écran pour une école de conduite. Mots-clés : Niveau : Bases de données relationnelles, Open Office, champs, relations,
Baccalauréat ES Polynésie (spécialité) 10 septembre 2014 Corrigé
 Baccalauréat ES Polynésie (spécialité) 10 septembre 2014 Corrigé A. P. M. E. P. Exercice 1 5 points 1. Réponse d. : 1 e Le coefficient directeur de la tangente est négatif et n est manifestement pas 2e
Baccalauréat ES Polynésie (spécialité) 10 septembre 2014 Corrigé A. P. M. E. P. Exercice 1 5 points 1. Réponse d. : 1 e Le coefficient directeur de la tangente est négatif et n est manifestement pas 2e
Continuité et dérivabilité d une fonction
 DERNIÈRE IMPRESSIN LE 7 novembre 014 à 10:3 Continuité et dérivabilité d une fonction Table des matières 1 Continuité d une fonction 1.1 Limite finie en un point.......................... 1. Continuité
DERNIÈRE IMPRESSIN LE 7 novembre 014 à 10:3 Continuité et dérivabilité d une fonction Table des matières 1 Continuité d une fonction 1.1 Limite finie en un point.......................... 1. Continuité
Théorie et codage de l information
 Théorie et codage de l information Les codes linéaires - Chapitre 6 - Principe Définition d un code linéaire Soient p un nombre premier et s est un entier positif. Il existe un unique corps de taille q
Théorie et codage de l information Les codes linéaires - Chapitre 6 - Principe Définition d un code linéaire Soient p un nombre premier et s est un entier positif. Il existe un unique corps de taille q
MO-Call pour les Ordinateurs. Guide de l utilisateur
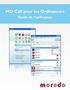 MO-Call pour les Ordinateurs Guide de l utilisateur Sommaire MO-CALL POUR ORDINATEURS...1 GUIDE DE L UTILISATEUR...1 SOMMAIRE...2 BIENVENUE CHEZ MO-CALL...4 MISE EN ROUTE...5 CONNEXION...5 APPELS...7 COMPOSITION
MO-Call pour les Ordinateurs Guide de l utilisateur Sommaire MO-CALL POUR ORDINATEURS...1 GUIDE DE L UTILISATEUR...1 SOMMAIRE...2 BIENVENUE CHEZ MO-CALL...4 MISE EN ROUTE...5 CONNEXION...5 APPELS...7 COMPOSITION
Programme de la classe de première année MPSI
 Objectifs Programme de la classe de première année MPSI I - Introduction à l analyse L objectif de cette partie est d amener les étudiants vers des problèmes effectifs d analyse élémentaire, d introduire
Objectifs Programme de la classe de première année MPSI I - Introduction à l analyse L objectif de cette partie est d amener les étudiants vers des problèmes effectifs d analyse élémentaire, d introduire
Note de cours. Introduction à Excel 2007
 Note de cours Introduction à Excel 2007 par Armande Pinette Cégep du Vieux Montréal Excel 2007 Page: 2 de 47 Table des matières Comment aller chercher un document sur CVMVirtuel?... 8 Souris... 8 Clavier
Note de cours Introduction à Excel 2007 par Armande Pinette Cégep du Vieux Montréal Excel 2007 Page: 2 de 47 Table des matières Comment aller chercher un document sur CVMVirtuel?... 8 Souris... 8 Clavier
