Représentation des informations Codage des nombres
|
|
|
- Carole Henry
- il y a 8 ans
- Total affichages :
Transcription
1 Chapitre 3 Représentation des informations Codage des nombres Objectif L objectif de ce chapitre est de découvrir comment sont représenté les informations en mémoire et plus particulièrement les nombres. 3.1 Introduction Les ordinateurs, cartes d acquisitions ou commande numériques sont des systèmes de traitement de l information. Cette information doit être codée sous une forme conventionnelle pour être comprise. Un microprocesseur ne traite que des «bits» : des 0 ou des 1. Les informations à représentées sont diverses et variés. On peut représenter : des nombres : entier ou réel, des complexes, des booléens des vecteurs des signaux, des courbes de R dans R des images des tests des sons, des films Les informations numériques sont nécessairement codés sur des BIT (binary digit) : 0 ou 1. Ces états 0 et 1 peuvent être obtenus : électriquement 0 à 1,5V mémoire MOS actif ou non (clé USB) disque dur : orientation identique ou opposé des aimants CD/DVD : trou ou absence de trou Le microprocesseur travaille essentiellement avec la mémoire vive et ses registres. La mémoire est organisé comme un grand tableau de largeur fixe : 8 bits, 16 bits, 32 bits, 64 bits, 128 bits... À chaque ligne du tableau correspond une adresse, et le bus de données vient lire ou écrire une ligne du tableau ou paquet de lignes. On parle d alignement des données en mémoire. Notion d octet : un octet est un groupe de 8 bits, en anglais on parle de Byte. 1 ko = 1 kb = 1024 octets = 8192 bits 1 Mo = 1024 ko 1 Go = 1024 Mo 1 To = 1024 Go 1
2 3.2 Numération Bases de numération Une base de numération permet de décrire tout nombre de manière unique. Usuellement nous utilisons la base 10, mais d autres bases pourraient être utilisés. Un nombre X réel s écrit dans la base B sous la forme suivante : X = a n B N + a n 1 B n a 0 B 0 + a 1 B a m 1 B m 1 = n i= m a i B i Remarque : Pour obtenir un nombre négatif, il suffit d ajouter le signe devant l expression. La notation d un nombre dans une base quelconque sera : X = (a n a n 1...a 0 a 1...a m ) B = a n a n 1...a 0 a 1...a m B La partie (a n a n 1...a 0 ) correspond à la partie entière du nombre et la partie (a 1...a m ) correspond à la partie décimale. Bases classiques Base 10 a i {0, 1,..., 9} chiffres Ex : 123,45 Base 2 a i {0, 1} bits Ex : 101,0011 Base 16 a i {0, 1,..., 9, A, B,...F } Ex : 5A5,FC2 Compléter le tableau ci-contre. On peut remarquer qu un élément de la base 16 permet de représenter exactement 4 éléments de la base 2. C est pourquoi pour des raisons de concision l affichage de grand nombre d éléments binaires sont affichés en base 16. Base 10 Base 2 Base Passage d une base B à la base 10 Ce sens de conversion est trivial, il suffit d appliquer la définition. (101,0011) 2 = = 5,1875 Convertir en base 10, les nombres suivant : (11001,101) 2 et (F 5G,8F ) Passage de la base 10 à la base B Détermination de la partie entière Pour déterminer la partie entière dans la nouvelle base, la méthode consiste à effectuer une décomposition en réalisant des divisions euclidiennes successives par B. On divise le nombre par B jusqu à obtenir un résultat non divisible (dans les entiers) par B. passage de 145 en base 2 et base 16. D après la figure ci-contre : 145 = ( ) 2 = (91) 16. Remarque : Il faut lire les résultats en remontant du bas vers le haut et en réécrivant de gauche à droite
3 Remarque : En regroupant les termes en base binaire par groupe de 4 (en partant de la droite), on peut passer à la base 16 directement en prenant la correspondance du quartet en héxadécimal : 145 = (1001 }{{} 0001 }{{}) 2 = (91) 16. (9) 16 (1) 16 Passer le nombre 2013 en base 2 puis 16. Détermination de la partie décimale L expression de la partie décimale dans une nouvelle base est obtenu par multiplication successive par B de la partie décimale du résultat précédent, l unité obtenu correspond à un chiffre de la décomposition. passage de 0,145 en base 2 et base 16. 0,145 2 = 0,29 0,29 2 = 0,58 0,58 2 = 1,16 0,16 2 = 0,32 0,32 2 = 0,64 0,64 2 = 1,28. 0,145 (0, ) 2 0, = 2,32 0,32 16 = 5,12 0,12 16 = 1,92 0,92 16 = 14,72 0,72 16 = 11,52 0,52 16 = 8,32. 0,145 (0,251EB8) 16 Remarque : La décomposition de la partie décimale peut conduire à une suite infinie de termes. Déterminer la partie décimale en base 2 et 16 de 0, Opérations Les opérations mathématiques +,, et / fonctionnent exactement de la même manière dans les bases B qu en base 10. On peut utiliser les mêmes techniques de calcul. Additionnons puis multiplier en binaire les nombres a = (10) 10 = (1010) 2 avec b = (7) 10 = (111) = On retrouve bien un résultat qui vaut (10001) 2 = (17) = On retrouve bien un résultat qui vaut ( ) 2 = (70) Représentation des nombres entiers en machine. Le stockage des données dans la machine est nécessairement sous forme de 0 et de 1. Dans une représentation binaire d un mot de plusieurs bits, rien n indique comme il doit être lu. Il est nécessaire de déclarer un type au mot binaire pour l interpréter correctement. Un mot binaire est stocké sur un ou plusieurs octets (bytes en anglais), donc un multiple de 8 bits. 3
4 3.3.1 Représentation des entiers naturels N type entier non signé (unsigned int) La représentation des entiers peut être est réalisée sur 1, 2, 4 ou 8 octets, soit 8, 16, 32 ou 64 bits, voir plus. Pour représenter les entiers positifs, il suffit d utiliser le codage en binaire vu précédemment. Si on note N ne nombre de bits de la représentation, il sera possible d écrire 2 N valeurs. Ainsi sur : 8 bits, il est possible de compter de 0 jusqu à = 255 (la première valeur étant 0) 16 bits, il est possible de compter de 0 jusqu à = bits, il est possible de compter de 0 jusqu à = Représentation des entiers relatifs Z type entier signé (int) Le problème pour représenter les nombres négatifs est qu il faut faire comprendre à la machine le symbole. Une solution élémentaire consiste à prendre un bit (généralement le bit de poids fort, le plus à gauche) pour déclarer le signe : 0 le nombre est positif, 1 le nombre est négatifs et le reste des bits permet de représenter la valeur absolue du nombre. Cette solution présente deux inconvénients : le 0 est défini deux fois et les opérations entre deux nombres ne sont plus élémentaires. On utilise le complément à 2 pour représenter a Z : 1 bit détermine le signe, le bit de poids fort à gauche les autres bits (7, 15, 31 et 63 en pratique) détermine la valeur : pour un nombre positif, on utilise le codage binaire naturel pour un nombre négatif, on utilise le complément à 2, on code en binaire naturel le nombre 2 N a Calcul du complément à 2 d un nombre : en pratique le calcul pour un nombre négatif est obtenu en prenant le complément du la représentation du nombre positif et en lui ajoutant 1 (le dépassement éventuelle de capacité du à la retenue de l addition est ignoré). Exemple : On a 110 = ( ) 2 Donc 110 = ( ) = ( ) 2 Vérifions que = = Il faut noter que 1+1 en binaire fait 0 et on retient 1. La dernière retenue du calcul est «oubliée». Un autre méthode pour déterminer le complètement à 2, consiste à garder tout les 0 à partir de la droite en conservant le premier 1 rencontré. Puis tout les autres bits sont inversés : on a 110 = ( ) 2 on conserve la partie droite jusqu au premier 1 : ( ) on prend le complètement des autres bits : ( ) d où la représentation de 110 en complément à 2 : ( ) 2 Déterminer la représentation de 145 en complément à 2. Avec cette représentation, sur : 8 bits, il est possible de compter de 128 jusqu à 127 (la première valeur étant 0) 16 bits, il est possible de compter de jusqu à bits, il est possible de compter de jusqu à
5 3.3.3 Particularité en Python On vient de voir que suivant le nombre d octet utiliser pour représenter un entier, on a une limitation du nombre de valeur représentable. Cela signifie que si on ne fait pas attention le résultat d une opération peut dépasser la capacité de représentation et une erreur de type overflow apparaitra. Il faut noter que le type int de Python est un type à représentation infinie. Il n y a aucune limitation, Python modifiera le nombre de bits nécessaire au stockage à la volée. >>> entier = 45 >>> type ( entier ) <class int > >>> entier. bit_ length () 6 >>> entier = >>> entier. bit_ length () 77 La fonction type renvoie le type de la variable. La méthode bit_length() renvoie le nombre de bit utilisé pour représenter l entier Opérations Comme on l a vu dans la partie précédente, les opérations mathématiques sont réalisés comme on le ferait à la main : addition : on somme les bits un par un en prenant en compte les retenus soustraction : on réalise un complément à 2 du nombre à soustraire pour obtenir la représentation de son opposé, puis on fait une addition multiplication : même méthode qu à la main. En pratique, on utilise les décalages des bits Représentation des nombres réels en machine. Nous avons vu comment écrire un réel dans n importe quelle base et notamment la base 2. Le problème est que cette écriture ne peut être utilisé dans un ordinateur en raison de la présence la virgule. La notation scientifique pour les nombres est adoptée depuis longtemps. Le principe du codage des réels en mémoire est basé sur cette représentation. Tout nombre x sera représenté sous la forme εm B e avec m la mantisse B la valeur de la base, ici B = 2 e l exposant ε le signe Représentation des réels NORME IEEE 754 L IEEE 754 est une norme de représentation des réels et plus précisément une norme de stockage du signe, de la mantisse et de l exposant. Elle définit également le 0, l infini et les NaN (Not a Number!). Forme générale Le mot binaire représentant le réel comportera : 1 bit, celui de poids fort pour représenter le signe n 1 bits pour représenter l exposant n 2 bits pour représenter la mantisse 1 bit n 1 bits n 2 bits signe exposant mantisse 5
6 La première remarque à faire est que l exposant pouvant être négatif, il faut prévoir le signe. Le choix aurait pu être fait d utiliser une notation de type complément à 2 mais c est un décalage qui est réalisé. La valeur du décalage est de decalage = 2 n L interprétation d un nombre est donc : x = signe mantisse 2 exposant decalage Particularités : le nombre est positif si le bit de signe est nul et négatif sinon, si tous les bits de l exposant sont à 1, alors le nombre est : l infini si la mantisse est nulle, Not a Number sinon. si tous les bits de l exposant sont à 0, alors le nombre est : nul si la mantisse est nul, non normalisé sinon (nous ne détaillerons pas ce cas). Format simple précision sur 32 bits Dans ce format, 1 bit est utilisé pour le signe, 8 bits pour l exposant et 23+1 bits pour la mantisse. Le +1 bit est un bit masqué. En effet, la mantisse est un nombre décimal compris entre 1 et 2 (< 2), donc le premier chiffre est nécessairement 1. Il n est donc pas représenté. On ne code que la mantisse réduite m telle que m = 1 + m. 1 bit 8 bits 23 bits signe exposant mantisse réduite Le décalage est égale à = 127. Représentation de 0, écriture en base binaire du nombre : nous avons vu que 0,145 (0,001001) 2, 2. mise sous forme scientifique : 0,145 = on code le bit signe : 0 4. on code l exposant décalé sur 8 bits : = 124 = ( ) 2 5. la mantisse réduite est directement la partie décimale de l écriture en base 2, complété par des 0 pour obtenir les 23 bits : ( ) 2 On en déduit que la représentation de 0,145 ( ) 2. Remarque : On peut observer que la limitation se situe à 23 chiffres significatifs sur la mantisse réduite. Si la décomposition exacte nécessite plus de chiffres alors le nombre représenté en mémoire sera approché. Le plus petit nombre représentable est ±2 126 = ±1, et le plus grand nombre représentable est ± ±2 128 = ±3, Donner la représentation en 32 bits du nombre 0,6875. Format double précision sur 64 bits Dans ce format, 1 bit est utilisé pour le signe, 11 bits pour l exposant et 52+1 bits pour la mantisse. 1 bit 11 bits 52 bits signe exposant mantisse réduite Le décalage est égale à = Le plus petit nombre représentable est ± = ±2, et le plus grand nombre représentable est ± ± = ±1, Remarque : En fonction de la précision du calcul souhaité, on choisira entre la simple precision ou la double precision. La conséquence de ce choix est un temps de calcul plus long en double précision (car plus de bits à manipuler) et un espace de stockage également plus important. 6
7 Représentation en Python Python utilise par défaut une représentation double precision nommé «float». >>> reel = >>> type ( reel ) <class float > Il existe un type decimal à précision infinie en utilisant le module Decimal Opérations Pour réaliser les opérations sur la représentation des nombres réelles, il faut : pour une multiplication/division : réaliser l opération sur les mantisses et définir la nouvelle mantisse car le résultat peut être supérieur à 2 ou inférieur à 1. additionner pour la multiplication ou soustraire pour la division les exposants pour une addition/soustraction : effectuer l opération sur les mantisses en pensant à décaler les représentations du nombre nécessaire de bits pour prendre en compte les exposants différents modifier le résultat pour être sous la bonne forme vérifier le non dépassement de capacité Les opérations directes sur les nombres réels sont très difficiles à illustrer. 3.5 Représentation d autres informations Caractères Ils ne peuvent pas être décrit sur une base de numération. Il faut donc définir un code binaire associé à chaque caractère. Il existe plusieurs codages : ASCII (1961) qui définit 128 caractères et est codé sur 7 bits (voir Figure 3.5.1). Les ordinateurs travaillant sur des octets, des versions étendus ont été proposées. ISO 8859 (1986) définit 15 jeux de 256 caractères codé sur 1 octet. Ce sont des extensions du code ASCII pour prendre en compte les caractères spéciaux des différentes langues Unicode (1991) et UTF8 (1993) définissent environ mais peuvent en contenir plus d un million. Il n y a plus de relation directe entre le codage d un caractère et son espace mémoire. Suivant la version de la norme choisie le nombre de bits nécessaire à la représentation peut varier fortement. Notons par exemple que pour l UTF8 il faut au plus 4 octets pour représenter les caractères. [Code ASCII 7 bits] [Enregistrement voix humaine : 200 points toutes les 5 ms environ] Figure 3.1: Représentation des caractères et des signaux temporels Signaux temporels Les signaux temporels ne peuvent être représentés que de façon discrète, c est-à-dire une suite de point de coordonnées (x, y) suffisamment proche pour bien représenter le signal (voir Figure 3.5.1). Chaque point peut être représenté sous la forme d un entier ou d un flottant et stocké dans un tableau/une liste Images matricielles Les images matricielles sont stockées et affichées sous forme d un tableau de pixel («picture element») colorés, on parle de carte de point («bitmap»). Le codage de chaque pixel peut être réalisé en : 7
8 noir et blanc : 1 bit par pixel niveau de gris : 4, 8 ou 16 bits par pixel couleur RGB : on décompose la couleur en sa composante rouge, verte et bleue et chaque composante est stocké sur 4, 8 ou 16 bits. une palette interne et chaque pixel est associé au numéro de la couleur dans la palette L image est ensuite généralement compressée et donne les différents de fichiers connus : sans compression : bmp, raw, tiff compression sans perte : png, tiff compression avec perte : jpg, tiff [Couleur (évidemment sur papier!)] [Niveau de gris] [Noir et blanc] Figure 3.2: Différentes palettes de couleurs pour une même image. 8
Informatique Générale
 Informatique Générale Guillaume Hutzler Laboratoire IBISC (Informatique Biologie Intégrative et Systèmes Complexes) [email protected] Cours Dokeos 625 http://www.ens.univ-evry.fr/modx/dokeos.html
Informatique Générale Guillaume Hutzler Laboratoire IBISC (Informatique Biologie Intégrative et Systèmes Complexes) [email protected] Cours Dokeos 625 http://www.ens.univ-evry.fr/modx/dokeos.html
Logiciel de Base. I. Représentation des nombres
 Logiciel de Base (A1-06/07) Léon Mugwaneza ESIL/Dépt. Informatique (bureau A118) [email protected] I. Représentation des nombres Codage et représentation de l'information Information externe formats
Logiciel de Base (A1-06/07) Léon Mugwaneza ESIL/Dépt. Informatique (bureau A118) [email protected] I. Représentation des nombres Codage et représentation de l'information Information externe formats
Codage d information. Codage d information : -Définition-
 Introduction Plan Systèmes de numération et Représentation des nombres Systèmes de numération Système de numération décimale Représentation dans une base b Représentation binaire, Octale et Hexadécimale
Introduction Plan Systèmes de numération et Représentation des nombres Systèmes de numération Système de numération décimale Représentation dans une base b Représentation binaire, Octale et Hexadécimale
Représentation des Nombres
 Chapitre 5 Représentation des Nombres 5. Representation des entiers 5.. Principe des représentations en base b Base L entier écrit 344 correspond a 3 mille + 4 cent + dix + 4. Plus généralement a n a n...
Chapitre 5 Représentation des Nombres 5. Representation des entiers 5.. Principe des représentations en base b Base L entier écrit 344 correspond a 3 mille + 4 cent + dix + 4. Plus généralement a n a n...
TD : Codage des images
 TD : Codage des images Les navigateurs Web (Netscape, IE, Mozilla ) prennent en charge les contenus textuels (au format HTML) ainsi que les images fixes (GIF, JPG, PNG) ou animée (GIF animée). Comment
TD : Codage des images Les navigateurs Web (Netscape, IE, Mozilla ) prennent en charge les contenus textuels (au format HTML) ainsi que les images fixes (GIF, JPG, PNG) ou animée (GIF animée). Comment
Conversion d un entier. Méthode par soustraction
 Conversion entre bases Pour passer d un nombre en base b à un nombre en base 10, on utilise l écriture polynomiale décrite précédemment. Pour passer d un nombre en base 10 à un nombre en base b, on peut
Conversion entre bases Pour passer d un nombre en base b à un nombre en base 10, on utilise l écriture polynomiale décrite précédemment. Pour passer d un nombre en base 10 à un nombre en base b, on peut
UEO11 COURS/TD 1. nombres entiers et réels codés en mémoire centrale. Caractères alphabétiques et caractères spéciaux.
 UEO11 COURS/TD 1 Contenu du semestre Cours et TDs sont intégrés L objectif de ce cours équivalent a 6h de cours, 10h de TD et 8h de TP est le suivant : - initiation à l algorithmique - notions de bases
UEO11 COURS/TD 1 Contenu du semestre Cours et TDs sont intégrés L objectif de ce cours équivalent a 6h de cours, 10h de TD et 8h de TP est le suivant : - initiation à l algorithmique - notions de bases
IFT2880 Organisation des ordinateurs et systèmes
 Représentation des nombres flottants Notation exponentielle Représentations équivalentes dans la base 10 de 1,234 1 2 3, 4 0 0. 0 x 1 0-2 1 2, 3 4 0. 0 x 1 0-1 1, 2 3 4. 0 x 1 0 1 2 3. 4 x 1 0 1 2. 3 4
Représentation des nombres flottants Notation exponentielle Représentations équivalentes dans la base 10 de 1,234 1 2 3, 4 0 0. 0 x 1 0-2 1 2, 3 4 0. 0 x 1 0-1 1, 2 3 4. 0 x 1 0 1 2 3. 4 x 1 0 1 2. 3 4
Formats d images. 1 Introduction
 Formats d images 1 Introduction Lorsque nous utilisons un ordinateur ou un smartphone l écran constitue un élément principal de l interaction avec la machine. Les images sont donc au cœur de l utilisation
Formats d images 1 Introduction Lorsque nous utilisons un ordinateur ou un smartphone l écran constitue un élément principal de l interaction avec la machine. Les images sont donc au cœur de l utilisation
Licence Sciences et Technologies Examen janvier 2010
 Université de Provence Introduction à l Informatique Licence Sciences et Technologies Examen janvier 2010 Année 2009-10 Aucun document n est autorisé Les exercices peuvent être traités dans le désordre.
Université de Provence Introduction à l Informatique Licence Sciences et Technologies Examen janvier 2010 Année 2009-10 Aucun document n est autorisé Les exercices peuvent être traités dans le désordre.
Structure du format BMP, sa lecture, sa construction et son écriture
 Structure du format BMP, sa lecture, sa construction et son écriture Claude Parisel Mars 2003 Table des matières : 1. Le choix du format 2. Commentaires sur les autres formats 3. Format BMP pour noir&blanc,
Structure du format BMP, sa lecture, sa construction et son écriture Claude Parisel Mars 2003 Table des matières : 1. Le choix du format 2. Commentaires sur les autres formats 3. Format BMP pour noir&blanc,
V- Manipulations de nombres en binaire
 1 V- Manipulations de nombres en binaire L ordinateur est constitué de milliards de transistors qui travaillent comme des interrupteurs électriques, soit ouverts soit fermés. Soit la ligne est activée,
1 V- Manipulations de nombres en binaire L ordinateur est constitué de milliards de transistors qui travaillent comme des interrupteurs électriques, soit ouverts soit fermés. Soit la ligne est activée,
Représentation d un entier en base b
 Représentation d un entier en base b 13 octobre 2012 1 Prérequis Les bases de la programmation en langage sont supposées avoir été travaillées L écriture en base b d un entier est ainsi défini à partir
Représentation d un entier en base b 13 octobre 2012 1 Prérequis Les bases de la programmation en langage sont supposées avoir été travaillées L écriture en base b d un entier est ainsi défini à partir
Définition 0,752 = 0,7 + 0,05 + 0,002 SYSTÈMES DE NUMÉRATION POSITIONNELS = 7 10 1 + 5 10 2 + 2 10 3
 8 Systèmes de numération INTRODUCTION SYSTÈMES DE NUMÉRATION POSITIONNELS Dans un système positionnel, le nombre de symboles est fixe On représente par un symbole chaque chiffre inférieur à la base, incluant
8 Systèmes de numération INTRODUCTION SYSTÈMES DE NUMÉRATION POSITIONNELS Dans un système positionnel, le nombre de symboles est fixe On représente par un symbole chaque chiffre inférieur à la base, incluant
Traitement numérique de l'image. Raphaël Isdant - 2009
 Traitement numérique de l'image 1/ L'IMAGE NUMÉRIQUE : COMPOSITION ET CARACTÉRISTIQUES 1.1 - Le pixel: Une image numérique est constituée d'un ensemble de points appelés pixels (abréviation de PICture
Traitement numérique de l'image 1/ L'IMAGE NUMÉRIQUE : COMPOSITION ET CARACTÉRISTIQUES 1.1 - Le pixel: Une image numérique est constituée d'un ensemble de points appelés pixels (abréviation de PICture
Les opérations binaires
 Les opérations binaires Compétences associées A2 : Analyser et interpréter une information numérique Objectifs Etre capable: - De coder les nombres entiers en code complément à 2. - De résoudre les opérations
Les opérations binaires Compétences associées A2 : Analyser et interpréter une information numérique Objectifs Etre capable: - De coder les nombres entiers en code complément à 2. - De résoudre les opérations
nom : Collège Ste Clotilde
 UNE CONFIGURATION INFORMATIQUE Objectif : Identifier les éléments principaux d une configuration L ordinateur enregistre des données qu il traite pour produire un résultat Sifflements 20 Notice 12 attache
UNE CONFIGURATION INFORMATIQUE Objectif : Identifier les éléments principaux d une configuration L ordinateur enregistre des données qu il traite pour produire un résultat Sifflements 20 Notice 12 attache
Chapitre 10 Arithmétique réelle
 Chapitre 10 Arithmétique réelle Jean Privat Université du Québec à Montréal INF2170 Organisation des ordinateurs et assembleur Automne 2013 Jean Privat (UQAM) 10 Arithmétique réelle INF2170 Automne 2013
Chapitre 10 Arithmétique réelle Jean Privat Université du Québec à Montréal INF2170 Organisation des ordinateurs et assembleur Automne 2013 Jean Privat (UQAM) 10 Arithmétique réelle INF2170 Automne 2013
Le codage informatique
 Outils de Bureautique Le codage informatique (exemple : du binaire au traitement de texte) PLAN 3) Le codage binaire 4) Représentation physique des bits 5) Le bit est un peu court... 6) Codage de texte
Outils de Bureautique Le codage informatique (exemple : du binaire au traitement de texte) PLAN 3) Le codage binaire 4) Représentation physique des bits 5) Le bit est un peu court... 6) Codage de texte
INITIATION AU LANGAGE C SUR PIC DE MICROSHIP
 COURS PROGRAMMATION INITIATION AU LANGAGE C SUR MICROCONTROLEUR PIC page 1 / 7 INITIATION AU LANGAGE C SUR PIC DE MICROSHIP I. Historique du langage C 1972 : naissance du C dans les laboratoires BELL par
COURS PROGRAMMATION INITIATION AU LANGAGE C SUR MICROCONTROLEUR PIC page 1 / 7 INITIATION AU LANGAGE C SUR PIC DE MICROSHIP I. Historique du langage C 1972 : naissance du C dans les laboratoires BELL par
JPEG, PNG, PDF, CMJN, HTML, Préparez-vous à communiquer!
 JPEG, PNG, PDF, CMJN, HTML, Préparez-vous à communiquer! 1 / Contexte L ordinateur La loi du nombre La numérisation = codage d une information en chiffres binaire : 0 1 («bit») 8 bits = 1 octet 1ko = 1024
JPEG, PNG, PDF, CMJN, HTML, Préparez-vous à communiquer! 1 / Contexte L ordinateur La loi du nombre La numérisation = codage d une information en chiffres binaire : 0 1 («bit») 8 bits = 1 octet 1ko = 1024
Chap17 - CORRECTİON DES EXERCİCES
 Chap17 - CORRECTİON DES EXERCİCES n 3 p528 Le signal a est numérique : il n y a que deux valeurs possibles pour la tension. Le signal b n est pas numérique : il y a alternance entre des signaux divers
Chap17 - CORRECTİON DES EXERCİCES n 3 p528 Le signal a est numérique : il n y a que deux valeurs possibles pour la tension. Le signal b n est pas numérique : il y a alternance entre des signaux divers
La mémoire. Un ordinateur. L'octet. Le bit
 Introduction à l informatique et à la programmation Un ordinateur Un ordinateur est une machine à calculer composée de : un processeur (ou unité centrale) qui effectue les calculs une mémoire qui conserve
Introduction à l informatique et à la programmation Un ordinateur Un ordinateur est une machine à calculer composée de : un processeur (ou unité centrale) qui effectue les calculs une mémoire qui conserve
TP SIN Traitement d image
 TP SIN Traitement d image Pré requis (l élève doit savoir): - Utiliser un ordinateur Objectif terminale : L élève doit être capable de reconnaître un format d image et d expliquer les différents types
TP SIN Traitement d image Pré requis (l élève doit savoir): - Utiliser un ordinateur Objectif terminale : L élève doit être capable de reconnaître un format d image et d expliquer les différents types
Outils permettant la diffusion de l information. Un point sur le droit numérique
 Technologies de l Information et de la Communication Introduction aux NTE/TICE Présentation des UNR UNT Outils permettant la diffusion de l information Conceptualisation d un module d apprentissage numérique
Technologies de l Information et de la Communication Introduction aux NTE/TICE Présentation des UNR UNT Outils permettant la diffusion de l information Conceptualisation d un module d apprentissage numérique
Algorithme. Table des matières
 1 Algorithme Table des matières 1 Codage 2 1.1 Système binaire.............................. 2 1.2 La numérotation de position en base décimale............ 2 1.3 La numérotation de position en base binaire..............
1 Algorithme Table des matières 1 Codage 2 1.1 Système binaire.............................. 2 1.2 La numérotation de position en base décimale............ 2 1.3 La numérotation de position en base binaire..............
Chapitre 13 Numérisation de l information
 DERNIÈRE IMPRESSION LE 2 septembre 2013 à 17:33 Chapitre 13 Numérisation de l information Table des matières 1 Transmission des informations 2 2 La numérisation 2 2.1 L échantillonage..............................
DERNIÈRE IMPRESSION LE 2 septembre 2013 à 17:33 Chapitre 13 Numérisation de l information Table des matières 1 Transmission des informations 2 2 La numérisation 2 2.1 L échantillonage..............................
Rappels Entrées -Sorties
 Fonctions printf et scanf Syntaxe: écriture, organisation Comportement Données hétérogènes? Gestion des erreurs des utilisateurs 17/11/2013 Cours du Langage C [email protected] ibrahimguelzim.atspace.co.uk
Fonctions printf et scanf Syntaxe: écriture, organisation Comportement Données hétérogènes? Gestion des erreurs des utilisateurs 17/11/2013 Cours du Langage C [email protected] ibrahimguelzim.atspace.co.uk
FORMATS DE FICHIERS. Quels sont les différents types d informations numériques dans un document multimédia?
 FORMATS DE FICHIERS Choisir et justifier un format de fichier pour réaliser un document multimédia 1 ) Le problème d Amélie Amélie et Léa ont publié leur premier article sur leur propre blog. Amélie constate
FORMATS DE FICHIERS Choisir et justifier un format de fichier pour réaliser un document multimédia 1 ) Le problème d Amélie Amélie et Léa ont publié leur premier article sur leur propre blog. Amélie constate
INFO 2 : Traitement des images
 INFO 2 : Traitement des images Objectifs : Comprendre la différence entre image vectorielle et bipmap. Comprendre les caractéristiques d'une image : résolution, définition, nombre de couleurs, poids Etre
INFO 2 : Traitement des images Objectifs : Comprendre la différence entre image vectorielle et bipmap. Comprendre les caractéristiques d'une image : résolution, définition, nombre de couleurs, poids Etre
Architecture de l ordinateur
 Architecture de l ordinateur Emmanuel Lazard Université Paris-Dauphine mars 2011 Computers are my forte! BRAZIL (Terry Gilliam, 1985) Ce document a initialement été publié sous forme de livre : Emmanuel
Architecture de l ordinateur Emmanuel Lazard Université Paris-Dauphine mars 2011 Computers are my forte! BRAZIL (Terry Gilliam, 1985) Ce document a initialement été publié sous forme de livre : Emmanuel
Architecture des ordinateurs TD1 - Portes logiques et premiers circuits
 Architecture des ordinateurs TD1 - Portes logiques et premiers circuits 1 Rappel : un peu de logique Exercice 1.1 Remplir la table de vérité suivante : a b a + b ab a + b ab a b 0 0 0 1 1 0 1 1 Exercice
Architecture des ordinateurs TD1 - Portes logiques et premiers circuits 1 Rappel : un peu de logique Exercice 1.1 Remplir la table de vérité suivante : a b a + b ab a + b ab a b 0 0 0 1 1 0 1 1 Exercice
Cours Informatique 1. Monsieur SADOUNI Salheddine
 Cours Informatique 1 Chapitre 2 les Systèmes Informatique Monsieur SADOUNI Salheddine Un Système Informatique lesystème Informatique est composé de deux parties : -le Matériel : constitué de l unité centrale
Cours Informatique 1 Chapitre 2 les Systèmes Informatique Monsieur SADOUNI Salheddine Un Système Informatique lesystème Informatique est composé de deux parties : -le Matériel : constitué de l unité centrale
Sur trois couches, on obtient donc 2563 = 16 777 216 de couleurs, soit 24bpp (Bit Per Pixel).
 Camera raw La fonction Camera Raw d'adobe Photoshop permet d'accéder facilement et rapidement aux images au format «raw» (brut), utilisé par de nombreux appareils photo numériques professionnels et milieu
Camera raw La fonction Camera Raw d'adobe Photoshop permet d'accéder facilement et rapidement aux images au format «raw» (brut), utilisé par de nombreux appareils photo numériques professionnels et milieu
Architecture des ordinateurs Introduction à l informatique
 Architecture des ordinateurs Introduction à l informatique 17 septembre 2004 1 2 3 4 5 6 Les interrupteurs... 0V 5V Ce sont des composants électroniques qui laissent pser un courant principal lorsque la
Architecture des ordinateurs Introduction à l informatique 17 septembre 2004 1 2 3 4 5 6 Les interrupteurs... 0V 5V Ce sont des composants électroniques qui laissent pser un courant principal lorsque la
IN 102 - Cours 1. 1 Informatique, calculateurs. 2 Un premier programme en C
 IN 102 - Cours 1 Qu on le veuille ou non, les systèmes informatisés sont désormais omniprésents. Même si ne vous destinez pas à l informatique, vous avez de très grandes chances d y être confrontés en
IN 102 - Cours 1 Qu on le veuille ou non, les systèmes informatisés sont désormais omniprésents. Même si ne vous destinez pas à l informatique, vous avez de très grandes chances d y être confrontés en
Bases de programmation. Cours 5. Structurer les données
 Bases de programmation. Cours 5. Structurer les données Pierre Boudes 1 er décembre 2014 This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike 3.0 License. Types char et
Bases de programmation. Cours 5. Structurer les données Pierre Boudes 1 er décembre 2014 This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike 3.0 License. Types char et
MICROINFORMATIQUE NOTE D APPLICATION 1 (REV. 2011) ARITHMETIQUE EN ASSEMBLEUR ET EN C
 Haute Ecole d Ingénierie et de Gestion Du Canton du Vaud MICROINFORMATIQUE NOTE D APPLICATION 1 (REV. 2011) ARITHMETIQUE EN ASSEMBLEUR ET EN C Programmation en mode simulation 1. DOCUMENTS DE RÉFÉRENCE...
Haute Ecole d Ingénierie et de Gestion Du Canton du Vaud MICROINFORMATIQUE NOTE D APPLICATION 1 (REV. 2011) ARITHMETIQUE EN ASSEMBLEUR ET EN C Programmation en mode simulation 1. DOCUMENTS DE RÉFÉRENCE...
Programmation C. Apprendre à développer des programmes simples dans le langage C
 Programmation C Apprendre à développer des programmes simples dans le langage C Notes de cours sont disponibles sur http://astro.u-strasbg.fr/scyon/stusm (attention les majuscules sont importantes) Modalités
Programmation C Apprendre à développer des programmes simples dans le langage C Notes de cours sont disponibles sur http://astro.u-strasbg.fr/scyon/stusm (attention les majuscules sont importantes) Modalités
Partie 1. Professeur : Haouati Abdelali. CPGE Lycée Omar Ibn Lkhattab - Meknès www.haouati.com [email protected]
 Partie 1 Professeur : Haouati Abdelali CPGE Lycée Omar Ibn Lkhattab - Meknès www.haouati.com [email protected] Partie I : Généralités et algorithmique de base 1. Environnement matériel et logiciel
Partie 1 Professeur : Haouati Abdelali CPGE Lycée Omar Ibn Lkhattab - Meknès www.haouati.com [email protected] Partie I : Généralités et algorithmique de base 1. Environnement matériel et logiciel
Représentation d un nombre en machine, erreurs d arrondis
 Chapitre Représentation d un nombre en machine, erreurs d arrondis Ce chapitre est une introduction à la représentation des nombres en machine et aux erreurs d arrondis, basé sur [], [].. Un exemple :
Chapitre Représentation d un nombre en machine, erreurs d arrondis Ce chapitre est une introduction à la représentation des nombres en machine et aux erreurs d arrondis, basé sur [], [].. Un exemple :
2 Comment fonctionne un ordinateur, dans les grandes lignes
 Programmation 1 Cours n 1 GB3, 2 nd semestre 2014-2015 Cours de Python Gilles Bernot Les notes de cours et les feuilles de TD sont disponibles (avec un peu de retard par rapport au déroulement du cours)
Programmation 1 Cours n 1 GB3, 2 nd semestre 2014-2015 Cours de Python Gilles Bernot Les notes de cours et les feuilles de TD sont disponibles (avec un peu de retard par rapport au déroulement du cours)
Chapitre 1 I:\ Soyez courageux!
 Chapitre 1 I:\ Soyez courageux! Pour ne rien vous cacher, le langage d'assembleur (souvent désigné sous le terme "Assembleur", bien que ce soit un abus de langage, puisque "Assembleur" désigne le logiciel
Chapitre 1 I:\ Soyez courageux! Pour ne rien vous cacher, le langage d'assembleur (souvent désigné sous le terme "Assembleur", bien que ce soit un abus de langage, puisque "Assembleur" désigne le logiciel
USTL - Licence ST-A 1ère année 2005-2006 Codage de l information TP 1 :
 USTL - Licence ST-A 1ère année 2005-2006 Codage de l information TP 1 : Objectifs du TP Ce TP a pour but 1. de découvrir quelques opérations logiques sur les nombres 2. et quelques formats de fichiers.
USTL - Licence ST-A 1ère année 2005-2006 Codage de l information TP 1 : Objectifs du TP Ce TP a pour but 1. de découvrir quelques opérations logiques sur les nombres 2. et quelques formats de fichiers.
Travaux pratiques. Compression en codage de Huffman. 1.3. Organisation d un projet de programmation
 Université de Savoie Module ETRS711 Travaux pratiques Compression en codage de Huffman 1. Organisation du projet 1.1. Objectifs Le but de ce projet est d'écrire un programme permettant de compresser des
Université de Savoie Module ETRS711 Travaux pratiques Compression en codage de Huffman 1. Organisation du projet 1.1. Objectifs Le but de ce projet est d'écrire un programme permettant de compresser des
Hiver 2013 IMN 259. Introduction à l analyse d images. Par Pierre-Marc Jodoin
 Hiver 2013 Analyse d images IMN 259 Introduction à l analyse d images Par Pierre-Marc Jodoin Où se situe l analyse d images? Traitement d images Imagerie Image Analyse d images/ Vision par ordinateur Infographie
Hiver 2013 Analyse d images IMN 259 Introduction à l analyse d images Par Pierre-Marc Jodoin Où se situe l analyse d images? Traitement d images Imagerie Image Analyse d images/ Vision par ordinateur Infographie
Cours 1 : Introduction Ordinateurs - Langages de haut niveau - Application
 Université de Provence Licence Math-Info Première Année V. Phan Luong Algorithmique et Programmation en Python Cours 1 : Introduction Ordinateurs - Langages de haut niveau - Application 1 Ordinateur Un
Université de Provence Licence Math-Info Première Année V. Phan Luong Algorithmique et Programmation en Python Cours 1 : Introduction Ordinateurs - Langages de haut niveau - Application 1 Ordinateur Un
Une version javascript sera disponible directement dans le cours prochainement.
 Author : Cédric Vanconingsloo Ce cours est principalement axé sur la compréhension du fonctionnement d'un ordinateur et l'étude du seul langage qu'il connaisse, le binaire. De ce fait, le cours est relativement
Author : Cédric Vanconingsloo Ce cours est principalement axé sur la compréhension du fonctionnement d'un ordinateur et l'étude du seul langage qu'il connaisse, le binaire. De ce fait, le cours est relativement
Manuel d utilisation 26 juin 2011. 1 Tâche à effectuer : écrire un algorithme 2
 éducalgo Manuel d utilisation 26 juin 2011 Table des matières 1 Tâche à effectuer : écrire un algorithme 2 2 Comment écrire un algorithme? 3 2.1 Avec quoi écrit-on? Avec les boutons d écriture........
éducalgo Manuel d utilisation 26 juin 2011 Table des matières 1 Tâche à effectuer : écrire un algorithme 2 2 Comment écrire un algorithme? 3 2.1 Avec quoi écrit-on? Avec les boutons d écriture........
Voici quelques-unes des questions auxquelles répond cette présentation.
 Qu est-ce que l édition d images? Quels sont les formats d image possibles? Quels sont les logiciels permettant de la pratiquer? Voici quelques-unes des questions auxquelles répond cette présentation.
Qu est-ce que l édition d images? Quels sont les formats d image possibles? Quels sont les logiciels permettant de la pratiquer? Voici quelques-unes des questions auxquelles répond cette présentation.
I- Définitions des signaux.
 101011011100 010110101010 101110101101 100101010101 Du compact-disc, au DVD, en passant par l appareil photo numérique, le scanner, et télévision numérique, le numérique a fait une entrée progressive mais
101011011100 010110101010 101110101101 100101010101 Du compact-disc, au DVD, en passant par l appareil photo numérique, le scanner, et télévision numérique, le numérique a fait une entrée progressive mais
INTRODUCTION A L ELECTRONIQUE NUMERIQUE ECHANTILLONNAGE ET QUANTIFICATION I. ARCHITECTURE DE L ELECRONIQUE NUMERIQUE
 INTRODUCTION A L ELECTRONIQUE NUMERIQUE ECHANTILLONNAGE ET QUANTIFICATION I. ARCHITECTURE DE L ELECRONIQUE NUMERIQUE Le schéma synoptique ci-dessous décrit les différentes étapes du traitement numérique
INTRODUCTION A L ELECTRONIQUE NUMERIQUE ECHANTILLONNAGE ET QUANTIFICATION I. ARCHITECTURE DE L ELECRONIQUE NUMERIQUE Le schéma synoptique ci-dessous décrit les différentes étapes du traitement numérique
Maintenir un service de traitement de son ou d image d ordinateur
 Maintenir un service de traitement de son ou d image d ordinateur Dominique Pagnier Table des matières 1. Introduction... 3 2. Les formats d image... 3 2.1. Formats d infographie : EPS et TIF... 4 2.2.
Maintenir un service de traitement de son ou d image d ordinateur Dominique Pagnier Table des matières 1. Introduction... 3 2. Les formats d image... 3 2.1. Formats d infographie : EPS et TIF... 4 2.2.
Projet Matlab : un logiciel de cryptage
 Projet Matlab : un logiciel de cryptage La stéganographie (du grec steganos : couvert et graphein : écriture) consiste à dissimuler une information au sein d'une autre à caractère anodin, de sorte que
Projet Matlab : un logiciel de cryptage La stéganographie (du grec steganos : couvert et graphein : écriture) consiste à dissimuler une information au sein d'une autre à caractère anodin, de sorte que
Initiation à linfographie
 Ce support de cours de l Agence universitaire de la Francophonie est distribué sous licence GNU FDL. Permission vous est donnée de copier, distribuer et/ou modifier ce document selon les termes de la Licence
Ce support de cours de l Agence universitaire de la Francophonie est distribué sous licence GNU FDL. Permission vous est donnée de copier, distribuer et/ou modifier ce document selon les termes de la Licence
Arithmétique binaire. Chapitre. 5.1 Notions. 5.1.1 Bit. 5.1.2 Mot
 Chapitre 5 Arithmétique binaire L es codes sont manipulés au quotidien sans qu on s en rende compte, et leur compréhension est quasi instinctive. Le seul fait de lire fait appel au codage alphabétique,
Chapitre 5 Arithmétique binaire L es codes sont manipulés au quotidien sans qu on s en rende compte, et leur compréhension est quasi instinctive. Le seul fait de lire fait appel au codage alphabétique,
Numérisation du signal
 Chapitre 12 Sciences Physiques - BTS Numérisation du signal 1 Analogique - Numérique. 1.1 Définitions. Signal analogique : un signal analogique s a (t)est un signal continu dont la valeur varie en fonction
Chapitre 12 Sciences Physiques - BTS Numérisation du signal 1 Analogique - Numérique. 1.1 Définitions. Signal analogique : un signal analogique s a (t)est un signal continu dont la valeur varie en fonction
 Chapitre 1 Introduction à la technologie des ordinateurs 1.1 DEFINITION DE L INFORMATIQUE L informatique (de information et automatique) est la «science du traitement rationnel (fondée sur la raison, conforme
Chapitre 1 Introduction à la technologie des ordinateurs 1.1 DEFINITION DE L INFORMATIQUE L informatique (de information et automatique) est la «science du traitement rationnel (fondée sur la raison, conforme
TP Codage numérique des caractères. Un ordinateur ne manipule que des 0 et des 1 : Comment alors code-t-il du texte?
 TP Codage numérique des caractères Un ordinateur ne manipule que des 0 et des 1 : Comment alors code-t-il du texte? I Le code ASCII 1. Une première approche Ouvrir un fichier Excell Sur la ligne 1 du tableau,
TP Codage numérique des caractères Un ordinateur ne manipule que des 0 et des 1 : Comment alors code-t-il du texte? I Le code ASCII 1. Une première approche Ouvrir un fichier Excell Sur la ligne 1 du tableau,
Comme chaque ligne de cache a 1024 bits. Le nombre de lignes de cache contenu dans chaque ensemble est:
 Travaux Pratiques 3. IFT 1002/IFT 1005. Structure Interne des Ordinateurs. Département d'informatique et de génie logiciel. Université Laval. Hiver 2012. Prof : Bui Minh Duc. Tous les exercices sont indépendants.
Travaux Pratiques 3. IFT 1002/IFT 1005. Structure Interne des Ordinateurs. Département d'informatique et de génie logiciel. Université Laval. Hiver 2012. Prof : Bui Minh Duc. Tous les exercices sont indépendants.
Jeux de caracte res et encodage (par Michel Michaud 2014)
 Jeux de caracte res et encodage (par Michel Michaud 2014) Les ordinateurs ne traitent que des données numériques. En fait, les codages électriques qu'ils conservent en mémoire centrale ne représentent
Jeux de caracte res et encodage (par Michel Michaud 2014) Les ordinateurs ne traitent que des données numériques. En fait, les codages électriques qu'ils conservent en mémoire centrale ne représentent
Compléments de documentation Scilab : affichage de texte et formatage de nombres
 Université des Sciences et Technologies de Lille U.F.R. de Mathématiques Pures et Appliquées Agrégation externe Année 2002-2003 Compléments de documentation Scilab : affichage de texte et formatage de
Université des Sciences et Technologies de Lille U.F.R. de Mathématiques Pures et Appliquées Agrégation externe Année 2002-2003 Compléments de documentation Scilab : affichage de texte et formatage de
IMAGES NUMÉRIQUES MATRICIELLES EN SCILAB
 IMAGES NUMÉRIQUES MATRICIELLES EN SCILAB Ce document, écrit par des animateurs de l IREM de Besançon, a pour objectif de présenter quelques unes des fonctions du logiciel Scilab, celles qui sont spécifiques
IMAGES NUMÉRIQUES MATRICIELLES EN SCILAB Ce document, écrit par des animateurs de l IREM de Besançon, a pour objectif de présenter quelques unes des fonctions du logiciel Scilab, celles qui sont spécifiques
ET LO GICIEL D UN S YS T EME IN FORMATIQUE
 C HAPIT RE 0 : ENVIRONNEMENT MATE RI EL ET LO GICIEL D UN S YS T EME IN FORMATIQUE Objectifs : 1. Présenter l ensemble des ressources physiques et logicielles d un système informatique. 2. Comprendre la
C HAPIT RE 0 : ENVIRONNEMENT MATE RI EL ET LO GICIEL D UN S YS T EME IN FORMATIQUE Objectifs : 1. Présenter l ensemble des ressources physiques et logicielles d un système informatique. 2. Comprendre la
Le poids et la taille des fichiers
 Le poids et la taille des fichiers Au tout départ des 0 et des 1 En français et en anglais on appelle cela un bit 8 bit donne un octet (ou byte en anglais) Exemple d octet : 11111111 10111010 00001000
Le poids et la taille des fichiers Au tout départ des 0 et des 1 En français et en anglais on appelle cela un bit 8 bit donne un octet (ou byte en anglais) Exemple d octet : 11111111 10111010 00001000
Glossaire des nombres
 Glossaire des nombres Numérisation et sens du nombre (4-6) Imprimeur de la Reine pour l'ontario, 008 Nombre : Objet mathématique qui représente une valeur numérique. Le chiffre est le symbole utilisé pour
Glossaire des nombres Numérisation et sens du nombre (4-6) Imprimeur de la Reine pour l'ontario, 008 Nombre : Objet mathématique qui représente une valeur numérique. Le chiffre est le symbole utilisé pour
Techniques de stockage. Techniques de stockage, P. Rigaux p.1/43
 Techniques de stockage Techniques de stockage, P. Rigaux p.1/43 Techniques de stockage Contenu de ce cours : 1. Stockage de données. Supports, fonctionnement d un disque, technologie RAID 2. Organisation
Techniques de stockage Techniques de stockage, P. Rigaux p.1/43 Techniques de stockage Contenu de ce cours : 1. Stockage de données. Supports, fonctionnement d un disque, technologie RAID 2. Organisation
ASR1 TD7 : Un microprocesseur RISC 16 bits
 {Â Ö Ñ º ØÖ Ý,È ØÖ ºÄÓ Ù,Æ ÓÐ ºÎ ÝÖ Ø¹ ÖÚ ÐÐÓÒ} Ò ¹ÐÝÓÒº Ö ØØÔ»»Ô Ö Óº Ò ¹ÐÝÓÒº Ö» Ö Ñ º ØÖ Ý»¼ Ö½» ASR1 TD7 : Un microprocesseur RISC 16 bits 13, 20 et 27 novembre 2006 Présentation générale On choisit
{Â Ö Ñ º ØÖ Ý,È ØÖ ºÄÓ Ù,Æ ÓÐ ºÎ ÝÖ Ø¹ ÖÚ ÐÐÓÒ} Ò ¹ÐÝÓÒº Ö ØØÔ»»Ô Ö Óº Ò ¹ÐÝÓÒº Ö» Ö Ñ º ØÖ Ý»¼ Ö½» ASR1 TD7 : Un microprocesseur RISC 16 bits 13, 20 et 27 novembre 2006 Présentation générale On choisit
6 - Le système de gestion de fichiers F. Boyer, UJF-Laboratoire Lig, [email protected]
 6 - Le système de gestion de fichiers F. Boyer, UJF-Laboratoire Lig, [email protected] Interface d un SGF Implémentation d un SGF Gestion de la correspondance entre la structure logique et la structure
6 - Le système de gestion de fichiers F. Boyer, UJF-Laboratoire Lig, [email protected] Interface d un SGF Implémentation d un SGF Gestion de la correspondance entre la structure logique et la structure
1 Introduction au codage
 CélestineOscarDésiréAnatoleGastonEugène 1 Introduction au codage 1.1 Les ensembles L ensemble de tout les ensembles est Dieu lui-même. Kantor Ensemble des parties d un ensemble désigne l ensemble des sous-ensembles
CélestineOscarDésiréAnatoleGastonEugène 1 Introduction au codage 1.1 Les ensembles L ensemble de tout les ensembles est Dieu lui-même. Kantor Ensemble des parties d un ensemble désigne l ensemble des sous-ensembles
Système binaire. Algèbre booléenne
 Algèbre booléenne Système binaire Système digital qui emploie des signaux à deux valeurs uniques En général, les digits employés sont 0 et 1, qu'on appelle bits (binary digits) Avantages: on peut utiliser
Algèbre booléenne Système binaire Système digital qui emploie des signaux à deux valeurs uniques En général, les digits employés sont 0 et 1, qu'on appelle bits (binary digits) Avantages: on peut utiliser
Base de l'informatique. Généralité et Architecture Le système d'exploitation Les logiciels Le réseau et l'extérieur (WEB)
 Base de l'informatique Généralité et Architecture Le système d'exploitation Les logiciels Le réseau et l'extérieur (WEB) Généralité Comment fonctionne un ordinateur? Nous définirons 3 couches Le matériel
Base de l'informatique Généralité et Architecture Le système d'exploitation Les logiciels Le réseau et l'extérieur (WEB) Généralité Comment fonctionne un ordinateur? Nous définirons 3 couches Le matériel
LECON 2 : PROPRIETES DE L'AFFICHAGE Version aout 2011
 LECON 2 : PROPRIETES DE L'AFFICHAGE Version aout 2011 COPIER LE FICHIER LECON 1_02 DU DISQUE D : VERS LA CLE USB Cliquez gauche deux fois sur l'icône POSTE DE TRAVAIL Cliquez gauche deux fois sur DONNEES
LECON 2 : PROPRIETES DE L'AFFICHAGE Version aout 2011 COPIER LE FICHIER LECON 1_02 DU DISQUE D : VERS LA CLE USB Cliquez gauche deux fois sur l'icône POSTE DE TRAVAIL Cliquez gauche deux fois sur DONNEES
Architecture matérielle des systèmes informatiques
 Architecture matérielle des systèmes informatiques IDEC, Renens. Version novembre 2003. Avertissement : ce support de cours n est pas destiné à l autoformation et doit impérativement être complété par
Architecture matérielle des systèmes informatiques IDEC, Renens. Version novembre 2003. Avertissement : ce support de cours n est pas destiné à l autoformation et doit impérativement être complété par
DE L ALGORITHME AU PROGRAMME INTRO AU LANGAGE C 51
 DE L ALGORITHME AU PROGRAMME INTRO AU LANGAGE C 51 PLAN DU COURS Introduction au langage C Notions de compilation Variables, types, constantes, tableaux, opérateurs Entrées sorties de base Structures de
DE L ALGORITHME AU PROGRAMME INTRO AU LANGAGE C 51 PLAN DU COURS Introduction au langage C Notions de compilation Variables, types, constantes, tableaux, opérateurs Entrées sorties de base Structures de
avec des nombres entiers
 Calculer avec des nombres entiers Effectuez les calculs suivants.. + 9 + 9. Calculez. 9 9 Calculez le quotient et le rest. : : : : 0 :. : : 9 : : 9 0 : 0. 9 9 0 9. Calculez. 9 0 9. : : 0 : 9 : :. : : 0
Calculer avec des nombres entiers Effectuez les calculs suivants.. + 9 + 9. Calculez. 9 9 Calculez le quotient et le rest. : : : : 0 :. : : 9 : : 9 0 : 0. 9 9 0 9. Calculez. 9 0 9. : : 0 : 9 : :. : : 0
Compter à Babylone. L écriture des nombres
 Compter à Babylone d après l article de Christine Proust «Le calcul sexagésimal en Mésopotamie : enseignement dans les écoles de scribes» disponible sur http://www.dma.ens.fr/culturemath/ Les mathématiciens
Compter à Babylone d après l article de Christine Proust «Le calcul sexagésimal en Mésopotamie : enseignement dans les écoles de scribes» disponible sur http://www.dma.ens.fr/culturemath/ Les mathématiciens
UE Programmation Impérative Licence 2ème Année 2014 2015
 UE Programmation Impérative Licence 2 ème Année 2014 2015 Informations pratiques Équipe Pédagogique Florence Cloppet Neilze Dorta Nicolas Loménie [email protected] 2 Programmation Impérative
UE Programmation Impérative Licence 2 ème Année 2014 2015 Informations pratiques Équipe Pédagogique Florence Cloppet Neilze Dorta Nicolas Loménie [email protected] 2 Programmation Impérative
Leçon N 5 PICASA Généralités
 Leçon N 5 PICASA Généralités Avec cette leçon N 5, nous allons commencer l étude du traitement de vos photos avec le logiciel de GOOGLE, PICASA, que vous avez téléchargé dans la leçon N 3. 1 Présentation
Leçon N 5 PICASA Généralités Avec cette leçon N 5, nous allons commencer l étude du traitement de vos photos avec le logiciel de GOOGLE, PICASA, que vous avez téléchargé dans la leçon N 3. 1 Présentation
Initiation à la programmation en Python
 I-Conventions Initiation à la programmation en Python Nom : Prénom : Une commande Python sera écrite en caractère gras. Exemples : print 'Bonjour' max=input("nombre maximum autorisé :") Le résultat de
I-Conventions Initiation à la programmation en Python Nom : Prénom : Une commande Python sera écrite en caractère gras. Exemples : print 'Bonjour' max=input("nombre maximum autorisé :") Le résultat de
Clé USB. Quel type de données peut contenir une clé USB?
 Qu est-ce qu une clé USB? Clé USB Une clé USB est un support de stockage amovible. Ce qui, en français, signifie que c est une mémoire que vous pouvez brancher et débrancher sur n importe quel ordinateur
Qu est-ce qu une clé USB? Clé USB Une clé USB est un support de stockage amovible. Ce qui, en français, signifie que c est une mémoire que vous pouvez brancher et débrancher sur n importe quel ordinateur
Cours d introduction à l informatique. Partie 2 : Comment écrire un algorithme? Qu est-ce qu une variable? Expressions et instructions
 Cours d introduction à l informatique Partie 2 : Comment écrire un algorithme? Qu est-ce qu une variable? Expressions et instructions Qu est-ce qu un Une recette de cuisine algorithme? Protocole expérimental
Cours d introduction à l informatique Partie 2 : Comment écrire un algorithme? Qu est-ce qu une variable? Expressions et instructions Qu est-ce qu un Une recette de cuisine algorithme? Protocole expérimental
TP 1 : 1 Calculs en binaire, octal et hexadécimal
 Univ. Lille 1 - Licence Informatique 2ème année 2013-14 Objectifs du TP Ce TP a pour but Codage de l'information TP 1 : 1. de découvrir quelques opérations logiques sur les nombres 2. et quelques formats
Univ. Lille 1 - Licence Informatique 2ème année 2013-14 Objectifs du TP Ce TP a pour but Codage de l'information TP 1 : 1. de découvrir quelques opérations logiques sur les nombres 2. et quelques formats
Introduction à NetCDF
 Introduction à NetCDF École normale supérieure L3 géosciences 2014/2015 Lionel GUEZ [email protected] Laboratoire de météorologie dynamique Explications préliminaires Deux distinctions générales sur les
Introduction à NetCDF École normale supérieure L3 géosciences 2014/2015 Lionel GUEZ [email protected] Laboratoire de météorologie dynamique Explications préliminaires Deux distinctions générales sur les
Organisation des Ordinateurs
 Organisation des Ordinateurs Bernard Boigelot E-mail : [email protected] URL : http://www.montefiore.ulg.ac.be/~boigelot/ http://www.montefiore.ulg.ac.be/~boigelot/cours/org/ 1 Chapitre 1 Les
Organisation des Ordinateurs Bernard Boigelot E-mail : [email protected] URL : http://www.montefiore.ulg.ac.be/~boigelot/ http://www.montefiore.ulg.ac.be/~boigelot/cours/org/ 1 Chapitre 1 Les
TP 1. Prise en main du langage Python
 TP. Prise en main du langage Python Cette année nous travaillerons avec le langage Python version 3. ; nous utiliserons l environnement de développement IDLE. Étape 0. Dans votre espace personnel, créer
TP. Prise en main du langage Python Cette année nous travaillerons avec le langage Python version 3. ; nous utiliserons l environnement de développement IDLE. Étape 0. Dans votre espace personnel, créer
Usage des photos pour Internet et pour la presse
 Usage des photos pour Internet et pour la presse Que ce soit sur Internet ou dans la presse, l'usage de photographies a la même fonction qui est d illustrer le propos. Pour bien jouer son rôle d information
Usage des photos pour Internet et pour la presse Que ce soit sur Internet ou dans la presse, l'usage de photographies a la même fonction qui est d illustrer le propos. Pour bien jouer son rôle d information
ET 24 : Modèle de comportement d un système Boucles de programmation avec Labview.
 ET 24 : Modèle de comportement d un système Boucles de programmation avec Labview. Sciences et Technologies de l Industrie et du Développement Durable Formation des enseignants parcours : ET24 Modèle de
ET 24 : Modèle de comportement d un système Boucles de programmation avec Labview. Sciences et Technologies de l Industrie et du Développement Durable Formation des enseignants parcours : ET24 Modèle de
1. Structure d un programme C. 2. Commentaire: /*..texte */ On utilise aussi le commentaire du C++ qui est valable pour C: 3.
 1. Structure d un programme C Un programme est un ensemble de fonctions. La fonction "main" constitue le point d entrée pour l exécution. Un exemple simple : #include int main() { printf ( this
1. Structure d un programme C Un programme est un ensemble de fonctions. La fonction "main" constitue le point d entrée pour l exécution. Un exemple simple : #include int main() { printf ( this
Création de maquette web
 Création de maquette web avec Fireworks Il faut travailler en 72dpi et en pixels, en RVB Fireworks étant un logiciel dédié à la création de maquettes pour le web il ne propose que les pixels pour le texte
Création de maquette web avec Fireworks Il faut travailler en 72dpi et en pixels, en RVB Fireworks étant un logiciel dédié à la création de maquettes pour le web il ne propose que les pixels pour le texte
Gestion de gros fichiers binaires (images) en APL*PLUS III
 Gestion de gros fichiers binaires (images) en APL*PLUS III par Gérard A. Langlet Lun des nombreux problèmes que nous avons rencontrés en APL concerne l impression d images, constituées en fait de grosses
Gestion de gros fichiers binaires (images) en APL*PLUS III par Gérard A. Langlet Lun des nombreux problèmes que nous avons rencontrés en APL concerne l impression d images, constituées en fait de grosses
TS 35 Numériser. Activité introductive - Exercice et démarche expérimentale en fin d activité Notions et contenus du programme de Terminale S
 FICHE Fiche à destination des enseignants TS 35 Numériser Type d'activité Activité introductive - Exercice et démarche expérimentale en fin d activité Notions et contenus du programme de Terminale S Compétences
FICHE Fiche à destination des enseignants TS 35 Numériser Type d'activité Activité introductive - Exercice et démarche expérimentale en fin d activité Notions et contenus du programme de Terminale S Compétences
Projet d informatique M1BI : Compression et décompression de texte. 1 Généralités sur la compression/décompression de texte
 Projet d informatique M1BI : Compression et décompression de texte Le but de ce projet est de coder un programme réalisant de la compression et décompression de texte. On se proposera de coder deux algorithmes
Projet d informatique M1BI : Compression et décompression de texte Le but de ce projet est de coder un programme réalisant de la compression et décompression de texte. On se proposera de coder deux algorithmes
Le multiplexage. Sommaire
 Sommaire Table des matières 1- GENERALITES... 2 1-1 Introduction... 2 1-2 Multiplexage... 4 1-3 Transmission numérique... 5 2- LA NUMERATION HEXADECIMALE Base 16... 8 3- ARCHITECTURE ET PROTOCOLE DES RESEAUX...
Sommaire Table des matières 1- GENERALITES... 2 1-1 Introduction... 2 1-2 Multiplexage... 4 1-3 Transmission numérique... 5 2- LA NUMERATION HEXADECIMALE Base 16... 8 3- ARCHITECTURE ET PROTOCOLE DES RESEAUX...
I. QU'EST-CE QU'UN ORDINATEUR? Un ordinateur est relié à plein de périphériques
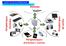 I. QU'EST-CE QU'UN ORDINATEUR? Un ordinateur est relié à plein de périphériques I. QU'EST-CE QU'UN ORDINATEUR? Branchements sur l'unité Centrale + Connexions SANS FILS : WIFI (vers la Box Internet) Bluetooth
I. QU'EST-CE QU'UN ORDINATEUR? Un ordinateur est relié à plein de périphériques I. QU'EST-CE QU'UN ORDINATEUR? Branchements sur l'unité Centrale + Connexions SANS FILS : WIFI (vers la Box Internet) Bluetooth
UFR de Mathématiques et Informatique Année 2009/2010. Réseaux Locaux TP 04 : ICMP, ARP, IP
 Université de Strasbourg Licence Pro ARS UFR de Mathématiques et Informatique Année 2009/2010 1 Adressage IP 1.1 Limites du nombre d adresses IP 1.1.1 Adresses de réseaux valides Réseaux Locaux TP 04 :
Université de Strasbourg Licence Pro ARS UFR de Mathématiques et Informatique Année 2009/2010 1 Adressage IP 1.1 Limites du nombre d adresses IP 1.1.1 Adresses de réseaux valides Réseaux Locaux TP 04 :
PROJET ALGORITHMIQUE ET PROGRAMMATION II
 PROJET 1 ALGORITHMIQUE ET PROGRAMMATION II CONTENU DU RAPPORT A RENDRE : o Fiche signalétique du binôme o Listing des différents fichiers sources o CD sources o Il sera tenu compte de la présentation du
PROJET 1 ALGORITHMIQUE ET PROGRAMMATION II CONTENU DU RAPPORT A RENDRE : o Fiche signalétique du binôme o Listing des différents fichiers sources o CD sources o Il sera tenu compte de la présentation du
STAGE IREM 0- Premiers pas en Python
 Université de Bordeaux 16-18 Février 2014/2015 STAGE IREM 0- Premiers pas en Python IREM de Bordeaux Affectation et expressions Le langage python permet tout d abord de faire des calculs. On peut évaluer
Université de Bordeaux 16-18 Février 2014/2015 STAGE IREM 0- Premiers pas en Python IREM de Bordeaux Affectation et expressions Le langage python permet tout d abord de faire des calculs. On peut évaluer
