La notion de fonction en classe de seconde,
|
|
|
- Claude Perrot
- il y a 10 ans
- Total affichages :
Transcription
1 IUFM Académie de Montpellier Site de Perpignan DURAN Arnaud La notion de fonction en classe de seconde, Enjeux et obstacles Discipline : Mathématiques Classe concernée : Seconde Etablissement : Lycée Déodat de Séverac, Céret Tuteur du mémoire : Yves Girmens Année universitaire
2 Résumé : Lors de cette étude, je me suis principalement intéressé aux obstacles liés à la notion de fonction. Après avoir exposé les raisons qui m ont poussé à m orienter vers un tel sujet, j ai développé une approche théorique à l issue de laquelle j ai pu identifier certaines de ces difficultés. Il apparaît que des passages réguliers entre les différents registres de représentation sémiotique, ainsi qu un travail régulier autour du langage courant, pourraient, entre autres, constituer des moyens pour clarifier le concept de fonction auprès des élèves. La partie expérimentale de ce mémoire nous a mené à confirmer ces hypothèses. My main concern throughout this study was to deal with the issues related to the notion of Function. After having reported the reasons which made me choose such a subject, I decided to take particular care to develop a theoretical approach so as to describe some of those issues. Additionaly, I noticed that a regular use of different types of semiotic representation combined with a constant work on our common language may be considered as an efficient means that could help pupils understand the notion of Function. Eventually, the experimental section of this memoire was meant to validate this hypothesis. Les mots clés : notion de fonction registre de représentation langue naturelle - obstacle 2
3 3
4 Table des matières I ] INTRODUCTION... 6 Les motivations... 6 Les points importants... 6 Les pistes de recherche...8 II] ETUDE THEORIQUE A. HISTOIRE DE LA NOTION DE FONCTION ) Un bref historique ) Les enjeux didactiques B. APPRENTISSAGE DE LA NOTION DE FONCTION DE LA 6 ème A LA SECONDE ) Sixième ) Cinquième ) Quatrième ) Troisième ) Seconde C. LES OBSTACLES ) Obstacles didactiques ) Obstacles épistémologiques ) Autres types d obstacles D. LES REGISTRES DE REPRESENTATION ) Eléments théoriques ) Le langage courant ) Formules et graphiques ) Tableaux de correspondance E. BATIR UNE AER ET DES ACTIVITES
5 III] LES EXPERIENCES A. ACTIVITE 1 : Introduction de la notion de fonction ) Présentation du problème ) L articulation des registres ) Passage du discret au continu ) Conclusions B. ACTIVITE 2 : Fonctions «discrètes», cloisonnement ) Les activités ) Un nouveau sondage...26 C. ACTIVITE 3 : Fonctions de référence : fonction carré/fonction inverse ) La fonction carré ) La fonction inverse ) Conclusions D. ACTIVITE 4 : Approche de la notion de fonction en 3 ème ) Présentation du problème ) Découverte la notion de fonction ) Conclusions IV] CONCLUSION ANNEXE 1 : Etude des manuels ANNEXE 2 : Une approche de la notion de fonction ANNEXE 3 : Activités diverses ANNEXE 4 : Approche de la fonction iuverse avec EXCEL ANNEXE 5 : Productions d élèves de 3 ème ANNEXE 6 : Bibliographie
6 I ] INTRODUCTION Les motivations Lors de l élaboration de ma progression, et en discutant avec mon tuteur, je me suis aperçu que le chapitre «fonctions» constituait un élément relativement difficile à introduire. Cette difficulté est liée à plusieurs facteurs. D une part, ce chapitre est sans doute un des plus importants pour la classe de seconde, c est pourquoi il est indispensable de le présenter de manière soignée et claire à des élèves pour qui la notion de fonction est, nous le verrons plus tard, encore assez vague. En second lieu, ce chapitre est très étoffé ; la majorité des professeurs que j ai interrogés m ont conseillé de le fragmenter en 4 ou 5 parties. J ai donc suivi ce conseil, d autant plus que le niveau de ma classe est relativement faible et m oblige à effectuer des séquences courtes pour ne pas les perdre ou les décourager. Le dernier point, et c est sans doute celui qui a soulevé le plus d interrogations, repose sur le fait que l éventail des entrées possibles pour aborder ce chapitre est très large : on peut présenter les fonctions à travers l étude d un tableau de valeurs, d une lecture graphique, d une formule, d un tableau de variations Mon tuteur de stage, curieux de savoir comment j allais procéder, ne m a volontairement pas fait part de manière détaillée de ce problème. J ai donc été amené à découvrir par moi-même la multiplicité des entrées possibles pour cette notion, et quelles difficultés cela pouvait engendrer. Pour amorcer ce chapitre j ai donc commencé par m intéresser à ce que proposaient tous les ouvrages à ma disposition. Je n ai pas tardé à remarquer l abondance des activités utilisées pour présenter la notion de fonction. Devant la multitude et la diversité des activités d étude et de recherche utilisées, une question toute simple s est posée : «Comment aborder le chapitre fonctions en seconde? Quels sont les enjeux et les obstacles de cette notion?» Les points importants D une part, en seconde, le chapitre «fonctions» tient une part primordiale dans les programmes. C est là qu on va véritablement définir cette notion, et ainsi donner à l élève les clés d un outil qui tiendra une place fondamentale tout au long de son cursus au lycée. Devant 6
7 cette responsabilité, il m a paru nécessaire de donner à ce chapitre une importance particulière. En second lieu, j ai été amené à constater que l introduction de cette notion constituait un enjeu didactique majeur. Pour le jeune professeur que je suis, le fait de rechercher à optimiser cette approche sur un plan pédagogique me semble être quelque chose de très formateur. Je pense donc, sur un plan plus personnel, que l étude détaillée de cette problématique peut s avérer très fructueuse. Cela me semble même être un problème central pour un professeur : un enseignant se doit de s efforcer d offrir à ses élèves les plus grandes chances de bien appréhender les notions qu il présente. Elaborer une séquence répondant à cette question constitue une étape indispensable pour ma formation. De manière plus générale, il pourrait m être bénéfique de savoir comment peuvent s introduire des chapitres importants, dans lesquels on manipule des notions pouvant s étudier à travers plusieurs registres. Je pense que cette étude pourrait m apporter quelques éléments théoriques qui pourront m aider à construire mon cours, et j aurai la possibilité de voir quels critères peuvent constituer des paramètres de choix concernant mes activités. Les différentes manières dont les collègues procèdent, ainsi que les raisons de leurs choix didactiques peuvent aussi s avérer d une grande richesse. L introduction de la notion de fonction est difficile. Pour un élève de seconde, qui, jusque là, dans son cursus de collège, n a étudié que les fonctions affines et linéaires, ce chapitre peut être la source de grandes difficultés ; des difficultés d autant plus importantes qu en seconde tous les aspects sont vus de manière quasi-simultanée, ce qui va obliger les élèves à mobiliser énormément de connaissances dans de divers domaines (algèbre, lecture graphique, lecture d un tableau de valeurs, calculs de base ). Ceci met en évidence que l apprentissage de cette notion met en jeu de multiples types d obstacles. Il me semble très intéressant de voir comment je pourrais faire en sorte qu ils ne deviennent pas insurmontables pour mes élèves. Sur un plan historique enfin, je pense que ce sujet pourrait m apporter des connaissances que je mettrais à profit dans le cadre de mon enseignement. Il me semble important, voire indispensable de voir comment s est construit l enseignement de cette notion au fil du temps. Dans un cadre plus global, je pense aussi que l étude de la construction même de cette notion au cours de l histoire m apportera surement beaucoup, à la fois sur un plan pédagogique et culturel. 7
8 Les pistes de recherche Dans le cadre de cette étude, il m a semblé fondamental de savoir ce qu était une fonction pour mes élèves. Leurs réponses (en particulier leurs erreurs) m aideront sans doute à mettre en évidence quelles sont les principales difficultés liées à cette notion ; peut être pourrais je en tirer une première idée sur principaux obstacles. De plus, l avantage de ce mini sondage réside dans le fait qu il me donnera des éléments me permettant de répondre directement aux besoins et aux difficultés de mes élèves. Ceci me permettra peut être de tirer mon étude de son cadre théorique et de l orienter légèrement pour le bien de ma propre classe, même si, je pense, les difficultés des élèves de seconde 8 du Lycée de Céret ne doivent surement pas être éloignées de celles des autres élèves de seconde. L étude de la construction de cette notion pourrait m apporter des pistes de réflexion intéressantes, notamment au niveau des raisons pour lesquelles elle est si difficile à concevoir pour certains élèves. J effectuerai donc des recherches dans cette direction. J ai pu constater que, pour la plupart de mes élèves, le passage du numérique à l algébrique (en particulier représenter un nombre pouvant prendre plusieurs valeurs par une lettre), présente un blocage important. Certains sont incapables d effectuer un calcul avec des «lettres», alors qu ils en sont tout à fait capables avec des nombres. C est sans doute une des difficultés principales que présente la notion de fonction. Je prendrai donc le soin de me pencher sur les difficultés liées à la sémiotique et à la notion de variable. Les manuels constituent une source de données très riche. J irai donc étudier ce qu ils proposent, comment ils présentent les différents registres et les articulent entre eux. En possédant un nombre assez conséquent, j essaierai d en effectuer une classification, et tenterai de voir quels registres sont le plus mis en avant. Enfin, je verrai comment ces résultats se situent par rapport aux programmes. La multiplicité des registres possibles est sans doute un point central dans l apprentissage du concept de fonction. J essaierai donc de voir autour de quels critères construire mes activités, et ainsi comment peuvent s articuler ces registres dans un chapitre introductif. Je rechercherai donc des ouvrages relatifs à cette problématique, et tenterai de structurer une approche cohérente. Dans cette optique, je m intéresserai notamment aux travaux de Raymond DUVAL. 8
9 Enfin, la majeure partie de mon travail consistant à trouver une ou plusieurs activités d étude et de recherche appropriés à l approche de cette notion, j essaierai de me renseigner sur la façon dont on peut construire et articuler une activité d étude et de recherche de la meilleure façon possible. L étude des programmes me sera certainement utile. 9
10 II] ETUDE THEORIQUE A. HISTOIRE DE LA NOTION DE FONCTION : La façon dont ce concept s est construit peut nous renseigner sur la nature des obstacles. Il semble qu une étude épistémologique de ce concept pourrait nous offrir des pistes de réflexions intéressantes. En particulier, nous essaierons de voir dans quels contextes et à travers quels registres cette notion a émergé et s est construite au fil des années. Nous essaierons, à la suite de cette étude, de mettre en évidence ce qui peut s avérer essentiel dans l apprentissage de cette notion. 1) Un bref historique : On attribue aux Babyloniens les premières esquisses de l apparition de fonctions. Ces dernières sont présentes, de manière implicite, derrière des tables de nombres, utilisées par les scribes pour gérer certaines transactions économiques. Certains exemplaires ont été retrouvés à Babylone et datent de 2000 ans avant notre ère. Il semblerait que le premier registre dans lequel cette notion ait émergé soit celui des tableaux de valeurs. Jusqu ici, le concept de variable n apparaît pas encore, il n est en aucun cas question de dépendance entre deux quantités. La notion de dépendance pourrait avoir émergé avec les pythagoriciens, lors de l établissement des premières lois de l acoustique. Ils ont formulé une relation de dépendance numérique entre la longueur d une corde vibrante et la hauteur du son qu elle produit. Là encore, ils ont traduit ces phénomènes à l aide de tableaux de correspondances. Au Moyen âge, l étude et l analyse d une dépendance entre deux quantités (grandeurs physiques) sera l objet de la construction de graphiques. Ils traduiront pour la première fois les correspondances faites à partir de quantités variables. L étude des mouvements et des phénomènes physiques va contribuer à enrichir et diversifier les différents aspects à travers lesquels la fonction peut se représenter. Au 16 ème et au début du 17 ème siècle, elle apparaît déjà à travers des courbes, des tableaux de correspondance, et même de formules algébriques. C est à cette période qu est utilisé pour la première fois le terme «fonction» (utilisée par Leibniz en 1673 : 10
11 «J'appelle fonctions toutes les portions des lignes droites, qu'on fait en menant des droites indéfinies, qui répondent au point fixe, et aux points de la courbe.») Bernouilli sera le premier à donner une définition générale de la notion de fonction, au début du 18 ème siècle : «On appelle fonction d'une grandeur variable une quantité composée de quelque manière que ce soit de cette grandeur variable et de constantes.» On commence à employer la notation «f(x)». A partir du 19 ème siècle, la fonction devient un objet d étude pour lui-même, on parle de «théorie des fonctions». On commence à étudier les fonctions composées Au 20 ème siècle, les fonctions deviennent le cadre d une théorie globale. On cherche à définir ce concept de manière générale. 2) Les enjeux didactiques : Le concept de fonction a mis plusieurs millénaires à se mettre en place. A l origine, la fonction est présente à travers des tables de correspondance, et est utilisée pour répondre à des problèmes concrets, liés à l économie. Elle établit un lien entre des quantités fixes. Il est évident qu à cette époque, en utilisant ces «correspondances tabulées», nos ancêtres n avaient aucune idée du concept de «fonction» en tant qu objet mathématique. L étude de phénomènes physiques donnera progressivement naissance à un second cadre d étude : les graphiques. Nous noterons aussi que la définition générale du mot «fonction» n est apparue qu au 18 ème siècle. Le caractère tardif de cette définition, et de l émergence de ce concept en général peut donc expliquer que cette notion peut s avérer difficile à appréhender. Dans le cadre de l enseignement au collège ou au lycée, cela peut donc expliquer pourquoi cette définition est donnée qu en classe de seconde, alors qu au collège la notion de fonction apparaît en tant qu outil dans la résolution de problèmes bien précis, dans des contextes particuliers (proportionnalité, lecture graphique, fonctions affines ). Cette disposition est directement liée aux obstacles que présente le chapitre «fonctions» ; nous essaierons de voir comment cette brève étude épistémologique peut apporter des éléments de réponse face à cette question. Pour cela, commençons par étudier de manière plus poussée comment la notion de fonction est abordée au cours du collège. 11
12 B. APPRENTISSAGE DE LA NOTION DE FONCTION DE LA 6 ème A LA SECONDE : 1) Sixième : En sixième, la notion de fonction est déjà sous-jacente dans plusieurs chapitres. Dans le chapitre «proportionnalité», elle intervient sous forme de correspondances tabulées, dans la résolution de problèmes concrets. Nous pourrons évoquer le parallèle avec l étude effectuée précédemment, où ce concept commence à prendre naissance sous forme de tableaux de valeurs, pour répondre à des problèmes précis faisant intervenir des grandeurs et des mesures. Dans ce contexte, la fonction intervient déjà sous forme de procédure, ce qui permet aux élèves de la décrire grâce au langage courant (une situation de proportionnalité peut être décrite par un élève par «je multiplie par»). On pourra déjà noter qu il est conseillé de montrer aux élèves qu il existe des situations «non proportionnelles». Nous verrons plus tard quel impact cela peut avoir dans l apprentissage du concept de fonction en classe de seconde. «Les problèmes à proposer (qui relèvent aussi bien de la proportionnalité que de la non proportionnalité) se situent dans le cadre des grandeurs (quantités, mesures).» Dans le chapitre «Organisation et traitement de données», les élèves auront un premier contact avec la notion de graphique. Ces travaux vont permettre de mettre en place les premières règles relatives au registre graphique, et sont d autant plus importants que c est à travers eux que la notion de dépendance va commencer à émerger. Les compétences visées vont de la simple lecture d une information (qui revient, par exemple, sur un graphique, à la lecture des coordonnées) à la capacité à faire une interprétation globale et qualitative de la représentation étudiée (évolution d une grandeur en fonction d une autre). 2) Cinquième : Dans la continuité du programme de sixième, le chapitre «proportionnalité» apporte des compléments intéressants : Les activités numériques ou graphiques font le plus souvent appel à des situations mettant en relation deux grandeurs. Le travail sur les tableaux de nombres sans lien avec un contexte doit occuper une place limitée. Il est possible d envisager, dans une formule, des variations d une grandeur en fonction d une autre grandeur, tout autre variable étant fixée [ ]. 12
13 Nous pourrons noter certains «mots clés» dans cet extrait, comme «formule», qui met en valeur un registre jusque là occulté par les programmes, ainsi que le mot «variable» et l expression «en fonction de» ; la notion de dépendance ne se voit plus seulement à travers le registre graphique comme c était le cas en classe de sixième ; les élèves doivent apprendre à lire et interpréter certaines formules simples, ce qui les oblige à avoir déjà des notions sur le statut des objets qu ils manipulent, distinguer ce qui varie de ce qui est fixé Le registre graphique est réinvesti et vu de manière plus poussée. En particulier, savoir utiliser le vocabulaire spécifique (coordonnées, repère, abscisse ), fait partie des compétences visées. 3) Quatrième : En quatrième, les élèves vont poursuivre les travaux effectués sur la proportionnalité et le traitement de données. Cette classe n apporte véritablement rien de nouveau par rapport au concept de fonction : les élèves vont approfondir leurs connaissances en continuant de manipuler certains types de fonction (en particulier des fonctions affines et linéaires) dans les registres déjà connus. Le programme de la classe de quatrième propose d approfondir et de prolonger l étude de notions introduites dans les classes antérieures [ ]. Comme en classe de cinquième, le mot fonction est employé, chaque fois que nécessaire, en situation, et sans qu une définition formelle de la notion de fonction soit donnée 4) Troisième : C est en classe de troisième qu apparaît pour la première fois de manière explicite un chapitre consacré à la notion de fonction (dans les nouveaux programmes). Les capacités attendues se limitent à des calculs d images dans les trois registres connus : registre «graphique», «formule» et «tableau de correspondance». On introduit la notion d antécédent (par lecture dans un tableau ou sur une courbe), et l utilisation de certaines notations (f(x), x α f(x)) vient enrichir le registre «formules». L accent est toutefois donné sur l étude des fonctions linéaires et affines. Ce chapitre va pouvoir être l objet d une synthèse des apprentissages réalisés depuis la sixième sur le concept de fonction. Dans ce chapitre, la définition formelle de cet objet mathématique est implicite : donnée sous forme d une formule, une fonction sera vue comme étant un procédé de calcul, que l on va pouvoir décrire grâce au langage courant. Par exemple, processus de correspondance x α ax + b peut être décrit comme : «je multiplie par a puis je rajoute b». 13
14 5) Seconde : C est en classe de seconde que l on va donner une définition formelle de la notion de fonction. Le travail autour de ce concept va être fondamental et très lourd : les différents registres, avec leur vocabulaire et technique respectifs vont devoir être réinvestis de manière quasi-simultanée, et on introduit un nouvel outil : celui des tableaux de variations. Là encore, il est préconisé par les programmes de motiver l introduction de ce concept autour de l étude d un problème dans un contexte précis (optimisation en géométrie, calcul d intérêts ). On étudie les principales fonctions de référence (fonctions affines, linéaires, carré, inverse, trigonométriques). 6) Synthèse : Nous pouvons voir que l apprentissage de la notion de fonction se fait de manière très progressive, même si c est véritablement en classe de seconde que l on va définir formellement ce concept. En réalité, nous pouvons établir sans difficulté un parallèle entre l évolution de cet enseignement avec la construction de cette notion au cours de l histoire. Dans les deux cas, c est la fonction en tant qu outil qui émerge, à travers des tableaux de correspondance, apportant des solutions à des situations et des problèmes concrets. La mise en place des deux autres principaux registres (graphiques et formules) se fera progressivement, et l étude de plus en plus approfondie de ces aspects nous poussera à basculer progressivement vers le concept «objet» de la notion de fonction. Si l on se réfère à la manière dont elle s est construite au fil de l histoire, il semble que la notion de fonction, telle qu elle est abordée au long du cursus du secondaire, est vue de manière relativement naturelle. Cette étude peut, de surcroît, nous permettre de mettre en évidence différents obstacles liés à son apprentissage. 14
15 C. LES OBSTACLES : La construction de la notion de fonction, ainsi que sa manière de l enseigner au collège, mettent en évidence de nombreuses difficultés liées à ce concept. Dans le but de mieux cibler et travailler sur ces difficultés, je me suis attardé sur leur nature et leur cause. Les travaux de Guy Brousseau nous amènent à identifier plusieurs catégories d obstacles, que nous essaierons d étudier plus en profondeur : 1) Obstacles didactiques : La première source de difficultés peut venir de l enseignement lui-même ; l étude effectuée précédemment révèle en effet que le fait de faire émerger le concept de fonction au niveau collège dans un cadre très particulier (on y étudie essentiellement les fonctions affines), peut s avérer problématique lorsqu on va vouloir présenter cette notion dans un cadre plus général au lycée. La prépondérance du chapitre «proportionnalité», par lequel on commence à mettre en place les premiers systèmes d étude et de langage des registres constitue un obstacle didactique. En effet, les seuls exemples de fonctions que les élèves ont étudiés de manière approfondie au collège sont les fonctions affines et linéaires. Il m a donc paru important d essayer de voir quel pouvait être l impact de cet apprentissage sur mes élèves fraîchement sortis du collège. J ai donc décidé d effectuer un sondage auprès de mes élèves, en leur posant une simple question : «Pour vous, qu est-ce qu une fonction?». La grande majorité de mes élèves font référence aux fonctions linéaires, affines et constantes. Pour la plupart d entre eux, il n y a que ces trois types de fonctions. Parmi les non redoublants, seuls trois élèves n ont pas fait d amalgame : «Une fonction, c'est un calcul qui dépend d'une lettre, on trouvera le résultat en fonction de la lettre (grandeur du chiffre ou du nombre)» «C'est un calcul qu'on peut représenter graphiquement. Je connais 3 types de fonctions : linéaire, affine, constante» «C'est un calcul avec une ou plusieurs inconnues (ex : 2X+3). On peut la représenter graphiquement grâce à des calculs, ou l'utiliser comme outil mathématique». On peut toutefois noter que même dans les deux dernières réponses, la notion de fonction affine est encore très présente. L un des objectifs de l introduction de ce chapitre va donc être de mettre l accent sur ce point, c'est-à-dire de détacher la notion de fonction du chapitre «proportionnalité / fonctions affines et linéaires». 15
16 Cet obstacle didactique est toutefois difficilement contournable. Il paraît en effet assez ambitieux de présenter la fonction sous son aspect le plus général, car la richesse de ce concept, et la diversité des cadres d étude va obliger l élève à mobiliser un grand nombre d outils et de connaissances, avec lesquelles il n est peut être pas encore à l aise. En faisant cela, on court donc le risque de noyer les élèves même moyens dans un chapitre qu ils auront du mal à appréhender, ces difficultés passant vite au premier plan. Toutefois, au moins en troisième, il me semble envisageable, voire important de présenter la notion de fonction dans un contexte global (sans pour autant en donner une définition formelle), en évoquant le fait qu il existe des fonctions de type «non linéaires». J ai eu la chance d effectuer mon stage de pratique accompagnée en classe troisième ; j ai donc pu observer la mise en pratique d une activité d approche répondant à cette problématique. 2) Obstacles épistémologiques : En second lieu, la notion de fonction présente aussi des obstacles d ordre épistémologiques. Ces difficultés, liées au savoir lui-même, sont en partie dues au caractère abstrait de cette notion ; l élève aura surement du mal à appréhender ce qu est réellement une fonction. Pour lui donner du sens, il sera forcément tenté de rattacher cet objet mathématique à un registre particulier. C est ce que R. DUVAL explique en affirmant : Le fonctionnement cognitif de la pensée humaine se révèle inséparable de l existence d une diversité de registres sémiotiques de représentation. Si on appelle sémiosis l appréhension, ou la production, d une représentation sémiotique, et noésis l appréhension conceptuelle d un objet, il faut affirmer que la noésis est inséparable de la sémiosis. Pour comprendre et donner réellement du sens à ce concept, il paraît donc indispensable de faire comprendre que ces différents modes de représentation sémiotiques sont des moyens de donner vie à la fonction, sont des outils qui vont traduire sa présence. La notion de dépendance est sans doute aussi un obstacle important. Dans le cadre algébrique, les élèves vont devoir travailler avec des grandeurs variables, manipuler des formules faisant intervenir des «inconnues». Je me suis rendu compte que la plupart des élèves de ma classe n étaient pas à l aise avec la signification de ces expressions. Ils savent globalement les manipuler, mais ont du mal à leur donner du sens, les interpréter. En corrélation avec le problème que nous venons de souligner, se pose le problème du passage du «discret» au «continu». Par exemple, les élèves sauront sans difficulté déterminer l aire d une surface dont les dimensions sont connues, mais lorsqu il s agira de 16
17 déterminer une aire qui dépend d une quantité variable (périmètre, longueur d un côté ), l élève obtiendra une formule dont il aura du mal à voir qu elle donne l aire «pour tout x» ; pour lui cette formule reste le résultat d un calcul ; c est quelque part son seul statut. Nous verrons plus tard que pour que cette formule puisse avoir une autre signification que celle d une simple étiquette, c est à dire se voir attribuer un sens lié au contexte de départ, il va falloir que l élève puisse trouver un moyen d exprimer ce qu elle signifie pour lui. C est en particulier dans ce contexte que l importance du vocabulaire, c'est-à-dire le registre du langage courant va pouvoir prendre une place centrale dans l apprentissage. 3) Autres types d obstacles : L étude des réponses de mes élèves m amène à soulever un autre problème : beaucoup de réponses sont une succession parfois incohérente de termes mathématiques liés à différents registres : «Il y a la fonction affine et la fonction linéaire. Une fonction sert à calculer les ordonnées et les coordonnées d'une droite dans un repère orthonormé» «C'est un nombre qui sert de repère» «Une fonction est notée f(x). Dans un graphe, la fonction d'un nombre est affine ou linéaire; On peut obtenir ensuite une droite, une courbe, des points non alignés. En faisant un graphique on calcule une moyenne» Certains élèves ont du mal à donner du sens aux termes techniques avec lesquels ils ont fait leur apprentissage. Ces impressions ont été largement confirmées lors des premières heures de cours sur ce chapitre. Cela révèle que, dans chaque registre, il règne une certaine confusion au niveau du sens de mots et du statut des objets que l on manipule. Une de mes tâches va donc être de réattribuer à chaque registre un vocabulaire et des règles de traitement précises. 17
18 D. LES REGISTRES DE REPRESENTATION : Le concept de fonction peut apparaître sous différentes formes. Il m a paru intéressant de répertorier sous quels aspects la fonction peut apparaître, et de voir comment on va pouvoir les faire intervenir dans le cadre de l apprentissage. Les travaux de R DUVAL m ont permis d apporter quelques éléments de réponse relatifs à ce sujet. 1) Eléments théoriques : L étude épistémologique permet de mettre en évidence quatre registres de représentation : tableau de correspondance, graphiques, formules, et langage courant. A celui - ci vient s ajouter, en classe de seconde, le registre «tableau de variations». Comme nous l avons vu précédemment, il y a de forts risques que les élèves confondent l objet mathématique qu est la fonction avec une de ses représentations. C est ce que R. DUVAL appelle le «cloisonnement des registres de représentation». Ce phénomène aura d autant plus de chances de se produire si l on étudie de manière séparée chacun de ces différents modes de représentation. La coordination de plusieurs registres peut être un moyen de surmonter cette difficulté. «Le recours à plusieurs registres semble même une condition nécessaire pour que les objets mathématiques ne soient pas confondus avec leurs représentations et qu ils puissent aussi être reconnus dans chacune de leurs représentations». Nous venons de répertorier les différents registres de représentations de fonctions que l on voit en seconde. A partir de là, j ai pensé qu il serait intéressant de pointer quelles étaient les particularités de ces cadres d étude, afin de pouvoir articuler mon cours de façon cohérente, et surtout de façon à répondre aux besoins de mes élèves. Ma réflexion, appuyée par les discussions échangées au cours de cette année, m a permis de faire émerger certains éléments de réponse, dont je présenterai ici les idées maîtresses. 2) Le langage courant : Dans de nombreux contextes, le langage courant peut s avérer être un moyen de faire face à certains obstacles. L analyse des ouvrages met d ailleurs en évidence son importance ; c est le second registre le plus présent dans les activités présentées sur l ensemble des manuels qui étaient à ma disposition. Dans la grande majorité des cas, cet outil intervient pour 18
19 que l élève donne du sens à la notion de fonction (traduire des phénomènes, des variations, lecture et interprétation de graphiques...). De la sorte, le professeur donne l occasion aux élèves de voir réellement l utilité d une fonction. En traduisant par son langage propre ce qu il peut observer à travers d autres registres, il acquiert petit à petit une meilleure appréhension de cet objet. Une telle démarche peut contribuer à lui ôter progressivement son aspect abstrait. En particulier, comme nous l avons précédemment évoqué, le registre de représentation sémiotique «formules» reste stérile s il est vu de manière isolée. Le langage courant lui donnera tout son sens et pourra mettre en valeur son utilité, ceci étant bien sur valable pour les autres registres de représentation. En résumé, en liaison avec les corrélations entre les différents cadres d étude évoqués précédemment, nous venons de voir l importance particulière que pourrait représenter l articulation d un registre de représentation avec celui du langage courant. 3) Formules et graphiques : Nous avons vu qu il y avait un risque pour qu un élève confonde une fonction avec son mode de représentation. Si l on analyse avec plus de précision le résultat du sondage effectué auprès de mes élèves, nous constaterons que les élèves confondent la plupart du temps une fonction avec sa représentation graphique ou sa formule. La formule est souvent vue comme une étiquette, c est en quelque sorte le nom de la fonction. ; pour ce qui est du graphique, il s agit encore là pour les élèves d un objet relativement vague auquel ils ont du mal à donner du sens ; c est en quelque sorte l image de la fonction, son «portrait». Nous avons déjà fait émerger quelques éléments pouvant nous permettre de donner quelques outils à l élève afin qu il puisse saisir la signification réelle de ces modes de représentation. Mais le problème posé ici ne repose pas seulement sur la question du «sens». Le but est de faire prendre conscience à l élève qu une fonction n est pas une formule ou un graphique ; c'est-à-dire d éviter le phénomène de cloisonnement. J ai donc essayé de trouver un moyen de mettre en place une activité pouvant éclairer mes élèves sur ce point. Même si les programmes préconisent d en présenter un nombre limité, il m a paru approprié de leur donner des exemples de fonctions ne pouvant pas se représenter par un graphique «traditionnel», ou par une formule. De la sorte, les élèves auront au moins quelques exemples de fonctions ne pouvant pas «vivre» à travers ces registres. Peut être cela leur permettra de prendre un peu de recul par rapport à ce concept et de mieux l appréhender. Là encore, le langage courant va sans doute nous être d une utilité non négligeable. 19
20 4) Tableaux de correspondance : Le tableau de valeurs est le premier mode représentation à être apparu ; c est aussi celui qui semble à priori le plus abordable pour les élèves, qui travaillent avec depuis la sixième. Cependant cet outil présente un risque : celui de considérer une fonction comme une succession de nombres ; il ôte à la fonction son caractère variationnel, dynamique. Ainsi, si l on construit le graphique associé à ce tableau de valeurs, deux risques sont envisageables. Dans un premier temps, il semblerait qu un élève reliant les points du graphique par une courbe puisse considérer qu il effectue une méthode d interpolation, lui donnant la valeur exacte de la fonction pour les points intermédiaires. D autre part, le risque contraire serait qu il conçoive le graphique de manière «discrète», en donnant crédit seulement aux points donnés. Une manière de minimiser ce problème serait de faire intervenir le langage courant afin de pouvoir intégrer la notion de dépendance, de variation. Une lecture du graphique élaborée à partir du tableau, relié au problème initial pourrait en effet être une solution pour atténuer ces risques. Voilà pourquoi il semblerait peu indiqué d étudier un tableau de correspondance et de tracer le graphique sans en effectuer une interprétation dynamique. J essaierai donc d en tenir compte dans l élaboration de mes activités. E. BATIR UNE AER ET DES ACTIVITES : Nous avons vu que les premiers édifices de la notion de fonction ont été construits pour répondre à des problèmes concrets. Par analogie, il paraît donc naturel de faire en sorte que le premier contact avec la notion de fonction s effectue autour d une situation de la vie courante ; il paraît difficilement envisageable d introduire ce concept de manière formelle en seconde. Les programmes mettent l accent sur ce point : «On étudiera des situations issues, entre autres, de la géométrie, de la physique, de l actualité ou de problèmes historiques. On réfléchira sur les expressions être fonction de et dépendre de dans le langage courant et en mathématiques.» Nous pouvons aussi souligner que les programmes insistent sur la place du langage courant, dont nous avons précédemment évoqué l importance L objectif ici est d arriver, à terme, à donner à l élève une vision globale et générale de cet objet mathématique. Il me semble donc approprié, dans le cadre d une activité d approche, de faire intervenir une situation permettant de mettre en jeu la notion de variable et de 20
21 dépendance, et dans laquelle la fonction serait un outil pouvant intervenir sous différents aspects. Il me semble intéressant de voir ce que proposent les ouvrages à ce sujet ; cela m aidera très certainement à orienter mes choix : ANNEXE 1. ( ) Outre l importance de l aspect «graphiques», nous pouvons souligner l importance primordiale du registre de la langue naturelle, qui revient presque de manière systématique, ce qui confirme bien que le langage courant tient une place centrale dans l apprentissage. Enfin, il me semble important de pointer le fait que chacune des activités présentées met en jeu l articulation d au moins deux registres de représentation différents. Ce phénomène parait d autant plus visible avec les livres correspondant aux nouveaux programmes, qui proposent des travaux dans lesquels la fonction est vue à travers trois, voire quatre aspects. A la lumière de cette étude, il me semble opportun de bâtir une activité qui puisse prendre en considération le plus grand nombre de paramètres que nous venons d évoquer, notamment ceux qui me paraissent primordiaux, à savoir insister sur le langage naturel l articulation des registres. 21
22 III] LES EXPERIENCES : L étude théorique précédente nous a permis de cibler les principaux enjeux liés à la notion de fonction, et de voir comment on pourrait tenter de travailler pour pallier aux principales difficultés inhérentes à ce concept. A. ACTIVITE 1 : Introduction de la notion de fonction J ai bâti et présenté cette activité en début d année : ANNEXE 2 ( ). Elle constitue pour ma classe la première approche de la notion de fonction. A cette époque, je n avais pas le bagage théorique exposé précédemment. Conscient de l enjeu que représentait ce premier contact, j ai pris le soin de tenter d élaborer une activité qui puisse tenir la route, malgré mon manque d expérience et de connaissances. Par chance, nous pouvons retrouver dans cet exercice de nombreuses questions qui peuvent paraître cohérentes par rapport à certains points que nous venons de développer. 1) Présentation du problème : Afin de rester en accord avec les programmes, j ai décidé d articuler ma première activité d approche autour d un contexte particulier, à savoir un problème d optimisation d aire en géométrie. Il s agit d une situation classique, qui va donner naissance à une fonction, dont l étude à travers les différents registres de représentation sémiotique aboutira à un encadrement de «la valeur de x pour laquelle l aire est maximale». Je me suis dit que cette activité assurerait la transition entre un chapitre de géométrie («quadrilatères»), et un chapitre d analyse («notion de fonction»). Nous verrons plus tard en quoi cette transition peut s avérer problématique pour les élèves. Cette activité présente 4 parties. Les parties I et II ont été traitées à part, en cours, et de manière individuelle par les élèves. La partie III a fait l objet d un travail de groupe lors d un module faisant intervenir la calculatrice. Le bilan s est effectué de manière collective au cours d une dernière séance. 2) L articulation des registres : Afin de rendre mon activité la plus riche possible, j ai jugé qu il serait intéressant de présenter une activité dans laquelle la fonction est vue à travers le plus grand nombre de d aspects possibles. Ainsi, chaque partie fait intervenir un domaine d étude différent, et on 22
23 demande systématiquement à l élève d avoir recours au langage courant pour donner du sens à ce qu il est en train d étudier. Tout en revenant régulièrement sur le sens et l interprétation des résultats par le biais du langage, l élève étudiera la fonction successivement à travers : une formule, un tableau de correspondance, un graphique, un tableur sur la calculatrice. Au cours du bilan nous avons donc eu l occasion de mettre en évidence tous les registres de représentation possibles connus, ou du moins mis en jeu dans cette activité. Nous devrions, en agissant de la sorte, éviter le problème du «cloisonnement des registres de représentation». L élève a au moins pu voir qu une fonction pouvait s étudier d une multitude de manières, et surtout de voir quelle pouvait en être l utilité dans la résolution de certains problèmes. Ainsi, j ose croire que ce dispositif leur a permis de donner un peu plus de sens au concept de fonction. 3) Passage du discret au continu : Attardons nous maintenant sur une question qui me paraît importante, voire centrale : le passage du discret au continu. Lors de l étude théorique, nous avons souligné le problème que pouvait représenter l algèbre et le statut des lettres. La première partie de cette activité s est avéré être un terrain propice pour essayer de trouver des solutions à cet obstacle. En effet, les élèves doivent dégager, à partir de l étude d un problème de géométrie, une formule donnant l aire d un triangle rectangle en fonction de la longueur d un segment. Si l on fait un schéma conforme aux consignes de l énoncé, et que l on place les points A et B, le segment AB aura une longueur fixe pour les élèves. Les élèves n ont aucune raison de penser que x puisse varier. L idée de trouver la formule de l aire du triangle ABC en fonction de x perd alors toute sa valeur, car elle sera dépourvue de sa signification : les élèves travailleront «à l aveugle» dans toute la suite du problème, x étant pour eux un nombre figé. Lorsqu il s agit de manipuler des nombres, et non des lettres, les élèves sont plus à l aise. J ai tenté d utiliser cet atout pour les mener à trouver par eux même une formule plus générale. Cette réflexion a abouti à la question 5) de la première partie : le calcul de l aire pour différentes valeurs de x va leur permettre de voir que l aire s obtient toujours en suivant le même procédé. Ceci leur permettra peut être de voir à quoi correspond véritablement cette formule, même s il est vrai qu elle demande à l esprit un certain effort qui n est sans doute pas à la portée de tous mes élèves. 4) Conclusions : 23
24 J ai du étaler cette activité sur 4 séances (un cours de deux heures, une heure de module, puis une nouvelle heure de cours pour le bilan). Autrement dit, j ai consacré une semaine entière à cette seule activité. Après réflexion, je me demande si ce choix était judicieux. Certes, l idée d avoir fait intervenir le plus grand éventail de domaines d étude de la fonction, ainsi que de les articuler le plus possible en les mettant en relation avec le langage courant me paraît intéressante, mais ce dispositif présente des difficultés d une autre nature : d une part, il oblige les élèves à réinvestir un grand nombre de connaissances dans des domaines divers. D autre part, le fait que cette activité débute par des questions faisant appel aux connaissances du cours précédent va alourdir le problème. En troisième lieu, cette activité présente des difficultés techniques qui ont de toute évidence posé problème à mes élèves. Je me suis rendu compte que les élèves n ont pas saisi quel était véritablement l enjeu de cette activité ; ils se sont contentés de répondre (avec un certain degré de difficulté) à chacune des questions qui leur était posée les unes après les autres ; dans un contexte plus global, il me semble que la plupart d entre eux ont été noyés par la difficulté et la lourdeur de l activité. Ce problème me paraît d autant plus évident maintenant qu à cette période de l année je n avais pas encore conscience de la relative faiblesse du niveau de ma classe. J ai pu mettre en évidence les difficultés de compréhension des élèves lors de l évaluation qui a suivi. Si j avais donc à refaire une activité introductive, je prendrai d une part le soin de ne pas la rendre trop complexe, de manière à pouvoir insister sur les points qui sont véritablement importants. Je chercherai donc à partir d une situation semblable, mais plus simple. Quitte à l étudier au cours d une autre activité, je n hésiterai pas non plus à «sacrifier» une registre de représentation, de manière à rendre mon approche moins laborieuse, et donc peut être plus accessible pour la plupart de mes élèves. Je me dis que j aurai sans doute du opter pour mettre en place deux activités plus légères, grâce auxquelles j aurai plus facilement pu faire émerger les principaux enjeux liés au concept de fonction. Cela aurait sans doute permis aux élèves d appréhender avec moins de difficultés certaines des notions que je désirais leur transmettre. 24
25 B. ACTIVITE 2 : Fonctions «discrètes», cloisonnement : 1) Les activités : Nous avons précédemment évoqué l importance de l obstacle que pouvait constituer le phénomène de cloisonnement des registres. Pour ce faire j ai donc essayé de construire des activités dans lesquelles la fonction n intervient ni sous forme de graphique, ni sous forme de formule, car il s agit là des deux principales sources de confusion. Ces activités vont obliger les élèves à se référer à la définition donnée en cours ; compte tenu du caractère formel de cette définition, il faudrait s attendre à ce que la plupart des élèves aient à réfléchir de manière assez poussée sur ces activités. J ai choisi de proposer ces travaux lors de séances faisant intervenir des petits groupes, en module, et même en aide individualisée. Après un travail individuel peu évident pour eux, je me suis dit que les échanges entre les élèves pourraient en revanche s avérer assez riches et déboucher sur des idées intéressantes. Ces deux activités sont présentées dans l annexe 3. ANNEXE 3 ( ). a) Fonction discrète qualitative : Les «codes postaux» (exercice 2) : J ai voulu rattacher le plus possible le premier exercice à un problème impliquant directement mes élèves. Je leur ai demandé de me donner les noms et les codes postaux de leurs villes. Une grande ville pouvant avoir plusieurs codes postaux, l objectif est de voir que l on peut trouver une fonction qui à chaque code postal associe la ville qui y est rattachée, le contraire étant impossible. Le fait de demander des informations personnelles à mes élèves les a surement amené à s impliquer personnellement dans la résolution du problème, et j ai pu bénéficier d une participation soutenue (et peu commune). Les nombreux échanges ont abouti a une solution collégiale qui, je pense, a été à la portée de la plupart de mes élèves. Cette activité s est principalement bâtie autour du seul registre du langage courant, mais je ne pense pas que cela soit problématique ; le but ici est justement d illustrer une situation ne pouvant pas s étudier à travers d autres registres. Il n y a pas de risque de cloisonnement : il semble peu probable qu un élève confonde une fonction et sa manière de la décrire avec ses propres mots ; du moins, ce n est pas apparu dans les résultats du sondage soumis à mes élèves. Ceci nous permet de pouvoir mettre l accent sur l importance et même sur le caractère indispensable du langage courant dans certains cas. Nous venons aussi de mettre en évidence une autre particularité liée à ce domaine d étude : dans ce type de problème, le registre du langage 25
26 courant est «autosuffisant» : il n est pas nécessaire d avoir recours à un autre pour lui donner du sens. Ayant recours à une définition schématique de la fonction à laquelle j ai régulièrement fait référence, j ai pu mener la classe à atteindre l objectif que je m étais fixé : une fonction n est pas un graphique, une fonction n est pas une formule. J ai pu mettre l accent et donner peut être un peu de sens à l aspect «procédure». Bien sur il s agit là d une étude ponctuelle, qui a éveillé les élèves à ce nouvel aspect. Nous verrons plus tard si cette activité les a marqués à plus long terme b) Fonction discrète quantitative (exercice 1) : L exemple précédent semble intéressant mais peut être un peu «artificiel» pour les élèves. Il est complètement détaché du contexte numérique et calculatoire dans lequel nous étions plongés jusque là. Aussi peuvent-ils s interroger sur l utilité d effectuer ce type de tâches, ou du moins, croire que ces exemples ne peuvent se trouver que dans des problèmes de nature «qualitative», qui correspondent plus à des problèmes de logique qu à des problèmes de nature purement mathématique. Ainsi il m a semblé indiqué de trouver un exercice de même nature que le précédent, mais dans lequel l aspect calculatoire est plus mis en avant. Ces exercices se trouvent sans trop de difficultés dans les ouvrages, et ils me semblent d autant plus riches que, outre le fait qu ils obligent les élèves à porter une réelle réflexion, ils apportent des éléments de réponse précieux dans le cadre de notre étude. J ai proposé de leur faire étudier la fonction qui à un nombre associe la somme des chiffres qui le constituent. Ce problème en est réellement un pour les élèves. La plupart sont restés complètement démunis devant la difficulté de la tâche. Le mot fonction les trouble. A la différence de l exercice précédent, l aspect «calcul» constitue un obstacle : comment déterminer l image d un nombre par une fonction sans en posséder la formule? C est vraisemblablement ce point précis qui les bloque, et qui représente tout l enjeu de l exercice. Leur donner un exemple pour les débloquer ne me semble pas approprié ; cela saboterait tout le travail de recherche, et donnerait l impression aux élèves que l on s intéresse plus à la résolution de l exercice qu à son réel objectif. J ai donc décidé d insister et de les guider, en faisant régulièrement référence à l exercice précédent, et à la définition. A terme, il a suffit d un exemple fourni par un élève pour débloquer l ensemble de la classe. J ose croire que cet exercice leur a fourni des éléments supplémentaires pour leur permettre de détacher le mot «fonction» du contexte formule et du contexte graphique. 2) Un nouveau sondage : 26
27 Au début de l année, j ai effectué un sondage auprès de mes élèves, leur demandant ce qu était pour eux une fonction. Après ces activités, je me suis dit que le meilleur moyen de savoir si mes objectifs avaient été atteints, ou du moins, de voir quelle a pu être l évolution conceptuelle de mes élèves, serait de leur soumettre le même sondage. Je leur ai donc demandé d y répondre, deux semaines après la rentrée des vacances de février, à la fin d un chapitre de géométrie. Je me suis dit qu à chaud, les réponses des élèves seraient biaisées par les activités qui viennent d être traitées. Voilà pourquoi, dans le souci d obtenir des réponses qui correspondent à ce qu ont globalement appris mes élèves, j ai décidé de le poser à cette date, hors contexte. Après une première lecture, je me suis rendu compte que mes élèves, pris «à froid», se sont raccrochés aux savoirs qu ils pensent être les plus solides pour eux, c'est-à-dire qu ils ont une nouvelle fois fait référence aux connaissances les plus profondément encrées ; j ai relevé chez certains élèves le même type de réponse qu au premier sondage, et le problème du cloisonnement est toujours présent. Ainsi j ai pu constater que l aspect procédural n apparaît pas non plus de manière significative, comme j aurai pu l espérer après avoir travaillé sur ce problème. En revanche, les réponses des élèves ont été très nettement plus riches, beaucoup plus détaillés. Après une lecture plus approfondie, j ai vu que notre travail avait en réalité été beaucoup plus efficace que ce que j aurai pu penser au premier abord. En fait, le phénomène de cloisonnement se retrouve dans seulement 4 ou 5 réponses, comme par exemple : «C est une courbe», ou encore, «C est un nombre suivi de x, comme par exemple 4x». Ensuite, chez deux ou trois élèves, on a le même type de réponse, mais cette fois ils font aussi intervenir au moins un autre registre de représentation pour illustrer leur pensée. Dans toutes les autres réponses, je me suis rendu compte de quelque choses de très intéressant : ce que j avais pris pour être du cloisonnement n en était en fait pas du tout. Détaillons cela : Dans le premier sondage, les élèves étaient très affirmatifs, catégoriques même : «une fonction c est une courbe», «une fonction, c est un graphique». Ici, tous les autres élèves ont pris la précaution d éviter ce genre de confusion : on passe à des réponses du type «on peut représenter une fonction graphiquement ou avec un tableau de variation», ou encore «il y a la représentation graphique d une fonction». Les élèves prennent la précaution de ne pas commettre cette erreur, même ceux pour qui le concept de fonction est encore très approximatif et qui ont encore pour seul exemple les fonctions affines : «une fonction est représentée sous la forme d une droite placée dans un repère». 27
28 En second lieu, la quasi-totalité des réponses fait intervenir au moins deux registres de représentation. Même si le phénomène de cloisonnement est encore sans doute présent, ou du moins se fait un peu ressentir dans leur raisonnement, c est un moyen qu ont les élèves de me faire comprendre qu ils ont conscience qu une fonction peut vivre à travers d autres aspects. C est une énorme évolution par rapport au sondage précédent, dans lequel on n a pu retrouver que très rarement cette forme de réponse. Ainsi, je pense que mes attentes par rapports aux réponses étaient une peu trop ambitieuses : l aspect «procédural» et le concept de fonction étant extrêmement abstrait et difficile, je ne pouvais pas m attendre à un changement radical de point de vue, et encore moins espérer de mes élèves qu ils m en redonnent la définition. Les élèves ont toujours besoin, pour faire vivre la fonction, de se rattacher à des situations, des représentations qui leur sont familières. Je trouve très positif et encourageant que leurs réponses aient évoluées de la sorte, en particulier sur les deux points évoqués précédemment. Je pense que c est par le biais de ce genre de travaux, et en continuant d insister sur l importance entre «est» et «peut se représenter par» qu ils pourront, à terme, se forger une idée de plus en plus claire du concept de fonction. L étude des réponses apportées me fait croire que la plupart de mes élèves ont franchi là une première étape importante. 28
29 C. ACTIVITE 3 : Fonctions de référence : fonction carré/fonction inverse 1) La fonction carré : a) Introduction des différents registres de représentation : N ayant pas pu le faire de manière très réfléchie dans les premières étapes de mon cours, j ai mis à profit les premiers éléments de cette étude dans le cadre des chapitres qui suivirent, comme par exemple, les fonctions de référence. J ai commencé par demander à mes élèves quels étaient les différents outils qui étaient en notre possession pour étudier des fonctions. Les réponses furent assez rapides. J ai pu dresser une liste dans laquelle figurait dans l ordre : tableau de valeurs graphiques formule tableau de variation. J ai du rajouter et souligner l importance du mode de représentation manquant : le langage courant. b) L articulation des registres : Dans un second temps, mon idée était de bâtir mon cours autour d une seule question : étudier la fonction qui à un nombre associe son carré. Mon idée était que mes élèves partent d un problème posé dans le langage courant, prenant ainsi une place privilégiée, et qu ils essaient de se plonger successivement dans chacun des autres registres ; de la sorte ils pourraient voir comment il paraît plus aisé de travailler, de souligner quelles sont les interactions entre ces différents modes de représentation dans ce contexte. A l issue de ce temps de recherche, je leur ai demandé de me produire un papier sur lequel figurerait «tout ce qu ils peuvent me dire sur la fonction carré». Conscient que cette tâche peut paraître un peu atypique, du fait qu elle propose un travail peu classique d une part, et qu elle offre aux élèves une liberté et une autonomie totale dans le travail, je me suis dit qu un travail de groupe pourrait être approprié. Ainsi donc, après un premier travail papier/crayon individuel visant à faire travailler chacun des élèves sur un ou plusieurs registres de leur choix, le travail de groupe a eu pour but de regrouper les résultats, les comparer, et surtout faire émerger des remarques. Cette tâche laisse une grande liberté aux élèves. De la sorte, soumis eux mêmes à la difficulté que représente la largeur de l éventail des entrées possibles pour étudier une fonction, ils pourront voir de manière concrète la multiplicité et les particularités de chacun des registres de représentation, et ce de manière «non cloisonnée» ; de plus, cette liberté leur permet aussi de pouvoir s attarder sur les aspects dans lequel ils se sentent le plus à l aise ; 29
30 ainsi, aucun élève ne devrait être découragé ou dépassé par la difficulté de la tâche, le remplissage d un tableau de correspondance étant à la portée de tous. c) Bilan : Ce dispositif dans le travail a troublé mes élèves. Bien que je m emploie régulièrement à rendre mes élèves autonomes, ils ne sont à l aise que lorsqu on leur donne des consignes très cadrées et précises. J ai tout de même jugé utile de les laisser travailler avec cette méthode, afin de voir ce qui pouvait émerger. Le travail proposé offrant de nombreuses pistes, je pense qu ils ont été perdus et n ont pas osé prendre l initiative de se lancer dans le problème. Aussi ai je du effectuer un bilan collectif intermédiaire afin de débloquer la situation et de pouvoir poursuivre. Notre discussion a abouti sur le fait qu il serait approprié dans un premier temps de construire un tableau de valeurs. A partir de là, le travail s est déclenché et s est déroulé de manière assez fluide. A l issue de cette séance, les élèves ont pu réaliser un travail dans lequel figurent tous les modes de représentation de la fonction carré. Lors du bilan de cette activité, nous avons donc pu insister sur les différentes façons dont on disposait pour représenter une fonction. Je pense que les élèves ont pu maintenant prendre un peu plus de recul face au concept de fonction, même si nous avons travaillé sur une fonction particulière. Il nous reste à mettre en évidence que cette étude peut se généraliser à de nombreuses autres fonctions, comme par exemple, la fonction inverse, qui fera l objet de notre prochaine séance. 2) La fonction inverse : a) Travail préliminaire : J ai demandé à mes élèves lors d une séance précédente d essayer de voir quelle pourrait être la représentation graphique de la fonction inverse, sans aucune autre consigne. En s appuyant sur le travail effectué avec la fonction carré, j espérais qu ils auraient eu l idée de dresser un tableau de correspondance et d ensuite essayer de construire le graphique. Ce travail n est pas évident car le «0» pose problème, et l étude de cette fonction est moins évidente que celle de la fonction carré. Ceci constitue un premier travail «papier/crayon». La difficulté de cette tâche et les erreurs qu ont produites mes élèves ont motivé l utilisation d un logiciel approprié. L utilisation du logiciel EXCEL est certes très pratique, mais peut s avérer dangereuse. Il est indéniable que pour un professeur, ou quelqu un qui sait précisément pour 30
31 quelles raisons il l utilise, il peut s avérer très efficace et permet un gain de temps certain. Pour les élèves, cela me semble moins évident. Dans notre problème, elle peut leur sembler relativement artificielle, d où l importance du travail écrit préalable. Je pense que cette fois, le sens de cette activité sera donné par la capacité du logiciel à contourner les obstacles auxquels ils se sont confrontés. b) Utilisation d EXCEL : ANNEXE 4 ( ) Dans cette situation il semble que le recours à ce logiciel soit efficace. A la différence de la fonction carré étudiée précédemment, la construction du graphique associé semble plus délicate, car cette fonction est discontinue : le «0» représente une difficulté importante. EXCEL va nous permettre d étudier cette fonction sur des intervalles particuliers, et de faire ressortir les principales propriétés par le biais de l assistant graphique. L outil informatique fait intervenir deux registres de représentation : tableau de correspondance et représentation graphique. L activité présentée va permettre de faire vivre la fonction inverse à travers deux autres aspects, à savoir la langue naturelle et le tableau de variations. Ainsi, à l issue de cette séance et d un bilan précis et complet, les élèves pourront avoir en leur possession une vision globale de cette fonction, détachée d un registre particulier. c) Bilan : Malgré le travail écrit, il m a semblé que la plupart de mes élèves ont toutefois eu du mal avec certains points de l activité. Je pense que ces difficultés auraient été bien plus importantes si on ne l avait pas effectué. L outil informatique a troublé les élèves qui n y étaient pas habitués. Une de mes principales tâches a été de leur faire comprendre que les résultats obtenus étaient quelque part «exploitables». Le tableau et le graphique obtenus sur l écran sont pour eux différents de ceux que l on étudie «à la main», ceci étant certainement dû à la disposition et la représentation des données ; ainsi par exemple, j ai du répondre à plusieurs reprises à des questions comme «sur le graphique, les x sont aussi sur l axe des abscisses?». Si mes élèves se posent ce genre de questions, c est qu ils ne voient pas un graphique «EXCEL» comme un graphique normal. Le langage courant, encore une fois, m a apporté des solutions précieuses : le fait de demander à mes élèves une interprétation «dynamique» du graphique (qui leur paraissait peut être sorti de nulle part, complètement artificiel) par le biais de 31
32 plusieurs questions basiques, a permis de lui donner crédit ; la construction du tableau de variations à partir de cette interprétation a été un autre moyen de rattacher ces résultats à quelque chose de concret et familier pour eux. Pour être régulièrement passé dans les rangs et avoir suivi de manière soutenue mes élèves, je pense que leur compréhension est passée par cette transition, c'est-à-dire le passage de l ordinateur à l écrit. En réalité je me suis d autant plus rendu compte que le sens passe par des phénomènes transitoires, c'est-à-dire, non seulement par le passage d un registre à un autre, mais aussi dans certains cas, par le passage de l utilisation de l outil papier crayon à l outil informatique (et inversement). Ici, l utilisation seule d un logiciel informatique, même s il articule deux registres de représentation, constitue quelque part une forme de cloisonnement. Le sens passera par le retour à l écrit, la traduction et l interprétation des résultats obtenus par le biais d autres registres de représentation sémiotique. Pour ces multiples raisons, l articulation entre les différents registres de représentation a été ici je pense extrêmement riche et porteuse de sens pour mes élèves. 3) Conclusions générales : Au cours de l apprentissage, j ai pu observer que globalement, en ce qui concerne ces deux fonctions de référence, les élèves ont pu suivre le cours et comprendre la plupart des points qui me paraissaient importants. Je suis maintenant convaincu que cette compréhension est en partie passée par le fait d avoir pris en compte les deux variables mises en évidences dans notre étude théorique : jouer sur les passages d un mode de représentation à un autre, et insister sur le langage courant. Ces deux points ont pu être développés grâce à un travail de recherche important de la part des élèves ; il est à mes yeux nécessaire de laisser aux élèves découvrir eux même les points délicats grâce à un temps de recherche qui les pousse à se concentrer réellement sur le problème. Cet aspect me paraît être aussi fondamental mais il dépasse le cadre de notre étude, car il s inscrit dans un contexte bien plus global. Mais que restera t il de cela à mes élèves sur le moyen terme? A l issue de ce chapitre, j ai proposé à mes élèves de réinvestir les connaissances acquises par le biais de brèves interrogations. J ai élaboré quelques activités faisant intervenir ces deux fonctions, comme par exemple des études comparatives, des lectures graphiques... Il s agit là de problèmes plus vastes, pas seulement ciblés sur les fonctions de référence elles-mêmes. J ai été surpris de voir à quelle vitesse les connaissances de mes élèves s évaporent Cela m a obligé à effectuer quelques rappels et revenir sur les points importants. Ainsi, pour que les élèves puissent se forger une idée de plus en plus précise des fonctions étudiées lors de leur 32
33 cursus, je pense qu il est nécessaire de revenir dessus (dans la mesure du possible) de manière régulière si l on ne veut pas qu un tel travail soit d une efficacité éphémère. 33
34 D. ACTIVITE 4 : Approche de la notion de fonction en 3 ème 1) Présentation du problème : Toutes les réponses d élèves et les apports théoriques nous mènent à effectuer les conclusions suivantes : l approche de la notion de fonction en classe de troisième présente un enjeu majeur. Pour éviter qu à l entrée en seconde les élèves partent avec un handicap qui les freinera dans leur apprentissage, je pense qu il est important de voir comment, en aval, nous pouvons travailler pour essayer de minimiser l impact de ce problème. J ai eu la chance d effectuer mon stage de pratique accompagnée en classe de troisième. J ai donc pu le mettre à profit pour pouvoir analyser un travail allant dans ce sens. L enjeu principal, à mon sens, est simple : il faut faire comprendre à l élève qu il existe d autres fonctions que les fonctions affines. Il existe une multitude de moyens pour illustrer ceci, et ce, même avant la troisième : dans l étude théorique, nous avons souligné que dans le chapitre proportionnalité en sixième, il était indiqué par les programmes de trouver des situations de type «non proportionnelles», mettant ainsi en jeu des correspondances entre des quantités qui sont définies par des fonctions autres que des fonctions affines. Ce travail, s il est poursuivi sur le long terme, permettra surement aux élèves d avoir une vision plus précise des notions qu il sera amené à étudier plus tard. Pour amorcer le chapitre «fonction linéaire, fonction affine», il me semble peu judicieux de travailler d emblée sur ce type de fonction si l on veut éviter le problème évoqué précédemment. Je pense qu un travail préalable sur une multitude d exemples de fonctions permettra aux élèves de voir d emblée toute l étendue du domaine d étude offert par le concept de fonction. Ainsi, à l issue de ce travail introductif, nous pourrons préciser que les fonctions affines et linéaires sont des fonctions particulières, et qu elles vont faire l objet de l étude du prochain chapitre. 2) Découverte la notion de fonction : ANNEXE 5 ( ) Mon tuteur de stage de pratique accompagnée a décidé de faire découvrir la notion de fonction à travers un travail de groupe. Il s avère que l activité qu il a proposée à ses élèves correspond aux critères que nous venons d évoquer. L analyse de cette activité, ainsi que des productions des ses élèves pourront très certainement nous apporter des informations précieuses et soulever des questions intéressantes dans le cadre de notre étude. 34
35 A partir d un tableau de signes, l élève doit retrouver par quel procédé permet de passer de la première ligne à la colonne. Il d agit donc là d un travail basé sur l articulation de deux registres de représentation : tableau de correspondance et langue naturelle. Cette activité permet à l élève d être en contact à la fois avec des fonctions affines et d autres types de fonctions. Ce brassage permet, je pense, de lui faire prendre conscience de manière tout à fait naturelle que ces fonctions là correspondent à des procédures au même titre que toutes les autres : elles n ont à priori aucun statut particulier au cours de cette activité. Donc, au premier abord, il n y a aucune raison qu un élève ne connaisse que ces fonctions là à l issue de cette activité. Le problème est qu au cours de ce chapitre, qui est au demeurant assez lourd, l élève moyen perdra surement de vue les véritables enjeux de cette activité, car, si elle constitue un moyen de présenter la notion de fonction dans son aspect le plus général, elle est aussi le point de départ d un chapitre dans lequel on va se recentrer très vite vers un type de fonction particulier. Ainsi il est donc tout à fait envisageable qu à l issue de quelques semaines de cours sur ce chapitre, les élèves ne retiennent plus que les grandes lignes et perdent les bénéfices tirés lors de cette activité introductive. Je trouve cette activité extrêmement riche et intéressante, mais si l on désire en tirer profit sur le long terme, il me semble indispensable d effectuer de manière régulière des retours sur ses enjeux principaux et ses objectifs. Par exemple, tout au cours du chapitre, ou même de l année, je tenterai de mettre en place des exercices ou des exemples nécessitant l étude (ou tout simplement évoquant) des fonctions non affines, et n hésiterai pas à faire des remarques le plus régulièrement possible sur ce point. A mon avis, si l on veut éviter que les élèves ne bâtissent leur vision de la fonction autour de la fonction affine, il faudra multiplier ce genre d activités, ou du moins tenter de faire un travail régulier allant dans ce sens. Cela ne peut en aucun cas faire l objet d une action ponctuelle. 3) Conclusions : Cet exercice de recherche peut aider l élève à constituer des bases solides autour du concept de fonction, car elle met complètement l accent sur son côté procédural, celui qui correspond le plus à sa définition, c'est-à-dire sans doute le plus abstrait. Cela dit, la manière dont l exercice est introduit va le faire intervenir de manière naturelle, et je ne pense pas que cela soit réellement problématique pour les élèves. J ai pu donner régulièrement des cours dans la classe de 3 ème 9, et j ai pu évaluer le niveau de certains élèves. La production d élèves N 1 correspond donc à des élèves que je connais un peu, c'est-à-dire à un groupe plutôt faible, mais volontaire. Il va sans dire qu à la vue de la production, il semble qu ils aient bien saisi 35
36 les enjeux de l exercice, et ont même pu saisir la portée générale des formules (donnée par la dernière colonne). Le fait d avoir rajouté cette dernière colonne me semble absolument fondamental : cela constitue un passage du «discret au continu», qui est terriblement difficile pour les élèves ; cela soulève aussi le délicat problème du statut des lettres. Ici, les élèves n ont apparemment eu aucune difficulté pour effectuer cette transition, et ainsi, ils font euxmêmes, sans le savoir, intervenir un troisième registre de représentation. La production du second groupe, dont je ne connais pas les élèves, m a semblé tout aussi intéressante, car elle met en évidence un autre avantage de cette activité. Il s agit en effet d une véritable activité de recherche : les élèves, pour pouvoir répondre, vont devoir émettre des conjectures, puis les mettre à l épreuve, les tester sur des calculs Ils ont réellement une démarche scientifique et autonome qui me semble très intéressante. Dans le cadre de notre étude, cette activité mathématique va solliciter je pense la curiosité et la motivation des élèves, qui seront sans doute plus aptes et désireux de comprendre «ce qui se cache derrière tout ça» ; c est donc en quelque sorte une mise en condition dans laquelle les élèves sont réellement acteurs, et qui va permettre de poser les bases d un travail efficace et porteur de sens sur le long terme. J envisage dans les années qui viennent de proposer de telles activités en classe de seconde, j ai la conviction qu elles viendront donner des points d appuis important dans la construction de ce «nouveau savoir» qu est le concept de fonction. 36
37 IV] CONCLUSION : L étude théorique nous a permis de cibler les obstacles majeurs inhérents au concept de fonction. Les expériences menées au sein du groupe classe me mènent à croire que l idée de jouer sur l articulation des registres pour éviter le phénomène de cloisonnement et donner à l élève une vision plus précise des objets qu il manipule semble être relativement efficace. Le fait de poser des mots sur les objets mathématiques permet aux élèves de leur donner vie. C est un aspect qui me semble maintenant absolument primordial dans l apprentissage. Je n avais pas soupçonné au début de mon mémoire que le langage naturel constituerait une des pierres angulaires de mon travail. Je pense pouvoir tirer bénéfice de cette étude dans un cadre bien plus vaste. Même dans d autres niveaux que la seconde, il me semble tout à fait opportun de prendre en considération ces deux variables dans l apprentissage d autres chapitres, notamment ceux qui sont basés sur des notions abstraites et qui offrent des possibilités de représentations diverses. Ainsi, l avantage de cette étude est double : d une part, à court terme, il m a offert des solutions qui m ont semblé efficaces face à la difficile tâche qui m était confiée d introduire la notion de fonction. D autre part, à long terme, elle m a apporté un bagage théorique que je pourrai sans doute mettre à profit dans d autres classes. Les expériences mettent en évidence une variable sur laquelle je n ai pas suffisamment insisté à mon goût : le temps. Au cours d apprentissage d une notion, nous avons la possibilité de faire des remarques aux élèves, nous insistons sur les enjeux et les réels objectifs des activités. Mais nous pouvons nous interroger sur ce qu il en restera après un intervalle de temps de quelques semaines, de quelques mois. Par exemple, dans la troisième activité présentée, nous avons vu que si l on demande après coup de réinvestir les connaissances relatives aux fonctions de référence, les résultats sont plutôt décevant par rapport à ce qu ils auraient été s ils avaient été posés à la fin même du chapitre. Une seconde illustration peut nous être donnée par les résultats du second sondage proposé aux élèves : il montre qu au cours de l année la vision de mes élèves a pu mûrir légèrement, même s ils n ont pas encore une idée tout à fait précise et correcte du concept. Ceci met évidence le fait que la notion de fonction est difficile à assimiler, et nécessite du temps. Je me demande donc s il n est pas nécessaire d étaler le chapitre «fonction» le plus possible au cours de l année, de manière à pouvoir faire des rappels de manière régulière sur les points fondamentaux. Ainsi on peut donner aux élèves des éléments qui contribueront à faire évoluer leur vision tout au long de l année ; on leur laisse le temps d appréhender ce concept de manière convenable. 37
38 Pour compléter cette étude, je proposerai d essayer de voir comment cette évolution est perçue à partir de la classe de troisième, jusqu en terminale. Dans chaque niveau, peut être pourrait on poser à certains moments de l année des types d activités (ou questions, sondages), qui constitueraient des indicateurs pouvant nous informer là-dessus ; il serait peut être envisageable de repérer les différentes étapes de cette évolution conceptuelle et de les classifier. 38
39 ANNEXE 1 Ce document répertorie les relations entre les différents registres de représentation sémiotiques présents dans les activités d études et de recherche de certains manuels. On comptabilise les occurrences des différents aspects pour l ensemble des ouvrages étudiés dans le diagramme ci-dessous. 1 : Expression, symbole algébrique. 2 : Langue naturelle. 3 : Tableau de variations. 4 : Tableau de correspondance. 5 : Représentation graphique. Ouvrage AER 1 AER 2 AER 3 AER 4 Dimathème (2000) Hyperbole (2000) Fractale (2000) Math x (programme actuel) Radial (programme actuel) Abscisse (programme actuel) Déclic (programme actuel) Modulo (programme actuel) Axiale (programme actuel) Hyperbole (programme actuel) Indice (programme actuel) Transmath (programme actuel) , , , , , , , 5 2, 4 2, , , Formule 14 Langue naturelle 26 Tableau de correspondance 19 Représentation graphique Tableau de variations Cliquer ici pour retourner au corps du mémoire : ( ) 39
40 ANNEXE 2 Une approche de la notion de fonction I MISE EN PLACE DU PROBLEME : 1-Construire un cercle de diamètre [AC] tel que AC = 1 et de centre O. Placer un point B sur ce cercle. D est le point d intersection de la droite (BO) avec. On pose AB = x 2-Prouver que ABCD est un rectangle. 3-Calculer BC en fonction de x (utiliser le théorème de Pythagore). 4-A partir de BC² > 0, prouver que 1-BC² < 1 En déduire que 0 < AB² < 1, puis que 0 < x < 1 5-Calculer l aire de ABC pour x = 0,5 ; x = 0,8 ; x=0,2. Etablir une formule donnant l aire de ABC pour x quelconque. On note A(x) l aire de ABC en fonction de x. II VERS LA FONCTION A... : D après la partie I, A(x) = x 1 x 2 1-Compléter le tableau de valeurs suivant : x 0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 Arrondi de A(x) à près 2-Placer les points (x,a(x)) dans un repère orthonormé et les relier par une courbe. 3-Comment l aire semble-t-elle varier lorsque B décrit l arc de cercle AC? 4-Aux alentours de quelle valeur de x l aire A(x) semble-t-elle maximale? On note a la valeur de x pour laquelle l aire est maximale. III RECHERCHE DU MINIMUM DE LA FONCTION A IV BILAN : 1-Que vaut BC si AB =? 2-Quelle est alors la nature du quadrilatère ABCD? Qu en conclut-on? 40
41 III RECHERCHE DU MAXIMUM DE LA FONCTION A : 1-Tracé du graphe de A à la calculatrice : On rappelle que A(x) = x 1 x 2 La séquence à effectuer est la suivante : f(x) alpha X x 2nde 1 - alpha X ^ 2 ) : 2 Il ne reste plus qu à taper sur la touche graphe pour visualiser le graphe de la fonction A. A l aide de la touche trace et en utilisant les touches directionnelles < et, >,dire aux alentours de quelles valeurs de x l aire A(x) semble maximale :.. 2-Utiliser le tableur : x 0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 Arrondi de A(x) à 3 décimales 1-On cherche à compléter le tableau de valeurs suivant : Une méthode possible consiste à demander à la calculatrice de calculer A(x) pour chaque valeur de x, mais il y a beaucoup plus simple : sur ce tableau, la différence entre deux valeurs consécutives de x est constante, égale à 0,1 ; c est ce qu on appelle le PAS. On demande donc toutes les valeurs que prend la fonction A «de 0,1 en 0,1», en partant de 0. Le tableur de la calculatrice peut nous donner directement ces valeurs : La séquence à effectuer est la suivante : 2nde déf table On rentre alors la valeur initiale et le pas : DébTable = 0 PasTable = 0,1 Ensuite : 2nde table et on peut ainsi compléter notre tableau de valeurs. x 0,67 0,68 0,69 0,7 0,71 0,72 0,73 Arrondi de A(x) à 6 décimales Pour quelle valeur de x le tableur donne la plus grande valeur de l aire?. 2-Utiliser le tableur pour compléter le tableau de valeurs suivant : Noter que le tableur n affiche que 5 chiffres après la virgule pour les valeurs de A. Ce n est pas suffisant pour pouvoir donner un arrondi à 6 décimales. Une fois dans le tableur, il faut utiliser les touches directionnelles et aller sur le nombre voulu pour obtenir les décimales supplémentaires. 3-A l aide du tableau ci-dessus, donner un encadrement d amplitude 2. de la valeur de x pour laquelle A(x) est maximale (on la notera a) :. < a < 3-Recherche du maximum d une fonction : On vient de voir que le tableur nous permet d obtenir un encadrement de a. Cependant on peut demander à la machine de nous en donner une valeur approchée très précise. La séquence à effectuer est la suivante : Puis descendre jusqu'à «4 : maximum» et appuyer sur graphe 2nde calculs entrer La calculatrice demande ensuite dans quel intervalle elle va rechercher ce maximum (BorneInf, BorneSup). Appuyer sur entrer après avoir indiqué chaque valeur, puis une nouvelle fois sur entrer : la calculatrice donne une valeur approchée de a Valeur approchée de a donnée par la calculatrice :. Cliquer ici pour retourner au corps du mémoire : ( ). 41
42 ANNEXE 3 Exercice 1 : On considère la fonction f qui à tout entier n, associe la somme des chiffres qui le constitue. 1) Quel est l ensemble de définition de f? 2) Déterminer les images de 1, de 18, de 81, de 999 3) Donner trois antécédents du nombre 5 par f. 4) Combien le nombre 9 possède-t-il d antécédents parmi les nombres inférieurs à 50? Exercice 2 : Les correspondances entre les grandeurs décrites par les phrases suivantes permettent-elles de définir des fonctions? 1. x est la taille et y le poids des élèves d une classe. 2. x est le code postal d une commune et y son département. 3. x est la longueur d un rectangle et y son aire. 4. x est la longueur du côté d un carré et y son aire. 5. x est le périmètre d un rectangle et y son aire. Les deux exercices suivants permettent de travailler sur le passage langage courant formule/calculs. L exercice 3 permet en outre de travailler sur l aspect procédural de la fonction. Dans les deux cas il est possible de travailler sur le passage «inverse». Exercice 3 : Associer à chaque phrase la fonction qui lui correspond : A) Je double 1) x α 2x + 3 B) Je prends la moitié 2) x α 2(x + 3) C) Je double puis j ajoute 3 3) x α 2x D) J ajoute 3 puis je double 4) x α 2(x 4) E) Je soustrais 4 puis je double 5) x α x 2 F) Je soustrais 4 puis je prends la moitié 6) x α 2x - 3 G) Je double puis je soustrais 3 7) x α x 4 2 Exercice 4 : Traduire chacune des phrases par une égalité : a. 1 a pour image 3 par f :... =.. b. Le point A(2 ; 3) appartient à C :... =.. c. 0 est un antécédent de 1 par f :... =.. d. 1 est l image de 2 :... =.. e. L ordonnée du point de C d abscisse 3 est 17 :... =.. A B C D E F G Cliquer ici pour retourner au corps du mémoire : ( ) 42
43 ANNEXE 4 APPROCHE DE LA FONCTION INVERSE AVEC EXCEL RAPPEL : La fonction inverse est la fonction f qui à tout nombre non nul associe son inverse. OBJECTIF : Découvrir quelques propriétés de la fonction inverse Pour étudier cette fonction, nous allons utiliser le logiciel EXCEL, qui va nous permettre de déterminer aisément les images d une grande quantité de nombres, ainsi que d obtenir l allure de sa courbe représentative. Nous choisirons pour cette étude des nombres compris entre 2 et 2. I] La colonne A (entrée des valeurs de x) : ETAPE 1 Dans la case A1, entrer le nombre 2 Dans la case A2, entrer le nombre 1,9 ETAPE 2 Sélectionnez les cases A1 et A2, puis placer le curseur en bas à droite de la case A2, jusqu à ce que la croix noire apparaisse. Cliquez à nouveau puis «tirez vers le bas» jusqu à la case A41. A l issue de cette étape, la colonne A doit vous donner une liste de 41 nombres successifs compris entre -2 et 2. La différence entre deux nombres successifs est égale à 0,1. On dit que 0,1 est le pas de cette liste de nombres. Nous désirons maintenant voir quels sont les inverses de ces nombres. II] La colonne B (calcul des valeurs de f(x)) : ETAPE 1 Dans la case B1, entrer la formule : = 1/A1 (N oubliez pas le signe «=») ETAPE 2 Cliquez sur la case B1, puis mettez le curseur en bas à droite de la case B1, jusqu à ce qu une croix noire apparaisse. Cliquez à nouveau puis «tirez vers le bas» jusqu à la case B41. 43
44 Questions : - Qu est il affiché dans la case correspondant au nombre 0 (B21)? - Comment expliquez-vous cela? Sélectionnez la case A21 puis effacez son contenu. Faites de même pour la case B21. Nous obtenons ainsi un tableau de correspondance entre les nombres de la colonne A et leur inverse situés dans la colonne B. A partir du tableau obtenu : Quel est l inverse de 2? de 2? Que remarque t on? De la même façon, comparer les inverses des nombres 1 et 1, puis des nombres 0,5 et 0,5. Recopier puis compléter : Plus généralement, il semble que pour tout x non nul de l intervalle [ 2 ; 2], f( x) et f(x) sont III] Représentation graphique : ETAPE 1 Cliquez sur la case A1. Lorsqu une croix blanche apparaît, cliquez à nouveau et «tirez vers le bas» jusqu à la case B41. L ensemble des valeurs sélectionnées doit apparaître en bleu. Cliquez sur l icône assistant graphique situé sur la barre d outils (en plus foncé sur la capture d écran ci-dessous). ETAPE 2 Dans l assistant graphique, cliquez sur «nuage de points», puis sélectionnez le cadre «nuage de points reliés par une courbe lissée» Cliquez sur terminer. La représentation graphique s affiche alors sur la fenêtre. Questions : A partir du graphique obtenu : - Que peut on dire de l inverse de x lorsque x est positif et de plus en plus grand? - Que peut on dire de l inverse de x lorsque x se rapproche de 0 en étant positif? en étant négatif? - Ce graphique donne l allure d une fonction. Quel est son ensemble de définition? - Dresser le tableau de variations de cette fonction. Cliquer ici pour retourner au corps du mémoire : ( ) 44
45 ANNEXE 5 Production d élèves n 1 : groupe d Angie, Natasha, Clément et Aude, élèves de 3 ème 8. 45
46 46
47 Production d élèves n 2 : groupe de Brahim, Florian, Mélanie et Maeva, élèves de 3 ème 9. 47
48 Cliquer ici pour retourner au corps du mémoire : ( ) 48
49 ANNEXE 6 Bibliographie : Raymond DUVAL, Registres de représentation sémiotique et fonctionnement cognitif de la pensée (Annales de Didactique et de Sciences Cognitives IREM de Strasbourg) Graphiques et Equations : l Articulation de deux registres (Annales de Didactique et de Sciences Cognitives IREM de Strasbourg) Guy BROUSSEAU, Théorie des situations didactiques ; recherche en didactique des mathématiques (LA PENSEE SAUVAGE, 1998) Jean DIEUDONNE, Abrégé d histoire des mathématiques (HERMANN, 1986) Nicolas BOURBAKI, Eléments d Histoire Des Mathématiques (SPRINGER, 1984) Amy DAHAN-DALMEDICO, Jeanne PEIFFER, Une Histoire des Mathématiques (SEUIL, 1986) 49
10 REPÈRES «PLUS DE MAÎTRES QUE DE CLASSES» JUIN 2013 POUR LA MISE EN ŒUVRE DU DISPOSITIF
 10 REPÈRES POUR LA MISE EN ŒUVRE DU DISPOSITIF «PLUS DE MAÎTRES QUE DE CLASSES» JUIN 2013 MEN-DGESCO 2013 Sommaire 1. LES OBJECTIFS DU DISPOSITIF 2. LES ACQUISITIONS PRIORITAIREMENT VISÉES 3. LES LIEUX
10 REPÈRES POUR LA MISE EN ŒUVRE DU DISPOSITIF «PLUS DE MAÎTRES QUE DE CLASSES» JUIN 2013 MEN-DGESCO 2013 Sommaire 1. LES OBJECTIFS DU DISPOSITIF 2. LES ACQUISITIONS PRIORITAIREMENT VISÉES 3. LES LIEUX
Chères collègues, chers collègues,
 Chères collègues, chers collègues, Les IREM ont été créés en 1969 avec les missions suivantes : - mener des recherches sur l enseignement des mathématiques ; - contribuer à la formation initiale et continue
Chères collègues, chers collègues, Les IREM ont été créés en 1969 avec les missions suivantes : - mener des recherches sur l enseignement des mathématiques ; - contribuer à la formation initiale et continue
SOCLE COMMUN - La Compétence 3 Les principaux éléments de mathématiques et la culture scientifique et technologique
 SOCLE COMMUN - La Compétence 3 Les principaux éléments de mathématiques et la culture scientifique et technologique DOMAINE P3.C3.D1. Pratiquer une démarche scientifique et technologique, résoudre des
SOCLE COMMUN - La Compétence 3 Les principaux éléments de mathématiques et la culture scientifique et technologique DOMAINE P3.C3.D1. Pratiquer une démarche scientifique et technologique, résoudre des
LES CARTES À POINTS : POUR UNE MEILLEURE PERCEPTION
 LES CARTES À POINTS : POUR UNE MEILLEURE PERCEPTION DES NOMBRES par Jean-Luc BREGEON professeur formateur à l IUFM d Auvergne LE PROBLÈME DE LA REPRÉSENTATION DES NOMBRES On ne conçoit pas un premier enseignement
LES CARTES À POINTS : POUR UNE MEILLEURE PERCEPTION DES NOMBRES par Jean-Luc BREGEON professeur formateur à l IUFM d Auvergne LE PROBLÈME DE LA REPRÉSENTATION DES NOMBRES On ne conçoit pas un premier enseignement
Synthèse «Le Plus Grand Produit»
 Introduction et Objectifs Synthèse «Le Plus Grand Produit» Le document suivant est extrait d un ensemble de ressources plus vastes construites par un groupe de recherche INRP-IREM-IUFM-LEPS. La problématique
Introduction et Objectifs Synthèse «Le Plus Grand Produit» Le document suivant est extrait d un ensemble de ressources plus vastes construites par un groupe de recherche INRP-IREM-IUFM-LEPS. La problématique
UE5 Mise en situation professionnelle M1 et M2. Note de cadrage Master MEEF enseignement Mention second degré
 UE5 Mise en situation professionnelle M1 et M2 Note de cadrage Master MEEF enseignement Mention second degré ESPE Lille Nord de France Année 2014-2015 Cette note de cadrage a pour but d aider les collègues
UE5 Mise en situation professionnelle M1 et M2 Note de cadrage Master MEEF enseignement Mention second degré ESPE Lille Nord de France Année 2014-2015 Cette note de cadrage a pour but d aider les collègues
Programme de la formation. Écrit : 72hdepréparation aux épreuves d admissibilité au CRPE
 Programme de la formation Écrit : 72hdepréparation aux épreuves d admissibilité au CRPE o 36 h pour la préparation à l'épreuve écrite de français Cette préparation comprend : - un travail sur la discipline
Programme de la formation Écrit : 72hdepréparation aux épreuves d admissibilité au CRPE o 36 h pour la préparation à l'épreuve écrite de français Cette préparation comprend : - un travail sur la discipline
Les «devoirs à la maison», une question au cœur des pratiques pédagogiques
 Les «devoirs à la maison», une question au cœur des pratiques pédagogiques Parmi les trois domaines d activités proposés aux élèves volontaires dans le cadre de l accompagnement éducatif, «l aide aux devoirs
Les «devoirs à la maison», une question au cœur des pratiques pédagogiques Parmi les trois domaines d activités proposés aux élèves volontaires dans le cadre de l accompagnement éducatif, «l aide aux devoirs
INF 1250 INTRODUCTION AUX BASES DE DONNÉES. Guide d étude
 INF 1250 INTRODUCTION AUX BASES DE DONNÉES Guide d étude Sous la direction de Olga Mariño Télé-université Montréal (Québec) 2011 INF 1250 Introduction aux bases de données 2 INTRODUCTION Le Guide d étude
INF 1250 INTRODUCTION AUX BASES DE DONNÉES Guide d étude Sous la direction de Olga Mariño Télé-université Montréal (Québec) 2011 INF 1250 Introduction aux bases de données 2 INTRODUCTION Le Guide d étude
N 163 - ROUX-PEREZ Thérèse. 1. Problématique
 N 163 - ROUX-PEREZ Thérèse CONSTRUCTION IDENTITAIRE DES ENSEIGNANTS EN FORMATION INTIALE : ENTRE REPRESENTATIONS PARTAGEES ET ELEMENTS DE DIFFERENCIATION DANS LE RAPPORT AU METIER 1. Problématique L étude
N 163 - ROUX-PEREZ Thérèse CONSTRUCTION IDENTITAIRE DES ENSEIGNANTS EN FORMATION INTIALE : ENTRE REPRESENTATIONS PARTAGEES ET ELEMENTS DE DIFFERENCIATION DANS LE RAPPORT AU METIER 1. Problématique L étude
Rédiger et administrer un questionnaire
 Rédiger et administrer un questionnaire Ce document constitue une adaptation, en traduction libre, de deux brochures distinctes : l une produite par l American Statistical Association (Designing a Questionnaire),
Rédiger et administrer un questionnaire Ce document constitue une adaptation, en traduction libre, de deux brochures distinctes : l une produite par l American Statistical Association (Designing a Questionnaire),
Une stratégie d enseignement de la pensée critique
 Une stratégie d enseignement de la pensée critique Jacques Boisvert Professeur de psychologie Cégep Saint-Jean-sur-Richelieu La pensée critique fait partie des capacités à développer dans la formation
Une stratégie d enseignement de la pensée critique Jacques Boisvert Professeur de psychologie Cégep Saint-Jean-sur-Richelieu La pensée critique fait partie des capacités à développer dans la formation
EXPLOITATIONS PEDAGOGIQUES DU TABLEUR EN STG
 Exploitations pédagogiques du tableur en STG Académie de Créteil 2006 1 EXPLOITATIONS PEDAGOGIQUES DU TABLEUR EN STG Commission inter-irem lycées techniques contact : [email protected] La maquette
Exploitations pédagogiques du tableur en STG Académie de Créteil 2006 1 EXPLOITATIONS PEDAGOGIQUES DU TABLEUR EN STG Commission inter-irem lycées techniques contact : [email protected] La maquette
«L utilisation d un intranet permet-il la mise en place d un travail collaboratif et/ou coopératifs? Pour quelles compétences?»
 «L utilisation d un intranet permet-il la mise en place d un travail collaboratif et/ou coopératifs? Pour quelles compétences?» Introduction Le travail que nous présentons ici repose sur une expérience
«L utilisation d un intranet permet-il la mise en place d un travail collaboratif et/ou coopératifs? Pour quelles compétences?» Introduction Le travail que nous présentons ici repose sur une expérience
Cabri et le programme de géométrie au secondaire au Québec
 Cabri et le programme de géométrie au secondaire au Québec Benoît Côté Département de mathématiques, UQAM, Québec [email protected] 1. Introduction - Exercice de didactique fiction Que signifie intégrer
Cabri et le programme de géométrie au secondaire au Québec Benoît Côté Département de mathématiques, UQAM, Québec [email protected] 1. Introduction - Exercice de didactique fiction Que signifie intégrer
APPRENDRE LA CHIMIE EN ZEP
 Résumé du rapport de recherche destiné au Centre Alain Savary, INRP APPRENDRE LA CHIMIE EN ZEP Martine Méheut, Olivier Prézeau INRP, Centre Alain Savary Apprendre la chimie en ZEP Résumé 1 Dans une perspective
Résumé du rapport de recherche destiné au Centre Alain Savary, INRP APPRENDRE LA CHIMIE EN ZEP Martine Méheut, Olivier Prézeau INRP, Centre Alain Savary Apprendre la chimie en ZEP Résumé 1 Dans une perspective
utiliser un Macintosh dans la classe
 utiliser un Macintosh dans la classe Philippe DESSUS Pascal MARQUET Le Macintosh Les dessins Les textes Les nombres Préparer et gérer sa classe Évaluer des logiciels SOMMAIRE AVANT-PROPOS...5 Les grandes
utiliser un Macintosh dans la classe Philippe DESSUS Pascal MARQUET Le Macintosh Les dessins Les textes Les nombres Préparer et gérer sa classe Évaluer des logiciels SOMMAIRE AVANT-PROPOS...5 Les grandes
Réguler son enseignement : Pourquoi? Comment?
 Mon enseignement, je l évalue, il évolue Réguler son enseignement : Pourquoi? Comment? Lucie Mottier Lopez Université de Genève 13 mai 2013 IFRES, Liège [email protected] 1 Plan Un cadre pour penser
Mon enseignement, je l évalue, il évolue Réguler son enseignement : Pourquoi? Comment? Lucie Mottier Lopez Université de Genève 13 mai 2013 IFRES, Liège [email protected] 1 Plan Un cadre pour penser
NOM : Prénom : Date de naissance : Ecole : CM2 Palier 2
 NOM : Prénom : Date de naissance : Ecole : CM2 Palier 2 Résultats aux évaluations nationales CM2 Annexe 1 Résultats de l élève Compétence validée Lire / Ecrire / Vocabulaire / Grammaire / Orthographe /
NOM : Prénom : Date de naissance : Ecole : CM2 Palier 2 Résultats aux évaluations nationales CM2 Annexe 1 Résultats de l élève Compétence validée Lire / Ecrire / Vocabulaire / Grammaire / Orthographe /
EXAMEN CRITIQUE D UN DOSSIER TECHNIQUE
 EXAMEN CRITIQUE D UN DOSSIER TECHNIQUE (Préparation : 5 heures -- Exposé et Questions : 1 heure) Rapport établi par : P.J. BARRE, E. JEAY, D. MARQUIS, P. RAY, A. THIMJO 1. PRESENTATION DE L EPREUVE 1.1.
EXAMEN CRITIQUE D UN DOSSIER TECHNIQUE (Préparation : 5 heures -- Exposé et Questions : 1 heure) Rapport établi par : P.J. BARRE, E. JEAY, D. MARQUIS, P. RAY, A. THIMJO 1. PRESENTATION DE L EPREUVE 1.1.
Stage à la Société Générale Ingénierie Financière. Note de Prise de Recul
 Stage à la Société Générale Ingénierie Financière Note de Prise de Recul I. Rôle et Missions Assignés a. Description de l environnement de travail Au cours de mon stage, je travaille au sein du département
Stage à la Société Générale Ingénierie Financière Note de Prise de Recul I. Rôle et Missions Assignés a. Description de l environnement de travail Au cours de mon stage, je travaille au sein du département
UNE EXPERIENCE, EN COURS PREPARATOIRE, POUR FAIRE ORGANISER DE L INFORMATION EN TABLEAU
 Odile VERBAERE UNE EXPERIENCE, EN COURS PREPARATOIRE, POUR FAIRE ORGANISER DE L INFORMATION EN TABLEAU Résumé : Cet article présente une réflexion sur une activité de construction de tableau, y compris
Odile VERBAERE UNE EXPERIENCE, EN COURS PREPARATOIRE, POUR FAIRE ORGANISER DE L INFORMATION EN TABLEAU Résumé : Cet article présente une réflexion sur une activité de construction de tableau, y compris
Cet exposé s intègre dans les travaux développés par une Equipe en Projet INRP-IUFM,
 15 Les nouvelles technologies et les stagiaires IUFM : une appropriation mal contrôlée Philippe Le Borgne IUFM de Franche-Comté [email protected] PRÉSENTATION Cet exposé s intègre dans les
15 Les nouvelles technologies et les stagiaires IUFM : une appropriation mal contrôlée Philippe Le Borgne IUFM de Franche-Comté [email protected] PRÉSENTATION Cet exposé s intègre dans les
FORMATION CONTINUE SUR L UTILISATION D EXCEL DANS L ENSEIGNEMENT Expérience de l E.N.S de Tétouan (Maroc)
 87 FORMATION CONTINUE SUR L UTILISATION D EXCEL DANS L ENSEIGNEMENT Expérience de l E.N.S de Tétouan (Maroc) Dans le cadre de la réforme pédagogique et de l intérêt que porte le Ministère de l Éducation
87 FORMATION CONTINUE SUR L UTILISATION D EXCEL DANS L ENSEIGNEMENT Expérience de l E.N.S de Tétouan (Maroc) Dans le cadre de la réforme pédagogique et de l intérêt que porte le Ministère de l Éducation
Site(s) (lieux où la formation est dispensée, y compris pour les diplômes délocalisés) :
 Evaluation des diplômes Masters Vague D Académie : Paris Etablissement déposant : Académie(s) : / Etablissement(s) co-habilité(s) : / Mention : Economie managériale et industrielle Domaine : Economie,
Evaluation des diplômes Masters Vague D Académie : Paris Etablissement déposant : Académie(s) : / Etablissement(s) co-habilité(s) : / Mention : Economie managériale et industrielle Domaine : Economie,
Méthode du commentaire de document en Histoire
 Méthode du commentaire de document en Histoire I. Qu est-ce qu un commentaire de document? En quelques mots, le commentaire de texte est un exercice de critique historique, fondé sur la démarche analytique.
Méthode du commentaire de document en Histoire I. Qu est-ce qu un commentaire de document? En quelques mots, le commentaire de texte est un exercice de critique historique, fondé sur la démarche analytique.
LA BATTERIE DU PORTABLE
 LA BATTERIE DU PORTABLE Table des matières Fiche professeur... 2 Fiche élève... 4 Narration de séance et productions d élèves... 5 1 Fiche professeur LA BATTERIE DU PORTABLE Niveaux et objectifs pédagogiques
LA BATTERIE DU PORTABLE Table des matières Fiche professeur... 2 Fiche élève... 4 Narration de séance et productions d élèves... 5 1 Fiche professeur LA BATTERIE DU PORTABLE Niveaux et objectifs pédagogiques
Le système d évaluation par contrat de confiance (EPCC) *
 André ANTIBI Le système d évaluation par contrat de confiance (EPCC) * * extrait du livre «LES NOTES : LA FIN DU CAUCHEMAR» ou «Comment supprimer la constante macabre» 1 Nous proposons un système d évaluation
André ANTIBI Le système d évaluation par contrat de confiance (EPCC) * * extrait du livre «LES NOTES : LA FIN DU CAUCHEMAR» ou «Comment supprimer la constante macabre» 1 Nous proposons un système d évaluation
Items étudiés dans le CHAPITRE N5. 7 et 9 p 129 D14 Déterminer par le calcul l'antécédent d'un nombre par une fonction linéaire
 CHAPITRE N5 FONCTIONS LINEAIRES NOTION DE FONCTION FONCTIONS LINEAIRES NOTION DE FONCTION FONCTIONS LINEAIRES NOTION DE FONCTION Code item D0 D2 N30[S] Items étudiés dans le CHAPITRE N5 Déterminer l'image
CHAPITRE N5 FONCTIONS LINEAIRES NOTION DE FONCTION FONCTIONS LINEAIRES NOTION DE FONCTION FONCTIONS LINEAIRES NOTION DE FONCTION Code item D0 D2 N30[S] Items étudiés dans le CHAPITRE N5 Déterminer l'image
Entraînement, consolidation, structuration... Que mettre derrière ces expressions?
 Entraînement, consolidation, structuration... Que mettre derrière ces expressions? Il est clair que la finalité principale d une démarche d investigation est de faire acquérir des connaissances aux élèves.
Entraînement, consolidation, structuration... Que mettre derrière ces expressions? Il est clair que la finalité principale d une démarche d investigation est de faire acquérir des connaissances aux élèves.
Attestation de maîtrise des connaissances et compétences au cours moyen deuxième année
 Attestation de maîtrise des connaissances et compétences au cours moyen deuxième année PALIER 2 CM2 La maîtrise de la langue française DIRE S'exprimer à l'oral comme à l'écrit dans un vocabulaire approprié
Attestation de maîtrise des connaissances et compétences au cours moyen deuxième année PALIER 2 CM2 La maîtrise de la langue française DIRE S'exprimer à l'oral comme à l'écrit dans un vocabulaire approprié
Le menu du jour, un outil au service de la mise en mémoire
 Le menu du jour, un outil au service de la mise en mémoire Type d outil : Outil pour favoriser la mise en mémoire et développer des démarches propres à la gestion mentale. Auteur(s) : Sarah Vercruysse,
Le menu du jour, un outil au service de la mise en mémoire Type d outil : Outil pour favoriser la mise en mémoire et développer des démarches propres à la gestion mentale. Auteur(s) : Sarah Vercruysse,
Qu est-ce qu une problématique?
 Fiche méthodologique préparée par Cécile Vigour octobre 2006 1 Qu est-ce qu une problématique? Trois étapes : 1. Définition de la problématique 2. Qu est-ce qu une bonne problématique? 3. Comment problématiser?
Fiche méthodologique préparée par Cécile Vigour octobre 2006 1 Qu est-ce qu une problématique? Trois étapes : 1. Définition de la problématique 2. Qu est-ce qu une bonne problématique? 3. Comment problématiser?
LE CADRE COMMUN DE REFERENCE LA CONVERGENCE DES DROITS 3 e forum franco-allemand
 LE CADRE COMMUN DE REFERENCE LA CONVERGENCE DES DROITS 3 e forum franco-allemand Guillaume Wicker Professeur à l Université Montesquieu - Bordeaux IV 1 Je commencerais par cette interrogation : est-il
LE CADRE COMMUN DE REFERENCE LA CONVERGENCE DES DROITS 3 e forum franco-allemand Guillaume Wicker Professeur à l Université Montesquieu - Bordeaux IV 1 Je commencerais par cette interrogation : est-il
Manuel de recherche en sciences sociales
 Résumé de QUIVY R; VAN CAMPENHOUDT L. 95, "Manuel de recherches en sciences sociales", Dunod Cours de TC5 du DEA GSI de l intergroupe des écoles Centrales 11/2002 Manuel de recherche en sciences sociales
Résumé de QUIVY R; VAN CAMPENHOUDT L. 95, "Manuel de recherches en sciences sociales", Dunod Cours de TC5 du DEA GSI de l intergroupe des écoles Centrales 11/2002 Manuel de recherche en sciences sociales
MASTER 1 MANAGEMENT PUBLIC ENVIRONNEMENTAL CONTENU DES ENSEIGNEMENTS
 MASTER 1 MANAGEMENT PUBLIC ENVIRONNEMENTAL CONTENU DES ENSEIGNEMENTS Le Master 1 : Management Public Environnemental forme aux spécialités de Master 2 suivantes : - Management de la qualité o Parcours
MASTER 1 MANAGEMENT PUBLIC ENVIRONNEMENTAL CONTENU DES ENSEIGNEMENTS Le Master 1 : Management Public Environnemental forme aux spécialités de Master 2 suivantes : - Management de la qualité o Parcours
Utilisation du TNI en classe d anglais. PROJET INNOVANT présenté par la SECTION D ANGLAIS du Lycée Jean-Paul de Rocca Serra, 20137 Porto-Vecchio
 Touch N Invent! Utilisation du TNI en classe d anglais PROJET INNOVANT présenté par la SECTION D ANGLAIS du Lycée Jean-Paul de Rocca Serra, 20137 Porto-Vecchio Sylvie Chiariglione, Brigitte Collomb, Régine
Touch N Invent! Utilisation du TNI en classe d anglais PROJET INNOVANT présenté par la SECTION D ANGLAIS du Lycée Jean-Paul de Rocca Serra, 20137 Porto-Vecchio Sylvie Chiariglione, Brigitte Collomb, Régine
Le management des risques de l entreprise Cadre de Référence. Synthèse
 Le management des risques de l entreprise Cadre de Référence Synthèse SYNTHESE L incertitude est une donnée intrinsèque à la vie de toute organisation. Aussi l un des principaux défis pour la direction
Le management des risques de l entreprise Cadre de Référence Synthèse SYNTHESE L incertitude est une donnée intrinsèque à la vie de toute organisation. Aussi l un des principaux défis pour la direction
La supervision en soins infirmiers
 La supervision en soins infirmiers (article en deux parties : version jumelée) La pratique de la supervision en soins infirmiers étant peu courante en France et les écrits la concernant de même, bien que
La supervision en soins infirmiers (article en deux parties : version jumelée) La pratique de la supervision en soins infirmiers étant peu courante en France et les écrits la concernant de même, bien que
Méthode universitaire du commentaire de texte
 Méthode universitaire du commentaire de texte Baptiste Mélès Novembre 2014 L objectif du commentaire de texte est de décrire la structure argumentative et de mettre au jour les concepts qui permettent
Méthode universitaire du commentaire de texte Baptiste Mélès Novembre 2014 L objectif du commentaire de texte est de décrire la structure argumentative et de mettre au jour les concepts qui permettent
Cahier des charges pour le tutorat d un professeur du second degré
 Cahier des charges pour le tutorat d un professeur du second degré Référence : Circulaire n 2010-037 du 25 février 2010 relative au dispositif d'accueil, d'accompagnement et de formation des enseignants
Cahier des charges pour le tutorat d un professeur du second degré Référence : Circulaire n 2010-037 du 25 février 2010 relative au dispositif d'accueil, d'accompagnement et de formation des enseignants
Portefeuille. Bénévolat. de compétences. Modes d emploi pour. Tout bénévole Les jeunes Les actifs Les responsables d associations
 Bénévolat Portefeuille de compétences Modes d emploi pour Tout bénévole Les jeunes Les actifs Les responsables d associations Tout bénévole Votre mode d emploi Le Portefeuille de compétences vous aide
Bénévolat Portefeuille de compétences Modes d emploi pour Tout bénévole Les jeunes Les actifs Les responsables d associations Tout bénévole Votre mode d emploi Le Portefeuille de compétences vous aide
Primaire. analyse a priori. Lucie Passaplan et Sébastien Toninato 1
 Primaire l ESCALIER Une activité sur les multiples et diviseurs en fin de primaire Lucie Passaplan et Sébastien Toninato 1 Dans le but d observer les stratégies usitées dans la résolution d un problème
Primaire l ESCALIER Une activité sur les multiples et diviseurs en fin de primaire Lucie Passaplan et Sébastien Toninato 1 Dans le but d observer les stratégies usitées dans la résolution d un problème
FICHE N 8 Photodiversité, d une banque d images à un portail d activités en ligne Anne-Marie Michaud, académie de Versailles
 FICHE N 8 Photodiversité, d une banque d images à un portail d activités en ligne Anne-Marie Michaud, académie de Versailles Niveaux et thèmes de programme Sixième : 1 ère partie : caractéristiques de
FICHE N 8 Photodiversité, d une banque d images à un portail d activités en ligne Anne-Marie Michaud, académie de Versailles Niveaux et thèmes de programme Sixième : 1 ère partie : caractéristiques de
Plates-formes de téléformation et modèles pédagogiques
 POYET Françoise, (7095) Introduction Plates-formes de téléformation et modèles pédagogiques Depuis quelques années, on assiste à une stabilisation informatique des Technologies de l Information et de la
POYET Françoise, (7095) Introduction Plates-formes de téléformation et modèles pédagogiques Depuis quelques années, on assiste à une stabilisation informatique des Technologies de l Information et de la
Nom de l application
 Ministère de l Enseignement Supérieur et de la Recherche Scientifique Direction Générale des Etudes Technologiques Institut Supérieur des Etudes Technologiques de Gafsa Département Technologies de l Informatique
Ministère de l Enseignement Supérieur et de la Recherche Scientifique Direction Générale des Etudes Technologiques Institut Supérieur des Etudes Technologiques de Gafsa Département Technologies de l Informatique
EVALUATION DES SERVICES GUIDE A L INTENTION DE LA CHEFFE OU DU CHEF DE SERVICE ET DE SES COLLABORATRICES ET COLLABORATEURS
 EVALUATION DES SERVICES GUIDE A L INTENTION DE LA CHEFFE OU DU CHEF DE SERVICE ET DE SES COLLABORATRICES ET COLLABORATEURS Ce document présente la procédure d évaluation des services centraux de l UNIL
EVALUATION DES SERVICES GUIDE A L INTENTION DE LA CHEFFE OU DU CHEF DE SERVICE ET DE SES COLLABORATRICES ET COLLABORATEURS Ce document présente la procédure d évaluation des services centraux de l UNIL
Chapitre 2 LE CAS PRATIQUE
 Chapitre 2 LE CAS PRATIQUE Demande de conseil. Le cas pratique est un exercice juridique qui, à l instar d une personne se trouvant en situation de litige avec autrui, demande conseil. C est un exercice
Chapitre 2 LE CAS PRATIQUE Demande de conseil. Le cas pratique est un exercice juridique qui, à l instar d une personne se trouvant en situation de litige avec autrui, demande conseil. C est un exercice
Complément d information concernant la fiche de concordance
 Sommaire SAMEDI 0 DÉCEMBRE 20 Vous trouverez dans ce dossier les documents correspondants à ce que nous allons travailler aujourd hui : La fiche de concordance pour le DAEU ; Page 2 Un rappel de cours
Sommaire SAMEDI 0 DÉCEMBRE 20 Vous trouverez dans ce dossier les documents correspondants à ce que nous allons travailler aujourd hui : La fiche de concordance pour le DAEU ; Page 2 Un rappel de cours
Organisation de dispositifs pour tous les apprenants : la question de l'évaluation inclusive
 Organisation de dispositifs pour tous les apprenants : la question de l'évaluation inclusive Transcription et traduction de la communication de Verity DONNELLY colloque Éducation inclusive, la question
Organisation de dispositifs pour tous les apprenants : la question de l'évaluation inclusive Transcription et traduction de la communication de Verity DONNELLY colloque Éducation inclusive, la question
2 e partie de la composante majeure (8 points) Les questions prennent appui sur six documents A, B, C, D, E, F (voir pages suivantes).
 SUJET DE CONCOURS Sujet Exploitation d une documentation scientifique sur le thème de l énergie 2 e partie de la composante majeure (8 points) Les questions prennent appui sur six documents A, B, C, D,
SUJET DE CONCOURS Sujet Exploitation d une documentation scientifique sur le thème de l énergie 2 e partie de la composante majeure (8 points) Les questions prennent appui sur six documents A, B, C, D,
Tâche complexe produite par l académie de Clermont-Ferrand. Mai 2012 LE TIR A L ARC. (d après une idée du collège des Portes du Midi de Maurs)
 (d après une idée du collège des Portes du Midi de Maurs) Table des matières Fiche professeur... 2 Fiche élève... 5 1 Fiche professeur Niveaux et objectifs pédagogiques 5 e : introduction ou utilisation
(d après une idée du collège des Portes du Midi de Maurs) Table des matières Fiche professeur... 2 Fiche élève... 5 1 Fiche professeur Niveaux et objectifs pédagogiques 5 e : introduction ou utilisation
Animer une association
 FICHE PRATIQUE N 7 www.animafac.net gestion de projet Animer une association Une association vit mieux si elle est composée de plusieurs membres partageant un projet collectif. Si la loi 1901 est une loi
FICHE PRATIQUE N 7 www.animafac.net gestion de projet Animer une association Une association vit mieux si elle est composée de plusieurs membres partageant un projet collectif. Si la loi 1901 est une loi
CONSEILS POUR LA REDACTION DU RAPPORT DE RECHERCHE. Information importante : Ces conseils ne sont pas exhaustifs!
 CONSEILS POUR LA REDACTION DU RAPPORT DE RECHERCHE Information importante : Ces conseils ne sont pas exhaustifs! Conseils généraux : Entre 25 et 60 pages (hormis références, annexes, résumé) Format d un
CONSEILS POUR LA REDACTION DU RAPPORT DE RECHERCHE Information importante : Ces conseils ne sont pas exhaustifs! Conseils généraux : Entre 25 et 60 pages (hormis références, annexes, résumé) Format d un
5.3. Bande numérique cartes numération et cartes à points pour apprendre les nombres de 0 à 99
 5.3. Bande numérique cartes numération et cartes à points pour apprendre les nombres de 0 à 99 Niveau CP pistes pour le CE1 Modèle proposé : modèles de séance Hypothèse de la difficulté : pour les élèves
5.3. Bande numérique cartes numération et cartes à points pour apprendre les nombres de 0 à 99 Niveau CP pistes pour le CE1 Modèle proposé : modèles de séance Hypothèse de la difficulté : pour les élèves
Evaluation des cursus «Information & Communication» 2009-2010
 Evaluation des cursus «Information & Communication» 2009-2010 RAPPORT FINAL DE SYNTHÈSE Université Catholique de Louvain (UCL) Comité des experts : M. Pascal LARDELLIER, président Mme Martine SIMONIS,
Evaluation des cursus «Information & Communication» 2009-2010 RAPPORT FINAL DE SYNTHÈSE Université Catholique de Louvain (UCL) Comité des experts : M. Pascal LARDELLIER, président Mme Martine SIMONIS,
Plan de formation 2nd degré 2015 2016 CREER, INNOVER
 Plan de formation 2nd degré 2015 2016 La carte heuristique, un outil au service des apprentissages PN009406 Les cartes heuristiques sont un réel outil pour apprendre à apprendre, et s avèrent un atout
Plan de formation 2nd degré 2015 2016 La carte heuristique, un outil au service des apprentissages PN009406 Les cartes heuristiques sont un réel outil pour apprendre à apprendre, et s avèrent un atout
Service d accompagnement pédagogique de l Université Sorbonne Paris Cité
 Service d accompagnement pédagogique de l Université Sorbonne Paris Cité CATALOGUE DE FORMATION POUR LES ENSEIGNANTS DE USPC 2014-2015 Le service SAPIENS créé en janvier 2014 propose durant l année 2014-2015
Service d accompagnement pédagogique de l Université Sorbonne Paris Cité CATALOGUE DE FORMATION POUR LES ENSEIGNANTS DE USPC 2014-2015 Le service SAPIENS créé en janvier 2014 propose durant l année 2014-2015
Problématique / Problématiser / Problématisation / Problème
 Problématique / Problématiser / Problématisation / PROBLÉMATIQUE : UN GROUPEMENT DE DÉFINITIONS. «Art, science de poser les problèmes. Voir questionnement. Ensemble de problèmes dont les éléments sont
Problématique / Problématiser / Problématisation / PROBLÉMATIQUE : UN GROUPEMENT DE DÉFINITIONS. «Art, science de poser les problèmes. Voir questionnement. Ensemble de problèmes dont les éléments sont
Eléments de Choix d Utilisation de l Informatique dans l Enseignement des Mathématiques en Classe de Cinquième
 GUYOT Stéphanie Professeur stagiaire en mathématiques au collège Lo Trentanel de GIGNAC I.U.F.M. de l académie de Montpellier Site de Montpellier Eléments de Choix d Utilisation de l Informatique dans
GUYOT Stéphanie Professeur stagiaire en mathématiques au collège Lo Trentanel de GIGNAC I.U.F.M. de l académie de Montpellier Site de Montpellier Eléments de Choix d Utilisation de l Informatique dans
Modulo Bank - Groupe E.S.C Chambéry - prérequis à la formation - doc. interne - Ecoute active.doc Page 1
 Généralités, l'écoute active : présentation et techniques... 3 Introduction... 3 Plan... 3 La présentation de l'écoute active... 4 Définition... 4 Fondement... 4 Application... 4 de l'écoute active...
Généralités, l'écoute active : présentation et techniques... 3 Introduction... 3 Plan... 3 La présentation de l'écoute active... 4 Définition... 4 Fondement... 4 Application... 4 de l'écoute active...
Évaluation en vue de l accréditation. Programme Master Européen en Médiation de l Institut Universitaire Kurt Bösch
 Évaluation en vue de l accréditation Programme Master Européen en Médiation de l Institut Universitaire Kurt Bösch Rapport final du Comité de visite de l OAQ 30 août 2005 I - Description du processus d
Évaluation en vue de l accréditation Programme Master Européen en Médiation de l Institut Universitaire Kurt Bösch Rapport final du Comité de visite de l OAQ 30 août 2005 I - Description du processus d
eduscol Ressources pour la voie professionnelle Français Ressources pour les classes préparatoires au baccalauréat professionnel
 eduscol Ressources pour la voie professionnelle Ressources pour les classes préparatoires au baccalauréat professionnel Français Présentation des programmes 2009 du baccalauréat professionnel Ces documents
eduscol Ressources pour la voie professionnelle Ressources pour les classes préparatoires au baccalauréat professionnel Français Présentation des programmes 2009 du baccalauréat professionnel Ces documents
I. LE CAS CHOISI PROBLEMATIQUE
 I. LE CAS CHOISI Gloria est une élève en EB4. C est une fille brune, mince avec un visage triste. Elle est timide, peureuse et peu autonome mais elle est en même temps, sensible, serviable et attentive
I. LE CAS CHOISI Gloria est une élève en EB4. C est une fille brune, mince avec un visage triste. Elle est timide, peureuse et peu autonome mais elle est en même temps, sensible, serviable et attentive
6 ème FONCTIONS. Pratiquer une démarche scientifique et technologique. Capacités
 6 ème FONCTIONS Les exercices de ce chapitre permettent de travailler des compétences scientifiques du socle commun. Pratiquer une démarche scientifique et technologique Capacités Rechercher, extraire
6 ème FONCTIONS Les exercices de ce chapitre permettent de travailler des compétences scientifiques du socle commun. Pratiquer une démarche scientifique et technologique Capacités Rechercher, extraire
Il y a trois types principaux d analyse des résultats : l analyse descriptive, l analyse explicative et l analyse compréhensive.
 L ANALYSE ET L INTERPRÉTATION DES RÉSULTATS Une fois les résultats d une investigation recueillis, on doit les mettre en perspective en les reliant au problème étudié et à l hypothèse formulée au départ:
L ANALYSE ET L INTERPRÉTATION DES RÉSULTATS Une fois les résultats d une investigation recueillis, on doit les mettre en perspective en les reliant au problème étudié et à l hypothèse formulée au départ:
CRÉER UN(E) E.N. 1 DANS CHAQUE I.U.F.M.?
 89 CRÉER UN(E) E.N. 1 DANS CHAQUE I.U.F.M.? L organisation des Instituts Universitaires de Formation des Maîtres est structurée autour de «sites» qui sont des implantations immobilières chargées d histoire
89 CRÉER UN(E) E.N. 1 DANS CHAQUE I.U.F.M.? L organisation des Instituts Universitaires de Formation des Maîtres est structurée autour de «sites» qui sont des implantations immobilières chargées d histoire
Formation certifiante au métier de coach scolaire
 Formation certifiante au métier de coach scolaire 1 Préambule CoachingMaestro est un portail de formations dédié à toute personne intéressée dans l accompagnement des jeunes. Préambule Ses missions sont
Formation certifiante au métier de coach scolaire 1 Préambule CoachingMaestro est un portail de formations dédié à toute personne intéressée dans l accompagnement des jeunes. Préambule Ses missions sont
Rapport d évaluation du master
 Section des Formations et des diplômes Rapport d évaluation du master Philosophie, psychanalyse de l Université Paul-Valéry Montpellier 3 Vague E 2015-2019 Campagne d évaluation 2013-2014 Section des Formations
Section des Formations et des diplômes Rapport d évaluation du master Philosophie, psychanalyse de l Université Paul-Valéry Montpellier 3 Vague E 2015-2019 Campagne d évaluation 2013-2014 Section des Formations
Exercices Alternatifs. Quelqu un aurait-il vu passer un polynôme?
 Exercices Alternatifs Quelqu un aurait-il vu passer un polynôme? c 2004 Frédéric Le Roux, François Béguin (copyleft LDL : Licence pour Documents Libres). Sources et figures: polynome-lagrange/. Version
Exercices Alternatifs Quelqu un aurait-il vu passer un polynôme? c 2004 Frédéric Le Roux, François Béguin (copyleft LDL : Licence pour Documents Libres). Sources et figures: polynome-lagrange/. Version
Exercices Alternatifs. Quelqu un aurait-il vu passer un polynôme?
 Exercices Alternatifs Quelqu un aurait-il vu passer un polynôme? c 2004 Frédéric Le Roux, François Béguin (copyleft LDL : Licence pour Documents Libres). Sources et figures: polynome-lagrange/. Version
Exercices Alternatifs Quelqu un aurait-il vu passer un polynôme? c 2004 Frédéric Le Roux, François Béguin (copyleft LDL : Licence pour Documents Libres). Sources et figures: polynome-lagrange/. Version
N 334 - SIMON Anne-Catherine
 N 334 - SIMON Anne-Catherine RÉALISATION D UN CDROM/DVD CONTENANT DES DONNÉES DU LANGAGE ORAL ORGANISÉES EN PARCOURS DIDACTIQUES D INITIATION LINGUISTIQUE A PARTIR DES BASES DE DONNÉES VALIBEL Introduction
N 334 - SIMON Anne-Catherine RÉALISATION D UN CDROM/DVD CONTENANT DES DONNÉES DU LANGAGE ORAL ORGANISÉES EN PARCOURS DIDACTIQUES D INITIATION LINGUISTIQUE A PARTIR DES BASES DE DONNÉES VALIBEL Introduction
Bilan de mission. Au collège : «Les clés de la culture»
 Bilan de mission Au collège : «Les clés de la culture» La co-intervention en 6 e La formation des Assistants pédagogiques Dans le R.A.R. : Accompagner le projet «chorale» par l histoire Histoire de Montpellier
Bilan de mission Au collège : «Les clés de la culture» La co-intervention en 6 e La formation des Assistants pédagogiques Dans le R.A.R. : Accompagner le projet «chorale» par l histoire Histoire de Montpellier
Introduction à la méthodologie de la recherche
 MASTER DE RECHERCHE Relations Économiques Internationales 2006-2007 Introduction à la méthodologie de la recherche [email protected] Les Etapes de la Recherche Les étapes de la démarche Etape
MASTER DE RECHERCHE Relations Économiques Internationales 2006-2007 Introduction à la méthodologie de la recherche [email protected] Les Etapes de la Recherche Les étapes de la démarche Etape
Licence professionnelle Intégration des systèmes voix / données
 Formations et diplômes Rapport d'évaluation Licence professionnelle Intégration des systèmes voix / données Université de Pau et des Pays de l Adour - UPPA Campagne d évaluation 2014-2015 (Vague A) Formations
Formations et diplômes Rapport d'évaluation Licence professionnelle Intégration des systèmes voix / données Université de Pau et des Pays de l Adour - UPPA Campagne d évaluation 2014-2015 (Vague A) Formations
Stages de recherche dans les formations d'ingénieur. Víctor Gómez Frías. École des Ponts ParisTech, Champs-sur-Marne, France
 Stages de recherche dans les formations d'ingénieur Víctor Gómez Frías École des Ponts ParisTech, Champs-sur-Marne, France [email protected] Résumé Les méthodes de l ingénierie ont été généralement
Stages de recherche dans les formations d'ingénieur Víctor Gómez Frías École des Ponts ParisTech, Champs-sur-Marne, France [email protected] Résumé Les méthodes de l ingénierie ont été généralement
Une école adaptée à tous ses élèves
 PRENDRE LE VIRAGE DU SUCCÈS Une école adaptée à tous ses élèves PLAN D'ACTION EN MATIÈRE D'ADAPTATION SCOLAIRE Québec Ministère de l'éducation Une école adaptée à tous ses élèves PRENDRE LE VIRAGE DU SUCCÈS
PRENDRE LE VIRAGE DU SUCCÈS Une école adaptée à tous ses élèves PLAN D'ACTION EN MATIÈRE D'ADAPTATION SCOLAIRE Québec Ministère de l'éducation Une école adaptée à tous ses élèves PRENDRE LE VIRAGE DU SUCCÈS
Eléments de présentation du projet de socle commun de connaissances, de compétences et de culture par le Conseil supérieur des programmes
 Eléments de présentation du projet de socle commun de connaissances, de compétences et de culture par le Conseil supérieur des programmes Le projet de socle de connaissances, de compétences et de culture,
Eléments de présentation du projet de socle commun de connaissances, de compétences et de culture par le Conseil supérieur des programmes Le projet de socle de connaissances, de compétences et de culture,
LE PROCESSUS ( la machine) la fonction f. ( On lit : «fonction f qui à x associe f (x)» )
 SYNTHESE ( THEME ) FONCTIONS () : NOTIONS de FONCTIONS FONCTION LINEAIRE () : REPRESENTATIONS GRAPHIQUES * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
SYNTHESE ( THEME ) FONCTIONS () : NOTIONS de FONCTIONS FONCTION LINEAIRE () : REPRESENTATIONS GRAPHIQUES * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
La construction du temps et de. Construction du temps et de l'espace au cycle 2, F. Pollard, CPC Bièvre-Valloire
 La construction du temps et de l espace au cycle 2 Rappel de la conférence de Pierre Hess -Démarche de recherche: importance de se poser des questions, de chercher, -Envisager la démarche mentale qui permet
La construction du temps et de l espace au cycle 2 Rappel de la conférence de Pierre Hess -Démarche de recherche: importance de se poser des questions, de chercher, -Envisager la démarche mentale qui permet
FICHE PEDAGOGIQUE 17
 FICHE PEDAGOGIQUE 17 THEME : NOM DE L EXERCICE : LA MEDIATION Séries de tableaux à double entrée Progressions numériques et suites logiques L EXERCICE COMPORTE PLUSIEURS VARIANTES D EXPLOITATION non REFERENCE
FICHE PEDAGOGIQUE 17 THEME : NOM DE L EXERCICE : LA MEDIATION Séries de tableaux à double entrée Progressions numériques et suites logiques L EXERCICE COMPORTE PLUSIEURS VARIANTES D EXPLOITATION non REFERENCE
Spécialité auxiliaire en prothèse dentaire du brevet d études professionnelles. ANNEXE IIb DEFINITION DES EPREUVES
 ANNEXE IIb DEFINITION DES EPREUVES 51 Epreuve EP1 : ANALYSE ET COMMUNICATION TECHNOLOGIQUES UP1 Coefficient 4 Finalité et objectifs de l épreuve L épreuve vise à évaluer la capacité du candidat à mobiliser
ANNEXE IIb DEFINITION DES EPREUVES 51 Epreuve EP1 : ANALYSE ET COMMUNICATION TECHNOLOGIQUES UP1 Coefficient 4 Finalité et objectifs de l épreuve L épreuve vise à évaluer la capacité du candidat à mobiliser
Principes de mathématiques 12 SÉRIE DE PROBLÈMES. Septembre 2001. Student Assessment and Program Evaluation Branch
 Principes de mathématiques 12 SÉRIE DE PROBLÈMES Septembre 2001 Student Assessment and Program Evaluation Branch REMERCIEMENTS Le Ministère de l Éducation tient à remercier chaleureusement les professionnels
Principes de mathématiques 12 SÉRIE DE PROBLÈMES Septembre 2001 Student Assessment and Program Evaluation Branch REMERCIEMENTS Le Ministère de l Éducation tient à remercier chaleureusement les professionnels
Les cinq premiers pas pour devenir vraiment agile à XP Day Suisse 2009 par Pascal Van Cauwenberghe et Portia Tung: La Rétrospective
 Ce qui était bien Ce qui n était pas bien Questions J ai appris Bon résumé des valeurs Simplicité du format Présentateurs sympathiques et joie communicative Bonbons Utilisation réelle du feedback Présentation
Ce qui était bien Ce qui n était pas bien Questions J ai appris Bon résumé des valeurs Simplicité du format Présentateurs sympathiques et joie communicative Bonbons Utilisation réelle du feedback Présentation
Indications pour une progression au CM1 et au CM2
 Indications pour une progression au CM1 et au CM2 Objectif 1 Construire et utiliser de nouveaux nombres, plus précis que les entiers naturels pour mesurer les grandeurs continues. Introduction : Découvrir
Indications pour une progression au CM1 et au CM2 Objectif 1 Construire et utiliser de nouveaux nombres, plus précis que les entiers naturels pour mesurer les grandeurs continues. Introduction : Découvrir
Point de situation sur la réforme du lycée. I. Les faiblesses du lycée actuel et la nécessité de le réformer
 1 Point de situation sur la réforme du lycée I. Les faiblesses du lycée actuel et la nécessité de le réformer Sur le diagnostic et la problématique de départ, l essentiel du travail est fait. D une part,
1 Point de situation sur la réforme du lycée I. Les faiblesses du lycée actuel et la nécessité de le réformer Sur le diagnostic et la problématique de départ, l essentiel du travail est fait. D une part,
Rapport d évaluation du master
 Section des Formations et des diplômes Rapport d évaluation du master Administration et gestion des entreprises de l Université de Versailles Saint- Quentin-en-Yvelines - UVSQ Vague E 2015-2019 Campagne
Section des Formations et des diplômes Rapport d évaluation du master Administration et gestion des entreprises de l Université de Versailles Saint- Quentin-en-Yvelines - UVSQ Vague E 2015-2019 Campagne
Conditions gagnantes pour démarrer sa transition Agile
 Conditions gagnantes pour démarrer sa transition Agile 1 4 Les De plus en plus d organisations voient l Agilité comme une piste de solution aux problèmes auxquels elles sont confrontées. Par ailleurs,
Conditions gagnantes pour démarrer sa transition Agile 1 4 Les De plus en plus d organisations voient l Agilité comme une piste de solution aux problèmes auxquels elles sont confrontées. Par ailleurs,
SECRÉTARIAT GÉNÉRAL SERVICE DES TECHNOLOGIES ET DES SYSTÈMES. Etude sur les usages des dispositifs TIC dans l enseignement scolaire.
 SECRÉTARIAT GÉNÉRAL SERVICE DES TECHNOLOGIES ET DES SYSTÈMES D INFORMATION SOUS-DIRECTION DES TECHNOLOGIES DE L INFORMATION ET DE LA COMMUNICATION POUR L ÉDUCATION BUREAU DES USAGES Etude sur les usages
SECRÉTARIAT GÉNÉRAL SERVICE DES TECHNOLOGIES ET DES SYSTÈMES D INFORMATION SOUS-DIRECTION DES TECHNOLOGIES DE L INFORMATION ET DE LA COMMUNICATION POUR L ÉDUCATION BUREAU DES USAGES Etude sur les usages
Enoncé et corrigé du brevet des collèges dans les académies d Aix- Marseille, Montpellier, Nice Corse et Toulouse en 2000. Énoncé.
 Enoncé et corrigé du brevet des collèges dans les académies d Aix- Marseille, Montpellier, Nice Corse et Toulouse en 2000. Énoncé. I- ACTIVITES NUMERIQUES (12 points) Exercice 1 (3 points) On considère
Enoncé et corrigé du brevet des collèges dans les académies d Aix- Marseille, Montpellier, Nice Corse et Toulouse en 2000. Énoncé. I- ACTIVITES NUMERIQUES (12 points) Exercice 1 (3 points) On considère
Lecture critique et pratique de la médecine
 1-00.qxp 24/04/2006 11:23 Page 13 Lecture critique appliquée à la médecine vasculaireecture critique et pratique de la médecine Lecture critique et pratique de la médecine Introduction Si la médecine ne
1-00.qxp 24/04/2006 11:23 Page 13 Lecture critique appliquée à la médecine vasculaireecture critique et pratique de la médecine Lecture critique et pratique de la médecine Introduction Si la médecine ne
Présentation du programme. de physique-chimie. de Terminale S. applicable en septembre 2012
 Présentation du programme de physique-chimie de Terminale S applicable en septembre 2012 Nicolas Coppens [email protected] Comme en Seconde et en Première, le programme mélange la physique
Présentation du programme de physique-chimie de Terminale S applicable en septembre 2012 Nicolas Coppens [email protected] Comme en Seconde et en Première, le programme mélange la physique
UN PROJET SCIENTIFIQUE ET CULTUREL POUR LA SOCIÉTÉ DE LA CONNAISSANCE
 UN PROJET SCIENTIFIQUE ET CULTUREL POUR LA SOCIÉTÉ DE LA CONNAISSANCE Le regroupement du Palais de la découverte et de la Cité des sciences et de l industrie en un seul établissement apporte les atouts
UN PROJET SCIENTIFIQUE ET CULTUREL POUR LA SOCIÉTÉ DE LA CONNAISSANCE Le regroupement du Palais de la découverte et de la Cité des sciences et de l industrie en un seul établissement apporte les atouts
Les services en ligne
 X Les services en ligne (ressources partagées, cahier de texte numérique, messagerie, forum, blog ) Extrait de l étude «Le développement des usages des TICE dans l enseignement secondaire», 2005-2008 SDTICE
X Les services en ligne (ressources partagées, cahier de texte numérique, messagerie, forum, blog ) Extrait de l étude «Le développement des usages des TICE dans l enseignement secondaire», 2005-2008 SDTICE
ENSEIGNEMENT DES SCIENCES ET DE LA TECHNOLOGIE A L ECOLE PRIMAIRE : QUELLE DEMARCHE?
 ENSEIGNEMENT DES SCIENCES ET DE LA TECHNOLOGIE A L ECOLE PRIMAIRE : QUELLE DEMARCHE? Les nouveaux programmes 2008 confirment que l observation, le questionnement, l expérimentation et l argumentation sont
ENSEIGNEMENT DES SCIENCES ET DE LA TECHNOLOGIE A L ECOLE PRIMAIRE : QUELLE DEMARCHE? Les nouveaux programmes 2008 confirment que l observation, le questionnement, l expérimentation et l argumentation sont
CFP Brest, CFP Guingamp, CFP Rennes, CFP Vannes et IFP de Bretagne. ISFEC BRETAGNE
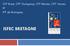 CFP Brest, CFP Guingamp, CFP Rennes, CFP Vannes et IFP de Bretagne. ISFEC BRETAGNE La formation: un double enjeu Recruter et Former de futurs «professionnels» de l enseignement pour l enseignement catholique
CFP Brest, CFP Guingamp, CFP Rennes, CFP Vannes et IFP de Bretagne. ISFEC BRETAGNE La formation: un double enjeu Recruter et Former de futurs «professionnels» de l enseignement pour l enseignement catholique
Le prof, cet incompris ; l élève, désinvesti? Enseignant, animateur, accompagnateur : quelle(s) posture(s) pour quels effets?
 Le prof, cet incompris ; l élève, désinvesti? Enseignant, animateur, accompagnateur : quelle(s) posture(s) pour quels effets? Résumé Christine Jacqmot et Elie Milgrom FA2L scrl «Mon cours intéresse-t-il
Le prof, cet incompris ; l élève, désinvesti? Enseignant, animateur, accompagnateur : quelle(s) posture(s) pour quels effets? Résumé Christine Jacqmot et Elie Milgrom FA2L scrl «Mon cours intéresse-t-il
Comment parler de sa pratique pour la faire partager?
 pour la faire partager? 1. Profiter de l expérience des autres 2. Comment raconter son expérience? 2.1. Théoriser sous forme de récit 2.2. Les ingrédients de la théorisation de pratique 3. Élargir le récit
pour la faire partager? 1. Profiter de l expérience des autres 2. Comment raconter son expérience? 2.1. Théoriser sous forme de récit 2.2. Les ingrédients de la théorisation de pratique 3. Élargir le récit
Bibliothèque des Compétences clés
 Bibliothèque des Compétences clés Modules Jours Heures S exprimer oralement 3 21 S exprimer à l écrit 4 28 Manipuler les chiffres et les ordres de grandeur 5 35 Utiliser les principaux outils bureautiques
Bibliothèque des Compétences clés Modules Jours Heures S exprimer oralement 3 21 S exprimer à l écrit 4 28 Manipuler les chiffres et les ordres de grandeur 5 35 Utiliser les principaux outils bureautiques
