5. Equivalences d automates
|
|
|
- Jules Pothier
- il y a 10 ans
- Total affichages :
Transcription
1 5. Equivalences d automates 5.1. Le problème du déterminisme 5.2. Différentes sortes d AEF 5.3. Déterminisation d un AEF 5.4. Déterminisation d un AEF avec ɛ-transitions 5.5. Minimisation d un AEF déterministe Anne Berry, Cours de Théorie des Langages Partie 1 : 5. Equivalences d automates 1/34
2 5. Equivalences d automates il existe plusieurs types d Automates d Etats Finis ils sont équivalents Anne Berry, Cours de Théorie des Langages Partie 1 : 5. Equivalences d automates 2/34
3 5.1. Le problème du déterminisme La définition d un automate d états finis n interdit pas les conflits. L = aab a + ab b Comment doit-on interpréter δ(q 0, a)? Anne Berry, Cours de Théorie des Langages Partie 1 : 5. Equivalences d automates 3/34
4 5.1. Le problème du déterminisme Le choix est non-déterministe. Anne Berry, Cours de Théorie des Langages Partie 1 : 5. Equivalences d automates 4/34
5 5.1. Le problème du déterminisme Définition Un automates d états finis déterministe (AEFD) (en anglais : Deterministic Finite Automaton (DFA) ) est un automate d états finis tel que, de chaque état q Q, il part Σ transitions, une pour chacune des lettres de l alphabet Σ. 1 dans la pratique, les transitions absentes partent vers l état poubelle, qui souvent est implicite. 2 pas d ɛ-transition! Anne Berry, Cours de Théorie des Langages Partie 1 : 5. Equivalences d automates 5/34
6 5.1. Le problème du déterminisme Exemple d automate déterministe : Anne Berry, Cours de Théorie des Langages Partie 1 : 5. Equivalences d automates 6/34
7 5.2. Différentes sortes d AEF On définit 3 sortes d automates d états finis : 1 les automates d états finis déterministes 2 les automates d états finis non-déterministes avec ɛ-transition (NFA-ɛ) 3 les automates d états finis non-déterministes sans ɛ-transition (NFA-W, W pour Without ) Anne Berry, Cours de Théorie des Langages Partie 1 : 5. Equivalences d automates 7/34
8 5.2. Différentes sortes d AEF Théorème La classe des langages reconnus par : - les automates d états finis déterministes - les automates d états finis non-déterministes sans ɛ-transition - les automates d états finis non-déterministes avec ɛ-transition est la même : celle des langages rationnels. Preuve : constructive (algorithmes de passage d un type d AEF à un autre) Anne Berry, Cours de Théorie des Langages Partie 1 : 5. Equivalences d automates 8/34
9 5.3. Déterminisation d un AEF sans ɛ-transition On part d un AEF non déterministe A 1 = (Q, Σ, δ, q 0, F ) sans ɛ-transition. On calcule un automate d états finis déterministe A 2 = (Q, Σ, δ, Q 0, F ), avec Q 0 = {q 0} Anne Berry, Cours de Théorie des Langages Partie 1 : 5. Equivalences d automates 9/34
10 5.3. Déterminisation d un AEF sans ɛ-transition Principe : On construit les états et la table de transition de δ : 1 On construit la table de transition de δ (qui comporte des ensembles d états) 2 Initialisation de δ - on commence par Q 0 ={q 0} - on applique chaque caractère x de Σ à Q 0 - on obtient un ensemble d états qui est sera état de Q Anne Berry, Cours de Théorie des Langages Partie 1 : 5. Equivalences d automates 10/34
11 5.3. Déterminisation d un AEF sans ɛ-transition 3 Construction de δ - on choisit un état Q de Q non encore traité - on applique chaque caractère x de Σ chaque état de Q avec δ - on obtient un ensemble d états 1 si cet ensemble ne correspond pas à un été déjà défini de Q, on crée un nouvel état (final) de Q 4 les états finaux de A 2 sont ceux qui contiennent au moins un état de F Anne Berry, Cours de Théorie des Langages Partie 1 : 5. Equivalences d automates 11/34
12 5.3. Déterminisation d un AEF sans ɛ-transition Algo DETERMINISATION Donnee : un automate A 1 = (Q, Σ, δ, q 0, F ) Resultat : un automate déterministe A 2 = (Q, Σ, δ, Q 0, F ). Initialisation : Q 0 {q 0};ATRAITER Q 0 = {q 0} ; Q {Q 0 } ; tant que ATRAITER faire CHOISIR Q dans ATRAITER ; ATRAITER ATRAITER - Q ; pour chaque caractère x de Σ faire pour chaque état Q de Q faire δ (Q, x) δ (Q, x) δ(q, x) ; si δ (Q, x) n est pas un état de Q alors Q δ (Q, x) ; Q Q + {Q } ; ATRAITER ATRAITER + {Q } ; pour chaque état Q de Q contenant un état de F faire AJOUTER Q à F ; Retourner((Q, Σ, δ, Q 0, F )). Anne Berry, Cours de Théorie des Langages Partie 1 : 5. Equivalences d automates 12/34
13 5.3. Déterminisation d un AEF sans ɛ-transition Exemple : L = {ab, ac} δ a b c q 0 {q 1,q 3 } { } { } q 1 { } {q 2 } { } q 2 { } { } { } q 3 { } { } {q 4 } q 4 { } { } { } Anne Berry, Cours de Théorie des Langages Partie 1 : 5. Equivalences d automates 13/34
14 5.3. Déterminisation d un AEF sans ɛ-transition Initialisation : Q 0 = {q 0} δ (Q 0, a) = {q 1, q 3 } : on crée un nouvel état Q 1 = {q 1, q 3 } δ (Q 0, b) = { } ; δ (Q 0, c) = { } Anne Berry, Cours de Théorie des Langages Partie 1 : 5. Equivalences d automates 14/34
15 5.3. Déterminisation d un AEF sans ɛ-transition On a un état Q 1 = {q 1, q 3 } qui n est pas traité : δ (Q 1, a) = δ (Q 0, b) = {q 2} : on crée un nouvel état Q 2 = {q 2} δ (Q 0, c) = {q 4} : on crée un nouvel état Q 3 = {q 4} Anne Berry, Cours de Théorie des Langages Partie 1 : 5. Equivalences d automates 15/34
16 5.3. Déterminisation d un AEF sans ɛ-transition On traite l état Q 2 = {q 2} : δ (Q 2, a) = δ (Q 2, b) = δ (Q 2, c) = On traite l état Q 3 = {q 4} : δ (Q 3, a) = δ (Q 3, b) = δ (Q 3, c) = Etats finaux : Q 2 parce qu il contient q 2, et Q 3 parce qu il contient q 4. Anne Berry, Cours de Théorie des Langages Partie 1 : 5. Equivalences d automates 16/34
17 5.3. Déterminisation d un AEF sans ɛ-transition A la fin, on obtient : δ a b c q 0 {q 1,q 3 } { } { } q 1 { } {q 2 } { } q 2 { } { } { } q 3 { } { } {q 4 } q 4 { } { } { } δ a b c Q 0 ={q 0} {q 1,q 3 }=Q 1 { } { } Q 1 ={q 1,q 3 } { } {q 2 }=Q 2 {q 4 }=Q 3 Q 2 =q 2 { } { } { } Q 3 =q 4 { } { } { } Anne Berry, Cours de Théorie des Langages Partie 1 : 5. Equivalences d automates 17/34
18 5.3. Déterminisation d un AEF sans ɛ-transition Remarque : Etant donné un AEF non déterministe à k états, l AEF déterministe correspondant peut avoir 2 k états. Anne Berry, Cours de Théorie des Langages Partie 1 : 5. Equivalences d automates 18/34
19 5.4. Déterminisation d un AEF avec ɛ-transitions On étend la technique de déterminisation en étendant la fonction de transition δ (Q i, x) à une fonction donnée par les mots ɛ xɛ. Anne Berry, Cours de Théorie des Langages Partie 1 : 5. Equivalences d automates 19/34
20 5.4. Déterminisation d un AEF avec ɛ-transitions Définition On appelle ɛ-fermeture d un état q l ensemble des états q i atteignables à partir de q par un chemin étiqueté uniquement par le mot vide ɛ. Définition On appelle ɛ-fermeture d un ensemble Q d états l union des ɛ-fermetures des états appartenant à Q. Anne Berry, Cours de Théorie des Langages Partie 1 : 5. Equivalences d automates 20/34
21 5.4. Déterminisation d un AEF avec ɛ-transitions Exemple : a b c ɛ-fermeture(q 0 ) = {q 0, q 1, q 2 } ɛ-fermeture(q 1 ) = {q 1, q 2 } ɛ-fermeture(q 2 ) = {q 2 } Anne Berry, Cours de Théorie des Langages Partie 1 : 5. Equivalences d automates 21/34
22 5.4. Déterminisation d un AEF avec ɛ-transitions Principe de déterminisation : Pour un état Q de l AEF déterministe en cours de calcul : 1 On part de l ɛ-fermeture de Q. 2 On calcule δ(q ) 3 On calcule l ɛ-fermeture de δ(q ) 4 On obtient un état du nouvel automate Les états finaux du nouvel automate sont ceux qui contiennent au moins un état de l automate de départ. Anne Berry, Cours de Théorie des Langages Partie 1 : 5. Equivalences d automates 22/34
23 5.4. Déterminisation d un AEF avec ɛ-transitions Exemple : δ a b c ɛ q 0 {q 0 } { } { } {q 0,q 1,q 2 } q 1 { } {q 1 } { } {q 1,q 2 } q 2 { } { } {q 2 } {q 2 } Construction de δ, Q 0 =ɛ-fermeture(q 0)={q 0,q 1,q 2 } Anne Berry, Cours de Théorie des Langages Partie 1 : 5. Equivalences d automates 23/34
24 5.4. Déterminisation d un AEF avec ɛ-transitions δ a b c Q 0 = {q 0, q 1, q 2 } {q 0 } Q 0 {q 1 } {q 1,q 2 }=Q 1 {q 2 } {q 2 }= Q 1 = {q 1, q 2 } { } {Q 1 } {Q 2 } Q 2 = {q 2} { } { } {Q 2 } Anne Berry, Cours de Théorie des Langages Partie 1 : 5. Equivalences d automates 24/34
25 5.4. Déterminisation d un AEF avec ɛ-transitions Tous les états sont finaux, on obtient l automate : Anne Berry, Cours de Théorie des Langages Partie 1 : 5. Equivalences d automates 25/34
26 5.5. Minimisation d un AEF déterministe Théorème (de Nérode - Myhill) : Pour un langage rationnel donné L, il existe un automate d états finis déterministe canonique (uniquement défini), et qui comporte un nombre minimum d états, reconnaissant L. Il existe un algorithme très efficace de minimisation. Anne Berry, Cours de Théorie des Langages Partie 1 : 5. Equivalences d automates 26/34
27 5.5. Minimisation d un AEF déterministe Principe de minimisation d un automate d états finis déterministe : utilise le principe algorithmique d éclatement de partitions. Anne Berry, Cours de Théorie des Langages Partie 1 : 5. Equivalences d automates 27/34
28 5.5. Minimisation d un AEF déterministe Rappel : une partition d un ensemble est la définition d un ensemble de classes, tel que l union de toutes les classes est l ensemble de départ et l intersection de deux classes est vide (une partition correspond à une relation d équivalence) Principe algorithmique d éclatement de partitions (ou d affinement de partitions) 1 on part d une (ou plusieurs) (grandes) classes 2 on a un critère qui permet de partitionner un classe en plusieurs classes plus petites 3 on arête quand chaque classe obtenue est non-partitionnable Anne Berry, Cours de Théorie des Langages Partie 1 : 5. Equivalences d automates 28/34
29 5.5. Minimisation d un AEF déterministe Pour minimiser un AEF déterministe : 1 on retire les états non atteignables ; 2 on partitionne l ensemble des états en deux classes : 1 les états finaux 2 les états non finaux (y compris l état poubelle ) Anne Berry, Cours de Théorie des Langages Partie 1 : 5. Equivalences d automates 29/34
30 5.5. Minimisation d un AEF déterministe Etape d éclatement d une classe C i : 1 appliquer à C i une transition par un caractère x de Σ ; 2 séparer les éléments de C i qui n aboutissent pas à la même classe Anne Berry, Cours de Théorie des Langages Partie 1 : 5. Equivalences d automates 30/34
31 5.5. Minimisation d un AEF déterministe On répète jusqu à ce qu il n y ait plus d éclatement possible. A la fin, on a pour toute classe C i obtenue : x Σ, q, q C i, δ(q, x) = δ(q, x) On obtient la description d un nouvel AEF déterministe, dont l état initial est l état contenant q 0 et dont les états finaux sont les états contenant un état final de de l automate de départ. Anne Berry, Cours de Théorie des Langages Partie 1 : 5. Equivalences d automates 31/34
32 5.5. Minimisation d un AEF déterministe Exemple : L = {ab, ac} On part de C 1 = {q 3, q 4 } et C 2 = {q 0, q 2, } (C 1, a), (C 1, b), (C 1, c), (C 2, a) C 2 C 2, b : (q 0, b) C 2, (q 2, b) C 1, (q 2, c) C 1 On sépare C 2 = {q 0, q 2 } en C 2 = {q 0, } et C 2 = {q 2} etc. On obtient un automate d états finis déterministe à trois états : Anne Berry, Cours de Théorie des Langages Partie 1 : 5. Equivalences d automates 32/34
33 5.5. Minimisation d un AEF déterministe Algo MINIMISATION Donnee : un automate déterministe A 1 = (Q, Σ, δ, q 0, F ) Resultat : l automate déterministe minimum A 2 = (Q, Σ, δ, Q 0, F ). Initialisation : C {Q F, F } ; b 1 ; SUPPRIMER de A 1 les états non atteignables ; tant que b=1 faire b 0 ; pour chaque classe C de C faire pour chaque caractère x de Σ faire si par δ on n aboutit pas dans une même classe de C alors REMPLACER C dans C par les classes obtenues ; b 1 ; δ fonction de passage d une classe de C à une autre ; F ensemble des classes de C classes contenant au moins un état de F ; Retourner(C, Σ, δ, q 0, F ). Anne Berry, Cours de Théorie des Langages Partie 1 : 5. Equivalences d automates 33/34
34 5.5. Minimisation d un AEF déterministe Théorème Pour un langage rationnel L donné, il existe un unique automate d états fini déterministe minimum engendrant L. Conséquence fondamentale : Les langages rationnels sont non ambigüs. Anne Berry, Cours de Théorie des Langages Partie 1 : 5. Equivalences d automates 34/34
INF 232: Langages et Automates. Travaux Dirigés. Université Joseph Fourier, Université Grenoble 1 Licence Sciences et Technologies
 INF 232: Langages et Automates Travaux Dirigés Université Joseph Fourier, Université Grenoble 1 Licence Sciences et Technologies Année Académique 2013-2014 Année Académique 2013-2014 UNIVERSITÉ JOSEPH
INF 232: Langages et Automates Travaux Dirigés Université Joseph Fourier, Université Grenoble 1 Licence Sciences et Technologies Année Académique 2013-2014 Année Académique 2013-2014 UNIVERSITÉ JOSEPH
Informatique Théorique : Théorie des Langages, Analyse Lexicale, Analyse Syntaxique Jean-Pierre Jouannaud Professeur
 Université Paris-Sud Licence d Informatique Informatique Théorique : Théorie des Langages, Analyse Lexicale, Analyse Syntaxique Jean-Pierre Jouannaud Professeur Adresse de l auteur : LIX École Polytechnique
Université Paris-Sud Licence d Informatique Informatique Théorique : Théorie des Langages, Analyse Lexicale, Analyse Syntaxique Jean-Pierre Jouannaud Professeur Adresse de l auteur : LIX École Polytechnique
Théorie des Langages
 Théorie des Langages Analyse syntaxique descendante Claude Moulin Université de Technologie de Compiègne Printemps 2010 Sommaire 1 Principe 2 Premiers 3 Suivants 4 Analyse 5 Grammaire LL(1) Exemple : Grammaire
Théorie des Langages Analyse syntaxique descendante Claude Moulin Université de Technologie de Compiègne Printemps 2010 Sommaire 1 Principe 2 Premiers 3 Suivants 4 Analyse 5 Grammaire LL(1) Exemple : Grammaire
CH.6 Propriétés des langages non contextuels
 CH.6 Propriétés des langages non contetuels 6.1 Le lemme de pompage 6.2 Les propriétés de fermeture 6.3 Les problèmes de décidabilité 6.4 Les langages non contetuels déterministes utomates ch6 1 6.1 Le
CH.6 Propriétés des langages non contetuels 6.1 Le lemme de pompage 6.2 Les propriétés de fermeture 6.3 Les problèmes de décidabilité 6.4 Les langages non contetuels déterministes utomates ch6 1 6.1 Le
Objets Combinatoires élementaires
 Objets Combinatoires élementaires 0-0 Permutations Arrangements Permutations pour un multi-ensemble mots sous-ensemble à k éléments (Problème du choix) Compositions LE2I 04 1 Permutations Supposons que
Objets Combinatoires élementaires 0-0 Permutations Arrangements Permutations pour un multi-ensemble mots sous-ensemble à k éléments (Problème du choix) Compositions LE2I 04 1 Permutations Supposons que
La classification automatique de données quantitatives
 La classification automatique de données quantitatives 1 Introduction Parmi les méthodes de statistique exploratoire multidimensionnelle, dont l objectif est d extraire d une masse de données des informations
La classification automatique de données quantitatives 1 Introduction Parmi les méthodes de statistique exploratoire multidimensionnelle, dont l objectif est d extraire d une masse de données des informations
Intégration et probabilités TD1 Espaces mesurés
 Intégration et probabilités TD1 Espaces mesurés 2012-2013 1 Petites questions 1) Est-ce que l ensemble des ouverts de R est une tribu? 2) Si F et G sont deux tribus, est-ce que F G est toujours une tribu?
Intégration et probabilités TD1 Espaces mesurés 2012-2013 1 Petites questions 1) Est-ce que l ensemble des ouverts de R est une tribu? 2) Si F et G sont deux tribus, est-ce que F G est toujours une tribu?
2.4 Représentation graphique, tableau de Karnaugh
 2 Fonctions binaires 45 2.4 Représentation graphique, tableau de Karnaugh On peut définir complètement une fonction binaire en dressant son tableau de Karnaugh, table de vérité à 2 n cases pour n variables
2 Fonctions binaires 45 2.4 Représentation graphique, tableau de Karnaugh On peut définir complètement une fonction binaire en dressant son tableau de Karnaugh, table de vérité à 2 n cases pour n variables
Introduction à la théorie des graphes. Solutions des exercices
 CAHIERS DE LA CRM Introduction à la théorie des graphes Solutions des exercices Didier Müller CAHIER N O 6 COMMISSION ROMANDE DE MATHÉMATIQUE 1 Graphes non orientés Exercice 1 On obtient le graphe biparti
CAHIERS DE LA CRM Introduction à la théorie des graphes Solutions des exercices Didier Müller CAHIER N O 6 COMMISSION ROMANDE DE MATHÉMATIQUE 1 Graphes non orientés Exercice 1 On obtient le graphe biparti
AC AB. A B C x 1. x + 1. d où. Avec un calcul vu au lycée, on démontre que cette solution admet deux solutions dont une seule nous intéresse : x =
 LE NOMBRE D OR Présentation et calcul du nombre d or Euclide avait trouvé un moyen de partager en deu un segment selon en «etrême et moyenne raison» Soit un segment [AB]. Le partage d Euclide consiste
LE NOMBRE D OR Présentation et calcul du nombre d or Euclide avait trouvé un moyen de partager en deu un segment selon en «etrême et moyenne raison» Soit un segment [AB]. Le partage d Euclide consiste
Théorie des Graphes Cours 3: Forêts et Arbres II / Modélisation
 IFIPS S7 - informatique Université Paris-Sud 11 1er semestre 2009/2010 Théorie des Graphes Cours 3: Forêts et Arbres II / 1 Forêts et arbres II Théorème 1.1. Les assertions suivantes sont équivalentes
IFIPS S7 - informatique Université Paris-Sud 11 1er semestre 2009/2010 Théorie des Graphes Cours 3: Forêts et Arbres II / 1 Forêts et arbres II Théorème 1.1. Les assertions suivantes sont équivalentes
Programmation linéaire
 1 Programmation linéaire 1. Le problème, un exemple. 2. Le cas b = 0 3. Théorème de dualité 4. L algorithme du simplexe 5. Problèmes équivalents 6. Complexité de l Algorithme 2 Position du problème Soit
1 Programmation linéaire 1. Le problème, un exemple. 2. Le cas b = 0 3. Théorème de dualité 4. L algorithme du simplexe 5. Problèmes équivalents 6. Complexité de l Algorithme 2 Position du problème Soit
PROTEGER SA CLE USB AVEC ROHOS MINI-DRIVE
 PROTEGER SA CLE USB AVEC ROHOS MINI-DRIVE Protéger sa clé USB avec un système de cryptage par mot de passe peut s avérer très utile si l on veut cacher certaines données sensibles, ou bien rendre ces données
PROTEGER SA CLE USB AVEC ROHOS MINI-DRIVE Protéger sa clé USB avec un système de cryptage par mot de passe peut s avérer très utile si l on veut cacher certaines données sensibles, ou bien rendre ces données
Intégration et probabilités TD1 Espaces mesurés Corrigé
 Intégration et probabilités TD1 Espaces mesurés Corrigé 2012-2013 1 Petites questions 1 Est-ce que l ensemble des ouverts de R est une tribu? Réponse : Non, car le complémentaire de ], 0[ n est pas ouvert.
Intégration et probabilités TD1 Espaces mesurés Corrigé 2012-2013 1 Petites questions 1 Est-ce que l ensemble des ouverts de R est une tribu? Réponse : Non, car le complémentaire de ], 0[ n est pas ouvert.
Théorie et codage de l information
 Théorie et codage de l information Les codes linéaires - Chapitre 6 - Principe Définition d un code linéaire Soient p un nombre premier et s est un entier positif. Il existe un unique corps de taille q
Théorie et codage de l information Les codes linéaires - Chapitre 6 - Principe Définition d un code linéaire Soient p un nombre premier et s est un entier positif. Il existe un unique corps de taille q
La demande Du consommateur. Contrainte budgétaire Préférences Choix optimal
 La demande Du consommateur Contrainte budgétaire Préférences Choix optimal Plan du cours Préambule : Rationalité du consommateur I II III IV V La contrainte budgétaire Les préférences Le choix optimal
La demande Du consommateur Contrainte budgétaire Préférences Choix optimal Plan du cours Préambule : Rationalité du consommateur I II III IV V La contrainte budgétaire Les préférences Le choix optimal
Continuité et dérivabilité d une fonction
 DERNIÈRE IMPRESSIN LE 7 novembre 014 à 10:3 Continuité et dérivabilité d une fonction Table des matières 1 Continuité d une fonction 1.1 Limite finie en un point.......................... 1. Continuité
DERNIÈRE IMPRESSIN LE 7 novembre 014 à 10:3 Continuité et dérivabilité d une fonction Table des matières 1 Continuité d une fonction 1.1 Limite finie en un point.......................... 1. Continuité
Pourquoi l apprentissage?
 Pourquoi l apprentissage? Les SE sont basés sur la possibilité d extraire la connaissance d un expert sous forme de règles. Dépend fortement de la capacité à extraire et formaliser ces connaissances. Apprentissage
Pourquoi l apprentissage? Les SE sont basés sur la possibilité d extraire la connaissance d un expert sous forme de règles. Dépend fortement de la capacité à extraire et formaliser ces connaissances. Apprentissage
Chapitre 5 : Flot maximal dans un graphe
 Graphes et RO TELECOM Nancy A Chapitre 5 : Flot maximal dans un graphe J.-F. Scheid 1 Plan du chapitre I. Définitions 1 Graphe Graphe valué 3 Représentation d un graphe (matrice d incidence, matrice d
Graphes et RO TELECOM Nancy A Chapitre 5 : Flot maximal dans un graphe J.-F. Scheid 1 Plan du chapitre I. Définitions 1 Graphe Graphe valué 3 Représentation d un graphe (matrice d incidence, matrice d
Décision Markovienne appliquée à un jeu de stop ou encore : Pickomino (Heckmeck Am Bratwurmeck)
 Décision Markovienne appliquée à un jeu de stop ou encore : Pickomino (Heckmeck Am Bratwurmeck) Stéphane Cardon Nathalie Chetcuti-Sperandio Fabien Delorme Sylvain agrue CRI - Université d Artois {cardon,chetcuti,delorme,lagrue}@cril.univ-artois.fr
Décision Markovienne appliquée à un jeu de stop ou encore : Pickomino (Heckmeck Am Bratwurmeck) Stéphane Cardon Nathalie Chetcuti-Sperandio Fabien Delorme Sylvain agrue CRI - Université d Artois {cardon,chetcuti,delorme,lagrue}@cril.univ-artois.fr
Plus courts chemins, programmation dynamique
 1 Plus courts chemins, programmation dynamique 1. Plus courts chemins à partir d un sommet 2. Plus courts chemins entre tous les sommets 3. Semi-anneau 4. Programmation dynamique 5. Applications à la bio-informatique
1 Plus courts chemins, programmation dynamique 1. Plus courts chemins à partir d un sommet 2. Plus courts chemins entre tous les sommets 3. Semi-anneau 4. Programmation dynamique 5. Applications à la bio-informatique
Polynômes à plusieurs variables. Résultant
 Polynômes à plusieurs variables. Résultant Christophe Ritzenthaler 1 Relations coefficients-racines. Polynômes symétriques Issu de [MS] et de [Goz]. Soit A un anneau intègre. Définition 1.1. Soit a A \
Polynômes à plusieurs variables. Résultant Christophe Ritzenthaler 1 Relations coefficients-racines. Polynômes symétriques Issu de [MS] et de [Goz]. Soit A un anneau intègre. Définition 1.1. Soit a A \
Résolution de systèmes linéaires par des méthodes directes
 Résolution de systèmes linéaires par des méthodes directes J. Erhel Janvier 2014 1 Inverse d une matrice carrée et systèmes linéaires Ce paragraphe a pour objet les matrices carrées et les systèmes linéaires.
Résolution de systèmes linéaires par des méthodes directes J. Erhel Janvier 2014 1 Inverse d une matrice carrée et systèmes linéaires Ce paragraphe a pour objet les matrices carrées et les systèmes linéaires.
Model checking temporisé
 Model checking temporisé Béatrice Bérard LAMSADE Université Paris-Dauphine & CNRS [email protected] ETR 07, 5 septembre 2007 1/44 Nécessité de vérifier des systèmes... 2/44 Nécessité de vérifier
Model checking temporisé Béatrice Bérard LAMSADE Université Paris-Dauphine & CNRS [email protected] ETR 07, 5 septembre 2007 1/44 Nécessité de vérifier des systèmes... 2/44 Nécessité de vérifier
Souad EL Bernoussi. Groupe d Analyse Numérique et Optimisation Rabat http ://www.fsr.ac.ma/ano/
 Recherche opérationnelle Les démonstrations et les exemples seront traités en cours Souad EL Bernoussi Groupe d Analyse Numérique et Optimisation Rabat http ://www.fsr.ac.ma/ano/ Table des matières 1 Programmation
Recherche opérationnelle Les démonstrations et les exemples seront traités en cours Souad EL Bernoussi Groupe d Analyse Numérique et Optimisation Rabat http ://www.fsr.ac.ma/ano/ Table des matières 1 Programmation
chapitre 4 Nombres de Catalan
 chapitre 4 Nombres de Catalan I Dénitions Dénition 1 La suite de Catalan (C n ) n est la suite dénie par C 0 = 1 et, pour tout n N, C n+1 = C k C n k. Exemple 2 On trouve rapidement C 0 = 1, C 1 = 1, C
chapitre 4 Nombres de Catalan I Dénitions Dénition 1 La suite de Catalan (C n ) n est la suite dénie par C 0 = 1 et, pour tout n N, C n+1 = C k C n k. Exemple 2 On trouve rapidement C 0 = 1, C 1 = 1, C
La NP-complétude. Johanne Cohen. PRISM/CNRS, Versailles, France.
 La NP-complétude Johanne Cohen PRISM/CNRS, Versailles, France. Références 1. Algorithm Design, Jon Kleinberg, Eva Tardos, Addison-Wesley, 2006. 2. Computers and Intractability : A Guide to the Theory of
La NP-complétude Johanne Cohen PRISM/CNRS, Versailles, France. Références 1. Algorithm Design, Jon Kleinberg, Eva Tardos, Addison-Wesley, 2006. 2. Computers and Intractability : A Guide to the Theory of
Définitions. Numéro à préciser. (Durée : )
 Numéro à préciser (Durée : ) On étudie dans ce problème l ordre lexicographique pour les mots sur un alphabet fini et plusieurs constructions des cycles de De Bruijn. Les trois parties sont largement indépendantes.
Numéro à préciser (Durée : ) On étudie dans ce problème l ordre lexicographique pour les mots sur un alphabet fini et plusieurs constructions des cycles de De Bruijn. Les trois parties sont largement indépendantes.
Cours de Probabilités et de Statistique
 Cours de Probabilités et de Statistique Licence 1ère année 2007/2008 Nicolas Prioux Université Paris-Est Cours de Proba-Stat 2 L1.2 Science-Éco Chapitre Notions de théorie des ensembles 1 1.1 Ensembles
Cours de Probabilités et de Statistique Licence 1ère année 2007/2008 Nicolas Prioux Université Paris-Est Cours de Proba-Stat 2 L1.2 Science-Éco Chapitre Notions de théorie des ensembles 1 1.1 Ensembles
Fondements de l informatique Logique, modèles, et calculs
 Fondements de l informatique Logique, modèles, et calculs Cours INF423 de l Ecole Polytechnique Olivier Bournez Version du 20 septembre 2013 2 Table des matières 1 Introduction 9 1.1 Concepts mathématiques........................
Fondements de l informatique Logique, modèles, et calculs Cours INF423 de l Ecole Polytechnique Olivier Bournez Version du 20 septembre 2013 2 Table des matières 1 Introduction 9 1.1 Concepts mathématiques........................
Chp. 4. Minimisation d une fonction d une variable
 Chp. 4. Minimisation d une fonction d une variable Avertissement! Dans tout ce chapître, I désigne un intervalle de IR. 4.1 Fonctions convexes d une variable Définition 9 Une fonction ϕ, partout définie
Chp. 4. Minimisation d une fonction d une variable Avertissement! Dans tout ce chapître, I désigne un intervalle de IR. 4.1 Fonctions convexes d une variable Définition 9 Une fonction ϕ, partout définie
Programmation Linéaire - Cours 1
 Programmation Linéaire - Cours 1 P. Pesneau [email protected] Université Bordeaux 1 Bât A33 - Bur 265 Ouvrages de référence V. Chvátal - Linear Programming, W.H.Freeman, New York, 1983.
Programmation Linéaire - Cours 1 P. Pesneau [email protected] Université Bordeaux 1 Bât A33 - Bur 265 Ouvrages de référence V. Chvátal - Linear Programming, W.H.Freeman, New York, 1983.
Big Data et Graphes : Quelques pistes de recherche
 Big Data et Graphes : Quelques pistes de recherche Hamamache Kheddouci http://liris.cnrs.fr/hamamache.kheddouci Laboratoire d'informatique en Image et Systèmes d'information LIRIS UMR 5205 CNRS/INSA de
Big Data et Graphes : Quelques pistes de recherche Hamamache Kheddouci http://liris.cnrs.fr/hamamache.kheddouci Laboratoire d'informatique en Image et Systèmes d'information LIRIS UMR 5205 CNRS/INSA de
Algorithmes d'apprentissage
 Algorithmes d'apprentissage 1 Agents qui apprennent à partir d'exemples La problématique : prise de décision automatisée à partir d'un ensemble d'exemples Diagnostic médical Réponse à une demande de prêt
Algorithmes d'apprentissage 1 Agents qui apprennent à partir d'exemples La problématique : prise de décision automatisée à partir d'un ensemble d'exemples Diagnostic médical Réponse à une demande de prêt
Bien lire l énoncé 2 fois avant de continuer - Méthodes et/ou Explications Réponses. Antécédents d un nombre par une fonction
 Antécédents d un nombre par une fonction 1) Par lecture graphique Méthode / Explications : Pour déterminer le ou les antécédents d un nombre a donné, on trace la droite (d) d équation. On lit les abscisses
Antécédents d un nombre par une fonction 1) Par lecture graphique Méthode / Explications : Pour déterminer le ou les antécédents d un nombre a donné, on trace la droite (d) d équation. On lit les abscisses
Excel 2007 Niveau 3 Page 1 www.admexcel.com
 Excel 2007 Niveau 3 Page 1 TABLE DES MATIERES UTILISATION DE LISTES DE DONNEES... 4 REMARQUES PREALABLES SUR LES LISTES DE DONNEES... 4 METTRE EN FORME LE TABLEAU... 6 METTRE LA LISTE A JOUR... 7 a/ Directement
Excel 2007 Niveau 3 Page 1 TABLE DES MATIERES UTILISATION DE LISTES DE DONNEES... 4 REMARQUES PREALABLES SUR LES LISTES DE DONNEES... 4 METTRE EN FORME LE TABLEAU... 6 METTRE LA LISTE A JOUR... 7 a/ Directement
Continuité d une fonction de plusieurs variables
 Chapitre 2 Continuité d une fonction de plusieurs variables Maintenant qu on a défini la notion de limite pour des suites dans R n, la notion de continuité s étend sans problème à des fonctions de plusieurs
Chapitre 2 Continuité d une fonction de plusieurs variables Maintenant qu on a défini la notion de limite pour des suites dans R n, la notion de continuité s étend sans problème à des fonctions de plusieurs
Outils logiciels pour la combinaison de vérification fonctionnelle et d évaluation de performances au sein de CADP
 Outils logiciels pour la combinaison de vérification fonctionnelle et d évaluation de performances au sein de CADP Christophe Joubert Séminaire VASY 2002 30 Octobre 2002 Aix les Bains Contexte du projet
Outils logiciels pour la combinaison de vérification fonctionnelle et d évaluation de performances au sein de CADP Christophe Joubert Séminaire VASY 2002 30 Octobre 2002 Aix les Bains Contexte du projet
LE MODELE CONCEPTUEL DE DONNEES
 LE MODELE CONCEPTUEL DE DONNEES Principe : A partir d'un cahier des charges, concevoir de manière visuelle les différents liens qui existent entre les différentes données. Les différentes étapes de réalisation.
LE MODELE CONCEPTUEL DE DONNEES Principe : A partir d'un cahier des charges, concevoir de manière visuelle les différents liens qui existent entre les différentes données. Les différentes étapes de réalisation.
La fonction exponentielle
 DERNIÈRE IMPRESSION LE 2 novembre 204 à :07 La fonction exponentielle Table des matières La fonction exponentielle 2. Définition et théorèmes.......................... 2.2 Approche graphique de la fonction
DERNIÈRE IMPRESSION LE 2 novembre 204 à :07 La fonction exponentielle Table des matières La fonction exponentielle 2. Définition et théorèmes.......................... 2.2 Approche graphique de la fonction
Etude d Algorithmes Parallèles de Data Mining
 REPUBLIQUE TUNISIENNE MINISTERE DE L ENSEIGNEMENT SUPERIEUR, DE LA TECHNOLOGIE ET DE LA RECHERCHE SCIENTIFIQUE UNIVERSITE DE TUNIS ELMANAR FACULTE DES SCIENCES DE TUNIS DEPARTEMENT DES SCIENCES DE L INFORMATIQUE
REPUBLIQUE TUNISIENNE MINISTERE DE L ENSEIGNEMENT SUPERIEUR, DE LA TECHNOLOGIE ET DE LA RECHERCHE SCIENTIFIQUE UNIVERSITE DE TUNIS ELMANAR FACULTE DES SCIENCES DE TUNIS DEPARTEMENT DES SCIENCES DE L INFORMATIQUE
Exercices - Polynômes : corrigé. Opérations sur les polynômes
 Opérations sur les polynômes Exercice 1 - Carré - L1/Math Sup - Si P = Q est le carré d un polynôme, alors Q est nécessairement de degré, et son coefficient dominant est égal à 1. On peut donc écrire Q(X)
Opérations sur les polynômes Exercice 1 - Carré - L1/Math Sup - Si P = Q est le carré d un polynôme, alors Q est nécessairement de degré, et son coefficient dominant est égal à 1. On peut donc écrire Q(X)
1S Modèles de rédaction Enoncés
 Par l équipe des professeurs de 1S du lycée Parc de Vilgénis 1S Modèles de rédaction Enoncés Produit scalaire & Corrigés Exercice 1 : définition du produit scalaire Soit ABC un triangle tel que AB, AC
Par l équipe des professeurs de 1S du lycée Parc de Vilgénis 1S Modèles de rédaction Enoncés Produit scalaire & Corrigés Exercice 1 : définition du produit scalaire Soit ABC un triangle tel que AB, AC
La programmation linéaire : une introduction. Qu est-ce qu un programme linéaire? Terminologie. Écriture mathématique
 La programmation linéaire : une introduction Qu est-ce qu un programme linéaire? Qu est-ce qu un programme linéaire? Exemples : allocation de ressources problème de recouvrement Hypothèses de la programmation
La programmation linéaire : une introduction Qu est-ce qu un programme linéaire? Qu est-ce qu un programme linéaire? Exemples : allocation de ressources problème de recouvrement Hypothèses de la programmation
Système binaire. Algèbre booléenne
 Algèbre booléenne Système binaire Système digital qui emploie des signaux à deux valeurs uniques En général, les digits employés sont 0 et 1, qu'on appelle bits (binary digits) Avantages: on peut utiliser
Algèbre booléenne Système binaire Système digital qui emploie des signaux à deux valeurs uniques En général, les digits employés sont 0 et 1, qu'on appelle bits (binary digits) Avantages: on peut utiliser
CHOIX OPTIMAL DU CONSOMMATEUR. A - Propriétés et détermination du choix optimal
 III CHOIX OPTIMAL DU CONSOMMATEUR A - Propriétés et détermination du choix optimal La demande du consommateur sur la droite de budget Résolution graphique Règle (d or) pour déterminer la demande quand
III CHOIX OPTIMAL DU CONSOMMATEUR A - Propriétés et détermination du choix optimal La demande du consommateur sur la droite de budget Résolution graphique Règle (d or) pour déterminer la demande quand
Big Data et Graphes : Quelques pistes de recherche
 Big Data et Graphes : Quelques pistes de recherche Hamamache Kheddouci Laboratoire d'informatique en Image et Systèmes d'information LIRIS UMR 5205 CNRS/INSA de Lyon/Université Claude Bernard Lyon 1/Université
Big Data et Graphes : Quelques pistes de recherche Hamamache Kheddouci Laboratoire d'informatique en Image et Systèmes d'information LIRIS UMR 5205 CNRS/INSA de Lyon/Université Claude Bernard Lyon 1/Université
Cours de mathématiques
 DEUG MIAS premier niveau Cours de mathématiques année 2003/2004 Guillaume Legendre (version révisée du 3 avril 2015) Table des matières 1 Éléments de logique 1 1.1 Assertions...............................................
DEUG MIAS premier niveau Cours de mathématiques année 2003/2004 Guillaume Legendre (version révisée du 3 avril 2015) Table des matières 1 Éléments de logique 1 1.1 Assertions...............................................
Cryptographie et fonctions à sens unique
 Cryptographie et fonctions à sens unique Pierre Rouchon Centre Automatique et Systèmes Mines ParisTech [email protected] Octobre 2012 P.Rouchon (Mines ParisTech) Cryptographie et fonctions
Cryptographie et fonctions à sens unique Pierre Rouchon Centre Automatique et Systèmes Mines ParisTech [email protected] Octobre 2012 P.Rouchon (Mines ParisTech) Cryptographie et fonctions
Théorie de la Mesure et Intégration
 Université Pierre & Marie Curie (Paris 6) Licence de Mathématiques L3 UE LM364 Intégration 1 & UE LM365 Intégration 2 Année 2010 11 Théorie de la Mesure et Intégration Responsable des cours : Amaury LAMBERT
Université Pierre & Marie Curie (Paris 6) Licence de Mathématiques L3 UE LM364 Intégration 1 & UE LM365 Intégration 2 Année 2010 11 Théorie de la Mesure et Intégration Responsable des cours : Amaury LAMBERT
Etude d un cas industriel : Optimisation de la modélisation de paramètre de production
 Revue des Sciences et de la Technologie RST- Volume 4 N 1 /janvier 2013 Etude d un cas industriel : Optimisation de la modélisation de paramètre de production A.F. Bernate Lara 1, F. Entzmann 2, F. Yalaoui
Revue des Sciences et de la Technologie RST- Volume 4 N 1 /janvier 2013 Etude d un cas industriel : Optimisation de la modélisation de paramètre de production A.F. Bernate Lara 1, F. Entzmann 2, F. Yalaoui
Intelligence Artificielle et Systèmes Multi-Agents. Badr Benmammar [email protected]
 Intelligence Artificielle et Systèmes Multi-Agents Badr Benmammar [email protected] Plan La première partie : L intelligence artificielle (IA) Définition de l intelligence artificielle (IA) Domaines
Intelligence Artificielle et Systèmes Multi-Agents Badr Benmammar [email protected] Plan La première partie : L intelligence artificielle (IA) Définition de l intelligence artificielle (IA) Domaines
Calcul différentiel sur R n Première partie
 Calcul différentiel sur R n Première partie Université De Metz 2006-2007 1 Définitions générales On note L(R n, R m ) l espace vectoriel des applications linéaires de R n dans R m. Définition 1.1 (différentiabilité
Calcul différentiel sur R n Première partie Université De Metz 2006-2007 1 Définitions générales On note L(R n, R m ) l espace vectoriel des applications linéaires de R n dans R m. Définition 1.1 (différentiabilité
Deux disques dans un carré
 Deux disques dans un carré Table des matières 1 Fiche résumé 2 2 Fiche élève Seconde - version 1 3 2.1 Le problème............................................... 3 2.2 Construction de la figure avec geogebra...............................
Deux disques dans un carré Table des matières 1 Fiche résumé 2 2 Fiche élève Seconde - version 1 3 2.1 Le problème............................................... 3 2.2 Construction de la figure avec geogebra...............................
Diagramme de classes
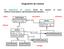 Diagramme de classes Un diagramme de classes décrit les classes et leurs relations (associations, généralisation/spécialisation, ). classe association méthodes attributs héritage Diagramme de classes :
Diagramme de classes Un diagramme de classes décrit les classes et leurs relations (associations, généralisation/spécialisation, ). classe association méthodes attributs héritage Diagramme de classes :
Algorithme. Table des matières
 1 Algorithme Table des matières 1 Codage 2 1.1 Système binaire.............................. 2 1.2 La numérotation de position en base décimale............ 2 1.3 La numérotation de position en base binaire..............
1 Algorithme Table des matières 1 Codage 2 1.1 Système binaire.............................. 2 1.2 La numérotation de position en base décimale............ 2 1.3 La numérotation de position en base binaire..............
Planche n o 22. Fonctions de plusieurs variables. Corrigé
 Planche n o Fonctions de plusieurs variables Corrigé n o : f est définie sur R \ {, } Pour, f, = Quand tend vers, le couple, tend vers le couple, et f, tend vers Donc, si f a une limite réelle en, cette
Planche n o Fonctions de plusieurs variables Corrigé n o : f est définie sur R \ {, } Pour, f, = Quand tend vers, le couple, tend vers le couple, et f, tend vers Donc, si f a une limite réelle en, cette
Cours d introduction à l informatique. Partie 2 : Comment écrire un algorithme? Qu est-ce qu une variable? Expressions et instructions
 Cours d introduction à l informatique Partie 2 : Comment écrire un algorithme? Qu est-ce qu une variable? Expressions et instructions Qu est-ce qu un Une recette de cuisine algorithme? Protocole expérimental
Cours d introduction à l informatique Partie 2 : Comment écrire un algorithme? Qu est-ce qu une variable? Expressions et instructions Qu est-ce qu un Une recette de cuisine algorithme? Protocole expérimental
1.1 Rappels sur le produit cartésien... 1. 1.2 Relations... 3. 1.3 Graphes dirigés... 8. 1.4 Arbres... 12. 1.5 Exercices... 19. 2.1 Motivation...
 Table des matières 1 Relations et graphes 1 1.1 Rappels sur le produit cartésien.................... 1 1.2 Relations.................................. 3 1.3 Graphes dirigés..............................
Table des matières 1 Relations et graphes 1 1.1 Rappels sur le produit cartésien.................... 1 1.2 Relations.................................. 3 1.3 Graphes dirigés..............................
Bases de données cours 4 Construction de requêtes en SQL. Catalin Dima
 Bases de données cours 4 Construction de requêtes en SQL Catalin Dima Requêtes SQL et langage naturel Énoncés en langage naturel. Traduction en SQL? Correspondance entre syntagmes/phrases et opérations
Bases de données cours 4 Construction de requêtes en SQL Catalin Dima Requêtes SQL et langage naturel Énoncés en langage naturel. Traduction en SQL? Correspondance entre syntagmes/phrases et opérations
TABLEAU CROISE DYNAMIQUE
 EXCEL NIVEAU III Mireille DUCELLIER MARS 2003 BASE DE DONNEES RAPPEL Une base de données est une plage de cellules contiguës située sur une la feuille 1. Elle commence en A1. On parle alors de champs,
EXCEL NIVEAU III Mireille DUCELLIER MARS 2003 BASE DE DONNEES RAPPEL Une base de données est une plage de cellules contiguës située sur une la feuille 1. Elle commence en A1. On parle alors de champs,
Exercices types Algorithmique et simulation numérique Oral Mathématiques et algorithmique Banque PT
 Exercices types Algorithmique et simulation numérique Oral Mathématiques et algorithmique Banque PT Ces exercices portent sur les items 2, 3 et 5 du programme d informatique des classes préparatoires,
Exercices types Algorithmique et simulation numérique Oral Mathématiques et algorithmique Banque PT Ces exercices portent sur les items 2, 3 et 5 du programme d informatique des classes préparatoires,
Calculabilité Cours 3 : Problèmes non-calculables. http://www.irisa.fr/lande/pichardie/l3/log/
 Calculabilité Cours 3 : Problèmes non-calculables http://www.irisa.fr/lande/pichardie/l3/log/ Problèmes et classes de décidabilité Problèmes et classes de décidabilité Nous nous intéressons aux problèmes
Calculabilité Cours 3 : Problèmes non-calculables http://www.irisa.fr/lande/pichardie/l3/log/ Problèmes et classes de décidabilité Problèmes et classes de décidabilité Nous nous intéressons aux problèmes
Algèbre binaire et Circuits logiques (2007-2008)
 Université Mohammed V Faculté des Sciences Département de Mathématiques et Informatique Filière : SMI Algèbre binaire et Circuits logiques (27-28) Prof. Abdelhakim El Imrani Plan. Algèbre de Boole 2. Circuits
Université Mohammed V Faculté des Sciences Département de Mathématiques et Informatique Filière : SMI Algèbre binaire et Circuits logiques (27-28) Prof. Abdelhakim El Imrani Plan. Algèbre de Boole 2. Circuits
Correction du baccalauréat ES/L Métropole 20 juin 2014
 Correction du baccalauréat ES/L Métropole 0 juin 014 Exercice 1 1. c.. c. 3. c. 4. d. 5. a. P A (B)=1 P A (B)=1 0,3=0,7 D après la formule des probabilités totales : P(B)=P(A B)+P(A B)=0,6 0,3+(1 0,6)
Correction du baccalauréat ES/L Métropole 0 juin 014 Exercice 1 1. c.. c. 3. c. 4. d. 5. a. P A (B)=1 P A (B)=1 0,3=0,7 D après la formule des probabilités totales : P(B)=P(A B)+P(A B)=0,6 0,3+(1 0,6)
LES DIFFERENTS TYPES DE MESURE
 LES DIFFERENTS TYPES DE MESURE Licence - Statistiques 2004/2005 REALITE ET DONNEES CHIFFREES Recherche = - mesure. - traduction d une réalité en chiffre - abouti à des tableaux, des calculs 1) Qu est-ce
LES DIFFERENTS TYPES DE MESURE Licence - Statistiques 2004/2005 REALITE ET DONNEES CHIFFREES Recherche = - mesure. - traduction d une réalité en chiffre - abouti à des tableaux, des calculs 1) Qu est-ce
IFT1215 Introduction aux systèmes informatiques
 Introduction aux circuits logiques de base IFT25 Architecture en couches Niveau 5 Niveau 4 Niveau 3 Niveau 2 Niveau Niveau Couche des langages d application Traduction (compilateur) Couche du langage d
Introduction aux circuits logiques de base IFT25 Architecture en couches Niveau 5 Niveau 4 Niveau 3 Niveau 2 Niveau Niveau Couche des langages d application Traduction (compilateur) Couche du langage d
Rappels sur les suites - Algorithme
 DERNIÈRE IMPRESSION LE 14 septembre 2015 à 12:36 Rappels sur les suites - Algorithme Table des matières 1 Suite : généralités 2 1.1 Déition................................. 2 1.2 Exemples de suites............................
DERNIÈRE IMPRESSION LE 14 septembre 2015 à 12:36 Rappels sur les suites - Algorithme Table des matières 1 Suite : généralités 2 1.1 Déition................................. 2 1.2 Exemples de suites............................
point On obtient ainsi le ou les points d inter- entre deux objets».
 Déplacer un objet Cliquer sur le bouton «Déplacer». On peut ainsi rendre la figure dynamique. Attraper l objet à déplacer avec la souris. Ici, on veut déplacer le point A du triangle point ABC. A du triangle
Déplacer un objet Cliquer sur le bouton «Déplacer». On peut ainsi rendre la figure dynamique. Attraper l objet à déplacer avec la souris. Ici, on veut déplacer le point A du triangle point ABC. A du triangle
Algorithmique des Systèmes Répartis Protocoles de Communications
 Algorithmique des Systèmes Répartis Protocoles de Communications Master Informatique Dominique Méry Université de Lorraine 1 er avril 2014 1 / 70 Plan Communications entre processus Observation et modélisation
Algorithmique des Systèmes Répartis Protocoles de Communications Master Informatique Dominique Méry Université de Lorraine 1 er avril 2014 1 / 70 Plan Communications entre processus Observation et modélisation
Le contexte. Le questionnement du P.E.R. :
 Le contexte Ce travail a débuté en janvier. Le P.E.R. engagé depuis fin septembre a permis de faire émerger ou de réactiver : Des raisons d être de la géométrie : Calculer des grandeurs inaccessibles et
Le contexte Ce travail a débuté en janvier. Le P.E.R. engagé depuis fin septembre a permis de faire émerger ou de réactiver : Des raisons d être de la géométrie : Calculer des grandeurs inaccessibles et
Construction d un cercle tangent à deux cercles donnés.
 Préparation au CAPES Strasbourg, octobre 2008 Construction d un cercle tangent à deux cercles donnés. Le problème posé : On se donne deux cercles C et C de centres O et O distincts et de rayons R et R
Préparation au CAPES Strasbourg, octobre 2008 Construction d un cercle tangent à deux cercles donnés. Le problème posé : On se donne deux cercles C et C de centres O et O distincts et de rayons R et R
LES TYPES DE DONNÉES DU LANGAGE PASCAL
 LES TYPES DE DONNÉES DU LANGAGE PASCAL 75 LES TYPES DE DONNÉES DU LANGAGE PASCAL CHAPITRE 4 OBJECTIFS PRÉSENTER LES NOTIONS D ÉTIQUETTE, DE CONS- TANTE ET DE IABLE DANS LE CONTEXTE DU LAN- GAGE PASCAL.
LES TYPES DE DONNÉES DU LANGAGE PASCAL 75 LES TYPES DE DONNÉES DU LANGAGE PASCAL CHAPITRE 4 OBJECTIFS PRÉSENTER LES NOTIONS D ÉTIQUETTE, DE CONS- TANTE ET DE IABLE DANS LE CONTEXTE DU LAN- GAGE PASCAL.
GUIDE D UTILISATION. Gestion de compte. à destination des intermédiaires
 GUIDE D UTILISATION Gestion de compte à destination des intermédiaires - 1 - Table des matières JE CRÉE MON COMPTE... 3 JE GÈRE MON COMPTE... 5 JE GÈRE PLUSIEURS SIRET... 6 ENREGISTRER PLUSIEURS SIRET...
GUIDE D UTILISATION Gestion de compte à destination des intermédiaires - 1 - Table des matières JE CRÉE MON COMPTE... 3 JE GÈRE MON COMPTE... 5 JE GÈRE PLUSIEURS SIRET... 6 ENREGISTRER PLUSIEURS SIRET...
Premiers exercices d Algèbre. Anne-Marie Simon
 Premiers exercices d Algèbre Anne-Marie Simon première version: 17 août 2005 version corrigée et complétée le 12 octobre 2010 ii Table des matières 1 Quelques structures ensemblistes 1 1.0 Ensembles, relations,
Premiers exercices d Algèbre Anne-Marie Simon première version: 17 août 2005 version corrigée et complétée le 12 octobre 2010 ii Table des matières 1 Quelques structures ensemblistes 1 1.0 Ensembles, relations,
* très facile ** facile *** difficulté moyenne **** difficile ***** très difficile I : Incontournable
 Eo7 Fonctions de plusieurs variables Eercices de Jean-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-francefr * très facile ** facile *** difficulté moenne **** difficile ***** très difficile I
Eo7 Fonctions de plusieurs variables Eercices de Jean-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-francefr * très facile ** facile *** difficulté moenne **** difficile ***** très difficile I
Probabilité. Table des matières. 1 Loi de probabilité 2 1.1 Conditions préalables... 2 1.2 Définitions... 2 1.3 Loi équirépartie...
 1 Probabilité Table des matières 1 Loi de probabilité 2 1.1 Conditions préalables........................... 2 1.2 Définitions................................. 2 1.3 Loi équirépartie..............................
1 Probabilité Table des matières 1 Loi de probabilité 2 1.1 Conditions préalables........................... 2 1.2 Définitions................................. 2 1.3 Loi équirépartie..............................
Encryptions, compression et partitionnement des données
 Encryptions, compression et partitionnement des données Version 1.0 Grégory CASANOVA 2 Compression, encryption et partitionnement des données Sommaire 1 Introduction... 3 2 Encryption transparente des
Encryptions, compression et partitionnement des données Version 1.0 Grégory CASANOVA 2 Compression, encryption et partitionnement des données Sommaire 1 Introduction... 3 2 Encryption transparente des
Aspects théoriques et algorithmiques du calcul réparti L agglomération
 Aspects théoriques et algorithmiques du calcul réparti L agglomération Patrick CIARLET Enseignant-Chercheur UMA [email protected] Françoise LAMOUR [email protected] Aspects théoriques
Aspects théoriques et algorithmiques du calcul réparti L agglomération Patrick CIARLET Enseignant-Chercheur UMA [email protected] Françoise LAMOUR [email protected] Aspects théoriques
Section «Maturité fédérale» EXAMENS D'ADMISSION Session de février 2014 RÉCAPITULATIFS DES MATIÈRES EXAMINÉES. Formation visée
 EXAMENS D'ADMISSION Admission RÉCAPITULATIFS DES MATIÈRES EXAMINÉES MATIÈRES Préparation en 3 ou 4 semestres Formation visée Préparation complète en 1 an 2 ème partiel (semestriel) Niveau Durée de l examen
EXAMENS D'ADMISSION Admission RÉCAPITULATIFS DES MATIÈRES EXAMINÉES MATIÈRES Préparation en 3 ou 4 semestres Formation visée Préparation complète en 1 an 2 ème partiel (semestriel) Niveau Durée de l examen
Géométrie Algorithmique Plan du cours
 Plan du cours Introduction Triangulation de polygones Recherche/localisation Diagrammes de Voronoï Triangulation de Delaunay Arbres de partition binaire 1 Intersection de segments de droite Intersection
Plan du cours Introduction Triangulation de polygones Recherche/localisation Diagrammes de Voronoï Triangulation de Delaunay Arbres de partition binaire 1 Intersection de segments de droite Intersection
Soit la fonction affine qui, pour représentant le nombre de mois écoulés, renvoie la somme économisée.
 ANALYSE 5 points Exercice 1 : Léonie souhaite acheter un lecteur MP3. Le prix affiché (49 ) dépasse largement la somme dont elle dispose. Elle décide donc d économiser régulièrement. Elle a relevé qu elle
ANALYSE 5 points Exercice 1 : Léonie souhaite acheter un lecteur MP3. Le prix affiché (49 ) dépasse largement la somme dont elle dispose. Elle décide donc d économiser régulièrement. Elle a relevé qu elle
SUR CERTAINS SYSTEMES D EQUATIONS AVEC CONTRAINTES DANS UN GROUPE LIBRE (*)
 PORTUGALIAE MATHEMATICA Vol. 56 Fasc. 4 1999 SUR CERTAINS SYSTEMES D EQUATIONS AVEC CONTRAINTES DANS UN GROUPE LIBRE (*) J. Almeida and M. Delgado Résumé: Le théorème principal trouvé par Ash pour sa preuve
PORTUGALIAE MATHEMATICA Vol. 56 Fasc. 4 1999 SUR CERTAINS SYSTEMES D EQUATIONS AVEC CONTRAINTES DANS UN GROUPE LIBRE (*) J. Almeida and M. Delgado Résumé: Le théorème principal trouvé par Ash pour sa preuve
Introduction au maillage pour le calcul scientifique
 Introduction au maillage pour le calcul scientifique CEA DAM Île-de-France, Bruyères-le-Châtel [email protected] Présentation adaptée du tutorial de Steve Owen, Sandia National Laboratories, Albuquerque,
Introduction au maillage pour le calcul scientifique CEA DAM Île-de-France, Bruyères-le-Châtel [email protected] Présentation adaptée du tutorial de Steve Owen, Sandia National Laboratories, Albuquerque,
Résolution d équations non linéaires
 Analyse Numérique Résolution d équations non linéaires Said EL HAJJI et Touria GHEMIRES Université Mohammed V - Agdal. Faculté des Sciences Département de Mathématiques. Laboratoire de Mathématiques, Informatique
Analyse Numérique Résolution d équations non linéaires Said EL HAJJI et Touria GHEMIRES Université Mohammed V - Agdal. Faculté des Sciences Département de Mathématiques. Laboratoire de Mathématiques, Informatique
www.h-k.fr/publications/objectif-agregation
 «Sur C, tout est connexe!» www.h-k.fr/publications/objectif-agregation L idée de cette note est de montrer que, contrairement à ce qui se passe sur R, «sur C, tout est connexe». Cet abus de langage se
«Sur C, tout est connexe!» www.h-k.fr/publications/objectif-agregation L idée de cette note est de montrer que, contrairement à ce qui se passe sur R, «sur C, tout est connexe». Cet abus de langage se
Fonctions de plusieurs variables, intégrales multiples, et intégrales dépendant d un paramètre
 IUFM du Limousin 2009-10 PLC1 Mathématiques S. Vinatier Rappels de cours Fonctions de plusieurs variables, intégrales multiples, et intégrales dépendant d un paramètre 1 Fonctions de plusieurs variables
IUFM du Limousin 2009-10 PLC1 Mathématiques S. Vinatier Rappels de cours Fonctions de plusieurs variables, intégrales multiples, et intégrales dépendant d un paramètre 1 Fonctions de plusieurs variables
TP 2 Réseaux. Adresses IP, routage et sous-réseaux
 TP 2 Réseaux Adresses IP, routage et sous-réseaux C. Pain-Barre INFO - IUT Aix-en-Provence version du 24/2/2 Adressage IP. Limites du nombre d adresses IP.. Adresses de réseaux valides Les adresses IP
TP 2 Réseaux Adresses IP, routage et sous-réseaux C. Pain-Barre INFO - IUT Aix-en-Provence version du 24/2/2 Adressage IP. Limites du nombre d adresses IP.. Adresses de réseaux valides Les adresses IP
Installation d un Contrôleur de Domaine Windows Server 2003
 Windows Server 2003 Installation d un Contrôleur de Domaine Windows Server 2003 Auteur : Frédéric DIAZ I Introduction : Lorsqu un disque dur est installé pour la première fois dans un PC, seul un formatage
Windows Server 2003 Installation d un Contrôleur de Domaine Windows Server 2003 Auteur : Frédéric DIAZ I Introduction : Lorsqu un disque dur est installé pour la première fois dans un PC, seul un formatage
MIS 102 Initiation à l Informatique
 MIS 102 Initiation à l Informatique Responsables et cours : Cyril Gavoille Catherine Pannier Matthias Robine Marc Zeitoun Planning : 6 séances de cours 5 séances de TD (2h40) 4 séances de TP (2h40) + environ
MIS 102 Initiation à l Informatique Responsables et cours : Cyril Gavoille Catherine Pannier Matthias Robine Marc Zeitoun Planning : 6 séances de cours 5 séances de TD (2h40) 4 séances de TP (2h40) + environ
Les emprunts indivis. Administration Économique et Sociale. Mathématiques XA100M
 Les emprunts indivis Administration Économique et Sociale Mathématiques XA100M Les emprunts indivis sont les emprunts faits auprès d un seul prêteur. On va étudier le cas où le prêteur met à disposition
Les emprunts indivis Administration Économique et Sociale Mathématiques XA100M Les emprunts indivis sont les emprunts faits auprès d un seul prêteur. On va étudier le cas où le prêteur met à disposition
Chapitre 3. Mesures stationnaires. et théorèmes de convergence
 Chapitre 3 Mesures stationnaires et théorèmes de convergence Christiane Cocozza-Thivent, Université de Marne-la-Vallée p.1 I. Mesures stationnaires Christiane Cocozza-Thivent, Université de Marne-la-Vallée
Chapitre 3 Mesures stationnaires et théorèmes de convergence Christiane Cocozza-Thivent, Université de Marne-la-Vallée p.1 I. Mesures stationnaires Christiane Cocozza-Thivent, Université de Marne-la-Vallée
Problème 1 : applications du plan affine
 Problème 1 : applications du plan affine Notations On désigne par GL 2 (R) l ensemble des matrices 2 2 inversibles à coefficients réels. Soit un plan affine P muni d un repère (O, I, J). Les coordonnées
Problème 1 : applications du plan affine Notations On désigne par GL 2 (R) l ensemble des matrices 2 2 inversibles à coefficients réels. Soit un plan affine P muni d un repère (O, I, J). Les coordonnées
Programmation linéaire et Optimisation. Didier Smets
 Programmation linéaire et Optimisation Didier Smets Chapitre 1 Un problème d optimisation linéaire en dimension 2 On considère le cas d un fabricant d automobiles qui propose deux modèles à la vente, des
Programmation linéaire et Optimisation Didier Smets Chapitre 1 Un problème d optimisation linéaire en dimension 2 On considère le cas d un fabricant d automobiles qui propose deux modèles à la vente, des
Les algorithmes de base du graphisme
 Les algorithmes de base du graphisme Table des matières 1 Traçage 2 1.1 Segments de droites......................... 2 1.1.1 Algorithmes simples.................... 3 1.1.2 Algorithmes de Bresenham (1965).............
Les algorithmes de base du graphisme Table des matières 1 Traçage 2 1.1 Segments de droites......................... 2 1.1.1 Algorithmes simples.................... 3 1.1.2 Algorithmes de Bresenham (1965).............
Date : 16 novembre 2011 Version : 1. 2 Nombre de pages : 13
 Politique de Signature EDF Commerce Division Entreprises et Collectivités Locales Pour la dématérialisation fiscale XML des Entreprises et Collectivités Locales Date : 16 novembre 2011 Version : 1. 2 Nombre
Politique de Signature EDF Commerce Division Entreprises et Collectivités Locales Pour la dématérialisation fiscale XML des Entreprises et Collectivités Locales Date : 16 novembre 2011 Version : 1. 2 Nombre
EN BLANC AVANT IMPRESSION»»»
 Ce modèle doit se trouver sous le répertoire C:\Users\toto\AppData\Roaming\Microsoft\Templates EN BLANC AVANT IMPRESSION»»» Version : 1.0.54 Date du livrable : Mars 2015. Pour rafraîchir le numéro de version,
Ce modèle doit se trouver sous le répertoire C:\Users\toto\AppData\Roaming\Microsoft\Templates EN BLANC AVANT IMPRESSION»»» Version : 1.0.54 Date du livrable : Mars 2015. Pour rafraîchir le numéro de version,
Manuel d utilisation 26 juin 2011. 1 Tâche à effectuer : écrire un algorithme 2
 éducalgo Manuel d utilisation 26 juin 2011 Table des matières 1 Tâche à effectuer : écrire un algorithme 2 2 Comment écrire un algorithme? 3 2.1 Avec quoi écrit-on? Avec les boutons d écriture........
éducalgo Manuel d utilisation 26 juin 2011 Table des matières 1 Tâche à effectuer : écrire un algorithme 2 2 Comment écrire un algorithme? 3 2.1 Avec quoi écrit-on? Avec les boutons d écriture........
1 Première section: La construction générale
 AMALGAMATIONS DE CLASSES DE SOUS-GROUPES D UN GROUPE ABÉLIEN. SOUS-GROUPES ESSENTIEL-PURS. Călugăreanu Grigore comunicare prezentată la Conferinţa de grupuri abeliene şi module de la Padova, iunie 1994
AMALGAMATIONS DE CLASSES DE SOUS-GROUPES D UN GROUPE ABÉLIEN. SOUS-GROUPES ESSENTIEL-PURS. Călugăreanu Grigore comunicare prezentată la Conferinţa de grupuri abeliene şi module de la Padova, iunie 1994
Mesure d angles et trigonométrie
 Thierry Ciblac Mesure d angles et trigonométrie Mesure de l angle de deux axes (ou de deux demi-droites) de même origine. - Mesures en degrés : Divisons un cercle en 360 parties égales définissant ainsi
Thierry Ciblac Mesure d angles et trigonométrie Mesure de l angle de deux axes (ou de deux demi-droites) de même origine. - Mesures en degrés : Divisons un cercle en 360 parties égales définissant ainsi
