La tâche complexe, un enjeu de l'enseignement des mathématiques
|
|
|
- Hubert Audy
- il y a 10 ans
- Total affichages :
Transcription
1 La tâche complexe, un enjeu de l'enseignement des mathématiques Frédéric Barôme page 1 La tâche complexe, un enjeu de l'enseignement des mathématiques Enseigner en accord avec l'activité scientifique Pratiquer une activité scientifique ne peut se borner à exécuter une succession de tâches simples. Cela consiste essentiellement à chercher, raisonner, argumenter, conjecturer, diversifier les outils, convaincre... actions demandant toutes de l'autonomie. Pour donner du sens aux mathématiques enseignées et cultiver chez les élèves le goût de faire des mathématiques, les programmes recommandent d utiliser une situation-problème, ou tâche complexe pour introduire certaines notions nouvelles et/ou pour réinvestir des connaissances et capacités acquises. Pour favoriser la mise en œuvre de l autonomie de l élève, les programmes se sont fixés trois grands objectifs : instaurer l activité de raisonnement qui est l essence même des mathématiques et qui contribue à la formation scientifique du futur citoyen ; développer des automatismes (travail sur des tâches simples au travers des exercices d'application) qui favorisent l autonomie et l initiative des élèves dans la résolution de problèmes ; permettre à tous les élèves d acquérir la maîtrise du calcul réfléchi, inséparable du sens des nombres et des opérations. Pour cela, la pratique pédagogique quotidienne conduit à mettre en oeuvre des activités très diversifiées de recherche et de production : résolution de problèmes, travaux d'investigation ; individuels, en petits groupes, de manière collaborative (ateliers tournants ou non, en mosaïque) ; productions écrites (narrations de recherche, schémas ) ou orales (exposés, interrogations individuelles, débat argumenté ). La résolution de problèmes doit constituer le vecteur principal de l évaluation, aussi bien pour l évaluation de l acquisition du programme que pour celle du socle commun : il n est pas possible de gérer, dans chaque classe et pour chaque élève deux systèmes d évaluation, un pour le programme et l autre pour le socle. Il est donc indispensable que les outils d évaluation actuellement utilisés (devoirs de contrôle, évaluation diagnostique, travaux pratiques, travaux à la maison, utilisation des TICE, ou TUIC) soient repensés de manière à permettre de mesurer à la fois la maîtrise du programme et l acquisition des aptitudes du socle commun. Qu'est-ce qu'une tâche complexe Une tâche complexe, ou tâche-problème, est une tâche mettant en œuvre une combinaison de plusieurs procédures simples, automatisées, connues. Elle nécessite l élaboration par l élève d une stratégie personnelle et non pas d'une stratégie experte automatisée et attendue. Elle mobilise des ressources internes (culture, capacités, connaissances, vécu ) et externes (aides méthodologiques, protocoles, fiches techniques, ressources documentaires ). Dans l'idéal, la tâche-problème doit être : COMPLEXE Ressources de natures différentes = savoir + savoir-faire + savoir-être Ressources d origines différentes = savoirs acquis internes + externes (livres, internet, experts,...). FINALISÉE Vers l action, dans un but concret (éventuellement fictif). INTERACTIVE Interaction avec le milieu OUVERTE La démarche comme le produit attendu n'est pas définie, car plusieurs solutions coexistent. INÉDITE Même pour des tâches relevant d une même famille, le contenu change, de manière à ne pas permettre la simple répétition d un acquis. En outre, elle : tient compte des motivations de l élève (proche de son vécu, de son questionnement) ; installe une compétence nouvelle ; permet différents niveaux de performance ; permet à l élève d être au centre de son propre apprentissage.
2 page 4 du vade-mecum Compétence 3 de 2010 page 25 du vade-mecum Mathématiques de 2009 Complexe ne veut pas dire compliqué La tâche complexe, un enjeu de l'enseignement des mathématiques Frédéric Barôme page 2 La notion de tâche complexe fait partie intégrante de celle de compétence, comme le rappelle le préambule du socle commun : «Maîtriser le socle commun, c est être capable de mobiliser ses acquis dans des tâches et des situations complexes, à l école puis dans la vie». Les situations choisies dans ce cadre doivent permettre à tout élève de s engager avec ses acquis du moment et donc, ne reposer que sur des consignes simples, n exiger que des connaissances solidement acquises. Il est important que les consignes de recherche et de production soient à la fois suffisamment ouvertes et précises pour permettre à l élève ou au groupe de s organiser pour développer sa propre démarche de résolution. Pour gérer la double exigence du programme et du socle commun et faire cohabiter harmonieusement tous les objectifs de formation visés, il est essentiel de veiller à ce que ce type de problème offre une véritable activité mathématique à tout élève, sans oublier celui qui n accèdera peut-être pas à la modélisation ou à la stratégie experte visée et qui aura mis en place une «procédure artisanale». Démarches expertes et empiriques Ainsi, une situation algébrique pourra être traitée par essais et erreurs (les problèmes à programmes de calculs s'y prêtent très bien), des grandeurs géométriques pourront être représentées par un graphique à une échelle pratique. On se retrouvera donc à valoriser des approches empiriques : l'enseignant de mathématiques devra alors accepter que faire des mathématiques, c'est parfois tâtonner (et, avouons-le, c'est vrai à plus haut niveau...), puis faire prendre conscience aux élèves des limites. Par exemple, un élève peut trouver le centre d'un cercle de manière fort correcte en piquant quelques fois dans la bonne zone, ou en pliant le disque en quatre. Un cercle tronqué, un cercle de grande taille sur le tableau suffisent à justifier une méthode experte. Un exemple extrait du vade-mecum Cet exemple met en œuvre la capacité «Calculer la longueur d un côté d un triangle rectangle à partir de celles des deux autres (théorème de Pythagore)», souvent évaluée comme tâche simple, et bénéficiant d'une procédure experte et automatisée. Cette tâche simple se voit ici plus ou moins cachée par une situation concrète, dans laquelle le formatage des figures mathématiques est oublié, l'angle droit n'étant pas codé ni renseigné par quelques horizontalité et verticalité. Mais la complexité de cet exemple vient principalement du fait que l'outil Pythagore n'est pas le but en soi : l'obtention de la hauteur de l'escalier n'est qu'une des étapes du problème. On peut étudier son respect des règles de la tâche-problème : complexe par la diversité des ressources mathématiques (mais peu de savoir-être mis en œuvre) ; finalisée vers un but concret fictif ; interactive avec les normes du monde du travail ; peu ouverte car peu de démarches conviennent (on peut néanmoins envisager un dessin à l'échelle) ; inédite, vraisemblablement. Aides à la démarche Des aides doivent être prévues pour les élèves qui ont besoin d être accompagnés pour réaliser la tâche complexe. Les aides proposées sont de différents types : aide à la démarche de résolution ; apport de savoir-faire, par exemple sous la forme d'une procédure de réalisation ; apport de connaissances nécessaires à la résolution.
3 La tâche complexe, un enjeu de l'enseignement des mathématiques Frédéric Barôme page 3 Il n'y a pas de hiérarchie entre ces types d'aide. Les aides ne sont pas destinées à donner des réponses mais à guider les élèves. Elles permettent de respecter le rythme d acquisition de chaque élève. Elles doivent être mises à disposition de l'élève en fonction des difficultés qu'il rencontre, seulement quand il en a besoin et dans l'ordre qui lui convient. Pour les élèves ayant utilisé une aide, on n évalue pas les connaissances et les capacités correspondant à l aide, mais on évalue positivement toutes celles qu'ils ont mises en œuvre sans aide. Exemple de l'escalier vu précédemment : aides à la démarche de résolution : - Quelle dimension te faudrait-il pour calculer la hauteur d'une seule marche? - Que peux-tu dire du sol et du mur? apport de connaissances : - Énoncé du théorème de Pythagore. apport de savoir-faire : - Exemple de calcul de longueur avec le théorème de Pythagore. Pédagogie différenciée La distribution des aides à la démarche marque donc une différenciation de la pédagogie dans le groupe classe. C'est la gestion de l'hétérogénéité. On peut également la pratiquer par l'utilisation de paramètres didactiques : le même problème peut être posé en utilisant des nombres entiers, des nombres décimaux ou des nombres fractionnaires. La difficulté intrinsèque du problème n'en sera pas changée, mais les différences dans les techniques opératoires rencontrées permettra de maintenir le groupe classe dans le même projet. Classiquement, on peut demande aux plus rapides de se confronter à des questions «défi». On peut également différencier le niveau de rédaction attendu. Tâches complexes et tâches automatisées La tâche complexe ne remplace pas les exercices d'application directe... Les apprentissages passent aussi par des tâches simples, automatisées, d'ordre procédural. Et si les programmes plaident pour des situations-problèmes donnant le goût des mathématiques, nous connaissons tous de nombreux élèves qui aiment les situations techniques et abstraites, et s'y sentent rassurés. Ces automatismes, nécessaires à la résolution de problèmes, s acquièrent par la pratique d exercices référés à des tâches simples : calculs isolés, récitation de résultats mémorisés, construction de figures de base, Ce sont les exigibles de la colonne centrale des programmes.... et inversement! La tâche complexe peut être proposée à n importe quel moment du processus d apprentissage. Proposée en début d'apprentissage, elle constitue un atout important pour les élèves car elle leur permet : d acquérir des compétences mobilisables dans la vie quotidienne ; de prendre davantage d'initiatives ; de relever un défi motivant ; de pouvoir bénéficier d'aides ciblées pour l accomplir. Gestion des tâches automatisées Lorsque les exercices d'application directe se sont révélés inefficaces pour maîtriser une technique, il est illusoire de penser «faire rentrer» celle-ci par une répétition de ces mêmes exercices. La réussite «à force de» se traduit par une acquisition éphémère. Adopter une pédagogie du détour est souvent beaucoup plus efficace : revenir souvent et par petites touches sur un entraînement ; aider les élèves à prendre conscience que c est parce qu ils maîtrisent mal telle ou telle technique qu ils sont freinés à un moment donné dans telle résolution de problème ; autoriser et interdire l'usage de la calculatrice à bon escient : l'autoriser peut permettre de centrer l'élève sur son problème, l'interdire peut obliger la réactivation de techniques opératoires. L organisation en spirale de la progression était déjà recommandée dans les programmes mais l apparition du socle commun en renforce notablement les avantages : elle permet de gérer la priorité à donner aux aptitudes du socle sur celles du programme qui sont hors socle : le premier épisode de travail sur un thème donné peut viser en priorité les aptitudes du socle et réserver pour la suite les autres objectifs fixés par le programme sur ce thème ;
4 La tâche complexe, un enjeu de l'enseignement des mathématiques Frédéric Barôme page 4 elle permet de multiples réinvestissements sur différents thèmes, favorisant l entretien et la consolidation dans la durée des aptitudes acquises ; elle permet aussi de multiplier et de renouveler au fil du temps les occasions d évaluation d aptitudes que certains élèves mettent plus de temps que d autres à construire. L' évaluation par compétence : explicite et positive On parle généralement d'évaluation par compétences, et c'est bien le titre du LPC, mais en l'occurrence, nous parlerons aussi d'évaluation de capacités, composantes des items, des domaines et des compétences (voir la terminologie utilisée dans le LPC). L'acquisition d'une capacité, c'est sa maîtrise technique et sa mobilisation hors contexte. Par définition, évaluer le socle commun, c'est évaluer le degré d'acquisition des capacités et compétences et non débusquer les erreurs commises pour enlever des points selon la gravité de ces erreurs. L'entrée par les aptitudes dans les programmes de mathématiques ne participe pas encore assez de la culture commune. Quelques principes généraux : l'évaluation de la maîtrise d une capacité ne peut pas se limiter à la seule vérification de son fonctionnement dans des exercices techniques ; prendre en compte la stabilité de la réponse : ce n'est qu'au bout de plusieurs évaluations positives espacées dans le temps qu'on considèrera la capacité acquise ; prendre en compte la variété du contexte : ce n'est qu'en pouvant la mobiliser, la réinvestir dans des situations variées, abstraites, concrètes, associée à d'autres capacités mathématiques, associée à des capacités d'autres matières, dans des situations où leur usage n est pas explicitement sollicité dans la question posée, qu'on considèrera la capacité acquise. Il ne s agit plus seulement pour l élève de connaître le théorème de Pythagore, ni même de l'appliquer correctement, mais de penser à l utiliser, ce qui présuppose que l élève prenne l habitude d analyser une situation concrète avec des outils mathématiques. Revoir la place de la note Les élèves qui obtiennent très souvent des notes basses finissent par se décourager, voire par déconstruire leur implication dans leur travail. Par exemple, un élève peut être capable de conduire un bon raisonnement et rencontrer une difficulté sur la réalisation technique ou, ce qui est très fréquent, rendre une mise en forme écrite de son raisonnement défectueuse. Pour autant, s ils ne mènent pas à bien les tâches données en évaluation du programme, ces élèves peuvent tout de même faire preuve de certaines compétences au sein même de ce travail. Ce que les notes permettent difficilement de mettre en évidence, ne donnant aucune information sur la maîtrise ou la non-maîtrise d une compétence. Il est bon de rappeler également le problème récurrent que posent à chaque enseignant les deux élèves qui ont eu 10/20 : celui qui a tout fait, mais avec la moitié des réalisations fausses, celui qui a tout fait juste, mais qui n'en a fait que la moitié. Évaluer les compétences acquises par ces deux élèves amènera à des constats bien différents... Explicitation La description et l'explicitation des attendus du LPC devront être faites en classe. Afin de rendre objective l évaluation de chaque capacité : la formulation des consignes doit permettre à l'élève de reconnaître ce qu'on attend de lui et/ou de s'auto-évaluer ; les critères d'évaluation, invariables pour une capacité donnée, définissent les qualités de la production attendue, et sont explicités. Exemple d'explicitation des critères Il convient tout d'abord de distinguer les domaines de la Compétence 3. Les domaines P3.C3.D3. et P3.C3.D4. concernent clairement les sciences expérimentales. Le domaine P3.C3.D2. concerne essentiellement les mathématiques. Quant au domaine P3.C3.D1. (Pratiquer une démarche scientifique et technologique, résoudre des problèmes), il concerne toutes les matières scientifiques. Considérons à évaluer la capacité «Extraire d un document, d un fait observé, les informations utiles.», en vue de renseigner l'item 1 (S'informer : rechercher, extraire et organiser l information utile).
5 La tâche complexe, un enjeu de l'enseignement des mathématiques Frédéric Barôme page 5 Il conviendra d'expliciter clairement et simplement les critères engagés dans son évaluation : Pour... Extraire d un document, d un fait observé, les informations utiles. tu dois - prendre en compte des informations ayant un rapport avec le sujet ; - ne pas être hors sujet ; - ne rien oublier ; - ne pas faire d'erreur de lecture ou de déformation de donnée. Cela pourra prendre la forme d'une fiche en annexe du cours réunissant ces capacités. Cette annexe pourra être autorisée lors du travail de l'élève, en prenant bien en compte le temps qui pourrait être perdu à sa mauvaise utilisation. Évidemment, il conviendra de ne pas expliciter des critères qui pourraient donner une indication simplifiant la tâche complexe! Dans l'exemple de l'escalier, il serait peu pertinent d'annoncer qu'on va évaluer l'utilisation du théorème de Pythagore... Indicateurs de réussite Lors de son traitement d'une tâche-problème, chaque élève va alors, dans le cadre de sa démarche personnelle de résolution et selon l ordre qui lui convient, mettre en oeuvre un certain nombre de capacités de la compétence 3. Pour mettre en oeuvre efficacement les ces critères d'évaluation (transversaux ou mathématiques), il est souvent utile de les décliner en indicateurs, signes observables ou mesurables, propres à chaque situation. Exemple de l'escalier vu précédemment : Capacités Proposer une méthode, un calcul, un algorithme, une procédure Indicateurs Tu as su proposer de calculer la hauteur de chaque marche à partir de la hauteur totale de l escalier, pour savoir si l' escalier est aux normes,. Utiliser les propriétés d une figure et les théorèmes de géométrie Tu as su reconnaître une configuration de Pythagore. Tu as su l appliquer correctement pour calculer la hauteur de l escalier. Mais, l évaluation des réussites au travers de solutions incomplètes ou partiellement erronées n est en effet possible que si l élève a osé garder trace de ses essais, de ses idées, de sa recherche. Trop d élèves n écrivent rien : ils préfèrent ne rien écrire plutôt que d écrire des choses fausses. D où la nécessité en formation de libérer leur inventivité et de valoriser leurs écrits intermédiaires, quitte à porter explicitement sur le texte du contrôle, par exemple : «Si tu ne trouves pas la solution, tu peux écrire les idées que tu as eues quand tu as cherché : si tes idées sont pertinentes, tu peux ainsi obtenir une partie des points.» Cela sous-entend une lecture inhabituelle des écrits imparfaits : l'enseignant-évaluateur ne cherche plus les erreurs mais doit extraire les éléments positifs d évaluation de certaines capacités du socle commun, puis les expliciter à l'élève en les référant aux indicateurs de réussite.
SOCLE COMMUN - La Compétence 3 Les principaux éléments de mathématiques et la culture scientifique et technologique
 SOCLE COMMUN - La Compétence 3 Les principaux éléments de mathématiques et la culture scientifique et technologique DOMAINE P3.C3.D1. Pratiquer une démarche scientifique et technologique, résoudre des
SOCLE COMMUN - La Compétence 3 Les principaux éléments de mathématiques et la culture scientifique et technologique DOMAINE P3.C3.D1. Pratiquer une démarche scientifique et technologique, résoudre des
b) Fiche élève - Qu est-ce qu une narration de recherche 2?
 Une tâche complexe peut-être traitée : Gestion d une tâche complexe A la maison : notamment les problèmes ouverts dont les connaissances ne sont pas forcément liées au programme du niveau de classe concerné
Une tâche complexe peut-être traitée : Gestion d une tâche complexe A la maison : notamment les problèmes ouverts dont les connaissances ne sont pas forcément liées au programme du niveau de classe concerné
SOCLE COMMUN: LA CULTURE SCIENTIFIQUE ET TECHNOLOGIQUE. alain salvadori IA IPR Sciences de la vie et de la Terre 2009-2010 ALAIN SALVADORI IA-IPR SVT
 SOCLE COMMUN: LA CULTURE SCIENTIFIQUE ET TECHNOLOGIQUE alain salvadori IA IPR Sciences de la vie et de la Terre 2009-2010 ALAIN SALVADORI IA-IPR SVT SOCLE COMMUN ET PROGRAMMES La référence pour la rédaction
SOCLE COMMUN: LA CULTURE SCIENTIFIQUE ET TECHNOLOGIQUE alain salvadori IA IPR Sciences de la vie et de la Terre 2009-2010 ALAIN SALVADORI IA-IPR SVT SOCLE COMMUN ET PROGRAMMES La référence pour la rédaction
Tâche complexe produite par l académie de Clermont-Ferrand. Mai 2012 LE TIR A L ARC. (d après une idée du collège des Portes du Midi de Maurs)
 (d après une idée du collège des Portes du Midi de Maurs) Table des matières Fiche professeur... 2 Fiche élève... 5 1 Fiche professeur Niveaux et objectifs pédagogiques 5 e : introduction ou utilisation
(d après une idée du collège des Portes du Midi de Maurs) Table des matières Fiche professeur... 2 Fiche élève... 5 1 Fiche professeur Niveaux et objectifs pédagogiques 5 e : introduction ou utilisation
Document ressource pour le socle commun dans l enseignement des mathématiques au collège
 Document ressource pour le socle commun dans l enseignement des mathématiques au collège SOMMAIRE : I. Le programme de mathématiques et le socle... 3 1. Introduction... 3 1. La formation des élèves en
Document ressource pour le socle commun dans l enseignement des mathématiques au collège SOMMAIRE : I. Le programme de mathématiques et le socle... 3 1. Introduction... 3 1. La formation des élèves en
Attestation de maîtrise des connaissances et compétences au cours moyen deuxième année
 Attestation de maîtrise des connaissances et compétences au cours moyen deuxième année PALIER 2 CM2 La maîtrise de la langue française DIRE S'exprimer à l'oral comme à l'écrit dans un vocabulaire approprié
Attestation de maîtrise des connaissances et compétences au cours moyen deuxième année PALIER 2 CM2 La maîtrise de la langue française DIRE S'exprimer à l'oral comme à l'écrit dans un vocabulaire approprié
Synthèse «Le Plus Grand Produit»
 Introduction et Objectifs Synthèse «Le Plus Grand Produit» Le document suivant est extrait d un ensemble de ressources plus vastes construites par un groupe de recherche INRP-IREM-IUFM-LEPS. La problématique
Introduction et Objectifs Synthèse «Le Plus Grand Produit» Le document suivant est extrait d un ensemble de ressources plus vastes construites par un groupe de recherche INRP-IREM-IUFM-LEPS. La problématique
Spécialité auxiliaire en prothèse dentaire du brevet d études professionnelles. ANNEXE IIb DEFINITION DES EPREUVES
 ANNEXE IIb DEFINITION DES EPREUVES 51 Epreuve EP1 : ANALYSE ET COMMUNICATION TECHNOLOGIQUES UP1 Coefficient 4 Finalité et objectifs de l épreuve L épreuve vise à évaluer la capacité du candidat à mobiliser
ANNEXE IIb DEFINITION DES EPREUVES 51 Epreuve EP1 : ANALYSE ET COMMUNICATION TECHNOLOGIQUES UP1 Coefficient 4 Finalité et objectifs de l épreuve L épreuve vise à évaluer la capacité du candidat à mobiliser
Culture scientifique et technologique
 Socle commun de connaissances et de compétences Collège Culture scientifique et technologique - Banque de situations d apprentissage et d évaluation - Ce document peut être utilisé librement dans le cadre
Socle commun de connaissances et de compétences Collège Culture scientifique et technologique - Banque de situations d apprentissage et d évaluation - Ce document peut être utilisé librement dans le cadre
O b s e r v a t o i r e E V A P M. Taxonomie R. Gras - développée
 O b s e r v a t o i r e E V A P M É q u i p e d e R e c h e r c h e a s s o c i é e à l ' I N R P Taxonomie R. Gras - développée Grille d'analyse des objectifs du domaine mathématique et de leurs relations
O b s e r v a t o i r e E V A P M É q u i p e d e R e c h e r c h e a s s o c i é e à l ' I N R P Taxonomie R. Gras - développée Grille d'analyse des objectifs du domaine mathématique et de leurs relations
NOM : Prénom : Date de naissance : Ecole : CM2 Palier 2
 NOM : Prénom : Date de naissance : Ecole : CM2 Palier 2 Résultats aux évaluations nationales CM2 Annexe 1 Résultats de l élève Compétence validée Lire / Ecrire / Vocabulaire / Grammaire / Orthographe /
NOM : Prénom : Date de naissance : Ecole : CM2 Palier 2 Résultats aux évaluations nationales CM2 Annexe 1 Résultats de l élève Compétence validée Lire / Ecrire / Vocabulaire / Grammaire / Orthographe /
LA BATTERIE DU PORTABLE
 LA BATTERIE DU PORTABLE Table des matières Fiche professeur... 2 Fiche élève... 4 Narration de séance et productions d élèves... 5 1 Fiche professeur LA BATTERIE DU PORTABLE Niveaux et objectifs pédagogiques
LA BATTERIE DU PORTABLE Table des matières Fiche professeur... 2 Fiche élève... 4 Narration de séance et productions d élèves... 5 1 Fiche professeur LA BATTERIE DU PORTABLE Niveaux et objectifs pédagogiques
6 ème FONCTIONS. Pratiquer une démarche scientifique et technologique. Capacités
 6 ème FONCTIONS Les exercices de ce chapitre permettent de travailler des compétences scientifiques du socle commun. Pratiquer une démarche scientifique et technologique Capacités Rechercher, extraire
6 ème FONCTIONS Les exercices de ce chapitre permettent de travailler des compétences scientifiques du socle commun. Pratiquer une démarche scientifique et technologique Capacités Rechercher, extraire
Programme de la formation. Écrit : 72hdepréparation aux épreuves d admissibilité au CRPE
 Programme de la formation Écrit : 72hdepréparation aux épreuves d admissibilité au CRPE o 36 h pour la préparation à l'épreuve écrite de français Cette préparation comprend : - un travail sur la discipline
Programme de la formation Écrit : 72hdepréparation aux épreuves d admissibilité au CRPE o 36 h pour la préparation à l'épreuve écrite de français Cette préparation comprend : - un travail sur la discipline
S entraîner au calcul mental
 E F C I - R E H S E S O S A PHOTOCOPIER S R U C Une collection dirigée par Jean-Luc Caron S entraîner au calcul mental CM Jean-François Quilfen Illustrations : Julie Olivier Sommaire Introduction au calcul
E F C I - R E H S E S O S A PHOTOCOPIER S R U C Une collection dirigée par Jean-Luc Caron S entraîner au calcul mental CM Jean-François Quilfen Illustrations : Julie Olivier Sommaire Introduction au calcul
Indications pour une progression au CM1 et au CM2
 Indications pour une progression au CM1 et au CM2 Objectif 1 Construire et utiliser de nouveaux nombres, plus précis que les entiers naturels pour mesurer les grandeurs continues. Introduction : Découvrir
Indications pour une progression au CM1 et au CM2 Objectif 1 Construire et utiliser de nouveaux nombres, plus précis que les entiers naturels pour mesurer les grandeurs continues. Introduction : Découvrir
INFO 2 : Traitement des images
 INFO 2 : Traitement des images Objectifs : Comprendre la différence entre image vectorielle et bipmap. Comprendre les caractéristiques d'une image : résolution, définition, nombre de couleurs, poids Etre
INFO 2 : Traitement des images Objectifs : Comprendre la différence entre image vectorielle et bipmap. Comprendre les caractéristiques d'une image : résolution, définition, nombre de couleurs, poids Etre
LA TABLETTE TACTILE, UN OUTIL AU SERVICE DES SCIENCES
 PASI NANCY-METZ LA TABLETTE TACTILE, UN OUTIL AU SERVICE DES SCIENCES Académie de Nancy-Metz PASI- CARDIE http://www4.ac-nancy-metz.fr/pasi/ ACTION CANDIDATE AU PRIX ACADEMIQUE DE L INNOVATION 2014 FICHE
PASI NANCY-METZ LA TABLETTE TACTILE, UN OUTIL AU SERVICE DES SCIENCES Académie de Nancy-Metz PASI- CARDIE http://www4.ac-nancy-metz.fr/pasi/ ACTION CANDIDATE AU PRIX ACADEMIQUE DE L INNOVATION 2014 FICHE
LIVRET PERSONNEL DE COMPÉTENCES
 Nom... Prénom... Date de naissance... Note aux parents Le livret personnel de compétences vous permet de suivre la progression des apprentissages de votre enfant à l école et au collège. C est un outil
Nom... Prénom... Date de naissance... Note aux parents Le livret personnel de compétences vous permet de suivre la progression des apprentissages de votre enfant à l école et au collège. C est un outil
Proposition de programmes de calculs en mise en train
 Proposition de programmes de calculs en mise en train Programme 1 : Je choisis un nombre, je lui ajoute 1, je calcule le carré du résultat, je retranche le carré du nombre de départ. Essai-conjecture-preuve.
Proposition de programmes de calculs en mise en train Programme 1 : Je choisis un nombre, je lui ajoute 1, je calcule le carré du résultat, je retranche le carré du nombre de départ. Essai-conjecture-preuve.
L'EPS à l'école primaire aucune modification des programmes
 L'EPS à l'école primaire aucune modification des programmes Les 3 objectifs sont poursuivis aussi bien à l'école maternelle, qu'à l école primaire MATERNELLE * Favoriser la construction des actions motrices
L'EPS à l'école primaire aucune modification des programmes Les 3 objectifs sont poursuivis aussi bien à l'école maternelle, qu'à l école primaire MATERNELLE * Favoriser la construction des actions motrices
LES NOMBRES DECIMAUX. I. Les programmes
 LES NOMBRES DECIMAUX I. Les programmes Au cycle des approfondissements (Cours Moyen), une toute première approche des fractions est entreprise, dans le but d aider à la compréhension des nombres décimaux.
LES NOMBRES DECIMAUX I. Les programmes Au cycle des approfondissements (Cours Moyen), une toute première approche des fractions est entreprise, dans le but d aider à la compréhension des nombres décimaux.
Organiser des groupes de travail en autonomie
 Organiser des groupes de travail en autonomie Frédérique MIRGALET Conseillère pédagogique L enseignant travaille avec un groupe de niveau de classe et le reste des élèves travaille en autonomie. Il s agira
Organiser des groupes de travail en autonomie Frédérique MIRGALET Conseillère pédagogique L enseignant travaille avec un groupe de niveau de classe et le reste des élèves travaille en autonomie. Il s agira
Document à l attention de l enseignant Grande section
 ÉCOLE : CLASSE : Numéro confidentiel de saisie : Document à l attention de l enseignant Grande section Passation 1 Évaluations «prévention de l illettrisme» - 31-2010-2011 Présentation générale Dans le
ÉCOLE : CLASSE : Numéro confidentiel de saisie : Document à l attention de l enseignant Grande section Passation 1 Évaluations «prévention de l illettrisme» - 31-2010-2011 Présentation générale Dans le
Le menu du jour, un outil au service de la mise en mémoire
 Le menu du jour, un outil au service de la mise en mémoire Type d outil : Outil pour favoriser la mise en mémoire et développer des démarches propres à la gestion mentale. Auteur(s) : Sarah Vercruysse,
Le menu du jour, un outil au service de la mise en mémoire Type d outil : Outil pour favoriser la mise en mémoire et développer des démarches propres à la gestion mentale. Auteur(s) : Sarah Vercruysse,
Document d aide au suivi scolaire
 Document d aide au suivi scolaire Ecoles Famille Le lien Enfant D une école à l autre «Enfants du voyage et de familles non sédentaires» Nom :... Prénom(s) :... Date de naissance :... Ce document garde
Document d aide au suivi scolaire Ecoles Famille Le lien Enfant D une école à l autre «Enfants du voyage et de familles non sédentaires» Nom :... Prénom(s) :... Date de naissance :... Ce document garde
Escalade durant l'e.p.s. à l'école primaire
 Escalade durant l'e.p.s. à l'école primaire Fabrice Paget B.E.E.S Escalade Tél : +336 88 31 14 72 [email protected] 1 Glossaire Effectifs Durée des séances Atelier escalade sans être encordée Traversées
Escalade durant l'e.p.s. à l'école primaire Fabrice Paget B.E.E.S Escalade Tél : +336 88 31 14 72 [email protected] 1 Glossaire Effectifs Durée des séances Atelier escalade sans être encordée Traversées
BACCALAURÉAT PROFESSIONNEL ÉPREUVE DE MATHEMATIQUES. EXEMPLE DE SUJET n 2
 Exemple de sujet n 2 Page 1/7 BACCALAURÉAT PROFESSIONNEL ÉPREUVE DE MATHEMATIQUES EXEMPLE DE SUJET n 2 Ce document comprend : Pour l examinateur : - une fiche descriptive du sujet page 2/7 - une fiche
Exemple de sujet n 2 Page 1/7 BACCALAURÉAT PROFESSIONNEL ÉPREUVE DE MATHEMATIQUES EXEMPLE DE SUJET n 2 Ce document comprend : Pour l examinateur : - une fiche descriptive du sujet page 2/7 - une fiche
Baccalauréat technologique
 Baccalauréat technologique Épreuve relative aux enseignements technologiques transversaux, épreuve de projet en enseignement spécifique à la spécialité et épreuve d'enseignement technologique en langue
Baccalauréat technologique Épreuve relative aux enseignements technologiques transversaux, épreuve de projet en enseignement spécifique à la spécialité et épreuve d'enseignement technologique en langue
Sciences de Gestion Spécialité : SYSTÈMES D INFORMATION DE GESTION
 Sciences de Gestion Spécialité : SYSTÈMES D INFORMATION DE GESTION Classe de terminale de la série Sciences et Technologie du Management et de la Gestion Préambule Présentation Les technologies de l information
Sciences de Gestion Spécialité : SYSTÈMES D INFORMATION DE GESTION Classe de terminale de la série Sciences et Technologie du Management et de la Gestion Préambule Présentation Les technologies de l information
Le graphisme et l écriture, en lien avec les apprentissages en maternelle
 Le graphisme et l écriture, en lien avec les apprentissages en maternelle Conférence de Marie-Thérèse Zerbato-Poudou : Les apprentissages à l école maternelle 12 novembre 2008, St Etienne de St Geoirs
Le graphisme et l écriture, en lien avec les apprentissages en maternelle Conférence de Marie-Thérèse Zerbato-Poudou : Les apprentissages à l école maternelle 12 novembre 2008, St Etienne de St Geoirs
Compétences documentaires et numériques (basées sur le PACIFI) à acquérir de la 6 à la terminale
 Compétences documentaires et numériques (basées sur le PACIFI) à acquérir de la 6 à la terminale En 6 : On attend d'un élève de 6 qu'il sache se repérer dans le CDI, trouver une fiction et un documentaire,
Compétences documentaires et numériques (basées sur le PACIFI) à acquérir de la 6 à la terminale En 6 : On attend d'un élève de 6 qu'il sache se repérer dans le CDI, trouver une fiction et un documentaire,
La notion de croissance (végétale) en sixième et en première S.
 La notion de croissance (végétale) en sixième et en première S. Activité proposée : La notion de croissance est abordée en classe de 6 ème et elle est traitée en première S. Montrez sur cet exemple qu
La notion de croissance (végétale) en sixième et en première S. Activité proposée : La notion de croissance est abordée en classe de 6 ème et elle est traitée en première S. Montrez sur cet exemple qu
MICRO-INFORMATIQUE DÉFINITION DU DOMAINE D'EXAMEN BASE DE DONNÉES CONSULTATION INF-5060-1
 MICRO-INFORMATIQUE DÉFINITION DU DOMAINE D'EXAMEN BASE DE DONNÉES CONSULTATION INF-5060-1 OCTOBRE 1996 MICRO-INFORMATIQUE DÉFINITION DU DOMAINE D'EXAMEN BASE DE DONNÉES CONSULTATION INF-5060-1 OCTOBRE
MICRO-INFORMATIQUE DÉFINITION DU DOMAINE D'EXAMEN BASE DE DONNÉES CONSULTATION INF-5060-1 OCTOBRE 1996 MICRO-INFORMATIQUE DÉFINITION DU DOMAINE D'EXAMEN BASE DE DONNÉES CONSULTATION INF-5060-1 OCTOBRE
Différencier, d accord oui mais comment organiser sa classe.
 Différencier, d accord oui mais comment organiser sa classe. Quand on est convaincu que l on ne peut pas travailler tout le temps avec toute sa classe en même temps et que l on souhaite mettre en place
Différencier, d accord oui mais comment organiser sa classe. Quand on est convaincu que l on ne peut pas travailler tout le temps avec toute sa classe en même temps et que l on souhaite mettre en place
Correspondance ancien / nouveau référentiel B2i pour le collège
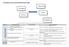 Correspondance ancien / nouveau référentiel B2i pour le collège Domaine Items B2i Réf 2006 1 s'approprier un environnement informatique de travail C.2.1 : connaître la charte d usage des TIC et la 2 adopter
Correspondance ancien / nouveau référentiel B2i pour le collège Domaine Items B2i Réf 2006 1 s'approprier un environnement informatique de travail C.2.1 : connaître la charte d usage des TIC et la 2 adopter
Exemples de différenciations pédagogiques en classe. Elémentaires Collèges. Ordinaires & ASH
 Exemples de différenciations pédagogiques en classe. Elémentaires Collèges Ordinaires & ASH PRESENTATION ESPRIT DES OUTILS PRESENTES L objectif de cette plaquette est de proposer des tours de mains aux
Exemples de différenciations pédagogiques en classe. Elémentaires Collèges Ordinaires & ASH PRESENTATION ESPRIT DES OUTILS PRESENTES L objectif de cette plaquette est de proposer des tours de mains aux
MAT2027 Activités sur Geogebra
 MAT2027 Activités sur Geogebra NOTE: Il n est pas interdit d utiliser du papier et un crayon!! En particulier, quand vous demandez des informations sur les différentes mesures dans une construction, il
MAT2027 Activités sur Geogebra NOTE: Il n est pas interdit d utiliser du papier et un crayon!! En particulier, quand vous demandez des informations sur les différentes mesures dans une construction, il
Dossier d autorisation à mettre en oeuvre le C2i2e
 Extrait du Dossier d autorisation à mettre en oeuvre le C2i2e déposé auprès de la Mission Numérique pour l'enseignement Supérieur par l Institut Catholique de Paris (ICP) - Mars 2011 Au cours du semestre,
Extrait du Dossier d autorisation à mettre en oeuvre le C2i2e déposé auprès de la Mission Numérique pour l'enseignement Supérieur par l Institut Catholique de Paris (ICP) - Mars 2011 Au cours du semestre,
Plan académique de formation. Le socle commun : formation, évaluation, validation
 ACADÉMIE DE BORDEAUX Plan académique de formation Le socle commun : formation, évaluation, validation Nous devons valider les sept compétences du palier 3 du Livret personnel de compétences (LPC). Nous
ACADÉMIE DE BORDEAUX Plan académique de formation Le socle commun : formation, évaluation, validation Nous devons valider les sept compétences du palier 3 du Livret personnel de compétences (LPC). Nous
Groupe de travail Tâches Complexes
 Inspection pédagogique régionale de Mathématiques I.R.E.M. section Guyane Groupe de travail Tâches Complexes Document réalisé par Michel VOISIN, conseiller pédagogique de Mathématiques et professeur au
Inspection pédagogique régionale de Mathématiques I.R.E.M. section Guyane Groupe de travail Tâches Complexes Document réalisé par Michel VOISIN, conseiller pédagogique de Mathématiques et professeur au
SOUTIEN INFORMATIQUE DEP 5229
 SOUTIEN INFORMATIQUE DEP 5229 Le Diplôme d études professionnelles D.E.P. en soutien informatique a une durée totale de 1800 heures à temps plein. Le programme permet de développer les compétences nécessaires
SOUTIEN INFORMATIQUE DEP 5229 Le Diplôme d études professionnelles D.E.P. en soutien informatique a une durée totale de 1800 heures à temps plein. Le programme permet de développer les compétences nécessaires
Document d accompagnement. de la 1 re à la 8 e année. Exemples de tâches et corrigés. 1 re année Tâche 1... 5 Corrigé... 7 Tâche 2... 8 Corrigé...
 Normes de performance de la Colombie-Britannique Document d accompagnement Mathématiques de la 1 re à la 8 e année Exemples de tâches et corrigés 1 re année Tâche 1... 5 Corrigé... 7 Tâche 2... 8 Corrigé...
Normes de performance de la Colombie-Britannique Document d accompagnement Mathématiques de la 1 re à la 8 e année Exemples de tâches et corrigés 1 re année Tâche 1... 5 Corrigé... 7 Tâche 2... 8 Corrigé...
RÉSULTAT DISCIPLINAIRE RÈGLE DE RÉUSSITE DISCIPLINAIRE Programme de formation de l école québécoise Secondaire - 1 er cycle
 RÉSULTAT DISCIPLINAIRE RÈGLE DE RÉUSSITE DISCIPLINAIRE Programme de formation de l école québécoise Secondaire - er cycle Direction générale de la formation des jeunes Octobre 006 Introduction Dans le
RÉSULTAT DISCIPLINAIRE RÈGLE DE RÉUSSITE DISCIPLINAIRE Programme de formation de l école québécoise Secondaire - er cycle Direction générale de la formation des jeunes Octobre 006 Introduction Dans le
3 e année (approximativement)
 3 e année (approximativement) 1. L élève s approprie les technologies de l information et de la communication en utilisant efficacement les outils informatiques 1.1 Avec aide, l élève manipule adéquatement
3 e année (approximativement) 1. L élève s approprie les technologies de l information et de la communication en utilisant efficacement les outils informatiques 1.1 Avec aide, l élève manipule adéquatement
Tapori France ATD Quart Monde 2014 1/5
 1/5 Les enfants, acteurs essentiels du combat contre les idées reçues. Prendre en compte leur parole et les actes concrets qu ils posent. Réfléchir et débattre ensemble PROPOSER UN DEBAT PHILO Il s'agit
1/5 Les enfants, acteurs essentiels du combat contre les idées reçues. Prendre en compte leur parole et les actes concrets qu ils posent. Réfléchir et débattre ensemble PROPOSER UN DEBAT PHILO Il s'agit
Jeux mathématiques en maternelle. Activités clés. Jeu des maisons et des jardins (Yvette Denny PEMF)
 Activités clés NIVEAU : PS/MS Jeu des maisons et des jardins (Yvette Denny PEMF) Compétences Construire les premiers nombres dans leur aspect cardinal Construire des collections équipotentes Situation
Activités clés NIVEAU : PS/MS Jeu des maisons et des jardins (Yvette Denny PEMF) Compétences Construire les premiers nombres dans leur aspect cardinal Construire des collections équipotentes Situation
LES REPRESENTATIONS DES NOMBRES
 LES CARTES A POINTS POUR VOIR LES NOMBRES INTRODUCTION On ne concevrait pas en maternelle une manipulation des nombres sans représentation spatiale. L enfant manipule des collections qu il va comparer,
LES CARTES A POINTS POUR VOIR LES NOMBRES INTRODUCTION On ne concevrait pas en maternelle une manipulation des nombres sans représentation spatiale. L enfant manipule des collections qu il va comparer,
Exemples d objectifs à atteindre pour un PPRE
 Exemples d objectifs à atteindre pour un PPRE A formuler ensuite, pour (et avec?) l élève en termes de : «À la fin du PPRE, tu auras atteint tel objectif» 1. Plus méthodologique Mieux gérer son matériel
Exemples d objectifs à atteindre pour un PPRE A formuler ensuite, pour (et avec?) l élève en termes de : «À la fin du PPRE, tu auras atteint tel objectif» 1. Plus méthodologique Mieux gérer son matériel
Contribution à la mise en œuvre du socle commun des connaissances et des compétences
 Contribution à la mise en œuvre du socle commun des connaissances et des compétences Des fiches et des outils pour répondre à certaines questions autour de la mise en œuvre, le suivi et la validation du
Contribution à la mise en œuvre du socle commun des connaissances et des compétences Des fiches et des outils pour répondre à certaines questions autour de la mise en œuvre, le suivi et la validation du
Entraînement, consolidation, structuration... Que mettre derrière ces expressions?
 Entraînement, consolidation, structuration... Que mettre derrière ces expressions? Il est clair que la finalité principale d une démarche d investigation est de faire acquérir des connaissances aux élèves.
Entraînement, consolidation, structuration... Que mettre derrière ces expressions? Il est clair que la finalité principale d une démarche d investigation est de faire acquérir des connaissances aux élèves.
Manuel d utilisation 26 juin 2011. 1 Tâche à effectuer : écrire un algorithme 2
 éducalgo Manuel d utilisation 26 juin 2011 Table des matières 1 Tâche à effectuer : écrire un algorithme 2 2 Comment écrire un algorithme? 3 2.1 Avec quoi écrit-on? Avec les boutons d écriture........
éducalgo Manuel d utilisation 26 juin 2011 Table des matières 1 Tâche à effectuer : écrire un algorithme 2 2 Comment écrire un algorithme? 3 2.1 Avec quoi écrit-on? Avec les boutons d écriture........
Organiser des séquences pédagogiques différenciées. Exemples produits en stage Besançon, Juillet 2002.
 Cycle 3 3 ème année PRODUCTION D'ECRIT Compétence : Ecrire un compte rendu Faire le compte rendu d'une visite (par exemple pour l'intégrer au journal de l'école ) - Production individuelle Précédée d'un
Cycle 3 3 ème année PRODUCTION D'ECRIT Compétence : Ecrire un compte rendu Faire le compte rendu d'une visite (par exemple pour l'intégrer au journal de l'école ) - Production individuelle Précédée d'un
Les finalités du B2i. Médiapôle d Argenteuil. Philippe da Silva
 Les finalités du B2i Les TIC font désormais partie du paysage économique, social, culturel et éducatif. Elles sont largement utilisées tout au long de la vie professionnelle et privée. «Il appartient à
Les finalités du B2i Les TIC font désormais partie du paysage économique, social, culturel et éducatif. Elles sont largement utilisées tout au long de la vie professionnelle et privée. «Il appartient à
GRILLE D ANALYSE D UNE SEQUENCE D APPRENTISSAGE
 GRILLE D ANALYSE D UNE SEQUENCE D APPRENTISSAGE 1 - LA DEFINITION DES OBJECTIFS DE LA SEQUENCE : - Ai-je bien identifié l objectif de la séquence? - Est-il clairement situé dans la progression générale
GRILLE D ANALYSE D UNE SEQUENCE D APPRENTISSAGE 1 - LA DEFINITION DES OBJECTIFS DE LA SEQUENCE : - Ai-je bien identifié l objectif de la séquence? - Est-il clairement situé dans la progression générale
2 Grad Info Soir Langage C++ Juin 2007. Projet BANQUE
 2 Grad Info Soir Langage C++ Juin 2007 Projet BANQUE 1. Explications L'examen comprend un projet à réaliser à domicile et à documenter : - structure des données, - objets utilisés, - relations de dépendance
2 Grad Info Soir Langage C++ Juin 2007 Projet BANQUE 1. Explications L'examen comprend un projet à réaliser à domicile et à documenter : - structure des données, - objets utilisés, - relations de dépendance
Cahier des charges pour le tutorat d un professeur du second degré
 Cahier des charges pour le tutorat d un professeur du second degré Référence : Circulaire n 2010-037 du 25 février 2010 relative au dispositif d'accueil, d'accompagnement et de formation des enseignants
Cahier des charges pour le tutorat d un professeur du second degré Référence : Circulaire n 2010-037 du 25 février 2010 relative au dispositif d'accueil, d'accompagnement et de formation des enseignants
PARTIE NUMERIQUE (18 points)
 4 ème DEVOIR COMMUN N 1 DE MATHÉMATIQUES 14/12/09 L'échange de matériel entre élèves et l'usage de la calculatrice sont interdits. Il sera tenu compte du soin et de la présentation ( 4 points ). Le barème
4 ème DEVOIR COMMUN N 1 DE MATHÉMATIQUES 14/12/09 L'échange de matériel entre élèves et l'usage de la calculatrice sont interdits. Il sera tenu compte du soin et de la présentation ( 4 points ). Le barème
LA MÉTHODOLOGIE DE TRAVAIL TRAVAILLER EXPLICITEMENT LES COMPÉTENCES 6 ET 7
 LA MÉTHODOLOGIE DE TRAVAIL TRAVAILLER EXPLIITEMENT LES OMPÉTENES 6 ET 7 Animation pédagogique novembre 2013 laire BEY -conseillère pédagogique irconscription de Tours Nord Programme : La méthodologie dans
LA MÉTHODOLOGIE DE TRAVAIL TRAVAILLER EXPLIITEMENT LES OMPÉTENES 6 ET 7 Animation pédagogique novembre 2013 laire BEY -conseillère pédagogique irconscription de Tours Nord Programme : La méthodologie dans
CORRIGE LES NOMBRES DECIMAUX RELATIFS. «Réfléchir avant d agir!»
 Corrigé Cours de Mr JULES v3.3 Classe de Quatrième Contrat 1 Page 1 sur 13 CORRIGE LES NOMBRES DECIMAUX RELATIFS. «Réfléchir avant d agir!» «Correction en rouge et italique.» I. Les nombres décimaux relatifs.
Corrigé Cours de Mr JULES v3.3 Classe de Quatrième Contrat 1 Page 1 sur 13 CORRIGE LES NOMBRES DECIMAUX RELATIFS. «Réfléchir avant d agir!» «Correction en rouge et italique.» I. Les nombres décimaux relatifs.
BREVET INFORMATIQUE ET INTERNET
 connaissances et capacités exigibles pour le B2i NOR : MENE0601490A RLR : 549-2 ARRÊTÉ DU 14-6-2006 JO DU 27-6-2006 MEN DGESCO A1-4 Vu code de l'éducation, not. articles L. 122-1-1, L. 311-1, L. 311-2,
connaissances et capacités exigibles pour le B2i NOR : MENE0601490A RLR : 549-2 ARRÊTÉ DU 14-6-2006 JO DU 27-6-2006 MEN DGESCO A1-4 Vu code de l'éducation, not. articles L. 122-1-1, L. 311-1, L. 311-2,
AP 2nde G.T : «Organiser l information de manière visuelle et créative»
 AP 2nde G.T : «Organiser l information de manière visuelle et créative» Les TICE, un mode d accès à mon autonomie bien sûr! «L'autonomie n'est pas un don! Elle ne survient pas par une sorte de miracle!
AP 2nde G.T : «Organiser l information de manière visuelle et créative» Les TICE, un mode d accès à mon autonomie bien sûr! «L'autonomie n'est pas un don! Elle ne survient pas par une sorte de miracle!
Temps forts départementaux. Le calcul au cycle 2 Technique opératoire La soustraction
 Temps forts départementaux Le calcul au cycle 2 Technique opératoire La soustraction Calcul au cycle 2 La soustraction fait partie du champ opératoire additif D un point de vue strictement mathématique,
Temps forts départementaux Le calcul au cycle 2 Technique opératoire La soustraction Calcul au cycle 2 La soustraction fait partie du champ opératoire additif D un point de vue strictement mathématique,
ENSEIGNEMENT DES SCIENCES ET DE LA TECHNOLOGIE A L ECOLE PRIMAIRE : QUELLE DEMARCHE?
 ENSEIGNEMENT DES SCIENCES ET DE LA TECHNOLOGIE A L ECOLE PRIMAIRE : QUELLE DEMARCHE? Les nouveaux programmes 2008 confirment que l observation, le questionnement, l expérimentation et l argumentation sont
ENSEIGNEMENT DES SCIENCES ET DE LA TECHNOLOGIE A L ECOLE PRIMAIRE : QUELLE DEMARCHE? Les nouveaux programmes 2008 confirment que l observation, le questionnement, l expérimentation et l argumentation sont
Propositions pour l élaboration de la «Charte informatique et Internet» au cycle 3
 Propositions pour l élaboration de la «Charte informatique et Internet» au cycle 3 Auteurs : Aurélia Beauval ( Ecole de Tostat ) & Pascal Nodenot ( Ien Lourdes-Bagnères) Document réalisé à partir du travail
Propositions pour l élaboration de la «Charte informatique et Internet» au cycle 3 Auteurs : Aurélia Beauval ( Ecole de Tostat ) & Pascal Nodenot ( Ien Lourdes-Bagnères) Document réalisé à partir du travail
REDIGER UN COMPTE RENDU DE TYPE JOURNALISTIQUE
 FICHE MEDIAS N 1 REDIGER UN COMPTE RENDU DE TYPE JOURNALISTIQUE A l'attention des enseignants des cycles II et III Initiative de sensibilisation au handicap mental l'écolensemble Objectifs pédagogiques
FICHE MEDIAS N 1 REDIGER UN COMPTE RENDU DE TYPE JOURNALISTIQUE A l'attention des enseignants des cycles II et III Initiative de sensibilisation au handicap mental l'écolensemble Objectifs pédagogiques
PRÉPARER SA CLASSE EN QUELQUES CLICS
 PROFESSEUR DES ÉCOLES PRÉPARER SA CLASSE EN QUELQUES CLICS Éric SEGOUIN Denis BASCANS Une méthode et un outil d aide à la conception et à la programmation de séquences d enseignement pour l école primaire
PROFESSEUR DES ÉCOLES PRÉPARER SA CLASSE EN QUELQUES CLICS Éric SEGOUIN Denis BASCANS Une méthode et un outil d aide à la conception et à la programmation de séquences d enseignement pour l école primaire
INTRANET: Pédagogie générale
 INTRANET: Pédagogie générale Les objectifs généraux : trois axes fondamentaux et trois types d activités associées. Les outils : A. Le cahier d ordinateur. B. Le projet de classe. C. Les projets personnels.
INTRANET: Pédagogie générale Les objectifs généraux : trois axes fondamentaux et trois types d activités associées. Les outils : A. Le cahier d ordinateur. B. Le projet de classe. C. Les projets personnels.
Enseigner la lecture analytique en 3ème avec une tablette numérique
 Enseigner les Langues et Cultures de l Antiquité avec les TICE http://lettres.ac-dijon.fr TraAM travaux académiques mutualisés, un accompagnement au développement des usages des TIC Enseigner la lecture
Enseigner les Langues et Cultures de l Antiquité avec les TICE http://lettres.ac-dijon.fr TraAM travaux académiques mutualisés, un accompagnement au développement des usages des TIC Enseigner la lecture
Solutions numériques d'apprentissage et de collaboration interactive
 Solutions numériques d'apprentissage et de collaboration interactive Chez Promethean, nous nous engageons à libérer le potentiel humain en révolutionnant les méthodes d'apprentissage et de collaboration
Solutions numériques d'apprentissage et de collaboration interactive Chez Promethean, nous nous engageons à libérer le potentiel humain en révolutionnant les méthodes d'apprentissage et de collaboration
Formation des formateurs en entreprise
 en entreprise Le (CQFA) du Cégep de Chicoutimi et le Service de formation continue de l'université du Québec à Chicoutimi (UQAC) unissent leurs efforts et leur expertise respective pour offrir aux organisations
en entreprise Le (CQFA) du Cégep de Chicoutimi et le Service de formation continue de l'université du Québec à Chicoutimi (UQAC) unissent leurs efforts et leur expertise respective pour offrir aux organisations
MINISTERE DE L'EDUCATION, DE LA RECHERCHE ET DE LA FORMATION ENSEIGNEMENT SECONDAIRE SPECIAL ORGANISE PAR LA COMMUNAUTE FRANCAISE
 MINISTERE DE L'EDUCATION, DE LA RECHERCHE ET DE LA FORMATION DIRECTION GENERALE DE L'ORGANISATION DES ETUDES ENSEIGNEMENT SECONDAIRE SPECIAL ORGANISE PAR LA COMMUNAUTE FRANCAISE ENSEIGNEMENT DE FORME 2
MINISTERE DE L'EDUCATION, DE LA RECHERCHE ET DE LA FORMATION DIRECTION GENERALE DE L'ORGANISATION DES ETUDES ENSEIGNEMENT SECONDAIRE SPECIAL ORGANISE PAR LA COMMUNAUTE FRANCAISE ENSEIGNEMENT DE FORME 2
MATHÉMATIQUES. Les préalables pour l algèbre MAT-P020-1 DÉFINITION DU DOMAINE D EXAMEN
 MATHÉMATIQUES Les préalables pour l algèbre MAT-P020-1 DÉFINITION DU DOMAINE D EXAMEN Mars 2001 MATHÉMATIQUES Les préalables pour l algèbre MAT-P020-1 DÉFINITION DU DOMAINE D EXAMEN Mars 2001 Direction
MATHÉMATIQUES Les préalables pour l algèbre MAT-P020-1 DÉFINITION DU DOMAINE D EXAMEN Mars 2001 MATHÉMATIQUES Les préalables pour l algèbre MAT-P020-1 DÉFINITION DU DOMAINE D EXAMEN Mars 2001 Direction
Projet d établissement
 Projet d établissement Le Lycée Expérimental de Saint-Nazaire est un établissement public assurant une formation de second cycle de l enseignement secondaire. Il regroupe des enseignants volontaires qui
Projet d établissement Le Lycée Expérimental de Saint-Nazaire est un établissement public assurant une formation de second cycle de l enseignement secondaire. Il regroupe des enseignants volontaires qui
Le contexte. Le questionnement du P.E.R. :
 Le contexte Ce travail a débuté en janvier. Le P.E.R. engagé depuis fin septembre a permis de faire émerger ou de réactiver : Des raisons d être de la géométrie : Calculer des grandeurs inaccessibles et
Le contexte Ce travail a débuté en janvier. Le P.E.R. engagé depuis fin septembre a permis de faire émerger ou de réactiver : Des raisons d être de la géométrie : Calculer des grandeurs inaccessibles et
Janvier 2011 CHIMIE. Camille de BATTISTI. Acquérir la démarche expérimentale en chimie. ACADEMIE DE MONTPELLIER
 CHIMIE Camille de BATTISTI Janvier 2011 Acquérir la démarche expérimentale en chimie. ACADEMIE DE MONTPELLIER TABLE DES MATIERES Pages 1. LES OBJECTIFS VISÉS ET LE SOCLE COMMUN 2 1.1. Objectifs disciplinaires
CHIMIE Camille de BATTISTI Janvier 2011 Acquérir la démarche expérimentale en chimie. ACADEMIE DE MONTPELLIER TABLE DES MATIERES Pages 1. LES OBJECTIFS VISÉS ET LE SOCLE COMMUN 2 1.1. Objectifs disciplinaires
360 feedback «Benchmarks»
 360 feedback «Benchmarks» La garantie d un coaching ciblé Pour préparer votre encadrement aux nouveaux rôles attendus des managers, Safran & Co vous propose un processus modulable, adapté aux réalités
360 feedback «Benchmarks» La garantie d un coaching ciblé Pour préparer votre encadrement aux nouveaux rôles attendus des managers, Safran & Co vous propose un processus modulable, adapté aux réalités
AC AB. A B C x 1. x + 1. d où. Avec un calcul vu au lycée, on démontre que cette solution admet deux solutions dont une seule nous intéresse : x =
 LE NOMBRE D OR Présentation et calcul du nombre d or Euclide avait trouvé un moyen de partager en deu un segment selon en «etrême et moyenne raison» Soit un segment [AB]. Le partage d Euclide consiste
LE NOMBRE D OR Présentation et calcul du nombre d or Euclide avait trouvé un moyen de partager en deu un segment selon en «etrême et moyenne raison» Soit un segment [AB]. Le partage d Euclide consiste
EXERCICES DE REVISIONS MATHEMATIQUES CM2
 EXERCICES DE REVISIONS MATHEMATIQUES CM2 NOMBRES ET CALCUL Exercices FRACTIONS Nommer les fractions simples et décimales en utilisant le vocabulaire : 3 R1 demi, tiers, quart, dixième, centième. Utiliser
EXERCICES DE REVISIONS MATHEMATIQUES CM2 NOMBRES ET CALCUL Exercices FRACTIONS Nommer les fractions simples et décimales en utilisant le vocabulaire : 3 R1 demi, tiers, quart, dixième, centième. Utiliser
Objectif. Développer son efficacité personnelle par une meilleure communication avec soi et les autres
 Développement personnel La programmation neurolinguistique (P.N.L.) Objectif. Développer son efficacité personnelle par une meilleure communication avec soi et les autres. Historique et postulats de la
Développement personnel La programmation neurolinguistique (P.N.L.) Objectif. Développer son efficacité personnelle par une meilleure communication avec soi et les autres. Historique et postulats de la
Les «devoirs à la maison», une question au cœur des pratiques pédagogiques
 Les «devoirs à la maison», une question au cœur des pratiques pédagogiques Parmi les trois domaines d activités proposés aux élèves volontaires dans le cadre de l accompagnement éducatif, «l aide aux devoirs
Les «devoirs à la maison», une question au cœur des pratiques pédagogiques Parmi les trois domaines d activités proposés aux élèves volontaires dans le cadre de l accompagnement éducatif, «l aide aux devoirs
Guide d utilisation en lien avec le canevas de base du plan d intervention
 Guide d utilisation en lien avec le canevas de base du plan d intervention Guide d utilisation en lien avec le canevas de base du plan d intervention À moins d indications contraires, toutes les définitions
Guide d utilisation en lien avec le canevas de base du plan d intervention Guide d utilisation en lien avec le canevas de base du plan d intervention À moins d indications contraires, toutes les définitions
TOUT CE QU IL FAUT SAVOIR POUR LE BREVET
 TOUT E QU IL FUT SVOIR POUR LE REVET NUMERIQUE / FONTIONS eci n est qu un rappel de tout ce qu il faut savoir en maths pour le brevet. I- Opérations sur les nombres et les fractions : Les priorités par
TOUT E QU IL FUT SVOIR POUR LE REVET NUMERIQUE / FONTIONS eci n est qu un rappel de tout ce qu il faut savoir en maths pour le brevet. I- Opérations sur les nombres et les fractions : Les priorités par
Logiciel SCRATCH FICHE 02
 1. Reprise de la fiche 1: 1.1. Programme Figure : Logiciel SCRATCH FICHE 02 SANS ORDINATEUR : Dessiner à droite le dessin que donnera l'exécution de ce programme : Unité : 50 pas : Remarque : vous devez
1. Reprise de la fiche 1: 1.1. Programme Figure : Logiciel SCRATCH FICHE 02 SANS ORDINATEUR : Dessiner à droite le dessin que donnera l'exécution de ce programme : Unité : 50 pas : Remarque : vous devez
Electricien automaticien Electricienne automaticienne
 Projet : Ecole Compétences -Entreprise Industrie Secteur : 2 orientation d'études : Electricien automaticien Electricienne automaticienne COMPETENCE PARTICULIERE VISEE: CP2 Monter des ensembles électriques
Projet : Ecole Compétences -Entreprise Industrie Secteur : 2 orientation d'études : Electricien automaticien Electricienne automaticienne COMPETENCE PARTICULIERE VISEE: CP2 Monter des ensembles électriques
Représentation géométrique d un nombre complexe
 CHAPITRE 1 NOMBRES COMPLEXES 1 Représentation géométrique d un nombre complexe 1. Ensemble des nombres complexes Soit i le nombre tel que i = 1 L ensemble des nombres complexes est l ensemble des nombres
CHAPITRE 1 NOMBRES COMPLEXES 1 Représentation géométrique d un nombre complexe 1. Ensemble des nombres complexes Soit i le nombre tel que i = 1 L ensemble des nombres complexes est l ensemble des nombres
Lecture critique et pratique de la médecine
 1-00.qxp 24/04/2006 11:23 Page 13 Lecture critique appliquée à la médecine vasculaireecture critique et pratique de la médecine Lecture critique et pratique de la médecine Introduction Si la médecine ne
1-00.qxp 24/04/2006 11:23 Page 13 Lecture critique appliquée à la médecine vasculaireecture critique et pratique de la médecine Lecture critique et pratique de la médecine Introduction Si la médecine ne
Date : 18.11.2013 Tangram en carré page
 Date : 18.11.2013 Tangram en carré page Titre : Tangram en carré Numéro de la dernière page : 14 Degrés : 1 e 4 e du Collège Durée : 90 minutes Résumé : Le jeu de Tangram (appelé en chinois les sept planches
Date : 18.11.2013 Tangram en carré page Titre : Tangram en carré Numéro de la dernière page : 14 Degrés : 1 e 4 e du Collège Durée : 90 minutes Résumé : Le jeu de Tangram (appelé en chinois les sept planches
I. LE CAS CHOISI PROBLEMATIQUE
 I. LE CAS CHOISI Gloria est une élève en EB4. C est une fille brune, mince avec un visage triste. Elle est timide, peureuse et peu autonome mais elle est en même temps, sensible, serviable et attentive
I. LE CAS CHOISI Gloria est une élève en EB4. C est une fille brune, mince avec un visage triste. Elle est timide, peureuse et peu autonome mais elle est en même temps, sensible, serviable et attentive
REFERENTIEL QUALITÉ ASSURANCE QUALITE DE DISPOSITIFS DE FORMATIONS SUPERIEURES PROFESSIONNELLES. Juin 2006
 ASSURANCE QUALITE DE DISPOSITIFS DE FORMATIONS SUPERIEURES PROFESSIONNELLES REFERENTIEL QUALITÉ Juin 2006 Groupe assurance qualité du réseau des écoles de service public Avertissement Ce référentiel constitue
ASSURANCE QUALITE DE DISPOSITIFS DE FORMATIONS SUPERIEURES PROFESSIONNELLES REFERENTIEL QUALITÉ Juin 2006 Groupe assurance qualité du réseau des écoles de service public Avertissement Ce référentiel constitue
Activités pour la maternelle PS MS GS
 Gcompris V.8.4.4 linux 1 Activités pour la maternelle SOMMAIRE : Gcompris : Qu est-ce que c est? 2 Remarques et problèmes rencontrés dans la mise en œuvre en classe 3 Liste des activités pour la maternelle
Gcompris V.8.4.4 linux 1 Activités pour la maternelle SOMMAIRE : Gcompris : Qu est-ce que c est? 2 Remarques et problèmes rencontrés dans la mise en œuvre en classe 3 Liste des activités pour la maternelle
CHARTE DES PROGRAMMES
 CHARTE DES PROGRAMMES Charte relative à l élaboration, à la mise en œuvre et au suivi des programmes d enseignement ainsi qu aux modalités d évaluation des élèves dans l enseignement scolaire CONSEIL SUPÉRIEUR
CHARTE DES PROGRAMMES Charte relative à l élaboration, à la mise en œuvre et au suivi des programmes d enseignement ainsi qu aux modalités d évaluation des élèves dans l enseignement scolaire CONSEIL SUPÉRIEUR
Dispositif : da01 - Animations pédagogiques. Module da-01 : 01 - Apprentissages coopératifs en maternelle
 Dispositif : da01 - Animations pédagogiques Identifiant : 13D0906003 Inscription : Public désigné, ne pas s'inscrire Objectifs généraux : Maîtrise de la langue, Mathématiques et culture scientifique, culture
Dispositif : da01 - Animations pédagogiques Identifiant : 13D0906003 Inscription : Public désigné, ne pas s'inscrire Objectifs généraux : Maîtrise de la langue, Mathématiques et culture scientifique, culture
Félicitations X pour ton sérieux et ton implication dans ton travail. Tes résultats sont excellents et ceci dans tous les domaines étudiés.
 Trimestre 1 X a fait énormément de progrès tout au long du trimestre et je ne peux que la féliciter. Il/elle s investit beaucoup en classe en participant activement. Les résultats en français/maths ont
Trimestre 1 X a fait énormément de progrès tout au long du trimestre et je ne peux que la féliciter. Il/elle s investit beaucoup en classe en participant activement. Les résultats en français/maths ont
Activités numériques [13 Points]
![Activités numériques [13 Points] Activités numériques [13 Points]](/thumbs/21/1117704.jpg) N du candidat L emploi de la calculatrice est autorisé. Le soin, la qualité de la présentation entrent pour 2 points dans l appréciation des copies. Les résultats seront soulignés. La correction est disponible
N du candidat L emploi de la calculatrice est autorisé. Le soin, la qualité de la présentation entrent pour 2 points dans l appréciation des copies. Les résultats seront soulignés. La correction est disponible
Chères collègues, chers collègues,
 Chères collègues, chers collègues, Les IREM ont été créés en 1969 avec les missions suivantes : - mener des recherches sur l enseignement des mathématiques ; - contribuer à la formation initiale et continue
Chères collègues, chers collègues, Les IREM ont été créés en 1969 avec les missions suivantes : - mener des recherches sur l enseignement des mathématiques ; - contribuer à la formation initiale et continue
PROBLEMES D'ORDONNANCEMENT AVEC RESSOURCES
 Leçon 11 PROBLEMES D'ORDONNANCEMENT AVEC RESSOURCES Dans cette leçon, nous retrouvons le problème d ordonnancement déjà vu mais en ajoutant la prise en compte de contraintes portant sur les ressources.
Leçon 11 PROBLEMES D'ORDONNANCEMENT AVEC RESSOURCES Dans cette leçon, nous retrouvons le problème d ordonnancement déjà vu mais en ajoutant la prise en compte de contraintes portant sur les ressources.
Banque d outils d aide à l évaluation diagnostique
 Banque d outils d aide à l évaluation diagnostique Url : http://www.banqoutils.education.gouv.fr/index.php Niveau : GS au Lycée Conditions d'utilisation : Pas d'inscription nécessaire. Format des ressources
Banque d outils d aide à l évaluation diagnostique Url : http://www.banqoutils.education.gouv.fr/index.php Niveau : GS au Lycée Conditions d'utilisation : Pas d'inscription nécessaire. Format des ressources
