Bloc 11 : La géométrie
|
|
|
- Marie Charbonneau
- il y a 9 ans
- Total affichages :
Transcription
1 Bloc 11 : La géométrie Trouvez le périmètre : 1. D un carré de 4 cm de côté : 4 x 4 cm = 16 cm. d un losange de 10 cm de côté :4 x 10 cm = 40 cm 3. d un rectangle de 4 cm par 6 cm : ( x 4) + ( x 6) = 0 cm 4. d un parallélogramme de 5 cm par 8 cm : ( x 5) + ( x 8) = 6 cm Pour tous les problèmes suivants : Dessiner la figure, écrire la formule et la démarche EXEMPLE 1. Un carré a un périmètre de 36 cm. Quelle est la mesure d un côté?. Un rectangle a 18 cm de périmètre. On transforme ce rectangle en doublant les mesures de ses côtés. Quel est le périmètre de ce nouveau rectangle? P = 4 C ou 36 = 4 x C 36 = C 4 Réponse : c = 9 cm x 18 = 36 cm 3. Quel est le périmètre d un rectangle dont la largeur mesure 5 cm et dont la longueur est de 3 cm de plus que la largeur? P = L + l P = x8 + x5 = 6 cm = 8 cm 5 cm 4. On a posé une corde autour d une piscine rectangulaire. La corde se vend 18 le mètre. Le coût de la corde utilisée est de 6,1 $. La piscine a une longueur de 11 m. Quelle est sa largueur? 0,18 1 m 6,1 x x = 6,1 x 1 0,18 = 34 m 34 (x11) = 1 1 = 6 La largeur est de 6 m 11 m?
2 5. On veut border une nappe de,8 m sur,5 m de dentelle. La dentelle nécessaire pour faire ce travail a coûté 3,18 $. Combien se vend un mètre de cette dentelle? P = x,8 + x,5 = 10,6 m 3,18 10,6 x 1 x = 3,18 x 1 10,6 = 0,30 $,8,5 6. Les dimensions d un rectangle sont de 6 cm sur 8 cm. À chaque coin, on coupe un coin carré de 1 cm². De combien de cm a-t-on diminué son périmètre? 7. Calculez l aire : - d un rectangle de 8 km par 6 km. On ne l a pas diminué; il reste de 8 cm, car : (4 après avoir coupé le coin) 8 (6 après avoir coupé le coin) A = L x l = 8 x 6 = 48 km - - d un carré qui mesure 6 dm de côté A = c = 6 =36 dm 8. Une fenêtre mesure m sur 1,5 m. P = x + x1,5 = 7 m - calculez son périmètre. - calculez son aire. A = L x l = x 1,5 = 3 m
3 9. On a peint sur les portes d une grange un losange dont les diagonales mesurent respectivement 4, m et,4 m. Calculez l aire de ce losange. A = (D x d) = (4, x,4) = 5,04 m 10. Mon écran a un problème et l image aperçue a la forme d un parallélogramme. Quelle est l aire de l image, si la hauteur mesure cm, la base 31 cm et le côté 5 cm? A = base x hauteur = 31 x = 341 cm 11. Quel est le périmètre d un losange dont les côtés mesurent 4 cm chacun? P = 4 x 4 cm = 16 cm
4 LE VOLUME Problèmes 1. Un prisme rectangulaire a 6 cm de longueur, 15 cm de largeur et 9 cm de hauteur. Trouvez le volume. V = Aire de la base x hauteur V = L x l x h = 6 x 15 x 9 = 810 cm 3. Un prisme dont la base est un triangle rectangle a les mesures suivantes : 3 cm, 4 cm et 5 cm. La hauteur du prisme est de 1 cm. Calculez le volume. V = aire de la base x hauteur V = (3x4) x 1 = 7 cm 3 3. Trouvez pour chaque figure le volume : 1 cm V = c 3 V = 1 x 1 x1 = 178 cm 3 1 cm 1 cm 8 cm 3,5 cm 5 cm V = aire de la base x hauteur V = 8 x 5 x 3,5 = 140 cm 3 3 cm 3 cm cm 1 cm V = aire de la base x hauteur V = 3x x 1 = 36 cm 3
5 4. La somme des longueurs de toutes les arêtes d un cube est de 96 cm. Calculez le volume du cube. Chaque côté mesure donc 96 cm 1 arêtes = 8 cm V = c 3 V = 8 x 8 x 8 = 51 cm 3 5. M. Dandurand a deux aquariums : celui du salon est deux fois plus long, trois fois plus large et deux fois plus profond que celui de la cuisine. Combien de fois l aquarium du salon est-il plus grand que celui de la cuisine? 6. On place des cubes de 3 cm d arête dans une boîte cube de 4 cm d arête. Combien de cubes pourra-t-on placer? Supposons que celui de la cuisine est un cube de 1 m, son volume est donc de 1 m 3 (1 x 1 x 1). Si on ajuste selon les agrandissements, cela devient : x 3 x = 1 m 3 Il est donc 1 fois plus grand. Volume grand cube : 4 x 4 x 4 = cm 3 Volume petit cube : 3 x 3 x 3 = 7 cm = 51 cubes
6 Exercices supplémentaires (aire et périmètre) 7. La grande base d un trapèze mesure 5 cm, la petite base mesure 3 cm, l un des côtés non parallèle mesure,3 cm et la hauteur cm. Trouvez le périmètre et l aire du trapèze. A = (B + b) x hauteur = 8 x = 8 cm P = B + b + c = x,3 = 1,46 8. Un parallélogramme a une base qui mesure 3 m, une hauteur de 4 m et des côtés de 5 m. Trouvez l aire de la figure. A = Base x hauteur = 3 x 4 = 6 m 9. Un nouveau jeu de table a la forme d un carré dont les diagonales mesurent 70 cm. Calculez l aire de la table. A = D x d = 70 x 70 = 450 cm 10. Un cerf-volant a la forme d un losange. Sa plus courte diagonale mesure 50 cm et sa plus longue diagonale mesure 30 cm de plus. Quelle est l aire de ce cerf-volant? A = D x d = 80 x 50 = 000 cm 11. Un trottoir de 1,5 m de largeur entoure une piscine rectangulaire. Calculez l aire totale du trottoir si la piscine mesure 1 m sur 8 m. A totale = 15 x 11 = 165 A piscine = 1 x 8 = 96 Donc A trottoir = = 69 m
7 1. Trouvez l aire de la figure suivante : m A = Base x hauteur = 8 x = 8 m 8 m 13. Trouvez l aire de la figure suivante : b AB = 5,3 cm AC = 4,4 cm BD =,1 cm A = Base x hauteur = 4,4 x,1 = 4,6 cm a d c 14. Trouvez l aire B D A BC = 7,8 cm AC = 7,5 cm AD = 3,4 cm A = Base x hauteur = 7,8 x 3,4 = 13,6 cm C 15. Trouvez l aire B A C D AB = cm BC = 3 cm CD =,9 cm AD = 5 cm A = (B + b) x hauteur = (5+3) x = 8 cm 16. Trouvez l aire B C BC =,16 cm CD = 3,1 cm AD = 4 cm CE = 3 cm A E D A = (B + b) x hauteur = (4+,16) x 3 = 9,4 cm
8 EXERCICES SUPPLEMENTAIRES LE VOLUME Trouvez le volume d un dé de 4 cm de côté. V = c 3 = 4 x 4 x 4 = 64 cm 3 Le périmètre d une face d un cube de rangement est de 8 m. Quel est le volume de ce cube? 8 4 = cm par côté donc V = x x = 8 cm 3 Trouvez la hauteur d une piscine dont le volume est de 500 m 3 si sa longueur est de 10 m et sa largeur de 6 m? V = L x l x h 500 = 10 x 6 x hauteur 500 = 60h 8,3 = h Donc hauteur est de 8,3 m
PROPORTIONNALITÉ LES ÉCHELLES. Dossier n 2 Juin 2005. Conçu et réalisé par : Marie-Christine LIEFOOGHE Bruno VANBAELINGHEM Annie VANDERSTRAELE
 PROPORTIONNALITÉ LES ÉCHELLES 0 000 000 Dossier n 2 Juin 2005 Tous droits réservés au réseau AGRIMÉDIA Conçu et réalisé par : Marie-Christine LIEFOOGHE Bruno VANBAELINGHEM Annie VANDERSTRAELE C.D.R. AGRIMEDIA
PROPORTIONNALITÉ LES ÉCHELLES 0 000 000 Dossier n 2 Juin 2005 Tous droits réservés au réseau AGRIMÉDIA Conçu et réalisé par : Marie-Christine LIEFOOGHE Bruno VANBAELINGHEM Annie VANDERSTRAELE C.D.R. AGRIMEDIA
315 et 495 sont dans la table de 5. 5 est un diviseur commun. Leur PGCD n est pas 1. Il ne sont pas premiers entre eux
 Exercice 1 : (3 points) Un sac contient 10 boules rouges, 6 boules noires et 4 boules jaunes. Chacune des boules a la même probabilité d'être tirée. On tire une boule au hasard. 1. Calculer la probabilité
Exercice 1 : (3 points) Un sac contient 10 boules rouges, 6 boules noires et 4 boules jaunes. Chacune des boules a la même probabilité d'être tirée. On tire une boule au hasard. 1. Calculer la probabilité
Les droites (d 1 ) et (d 2 ) sont sécantes en A Le point A est le point d intersection des 2 droites
 I Droites perpendiculaires Lorsque deux droites se coupent, on dit qu elles sont sécantes Les droites (d 1 ) et (d 2 ) sont sécantes en A Le point A est le point d intersection des 2 droites Lorsque deux
I Droites perpendiculaires Lorsque deux droites se coupent, on dit qu elles sont sécantes Les droites (d 1 ) et (d 2 ) sont sécantes en A Le point A est le point d intersection des 2 droites Lorsque deux
Thème 17: Optimisation
 OPTIMISATION 45 Thème 17: Optimisation Introduction : Dans la plupart des applications, les grandeurs physiques ou géométriques sont exprimées à l aide d une formule contenant une fonction. Il peut s agir
OPTIMISATION 45 Thème 17: Optimisation Introduction : Dans la plupart des applications, les grandeurs physiques ou géométriques sont exprimées à l aide d une formule contenant une fonction. Il peut s agir
EXAMEN : CAP ADAL SESSION 2011 N du sujet : 02.11 SPECIALITE : CEB - GEPER SUJET SECTEUR : FOLIO : 1/6 EPREUVE : EG2 (MATH-SCIENCES)
 EXAMEN : CAP ADAL SESSION 20 N du sujet : 02. FOLIO : /6 Rédiger les réponses sur ce document qui sera intégralement remis à la fin de l épreuve. L usage de la calculatrice est autorisé. Exercice : (7
EXAMEN : CAP ADAL SESSION 20 N du sujet : 02. FOLIO : /6 Rédiger les réponses sur ce document qui sera intégralement remis à la fin de l épreuve. L usage de la calculatrice est autorisé. Exercice : (7
Sommaire de la séquence 12
 Sommaire de la séquence 12 Séance 1................................................................................................... 367 Je redécouvre le parallélépipède rectangle..........................................................
Sommaire de la séquence 12 Séance 1................................................................................................... 367 Je redécouvre le parallélépipède rectangle..........................................................
AC AB. A B C x 1. x + 1. d où. Avec un calcul vu au lycée, on démontre que cette solution admet deux solutions dont une seule nous intéresse : x =
 LE NOMBRE D OR Présentation et calcul du nombre d or Euclide avait trouvé un moyen de partager en deu un segment selon en «etrême et moyenne raison» Soit un segment [AB]. Le partage d Euclide consiste
LE NOMBRE D OR Présentation et calcul du nombre d or Euclide avait trouvé un moyen de partager en deu un segment selon en «etrême et moyenne raison» Soit un segment [AB]. Le partage d Euclide consiste
Si deux droites sont parallèles à une même troisième. alors les deux droites sont parallèles entre elles. alors
 N I) Pour démontrer que deux droites (ou segments) sont parallèles (d) // (d ) (d) // (d ) deux droites sont parallèles à une même troisième les deux droites sont parallèles entre elles (d) // (d) deux
N I) Pour démontrer que deux droites (ou segments) sont parallèles (d) // (d ) (d) // (d ) deux droites sont parallèles à une même troisième les deux droites sont parallèles entre elles (d) // (d) deux
Activités numériques [13 Points]
![Activités numériques [13 Points] Activités numériques [13 Points]](/thumbs/21/1117704.jpg) N du candidat L emploi de la calculatrice est autorisé. Le soin, la qualité de la présentation entrent pour 2 points dans l appréciation des copies. Les résultats seront soulignés. La correction est disponible
N du candidat L emploi de la calculatrice est autorisé. Le soin, la qualité de la présentation entrent pour 2 points dans l appréciation des copies. Les résultats seront soulignés. La correction est disponible
EVALUATIONS FIN CM1. Mathématiques. Livret élève
 Les enseignants de CM1 de la circonscription de METZ-SUD proposent EVALUATIONS FIN CM1 Mathématiques Livret élève Circonscription de METZ-SUD page 1 NOMBRES ET CALCUL Exercice 1 : Écris en chiffres les
Les enseignants de CM1 de la circonscription de METZ-SUD proposent EVALUATIONS FIN CM1 Mathématiques Livret élève Circonscription de METZ-SUD page 1 NOMBRES ET CALCUL Exercice 1 : Écris en chiffres les
Soit la fonction affine qui, pour représentant le nombre de mois écoulés, renvoie la somme économisée.
 ANALYSE 5 points Exercice 1 : Léonie souhaite acheter un lecteur MP3. Le prix affiché (49 ) dépasse largement la somme dont elle dispose. Elle décide donc d économiser régulièrement. Elle a relevé qu elle
ANALYSE 5 points Exercice 1 : Léonie souhaite acheter un lecteur MP3. Le prix affiché (49 ) dépasse largement la somme dont elle dispose. Elle décide donc d économiser régulièrement. Elle a relevé qu elle
PROBLEME(12) Première partie : Peinture des murs et du plafond.
 PROBLEME(12) Une entreprise doit rénover un local. Ce local a la forme d'un parallélépipède rectangle. La longueur est 6,40m, la largeur est 5,20m et la hauteur est 2,80m. Il comporte une porte de 2m de
PROBLEME(12) Une entreprise doit rénover un local. Ce local a la forme d'un parallélépipède rectangle. La longueur est 6,40m, la largeur est 5,20m et la hauteur est 2,80m. Il comporte une porte de 2m de
Révision mars 2015. 2. Un terrain que la famille Boisvert veut acheter mesure 100m par 200m. Calcule la longueur de ses diagonales.
 Révision mars 2015 1. Mario part de sa maison. Pour se rendre au restaurant, sa famille doit conduire 11,5 km vers le nord et ensuite ils doivent tourner vers l ouest pendant 5,4km. Calcule la distance
Révision mars 2015 1. Mario part de sa maison. Pour se rendre au restaurant, sa famille doit conduire 11,5 km vers le nord et ensuite ils doivent tourner vers l ouest pendant 5,4km. Calcule la distance
Priorités de calcul :
 EXERCICES DE REVISION POUR LE PASSAGE EN QUATRIEME : Priorités de calcul : Exercice 1 : Calcule en détaillant : A = 4 + 5 6 + 7 B = 6 3 + 5 C = 35 5 3 D = 6 7 + 8 E = 38 6 3 + 7 Exercice : Calcule en détaillant
EXERCICES DE REVISION POUR LE PASSAGE EN QUATRIEME : Priorités de calcul : Exercice 1 : Calcule en détaillant : A = 4 + 5 6 + 7 B = 6 3 + 5 C = 35 5 3 D = 6 7 + 8 E = 38 6 3 + 7 Exercice : Calcule en détaillant
Items étudiés dans le CHAPITRE N5. 7 et 9 p 129 D14 Déterminer par le calcul l'antécédent d'un nombre par une fonction linéaire
 CHAPITRE N5 FONCTIONS LINEAIRES NOTION DE FONCTION FONCTIONS LINEAIRES NOTION DE FONCTION FONCTIONS LINEAIRES NOTION DE FONCTION Code item D0 D2 N30[S] Items étudiés dans le CHAPITRE N5 Déterminer l'image
CHAPITRE N5 FONCTIONS LINEAIRES NOTION DE FONCTION FONCTIONS LINEAIRES NOTION DE FONCTION FONCTIONS LINEAIRES NOTION DE FONCTION Code item D0 D2 N30[S] Items étudiés dans le CHAPITRE N5 Déterminer l'image
SOMMAIRE... SOMMAIRE... SOMMAIRE... SOMMAIRE... SOMMAIRE... SOMMAIRE... LES MESURES
 SOMMAIRE... SOMMAIRE... SOMMAIRE... SOMMAIRE... SOMMAIRE... SOMMAIRE... LES MESURES MES 1 Les mesures de longueurs MES 2 Lecture de l heure MES 3 Les mesures de masse MES 4 Comparer des longueurs, périmètres.
SOMMAIRE... SOMMAIRE... SOMMAIRE... SOMMAIRE... SOMMAIRE... SOMMAIRE... LES MESURES MES 1 Les mesures de longueurs MES 2 Lecture de l heure MES 3 Les mesures de masse MES 4 Comparer des longueurs, périmètres.
Si un quadrilatère a. Si un quadrilatère a. Si un quadrilatère a. Si un quadrilatère a. ses côtés opposés. ses côtés opposés de. deux côtés opposés
 P1 P2 P3 P4 a a a a ses côtés opposés ses côtés opposés de deux côtés opposés ses diagonales qui se parallèles, alors c est même longueur alors parallèles et de même coupent en leur un c est un longueur
P1 P2 P3 P4 a a a a ses côtés opposés ses côtés opposés de deux côtés opposés ses diagonales qui se parallèles, alors c est même longueur alors parallèles et de même coupent en leur un c est un longueur
FORD C-MAX + FORD GRAND C-MAX CMAX_Main_Cover_2013_V3.indd 1-3 22/08/2012 15:12
 1 2 3 4 5 6 7 8 9 10 12,999,976 km 9,136,765 km 1,276,765 km 499,892 km 245,066 km 112,907 km 36,765 km 24,159 km 7899 km 2408 km 76 km 12 14 16 1 12 7 3 1 6 2 5 4 3 11 9 10 8 18 20 21 22 23 24 26 28 30
1 2 3 4 5 6 7 8 9 10 12,999,976 km 9,136,765 km 1,276,765 km 499,892 km 245,066 km 112,907 km 36,765 km 24,159 km 7899 km 2408 km 76 km 12 14 16 1 12 7 3 1 6 2 5 4 3 11 9 10 8 18 20 21 22 23 24 26 28 30
ÉVALUATION EN FIN DE CM1. Année scolaire 2014 2015 LIVRET DE L'ÉLÈVE MATHÉMATIQUES
 ÉVALUATION EN FIN DE CM1 Année scolaire 2014 2015 LIVRET DE L'ÉLÈVE MATHÉMATIQUES NOM :....... Prénom :....... Né le :./../ École :............ Classe : Domaine Score de réussite NOMBRES ET CALCUL GÉOMÉTRIE
ÉVALUATION EN FIN DE CM1 Année scolaire 2014 2015 LIVRET DE L'ÉLÈVE MATHÉMATIQUES NOM :....... Prénom :....... Né le :./../ École :............ Classe : Domaine Score de réussite NOMBRES ET CALCUL GÉOMÉTRIE
Les problèmes de la finale du 21éme RMT
 21 e RMT Finale mai - juin 2013 armt2013 1 Les problèmes de la finale du 21éme RMT Titre Catégorie Ar Alg Geo Lo/Co Origine 1. La boucle (I) 3 4 x x rc 2. Les verres 3 4 x RZ 3. Les autocollants 3 4 x
21 e RMT Finale mai - juin 2013 armt2013 1 Les problèmes de la finale du 21éme RMT Titre Catégorie Ar Alg Geo Lo/Co Origine 1. La boucle (I) 3 4 x x rc 2. Les verres 3 4 x RZ 3. Les autocollants 3 4 x
Maîtriser les fonctionnalités d un traitement de texte (Word OpenOffice)
 Utilisation de l'ordinateur et apport des TIC en enseignement (1NP) Module 03 Maîtriser les fonctionnalités d un traitement de texte. Sens du Module De nombreux documents remis aux enfants sont réalisés
Utilisation de l'ordinateur et apport des TIC en enseignement (1NP) Module 03 Maîtriser les fonctionnalités d un traitement de texte. Sens du Module De nombreux documents remis aux enfants sont réalisés
MATHEMATIQUES GRANDEURS ET MESURES
 FICHE GM.01 Objectif : Choisir la bonne unité de mesure Pour chaque objet, choisis entre les trois propositions celle qui te paraît la plus juste : ta règle ton cahier une coccinelle ta trousse la Tour
FICHE GM.01 Objectif : Choisir la bonne unité de mesure Pour chaque objet, choisis entre les trois propositions celle qui te paraît la plus juste : ta règle ton cahier une coccinelle ta trousse la Tour
Le théorème de Thalès et sa réciproque
 Le théorème de Thalès et sa réciproque I) Agrandissement et Réduction d une figure 1) Définition : Lorsque toutes les longueurs d une figure F sont multipliées par un même nombre k on obtient une autre
Le théorème de Thalès et sa réciproque I) Agrandissement et Réduction d une figure 1) Définition : Lorsque toutes les longueurs d une figure F sont multipliées par un même nombre k on obtient une autre
Problèmes de dénombrement.
 Problèmes de dénombrement. 1. On se déplace dans le tableau suivant, pour aller de la case D (départ) à la case (arrivée). Les déplacements utilisés sont exclusivement les suivants : ller d une case vers
Problèmes de dénombrement. 1. On se déplace dans le tableau suivant, pour aller de la case D (départ) à la case (arrivée). Les déplacements utilisés sont exclusivement les suivants : ller d une case vers
EVALUATIONS MI-PARCOURS CM2
 Les enseignants de CM2 de la circonscription de METZ-SUD proposent EVALUATIONS MI-PARCOURS CM2 Mathématiques Livret enseignant NOMBRES ET CALCUL Circonscription de METZ-SUD Page 1 Séquence 1 : Exercice
Les enseignants de CM2 de la circonscription de METZ-SUD proposent EVALUATIONS MI-PARCOURS CM2 Mathématiques Livret enseignant NOMBRES ET CALCUL Circonscription de METZ-SUD Page 1 Séquence 1 : Exercice
Problèmes sur le chapitre 5
 Problèmes sur le chapitre 5 (Version du 13 janvier 2015 (10h38)) 501 Le calcul des réactions d appui dans les problèmes schématisés ci-dessous est-il possible par les équations de la statique Si oui, écrire
Problèmes sur le chapitre 5 (Version du 13 janvier 2015 (10h38)) 501 Le calcul des réactions d appui dans les problèmes schématisés ci-dessous est-il possible par les équations de la statique Si oui, écrire
6 ème. Rallye mathématique de la Sarthe 2013/2014. 1 ère épreuve de qualification : Problèmes Jeudi 21 novembre 2013
 Retrouver tous les sujets, les corrigés, les annales, les finales sur le site du rallye : http://sarthe.cijm.org I Stéphane, Eric et Christophe sont 3 garçons avec des chevelures différentes. Stéphane
Retrouver tous les sujets, les corrigés, les annales, les finales sur le site du rallye : http://sarthe.cijm.org I Stéphane, Eric et Christophe sont 3 garçons avec des chevelures différentes. Stéphane
3 ème 2 DÉVELOPPEMENT FACTORISATIONS ET IDENTITÉS REMARQUABLES 1/5 1 - Développements
 3 ème 2 DÉVELOPPEMENT FACTORISATIONS ET IDENTITÉS REMARQUABLES 1/5 1 - Développements Développer une expression consiste à transformer un produit en une somme Qu est-ce qu une somme? Qu est-ce qu un produit?
3 ème 2 DÉVELOPPEMENT FACTORISATIONS ET IDENTITÉS REMARQUABLES 1/5 1 - Développements Développer une expression consiste à transformer un produit en une somme Qu est-ce qu une somme? Qu est-ce qu un produit?
UN TOURNOI A GAGNER ENSEMBLE
 UN TOURNOI A GAGNER ENSEMBLE Ce tournoi réunit 3 classes de CM1, CM2 et 6, chaque équipe essaye de réussir le plus grand nombre possible des 82 exercices proposés. Objectifs généraux : Pour les 6, accueillir
UN TOURNOI A GAGNER ENSEMBLE Ce tournoi réunit 3 classes de CM1, CM2 et 6, chaque équipe essaye de réussir le plus grand nombre possible des 82 exercices proposés. Objectifs généraux : Pour les 6, accueillir
Notion de fonction. Série 1 : Tableaux de données. Série 2 : Graphiques. Série 3 : Formules. Série 4 : Synthèse
 N7 Notion de fonction Série : Tableaux de données Série 2 : Graphiques Série 3 : Formules Série 4 : Synthèse 57 SÉRIE : TABLEAUX DE DONNÉES Le cours avec les aides animées Q. Si f désigne une fonction,
N7 Notion de fonction Série : Tableaux de données Série 2 : Graphiques Série 3 : Formules Série 4 : Synthèse 57 SÉRIE : TABLEAUX DE DONNÉES Le cours avec les aides animées Q. Si f désigne une fonction,
Développer, factoriser pour résoudre
 Développer, factoriser pour résoudre Avec le vocabulaire Associer à chaque epression un terme A B A différence produit A+ B A B inverse quotient A B A opposé somme Écrire la somme de et du carré de + Écrire
Développer, factoriser pour résoudre Avec le vocabulaire Associer à chaque epression un terme A B A différence produit A+ B A B inverse quotient A B A opposé somme Écrire la somme de et du carré de + Écrire
Le seul ami de Batman
 Le seul ami de Batman Avant de devenir un héros de cinéma en 1989, Batman est depuis plus de 50 ans un fameux personnage de bandes dessinées aux États-Unis. Il fut créé en mai 1939 dans les pages de Détective
Le seul ami de Batman Avant de devenir un héros de cinéma en 1989, Batman est depuis plus de 50 ans un fameux personnage de bandes dessinées aux États-Unis. Il fut créé en mai 1939 dans les pages de Détective
MAT2027 Activités sur Geogebra
 MAT2027 Activités sur Geogebra NOTE: Il n est pas interdit d utiliser du papier et un crayon!! En particulier, quand vous demandez des informations sur les différentes mesures dans une construction, il
MAT2027 Activités sur Geogebra NOTE: Il n est pas interdit d utiliser du papier et un crayon!! En particulier, quand vous demandez des informations sur les différentes mesures dans une construction, il
Exercice 6 Associer chaque expression de gauche à sa forme réduite (à droite) :
 Eercice a Développer les epressions suivantes : A-(-) - + B-0(3 ²+3-0) -0 3²+-0 3+00 B -30²-30+00 C-3(-) -3 + 3-3²+6 D-(-) + ² Eerciceb Parmi les epressions suivantes, lesquelles sont sous forme réduite?
Eercice a Développer les epressions suivantes : A-(-) - + B-0(3 ²+3-0) -0 3²+-0 3+00 B -30²-30+00 C-3(-) -3 + 3-3²+6 D-(-) + ² Eerciceb Parmi les epressions suivantes, lesquelles sont sous forme réduite?
Découverte et prise en main de SWEET HOME 3D
 Découverte et prise en main de SWEET HOME 3D Auteur du tutoriel : ALLARDIN Jérémie - Prof. Génie Mécanique. Site : http://www.technologie-tutoriel.fr/ Dans la première partie du TP, vous créerez les murs
Découverte et prise en main de SWEET HOME 3D Auteur du tutoriel : ALLARDIN Jérémie - Prof. Génie Mécanique. Site : http://www.technologie-tutoriel.fr/ Dans la première partie du TP, vous créerez les murs
Découverte du logiciel ordinateur TI-n spire / TI-n spire CAS
 Découverte du logiciel ordinateur TI-n spire / TI-n spire CAS Mémento Ouvrir TI-Nspire CAS. Voici la barre d outils : L insertion d une page, d une activité, d une page où l application est choisie, pourra
Découverte du logiciel ordinateur TI-n spire / TI-n spire CAS Mémento Ouvrir TI-Nspire CAS. Voici la barre d outils : L insertion d une page, d une activité, d une page où l application est choisie, pourra
Eté 2015. LIVRET de RÉVISIONS en MATHÉMATIQUES
 Eté 2015 LIVRET de RÉVISIONS en MATHÉMATIQUES Destiné aux élèves entrant en Seconde au Lycée Honoré d Estienne d Orves Elaboré par les professeurs de mathématiques des collèges et lycées du secteur Une
Eté 2015 LIVRET de RÉVISIONS en MATHÉMATIQUES Destiné aux élèves entrant en Seconde au Lycée Honoré d Estienne d Orves Elaboré par les professeurs de mathématiques des collèges et lycées du secteur Une
CHAPITRE 2 SYSTEMES D INEQUATIONS A DEUX INCONNUES
 CHAPITRE 2 SYSTEMES D INEQUATIONS A DEUX INCONNUES Exercice 1 Dans un repère orthonormé on donne les points A( 1;2 ), ( 5; 6) et les droites a 3x + 2y = 5 et b 4x 3y + 10 = 0. B, 1 C 5; 2, 1 D 7; 2 1)
CHAPITRE 2 SYSTEMES D INEQUATIONS A DEUX INCONNUES Exercice 1 Dans un repère orthonormé on donne les points A( 1;2 ), ( 5; 6) et les droites a 3x + 2y = 5 et b 4x 3y + 10 = 0. B, 1 C 5; 2, 1 D 7; 2 1)
2.4 Représentation graphique, tableau de Karnaugh
 2 Fonctions binaires 45 2.4 Représentation graphique, tableau de Karnaugh On peut définir complètement une fonction binaire en dressant son tableau de Karnaugh, table de vérité à 2 n cases pour n variables
2 Fonctions binaires 45 2.4 Représentation graphique, tableau de Karnaugh On peut définir complètement une fonction binaire en dressant son tableau de Karnaugh, table de vérité à 2 n cases pour n variables
Sommaire de la séquence 10
 Sommaire de la séquence 10 Séance 1................................................................................................... 305 Je calcule la longueur d un cercle.......................................................................
Sommaire de la séquence 10 Séance 1................................................................................................... 305 Je calcule la longueur d un cercle.......................................................................
TSTI 2D CH X : Exemples de lois à densité 1
 TSTI 2D CH X : Exemples de lois à densité I Loi uniforme sur ab ; ) Introduction Dans cette activité, on s intéresse à la modélisation du tirage au hasard d un nombre réel de l intervalle [0 ;], chacun
TSTI 2D CH X : Exemples de lois à densité I Loi uniforme sur ab ; ) Introduction Dans cette activité, on s intéresse à la modélisation du tirage au hasard d un nombre réel de l intervalle [0 ;], chacun
UNITÉS ET MESURES UNITÉS DE MESURE DES LONGUEURS. Dossier n 1 Juin 2005
 UNITÉS ET MESURES UNITÉS DE MESURE DES LONGUEURS Dossier n 1 Juin 2005 Tous droits réservés au réseau AGRIMÉDIA Conçu et réalisé par : Marie-Christine LIEFOOGHE Bruno VANBAELINGHEM Annie VANDERSTRAELE
UNITÉS ET MESURES UNITÉS DE MESURE DES LONGUEURS Dossier n 1 Juin 2005 Tous droits réservés au réseau AGRIMÉDIA Conçu et réalisé par : Marie-Christine LIEFOOGHE Bruno VANBAELINGHEM Annie VANDERSTRAELE
ÉQUATIONS MISE EN ÉQUATION ET RÉSOLUTION D UN PROBLÈME. 3 x + 5 = 11. x + 4 = 0-5 + 3 x = 4 Mais qui sont ces inconnues?
 ÉQUATIONS MISE EN ÉQUATION ET RÉSOLUTION D UN PROBLÈME Utilisation des équations du er degré à une inconnue x + 5 = - z = x + = 0-5 + x = Mais qui sont ces inconnues? Dossier n Juin 005 Tous droits réservés
ÉQUATIONS MISE EN ÉQUATION ET RÉSOLUTION D UN PROBLÈME Utilisation des équations du er degré à une inconnue x + 5 = - z = x + = 0-5 + x = Mais qui sont ces inconnues? Dossier n Juin 005 Tous droits réservés
Catalogue de location
 Catalogue de location 514-523-2211 1-877-677-2211 2600, William-Tremblay, suite 128 Montréal (QC) H1Y 3J2 location Nous disposons de près d un millier de pièces en location pour vos projets temporaires
Catalogue de location 514-523-2211 1-877-677-2211 2600, William-Tremblay, suite 128 Montréal (QC) H1Y 3J2 location Nous disposons de près d un millier de pièces en location pour vos projets temporaires
Note de cours. Introduction à Excel 2007
 Note de cours Introduction à Excel 2007 par Armande Pinette Cégep du Vieux Montréal Excel 2007 Page: 2 de 47 Table des matières Comment aller chercher un document sur CVMVirtuel?... 8 Souris... 8 Clavier
Note de cours Introduction à Excel 2007 par Armande Pinette Cégep du Vieux Montréal Excel 2007 Page: 2 de 47 Table des matières Comment aller chercher un document sur CVMVirtuel?... 8 Souris... 8 Clavier
www.imprimermonlivre.com
 0 www.imprimermonlivre.com Composition d une couverture avec Word L objectif de ce guide est de vous proposer un mode opératoire pour créer une couverture avec Word. Nous vous rappelons toutefois que Word
0 www.imprimermonlivre.com Composition d une couverture avec Word L objectif de ce guide est de vous proposer un mode opératoire pour créer une couverture avec Word. Nous vous rappelons toutefois que Word
Comment insérer une image de fond?
 COMMUNICATION VISUELLE Mise en page à l aide d un traitement de texte Comment insérer une image de fond? Image Plein papier ou au Format utile qu est-ce que cela veut dire? La mise en page d un document
COMMUNICATION VISUELLE Mise en page à l aide d un traitement de texte Comment insérer une image de fond? Image Plein papier ou au Format utile qu est-ce que cela veut dire? La mise en page d un document
B = A = B = A = B = A = B = A = Recopier sur la copie chaque expression numérique et la réponse exacte. Réponse A Réponse B Réponse C Solution
 Q.C.M. Recopier sur la copie chaque expression numérique et la réponse exacte. Réponse A Réponse B Réponse C Solution Exercice 1 On considère les trois nombres A, B et C : 2 x (60 5 x 4 ²) (8 15) Calculer
Q.C.M. Recopier sur la copie chaque expression numérique et la réponse exacte. Réponse A Réponse B Réponse C Solution Exercice 1 On considère les trois nombres A, B et C : 2 x (60 5 x 4 ²) (8 15) Calculer
SPECIALITE : RESTAURATION À LIRE ATTENTIVEMENT AVANT DE TRAITER LE SUJET
 AGENT DE MAÎTRISE TERRITORIAL Concours interne et de 3 ème voie Centre Interdépartemental de Gestion de la Grande Couronne de la Région d Île-de-France SESSION 2015 Epreuve écrite d admissibilité Vérification
AGENT DE MAÎTRISE TERRITORIAL Concours interne et de 3 ème voie Centre Interdépartemental de Gestion de la Grande Couronne de la Région d Île-de-France SESSION 2015 Epreuve écrite d admissibilité Vérification
1S Modèles de rédaction Enoncés
 Par l équipe des professeurs de 1S du lycée Parc de Vilgénis 1S Modèles de rédaction Enoncés Produit scalaire & Corrigés Exercice 1 : définition du produit scalaire Soit ABC un triangle tel que AB, AC
Par l équipe des professeurs de 1S du lycée Parc de Vilgénis 1S Modèles de rédaction Enoncés Produit scalaire & Corrigés Exercice 1 : définition du produit scalaire Soit ABC un triangle tel que AB, AC
Sommaire de la séquence 10
 Sommaire de la séquence 10 Séance 1........................................................................................................ J étudie un problème concret................................................................................
Sommaire de la séquence 10 Séance 1........................................................................................................ J étudie un problème concret................................................................................
Les problèmes. Répond aux questions des problèmes en utilisant le tableau.
 Les problèmes Répond aux questions des problèmes en utilisant le tableau. 1. Monsieur Pierre pèse 53 kg. Pendant les vacances, il a grossi de 5 kg. Combien pèse-t-il maintenant? Il grossit Combien? Monsieur
Les problèmes Répond aux questions des problèmes en utilisant le tableau. 1. Monsieur Pierre pèse 53 kg. Pendant les vacances, il a grossi de 5 kg. Combien pèse-t-il maintenant? Il grossit Combien? Monsieur
Comment réaliser une capture d écran dans Word. Alors comment ouvrir une page Word?
 Comment réaliser une capture d écran dans Word Pour réaliser une capture d écran dans Word, l idéal est d ouvrir d abord la page Word. Mais on peut bien l ouvrir après la capture d écran. Alors comment
Comment réaliser une capture d écran dans Word Pour réaliser une capture d écran dans Word, l idéal est d ouvrir d abord la page Word. Mais on peut bien l ouvrir après la capture d écran. Alors comment
Correction : E = Soit E = -1,6. F = 12 Soit F = -6 3 + 45. y = 11. et G = -2z + 4y G = 2 6 = 3 G = G = -2 5 + 4 11
 Correction : EXERCICE : Calculer en indiquant les étapes: (-6 +9) ( ) ( ) B = -4 (-) (-8) B = - 8 (+ 6) B = - 8 6 B = - 44 EXERCICE : La visite médicale Calcul de la part des élèves rencontrés lundi et
Correction : EXERCICE : Calculer en indiquant les étapes: (-6 +9) ( ) ( ) B = -4 (-) (-8) B = - 8 (+ 6) B = - 8 6 B = - 44 EXERCICE : La visite médicale Calcul de la part des élèves rencontrés lundi et
«Aucune investigation humaine ne peut être qualifiée de science véritable si elle ne peut être démontrée mathématiquement.
 «Aucune investigation humaine ne peut être qualifiée de science véritable si elle ne peut être démontrée mathématiquement.» Léonard de Vinci MATHEMATIQUES Les mathématiques revêtaient un caractère particulier
«Aucune investigation humaine ne peut être qualifiée de science véritable si elle ne peut être démontrée mathématiquement.» Léonard de Vinci MATHEMATIQUES Les mathématiques revêtaient un caractère particulier
Exprimer ce coefficient de proportionnalité sous forme de pourcentage : 3,5 %
 23 CALCUL DE L INTÉRÊT Tau d intérêt Paul et Rémi ont reçu pour Noël, respectivement, 20 et 80. Ils placent cet argent dans une banque, au même tau. Au bout d une année, ce placement leur rapportera une
23 CALCUL DE L INTÉRÊT Tau d intérêt Paul et Rémi ont reçu pour Noël, respectivement, 20 et 80. Ils placent cet argent dans une banque, au même tau. Au bout d une année, ce placement leur rapportera une
Diviser un nombre décimal par 10 ; 100 ; 1 000
 Diviser un nombre décimal par 10 ; 100 ; 1 000 Diviser un nombre décimal par 10 ; 100 ; 1 000. 23 1 et 2 Pauline collectionne les cartes «Tokéron» depuis plusieurs mois. Elle en possède 364 et veut les
Diviser un nombre décimal par 10 ; 100 ; 1 000 Diviser un nombre décimal par 10 ; 100 ; 1 000. 23 1 et 2 Pauline collectionne les cartes «Tokéron» depuis plusieurs mois. Elle en possède 364 et veut les
Deux disques dans un carré
 Deux disques dans un carré Table des matières 1 Fiche résumé 2 2 Fiche élève Seconde - version 1 3 2.1 Le problème............................................... 3 2.2 Construction de la figure avec geogebra...............................
Deux disques dans un carré Table des matières 1 Fiche résumé 2 2 Fiche élève Seconde - version 1 3 2.1 Le problème............................................... 3 2.2 Construction de la figure avec geogebra...............................
Situations d apprentissage. Mat-2101-3
 Situations d apprentissage Mat-2101-3 Un vendredi au chalet (Activités 1, 2 et 3) Le taxi (Activités 1 et 2) Un entrepôt «sans dessus dessous» (Activités 1, 2, 3 et 4) France Dugal Diane Garneau Commission
Situations d apprentissage Mat-2101-3 Un vendredi au chalet (Activités 1, 2 et 3) Le taxi (Activités 1 et 2) Un entrepôt «sans dessus dessous» (Activités 1, 2, 3 et 4) France Dugal Diane Garneau Commission
TBI et mathématique. Pour vous soutenir dans votre enseignement des mathématiques. Les outils du logiciel Notebook. les ressources internet
 TBI et mathématique Pour vous soutenir dans votre enseignement des mathématiques Dessin tiré du site www.recitus.qc.ca Les outils du logiciel Notebook et les ressources internet Document préparé par France
TBI et mathématique Pour vous soutenir dans votre enseignement des mathématiques Dessin tiré du site www.recitus.qc.ca Les outils du logiciel Notebook et les ressources internet Document préparé par France
"#$%&!'#$'$&%(%$)&!*$++,)(-,&!.,!/0! 123456768!'$9#!/,&!&9:,(&!;!.,!/<-'#,9=,!.,!+0(>-+0(%?9,&!.9!1536!&,&&%$)!@;AB!
 !!! "#$%&!'#$'$&%(%$)&!*$++,)(-,&!.,!/0! 123456768!'$9#!/,&!&9:,(&!;!.,!/
!!! "#$%&!'#$'$&%(%$)&!*$++,)(-,&!.,!/0! 123456768!'$9#!/,&!&9:,(&!;!.,!/
Enoncé et corrigé du brevet des collèges dans les académies d Aix- Marseille, Montpellier, Nice Corse et Toulouse en 2000. Énoncé.
 Enoncé et corrigé du brevet des collèges dans les académies d Aix- Marseille, Montpellier, Nice Corse et Toulouse en 2000. Énoncé. I- ACTIVITES NUMERIQUES (12 points) Exercice 1 (3 points) On considère
Enoncé et corrigé du brevet des collèges dans les académies d Aix- Marseille, Montpellier, Nice Corse et Toulouse en 2000. Énoncé. I- ACTIVITES NUMERIQUES (12 points) Exercice 1 (3 points) On considère
AGASC / BUREAU INFORMATION JEUNESSE 06700 Saint Laurent du Var - E mail : [email protected] / Tel : 04.93.07.00.66 CONSIGNE N 1 :
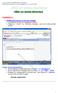 CONSIGNE N 1 : Rédiger puis envoyer un nouveau message La fenêtre de la boîte de messagerie s affiche Cliquer sur «Ecrire» ou «Nouveau message» pour ouvrir cette nouvelle fenêtre. Ensuite, suivre cette
CONSIGNE N 1 : Rédiger puis envoyer un nouveau message La fenêtre de la boîte de messagerie s affiche Cliquer sur «Ecrire» ou «Nouveau message» pour ouvrir cette nouvelle fenêtre. Ensuite, suivre cette
Alarme intrusion filaire AEI HA-981 6 zones
 Alarme intrusion filaire AEI HA-981 6 zones Lycée de l Aa Page 1 sur 11 1) Mise en situation Vous devez assurer une protection périmétrique et volumétrique de la maison de M r X. Le schéma architectural
Alarme intrusion filaire AEI HA-981 6 zones Lycée de l Aa Page 1 sur 11 1) Mise en situation Vous devez assurer une protection périmétrique et volumétrique de la maison de M r X. Le schéma architectural
Préparation à l épreuve de Mathématiques du concours d entrée en première année d IUFM (niveau 2) Responsable : Nathalie Villa villa@univ-tlse2
 Préparation à l épreuve de Mathématiques du concours d entrée en première année d IUFM (niveau 2) Responsable : Nathalie Villa villa@univ-tlse2 Algèbre : Exercices Equations linéaires du premier degré
Préparation à l épreuve de Mathématiques du concours d entrée en première année d IUFM (niveau 2) Responsable : Nathalie Villa villa@univ-tlse2 Algèbre : Exercices Equations linéaires du premier degré
LE PROJOPHONE de Fresnel
 LE PROJOPHONE de Fresnel Le principe général est assez simple : l'image de l écran est agrandie et projetée à l'aide de la lentille optique. Nous allons commencer par créer un élément dans lequel le téléphone
LE PROJOPHONE de Fresnel Le principe général est assez simple : l'image de l écran est agrandie et projetée à l'aide de la lentille optique. Nous allons commencer par créer un élément dans lequel le téléphone
EQUATIONS ET INEQUATIONS Exercices 1/8
 EQUATIONS ET INEQUATIONS Exercices 1/8 01 Résoudre les équation suivantes : x + 7 = 0 x 1 = 0 x + 4 = 0 3x 9 = 0 9x + 1 = 0 - x + 4 = 0-6x + = 0-5x 15 = 0-1 + 8x = 0-4 - 3x = 0-5x 3 + 7x = 0 + 6x 4 = 0
EQUATIONS ET INEQUATIONS Exercices 1/8 01 Résoudre les équation suivantes : x + 7 = 0 x 1 = 0 x + 4 = 0 3x 9 = 0 9x + 1 = 0 - x + 4 = 0-6x + = 0-5x 15 = 0-1 + 8x = 0-4 - 3x = 0-5x 3 + 7x = 0 + 6x 4 = 0
Créer des documents interactifs
 Créer des documents interactifs 14 Au cours de cette leçon, vous apprendrez à : créer un document en ligne de base ; ajouter des boutons, des transitions de page et des hyperliens ; exporter au format
Créer des documents interactifs 14 Au cours de cette leçon, vous apprendrez à : créer un document en ligne de base ; ajouter des boutons, des transitions de page et des hyperliens ; exporter au format
Exo7. Calculs de déterminants. Fiche corrigée par Arnaud Bodin. Exercice 1 Calculer les déterminants des matrices suivantes : Exercice 2.
 Eo7 Calculs de déterminants Fiche corrigée par Arnaud Bodin Eercice Calculer les déterminants des matrices suivantes : Correction Vidéo ( ) 0 6 7 3 4 5 8 4 5 6 0 3 4 5 5 6 7 0 3 5 4 3 0 3 0 0 3 0 0 0 3
Eo7 Calculs de déterminants Fiche corrigée par Arnaud Bodin Eercice Calculer les déterminants des matrices suivantes : Correction Vidéo ( ) 0 6 7 3 4 5 8 4 5 6 0 3 4 5 5 6 7 0 3 5 4 3 0 3 0 0 3 0 0 0 3
Brevet 2007 L intégrale d avril 2007 à mars 2008
 Brevet 2007 L intégrale d avril 2007 à mars 2008 Pondichéry avril 2007................................................. 3 Amérique du Nord juin 2007......................................... 7 Antilles
Brevet 2007 L intégrale d avril 2007 à mars 2008 Pondichéry avril 2007................................................. 3 Amérique du Nord juin 2007......................................... 7 Antilles
Introduction au maillage pour le calcul scientifique
 Introduction au maillage pour le calcul scientifique CEA DAM Île-de-France, Bruyères-le-Châtel [email protected] Présentation adaptée du tutorial de Steve Owen, Sandia National Laboratories, Albuquerque,
Introduction au maillage pour le calcul scientifique CEA DAM Île-de-France, Bruyères-le-Châtel [email protected] Présentation adaptée du tutorial de Steve Owen, Sandia National Laboratories, Albuquerque,
Logistique, Transports
 Baccalauréat Professionnel Logistique, Transports 1. France, juin 2006 1 2. Transport, France, juin 2005 2 3. Transport, France, juin 2004 4 4. Transport eploitation, France, juin 2003 6 5. Transport,
Baccalauréat Professionnel Logistique, Transports 1. France, juin 2006 1 2. Transport, France, juin 2005 2 3. Transport, France, juin 2004 4 4. Transport eploitation, France, juin 2003 6 5. Transport,
Tests de logique. Valérie CLISSON Arnaud DUVAL. Groupe Eyrolles, 2003 ISBN : 2-7081-3524-4
 Valérie CLISSON Arnaud DUVAL Tests de logique Groupe Eyrolles, 2003 ISBN : 2-7081-3524-4 CHAPITRE 1 Mise en bouche Les exemples qui suivent constituent un panorama de l ensemble des tests de logique habituellement
Valérie CLISSON Arnaud DUVAL Tests de logique Groupe Eyrolles, 2003 ISBN : 2-7081-3524-4 CHAPITRE 1 Mise en bouche Les exemples qui suivent constituent un panorama de l ensemble des tests de logique habituellement
PAGE 1. L écran du logiciel d Open Office Draw. Barre de menu: Les commandes du logiciel
 PAGE L écran du logiciel d Open Office Draw Nom du document : Nom d enregistrement Barre de mise forme: Ligne, couleurs, fond,... Barre de menu: Les commandes du logiciel Barre d outils: Les boutons de
PAGE L écran du logiciel d Open Office Draw Nom du document : Nom d enregistrement Barre de mise forme: Ligne, couleurs, fond,... Barre de menu: Les commandes du logiciel Barre d outils: Les boutons de
Proposition de programmes de calculs en mise en train
 Proposition de programmes de calculs en mise en train Programme 1 : Je choisis un nombre, je lui ajoute 1, je calcule le carré du résultat, je retranche le carré du nombre de départ. Essai-conjecture-preuve.
Proposition de programmes de calculs en mise en train Programme 1 : Je choisis un nombre, je lui ajoute 1, je calcule le carré du résultat, je retranche le carré du nombre de départ. Essai-conjecture-preuve.
Evaluation diagnostique de CM1 Circonscription de Saint Just en Chaussée Livret du maître partie Français
 Evaluation diagnostique de CM1 Circonscription de Saint Just en Chaussée Livret du maître partie Français Avant de débuter, demander aux élèves de préparer le matériel suivant : crayon à papier, gomme,
Evaluation diagnostique de CM1 Circonscription de Saint Just en Chaussée Livret du maître partie Français Avant de débuter, demander aux élèves de préparer le matériel suivant : crayon à papier, gomme,
Silhouette Studio Leçon N 2
 Silhouette Studio Leçon N 2 Apprendre comment utiliser Ma Bibliothèque et la Boutique en Ligne Silhouette pour importer des nouveaux modèles. Matériels nécessaires Silhouette SD Feuille de transport colle
Silhouette Studio Leçon N 2 Apprendre comment utiliser Ma Bibliothèque et la Boutique en Ligne Silhouette pour importer des nouveaux modèles. Matériels nécessaires Silhouette SD Feuille de transport colle
Utilisation de la plateforme VIA ecollaboration
 Entrer sur la plateforme L invitation que vous avez reçue comporte un lien vers la plateforme VIA ecollaboration (salle privée de François Guérin de Communagir). Pour y accéder, cliquez simplement sur
Entrer sur la plateforme L invitation que vous avez reçue comporte un lien vers la plateforme VIA ecollaboration (salle privée de François Guérin de Communagir). Pour y accéder, cliquez simplement sur
Durée de L épreuve : 2 heures. Barème : Exercice n 4 : 1 ) 1 point 2 ) 2 points 3 ) 1 point
 03 Mai 2013 Collège Oasis Durée de L épreuve : 2 heures. apple Le sujet comporte 4 pages et est présenté en livret ; apple La calculatrice est autorisée ; apple 4 points sont attribués à la qualité de
03 Mai 2013 Collège Oasis Durée de L épreuve : 2 heures. apple Le sujet comporte 4 pages et est présenté en livret ; apple La calculatrice est autorisée ; apple 4 points sont attribués à la qualité de
Prénom : MATHÉMATIQUES. 120 minutes Compas, règle métrique, rapporteur, équerre, calculatrice non programmable
 Admission en 8 VSG 8 VSB cocher la voie visée MATHÉMATIQUES Durée Matériel à disposition 120 minutes Compas, règle métrique, rapporteur, équerre, calculatrice non programmable Rappel des objectifs fondamentaux
Admission en 8 VSG 8 VSB cocher la voie visée MATHÉMATIQUES Durée Matériel à disposition 120 minutes Compas, règle métrique, rapporteur, équerre, calculatrice non programmable Rappel des objectifs fondamentaux
PARTIE NUMERIQUE (18 points)
 4 ème DEVOIR COMMUN N 1 DE MATHÉMATIQUES 14/12/09 L'échange de matériel entre élèves et l'usage de la calculatrice sont interdits. Il sera tenu compte du soin et de la présentation ( 4 points ). Le barème
4 ème DEVOIR COMMUN N 1 DE MATHÉMATIQUES 14/12/09 L'échange de matériel entre élèves et l'usage de la calculatrice sont interdits. Il sera tenu compte du soin et de la présentation ( 4 points ). Le barème
Sommaire. Images Actives Logiciel libre développé par le CRDP de l académie de Versailles 2 Rue Pierre Bourdan Marly le Roi - 78160
 Sommaire Choisir son image... 2 Enregistrer son travail... 3 Créer les détails... 4 Supprimer une zone ou un détail... 6 Les commentaires... 6 Créer un lien hypertexte... 8 Appliquer un modèle... 8 Personnaliser
Sommaire Choisir son image... 2 Enregistrer son travail... 3 Créer les détails... 4 Supprimer une zone ou un détail... 6 Les commentaires... 6 Créer un lien hypertexte... 8 Appliquer un modèle... 8 Personnaliser
ÉQUATIONS. Quel système!!!! PROBLÈMES À DEUX INCONNUES : - MISE EN ÉQUATIONS - RÉSOLUTION. Dossier n 3 Juin 2005
 ÉQUATIONS PROBLÈMES À DEUX INCONNUES : - MISE EN ÉQUATIONS - RÉSOLUTION 3 x + 5 y = 12 6 x + 4 y = 0 Quel système!!!! Dossier n 3 Juin 2005 Tous droits réservés au réseau AGRIMÉDIA Conçu et réalisé par
ÉQUATIONS PROBLÈMES À DEUX INCONNUES : - MISE EN ÉQUATIONS - RÉSOLUTION 3 x + 5 y = 12 6 x + 4 y = 0 Quel système!!!! Dossier n 3 Juin 2005 Tous droits réservés au réseau AGRIMÉDIA Conçu et réalisé par
EXERCICES DE REVISIONS MATHEMATIQUES CM2
 EXERCICES DE REVISIONS MATHEMATIQUES CM2 NOMBRES ET CALCUL Exercices FRACTIONS Nommer les fractions simples et décimales en utilisant le vocabulaire : 3 R1 demi, tiers, quart, dixième, centième. Utiliser
EXERCICES DE REVISIONS MATHEMATIQUES CM2 NOMBRES ET CALCUL Exercices FRACTIONS Nommer les fractions simples et décimales en utilisant le vocabulaire : 3 R1 demi, tiers, quart, dixième, centième. Utiliser
Fonction quadratique et trajectoire
 Fonction quadratique et trajectoire saé La sécurité routière On peut établir que la vitesse maimale permise sur une chaussée mouillée doit être inférieure à celle permise sur une chaussée sèche La vitesse
Fonction quadratique et trajectoire saé La sécurité routière On peut établir que la vitesse maimale permise sur une chaussée mouillée doit être inférieure à celle permise sur une chaussée sèche La vitesse
CONJUGUÉ D'UN POINT PAR RAPPORT À UN TRIANGLE
 CONJUGUÉ D'UN POINT PAR RAPPORT À UN TRIANGLE Jean Luc Bovet, Auvernier L'article de Monsieur Jean Piquerez (Bulletin de la SSPMP No 86), consacré aux symédianes me paraît appeler une généralisation. En
CONJUGUÉ D'UN POINT PAR RAPPORT À UN TRIANGLE Jean Luc Bovet, Auvernier L'article de Monsieur Jean Piquerez (Bulletin de la SSPMP No 86), consacré aux symédianes me paraît appeler une généralisation. En
Maison au bord de l eau 5 chambres Piscine Jacuzzi Dock A proximité immédiate du Normandy Shores Golf Club. www.selogeramiami.com
 Villa Miramar Maison au bord de l eau 5 chambres Piscine Jacuzzi Dock A proximité immédiate du Normandy Shores Golf Club www.selogeramiami.com Adresse : 480 S Shore Drive 33141 Miami Beach Florida Sur
Villa Miramar Maison au bord de l eau 5 chambres Piscine Jacuzzi Dock A proximité immédiate du Normandy Shores Golf Club www.selogeramiami.com Adresse : 480 S Shore Drive 33141 Miami Beach Florida Sur
Création d un petit livre Avec le logiciel «Didapages» Version Didapages 1.1 PC
 Création d un petit livre Avec le logiciel «Didapages» Version Didapages 1.1 PC Pascale-Dominique Chaillez Lynda O Connell Conseillères pédagogiques au Service national du RÉCIT à l éducation préscolaire
Création d un petit livre Avec le logiciel «Didapages» Version Didapages 1.1 PC Pascale-Dominique Chaillez Lynda O Connell Conseillères pédagogiques au Service national du RÉCIT à l éducation préscolaire
MODE D EMPLOI V.2.0. Installation. Nouveautés V.02. Fais ton journal - version 2.0 - mars 2008 - Mode d emploi -
 MODE D EMPLOI V.2.0 En cas de problème d utilsation, écrire à notre assistance : [email protected] Nouveautés V.02 - Résolution des bugs d enregistrement des journaux - Ajout du dictionnaire des mots de la
MODE D EMPLOI V.2.0 En cas de problème d utilsation, écrire à notre assistance : [email protected] Nouveautés V.02 - Résolution des bugs d enregistrement des journaux - Ajout du dictionnaire des mots de la
métallerie LA QUALITÉ & LE SERVICE AU COEUR DE NOTRE DÉMARCHE Notre indépendance fait la différence
 Gamme métallerie LA QUALITÉ & LE SERVICE AU COEUR DE NOTRE DÉMARCHE GRILLAGE SERRURIER Le grillage serrurier résulte d un process d assemblage par soudure de fils entre eux. Les fils assemblés peuvent
Gamme métallerie LA QUALITÉ & LE SERVICE AU COEUR DE NOTRE DÉMARCHE GRILLAGE SERRURIER Le grillage serrurier résulte d un process d assemblage par soudure de fils entre eux. Les fils assemblés peuvent
Chapitre. Conquérant est une toile de 1930 qui se trouve au Centre Paul Klee à Berne (Suisse). Paul Klee (1879-
 Chapitre 9 REVOIR > les notions de points, droites, segments ; > le milieu d un segment ; > l utilisation du compas. DÉCOUVRIR > la notion de demi-droite ; > de nouvelles notations ; > le codage d une
Chapitre 9 REVOIR > les notions de points, droites, segments ; > le milieu d un segment ; > l utilisation du compas. DÉCOUVRIR > la notion de demi-droite ; > de nouvelles notations ; > le codage d une
Chapitre 14. La diagonale du carré
 Chapitre 4 La diagonale du carré Préambule Examinons un puzzle tout simple : on se donne deux carrés de même aire et on demande, au moyen de quelques découpages, de construire un nouveau carré qui aurait
Chapitre 4 La diagonale du carré Préambule Examinons un puzzle tout simple : on se donne deux carrés de même aire et on demande, au moyen de quelques découpages, de construire un nouveau carré qui aurait
Création d un petit livre Avec le logiciel «Didapages 1.1»
 Création d un petit livre Avec le logiciel «Didapages 1.1» Version Didapages 1.1 PC Pascale-Dominique Chaillez Lynda O Connell Conseillères pédagogiques Service national du RÉCIT à l éducation préscolaire
Création d un petit livre Avec le logiciel «Didapages 1.1» Version Didapages 1.1 PC Pascale-Dominique Chaillez Lynda O Connell Conseillères pédagogiques Service national du RÉCIT à l éducation préscolaire
Excel 2007 Niveau 3 Page 1 www.admexcel.com
 Excel 2007 Niveau 3 Page 1 TABLE DES MATIERES UTILISATION DE LISTES DE DONNEES... 4 REMARQUES PREALABLES SUR LES LISTES DE DONNEES... 4 METTRE EN FORME LE TABLEAU... 6 METTRE LA LISTE A JOUR... 7 a/ Directement
Excel 2007 Niveau 3 Page 1 TABLE DES MATIERES UTILISATION DE LISTES DE DONNEES... 4 REMARQUES PREALABLES SUR LES LISTES DE DONNEES... 4 METTRE EN FORME LE TABLEAU... 6 METTRE LA LISTE A JOUR... 7 a/ Directement
Je découvre le diagramme de Venn
 Activité 8 Je découvre le diagramme de Venn Au cours de cette activité, l élève découvre le diagramme de Venn et se familiarise avec lui. Pistes d observation L élève : reconnaît les éléments du diagramme
Activité 8 Je découvre le diagramme de Venn Au cours de cette activité, l élève découvre le diagramme de Venn et se familiarise avec lui. Pistes d observation L élève : reconnaît les éléments du diagramme
Livret de formules. Calcul Professionnel Boulangère-Pâtissière-Confiseuse AFP Boulanger-Pâtissier-Confiseur AFP
 Version 2: 13.11.2014 Livret de formules Calcul Professionnel Boulangère-Pâtissière-Confiseuse AFP Boulanger-Pâtissier-Confiseur AFP Economie d entreprise Boulangère-Pâtissière-Confiseuse CFC Boulanger-Pâtissier-Confiseur
Version 2: 13.11.2014 Livret de formules Calcul Professionnel Boulangère-Pâtissière-Confiseuse AFP Boulanger-Pâtissier-Confiseur AFP Economie d entreprise Boulangère-Pâtissière-Confiseuse CFC Boulanger-Pâtissier-Confiseur
Programme de calcul et résolution d équation
 Programme de calcul et résolution d équation On appelle «programme de calcul» tout procédé mathématique qui permet de passer d un nombre à un autre suivant une suite d opérations déterminée. Un programme
Programme de calcul et résolution d équation On appelle «programme de calcul» tout procédé mathématique qui permet de passer d un nombre à un autre suivant une suite d opérations déterminée. Un programme
Trois personnes mangent dans un restaurant. Le serveur
 29=30 Trois personnes mangent dans un restaurant. Le serveur leur amène une addition de 30 francs. Les trois personnes décident de partager la facture en trois, soit 10 francs chacun. Le serveur rapporte
29=30 Trois personnes mangent dans un restaurant. Le serveur leur amène une addition de 30 francs. Les trois personnes décident de partager la facture en trois, soit 10 francs chacun. Le serveur rapporte
Angles orientés et trigonométrie
 Chapitre Angles orientés et trigonométrie Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES Trigonométrie Cercle trigonométrique. Radian. Mesure d un angle orienté, mesure principale.
Chapitre Angles orientés et trigonométrie Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES Trigonométrie Cercle trigonométrique. Radian. Mesure d un angle orienté, mesure principale.
Procédure de sauvegarde pour AB Magique
 Procédure de sauvegarde pour AB Magique Importance de la copie de sauvegarde : Il est très important de saisir l utilité d une copie de sauvegarde de votre logiciel AB Magique. Si un problème informatique
Procédure de sauvegarde pour AB Magique Importance de la copie de sauvegarde : Il est très important de saisir l utilité d une copie de sauvegarde de votre logiciel AB Magique. Si un problème informatique
