Circuits logiques. Eric Cariou. Université de Pau et des Pays de l'adour Département Informatique.
|
|
|
- Eric Alexandre Sylvain
- il y a 8 ans
- Total affichages :
Transcription
1 Circuits logiques Eric Cariou Université de Pau et des Pays de l'adour Département Informatique 1
2 Circuit logique Circuit électronique réalisant une ou plusieurs fonctions logiques Un circuit logique est composé D'un ensemble de portes logiques De circuits logiques Le tout interconnectés entre eux 2 types de circuits logiques Circuits combinatoires : S = f(e) Circuits séquentiels : notion d'état et de mémoire 2
3 Circuits Logiques (1) Circuits Combinatoires 3
4 Sj= f(ei) Circuit combinatoire Les sorties Sj sont fonctions uniquement de la valeur des entrées Ei Un circuit combinatoire est défini par une ou plusieurs fonctions logiques Définition de la valeur des sorties en fonction des entrées du circuit Algèbre de Boole et les fonctions logiques sont donc le support théorique des circuits combinatoires Un circuit se représente par un logigramme 4
5 Une porte logique Portes logiques Circuit combinatoire de base Réalisant une opération logique de base Exemple : OU, ET, NON, correspondant aux opérateurs de l'algèbre de Boole Une porte possède Une table de vérité et/ou une expression logique définissant son résultat en fonction de son/ses entrée(s) Un symbole graphique 5
6 Porte NON Porte NON (NOT) 1 entrée, 1 sortie NON a est noté a _ a a
7 Porte ET Porte ET (AND) 2 entrées, 1 sortie a ET b est noté a.b ou ab ou a^b a b a.b
8 Porte OU Porte OU (OR) 2 entrées, 1 sortie a OU b est noté a + b ou avb a b a + b
9 Porte OU exclusif Porte OU-exclusif (XOR) 2 entrées, 1 sortie a OU-exclusif b est noté a b a b a b
10 Porte NON ET Porte NON ET (NAND) 2 entrées, 1 sortie a NAND b est noté a.b a.b a b
11 Porte NON OU Porte NON OU (NOR) 2 entrées, 1 sortie a NOR b est noté a + b a + b a b
12 Autres portes Pour chaque porte à 2 entrées Variantes à 3, 4,... entrées (mais toujours une seule sortie) Généralisation de la fonction logique de base à plus de 2 variables en entrée Le symbole graphique utilisé est identique mais avec plus de 2 entrées Exemples Porte ET à 3 entrées a, b et c a pour expression logique : abc Porte NOR à 4 entrées a, b, c et d a pour expression logique : a + b + c + d 12
13 Synthèse d'un circuit logique A partir d'une fonction logique Trouver le logigramme correspondant à cette fonction Principe Simplifier la fonction logique avec 2 méthodes La méthode algébrique (algèbre de Boole) La méthode des tableaux de Karnaugh En déduire le logigramme correspondant 13
14 Analyse de circuit logique A partir du logigramme d'un circuit Trouver sa fonction logique Principe Donner l'expression des sorties de chaque porte/composant en fonction des valeurs de ses entrées En déduire au final la (ou les) fonction(s) logique(s) du circuit On peut ensuite Déterminer la table de vérité du circuit Simplifier la fonction logique à l'aide des propriétés de l'algèbre de Boole ou les tableaux de Karnaugh 14
15 Exemple d'analyse de circuit Exemple de circuit logique 3 entrées, 1 sortie Composé uniquement de portes logiques 15
16 Exemple d'analyse de circuit Quelle est la fonction logique de ce circuit? A partir de son logigramme Après simplification fa, b,c=ab.b.c fa, b,c=abc En nombre de portes minimales fa, b,c=acb 16
17 Exemple d'analyse de circuit Table de vérité de l'exemple a b c a+b=x b b.c=y x.y x.y
18 Exemple d'analyse de circuit Table de vérité de la fonction simplifiée a b c a c a+b+c On trouve les mêmes valeurs dans les 2 tables Les fonctions sont bien égales 18
19 Exemple de synthèse de circuit Soit la fonction fa, b,c=abca bca bca bc Après simplification, on obtient fa, b,c=acbc 19
20 Additionneur demi-bit Exemple de circuit : un additionneur demi-bit Réalise l'addition de 2 nombres codés chacun sur 1 bit Doit pouvoir gérer l'éventuel débordement Table de vérité du circuit avec : S : la somme des 2 bits R : la retenue x y S R Note : on parle de «demi-bit» car ne prend pas en compte une retenue en entrée (voir suite) 20
21 Additionneur demi-bit Fonctions logiques de S et R S=x yxy=x y R=xy 21
22 Additionneur demi-bit Additionneur n bits Fait une somme de 2 bits Additionneur n bits Fait l'addition de 2 nombres de n bits Deux réalisations possibles Concevoir entièrement l'additionneur à partir de rien Concevoir l'additionneur en réutilisant d'autres composants : des additionneurs 1 bit 22
23 Additionneur n bits Additionneur n bits Si on veut le construire à partir de n additionneurs 1 bit Doit prendre en compte les retenues intermédiaires générées et leur propagation 1 > retenue générée par l'addition des chiffres 010 précédents à additionner en plus aux 2 chiffres Additionneur demi-bit précédent Insuffisant : prend seulement 2 bits en entrée, pas la retenue On parlait donc de demi-additionneur Additionneur qui prend en compte une retenue en entrée : additionneur 1 bit complet 23
24 Additionneur 1 bit complet Additionneur 1 bit complet Entrées : bits x, y et retenue R 0 Sorties : résultat S et retenue R 1 2 idées pour définir l'additionneur 1 bit complet Déterminer la table de vérité de {S, R 1 } = f(x,y,r 0 ) On obtient un nouveau circuit, plus complexe Utiliser le demi-additionneur vu précedemment On réutilise le circuit déjà défini 24
25 Additionneur 1 bit complet En réutilisant le demi-additionneur Le calcul de S se fait via 2 additions x + y = z et S = z + R 0 Chaque addition est effectuée par un demi-additionneur La retenue finale R 1 est le OU des 2 retenues générées par les 2 additions Si la première addition génère une retenue : on aura forcément une retenue au final Si la seconde addition génère une retenue : on aura aussi une retenue au final Donc on fait le OU des 2 retenues 25
26 Additionneur 1 bit complet Additionneur 1 bit complet S : résultat de l'addition des bits a et b et de la retenue R 0 R1 : retenue générée 26
27 Additionneur n bits Exemple pour additionneur 4 bits On enchaîne en série 4 additionneurs 1 bit complet Le résultat est connu après propagation des valeurs calculées le long de tout le circuit C = A + B, en précision 4 bits. R : retenue globale 27
28 Ensembles complets de fonctions logiques de base Dans les exemples précédents On a construit des circuits avec n'importe quelles portes : ET, OU, NON, NAND, NOR, XOR... Il existe des ensembles complets de portes (fonctions logiques de base) Les portes d'un ensemble complet permettent de réaliser n'importe quel circuit (fonction logique) Peut être utile pour limiter le coût d'un circuit Le nombre de transistors utilisés pour réaliser une porte peut varier du simple au double selon les portes 28
29 Ensembles complets de fonctions logiques de base 3 ensembles complets de fonctions {ET, OU, NON} {NOR} {NAND} Pour prouver que ces ensembles sont complets Montrer qu'on peut spécifier toutes les fonctions de base à partir des fonctions d'un ensemble 29
30 Ensembles complets de fonctions logiques de base Ensembles complets minimaux : contenant le moins d'éléments {ET, OU, NON} : pas minimal car ab=a. b a. b=ab : OU se définit avec ET et NON : ET se définit avec OU et NON {ET, NON} et {OU, NON} sont 2 ensembles complets mais on ne peut pas les simplifier plus 30
31 Ensembles complets de fonctions logiques de base Au final : 2 ensembles complets minimaux {NAND} et {NOR} Preuve pour NAND On doit pouvoir définir à partir d'un NAND : NON : NON(a) = NAND(a,a) OU : OU(a,b) = NAND(NAND(a,a),NAND(b,b)) ab=a.a. b.b a=a.a ET : ET(a,b) = NAND(NAND(a,b),NAND(a,b)) a.b=a.b. a.b NOR, XOR : combinaisons de NON, ET et OU donc peut s'exprimer avec des NAND 31
32 Simplification des fonctions/circuits Pour une fonction logique, pour une question de lisibilité, on préfère la version Avec les termes les plus simples Reliés par le moins d'opérateurs En pratique, lors de la réalisation du circuit Ca ne sera pas forcément la version la moins coûteuse en terme d'éléments électroniques (transistors) Une porte NAND ou NOR est moins coûteuse en transistors qu'une porte OU ou ET 32
33 Simplification des fonctions/circuits Pour un circuit logique, on cherchera donc à le réaliser avec des portes NAND ou NOR Permet de diminuer le nombre total de transistors Permet de ne pas multiplier le nombre de portes différentes à utiliser Exemple : demi-additionneur 1 bit Sx,y=xyx y On va exprimer R et S avec des NAND et R=xy On utilise également des NON pour simplifier 33
34 Demi-additionneur avec NAND Pour transformer R et S, on passe par l'involution Sx,y=x yx y S(x,y)=x yxy=x y xy R=xy=xy=xy 34
35 Table de vérité -> circuit en portes NAND Méthode pour passer de la table de vérité au circuit réalisé avec des NAND (et des ET) 2 couches de portes NAND Première couche : Pour chaque valeur de f(x i ) égale à 1 On fait un NAND de tous les Xi en prenant Xi si Xi =1 ou Xi si Xi =0 Deuxième couche : on fait un NAND de toutes les sorties des NAND de la première couche Nécessite des portes NAND a plus de 2 entrées 35
36 Table de vérité -> circuit en portes NAND Exemple : avec additionneur complet 1 bit R0 x y S R Avantage de la méthode : construction systématique Inconvénient : pas toujours optimal en nb de portes 36
37 Logique à 3 états Algébre de Boole et circuits logiques : logique à 2 états Etat 0 (état «faux» ou état physique «courant électrique nul») Etat 1 (état «vrai» ou état physique «courant électrique non nul») Logique à 3 états Extension de la logique à 2 états avec un troisième état : «état indéfini» Utilité principale : activer ou désactiver des parties d'un circuit liées aux mêmes sorties ou éléments 37
38 Logique à 3 états Une porte, un élément de circuit de logique à 3 états possède une entrée supplémentaire E : Enable Si E = 1, alors les sorties de cette porte/élément sont actives et ont une valeur de 0 ou 1 Si E = 0, alors les sorties ne sont pas activées et n'ont pas de signification, comme si les sorties étaient «déconnectées» E : variante complémentée Activé à 0 et désactivé à 1 On peut connecter deux sorties ensemble, seule celle qui est activée positionnera la valeur (0 ou 1) du conducteur connectant ces deux sorties Multiplexage (voir suite) 38
39 Logique à 3 états Exemples de portes/composants de logique à 3 états Portes (1) et (2) (1) (2) (3) Eléments les plus simples : active ou désactive la sortie o selon la valeur de E Pour (1) : si E = 1 alors o = i, si E = 0, alors o =? (indéfini) Pour (2) : si E = 0 alors o = i, si E = 1, alors o =? (indéfini) Porte (3) : active les 4 sorties en fonction de E Si E = 1, alors chaque o x = i x pour tous les x, sinon tous les o x sont indéfinis 39
40 Exemple de circuit Logique à 3 états Selon la valeur de x, S correspond à la sortie d'une des 2 portes Si x = 0 alors S=a b Si x = 1 alors S=ab=a b 40
41 Circuits logiques de base Dans beaucoup de circuits, on retrouvera certaines fonctionnalités/composants logiques Additionneur 1 bit complet et additionneur n bits Multiplexeur : une des X entrées vers 1 sortie Démultiplexeur : 1 entrée vers une des X sorties Décodeur : active une des X sorties selon un code en entrée Codeur : pour 1 entrée active, fournit un code Transcodeur : pour un code A fournit un code B 41
42 Multiplexeur X entrées et 1 sortie Selon une adresse, la sortie prend la valeur d'une des X entrées Circuit combinatoire avec Une sortie K Une adresse codée sur n bits 2 n entrées k x 42
43 Multiplexeur à 4 entrées 4 entrées, adresse sur 2 bits : a et b Table de vérité a b K k k k K 3 Ka, b=k 0 a bk 1 a bk 2 a bk 3 a b D'autres choix de multiplexage sont possibles 43
44 Multiplexeur 4 entrées Logigramme et symbole pour le multiplexeur à 4 entrées 44
45 Multiplexeur 4 entrées Variante avec logique à 3 états Selon la valeur de a et b, on ne redirige qu'un des quatre k x vers K 45
46 Démultiplexeur 1 entrée, X sorties Selon une adresse, une des X sorties prend la valeur de l'entrée Circuit combinatoire avec 2n sorties k x 1 entrée K Une adresse codée sur n bits 46
47 Démultiplexeur à 4 sorties 4 sorties, adresse sur 2 bits : a et b Valeurs des k x sorties selon a et b a b k0 k1 k2 k K K K K k0=a bk k2=a bk k1=a bk k3=a bk 47
48 Démultiplexeur à 4 sorties Logigramme et symbole pour le démultiplexeur à 4 sorties 48
49 Codeur Active un code selon l'une des X entrées actives 2n (en général) entrées 1 entrée active (valeur 1) Les autres sont toutes désactivées (valeur 0) Code en sortie : sur n bits Exemple classique de codeur Numérotation de 0 à 2 n -1 des entrées Le code représente le numéro de l'entrée codé en binaire 49
50 Codeur sur 3 bits 3 bits S x en sortie et 8 entrées E y E0 E1 E2 E3 E4 E5 E6 E7 S0 S1 S
51 Décodeur Active une des X sorties selon un code Code : sur n bits Nombre de sorties : 2 n (en général) Exemple classique de décodeur Numérotation de 0 à 2 n -1 des sorties Le code représente le numéro codé en binaire de la sortie à activer 51
52 Décodeur sur 3 bits 3 bits S x : 8 sorties E y S2 S1 S0 E0 E1 E2 E3 E4 E5 E6 E
53 Transcodeur Fait correspondre un code A en entrée sur n lignes à un code B en sortie sur m lignes Exemple avec n = 3 et m = 5 a2 a1 a0 b4 b3 b2 b1 b
54 Circuits Logiques (2) Circuits Séquentiels 54
55 Circuits combinatoires Circuits séquentiels Les sorties ne dépendent que des valeurs des entrées Circuits séquentiels Ajout des notions d'état et de mémoire Ajout de la notion de temps (horloge) 55
56 Circuits séquentiels Les valeurs de sorties du circuit dépendent Des valeurs en entrée De valeurs calculées précédemment De l'état dans lequel on se trouve Théories utilisées pour étudier/spécifier les différents types de circuits Circuits combinatoires : algèbre de Boole Circuits séquentiels : théorie des automates finis 56
57 Automate fini Un automate fini possède un nombre fini d'états Il est caractérisé, pour un couple d'instants (t, t+1), par Sa réponse S Son entrée E Son état Q 57
58 Automate fini 3 façons de déterminer un automate Fonctions de transfert S(t+1) = f( Q(t), E(t) ) : sortie à t+1 dépend des entrées et états à t Q(t+1) = g ( Q(t), E(t) ) : état à t+1 dépend des entrées et états à t Tables de transition : tables des fonctions f et g Valeurs de Q(t+1) et S(t+1) pour chaque combinaison de valeurs de E(t) et Q(t) Diagrammes d'états ou de transitions 58
59 Exemple d'automate fini Mémoire binaire : stocke 1 bit 1 entrée Si 0, on mémorise la valeur 0 Si 1, on mémorise la valeur 1 2 états : valeur 0 ou valeur 1 Principe A t on est dans un état X, à t+1, on passe dans un état Y selon la valeur de l'entrée à t La sortie S à t+1 prend la valeur de l'état à t 59
60 Exemple d'automate fini Fonctions de transfert S(t+1) = Q(t) : la sortie à t +1 est égale à l'état à t Q(t+1) = E(t) : l'état à t +1 est égal à l'entrée passée à l'état t Tables de transitions : valeurs de Q(t+1) et S (t+1) en fonction de E(t) et Q(t) \ E(T) 0 1 \ E(t) 0 1 Q(t) + Q(t) S(t+1) Q(t+1) 60
61 Exemple d'automate fini Diagramme d'états/transitions 61
62 Caractéristiques électriques et temporelles D'un point de vue électrique et idéal Un 0 correspond à 0 volt (parfois à -V m volts) Un 1 correspond à +V m volts En pratique 2 niveaux : niveau haut V h et niveau bas V b 0 < V b < V h < V m Pour un voltage v 0 < v < V b : représente un 0 V h < v < V m : représente un 1 V b < v < V h : indéfini 62
63 Caractéristiques électriques et temporelles Changement de valeur (0 -> 1 ou 1 -> 0) Idéalement : instantané En pratique : prend un certain temps, délai de montée (0 -> 1) et de descente (1 -> 0) Passage d'un signal au travers d'une porte Idéalement : instantané En pratique : prend un certain temps Délai de propagation 63
64 Délais Exemple : traversée d'une porte NON E = 1 puis passe à 0, S = E 64
65 Délais Voltages V m : voltage correspondant au 1 idéal V h : voltage haut, minimum pour avoir un 1 V b : voltage bas, maximum pour avoir un 0 Délais t d : temps de descente, passage de 0 à 1 (voltage de V h à V b ) t m : temps de montée, passage de 0 à 1 (voltage de V b à V h ) t p : temps de propagation dans la porte (pris à la moyenne de V h et V b ) 65
66 Délais Si temps de montée ou de descente trop long On reste relativement longtemps entre V b et V h : état indéfini La sortie oscille alors entre 0 et 1 66
67 Contraintes temporelles des circuits Un circuit est formé de plusieurs portes Chemin critique : chemin le «plus long» pour la propagation des signaux à travers le circuit Détermine le temps total de propagation des signaux à travers tout le circuit Temps minimal à attendre pour avoir une sortie valide Intuitivement : chemin passant par le plus grand nombre de portes Mais dépend aussi du temps de propagation de chaque type de porte 67
68 Horloge A cause de tous les délais (montée, descente, propagation) Un signal n'est pas dans un état valide en permanence Idée : on ne lit ses valeurs qu'à des instants précis et à des intervalles réguliers Instants donnés par une horloge Horloge Indispensable aussi dans le cas des circuits séquentiels synchrones pour savoir quand on passe de t à t +1 68
69 Horloge Horloge Signal périodique 1 demi-période à 0, l'autre à 1 Début d'une nouvelle période : instant t i Pour exemple précédent du NON Instant t 1 : E = 1, S = 0 Instant t 2 : E = 0, S = 1 CLK = Clock = signal d'horloge 69
70 Mémoire sur 1 bit Circuit séquentiel basique : mémoire sur 1 bit Possède une variable binaire codée sur 1 bit Sa valeur est conservée ou modifiable dans le temps Mémoires 1 bit peuvent être réalisées avec des bascules 70
71 Bistable et bascule Bistable : 2 états stables dans le temps Principe général d'une bistable : 2 portes non (inverseurs) en opposition Bascule : composant qui met en oeuvre une bistable Possibilité de passer d'un état à l'autre, de changer l'état mémorisé Plusieurs façons de gérer et changer l'état Plusieurs types de bascules : RS, D, JK... 71
72 Entrée/sorties Bascule RS 2 entrées : R et S 1 sortie Q qui correspond à l'état stocké Principe : la valeur de Q à t+1 dépend de R, S et de la valeur de Q à t R = reset : remise à 0 de Q S = set : mise à 1 de Q S=1 et R=0 : Q mis à 1 S=0 et R=1 : Q mis à 0 S=0 et R=0 : Q garde sa valeur, maintien S=1 et R=1 : Q indéterminé 72
73 Bascule RS Table de vérité/transition du circuit et son tableau de Karnaugh Q R S Q \ RS Q \ X X X X Q+=SQR Q + : valeur de Q à l'instant suivant Dans tableau : X = valeur non connue mais sans influence, on peut regrouper dans les blocs à 1 73
74 Bascule RS Tables de vérité/transition dérivées R S Q+ Q > Q+ R S Q 0 0 X X X Logigramme de la bascule RS, avec des portes NOR 74
75 3 types de bascules Bascule asynchrone Sorties recalculées à chaque changement des valeurs en entrée Plus précisement : recalculées «en permanence» Exemple : la bascule RS précédente Bascule synchrone Sorties recalculées en fonction d'un signal d'horloge en entrée Nécessite une entrée de contrôle pour ce signal d'horloge 2 modes Sur niveau (dit «latch») Recalcule les sorties et l'état quand le signal d'horloge est à 1 Sur front (dit «flip-flop») Recalcule au moment où le signal d'horloge change de valeur Front montant : passage de 0 à 1 Front descendant : passage de 1 à 0 Note : on utilise en général un signal d'horloge sur l'entrée de contrôle, mais n'importe quel signal peut être utilisé en pratique 75
76 3 types de bascules Détermination du temps suivant (passage de t à t + 1) selon le type de bascule Asynchrone Quand les entrées changent et la sortie est recalculée Synchrone sur niveau Quand le niveau (1 en général, mais 0 aussi) est atteint Synchrone sur front Au moment du passage de 0 à 1 ou de 1 à 0 selon le type de front utilisé par la bascule Dans tous les cas Quand on recalcule, les valeurs prises pour l'état et les entrées sont celles juste avant de passer à t + 1, quand on est encore à t 76
77 D = delay Bascule D latch 2 entrées D : la valeur en entrée C : entrée de contrôle, généralement un signal d'horloge 1 sortie Q Q + = D si C = 1 Q + = Q si C = 0 Si C est un signal d'horloge Retarde le signal en entrée D d'une période d'horloge 77
78 Bascule D latch Table de vérité de la bascule D D C Q Q Q+=DCQC Versions condensées : (C=1) D Q+ C Q Q D 78
79 Bascule D latch Réalisation d'une bascule D à partir d'une bascule RS S = CD et R = CD Pour S Pour bascule D, Q+ = 1 si C = 1 et D = 1 Pour bascule RS, Q+ = 1 si S = 1 et R = 0 Pour R Pour bascule D, Q+ = 0 si C = 1 et D = 0 Pour bascule RS, Q+ = 0 si S = 0 et R = 1 Avec S = CD et R = CD, tout est cohérent Et le maintien Q += Q de la bascule D lorsque C=0 est cohérent avec le maintien de la RS : R=S=0 79
80 Bascule D latch Logigramme de la bascule D latch 80
81 Bascule D flip-flop Bascule D flip-flop Variante de la D latch Passage à t + 1 quand front montant de l'horloge En pratique, la D latch fonctionne de la même façon Exemple de chronogramme avec D = et Q(0) = 0 81
82 Bascule JK asynchrone JK = «rien de particulier», variante de RS Comme pour RS mais ajoute le cas de R=S=1 Si J = K = 1 alors Q+ = Q J K Q Q+ + Q+=J QKQ \ JK Q \ J K Q Q Q
83 Représentation des différents Bascule asynchrone types de bascule Pas d'entrée CLK ou de contrôle Bascule synchrone Entrée CLK Synchrone sur front : rajoute un triangle sur l'entrée de contrôle Si «rond inverseur» Bascule latch Modifie la sortie quand valeur d'horloge à 0 (1 par défaut) Bascule flip-flop Actif sur front descendant (montant par défaut) 83
84 Représentation des différents types de bascule De gauche à droite Bascule RS asynchrone Bascule D latch sur niveau 1 Bascule D flip-flop sur front montant Bascule D latch sur niveau 0 Bascule D flip-flop sur front descendant 84
85 Utilisation des bascules Utilisation des bascules pour créer des circuits ayant un état Compteurs Registres Mémorisation d'un mot mémoire, décalage vers la droite/gauche du mot... Mémoires (voir le cours sur les mémoires) Exemple : compteur cyclique sur 3 bits Valeur en décimal sur 3 bits Incrémentation de +1 à chaque période d'horloge Repasse à 0 après 7 85
86 Compteur 3 bits Utilisation de 3 bascules D Principe Chaque bascule prend en entrée D un signal d'horloge Fournit en sortie un signal d'horloge de fréquence divisée par 2 En mettant en série les 3 bascules 3 signaux d'horloge à 3 fréquences différentes Représente les combinaisons de bits pour les valeurs de 0 à 7 86
87 Compteur 3 bits Chronogramme du compteur 3 bits Version idéale, ne prend pas en compte les temps de propagation à travers les bascules (voir TD/TP) 87
88 Registre Registre : mot mémoire de X bits Composant utilisé en interne dans un processeur pour stocker des valeurs lors de l'exécution d'un programme par ce processeur Exemple : registre 4 bits 4 bascules D stockent les 4 bits 4 bits Ix en entrée pour écrire le mot 4 bits Ox en sortie pour récupérer la valeur du mot Une entrée L (pour «load») précise si on conserve la valeur du mot stocké (valeur 0) ou écrit le mot avec les 4 bits en entrée (valeur 1) 88
89 Registre 4 bits Selon la valeur de L, à chaque front montant de l'horloge, les sorties des multiplexeurs prennent les valeurs i x ou reprennent les valeurs déjà stockées par les bascules 89
90 Circuits synchrone et asynchrone Circuit synchrone Tous les éléments/composants du circuit devant être synchronisés le sont avec le même signal d'horloge Circuit asynchrone Tous les éléments/composants du circuit devant être synchronisés ne le sont pas avec le même signal d'horloge 90
91 Circuits synchrone et asynchrone Exemple du compteur 3 bits Circuit est asynchrone car plusieurs signaux d'horloges différents utilisés par les bascules Chaque bascule calcule donc sa sortie à des moments différents Même si certains sont communs à plusieurs bascules Les bascules D utilisées sont des bascules synchrones flipflop mais le circuit lui est bien asynchrone Exemple du registre 4 bits Synchrone car les 4 bascules D flip-flop utilisent toutes les 4 le même signal d'horloge 91
IFT1215 Introduction aux systèmes informatiques
 Introduction aux circuits logiques de base IFT25 Architecture en couches Niveau 5 Niveau 4 Niveau 3 Niveau 2 Niveau Niveau Couche des langages d application Traduction (compilateur) Couche du langage d
Introduction aux circuits logiques de base IFT25 Architecture en couches Niveau 5 Niveau 4 Niveau 3 Niveau 2 Niveau Niveau Couche des langages d application Traduction (compilateur) Couche du langage d
Architecture des ordinateurs TD1 - Portes logiques et premiers circuits
 Architecture des ordinateurs TD1 - Portes logiques et premiers circuits 1 Rappel : un peu de logique Exercice 1.1 Remplir la table de vérité suivante : a b a + b ab a + b ab a b 0 0 0 1 1 0 1 1 Exercice
Architecture des ordinateurs TD1 - Portes logiques et premiers circuits 1 Rappel : un peu de logique Exercice 1.1 Remplir la table de vérité suivante : a b a + b ab a + b ab a b 0 0 0 1 1 0 1 1 Exercice
Système binaire. Algèbre booléenne
 Algèbre booléenne Système binaire Système digital qui emploie des signaux à deux valeurs uniques En général, les digits employés sont 0 et 1, qu'on appelle bits (binary digits) Avantages: on peut utiliser
Algèbre booléenne Système binaire Système digital qui emploie des signaux à deux valeurs uniques En général, les digits employés sont 0 et 1, qu'on appelle bits (binary digits) Avantages: on peut utiliser
VIII- Circuits séquentiels. Mémoires
 1 VIII- Circuits séquentiels. Mémoires Maintenant le temps va intervenir. Nous avions déjà indiqué que la traversée d une porte ne se faisait pas instantanément et qu il fallait en tenir compte, notamment
1 VIII- Circuits séquentiels. Mémoires Maintenant le temps va intervenir. Nous avions déjà indiqué que la traversée d une porte ne se faisait pas instantanément et qu il fallait en tenir compte, notamment
FONCTION COMPTAGE BINAIRE ET DIVISION DE FRÉQUENCE
 I/ GÉNÉRALITÉS I.1/ Fonction Un compteur binaire est utilisé : -pour compter un certain nombre d'évènements binaires -pour diviser la fréquence d'un signal logique par 2 m Page 1 FONCTION COMPTAGE BINAIRE
I/ GÉNÉRALITÉS I.1/ Fonction Un compteur binaire est utilisé : -pour compter un certain nombre d'évènements binaires -pour diviser la fréquence d'un signal logique par 2 m Page 1 FONCTION COMPTAGE BINAIRE
Les fonctions logiques
 1 Les fonctions logiques Le fonctionnement des ordinateurs tout comme d autres appareils électroniques repose sur l emploi des circuits électroniques de logique binaire ou électronique numérique. Dans
1 Les fonctions logiques Le fonctionnement des ordinateurs tout comme d autres appareils électroniques repose sur l emploi des circuits électroniques de logique binaire ou électronique numérique. Dans
Les portes logiques. Voici les symboles des trois fonctions de base. Portes AND. Portes OR. Porte NOT
 Les portes logiques Nous avons jusqu ici utilisé des boutons poussoirs et une lampe pour illustrer le fonctionnement des opérateurs logiques. En électronique digitale, les opérations logiques sont effectuées
Les portes logiques Nous avons jusqu ici utilisé des boutons poussoirs et une lampe pour illustrer le fonctionnement des opérateurs logiques. En électronique digitale, les opérations logiques sont effectuées
Logique binaire. Aujourd'hui, l'algèbre de Boole trouve de nombreuses applications en informatique et dans la conception des circuits électroniques.
 Logique binaire I. L'algèbre de Boole L'algèbre de Boole est la partie des mathématiques, de la logique et de l'électronique qui s'intéresse aux opérations et aux fonctions sur les variables logiques.
Logique binaire I. L'algèbre de Boole L'algèbre de Boole est la partie des mathématiques, de la logique et de l'électronique qui s'intéresse aux opérations et aux fonctions sur les variables logiques.
RESUME DE COURS ET CAHIER D'EXERCICES
 ARCITECTURE INFO-UP REUME DE COUR ET CAIER D'EXERCICE EPITA F. GABON Architecture EPITA INFO-UP F. Gabon COUR LIVRE D ARCITECTURE 3 REUME D'ELECTRONIUE LOGIUE 4 YTEME DE NUMERATION 6 ALGEBRE DE BOOLE 6
ARCITECTURE INFO-UP REUME DE COUR ET CAIER D'EXERCICE EPITA F. GABON Architecture EPITA INFO-UP F. Gabon COUR LIVRE D ARCITECTURE 3 REUME D'ELECTRONIUE LOGIUE 4 YTEME DE NUMERATION 6 ALGEBRE DE BOOLE 6
Algèbre binaire et Circuits logiques (2007-2008)
 Université Mohammed V Faculté des Sciences Département de Mathématiques et Informatique Filière : SMI Algèbre binaire et Circuits logiques (27-28) Prof. Abdelhakim El Imrani Plan. Algèbre de Boole 2. Circuits
Université Mohammed V Faculté des Sciences Département de Mathématiques et Informatique Filière : SMI Algèbre binaire et Circuits logiques (27-28) Prof. Abdelhakim El Imrani Plan. Algèbre de Boole 2. Circuits
Patentamt JEuropaisches. European Patent Office Numéro de publication: 0 1 1 0 7 6 7 Office européen des brevets DEMANDE DE BREVET EUROPEEN
 Patentamt JEuropaisches European Patent Office Numéro de publication: 0 1 1 0 7 6 7 Office européen des brevets ^ DEMANDE DE BREVET EUROPEEN Numéro de dépôt: 83402232.9 @ Int. Cl.3: G 06 F 7/52 Date de
Patentamt JEuropaisches European Patent Office Numéro de publication: 0 1 1 0 7 6 7 Office européen des brevets ^ DEMANDE DE BREVET EUROPEEN Numéro de dépôt: 83402232.9 @ Int. Cl.3: G 06 F 7/52 Date de
Livret - 1. Informatique : le matériel. --- Ordinateur, circuits, codage, système, réseau. Cours informatique programmation.
 Livret - 1 Informatique : le matériel --- Ordinateur, circuits, codage, système, réseau. RM di scala Cours informatique programmation Rm di Scala - http://www.discala.net SOMMAIRE Introduction 2 Notations
Livret - 1 Informatique : le matériel --- Ordinateur, circuits, codage, système, réseau. RM di scala Cours informatique programmation Rm di Scala - http://www.discala.net SOMMAIRE Introduction 2 Notations
GPA770 Microélectronique appliquée Exercices série A
 GPA770 Microélectronique appliquée Exercices série A 1. Effectuez les calculs suivants sur des nombres binaires en complément à avec une représentation de 8 bits. Est-ce qu il y a débordement en complément
GPA770 Microélectronique appliquée Exercices série A 1. Effectuez les calculs suivants sur des nombres binaires en complément à avec une représentation de 8 bits. Est-ce qu il y a débordement en complément
La conversion de données : Convertisseur Analogique Numérique (CAN) Convertisseur Numérique Analogique (CNA)
 La conversion de données : Convertisseur Analogique Numérique (CAN) Convertisseur Numérique Analogique (CNA) I. L'intérêt de la conversion de données, problèmes et définitions associés. I.1. Définitions:
La conversion de données : Convertisseur Analogique Numérique (CAN) Convertisseur Numérique Analogique (CNA) I. L'intérêt de la conversion de données, problèmes et définitions associés. I.1. Définitions:
MPI Activité.10 : Logique binaire Portes logiques
 MPI Activité.10 : Logique binaire Portes logiques I. Introduction De nombreux domaines font appel aux circuits logiques de commutation : non seulement l'informatique, mais aussi les technologies de l'asservissement
MPI Activité.10 : Logique binaire Portes logiques I. Introduction De nombreux domaines font appel aux circuits logiques de commutation : non seulement l'informatique, mais aussi les technologies de l'asservissement
QUESTION 1 {2 points}
 ELE4301 Systèmes logiques II Page 1 de 8 QUESTION 1 {2 points} En se servant de paramètres électriques donnés dans le Tableau 1 ci-dessous, on désire déterminer la fréquence d opération du compteur présenté
ELE4301 Systèmes logiques II Page 1 de 8 QUESTION 1 {2 points} En se servant de paramètres électriques donnés dans le Tableau 1 ci-dessous, on désire déterminer la fréquence d opération du compteur présenté
Arithmétique binaire. Chapitre. 5.1 Notions. 5.1.1 Bit. 5.1.2 Mot
 Chapitre 5 Arithmétique binaire L es codes sont manipulés au quotidien sans qu on s en rende compte, et leur compréhension est quasi instinctive. Le seul fait de lire fait appel au codage alphabétique,
Chapitre 5 Arithmétique binaire L es codes sont manipulés au quotidien sans qu on s en rende compte, et leur compréhension est quasi instinctive. Le seul fait de lire fait appel au codage alphabétique,
Logique séquentielle
 Bascules et logique séquentielle aniel Etiemble de@lri.fr Logique séquentielle Logique séquentielle Le système a des «états» ans un système séquentiel Éléments de mémorisation Les sorties dépendent des
Bascules et logique séquentielle aniel Etiemble de@lri.fr Logique séquentielle Logique séquentielle Le système a des «états» ans un système séquentiel Éléments de mémorisation Les sorties dépendent des
ELP 304 : Électronique Numérique. Cours 1 Introduction
 ELP 304 : Électronique Numérique Cours 1 Introduction Catherine Douillard Dépt Électronique Les systèmes numériques : généralités (I) En électronique numérique, le codage des informations utilise deux
ELP 304 : Électronique Numérique Cours 1 Introduction Catherine Douillard Dépt Électronique Les systèmes numériques : généralités (I) En électronique numérique, le codage des informations utilise deux
- Instrumentation numérique -
 - Instrumentation numérique - I.Présentation du signal numérique. I.1. Définition des différents types de signaux. Signal analogique: Un signal analogique a son amplitude qui varie de façon continue au
- Instrumentation numérique - I.Présentation du signal numérique. I.1. Définition des différents types de signaux. Signal analogique: Un signal analogique a son amplitude qui varie de façon continue au
Université de La Rochelle. Réseaux TD n 6
 Réseaux TD n 6 Rappels : Théorème de Nyquist (ligne non bruitée) : Dmax = 2H log 2 V Théorème de Shannon (ligne bruitée) : C = H log 2 (1+ S/B) Relation entre débit binaire et rapidité de modulation :
Réseaux TD n 6 Rappels : Théorème de Nyquist (ligne non bruitée) : Dmax = 2H log 2 V Théorème de Shannon (ligne bruitée) : C = H log 2 (1+ S/B) Relation entre débit binaire et rapidité de modulation :
2.4 Représentation graphique, tableau de Karnaugh
 2 Fonctions binaires 45 2.4 Représentation graphique, tableau de Karnaugh On peut définir complètement une fonction binaire en dressant son tableau de Karnaugh, table de vérité à 2 n cases pour n variables
2 Fonctions binaires 45 2.4 Représentation graphique, tableau de Karnaugh On peut définir complètement une fonction binaire en dressant son tableau de Karnaugh, table de vérité à 2 n cases pour n variables
Vers l'ordinateur quantique
 Cours A&G Vers l'ordinateur quantique Données innies On a vu dans les chapîtres précédents qu'un automate permet de représenter de manière nie (et même compacte) une innité de données. En eet, un automate
Cours A&G Vers l'ordinateur quantique Données innies On a vu dans les chapîtres précédents qu'un automate permet de représenter de manière nie (et même compacte) une innité de données. En eet, un automate
V- Manipulations de nombres en binaire
 1 V- Manipulations de nombres en binaire L ordinateur est constitué de milliards de transistors qui travaillent comme des interrupteurs électriques, soit ouverts soit fermés. Soit la ligne est activée,
1 V- Manipulations de nombres en binaire L ordinateur est constitué de milliards de transistors qui travaillent comme des interrupteurs électriques, soit ouverts soit fermés. Soit la ligne est activée,
CONVERTISSEURS NA ET AN
 Convertisseurs numériques analogiques (xo Convertisseurs.doc) 1 CONVTIU NA T AN NOT PLIMINAI: Tous les résultats seront exprimés sous formes littérales et encadrées avant les applications numériques. Les
Convertisseurs numériques analogiques (xo Convertisseurs.doc) 1 CONVTIU NA T AN NOT PLIMINAI: Tous les résultats seront exprimés sous formes littérales et encadrées avant les applications numériques. Les
J AUVRAY Systèmes Electroniques TRANSMISSION DES SIGNAUX NUMERIQUES : SIGNAUX EN BANDE DE BASE
 RANSMISSION DES SIGNAUX NUMERIQUES : SIGNAUX EN BANDE DE BASE Un message numérique est une suite de nombres que l on considérera dans un premier temps comme indépendants.ils sont codés le plus souvent
RANSMISSION DES SIGNAUX NUMERIQUES : SIGNAUX EN BANDE DE BASE Un message numérique est une suite de nombres que l on considérera dans un premier temps comme indépendants.ils sont codés le plus souvent
Manipulations du laboratoire
 Manipulations du laboratoire 1 Matériel Les manipulations de ce laboratoire sont réalisées sur une carte électronique comprenant un compteur 4-bit asynchrone (74LS93) avec possibilité de déclenchement
Manipulations du laboratoire 1 Matériel Les manipulations de ce laboratoire sont réalisées sur une carte électronique comprenant un compteur 4-bit asynchrone (74LS93) avec possibilité de déclenchement
Organisation des Ordinateurs
 Organisation des Ordinateurs Bernard Boigelot E-mail : boigelot@montefiore.ulg.ac.be URL : http://www.montefiore.ulg.ac.be/~boigelot/ http://www.montefiore.ulg.ac.be/~boigelot/cours/org/ 1 Chapitre 1 Les
Organisation des Ordinateurs Bernard Boigelot E-mail : boigelot@montefiore.ulg.ac.be URL : http://www.montefiore.ulg.ac.be/~boigelot/ http://www.montefiore.ulg.ac.be/~boigelot/cours/org/ 1 Chapitre 1 Les
ET 24 : Modèle de comportement d un système Boucles de programmation avec Labview.
 ET 24 : Modèle de comportement d un système Boucles de programmation avec Labview. Sciences et Technologies de l Industrie et du Développement Durable Formation des enseignants parcours : ET24 Modèle de
ET 24 : Modèle de comportement d un système Boucles de programmation avec Labview. Sciences et Technologies de l Industrie et du Développement Durable Formation des enseignants parcours : ET24 Modèle de
TD Architecture des ordinateurs. Jean-Luc Dekeyser
 TD Architecture des ordinateurs Jean-Luc Dekeyser Fiche 1 Nombres de l informatique Exercice 1 Une entreprise désire réaliser la sauvegarde de ses données sur un site distant. Le volume de données à sauvegarder
TD Architecture des ordinateurs Jean-Luc Dekeyser Fiche 1 Nombres de l informatique Exercice 1 Une entreprise désire réaliser la sauvegarde de ses données sur un site distant. Le volume de données à sauvegarder
SUR MODULE CAMÉRA C38A (OV7620)
 Applications maquette d'étude EP10K20 DÉMULTIPLEXEUR BT.656 SUR MODULE CAMÉRA C38A OV7620 SCHÉMAS ET DESCRIPTIONS AHDL 1. Schéma principal Le démultiplexeur proprement dit est la fonction "Decod_BT656_1".
Applications maquette d'étude EP10K20 DÉMULTIPLEXEUR BT.656 SUR MODULE CAMÉRA C38A OV7620 SCHÉMAS ET DESCRIPTIONS AHDL 1. Schéma principal Le démultiplexeur proprement dit est la fonction "Decod_BT656_1".
Modules d automatismes simples
 Modules d automatismes simples Solutions pour automatiser Modules d'automatismes Enfin, vraiment simple! Un concentré de solution Pour vos petites applications d'automatismes millenium gère : Temporisations
Modules d automatismes simples Solutions pour automatiser Modules d'automatismes Enfin, vraiment simple! Un concentré de solution Pour vos petites applications d'automatismes millenium gère : Temporisations
2.1 Le point mémoire statique Le point mémoire statique est fondé sur le bistable, dessiné de manière différente en Figure 1.
 Mémoires RAM 1. LOGIUE STATIUE ET LOGIUE DYNAMIUE Le point mémoire est l élément de base, capable de mémoriser un bit. Il y a deux approches possibles. L approche statique est fondée sur la l'utilisation
Mémoires RAM 1. LOGIUE STATIUE ET LOGIUE DYNAMIUE Le point mémoire est l élément de base, capable de mémoriser un bit. Il y a deux approches possibles. L approche statique est fondée sur la l'utilisation
Les opérations binaires
 Les opérations binaires Compétences associées A2 : Analyser et interpréter une information numérique Objectifs Etre capable: - De coder les nombres entiers en code complément à 2. - De résoudre les opérations
Les opérations binaires Compétences associées A2 : Analyser et interpréter une information numérique Objectifs Etre capable: - De coder les nombres entiers en code complément à 2. - De résoudre les opérations
REALISATION d'un. ORDONNANCEUR à ECHEANCES
 REALISATION d'un ORDONNANCEUR à ECHEANCES I- PRÉSENTATION... 3 II. DESCRIPTION DU NOYAU ORIGINEL... 4 II.1- ARCHITECTURE... 4 II.2 - SERVICES... 4 III. IMPLÉMENTATION DE L'ORDONNANCEUR À ÉCHÉANCES... 6
REALISATION d'un ORDONNANCEUR à ECHEANCES I- PRÉSENTATION... 3 II. DESCRIPTION DU NOYAU ORIGINEL... 4 II.1- ARCHITECTURE... 4 II.2 - SERVICES... 4 III. IMPLÉMENTATION DE L'ORDONNANCEUR À ÉCHÉANCES... 6
BCI - TPSP - Processeurs et Architectures Numériques
 BCI - TPSP - Processeurs et Architectures Numériques Jean-Luc Danger Guillaume Duc Tarik Graba Philippe Matherat Yves Mathieu Lirida Naviner Alexis Polti Jean Provost c 2002-2011 groupe SEN, Télécom ParisTech
BCI - TPSP - Processeurs et Architectures Numériques Jean-Luc Danger Guillaume Duc Tarik Graba Philippe Matherat Yves Mathieu Lirida Naviner Alexis Polti Jean Provost c 2002-2011 groupe SEN, Télécom ParisTech
I- Définitions des signaux.
 101011011100 010110101010 101110101101 100101010101 Du compact-disc, au DVD, en passant par l appareil photo numérique, le scanner, et télévision numérique, le numérique a fait une entrée progressive mais
101011011100 010110101010 101110101101 100101010101 Du compact-disc, au DVD, en passant par l appareil photo numérique, le scanner, et télévision numérique, le numérique a fait une entrée progressive mais
Cours Informatique 1. Monsieur SADOUNI Salheddine
 Cours Informatique 1 Chapitre 2 les Systèmes Informatique Monsieur SADOUNI Salheddine Un Système Informatique lesystème Informatique est composé de deux parties : -le Matériel : constitué de l unité centrale
Cours Informatique 1 Chapitre 2 les Systèmes Informatique Monsieur SADOUNI Salheddine Un Système Informatique lesystème Informatique est composé de deux parties : -le Matériel : constitué de l unité centrale
3. SPÉCIFICATIONS DU LOGICIEL. de l'expression des besoins à la conception. Spécifications fonctionnelles Analyse fonctionnelle et méthodes
 PLAN CYCLE DE VIE D'UN LOGICIEL EXPRESSION DES BESOINS SPÉCIFICATIONS DU LOGICIEL CONCEPTION DU LOGICIEL LA PROGRAMMATION TESTS ET MISE AU POINT DOCUMENTATION CONCLUSION C.Crochepeyre Génie Logiciel Diapason
PLAN CYCLE DE VIE D'UN LOGICIEL EXPRESSION DES BESOINS SPÉCIFICATIONS DU LOGICIEL CONCEPTION DU LOGICIEL LA PROGRAMMATION TESTS ET MISE AU POINT DOCUMENTATION CONCLUSION C.Crochepeyre Génie Logiciel Diapason
ASR1 TD7 : Un microprocesseur RISC 16 bits
 {Â Ö Ñ º ØÖ Ý,È ØÖ ºÄÓ Ù,Æ ÓÐ ºÎ ÝÖ Ø¹ ÖÚ ÐÐÓÒ} Ò ¹ÐÝÓÒº Ö ØØÔ»»Ô Ö Óº Ò ¹ÐÝÓÒº Ö» Ö Ñ º ØÖ Ý»¼ Ö½» ASR1 TD7 : Un microprocesseur RISC 16 bits 13, 20 et 27 novembre 2006 Présentation générale On choisit
{Â Ö Ñ º ØÖ Ý,È ØÖ ºÄÓ Ù,Æ ÓÐ ºÎ ÝÖ Ø¹ ÖÚ ÐÐÓÒ} Ò ¹ÐÝÓÒº Ö ØØÔ»»Ô Ö Óº Ò ¹ÐÝÓÒº Ö» Ö Ñ º ØÖ Ý»¼ Ö½» ASR1 TD7 : Un microprocesseur RISC 16 bits 13, 20 et 27 novembre 2006 Présentation générale On choisit
Informatique Générale
 Informatique Générale Guillaume Hutzler Laboratoire IBISC (Informatique Biologie Intégrative et Systèmes Complexes) guillaume.hutzler@ibisc.univ-evry.fr Cours Dokeos 625 http://www.ens.univ-evry.fr/modx/dokeos.html
Informatique Générale Guillaume Hutzler Laboratoire IBISC (Informatique Biologie Intégrative et Systèmes Complexes) guillaume.hutzler@ibisc.univ-evry.fr Cours Dokeos 625 http://www.ens.univ-evry.fr/modx/dokeos.html
Concevoir son microprocesseur
 Concevoir son microprocesseur structure des systèmes logiques Jean-Christophe Buisson Collection Technosup Ellipses Avant-propos Ce livre s adresse aux étudiants en informatique de licence et maîtrise,
Concevoir son microprocesseur structure des systèmes logiques Jean-Christophe Buisson Collection Technosup Ellipses Avant-propos Ce livre s adresse aux étudiants en informatique de licence et maîtrise,
Les diagrammes de modélisation
 L approche Orientée Objet et UML 1 Plan du cours Introduction au Génie Logiciel L approche Orientée Objet et Notation UML Les diagrammes de modélisation Relations entre les différents diagrammes De l analyse
L approche Orientée Objet et UML 1 Plan du cours Introduction au Génie Logiciel L approche Orientée Objet et Notation UML Les diagrammes de modélisation Relations entre les différents diagrammes De l analyse
Cours Premier semestre
 C.Belleudy, D.Gaffé Université de Nice-Sophia Antipolis DEUG Première année SM,MP,MI UECS EEA Électronique Numérique Cours Premier semestre C. Belleudy, D.Gaffé version 3. 2 Électronique Numérique Chapitre
C.Belleudy, D.Gaffé Université de Nice-Sophia Antipolis DEUG Première année SM,MP,MI UECS EEA Électronique Numérique Cours Premier semestre C. Belleudy, D.Gaffé version 3. 2 Électronique Numérique Chapitre
CHAPITRE VIII : Les circuits avec résistances ohmiques
 CHAPITRE VIII : Les circuits avec résistances ohmiques VIII. 1 Ce chapitre porte sur les courants et les différences de potentiel dans les circuits. VIII.1 : Les résistances en série et en parallèle On
CHAPITRE VIII : Les circuits avec résistances ohmiques VIII. 1 Ce chapitre porte sur les courants et les différences de potentiel dans les circuits. VIII.1 : Les résistances en série et en parallèle On
CHAPITRE VI ALEAS. 6.1.Généralités.
 CHAPITRE VI ALEAS 6.1.Généralités. Lors de la synthèse des systèmes logique (combinatoires ou séquentiels), nous avons supposé, implicitement, qu une même variable secondaire avait toujours la même valeur
CHAPITRE VI ALEAS 6.1.Généralités. Lors de la synthèse des systèmes logique (combinatoires ou séquentiels), nous avons supposé, implicitement, qu une même variable secondaire avait toujours la même valeur
CHAPITRE XIII : Les circuits à courant alternatif : déphasage, représentation de Fresnel, phaseurs et réactance.
 XIII. 1 CHAPITRE XIII : Les circuits à courant alternatif : déphasage, représentation de Fresnel, phaseurs et réactance. Dans les chapitres précédents nous avons examiné des circuits qui comportaient différentes
XIII. 1 CHAPITRE XIII : Les circuits à courant alternatif : déphasage, représentation de Fresnel, phaseurs et réactance. Dans les chapitres précédents nous avons examiné des circuits qui comportaient différentes
UE 503 L3 MIAGE. Initiation Réseau et Programmation Web La couche physique. A. Belaïd
 UE 503 L3 MIAGE Initiation Réseau et Programmation Web La couche physique A. Belaïd abelaid@loria.fr http://www.loria.fr/~abelaid/ Année Universitaire 2011/2012 2 Le Modèle OSI La couche physique ou le
UE 503 L3 MIAGE Initiation Réseau et Programmation Web La couche physique A. Belaïd abelaid@loria.fr http://www.loria.fr/~abelaid/ Année Universitaire 2011/2012 2 Le Modèle OSI La couche physique ou le
Les techniques de multiplexage
 Les techniques de multiplexage 1 Le multiplexage et démultiplexage En effet, à partir du moment où plusieurs utilisateurs se partagent un seul support de transmission, il est nécessaire de définir le principe
Les techniques de multiplexage 1 Le multiplexage et démultiplexage En effet, à partir du moment où plusieurs utilisateurs se partagent un seul support de transmission, il est nécessaire de définir le principe
Représentation d un entier en base b
 Représentation d un entier en base b 13 octobre 2012 1 Prérequis Les bases de la programmation en langage sont supposées avoir été travaillées L écriture en base b d un entier est ainsi défini à partir
Représentation d un entier en base b 13 octobre 2012 1 Prérequis Les bases de la programmation en langage sont supposées avoir été travaillées L écriture en base b d un entier est ainsi défini à partir
Calculons avec Albert!
 Calculons avec Albert! Par : Guy Lefebvre, 1257 rue Principale, St-Prime, G8J 1V2, 418-251-2170 Guillaume Rainville, 610 8 e rue, St-Prime, G8J 1P6, 418-251-8290 Résumé : Lefebvre G. et Rainville G., 2001,
Calculons avec Albert! Par : Guy Lefebvre, 1257 rue Principale, St-Prime, G8J 1V2, 418-251-2170 Guillaume Rainville, 610 8 e rue, St-Prime, G8J 1P6, 418-251-8290 Résumé : Lefebvre G. et Rainville G., 2001,
Codage d information. Codage d information : -Définition-
 Introduction Plan Systèmes de numération et Représentation des nombres Systèmes de numération Système de numération décimale Représentation dans une base b Représentation binaire, Octale et Hexadécimale
Introduction Plan Systèmes de numération et Représentation des nombres Systèmes de numération Système de numération décimale Représentation dans une base b Représentation binaire, Octale et Hexadécimale
Structures algébriques
 Structures algébriques 1. Lois de composition s Soit E un ensemble. Une loi de composition interne sur E est une application de E E dans E. Soient E et F deux ensembles. Une loi de composition externe
Structures algébriques 1. Lois de composition s Soit E un ensemble. Une loi de composition interne sur E est une application de E E dans E. Soient E et F deux ensembles. Une loi de composition externe
IV- Comment fonctionne un ordinateur?
 1 IV- Comment fonctionne un ordinateur? L ordinateur est une alliance du hardware (le matériel) et du software (les logiciels). Jusqu à présent, nous avons surtout vu l aspect «matériel», avec les interactions
1 IV- Comment fonctionne un ordinateur? L ordinateur est une alliance du hardware (le matériel) et du software (les logiciels). Jusqu à présent, nous avons surtout vu l aspect «matériel», avec les interactions
OPÉRATIONS SUR LES FRACTIONS
 OPÉRATIONS SUR LES FRACTIONS Sommaire 1. Composantes d'une fraction... 1. Fractions équivalentes... 1. Simplification d'une fraction... 4. Règle d'addition et soustraction de fractions... 5. Règle de multiplication
OPÉRATIONS SUR LES FRACTIONS Sommaire 1. Composantes d'une fraction... 1. Fractions équivalentes... 1. Simplification d'une fraction... 4. Règle d'addition et soustraction de fractions... 5. Règle de multiplication
Chapitre 4 : Les mémoires
 1. Introduction: Chapitre 4 : Les mémoires Nous savons que dans un ordinateur toutes les informations : valeur numérique, instruction, adresse, symbole (chiffre, lettre,... etc.) sont manipulées sous une
1. Introduction: Chapitre 4 : Les mémoires Nous savons que dans un ordinateur toutes les informations : valeur numérique, instruction, adresse, symbole (chiffre, lettre,... etc.) sont manipulées sous une
Logiciel de Base. I. Représentation des nombres
 Logiciel de Base (A1-06/07) Léon Mugwaneza ESIL/Dépt. Informatique (bureau A118) mugwaneza@univmed.fr I. Représentation des nombres Codage et représentation de l'information Information externe formats
Logiciel de Base (A1-06/07) Léon Mugwaneza ESIL/Dépt. Informatique (bureau A118) mugwaneza@univmed.fr I. Représentation des nombres Codage et représentation de l'information Information externe formats
Cours de Génie Logiciel
 Cours de Génie Logiciel Sciences-U Lyon Diagrammes UML (2) http://www.rzo.free.fr Pierre PARREND 1 Avril 2005 Sommaire Les Diagrammes UML Diagrammes de Collaboration Diagrammes d'etats-transitions Diagrammes
Cours de Génie Logiciel Sciences-U Lyon Diagrammes UML (2) http://www.rzo.free.fr Pierre PARREND 1 Avril 2005 Sommaire Les Diagrammes UML Diagrammes de Collaboration Diagrammes d'etats-transitions Diagrammes
UEO11 COURS/TD 1. nombres entiers et réels codés en mémoire centrale. Caractères alphabétiques et caractères spéciaux.
 UEO11 COURS/TD 1 Contenu du semestre Cours et TDs sont intégrés L objectif de ce cours équivalent a 6h de cours, 10h de TD et 8h de TP est le suivant : - initiation à l algorithmique - notions de bases
UEO11 COURS/TD 1 Contenu du semestre Cours et TDs sont intégrés L objectif de ce cours équivalent a 6h de cours, 10h de TD et 8h de TP est le suivant : - initiation à l algorithmique - notions de bases
Conversion d un entier. Méthode par soustraction
 Conversion entre bases Pour passer d un nombre en base b à un nombre en base 10, on utilise l écriture polynomiale décrite précédemment. Pour passer d un nombre en base 10 à un nombre en base b, on peut
Conversion entre bases Pour passer d un nombre en base b à un nombre en base 10, on utilise l écriture polynomiale décrite précédemment. Pour passer d un nombre en base 10 à un nombre en base b, on peut
REALISATION D UNE CALCULATRICE GRACE AU LOGICIEL CROCODILE CLIPS 3.
 1 sur 6 REALISATION D UNE CALCULATRICE GRACE AU LOGICIEL CROCODILE CLIPS 3. OBJECTIF - PUBLIC - LOGICIEL - MATERIEL - METHODE - BIBLIOGRAPHIE - AVANTAGES - DIFFICULTES - AUTEUR DU DOCUMENT - LE DOCUMENT
1 sur 6 REALISATION D UNE CALCULATRICE GRACE AU LOGICIEL CROCODILE CLIPS 3. OBJECTIF - PUBLIC - LOGICIEL - MATERIEL - METHODE - BIBLIOGRAPHIE - AVANTAGES - DIFFICULTES - AUTEUR DU DOCUMENT - LE DOCUMENT
Géométrie dans l espace Produit scalaire et équations
 Chapitre 11. 2ème partie Géométrie dans l espace Produit scalaire et équations Terminale S Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES 2ème partie Produit scalaire Produit scalaire
Chapitre 11. 2ème partie Géométrie dans l espace Produit scalaire et équations Terminale S Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES 2ème partie Produit scalaire Produit scalaire
Diagramme de classes
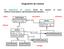 Diagramme de classes Un diagramme de classes décrit les classes et leurs relations (associations, généralisation/spécialisation, ). classe association méthodes attributs héritage Diagramme de classes :
Diagramme de classes Un diagramme de classes décrit les classes et leurs relations (associations, généralisation/spécialisation, ). classe association méthodes attributs héritage Diagramme de classes :
Représentation des Nombres
 Chapitre 5 Représentation des Nombres 5. Representation des entiers 5.. Principe des représentations en base b Base L entier écrit 344 correspond a 3 mille + 4 cent + dix + 4. Plus généralement a n a n...
Chapitre 5 Représentation des Nombres 5. Representation des entiers 5.. Principe des représentations en base b Base L entier écrit 344 correspond a 3 mille + 4 cent + dix + 4. Plus généralement a n a n...
Atelier C TIA Portal CTIA06 : programmation des automates S7-300 Blocs d organisation
 Atelier C TIA Portal CTIA06 : programmation des automates S7-300 Blocs d organisation CTIA06 Page 1 1. Types de blocs de programme L automate met à disposition différents types de blocs qui contiennent
Atelier C TIA Portal CTIA06 : programmation des automates S7-300 Blocs d organisation CTIA06 Page 1 1. Types de blocs de programme L automate met à disposition différents types de blocs qui contiennent
Tout savoir sur le matériel informatique
 Tout savoir sur le matériel informatique Thème de l exposé : Les Processeurs Date : 05 Novembre 2010 Orateurs : Hugo VIAL-JAIME Jérémy RAMBAUD Sommaire : 1. Introduction... 3 2. Historique... 4 3. Relation
Tout savoir sur le matériel informatique Thème de l exposé : Les Processeurs Date : 05 Novembre 2010 Orateurs : Hugo VIAL-JAIME Jérémy RAMBAUD Sommaire : 1. Introduction... 3 2. Historique... 4 3. Relation
Architecture des ordinateurs Introduction à l informatique
 Architecture des ordinateurs Introduction à l informatique 17 septembre 2004 1 2 3 4 5 6 Les interrupteurs... 0V 5V Ce sont des composants électroniques qui laissent pser un courant principal lorsque la
Architecture des ordinateurs Introduction à l informatique 17 septembre 2004 1 2 3 4 5 6 Les interrupteurs... 0V 5V Ce sont des composants électroniques qui laissent pser un courant principal lorsque la
Licence Sciences et Technologies Examen janvier 2010
 Université de Provence Introduction à l Informatique Licence Sciences et Technologies Examen janvier 2010 Année 2009-10 Aucun document n est autorisé Les exercices peuvent être traités dans le désordre.
Université de Provence Introduction à l Informatique Licence Sciences et Technologies Examen janvier 2010 Année 2009-10 Aucun document n est autorisé Les exercices peuvent être traités dans le désordre.
t 100. = 8 ; le pourcentage de réduction est : 8 % 1 t Le pourcentage d'évolution (appelé aussi taux d'évolution) est le nombre :
 Terminale STSS 2 012 2 013 Pourcentages Synthèse 1) Définition : Calculer t % d'un nombre, c'est multiplier ce nombre par t 100. 2) Exemples de calcul : a) Calcul d un pourcentage : Un article coûtant
Terminale STSS 2 012 2 013 Pourcentages Synthèse 1) Définition : Calculer t % d'un nombre, c'est multiplier ce nombre par t 100. 2) Exemples de calcul : a) Calcul d un pourcentage : Un article coûtant
Introduction à l architecture des ordinateurs. Adrien Lebre Décembre 2007
 Introduction à l architecture des ordinateurs Adrien Lebre Décembre 2007 Plan - partie 1 Vue d ensemble La carte mère Le processeur La mémoire principal Notion de bus Introduction à l architecture des
Introduction à l architecture des ordinateurs Adrien Lebre Décembre 2007 Plan - partie 1 Vue d ensemble La carte mère Le processeur La mémoire principal Notion de bus Introduction à l architecture des
CORRIGE LES NOMBRES DECIMAUX RELATIFS. «Réfléchir avant d agir!»
 Corrigé Cours de Mr JULES v3.3 Classe de Quatrième Contrat 1 Page 1 sur 13 CORRIGE LES NOMBRES DECIMAUX RELATIFS. «Réfléchir avant d agir!» «Correction en rouge et italique.» I. Les nombres décimaux relatifs.
Corrigé Cours de Mr JULES v3.3 Classe de Quatrième Contrat 1 Page 1 sur 13 CORRIGE LES NOMBRES DECIMAUX RELATIFS. «Réfléchir avant d agir!» «Correction en rouge et italique.» I. Les nombres décimaux relatifs.
Transmission de données. A) Principaux éléments intervenant dans la transmission
 Page 1 / 7 A) Principaux éléments intervenant dans la transmission A.1 Equipement voisins Ordinateur ou terminal Ordinateur ou terminal Canal de transmission ETTD ETTD ETTD : Equipement Terminal de Traitement
Page 1 / 7 A) Principaux éléments intervenant dans la transmission A.1 Equipement voisins Ordinateur ou terminal Ordinateur ou terminal Canal de transmission ETTD ETTD ETTD : Equipement Terminal de Traitement
Architecture : Circuits numériques et éléments d architecture
 Ecole Nationale Supérieure d Informatique et de Mathématiques Appliquées Architecture : Circuits numériques et éléments d architecture 1 ère année Année scolaire 2014 2015 Consignes Les exercices de ce
Ecole Nationale Supérieure d Informatique et de Mathématiques Appliquées Architecture : Circuits numériques et éléments d architecture 1 ère année Année scolaire 2014 2015 Consignes Les exercices de ce
LE PROBLEME DU PLUS COURT CHEMIN
 LE PROBLEME DU PLUS COURT CHEMIN Dans cette leçon nous définissons le modèle de plus court chemin, présentons des exemples d'application et proposons un algorithme de résolution dans le cas où les longueurs
LE PROBLEME DU PLUS COURT CHEMIN Dans cette leçon nous définissons le modèle de plus court chemin, présentons des exemples d'application et proposons un algorithme de résolution dans le cas où les longueurs
INF 232: Langages et Automates. Travaux Dirigés. Université Joseph Fourier, Université Grenoble 1 Licence Sciences et Technologies
 INF 232: Langages et Automates Travaux Dirigés Université Joseph Fourier, Université Grenoble 1 Licence Sciences et Technologies Année Académique 2013-2014 Année Académique 2013-2014 UNIVERSITÉ JOSEPH
INF 232: Langages et Automates Travaux Dirigés Université Joseph Fourier, Université Grenoble 1 Licence Sciences et Technologies Année Académique 2013-2014 Année Académique 2013-2014 UNIVERSITÉ JOSEPH
Introduction à l'informatique. Vincent Boyer et Jean Méhat
 Introduction à l'informatique Vincent Boyer et Jean Méhat 19 février 2010 Copyright (C) 2009 Jean Méhat Permission is granted to copy, distribute and/or modify this document under the terms of the GNU
Introduction à l'informatique Vincent Boyer et Jean Méhat 19 février 2010 Copyright (C) 2009 Jean Méhat Permission is granted to copy, distribute and/or modify this document under the terms of the GNU
TP Modulation Démodulation BPSK
 I- INTRODUCTION : TP Modulation Démodulation BPSK La modulation BPSK est une modulation de phase (Phase Shift Keying = saut discret de phase) par signal numérique binaire (Binary). La phase d une porteuse
I- INTRODUCTION : TP Modulation Démodulation BPSK La modulation BPSK est une modulation de phase (Phase Shift Keying = saut discret de phase) par signal numérique binaire (Binary). La phase d une porteuse
KL5121. Pour activer des sorties en fonction de la position d'un codeur
 KL5121 Pour activer des sorties en fonction de la position d'un codeur VERSION : 1.0 / PH DATE : 07 Février 2006 Sommaire Ce manuel explique de manière pratique les étapes successives pour mettre en œuvre
KL5121 Pour activer des sorties en fonction de la position d'un codeur VERSION : 1.0 / PH DATE : 07 Février 2006 Sommaire Ce manuel explique de manière pratique les étapes successives pour mettre en œuvre
INITIATION AU LANGAGE C SUR PIC DE MICROSHIP
 COURS PROGRAMMATION INITIATION AU LANGAGE C SUR MICROCONTROLEUR PIC page 1 / 7 INITIATION AU LANGAGE C SUR PIC DE MICROSHIP I. Historique du langage C 1972 : naissance du C dans les laboratoires BELL par
COURS PROGRAMMATION INITIATION AU LANGAGE C SUR MICROCONTROLEUR PIC page 1 / 7 INITIATION AU LANGAGE C SUR PIC DE MICROSHIP I. Historique du langage C 1972 : naissance du C dans les laboratoires BELL par
Architecture Matérielle et Logicielle (LIF6) Cahier d'exercices, automne 2014
 Architecture Matérielle et Logicielle (LIF6) Cahier d'exercices, automne 2014 Table des matières 1 Vue d'ensemble de l'ordinateur 4 11 Taille du bus, volume de mémoire centrale 4 12 Petits calculs autour
Architecture Matérielle et Logicielle (LIF6) Cahier d'exercices, automne 2014 Table des matières 1 Vue d'ensemble de l'ordinateur 4 11 Taille du bus, volume de mémoire centrale 4 12 Petits calculs autour
Electronique Numérique
 Electronique Numérique 1er tome Systèmes combinatoires Etienne Messerli Yves Meyer Septembre 2010 Version 1.4 Mise à jour de ce manuel La base du présent manuel a été écrit par M. Yves Meyer de l'école
Electronique Numérique 1er tome Systèmes combinatoires Etienne Messerli Yves Meyer Septembre 2010 Version 1.4 Mise à jour de ce manuel La base du présent manuel a été écrit par M. Yves Meyer de l'école
CONFIGURATION DE L AUTOMATE SIEMENS
 CONFIGURATION DE L AUTOMATE SIEMENS Créer un projet Dans le bureau de Windows, double-cliquer sur l icône «SIMATIC Manager» : Cliquer ensuite sur l icône «nouveau» : Choisir un nom de projet et valider
CONFIGURATION DE L AUTOMATE SIEMENS Créer un projet Dans le bureau de Windows, double-cliquer sur l icône «SIMATIC Manager» : Cliquer ensuite sur l icône «nouveau» : Choisir un nom de projet et valider
Algorithme. Table des matières
 1 Algorithme Table des matières 1 Codage 2 1.1 Système binaire.............................. 2 1.2 La numérotation de position en base décimale............ 2 1.3 La numérotation de position en base binaire..............
1 Algorithme Table des matières 1 Codage 2 1.1 Système binaire.............................. 2 1.2 La numérotation de position en base décimale............ 2 1.3 La numérotation de position en base binaire..............
Manuel de référence du langage Exemples Les aventures de Docteur R. www.irai.com
 Manuel de référence du langage Exemples Les aventures de Docteur R. www.irai.com 1. Eléments communs... 7 1.1. Les variables... 7 1.1.1. Les variables booléennes... 7 1.1.2. Les variables numériques...
Manuel de référence du langage Exemples Les aventures de Docteur R. www.irai.com 1. Eléments communs... 7 1.1. Les variables... 7 1.1.1. Les variables booléennes... 7 1.1.2. Les variables numériques...
3 ÉLÉMENTS forment un LABoratoire.
 3 ÉLÉMENTS forment un LABoratoire. L environnement d apprentissage COM3LAB combine l expérimentation et les avantages du e-learning interactif. La nouvelle unité centrale (console) est la jonction entre
3 ÉLÉMENTS forment un LABoratoire. L environnement d apprentissage COM3LAB combine l expérimentation et les avantages du e-learning interactif. La nouvelle unité centrale (console) est la jonction entre
Initiation à LabView : Les exemples d applications :
 Initiation à LabView : Les exemples d applications : c) Type de variables : Créer un programme : Exemple 1 : Calcul de c= 2(a+b)(a-3b) ou a, b et c seront des réels. «Exemple1» nom du programme : «Exemple
Initiation à LabView : Les exemples d applications : c) Type de variables : Créer un programme : Exemple 1 : Calcul de c= 2(a+b)(a-3b) ou a, b et c seront des réels. «Exemple1» nom du programme : «Exemple
Conception de circuits numériques et architecture des ordinateurs
 Conception de circuits numériques et architecture des ordinateurs Frédéric Pétrot et Sébastien Viardot Année universitaire 2011-2012 Structure du cours C1 C2 C3 C4 C5 C6 C7 C8 C9 C10 C11 C12 Codage des
Conception de circuits numériques et architecture des ordinateurs Frédéric Pétrot et Sébastien Viardot Année universitaire 2011-2012 Structure du cours C1 C2 C3 C4 C5 C6 C7 C8 C9 C10 C11 C12 Codage des
Matériel & Logiciels (Hardware & Software)
 CHAPITRE 2 HARDWARE & SOFTWARE P. 1 Chapitre 2 Matériel & Logiciels (Hardware & Software) 2.1 Matériel (Hardware) 2.1.1 Présentation de l'ordinateur Un ordinateur est un ensemble de circuits électronique
CHAPITRE 2 HARDWARE & SOFTWARE P. 1 Chapitre 2 Matériel & Logiciels (Hardware & Software) 2.1 Matériel (Hardware) 2.1.1 Présentation de l'ordinateur Un ordinateur est un ensemble de circuits électronique
MICROCONTROLEURS PIC PROGRAMMATION EN C. V. Chollet - cours-pic-13b - 09/12/2012 Page 1 sur 44
 MICROCONTROLEURS PIC PROGRAMMATION EN C V. Chollet - cours-pic-13b - 09/12/2012 Page 1 sur 44 Chapitre 1 GENERALITES 1 DEFINITION Un microcontrôleur est un microprocesseur RISC (Reduced Instruction Set
MICROCONTROLEURS PIC PROGRAMMATION EN C V. Chollet - cours-pic-13b - 09/12/2012 Page 1 sur 44 Chapitre 1 GENERALITES 1 DEFINITION Un microcontrôleur est un microprocesseur RISC (Reduced Instruction Set
Architecture des ordinateurs
 Architecture des ordinateurs Cours 4 5 novembre 2012 Archi 1/22 Micro-architecture Archi 2/22 Intro Comment assembler les différents circuits vus dans les cours précédents pour fabriquer un processeur?
Architecture des ordinateurs Cours 4 5 novembre 2012 Archi 1/22 Micro-architecture Archi 2/22 Intro Comment assembler les différents circuits vus dans les cours précédents pour fabriquer un processeur?
Notice d'utilisation Afficheur multifonctions et système d'évaluation FX 360. Mode/Enter
 Notice d'utilisation Afficheur multifonctions et système d'évaluation FR FX 360 7390275 / 08 07 / 2009 Mode/Enter Set Consignes de sécurité Cette notice fait partie de l'appareil. Elle fournit des textes
Notice d'utilisation Afficheur multifonctions et système d'évaluation FR FX 360 7390275 / 08 07 / 2009 Mode/Enter Set Consignes de sécurité Cette notice fait partie de l'appareil. Elle fournit des textes
SIN-FPGA DESCRIPTION PAR SCHEMA
 SIN-FPGA DESCRIPTION PAR SCHEMA Documents ressources: http://www.altera.com/literature/lit-index.html Introduction to Quartus II : intro_to_quartus2.pdf Documentation QUARTUS II : quartusii_handbook.pdf
SIN-FPGA DESCRIPTION PAR SCHEMA Documents ressources: http://www.altera.com/literature/lit-index.html Introduction to Quartus II : intro_to_quartus2.pdf Documentation QUARTUS II : quartusii_handbook.pdf
DU BINAIRE AU MICROPROCESSEUR - D ANGELIS CIRCUITS CONFIGURABLES NOTION DE PROGRAMMATION
 145 NOTION DE PROGRAMMATION 1/ Complétons notre microprocesseur Nous avons, dans les leçons précédentes décrit un microprocesseur théorique, cependant il s inspire du 6800, premier microprocesseur conçu
145 NOTION DE PROGRAMMATION 1/ Complétons notre microprocesseur Nous avons, dans les leçons précédentes décrit un microprocesseur théorique, cependant il s inspire du 6800, premier microprocesseur conçu
Convertisseurs statiques d'énergie électrique
 Convertisseurs statiques d'énergie électrique I. Pourquoi des convertisseurs d'énergie électrique? L'énergie électrique utilisée dans l'industrie et chez les particuliers provient principalement du réseau
Convertisseurs statiques d'énergie électrique I. Pourquoi des convertisseurs d'énergie électrique? L'énergie électrique utilisée dans l'industrie et chez les particuliers provient principalement du réseau
Transmissions série et parallèle
 1. Introduction : Un signal numérique transmet généralement plusieurs digits binaires. Exemple : 01000001 ( huit bits). Dans une transmission numérique on peut envisager deux modes : les envoyer tous en
1. Introduction : Un signal numérique transmet généralement plusieurs digits binaires. Exemple : 01000001 ( huit bits). Dans une transmission numérique on peut envisager deux modes : les envoyer tous en
«SESSION 2009» Thème : GESTION DU SYSTEME D INFORMATION. Durée : 2 h 00 (Coef. 3) Chaque question peut comporter plus d'une bonne réponse
 CONCOURS DE TECHNICIEN DES SYSTEMES D INFORMATION ET DE COMMUNICATION «SESSION 2009» CONCOURS INTERNE Questionnaire à choix multiple, soumis au choix du candidat, portant sur le thème suivant : Thème :
CONCOURS DE TECHNICIEN DES SYSTEMES D INFORMATION ET DE COMMUNICATION «SESSION 2009» CONCOURS INTERNE Questionnaire à choix multiple, soumis au choix du candidat, portant sur le thème suivant : Thème :
LA MESURE INDUSTRIELLE
 E02 LA MESURE INDUSTRIELLE 20 Heures Technicien responsable de la maintenance Approfondir les techniques de mesure; Prendre en compte l aspect métrologie. Connaître les limites et les facteurs d influences
E02 LA MESURE INDUSTRIELLE 20 Heures Technicien responsable de la maintenance Approfondir les techniques de mesure; Prendre en compte l aspect métrologie. Connaître les limites et les facteurs d influences
UNIVERSITE D'ORLEANS ISSOUDUN CHATEAUROUX
 UNIVERSITE D'ORLEANS ISSOUDUN CHATEAUROUX PLAN
UNIVERSITE D'ORLEANS ISSOUDUN CHATEAUROUX PLAN
Conception de circuits numériques et architecture des ordinateurs
 Conception de circuits numériques et architecture des ordinateurs Frédéric Pétrot Année universitaire 2014-2015 Structure du cours C1 C2 C3 C4 C5 C6 C7 C8 C9 C10 C11 Codage des nombres en base 2, logique
Conception de circuits numériques et architecture des ordinateurs Frédéric Pétrot Année universitaire 2014-2015 Structure du cours C1 C2 C3 C4 C5 C6 C7 C8 C9 C10 C11 Codage des nombres en base 2, logique
