Compilation. Algorithmes d'analyse syntaxique
|
|
|
- Antonin Bouffard
- il y a 8 ans
- Total affichages :
Transcription
1 Compilation Algorithmes d'analyse syntaxique
2 Préliminaires Si A est un non-terminal et γ une suite de terminaux et de non-terminaux, on note : A γ si en partant de A on peut arriver à γ par dérivations successives (y compris aucune donc A A).
3 Préliminaires Non-terminaux : E Terminaux : '+' 'n' 'id' E ::= E '+' E 'id' 'n' E E '+' E 'id' '+' E 'id' '+' E '+' E 'id' '+' E '+' 'n' E E E 'id' '+' E '+' E E 'id' '+' E '+' 'n' 'id' '+' E 'id' '+' E '+' 'n'
4 Algorithmes d'analyse syntaxique Il existe deux principaux types algorithmes d'analyse syntaxique : prédictifs ou descendants ou LL Left-to-right Leftmost ascendants ou LR Left-to-right Rightmost
5 Algorithmes d'analyse syntaxique Ces deux algorithmes nécessitent de calculer, à partir de la grammaire algébrique : l'ensemble Annulable (nullable) la fonction Premier (first) la fonction Suivant (follow)
6 Annulable, premier et suivant Les algorithmes pour calculer ces trois objets ont tous le même déroulement : On dispose de propriétés caractéristiques sur ces objets On applique les propriétés pour obtenir des équations ensemblistes entre ces objets On résoud le système d'équations ensemblistes
7 Annulable, premier et suivant Dans les propriétés qui suivent : On apprend quelque chose sur X [à l'aide de Y] [quand les Z i sont annulables]
8 L'ensemble Annulable L'ensemble Annulable contient l'ensemble des non terminaux annulables, c'est-à-dire ceux qui peuvent se dériver en ε, éventuellement en appliquant plusieurs productions : X Annulable si X ε
9 L'ensemble Annulable Non-terminaux : S X Y Terminaux : 'a' 'c' 'd' Productions : S ::= X Y S 'd' Y ::= 'c' ε X ::= Y 'a' Annulable = {X,Y}
10 Propriétés de Annulable Propriétés : 1)Si X ::= ε est une productions, alors X est annulable 2)Si X ::= Z 1 Z 2 Z k est une production, et que tous les nonterminaux Z i sont annulables, alors X est annulable. Remarques : S'il n'y a aucune production de type X ::= ε, aucun nonterminal n'est annulable Seules les production dont le membre droit est ε ou ne contient que des non-terminaux sont à considérer Les productions qui donnent des informations sur X sont celles dont le membre gauche est X
11 Calcul de Annulable On commence par déclarer annulable les non-terminaux X pour lesquels il y a une production X ::= ε À l'aide des productions dont le membre droit ne contient que des non-terminaux, ajouter à l'ensemble Annulable les non-terminaux rendus annulables par la propriété 2) Remarques Une fois que l'on sait un non-terminal annulable, on n'a plus besoin de considérer les productions associées
12 Exemple Non-terminaux : S X Y Terminaux : 'a' 'c' 'd' Productions : S ::= X Y S 'd' Y ::= 'c' ε X ::= Y 'a' 1)Y est annulable avec Y ::= ε 2)Les productions potentiellement utiles sont X ::= Y et S ::= X Y S 3)X est annulable avec X ::= Y 4)On n'apprend plus rien donc seuls X et Y sont annulables
13 La fonction Premier La fonction Premier associe à un non-terminal l'ensemble des terminaux qui peuvent apparaître en premier une fois appliquées une ou plusieurs dérivations à partir de ce non-terminal : a Premier(X) si X aγ γ est une suite de terminaux et non-terminaux, éventuellement vide
14 La fonction Premier Non-terminaux : S E T F Terminaux : '+' '-' ' ' '*' '(' ')' 'id' 'n' '$' Productions : S ::= E '$' E ::= E '+' T '-' T T T ::= T ' ' F '*' F F F ::= 'id' 'n' '(' E ')' Premier(E) = {'(','id','n','*','-'} Premier(T) = {'(','id','n','*'} Premier(F) = {'(','id','n'}
15 Propriétés de Premier Propriétés : 1)Si X ::= 'a' γ est une production alors 'a' Premier(X) 2)Si X ::= Y γ est une production alors Premier(X) contient tous les terminaux de Premier(Y) 3)Si X ::= Z 1 Z 2 Z k 'a' γ est une production et que les Z i sont annulables alors 'a' Premier(X) (et Premier(X) contient tous les terminaux des Premier(Z i )) 4)Si X ::= Z 1 Z 2 Z k Y γ est une production et que les Z i sont annulables alors Premier(X) contient tous les terminaux de Premier(Y) (et des Premier(Z i ))
16 Propriétés de Premier Remarques 1)Les productions qui donnent des informations sur X sont celles dont le membre gauche est X 2)La production E ::= E γ enseigne que Premier(E) contient Premier(E), ce que l'on savait déjà, mais attention si E est annulable
17 Calcul de Premier Calculer l'ensemble Annulable Pour chaque non-terminal E, appliquer les propriétés aux productions dont le membre gauche est E pour trouver Premier(E) en fonction des autres ensembles Premier on abrégera Premier(X) en P(X) Résoudre les équations ensemblistes pour trouver ces ensembles en remplaçant les ensembles connus dans les équations si cela ne suffit pas, réfléchir!
18 Exemple Non-terminaux : S E T F Terminaux : '+' '-' ' ' '*' '(' ')' 'id' 'n' '$' Productions : S ::= E '$' E ::= E '+' T '-' T T T ::= T ' ' F '*' F F F ::= 'id' 'n' '(' E ')' Premier(S) : P(E) Premier(E) : '-',P(T) Premier(T) : '*',P(F) Premier(F) : 'id','n','(' Premier(T) : '*','id','n','(' Premier(E) : '-','*','id','n','(' Premier(S) : '-','*','id','n','('
19 Exemple Non-terminaux : S X Y Terminaux : 'a' 'c' 'd' Productions : S ::= X Y S 'd' Y ::= 'c' ε X ::= Y 'a' Annulable = {X,Y} Premier(S) : P(X),P(Y),'d' Premier(Y) : 'c' Premier(X) : P(Y),'a' Premier(X) : 'c','a' Premier(S) : 'c','a','d'
20 Exemple Non-terminaux : S Y Terminaux : 'c' 'd' Productions : S ::= Y 'd' ε Y ::= S 'c' ε Annulable = {S,Y} Premier(S) : P(Y),'d' Premier(Y) : P(S),'c' En réfléchissant : Premier(S)={'c','d'} Premier(Y)={'c','d'}
21 La fonction Suivant La fonction Suivant associe à un non-terminal, les terminaux qui peuvent apparaître après ce non-terminal dans une suite de dérivations issues du start : b Suivant(X) si S γxbδ γ et δ sont des suites de non-terminaux et de terminaux, éventuellement vides
22 La fonction Suivant Non-terminaux : S E T F Terminaux : '+' '-' ' ' ' ' '(' ')' 'id' 'n' '$' Productions : S ::= E '$' E ::= E '+' T E '-' T T T ::= T ' ' F T ' ' F F F ::= 'n' 'id' '(' E ')' Suivant(E)={+,-,),$} Suivant(T)={,,+,-,),$} Suivant(F)={,,+,-,),$}
23 Propriétés de Suivant Propriétés : 1)Si A ::= γ X 'a' δ alors 'a' est dans Suivant(X) 2)Si A ::= γ X Y δ alors Premier(Y) est dans Suivant(X) 3)Si Y ::= γ X alors Suivant(X) contient Suivant(Y) 4)Si A ::= γ X Z 1 Z 2 Z n 'a' δ et que tous les Z i sont annulables alors 'a' est dans Suivant(X) (ainsi que les Premier(Z i )) 5)Si A ::= γ X Z 1 Z 2 Z n Y δ et que tous les Z i sont annulables alors Premier(Y) est dans Suivant(X) (ainsi que les Premier(Z i )) 6)Si Y ::= γ X Z 1 Z 2 Z n et que tous les Z i sont annulables alors Suivant(X) contient Suivant(Y) (ainsi que les Premier(Z i ))
24 Propriétés de Suivant Remarques 1)Les productions qui donnent des informations sur X sont celles dont le membre droit contient X, pour chaque occurrence de X 2)La production E ::= γ E enseigne que Suivant(E) contient Suivant(E), ce que l'on savait déjà
25 Calcul de Suivant Calculer Annulable et Premier Pour chaque non-terminal E, appliquer les propriétés à chaque occurrence de E dans les membres droits des productions on abrégera Suivant(X) en S(X) : regarder ce qui suit : si c'est un terminal 'x', ajouter 'x' à Suivant(E) si c'est un non-terminal Y, ajouter P(Y) à Suivant(E) si Y est annulable, reprendre à partir de ce qui suit Y là si rien ne suit, ajouter S(A) à Suivant(E), où A est le membre gauche de la production Résoudre les inéquations ensemblistes.
26 Exemple Non-terminaux : S E T F Terminaux : '+' '-' ' ' ' ' '(' ')' 'id' 'n' '$' Productions : S ::= E '$' E ::= E '+' T E '-' T T T ::= T ' ' F T ' ' F F F ::= 'n' 'id' '(' E ')' Suivant(E) : '$','+','-',')' Suivant(T) : S(E),' ',' ' Suivant(F) : S(T) Suivant(T)='+','-',')','$',' ',' ' Suivant(F)='+','-',')','$',' ',' '
27 Exemple Non-terminaux : S X Y Terminaux : 'a' 'c' 'd' Productions : S ::= X Y S 'd' Y ::= 'c' ε X ::= Y 'a' Annulable = {X,Y} Premier(Y) : 'c' Premier(X) : 'c','a' Premier(S) : 'c','a','d' Suivant(S) : vide Suivant(Y) : P(S),S(S),S(X) Suivant(X) : P(Y),P(S),S(S) Suivant(X) : 'c','a','d' Suivant(Y) : 'c','a','d'
28 Exemple Non-terminaux : S E O F Terminaux : '+' '-' 'n' '(' ')' Productions : S ::= E '$' E ::= E O E F O ::= '+' '-' ε F ::= 'n' '(' E ')' Annulable={O} Premier(O)={+,-} Premier(E)={n,(} Suivant(S) : vide Suivant(E) : P(O),P(E),')' Suivant(O) : P(E) Suivant(F) : S(E) Suivant(O) : 'id','n','(' Suivant(E) : '+','-','n','(',')' Suivant(F) : '+','-','n','(',')'
29 Exercice Non-terminaux : S E E2 T T2 F Terminaux : '$' '+' '-' ' ' ' ' '(' ')' 'id' 'n' Productions : S ::= E '$' E ::= T E2 E2 ::= '+' T E2 '-' T E2 ε T ::= F T2 T2 ::= ' ' F T2 ' ' F T2 ε F ::= 'n' 'id' '('E')' Annulable Premier Suivant S P(E) E P(T) ) $ E2 oui + - S(E) T P(F) P(E2),S(E2),S(E) T2 oui S(T) F ( id n P(T2),S(T2),S(T)
30 Exercice Non-terminaux : S E E2 T T2 F Terminaux : '$' '+' '-' ' ' ' ' '(' ')' 'id' 'n' Productions : S ::= E '$' E ::= T E2 E2 ::= '+' T E2 '-' T E2 ε T ::= F T2 T2 ::= ' ' F T2 ' ' F T2 ε F ::= 'n' 'id' '('E')' Annulable Premier Suivant S ( id n E ( id n ) $ E2 oui + - ) $ T ( id n ) + - $ T2 oui ) + - $ F ( id n ) + - $
31 Extensions On peut étendre Premier et Annulable (pas Suivant) aux suite de terminaux et non-terminaux : γ est annulable si elle ne contient que des non terminaux annulables Premier('a'γ) = { a } Si Z est annulable, Premier(Zγ) = P(Z) + Premier(γ) Si A n'est pas annulable, Premier(Aγ) = P(A)
32 Exemple Non-terminaux : S E O F Terminaux : '+' '-' 'n' '(' ')' Productions : Premier(OE) : '+','-','n','(' S ::= E '$' E ::= E O E F O ::= '+' '-' ε F ::= 'n' '(' E ')'
33 Notion de lookahead Lors de l analyse du code, on lira un certain nombre de lexèmes (en général un) à l avance, par rapport à ce que l on a déjà analysé Ces lexèmes constituent le lookahead Les algorithmes agissent en fonction des valeurs de ces lookahead
34 Grammaire augmentée Pour effectuer le parsing, il faut spécifier aux algorithmes quand arrive la fin du fichier : on ajoute un terminal spécial (en général '$') qui sera envoyé par le lexer un fois la fin du fichier atteinte en plus des actions usuelles, ce terminal est utilisé par les algorithmes pour savoir quand le parsing est terminé Pour cela, on augmente les grammaires : On ajoute un nouveau start, et un nouvel terminal '$' On ajoute la production nouveaustart ::= ancienstart '$'
35 Exemple Non-terminaux : S X Y Start : S Terminaux : 'a' 'c' 'd' Productions : S ::= X Y S 'd' Y ::= 'c' ε X ::= Y 'a' Non-terminaux : R S X Y Start : R Terminaux : 'a' 'c' 'd' '$' Productions : R ::= S '$' S ::= X Y S 'd' Y ::= 'c' ε X ::= Y 'a'
Chap 4: Analyse syntaxique. Prof. M.D. RAHMANI Compilation SMI- S5 2013/14 1
 Chap 4: Analyse syntaxique 1 III- L'analyse syntaxique: 1- Le rôle d'un analyseur syntaxique 2- Grammaires non contextuelles 3- Ecriture d'une grammaire 4- Les méthodes d'analyse 5- L'analyse LL(1) 6-
Chap 4: Analyse syntaxique 1 III- L'analyse syntaxique: 1- Le rôle d'un analyseur syntaxique 2- Grammaires non contextuelles 3- Ecriture d'une grammaire 4- Les méthodes d'analyse 5- L'analyse LL(1) 6-
t 100. = 8 ; le pourcentage de réduction est : 8 % 1 t Le pourcentage d'évolution (appelé aussi taux d'évolution) est le nombre :
 Terminale STSS 2 012 2 013 Pourcentages Synthèse 1) Définition : Calculer t % d'un nombre, c'est multiplier ce nombre par t 100. 2) Exemples de calcul : a) Calcul d un pourcentage : Un article coûtant
Terminale STSS 2 012 2 013 Pourcentages Synthèse 1) Définition : Calculer t % d'un nombre, c'est multiplier ce nombre par t 100. 2) Exemples de calcul : a) Calcul d un pourcentage : Un article coûtant
Théorie des Langages
 Théorie des Langages Analyse syntaxique descendante Claude Moulin Université de Technologie de Compiègne Printemps 2010 Sommaire 1 Principe 2 Premiers 3 Suivants 4 Analyse 5 Grammaire LL(1) Exemple : Grammaire
Théorie des Langages Analyse syntaxique descendante Claude Moulin Université de Technologie de Compiègne Printemps 2010 Sommaire 1 Principe 2 Premiers 3 Suivants 4 Analyse 5 Grammaire LL(1) Exemple : Grammaire
Les formations de remise à niveau(!) l'entrée des licences scientifiques. Patrick Frétigné CIIU
 Les formations de remise à niveau(!) pour les bacheliers «non-s» à l'entrée des licences scientifiques. Patrick Frétigné CIIU Cinq exemples Nantes Clermont Ferrand Lorraine Rennes 1 Rouen Nantes REUSCIT
Les formations de remise à niveau(!) pour les bacheliers «non-s» à l'entrée des licences scientifiques. Patrick Frétigné CIIU Cinq exemples Nantes Clermont Ferrand Lorraine Rennes 1 Rouen Nantes REUSCIT
Baccalauréat ES Antilles Guyane 12 septembre 2014 Corrigé
 Baccalauréat ES Antilles Guyane 12 septembre 2014 Corrigé EXERCICE 1 5 points Commun à tous les candidats 1. Réponse c : ln(10)+2 ln ( 10e 2) = ln(10)+ln ( e 2) = ln(10)+2 2. Réponse b : n 13 0,7 n 0,01
Baccalauréat ES Antilles Guyane 12 septembre 2014 Corrigé EXERCICE 1 5 points Commun à tous les candidats 1. Réponse c : ln(10)+2 ln ( 10e 2) = ln(10)+ln ( e 2) = ln(10)+2 2. Réponse b : n 13 0,7 n 0,01
Structures algébriques
 Structures algébriques 1. Lois de composition s Soit E un ensemble. Une loi de composition interne sur E est une application de E E dans E. Soient E et F deux ensembles. Une loi de composition externe
Structures algébriques 1. Lois de composition s Soit E un ensemble. Une loi de composition interne sur E est une application de E E dans E. Soient E et F deux ensembles. Une loi de composition externe
Fonction inverse Fonctions homographiques
 Fonction inverse Fonctions homographiques Année scolaire 203/204 Table des matières Fonction inverse 2. Définition Parité............................................ 2.2 Variations Courbe représentative...................................
Fonction inverse Fonctions homographiques Année scolaire 203/204 Table des matières Fonction inverse 2. Définition Parité............................................ 2.2 Variations Courbe représentative...................................
RÉSOLUTION DE SYSTÈMES À DEUX INCONNUES
 RÉSOLUTION DE SYSTÈMES À DEUX INCONNUES Sommaire 1 Méthodes de résolution... 3 1.1. Méthode de Substitution... 3 1.2. Méthode des combinaisons linéaires... 6 La rubrique d'aide qui suit s'attardera aux
RÉSOLUTION DE SYSTÈMES À DEUX INCONNUES Sommaire 1 Méthodes de résolution... 3 1.1. Méthode de Substitution... 3 1.2. Méthode des combinaisons linéaires... 6 La rubrique d'aide qui suit s'attardera aux
2. RAPPEL DES TECHNIQUES DE CALCUL DANS R
 2. RAPPEL DES TECHNIQUES DE CALCUL DANS R Dans la mesure où les résultats de ce chapitre devraient normalement être bien connus, il n'est rappelé que les formules les plus intéressantes; les justications
2. RAPPEL DES TECHNIQUES DE CALCUL DANS R Dans la mesure où les résultats de ce chapitre devraient normalement être bien connus, il n'est rappelé que les formules les plus intéressantes; les justications
Fonctions de plusieurs variables
 Module : Analyse 03 Chapitre 00 : Fonctions de plusieurs variables Généralités et Rappels des notions topologiques dans : Qu est- ce que?: Mathématiquement, n étant un entier non nul, on définit comme
Module : Analyse 03 Chapitre 00 : Fonctions de plusieurs variables Généralités et Rappels des notions topologiques dans : Qu est- ce que?: Mathématiquement, n étant un entier non nul, on définit comme
* très facile ** facile *** difficulté moyenne **** difficile ***** très difficile I : Incontournable T : pour travailler et mémoriser le cours
 Exo7 Continuité (étude globale). Diverses fonctions Exercices de Jean-Louis Rouget. Retrouver aussi cette fiche sur www.maths-france.fr * très facile ** facile *** difficulté moyenne **** difficile *****
Exo7 Continuité (étude globale). Diverses fonctions Exercices de Jean-Louis Rouget. Retrouver aussi cette fiche sur www.maths-france.fr * très facile ** facile *** difficulté moyenne **** difficile *****
Exercice 3 (5 points) A(x) = 1-e -0039' -0 156e- 0,039x A '() -'-,..--,-,--,------:-- X = (l_e-0,039x)2
 Les parties A et B sont indépendantes. Partie A Exercice 3 (5 points) Commun à tous les candidats On considère la fonction A définie sur l'intervalle [1 ; + 00 [ par A(x) = 1-e -0039' ' x 1. Calculer la
Les parties A et B sont indépendantes. Partie A Exercice 3 (5 points) Commun à tous les candidats On considère la fonction A définie sur l'intervalle [1 ; + 00 [ par A(x) = 1-e -0039' ' x 1. Calculer la
Complément d information concernant la fiche de concordance
 Sommaire SAMEDI 0 DÉCEMBRE 20 Vous trouverez dans ce dossier les documents correspondants à ce que nous allons travailler aujourd hui : La fiche de concordance pour le DAEU ; Page 2 Un rappel de cours
Sommaire SAMEDI 0 DÉCEMBRE 20 Vous trouverez dans ce dossier les documents correspondants à ce que nous allons travailler aujourd hui : La fiche de concordance pour le DAEU ; Page 2 Un rappel de cours
La fonction exponentielle
 DERNIÈRE IMPRESSION LE 2 novembre 204 à :07 La fonction exponentielle Table des matières La fonction exponentielle 2. Définition et théorèmes.......................... 2.2 Approche graphique de la fonction
DERNIÈRE IMPRESSION LE 2 novembre 204 à :07 La fonction exponentielle Table des matières La fonction exponentielle 2. Définition et théorèmes.......................... 2.2 Approche graphique de la fonction
NOTATIONS PRÉLIMINAIRES
 Pour le Jeudi 14 Octobre 2010 NOTATIONS Soit V un espace vectoriel réel ; l'espace vectoriel des endomorphismes de l'espace vectoriel V est désigné par L(V ). Soit f un endomorphisme de l'espace vectoriel
Pour le Jeudi 14 Octobre 2010 NOTATIONS Soit V un espace vectoriel réel ; l'espace vectoriel des endomorphismes de l'espace vectoriel V est désigné par L(V ). Soit f un endomorphisme de l'espace vectoriel
Rapport d'analyse des besoins
 Projet ANR 2011 - BR4CP (Business Recommendation for Configurable products) Rapport d'analyse des besoins Janvier 2013 Rapport IRIT/RR--2013-17 FR Redacteur : 0. Lhomme Introduction...4 La configuration
Projet ANR 2011 - BR4CP (Business Recommendation for Configurable products) Rapport d'analyse des besoins Janvier 2013 Rapport IRIT/RR--2013-17 FR Redacteur : 0. Lhomme Introduction...4 La configuration
CHAPITRE VIII : Les circuits avec résistances ohmiques
 CHAPITRE VIII : Les circuits avec résistances ohmiques VIII. 1 Ce chapitre porte sur les courants et les différences de potentiel dans les circuits. VIII.1 : Les résistances en série et en parallèle On
CHAPITRE VIII : Les circuits avec résistances ohmiques VIII. 1 Ce chapitre porte sur les courants et les différences de potentiel dans les circuits. VIII.1 : Les résistances en série et en parallèle On
Cours 1 : Qu est-ce que la programmation?
 1/65 Introduction à la programmation Cours 1 : Qu est-ce que la programmation? Yann Régis-Gianas yrg@pps.univ-paris-diderot.fr Université Paris Diderot Paris 7 2/65 1. Sortez un appareil qui peut se rendre
1/65 Introduction à la programmation Cours 1 : Qu est-ce que la programmation? Yann Régis-Gianas yrg@pps.univ-paris-diderot.fr Université Paris Diderot Paris 7 2/65 1. Sortez un appareil qui peut se rendre
Résolution d équations non linéaires
 Analyse Numérique Résolution d équations non linéaires Said EL HAJJI et Touria GHEMIRES Université Mohammed V - Agdal. Faculté des Sciences Département de Mathématiques. Laboratoire de Mathématiques, Informatique
Analyse Numérique Résolution d équations non linéaires Said EL HAJJI et Touria GHEMIRES Université Mohammed V - Agdal. Faculté des Sciences Département de Mathématiques. Laboratoire de Mathématiques, Informatique
Probabilités conditionnelles Exercices corrigés
 Terminale S Probabilités conditionnelles Exercices corrigés Exercice : (solution Une compagnie d assurance automobile fait un bilan des frais d intervention, parmi ses dossiers d accidents de la circulation.
Terminale S Probabilités conditionnelles Exercices corrigés Exercice : (solution Une compagnie d assurance automobile fait un bilan des frais d intervention, parmi ses dossiers d accidents de la circulation.
INTRODUCTION. A- Modélisation et paramétrage : CHAPITRE I : MODÉLISATION. I. Paramétrage de la position d un solide : (S1) O O1 X
 INTRODUCTION La conception d'un mécanisme en vue de sa réalisation industrielle comporte plusieurs étapes. Avant d'aboutir à la maquette numérique du produit définitif, il est nécessaire d'effectuer une
INTRODUCTION La conception d'un mécanisme en vue de sa réalisation industrielle comporte plusieurs étapes. Avant d'aboutir à la maquette numérique du produit définitif, il est nécessaire d'effectuer une
Probabilités et Statistiques. Feuille 2 : variables aléatoires discrètes
 IUT HSE Probabilités et Statistiques Feuille : variables aléatoires discrètes 1 Exercices Dénombrements Exercice 1. On souhaite ranger sur une étagère 4 livres de mathématiques (distincts), 6 livres de
IUT HSE Probabilités et Statistiques Feuille : variables aléatoires discrètes 1 Exercices Dénombrements Exercice 1. On souhaite ranger sur une étagère 4 livres de mathématiques (distincts), 6 livres de
Chapitre 1 : Introduction aux bases de données
 Chapitre 1 : Introduction aux bases de données Les Bases de Données occupent aujourd'hui une place de plus en plus importante dans les systèmes informatiques. Les Systèmes de Gestion de Bases de Données
Chapitre 1 : Introduction aux bases de données Les Bases de Données occupent aujourd'hui une place de plus en plus importante dans les systèmes informatiques. Les Systèmes de Gestion de Bases de Données
chapitre 4 Nombres de Catalan
 chapitre 4 Nombres de Catalan I Dénitions Dénition 1 La suite de Catalan (C n ) n est la suite dénie par C 0 = 1 et, pour tout n N, C n+1 = C k C n k. Exemple 2 On trouve rapidement C 0 = 1, C 1 = 1, C
chapitre 4 Nombres de Catalan I Dénitions Dénition 1 La suite de Catalan (C n ) n est la suite dénie par C 0 = 1 et, pour tout n N, C n+1 = C k C n k. Exemple 2 On trouve rapidement C 0 = 1, C 1 = 1, C
Programme et contenus 2010-2011. Licence d'informatique de Lille, parcours MIAGE, en alternance ou en formation continue 01-04-2011 (13:40)
 Programme et contenus 2010-2011 L3 MIAGE FA/FC Licence d'informatique de Lille, parcours MIAGE, en alternance ou en formation continue 01-04-2011 (13:40) PROGRAMME ET CONTENUS 2010-2011 Séminaire de rentrée
Programme et contenus 2010-2011 L3 MIAGE FA/FC Licence d'informatique de Lille, parcours MIAGE, en alternance ou en formation continue 01-04-2011 (13:40) PROGRAMME ET CONTENUS 2010-2011 Séminaire de rentrée
BANQUES DE DONNÉES PÉDAGOGIQUES
 223 Daniel BURET, Jean-Claude BLANCHARD. HISTORIQUE L'EPI a entrepris en 1989 de créer des bases d'énoncés mathématiques destinées aux enseignants pour la production de documents et accompagnées d'un outil
223 Daniel BURET, Jean-Claude BLANCHARD. HISTORIQUE L'EPI a entrepris en 1989 de créer des bases d'énoncés mathématiques destinées aux enseignants pour la production de documents et accompagnées d'un outil
Pour l épreuve d algèbre, les calculatrices sont interdites.
 Les pages qui suivent comportent, à titre d exemples, les questions d algèbre depuis juillet 003 jusqu à juillet 015, avec leurs solutions. Pour l épreuve d algèbre, les calculatrices sont interdites.
Les pages qui suivent comportent, à titre d exemples, les questions d algèbre depuis juillet 003 jusqu à juillet 015, avec leurs solutions. Pour l épreuve d algèbre, les calculatrices sont interdites.
SINE QUA NON. Découverte et Prise en main du logiciel Utilisation de bases
 SINE QUA NON Découverte et Prise en main du logiciel Utilisation de bases Sine qua non est un logiciel «traceur de courbes planes» mais il possède aussi bien d autres fonctionnalités que nous verrons tout
SINE QUA NON Découverte et Prise en main du logiciel Utilisation de bases Sine qua non est un logiciel «traceur de courbes planes» mais il possède aussi bien d autres fonctionnalités que nous verrons tout
1. Introduction... 2. 2. Création d'une macro autonome... 2. 3. Exécuter la macro pas à pas... 5. 4. Modifier une macro... 5
 1. Introduction... 2 2. Création d'une macro autonome... 2 3. Exécuter la macro pas à pas... 5 4. Modifier une macro... 5 5. Création d'une macro associée à un formulaire... 6 6. Exécuter des actions en
1. Introduction... 2 2. Création d'une macro autonome... 2 3. Exécuter la macro pas à pas... 5 4. Modifier une macro... 5 5. Création d'une macro associée à un formulaire... 6 6. Exécuter des actions en
LE PROBLEME DU PLUS COURT CHEMIN
 LE PROBLEME DU PLUS COURT CHEMIN Dans cette leçon nous définissons le modèle de plus court chemin, présentons des exemples d'application et proposons un algorithme de résolution dans le cas où les longueurs
LE PROBLEME DU PLUS COURT CHEMIN Dans cette leçon nous définissons le modèle de plus court chemin, présentons des exemples d'application et proposons un algorithme de résolution dans le cas où les longueurs
Rappel. Analyse de Données Structurées - Cours 12. Un langage avec des déclaration locales. Exemple d'un programme
 Rappel Ralf Treinen Université Paris Diderot UFR Informatique Laboratoire Preuves, Programmes et Systèmes treinen@pps.univ-paris-diderot.fr 6 mai 2015 Jusqu'à maintenant : un petit langage de programmation
Rappel Ralf Treinen Université Paris Diderot UFR Informatique Laboratoire Preuves, Programmes et Systèmes treinen@pps.univ-paris-diderot.fr 6 mai 2015 Jusqu'à maintenant : un petit langage de programmation
LES OUTILS D ALIMENTATION DU REFERENTIEL DE DB-MAIN
 LES OUTILS D ALIMENTATION DU REFERENTIEL DE DB-MAIN Les contenues de ce document sont la propriété exclusive de la société REVER. Ils ne sont transmis qu à titre d information et ne peuvent en aucun cas
LES OUTILS D ALIMENTATION DU REFERENTIEL DE DB-MAIN Les contenues de ce document sont la propriété exclusive de la société REVER. Ils ne sont transmis qu à titre d information et ne peuvent en aucun cas
Dérivation : Résumé de cours et méthodes
 Dérivation : Résumé de cours et métodes Nombre dérivé - Fonction dérivée : DÉFINITION (a + ) (a) Etant donné est une onction déinie sur un intervalle I contenant le réel a, est dérivable en a si tend vers
Dérivation : Résumé de cours et métodes Nombre dérivé - Fonction dérivée : DÉFINITION (a + ) (a) Etant donné est une onction déinie sur un intervalle I contenant le réel a, est dérivable en a si tend vers
M2 IAD UE MODE Notes de cours (3)
 M2 IAD UE MODE Notes de cours (3) Jean-Yves Jaffray Patrice Perny 16 mars 2006 ATTITUDE PAR RAPPORT AU RISQUE 1 Attitude par rapport au risque Nousn avons pas encore fait d hypothèse sur la structure de
M2 IAD UE MODE Notes de cours (3) Jean-Yves Jaffray Patrice Perny 16 mars 2006 ATTITUDE PAR RAPPORT AU RISQUE 1 Attitude par rapport au risque Nousn avons pas encore fait d hypothèse sur la structure de
Chapitre 4 : les stocks
 Chapitre 4 : les stocks Stocks et actifs Une entreprise achète généralement des biens pour les utiliser dans son processus de production, ce sont les matières premières et les fournitures, elle peut également
Chapitre 4 : les stocks Stocks et actifs Une entreprise achète généralement des biens pour les utiliser dans son processus de production, ce sont les matières premières et les fournitures, elle peut également
Calculs de probabilités avec la loi normale
 Calculs de probabilités avec la loi normale Olivier Torrès 20 janvier 2012 Rappels pour la licence EMO/IIES Ce document au format PDF est conçu pour être visualisé en mode présentation. Sélectionnez ce
Calculs de probabilités avec la loi normale Olivier Torrès 20 janvier 2012 Rappels pour la licence EMO/IIES Ce document au format PDF est conçu pour être visualisé en mode présentation. Sélectionnez ce
Transducteurs d arbres et (peut-être un peu) apprentissage
 Transducteurs d arbres et (peut-être un peu) apprentissage A. Lemay 2006 Taxonomie des transducteurs d arbres Syntax Directed translation (Irons 60) Attributed Tree Transducers (Knuth 68, Fülop 81) Rational
Transducteurs d arbres et (peut-être un peu) apprentissage A. Lemay 2006 Taxonomie des transducteurs d arbres Syntax Directed translation (Irons 60) Attributed Tree Transducers (Knuth 68, Fülop 81) Rational
Pourquoi l apprentissage?
 Pourquoi l apprentissage? Les SE sont basés sur la possibilité d extraire la connaissance d un expert sous forme de règles. Dépend fortement de la capacité à extraire et formaliser ces connaissances. Apprentissage
Pourquoi l apprentissage? Les SE sont basés sur la possibilité d extraire la connaissance d un expert sous forme de règles. Dépend fortement de la capacité à extraire et formaliser ces connaissances. Apprentissage
CH.6 Propriétés des langages non contextuels
 CH.6 Propriétés des langages non contetuels 6.1 Le lemme de pompage 6.2 Les propriétés de fermeture 6.3 Les problèmes de décidabilité 6.4 Les langages non contetuels déterministes utomates ch6 1 6.1 Le
CH.6 Propriétés des langages non contetuels 6.1 Le lemme de pompage 6.2 Les propriétés de fermeture 6.3 Les problèmes de décidabilité 6.4 Les langages non contetuels déterministes utomates ch6 1 6.1 Le
Algorithmes de recherche
 Algorithmes de recherche 1 Résolution de problèmes par recherche On représente un problème par un espace d'états (arbre/graphe). Chaque état est une conguration possible du problème. Résoudre le problème
Algorithmes de recherche 1 Résolution de problèmes par recherche On représente un problème par un espace d'états (arbre/graphe). Chaque état est une conguration possible du problème. Résoudre le problème
Simulation de variables aléatoires
 Chapter 1 Simulation de variables aléatoires Références: [F] Fishman, A first course in Monte Carlo, chap 3. [B] Bouleau, Probabilités de l ingénieur, chap 4. [R] Rubinstein, Simulation and Monte Carlo
Chapter 1 Simulation de variables aléatoires Références: [F] Fishman, A first course in Monte Carlo, chap 3. [B] Bouleau, Probabilités de l ingénieur, chap 4. [R] Rubinstein, Simulation and Monte Carlo
Articles sur le thème "Sécurité" http://thegeekcorner.free.fr
 Articles sur le thème "Sécurité" Sommaire TUTORIEL Installation et configuration de Xplico sous Backtrack I-Pré-requis...p. II-Installation et configuration...p. a) Installation de Xplico... p. b) Configuration
Articles sur le thème "Sécurité" Sommaire TUTORIEL Installation et configuration de Xplico sous Backtrack I-Pré-requis...p. II-Installation et configuration...p. a) Installation de Xplico... p. b) Configuration
Sauvegarder et restaurer les données PMB
 Fiche technique PMB n 2.9 Sauvegarder et restaurer les données PMB Objectif : Savoir sauvegarder les paramètres, les notices, les exemplaires, les prêts... avec PMB Notez bien : Le documentaliste est responsable
Fiche technique PMB n 2.9 Sauvegarder et restaurer les données PMB Objectif : Savoir sauvegarder les paramètres, les notices, les exemplaires, les prêts... avec PMB Notez bien : Le documentaliste est responsable
CALCUL DES PROBABILITES
 CALCUL DES PROBABILITES Exemple On lance une pièce de monnaie une fois. Ensemble des événements élémentaires: E = pile, face. La chance pour obtenir pile vaut 50 %, pour obtenir face vaut aussi 50 %. Les
CALCUL DES PROBABILITES Exemple On lance une pièce de monnaie une fois. Ensemble des événements élémentaires: E = pile, face. La chance pour obtenir pile vaut 50 %, pour obtenir face vaut aussi 50 %. Les
Cours3. Applications continues et homéomorphismes. 1 Rappel sur les images réciproques
 Université de Provence Topologie 2 Cours3. Applications continues et homéomorphismes 1 Rappel sur les images réciproques Soit une application f d un ensemble X vers un ensemble Y et soit une partie P de
Université de Provence Topologie 2 Cours3. Applications continues et homéomorphismes 1 Rappel sur les images réciproques Soit une application f d un ensemble X vers un ensemble Y et soit une partie P de
Baccalauréat ES/L Amérique du Sud 21 novembre 2013
 Baccalauréat ES/L Amérique du Sud 21 novembre 2013 A. P. M. E. P. EXERCICE 1 Commun à tous les candidats 5 points Une entreprise informatique produit et vend des clés USB. La vente de ces clés est réalisée
Baccalauréat ES/L Amérique du Sud 21 novembre 2013 A. P. M. E. P. EXERCICE 1 Commun à tous les candidats 5 points Une entreprise informatique produit et vend des clés USB. La vente de ces clés est réalisée
Exo7. Probabilité conditionnelle. Exercices : Martine Quinio
 Exercices : Martine Quinio Exo7 Probabilité conditionnelle Exercice 1 Dans la salle des profs 60% sont des femmes ; une femme sur trois porte des lunettes et un homme sur deux porte des lunettes : quelle
Exercices : Martine Quinio Exo7 Probabilité conditionnelle Exercice 1 Dans la salle des profs 60% sont des femmes ; une femme sur trois porte des lunettes et un homme sur deux porte des lunettes : quelle
FctsAffines.nb 1. Mathématiques, 1-ère année Edition 2007-2008. Fonctions affines
 FctsAffines.nb 1 Mathématiques, 1-ère année Edition 2007-2008 Fonctions affines Supports de cours de mathématiques de degré secondaire II, lien hpertete vers la page mère http://www.deleze.name/marcel/sec2/inde.html
FctsAffines.nb 1 Mathématiques, 1-ère année Edition 2007-2008 Fonctions affines Supports de cours de mathématiques de degré secondaire II, lien hpertete vers la page mère http://www.deleze.name/marcel/sec2/inde.html
Méthodes de quadrature. Polytech Paris-UPMC. - p. 1/48
 Méthodes de Polytech Paris-UPMC - p. 1/48 Polynôme d interpolation de Preuve et polynôme de Calcul de l erreur d interpolation Étude de la formule d erreur Autres méthodes - p. 2/48 Polynôme d interpolation
Méthodes de Polytech Paris-UPMC - p. 1/48 Polynôme d interpolation de Preuve et polynôme de Calcul de l erreur d interpolation Étude de la formule d erreur Autres méthodes - p. 2/48 Polynôme d interpolation
INF 232: Langages et Automates. Travaux Dirigés. Université Joseph Fourier, Université Grenoble 1 Licence Sciences et Technologies
 INF 232: Langages et Automates Travaux Dirigés Université Joseph Fourier, Université Grenoble 1 Licence Sciences et Technologies Année Académique 2013-2014 Année Académique 2013-2014 UNIVERSITÉ JOSEPH
INF 232: Langages et Automates Travaux Dirigés Université Joseph Fourier, Université Grenoble 1 Licence Sciences et Technologies Année Académique 2013-2014 Année Académique 2013-2014 UNIVERSITÉ JOSEPH
Cours 1 : La compilation
 /38 Interprétation des programmes Cours 1 : La compilation Yann Régis-Gianas yrg@pps.univ-paris-diderot.fr PPS - Université Denis Diderot Paris 7 2/38 Qu est-ce que la compilation? Vous avez tous déjà
/38 Interprétation des programmes Cours 1 : La compilation Yann Régis-Gianas yrg@pps.univ-paris-diderot.fr PPS - Université Denis Diderot Paris 7 2/38 Qu est-ce que la compilation? Vous avez tous déjà
Manuel utilisateur. Version 1.6b
 Manuel utilisateur Version 1.6b Table des matières Table des matières... 2 1. Introduction... 3 a. But de ce document... 3 b. Objet de ce document... 3 c. Remarques et commentaires... 3 2. Premiers pas
Manuel utilisateur Version 1.6b Table des matières Table des matières... 2 1. Introduction... 3 a. But de ce document... 3 b. Objet de ce document... 3 c. Remarques et commentaires... 3 2. Premiers pas
Limites finies en un point
 8 Limites finies en un point Pour ce chapitre, sauf précision contraire, I désigne une partie non vide de R et f une fonction définie sur I et à valeurs réelles ou complees. Là encore, les fonctions usuelles,
8 Limites finies en un point Pour ce chapitre, sauf précision contraire, I désigne une partie non vide de R et f une fonction définie sur I et à valeurs réelles ou complees. Là encore, les fonctions usuelles,
Problème : Calcul d'échéanciers de prêt bancaire (15 pt)
 Problème : Calcul d'échéanciers de prêt bancaire (15 pt) 1 Principe d'un prêt bancaire et dénitions Lorsque vous empruntez de l'argent dans une banque, cet argent (appelé capital) vous est loué. Chaque
Problème : Calcul d'échéanciers de prêt bancaire (15 pt) 1 Principe d'un prêt bancaire et dénitions Lorsque vous empruntez de l'argent dans une banque, cet argent (appelé capital) vous est loué. Chaque
DÉRIVÉES. I Nombre dérivé - Tangente. Exercice 01 (voir réponses et correction) ( voir animation )
 DÉRIVÉES I Nombre dérivé - Tangente Eercice 0 ( voir animation ) On considère la fonction f définie par f() = - 2 + 6 pour [-4 ; 4]. ) Tracer la représentation graphique (C) de f dans un repère d'unité
DÉRIVÉES I Nombre dérivé - Tangente Eercice 0 ( voir animation ) On considère la fonction f définie par f() = - 2 + 6 pour [-4 ; 4]. ) Tracer la représentation graphique (C) de f dans un repère d'unité
MICROINFORMATIQUE NOTE D APPLICATION 1 (REV. 2011) ARITHMETIQUE EN ASSEMBLEUR ET EN C
 Haute Ecole d Ingénierie et de Gestion Du Canton du Vaud MICROINFORMATIQUE NOTE D APPLICATION 1 (REV. 2011) ARITHMETIQUE EN ASSEMBLEUR ET EN C Programmation en mode simulation 1. DOCUMENTS DE RÉFÉRENCE...
Haute Ecole d Ingénierie et de Gestion Du Canton du Vaud MICROINFORMATIQUE NOTE D APPLICATION 1 (REV. 2011) ARITHMETIQUE EN ASSEMBLEUR ET EN C Programmation en mode simulation 1. DOCUMENTS DE RÉFÉRENCE...
Le chiffre est le signe, le nombre est la valeur.
 Extrait de cours de maths de 6e Chapitre 1 : Les nombres et les opérations I) Chiffre et nombre 1.1 La numération décimale En mathématique, un chiffre est un signe utilisé pour l'écriture des nombres.
Extrait de cours de maths de 6e Chapitre 1 : Les nombres et les opérations I) Chiffre et nombre 1.1 La numération décimale En mathématique, un chiffre est un signe utilisé pour l'écriture des nombres.
Fonctions de plusieurs variables : dérivés partielles, diérentielle. Fonctions composées. Fonctions de classe C 1. Exemples
 45 Fonctions de plusieurs variables : dérivés partielles, diérentielle. Fonctions composées. Fonctions de classe C 1. Exemples Les espaces vectoriels considérés sont réels, non réduits au vecteur nul et
45 Fonctions de plusieurs variables : dérivés partielles, diérentielle. Fonctions composées. Fonctions de classe C 1. Exemples Les espaces vectoriels considérés sont réels, non réduits au vecteur nul et
Suivant les langages de programmation, modules plus avancés : modules imbriqués modules paramétrés par des modules (foncteurs)
 Modularité Extensions Suivant les langages de programmation, modules plus avancés : modules imbriqués modules paramétrés par des modules (foncteurs) généricité modules de première classe : peuvent être
Modularité Extensions Suivant les langages de programmation, modules plus avancés : modules imbriqués modules paramétrés par des modules (foncteurs) généricité modules de première classe : peuvent être
Introduction. I Étude rapide du réseau - Apprentissage. II Application à la reconnaissance des notes.
 Introduction L'objectif de mon TIPE est la reconnaissance de sons ou de notes de musique à l'aide d'un réseau de neurones. Ce réseau doit être capable d'apprendre à distinguer les exemples présentés puis
Introduction L'objectif de mon TIPE est la reconnaissance de sons ou de notes de musique à l'aide d'un réseau de neurones. Ce réseau doit être capable d'apprendre à distinguer les exemples présentés puis
Correction du baccalauréat ES/L Métropole 20 juin 2014
 Correction du baccalauréat ES/L Métropole 0 juin 014 Exercice 1 1. c.. c. 3. c. 4. d. 5. a. P A (B)=1 P A (B)=1 0,3=0,7 D après la formule des probabilités totales : P(B)=P(A B)+P(A B)=0,6 0,3+(1 0,6)
Correction du baccalauréat ES/L Métropole 0 juin 014 Exercice 1 1. c.. c. 3. c. 4. d. 5. a. P A (B)=1 P A (B)=1 0,3=0,7 D après la formule des probabilités totales : P(B)=P(A B)+P(A B)=0,6 0,3+(1 0,6)
Al attention du praticien et des étudiants, nous avons développé
 Chapitre 15 Applications informatiques Al attention du praticien et des étudiants, nous avons développé deux applications informatiques téléchargeables gratuitement sur le site www.digilex.ch. La première
Chapitre 15 Applications informatiques Al attention du praticien et des étudiants, nous avons développé deux applications informatiques téléchargeables gratuitement sur le site www.digilex.ch. La première
TSTI 2D CH X : Exemples de lois à densité 1
 TSTI 2D CH X : Exemples de lois à densité I Loi uniforme sur ab ; ) Introduction Dans cette activité, on s intéresse à la modélisation du tirage au hasard d un nombre réel de l intervalle [0 ;], chacun
TSTI 2D CH X : Exemples de lois à densité I Loi uniforme sur ab ; ) Introduction Dans cette activité, on s intéresse à la modélisation du tirage au hasard d un nombre réel de l intervalle [0 ;], chacun
Raisonnement probabiliste
 Plan Raisonnement probabiliste IFT-17587 Concepts avancés pour systèmes intelligents Luc Lamontagne Réseaux bayésiens Inférence dans les réseaux bayésiens Inférence exacte Inférence approximative 1 2 Contexte
Plan Raisonnement probabiliste IFT-17587 Concepts avancés pour systèmes intelligents Luc Lamontagne Réseaux bayésiens Inférence dans les réseaux bayésiens Inférence exacte Inférence approximative 1 2 Contexte
Exercices de dénombrement
 Exercices de dénombrement Exercice En turbo Pascal, un entier relatif (type integer) est codé sur 6 bits. Cela signifie que l'on réserve 6 cases mémoires contenant des "0" ou des "" pour écrire un entier.
Exercices de dénombrement Exercice En turbo Pascal, un entier relatif (type integer) est codé sur 6 bits. Cela signifie que l'on réserve 6 cases mémoires contenant des "0" ou des "" pour écrire un entier.
La syllabe (1/5) Unité intuitive (différent du phonème) Constituant essentiel pour la phonologie au même titre que phonème et trait
 La syllabe (1/5) Unité intuitive (différent du phonème) Variation des structures syllabiques d une langue à une autre et dans une même langue (cf strict vs à : une seule syllabe mais des structures bien
La syllabe (1/5) Unité intuitive (différent du phonème) Variation des structures syllabiques d une langue à une autre et dans une même langue (cf strict vs à : une seule syllabe mais des structures bien
Continuité et dérivabilité d une fonction
 DERNIÈRE IMPRESSIN LE 7 novembre 014 à 10:3 Continuité et dérivabilité d une fonction Table des matières 1 Continuité d une fonction 1.1 Limite finie en un point.......................... 1. Continuité
DERNIÈRE IMPRESSIN LE 7 novembre 014 à 10:3 Continuité et dérivabilité d une fonction Table des matières 1 Continuité d une fonction 1.1 Limite finie en un point.......................... 1. Continuité
TP n 2 Concepts de la programmation Objets Master 1 mention IL, semestre 2 Le type Abstrait Pile
 TP n 2 Concepts de la programmation Objets Master 1 mention IL, semestre 2 Le type Abstrait Pile Dans ce TP, vous apprendrez à définir le type abstrait Pile, à le programmer en Java à l aide d une interface
TP n 2 Concepts de la programmation Objets Master 1 mention IL, semestre 2 Le type Abstrait Pile Dans ce TP, vous apprendrez à définir le type abstrait Pile, à le programmer en Java à l aide d une interface
Arithmétique binaire. Chapitre. 5.1 Notions. 5.1.1 Bit. 5.1.2 Mot
 Chapitre 5 Arithmétique binaire L es codes sont manipulés au quotidien sans qu on s en rende compte, et leur compréhension est quasi instinctive. Le seul fait de lire fait appel au codage alphabétique,
Chapitre 5 Arithmétique binaire L es codes sont manipulés au quotidien sans qu on s en rende compte, et leur compréhension est quasi instinctive. Le seul fait de lire fait appel au codage alphabétique,
Développements limités. Notion de développement limité
 MT12 - ch2 Page 1/8 Développements limités Dans tout ce chapitre, I désigne un intervalle de R non vide et non réduit à un point. I Notion de développement limité Dans tout ce paragraphe, a désigne un
MT12 - ch2 Page 1/8 Développements limités Dans tout ce chapitre, I désigne un intervalle de R non vide et non réduit à un point. I Notion de développement limité Dans tout ce paragraphe, a désigne un
Fonctions de deux variables. Mai 2011
 Fonctions de deux variables Dédou Mai 2011 D une à deux variables Les fonctions modèlisent de l information dépendant d un paramètre. On a aussi besoin de modéliser de l information dépendant de plusieurs
Fonctions de deux variables Dédou Mai 2011 D une à deux variables Les fonctions modèlisent de l information dépendant d un paramètre. On a aussi besoin de modéliser de l information dépendant de plusieurs
Théorème du point fixe - Théorème de l inversion locale
 Chapitre 7 Théorème du point fixe - Théorème de l inversion locale Dans ce chapitre et le suivant, on montre deux applications importantes de la notion de différentiabilité : le théorème de l inversion
Chapitre 7 Théorème du point fixe - Théorème de l inversion locale Dans ce chapitre et le suivant, on montre deux applications importantes de la notion de différentiabilité : le théorème de l inversion
Représentation des Nombres
 Chapitre 5 Représentation des Nombres 5. Representation des entiers 5.. Principe des représentations en base b Base L entier écrit 344 correspond a 3 mille + 4 cent + dix + 4. Plus généralement a n a n...
Chapitre 5 Représentation des Nombres 5. Representation des entiers 5.. Principe des représentations en base b Base L entier écrit 344 correspond a 3 mille + 4 cent + dix + 4. Plus généralement a n a n...
Diagramme de classes
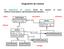 Diagramme de classes Un diagramme de classes décrit les classes et leurs relations (associations, généralisation/spécialisation, ). classe association méthodes attributs héritage Diagramme de classes :
Diagramme de classes Un diagramme de classes décrit les classes et leurs relations (associations, généralisation/spécialisation, ). classe association méthodes attributs héritage Diagramme de classes :
Introduction à MATLAB R
 Introduction à MATLAB R Romain Tavenard 10 septembre 2009 MATLAB R est un environnement de calcul numérique propriétaire orienté vers le calcul matriciel. Il se compose d un langage de programmation, d
Introduction à MATLAB R Romain Tavenard 10 septembre 2009 MATLAB R est un environnement de calcul numérique propriétaire orienté vers le calcul matriciel. Il se compose d un langage de programmation, d
U102 Devoir sur les suites (TST2S)
 LES SUITES - DEVOIR 1 EXERCICE 1 L'objectif de cet exercice est de comparer l'évolution des économies de deux personnes au cours d'une année. Pierre possède 500 euros d'économies le 1 er janvier. Il décide
LES SUITES - DEVOIR 1 EXERCICE 1 L'objectif de cet exercice est de comparer l'évolution des économies de deux personnes au cours d'une année. Pierre possède 500 euros d'économies le 1 er janvier. Il décide
Post-production ~ captation audio/vidéo ~ RMLL 2010, Bordeaux
 Post-production ~ captation audio/vidéo ~ RMLL 2010, Bordeaux version 1.0 du 20 juillet 2010 Introduction Ce document détaille l'ensemble des procédures, fichiers, emplacements et comptes permettant de
Post-production ~ captation audio/vidéo ~ RMLL 2010, Bordeaux version 1.0 du 20 juillet 2010 Introduction Ce document détaille l'ensemble des procédures, fichiers, emplacements et comptes permettant de
Présentation du langage et premières fonctions
 1 Présentation de l interface logicielle Si les langages de haut niveau sont nombreux, nous allons travaillé cette année avec le langage Python, un langage de programmation très en vue sur internet en
1 Présentation de l interface logicielle Si les langages de haut niveau sont nombreux, nous allons travaillé cette année avec le langage Python, un langage de programmation très en vue sur internet en
Guide de démarrage rapide Centre de copies et d'impression Bureau en Gros en ligne
 Guide de démarrage rapide Centre de copies et d'impression Bureau en Gros en ligne Aperçu du Centre de copies et d'impression Bureau en Gros en ligne Pour accéder à «copies et impression Bureau en Gros
Guide de démarrage rapide Centre de copies et d'impression Bureau en Gros en ligne Aperçu du Centre de copies et d'impression Bureau en Gros en ligne Pour accéder à «copies et impression Bureau en Gros
GEA II Introduction aux probabilités Poly. de révision. Lionel Darondeau
 GEA II Introduction aux probabilités Poly. de révision Lionel Darondeau Table des matières Énoncés 4 Corrigés 10 TD 1. Analyse combinatoire 11 TD 2. Probabilités élémentaires 16 TD 3. Probabilités conditionnelles
GEA II Introduction aux probabilités Poly. de révision Lionel Darondeau Table des matières Énoncés 4 Corrigés 10 TD 1. Analyse combinatoire 11 TD 2. Probabilités élémentaires 16 TD 3. Probabilités conditionnelles
Analyse stochastique de la CRM à ordre partiel dans le cadre des essais cliniques de phase I
 Analyse stochastique de la CRM à ordre partiel dans le cadre des essais cliniques de phase I Roxane Duroux 1 Cadre de l étude Cette étude s inscrit dans le cadre de recherche de doses pour des essais cliniques
Analyse stochastique de la CRM à ordre partiel dans le cadre des essais cliniques de phase I Roxane Duroux 1 Cadre de l étude Cette étude s inscrit dans le cadre de recherche de doses pour des essais cliniques
Fonctions linéaires et affines. 1 Fonctions linéaires. 1.1 Vocabulaire. 1.2 Représentation graphique. 3eme
 Fonctions linéaires et affines 3eme 1 Fonctions linéaires 1.1 Vocabulaire Définition 1 Soit a un nombre quelconque «fixe». Une fonction linéaire associe à un nombre x quelconque le nombre a x. a s appelle
Fonctions linéaires et affines 3eme 1 Fonctions linéaires 1.1 Vocabulaire Définition 1 Soit a un nombre quelconque «fixe». Une fonction linéaire associe à un nombre x quelconque le nombre a x. a s appelle
3- FONDEMENTS. Politique relat ve aux contributions financières exigées des parents ou des usagers
 Centre administratif 3644, rue Saint-Jules, C.P 1600, Jonquière (Québec) G7X 7X4 Téléphone : 41 8 542-7551. Télécopieur : 41 8 542-1 505 sgeneral@csjonquiere.qc.ca. www.csjonquiere.qc.ca Politique relat
Centre administratif 3644, rue Saint-Jules, C.P 1600, Jonquière (Québec) G7X 7X4 Téléphone : 41 8 542-7551. Télécopieur : 41 8 542-1 505 sgeneral@csjonquiere.qc.ca. www.csjonquiere.qc.ca Politique relat
1. Introduction...2. 2. Création d'une requête...2
 1. Introduction...2 2. Création d'une requête...2 3. Définition des critères de sélection...5 3.1 Opérateurs...5 3.2 Les Fonctions...6 3.3 Plusieurs critères portant sur des champs différents...7 3.4 Requête
1. Introduction...2 2. Création d'une requête...2 3. Définition des critères de sélection...5 3.1 Opérateurs...5 3.2 Les Fonctions...6 3.3 Plusieurs critères portant sur des champs différents...7 3.4 Requête
1 Introduction C+ + Algorithm e. languag. Algorigramm. machine binaire. 1-1 Chaîne de développement. Séance n 4
 1 Introduction 1-1 Chaîne de développement Algorithm e C+ + Algorigramm e languag e machine binaire Le programme est écrit à l aide de Multiprog sous forme d algorigramme puis introduit dans le microcontrôleur
1 Introduction 1-1 Chaîne de développement Algorithm e C+ + Algorigramm e languag e machine binaire Le programme est écrit à l aide de Multiprog sous forme d algorigramme puis introduit dans le microcontrôleur
AGRÉGATION «ÉCONOMIE ET GESTION»
 AGRÉGATION «ÉCONOMIE ET GESTION» CONCOURS INTERNE SESSION 2002 ÉPREUVE SUR LES TECHNIQUES DE GESTION ET COMPORTANT DES ASPECTS PÉDAGOGIQUES DOMAINE : économie et gestion informatique Durée de préparation
AGRÉGATION «ÉCONOMIE ET GESTION» CONCOURS INTERNE SESSION 2002 ÉPREUVE SUR LES TECHNIQUES DE GESTION ET COMPORTANT DES ASPECTS PÉDAGOGIQUES DOMAINE : économie et gestion informatique Durée de préparation
P our appeler : Décrochez le combiné et composez le numéro OU Composez le numéro et décrochez le combiné
 Appareil analogique Meridian Fonctions du système téléphonique Numéro d'appel Haut parleur Touche de libération Touche de garde Touche de commande de volume Indicateur ICL Voyant de message en attente
Appareil analogique Meridian Fonctions du système téléphonique Numéro d'appel Haut parleur Touche de libération Touche de garde Touche de commande de volume Indicateur ICL Voyant de message en attente
Chapitre 4: Dérivée d'une fonction et règles de calcul
 DERIVEES ET REGLES DE CALCULS 69 Chapitre 4: Dérivée d'une fonction et règles de calcul Prérequis: Généralités sur les fonctions, Introduction dérivée Requis pour: Croissance, Optimisation, Études de fct.
DERIVEES ET REGLES DE CALCULS 69 Chapitre 4: Dérivée d'une fonction et règles de calcul Prérequis: Généralités sur les fonctions, Introduction dérivée Requis pour: Croissance, Optimisation, Études de fct.
Souad EL Bernoussi. Groupe d Analyse Numérique et Optimisation Rabat http ://www.fsr.ac.ma/ano/
 Recherche opérationnelle Les démonstrations et les exemples seront traités en cours Souad EL Bernoussi Groupe d Analyse Numérique et Optimisation Rabat http ://www.fsr.ac.ma/ano/ Table des matières 1 Programmation
Recherche opérationnelle Les démonstrations et les exemples seront traités en cours Souad EL Bernoussi Groupe d Analyse Numérique et Optimisation Rabat http ://www.fsr.ac.ma/ano/ Table des matières 1 Programmation
Augmenter la portée de votre WiFi avec un répéteur
 Augmenter la portée de votre WiFi avec un répéteur Vous utilisez le réseau sans fil Wifi de votre box pour vous connecter à Internet mais vous avez du mal à capter le signal à certains endroits de votre
Augmenter la portée de votre WiFi avec un répéteur Vous utilisez le réseau sans fil Wifi de votre box pour vous connecter à Internet mais vous avez du mal à capter le signal à certains endroits de votre
LE PROCESSUS ( la machine) la fonction f. ( On lit : «fonction f qui à x associe f (x)» )
 SYNTHESE ( THEME ) FONCTIONS () : NOTIONS de FONCTIONS FONCTION LINEAIRE () : REPRESENTATIONS GRAPHIQUES * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
SYNTHESE ( THEME ) FONCTIONS () : NOTIONS de FONCTIONS FONCTION LINEAIRE () : REPRESENTATIONS GRAPHIQUES * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
JEU BOURSIER 2015. Séance d introduction à la plateforme de trading SaxoWebTrader. - Pour débutants -
 JEU BOURSIER 2015 Séance d introduction à la plateforme de trading SaxoWebTrader - Pour débutants - A partir d un ordinateur: a) Rends-toi sur le site suisse de SaxoBank: https://webtrader.saxobank.ch/sim/login/
JEU BOURSIER 2015 Séance d introduction à la plateforme de trading SaxoWebTrader - Pour débutants - A partir d un ordinateur: a) Rends-toi sur le site suisse de SaxoBank: https://webtrader.saxobank.ch/sim/login/
Plateforme de support en ligne. Guide d utilisation
 Plateforme de support en ligne Guide d utilisation Sommaire Sommaire...2 Procédure de la plateforme de support...3 Accès à la plateforme de support en ligne...4 Créer un compte utilisateur...5 Oubli de
Plateforme de support en ligne Guide d utilisation Sommaire Sommaire...2 Procédure de la plateforme de support...3 Accès à la plateforme de support en ligne...4 Créer un compte utilisateur...5 Oubli de
Capacité d un canal Second Théorème de Shannon. Théorie de l information 1/34
 Capacité d un canal Second Théorème de Shannon Théorie de l information 1/34 Plan du cours 1. Canaux discrets sans mémoire, exemples ; 2. Capacité ; 3. Canaux symétriques ; 4. Codage de canal ; 5. Second
Capacité d un canal Second Théorème de Shannon Théorie de l information 1/34 Plan du cours 1. Canaux discrets sans mémoire, exemples ; 2. Capacité ; 3. Canaux symétriques ; 4. Codage de canal ; 5. Second
BICS Fiche d instruction
 BICS Fiche d instruction Signalement de cargaisons Water. Wegen. Werken. Rijkswaterstaat. 1 Nous vous exposerons dans cette instruction comment les cargaisons isées devront être signalées à l IVS90 aux
BICS Fiche d instruction Signalement de cargaisons Water. Wegen. Werken. Rijkswaterstaat. 1 Nous vous exposerons dans cette instruction comment les cargaisons isées devront être signalées à l IVS90 aux
Aide - mémoire gnuplot 4.0
 Aide - mémoire gnuplot 4.0 Nicolas Kielbasiewicz 20 juin 2008 L objet de cet aide-mémoire est de présenter les commandes de base pour faire rapidement de très jolis graphiques et courbes à l aide du logiciel
Aide - mémoire gnuplot 4.0 Nicolas Kielbasiewicz 20 juin 2008 L objet de cet aide-mémoire est de présenter les commandes de base pour faire rapidement de très jolis graphiques et courbes à l aide du logiciel
Congé de soutien/solidarité familiale
 Congé de soutien/solidarité familiale Si un membre de votre famille, handicapé ou dépendant, a besoin de votre présence pour quelques temps, sachez que vous pouvez désormais bénéficier d'un congé spécifique.
Congé de soutien/solidarité familiale Si un membre de votre famille, handicapé ou dépendant, a besoin de votre présence pour quelques temps, sachez que vous pouvez désormais bénéficier d'un congé spécifique.
Guide de démarrage rapide
 Guide de démarrage rapide 1 Sommaire 1.Préambule...3 2.Démarrage du programme...4 3.Prise en main...6 3.1.Les saisies...6 3.2.Les listes...10 4.Gestion courante...13 4.1.Saisie d'un devis...13 4.2.Transformation
Guide de démarrage rapide 1 Sommaire 1.Préambule...3 2.Démarrage du programme...4 3.Prise en main...6 3.1.Les saisies...6 3.2.Les listes...10 4.Gestion courante...13 4.1.Saisie d'un devis...13 4.2.Transformation
TP 4 de familiarisation avec Unix
 TP 4 de familiarisation avec Unix Réseau Filtres (suite) Variables Scripts Vincent Berry - vberry@lirmm.fr IMPORTANT : la prise de notes est une pratique très importante et pourtant négligée, elle est
TP 4 de familiarisation avec Unix Réseau Filtres (suite) Variables Scripts Vincent Berry - vberry@lirmm.fr IMPORTANT : la prise de notes est une pratique très importante et pourtant négligée, elle est
