Laboratoire 2 Extraction des caractéristiques
|
|
|
- Edgar Thomas Simoneau
- il y a 9 ans
- Total affichages :
Transcription
1 Laboratoire 2 Extraction des caractéristiques L objectif de l extraction et de la sélection de caractéristiques est d identifier les caractéristiques importantes pour la discrimination entre classes. Après avoir choisi le meilleur ensemble de caractéristiques, il s agit de réduire la dimensionnalité de l ensemble des caractéristiques en trouvant un nouvel ensemble, plus petit que l ensemble original, qui néanmoins, contient la plupart de l information. Contrairement à ce que l intuition peut laisser penser, la performance des classificateurs n augmente pas indéfiniment avec la taille du vecteur de caractéristiques. Après avoir augmenté en fonction du nombre de caractéristiques, l efficacité atteint un plateau et quelquefois se met à décroître au-delà d un certain nombre de caractéristiques. Ce phénomène est appelé malédiction de la dimensionnalité. En plus, le coût (temps + mémoire) de la classification augmente avec la taille de ce vecteur. On a toujours intérêt à réduire le nombre de caractéristiques pour qu il corresponde à la dimensionnalité intrinsèque du problème ou pour de simples raisons pratiques. Les méthodes d extraction de caractéristiques à partir de l intensité d une image du visage peuvent être divisées en trois catégories : les méthodes globales (exploitant toute la région visage), les méthodes locales (exploitant des caractéristiques locales : yeux, nez, etc.), et les méthodes hybrides. On se limite principalement aux méthodes globales où l image du visage au complet peut être vue comme un vecteur dans un espace ayant autant de dimensions que de pixels dans l image, et représentant la variation d intensité (en niveau de gris). L image du visage, une matrice de pixel M, peut être représentée, par concaténation de colonnes, comme un vecteur x de dimension I = largeur hauteur. Chaque visage peut donc être considéré comme un vecteur à I composantes dans un espace R I. L ensemble des visages forme alors la matrice d images X, où chaque vecteur colonne x j représente un visage dont chaque élément x ij est l intensité du pixel i. Dans notre cas, la dimension (I = = pixels) du vecteur de caractéristiques est très grande, mais la vraie dimension de l espace dans laquelle les visages observés sont situés peut être plus petite. En plus, le nombre d échantillons réservés à l apprentissage est considérablement inférieur au nombre de caractéristiques. Parmi les techniques de réduction de dimensionnalité, les analyses statistiques linéaires consistent à transformer les données originales par une transformation linéaire (changement de base) optimisant un critère géométrique ou statistique. Pour J images, on cherche une matrice de transformation W pour obtenir la projection R I R K de la matrice d images X : où Y est la matrice résultante de la projection telle que K < I. Y K J = W T I KX I J, (1) 2.1 Analyse en composantes principales (Eigenfaces) L analyse en composantes principales (PCA pour Principal Component Analysis ) 1 est une méthode classique de réduction de dimension Cette méthode permet de représenter le nuage des points originel dans un sous-espace orthogonale de dimension inférieure, tout en limitant au maximum la perte d information. Les axes principaux sont ceux qui contiennent le plus d information 1. Également connue sous le nom de transformée de Karhunen-Loève ou de transformée de Hotelling. 1
2 (a) (b) Figure 1 Représentation d une image de visage. (a) Un vecteur image formé par concaténation de colonnes. (b) Illustration d un visage représenté par un point dans l espace de visages de K dimensions (en supposant K = 3) pertinente c est-à-dire qui maximisent l inertie 2 du nuage projeté. Les composantes principales sont les vecteurs ayant pour coordonnées celles des projections orthogonales des points du nuage sur les axes principaux. La PCA fournit donc une base de représentation dans laquelle les composantes sont simplement dé-corrélées et rendant compte de la variation maximale, ce qui permet : une réduction des données de D à K nouvelles caractéristiques une visualisation des données à 2 ou 3 dimensions (si K = 2 ou 3) une interprétation des données Soit J images en format de vecteur colonne x j (j = 1,..., J) dans R I, l objectif est de transformer l espace initial R I des images à un espace visage de dimensions R K (K < I) de manière à ce que la variance observée dans chacune de ces nouvelles dimensions soit décroissante. Le calcul des composantes principales consiste à : A) Calculer la valeur moyenne des visages (visage moyen) : µ = 1 J J x j (2) j=1 B) Centrer les images de manière à avoir une matrice de données D dont la moyenne est de zéro : D = [x 1 µ, x 2 µ,..., x J µ] (3) C) Calculer la matrice de covariance de la matrice centrée A : J C = (x j µ)(x j µ) T = DD T (4) j=1 2. La moyenne pondérée des carrés des distances des points projetés à leur centre de gravité. 2
3 D) Décomposer C en vecteurs propres v i et leurs valeurs propres λ i : Sv i = λ i v i, j = 1,..., I (5) où, Λ = diag(λ k ) et V = [v 1,, v I ] est la matrice de tous les I vecteurs propres. Cette opération revient à poser S = VΛV T. E) Trier les valeurs propres et les vecteurs propres correspondants : λ 1 λ 2... λ I 0 v 1 v 2... v I 0 (6) F) Choisir les K premiers vecteurs propres (composantes principales) : G) Finalement, projeter les données sur les K < I nouveaux axes : W = [v 1,..., v K ] (7) Y = W T (X µ), X R I, Y R K (8) Les vecteurs propres d un visage (Eigenfaces) associées aux plus fortes valeurs propres sont les plus pertinentes et représentent dans l espace des images les fortes variations d un visage. Le nombre possible de visages propres peut être donc approximé en utilisant seulement les meilleurs visages propres qui correspondent aux plus grandes valeurs propres. 2.2 Analyse en composantes principales avec noyau L analyse par composante principale avec noyau (kpca, pour kernel PCA ) est une variation de la méthode précédente avec l utilisation de la technique du noyau. Soit J vecteurs x d image centrée (voir éq. 3) dans un espace R I, ces données ne seront généralement pas linéairement séparables si I < J. Par contre, si nous effectuons la projection Φ : R I R I, où I J, les données seront alors pratiquement toujours linéairement séparable et il sera facile de construire des hyperplans séparant les données en sous-groupes de données (dans notre cas des classes). Contrairement à PCA, la projection Φ créée des vecteurs linéairement indépendants et il est donc impossible d obtenir des vecteurs propres à partir d un matrice de covariance. À la place, une fonction arbitraire Φ, de dimension I J, est utilisée pour créer un noyau (en anglais, kernel ) J J défini par le produit scalaire N ij = k(x i, x j ) = Φ(x i ) Φ(x j ) = Φ(x i ) T Φ(x j ). (9) Notons que la matrice N est le résultat d un produit scalaire effectué avec la fonction Φ(x). Chaque élément du noyau N est donc le résultat de la projection des données sur les vecteurs propres v k et non les vecteurs propres en tant que tels, comme la matrice W obtenu avec PCA. Puisque les opérations avec la projection Φ(x) ne sont jamais calculée explicitement, ceci nous permet donc de travailler dans un espace R D de très haute dimensionnalité et de satisfaire D J. 3
4 Pour évaluer la projection d un vecteur x 3 sur le k ième vecteur propre (v k ), il suffit d exécuter l opération I v k Φ(x) = α ik Φ(x i ) T Φ(x) (10) i=1 où les produit scalaires Φ(x i ) T Φ(x) sont les éléments de la matrice N, αi k est le i ième élément du k ième vecteur propre de la matrice N. Il reste alors à calculer et normaliser les vecteurs propres de N, α k. Étant donné que les visage ont été centrés, le calcul des α k se fait en solutionnant l équation de vecteurs propres JλA = NA, (11) où A est la matrice des vecteurs propres de N, A = [α 1,..., α J, et λ est le vecteur des valeurs propres. La normalisation des vecteurs propres α k est effectuée de manière à satisfaire l équation 1 = λ k (α k α k ). (12) Le principal désavantage de cette démarche est que les vecteurs propres v k ne sont jamais calculés et, contrairement à PCA, il n est donc pas possible de trouver les K meilleurs vecteurs explicitement. Ceci entraîne que pour de grandes bases de données, l utilisation de kpca nécessitera l utilisation de très grandes matrices N, ce qui peut s avérer problématique. Il est alors nécessaire de faire une première catégorisation ( clustering ) des données et d utiliser le centre des catégories pour remplir la matrice N. 2.3 Expérimentations Utiliser le script exp2_dimensions.m pour expérimenter avec PCA et kpca sur des données synthétiques afin de voir les avantages et les inconvénients des deux méthodes. Voir help pca, kernel_pca et compute_mapping pour bien comprendre les fonctions. 2.4 Préparation de la base de donnée de visages Vous pouvez télécharger la base de visage de AT&T 4 du site web : uk/research/dtg/attarchive/pub/data/att_faces.zip, puis l extraire (par exemple dans un répertoire nommé : att ). Les images sont organisées dans 40 répertoires (un pour chaque individu) nommé : s1,..., s40. Dans chacun de ces répertoires, il y a dix images de visage différentes pour chaque individu numérotées de 1 à 10. Les fichiers sont en format PGM. La taille de chaque image est de 92x112 pixels, avec 256 niveaux de gris par pixel. Écrire un script pour : faces_to_prtools_data.m Charger les images de chaque individu, les transformer en PRTools datasets, et les sauvegarder en format.mat. Par exemple, face1.mat : (les images du premier individu dans le répertoire s1) doit être une dataset de : 10 images par caractéristiques de classe Les vecteurs x proviennent des données utilisées pour construire la matrice N 4. http :// 4
5 (a) (b) Figure 2 Les 5 premières images appartenant au 10 premiers individus de la base AT&T (2a), avec les 3 premiers Eigenfaces (2b) read_faces(path,subject,photo) Charger (dans une même dataset ) les images déjà sauvegardées (facexx.mat) en choisissant le numéro de l individu (subject) et le nombre des images (bien sur en gardant les étiquettes). Il est préférable si la fonction accepte des vecteurs en entrée pour faciliter la division des données en apprentissage et test (pour les séances prochaines). Par exemple, Train = read_faces(./att,1:10,1:5); % charge les 5 premières images pour les 10 premier individus dans Train Test = read_faces(./att,1:10,6:10); % charge les 5 dernières images pour les 10 premier individus dans Test Fonctions utiles : Matlab : imread, imshow, sprintf, save, load. PRTools : show, im2obj. 2.5 Application de PCA/kPCA sur notre problème On va appliquer et comparer PCA et kpca sur notre problème d identification de visage. Dans le cadre de cette séance on ne va pas aller au-delà de la réduction de dimensions. Charger les images, par exemple (figure 2a) : Train = read_faces(./att,1:10,1:5) Appliquer la PCA et la LDA sur la base Train Reconstruire quelques images (projetées dans le nouvel espace) pour visualiser l effet de chaque méthode. Par exemple, pour les 3 premiers vectteur pour Eigenfaces, vous devriez obtenir des images similaires à la figure 2b Comparer les dispersions de données en utilisant les 2 (ou 3) premières caractéristiques (avec la fonction scatterd) provenant des données brutes, de PCA et de kpca. Choisir et comparer aussi autres vecteurs caractéristiques (e.g., les derniers, etc.) Expérimenter en variant le nombre : de composantes retenues des individus 5
L ANALYSE EN COMPOSANTES PRINCIPALES (A.C.P.) Pierre-Louis GONZALEZ
 L ANALYSE EN COMPOSANTES PRINCIPALES (A.C.P.) Pierre-Louis GONZALEZ INTRODUCTION Données : n individus observés sur p variables quantitatives. L A.C.P. permet d eplorer les liaisons entre variables et
L ANALYSE EN COMPOSANTES PRINCIPALES (A.C.P.) Pierre-Louis GONZALEZ INTRODUCTION Données : n individus observés sur p variables quantitatives. L A.C.P. permet d eplorer les liaisons entre variables et
Extraction d informations stratégiques par Analyse en Composantes Principales
 Extraction d informations stratégiques par Analyse en Composantes Principales Bernard DOUSSET IRIT/ SIG, Université Paul Sabatier, 118 route de Narbonne, 31062 Toulouse cedex 04 [email protected] 1 Introduction
Extraction d informations stratégiques par Analyse en Composantes Principales Bernard DOUSSET IRIT/ SIG, Université Paul Sabatier, 118 route de Narbonne, 31062 Toulouse cedex 04 [email protected] 1 Introduction
1 Complément sur la projection du nuage des individus
 TP 0 : Analyse en composantes principales (II) Le but de ce TP est d approfondir nos connaissances concernant l analyse en composantes principales (ACP). Pour cela, on reprend les notations du précédent
TP 0 : Analyse en composantes principales (II) Le but de ce TP est d approfondir nos connaissances concernant l analyse en composantes principales (ACP). Pour cela, on reprend les notations du précédent
Analyse en Composantes Principales
 Analyse en Composantes Principales Anne B Dufour Octobre 2013 Anne B Dufour () Analyse en Composantes Principales Octobre 2013 1 / 36 Introduction Introduction Soit X un tableau contenant p variables mesurées
Analyse en Composantes Principales Anne B Dufour Octobre 2013 Anne B Dufour () Analyse en Composantes Principales Octobre 2013 1 / 36 Introduction Introduction Soit X un tableau contenant p variables mesurées
Déroulement d un projet en DATA MINING, préparation et analyse des données. Walid AYADI
 1 Déroulement d un projet en DATA MINING, préparation et analyse des données Walid AYADI 2 Les étapes d un projet Choix du sujet - Définition des objectifs Inventaire des données existantes Collecte, nettoyage
1 Déroulement d un projet en DATA MINING, préparation et analyse des données Walid AYADI 2 Les étapes d un projet Choix du sujet - Définition des objectifs Inventaire des données existantes Collecte, nettoyage
Laboratoire 4 Développement d un système intelligent
 DÉPARTEMENT DE GÉNIE LOGICIEL ET DES TI LOG770 - SYSTÈMES INTELLIGENTS ÉTÉ 2012 Laboratoire 4 Développement d un système intelligent 1 Introduction Ce quatrième et dernier laboratoire porte sur le développement
DÉPARTEMENT DE GÉNIE LOGICIEL ET DES TI LOG770 - SYSTÈMES INTELLIGENTS ÉTÉ 2012 Laboratoire 4 Développement d un système intelligent 1 Introduction Ce quatrième et dernier laboratoire porte sur le développement
BASE. Vous avez alors accès à un ensemble de fonctionnalités explicitées ci-dessous :
 BASE BioArray Software Environment (BASE) est une base de données permettant de gérer l importante quantité de données générées par des analyses de bio-puces. BASE gère les informations biologiques, les
BASE BioArray Software Environment (BASE) est une base de données permettant de gérer l importante quantité de données générées par des analyses de bio-puces. BASE gère les informations biologiques, les
La structure de la base de données et l utilisation de PAST. Musée Royal de l Afrique Centrale (MRAC Tervuren)
 La structure de la base de données et l utilisation de PAST La structure de la base de données données originales SPÉCIMENS Code des spécimens: Identification des spécimens individuels. Dépend du but de
La structure de la base de données et l utilisation de PAST La structure de la base de données données originales SPÉCIMENS Code des spécimens: Identification des spécimens individuels. Dépend du but de
La classification automatique de données quantitatives
 La classification automatique de données quantitatives 1 Introduction Parmi les méthodes de statistique exploratoire multidimensionnelle, dont l objectif est d extraire d une masse de données des informations
La classification automatique de données quantitatives 1 Introduction Parmi les méthodes de statistique exploratoire multidimensionnelle, dont l objectif est d extraire d une masse de données des informations
Analyse de la vidéo. Chapitre 4.1 - La modélisation pour le suivi d objet. 10 mars 2015. Chapitre 4.1 - La modélisation d objet 1 / 57
 Analyse de la vidéo Chapitre 4.1 - La modélisation pour le suivi d objet 10 mars 2015 Chapitre 4.1 - La modélisation d objet 1 / 57 La représentation d objets Plan de la présentation 1 La représentation
Analyse de la vidéo Chapitre 4.1 - La modélisation pour le suivi d objet 10 mars 2015 Chapitre 4.1 - La modélisation d objet 1 / 57 La représentation d objets Plan de la présentation 1 La représentation
Introduction à MATLAB R
 Introduction à MATLAB R Romain Tavenard 10 septembre 2009 MATLAB R est un environnement de calcul numérique propriétaire orienté vers le calcul matriciel. Il se compose d un langage de programmation, d
Introduction à MATLAB R Romain Tavenard 10 septembre 2009 MATLAB R est un environnement de calcul numérique propriétaire orienté vers le calcul matriciel. Il se compose d un langage de programmation, d
INTRODUCTION À L ANALYSE FACTORIELLE DES CORRESPONDANCES
 INTRODUCTION À L ANALYSE FACTORIELLE DES CORRESPONDANCES Dominique LAFFLY Maître de Conférences, Université de Pau Laboratoire Société Environnement Territoire UMR 5603 du CNRS et Université de Pau Domaine
INTRODUCTION À L ANALYSE FACTORIELLE DES CORRESPONDANCES Dominique LAFFLY Maître de Conférences, Université de Pau Laboratoire Société Environnement Territoire UMR 5603 du CNRS et Université de Pau Domaine
Exercice : la frontière des portefeuilles optimaux sans actif certain
 Exercice : la frontière des portefeuilles optimaux sans actif certain Philippe Bernard Ingénierie Economique & Financière Université Paris-Dauphine Février 0 On considère un univers de titres constitué
Exercice : la frontière des portefeuilles optimaux sans actif certain Philippe Bernard Ingénierie Economique & Financière Université Paris-Dauphine Février 0 On considère un univers de titres constitué
Projet Matlab/Octave : segmentation d'un ballon de couleur dans une image couleur et insertion d'un logo
 Projet Matlab/Octave : segmentation d'un ballon de couleur dans une image couleur et insertion d'un logo Dans ce projet, nous allons réaliser le code qui permet d'insérer sur une image, un logo sur un
Projet Matlab/Octave : segmentation d'un ballon de couleur dans une image couleur et insertion d'un logo Dans ce projet, nous allons réaliser le code qui permet d'insérer sur une image, un logo sur un
Chapitre 3. Les distributions à deux variables
 Chapitre 3. Les distributions à deux variables Jean-François Coeurjolly http://www-ljk.imag.fr/membres/jean-francois.coeurjolly/ Laboratoire Jean Kuntzmann (LJK), Grenoble University 1 Distributions conditionnelles
Chapitre 3. Les distributions à deux variables Jean-François Coeurjolly http://www-ljk.imag.fr/membres/jean-francois.coeurjolly/ Laboratoire Jean Kuntzmann (LJK), Grenoble University 1 Distributions conditionnelles
IMAGES NUMÉRIQUES MATRICIELLES EN SCILAB
 IMAGES NUMÉRIQUES MATRICIELLES EN SCILAB Ce document, écrit par des animateurs de l IREM de Besançon, a pour objectif de présenter quelques unes des fonctions du logiciel Scilab, celles qui sont spécifiques
IMAGES NUMÉRIQUES MATRICIELLES EN SCILAB Ce document, écrit par des animateurs de l IREM de Besançon, a pour objectif de présenter quelques unes des fonctions du logiciel Scilab, celles qui sont spécifiques
Introduction au Data-Mining
 Introduction au Data-Mining Alain Rakotomamonjy - Gilles Gasso. INSA Rouen -Département ASI Laboratoire PSI Introduction au Data-Mining p. 1/25 Data-Mining : Kèkecé? Traduction : Fouille de données. Terme
Introduction au Data-Mining Alain Rakotomamonjy - Gilles Gasso. INSA Rouen -Département ASI Laboratoire PSI Introduction au Data-Mining p. 1/25 Data-Mining : Kèkecé? Traduction : Fouille de données. Terme
Projet de traitement d'image - SI 381 reconstitution 3D d'intérieur à partir de photographies
 Projet de traitement d'image - SI 381 reconstitution 3D d'intérieur à partir de photographies Régis Boulet Charlie Demené Alexis Guyot Balthazar Neveu Guillaume Tartavel Sommaire Sommaire... 1 Structure
Projet de traitement d'image - SI 381 reconstitution 3D d'intérieur à partir de photographies Régis Boulet Charlie Demené Alexis Guyot Balthazar Neveu Guillaume Tartavel Sommaire Sommaire... 1 Structure
Projet Matlab : un logiciel de cryptage
 Projet Matlab : un logiciel de cryptage La stéganographie (du grec steganos : couvert et graphein : écriture) consiste à dissimuler une information au sein d'une autre à caractère anodin, de sorte que
Projet Matlab : un logiciel de cryptage La stéganographie (du grec steganos : couvert et graphein : écriture) consiste à dissimuler une information au sein d'une autre à caractère anodin, de sorte que
Analyses multivariées avec R Commander (via le package FactoMineR) Qu est ce que R? Introduction à R Qu est ce que R?
 Analyses multivariées avec R Commander Analyses multivariées avec R Commander (via le package FactoMineR) Plate-forme de Support en Méthodologie et Calcul Statistique (SMCS) - UCL 1 Introduction à R 2
Analyses multivariées avec R Commander Analyses multivariées avec R Commander (via le package FactoMineR) Plate-forme de Support en Méthodologie et Calcul Statistique (SMCS) - UCL 1 Introduction à R 2
21 mars 2012. Simulations et Méthodes de Monte Carlo. DADI Charles-Abner. Objectifs et intérêt de ce T.E.R. Générer l'aléatoire.
 de 21 mars 2012 () 21 mars 2012 1 / 6 de 1 2 3 4 5 () 21 mars 2012 2 / 6 1 de 2 3 4 5 () 21 mars 2012 3 / 6 1 2 de 3 4 5 () 21 mars 2012 4 / 6 1 2 de 3 4 de 5 () 21 mars 2012 5 / 6 de 1 2 3 4 5 () 21 mars
de 21 mars 2012 () 21 mars 2012 1 / 6 de 1 2 3 4 5 () 21 mars 2012 2 / 6 1 de 2 3 4 5 () 21 mars 2012 3 / 6 1 2 de 3 4 5 () 21 mars 2012 4 / 6 1 2 de 3 4 de 5 () 21 mars 2012 5 / 6 de 1 2 3 4 5 () 21 mars
INF6304 Interfaces Intelligentes
 INF6304 Interfaces Intelligentes filtres collaboratifs 1/42 INF6304 Interfaces Intelligentes Systèmes de recommandations, Approches filtres collaboratifs Michel C. Desmarais Génie informatique et génie
INF6304 Interfaces Intelligentes filtres collaboratifs 1/42 INF6304 Interfaces Intelligentes Systèmes de recommandations, Approches filtres collaboratifs Michel C. Desmarais Génie informatique et génie
Dossier I Découverte de Base d Open Office
 ETUDE D UN SYSTEME DE GESTION DE BASE DE DONNEES RELATIONNELLES Définition : Un SGBD est un logiciel de gestion des données fournissant des méthodes d accès aux informations. Un SGBDR permet de décrire
ETUDE D UN SYSTEME DE GESTION DE BASE DE DONNEES RELATIONNELLES Définition : Un SGBD est un logiciel de gestion des données fournissant des méthodes d accès aux informations. Un SGBDR permet de décrire
Projet SINF2275 «Data mining and decision making» Projet classification et credit scoring
 Projet SINF2275 «Data mining and decision making» Projet classification et credit scoring Année académique 2006-2007 Professeurs : Marco Saerens Adresse : Université catholique de Louvain Information Systems
Projet SINF2275 «Data mining and decision making» Projet classification et credit scoring Année académique 2006-2007 Professeurs : Marco Saerens Adresse : Université catholique de Louvain Information Systems
Chapitre 7. Statistique des échantillons gaussiens. 7.1 Projection de vecteurs gaussiens
 Chapitre 7 Statistique des échantillons gaussiens Le théorème central limite met en évidence le rôle majeur tenu par la loi gaussienne en modélisation stochastique. De ce fait, les modèles statistiques
Chapitre 7 Statistique des échantillons gaussiens Le théorème central limite met en évidence le rôle majeur tenu par la loi gaussienne en modélisation stochastique. De ce fait, les modèles statistiques
Une comparaison de méthodes de discrimination des masses de véhicules automobiles
 p.1/34 Une comparaison de méthodes de discrimination des masses de véhicules automobiles A. Rakotomamonjy, R. Le Riche et D. Gualandris INSA de Rouen / CNRS 1884 et SMS / PSA Enquêtes en clientèle dans
p.1/34 Une comparaison de méthodes de discrimination des masses de véhicules automobiles A. Rakotomamonjy, R. Le Riche et D. Gualandris INSA de Rouen / CNRS 1884 et SMS / PSA Enquêtes en clientèle dans
Introduction. Préambule. Le contexte
 Préambule... INTRODUCTION... BREF HISTORIQUE DE L ACP... 4 DOMAINE D'APPLICATION... 5 INTERPRETATIONS GEOMETRIQUES... 6 a - Pour les n individus... 6 b - Pour les p variables... 7 c - Notion d éléments
Préambule... INTRODUCTION... BREF HISTORIQUE DE L ACP... 4 DOMAINE D'APPLICATION... 5 INTERPRETATIONS GEOMETRIQUES... 6 a - Pour les n individus... 6 b - Pour les p variables... 7 c - Notion d éléments
Lecture critique et pratique de la médecine
 1-00.qxp 24/04/2006 11:23 Page 13 Lecture critique appliquée à la médecine vasculaireecture critique et pratique de la médecine Lecture critique et pratique de la médecine Introduction Si la médecine ne
1-00.qxp 24/04/2006 11:23 Page 13 Lecture critique appliquée à la médecine vasculaireecture critique et pratique de la médecine Lecture critique et pratique de la médecine Introduction Si la médecine ne
Traitement bas-niveau
 Plan Introduction L approche contour (frontière) Introduction Objectifs Les traitements ont pour but d extraire l information utile et pertinente contenue dans l image en regard de l application considérée.
Plan Introduction L approche contour (frontière) Introduction Objectifs Les traitements ont pour but d extraire l information utile et pertinente contenue dans l image en regard de l application considérée.
Revue des algorithmes PCA, LDA et EBGM utilisés en reconnaissance 2D du visage pour la biométrie
 Revue des algorithmes PCA, LDA et EBGM utilisés en reconnaissance 2D du visage pour la biométrie Nicolas MORIZET, Thomas EA, Florence ROSSANT, Frédéric AMIEL, Amara AMARA Institut Supérieur d Électronique
Revue des algorithmes PCA, LDA et EBGM utilisés en reconnaissance 2D du visage pour la biométrie Nicolas MORIZET, Thomas EA, Florence ROSSANT, Frédéric AMIEL, Amara AMARA Institut Supérieur d Électronique
Programmation linéaire
 1 Programmation linéaire 1. Le problème, un exemple. 2. Le cas b = 0 3. Théorème de dualité 4. L algorithme du simplexe 5. Problèmes équivalents 6. Complexité de l Algorithme 2 Position du problème Soit
1 Programmation linéaire 1. Le problème, un exemple. 2. Le cas b = 0 3. Théorème de dualité 4. L algorithme du simplexe 5. Problèmes équivalents 6. Complexité de l Algorithme 2 Position du problème Soit
Statistiques Descriptives à une dimension
 I. Introduction et Définitions 1. Introduction La statistique est une science qui a pour objectif de recueillir et de traiter les informations, souvent en très grand nombre. Elle regroupe l ensemble des
I. Introduction et Définitions 1. Introduction La statistique est une science qui a pour objectif de recueillir et de traiter les informations, souvent en très grand nombre. Elle regroupe l ensemble des
Analyse d images. [email protected]. Edmond Boyer UFRIMA 1
 Analyse d images [email protected] Edmond Boyer UFRIMA 1 1 Généralités Analyse d images (Image Analysis) : utiliser un ordinateur pour interpréter le monde extérieur au travers d images. Images Objets
Analyse d images [email protected] Edmond Boyer UFRIMA 1 1 Généralités Analyse d images (Image Analysis) : utiliser un ordinateur pour interpréter le monde extérieur au travers d images. Images Objets
Ne cherchez plus, soyez informés! Robert van Kommer
 Ne cherchez plus, soyez informés! Robert van Kommer Le sommaire La présentation du contexte applicatif Le mariage: Big Data et apprentissage automatique Dialogues - interactions - apprentissages 2 Le contexte
Ne cherchez plus, soyez informés! Robert van Kommer Le sommaire La présentation du contexte applicatif Le mariage: Big Data et apprentissage automatique Dialogues - interactions - apprentissages 2 Le contexte
Les bases de données
 Les bases de données Introduction aux fonctions de tableur et logiciels ou langages spécialisés (MS-Access, Base, SQL ) Yves Roggeman Boulevard du Triomphe CP 212 B-1050 Bruxelles (Belgium) Idée intuitive
Les bases de données Introduction aux fonctions de tableur et logiciels ou langages spécialisés (MS-Access, Base, SQL ) Yves Roggeman Boulevard du Triomphe CP 212 B-1050 Bruxelles (Belgium) Idée intuitive
Intelligence Artificielle et Systèmes Multi-Agents. Badr Benmammar [email protected]
 Intelligence Artificielle et Systèmes Multi-Agents Badr Benmammar [email protected] Plan La première partie : L intelligence artificielle (IA) Définition de l intelligence artificielle (IA) Domaines
Intelligence Artificielle et Systèmes Multi-Agents Badr Benmammar [email protected] Plan La première partie : L intelligence artificielle (IA) Définition de l intelligence artificielle (IA) Domaines
Vérification audiovisuelle de l identité
 Vérification audiovisuelle de l identité Rémi Landais, Hervé Bredin, Leila Zouari, et Gérard Chollet École Nationale Supérieure des Télécommunications, Département Traitement du Signal et des Images, Laboratoire
Vérification audiovisuelle de l identité Rémi Landais, Hervé Bredin, Leila Zouari, et Gérard Chollet École Nationale Supérieure des Télécommunications, Département Traitement du Signal et des Images, Laboratoire
2 Serveurs OLAP et introduction au Data Mining
 2-1 2 Serveurs OLAP et introduction au Data Mining 2-2 Création et consultation des cubes en mode client-serveur Serveur OLAP Clients OLAP Clients OLAP 2-3 Intérêt Systèmes serveurs et clients Fonctionnalité
2-1 2 Serveurs OLAP et introduction au Data Mining 2-2 Création et consultation des cubes en mode client-serveur Serveur OLAP Clients OLAP Clients OLAP 2-3 Intérêt Systèmes serveurs et clients Fonctionnalité
L'analyse des données à l usage des non mathématiciens
 Montpellier L'analyse des données à l usage des non mathématiciens 2 ème Partie: L'analyse en composantes principales AGRO.M - INRA - Formation Permanente Janvier 2006 André Bouchier Analyses multivariés.
Montpellier L'analyse des données à l usage des non mathématiciens 2 ème Partie: L'analyse en composantes principales AGRO.M - INRA - Formation Permanente Janvier 2006 André Bouchier Analyses multivariés.
L'analyse de données. Polycopié de cours ENSIETA - Réf. : 1463. Arnaud MARTIN
 L'analyse de données Polycopié de cours ENSIETA - Réf : 1463 Arnaud MARTIN Septembre 2004 Table des matières 1 Introduction 1 11 Domaines d'application 2 12 Les données 2 13 Les objectifs 3 14 Les méthodes
L'analyse de données Polycopié de cours ENSIETA - Réf : 1463 Arnaud MARTIN Septembre 2004 Table des matières 1 Introduction 1 11 Domaines d'application 2 12 Les données 2 13 Les objectifs 3 14 Les méthodes
Trépier avec règle, ressort à boudin, chronomètre, 5 masses de 50 g.
 PHYSQ 130: Hooke 1 LOI DE HOOKE: CAS DU RESSORT 1 Introduction La loi de Hooke est fondamentale dans l étude du mouvement oscillatoire. Elle est utilisée, entre autres, dans les théories décrivant les
PHYSQ 130: Hooke 1 LOI DE HOOKE: CAS DU RESSORT 1 Introduction La loi de Hooke est fondamentale dans l étude du mouvement oscillatoire. Elle est utilisée, entre autres, dans les théories décrivant les
Séries Statistiques Simples
 1. Collecte et Représentation de l Information 1.1 Définitions 1.2 Tableaux statistiques 1.3 Graphiques 2. Séries statistiques simples 2.1 Moyenne arithmétique 2.2 Mode & Classe modale 2.3 Effectifs &
1. Collecte et Représentation de l Information 1.1 Définitions 1.2 Tableaux statistiques 1.3 Graphiques 2. Séries statistiques simples 2.1 Moyenne arithmétique 2.2 Mode & Classe modale 2.3 Effectifs &
GROUPE DE TRAVAIL «ARTICLE 29» SUR LA PROTECTION DES DONNÉES
 GROUPE DE TRAVAIL «ARTICLE 29» SUR LA PROTECTION DES DONNÉES 00727/12/FR WP 192 Avis 02/2012 sur la reconnaissance faciale dans le cadre des services en ligne et mobiles Adopté le 22 mars 2012 Le groupe
GROUPE DE TRAVAIL «ARTICLE 29» SUR LA PROTECTION DES DONNÉES 00727/12/FR WP 192 Avis 02/2012 sur la reconnaissance faciale dans le cadre des services en ligne et mobiles Adopté le 22 mars 2012 Le groupe
= 1 si n = m& où n et m sont souvent des indices entiers, par exemple, n, m = 0, 1, 2, 3, 4... En fait,! n m
 1 épartement de Physique, Université Laval, Québec Pierre Amiot, 1. La fonction delta et certaines de ses utilisations. Clientèle Ce texte est destiné aux physiciens, ingénieurs et autres scientifiques.
1 épartement de Physique, Université Laval, Québec Pierre Amiot, 1. La fonction delta et certaines de ses utilisations. Clientèle Ce texte est destiné aux physiciens, ingénieurs et autres scientifiques.
Franck VAUTIER, Jean-Pierre TOUMAZET, Erwan ROUSSEL, Marlène FAURE, Mohamed ABADI, Marta FLOREZ, Bertrand DOUSTEYSSIER
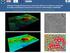 Utilisation d images dérivées d un jeu de données LIDAR pour la détection automatisée de vestiges archéologiques (programme de recherche méthodologique LiDARCHEO) Franck VAUTIER, Jean-Pierre TOUMAZET,
Utilisation d images dérivées d un jeu de données LIDAR pour la détection automatisée de vestiges archéologiques (programme de recherche méthodologique LiDARCHEO) Franck VAUTIER, Jean-Pierre TOUMAZET,
Relation entre deux variables : estimation de la corrélation linéaire
 CHAPITRE 3 Relation entre deux variables : estimation de la corrélation linéaire Parmi les analyses statistiques descriptives, l une d entre elles est particulièrement utilisée pour mettre en évidence
CHAPITRE 3 Relation entre deux variables : estimation de la corrélation linéaire Parmi les analyses statistiques descriptives, l une d entre elles est particulièrement utilisée pour mettre en évidence
Cours d analyse numérique SMI-S4
 ours d analyse numérique SMI-S4 Introduction L objet de l analyse numérique est de concevoir et d étudier des méthodes de résolution de certains problèmes mathématiques, en général issus de problèmes réels,
ours d analyse numérique SMI-S4 Introduction L objet de l analyse numérique est de concevoir et d étudier des méthodes de résolution de certains problèmes mathématiques, en général issus de problèmes réels,
La segmentation à l aide de EG-SAS. A.Bouhia Analyste principal à la Banque Nationale du Canada. Chargé de cours à l UQAM
 La segmentation à l aide de EG-SAS A.Bouhia Analyste principal à la Banque Nationale du Canada. Chargé de cours à l UQAM Définition de la segmentation - Au lieu de considérer une population dans son ensemble,
La segmentation à l aide de EG-SAS A.Bouhia Analyste principal à la Banque Nationale du Canada. Chargé de cours à l UQAM Définition de la segmentation - Au lieu de considérer une population dans son ensemble,
La Licence Mathématiques et Economie-MASS Université de Sciences Sociales de Toulouse 1
 La Licence Mathématiques et Economie-MASS Université de Sciences Sociales de Toulouse 1 La licence Mathématiques et Economie-MASS de l Université des Sciences Sociales de Toulouse propose sur les trois
La Licence Mathématiques et Economie-MASS Université de Sciences Sociales de Toulouse 1 La licence Mathématiques et Economie-MASS de l Université des Sciences Sociales de Toulouse propose sur les trois
Calcul Formel et Numérique, Partie I
 Calcul Formel et Numérique N.Vandenberghe [email protected] Table des matières 1 Introduction à Matlab 2 1.1 Quelques généralités.......................... 2 2 Où trouver des informations 2 3 Opérations
Calcul Formel et Numérique N.Vandenberghe [email protected] Table des matières 1 Introduction à Matlab 2 1.1 Quelques généralités.......................... 2 2 Où trouver des informations 2 3 Opérations
Reconnaissance et suivi de visages et implémentation en robotique temps-réel
 Université Catholique de Louvain Ecole Polytechnique de Louvain Mémoire de fin d études Reconnaissance et suivi de visages et implémentation en robotique temps-réel Réalisé par Mathieu Van Wambeke en vue
Université Catholique de Louvain Ecole Polytechnique de Louvain Mémoire de fin d études Reconnaissance et suivi de visages et implémentation en robotique temps-réel Réalisé par Mathieu Van Wambeke en vue
Optimisation de la compression fractale D images basée sur les réseaux de neurones
 Optimisation de la compression fractale D images basée sur les réseaux de neurones D r BOUKELIF Aoued Communication Networks,Architectures and Mutimedia laboratory University of S.B.A [email protected]
Optimisation de la compression fractale D images basée sur les réseaux de neurones D r BOUKELIF Aoued Communication Networks,Architectures and Mutimedia laboratory University of S.B.A [email protected]
Séance 0 : Linux + Octave : le compromis idéal
 Séance 0 : Linux + Octave : le compromis idéal Introduction Linux est un système d'exploitation multi-tâches et multi-utilisateurs, basé sur la gratuité et développé par une communauté de passionnés. C'est
Séance 0 : Linux + Octave : le compromis idéal Introduction Linux est un système d'exploitation multi-tâches et multi-utilisateurs, basé sur la gratuité et développé par une communauté de passionnés. C'est
Initiation à l analyse en composantes principales
 Fiche TD avec le logiciel : tdr601 Initiation à l analyse en composantes principales A.B. Dufour & J.R. Lobry Une première approche très intuitive et interactive de l ACP. Centrage et réduction des données.
Fiche TD avec le logiciel : tdr601 Initiation à l analyse en composantes principales A.B. Dufour & J.R. Lobry Une première approche très intuitive et interactive de l ACP. Centrage et réduction des données.
FORMULAIRE DE STATISTIQUES
 FORMULAIRE DE STATISTIQUES I. STATISTIQUES DESCRIPTIVES Moyenne arithmétique Remarque: population: m xμ; échantillon: Mx 1 Somme des carrés des écarts "# FR MOYENNE(série) MOYENNE(série) NL GEMIDDELDE(série)
FORMULAIRE DE STATISTIQUES I. STATISTIQUES DESCRIPTIVES Moyenne arithmétique Remarque: population: m xμ; échantillon: Mx 1 Somme des carrés des écarts "# FR MOYENNE(série) MOYENNE(série) NL GEMIDDELDE(série)
Première partie. Préliminaires : noyaux itérés. MPSI B 6 juin 2015
 Énoncé Soit V un espace vectoriel réel. L espace vectoriel des endomorphismes de V est désigné par L(V ). Lorsque f L(V ) et k N, on désigne par f 0 = Id V, f k = f k f la composée de f avec lui même k
Énoncé Soit V un espace vectoriel réel. L espace vectoriel des endomorphismes de V est désigné par L(V ). Lorsque f L(V ) et k N, on désigne par f 0 = Id V, f k = f k f la composée de f avec lui même k
Arbres binaires de décision
 1 Arbres binaires de décision Résumé Arbres binaires de décision Méthodes de construction d arbres binaires de décision, modélisant une discrimination (classification trees) ou une régression (regression
1 Arbres binaires de décision Résumé Arbres binaires de décision Méthodes de construction d arbres binaires de décision, modélisant une discrimination (classification trees) ou une régression (regression
Enjeux mathématiques et Statistiques du Big Data
 Enjeux mathématiques et Statistiques du Big Data Mathilde Mougeot LPMA/Université Paris Diderot, [email protected] Mathématique en Mouvements, Paris, IHP, 6 Juin 2015 M. Mougeot (Paris
Enjeux mathématiques et Statistiques du Big Data Mathilde Mougeot LPMA/Université Paris Diderot, [email protected] Mathématique en Mouvements, Paris, IHP, 6 Juin 2015 M. Mougeot (Paris
Travaux pratiques avec RapidMiner
 Travaux pratiques avec RapidMiner Master Informatique de Paris 6 Spécialité IAD Parcours EDOW Module Algorithmes pour la Fouille de Données Janvier 2012 Prise en main Généralités RapidMiner est un logiciel
Travaux pratiques avec RapidMiner Master Informatique de Paris 6 Spécialité IAD Parcours EDOW Module Algorithmes pour la Fouille de Données Janvier 2012 Prise en main Généralités RapidMiner est un logiciel
Apprentissage Automatique
 Apprentissage Automatique Introduction-I [email protected] www.lia.univ-avignon.fr Définition? (Wikipedia) L'apprentissage automatique (machine-learning en anglais) est un des champs
Apprentissage Automatique Introduction-I [email protected] www.lia.univ-avignon.fr Définition? (Wikipedia) L'apprentissage automatique (machine-learning en anglais) est un des champs
Introduction: 1. définition d un ETL 2. importance et diversité des données spatiales utilitédes ETL géographiques
 1 2 Introduction: 1. définition d un ETL 2. importance et diversité des données spatiales utilitédes ETL géographiques 3 ETL = extracto-chargeur = datadumping La Business Intelligence, BI, (ou informatique
1 2 Introduction: 1. définition d un ETL 2. importance et diversité des données spatiales utilitédes ETL géographiques 3 ETL = extracto-chargeur = datadumping La Business Intelligence, BI, (ou informatique
aux différences est appelé équation aux différences d ordre n en forme normale.
 MODÉLISATION ET SIMULATION EQUATIONS AUX DIFFÉRENCES (I/II) 1. Rappels théoriques : résolution d équations aux différences 1.1. Équations aux différences. Définition. Soit x k = x(k) X l état scalaire
MODÉLISATION ET SIMULATION EQUATIONS AUX DIFFÉRENCES (I/II) 1. Rappels théoriques : résolution d équations aux différences 1.1. Équations aux différences. Définition. Soit x k = x(k) X l état scalaire
ACP Voitures 1- Méthode
 acp=princomp(voit,cor=t) ACP Voitures 1- Méthode Call: princomp(x = voit, cor = T) Standard deviations: Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 2.1577815 0.9566721 0.4903373 0.3204833 0.2542759 0.1447788
acp=princomp(voit,cor=t) ACP Voitures 1- Méthode Call: princomp(x = voit, cor = T) Standard deviations: Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 2.1577815 0.9566721 0.4903373 0.3204833 0.2542759 0.1447788
3. Conditionnement P (B)
 Conditionnement 16 3. Conditionnement Dans cette section, nous allons rappeler un certain nombre de définitions et de propriétés liées au problème du conditionnement, c est à dire à la prise en compte
Conditionnement 16 3. Conditionnement Dans cette section, nous allons rappeler un certain nombre de définitions et de propriétés liées au problème du conditionnement, c est à dire à la prise en compte
Introduction au Data-Mining
 Introduction au Data-Mining Gilles Gasso, Stéphane Canu INSA Rouen -Département ASI Laboratoire LITIS 8 septembre 205. Ce cours est librement inspiré du cours DM de Alain Rakotomamonjy Gilles Gasso, Stéphane
Introduction au Data-Mining Gilles Gasso, Stéphane Canu INSA Rouen -Département ASI Laboratoire LITIS 8 septembre 205. Ce cours est librement inspiré du cours DM de Alain Rakotomamonjy Gilles Gasso, Stéphane
L analyse d images regroupe plusieurs disciplines que l on classe en deux catégories :
 La vision nous permet de percevoir et d interpreter le monde qui nous entoure. La vision artificielle a pour but de reproduire certaines fonctionnalités de la vision humaine au travers de l analyse d images.
La vision nous permet de percevoir et d interpreter le monde qui nous entoure. La vision artificielle a pour but de reproduire certaines fonctionnalités de la vision humaine au travers de l analyse d images.
Modèles pour données répétées
 Résumé Les données répétées, ou données longitudinales, constituent un domaine à la fois important et assez particulier de la statistique. On entend par données répétées des données telles que, pour chaque
Résumé Les données répétées, ou données longitudinales, constituent un domaine à la fois important et assez particulier de la statistique. On entend par données répétées des données telles que, pour chaque
Excel Avancé. Plan. Outils de résolution. Interactivité dans les feuilles. Outils de simulation. La valeur cible Le solveur
 Excel Avancé Plan Outils de résolution La valeur cible Le solveur Interactivité dans les feuilles Fonctions de recherche (ex: RechercheV) Utilisation de la barre d outils «Formulaires» Outils de simulation
Excel Avancé Plan Outils de résolution La valeur cible Le solveur Interactivité dans les feuilles Fonctions de recherche (ex: RechercheV) Utilisation de la barre d outils «Formulaires» Outils de simulation
PRÉSENTATION PRODUIT. Plus qu un logiciel, la méthode plus efficace de réconcilier.
 PRÉSENTATION PRODUIT Plus qu un logiciel, la méthode plus efficace de réconcilier. Automatiser les réconciliations permet d optimiser l utilisation des ressources et de générer plus de rentabilité dans
PRÉSENTATION PRODUIT Plus qu un logiciel, la méthode plus efficace de réconcilier. Automatiser les réconciliations permet d optimiser l utilisation des ressources et de générer plus de rentabilité dans
LA NOTATION STATISTIQUE DES EMPRUNTEURS OU «SCORING»
 LA NOTATION STATISTIQUE DES EMPRUNTEURS OU «SCORING» Gilbert Saporta Professeur de Statistique Appliquée Conservatoire National des Arts et Métiers Dans leur quasi totalité, les banques et organismes financiers
LA NOTATION STATISTIQUE DES EMPRUNTEURS OU «SCORING» Gilbert Saporta Professeur de Statistique Appliquée Conservatoire National des Arts et Métiers Dans leur quasi totalité, les banques et organismes financiers
Vision industrielle et télédétection - Détection d ellipses. Guillaume Martinez 17 décembre 2007
 Vision industrielle et télédétection - Détection d ellipses Guillaume Martinez 17 décembre 2007 1 Table des matières 1 Le projet 3 1.1 Objectif................................ 3 1.2 Les choix techniques.........................
Vision industrielle et télédétection - Détection d ellipses Guillaume Martinez 17 décembre 2007 1 Table des matières 1 Le projet 3 1.1 Objectif................................ 3 1.2 Les choix techniques.........................
Classification non supervisée
 AgroParisTech Classification non supervisée E. Lebarbier, T. Mary-Huard Table des matières 1 Introduction 4 2 Méthodes de partitionnement 5 2.1 Mesures de similarité et de dissimilarité, distances.................
AgroParisTech Classification non supervisée E. Lebarbier, T. Mary-Huard Table des matières 1 Introduction 4 2 Méthodes de partitionnement 5 2.1 Mesures de similarité et de dissimilarité, distances.................
Introduction au datamining
 Introduction au datamining Patrick Naïm janvier 2005 Définition Définition Historique Mot utilisé au départ par les statisticiens Le mot indiquait une utilisation intensive des données conduisant à des
Introduction au datamining Patrick Naïm janvier 2005 Définition Définition Historique Mot utilisé au départ par les statisticiens Le mot indiquait une utilisation intensive des données conduisant à des
AICp. Vincent Vandewalle. To cite this version: HAL Id: inria-00386678 https://hal.inria.fr/inria-00386678
 Sélection prédictive d un modèle génératif par le critère AICp Vincent Vandewalle To cite this version: Vincent Vandewalle. Sélection prédictive d un modèle génératif par le critère AICp. 41èmes Journées
Sélection prédictive d un modèle génératif par le critère AICp Vincent Vandewalle To cite this version: Vincent Vandewalle. Sélection prédictive d un modèle génératif par le critère AICp. 41èmes Journées
Optimisation, traitement d image et éclipse de Soleil
 Kléber, PCSI1&3 014-015 I. Introduction 1/8 Optimisation, traitement d image et éclipse de Soleil Partie I Introduction Le 0 mars 015 a eu lieu en France une éclipse partielle de Soleil qu il était particulièrement
Kléber, PCSI1&3 014-015 I. Introduction 1/8 Optimisation, traitement d image et éclipse de Soleil Partie I Introduction Le 0 mars 015 a eu lieu en France une éclipse partielle de Soleil qu il était particulièrement
Importation de fichiers Eagle
 Importation de fichiers Eagle 2 Mention de réserve sur les droits d'auteur Les droits d auteur rattachés à tout ou partie des présents logiciel et manuel appartiennent à RS Components et ne peuvent être
Importation de fichiers Eagle 2 Mention de réserve sur les droits d'auteur Les droits d auteur rattachés à tout ou partie des présents logiciel et manuel appartiennent à RS Components et ne peuvent être
LA PHYSIQUE DES MATERIAUX. Chapitre 1 LES RESEAUX DIRECT ET RECIPROQUE
 LA PHYSIQUE DES MATERIAUX Chapitre 1 LES RESEAUX DIRECT ET RECIPROQUE Pr. A. Belayachi Université Mohammed V Agdal Faculté des Sciences Rabat Département de Physique - L.P.M [email protected] 1 1.Le réseau
LA PHYSIQUE DES MATERIAUX Chapitre 1 LES RESEAUX DIRECT ET RECIPROQUE Pr. A. Belayachi Université Mohammed V Agdal Faculté des Sciences Rabat Département de Physique - L.P.M [email protected] 1 1.Le réseau
Fonctions de plusieurs variables
 Module : Analyse 03 Chapitre 00 : Fonctions de plusieurs variables Généralités et Rappels des notions topologiques dans : Qu est- ce que?: Mathématiquement, n étant un entier non nul, on définit comme
Module : Analyse 03 Chapitre 00 : Fonctions de plusieurs variables Généralités et Rappels des notions topologiques dans : Qu est- ce que?: Mathématiquement, n étant un entier non nul, on définit comme
Sillage Météo. Notion de sillage
 Sillage Météo Les représentations météorologiques sous forme d animation satellites image par image sont intéressantes. Il est dommage que les données ainsi visualisées ne soient pas utilisées pour une
Sillage Météo Les représentations météorologiques sous forme d animation satellites image par image sont intéressantes. Il est dommage que les données ainsi visualisées ne soient pas utilisées pour une
Programmation linéaire
 Programmation linéaire DIDIER MAQUIN Ecole Nationale Supérieure d Electricité et de Mécanique Institut National Polytechnique de Lorraine Mathématiques discrètes cours de 2ème année Programmation linéaire
Programmation linéaire DIDIER MAQUIN Ecole Nationale Supérieure d Electricité et de Mécanique Institut National Polytechnique de Lorraine Mathématiques discrètes cours de 2ème année Programmation linéaire
Simulation d'un examen anthropomorphique en imagerie TEMP à l iode 131 par simulation Monte Carlo GATE
 Simulation d'un examen anthropomorphique en imagerie TEMP à l iode 131 par simulation Monte Carlo GATE LAURENT Rémy [email protected] http://clrpcsv.in2p3.fr Journées des LARD Septembre 2007 M2R
Simulation d'un examen anthropomorphique en imagerie TEMP à l iode 131 par simulation Monte Carlo GATE LAURENT Rémy [email protected] http://clrpcsv.in2p3.fr Journées des LARD Septembre 2007 M2R
Avant-après, amont-aval : les couples de tableaux totalement appariés
 ADE-4 Avant-après, amont-aval : les couples de tableaux totalement appariés Résumé La fiche décrit les méthodes d analyse des couples de tableaux complètement appariés (mêmes individus, mêmes variables).
ADE-4 Avant-après, amont-aval : les couples de tableaux totalement appariés Résumé La fiche décrit les méthodes d analyse des couples de tableaux complètement appariés (mêmes individus, mêmes variables).
Optimisation non linéaire Irène Charon, Olivier Hudry École nationale supérieure des télécommunications
 Optimisation non linéaire Irène Charon, Olivier Hudry École nationale supérieure des télécommunications A. Optimisation sans contrainte.... Généralités.... Condition nécessaire et condition suffisante
Optimisation non linéaire Irène Charon, Olivier Hudry École nationale supérieure des télécommunications A. Optimisation sans contrainte.... Généralités.... Condition nécessaire et condition suffisante
MATLAB : COMMANDES DE BASE. Note : lorsqu applicable, l équivalent en langage C est indiqué entre les délimiteurs /* */.
 Page 1 de 9 MATLAB : COMMANDES DE BASE Note : lorsqu applicable, l équivalent en langage C est indiqué entre les délimiteurs /* */. Aide help, help nom_de_commande Fenêtre de travail (Command Window) Ligne
Page 1 de 9 MATLAB : COMMANDES DE BASE Note : lorsqu applicable, l équivalent en langage C est indiqué entre les délimiteurs /* */. Aide help, help nom_de_commande Fenêtre de travail (Command Window) Ligne
Aide-mémoire de statistique appliquée à la biologie
 Maxime HERVÉ Aide-mémoire de statistique appliquée à la biologie Construire son étude et analyser les résultats à l aide du logiciel R Version 5(2) (2014) AVANT-PROPOS Les phénomènes biologiques ont cela
Maxime HERVÉ Aide-mémoire de statistique appliquée à la biologie Construire son étude et analyser les résultats à l aide du logiciel R Version 5(2) (2014) AVANT-PROPOS Les phénomènes biologiques ont cela
PRODIGE V3. Manuel utilisateurs. Consultation des métadonnées
 PRODIGE V3 Manuel utilisateurs Consultation des métadonnées Pour plus d'information sur le dispositif : à remplir par chaque site éventuellement 2 PRODIGE V3 : Consultation des métadonnées SOMMAIRE 1.
PRODIGE V3 Manuel utilisateurs Consultation des métadonnées Pour plus d'information sur le dispositif : à remplir par chaque site éventuellement 2 PRODIGE V3 : Consultation des métadonnées SOMMAIRE 1.
Introduction à la Visualisation Scientifique
 à la Visualisation Scientifique CEA, DAM, DIF [email protected] 5 décembre 2008 à la Visualisation Scientifique p. 1 / 22 1 2 à 3 4 à 5 à la Visualisation Scientifique p. 2 / 22 à Ces dernières
à la Visualisation Scientifique CEA, DAM, DIF [email protected] 5 décembre 2008 à la Visualisation Scientifique p. 1 / 22 1 2 à 3 4 à 5 à la Visualisation Scientifique p. 2 / 22 à Ces dernières
IMPORTATION, CRÉATION, MANIPULATION, EXPORTATION DE DONNÉES STATISTIQUES
 IMPRTATIN, CRÉATIN, MANIPULATIN, EXPRTATIN DE DNNÉES STATISTIQUES Bernard Dupont [email protected] [email protected] Bien que l'analyse et le traitement des données ne soient pas sa vocation
IMPRTATIN, CRÉATIN, MANIPULATIN, EXPRTATIN DE DNNÉES STATISTIQUES Bernard Dupont [email protected] [email protected] Bien que l'analyse et le traitement des données ne soient pas sa vocation
Business Intelligence avec Excel, Power BI et Office 365
 Avant-propos A. À qui s adresse ce livre? 9 1. Pourquoi à chaque manager? 9 2. Pourquoi à tout informaticien impliqué dans des projets «BI» 9 B. Obtention des données sources 10 C. Objectif du livre 10
Avant-propos A. À qui s adresse ce livre? 9 1. Pourquoi à chaque manager? 9 2. Pourquoi à tout informaticien impliqué dans des projets «BI» 9 B. Obtention des données sources 10 C. Objectif du livre 10
Manuel d utilisation email NETexcom
 Manuel d utilisation email NETexcom Table des matières Vos emails avec NETexcom... 3 Présentation... 3 GroupWare... 3 WebMail emails sur internet... 4 Se connecter au Webmail... 4 Menu principal... 5 La
Manuel d utilisation email NETexcom Table des matières Vos emails avec NETexcom... 3 Présentation... 3 GroupWare... 3 WebMail emails sur internet... 4 Se connecter au Webmail... 4 Menu principal... 5 La
Cours de méthodes de scoring
 UNIVERSITE DE CARTHAGE ECOLE SUPERIEURE DE STATISTIQUE ET D ANALYSE DE L INFORMATION Cours de méthodes de scoring Préparé par Hassen MATHLOUTHI Année universitaire 2013-2014 Cours de méthodes de scoring-
UNIVERSITE DE CARTHAGE ECOLE SUPERIEURE DE STATISTIQUE ET D ANALYSE DE L INFORMATION Cours de méthodes de scoring Préparé par Hassen MATHLOUTHI Année universitaire 2013-2014 Cours de méthodes de scoring-
MODULES 3D TAG CLOUD. Par GENIUS AOM
 MODULES 3D TAG CLOUD Par GENIUS AOM 1 Sommaire I. INTRODUCTIONS :... 3 II. INSTALLATION MANUELLE D UN MODULE PRESTASHOP... 3 III. CONFIGURATION DU MODULE... 7 3.1. Préférences... 7 3.2. Options... 8 3.3.
MODULES 3D TAG CLOUD Par GENIUS AOM 1 Sommaire I. INTRODUCTIONS :... 3 II. INSTALLATION MANUELLE D UN MODULE PRESTASHOP... 3 III. CONFIGURATION DU MODULE... 7 3.1. Préférences... 7 3.2. Options... 8 3.3.
TRAITEMENT DES DONNEES MANQUANTES AU MOYEN DE L ALGORITHME DE KOHONEN
 TRAITEMENT DES DONNEES MANQUANTES AU MOYEN DE L ALGORITHME DE KOHONEN Marie Cottrell, Smaïl Ibbou, Patrick Letrémy SAMOS-MATISSE UMR 8595 90, rue de Tolbiac 75634 Paris Cedex 13 Résumé : Nous montrons
TRAITEMENT DES DONNEES MANQUANTES AU MOYEN DE L ALGORITHME DE KOHONEN Marie Cottrell, Smaïl Ibbou, Patrick Letrémy SAMOS-MATISSE UMR 8595 90, rue de Tolbiac 75634 Paris Cedex 13 Résumé : Nous montrons
Python - introduction à la programmation et calcul scientifique
 Université de Strasbourg Environnements Informatique Python - introduction à la programmation et calcul scientifique Feuille de TP 1 Avant de commencer Le but de ce TP est de vous montrer les bases de
Université de Strasbourg Environnements Informatique Python - introduction à la programmation et calcul scientifique Feuille de TP 1 Avant de commencer Le but de ce TP est de vous montrer les bases de
Recherche d Information(RI): Fondements et illustration avec Apache Lucene. par Majirus Fansi @majirus
 1 Recherche d Information(RI): Fondements et illustration avec Apache Lucene par Majirus Fansi @majirus Résumé Fondements de la Recherche d Information (RI) Noyau de toute application de RI Éléments à
1 Recherche d Information(RI): Fondements et illustration avec Apache Lucene par Majirus Fansi @majirus Résumé Fondements de la Recherche d Information (RI) Noyau de toute application de RI Éléments à
Impact du mobile banking sur les comportements d épargne et de transferts à Madagascar. Florence Arestoff Baptiste Venet
 Impact du mobile banking sur les comportements d épargne et de transferts à Madagascar Florence Arestoff Baptiste Venet 1 Introduction : contexte du contrat de recherche Ce contrat de recherche fait suite
Impact du mobile banking sur les comportements d épargne et de transferts à Madagascar Florence Arestoff Baptiste Venet 1 Introduction : contexte du contrat de recherche Ce contrat de recherche fait suite
Sujet proposé par Yves M. LEROY. Cet examen se compose d un exercice et de deux problèmes. Ces trois parties sont indépendantes.
 Promotion X 004 COURS D ANALYSE DES STRUCTURES MÉCANIQUES PAR LA MÉTHODE DES ELEMENTS FINIS (MEC 568) contrôle non classant (7 mars 007, heures) Documents autorisés : polycopié ; documents et notes de
Promotion X 004 COURS D ANALYSE DES STRUCTURES MÉCANIQUES PAR LA MÉTHODE DES ELEMENTS FINIS (MEC 568) contrôle non classant (7 mars 007, heures) Documents autorisés : polycopié ; documents et notes de
Comparaison de Relevés 3D issus de plusieurs Systèmes de Numérisation
 Laboratoire Vision & Robotique Comparaison de Relevés 3D issus de plusieurs Systèmes de Numérisation Emilie KOENIG, Benjamin ALBOUY, Sylvie TREUILLET, Yves Lucas Contact : Sylvie Treuillet Polytech'Orléans
Laboratoire Vision & Robotique Comparaison de Relevés 3D issus de plusieurs Systèmes de Numérisation Emilie KOENIG, Benjamin ALBOUY, Sylvie TREUILLET, Yves Lucas Contact : Sylvie Treuillet Polytech'Orléans
UNE EXPERIENCE, EN COURS PREPARATOIRE, POUR FAIRE ORGANISER DE L INFORMATION EN TABLEAU
 Odile VERBAERE UNE EXPERIENCE, EN COURS PREPARATOIRE, POUR FAIRE ORGANISER DE L INFORMATION EN TABLEAU Résumé : Cet article présente une réflexion sur une activité de construction de tableau, y compris
Odile VERBAERE UNE EXPERIENCE, EN COURS PREPARATOIRE, POUR FAIRE ORGANISER DE L INFORMATION EN TABLEAU Résumé : Cet article présente une réflexion sur une activité de construction de tableau, y compris
