Morphologie mathématique
|
|
|
- Michelle Pellerin
- il y a 7 ans
- Total affichages :
Transcription
1 Morphologie mathématique Squelette, squelette par zone d influence et ligne de partage des eaux Luc Brun (d après le cours de M. Coster) Morphologie mathématique p.1/50
2 Plan Squelette (SK) Définitions propriétés Le squelette et les transformations morphologiques de base Configurations de voisinage et les éléments structurants bi-colorés, les transformations en tout ou rien Amincissement et épaississement, squelette et amincissement homotopique, Points particuliers du squelette La bissectrice conditionnelle Squelette par zone d influence (SKIZ) Segmentation par ligne de partage des eaux (LPE) Approche par écoulement, LPE 1D par inondation, LPE 2D par inondation, Techniques de Marquage Swamping Dynamique des bassins LPE hiérarchique Waterfall Dynamique des contours Morphologie mathématique p.2/50
3 Le squelette Boule maximale : Une boule B(x,ρ) est maximale dans X s il n existe pas B (x,ρ ) tel que x x B(x,ρ) B (x,ρ ) X Squelette : Le squelette Sk (X) est l union des centres des disques maximaux B contenus dans X. En pratique les disques maximaux touchent X en au moins 2 points. x y : X : Sk(X) r(y) Morphologie mathématique p.3/50
4 Propriétés du squelette Dans l espace continu : Le squelette n est pas une transformation croissante Le squelette n est pas une transformation continue (Le squelette est très sensible au bruit) Le squelette est une transformation homotopique et idempotente Discontinuité de la squelettisation Homotopie Morphologie mathématique p.4/50
5 Squelette et transformations morphologiques de Algorithme de Lantuéjoul : Le squelette est l union (pour tout les λ > 0) de l intersection (pour tout les µ > 0) de la différence entre l érosion de X par λb, et de l érosion de X par λb ouverte par µb. Sk(X) = λ E λb (X) γ µb (E λb (X)) µ + + : X + : E λb (X) : γ µb (E λb (X)) : E λb (X) γ µb (E λb (X)) Morphologie mathématique p.5/50
6 Squelettes et résidus Squelette par ouverture (de Lantuéjoul) Sk(X) = i E ib (X) γ 1B (E ib (X)) Érodés ultimes : Sk(X) = i U i (X) = i E ib (X) γ Rec (E (i+1)b (X) : E ib (X)) Bissectrice conditionnelle : B(X) = i B i (X) = i E ib (X) δ nb (E (i+1)b (X) : E ib (X)) Morphologie mathématique p.6/50
7 Squelette par Ouverture : Illustration erosion ouverture residus Morphologie mathématique p.7/50
8 Érosion Ultime : Illustration erosion erosion erosion ouverture par reconstruction erosion ultime Morphologie mathématique p.8/50
9 Bissectrice conditionnelle Remarque : La bissectrice conditionnelle à un comportement intermédiaire entre l ensemble des érodés ultimes et le squelette par ouverture. Elle dépend d un paramètre n lié à la variation de taille des disques maximaux inscrits. Morphologie mathématique p.9/50
10 Squelettes et Résidus : Récapitulatif Sk(X) = i F i 1(X) F i 2(X) Résidus F 1 F 2 Squelette par ouverture érosion ouverture unitaire Résidus ultimes érosion ouverture par reconstruction Bissectrice érosion ouverture géodésique Morphologie mathématique p.10/50
11 Propriétés de la squelettisation Dans le cas numérique, L intersection des ouvertures par µb est remplacée par une ouverture avec 1B, le squelette par ouverture n est pas connexe. La topologie (homotopie) n est pas préservée. Le squelette homotopique est obtenu par amincissement Formes Squelette par ouverture Morphologie mathématique p.11/50
12 Amincissements et épaississement Les amincissements et épaississement sont obtenus comme résidu de transformations bi-colorées. Amincissement : L amincissement de l ensemble X consiste à enlever les points qui correspondent à une configuration donnée. C est le résidu morphologique entre l image initiale et la transformation en tout ou rien correspondant à cette configuration. θ T (X) = X η T (X) Épaississement : L épaississement d un ensemble X consiste à ajouter les points correspondant à une configuration donnée. ξ T (X) = X η T (X) Morphologie mathématique p.12/50
13 Exemple T = η B (X) θ B (X) Morphologie mathématique p.13/50
14 Exemple de séquence d amincissement θ T (X) θ T (θ T (X)) θ T (θ T (θ T (X))) résultat stable Morphologie mathématique p.14/50
15 Amincissements et épaississements homotopiqu Définition : Un amincissement (épaississement) homotopique conserve la topologie de l ensemble de départ. Règles de construction des éléments bicolorés Le pixel central est à 1 (amincissement) ou 0 (épaississement) L inversion de la couleur du point central ne doit pas modifier la topologie associée inversion Transformation homotopique inversion Transformation non homotopiqu Morphologie mathématique p.15/50
16 Squelettes par amincissements Définition : Le squelette par amincissement utilise une famille d éléments structurants qui préservent l homotopie (M, L ou D). La famille est obtenue par rotation de la configuration L, M ou D. L amincissement s arrête lorsqu il n y a plus de modification des pixels de l image. Sk L (X) = (θ L (X)) = (X η L (X)) Afin d amincir dans toutes les directions il nous faut une famille d éléments structurants se déduisant les un des autres par rotations. Pour une maille carré on obtient 8 éléments avec une rotation de π 4. Pour une maille triangulaire on a 6 éléments avec une rotation de π 3. Morphologie mathématique p.16/50
17 Exemple avec l élément L en 8 connexité On a 8 éléments L 1,...,L 8 θ 1L (X) = θ L8 (...θ L3 (θ L2 (θ L1 (X)))) L 1 L 2 L 3 L 4 L 5 L 6 L 7 L 8 Morphologie mathématique p.17/50
18 Différentes familles d éléments structurants (1/2 Famille Amincissement L Squelette homotopique L : Lskel En 6 connexité M Squelette homotopique M : Mskel D Squelette homotopique D : Dskel E Ébarbage Morphologie mathématique p.18/50
19 Différentes familles d éléments structurants (2/2 En 8 connexité Famille L M E Amincissement Squelette homotopique L : Lskel Squelette homotopique M : Mskel Ébarbage Morphologie mathématique p.19/50
20 Exemples en 6 connexité Lsk(X) M sk(x) Dsk(X) Lsk(X) Ébardé par E. Morphologie mathématique p.20/50
21 Exemples en 8 connexité Lsk(X) Msk(X) Lsk(X) ébardé par E. Morphologie mathématique p.21/50
22 Points particuliers Les points particuliers d un squelette sont les points ayant moins ou plus de deux voisins. Les points extêmes (arité 1), Les points multiples (arité 3) Point extrême Point multiple Morphologie mathématique p.22/50
23 Détection des points particuliers En maille triangulaire Famille E F F Points particuliers Points extrêmes Points triples Points triples Morphologie mathématique p.23/50
24 Détection des points particuliers Famille Points particuliers E Points extrêmes En maille 8 connexe F Points multiples F Points multiples F Points multiples Morphologie mathématique p.24/50
25 Squelette par zone d influence (SKIZ) Squelette (SK) Définitions propriétés Le squelette et les transformations morphologiques de base Configurations de voisinage et les éléments structurants bi-colorés, les transformations en tout ou rien Amincissement et épaississement, squelette et amincissement homotopique, Points particuliers du squelette La bissectrice conditionnelle Squelette par zone d influence Approche par écoulement, LPE 1D par inondation, LPE 2D par inondation, Techniques de Marquage Swamping Dynamique des bassins LPE hiérarchique Waterfall Dynamique des contours Morphologie mathématique p.25/50
26 Squelette par zone d influence (SKIZ) Soit un ensemble X composé d objets disjoints. A chaque objet X i on peut associer une zone d influence Y i, telle que chaque point y de Y i est plus proche de X i que de tout autre objet X j (i j). Y i = {y j i,d(y,x i ) < d(y,x j )} Le squelette par zone d influence (ou SKIZ) de X, noté Skiz(X), est par définition le complément de l union de tout les Y i (zones d influence) ; Skiz(X) = C E ( i Y i ) Morphologie mathématique p.26/50
27 Propriétés du SKIZ Le squelette par zone d influence (SKIZ) partage l espace en autant de parties qu il y a de composantes connexes. Le SKIZ n est pas une transformation homotopique. En effet, la zone d influence d un objet est une composante simplement connexe que l objet soit sans trou ou avec trou. Le SKIZ n est pas une transformation croissante. Le SKIZ est une transformation anti-extensive par rapport à C E (X). Le SKIZ est une transformation semi-continue supérieure. La transformation est nettement plus stable que la squelettisation. Morphologie mathématique p.27/50
28 Calcul du SKIZ Dans le cas numérique, le SKIZ est obtenu à partir du squelette de l ensemble complémentaire, appelé exo-squelette. L ébarbage de l exosquelette donne le SKIZ. Exo Squelette SKIZ Morphologie mathématique p.28/50
29 Amincissements et Épaississements Géodesique Un épaississement par un élément structurant T 1 est défini par : ξ T (Y ) = ξ Tn (...ξ T2 (ξ T1 (Y ))) où T i est l élément structurant défini par une rotation i.α de l élément T 1. L épaississement géodésique de Y par rapport à X avec l élément structurant mt est obtenu en intersectant chaque épaississement avec X. ξ X,mT (Y ) = (...ξ 1T (ξ 1T (ξ 1T (Y ) X) X) X) m fois L amincissement géodésique est défini à partir de l épaississement géodésique de la différence symétrique de X et Y, suivi à nouveau d une différence symétrique : θ X,nT (Y ) = X/ξ X,nT (X/Y ) Morphologie mathématique p.29/50
30 SKIZ Géodésique Le SKIZ géodésique de Y par rapport à X (Gskiz X (Y )) est défini par l application jusqu à stabilité : d un épaississements avec L C (inversion blue rouge), d un épaississements avec E C, d une intersection avec X La zone associée a une composante connexe Y i de Y est notée iz X (Y i ). Gskiz X (Y ) = skiz(y ) = X = X = Y = Y = Morphologie mathématique p.30/50
31 Segmentation par ligne de partage des eaux (LPE Squelette (SK) Définitions propriétés Le squelette et les transformations morphologiques de base Configurations de voisinage et les éléments structurants bi-colorés, les transformations en tout ou rien Amincissement et épaississement, squelette et amincissement homotopique, Points particuliers du squelette La bissectrice conditionnelle Squelette par zone d influence (SKIZ) Segmentation par ligne de partage des Approche par écoulement, LPE 1D par inondation, LPE 2D par inondation, Techniques de Marquage Swamping Dynamique des bassins LPE hiérarchique Waterfall Dynamique des contours Morphologie mathématique p.31/50
32 Ligne de partage des eaux La notion de ligne de partage des eaux est Topographique. Vision Inondation : Supposons que les pôles fondent et que les océans débordent : Où vont se rencontrer les eaux des différentes mers (du nord, manche, atlantique,méditerranée)? Les lignes de rencontre constituent les lignes de partage des eaux. Par exemple la ligne de partage des eaux entre la mer du nord et la méditerranée passe entre Troyes et Dijon. Les zones envahies par les différentes mers constituent leurs bassins versant Les mers constituent les minimums des bassins versants. Vision Écoulement : Supposons le sol absolument imperméable. Si une goutte d eau tombe sur un point du relief dans quel océan va-t-elle se jeter? Si une seule solution : le point appartient a un bassin versant. Sinon il appartient à une ligne de partage des eaux. Morphologie mathématique p.32/50
33 Approche par Écoulement en Traitement d imag Question : Peut on décrémenter la valeur d un pixel sans changer l écoulement? Grille Initiale LPE Travail de Gille Bertrand et Michel Couprie Notion de point Simple (géométrie discrète) Remarque : On préserve la valeur minimale le long d un contour mais pas son profil d intensité. Morphologie mathématique p.33/50
34 LPE 1D par inondation On suppose qu un trou a été percé sur chaque minimum local et que la surface est inondée à partir de ces trous. Progressivement le niveau de l eau augmente. Pour empêcher la réunion des eaux provenant des différents trous, Une digue est construite à chaque point de contact. Finalement, l union de toutes les digues forment la ligne de partage des eaux. Morphologie mathématique p.34/50
35 LPE 2D par inondation (1/4) Soient C(M) le bassin associé au minimum M et { T h (I) = {p D I,I(p) h} C h (M) = {p C(M),I(p) h} = C(M) T h (I) X h l ensemble des pixels appartenant à un bassin et d altitude inférieure à h : ( ) X h = C(M i ) T h (I) = C h (M i ) i I i I Soit h min l altitude minimale de I. T hmin correspond aux minima (aux mers) de l image I. On a donc : X hmin = T hmin (I) Soit Y une composante connexe de T hmin +1(I). Morphologie mathématique p.35/50
36 LPE 2D par inondation (2/4) Étudions les 3 configurations de Y X hmin : 1. Y X hmin = : Y est un nouveau minimum d altitude h min Y X hmin et est connexe : Y correspond aux pixels du bassin associé au minimum Y X hmin et d altitude inférieure à h min + 1. Y = C hmin +1(Y X hmin ) 3. Y X hmin et n est pas connexe. Soient Z 1...Z k les composantes connexes de Y X hmin. Z i correspond à une minimum dont le bassin à l altitude h min + 1 est défini par C hmin +1(Z i ) = iz Y (Z i ) Z1 Z1 iz (Z1) Y iz (Z2) Y Z2 Y Y Y Morphologie mathématique p.36/50
37 LPE 2D par inondation (3/4) L ensemble des pixels appartenant aux bassins et d altitude inférieure à h min + 1 est donc constitué : 1. Des minima isolés d altitude h min + 1 (cas Y X hmin = ). 2. Des zones d influence géodésique des minimums de X hmin dans T hmin +1 (cas Y X hmin ) On a donc : X hmin +1 = min hmin +1 IZ Thmin +1(I)(X hmin ) On a donc une suite d ensembles définie par : 1. X hmin = T hmin (I), 2. pour tout h {h min,...,h max 1} X h+1 = min h+1 IZ Th+1 (I)(X h ) Morphologie mathématique p.37/50
38 LPE 2D par inondation (4/4) X hmax contient l ensemble des bassins. L ensemble des pixels appartenant à une ligne de partage des eaux est défini par D I X hmax. Historique (Rapide) : Beucher et Lantuéjoul (1979) : Épaississements avec éléments M et E Meyer (1989) :squeletisation d images en niveaux de gris Vincent et Soille (1991) : Propagation avec tri des pixels Meyer 1991 : Files d attentes hiérarchiques Morphologie mathématique p.38/50
39 LPE 2D : Exemple Lenna Gradient couleur Lignes de partage des e Morphologie mathématique p.39/50
40 LPE : Remarques Propriétés de la LPE Les contours sont généralement bien positionnés Chaque minima induit un bassin Sur Segmentation. Comment lutter contre la sur segmentation? Techniques de marquages ( swamping) suppression de minimums par h minima, Lignes de partage des eaux hiérarchiques Original Gradient couleur Lignes de partage des eaux Morphologie mathématique p.40/50
41 Les techniques de marquage Supposons que l on dispose d une connaissance a priori sur les zones à segmenter. Soit M l ensemble des zones ne devant pas posséder de contours internes. { h max si p M On définit la fonction g par : g(p) = 0 sinon On construit la ligne de partage des eaux sur l érosion géodésique de g par min(f,g) (ϕ Rec (g : g f)) f g marqueurs Morphologie mathématique p.41/50
42 Simplification de LPE & Dynamique des bassin Définition : Dynamique des bassins. Soir M un minima de f. La dynamique de M est le nombre : min γ {max s {f(γ(s)) f(γ(0)) γ : [0, 1] IR 2,f(γ(1)) < f(γ(0)),γ(0) M} qui correspond à l altitude minimal qu il faudra monter pour pouvoir descendre plus bas que l altitude de M. Morphologie mathématique p.42/50
43 Suppression des bassins La suppression des bassins de dynamique inférieure à h est réalisé en effectuant la LPE sur l érosion géodésique de f(x) + h sur f(x)(ϕ Rec (f + h : f)). f+h h f h L érosion remplie les bassins jusqu à une hauteur h. Tous les bassins de dynamique inférieure à h sont supprimés. Morphologie mathématique p.43/50
44 LPE Hiérarchique : Waterfall Soit f une fonction (ou une image) et M l ensemble de ses pixels watersheds. On construit la fonction g définie par : { f(p) si p M g(p) = sinon h max L érosion géodésique de g sur f supprime les minima les moins significatifs. Morphologie mathématique p.44/50
45 Waterfall : Exemple extrait de Fast Implementation of Waterfall Based on Graphs (B. Marcotegui and S. Beucher, 2005) Original Watershed Waterfall (iter. 1) Waterfall (iter. 2 : Waterfall (iter. 3) Morphologie mathématique p.45/50
46 Dynamique des contours Auteur Laurent Najman & Michel Schmitt Soit a le point le plus bas d un contour entre 2 bassins. Soit Bas(a) = {b D I γ,γ(0) = a,γ(1) = b et f(γ(s)) < f(a) s [0, 1]} L ensemble des points pouvant être atteint à partir de a sans jamais remonter au dessus de a. B 1,...,B n l ensemble des composantes connexes de Bas(a) = n i=1 B i. On définit la dynamique de a par : dyn(a) = min i max b i B i (f(a) f(b i )) dyn(a) correspond à la plus haute valeur h pour laquelle a est un pixel watershed de ϕ Rec (f + h : f). Morphologie mathématique p.46/50
47 Dynamique des contours : Illustration & Algorit Illustration : dyn(a) B1 a B2 Algorithme : Effectuer une inondation sur l ensemble des bassins Pour chaque contour inonde C : dyn(c) = pass_value(c) MAX(Profondeur(B 1 ),Profondeur(B 2 )) avec B 1,B 2 bassins bordant C, pass_value(c) altitude minimale de C. Positionner Profondeur(B 1 B 2 ) = min(profondeur(b 1 ),Profondeur(B 2 )) Morphologie mathématique p.47/50
48 Dynamique des contours : Applications & Probl Applications : Fusionner tous les bassins adjacents par un contour de dynamique inférieure à ǫ. Trier les contours par ordre croissant de dynamique et les supprimer si les bassins satisfont un critère de fusion (test statistique sur les couleurs des pixels contenus dans les bassins). Problèmes : La valeur pass_value(c) est sensible au bruit (comme tout opérateur min).. les contours initiaux sont courts pass_value(c) peu significatif même sans bruit. Morphologie mathématique p.48/50
49 Dynamique des contours : Améliorations Auteur Luc Brun. Effectuer un waterfall sur le profil d intensité de C, Calculer le volume de chaque bassin inondé, Soit b 1...,b n l ensemble des bassins inondés. Positionner pass_value(c) à : pass_value(c) = Min{ Profondeur(b i ), V olume(b i ) = max V olume(b j)} j {1,...,n} La valeur de passage est la profondeur du bassin de volume maximal. Fusionner les contours de plus faible dynamique et mettre à jour les dynamiques des contours restants. pass_value(c) Morphologie mathématique p.49/50
50 Dynamique des contours améliorée : Exemple Lenna Itération 1 Itération 5 Itération 9 Itération 13 Itération 17 Itération 21 Itération 25 Morphologie mathématique p.50/50
Master IMA - UMPC Paris 6 RDMM - Année 2009-2010 Fiche de TP
 Master IMA - UMPC Paris 6 RDMM - Année 2009-200 Fiche de TP Préliminaires. Récupérez l archive du logiciel de TP à partir du lien suivant : http://www.ensta.fr/~manzaner/cours/ima/tp2009.tar 2. Développez
Master IMA - UMPC Paris 6 RDMM - Année 2009-200 Fiche de TP Préliminaires. Récupérez l archive du logiciel de TP à partir du lien suivant : http://www.ensta.fr/~manzaner/cours/ima/tp2009.tar 2. Développez
Chapitre VI. Connexions et fonctions numériques
 Chapitre VI Connexions et fonctions numériques Concepts : -> Extension aux fonctions -> Opérateurs connexes -> Géodésie numérique -> Nivellements et auto-dualité Applications : -> Etude des extrema ->
Chapitre VI Connexions et fonctions numériques Concepts : -> Extension aux fonctions -> Opérateurs connexes -> Géodésie numérique -> Nivellements et auto-dualité Applications : -> Etude des extrema ->
FONCTIONS DE PLUSIEURS VARIABLES (Outils Mathématiques 4)
 FONCTIONS DE PLUSIEURS VARIABLES (Outils Mathématiques 4) Bernard Le Stum Université de Rennes 1 Version du 13 mars 2009 Table des matières 1 Fonctions partielles, courbes de niveau 1 2 Limites et continuité
FONCTIONS DE PLUSIEURS VARIABLES (Outils Mathématiques 4) Bernard Le Stum Université de Rennes 1 Version du 13 mars 2009 Table des matières 1 Fonctions partielles, courbes de niveau 1 2 Limites et continuité
Résolution d équations non linéaires
 Analyse Numérique Résolution d équations non linéaires Said EL HAJJI et Touria GHEMIRES Université Mohammed V - Agdal. Faculté des Sciences Département de Mathématiques. Laboratoire de Mathématiques, Informatique
Analyse Numérique Résolution d équations non linéaires Said EL HAJJI et Touria GHEMIRES Université Mohammed V - Agdal. Faculté des Sciences Département de Mathématiques. Laboratoire de Mathématiques, Informatique
Chapitre 5 : Flot maximal dans un graphe
 Graphes et RO TELECOM Nancy A Chapitre 5 : Flot maximal dans un graphe J.-F. Scheid 1 Plan du chapitre I. Définitions 1 Graphe Graphe valué 3 Représentation d un graphe (matrice d incidence, matrice d
Graphes et RO TELECOM Nancy A Chapitre 5 : Flot maximal dans un graphe J.-F. Scheid 1 Plan du chapitre I. Définitions 1 Graphe Graphe valué 3 Représentation d un graphe (matrice d incidence, matrice d
Analyse Sémantique de Nuages de Points 3D et d Images dans les Milieux Urbains
 Analyse Sémantique de Nuages de Points 3D et d Images dans les Milieux Urbains Andrés Felipe SERNA MORALES Directrice de thèse: Beatriz MARCOTEGUI ITURMENDI serna@cmm.ensmp.fr MINES ParisTech, Mathématiques
Analyse Sémantique de Nuages de Points 3D et d Images dans les Milieux Urbains Andrés Felipe SERNA MORALES Directrice de thèse: Beatriz MARCOTEGUI ITURMENDI serna@cmm.ensmp.fr MINES ParisTech, Mathématiques
M2R IMA UE CONF Présentation
 M2R IMA UE CONF Présentation L objectif de l UE «Conférences» est de : 1. Présenter des applications du traitement d images dans divers domaines industriels ou académiques. 2. Apporter des compléments
M2R IMA UE CONF Présentation L objectif de l UE «Conférences» est de : 1. Présenter des applications du traitement d images dans divers domaines industriels ou académiques. 2. Apporter des compléments
Traitement bas-niveau
 Plan Introduction L approche contour (frontière) Introduction Objectifs Les traitements ont pour but d extraire l information utile et pertinente contenue dans l image en regard de l application considérée.
Plan Introduction L approche contour (frontière) Introduction Objectifs Les traitements ont pour but d extraire l information utile et pertinente contenue dans l image en regard de l application considérée.
Intégration et probabilités TD1 Espaces mesurés Corrigé
 Intégration et probabilités TD1 Espaces mesurés Corrigé 2012-2013 1 Petites questions 1 Est-ce que l ensemble des ouverts de R est une tribu? Réponse : Non, car le complémentaire de ], 0[ n est pas ouvert.
Intégration et probabilités TD1 Espaces mesurés Corrigé 2012-2013 1 Petites questions 1 Est-ce que l ensemble des ouverts de R est une tribu? Réponse : Non, car le complémentaire de ], 0[ n est pas ouvert.
Rallye Mathématiques de liaison 3 ème /2 nde et 3 ème /2 nde pro Epreuve finale Jeudi 21 mai 2015 Durée : 1h45
 Rallye Mathématiques de liaison 3 ème /2 nde et 3 ème /2 nde pro Epreuve finale Jeudi 21 mai 2015 Durée : 1h45 Précisions pour les problèmes 1 et 2 : Pour ces problèmes, on attend une narration de recherche
Rallye Mathématiques de liaison 3 ème /2 nde et 3 ème /2 nde pro Epreuve finale Jeudi 21 mai 2015 Durée : 1h45 Précisions pour les problèmes 1 et 2 : Pour ces problèmes, on attend une narration de recherche
Présentation du Master Ingénierie Informatique et du Master Science Informatique 2007-2008, Année 2 Université Paris-Est Marne-la-Vallée
 Présentation du Master Ingénierie Informatique et du Master Science Informatique 2007-2008, Année 2 Université Paris-Est Marne-la-Vallée Responsable du Master Informatique : Marc Zipstein Responsable de
Présentation du Master Ingénierie Informatique et du Master Science Informatique 2007-2008, Année 2 Université Paris-Est Marne-la-Vallée Responsable du Master Informatique : Marc Zipstein Responsable de
Continuité et dérivabilité d une fonction
 DERNIÈRE IMPRESSIN LE 7 novembre 014 à 10:3 Continuité et dérivabilité d une fonction Table des matières 1 Continuité d une fonction 1.1 Limite finie en un point.......................... 1. Continuité
DERNIÈRE IMPRESSIN LE 7 novembre 014 à 10:3 Continuité et dérivabilité d une fonction Table des matières 1 Continuité d une fonction 1.1 Limite finie en un point.......................... 1. Continuité
8.1 Généralités sur les fonctions de plusieurs variables réelles. f : R 2 R (x, y) 1 x 2 y 2
 Chapitre 8 Fonctions de plusieurs variables 8.1 Généralités sur les fonctions de plusieurs variables réelles Définition. Une fonction réelle de n variables réelles est une application d une partie de R
Chapitre 8 Fonctions de plusieurs variables 8.1 Généralités sur les fonctions de plusieurs variables réelles Définition. Une fonction réelle de n variables réelles est une application d une partie de R
Fonctions de plusieurs variables
 Module : Analyse 03 Chapitre 00 : Fonctions de plusieurs variables Généralités et Rappels des notions topologiques dans : Qu est- ce que?: Mathématiquement, n étant un entier non nul, on définit comme
Module : Analyse 03 Chapitre 00 : Fonctions de plusieurs variables Généralités et Rappels des notions topologiques dans : Qu est- ce que?: Mathématiquement, n étant un entier non nul, on définit comme
Programmation Linéaire - Cours 1
 Programmation Linéaire - Cours 1 P. Pesneau pierre.pesneau@math.u-bordeaux1.fr Université Bordeaux 1 Bât A33 - Bur 265 Ouvrages de référence V. Chvátal - Linear Programming, W.H.Freeman, New York, 1983.
Programmation Linéaire - Cours 1 P. Pesneau pierre.pesneau@math.u-bordeaux1.fr Université Bordeaux 1 Bât A33 - Bur 265 Ouvrages de référence V. Chvátal - Linear Programming, W.H.Freeman, New York, 1983.
Image d un intervalle par une fonction continue
 DOCUMENT 27 Image d un intervalle par une fonction continue La continuité d une fonction en un point est une propriété locale : une fonction est continue en un point x 0 si et seulement si sa restriction
DOCUMENT 27 Image d un intervalle par une fonction continue La continuité d une fonction en un point est une propriété locale : une fonction est continue en un point x 0 si et seulement si sa restriction
Jean-Philippe Préaux http://www.i2m.univ-amu.fr/~preaux
 Colonies de fourmis Comment procèdent les colonies de fourmi pour déterminer un chemin presque géodésique de la fourmilière à un stock de nourriture? Les premières fourmis se déplacent au hasard. Les fourmis
Colonies de fourmis Comment procèdent les colonies de fourmi pour déterminer un chemin presque géodésique de la fourmilière à un stock de nourriture? Les premières fourmis se déplacent au hasard. Les fourmis
De même, le périmètre P d un cercle de rayon 1 vaut P = 2π (par définition de π). Mais, on peut démontrer (difficilement!) que
 Introduction. On suppose connus les ensembles N (des entiers naturels), Z des entiers relatifs et Q (des nombres rationnels). On s est rendu compte, depuis l antiquité, que l on ne peut pas tout mesurer
Introduction. On suppose connus les ensembles N (des entiers naturels), Z des entiers relatifs et Q (des nombres rationnels). On s est rendu compte, depuis l antiquité, que l on ne peut pas tout mesurer
LES OUTILS D ALIMENTATION DU REFERENTIEL DE DB-MAIN
 LES OUTILS D ALIMENTATION DU REFERENTIEL DE DB-MAIN Les contenues de ce document sont la propriété exclusive de la société REVER. Ils ne sont transmis qu à titre d information et ne peuvent en aucun cas
LES OUTILS D ALIMENTATION DU REFERENTIEL DE DB-MAIN Les contenues de ce document sont la propriété exclusive de la société REVER. Ils ne sont transmis qu à titre d information et ne peuvent en aucun cas
Souad EL Bernoussi. Groupe d Analyse Numérique et Optimisation Rabat http ://www.fsr.ac.ma/ano/
 Recherche opérationnelle Les démonstrations et les exemples seront traités en cours Souad EL Bernoussi Groupe d Analyse Numérique et Optimisation Rabat http ://www.fsr.ac.ma/ano/ Table des matières 1 Programmation
Recherche opérationnelle Les démonstrations et les exemples seront traités en cours Souad EL Bernoussi Groupe d Analyse Numérique et Optimisation Rabat http ://www.fsr.ac.ma/ano/ Table des matières 1 Programmation
Université Paris-Dauphine DUMI2E 1ère année, 2009-2010. Applications
 Université Paris-Dauphine DUMI2E 1ère année, 2009-2010 Applications 1 Introduction Une fonction f (plus précisément, une fonction réelle d une variable réelle) est une règle qui associe à tout réel x au
Université Paris-Dauphine DUMI2E 1ère année, 2009-2010 Applications 1 Introduction Une fonction f (plus précisément, une fonction réelle d une variable réelle) est une règle qui associe à tout réel x au
Dérivées d ordres supérieurs. Application à l étude d extrema.
 Chapitre 5 Dérivées d ordres supérieurs. Application à l étude d extrema. On s intéresse dans ce chapitre aux dérivées d ordre ou plus d une fonction de plusieurs variables. Comme pour une fonction d une
Chapitre 5 Dérivées d ordres supérieurs. Application à l étude d extrema. On s intéresse dans ce chapitre aux dérivées d ordre ou plus d une fonction de plusieurs variables. Comme pour une fonction d une
Durée de L épreuve : 2 heures. Barème : Exercice n 4 : 1 ) 1 point 2 ) 2 points 3 ) 1 point
 03 Mai 2013 Collège Oasis Durée de L épreuve : 2 heures. apple Le sujet comporte 4 pages et est présenté en livret ; apple La calculatrice est autorisée ; apple 4 points sont attribués à la qualité de
03 Mai 2013 Collège Oasis Durée de L épreuve : 2 heures. apple Le sujet comporte 4 pages et est présenté en livret ; apple La calculatrice est autorisée ; apple 4 points sont attribués à la qualité de
Introduction à la théorie des graphes. Solutions des exercices
 CAHIERS DE LA CRM Introduction à la théorie des graphes Solutions des exercices Didier Müller CAHIER N O 6 COMMISSION ROMANDE DE MATHÉMATIQUE 1 Graphes non orientés Exercice 1 On obtient le graphe biparti
CAHIERS DE LA CRM Introduction à la théorie des graphes Solutions des exercices Didier Müller CAHIER N O 6 COMMISSION ROMANDE DE MATHÉMATIQUE 1 Graphes non orientés Exercice 1 On obtient le graphe biparti
Sujet 4: Programmation stochastique propriétés de fonction de recours
 Sujet 4: Programmation stochastique propriétés de fonction de recours MSE3313: Optimisation Stochastiqe Andrew J. Miller Dernière mise au jour: October 19, 2011 Dans ce sujet... 1 Propriétés de la fonction
Sujet 4: Programmation stochastique propriétés de fonction de recours MSE3313: Optimisation Stochastiqe Andrew J. Miller Dernière mise au jour: October 19, 2011 Dans ce sujet... 1 Propriétés de la fonction
Développement de lois et de structures de réglages destinées à la téléopération avec retour d effort
 Développement de lois et de structures de réglages destinées à la téléopération avec retour d effort Thomas Delwiche, Laurent Catoire et Michel Kinnaert Faculté des Sciences Appliquées Service d Automatique
Développement de lois et de structures de réglages destinées à la téléopération avec retour d effort Thomas Delwiche, Laurent Catoire et Michel Kinnaert Faculté des Sciences Appliquées Service d Automatique
Exercices types Algorithmique et simulation numérique Oral Mathématiques et algorithmique Banque PT
 Exercices types Algorithmique et simulation numérique Oral Mathématiques et algorithmique Banque PT Ces exercices portent sur les items 2, 3 et 5 du programme d informatique des classes préparatoires,
Exercices types Algorithmique et simulation numérique Oral Mathématiques et algorithmique Banque PT Ces exercices portent sur les items 2, 3 et 5 du programme d informatique des classes préparatoires,
Équations non linéaires
 Équations non linéaires Objectif : trouver les zéros de fonctions (ou systèmes) non linéaires, c-à-d les valeurs α R telles que f(α) = 0. y f(x) α 1 α 2 α 3 x Equations non lineaires p. 1/49 Exemples et
Équations non linéaires Objectif : trouver les zéros de fonctions (ou systèmes) non linéaires, c-à-d les valeurs α R telles que f(α) = 0. y f(x) α 1 α 2 α 3 x Equations non lineaires p. 1/49 Exemples et
Intégration et probabilités TD1 Espaces mesurés
 Intégration et probabilités TD1 Espaces mesurés 2012-2013 1 Petites questions 1) Est-ce que l ensemble des ouverts de R est une tribu? 2) Si F et G sont deux tribus, est-ce que F G est toujours une tribu?
Intégration et probabilités TD1 Espaces mesurés 2012-2013 1 Petites questions 1) Est-ce que l ensemble des ouverts de R est une tribu? 2) Si F et G sont deux tribus, est-ce que F G est toujours une tribu?
Les algorithmes de base du graphisme
 Les algorithmes de base du graphisme Table des matières 1 Traçage 2 1.1 Segments de droites......................... 2 1.1.1 Algorithmes simples.................... 3 1.1.2 Algorithmes de Bresenham (1965).............
Les algorithmes de base du graphisme Table des matières 1 Traçage 2 1.1 Segments de droites......................... 2 1.1.1 Algorithmes simples.................... 3 1.1.2 Algorithmes de Bresenham (1965).............
Cours Fonctions de deux variables
 Cours Fonctions de deux variables par Pierre Veuillez 1 Support théorique 1.1 Représentation Plan et espace : Grâce à un repère cartésien ( ) O, i, j du plan, les couples (x, y) de R 2 peuvent être représenté
Cours Fonctions de deux variables par Pierre Veuillez 1 Support théorique 1.1 Représentation Plan et espace : Grâce à un repère cartésien ( ) O, i, j du plan, les couples (x, y) de R 2 peuvent être représenté
Introduction au Data-Mining
 Introduction au Data-Mining Alain Rakotomamonjy - Gilles Gasso. INSA Rouen -Département ASI Laboratoire PSI Introduction au Data-Mining p. 1/25 Data-Mining : Kèkecé? Traduction : Fouille de données. Terme
Introduction au Data-Mining Alain Rakotomamonjy - Gilles Gasso. INSA Rouen -Département ASI Laboratoire PSI Introduction au Data-Mining p. 1/25 Data-Mining : Kèkecé? Traduction : Fouille de données. Terme
Extraction et reconstruction de bâtiments en 3D à partir de relevés lidar aéroportés
 Thèse présentée pour obtenir le grade de Docteur de l Université Louis Pasteur Strasbourg I Discipline : Sciences pour l Ingénieur Spécialité : Topographie-Géomatique Par : Fayez TARSHA KURDI Extraction
Thèse présentée pour obtenir le grade de Docteur de l Université Louis Pasteur Strasbourg I Discipline : Sciences pour l Ingénieur Spécialité : Topographie-Géomatique Par : Fayez TARSHA KURDI Extraction
Fonctions de deux variables. Mai 2011
 Fonctions de deux variables Dédou Mai 2011 D une à deux variables Les fonctions modèlisent de l information dépendant d un paramètre. On a aussi besoin de modéliser de l information dépendant de plusieurs
Fonctions de deux variables Dédou Mai 2011 D une à deux variables Les fonctions modèlisent de l information dépendant d un paramètre. On a aussi besoin de modéliser de l information dépendant de plusieurs
Chp. 4. Minimisation d une fonction d une variable
 Chp. 4. Minimisation d une fonction d une variable Avertissement! Dans tout ce chapître, I désigne un intervalle de IR. 4.1 Fonctions convexes d une variable Définition 9 Une fonction ϕ, partout définie
Chp. 4. Minimisation d une fonction d une variable Avertissement! Dans tout ce chapître, I désigne un intervalle de IR. 4.1 Fonctions convexes d une variable Définition 9 Une fonction ϕ, partout définie
Fonctions Analytiques
 5 Chapitre Fonctions Analytiques. Le plan complexe.. Rappels Soit z C, alors!(x,y) IR 2 tel que z = x + iy. On définit le module de z comme z = x 2 + y 2. On peut aussi repérer z par des coordonnées polaires,
5 Chapitre Fonctions Analytiques. Le plan complexe.. Rappels Soit z C, alors!(x,y) IR 2 tel que z = x + iy. On définit le module de z comme z = x 2 + y 2. On peut aussi repérer z par des coordonnées polaires,
Fonctions de plusieurs variables
 Maths MP Exercices Fonctions de plusieurs variables Les indications ne sont ici que pour être consultées après le T (pour les exercices non traités). Avant et pendant le T, tenez bon et n allez pas les
Maths MP Exercices Fonctions de plusieurs variables Les indications ne sont ici que pour être consultées après le T (pour les exercices non traités). Avant et pendant le T, tenez bon et n allez pas les
Statistique : Résumé de cours et méthodes
 Statistique : Résumé de cours et méthodes 1 Vocabulaire : Population : c est l ensemble étudié. Individu : c est un élément de la population. Effectif total : c est le nombre total d individus. Caractère
Statistique : Résumé de cours et méthodes 1 Vocabulaire : Population : c est l ensemble étudié. Individu : c est un élément de la population. Effectif total : c est le nombre total d individus. Caractère
Franck VAUTIER, Jean-Pierre TOUMAZET, Erwan ROUSSEL, Marlène FAURE, Mohamed ABADI, Marta FLOREZ, Bertrand DOUSTEYSSIER
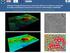 Utilisation d images dérivées d un jeu de données LIDAR pour la détection automatisée de vestiges archéologiques (programme de recherche méthodologique LiDARCHEO) Franck VAUTIER, Jean-Pierre TOUMAZET,
Utilisation d images dérivées d un jeu de données LIDAR pour la détection automatisée de vestiges archéologiques (programme de recherche méthodologique LiDARCHEO) Franck VAUTIER, Jean-Pierre TOUMAZET,
CARTE DE VOEUX À L ASSOCIAEDRE
 CARTE DE VOEUX À L ASSOCIAEDRE JEAN-LOUIS LODAY Il y a cinq ans le Centre International de Rencontres Mathématiques de Luminy a envoyé ses voeux avec la carte ci-dessus. L illustration choisie par Robert
CARTE DE VOEUX À L ASSOCIAEDRE JEAN-LOUIS LODAY Il y a cinq ans le Centre International de Rencontres Mathématiques de Luminy a envoyé ses voeux avec la carte ci-dessus. L illustration choisie par Robert
Chapitre 2 Le problème de l unicité des solutions
 Université Joseph Fourier UE MAT 127 Mathématiques année 2011-2012 Chapitre 2 Le problème de l unicité des solutions Ce que nous verrons dans ce chapitre : un exemple d équation différentielle y = f(y)
Université Joseph Fourier UE MAT 127 Mathématiques année 2011-2012 Chapitre 2 Le problème de l unicité des solutions Ce que nous verrons dans ce chapitre : un exemple d équation différentielle y = f(y)
Bases de données documentaires et distribuées Cours NFE04
 Bases de données documentaires et distribuées Cours NFE04 Introduction a la recherche d information Auteurs : Raphaël Fournier-S niehotta, Philippe Rigaux, Nicolas Travers prénom.nom@cnam.fr Département
Bases de données documentaires et distribuées Cours NFE04 Introduction a la recherche d information Auteurs : Raphaël Fournier-S niehotta, Philippe Rigaux, Nicolas Travers prénom.nom@cnam.fr Département
Quelques algorithmes simples dont l analyse n est pas si simple
 Quelques algorithmes simples dont l analyse n est pas si simple Michel Habib habib@liafa.jussieu.fr http://www.liafa.jussieu.fr/~habib Algorithmique Avancée M1 Bioinformatique, Octobre 2008 Plan Histoire
Quelques algorithmes simples dont l analyse n est pas si simple Michel Habib habib@liafa.jussieu.fr http://www.liafa.jussieu.fr/~habib Algorithmique Avancée M1 Bioinformatique, Octobre 2008 Plan Histoire
La programmation linéaire : une introduction. Qu est-ce qu un programme linéaire? Terminologie. Écriture mathématique
 La programmation linéaire : une introduction Qu est-ce qu un programme linéaire? Qu est-ce qu un programme linéaire? Exemples : allocation de ressources problème de recouvrement Hypothèses de la programmation
La programmation linéaire : une introduction Qu est-ce qu un programme linéaire? Qu est-ce qu un programme linéaire? Exemples : allocation de ressources problème de recouvrement Hypothèses de la programmation
Problèmes de dénombrement.
 Problèmes de dénombrement. 1. On se déplace dans le tableau suivant, pour aller de la case D (départ) à la case (arrivée). Les déplacements utilisés sont exclusivement les suivants : ller d une case vers
Problèmes de dénombrement. 1. On se déplace dans le tableau suivant, pour aller de la case D (départ) à la case (arrivée). Les déplacements utilisés sont exclusivement les suivants : ller d une case vers
Programmation linéaire
 1 Programmation linéaire 1. Le problème, un exemple. 2. Le cas b = 0 3. Théorème de dualité 4. L algorithme du simplexe 5. Problèmes équivalents 6. Complexité de l Algorithme 2 Position du problème Soit
1 Programmation linéaire 1. Le problème, un exemple. 2. Le cas b = 0 3. Théorème de dualité 4. L algorithme du simplexe 5. Problèmes équivalents 6. Complexité de l Algorithme 2 Position du problème Soit
Algorithmes récursifs
 Licence 1 MASS - Algorithmique et Calcul Formel S. Verel, M.-E. Voge www.i3s.unice.fr/ verel 23 mars 2007 Objectifs de la séance 3 écrire des algorithmes récursifs avec un seul test rechercher un élément
Licence 1 MASS - Algorithmique et Calcul Formel S. Verel, M.-E. Voge www.i3s.unice.fr/ verel 23 mars 2007 Objectifs de la séance 3 écrire des algorithmes récursifs avec un seul test rechercher un élément
Continuité d une fonction de plusieurs variables
 Chapitre 2 Continuité d une fonction de plusieurs variables Maintenant qu on a défini la notion de limite pour des suites dans R n, la notion de continuité s étend sans problème à des fonctions de plusieurs
Chapitre 2 Continuité d une fonction de plusieurs variables Maintenant qu on a défini la notion de limite pour des suites dans R n, la notion de continuité s étend sans problème à des fonctions de plusieurs
Coup de Projecteur sur les Réseaux de Neurones
 Coup de Projecteur sur les Réseaux de Neurones Les réseaux de neurones peuvent être utilisés pour des problèmes de prévision ou de classification. La représentation la plus populaire est le réseau multicouche
Coup de Projecteur sur les Réseaux de Neurones Les réseaux de neurones peuvent être utilisés pour des problèmes de prévision ou de classification. La représentation la plus populaire est le réseau multicouche
OM 1 Outils mathématiques : fonction de plusieurs variables
 Outils mathématiques : fonction de plusieurs variables PCSI 2013 2014 Certaines partie de ce chapitre ne seront utiles qu à partir de l année prochaine, mais une grande partie nous servira dès cette année.
Outils mathématiques : fonction de plusieurs variables PCSI 2013 2014 Certaines partie de ce chapitre ne seront utiles qu à partir de l année prochaine, mais une grande partie nous servira dès cette année.
Eteindre. les. lumières MATH EN JEAN 2013-2014. Mme BACHOC. Elèves de seconde, première et terminale scientifiques :
 MTH EN JEN 2013-2014 Elèves de seconde, première et terminale scientifiques : Lycée Michel Montaigne : HERITEL ôme T S POLLOZE Hélène 1 S SOK Sophie 1 S Eteindre Lycée Sud Médoc : ROSIO Gauthier 2 nd PELGE
MTH EN JEN 2013-2014 Elèves de seconde, première et terminale scientifiques : Lycée Michel Montaigne : HERITEL ôme T S POLLOZE Hélène 1 S SOK Sophie 1 S Eteindre Lycée Sud Médoc : ROSIO Gauthier 2 nd PELGE
Cours de Recherche Opérationnelle IUT d Orsay. Nicolas M. THIÉRY. E-mail address: Nicolas.Thiery@u-psud.fr URL: http://nicolas.thiery.
 Cours de Recherche Opérationnelle IUT d Orsay Nicolas M. THIÉRY E-mail address: Nicolas.Thiery@u-psud.fr URL: http://nicolas.thiery.name/ CHAPTER 1 Introduction à l optimisation 1.1. TD: Ordonnancement
Cours de Recherche Opérationnelle IUT d Orsay Nicolas M. THIÉRY E-mail address: Nicolas.Thiery@u-psud.fr URL: http://nicolas.thiery.name/ CHAPTER 1 Introduction à l optimisation 1.1. TD: Ordonnancement
Une nouvelle approche de détection de communautés dans les réseaux sociaux
 UNIVERSITÉ DU QUÉBEC EN OUTAOUAIS Département d informatique et d ingénierie Une nouvelle approche de détection de communautés dans les réseaux sociaux Mémoire (INF 6021) pour l obtention du grade de Maîtrise
UNIVERSITÉ DU QUÉBEC EN OUTAOUAIS Département d informatique et d ingénierie Une nouvelle approche de détection de communautés dans les réseaux sociaux Mémoire (INF 6021) pour l obtention du grade de Maîtrise
C algèbre d un certain groupe de Lie nilpotent.
 Université Paul Verlaine - METZ LMAM 6 décembre 2011 1 2 3 4 Les transformations de Fourier. Le C algèbre de G/ Z. Le C algèbre du sous-groupe G 5 / vect{u,v }. Conclusion. G un groupe de Lie, Ĝ l ensemble
Université Paul Verlaine - METZ LMAM 6 décembre 2011 1 2 3 4 Les transformations de Fourier. Le C algèbre de G/ Z. Le C algèbre du sous-groupe G 5 / vect{u,v }. Conclusion. G un groupe de Lie, Ĝ l ensemble
Théorème du point fixe - Théorème de l inversion locale
 Chapitre 7 Théorème du point fixe - Théorème de l inversion locale Dans ce chapitre et le suivant, on montre deux applications importantes de la notion de différentiabilité : le théorème de l inversion
Chapitre 7 Théorème du point fixe - Théorème de l inversion locale Dans ce chapitre et le suivant, on montre deux applications importantes de la notion de différentiabilité : le théorème de l inversion
Objectifs. Clustering. Principe. Applications. Applications. Cartes de crédits. Remarques. Biologie, Génomique
 Objectifs Clustering On ne sait pas ce qu on veut trouver : on laisse l algorithme nous proposer un modèle. On pense qu il existe des similarités entre les exemples. Qui se ressemble s assemble p. /55
Objectifs Clustering On ne sait pas ce qu on veut trouver : on laisse l algorithme nous proposer un modèle. On pense qu il existe des similarités entre les exemples. Qui se ressemble s assemble p. /55
Corrigé du baccalauréat S Asie 21 juin 2010
 Corrigé du baccalauréat S Asie juin 00 EXERCICE Commun à tous les candidats 4 points. Question : Le triangle GBI est : Réponse a : isocèle. Réponse b : équilatéral. Réponse c : rectangle. On a GB = + =
Corrigé du baccalauréat S Asie juin 00 EXERCICE Commun à tous les candidats 4 points. Question : Le triangle GBI est : Réponse a : isocèle. Réponse b : équilatéral. Réponse c : rectangle. On a GB = + =
Modélisation multi-agents - Agents réactifs
 Modélisation multi-agents - Agents réactifs Syma cursus CSI / SCIA Julien Saunier - julien.saunier@ifsttar.fr Sources www-lih.univlehavre.fr/~olivier/enseignement/masterrecherche/cours/ support/algofourmis.pdf
Modélisation multi-agents - Agents réactifs Syma cursus CSI / SCIA Julien Saunier - julien.saunier@ifsttar.fr Sources www-lih.univlehavre.fr/~olivier/enseignement/masterrecherche/cours/ support/algofourmis.pdf
Projet L1, S2, 2015: Simulation de fourmis, Soutenance la semaine du 4 mai.
 Projet L1, S2, 2015: Simulation de fourmis, Soutenance la semaine du 4 mai. 1 Introduction On considère une grille de 20 lignes 20 colonnes. Une case de la grille peut être vide, ou contenir une et une
Projet L1, S2, 2015: Simulation de fourmis, Soutenance la semaine du 4 mai. 1 Introduction On considère une grille de 20 lignes 20 colonnes. Une case de la grille peut être vide, ou contenir une et une
LIDAR LAUSANNE 2012. Nouvelles données altimétriques sur l agglomération lausannoise par technologie laser aéroporté et ses produits dérivés
 LIDAR LAUSANNE 2012 Nouvelles données altimétriques sur l agglomération lausannoise par technologie laser aéroporté et ses produits dérivés LIDAR 2012, nouveaux modèles altimétriques 1 Affaire 94022 /
LIDAR LAUSANNE 2012 Nouvelles données altimétriques sur l agglomération lausannoise par technologie laser aéroporté et ses produits dérivés LIDAR 2012, nouveaux modèles altimétriques 1 Affaire 94022 /
MABioVis. Bio-informatique et la
 MABioVis Modèles et Algorithmes pour la Bio-informatique et la Visualisation Visite ENS Cachan 5 janvier 2011 MABioVis G GUY MELANÇON (PR UFR Maths Info / EPI GRAVITE) (là, maintenant) - MABioVis DAVID
MABioVis Modèles et Algorithmes pour la Bio-informatique et la Visualisation Visite ENS Cachan 5 janvier 2011 MABioVis G GUY MELANÇON (PR UFR Maths Info / EPI GRAVITE) (là, maintenant) - MABioVis DAVID
Optimisation des fonctions de plusieurs variables
 Optimisation des fonctions de plusieurs variables Hervé Hocquard Université de Bordeaux, France 8 avril 2013 Extrema locaux et globaux Définition On étudie le comportement d une fonction de plusieurs variables
Optimisation des fonctions de plusieurs variables Hervé Hocquard Université de Bordeaux, France 8 avril 2013 Extrema locaux et globaux Définition On étudie le comportement d une fonction de plusieurs variables
Axe " Génie des Procédés", centre SPIN, Ecole des Mines de Saint-Etienne ECOLE DES MINES SAINT-ETIENNE ANALYSE D IMAGE
 ANALYSE D IMAGE 1. PRESENTATION DE L ANALYSE D IMAGE. 4 1.1. OJECTIF ET BUT DE L ANALYSE D IMAGE 4 1.2. PRINCIPE 4 1.2.1. FORMATION DE L IMAGE NUMERIQUE 4 1.2.2. TRANSFORMATION DE L IMAGE NUMERIQUE EN
ANALYSE D IMAGE 1. PRESENTATION DE L ANALYSE D IMAGE. 4 1.1. OJECTIF ET BUT DE L ANALYSE D IMAGE 4 1.2. PRINCIPE 4 1.2.1. FORMATION DE L IMAGE NUMERIQUE 4 1.2.2. TRANSFORMATION DE L IMAGE NUMERIQUE EN
Probabilités. Rappel : trois exemples. Exemple 2 : On dispose d un dé truqué. On sait que : p(1) = p(2) =1/6 ; p(3) = 1/3 p(4) = p(5) =1/12
 Probabilités. I - Rappel : trois exemples. Exemple 1 : Dans une classe de 25 élèves, il y a 16 filles. Tous les élèves sont blonds ou bruns. Parmi les filles, 6 sont blondes. Parmi les garçons, 3 sont
Probabilités. I - Rappel : trois exemples. Exemple 1 : Dans une classe de 25 élèves, il y a 16 filles. Tous les élèves sont blonds ou bruns. Parmi les filles, 6 sont blondes. Parmi les garçons, 3 sont
Microscopie de fluorescence Etat de l art
 Etat de l art Bibliométrie (Web of sciences) CLSM GFP & TPE EPI-FLUORESCENCE 1 Fluorescence Diagramme de JABLONSKI S2 S1 10-12 s Excitation Eex Eem 10-9 s Émission Courtoisie de C. Spriet
Etat de l art Bibliométrie (Web of sciences) CLSM GFP & TPE EPI-FLUORESCENCE 1 Fluorescence Diagramme de JABLONSKI S2 S1 10-12 s Excitation Eex Eem 10-9 s Émission Courtoisie de C. Spriet
La classification automatique de données quantitatives
 La classification automatique de données quantitatives 1 Introduction Parmi les méthodes de statistique exploratoire multidimensionnelle, dont l objectif est d extraire d une masse de données des informations
La classification automatique de données quantitatives 1 Introduction Parmi les méthodes de statistique exploratoire multidimensionnelle, dont l objectif est d extraire d une masse de données des informations
CCP PSI - 2010 Mathématiques 1 : un corrigé
 CCP PSI - 00 Mathématiques : un corrigé Première partie. Définition d une structure euclidienne sur R n [X]... B est clairement symétrique et linéaire par rapport à sa seconde variable. De plus B(P, P
CCP PSI - 00 Mathématiques : un corrigé Première partie. Définition d une structure euclidienne sur R n [X]... B est clairement symétrique et linéaire par rapport à sa seconde variable. De plus B(P, P
Chapitre V : La gestion de la mémoire. Hiérarchie de mémoires Objectifs Méthodes d'allocation Simulation de mémoire virtuelle Le mapping
 Chapitre V : La gestion de la mémoire Hiérarchie de mémoires Objectifs Méthodes d'allocation Simulation de mémoire virtuelle Le mapping Introduction Plusieurs dizaines de processus doivent se partager
Chapitre V : La gestion de la mémoire Hiérarchie de mémoires Objectifs Méthodes d'allocation Simulation de mémoire virtuelle Le mapping Introduction Plusieurs dizaines de processus doivent se partager
3 Approximation de solutions d équations
 3 Approximation de solutions d équations Une équation scalaire a la forme générale f(x) =0où f est une fonction de IR dans IR. Un système de n équations à n inconnues peut aussi se mettre sous une telle
3 Approximation de solutions d équations Une équation scalaire a la forme générale f(x) =0où f est une fonction de IR dans IR. Un système de n équations à n inconnues peut aussi se mettre sous une telle
TP3 Intégration de pratiques agiles. 1. User Stories (1) Scénario d intégration agile. En direct-live du château
 Rappel TP3 Intégration de pratiques agiles En direct-live du château 40 41 Scénario d intégration agile 1. User Stories (1) 1. Rédiger les User Stories (exigences) 2. Planifier les Itérations (quoi / quand)
Rappel TP3 Intégration de pratiques agiles En direct-live du château 40 41 Scénario d intégration agile 1. User Stories (1) 1. Rédiger les User Stories (exigences) 2. Planifier les Itérations (quoi / quand)
Savoir lire une carte, se situer et s orienter en randonnée
 Savoir lire une carte, se situer et s orienter en randonnée Le b.a.-ba du randonneur Fiche 2 Lire une carte topographique Mais c est où le nord? Quel Nord Le magnétisme terrestre attire systématiquement
Savoir lire une carte, se situer et s orienter en randonnée Le b.a.-ba du randonneur Fiche 2 Lire une carte topographique Mais c est où le nord? Quel Nord Le magnétisme terrestre attire systématiquement
L E Ç O N. Marches aléatoires. Niveau : Terminale S Prérequis : aucun
 9 L E Ç O N Marches aléatoires Niveau : Terminale S Prérequis : aucun 1 Chaînes de Markov Définition 9.1 Chaîne de Markov I Une chaîne de Markov est une suite de variables aléatoires (X n, n N) qui permet
9 L E Ç O N Marches aléatoires Niveau : Terminale S Prérequis : aucun 1 Chaînes de Markov Définition 9.1 Chaîne de Markov I Une chaîne de Markov est une suite de variables aléatoires (X n, n N) qui permet
Notice de pose NOTICE DE POSE 1-2. 1. Fond: 2. IMPORTANT:
 Panneaux de terrasse TimberStar Notice de pose NOTICE DE POSE 1-2 Veuillez lire l intégralité de la notice de pose avant de commencer le montage! Les panneaux de terrasse TimberStar peuvent être sciés,
Panneaux de terrasse TimberStar Notice de pose NOTICE DE POSE 1-2 Veuillez lire l intégralité de la notice de pose avant de commencer le montage! Les panneaux de terrasse TimberStar peuvent être sciés,
LAURENT FABIUS, MINISTRE DES AFFAIRES ETRANGERES
 LAURENT FABIUS, MINISTRE DES AFFAIRES ETRANGERES Tout à l heure, le Président de la République m a demandé, avec le Premier ministre, de vous apporter un certain nombre d éléments sur le contexte dans
LAURENT FABIUS, MINISTRE DES AFFAIRES ETRANGERES Tout à l heure, le Président de la République m a demandé, avec le Premier ministre, de vous apporter un certain nombre d éléments sur le contexte dans
Cours d Analyse. Fonctions de plusieurs variables
 Cours d Analyse Fonctions de plusieurs variables Licence 1ère année 2007/2008 Nicolas Prioux Université de Marne-la-Vallée Table des matières 1 Notions de géométrie dans l espace et fonctions à deux variables........
Cours d Analyse Fonctions de plusieurs variables Licence 1ère année 2007/2008 Nicolas Prioux Université de Marne-la-Vallée Table des matières 1 Notions de géométrie dans l espace et fonctions à deux variables........
Reconstruction de bâtiments en 3D à partir de nuages de points LIDAR
 Reconstruction de bâtiments en 3D à partir de nuages de points LIDAR Mickaël Bergem 25 juin 2014 Maillages et applications 1 Table des matières Introduction 3 1 La modélisation numérique de milieux urbains
Reconstruction de bâtiments en 3D à partir de nuages de points LIDAR Mickaël Bergem 25 juin 2014 Maillages et applications 1 Table des matières Introduction 3 1 La modélisation numérique de milieux urbains
Géométrie discrète Chapitre V
 Géométrie discrète Chapitre V Introduction au traitement d'images Géométrie euclidienne : espace continu Géométrie discrète (GD) : espace discrétisé notamment en grille de pixels GD définition des objets
Géométrie discrète Chapitre V Introduction au traitement d'images Géométrie euclidienne : espace continu Géométrie discrète (GD) : espace discrétisé notamment en grille de pixels GD définition des objets
P.L.U. Plan Local d'urbanisme PRESCRIPTION D'ISOLEMENT ACOUSTIQUE AU VOISINAGE DES INFRASTRUCTURES TERRESTRES DOCUMENT OPPOSABLE
 Commune du Département de l'oise P.L.U Plan Local d'urbanisme PRESCRIPTION D'ISOLEMENT ACOUSTIQUE AU VOISINAGE DES INFRASTRUCTURES TERRESTRES DOCUMENT OPPOSABLE Document Établi le 20 septembre 2013 Le
Commune du Département de l'oise P.L.U Plan Local d'urbanisme PRESCRIPTION D'ISOLEMENT ACOUSTIQUE AU VOISINAGE DES INFRASTRUCTURES TERRESTRES DOCUMENT OPPOSABLE Document Établi le 20 septembre 2013 Le
Indications pour une progression au CM1 et au CM2
 Indications pour une progression au CM1 et au CM2 Objectif 1 Construire et utiliser de nouveaux nombres, plus précis que les entiers naturels pour mesurer les grandeurs continues. Introduction : Découvrir
Indications pour une progression au CM1 et au CM2 Objectif 1 Construire et utiliser de nouveaux nombres, plus précis que les entiers naturels pour mesurer les grandeurs continues. Introduction : Découvrir
Cryptologie. Algorithmes à clé publique. Jean-Marc Robert. Génie logiciel et des TI
 Cryptologie Algorithmes à clé publique Jean-Marc Robert Génie logiciel et des TI Plan de la présentation Introduction Cryptographie à clé publique Les principes essentiels La signature électronique Infrastructures
Cryptologie Algorithmes à clé publique Jean-Marc Robert Génie logiciel et des TI Plan de la présentation Introduction Cryptographie à clé publique Les principes essentiels La signature électronique Infrastructures
Statistiques Descriptives à une dimension
 I. Introduction et Définitions 1. Introduction La statistique est une science qui a pour objectif de recueillir et de traiter les informations, souvent en très grand nombre. Elle regroupe l ensemble des
I. Introduction et Définitions 1. Introduction La statistique est une science qui a pour objectif de recueillir et de traiter les informations, souvent en très grand nombre. Elle regroupe l ensemble des
Calcul différentiel sur R n Première partie
 Calcul différentiel sur R n Première partie Université De Metz 2006-2007 1 Définitions générales On note L(R n, R m ) l espace vectoriel des applications linéaires de R n dans R m. Définition 1.1 (différentiabilité
Calcul différentiel sur R n Première partie Université De Metz 2006-2007 1 Définitions générales On note L(R n, R m ) l espace vectoriel des applications linéaires de R n dans R m. Définition 1.1 (différentiabilité
Cours3. Applications continues et homéomorphismes. 1 Rappel sur les images réciproques
 Université de Provence Topologie 2 Cours3. Applications continues et homéomorphismes 1 Rappel sur les images réciproques Soit une application f d un ensemble X vers un ensemble Y et soit une partie P de
Université de Provence Topologie 2 Cours3. Applications continues et homéomorphismes 1 Rappel sur les images réciproques Soit une application f d un ensemble X vers un ensemble Y et soit une partie P de
ARBRES BINAIRES DE RECHERCHE
 ARBRES BINAIRES DE RECHERCHE Table de symboles Recherche : opération fondamentale données : éléments avec clés Type abstrait d une table de symboles (symbol table) ou dictionnaire Objets : ensembles d
ARBRES BINAIRES DE RECHERCHE Table de symboles Recherche : opération fondamentale données : éléments avec clés Type abstrait d une table de symboles (symbol table) ou dictionnaire Objets : ensembles d
La base de données régionale sur les sols. d Alsace. La base de données régionale sur les sols d Alsace
 3 outils complémentaires pour connaître les sols en Alsace La base de données régionale sur les sols d Alsace Le guide des sols d Alsace La base de données régionale sur les sols Le réseau de mesure de
3 outils complémentaires pour connaître les sols en Alsace La base de données régionale sur les sols d Alsace Le guide des sols d Alsace La base de données régionale sur les sols Le réseau de mesure de
Géoréférencement et RGF93
 Géoréférencement et RGF93 Théorie et concepts - Fiche T3 Les projections coniques conformes 9 zones T3 Décembre 2008 2008/54 Historique Ces projections ont été définies par l'ign, suite à une recommandation
Géoréférencement et RGF93 Théorie et concepts - Fiche T3 Les projections coniques conformes 9 zones T3 Décembre 2008 2008/54 Historique Ces projections ont été définies par l'ign, suite à une recommandation
Laboratoire d informatique Gaspard-Monge UMR 8049. Journée Labex Bézout- ANSES
 Laboratoire d informatique Gaspard-Monge UMR 8049 Journée Labex Bézout- ANSES Présentation du laboratoire 150 membres, 71 chercheurs et enseignants-chercheurs, 60 doctorants 4 tutelles : CNRS, École des
Laboratoire d informatique Gaspard-Monge UMR 8049 Journée Labex Bézout- ANSES Présentation du laboratoire 150 membres, 71 chercheurs et enseignants-chercheurs, 60 doctorants 4 tutelles : CNRS, École des
Architecture des Systèmes d Information Architecture des Systèmes d Information
 Plan... Tableaux et tris I3 - Algorithmique et programmation 1 Rappels Nicol Delestre 2 Tableaux à n dimensions 3 Initiation aux tris Tableaux - v2.0.1 1 / 27 Tableaux - v2.0.1 2 / 27 Rappels : tableau
Plan... Tableaux et tris I3 - Algorithmique et programmation 1 Rappels Nicol Delestre 2 Tableaux à n dimensions 3 Initiation aux tris Tableaux - v2.0.1 1 / 27 Tableaux - v2.0.1 2 / 27 Rappels : tableau
Intelligence Artificielle Planification
 Intelligence Artificielle Planification Bruno Bouzy http://web.mi.parisdescartes.fr/~bouzy bruno.bouzy@parisdescartes.fr Licence 3 Informatique UFR Mathématiques et Informatique Université Paris Descartes
Intelligence Artificielle Planification Bruno Bouzy http://web.mi.parisdescartes.fr/~bouzy bruno.bouzy@parisdescartes.fr Licence 3 Informatique UFR Mathématiques et Informatique Université Paris Descartes
Modèles à Événements Discrets. Réseaux de Petri Stochastiques
 Modèles à Événements Discrets Réseaux de Petri Stochastiques Table des matières 1 Chaînes de Markov Définition formelle Idée générale Discrete Time Markov Chains Continuous Time Markov Chains Propriétés
Modèles à Événements Discrets Réseaux de Petri Stochastiques Table des matières 1 Chaînes de Markov Définition formelle Idée générale Discrete Time Markov Chains Continuous Time Markov Chains Propriétés
A. CARACTERISTIQUES TECHNIQUES.
 Page : 2 A. CARACTERISTIQUES TECHNIQUES. A.1. VUE D ENSEMBLE A.2. PRINCIPE DE FONCTIONNEMENT!" #! $! %&' ( ) * µ +, µ $# (& % ± -. /01)0$ ' &%(% 2 3,)/4 $ A.3. CARACTERISTIQUES MECANIQUES. PARAMETRES Valeur
Page : 2 A. CARACTERISTIQUES TECHNIQUES. A.1. VUE D ENSEMBLE A.2. PRINCIPE DE FONCTIONNEMENT!" #! $! %&' ( ) * µ +, µ $# (& % ± -. /01)0$ ' &%(% 2 3,)/4 $ A.3. CARACTERISTIQUES MECANIQUES. PARAMETRES Valeur
Resolution limit in community detection
 Introduction Plan 2006 Introduction Plan Introduction Introduction Plan Introduction Point de départ : un graphe et des sous-graphes. But : quantifier le fait que les sous-graphes choisis sont des modules.
Introduction Plan 2006 Introduction Plan Introduction Introduction Plan Introduction Point de départ : un graphe et des sous-graphes. But : quantifier le fait que les sous-graphes choisis sont des modules.
Opérations de base sur ImageJ
 Opérations de base sur ImageJ TPs d hydrodynamique de l ESPCI, J. Bico, M. Reyssat, M. Fermigier ImageJ est un logiciel libre, qui fonctionne aussi bien sous plate-forme Windows, Mac ou Linux. Initialement
Opérations de base sur ImageJ TPs d hydrodynamique de l ESPCI, J. Bico, M. Reyssat, M. Fermigier ImageJ est un logiciel libre, qui fonctionne aussi bien sous plate-forme Windows, Mac ou Linux. Initialement
Fête de la science Initiation au traitement des images
 Fête de la science Initiation au traitement des images Détection automatique de plaques minéralogiques à partir d'un téléphone portable et atelier propose de créer un programme informatique pour un téléphone
Fête de la science Initiation au traitement des images Détection automatique de plaques minéralogiques à partir d'un téléphone portable et atelier propose de créer un programme informatique pour un téléphone
AC AB. A B C x 1. x + 1. d où. Avec un calcul vu au lycée, on démontre que cette solution admet deux solutions dont une seule nous intéresse : x =
 LE NOMBRE D OR Présentation et calcul du nombre d or Euclide avait trouvé un moyen de partager en deu un segment selon en «etrême et moyenne raison» Soit un segment [AB]. Le partage d Euclide consiste
LE NOMBRE D OR Présentation et calcul du nombre d or Euclide avait trouvé un moyen de partager en deu un segment selon en «etrême et moyenne raison» Soit un segment [AB]. Le partage d Euclide consiste
Optimisation for Cloud Computing and Big Data
 1 / 23 Optimisation for Cloud Computing and Big Data Olivier Beaumont, Lionel Eyraud-Dubois 2 / 23 Aujourd hui Problèmes de fiabilité on va oublier la dynamicité Placement de VMs en programmation par contraintes
1 / 23 Optimisation for Cloud Computing and Big Data Olivier Beaumont, Lionel Eyraud-Dubois 2 / 23 Aujourd hui Problèmes de fiabilité on va oublier la dynamicité Placement de VMs en programmation par contraintes
TOUT CE QU IL FAUT SAVOIR POUR LE BREVET
 TOUT E QU IL FUT SVOIR POUR LE REVET NUMERIQUE / FONTIONS eci n est qu un rappel de tout ce qu il faut savoir en maths pour le brevet. I- Opérations sur les nombres et les fractions : Les priorités par
TOUT E QU IL FUT SVOIR POUR LE REVET NUMERIQUE / FONTIONS eci n est qu un rappel de tout ce qu il faut savoir en maths pour le brevet. I- Opérations sur les nombres et les fractions : Les priorités par
DOCM 2013 http://docm.math.ca/ Solutions officielles. 1 2 10 + 1 2 9 + 1 2 8 = n 2 10.
 A1 Trouvez l entier positif n qui satisfait l équation suivante: Solution 1 2 10 + 1 2 9 + 1 2 8 = n 2 10. En additionnant les termes du côté gauche de l équation en les mettant sur le même dénominateur
A1 Trouvez l entier positif n qui satisfait l équation suivante: Solution 1 2 10 + 1 2 9 + 1 2 8 = n 2 10. En additionnant les termes du côté gauche de l équation en les mettant sur le même dénominateur
INTRODUCTION A L ELECTRONIQUE NUMERIQUE ECHANTILLONNAGE ET QUANTIFICATION I. ARCHITECTURE DE L ELECRONIQUE NUMERIQUE
 INTRODUCTION A L ELECTRONIQUE NUMERIQUE ECHANTILLONNAGE ET QUANTIFICATION I. ARCHITECTURE DE L ELECRONIQUE NUMERIQUE Le schéma synoptique ci-dessous décrit les différentes étapes du traitement numérique
INTRODUCTION A L ELECTRONIQUE NUMERIQUE ECHANTILLONNAGE ET QUANTIFICATION I. ARCHITECTURE DE L ELECRONIQUE NUMERIQUE Le schéma synoptique ci-dessous décrit les différentes étapes du traitement numérique
2x 9 =5 c) 4 2 x 5 1= x 1 x = 1 9
 Partie #1 : La jonglerie algébrique... 1. Résous les (in)équations suivantes a) 3 2x 8 =x b) Examen maison fonctions SN5 NOM : 2x 9 =5 c) 4 2 x 5 1= x 1 x d) 2 x 1 3 1 e) x 2 5 = 1 9 f) 2 x 6 7 3 2 2.
Partie #1 : La jonglerie algébrique... 1. Résous les (in)équations suivantes a) 3 2x 8 =x b) Examen maison fonctions SN5 NOM : 2x 9 =5 c) 4 2 x 5 1= x 1 x d) 2 x 1 3 1 e) x 2 5 = 1 9 f) 2 x 6 7 3 2 2.
