STATISTIQUE Notion de test et niveau de signification
|
|
|
- Oscar Mongeau
- il y a 9 ans
- Total affichages :
Transcription
1 STATISTIQUE Notion de test et niveau de signification Sept.-Nov.2010 Bruno Depay
2 Le Figaro, lundi 18 octobre 2010
3 «Le téléphone sonne»émission de radio consacrée aux statistiques France Inter 20 octobre 2010
4 Données du problème La consommation X de boissons au cola suit habituellement une loi N(µ 0 =5, σ). Une campagne de promotion est organisée. Après la campagne, on a obtenu sur un échantillon de 40 personnes une consommation moyenne de 5.88 avec un écart-type de On suppose qu après la campagne X N(µ, σ). La campagne de promotion est considérée comme un succès si µ > 5.
5 Question Au vu des résultats sur l échantillon, peut-on considérer, avec une faible probabilité d erreur, que la campagne de promotion a été un succès? Autrement dit : La moyenne µ estimée par x = 5.88 est-elle significativement supérieure à µ 0 = 5?
6 Rappel Nous savons comment répondre à cette question en utilisant un intervalle de confiance. [ x t ( n 1 ) s ; x ( n 1 ) α α n 2 n + t s ]
7 Conclusion? On ne peut pas affirmer, avec un risque de 5% d erreur, que la consommation µ est significativement supérieure à µ 0.
8 Conclusion? On peut affirmer, avec un risque de 10% d erreur, que la consommation µ est significativement supérieure à µ 0.
9 Conclusion? 7% est le risque d erreur seuil que l on accepte pour affirmer que la consommation µ 0 est significativement supérieure à µ.
10 Niveau de signification α=5% α=10% α=7% Le niveau de signification (SIG) correspond à la valeur minimum du risque que l on peut accepter pour rejeter l hypothèse de départ. Ici l hypothèse de départ est : µ = µ 0 et on a SIG = 7%
11 Test d hypothèse Le test d hypothèse est une méthode qui permet de comparer une moyenne µ à un standard µ 0 Il nous donne directement le niveau de signification (SIG), que nous utiliserons lors de l étude de la régression multiple.
12 Test d hypothèse : démarche On pose une hypothèse de départ H 0 considérée comme vraie, et une hypothèse alternative H 1. On définit une statistique qui suit une loi de probabilité connue pour H 0. On fixe une règle de décision qui permettra ou non de rejeter H 0 au profit de H 1.
13 Test de comparaison bilatéral d une moyenne µ à un standard µ 0 Test : H 0 : µ = µ 0 H 1 : µ µ 0 Statistique utilisée : x µ t = 0 s / n Règle de décision : On rejette H 0 au profit de H 1, au risque α de se tromper, si t t 1-(α/2) (n-1) Niveau de signification (Sig) du t observé : Plus petite valeur de α conduisant au rejet de H 0 : Sig/2 = Prob(t(n-1) t )
14 Niveau de signification (Sig) La plus petite valeur de α avec laquelle on rejette H 0 Loi de Student à (n-1) ddl Sig/2 α/2 Sig/2 - t 0 t t 1-α/2 (n-1) On peut rejeter H 0 avec un risque α si t >t 1-α/2 (n-1) (soit Sig α)
15 Application : t =? t = x s µ 0 / n One-Sample Statistics Consommation de boisson au cola N Mean Std. Deviation Std. Error Mean 40 5,88 2,972,470 One-Sample Test Consommation de boisson au cola t df Sig. (2-tailed) Test Value = 5 95% Confidence Interval of the Mean Difference Difference Lower Upper 1,862 39,070,875 -,08 1,83
16
17 Conclusion de ce test pour Rola-Cola On ne peut pas rejeter, avec un risque α<7%, l hypothèse que µ = µ 0. Autrement dit : Si on prend un risque α<7%, on ne peut pas dire que la consommation de Rola- Cola suite à la campagne de promotion est significativement différente.
18 Test de comparaison unilatéral Dans notre exemple on peut utiliser un test de comparaison unilatéral si on part de l hypothèse que la moyenne de consommation ne peut qu avoir augmentée après la campagne de publicité. On ne cherche plus à savoir si µ µ 0 mais seulement si µ > µ 0
19 Test de comparaison unilatéral (à droite) d une moyenne µ à un standard µ 0 Test : H 0 : µ = µ 0 H 1 : µ > µ 0 Statistique utilisée : x µ t = 0 s / n Règle de décision : On rejette H 0 au profit de H 1, au risque α de se tromper, si t t 1-α (n-1) Niveau de signification (Sig) du t observé : Plus petite valeur de α conduisant au rejet de H 0 : Sig = Prob(t(n-1) t)
20 Niveau de signification (Sig) La plus petite valeur de α avec laquelle on rejette H 0 Loi de Student α Sig 0 t t 1-α (n-1) On peut rejeter H 0 avec un risque α si t >t 1-α (n-1) (soit Sig α)
21 Application t = 1,862 (inchangé) t 0,95 (39)=1,685 Donc t > t 0,95 (39) Le niveau de signification vaut : Sig = Prob(t(39)>1,862)=3,5% Donc en prenant un test de comparaison unilatéral à droite, le niveau de signification est de 3,5%
22 Importance de l hypothèse H 1 On peut rejeter avec un risque d erreur α=5% l hypothèse H 0 : µ = µ 0 au profit de H 1 : µ > µ 0 Ainsi dans notre exemple avec : -les mêmes données -le même risque d erreur α -la même hypothèse de départ H 0 On rejette ou non H 0 selon la nature de H 1
23 Importance de l hypothèse H 1 Après la campagne de publicité 1/ Je ne peux pas affirmer avec 5% d erreur que la consommation est différente 2/ Je peux affirmer avec 5% d erreur que la consommation a augmentée (= j ai 95% de chance d avoir raison qu elle a augmenté en supposant dès le départ qu elle ne peut pas diminuer)
24 Importance de l hypothèse H 1 Conclusion : lorsqu on utilise les tests en statistique, attention aux formulations. De la même façon que précédemment, nous pouvons faire un test de comparaison unilatéral à gauche.
25 Test de comparaison unilatéral (à gauche) d une moyenne µ à un standard µ 0 Test : H 0 : µ = µ 0 H 1 : µ < µ 0 Statistique utilisée : x µ t = 0 s / n Règle de décision : On rejette H 0 au profit de H 1, au risque α de se tromper, si t -t 1-α (n-1) Niveau de signification (Sig) du t observé : Plus petite valeur de α conduisant au rejet de H 0 : Sig = Prob(t(n-1) t)
26 Remarques importantes Tout est important dans la construction d un test statistique : la définition de l hypothèse H 0 : elle doit être solidement établie et on doit avoir une bonne raison de la rejeter La définition de l hypothèse H 1 Le niveau d erreur que l on se fixe : 5% est standard, 1% pour les cas où le rejet de H 0 a des conséquences importantes
27 Remarques importantes Ce niveau seuil d erreur acceptable est fixé par le décideur, et non le statisticien. La statistique est une aide à la décision, ce n est pas elle qui la prend.
28 Application pour la régression Cor(X,Y) est-il significatif avec α = 5%? Test : H 0 : Cor(X,Y) = 0 (= le modèle n est pas bon) H 1 : Cor (X,Y) 0 (= le modèle est bon) Règle de décision On rejette H 0 avec un risque d erreur α = 5% si Cor( X, Y ) 2 n (il faut n > 20) 28
29 Cor(X,Y) est-il significatif avec α choisi? Test : H 0 : Cor(X,Y) = 0 H 1 : Cor(X,Y) 0 Règle de décision On rejette H 0 avec un risque d erreur α si Cor( X, Y ) t t 1 α / α / 2 ( n 2 ) ( n 2 ) + n 2 α
30 -1 -a 0 a 1 R: cor. négative Pas de corrélation Cor. positive (bon) (pas bon) (bon) Ici on note a = t t 1 α / α / 2 ( n 2 ) ( n 2 ) + n 2 Exemple avec n= 36 et R=Cor(X,Y)=0.41 : Que peut-on dire avec = 2%? = 1%? 30
31
32 Résultats : Avec α = 2%, t 1-α/2 (34) = 2,441 et a=0,3861 donc R >a. On rejette avec α = 2% l hypothèse que le modèle est mauvais. Avec α = 1%, t 1-α/2 (34) = 2,728 et a=0,4237 donc R <a. On ne rejette pas avec α = 1% l hypothèse que le modèle est mauvais. donc 1%< SIG <2% 32
33 Exemple d un R non significatif Correlations PRIXM2 Pearson Correlation Sig. (2-tailed) N SURFACE Prix au m Surface Rouge : droite des moindres carrés ( y= bo + b1x ) Bleu : moyenne des prix (y = y) Rsq =. On a 30.9% de chance de se tromper si on dit qu il y a une corrélation linéaire entre le prix au m² et la surface. On considère que la corrélation entre le prix au m² et la surface (0.199) n est pas significative. 33
34 Ex : appartements du XIX arrondissement Model 1 (Constant) Surface en m a. Dependent Variable: Prix en k Unstandardized Coefficients Coefficients a Standardized Coefficients B Std. Error Beta t Sig. 28,519 17,077 1,670,105 5,390,184,983 29,342,000 SIG < 0,1%
35 Ce qu il faut retenir La démarche d un test : importance des hypothèses H 0 (hypothèse de prudence) et H 1. Statistique utilisée pour un test de comparaison à une moyenne : x t = s µ 0 / n
36 Ce qu il faut retenir Test de comparaison bilatéral d une moyenne µ à un standard µ 0 : on rejette H 0 au profit de H 1 si t t 1-(α/2) (n-1) Niveau de signification (SIG) : la plus petite valeur de α conduisant au rejet de H 0 C est le décideuret non le statisticien qui fixe les hypothèses et qui se situe par rapport au niveau de signification (ou qui fixe le seuil d erreur acceptable).
37 «42.7 percent of all statistics are made up on the spot.» Steven Wright
38 Prochain cours Mercredi 27 octobre Exercice : régression simple
Tests de comparaison de moyennes. Dr Sahar BAYAT MASTER 1 année 2009-2010 UE «Introduction à la biostatistique»
 Tests de comparaison de moyennes Dr Sahar BAYAT MASTER 1 année 2009-2010 UE «Introduction à la biostatistique» Test de Z ou de l écart réduit Le test de Z : comparer des paramètres en testant leurs différences
Tests de comparaison de moyennes Dr Sahar BAYAT MASTER 1 année 2009-2010 UE «Introduction à la biostatistique» Test de Z ou de l écart réduit Le test de Z : comparer des paramètres en testant leurs différences
distribution quelconque Signe 1 échantillon non Wilcoxon gaussienne distribution symétrique Student gaussienne position
 Arbre de NESI distribution quelconque Signe 1 échantillon distribution symétrique non gaussienne Wilcoxon gaussienne Student position appariés 1 échantillon sur la différence avec référence=0 2 échantillons
Arbre de NESI distribution quelconque Signe 1 échantillon distribution symétrique non gaussienne Wilcoxon gaussienne Student position appariés 1 échantillon sur la différence avec référence=0 2 échantillons
Analyse de variance à deux facteurs (plan inter-sujets à deux facteurs) TP9
 Analyse de variance à deux facteurs (plan inter-sujets à deux facteurs) TP9 L analyse de variance à un facteur permet de vérifier, moyennant certaines hypothèses, si un facteur (un critère de classification,
Analyse de variance à deux facteurs (plan inter-sujets à deux facteurs) TP9 L analyse de variance à un facteur permet de vérifier, moyennant certaines hypothèses, si un facteur (un critère de classification,
Cours (7) de statistiques à distance, élaboré par Zarrouk Fayçal, ISSEP Ksar-Said, 2011-2012 LES STATISTIQUES INFERENTIELLES
 LES STATISTIQUES INFERENTIELLES (test de Student) L inférence statistique est la partie des statistiques qui, contrairement à la statistique descriptive, ne se contente pas de décrire des observations,
LES STATISTIQUES INFERENTIELLES (test de Student) L inférence statistique est la partie des statistiques qui, contrairement à la statistique descriptive, ne se contente pas de décrire des observations,
Chapitre 3 : Principe des tests statistiques d hypothèse. José LABARERE
 UE4 : Biostatistiques Chapitre 3 : Principe des tests statistiques d hypothèse José LABARERE Année universitaire 2010/2011 Université Joseph Fourier de Grenoble - Tous droits réservés. Plan I. Introduction
UE4 : Biostatistiques Chapitre 3 : Principe des tests statistiques d hypothèse José LABARERE Année universitaire 2010/2011 Université Joseph Fourier de Grenoble - Tous droits réservés. Plan I. Introduction
Analyse de la variance Comparaison de plusieurs moyennes
 Analyse de la variance Comparaison de plusieurs moyennes Biostatistique Pr. Nicolas MEYER Laboratoire de Biostatistique et Informatique Médicale Fac. de Médecine de Strasbourg Mars 2011 Plan 1 Introduction
Analyse de la variance Comparaison de plusieurs moyennes Biostatistique Pr. Nicolas MEYER Laboratoire de Biostatistique et Informatique Médicale Fac. de Médecine de Strasbourg Mars 2011 Plan 1 Introduction
Introduction aux Statistiques et à l utilisation du logiciel R
 Introduction aux Statistiques et à l utilisation du logiciel R Christophe Lalanne Christophe Pallier 1 Introduction 2 Comparaisons de deux moyennes 2.1 Objet de l étude On a mesuré le temps de sommeil
Introduction aux Statistiques et à l utilisation du logiciel R Christophe Lalanne Christophe Pallier 1 Introduction 2 Comparaisons de deux moyennes 2.1 Objet de l étude On a mesuré le temps de sommeil
Tests paramétriques de comparaison de 2 moyennes Exercices commentés José LABARERE
 Chapitre 5 UE4 : Biostatistiques Tests paramétriques de comparaison de 2 moyennes Exercices commentés José LABARERE Année universitaire 2010/2011 Université Joseph Fourier de Grenoble - Tous droits réservés.
Chapitre 5 UE4 : Biostatistiques Tests paramétriques de comparaison de 2 moyennes Exercices commentés José LABARERE Année universitaire 2010/2011 Université Joseph Fourier de Grenoble - Tous droits réservés.
Principe d un test statistique
 Biostatistiques Principe d un test statistique Professeur Jean-Luc BOSSON PCEM2 - Année universitaire 2012/2013 Faculté de Médecine de Grenoble (UJF) - Tous droits réservés. Objectifs pédagogiques Comprendre
Biostatistiques Principe d un test statistique Professeur Jean-Luc BOSSON PCEM2 - Année universitaire 2012/2013 Faculté de Médecine de Grenoble (UJF) - Tous droits réservés. Objectifs pédagogiques Comprendre
Exercices M1 SES 2014-2015 Ana Fermin (http:// fermin.perso.math.cnrs.fr/ ) 14 Avril 2015
 Exercices M1 SES 214-215 Ana Fermin (http:// fermin.perso.math.cnrs.fr/ ) 14 Avril 215 Les exemples numériques présentés dans ce document d exercices ont été traités sur le logiciel R, téléchargeable par
Exercices M1 SES 214-215 Ana Fermin (http:// fermin.perso.math.cnrs.fr/ ) 14 Avril 215 Les exemples numériques présentés dans ce document d exercices ont été traités sur le logiciel R, téléchargeable par
MODELE A CORRECTION D ERREUR ET APPLICATIONS
 MODELE A CORRECTION D ERREUR ET APPLICATIONS Hélène HAMISULTANE Bibliographie : Bourbonnais R. (2000), Econométrie, DUNOD. Lardic S. et Mignon V. (2002), Econométrie des Séries Temporelles Macroéconomiques
MODELE A CORRECTION D ERREUR ET APPLICATIONS Hélène HAMISULTANE Bibliographie : Bourbonnais R. (2000), Econométrie, DUNOD. Lardic S. et Mignon V. (2002), Econométrie des Séries Temporelles Macroéconomiques
Statistiques. Rappels de cours et travaux dirigés. Master 1 Biologie et technologie du végétal. Année 2010-2011
 Master 1 Biologie et technologie du végétal Année 010-011 Statistiques Rappels de cours et travaux dirigés (Seul ce document sera autorisé en examen) auteur : Jean-Marc Labatte [email protected]
Master 1 Biologie et technologie du végétal Année 010-011 Statistiques Rappels de cours et travaux dirigés (Seul ce document sera autorisé en examen) auteur : Jean-Marc Labatte [email protected]
La problématique des tests. Cours V. 7 mars 2008. Comment quantifier la performance d un test? Hypothèses simples et composites
 La problématique des tests Cours V 7 mars 8 Test d hypothèses [Section 6.1] Soit un modèle statistique P θ ; θ Θ} et des hypothèses H : θ Θ H 1 : θ Θ 1 = Θ \ Θ Un test (pur) est une statistique à valeur
La problématique des tests Cours V 7 mars 8 Test d hypothèses [Section 6.1] Soit un modèle statistique P θ ; θ Θ} et des hypothèses H : θ Θ H 1 : θ Θ 1 = Θ \ Θ Un test (pur) est une statistique à valeur
Cours de Tests paramétriques
 Cours de Tests paramétriques F. Muri-Majoube et P. Cénac 2006-2007 Licence Ce document est sous licence ALC TYPE 2. Le texte de cette licence est également consultable en ligne à l adresse http://www.librecours.org/cgi-bin/main?callback=licencetype2.
Cours de Tests paramétriques F. Muri-Majoube et P. Cénac 2006-2007 Licence Ce document est sous licence ALC TYPE 2. Le texte de cette licence est également consultable en ligne à l adresse http://www.librecours.org/cgi-bin/main?callback=licencetype2.
Relation entre deux variables : estimation de la corrélation linéaire
 CHAPITRE 3 Relation entre deux variables : estimation de la corrélation linéaire Parmi les analyses statistiques descriptives, l une d entre elles est particulièrement utilisée pour mettre en évidence
CHAPITRE 3 Relation entre deux variables : estimation de la corrélation linéaire Parmi les analyses statistiques descriptives, l une d entre elles est particulièrement utilisée pour mettre en évidence
Introduction à la statistique non paramétrique
 Introduction à la statistique non paramétrique Catherine MATIAS CNRS, Laboratoire Statistique & Génome, Évry http://stat.genopole.cnrs.fr/ cmatias Atelier SFDS 27/28 septembre 2012 Partie 2 : Tests non
Introduction à la statistique non paramétrique Catherine MATIAS CNRS, Laboratoire Statistique & Génome, Évry http://stat.genopole.cnrs.fr/ cmatias Atelier SFDS 27/28 septembre 2012 Partie 2 : Tests non
Lire ; Compter ; Tester... avec R
 Lire ; Compter ; Tester... avec R Préparation des données / Analyse univariée / Analyse bivariée Christophe Genolini 2 Table des matières 1 Rappels théoriques 5 1.1 Vocabulaire....................................
Lire ; Compter ; Tester... avec R Préparation des données / Analyse univariée / Analyse bivariée Christophe Genolini 2 Table des matières 1 Rappels théoriques 5 1.1 Vocabulaire....................................
TESTS D'HYPOTHESES Etude d'un exemple
 TESTS D'HYPOTHESES Etude d'un exemple Un examinateur doit faire passer une épreuve type QCM à des étudiants. Ce QCM est constitué de 20 questions indépendantes. Pour chaque question, il y a trois réponses
TESTS D'HYPOTHESES Etude d'un exemple Un examinateur doit faire passer une épreuve type QCM à des étudiants. Ce QCM est constitué de 20 questions indépendantes. Pour chaque question, il y a trois réponses
Chapitre 3. Les distributions à deux variables
 Chapitre 3. Les distributions à deux variables Jean-François Coeurjolly http://www-ljk.imag.fr/membres/jean-francois.coeurjolly/ Laboratoire Jean Kuntzmann (LJK), Grenoble University 1 Distributions conditionnelles
Chapitre 3. Les distributions à deux variables Jean-François Coeurjolly http://www-ljk.imag.fr/membres/jean-francois.coeurjolly/ Laboratoire Jean Kuntzmann (LJK), Grenoble University 1 Distributions conditionnelles
VI. Tests non paramétriques sur un échantillon
 VI. Tests non paramétriques sur un échantillon Le modèle n est pas un modèle paramétrique «TESTS du CHI-DEUX» : VI.1. Test d ajustement à une loi donnée VI.. Test d indépendance de deux facteurs 96 Différentes
VI. Tests non paramétriques sur un échantillon Le modèle n est pas un modèle paramétrique «TESTS du CHI-DEUX» : VI.1. Test d ajustement à une loi donnée VI.. Test d indépendance de deux facteurs 96 Différentes
Introduction à l approche bootstrap
 Introduction à l approche bootstrap Irène Buvat U494 INSERM buvat@imedjussieufr 25 septembre 2000 Introduction à l approche bootstrap - Irène Buvat - 21/9/00-1 Plan du cours Qu est-ce que le bootstrap?
Introduction à l approche bootstrap Irène Buvat U494 INSERM buvat@imedjussieufr 25 septembre 2000 Introduction à l approche bootstrap - Irène Buvat - 21/9/00-1 Plan du cours Qu est-ce que le bootstrap?
Bureau : 238 Tel : 04 76 82 58 90 Email : [email protected]
 Dominique Muller Laboratoire Inter-universitaire de Psychologie Bureau : 238 Tel : 04 76 82 58 90 Email : [email protected] Supports de cours : webcom.upmf-grenoble.fr/lip/perso/dmuller/m2r/acm/
Dominique Muller Laboratoire Inter-universitaire de Psychologie Bureau : 238 Tel : 04 76 82 58 90 Email : [email protected] Supports de cours : webcom.upmf-grenoble.fr/lip/perso/dmuller/m2r/acm/
Cahiers de l IMA. Fascicule SPSS
 Octobre 2008 Numéro 41 Cahiers de l IMA Fascicule SPSS Ingrid Gilles Eva G. T. Green Paola Ricciardi Joos Régis Scheidegger Chiara Storari Thomas Tuescher Pascal Wagner-Egger Ricciardi-Joos Ricciardi-Joos
Octobre 2008 Numéro 41 Cahiers de l IMA Fascicule SPSS Ingrid Gilles Eva G. T. Green Paola Ricciardi Joos Régis Scheidegger Chiara Storari Thomas Tuescher Pascal Wagner-Egger Ricciardi-Joos Ricciardi-Joos
Équivalence et Non-infériorité
 Équivalence et Non-infériorité Éléments d Introduction Lionel RIOU FRANÇA INSERM U669 Mars 2009 Essais cliniques de supériorité Exemple d Introduction Données tirées de Brinkhaus B et al. Arch Intern Med.
Équivalence et Non-infériorité Éléments d Introduction Lionel RIOU FRANÇA INSERM U669 Mars 2009 Essais cliniques de supériorité Exemple d Introduction Données tirées de Brinkhaus B et al. Arch Intern Med.
ELEC2753 Electrotechnique examen du 11/06/2012
 ELEC2753 Electrotechnique examen du 11/06/2012 Pour faciliter la correction et la surveillance, merci de répondre aux 3 questions sur des feuilles différentes et d'écrire immédiatement votre nom sur toutes
ELEC2753 Electrotechnique examen du 11/06/2012 Pour faciliter la correction et la surveillance, merci de répondre aux 3 questions sur des feuilles différentes et d'écrire immédiatement votre nom sur toutes
Statistiques Décisionnelles L3 Sciences Economiques & Gestion Faculté d économie, gestion & AES Université Montesquieu - Bordeaux 4 2013-2014
 Tests du χ 2 Statistiques Décisionnelles L3 Sciences Economiques & Gestion Faculté d économie, gestion & AES Université Montesquieu - Bordeaux 4 2013-2014 A. Lourme http://alexandrelourme.free.fr Outline
Tests du χ 2 Statistiques Décisionnelles L3 Sciences Economiques & Gestion Faculté d économie, gestion & AES Université Montesquieu - Bordeaux 4 2013-2014 A. Lourme http://alexandrelourme.free.fr Outline
Biostatistiques Biologie- Vétérinaire FUNDP Eric Depiereux, Benoît DeHertogh, Grégoire Vincke
 www.fundp.ac.be/biostats Module 140 140 ANOVA A UN CRITERE DE CLASSIFICATION FIXE...2 140.1 UTILITE...2 140.2 COMPARAISON DE VARIANCES...2 140.2.1 Calcul de la variance...2 140.2.2 Distributions de référence...3
www.fundp.ac.be/biostats Module 140 140 ANOVA A UN CRITERE DE CLASSIFICATION FIXE...2 140.1 UTILITE...2 140.2 COMPARAISON DE VARIANCES...2 140.2.1 Calcul de la variance...2 140.2.2 Distributions de référence...3
Exemples d application
 AgroParisTech Exemples d application du modèle linéaire E Lebarbier, S Robin Table des matières 1 Introduction 4 11 Avertissement 4 12 Notations 4 2 Régression linéaire simple 7 21 Présentation 7 211 Objectif
AgroParisTech Exemples d application du modèle linéaire E Lebarbier, S Robin Table des matières 1 Introduction 4 11 Avertissement 4 12 Notations 4 2 Régression linéaire simple 7 21 Présentation 7 211 Objectif
Package TestsFaciles
 Package TestsFaciles March 26, 2007 Type Package Title Facilite le calcul d intervalles de confiance et de tests de comparaison avec prise en compte du plan d échantillonnage. Version 1.0 Date 2007-03-26
Package TestsFaciles March 26, 2007 Type Package Title Facilite le calcul d intervalles de confiance et de tests de comparaison avec prise en compte du plan d échantillonnage. Version 1.0 Date 2007-03-26
Biostatistiques : Petits effectifs
 Biostatistiques : Petits effectifs Master Recherche Biologie et Santé P. Devos DRCI CHRU de Lille EA2694 [email protected] Plan Données Générales : Définition des statistiques Principe de l
Biostatistiques : Petits effectifs Master Recherche Biologie et Santé P. Devos DRCI CHRU de Lille EA2694 [email protected] Plan Données Générales : Définition des statistiques Principe de l
Le Data Mining au service du Scoring ou notation statistique des emprunteurs!
 France Le Data Mining au service du Scoring ou notation statistique des emprunteurs! Comme le rappelle la CNIL dans sa délibération n 88-083 du 5 Juillet 1988 portant adoption d une recommandation relative
France Le Data Mining au service du Scoring ou notation statistique des emprunteurs! Comme le rappelle la CNIL dans sa délibération n 88-083 du 5 Juillet 1988 portant adoption d une recommandation relative
Une étude de différentes analyses réalisées par le BIT
 Association internationale de la sécurité sociale Quinzième Conférence internationale des actuaires et statisticiens de la sécurité sociale Helsinki, Finlande, 23-25 mai 2007 Comparaison des hypothèses
Association internationale de la sécurité sociale Quinzième Conférence internationale des actuaires et statisticiens de la sécurité sociale Helsinki, Finlande, 23-25 mai 2007 Comparaison des hypothèses
Analyses de Variance à un ou plusieurs facteurs Régressions Analyse de Covariance Modèles Linéaires Généralisés
 Analyses de Variance à un ou plusieurs facteurs Régressions Analyse de Covariance Modèles Linéaires Généralisés Professeur Patrice Francour [email protected] Une grande partie des illustrations viennent
Analyses de Variance à un ou plusieurs facteurs Régressions Analyse de Covariance Modèles Linéaires Généralisés Professeur Patrice Francour [email protected] Une grande partie des illustrations viennent
La crise économique vue par les salariés français
 La crise économique vue par les salariés français Étude du lien entre la performance sociale et le contexte socioéconomique Baggio, S. et Sutter, P.-E. La présente étude s intéresse au lien entre cette
La crise économique vue par les salariés français Étude du lien entre la performance sociale et le contexte socioéconomique Baggio, S. et Sutter, P.-E. La présente étude s intéresse au lien entre cette
Les relations commerciales UE-Japon: la question des marchés publics
 Les relations commerciales UE-Japon: la question des marchés publics Patrick A. Messerlin et Sébastien Miroudot Groupe d Economie Mondiale de Sciences Po A la recherche de la croissance: Quel avenir pour
Les relations commerciales UE-Japon: la question des marchés publics Patrick A. Messerlin et Sébastien Miroudot Groupe d Economie Mondiale de Sciences Po A la recherche de la croissance: Quel avenir pour
Utilisation du Logiciel de statistique SPSS 8.0
 Utilisation du Logiciel de statistique SPSS 8.0 1 Introduction Etude épidémiologique transversale en population générale dans 4 pays d Afrique pour comprendre les différences de prévalence du VIH. 2000
Utilisation du Logiciel de statistique SPSS 8.0 1 Introduction Etude épidémiologique transversale en population générale dans 4 pays d Afrique pour comprendre les différences de prévalence du VIH. 2000
T de Student Khi-deux Corrélation
 Les tests d inférence statistiques permettent d estimer le risque d inférer un résultat d un échantillon à une population et de décider si on «prend le risque» (si 0.05 ou 5 %) Une différence de moyennes
Les tests d inférence statistiques permettent d estimer le risque d inférer un résultat d un échantillon à une population et de décider si on «prend le risque» (si 0.05 ou 5 %) Une différence de moyennes
La fumée de tabac secondaire (FTS) en Mauricie et au Centre-du- Québec, indicateurs du plan commun tirés de l ESCC de 2007-2008
 La fumée de tabac secondaire (FTS) en Mauricie et au Centre-du- Québec, indicateurs du plan commun tirés de l ESCC de 2007-2008 Ce document se veut une analyse succincte des indicateurs se rapportant à
La fumée de tabac secondaire (FTS) en Mauricie et au Centre-du- Québec, indicateurs du plan commun tirés de l ESCC de 2007-2008 Ce document se veut une analyse succincte des indicateurs se rapportant à
L'évaluation par les pairs dans un MOOC. Quelle fiabilité et quelle légitimité? Rémi Bachelet Ecole Centrale de Lille 24 novembre 2014, Université
 L'évaluation par les pairs dans un MOOC. Quelle fiabilité et quelle légitimité? Rémi Bachelet Ecole Centrale de Lille 24 novembre 2014, Université Paris-Est séminaire annuel IDEA Les diapos seront tweetées
L'évaluation par les pairs dans un MOOC. Quelle fiabilité et quelle légitimité? Rémi Bachelet Ecole Centrale de Lille 24 novembre 2014, Université Paris-Est séminaire annuel IDEA Les diapos seront tweetées
UFR de Sciences Economiques Année 2008-2009 TESTS PARAMÉTRIQUES
 Université Paris 13 Cours de Statistiques et Econométrie I UFR de Sciences Economiques Année 2008-2009 Licence de Sciences Economiques L3 Premier semestre TESTS PARAMÉTRIQUES Remarque: les exercices 2,
Université Paris 13 Cours de Statistiques et Econométrie I UFR de Sciences Economiques Année 2008-2009 Licence de Sciences Economiques L3 Premier semestre TESTS PARAMÉTRIQUES Remarque: les exercices 2,
Degré de confiance pour les indicateurs de performance : degré de fiabilité du processus de production et écart significatif 1
 Degré de confiance pour les indicateurs de performance : degré de fiabilité du processus de production et écart significatif 1 L utilisation des indicateurs de performance ne peut se faire de manière pertinente
Degré de confiance pour les indicateurs de performance : degré de fiabilité du processus de production et écart significatif 1 L utilisation des indicateurs de performance ne peut se faire de manière pertinente
Probabilités III Introduction à l évaluation d options
 Probabilités III Introduction à l évaluation d options Jacques Printems Promotion 2012 2013 1 Modèle à temps discret 2 Introduction aux modèles en temps continu Limite du modèle binomial lorsque N + Un
Probabilités III Introduction à l évaluation d options Jacques Printems Promotion 2012 2013 1 Modèle à temps discret 2 Introduction aux modèles en temps continu Limite du modèle binomial lorsque N + Un
La nouvelle planification de l échantillonnage
 La nouvelle planification de l échantillonnage Pierre-Arnaud Pendoli Division Sondages Plan de la présentation Rappel sur le Recensement de la population (RP) en continu Description de la base de sondage
La nouvelle planification de l échantillonnage Pierre-Arnaud Pendoli Division Sondages Plan de la présentation Rappel sur le Recensement de la population (RP) en continu Description de la base de sondage
LIVRET DE RÈGLES. @AsmadiGames. facebook.com/asmadigames
 LIVRET DE RÈGLES @AsmadiGames facebook.com/asmadigames VOUS JOUEZ À RED La règle pour gagner au Rouge est simple : avoir la plus haute carte! Mais jouerez-vous toujours au même jeu lorsque votre tour prendra
LIVRET DE RÈGLES @AsmadiGames facebook.com/asmadigames VOUS JOUEZ À RED La règle pour gagner au Rouge est simple : avoir la plus haute carte! Mais jouerez-vous toujours au même jeu lorsque votre tour prendra
Parole d utilisateur. Témoignage Gestion de la relation client. L Oréal fidélise ses clients en réduisant sa charge de travail
 Parole d utilisateur Témoignage Gestion de la relation client L Oréal fidélise ses clients en réduisant sa charge de travail Témoignage Gestion de la relation client L Oréal fidélise ses clients en réduisant
Parole d utilisateur Témoignage Gestion de la relation client L Oréal fidélise ses clients en réduisant sa charge de travail Témoignage Gestion de la relation client L Oréal fidélise ses clients en réduisant
Exposition. VLR plongée e commission photo
 Exposition VLR plongée e commission photo Agenda Définitions Exposition / analogie du verre d eau (de vin?) Ouverture Vitesse Sensibilité La notion d EV Pourquoi cela ne suffit pas? Dynamique des capteurs
Exposition VLR plongée e commission photo Agenda Définitions Exposition / analogie du verre d eau (de vin?) Ouverture Vitesse Sensibilité La notion d EV Pourquoi cela ne suffit pas? Dynamique des capteurs
B B A C U C C U C G 2 E 0 B 0
 Test psychotechnique ISI : Mastermind Test psychotechnique ISI : Mastermind Le Mastermind est un jeu de société, créé danss les années 70, opposant deux adversaires et dans lequel l un des joueurs doit
Test psychotechnique ISI : Mastermind Test psychotechnique ISI : Mastermind Le Mastermind est un jeu de société, créé danss les années 70, opposant deux adversaires et dans lequel l un des joueurs doit
Activité au 31 décembre 2014. Conférence téléphonique du 3 février 2015
 Activité au 31 décembre 2014 Conférence téléphonique du 3 février 2015 Stabilité de l activité en 2014 T4 dynamique CA hors IFRIC 12 au 31 décembre 2014 : 436,6 M vs. 444,0 M soit -1,5% à taux de change
Activité au 31 décembre 2014 Conférence téléphonique du 3 février 2015 Stabilité de l activité en 2014 T4 dynamique CA hors IFRIC 12 au 31 décembre 2014 : 436,6 M vs. 444,0 M soit -1,5% à taux de change
ICHEC MANAGEMENT SCHOOL
 CASE TELECOMMUNICATION - MOBISTAR BUSINESS CASE TELECOMMUNICATIONS - MOBISTAR Defort Florence De Veyt Marie-Laure Dierickx Arnaud Leruite Julien Marlot Camille ICHEC MANAGEMENT SCHOOL MOBISTAR, EN ROUTE
CASE TELECOMMUNICATION - MOBISTAR BUSINESS CASE TELECOMMUNICATIONS - MOBISTAR Defort Florence De Veyt Marie-Laure Dierickx Arnaud Leruite Julien Marlot Camille ICHEC MANAGEMENT SCHOOL MOBISTAR, EN ROUTE
1 Définition de la non stationnarité
 Chapitre 2: La non stationnarité -Testsdedétection Quelques notes de cours (non exhaustives) 1 Définition de la non stationnarité La plupart des séries économiques sont non stationnaires, c est-à-direqueleprocessusquiles
Chapitre 2: La non stationnarité -Testsdedétection Quelques notes de cours (non exhaustives) 1 Définition de la non stationnarité La plupart des séries économiques sont non stationnaires, c est-à-direqueleprocessusquiles
EVALUATION DE LA QUALITE DES SONDAGES EN LIGNE : CAS D UN SONDAGE D OPINION AU BURKINA FASO
 EVALUATION DE LA QUALITE DES SONDAGES EN LIGNE : CAS D UN SONDAGE D OPINION AU BURKINA FASO Auteur Baguinébié Bazongo 1 Ingénieur Statisticien Economiste Chef de l Unité de recherche à l Institut national
EVALUATION DE LA QUALITE DES SONDAGES EN LIGNE : CAS D UN SONDAGE D OPINION AU BURKINA FASO Auteur Baguinébié Bazongo 1 Ingénieur Statisticien Economiste Chef de l Unité de recherche à l Institut national
COMPARAISON DE LOGICIELS TESTANT L INDEPENDANCE DE VARIABLES BINAIRES
 J. sci. pharm. biol., Vol.9, n - 00, pp. 9-0 EDUCI 00 9 VALLEE POLNEAU S.* DIAINE C. COMPARAISON DE LOGICIELS TESTANT L INDEPENDANCE DE VARIABLES BINAIRES Notre étude visait à comparer les résultats obtenus
J. sci. pharm. biol., Vol.9, n - 00, pp. 9-0 EDUCI 00 9 VALLEE POLNEAU S.* DIAINE C. COMPARAISON DE LOGICIELS TESTANT L INDEPENDANCE DE VARIABLES BINAIRES Notre étude visait à comparer les résultats obtenus
Ecran : Processeur : OS : Caméra : Communication : Mémoire : Connectique : Audio : Batterie : Autonomie : Dimensions : Poids : DAS :
 SMARTPHONE - DUAL-CORE - NOIR 3483072425242 SMARTPHONE - DUAL-CORE - BLEU XXXX SMARTPHONE - DUAL-CORE - BLANC 3483072485246 SMARTPHONE - DUAL-CORE - ROSE 3483073704131 SMARTPHONE - DUAL-CORE - ROUGE XXXX
SMARTPHONE - DUAL-CORE - NOIR 3483072425242 SMARTPHONE - DUAL-CORE - BLEU XXXX SMARTPHONE - DUAL-CORE - BLANC 3483072485246 SMARTPHONE - DUAL-CORE - ROSE 3483073704131 SMARTPHONE - DUAL-CORE - ROUGE XXXX
Introduction à la Statistique Inférentielle
 UNIVERSITE MOHAMMED V-AGDAL SCIENCES FACULTE DES DEPARTEMENT DE MATHEMATIQUES SMI semestre 4 : Probabilités - Statistique Introduction à la Statistique Inférentielle Prinemps 2013 0 INTRODUCTION La statistique
UNIVERSITE MOHAMMED V-AGDAL SCIENCES FACULTE DES DEPARTEMENT DE MATHEMATIQUES SMI semestre 4 : Probabilités - Statistique Introduction à la Statistique Inférentielle Prinemps 2013 0 INTRODUCTION La statistique
Jabra CLEAR. Jabra MODE D EMPLOI
 Jabra CLEAR Jabra MODE D EMPLOI TABLE DES MATIÈRES MERCI...2 À PROPOS DE VOTRE...2 FONCTIONNALITÉS DE VOTRE OREILLETTE....3 MISE EN ROUTE...4 CHARGEMENT DE VOTRE OREILLETTE....4 MISE EN MARCHE ET ARRÊT
Jabra CLEAR Jabra MODE D EMPLOI TABLE DES MATIÈRES MERCI...2 À PROPOS DE VOTRE...2 FONCTIONNALITÉS DE VOTRE OREILLETTE....3 MISE EN ROUTE...4 CHARGEMENT DE VOTRE OREILLETTE....4 MISE EN MARCHE ET ARRÊT
Lecture critique d article. Bio statistiques. Dr MARC CUGGIA MCU-PH Laboratoire d informatique médicale EA-3888
 Lecture critique d article Rappels Bio statistiques Dr MARC CUGGIA MCU-PH Laboratoire d informatique médicale EA-3888 Plan du cours Rappels fondamentaux Statistiques descriptives Notions de tests statistiques
Lecture critique d article Rappels Bio statistiques Dr MARC CUGGIA MCU-PH Laboratoire d informatique médicale EA-3888 Plan du cours Rappels fondamentaux Statistiques descriptives Notions de tests statistiques
Recherche dans un tableau
 Chapitre 3 Recherche dans un tableau 3.1 Introduction 3.1.1 Tranche On appelle tranche de tableau, la donnée d'un tableau t et de deux indices a et b. On note cette tranche t.(a..b). Exemple 3.1 : 3 6
Chapitre 3 Recherche dans un tableau 3.1 Introduction 3.1.1 Tranche On appelle tranche de tableau, la donnée d'un tableau t et de deux indices a et b. On note cette tranche t.(a..b). Exemple 3.1 : 3 6
Coup de Projecteur sur les Réseaux de Neurones
 Coup de Projecteur sur les Réseaux de Neurones Les réseaux de neurones peuvent être utilisés pour des problèmes de prévision ou de classification. La représentation la plus populaire est le réseau multicouche
Coup de Projecteur sur les Réseaux de Neurones Les réseaux de neurones peuvent être utilisés pour des problèmes de prévision ou de classification. La représentation la plus populaire est le réseau multicouche
Groupe Eyrolles, 2006, ISBN : 2-212-11959-3
 Groupe Eyrolles, 2006, ISBN : 2-212-11959-3 annexe B Piano Corner, (c) 2005 par Zsolt Stefan : http://deeppixel.uw.hu/gallery.html YafRay, le moteur de rendu photoréaliste Dès sa création, par une équipe
Groupe Eyrolles, 2006, ISBN : 2-212-11959-3 annexe B Piano Corner, (c) 2005 par Zsolt Stefan : http://deeppixel.uw.hu/gallery.html YafRay, le moteur de rendu photoréaliste Dès sa création, par une équipe
CH IV) Courant alternatif Oscilloscope.
 CH IV) Courant alternatif Oscilloscope. Il existe deux types de courant, le courant continu et le courant alternatif. I) Courant alternatif : Observons une coupe transversale d une «dynamo» de vélo. Galet
CH IV) Courant alternatif Oscilloscope. Il existe deux types de courant, le courant continu et le courant alternatif. I) Courant alternatif : Observons une coupe transversale d une «dynamo» de vélo. Galet
Probabilité et Statistique pour le DEA de Biosciences. Avner Bar-Hen
 Probabilité et Statistique pour le DEA de Biosciences Avner Bar-Hen Université Aix-Marseille III 2000 2001 Table des matières 1 Introduction 3 2 Introduction à l analyse statistique 5 1 Introduction.................................
Probabilité et Statistique pour le DEA de Biosciences Avner Bar-Hen Université Aix-Marseille III 2000 2001 Table des matières 1 Introduction 3 2 Introduction à l analyse statistique 5 1 Introduction.................................
Mesure du surendettement en Europe
 Mesure du surendettement en Europe Conférence du 24 juin 2008 Didier Davydoff, Directeur de l OEE 0EE - Observatoire de l'épargne européenne 1 Introduction: l augmentation des encours de crédit aux ménages
Mesure du surendettement en Europe Conférence du 24 juin 2008 Didier Davydoff, Directeur de l OEE 0EE - Observatoire de l'épargne européenne 1 Introduction: l augmentation des encours de crédit aux ménages
STATISTIQUES. UE Modélisation pour la biologie
 STATISTIQUES UE Modélisation pour la biologie 2011 Cadre Général n individus: 1, 2,..., n Y variable à expliquer : Y = (y 1, y 2,..., y n ), y i R Modèle: Y = Xθ + ε X matrice du plan d expériences θ paramètres
STATISTIQUES UE Modélisation pour la biologie 2011 Cadre Général n individus: 1, 2,..., n Y variable à expliquer : Y = (y 1, y 2,..., y n ), y i R Modèle: Y = Xθ + ε X matrice du plan d expériences θ paramètres
Le chi carré. Le sommaire. Approche quantitative
 Approche quantitative Le chi carré Les objectifs pédagogiques Définir le test du chi carré Déterminer la nature des données propres au chi carré Savoir calculer le chi carré Savoir déterminer les fréquences
Approche quantitative Le chi carré Les objectifs pédagogiques Définir le test du chi carré Déterminer la nature des données propres au chi carré Savoir calculer le chi carré Savoir déterminer les fréquences
Louis Laurencelle, a. 2015 vol. 11 no. 1. Introduction
 Un indice d association non-linéaire entre deux variables continues, en version non-paramétrique A general non-linear index of association between two continuous rank-order variables Louis Laurencelle,
Un indice d association non-linéaire entre deux variables continues, en version non-paramétrique A general non-linear index of association between two continuous rank-order variables Louis Laurencelle,
Introduction au pricing d option en finance
 Introduction au pricing d option en finance Olivier Pironneau Cours d informatique Scientifique 1 Modélisation du prix d un actif financier Les actions, obligations et autres produits financiers cotés
Introduction au pricing d option en finance Olivier Pironneau Cours d informatique Scientifique 1 Modélisation du prix d un actif financier Les actions, obligations et autres produits financiers cotés
L Equilibre Macroéconomique en Economie Ouverte
 L Equilibre Macroéconomique en Economie Ouverte Partie 3: L Equilibre Macroéconomique en Economie Ouverte On abandonne l hypothèse d économie fermée Les échanges économiques entre pays: importants, en
L Equilibre Macroéconomique en Economie Ouverte Partie 3: L Equilibre Macroéconomique en Economie Ouverte On abandonne l hypothèse d économie fermée Les échanges économiques entre pays: importants, en
Etude du niveau stress ressenti par les salariés de plusieurs entreprises du tertiaire. Un outil de mesure.
 Etude du niveau stress ressenti par les salariés de plusieurs entreprises du tertiaire. Un outil de mesure. Participants : Dr Evelyne Barraud, Martine Chevillard, Marie-José Dureau Mer, Isabelle Gouget,
Etude du niveau stress ressenti par les salariés de plusieurs entreprises du tertiaire. Un outil de mesure. Participants : Dr Evelyne Barraud, Martine Chevillard, Marie-José Dureau Mer, Isabelle Gouget,
SELENE : Guide d utilisation de l outil de remontée des fichiers de promouvables
 SELENE : Guide d utilisation de l outil de remontée des fichiers de promouvables DGRH-A 1 19/11/2013 Sommaire SELENE Guide d utilisation de l outil de remontée des fichiers de promouvables IDENTIFICATION
SELENE : Guide d utilisation de l outil de remontée des fichiers de promouvables DGRH-A 1 19/11/2013 Sommaire SELENE Guide d utilisation de l outil de remontée des fichiers de promouvables IDENTIFICATION
Comment la recherche en sciences humaines est-elle utilisée? Observations tirées du sondage du groupe d experts chargé de l examen des pratiques d
 Comment la recherche en sciences humaines est-elle utilisée? Observations tirées du sondage du groupe d experts chargé de l examen des pratiques d évaluation par les pairs du CRSH Où la recherche est-elle
Comment la recherche en sciences humaines est-elle utilisée? Observations tirées du sondage du groupe d experts chargé de l examen des pratiques d évaluation par les pairs du CRSH Où la recherche est-elle
Tarifs 2012 - WebArtDesign à Grenoble: Création Site Internet, Référencement, Création Graphique, Création Log...
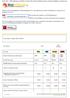 Votre Site e-vitrine PRO et PRO+ Site e-vitrine PRO PRO+ (autogéré) Formule Vert Bleu Orange Rouge Prix d'achat de votre site internet 199 599 1 390 1 190 1 790 1 590 Nombre de pages 1 page 5 pages Illimité
Votre Site e-vitrine PRO et PRO+ Site e-vitrine PRO PRO+ (autogéré) Formule Vert Bleu Orange Rouge Prix d'achat de votre site internet 199 599 1 390 1 190 1 790 1 590 Nombre de pages 1 page 5 pages Illimité
Exercices - Fonctions de plusieurs variables : corrigé. Pour commencer
 Pour commencer Exercice 1 - Ensembles de définition - Première année - 1. Le logarithme est défini si x + y > 0. On trouve donc le demi-plan supérieur délimité par la droite d équation x + y = 0.. 1 xy
Pour commencer Exercice 1 - Ensembles de définition - Première année - 1. Le logarithme est défini si x + y > 0. On trouve donc le demi-plan supérieur délimité par la droite d équation x + y = 0.. 1 xy
1. Structure d un programme C. 2. Commentaire: /*..texte */ On utilise aussi le commentaire du C++ qui est valable pour C: 3.
 1. Structure d un programme C Un programme est un ensemble de fonctions. La fonction "main" constitue le point d entrée pour l exécution. Un exemple simple : #include int main() { printf ( this
1. Structure d un programme C Un programme est un ensemble de fonctions. La fonction "main" constitue le point d entrée pour l exécution. Un exemple simple : #include int main() { printf ( this
Logitech Tablet Keyboard for Windows 8, Windows RT and Android 3.0+ Setup Guide Guide d installation
 Logitech Tablet Keyboard for Windows 8, Windows RT and Android 3.0+ Setup Guide Guide d installation English.......................................... 3 Français.........................................
Logitech Tablet Keyboard for Windows 8, Windows RT and Android 3.0+ Setup Guide Guide d installation English.......................................... 3 Français.........................................
Principaux partenaires commerciaux de l UE, 2002-2014 (Part dans le total des échanges de biens extra-ue, sur la base de la valeur commerciale)
 55/2015-27 mars 2015 Commerce international de biens en 2014 Principaux partenaires commerciaux de l UE en 2014: les États-Unis pour les exportations, la Chine pour les importations Le commerce entre États
55/2015-27 mars 2015 Commerce international de biens en 2014 Principaux partenaires commerciaux de l UE en 2014: les États-Unis pour les exportations, la Chine pour les importations Le commerce entre États
Incertitudes expérimentales
 Incertitudes expérimentales F.-X. Bally et J.-M. Berroir Février 2013 Table des matières Introduction 4 1 Erreur et incertitude 4 1.1 Erreurs............................................. 4 1.1.1 Définition
Incertitudes expérimentales F.-X. Bally et J.-M. Berroir Février 2013 Table des matières Introduction 4 1 Erreur et incertitude 4 1.1 Erreurs............................................. 4 1.1.1 Définition
Comment bien régresser: La statistique peut-elle se passer d artefacts?
 Comment bien régresser: La statistique peut-elle se passer d artefacts? Jean-Bernard Chatelain To cite this version: Jean-Bernard Chatelain. Comment bien régresser: La statistique peut-elle se passer d
Comment bien régresser: La statistique peut-elle se passer d artefacts? Jean-Bernard Chatelain To cite this version: Jean-Bernard Chatelain. Comment bien régresser: La statistique peut-elle se passer d
UNIVERSITY OF MALTA FACULTY OF ARTS. French as Main Area in an ordinary Bachelor s Degree
 French Programme of Studies (for courses commencing October 2009 and later) YEAR ONE (2009/10) Year (These units start in and continue in.) FRE1001 Linguistique théorique 1 4 credits Non Compensatable
French Programme of Studies (for courses commencing October 2009 and later) YEAR ONE (2009/10) Year (These units start in and continue in.) FRE1001 Linguistique théorique 1 4 credits Non Compensatable
Didacticiel - Études de cas. Description de quelques fonctions du logiciel PSPP, comparaison des résultats avec ceux de Tanagra, R et OpenStat.
 1 Objectif Description de quelques fonctions du logiciel PSPP, comparaison des résultats avec ceux de Tanagra, R et OpenStat. Tout le monde l aura compris, je passe énormément de temps à analyser les logiciels
1 Objectif Description de quelques fonctions du logiciel PSPP, comparaison des résultats avec ceux de Tanagra, R et OpenStat. Tout le monde l aura compris, je passe énormément de temps à analyser les logiciels
Problèmes de crédit et coûts de financement
 Chapitre 9 Problèmes de crédit et coûts de financement Ce chapitre aborde un ensemble de préoccupations devenues essentielles sur les marchés dedérivésdecréditdepuislacriseducréditde2007.lapremièredecespréoccupations
Chapitre 9 Problèmes de crédit et coûts de financement Ce chapitre aborde un ensemble de préoccupations devenues essentielles sur les marchés dedérivésdecréditdepuislacriseducréditde2007.lapremièredecespréoccupations
DESS INGENIERIE FINANCIERE
 DESS INGENIERIE FINANCIERE Mercredi 27 mars 2005 Philippe TESTIER - CFCM Brest 1 SOMMAIRE Le Change au comptant (spot) ; Le Change à Terme (termes secs, swaps de change) ; Les Options de Change ; Les Options
DESS INGENIERIE FINANCIERE Mercredi 27 mars 2005 Philippe TESTIER - CFCM Brest 1 SOMMAIRE Le Change au comptant (spot) ; Le Change à Terme (termes secs, swaps de change) ; Les Options de Change ; Les Options
Title Text. Gestion de données de mobilité Mobility data management
 Title Text Gestion de données de mobilité Mobility data management Contenu de la présentation Content Entrepôt de données de mobilité et exportation Automatisation de la génération d objets dynamiques
Title Text Gestion de données de mobilité Mobility data management Contenu de la présentation Content Entrepôt de données de mobilité et exportation Automatisation de la génération d objets dynamiques
Chapitre 4 : Régression linéaire
 Exercice 1 Méthodes statistiques appliquées aux sciences sociales (STAT-D-203) Titulaire : Catherine Vermandele Chapitre 4 : Régression linéaire Le diplôme de Master of Business Administration ou MBA est
Exercice 1 Méthodes statistiques appliquées aux sciences sociales (STAT-D-203) Titulaire : Catherine Vermandele Chapitre 4 : Régression linéaire Le diplôme de Master of Business Administration ou MBA est
FORMULAIRE DE STATISTIQUES
 FORMULAIRE DE STATISTIQUES I. STATISTIQUES DESCRIPTIVES Moyenne arithmétique Remarque: population: m xμ; échantillon: Mx 1 Somme des carrés des écarts "# FR MOYENNE(série) MOYENNE(série) NL GEMIDDELDE(série)
FORMULAIRE DE STATISTIQUES I. STATISTIQUES DESCRIPTIVES Moyenne arithmétique Remarque: population: m xμ; échantillon: Mx 1 Somme des carrés des écarts "# FR MOYENNE(série) MOYENNE(série) NL GEMIDDELDE(série)
Évaluation de la régression bornée
 Thierry Foucart UMR 6086, Université de Poitiers, S P 2 M I, bd 3 téléport 2 BP 179, 86960 Futuroscope, Cedex FRANCE Résumé. le modèle linéaire est très fréquemment utilisé en statistique et particulièrement
Thierry Foucart UMR 6086, Université de Poitiers, S P 2 M I, bd 3 téléport 2 BP 179, 86960 Futuroscope, Cedex FRANCE Résumé. le modèle linéaire est très fréquemment utilisé en statistique et particulièrement
1 er Avril 2015 Data Science & Big Data Etat de l art Donner plus d intelligence aux données
 1 er Avril 2015 Data Science & Big Data Etat de l art Donner plus d intelligence aux données Votre interlocuteur Didier Gaultier Directeur Data Science Business & Decision Professeur de Statistique à l
1 er Avril 2015 Data Science & Big Data Etat de l art Donner plus d intelligence aux données Votre interlocuteur Didier Gaultier Directeur Data Science Business & Decision Professeur de Statistique à l
Les débats sur l évolution des
 D o c u m e n t d e t r a v a i l d e l a B r a n c h e R e t r a i t e s d e l a C a i s s e d e s d é p ô t s e t c o n s i g n a t i o n s n 9 8-0 7 C o n t a c t : La u re nt V e r n i è r e 0 1 4
D o c u m e n t d e t r a v a i l d e l a B r a n c h e R e t r a i t e s d e l a C a i s s e d e s d é p ô t s e t c o n s i g n a t i o n s n 9 8-0 7 C o n t a c t : La u re nt V e r n i è r e 0 1 4
CONCOURS D ENTREE A L ECOLE DE 2007 CONCOURS EXTERNE. Cinquième épreuve d admissibilité STATISTIQUE. (durée : cinq heures)
 CONCOURS D ENTREE A L ECOLE DE 2007 CONCOURS EXTERNE Cinquième épreuve d admissibilité STATISTIQUE (durée : cinq heures) Une composition portant sur la statistique. SUJET Cette épreuve est composée d un
CONCOURS D ENTREE A L ECOLE DE 2007 CONCOURS EXTERNE Cinquième épreuve d admissibilité STATISTIQUE (durée : cinq heures) Une composition portant sur la statistique. SUJET Cette épreuve est composée d un
La légalité du «marketing viral»
 SERVICE PUBLIC FÉDÉRAL ÉCONOMIE, PME, CLASSES MOYENNES ET ÉNERGIE Direction générale Régulation et Organisation du Marché Cellule Economie électronique La légalité du «marketing viral» Septembre 2005 1
SERVICE PUBLIC FÉDÉRAL ÉCONOMIE, PME, CLASSES MOYENNES ET ÉNERGIE Direction générale Régulation et Organisation du Marché Cellule Economie électronique La légalité du «marketing viral» Septembre 2005 1
Principe de symétrisation pour la construction d un test adaptatif
 Principe de symétrisation pour la construction d un test adaptatif Cécile Durot 1 & Yves Rozenholc 2 1 UFR SEGMI, Université Paris Ouest Nanterre La Défense, France, [email protected] 2 Université
Principe de symétrisation pour la construction d un test adaptatif Cécile Durot 1 & Yves Rozenholc 2 1 UFR SEGMI, Université Paris Ouest Nanterre La Défense, France, [email protected] 2 Université
Leçon N 4 : Statistiques à deux variables
 Leçon N 4 : Statistiques à deux variables En premier lieu, il te faut relire les cours de première sur les statistiques à une variable, il y a tout un langage à se remémorer : étude d un échantillon d
Leçon N 4 : Statistiques à deux variables En premier lieu, il te faut relire les cours de première sur les statistiques à une variable, il y a tout un langage à se remémorer : étude d un échantillon d
Tableau récapitulatif de l analyse fréquentielle
 Tableau récapitulatif de l analyse fréquentielle Très Plutôt Quelque Ni Quelque Plutôt Très TOTAL peu ni peu 1. L utilité du d inclure le contexte dans la note de stratégie 4% 4% 4% 8% 64% 16% 100% 2.
Tableau récapitulatif de l analyse fréquentielle Très Plutôt Quelque Ni Quelque Plutôt Très TOTAL peu ni peu 1. L utilité du d inclure le contexte dans la note de stratégie 4% 4% 4% 8% 64% 16% 100% 2.
quelques Repères pour Doctorants
 Gilles HUNAULT 2005 quelques Repères en STATISTIQUES pour Doctorants Université d Angers c [email protected] http ://www.info.univ-angers.fr/pub/gh/ 3 Le principe consistant à ne pouvoir affirmer
Gilles HUNAULT 2005 quelques Repères en STATISTIQUES pour Doctorants Université d Angers c [email protected] http ://www.info.univ-angers.fr/pub/gh/ 3 Le principe consistant à ne pouvoir affirmer
Estimation du coût de l incessibilité des BSA
 Estimation du coût de l incessibilité des BSA Jean-Michel Moinade Oddo Corporate Finance 22 Juin 2012 Incessibilité des BSA Pas de méthode académique reconnue Plusieurs méthodes «pratiques», dont une usuelle
Estimation du coût de l incessibilité des BSA Jean-Michel Moinade Oddo Corporate Finance 22 Juin 2012 Incessibilité des BSA Pas de méthode académique reconnue Plusieurs méthodes «pratiques», dont une usuelle
TABLE DES MATIERES. C Exercices complémentaires 42
 TABLE DES MATIERES Chapitre I : Echantillonnage A - Rappels de cours 1. Lois de probabilités de base rencontrées en statistique 1 1.1 Définitions et caractérisations 1 1.2 Les propriétés de convergence
TABLE DES MATIERES Chapitre I : Echantillonnage A - Rappels de cours 1. Lois de probabilités de base rencontrées en statistique 1 1.1 Définitions et caractérisations 1 1.2 Les propriétés de convergence
Limitations of the Playstation 3 for High Performance Cluster Computing
 Introduction Plan Limitations of the Playstation 3 for High Performance Cluster Computing July 2007 Introduction Plan Introduction Intérêts de la PS3 : rapide et puissante bon marché L utiliser pour faire
Introduction Plan Limitations of the Playstation 3 for High Performance Cluster Computing July 2007 Introduction Plan Introduction Intérêts de la PS3 : rapide et puissante bon marché L utiliser pour faire
Leçon n 4. Analyse graphique Techniques de construction de barres et styles de. Fenêtres d analyse graphique. Leçon n 4
 Leçon n 4 Table des matières Fenêtre d analyse graphique... 1 Demande de données avec le gestionnaire de téléchargement... 7 Formater le symbole dans un graphique 2 Changer le style d un symbole... 8 Modifier
Leçon n 4 Table des matières Fenêtre d analyse graphique... 1 Demande de données avec le gestionnaire de téléchargement... 7 Formater le symbole dans un graphique 2 Changer le style d un symbole... 8 Modifier
Tutoriel Sage One Edition Expert-Comptable. - Le cabinet d Expertise-Comptable doit appeler le Service Client Sage One au 0825 95 00 70.
 Tutoriel Sage One Edition Expert-Comptable Sage One Edition Expert-Comptable : inscription et identifiants - Le cabinet d Expertise-Comptable doit appeler le Service Client Sage One au 0825 95 00 70. -
Tutoriel Sage One Edition Expert-Comptable Sage One Edition Expert-Comptable : inscription et identifiants - Le cabinet d Expertise-Comptable doit appeler le Service Client Sage One au 0825 95 00 70. -
TESTS D HYPOTHÈSE FONDÉS SUR LE χ². http://fr.wikipedia.org/wiki/eugénisme
 TESTS D HYPOTHÈSE FONDÉS SUR LE χ² http://fr.wikipedia.org/wiki/eugénisme Logo du Second International Congress of Eugenics 1921. «Comme un arbre, l eugénisme tire ses constituants de nombreuses sources
TESTS D HYPOTHÈSE FONDÉS SUR LE χ² http://fr.wikipedia.org/wiki/eugénisme Logo du Second International Congress of Eugenics 1921. «Comme un arbre, l eugénisme tire ses constituants de nombreuses sources
