TOPOGRAPHIE. Relevé. 1. Introduction
|
|
|
- Claude Larrivée
- il y a 8 ans
- Total affichages :
Transcription
1 TOPOGRAPHIE 1 Avant de concevoir un projet, il est nécessaire de connaître le site dans lequel il s inscrit et d en faire un relevé précis. Ce chapitre traite des techniques de relevé (étude de l existant) et d implantation d un bâtiment, ces éléments constituent les fondements de la topographie. Ils sont nécessaires au démarrage d un projet : d une part, le relevé de l existant en vue d une rénovation ou d une réhabilitation et d autre part l implantation du futur bâtiment (neuf). A Relevé 1. Introduction Le relevé consiste à prendre des mesures afin de se représenter l élément étudié. Il peut s agir d une route, d un bâtiment ou de tout autre chose. Diverses caractéristiques sont regardées : Les longueurs. Les hauteurs. Les angles. Concernant les longueurs et les angles, il s agit de mesures faites à l horizontale, tandis que la hauteur d un bâtiment se mesure verticalement. L al métrie est la position en hauteur d un ouvrage. Elle est très importante, quel que soit le type d ouvrage. Par exemple, dans les Plans Locaux d Urbanisme (PLU), les mairies imposent des limitations de taille aux bâtiments afin de garantir une homogénéité du paysage. On distingue donc deux types de relevés : Les relevés plans (longueurs, angles). Et les relevés altimétriques (hauteurs relatives : altimétrie ou hauteurs réelles). On peut inclure un troisième type, mais qui correspond aux deux précédents, incluant des mesures automatisées dans l espace. Ce relevé en trois dimensions ne présente pas d intérêt pédagogique, mais existe de plus en plus dans les entreprises. À noter qu un long travail d interprétation des données est nécessaire, car des milliers de points sont pris. TOPOGRAPHIE 7
2 2. Relevé plan Le relevé plan consiste à mesurer des longueurs (distance entre deux points) et des angles. On utilise pour cela une multitude d outils. Il est nécessaire d effectuer ces relevés avec une certaine rigueur, afin d obtenir des résultats cohérents. L outil le plus couramment utilisé est le décamètre. Il s agit d un ruban gradué permettant de connaître la distance entre deux points (dont la précision est donnée par le fabricant du décamètre). Il faut manier le décamètre avec rigueur : le ruban doit être horizontal afin de connaître la distance en plan séparant les deux points de la mesure, il faut donc le tendre et si possible utiliser un niveau afin de vérifier son horizontalité. Si la pente est trop importante, la mesure s effectuera en plusieurs fois, avec l utilisation d un fil à plomb afin de marquer le ou les points intermédiaires. Cette démarche en escalier est appelée cultella on. Les autres outils disponibles sont les suivants (la liste est non exhaustive, elle contient les plus utilisés) : Télémètre laser : fournit une distance immédiatement. Odomètre : fournit le chemin parcouru par la roue, souvent utilisé lors de compétitions sportives. Pour mesurer les angles horizontaux, il suffit d utiliser le principe de la triangulation. Cette technique permet de représenter des triangles, et ainsi de connaître les angles formés par les différents segments entre eux. 3. Relevé altimétrique On mesure l altitude d un élément par rapport à un référentiel (niveau 0) identique à tout le monde. Ce niveau 0 a été arrêté arbitrairement et correspond au niveau moyen de la Méditerranée. La mesure est faite à Marseille à l aide d un marégraphe. Le principe du relevé altimétrique est de mesurer la différence de hauteur entre deux points, dont l un est connu en altimétrie. La différence de hauteur est appelée dénivelée. Comme il est impossible de faire ce relevé par rapport au niveau du marégraphe, des centaines de points sont implantés en France, dont les coordonnées sont connues, afin de permettre une utilisation simplifiée de ce référentiel. Ces points sont des repères. Le référentiel a changé plusieurs fois. Celui qui est utilisé 8 CHAPITRE 1
3 actuellement est le NGF69 (Nivellement Général de France), finalisé en Il est plus précis que le précédent et prend en compte les variations de la croûte terrestre. Les repères sont donc très importants, ils sont censés être positionnés précisément. Ils sont souvent mis en place sur les édifices publics tels que les mairies ou les églises, car ces bâtiments sont par nature pérennes. On utilise le niveau pour mesurer la dénivelée. Le niveau est un outil simple, s apparentant à une lunette et permettant une visée horizontale sur des objectifs appelés mires. La mire est positionnée au niveau du point dont on souhaite mesurer la hauteur. Le niveau est une lunette qui pivote sur sa base dont l horizontalité est assurée lors de la mise en station par l opérateur. La base est un trépied, permettant une bonne stabilité. La lecture sur la mire permet de noter trois valeurs : La lecture principale n : ici n = 1,005 m. Le fil stadimétrique haut s, ici s = 1,040 m. Et le fil stadimétrique bas s : ici s = 0,970 m. Il faut donc à chaque mesure vérifier que : s s' n 2 Un fil vertical ou un niveau à bulle permet de vérifier la bonne verticalité de la mire. De plus, il faut essayer de se mettre à équidistance des deux points qui vont faire l objet de la mesure afin d éviter des erreurs imputables à la lecture distante. Une fois la valeur de n A déterminée (soit l altimétrie relative du point A) et l altimétrie relative n B du deuxième point noté B déterminée, il suffit de soustraire la valeur du point connu (ici A pour l exemple) à celle du point inconnu (ici B) afin de connaître la dénivelée, ΔH AB [en m], entre ces deux points : ΔH AB = n A n B. Donc l altitude du point B : H B [en m] est : H B = H A + ΔH AB. Il est possible d effectuer des relevés altimétriques par la technique du cheminement. Cette technique s utilise lorsque le point à étudier est éloigné d un repère. On utilise plusieurs points intermédiaires afin d arriver au point étudié puis on retourne au point de départ (cheminement fermé) ou on termine le cheminement sur un autre point connu en altitude. Il faut absolument connaître les altitudes des points de départ et d arrivée. TOPOGRAPHIE 9
4 Exemple de relevé par cheminement fermé (départ et arrivée au point A) Autre technique, le rayonnement, utilisé lorsque les points étudiés sont proches du point connu. Exemple de relevé par rayonnement 4. Relevé complet Le relevé complet s effectue à l aide d appareils totalement automatisés, et fournit ce que l on appelle un nuage de points, découlant du relevé. L appareil le plus utilisé est le théodolite, dans sa version la plus récente. On peut également utiliser des drones, mais cette technique n est pas encore totalement opérationnelle. 10 CHAPITRE 1
5 B Implantation 1. Introduction L implantation d un bâtiment consiste à mettre en place des repères (piquets en bois généralement) sur le terrain du futur chantier pour représenter les angles ou tout autre point nécessaire aux travaux. Peu de points sont implantés par un géomètre, car cette opération est coûteuse. Par la suite, les futurs autres points seront implantés par les équipes de gros œuvre à l aide des deux techniques suivantes : Une implantation que l on nommera linéaire, avec l utilisation exclusive de distances. Une implantation polaire, où l on utilise des distances et des angles. 2. Implantation linéaire a. Méthode du L implantation linéaire consiste à utiliser des segments. La première méthode est appelée méthode du : on crée un triangle rectangle afin de tracer une perpendiculaire à un point, en utilisant la relation : = 5 2 découlant du théorème de Pythagore. Par exemple, on cherche à tracer la perpendiculaire à AB passant par C, dans l hypothèse où un géomètre est venu mettre deux piquets correspondants aux points A et B pour l implantation du bâtiment. On place à 3 m de C sur la droite (AB) un point D, puis on trace à l aide d un décamètre des arcs de cercle : un de 4 m partant de C et un de 5 m partant de D. Le point d intersection est le point E, avec comme propriété que (CE) et perpendiculaire à (AB). Il suffit par la suite de mettre le point souhaité à la bonne distance de C. TOPOGRAPHIE 11
6 b. Méthode du triangle isocèle Pour tracer une perpendiculaire, on peut également utiliser la méthode du triangle isocèle, car la bissectrice de l angle est également la hauteur, donc perpendiculaire au côté opposé. Par exemple, on cherche toujours à tracer la perpendiculaire à (AB) passant par C. On implante donc deux points, G et H, équidistants de C sur la droite (AB). On trace ensuite des arcs de cercle de la distance [GH] partant de G et de H. Le point d intersection obtenu, I, permet de former le triangle isocèle GHI. La droite (IC) est donc perpendiculaire à (AB). Il suffit ensuite de mettre le point souhaité à la bonne distance de C sur la droite (IC). 12 CHAPITRE 1
7 c. Méthode du rayonnement Pour implanter un point, on peut simplement utiliser une méthode dite du rayonnement (ou de la triangulation), qui consiste à calculer les distances du futur point avec les deux points A et B connus. Cette technique est la plus simple, elle permet de ne pas cumuler d erreurs en implantant des points à partir d autres points eux-mêmes déjà implantés à partir d autres, mais la limite de cette technique est la taille des implantations à faire, car le terrain ne se prête pas forcément à des implantations sur de longues distances (talus, mauvaise qualité de sol, passage d engins). 3. Implantation polaire L implantation polaire est beaucoup plus précise que l implantation linéaire, car on se base sur un seul point, et non sur deux ou sur des constructions complexes à tracer. Pour réaliser une implantation dite polaire, on se sert d un théodolite (en photographie). Cet appareil permet de donner un angle et une distance, donc d implanter des points en coordonnées polaires. De plus, il s agit d une technique faisant abstraction des conditions environnementales (terrain, engins ). L appareil doit être mis en station comme le niveau, sauf que le théodolite doit être au-dessus du point de référence (A dans notre exemple), cette mise en station est donc très précise. Une fois mis en station, il suffit de faire pivoter l appareil jusqu à atteindre l angle voulu (attention l angle est en gradian, degré centésimal par opposition au degré sexagésimal : 400 grd = 360 ). Une fois l angle atteint, le télémètre laser incorporé permet de pointer la bonne distance au sol avec le laser. Si le théodolite n en possède pas, on peut se servir d un décamètre pour mesurer la distance à avoir par rapport au point de départ (l opérateur pointera l angle sur le ruban du décamètre, et il suffira de noter la bonne distance du point de référence). TOPOGRAPHIE 13
8 Exercices Exercice 1. Relevé : création de courbes de niveaux Un géomètre a réalisé le relevé par rayonnement ci-dessous. On souhaite représenter les courbes de niveaux afin d augmenter la lisibilité du relevé. Exercice 2. Relevé : exploitation d un relevé altimétrique par cheminement 1. Déterminer l altitude du point inconnu (noté D ici) en complétant la fiche de mesures. On part du point connu en altitude A (398,656 m) et on finit sur l autre point connu H (400,592). 14 CHAPITRE 1
Le contexte. Le questionnement du P.E.R. :
 Le contexte Ce travail a débuté en janvier. Le P.E.R. engagé depuis fin septembre a permis de faire émerger ou de réactiver : Des raisons d être de la géométrie : Calculer des grandeurs inaccessibles et
Le contexte Ce travail a débuté en janvier. Le P.E.R. engagé depuis fin septembre a permis de faire émerger ou de réactiver : Des raisons d être de la géométrie : Calculer des grandeurs inaccessibles et
Si deux droites sont parallèles à une même troisième. alors les deux droites sont parallèles entre elles. alors
 N I) Pour démontrer que deux droites (ou segments) sont parallèles (d) // (d ) (d) // (d ) deux droites sont parallèles à une même troisième les deux droites sont parallèles entre elles (d) // (d) deux
N I) Pour démontrer que deux droites (ou segments) sont parallèles (d) // (d ) (d) // (d ) deux droites sont parallèles à une même troisième les deux droites sont parallèles entre elles (d) // (d) deux
PROBLEME(12) Première partie : Peinture des murs et du plafond.
 PROBLEME(12) Une entreprise doit rénover un local. Ce local a la forme d'un parallélépipède rectangle. La longueur est 6,40m, la largeur est 5,20m et la hauteur est 2,80m. Il comporte une porte de 2m de
PROBLEME(12) Une entreprise doit rénover un local. Ce local a la forme d'un parallélépipède rectangle. La longueur est 6,40m, la largeur est 5,20m et la hauteur est 2,80m. Il comporte une porte de 2m de
AC AB. A B C x 1. x + 1. d où. Avec un calcul vu au lycée, on démontre que cette solution admet deux solutions dont une seule nous intéresse : x =
 LE NOMBRE D OR Présentation et calcul du nombre d or Euclide avait trouvé un moyen de partager en deu un segment selon en «etrême et moyenne raison» Soit un segment [AB]. Le partage d Euclide consiste
LE NOMBRE D OR Présentation et calcul du nombre d or Euclide avait trouvé un moyen de partager en deu un segment selon en «etrême et moyenne raison» Soit un segment [AB]. Le partage d Euclide consiste
Lecture graphique. Table des matières
 Lecture graphique Table des matières 1 Lecture d une courbe 2 1.1 Définition d une fonction.......................... 2 1.2 Exemple d une courbe........................... 2 1.3 Coût, recette et bénéfice...........................
Lecture graphique Table des matières 1 Lecture d une courbe 2 1.1 Définition d une fonction.......................... 2 1.2 Exemple d une courbe........................... 2 1.3 Coût, recette et bénéfice...........................
PROGRAMME D HABILETÉS EN FAUTEUIL ROULANT (WSP-F)
 PROGRAMME D HABILETÉS EN FAUTEUIL ROULANT (WSP-F) LIGNES DIRECTRICES POUR LE PARCOURS À OBSTACLES VERSION 4.1 CANADIENNE-FRANÇAISE Les activités d entraînement et d évaluation du WSP-F 4.1 peuvent se dérouler
PROGRAMME D HABILETÉS EN FAUTEUIL ROULANT (WSP-F) LIGNES DIRECTRICES POUR LE PARCOURS À OBSTACLES VERSION 4.1 CANADIENNE-FRANÇAISE Les activités d entraînement et d évaluation du WSP-F 4.1 peuvent se dérouler
Enoncé et corrigé du brevet des collèges dans les académies d Aix- Marseille, Montpellier, Nice Corse et Toulouse en 2000. Énoncé.
 Enoncé et corrigé du brevet des collèges dans les académies d Aix- Marseille, Montpellier, Nice Corse et Toulouse en 2000. Énoncé. I- ACTIVITES NUMERIQUES (12 points) Exercice 1 (3 points) On considère
Enoncé et corrigé du brevet des collèges dans les académies d Aix- Marseille, Montpellier, Nice Corse et Toulouse en 2000. Énoncé. I- ACTIVITES NUMERIQUES (12 points) Exercice 1 (3 points) On considère
Mesurer les altitudes avec une carte
 www.ign.fr > Espace éducatif > Les fiches thématiques > Lecture de la carte Mesurer les altitudes avec une carte Les cartes topographiques ne sont pas uniquement une représentation plane de la surface
www.ign.fr > Espace éducatif > Les fiches thématiques > Lecture de la carte Mesurer les altitudes avec une carte Les cartes topographiques ne sont pas uniquement une représentation plane de la surface
Cours de tracés de Charpente, Le TRAIT
 Page 1/5 Cours de tracés de Charpente, Le TRAIT Recherches de vraies grandeurs, angles de coupes, surfaces. Les Méthodes : Le tracé et les calculs Chaque chapitre ou fichier comportent une explication
Page 1/5 Cours de tracés de Charpente, Le TRAIT Recherches de vraies grandeurs, angles de coupes, surfaces. Les Méthodes : Le tracé et les calculs Chaque chapitre ou fichier comportent une explication
Priorités de calcul :
 EXERCICES DE REVISION POUR LE PASSAGE EN QUATRIEME : Priorités de calcul : Exercice 1 : Calcule en détaillant : A = 4 + 5 6 + 7 B = 6 3 + 5 C = 35 5 3 D = 6 7 + 8 E = 38 6 3 + 7 Exercice : Calcule en détaillant
EXERCICES DE REVISION POUR LE PASSAGE EN QUATRIEME : Priorités de calcul : Exercice 1 : Calcule en détaillant : A = 4 + 5 6 + 7 B = 6 3 + 5 C = 35 5 3 D = 6 7 + 8 E = 38 6 3 + 7 Exercice : Calcule en détaillant
Fonctions de plusieurs variables
 Module : Analyse 03 Chapitre 00 : Fonctions de plusieurs variables Généralités et Rappels des notions topologiques dans : Qu est- ce que?: Mathématiquement, n étant un entier non nul, on définit comme
Module : Analyse 03 Chapitre 00 : Fonctions de plusieurs variables Généralités et Rappels des notions topologiques dans : Qu est- ce que?: Mathématiquement, n étant un entier non nul, on définit comme
TOUT CE QU IL FAUT SAVOIR POUR LE BREVET
 TOUT E QU IL FUT SVOIR POUR LE REVET NUMERIQUE / FONTIONS eci n est qu un rappel de tout ce qu il faut savoir en maths pour le brevet. I- Opérations sur les nombres et les fractions : Les priorités par
TOUT E QU IL FUT SVOIR POUR LE REVET NUMERIQUE / FONTIONS eci n est qu un rappel de tout ce qu il faut savoir en maths pour le brevet. I- Opérations sur les nombres et les fractions : Les priorités par
1S Modèles de rédaction Enoncés
 Par l équipe des professeurs de 1S du lycée Parc de Vilgénis 1S Modèles de rédaction Enoncés Produit scalaire & Corrigés Exercice 1 : définition du produit scalaire Soit ABC un triangle tel que AB, AC
Par l équipe des professeurs de 1S du lycée Parc de Vilgénis 1S Modèles de rédaction Enoncés Produit scalaire & Corrigés Exercice 1 : définition du produit scalaire Soit ABC un triangle tel que AB, AC
Durée de L épreuve : 2 heures. Barème : Exercice n 4 : 1 ) 1 point 2 ) 2 points 3 ) 1 point
 03 Mai 2013 Collège Oasis Durée de L épreuve : 2 heures. apple Le sujet comporte 4 pages et est présenté en livret ; apple La calculatrice est autorisée ; apple 4 points sont attribués à la qualité de
03 Mai 2013 Collège Oasis Durée de L épreuve : 2 heures. apple Le sujet comporte 4 pages et est présenté en livret ; apple La calculatrice est autorisée ; apple 4 points sont attribués à la qualité de
Mesurer en toute simplicité
 Mesurer en toute simplicité Avant-propos Chers étudiants et enseignants, ainsi que toutes personnes passionnées de topographie, au cours des dernières années, le développement d'instruments modernes et
Mesurer en toute simplicité Avant-propos Chers étudiants et enseignants, ainsi que toutes personnes passionnées de topographie, au cours des dernières années, le développement d'instruments modernes et
Savoir lire une carte, se situer et s orienter en randonnée
 Savoir lire une carte, se situer et s orienter en randonnée Le b.a.-ba du randonneur Fiche 2 Lire une carte topographique Mais c est où le nord? Quel Nord Le magnétisme terrestre attire systématiquement
Savoir lire une carte, se situer et s orienter en randonnée Le b.a.-ba du randonneur Fiche 2 Lire une carte topographique Mais c est où le nord? Quel Nord Le magnétisme terrestre attire systématiquement
I - PUISSANCE D UN POINT PAR RAPPORT A UN CERCLE CERCLES ORTHOGONAUX POLES ET POLAIRES
 I - PUISSANCE D UN POINT PAR RAPPORT A UN CERCLE CERCLES ORTHOGONAUX POLES ET POLAIRES Théorème - Définition Soit un cercle (O,R) et un point. Une droite passant par coupe le cercle en deux points A et
I - PUISSANCE D UN POINT PAR RAPPORT A UN CERCLE CERCLES ORTHOGONAUX POLES ET POLAIRES Théorème - Définition Soit un cercle (O,R) et un point. Une droite passant par coupe le cercle en deux points A et
Correction : E = Soit E = -1,6. F = 12 Soit F = -6 3 + 45. y = 11. et G = -2z + 4y G = 2 6 = 3 G = G = -2 5 + 4 11
 Correction : EXERCICE : Calculer en indiquant les étapes: (-6 +9) ( ) ( ) B = -4 (-) (-8) B = - 8 (+ 6) B = - 8 6 B = - 44 EXERCICE : La visite médicale Calcul de la part des élèves rencontrés lundi et
Correction : EXERCICE : Calculer en indiquant les étapes: (-6 +9) ( ) ( ) B = -4 (-) (-8) B = - 8 (+ 6) B = - 8 6 B = - 44 EXERCICE : La visite médicale Calcul de la part des élèves rencontrés lundi et
Une solution pour les experts! Les relevés de surfaces. solution? On y retourne!
 Relevé de surfaces, Repérage amiante, Diagnostic plomb, Etat parasitaire, avec une TabletPC Une solution pour les experts! DISTOTABLET La réhabilitation de bâtiments existants constitue désormais une partie
Relevé de surfaces, Repérage amiante, Diagnostic plomb, Etat parasitaire, avec une TabletPC Une solution pour les experts! DISTOTABLET La réhabilitation de bâtiments existants constitue désormais une partie
Tâche complexe produite par l académie de Clermont-Ferrand. Mai 2012 LE TIR A L ARC. (d après une idée du collège des Portes du Midi de Maurs)
 (d après une idée du collège des Portes du Midi de Maurs) Table des matières Fiche professeur... 2 Fiche élève... 5 1 Fiche professeur Niveaux et objectifs pédagogiques 5 e : introduction ou utilisation
(d après une idée du collège des Portes du Midi de Maurs) Table des matières Fiche professeur... 2 Fiche élève... 5 1 Fiche professeur Niveaux et objectifs pédagogiques 5 e : introduction ou utilisation
Ce guide se divise en six chapitres, dont quatre sont dédiés à une catégorie de bâtiment :
 INTRODUCTION Constructions de pointe et d usage courant, les escaliers métalliques doivent répondre à d autres exigences, que celle de pouvoir passer d un niveau à un autre. L un des principaux points
INTRODUCTION Constructions de pointe et d usage courant, les escaliers métalliques doivent répondre à d autres exigences, que celle de pouvoir passer d un niveau à un autre. L un des principaux points
Activités numériques [13 Points]
![Activités numériques [13 Points] Activités numériques [13 Points]](/thumbs/21/1117704.jpg) N du candidat L emploi de la calculatrice est autorisé. Le soin, la qualité de la présentation entrent pour 2 points dans l appréciation des copies. Les résultats seront soulignés. La correction est disponible
N du candidat L emploi de la calculatrice est autorisé. Le soin, la qualité de la présentation entrent pour 2 points dans l appréciation des copies. Les résultats seront soulignés. La correction est disponible
EXERCICES DE REVISIONS MATHEMATIQUES CM2
 EXERCICES DE REVISIONS MATHEMATIQUES CM2 NOMBRES ET CALCUL Exercices FRACTIONS Nommer les fractions simples et décimales en utilisant le vocabulaire : 3 R1 demi, tiers, quart, dixième, centième. Utiliser
EXERCICES DE REVISIONS MATHEMATIQUES CM2 NOMBRES ET CALCUL Exercices FRACTIONS Nommer les fractions simples et décimales en utilisant le vocabulaire : 3 R1 demi, tiers, quart, dixième, centième. Utiliser
Mesure d angles et trigonométrie
 Thierry Ciblac Mesure d angles et trigonométrie Mesure de l angle de deux axes (ou de deux demi-droites) de même origine. - Mesures en degrés : Divisons un cercle en 360 parties égales définissant ainsi
Thierry Ciblac Mesure d angles et trigonométrie Mesure de l angle de deux axes (ou de deux demi-droites) de même origine. - Mesures en degrés : Divisons un cercle en 360 parties égales définissant ainsi
PRATIQUE DU COMPAS ou
 PRTQU U OMPS ou Traité élémentaire de tous les traits servant aux rts et Métiers et à la construction des âtiments ZR, éomètre ii Reproduction de l édition de 1833, VNN, imprimerie TMON Père et ils, par
PRTQU U OMPS ou Traité élémentaire de tous les traits servant aux rts et Métiers et à la construction des âtiments ZR, éomètre ii Reproduction de l édition de 1833, VNN, imprimerie TMON Père et ils, par
Exprimer ce coefficient de proportionnalité sous forme de pourcentage : 3,5 %
 23 CALCUL DE L INTÉRÊT Tau d intérêt Paul et Rémi ont reçu pour Noël, respectivement, 20 et 80. Ils placent cet argent dans une banque, au même tau. Au bout d une année, ce placement leur rapportera une
23 CALCUL DE L INTÉRÊT Tau d intérêt Paul et Rémi ont reçu pour Noël, respectivement, 20 et 80. Ils placent cet argent dans une banque, au même tau. Au bout d une année, ce placement leur rapportera une
Séquence 2. Repérage dans le plan Équations de droites. Sommaire
 Séquence Repérage dans le plan Équations de droites Sommaire 1 Prérequis Repérage dans le plan 3 Équations de droites 4 Synthèse de la séquence 5 Exercices d approfondissement Séquence MA0 1 1 Prérequis
Séquence Repérage dans le plan Équations de droites Sommaire 1 Prérequis Repérage dans le plan 3 Équations de droites 4 Synthèse de la séquence 5 Exercices d approfondissement Séquence MA0 1 1 Prérequis
Cours Fonctions de deux variables
 Cours Fonctions de deux variables par Pierre Veuillez 1 Support théorique 1.1 Représentation Plan et espace : Grâce à un repère cartésien ( ) O, i, j du plan, les couples (x, y) de R 2 peuvent être représenté
Cours Fonctions de deux variables par Pierre Veuillez 1 Support théorique 1.1 Représentation Plan et espace : Grâce à un repère cartésien ( ) O, i, j du plan, les couples (x, y) de R 2 peuvent être représenté
Chapitre 2 : Caractéristiques du mouvement d un solide
 Chapitre 2 : Caractéristiques du mouvement d un solide I Rappels : Référentiel : Le mouvement d un corps est décris par rapport à un corps de référence et dépend du choix de ce corps. Ce corps de référence
Chapitre 2 : Caractéristiques du mouvement d un solide I Rappels : Référentiel : Le mouvement d un corps est décris par rapport à un corps de référence et dépend du choix de ce corps. Ce corps de référence
Exercice numéro 1 - L'escalier
 Exercice numéro 1 - L'escalier On peut monter un escalier une ou deux marches à la fois. La figure de droite montre un exemple. 1. De combien de façons différentes peut-on monter un escalier de une marche?
Exercice numéro 1 - L'escalier On peut monter un escalier une ou deux marches à la fois. La figure de droite montre un exemple. 1. De combien de façons différentes peut-on monter un escalier de une marche?
COMPTE-RENDU «MATHS EN JEANS» LYCEE OZENNE Groupe 1 : Comment faire une carte juste de la Terre?
 Claire FORGACZ Marion GALLART Hasnia GOUDJILI COMPTERENDU «MATHS EN JEANS» LYCEE OZENNE Groupe 1 : Comment faire une carte juste de la Terre? Si l on se pose la question de savoir comment on peut faire
Claire FORGACZ Marion GALLART Hasnia GOUDJILI COMPTERENDU «MATHS EN JEANS» LYCEE OZENNE Groupe 1 : Comment faire une carte juste de la Terre? Si l on se pose la question de savoir comment on peut faire
Calcul intégral élémentaire en plusieurs variables
 Calcul intégral élémentaire en plusieurs variables PC*2 2 septembre 2009 Avant-propos À part le théorème de Fubini qui sera démontré dans le cours sur les intégrales à paramètres et qui ne semble pas explicitement
Calcul intégral élémentaire en plusieurs variables PC*2 2 septembre 2009 Avant-propos À part le théorème de Fubini qui sera démontré dans le cours sur les intégrales à paramètres et qui ne semble pas explicitement
PARTIE NUMERIQUE (18 points)
 4 ème DEVOIR COMMUN N 1 DE MATHÉMATIQUES 14/12/09 L'échange de matériel entre élèves et l'usage de la calculatrice sont interdits. Il sera tenu compte du soin et de la présentation ( 4 points ). Le barème
4 ème DEVOIR COMMUN N 1 DE MATHÉMATIQUES 14/12/09 L'échange de matériel entre élèves et l'usage de la calculatrice sont interdits. Il sera tenu compte du soin et de la présentation ( 4 points ). Le barème
DOCM 2013 http://docm.math.ca/ Solutions officielles. 1 2 10 + 1 2 9 + 1 2 8 = n 2 10.
 A1 Trouvez l entier positif n qui satisfait l équation suivante: Solution 1 2 10 + 1 2 9 + 1 2 8 = n 2 10. En additionnant les termes du côté gauche de l équation en les mettant sur le même dénominateur
A1 Trouvez l entier positif n qui satisfait l équation suivante: Solution 1 2 10 + 1 2 9 + 1 2 8 = n 2 10. En additionnant les termes du côté gauche de l équation en les mettant sur le même dénominateur
Représentation géométrique d un nombre complexe
 CHAPITRE 1 NOMBRES COMPLEXES 1 Représentation géométrique d un nombre complexe 1. Ensemble des nombres complexes Soit i le nombre tel que i = 1 L ensemble des nombres complexes est l ensemble des nombres
CHAPITRE 1 NOMBRES COMPLEXES 1 Représentation géométrique d un nombre complexe 1. Ensemble des nombres complexes Soit i le nombre tel que i = 1 L ensemble des nombres complexes est l ensemble des nombres
La perspective conique
 La perspective conique Définitions et principes. Deux cas de la perspective conique : la perspective conique oblique et la perspective conique centrale. Principe de la perspective conique : . La perspective
La perspective conique Définitions et principes. Deux cas de la perspective conique : la perspective conique oblique et la perspective conique centrale. Principe de la perspective conique : . La perspective
Items étudiés dans le CHAPITRE N5. 7 et 9 p 129 D14 Déterminer par le calcul l'antécédent d'un nombre par une fonction linéaire
 CHAPITRE N5 FONCTIONS LINEAIRES NOTION DE FONCTION FONCTIONS LINEAIRES NOTION DE FONCTION FONCTIONS LINEAIRES NOTION DE FONCTION Code item D0 D2 N30[S] Items étudiés dans le CHAPITRE N5 Déterminer l'image
CHAPITRE N5 FONCTIONS LINEAIRES NOTION DE FONCTION FONCTIONS LINEAIRES NOTION DE FONCTION FONCTIONS LINEAIRES NOTION DE FONCTION Code item D0 D2 N30[S] Items étudiés dans le CHAPITRE N5 Déterminer l'image
EVALUATIONS FIN CM1. Mathématiques. Livret élève
 Les enseignants de CM1 de la circonscription de METZ-SUD proposent EVALUATIONS FIN CM1 Mathématiques Livret élève Circonscription de METZ-SUD page 1 NOMBRES ET CALCUL Exercice 1 : Écris en chiffres les
Les enseignants de CM1 de la circonscription de METZ-SUD proposent EVALUATIONS FIN CM1 Mathématiques Livret élève Circonscription de METZ-SUD page 1 NOMBRES ET CALCUL Exercice 1 : Écris en chiffres les
mesure des débits et des volumes dérivés par les canaux gravitaires
 mesures limnimétriques 2009 Depuis la loi sur l Eau de 1992, précisée par celle de 2006, tous les volumes d eau prélevés dans le milieu naturel doivent être mesurés, et ce, pour permettre une meilleure
mesures limnimétriques 2009 Depuis la loi sur l Eau de 1992, précisée par celle de 2006, tous les volumes d eau prélevés dans le milieu naturel doivent être mesurés, et ce, pour permettre une meilleure
point On obtient ainsi le ou les points d inter- entre deux objets».
 Déplacer un objet Cliquer sur le bouton «Déplacer». On peut ainsi rendre la figure dynamique. Attraper l objet à déplacer avec la souris. Ici, on veut déplacer le point A du triangle point ABC. A du triangle
Déplacer un objet Cliquer sur le bouton «Déplacer». On peut ainsi rendre la figure dynamique. Attraper l objet à déplacer avec la souris. Ici, on veut déplacer le point A du triangle point ABC. A du triangle
COMMENT FAIRE DES ESCALIERS?
 COMMENT FAIRE DES ESCALIERS? Conception et mise en œuvre GUIDE TECHNIQUE 2012 Union des Métalliers C O L L E CT I O N R E C H E R C H E D É V E LO P P E M E N T M É T I E R 4 INTRODUCTION 13 PARTIE I GÉNÉR
COMMENT FAIRE DES ESCALIERS? Conception et mise en œuvre GUIDE TECHNIQUE 2012 Union des Métalliers C O L L E CT I O N R E C H E R C H E D É V E LO P P E M E N T M É T I E R 4 INTRODUCTION 13 PARTIE I GÉNÉR
Problèmes sur le chapitre 5
 Problèmes sur le chapitre 5 (Version du 13 janvier 2015 (10h38)) 501 Le calcul des réactions d appui dans les problèmes schématisés ci-dessous est-il possible par les équations de la statique Si oui, écrire
Problèmes sur le chapitre 5 (Version du 13 janvier 2015 (10h38)) 501 Le calcul des réactions d appui dans les problèmes schématisés ci-dessous est-il possible par les équations de la statique Si oui, écrire
Seconde MESURER LA TERRE Page 1 MESURER LA TERRE
 Seconde MESURER LA TERRE Page 1 TRAVAUX DIRIGES MESURER LA TERRE -580-570 -335-230 +400 IX - XI siècles 1670 1669/1716 1736/1743 THALES (-à Milet) considère la terre comme une grande galette, dans une
Seconde MESURER LA TERRE Page 1 TRAVAUX DIRIGES MESURER LA TERRE -580-570 -335-230 +400 IX - XI siècles 1670 1669/1716 1736/1743 THALES (-à Milet) considère la terre comme une grande galette, dans une
Un pavillon se compose de murs et d'un toit qui peuvent être réalisés de différentes façons suivant le budget donné :
 Un pavillon se compose de murs et d'un toit qui peuvent être réalisés de différentes façons suivant le budget donné : l'assemblage de parpaings le moulage dans un coffrage donnant une forme circulaire
Un pavillon se compose de murs et d'un toit qui peuvent être réalisés de différentes façons suivant le budget donné : l'assemblage de parpaings le moulage dans un coffrage donnant une forme circulaire
Franck VAUTIER, Jean-Pierre TOUMAZET, Erwan ROUSSEL, Marlène FAURE, Mohamed ABADI, Marta FLOREZ, Bertrand DOUSTEYSSIER
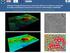 Utilisation d images dérivées d un jeu de données LIDAR pour la détection automatisée de vestiges archéologiques (programme de recherche méthodologique LiDARCHEO) Franck VAUTIER, Jean-Pierre TOUMAZET,
Utilisation d images dérivées d un jeu de données LIDAR pour la détection automatisée de vestiges archéologiques (programme de recherche méthodologique LiDARCHEO) Franck VAUTIER, Jean-Pierre TOUMAZET,
Trois personnes mangent dans un restaurant. Le serveur
 29=30 Trois personnes mangent dans un restaurant. Le serveur leur amène une addition de 30 francs. Les trois personnes décident de partager la facture en trois, soit 10 francs chacun. Le serveur rapporte
29=30 Trois personnes mangent dans un restaurant. Le serveur leur amène une addition de 30 francs. Les trois personnes décident de partager la facture en trois, soit 10 francs chacun. Le serveur rapporte
1 Création d une pièce. 2 Travail complémentaire. 1-1 Réglage des barres d outils. 1-2 Exemples de réalisation de pièces à l aide d un modeleur 3D
 SolidWorks Logiciel de DAO (Dessin Assisté par Ordinateur) Palonnier Servomoteur SOMMAIRE : 1 Création d une pièce 1-1 Réglage des barres d outils 1-2 Exemples de réalisation de pièces à l aide d un modeleur
SolidWorks Logiciel de DAO (Dessin Assisté par Ordinateur) Palonnier Servomoteur SOMMAIRE : 1 Création d une pièce 1-1 Réglage des barres d outils 1-2 Exemples de réalisation de pièces à l aide d un modeleur
Deux disques dans un carré
 Deux disques dans un carré Table des matières 1 Fiche résumé 2 2 Fiche élève Seconde - version 1 3 2.1 Le problème............................................... 3 2.2 Construction de la figure avec geogebra...............................
Deux disques dans un carré Table des matières 1 Fiche résumé 2 2 Fiche élève Seconde - version 1 3 2.1 Le problème............................................... 3 2.2 Construction de la figure avec geogebra...............................
ÉTUDE DE L EFFICACITÉ DE GÉOGRILLES POUR PRÉVENIR L EFFONDREMENT LOCAL D UNE CHAUSSÉE
 ÉTUDE DE L EFFICACITÉ DE GÉOGRILLES POUR PRÉVENIR L EFFONDREMENT LOCAL D UNE CHAUSSÉE ANALYSIS OF THE EFFICIENCY OF GEOGRIDS TO PREVENT A LOCAL COLLAPSE OF A ROAD Céline BOURDEAU et Daniel BILLAUX Itasca
ÉTUDE DE L EFFICACITÉ DE GÉOGRILLES POUR PRÉVENIR L EFFONDREMENT LOCAL D UNE CHAUSSÉE ANALYSIS OF THE EFFICIENCY OF GEOGRIDS TO PREVENT A LOCAL COLLAPSE OF A ROAD Céline BOURDEAU et Daniel BILLAUX Itasca
Produits concernés: CS10, CS15, TS11, TS15, GS05, GS06, GS08, GS10, GS15
 V3.50 Apports et bénéfices Produits concernés: CS10, CS15, TS11, TS15, GS05, GS06, GS08, GS10, GS15 Ce document contient d importantes informations au sujet de la version 3.50 de SmartWorx Viva et des
V3.50 Apports et bénéfices Produits concernés: CS10, CS15, TS11, TS15, GS05, GS06, GS08, GS10, GS15 Ce document contient d importantes informations au sujet de la version 3.50 de SmartWorx Viva et des
Exercices Alternatifs. Une fonction continue mais dérivable nulle part
 Eercices Alternatifs Une fonction continue mais dérivable nulle part c 22 Frédéric Le Rou (copyleft LDL : Licence pour Documents Libres). Sources et figures: applications-continues-non-derivables/. Version
Eercices Alternatifs Une fonction continue mais dérivable nulle part c 22 Frédéric Le Rou (copyleft LDL : Licence pour Documents Libres). Sources et figures: applications-continues-non-derivables/. Version
OBLIGATION D INSTALLATION D UN GARDE-CORPS
 2 CHAPITRE OBLIGATION D INSTALLATION D UN GARDE-CORPS 2.1. CAS GÉNÉRAL L installation d un garde-corps est obligatoire lorsque la hauteur de chute comptée à partir de la zone de stationnement normal (ZSN)
2 CHAPITRE OBLIGATION D INSTALLATION D UN GARDE-CORPS 2.1. CAS GÉNÉRAL L installation d un garde-corps est obligatoire lorsque la hauteur de chute comptée à partir de la zone de stationnement normal (ZSN)
MAT2027 Activités sur Geogebra
 MAT2027 Activités sur Geogebra NOTE: Il n est pas interdit d utiliser du papier et un crayon!! En particulier, quand vous demandez des informations sur les différentes mesures dans une construction, il
MAT2027 Activités sur Geogebra NOTE: Il n est pas interdit d utiliser du papier et un crayon!! En particulier, quand vous demandez des informations sur les différentes mesures dans une construction, il
ESCALIERS. passer des dénivellations supérieures à 7%
 ESCALIERS passer des dénivellations supérieures à 7% 2 définitions essentielles : Contremarche et giron Le rapport H/G donne la pente d une volée de marches ex : 16 cm / 32 cm = 50% Emmarchement, emprise,
ESCALIERS passer des dénivellations supérieures à 7% 2 définitions essentielles : Contremarche et giron Le rapport H/G donne la pente d une volée de marches ex : 16 cm / 32 cm = 50% Emmarchement, emprise,
Vision industrielle et télédétection - Détection d ellipses. Guillaume Martinez 17 décembre 2007
 Vision industrielle et télédétection - Détection d ellipses Guillaume Martinez 17 décembre 2007 1 Table des matières 1 Le projet 3 1.1 Objectif................................ 3 1.2 Les choix techniques.........................
Vision industrielle et télédétection - Détection d ellipses Guillaume Martinez 17 décembre 2007 1 Table des matières 1 Le projet 3 1.1 Objectif................................ 3 1.2 Les choix techniques.........................
DURÉE DU JOUR EN FONCTION DE LA DATE ET DE LA LATITUDE
 DURÉE DU JUR E FCTI DE LA DATE ET DE LA LATITUDE ous allons nous intéresser à la durée du jour, prise ici dans le sens de période d éclairement par le Soleil dans une journée de 4 h, en un lieu donné de
DURÉE DU JUR E FCTI DE LA DATE ET DE LA LATITUDE ous allons nous intéresser à la durée du jour, prise ici dans le sens de période d éclairement par le Soleil dans une journée de 4 h, en un lieu donné de
Nom : Groupe : Date : 1. Quels sont les deux types de dessins les plus utilisés en technologie?
 Nom : Groupe : Date : Verdict Chapitre 11 1 La communication graphique Pages 336 et 337 1. Quels sont les deux types de dessins les plus utilisés en technologie? Les dessins de fabrication. Les schémas.
Nom : Groupe : Date : Verdict Chapitre 11 1 La communication graphique Pages 336 et 337 1. Quels sont les deux types de dessins les plus utilisés en technologie? Les dessins de fabrication. Les schémas.
Dimensionnement d une roue autonome pour une implantation sur un fauteuil roulant
 Dimensionnement d une roue autonome pour une implantation sur un fauteuil roulant I Présentation I.1 La roue autonome Ez-Wheel SAS est une entreprise française de technologie innovante fondée en 2009.
Dimensionnement d une roue autonome pour une implantation sur un fauteuil roulant I Présentation I.1 La roue autonome Ez-Wheel SAS est une entreprise française de technologie innovante fondée en 2009.
«Aucune investigation humaine ne peut être qualifiée de science véritable si elle ne peut être démontrée mathématiquement.
 «Aucune investigation humaine ne peut être qualifiée de science véritable si elle ne peut être démontrée mathématiquement.» Léonard de Vinci MATHEMATIQUES Les mathématiques revêtaient un caractère particulier
«Aucune investigation humaine ne peut être qualifiée de science véritable si elle ne peut être démontrée mathématiquement.» Léonard de Vinci MATHEMATIQUES Les mathématiques revêtaient un caractère particulier
Angles orientés et trigonométrie
 Chapitre Angles orientés et trigonométrie Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES Trigonométrie Cercle trigonométrique. Radian. Mesure d un angle orienté, mesure principale.
Chapitre Angles orientés et trigonométrie Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES Trigonométrie Cercle trigonométrique. Radian. Mesure d un angle orienté, mesure principale.
Mesures de l état du réseau Domaine Voie Tendances, perspectives et innovations
 Mesures de l état du réseau Domaine Voie Tendances, perspectives et innovations Symposium Infra - Direction de la maintenance du réseau : Régis Ambert, Division Ingénierie de la Maintenance de la Voie
Mesures de l état du réseau Domaine Voie Tendances, perspectives et innovations Symposium Infra - Direction de la maintenance du réseau : Régis Ambert, Division Ingénierie de la Maintenance de la Voie
Vu le dahir du 7 kaada 1371 (30 Juillet 1952) relatif à l urbanisme et, notamment, son article 18 ;
 Décret n 2-64-445 du 21 chaabane 1384 (26 décembre 1964) définissant les zones d habitat économique et approuvant le règlement général de construction applicable à ces zones. (B.O. n 2739 du 28-4-1965,
Décret n 2-64-445 du 21 chaabane 1384 (26 décembre 1964) définissant les zones d habitat économique et approuvant le règlement général de construction applicable à ces zones. (B.O. n 2739 du 28-4-1965,
Cours IV Mise en orbite
 Introduction au vol spatial Cours IV Mise en orbite If you don t know where you re going, you ll probably end up somewhere else. Yogi Berra, NY Yankees catcher v1.2.8 by-sa Olivier Cleynen Introduction
Introduction au vol spatial Cours IV Mise en orbite If you don t know where you re going, you ll probably end up somewhere else. Yogi Berra, NY Yankees catcher v1.2.8 by-sa Olivier Cleynen Introduction
CLUB DE MARCHE Ballade et Randonnée
 CLUB DE MARCHE Ballade et Randonnée SOMMAIRE 1 LA CARTE 1.1 Les types de carte 1.2 Les différentes échelles 1.3 - Les informations figurants sur les cartes au 1/25000 ème 1.3.1 - Le cadre 1.3.2 Les couleurs
CLUB DE MARCHE Ballade et Randonnée SOMMAIRE 1 LA CARTE 1.1 Les types de carte 1.2 Les différentes échelles 1.3 - Les informations figurants sur les cartes au 1/25000 ème 1.3.1 - Le cadre 1.3.2 Les couleurs
1. Introduction 2. Localiser un séisme 3. Déterminer la force d un séisme 4. Caractériser le mécanisme de rupture d un séisme
 Partie II Les paramètres des séismes Séisme: libération d énergie destructrice à partir de la magnitude 5 Prévision sismique: déterminer l aléa sismique Étude du mécanisme de rupture de la faille 1. Introduction
Partie II Les paramètres des séismes Séisme: libération d énergie destructrice à partir de la magnitude 5 Prévision sismique: déterminer l aléa sismique Étude du mécanisme de rupture de la faille 1. Introduction
Reconstruction de bâtiments en 3D à partir de nuages de points LIDAR
 Reconstruction de bâtiments en 3D à partir de nuages de points LIDAR Mickaël Bergem 25 juin 2014 Maillages et applications 1 Table des matières Introduction 3 1 La modélisation numérique de milieux urbains
Reconstruction de bâtiments en 3D à partir de nuages de points LIDAR Mickaël Bergem 25 juin 2014 Maillages et applications 1 Table des matières Introduction 3 1 La modélisation numérique de milieux urbains
315 et 495 sont dans la table de 5. 5 est un diviseur commun. Leur PGCD n est pas 1. Il ne sont pas premiers entre eux
 Exercice 1 : (3 points) Un sac contient 10 boules rouges, 6 boules noires et 4 boules jaunes. Chacune des boules a la même probabilité d'être tirée. On tire une boule au hasard. 1. Calculer la probabilité
Exercice 1 : (3 points) Un sac contient 10 boules rouges, 6 boules noires et 4 boules jaunes. Chacune des boules a la même probabilité d'être tirée. On tire une boule au hasard. 1. Calculer la probabilité
Trait de côte Histolitt v1.0 Descriptif technique Version du document 1.0 *** Sommaire
 Trait de côte Histolitt v1.0 Descriptif technique Version du document 1.0 *** Sommaire 1 Producteurs 2 Dénomination du produit 3 Protection militaire 4 Abréviations 5 Description générale 1. Définition
Trait de côte Histolitt v1.0 Descriptif technique Version du document 1.0 *** Sommaire 1 Producteurs 2 Dénomination du produit 3 Protection militaire 4 Abréviations 5 Description générale 1. Définition
KIT D AIDE A LA MISE EN ACCESSIBILITE DES ETABLISSEMENTS DE TOURISME ET DE COMMERCE Édition Janvier 2015 FICHE N 2D RENDRE MON COMMERCE ACCESSIBLE
 KIT D AIDE A LA MISE EN ACCESSIBILITE DES ETABLISSEMENTS DE TOURISME ET DE COMMERCE Édition Janvier 2015 FICHE N 2D RENDRE MON COMMERCE ACCESSIBLE RAPPEL : Pour les ERP classés 1, 2, 3, 4e catégorie :
KIT D AIDE A LA MISE EN ACCESSIBILITE DES ETABLISSEMENTS DE TOURISME ET DE COMMERCE Édition Janvier 2015 FICHE N 2D RENDRE MON COMMERCE ACCESSIBLE RAPPEL : Pour les ERP classés 1, 2, 3, 4e catégorie :
METEOROLOGIE CAEA 1990
 METEOROLOGIE CAEA 1990 1) Les météorologistes mesurent et prévoient le vent en attitude à des niveaux exprimés en pressions atmosphériques. Entre le niveau de la mer et 6000 m d'altitude, quels sont les
METEOROLOGIE CAEA 1990 1) Les météorologistes mesurent et prévoient le vent en attitude à des niveaux exprimés en pressions atmosphériques. Entre le niveau de la mer et 6000 m d'altitude, quels sont les
6 ème. Rallye mathématique de la Sarthe 2013/2014. 1 ère épreuve de qualification : Problèmes Jeudi 21 novembre 2013
 Retrouver tous les sujets, les corrigés, les annales, les finales sur le site du rallye : http://sarthe.cijm.org I Stéphane, Eric et Christophe sont 3 garçons avec des chevelures différentes. Stéphane
Retrouver tous les sujets, les corrigés, les annales, les finales sur le site du rallye : http://sarthe.cijm.org I Stéphane, Eric et Christophe sont 3 garçons avec des chevelures différentes. Stéphane
Comment démontrer que deux droites sont perpendiculaires?
 omment démontrer que deux droites sont perpendiculaires? Utilisons On sait que (hypothèses) or...(propriété, définition) donc...(conclusion) Réciproque de Pythagore,5 1,5 = + Si dans un triangle le carré
omment démontrer que deux droites sont perpendiculaires? Utilisons On sait que (hypothèses) or...(propriété, définition) donc...(conclusion) Réciproque de Pythagore,5 1,5 = + Si dans un triangle le carré
ÉVALUATION EN FIN DE CM1. Année scolaire 2014 2015 LIVRET DE L'ÉLÈVE MATHÉMATIQUES
 ÉVALUATION EN FIN DE CM1 Année scolaire 2014 2015 LIVRET DE L'ÉLÈVE MATHÉMATIQUES NOM :....... Prénom :....... Né le :./../ École :............ Classe : Domaine Score de réussite NOMBRES ET CALCUL GÉOMÉTRIE
ÉVALUATION EN FIN DE CM1 Année scolaire 2014 2015 LIVRET DE L'ÉLÈVE MATHÉMATIQUES NOM :....... Prénom :....... Né le :./../ École :............ Classe : Domaine Score de réussite NOMBRES ET CALCUL GÉOMÉTRIE
Ch.G3 : Distances et tangentes
 4 e - programme 2011 mathématiques ch.g3 cahier élève Page 1 sur 14 1 DISTC D U PIT À U DRIT Ch.G3 : Distances et tangentes 1.1 Définition ex 1 DÉFIITI 1 : Soit une droite et un point n'appartenant pas
4 e - programme 2011 mathématiques ch.g3 cahier élève Page 1 sur 14 1 DISTC D U PIT À U DRIT Ch.G3 : Distances et tangentes 1.1 Définition ex 1 DÉFIITI 1 : Soit une droite et un point n'appartenant pas
Géométrie dans la rue : mesure d un bâtiment avec les étudiants
 Géométrie dans la rue : mesure d un bâtiment avec les étudiants Claude Archer Haute école Francisco Ferrer E-mail : [email protected] Abstract Mais Monsieur, un triangle dans la rue ce n est pas la
Géométrie dans la rue : mesure d un bâtiment avec les étudiants Claude Archer Haute école Francisco Ferrer E-mail : [email protected] Abstract Mais Monsieur, un triangle dans la rue ce n est pas la
Présentation d un télescope, de ses composants et de quelques consignes d utilisation
 Présentation d un télescope, de ses composants et de quelques consignes d utilisation Nous vous présentons ici très brièvement les différentes parties d un télescope, en prenant l exemple d un type de
Présentation d un télescope, de ses composants et de quelques consignes d utilisation Nous vous présentons ici très brièvement les différentes parties d un télescope, en prenant l exemple d un type de
(B.O. n 2739 du 28-4-1965, page 489) LE PREMIER MINISTRE,
 DECRET N 2-64-445 DU 21 CHAABANE 1384 (26 DECEMBRE 1964) DEFINISSANT LES ZONES D HABITAT ECONOMIQUE ET APPROUVANT LE REGLEMENT GENERAL DE CONSTRUCTION APPLIABLE A CES ZONES (B.O. n 2739 du 28-4-1965, page
DECRET N 2-64-445 DU 21 CHAABANE 1384 (26 DECEMBRE 1964) DEFINISSANT LES ZONES D HABITAT ECONOMIQUE ET APPROUVANT LE REGLEMENT GENERAL DE CONSTRUCTION APPLIABLE A CES ZONES (B.O. n 2739 du 28-4-1965, page
Diviser un nombre décimal par 10 ; 100 ; 1 000
 Diviser un nombre décimal par 10 ; 100 ; 1 000 Diviser un nombre décimal par 10 ; 100 ; 1 000. 23 1 et 2 Pauline collectionne les cartes «Tokéron» depuis plusieurs mois. Elle en possède 364 et veut les
Diviser un nombre décimal par 10 ; 100 ; 1 000 Diviser un nombre décimal par 10 ; 100 ; 1 000. 23 1 et 2 Pauline collectionne les cartes «Tokéron» depuis plusieurs mois. Elle en possède 364 et veut les
Fonctions de deux variables. Mai 2011
 Fonctions de deux variables Dédou Mai 2011 D une à deux variables Les fonctions modèlisent de l information dépendant d un paramètre. On a aussi besoin de modéliser de l information dépendant de plusieurs
Fonctions de deux variables Dédou Mai 2011 D une à deux variables Les fonctions modèlisent de l information dépendant d un paramètre. On a aussi besoin de modéliser de l information dépendant de plusieurs
Proposition de programmes de calculs en mise en train
 Proposition de programmes de calculs en mise en train Programme 1 : Je choisis un nombre, je lui ajoute 1, je calcule le carré du résultat, je retranche le carré du nombre de départ. Essai-conjecture-preuve.
Proposition de programmes de calculs en mise en train Programme 1 : Je choisis un nombre, je lui ajoute 1, je calcule le carré du résultat, je retranche le carré du nombre de départ. Essai-conjecture-preuve.
Chapitre 3. Quelques fonctions usuelles. 1 Fonctions logarithme et exponentielle. 1.1 La fonction logarithme
 Chapitre 3 Quelques fonctions usuelles 1 Fonctions logarithme et eponentielle 1.1 La fonction logarithme Définition 1.1 La fonction 7! 1/ est continue sur ]0, +1[. Elle admet donc des primitives sur cet
Chapitre 3 Quelques fonctions usuelles 1 Fonctions logarithme et eponentielle 1.1 La fonction logarithme Définition 1.1 La fonction 7! 1/ est continue sur ]0, +1[. Elle admet donc des primitives sur cet
Les Cheminements piétons
 Les Cheminements piétons 2 Les cheminements Le cheminement usuel doit être le plus court possible. Il lie entre eux tous les maillons de la vie sociale. Domicile Services publics Écoles Transports Travail
Les Cheminements piétons 2 Les cheminements Le cheminement usuel doit être le plus court possible. Il lie entre eux tous les maillons de la vie sociale. Domicile Services publics Écoles Transports Travail
Diplômes. Expériences professionnelles en Archéologie Préventive
 COUSIN Colin 30, rue Burdeau 69001 LYON 0673185568 [email protected] Diplômes 2012 : Master 2 Professionnel - «Archéologie de l objet, du site et du bâti», Université Lumière Lyon (69) 2011: Master
COUSIN Colin 30, rue Burdeau 69001 LYON 0673185568 [email protected] Diplômes 2012 : Master 2 Professionnel - «Archéologie de l objet, du site et du bâti», Université Lumière Lyon (69) 2011: Master
8.1 Généralités sur les fonctions de plusieurs variables réelles. f : R 2 R (x, y) 1 x 2 y 2
 Chapitre 8 Fonctions de plusieurs variables 8.1 Généralités sur les fonctions de plusieurs variables réelles Définition. Une fonction réelle de n variables réelles est une application d une partie de R
Chapitre 8 Fonctions de plusieurs variables 8.1 Généralités sur les fonctions de plusieurs variables réelles Définition. Une fonction réelle de n variables réelles est une application d une partie de R
Exercices Alternatifs. Une fonction continue mais dérivable nulle part
 Eercices Alternatifs Une fonction continue mais dérivable nulle part c 22 Frédéric Le Rou (copleft LDL : Licence pour Documents Libres). Sources et figures: applications-continues-non-derivables/. Version
Eercices Alternatifs Une fonction continue mais dérivable nulle part c 22 Frédéric Le Rou (copleft LDL : Licence pour Documents Libres). Sources et figures: applications-continues-non-derivables/. Version
CHAPITRE 2 POSITIONNEMENT
 35 CHPITRE POSITIONNEMENT 1. INTRODUCTION La détermination d une position précise est le problème fondamental d un Système d Information Géographique (SIG) et l objet principal de la géodésie. La position
35 CHPITRE POSITIONNEMENT 1. INTRODUCTION La détermination d une position précise est le problème fondamental d un Système d Information Géographique (SIG) et l objet principal de la géodésie. La position
NOUVEAU DISPOSITIF REGLEMENTAIRE Les ERP
 Loi pour l Égalité des Droits et des Chances, la Participation et la Citoyenneté des Personnes Handicapées (EDCPCPH) NOUVEAU DISPOSITIF REGLEMENTAIRE Les ERP 1 1 Quel classement pour les ERP? Le classement
Loi pour l Égalité des Droits et des Chances, la Participation et la Citoyenneté des Personnes Handicapées (EDCPCPH) NOUVEAU DISPOSITIF REGLEMENTAIRE Les ERP 1 1 Quel classement pour les ERP? Le classement
L ANALYSE EN COMPOSANTES PRINCIPALES (A.C.P.) Pierre-Louis GONZALEZ
 L ANALYSE EN COMPOSANTES PRINCIPALES (A.C.P.) Pierre-Louis GONZALEZ INTRODUCTION Données : n individus observés sur p variables quantitatives. L A.C.P. permet d eplorer les liaisons entre variables et
L ANALYSE EN COMPOSANTES PRINCIPALES (A.C.P.) Pierre-Louis GONZALEZ INTRODUCTION Données : n individus observés sur p variables quantitatives. L A.C.P. permet d eplorer les liaisons entre variables et
Triangles isométriques Triangles semblables
 Triangles isométriques Triangles semblables Les transformations du plan ont permis de dégager des propriétés de figures superposables. Le théorème de Thalès a permis de s initier aux notions de réduction
Triangles isométriques Triangles semblables Les transformations du plan ont permis de dégager des propriétés de figures superposables. Le théorème de Thalès a permis de s initier aux notions de réduction
Le seul ami de Batman
 Le seul ami de Batman Avant de devenir un héros de cinéma en 1989, Batman est depuis plus de 50 ans un fameux personnage de bandes dessinées aux États-Unis. Il fut créé en mai 1939 dans les pages de Détective
Le seul ami de Batman Avant de devenir un héros de cinéma en 1989, Batman est depuis plus de 50 ans un fameux personnage de bandes dessinées aux États-Unis. Il fut créé en mai 1939 dans les pages de Détective
Paris et New-York sont-ils les sommets d'un carré?
 page 95 Paris et New-York sont-ils les sommets d'un carré? par othi Mok (3 ), Michel Vongsavanh (3 ), Eric hin (3 ), iek-hor Lim ( ), Eric kbaraly ( ), élèves et anciens élèves du ollège Victor Hugo (2
page 95 Paris et New-York sont-ils les sommets d'un carré? par othi Mok (3 ), Michel Vongsavanh (3 ), Eric hin (3 ), iek-hor Lim ( ), Eric kbaraly ( ), élèves et anciens élèves du ollège Victor Hugo (2
ASSURANCE QUALITE WORLDSKILLS
 5 Date Approuvé ASSURANCE QUALITE WORLDSKILLS Description technique Conception et dessin industriel en mécanique/cdao Document No. TD5 Révision Projet de texte Suite à une résolution votée par le Comité
5 Date Approuvé ASSURANCE QUALITE WORLDSKILLS Description technique Conception et dessin industriel en mécanique/cdao Document No. TD5 Révision Projet de texte Suite à une résolution votée par le Comité
FONCTIONS DE PLUSIEURS VARIABLES (Outils Mathématiques 4)
 FONCTIONS DE PLUSIEURS VARIABLES (Outils Mathématiques 4) Bernard Le Stum Université de Rennes 1 Version du 13 mars 2009 Table des matières 1 Fonctions partielles, courbes de niveau 1 2 Limites et continuité
FONCTIONS DE PLUSIEURS VARIABLES (Outils Mathématiques 4) Bernard Le Stum Université de Rennes 1 Version du 13 mars 2009 Table des matières 1 Fonctions partielles, courbes de niveau 1 2 Limites et continuité
Bac Blanc Terminale ES - Février 2011 Épreuve de Mathématiques (durée 3 heures)
 Bac Blanc Terminale ES - Février 2011 Épreuve de Mathématiques (durée 3 heures) Eercice 1 (5 points) pour les candidats n ayant pas choisi la spécialité MATH Le tableau suivant donne l évolution du chiffre
Bac Blanc Terminale ES - Février 2011 Épreuve de Mathématiques (durée 3 heures) Eercice 1 (5 points) pour les candidats n ayant pas choisi la spécialité MATH Le tableau suivant donne l évolution du chiffre
a et b étant deux nombres relatifs donnés, une fonction affine est une fonction qui a un nombre x associe le nombre ax + b
 I Définition d une fonction affine Faire l activité 1 «une nouvelle fonction» 1. définition générale a et b étant deux nombres relatifs donnés, une fonction affine est une fonction qui a un nombre x associe
I Définition d une fonction affine Faire l activité 1 «une nouvelle fonction» 1. définition générale a et b étant deux nombres relatifs donnés, une fonction affine est une fonction qui a un nombre x associe
Station Totale Geomax Série Zoom30
 Station Totale Geomax Série Zoom30 GeoMax Profil de l entreprise GeoMax est une entreprise fort de solides positions sur L étroite collaboration qui présente à l international et le marché des technologies
Station Totale Geomax Série Zoom30 GeoMax Profil de l entreprise GeoMax est une entreprise fort de solides positions sur L étroite collaboration qui présente à l international et le marché des technologies
COURS EULER: PROGRAMME DE LA PREMIÈRE ANNÉE
 COURS EULER: PROGRAMME DE LA PREMIÈRE ANNÉE Le cours de la première année concerne les sujets de 9ème et 10ème années scolaires. Il y a bien sûr des différences puisque nous commençons par exemple par
COURS EULER: PROGRAMME DE LA PREMIÈRE ANNÉE Le cours de la première année concerne les sujets de 9ème et 10ème années scolaires. Il y a bien sûr des différences puisque nous commençons par exemple par
REPRESENTER LA TERRE Cartographie et navigation
 REPRESENTER LA TERRE Seconde Page 1 TRAVAUX DIRIGES REPRESENTER LA TERRE Cartographie et navigation Casterman TINTIN "Le trésor de Rackham Le Rouge" 1 TRIGONOMETRIE : Calcul du chemin le plus court. 1)
REPRESENTER LA TERRE Seconde Page 1 TRAVAUX DIRIGES REPRESENTER LA TERRE Cartographie et navigation Casterman TINTIN "Le trésor de Rackham Le Rouge" 1 TRIGONOMETRIE : Calcul du chemin le plus court. 1)
La géométrie du triangle III IV - V Cercles remarquables - Lieux géométriques - Relations métriques
 La géométrie du triangle III IV - V Cercles remarquables - Lieux géométriques - Relations métriques III. Cercles 1. Cercle d'euler 2. Droite d'euler 3. Théorème de Feuerbach 4. Milieux des segments joignant
La géométrie du triangle III IV - V Cercles remarquables - Lieux géométriques - Relations métriques III. Cercles 1. Cercle d'euler 2. Droite d'euler 3. Théorème de Feuerbach 4. Milieux des segments joignant
Exercice n o 54 : Tracer le graphique d une fonction
 Eercice n o 54 : Tracer le graphique d une fonction G- Pour chaque fonction donnée dans les problèmes à 6 : a) Dessine le graphique correspondant. b) Indique le domaine et l'image. c) Évalue f(0). d) Trouve
Eercice n o 54 : Tracer le graphique d une fonction G- Pour chaque fonction donnée dans les problèmes à 6 : a) Dessine le graphique correspondant. b) Indique le domaine et l'image. c) Évalue f(0). d) Trouve
