Romain Vernoux. Reconstruction d une scène 3D par stéréovision
|
|
|
- Marianne Boudreau
- il y a 9 ans
- Total affichages :
Transcription
1 Romain Vernoux Reconstruction d une scène 3D par stéréovision TIPE Informatique
2 Table des matières Introduction 3 I. Modélisation des caméras 4 1. Espace projectif La projection de E 3 dans E 2 est linéaire Les rotations et les translations sont linéaires Les projections perspectives sont linéaires Calcul de la matrice de projection Situation Décomposition en Valeurs Singulières (SVD) Trouver x qui minimise Ax et tel que x = Algorithme de calcul de P par Transformation Linéaire Directe (DLT) II. Triangulation 9 1. Situation Algorithme de triangulation DLT Condition d existence d une solution III. Suivi de la trajectoire Algorithme naïf de détection de l objet Algorithme de suivi de trajectoire IV. Un premier essai : cas idéal Description de l expérience Résultats V. Deuxième essai : en situation réelle Description de l expérience Résultats VI. Généralisation et extensions Retour sur les hypothèses simplificatrices Vision à n caméras D autres utilisations de la stéréovision Bibliographie 15 2
3 Introduction La stéréovision consiste en la localisation dans l espace d objets filmés simultanément sous des angles différents par au moins deux caméras en position générale. Cette opération se décompose en trois phases principales : La calibration des caméras, c est-à-dire la détermination des paramètres intrinsèques des capteurs L association (ou appariement), fait de reconnaitre sur chaque paire d images les pixels correspondant au même objet réel La reconstruction de la scène, ou le calcul des coordonnées des objets la constituant uniquement à partir des images fournies par les capteurs. Mon objectif est d étudier l aspect théorique de la reconstruction d une scène en trois dimensions, puis d implémenter ces algorithmes et de construire une version simplifiée du système Hawk-Eye. Actuellement utilisé dans les tournois de tennis comme une aide à l arbitrage, celui-ci propose une simulation en 3D du dernier échange et donne la position des impacts de balles avec une erreur moyenne annoncée de 3.6 mm, et cela uniquement à partir d images filmées par six caméras disposées autour du terrain. Figure 1 Ralenti 3D et jugement de l impact donnés par un système Hawk-Eye Ce modèle fera plusieurs hypothèses simplificatrices. Tout d abord, on s affranchira de l étape d appariement en nous limitant à la détection d une balle lumineuse sur un fond sombre. Ensuite, on remplacera, dans les calculs, l ensemble des lentilles composant les optiques des capteurs par une unique lentille équivalente convergente. Enfin, nous supposerons que cette lentille est immobile au cours du déplacement de l objet, une approximation correcte si celui-ci ne s écarte pas trop de sa position initiale. Nous verrons enfin que si la première simplification correspond à un épineux problème, les deux autres peuvent être aisément contournées. 3
4 I. Modélisation des caméras Afin de pouvoir exploiter les images filmées dans le processus de reconstruction de la scène, il est nécessaire de déterminer l application P qui à un point X de l espace associe son projeté x sur le capteur d une caméra. Après une courte introduction sur les espaces projectifs, nous montrerons que P est linéaire et calculerons sa matrice. 1. Espace projectif On définit l espace projectif E n comme suit. À chaque vecteur (x 1,..., x n ) de R n, on associe la classe d équivalence des vecteurs colinéaires à (x 1,..., x n, 1). On appelle E n l ensemble de ces classes d équivalence. En somme, on associe (x 1,..., x n ) à R (x 1,..., x n, 1) et inversement (z 1,..., z n, d) est associé à ( z 1 d,..., zn ). On appelle d coordonnées homogènes de x R n les composantes de n importe quel vecteur de E n associé à x. Figure 2 Interprétation graphique : on associe R n à l hyperplan affine d équation x n+1 = 1 dans R n+1 représentant E n. À tout vecteur (x 1,..., x n ) de R n, on associe la droite vectorielle passant par (x 1,..., x n, 1) et O. L espace projectif possède de nombreuses propriétés utiles dans la construction de scènes 3D. En particulier, certaines transformations non linéaires de R 3 le deviennent une fois que l on passe dans E 3. Nous allons ainsi montrer que l application P est linéaire. Dans toute la suite, on utilisera les coordonnées homogènes de manière systématique. 2. La projection de E 3 dans E 2 est linéaire On décompose cette transformation en un changement de repère d une part, nous permettant de passer du repère-monde R M à un repère R CAM aligné sur le centre optique de la lentille convergente de la caméra, et une projection perspective sur le capteur d autre part. Figure 3 Changement de référentiel : R M R CAM 4
5 2.1. Les rotations et les translations sont linéaires On décompose le premier changement de repère en une translation selon le vecteur T = O M O CAM puis une rotation R bien choisie. Cela constitue une application non linéaire de R 3 mais linéaire de E 3, dont voici la matrice : R T X 1 = RX + T Les projections perspectives sont linéaires Figure 4 Projection perspective dans R CAM Une fois dans le repère R CAM, la projection perspective sur R CAP T réalisée par la lentille équivalente convergente s écrit simplement : x = f X Z y = f Y Z Encore une fois, c est une transformation non linéaire de R 3 dans R 2, mais linéaire de E 3 dans E 2 ; en voici la matrice : f f X Y Z 1 = fx fy Z = f X Z f Y Z 1 5
6 3. Calcul de la matrice de projection 3.1. Situation J ai tout d abord tenté d établir la matrice P de projection correspondant à une caméra à partir des matrices précédemment données. Cependant, cela nécessite une connaissance précise de la position de O CAP T, le centre optique de la lentille et de la valeur de f, des données inconnues si l on utilise des caméras grand public. Une estimation de ces valeurs de l ordre du centimètre m a permis de construire un système commettant une erreur de 5 à 10% sur les mesures qu il effectue. Je propose ici une méthode de calcul de P bien plus précise et facilement automatisable. On place une mire de calibration dans le champ de la caméra. Cette mire est composée de n points X i dont on mesure les coordonnées dans le repère R M. On mesure par ailleurs la position de leurs projetés respectifs x i sur une image de la caméra. On dispose donc de n correspondances X i x i. Soit i {1,..., n}, alors x i = P X i. En coordonnées homogènes, les facteurs scalaires n ont pas d importance, on ne perd donc pas d information en écrivant x i P X i = 0. x y w P 1 P 2 P 3 yp 3 X i wp 2 X i X i = wp 1 X i xp 3 X i xp 2 X i yp 1 X i = w t X i y t X i w t X i x t X i y t X i x t X i t P 1 t P 2 t P 3 = A 3,12. P = 0 Chaque correspondance ne fournit en fait que deux équations indépendantes étant donné que xl 1 + yl 2 = wl 3. Cela nous donne donc un système à 2n équations et 12 inconnues : A 2n,12. P = 0. On pourrait ne conserver que 11 équations indépendantes et trouver P comme un vecteur du noyau de A 11,12, mais cela donne trop d importance à une possible erreur de mesure ponctuelle. On prendra donc n > 6 et on cherchera à minimiser A 2n,12. P, tout en sachant que la solution P = 0 ne nous intéresse pas. Comme les facteurs scalaires n importent pas, on va minimiser A 2n,12. P avec la contrainte P = 1. 6
7 3.2. Décomposition en Valeurs Singulières (SVD) Soit m n et A M m,n (R). Il existe U M m,n (R) à vecteurs colonnes orthonormaux, V O n (R) et S D + n (R) à entrées décroissantes tels que Démonstration : A = US t V t MM S + n (R), donc d après le théorème spectral, il existe V O n (R), r n et D D + r (R) à entrées décroissantes tels que t V t MMV = D 0 r,n r 0 n r,r 0 n r,n r Soit, en décomposant en blocs compatibles de tailles bien choisies : t V 1 t V 2 t MM ( V 1 V 2 ) = t V t 1MMV 1 t V t 2MMV 1 t V t 1MMV 2 t V t 2MMV 2 = D (0) (0) (0) On note alors que t V1MMV t 1 = D, MV 2 = 0 et on rappelle que V O n (R) donc V1 t V 1 + V2 t V 2 = I n Reste à poser U 1 = MV 1 D 1/2 M m,r (R) et à la compléter avec U 2 M m,n r (R) formée de vecteurs orthogonaux entre eux et orthogonaux aux vecteurs colonnes de U 1 de manière à former U = (U 1 U 2 ) M m,n (R). On vérifie alors que t U 1 U 1 = D 1/2. t V 1. t M.M.V 1.D 1/2 = D 1/2.D.D 1/2 = I r t UU = t U 1 t U 2 ( U 1 U 2 ) = t U 1 U 1 t U 1 U 2 t U 2 U 1 t U 2 U 2 = I r (0) (0) I n r = I n D 1/2 (0) En prenant par ailleurs S =, on vérifie que (0) (0) ( ) U.S. t V = MV 1 D 1/2 D 1/2 (0) t V 1 U 2 = MV 1 t V 1 = M(I n V2 t V 2 ) = M (0) (0) t V 2 Soit le résultat annoncé. 7
8 3.3. Trouver x qui minimise Ax et tel que x = 1 Soit m n et A M m,n (R). On effectue la décomposition SVD de A. Ax = US t V x = S t V x et x = t V x. En posant y = t V x, cela revient à minimiser Sy y. S étant diagonale à entrées positives décroissantes, on trouve y = (0,..., 0, 1) et comme x = V y, x est la dernière colonne de V Algorithme de calcul de P par Transformation Linéaire Directe (DLT) Objectif : À partir de n 6 correspondances X i x i, déterminer la matrice de projection P telle que x = P X. Algorithme : Pour tout i {1,..., n} calculer A (i) 2,12. Fusionner les n matrices A (i) 2,12 pour former A 2n,12. Effectuer la décomposition SVD de A 2n,12. La dernière colonne de V contient les coefficients de P. Amélioration : Le système dont on cherche une solution approchée est l intersection de n systèmes yp 3 X i wp 2 X i = 0 wp 1 X i xp 3 X i Or en pratique, x et y sont de l ordre de 10 2 et w = 1. En minimisant A 2n,12 P, on fait donc de plus grosses erreurs sur P 1 et P 2 que sur P 3. On voudrait ainsi x, y et w du même ordre de grandeur. De même, on veut éviter qu une partie A (i) 2,12 du système ait un plus grand «poids» qu une autre, il faudrait donc que cet ordre de grandeur soit le même pour tous les x i. Ce raisonnement s applique aussi aux X i. On rajoute de ce fait une étape préliminaire à l algorithme précédent : on calcule une matrice T (resp. T ) qui centre le nuage des x i (resp. X i ) sur l origine et telle que la moyenne des normes des x i (resp. X i ) égale 2 (resp. 3). On aura alors les T x i de l ordre de (1, 1, 1) et les T X i de (1, 1, 1, 1). On applique notre algorithme à ces nouvelles correspondances T x i T X i et l on retourne T 1 P T au lieu de P. 8
9 II. Triangulation Maintenant que l on connait les matrices de projection associées aux différentes caméras, on souhaite retrouver la position X d un objet de l espace uniquement à partir des positions x i des images de cet objet sur les capteurs des caméras. 1. Situation Figure 5 Objet vu par deux caméras Pour une caméra, on a x = P X, que l on écrira plutôt x P X = 0 : x P 1 yp 3 wp 2 y P 2 X = wp 1 xp 3 X = 0 w P 3 xp 2 yp 1 Encore une fois, ce système ne contient que deux équations indépendantes. On en conserve les deux premières, auxquelles on joint les équations provenant de la deuxième caméra : yp 3 wp 2 wp 1 xp 3 y P 3 w X = A 4,4.X = 0 P 2 w P 1 x P 3 2. Algorithme de triangulation DLT Objectif : À partir d un couple (x, x ) d images par deux caméras (P, P ) du même point réel, calculer les coordonnées de ce point. Algorithme : Calculer A 4,4. Effectuer sa décomposition SVD. X est la dernière colonne de V. 9
10 3. Condition d existence d une solution En pratique, à cause des erreurs de mesure et de l utilisation de flottants, ce système est déterminé, d où l intérêt d appliquer le même algorithme DLT, qui nous fournit lui une solution approchée non nulle. Figure 6 Cas idéal (en haut) et cas pratique (en bas) À quelle condition un point de l espace est-il filmé par les deux caméras? Figure 7 L objet doit être dans l intersection des champs de deux caméras 10
11 III. Suivi de la trajectoire On sait désormais, à partir des images de l objet sur les capteurs, déterminer sa position dans l espace. Reste donc d une part à produire un algorithme capable de détecter effectivement l objet sur une image et d autre part à appliquer tous les algorithmes précédents à une série d images correspondant au film de l objet en mouvement. 1. Algorithme naïf de détection de l objet Objectif : Détecter un objet lumineux unique sur une image de p q pixels. Algorithme : Convertir l image en une matrice p q. Pour chaque pixel, calculer sa luminance Y = 0, 299R + 0, 587G + 0, 114B. Calculer le contraste moyen et établir un seuil de détection. Le point cherché est le barycentre des pixels dont la luminance est supérieure à ce seuil. 2. Algorithme de suivi de trajectoire Objectif : À partir de deux séries de photographies simultanées de la même scène en mouvement, déterminer la trajectoire d un objet donné. Algorithme : Calibrer les deux caméras avec l algorithme DLT. Pour chaque image, détecter l objet avec l algorithme précédent. Avec chaque couple d images, déterminer la position de l objet par triangulation DLT. Tracer la trajectoire en reliant les positions obtenues. 11
12 IV. Un premier essai : cas idéal 1. Description de l expérience Afin de tester ce système, j ai simulé une scène représentant le déplacement d une balle à l aide du logiciel 3ds Max. Celui-ci donne la position exacte de l objet au cours du temps et produit des images de la scène vue par des caméras virtuelles. Figure 8 Vue d ensemble de la scène et balle filmée par la caméra 2 2. Résultats Voici la superposition de la trajectoire exacte de la balle d une part, et de la trajectoire calculée avec l algorithme de suivi à partir des images simulées : Figure 9 Trajectoires théorique et expérimentale superposées, vues d ensemble et rapprochée L erreur relative mesurée (en module) est de l ordre de 0.10%. Si un tel système surveillait une surface de la taille d un demi-court de tennis, il ferait une erreur moyenne d environ 1 cm. 12
13 V. Deuxième essai : en situation réelle 1. Description de l expérience J ai enfin testé la capacité de ce système à suivre, en situation réelle, le mouvement d une balle de tennis rebondissant au sol. J ai pour cela utilisé deux appareils photo numériques grand public différents en mode vidéo. Figure 10 Mire de calibration et balle filmée par la caméra 2 2. Résultats La calibration n a pas posé de problèmes et la trajectoire déterminée correspond qualitativement au mouvement observé de la balle. Figure 11 Trajectoires estimées pour deux jets différents Il faut toutefois noter que l algorithme naïf de détection de la balle lumineuse a échoué sur plusieurs images et que la fin de la trajectoire, située dans l extrémité droite du champ de la caméra 1, a fait les frais des aberrations géométriques inhérentes à l objectif grand-angle de celle-ci. 13
14 VI. Généralisation et extensions 1. Retour sur les hypothèses simplificatrices Nous avons ici montré comment fabriquer un système de stéréovision relativement précis. Donnons maintenant quelques pistes d améliorations. Rappelons tout d abord les simplifications faites lors de l élaboration de ce système : le suivi d une unique balle lumineuse sur un fond sombre, la possibilité de modéliser l optique du capteur par une seule lentille convergente et enfin l immobilité de cette lentille. Sans revenir sur la première d entre elles, les deux dernières peuvent être écartées assez facilement. Pour ce qui est de la modélisation par une lentille convergente, il faudrait compenser les aberrations géométriques observées sur les bords des images. En fait, notre méthode de calibration, qui ne fait, en dehors de la linéarité, aucune hypothèse sur le type de projection, prend en compte toutes les déformations linéaires (dans l espace projectif). Pour les phénomènes plus complexes, on dispose de même déjà d une correction au premier ordre. Sans nous plonger davantage dans la gestion des aberrations, il serait relativement simple de calculer une matrice P générale pour l ensemble du champ de vision, puis des matrices plus précises pour chaque subdivision de l espace, réalisant une correction linéaire plus fine des aberrations dans une zone plus petite. La première nous fournirait une estimation de la position, la deuxième une mesure précise. Cette amélioration permettrait aussi de régler le problème de la lentille mobile, sa position dépendant de la mise au point donc de la position de l objet dans l espace. 2. Vision à n caméras Notre algorithme de triangulation DLT possède l avantage de facilement se généraliser à un système à n caméras. Le système A 4,4 X = 0 ayant pour solution la position de l objet est l intersection de deux systèmes A 2,4 X = 0 provenant des deux caméras. Pour n caméras, on obtiendra simplement un système A 2n,4 X = 0 duquel on pourra de la même manière obtenir une décomposition SVD. En ne joignant à ce système que les équations venant des caméras qui ont l objet dans leur champ de vision, on peut ainsi créer un système dont les capteurs se partagent l étendue d un court de tennis, par exemple. 3. D autres utilisations de la stéréovision Les systèmes permettant d effectuer des mesures en 3D à partir d image fournies par des caméras ont l avantage de ne pas être intrusifs et sont de plus en plus utilisés, dans des domaines très divers. Citons par exemple la restitution des reliefs à partir de photographies aériennes, les systèmes d aide au créneau pour les voitures et à l accostage en aérospatiale, de «Motion Capture» au cinéma, la détection des fronts de flamme dans les feux de forêts, la surveillance des piscines, la vision de robots et bien sûr les systèmes d arbitrage vidéo comme le Hawk-Eye. 14
15 Bibliographie Orteu, Jean-José, Calibrage géométrique d une caméra ou d un capteur de vision stéréoscopique, SCIRN-PRN Université du Maine, Durou, Jean-Denis et Pocquet, Anne-Marie, Vision par ordinateur, IRIT, Hartley, Richard et Zisserman, Andrew, Multiple View Geometry in computer vision, Cambridge University Press, Merci à Cédric Awanzino de Bertin Technologies pour ses précieux conseils et sa patience. 15
Exercices Corrigés Premières notions sur les espaces vectoriels
 Exercices Corrigés Premières notions sur les espaces vectoriels Exercice 1 On considére le sous-espace vectoriel F de R formé des solutions du système suivant : x1 x 2 x 3 + 2x = 0 E 1 x 1 + 2x 2 + x 3
Exercices Corrigés Premières notions sur les espaces vectoriels Exercice 1 On considére le sous-espace vectoriel F de R formé des solutions du système suivant : x1 x 2 x 3 + 2x = 0 E 1 x 1 + 2x 2 + x 3
3 Approximation de solutions d équations
 3 Approximation de solutions d équations Une équation scalaire a la forme générale f(x) =0où f est une fonction de IR dans IR. Un système de n équations à n inconnues peut aussi se mettre sous une telle
3 Approximation de solutions d équations Une équation scalaire a la forme générale f(x) =0où f est une fonction de IR dans IR. Un système de n équations à n inconnues peut aussi se mettre sous une telle
Comparaison de Relevés 3D issus de plusieurs Systèmes de Numérisation
 Laboratoire Vision & Robotique Comparaison de Relevés 3D issus de plusieurs Systèmes de Numérisation Emilie KOENIG, Benjamin ALBOUY, Sylvie TREUILLET, Yves Lucas Contact : Sylvie Treuillet Polytech'Orléans
Laboratoire Vision & Robotique Comparaison de Relevés 3D issus de plusieurs Systèmes de Numérisation Emilie KOENIG, Benjamin ALBOUY, Sylvie TREUILLET, Yves Lucas Contact : Sylvie Treuillet Polytech'Orléans
 Utilisation d informations visuelles dynamiques en asservissement visuel Armel Crétual IRISA, projet TEMIS puis VISTA L asservissement visuel géométrique Principe : Réalisation d une tâche robotique par
Utilisation d informations visuelles dynamiques en asservissement visuel Armel Crétual IRISA, projet TEMIS puis VISTA L asservissement visuel géométrique Principe : Réalisation d une tâche robotique par
Projet de traitement d'image - SI 381 reconstitution 3D d'intérieur à partir de photographies
 Projet de traitement d'image - SI 381 reconstitution 3D d'intérieur à partir de photographies Régis Boulet Charlie Demené Alexis Guyot Balthazar Neveu Guillaume Tartavel Sommaire Sommaire... 1 Structure
Projet de traitement d'image - SI 381 reconstitution 3D d'intérieur à partir de photographies Régis Boulet Charlie Demené Alexis Guyot Balthazar Neveu Guillaume Tartavel Sommaire Sommaire... 1 Structure
a et b étant deux nombres relatifs donnés, une fonction affine est une fonction qui a un nombre x associe le nombre ax + b
 I Définition d une fonction affine Faire l activité 1 «une nouvelle fonction» 1. définition générale a et b étant deux nombres relatifs donnés, une fonction affine est une fonction qui a un nombre x associe
I Définition d une fonction affine Faire l activité 1 «une nouvelle fonction» 1. définition générale a et b étant deux nombres relatifs donnés, une fonction affine est une fonction qui a un nombre x associe
Analyse d images. [email protected]. Edmond Boyer UFRIMA 1
 Analyse d images [email protected] Edmond Boyer UFRIMA 1 1 Généralités Analyse d images (Image Analysis) : utiliser un ordinateur pour interpréter le monde extérieur au travers d images. Images Objets
Analyse d images [email protected] Edmond Boyer UFRIMA 1 1 Généralités Analyse d images (Image Analysis) : utiliser un ordinateur pour interpréter le monde extérieur au travers d images. Images Objets
Fonctions linéaires et affines. 1 Fonctions linéaires. 1.1 Vocabulaire. 1.2 Représentation graphique. 3eme
 Fonctions linéaires et affines 3eme 1 Fonctions linéaires 1.1 Vocabulaire Définition 1 Soit a un nombre quelconque «fixe». Une fonction linéaire associe à un nombre x quelconque le nombre a x. a s appelle
Fonctions linéaires et affines 3eme 1 Fonctions linéaires 1.1 Vocabulaire Définition 1 Soit a un nombre quelconque «fixe». Une fonction linéaire associe à un nombre x quelconque le nombre a x. a s appelle
Analyse de la vidéo. Chapitre 4.1 - La modélisation pour le suivi d objet. 10 mars 2015. Chapitre 4.1 - La modélisation d objet 1 / 57
 Analyse de la vidéo Chapitre 4.1 - La modélisation pour le suivi d objet 10 mars 2015 Chapitre 4.1 - La modélisation d objet 1 / 57 La représentation d objets Plan de la présentation 1 La représentation
Analyse de la vidéo Chapitre 4.1 - La modélisation pour le suivi d objet 10 mars 2015 Chapitre 4.1 - La modélisation d objet 1 / 57 La représentation d objets Plan de la présentation 1 La représentation
IMAGES NUMÉRIQUES MATRICIELLES EN SCILAB
 IMAGES NUMÉRIQUES MATRICIELLES EN SCILAB Ce document, écrit par des animateurs de l IREM de Besançon, a pour objectif de présenter quelques unes des fonctions du logiciel Scilab, celles qui sont spécifiques
IMAGES NUMÉRIQUES MATRICIELLES EN SCILAB Ce document, écrit par des animateurs de l IREM de Besançon, a pour objectif de présenter quelques unes des fonctions du logiciel Scilab, celles qui sont spécifiques
Théorème du point fixe - Théorème de l inversion locale
 Chapitre 7 Théorème du point fixe - Théorème de l inversion locale Dans ce chapitre et le suivant, on montre deux applications importantes de la notion de différentiabilité : le théorème de l inversion
Chapitre 7 Théorème du point fixe - Théorème de l inversion locale Dans ce chapitre et le suivant, on montre deux applications importantes de la notion de différentiabilité : le théorème de l inversion
Optimisation, traitement d image et éclipse de Soleil
 Kléber, PCSI1&3 014-015 I. Introduction 1/8 Optimisation, traitement d image et éclipse de Soleil Partie I Introduction Le 0 mars 015 a eu lieu en France une éclipse partielle de Soleil qu il était particulièrement
Kléber, PCSI1&3 014-015 I. Introduction 1/8 Optimisation, traitement d image et éclipse de Soleil Partie I Introduction Le 0 mars 015 a eu lieu en France une éclipse partielle de Soleil qu il était particulièrement
Reconstruction de bâtiments en 3D à partir de nuages de points LIDAR
 Reconstruction de bâtiments en 3D à partir de nuages de points LIDAR Mickaël Bergem 25 juin 2014 Maillages et applications 1 Table des matières Introduction 3 1 La modélisation numérique de milieux urbains
Reconstruction de bâtiments en 3D à partir de nuages de points LIDAR Mickaël Bergem 25 juin 2014 Maillages et applications 1 Table des matières Introduction 3 1 La modélisation numérique de milieux urbains
Résolution d équations non linéaires
 Analyse Numérique Résolution d équations non linéaires Said EL HAJJI et Touria GHEMIRES Université Mohammed V - Agdal. Faculté des Sciences Département de Mathématiques. Laboratoire de Mathématiques, Informatique
Analyse Numérique Résolution d équations non linéaires Said EL HAJJI et Touria GHEMIRES Université Mohammed V - Agdal. Faculté des Sciences Département de Mathématiques. Laboratoire de Mathématiques, Informatique
PHYSIQUE 2 - Épreuve écrite
 PHYSIQUE - Épreuve écrite WARIN André I. Remarques générales Le sujet de physique de la session 010 comprenait une partie A sur l optique et une partie B sur l électromagnétisme. - La partie A, à caractère
PHYSIQUE - Épreuve écrite WARIN André I. Remarques générales Le sujet de physique de la session 010 comprenait une partie A sur l optique et une partie B sur l électromagnétisme. - La partie A, à caractère
de calibration Master 2: Calibration de modèles: présentation et simulation d
 Master 2: Calibration de modèles: présentation et simulation de quelques problèmes de calibration Plan de la présentation 1. Présentation de quelques modèles à calibrer 1a. Reconstruction d une courbe
Master 2: Calibration de modèles: présentation et simulation de quelques problèmes de calibration Plan de la présentation 1. Présentation de quelques modèles à calibrer 1a. Reconstruction d une courbe
Opérations de base sur ImageJ
 Opérations de base sur ImageJ TPs d hydrodynamique de l ESPCI, J. Bico, M. Reyssat, M. Fermigier ImageJ est un logiciel libre, qui fonctionne aussi bien sous plate-forme Windows, Mac ou Linux. Initialement
Opérations de base sur ImageJ TPs d hydrodynamique de l ESPCI, J. Bico, M. Reyssat, M. Fermigier ImageJ est un logiciel libre, qui fonctionne aussi bien sous plate-forme Windows, Mac ou Linux. Initialement
Notion de fonction. Résolution graphique. Fonction affine.
 TABLE DES MATIÈRES 1 Notion de fonction. Résolution graphique. Fonction affine. Paul Milan LMA Seconde le 12 décembre 2011 Table des matières 1 Fonction numérique 2 1.1 Introduction.................................
TABLE DES MATIÈRES 1 Notion de fonction. Résolution graphique. Fonction affine. Paul Milan LMA Seconde le 12 décembre 2011 Table des matières 1 Fonction numérique 2 1.1 Introduction.................................
Programmation linéaire et Optimisation. Didier Smets
 Programmation linéaire et Optimisation Didier Smets Chapitre 1 Un problème d optimisation linéaire en dimension 2 On considère le cas d un fabricant d automobiles qui propose deux modèles à la vente, des
Programmation linéaire et Optimisation Didier Smets Chapitre 1 Un problème d optimisation linéaire en dimension 2 On considère le cas d un fabricant d automobiles qui propose deux modèles à la vente, des
Cours de Mécanique du point matériel
 Cours de Mécanique du point matériel SMPC1 Module 1 : Mécanique 1 Session : Automne 2014 Prof. M. EL BAZ Cours de Mécanique du Point matériel Chapitre 1 : Complément Mathématique SMPC1 Chapitre 1: Rappels
Cours de Mécanique du point matériel SMPC1 Module 1 : Mécanique 1 Session : Automne 2014 Prof. M. EL BAZ Cours de Mécanique du Point matériel Chapitre 1 : Complément Mathématique SMPC1 Chapitre 1: Rappels
Sujet. calculatrice: autorisée durée: 4 heures
 DS SCIENCES PHYSIQUES MATHSPÉ calculatrice: autorisée durée: 4 heures Sujet Approche d'un projecteur de diapositives...2 I.Questions préliminaires...2 A.Lentille divergente...2 B.Lentille convergente et
DS SCIENCES PHYSIQUES MATHSPÉ calculatrice: autorisée durée: 4 heures Sujet Approche d'un projecteur de diapositives...2 I.Questions préliminaires...2 A.Lentille divergente...2 B.Lentille convergente et
Développement mobile MIDP 2.0 Mobile 3D Graphics API (M3G) JSR 184. Frédéric BERTIN [email protected]
 Développement mobile MIDP 2.0 Mobile 3D Graphics API (M3G) JSR 184 Frédéric BERTIN [email protected] Présentaion : Mobile 3D Graphics API JSR 184 M3G :présentation Package optionnel de l api J2ME. Prend
Développement mobile MIDP 2.0 Mobile 3D Graphics API (M3G) JSR 184 Frédéric BERTIN [email protected] Présentaion : Mobile 3D Graphics API JSR 184 M3G :présentation Package optionnel de l api J2ME. Prend
TESTS PORTMANTEAU D ADÉQUATION DE MODÈLES ARMA FAIBLES : UNE APPROCHE BASÉE SUR L AUTO-NORMALISATION
 TESTS PORTMANTEAU D ADÉQUATION DE MODÈLES ARMA FAIBLES : UNE APPROCHE BASÉE SUR L AUTO-NORMALISATION Bruno Saussereau Laboratoire de Mathématiques de Besançon Université de Franche-Comté Travail en commun
TESTS PORTMANTEAU D ADÉQUATION DE MODÈLES ARMA FAIBLES : UNE APPROCHE BASÉE SUR L AUTO-NORMALISATION Bruno Saussereau Laboratoire de Mathématiques de Besançon Université de Franche-Comté Travail en commun
Transmission d informations sur le réseau électrique
 Transmission d informations sur le réseau électrique Introduction Remarques Toutes les questions en italique devront être préparées par écrit avant la séance du TP. Les préparations seront ramassées en
Transmission d informations sur le réseau électrique Introduction Remarques Toutes les questions en italique devront être préparées par écrit avant la séance du TP. Les préparations seront ramassées en
Programmes des classes préparatoires aux Grandes Ecoles
 Programmes des classes préparatoires aux Grandes Ecoles Filière : scientifique Voie : Biologie, chimie, physique et sciences de la Terre (BCPST) Discipline : Mathématiques Seconde année Préambule Programme
Programmes des classes préparatoires aux Grandes Ecoles Filière : scientifique Voie : Biologie, chimie, physique et sciences de la Terre (BCPST) Discipline : Mathématiques Seconde année Préambule Programme
1 Définition. 2 Systèmes matériels et solides. 3 Les actions mécaniques. Le système matériel : Il peut être un ensemble.un sous-ensemble..
 1 Définition GÉNÉRALITÉS Statique 1 2 Systèmes matériels et solides Le système matériel : Il peut être un ensemble.un sous-ensemble..une pièce mais aussi un liquide ou un gaz Le solide : Il est supposé
1 Définition GÉNÉRALITÉS Statique 1 2 Systèmes matériels et solides Le système matériel : Il peut être un ensemble.un sous-ensemble..une pièce mais aussi un liquide ou un gaz Le solide : Il est supposé
Vision industrielle et télédétection - Détection d ellipses. Guillaume Martinez 17 décembre 2007
 Vision industrielle et télédétection - Détection d ellipses Guillaume Martinez 17 décembre 2007 1 Table des matières 1 Le projet 3 1.1 Objectif................................ 3 1.2 Les choix techniques.........................
Vision industrielle et télédétection - Détection d ellipses Guillaume Martinez 17 décembre 2007 1 Table des matières 1 Le projet 3 1.1 Objectif................................ 3 1.2 Les choix techniques.........................
Première partie. Préliminaires : noyaux itérés. MPSI B 6 juin 2015
 Énoncé Soit V un espace vectoriel réel. L espace vectoriel des endomorphismes de V est désigné par L(V ). Lorsque f L(V ) et k N, on désigne par f 0 = Id V, f k = f k f la composée de f avec lui même k
Énoncé Soit V un espace vectoriel réel. L espace vectoriel des endomorphismes de V est désigné par L(V ). Lorsque f L(V ) et k N, on désigne par f 0 = Id V, f k = f k f la composée de f avec lui même k
La programmation linéaire : une introduction. Qu est-ce qu un programme linéaire? Terminologie. Écriture mathématique
 La programmation linéaire : une introduction Qu est-ce qu un programme linéaire? Qu est-ce qu un programme linéaire? Exemples : allocation de ressources problème de recouvrement Hypothèses de la programmation
La programmation linéaire : une introduction Qu est-ce qu un programme linéaire? Qu est-ce qu un programme linéaire? Exemples : allocation de ressources problème de recouvrement Hypothèses de la programmation
L analyse d images regroupe plusieurs disciplines que l on classe en deux catégories :
 La vision nous permet de percevoir et d interpreter le monde qui nous entoure. La vision artificielle a pour but de reproduire certaines fonctionnalités de la vision humaine au travers de l analyse d images.
La vision nous permet de percevoir et d interpreter le monde qui nous entoure. La vision artificielle a pour but de reproduire certaines fonctionnalités de la vision humaine au travers de l analyse d images.
LE PROJOPHONE de Fresnel
 LE PROJOPHONE de Fresnel Le principe général est assez simple : l'image de l écran est agrandie et projetée à l'aide de la lentille optique. Nous allons commencer par créer un élément dans lequel le téléphone
LE PROJOPHONE de Fresnel Le principe général est assez simple : l'image de l écran est agrandie et projetée à l'aide de la lentille optique. Nous allons commencer par créer un élément dans lequel le téléphone
Chapitre 3. Mesures stationnaires. et théorèmes de convergence
 Chapitre 3 Mesures stationnaires et théorèmes de convergence Christiane Cocozza-Thivent, Université de Marne-la-Vallée p.1 I. Mesures stationnaires Christiane Cocozza-Thivent, Université de Marne-la-Vallée
Chapitre 3 Mesures stationnaires et théorèmes de convergence Christiane Cocozza-Thivent, Université de Marne-la-Vallée p.1 I. Mesures stationnaires Christiane Cocozza-Thivent, Université de Marne-la-Vallée
Fonctions de plusieurs variables
 Module : Analyse 03 Chapitre 00 : Fonctions de plusieurs variables Généralités et Rappels des notions topologiques dans : Qu est- ce que?: Mathématiquement, n étant un entier non nul, on définit comme
Module : Analyse 03 Chapitre 00 : Fonctions de plusieurs variables Généralités et Rappels des notions topologiques dans : Qu est- ce que?: Mathématiquement, n étant un entier non nul, on définit comme
Caractéristiques des ondes
 Caractéristiques des ondes Chapitre Activités 1 Ondes progressives à une dimension (p 38) A Analyse qualitative d une onde b Fin de la Début de la 1 L onde est progressive puisque la perturbation se déplace
Caractéristiques des ondes Chapitre Activités 1 Ondes progressives à une dimension (p 38) A Analyse qualitative d une onde b Fin de la Début de la 1 L onde est progressive puisque la perturbation se déplace
F411 - Courbes Paramétrées, Polaires
 1/43 Courbes Paramétrées Courbes polaires Longueur d un arc, Courbure F411 - Courbes Paramétrées, Polaires Michel Fournié [email protected] http://www.math.univ-toulouse.fr/ fournie/ Année 2012/2013
1/43 Courbes Paramétrées Courbes polaires Longueur d un arc, Courbure F411 - Courbes Paramétrées, Polaires Michel Fournié [email protected] http://www.math.univ-toulouse.fr/ fournie/ Année 2012/2013
Cours d analyse numérique SMI-S4
 ours d analyse numérique SMI-S4 Introduction L objet de l analyse numérique est de concevoir et d étudier des méthodes de résolution de certains problèmes mathématiques, en général issus de problèmes réels,
ours d analyse numérique SMI-S4 Introduction L objet de l analyse numérique est de concevoir et d étudier des méthodes de résolution de certains problèmes mathématiques, en général issus de problèmes réels,
CHAPITRE. Le mouvement en deux dimensions CORRIGÉ DES EXERCICES
 CHAPITRE Le mouvement en deux dimensions CORRIGÉ DES EXERCICES Exercices. Les vecteurs du mouvement SECTION. 5. Une montgolfière, initialement au repos, se déplace à vitesse constante. En 5 min, elle
CHAPITRE Le mouvement en deux dimensions CORRIGÉ DES EXERCICES Exercices. Les vecteurs du mouvement SECTION. 5. Une montgolfière, initialement au repos, se déplace à vitesse constante. En 5 min, elle
Le théorème de Perron-Frobenius, les chaines de Markov et un célèbre moteur de recherche
 Le théorème de Perron-Frobenius, les chaines de Markov et un célèbre moteur de recherche Bachir Bekka Février 2007 Le théorème de Perron-Frobenius a d importantes applications en probabilités (chaines
Le théorème de Perron-Frobenius, les chaines de Markov et un célèbre moteur de recherche Bachir Bekka Février 2007 Le théorème de Perron-Frobenius a d importantes applications en probabilités (chaines
Optimisation non linéaire Irène Charon, Olivier Hudry École nationale supérieure des télécommunications
 Optimisation non linéaire Irène Charon, Olivier Hudry École nationale supérieure des télécommunications A. Optimisation sans contrainte.... Généralités.... Condition nécessaire et condition suffisante
Optimisation non linéaire Irène Charon, Olivier Hudry École nationale supérieure des télécommunications A. Optimisation sans contrainte.... Généralités.... Condition nécessaire et condition suffisante
Cours 02 : Problème général de la programmation linéaire
 Cours 02 : Problème général de la programmation linéaire Cours 02 : Problème général de la Programmation Linéaire. 5 . Introduction Un programme linéaire s'écrit sous la forme suivante. MinZ(ou maxw) =
Cours 02 : Problème général de la programmation linéaire Cours 02 : Problème général de la Programmation Linéaire. 5 . Introduction Un programme linéaire s'écrit sous la forme suivante. MinZ(ou maxw) =
Représentation géométrique d un nombre complexe
 CHAPITRE 1 NOMBRES COMPLEXES 1 Représentation géométrique d un nombre complexe 1. Ensemble des nombres complexes Soit i le nombre tel que i = 1 L ensemble des nombres complexes est l ensemble des nombres
CHAPITRE 1 NOMBRES COMPLEXES 1 Représentation géométrique d un nombre complexe 1. Ensemble des nombres complexes Soit i le nombre tel que i = 1 L ensemble des nombres complexes est l ensemble des nombres
M6 MOMENT CINÉTIQUE D UN POINT MATÉRIEL
 M6 MOMENT CINÉTIQUE D UN POINT MATÉRIEL OBJECTIFS Jusqu à présent, nous avons rencontré deux méthodes pour obtenir l équation du mouvement d un point matériel : - l utilisation du P.F.D. - et celle du
M6 MOMENT CINÉTIQUE D UN POINT MATÉRIEL OBJECTIFS Jusqu à présent, nous avons rencontré deux méthodes pour obtenir l équation du mouvement d un point matériel : - l utilisation du P.F.D. - et celle du
Q6 : Comment calcule t-on l intensité sonore à partir du niveau d intensité?
 EXERCICE 1 : QUESTION DE COURS Q1 : Qu est ce qu une onde progressive? Q2 : Qu est ce qu une onde mécanique? Q3 : Qu elle est la condition pour qu une onde soit diffractée? Q4 : Quelles sont les différentes
EXERCICE 1 : QUESTION DE COURS Q1 : Qu est ce qu une onde progressive? Q2 : Qu est ce qu une onde mécanique? Q3 : Qu elle est la condition pour qu une onde soit diffractée? Q4 : Quelles sont les différentes
MESURE ET PRECISION. Il est clair que si le voltmètre mesure bien la tension U aux bornes de R, l ampèremètre, lui, mesure. R mes. mes. .
 MESURE ET PRECISIO La détermination de la valeur d une grandeur G à partir des mesures expérimentales de grandeurs a et b dont elle dépend n a vraiment de sens que si elle est accompagnée de la précision
MESURE ET PRECISIO La détermination de la valeur d une grandeur G à partir des mesures expérimentales de grandeurs a et b dont elle dépend n a vraiment de sens que si elle est accompagnée de la précision
Items étudiés dans le CHAPITRE N5. 7 et 9 p 129 D14 Déterminer par le calcul l'antécédent d'un nombre par une fonction linéaire
 CHAPITRE N5 FONCTIONS LINEAIRES NOTION DE FONCTION FONCTIONS LINEAIRES NOTION DE FONCTION FONCTIONS LINEAIRES NOTION DE FONCTION Code item D0 D2 N30[S] Items étudiés dans le CHAPITRE N5 Déterminer l'image
CHAPITRE N5 FONCTIONS LINEAIRES NOTION DE FONCTION FONCTIONS LINEAIRES NOTION DE FONCTION FONCTIONS LINEAIRES NOTION DE FONCTION Code item D0 D2 N30[S] Items étudiés dans le CHAPITRE N5 Déterminer l'image
Ligne Dentaire. Système Dentaire Panoramique et 3D
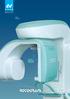 Ligne Dentaire Système Dentaire Panoramique et 3D La Société Villa Sistemi Medicali est fière de présenter son nouveau panoramique Rotograph Evo 3D, un système d'imagerie dentaire avec fonctionnalité 3-en-1:
Ligne Dentaire Système Dentaire Panoramique et 3D La Société Villa Sistemi Medicali est fière de présenter son nouveau panoramique Rotograph Evo 3D, un système d'imagerie dentaire avec fonctionnalité 3-en-1:
Exo7. Matrice d une application linéaire. Corrections d Arnaud Bodin.
 Exo7 Matrice d une application linéaire Corrections d Arnaud odin. Exercice Soit R muni de la base canonique = ( i, j). Soit f : R R la projection sur l axe des abscisses R i parallèlement à R( i + j).
Exo7 Matrice d une application linéaire Corrections d Arnaud odin. Exercice Soit R muni de la base canonique = ( i, j). Soit f : R R la projection sur l axe des abscisses R i parallèlement à R( i + j).
Les algorithmes de base du graphisme
 Les algorithmes de base du graphisme Table des matières 1 Traçage 2 1.1 Segments de droites......................... 2 1.1.1 Algorithmes simples.................... 3 1.1.2 Algorithmes de Bresenham (1965).............
Les algorithmes de base du graphisme Table des matières 1 Traçage 2 1.1 Segments de droites......................... 2 1.1.1 Algorithmes simples.................... 3 1.1.2 Algorithmes de Bresenham (1965).............
Better data. Better decisions. La carière digitale, nouvel outil de suivi et de gestion de l exploitation
 Better data. Better decisions. La carière digitale, nouvel outil de suivi et de gestion de l exploitation CIGO Juin 2015 Nous vivons dans un environnement digital De nombreux éléments personnels ou professionnels
Better data. Better decisions. La carière digitale, nouvel outil de suivi et de gestion de l exploitation CIGO Juin 2015 Nous vivons dans un environnement digital De nombreux éléments personnels ou professionnels
Chap 8 - TEMPS & RELATIVITE RESTREINTE
 Chap 8 - TEMPS & RELATIVITE RESTREINTE Exercice 0 page 9 On considère deux évènements E et E Référentiel propre, R : la Terre. Dans ce référentiel, les deux évènements ont lieu au même endroit. La durée
Chap 8 - TEMPS & RELATIVITE RESTREINTE Exercice 0 page 9 On considère deux évènements E et E Référentiel propre, R : la Terre. Dans ce référentiel, les deux évènements ont lieu au même endroit. La durée
Souad EL Bernoussi. Groupe d Analyse Numérique et Optimisation Rabat http ://www.fsr.ac.ma/ano/
 Recherche opérationnelle Les démonstrations et les exemples seront traités en cours Souad EL Bernoussi Groupe d Analyse Numérique et Optimisation Rabat http ://www.fsr.ac.ma/ano/ Table des matières 1 Programmation
Recherche opérationnelle Les démonstrations et les exemples seront traités en cours Souad EL Bernoussi Groupe d Analyse Numérique et Optimisation Rabat http ://www.fsr.ac.ma/ano/ Table des matières 1 Programmation
Structures algébriques
 Structures algébriques 1. Lois de composition s Soit E un ensemble. Une loi de composition interne sur E est une application de E E dans E. Soient E et F deux ensembles. Une loi de composition externe
Structures algébriques 1. Lois de composition s Soit E un ensemble. Une loi de composition interne sur E est une application de E E dans E. Soient E et F deux ensembles. Une loi de composition externe
Immersion - Vision 3D dans la RV.
 Cours RVS Master II IVA Immersion - Vision 3D dans la RV. Cours de Réalité Virtuelle et Simulation Master II - IVA A. Mebarki - Maître de Conférences Département d'informatique Faculté des Mathématiques
Cours RVS Master II IVA Immersion - Vision 3D dans la RV. Cours de Réalité Virtuelle et Simulation Master II - IVA A. Mebarki - Maître de Conférences Département d'informatique Faculté des Mathématiques
Baccalauréat S Antilles-Guyane 11 septembre 2014 Corrigé
 Baccalauréat S ntilles-guyane 11 septembre 14 Corrigé EXERCICE 1 6 points Commun à tous les candidats Une entreprise de jouets en peluche souhaite commercialiser un nouveau produit et à cette fin, effectue
Baccalauréat S ntilles-guyane 11 septembre 14 Corrigé EXERCICE 1 6 points Commun à tous les candidats Une entreprise de jouets en peluche souhaite commercialiser un nouveau produit et à cette fin, effectue
La Licence Mathématiques et Economie-MASS Université de Sciences Sociales de Toulouse 1
 La Licence Mathématiques et Economie-MASS Université de Sciences Sociales de Toulouse 1 La licence Mathématiques et Economie-MASS de l Université des Sciences Sociales de Toulouse propose sur les trois
La Licence Mathématiques et Economie-MASS Université de Sciences Sociales de Toulouse 1 La licence Mathématiques et Economie-MASS de l Université des Sciences Sociales de Toulouse propose sur les trois
Comment choisir sa tablette?
 Comment choisir sa tablette? Sommaire Ø Critère n 1 : le système d exploitation Ø Critère n 2 : Les caractéristiques techniques Ø Les petits plus Ø Nos bons plans Ø Ils comparent pour vous Lancée en 2010
Comment choisir sa tablette? Sommaire Ø Critère n 1 : le système d exploitation Ø Critère n 2 : Les caractéristiques techniques Ø Les petits plus Ø Nos bons plans Ø Ils comparent pour vous Lancée en 2010
Chapitre 3. Les distributions à deux variables
 Chapitre 3. Les distributions à deux variables Jean-François Coeurjolly http://www-ljk.imag.fr/membres/jean-francois.coeurjolly/ Laboratoire Jean Kuntzmann (LJK), Grenoble University 1 Distributions conditionnelles
Chapitre 3. Les distributions à deux variables Jean-François Coeurjolly http://www-ljk.imag.fr/membres/jean-francois.coeurjolly/ Laboratoire Jean Kuntzmann (LJK), Grenoble University 1 Distributions conditionnelles
DURÉE DU JOUR EN FONCTION DE LA DATE ET DE LA LATITUDE
 DURÉE DU JUR E FCTI DE LA DATE ET DE LA LATITUDE ous allons nous intéresser à la durée du jour, prise ici dans le sens de période d éclairement par le Soleil dans une journée de 4 h, en un lieu donné de
DURÉE DU JUR E FCTI DE LA DATE ET DE LA LATITUDE ous allons nous intéresser à la durée du jour, prise ici dans le sens de période d éclairement par le Soleil dans une journée de 4 h, en un lieu donné de
Calcul matriciel. Définition 1 Une matrice de format (m,n) est un tableau rectangulaire de mn éléments, rangés en m lignes et n colonnes.
 1 Définitions, notations Calcul matriciel Définition 1 Une matrice de format (m,n) est un tableau rectangulaire de mn éléments, rangés en m lignes et n colonnes. On utilise aussi la notation m n pour le
1 Définitions, notations Calcul matriciel Définition 1 Une matrice de format (m,n) est un tableau rectangulaire de mn éléments, rangés en m lignes et n colonnes. On utilise aussi la notation m n pour le
Soit la fonction affine qui, pour représentant le nombre de mois écoulés, renvoie la somme économisée.
 ANALYSE 5 points Exercice 1 : Léonie souhaite acheter un lecteur MP3. Le prix affiché (49 ) dépasse largement la somme dont elle dispose. Elle décide donc d économiser régulièrement. Elle a relevé qu elle
ANALYSE 5 points Exercice 1 : Léonie souhaite acheter un lecteur MP3. Le prix affiché (49 ) dépasse largement la somme dont elle dispose. Elle décide donc d économiser régulièrement. Elle a relevé qu elle
10 leçon 2. Leçon n 2 : Contact entre deux solides. Frottement de glissement. Exemples. (PC ou 1 er CU)
 0 leçon 2 Leçon n 2 : Contact entre deu solides Frottement de glissement Eemples (PC ou er CU) Introduction Contact entre deu solides Liaisons de contact 2 Contact ponctuel 2 Frottement de glissement 2
0 leçon 2 Leçon n 2 : Contact entre deu solides Frottement de glissement Eemples (PC ou er CU) Introduction Contact entre deu solides Liaisons de contact 2 Contact ponctuel 2 Frottement de glissement 2
Représentation des Nombres
 Chapitre 5 Représentation des Nombres 5. Representation des entiers 5.. Principe des représentations en base b Base L entier écrit 344 correspond a 3 mille + 4 cent + dix + 4. Plus généralement a n a n...
Chapitre 5 Représentation des Nombres 5. Representation des entiers 5.. Principe des représentations en base b Base L entier écrit 344 correspond a 3 mille + 4 cent + dix + 4. Plus généralement a n a n...
NOTICE DOUBLE DIPLÔME
 NOTICE DOUBLE DIPLÔME MINES ParisTech / HEC MINES ParisTech/ AgroParisTech Diplômes obtenus : Diplôme d ingénieur de l Ecole des Mines de Paris Diplôme de HEC Paris Ou Diplôme d ingénieur de l Ecole des
NOTICE DOUBLE DIPLÔME MINES ParisTech / HEC MINES ParisTech/ AgroParisTech Diplômes obtenus : Diplôme d ingénieur de l Ecole des Mines de Paris Diplôme de HEC Paris Ou Diplôme d ingénieur de l Ecole des
TP SIN Traitement d image
 TP SIN Traitement d image Pré requis (l élève doit savoir): - Utiliser un ordinateur Objectif terminale : L élève doit être capable de reconnaître un format d image et d expliquer les différents types
TP SIN Traitement d image Pré requis (l élève doit savoir): - Utiliser un ordinateur Objectif terminale : L élève doit être capable de reconnaître un format d image et d expliquer les différents types
LA PHYSIQUE DES MATERIAUX. Chapitre 1 LES RESEAUX DIRECT ET RECIPROQUE
 LA PHYSIQUE DES MATERIAUX Chapitre 1 LES RESEAUX DIRECT ET RECIPROQUE Pr. A. Belayachi Université Mohammed V Agdal Faculté des Sciences Rabat Département de Physique - L.P.M [email protected] 1 1.Le réseau
LA PHYSIQUE DES MATERIAUX Chapitre 1 LES RESEAUX DIRECT ET RECIPROQUE Pr. A. Belayachi Université Mohammed V Agdal Faculté des Sciences Rabat Département de Physique - L.P.M [email protected] 1 1.Le réseau
Baccalauréat ES Polynésie (spécialité) 10 septembre 2014 Corrigé
 Baccalauréat ES Polynésie (spécialité) 10 septembre 2014 Corrigé A. P. M. E. P. Exercice 1 5 points 1. Réponse d. : 1 e Le coefficient directeur de la tangente est négatif et n est manifestement pas 2e
Baccalauréat ES Polynésie (spécialité) 10 septembre 2014 Corrigé A. P. M. E. P. Exercice 1 5 points 1. Réponse d. : 1 e Le coefficient directeur de la tangente est négatif et n est manifestement pas 2e
Comment tracer une droite représentative d'une fonction et méthode de calcul de l'équation d'une droite.
 Comment tracer une droite représentative d'une fonction et méthode de calcul de l'équation d'une droite. Introduction : Avant de commencer, il est nécessaire de prendre connaissance des trois types de
Comment tracer une droite représentative d'une fonction et méthode de calcul de l'équation d'une droite. Introduction : Avant de commencer, il est nécessaire de prendre connaissance des trois types de
Baccalauréat ES Antilles Guyane 12 septembre 2014 Corrigé
 Baccalauréat ES Antilles Guyane 12 septembre 2014 Corrigé EXERCICE 1 5 points Commun à tous les candidats 1. Réponse c : ln(10)+2 ln ( 10e 2) = ln(10)+ln ( e 2) = ln(10)+2 2. Réponse b : n 13 0,7 n 0,01
Baccalauréat ES Antilles Guyane 12 septembre 2014 Corrigé EXERCICE 1 5 points Commun à tous les candidats 1. Réponse c : ln(10)+2 ln ( 10e 2) = ln(10)+ln ( e 2) = ln(10)+2 2. Réponse b : n 13 0,7 n 0,01
Chapitre 7. Statistique des échantillons gaussiens. 7.1 Projection de vecteurs gaussiens
 Chapitre 7 Statistique des échantillons gaussiens Le théorème central limite met en évidence le rôle majeur tenu par la loi gaussienne en modélisation stochastique. De ce fait, les modèles statistiques
Chapitre 7 Statistique des échantillons gaussiens Le théorème central limite met en évidence le rôle majeur tenu par la loi gaussienne en modélisation stochastique. De ce fait, les modèles statistiques
Méthodes de quadrature. Polytech Paris-UPMC. - p. 1/48
 Méthodes de Polytech Paris-UPMC - p. 1/48 Polynôme d interpolation de Preuve et polynôme de Calcul de l erreur d interpolation Étude de la formule d erreur Autres méthodes - p. 2/48 Polynôme d interpolation
Méthodes de Polytech Paris-UPMC - p. 1/48 Polynôme d interpolation de Preuve et polynôme de Calcul de l erreur d interpolation Étude de la formule d erreur Autres méthodes - p. 2/48 Polynôme d interpolation
I. Polynômes de Tchebychev
 Première épreuve CCP filière MP I. Polynômes de Tchebychev ( ) 1.a) Tout réel θ vérifie cos(nθ) = Re ((cos θ + i sin θ) n ) = Re Cn k (cos θ) n k i k (sin θ) k Or i k est réel quand k est pair et imaginaire
Première épreuve CCP filière MP I. Polynômes de Tchebychev ( ) 1.a) Tout réel θ vérifie cos(nθ) = Re ((cos θ + i sin θ) n ) = Re Cn k (cos θ) n k i k (sin θ) k Or i k est réel quand k est pair et imaginaire
Contexte. Pour cela, elles doivent être très compliquées, c est-à-dire elles doivent être très différentes des fonctions simples,
 Non-linéarité Contexte Pour permettre aux algorithmes de cryptographie d être sûrs, les fonctions booléennes qu ils utilisent ne doivent pas être inversées facilement. Pour cela, elles doivent être très
Non-linéarité Contexte Pour permettre aux algorithmes de cryptographie d être sûrs, les fonctions booléennes qu ils utilisent ne doivent pas être inversées facilement. Pour cela, elles doivent être très
= constante et cette constante est a.
 Le problème Lorsqu on sait que f(x 1 ) = y 1 et que f(x 2 ) = y 2, comment trouver l expression de f(x 1 )? On sait qu une fonction affine a une expression de la forme f(x) = ax + b, le problème est donc
Le problème Lorsqu on sait que f(x 1 ) = y 1 et que f(x 2 ) = y 2, comment trouver l expression de f(x 1 )? On sait qu une fonction affine a une expression de la forme f(x) = ax + b, le problème est donc
La solution à vos mesures de pression
 Mesure de force linéique La solution à vos mesures de pression Sensibilité Répétabilité Stabilité Le système X3 de XSENSOR propose un concept innovant spécialement adapté pour vos applications de mesure
Mesure de force linéique La solution à vos mesures de pression Sensibilité Répétabilité Stabilité Le système X3 de XSENSOR propose un concept innovant spécialement adapté pour vos applications de mesure
Concours EPITA 2009 Epreuve de Sciences Industrielles pour l ingénieur La suspension anti-plongée de la motocyclette BMW K1200S
 Concours EPIT 2009 Epreuve de Sciences Industrielles pour l ingénieur La suspension anti-plongée de la motocyclette MW K1200S Durée : 2h. Calculatrices autorisées. Présentation du problème Le problème
Concours EPIT 2009 Epreuve de Sciences Industrielles pour l ingénieur La suspension anti-plongée de la motocyclette MW K1200S Durée : 2h. Calculatrices autorisées. Présentation du problème Le problème
Analyse en Composantes Principales
 Analyse en Composantes Principales Anne B Dufour Octobre 2013 Anne B Dufour () Analyse en Composantes Principales Octobre 2013 1 / 36 Introduction Introduction Soit X un tableau contenant p variables mesurées
Analyse en Composantes Principales Anne B Dufour Octobre 2013 Anne B Dufour () Analyse en Composantes Principales Octobre 2013 1 / 36 Introduction Introduction Soit X un tableau contenant p variables mesurées
INTRODUCTION À L ANALYSE FACTORIELLE DES CORRESPONDANCES
 INTRODUCTION À L ANALYSE FACTORIELLE DES CORRESPONDANCES Dominique LAFFLY Maître de Conférences, Université de Pau Laboratoire Société Environnement Territoire UMR 5603 du CNRS et Université de Pau Domaine
INTRODUCTION À L ANALYSE FACTORIELLE DES CORRESPONDANCES Dominique LAFFLY Maître de Conférences, Université de Pau Laboratoire Société Environnement Territoire UMR 5603 du CNRS et Université de Pau Domaine
Introduction. I Étude rapide du réseau - Apprentissage. II Application à la reconnaissance des notes.
 Introduction L'objectif de mon TIPE est la reconnaissance de sons ou de notes de musique à l'aide d'un réseau de neurones. Ce réseau doit être capable d'apprendre à distinguer les exemples présentés puis
Introduction L'objectif de mon TIPE est la reconnaissance de sons ou de notes de musique à l'aide d'un réseau de neurones. Ce réseau doit être capable d'apprendre à distinguer les exemples présentés puis
1 radian. De même, la longueur d un arc de cercle de rayon R et dont l angle au centre a pour mesure α radians est α R. R AB =R.
 Angles orientés Trigonométrie I. Préliminaires. Le radian Définition B R AB =R C O radian R A Soit C un cercle de centre O. Dire que l angle géométrique AOB a pour mesure radian signifie que la longueur
Angles orientés Trigonométrie I. Préliminaires. Le radian Définition B R AB =R C O radian R A Soit C un cercle de centre O. Dire que l angle géométrique AOB a pour mesure radian signifie que la longueur
Exercices types Algorithmique et simulation numérique Oral Mathématiques et algorithmique Banque PT
 Exercices types Algorithmique et simulation numérique Oral Mathématiques et algorithmique Banque PT Ces exercices portent sur les items 2, 3 et 5 du programme d informatique des classes préparatoires,
Exercices types Algorithmique et simulation numérique Oral Mathématiques et algorithmique Banque PT Ces exercices portent sur les items 2, 3 et 5 du programme d informatique des classes préparatoires,
De même, le périmètre P d un cercle de rayon 1 vaut P = 2π (par définition de π). Mais, on peut démontrer (difficilement!) que
 Introduction. On suppose connus les ensembles N (des entiers naturels), Z des entiers relatifs et Q (des nombres rationnels). On s est rendu compte, depuis l antiquité, que l on ne peut pas tout mesurer
Introduction. On suppose connus les ensembles N (des entiers naturels), Z des entiers relatifs et Q (des nombres rationnels). On s est rendu compte, depuis l antiquité, que l on ne peut pas tout mesurer
Exo7. Calculs de déterminants. Fiche corrigée par Arnaud Bodin. Exercice 1 Calculer les déterminants des matrices suivantes : Exercice 2.
 Eo7 Calculs de déterminants Fiche corrigée par Arnaud Bodin Eercice Calculer les déterminants des matrices suivantes : Correction Vidéo ( ) 0 6 7 3 4 5 8 4 5 6 0 3 4 5 5 6 7 0 3 5 4 3 0 3 0 0 3 0 0 0 3
Eo7 Calculs de déterminants Fiche corrigée par Arnaud Bodin Eercice Calculer les déterminants des matrices suivantes : Correction Vidéo ( ) 0 6 7 3 4 5 8 4 5 6 0 3 4 5 5 6 7 0 3 5 4 3 0 3 0 0 3 0 0 0 3
Fonctions de plusieurs variables
 Maths MP Exercices Fonctions de plusieurs variables Les indications ne sont ici que pour être consultées après le T (pour les exercices non traités). Avant et pendant le T, tenez bon et n allez pas les
Maths MP Exercices Fonctions de plusieurs variables Les indications ne sont ici que pour être consultées après le T (pour les exercices non traités). Avant et pendant le T, tenez bon et n allez pas les
Lecture graphique. Table des matières
 Lecture graphique Table des matières 1 Lecture d une courbe 2 1.1 Définition d une fonction.......................... 2 1.2 Exemple d une courbe........................... 2 1.3 Coût, recette et bénéfice...........................
Lecture graphique Table des matières 1 Lecture d une courbe 2 1.1 Définition d une fonction.......................... 2 1.2 Exemple d une courbe........................... 2 1.3 Coût, recette et bénéfice...........................
* très facile ** facile *** difficulté moyenne **** difficile ***** très difficile I : Incontournable
 Eo7 Fonctions de plusieurs variables Eercices de Jean-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-francefr * très facile ** facile *** difficulté moenne **** difficile ***** très difficile I
Eo7 Fonctions de plusieurs variables Eercices de Jean-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-francefr * très facile ** facile *** difficulté moenne **** difficile ***** très difficile I
LPP SAINT JOSEPH BELFORT MODE OPERATOIRE ACTIVINSPIRE. Bonne utilisation à toutes et tous! UTILISATION DES TBI LE LOGICIEL ACTIVINSPIRE
 LPP SAINT JOSEPH BELFORT MODE OPERATOIRE ACTIVINSPIRE Utilisation des TBI UTILISATION DES TBI LE LOGICIEL ACTIVINSPIRE T B utoriel de base, ce mode d emploi a pour objectif de vous présenter les principales
LPP SAINT JOSEPH BELFORT MODE OPERATOIRE ACTIVINSPIRE Utilisation des TBI UTILISATION DES TBI LE LOGICIEL ACTIVINSPIRE T B utoriel de base, ce mode d emploi a pour objectif de vous présenter les principales
Le produit semi-direct
 Le produit semi-direct Préparation à l agrégation de mathématiques Université de Nice - Sophia Antipolis Antoine Ducros Octobre 2007 Ce texte est consacré, comme son titre l indique, au produit semi-direct.
Le produit semi-direct Préparation à l agrégation de mathématiques Université de Nice - Sophia Antipolis Antoine Ducros Octobre 2007 Ce texte est consacré, comme son titre l indique, au produit semi-direct.
Découverte du logiciel ordinateur TI-n spire / TI-n spire CAS
 Découverte du logiciel ordinateur TI-n spire / TI-n spire CAS Mémento Ouvrir TI-Nspire CAS. Voici la barre d outils : L insertion d une page, d une activité, d une page où l application est choisie, pourra
Découverte du logiciel ordinateur TI-n spire / TI-n spire CAS Mémento Ouvrir TI-Nspire CAS. Voici la barre d outils : L insertion d une page, d une activité, d une page où l application est choisie, pourra
Planche n o 22. Fonctions de plusieurs variables. Corrigé
 Planche n o Fonctions de plusieurs variables Corrigé n o : f est définie sur R \ {, } Pour, f, = Quand tend vers, le couple, tend vers le couple, et f, tend vers Donc, si f a une limite réelle en, cette
Planche n o Fonctions de plusieurs variables Corrigé n o : f est définie sur R \ {, } Pour, f, = Quand tend vers, le couple, tend vers le couple, et f, tend vers Donc, si f a une limite réelle en, cette
Sommaire. Bertrand PECUCHET
 Sommaire I. Introduction... 2 II. Présentation de la Kinect... 3 1. Caractéristiques :... 4 III. Focus sur les différents capteurs de la Kinect... 5 1. Le capteur RGB... 5 2. Capteur et émetteur Infrarouge...
Sommaire I. Introduction... 2 II. Présentation de la Kinect... 3 1. Caractéristiques :... 4 III. Focus sur les différents capteurs de la Kinect... 5 1. Le capteur RGB... 5 2. Capteur et émetteur Infrarouge...
Netbook Asus 1000H / Samsung NC10 et Ecran 3D ZALMAN
 Netbook Asus 1000H / Samsung NC10 et Ecran 3D ZALMAN Les Netbooks par Daniel Chailloux et Jacques Claverie Récemment de nouveaux ordinateurs portables ont vu le jour. Ils font partie de la famille des
Netbook Asus 1000H / Samsung NC10 et Ecran 3D ZALMAN Les Netbooks par Daniel Chailloux et Jacques Claverie Récemment de nouveaux ordinateurs portables ont vu le jour. Ils font partie de la famille des
Fonctions de plusieurs variables, intégrales multiples, et intégrales dépendant d un paramètre
 IUFM du Limousin 2009-10 PLC1 Mathématiques S. Vinatier Rappels de cours Fonctions de plusieurs variables, intégrales multiples, et intégrales dépendant d un paramètre 1 Fonctions de plusieurs variables
IUFM du Limousin 2009-10 PLC1 Mathématiques S. Vinatier Rappels de cours Fonctions de plusieurs variables, intégrales multiples, et intégrales dépendant d un paramètre 1 Fonctions de plusieurs variables
1 Complément sur la projection du nuage des individus
 TP 0 : Analyse en composantes principales (II) Le but de ce TP est d approfondir nos connaissances concernant l analyse en composantes principales (ACP). Pour cela, on reprend les notations du précédent
TP 0 : Analyse en composantes principales (II) Le but de ce TP est d approfondir nos connaissances concernant l analyse en composantes principales (ACP). Pour cela, on reprend les notations du précédent
LIDAR LAUSANNE 2012. Nouvelles données altimétriques sur l agglomération lausannoise par technologie laser aéroporté et ses produits dérivés
 LIDAR LAUSANNE 2012 Nouvelles données altimétriques sur l agglomération lausannoise par technologie laser aéroporté et ses produits dérivés LIDAR 2012, nouveaux modèles altimétriques 1 Affaire 94022 /
LIDAR LAUSANNE 2012 Nouvelles données altimétriques sur l agglomération lausannoise par technologie laser aéroporté et ses produits dérivés LIDAR 2012, nouveaux modèles altimétriques 1 Affaire 94022 /
Cours d Analyse. Fonctions de plusieurs variables
 Cours d Analyse Fonctions de plusieurs variables Licence 1ère année 2007/2008 Nicolas Prioux Université de Marne-la-Vallée Table des matières 1 Notions de géométrie dans l espace et fonctions à deux variables........
Cours d Analyse Fonctions de plusieurs variables Licence 1ère année 2007/2008 Nicolas Prioux Université de Marne-la-Vallée Table des matières 1 Notions de géométrie dans l espace et fonctions à deux variables........
Nombres, mesures et incertitudes en sciences physiques et chimiques. Groupe des Sciences physiques et chimiques de l IGEN
 Nombres, mesures et incertitudes en sciences physiques et chimiques. Groupe des Sciences physiques et chimiques de l IGEN Table des matières. Introduction....3 Mesures et incertitudes en sciences physiques
Nombres, mesures et incertitudes en sciences physiques et chimiques. Groupe des Sciences physiques et chimiques de l IGEN Table des matières. Introduction....3 Mesures et incertitudes en sciences physiques
Oscillations libres des systèmes à deux degrés de liberté
 Chapitre 4 Oscillations libres des systèmes à deux degrés de liberté 4.1 Introduction Les systèmes qui nécessitent deux coordonnées indépendantes pour spécifier leurs positions sont appelés systèmes à
Chapitre 4 Oscillations libres des systèmes à deux degrés de liberté 4.1 Introduction Les systèmes qui nécessitent deux coordonnées indépendantes pour spécifier leurs positions sont appelés systèmes à
Introduction à l étude des Corps Finis
 Introduction à l étude des Corps Finis Robert Rolland (Résumé) 1 Introduction La structure de corps fini intervient dans divers domaines des mathématiques, en particulier dans la théorie de Galois sur
Introduction à l étude des Corps Finis Robert Rolland (Résumé) 1 Introduction La structure de corps fini intervient dans divers domaines des mathématiques, en particulier dans la théorie de Galois sur
Baccalauréat ES Pondichéry 7 avril 2014 Corrigé
 Baccalauréat ES Pondichéry 7 avril 204 Corrigé EXERCICE 4 points Commun à tous les candidats. Proposition fausse. La tangente T, passant par les points A et B d abscisses distinctes, a pour coefficient
Baccalauréat ES Pondichéry 7 avril 204 Corrigé EXERCICE 4 points Commun à tous les candidats. Proposition fausse. La tangente T, passant par les points A et B d abscisses distinctes, a pour coefficient
