Maîtriser la topographie
|
|
|
- Danièle Lavallée
- il y a 9 ans
- Total affichages :
Transcription
1 Maîtriser la topographie Des observations au plan Michel BRABANT Professeur agrégé de génie civil Géomètre expert DPLG Deuxième édition 2003 ISBN
2 SOMMAIRE CHAPITRE 1. CONNAISSANCES DE BASE TRAVAUX TOPOGRAPHIQUES Le levé topographique Les calculs topométriques Les dessins topographiques Projets d aménagement Implantations Suivi et contrôle des ouvrages COORDONNÉES GÉOGRAPHIQUES ET ALTITUDES Coordonnées géographiques Altitudes SYSTÈMES DE PROJECTION Caractéristiques générales Les systèmes Lambert La projection Lambert I, II, III, IV Altérations linéaires
3 M aîtriser la topographie Correction de réduction à la corde ou correction de dv Lambert II étendu Lambert Projection UTM (Universal Transverse Mercator) LE RGF (RÉSEAU GÉODÉSIQUE FRANÇAIS) La NTF (Nouvelle Triangulation de la France) Le RGF LE NGF (NIVELLEMENT GÉNÉRAL DE LA FRANCE) Le réseau Lallemand Les réseaux IGN 69 en métropole et IGN 78 en Corse OBSERVATIONS TOPOGRAPHIQUES Angles ( 2) Distances ( 3) Dénivelées ( 4) GPS (Global Positioning System) PRÉCISION DES OBSERVATIONS Définitions Erreurs parasites ou fautes Erreurs systématiques Erreur de justesse Évaluation sommaire de l erreur de justesse Droite moyenne Erreurs accidentelles des mesures directes Erreur absolue Répartition expérimentale Probabilité Espérance mathématique Loi normale ou loi de Laplace-Gauss Indices de dispersion Estimation de la moyenne Tolérances Erreurs accidentelles des mesures indirectes Principe de l indépendance des erreurs Composition des écarts-types d une mesure indirecte Observations d inégales précisions Moyenne pondérée
4 Sommaire Précision Classes de précision des travaux topographiques LA CARTE Série bleue et TOP Exactitude Mesures planimétriques Orographie Exploitation de l orographie La BD Topo CHAPITRE 2. MESURES DES ANGLES LE THÉODOLITE Conception Pivot Embase Calage du pivot Cercle horizontal Goniomètre Lecture optique Lecture électronique Mouvements Cercle vertical Axe optique Lunette Mise au point Qualités d une lunette PRÉCISION DES MESURES D ANGLES Erreurs parasites Erreurs systématiques Erreurs accidentelles Écarts-types MESURAGE D UN ANGLE HORIZONTAL Mises en station Séquence Paires de séquences Tour d horizon
5 M aîtriser la topographie 2.4. MESURAGE D UN ANGLE ZÉNITHAL Observations Correction d index Application ORIENTATION Orientation dans le système de projection Orientation magnétique Orientation gyroscopique Orientation astronomique CHAPITRE 3. MESURES DES DISTANCES MESURAGE AU RUBAN Jalonnement Jalonnement sans obstacle Franchissement d une butte Obstacle de faible largeur Obstacle important Prolongement Méthodes de mesurage À plat Étalonnage et dilatation Ruban suspendu horizontal Précision Erreurs parasites Erreurs systématiques Erreurs accidentelles Écarts-types Réductions des mesures à plat MESURAGE OPTIQUE Méthode parallactique Mesure stadimétrique Lecture sur mire ordinaire Distance stadimétrique Méthode clisimétrique MESURAGE ÉLECTRONIQUE Principe
6 Sommaire Onde modulée Mesure du déphasage Synoptique Distancemètres de topographie Précision Erreurs parasites Erreurs systématiques Erreurs accidentelles Écarts-types Réductions des distances CHAPITRE 4. NIVELLEMENT NIVELLEMENT DIRECT ORDINAIRE Observations Niveaux et mires Niveaux-blocs à nivelle torique Niveaux automatiques Niveaux numériques, mires codes-barres Dénivelée élémentaire Cheminement encadré Observations Calcul des altitudes Algorithme Application Point nodal et cheminements nodaux Cheminement fermé Nivellement simultané d un cheminement et de points de détail Précision Erreurs parasites Erreurs systématiques Erreurs accidentelles Écart-type Vérification et réglage de la collimation NIVELLEMENT GÉOMÉTRIQUE DE PRÉCISION Matériels Cheminement aller et retour Cheminement double à doubles stations Cheminement double à doubles points de mire
7 M aîtriser la topographie Précision Nivellement géométrique motorisé NIVELLEMENT GÉODÉSIQUE Dénivelée instrumentale Niveau apparent Visée unilatérale Visées réciproques non simultanées Visées réciproques simultanées NIVELLEMENT TRIGONOMÉTRIQUE Visée unilatérale Visées réciproques Cheminements NIVELLEMENT STADIMÉTRIQUE CANEVAS DE NIVELLEMENT Avant-projet et reconnaissance Projet et matérialisation Observations et calculs Dossier et vérification CHAPITRE 5. CANEVAS D ENSEMBLE CARACTÉRISTIQUES DÉTERMINATION PAR POINTS ISOLÉS OU «POINT PAR POINT» Intersection Observations Calcul par la méthode du point approché Nivellement Application Relèvement Observations Calcul par la méthode du point approché Nivellement Application
8 Sommaire Recoupement Observations Calcul par la méthode du point approché Nivellement Application Insertion Observations Calcul par la méthode du point approché Nivellement Application Compensation par la méthode des moindres carrés Linéarisation des relations d observation Normalisation des relations d observation Résolution du système d équations normalisées Intersection Relèvement Distance Application CALCUL EN BLOC Amélioration de la méthode point par point Mappe des observations Compensation Application Réseaux de triangles CHRONOLOGIE DES TRAVAUX Avant-projet Reconnaissance Projet Matérialisation et signalisation Repérage Observations Traitements numériques Dossier et vérification CANEVAS GPS Le système WGS Géodésie tridimensionnelle Composition du système Mesures
9 M aîtriser la topographie Méthodes d observation Statiques Cinématiques Temps réel Missions Procédures Préparation Qualité des mesures Redondance GDOP Temps d observation Traitement des observations Transfert des données Calculs et validation des vecteurs Compensation Adaptation Application CHAPITRE 6. CANEVAS POLYGONAL CHEMINEMENTS PLANIMÉTRIQUES CHEMINEMENT OUVERT Observations Calculs Première phase : orientation Seconde phase : coordonnées Exemple Valeur des résultats CHEMINEMENT ENCADRÉ Observations Calculs Première phase : orientation Réorientation Seconde phase : coordonnées Exemple Exploitation des coordonnées LOCALISATION DES ERREURS PARASITES Erreur parasite d observation sur un angle
10 Sommaire Graphique Calcul aller-retour Coordonnées du sommet d angle erroné Erreur parasite d observation sur une distance Graphique Calcul du gisement du côté erroné Erreurs simultanées d angles ou de distances POINT NODAL ET CHEMINEMENTS NODAUX PLANIMÉTRIQUES Observations Calculs Première phase : orientation Seconde phase : coordonnées Points nodaux multiples CHEMINEMENT FERMÉ L orientation et les coordonnées à l origine sont connues Orientation sommaire, origine inconnue L origine est inconnue en coordonnées, mais l orientation du premier côté est strictement imposée CANEVAS POLYGONAL ORDINAIRE Cheminements principaux et cheminements secondaires Canevas de polygonation et désignations Cas particulier des grands chantiers Matérialisation des sommets et fiches signalétiques Observations et calculs CANEVAS POLYGONAL DE PRÉCISION CHAPITRE 7. LEVÉ DES DÉTAILS ET IMPLANTATIONS LEVÉ DES DÉTAILS PLANIMÉTRIQUES Points à lever Reconnaissance Techniques de levé Limites et points Abscisses et ordonnées Multilatération des détails
11 M aîtriser la topographie Rayonnement Saisie des données LEVÉ DU RELIEF Lignes caractéristiques et semis de points Balayage et quadrillage Profils Filage des courbes de niveau TACHÉOMÉTRIE Tachéométrie optique Rôle du chef d équipe Chronologie des observations d une station Calculs et dessin Tachéométrie électro-optique Instruments Méthode Traitements numériques et graphiques Tachéométrie automatique Performances des instruments et ergonomie de la méthode Enregistrement Géocodification LEVÉ DES DÉTAILS PAR GPS Post-traitement Temps réel IMPLANTATIONS Caractères généraux Alignements Points alignés Parallèle à un mur Piquetage planimétrique Repères altimétriques Chronologie des travaux d implantation LA TOPOMATIQUE Automatisation des observations Travail au point levé ou implanté Gestion des données
12 Sommaire Visualisation graphique Traitement en temps réel Standardisation Nuages de points 3D par laser scanner CHAPITRE 8. TRAVAUX TOPOGRAPHIQUES SPÉCIFIQUES BÂTIMENT Levé d intérieur Saisie manuelle Chaîne numérique Levé des façades Contrôles de verticalité Chaises Le GPS dans le monde de la construction TRAVAUX PUBLICS Tracés routiers Implantation des arcs de cercle tangents à des alignements droits Points de tangence Abscisses et ordonnées Implantation polaire Intersection Raccordement circulaire double Clothoïde Caractéristiques géométriques et formules Calculs des éléments d implantation Entrées en terre et gabarits de talutage Entrées en terre Gabarits Localisation et guidage des engins de chantier Travaux topographiques en génie civil Sécurité TOPOGRAPHIE SOUTERRAINE Creusement d un puits Descente d une orientation Descente optique Descente optico-mécanique
13 M aîtriser la topographie Mesure de la profondeur Transfert des coordonnées au fond Creusement d une galerie Contrôle des profils en travers MÉTROLOGIE Métrologie d atelier Métrologie géodésique Autocollimation Rayonnement spatial Intersection spatiale Nivellement géométrique de très haute précision Métrologie photogrammétrique Auscultation d ouvrage PHOTOGRAMMÉTRIE Prise de vue et clichés Photo-interprétation Stéréophotogrammétrie BATHYMÉTRIE SIG Un SIG, pour quoi faire? Architecture et fonctionnalités Modélisation et articulation des données Nomenclatures d échange Les sources de données CHAPITRE 9. CALCULS TOPOMÉTRIQUES MODES DE CALCUL Rappels mathématiques Trigonométrie circulaire Équation du second degré Développements limités Dérivées et différentielles Géométrie Calcul séquentiel Traitement informatique COORDONNÉES
14 Sommaire Conversions Conversion des coordonnées polaires en coordonnées rectangulaires (P R) Conversion des coordonnées rectangulaires en coordonnées polaires (R P) Application Distance d un point à une droite G0 de station Stations excentrées Rattachement Rabattement Changement de repère orthonormé Angle des repères Formules Algorithme Application INTERSECTIONS DE DROITES ET CERCLES Intersection de deux visées Intersection de deux droites Intersections de deux cercles Centre et rayon d un cercle défini par les coordonnées de trois de ses points Relèvement sur trois points Intersection des arcs capables Méthode de Gauss Relèvement italien Formule de Delambre Relèvement double Intersections d une droite et d un cercle Intersections d une visée et d un arc capable SUPERFICIES Superficies graphiques Décomposition d un polygone en triangles et trapèzes Équerres et glaces divisées Surfaces à limites sinueuses Jeu du papier Superficies numériques élémentaires Triangles Trapèzes Quadrilatères Secteur et segment circulaires
15 M aîtriser la topographie Superficie d un polygone défini en coordonnées polaires Superficie d un polygone défini en coordonnées rectangulaires Superficie positive Superficie négative Polygone quelconque Formule polygonale ou formule de Sarron Notations Formule Calcul direct du côté inconnu Calcul des angles inconnus Arrondis et troncatures Planimètres Planimètre polaire à pôle fixe Surface-chiffre ou unité du vernier Planimètre polaire à chariot Surfaces digitalisées Redressement des limites Segment de redressement Ligne brisée DIVISIONS DES SURFACES Triangles Diviser un triangle en superficies successives S 1, S 2, S3, etc., respectivement proportionnelles aux nombres m, n, p, etc., par des droites issues d un sommet Diviser un triangle en superficies S 1, S 2, S 3, etc., respectivement proportionnelles aux nombres m, n, p, etc., par des droites issues d un point connu sur un côté Diviser un triangle en superficies S 1, S 2, S 3, etc., respectivement proportionnelles aux nombres m, n, p, etc., par des parallèles à un côté Transformer un triangle ABC donné en un triangle AMN équivalent par une parallèle à une direction D connue Diviser un triangle en superficies successives S 1, S 2, S 3, etc., respectivement proportionnelles aux nombres m, n, p, etc., par des parallèles à une direction connue Diviser un triangle en superficies successives S 1, S 2, S 3, etc., respectivement proportionnelles aux nombres m, n, p, etc., par des perpendiculaires à un côté
16 Sommaire Diviser un triangle en deux superficies S 1 et S 2, respectivement proportionnelles aux nombres m et n, par une droite passant par un point donné à l intérieur du triangle Trapèzes Diviser un trapèze en deux superficies S 1 et S 2, respectivement proportionnelles aux nombres m et n, par une droite passant par un point donné à l intérieur du trapèze et coupant les deux bases Diviser un trapèze en superficies successives S 1, S 2, S 3, etc., respectivement proportionnelles aux nombres m, n, p, etc., par des parallèles aux bases Quadrilatères Diviser un quadrilatère en superficies successives S 1, S 2, S 3, etc., respectivement proportionnelles aux nombres m, n, p, etc., par des droites issues d un sommet Diviser un quadrilatère en superficies successives S 1, S 2, S 3, etc., respectivement proportionnelles aux nombres m, n, p, etc., par des droites issues d un point connu sur un côté Implanter dans un quadrilatère une superficie connue, par une parallèle à un côté Dans un quadrilatère, implanter une superficie par une parallèle à une direction connue Dans un quadrilatère, implanter une superficie par une perpendiculaire à un côté Dans un quadrilatère, implanter une superficie par une droite délimitant des façades opposées dans un rapport donné Dans un quadrilatère, implanter une superficie par une droite délimitant des façades opposées égales Par un point donné à l intérieur d un quadrilatère, implanter une superficie S connue Partage des pointes PROGRAMMATION DES FONCTIONS DE CALCUL TOPOMÉTRIQUE CALCULS ITÉRATIFS Racines d une équation à une inconnue Approximations successives Linéarisation ou méthode de Newton
17 M aîtriser la topographie Dichotomie Incrémentation Algorithmes itératifs CHAPITRE 10. DESSINS TOPOGRAPHIQUES PLANS GRAPHIQUES Minutes et calques Reports par multilatération Quadrillage et points connus en coordonnées ; échelles 1/100 à 1/ Dessin des courbes de niveau Profils Tracé en plan Profil en long Profils en travers Cubature des terrassements Principe Moyenne des aires Distances des profils encadrants à la ligne de passage Moyenne des entre-profils Cubature simplifiée PLANS NUMÉRIQUES Infographie Le poste de travail Les logiciels Interactivité PLANS NUMÉRISÉS PRÉSENTATION VÉRIFICATION TIRAGES ET ARCHIVAGE BIBLIOGRAPHIE INDEX
Savoir lire une carte, se situer et s orienter en randonnée
 Savoir lire une carte, se situer et s orienter en randonnée Le b.a.-ba du randonneur Fiche 2 Lire une carte topographique Mais c est où le nord? Quel Nord Le magnétisme terrestre attire systématiquement
Savoir lire une carte, se situer et s orienter en randonnée Le b.a.-ba du randonneur Fiche 2 Lire une carte topographique Mais c est où le nord? Quel Nord Le magnétisme terrestre attire systématiquement
CLUB DE MARCHE Ballade et Randonnée
 CLUB DE MARCHE Ballade et Randonnée SOMMAIRE 1 LA CARTE 1.1 Les types de carte 1.2 Les différentes échelles 1.3 - Les informations figurants sur les cartes au 1/25000 ème 1.3.1 - Le cadre 1.3.2 Les couleurs
CLUB DE MARCHE Ballade et Randonnée SOMMAIRE 1 LA CARTE 1.1 Les types de carte 1.2 Les différentes échelles 1.3 - Les informations figurants sur les cartes au 1/25000 ème 1.3.1 - Le cadre 1.3.2 Les couleurs
Le contexte. Le questionnement du P.E.R. :
 Le contexte Ce travail a débuté en janvier. Le P.E.R. engagé depuis fin septembre a permis de faire émerger ou de réactiver : Des raisons d être de la géométrie : Calculer des grandeurs inaccessibles et
Le contexte Ce travail a débuté en janvier. Le P.E.R. engagé depuis fin septembre a permis de faire émerger ou de réactiver : Des raisons d être de la géométrie : Calculer des grandeurs inaccessibles et
Mesurer en toute simplicité
 Mesurer en toute simplicité Avant-propos Chers étudiants et enseignants, ainsi que toutes personnes passionnées de topographie, au cours des dernières années, le développement d'instruments modernes et
Mesurer en toute simplicité Avant-propos Chers étudiants et enseignants, ainsi que toutes personnes passionnées de topographie, au cours des dernières années, le développement d'instruments modernes et
Franck VAUTIER, Jean-Pierre TOUMAZET, Erwan ROUSSEL, Marlène FAURE, Mohamed ABADI, Marta FLOREZ, Bertrand DOUSTEYSSIER
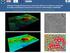 Utilisation d images dérivées d un jeu de données LIDAR pour la détection automatisée de vestiges archéologiques (programme de recherche méthodologique LiDARCHEO) Franck VAUTIER, Jean-Pierre TOUMAZET,
Utilisation d images dérivées d un jeu de données LIDAR pour la détection automatisée de vestiges archéologiques (programme de recherche méthodologique LiDARCHEO) Franck VAUTIER, Jean-Pierre TOUMAZET,
Tâche complexe produite par l académie de Clermont-Ferrand. Mai 2012 LE TIR A L ARC. (d après une idée du collège des Portes du Midi de Maurs)
 (d après une idée du collège des Portes du Midi de Maurs) Table des matières Fiche professeur... 2 Fiche élève... 5 1 Fiche professeur Niveaux et objectifs pédagogiques 5 e : introduction ou utilisation
(d après une idée du collège des Portes du Midi de Maurs) Table des matières Fiche professeur... 2 Fiche élève... 5 1 Fiche professeur Niveaux et objectifs pédagogiques 5 e : introduction ou utilisation
BACCALAURÉAT GÉNÉRAL SESSION 2012 OBLIGATOIRE MATHÉMATIQUES. Série S. Durée de l épreuve : 4 heures Coefficient : 7 ENSEIGNEMENT OBLIGATOIRE
 BACCALAURÉAT GÉNÉRAL SESSION 2012 MATHÉMATIQUES Série S Durée de l épreuve : 4 heures Coefficient : 7 ENSEIGNEMENT OBLIGATOIRE Les calculatrices électroniques de poche sont autorisées, conformément à la
BACCALAURÉAT GÉNÉRAL SESSION 2012 MATHÉMATIQUES Série S Durée de l épreuve : 4 heures Coefficient : 7 ENSEIGNEMENT OBLIGATOIRE Les calculatrices électroniques de poche sont autorisées, conformément à la
CHAPITRE 2 POSITIONNEMENT
 35 CHPITRE POSITIONNEMENT 1. INTRODUCTION La détermination d une position précise est le problème fondamental d un Système d Information Géographique (SIG) et l objet principal de la géodésie. La position
35 CHPITRE POSITIONNEMENT 1. INTRODUCTION La détermination d une position précise est le problème fondamental d un Système d Information Géographique (SIG) et l objet principal de la géodésie. La position
Si deux droites sont parallèles à une même troisième. alors les deux droites sont parallèles entre elles. alors
 N I) Pour démontrer que deux droites (ou segments) sont parallèles (d) // (d ) (d) // (d ) deux droites sont parallèles à une même troisième les deux droites sont parallèles entre elles (d) // (d) deux
N I) Pour démontrer que deux droites (ou segments) sont parallèles (d) // (d ) (d) // (d ) deux droites sont parallèles à une même troisième les deux droites sont parallèles entre elles (d) // (d) deux
AC AB. A B C x 1. x + 1. d où. Avec un calcul vu au lycée, on démontre que cette solution admet deux solutions dont une seule nous intéresse : x =
 LE NOMBRE D OR Présentation et calcul du nombre d or Euclide avait trouvé un moyen de partager en deu un segment selon en «etrême et moyenne raison» Soit un segment [AB]. Le partage d Euclide consiste
LE NOMBRE D OR Présentation et calcul du nombre d or Euclide avait trouvé un moyen de partager en deu un segment selon en «etrême et moyenne raison» Soit un segment [AB]. Le partage d Euclide consiste
EXERCICES DE REVISIONS MATHEMATIQUES CM2
 EXERCICES DE REVISIONS MATHEMATIQUES CM2 NOMBRES ET CALCUL Exercices FRACTIONS Nommer les fractions simples et décimales en utilisant le vocabulaire : 3 R1 demi, tiers, quart, dixième, centième. Utiliser
EXERCICES DE REVISIONS MATHEMATIQUES CM2 NOMBRES ET CALCUL Exercices FRACTIONS Nommer les fractions simples et décimales en utilisant le vocabulaire : 3 R1 demi, tiers, quart, dixième, centième. Utiliser
Bac Blanc Terminale ES - Février 2011 Épreuve de Mathématiques (durée 3 heures)
 Bac Blanc Terminale ES - Février 2011 Épreuve de Mathématiques (durée 3 heures) Eercice 1 (5 points) pour les candidats n ayant pas choisi la spécialité MATH Le tableau suivant donne l évolution du chiffre
Bac Blanc Terminale ES - Février 2011 Épreuve de Mathématiques (durée 3 heures) Eercice 1 (5 points) pour les candidats n ayant pas choisi la spécialité MATH Le tableau suivant donne l évolution du chiffre
GÉODÉSIE, COORDONNÉES ET GPS
 GÉODÉSIE, COORDONNÉES ET GPS LES PROJECTIONS La représentation du globe terrestre sur un plan en deux dimensions exige une opération nommée projection. Une projection s appuie sur un géoïde, qui est une
GÉODÉSIE, COORDONNÉES ET GPS LES PROJECTIONS La représentation du globe terrestre sur un plan en deux dimensions exige une opération nommée projection. Une projection s appuie sur un géoïde, qui est une
LES LOIS PHYSIQUES APPLIQUÉES AUX DEUX-ROUES : 1. LA FORCE DE GUIDAGE
 LES LOIS PHYSIQUES APPLIQUÉES AUX DEUX-ROUES : 1. LA FORCE DE GUIDAGE 2. L EFFET GYROSCOPIQUE Les lois physiques qui régissent le mouvement des véhicules terrestres sont des lois universelles qui s appliquent
LES LOIS PHYSIQUES APPLIQUÉES AUX DEUX-ROUES : 1. LA FORCE DE GUIDAGE 2. L EFFET GYROSCOPIQUE Les lois physiques qui régissent le mouvement des véhicules terrestres sont des lois universelles qui s appliquent
Trait de côte Histolitt v1.0 Descriptif technique Version du document 1.0 *** Sommaire
 Trait de côte Histolitt v1.0 Descriptif technique Version du document 1.0 *** Sommaire 1 Producteurs 2 Dénomination du produit 3 Protection militaire 4 Abréviations 5 Description générale 1. Définition
Trait de côte Histolitt v1.0 Descriptif technique Version du document 1.0 *** Sommaire 1 Producteurs 2 Dénomination du produit 3 Protection militaire 4 Abréviations 5 Description générale 1. Définition
Calcul intégral élémentaire en plusieurs variables
 Calcul intégral élémentaire en plusieurs variables PC*2 2 septembre 2009 Avant-propos À part le théorème de Fubini qui sera démontré dans le cours sur les intégrales à paramètres et qui ne semble pas explicitement
Calcul intégral élémentaire en plusieurs variables PC*2 2 septembre 2009 Avant-propos À part le théorème de Fubini qui sera démontré dans le cours sur les intégrales à paramètres et qui ne semble pas explicitement
Cours Fonctions de deux variables
 Cours Fonctions de deux variables par Pierre Veuillez 1 Support théorique 1.1 Représentation Plan et espace : Grâce à un repère cartésien ( ) O, i, j du plan, les couples (x, y) de R 2 peuvent être représenté
Cours Fonctions de deux variables par Pierre Veuillez 1 Support théorique 1.1 Représentation Plan et espace : Grâce à un repère cartésien ( ) O, i, j du plan, les couples (x, y) de R 2 peuvent être représenté
Fonctions de plusieurs variables
 Module : Analyse 03 Chapitre 00 : Fonctions de plusieurs variables Généralités et Rappels des notions topologiques dans : Qu est- ce que?: Mathématiquement, n étant un entier non nul, on définit comme
Module : Analyse 03 Chapitre 00 : Fonctions de plusieurs variables Généralités et Rappels des notions topologiques dans : Qu est- ce que?: Mathématiquement, n étant un entier non nul, on définit comme
Enoncé et corrigé du brevet des collèges dans les académies d Aix- Marseille, Montpellier, Nice Corse et Toulouse en 2000. Énoncé.
 Enoncé et corrigé du brevet des collèges dans les académies d Aix- Marseille, Montpellier, Nice Corse et Toulouse en 2000. Énoncé. I- ACTIVITES NUMERIQUES (12 points) Exercice 1 (3 points) On considère
Enoncé et corrigé du brevet des collèges dans les académies d Aix- Marseille, Montpellier, Nice Corse et Toulouse en 2000. Énoncé. I- ACTIVITES NUMERIQUES (12 points) Exercice 1 (3 points) On considère
COVADIS version 14.0
 COVADIS version 14.0 NOUVEAUTÉS, AMÉLIORATIONS ET CORRECTIONS PAR RAPPORT À LA VERSION 13.0h GÉNÉRALITÉS 1. Modification de la procédure d installation Installation automatique du logiciel complémentaire
COVADIS version 14.0 NOUVEAUTÉS, AMÉLIORATIONS ET CORRECTIONS PAR RAPPORT À LA VERSION 13.0h GÉNÉRALITÉS 1. Modification de la procédure d installation Installation automatique du logiciel complémentaire
Baccalauréat technique de la musique et de la danse Métropole septembre 2008
 Baccalauréat technique de la musique et de la danse Métropole septembre 008 EXERCICE 5 points Pour chacune des cinq questions à 5, trois affirmations sont proposées dont une seule est exacte. Pour chaque
Baccalauréat technique de la musique et de la danse Métropole septembre 008 EXERCICE 5 points Pour chacune des cinq questions à 5, trois affirmations sont proposées dont une seule est exacte. Pour chaque
PROGRAMME D HABILETÉS EN FAUTEUIL ROULANT (WSP-F)
 PROGRAMME D HABILETÉS EN FAUTEUIL ROULANT (WSP-F) LIGNES DIRECTRICES POUR LE PARCOURS À OBSTACLES VERSION 4.1 CANADIENNE-FRANÇAISE Les activités d entraînement et d évaluation du WSP-F 4.1 peuvent se dérouler
PROGRAMME D HABILETÉS EN FAUTEUIL ROULANT (WSP-F) LIGNES DIRECTRICES POUR LE PARCOURS À OBSTACLES VERSION 4.1 CANADIENNE-FRANÇAISE Les activités d entraînement et d évaluation du WSP-F 4.1 peuvent se dérouler
Deux disques dans un carré
 Deux disques dans un carré Table des matières 1 Fiche résumé 2 2 Fiche élève Seconde - version 1 3 2.1 Le problème............................................... 3 2.2 Construction de la figure avec geogebra...............................
Deux disques dans un carré Table des matières 1 Fiche résumé 2 2 Fiche élève Seconde - version 1 3 2.1 Le problème............................................... 3 2.2 Construction de la figure avec geogebra...............................
Section «Maturité fédérale» EXAMENS D'ADMISSION Session de février 2014 RÉCAPITULATIFS DES MATIÈRES EXAMINÉES. Formation visée
 EXAMENS D'ADMISSION Admission RÉCAPITULATIFS DES MATIÈRES EXAMINÉES MATIÈRES Préparation en 3 ou 4 semestres Formation visée Préparation complète en 1 an 2 ème partiel (semestriel) Niveau Durée de l examen
EXAMENS D'ADMISSION Admission RÉCAPITULATIFS DES MATIÈRES EXAMINÉES MATIÈRES Préparation en 3 ou 4 semestres Formation visée Préparation complète en 1 an 2 ème partiel (semestriel) Niveau Durée de l examen
Chapitre 3. Quelques fonctions usuelles. 1 Fonctions logarithme et exponentielle. 1.1 La fonction logarithme
 Chapitre 3 Quelques fonctions usuelles 1 Fonctions logarithme et eponentielle 1.1 La fonction logarithme Définition 1.1 La fonction 7! 1/ est continue sur ]0, +1[. Elle admet donc des primitives sur cet
Chapitre 3 Quelques fonctions usuelles 1 Fonctions logarithme et eponentielle 1.1 La fonction logarithme Définition 1.1 La fonction 7! 1/ est continue sur ]0, +1[. Elle admet donc des primitives sur cet
Résolution d équations non linéaires
 Analyse Numérique Résolution d équations non linéaires Said EL HAJJI et Touria GHEMIRES Université Mohammed V - Agdal. Faculté des Sciences Département de Mathématiques. Laboratoire de Mathématiques, Informatique
Analyse Numérique Résolution d équations non linéaires Said EL HAJJI et Touria GHEMIRES Université Mohammed V - Agdal. Faculté des Sciences Département de Mathématiques. Laboratoire de Mathématiques, Informatique
Extraction et reconstruction de bâtiments en 3D à partir de relevés lidar aéroportés
 Thèse présentée pour obtenir le grade de Docteur de l Université Louis Pasteur Strasbourg I Discipline : Sciences pour l Ingénieur Spécialité : Topographie-Géomatique Par : Fayez TARSHA KURDI Extraction
Thèse présentée pour obtenir le grade de Docteur de l Université Louis Pasteur Strasbourg I Discipline : Sciences pour l Ingénieur Spécialité : Topographie-Géomatique Par : Fayez TARSHA KURDI Extraction
Vision industrielle et télédétection - Détection d ellipses. Guillaume Martinez 17 décembre 2007
 Vision industrielle et télédétection - Détection d ellipses Guillaume Martinez 17 décembre 2007 1 Table des matières 1 Le projet 3 1.1 Objectif................................ 3 1.2 Les choix techniques.........................
Vision industrielle et télédétection - Détection d ellipses Guillaume Martinez 17 décembre 2007 1 Table des matières 1 Le projet 3 1.1 Objectif................................ 3 1.2 Les choix techniques.........................
Géoréférencement et RGF93
 Géoréférencement et RGF93 Théorie et concepts - Fiche T3 Les projections coniques conformes 9 zones T3 Décembre 2008 2008/54 Historique Ces projections ont été définies par l'ign, suite à une recommandation
Géoréférencement et RGF93 Théorie et concepts - Fiche T3 Les projections coniques conformes 9 zones T3 Décembre 2008 2008/54 Historique Ces projections ont été définies par l'ign, suite à une recommandation
Angles orientés et fonctions circulaires ( En première S )
 Angles orientés et fonctions circulaires ( En première S ) Dernière mise à jour : Jeudi 01 Septembre 010 Vincent OBATON, Enseignant au lycée Stendhal de Grenoble (Année 006-007) Lycée Stendhal, Grenoble
Angles orientés et fonctions circulaires ( En première S ) Dernière mise à jour : Jeudi 01 Septembre 010 Vincent OBATON, Enseignant au lycée Stendhal de Grenoble (Année 006-007) Lycée Stendhal, Grenoble
Institut Technique de Formation Professionnelle en Bâtiment, Travaux Publics et Génie Civil (Privé) Plan de Formation
 Plan de Formation Adresse : 66 Rue Melouiya, 4 ème étage, plateau N 11, Agdal Rabat (angle Avenue de France et Rue Melouiya) Tel/Fax : 05 37 68 60 62 Email : [email protected] Site : www.itechbtp.ma
Plan de Formation Adresse : 66 Rue Melouiya, 4 ème étage, plateau N 11, Agdal Rabat (angle Avenue de France et Rue Melouiya) Tel/Fax : 05 37 68 60 62 Email : [email protected] Site : www.itechbtp.ma
1 radian. De même, la longueur d un arc de cercle de rayon R et dont l angle au centre a pour mesure α radians est α R. R AB =R.
 Angles orientés Trigonométrie I. Préliminaires. Le radian Définition B R AB =R C O radian R A Soit C un cercle de centre O. Dire que l angle géométrique AOB a pour mesure radian signifie que la longueur
Angles orientés Trigonométrie I. Préliminaires. Le radian Définition B R AB =R C O radian R A Soit C un cercle de centre O. Dire que l angle géométrique AOB a pour mesure radian signifie que la longueur
- Notice explicative Hôtels
 - Notice explicative Hôtels Ce document apporte des précisions référencées à la grille d auto-évaluation (dernière colonne) pour permettre de comprendre les attendus de la réglementation en matière d accessibilité.
- Notice explicative Hôtels Ce document apporte des précisions référencées à la grille d auto-évaluation (dernière colonne) pour permettre de comprendre les attendus de la réglementation en matière d accessibilité.
Référentiel Handicap. Référentiel Handicap. 2 e seuil de bonification. Logement collectif neuf. Logement individuel neuf
 2 e seuil de bonification page 1/5 identification du/des logement(s) concerné(s) Nom du bailleur Nom de l opération Logement individuel neuf Adresse de l opération Référence du/des logement(s) concerné(s)
2 e seuil de bonification page 1/5 identification du/des logement(s) concerné(s) Nom du bailleur Nom de l opération Logement individuel neuf Adresse de l opération Référence du/des logement(s) concerné(s)
Continuité et dérivabilité d une fonction
 DERNIÈRE IMPRESSIN LE 7 novembre 014 à 10:3 Continuité et dérivabilité d une fonction Table des matières 1 Continuité d une fonction 1.1 Limite finie en un point.......................... 1. Continuité
DERNIÈRE IMPRESSIN LE 7 novembre 014 à 10:3 Continuité et dérivabilité d une fonction Table des matières 1 Continuité d une fonction 1.1 Limite finie en un point.......................... 1. Continuité
Produits concernés: CS10, CS15, TS11, TS15, GS05, GS06, GS08, GS10, GS15
 V3.50 Apports et bénéfices Produits concernés: CS10, CS15, TS11, TS15, GS05, GS06, GS08, GS10, GS15 Ce document contient d importantes informations au sujet de la version 3.50 de SmartWorx Viva et des
V3.50 Apports et bénéfices Produits concernés: CS10, CS15, TS11, TS15, GS05, GS06, GS08, GS10, GS15 Ce document contient d importantes informations au sujet de la version 3.50 de SmartWorx Viva et des
Lot n 05 SERRURERIE EXTERIEURE
 Lot n 05 SERRURERIE EXTERIEURE 05.1 CONSISTANCE DES TRAVAUX... 2 05.2 TEXTES ET REGLEMENTS... 2 05.3 PRESCRIPTIONS GÉNÉRALES... 2 05.4 PRESCRIPTIONS PARTICULIÈRES... 3 05.4.1 GENERALITES... 3 05.4.2 SERRURERIE...
Lot n 05 SERRURERIE EXTERIEURE 05.1 CONSISTANCE DES TRAVAUX... 2 05.2 TEXTES ET REGLEMENTS... 2 05.3 PRESCRIPTIONS GÉNÉRALES... 2 05.4 PRESCRIPTIONS PARTICULIÈRES... 3 05.4.1 GENERALITES... 3 05.4.2 SERRURERIE...
Territoire3D. Descriptif de contenu. Institut Géographique National. www.ign.fr. Date du Document : Mars 2011
 Territoire3D Descriptif de contenu Date du Document : Mars 2011 Institut Géographique National 73 avenue de Paris 94165 Saint-Mandé Cedex www.ign.fr Révision : Spécifications externes A 18/03/2011 Création
Territoire3D Descriptif de contenu Date du Document : Mars 2011 Institut Géographique National 73 avenue de Paris 94165 Saint-Mandé Cedex www.ign.fr Révision : Spécifications externes A 18/03/2011 Création
DIAGNOSTIQUEUR IMMOBILIER
 OBJECTIFS Réaliser le dossier dans chaque domaine de diagnostique immobilier : amiante, plomb, diagnostic de performance énergétique, termites, gaz et installations intérieures électriques, mesurage des
OBJECTIFS Réaliser le dossier dans chaque domaine de diagnostique immobilier : amiante, plomb, diagnostic de performance énergétique, termites, gaz et installations intérieures électriques, mesurage des
Banc d études des structures Etude de résistances de matériaux (RDM) et structures mécaniques
 Banc d études des structures Etude de résistances de matériaux (RDM) et structures mécaniques Descriptif du support pédagogique Le banc d essais des structures permet de réaliser des essais et des études
Banc d études des structures Etude de résistances de matériaux (RDM) et structures mécaniques Descriptif du support pédagogique Le banc d essais des structures permet de réaliser des essais et des études
Cahier des Clauses techniquesparticulières
 ARCHES PUBLICS MAIRIE DE BASTIA Avenue Pierre Guidicelli 20410 BASTIA CEDEX MARCHE D ETUDES A MAITRISE D OUVRAGE EN VUE DE L ORIENTATION ET DU DEVELOPPEMENT DU SYTEME D INFORMATION GEOGRAPHIQUE SERVICE
ARCHES PUBLICS MAIRIE DE BASTIA Avenue Pierre Guidicelli 20410 BASTIA CEDEX MARCHE D ETUDES A MAITRISE D OUVRAGE EN VUE DE L ORIENTATION ET DU DEVELOPPEMENT DU SYTEME D INFORMATION GEOGRAPHIQUE SERVICE
point On obtient ainsi le ou les points d inter- entre deux objets».
 Déplacer un objet Cliquer sur le bouton «Déplacer». On peut ainsi rendre la figure dynamique. Attraper l objet à déplacer avec la souris. Ici, on veut déplacer le point A du triangle point ABC. A du triangle
Déplacer un objet Cliquer sur le bouton «Déplacer». On peut ainsi rendre la figure dynamique. Attraper l objet à déplacer avec la souris. Ici, on veut déplacer le point A du triangle point ABC. A du triangle
Éditorial. Tangente ÉDUCATION. Scratch, AlgoBox, Python. Trimestriel - n 15 - janvier 2011 Numéro spécial 16 activités TICE pour le lycée
 Tangente ÉDUCATION Trimestriel - n 15 - janvier 2011 Numéro spécial 16 activités TICE pour le lycée et leurs programmes dans les trois langages les plus utilisés : Scratch, AlgoBox, Python Python Éditorial
Tangente ÉDUCATION Trimestriel - n 15 - janvier 2011 Numéro spécial 16 activités TICE pour le lycée et leurs programmes dans les trois langages les plus utilisés : Scratch, AlgoBox, Python Python Éditorial
Chapitre 1 Cinématique du point matériel
 Chapitre 1 Cinématique du point matériel 7 1.1. Introduction 1.1.1. Domaine d étude Le programme de mécanique de math sup se limite à l étude de la mécanique classique. Sont exclus : la relativité et la
Chapitre 1 Cinématique du point matériel 7 1.1. Introduction 1.1.1. Domaine d étude Le programme de mécanique de math sup se limite à l étude de la mécanique classique. Sont exclus : la relativité et la
Repérage d un point - Vitesse et
 PSI - écanique I - Repérage d un point - Vitesse et accélération page 1/6 Repérage d un point - Vitesse et accélération Table des matières 1 Espace et temps - Référentiel d observation 1 2 Coordonnées
PSI - écanique I - Repérage d un point - Vitesse et accélération page 1/6 Repérage d un point - Vitesse et accélération Table des matières 1 Espace et temps - Référentiel d observation 1 2 Coordonnées
TOUT CE QU IL FAUT SAVOIR POUR LE BREVET
 TOUT E QU IL FUT SVOIR POUR LE REVET NUMERIQUE / FONTIONS eci n est qu un rappel de tout ce qu il faut savoir en maths pour le brevet. I- Opérations sur les nombres et les fractions : Les priorités par
TOUT E QU IL FUT SVOIR POUR LE REVET NUMERIQUE / FONTIONS eci n est qu un rappel de tout ce qu il faut savoir en maths pour le brevet. I- Opérations sur les nombres et les fractions : Les priorités par
Chapitre 6. Fonction réelle d une variable réelle
 Chapitre 6 Fonction réelle d une variable réelle 6. Généralités et plan d étude Une application de I dans R est une correspondance entre les éléments de I et ceu de R telle que tout élément de I admette
Chapitre 6 Fonction réelle d une variable réelle 6. Généralités et plan d étude Une application de I dans R est une correspondance entre les éléments de I et ceu de R telle que tout élément de I admette
STATIQUE GRAPHIQUE ET STATIQUE ANALYTIQUE
 ÉCOLE D'INGÉNIEURS DE FRIBOURG (E.I.F.) SECTION DE MÉCANIQUE G.R. Nicolet, revu en 2006 STATIQUE GRAPHIQUE ET STATIQUE ANALYTIQUE Eléments de calcul vectoriel Opérations avec les forces Equilibre du point
ÉCOLE D'INGÉNIEURS DE FRIBOURG (E.I.F.) SECTION DE MÉCANIQUE G.R. Nicolet, revu en 2006 STATIQUE GRAPHIQUE ET STATIQUE ANALYTIQUE Eléments de calcul vectoriel Opérations avec les forces Equilibre du point
t 100. = 8 ; le pourcentage de réduction est : 8 % 1 t Le pourcentage d'évolution (appelé aussi taux d'évolution) est le nombre :
 Terminale STSS 2 012 2 013 Pourcentages Synthèse 1) Définition : Calculer t % d'un nombre, c'est multiplier ce nombre par t 100. 2) Exemples de calcul : a) Calcul d un pourcentage : Un article coûtant
Terminale STSS 2 012 2 013 Pourcentages Synthèse 1) Définition : Calculer t % d'un nombre, c'est multiplier ce nombre par t 100. 2) Exemples de calcul : a) Calcul d un pourcentage : Un article coûtant
LA PHYSIQUE DES MATERIAUX. Chapitre 1 LES RESEAUX DIRECT ET RECIPROQUE
 LA PHYSIQUE DES MATERIAUX Chapitre 1 LES RESEAUX DIRECT ET RECIPROQUE Pr. A. Belayachi Université Mohammed V Agdal Faculté des Sciences Rabat Département de Physique - L.P.M [email protected] 1 1.Le réseau
LA PHYSIQUE DES MATERIAUX Chapitre 1 LES RESEAUX DIRECT ET RECIPROQUE Pr. A. Belayachi Université Mohammed V Agdal Faculté des Sciences Rabat Département de Physique - L.P.M [email protected] 1 1.Le réseau
Niveaux numériques Leica DNA Des avancées qui vous mènent plus loin
 Niveaux numériques Leica DNA Des avancées qui vous mènent plus loin Niveaux numériques Leica DNA l avance grâce à l expérience Avec les niveaux numériques DNA de Leica découvrez un nouveau monde d avantages
Niveaux numériques Leica DNA Des avancées qui vous mènent plus loin Niveaux numériques Leica DNA l avance grâce à l expérience Avec les niveaux numériques DNA de Leica découvrez un nouveau monde d avantages
RÉFÉRENTIEL PROFESSIONNEL DES AGENTS AFIS
 RÉFÉRENTIEL PROFESSIONNEL DES AGENTS AFIS Les missions de l agent AFIS s articulent autour de trois objets L exécution de fonctions opérationnelles La tenue de documents L exercice de relations avec la
RÉFÉRENTIEL PROFESSIONNEL DES AGENTS AFIS Les missions de l agent AFIS s articulent autour de trois objets L exécution de fonctions opérationnelles La tenue de documents L exercice de relations avec la
PAUL CORREIA 6 e édition
 GUIDE PRATIQUE DU PAUL CORREIA 6 e édition Groupe Eyrolles, 2012, ISBN : 978-2-212-13367-7 Table des matières AVANT-PROPOS.......................................................... 1 Organisation de l
GUIDE PRATIQUE DU PAUL CORREIA 6 e édition Groupe Eyrolles, 2012, ISBN : 978-2-212-13367-7 Table des matières AVANT-PROPOS.......................................................... 1 Organisation de l
Glossaire. base de données géographiques Voir géodatabase (GDB).
 Glossaire analyse Processus d identification d une question ou d un problème à résoudre, de modélisation de ce problème, de recherche des résultats de modélisation, d interprétation des résultats, d élaboration
Glossaire analyse Processus d identification d une question ou d un problème à résoudre, de modélisation de ce problème, de recherche des résultats de modélisation, d interprétation des résultats, d élaboration
Scanner laser HDS7000 Ultra rapide, à portée étendue
 > 1 million de points / sec Scanner laser HDS7000 Ultra rapide, à portée étendue > 180 m de portée HDS7000 Scanner laser ultra rapide pour les professionnels exigeants Les scanners à mesure de phase sont
> 1 million de points / sec Scanner laser HDS7000 Ultra rapide, à portée étendue > 180 m de portée HDS7000 Scanner laser ultra rapide pour les professionnels exigeants Les scanners à mesure de phase sont
Introduction à Adobe Illustrator pour la cartographie et la mise en page
 Atelier Carto. Septembre 2009 Dept. Géographie / Université de Toulouse-Le Mirail Laurent Jégou Introduction à Adobe Illustrator pour la cartographie et la mise en page Le présent support n'a pas prétention
Atelier Carto. Septembre 2009 Dept. Géographie / Université de Toulouse-Le Mirail Laurent Jégou Introduction à Adobe Illustrator pour la cartographie et la mise en page Le présent support n'a pas prétention
Introduction à MATLAB R
 Introduction à MATLAB R Romain Tavenard 10 septembre 2009 MATLAB R est un environnement de calcul numérique propriétaire orienté vers le calcul matriciel. Il se compose d un langage de programmation, d
Introduction à MATLAB R Romain Tavenard 10 septembre 2009 MATLAB R est un environnement de calcul numérique propriétaire orienté vers le calcul matriciel. Il se compose d un langage de programmation, d
G.P. DNS02 Septembre 2012. Réfraction...1 I.Préliminaires...1 II.Première partie...1 III.Deuxième partie...3. Réfraction
 DNS Sujet Réfraction...1 I.Préliminaires...1 II.Première partie...1 III.Deuxième partie...3 Réfraction I. Préliminaires 1. Rappeler la valeur et l'unité de la perméabilité magnétique du vide µ 0. Donner
DNS Sujet Réfraction...1 I.Préliminaires...1 II.Première partie...1 III.Deuxième partie...3 Réfraction I. Préliminaires 1. Rappeler la valeur et l'unité de la perméabilité magnétique du vide µ 0. Donner
Séquence 2. Repérage dans le plan Équations de droites. Sommaire
 Séquence Repérage dans le plan Équations de droites Sommaire 1 Prérequis Repérage dans le plan 3 Équations de droites 4 Synthèse de la séquence 5 Exercices d approfondissement Séquence MA0 1 1 Prérequis
Séquence Repérage dans le plan Équations de droites Sommaire 1 Prérequis Repérage dans le plan 3 Équations de droites 4 Synthèse de la séquence 5 Exercices d approfondissement Séquence MA0 1 1 Prérequis
Chapitre 4: Dérivée d'une fonction et règles de calcul
 DERIVEES ET REGLES DE CALCULS 69 Chapitre 4: Dérivée d'une fonction et règles de calcul Prérequis: Généralités sur les fonctions, Introduction dérivée Requis pour: Croissance, Optimisation, Études de fct.
DERIVEES ET REGLES DE CALCULS 69 Chapitre 4: Dérivée d'une fonction et règles de calcul Prérequis: Généralités sur les fonctions, Introduction dérivée Requis pour: Croissance, Optimisation, Études de fct.
COURS EULER: PROGRAMME DE LA PREMIÈRE ANNÉE
 COURS EULER: PROGRAMME DE LA PREMIÈRE ANNÉE Le cours de la première année concerne les sujets de 9ème et 10ème années scolaires. Il y a bien sûr des différences puisque nous commençons par exemple par
COURS EULER: PROGRAMME DE LA PREMIÈRE ANNÉE Le cours de la première année concerne les sujets de 9ème et 10ème années scolaires. Il y a bien sûr des différences puisque nous commençons par exemple par
Le projet 3D de la Ville de Liège: réflexions sur l'exploitation des données. Bernard Lechanteur, Responsable Cellule cartographie Ville de Liège
 Le projet 3D de la Ville de Liège: réflexions sur l'exploitation des données Bernard Lechanteur, Responsable Cellule cartographie Ville de Liège La cellule cartographie La cellule cartographie n est pas
Le projet 3D de la Ville de Liège: réflexions sur l'exploitation des données Bernard Lechanteur, Responsable Cellule cartographie Ville de Liège La cellule cartographie La cellule cartographie n est pas
Paris et New-York sont-ils les sommets d'un carré?
 page 95 Paris et New-York sont-ils les sommets d'un carré? par othi Mok (3 ), Michel Vongsavanh (3 ), Eric hin (3 ), iek-hor Lim ( ), Eric kbaraly ( ), élèves et anciens élèves du ollège Victor Hugo (2
page 95 Paris et New-York sont-ils les sommets d'un carré? par othi Mok (3 ), Michel Vongsavanh (3 ), Eric hin (3 ), iek-hor Lim ( ), Eric kbaraly ( ), élèves et anciens élèves du ollège Victor Hugo (2
MOTO ELECTRIQUE. CPGE / Sciences Industrielles pour l Ingénieur TD06_08 Moto électrique DIAGRAMME DES INTER-ACTEURS UTILISATEUR ENVIRONNEMENT HUMAIN
 MOTO ELECTRIQUE MISE EN SITUATION La moto électrique STRADA EVO 1 est fabriquée par une société SUISSE, située à LUGANO. Moyen de transport alternatif, peut-être la solution pour concilier contraintes
MOTO ELECTRIQUE MISE EN SITUATION La moto électrique STRADA EVO 1 est fabriquée par une société SUISSE, située à LUGANO. Moyen de transport alternatif, peut-être la solution pour concilier contraintes
Chapitre 9 : Applications des lois de Newton et Kepler à l'étude du mouvement des planètes et des satellites
 I- Les trois lois de Kepler : Chapitre 9 : Applications des lois de Newton et Kepler à l'étude du mouvement des planètes et des satellites Les lois de Kepler s'applique aussi bien pour une planète en mouvement
I- Les trois lois de Kepler : Chapitre 9 : Applications des lois de Newton et Kepler à l'étude du mouvement des planètes et des satellites Les lois de Kepler s'applique aussi bien pour une planète en mouvement
I - PUISSANCE D UN POINT PAR RAPPORT A UN CERCLE CERCLES ORTHOGONAUX POLES ET POLAIRES
 I - PUISSANCE D UN POINT PAR RAPPORT A UN CERCLE CERCLES ORTHOGONAUX POLES ET POLAIRES Théorème - Définition Soit un cercle (O,R) et un point. Une droite passant par coupe le cercle en deux points A et
I - PUISSANCE D UN POINT PAR RAPPORT A UN CERCLE CERCLES ORTHOGONAUX POLES ET POLAIRES Théorème - Définition Soit un cercle (O,R) et un point. Une droite passant par coupe le cercle en deux points A et
C - ICM LTE Gamme DE
 Gamme DELTEC - ICM ICM micro Projecteur de profil numérique 2D Système de mesure 2D, fruit de plus de 25 ans d expérience dans la métrologie par vision! Déposer c est mesurer! - Reconnaissance de la pièce
Gamme DELTEC - ICM ICM micro Projecteur de profil numérique 2D Système de mesure 2D, fruit de plus de 25 ans d expérience dans la métrologie par vision! Déposer c est mesurer! - Reconnaissance de la pièce
I Mise en place d un SIG pour la gestion des équipements sur les routes départementales de la Loire I
 I Mise en place d un SIG pour la gestion des équipements sur les routes départementales de la Loire I I Déroulement de la présentation I Les missions de la cellule programmation Le patrimoine routier Le
I Mise en place d un SIG pour la gestion des équipements sur les routes départementales de la Loire I I Déroulement de la présentation I Les missions de la cellule programmation Le patrimoine routier Le
Zone 2 L aventure de la copie
 EXPOSITION INTERNATIONALE INTERNATIONAL EXHIBITION Zone 2 L aventure de la copie 1. Synopsis... 2 2. Scénographie... 3 3. Mobiliers... 3 4. Supports graphiques... 4 5. Eclairage... 4 6. Audiovisuels...
EXPOSITION INTERNATIONALE INTERNATIONAL EXHIBITION Zone 2 L aventure de la copie 1. Synopsis... 2 2. Scénographie... 3 3. Mobiliers... 3 4. Supports graphiques... 4 5. Eclairage... 4 6. Audiovisuels...
Leica System 1200 Software Des programmes intégrés pour GPS1200 et TPS1200
 Leica System 1200 Software Des programmes intégrés pour GPS1200 et TPS1200 Leica System 1200 Logiciels L'ensemble de logiciels du System 1200 se nomme Smart- Worx les programmes TPS, GPS et RX1250 embarqués
Leica System 1200 Software Des programmes intégrés pour GPS1200 et TPS1200 Leica System 1200 Logiciels L'ensemble de logiciels du System 1200 se nomme Smart- Worx les programmes TPS, GPS et RX1250 embarqués
Les algorithmes de base du graphisme
 Les algorithmes de base du graphisme Table des matières 1 Traçage 2 1.1 Segments de droites......................... 2 1.1.1 Algorithmes simples.................... 3 1.1.2 Algorithmes de Bresenham (1965).............
Les algorithmes de base du graphisme Table des matières 1 Traçage 2 1.1 Segments de droites......................... 2 1.1.1 Algorithmes simples.................... 3 1.1.2 Algorithmes de Bresenham (1965).............
Série T modèle TES et TER
 6-8 rue des Casernes Tél. : 03.84.29.55.55 F 90200 GIROMAGNY Fax : 03.84.29.09.91 E-mail : [email protected] http://www.ultralu.com NOTICE DE MONTAGE ET D UTILISATION ECHAFAUDAGE ROULANT ALUMINIUM Série
6-8 rue des Casernes Tél. : 03.84.29.55.55 F 90200 GIROMAGNY Fax : 03.84.29.09.91 E-mail : [email protected] http://www.ultralu.com NOTICE DE MONTAGE ET D UTILISATION ECHAFAUDAGE ROULANT ALUMINIUM Série
CONSTRUCTION DES PROJECTIONS TYPES DE PROJECTION. Projection => distorsions. Orientations des projections
 A.Charbonnel SYNTHÈSE SUR LES PROJECTIONS CARTOGRAPHIQUES SIMPLES 1/6 TYPES DE PROJECTION Pour passer de la représentation en 3D de la terre (globe terrestre) à une représentation en 2D (la carte), on
A.Charbonnel SYNTHÈSE SUR LES PROJECTIONS CARTOGRAPHIQUES SIMPLES 1/6 TYPES DE PROJECTION Pour passer de la représentation en 3D de la terre (globe terrestre) à une représentation en 2D (la carte), on
Cabri et le programme de géométrie au secondaire au Québec
 Cabri et le programme de géométrie au secondaire au Québec Benoît Côté Département de mathématiques, UQAM, Québec [email protected] 1. Introduction - Exercice de didactique fiction Que signifie intégrer
Cabri et le programme de géométrie au secondaire au Québec Benoît Côté Département de mathématiques, UQAM, Québec [email protected] 1. Introduction - Exercice de didactique fiction Que signifie intégrer
L.T.Mohammedia CHAINE D ENERGIE - DESSIN TECHNIQUE S.CHARI
 I. Introduction Pourquoi le dessin technique? Le Dessin Technique est une façon de représenter des pièces réelles (donc en 3 dimensions) sur une feuille de papier (donc en 2 dimensions) que l on appelle
I. Introduction Pourquoi le dessin technique? Le Dessin Technique est une façon de représenter des pièces réelles (donc en 3 dimensions) sur une feuille de papier (donc en 2 dimensions) que l on appelle
Sujet proposé par Yves M. LEROY. Cet examen se compose d un exercice et de deux problèmes. Ces trois parties sont indépendantes.
 Promotion X 004 COURS D ANALYSE DES STRUCTURES MÉCANIQUES PAR LA MÉTHODE DES ELEMENTS FINIS (MEC 568) contrôle non classant (7 mars 007, heures) Documents autorisés : polycopié ; documents et notes de
Promotion X 004 COURS D ANALYSE DES STRUCTURES MÉCANIQUES PAR LA MÉTHODE DES ELEMENTS FINIS (MEC 568) contrôle non classant (7 mars 007, heures) Documents autorisés : polycopié ; documents et notes de
Equipement. électronique
 MASTER ISIC Les générateurs de fonctions 1 1. Avant-propos C est avec l oscilloscope, le multimètre et l alimentation stabilisée, l appareil le plus répandu en laboratoire. BUT: Fournir des signau électriques
MASTER ISIC Les générateurs de fonctions 1 1. Avant-propos C est avec l oscilloscope, le multimètre et l alimentation stabilisée, l appareil le plus répandu en laboratoire. BUT: Fournir des signau électriques
1 Création d une pièce. 2 Travail complémentaire. 1-1 Réglage des barres d outils. 1-2 Exemples de réalisation de pièces à l aide d un modeleur 3D
 SolidWorks Logiciel de DAO (Dessin Assisté par Ordinateur) Palonnier Servomoteur SOMMAIRE : 1 Création d une pièce 1-1 Réglage des barres d outils 1-2 Exemples de réalisation de pièces à l aide d un modeleur
SolidWorks Logiciel de DAO (Dessin Assisté par Ordinateur) Palonnier Servomoteur SOMMAIRE : 1 Création d une pièce 1-1 Réglage des barres d outils 1-2 Exemples de réalisation de pièces à l aide d un modeleur
Décrets, arrêtés, circulaires
 Décrets, arrêtés, circulaires TEXTES GÉNÉRAUX MINISTÈRE DES TRANSPORTS, DE L ÉQUIPEMENT, DU TOURISME ET DE LA MER Arrêté du 15 janvier 2007 portant application du décret n o 2006-1658 du 21 décembre 2006
Décrets, arrêtés, circulaires TEXTES GÉNÉRAUX MINISTÈRE DES TRANSPORTS, DE L ÉQUIPEMENT, DU TOURISME ET DE LA MER Arrêté du 15 janvier 2007 portant application du décret n o 2006-1658 du 21 décembre 2006
La spectro, c'est facile
 La spectro, c'est facile OHP Spectro Party Observatoire de Haute Provence 25-30 juillet 2014 François Cochard [email protected] La spectro, c'est facile à certaines conditions OHP Spectro Party
La spectro, c'est facile OHP Spectro Party Observatoire de Haute Provence 25-30 juillet 2014 François Cochard [email protected] La spectro, c'est facile à certaines conditions OHP Spectro Party
Station Totale Geomax Série Zoom30
 Station Totale Geomax Série Zoom30 GeoMax Profil de l entreprise GeoMax est une entreprise fort de solides positions sur L étroite collaboration qui présente à l international et le marché des technologies
Station Totale Geomax Série Zoom30 GeoMax Profil de l entreprise GeoMax est une entreprise fort de solides positions sur L étroite collaboration qui présente à l international et le marché des technologies
TBI et mathématique. Pour vous soutenir dans votre enseignement des mathématiques. Les outils du logiciel Notebook. les ressources internet
 TBI et mathématique Pour vous soutenir dans votre enseignement des mathématiques Dessin tiré du site www.recitus.qc.ca Les outils du logiciel Notebook et les ressources internet Document préparé par France
TBI et mathématique Pour vous soutenir dans votre enseignement des mathématiques Dessin tiré du site www.recitus.qc.ca Les outils du logiciel Notebook et les ressources internet Document préparé par France
DISQUE DUR. Figure 1 Disque dur ouvert
 DISQUE DUR Le sujet est composé de 8 pages et d une feuille format A3 de dessins de détails, la réponse à toutes les questions sera rédigée sur les feuilles de réponses jointes au sujet. Toutes les questions
DISQUE DUR Le sujet est composé de 8 pages et d une feuille format A3 de dessins de détails, la réponse à toutes les questions sera rédigée sur les feuilles de réponses jointes au sujet. Toutes les questions
BROCHURE PRODUIT. Swift-fix Solutions de fixation des pièces pour les applications de mesure
 BROCHURE PRODUIT Swift-fix Solutions de fixation des pièces pour les applications de mesure swift-fix Une gamme unique de systèmes de fixation et de serrage de pièces, signée Hexagon Metrology Swift-fix
BROCHURE PRODUIT Swift-fix Solutions de fixation des pièces pour les applications de mesure swift-fix Une gamme unique de systèmes de fixation et de serrage de pièces, signée Hexagon Metrology Swift-fix
Plan présentation RATP
 Plan présentation RATP Présentation réseau RATP Présentation de la maintenance des caténaires Risques rupture caténaire Sélection du nouveau système Présentation du réseau RATP NANTERRE T1 T2 T3 VAL DE
Plan présentation RATP Présentation réseau RATP Présentation de la maintenance des caténaires Risques rupture caténaire Sélection du nouveau système Présentation du réseau RATP NANTERRE T1 T2 T3 VAL DE
Mesurer les altitudes avec une carte
 www.ign.fr > Espace éducatif > Les fiches thématiques > Lecture de la carte Mesurer les altitudes avec une carte Les cartes topographiques ne sont pas uniquement une représentation plane de la surface
www.ign.fr > Espace éducatif > Les fiches thématiques > Lecture de la carte Mesurer les altitudes avec une carte Les cartes topographiques ne sont pas uniquement une représentation plane de la surface
I Stabilité, Commandabilité et Observabilité 11. 1 Introduction 13 1.1 Un exemple emprunté à la robotique... 13 1.2 Le plan... 18 1.3 Problème...
 TABLE DES MATIÈRES 5 Table des matières I Stabilité, Commandabilité et Observabilité 11 1 Introduction 13 1.1 Un exemple emprunté à la robotique................... 13 1.2 Le plan...................................
TABLE DES MATIÈRES 5 Table des matières I Stabilité, Commandabilité et Observabilité 11 1 Introduction 13 1.1 Un exemple emprunté à la robotique................... 13 1.2 Le plan...................................
Cours IV Mise en orbite
 Introduction au vol spatial Cours IV Mise en orbite If you don t know where you re going, you ll probably end up somewhere else. Yogi Berra, NY Yankees catcher v1.2.8 by-sa Olivier Cleynen Introduction
Introduction au vol spatial Cours IV Mise en orbite If you don t know where you re going, you ll probably end up somewhere else. Yogi Berra, NY Yankees catcher v1.2.8 by-sa Olivier Cleynen Introduction
EVALUATIONS MI-PARCOURS CM2
 Les enseignants de CM2 de la circonscription de METZ-SUD proposent EVALUATIONS MI-PARCOURS CM2 Mathématiques Livret enseignant NOMBRES ET CALCUL Circonscription de METZ-SUD Page 1 Séquence 1 : Exercice
Les enseignants de CM2 de la circonscription de METZ-SUD proposent EVALUATIONS MI-PARCOURS CM2 Mathématiques Livret enseignant NOMBRES ET CALCUL Circonscription de METZ-SUD Page 1 Séquence 1 : Exercice
INTRODUCTION À L ANALYSE FACTORIELLE DES CORRESPONDANCES
 INTRODUCTION À L ANALYSE FACTORIELLE DES CORRESPONDANCES Dominique LAFFLY Maître de Conférences, Université de Pau Laboratoire Société Environnement Territoire UMR 5603 du CNRS et Université de Pau Domaine
INTRODUCTION À L ANALYSE FACTORIELLE DES CORRESPONDANCES Dominique LAFFLY Maître de Conférences, Université de Pau Laboratoire Société Environnement Territoire UMR 5603 du CNRS et Université de Pau Domaine
 Utilisation d informations visuelles dynamiques en asservissement visuel Armel Crétual IRISA, projet TEMIS puis VISTA L asservissement visuel géométrique Principe : Réalisation d une tâche robotique par
Utilisation d informations visuelles dynamiques en asservissement visuel Armel Crétual IRISA, projet TEMIS puis VISTA L asservissement visuel géométrique Principe : Réalisation d une tâche robotique par
Soit la fonction affine qui, pour représentant le nombre de mois écoulés, renvoie la somme économisée.
 ANALYSE 5 points Exercice 1 : Léonie souhaite acheter un lecteur MP3. Le prix affiché (49 ) dépasse largement la somme dont elle dispose. Elle décide donc d économiser régulièrement. Elle a relevé qu elle
ANALYSE 5 points Exercice 1 : Léonie souhaite acheter un lecteur MP3. Le prix affiché (49 ) dépasse largement la somme dont elle dispose. Elle décide donc d économiser régulièrement. Elle a relevé qu elle
Les moments de force. Ci-contre, un schéma du submersible MIR où l on voit les bras articulés pour la récolte d échantillons [ 1 ]
![Les moments de force. Ci-contre, un schéma du submersible MIR où l on voit les bras articulés pour la récolte d échantillons [ 1 ] Les moments de force. Ci-contre, un schéma du submersible MIR où l on voit les bras articulés pour la récolte d échantillons [ 1 ]](/thumbs/20/424260.jpg) Les moments de force Les submersibles Mir peuvent plonger à 6 000 mètres, rester en immersion une vingtaine d heures et abriter 3 personnes (le pilote et deux observateurs), dans une sphère pressurisée
Les moments de force Les submersibles Mir peuvent plonger à 6 000 mètres, rester en immersion une vingtaine d heures et abriter 3 personnes (le pilote et deux observateurs), dans une sphère pressurisée
Priorités de calcul :
 EXERCICES DE REVISION POUR LE PASSAGE EN QUATRIEME : Priorités de calcul : Exercice 1 : Calcule en détaillant : A = 4 + 5 6 + 7 B = 6 3 + 5 C = 35 5 3 D = 6 7 + 8 E = 38 6 3 + 7 Exercice : Calcule en détaillant
EXERCICES DE REVISION POUR LE PASSAGE EN QUATRIEME : Priorités de calcul : Exercice 1 : Calcule en détaillant : A = 4 + 5 6 + 7 B = 6 3 + 5 C = 35 5 3 D = 6 7 + 8 E = 38 6 3 + 7 Exercice : Calcule en détaillant
Commune X. Quelles nouvelles exigences pour l accessibilité de la voirie? Les prescriptions techniques de l arrêté du 15 janvier 2007
 Commune X Quelles nouvelles exigences pour l accessibilité de la voirie? Les prescriptions techniques de l arrêté du 15 janvier 2007 Centre d'études Techniques de l'équipement Méditerranée Les cheminements
Commune X Quelles nouvelles exigences pour l accessibilité de la voirie? Les prescriptions techniques de l arrêté du 15 janvier 2007 Centre d'études Techniques de l'équipement Méditerranée Les cheminements
BD ADRESSE. Version 2.1. Descriptif de contenu. Institut Géographique National. www.ign.fr. Date du Document : Octobre 2011
 BD ADRESSE Version 2.1 Descriptif de contenu Date du Document : Octobre 2011 Institut Géographique National 73 avenue de Paris 94165 Saint-Mandé Cedex www.ign.fr 1. GÉNÉRALITÉS...3 1.1 Ce que contient
BD ADRESSE Version 2.1 Descriptif de contenu Date du Document : Octobre 2011 Institut Géographique National 73 avenue de Paris 94165 Saint-Mandé Cedex www.ign.fr 1. GÉNÉRALITÉS...3 1.1 Ce que contient
Concevoir et réaliser des systèmes constructifs ossature bois
 Concevoir et réaliser des systèmes constructifs ossature bois Cette vous permettra d appréhender les principes fondamentaux du système constructif ossature bois selon les normes et DTU en vigueur. Elle
Concevoir et réaliser des systèmes constructifs ossature bois Cette vous permettra d appréhender les principes fondamentaux du système constructif ossature bois selon les normes et DTU en vigueur. Elle
Cours d Analyse. Fonctions de plusieurs variables
 Cours d Analyse Fonctions de plusieurs variables Licence 1ère année 2007/2008 Nicolas Prioux Université de Marne-la-Vallée Table des matières 1 Notions de géométrie dans l espace et fonctions à deux variables........
Cours d Analyse Fonctions de plusieurs variables Licence 1ère année 2007/2008 Nicolas Prioux Université de Marne-la-Vallée Table des matières 1 Notions de géométrie dans l espace et fonctions à deux variables........
Exprimer ce coefficient de proportionnalité sous forme de pourcentage : 3,5 %
 23 CALCUL DE L INTÉRÊT Tau d intérêt Paul et Rémi ont reçu pour Noël, respectivement, 20 et 80. Ils placent cet argent dans une banque, au même tau. Au bout d une année, ce placement leur rapportera une
23 CALCUL DE L INTÉRÊT Tau d intérêt Paul et Rémi ont reçu pour Noël, respectivement, 20 et 80. Ils placent cet argent dans une banque, au même tau. Au bout d une année, ce placement leur rapportera une
Cartes de bruit stratégiques
 Département de la Sarthe Cartes de bruit stratégiques Grandes infrastructures de transports Réseau autoroutier COFIROUTE Résumé non technique Article R 572-5 du code de l environnement Vu pour être annexé
Département de la Sarthe Cartes de bruit stratégiques Grandes infrastructures de transports Réseau autoroutier COFIROUTE Résumé non technique Article R 572-5 du code de l environnement Vu pour être annexé
