THÈSE. présentée DEVANT L UNIVERSITÉ DE RENNES I. pour obtenir. Mention : Génie Biologique et Médical PAR. Christophe Grova
|
|
|
- Maxime Beaudoin
- il y a 8 ans
- Total affichages :
Transcription
1 N o d ordre : 68 THÈSE présentée DEVANT L UNIVERSITÉ DE RENNES I pour obtenir le grade de : DOCTEUR DE L UNIVERSITÉ DE RENNES I Mention : Génie Biologique et Médical PAR Christophe Grova Équipe d accueil : Laboratoire IDM - UPRES EA 3192 Intégration de données multimedia en anatomie et physiologie cérébrale pour l aide à la décision et l enseignement (Faculté de Médecine, Rennes) École doctorale : Vie, Agro, Santé (VAS) Titre de la thèse : Simulations réalistes de données de tomographie d émission monophotonique (TEMP) pour l évaluation de méthodes de recalage TEMP/IRM utilisant des mesures statistiques de similarité : application dans le contexte de la fusion de données en épilepsie Soutenue le 23 décembre 2002, devant la commission d examen COMPOSITION DU JURY: M. Jean-Marie SCARABIN Directeur de thèse MM. Nicholas AYACHE Rapporteurs Jacques DARCOURT MM. Habib BENALI Examinateurs Jean-Yves BOIRE Bernard GIBAUD M. Arnaud BIRABEN Membre invité
2
3 3 Remerciements Si c est possible, c est fait; Si c est impossible, cela se fera C.A. de Calonne Ce travail de thèse a été réalisé au sein du laboratoire IDM de l université de Rennes 1, il s agit d un environnement hautement pluridisciplinaire, en lien direct avec le CHU de Rennes, qui m a permis de comprendre au mieux les enjeux de ce domaine de recherche très complexe et passionnant qu est l épileptologie. La laboratoire IDM ainsi que les services de neurologie, neurochirurgie, radiologie et explorations fonctionnelles du CHU Pontchaillou de Rennes m ont permis de m épanouir dans un cadre humain et technique unique de part les compétences et moyens mis à ma disposition. Je tiens tout d abord à témoigner ma profonde reconnaissance à Monsieur le professeur Jean Marie Scarabin, Professeur des Universités, pour avoir accepté de diriger ce travail de thèse au sein du laboratoire IDM. Je tiens à lui témoigner toute ma gratitude pour sa confiance ainsi que pour m avoir appris à considérer l application clinique comme une priorité dans toutes mes approches. Je tiens à remercier particulièrement Messieurs Nicholas Ayache, directeur de recherche INRIA, et Jacques Darcourt, Professeur des Universités, pour m avoir fait l honneur de rapporter cette thèse, ainsi que pour l intérêt qu ils ont porté à mes travaux et la qualité de leurs rapports. Je tiens finalement à remercier Messieurs Habib Benali, directeur de recherche IN- SERM, Arnaud Biraben, neurologue, Jean-Yves Boire, Maître de Conférence Universitaire, et Bernard Gibaud, chargé de recherche INSERM, pour avoir accepté de participer à mon jury. J exprime particulièrement ma reconnaissance à Bernard Gibaud et Pierre Jannin du laboratoire IDM, pour lesquels l encadrement de ce travail de thèse a été un travail quotidien. Ils ont contribué pour beaucoup à ma formation au monde de la recherche, ont réussi à me convaincre qu une recherche appliquée et proche des problématiques des cliniciens est tout à fait valorisante et passionnante. Ils ont su me guider tout au long de ses années, m éclairer par leur vision d ensemble des différentes problématiques et surtout me recentrer sur ma problématique quand je voulais apprendre tout sur tout. Je tiens surtout à saluer leur patience et leur grande disponibilité. Je me souviendrais longtemps d un plan de thèse discuté avec Pierre sur le pont de la bisquine Cancalaise dans le port de Douarnenez.
4 4 Un grand merci aux personnes des l unité INSERM U494 de la Pitié Salpétrière, notamment Habib Benali, Irène Buvat et Sébastien Hapdey. Ils étaient toujours là pour répondre à mes nombreuses interrogations sur la formation et la simulation des images en médecine nucléaire et sur des questions statistiques. Je remercie particulièrement Habib Benali d avoir accepté d être mon tuteur scientifique pour cette thèse. Nos nombreuses réunions furent toujours très enrichissantes et pleines de nouvelles idées sur la manière d aborder mon travail. Merci, encore pour m avoir appris à me poser la fameuse question en statistique: qu est ce qu on fait lorsque ce n est pas gaussien?. Je tiens à exprimer ma reconnaissance au docteur Leighton Barnden (Woodville, Australie), pour m avoir donner accès à sa base de données TEMP de sujets sains, ainsi qu à Alexis Roche (INRIA Sophia Antipolis) pour ses conseils sur le rapport de corrélation. Je tiens à remercier également tous les cliniciens avec qui j ai collaboré au cours de ma thèse. Je remercie surtout le docteur Arnaud Biraben, pour m avoir permis d assister régulièrement au staff du service d épilepsie, et m avoir ainsi fait prendre conscience de l intérêt des méthodes de fusion pour assister l analyse des épileptologues. J en profite pour remercier les docteurs Pierre Toulouse, Delphine Taussig, Claire Haegelen, Eric Seigneuret et Xavier Morandi ainsi que toutes les personnes des services de neurochirurgie, neurologie et explorations fonctionnelles que j ai cotoyées. Je remercie le Centre Eugène Marquis et en particulier le docteur Anne-Marie Bernard et Olivier Schill pour leurs conseils sur l acquisition et le traitement des données TEMP. Merci également aux collègues de l IRISA, notamment à Christian Barillot pour m avoir fait découvrir ce monde obscure du recalage d images médicales, et aussi à son équipe, Pierre et Isabelle notamment. Merci également à Elisabeth Le Rumeur pour son aide sur l analyse des données IRMf, ainsi qu à Jean- Yves Bansard et Michel Kerbaol pour leur conseils concernant l analyse factorielle des correspondences des données TEMP. Bien évidemment un grand grand merci à tous mes collègues et amis du laboratoire IDM, qui m ont permis de réaliser ces travaux dans une ambiance très sympathique et motivante. Merci à Oliver pour ce travail d équipe qui nous a permis de mettre en place un environnement multimodal utilisable au laboratoire et par les neurochirurgiens, et surtout pour avoir toujours su répondre aux questions du style: pourquoi ça ne compile pas?. Merci à Bérengère et Mélanie, je leur serai toujours reconnaissant pour leur aide et leur support à la fin de la rédaction de ce manuscrit, et puis merci pour leur sourire et leur bonne humeur de tous les jours. Un clin d œil au marin Olivier, et merci pour les nombreuses soirées labo qui ont fini à la Lupa et au Couleur Caf avec Isabelle. Outre cette joyeuse bande de thésards, un grand merci aux nombreuses autres personnes que j ai côtoyées au laboratoire SIM devenu IDM, je cite dans le désordre: Eric, Chantal, Alain, Benoît, Laurent, Claudine, toute l équipe du CRITT, Jérémie, Solène, Didier, Denis... et à tous ceux que je risque certainement d oublier, car il y en a eu du monde... Cette thèse n aurait certainement jamais abouti, sans le soutien et la confiance de mes proches, je leur suis extrêmement reconnaissant, je pense particulièrement à mes parents, à ma sœur Nathalie, et aussi à ma cousine Christine, tous toujours là au bout du fil quand on en a besoin! Merci à tous d avoir gardé confiance en moi et de m avoir soutenu pendant
5 toutes ces années. Cette thèse a été également pour moi l occasion de découvrir la Bretagne, de réaliser qu il ne pleuvait pas tout le temps et surtout d apprécier la chaleur des bretons. Merci aux doctoriales de Saint Malo, sans qui je n aurais pas rencontré mes compagnons thésards, embarqués dans la même galère, et devenus de vrais amis particulièrement Jean René, Anthony, Malika, Frédérique, Olivier et Nico. Merci à vous tous les marins, on est tous arrivé à bon port. Merci encore merci à tous les rennais pour votre soutien et amitié, Géraldine, alias la meilleure des voisines, Sabrina, Bich Thuy, Luce, Eric, Anne, les complices d Yfonkdufonk, les amis de la Bisquine... et puis aussi aux amis de toujours Franky, Franck à la guitare, Dan et Fred. Je terminerai par un petit clin d œil tout spécial à Maggye pour son soutien venu d outre Atlantique pendant les longues nuits de rédaction. Voilà cela fait beaucoup de merci tout ça, et je suis sur que j en oublie pas mal... Merci à vous tous... 5
6 6
7 Table des matières 7 Table des matières Introduction générale 16 I FUSION DE DONNEES EN EPILEPSIE, RECALAGE ET VALI- DATION 21 1 Fusion de données multimodales anatomo-fonctionnelles en épilepsie Chirurgie de l épilepsie et réseau épileptogène Historique de l épilepsie La chirurgie de l épilepsie Définition du réseau épileptogène Techniques d exploration du réseau épileptogène Notions de neurophysiologie : origine de l activité cérébrale? Examens statiques La Tomodensitométrie ou Scanner X L Imagerie par Résonance Magnétique(IRM) morphologique La spectroscopie RMN La Tomographie d Emission de Positons (TEP): Examens dynamiques de l état inter-critique Approches électrophysiologiques Mesures de perfusion en médecine nucléaire : TEP et TEMP inter-critiques Imagerie par Résonance Magnétique (IRM) dynamique et fonctionnelle : Examens dynamiques de l état critique Approches électrophysiologiques Tomographie d Emission MonoPhotonique (TEMP) critique Analyse de l environnement fonctionnel Potentiels évoqués: EEG, MEG, ECoG, SEEG Imagerie d activation : IRMf, TEP Explorations invasives Méthodes d analyse et de fusion de données: besoins pour l épilepsie Fusion de données guidée par le problème clinique Aide au repérage sur l anatomie du patient
8 8 Table des matières Aide à la détection et quantification d aires pathologiques ou fonctionnelles spécifiques au sujet exploré Aider à une meilleure détection, localisation ou quantification des anomalies épileptogènes: Construction de nouvelles images dites de fusion : Comparaison d informations fonctionnelles: Fusion coopérative et méthodes de reconstruction de sources en MEG/EEG: Identification de patterns caractérisant des aires pathologiques ou fonctionnelles au sein d une population de sujets Analyse par standardisation anatomique : Cartographies statistiques d activation : Aide à la réalisation d un acte chirurgical Méthodes de recalage par mesures statistiques de similarité Revue générale des méthodes de recalage Contextes de mise en œuvre de procédures de recalage Contexte de fusion 1 : recalage intra-sujet et intra-modalité Contexte de fusion 2 : recalage intra-sujet et inter-modalité Contexte de fusion 3 : recalage sujet réel et modalités Contexte 4 : recalage inter-sujet et intra- ou inter-modalité Classification des méthodes de recalage Définition des repères géométriques utilisés Espace de recherche : type de transformation géométrique Espace des paramètres: type d information homologue Métrique de qualité de la mise en correspondance : fonction de coût Stratégie de recherche : méthodes d optimisation Recalage basé sur des mesures statistiques de similarité Pourquoi s intéresser aux mesures statistiques de similarité? Principe de la mise en correspondance par mesures statistiques de similarité Position du problème L image médicale : une variable aléatoire discrète Principales notations utilisées Interpolation et estimation des lois de probabilité Normalisation : gestion du recouvrement partiel Éléments de théorie de l information Géométrie des variables aléatoires de carré intégrable Mesures de quantité d information Métriques de comparaison des quantités d information Classification des mesures statistiques de similarité Mesures considérant les images comme des variables quantitatives Mesures considérant les images comme des variables qualitatives
9 Table des matières Approches hybrides Mesures basées sur une modélisation de la similarité entre les données à recaler Modélisation de la similarité à partir des données Modélisation du processus de génération des données Mise en œuvre du recalage : pré-traitements et méthodes d optimisation Synthèse Validation de méthodes de recalage : application aux recalages TEMP/IRM ou TEMP/TEMP Classification des procédures de validation Méthodes de recalage évaluées Hypothèse de validation Mise en œuvre d une procédure de validation : Type de gold standard Données de validation Calcul de la transformation de référence Paramètres Métrique de validation : Type de divergence (discrepancy) : erreur (E) ou inconsistence (I) Objet de la mesure Etude de la distribution des divergences Test d hypothèse Evaluation clinique qualitative II SIMULATIONS REALISTES D IMAGERIE TEMP POUR L EVA- LUATION DU RECALAGE TEMP/IRM 135 Position du problème Construction d un modèle théorique de perfusion par une analyse par standardisation anatomique Méthodes de reconstruction tomographique et de correction pour la quantification en TEMP Quels phénomènes dégradent le signal en TEMP? Interactions rayonnement - matière Bruit stochastique d acquisition Limitations technologiques du détecteur Perte de résolution en profondeur : L effet de volume partiel : Techniques de reconstruction tomographique Rétroprojection filtrée : Méthodes itératives Modélisation du projecteur : Mesure de la résolution spatiale :
10 10 Table des matières Méthodes usuelles de correction Correction de l atténuation : méthode de Chang Correction de la diffusion : méthode de la fenêtre de Jaszczak Correction de la perte de résolution en profondeur Correction de volume partiel Etat de l art des méthodes d analyse de données TEMP ou TEP par standardisation anatomique Définition d une méthode d analyse par standardisation anatomique Quels contextes cliniques? Méthodes de normalisation spatiale Evaluation de la normalisation spatiale Approches utilisant des ROIs ou VOIs Approches basées voxels Comparaison des approches basées VOIs et des approches basées voxels Méthode de construction d un modèle théorique de perfusion Modèle spatial de l anatomie cérébrale Carte d activité : modèle théorique de perfusion cérébrale Choix d une population homogène : Acquisition et prétraitement des données: Normalisation spatiale des données: Normalisation en intensité des données TEMP : Mesures de perfusion sur des données TEMP réelles: Création de la carte théorique d activité : Analyse statistique des mesures de perfusion Présentation des résultats des mesures Phase 1 : analyse statistique descriptive Méthode : estimateurs et erreurs standard bootstrap Résultats Analyse statistique descriptive de la perfusion chez les sujets sains Analyse statistique descriptive de la perfusion ictale chez les sujets épileptiques Phase 2 : Effet de la localisation anatomique Méthode : analyse de la variance (ANOVA) Résultats Analyse de la variance de la perfusion chez les sujets sains en fonction des VOIs Analyse de la variance de la perfusion ictale chez les sujets épileptiques en fonction des VOIs Phase 2 (suite) : comparaison inter-hémisphérique Méthode : test t standard et bootstrapé Résultats Analyse des asymétries inter-hémisphériques de la perfusion chez les sujets sains Analyse des asymétries inter-hémisphériques de la perfusion ictale chez les sujets épileptiques
11 Table des matières Phase 3 : étude des dépendances statistiques entre structures anatomiques Méthode : Analyse Factorielle des Correspondances (AFC) Résultats AFC des mesures de perfusion chez les sujets sains (données corrigées du diffusé) AFC des mesures de perfusion ictale chez les sujets épileptiques en fonction des VOIs Discussion : des mesures au modèle de perfusion Méthode d analyse par standardisation anatomique Nécessité d un modèle spatial de l anatomie pour modéliser la perfusion Compensation de la variabilité anatomique inter-individuelle Mesure de la variabilité fonctionnelle inter-individuelle Intérêt clinique des modèles de perfusion normaux et pathologiques Analyse de la perfusion TEMP chez le sujet sain Analyse de la perfusion en épilepsie temporo-mésiale Qualité des données TEMP pour la quantification et la modélisation Perspectives de ces travaux de modélisation Simulation réaliste de données TEMP Méthodes de simulation réaliste de données TEMP Carte d activité et carte d atténuation des photons Simulations analytiques Simulations réalistes par techniques de Monte Carlo Reconstruction tomographique à partir des projections simulées Cartes d activité et résultats des simulations réalistes de données TEMP Simulations par techniques de Monte Carlo Perfusion normale moyenne Perfusion ictale moyenne caractéristique d une épilepsie temporomésiale Simulations analytiques Effet du niveau du bruit de comptage Simulations d activité extra-cérébrale Simulations d activités pathologiques extrêmes Discussion : réalisme des simulations Simulations TEMP comme données de validation Réalisme des simulations proposées Evaluation de méthodes de recalage TEMP/IRM utilisant des mesures statistiques de similarités Présentation des méthodes de recalage évaluées Prétraitements Modèle de transformation géométrique et repère Mesures statistiques de similarité
12 12 Table des matières Méthode d optimisation Stratégie de recherche Résultat du recalage Hypothèse de validation Niveau d évaluation Description des modalités Contexte clinique Objectif de validation Mise en œuvre de la procédure de validation Gold standard Données de validation Transformation de référence Métriques de validation Type de divergence : une erreur absolue Objet de la mesure de l erreur Etude de la distribution des erreurs Précision Résolution Pourcentage d échec Test d hypothèse Résultats de l évaluation comparative de méthodes de recalage Recalage multimodal TEMP/IRM Perfusion moyenne normale et ictale Niveau de bruit poissonnien Dissimilarités intrinsèques extrêmes Analyses de la variance Recalage monomodal TEMP/TEMP Analyses de la variance Discussion Synthèse sur l évaluation du recalage TEMP/IRM par mesures statistiques de similarité Simulations analytiques versus simulations de Monte Carlo Explication du comportement instable du critère de Woods avec nos simulations Synthèse de l évaluation du recalage TEMP/TEMP basé par mesures statistiques de similarité Comparaison avec les résultats de la littérature Perspectives Quelques conseils pour le recalage des données cliniques Vers une modélisation complète du processus lié au recalage TEMP/IRM Une meilleure modélisation pour les méthodes de recalage par inférence statistique
13 Table des matières 13 Conclusion générale 260 A Annexe : suite des résultats de l AFC 263 Bibliographie 281 Publications 302
14
15 Table des matières 15 Principales abbréviations BHE : Barrière Hémato-Encéphalique CC : Coefficient de Corrélation CT : Scanner X CW : Critère de Woods DSCr : Débit Sanguin Cérébral Régional EEG: Electro-EncéphaloGraphie GS : Gold Standard IM : Information Mutuelle IMN: Information Mutuelle Normalisée IRM : Imagerie par Résonance Magnétique LCR : Liquide Céphalo-Rachidien LMH: Largeur à Mi-Hauteur MEG: Magnéto-EncéphaloGraphie RCL1 : Rapport de Corrélation en Norme L1 RCL2 : Rapport de Corrélation en norme L2 RMN: Résonance Magnétique Nucléaire ROI : Region Of Interest SEEG: Stéréo-Electro-EncéphaloGraphie TEMP : Tomographie d Emission MonoPhotonique TEP : Tomographie d Emission de Positons VOI : Volume Of Interest ZE : Zone Epileptogène ZI : Zone Irritative ZL : Zone Lésionnelle
16
17 Introduction Générale 17 Introduction La prise en charge chirurgicale des épilepsies partielles dites pharmaco-résistantes est un domaine de recherche particulièrement porteur en imagerie médicale et principalement dans le domaine de la fusion de données multimodales anatomo-fonctionnelles. En effet, la décision thérapeutique liée à ces épilepsies sévères nécessite la compréhension du réseau épileptogène qui caractérise la maladie et son environnement fonctionnel proche, afin de s assurer que le foyer épileptogène est résécable sans causer de déficit fonctionnel significatif. La compréhension du dit réseau épileptogène passe par la définition de trois zones que sont la zone lésionnelle (ZL), la zone irritative (ZI) et la zone épileptogène (ZE). Toutes les situations peuvent se rencontrer, depuis le recouvrement parfait entre ces zones, leur chevauchement partiel, jusqu à leur distinction complète. La notion très récente de réseau provient plus particulièrement du fait que chacune de ces zones peut concerner un ou plusieurs territoires cérébraux mais aussi du fait qu il est nécessaire d identifier leur organisation dynamique ainsi que leurs interconnexions et synchronisations potentielles, pendant et entre les crises, pour comprendre les manifestations de la maladie. De l identification de ce réseau et de son environnement fonctionnel dépend la décision éventuelle d un acte thérapeutique chirurgical, et ainsi la possibilité d une rémission complète de la maladie. Pour caractériser ces réseaux, le clinicien dispose de sources d informations diverses provenant soit de l investigation clinique habituelle (histoire de la maladie, sémiologie des crises), mais aussi de divers signaux et images. Les images renseignent sur l organisation morphologique et fonctionnelle du réseau épileptogène. Ainsi, la tomodensitométrie et surtout l Imagerie par Résonance Magnétique (IRM) permettent la détection d altérations morphologiques du tissu nerveux. La Tomographie d Emission de Positons (TEP) reflète une activité métabolique comme la capture du glucose. La Tomographie d Emission MonoPhotonique (TEMP) est un indicateur de la perfusion cérébrale au cours d une crise (TEMP ictale) ou entre les crises (TEMP inter-ictale). Les signaux disponibles apportent quant à eux des informations sur les phénomènes électrophysiologiques mis en jeu en période ictale ou inter-ictale (ElectroEncéphaloGraphie EEG, MagnétoEncéphaloGraphie MEG, électrodes profondes: Stéréo-EEG, ElectroCorticoGraphie ECoG). L aspect complémentaire des divers phénomènes physiologiques observés ainsi que les différentes résolutions temporelles et spatiales de ces techniques d exploration rendent la confrontation de ces données très informative. En pratique clinique courante, le clinicien fusionne mentalement ces informations d origines et de natures diverses. Le traitement numérique de ces données permet de rendre cette fusion plus objective et plus précise. Les méthodes numériques de fusion de données apportent de nouvelles solutions en matière de mise en correspondance des données (ou recalage), de représentation des données fusionnées et d analyse quantitative des informations notamment fonctionnelles. La prise en charge
18 18 Introduction Générale chirurgicale des épilepsie partielles pharmaco-résistantes est donc un contexte clinique idéal pour mettre en œuvre une méthodologie de fusion de données. Dans ce travail, nous nous sommes particulièrement intéressés à la TEMP ictale, qui consiste à l heure actuelle en la principale technique d imagerie dynamique permettant d accéder au fonctionnement du cerveau pendant les premières dizaines de secondes de la crise d épilepsie. La faible résolution spatiale de ces données en rend l interprétation difficile, notamment au niveau de la localisation des structures internes telles que les noyaux gris. Pour cela la mise en correspondance et la fusion des données de TEMP ictale sur l IRM 3D morphologique du patient s avère très informative pour le clinicien. L objectif principal de ces travaux de thèse est l évaluation de la précision de méthodes de recalage utilisant des critères statistiques de similarité, dans ce contexte bien particulier qu est la mise en correspondance TEMP ictale / IRM. Pour réaliser cette évaluation quantitative, nous proposons une méthode permettant de générer des simulations réalistes de données TEMP à partir d une IRM. Pour cela nous construisons à la résolution de l IRM, un modèle théorique de perfusion caractéristique du contexte clinique étudié (sujets sains ou épileptiques), à partir de mesures sur des examens réels et nous modélisons la géométrie et les processus physiques d une acquisition TEMP via des techniques de Monte Carlo. Ce document est organisé en deux parties. La première partie consiste principalement en un état de l art présentant successivement la fusion de données dans le contexte de l épilepsie, les méthodes de recalage basées sur l optimisation de critères statistiques de similarité et une classification des études portant sur l évaluation de méthodes de recalage impliquant des données TEMP ou utilisant des mesures statistiques de similarité. La deuxième partie présente la méthode qui a été mise en œuvre pour l évaluation du recalage TEMP ictale / IRM. Elle consiste tout d abord en une modélisation du profil de perfusion que l on cherche à étudier, à partir d une méthode d analyse par standardisation anatomique de données TEMP réelles. Suivent ensuite une présentation des outils utilisés pour simuler les aspects géométriques et physiques de l acquisition TEMP, ainsi que des simulations réalisées. Dans le dernier chapitre ces simulations sont utilisées pour l évaluation comparative de méthodes de recalage utilisant des mesures statistiques de similarité. Ainsi, l objectif du premier chapitre est de présenter l enjeu de l utilisation de données d imagerie anatomique et fonctionnelle ou d électrophysiologie pour aider à la caractérisation du réseau épileptogène et de son environnement fonctionnel, pour assister un éventuel traitement chirurgical. Après avoir défini les différentes zones participant au réseau épileptogène, nous présentons de quelle manière elles peuvent être appréhendées par différentes techniques de neuroimagerie ou d électrophysiologie. Finalement, après avoir défini ce que nous entendons par fusion de données dans ce contexte clinique, les besoins en matière de fusion de données que soulève cette caractérisation du réseau épileptogène sont soulignés. Certains de ces aspects sont illustrés à partir de travaux réalisés au laboratoire. Ces éléments soulignent l importance des techniques de recalage comme composante de base de toute méthode de fusion et les besoins en matière de validation, essentielle avant d envisager toute utilisation en clinique. Le deuxième chapitre débute par une revue générale et une classification des différentes méthodes de recalage utilisables pour la mise en correspondance d images médicales suivant leur contexte d utilisation et suivant leurs différentes composantes intrinsèques: espace de recherche, espace des paramètres, métrique de la qualité de la mise en correspondance et stratégie de recherche. La seconde partie de ce chapitre souligne l importance
19 Introduction Générale 19 des méthodes basées sur des mesures statistiques de similarité pour la mise en correspondance automatique de données volumiques. Après un rappel des éléments de théorie de l information permettant de poser leurs fondements, nous proposons une classification des principales mesures statistiques de similarité utilisées dans la littérature, ainsi que leur implémentation notamment pour répondre au problème du recalage TEMP/IRM. Le troisième chapitre souligne la nécessité d une évaluation objective des méthodes de recalage, étape préliminaire à l évaluation de toute méthode de fusion de données. S inspirant de travaux menés au laboratoire sur la standardisation des procédures de validation, nous commençons par définir les notions clés: hypothèses et objectifs de validation, données de validation et gold standard, métriques de validation. A partir de ces définitions, nous proposons une classification des différentes techniques de validation de méthodes de recalage. Cet état de l art se limite principalement aux méthodes de recalage faisant intervenir des données de TEMP ou de TEP ou des techniques de recalage basées sur l optimisation de mesures statistiques de similarité. La partie II débute par l énoncé de la problématique principale de ces travaux de thèse, à savoir l étude et l évaluation du recalage TEMP/IRM à partir de méthodes de recalage utilisant des mesures statistiques de similarité. Nous introduisons alors l approche adoptée pour répondre à cette problématique. Nous cherchons plus particulièrement à étudier le comportement de ces méthodes de recalage dans le contexte de l épilepsie, où les acquisitions de TEMP ictale génèrent des dissimilarités intrinsèques entre les données TEMP et IRM (fonction vs anatomie). Le quatrième chapitre expose la première partie de la méthode proposée qui est l identification d un modèle théorique de perfusion cérébrale, caractéristique de la situation physiologique ou physiopathologique à laquelle on s intéresse. Une méthode de mesure par standardisation anatomique est proposée et appliquée à des données réelles obtenues sur des sujets sains et épileptiques. La seconde partie de ce chapitre consiste en l analyse statistique de ces mesures de perfusion afin d en extraire des caractéristiques pouvant être utilisées à des fins de modélisation. Dans le cinquième chapitre, nous présentons les méthodes de simulation réaliste de données TEMP qui ont été mises en œuvre, simulations analytiques et de Monte Carlo. Les données obtenues grâce à ces simulations constituent les données de validation utilisées dans le cadre de l évaluation présentée au dernier chapitre. Différents contextes ont été simulés, tels qu un profil moyen de perfusion normale et ictale à partir de techniques de Monte Carlo. A l aide de simulations analytiques, nous ajustons différents paramètres à partir des profils moyens de perfusion normale ou ictale : simulation de différents niveaux de bruit de comptage poissonnien, simulation d asymétries fonctionnelles hyperperfusées, contraintes ou non à la matière grise, simulation d activités extra-cérébrales. Le sixième chapitre présente les résultats de l évaluation de méthodes de recalage utilisant différentes mesures statistiques de similarité, ainsi que les données créées par les processus de simulation décrits au chapitre précédent. En ce qui concerne la validation du recalage multimodalité TEMP/IRM, cinq méthodes de recalage sont étudiées. Elle sont basées sur l optimisation des critères suivants: l information mutuelle, l information mutuelle normalisée, les rapports de corrélation en norme L1 et L2 et le critère de Woods. Ces mêmes méthodes de recalage ainsi que les simulations de Monte Carlo sont finalement utilisées pour étudier le recalage monomodalité TEMP/TEMP.
20 20 Introduction Générale
21 21 Première partie FUSION DE DONNEES EN EPILEPSIE, RECALAGE ET VALIDATION
22
23 Fusion de données multimodales anatomo-fonctionnelles en épilepsie 23 Chapitre 1 Fusion de données multimodales anatomo-fonctionnelles en épilepsie 1.1 Chirurgie de l épilepsie et réseau épileptogène Historique de l épilepsie Dérivé du verbe grec epilambanein, le terme épilepsie signifie : saisir, attaquer par surprise. Considérée comme une possession démoniaque pendant tout le Moyen Age, l épilepsie fut pour la première fois considérée comme une maladie par le Traité de l épilepsie de Tissot en 1770 qui propose une vision scientifique déjà très moderne de celle-ci : pour produire l épilepsie, il faut nécessairement deux choses: 1) une disposition du cerveau à entrer en contraction plus aisément qu en santé ; 2) une cause d irritation qui mette en action cette disposition. De nombreux progrès concernant la terminologie et la neuropathologie des épilepsies sont réalisés au cours du XIX ième siècle, et c est à partir des travaux de J.H. Jackson ( ) que l épilepsie passe définitivement du champ de la psychiatrie à la neurologie [Jackson 38]. De nombreux progrès concernant le diagnostic des épilepsies sont réalisés par l utilisation des techniques d ElectroEncéphaloGraphie (EEG) introduites par Hans Berger en Le traitement chirurgical des épilepsies a été proposé dans les années 50 avec les travaux de Penfield et Jaspers à Montréal [Penfield 54]. Ils utilisaient des enregistrements et stimulations électriques sur la surface du cortex (électrocorticographie peropératoire) afin d identifier le foyer épileptogène, de proposer une cartographie anatomo-fonctionnelle du cortex et de décider au mieux de la zone d exérèse. Grâce à ces travaux, Penfield et Jaspers ont réalisé les premières observations directes qu une activité électrique épileptique, notamment une activité électrique rapide pendant la crise, est associée à une augmentation locale de la perfusion cérébrale. Cette observation princeps est fondamentale, vu l importance encore actuelle que prennent les mesures liées à l électrophysiologie et à la perfusion cérébrale pour l étude des épilepsies. L œuvre de l école de Montréal trouva naturellement un prolongement en France par les travaux de Bancaud et Talairach [Bancaud 65] qui proposèrent l étude du décours spatio-temporel d une crise à partir d enregistrements intra-cérébraux via des électrodes profondes implantées après repérage stéréotaxique : la stéréo-electroencéphalographie (SEEG).
24 Chirurgie de l épilepsie et réseau épileptogène La chirurgie de l épilepsie En France, on compte de à sujets épileptiques parmi lesquels 50% présentent une épilepsie dite partielle [Devaux 01]. Les crises d épilepsie sont dites focales ou partielles lorsqu elles prennent naissance dans une ou plusieurs régions cérébrales limitées et entraînent des signes cliniques en rapport avec la fonction de la zone affectée par la décharge. Pour 25% de ces épilepsies partielles, les traitements médicamenteux s avèrent incapables de contrôler les crises, on parle alors d épilepsies partielles pharmaco-résistantes pour lesquelles un traitement chirurgical peut être envisagé. Ainsi, on estime de à le nombre de patients en France qui pourraient bénéficier d une chirurgie de l épilepsie. Or seulement 200 à 300 interventions chirurgicales sont pratiquées chaque année en France, dont une trentaine au Centre Hospitalier Universitaire (CHU) de Rennes. Du fait du caractère phasique et aléatoire de la survenue des crises, la prise en charge chirurgicale des épilepsies est lourde à mettre en œuvre, surtout lorsque le planning préchirurgical nécessite d avoir recours à des enregistrements intra-cérébraux en SEEG. Les indications suivantes sont nécessaires pour envisager un traitement chirurgical [SaintHilaire 90] : l épilepsie doit être résistante au traitement médical : épilepsie partielle pharmacorésistante dite grave, le foyer épileptogène doit être bien limité et unique, le foyer épileptogène doit être résécable sans déficit fonctionnel significatif. Le premier point comprend en plus de la pharmaco-résistance une évaluation de l influence des crises dans la vie de tous les jours et sur la qualité de vie du patient (e.g. fréquence des crises, gravité des crises). Il est d ailleurs fondamental d étudier si le patient est apte à collaborer avec les cliniciens au cours des investigations nécessaires avant la chirurgie. Des troubles comportementaux ou un retard mental peuvent par exemple contre-indiquer une prise en charge chirurgicale, car dangereuse pour le patient. L étude des deux autres indications est appréhendée pendant le bilan préopératoire. La méthode consiste à confronter les résultats des investigations cliniques à ceux des examens d électrophysiologie et de neuroimagerie, afin de caractériser le foyer épileptogène sousjacent ainsi que son environnement fonctionnel. Si l indication chirurgicale est confortée après ce bilan préopératoire, l intervention consiste soit en une cortectomie standardisée (principalement temporale), soit en une cortectomie sélective, réalisée à façon, après un repérage préopératoire très précis de l épilepsie du patient. Cette dernière technique, nécessitant souvent un recours aux explorations SEEG, a été principalement développée par l école parisienne de Sainte Anne [Bancaud 65] Définition du réseau épileptogène L objectif de la chirurgie de l épilepsie étant de traiter le principal symptôme de la maladie qu est la crise, il faut identifier la zone cérébrale dont la resection permet l arrêt de ces crises. Alors que certaines lésions morphologiques peuvent être à l origine ou liées à la maladie, il est fondamental de prendre en compte l aspect dynamique de la crise d épilepsie et de bien identifier la ou les aires de déclenchement et de propagation des crises. Les premiers enregistrements SEEG réalisés par Bancaud et Talairach en 1966 [Talairach 66] ont permis de mettre en évidence que la distribution topographique des anomalies fonctionnelles électriques en période critique ou ictale (i.e. pendant la crise) et en période
25 Fusion de données multimodales anatomo-fonctionnelles en épilepsie 25 inter-critique ou inter-ictale (i.e. après une période d au moins 24h sans crises) ne se recouvraient que rarement. Ils proposent ainsi de caractériser la maladie par la définition des trois zones suivantes: Zone Epileptogène (ZE): D un point de vue pragmatique, la zone épileptogène est par définition l aire cérébrale dont l ablation est nécessaire et suffisante pour guérir le patient. Cette zone inclut essentiellement la zone primaire. Pour Bancaud, la ZE est la zone dont la décharge électrique est corrélée à l apparition des signes cliniques des crises. Cette définition a été proposée à partir des enregistrements de crises en SEEG. Cette zone inclut la zone primaire d origine des crises et les zones de propagation. Zone Irritative (ZI): Les enregistrements SEEG ont également permis de localiser précisément des Episodes Paroxystiques Inter Critiques (EPIC) qui se manifestent sous la forme de pointes et de pointes-ondes. Les aires cérébrales étant le siège de ces EPIC définissent la zone irritative. Zone Lésionnelle (ZL): La zone lésionnelle caractérise une altération morphologique du tissu nerveux, et/ou une altération métabolique comme une diminution de la capture du glucose, ou une diminution du débit sanguin loco-régional, en période inter-ictale. En SEEG, il s agit la plupart du temps d une zone étant le siège d ondes lentes, témoignant la présence d une lésion ou d une souffrance fonctionnelle. La ZL est souvent en rapport avec des lésions maintenant vues sur l imagerie. Par extension est née la notion de réseau épileptogène. L expérience démontre que la zone épileptogène n est jamais ponctuelle, mais que l activation simultanée de plusieurs groupes de neurones est nécessaire à la naissance d une crise. Ayant permis la définition de ces trois zones, la technique invasive qu est la SEEG est considérée comme une des techniques de référence, ou gold standard, pour la compréhension de l organisation du réseau épileptogène. En enregistrant des états critiques et inter-critiques du patient simultanément avec un enregistrement vidéo, la SEEG autorise des corrélations anatomo-électro-cliniques, permettant d étudier l articulation des zones impliquées et de poser des hypothèses localisatrices. La SEEG peut également être utilisée pour conforter ces hypothèses en provoquant des crises par stimulation électrique intracérébrale. En pratique, toutes les situations peuvent se rencontrer, depuis le recouvrement parfait entre ces trois zones, leur chevauchement partiel, jusqu à leur distinction complète, voire la coexistence de plusieurs ZE, ZI ou ZL (cf. Figure 1.1). Cependant, cette organisation en trois zones circonscrites peut s avérer trop réductionniste. La complexité des phénomènes étudiés a conduit Chauvel et al. [Chauvel 96] à proposer la notion de réseau épileptogène faisant intervenir plusieurs régions anatomiques inter-connectées en période critique et inter-critique : Les épilepsies à crises partielles ou focales sont caractérisées par des événements paroxystiques inter-critiques (EPIC ou pointes inter-critiques) et par des crises. Les EPIC, accidents transitoires phasiques, expriment la synchronie anormale d un ensemble neuronal au sein d une ou plusieurs régions anatomiques; les crises, oscillations périodiques (ou non) généralement de haute fréquence (décharges rapides) activent de façon durable et inhibent fonctionnellement cet ensemble neuronal, et se propagent souvent au delà de ses limites propres. Les tenants et les aboutissants de l identification d un tel réseau épileptogène doivent donc passer par la résolution d un problème de liaison entre d éventuelles lésions morphologiques, des zones cérébrales qui sont le siège d EPIC et des zones cérébrales impliquées au départ et au cours des crises.
26 Techniques d exploration du réseau épileptogène Fig. 1.1 Représentation schématique des concepts de Zone Épileptogène (EZ), Zone Irritative (IZ et IZ II) et Zone Lésionnelle (LZ): les différentes entités du réseau épileptogène sont représentées sur une IRM 3D du cerveau segmenté, sur laquelle a été recalée la vue peropératoire du patient. Les neurones et leurs interconnections représentés dans les zones décrivent les différentes relations possibles entre ces structures 1.2 Techniques d exploration du réseau épileptogène L essor de nombreuses techniques d exploration, que ce soit en électrophysiologie ou en neuroimagerie, permet d assister la caractérisation de ce réseau épileptogène. Il n existe pas une technique d exploration qui va supplanter toutes les autres, mais c est l analyse combinée de ces nombreuses méthodes qui permettra une meilleure compréhension de ce réseau épileptogène, tout en s efforçant d utiliser les techniques d investigation les moins invasives possibles. Les paragraphes précédents ont montré l importance de la SEEG, considérée comme technique de référence, mais le nombre limité d électrodes implantables (en général, une dizaine) souligne l importance de définir au mieux le schéma d implantation par un bilan préalable poussé permettant d avoir des hypothèses solides. La grande précision anatomique est apportée par un repérage stéréotaxique. Ce schéma est décidé après une première phase d examens non invasifs (e.g. vidéo-eeg, Imagerie par Résonance Magnétique - IRM, Tomographie d Emission MonoPhotonique - TEMP) au cours de laquelle les principales hypothèses sur l organisation du réseau sont posées et seront à confirmer par la SEEG. L enjeu principal de l utilisation de ces nouvelles techniques d exploration est, à terme, de limiter le recours à des méthodes invasives et difficiles à mettre en œuvre, comme la SEEG. Dans cette optique, la SEEG est également un élément fondamental pour valider la pertinence des résultats issus des techniques d exploration non invasives. L objectif de cette partie est de présenter les principales techniques d exploration utilisée en routine clinique ou en recherche pour aider à la caractérisation du réseau épileptogène. Pour chaque technique présentée, nous décrivons succinctement les principes d acquisition et de reconstruction des données, la nature physiologique de l information mesurée, les limites en matière de résolution spatiale et temporelle, ainsi que l intérêt de
27 Fusion de données multimodales anatomo-fonctionnelles en épilepsie 27 la technique pour l épilepsie. La Figure 1.2 décrit la place respective de ces techniques lors de la prise en charge chirurgicale d un patient épileptique, selon l organisation en place au CHU de Rennes. D après Chauvel [Chauvel 99], il est nécessaire de disposer d une vision méthodique des articulations entre les différents outils et techniques d exploration, pour fournir à terme une synthèse anatomo-fonctionnelle capable de définir pour chaque patient son épilepsie, mais aussi de rationaliser les classifications pour tous les patients. Notre ambition est ici de présenter les grandes tendances actuelles liées à l utilisation de ces techniques, afin de mettre en exergue les besoins qui s expriment en matière de méthodes de traitement d image ou du signal, et plus particulièrement de fusion de données anatomiques et fonctionnelles. Pour une description plus exhaustive des principaux résultats cliniques en épilepsie, nous renvoyons le lecteur vers différents articles de revue sur la neuroimagerie de l épilepsie [Mauguière 96, Duncan 97a, Richardson 01], ainsi que vers le livre de P. Thomas et P. Genton [Thomas 94] sur l électrophysiologie en épilepsie. Après quelques rappels sur la physiologie de l activité cérébrale, nous proposons une classification des différentes techniques utilisées en épileptologie, en distinguant les méthodes d exploration dite statique, des méthodes d exploration dynamique des états inter-critiques et critiques du patient, et des méthodes permettant d analyser l environnement fonctionnel du réseau épileptogène.
28 Techniques d exploration du réseau épileptogène PHASE I Examens "statiques" Recherche d une ZL neuro psychologie scanner X IRM morpho spectoscopie RMN TEP Examens "dynamiques" Recherche des ZI et ZE INTERCRITIQUE EEG, MEG TEP, TEMP IRM de perfusion IRM de diffusion CRITIQUE vidéo EEG TEMP Etude de la fonctionnalité des ZL, ZE, ZI et de l environnement potentiels évoqués EEG, MEG TEP, IRMf CONCORDANCE zone bien déterminée zone non fonctionnelle déficit prévu tolérable PROBLEMES non concordance plusieurs zones proche des zones fonctionnelles CONTRE INDICATION PHASE II Examens "dynamiques" vidéo SEEG Etude de la fonctionnalité des ZL, ZE, ZI et de l environnement test de Wada SEEG stim. électriques perop. CONCORDANCE CONTRE INDICATION CHIRURGIE RESULTAT POST OPERATOIRE Fig. 1.2 Schéma décrivant les techniques d exploration mises en jeu pendant le planning préchirurgical d un patient épileptique
29 Fusion de données multimodales anatomo-fonctionnelles en épilepsie Notions de neurophysiologie : origine de l activité cérébrale? Fig. 1.3 Vue externe du cerveau présentant les différents lobes (rouge:lobe frontal, jaune:lobe temporal, bleu:lobe pariétal, vert:lobe occipital) L unité de base à l origine de l activité cérébrale est le neurone. Le neurone est une cellule, dite excitable, capable de transférer de l information de nature électro-chimique à d autres neurones. Les techniques d imagerie dites morphologiques permettent naturellement d étudier à une échelle macroscopique l organisation des tissus cérébraux. L activité cérébrale peut quant à elle être appréhendée, soit directement en mesurant l activité électromagnétique générée par le fonctionnement des neurones, soit indirectement en mesurant la consommation de glucose ou d oxygène ou encore la perfusion sanguine destinées à alimenter ces neurones en énergie. Les tissus cérébraux: Les tissus cérébraux sont principalement constitués de deux types de cellules, les neurones et les cellules gliales. Ces dernières sont beaucoup plus nombreuses et ont un rôle de soutien et de protection. Le tout baigne dans un liquide nourricier, le Liquide Céphalo-Rachidien (LCR). Les échanges entre les neurones et le sang se font nécessairement par l intermédiaire de ces cellules gliales, de ce fait ces échanges sont assez restrictifs: on parle de barrière hémato-encéphalique. Alors que le gaz carbonique, l oxygène et l eau traversent librement cette barrière, d autres substances, dont le glucose, nécessitent un recours à des mécanismes de transport particuliers. La substance grise est caractérisée par une disposition organisée des corps cellulaires des neurones, sous forme de noyaux au niveau des structures internes, et sous forme d une couche couvrant toute la périphérie du cerveau, le cortex (cf. Figures 1.3 et 1.4). Pour gagner en superficie, le cortex est une structure hautement repliée dont la surface couvre environ 1600 cm 2. Les crêtes de ces circonvolutions sont appelées des gyri, et les creux des sillons. Ils constituent des repères anatomiques fondamentaux pour le clinicien, notamment les sillons qui coincident parfois avec de véritables frontières entre différentes zones fonctionnelles. Ainsi, le sillon central ou sillon de Rolando sépare les aires primaires de la motricité des aires
30 Techniques d exploration du réseau épileptogène Fig. 1.4 Coupe anatomique coronale du lobe temporal (1:hippocampe, 2:corne temporale inférieure du ventricule latéral, 3:amygdale, 8:gyrus temporal inférieur, 9:gyrus temporal central, 10:sillon temporal supérieur, 11:gyrus temporal supérieur, 14:insula, 23:ventricule latéral, 24:noyau caudé, 26:queue du noyau caudé, 27:putamen, 28: partie latérale du pallidum, 29: partie mésiale du pallidum) de la somesthésie 1. La substance blanche représente les fibres neuronales assurant les connexions nerveuses à longue distance (entre deux gyri, entre le cortex et les structures internes, entre les deux hémisphères). Lors du développement fœtal du cerveau, les corps cellulaires des neurones migrent de la couche germinative périventriculaire vers le cortex. Diverses malformations du développement cortical, comme par exemple une anomalie de migration des corps cellulaires, génèrent des tissus fortement enclins à devenir épileptogène. Nous montrerons comment ces malformations sont détectables par l imagerie. Électrophysiologie du neurone: L unité fonctionnelle élémentaire de l activité cérébrale est le neurone (cf. figure 1.5). Cette cellule est composée d un corps cellulaire, ou soma, où se trouve le noyau de la cellule, de dendrites et d un axone. Les dendrites constituent les entrées du neurone, ou voies afférentes, par lesquelles lui parvient l information en provenance des autres neurones. L axone constitue la sortie de neurone, ou voie efférente, et permet au neurone de transmettre de l information à un ou plusieurs autres neurones, pouvant être situés à longue distance. Ce sont principalement les axones des neurones qui constituent la substance blanche. Les neurones sont des cellules dites excitables, car au repos ils présentent une différence de potentiel négative entre les milieux intra- et extra- cellulaires de 70 mv. Cette polarisation est maintenue par le transport actif des ions Na + et K + de part et d autre de la membrane cellulaire via des canaux ioniques spécifiques. Lorsque cet équilibre est rompu et que cette différence de potentiel dépasse un seuil d environ 50 mv, une modification temporaire du comportement des canaux ioniques va permettre la gé- 1. La somesthésie désigne la sensibilité liée au toucher.
31 Fusion de données multimodales anatomo-fonctionnelles en épilepsie 31 Fig. 1.5 Représentation schématique d un neurone (dendrites, corps cellulaire, axone) nération d un potentiel d action (PA) et ainsi la transmission de l influx nerveux. En fait, le PA est une onde électrique correspondant à une dépolarisation suivie d une repolarisation de la membrane cellulaire qui se propage de proche en proche le long de l axone. La transmission d information d un neurone à un autre se fait au niveau des synapses, zones particulières situées sur les dendrites ou au bout de l axone et où les membranes des deux neurones connectés sont particulièrement proches ( 30 nm). La transmission électrochimique de l information se décompose en trois étapes: 1. Arrivée d un PA au niveau de la membrane présynaptique. 2. Libération de neurotransmetteurs dans la fente synaptique. Ces neurotransmetteurs vont aller se fixer sur des récepteurs qui leur sont spécifiques sur la membrane postsynaptique. 3. La stimulation de ces récepteurs entraîne des modifications du comportement des canaux ioniques, permettant de modifier localement la polarisation de la membrane postsynaptique. S il s ensuit une dépolarisation de la membrane, on parle de Potentiel PostSynaptique Excitateur (PPSE). Par contre, dans le cas d une hyperpolarisation de la membrane, on parle de Potentiel PostSynaptique Inhibiteur (PPSI). La sommation spatiale et temporelle des PPSE et des PPSI au niveau de toutes les dendrites va permettre la génération d un PA, si la polarisation moyenne dépasse 50mV pendant une durée suffisante. Ces phénomènes sont à l origine des signaux électromagnétiques qu il est possible d explorer par les techniques d électrophysiologie. Phénomènes physiologiques nécessaires au fonctionnement du neurone: Pour pouvoir être activés, les neurones ont besoin d énergie. En effet, on estime que l activité des canaux ioniques membranaires et la génération des activités électriques sont responsables de 80 % des dépenses énergétiques cérébrales au repos. Or, le cerveau est le seul organe ne possédant pratiquement aucun système de stockage d énergie. Au niveau cellulaire, l énergie est obtenue lors de la dégradation des molécules d Adénosine TriPhosphate (ATP). Ces molécules, stockées en quantité insuffisante dans la cellule, nécessitent d être synthétisées. Les mécanismes de synthèse de l ATP impliquent une consommation de glucose et d oxygène : c est le cycle de Krebs. Le glucose et l oxy-
32 Techniques d exploration du réseau épileptogène Tab. 1.1 Besoins cérébraux moyens en perfusion et métabolisme d après [Catafau 01] Paramètre Besoins Pourcentage du poids du corps entier 2% Pourcentage de la perfusion cardiaque globale 20% Volume sanguin cérébral 120 ml Débit artériel 750 ml/min Oxygène 50 ml/min Glucose 100 mg/min Débit sanguin cérébral global 55 ml/100g/min Débit sanguin dans la substance grise 80 ml/100g/min Débit sanguin dans la substance blanche 20 ml/100g/min gène sont amenés par le sang au niveau des neurones après avoir passé la barrière hémato-encéphalique. Le réseau vasculaire se divise progressivement jusqu à former un réseau dense de capillaires qui irriguent tous les éléments corticaux et les structures internes. Ainsi, la consommation de glucose au niveau des neurones, de même que la consommation d oxygène sur le versant artériel ou veineux, sont autant de pistes permettant d explorer indirectement le fonctionnement des neurones. De plus, divers processus physiologiques de régulation permettent d adapter le débit sanguin en fonction des besoins énergétiques des neurones. En effet, ce sont, entre autres médiateurs, des métabolites sécrétés lors de l activation des neurones qui entraînent une vasodilatation des capillaires et par là même une augmentation du débit sanguin cérébral régional (DSCr). Ainsi, l étude de la perfusion sanguine par mesure de débit (DSCr) ou de volume (VSCr) sanguin cérébral régional permet d appréhender l activité cérébrale. Ces dépendances font du cerveau l organe de loin le plus vulnérable aux variations de DSCr (cf. Table 1.1) Examens statiques L objectif des examens dits statiques est principalement la détection d anomalies morphologiques pouvant être associées à l épilepsie. C est principalement grâce à ces techniques qu il est possible d identifier une éventuelle ZL. L enjeu de ces techniques est l identification d une base structurelle permettant de guider la diagnostic de l épilepsie mais également de donner des pronostics quant à l issue d un traitement chirurgical. En effet, il a été montré que les résultats de la chirurgie étaient significativement meilleurs lorsqu une ZL était identifiée [Devaux 01]. Les progrès récents des examens statiques permettent d ailleurs d identifier une anomalie morphologique dans de nombreux cas d épilepsies considérées préalablement comme cryptogéniques La Tomodensitométrie ou Scanner X Principe physique et technique d acquisition: La tomodensitométrie est une technique d imagerie utilisant la transmission de rayons X. La rotation, autour de la tête 2. Les épilepsies cryptogéniques sont des épilepsies pour lesquelles la cause de la maladie est cachée ou occulte
33 Fusion de données multimodales anatomo-fonctionnelles en épilepsie 33 du patient, d un couple générateur/détecteur de rayons X permet l acquisition successive de projections correspondant aux photons X atténués par la traversée d un même plan de détection axial. L utilisation de techniques de reconstruction tomographique, comme par exemple la rétroprojection filtrée, permet de reconstruire, à partir des projections, les valeurs d atténuation de ce plan de détection. Une acquisition volumique complète est réalisable soit de manière incrémentale en avançant la table du patient après l acquisition de chaque coupe (scanner séquentiel), soit en combinant simultanément la rotation du couple émetteur/détecteur et la translation de la table (scanner spiralé). Type d information explorée: Lorsqu il traverse des tissus biologiques, un faisceau de rayons X est atténué en fonction des coefficients d atténuation caractéristiques des tissus traversés. Après reconstruction, la tomodensitométrie fournit une cartographie des coefficients d atténuation du volume exploré. Ainsi, les tissus denses très atténuants tels que l os présenteront un signal intense alors que les tissus mous nettement moins denses, donc moins atténuants, présenteront un signal plus faible. La tomodensitométrie possède une excellente résolution spatiale, de l ordre de 0.5mm. Apport pour l épilepsie: De moins en moins utilisée en raison des progrès de l IRM, la tomodensitométrie est capable de mettre en évidence des lésions associées à une épilepsie avec une sensibilité plutôt faible (15 à 35 %). Outre ses indications habituelles en neurologie (par exemple accidents vasculaires cérébraux ischémiques ou hémorragiques, fractures crâniennes, tumeurs), elle peut s avérer utile pour la détection d éventuelles calcifications intracrâniennes difficilement détectables en IRM. Finalement, le scanner X reste la seule technique d imagerie morphologique accessible lorsque l IRM est contre-indiquée ou difficile à réaliser, notamment en condition d urgence L Imagerie par Résonance Magnétique(IRM) morphologique Principe physique et technique d acquisition : Certains noyaux atomiques dits polarisés ont la propriété d absorber sélectivement l énergie d une onde radio-fréquence (RF) lorsqu ils sont placés dans un champ magnétique intense : c est le phénomène de Résonance Magnétique Nucléaire (RMN). La RMN du proton de l hydrogène est à l origine du signal mesuré en IRM (pour une description complète de l IRM et des protocoles d acquisition voir Doyon et al. [Doyon 94]). Resonance Magnétique Nucléaire et excitation radio-fréquence: Les protons, particules élémentaires du noyau chargées positivement, ont la propriété de tourner naturellement autour d eux mêmes (mouvement de spin), générant ainsi un moment magnétique aligné sur leur axe de rotation. Les atomes dits polarisés présentent un nombre de protons impair et donc un moment magnétique résultant non nul (e.g. hydrogène, carbone 13, phosphore 31). Placés dans un champ magnétique intense B 0 (de 0.5 à 4 Tesla), ces moments magnétiques s orientent dans la direction de B 0, soit dans le sens de celui-ci (parallèle) soit dans le sens contraire (antiparallèle), et tournent autour de l axe de B 0 (mouvement de précession) à une vitesse angulaire ω 0 = γ.b 0. ω 0 est définie comme la fréquence de Larmor et γ représente le rapport gyromagnétique qui est caractéristique du noyau étudié (γ = 42.6MHz/Tesla pour
34 Techniques d exploration du réseau épileptogène le noyau d hydrogène). A l équilibre, il apparaît une aimantation résultante non nulle M dans le même sens que B 0. L excitation par une onde radio-fréquence (RF) consiste en l application d un champ magnétique B 1 perpendiculaire à B 0 et tournant autour de l axe de celui-ci exactement à la vitesse ω 0. Grâce à cette excitation, le phénomène de résonance permet la mise en phase des différents moments magnétiques qui précessent désormais à la fois autour de B 0 et de B 1. L aimantation résultante M décrit alors une spirale sur une calotte sphérique (cf. Figure 1.6) et une composante transversale M xy non-nulle de M apparaît dans le plan perpendiculaire à B 0. Une impulsion RF à 90 correspondra alors à une excitation permettant le basculement complet de M dans ce plan transversal. z z M y y Mz Mxy M x x Fig. 1.6 Mouvement de la magnétisation résultante M pendant l excitation par une impulsion RF Fig. 1.7 Mouvement de la magnétisation résultante M pendant la phase de relaxation Relaxation et acquisition du signal: Après cette excitation instantanée, l aimantation M entre dans une phase de relaxation plus lente afin de retrouver sa position d équilibre (cf. Figure 1.7). La restitution de l énergie apportée par l onde RF provoque une repousse de la composante longitudinale M z de M le long de B 0 suivant une exponentielle croissante avec une constante de temps T1 (entre 300 et ms). Causée principalement par le déphasage progressif des différentes magnétisations, la décroissance de la composante transversale M xy de M se fait plus rapidement suivant une exponentielle décroissante avec une constante de temps T2 (entre 30 et 200 ms). L acquisition du signal se fait de ce plan transversal à l aide de la même antenne ayant permis l excitation RF. Sélection des contrastes, du plan de coupe et reconstruction: L application de gradients de champs magnétiques s additionnant à B 0, ajustables dans les trois directions de l espace permet de sélectionner précisément le volume ou le plan de coupe à exciter, puis à acquérir. Le choix des séquences d acquisition permet, en ajustant impulsions RF et gradients, de remettre en phase les magnétisations afin d acquérir un signal dans le plan transversal sous forme d un écho. On montre que le signal mesuré correspond directement à la transformée de Fourier de la densité de protons ρ modulée par une porteuse à la fréquence ω 0. La reconstruction des images se fait
35 Fusion de données multimodales anatomo-fonctionnelles en épilepsie 35 donc par démodulation puis transformée de Fourier 2D inverse. Type d information explorée : Le proton de l atome d hydrogène étant à l origine du signal mesuré, l IRM est une technique d imagerie idéale pour l étude des tissus mous, notamment cérébraux, qui contiennent beaucoup d eau et donc d hydrogène. L IRM présente une excellente résolution en contraste et une résolution spatiale millimétrique. Par contre, l os contenant très peu d eau n est pratiquement pas visible en IRM, contrairement au scanner X. Le réglage des différentes séquences d acquisition permet d obtenir des images pondérées suivant la densité de protons ρ ou suivant les paramètres T1 et T2 caractéristiques des tissus. Caractérisant la repousse longitudinale de la magnétisation M, le paramètre T1 est lié à la capacité du milieu à restituer l énergie transmise par l onde RF, il sera plus court dans un milieu où les molécules sont organisées comme les lipides, que dans un milieu où les molécules sont totalement libres de leurs déplacements, comme l eau ou le liquide céphalo-rachidien (LCR). Le paramètre T2 est lié à la présence d inhomogénéités locales du champ B 0 causées par des éléments magnétiques naturels de l environnement moléculaire. Ainsi, dans les liquides, l agitation moléculaire annule par moyennage ces champs magnétiques locaux et il en résulte un T2 long, alors que dans d autres tissus (solides, lipides), l organisation moléculaire permet un maintien de ces champs locaux et il en résulte donc un T2 plus court. De par ces propriétés, les acquisitions pondérées en T1 et en T2 présentent une inversion des contrastes entre la substance grise et la substance blanche (cf. Figures 1.8 et 1.9). En ajustant les échos de telles séquences et les instants auxquels les magnétisations de chaque tissu se remettent en phase, il est possible aussi d éteindre sélectivement le signal d un tissu au moment de l acquisition. Ainsi, les séquences FLAIR (FLuid Attenuated Inversion Recovery) permettent de supprimer les liquides au moment de l acquisition, permettant une analyse différentielle par rapport aux données pondérées en T2. Apport pour l épilepsie : Surtout lorsqu un traitement chirurgical est pressenti, l exploration IRM doit être la plus complète possible. Elle consiste en général en une exploration détaillée de tout le volume cérébral, à partir d acquisition pondérées en T1 et en T2, et en utilisant la meilleure résolution possible. Jackson et al. [Jackson 94] ont montré que sur une série de 330 cas, dont 244 épilepsies temporales, l IRM réalisée dans des conditions optimales a permis de détecter des anomalies morphologiques dans 92% des cas, dont 57% de scléroses hippocampiques, 13.5% de tumeurs et 10.5% de dysplasies corticales. La sclérose de l hippocampe, notamment l atrophie, est la pathologie la plus courante associée à l épilepsie partielle pharmaco-résistante du lobe temporal. L étude de l ampleur et de la latéralité de l atrophie évaluée en IRM par rapport à l hémisphère dominant et à l hémisphère siège des anomalies électriques permet de garantir de très bons résultats au traitement chirurgical [Duncan 97a]. L exploration rigoureuse de l hippocampe nécessite l acquisition de coupes axiales, orientées suivant le grand axe du lobe temporal, et ainsi que l acquisition de coupes coronales perpendiculaires aux précédentes (cf. Figures 1.8 et 1.9). Le diagnostic est posé en analysant la forme de l hippocampe sur les images pondérées en T1, et en mettant en évidence un hypersignal sur les images pondérées en T2. Une meilleure sensibilité peut être obtenue par des analyses volumétriques quantitatives de l hippocampe à partir des images en T1 [Jack 94], ou par la mesure quantitative du temps de relaxométrie T2 de l hippocampe [Jackson 94].
36 Techniques d exploration du réseau épileptogène Outre la détection de tumeurs ayant donné naissance à l épilepsie, l IRM permet la détection des malformations du développement cortical, notamment les dysplasies corticales focales qui consistent en une désorganisation locale de l architecture du cortex [Taylor 71]. L étude précise des contrastes entre substance grise et substance blanche, la détection d épaississement cortical en T1 ou de lésions parenchymateuses hyperintenses en FLAIR (cf. Figure 1.10) ont permis de donner une origine à de nombreuses épilepsies considérées auparavant comme cryptogéniques. La détection de ces malformations à l aide de séquences d acquisition toujours plus performantes est un enjeu considérable, même si d après Duncan [Duncan 97a], l IRM ne nous révèle pour l instant que la partie émergée de l iceberg des anomalies du développement cortical. Fig. 1.8 Coupe coronale du lobe temporal pondérée en T1: la substance grise est moins intense que la substance blanche, et il n y a pratiquement aucun signal dans le LCR - élargissement de la corne ventriculaire dans l hémisphère gauche Fig. 1.9 Coupe coronale du lobe temporal pondérée en T2: la substance grise est plus intense que la substance blanche, c est dans le LCR que le signal est le plus intense - hypersignal des structures hippocampiques La spectroscopie RMN Principe physique et technique d acquisition: Le signal à l origine de la spectroscopie RMN est l excitation RMN des principaux noyaux polarisés, à savoir l hydrogène 1, le phosphore 31 ou le carbone 13. Placés dans un champ magnétique intense B 0, les moments magnétiques de ces noyaux précessent à la fréquence de Larmor ω 0 qui leur est spécifique. En fait, cette fréquence est légèrement modifiée par les électrons voisins de ces noyaux qui créent un très faible champ magnétique local. Ces décalages de fréquence de résonance, appelés déplacements chimiques, sont caractéristiques des groupements chimiques de ces atomes. L analyse du signal mesuré après l exploration de cette gamme de fréquences permet d obtenir des spectres caractéristiques de certaines molécules. Technique classique d analyse chimique in vitro, la spectroscopie RMN devient accessible in vivo comme une technique d imagerie permettant une quantification absolue de certains métabolites. Les molécules recherchées étant nettement moins présentes que l eau, le faible rapport signal/bruit et la faible sensibilité
37 Fusion de données multimodales anatomo-fonctionnelles en épilepsie 37 Fig Dysplasie corticale focale caractérisée par un hypersignal sur une acquisition IRM FLAIR de la technique imposent des temps d acquisition plutôt longs de par la nécessité d acquérir plusieurs fois le même signal. L acquisition en mode simple voxel se fait en analysant les spectres RMN des molécules contenues dans un volume d intérêt d environ 2cm 3 délimité manuellement sur une séquence anatomique de repérage. Des séquences plus complexes d imagerie du déplacement chimique dans un plan de coupe ont également été proposées, mais n autorisent qu une résolution spatiale limitée (de l ordre du cm). Type d information explorée: La spectroscopie RMN est une technique prometteuse d exploration in vivo du métabolisme cérébral. C est principalement la spectroscopie de l hydrogène qui trouve aujourd hui des applications en pathologie cérébrale. Citons entre autres le N-acétyl-aspartate (NAA), considéré comme un marqueur de la viabilité neuronale, la Choline (Ch), indicateur du métabolisme membranaire, ou la Créatine (Cr) et la phosphocréatine (PCr), indicateurs de bioénergétique cellulaire. Apport pour l épilepsie: De nombreuses études de quantification de ces métabolites au niveau du foyer épileptogène ont été réalisées, soit par comparaison interhémisphérique, soit par comparaison population saine / population pathologique. Les résultats les plus probants concernent la diminution des rapports NAA/Ch ou NAA/(Ch+Cr) dans l hippocampe pour les épilepsies du lobe temporal, latéralisant le foyer épileptogène dans plus de 75 % des cas [Cendes 94]. Ces méthodes s avèrent prometteuses en pharmacologie pour étudier l effet de certains anti-épileptiques, notamment GABAergiques Le GABA est le principal neurotransmetteur inhibiteur du cerveau, sa transmission serait altérée dans l épilepsie mais son rôle précis est toujours discuté.
38 Techniques d exploration du réseau épileptogène La Tomographie d Emission de Positons (TEP): Principe physique et technique d acquisition: En tant que technique d imagerie de médecine nucléaire, la Tomographie d Emission de Positons (TEP) est basée sur la détection de rayons γ émis par une molécule radioactive injectée au patient. Les radio-isotopes utilisés en TEP sont des émetteurs de positons β +, dont l annihilation quasi-immédiate consécutive à la rencontre avec un électron libre, provoque l émission simultanée de deux photons γ de haute énergie (511 kev) se déplaçant en sens inverses sur la même trajectoire. Les principaux radio-isotopes utilisés (fluor 18 F, oxygène 15 O, carbone 11 C) sont des éléments organiques très répandus, facilement incorporables dans des molécules biologiques ou pharmacologiques que l on nommera traceurs. En raison de la courte demi-vie de ces éléments ( 18 F : 110 min., 15 O : 2 min., 11 C : 20 min.), il est nécessaire de disposer d un cyclotron à côté de l imageur afin de produire le traceur juste avant l acquisition. Cette contrainte fait de la TEP une technique encore difficilement accessible en pratique clinique sauf dans quelques grands centres spécialisés. Les deux photons γ émis simultanément sont détectés en coïncidence par une couronne de détecteurs (cf. Figure 1.11) et définissent ainsi une ligne de coïncidence. Chaque détecteur comprend un cristal scintillateur et un photomultiplicateur permettant de convertir l énergie du photon détecté en signal électrique (voir I ). La détection d un nombre suffisant de photons détectés en coïncidence permet la reconstruction tomographique de la distribution volumique du traceur injecté. Le déplacement moyen des positons avant l annihilation est de l ordre de 2 mm, ce qui constitue en soi une limite à la résolution spatiale. Les caméras TEP actuelles permettent d atteindre des résolutions spatiales de l ordre de 5 mm. Type d information explorée: De nombreux aspects du métabolisme cérébral peuvent être explorés en TEP. Citons surtout le 2-Déoxy-D-Glucose marqué au Fluor 18, ou FDG, comme marqueur du métabolisme du glucose. L utilisation d un cathéter artériel, permettant le suivi de la radioactivité circulante et de la glycémie, ce qui, moyennant un modèle compartimental, permet une quantification absolue de la consommation du glucose à partir de la distribution du traceur. Ce modèle de quantification est valide si l activité métabolique est stable. En épilepsie, ceci suppose donc que le patient soit dans un état inter-critique. Le glucose étant une source d énergie nécessaire au fonctionnement des neurones, son métabolisme est un paramètre important permettant de mesurer indirectement l activité neuronale. L acquisition est réalisée entre 40 et 60 min. après l injection du traceur, ce qui garantit que la majorité de la radioactivité est piégée dans les cellules et que les hypothèses du modèle de quantification sont vérifiées. La TEP est également une technique de choix pour l étude in vivo de très nombreux récepteurs de neurotransmetteurs 4. Citons notamment les récepteurs centraux aux benzodiazépines (RCBZ) qui jouent une rôle régulateur dans la transmission du GABA (neurotransmetteur inhibiteur). La distribution de ces récepteurs est appréhendée en TEP à l aide du flumazénil (FMZ) marqué au 11 C, antagoniste spécifique des récepteurs aux benzodiazépines. On peut de plus considérer que cartographier la 4. Ces récepteurs jouent un rôle fondamental dans la conduction de l influx nerveux, en autorisant la génération de PPSE ou PPSI.
39 Fusion de données multimodales anatomo-fonctionnelles en épilepsie 39 distribution des RCBZ est un bon indicateur de la densité neuronale. Néanmoins, il reste discuté qu une diminution du nombre de RCBZ soit due à une baisse du nombre de neurones ou à des modifications fonctionnelles [Ryvlin 98]. Dans ce cas également, toute quantification absolue nécessite des mesures répétées de la radioactivité du sang artériel et d un modèle mathématique. Apport pour l épilepsie: L étude du métabolisme du glucose à partir du FDG est la technique la plus référencée en épilepsie [Theodore 92, Mauguière 96, VanBogaert 00, Kang 01]. Le principal dysfonctionnement cérébral focal observé en épilepsie est un hypométabolisme loco-régional (cf. Figure 1.12). La sensibilité est de l ordre de 70 à 80 % et avoisine les 100 % pour les épilepsies temporales surtout lorsqu une sclérose de l hippocampe a été détectée en IRM [Mauguière 96]. L intérêt de la TEP FDG dans le bilan préchirurgical des épilepsies a été renforcé par la mise en évidence d une corrélation positive entre la présence d un hypométabolisme et de son degré et la qualité du résultat postopératoire [Theodore 92]. L explication de cet hypométabolisme focal, détectable même lorsqu aucune anomalie n est décelable à l IRM, reste encore discutée. Les hypothèses actuelles concernent une éventuelle perte neuronale ou une déafférentation 5. Néanmoins, les progrès récents de l IRM pour la détection d une ZL amènent à reconsidérer le rôle du TEP FDG au cours de cette investigation préchirurgicale. Notamment, les hypométabolismes observés en TEP sont généralement plus vastes que la lésion identifiée à l IRM et que la zone épileptogène définie électrophysiologiquement. La capacité de la TEP à étudier in vivo la fixation de traceurs sur des récepteurs aux neurotransmetteurs présente un intérêt double, d une part mettre en évidence des anomalies plus focalisées que celles mises en lumière dans les études du métabolisme, et d autre part, fournir des renseignements sur des phénomènes impliqués dans l épileptogénèse. De nombreuses études au 11 C-FMZ ont montré une diminution de la densité des récepteurs centraux aux benzodiazépines au niveau du foyer épileptogène [Savic 88, Ryvlin 98], beaucoup plus limitée spatialement que l hypométabolisme inter-critique. Une des principales explications de ce phénomène serait une perte neuronale. La TEP au FMZ permettrait alors, au même titre que l IRM, la détection d une ZL structurelle associée à l épilepsie. Bien que la signification exacte de cette diminution de densité des récepteurs centraux aux benzodiazépines reste encore discutée, des études comparatives avec l IRM doivent être menées afin de bien caractériser la place de chaque technique dans l identification d une ZL Examens dynamiques de l état inter-critique L étude d anomalies fonctionnelles inter-critiques, permettant l étude de la zone irritative (ZI), fait naturellement appel à des techniques autorisant une étude dynamique de ces phénomènes. Nous allons donc présenter ici des méthodes d exploration privilégiant de meilleures résolutions temporelles, dont les techniques d électrophysiologie, capables d étudier le fonctionnement du cerveau en temps réel. Ce gain en résolution temporelle 5. Perte des connexions afférentes des neurones, i.e. au niveau des dendrites. Il est montré que lorsque les connexions neuronales ne sont plus entretenues, elles ont tendance à disparaître.
40 Techniques d exploration du réseau épileptogène Fig Principe de la détection en coïncidence lors de l acquisition de données de TEP (d après [Bruyant 02b]) Fig Hypométabolisme glucidique temporal observé en TEP- FDG nécessaire pour appréhender la dynamique des phénomènes inter-critiques, mais aussi critiques, se fait souvent au prix d une résolution spatiale moindre. De ce fait, il en résulte une grande complémentarité entre ces techniques d exploration fonctionnelle, et les examens morphologiques, surtout l IRM Approches électrophysiologiques Enregistrements surfaciques non-invasifs : ElectroEncéphaloGraphie (EEG) et MagnétoEncéphalographie (MEG) Principe physique et technique d acquisition: L activité électrique ou magnétique générée par l activation d une population suffisante de neurones permet de générer des signaux qui se propagent et qu il est possible de mesurer directement sur le scalp. L ElectroEncéphaloGraphie (EEG) permet d étudier les champs électriques ainsi générés, par la mesure de différences de potentiels grâce à des électrodes placées sur le scalp. La MagnétoEncéphaloGraphie (MEG) quant à elle permet de mesurer des variations infimes de champ magnétique à partir de capteurs supraconducteurs placés à proximité du scalp. L EEG est de loin la technique d exploration la moins contraignante et la moins onéreuse. Pour rendre les mesures reproductibles et comparables d un centre à l autre, le positionnement des électrodes sur le scalp a été standardisé au niveau international : le système 10-20, qui comprend 19 électrodes. Les mesures de potentiel se font, soit par rapport à une électrode de référence (montage référentiel), soit en mesurant les différences de potentiels entre deux électrodes adjacentes dans une direction longitudinale ou transverse (montage bipolaire). La numérisation des signaux permet de choisir a posteriori différents montages lors de l analyse des signaux, et facilite l interprétation. La fréquence d échantillonnage temporel est de l ordre de 1kHz, ce qui correspond à une résolution temporelle de l ordre de la milliseconde, et donc au temps de fonctionnement des activations neuronales. L échantillonnage
41 Fusion de données multimodales anatomo-fonctionnelles en épilepsie 41 spatial peut être amélioré par l utilisation de systèmes d enregistrement comprenant 32, 64, 128 voire même 256 électrodes. Pour plus de commodité, ces électrodes sont fixées sur un casque ajustable au crâne de chaque sujet. La MEG est beaucoup plus lourde à mettre en œuvre, principalement du fait des infimes variations du champ magnétique que l on cherche à mesurer (de l ordre du femtotesla = Tesla 6 ). Le principe de base étant de mesurer un courant électrique induit dans une bobine lors d une variation du champ magnétique, c est la mise au point de capteurs supraconducteurs, les SQUIDs (Superconducting QUantum Interference Device) qui a permis d atteindre une telle précision. Les SQUIDs fonctionnent à très basse température (de l ordre de -269 C) et doivent pour cela être plongés dans de l hélium liquide, ce qui induit un coût de fonctionnement non négligeable de la MEG. De plus, pour ne pas être perturbées par le bruit magnétique ambiant, terrestre et urbain, les mesures doivent être réalisées dans une chambre d isolation magnétique (cage de Faraday en µ-métal). Les fréquences d échantillonnage temporel des signaux sont du même ordre de grandeur qu en EEG. Nous disposons à Rennes d un système comprenant 37 capteurs répartis sur un disque de 10 cm de diamètre (cf. Figure 1.13). Les systèmes plus récents sont constitués d un casque couvrant toute la surface de la tête et comprenant de 100 à 300 capteurs, permettant éventuellement une acquisition EEG simultanée. La principale limitation des techniques EEG et MEG reste leur mauvaise résolution spatiale, vu que les signaux sont enregistrés à distance de la source d activité. L utilisation de méthodes de localisation de sources permet d améliorer celle-ci, mais nécessite la résolution d un problème inverse mal posé [Schwartz 98, Mattout 02]. Fig Système MEG à 37 capteurs (Magnes, 4D Neuroimaging) installé au CHU de Rennes 6. Ces champs magnétiques sont fois plus petits que le champ magnétique terrestre, de l ordre de 10 4 Tesla.
42 Techniques d exploration du réseau épileptogène Type d information explorée: Lors de l arrivée d un potentiel d action (PA) au niveau d une synapse, des courants transmembranaires d ions Na + sont à l origine des changements de polarisation de la membrane postsynaptique. Afin de rééquilibrer les charges à l intérieur de la cellule, il apparaît alors un courant intra-cellulaire qui est principalement à l origine des variations de champs magnétiques mesurables en MEG. Parallèlement à ces courants intra-cellulaires, les charges se redistribuent à l extérieur de la membrane et génèrent des courants extracellulaires se propageant dans le milieu. Ces courants sont à l origine des différences de potentiel mesurables sur le scalp en EEG (cf. Figure 1.14). Au niveau de la synapse, la membrane postsynaptique se comporte donc comme un puit de courant, et le reste de la membrane comme une source de courant, de sorte qu à distance un neurone activé peut être assimilé à un dipôle de courant. Pour que ces signaux soient mesurables en surface, il est nécessaire qu un grand nombre de neurones, généralement entre 10 7 et 10 9 [Nunez 81], se synchronisent, s activent simultanément et soient organisés spatialement de manière à générer un dipôle de courant équivalent. Ainsi, les signaux surfaciques sont principalement causés par les PPSE et PPSI des cellules dites pyramidales, dont les nombreuses dendrites sont disposées perpendiculairement au ruban cortical et parallèles entre elles (cf Figure 1.15). La modélisation dipôlaire pose que l intensité des champs électriques et magnétiques en tout point de l espace diminue proportionnellement au carré de la distance au dipôle. Ainsi, ce sont principalement les activités corticales qui sont visibles en surface, alors que l activité des structures internes est rarement accessible. Les signaux EEG et MEG ne reflètent donc qu une partie de l activité cérébrale et sont de plus complémentaires. En effet, alors que les sources radiales ne sont pas visibles en MEG, les signaux MEG sont nettement moins perturbés par l inhomogénéité des tissus (et notamment la traversée de l os) que les signaux EEG 7. Fig Modélisation des courants lors d une activation synaptique (d après [Schwartz 98]) Fig Organisation des cellules pyramidales du cortex par rapport aux différents milieux (d après [Schwartz 98]) 7. La permitivité électrique de l os est largement supérieure à celles des autres tissus cérébraux, alors que tous ces tissus possèdent des perméabilités magnétiques du même ordre de grandeur.
43 Fusion de données multimodales anatomo-fonctionnelles en épilepsie 43 Apport pour l épilepsie: En clinique, il est possible de faciliter l apparition de signaux caractéristiques de l épilepsie, voire de crises par une hyperpnée, des ouverturesfermetures oculaires, des stimulations visuelles intermittentes ou encore par un sevrage du traitement médicamenteux. La détection d Événements Paroxystiques Inter- Critiques (EPIC) en EEG est un élément diagnostique fondamental permettant de caractériser l épilepsie. Combinée à un examen clinique, c est d abord l étude des EPIC et des crises en EEG qui permet de classifier les épilepsies [Thomas 94] et d identifier celles susceptibles d être traitées par la chirurgie. La Ligue Internationale contre l Epilepsie a décrit ces EPIC par un certain nombre de figures épileptiques caractéristiques: la pointe, la pointe-onde, la pointe lente, la polypointe et la polypointe-onde. Leur description morphologique en terme de fréquence, de durée et d amplitude a été précisément définie en EEG. Ces EPIC sont des indicateurs essentiels d anomalies de fonctionnement de la transmission neuronale en période inter-critique, et participent à la caractérisation de la ZI. Ainsi, la pointe est principalement liée à une activité synaptique sous-jacente de type décharge de potentiel excitateur, alors que l onde lente correspond à la traduction d une somme de potentiels inhibiteurs. En raison de la complémentarité des enregistrements MEG et EEG, des pointes peuvent être visibles en MEG et pas en EEG, et inversement. Enregistrements in situ invasifs : Electro-CorticoGraphie (ECoG) et Stéréo- ElectroEncéphaloGraphie (SEEG) Principe physique et technique d acquisition: Afin de remédier à la faible résolution spatiale des signaux surfaciques, il est possible de mesurer l activité cérébrale in situ dans certains contextes pathologiques, dont l investigation préchirurgicale des épilepsies. Ces méthodes consistent soit à mesurer directement l activité corticale à l aide de grilles d électrodes posées sur la surface du cortex (ElectroCorticoGraphie, ECoG), soit à implanter en profondeur des électrodes semi-flexibles après un repérage stéréotaxique 8 (Stéréo-ElectroEncéphaloGraphie, SEEG). De ce fait, ces techniques d exploration sont relativement invasives; elles nécessitent une anesthésie et un geste chirurgical d implantation non totalement dénués de risques. Mise au point par Bancaud et Talairach [Bancaud 65], seule la SEEG permet réellement l exploration de structures internes (par exemple, amygdale, hippocampe), dont l exploration à partir d enregistrements surfaciques ou corticaux est souvent délicate voire impossible. Les électrodes utilisées ont un diamètre de 0.8mm et comportent 5 à 18 plots d enregistrement de 2mm de long séparés par des parties isolantes de 1.5 mm (cf. figure 1.16). Généralement, une angiographie stéréoscopique aux rayons X est réalisée avant l implantation des électrodes afin d éviter de léser tout vaisseau sanguin pendant l implantation. Type d information explorée: Ces méthodes permettent ainsi un enregistrement in situ de l activité cérébrale. De même qu en MEG et EEG, l ECoG et la SEEG béné- 8. Le repérage stéréotaxique consiste en l utilisation d un cadre vissé au crâne du patient, par exemple le cadre de Talairach, pour guider l implantation des électrodes. Ce cadre permet en outre de définir un référentiel moyen largement utilisé en neurochirurgie et donc de se repérer dans l atlas de Talairach et Tournoux [Talairach 88]. D un point de vue anatomique, ce référentiel est défini par l identification du plan inter-hémisphérique, des commissures antérieure (CA) et postérieure (CP) et de la boîte englobante du cerveau.
44 Techniques d exploration du réseau épileptogène ficient également d une excellente résolution temporelle, du même ordre de grandeur que la plupart des phénomènes électrophysiologiques (i.e. la milliseconde). En SEEG, une localisation spatiale très précise des générateurs d activité cérébrale est possible par la détection d une inversion de polarité franche du signal entre deux plots consécutifs d une même électrode. Le générateur sera alors localisé entre ces deux plots. De la même manière, il est possible de localiser un générateur entre deux électrodes à condition qu elles soient suffisamment proches l une de l autre. En effet, contrairement aux autres capteurs, un plot de SEEG n est sensible qu aux générateurs présents dans son voisinage immédiat (i.e. quelques millimètres). La principale limitation de la SEEG est son mauvais échantillonnage spatial. En effet, il n est pas concevable d explorer ainsi toute l anatomie cérébrale. Les sites d implantation à explorer doivent être choisis avec soin en fonction d hypothèses localisatrices issues du bilan de phase 1 (cf. Figure 1.2) réalisé à partir d examens non invasifs statiques ou dynamiques. Apport pour l épilepsie: Le rôle de la SEEG dans la caractérisation de la ZI est fondamentale, vu que c est à partir de la SEEG qu a été définie la notion même de ZI. L étude de l état inter-critique d un patient en SEEG consiste donc essentiellement en la détection et la localisation d EPIC, notamment les pointes inter-critiques (cf. figure 1.17), ou encore l éventuel décours spatio-temporel de ces EPIC. Pour cela, après l implantation SEEG, le patient est hospitalisé pendant une dizaine de jours afin d acquérir des enregistrements inter-critiques et critiques sous contrôle vidéo : c est la phase 2 (cf. Figure 1.2). Fig Position de deux électrodes dans le lobe temporal permettant l enregistrement in situ de l activité électrique de l amygdale (A ) et de l hippocampe (B ) Mesures de perfusion en médecine nucléaire: TEP et TEMP intercritiques Tomographie d Emission de Positons inter-critique L utilisation de l oxygène 15 O comme émetteur de positons en TEP permet de quantifier le débit sanguin cérébral régio-
45 Fusion de données multimodales anatomo-fonctionnelles en épilepsie 45 Fig Pointes inter-critiques suivies d une crise (décharges rapides) au niveau des plots p1-p2 et p2-p3 de l électrode B (cf. position de ces électrodes sur la figure 1.16) nal (DSCr), soit par injection intraveineuse d eau marquée H 2 [ 15 O] soit par inhalation continue d 15 O. Les techniques d acquisition et de reconstruction sont identiques à celles des examens statiques (voir I ). La résolution spatiale de ces acquisitions est de l ordre de 8 mm, alors qu elle peut atteindre 5 mm en imagerie statique au TEP-FDG. Vue la courte demi-vie de 15 O (2 minutes), l acquisition de tout le volume cérébral prend environ 90 secondes après l injection du traceur. Il s agit donc bien d un examen dynamique permettant une quantification absolue du DSCr, par opposition au TEP-FDG qui nécessite l établissement d un état stable pendant 40 minutes après l injection pour pouvoir explorer le métabolisme du glucose. Le choix des temps d acquisition résulte classiquement d un compromis entre résolution temporelle et statistique de comptage. Pour améliorer la statistique de comptage, il est également possible de réaliser plusieurs acquisitions successives tout en respectant une irradiation raisonnable du patient. Principalement utilisée pour les études de neuroactivation (voir I ), la TEP à l eau marquée a également été utilisée pour étudier la perfusion cérébrale de l état intercritique en épilepsie. Classiquement, un hypodébit est observé au même niveau que l hypométabolisme détecté en TEP-FDG, mais souvent moins focal et moins fiable [Theodore 94]. Les raisons de la sensibilité moyenne de ces examens sont certainement les mêmes que celles évoquées à propos de la TEMP inter-critique dans le paragraphe suivant. Tomographie d Emission MonoPhotonique (TEMP) inter-critique L étude de la perfusion cérébrale en Tomographie d Emission MonoPhotonique (TEMP) dans le contexte
46 Techniques d exploration du réseau épileptogène Fig Imageur TEMP à deux têtes utilisé au service de médecine nucléaire de Rennes (Caméra DST- XL de General Electric Medical Systems) Fig Schéma des principaux éléments constituant une γ caméra (d après [Bruyant 02b]) de l épilepsie constitue un aspect central de ce travail de thèse. C est pourquoi le principe d acquisition des données TEMP et son rôle dans le planning préchirurgical des épilepsies seront détaillés ici. Les méthodes de reconstruction, les phénomènes responsables de la dégradation des signaux et les principales méthodes de correction, seront présentés au II.4.1 avant l exposé de nos travaux sur la création d un modèle théorique de perfusion à partir de mesures sur des données TEMP réelles. Principe physique et technique d acquisition: De même qu en TEP, le principe de la TEMP est de suivre l évolution dans le corps humain d un radio-élément, qui est dans ce cas un émetteur naturel de simples photons γ. Le radio-élément est en général fixé sur une molécule (appelée radio-traceur) intervenant dans un processus métabolique caractéristique de la fonction à explorer. Seule l étude de la perfusion cérébrale en TEMP sera traitée ici. Les radio-éléments utilisés en TEMP (cf. Table 1.2) ont une demi-vie longue, comparée à celle des radioéléments utilisés en TEP, et ne nécessitent pas d être produits sur site. Par contre, on ne les compte pas parmi les éléments standards du vivant : ils doivent donc marquer des molécules spécifiques dont on va suivre le métabolisme. Bien qu elle possède une moins bonne résolution spatiale que la TEP en raison de la détection de photons simples (résolution spatiale de l ordre du cm), la TEMP est une technique intéressante et nettement moins onéreuse que la TEP. De ce fait, elle est plus facilement disponible sur un grand nombre de sites. La TEMP constitue ainsi une technique d exploration de la perfusion cérébrale largement utilisée dans la pratique clinique quotidienne et particulièrement en épilepsie [Catafau 01]. La détection de photons γ émis par le corps dans une direction privilégiée est réalisée grâce à une gamma caméra, appareil inventé par Hal Anger en Un tel détecteur est capable de fournir une image dite de projection de la distribution tridimension-
47 Fusion de données multimodales anatomo-fonctionnelles en épilepsie 47 nelle du radio-traceur suivant cette direction. L acquisition d un nombre suffisant de projections par rotations successives de la caméra autour du patient permet de résoudre les problèmes de superposition des structures dans les images de projection et de reconstruire la distribution tridimensionnelle du radio-traceur : on parle de reconstruction tomographique. Les systèmes actuels sont pour la plupart équipés de 2 voire 3 γ cameras (cf. Figure 1.18). Chaque détecteur est principalement constitué de 3 composantes [Patterson 97, ElFakhri 98] : le collimateur, le cristal scintillant et les photomultiplicateurs (PM) (cf. Figure 1.19) : 1. Le collimateur : Alors que l émission des photons γ du radiotraceur est isotropique, le collimateur va permettre de ne sélectionner que les photons incidents perpendiculaires au plan de la caméra, i.e. au plan de projection. Le principe est d empêcher les autres photons d atteindre la caméra en les arrêtant grâce à un matériau possédant un numéro atomique élevé qu ils ne traversent pas, généralement du Plomb. Un collimateur est donc constitué d un assemblage de canaux séparés de septa en Plomb. Les collimateurs principalement utilisés en imagerie cérébrale possèdent, soit des canaux parallèles, soit des canaux en éventail divergents (Fan Beam). Les collimateurs Fan Beam permettent un gain en sensibilité de détection et sont particulièrement adaptés pour l étude des gros organes comme le cerveau [DeBreuille 98], mais nécessitent une correction de la géométrie d acquisition ( rebinnage ) avant la reconstruction tomographique. En pratique clinique, on utilise généralement des collimateurs parallèles ultra-haute résolution ou des collimateurs Fan Beam ultra-haute résolution. 2. Le cristal scintillant : Le cristal scintillant, constitué de iodure de sodium activé au thallium (NaI(Tl)), permet de convertir l énergie des photons γ incidents ayant passé le collimateur en énergie lumineuse. Les principales interactions des photons γ dans le cristal sont du type effet photoélectrique et diffusion Compton (voir II ). Ces transferts d énergie permettent l excitation des atomes de thallium avoisinant, qui, à leur tour excités, émettent des photons visibles dans le proche UV: on parle de flashs lumineux. Seule une très faible partie de l énergie des photons γ est convertie en énergie lumineuse ( 3%). L arrivée d un photon en un point du cristal va générer une tache lumineuse, définissant ainsi la résolution intrinsèque du cristal. 3. Les photomultiplicateurs et l électronique associée : Ces photons lumineux suivent ensuite un guide de lumière avant d atteindre les photomultiplicateurs qui permettront de transformer cette énergie lumineuse en courant électrique. Ainsi lorsqu un photon lumineux frappe la photocathode d un tube photomultiplicateur, il en arrache quelques électrons qui sont ensuite accélérés par un champ électrique avant d aller frapper une dynode. De plus en plus d électrons sont ainsi arrachés et accélérés de dynode en dynode, si bien qu on obtient un facteur d amplification du courant de l ordre de 10 6 en sortie du photomultiplicateur. L électronique associée aux différents photomultiplicateurs réalise ensuite une sommation pondérée des différents courants lui permettant de localiser spatialement le photon incident et de quantifier son énergie. Le choix de la fenêtre spectrométrique d acquisition 9 permet alors soit d éliminer des photons 9. Intervalle d énergie des photons acceptés pour constituer l image.
48 Techniques d exploration du réseau épileptogène qui ont subi différentes interactions avec la matière avant d atteindre le détecteur (élimination des photons diffusés), soit d autoriser l acquisition simultanée des données dans différentes fenêtres spectrométriques (par exemple, acquisition simultanée à partir de deux radio-éléments 99m Tc et 123 I). La résolution spatiale des données TEMP dépend non seulement des caractéristiques de tout ce système de détection (collimateur + cristal + photomultiplicateurs), mais aussi de la méthode de reconstruction tomographique utilisée et surtout du filtrage. Une mesure précise de la résolution spatiale des données TEMP utilisées pour créer le modèle de perfusion présenté au chapitre II.4, a d ailleurs été réalisée par l acquisition de sources linéiques (voir II ). La qualité des images reconstruites en TEMP résulte classiquement d un compromis entre sensibilité de détection et donc niveau du rapport signal / bruit et résolution spatiale. Différents paramètres d acquisition permettent d ajuster ce compromis: la dose de traceur injectée, le type de collimateur, la taille du pixel (échantillonnage spatial), le temps d acquisition, le nombre de projections, l algorithme de reconstruction et le filtrage. En moyenne, les systèmes actuels permettent d obtenir des résolutions spatiales des données reconstruites entre 10 et 15mm. Type d information explorée: L information physiologique que l on cherche à mesurer en TEMP est la perfusion cérébrale et notamment le DSCr. Pour cela, différents radio-traceurs sont utilisables [Patterson 97, Steinling 99, Catafau 01], dont nous présentons ici les propriétés. Un traceur idéal de perfusion doit présenter les propriétés suivantes: une extraction maximale (i.e. passage de la BHE) lors du premier passage après injection, une captation cellulaire dépendante du flux sanguin, et l absence de redistribution du traceur dans la circulation sanguine. Dans ces conditions, la concentration de traceur dans les tissus sera proportionnelle au DSCr moyen pendant cette période de captation cellulaire. Pour pouvoir traverser la BHE par diffusion passive, une telle molécule doit être de faible poids moléculaire, neutre et surtout lipophile 10. Lors de la captation cellulaire, le traceur à caractère lipophile devient hydrophile et se retrouve piégé dans les cellules. Une fois établi, cet état reste stable pendant quelques heures, autorisant alors l acquisition des données. La TEMP réalise ainsi un cliché figé, ou shoot, des variations de DSCr au cours de cette captation cellulaire. Cette caractéristique fait bien de la TEMP une imagerie dynamique, dont la résolution temporelle dépend de la cinétique du traceur. La TEMP est de ce fait une des seules techniques de neuroimagerie fonctionnelle où l injection du radio-traceur peut être réalisée de façon anticipée par rapport à l exploration dans l imageur, caractéristique fondamentale pour l exploration de l état critique en épilepsie. Les principaux traceurs utilisés en TEMP pour mesurer le DSCr sont les suivants (cf. Table 1.2): Le Xenon 133 ( 133 Xe) : Après inhalation de ce gaz, le 133 Xe est passivement diffusable à travers la BHE, et le suivi de sa cinétique de captation et de son 10. Le caractère lipophile d une molécule désigne son affinité pour les milieux contenant des lipides, comme notamment les membranes cellulaires. Par opposition, on désignera par hydrophile une substance présentant plus d affinité pour les milieux riches en eau, comme notamment les espaces intra- et intercellulaires.
49 Fusion de données multimodales anatomo-fonctionnelles en épilepsie 49 Tab. 1.2 Propriétés des principaux traceurs de perfusion utilisés en TEMP (pi: post-injection) Radio-élément Demi-vie Emission γ Traceur Mesure de DSCr Avantages Inconvénients 133 Xe 5.3 jours 81 kev / absolue Clairance Rapide Équipement dédié Acqu. dyn. (5 min) Mauvaise rés. spatiale Emission β I 13 h 159 kev IAMP relative Équilibre : 20 min pi Cher et peu disponible Stabilité : 1h pi Recirculation Protection de la thyroïde 99m Tc 6.02 h 140 kev HMPAO relative Équilibre : 2 min pi Instable in vitro Stabilité : 4h pi Rétrodiffusion initiale Ne mesure que du flux 99m Tc 6.02 h 140 kev ECD relative Équilibre : 2 min pi Instable in vitro Stabilité : 2h pi Rétrodiffusion initiale Meilleur contraste Comportement métabolique
50 Techniques d exploration du réseau épileptogène washout permet une quantification absolue du DSCr en ml/min/100 g de tissu. C est le seul traceur permettant une quantification absolue en TEMP, et cette technique est de ce fait considérée comme un gold standard de la mesure du DSCr. Contrairement aux autres traceurs présentés ci-dessous, le 133 Xe ne reste pas piégé dans les cellules et sa clairance courte impose des acquisitions dynamiques rapides, de l ordre de 5 min pendant l inhalation du gaz. Ainsi, de telles explorations ne sont réalisables que sur un imageur dédié, présentant un grande sensibilité de détection pour palier ces contraintes dynamiques. De ce fait, cette méthode ne peut fournir qu une faible résolution spatiale. De tels imageurs ne sont accessibles que dans certains centres spécialisés. Finalement, le 133 Xe est un émetteur γ à 81keV mais aussi un émetteur de rayonnements β +, conduisant à une irradiation plus importante. L Iode 123 ( 123 I) : Le 123 I-N-Isopropyl-p-Iodoamphétamine ( 123 I-IAMP) franchit la BHE avec une extraction au premier passage de 90 à 100 % et une rétention cérébrale de 6 à 9 %. Après captation cellulaire, un plateau d équilibre de l activité est atteint entre 15 et 20 minutes après l injection, puis l activité reste constante pendant une heure environ. Mais il existe une redistribution dans la circulation au cours du temps. De plus, le produit est cher, difficilement disponible et nécessite quelques précautions particulières liées à l utilisation de l 123 I (protection de la thyroïde notamment). Le Technetium 99m ( 99m Tc) : Les traceurs utilisant le 99m Tc sont de loin les plus utilisés en clinique, et se rapprochent le plus des propriétés du traceur idéal. Le 99m Tc-L-Héxaméthyl-Propylène-Amine-Oxyme ( 99m Tc-HMPAO) est extrait à 80 % lors du premier passage et présente un taux de fixation cérébrale d environ 5%. La stabilité in vivo intra-cellulaire est obtenue très rapidement entre 1 et 2 minutes après injection. Ainsi la TEMP réalise une photographie de la perfusion cérébrale qui correspond à une intégration des variations de DSCr qui ont eu lieu pendant une période de 15 sec à 1 min après l injection du traceur [Patterson 97]. Par contre, le marquage de l HMPAO au 99m Tc conduit à une molécule instable in vitro, qui ne peut être conservée plus de 30 min. Il est donc nécessaire de faire ce marquage juste avant l injection. Le 99m Tc-Ethyl-Cystéinate-Dimer ( 99m Tc-ECD) présente une extraction plus modérée (57 %) avec une rétention cérébrale de l ordre de 6 % de l activité injectée. Dans ce cas aussi, la rétention du marqueur se fait par transformation du complexe lipophile en complexe hydrophile mais cette fois via une action enzymatique. Comme pour l HMPAO, la stabilité intra-cellulaire est obtenue environ 2 min après l injection. L avantage principal de l ECD est qu il est nettement plus stable que l HMPAO après son marquage au 99m Tc, et peut être préparé plusieurs heures avant l injection. Le mode de rétention de l ECD faisant appel à des procédés métaboliques (cf. action enzymatique permettant la conversion lipophile ->hydrophile), il peut ne pas détecter des modifications rapides de flux, par contre il fournit des données mieux contrastées que l HMPAO. Même si des patterns de perfusion différents en HMPAO et ECD ont été observés chez le sujet sain [Koyama 97], leurs propriétés similaires font qu en pratique clinique le choix de l un ou l autre dépend essentiellement de la disponibilité du produit
51 Fusion de données multimodales anatomo-fonctionnelles en épilepsie 51 au moment de l injection. L état du patient et de son environnement au moment de l injection sont aussi à prendre en compte au moment de l analyse des données [Catafau 01]. Par exemple, il sera utile de savoir si le patient avait ou non les yeux ouverts au moment de l injection avant d interpréter une prise de contraste au niveau occipital. Apport pour l épilepsie: Les propriétés dynamiques de la TEMP en font une technique de choix pour l étude du DSCr en épilepsie [Duncan 97b, Devous 98, Biraben 99]. Nous avons déjà insisté sur l importance des examens dynamiques pour l étude du réseau épileptogène. Ainsi, au sein du service d épileptologie de Rennes, tous les patients admis en phase 1 bénéficient d un examen TEMP en période inter-critique, et si possible d un examen TEMP en période critique. La définition de la période inter-critique, ou inter-ictale, n est pas évidente en pratique, car il existe des crises qui ne sont pas détectées par le patient (amnésie, par exemple) ou par son entourage. De plus, certaines anomalies postcritiques du fonctionnement cérébral peuvent persister jusqu à 24 h après la crise. Généralement, on a recours à l EEG pour vérifier qu il s agit bien d un état inter-critique, même si la SEEG a montré que certaines crises impliquant les structures temporales internes pouvaient n avoir aucune traduction sur l EEG de surface. Ainsi, en pratique, la plupart des auteurs définissent l état inter-ictal stable comme atteint après une période d au moins 24h sans crise décelable cliniquement. De manière analogue à l hypométabolisme généralement observé en FDG-TEP, l aspect le plus fréquemment observé en TEMP inter-ictale est une hypoperfusion (cf. Figure 1.20). Cependant, à elle seule, la TEMP inter-ictale souffre d une faible sensibilité, elle est plus communément utilisée pour définir un niveau de base lors de l analyse des données critiques. La méta-analyse de Devous et al. [Devous 98] montre que pour l épilepsie du lobe temporal, la TEMP inter-ictale localise le lobe temporal pathologique dans 44 % des cas, l hémisphère pathologique dans 58 % des cas (dans 67 % des cas dans les séries chirurgicales). Sa spécificité également est discutée, vu que certains auteurs observent jusqu à 40 % de discordance entre l EEG et la TEMP. Ces résultats sont néanmoins à relativiser et peuvent être biaisés par la définition incertaine de l état inter-ictal, la technique de détection de l hypodébit (généralement visuelle et subjective), ou encore par la sélection des patients sur les séries courtes. Alors que l existence d une hypoperfusion en présence d une lésion (détectée en IRM) n a d autre signification que la présence de cette lésion, plusieurs hypothèses ont été posées pour expliquer cette hypoperfusion dans les cas où aucune lésion n a pu être observée [Biraben 99] : une raréfaction neuronale (e.g. sclérose de l hippocampe), un hypofonctionnement des structures impliquées dans l épilepsie, ou la notion de surround inhibition associée à une activité épileptiforme inter-critique focale (e.g. pointes). En épilepsie temporale, l étude de Guillon et al. [Guillon 98] réalisée au service de neurologie de Rennes a d ailleurs montré une corrélation positive entre deux patterns de localisation de pointes inter-critiques en SEEG et deux patterns d hypoperfusion en TEMP inter-critique. Ces patterns intéressaient soit uniquement la partie mésiale du lobe temporal (5 cas sur 20), soit tout le lobe temporal (8 cas sur 20). Ce résultat est fondamental car il suggère l étude des hypoperfusions en TEMP inter-critique comme une technique non invasive d investigation de la ZI.
52 Techniques d exploration du réseau épileptogène Par contre, cette corrélation n était pas absolue, car si un hypodébit en TEMP prédit correctement la présence de pointes en SEEG, l inverse n est pas vrai. En effet, des pointes ont été enregistrées dans 5 cas où la TEMP inter-critique a été considérée comme normale. L étude plus approfondie du lien entre la ZI et la TEMP devrait pouvoir bénéficier de développements méthodologiques afin d être abordée de manière plus objective et quantitative ; la méthode d analyse de données TEMP par standardisation anatomique qui sera présentée au chapitre II.4 peut être considérée comme une contribution de ce travail de thèse allant dans ce sens Imagerie par Résonance Magnétique (IRM) dynamique et fonctionnelle: Origine des signaux - effets de susceptibilité magnétique et pondération T2 : En utilisant principalement les effets de susceptibilité magnétique créant des inhomogénéités locales de champ magnétique, des nouvelles séquences d IRM permettent d explorer sélectivement le compartiment vasculaire capillaire (IRM de perfusion), le compartiment intersticiel et extra-cellulaire séparé du précédent par la BHE (IRM de diffusion), et indirectement le compartiment cellulaire par la consommation en oxygène des neurones (effet BOLD - Blood Oxygenation Level Dependent - en IRM fonctionnelle). Quelles que soient leurs origines (e.g. agent de contraste endogène ou exogène, interface air/os), ces inhomogénéités locales du champ magnétique B 0 accentuent le déphasage des magnétisations et entraînent une décroissance plus rapide de la composante transversale de la magnétisation : décroissance exponentielle en T2 avec T 2 < T 2. Alors que certaines séquences permettent d annuler ces effets au moment de l écho (e.g. séquences spin-echo) afin d obtenir une vraie pondération en T2, d autres séquences tendent au contraire à être sensibles au T2 : c est notamment le cas des acquisitions rapides en écho de gradient, les séquences Echo-Planar Imaging (EPI). En plus d être pondérées en T2, ces séquences d acquisition sont rapides et peuvent donc être utilisées pour explorer des phénomènes dynamiques. Mesure de l effet BOLD en IRM fonctionnelle (IRMf) : Lorsqu une population de neurones est activée, l oxygène nécessaire à leur fonctionnement est apporté via la circulation sanguine, notamment grâce aux molécules d hémoglobine présentes dans les globules rouges. L augmentation locale de la consommation en oxygène va entraîner localement une augmentation du taux de désoxy-hémoglobine par rapport à l oxy-hémoglobine. Dans un second temps, la vasodilatation des vaisseaux liée à cette activité neuronale provoque une augmentation du DSCr. L apport en oxygène devient alors largement excédentaire par rapport aux besoins métaboliques. Il en résulte localement une diminution du taux de désoxy-hémoglobine par rapport à l oxy-hémoglobine : c est l effet BOLD. Cet effet apparaît 1 à 2 secondes après le début de l activité électrique neuronale, et persiste pendant environ 6 secondes après la fin de l activation. Or en IRM, la désoxy-hémoglobine étant paramagnétique, elle modifie le signal dû aux molécules d eau avoisinantes, alors que l oxyhémoglobine, diamagnétique, est sans effet. L utilisation des séquences EPI sensibles à cet effet BOLD permet l exploration d états de fonctionnement du cerveau. Les modifications du signal engendrées par l effet BOLD sont infimes et non repérables visuellement. En pratique, il est nécessaire de comparer par des méthodes statistiques différents états du
53 Fusion de données multimodales anatomo-fonctionnelles en épilepsie 53 cerveau, en général un état actif et un état de repos. Largement utilisées pour réaliser des cartographies fonctionnelles préchirurgicales, ces techniques peuvent également être utilisées pour explorer l état inter-critique d un patient épileptique. Les méthodes consistent généralement à comparer des acquisitions réalisées en présence ou non de pointes intercritiques, et nécessitent un enregistrement simultané de l EEG dans l imageur. L IRM de perfusion : L IRM de perfusion est basée sur l utilisation d un agent de contraste endogène (arterial spin labelling) ou exogène (injection de chélate de Gadolinium) modifiant localement la susceptibilité magnétique. Le passage de l agent de contraste est suivi par l acquisition de séquences pondérées en T2. A partir d un modèle compartimental, il est alors possible de reconstruire une cartographie du volume sanguin cérébral local. L IRM de perfusion fournit en fait un indice de micro-vascularisation. Il s agit d une technique prometteuse pour l analyse de la perfusion en période intercritique. Une étude menée au laboratoire a mis en évidence trois patterns spécifiques de perfusion, correspondant à deux type d épilepsies temporales et à un pattern caractérisant les épilepsies associées à des dysplasies corticales focales [Scarabin 02]. L IRM de diffusion : L IRM de diffusion est basée sur l utilisation de séquences d acquisition spécifiques sensibles aux micro-déplacements des molécules d eau. Le principe physique est de suivre les modifications de phase des molécules d eau en mouvement. A partir de séquences permettant d explorer la diffusion dans les différentes directions de l espace, il est possible d estimer en tout point du cerveau un tenseur de diffusion et d en déduire un coefficient de diffusion apparent. Le déplacement des molécules d eau dépend de la structure du tissu et donc de l orientation des fibres de substance blanche. L IRM de diffusion est donc particulièrement sensible à l anisotropie des tissus. En période inter-ictale, il existe une augmentation de l anisotropie et du coefficient de diffusion apparent dans les épilepsies du lobe temporal Examens dynamiques de l état critique La délimitation de la ZE est de loin le principal enjeu du planning préchirurgical, car c est par définition l exérèse de la ZE qui permettra de traiter le patient, en arrêtant ou diminuant la fréquence de ses crises. La caractérisation précise de la ZE est une tâche délicate vu qu elle nécessite d explorer l état critique du patient, c est à dire qu il faut être capable d acquérir des données au cours de la crise d épilepsie. Quelques rares cas d analyse de l état critique en TEP, IRMf ou MEG ont été répertoriés, mais dans la plupart des cas il s agit de crises survenues par hasard pendant l acquisition ou de protocoles de recherche très spécifiques. En effet, seules certaines crises ne présentant pas ou peu de signes cliniques (par exemple, des absences) sont compatibles avec ces techniques d acquisition. Ainsi, nous présentons ici les seules techniques d exploration applicables à tout type de crise, à savoir l EEG et la SEEG enregistrés simultanément avec la vidéo du patient et la TEMP critique Approches électrophysiologiques Vidéo Electro-EncéphaloGraphie (EEG) La principale technique d investigation de l état critique consiste à coupler l EEG à un enregistrement vidéo. Ce mode opératoire
54 Techniques d exploration du réseau épileptogène permet d enregistrer de façon synchrone les manifestations électriques et la sémiologie clinique des crises; la vidéo-eeg autorise donc des corrélations électro-cliniques. Tout comme l EEG traditionnelle, cette technique fournit une excellente résolution temporelle compatible avec les temps de fonctionnement de l activité neuronale et donc des crises, mais une résolution spatiale médiocre. Cependant, en raison des mouvements du patient pendant la crise, l électromyogramme 11 peut fortement entacher l EEG, même si généralement ce n est pas le cas en tout début de crise. De plus, des crises intéressant les structures internes peuvent ne pas générer de signal mesurable en surface, ou peuvent apparaître retardées après propagation vers des structures externes. L interaction directe du médecin ou d un technicien pendant ou juste après la crise permet de retirer de cet examen une grande quantité d informations pertinentes sur le début de la crise et ses voies de propagation (e.g. tests du langage, de l état de conscience). Techniquement, deux caméras enregistrent respectivement le corps entier du patient et son visage. Pour synchroniser la vidéo et l EEG, les premières techniques consistaient simplement à filmer l enregistreur papier de l EEG. Si l EEG est stocké numériquement, on peut soit enregistrer un signal de synchronisation pendant l enregistrement vidéo analogique, soit disposer également d un enregistrement vidéo numérique. D un point de vue clinique, il est nécessaire d enregistrer plusieurs crises (en pratique 2 ou 3), afin de vérifier qu elles sont stéréotypées et/ou en extraire la partie commune essentielle. Il est important que la sémiologie clinique et les manifestations électriques soient suffisamment reproductibles d une crise à l autre afin de pouvoir poser des hypothèses localisatrices. Pour cela, cet examen nécessite plusieurs jours d hospitalisation pendant lesquels le patient est enregistré en continu (soit la journée, soit 24h/24h) : c est la phase 1 (cf. Figure 1.2), étape indispensable de toute prise en charge chirurgicale d une épilepsie partielle pharmaco-résistante. La vidéo-eeg est donc la principale technique non-invasive d identification de la ZE. Vidéo-SEEG Comme déjà précisé, la SEEG est une des techniques de référence qui a permis la définition des notions de ZE, ZI et ZL. Synchronisés à la vidéo, les enregistrements SEEG fournissent les informations les plus précises sur le départ et la propagation des crises. L enregistrement vidéo des manifestations cliniques, couplé à des enregistrements in situ, bénéficiant d une excellente résolution spatiale et temporelle, autorise la réalisation de corrélations anatomo-électro-cliniques. De même que lors de la phase 1, le patient auquel on a implanté des électrodes intra-cérébrales, est hospitalisé pendant une dizaine de jours pour permettre l enregistrement de plusieurs crises, spontanées ou déclenchées: c est la phase 2. En effet, les plots des électrodes intra-cérébrales peuvent également être utilisés pour réaliser des stimulations électriques intra-cérébrales, afin de provoquer des crises ou de cartographier l environnement fonctionnel du réseau épileptogène. Le recours à ces explorations invasives de phase 2 est de plus en plus rarement nécessaire pour les épilepsies temporales, qui sont les plus courantes et les mieux connues. Par contre, cette étape est fondamentale avant la décision chirurgicale pour la plupart des épilepsies extra-temporales, et notamment les épilepsies frontales. En effet, les crises frontales sont généralement très rapides et se propagent sur un territoire cérébral important, si bien que la localisation de l origine des crises est loin d être évidente. Cependant, toute exploration 11. Signal électrique généré lors de l activité d un muscle.
55 Fusion de données multimodales anatomo-fonctionnelles en épilepsie 55 SEEG est biaisée par son échantillonnage spatial limité ; en effet 5 à 15 électrodes sont en général implantées, ce qui exclut l exploration de tout le volume cérébral. La définition du schéma d implantation est réalisée lors de l investigation non invasive très précise à partir des différentes techniques d exploration précédemment décrites. A ce stade, les deux seules techniques d exploration de l état critique sont la vidéo-eeg des crises et la TEMP ictale (cf. paragraphe suivant). D après Biraben et al. [Biraben 97], le choix du schéma d implantation se fait en 4 étapes: 1. Placement des électrodes au niveau des sites suspectés comme étant à l origine des crises, et suivant les principales voies de propagation, connues ou suspectées de jouer un rôle dans la propagation de la crise (exploration de la ZE). 2. Si une lésion a été détectée lors des examens morphologiques, placement d électrodes dans la lésion et dans son environnement pour étudier l épileptogénicité de ces tissus (exploration de la ZL). 3. Exploration d autres zones dont on suspecte le caractère épileptogène, du fait d événements cliniques ou paracliniques, ainsi que de zones qui sont le siège d anomalies intercritiques (exploration de la ZI). 4. Ajustement définitif: cette étape consiste à prendre en compte les trois étapes précédentes afin de définir un schéma d implantation optimal permettant d explorer sans risque et avec un nombre minimal d électrodes les zones décrites précédemment et leur environnement fonctionnel proche (pour réaliser une cartographie fonctionnelle préchirurgicale afin d éviter tout déficit fonctionnel postopératoire). La réalisation d une angiographie stéréoscopique aux rayons X de haute résolution spatiale (environ 0.5 mm) permet en outre de choisir le lieu précis de l implantation de façon à éviter de léser les éléments vasculaires pendant l implantation Tomographie d Emission MonoPhotonique (TEMP) critique Fig TEMP inter-critique d une épilepsie à point de départ temporal mésial Fig TEMP critique d une épilepsie à point de départ temporal mésial
56 Techniques d exploration du réseau épileptogène Principe physique et technique d acquisition: Le principe est de réaliser l injection du radio-traceur au moment du déclenchement de la crise ou immédiatement après. La survenue d une crise étant toujours inopinée, le radio-traceur ( 99m Tc-HMPAO ou 99m Tc-ECD) doit être stocké à proximité du patient. Un tel examen est réalisable pendant que le patient est pris en charge en phase 1. Ainsi, l enregistrement vidéo- EEG permet de repérer à quel moment de la crise le radio-traceur a été injecté, ce qui a une grande importance pour l interprétation des données. Si l on utilise du HMPAO, le marquage au 99m Tc est alors réalisé juste avant l injection. Cependant, une forme stabilisée du HMPAO marqué au 99m Tc est désormais disponible. En général, il est recommandé d injecter une dose de 740 à 825 MBq. Après l injection, le patient est transféré dans le service de médecine nucléaire, et l acquisition est réalisée dans l heure qui suit. D un point de vue organisationnel, la réalisation de tels examens nécessite une parfaite collaboration entre les services de neurologie et de médecine nucléaire et la disponibilité d une caméra sans rendez-vous. Type d information explorée: Historiquement, aux débuts de la chirurgie de l épilepsie, Penfield et ses collaborateurs observèrent une hyperperfusion locale à l endroit où une crise ou une aura avaient été déclenchées par stimulation électrique corticale. Des études systématiques de ces augmentations du débit sanguin, mesurées à l aide d un thermocouple sur la surface du cortex, les amenèrent à montrer que celles-ci apparaissent entre 4 à 10 secondes après le début de la décharge EEG ictale, restent bien localisées et persistent après la crise, avant de devenir une hypoperfusion locale [Penfield 39]. Les propriétés de captation cellulaire rapide des radio-traceurs que sont le 99m Tc-HMPAO et le 99m Tc-ECD (entre 1 et 2 min), en font des traceurs idéaux pour l étude de tels phénomènes. Ainsi, on estime qu en injection ictale cette captation débute environ 15 s après l injection et dure environ 40 s. Les données de TEMP ictale représentent donc une intégration du DSCr pendant une courte période qu il est fondamental de repérer par rapport au début de la crise sur la vidéo-eeg. Apport pour l épilepsie: La possibilité d injecter le radio-traceur en salle de vidéo- EEG fait de la TEMP critique la seule technique d imagerie capable d explorer la ZE. La TEMP critique fournit la meilleure résolution spatiale (de l ordre du cm) parmi tous les examens non invasifs de l état critique. Vu que la crise n a pas lieu dans l imageur, la plupart des crises peuvent être explorées ainsi. Cet examen est réalisé dès que possible pendant la phase 1. La principale difficulté consiste à détecter suffisamment tôt le début de la crise pour permettre l injection. En épilepsie temporale, la méta-analyse de Devous et al. [Devous 98] annonce une sensibilité très élevée, de l ordre de 97%, lorsque l injection est bien réalisée en perictal. Sensibilité et spécificité atteignent 100 % dans les séries chirurgicales. Néanmoins, dans 15 à 20 % des cas, l interprétation est rendue difficile par la présence d une hyperperfusion bilatérale. En fonction du moment de l injection, l hyperperfusion est localisée au niveau de la ZE et éventuellement au niveau des principales voies de propagation (cf. Figure 1.21) [Duncan 97b, Devous 98, Biraben 99]. Cet hyperdébit peut intéresser également certaines structures internes (e.g. thalamus, noyaux lenticulaires ou noyaux caudés), dont le lien avec la sémiologie des crises reste une question ouverte. Généralement, l hyperperfusion est entourée d une large zone d hypoperfusion pouvant intéresser jusqu à tout le reste de l hémisphère, phénomène comparable à la surround inhibition décrite en inter-critique. Lorsque l injection est tardive par
57 Fusion de données multimodales anatomo-fonctionnelles en épilepsie 57 rapport au début de la crise, TEMP post-critique, l hyperperfusion est remplacée par une hypoperfusion. Différents patterns spécifiques de perfusion ictale associés à 4 types d épilepsies temporales ont été décrits par Ho et al. [Ho 96, Ho 97]. J insiste un peu sur les résultats cliniques concernant les épilepsies temporales, d une part parce que ce sont de loin les épilepsies les plus connues, les plus étudiées et les plus faciles à traiter, d autre part parce que c est précisément la perfusion de l épilepsie à point de départ temporal mésial qui a été modélisée au chapitre II.4. Concernant les épilepsies extra-temporales, les études systématiques sont plus rares et l identification de patterns plus difficile, néanmoins la TEMP ictale apporte généralement des informations pertinentes sur la ZE. La comparaison avec la TEMP inter-critique permet d assister l interprétation. Alors que la dynamique des traceurs est compatible avec la durée des crises temporales, ce n est généralement pas le cas pour les crises frontales qui sont brèves, se propagent très vite et généralisent souvent. Dans ces conditions le recours à la SEEG reste nécessaire, et chaque épilepsie est différente. R. Duncan [Duncan 97b] précise que lorsqu une hyperperfusion ictale est observée dans la partie mésiale du lobe temporal, alors il est possible d avoir recours à la chirurgie sans recours à la SEEG. Par contre, la présence d un hyperdébit ictal extra-temporal doit être pris en compte pour guider l implantation des électrodes intra-cérébrales Analyse de l environnement fonctionnel L objectif de ces techniques est de caractériser l environnement fonctionnel du réseau épileptogène afin de s assurer que la cortectomie est envisageable sans générer de troubles fonctionnels significatifs. La fonction à explorer dépend de la région anatomique où a été localisé le réseau épileptogène : aires motrices, somesthésiques, auditives, visuelles, aires impliquées dans le langage. Il existe de nombreux paradigmes d exploration de ces fonctions, ce n est pas l objet de ce paragraphe Potentiels évoqués: EEG, MEG, ECoG, SEEG Principe physique et technique d acquisition: Les potentiels évoqués sont obtenus par application répétée d un stimulus synchronisé avec l acquisition des signaux. Le moyennage de ces signaux permet de n extraire que le signal correspondant à l information électrophysiologique synchronisée et en phase avec le stimulus. Type d information explorée: L information électrique ou magnétique générée au niveau d une population de neurones activés est à l origine du signal mesuré par ces techniques. Elles bénéficient ainsi d une excellente résolution temporelle et autorisent un suivi spatio-temporel des activations. Par contre, les enregistrements surfaciques souffrent d une faible résolution spatiale et nécessitent généralement d avoir recours à des méthodes de localisation de sources Imagerie d activation: IRMf, TEP Principe physique, technique d acquisition et pré-traitements: Le principe de la neuroimagerie d activation est l acquisition d une série de données pendant des phases successives de repos ou d activité en exécutant une tâche
58 Méthodes d analyse et de fusion de données : besoins pour l épilepsie spécifique de la fonction à étudier. Il peut s agir de stimulation par bloc ou monoévénementielle. L analyse statistique du signal voxel/voxel permet de détecter et de localiser les aires cérébrales significativement corrélées au paradigme d activation. Ces méthodes autorisent une très bonne résolution spatiale (2 mm), mais ne permettent qu une faible résolution temporelle. Les limites en matière de résolution temporelle s expliquent principalement par le fait que ces techniques explorent de manière indirecte l activité du neurone, via la consommation O 2 notamment. De part sa non-invasivité et surtout sa facilité d accès sur de nombreux sites cliniques, l IRMf a tendance à remplacer la TEP pour les études en neuroimagerie fonctionnelle Explorations invasives Le test de Wada permet de déterminer la latéralisation des fonctions du langage et d évaluer les capacités mnésiques, lors de bilans préopératoires de neurochirurgies susceptibles de toucher les aires du langage ou de la mémoire. Il consiste en une injection intracarotidienne unilatérale d un barbiturique de durée d action intermédiaire, l amobarbital. Son injection provoque une hémiplégie après quelques secondes et pendant environ 5 minutes. Il est réalisé avant certaines cortectomies temporales et permet d analyser le déficit envisagé par une ablation de l hippocampe (notamment par la prédiction des effets sur la mémoire verbale). Ses résultats peuvent contre-indiquer la chirurgie, s il existe un doute sur la latéralisation ou la fonctionnalité du côté sain. Les stimulations électriques corticales peropératoire ou en profondeur (SEEG) sont des méthodes considérées comme un gold standard pour la réalisation d une cartographie anatomo-fonctionnelle. 1.3 Méthodes d analyse et de fusion de données: besoins pour l épilepsie Fig Répartition des résolutions spatiales et temporelles accessibles par les principales techniques d exploration fonctionnelle Après avoir présenté les principales techniques d exploration du réseau épileptogène et de son environnement fonctionnel, l objectif de cette partie est de définir la notion de fusion
59 Fusion de données multimodales anatomo-fonctionnelles en épilepsie 59 de données dans le contexte clinique qu est la prise en charge chirurgicale de l épilepsie. Tout en insistant sur le fait que la fusion ne se limite pas qu au problème du recalage, i.e., à une mise en correspondance géométrique des données, nous montrerons à quel point le recalage est une étape incontournable avant toute méthode dite de fusion de données. Nous justifierons ainsi la nécessité d une évaluation précise et objective des méthodes de recalage dans le contexte clinique de l épilepsie. Une telle évaluation, pour le recalage TEMP ictale / IRM notamment, fait précisément l objet de ce travail de thèse. La Figure 1.22 rappelle la complémentarité des différentes techniques d exploration en montrant notamment la gamme des résolutions spatiales et temporelles accessibles. De plus, l origine physiologique de ces informations est à la fois diverse et complémentaire, soit de nature purement morphologique, soit explorant le métabolisme ou la perfusion cérébrale, ou encore mesurant de façon directe le fonctionnement électro-magnétique des neurones. D autres paramètres liés à la clinique (e.g., histoire de la maladie, antécédents, facteurs génétiques) et à la sémiologie des crises constituent autant d informations complémentaires qu il est fondamental de prendre en compte lors du diagnostic, bien qu elles soient plus difficiles à formaliser que des images ou des signaux. La compréhension et la caractérisation d une épilepsie partielle pharmaco-résistante est par nature un processus de fusion de données hautement multimodal, qui intègre les informations rassemblées au fur et à mesure de la prise en charge : Examen clinique : caractéristiques du patient (âge, sexe, latéralisation, etc), historique de la maladie, antécédents (e.g. traumatismes, facteurs génétiques), types de crises, fréquence des crises, moment d apparition des crise (e.g. nuit, lever), etc. La plupart de ces données sont obtenues après l interview du patient et de son entourage par le neurologue. Etude de la sémiologie de crises: analyse de la ou des crises stéréotypées du patient enregistrées par vidéo EEG. Les crises sont revisionnées minutieusement afin de faire des corrélations entre la sémiologie et les signaux EEG. Recherche d une zone lésionnelle : analyse des examens morphologiques (IRM). Etude du début de la crise et de l état inter-critique : analyse des signaux EEG. Exploration complémentaire du réseau épileptogène et étude de son environnement fonctionnel : analyse des autres données fonctionnelles disponibles (e.g., TEMP interictale et/ou ictale, TEP, IRMf, MEG). Ces différentes informations, combinées à l expertise du neurologue (connaissances théoriques et pratique quotidienne) vont permettre de poser des hypothèses sur l organisation du réseau épileptogène. Soit ces éléments plaident en faveur d un cas stéréotypé et la décision d une exérèse chirurgicale est décidée ou contre-indiquée (cf. Figure 1.2), soit ces hypothèses nécessitent d être vérifiées par des explorations plus poussées et une exploration SEEG est alors envisagée. Le schéma d implantation des électrodes résulte d une discussion entre le neurologue et le neurochirurgien qui pratique l implantation. Il s agit de choisir judicieusement les zones à explorer, tout en limitant les risques liés à l implantation. Ainsi, dans tout le processus aboutissant à une éventuelle chirurgie, on assiste à une intégration de données multimodales 12. Cette intégration des données s opère pendant les 12. Dans ce contexte, la notion de modalité ne désigne pas seulement un type d imagerie mais est bien plus générale. Ces données regroupent les résultats de diverses techniques d exploration anatomique et fonctionnelle, mais également de nombreuses informations liées à la clinique du patient et à la sémiologie
60 Méthodes d analyse et de fusion de données : besoins pour l épilepsie phases d exploration non invasives et invasives du réseau épileptogène, pendant la préparation de l acte chirurgical (cartographie fonctionnelle préchirurgicale), voire même au cours de la réalisation de cet acte chirurgical (neuronavigation multimodalité). Le raisonnement du neurologue peut donc être assimilé à un processus de fusion mentale des ces informations. Depuis une dizaine d années, l essor de nouvelles techniques de traitement du signal et de l image a suscité de nouveaux besoins et possibilités en matière de fusion de données, permettant d aboutir à une définition plus objective voire quantitative de la fusion de données multimodales en imagerie médicale. Après avoir défini le concept de fusion de données dans le contexte clinique de l épilepsie, nous présentons un certain nombre de méthodes d analyse couramment utilisées en neuroimagerie et considérées comme des méthodes dites de fusion de données Fusion de données guidée par le problème clinique Ce paragraphe applique au contexte de l épilepsie une définition plus générique d une application clinique de fusion de données que nous avons proposée dans [Jannin 01a, Jannin 01b]. Afin de mettre en œuvre une application de fusion de données, il convient de définir quels sont les objectifs cliniques et d identifier quel est le contexte de fusion. Lors de la prise en charge chirurgicale des épilepsies pharmaco-résistante, l objectif clinique principal concerne la caractérisation du réseau épileptogène et de son environnement fonctionnel afin d assister au mieux une éventuelle chirurgie. La caractérisation du réseau épileptogène consiste en l identification des éventuelles ZE, ZI et ZL. Cette caractérisation permet à la fois de mieux comprendre l épilepsie du patient et d enrichir les connaissances théoriques sur ce type d épilepsie. Lorsqu un acte chirurgical est envisagé, les techniques de fusion vont permettre d assister au mieux la préparation et la réalisation de ce dernier. Ces aspects incluent la réalisation d une cartographie anatomo-fonctionnelle préchirurgicale et l utilisation de systèmes de chirurgie guidée par l image (neuronavigation). Nous distinguerons donc quatre types de problèmes cliniques pour lesquels les méthodes dites de fusion de données permettent d assister la démarche du clinicien : Repérage des résultats des différentes explorations anatomo-fonctionnelles sur l anatomie du patient Détection et quantification d aires pathologiques ou fonctionnelles spécifiques du patient exploré Identification de patterns caractérisant des aires pathologiques ou fonctionnelles au sein d une population de sujets, prise en compte de la variabilité inter-individuelle Aide à la réalisation d un acte chirurgical. Le contexte de fusion d une application de fusion de données est ensuite défini comme l ensemble des données qu il convient de mettre en correspondance et d intégrer, leurs caractéristiques intrinsèques (e.g. type de modalité, dimension, résolution spatiale et temporelle), et les hypothèses caractérisant quelles sont les informations homologues, les informations complémentaires et les perturbations entre ces données. [Brown 92] pose le problème du recalage comme étant le moyen de compenser des perturbations entre les données, tout des crises.
61 Fusion de données multimodales anatomo-fonctionnelles en épilepsie 61 en conservant les informations complémentaires qui constituent précisément ce que l on cherche à mettre en évidence (e.g. assister la localisation d une fonction à partir de données anatomiques). Cette définition est généralisable à toute application de fusion de données. [Brown 92] distingue trois types de perturbations: les distortions corrigées, les distortions non corrigées et les variations d intérêt. Les distortions corrigées sont celles qui peuvent être modélisées lors de la formalisation du problème de fusion de données. Dans le cas du recalage, ce sont notamment des changements de point de vue ou de perspective de la scène imagée ou des changements de forme de l objet étudié, que l on peut modéliser par une transformation géométrique qu il faudra estimer. Les distortions non corrigées sont difficilement modélisables, mais les méthodes de fusion devront y être les moins sensibles que possible lors de l estimation des distortions modélisées. Ces perturbations sont notamment liées au bruit, au changement d éclairage de la scène (en vision par ordinateur), au changement de capteur (imagerie multimodalité) ou encore à des phénomènes physiologiques non modélisés. Enfin, les variations d intérêt constituent précisément l information que les méthodes de fusion de données cherchent à mettre en évidence (e.g. détection, localisation, quantification d une aire pathologique ou fonctionnelle, étude de la variabilité fonctionnelle inter-individuelle). Les sources d information mises en jeu dans ces processus de fusion sont les nombreuses techniques d exploration présentées précédemment. Dans la plupart des cas, les processus de fusion de données n impliquent que des images ou des signaux, mais ils pourraient théoriquement faire intervenir des informations ou connaissances d un plus haut niveau sémantique, comme par exemple les connaissances du neurologue, la clinique ou la sémiologie des crises. Nous désignerons donc par méthode de fusion de données toute méthodologie qui a pour finalité d assister le clinicien vis à vis des différents objectifs cliniques précédemment cités, en utilisant de manière combinée les différentes sources d informations disponibles. De telles approches, dites de fusion de données, font généralement appel à des méthodes issues du traitement de l image et du signal, des statistiques ou de l analyse de données. Cette définition est très vaste et déborde très largement du domaine couvert par nos travaux. La position de la tête du patient dans l imageur étant rarement contrôlée d un examen médical à l autre, le recalage apparaît néanmoins comme une étape incontournable avant d envisager toute fusion de données. Une fois les données recalées, différentes techniques dites de fusion permettent d assister le clinicien, citons par exemple : Outils de visualisation interactifs, Synthèse d une nouvelle donnée dite fusionnée, Analyse statistique des mesures réalisées de manière supervisée ou non, Fusion coopérative : utilisation de données multimodales, pour assister un problème de reconstruction, de localisation ou de détection,... Pour finir ce premier chapitre, nous allons présenter la fusion de données dans le contexte de l épilepsie, en l abordant sous l angle des quatre problématiques cliniques citées précédemment. Dans chacun des cas, sont présentées des méthodes couramment utilisées en neuroimagerie et que nous considérons comme des méthodes de fusion de données. Certaines méthodes seront illustrées à partir de réalisations issues de l environnement de fusion développé au laboratoire IDM et à partir de cas cliniques provenant des services de neurologie et de neurochirurgie du CHU de Rennes.
62 Méthodes d analyse et de fusion de données : besoins pour l épilepsie Aide au repérage sur l anatomie du patient Le contexte clinique abordé ici concerne la compréhension de l épilepsie d un patient bien particulier. L objectif est de fournir un substrat anatomique commun permettant la mise en correspondance des résultats des différents examens morphologiques et fonctionnels afin d assister la caractérisation du réseau épileptogène (ZL, ZI et ZE) et de son environnement fonctionnel. Cet aspect se limite dans la plupart des cas à un problème de recalage et de visualisation. Le substrat anatomique commun est en général une IRM 3D haute résolution pondérée en T1. Les différents examens anatomiques et/ou fonctionnels qu il est nécessaire de fusionner sont donc tout d abord recalés, puis présentés au clinicien à l aide d outils de visualisation et d interaction adaptés. Il s agit donc principalement d un problème de recalage intra-patient, pouvant être monomodalité ou multimodalité. Le chapitre I.2 présente un état de l art des différentes techniques de recalage utilisables. En ce qui concerne les outils de visualisation et d interaction sur les données recalées, on distingue les approches basées curseur et les approches basées superposition de données. L approche basée curseur permet de mettre en correspondance plusieurs jeux de données en partageant un curseur entre des modules de visualisation synchronisés. Un événement souris dans une image correspond à la désignation d un point dans les données affichées par le module. Les coordonnées de ce point sont envoyées aux autres modules de visualisation, transformées selon les transformations géométriques calculées par le recalage, provoquant l affichage des images contenant le point correspondant. Néanmoins, il est souvent plus commode pour le clinicien de ré-échantillonner les données dans le même référentiel, e.g., celui de l IRM 3D, avant de permettre ce mode de visualisation. En effet, il est plus facile d intégrer visuellement un même plan de coupe appliqué à deux examens différents, que simplement un point correspondant à l intersection de deux plans de coupes différents. Soulignons cependant qu un tel ré-échantillonnage fait intervenir des données présentant des résolutions spatiales diverses. Dans la plupart des cas, les données fonctionnelles de faible résolution spatiale seront sur-échantillonnées avant d être superposées aux données anatomiques. Le clinicien devra donc garder à l esprit ces différences de résolution spatiale avant d interpréter ces données fusionnées. L approche basée superposition visuelle consiste à visualiser sur une même image l information de différents jeux de données recalés entre eux. Dans une première solution, les données multimodales sont superposées point à point au sein d une seule image. Cette superposition peut être réalisée par une opération arithmétique sur les intensités des pixels ou des voxels (transparence par exemple), par codage de couleurs ou codage par spectres. En 2D, des techniques comme le remplacement des valeurs peuvent aussi être utilisées. Ainsi il peut s agir d une fenêtre glissante déplacée par l utilisateur dans laquelle les valeurs des pixels d un jeu de données sont remplacées par les valeurs de l autre jeu de données, ou encore de la visualisation en échiquier 2D. Un inconvénient de ces méthodes est que l image ou le volume résultant ne correspond plus à une modalité réelle, ce qui peut gêner le clinicien. Quand plus de deux ensembles de données doivent être superposés, il est préférable d utiliser les approches curseur. Une solution, pour réduire la complexité de la scène, est d extraire les surfaces des structures d intérêt (e.g., sillons corticaux, contours d une lésion, zone activée en IRMf), et de les fusionner dans une nouvelle scène, en utilisant les techniques de rendu de surface 3D. Les méthodes utilisant des textures couleur afin de coder l information fonctionnelle et
63 Fusion de données multimodales anatomo-fonctionnelles en épilepsie 63 de la superposer sur l anatomie (IRM) sont classiquement utilisées en médecine nucléaire (TEP ou TEMP). En effet, la TEP et la TEMP sont des données que les cliniciens sont habitués à visualiser à l aide de tables de couleur. Il existe différents modes de création d une image dite fusionnée à partir de textures couleur [Foehrenbach 99, Alpert 96]. Un premier mode consiste à choisir une échelle de couleur pour l image fonctionnelle (e.g., TEMP ou TEP), et, de manière indépendante, une échelle de niveaux de gris pour l image anatomique (IRM). Un autre mode de superposition est de réaliser une combinaison linéaire ou géométrique des composantes Rouge/Vert/Bleu des données anatomiques et fonctionnelles pour générer l image fusionnée. Un troisième mode de superposition, consiste à utiliser un codage teinte/saturation/luminance. La teinte et la saturation sont dérivées de l image fonctionnelle et la luminance (en niveaux de gris) est déduite des intensités de l image anatomique. L utilisation de techniques de rendu volumique tridimensionnel de ces données fusionnées est hautement informative, car elle permet une vision synthétique de l organisation sulco-gyrale et des données fonctionnelles. Habituellement, l information fonctionnelle, codée en couleur sur la surface corticale, est intégrée sur une épaisseur de quelques voxels suivant la direction d observation. Stokking et al. [Stokking 97] ont proposé une technique où cette intégration se fait dans la direction de la normale à la surface du cerveau. Particulièrement adaptées pour la médecine nucléaire, ces techniques de visualisation peuvent également être utilisées pour fusionner sur l anatomie des cartes statistiques d activation (e.g. en TEP ou IRMf), ou encore les résultats de méthodes tomographiques de localisation de sources en MEG ou EEG. Ces différentes approches de visualisation multimodalités, sont illustrées par l exploration du réseau épileptogène de deux cas cliniques provenant des services de neurologie et de neurochirurgie du CHU de Rennes. La plupart des méthodes de recalage utilisées ici sont celles dont l évaluation fait précisément l objet de ce travail de thèse. Les figures 1.23 et 1.24 illustrent l intérêt du recalage et de la fusion TEMP/IRM dans le contexte de l épilepsie. Il s agit d un examen TEMP inter-ictal (Fig. 1.23) et d un examen TEMP ictal (Fig. 1.24) du même patient épileptique. Ces deux examens ont été préalablement recalés sur l IRM par maximisation de l information mutuelle, puis ré-échantillonnés dans le référentiel spatial de l IRM. Les données TEMP ont ensuite été fusionnées sur l IRM à l aide de textures couleur. Le mode de calcul de l image fusionnée correspond à un mode de rendu intégral (intégration des niveaux de gris et de la texture couleur sur quelques voxels depuis la surface). Ces images montrent distinctement une hyper-perfusion pendant la crise d épilepsie se projetant exactement le long d un sillon (cf. ellipse jaune sur la figure 1.24). Cette même région montrait une légère hypo-perfusion en période inter-critique (cf. Fig. 1.23). Cette information a été fondamentale pour guider l implantation d électrodes profondes SEEG et pour préparer l intervention chirurgicale. Nous présentons un deuxième cas clinique pour lequel une procédure complète a été réalisée, à savoir : caractérisation du réseau épileptogène, cartographie fonctionnelle préchirurgicale, et chirurgie assistée par l image (cf. I.1.3.5). Les figures 1.25, 1.26 et 1.27 illustrent l apport de techniques de recalage et de fusion pour apprécier la concordance de différentes anomalies morphologiques ou fonctionnelles détectées lors de la prise en charge chirurgicale de ce patient épileptique présentant une dysplasie corticale focale. Les recalages TEMP/IRM T1 et IRM FLAIR/IRM T1 ont été réalisés par maximisation de l information mutuelle. L information MEG a été localisée par une méthode dipôlaire développée et validée au laboratoire [Schwartz 99], basée sur une localisation des sources dans un sous-espace
64 Méthodes d analyse et de fusion de données : besoins pour l épilepsie Fig Fusion de données TEMP inter-ictale/irm Fig Fusion de données TEMP ictale/irm signal sélectionné par analyse en composantes principales d une fenêtre spatio-temporelle du signal. Cette méthode a été appliquée pour localiser les sources à l origine de pointes inter-critiques enregistrées sur le scalp en MEG. Le dipôle le plus représentatif de chaque pointe a été sélectionné, et un cluster d un cinquantaine de pointes ainsi traitées est représenté sur les figures 1.25 et Le recalage MEG/IRM est réalisé à l aide d un recalage basé surface entre la peau extraite des données IRM et la numérisation de la surface 3D de la tête du patient, réalisée par un localisateur magnétique au moment de l acquisition MEG. L algorithme de recalage utilise une transformée en distance de Chanfrein à partir de la surface de la peau en IRM et minimise la distance moyenne à cette surface des points numérisés en MEG par l algorithme de Powell [Schwartz 96, Schwartz 98]. La fusion de ces diverses informations sur l IRM du patient met en évidence des anomalies électrophysiologiques caractérisant la ZI ( cluster de pointes sur les figures 1.25 et 1.26), des anomalies de perfusion ictale caractérisant la ZE (hyperperfusion en TEMP ictale sur la figure 1.25) ainsi qu une ZL par la détection d une dysplasie corticale focale (hypersignal sur séquence FLAIR, figure 1.26). Cette caractérisation du réseau épileptogène à partir de techniques d exploration non invasives a été validée par l implantation d une électrode intra-cérébrale SEEG au niveau de la zone considérée (Fig. 1.27). Ces méthodes de fusion assistent ainsi la caractérisation précise des ZL, ZI et ZE. Mais de nombreuses questions restent ouvertes sur les choix de la limite d exérèse notamment lorsque les anomalies morphologiques et fonctionnelles ne se superposent pas complètement. Ainsi, dans l exemple présenté sur les figures 1.25, 1.26 et 1.27, l exérèse doit-elle être limitée à la dysplasie détectée en FLAIR, ou inclure le tissu environnant, où un comportement épileptogène a été détecté en TEMP et en MEG? Dans le cas des dysplasies, il est reconnu qu il faut faire plus confiance aux données électrophysiologiques qu à l IRM. Il s agit de questions délicates au sein de la communauté d épileptologie, et l utilisation de techniques de fusion de données permettra de les aborder de manière plus objective et plus systématique.
65 Fusion de données multimodales anatomo-fonctionnelles en épilepsie 65 Fig Fusion de données TEMP ictale/irm et cluster de pointes inter-ictales en MEG (carrés blancs) Aide à la détection et quantification d aires pathologiques ou fonctionnelles spécifiques au sujet exploré L objectif clinique des méthodes de fusion présentées dans ce paragraphe est d aider à la détection, la localisation et la quantification des différentes aires cérébrales impliquées dans le réseau épileptogène, ou caractérisant son environnement fonctionnel. Les méthodes décrites dans le paragraphe précédent permettent d aider le clinicien à se repérer au mieux par rapport à l anatomie du patient. A présent, nous allons montrer comment des méthodes de fusion permettent de caractériser de manière plus quantitative le réseau épileptogène et son environnement fonctionnel. L étude d un réseau épileptogène est une analyse avant tout intra-patient ayant pour but de comprendre au mieux l épilepsie du sujet en question, et de préparer au mieux l intervention chirurgicale Aider à une meilleure détection, localisation ou quantification des anomalies épileptogènes: Ce domaine intéresse plus particulièrement les examens de médecine nucléaire (TEP et TEMP), qui sont difficiles à analyser en raison d une faible résolution spatiale, en général de l ordre du centimètre. Dans la plupart des cas, les méthodes de fusion de données permettent de réaliser des études de quantification relative et non absolue. En effet, les données TEMP au 99m Tc-
66 Méthodes d analyse et de fusion de données : besoins pour l épilepsie Fig Fusion de données IRM FLAIR et cluster de pointes interictales en MEG (carrés rouges) Fig Positionnement d une électrode SEEG (L) sur l IRM HMPAO ou au 99m Tc-ECD ne donnent accès qu à une mesure relative de la perfusion cérébrale, alors qu une quantification absolue est envisageable en TEP. Les méthodes de fusion permettent d assister l analyse de données de médecine nucléaire en permettant un meilleur repérage sur l anatomie. Ces méthodes s appliquent de la même manière qu il s agisse de mesures absolues ou relatives. Les principales techniques d analyse de données TEMP ou TEP concernent la comparaison inter-hémisphérique, la comparaison entre différentes conditions d acquisition du même sujet, ou encore la comparaison inter-individuelle entre différents groupes de sujets. Pour l étude de l épilepsie d un patient précis, nous nous limiterons aux deux premiers points qui ne nécessitent généralement pas de déformation non linéaire de l anatomie de celui-ci. Un premier moyen d assister l analyse des données TEMP ou TEP est d utiliser l IRM recalée pour guider de manière automatique ou semi-automatique le positionnement de régions d intérêt (ROIs) ou de volumes d intérêt (VOIs) sur les données fonctionnelles [Harris 93, Iida 98]. La plupart des autres méthodes guidant le positionnement de VOIs ou permettant une analyse voxel/voxel sont dites méthodes d analyse par standardisation anatomique. Elles nécessitent de localiser les données dans un référentiel géométrique moyen et seront présentées dans le paragraphe I Parmi les techniques qui analysent les données à partir de l IRM originale du patient, citons la méthode proposée par Aubert-Broche et al. [AubertBroche 02] développée au laboratoire, qui permet de réaliser une comparaison inter-hémisphérique non supervisée en TEMP. Le principe est d identifier dans l IRM des couples de points symétriquement homologues (après correction linéaire ou non-linéaire des asymétries morphologiques), et d utiliser un voisinage autour de chacun de ces points pour créer une carte d indice d asymétrie en TEMP. Cette méthode a été développée pour mettre en évidence des fines hypoperfusions en TEMP inter-ictale, difficilement détectables visuellement. Elle est actuellement en cours d évaluation sur données simulées et cliniques.
67 Fusion de données multimodales anatomo-fonctionnelles en épilepsie 67 La principale méthode d analyse TEMP basée sur l IRM originale d un patient est la soustraction TEMP ictale / TEMP inter-ictale fusionnée sur l IRM : SISCOM - Subtracted Ictal Spect CO-registered to MRI [Zubal 95, O Brien 98, Pérault 02]. Après recalage des trois examens, la méthode consiste à considérer la TEMP inter-ictale comme un niveau de base ou de référence pour l analyse des données de TEMP ictale. L aspect délicat de ces méthodes est le choix d une méthode adéquate de normalisation des intensités avant la soustraction. Ce problème est abordé par Pérault et al. [Pérault 02], qui évaluent trois méthodes de normalisation. Le deuxième enjeu est d être capable de seuiller la carte de différence, et pour cela d estimer la significativité de celle-ci. Ce point est également délicat, dans la mesure où il est difficile d obtenir un test statistique suffisamment puissant à partir de seulement deux échantillons. O Brien et al. [O Brien 98] proposent d utiliser la variabilité des données TEMP mesurée au sein d une population de sujets sains afin d identifier quelles différences de signal sont réellement dues à une différence de perfusion ictale / inter-ictale Construction de nouvelles images dites de fusion: Alors qu au I.1.3.2, nous avons présenté comment superposer visuellement des informations TEMP ou TEP sur l IRM, certains auteurs ont proposé la construction à partir des images recalées de nouvelles données dites fusionnées. Il ne s agit plus de visualiser la superposition de deux volumes, mais réellement de synthétiser un nouveau volume. Ainsi, Migneco et al. [Migneco 00] proposent de combiner les propriétés de quantification absolue de la TEMP au 133 Xe avec la meilleure résolution spatiale des données TEMP au 99m Tc- HMPAO, afin de générer une image TEMP calibrée. Le principe est de recaler les deux jeux de données TEMP à partir de critères statistiques de similarité (voir I.2.2), et d utiliser l histogramme joint obtenu lorsque les données sont recalées pour estimer la relation entre les intensités en 133 Xe, représentant une quantification absolue, et celles en 99m Tc- HMPAO, représentant une quantification relative. Il est alors possible d estimer l allure de la saturation de la mesure de flux en 99m Tc-HMPAO pour les débits élevés [Patterson 97], et ainsi de calibrer à partir de cette relation les intensités observées en 99m Tc-HMPAO : il en résulte une image présentant des mesures de débit absolu avec une résolution spatiale centimétrique. Barra et al. [Barra 01, Colin 99] proposent une formalisation intéressante du concept de fusion de données basée sur la logique des possibilités. Ils appliquent cette approche pour créer des images fonctionnelles à haute résolution à partir d acquisitions IRM, TEMP et/ou TEP. L utilisation de la notion de possibilité et non de probabilité est particulièrement adaptée dans ce contexte où l on ne dispose généralement que de très peu d échantillons voire d un seul, sachant que l on s intéresse à un seul patient particulier. Contrairement aux probabilités, un événement A et son contraire Ā peuvent être totalement possibles. Dans ce cas, leurs distributions de possibilité π valent π(a) = π(ā) = 1. Les auteurs proposent d utiliser ces concepts pour tenir compte des incertitudes (bruit) et imprécisions (effet de volume partiel en raison d une résolution spatiale limitée) particulièrement importantes en imagerie fonctionnelle. Les données étant préalablement recalées, ils appliquent un algorithme de classification floue aux données issues de chaque modalité en 4 classes (substance grise, substance blanche, LCR et fond), puis définissent un opérateur de fusion issu de la théorie de l information entre classes de tissus, l opérateur M IM (Mutual Information Maps) :
68 Méthodes d analyse et de fusion de données : besoins pour l épilepsie le voxel v, la classe de tisssu k MIM(π A k (v),πf k (v)) = [min(πa k (v),πf k (v))]mi(av,fv) [max(π A k (v),πf k (v))]1 MI(av,fv) (1.1) où πk A(v) (respectivement πf k (v)) représente la densité de possibilité qu à le voxel v de l image anatomique A (respectivement fonctionnelle F) d appartenir à la classe de tissu k. Ces mesures de possibilité s apparentent à des coefficients flous d appartenance à une classe de tissu. Les opérateurs min et max sont des opérateurs de fusion standard en logique des possibilités (resp. fusion conjonctive et fusion disjonctive). Cependant, ils sont pondérés par MI, qui est à rapprocher de la mesure d information mutuelle qui sera introduite plus loin comme critère de similarité pour le recalage, elle est définie par : ( ) pa,f (a v,f v ) MI(a v,f v ) = ln (1.2) p A (a v )p F (f v ) où a v (resp. f v ) désigne l intensité de l image A (resp. F) au voxel v, et p A,F, p A et p F les probabilités jointe et marginales, estimées à partir de l histogramme joint des intensités des deux images 13. Grâce à cet opérateur de fusion, Barra et al. construisent de nouvelles classes de tissu normales ou pathologiques (e.g. matière grise hypoperfusée). Ils génèrent alors soit une classification des données suivant ces différentes classes (on associe chaque voxel à sa classe la plus possible), soit une image de synthèse ou de fusion (l intensité de chaque voxel est une moyenne des valeurs d activité caractéristiques de chaque classe, pondérée par le degré d appartenance à chaque classe). Ils appliquent cette méthode pour générer une image combinant des informations IRM, TEP et TEMP ictale et inter-ictale. Cependant, l évaluation clinique de la plus value de toute nouvelle image ainsi synthétisée (auxquelles les cliniciens ne sont pas habitués) est loin d être évidente, notamment du fait de l absence de gold standard. Il est finalement intéressant de noter que les deux méthodes de fusion présentées dans ce paragraphe utilisent l histogramme joint pour quantifier l information dite fusionnée. Or, de nombreuses mesures de similarité estimées à partir de l histogramme joint ont été proposées pour recaler les données. L influence des données de TEMP ictale sur ces critères de recalage fait justement l objet du chapitre II.6. L utilisation de ces mesures de similarité pour caractériser le contenu des images, une fois recalées, s avère un domaine d étude tout à fait novateur. Sarrut [Sarrut 00] aborde également cet aspect en proposant d utiliser divers critères de similarité statistique pour indexer par leur contenu de grandes bases de données d images, médicales notamment Comparaison d informations fonctionnelles: La notion de fusion au sens de comparaison objective de différents résultats d examens fonctionnels est envisageable pendant la phase de cartographie fonctionnelle préchirurgicale. L utilisation de techniques d exploration non invasives comme les études de neuroactivation en TEP ou IRMf ou de potentiels évoqués en MEG/EEG permettent de cartographier les aires fonctionnelles. La réalisation de telles cartographies permet d identifier précisément les aires qu il sera indispensable de préserver lors de l acte chirurgical 13. Notons que le critère d information mutuelle utilisé en recalage n est autre que l espérance mathématique de cette statistique, estimée sur tout l histogramme joint.
69 Fusion de données multimodales anatomo-fonctionnelles en épilepsie 69 (e.g., somesthésie, motricité, langage). Ces techniques présentent des limitations en terme de résolution spatiale et temporelle et posent des problèmes de localisation ou de détection délicats (e.g. analyse statistique voxel par voxel en IRMf ou TEP, localisation de sources en MEG/EEG). Le choix du paradigme d activation est également délicat, notamment lorsqu on cherche à cartographier les aires cérébrales impliquées dans des fonctions complexes comme le langage ou la mémoire. Dans ces conditions, le fait d observer des concordances entre des techniques d explorations fonctionnelles différentes, utilisant des protocoles d activation équivalents, est plutôt rassurant pour le chirurgien. Il faut cependant tenir compte de l origine physiologique différente des signaux observés, qui peut dans certains cas expliquer que la superposition des activations ne soit pas parfaite. Ainsi, en comparant des localisations MEG/IRMf liées à une activation motrice chez 13 volontaires sains, Sanders et al. [Sanders 96] estiment une distance moyenne entre localisations MEG et IRMf de l ordre du centimètre. Nous avons obtenu des résultats du même ordre de grandeur par comparaison qualitative par un neurochirurgien de localisations MEG / IRMf fusionnées sur l IRM 3D chez 12 patients candidats à une procédure neurochirurgicale ; il s agissait d activations motrices, somesthésiques (voir figure 1.28) et du langage [Grova 00]. Cette approche est à présent utilisée en clinique lors du planning préchirurgical, et permet la réalisation du geste chirurgical sans recours à des stimulations électriques peropératoires. Réaliser une comparaison quantitative de ces informations fonctionnelles demeure néanmoins un problème délicat. Notamment, les différentes résolutions spatiale et temporelle des modalités considérées (cf. figure 1.22) devraient être estimées à partir des données et prises en compte par toute métrique de comparaison. Ce problème n est pas trivial, vu que ces résolutions ne sont pas forcément constantes au sein d un même examen (e.g., anisotropie du voxel en IRMf, méthodes de localisation utilisées en MEG/EEG plus précises en surface qu en profondeur) Fusion coopérative et méthodes de reconstruction de sources en MEG/EEG: Le problème de la localisation de sources électromagnétiques d activité cérébrale à partir de signaux surfaciques acquis en MEG ou EEG est un problème mal posé au sens d Hadamard. En effet, si dans le plupart des cas il existe une solution à un tel problème inverse, elle n est jamais unique et peut ne pas être stable. Ainsi, afin d obtenir un localisation pertinente en MEG/EEG il convient d introduire des a priori dans la résolution du problème inverse. On dénotera alors par le terme de fusion coopérative l utilisation d une autre source d information, en général une autre modalité, pour assister ou contraindre un problème de localisation [Schwartz 98, Mattout 02]. La localisation de sources électromagnétiques nécessite tout d abord la formalisation et la résolution du problème direct, i.e., être capable de calculer les champs électriques et magnétiques générés sur le scalp à partir d une source connue. Le problème direct nécessite une modélisation de la source et du milieu conducteur. La source d activité est généralement modélisée par un dipôle de courant (voir I ). La modélisation réaliste du milieu conducteur, de son inhomogénéité et de son anisotropie, nécessitent d avoir recours à une segmentation et à une classification des différents tissus de la tête à partir de l IRM (voir par exemple [Mangin 95, Schattuck 01]). Alors qu en MEG, une modélisation de la tête par des sphères concentriques s avère suffisamment précise et permet une résolution analytique du problème direct, l utilisation de modèles réalistes du milieu est souhaitable en EEG,
70 Méthodes d analyse et de fusion de données : besoins pour l épilepsie Fig Résultats de localisations fonctionnelles en MEG (vert) et IRMf (rouge), fusionnées sur l IRM 3D d un sujet: exploration somesthésique par stimulation du pouce droit du fait des grandes différences de conduction électrique des différents tissus et notamment de l os. L IRM, pondérée en T1 notamment, ne permettant pas une segmentation précise des tissus osseux, on peut avoir recours au scanner X ou à des méthodes de classification des tissus dédiées. Ces modélisations dites réalistes fournissent un maillage (surfacique ou volumique) de l anatomie du sujet étudié à partir duquel des méthodes de résolution numérique du problème direct ont été proposées (e.g. méthode des intégrales de frontières ou des éléments finis). De nombreuses méthodes récentes posent le problème inverse comme un problème d identification de l intensité d un système de sources distribuées. L identification précise de l interface matière grise / matière blanche [Mangin 95], permet de contraindre la position des sources dipôlaires au ruban cortical, voire leur orientation de façon perpendiculaire à ce dernier. La résolution du problème inverse revient alors à estimer à chaque instant l activité de chacune de ces sources (de à sources). Même s il se linéarise [Dale 93], ce problème d estimation de l intensité de chaque source devient fortement sous-déterminé. Ces modèles de sources distribuées font appel à des techniques de reconstruction tomographique. La résolution nécessite également l introduction d a priori pour restreindre l espace
71 Fusion de données multimodales anatomo-fonctionnelles en épilepsie 71 des solutions et mieux conditionner le problème inverse. La figure 1.29 illustre l introduction de contraintes anatomiques (points de la matière grise) lors de la localisation d une pointe inter-critique dans le cadre d une méthode spatio-temporelle développée au laboratoire IDM [Schwartz 99]. La figure 1.29 montre la concordance entre les deux approches, à savoir la méthode estimant à chaque latence du signal un ou plusieurs dipôles de courant équivalents, et l approche avec contraintes de localisation dans la matière grise. Il s agit du même cas clinique déjà présenté dans les figures 1.25, 1.26 et La localisation des pointes inter-critiques enregistrées en MEG a pu être validée par SEEG. Ces méthodes permettent ainsi de fournir de véritables cartographies spatio-temporelles d activation que l on peut superposer sur l IRM anatomique, s avérant très informatives à la fois pour la cartographie fonctionnelle mais également pour l étude de pointes inter-critiques en épilepsie. Des développements récents ont montré qu il était important d incorporer des a priori fonctionnels dans la résolution du problème inverse, comme par exemple des régions activées en IRMf [Dale 00, Mattout 02]. L application à l épilepsie de ces approches, et l utilisation de différentes sources d imagerie anatomique ou fonctionnelle (e.g. TEMP, TEP, IRM FLAIR) nous paraît une approche prometteuse pour l étude du réseau épileptogène et notamment de sa dynamique spatio-temporelle. Fig Fusion sur l IRM de la localisation d une pointe inter-ictale, à une latence précise, par la méthode spatio-temporelle avec contraintes anatomiques (texture couleur) et d un cluster de pointes inter-ictales localisées avec la méthode non contrainte (carrés blancs)
72 Méthodes d analyse et de fusion de données : besoins pour l épilepsie Identification de patterns caractérisant des aires pathologiques ou fonctionnelles au sein d une population de sujets Ce paragraphe introduit des méthodes de fusion utilisées afin d extraire des connaissances d ordre plus général concernant un type d épilepsie. Un tel objectif clinique nécessite d avoir recours à des analyses inter-individuelles. De nombreuses méthodes d analyse statistique inter-individuelles sont utilisées de manière quasi-standard en neuroimagerie, notamment pour des études d activation en TEP ou en IRMf. Ces approches s avèrent également intéressantes en épilepsie pour aider à la rationalisation des connaissances. Il s agit plutôt dans ce cas de comprendre tel ou tel aspect générique et reproductible de la maladie. De telles études sont pour l instant limitées aux domaines où les connaissances sur la maladie peuvent être traitées ainsi. Jusqu à présent seule l épilepsie du lobe temporal, la plus connue et reproductible, a été analysée à l aide d outils de comparaisons inter-individuelles [VanBogaert 00, Lee 00a, Kang 01]. Afin de comparer entre eux différents individus, les méthodes d analyse de données fonctionnelles présentées ici nécessitent un recalage et rééchantillonnage préalable des données vers un référentiel géométrique moyen. Ces approchent utilisent donc en amont des procédures de recalage, linéaires ou non linéaires. Un tel référentiel peut provenir soit d un atlas éventuellement numérique [Talairach 88, Seitz 90, Roland 94, Mazziotta 95, Evans 93], soit d un examen type, appelé template, résultat du moyennage d un grand nombre d examens de la même modalité et préalablement recalés (généralement de manière non linéaire). Notons que le logiciel Statistical Parametric Mapping 99 (SPM99) 14, largement utilisé en neuroimagerie, met à disposition de tels templates réalisés à partir de sujets sains, correspondants aux modalités d imagerie les plus courantes (e.g. IRM T1, T2, densité de proton, TEP, TEMP). Ces approches, dites d analyse par standardisation anatomique, permettent des comparaisons inter-groupes d individus, mais également l analyse d un sujet particulier par rapport à une population de référence. Elles permettent en outre de faciliter et d uniformiser les résultats d expériences de neuroactivation (en IRMf ou en TEP). Dans la mesure où les transformations, mêmes non linéaires, utilisées lors de cette standardisation anatomique sont inversibles, les résultats des diverses analyses statistiques peuvent à nouveau être fusionnés sur l IRM anatomique d origine du patient étudié, afin de préparer au mieux l intervention chirurgicale Analyse par standardisation anatomique: Nous reviendrons au II.4.2 sur une description plus détaillée des différentes techniques d analyse par standardisation anatomique principalement utilisées en TEP ou en TEMP. Suivant les études référencées, l étape de recalage vers le référentiel anatomique moyen est soit manuelle et interactive, soit semi-automatique, soit entièrement automatique. Le type de transformation géométrique utilisé est au minimum affine, plus généralement non linéaire, résultant d une décomposition sur des fonctions de déformation définies globalement ou localement (e.g. fonctions polynomiales, fonctions de base radiale), ou encore représentée par un champ dense de déformation. Les principales méthodes employées pour assister l analyse quantitative en TEP ou en 14. Logiciel SPM99 développé au Functional Imaging Laboratory à Londres (
73 Fusion de données multimodales anatomo-fonctionnelles en épilepsie 73 TEMP utilisent des ROIs positionnées de manière semi-automatique, grâce au recalage vers un atlas [Migneco 94, Tanaka 00]. L analyse par standardisation anatomique peut également être réalisée au moyen de VOIs représentant diverses structures anatomiques, positionnés automatiquement sur les données standardisées spatialement [Lobaugh 00, Liow 00, Lee 00b, VanLaere 01b, VanLaere 01a, VanLaere 02, Kang 01]. De par la définition de ces VOIs, ces méthodes imposent un a priori sur la distribution anatomique du phénomène que l on cherche à étudier. La troisième technique, largement utilisée, consiste en une analyse voxel/voxel des données normalisées spatialement [Minoshima 94b, Houston 94, Ito 96, Koyama 97, Liow 00, VanLaere 01b, VanLaere 01a, VanLaere 02] Cartographies statistiques d activation: L analyse voxel/voxel après standardisation anatomique est particulièrement adaptée à des analyses statistiques traitant de manière indépendante chaque voxel. Il est alors possible de générer une carte statistique d activation représentant en chaque voxel la valeur de significativité du test d hypothèse utilisé (ou p-value ), c est à dire une Statistical Parametric Map (SPM). De nombreux tests statistiques sont réalisables allant d un simple test de Student de comparaison de moyennes de deux populations, à des analyses de la variance permettant l analyse de différents facteurs (e.g. sexe, âge). La plupart de ces méthodes d analyse peuvent être formalisées à l aide du modèle linéaire généralisé (MLG) proposé par Friston et al. [Friston 95b]. Un seuillage de cette carte d activation permettrait alors d apporter une décision au test d hypothèse correspondant : e.g. il y a une activation IRMf, i.e. le signal est fortement corrélé avec le paradigme d activation, il y a une différence significative des moyennes du signal entre deux populations, etc... Cependant, le même test est appliqué de manière indépendante en chaque voxel appartenant à un masque du cerveau. On est donc confronté à un problème de comparaisons multiples, vu qu il s agit de réaliser des milliers de tests dont les statistiques sont spatialement corrélées. La principale méthode de correction utilisée pour tenir compte des corrélations spatiales est issue de la théorie des champs aléatoires gaussiens [Poline 97]. Après seuillage de la carte de p-values préalablement gaussiennisées, la méthode de correction utilise l espérance mathématique de la caractéristique d Euler, correspondant à la différence entre le nombre de composantes connexes et le nombre de trous après seuillage, ainsi qu une estimation de la résolution spatiale des données. Il est alors possible de tester à la fois les statistiques issues du modèle linéaire généralisé et l extension spatiale des régions activées. Cette approche a été appliquée avec succès dans de nombreuses études de neuroactivation en TEP et en IRMf. L analyse étant généralement de type intra-sujet (notamment en IRMf), la standardisation anatomique vers un référentiel moyen ou un atlas a surtout pour fonction de permettre la comparaison de résultats au sein de la communauté des neurosciences 15. Néanmoins, une étape préalable de correction du bougé entre les différents examens est fondamentale. En effet, une erreur minime liée au bougé entre les acquisitions peut avoir des conséquences désastreuses sur l analyse statistique du signal [Worsley 95]. Le modèle linéaire généralisé est largement utilisé en neurosciences et de plus en plus en clinique. Il constitue une méthode de référence vu sa grande souplesse d utilisation et d accès via la distribution gratuite du logiciel SPM99. En neuroactivation, le paradigme d acti- 15. Dans de nombreuses études utilisant SPM, les zones activées sont repérées par leurs coordonnées dans le quadrillage proportionnel de Talairach.
74 Méthodes d analyse et de fusion de données : besoins pour l épilepsie vation (e.g. stimulation par blocs ou monoévènementielle) est le principal régresseur du MLG. En IRMf, il est possible de le convoluer par un modèle de la réponse impulsionnelle hémodynamique. En TEP, le modèle prend en compte la question de la normalisation en intensité globale (DSC global), nécessaire à la comparaison de différents examens: cet effet moyen peut être modélisé de manière additive (classiquement en analyse de la variance), ou de manière multiplicative (normalisation dite proportional scaling ). Dans les modèles d analyse de la variance ou de la covariance au sein de populations de sujets ou de patients, il est possible de modéliser l effet de facteurs comme le sexe, l âge, les résultats d un test neuropsychologique, etc... Néanmoins, le choix du modèle est loin d être évident. Si on n utilise pas assez de régresseurs, on aura du mal à expliquer le signal. A l inverse, si on contraint trop le modèle en utilisant de nombreux régresseurs, on perdra en puissance statistique des tests. Notons qu il existe d autres approches non paramétriques qui tentent d expliquer le signal essentiellement à partir des données (voir par exemple [Benali 01] en IRMf, ou [Houston 94] en TEMP). Le MLG a été aussi utilisé dans le contexte de l épilepsie. Vu qu il s agit d identifier les caractéristiques reproductibles de la maladie au sein d une population, ces études sont restreintes à l étude de l épilepsie temporale. Ces études, utilisant des données TEP ou TEMP, consistent généralement en des comparaisons de groupes (e.g. sujets sains vs sujets épileptiques, données ictales vs données inter-ictales) [VanBogaert 00, Ring 99, Muzik 00, Lee 00a], en la comparaison d un seul sujet par rapport à une population de référence [Signorini 99, VanBogaert 00, Lee 00a], ou encore en l analyse des asymétries inter-hémisphériques d un sujet épileptique par rapport aux asymétries d une population de sujets sains [VanBogaert 00]. Acton et al. [Acton 98] montrent que les approches mises en œuvre dans le logiciel SPM99, initialement développées pour l analyse des données TEP ou IRMf, sont applicables en TEMP. Néanmoins, ils précisent que les tests statistiques sont souvent trop conservateurs, du fait de la résolution spatiale moindre des données TEMP, et surtout du fait du nombre souvent limité des examens disponibles. Ces approches ont récemment été utilisées pour étudier la distribution du DSCr en TEMP au sein d une population de sujets sains [VanLaere 01b, VanLaere 02]. Après classification des tissus (substance grise, substance blanche et LCR) à partir de données IRM standardisées anatomiquement, il est aussi possible d utiliser le MLG pour analyser voxel/voxel la concentration de matière grise au sein de deux populations de sujets: voxel based morphometry [Ashburner 00]. Cette approche a été appliquée avec succès pour détecter de manière objective des anomalies morphologiques de l hippocampe associées à l épilepsie temporale [Keller 02] Aide à la réalisation d un acte chirurgical Une fois les différents jeux de données analysés, le clinicien dispose d un certain nombre d informations caractérisant le réseau épileptogène et son environnement fonctionnel, spécifiques du patient étudié. Ces informations peuvent être segmentées et localisées sur l IRM morphologique du patient. La figure 1.30 présente un exemple de scène 3D générée à partir de l analyse des données anatomo-fonctionnelles du patient présenté au I On y retrouve des zones identifiées comme cible, caractéristiques du réseau épileptogène, des zones constituant des repères anatomiques, comme les principaux sillons corticaux segmentés à partir de l IRM [LeGoualher 99], et des zones fonctionnelles à éviter. Différents systèmes de localisation 3D permettent de mettre en correspondance le patient au bloc opératoire et ses
75 Fusion de données multimodales anatomo-fonctionnelles en épilepsie 75 données préopératoires. Cette mise en correspondance permet au chirurgien de bénéficier, pendant la réalisation de son geste, des différentes entités identifiées pendant le planning préchirurgical. En effet, il peut par exemple utiliser un pointeur 3D pour identifier un point sur le patient et voir son correspondant apparaître sur la scene 3D du planning, visualisée sur une station de travail dans le bloc opératoire. Un autre mode de visualisation du résultat du planning est de superposer dans les oculaires du microscope présentant la vue réelle peropératoire, les contours des entités identifiées comme nécessaires sur les données préopératoires (voir figure 1.31). Nous désignons cette approche sous le terme de neuronavigation multimodalité [Jannin 00]. Elle est particulièrement intéressante pour la chirurgie de l épilepsie où, dans de nombreux cas, il n y a pas de lésion anatomique détectable visuellement. Elle permet de bénéficier pendant la réalisation du geste des principaux résultats d examens multimodalité caractérisant le réseau épileptogène et son environnement fonctionnel [Murphy 01]. En amont de la chirurgie, la mise en correspondance d une IRM anatomique 3D et d angiographies RX permet d assister l implantation d électrodes SEEG en conditions stéréotaxiques, la rendant plus précise et limitant les risques de lésions des vaisseaux [Scarabin 99]. Il nous paraît évident que d autres informations multimodales déjà utilisées lors du geste chirurgical pourraient également être utilisées lors de l implantation d électrodes SEEG. (a) (b) Fig Scènes 3D volumique (a) et surfacique (b) représentant le foyer épileptogène (en rouge, VOI représentant une hypoperfusion en IRM de perfusion) et son environnement anatomique (principaux sillons segmentés automatiquement) obtenue lors du planning préchirurgical d un patient épileptique
76 Méthodes d analyse et de fusion de données : besoins pour l épilepsie Fig Neuronavigation multimodalité en chirurgie de l épilepsie: superposition dans les oculaires du microscope des informations selectionnées lors du planning pré-chirurgical (cf. figure 1.30)
77 Méthodes de recalage par mesures statistiques de similarité 77 Chapitre 2 Méthodes de recalage par mesures statistiques de similarité Notre objectif étant la validation de méthodes de recalage TEMP/IRM dans le contexte de l épilepsie, ce chapitre est dédié à l exposé d une revue générale des méthodes de recalage utilisées en imagerie médicale. Après avoir introduit les principaux contextes de fusion dans lesquels se posent des problèmes de mise en correspondance, la première partie de ce chapitre présente un état de l art des méthodes de recalage, principalement inspiré de celui que nous avons proposé dans [Jannin 01a, Jannin 01b]. Nous définissons ainsi un problème de recalage par la spécification des quatre points suivants: l espace de recherche des transformations géométriques entre les données, la nature de l information considérée comme homologue entre les données, le critère ou la fonction de coût évaluant la qualité de la mise en correspondance de ces structures homologues et finalement la stratégie d optimisation de ce critère. La seconde partie est dédiée à une revue beaucoup plus détaillée des méthodes de recalage fondées sur l optimisation d un critère statistique de similarité qui font l objet de ce travail d évaluation de méthodes de recalage. Les aspects théoriques de ces mesures statistiques de similarité, introduits ici, seront réutilisés lors de l interprétation des résultats de l évaluation de telles méthodes appliquées au recalage TEMP/IRM (voir chapitre II.6). 2.1 Revue générale des méthodes de recalage Cette revue issue de [Jannin 01a, Jannin 01b] ne se veut pas exhaustive vis à vis des aspects purement méthodologiques. Nous cherchons plutôt à insister sur la manière dont se met en place une méthode de mise en correspondance de données vis à vis du problème clinique posé. Ainsi nous rappelons tout d abord les différents contextes de fusion de données dans lesquels se posent des problèmes de recalage. Nous avons vu au chapitre précédent que les quatre contextes présentés ici sont rencontrés lors de la prise en charge chirurgicale d un patient épileptique. Pour une revue plus complète des différentes méthodes de recalage utilisées en imagerie médicale, nous renvoyons le lecteur vers quelques articles de revue fondamentaux [Brown 92, Maurer 93, VanDenElsen 93, Maintz 98, Hawkes 98, Duncan 00, Hill 01]. Notons néanmoins que l état de l art proposé par Hill et al. [Hill 01], étant le plus récent,
78 Revue générale des méthodes de recalage est le plus complet en ce qui concerne les méthodes basées mesures statistiques de similarité. En effet, nous assistons à une utilisation accrue de telles méthodes au sein de la communauté depuis environ 5 ans, date à laquelle ont été publiés les premiers articles proposant pour le recalage un critère issu de la théorie de l information : l information mutuelle [WellsIII 96, Maes 97]. L article de Duncan et al. [Duncan 00] n est pas dédié au seul problème du recalage, mais propose une présentation chronologique et parallèle de plusieurs thématiques de l imagerie médicale (e.g. segmentation, recalage, analyse du mouvement) permettant de mettre l accent sur les principales tendances du domaine Contextes de mise en œuvre de procédures de recalage Nous présentons quatre contextes de fusion qu il est fondamental d identifier lors de la mise en place d une procédure de recalage. En effet, ils permettent de choisir au mieux le type de transformation géométrique ou en intensité recherchée, ou encore d identifier la nature de l information homologue entre les données à recaler Contexte de fusion 1: recalage intra-sujet et intra-modalité Ce contexte concerne la fusion entre différents jeux de données provenant d une même modalité pour un sujet. Trois principaux objectifs cliniques sont associés à ce contexte de fusion : (1) suivi dans le temps de modifications dans l anatomie du patient, (2) comparaison de différents états et (3) imagerie par soustraction. (1) Le suivi dans le temps de modifications dans l anatomie du patient permet, par exemple, de suivre la croissance ou d étudier l évolution d une zone lésionnelle ou les effets d un traitement thérapeutique. En chirurgie ou en radiothérapie, ce contexte de fusion permet de comparer des images préet post-opératoires ou pré- et post-traitement. (2) Ce contexte de fusion peut aussi être utilisé pour permettre la comparaison de différents états du sujet. La comparaison d un examen de TEMP ictale en utilisant l examen inter-ictal comme niveau de référence aide à la localisation de la zone épileptogène [Duncan 97b]. En IRM fonctionnelle, les mesures d activations fonctionnelles peuvent être réalisées par la comparaison statistique d images acquises respectivement dans des états successifs d activité et de repos [Friston 95b]. Le recalage intra-sujet et intra-modalité peut aussi être utilisé pour corriger les éventuels mouvements du sujet pendant une acquisition, notamment dans le cas de séries temporelles en IRM fonctionnelle où un léger déplacement pendant l acquisition peut influer de manière importante sur l analyse statistique [Worsley 95]. (3) L imagerie par soustraction est généralement basée sur le calcul d une différence entre deux jeux de données image correspondant à deux acquisitions différentes réalisées par exemple avec et sans traceur ou agent de contraste. En imagerie vasculaire, ce processus de soustraction permet une meilleure visualisation de l arbre vasculaire. Un autre exemple d imagerie par soustraction est la différence TEMP ictale / TEMP inter-ictale recalées et fusionnées sur l IRM : SIS- COM - Subtracted Ictal Spect CO-registered to MRI [Zubal 95, O Brien 98, Pérault 02]. Pour ces différentes applications la transformation géométrique reliant les données à recaler peut, la plupart du temps, être considérée comme rigide, i.e., uniquement composée de rotations et de translations.
79 Méthodes de recalage par mesures statistiques de similarité Contexte de fusion 2: recalage intra-sujet et inter-modalité Cette deuxième catégorie de contextes de fusion permet de profiter de la nature complémentaire des différentes modalités d imagerie. La mise en correspondance entre données CT et IRM facilite la localisation anatomique conjointe des structures osseuses et des tissus mous. La mise en correspondance de données d IRM fonctionnelle, de MEG, de TEP ou de TEMP avec une IRM anatomique permet une corrélation anatomo-fonctionnelle, particulièrement utile lors d études préchirurgicales. Dans le contexte de la chirurgie de l épilepsie, nous avons montré au chapitre I.1 comment l analyse d informations multimodales anatomiques et fonctionnelles permettait une meilleure caractérisation du réseau épileptogène (voir par exemple [Stefan 92]). Pendant la réalisation d une procédure neurochirurgicale, les tissus mous, et notamment les structures corticales, sont sujets à des déformations (effondrement ou dilatation du cortex, cortectomie, etc.). Ainsi, les images pré-opératoires qui peuvent avoir servi à la préparation du geste chirurgical ne correspondent plus à la réalité anatomique courante du patient. Une façon de corriger ces modifications est d acquérir des images en salle d opération (appelées images per-opératoires, comme l échographie, l IRM ou le scanner X interventionnels, par exemple) qui fournissent une information permettant, une fois recalées avec les images pré-opératoires, de calculer les déformations à appliquer à ces dernières [Maurer 98, Comeau 98]. Le choix du type de transformation géométrique (rigide ou élastique) est ainsi complètement dépendant de l application clinique. La nature de l information homologue entre les données peut, quant à elle, ne pas être évidente surtout lorsqu une modalité représente l anatomie et l autre une fonction cérébrale (e.g. perfusion en TEMP) Contexte de fusion 3: recalage sujet réel et modalités Ce contexte de fusion concerne la mise en correspondance entre le sujet réel, les outils thérapeutiques (outils chirurgicaux, systèmes robotiques, systèmes d imagerie interventionnelle, etc.) et des images ou mesures pré- ou per-opératoires. Grâce à des localisateurs 3D (mécaniques [Olivier 94], magnétiques [Doyle 95], optiques [Tebo 96] ou à ultrasons), il est possible de connaître la position tridimensionnelle du sujet dans un repère défini dans le monde réel. Connaissant cette position (en salle d opération, dans la salle de radiothérapie ou par rapport à un imageur), il est possible de calculer la transformation géométrique entre le repère lié au sujet et un repère lié aux images. Les localisateurs 3D permettent aussi de suivre des outils chirurgicaux, repérables, par exemple, à l aide de diodes électroluminescentes pour les localisateurs à infra-rouge, et donc de localiser l extrémité des outils, ainsi que leur orientation par rapport aux images. De tels systèmes, appelés systèmes de neuronavigation, font partie des systèmes les plus utilisés en chirurgie guidée par l image. Ils remplacent progressivement les approches utilisant des cadres de stéréotaxie comme porte-instrument et auxquels sont attachés des marqueurs permettant le recalage cadre/image. Ces cadres sont fixés sur la tête du patient et optimisent la définition et la réalisation de trajectoires chirurgicales rectilignes pour des biopsies [Jannin 94] ou pour l implantation d électrodes profondes en SEEG [Scarabin 99]. En ce qui concerne les systèmes robotisés, ce contexte de fusion correspond à l interaction entre robots, images et patient. Les applications, utilisant des systèmes robotiques ou de neuronavigation, sont fréquemment utilisées en neurochirurgie ou en radiologie interventionnelle. Les systèmes de thérapie guidée par l image, notamment les systèmes de neuronavigation, sont aujour-
80 Revue générale des méthodes de recalage d hui parmi les applications de fusion de données les plus utilisées en routine clinique. Leur utilisation clinique croissante a notamment permis de souligner la plus value apportée par la fusion de données Contexte 4: recalage inter-sujet et intra- ou inter-modalité Ce contexte intéresse la fusion entre des données mono- ou multimodalité concernant des sujets différents. Les applications principales de cette catégorie de contextes de fusion sont liées à l étude de la variabilité anatomique ou fonctionnelle au sein d une population de sujets (sujets sains ou patients). Ce type de recalage permet de construire des modèles moyens correspondant à chaque modalité d imagerie ou template [Evans 93], de comparer les données d un sujet à un atlas ou à un template, de comparer des données concernant des sujets différents appartenant à une même population ou, enfin, de comparer deux populations de sujets. Ce type de fusion nécessite préalablement une étape de normalisation spatiale vers un atlas ou template [Friston 95a]. Ces approches sont appelées analyses par standardisation anatomique. Le recalage, vers un référentiel commun, de données provenant de sujets différents, mais d une même modalité et utilisant un même protocole d acquisition, autorise une analyse statistique inter-individuelle des données. Une telle démarche peut être utilisée pour des études statistiques sur la fonction ou la morphologie de données normales ou pathologiques. Un des principaux domaines d application de ces méthodes est l étude de la cartographie fonctionnelle cérébrale (Human Brain Mapping project [Mazziotta 95], Statistical Parametric Mapping, etc.) Classification des méthodes de recalage Le recalage consiste à calculer une transformation entre deux jeux de données pour compenser des variations spatiales ou d intensité dues, par exemple, à l utilisation de systèmes d acquisition différents ou à des différences de conditions ou de géométrie d acquisition. Par la suite, et dans cet article, nous nous focaliserons sur les méthodes de recalage qui cherchent à compenser les variations spatiales. L objectif d une méthode de recalage est précisément de compenser ce qui peut être variable entre les données à recaler, du fait par exemple de conditions d acquisition différentes, tout en préservant l information qui est complémentaire, que l on cherche généralement à mettre en évidence par une approche de type fusion de données. En reprenant le formalisme introduit par L. Brown [Brown 92], nous définissons une méthode de recalage par la définition d un espace de recherche, d un espace des paramètres, d une métrique de similarité et d une stratégie de recherche. L espace de recherche est défini par la classe de transformations qui modélise les variations entre les données. L espace des paramètres est défini par les informations homologues entre les données à recaler. La métrique de similarité, ou fonction de coût, fournit une mesure sur la qualité de la mise en correspondance d un ensemble de structures homologues, pour une transformation donnée. La stratégie de recherche correspond notamment au choix d une méthode d optimisation, utilisée pour calculer la meilleure mise en correspondance au sens de la métrique de similarité. En d autres termes, le recalage entre deux jeux de données consiste en l optimisation d un critère de similarité mesuré sur les informations homologues extraites des données. La transformation ainsi estimée peut alors être appliquée aux jeux de données dans leur tota-
81 Méthodes de recalage par mesures statistiques de similarité 81 lité. Ainsi, à chaque point du premier jeu de données est associé un point correspondant dans l autre jeu de données. Dans la plupart des classifications des méthodes de recalage [Maurer 93, Maintz 98, Hawkes 98], la distinction n est pas toujours faite entre information homologue et fonctions de coût. Dans notre formalisme, l information homologue est une caractéristique intrinsèque aux données, contrairement à la fonction de coût, qui est plutôt homogène à une mesure de distance entre structures homologues Définition des repères géométriques utilisés Dans le processus de recalage, la définition précise des différents repères géométriques servant de support aux transformations est une première étape indispensable. Traditionnellement, trois repères géométriques sont définis: un repère lié aux données, un repère lié au sujet et un repère appelé mondial. Le repère lié aux données est basé sur la grille de pixels ou de voxels. Le repère lié au sujet est généralement centré par rapport aux données et utilise une métrique millimétrique standard, calculée à partir de la taille du pixel ou du voxel fournie par le système d acquisition d images. Enfin, le repère mondial est la combinaison du repère sujet et d informations liées à la position et à l orientation du sujet pendant l acquisition. Ces informations sont généralement fournies par les systèmes d acquisition, elles sont stockées avec les images et permettent d initialiser la procédure de recalage. D autres repères peuvent être définis en fonction des contextes applicatifs (repère lié à un cadre de stéréotaxie, repère anatomique de Talairach [Talairach 88] etc.). Ainsi, nous définissons ici le repère mondial, comme le repère des acquisitions sagittales. Ainsi, pour les différents résultats présentés dans le chapitre II.6 portant sur l évaluation de méthodes de recalage, l axe x désignera l axe avant vers arrière, l axe y l axe haut vers bas et l axe z l axe gauche vers droite Espace de recherche: type de transformation géométrique Les types de transformations géométriques permettent de modéliser les variations géométriques qu on cherche à compenser entre les données à recaler. Ces transformations peuvent être caractérisées par leur nature (rigide, affine ou non linéaire) et par leur domaine d application (local ou global). Transformations géométriques linéaires : Une transformation T est dite linéaire si et seulement si pour tous points de l espace x 1 et x 2 elle vérifie : (λ 1,λ 2 ) R 2 T(λ 1 x 1 + λ 2 x 2 ) = λ 1 T(x 1 ) + λ 2 T(x 2 ) (2.1) Les transformations linéaires sont utilisées quand des connaissances a priori sur les données sont disponibles, justifiant les hypothèses de linéarité des variations spatiales (conditions d acquisition, propriétés de rigidité des objets, etc.). L utilisation de ce type de transformations permet de simplifier le problème du recalage, en limitant considérablement la dimension de l espace de recherche des transformations géométriques. Une transformation T est dite affine si et seulement si T(x) T(0) est linéaire (0 étant par exemple l origine du repère géométrique). L expression d une transformation affine entre deux espaces de dimension N est : T(x) = Ax + b où x et b sont deux vecteurs
82 Revue générale des méthodes de recalage colonnes de dimension N et A une matrice N N. Les transformations affines permettent de modéliser une grande partie des distorsions spatiales usuelles, car elles représentent la combinaison de N translations (vecteur b), N rotations, N facteurs d échelle et N facteurs de torsion (ou de cisaillements). Dans le cas du recalage de données tridimensionnelles ou volumes, les transformations affines s expriment à l aide de 12 degrés de liberté. Dans certains contextes applicatifs particuliers, il est possible de poser des hypothèses fortes sur les données à recaler. Par exemple, les entités anatomiques contenues dans les images peuvent être considérées comme rigides; la valeur de l échantillonnage spatial des données peut être connue (ou facilement calculée), des distorsions lors de l acquisition des images peuvent avoir été corrigées lors d un processus de calibrage. Sous de telles hypothèses, une nouvelle catégorie de transformations est communément utilisée : les transformations rigides. Une transformation rigide est un sous-ensemble des transformations affines, elle est composée de translations, de rotations et d un facteur d échelle le plus souvent isotropique. Dans le cas du recalage de volumes, les transformations rigides s expriment à l aide de 7 paramètres. Souvent, le facteur d échelle peut être déduit de l échantillonnage spatial des données (taille du pixel ou du voxel), réduisant ainsi à 6 le nombre de paramètres à estimer. Une transformation linéaire globale est uniformément appliquée à l ensemble du volume, alors qu une transformation linéaire locale est définie sur un sousensemble du volume. Par exemple, la transformation associée au quadrillage proportionnel de Talairach correspond à une transformation affine par morceaux constituée de 12 transformations affines locales différentes, chacune associée à l un des 12 sous-volumes délimités anatomiquement. Cette transformation est utilisée pour recaler des images de sujets vers l atlas anatomique de Talairach et Tournoux [Talairach 88]. Transformations géométriques non linéaires : Les transformations non linéaires modélisent des variations spatiales complexes. Parmi celles-ci, les transformations projectives sont un cas particulier utilisé quand les données sont projetées via un système idéal d acquisition d images et où une dimension, ou plus, est perdue lors de cette transformation. Ce type de transformation est principalement rencontré dans des problèmes de recalage 3D/2D. Les transformations non linéaires sont généralement appelées transformations élastiques ou déformations. Ces transformations peuvent être modélisées soit par une simple fonction non linéaire (fonction paramétrique) définie sur l ensemble du volume (dans le cas de transformations 3D), soit par des déformations locales non linéaires. Ces dernières sont mieux adaptées à des variations complexes et peuvent être estimées à l aide de champs denses de déformation où un vecteur de déplacement local est associé à chaque nœud d une grille définie sur les données. Ces transformations sont généralement définies à l aide d un terme lié aux données (correspondant à la mesure d une fonctionnelle de coût entre les nœuds) et d un second terme énergétique qui permet de s assurer du degré de régularité spatiale de la transformation. Des méthodes d interpolation sont ensuite utilisées pour calculer le champ de déformation sur la totalité du volume et/ou localement en chaque nœud de la grille, permettant d assurer la régularisation du champ. Nous renvoyons le lecteur vers [Cachier 03], pour une classification des différents modèles de déformations et des termes d attache aux données correspondant. Dans le cas d informations homologues de type point, la régularisation est effectuée par des techniques d interpolation basées sur des fonctions de base radiale [Bookstein 89]. Dans le cas d informations homologues de type surfaces, la régularisation
83 Méthodes de recalage par mesures statistiques de similarité 83 est obtenue par l utilisation de modèles élastiques mécaniques [Sandor 97], de déformations de type super-quadriques [Thompson 96] ou splines [Szeliski 96]. Dans le cas d informations homologues basées sur des mesures statistiques de similarité locale, les schémas de régularisation peuvent être fondés sur des propriétés mécaniques [Bajcsy 89, Gee 93] (comme l élasticité, la plasticité ou la viscosité) ou de type fluide [Miller 93, Christensen 95]. Citons également les déformations multi-échelle [Collins 94] ou celles utilisant le concept de diffusion [Thirion 98] par opposition au concept d attraction. Les transformations nonlinéaires peuvent aussi modéliser les variations d intensité entre les données à recaler, e.g., [Guimond 01] proposent de résoudre un problème de recalage non linéaire multimodal en combinant l estimation d une transformation en intensité entre les deux modalités et une méthode de recalage non linéaire monomodal sur les données ainsi transformées en intensité. Les transformations non linéaires sont principalement utilisées dans deux types de situations: (1) quand les jeux de données à recaler ne correspondent pas à la même instance du substrat anatomique (dans le cas, par exemple, de recalage inter-sujet, ou de recalage vers un atlas ou vers un modèle) et (2) quand un substrat anatomique commun existe entre les données mais qu il est distordu par une déformation non-rigide : correction de déformations liées à l acquisition ou à des structures ayant des états différents (dû, par exemple, à la croissance de la structure anatomique ou pathologique, à la comparaison d une structure saine avec une structure pathologique, ou la comparaison de données pré-opératoires avec des données post-opératoires ou per-opératoires) Espace des paramètres: type d information homologue L information homologue correspond à une information extraite des données à recaler et sur laquelle est basée la recherche de la transformation géométrique optimale au sens de l optimisation d une fonctionnelle de coût. L information homologue peut être classifiée par sa dimension : 0 D (point), 1 D (contour), 2 D (surface), 3 D (volume) ou n D (hypersurface) et par la dimension de son espace d évolution : 2 D (image, surface ou projection), 3 D (volume, hypersurface) ou n D (hypersurface) avec ou sans une dimension temporelle supplémentaire [Barillot 99a]. L information homologue est aussi fréquemment classifiée par son type, notamment extrinsèque versus intrinsèque. Les méthodes de recalage basées sur une information homologue extrinsèque utilisent des objets artificiels liés au sujet et conçus pour être facilement identifiables dans les images. Par conséquent, ces méthodes nécessitent un protocole particulier d acquisition d images. Parmi ces méthodes, les techniques invasives utilisent, notamment, des marqueurs osseux vissés directement dans les structures osseuses du patient ou des cadres de stéréotaxie. Les techniques noninvasives utilisent, par exemple, des marqueurs adhésifs collés sur la peau du patient. Les méthodes utilisant de l information de nature intrinsèque utilisent différentes caractéristiques anatomiques, géométriques ou des caractéristiques liées à l intensité des voxels de l image entière. Les caractéristiques anatomiques peuvent être des points anatomiques connus (par exemple, commissure antérieure et commissure postérieure dans le cas d images cérébrales [Talairach 88]), des lignes ou des surfaces anatomiques remarquables (surface de la peau, surface des ventricules, sillons corticaux [Collins 98a], etc.) ou enfin des volumes anatomiques (cerveau, structures osseuses, vaisseaux, etc.). Les points anatomiques sont généralement choisis manuellement alors que les lignes, surfaces ou volumes nécessitent une procédure de segmentation initiale. Les caractéristiques géométriques ou primitives
84 Revue générale des méthodes de recalage géométriques consistent en des points, lignes, surfaces ou volumes qui ne correspondent pas directement à des structures anatomiques mais à des caractéristiques calculées à partir des images (gradients, extremum local de courbures [VanDenElsen 95], lignes de crêtes [Subsol 94], etc.). Parce qu elles sont directement liées à une connaissance anatomique a priori, les informations homologues basées sur des repères anatomiques sont généralement préférées aux informations basées sur des caractéristiques géométriques. Le calcul d une information homologue intrinsèque à partir des intensités (appelée aussi approche iconique) utilise soit directement les intensités de l image en les considérant comme des réalisations d une variable aléatoire quantitative ou qualitative, soit les intensités pondérées par la localisation du pixel ou du voxel (axes principaux, moments d inertie, etc.). L information homologue intrinsèque est notamment préférée quand il est difficile d extraire des structures communes des jeux de données. Elle permet aussi de faciliter l automatisation des méthodes de recalage Métrique de qualité de la mise en correspondance: fonction de coût La fonction de coût correspond à un critère objectif, utilisé pour estimer la qualité du recalage pour une transformation donnée. Elle est définie en fonction de l information homologue et du type de la transformation à estimer. En utilisant le formalisme défini par L. Brown [Brown 92], la fonction de coût définit une métrique de similarité des structures homologues grâce à laquelle est mesurée la qualité de l estimation de la transformation, étant donnés un espace de paramètres et un espace de recherche. On peut distinguer deux principales familles de fonctions de coût : celles utilisant des distances euclidiennes dans l espace et celles utilisant des mesures de similarité statistique dans l espace des intensités des images. Lorsque l information homologue est de nature extrinsèque aux données, la fonction de coût correspond souvent à une estimation de distance euclidienne moyenne. Le problème de la mise en correspondance de points de type marqueurs externes ou références anatomiques est généralement formulé par une approche de type minimisation des moindres carrés. Quand les structures homologues sont plus complexes, d autres critères de distance sont utilisés comme la méthode head-hat [Pelizzari 89] ou des transformées en distance comme la distance de chanfrein [Borgefors 88, VanHerk 94, demunck 98, Foehrenbach 99]. La distance euclidienne entre points est calculée dans un espace continu alors que la distance de chanfrein est calculée sur une grille discrète et dans un espace discret. Ces méthodes ont prouvé leur efficacité et leur robustesse dans le recalage multimodalité intra-sujet en utilisant, par exemple, la surface de la peau comme information homologue, celle-ci étant facilement identifiable dans les images IRM, Scanner X et à moindre degré TEP et suffisante pour contraindre le calcul d une transformation rigide. Quand le recalage est basé sur une information homologue qui utilise la distribution des intensités de l image, des critères s appuyant sur des mesures statistiques de similarité sont utilisés. Ces critères posent généralement des hypothèses sur la nature de la dépendance statistique entre les données à recaler. Une description détaillées de tels critères fait l objet de la deuxième partie de ce chapitre.
85 Méthodes de recalage par mesures statistiques de similarité Stratégie de recherche: méthodes d optimisation La stratégie de recherche consiste en la définition d une méthode qui permet de calculer la mise en correspondance optimale entre des jeux de données, i.e., une méthode qui permet de calculer la meilleure transformation au sens de la fonctionnelle de coût mesurée entre les informations homologues. En fonction des hypothèses ou des contraintes, le problème de l optimisation peut avoir une solution analytique (e.g. solution analytique d un problème de régression linéaire au sens des moindres carrés) ou peut nécessiter l utilisation de méthodes itératives. De nombreuses méthodes existent dans la littérature (citons [Press 92]). Le choix d une méthode d optimisation est un choix algorithmique qui dépend de la fonction de coût et de ses propriétés mathématiques, plus que du contexte clinique. Dans le contexte des problèmes de recalage d images médicales, les méthodes d optimisation peuvent être classifiées comme suit [Barillot 99a] : Approches quadratiques ou semi-quadratiques: Ces méthodes sont basées sur l hypothèse de convexité ou de quasi-convexité de la fonction de coût au voisinage de la solution optimale. Parmi celles-ci, on trouve les méthodes de descente de gradient, de Powell, de Newton-Raphson, du Simplex, pour la convexité ou la méthode dite ICP (Iterative Closest Point) pour la quasi-convexité. Ces méthodes sont bien adaptées aux problèmes bien contraints. Généralement, ce sont les propriétés de la fonction de coût (comme, par exemple, sa différentiabilité ou sa régularité) qui conduisent au choix de la méthode d optimisation. Les approches stochastiques ou basées statistiques: Les méthodes comme le recuit simulé ou les algorithmes génétiques se comportent de manière efficace en présence de points aberrants. Elles sont donc plus fiables pour la résolution de problèmes faiblement contraints (dits sous déterminés) et évitent les minima locaux. Néanmoins, les avantages en terme de robustesse sont font au prix des temps de calcul importants. Les approches structurelles: Ces méthodes s appuient sur des techniques d optimisation basées sur l utilisation d arbres ou de graphes. Elles nécessitent l étude exhaustive de l espace de recherche pour trouver la solution optimale. Un optimum global est toujours atteint nécessitant un temps de calcul important. Les méthodes structurelles sont bien adaptées aux cas où les mesures de similarité peuvent être formalisées par une structure hiérarchique. Les approches heuristiques: Ces méthodes consistent généralement en une recherche interactive d un optimum, en cherchant, par exemple, à optimiser visuellement les mesures de similarité. De plus, il peut être intéressant d associer à la méthode d optimisation une stratégie d optimisation pour résoudre les problèmes classiques liés à toute optimisation : éviter les extrema locaux et/ou réduire le temps de calcul. Pour cela, des stratégies de type multirésolution ou multi-échelle peuvent être utilisées (voir par exemple [Hellier 01b]), permettant de travailler à des résolutions croissantes pour une meilleure mise en correspondance à chaque résolution. En ce qui concerne la définition d une stratégie d optimisation, on peut aussi trouver l initialisation de la recherche avec une solution adaptée, l adaptation des contraintes (i.e. informations homologues) durant le processus d optimisation ou l utilisation combinée de plusieurs méthodes d optimisation.
86 Recalage basé sur des mesures statistiques de similarité 2.2 Recalage basé sur des mesures statistiques de similarité Pourquoi s intéresser aux mesures statistiques de similarité? Les méthodes de recalage basées sur des mesures statistiques de similarité ou encore iconiques occupent une place privilégiée parmi les méthodes de recalage de données médicales. C est surtout le cas des approches entropiques, comme l information mutuelle, qui ont montré leur efficacité et leur robustesse dans un grand nombre de situations, notamment les problèmes de recalage mono- ou multi-modalité rigide ou non linéaire. J. Duncan et N. Ayache [Duncan 00] suggèrent que les excellents résultats obtenus avec ces approches iconiques, publiés dans la principale étude multicentrique d évaluation de méthodes de recalage rigide [West 96, West 97], ont suscité de nombreux efforts au sein de la communauté et conduit à la mise au point de nouvelles mesures. De manière générale, les approches déduites de la théorie de l information sont de plus en plus envisagées par d autres domaines du traitement d images médicales que le recalage comme par exemple l analyse du signal IRMf [Tsai 99], la reconstruction tomographique [Amblard 01], la fusion TEMP/TEP/IRM [Barra 01], ou encore l application de l analyse en composantes indépendantes [Cardoso 98] à la localisation de sources en MEG/EEG [Vigario 00]. Sans prétendre fournir une bibliographie exhaustive des travaux traitant du recalage basé sur des mesures statistiques de similarité, nous avons plutôt tenté de recenser les articles caractéristiques de chaque méthode. Nous nous restreignons également au cas du recalage rigide ou affine. Nous proposons ainsi une classification des mesures statistiques de similarité, en faisant la synthèse notamment de trois travaux de thèse considérant les intensités des images soit comme des variables quantitatives [Roche 01a], soit comme des variables qualitatives [Pluim 00b, Sarrut 00]. Un autre intérêt du recalage utilisant des mesures statistiques de similarité est que ces méthodes ne requièrent en général aucun pré-traitement. Les hypothèses quant aux caractéristiques homologues des images qui vont permettre le recalage sont nettement moins formalisées que dans les méthodes utilisant des caractéristiques géométriques des images (e.g. recalage basé surface). En effet, dans les approches géométriques, ces caractéristiques homologues doivent être clairement identifiées dans les données avant la mise en correspondance, et nécessitent sinon d être segmentées, au moins d être réhaussées. Ainsi, l évaluation de ces méthodes requiert à la fois l évaluation des performances de la méthode d extraction ou de segmentation de ces caractéristiques et l évaluation de la méthode de mise en correspondance elle-même. Les diverses méthodes de recalage utilisant des mesures statistiques de similarité, s appliquant directement à tous les niveaux de gris des images, peuvent être mise en œuvre de la même manière, et sont donc aisément comparables entre elles. Néanmoins, ces méthodes utilisent également des caractéristiques homologues, même si elles sont plus difficiles à relier au contenu de l image (en terme de contenu anatomique et physiologique) : ce sont les hypothèses caractérisant le lien entre les images à recaler. Ainsi, lorsque l on décide d utiliser une mesure statistique de similarité, il est fondamental de prendre en compte les hypothèses sous-jacentes, déduites de la nature de la similarité reliant les intensités des données. Nous préciserons ces hypothèses pour les différentes mesures que nous allons présenter. Néanmoins, il est relativement difficile de caractériser ce lien sur des données cliniques, surtout en condition pathologique. Or, nous montrerons que la plupart de ces méthodes
87 Méthodes de recalage par mesures statistiques de similarité 87 s avèrent efficaces et robustes lors du recalage IRM / TEMP ictale ou inter-ictale. L un des objectifs de cette thèse est ainsi d aider à comprendre ce côté un peu magique du fonctionnement de ces méthodes notamment dans des conditions pathologiques, lorsque les hypothèses ne sont certainement pas valides ou difficiles à vérifier. A plus long terme, notre étude vise à faire le lien entre la connaissance de la nature théorique de ce lien et le choix de la mesure idéale pour obtenir la meilleure mise en correspondance possible, voire modéliser au mieux celui-ci à partir du type de données que l on cherche à traiter, afin de proposer une méthode de recalage adaptée au contexte clinique. Nous allons tout d abord présenter quel est le principe générique d une méthode de recalage basée sur l optimisation d un critère de similarité. En rappelant les contraintes spécifiques liées aux volumes 3D discrets qui constituent la majeure partie des données médicales que l on cherche à mettre en correspondance, nous présenterons quelles doivent être les propriétés d une mesure statistique de similarité idéale. Quelques éléments théoriques, venant notamment de la théorie de l information, présenteront les principaux éléments permettant de construire un mesure de similarité. Comment mesurer l information dans les données? Quelle métrique utiliser pour caractériser un lien entre deux quantités d information? Nous présenterons ensuite une classification des différentes mesures statistiques de similarité couramment utilisées pour le recalage mono- ou multi-modalité. Nous avons fait le choix de distinguer les méthodes considérant les intensités des images comme des variables quantitatives, de celles considérant les intensités des images comme des variables qualitatives. Nous finirons par la présentation de quelques méthodes proposant une mesure statistique de similarité à partir d une modélisation du processus ayant permis de générer les données à recaler : ces approches posent le problème du recalage basé sur des mesures statistiques de similarité comme un problème d inférence statistique des différents paramètres du modèle à partir des données Principe de la mise en correspondance par mesures statistiques de similarité Position du problème Le principe des méthodes de recalage utilisant des mesures statistiques de similarité est précisément de trouver la transformation géométrique T qui permet de garantir que les intensités des données sont les plus similaires possibles lorsqu elles sont en parfaite mise en correspondance géométrique. La particularité de ces méthodes est de se baser uniquement sur les intensités des voxels pour quantifier cette similarité ou lien statistique entre les données. Alors qu en recalage monomodalité, ce lien peut se quantifier de manière très simple par une formulation de type moindres carrés, en recalage multimodalité il est fondamental de tenir compte du fait que les intensités des images à recaler reflètent des informations homologues mais également complémentaires. C est le cas lorsqu une des données caractérise l anatomie (e.g. l IRM) et l autre une fonction (e.g. perfusion en TEMP ictale). Ainsi, de manière générique, une mesure statistique de similarité devra formaliser cet aspect par une transformation en intensité f permettant de rendre les données comparables. Ainsi, de manière générique, pour recaler deux volumes de données (la plupart du temps 3D) A et B, il faut construire une mesure statistique de similarité S définie par :
88 Recalage basé sur des mesures statistiques de similarité S T,f (A,B) = A,f B T (2.2) où A désigne l image de référence et B l image flottante. Pour pouvoir être comparé à l intensité de A en un voxel x k, on transforme les coordonnées de ce voxel par T afin de se situer dans le référentiel de l image B, on est alors capable de calculer l intensité de ce point dans l image B puis de la transformer par f. En résumé, s il s agit d une mesure locale au voxel x k, on compare A(x k ) et f(b(t(x k )))., désigne une mesure quantifiant la similarité entre A et f B T. Elle peut s exprimer comme la négation d une norme sur un espace Hilbertien L p mesurant une distance entre les valeurs des intensités des images (e.g. norme de L 2 : norme quadratique, norme de L 1 : distance de Manhattan)., peut également représenter une métrique quantifiant la similarité des images à partir des distributions de probabilité de leurs intensités, considérées dès lors comme des variables qualitatives. La transformation géométrique T appartient à l espace des transformations géométriques possibles T (e.g. transformations rigides, affines, non linéaires). De même, f appartient à un espace F des transformations en intensité. De manière générale, f peut être considérée comme instationnaire et dépendra alors à la fois des intensités de B mais aussi de la position dans l espace des voxels en lesquels elle est évaluée. La résolution d un problème de recalage basé sur des mesures statistiques de similarité consiste à estimer la transformation géométrique ˆT qui maximise la similarité entre deux données: ˆT = argmax T T,f F (S T,f (A,B)) (2.3) L image médicale: une variable aléatoire discrète Les images A et B sont les entités à partir desquelles vont être estimés les différents critères statistiques de similarité. Faire le lien entre l expression théorique de ces mesures de similarité et leur estimation à partir des images A et B n est pas immédiat et nécessite au préalable une description de la structure d une image médicale. Revenons préalablement à la définition d une variable aléatoire. Une variable aléatoire (v.a.) réelle X est par définition une application mesurable d un espace probabilisé (Ω,A,Pr) dans l espace probabilisable (R,B). Ω désigne l ensemble des événements aléatoires élémentaires, A désigne la tribu maximale associée à Ω, à savoir l ensemble maximal des sous-ensembles de Ω qui sont aussi des événements, et auxquels on peut donc associer une probabilité Pr [0,1]. R désigne la droite réelle et B la tribu des boréliens 1. La condition de mesurabilité implique que : borélien B B, {ω Ω tq X(ω) B} est un élément de A (2.4) Il est alors possible d associer à la variable aléatoire X une loi de probabilité P X définie par : P X : (R,B) [0,1] B B P X (B) = Pr({ω Ω tq X(ω) B}) (2.5) 1. La tribu des boréliens est la tribu maximale associée à la droite réelle R. On montre qu elle est constituée de la réunion d un nombre dénombrable d intervalles ouverts.
89 Méthodes de recalage par mesures statistiques de similarité 89 Par abus de notation, on notera généralement P X (B) = P(X B). Ces définitions peuvent s appliquer aux images A et B. Ainsi, l image A peut être considérée comme une variable aléatoire définie sur une grille de voxels Ω A et à valeur dans un alphabet d intensités I. Pour des données où chaque voxel est codé par un octet, on aura typiquement I = {0,1,2,...,255}. Ainsi, la grille voxel Ω A définit l ensemble des événements élémentaires, et la probabilité Pr est choisie comme étant uniforme sur Ω A. Ainsi, on considère tous les voxels de l image de la même manière. A est donc une variable aléatoire discrète, définie sur l ensemble des événements élémentaires Ω A également discret et fini. Il est possible de considérer A comme une variable aléatoire continue à valeur dans R, notamment lorsque l on utilise la méthode de Parzen [WellsIII 96] pour estimer la densité de probabilité de A. Dans le cas où A est considérée comme une variable aléatoire discrète, on lui attribue une loi de probabilité P A, définie comme suit : P A : I [0,1] i P A (i) = P(A = i) = Pr({ω Ω A tq A(ω) = i}) (2.6) Ainsi, une des caractéristiques principales des images A et B que l on va chercher à recaler, est qu elles sont respectivement définies sur des espaces dénombrables finis, i.e., les grilles de voxels Ω A et Ω B. Pour les données que l on va considérer ici, les données et donc les grilles de voxels sont tridimensionnelles. Elles sont caractérisées par un échantillonnage spatial dans les trois directions de l espace rx A, ry A et rz A (respectivement rx B, ry B et rz B ). Cet échantillonnage est complètement dépendant de la modalité d imagerie utilisée, et souvent une estimation, plus ou moins précise, est fournie par le constructeur. De manière générale, si l échantillonnage n est pas identique dans les 3 directions de l espace, on parle de voxel anisotrope. L échantillonnage spatial est en général différent entre deux données surtout lorsqu elles sont multimodales. Ainsi, en pratique il y a très peu de chances que la grille de voxels Ω A coïncide avec la grille Ω B, et encore moins lorsque B est transformée spatialement par la transformation géométrique T. En effet, pour gagner en précision, l espace de recherche T de la transformation géométrique T est généralement considéré comme continu. De ce fait, l estimation de S T,f (A,B) nécessite d avoir recours à des méthodes d interpolation des données. En plus de l échantillonnage, les images médicales sont caractérisées par l exploration d un champ de vue fini, très variable également d une modalité à l autre. Ce champ de vue peut, suivant les cas, couvrir largement toute la tête du sujet ou dans d autres cas n être limité qu à une partie du cerveau (quelques coupes généralement). L estimation d un critère statistique de similarité ne sera ainsi possible que dans la zone de recouvrement partiel de A et de B T. Nous noterons Ω T A,B cette zone de recouvrement partiel, caractérisée par l ensemble de voxels de A pour lesquels il est possible de calculer par interpolation l intensité du point correspondant de B T. De même que pour A, on peut considérer B T comme une variable aléatoire définie sur la zone de recouvrement partiel de A et de B T, Ω T A,B, comme ensemble des événements élémentaires. Dans le cas de variables aléatoires discrètes, on lui attribue une loi de probabilité P B T, définie comme suit : P B T : I [0,1] i P B T (i) = Pr({ω Ω T A,B tq B(T(ω)) = i}) (2.7) Notons cependant que vu que T(ω) ne coïncide que rarement avec un nœud de la grille Ω B, le calcul de B(T(ω)) qui nécessite d avoir recours à une interpolation, a été omis ici
90 Recalage basé sur des mesures statistiques de similarité (voir I ). Par souci d alléger les notations, nous utiliserons P B pour P B T. La flèche orientée vers le bas sera utilisée pour indiquer une dépendance en T et la nécessité d avoir recours à une interpolation lors de l estimation. Nous verrons que la plupart des mesures de similarité consistent de manière plus ou moins directe à comparer les intensités A(x k ) et f(b(t(x k ))). Cette comparaison peut nécessiter d avoir recours à la loi de probabilité jointe du couple de variable aléatoire (A,B T) que l on définit alors par : P A,B T : I I [0,1] (i,j) P A,B T (i,j) = Pr({ω Ω T A,B tq A(ω) = i et B(T(ω)) = j}) (2.8) On définit de manière analogue la loi jointe du couple de variables aléatoires (A,f B T), vu que l on pose f comme une fonction déterministe. Pour les mêmes raisons que précédemment, nous utiliserons la notation P A,B pour P A,B T.
91 Méthodes de recalage par mesures statistiques de similarité Principales notations utilisées A image de référence B image flottante à recaler avec A Ω A grille voxel de l image de référence A N A = Card(Ω A ) nombre de voxels de l image de référence A Ω B grille voxel de l image flottante B N B = Card(Ω B ) nombre de voxels de l image flottante B T transformation géométrique de A vers B T espace des transformations géométriques f transformation en intensité de B F espace des transformations en intensité ω un voxel d une des différentes grilles x k = (x k 1,xk 2,xk 3 ) coordonnées du k ième voxel de la grille Ω A dans référentiel mondial (sagittal, centré, millimétrique) y k = (y1 k,yk 2,yk 3 ) coordonnées du k ième voxel de la grille Ω B dans référentiel mondial axe 1 ou x antérieur vers postérieur axe 2 ou y tête vers pieds axe 3 ou z gauche vers droite I espace des intensités des images (continu ou discret) a k = A(x k ) intensité dans A du k ième voxel de Ω A b k intensité dans B au point T(x k ) après interpolation B Ω T A,B image B rééchantillonnée dans le référentiel de A (ensemble des b k ) zone de recouvrement partiel de A et de B T i.e., ensemble des x k de Ω A tels que l on peut calculer b k N = Card(Ω T A,B ) nombre de voxels de la zone de recouvrement partiel w kl coefficient de pondération lié à la distance entre T(x k ) et son l ième voisin sur la grille Ω B S T,f (A,B) mesure statistique de similarité entre A et f B T ˆT estimation de la transformation géométrique au maximum de S ˆf estimation de la transformation en intensité au maximum de S P A loi de probabilité de l image A considérée comme une v.a. sur Ω A P B = P B T loi de probabilité de l image B T considérée comme une v.a. sur Ω T A,B P A,B = P A,B T loi de probabilité jointe des images A et B T ˆp A estimation de P A à partir des réalisations de A sur Ω T A,B ˆp B ˆp A,B estimation de P B à partir des réalisations de B T sur Ω T A,B estimation de P A,B à partir des réalisations de A et de B T sur ΩT A,B
92 Recalage basé sur des mesures statistiques de similarité X une variable aléatoire réelle x réalisation de la variable aléatoire X P X loi de probabilité de X p X densité de probabilité de X Y une variable aléatoire réelle y réalisation de la variable aléatoire Y P Y loi de probabilité de Y p Y densité de probabilité de Y P X,Y loi de probabilité jointe du couple de (X,Y ) p X,Y densité de probabilité jointe du couple de (X,Y ) Interpolation et estimation des lois de probabilité Interpolation : Pour gagner en précision, la transformation géométrique T utilisée pour le recalage est choisie dans un espace continu (e.g. pour une transformation rigide les translations sont exprimées en mm et les rotations en ). Ainsi, pour tout voxel x k de la grille Ω A, le correspondant de ce point dans l image B, T(x k ), ne coïncide qu exceptionnellement avec un point de la grille Ω B. L estimation de l intensité de B au point T(x k ) nécessite donc d avoir recours à une méthode d interpolation à partir des intensités des points de la grille Ω B voisins de T(x k ). On notera b k cette estimation. La théorie de l échantillonnage de Shannon annonce qu il est possible d interpoler parfaitement un signal à bande fréquentielle limitée échantillonné périodiquement à partir de fonctions sinus cardinal (sinc). Néanmoins, Hill et al. [Hill 01] précisent que les images médicales ne sont pas à bande limitées, vu qu elles résultent généralement d un fenêtrage par une fonction rectangulaire sur le champ de vue exploré. De plus, la fonction sinc étant de support infini, elle n est pas utilisable en pratique sans troncature. A. Roche [Roche 01a] rappelle que l interpolation par décomposition sur une base de fonctions B-splines de degré d est intéressante d un point de vue calculatoire, et converge vers la fonction sinc lorsque d tend vers l infini. La plupart des méthodes de recalage basées sur des mesures statistiques de similarité utilisent des méthodes itératives d optimisation et requièrent ainsi plusieurs évaluations successives de la mesure de similarité S. Chaque estimation de S nécessite, directement ou indirectement, un rééchantillonnage de B dans le référentiel de A via la transformation T, et donc le recours à une interpolation des intensités de B. De ce fait, pour limiter la complexité calculatoire, les techniques d interpolation couramment utilisées se basent sur des fonctions B-splines de degré 0, l interpolation plus proche voisin, ou de degré 1, l interpolation trilinéaire. Pour les mêmes raisons, l estimation de l intensité de B en T(x k ) ne considérera que ses 8 plus proches voisins y l dans la grille Ω B, et sera de la forme : Interpolation plus proche voisin : l=8 b k w kl B(y l) (2.9) l=1 w kl = { 1 si yl est le plus proche voisin de T(x k ) 0 sinon (2.10)
93 Méthodes de recalage par mesures statistiques de similarité 93 Interpolation trilinéaire : avec w kl = β1 3(T(x k ) y l ) (2.11) { β3(z) 1 (1 z1 )(1 z = 2 )(1 z 3 ) si z [ 1; 1] 3 0 sinon où β3 1 désigne justement une B-spline de degré 1 en dimension 3. z désigne un vecteur tridimensionnel. Pour simplifier les notations, on suppose ici que les dimensions du voxel de Ω B sont toutes égales à 1, ce qui revient à considérer les coordonnées du vecteur T(x k ) y l dans le référentiel data de la grille Ω B (voir I ). Estimation des lois jointes et marginales : Quantifier la similarité entre deux images, considérées comme des variables aléatoires, peut nécessiter une estimation des lois de probabilité de ces variables aléatoires. De nombreuses mesures de similarité issue de la théorie de l information, dont l information mutuelle, requièrent l estimation de la loi jointe P A,B T. Rappelons que l image A est une variable aléatoire définie sur l espace probabilisé constitué de Ω A, de sa tribu maximale et de la probabilité Pr uniforme. La proportion empirique étant l estimateur habituel permettant de caractériser une distribution uniforme, on en déduit une estimation de P A (i) pour tout i I : ˆp A (i) = #{ω Ω A tq A(w) = i} #{ω Ω A } (2.12) où la notation # représente le cardinal de l ensemble. On reconnaît alors la notion d histogramme des intensités d une image. Pour que l histogramme soit un bon estimateur de P A, il est nécessaire que le nombre d échantillons observés, i.e. le nombre de voxels, soit grand devant le nombre possible de valeurs d intensité. C est généralement le cas pour la plupart des images 3D lorsque les données sont codées sur 1 octet (I = {1,2,...,255}). Cette condition n est par contre plus vérifiée dès lors que les intensités de l image sont codées sur 2 voire 4 octets. Il est dans ce cas nécessaire de regrouper les intensités. On définit alors de manière générale un histogramme, ou une loi de probabilité, sur la grille αz par : ˆp A (i) = 1 N A x k Ω A K α (i a k ) i {αp, p Z} (2.13) où a k désigne l intensité de A en x k, N A le nombre de voxels de l image A et K α la fonction indicatrice de [ α 2 ; α 2 [, à savoir : { 1 si i [ α K α (i) = 2 ; α 2 [ (2.14) 0 sinon De manière analogue, on définit un estimateur de la loi de probabilité jointe P A,B T comme suit : ˆp A,B (i,j) = 1 N x k Ω A,B K α,β (i a k,j b k ) (i,j) {(αp,βq), (p,q) Z2 } (2.15)
94 Recalage basé sur des mesures statistiques de similarité où b k désigne l intensité interpolée de B en T(x k) évaluée d après l équation (2.9), N désigne le nombre de voxels de la zone de recouvrement partiel Ω A,B et K α,β la fonction indicatrice du pavé [ α 2 ; α 2 [ [ β 2 ; β 2 [. On reconnaît bien la formule habituelle du calcul d un histogramme joint, ou table de co-occurrence des intensités de deux variables aléatoires discrètes. Le fait de créer une intensité interpolée b k qui n a pas été observée parmi les échantillons disponibles n est pas un principe habituel vis à vis de l estimation. Pour gérer cela, Maes et al. [Maes 97] proposent une manière astucieuse d utiliser les coefficients de pondération w kl de l interpolation trilinéaire pour incrémenter les cases de l histogramme joint, plutôt que de créer de nouvelles intensités artificielles. Il vient : ˆp A,B (i,j) = 1 N l=8 w kl K α,β(i a k,j b l ) (i,j) {(αp,βq), (p,q) Z 2 } (2.16) x k Ω l=1 A,B On parle alors de technique d interpolation intrinsèque, ou partial volume en anglais. b l désigne l intensité de B au l ième voisin y l de T(x k ) sur la grille Ω B et les poids w kl sont évalués d après l équation (2.11). Cette formulation confère à l estimation de la loi jointe plus de régularité en fonction des variations T, vu que les incréments minimaux de l histogramme sont inférieurs à 1/N. Maes et al. montrent qu il est alors possible de différencier l histogramme joint, et par suite l information mutuelle, suivant la transformation géométrique T [Maes 99]. Une autre approche revient à considérer les images comme des variables aléatoires réelles, et donc continues, et de supposer qu elles acceptent une densité de probabilité. Pour l image A, on définit sa densité de probabilité p A par : P A : (R,B) [0,1] B B P A (B) = P(A B) = λ B p A(λ)dλ (2.17) Notons qu ici B désigne un élément de la tribu des Boréliens B, donc un intervalle de R. Pour que la fonction p A soit bien une densité de probabilité, il faut qu elle vérifie : λ R p A(λ)dλ = 1. On peut alors utiliser la méthode de noyaux pour estimer p A. Le principe est d utiliser une formule analogue à l équation (2.13), en remplaçant K α par un noyau quelconque K défini sur R et d intégrale sur R égale à 1, afin de s assurer que ˆp A est bien une densité de probabilité. C est la technique du fenêtrage de Parzen qui a été utilisée par Wells, Viola et al. [WellsIII 96] pour estimer l histogramme joint comme suit : ˆp A,B (i,j) = 1 N x k Ω A,B K σ (i a k,j b k ) (i,j) R2 (2.18) où le noyau K σ peut, par exemple, être choisi comme une gaussienne de moyenne nulle et d écart-type σ. Le choix de σ dépend des données, et permet de gérer différents niveaux de lissage de l histogramme joint. Le choix de tels noyaux confère à l histogramme joint de bonnes propriétés de régularité et notamment sa différentiabilité [WellsIII 96, Leventon 98].
95 Méthodes de recalage par mesures statistiques de similarité Normalisation: gestion du recouvrement partiel Un critère idéal de similarité ne devrait pas être sensible à la taille de la zone de recouvrement partiel. Cependant, vu que de manière générale, on cherche une transformation géométrique T et une transformation en intensité f telles que A et f B T soient les plus similaires possibles, il est possible de rencontrer des cas de dépendance dégénérée entre les données. Une dépendance dégénérée peut par exemple correspondre au cas où B T se retrouve complètement à l extérieur du champ de vue de A, et si f est alors choisie comme une fonction constante, on peut aboutir à une mesure de similarité optimale. Parmi les critères de similarité principalement utilisés dans la littérature et présentés au I.2.2.4, tous ne prennent pas en compte cet aspect et y sont plus ou moins sensibles. Ces problèmes se posent en pratique lorsque les champs de vue des images à recaler sont très différents et ne couvrent pas toute la partie anatomique étudiée. Dans le cas où la mesure de similarité S est définie comme l opposée d une distance entre les intensités de A et de f B T, caractérisant ainsi une dissimilarité D, A. Roche [Roche 01a] propose une normalisation permettant d éviter ces cas de dépendance dégénérée. Un tel critère de dissimilarité s écrit dans ce cas: D T,f (A,B) = S T,f (A,B) = A f B T (2.19) où désigne une norme sur l espace des intensités. On a donc toujours D T,f (A,B) 0 et ce critère est à minimiser. Les cas de dépendance dégénérée peuvent être rencontrés lorsque f est considérée comme constante. A. Roche propose alors d imposer la contrainte suivante au critère de dissimilarité que l on cherche à construire : avec par définition : 0 D T (A,B) D 0 T(A,B) (2.20) { DT (A,B) = argmin f F D T,f (A,B) D 0 T (A,B) = argmin f constante D T,f (A,B) (2.21) On peut par exemple chercher un critère de dissimilarité optimal DT comme une fonction g de D T et de DT 0 à laquelle on impose les propriétés suivantes: 1. g(d T,DT 0 ) [0; 1] 2. A DT 0 fixé, g(d T,DT 0 ) est une fonction croissante de D T 3. Si D T = 0 et DT 0 0, g(d T,DT 0 ) = 0 4. Si D T = DT 0, g(d T,DT 0 ) = 1 En cherchant g comme une fonction affine de D T et de DT 0, on montre à partir des propriétés précédentes et de la contrainte 2.20, qu un critère de dissimilarité idéal, i.e. insensible à la zone de recouvrement partiel, s écrit : D T (A,B) = D T(A,B) D 0 T (A,B) = argmin f F D T,f (A,B) argmin f constante D T,f (A,B) (2.22) avec D T (A,B) = 1 si D 0 T (A,B) = 0. Ainsi, on évite les cas de dépendance dégénérée car un tel critère sera nul s il y a une correspondance parfaite entre les intensités des images à condition que f ne soit pas constante. De même, les cas de dépendance dégénérée seront caractérisés par un maximum absolu du critère D T (A,B) qui sera égal à 1.
96 Recalage basé sur des mesures statistiques de similarité Éléments de théorie de l information L objectif de ce paragraphe est d introduire quelques outils théoriques permettant de mesurer une quantité d information à partir des données considérées comme des variables aléatoires. Nous rappellerons tout d abord les méthodes les plus conventionnelles pour caractériser la loi d une variable aléatoire, notamment par ses moments. Ensuite nous présenterons comment mesurer une quantité d information à partir de la loi de probabilité d une variable aléatoire, en s appuyant sur des notions issues de la théorie de l information, notamment l entropie. Nous terminerons par la présentation des quelques métriques permettant de comparer l information contenue dans deux variables aléatoires. Nous distinguerons les métriques portant sur la comparaison de lois de probabilité, ou divergences, des métriques portant sur les valeurs prises par les variables aléatoire, i.e. les intensités des images (norme L2, norme L1 et normes robustes). Dans ce paragraphe, nous considérerons que nous cherchons à caractériser la loi de probabilité ou une quantité d information d une variable aléatoire réelle X, ou à comparer deux variables aléatoires réelles X et Y. Nous désignerons par x (respectivement y) les réalisations de X (respectivement de Y ). On considérera donc X et Y comme des variables aléatoires continues, et on supposera qu elles acceptent une densité de probabilité p X (respectivement p Y ). Au I.2.2.4, nous montrerons comment les principales mesures de similarité utilisées en recalage d images utilisent ces éléments théoriques. Dès lors que nous appliquerons ces notions aux images A et B, toutes les formules seront alors présentées dans le cas discret Géométrie des variables aléatoires de carré intégrable Une variable aléatoire X est complètement définie par la donnée de sa loi de probabilité P X, ce qui revient à connaître sa fonction de répartition F X (x) = P X (X x). Si X et donc P X est continue, on peut en général définir la mesure élémentaire dp X par rapport à une mesure de référence λ à l aide de la densité de probabilité p X par : dp X (λ) = p X (λ)dλ (2.23) Moments d une loi : Plutôt que de spécifier la fonction de répartition ou la densité de probabilité qui ne sont pas très simples à manipuler, il est intéressant de décrire une loi en la résumant par ses caractéristiques principales. Pour cela, on utilise les moments. Le premier moment non-centré d une variable aléatoire X est son espérance mathématique qui, si elle existe, s écrit : E(X) = λdp X (λ) = λp X (λ)dλ (2.24) λ R On utilise cette définition pour définir l espérance mathématique d une fonction g(x) qui est aussi une variable aléatoire : E(g(X)) = g(λ)p X (λ)dλ (2.25) λ R λ R
97 Méthodes de recalage par mesures statistiques de similarité 97 Outre la spécification d une fonction de répartition ou d une densité de probabilité, une loi de probabilité peut être entièrement décrite par sa fonction caractéristique ϕ X, qui n est autre que le transformée de Fourier de sa densité de probabilité p X : ϕ X (t) = e itλ p X (λ)dλ = E(e itx ) (2.26) Si ϕ X (t) est infiniment dérivable, on a d après la formule de Mac-Laurin [Saporta 90] : ϕ X (t) = + n=0 t n n! in E(X n ) (2.27) E(X n ) est par définition le moment non-centré d ordre n de X. Cette formule est très intéressante vu qu elle montre que la loi de probabilité d une variable aléatoire X peut être complètement décrite par la connaissance de tous ses moments non-centrés. En pratique, on s intéresse principalement aux moments d ordres 1 et 2. On définit d ailleurs la variance d une variable aléatoire X comme son moment centré d ordre 2 : V ar(x) = E[(X E(X)) 2 ] (2.28) Géométrie de L2 : Le cas où on n étudie que des variables aléatoires réelles de moment d ordre 2 fini est l un des plus importants en pratique, et est susceptible d interprétations géométriques très éclairantes. De telles variables appartiennent à l espace Hilbertien L2 défini comme l ensemble des variables réelles de carré intégrable, c est à dire qui vérifient : E(X 2 ) = λ 2 dp X (λ) < + (2.29) λ R L espace L2 est muni du produit scalaire suivant : X,Y = E(XY ) = xy p X,Y (x,y)dxdy (2.30) R 2 où p X,Y désigne la densité de probabilité jointe du couple de variable aléatoire (X,Y). On définit alors la norme de L2, ou norme quadratique, par : X = E(X 2 ). Ce formalisme nous permet de définir E(X) comme la meilleure approximation de X par une constante a R au sens de la norme L2, en effet on montre que : E(X) = argmin a R X a (2.31) E(X) s interprète ainsi comme la projection orthogonale, au sens du produit scalaire de L2, de X sur la droite C des variables aléatoires constantes. De la même manière, on peut chercher à expliquer une variable aléatoire Y comme une fonction φ de la variable aléatoire X. L existence d un tel lien entre les variables X et Y définit ce que l on appelle une dépendance fonctionnelle entre X et Y. Ainsi, si on cherche φ parmi l ensemble F X de toutes les fonctions réelles qui assurent que E(φ(X) 2 ) < + (i.e. telle que φ(x) L2), alors on montre que [Saporta 90, Roche 98a] : E(Y X) = argmin φ FX Y φ(x) (2.32)
98 Recalage basé sur des mesures statistiques de similarité où E(Y X) est l espérance conditionnelle de Y sachant X, elle est définie par : E(Y X) = y p Y X (y)dy = y p X,Y (x,y) dy (2.33) p X (x) où p Y X désigne la densité de probabilité de Y sachant X, elle se déduit des lois de Bayes sur les probabilités, et vaut par définition p X,Y (x,y)/p X (x). De même que pour E(X) sur la droite des variables aléatoires constantes C, E(Y X) est la projection orthogonale de Y sur le sous-espace de L2 engendré par les fonctions de X. Les résultats (2.31) et (2.32) nous montrent ainsi que la meilleure manière d approcher une variable X par une constante est de prendre son espérance mathématique, et que la meilleure façon d approcher une variable Y par une fonction de la variable X est de prendre l espérance conditionnelle de Y sachant X. Ainsi, l espérance mathématique de X décrit le comportement moyen et constant de la variable aléatoire X. On la désignera d ailleurs comme sa moyenne. Les variations de X autour de sa moyenne E(X) seront décrites par sa variance V ar(x) qui n est autre que le carré de la distance de X à son projeté orthogonal sur la droite des constantes C. Lien entre deux variables aléatoires - indépendance, corrélation et dépendance fonctionnelle : Les différents éléments théoriques sur la géométrie des variables aléatoires qui viennent d être présentés nous permettent d introduire différentes méthodes pour étudier le lien statistique reliant deux variables aléatoires. Deux variables aléatoires X et Y sont indépendantes si et seulement si, par définition, quelles que soient les fonctions réelles g 1 et g 2 on a : E[g 1 (X)g 2 (Y )] = E(g 1 (X))E(g 2 (Y )) (2.34) On en déduit un résultat fondamental qui est que la loi jointe d un couple de variables aléatoires indépendantes (X,Y ) est la loi produit des lois marginales, ce qui s écrit : Mesure élémentaire : Fonction de répartition : Densité de probabilité : dp X,Y (x,y) = dp X (x).dp Y (y) F X,Y (x,y) = F X (x).f Y (y) p X,Y (x,y) = p X (x).p Y (y) (2.35) Ainsi une manière d apprécier l indépendance de deux variables aléatoires est de mesurer l écart entre la loi de probabilité jointe et la loi produit des lois marginales. Nous verrons au I quelques métriques permettant de quantifier cet écart. Une méthode standard pour analyser un lien entre deux variables aléatoires X et Y est d estimer leur covariance, qui est défini par : Cov(X,Y ) = E[(X E(X))(Y E(Y ))] = (X E(X)),(Y E(Y )) = X E(X). Y E(Y ).cos(θ) (2.36) La covariance n est autre que le produit scalaire des variables centrées X E(X) et Y E(Y ). θ indique l angle entre ces deux variables dans l interprétation géométrique de L2. En pratique, on préférera utiliser le coefficient de corrélation linéaire ρ X,Y qui est une version normalisée de la covariance :
99 Méthodes de recalage par mesures statistiques de similarité 99 ρ X,Y = Cov(X,Y ) V ar(x) V ar(y ) = cos(θ) (2.37) Le coefficient de corrélation linéaire n est autre que le cosinus de l angle θ entre les variables centrées X E(X) et Y E(Y ). Il prend donc des valeurs entre -1 et 1. Deux variables aléatoires sont dites non-corrélées lorsque leur coefficient de corrélation linéaire est nul, ce qui correspond à deux variables centrées orthogonales d après le produit scalaire de L2. Le lien entre X et Y est optimal au sens du coefficient de corrélation, lorsque celui-ci vaut 1, variables positivement corrélées, ou -1, variables négativement corrélées. Ces deux limites sont atteintes lorsque l angle θ vaut 0 ou π, c est à dire lorsque les variables centrées sont colinéaires. Ainsi le coefficient de corrélation linéaire ρ X,Y mesure une dépendance linéaire entre X et Y. Il est optimal (égal à 1 ou -1) lorsque Y est une fonction linéaire de X, de la forme Y = αx + β avec (α,β) R 2. Les définitions (2.34) et (2.36) permettent de montrer que l indépendance de deux variables aléatoires entraîne leur non-corrélation, c est à dire l orthogonalité dans L2. A l exception du cas gaussien, la réciproque est en générale fausse. Plutôt que de se restreindre à une relation linéaire, une autre manière d étudier le lien entre X et Y est de rechercher si Y peut s exprimer comme une fonction quelconque φ de X (avec φ F X ). Il s agit d étudier s il existe une dépendance fonctionnelle entre X et Y, et donc si la connaissance de X permet de prédire le comportement de Y. Or, nous avons déjà précisé que la projection orthogonale de Y sur le sous-espace de L2 engendré par les variables {φ(x),φ F X } n était autre que l espérance conditionnelle E(Y X). De plus, vu qu une constante est également une fonction de X, E(Y ) appartient également à ce sousespace de L2. En utilisant le théorème de Pythagore sur le triangle (Y,E(Y X),E(Y )), on montre le théorème de la variance totale [Saporta 90] : V ar(y ) = V ar[e(y X)] + E[V ar(y X)] (2.38) où V ar(y X) désigne la variance conditionnelle de Y sachant X, elle est définie par : V ar(y X) = (y E(Y X = x)) 2 p Y X (y)dy (2.39) L équation (2.38) peut être vue comme une équation de conservation de l énergie de Y et permet de proposer une mesure de la dépendance fonctionnelle : le rapport de corrélation η Y X de Y sachant X [Saporta 90, Roche 98a] : η Y X = V ar[e(y X)] V ar(y ) (2.40) Si η Y X = 0, alors V ar[e(y X)] = 0 et donc E(Y X) est presque sûrement une constante, donc E(Y X) = E(Y ). Il n y a pas de dépendance fonctionnelle entre X et Y. Si η Y X = 1, alors E[V ar(y X)] = 0 et donc V ar(y X) = 0 (une variable positive de moyenne nulle est nécessairement nulle partout). Ainsi à X fixé, la variance de Y est nulle, Y ne peut donc prendre qu une seule valeur, ainsi φ F X telle que Y = φ(x). On dit qu il y a dépendance fonctionnelle parfaite.
100 Recalage basé sur des mesures statistiques de similarité Mesures de quantité d information Mesure d information d un signal d après Hartley : La nécessité de devoir mesurer une quantité d information contenue par un signal est apparue avec le début des communications télégraphiques ou radio où l on cherchait à quantifier l information contenue dans un message émis par un émetteur et reçu par un récepteur. En 1928, Hartley propose une mesure de l information d un message encore largement utilisée dans toute la théorie de l information [Hartley 28]. Pour caractériser un message en Morse ou un mot, il définit un message comme étant une suite de n caractères choisis parmi s symboles possibles. Ainsi, un message de longueur n correspond à s n messages possibles. Utiliser s n pour mesurer l information contenue dans un message entraînerait une augmentation exponentielle de la quantité d information avec la longueur des messages, et n est donc pas envisageable. Cherchant à définir une mesure d information H qui croît de manière linéaire avec la longueur du message n, et qui soit telle que deux messages de longueur n 1 et n 2 utilisant respectivement s 1 et s 2 symboles présentent la même mesure d information si s n 1 1 = s n 2 2, Hartley proposa la mesure d information H suivante : H = ln(s n ) = n lns (2.41) Entropie de Shannon : La principale limitation de la mesure proposée par Hartley provient du fait que tous les symboles parmi les s utilisés pour construire un message sont considérés comme équiprobables. C est rarement le cas en pratique, si l on considère par exemple les mots de langue française, il est évident que la lettre e sera beaucoup plus souvent rencontrée que la lettre w. Certains messages seront donc plus probables que d autres. En attribuant à chacun des messages choisis parmi les s n messages possibles une probabilité P i, Shannon propose de mesurer la quantité d information moyenne obtenue lors de la réception d un message de longueur n de la façon suivante : H = i=s n i=1 ( ) i=s 1 n P i ln = P i i=1 P i ln(p i ) (2.42) Cette mesure d information définit l entropie de Shannon [Shannon 48]. Cela revient à associer à chaque message une quantité d information élémentaire représentée par ln( 1 P i ), définie également comme la quantité d information de Fisher. Ainsi, un message rare ou peu probable apporte plus d information qu un message fréquent ou très probable. Si un seul type de message est transmis, il contiendra très peu d information, car le récepteur sera toujours sûr du message qu il reçoit. A l inverse si tous les messages sont équiprobables, il existe une grande diversité de messages susceptibles d être reçus, ils sont très difficiles à prévoir, et la réception de chacun apporte en soi beaucoup plus d information. La formule de l entropie de Shannon, dont l équation (2.42) est la définition dans le cas discret, n est autre que l espérance mathématique de la quantité d information de Fisher : il s agit donc d une mesure moyenne de l information contenue dans tous les messages de longueur n. Elle sera maximale lorsque tous les messages sont équiprobables (i.e. i P i = 1/s n ), on retrouve alors la mesure d information proposée par Hartley (2.41). L entropie de Shannon, comme mesure moyenne de la quantité d information de Fisher, peut également être vue comme une mesure d incertitude. On retrouve, par analogie, sa
101 Méthodes de recalage par mesures statistiques de similarité 101 signification en thermodynamique comme un indicateur de désordre. Pour revenir aux notations du paragraphe précédent, on définit l entropie de Shannon d une variable aléatoire X à partir de sa densité de probabilité p X : H(P X ) = λ R ( ) 1 p X (λ)ln dλ = p X (λ)ln(p X (λ))dλ = E(ln(p X )) (2.43) p X (λ) λ R Définir l entropie de Shannon non pas comme une fonction de X mais comme une fonction de la loi de probabilité de P X, permet d insister sur le fait que, contrairement aux moments, l entropie est une mesure portant uniquement sur la loi de X : l espérance mathématique de ln(1/p X ). Définition générique de la notion d entropie : L entropie de Shannon n est en fait qu un cas particulier d une famille plus générique d entropies qui sont toutes des mesures de la quantité d information d une loi de probabilité. On définit ainsi l entropie d une loi de probabilité P X de manière relative à une mesure de référence λ, par la forme fonctionnelle intégrale suivante [Basseville 96] : ( ) dpx (λ) H λ (P X ) = h dλ (2.44) λ dλ La fonction h est le plus souvent choisie convexe 2. M. Basseville [Basseville 96] propose également une définition de l entropie à partir d une forme fonctionnelle non intégrale, ainsi que plusieurs exemples de fonctions h. Si on choisit h comme la fonction h(u) = u ln(u), on retrouve l entropie de Shannon définie en (2.43). D. Sarrut a utilisé différentes définitions de l entropie afin de proposer différents critères statistiques de similarité pour le recalage multimodalité [Sarrut 00] Métriques de comparaison des quantités d information Nous venons de présenter différents outils permettant de caractériser l information d une variable aléatoire soit par ses moments soit par des mesures portant sur sa loi de probabilité, comme l entropie. Vu que l objectif de ce chapitre est de présenter des mesures de similarité, nous présentons ici quelques métriques permettant de comparer ces informations pour caractériser un lien entre deux variables aléatoires X et Y. Nous distinguons les métriques portant directement sur les valeurs des variables aléatoires, de celles portant sur les lois de probabilités. Les premières permettront de définir différentes mesures statistiques de similarité considérant les intensités des images comme des variables quantitatives alors que les secondes donneront lieu à des mesures de similarité considérant les intensités des images comme des variables qualitatives. Métriques portant sur les variables aléatoires : Ces métriques sont utilisées lorsque la mesure de similarité est en fait une mesure de dissimilarité estimant une distance entre les intensités des images à recaler qu il faut alors minimiser. Une telle dissimilarité D s exprime de manière générale par : 2. Une fonction h est convexe si elle vérifie : h(x) αh(x 1) + (1 α)h(x 2) pour tout couple (x 1,x 2) du domaine de h, et pour tout x tel que 0 < α < 1 et x = αx 1 + (1 α)x 2
102 Recalage basé sur des mesures statistiques de similarité D T,f (A,B) = S T,f (A,B) = A f B T (2.45) L objectif de ce paragraphe est de présenter quelques métriques ou normes couramment utilisées pour définir des critères statistiques de similarité. Nous avons déjà montré que les propriétés géométriques de L2 étaient très intéressantes pour étudier les relations entre deux variables aléatoires à partir des moments. Ainsi le coefficient de corrélation (2.37) permet de caractériser une dépendance linéaire entre deux variables aléatoires X et Y, alors que le rapport de corrélation (2.40) caractérise une dépendance fonctionnelle. Or ces critères ne sont autres que des mesures de distance, au sens de la norme de L2, entre Y et sa meilleure approximation dans L2 par une fonction linéaire de X (respectivement par une fonction quelconque de X). Nous avons vu que cette notion de meilleure approximation était en fait une projection orthogonale sur le sous-espace en question (voit I ). Une approche analogue est applicable à d autres espaces Hilbertiens de variables aléatoires. C est notamment le cas de l espace L1 défini comme l ensemble des variables réelles intégrables en valeur absolue, c est à dire qui vérifient : E( X ) = λ dp X (λ) < + (2.46) On définit alors la norme de L1 par : λ R X L1 = E( X ) (2.47) De manière analogue au cas de L2, on montre ainsi que la meilleure approximation de X par une constante au sens de cette norme L1 est en fait la médiane de X définie par : P X (X Med(X)) = F X (Med(X)) = 0.5 (2.48) De même que pour la variance dans L2, la mesure de dispersion d une variable aléatoire dans L1 sera estimée par sa distance à la meilleure approximation constante. Cette mesure de dispersion dans L1, Disp L1, correspond donc à la moyenne des écarts en valeur absolue de X à sa médiane : Disp L1 (X) = E( X Med(X) ) (2.49) La norme L1 peut être utilisée directement pour quantifier un écart entre les intensités des images ou pour définir par analogie à la géométrie de L2, un rapport de corrélation dans L1 [Roche 01a]. L utilisation de la norme L1 est souvent préférée en statistique à la norme L2, car bien qu elle possède de moins bonnes propriétés mathématiques (e.g. régularité), elle est moins sensible aux valeurs aberrantes que la norme quadratique. La norme L1 est dite faiblement robuste alors que la norme quadratique est non-robuste. Or il s avère difficile en pratique de modéliser correctement la similarité entre les intensités des images à recaler. Malgré la transformation de l image B en f B T, il peut subsister des voxels où l écart entre les intensités de A et f B T est anormalement important. Ces points sont considérés comme des points aberrants, non pris en compte par le modèle de transformation géométrique et en intensité de B. De telles situations
103 Méthodes de recalage par mesures statistiques de similarité 103 peuvent être rencontrées en pratique lorsque par exemple une seule des deux images à recaler contient une information pathologique, comme c est souvent le cas lors du recalage de données anatomo-fonctionnelles. Or le recalage ne doit justement pas compenser cette information pathologique, que l on cherche à mettre en évidence par cette mise en correspondance. Il peut donc s avérer utile de disposer de métriques permettant de ne pas prendre en compte ces points aberrants lors du recalage : c est précisément le but des métriques dites robustes. De manière générale, le critère de dissimilarité (2.19) peut s écrire : D T,f (A,B) = E[ρ(A f B T)] (2.50) où lorsque ρ(x) = x 2, on retrouve la norme quadratique de L2, et lorsque ρ(x) = x, on retrouve la norme de L1. On définit alors un M-estimateur robuste [Black 96], ou norme robuste, par une fonction ρ vérifiant les propriétés suivantes: 1. ρ est croissante sur R + 2. φ(x) = ρ( x) est strictement concave sur R + 3. lim x + ρ (x) < + Un M-estimateur robuste est caractérisé par son point de rupture, représentant le pourcentage de points aberrants que peut tolérer l estimateur sans être perturbé. Par exemple, la médiane est un estimateur de la tendance centrale d une variable aléatoire avec un point de rupture de 50%, i.e. on peut avoir dans un échantillon jusqu à 50% de valeurs aberrantes sans modifier la valeur de la médiane. On caractérise un estimateur robuste par sa fonction d influence, qui n est autre que sa dérivée ρ. Ainsi, le fait d imposer que la fonction d influence soit de limite finie en +, permet de garantir que, lorsque l écart entre deux intensités dépasse un certain seuil, son influence sur la mesure de dissimilarité stagne voire décroît. De telles approches ont été utilisées en recalage d images à partir de M-estimateurs robustes [Nikou 98, Hellier 01b], ou de S-estimateurs instantanés [Roche 01a]. Un exemple de métrique robuste couramment utilisée est la fonction de Geman-McClure définie par : ρ(x) = (2.51) 1 + x2 c 2 où le réel c permet de régler le point de rupture de la métrique. Métriques portant sur les lois de probabilité : Une seconde approche pour étudier le lien statistique entre deux variables aléatoires est de ne s intéresser qu à leurs lois de probabilité. Nous avons déjà vu qu il était possible de caractériser la quantité d information d une variable aléatoire à partir de mesure ne portant que sur la loi de probabilité, notamment grâce à l entropie de Shannon (2.43). On définit alors la f-divergence entre deux mesures ν et λ, comme l opposé de l entropie de la mesure ν relativement à λ [Basseville 96] : ( ) dν I(ν,λ) = H λ (ν) = h dλ (2.52) dλ x2 λ
104 Recalage basé sur des mesures statistiques de similarité La notion de divergence peut être interprétée comme un gain d information de ν par rapport à λ. On définit alors la f-divergence de deux lois de probabilité P X et P Y, possédant respectivement pour densités de probabilité p X et p Y, par : I(P X,P Y ) = ( dpx h dp Y ) dp Y = h µ ( ) [ px (µ) p Y (µ)dµ = E Y h p Y (µ) ( px p Y )] (2.53) où la fonction h est en général choisie convexe, et vérifie h(1) = 0. Cette dernière condition sur h garantit que I(P X,P X ) = 0, ce qui signifie que la divergence entre une loi de probabilité et elle même est nulle, ou encore il n y a pas de gain d information d une loi de probabilité par elle-même. De même que pour la formule générique de l entropie (2.44), il s agit d une définition à partir d une forme fonctionnelle intégrale. D autres définitions de la divergence à partir de formes fonctionnelles non intégrales ainsi que quelques exemples sont présentés dans [Basseville 96]. Un cas particulier très connu est la divergence obtenue à partir de l entropie de Shannon, ce qui correspond à choisir la fonction h(u) = u ln(u), on aboutit alors à la divergence de Kullback-Leibler ou entropie relative, mesure largement utilisée comme distance entre deux lois de probabilité : ( ) ( ) [ ( )] dpx dpx px (µ) px K(P X,P Y ) = ln dp Y = ln p X (µ)dµ = E X ln dp Y dp Y µ p Y (µ) p Y (2.54) Par analogie à la géométrie de variables aléatoires dans L2, il est d ailleurs possible de définir une géométrie des lois de probabilité dans laquelle les points correspondent à des lois de probabilité, les espaces affines ou plans à des familles exponentielles, le carré de la norme de L2 à la divergence de Kullback-Leibler [Cardoso 01]. Nous verrons plus loin que c est à partir de cette divergence qu est déduite l information mutuelle [WellsIII 96, Maes 97, Zhu 02a], qui est certainement un des critères de similarité les plus couramment utilisés en recalage d images. D autres f-divergences connues ont été utilisées pour construire des critères de similarité utilisables en recalage d images [Pluim 00b, Pluim 01a, Sarrut 99, Sarrut 00]. Citons entre autres la distance de Kolmogorov V obtenue en choisissant h(u) = 1 2 u 1, la I α-divergence de Csiszàr obtenue en choisissant la fonction h comme : h(u) = 1 α(α 1) (uα αu + α 1) α 0 ou 1 (2.55) Notons que lorsque α tend vers 1, la I α -divergence tend vers la divergence de Kullback- Leibler. Citons finalement la famille des χ α -divergences obtenues en choisissant la fonction h comme suit : h(u) = { 1 u α 1 α si 0 < α 1 1 u α α si α > 1 (2.56) Les mesures statistiques de similarité déduites de ces différentes mesures de distance entre lois de probabilité seront détaillées au I
105 Méthodes de recalage par mesures statistiques de similarité Classification des mesures statistiques de similarité Nous présentons ici une classification des principales mesures statistiques de similarité utilisées pour recaler les images A et B. Nous présentons tout d abord les mesures qui utilisent A et B comme des variables aléatoires quantitatives, on se ramène alors à une mesure de distance dans l espace des intensités des images. La deuxième catégorie de méthodes considère les images A et B comme des variables aléatoires qualitatives, on se ramène alors à étudier les propriétés des lois de probabilité P A et P B et de la loi jointe P A,B. Sauf pour quelques approches heuristiques, nous caractérisons chaque méthode par le type de lien statistique exploré entre les variables et par la métrique utilisée pour le quantifier. Dans ce paragraphe, les notations introduites au paragraphe I seront utilisées. Toutes les mesures présentées dans ce paragraphe seront estimées à partir de la zone de recouvrement partiel des données Ω A,B, ayant pour cardinal N voxels. Pour tout voxel k de cette zone de recouvrement partiel, on désignera par a k l intensité de ce voxel dans A, et b k l intensité de son correspondant dans B T après interpolation (voir I ). La plupart des critères de similarité présentés peuvent être évalués à partir des densités de probabilité jointes et marginales. Nous désignons par ˆp A,B, ˆp A et ˆp B, respectivement, les estimateurs sur Ω A,B des densités de probabilité jointe p A,B T et marginales p A et p B T. Comme montré précédemment, ces estimateurs peuvent soit utiliser un rééchantillonnage de l image B et donc la création d intensités artificielles (i.e. non observées), soit utiliser une interpolation intrinsèque (voir équation 2.16). Tous les critères présentés dépendront de la transformation géométrique T et de la transformation en intensité f (si elle apparaît de manière explicite). Pour alléger les notations, nous omettrons de préciser explicitement cette dépendance Mesures considérant les images comme des variables quantitatives De manière générale, les mesures quantitatives de similarité reviennent à minimiser une dissimilarité, ou distance, entre les intensités des images, à savoir : ˆT = argmin T T,f F (D T,f (A,B)) = argmin T T,f F A f B T (2.57) avec la transformation géométrique T recherchée dans l espace des transformations géométriques T et la transformation en intensité f choisie parmi l espace de fonctions F. Pour l essentiel des applications citées dans cette classification, nous nous limitons à la recherche de transformations géométriques rigides ou affines. La plupart des mesures de similarité présentées ici peuvent s appliquer directement dans le cas de transformations géométriques non linéaires, mais il est souvent nécessaire de rajouter un terme énergétique permettant de régulariser le champ de déformation (voir par exemple [Hellier 01b]). Mesures de distance sur les intensités: Distance entre intensités au sens de L2: Lorsque l on utilise la norme quadratique ou norme de L2 pour quantifier la distance entre les intensités, on se ramène au critère dit de somme des carrés (SDC) :
106 Recalage basé sur des mesures statistiques de similarité SDC(A,B) = 1 N x k Ω A,B (a k f(b k ))2 (2.58) Lorsque la fonction f est choisie comme l identité, on se ramène à une méthode standard de minimisation de l erreur des moindres carrés couramment utilisée en recalage monomodalité, comme par exemple pour le recalage TEP/TEP [Woods 98] ou IRM/IRM [Holden 00]. Ce critère est optimal lorsque les données ne diffèrent que par un bruit blanc additif gaussien : A = B + ǫ où le résidu ǫ est un échantillon indépendant identiquement distribué (iid) issu d une distribution gaussienne centrée. Ainsi, ce critère est bien adapté au recalage intra-sujet et monomodalité, même si en réalité le bruit des images médicales est rarement gaussien. Lorsque f est l identité, la relation supposée entre A et B T est également connue comme l hypothèse du flot optique ou de conservation de la luminance. Si de plus, on suppose que les déplacements de l image B via T par rapport à l image A sont petits, le critère (2.58) se linéarise en fonction de T via un développement de Taylor [Barber 95]. On se ramène alors à un problème de régression linéaire au sens des moindres carrés. De nombreux travaux sur la régression linéaire ont été menés en statistiques. Ce problème admet une solution analytique et on dispose de nombreux résultats sur les propriétés des estimateurs des régresseurs (e.g. biais, variance) [Lebart 79, Saporta 90], donc dans notre cas des paramètres de T. Cette approche a été généralisée par Friston et al. [Friston 95a], qui utilisent également un développement de Taylor pour linéariser le problème. Par contre, les espaces de recherche des transformations géométriques T et des transformations en intensité F peuvent être choisis de manière très générique. Par exemple, ils proposent d estimer une transformation géométrique non linéaire en linéarisant le critère par décomposition de la transformation géométrique sur une base de fonctions correspondant aux modes de Fourier. La transformation en intensité peut également être très générique et notamment non-stationnaire 3. Le recalage est alors vu comme la résolution d un problème de régression linéaire généralisée, et permet d estimer les paramètres des transformations géométrique et en intensité, qui peuvent être nombreux. Cette approche est notamment utilisée pour du recalage monomodalité inter-sujets entre un examen et un examen moyen de la même modalité, que l on appellera template : c est la normalisation spatiale proposée par le logiciel SPM. Elle est applicable à toute modalité à condition de disposer d un template adéquat. Dans le cas du recalage rigide monomodalité intra-sujet, cette approche générique peut par exemple être appliquée à la correction de bougé pour des séquences d IRMf. L hypothèse de petits déplacements justifiant le développement de Taylor et donc la linéarisation du problème n est pas toujours vérifiée en pratique. Cet aspect est généralement pris en compte lors de l optimisation du critère de similarité par des approches itératives et multi-échelles. Dans le contexte du recalage affine TEMP/TEMP inter-sujets, Alpert et al. [Alpert 96] proposent d utiliser pour fonction f une mise a l échelle des intensités moyennes des images: 3. La non-stationnarité signifie que f dépend de l intensité mais aussi de la position dans l espace du voxel en lequel elle est évaluée.
107 Méthodes de recalage par mesures statistiques de similarité 107 SDC Alpert (A,B) = 1 N x k Ω A,B (a k ā bb k )2 (2.59) où ā et b désignent respectivement les moyennes empiriques des intensités des images A et B. Distance entre intensités au sens de L1: Lorsque l on utilise la norme de L1 pour quantifier la distance entre les intensités et que l on choisit f comme l identité, on se ramène au critère dit de somme des différences absolues (SDA) : SDA(A,B) = 1 N x k Ω A,B a k b k (2.60) Nous avons déjà vu que la norme L1 était faiblement robuste. Elle est donc moins sensible que le critère SDC aux écarts importants entre les intensités des images. Vu qu ici aussi le modèle sous-jacent est que les images A et B sont identiques à une transformation géométrique près, ce critère est principalement utilisable dans le cas du recalage monomodalité. Il a été utilisé en recalage TEMP/TEMP [Eberl 96, Radau 01] ou TEP/TEP [Eberl 96]. Eberl et al. ont néanmoins utilisé ce critère pour du recalage multimodalité TEP/TEMP. Utilisation d une métrique robuste: La prise en compte des écarts aberrants entre intensités peut être mieux assurée par l utilisation d une métrique robuste ρ. On aboutit ainsi à une mesure de similarité communément appelée erreur des moindres carrés robuste : SDC robuste (A,B) = 1 N x k Ω A,B ρ(a k b k ) (2.61) Nikou et al. [Nikou 98, Nikou 99b] proposent d utiliser la métrique de Geman-MacClure (voir équation 2.51) et l appliquent au recalage rigide monomodalité de données IRM. Radau et al. [Radau 01] appliquent ce même critère dans le cadre du recalage affine des données TEMP vers un template TEMP. Hellier et al. [Hellier 01b] proposent une formulation robuste de l hypothèse du flot optique dans un contexte de recalage non linéaire monomodalité. Quelques approches heuristiques en recalage mononomodalité: Il existe quantité d autres critères statistiques de similarité qui ont été proposés à des fins de recalage monomodalité. Ils résultent principalement d approches heuristiques et s expriment difficilement comme une distance entre intensités. Citons par exemple le nombre de changements de signes de l image de différence D ou la somme des intensités du produit voxel par voxel des deux images. Ces deux derniers critères ont été étudiés par Eberl et al. dans le cadre du recalage mono- ou multi-modalité des données TEMP et TEP [Eberl 96].
108 Recalage basé sur des mesures statistiques de similarité Mesures de dépendance linéaire : Coefficient de corrélation: Si on peut supposer que la transformation en intensité entre les deux images est de nature linéaire (f(i) = α i + β), nous avons montré que le coefficient de corrélation était la mesure optimale au sens de L2. Lorsqu il est proche de 1 en valeur absolue, il garantit ainsi que A est approchée au mieux, au sens de L2, par une fonction linéaire B. L estimateur du coefficient de corrélation est défini par : ρ 2 A,B = ( ) 2 xk Ω (a k ā)(b k b k ) A,B x k Ω A,B(a k ā) 2 x k Ω (b k b (2.62) k )2 A,B où ā et b k désignent respectivement les moyennes empiriques des intensités de A et de B sur la zone de recouvrement partiel Ω A,B. Elles sont définies par : ā = 1 N a k et b k = 1 N b k (2.63) x k Ω A,B x k Ω A,B En pratique, cette hypothèse de dépendance linéaire entre les intensités des images est plutôt adaptée au contexte du recalage monomodalité, IRM/IRM par exemple [Holden 00]. Il a malgré tout été étudié en recalage multimodal, comme par exemple le recalage IRM/TEP [Studholme 95]. Uniformité du rapport des intensités: Une manière indirecte d étudier une dépendance linéaire entre les images à recaler est d étudier l uniformité de leur rapport. Minimiser la variance normalisée du rapport des intensités (ou coefficient de variation) revient à supposer qu à l optimum les intensités des images ne diffèrent que par un facteur multiplicatif uniforme sur tout le volume (f(i) = α i). Ce critère qui a été proposé par Woods et al. [Woods 92, Woods 98] est défini par : URI(A,B) = 1 µ ( ) 1 A N B x k Ω A,B ( a k b k µ ( ) ) 2 A B (2.64) Avec par définition : µ ( ) A = 1 B N x k Ω A,B ( a k b k ) (2.65) En général, l estimation de ce critère ne se fait pas sur toute la zone de recouvrement partiel Ω A,B, mais uniquement à l intérieur d un masque se limitant par exemple au volume cérébral. En effet, l évaluation du rapport des intensités peut être instable numériquement surtout au niveau du bruit de fond des images. En TEP ou en TEMP, on sélectionne ce masque en ne tenant compte que des intensités supérieures à un seuil fixé [Woods 92, Woods 98, Eberl 96]. Pour d autres modalités, comme par exemple
109 Méthodes de recalage par mesures statistiques de similarité 109 l IRM, il peut être nécessaire d avoir recours à une méthode de segmentation du cerveau manuelle ou automatique [Woods 98, Holden 00]. Afin d éviter une pondération inégale des paires d intensités, notamment lorsque le dénominateur du rapport est proche de zéro, Holden et al. [Holden 00] proposent une variante de l U RI plus stable numériquement : URI Holden (A,B) = 1 µ ( ) 1 A N B x k Ω A,B ( ( ) ) 2 a k + c A + c b k + c µ B + c (2.66) où c est une constante choisie par exemple comme le maximum d intensité de l image B. Mesures de dépendance fonctionnelle : Rapport de corrélation généralisé: L hypothèse statistique de dépendance fonctionnelle entre deux variables A et B revient à supposer que l on peut prédire le comportement de A comme une fonction φ(b). Nous rappelons qu au sens de la norme L2, la meilleure approximation de A par une fonction φ(b) n est autre que l espérance conditionnelle de A sachant B : E(A B). Le théorème de la variance totale permet d introduire le rapport de corrélation η A B comme un indice de qualité de cette approximation 4 (voir I ). Critère classique en statistique, Roche et al. [Roche 98b, Roche 98a] sont les premiers à proposer son utilisation dans le contexte du recalage mono- ou multimodalité. A. Roche [Roche 01a] propose en fait un cadre plus général de l étude de la dépendance fonctionnelle entre deux variables aléatoires, le rapport de corrélation généralisé défini par : D(A,B) = D T(A,B) D 0 T (A,B) = argmin f F argmin f constante x k Ω A,B x k Ω A,B ρ(a k f(b k )) ρ(a k f(b k )) (2.67) Ce critère n est autre que la mesure de dissimilarité (2.22) présentée au I Il est donc à minimiser suivant T. Contrairement à tous les autres critères présentés jusqu à présent, le rapport de corrélation généralisé est par construction insensible à la zone de recouvrement partiel, et permet d éviter des cas de dépendance dégénérée lorsqu une image est par exemple recalée dans le fond de l autre. F est l espace dans lequel est cherchée la transformation en intensité f, et ρ est une métrique de l espace des intensités. Rapport de corrélation L2: Considérons tout d abord le cas où F est l ensemble des fonctions constantes par morceaux et où ρ est la métrique quadratique de L2 (ρ(x) = x 2 ). Notons qu en plus les images sont considérées ici comme des variables aléatoires discrètes à valeur dans I = {0,1,2,...,255}. L ensemble des fonctions constantes par morceaux définies sur des intervalles du type [j 1/2; j + 1/2[ j I, n est autre que l ensemble de toutes 4. En rappelant que E(A B) est la projection orthogonale de A sur l espace des variables aléatoires généré par les variables fonction de B, le rapport de corrélation n est autre que le cosinus de l angle de cette projection au point E(A).
110 Recalage basé sur des mesures statistiques de similarité les fonctions qu il est possible de définir sur les intensités d une image discrète. Dans ces conditions, la résolution explicite en fonction de f de l équation (2.67) permet d aboutir au critère suivant (voir [Roche 01a]): D L2 (A B) = j I x k Ω j x k Ω A,B (a k ā j ) 2 (a k ā) 2 (2.68) où Ω j est la partition des voxels de Ω A,B B, à savoir : d intensité j dans l image rééchantillonnée Ω j = {x k Ω A,B tq b k [j 1/2; j + 1/2[} (2.69) On désignera par N j le nombre de voxels appartenant à cette partition Ω j. ā et ā j désignent respectivement les moyennes empiriques de A et de A sachant B = j, à savoir : ā = 1 N x k Ω A,B a k et ā j = 1 N j x k Ω j a k (2.70) Ces expressions correspondent au cas où une interpolation extrinsèque est utilisée (e.g. calcul de b k par interpolation trilinéaire). L utilisation d une interpolation intrinsèque donnerait lieu à des expressions analogues faisant intervenir les poids w kl. Ce même critère peut également s exprimer à partir des estimateurs des densités de probabilité jointes et marginales ˆp A,B, ˆp A et ˆp B évaluées sur la zone de recouvrement partiel Ω A,B (voir I pour les expressions de ces estimateurs) : avec : D L2 (A B) = 1 σ 2 p j σj 2 = 1 ˆη A B (2.71) j I ā = i p i i et ā j = i p i j i (2.72) σ 2 = i p i i 2 ā 2 et σ 2 j = i p i j i 2 ā 2 j (2.73) p j = ˆp B (j) = ˆp A,B (i,j) et p i j = ˆp A B (i) = ˆp A,B (i,j) i ˆp B (j) (2.74) L interprétation statistique de cette dernière expression (2.71) fait apparaître le critère D L2 (A B) comme un estimateur de E B [V ar(a B )] V ar(a), d où le lien avec l estimateur du rapport de corrélation L2 : ˆη A B (voir équation 2.40). De plus, le fait d utiliser une interpolation extrinsèque ou intrinsèque donne lieu à la même expression en fonction des densités de probabilité. Notons également que la résolution de l équation (2.67) en considérant toujours une métrique quadratique, mais en choisissant f comme une fonction affine des intensités permet d aboutir au coefficient de corrélation (2.62).
111 Méthodes de recalage par mesures statistiques de similarité 111 Rapport de corrélation L1: Considérons désormais le cas où F est l ensemble des fonctions constantes par morceaux sur des intervalles du type [j 1/2; j + 1/2[ j I et où ρ est la métrique de L1 (ρ(x) = x ). Dans ces conditions, la résolution explicite en fonction de f de l équation (2.67) permet d aboutir au critère (voir [Roche 01a]): avec : D L1 (A B) = 1 DispL1 p j DispL1 j (2.75) j I Med = Mediane{a k tq x k Ω A,B } et Med j = Mediane{a k tq x k Ω j } (2.76) DispL1 = i p i i Med et DispL1 j = i p i j i Med j (2.77) On retrouve donc bien une formule analogue au rapport de corrélation en norme L2, en remplaçant les moyennes empiriques par des médianes, et les variances par des mesures de dispersion en valeur absolue (dispersion L1 : DispL1). L estimation des médianes se fait également à partir des densités de probabilité, vu que la médiane d un autre échantillon n est autre que la valeur en laquelle sa fonction de répartition vaut 0.5. Critère de Woods et ses variantes: Dans le contexte du recalage multimodalité, Woods et al. [Woods 93] posent l hypothèse que, si une même structure est observée au travers de deux systèmes d imagerie, elle devrait correspondre à des régions dont l intensité est uniforme dans chacune des images. Par contre, la fonction caractérisant la valeur de l intensité moyenne de cette structure dans chacune des images peut quant à elle être relativement complexe, et n a pas besoin d être connue. Cette approche heuristique, qui revient également à faire l hypothèse qu il existe une relation de type dépendance fonctionnelle entre les images, a conduit Woods et al. à poser le critère suivant : CW(A B) = j I p j σ j ā j (2.78) On utilise les mêmes définitions des moyennes et variances conditionnelles introduites pour le rapport de corrélation L2. On remarque que cette approche heuristique a conduit Woods à proposer un critère exprimant relativement la même idée que le critère D L2 (A B). L interprétation statistique de ce critère montre qu il s agit en fait de l estimateur de la moyenne du coefficient de variation (ou écart-type standardisé) de A sachant B, à savoir : CW(A B) = E B ( ) V ar(a B ) E(A B ) (2.79) Ce critère a été développé dans le contexte du recalage IRM/TEP. En général, on choisit l IRM pour l image B. Minimiser ce critère revient à classifier l IRM en 256
112 Recalage basé sur des mesures statistiques de similarité régions d intensité homogène (correspondant aux 256 valeurs possibles d intensité), et de minimiser l écart-type standardisé des intensités des 256 régions correspondantes dans l image TEP : on s assure ainsi que ces régions soient les plus homogènes possibles lorsque les données sont recalées. Néanmoins, de telles hypothèses d uniformité ne sont relativement bien vérifiées qu au niveau du cerveau, et Woods suggère de segmenter le cerveau à partir de l IRM avant d utiliser ce critère. Cette idée générale a conduit à la définition de critères similaires estimés à partir de classifications plus réalistes des tissus de l IRM [Ardekani 95, Ashburner 97]. Ainsi, Ardekani et al. [Ardekani 95] utilisent un algorithme des K-moyennes pour classifier la substance blanche, la substance grise et le LCR à partir de l IRM, avant d estimer un critère d uniformité sur ces partitions reportées dans l image TEP. Ashburner et al. [Ashburner 97] proposent de commencer par une normalisation spatiale monomodalité des données TEP et IRM vers leurs templates respectifs [Friston 95a], puis ils reportent la classification a priori des tissus de ces templates sur les données à recaler pour estimer un critère d uniformité : c est l algorithme de recalage multimodalité implémenté dans le logiciel SPM. En recalage monomodalité intra-sujet, Holden et al. [Holden 00] proposent une mesure qui revient à s assurer que la somme des carrés de l image de différences soit localement uniforme autour d une sphère de rayon r : le Profil d Intensité (PI ou Pattern Intensity). Cette approche revient à choisir f non-stationnaire et caractérise également une dépendance fonctionnelle entre les données. Cette mesure est à maximiser et s écrit à partir de l image de différence D = A B T : PI(D) = 1 N x k Ω A,B x l tq x k x l 2 r 2 c2 c 2 + (d k d l ) 2 (2.80) où c est une constante arbitraire et par définition d k = a k b k est l intensité en x k de l image de différence D. Approches robustes: Nikou et al. [Nikou 98, Nikou 99b] proposent une variante robuste du critère de Woods, en remplaçant la métrique quadratique pour le calcul des variances par une métrique robuste, en l occurrence celle de Geman-McClure. Le rapport de corrélation L1 déjà présenté est une formulation faiblement robuste du concept de rapport de corrélation. L équation générique du rapport de corrélation généralisé (2.67) peut être envisagée à partir d autres normes robustes, comme par exemple celle de Geman-McClure. A. Roche propose une solution utilisant des S-estimateurs instantanés [Roche 01a] Mesures considérant les images comme des variables qualitatives Nous abordons à présent une deuxième classe de critères statistiques de similarité issus principalement des éléments de théorie de l information présentés au paragraphe I Les images A et B sont désormais considérées comme des variables qualitatives, ce qui signifie que les intensités des images peuvent prendre 256 valeurs différentes sans forcément présumer de relation d ordre sur ces intensités. Concrètement, de telles mesures ne sont déduites que de propriétés de la loi jointe P A,B et des lois de probabilité marginales P A et
113 Méthodes de recalage par mesures statistiques de similarité 113 P B. Ainsi, si l estimation de ces densités de probabilité ne nécessitait pas d interpolation, le fait de redistribuer aléatoirement dans l espace les intensités des deux images tout en conservant les mêmes lois jointes et marginales n aurait aucune influence sur les critères de similarité présentés ici. Propriétés statistiques de la loi jointe : La loi de probabilité jointe entre les variables A et B T est un indicateur important de la quantité d information partagée par les données, d où l intérêt de l utiliser à des fins de recalage. En effet, les images que l on cherche à recaler représentent des structures (anatomiques) identiques, que la mise en correspondance cherche à faire se superposer, comme par exemple le nez, le scalp, les oreilles ou les yeux. Or, lorsque les données sont mal recalées, la loi jointe reflète une complexité accrue vu qu elle considérera que la personne possède 2 nez, 2 scalps, 4 oreilles, ou encore 4 yeux. Ce petit exemple permet d illustrer que le recalage des données revient à simplifier la scène jointe, ce qui peut s interpréter comme une diminution de la quantité d information contenue dans la loi jointe. Hill et al. [Hill 92] proposent de visualiser sous forme d image l histogramme joint des images pour étudier ces phénomènes (voir [Studholme 99] pour une explication très intuitive de ces comportements à partir d exemples simples). Ainsi, Hill et al. remarquent que lorsque l on s éloigne du recalage optimal, les pics de l histogramme joint ont tendance à diminuer et la dispersion augmente. Apparaissent notamment de nombreuses faibles valeurs dans certains cas où la probabilité était nulle à l optimum du recalage. Ils suggèrent ainsi d utiliser pour le recalage une minimisation des moments d ordre n de la distribution des estimations de la loi jointe p A,B (i,j) (i,j) I2, ce qui revient à minimiser la dispersion de la loi jointe : ( ) M n (A,B) = p A,B (i,j) 1 n (2.81) i,j (i,j) I 2 Une telle mesure revient à considérer les valeurs p A,B (i,j) (i,j) I2 comme les réalisations d une variable aléatoire et d en étudier sa distribution via l estimation des moments. Le moment d ordre 3 ou plutôt le coefficient d asymétrie (ou skewness ) a été utilisé comme mesure de dispersion à minimiser lors du recalage de données IRM et TEP [Hill 92, Studholme 95]. Afin d étudier quantitativement les effets de l interpolation extrinsèque ou intrinsèque sur les méthodes de recalage construites à partir de l histogramme joint (notamment l information mutuelle, voir plus loin), Pluim et al. [Pluim 00a] utilisent les propriétés de l histogramme 1D de la distribution des valeurs p A,B (i,j). Pour caractériser la dispersion de la loi jointe entre un alignement parfait des données sur la grille des voxels ou hors grille, ces données utilisent notamment la fréquence des probabilités p A,B (i,j) faibles, le nombre de cases non nulles de l histogramme joint et l entropie de cette distribution 1D. Recaler deux images revenant donc à diminuer la dispersion, ou encore à réduire la quantité d information de la loi jointe, l entropie de Shannon apparaît comme une mesure idéale d une telle quantité d information. Ainsi, il est possible de recaler deux images A et B en minimisant leur entropie jointe définie par : H(A,B) = p A,B (i,j)ln(p A,B (i,j)) (2.82) i,j (i,j) I 2
114 Recalage basé sur des mesures statistiques de similarité Ce critère a été utilisé à des fins de recalage mono- ou multimodalité, comme par exemple le recalage IRM/TEP [Studholme 95, Studholme 99]. Néanmoins, l objectif de ce critère étant de réduire la complexité de la scène jointe, il a tendance à favoriser des situations de dépendance dégénérée entre les deux images, en recalant une image dans le fond de l autre, par exemple. Ainsi, ce critère est reconnu pour être très sensible à la zone de recouvrement partiel des données [Studholme 99]. Mesures d un écart à l indépendance : Alors que les mesures dites quantitatives de similarité présentées au paragraphe I utilisaient à des fins de recalage des propriétés telles que la dépendance linéaire ou la dépendance fonctionnelle, nous allons utiliser ici une autre propriété : l indépendance statistique. Rappelons que par définition deux variables aléatoires sont indépendantes si et seulement si leur loi jointe est le produit des lois marginales. Ainsi, A et B T sont indépendantes si et seulement si on a : p A,B (i,j) = p A(i) p B (j) (i,j) I2 (2.83) La notion d indépendance statistique est très intéressante vis à vis du recalage car elle est très générique et ne fait aucune hypothèse quant à la nature du lien statistique entre les images à recaler, sauf justement cette notion de dépendance. Les hypothèses de dépendance fonctionnelle et surtout de dépendance linéaire peuvent en effet s avérer trop restrictives en recalage multimodalité, et surtout difficiles à vérifier objectivement. Pour le recalage, nous allons donc supposer que la dépendance statistique entre les données sera maximale lorsque celles-ci seront en correspondance parfaite. Les critères présentés ici consisteront donc à recaler les données en maximisant leur écart à la situation d indépendance statistique. De la f-divergence à la f-information: Nous avons précédemment introduit la notion très générique de f-divergence comme une métrique permettant de comparer des densités de probabilité. Ces métriques permettent notamment de quantifier l écart à l indépendance de deux variables aléatoires. Nous définissons ainsi la f-information [Pluim 00b] comme la f-divergence entre la loi jointe et la loi produit des marginales qui serait observée en cas de parfaite indépendance. Le recalage consistera à estimer la transformation géométrique qui assure une f-information maximale, à savoir : ˆT = argmax T T I(P A,B,P A P B ) (2.84) où I désigne la f-divergence définie en (2.52). J. Pluim [Pluim 00b, Pluim 01a] et D. Sarrut [Sarrut 99, Sarrut 00] ont étudié quantité de critères statistiques de similarité déduits de ce principe (20 pour J. Pluim et 14 pour D. Sarrut), dont certains déduits d autres définitions de la divergence (forme fonctionnelle non intégrale notamment [Basseville 96]). Nous présentons ici les critères les plus couramment utilisés à des fins de recalage, comme l information mutuelle, mais aussi certains critères très connus en statistiques qu il nous a paru intéressant de situer dans cette même famille : la distance de Kolmogorov et la statistique du χ 2.
115 Méthodes de recalage par mesures statistiques de similarité 115 Divergence de Kullback-Leibler et information mutuelle: L information mutuelle est le critère statistique de similarité issu de ce formalisme de loin le plus connu pour le recalage d image. Elle se déduit en choisissant la divergence de Kullback-Leibler comme mesure de divergence, on en déduit l estimateur de l information mutuelle : I(A,B) = K(P A,B,P A P B ) = (i,j) I 2 p A,B (i,j) ln ( p A,B (i,j) p A (i) p B (j) ) (2.85) L utilisation de l information mutuelle pour le recalage d images médicales a été proposé de manière simultanée par deux équipes, celle de Maes et al.[maes 97] à Louvain, et celle de Wells et al. [WellsIII 96] au MIT(Boston). Depuis, établir une liste exhaustive de toutes les études basées sur ce critère qui ont été publiées s avérerait une tâche difficile vu la quantité impressionnante de telles références. Notons de plus que déjà dans ces deux articles, considérés comme les références en la matière, Maes et al. proposent la méthode d interpolation intrinsèque, dite partial volume, et Wells et al. proposent d utiliser le fenêtrage de Parzen pour l estimation des lois de probabilité et en déduisent la dérivée de l information mutuelle en fonction de T. Pour aider à la compréhension du mode de fonctionnement de l information mutuelle, il est utile de l interpréter à partir des entropies de Shannon des lois jointe et marginales, que l on peut envisager comme des mesures de quantité d information. On montre aisément à partir de l équation (2.85), que l information mutuelle peut également s écrire : I(A,B) = H(A) + H(B ) H(A,B ) = H(A) H(A B ) = H(B ) H(B A) (2.86) où H(A,B ), H(A), H(B ), H(A B ) et H(B A) désignent respectivement les entropies de Shannon des densités de probabilité p A,B, p A, p B, p A B et p B A. La première expression montre que maximiser l information mutuelle revient à minimiser l entropie jointe, c est à dire à diminuer la quantité d information et donc la complexité de la scène jointe. Néanmoins, la présence des entropies marginales H(A) et H(B ) qu il faut maximiser, garantit que dans la zone de recouvrement partiel les images contiennent suffisamment d information. Ce dernier point permet d éviter des cas de dépendance dégénérée, lorsqu une image se recale sur le fond de l autre. Ainsi, l information mutuelle permet de stabiliser le comportement de la minimisation de l entropie jointe, en rendant le critère moins sensible à la zone de recouvrement partiel. La seconde interprétation utilise la notion d entropie conditionnelle. Nous avons vu que l entropie pouvait être considérée comme une mesure de quantité d information ou comme une mesure de degré d incertitude 5. Ainsi, on peut interpréter l information mutuelle comme la diminution du degré d incertitude de l image A (H(A)) 5. Les deux points de vue sont équivalents, puisque l on peut considérer qu une image qui contient beaucoup d événement peu probables, i.e. un important degré d incertitude, contient en fait beaucoup plus d information qu une image présentant une intensité uniforme.
116 Recalage basé sur des mesures statistiques de similarité lorsque l on dispose de l image B comme information a priori (H(A B ), et inversement. Ainsi, lorsque les données sont en parfaite correspondance, cette perte d incertitude sera maximale. L information mutuelle caractérise ainsi l information qui est partagée entre A et B. En théorie de l information, elle est considérée comme la quantité d information partagée entre un récepteur et un émetteur dans un canal de communication. Une interprétation graphique très intuitive de l entropie jointe et de l information mutuelle à partir des diagrammes de Venn est présentée dans [Studholme 99]. Information mutuelle normalisée: Bien que nettement moins sensible que l entropie jointe à la zone de recouvrement partiel, Studholme et al. [Studholme 99] montrent que l information mutuelle y est également sensible. Ils justifient cela à partir de quelques petits exemples analytiques et de vraies données IRM. Cette étude les a conduit à proposer un critère de similarité mesurant l écart à l indépendance, complètement insensible à la zone de recouvrement partiel. Il s agit de l information mutuelle normalisée, qui s écrit : IMN(A,B) = H(A) + H(B ) H(A,B ) (2.87) F. Maes [Maes 98] a proposé un critère sensiblement identique, le coefficient de corrélation entropique, défini par : CCE(A,B) = 2I(A,B) H(A) + H(B = 2 2/IMN(A,B) (2.88) ) Notons que le coefficient de corrélation entropique peut également se déduire en utilisant une autre définition plus générale de la divergence que celle de Kullback- Leibler [Sarrut 00]. V -information ou statistique de Kolmogorov: La distance de Kolmogorov est obtenue en choisissant la fonction h(u) = 1/2 1 u dans la formule générique de la f-divergence (2.53). Lorsqu on utilise cette divergence pour quantifier l écart à l indépendance, on aboutit à la V -information ou statistique de Kolmogorov : V (A,B) = 1 p A,B 2 (i,j) p A(i) p B (j) (2.89) (i,j) I 2 Ce critère est à rapprocher de la mesure classique utilisée dans le test d adéquation de Kolmogorov-Smirnov qui utilise également la valeur absolue de la différence entre une loi empirique observée et une loi a priori que l on cherche à comparer. I α -information: La I α -divergence est obtenue en choisissant la fonction h comme dans l équation (2.55) dans la formule générique de la f-divergence (2.53). On aboutit ainsi au critère de I α -information pour caractériser l indépendance de deux variables aléatoires: I α (A,B) = 1 α(α 1) (i,j) I 2 p A,B (i,j)α (p A (i) p 1 α 0,1 (2.90) B (j))α 1
117 Méthodes de recalage par mesures statistiques de similarité 117 On retrouve l information mutuelle lorsque α tend vers 1. J. Pluim a étudié le comportement de ce critère en utilisant plusieurs valeurs de α dans le contexte du recalage IRM/TEP et IRM/Scanner X [Pluim 00b, Pluim 01a]. Elle montre notamment qu à partir de α = 3 et au-delà, l allure de la fonction de coût autour de l optimum est très perturbée, plus du tout quadratique, et que ce critère n est plus utilisable dans ces conditions. χ α -information: La χ α -divergence est obtenue en choisissant la fonction h comme dans l équation (2.56) dans la formule générique de la f-divergence (2.53). On aboutit ainsi au critère de χ α -information pour caractériser l indépendance de deux variables aléatoires. Dans le cas où α = 2, on obtient : χ 2 (A,B) = (i,j) I 2 (p A,B (i,j) p A(i) p B (j))2 p A (i) p B (j) (2.91) On aboutit donc à la mesure du χ 2 très connue en statistiques pour caractériser l indépendance de deux variables aléatoires qualitatives [Saporta 90]. Notons également que lorsque α vaut 1, la χ 1 -information n est autre que la statistique de Kolmogorov. Lorsque α 1, la χ α -information est encore appelée M α -information de Matusita. Les études menées par J. Pluim et D. Sarrut sur l évaluation des performances de ces derniers critères parmi d autres pour le recalage de données TEP, Scanner X ou IRM ont montré que certains se comportent beaucoup mieux que d autres. En général ces résultats sont très dépendants de la modalité utilisée, et dans tous les cas, l information mutuelle et l information mutuelle normalisée font partie des critères les plus performants en terme de précision, mais aussi de robustesse Approches hybrides Toutes les mesures de similarité que nous venons de présenter, qu elles soient quantitatives ou qualitatives, n utilisent que les intensités des images. Plus encore, nous avons vu que les mesures issues de la théorie de l information comme l information mutuelle, ne prenaient en compte l organisation spatiale des intensités que de manière indirecte, via les besoins d interpolation. Or, dans certains contextes, il peut s avérer utile de mettre en avant cette organisation spatiale lors de la procédure de recalage. Ainsi certains critères, dits hybrides ont été développés pour répondre à ces besoins. Par exemple, en recalage monomodalité IRM/IRM, Holden et al. [Holden 00] utilisent, entre autres, un critère qui mélange les approches quantitatives et qualitatives: ils minimisent l entropie de l image de différence. Partant du principe que l os du crâne est une caractéristique spatiale importante pour le recalage, Van den Elsen et al. [VanDenElsen 95] proposent d appliquer un opérateur de courbure issu de la géométrie différentielle sur des données IRM et Scanner X, avant de maximiser le coefficient de corrélation entre ces deux volumes de courbures. En effet, rappelons que l os du crâne apparaît hyper-intense en scanner X et ne présente pratiquement aucun signal en IRM. Dans les deux cas, il se situe à un optimum de courbure, positive ou négative. Plus récemment, des études ont proposé l utilisation combinée de critères statistiques de similarité et d information sur les contours de l image provenant du gradient. Ainsi,
118 Recalage basé sur des mesures statistiques de similarité Pluim et al. [Pluim 00c] proposent un critère obtenu en combinant l information mutuelle et le gradient des images, et l appliquent pour le recalage multimodalité de données Scanner X, IRM et TEP. De manière analogue, Roche et al. [Roche 01b] suggèrent que l utilisation combinée du gradient des images et du rapport de corrélation généralisé est particulièrement bien adaptée pour le recalage rigide IRM/échographie. En effet, l échographie étant par nature une imagerie d interface, utiliser une information provenant des contours de l IRM ne peut que favoriser le recalage Mesures basées sur une modélisation de la similarité entre les données à recaler Modélisation de la similarité à partir des données Alors que la plupart des mesures qualitatives présentées cherchent à recaler les images en les éloignant le plus possible de la situation d indépendance statistique, quelques approches récemment proposées consistent au contraire à minimiser la divergence entre la loi jointe observée et une loi jointe a priori, caractéristique du type de données que l on cherche à recaler. On montre que formuler ce problème comme une maximisation de la log-vraisemblance entre la loi jointe estimée et la loi jointe a priori revient à minimiser la divergence de Kullback-Leibler entre ces deux densités de probabilité. Cette approche a été utilisée par Leventon et al. [Leventon 98] pour le recalage de différentes séquences IRM, et par Zhu pour le recalage IRM/TEMP [Zhu 02a]. La loi jointe a priori peut être estimée à partir d une base de données préalablement recalées de même nature que les données que l on cherche précisément à recaler. Zhu estime cette loi jointe a priori à partir de 5 recalages manuels réalisés par un expert sur les données TEMP/IRM de 4 patients. Sur une base de données de 37 sujets, Leventon et al. utilisent les données d un seul sujet pour estimer la loi jointe a priori par une méthode de mélange de Gaussiennes ou fenêtrage de Parzen, et utilisent les données des 36 autres sujets pour tester l algorithme. Dans les deux études, ce nouveau type d approche semble très prometteur, Zhu le compare notamment à la maximisation de l information mutuelle Modélisation du processus de génération des données La méthode proposée par A. Roche [Roche 01a] revient à estimer cette loi jointe a priori directement à partir des données à recaler, en modélisant le processus de génération de celles-ci. Ainsi, il part d un modèle spatial de l anatomie cérébrale, à partir duquel sont générées les données à recaler grâce à une transformation en intensité et l ajout de bruit. La transformation géométrique que la méthode de recalage est censée estimer est appliquée à l un des deux jeux de données. Après quelques hypothèses simplificatrices, comme notamment l indépendance du bruit en chaque voxel, un critère de recalage idéal est proposé en estimant les différentes composantes du modèle (modèle de l anatomie, transformations en intensité et transformation spatiale) par maximisation de la log-vraisemblance. Une telle approche revient à poser le problème du recalage basé sur l optimisation d un critère de similarité comme un problème d inférence statistique de ce modèle de génération des données. Dans le contexte du recalage multimodal non linéaire, cette modélisation a été utilisée par [Guimond 01] afin d estimer une transformation en intensité entre données
119 Méthodes de recalage par mesures statistiques de similarité 119 multimodales, dans le but d appliquer des techniques de recalage monomodal non linéaire sur les données ainsi transformées en intensité Mise en œuvre du recalage : pré-traitements et méthodes d optimisation De nombreux auteurs suggèrent certains pré-traitements comme l utilisation d un masque pour n utiliser que les intensités du cerveau lors du recalage, ou encore le lissage des données. Alors que ces pré-traitements sont fondamentaux pour certaines approches heuristiques comme notamment le critère de Woods [Woods 98], la plupart des critères récents tels que l information mutuelle normalisée ou non, les rapports de corrélation ou les approches robustes, s avèrent particulièrement fiables sans recourir à aucun pré-traitement. Pour une description détaillée des différentes méthodes d optimisation auxquelles nous faisons allusion ici, nous renvoyons le lecteur vers [Press 92]. En ce qui concerne la stratégie d optimisation du critère, les méthodes itératives ne nécessitant pas de dériver le critère s avèrent de loin les plus utilisées. Citons notamment l algorithme de Powell [Pluim 00c, Pluim 00b, Pluim 01a, Sarrut 99, Sarrut 00, Roche 01a, Maes 97, Leventon 98, Zhu 02a] ou l algorithme du Simplex [Eberl 96, Brinkmann 99, Pfluger 00, Radau 01]. Ces deux approches sont des méthodes d optimisation locale. La méthode de Powell recherche l optimum d une fonction multi-dimensionnelle par optimisations 1D successives selon des directions mutuellement conjuguées dans l espace des paramètres. Chaque optimisation monodimensionnelle est généralement réalisée à l aide de la méthode de Brent. Si la fonctionnelle de coût à optimiser est quadratique, ces algorithmes convergent en un nombre fini d itérations. Pour certains critères, il est possible de disposer d une formulation analytique de la solution, c est notamment le cas lorsque l on se ramène à un problème de régression linéaire au sens des moindres carrés pour des petits déplacements [Barber 95, Friston 95a]. En pratique, la résolution peut nécessiter quelques itérations. Une approche similaire a été proposée par A. Roche [Roche 01a] pour rechercher la fonction de transformation en intensité f optimale (parmi les fonctions constantes par morceaux ou polynomiales, par exemple). Il combine séquentiellement l optimisation du rapport de corrélation généralisé suivant f par une méthode des moindres carrés itérés et suivant T par l algorithme de Powell : il s agit d une optimisation alternée. Des approches heuristiques de recherche exhaustive par un échantillonnage adaptatif de l espace des paramètres de T ont également été proposées: hill climbing optimization [Studholme 99, Studholme 95, Pluim 00b, Holden 00]. Ces approches sont couplées à une approche multirésolution, évoluant vers un échantillonnage de plus en plus fin de l espace des paramètres de T. D autres méthodes ont également été utilisées telles l algorithme de Levenberg-Marquardt [Alpert 96, Woods 98], ou des approches nécessitant de dériver le critère, comme l algorithme de Newton-Raphson [Woods 92, Woods 93, Woods 98]. Toutes ces méthodes d optimisation ne garantissent que le fait que la solution soit un optimum local. Quelques approches stochastiques permettant une optimisation globale ont également été proposées. Ainsi, Nikou et al. [Nikou 98, Nikou 99b] proposent une approche stochastique de type recuit simulé pour initialiser rapidement et grossièrement la solution dans le bon bassin d attraction, puis ils utilisent une approche locale pour affiner la solution. Wells et al. [WellsIII 96] proposent une descente de gradient stochastique pour maximiser l information mutuelle, dont la dérivée est évaluée grâce à l utilisation de la méthode de
120 Recalage basé sur des mesures statistiques de similarité Parzen pour le calcul de l histogramme joint. En pratique, pour éviter de tomber dans un optimum local et accélérer la recherche, de nombreuses stratégies multirésolution ont également été proposées. Elles consistent à initialiser le recalage en utilisant des données sous-échantillonnées, puis à se servir de ce résultat pour initialiser la recherche à une résolution plus fine et ainsi de suite. Différentes stratégies sont envisagées pour rééchantillonner les données, utilisant soit un simple souséchantillonnage, soit le calcul de la valeur moyenne des intensités du cube correspondant à la résolution plus fine, soit un lissage gaussien avant le sous-échantillonnage. Quelques études se sont intéressées à l influence de l algorithme d optimisation et de la stratégie multirésolution employés sur la qualité du recalage. Ainsi, Maes et al. [Maes 99] comparent 6 méthodes de maximisation de l information mutuelle, à savoir les méthodes de Powell, du simplex, de la descente de gradient, du gradient conjugué, de quasi-newton et de Levenberg-Marquardt. Ils proposent d ailleurs une méthode de calcul des dérivées de l information mutuelle lorsque l histogramme joint est estimé à l aide d une interpolation intrinsèque. Pluim et al. [Pluim 01b] étudient l impact sur la précision du recalage de différentes stratégie multirésolution, et mettent en garde sur le fait qu il ne faut pas trop sous-échantillonner des données de faible résolution spatiale comme la TEP. Concernant le recalage TEMP/IRM par maximisation de l information mutuelle, Thurjfell et al. [Thurjfell 00] étudient l influence sur la précision du recalage, de l échantillonnage en intensité des données lors de l estimation de l histogramme joint (nombre de bins de l histogramme). Il proposent d ailleurs une réduction adaptative du nombre de bins de l histogramme au cours d un processus de recherche multirésolution. Enfin, Zhu et al. [Zhu 02b] étudient l influence de la méthode d optimisation (Powell ou simplex) et de différentes approches multirésolution sur le recalage IRM/TEMP par maximisation de l information mutuelle Synthèse Nous venons de proposer une classification des divers critères statistiques de similarité utilisables à des fins de recalage. Notre classification distingue les critères considérant les images comme des variables aléatoires quantitatives et qualitatives. Au regard de cette distinction, nous proposons ici un travail de synthèse principalement réalisé à partir des travaux d A. Roche [Roche 01a] sur les approches quantitatives, et à partir de ceux de J. Pluim [Pluim 00b] et de D. Sarrut [Sarrut 00] sur les approches qualitatives. Pour chacun des critères statistiques présentés, l accent a été mis sur la manière dont l information est mesurée au sein d une image et sur la métrique utilisée pour comparer deux quantités d information, i.e., pour mesurer un lien statistique entre deux images. Ainsi, chacun des critères présentés pose des hypothèses sur la nature d un tel lien statistique (dépendance linéaire, dépendance fonctionnelle, écart à l indépendance). Quelques approches récentes tentent d estimer un tel lien à partir des données en posant le problème du recalage comme un problème d inférence statistique. La nature de ce lien statistique est en général difficilement identifiable en pratique, surtout lorsque l on cherche à recaler des données réelles, pathologiques notamment. Les performances des différentes méthodes de recalage, au regard de la validité des hypothèses concernant la nature du lien statistique sous-jacent, ne peuvent être appréhendées qu à partir de procédures d évaluation dédiées. L objet du prochain chapitre est de présenter de telles procédures de validation de méthodes de recalage.
121 Validation de méthodes de recalage : application aux recalages TEMP/IRM ou TEMP/TEMP 121 Chapitre 3 Validation de méthodes de recalage: application aux recalages TEMP/IRM ou TEMP/TEMP L utilisation en clinique de plus en plus répandue de techniques de traitement d image et principalement de méthodes de fusion et de recalage font de la validation une étape clé et incontournable lors de la mise au point de toute nouvelle méthode. La validation d une méthode de traitement d images médicales a pour objet la mise en évidence des caractéristiques intrinsèques de cette méthode, ainsi que l évaluation de ses performances et limites d utilisation. La validation permet alors de mettre clairement en évidence dans quel contexte clinique telle ou telle méthode est utilisable. La validation peut également démontrer la valeur ajoutée de l utilisation de telle méthode vis à vis d un impact sur l aide au diagnostic, la thérapie, la société ou encore l économie. La validation de méthodes de recalage utilisant des mesures statistiques de similarité, dans le contexte clinique qu est la mise en correspondance TEMP ictale/irm, est un aspect central de ce travail de thèse. Après avoir présenté au chapitre précédent une classification des mesures statistiques de similarité utilisables à des fins de recalage, nous allons présenter une classification des procédures de validation de ces méthodes de recalage. Pour cela, nous nous restreignons aux études portant sur la validation de méthodes de recalage basées mesures statistiques de similarité ou sur la validation de méthodes s adressant spécifiquement au problème du recalage de données TEMP ou TEP. Pour réaliser cette classification, nous nous sommes principalement inspiré d un modèle des procédures de validation de méthodes de traitement d images médicales qui est en cours de réalisation au laboratoire [Jannin 02] et qui n a pas encore fait l objet d une publication. Nous avons ainsi sélectionné les publications qui nous ont semblé les plus représentatives des études portant sur le recalage basé mesures statistiques de similarité ou du recalage intéressant des données TEMP ou TEP. Nous présentons ces études en distinguant les trois étapes clé d une procédure de validation : l énoncé d une hypothèse de validation, la mise en œuvre de la procédure de validation et notamment le choix de la transformation géométrique de référence, et le choix d une métrique de validation.
122 Classification des procédures de validation 3.1 Classification des procédures de validation La classification des références bibliographiques portant sur l évaluation de méthodes de recalage sélectionnées est présentée sur les tableaux 3.1, 3.3, 3.4 et 3.5. Nous avons opté pour classer les études en question en fonction du type de transformation géométrique de référence qui a été utilisé. En effet, l évaluation quantitative des performances d une méthode de recalage nécessite en général de comparer à une transformation géométrique de référence, la transformation géométrique fournie par la méthode de recalage en question. Ainsi, nous distinguons quatre familles de procédures de validation. La première consiste en l utilisation d une transformation géométrique de référence connue de manière absolue (voir table 3.1), on parle de gold standard (GS) absolu. Elle est principalement liée à l utilisation de fantômes physiques ou de simulations numériques. La seconde famille de procédures de validation concerne l utilisation de données prospectives acquises afin d obtenir une transformation géométrique de référence approchée. Parmi ces procédures de validation, on compte principalement les études utilisant des données prospectives acquises de manière invasive (voir table 3.3), comme par exemple l utilisation de cadres de stéréotaxie ou de marqueurs directement vissés sur le crâne du patient. La troisième catégorie de procédures de validation (voir table 3.4) ne donne accès également qu à une transformation géométrique de référence approchée, mais moins précise que la précédente, vu qu elle est obtenue par l acquisition de données prospectives via des techniques noninvasives (e.g. marqueurs collés sur la peau, systèmes de contention pendant l acquisition). Enfin, dans la dernière catégorie de procédures de validation présentée dans la table 3.5, nous présentons les études d évaluation dites sans gold standard, pour lesquelles aucune technique n a été spécifiquement mise en œuvre à des fins des validation avant l acquisition des données. La transformation géométrique de référence peut dans ce cas être une transformation géométrique moyenne issue de divers essais de recalage ou une transformation géométrique issue d une autre méthode de recalage. Lorsque plusieurs de ces approches sont mises en jeu dans une même publication, nous les avons indiqué sur la même ligne du tableau (entre deux traits continus). Par contre, une telle publication ne figurera que dans un seul des quatre tableaux. L approche qui nous a paru la plus significative nous a permis de choisir dans quel tableau placer une telle référence. La première colonne Référence indique le pointeur bibliographique dont il est question. Nous présentons maintenant une description des différentes colonnes du tableau, qui correspondent aux étapes clé du modèle des procédures de validation, précédemment mentionné. 3.2 Méthodes de recalage évaluées La colonne Méthodes décrit la ou les méthodes de recalage faisant l objet d un travail de validation ou de comparaison dans la publication en question. Nous ne précisons que la fonctionnelle de coût utilisée par la méthode de recalage. Même si les résultats ne figurent pas dans les tableaux, ce travail de classification nous a permis de proposer une revue des méthodes d optimisation et pré-traitements classiquement utilisés par les méthodes basées sur l optimisation d une mesure statistique de similarité (cf. I.2.2.6).
123 Validation de méthodes de recalage : application aux recalages TEMP/IRM ou TEMP/TEMP 123 Tab. 3.1 Etat de l art de méthodes de recalage basées mesures statistiques de similarité et de méthodes de recalage intéressant des données TEMP: Approches utilisant un GS absolu Hyp. de validation Mise en oeuvre Métrique de validation Référence Méthodes Niveau Modalités GS Données de Transfo. de Paramètres Type Mesurée Stat Desc. d éval. et contexte type validation réf. sur clin. [Strother 94] cadre Z, CA-CP, HH, PIE, CW ou URI [Barber 95] SDC (flot optique) [Nikou 98] SDC, CW, IM, SDCr, CWr [Brinkmann 99] Surf(Chamf.), IM, URI [Holden 00] SDC, CC, IM, IMN, H(diff),PI, URI, URI Holden [Stamatakis 01] SDC (norm. spatiale SPM), diff. fonct. non lin. T T IRM/TEP sujets sains TEMP intra- et inter-sujets T IRM/IRM (1 sujet) T/C T/C absolu simulations connue(aléat) 2 opérateurs E pts (cerveau) I(moy,max), G(moy,std) approx prospectives (contention) contrôle position 2 opérateurs E intensités I(CC), G(moy,std) absolu simulations connue bruit Poissonien E paramètres G(moy,std) approx prospectives contrôle position (Id) rec. vers template ou une donnée E intensités I(SDC), G(moy,std) absolu simulations connue(aléat) bruit E paramètres G(moy,std) objet test absolu fantôme contrôle position (par seq. IRM) TEMP interictale /IRM (1 sujet) TEMP ictale et inter-ictale IRM/IRM (sains ou déf. en hormone de croissance) T TEMP (lésions hypoperfusées) aucun rétrospectives rec. manuel par l expert E paramètres G(moy,std) bruit I paramètres G(moy,std) absolu fantôme connue E 1 seul pt G(moy) aov approx fantôme contrôle position E 1 seul pt G(moy) aov absolu simulations connue E 1 seul pt G(moy) aov aucun rétrospectives I Intensités I(std(diff)), G(moy) aov absolu simulations connue seg. cerveau, E pts (cerveau) I(moy, bruit, inhom. eqm,max), RF G(moy,std) aucun rétrospectives Id: consistence à 2 ou 3 niveaux absolu simulations Id amplitude et extension des zones patho. simulées seg. cerveau I pts (cerveau) I(moy, eqm,max), G(moy,std) E intensité I(% vol. patho, SDC) Test stat. t-tests appariés test du signe ou Wilcoxon
124 Méthodes de recalage évaluées Tab. 3.3 Etat de l art de méthodes de recalage basées mesures statistiques de similarité et de méthodes de recalage intéressant des données TEMP: Approches utilisant un GS approché par méthodes invasives (base de données Vanderbilt essentiellement) Hyp. de validation Mise en oeuvre Métrique de validation Référence Méthodes Niveau Modalités GS Données de Transfo. de Paramètres Type Mesurée Stat Desc. d éval. et contexte type validation réf. sur clin. [Woods 93] CW C IRM / TEP sujets sains et épileptiques [West 96] Surf(Chamf), T IRM / CT / approx prospectives [West 97] IM, CC, HH, TEP (vdb) PIE, CW,...16 méthodes [WellsIII 96] IM T IRM / CT approx prospectives (vdb) [Maes 97] IM T IRM / CT / TEP approx prospectives marqueurs osseux marqueurs osseux marqueurs osseux + connue(aléat) marqueurs approx prospectives (vdb) osseux IRM / CT aucun rétrospectives rec. avec CC sur courbures [Maes 99] IM T IRM / CT approx prospectives (vdb) [Studholme 99] H, IM, IMN T IRM / CT approx prospectives /TEP (vdb) [Nikou 99a] Chap. 5 [Sarrut 00] Chap. 2 CWr T IRM / CT /TEP 19 mes. de similarité : f- info, RC,... [Pluim 00c] IM, IMN, Gr., IM+Gr [Pluim 01a] [Roche 01a] Chap mes. de similarité : f- info,... IM, 6 versions du RCg T T T T IRM / CT /TEP IRM / CT /TEP IRM / CT /TEP IRM / CT /TEP a correction ou non des distorsions géométriques b choix de l ordre volume de référence / volume flottant approx approx approx approx approx prospectives (vdb) prospectives (vdb) prospectives (vdb) prospectives (vdb) prospectives (vdb) [VanDenElsen 95] marqueurs osseux marqueurs osseux + connue(aléat) marqueurs osseux marqueurs osseux marqueurs osseux marqueurs osseux marqueurs osseux multirés. E pts (cerveau) dist. géom. a E pts (10 VOIs) I(moy,max), G(moy) G(med, max) E paramètres G(std) t-tests appariés E pts (8) et interpolation, I(moy,max) ordre b param. interpolation, E pts (8) et I(moy,max) ordre, souséch., param. recouv. partiel optimisation, E paramètres G(moy,min, multirés. max,std) recouv. partiel E pts (8) I(moy) Test stat. t-tests échantillonnage E pts (6-10) G(med,max) class. med par rapport à [West 97] dist. géom., E pts (10) I(eqm), sous-éch. G(moy) dist. géom. E pts (8) I(eqm), G(med,max) dist. géom. E pts (8) I(eqm), G(moy,std, med,q90) initialisation E 1 pt + param. (rot.) I(eqm), G(eqm,med) t-tests appariés, Wilcoxon t-tests appariés
125 Validation de méthodes de recalage : application aux recalages TEMP/IRM ou TEMP/TEMP 125 Tab. 3.4 Etat de l art de méthodes de recalage basées mesures statistiques de similarité et de méthodes de recalage intéressant des données TEMP: Approches utilisant un GS approché par méthodes non invasives (marqueurs peau, fantômes, contrôle de la position lors de l acquisition) Hyp. de validation Mise en oeuvre Métrique de validation Référence Méthodes Niveau Modalités GS Données de Transfo. de Paramètres Type Mesurée Stat Desc. d éval. et contexte type validation réf. sur clin. [Barnden 00] IM, SDC SPM, RCL2, CW, CW Ardekani [Eberl 96] SDA, CSS, SDP, URI [Ardekani 95] CW à partir de classif. IRM C IRM / TEMP T/C TEP / TEMP Em + Trans. a C TEMP ictale, interictale IRM / TEP (sujets sains) approx prospectives marqueurs peau approx fantôme marqueurs peau approx fantôme contrôle position aucun rétrospectives points anatomiques désignés visuellement approx prospectives contrôle position (contention) (Id) approx prospectives 3 marqueurs peau [Woods 92] URI T TEP approx fantôme contrôle position [Leventon 98] Log. vraisemblance [Zhu 02a] IM, H, H cond. Log. vraisemblance approx prospectives contrôle position T IRM / IRM approx prospectives contrôle position (Id) + connue T/C TEMP Em. approx prospectives contrôle position + Trans. (Id) IRM / approx prospectives contrôle position TEMP Em. TEMP + Trans. (Id) + consistence via IRM / TEMP Em. IRM aucun rétrospectives transfo. moy (5 rec. manuels) + connue(aléat) lissage, foyers hyperperfusés E E points (marqueurs, cerveau, surface) points (marqueurs) I(moy) G(moy,max, std) G(moy,max, std) E paramètres G(moy,max, std) I pts G(moy,max, std) E paramètres G(moy,std) E pts (3) G(moy) E pts (cerveau) I(moy,max) E pts (cerveau) I(moy,max) E pts (8) I(moy) E paramètres G(moy,std) E paramètres G(moy,std) I paramètres G(moy,std) Test stat. a acquisitions en émission et transmission
126 Tab. 3.5 Etat de l art de méthodes de recalage basées mesures statistiques de similarité et de méthodes de recalage intéressant des données TEMP: Approches sans GS Méthodes de recalage évaluées Hyp. de validation Mise en oeuvre Métrique de validation Référence Méthodes Niveau Modalités GS Données de Transfo. de Paramètres Type Mesurée Stat Desc. d éval. et contexte type validation réf. sur clin. [VanHerk 94] Surf (Chamf.) C IRM / CT / TEMP aucun rétrospectives rec. haute rés. (ts les pts) + connue(aléat) T/C TEP / TEP aucun rétrospectives URI (implém. [Studholme 95] CC, CW, C IRM / TEP aucun rétrospectives rec. manuel M 3 (H), H basé pts anat. + connue(aléat) [Alpert 96] SDC, URI, SDC Alpert AIR) CW Alpert, IRM / TEP aucun rétrospectives CW (implém. CW AIR) [demunck 98] Surf(Chamf.) T/C IRM / aucun rétrospectives rec. haute rés. TEMP optimal + connue(aléat) [Woods 98] [Pfluger 00] [Radau 01] SDC, SDC Alpert, URI Interactif, HH, CW SDA, SDCr, IMN T/C IRM / IRM aucun rétrospectives transfo. moy. accordante (reconciled) : consistence C IRM / TEMP nb pts surface, Coût = dist. moy, eqm ou max recouv. partiel seg. cerveau (seuils) TEP / TEP approx fantôme contrôle pos. lissage, souséch,... TEP / TEP aucun fantôme contrôle pos. lissage, souséch, + consistence... aucun rétrospectives transfo moy sur essais semiautomatiques + connue(aléat) T/C TEMP sujets sains et Alzheimer (inter-sujet) t-tests appariés TEMP sujets sains (inter-sujet) [Zhu 02b] IM C IRM / TEMP Em + Trans aucun rétrospectives 3 rec de réf (avec seg., interp. et moy sur essais) + connue(aléat) aucun a test de Kolmogorov de comparaison des distributions des erreurs simulations (patho) rec. sans patho simulée aucun rétrospectives rec. IM [Maes 97] I pts (surface) I(dist. moy), G(moy,std, étendue) I paramètre I(eqm), G(moy,std) I paramètres G(moy,eqm, max) I paramètres G(moy,eqm, max) I pts (surface) I(dist. moy), G(moy,std, étendue) lissage I pts (cerveau) E pts (cerveau) I pts (cerveau) opérateurs I pts (cerveau) interpolation, optimisation, multirés.... I(moy,max), G(moy,max) G(moy,eqm, max) G(moy,eqm, max) I(moy), G(moy,std, max) I pts (6) I(max), G(moy,med, std, Q70,Q90) I pts (6) I(max), G(moy,std) I paramètres G(moy,std) Test stat. tests K. a de tests de K. tests de K. t-tests appariés, aov
127 Validation de méthodes de recalage : application aux recalages TEMP/IRM ou TEMP/TEMP 127 Les notations suivantes ont été utilisées dans les tableaux. Lorsqu il s agit d une mesure statistique de similarité présentée au chapitre I.2, le numéro de l équation correspondante est indiqué : Cadre Z: ajustement des formes en Z du cadre de stéréotaxie de Fisher CA-CP : Recalage vers le quadrillage proportionnel de Talairach et Tournoux [Talairach 88] HH - Head-Hat : recalage basé mise en correspondance de surfaces proposé par Pelizzari et al. [Pelizzari 89] PIE : points internes équivalents: désignation interactive de points anatomiques homologues dans les deux images diff: image de différence CSS : changements de signe stochastiques H: entropie jointe (équation 2.82) H cond. : entropie conditionnelle H(diff) : entropie de l image de différence M 3 (H): moment d ordre 3 de l entropie jointe (équation 2.81) PI : Profil d intensité (équation 2.80) IM : information mutuelle (équation 2.85) IMN: information mutuelle normalisée (équation 2.87) CW : critère de Woods (équation 2.78) CW Alpert : critère de Woods formalisé comme une erreur des moindres carrés avec une mise à l échelle des intensités CWr : critère de Woods avec norme robuste URI : uniformité du rapport des intensités (équation 2.64) CC : coefficient de corrélation (équation 2.62) SDC : somme des différences au carré ou erreur des moindres carrés (équation 2.58) SDC Alpert : erreur des moindres carrés avec mise à l échelle des intensités (équation 2.59) SDA: somme des différences absolues en norme L1 (équation 2.60) SDP : somme des produits SDCr : erreur des moindres carrés avec norme robuste RCg : rapport de corrélation généralisé (équation 2.67) RCL2 : rapport de corrélation en norme quadratique L2 (équation 2.71) RCL1 : rapport de corrélation en norme L1 (équation 2.75) Gr : information provenant du gradient des images IM+Gr : combinaison de IM et du Gr. 3.3 Hypothèse de validation Définir un objectif de validation revient à formaliser la ou les questions auxquelles devra répondre la procédure de validation. Nous introduisons pour cela la notion d hypothèse de validation. L objectif d une procédure de validation est de confirmer ou non une hypothèse de validation, qui consiste en un postulat sur les performances de la méthode dans un
128 Mise en œuvre d une procédure de validation : contexte d utilisation précis. Une hypothèse de validation se formalise par la spécification d un niveau d évaluation, des caractéristiques des données mises en jeu (modalité, dimensions, résolutions) et d un contexte clinique. Confirmer ou non une hypothèse de validation peut se formaliser par la décision d un test d hypothèse, nécessitant alors le recours à une métrique de validation. En général, les références que nous avons étudiées ne répondent que rarement à une seule question bien précise vis à vis de leurs objectifs de validation, mais étudient plutôt plusieurs aspects de la méthode de recalage. Qui plus est, lorsqu un objectif de validation est clairement affiché, ils n y répondent que rarement à l aide de tests d hypothèse. Ainsi, nous omettrons de formuler précisément toutes les hypothèses de validation de chaque référence. Par contre, dans chaque cas, nous précisons les éléments fondamentaux pour l énoncé d une hypothèse de validation : le niveau d évaluation, les caractéristiques intrinsèques des données mises en jeu et le contexte clinique. Niveau d évaluation: Pour chaque référence, nous précisons si le niveau d évaluation de la procédure de validation est technique (T), clinique(c) ou les deux (T/C). Un niveau d évaluation technique correspond à une phase de réglage des paramètres de la méthode, afin d obtenir des performances optimales. Cela peut consister par exemple en l étude de différentes stratégies d optimisation [Maes 99]. Un niveau d évaluation clinique consiste en l étude des performances de telle méthode dans un contexte clinique d utilisation précis. Citons par exemple, l étude de l influence de zones pathologiques hyper- ou hypo-perfusées en TEMP sur la précision du recalage [Brinkmann 99, Stamatakis 01, Radau 01]. Caractéristiques intrinsèques des données: Il s agit de préciser le type de modalités d imagerie utilisées par l étude ainsi que diverses caractéristiques intrinsèques à ces données telles que les dimensions du champ de vue et de l échantillonnage, ou encore la résolution spatiale. Des propriétés informant sur le type de données à recaler permettent également de poser des a priori sur le type de transformation géométrique recherchée (rigide, affine ou non linéaire). Dans les tableaux, seuls les types de modalités d imagerie utilisées sont indiqués. Contexte clinique: Le contexte clinique permet de préciser en vue de quelle utilisation clinique est mise en œuvre la procédure d évaluation. Lorsque ce contexte clinique est indiqué par les auteurs, nous précisons si l étude porte sur des données provenant de sujets sains ou pathologiques. Dans ce dernier cas, nous indiquons de quelle pathologie il est question. 3.4 Mise en œuvre d une procédure de validation: La mise en œuvre d une procédure de validation de méthodes de recalage nécessite de se doter de données dites de validation et de paramètres en entrée de la procédure. Ces données et paramètres sont alors utilisés à la fois par la méthode de recalage à valider et par la méthode de calcul d une transformation géométrique de référence. Il est alors possible de valider la méthode dans différentes configurations en faisant varier les paramètres. Si la transformation géométrique de référence correspond à une vérité terrain, on parle d évaluation avec gold standard (GS). Une évaluation sera dite sans gold standard lorsque rien n aura été mis en œuvre pour contrôler la position de la tête du sujet au moment de
129 Validation de méthodes de recalage : application aux recalages TEMP/IRM ou TEMP/TEMP 129 l acquisition. Dans les tableaux, nous indiquons successivement le type de GS, les données de validation, la méthode de calcul de la transformation de référence et les paramètres Type de gold standard Dans la colonne GS type, on précise si la procédure de validation en question fait appel à un gold standard absolu ( absolu ), approché ( approx ) ou si elle ne fait appel à aucun gold standard ( aucun ) Données de validation Les données de validation sont par définition les données images utilisées par la procédure de validation. Le type de GS utilisé dépend du choix des données de validation. Nous distinguons quatre types de données de validation : les fantômes physiques, les simulations numériques, les données prospectives et les données rétrospectives. Fantômes physiques: Le fantôme de tête proposé par Hoffman et al. [Hoffman 90] est certainement le plus couramment utilisé en médecine nucléaire. Il permet de tenir compte d acquisitions réelles. Son modèle à trois compartiments (moules de plexyglass) le rend néanmoins difficilement utilisable pour simuler des contextes pathologiques complexes. Il a été largement utilisé à des fins d évaluation de méthodes de recalage en TEP [Woods 92, Woods 98] ou en TEMP [Eberl 96, Brinkmann 99]. Suivant les précautions prises à l acquisition, le GS associé peut être absolu ou approché. Simulations numériques: Les simulations numériques donnent en principe accès à un GS absolu, vu qu en général les données simulées sont déduites d une même donnée d origine (souvent une IRM). Les méthodes les plus utilisées simulent les processus physiques liés à la génération et à l acquisition des données TEMP [Barber 95], TEP [Strother 94] ou IRM [Holden 00]. D autres auteurs ont proposé de simuler des zones pathologiques par modification locale des contrastes de données réelles et étudient leurs influences sur la précision des méthodes de recalage [Brinkmann 99, Stamatakis 01, Radau 01]. Données prospectives: Les données prospectives sont des données cliniques qui ont été spécialement acquises à des fins de recalage ou de validation de méthodes de recalage. Différents systèmes, invasifs ou non invasifs, sont envisageables pour contrôler la position du sujet dans l imageur au moment de l acquisition. Parmi les techniques invasives, citons l utilisation de marqueurs extrinsèques tels que la pose de cadres de stéréotaxie ou de marqueurs vissés sur le crâne, réalisée sur des patients candidats à une neurochirurgie. Ces approches donnent accès à un GS approché, vu qu il doit être estimé à partir des données, mais ce GS est néanmoins très précis. Acquises sur ce principe, les données Scanner X (CT), IRM et TEP mises à disposition de la communauté par l université de Vanderbilt constituent la base de données la plus connue pour l évaluation de méthodes de recalage (cf. toutes les références de la table 3.3). Ce sont les données qui ont été utilisées par le projet d évaluation rétrospective de méthodes de recalage mené par J. Fitzpatrick de l université de Vanderbilt [West 96, West 97]. Ce projet consistait en une évaluation multicentrique et en aveugle de différentes méthodes de recalage. La position des marqueurs
130 Mise en œuvre d une procédure de validation : sur les données avait été artificiellement effacée et n était connue que par les responsables du projet. Dans les tableaux, nous indiquons par vdb toutes les études qui utilisent cette base de données. Des données de validation prospectives peuvent également être obtenues à partir de méthodes nettement moins invasives (cf. table 3.4) comme par exemple l utilisation de marqueurs collés sur la peau [Barnden 00] ou encore l utilisation de systèmes de contention ou simplement de consignes pour éviter au maximum les mouvements de la tête du sujet entre deux acquisitions successives sur le même imageur [Ardekani 95, Zhu 02a]. Données rétrospectives: Les données dites rétrospectives sont des données cliniques pour lesquelles aucun système de contrôle de la position de la tête n a été utilisé lors de l acquisition. De telles données sont utilisées par les procédures d évaluation sans GS (cf. table 3.5) Calcul de la transformation de référence La colonne Transfo. de réf. indique la méthode utilisée pour calculer la transformation géométrique de référence. Lorsqu il s agit d une procédure d évaluation de méthodes de recalage avec GS, la transformation géométrique de référence est par définition ce GS. Suivant les cas, elle peut être parfaitement connue ou nécessiter d être estimée à partir des données. Lorsque des marqueurs extrinsèques sont utilisés (e.g. marqueurs vissés sur le crâne ou collés sur la peau), le calcul de la transformation géométrique de référence est en général obtenu par minimisation d une distance quadratique entre points homologues. Ces points homologues représentent les marqueurs dans les différentes images. La transformation géométrique de référence peut également être déduite de l utilisation de systèmes de contrôle de la position du sujet au moment de l acquisition. Citons par exemple l utilisation de systèmes de contention, la transformation géométrique de référence sera alors l identité ( Id ), ou encore le déplacement contrôlé du lit dans l imageur [Woods 92]. Dans le cas d une procédure d évaluation sans GS, la transformation géométrique de référence peut être simplement le résultat d une autre méthode de recalage [VanHerk 94, Alpert 96, demunck 98, Zhu 02b] éventuellement manuelle [Studholme 95, Nikou 98]. Elle peut également consister en une transformation géométrique moyenne déduite de plusieurs essais de recalages, souvent manuels, sur le même couple de données [Pfluger 00, Radau 01]. Pour les études de consistence, Woods et al. [Woods 98] introduisent la notion de transformation accordante moyenne ( reconciled mean transformation ) qu ils utilisent comme transformation de référence. Lorsque l on dispose d au minimum deux acquisitions du même sujet, une telle transformation est définie comme la transformation géométrique qui minimise les écarts entre points d une même donnée auxquels on applique toutes les combinaisons non redondantes de recalages permettant de réaliser un circuit fermé, et de se retrouver sur cette même donnée. Lorsqu on réalise un tel circuit fermé, la transformation géométrique de référence peut également être définie comme l identité [Holden 00]. Finalement, nombreux auteurs étudient également le comportement des méthodes de recalage lorsqu ils appliquent une transformation géométrique connue à l une des données. Cette technique permet d étudier les performances de la méthode d optimisation en évitant de partir d une position trop proche de la solution (fournie par le GS). Les paramètres d une telle transformation sont en général échantillonnés de manière aléatoire (cf. cases
131 Validation de méthodes de recalage : application aux recalages TEMP/IRM ou TEMP/TEMP 131 connue(aléat) dans les tableaux) Paramètres Les paramètres en entrée d une procédure de validation peuvent concerner la qualité des données à recaler comme par exemple l ajout d inhomogénéités RF en IRM ou de bruit, la correction ou non des distortions géométriques ( dist. géom. ), la segmentation préalable ou non du cerveau ( seg. cerveau ), la simulation de zones pathologiques ou encore le recouvrement partiel des données ( recouv. partiel ). Pour une même fonctionnelle de coût, ces paramètres concernent également l ajustement des différentes composantes de la méthode de recalage comme par exemple l algorithme d optimisation, la stratégie multirésolution ( multirés. ), la méthode de sous-échantillonnage ( sous-ech. ) ou de lissage des données, la méthode d interpolation, ou encore le nombre d opérateurs lorsqu il s agit d une méthode de recalage semi-automatique. 3.5 Métrique de validation: L évaluation quantitative d une méthode de recalage est obtenue par l estimation de l écart ou divergence ( discrepancy d après [Woods 98]) entre la transformation géométrique ˆT obtenue par la méthode de recalage à valider et la transformation géométrique de référence T ref Type de divergence (discrepancy) : erreur (E) ou inconsistence (I) Lorsque la transformation géométrique de référence T ref correspond à une vérité terrain (validation avec GS) alors cette mesure de divergence revient à une mesure d erreur (E) de recalage. Par contre, lorsque T ref ne correspond pas à une vérité terrain mais plutôt au résultat d une autre méthode de recalage ou à une transformation moyenne, Woods et al. [Woods 98] introduisent la notion de mesure d inconsistence (I) Objet de la mesure Dans la colonne Mesurée sur..., nous indiquons à partir de quelles informations est estimée cette mesure de divergence entre ˆT et T ref. Elle peut être réalisée directement à partir des paramètres des transformations (e.g. translations et rotations). Il est plus commode de fournir au clinicien une distribution spatiale de cette divergence, ainsi nombreux auteurs estiment cette divergence à partir d une liste de points comme par exemple les huit sommets de la boîte englobante de la tête du sujet (cf. pts(8) ), des points correspondant à des structures anatomiques d intérêt ou encore des points uniformément répartis sur la surface de la peau ou dans le cerveau. Pour quantifier cette divergence, certains auteurs utilisent également une mesure de similarité sur les intensités des images rééchantillonnées après recalage comme par exemple le coefficient de corrélation [Strother 94] ou la somme des différences au carré (SDC) [Barber 95].
132 Test d hypothèse Etude de la distribution des divergences La distribution des divergences (erreurs ou inconsistences) peut être appréhendée à différents niveaux. Nous reprenons et complétons ici les définitions proposées par Woods et al. [Woods 98] qui distinguent un niveau local, moyen, plural et global. Le niveau local (L) fait référence à une mesure de divergence réalisée en un seul point. Nous définissons le niveau intrinsèque (I) pour caractériser, à l aide de statistiques descriptives, la distribution spatiale des divergences pour un essai de recalage (i.e. un réglage des paramètres) sur un couple de données de validation d un même sujet. Lorsque pour un même sujet, plusieurs données de validation sont disponibles et plusieurs essais de recalage sont réalisés, le niveau plural (P) est défini pour caractériser la distribution de ces divergences. On utilisera la notion de divergence globale (G) pour caractériser les mesures de divergence obtenues lorsque la même procédure de validation est appliquée à des données de différents sujets. Pour plus de lisibilité dans les tableaux, nous n avons pas distingué les niveaux P et G, ils sont tous deux indiqués par la lettre G. Dans la colonne statistiques descriptives ( stat. desc. ), nous indiquons entre parenthèses, pour les niveaux intrinsèques I et globaux G, les statistiques descriptives utilisées pour caractériser la distribution des divergences à savoir : la moyenne empirique ( moy ), l erreur quadratique moyenne ( eqm ), la médiane ( med ), l écart-type ( std ), la dispersion en norme L1 ( displ1 ), le 90 ième quantile de la distribution ( Q90 ) ou encore la valeur maximale ( max ). Précision ( accuracy en anglais): Quel que soit le niveau où on l estime, la précision indique à quel degré une mesure est vraie ou correcte. On estime généralement la précision à partir de la tendance centrale de la distribution des divergences (e.g. moyenne empirique, erreur quadratique moyenne, médiane). Résolution ( precision en anglais): Par définition, si la divergence entre deux mises en correspondance théoriques est inférieure à la résolution, alors la méthode de recalage fournira la même solution dans les deux cas. La notion de résolution est donc liée à la notion de reproductibilité lorsqu on simule de faibles fluctuations autour de la solution. Elle est généralement estimée par une mesure de dispersion sur la distribution des divergences (e.g. écart-type, dispersion en norme L1). Robustesse: La robustesse fait référence à l étude des performances de la méthode en présence d éléments perturbateurs. Une telle étude est donc liée à la façon dont on fait varier les paramètres de validation. 3.6 Test d hypothèse L analyse statistique des résultats fournis par les métriques de validation peut être envisagée sous forme de tests d hypothèse (cf. colonne Test stat. ). La décision du test permet alors de rejeter ou non l hypothèse de validation que l on s était fixée au début de la procédure de validation. Dans la plupart des cas, il s agit de comparer la précision des méthodes entre elles à l aide de tests de comparaison de moyennes (tests de Student 2 à 2 : t-tests appariés ) [Barber 95, West 96, West 97, Maes 99, Pluim 00c, Pluim 01a, Radau 01], ou alors d évaluer de manière plus globale l effet du choix de la méthode ou de son implémentation sur la précision des résultats par une analyse de la variance ( aov )[Brinkmann 99,
133 Validation de méthodes de recalage : application aux recalages TEMP/IRM ou TEMP/TEMP 133 Radau 01]. Quelques approches non paramétriques ont également été utilisées (test du signe, test de Wilcoxon ou test de Kolmogorov)[Holden 00, Pluim 00c, Woods 98]. 3.7 Evaluation clinique qualitative L objectif de ces travaux est l évaluation quantitative du recalage TEMP/IRM à l aide de méthodes utilisant de critères statistiques de similarité, dans le contexte clinique du recalage TEMP ictale / IRM. La partie II de ce manuscrit expose la démarche mise en œuvre pour réaliser cette validation quantitative, elle constitue la principale contribution de ces travaux de thèse. Les différents concepts nécessaires à une procédure de validation, que nous venons de présenter, y sont alors exposés: hypothèse de validation, mise en œuvre (choix du Gold Standard, génération des données de validation, paramètres étudiés), métrique de validation et analyse statistique. En préambule, nous présentons ici les résultats d une pré-évaluation visuelle et qualitative du recalage de données cliniques TEMP / IRM dans le contexte de l épilepsie. Les données ictales et inter-ictales analysées sont celles qui ont permis la création des modèles théoriques de perfusion présentés au chapitre II.4 (cf II : choix d une population homogène). Trois mesures statistiques de similarité ont été étudiées, à savoir l information mutuelle (IM), le rapport de corrélation en norme L1 (RCL1) et le rapport de corrélation en norme L2 (RCL2). Les données TEMP ont été recalées soit directement à l IRM, soit aux données IRM après segmentation du cerveau. L optimisation des différents critères de similarité a été réalisée à l aide de la méthode d optimisation multi-dimensionnelle de Powell, associée à l algorithme de recherche mono-dimensionnelle de Brent [Press 92]. Une fois les différents recalages réalisés, l évaluation a été réalisée de manière visuelle vu qu aucun gold standard n était disponible. Les données TEMP ont été rééchantillonnées dans le référentiel de l IRM à l aide de la transformation géométrique estimée par la méthode de recalage évaluée. Deux types deux représentations ont alors été utilisées: (1) fusion des données TEMP sur l IRM à l aide d une texture couleur (2) fusion du masque de la matière grise segmenté à partir de l IRM sur les données TEMP à l aide d une texture couleur. La qualité du recalage a alors été jugée visuellement et un indice de qualité allant de 0 à 3 a été attribué à chaque recalage (0: recalage complètement aberrant, 1: erreur de quelques centimètres aisément détectable visuellement, 2: légère erreur de recalage à peine détectable visuellement, 3: recalage considéré comme de bonne qualité). La table 3.6 présente les résultats de cette pré-évaluation qualitative. Ces résultats montrent qu il est possible d atteindre 75% de recalages de bonne qualité. Ils semblent suggérer que la segmentation préalable du cerveau sur les données IRM a plus d impact sur le recalage utilisant le rapport de corrélation que sur celui utilisant l information mutuelle. Il existe néanmoins un certain nombre de cas où des erreurs importantes de recalage ont été observées, mais aucune tendance permet réellement de favoriser telle ou telle méthode par rapport aux autres. C est dans le but de mieux comprendre de telles observations qu une évaluation quantitative a été mise en œuvre.
134 Evaluation clinique qualitative sans segmentation avec segmentation du cerveau en IRM du cerveau en IRM Nom Données IM RCL1 RCL2 IM RCL1 RCL2 ARN. Ictal Interictal BLI. Ictal BLI. Interictal GRAV. Ictal LEB. Ictal InterIctal LECa. Ictal InterIctal LECb. Ictal LEVa. Ictal InterIctal LEVb. Ictal InterIctal AUG. Ictal GUE. Ictal Pourcentage % 81.25% 87.50% 87.50% 75% 93.75% Pourcentage 3 75% 37.50% 62.50% 75% 75% 75% Tab. 3.6 Résultat de l évaluation qualitative du recalage TEMP/IRM à partir de données cliniques ictales et inter-ictales. Méthodes de recalage évaluées: information mutuelle (IM), rapport de corrélation en norme L1 (RCL1), rapport de corrélation en norme L2 (RCL2). Indices de qualité utilisés: 0: recalage complètement aberrant, 1: erreur de quelques centimètres aisément détectable visuellement, 2: légère erreur de recalage à peine détectable visuellement, 3: recalage considéré comme de bonne qualité
135 135 Deuxième partie SIMULATIONS REALISTES D IMAGERIE TEMP POUR L EVALUATION DU RECALAGE TEMP/IRM
136
137 Position du problème 137 Position du problème : évaluation des méthodes de recalage utilisant des mesures statistiques de similarité entre des données de TEMP ictale et d IRM Dans le chapitre I.1, nous avons souligné l importance de la TEMP, acquise en condition ictale notamment, pour l exploration de la zone épileptogène. Or, l analyse objective des données TEMP est principalement limitée par le manque de repères anatomiques précis du fait de sa faible résolution spatiale. Un certain nombre de techniques de fusion de données permettent d assister son interprétation (e.g. superposition sur l IRM, soustraction TEMP ictale / TEMP inter-ictale, analyses inter-individuelles après normalisation spatiale). L étape de mise en correspondance géométrique des données apparaît comme incontournable lors de la mise en œuvre de ces méthodes de fusion. L objectif de ce travail de thèse est d évaluer les performances et la précision de méthodes de recalage TEMP/IRM, principalement lorsqu il s agit de traiter des données ictales. Nous avons montré au chapitre I.3 que les travaux d évaluation de méthodes de recalage mettant en jeu des données TEMP sont nettement moins nombreux que ceux impliquant des données IRM, Scanner X ou TEP. Ce constat peut notamment s expliquer par la difficulté de disposer d un gold standard précis en TEMP et par le fait qu il n existe pas de bases de données TEMP pour l évaluation, accessibles librement par la communauté scientifique. Concernant les données IRM, Scanner X ou TEP, le projet multicentrique d évaluation rétrospective de méthodes de recalage mené par l université de Vanderbilt [West 96, West 97] a mis à disposition de la communauté de telles données, pour lesquelles le gold standard était connu par l utilisation de cadres de stéréotaxie. Ces données ont été largement utilisées dans la section évaluation de nombreux articles portant sur le recalage (cf. tableau 3.3 du chapitre I.3). Les principales études portant spécifiquement sur l évaluation de méthodes de recalage TEMP/IRM ou TEMP/Scanner X n utilisent généralement pas de gold standard aussi précis que celui obtenu par l utilisation de cadres de stéréotaxie. A part Barnden et al. qui utilisent des marqueurs placés sur la peau [Barnden 00], la plupart de ces évaluations consistent en fait en une comparaison avec une technique de recalage particulière considérée comme référence ou en une comparaison avec une transformation géométrique moyenne [demunck 98, Nikou 98, Foehrenbach 99, Pfluger 00, Zhu 02a, Zhu 02b]. Parmi
138 138 Position du problème ces travaux, seuls Nikou et al. [Nikou 98] s intéressent au recalage TEMP ictale/irm et utilisent comme référence un recalage manuel réalisé par un expert. Les autres travaux étudient des données TEMP de sujets sains ou de sujets pathologiques présentant des maladies diffuses (e.g. Parkinson, Alzheimer). Or, il nous semble important de prendre en compte les perturbations souvent extrêmes de perfusion en condition ictale, lors de l évaluation du recalage. Quelques auteurs se sont intéressés à l influence des données ictales dans le cadre du recalage TEMP/TEMP [Eberl 96, Brinkmann 99] ou TEMP/TEP [Eberl 96], ou à l influence de foyers hypofixants sur la normalisation spatiale de données TEMP [Stamatakis 01, Radau 01]. En ce qui concerne l influence de foyers hypo- ou hyperfixants pathologiques sur le recalage, l utilisation de fantômes physiques [Woods 92] ou de simulations numériques [Brinkmann 99, Thurjfell 00, Stamatakis 01, Radau 01] permet alors d avoir accès à une référence absolue lors de l évaluation. L évaluation quantitative de l influence de foyers d hyperfixation en TEMP ictale sur les performances du recalage TEMP/IRM n a par contre pas été étudiée à notre connaissance. Une évaluation qualitative du recalage TEMP ictale/irm réalisée à partir des données cliniques analysées dans ce chapitre (cf. I.3.7), nous a montré la robustesse des méthodes de recalage basées mesures statistiques de similarité dans ce contexte. Les méthodes utilisant comme critère de similarité l information mutuelle, qu elle soit normalisée ou non, ou le rapport de corrélation, en norme L1 ou L2, se sont avérées particulièrement performantes. Malgré tout, il subsiste des cas de convergence du critère vers un optimum local qui a donné lieu à des erreurs de recalage détectables visuellement, voire à des mises en correspondance aberrantes. Pour comprendre de telles situations, notre objectif est de mener une évaluation quantitative et objective de ces méthodes de recalage utilisant des mesures statistiques de similarité, dans le contexte clinique mettant en jeu des données TEMP ictale et IRM. Nous nous proposons d étudier dans quelles mesures ce que l on pourrait appeler des dissimilarités intrinsèques entre les données TEMP ictales et IRM, influencent les performances des méthodes de recalage. Par dissimilarités intrinsèques, nous comprenons les situations complexes où de vastes régions hyperperfusées caractérisent la zone épileptogène en TEMP ictale, alors que l IRM morphologique est généralement considérée comme normale. Un des enjeux de ce travail est également de se doter d un environnement d expérimentation permettant d étudier quelles sont les limites de validité, en présence de telles dissimilarités intrinsèques, des hypothèses de similarité habituellement posées par les différents critères statistiques (e.g. dépendance linéaire, dépendance fonctionnelle, écart à l indépendance), et quelles en sont les conséquences sur les performances du recalage. Pour répondre à ces questions, nous avons mis en place un environnement d étude contrôlé permettant l accès à une référence absolue pour l évaluation de méthodes de recalage, mais aussi au contrôle du degré de dissimilarités intrinsèques entre données TEMP et IRM. Ainsi, nous proposons de générer des données de validation pour l évaluation de méthodes de recalage en simulant de façon réaliste des données TEMP à partir d une IRM. Notre méthode fournit une référence absolue pour la géométrie d acquisition, les simulations TEMP étant par construction en parfaite correspondance avec l IRM. La méthode proposée consiste en fait à coupler une méthode d analyse inter-individuelle de données TEMP par standardisation anatomique avec l utilisation d un simulateur de données TEMP réalistes. L aspect réaliste des simulations TEMP a tout d abord été géré par la modélisation de la géométrie et des différents processus physiques liés à la génération et à l acquisition de données TEMP. Pour cela, nous avons utilisé une modélisation haute-résolution de l ana-
139 Position du problème 139 tomie cérébrale, le modèle anthropomorphique proposé par Zubal et al. [Zubal 94], qui consiste en une IRM pondérée en T1 segmentée et étiquetée manuellement. La méthode de simulation consiste alors à définir, à partir de ce modèle de l anatomie, une carte théorique d atténuation des photons ainsi qu une carte théorique d activité représentant la distribution du radiotraceur de perfusion ( 99m Tc-HMPAO ou 99m Tc-ECD). La géométrie et la physique d une acquisition TEMP sont alors modélisées à partir de ces cartes d atténuation ou d activité, en utilisant des simulations analytiques ou de Monte Carlo. Notre méthode permet également de gérer le réalisme des simulations vis à vis de l information physiologique ou physiopathologique modélisée lors de la création de cette carte d activité. Ainsi, afin de contrôler, dans nos simulations, la fonction perfusion cérébrale et donc le degré de dissimilarités intrinsèques entre les données TEMP et IRM, nous proposons une méthode d analyse par standardisation anatomique de données TEMP d une population de sujets donnée, qui permet de créer, à la résolution de l IRM, un modèle théorique de perfusion normale ou pathologique. Cette méthode est appliquée à l étude d une population de sujets sains et à l étude de la perfusion ictale et inter-ictale d une population de sujets présentant une épilepsie temporo-mésiale. Au delà de la génération de cartes d activité réalistes et contrôlées pour l évaluation de méthodes de recalage, la méthode d analyse proposée nous semble prometteuse et informative vis à vis de la compréhension plus fondamentale d un profil de perfusion caractéristique d une population normale ou pathologique. Nous en présentons quelques résultats. Ces différents aspects vont être exposés dans les prochains chapitres selon l organisation suivante : Dans le chapitre II.4: Construction d un modèle théorique de perfusion ; nous présentons la méthode d analyse de données TEMP par standardisation anatomique. Nous l appliquons à l étude de la perfusion chez une population de sujets sains et à l étude de la perfusion inter-ictale et ictale chez une population de sujets présentant une épilepsie temporo-mésiale. L analyse statistique des résultats fournit quelques éléments de compréhension sur l organisation de ces patterns de perfusion. Dans le chapitre II.5: Génération des données de validation ; après un exposé des méthodes de simulations analytiques et de Monte Carlo utilisées, nous définissons, à partir des résultats du chapitre précédent, différentes cartes d activité modélisant différents contextes de dissimilarités intrinsèques entre données TEMP et IRM, avant de présenter les résultats des simulations. Dans le chapitre II.6: Evaluation de méthodes de recalage utilisant des mesures statistiques de similarité ; ce chapitre expose l utilisation de ces simulations pour évaluer des méthodes de recalage TEMP/IRM ou TEMP/TEMP dans les différents contextes de perfusion normale ou ictale présentés dans le chapitre précédent. L évaluation porte sur les cinq critères suivants: l information mutuelle, l information mutuelle normalisée, les rapports de corrélation en norme L1 et L2 et le critère de Woods.
140 140 Position du problème
141 Construction d un modèle théorique de perfusion par une analyse par standardisation anatomique 141 Chapitre 4 Construction d un modèle théorique de perfusion par une analyse par standardisation anatomique Notre objectif étant de simuler de manière réaliste des examens de TEMP caractéristiques d un profil de perfusion précis, l objectif de ce chapitre est précisément de proposer une méthode d analyse de données TEMP par standardisation anatomique pour permettre l identification d un tel profil de perfusion. Cette analyse de données TEMP réelles a ainsi pour objectif la création d un modèle théorique de perfusion. Le chapitre II.5 montrera alors comment simuler de manière réaliste des données TEMP, à partir de ce modèle théorique de perfusion, en modélisant également les processus liés à la géométrie et à la physique de l acquisition. Caractériser un profil de perfusion en TEMP, ou pattern, est une tâche délicate car elle nécessite à la fois une analyse quantitative des données TEMP (quantification relative) et une analyse inter-individuelle d une série d examens réalisés sur une population de sujets considérée comme homogène. La sélection de cette population dépend complètement du profil de perfusion que l on cherche à modéliser. Ainsi, nous appliquerons la méthode d analyse proposée ici à l étude de la perfusion chez une population de sujets sains, ainsi qu à l étude de la perfusion ictale et inter-ictale chez une population de patients présentant une épilepsie temporo-mésiale. Nous convenons néanmoins que l emploi de la terminologie modèle de perfusion peut paraître abusive, dans la mesure où aucun aspect dynamique n a été modélisé (notre objectif n est pas de proposer un modèle physiologique de la perfusion cérébrale). Idéalement, un tel modèle physiologique de perfusion cérébrale se devrait d être dynamique et de prendre en compte une modélisation hémodynamique du réseau vasculaire et surtout capillaire, ainsi qu une modélisation des échanges membranaires au niveau des capillaires et des cellules cérébrales (modèles compartimentaux notamment). Or, la TEMP ne donne accès qu à une photographie des variations moyennes de Débit Sanguin Cérébral régional (DSCr) qui ont eu lieu pendant une période de 15 secondes à 1 minute après l injection du traceur [Patterson 97], comme nous l avons vu au paragraphe I Qui plus est, si on utilise des traceurs tels que le 99m Tc-HMPAO ou le 99m Tc- ECD, il ne s agit que d une mesure relative et non absolue de DSCr. Ainsi, dans la suite de ce document, nous désignerons par modèle théorique de perfusion la modélisation des
142 Méthodes de reconstruction tomographique et de correction pour la quantification en TEMP mesures relatives de DSCr de cette photographie, caractéristique d un contexte clinique bien défini (par exemple, perfusion normale, perfusion ictale en épilepsie temporo-mésiale). La création d un modèle théorique de perfusion nécessite l analyse d une série d examens TEMP issus d une population homogène. Nous présentons donc tout d abord les principales limitations rencontrées lors d une analyse quantitative (même relative) en TEMP. Nous présentons les principaux phénomènes à l origine d une dégradation du signal en TEMP, et nous décrivons les méthodes de correction les plus couramment utilisées. Comme il s agit ensuite de réaliser une analyse inter-individuelle, une revue bibliographique des principales méthodes d analyse des données TEMP ou TEP par standardisation anatomique est présentée. Pour cette analyse, notre méthode consiste en la réalisation de mesures de l activité à l aide de volumes d intérêt (VOIs) positionnés automatiquement sur les données TEMP, préalablement normalisées spatialement. Ces VOIs sont déduits d un modèle spatial de l anatomie cérébrale, à savoir le fantôme anthropomorphique proposé par Zubal et al. [Zubal 94], que nous avons resegmenté pour l adapter à l étude des épilepsies. Les résultats des mesures réalisées sur les données de 27 sujets sains et de 10 sujets épileptiques sont ensuite présentés et analysés. Les données TEMP des 27 sujets sains nous ont été aimablement fournies par Dr. Leighton Barnden Ph.D. du service de Médecine Nucléaire du Queen Elizabeth Hospital (Woodville, Australie). Les 10 patients épileptiques étudiés ont été pris en charge et guéris par les services d épileptologie et de neurochirurgie de l hôpital de Rennes. L inférence statistique d un modèle théorique de perfusion à partir de ces mesures est une tâche délicate, surtout si l on veut gérer une certaine variabilité fonctionnelle physiologique ou physiopathologique au sein de chaque population. Afin d extraire de ces mesures de perfusion les informations pertinentes caractérisant les patterns étudiés, nous proposons quelques analyses statistiques: analyse statistique descriptive, étude de l effet de la localisation anatomique sur la perfusion et comparaisons inter-hémisphérique (comparaison de moyennes et analyse de la variance), utilisation de techniques de rééchantillonnage bootstrap pour palier le faible nombre d échantillons disponibles, et analyse factorielle des correspondances pour explorer la variabilité fonctionnelle au sein de chaque population. 4.1 Méthodes de reconstruction tomographique et de correction pour la quantification en TEMP Quels phénomènes dégradent le signal en TEMP? Interactions rayonnement - matière Lorsqu un photon électro-magnétique est émis, il interagit avec la matière selon quatre mécanismes indépendants [ElFakhri 98]: l absorption photoélectrique, la diffusion Compton (ou non cohérente), la diffusion Rayleigh (ou cohérente) et la création de paires. De ces phénomènes physiques à l échelle atomique, il résulte trois effets au niveau macroscopique, qui sont l atténuation, la diffusion et l émission de photons de fluorescence. Atténuation des photons : Lorsqu un faisceau de photons traverse une matière ou un tissu homogène d épaisseur d, il est progressivement atténué. Ceci signifie que les photons qui émergent dans la même direction que le faisceau incident ont la même énergie que les
143 Construction d un modèle théorique de perfusion par une analyse par standardisation anatomique 143 photons incidents, mais qu ils sont moins nombreux. L atténuation des photons traversant la matière suit une loi exponentielle décrite par : N = N 0 exp( µd) (4.1) où N et N 0 sont les nombres de photons après et avant le passage du faisceau à travers un milieu atténuant homogène d épaisseur d. µ (en cm 1 ) désigne le coefficient d atténuation linéaire, qui est spécifique du milieu traversé par le faisceau. Ce coefficient d atténuation linéaire résume au niveau macroscopique les différents phénomènes d interaction rayonnement-matière ayant lieu au niveau atomique. Il est relié au coefficient d atténuation atomique total µ a par : µ = µ a N 0 A ρ (4.2) où N 0 est le nombre d Avogadro, A le nombre de masse atomique de l élément rencontré par le faisceau et ρ sa densité. Le coefficient d atténuation atomique est alors défini comme la somme des sections efficaces de l effet photoélectrique, de la diffusion Compton, de la diffusion cohérente et de la création de paires: µ a = τ photo + σ Comp + σ coh + π pair (4.3) Comme nous nous limitons à l étude de la TEMP au 99m Tc (pic d émission à 140keV ), la création de paires sera négligée. En effet, elle n apparaît que pour des photons ayant une énergie supérieure à 1MeV. La répartition de ces sections efficaces est dépendante de l élément rencontré mais également de l énergie du photon incident. Effet photoélectrique : Cet effet est le phénomène essentiel permettant la détection de photons γ en TEMP. Lors d un effet photoélectrique, le photon γ percute un électron d une orbitale interne d un atome. Le photon est alors complètement absorbé et l électron est alors expulsé de son orbitale : on l appelle alors photo-électron. Ainsi, toute l énergie du photon γ se répartit entre l énergie nécessaire pour arracher l électron de son orbitale (énergie de liaison) et en énergie cinétique communiquée à cet électron. Lorsqu un électron d une orbitale supérieure (donc plus énergétique) vient prendre la place de l électron expulsé, il perd donc de l énergie, ce qui provoque l émission d un photon dit photon de fluorescence (voir figure 4.1). C est précisément ce phénomène qui, dans le cristal scintillant, permet la conversion de l énergie des photons γ incidents en énergie lumineuse qui atteindra les photomultiplicateurs. Par contre, lorsqu une interaction de type photoélectrique a lieu avant le cristal (dans la tête du sujet ou dans le collimateur), le photon est alors perdu pour la détection. Diffusion Compton : Lors de la diffusion Compton, les photons γ interagissent avec les électrons faiblement liés à l atome. Ils transfèrent alors une partie de leur énergie E sous forme d énergie cinétique E c et sont légèrement déviés d un angle θ par rapport à la trajectoire incidente (voir figure 4.2). L énergie du photon diffusé E d est donnée par : E d = E 1 + E (1 cosθ) mc 2 (4.4)
144 Méthodes de reconstruction tomographique et de correction pour la quantification en TEMP Fig. 4.1 L effet photo-électrique (d après [Bruyant 02b]) Fig. 4.2 Principe de la diffusion Compton (d après [Bruyant 02b]) où m désigne la masse de l électron et c la vitesse de la lumière (mc 2 = 511keV ). Aux énergies habituellement utilisées en TEMP, c est la diffusion Compton qui est le phénomène d interaction prédominant dans les tissus mous de l organisme. Diffusion Cohérente ou diffusion Rayleigh : Lors d une diffusion cohérente, le photon est également dévié mais ne subit pas une perte d énergie appréciable car la variation de sa quantité de mouvement est transmise à l atome tout entier et non à un seul électron Bruit stochastique d acquisition C est précisément l émission radioactive qui est à l origine de la composante stochastique du signal étudié en médecine nucléaire. La probabilité qu un radiotraceur émette un photon γ pendant un intervalle de temps τ infiniment petit par rapport à sa période de décroissance est proportionnelle à la durée de cet intervalle τ [MarianoGoulart 98]. Ainsi, on peut considérer qu un seul photon est émis à la fois, que le nombre de photons émis pendant un intervalle de temps τ ne dépend que de cet intervalle, et que les émissions sont indépendantes les unes des autres: ces propriétés décrivent donc un processus de Poisson. Ainsi, le nombre de photons N émis par unité de temps peut être considéré comme une variable aléatoire qui suit une loi de Poisson P(λ): Prob(N = n) = exp( λ)λn (4.5) λ! où λ désigne le nombre moyen d émissions par unité de temps. Une loi de Poisson P(λ) admet pour espérance mathématique E(N) = λ et pour variance V ar(n) = λ. Ainsi, si on caractérise le rapport signal sur bruit par le rapport moyenne sur écart-type, il vaudra (λ). Vu que la somme de variables aléatoires indépendantes suivant une loi de Poisson est également une variable aléatoire suivant une loi de Poisson, on considérera le nombre de coups obtenu dans chaque pixel des projections comme la réalisation d une variable aléatoire suivant une loi de Poisson. Vu les faibles doses injectées en imagerie diagnostique, le paramètre λ est en général faible. De ce fait, la loi de Poisson ne peut pas être approchée de façon satisfaisante par une loi gaussienne.
145 Construction d un modèle théorique de perfusion par une analyse par standardisation anatomique Limitations technologiques du détecteur Nous avons que vu les interactions rayonnement-matière à l origine de l atténuation des faisceaux de photons contribuaient à la dégradation du signal recueilli en TEMP. Il est cependant nécessaire de considérer à présent les limitations technologiques intrinsèques au détecteur. Notons que les différentes interactions décrites précédemment ont également lieu dans le détecteur (c est d ailleurs l effet photoélectrique au niveau du cristal scintillant qui permet l acquisition du signal). Résolution spatiale du détecteur : La fonction du collimateur est de sélectionner les photons qui arrivent jusqu au détecteur suivant une direction perpendiculaire au plan de projection (pour les collimateurs parallèles). Les photons qui arrivent suivant une direction faisant un angle α avec la normale au plan de projection sont arrêtés par les septa de plomb du collimateur, si α > alpha acc. alpha acc est l angle d acceptance du collimateur, et dépend des caractéristiques géométriques de celui-ci. Les caractéristiques géométriques du collimateur (diamètre et longueur des trous, épaisseur des septa, géométrie parallèle ou Fan Beam) permettent de définir la composante géométrique de la résolution spatiale du collimateur R c, pour laquelle un formulation analytique est disponible [ElFakhri 98]. Ainsi, deux photons qui atteignent le collimateur suivant une direction acceptée, ne pourront être détectés séparément que s ils sont distants de plus de R c. Lorsqu il arrive au niveau du cristal, le photon interagit principalement par effet photoélectrique permettant l émission d un photo-électron et d un photon de fluorescence. Ce photo-électron a une énergie suffisante pour provoquer à son tour l expulsion de nombreux autres électrons dans le cristal par effet photoélectrique. Il s en suit donc l émission de plusieurs photons de fluorescence dans le proche UV: c est la scintillation. Ainsi, l arrivée d un photon sur le cristal va provoquer la création d une tâche lumineuse. Combinée à la précision du système de localisation d un événement par les photomultiplicateurs, les dimensions de cette tâche permettent de définir la résolution spatiale intrinsèque R i du système de détection (cristal+photomultiplicateur). La résolution spatiale résultante du détecteur R sera alors définie par : R 2 = R 2 i + R 2 c (4.6) Rappelons que par définition, la résolution spatiale est la distance minimale à partir de laquelle deux sources distinctes peuvent être considérées comme distinctes dans l image. Résolution énergétique finie : Le système (cristal+photomultiplicateur) est caractérisé par une résolution spatiale intrinsèque R i mais aussi par une résolution énergétique finie. Les photomultiplicateurs permettent d estimer l énergie de l événement détecté (par intégration spatio-temporelle du signal sur les photomultiplicateurs voisins). Ainsi, en théorie, la détection d un photon primaire arrivant sur le cristal devrait correspondre à un pic d énergie au niveau du signal (dirac). Or, on observe plutôt un spectre continu d énergie autour du principal pic d émission. Ainsi, le système ne pourra différencier des photons primaires et diffusés ayant des énergies très proches. On caractérise généralement cette résolution en énergie par une gaussienne de largeur à mi-hauteur (LMH) de l ordre de 10% du pic primaire d émission (e.g. 140 kev pour le 99m Tc).
146 Méthodes de reconstruction tomographique et de correction pour la quantification en TEMP Perte de résolution en profondeur: La perte de résolution est liée à la fonction de réponse du collimateur. Celle ci peut être modélisée par une gaussienne dont la LMH augmente avec la distance de la source au collimateur. Pour être modélisé ou corrigé, cet effet doit être calibré en réalisant l acquisition d une source ponctuelle à différentes distances du détecteur, et en mesurant la LMH sur l image de projection obtenue L effet de volume partiel: La résolution spatiale limitée du détecteur introduit un effet dit de volume partiel lorsque la taille des structures considérées est inférieure à trois fois la LMH de la réponse impulsionnelle du système. L effet de volume partiel résulte donc d une inadéquation entre le taille de la structure imagée, la résolution spatiale du système d imagerie et l échantillonnage spatial du système d imagerie (taille du pixel). L effet de volume partiel résulte de la convolution d un tel profil par la réponse impulsionnelle du système d imagerie (de LMH supérieure), on observe alors une diminution du maximum du signal et une dispersion plus importante. Ainsi, l effet de volume partiel se manifeste par une sous-estimation du signal au niveau des structures de petites tailles, ainsi que par une contamination du signal de cette structure sur les pixels voisins Techniques de reconstruction tomographique Nous présentons à présent les principales techniques de reconstruction tomographique qui permettent de reconstruire la distribution tridimensionnelle du traceur à partir d une série de projections. Nous détaillons un peu plus la méthode de rétroprojection filtrée vu qu il s agit de la seule méthode qui a été utilisée pour ce travail. Pour une revue plus détaillée des méthodes de reconstruction tomographique par rétroprojection filtrée ou par des méthodes itératives, nous renvoyons le lecteur vers [Barrett 92, Dubois 98, Darcourt 98, Bruyant 02a]. La plupart des méthodes de reconstruction peuvent être considérées comme la reconstruction séquentielle par la même méthode de chaque coupe axiale de l objet imagé (coupes perpendiculaires à l axe de rotation du tomographe) afin d en reconstruire le volume. Ainsi, pour plus de clarté, nous limitons l exposé de ces méthodes dans le cas de la reconstruction d une image bidimensionnelle. On désigne par f(x,y) la fonction décrivant la répartition théorique du radiotraceur dans l image. L objectif de la reconstruction tomographique est d estimer f à partir d une série de projections P θ (u). Soit (Ox,Oy) le repère de l image f, on désigne par (Ou,Ov) le repère tournant faisant un angle θ avec Ox. P θ (u) n est autre que la projection orthogonale de f(x,y) suivant la direction 0v (voir figure 4.3). Dans le cas discret, on désignera par dim x et dim y les dimensions de l image f, par td le nombre d échantillons mesurés sur P θ (nombre de dexels ou bins de la projection) et par P le nombre de projections. En pratique, on aura typiquement dim x = dim y = 128, td = 128 et p = 64.
147 Construction d un modèle théorique de perfusion par une analyse par standardisation anatomique 147 Ov P(u) θ Ou Oy Ou f(x,y) θ Ox Fig. 4.3 Géométrie de l acquisition en projection Rétroprojection filtrée: Si l on considère l image f et la projection P θ comme des fonctions continues, alors il vient : { x = ucosθ vsinθ P θ (u) = f(x,y)dv = R(f) avec : (4.7) y = usinθ + vcosθ v Cette transformation désigne par définition la transformée de Radon R d une image f. En prenant la transformée de Fourier de la projection P θ (u) et en utilisant un changement de repère pour passer en coordonnées polaires, on montre alors le théorème de la coupe centrale qui énonce : P θ (ν) = f(ν x,ν y ) avec : { νx = νcosθ ν y = νsinθ (4.8) où P θ désigne la transformée de Fourier monodimensionnelle de P θ comme fonction de u (ν étant la fréquence spatiale correspondante). De même, f désigne la transformée de Fourier bidimensionnelle de l image f (ν x et ν y sont les fréquences spatiales correspondantes). Ce théorème est fondamental vu qu il montre qu à l aide des transformées de Fourier 1D de projections successives, il est possible de remplir le plan de Fourier 2D de l image. On utilisera alors une transformée de Fourier 2D inverse pour retrouver l image. On montre ainsi qu il est possible de reconstruire l image f à partir des projections, à savoir : f(x,y) = π 0 ˆP θ (u)dθ avec : ˆPθ (u) = P θ (ν) ν exp(2iπνu) dν (4.9) où ˆP θ (u) résulte de la transformée de Fourier inverse de P θ (ν) préalablement multipliée par ν. Ainsi, ˆPθ (u) est en fait une version filtrée des projections d origine P θ (u), et la
148 Méthodes de reconstruction tomographique et de correction pour la quantification en TEMP transformée de Fourier de la réponse impulsionnelle du filtre utilisé n est autre que ν. Il s agit donc d un filtre passe haut qui annule la composante continue et amplifie considérablement les hautes fréquences: le filtre rampe. L équation 4.9 montre alors qu il est possible de reconstruire l image f par épandages successifs sur l image des différentes projections préalablement filtrées. Le filtrage rampe permet notamment de limiter les artéfacts en étoile causés par l épandage. La formulation dans le cas discret de cette reconstruction impose de tenir compte des contraintes habituelles liées à l échantillonnage, notamment du fait de la théorie de Shannon 1. Du fait du théorème de la coupe centrale, l échantillonnage doit être réalisé de manière radiale. L échantillonnage sur chaque projection et le nombre de projections doivent être choisis pour satisfaire aux contraintes d échantillonnage (voir [Barrett 92]). Le filtre rampe présente néanmoins un problème, vu qu il amplifie considérablement les hautes fréquences du signal, et, par là même, le bruit. Il est donc nécessaire de l associer à un filtre lissant (on parle d apodisation). Plusieurs stratégies sont envisageables: on filtre les projections avec un filtre lissant en même temps que le filtre rampe pendant la reconstruction (multiplication dans le domaine fréquentiel par exemple), on filtre préalablement les projections avec un filtre lissant 1D, puis on reconstruit les données avec un filtre rampe, on reconstruit les données avec un filtre rampe, puis on filtre chaque coupe reconstruite avec un filtre lissant 2D, on reconstruit toutes les coupes avec un filtre rampe, puis on filtre tout le volume ainsi reconstruit avec un filtre lissant 3D. Il n existe pas de technique optimale pour choisir et régler le filtre lissant. Le choix d un filtre et notamment de sa fréquence de coupure résulte classiquement d un compromis entre sensibilité de l image et résolution spatiale. La détermination de la fréquence de coupure dépend du niveau de bruit statistique. Pour toutes les données reconstruites que nous présenterons par la suite, qu il s agisse d acquisitions réelles ou simulées, nous avons toujours utilisé la même technique de reconstruction. Ainsi, toutes les données sont reconstruites par rétroprojection filtrée avec un filtre rampe de fréquence de coupure égale à la fréquence de Nyquist (moitié de la fréquence d échantillonnage). Le volume reconstruit est ensuite postfiltré à l aide d un filtre gaussien 3D (voir figure 4.4). Le réglage de la LMH du filtre est fonction de la résolution spatiale attendue dans les données reconstruites (voir II ) Méthodes itératives La deuxième grande famille de méthodes de reconstruction tomographique concerne les méthodes itératives qui posent directement le problème sous sa forme discrète. La méthode revient à modéliser le signal mesuré en chaque dexel de P θ (i.e. chaque échantillon ou bin de la ligne de projection) comme étant une combinaison linéaire de tous les pixels de l image théorique f, et ce pour toutes les projections. Ainsi, si on note p le vecteur 1. Pour pouvoir être reconstruit intégralement à partir de sa version discrétisée, la fréquence d échantillonnage d un signal doit être supérieure ou égale au double de la fréquence maximale contenue dans le signal d origine.
149 Construction d un modèle théorique de perfusion par une analyse par standardisation anatomique 149 (a) (b) (c) Fig. 4.4 Reconstruction d un examen TEMP de la base des 27 sujets sains étudiés: (a) sinogramme des projections, (b) reconstruction avec un filtre rampe, (c) post-filtrage gaussien 3D (LMH = 8mm) colonne comprenant, les unes après les autres, les intensités de tous les dexels de chacune des projections (typiquement de dimension td = 128 dexels p = 64 projections), et f le vecteur colonne comprenant tous les pixels de l image f (typiquement de dimension dim x dim y = pixels), le modèle s écrit : p = R f (4.10) La matrice R représente les coefficients de la contribution de chaque pixel de l image à chaque dexel de chaque projection, c est le projecteur. Sa transposée t R est la matrice des coefficients de la contribution de chaque dexel de chaque projection à chaque pixel de l image : c est le rétroprojecteur. R est calculée par une modélisation de la géométrie d acquisition. Résoudre le problème de la reconstruction tomographique revient donc à inverser le système Or, les grandes dimensions de la matrice R ( (td p) (dim x dim y )) et son mauvais conditionnement 2 en font un problème inverse mal posé. Il est donc nécessaire de le résoudre de manière itérative, et des informations a priori ou contraintes peuvent s avérer nécessaire pour régulariser le problème (e.g., contrainte de positivité de l image reconstruite). De manière générale, la reconstruction par méthode itérative consiste en la recherche d un estimateur ˆf de f, qui minimise l erreur quadratique entre les projections calculées et les projections observées p Rˆf 2. On estime ˆf en réduisant cette erreur à chaque itération. Différentes approches ont été proposées dans la littérature, comme par exemple l algorithme EM (Expectation Maximisation) ou la méthode du Gradient Conjugué. Le problème peut être formulé de manière Bayésienne, il est alors possible d injecter des contraintes a priori pour régulariser la solution (méthode du Maximum A Posteriori ou MAP). Le choix du critère d arrêt est délicat, étant donné qu au départ l erreur diminue, et l algorithme converge, mais au fur et à mesure des itérations, une forte amplification du bruit peut entraîner une divergence de l algorithme. Ainsi, plus on s arrête tôt, plus la reconstruction sera lissée, et plus on s arrête tard, plus elle sera bruitée. Le choix du critère 2. Seuls les pixels appartenant au voisinage du faisceau issu du dexel et orienté suivant la direction de projection contribuent principalement à l intensité de celui-ci.
150 Méthodes de reconstruction tomographique et de correction pour la quantification en TEMP d arrêt résulte donc d un compromis entre résolution spatiale et niveau de bruit, il en est de même pour le réglage de la fréquence de coupure du filtre pour les méthodes analytiques par rétroprojection filtrée Modélisation du projecteur: Le principal avantage des méthodes de reconstruction itératives est qu une modélisation précise du projecteur R permet de tenir compte de l atténuation, de la perte de résolution en profondeur, voire même de la diffusion (via des simulations de Monte Carlo). Il est alors possible de combiner reconstruction des données et correction des principaux effets perturbateurs du signal TEMP. La littérature sur les méthodes combinant correction et reconstruction itérative est très riche, mais sort du cadre de notre étude Mesure de la résolution spatiale: Les données de sujets sains et épileptiques que nous nous proposons d analyser dans ce chapitre proviennent de systèmes d imagerie différents (voir II ). Nous avons tout d abord procédé à la mesure de la résolution spatiale des deux systèmes d imagerie par l acquisition de sources linéiques, afin de régler les méthodes de reconstruction, et notamment la largeur à mi-hauteur du filtre 3D gaussien, pour s assurer que les données analysées aient la même résolution spatiale. L ajustement des résolutions spatiales est une précaution nécessaire afin de rendre les mesures issues de systèmes d acquisitions différents relativement comparables [Lobaugh 00, VanLaere 01a]. Une source linéique de 1mm de diamètre et remplie d une solution contenant une solution de 99m Tc a été acquise sur chacun des imageurs, en utilisant la même configuration (e.g. collimateur, distance de la caméra, nombre de projections) que pour les acquisitions correspondant aux données de sujets sains ou épileptiques. L. Barnden a réalisé la même expérience sur leur imageur en Australie. Les données ont ensuite été reconstruites par rétroprojection avec un filtre rampe à la fréquence de coupure de Nyquist. Différents postfiltrages gaussiens ont été réalisés en utilisant respectivement une LMH de 6, 7, 8, 9 et 10 mm, et une mesure de la résolution spatiale a été réalisée dans chaque cas. La mesure de la résolution spatiale a été réalisée en estimant sur les données reconstruites la largeur à mi-hauteur d un profil d activité mesuré sur une ligne passant par le centre de la source linéique. L estimation a été réalisée en ajustant une fonction gaussienne sur ce profil mesuré, par minimisation de l erreur au sens des moindres carrés, à l aide de l algorithme de Levenberg-Marquardt. L écart-type estimé σ de la gaussienne permettant le meilleur ajustement au profil mesuré permet alors de déduire la mesure de la résolution spatiale en calculant la largeur à mi-hauteur correspondante, à l aide de la relation LMH = σ 2 2 ln(2) Les résultats des mesures de résolution spatiale sont présentés par la table 4.1. On observe qu en post-filtrant les données avec un filtre gaussien 3D de largeur à mi-hauteur 8mm, les deux imageurs fournissent quasiment la même résolution spatiale, à savoir une largeur à mi-hauteur de 12.2mm. Ainsi, toutes les données analysées ont été reconstruites par rétroprojection filtrée avec un filtre rampe, suivi d un post-filtrage gaussien 3D avec une largeur à mi-hauteur de 8mm (voir figure 4.4).
151 Construction d un modèle théorique de perfusion par une analyse par standardisation anatomique 151 Tab. 4.1 Mesures de résolution spatiale (LMH) en mm pour différents post-filtrages gaussiens des données reconstruites, sur l imageur du service de médecine nucléaire de Rennes utilisé pour l acquisition des sujets épileptiques (imageur à deux têtes DST-XL de General Electric Medical Systems) et sur l imageur utilisé par L. Barnden pour l acquisition des sujets sains (trois têtes IRIX de Philips Medical Systems) Type de filtre Résolution en mm de l imageur Résolution en mm de l imageur à 2 têtes DST-XL de GEMS à 3 têtes IRIX de Philips MS (Rennes) (Woodville, Australie) Rampe Rampe + gaussienne 3D (LMH = 6 mm) Rampe + gaussienne 3D (LMH = 7 mm) Rampe + gaussienne 3D (LMH = 8 mm) Rampe + gaussienne 3D (LMH = 9 mm) Rampe + gaussienne 3D (LMH = 10 mm) Méthodes usuelles de correction Après avoir présenté les principaux phénomènes à l origine du biais de quantification en TEMP, tels l atténuation, la diffusion, la perte de résolution en profondeur ou encore l effet de volume partiel, nous présentons les méthodes de correction les plus couramment utilisées en clinique. D autres phénomènes peuvent occasionner une dégradation du signal TEMP. C est notamment le cas du bougé lors des acquisitions, qu il faut également corriger ou du moins contrôler en cours d acquisition. Nous n aborderons pas ces aspects. De même que pour les méthodes de reconstruction, il existe une littérature abondante concernant les techniques de correction, cependant l étude de ces différentes méthodes sort du cadre de ce travail. Pour un exposé plus détaillé de ces différentes méthodes ainsi que pour l évaluation de leurs performances, nous reportons le lecteur aux références suivantes [ElFakhri 98, Buvat 99]. Dans ce paragraphe, nous présentons notamment les méthodes de correction d atténuation et de la diffusion mises en œuvre sur les données de notre étude, à savoir la méthode de Chang pour la correction d atténuation, et la méthode de soustraction de Jaszczak pour la correction de la diffusion Correction de l atténuation: méthode de Chang La méthode de Chang [Chang 78] permet de corriger l effet de l atténuation à partir des données déjà reconstruites: il s agit d une post-correction. Il s agit de la méthode la plus couramment utilisée et disponible sur de nombreux équipements cliniques. Le principe est d estimer, à partir d une cartographie des coefficients d atténuation, l atténuation moyenne subie en chaque point de l image. On calcule ainsi en chaque pixel de l image un coefficient d atténuation moyen A(x,y) de la manière suivante : ( A(x,y) = 1 p exp ) 1 ij µ i (4.11) p j=1 i où 1 ij est l indicatrice de tous les pixels de l image situés sur la ligne passant par le point (x,y) et orientée dans la direction de l axe de la j ième projection. L indice i indique tous les
152 Méthodes de reconstruction tomographique et de correction pour la quantification en TEMP pixels de l image traversés par cette ligne entre le point (x,y) et le détecteur, et µ i indique le coefficient d atténuation en chacun de ces points. A partir de ces coefficients A(x,y), on corrige en atténuation l image ˆf obtenue après reconstruction tomographique, on en déduit ainsi l image corrigée ˆf corr : ˆf corr (x,y) = ˆf(x,y) A(x,y) (4.12) L équation (4.11) montre qu il est nécessaire de connaître les coefficients d atténuation en tout point de l image. En pratique, cette carte d atténuation non-uniforme peut être estimée en réalisant une acquisition en transmission à l aide d une source externe, juste après ou avant l acquisition habituelle en émission. Souvent, il ne s agit pas du même radio-élément utilisé en émission et en transmission, il est alors nécessaire de convertir les coefficients d atténuation d un élément à l autre en les multipliant par un facteur d échelle [Rajeevan 98, Iida 98]. Ce facteur d échelle peut être mesuré lors d une phase de calibration [Rajeevan 98]. Dans ce cas, on montre que la formule de correction 4.12 est exacte pour une source ponctuelle et approximative dans le cas général. Lorsque l on ne dispose pas d acquisition en transmission, en raison de problèmes de réglementation en France notamment, il est possible de considérer toute la tête du patient comme un milieu atténuant uniforme. Pour le 99m Tc, on choisit habituellement comme coefficient d atténuation moyen celui de l eau à 140keV à savoir µ = 0.15cm 1. Les études de Rajeevan et al. et de Iida et al., utilisant un marqueur de la dopamine marqué à l 123 I [Rajeevan 98] ou le marqueur de perfusion cérébrale 123 I-IAMP [Iida 98], ont évalué l effet d une correction d atténuation uniforme ou non-uniforme sur les capacités de quantification en TEMP. De manière générale, les méthodes de correction uniforme sous-corrigent les régions proches du crâne et sur-corrigent les régions internes où il y a peu d activité comme les sinus. Ainsi, ces différences se font sentir surtout sur le haut du crâne (interface avec l os importante) et sur le bas de la tête (os et nombreuses cavités comprenant de l air). Ces auteurs ont montré qu au niveau cérébral, le gain en précision des méthodes de correction non-uniforme était relativement limité. Les erreurs de quantification liées à une correction d atténuation uniforme ne dépassent pas 5% par rapport à l utilisation de méthodes de correction non-uniforme. Par contre, Rajeevan et al. ont montré qu une mauvaise détection de la surface de la tête pouvait entraîner des erreurs de quantification de l ordre de 15%. Pour notre étude concernant notamment l épilepsie temporale, il conviendrait d étudier plus particulièrement la précision obtenue par une correction d atténuation uniforme ou non-uniforme au niveau du lobe temporal. Nous avons donc appliqué une correction de Chang en supposant un milieu atténuant uniforme sur les données de sujets sains et épileptiques faisant l objet de cette étude. La figure 4.5 illustre le résultat de cette correction sur une des données ictales pour laquelle le masque de la tête a été précisément déduit de l IRM du même sujet préalablement recalée. Cette méthode de correction est dite méthode de Chang d ordre 1. Le procédé peut être itéré. Ainsi, les données corrigées ˆf corr peuvent être projetées (voir équation 4.10) et les projections calculées soustraites aux projections mesurées. On rétroprojette l erreur obtenue, on corrige le résultat de la même manière (équation 4.12), et on ajoute cette carte d erreur corrigée en atténuation à ˆf corr. Ce procédé peut être itéré plusieurs fois de la même manière, mais en pratique on se limite à une ou deux itérations pour éviter une amplification du bruit. D autres méthodes de correction d atténuation sont également disponibles. Citons
153 Construction d un modèle théorique de perfusion par une analyse par standardisation anatomique 153 (a) (b) Fig. 4.5 Illustration de la correction d atténuation uniforme par la méthode de Chang d ordre 1 sur un examen de TEMP de sujet sain: (a) Données d origine reconstruite (b) Données corrigées par exemple, l approche heuristique qui consiste à considérer la moyenne géométrique des projections diamétralement opposées, ou les techniques modélisant l atténuation uniforme ou non-uniforme dans le projecteur utilisé par les méthodes de reconstruction itératives Correction de la diffusion: méthode de la fenêtre de Jaszczak La méthode de la fenêtre de Jaszczak [Jaszczak 85] est certainement la méthode de correction de la diffusion la plus connue. Elle peut être utilisée sur n importe quelle caméra à condition d être capable d acquérir les données simultanément dans deux fenêtres d énergie : la fenêtre à 20% du pic principal d émission du radioélément, et une fenêtre adjacente, dite de Compton, ne contenant que des photons diffusés. Le principe est de considérer que la quantité de photons diffusés compris dans la fenêtre à 20% du pic principal d émission est liée à la quantité de photons diffusés mesurés dans la fenêtre Compton, par un coefficient multiplicatif k. Si on note P θ les projections mesurées dans la fenêtre à 20% du pic principal d émission et Pθ C les projections mesurées dans la fenêtre Compton, on obtient des projections corrigées de la diffusion Pθ corr en réalisant la soustraction : P corr θ = P θ k P C θ (4.13) Cette correction peut s appliquer soit sur les projections, soit sur les données reconstruites. Généralement, la soustraction génère des valeurs négatives qui n ont aucune signification physique et qu il convient de remplacer par zéro. Typiquement, pour une fenêtre à 20% du pic d émission du 99m Tc ( keV ), Jaszczak propose d utiliser l intervalle (92 125keV ) pour la fenêtre Compton. Le coefficient k peut alors être mesuré soit de manière expérimentale, soit à partir de simulations de Monte Carlo [Gustafsson 00], il est reconnu d utiliser k = 0.5 pour de telles fenêtres d énergie [Jaszczak 85]. Alors qu au paragraphe précédent nous avons justifié qu il était raisonnable de se limiter à une correction d atténuation uniforme, la correction de la diffusion semble quant à elle fondamentale pour assurer un bon contraste dans les images 3. Ainsi, Iida et al. [Iida 98] 3. Le contraste peut être défini comme l écart relatif entre une région hyper-intense H et une région hypo-intense L par: (H L)/(H + L) 100.
154 Méthodes de reconstruction tomographique et de correction pour la quantification en TEMP annoncent que, sans correction de la diffusion, l intensité de la matière grise est sous-estimée de 20 à 30% et celle de la matière blanche est sur-estimée de 10 à 20%. Nous ne disposions pas d acquisition en double fenêtre d énergie pour les données des sujets épileptiques provenant du service de médecine nucléaire de Rennes, donc aucune correction de la diffusion n a pu être réalisée. Par contre, pour les données de sujets sains acquises dans le service de L. Barnden, nous disposions d une acquisition simultanée dans la fenêtre d énergie à 20% du pic d émission du 99m Tc ( keV ) ainsi qu une acquisition dans une fenêtre Compton mais de ( keV ). Pour cette fenêtre Compton, Barnden et al. ont proposé d utiliser un coefficient k = 1.3 après avoir optimisé la précision en quantification de leur imageur [Barnden 02] à partir d acquisitions utilisant le fantôme physique d Hoffmann [Hoffman 90, Hoffman 91]. La figure 4.6 illustre, pour une de ces acquisitions, l effet de cette correction de la diffusion. (a) (b) (c) Fig. 4.6 Illustration de la correction de la diffusion par la méthode de la fenêtre de Jaszczak sur un examen TEMP de sujet sain (k = 1.3): (a) Données d origine reconstruites (b) Données de la fenêtre Compton reconstruites (c) Données corrigées de la diffusion Jaszczak précise de plus qu il est possible de tenir compte de la diffusion lors de la correction d atténuation en diminuant le coefficient d atténuation uniforme moyen à µ = 0.12cm 1 au lieu de µ = 0.15cm 1. Cette valeur a été mesurée expérimentalement [Jaszczak 85, Rajeevan 98]. Nous avons appliqué ce choix lors de la correction en atténuation des données des sujets épileptiques pour lesquelles nous ne disposions pas d acquisition en double fenêtre d énergie. De nombreuses autres méthodes de correction de la diffusion ont été proposées. Citons, par exemple, l utilisation d une triple fenêtre d énergie [Buvat 99], l analyse factorielle d une série de fenêtres spectrales adjacentes, l utilisation d un facteur k dépendant de l atténuation en chaque point de l image [Iida 98], l utilisation de méthodes de déconvolution supposant les projections des photons diffusés comme issues du lissage des projections des photons primaires [Jaszczak 85], ou encore la modélisation du phénomène lors de la reconstruction (par des techniques de Monte Carlo notamment) Correction de la perte de résolution en profondeur Les principales méthodes de correction de la perte de résolution en profondeur sont le principe fréquence-distance et la modélisation du phénomène pendant la reconstruction par des méthodes itératives [Koulibaly 98]. Dans les deux cas, il est nécessaire de connaître la fonction de dispersion ponctuelle du détecteur. Cette fonction est mesurée expérimenta-
155 Construction d un modèle théorique de perfusion par une analyse par standardisation anatomique 155 lement par l acquisition d une source ponctuelle à différentes distances du détecteur, et en mesurant la LMH correspondante sur chacune des projections. La relation entre la LMH caractérisant la réponse du détecteur et la distance entre la source et le détecteur est généralement modélisée par une régression linéaire. Le principe fréquence-distance consiste en un filtrage non-stationnaire. Ainsi, la distance d un point source au centre de rotation du tomographe peut se retrouver dans la transformée de Fourier du sinogramme. On utilise cette relation pour déconvoluer sélectivement les points situés à une certaine distance du détecteur, en s aidant de la relation LMH du détecteur - distance de la source préalablement calibrée. Dans les méthodes de reconstruction itératives, on modélise la perte de résolution en profondeur dans la matrice R de projection. Ainsi, ce sont les pixels les plus éloignés du détecteur qui contribueront au plus grand nombre de dexels sur la projection. Vu que nous ne disposions pas de la calibration mesurant la résolution spatiale (LMH) du détecteur en fonction de la distance, aucune correction de la perte de résolution en profondeur n a été appliquée sur les données analysées ici Correction de volume partiel La correction de l effet de volume partiel intéresse principalement la quantification de l activité au niveau des structures de petite taille. La méthode nécessite de se doter d un modèle à haute-résolution de l anatomie sous-jacente pour déconvoluer le lissage causé justement par l effet de volume partiel. Ce modèle de l anatomie est généralement fourni par l IRM préalablement recalée et segmentée. Par exemple, Buvat et al. [Buvat 00] corrigent l effet de volume partiel de l activité des noyaux caudés sur des données TEMP utilisant un marqueur de la dopamine, en identifiant préalablement les noyaux caudés et le putamen sur l anatomie. Nous n avons pas réalisé de correction de volume partiel en tant que pré-traitement des données étudiées. Par contre, cet effet a été pris en compte au moment des mesures de perfusion lors de la mise en œuvre de notre méthode d analyse par standardisation anatomique (voir II ). 4.2 Etat de l art des méthodes d analyse de données TEMP ou TEP par standardisation anatomique Définition d une méthode d analyse par standardisation anatomique L objectif des méthodes d analyse par standardisation anatomique est principalement d aider à une analyse plus objective et systématique d un grand nombre de données et de permettre des analyses inter-individuelles. Nous présentons ici les méthodes qui ont été proposées pour assister l analyse de données TEP ou TEMP. En pratique clinique, l analyse des données TEP et surtout TEMP est encore essentiellement réalisée de manière subjective et visuelle. Les principales approches quantitatives se limitent en la mesure du signal au sein de régions d intérêt (ROIs) positionnées manuellement sur les données (voir par exemple [Ho 96]). En plus de leur résolution spatiale limitée (de l ordre de 5 mm en TEP et de 10 mm en TEMP), l information contenue dans de
156 Etat de l art des méthodes d analyse de données TEMP ou TEP par standardisation anatomique telles données étant de nature essentiellement fonctionnelle, le repérage précis des structures anatomiques lors de l analyse est une tâche délicate. Lobaugh et al. [Lobaugh 00] précisent qu une analyse idéale de données TEMP serait d identifier, pour chaque sujet, les principales structures anatomiques sur l IRM préalablement recalée et de les reporter sur les données TEMP. Une telle analyse est cependant difficile à automatiser, la segmentation fine de l IRM se faisant le plus souvent manuellement, et devient vite lourde à gérer pour analyser un grand nombre d individus, d où le recours à des méthodes d analyse par standardisation anatomique. Le principe des méthodes d analyse par standardisation anatomique est de repositionner les données d origine dans le référentiel d un modèle moyen de l anatomie : c est l étape dite de normalisation spatiale. Ce modèle moyen de l anatomie peut être soit un atlas anatomique numérisé (atlas papier, coupes anatomiques numérisées) ou numérique (construit à partir de données images: IRM) ou un examen moyen issu du moyennage après mise en correspondance non linéaire d un grand nombre de données de la même modalité. On appelle template un tel examen moyen 4. L étape de normalisation spatiale est une étape de recalage, affine ou non linéaire, des données d origine vers l atlas ou le template. Une fois les données normalisées spatialement, il est possible de les comparer. On distingue alors deux approches. La première consiste à utiliser un découpage anatomique du modèle spatial (atlas ou template), sous forme de régions d intérêt (ROIs) ou de volumes d intérêt (VOIs) prédéfinis, et de le reporter sur les données pour mesurer l activité. La deuxième approche consiste à comparer les données entre elles, voxel par voxel Quels contextes cliniques? L objectif principal des méthodes d analyse par standardisation anatomique est une analyse par comparaison inter-individuelle. Elles cherchent donc à étudier et caractériser les aspects reproductibles et variables au sein d une population homogène de sujets sains ou pathologiques. Elles permettent l identification de profils d activité (du métabolisme ou de la perfusion cérébrale) reproductibles d un individu à l autre et caractéristiques d une situation physiologique ou physiopathologique : on appellera patterns de tels profils. L étude de tels patterns ou leur comparaison est une voie d accès à des connaissances fondamentales sur les phénomènes sous-jacents. Ainsi, ces approches sont essentiellement adaptées au cas où le phénomène étudié est relativement reproductible d un individu à l autre. Ces méthodes intéressent donc plus particulièrement les maladies dites diffuses. Elles ont principalement été appliquées à l étude de la maladie d Alzheimer en TEP [Minoshima 94b, Ishii 01, Herholz 02] ou en TEMP [Houston 94, Donnemiller 97, Bartenstein 97, Ebmeier 98, Imran 99, VanLaere 02] ou à l étude de l épilepsie du lobe temporal en TEP [VanBogaert 00, Muzik 00, Lee 00b, Kang 01] ou en TEMP [Ring 99, Lee 00a]. Par contre, ces méthodes ne sont pas dédiées à l étude des pathologies d origine lésionnelle, la localisation de la lésion étant rarement reproductible d un individu à l autre, sauf en comparant les données d un seul sujet pathologique à une population de sujets sains [Signorini 99, Stamatakis 99]. La détection d anomalies pathologiques de métabolisme ou de perfusion n étant envisageable que via la connaissance préalable du métabolisme ou de la perfusion cérébrale normale, de nombreuses 4. Rappelons que le logiciel Statistical Parametric Mapping (SPM) met à disposition des templates IRM (T1, T2, EPI, densité de proton), Scanner X, TEP et TEMP.
157 Construction d un modèle théorique de perfusion par une analyse par standardisation anatomique 157 études ont été menées chez le sujet sain notamment en TEMP [Houston 94, Koyama 97, Tanaka 00, Lobaugh 00, VanLaere 01b, VanLaere 01a]. L enjeu de ces méthodes d analyse est souvent d étudier la part de reproductibilité et de variabilité fonctionnelle caractérisant un état normal ou pathologique Méthodes de normalisation spatiale La méthode de normalisation spatiale la plus ancienne, et largement reconnue en neurochirurgie et neurologie, est le quadrillage proportionnel proposé par Talairach et Tournoux [Talairach 88]. Cette méthode permet de repérer tout examen de neuroimagerie dans l atlas proposé par ces mêmes auteurs. L atlas de Talairach et Tournoux est constitué de planches dessinées à partir de photographies de coupes anatomiques du cerveau d un sujet décédé. Le quadrillage proportionnel est défini par la désignation du plan inter-hémisphérique, des commissures antérieure (CA) et postérieure (CP), et de la boîte englobante du cerveau : on définit ainsi 12 parallélépipèdes. L identification de ces points et de ce quadrillage est généralement réalisée de manière interactive par l expert sur l IRM du sujet. La normalisation spatiale est alors réalisée à l aide d une transformation affine par morceaux permettant d ajuster chacun des 12 parallélépipèdes du sujet sur ceux de l atlas. La désignation des coordonnées d un point dans ce référentiel, communément appelé référentiel CA-CP, permet aux cliniciens de se repérer dans l anatomie du patient. Pour cela, l atlas est divisé en un certain nombre de cases identifiées par des lettres et numéros. Il est reconnu que cette méthode est suffisamment précise pour l identification des structures internes, par contre au niveau du cortex, elle ne rend que partiellement compte de la variabilité interindividuelle de l anatomie sulco-gyrale. Concernant les données TEMP ou TEP, Minoshima et al. [Minoshima 94a] ont proposé un atlas stéréotaxique TEP pour assister l analyse visuelle en TEP. Cet atlas a été réalisé par recalage interactif d un examen TEP dans CA-CP suivi d un étiquetage manuel d un certain nombre d entités anatomiques. Migneco et al. [Migneco 94] proposent une méthode semi-automatique d identification de CA-CP sur des données TEMP, permettant de reporter sur les données des ROIs du lobe temporal définies sur l atlas. D autres approches de normalisation spatiale basées atlas ont été proposées. Elles consistent principalement en un recalage non linéaire interactif de l atlas sur l IRM ou le scanner X d un sujet [Seitz 90, Roland 94]. Pour cela, l utilisateur dispose d une batterie de transformations linéaires ou non, applicables globalement ou localement. La méthode proposée par Roland et al. a été utilisée pour normaliser spatialement des données TEP [Koyama 97] ou TEMP [Ito 96, Koyama 97] en combinant un recalage non linéaire interactif du scanner X de chaque sujet vers l atlas et un recalage rigide entre le scanner X et les données de médecine nucléaire. Des méthodes de normalisation spatiale utilisant des approches complètement automatiques ont également été proposées. Citons par exemple l approche proposée pour la TEP par Minoshima et al. [Minoshima 94b]. La méthode consiste tout d abord par une identification automatique de CA-CP par des critères de géométrie et de symétrie, suivie d une mise à l échelle globale de la taille du cerveau, et finalement d une déformation locale des données à partir de points de contrôle situés principalement au centre de la matière blanche et sur le cortex, afin d ajuster les données sur l atlas. Après la mise en correspondance des points de contrôle, la déformation est appliquée à tout le volume par
158 Etat de l art des méthodes d analyse de données TEMP ou TEP par standardisation anatomique interpolation sur des fonctions spline plaque-mince [Bookstein 89]. Les auteurs précisent que leur méthode mime les déformations du cerveau le long des fibres nerveuses. C est la méthode implémentée dans le logiciel Neurostat, évaluée dans [Ishii 01]. Cette méthode a aussi été appliquée à la normalisation spatiale de données TEMP [Bartenstein 97]. La méthode de normalisation spatiale certainement la plus utilisée en neuroimagerie est l approche proposée par Friston et al. [Friston 95a], basée sur une minimisation de l erreur quadratique entre les intensités de l image et du template (voir equation 2.58) et une paramétrisation adaptée de la transformation spatiale et en intensité (généralement transformations non linéaires et non stationnaires). Cette méthode est implémentée dans le logiciel Statistical Parametric Mapping (SPM). Étant donné que le logiciel SPM permet également une analyse statistique basée voxel des données (voir II.4.2.6), la plupart des travaux utilisant ces approches voxel utilisent également la méthode de normalisation spatiale SPM, citons par exemple [Ebmeier 98, Stamatakis 99, Signorini 99, Lee 00a, Herholz 02]. Il existe également de nombreux travaux sur le recalage non linéaire inter-sujets IRM/IRM, dont les résultats sont potentiellement applicables dans ce contexte (voir [Hellier 01a] pour une évaluation comparative de ces principales méthodes). Néanmoins, de nombreux auteurs suggèrent que lorsqu on normalise spatialement des données TEMP pathologiques, il est préférable de se limiter à un recalage affine, afin d éviter des déformations aberrantes [Acton 98, Stamatakis 01]. Différentes mesures statistiques de similarité présentées au chapitre I.2 ont été utilisées pour normaliser spatialement les données vers un template, en recherchant une transformation géométrique affine. Citons par exemple l utilisation de la somme des différences absolues (équation 2.60) [Ring 99, VanLaere 01b, VanLaere 01a], la linéarisation de la somme des carrés sous l hypothèse du flot optique (équation 2.58) [Houston 94], ou encore l uniformité du rapport des intensités (équation 2.64) [Imran 99, Lobaugh 00, Liow 00] tel qu il est implémenté dans le logiciel Automated Image Registration (AIR) Evaluation de la normalisation spatiale L évaluation de la précision des méthodes de normalisation spatiale est un problème méthodologique délicat, étant donnée l impossibilité de disposer d une référence absolue pour le recalage inter-sujets. Nous nous contentons de présenter les travaux de quelques auteurs qui se sont intéressés à l étude des performances des méthodes de normalisation spatiale que nous venons de présenter, et à l influence des erreurs de recalage sur l analyse statistique des données. Les premières études sur les atlas ont été évaluées en quantifiant, après normalisation, une diminution de la variabilité inter-individuelle résiduelle au niveau de points anatomiques ou de mesures de distances [Roland 94]. Pour les données de médecine nucléaire, la méthode d évaluation la plus couramment utilisée consiste à appliquer à l IRM ou au scanner X la transformation calculée à partir de la TEP ou de la TEMP. Il est alors possible de définir différents critères comme le positionnement de CA [Migneco 94, Sugiura 99], la comparaison des contours du cerveau ou des principaux sillons [Sugiura 99, Imran 99, Muzik 00], ou encore une mesure de recouvrement du cerveau ou de la matière grise [Imran 99, Ishii 01]. Lors de l évaluation comparative de méthodes de recalage non linéaires IRM/IRM, Hellier et al. [Hellier 01a, Hellier 02] utilisent également comme critère 5. Logiciel AIR:
159 Construction d un modèle théorique de perfusion par une analyse par standardisation anatomique 159 d évaluation des taux de recouvrement matière grise / matière blanche et des distances entre sillons, mais segmentés automatiquement à partir de l IRM. Dans [Hellier 02], ils montrent d ailleurs de très bons résultats de la méthode de Friston et al. [Friston 95a] au niveau des distances entre sillons. Par contre, Ishii et al. [Ishii 01] mesurent des erreurs de recouvrement de la matière grise de 20% de plus pour la méthode implémentée dans SPM par rapport à celle implémentée dans Neurostat. Mais de telles études étant difficilement comparables entre elles, nous n irons pas plus loin dans l analyse. Une autre manière d évaluer la normalisation spatiale est de comparer les résultats de l analyse statistique (e.g. comparaison de groupes de sujets sains et pathologiques) en utilisant l une ou l autre des méthodes de normalisation spatiale [Minoshima 94b, Muzik 00, Ishii 01]. L influence de zones fonctionnelles pathologiques ou activées sur la normalisation spatiale et sur l analyse statistique peut être étudiée de manière objective en utilisant des simulations numériques. La simulation de zones pathologiques hypoperfusées en TEMP a été utilisée pour étudier la précision de la normalisation spatiale [Stamatakis 01, Radau 01] et ses conséquences sur les performances de détection de ces zones pathologiques [Stamatakis 99]. Lahorte et al. [Lahorte 00] simulent des zones hyperperfusées pour évaluer les performances de détection des expériences de neuroactivation en TEMP. Les études quantitatives de Radau et al. et de Stamatakis et al. confirment qu il est préférable d utiliser une transformation géométrique affine pour normaliser spatialement des données TEMP pathologiques Approches utilisant des ROIs ou VOIs Une fois les données normalisées spatialement, il est possible d assister le positionnement de régions d intérêt (ROIs) sur les données de manière semi-automatique à partir d un atlas [Donnemiller 97, Tanaka 00] ou de manière automatique [Migneco 94, Lobaugh 00]. Il est aussi possible de réaliser des mesures volumiques en utilisant des volumes d intérêt (VOIs) prédéfinis dans un atlas ou un template et en les reportant automatiquement sur les données normalisées spatialement [Liow 00, Lee 00b, VanLaere 01b, VanLaere 01a, VanLaere 02, Kang 01]. L origine du découpage en VOIs n est pas toujours précisée dans les références. En s aidant de l atlas de Talairach et Tournoux, Lobaugh et al. [Lobaugh 00] définissent manuellement des ROIs sur l IRM d un sujet sain âgé, la TEMP de ce même sujet sert de référence pour l analyse inter-individuelle : ils proposent ainsi un découpage en ROIs caractéristiques du sujet âgé et l utilisent pour étudier la maladie d Alzheimer. Lee et al. [Lee 00b] utilisent un découpage en VOIs prédéfinis sur le template TEP de SPM. Kang et al. [Kang 01] utilisent comme VOIs des cartes de probabilité de présence de structures anatomiques (Statistical Probabilistic Anatomical Map : SPAM [Evans 96]). Ces cartes consistent en une classification floue de 98 structures anatomiques et reflètent la variabilité anatomique inter-individuelle, elles ont été construites à partir de la segmentation de 152 IRM de sujets sains normalisés. Quelques auteurs ont également proposé l utilisation de ROIs sur les cartes obtenues après une analyse statistique voxel par voxel comme sur une carte de moyenne ou d écart-type [Koyama 97], ou sur une carte de Z-score 6 [Bartenstein 97]. A part [Donnemiller 97, Bartenstein 97] pour la maladie d Alzheimer en TEMP, [Kang 01, Lee 00b] pour l épilepsie en TEP et [Liow 00] pour le HIV en TEP, 6. Le Z-score est utilisé pour comparer un individu à une population, on soustrait à cet individu la moyenne de la population et on divise le résultat par l écart-type de la population
160 Etat de l art des méthodes d analyse de données TEMP ou TEP par standardisation anatomique toutes les autres études citées ici s intéressent à l étude de la perfusion en TEMP chez le sujet sain. Une fois les mesures réalisées à partir de ces VOIs, l analyse dépend bien évidemment des objectifs de chacun, mais on retrouve le plus souvent des approches statistiques de type régression linéaire. Les études les plus courantes consistent en des comparaisons de populations en fonction du type de pathologie (ou comparaison sujets sains vs sujets pathologiques) [Donnemiller 97, Tanaka 00, VanLaere 02], de la modalité d imagerie (comparaison TEMP/TEP) [Koyama 97], de systèmes d imagerie différents [Lobaugh 00, VanLaere 01a], du sexe [Tanaka 00]. Ces comparaisons de groupes sont le plus généralement réalisées à partir de tests de Student lorsque l on compare deux populations, et par des analyses de la variance au delà. Des comparaisons inter-hémisphériques sont pratiquement réalisées à chaque fois en utilisant des indices d asymétrie suivis de tests de Student pour tester la non nullité de l asymétrie [Kang 01, Lobaugh 00, Tanaka 00]. Finalement, lorsque l on étudie l effet d un facteur quantitatif, une étude par régression linéaire ou de corrélation est généralement utilisée, comme par exemple l âge [Tanaka 00] ou le résultat d un test neuropsychologique. Pour une analyse très complète de la perfusion chez le sujet sain en TEMP nous renvoyons le lecteur vers les études de van Laere et al. [VanLaere 01b, VanLaere 01a], dans lesquelles la plupart de ces effets (localisation anatomique, type d imageur, sexe, âge, latéralité, etc) sont étudiés. D autres approches d analyse de données ont été proposées pour faire de la comparaison et de la classification automatique sujets sains/sujets pathologiques à partir des mesures basées VOIs. Ainsi, Liow et al. [Liow 00] proposent une analyse en composante principale suivie d une analyse discriminante pour classifier des sujets sains et HIV+ en TEP. Lee et al. [Lee 00b] utilisent ces mesures pour classifier, à l aide de réseaux de neurones artificiels, trois patterns TEP liés à l épilepsie temporale (hypométabolisme droit, hypométabolisme gauche ou pas d anomalie). Classiquement, ces études nécessitent de disposer d une base de données d apprentissage, puis les capacités de généralisation de la méthode de classification sont évaluées à partir d une base de données de test. Certains auteurs fournissent de plus les résultats de leurs mesures, généralement par moyenne et écart-type pour chaque structure anatomique, comme par exemple [Koyama 97, VanLaere 01a, VanLaere 01b] pour la perfusion normale en TEMP et [Lobaugh 00] pour la perfusion chez le sujet sain âgé. De telles mesures peuvent être utiles pour définir un modèle théorique de perfusion à des fins de simulation. Nous présentons par la suite (voir II.4.3) une autre méthode d analyse basée VOI et nous l utilisons pour définir un modèle de perfusion. Enfin, toutes les approches qui viennent d être présentées dépendent complètement du découpage en ROIs ou VOIs utilisé. Nous définissons ce découpage comme un modèle spatial de l anatomie cérébrale. Ainsi, les méthodes d analyse basées ROIs ou VOIs posent un a priori sur la distribution anatomique de la fonction (perfusion ou métabolisme) étudiée. Typiquement, des modifications très locales de la fonction étudiée risquent d être masquées par la réalisation d une mesure moyenne dans un VOI plus étendu. Inversement, ces approches permettent d aller étudier des activations spécifiques dans certaines structures internes de petites tailles, en autorisant, le cas échéant, une correction de l effet de volume partiel. Cet a priori est défini par le modèle spatial de l anatomie cérébrale. Nous y reviendrons en définissant pour notre méthode un modèle spatial de l anatomie cérébrale dédié à l étude de l épilepsie temporale.
161 Construction d un modèle théorique de perfusion par une analyse par standardisation anatomique Approches basées voxels A contrario, les méthodes consistant en l analyse voxel par voxel des données n ont aucun a priori sur la répartition anatomique du phénomène étudié. Elles sont donc complètement exploratoires. Le principe est d analyser les valeurs d un même voxel dans les différentes données normalisées spatialement. La même analyse est alors réalisée de manière indépendante pour tous les voxels du cerveau. De même que pour les approches utilisant des VOIs, l objectif des analyses statistiques des approches basées voxels est généralement la comparaison de groupes de sujets sains/sujets pathologiques comme par exemple dans le contexte de la maladie d Alzheimer [Minoshima 94b, Ito 96, Ebmeier 98], ou de l épilepsie [Ring 99, Lee 00a, VanBogaert 00]. On retrouve également des cas de comparaison de modalités d imagerie (TEMP/TEP) et des études de corrélations avec des facteurs quantitatifs comme le résultat d un test neuropsychologique (voir par exemple [Herholz 02] pour la maladie d Alzheimer). La plupart de ces analyses peuvent se formaliser dans le cadre du modèle linéaire généralisé proposé par Friston et al. [Friston 95b] pour générer des cartes statistiques d activation (Statistical Parametric Map - SPM). De plus, pour pouvoir appréhender l extension spatiale des zones détectées et corriger des comparaisons multiples dans le cadre de la théorie des champs aléatoires gaussiens, les données doivent être préalablement lissées par un filtre gaussien [Poline 97]. L utilisation de ces méthodes est reconnue en TEP, du fait d une très large utilisation au sein de la communauté des neurosciences. L éditorial de P. Acton et K. Friston [Acton 98] définit quelques principes de base pour appliquer ces méthodes à la TEMP. Ils insistent essentiellement sur la nécessité de se limiter à une transformation affine lors de l étape de normalisation spatiale, et sur la faible puissance des tests et leur caractère trop conservateur du fait du faible nombre d examens généralement disponibles, et donc du faible nombre de degrés de liberté. Signorini et al. [Signorini 99] ont proposé une méthode permettant de comparer en TEP un sujet particulier à une population de sujets sains. La sensibilité et spécificité de la méthode est évaluée en analysant des sujets sains ou pathologiques. Une telle approche est prometteuse pour analyser les pathologies où la localisation de la zone pathologique n est pas reproductible d un patient à l autre. C est notamment le cas des lésions et des épilepsies extra-temporales. Cette méthode a notamment été employée pour l étude des épilepsies temporales en TEP [VanBogaert 00] ou en TEMP ictale [Lee 00a], ainsi que pour la détection de lésions en TEMP [Stamatakis 99]. L analyse des asymétries inter-hémisphériques est par contre nettement moins évidente que pour les approches basées VOIs. De fait, on observe de manière générale beaucoup plus d analyses par indice d asymétrie pour les approches basées VOIs, et beaucoup plus d analyses par comparaison de populations par les approches basées voxel. Une explication peut être liée à la difficulté d assigner à chaque voxel son voxel symétriquement homologue dans l autre hémisphère, alors que c est immédiat pour les VOIs. En TEP, van Bogaert et al. [VanBogaert 00] proposent de normaliser spatialement les données vers un template TEP parfaitement symétrique, et inversent les données normalisées par symétrie droite/gauche. Ils proposent une analyse de type un sujet seul versus groupe ou une comparaison de groupes pour étudier les asymétries pathologiques en épilepsie par rapport aux asymétries physiologiques mesurées au sein d une population de sujets sains. D autres méthodes d analyse qui ne s appuient par sur le modèle linéaire généralisé de SPM, mais plutôt sur des méthodes d analyse factorielle ont également été proposées.
162 Méthode de construction d un modèle théorique de perfusion Ainsi, Houston et al. [Houston 94] utilisent une analyse en composante principale pour caractériser la perfusion en TEMP d une base de données de sujets sains. Les composantes principales correspondant aux valeurs propres les plus fortes définissent ainsi un sous-espace caractérisant la variabilité fonctionnelle de la perfusion de ces sujets sains. Ils proposent alors une méthode de détection de données pathologiques en mesurant la distance entre un examen TEMP et sa projection orthogonale sur ce sous-espace (i.e. l image TEMP normale la plus proche de l examen en question). Utilisant également les intensités voxels des données TEMP normalisées spatialement comme seule caractéristique, Stoeckel et al. [Stoeckel 01] proposent une méthode de classification par analyse discriminante entre des sujets sains et des sujets atteints de la maladie d Alzheimer Comparaison des approches basées VOIs et des approches basées voxels Quelques études de comparaison des deux approches ont été proposées dans la littérature. Ainsi, Van Laere et al. [VanLaere 01b] utilisent les deux méthodes pour analyser très précisément des données TEMP provenant d une base de données de 89 sujets sains. Dans ce cas, il s agit plutôt d une approche exploratoire permettant de caractériser la perfusion en TEMP chez le sujet sain à partir des deux méthodes. Mais les méthodes ne sont pas explicitement comparées. Les capacités de détection de pathologie des approches basées VOIs et des approches basées voxel ont également été comparées [Liow 00, VanLaere 02]. Ainsi, Liow et al. [Liow 00] comparent les performances de détection de leur méthode d analyse discriminante suivant qu ils utilisent comme entrées les intensités des voxels ou les intensités moyennes mesurées en chaque VOI. Van Laere et al. [VanLaere 02] comparent les performances de détection de cas pathologiques par quatre méthodes: une analyse visuelle qualitative, une analyse basée VOIs, et deux approches basées voxels, dont l approche SPM. Pour ces deux études, la connaissance théorique du diagnostic des données testées permet de quantifier la sensibilité et spécificité des méthodes. Les capacités de détection et la comparaison de performances des différentes méthodes sont évaluées à l aide d analyses par courbe ROC (Receiver Operating Curves [Metz 86]). Globalement, les deux études montrent des performances équivalentes. 4.3 Méthode de construction d un modèle théorique de perfusion Nous présentons à présent la méthode d analyse par standardisation anatomique qui a tout d abord été développée à des fins de simulation des données TEMP. Ainsi notre objectif était de développer un méthode de modélisation d un profil de perfusion particulier en TEMP, et de l utiliser pour simuler de manière réaliste des données TEMP. Notre choix s est donc naturellement porté vers une approche basée VOIs. L objectif premier de la méthode n est pas d assister la détection d anomalies de perfusion, mais plutôt de caractériser et donc de modéliser la perfusion en TEMP d une population homogène de sujets. La méthode est assez générique pour s appliquer à différentes populations de sujets sains ou pathologiques. Nous l appliquons ici à l analyse de la perfusion d une population de 27 sujets sains et
163 Construction d un modèle théorique de perfusion par une analyse par standardisation anatomique 163 à l analyse de la perfusion ictale et inter-ictale de 10 patients présentant une épilepsie à point de départ temporo-mésial. L idée est de se doter d un outil permettant d identifier la distribution moyenne de la perfusion qui est reproductible d un sujet à l autre au sein de cette population, mais aussi la part de variabilité fonctionnelle qui caractérise également cette population. Cette méthode présente un intérêt pour la simulation, mais également vis à vis de connaissances plus fondamentales sur la population et donc éventuellement la pathologie étudiée. Nous montrerons à la fin de ce chapitre comment l analyse des résultats a permis de mettre en évidence certaines dépendances au niveau de la perfusion de différentes structures anatomiques. La simulation réaliste de données TEMP, via des techniques de simulation analytique ou de Monte Carlo, nécessite la définition à partir d une IRM morphologique d une carte théorique d atténuation des photons ainsi que d une carte théorique d activité représentant la distribution du radiotraceur de perfusion ( 99m Tc-HMPAO ou 99m Tc-ECD). La construction de ces cartes nécessite de se doter d un modèle spatial de l anatomie cérébrale afin d assigner une valeur théorique d atténuation et d activité à chaque structure anatomique identifiée par ce modèle. La définition d une carte d activité réaliste passe par la modélisation du profil de perfusion à simuler. C est justement l analyse inter-individuelle de données TEMP d une population homogène par une méthode basée VOIs, qui permet cette modélisation. Ainsi, ce sont les VOIs définis par le modèle spatial de l anatomie cérébrale qui ont été utilisés pour mettre en place une méthode d analyse par standardisation anatomique basée VOIs Modèle spatial de l anatomie cérébrale Le modèle spatial de l anatomie cérébrale utilisé a été déduit du fantôme anthropomorphique de tête proposé par Zubal et al. [Zubal 90, Zubal 94]. Ce fantôme consiste en une IRM 3D haute-résolution pondérée en T1 d un sujet sain à partir de laquelle soixante trois structures anatomiques ou Volumes d Intérêt (VOIs) intra- et extra-cérébraux ont été segmentés manuellement et étiquetés. Afin de simuler des données TEMP caractéristiques de l épilepsie, les VOIs du fantôme de Zubal ont été latéralisés et resegmentés. En effet, la plupart des études de perfusion cérébrale en épilepsie se font en comparant l hémisphère sain à l hémisphère pathologique [Ho 96, Ho 97, Duncan 97b]. De plus les découpages anatomiques habituellement utilisés par les épileptologues nécessitent de distinguer différentes zones corticales au niveau des différents lobes, comme, par exemple, différentes parties du lobe temporal [Bartolomei 99]. Ainsi, l objectif était de distinguer au sein du lobe temporal, les régions temporo-mésiale (ou interne), temporo-latérale (ou externe), pôle temporal et temporo-postérieure. De même, au sein du lobe frontal, les régions fronto-mésiale, fronto-latérale, fronto-orbitaire et pôle frontal ont été identifiées. Les régions occipito-mésiale et occipito-latéral ont été distinguées au sein du lobe occipital. Ces segmentations ou redécoupages ont été réalisés de manière semi-automatique et guidée par l atlas de Talairach et Tournoux [Talairach 88]. Cette étape a été réalisée avec l aide d un expert, A. Biraben (neurologue), de la manière suivante : La mise en correspondance de l IRM pondérée en T1 du fantôme de Zubal avec l atlas a été réalisée par désignation interactive du quadrillage proportionnel sur l IRM : désignation du plan inter-hémisphérique, des commissures antérieure et postérieure
164 Méthode de construction d un modèle théorique de perfusion et de la boîte englobante du cerveau. En analysant une à une les planches coronales de l atlas, les cases ou demi-cases de l atlas appartenant à la structure anatomique à segmenter ont été identifiées (e.g. pôle temporal). La segmentation des VOIs du fantôme de Zubal a été réalisée en prenant l intersection entre chacun de ces VOIs (e.g. lobe temporal) et les cases de l atlas, identifiées comme appartenant à l entité à segmenter (e.g. pôle temporal). Les VOIs du fantôme de Zubal étant définis dans le référentiel de l IRM de celui-ci, le quadrillage proportionnel est utilisé pour la mise en correspondance lors de cette intersection. Les VOIs resegmentés sont ainsi également définis dans le référentiel d origine de l IRM du fantôme de Zubal. Tous les VOIs, d origine ou resegmentés, sont latéralisés grâce au plan inter-hémisphérique préalablement désigné. L ensemble de ces VOIs, ceux resegmentés et ceux du fantôme n ayant subi aucune transformation sauf la latéralisation, définissent les entités de notre modèle spatial de l anatomie cérébrale. Afin de simuler des asymétries purement fonctionnelles, ce modèle a été symétrisé par rapport au plan inter-hémisphérique. L IRM d origine du fantôme a été symétrisée de la même manière en utilisant une interpolation trilinéaire. La figure 4.7 illustre cette resegmentation du fantôme de Zubal au niveau du lobe temporal. Ces mêmes VOIs ont été utilisés lors de l analyse par standardisation anatomique de données TEMP réelles, afin de construire un modèle théorique de perfusion (voir prochain paragraphe). Dans le cadre de cette analyse, certains VOIs ont également été fusionnés. La table 4.2 présente la liste des VOIs ainsi obtenus après redécoupage ou fusion. Ainsi, le VOI temporo-mésial correspond en fait à la réunion de la portion resegmentée du VOI lobe temporal et des VOIs Hippocampe et Amygdale. Le VOI Cortex a été construit en regroupant les VOIs lobe temporal, lobe frontal, lobe pariétal et lobe occipital. Comme la pathologie faisant l objet de cette étude est l épilepsie temporale, nous avons défini le VOI Cortex Sain comme le regroupement des VOIs lobe frontal, lobe pariétal et lobe occipital externe. Les VOIs thalamus, putamen et pallidum ont été regroupés pour construire le VOI Noyau Gris. De même, la réunion des VOIs putamen et pallidum a permis de définir le VOI Noyau Lenticulaire Carte d activité: modèle théorique de perfusion cérébrale La création d un modèle théorique de perfusion cérébrale à partir de mesures sur des données TEMP réelles, utilisant une approche de type standardisation anatomique basée VOIs, est résumée sur la figure 4.7. La méthode consiste à normaliser spatialement les données TEMP à étudier vers un référentiel anatomique moyen et à réaliser des mesures quantitatives à partir des VOIs que nous venons de décrire Choix d une population homogène: Afin de construire un modèle théorique de perfusion, la première étape a consisté à sélectionner une population homogène de sujets, caractéristique du type de perfusion que l on cherche à modéliser. Les examens TEMP de 27 sujets sains (12 hommes et 15 femmes âgés de 20 à 56 ans) ont été utilisés pour construire un modèle théorique de perfusion
165 Construction d un modèle théorique de perfusion par une analyse par standardisation anatomique 165 Tab. 4.2 Correspondances entre les VOIs du fantôme de Zubal (colonnes) et ceux de notre modèle spatial de l anatomie cérébrale utilisés pour l analyse par standardisation anatomique (lignes) - o : fusion des VOIs du fantôme de Zubal, : découpage des VOIs du fantôme de Zubal à partir de l atlas stéréotaxique de Talairach (Amyg: amygdale, Hipp.: hippocampe, Temp.: Temporal, Front.: Frontal, Par.: Parietal, Occ.: Occipital Amyg. Hipp. Temp. Front. Par. Occ. Thalamus Putamen Pallidum Cortex o o o o CortexSain o o o NoyauGris o o o NoyauLenticulaire o o TempPole TemporoMesial o o TemporoLateral TemporoPostérieur FrontalPole FrontoOrbitaire FrontoMesial FrontoLateral OccipitoMesial OccipitoLateral normale. Ces données nous ont été aimablement fournies par Leighton Barnden du service de Médecine Nucléaire du Queen Elizabeth Hospital (Woodville, Australie). Pour analyser la perfusion ictale et inter-ictale de l épilepsie temporo-mésiale, une population constituée de 10 sujets épileptiques (6 hommes et 4 femmes âgés de de 19 à 43 ans) a été sélectionnée. Tous ces patients ont été pris en charge par les services d épileptologie et de neurochirurgie de l hôpital de Rennes. Ils ont tous été opérés et guéris (score de Engel de 1a [Engel 87]). Le diagnostic d épilepsie à point de départ temporo-mésial suivi d une propagation temporolatérale, a été posé à partir des données électrocliniques selon la classification des crises temporales proposée par Bartolomei et al. [Bartolomei 99]. Les données ont été acquises après injection perictale du radiotraceur effectuée dans des conditions reproductibles grâce à un contrôle du début de la crise par vidéo-electroencéphalographie Acquisition et prétraitement des données: Après une injection de 500 MBq de 99m Tc-HMPAO, les acquisitions TEMP des 27 sujets sains ont été réalisées sur une Gamma camera à trois têtes IRIX (Philips Medical Systems), munie de collimateurs parallèles à ultra-haute résolution. 120 projections couvrant 360 (matrice= , taille du pixel=3.59mm) ont été acquises en utilisant simultanément une fenêtre d énergie à 20% du pic d activité du 99m Tc ( keV ), ainsi qu une fenêtre Compton ( keV ). Une correction du diffusé par la méthode de Jasczsak [Jaszczak 85] a été réalisée en soustrayant aux 120 projections acquises dans la fenêtre à 20% du pic d activité du 99m Tc celles acquises dans la fenêtre Compton considérée. Ces dernières projections ont été multipliées par un coefficient k = 1.3 avant la soustraction (voir II ). En ce qui concerne les 10 sujets épileptiques, les acquisitions de TEMP ictales et interictales ont été réalisées sur un imageur à deux têtes DST-XL (General Electric Medical
166 Méthode de construction d un modèle théorique de perfusion Anatomie : IRM T1 étiquetée = fantôme de Zubal Entités anatomiques = Volumes d intérêt (VOIs) après resegmentation Modèle de Perfusion Théorique Analyse Statistique Fonction : Données TEMP et IRM issues d une population homogène (normale ou pathologique) Référentiel Anatomique Moyen Normalisation Spatiale vers le template T1 (SPM) VOI normalisé Moyenne du signal TEMP pondérée par le masque lissé du VOI TEMP normalisée Fig. 4.7 Construction du modèle de perfusion théorique à partir des mesures sur des données TEMP réelles Systems) muni de collimateurs Fan Beam à ultra-haute résolution (7 cas) ou parallèles ultra-haute résolution (3 cas). Une injection moyenne de 740 MBq de 99m Tc-HMPAO ou de 99m Tc-ECD a été réalisée suivant la disponibilité du traceur. 64 projections couvrant 360 (matrice= , taille du pixel=4.51mm) ont ainsi été acquises. Parmi les examens inter-ictaux, 4 ont été en fait acquis sur un ancien imageur, de moins bonne résolution spatiale (matrice=64 64, taille du pixel=6.78mm). N ayant pu mesurer précisément cette résolution spatiale, ces 4 examens ont été écartés de l étude afin de n analyser que des données homogènes en terme de résolution spatiale. Pour chacun des 10 sujets épileptiques, une acquisition IRM 3D pondérée en T1 a été réalisée sur un imageur Signa 1.5T (General Electric Medical Systems) : 124 coupes sagittales , voxel= mm 3, séquence SPGR (FOV = 24 cm, α = 30, TE = 3 ms et TR = 33 ms). La reconstruction tomographique de toutes ces données TEMP a été réalisée par rétroprojection filtrée en utilisant un filtre rampe à la fréquence de coupure de Nyquist. Les données reconstruites ont été post-filtrées à l aide d un filtre Gaussien 3D de largeur à mi-hauteur (LMH) 8mm. Ainsi, la résolution spatiale de toutes les données reconstruites est de 12.2mm (voir II ). Les données ont été corrigées en atténuation par la méthode de Chang d ordre 1 [Chang 78] en considérant la tête comme un milieu atténuant uniforme (voir II ). Un coefficient d atténuation de µ = 0.15cm 1 a été utilisé pour les données corrigées de la diffusion et de µ = 0.12cm 1 pour les données non corrigées (voir II ). Rajeevan et al. [Rajeevan 98] ont montré que la correction d atténuation uniforme était suffisamment précise en quantification relative à condition d identifier précisément la frontière de la peau sur les données TEMP. Ainsi, pour les sujets sains, le masque de la tête a été déduit par binarisation des volumes reconstruits à partir des données de la fenêtre Compton, comme conseillé par Rajeevan et al. lorsqu on ne dispose pas d acquisition en transmission. Pour les sujets épileptiques, le masque de la tête a été déduit par binarisation de l IRM préalablement recalée sur les données TEMP.
Le logiciel EduAnatomist.
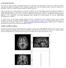 Le logiciel EduAnatomist. Les travaux de l équipe ACCES (Actualisation Continue des Connaissances des Enseignants en Sciences) de l INRP restent, hélas, largement méconnus des enseignants de SVT. Pourtant,
Le logiciel EduAnatomist. Les travaux de l équipe ACCES (Actualisation Continue des Connaissances des Enseignants en Sciences) de l INRP restent, hélas, largement méconnus des enseignants de SVT. Pourtant,
Les atouts et faiblesses des caméras TEP dédiées, TEP corps entier, TEP-CT, TEMP pour la quantification
 Les atouts et faiblesses des caméras TEP dédiées, TEP corps entier, TEP-CT, TEMP pour la quantification Irène Buvat U494 INSERM CHU Pitié-Salpêtrière, Paris buvat@imed.jussieu.fr http://www.guillemet.org/irene
Les atouts et faiblesses des caméras TEP dédiées, TEP corps entier, TEP-CT, TEMP pour la quantification Irène Buvat U494 INSERM CHU Pitié-Salpêtrière, Paris buvat@imed.jussieu.fr http://www.guillemet.org/irene
1ST2S Biophysiopathologie : Motricité et système nerveux. 2012-2013. La physiologie neuro-musculaire :
 La physiologie neuro-musculaire : Introduction : Le neurone possède 3 propriétés indispensables pour assurer sa fonction au sein de l organisme : -l excitabilité : capacité à répondre à un stimulus -la
La physiologie neuro-musculaire : Introduction : Le neurone possède 3 propriétés indispensables pour assurer sa fonction au sein de l organisme : -l excitabilité : capacité à répondre à un stimulus -la
Simulation d'un examen anthropomorphique en imagerie TEMP à l iode 131 par simulation Monte Carlo GATE
 Simulation d'un examen anthropomorphique en imagerie TEMP à l iode 131 par simulation Monte Carlo GATE LAURENT Rémy laurent@clermont.in2p3.fr http://clrpcsv.in2p3.fr Journées des LARD Septembre 2007 M2R
Simulation d'un examen anthropomorphique en imagerie TEMP à l iode 131 par simulation Monte Carlo GATE LAURENT Rémy laurent@clermont.in2p3.fr http://clrpcsv.in2p3.fr Journées des LARD Septembre 2007 M2R
La migraine. Foramen ovale perméable. Infarctus cérébral (surtout chez la femme)
 La migraine 1/Introduction : Céphalée primaire (sans lésion sous-jacente). Deux variétés principales: Migraine sans aura (migraine commune). Migraine avec aura (migraine accompagnée). Diagnostic: interrogatoire
La migraine 1/Introduction : Céphalée primaire (sans lésion sous-jacente). Deux variétés principales: Migraine sans aura (migraine commune). Migraine avec aura (migraine accompagnée). Diagnostic: interrogatoire
Les mécanismes de la récupération neurologique. PPradat-Diehl DU de Rehabilitation neuropsychologique 2007
 Les mécanismes de la récupération neurologique PPradat-Diehl DU de Rehabilitation neuropsychologique 2007 Introduction Plasticité cérébrale / Récupération après lésion cérébrale Récupération spontanée
Les mécanismes de la récupération neurologique PPradat-Diehl DU de Rehabilitation neuropsychologique 2007 Introduction Plasticité cérébrale / Récupération après lésion cérébrale Récupération spontanée
LASER DOPPLER. Cependant elle n est pas encore utilisée en routine mais reste du domaine de la recherche et de l évaluation.
 LASER DOPPLER INTRODUCTION La technique qui utilise l effet Doppler à partir d un faisceau laser est l une des seules qui permette d enregistrer en continu le reflet de la perfusion superficielle de tissus
LASER DOPPLER INTRODUCTION La technique qui utilise l effet Doppler à partir d un faisceau laser est l une des seules qui permette d enregistrer en continu le reflet de la perfusion superficielle de tissus
Migraine et céphalées de tension: diagnostic différentiel et enjeux thérapeutiques
 Migraine et céphalées de tension: diagnostic différentiel et enjeux thérapeutiques Dr Solène de Gaalon Service de neurologie- CHU Nantes Société française des migraines et céphalées Céphalées de tension
Migraine et céphalées de tension: diagnostic différentiel et enjeux thérapeutiques Dr Solène de Gaalon Service de neurologie- CHU Nantes Société française des migraines et céphalées Céphalées de tension
Foscolo (1), J Felblinger (2), S Bracard (1) CHU Hôpital central, service de neuroradiologie, Nancy (1) CHU BRABOIS, Centre d investigation clinique
 S A l (1) G H (2) S S Aptel (1), G Hossu (2), S Foscolo (1), J Felblinger (2), S Bracard (1) CHU Hôpital central, service de neuroradiologie, Nancy (1) CHU BRABOIS, Centre d investigation clinique innovation
S A l (1) G H (2) S S Aptel (1), G Hossu (2), S Foscolo (1), J Felblinger (2), S Bracard (1) CHU Hôpital central, service de neuroradiologie, Nancy (1) CHU BRABOIS, Centre d investigation clinique innovation
Peut-on reconnaître une tumeur de bas-grade en imagerie conventionnelle? S. Foscolo, L. Taillandier, E. Schmitt, A.S. Rivierre, S. Bracard, CHU NANCY
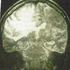 Peut-on reconnaître une tumeur de bas-grade en imagerie conventionnelle? S. Foscolo, L. Taillandier, E. Schmitt, A.S. Rivierre, S. Bracard, CHU NANCY A quoi sert l imagerie conventionnelle dans le diagnostic
Peut-on reconnaître une tumeur de bas-grade en imagerie conventionnelle? S. Foscolo, L. Taillandier, E. Schmitt, A.S. Rivierre, S. Bracard, CHU NANCY A quoi sert l imagerie conventionnelle dans le diagnostic
Dr E. CHEVRET UE2.1 2013-2014. Aperçu général sur l architecture et les fonctions cellulaires
 Aperçu général sur l architecture et les fonctions cellulaires I. Introduction II. Les microscopes 1. Le microscope optique 2. Le microscope à fluorescence 3. Le microscope confocal 4. Le microscope électronique
Aperçu général sur l architecture et les fonctions cellulaires I. Introduction II. Les microscopes 1. Le microscope optique 2. Le microscope à fluorescence 3. Le microscope confocal 4. Le microscope électronique
L ELECTRICITE : SON IMPLICATION DANS LE FONCTIONNEMENT DU CERVEAU ET DANS LES SOINS
 LES RENDEZ-VOUS PRESSE DU NEURODON L ELECTRICITE : SON IMPLICATION DANS LE FONCTIONNEMENT DU CERVEAU ET DANS LES SOINS Dossier réalisé avec l aide des : Professeur Yehezkel BEN ARI Directeur de l INMED
LES RENDEZ-VOUS PRESSE DU NEURODON L ELECTRICITE : SON IMPLICATION DANS LE FONCTIONNEMENT DU CERVEAU ET DANS LES SOINS Dossier réalisé avec l aide des : Professeur Yehezkel BEN ARI Directeur de l INMED
La prise en charge de votre épilepsie
 G U I D E - A F F E C T I O N D E L O N G U E D U R É E La prise en charge de votre épilepsie Vivre avec une épilepsie sévère Novembre 2007 Pourquoi ce guide? Votre médecin traitant vous a remis ce guide
G U I D E - A F F E C T I O N D E L O N G U E D U R É E La prise en charge de votre épilepsie Vivre avec une épilepsie sévère Novembre 2007 Pourquoi ce guide? Votre médecin traitant vous a remis ce guide
Dossier thématique de la. Fondation de l'avenir. Chirurgie du futur SOMMAIRE
 Dossier thématique de la Fondation de l'avenir Chirurgie du futur SOMMAIRE I L évolution de la chirurgie A La vidéochirurgie : une chirurgie mini-invasive 1 En quoi consiste la vidéochirurgie 2 - Les bénéfices
Dossier thématique de la Fondation de l'avenir Chirurgie du futur SOMMAIRE I L évolution de la chirurgie A La vidéochirurgie : une chirurgie mini-invasive 1 En quoi consiste la vidéochirurgie 2 - Les bénéfices
Les sciences de l ingénieur appliquées à la prise en charge du
 Les sciences de l ingénieur appliquées à la prise en charge du cancer : enjeux et opportunités Début de cartographie des enjeux cliniques et technologiques gq Jean-François MENUDET, Cluster I-Care Cartographie
Les sciences de l ingénieur appliquées à la prise en charge du cancer : enjeux et opportunités Début de cartographie des enjeux cliniques et technologiques gq Jean-François MENUDET, Cluster I-Care Cartographie
Tout ce que vous avez toujours voulu savoir sur la scintigraphie osseuse et le TEP-SCAN
 Tout ce que vous avez toujours voulu savoir sur la scintigraphie osseuse et le TEP-SCAN Docteur Antoine MONET Centre d Imagerie Fonctionnelle Clinique Saint Augustin Jeudi 25 Septembre 2008 Un peu d histoire
Tout ce que vous avez toujours voulu savoir sur la scintigraphie osseuse et le TEP-SCAN Docteur Antoine MONET Centre d Imagerie Fonctionnelle Clinique Saint Augustin Jeudi 25 Septembre 2008 Un peu d histoire
sur la valve mitrale À propos de l insuffisance mitrale et du traitement par implantation de clip
 À propos de l insuffisance mitrale et du traitement par implantation de clip sur la valve mitrale Support destiné aux médecins en vue d informer les patients. À propos de l insuffisance mitrale L insuffisance
À propos de l insuffisance mitrale et du traitement par implantation de clip sur la valve mitrale Support destiné aux médecins en vue d informer les patients. À propos de l insuffisance mitrale L insuffisance
MIEUX COMPRENDRE CE QU EST UN ACCIDENT VASCULAIRE CÉRÉBRAL AVC
 MIEUX COMPRENDRE CE QU EST UN ACCIDENT VASCULAIRE CÉRÉBRAL AVC SOMMAIRE UN QUIZ POUR FAIRE UN POINT SUR MES CONNAISSANCES Un quiz pour faire un point sur mes connaissances 3 Vrai Faux Qu est-ce que l on
MIEUX COMPRENDRE CE QU EST UN ACCIDENT VASCULAIRE CÉRÉBRAL AVC SOMMAIRE UN QUIZ POUR FAIRE UN POINT SUR MES CONNAISSANCES Un quiz pour faire un point sur mes connaissances 3 Vrai Faux Qu est-ce que l on
7- Les Antiépileptiques
 7- Les Antiépileptiques 1 Définition L épilepsie est un trouble neurologique chronique caractérisé par la survenue périodique et imprévisible de crises convulsives dues à l émission de décharges électriques
7- Les Antiépileptiques 1 Définition L épilepsie est un trouble neurologique chronique caractérisé par la survenue périodique et imprévisible de crises convulsives dues à l émission de décharges électriques
Item 169 : Évaluation thérapeutique et niveau de preuve
 Item 169 : Évaluation thérapeutique et niveau de preuve COFER, Collège Français des Enseignants en Rhumatologie Date de création du document 2010-2011 Table des matières ENC :...3 SPECIFIQUE :...3 I Différentes
Item 169 : Évaluation thérapeutique et niveau de preuve COFER, Collège Français des Enseignants en Rhumatologie Date de création du document 2010-2011 Table des matières ENC :...3 SPECIFIQUE :...3 I Différentes
Notions de base Gestion du patient au bloc opératoire
 Notions de base Gestion du patient au bloc opératoire Vieillissement de la population Augmentation du nombre de patients porteurs de stimulateurs cardiaques et défibrillateurs implantables Augmentation
Notions de base Gestion du patient au bloc opératoire Vieillissement de la population Augmentation du nombre de patients porteurs de stimulateurs cardiaques et défibrillateurs implantables Augmentation
Le patient ouvre les yeux et regarde dans. Les yeux ouverts, mais l esprit absent. Médecine
 NEUROBIOLOGIE «Il faut parler à une personne dans le coma» entend-on souvent dans les films.tout dépend de ce qu on appelle coma. Entre l état végétatif, où le patient peut encore remuer, sourire ou sursauter
NEUROBIOLOGIE «Il faut parler à une personne dans le coma» entend-on souvent dans les films.tout dépend de ce qu on appelle coma. Entre l état végétatif, où le patient peut encore remuer, sourire ou sursauter
Le Crédit-bail mobilier dans les procédures collectives
 Aimé Diaka Le Crédit-bail mobilier dans les procédures collectives Publibook Retrouvez notre catalogue sur le site des Éditions Publibook : http://www.publibook.com Ce texte publié par les Éditions Publibook
Aimé Diaka Le Crédit-bail mobilier dans les procédures collectives Publibook Retrouvez notre catalogue sur le site des Éditions Publibook : http://www.publibook.com Ce texte publié par les Éditions Publibook
Votre guide des définitions des maladies graves de l Assurance maladies graves express
 Votre guide des définitions des maladies graves de l Assurance maladies graves express Votre guide des définitions des maladies graves de l Assurance maladies graves express Ce guide des définitions des
Votre guide des définitions des maladies graves de l Assurance maladies graves express Votre guide des définitions des maladies graves de l Assurance maladies graves express Ce guide des définitions des
PHYSIQUE Discipline fondamentale
 Examen suisse de maturité Directives 2003-2006 DS.11 Physique DF PHYSIQUE Discipline fondamentale Par l'étude de la physique en discipline fondamentale, le candidat comprend des phénomènes naturels et
Examen suisse de maturité Directives 2003-2006 DS.11 Physique DF PHYSIQUE Discipline fondamentale Par l'étude de la physique en discipline fondamentale, le candidat comprend des phénomènes naturels et
Document d information dans le cadre de l installation d un cyclotron. à Saint-Louis
 Document d information dans le cadre de l installation d un cyclotron à Saint-Louis Cancers & imagerie médicale Un progrès majeur pour une meilleure prise en charge des patients. Accroitre les possibilités
Document d information dans le cadre de l installation d un cyclotron à Saint-Louis Cancers & imagerie médicale Un progrès majeur pour une meilleure prise en charge des patients. Accroitre les possibilités
I - CLASSIFICATION DU DIABETE SUCRE
 I - CLASSIFICATION DU DIABETE SUCRE 1- Définition : Le diabète sucré se définit par une élévation anormale et chronique de la glycémie. Cette anomalie est commune à tous les types de diabète sucré, mais
I - CLASSIFICATION DU DIABETE SUCRE 1- Définition : Le diabète sucré se définit par une élévation anormale et chronique de la glycémie. Cette anomalie est commune à tous les types de diabète sucré, mais
Médecine en 2014. Médecine en 2014. Exigences techniques
 Pierre Bonnet, Félix Scholtes - Université de Liège - Sciences biomédicales Michel Raze - Centre Hospitalier Universitaire de Liège Stéphane Safin - Université de Paris 8 - laboratoire Paragraphe-C3U Médecine
Pierre Bonnet, Félix Scholtes - Université de Liège - Sciences biomédicales Michel Raze - Centre Hospitalier Universitaire de Liège Stéphane Safin - Université de Paris 8 - laboratoire Paragraphe-C3U Médecine
Insuffisance cardiaque
 Insuffisance cardiaque Connaître son évolution pour mieux la vivre Guide d accompagnement destiné au patient et ses proches Table des matières L évolution habituelle de l insuffisance cardiaque 5 Quelles
Insuffisance cardiaque Connaître son évolution pour mieux la vivre Guide d accompagnement destiné au patient et ses proches Table des matières L évolution habituelle de l insuffisance cardiaque 5 Quelles
Modélisation aléatoire en fiabilité des logiciels
 collection Méthodes stochastiques appliquées dirigée par Nikolaos Limnios et Jacques Janssen La sûreté de fonctionnement des systèmes informatiques est aujourd hui un enjeu économique et sociétal majeur.
collection Méthodes stochastiques appliquées dirigée par Nikolaos Limnios et Jacques Janssen La sûreté de fonctionnement des systèmes informatiques est aujourd hui un enjeu économique et sociétal majeur.
 Les Migraines et les céphalées. Dr G.Hinzelin Migraines et Céphalées Migraines et Céphalées La migraine représente entre 5 à 18% de la population française selon le sexe et en fonction des études. Est
Les Migraines et les céphalées. Dr G.Hinzelin Migraines et Céphalées Migraines et Céphalées La migraine représente entre 5 à 18% de la population française selon le sexe et en fonction des études. Est
Epilepsies : Parents, enseignants, comment accompagner l enfant pour éviter l échec scolaire?
 Epilepsies : Parents, enseignants, comment accompagner l enfant pour éviter l échec scolaire? L épilepsie concerne plus de 500 000 personnes en France, dont la moitié sont des enfants ou des adolescents.
Epilepsies : Parents, enseignants, comment accompagner l enfant pour éviter l échec scolaire? L épilepsie concerne plus de 500 000 personnes en France, dont la moitié sont des enfants ou des adolescents.
Guide de rédaction d un protocole de recherche clinique à. l intention des chercheurs évoluant en recherche fondamentale
 V E R S I O N A V R I L 2 0 1 2 C E N T R E D E R E C H E R C H E C L I N I Q U E É T I E N N E - L E B E L D U C H U S Guide de rédaction d un protocole de recherche clinique à l intention des chercheurs
V E R S I O N A V R I L 2 0 1 2 C E N T R E D E R E C H E R C H E C L I N I Q U E É T I E N N E - L E B E L D U C H U S Guide de rédaction d un protocole de recherche clinique à l intention des chercheurs
Le cavernome cérébral
 La maladie Le diagnostic Les aspects génétiques Le traitement, la prise en charge, la prévention Vivre avec En savoir plus Madame, Monsieur, Cette fiche est destinée à vous informer sur le cavernome cérébral.
La maladie Le diagnostic Les aspects génétiques Le traitement, la prise en charge, la prévention Vivre avec En savoir plus Madame, Monsieur, Cette fiche est destinée à vous informer sur le cavernome cérébral.
Que mesure la neuro-imagerie fonctionnelle :
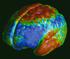 Que mesure la neuro-imagerie fonctionnelle : IRMf, TEP & MEG? O. Go s s e r i e s (1), A. De m e rt z i (1), Q. No i r ho m m e (1), J. Ts h i ba n d a (6), M. Bo ly (1), M. Op d e Be e c k (2), R. Hu
Que mesure la neuro-imagerie fonctionnelle : IRMf, TEP & MEG? O. Go s s e r i e s (1), A. De m e rt z i (1), Q. No i r ho m m e (1), J. Ts h i ba n d a (6), M. Bo ly (1), M. Op d e Be e c k (2), R. Hu
Sujets présentés par le Professeur Olivier CUSSENOT
 ANAMACaP Association Nationale des Malades du Cancer de la Prostate 17, bis Avenue Poincaré. 57400 SARREBOURG Sujets présentés par le Professeur Olivier CUSSENOT Place des nouvelles techniques d imagerie
ANAMACaP Association Nationale des Malades du Cancer de la Prostate 17, bis Avenue Poincaré. 57400 SARREBOURG Sujets présentés par le Professeur Olivier CUSSENOT Place des nouvelles techniques d imagerie
LIRE UN E.C.G. Formation sur le langage et la lecture d un ECG destinée aux techniciens ambulanciers de la région Chaudière-Appalaches
 LIRE UN E.C.G. Formation sur le langage et la lecture d un ECG destinée aux techniciens ambulanciers de la région Chaudière-Appalaches Denise Hébert, chargée de projet UCCSPU Février 2006 Le langage et
LIRE UN E.C.G. Formation sur le langage et la lecture d un ECG destinée aux techniciens ambulanciers de la région Chaudière-Appalaches Denise Hébert, chargée de projet UCCSPU Février 2006 Le langage et
Hospices cantonaux Centre Hospitalier Universitaire Vaudois DOSSIER DE PRESSE. Création du Centre romand hospitalo-universitaire de neurochirurgie
 Hospices cantonaux Centre Hospitalier Universitaire Vaudois DOSSIER DE PRESSE Création du Centre romand hospitalo-universitaire de neurochirurgie 1. Le Centre romand hospitalo-universitaire de neurochirurgie
Hospices cantonaux Centre Hospitalier Universitaire Vaudois DOSSIER DE PRESSE Création du Centre romand hospitalo-universitaire de neurochirurgie 1. Le Centre romand hospitalo-universitaire de neurochirurgie
La filtration glomérulaire et sa régulation
 UE3-2 - Physiologie rénale Chapitre 4 : La filtration glomérulaire et sa régulation Professeur Diane GODIN-RIBUOT Année universitaire 2010/2011 Université Joseph Fourier de Grenoble - Tous droits réservés.
UE3-2 - Physiologie rénale Chapitre 4 : La filtration glomérulaire et sa régulation Professeur Diane GODIN-RIBUOT Année universitaire 2010/2011 Université Joseph Fourier de Grenoble - Tous droits réservés.
L indépendance à chaque pas de la vie. Groupe. Votre meilleur allié. Visitez notre site : www.groupe-g2m.com
 L indépendance à chaque pas de la vie. Votre meilleur allié. Groupe Visitez notre site : www.groupe-g2m.com : Votre meilleur allié. Dispositif médical unique Le système WalkAide est une neuro-orthèse de
L indépendance à chaque pas de la vie. Votre meilleur allié. Groupe Visitez notre site : www.groupe-g2m.com : Votre meilleur allié. Dispositif médical unique Le système WalkAide est une neuro-orthèse de
L APS ET LE DIABETE. Le diabète se caractérise par un taux de glucose ( sucre ) trop élevé dans le sang : c est l hyperglycémie.
 1. Qu est-ce que le diabète? L APS ET LE DIABETE Le diabète se caractérise par un taux de glucose ( sucre ) trop élevé dans le sang : c est l hyperglycémie. Cette hyperglycémie est avérée si à 2 reprises
1. Qu est-ce que le diabète? L APS ET LE DIABETE Le diabète se caractérise par un taux de glucose ( sucre ) trop élevé dans le sang : c est l hyperglycémie. Cette hyperglycémie est avérée si à 2 reprises
Méthodologie de conception des Systèmes d Aide à l Exploitation des Simulateurs d Entraînement
 Méthodologie de conception des Systèmes d Aide à l Exploitation des Simulateurs d Entraînement Michelle Joab LIP6 Systèmes d Aide à la Décision et à la Formation (SYSDEF) Université Pierre-et-Marie Curie
Méthodologie de conception des Systèmes d Aide à l Exploitation des Simulateurs d Entraînement Michelle Joab LIP6 Systèmes d Aide à la Décision et à la Formation (SYSDEF) Université Pierre-et-Marie Curie
Référentiel Officine
 Référentiel Officine Inscrire la formation dans la réalité et les besoins de la pharmacie d officine de demain - Ce référentiel décrit dans le cadre des missions et des activités du pharmacien d officine
Référentiel Officine Inscrire la formation dans la réalité et les besoins de la pharmacie d officine de demain - Ce référentiel décrit dans le cadre des missions et des activités du pharmacien d officine
Service évaluation des actes professionnels
 TRAITEMENT DES AGÉNÉSIES DENTAIRES MULTIPLES LIÉES AUX DYSPLASIES ECTODERMIQUES OU À D'AUTRES MALADIES RARES, CHEZ L ENFANT ATTEINT D OLIGODONTIE, AVEC POSE DE 2 IMPLANTS (VOIRE 4 MAXIMUM) UNIQUEMENT DANS
TRAITEMENT DES AGÉNÉSIES DENTAIRES MULTIPLES LIÉES AUX DYSPLASIES ECTODERMIQUES OU À D'AUTRES MALADIES RARES, CHEZ L ENFANT ATTEINT D OLIGODONTIE, AVEC POSE DE 2 IMPLANTS (VOIRE 4 MAXIMUM) UNIQUEMENT DANS
Le GRAND CONSEIL de la République et canton de Genève décrète ce qui suit :
 Secrétariat du Grand Conseil PL 10267 Projet présenté par le Conseil d Etat Date de dépôt: 22 mai 2008 Projet de loi ouvrant un crédit au titre d'indemnité cantonale d'investissement de 3 000 000 F, pour
Secrétariat du Grand Conseil PL 10267 Projet présenté par le Conseil d Etat Date de dépôt: 22 mai 2008 Projet de loi ouvrant un crédit au titre d'indemnité cantonale d'investissement de 3 000 000 F, pour
La Dysplasie Ventriculaire Droite Arythmogène
 1 La Dysplasie Ventriculaire Droite Arythmogène Document rédigé par l équipe pluridisciplinaire du centre de référence pour les maladies cardiaques héréditaires (Paris), en collaboration avec des patients
1 La Dysplasie Ventriculaire Droite Arythmogène Document rédigé par l équipe pluridisciplinaire du centre de référence pour les maladies cardiaques héréditaires (Paris), en collaboration avec des patients
sentée e et soutenue publiquement pour le Doctorat de l Universitl
 Du rôle des signaux faibles sur la reconfiguration des processus de la chaîne de valeur de l organisation : l exemple d une centrale d achats de la grande distribution française Thèse présent sentée e
Du rôle des signaux faibles sur la reconfiguration des processus de la chaîne de valeur de l organisation : l exemple d une centrale d achats de la grande distribution française Thèse présent sentée e
Applications en imagerie cérébrale (MEG/EEG)
 EEG : mesure du potentiel électrique Ordre de grandeur : qq µ-volts Capteurs : électrodes MEG : mesure du champ magnétique Ordre de grandeur : 10 13 Tesla Capteurs SQUID couplés à des bobines VI. Applications
EEG : mesure du potentiel électrique Ordre de grandeur : qq µ-volts Capteurs : électrodes MEG : mesure du champ magnétique Ordre de grandeur : 10 13 Tesla Capteurs SQUID couplés à des bobines VI. Applications
des banques pour la recherche
 ADN, cellules, tissus... des banques pour la recherche FÉVRIER 2009 Les banques d échantillons de matériel biologique (tissus, cellules, ADN ), appelées biobanques, mettent à disposition des chercheurs
ADN, cellules, tissus... des banques pour la recherche FÉVRIER 2009 Les banques d échantillons de matériel biologique (tissus, cellules, ADN ), appelées biobanques, mettent à disposition des chercheurs
Pierre OLIVIER - Médecine Nucléaire
 Diplôme Universitaire Corrélations anatomo-physio-pathologiques en imagerie thoracique 25 mai 2011 Imagerie TEP et pathologie tumorale bronchique Pierre OLIVIER - Médecine Nucléaire Détection en coincidence
Diplôme Universitaire Corrélations anatomo-physio-pathologiques en imagerie thoracique 25 mai 2011 Imagerie TEP et pathologie tumorale bronchique Pierre OLIVIER - Médecine Nucléaire Détection en coincidence
JEU VIDEO : UN NOUVEAU COMPAGNON par Colette KELLER-DIDIER
 JEU VIDEO : UN NOUVEAU COMPAGNON par Colette KELLER-DIDIER JEU VIDEO : UN NOUVEAU COMPAGNON par Colette KELLER-DIDIER ALS (séance du 11 mai 2003) 48 Jeu video : un nouveau compagnon (Colette KELLER-DIDIER)
JEU VIDEO : UN NOUVEAU COMPAGNON par Colette KELLER-DIDIER JEU VIDEO : UN NOUVEAU COMPAGNON par Colette KELLER-DIDIER ALS (séance du 11 mai 2003) 48 Jeu video : un nouveau compagnon (Colette KELLER-DIDIER)
Quel apport de l imagerie dans les traitements anti-angiogéniques?
 Quel apport de l imagerie dans les traitements anti-angiogéniques? L Fournier, D Balvay, CA Cuénod Service de radiologie, Hôpital Européen Georges Pompidou Laboratoire de Recherche en Imagerie, Equipe
Quel apport de l imagerie dans les traitements anti-angiogéniques? L Fournier, D Balvay, CA Cuénod Service de radiologie, Hôpital Européen Georges Pompidou Laboratoire de Recherche en Imagerie, Equipe
DIPLÔME INTERUNIVERSITAIRE D ECHOGRAPHIE. Examen du Tronc Commun sous forme de QCM. Janvier 2012 14 h à 16 h
 ANNEE UNIVERSITAIRE 2011-2012 DIPLÔME INTERUNIVERSITAIRE D ECHOGRAPHIE Examen du Tronc Commun sous forme de QCM Janvier 2012 14 h à 16 h Les modalités de contrôle se dérouleront cette année sous forme
ANNEE UNIVERSITAIRE 2011-2012 DIPLÔME INTERUNIVERSITAIRE D ECHOGRAPHIE Examen du Tronc Commun sous forme de QCM Janvier 2012 14 h à 16 h Les modalités de contrôle se dérouleront cette année sous forme
Présentation du programme. de physique-chimie. de Terminale S. applicable en septembre 2012
 Présentation du programme de physique-chimie de Terminale S applicable en septembre 2012 Nicolas Coppens nicolas.coppens@iufm.unistra.fr Comme en Seconde et en Première, le programme mélange la physique
Présentation du programme de physique-chimie de Terminale S applicable en septembre 2012 Nicolas Coppens nicolas.coppens@iufm.unistra.fr Comme en Seconde et en Première, le programme mélange la physique
simulation c est [parfois] formidable
![simulation c est [parfois] formidable simulation c est [parfois] formidable](/thumbs/22/1310659.jpg) La simulation c est [parfois] formidable Thierry PELACCIA Faculté de médecine de Strasbourg SAMU - CESU 67 La simulation c est [parfois] formidable Thierry PELACCIA Faculté de médecine de Strasbourg SAMU
La simulation c est [parfois] formidable Thierry PELACCIA Faculté de médecine de Strasbourg SAMU - CESU 67 La simulation c est [parfois] formidable Thierry PELACCIA Faculté de médecine de Strasbourg SAMU
Projets proposés par le Laboratoire de Physique de l'université de Bourgogne
 Projets proposés par le Laboratoire de Physique de l'université de Bourgogne Titre : «Comprendre la couleur» Public : Collégiens, Lycéens. Nombre de participants : 5 à 10 (10 Maxi ) Lieu : Campus Universitaire
Projets proposés par le Laboratoire de Physique de l'université de Bourgogne Titre : «Comprendre la couleur» Public : Collégiens, Lycéens. Nombre de participants : 5 à 10 (10 Maxi ) Lieu : Campus Universitaire
Mention : STAPS. Sport, Prévention, Santé, Bien-être. Objectifs de la spécialité
 Mention : STAPS Sport, Prévention, Santé, Bien-être Objectifs de la spécialité L'objectif de la spécialité «Sport, Prévention, Santé, Bien être» est de doter les étudiants de compétences scientifiques,
Mention : STAPS Sport, Prévention, Santé, Bien-être Objectifs de la spécialité L'objectif de la spécialité «Sport, Prévention, Santé, Bien être» est de doter les étudiants de compétences scientifiques,
Modules optionnels. Passer à l acte en implantologie
 Passer à l acte en implantologie Modules optionnels est un cycle de formation basé sur des travaux pratiques de chirurgie implantaire, permettant de confirmer les acquis théoriques. À l issue du cursus,
Passer à l acte en implantologie Modules optionnels est un cycle de formation basé sur des travaux pratiques de chirurgie implantaire, permettant de confirmer les acquis théoriques. À l issue du cursus,
G U I D E - A F F E C T I O N D E L O N G U E D U R É E. La prise en charge de votre mélanome cutané
 G U I D E - A F F E C T I O N D E L O N G U E D U R É E La prise en charge de votre mélanome cutané Mars 2010 Pourquoi ce guide? Votre médecin traitant vous a remis ce guide pour vous informer sur le mélanome
G U I D E - A F F E C T I O N D E L O N G U E D U R É E La prise en charge de votre mélanome cutané Mars 2010 Pourquoi ce guide? Votre médecin traitant vous a remis ce guide pour vous informer sur le mélanome
MASTER 2 SCIENCES HUMAINES ET SOCIALES Mention Psychologie. Spécialité : Recherches en psychologie
 S3 Spécialité : Recherches en psychologie UE OBLIGATOIRES UE 1 : Epistémologie et méthodes de recherche en psychologie Ce séminaire aborde plusieurs aspects de la recherche en psychologie. Il présente
S3 Spécialité : Recherches en psychologie UE OBLIGATOIRES UE 1 : Epistémologie et méthodes de recherche en psychologie Ce séminaire aborde plusieurs aspects de la recherche en psychologie. Il présente
Consensus Scientifique sur. les. Champs statiques
 page 1/8 Consensus Scientifique sur Source : OMS (2006) les Champs statiques Résumé & Détails: GreenFacts Contexte - Les équipements d imagerie médicale par résonance magnétique (IRM), les trains et les
page 1/8 Consensus Scientifique sur Source : OMS (2006) les Champs statiques Résumé & Détails: GreenFacts Contexte - Les équipements d imagerie médicale par résonance magnétique (IRM), les trains et les
«Une bonne thèse répond à une question très précise!» : comment l enseigner?
 «Une bonne thèse répond à une question très précise!» : comment l enseigner? Congrès du CNGE Angers Novembre 2008 Sébastien Cadier*, Isabelle Aubin**, Pierre Barraine* *Département de médecine générale
«Une bonne thèse répond à une question très précise!» : comment l enseigner? Congrès du CNGE Angers Novembre 2008 Sébastien Cadier*, Isabelle Aubin**, Pierre Barraine* *Département de médecine générale
Compléments - Chapitre 5 Spectroscopie
 ompléments - hapitre 5 Spectroscopie Spectroscopie par résonance magnétique nucléaire (RMN 13 ) Tandis que la spectroscopie RMN 1 H fournit des données sur la disposition des atomes d'hydrogène dans une
ompléments - hapitre 5 Spectroscopie Spectroscopie par résonance magnétique nucléaire (RMN 13 ) Tandis que la spectroscopie RMN 1 H fournit des données sur la disposition des atomes d'hydrogène dans une
Surveillance et Detection des Anomalies. Diagnostic d une digue: rappel méthodologique
 Surveillance et Detection des Anomalies Diagnostic d une digue: rappel méthodologique issu de l expérience d EDF Jean-Paul BLAIS Service Géologie - Géotechnique EDF 1 La méthodologie utilisée par EDF,
Surveillance et Detection des Anomalies Diagnostic d une digue: rappel méthodologique issu de l expérience d EDF Jean-Paul BLAIS Service Géologie - Géotechnique EDF 1 La méthodologie utilisée par EDF,
admission aux urgences
 Société française de neurologie RÉFÉRENTIEL D AUTO-ÉVALUATION DES PRATIQUES EN NEUROLOGIE Prise en charge hospitalière initiale des personnes ayant fait un accident vasculaire cérébral (AVC) : admission
Société française de neurologie RÉFÉRENTIEL D AUTO-ÉVALUATION DES PRATIQUES EN NEUROLOGIE Prise en charge hospitalière initiale des personnes ayant fait un accident vasculaire cérébral (AVC) : admission
23. Interprétation clinique des mesures de l effet traitement
 23. Interprétation clinique des mesures de l effet traitement 23.1. Critères de jugement binaires Plusieurs mesures (indices) sont utilisables pour quantifier l effet traitement lors de l utilisation d
23. Interprétation clinique des mesures de l effet traitement 23.1. Critères de jugement binaires Plusieurs mesures (indices) sont utilisables pour quantifier l effet traitement lors de l utilisation d
Fonctionnement neural et troubles cognitifs chez le patient bipolaire: preuve ou surinterprétation
 DIALOGUE ESPRIT / CERVEAU : CIRCULARITE CRP -OU Santé ANTAGONISME? Fonctionnement neural et troubles cognitifs chez le patient bipolaire: preuve ou surinterprétation Charles Pull Directeur du «Laboratoire
DIALOGUE ESPRIT / CERVEAU : CIRCULARITE CRP -OU Santé ANTAGONISME? Fonctionnement neural et troubles cognitifs chez le patient bipolaire: preuve ou surinterprétation Charles Pull Directeur du «Laboratoire
Haïti, Projet d appui technique en Haïti (PATH) Houcine AKHNIF & Lucien ALBERT Avril 2015
 ETUDE DES COÛTS DES ACTES MEDICAUX EN HAÏTI: Résultats préliminaires et perspectives d utilisation dans la prise de décision Haïti, Projet d appui technique en Haïti (PATH) Houcine AKHNIF & Lucien ALBERT
ETUDE DES COÛTS DES ACTES MEDICAUX EN HAÏTI: Résultats préliminaires et perspectives d utilisation dans la prise de décision Haïti, Projet d appui technique en Haïti (PATH) Houcine AKHNIF & Lucien ALBERT
Céphalées de tension. Hélène Massiou Hôpital Lariboisière, Paris
 Céphalées de tension Hélène Massiou Hôpital Lariboisière, Paris Céphalée de tension : une maladie hétérogène La plus fréquente des céphalées primaires Diagnostic basé sur l interrogatoire Manque de spécificité
Céphalées de tension Hélène Massiou Hôpital Lariboisière, Paris Céphalée de tension : une maladie hétérogène La plus fréquente des céphalées primaires Diagnostic basé sur l interrogatoire Manque de spécificité
Photons, expériences de pensée et chat de Schrödinger: une promenade quantique
 Photons, expériences de pensée et chat de Schrödinger: une promenade quantique J.M. Raimond Université Pierre et Marie Curie Institut Universitaire de France Laboratoire Kastler Brossel Département de
Photons, expériences de pensée et chat de Schrödinger: une promenade quantique J.M. Raimond Université Pierre et Marie Curie Institut Universitaire de France Laboratoire Kastler Brossel Département de
Qu est-ce que la maladie de Huntington?
 Qu est-ce que la maladie de Huntington? Description sommaire Qu est-ce que la maladie de Huntington? La maladie de Huntington (MH) est une maladie neurodégénérative longtemps connue sous le nom de Chorée
Qu est-ce que la maladie de Huntington? Description sommaire Qu est-ce que la maladie de Huntington? La maladie de Huntington (MH) est une maladie neurodégénérative longtemps connue sous le nom de Chorée
Nom de l application
 Ministère de l Enseignement Supérieur et de la Recherche Scientifique Direction Générale des Etudes Technologiques Institut Supérieur des Etudes Technologiques de Gafsa Département Technologies de l Informatique
Ministère de l Enseignement Supérieur et de la Recherche Scientifique Direction Générale des Etudes Technologiques Institut Supérieur des Etudes Technologiques de Gafsa Département Technologies de l Informatique
Télémédecine. F. Brunet 28 octobre 2010
 Télémédecine F. Brunet 28 octobre 2010 Définition Idée générale : Faire voyager les informations plutôt que les patients Selon le CNOM (Conseil National de l Ordre des Médecins) : La télémédecine est une
Télémédecine F. Brunet 28 octobre 2010 Définition Idée générale : Faire voyager les informations plutôt que les patients Selon le CNOM (Conseil National de l Ordre des Médecins) : La télémédecine est une
Troubles de la vigilance au travail. Tests d aide à la décision d aptitude et structures de dépistage du syndrome d apnées du sommeil à Grenoble
 Troubles de la vigilance au travail Tests d aide à la décision d aptitude et structures de dépistage du syndrome d apnées du sommeil à Grenoble Sandrine Launois-Rollinat Patrick Lévy, Jean-Louis Pépin,
Troubles de la vigilance au travail Tests d aide à la décision d aptitude et structures de dépistage du syndrome d apnées du sommeil à Grenoble Sandrine Launois-Rollinat Patrick Lévy, Jean-Louis Pépin,
Bases physiques de l imagerie en
 Bases physiques de l imagerie en Médecine Nucléaire (MN) Pr. Malika ÇAOUI Service de Médecine Nucléaire CHU International Cheikh Zaid Faculté de Médecine et de Pharmacie - Rabat- 02/12/2010 Pr. Malika
Bases physiques de l imagerie en Médecine Nucléaire (MN) Pr. Malika ÇAOUI Service de Médecine Nucléaire CHU International Cheikh Zaid Faculté de Médecine et de Pharmacie - Rabat- 02/12/2010 Pr. Malika
SIMULATION HYBRIDE EN TEMPOREL D UNE CHAMBRE REVERBERANTE
 SIMULATION HYBRIDE EN TEMPOREL D UNE CHAMBRE REVERBERANTE Sébastien LALLECHERE - Pierre BONNET - Fatou DIOUF - Françoise PALADIAN LASMEA / UMR6602, 24 avenue des landais, 63177 Aubière pierre.bonnet@lasmea.univ-bpclermont.fr
SIMULATION HYBRIDE EN TEMPOREL D UNE CHAMBRE REVERBERANTE Sébastien LALLECHERE - Pierre BONNET - Fatou DIOUF - Françoise PALADIAN LASMEA / UMR6602, 24 avenue des landais, 63177 Aubière pierre.bonnet@lasmea.univ-bpclermont.fr
L IRM pas à pas Un module d enseignement interactif des bases physiques de l Imagerie par Résonance Magnétique. http://www.e-mri.
 L IRM pas à pas Un module d enseignement interactif des bases physiques de l Imagerie par Résonance Magnétique http://www.e-mri.org D HOA, A MICHEAU, G GAHIDE, E LE BARS, C CYTEVAL, M ZANCA, P DUJOLS,
L IRM pas à pas Un module d enseignement interactif des bases physiques de l Imagerie par Résonance Magnétique http://www.e-mri.org D HOA, A MICHEAU, G GAHIDE, E LE BARS, C CYTEVAL, M ZANCA, P DUJOLS,
Hôpital performant et soins de qualité. La rencontre des extrêmes estelle
 Hôpital performant et soins de qualité. La rencontre des extrêmes estelle possible? 18 octobre 2012 Professeur Philippe KOLH CIO, Directeur du Service des Informations Médico-Economiques CHU de LIEGE Plan
Hôpital performant et soins de qualité. La rencontre des extrêmes estelle possible? 18 octobre 2012 Professeur Philippe KOLH CIO, Directeur du Service des Informations Médico-Economiques CHU de LIEGE Plan
Ce qu il faut savoir sur l épilepsie.
 Ce qu il faut savoir sur l épilepsie. Sommaire Que faut-il savoir sur l épilepsie? 4 Qu est-ce que l épilepsie? 7 Qu est-ce qui cause l épilepsie? 8 Facteurs génétiques 9 Autres maladies 10 Blessures à
Ce qu il faut savoir sur l épilepsie. Sommaire Que faut-il savoir sur l épilepsie? 4 Qu est-ce que l épilepsie? 7 Qu est-ce qui cause l épilepsie? 8 Facteurs génétiques 9 Autres maladies 10 Blessures à
Introduction au datamining
 Introduction au datamining Patrick Naïm janvier 2005 Définition Définition Historique Mot utilisé au départ par les statisticiens Le mot indiquait une utilisation intensive des données conduisant à des
Introduction au datamining Patrick Naïm janvier 2005 Définition Définition Historique Mot utilisé au départ par les statisticiens Le mot indiquait une utilisation intensive des données conduisant à des
Pour un principe matérialiste fort. Jean-Paul Baquiast
 Pour un principe matérialiste fort Jean-Paul Baquiast Plan détaillé :. Pour un matérialisme fort Le retour en force du dogmatisme religieux Nécessité d un renouvellement du matérialisme Que sont les nouvelles
Pour un principe matérialiste fort Jean-Paul Baquiast Plan détaillé :. Pour un matérialisme fort Le retour en force du dogmatisme religieux Nécessité d un renouvellement du matérialisme Que sont les nouvelles
Compétence 3-1 S EXPRIMER A L ECRIT Fiche professeur
 Compétence 3-1 S EXPRIMER A L ECRIT Fiche professeur Nature de l activité : Réaliser 3 types de productions écrites (réécriture de notes, production d une synthèse de documents, production d une argumentation)
Compétence 3-1 S EXPRIMER A L ECRIT Fiche professeur Nature de l activité : Réaliser 3 types de productions écrites (réécriture de notes, production d une synthèse de documents, production d une argumentation)
INAUGURATION LABORATOIRE DE THERAPIE CELLULAIRE 16 FEVRIER 2012 DOSSIER DE PRESSE
 INAUGURATION LABORATOIRE DE THERAPIE CELLULAIRE 16 FEVRIER 2012 DOSSIER DE PRESSE Contact presse : Cathy Josse 03 22 66 87 83 / 06 86 30 46 57 josse.cathy@chu-amiens.fr 1 COMMUNIQUE DE SYNTHESE Le 16 février
INAUGURATION LABORATOIRE DE THERAPIE CELLULAIRE 16 FEVRIER 2012 DOSSIER DE PRESSE Contact presse : Cathy Josse 03 22 66 87 83 / 06 86 30 46 57 josse.cathy@chu-amiens.fr 1 COMMUNIQUE DE SYNTHESE Le 16 février
Mises en relief. Information supplémentaire relative au sujet traité. Souligne un point important à ne pas négliger.
 Cet ouvrage est fondé sur les notes d un cours dispensé pendant quelques années à l Institut universitaire de technologie de Grenoble 2, au sein du Département statistique et informatique décisionnelle
Cet ouvrage est fondé sur les notes d un cours dispensé pendant quelques années à l Institut universitaire de technologie de Grenoble 2, au sein du Département statistique et informatique décisionnelle
WHITE PAPER Une revue de solution par Talend & Infosense
 WHITE PAPER Une revue de solution par Talend & Infosense Master Data Management pour les données de référence dans le domaine de la santé Table des matières CAS D ETUDE : COLLABORATION SOCIALE ET ADMINISTRATION
WHITE PAPER Une revue de solution par Talend & Infosense Master Data Management pour les données de référence dans le domaine de la santé Table des matières CAS D ETUDE : COLLABORATION SOCIALE ET ADMINISTRATION
Dan Istrate. Directeur de thèse : Eric Castelli Co-Directeur : Laurent Besacier
 Détection et reconnaissance des sons pour la surveillance médicale Dan Istrate le 16 décembre 2003 Directeur de thèse : Eric Castelli Co-Directeur : Laurent Besacier Thèse mené dans le cadre d une collaboration
Détection et reconnaissance des sons pour la surveillance médicale Dan Istrate le 16 décembre 2003 Directeur de thèse : Eric Castelli Co-Directeur : Laurent Besacier Thèse mené dans le cadre d une collaboration
Formation des enseignants. Le tensiomètre. Objet technique modélisable issu de l environnement des élèves
 Le tensiomètre Objet technique modélisable issu de l environnement des élèves Un peu d'histoire C'est en 1628 que W. Harvey découvrit la circulation du sang. C'est pourtant seulement en 1730 que la pression
Le tensiomètre Objet technique modélisable issu de l environnement des élèves Un peu d'histoire C'est en 1628 que W. Harvey découvrit la circulation du sang. C'est pourtant seulement en 1730 que la pression
Bienvenue aux Soins Intensifs Pédiatriques
 SIP Août 2010 Route : 354 Bienvenue aux Soins Intensifs Pédiatriques Août 2010 1 Table des matières 1. Présentation du service p 3 2. Pathologies les plus courantes aux SIP. P 5 3. Objectifs de stage p
SIP Août 2010 Route : 354 Bienvenue aux Soins Intensifs Pédiatriques Août 2010 1 Table des matières 1. Présentation du service p 3 2. Pathologies les plus courantes aux SIP. P 5 3. Objectifs de stage p
La prise en charge de votre insuffisance cardiaque
 G U I D E - A F F E C T I O N D E L O N G U E D U R É E La prise en charge de votre insuffisance cardiaque Vivre avec une insuffisance cardiaque Décembre 2007 Pourquoi ce guide? Votre médecin traitant
G U I D E - A F F E C T I O N D E L O N G U E D U R É E La prise en charge de votre insuffisance cardiaque Vivre avec une insuffisance cardiaque Décembre 2007 Pourquoi ce guide? Votre médecin traitant
- MANIP 2 - APPLICATION À LA MESURE DE LA VITESSE DE LA LUMIÈRE
 - MANIP 2 - - COÏNCIDENCES ET MESURES DE TEMPS - APPLICATION À LA MESURE DE LA VITESSE DE LA LUMIÈRE L objectif de cette manipulation est d effectuer une mesure de la vitesse de la lumière sur une «base
- MANIP 2 - - COÏNCIDENCES ET MESURES DE TEMPS - APPLICATION À LA MESURE DE LA VITESSE DE LA LUMIÈRE L objectif de cette manipulation est d effectuer une mesure de la vitesse de la lumière sur une «base
Interactions des rayonnements avec la matière
 UE3-1 : Biophysique Chapitre 2 : Interactions des rayonnements avec la matière Professeur Jean-Philippe VUILLEZ Année universitaire 2011/2012 Université Joseph Fourier de Grenoble - Tous droits réservés.
UE3-1 : Biophysique Chapitre 2 : Interactions des rayonnements avec la matière Professeur Jean-Philippe VUILLEZ Année universitaire 2011/2012 Université Joseph Fourier de Grenoble - Tous droits réservés.
La maladie de Huntington, une maladie du cerveau
 Actualités à propos de la recherche sur la maladie de Huntington. Expliqué simplement. Écrit par des scientifiques. Pour la communauté mondiale HD. La greffe de moelle osseuse dans la maladie de Huntington
Actualités à propos de la recherche sur la maladie de Huntington. Expliqué simplement. Écrit par des scientifiques. Pour la communauté mondiale HD. La greffe de moelle osseuse dans la maladie de Huntington
L agénésie isolée du corps calleux
 L agénésie isolée du corps calleux Agénésie calleuse Dysgénésie du corps calleux La maladie Le diagnostic Les aspects génétiques Le traitement, la prise en charge, la prévention Vivre avec En savoir plus
L agénésie isolée du corps calleux Agénésie calleuse Dysgénésie du corps calleux La maladie Le diagnostic Les aspects génétiques Le traitement, la prise en charge, la prévention Vivre avec En savoir plus
Transplantation hépatique à donneur vivant apparenté. Olivier Scatton, Olivier Soubrane, Service de chirurgie Cochin
 Transplantation hépatique à donneur vivant apparenté Olivier Scatton, Olivier Soubrane, Service de chirurgie Cochin Introduction Le prélèvement d une partie du foie chez une personne «vivante» et apparentée
Transplantation hépatique à donneur vivant apparenté Olivier Scatton, Olivier Soubrane, Service de chirurgie Cochin Introduction Le prélèvement d une partie du foie chez une personne «vivante» et apparentée
TECHNIQUES D AVENIR LASER DOPPLER IMAGING LASER DOPPLER IMAGING LASER DOPPLER IMAGING
 TECHNIQUES D AVENIR Jonathan LONDNER, Aurélie HAUTIER Centre Régional de Traitement des Grands Brûlés Service de chirurgie Plastique, Hôpital de la Conception, Marseille. DIAGNOSTIC DÉTERSION BOURGEONNEMENT
TECHNIQUES D AVENIR Jonathan LONDNER, Aurélie HAUTIER Centre Régional de Traitement des Grands Brûlés Service de chirurgie Plastique, Hôpital de la Conception, Marseille. DIAGNOSTIC DÉTERSION BOURGEONNEMENT
Télé-expertise et surveillance médicale à domicile au service de la médecine générale :
 Télé-expertise et surveillance médicale à domicile au service de la médecine générale : Docteur DARY Patrick, Cardiologue, Praticien Hospitalier Centre Hospitalier de St YRIEIX - Haute Vienne 87500 Situé
Télé-expertise et surveillance médicale à domicile au service de la médecine générale : Docteur DARY Patrick, Cardiologue, Praticien Hospitalier Centre Hospitalier de St YRIEIX - Haute Vienne 87500 Situé
Sensibilisation à la Sécurité LASER. Aspet, le 26/06/2013
 Sensibilisation à la Sécurité LASER Aspet, le 26/06/2013 Modes d émission LASER P c P 0 P moy 0 Emission pulsée Salve ou train de N impulsions Emission continue Q i t i t Longueur d onde λ Emission continue
Sensibilisation à la Sécurité LASER Aspet, le 26/06/2013 Modes d émission LASER P c P 0 P moy 0 Emission pulsée Salve ou train de N impulsions Emission continue Q i t i t Longueur d onde λ Emission continue
Formation L.M.D. en instrumentation biomédicale. Mise en œuvre dans une université scientifique et médicale : Claude Bernard Lyon I
 J3eA, Journal sur l enseignement des sciences et technologies de l information et des systèmes, Volume 3, Hors-Série 1, 11 (2004) DOI : http://dx.doi.org/10.1051/bib-j3ea:2004611 EDP Sciences, 2004 Formation
J3eA, Journal sur l enseignement des sciences et technologies de l information et des systèmes, Volume 3, Hors-Série 1, 11 (2004) DOI : http://dx.doi.org/10.1051/bib-j3ea:2004611 EDP Sciences, 2004 Formation
