Applications en imagerie cérébrale (MEG/EEG)
|
|
|
- Adeline Fontaine
- il y a 10 ans
- Total affichages :
Transcription
1 EEG : mesure du potentiel électrique Ordre de grandeur : qq µ-volts Capteurs : électrodes MEG : mesure du champ magnétique Ordre de grandeur : Tesla Capteurs SQUID couplés à des bobines VI. Applications en imagerie cérébrale (MEG/EEG) VI. Applications en imagerie cérébrale 2 Problème direct/inverse en (MEG/EEG) Électroencéphalographie (EEG) Activité électrique neuronale Résolution temporelle : 1ms Magnétoencéphalographie (MEG)
2 VI. Applications en imagerie cérébrale 3 MEG/EEG : courants macroscopiques Mesure à l échelle du cm 2 de l activité électrique des cellules pyramidales synchrone temporellement et spatialement Dipôle de courant Macro-colonne corticale 10 5 neurones pyramidaux Q = I d 10 nam Dipôles sur la surface corticale VI. Applications en imagerie cérébrale 4 Les réponses de la MEG et de l EEG Données spatio-temporelles
3 VI. Applications en imagerie cérébrale 5 Réponse simultanée MEG et EEG Réponse auditive 100 millisecondes après l arrivée du son VI. Applications en imagerie cérébrale 6 MEG/EEG : Réponses topographiques Champ <0 Champ >0 Potentiel >0 Réponse dipolaire direction dipôle Réponse dipolaire à direction dipôle
4 VI. Applications en imagerie cérébrale 7 Imagerie MEG/EEG : localisation Reconstruire dans le temps et l espace les sources neuronales j à l origine des signaux MEG et EEG mesurés en surface Nécessité de résoudre le problème direct et le problème inverse VI. Applications en imagerie cérébrale 8 Problème direct en MEG/EEG Déf. : Connaissant la distribution des sources de courant j, calculer le champ électromagnétique ( E(r), B(r)), r S scalp Loi physiques : éq. de Maxwell, régime quasi-statique car f < 100 Hz Courants dans la tête : j = Courants primaires { }} { j p + Courants de conduction { }} { j c Loi d Ohm : jc = σ E = σ V Conservation de la charge : j = 0 (σ V ) = j p Loi Biot et Savart : r point de mesure à l extérieur de la tête (vol. conducteur) r : point à l intérieur du volume B( r) = µ 0 ( j 4π p + j r c )( r r ) r r 3 dv V tete
5 VI. Applications en imagerie cérébrale 9 Problème direct en MEG/EEG Difficultés : complexité du milieu physique [Hämäläinen et coll. 1993] Prise en compte de la géométrie des tissus (peau/os/lcr/subst. blanche) Connaissance imparfaite des conductivités : mesures in vivo difficiles Milieu homogène par morceaux (cas sphérique) B( r) = B 0 ( r) µ 0 4π n (σ j σ j+1 ) j=1 avec B0 ( r) = µ 0 4π V tete S j V ( r ) n( r ) jp ( r ) r r r r 3 dv r r r r 3 ds j Composante radiale calculée par B( r) n et n r le 2ème terme s annule B indépendant des conductivités Sources radiales silencieuses : j p n B 0 ( r) n = 0 [Sarvas 1987] VI. Applications en imagerie cérébrale 10 Problème direct en MEG/EEG : mileux homogènes Potentiel en un point appartenant à une surface [Hämäläinen et coll. 1993] σ j + σ j+1 V ( r) = σ n V 0 ( r) 2 avec r S j et V 0 ( r) = 1 4πσ n n j=1 V tete σ j σ j+1 4π jp ( r ) S j V ( r ) n( r ) r r r r 3 dv r r r r 3 ds j Solution analytique dans cas sphérique uniquement Modèle de source dipolaire : dipôle de courant équivalent q Activation en r p et observation en r j p ( r ) = qδ( r r p )avec q = j p ( r ) dv Conséquences cas sphérique : B0 ( r) n = µ 0 r r p 4π r r p 3 q
6 VI. Applications en imagerie cérébrale 11 Problème direct en MEG/EEG : Modèle de tête réaliste Calcul des champs sur un espace discret [Ermer et coll. 2001] m(r) = p g(r, r q p ) t q p, q p = [ q x p, q y p, q z p g(r, r qp ) : champ de sensibilité du capteur placé en r vis-à-vis du dipôle q p en r qp m = [m(r 1 ),..., m(r N )] t : potentiels/champs aux électrodes/capteurs, resp. g(r 1, r q1 ) t g(r 1, r qp ) t q 1 m = = G q g(r N, r q1 ) t g(r N, r qp ) t q P ] t Intégrales de frontières σ homogène isotrope Éléments/Différences fini(e)s σ variable VI. Applications en imagerie cérébrale 12 Modèles spatio-temporels k = 1,..., K, m tk = G q tk + b tk M = GQ avec M = [m t1 m tk ] q 1 (t) q avec Q = [ q t1... q tk ] t p x (t 1 ) q x p (t K ). =. et q p (t) = qp(t y 1 ) qp(t y K ) q P (t) qp(t z 1 ) qp(t z K ) Contrainte sur les dipôles : orientation u p fixe p = 1,..., P u x p q p (t) = u y p [s p (t 1 ),..., s p (t K )] = u p s t p, u = 1 u z p g(r 1, r q1 ) t u 1 g(r 1, r qp ) t u P s t 1 M = = A({r p, u p })S t g(r N, r q1 ) t u 1 g(r N, r qp ) t u P s t P Paramètres des sources : position/orientation {r p, u p } fixes au cours du temps
7 VI. Applications en imagerie cérébrale 13 Problème inverse MEG/EEG : approche Déf. : Reconstruire dans le temps et l espace les dipôles de courant neuronaux à partir des signaux MEG et EEG bruités mesurés en surface Difficultés : problème mal posé Non unicité de la solution (loi fondamentales de la physique, (Helmholtz 1853)) A chaque instant, nombre données faible (< 300) Instabilité due au bruit restreindre espace des solutions par régularisation par contrôle de dimension : modèles dipolaires ou paramétriques par pénalisation : modèles distribués VI. Applications en imagerie cérébrale 14 Problème inverse MEG/EEG : modèles dipolaires Identifier {r p, u p } et S t à partir de M = A({r p, u p })S t + N Hypothèse très forte : nombre de sources P connu a priori (P 10)! Méthode des moindres carrés arg min { J ({r p, u p }, S) = M A({r p, u p })S t 2 F }, Norme Frobenius 1 Linéaire en fonction des amplitudes S : calcul solution inverse généralisé {r p, u p }, fixé, ŜIG = A M avec A A = I et A = A({r p, u p }) 2 Problème non/quasi linéaire vis-à-vis de la position {r p }/orientation {u p } [ arg min J ({rp, u p }) = (I AA )M) 2 ] F = arg min P A M 2 r p,u p r p,u p Minimisation : algorithme du simplexe, de Levenberg-Marquart Quand P non convexité de J ({r p, u p }) Approche la plus utilisée en MEG/EEG sur données expérimentales et cliniques
8 VI. Applications en imagerie cérébrale 15 Résolution du problème inverse : modèle distribué Estimation des ampltiudes de dipôles de courant distribués au préalable sur la surface corticale (source distribuées) Imagerie de la densité corticale de courant Extraction de la surface corticale par segmentation de l IRM anatomique [Mangin et coll. 1995] Positions {r p } et orientations {u p } fixées :r p S cortex et u p S cortex Estimation des amplitudes S : pb linéaire mais indéterminé + mal conditionné! Approche bayésienne : estimateur du Maximum A Posteriori Ŝ = arg max p(s M) = arg max ln p(m S) + ln p(s) VI. Applications en imagerie cérébrale 16 Résolution du problème inverse : modèle distribué Méthodes linéaires : a priori spatial Gaussien S t N (0, C 1 { Ŝ t = arg min M AS t 2 + λtr [ SC 1 C 1 S S t] } ) N Ŝ t = F λ M avec F = C 1 N S ) A t (AC 1 N A t + λc 1 N ) Méthode de norme minimale/pondérée : C S = I ou C S = diagw, w p = A p 2 [Okada 1983, Jeffs et coll. 1987] Dérivée spatiale 1er ordre C 1 S = D t (1) D (1) [Wang 1993] Laplacien (Loreta) : C 1 S = D t (2) D (2) [Pascual-Marqui et coll. 1994] Limite des approches linéaires Manque de réalité neurophysiologique (solutions basse résolution) Interface entre régions fonctionnelles différentes mal gérée car norme L 2 Indépendance temporelle a priori
9 VI. Applications en imagerie cérébrale 17 Problème inverse : comparaison modèles distribués (Logiciel Curry) Dans le volume entier Surface corticale L 2 Norme minimale Loreta L 1 VI. Applications en imagerie cérébrale 18 Résolution du problème inverse : modèle distribué A priori spatiaux non gaussiens Solution sparses et focales : norme L p, p < 2 [Matsuura et Okabe 1995] A priori markoviens [Geman et Geman 1984, Idier 2001] ln p(s) = Ω(S) = J φ c ( (j) S c ) c C j=1 Exemple : champ de Markov d ordre 1, i.e., aux plus proches voisins Ω(S) = φ(s r s q ) {r,q} C C = {{r, q}, r q = 1} = {, } N s =
10 VI. Applications en imagerie cérébrale 19 Résolution du problème inverse : modèle distribué φ 22 (s) = s 2 φ 21 (s) = τ 2 + s 2 τ φ 20 (s) = min{s 2, τ 2 } Application en MEG/EEG j = 1, C = C : φ c ( S c ) = [Baillet et Garnero 1997, Geman et McClure 1987] K φ c ( x s c (t k )) + φ c ( y s 2 s c (t k )), avec φ c (s) = 1 + s 2 /τc 2 k=1 A priori spatio-temporel markovien [Baillet et coll. 1999] K Ω S,T (S) = Ω S (S) + β P t k 1 S tk 2 ou S tk : k ème col. de S, k=1 P t k 1 = I S tk 1 S t t k 1 / S tk 1 2 : projecteur sur hyperplan orthogonal à S tk 1 VI. Applications en imagerie cérébrale 20 Validation ST-MAP sur fantôme [Baillet et coll. 2001] Acquisition Crâne + gélatine + 6 sources Casque à 61 éléctrodes Traitement Cortex virtuel Norme minimale ST-MAP
11 VI. Applications en imagerie cérébrale 21 Données réelles MEG : somesthésie Somatotopie des doigts Contrôle VI. Applications en imagerie cérébrale 22 Modèles distribués : somesthésie ST-MAP et focalisation [Gavit et coll. 2001] Doigt 1 Doigt 3 Doigt 2 Doigt 5
12 Bibliographie 23 Bibliographie 24 [Baillet et Garnero 1997] S. Baillet et L. Garnero (1997), < A Bayesian approach to introducing Anatomo-functional priors in the EEG/MEG inverse problem >, IEEE Transactions on Biomedical Engineering, 44, 5, pages [Baillet et coll. 1999] S. Baillet, L. Garnero, G. Marin et J.-P. Hugonin (1999), < Combining MEG and EEG source imaging by minimization of mutual information >, IEEE Transactions on Biomedical Engineering, 46, 5, pages [Baillet et coll. 2001] S. Baillet, J.-J. Riera, G. Marin, J.-F. Mangin, J. Aubert et L. Garnero (2001), < Evaluation of Inverse Methods and Head Models for EEG Source Localization Using a Human Skull Phantom >, Physics in Medicine and Biology, 46. [Ermer et coll. 2001] J. J. Ermer, J. C. Mosher, S. Baillet et R. M. Leahy (2001), < Rapidly Re-computable EEG Forward Models for Realistic Head Shapes >, Physics in Medicine and Biology, 46, 4, pages [Gavit et coll. 2001] L. Gavit, S. Baillet, J.-F. Mangin, J. Pescatore et L. Garnero (2001), < A Multiresolution framework to the MEG/EEG source imaging >, IEEE Transactions on Biomedical Engineering, 48, 10, pages [Geman et Geman 1984] S. Geman et D. Geman (1984), < Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images >, IEEE Transactions on Pattern Analysis and Machine Intelligence, PAMI-6, 6, pages
MCMC et approximations en champ moyen pour les modèles de Markov
 MCMC et approximations en champ moyen pour les modèles de Markov Gersende FORT LTCI CNRS - TELECOM ParisTech En collaboration avec Florence FORBES (Projet MISTIS, INRIA Rhône-Alpes). Basé sur l article:
MCMC et approximations en champ moyen pour les modèles de Markov Gersende FORT LTCI CNRS - TELECOM ParisTech En collaboration avec Florence FORBES (Projet MISTIS, INRIA Rhône-Alpes). Basé sur l article:
Introduction au datamining
 Introduction au datamining Patrick Naïm janvier 2005 Définition Définition Historique Mot utilisé au départ par les statisticiens Le mot indiquait une utilisation intensive des données conduisant à des
Introduction au datamining Patrick Naïm janvier 2005 Définition Définition Historique Mot utilisé au départ par les statisticiens Le mot indiquait une utilisation intensive des données conduisant à des
Filtrage stochastique non linéaire par la théorie de représentation des martingales
 Filtrage stochastique non linéaire par la théorie de représentation des martingales Adriana Climescu-Haulica Laboratoire de Modélisation et Calcul Institut d Informatique et Mathématiques Appliquées de
Filtrage stochastique non linéaire par la théorie de représentation des martingales Adriana Climescu-Haulica Laboratoire de Modélisation et Calcul Institut d Informatique et Mathématiques Appliquées de
Séparation de sources en ingénierie biomédicale
 http://perso.univ-rennes1.fr/laurent.albera/ Séparation de sources en ingénierie biomédicale Laurent Albera SAS en SRM Conclusion 1 I. Applications, signaux et méthodes 1. Modalités d acquisitions 2. Problèmes
http://perso.univ-rennes1.fr/laurent.albera/ Séparation de sources en ingénierie biomédicale Laurent Albera SAS en SRM Conclusion 1 I. Applications, signaux et méthodes 1. Modalités d acquisitions 2. Problèmes
Que mesure la neuro-imagerie fonctionnelle :
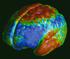 Que mesure la neuro-imagerie fonctionnelle : IRMf, TEP & MEG? O. Go s s e r i e s (1), A. De m e rt z i (1), Q. No i r ho m m e (1), J. Ts h i ba n d a (6), M. Bo ly (1), M. Op d e Be e c k (2), R. Hu
Que mesure la neuro-imagerie fonctionnelle : IRMf, TEP & MEG? O. Go s s e r i e s (1), A. De m e rt z i (1), Q. No i r ho m m e (1), J. Ts h i ba n d a (6), M. Bo ly (1), M. Op d e Be e c k (2), R. Hu
Champ électromagnétique?
 Qu est-ce qu un Champ électromagnétique? Alain Azoulay Consultant, www.radiocem.com 3 décembre 2013. 1 Définition trouvée à l article 2 de la Directive «champs électromagnétiques» : des champs électriques
Qu est-ce qu un Champ électromagnétique? Alain Azoulay Consultant, www.radiocem.com 3 décembre 2013. 1 Définition trouvée à l article 2 de la Directive «champs électromagnétiques» : des champs électriques
Les Conditions aux limites
 Chapitre 5 Les Conditions aux limites Lorsque nous désirons appliquer les équations de base de l EM à des problèmes d exploration géophysique, il est essentiel, pour pouvoir résoudre les équations différentielles,
Chapitre 5 Les Conditions aux limites Lorsque nous désirons appliquer les équations de base de l EM à des problèmes d exploration géophysique, il est essentiel, pour pouvoir résoudre les équations différentielles,
Chapitre 7. Circuits Magnétiques et Inductance. 7.1 Introduction. 7.1.1 Production d un champ magnétique
 Chapitre 7 Circuits Magnétiques et Inductance 7.1 Introduction 7.1.1 Production d un champ magnétique Si on considère un conducteur cylindrique droit dans lequel circule un courant I (figure 7.1). Ce courant
Chapitre 7 Circuits Magnétiques et Inductance 7.1 Introduction 7.1.1 Production d un champ magnétique Si on considère un conducteur cylindrique droit dans lequel circule un courant I (figure 7.1). Ce courant
Fonctions de plusieurs variables
 Module : Analyse 03 Chapitre 00 : Fonctions de plusieurs variables Généralités et Rappels des notions topologiques dans : Qu est- ce que?: Mathématiquement, n étant un entier non nul, on définit comme
Module : Analyse 03 Chapitre 00 : Fonctions de plusieurs variables Généralités et Rappels des notions topologiques dans : Qu est- ce que?: Mathématiquement, n étant un entier non nul, on définit comme
4.2 Unités d enseignement du M1
 88 CHAPITRE 4. DESCRIPTION DES UNITÉS D ENSEIGNEMENT 4.2 Unités d enseignement du M1 Tous les cours sont de 6 ECTS. Modélisation, optimisation et complexité des algorithmes (code RCP106) Objectif : Présenter
88 CHAPITRE 4. DESCRIPTION DES UNITÉS D ENSEIGNEMENT 4.2 Unités d enseignement du M1 Tous les cours sont de 6 ECTS. Modélisation, optimisation et complexité des algorithmes (code RCP106) Objectif : Présenter
Analyse de la vidéo. Chapitre 4.1 - La modélisation pour le suivi d objet. 10 mars 2015. Chapitre 4.1 - La modélisation d objet 1 / 57
 Analyse de la vidéo Chapitre 4.1 - La modélisation pour le suivi d objet 10 mars 2015 Chapitre 4.1 - La modélisation d objet 1 / 57 La représentation d objets Plan de la présentation 1 La représentation
Analyse de la vidéo Chapitre 4.1 - La modélisation pour le suivi d objet 10 mars 2015 Chapitre 4.1 - La modélisation d objet 1 / 57 La représentation d objets Plan de la présentation 1 La représentation
de calibration Master 2: Calibration de modèles: présentation et simulation d
 Master 2: Calibration de modèles: présentation et simulation de quelques problèmes de calibration Plan de la présentation 1. Présentation de quelques modèles à calibrer 1a. Reconstruction d une courbe
Master 2: Calibration de modèles: présentation et simulation de quelques problèmes de calibration Plan de la présentation 1. Présentation de quelques modèles à calibrer 1a. Reconstruction d une courbe
Une comparaison de méthodes de discrimination des masses de véhicules automobiles
 p.1/34 Une comparaison de méthodes de discrimination des masses de véhicules automobiles A. Rakotomamonjy, R. Le Riche et D. Gualandris INSA de Rouen / CNRS 1884 et SMS / PSA Enquêtes en clientèle dans
p.1/34 Une comparaison de méthodes de discrimination des masses de véhicules automobiles A. Rakotomamonjy, R. Le Riche et D. Gualandris INSA de Rouen / CNRS 1884 et SMS / PSA Enquêtes en clientèle dans
10ème Congrès Français d'acoustique Lyon, 12-16 Avril 2010
 10ème Congrès Français d'acoustique Lyon, 12-16 Avril 2010 Le compressed sensing pour l holographie acoustique de champ proche II: Mise en œuvre expérimentale. Antoine Peillot 1, Gilles Chardon 2, François
10ème Congrès Français d'acoustique Lyon, 12-16 Avril 2010 Le compressed sensing pour l holographie acoustique de champ proche II: Mise en œuvre expérimentale. Antoine Peillot 1, Gilles Chardon 2, François
AUTRES ASPECTS DU GPS. Partie I : tolérance de Battement Partie II : tolérancement par frontières
 AUTRES ASPECTS DU GPS Partie I : tolérance de Battement Partie II : tolérancement par frontières 1 Partie I Tolérance de battement Défaut de Battement Défautconjuguéde forme, orientation et position, constatélorsde
AUTRES ASPECTS DU GPS Partie I : tolérance de Battement Partie II : tolérancement par frontières 1 Partie I Tolérance de battement Défaut de Battement Défautconjuguéde forme, orientation et position, constatélorsde
IMAGERIE PAR TOMOGRAPHIE ÉLECTRIQUE RÉSISTIVE DE LA DISTRIBUTION DES PHASES DANS UNE COLONNE À BULLES
 IMAGERIE PAR TOMOGRAPHIE ÉLECTRIQUE RÉSISTIVE DE LA DISTRIBUTION DES PHASES DANS UNE COLONNE À BULLES E. Fransolet, M. Crine, G. L Homme, Laboratoires de Génie Chimique, P. Marchot, D. Toye. Université
IMAGERIE PAR TOMOGRAPHIE ÉLECTRIQUE RÉSISTIVE DE LA DISTRIBUTION DES PHASES DANS UNE COLONNE À BULLES E. Fransolet, M. Crine, G. L Homme, Laboratoires de Génie Chimique, P. Marchot, D. Toye. Université
I - Quelques propriétés des étoiles à neutrons
 Formation Interuniversitaire de Physique Option de L3 Ecole Normale Supérieure de Paris Astrophysique Patrick Hennebelle François Levrier Sixième TD 14 avril 2015 Les étoiles dont la masse initiale est
Formation Interuniversitaire de Physique Option de L3 Ecole Normale Supérieure de Paris Astrophysique Patrick Hennebelle François Levrier Sixième TD 14 avril 2015 Les étoiles dont la masse initiale est
Contents. 1 Introduction Objectifs des systèmes bonus-malus Système bonus-malus à classes Système bonus-malus : Principes
 Université Claude Bernard Lyon 1 Institut de Science Financière et d Assurances Système Bonus-Malus Introduction & Applications SCILAB Julien Tomas Institut de Science Financière et d Assurances Laboratoire
Université Claude Bernard Lyon 1 Institut de Science Financière et d Assurances Système Bonus-Malus Introduction & Applications SCILAB Julien Tomas Institut de Science Financière et d Assurances Laboratoire
Cours d électricité. Circuits électriques en courant constant. Mathieu Bardoux. 1 re année
 Cours d électricité Circuits électriques en courant constant Mathieu Bardoux [email protected] IUT Saint-Omer / Dunkerque Département Génie Thermique et Énergie 1 re année Objectifs du chapitre
Cours d électricité Circuits électriques en courant constant Mathieu Bardoux [email protected] IUT Saint-Omer / Dunkerque Département Génie Thermique et Énergie 1 re année Objectifs du chapitre
Les atouts et faiblesses des caméras TEP dédiées, TEP corps entier, TEP-CT, TEMP pour la quantification
 Les atouts et faiblesses des caméras TEP dédiées, TEP corps entier, TEP-CT, TEMP pour la quantification Irène Buvat U494 INSERM CHU Pitié-Salpêtrière, Paris [email protected] http://www.guillemet.org/irene
Les atouts et faiblesses des caméras TEP dédiées, TEP corps entier, TEP-CT, TEMP pour la quantification Irène Buvat U494 INSERM CHU Pitié-Salpêtrière, Paris [email protected] http://www.guillemet.org/irene
chargement d amplitude variable à partir de mesures Application à l approche fiabiliste de la tolérance aux dommages Modélisation stochastique d un d
 Laboratoire de Mécanique et Ingénieriesnieries EA 3867 - FR TIMS / CNRS 2856 ER MPS Modélisation stochastique d un d chargement d amplitude variable à partir de mesures Application à l approche fiabiliste
Laboratoire de Mécanique et Ingénieriesnieries EA 3867 - FR TIMS / CNRS 2856 ER MPS Modélisation stochastique d un d chargement d amplitude variable à partir de mesures Application à l approche fiabiliste
Magnétisme - Electromagnétisme
 Magnétisme - Electromagnétisme D re Colette Boëx, PhD, Ingénieur biomédical Neurologie, HUG et Faculté de médecine Figures principalement issues de : - "Physics for scientists and engineers, with modern
Magnétisme - Electromagnétisme D re Colette Boëx, PhD, Ingénieur biomédical Neurologie, HUG et Faculté de médecine Figures principalement issues de : - "Physics for scientists and engineers, with modern
Les mécanismes de la récupération neurologique. PPradat-Diehl DU de Rehabilitation neuropsychologique 2007
 Les mécanismes de la récupération neurologique PPradat-Diehl DU de Rehabilitation neuropsychologique 2007 Introduction Plasticité cérébrale / Récupération après lésion cérébrale Récupération spontanée
Les mécanismes de la récupération neurologique PPradat-Diehl DU de Rehabilitation neuropsychologique 2007 Introduction Plasticité cérébrale / Récupération après lésion cérébrale Récupération spontanée
Programmation linéaire
 Programmation linéaire DIDIER MAQUIN Ecole Nationale Supérieure d Electricité et de Mécanique Institut National Polytechnique de Lorraine Mathématiques discrètes cours de 2ème année Programmation linéaire
Programmation linéaire DIDIER MAQUIN Ecole Nationale Supérieure d Electricité et de Mécanique Institut National Polytechnique de Lorraine Mathématiques discrètes cours de 2ème année Programmation linéaire
Une fréquence peut-elle être instantanée?
 Fréquence? Variable? Instantané vs. local? Conclure? Une fréquence peut-elle être instantanée? Patrick Flandrin CNRS & École Normale Supérieure de Lyon, France Produire le temps, IRCAM, Paris, juin 2012
Fréquence? Variable? Instantané vs. local? Conclure? Une fréquence peut-elle être instantanée? Patrick Flandrin CNRS & École Normale Supérieure de Lyon, France Produire le temps, IRCAM, Paris, juin 2012
Annexe 6. Notions d ordonnancement.
 Annexe 6. Notions d ordonnancement. APP3 Optimisation Combinatoire: problèmes sur-contraints et ordonnancement. Mines-Nantes, option GIPAD, 2011-2012. [email protected] Résumé Ce document
Annexe 6. Notions d ordonnancement. APP3 Optimisation Combinatoire: problèmes sur-contraints et ordonnancement. Mines-Nantes, option GIPAD, 2011-2012. [email protected] Résumé Ce document
TABLE DES MATIÈRES. PRINCIPES D EXPÉRIMENTATION Planification des expériences et analyse de leurs résultats. Pierre Dagnelie
 PRINCIPES D EXPÉRIMENTATION Planification des expériences et analyse de leurs résultats Pierre Dagnelie TABLE DES MATIÈRES 2012 Presses agronomiques de Gembloux [email protected] www.pressesagro.be
PRINCIPES D EXPÉRIMENTATION Planification des expériences et analyse de leurs résultats Pierre Dagnelie TABLE DES MATIÈRES 2012 Presses agronomiques de Gembloux [email protected] www.pressesagro.be
Modélisation aléatoire en fiabilité des logiciels
 collection Méthodes stochastiques appliquées dirigée par Nikolaos Limnios et Jacques Janssen La sûreté de fonctionnement des systèmes informatiques est aujourd hui un enjeu économique et sociétal majeur.
collection Méthodes stochastiques appliquées dirigée par Nikolaos Limnios et Jacques Janssen La sûreté de fonctionnement des systèmes informatiques est aujourd hui un enjeu économique et sociétal majeur.
Rapport. Mesures de champ de très basses fréquences à proximité d antennes de stations de base GSM et UMTS
 Rapport Mesures de champ de très basses fréquences à proximité d antennes de stations de base GSM et UMTS A.AZOULAY T.LETERTRE R. DE LACERDA Convention AFSSET / Supélec 2009-1 - 1. Introduction Dans le
Rapport Mesures de champ de très basses fréquences à proximité d antennes de stations de base GSM et UMTS A.AZOULAY T.LETERTRE R. DE LACERDA Convention AFSSET / Supélec 2009-1 - 1. Introduction Dans le
Apprentissage Automatique
 Apprentissage Automatique Introduction-I [email protected] www.lia.univ-avignon.fr Définition? (Wikipedia) L'apprentissage automatique (machine-learning en anglais) est un des champs
Apprentissage Automatique Introduction-I [email protected] www.lia.univ-avignon.fr Définition? (Wikipedia) L'apprentissage automatique (machine-learning en anglais) est un des champs
Méthodes de Simulation
 Méthodes de Simulation JEAN-YVES TOURNERET Institut de recherche en informatique de Toulouse (IRIT) ENSEEIHT, Toulouse, France Peyresq06 p. 1/41 Remerciements Christian Robert : pour ses excellents transparents
Méthodes de Simulation JEAN-YVES TOURNERET Institut de recherche en informatique de Toulouse (IRIT) ENSEEIHT, Toulouse, France Peyresq06 p. 1/41 Remerciements Christian Robert : pour ses excellents transparents
Foscolo (1), J Felblinger (2), S Bracard (1) CHU Hôpital central, service de neuroradiologie, Nancy (1) CHU BRABOIS, Centre d investigation clinique
 S A l (1) G H (2) S S Aptel (1), G Hossu (2), S Foscolo (1), J Felblinger (2), S Bracard (1) CHU Hôpital central, service de neuroradiologie, Nancy (1) CHU BRABOIS, Centre d investigation clinique innovation
S A l (1) G H (2) S S Aptel (1), G Hossu (2), S Foscolo (1), J Felblinger (2), S Bracard (1) CHU Hôpital central, service de neuroradiologie, Nancy (1) CHU BRABOIS, Centre d investigation clinique innovation
Soutenance de stage Laboratoire des Signaux et Systèmes
 Soutenance de stage Laboratoire des Signaux et Systèmes Bornes inférieures bayésiennes de l'erreur quadratique moyenne. Application à la localisation de points de rupture. M2R ATSI Université Paris-Sud
Soutenance de stage Laboratoire des Signaux et Systèmes Bornes inférieures bayésiennes de l'erreur quadratique moyenne. Application à la localisation de points de rupture. M2R ATSI Université Paris-Sud
CAPTEURS - CHAINES DE MESURES
 CAPTEURS - CHAINES DE MESURES Pierre BONNET Pierre Bonnet Master GSI - Capteurs Chaînes de Mesures 1 Plan du Cours Propriétés générales des capteurs Notion de mesure Notion de capteur: principes, classes,
CAPTEURS - CHAINES DE MESURES Pierre BONNET Pierre Bonnet Master GSI - Capteurs Chaînes de Mesures 1 Plan du Cours Propriétés générales des capteurs Notion de mesure Notion de capteur: principes, classes,
Renforcement des trois compétences : compréhension orale, expression orale et expression écrite à partir de documents et vidéos.
 Master Mathématiques et Applications Spécialité : Ingénierie mathématique et modélisation Parcours : Mathématique et Informatique : Statistique, Signal, Santé (MI3S) 2015-2016 RÉSUMÉ DES COURS : (dernière
Master Mathématiques et Applications Spécialité : Ingénierie mathématique et modélisation Parcours : Mathématique et Informatique : Statistique, Signal, Santé (MI3S) 2015-2016 RÉSUMÉ DES COURS : (dernière
Sur les vols en formation.
 Sur les vols en formation. Grasse, 8 Février 2006 Plan de l exposé 1. Missions en cours et prévues 2. Le problème du mouvement relatif 2.1 Positionnement du problème 2.2 Les équations de Hill 2.2 Les changements
Sur les vols en formation. Grasse, 8 Février 2006 Plan de l exposé 1. Missions en cours et prévues 2. Le problème du mouvement relatif 2.1 Positionnement du problème 2.2 Les équations de Hill 2.2 Les changements
Programmation Linéaire - Cours 1
 Programmation Linéaire - Cours 1 P. Pesneau [email protected] Université Bordeaux 1 Bât A33 - Bur 265 Ouvrages de référence V. Chvátal - Linear Programming, W.H.Freeman, New York, 1983.
Programmation Linéaire - Cours 1 P. Pesneau [email protected] Université Bordeaux 1 Bât A33 - Bur 265 Ouvrages de référence V. Chvátal - Linear Programming, W.H.Freeman, New York, 1983.
TP N 57. Déploiement et renouvellement d une constellation de satellites
 TP N 57 Déploiement et renouvellement d une constellation de satellites L objet de ce TP est d optimiser la stratégie de déploiement et de renouvellement d une constellation de satellites ainsi que les
TP N 57 Déploiement et renouvellement d une constellation de satellites L objet de ce TP est d optimiser la stratégie de déploiement et de renouvellement d une constellation de satellites ainsi que les
Plan du chapitre «Milieux diélectriques»
 Plan du chapitre «Milieux diélectriques» 1. Sources microscopiques de la polarisation en régime statique 2. Etude macroscopique de la polarisation en régime statique 3. Susceptibilité diélectrique 4. Polarisation
Plan du chapitre «Milieux diélectriques» 1. Sources microscopiques de la polarisation en régime statique 2. Etude macroscopique de la polarisation en régime statique 3. Susceptibilité diélectrique 4. Polarisation
Méthodes de Caractérisation des Matériaux. Cours, annales http://www.u-picardie.fr/~dellis/
 Méthodes de Caractérisation des Matériaux Cours, annales http://www.u-picardie.fr/~dellis/ 1. Symboles standards et grandeurs électriques 3 2. Le courant électrique 4 3. La résistance électrique 4 4. Le
Méthodes de Caractérisation des Matériaux Cours, annales http://www.u-picardie.fr/~dellis/ 1. Symboles standards et grandeurs électriques 3 2. Le courant électrique 4 3. La résistance électrique 4 4. Le
Contenu pédagogique des unités d enseignement Semestre 1(1 ère année) Domaine : Sciences et techniques et Sciences de la matière
 Contenu pédagogique des unités d enseignement Semestre 1(1 ère année) Domaine : Sciences et techniques et Sciences de la matière Algèbre 1 : (Volume horaire total : 63 heures) UE1 : Analyse et algèbre
Contenu pédagogique des unités d enseignement Semestre 1(1 ère année) Domaine : Sciences et techniques et Sciences de la matière Algèbre 1 : (Volume horaire total : 63 heures) UE1 : Analyse et algèbre
Microscopie de fluorescence Etat de l art
 Etat de l art Bibliométrie (Web of sciences) CLSM GFP & TPE EPI-FLUORESCENCE 1 Fluorescence Diagramme de JABLONSKI S2 S1 10-12 s Excitation Eex Eem 10-9 s Émission Courtoisie de C. Spriet
Etat de l art Bibliométrie (Web of sciences) CLSM GFP & TPE EPI-FLUORESCENCE 1 Fluorescence Diagramme de JABLONSKI S2 S1 10-12 s Excitation Eex Eem 10-9 s Émission Courtoisie de C. Spriet
NON-LINEARITE ET RESEAUX NEURONAUX
 NON-LINEARITE ET RESEAUX NEURONAUX Vêlayoudom MARIMOUTOU Laboratoire d Analyse et de Recherche Economiques Université de Bordeaux IV Avenue. Leon Duguit, 33608 PESSAC, France tel. 05 56 84 85 77 e-mail
NON-LINEARITE ET RESEAUX NEURONAUX Vêlayoudom MARIMOUTOU Laboratoire d Analyse et de Recherche Economiques Université de Bordeaux IV Avenue. Leon Duguit, 33608 PESSAC, France tel. 05 56 84 85 77 e-mail
Chapitre XIV BASES PHYSIQUES QUANTITATIVES DES LOIS DE COMPORTEMENT MÉCANIQUE. par S. CANTOURNET 1 ELASTICITÉ
 Chapitre XIV BASES PHYSIQUES QUANTITATIVES DES LOIS DE COMPORTEMENT MÉCANIQUE par S. CANTOURNET 1 ELASTICITÉ Les propriétés mécaniques des métaux et alliages sont d un grand intérêt puisqu elles conditionnent
Chapitre XIV BASES PHYSIQUES QUANTITATIVES DES LOIS DE COMPORTEMENT MÉCANIQUE par S. CANTOURNET 1 ELASTICITÉ Les propriétés mécaniques des métaux et alliages sont d un grand intérêt puisqu elles conditionnent
Le logiciel EduAnatomist.
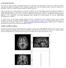 Le logiciel EduAnatomist. Les travaux de l équipe ACCES (Actualisation Continue des Connaissances des Enseignants en Sciences) de l INRP restent, hélas, largement méconnus des enseignants de SVT. Pourtant,
Le logiciel EduAnatomist. Les travaux de l équipe ACCES (Actualisation Continue des Connaissances des Enseignants en Sciences) de l INRP restent, hélas, largement méconnus des enseignants de SVT. Pourtant,
L analyse d images regroupe plusieurs disciplines que l on classe en deux catégories :
 La vision nous permet de percevoir et d interpreter le monde qui nous entoure. La vision artificielle a pour but de reproduire certaines fonctionnalités de la vision humaine au travers de l analyse d images.
La vision nous permet de percevoir et d interpreter le monde qui nous entoure. La vision artificielle a pour but de reproduire certaines fonctionnalités de la vision humaine au travers de l analyse d images.
Simulation d'un examen anthropomorphique en imagerie TEMP à l iode 131 par simulation Monte Carlo GATE
 Simulation d'un examen anthropomorphique en imagerie TEMP à l iode 131 par simulation Monte Carlo GATE LAURENT Rémy [email protected] http://clrpcsv.in2p3.fr Journées des LARD Septembre 2007 M2R
Simulation d'un examen anthropomorphique en imagerie TEMP à l iode 131 par simulation Monte Carlo GATE LAURENT Rémy [email protected] http://clrpcsv.in2p3.fr Journées des LARD Septembre 2007 M2R
Objectifs. Clustering. Principe. Applications. Applications. Cartes de crédits. Remarques. Biologie, Génomique
 Objectifs Clustering On ne sait pas ce qu on veut trouver : on laisse l algorithme nous proposer un modèle. On pense qu il existe des similarités entre les exemples. Qui se ressemble s assemble p. /55
Objectifs Clustering On ne sait pas ce qu on veut trouver : on laisse l algorithme nous proposer un modèle. On pense qu il existe des similarités entre les exemples. Qui se ressemble s assemble p. /55
Reconnaissance de visages 2.5D par fusion des indices de texture et de profondeur ICI 12/12/12
 Reconnaissance de visages 2.5D par fusion des indices de texture et de profondeur ICI 12/12/12 2 Discrimination Invariance Expressions faciales Age Pose Eclairage 11/12/2012 3 Personne Inconnue Identité
Reconnaissance de visages 2.5D par fusion des indices de texture et de profondeur ICI 12/12/12 2 Discrimination Invariance Expressions faciales Age Pose Eclairage 11/12/2012 3 Personne Inconnue Identité
Détection en environnement non-gaussien Cas du fouillis de mer et extension aux milieux
 Détection en environnement non-gaussien Cas du fouillis de mer et extension aux milieux hétérogènes Laurent Déjean Thales Airborne Systems/ENST-Bretagne Le 20 novembre 2006 Laurent Déjean Détection en
Détection en environnement non-gaussien Cas du fouillis de mer et extension aux milieux hétérogènes Laurent Déjean Thales Airborne Systems/ENST-Bretagne Le 20 novembre 2006 Laurent Déjean Détection en
Master IMA - UMPC Paris 6 RDMM - Année 2009-2010 Fiche de TP
 Master IMA - UMPC Paris 6 RDMM - Année 2009-200 Fiche de TP Préliminaires. Récupérez l archive du logiciel de TP à partir du lien suivant : http://www.ensta.fr/~manzaner/cours/ima/tp2009.tar 2. Développez
Master IMA - UMPC Paris 6 RDMM - Année 2009-200 Fiche de TP Préliminaires. Récupérez l archive du logiciel de TP à partir du lien suivant : http://www.ensta.fr/~manzaner/cours/ima/tp2009.tar 2. Développez
Introduction au Data-Mining
 Introduction au Data-Mining Alain Rakotomamonjy - Gilles Gasso. INSA Rouen -Département ASI Laboratoire PSI Introduction au Data-Mining p. 1/25 Data-Mining : Kèkecé? Traduction : Fouille de données. Terme
Introduction au Data-Mining Alain Rakotomamonjy - Gilles Gasso. INSA Rouen -Département ASI Laboratoire PSI Introduction au Data-Mining p. 1/25 Data-Mining : Kèkecé? Traduction : Fouille de données. Terme
Programmation linéaire
 1 Programmation linéaire 1. Le problème, un exemple. 2. Le cas b = 0 3. Théorème de dualité 4. L algorithme du simplexe 5. Problèmes équivalents 6. Complexité de l Algorithme 2 Position du problème Soit
1 Programmation linéaire 1. Le problème, un exemple. 2. Le cas b = 0 3. Théorème de dualité 4. L algorithme du simplexe 5. Problèmes équivalents 6. Complexité de l Algorithme 2 Position du problème Soit
Echantillonnage Non uniforme
 Echantillonnage Non uniforme Marie CHABERT IRIT/INP-ENSEEIHT/ ENSEEIHT/TéSASA Patrice MICHEL et Bernard LACAZE TéSA 1 Plan Introduction Echantillonnage uniforme Echantillonnage irrégulier Comparaison Cas
Echantillonnage Non uniforme Marie CHABERT IRIT/INP-ENSEEIHT/ ENSEEIHT/TéSASA Patrice MICHEL et Bernard LACAZE TéSA 1 Plan Introduction Echantillonnage uniforme Echantillonnage irrégulier Comparaison Cas
Quantification Scalaire et Prédictive
 Quantification Scalaire et Prédictive Marco Cagnazzo Département Traitement du Signal et des Images TELECOM ParisTech 7 Décembre 2012 M. Cagnazzo Quantification Scalaire et Prédictive 1/64 Plan Introduction
Quantification Scalaire et Prédictive Marco Cagnazzo Département Traitement du Signal et des Images TELECOM ParisTech 7 Décembre 2012 M. Cagnazzo Quantification Scalaire et Prédictive 1/64 Plan Introduction
Sujets présentés par le Professeur Olivier CUSSENOT
 ANAMACaP Association Nationale des Malades du Cancer de la Prostate 17, bis Avenue Poincaré. 57400 SARREBOURG Sujets présentés par le Professeur Olivier CUSSENOT Place des nouvelles techniques d imagerie
ANAMACaP Association Nationale des Malades du Cancer de la Prostate 17, bis Avenue Poincaré. 57400 SARREBOURG Sujets présentés par le Professeur Olivier CUSSENOT Place des nouvelles techniques d imagerie
Data Mining. Vincent Augusto 2012-2013. École Nationale Supérieure des Mines de Saint-Étienne. Data Mining. V. Augusto.
 des des Data Mining Vincent Augusto École Nationale Supérieure des Mines de Saint-Étienne 2012-2013 1/65 des des 1 2 des des 3 4 Post-traitement 5 représentation : 6 2/65 des des Définition générale Le
des des Data Mining Vincent Augusto École Nationale Supérieure des Mines de Saint-Étienne 2012-2013 1/65 des des 1 2 des des 3 4 Post-traitement 5 représentation : 6 2/65 des des Définition générale Le
Dan Istrate. Directeur de thèse : Eric Castelli Co-Directeur : Laurent Besacier
 Détection et reconnaissance des sons pour la surveillance médicale Dan Istrate le 16 décembre 2003 Directeur de thèse : Eric Castelli Co-Directeur : Laurent Besacier Thèse mené dans le cadre d une collaboration
Détection et reconnaissance des sons pour la surveillance médicale Dan Istrate le 16 décembre 2003 Directeur de thèse : Eric Castelli Co-Directeur : Laurent Besacier Thèse mené dans le cadre d une collaboration
Introduction au Data-Mining
 Introduction au Data-Mining Gilles Gasso, Stéphane Canu INSA Rouen -Département ASI Laboratoire LITIS 8 septembre 205. Ce cours est librement inspiré du cours DM de Alain Rakotomamonjy Gilles Gasso, Stéphane
Introduction au Data-Mining Gilles Gasso, Stéphane Canu INSA Rouen -Département ASI Laboratoire LITIS 8 septembre 205. Ce cours est librement inspiré du cours DM de Alain Rakotomamonjy Gilles Gasso, Stéphane
Master Informatique Aix-Marseille Université
 Aix-Marseille Université http://masterinfo.univ-mrs.fr/ Département Informatique et Interactions UFR Sciences Laboratoire d Informatique Fondamentale Laboratoire des Sciences de l Information et des Systèmes
Aix-Marseille Université http://masterinfo.univ-mrs.fr/ Département Informatique et Interactions UFR Sciences Laboratoire d Informatique Fondamentale Laboratoire des Sciences de l Information et des Systèmes
Cours 2012: Le cerveau statisticien:
 Cours 2012: Le cerveau statisticien: La révolution Bayésienne en sciences cognitives Stanislas Dehaene Chaire de Psychologie Cognitive Expérimentale Cours n 7 Le cerveau vu comme un système prédictif La
Cours 2012: Le cerveau statisticien: La révolution Bayésienne en sciences cognitives Stanislas Dehaene Chaire de Psychologie Cognitive Expérimentale Cours n 7 Le cerveau vu comme un système prédictif La
La Licence Mathématiques et Economie-MASS Université de Sciences Sociales de Toulouse 1
 La Licence Mathématiques et Economie-MASS Université de Sciences Sociales de Toulouse 1 La licence Mathématiques et Economie-MASS de l Université des Sciences Sociales de Toulouse propose sur les trois
La Licence Mathématiques et Economie-MASS Université de Sciences Sociales de Toulouse 1 La licence Mathématiques et Economie-MASS de l Université des Sciences Sociales de Toulouse propose sur les trois
CarrotAge, un logiciel pour la fouille de données agricoles
 CarrotAge, un logiciel pour la fouille de données agricoles F. Le Ber (engees & loria) J.-F. Mari (loria) M. Benoît, C. Mignolet et C. Schott (inra sad) Conférence STIC et Environnement, Rouen, 19-20 juin
CarrotAge, un logiciel pour la fouille de données agricoles F. Le Ber (engees & loria) J.-F. Mari (loria) M. Benoît, C. Mignolet et C. Schott (inra sad) Conférence STIC et Environnement, Rouen, 19-20 juin
Chp. 4. Minimisation d une fonction d une variable
 Chp. 4. Minimisation d une fonction d une variable Avertissement! Dans tout ce chapître, I désigne un intervalle de IR. 4.1 Fonctions convexes d une variable Définition 9 Une fonction ϕ, partout définie
Chp. 4. Minimisation d une fonction d une variable Avertissement! Dans tout ce chapître, I désigne un intervalle de IR. 4.1 Fonctions convexes d une variable Définition 9 Une fonction ϕ, partout définie
Relever les défis des véhicules autonomes
 EMM 2014 12eme rencontre européenne de mécatronique Relever les défis des véhicules autonomes Mathias Perrollaz Ingénieur expert Inria Christian Laugier Directeur de recherche Inria E-Motion Team Annecy,
EMM 2014 12eme rencontre européenne de mécatronique Relever les défis des véhicules autonomes Mathias Perrollaz Ingénieur expert Inria Christian Laugier Directeur de recherche Inria E-Motion Team Annecy,
Traitement bas-niveau
 Plan Introduction L approche contour (frontière) Introduction Objectifs Les traitements ont pour but d extraire l information utile et pertinente contenue dans l image en regard de l application considérée.
Plan Introduction L approche contour (frontière) Introduction Objectifs Les traitements ont pour but d extraire l information utile et pertinente contenue dans l image en regard de l application considérée.
Journée SITG, Genève 15 octobre 2013. Nicolas Lachance-Bernard M.ATDR Doctorant, Laboratoire de systèmes d information géographique
 Monitorint spatio-temporel intégré de la mobilité urbaine Monitoring spatio-temporel de l ADN urbain Une réponse aux défis, problèmes, enjeux et risques des milieux urbains Nicolas Lachance-Bernard M.ATDR
Monitorint spatio-temporel intégré de la mobilité urbaine Monitoring spatio-temporel de l ADN urbain Une réponse aux défis, problèmes, enjeux et risques des milieux urbains Nicolas Lachance-Bernard M.ATDR
Projet : Recalage par maximisation de l information mutuelle
 École Polytechnique de Montréal Automne 25, 12 décembre 25 Projet : Recalage par maximisation de l information mutuelle GBM613, Application médicales de l informatique Nom Matricule Groupe Herve Lombaert
École Polytechnique de Montréal Automne 25, 12 décembre 25 Projet : Recalage par maximisation de l information mutuelle GBM613, Application médicales de l informatique Nom Matricule Groupe Herve Lombaert
La (les) mesure(s) GPS
 La (les) mesure(s) GPS I. Le principe de la mesure II. Equation de mesure GPS III. Combinaisons de mesures (ionosphère, horloges) IV. Doubles différences et corrélation des mesures V. Doubles différences
La (les) mesure(s) GPS I. Le principe de la mesure II. Equation de mesure GPS III. Combinaisons de mesures (ionosphère, horloges) IV. Doubles différences et corrélation des mesures V. Doubles différences
Health Monitoring pour la Maintenance Prévisionnelle, Modélisation de la Dégradation
 Health Monitoring pour la Maintenance Prévisionnelle, Modélisation de la Dégradation Laurent Denis STATXPERT Journée technologique "Solutions de maintenance prévisionnelle adaptées à la production" FIGEAC,
Health Monitoring pour la Maintenance Prévisionnelle, Modélisation de la Dégradation Laurent Denis STATXPERT Journée technologique "Solutions de maintenance prévisionnelle adaptées à la production" FIGEAC,
TRAUMATISME CRANIEN DE L ENFANT : conduite à tenir?
 TRAUMATISME CRANIEN DE L ENFANT : conduite à tenir? H Le Hors-Albouze Urgences pédiatriques Timone enfants Marseille Traumatismes crâniens (TC) de l enfant Grande fréquence même si incidence réelle mal
TRAUMATISME CRANIEN DE L ENFANT : conduite à tenir? H Le Hors-Albouze Urgences pédiatriques Timone enfants Marseille Traumatismes crâniens (TC) de l enfant Grande fréquence même si incidence réelle mal
Introduction à la relativité générale
 Introduction à la relativité générale Bartolomé Coll Systèmes de référence relativistes SYRTE - CNRS Observatoire de Paris Introduction à la Relativité Générale Préliminaires Caractère théorique (formation)
Introduction à la relativité générale Bartolomé Coll Systèmes de référence relativistes SYRTE - CNRS Observatoire de Paris Introduction à la Relativité Générale Préliminaires Caractère théorique (formation)
Introduction à l informatique temps réel Pierre-Yves Duval (cppm)
 Introduction à l informatique temps réel Pierre-Yves Duval (cppm) Ecole d informatique temps réel - La Londes les Maures 7-11 Octobre 2002 -Définition et problématique - Illustration par des exemples -Automatisme:
Introduction à l informatique temps réel Pierre-Yves Duval (cppm) Ecole d informatique temps réel - La Londes les Maures 7-11 Octobre 2002 -Définition et problématique - Illustration par des exemples -Automatisme:
Module d Electricité. 2 ème partie : Electrostatique. Fabrice Sincère (version 3.0.1) http://pagesperso-orange.fr/fabrice.sincere
 Module d Electricité 2 ème partie : Electrostatique Fabrice Sincère (version 3.0.1) http://pagesperso-orange.fr/fabrice.sincere 1 Introduction Principaux constituants de la matière : - protons : charge
Module d Electricité 2 ème partie : Electrostatique Fabrice Sincère (version 3.0.1) http://pagesperso-orange.fr/fabrice.sincere 1 Introduction Principaux constituants de la matière : - protons : charge
Application de K-means à la définition du nombre de VM optimal dans un cloud
 Application de K-means à la définition du nombre de VM optimal dans un cloud EGC 2012 : Atelier Fouille de données complexes : complexité liée aux données multiples et massives (31 janvier - 3 février
Application de K-means à la définition du nombre de VM optimal dans un cloud EGC 2012 : Atelier Fouille de données complexes : complexité liée aux données multiples et massives (31 janvier - 3 février
Bac Blanc Terminale ES - Février 2011 Épreuve de Mathématiques (durée 3 heures)
 Bac Blanc Terminale ES - Février 2011 Épreuve de Mathématiques (durée 3 heures) Eercice 1 (5 points) pour les candidats n ayant pas choisi la spécialité MATH Le tableau suivant donne l évolution du chiffre
Bac Blanc Terminale ES - Février 2011 Épreuve de Mathématiques (durée 3 heures) Eercice 1 (5 points) pour les candidats n ayant pas choisi la spécialité MATH Le tableau suivant donne l évolution du chiffre
un module de simulation des évolutions urbaines http://geopensim.ign.fr Présentation
 un module de simulation des évolutions urbaines http://geopensim.ign.fr 12 mars 2009 Anne Ruas Annabelle Mas Julien Perret Présentation Plateforme open source d analyse et de simulation des évolutions
un module de simulation des évolutions urbaines http://geopensim.ign.fr 12 mars 2009 Anne Ruas Annabelle Mas Julien Perret Présentation Plateforme open source d analyse et de simulation des évolutions
Intérêt du découpage en sous-bandes pour l analyse spectrale
 Intérêt du découpage en sous-bandes pour l analyse spectrale David BONACCI Institut National Polytechnique de Toulouse (INP) École Nationale Supérieure d Électrotechnique, d Électronique, d Informatique,
Intérêt du découpage en sous-bandes pour l analyse spectrale David BONACCI Institut National Polytechnique de Toulouse (INP) École Nationale Supérieure d Électrotechnique, d Électronique, d Informatique,
23. Interprétation clinique des mesures de l effet traitement
 23. Interprétation clinique des mesures de l effet traitement 23.1. Critères de jugement binaires Plusieurs mesures (indices) sont utilisables pour quantifier l effet traitement lors de l utilisation d
23. Interprétation clinique des mesures de l effet traitement 23.1. Critères de jugement binaires Plusieurs mesures (indices) sont utilisables pour quantifier l effet traitement lors de l utilisation d
Sujet proposé par Yves M. LEROY. Cet examen se compose d un exercice et de deux problèmes. Ces trois parties sont indépendantes.
 Promotion X 004 COURS D ANALYSE DES STRUCTURES MÉCANIQUES PAR LA MÉTHODE DES ELEMENTS FINIS (MEC 568) contrôle non classant (7 mars 007, heures) Documents autorisés : polycopié ; documents et notes de
Promotion X 004 COURS D ANALYSE DES STRUCTURES MÉCANIQUES PAR LA MÉTHODE DES ELEMENTS FINIS (MEC 568) contrôle non classant (7 mars 007, heures) Documents autorisés : polycopié ; documents et notes de
Voir le cerveau en fonctionnement
 Voir le cerveau en fonctionnement évolution des techniques évolution des idées... http://www.atoute.org/n/img/jpg/neurone.jpg Françoise Jauzein, février 2009 Lien techniques-connaissances Socle commun
Voir le cerveau en fonctionnement évolution des techniques évolution des idées... http://www.atoute.org/n/img/jpg/neurone.jpg Françoise Jauzein, février 2009 Lien techniques-connaissances Socle commun
Méthodes de quadrature. Polytech Paris-UPMC. - p. 1/48
 Méthodes de Polytech Paris-UPMC - p. 1/48 Polynôme d interpolation de Preuve et polynôme de Calcul de l erreur d interpolation Étude de la formule d erreur Autres méthodes - p. 2/48 Polynôme d interpolation
Méthodes de Polytech Paris-UPMC - p. 1/48 Polynôme d interpolation de Preuve et polynôme de Calcul de l erreur d interpolation Étude de la formule d erreur Autres méthodes - p. 2/48 Polynôme d interpolation
Etude des propriétés empiriques du lasso par simulations
 Etude des propriétés empiriques du lasso par simulations L objectif de ce TP est d étudier les propriétés empiriques du LASSO et de ses variantes à partir de données simulées. Un deuxième objectif est
Etude des propriétés empiriques du lasso par simulations L objectif de ce TP est d étudier les propriétés empiriques du LASSO et de ses variantes à partir de données simulées. Un deuxième objectif est
Contribution à la conception par la simulation en électronique de puissance : application à l onduleur basse tension
 Contribution à la conception par la simulation en électronique de puissance : application à l onduleur basse tension Cyril BUTTAY CEGELY VALEO 30 novembre 2004 Cyril BUTTAY Contribution à la conception
Contribution à la conception par la simulation en électronique de puissance : application à l onduleur basse tension Cyril BUTTAY CEGELY VALEO 30 novembre 2004 Cyril BUTTAY Contribution à la conception
Modèles à Événements Discrets. Réseaux de Petri Stochastiques
 Modèles à Événements Discrets Réseaux de Petri Stochastiques Table des matières 1 Chaînes de Markov Définition formelle Idée générale Discrete Time Markov Chains Continuous Time Markov Chains Propriétés
Modèles à Événements Discrets Réseaux de Petri Stochastiques Table des matières 1 Chaînes de Markov Définition formelle Idée générale Discrete Time Markov Chains Continuous Time Markov Chains Propriétés
choisir H 1 quand H 0 est vraie - fausse alarme
 étection et Estimation GEL-64943 Hiver 5 Tests Neyman-Pearson Règles de Bayes: coûts connus min π R ( ) + ( π ) R ( ) { } Règles Minimax: coûts connus min max R ( ), R ( ) Règles Neyman Pearson: coûts
étection et Estimation GEL-64943 Hiver 5 Tests Neyman-Pearson Règles de Bayes: coûts connus min π R ( ) + ( π ) R ( ) { } Règles Minimax: coûts connus min max R ( ), R ( ) Règles Neyman Pearson: coûts
Nouvelles propositions pour la résolution exacte du sac à dos multi-objectif unidimensionnel en variables binaires
 Nouvelles propositions pour la résolution exacte du sac à dos multi-objectif unidimensionnel en variables binaires Julien Jorge [email protected] Laboratoire d Informatique de Nantes Atlantique,
Nouvelles propositions pour la résolution exacte du sac à dos multi-objectif unidimensionnel en variables binaires Julien Jorge [email protected] Laboratoire d Informatique de Nantes Atlantique,
Projet de Traitement du Signal Segmentation d images SAR
 Projet de Traitement du Signal Segmentation d images SAR Introduction En analyse d images, la segmentation est une étape essentielle, préliminaire à des traitements de haut niveau tels que la classification,
Projet de Traitement du Signal Segmentation d images SAR Introduction En analyse d images, la segmentation est une étape essentielle, préliminaire à des traitements de haut niveau tels que la classification,
Capteurs de déplacement LVDT
 Capteurs de déplacement LVDT Source d'innovation smart engineering for extreme environments Technologies Avantages Concurrentiels Sensorex, leader EUROPÉEN dans le domaine des capteurs LVDT, vous propose
Capteurs de déplacement LVDT Source d'innovation smart engineering for extreme environments Technologies Avantages Concurrentiels Sensorex, leader EUROPÉEN dans le domaine des capteurs LVDT, vous propose
Reconnaissance de gestes : approches 2D & 3D
 Reconnaissance de gestes : approches 2D & 3D Maher Mkhinini et Patrick Horain Institut Mines-Télécom/Télécom SudParis Département Électronique et Physique, 9 rue Charles Fourier, 91011 Evry, France Email
Reconnaissance de gestes : approches 2D & 3D Maher Mkhinini et Patrick Horain Institut Mines-Télécom/Télécom SudParis Département Électronique et Physique, 9 rue Charles Fourier, 91011 Evry, France Email
M HAMED EL GADDAB & MONGI SLIM
 Sous la direction : M HAMED EL GADDAB & MONGI SLIM Préparation et élaboration : AMOR YOUSSEF Présentation et animation : MAHMOUD EL GAZAH MOHSEN BEN LAMINE AMOR YOUSSEF Année scolaire : 2007-2008 RECUEIL
Sous la direction : M HAMED EL GADDAB & MONGI SLIM Préparation et élaboration : AMOR YOUSSEF Présentation et animation : MAHMOUD EL GAZAH MOHSEN BEN LAMINE AMOR YOUSSEF Année scolaire : 2007-2008 RECUEIL
LA PHYSIQUE DES MATERIAUX. Chapitre 1 LES RESEAUX DIRECT ET RECIPROQUE
 LA PHYSIQUE DES MATERIAUX Chapitre 1 LES RESEAUX DIRECT ET RECIPROQUE Pr. A. Belayachi Université Mohammed V Agdal Faculté des Sciences Rabat Département de Physique - L.P.M [email protected] 1 1.Le réseau
LA PHYSIQUE DES MATERIAUX Chapitre 1 LES RESEAUX DIRECT ET RECIPROQUE Pr. A. Belayachi Université Mohammed V Agdal Faculté des Sciences Rabat Département de Physique - L.P.M [email protected] 1 1.Le réseau
Laboratoire 4 Développement d un système intelligent
 DÉPARTEMENT DE GÉNIE LOGICIEL ET DES TI LOG770 - SYSTÈMES INTELLIGENTS ÉTÉ 2012 Laboratoire 4 Développement d un système intelligent 1 Introduction Ce quatrième et dernier laboratoire porte sur le développement
DÉPARTEMENT DE GÉNIE LOGICIEL ET DES TI LOG770 - SYSTÈMES INTELLIGENTS ÉTÉ 2012 Laboratoire 4 Développement d un système intelligent 1 Introduction Ce quatrième et dernier laboratoire porte sur le développement
Cours d Analyse. Fonctions de plusieurs variables
 Cours d Analyse Fonctions de plusieurs variables Licence 1ère année 2007/2008 Nicolas Prioux Université de Marne-la-Vallée Table des matières 1 Notions de géométrie dans l espace et fonctions à deux variables........
Cours d Analyse Fonctions de plusieurs variables Licence 1ère année 2007/2008 Nicolas Prioux Université de Marne-la-Vallée Table des matières 1 Notions de géométrie dans l espace et fonctions à deux variables........
 Utilisation d informations visuelles dynamiques en asservissement visuel Armel Crétual IRISA, projet TEMIS puis VISTA L asservissement visuel géométrique Principe : Réalisation d une tâche robotique par
Utilisation d informations visuelles dynamiques en asservissement visuel Armel Crétual IRISA, projet TEMIS puis VISTA L asservissement visuel géométrique Principe : Réalisation d une tâche robotique par
La programmation linéaire : une introduction. Qu est-ce qu un programme linéaire? Terminologie. Écriture mathématique
 La programmation linéaire : une introduction Qu est-ce qu un programme linéaire? Qu est-ce qu un programme linéaire? Exemples : allocation de ressources problème de recouvrement Hypothèses de la programmation
La programmation linéaire : une introduction Qu est-ce qu un programme linéaire? Qu est-ce qu un programme linéaire? Exemples : allocation de ressources problème de recouvrement Hypothèses de la programmation
Théorie et Codage de l Information (IF01) exercices 2013-2014. Paul Honeine Université de technologie de Troyes France
 Théorie et Codage de l Information (IF01) exercices 2013-2014 Paul Honeine Université de technologie de Troyes France TD-1 Rappels de calculs de probabilités Exercice 1. On dispose d un jeu de 52 cartes
Théorie et Codage de l Information (IF01) exercices 2013-2014 Paul Honeine Université de technologie de Troyes France TD-1 Rappels de calculs de probabilités Exercice 1. On dispose d un jeu de 52 cartes
Utilisation des matériaux magnétostrictifs filaires comme capteurs de mesure de champ magnétique
 Utilisation des matériaux magnétostrictifs filaires comme capteurs de mesure de champ magnétique Eric CRESCENZO 1 Evagelos HRISTOFOROU 2 1) IXTREM 9 rue Edouard Denis Baldus, F-711 CHALON SUR SAONE Tél
Utilisation des matériaux magnétostrictifs filaires comme capteurs de mesure de champ magnétique Eric CRESCENZO 1 Evagelos HRISTOFOROU 2 1) IXTREM 9 rue Edouard Denis Baldus, F-711 CHALON SUR SAONE Tél
Une application de méthodes inverses en astrophysique : l'analyse de l'histoire de la formation d'étoiles dans les galaxies
 Une application de méthodes inverses en astrophysique : l'analyse de l'histoire de la formation d'étoiles dans les galaxies Ariane Lançon (Observatoire de Strasbourg) en collaboration avec: Jean-Luc Vergely,
Une application de méthodes inverses en astrophysique : l'analyse de l'histoire de la formation d'étoiles dans les galaxies Ariane Lançon (Observatoire de Strasbourg) en collaboration avec: Jean-Luc Vergely,
Déroulement d un projet en DATA MINING, préparation et analyse des données. Walid AYADI
 1 Déroulement d un projet en DATA MINING, préparation et analyse des données Walid AYADI 2 Les étapes d un projet Choix du sujet - Définition des objectifs Inventaire des données existantes Collecte, nettoyage
1 Déroulement d un projet en DATA MINING, préparation et analyse des données Walid AYADI 2 Les étapes d un projet Choix du sujet - Définition des objectifs Inventaire des données existantes Collecte, nettoyage
