1) Déterminer en utilisant la représentation graphique donnée :
|
|
|
- Corentin Bonnet
- il y a 9 ans
- Total affichages :
Transcription
1 EXERCICES SUR LES FONCTIONS AFFINES ET LINÉAIRES Exercice 1 Un chef de chantier vient d acheter un récipient isotherme pour tenir sa boisson au chaud. Le graphique ci-contre figure sur le carton d emballage. 76 C 65 C 50 C Le graphique représente l évolution de la température en degré Celsius de la boisson contenue dans le récipient isotherme en fonction de la durée en heure. 1) Déterminer en utilisant la représentation graphique donnée : a) les coordonnées des 3 points qui figurent sur ce graphique ; b) la température de la boisson après neuf heures passées dans le récipient isotherme ; c) la durée qui correspond à une température de la boisson de 55 C. 2) Pour améliorer la précision des résultats de la lecture graphique, cette situation est modélisée par la fonction f telle que : f (t) = 1,5 t + 85 pour t appartenant à l intervalle [6 ; 24]. a) Compléter le tableau de valeurs de la fonction f. t valeur de f(t) b) Tracer la représentation graphique de f à l aide de la calculatrice graphique ou d un logiciel. 3) Déterminer en utilisant la représentation graphique : a) f(13) ; b) t 0 tel que f (t 0 ) = 60. 4) Le chef de chantier n aime pas sa boisson quand sa température est inférieure à 60 C. Après une durée de 6 h dans le récipient isotherme rempli le matin, la boisson est à 76 C à midi. Indiquer s'il pourra boire sa boisson comme il l aime sept heures plus tard. (D après sujet de BEP Secteur 2 Métropole Mayotte Réunion Session juin 2011) Exercices sur les fonctions affines et linéaires 1/9
2 Exercice 2 La quantité quotidienne de lait (en ml) recommandée pour un bébé peut être déterminée par la règle d Appert selon la formule suivante : Masse du bébé ( en gramme ) Quantité quotidienne de lait (en ml) = ) Calculer, en ml, la quantité quotidienne de lait recommandée pour un bébé de 4 kilogrammes. 2) La directrice de la crèche souhaite mettre à disposition du personnel un graphique permettant de visualiser directement la quantité quotidienne de lait recommandée pour les bébés en fonction de leur masse. La quantité quotidienne de lait en ml est modélisée par la fonction f définie par : f(x) = 0,1 x x représente la masse du bébé en gramme et f(x) représente la quantité quotidienne de lait recommandée en ml, pour x appartenant à l intervalle [2 500 ; 7 000]. a) Compléter le tableau de valeurs suivant. x Valeurs de f(x) 500 b) Représenter graphiquement la fonction f dans le repère suivant. Quantité quotidienne de lait (en ml) Masse du bébé (en g) c) Déterminer graphiquement, en ml, la quantité de lait quotidienne recommandée pour un bébé de g. Laisser apparents les traits utiles à la lecture. (D après sujet de BEP Secteur 4 DOM TOM Session juin 2011) Exercices sur les fonctions affines et linéaires 2/9
3 Exercice 3 Un particulier souhaite installer des panneaux photovoltaïques pour sa résidence principale. Pour réaliser son projet, il consulte deux installateurs dont les conditions de vente sont données ci-dessous : Entreprise Chardon : prix hors taxes (H.T.) du matériel : 5,20 par Watt-crête (Wc). forfait pour la pose : Entreprise Luminon : prix hors taxes (H.T.) du matériel : 6,60 par Watt-crête (Wc). pose gratuite. I) Étude de la proposition faite par l entreprise Chardon : 1) Calculer le prix à payer hors taxes pour une installation de panneaux photovoltaïques dont la puissance est égale à Wc. 2) On considère la fonction f définie par f(x) = 5,2x sur l intervalle [0 ; 3 000] où - x représente la puissance (en Wc) de l installation ; - f(x) représente le prix hors taxes (H.T.) de l installation. a) Compléter le tableau de valeurs de la fonction f ci-dessous. Puissance (en Wc) x Prix à payer H.T. (en ) f(x) = 5,2x b) Tracer la représentation graphique de la fonction f à d un logiciel ou de la calculatrice. II) Comparaison des propositions faites par les deux entreprises On considère la fonction g définie par g(x) = 6,6x sur l intervalle [0 ; 3 000] où - x représente la puissance (en Wc) de l installation ; - g(x) représente le prix hors taxes (H.T.) de l installation réalisée par l entreprise Luminon. 1) Tracer sa représentation graphique Dg dans le repère précédent. 2) Déterminer graphiquement l entreprise pour laquelle l installation de panneaux photovoltaïques de Wc est la moins chère. 3) Résoudre l équation f(x) = g(x). 4) En déduire l entreprise la plus avantageuse selon la puissance (en Wc) des panneaux photovoltaïques installés. III) Finalisation du projet Ce particulier opte pour une installation de panneaux photovoltaïques de puissance égale à Wc. Il bénéficie de la T.V.A. à 5,5 %. Calculer le prix toutes taxes comprises (T.T.C.) qu il devra payer pour cette installation dont le prix hors taxes (H.T.) pose comprise est égal à (D après sujet de BEP Secteur 6 DOM TOM Session juin 2011) Exercices sur les fonctions affines et linéaires 3/9
4 Exercice 4 Dans un magasin de sport, les vendeurs ont le choix entre deux possibilités de rémunération mensuelle. option A : mensuel quel que soit le montant des ventes. option B : Une partie fixe de mensuel et une partie variable correspondant à 6 % des ventes réalisées. 1) Calculer le montant du salaire mensuel perçu par une vendeuse ayant choisi l option B lorsqu elle réalise des ventes pour un montant de ) Pour l option B, le montant s du salaire mensuel perçu par une vendeuse en fonction du montant v des ventes réalisées est exprimé par l une des relations suivantes : s = ,06 v s = ,06 v s = ,06 v s = ,06 v Recopier la relation correcte parmi les quatre propositions données ci-dessus. 3) On considère la fonction f définie sur l intervalle [0 ; ] par f(x) = 0,06 x où x représente le montant des ventes réalisées f(x) représente le montant du salaire mensuel perçu correspondant au choix B. a) Compléter le tableau de valeurs de la fonction f. x f(x) = 0,06 x+1320 b) En utilisant le repère ci-dessous, tracer la représentation graphique de la fonction f D O ) Pour l option A, le montant du salaire mensuel perçu par une vendeuse est représenté par la droite D tracée sur le graphique précédent. Déterminer graphiquement le montant des ventes que doit réaliser une vendeuse ayant choisie l option B pour que son salaire mensuel soit identique à celui d une vendeuse ayant choisie l option A. Laisser apparents les traits nécessaires à la lecture. (D après sujet de BEP Secteur 6 Métropole la Réunion - Mayotte Session juin 2011) Exercices sur les fonctions affines et linéaires 4/9
5 y Exercice 5 La directrice d une maison de retraite souhaite bénéficier des services d une entreprise de nettoyage. L entreprise VAPEUR propose un tarif de 1,10 par m 2 de surface à nettoyer et ne facture aucun frais de déplacement. L entreprise DECAP facture 40 de déplacement et 0,80 par m 2 de surface à nettoyer. 1) Le prix facturé par l entreprise VAPEUR est modélisé par la fonction f définie par : f(x) = 1,1 x x représente la valeur de la surface à nettoyer en m 2 et f(x) représente le prix à payer, en euro, pour x appartenant à l intervalle. En utilisant le repère suivant, tracer la représentation graphique de la fonction f. 0 ; x 2) Le prix facturé par l entreprise DECAP est modélisé par la fonction g définie par : g(x) = 0,8 x + 40 x représente la valeur de la surface à nettoyer en m 2 et g(x) représente le prix à payer, en euro, pour x appartenant à l intervalle. 0 ; 400 a) Compléter le tableau de valeurs suivant. x g(x) = 0,8x Exercices sur les fonctions affines et linéaires 5/9
6 b) En utilisant le repère précédent, tracer la représentation graphique de la fonction g. 3) La surface à nettoyer de la maison de retraite est de 350 m 2. a) À l aide du graphique précédent, indiquer l entreprise la plus avantageuse. Laisser apparents les traits utiles à la lecture. b) Parmi les inéquations suivantes, relever celle qui traduit la situation précédente. 1,1x 0,8x + 40 ; 1,1x > 0,8x + 40 ; 0,8x < 1,1x + 40 ; 0,8x > 1,1x + 40 c) Résoudre cette inéquation dans l intervalle [0 ; 400]. Comparer le résultat obtenu avec celui de la question 3) a). Exercice 6 (D après sujet de BEP Secteur 4 Métropole la Réunion - Mayotte Session juin 2011) L unité monétaire est l euro. À l occasion du championnat du monde de course d orientation, le président d un club organise un voyage de deux jours en Suisse. Le nombre de participants est limité à 40 personnes. 1) Pour ce voyage en Suisse, une agence propose deux formules : - Formule A : 75 par personne. - Formule B : un forfait de 600 plus 50 par personne. Dix personnes participent au voyage. a) Calculer le prix à payer à l agence avec la formule A. b) Calculer le prix à payer à l agence avec la formule B. c) Indiquer, pour le président du club, la formule la plus avantageuse pour un voyage de dix personnes. Justifier la réponse par une phrase. 2) Soit la fonction f définie pour tout x de l intervalle [0 ; 40] par f (x) = 75x. La représentation graphique C f de la fonction f est tracée dans le plan rapporté au repère de suivant. Soit la fonction g définie pour tout x de l intervalle [0 ; 40] par g (x) = 50x a) Compléter le tableau de valeurs de la fonction g ci-dessous. x g(x) b) Placer dans le plan, les points de coordonnées (x ; g (x)) du tableau de valeurs de la fonction g. 3) a) Tracer la représentation graphique Cg de la fonction g dans le plan. Exercices sur les fonctions affines et linéaires 6/9
7 b) En utilisant les représentations graphiques, résoudre l inéquation : g (x) f (x). Laisser apparent le trait utile à la lecture. Présenter les solutions sous forme d un intervalle. c) La situation correspondant à la formule A est modélisée par la fonction f. La situation correspondant à la formule B est modélisée par la fonction g. Le président du club a réuni 35 personnes. En utilisant le résultat précédent, indiquer la formule la plus avantageuse pour le président du club. Justifier la réponse. y C f x' O y' x (D après sujet de BEP Secteur 7 Métropole la Réunion - Mayotte Session juin 2011) Exercices sur les fonctions affines et linéaires 7/9
8 Exercice 7 La société SURGELY invite son personnel à une fête de fin d année. Elle fait appel à deux fournisseurs proposant les mêmes plats cuisinés, conditionnés dans des barquettes de 1 kg. Fournisseur A : 11 la barquette de plats cuisinés, les frais de transport sont gratuits. Fournisseur B : 9 la barquette de plats cuisinés, les frais de transport sont de 13 par commande. 1 ère partie 1) On considère le fournisseur A. Calculer le prix à payer pour une commande de 5 barquettes de plats cuisinés. Présenter le résultat à l'aide d'une phrase. 2) On considère le fournisseur B. Calculer le prix à payer pour une commande de 5 barquettes de plats cuisinés. Présenter le résultat à l'aide d'une phrase. 3) Indiquer, pour la société SURGELY, le fournisseur le plus avantageux pour une commande de 5 barquettes de plats cuisinés. Justifier la réponse par une phrase. 4) Indiquer, pour la société SURGELY, le fournisseur le plus avantageux pour une commande de 10 barquettes de plats cuisinés. Justifier la réponse par des calculs et par une phrase. 5) n est le nombre de barquettes de plats cuisinés. Avec le fournisseur A, l expression du prix à payer P A, en fonction de n, est : P A = 11 n. Avec le fournisseur B, une seule des expressions suivantes permet de calculer le prix à payer P B en fonction de n. P B = 9n P B = 9n + 13 P B = 13n + 9 Recopier cette expression sur la copie. 2 eme partie Soient les fonctions f et g, de la variable x, définies sur l'intervalle [0 ; 10] par : f (x) = 11x et g (x) = 9x + 13 La représentation graphique D f de la fonction f figure dans le plan rapporté au repère orthogonal ci-dessous. 1) Compléter le tableau de valeurs de la fonction g. x g(x) 40 Exercices sur les fonctions affines et linéaires 8/9
9 2) Placer, dans le plan, les points de coordonnées (x ; g(x)) du tableau de valeurs précédent. 3) Tracer, dans le plan, la représentation graphique D g de la fonction g. 4) Les deux représentations graphiques se coupent en un point M. a) Placer le point M dans le plan. b) Proposer, par lecture graphique, l abscisse du point M. Laisser apparent le trait utile à la lecture. y D f x' O x y' 3 ème partie Indiquer le nombre minimal de barquettes de plats cuisinés qu il faut commander pour que le fournisseur B soit moins cher que le fournisseur A. Présenter la réponse à l'aide d'une phrase. (D après sujet de BEP Secteur 7 DOM TOM Session juin 2011) Exercices sur les fonctions affines et linéaires 9/9
Items étudiés dans le CHAPITRE N5. 7 et 9 p 129 D14 Déterminer par le calcul l'antécédent d'un nombre par une fonction linéaire
 CHAPITRE N5 FONCTIONS LINEAIRES NOTION DE FONCTION FONCTIONS LINEAIRES NOTION DE FONCTION FONCTIONS LINEAIRES NOTION DE FONCTION Code item D0 D2 N30[S] Items étudiés dans le CHAPITRE N5 Déterminer l'image
CHAPITRE N5 FONCTIONS LINEAIRES NOTION DE FONCTION FONCTIONS LINEAIRES NOTION DE FONCTION FONCTIONS LINEAIRES NOTION DE FONCTION Code item D0 D2 N30[S] Items étudiés dans le CHAPITRE N5 Déterminer l'image
annexe 6.3.6 b : pénalités
 annexe 6.3.6 b : pénalités Collecte Ethernet Optique Opérateurs Annexe applicable à compter de la date du 1er juillet 201215 janvier 2013. La présente annexe est établie notamment par application des paragraphes
annexe 6.3.6 b : pénalités Collecte Ethernet Optique Opérateurs Annexe applicable à compter de la date du 1er juillet 201215 janvier 2013. La présente annexe est établie notamment par application des paragraphes
Logistique, Transports
 Baccalauréat Professionnel Logistique, Transports 1. France, juin 2006 1 2. Transport, France, juin 2005 2 3. Transport, France, juin 2004 4 4. Transport eploitation, France, juin 2003 6 5. Transport,
Baccalauréat Professionnel Logistique, Transports 1. France, juin 2006 1 2. Transport, France, juin 2005 2 3. Transport, France, juin 2004 4 4. Transport eploitation, France, juin 2003 6 5. Transport,
Chapitre 7 : Intégration sur un intervalle quelconque
 Universités Paris 6 et Paris 7 M1 MEEF Analyse (UE 3) 2013-2014 Chapitre 7 : Intégration sur un intervalle quelconque 1 Fonctions intégrables Définition 1 Soit I R un intervalle et soit f : I R + une fonction
Universités Paris 6 et Paris 7 M1 MEEF Analyse (UE 3) 2013-2014 Chapitre 7 : Intégration sur un intervalle quelconque 1 Fonctions intégrables Définition 1 Soit I R un intervalle et soit f : I R + une fonction
Monnaie. Options de paiement Il y a différentes façons de paiement pour les produits et services en Estonie:
 Monnaie L Euro ( ) est la monnaie officielle de l Estonie depuis le 1er janvier 2011. 1 euro = 100 centimes. Les pièces suivantes sont utilisées: 1, 2, 5, 10, 20 & 50 centimes et 1 & 2 euros. Les dénominations
Monnaie L Euro ( ) est la monnaie officielle de l Estonie depuis le 1er janvier 2011. 1 euro = 100 centimes. Les pièces suivantes sont utilisées: 1, 2, 5, 10, 20 & 50 centimes et 1 & 2 euros. Les dénominations
Comparer des prix. Comparer des gains. Prix du gazole dans deux stations service. Comparer des salaires entre pays. Encadrer des salaires
 Comparer des prix Prix du gazole dans deux stations service Voici des prix affichés du gazole dans deux stations service : 1,403 e/l dans la première et 1,51 e/ L dans la seconde. 1. Quelle est la station
Comparer des prix Prix du gazole dans deux stations service Voici des prix affichés du gazole dans deux stations service : 1,403 e/l dans la première et 1,51 e/ L dans la seconde. 1. Quelle est la station
Quelles sont les principales formules utiles pour l étude de cas de vente?
 Quelles sont les principales formules utiles pour l étude de cas de vente? Approvisionnement et gestion des stocks : des quantités vendues dans un Du stock initial, final et des livraisons, des commandes
Quelles sont les principales formules utiles pour l étude de cas de vente? Approvisionnement et gestion des stocks : des quantités vendues dans un Du stock initial, final et des livraisons, des commandes
ARCHITECTE-FICHES RESSOURCES
 ARCHITECTE-FICHES RESSOURCES Vue du terrain à bâtir Plan de masse Surface plancher La «surface de plancher» s entend comme la somme des surfaces de plancher dans la maison dans les pièces où la hauteur
ARCHITECTE-FICHES RESSOURCES Vue du terrain à bâtir Plan de masse Surface plancher La «surface de plancher» s entend comme la somme des surfaces de plancher dans la maison dans les pièces où la hauteur
Les pourcentages. Un pourcentage est défini par un rapport dont le dénominateur est 100. Ce rapport appelé taux de pourcentage est noté t.
 Les pourcentages I Définition : Un pourcentage est défini par un rapport dont le dénominateur est 100. Ce rapport appelé taux de pourcentage est noté t. Exemple : Ecrire sous forme décimale les taux de
Les pourcentages I Définition : Un pourcentage est défini par un rapport dont le dénominateur est 100. Ce rapport appelé taux de pourcentage est noté t. Exemple : Ecrire sous forme décimale les taux de
Développements limités, équivalents et calculs de limites
 Développements ités, équivalents et calculs de ites Eercice. Déterminer le développement ité en 0 à l ordre n des fonctions suivantes :. f() e (+) 3 n. g() sin() +ln(+) n 3 3. h() e sh() n 4. i() sin(
Développements ités, équivalents et calculs de ites Eercice. Déterminer le développement ité en 0 à l ordre n des fonctions suivantes :. f() e (+) 3 n. g() sin() +ln(+) n 3 3. h() e sh() n 4. i() sin(
Social. Précisions ministérielles. Avantages en nature et frais professionnels
 Avantages en nature et frais professionnels Précisions ministérielles L administration vient de diffuser une troisième série de questions/réponses. S agissant des avantages en nature, elle revient notamment
Avantages en nature et frais professionnels Précisions ministérielles L administration vient de diffuser une troisième série de questions/réponses. S agissant des avantages en nature, elle revient notamment
Durée de L épreuve : 2 heures. Barème : Exercice n 4 : 1 ) 1 point 2 ) 2 points 3 ) 1 point
 03 Mai 2013 Collège Oasis Durée de L épreuve : 2 heures. apple Le sujet comporte 4 pages et est présenté en livret ; apple La calculatrice est autorisée ; apple 4 points sont attribués à la qualité de
03 Mai 2013 Collège Oasis Durée de L épreuve : 2 heures. apple Le sujet comporte 4 pages et est présenté en livret ; apple La calculatrice est autorisée ; apple 4 points sont attribués à la qualité de
Affiliation Cash Livre PDF Gratuit Cliquez Ici Pour Télécharger Merci!
 Enfin, Voici l'information que VOUS attendiez depuis longtemps. Vous allez découvrir une méthode inédite et des secrets que la plupart des affiliés ne connaitront jamais... Par: Mustapha GASSEM Le Dans
Enfin, Voici l'information que VOUS attendiez depuis longtemps. Vous allez découvrir une méthode inédite et des secrets que la plupart des affiliés ne connaitront jamais... Par: Mustapha GASSEM Le Dans
GUIDE DE DÉMARRAGE SOMMAIRE INTRODUCTION 1. SUIVI DE CAISSE PRÉSENTATION DU CALENDRIER PRINCIPES DE SAISIE N GESTIONSAISIE D'UNE JOURNÉE DE CAISSE
 PERT N ION RTGESTION N M E M M E E LA GESTION EN LIGNE DE VOTRE ENTREPRISE MODULE isse est un module de Mon-Expert-en Gestion. Mon-Expert-en-Gestion est un portail collaboratif 100% Web, constitué de plusieurs
PERT N ION RTGESTION N M E M M E E LA GESTION EN LIGNE DE VOTRE ENTREPRISE MODULE isse est un module de Mon-Expert-en Gestion. Mon-Expert-en-Gestion est un portail collaboratif 100% Web, constitué de plusieurs
PRÊT D HONNEUR / PRÊT NACRE DOSSIER DE DEMANDE
 PRÊT D HONNEUR / PRÊT NACRE DOSSIER DE DEMANDE NOM, Prénom : Activité : Commune : Tél. personnel : Tél. entreprise : E-mail : LE DEMANDEUR NOM, Prénom : Organisme : Téléphone : E-mail : L ACCOMPAGNATEUR
PRÊT D HONNEUR / PRÊT NACRE DOSSIER DE DEMANDE NOM, Prénom : Activité : Commune : Tél. personnel : Tél. entreprise : E-mail : LE DEMANDEUR NOM, Prénom : Organisme : Téléphone : E-mail : L ACCOMPAGNATEUR
COMMUNE D HAUTERIVE CONSEIL GENERAL
 COMMUNE D HAUTERIVE CONSEIL GENERAL RAPPORT DU CONSEIL COMMUNAL AU CONSEIL GENERAL A L APPUI D UNE DEMANDE DE CREDIT POUR LA RENOVATION DE LA CUISINE ET DES SANITAIRES DU CLUB-HOUSE DU FC HAUTERIVE Monsieur
COMMUNE D HAUTERIVE CONSEIL GENERAL RAPPORT DU CONSEIL COMMUNAL AU CONSEIL GENERAL A L APPUI D UNE DEMANDE DE CREDIT POUR LA RENOVATION DE LA CUISINE ET DES SANITAIRES DU CLUB-HOUSE DU FC HAUTERIVE Monsieur
Une nouvelle résidence à Strasbourg
 Une nouvelle résidence à Strasbourg RSS «Les Allées des Brasseurs» Strasbourg (67) 1 Eco-quartier de la Brasserie Sur près de 3,7 Hectares 400 logements, commerces et services Développement durable et
Une nouvelle résidence à Strasbourg RSS «Les Allées des Brasseurs» Strasbourg (67) 1 Eco-quartier de la Brasserie Sur près de 3,7 Hectares 400 logements, commerces et services Développement durable et
Seconde Généralités sur les fonctions Exercices. Notion de fonction.
 Seconde Généralités sur les fonctions Exercices Notion de fonction. Exercice. Une fonction définie par une formule. On considère la fonction f définie sur R par = x + x. a) Calculer les images de, 0 et
Seconde Généralités sur les fonctions Exercices Notion de fonction. Exercice. Une fonction définie par une formule. On considère la fonction f définie sur R par = x + x. a) Calculer les images de, 0 et
GENERALITES... 2. Sélection du fichier... 7 TRANSFERT DES ECRITURES... 8
 GENERALITES... 2 Présentation... 2 Définition du format du fichier d import/export... 4 Gestion des Profils... 6 Sélection d un profil existant... 6 Création d un profil... 6 Sélection du fichier... 7
GENERALITES... 2 Présentation... 2 Définition du format du fichier d import/export... 4 Gestion des Profils... 6 Sélection d un profil existant... 6 Création d un profil... 6 Sélection du fichier... 7
LE PORTAGE SALARIAL. Jean Michel RAUX. Présentation du 18 et 19 septembre 2014
 LE PORTAGE SALARIAL Jean Michel RAUX Présentation du 18 et 19 septembre 2014 3. Le groupe JAM en bref Leader dans son secteur, le groupe JAM (créé en 1991) a réalisé un CA de 35 M et a porté 4.000 salariés
LE PORTAGE SALARIAL Jean Michel RAUX Présentation du 18 et 19 septembre 2014 3. Le groupe JAM en bref Leader dans son secteur, le groupe JAM (créé en 1991) a réalisé un CA de 35 M et a porté 4.000 salariés
LETTRE CIRCULAIRE N 2003-103
 PARIS, le 09/07/2003 DIRECTION DE LA REGLEMENTATION ET DES ORIENTATIONS DU RECOUVREMENT DIROR LETTRE CIRCULAIRE N 2003-103 OBJET : Mise en oeuvre de la nouvelle réglementation relative à l'évaluation des
PARIS, le 09/07/2003 DIRECTION DE LA REGLEMENTATION ET DES ORIENTATIONS DU RECOUVREMENT DIROR LETTRE CIRCULAIRE N 2003-103 OBJET : Mise en oeuvre de la nouvelle réglementation relative à l'évaluation des
FORMULAIRE D AUTO-EVALUATION POUR PATIENTS SLA
 1 FORMULAIRE D AUTO-EVALUATION POUR PATIENTS SLA Afin de donner un bon aperçu de mes possibilités et mes limitations à la DG Personnes handicapés, je coche ce que je peux faire ou ne plus faire. Ci-dessous
1 FORMULAIRE D AUTO-EVALUATION POUR PATIENTS SLA Afin de donner un bon aperçu de mes possibilités et mes limitations à la DG Personnes handicapés, je coche ce que je peux faire ou ne plus faire. Ci-dessous
Groupage Tarifaire***
 (1) moyens indicatifs. Les délais s entendent pour une prise en charge du lundi Remise mensuelle - Tarifs de base < 2 envois 0,5 15,46 26,25 55,51 45,94 40,69 29,89 57,96 65,82 1 16,18 35,88 70,25 59,50
(1) moyens indicatifs. Les délais s entendent pour une prise en charge du lundi Remise mensuelle - Tarifs de base < 2 envois 0,5 15,46 26,25 55,51 45,94 40,69 29,89 57,96 65,82 1 16,18 35,88 70,25 59,50
EXERCICE 4 (7 points ) (Commun à tous les candidats)
 EXERCICE 4 (7 points ) (Commun à tous les candidats) On cherche à modéliser de deux façons différentes l évolution du nombre, exprimé en millions, de foyers français possédant un téléviseur à écran plat
EXERCICE 4 (7 points ) (Commun à tous les candidats) On cherche à modéliser de deux façons différentes l évolution du nombre, exprimé en millions, de foyers français possédant un téléviseur à écran plat
AbaWebFiduciaire Software issu du Cloud. Votre partenaire pour
 AbaWebFiduciaire Software issu du Cloud Votre partenaire pour AbaWebFiduciaire à votre avantage Frais mensuels avantageu, clairement définis et prévisibles Aucune installation de logiciel ABACUS, en conséquence
AbaWebFiduciaire Software issu du Cloud Votre partenaire pour AbaWebFiduciaire à votre avantage Frais mensuels avantageu, clairement définis et prévisibles Aucune installation de logiciel ABACUS, en conséquence
Sonde tensiométrique WATERMARK. Construire en préservant les sols Surveiller le chantier à distance Monitor
 Sonde tensiométrique WATERMARK Construire en préservant les sols Surveiller le chantier à distance Monitor mesure automatiquement la tension de l'eau du sol Transmission GPRS par module additionnel Le
Sonde tensiométrique WATERMARK Construire en préservant les sols Surveiller le chantier à distance Monitor mesure automatiquement la tension de l'eau du sol Transmission GPRS par module additionnel Le
IV - DETERMINATION DES COUTS
 Cterrier.com 1/6 06/01/2005 Initiation à la gestion Quantitative d une entreprise Auteur : C. Terrier ; mailto:[email protected] ; http://www.cterrier.com Utilisation : Reproduction libre pour des
Cterrier.com 1/6 06/01/2005 Initiation à la gestion Quantitative d une entreprise Auteur : C. Terrier ; mailto:[email protected] ; http://www.cterrier.com Utilisation : Reproduction libre pour des
Amortissement annuité 1 180 000 14 400 12 425,31 26 825,31 2. 2) Indiquer ce que sera la deuxième ligne du tableau en justifiant chacun des résultats.
 EXERCICES SUR LES EMPRUNTS INDIVIS Exercice 1 Pour financer l extension de son magasin, un responsable a contracté un emprunt remboursable, intérêts compris, sur 10 ans par annuités constantes. Voici le
EXERCICES SUR LES EMPRUNTS INDIVIS Exercice 1 Pour financer l extension de son magasin, un responsable a contracté un emprunt remboursable, intérêts compris, sur 10 ans par annuités constantes. Voici le
ici Au 9 juillet 2015
 ici Au BIENVENUE dans la Bourse aux Locaux Commerciaux de la commune de Châteauneuf-les-Martigues La Mède Vous êtes à la recherche d un site pour implanter votre activité sur notre territoire. Vous pouvez
ici Au BIENVENUE dans la Bourse aux Locaux Commerciaux de la commune de Châteauneuf-les-Martigues La Mède Vous êtes à la recherche d un site pour implanter votre activité sur notre territoire. Vous pouvez
RAPPORT COMPLET D'ETUDE DUALSYS
 RAPPORT COMPLET D'ETUDE DUALSYS 1 SITUATION DE L ÉTUDE Les données météorologiques sont des données primordiales pour le bon déroulement des calculs et pour avoir des résultats les plus proches de la réalité.
RAPPORT COMPLET D'ETUDE DUALSYS 1 SITUATION DE L ÉTUDE Les données météorologiques sont des données primordiales pour le bon déroulement des calculs et pour avoir des résultats les plus proches de la réalité.
Notion de fonction. Série 1 : Tableaux de données. Série 2 : Graphiques. Série 3 : Formules. Série 4 : Synthèse
 N7 Notion de fonction Série : Tableaux de données Série 2 : Graphiques Série 3 : Formules Série 4 : Synthèse 57 SÉRIE : TABLEAUX DE DONNÉES Le cours avec les aides animées Q. Si f désigne une fonction,
N7 Notion de fonction Série : Tableaux de données Série 2 : Graphiques Série 3 : Formules Série 4 : Synthèse 57 SÉRIE : TABLEAUX DE DONNÉES Le cours avec les aides animées Q. Si f désigne une fonction,
Gestion du budget familial-1
 Gestion du budget familial-1 Qu est-ce qu un budget? A quoi cela sert-il? C est un plan prévisionnel qui nous sert à bien gérer notre argent dans le temps. Le budget est un tableau qui enregistre pour
Gestion du budget familial-1 Qu est-ce qu un budget? A quoi cela sert-il? C est un plan prévisionnel qui nous sert à bien gérer notre argent dans le temps. Le budget est un tableau qui enregistre pour
DPGF - LOT 3 - CVC / PLOMBERIE
 4, rue Dolorès Ibarruri DPGF - LOT 3 - CVC / PLOMBERIE L entreprise a la responsabilité de prévoir les bonnes quantités de fourniture pour la réalisation des travaux : - faire les métrés et renseigner
4, rue Dolorès Ibarruri DPGF - LOT 3 - CVC / PLOMBERIE L entreprise a la responsabilité de prévoir les bonnes quantités de fourniture pour la réalisation des travaux : - faire les métrés et renseigner
SOMMAIRE... SOMMAIRE... SOMMAIRE... SOMMAIRE... SOMMAIRE... SOMMAIRE... LES MESURES
 SOMMAIRE... SOMMAIRE... SOMMAIRE... SOMMAIRE... SOMMAIRE... SOMMAIRE... LES MESURES MES 1 Les mesures de longueurs MES 2 Lecture de l heure MES 3 Les mesures de masse MES 4 Comparer des longueurs, périmètres.
SOMMAIRE... SOMMAIRE... SOMMAIRE... SOMMAIRE... SOMMAIRE... SOMMAIRE... LES MESURES MES 1 Les mesures de longueurs MES 2 Lecture de l heure MES 3 Les mesures de masse MES 4 Comparer des longueurs, périmètres.
Créer un tableau avec LibreOffice / Calc
 Créer un tableau avec LibreOffice / Calc Réaliser des tableaux LibreOffice / Calc permet de créer des tableaux facilement en utilisant les cellules. En premier lieu, il faut prévoir le nombre de colonnes
Créer un tableau avec LibreOffice / Calc Réaliser des tableaux LibreOffice / Calc permet de créer des tableaux facilement en utilisant les cellules. En premier lieu, il faut prévoir le nombre de colonnes
Marketing III. Calcul du prix & Indicateurs. Contenu
 Calcul du prix & Indicateurs Pour la gestion économique de l'entreprise, il est essentiel que les prix des biens et services soient soigneusement calculés en tenant compte de tous les facteurs internes
Calcul du prix & Indicateurs Pour la gestion économique de l'entreprise, il est essentiel que les prix des biens et services soient soigneusement calculés en tenant compte de tous les facteurs internes
Dépaysez! Station sports de nature
 Dépaysez! Station sports de nature Le domaine de Lieu Dieu est situé au cœur de la nature, un écrin de verdure idéal pour se ressourcer. C est un site naturel exceptionnel de 70 hectares avec rivière,
Dépaysez! Station sports de nature Le domaine de Lieu Dieu est situé au cœur de la nature, un écrin de verdure idéal pour se ressourcer. C est un site naturel exceptionnel de 70 hectares avec rivière,
LES FORMULES D ENVOI E.CARDS 2013
 LES FORMULES D ENVOI E.CARDS 2013 Nous proposons un module de personnalisation simple et performant, qui vous permettra d envoyer et de contrôler vos envois d e.cards. Vous serez guidé pas à pas dans la
LES FORMULES D ENVOI E.CARDS 2013 Nous proposons un module de personnalisation simple et performant, qui vous permettra d envoyer et de contrôler vos envois d e.cards. Vous serez guidé pas à pas dans la
LA TRESORERIE. mois. Cette donnée est importante pour établir le budget de trésorerie prévisionnel. TOTAL 30 000
 LA TRESORERIE 1. Présentation des composantes de la trésorerie 3.2. La TVA à décaisser 1.1. Qu est ce que la trésorerie 2. Les encaissements : de la prévision des ventes au budget prévisionnel des recettes
LA TRESORERIE 1. Présentation des composantes de la trésorerie 3.2. La TVA à décaisser 1.1. Qu est ce que la trésorerie 2. Les encaissements : de la prévision des ventes au budget prévisionnel des recettes
Les fonction affines
 Les fonction affines EXERCICE 1 : Voir le cours EXERCICE 2 : Optimisation 1) Traduire, pour une semaine de location, chaque formule par une écriture de la forme (où x désigne le nombre de kilomètres parcourus
Les fonction affines EXERCICE 1 : Voir le cours EXERCICE 2 : Optimisation 1) Traduire, pour une semaine de location, chaque formule par une écriture de la forme (où x désigne le nombre de kilomètres parcourus
DÉRIVÉES. I Nombre dérivé - Tangente. Exercice 01 (voir réponses et correction) ( voir animation )
 DÉRIVÉES I Nombre dérivé - Tangente Eercice 0 ( voir animation ) On considère la fonction f définie par f() = - 2 + 6 pour [-4 ; 4]. ) Tracer la représentation graphique (C) de f dans un repère d'unité
DÉRIVÉES I Nombre dérivé - Tangente Eercice 0 ( voir animation ) On considère la fonction f définie par f() = - 2 + 6 pour [-4 ; 4]. ) Tracer la représentation graphique (C) de f dans un repère d'unité
I - La définition des avantages en nature. A) Les avantages en nature font partie du salaire. 1/ Solutions générales. 058 Les avantages en nature
 058 Les avantages en nature Tableau des principaux avantages en nature et leur régime d évaluation Mise à disposition d outils issus des NTIC (nouvelles technologies d information et de communication :
058 Les avantages en nature Tableau des principaux avantages en nature et leur régime d évaluation Mise à disposition d outils issus des NTIC (nouvelles technologies d information et de communication :
Juriste d'entreprise
 Service des formations professionnalisées Licence Juriste d'entreprise UE4 Fiscal des affaires (Cours de M. Lamailloux) 23 mars 2015 9h à 12h -------------------------------------------------------------------------------------------------------
Service des formations professionnalisées Licence Juriste d'entreprise UE4 Fiscal des affaires (Cours de M. Lamailloux) 23 mars 2015 9h à 12h -------------------------------------------------------------------------------------------------------
Valeur cible et solveur. Les calculs effectués habituellement avec Excel utilisent des valeurs numériques qui constituent les données d'un problème.
 Valeur cible et solveur Atteindre une valeur cible Les calculs effectués habituellement avec Excel utilisent des valeurs numériques qui constituent les données d'un problème. A l'aide d'un certain nombre
Valeur cible et solveur Atteindre une valeur cible Les calculs effectués habituellement avec Excel utilisent des valeurs numériques qui constituent les données d'un problème. A l'aide d'un certain nombre
CARTES DE CREDIT CARTES DE CREDITS BCVS CARTES PREPAID CARTES EN MONNAIES BUSINESS CARD
 Tarif des frais GESTION DES COMPTES Compte courant 1 de gestion CHF 0.40 par opération de bouclement CHF 10. de port Selon tarif appliqué par la Poste Compte privé / gestion / cash management / senior
Tarif des frais GESTION DES COMPTES Compte courant 1 de gestion CHF 0.40 par opération de bouclement CHF 10. de port Selon tarif appliqué par la Poste Compte privé / gestion / cash management / senior
Choisir le bon compte-chèques et forfait bancaire
 OPÉRATIONS BANCAIRES Choisir le bon compte-chèques et forfait bancaire Pour la plupart des gens, un compte-chèques est un bon moyen de gérer leurs opérations bancaires courantes. Les banques, les coopératives
OPÉRATIONS BANCAIRES Choisir le bon compte-chèques et forfait bancaire Pour la plupart des gens, un compte-chèques est un bon moyen de gérer leurs opérations bancaires courantes. Les banques, les coopératives
ÉVALUATION EN FIN DE CM1. Année scolaire 2014 2015 LIVRET DE L'ÉLÈVE MATHÉMATIQUES
 ÉVALUATION EN FIN DE CM1 Année scolaire 2014 2015 LIVRET DE L'ÉLÈVE MATHÉMATIQUES NOM :....... Prénom :....... Né le :./../ École :............ Classe : Domaine Score de réussite NOMBRES ET CALCUL GÉOMÉTRIE
ÉVALUATION EN FIN DE CM1 Année scolaire 2014 2015 LIVRET DE L'ÉLÈVE MATHÉMATIQUES NOM :....... Prénom :....... Né le :./../ École :............ Classe : Domaine Score de réussite NOMBRES ET CALCUL GÉOMÉTRIE
Tableau récapitulatif des textes portant sur le devis août 2015
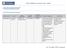 I - liés à une activité commerciale II - liés aux professions de santé I - liés à une activité commerciale Déménagement Arrêté du 27 avril 2010 Déménagement organisé ou spécial ment Mentions s - référence
I - liés à une activité commerciale II - liés aux professions de santé I - liés à une activité commerciale Déménagement Arrêté du 27 avril 2010 Déménagement organisé ou spécial ment Mentions s - référence
C f tracée ci- contre est la représentation graphique d une
 TLES1 DEVOIR A LA MAISON N 7 La courbe C f tracée ci- contre est la représentation graphique d une fonction f définie et dérivable sur R. On note f ' la fonction dérivée de f. La tangente T à la courbe
TLES1 DEVOIR A LA MAISON N 7 La courbe C f tracée ci- contre est la représentation graphique d une fonction f définie et dérivable sur R. On note f ' la fonction dérivée de f. La tangente T à la courbe
Informations aux athlètes en matière de fiscalité et de finances
 Table des matières 1. Introduction 2. Revenus 3. Dépenses 4. Impôts 5. Budget 6. Planification financière 7. Assurances 8. Épargne-retraite 9. Autres responsabilités 10. Remarques finales 1 1. Introduction
Table des matières 1. Introduction 2. Revenus 3. Dépenses 4. Impôts 5. Budget 6. Planification financière 7. Assurances 8. Épargne-retraite 9. Autres responsabilités 10. Remarques finales 1 1. Introduction
Avant-propos. Chère lectrice, cher lecteur,
 Avant-propos Chère lectrice, cher lecteur, En ces temps économiquement difficiles, il est important de savoir ce que je peux exiger comme salaire en tant qu entraîneur ou entraîneuse. En particulier, en
Avant-propos Chère lectrice, cher lecteur, En ces temps économiquement difficiles, il est important de savoir ce que je peux exiger comme salaire en tant qu entraîneur ou entraîneuse. En particulier, en
Programme de calcul et résolution d équation
 Programme de calcul et résolution d équation On appelle «programme de calcul» tout procédé mathématique qui permet de passer d un nombre à un autre suivant une suite d opérations déterminée. Un programme
Programme de calcul et résolution d équation On appelle «programme de calcul» tout procédé mathématique qui permet de passer d un nombre à un autre suivant une suite d opérations déterminée. Un programme
Création de comptes espace Client et direct Déclaration
 Cahier technique Création de comptes espace Client et direct Déclaration Logiciels Sage pour Artisans et Petites Sage Création de comptes Espace client et direct Déclaration - Page 1 sur 15 Entreprises
Cahier technique Création de comptes espace Client et direct Déclaration Logiciels Sage pour Artisans et Petites Sage Création de comptes Espace client et direct Déclaration - Page 1 sur 15 Entreprises
Nourriture Boissons Nettoyage
 Services généraux Pris net dès 1. décembre 2014 dans la limite des stocks disponibles Nourriture Boissons Nettoyage Hygiène 2 Café et accessoires, plats cuisinés 156438 600 quenelles de viande 156531 600
Services généraux Pris net dès 1. décembre 2014 dans la limite des stocks disponibles Nourriture Boissons Nettoyage Hygiène 2 Café et accessoires, plats cuisinés 156438 600 quenelles de viande 156531 600
INVESTISSEMENTS LOCATIFS : PLAFONDS 2014
 Février 2014 INVESTISSEMENTS LOCATIFS : PLAFONDS 2014 FISCALITE L'administration fiscale actualise les plafonds de loyers et de ressources applicables aux dispositifs Duflot, Scellier, Robien, Borloo et
Février 2014 INVESTISSEMENTS LOCATIFS : PLAFONDS 2014 FISCALITE L'administration fiscale actualise les plafonds de loyers et de ressources applicables aux dispositifs Duflot, Scellier, Robien, Borloo et
Extrait gratuit de la publication «Comptabilité, fiscalité et paie pour les entreprises du BTP»
 Extrait gratuit de la publication «Comptabilité, fiscalité et paie pour les entreprises du BTP» Calculer et régler les cotisations sociales Calculer les cotisations URSSAF (vieillesse, CSG CRDS, maternité,
Extrait gratuit de la publication «Comptabilité, fiscalité et paie pour les entreprises du BTP» Calculer et régler les cotisations sociales Calculer les cotisations URSSAF (vieillesse, CSG CRDS, maternité,
Le verbe être au présent - 1
 Le verbe être au présent - 1 A. Je conjugue le verbe être. Je.............................. B. Je réponds aux questions à la forme affirmative. Exemples : Est-elle malade? Oui, elle est malade. Sont-ils
Le verbe être au présent - 1 A. Je conjugue le verbe être. Je.............................. B. Je réponds aux questions à la forme affirmative. Exemples : Est-elle malade? Oui, elle est malade. Sont-ils
Site portail des Urssaf www.urssaf.fr Employeurs > Comité d'entreprise > Vous - Vos Cotisations > Les prestations
 Les prestations Aide financière finançant des activités de services à la personne et de garde d enfant Régime social de l aide destinée à financer des activités de services à la personne et de garde d
Les prestations Aide financière finançant des activités de services à la personne et de garde d enfant Régime social de l aide destinée à financer des activités de services à la personne et de garde d
New Famille Abgottspon-Schell
 Semaines avantageuses hiver 14/15 12 Nous attendons votre venue avec grand plaisir! Famille Abgottspon-Schell werbstatt.net New Famille Abgottspon-Schell Vispastrasse 52 CH-3920 Zermatt Téléphone +41 (0)27
Semaines avantageuses hiver 14/15 12 Nous attendons votre venue avec grand plaisir! Famille Abgottspon-Schell werbstatt.net New Famille Abgottspon-Schell Vispastrasse 52 CH-3920 Zermatt Téléphone +41 (0)27
guide immobilier Tout savoir pour se loger ou investir
 guide immobilier Tout savoir pour se loger ou investir Vous achetez pour vous loger Vous recherchez votre futur domicile? Appartement, maison, neuf ou ancien... Quel que soit le type de bien ou de surface,
guide immobilier Tout savoir pour se loger ou investir Vous achetez pour vous loger Vous recherchez votre futur domicile? Appartement, maison, neuf ou ancien... Quel que soit le type de bien ou de surface,
Thème 17: Optimisation
 OPTIMISATION 45 Thème 17: Optimisation Introduction : Dans la plupart des applications, les grandeurs physiques ou géométriques sont exprimées à l aide d une formule contenant une fonction. Il peut s agir
OPTIMISATION 45 Thème 17: Optimisation Introduction : Dans la plupart des applications, les grandeurs physiques ou géométriques sont exprimées à l aide d une formule contenant une fonction. Il peut s agir
Implantée sur TOULOUGES, dans les Pyrénées Orientales, la société ACTIV PORTAGE vous apporte :
 1/9 Implantée sur TOULOUGES, dans les Pyrénées Orientales, la société ACTIV PORTAGE vous apporte : - Pour vous tous : Devenez indépendant avec un statut salarié : Saisissez toutes les opportunités de mission
1/9 Implantée sur TOULOUGES, dans les Pyrénées Orientales, la société ACTIV PORTAGE vous apporte : - Pour vous tous : Devenez indépendant avec un statut salarié : Saisissez toutes les opportunités de mission
E. Avantages alloués par le comité d entreprise
 E. Avantages alloués par le comité d entreprise 1) Bons d achat et cadeaux Les bons d achat et cadeaux alloués par le comité d entreprise doivent en principe être assujettis aux cotisations de Sécurité
E. Avantages alloués par le comité d entreprise 1) Bons d achat et cadeaux Les bons d achat et cadeaux alloués par le comité d entreprise doivent en principe être assujettis aux cotisations de Sécurité
Compte rendu : Bourse Explora Sup
 Compte rendu : Bourse Explora Sup J ai effectué un stage d un mois et demi passionnant au sein de l école de langue anglaise LTC à Brighton. J ai eu par la suite la chance d être embauchée durant un mois
Compte rendu : Bourse Explora Sup J ai effectué un stage d un mois et demi passionnant au sein de l école de langue anglaise LTC à Brighton. J ai eu par la suite la chance d être embauchée durant un mois
COMPTA.COM. Compta.com v7 Nouvelles fonctionnalités
 COMPTA.COM Compta.com v7 Nouvelles fonctionnalités Date de la version : 23/04/2012 SOMMAIRE 1. Nouvelle charte graphique, nouvelle page d accueil... 3 2. Comptabilisation automatique des factures... 4
COMPTA.COM Compta.com v7 Nouvelles fonctionnalités Date de la version : 23/04/2012 SOMMAIRE 1. Nouvelle charte graphique, nouvelle page d accueil... 3 2. Comptabilisation automatique des factures... 4
www.jpad.fr.st JPAD portage - portage 1/5 Pour qui? Comment? Les avantages Portage - Pour qui?
 JPAD portage - portage 1/5 Pour qui? Comment? Les avantages Portage - Pour qui? Une nouvelle façon de travailler : le portage permet à des consultants (experts ou formateurs) d'être salariés pour une mission
JPAD portage - portage 1/5 Pour qui? Comment? Les avantages Portage - Pour qui? Une nouvelle façon de travailler : le portage permet à des consultants (experts ou formateurs) d'être salariés pour une mission
FONCTIONS DE PLUSIEURS VARIABLES (Outils Mathématiques 4)
 FONCTIONS DE PLUSIEURS VARIABLES (Outils Mathématiques 4) Bernard Le Stum Université de Rennes 1 Version du 13 mars 2009 Table des matières 1 Fonctions partielles, courbes de niveau 1 2 Limites et continuité
FONCTIONS DE PLUSIEURS VARIABLES (Outils Mathématiques 4) Bernard Le Stum Université de Rennes 1 Version du 13 mars 2009 Table des matières 1 Fonctions partielles, courbes de niveau 1 2 Limites et continuité
EdIntégral. Module ENCAISSEMENT. Le logiciel d encaissement multifonctions, évolutif et tactile
 EdIntégral Module ENCAISSEMENT Le logiciel d encaissement multifonctions, évolutif et tactile La gestion de la caisse, des stocks, de la fidélisation, les nombreuses et puissantes statistiques, sont autant
EdIntégral Module ENCAISSEMENT Le logiciel d encaissement multifonctions, évolutif et tactile La gestion de la caisse, des stocks, de la fidélisation, les nombreuses et puissantes statistiques, sont autant
Les Crédits et ouverture de crédit
 Les Crédits et ouverture de crédit Contexte général Besoin d une nouvelle voiture, votre machine à lessiver tombe en panne ou besoin d effectuer quelques travaux dans votre maison? De grosses dépenses
Les Crédits et ouverture de crédit Contexte général Besoin d une nouvelle voiture, votre machine à lessiver tombe en panne ou besoin d effectuer quelques travaux dans votre maison? De grosses dépenses
Cotisations et points de la retraite complémentaire. n o 3
 Guide retraite complémentaire Agirc et Arrco Cotisations et points de la retraite complémentaire Guide salariés n o 3 avril 2014 Cotisations et points de la retraite complémentaire Sommaire La retraite,
Guide retraite complémentaire Agirc et Arrco Cotisations et points de la retraite complémentaire Guide salariés n o 3 avril 2014 Cotisations et points de la retraite complémentaire Sommaire La retraite,
GUIDE DES PRINCIPAUX PRODUITS, SERVICES ET TARIFS
 Professionnels Entrepreneurs GUIDE DES PRINCIPAUX PRODUITS, SERVICES ET TARIFS janvier 2014 Professionnels Entrepreneurs Sommaire Vous êtes artisan, commerçant, agriculteur, profes sionnel libéral, dirigeant
Professionnels Entrepreneurs GUIDE DES PRINCIPAUX PRODUITS, SERVICES ET TARIFS janvier 2014 Professionnels Entrepreneurs Sommaire Vous êtes artisan, commerçant, agriculteur, profes sionnel libéral, dirigeant
CRÉER DES LEÇONS AVEC L'ÉDITEUR DU LOGICIEL 1000 MOTS POUR APPRENDRE À LIRE EN FRANÇAIS, ANGLAIS ET ALLEMAND
 93 CRÉER DES LEÇONS AVEC L'ÉDITEUR DU LOGICIEL 1000 MOTS POUR APPRENDRE À LIRE EN FRANÇAIS, ANGLAIS ET ALLEMAND 1 - LE LOGICIEL 1000 MOTS 1000 mots est un logiciel destiné aux classes du cycle II en France
93 CRÉER DES LEÇONS AVEC L'ÉDITEUR DU LOGICIEL 1000 MOTS POUR APPRENDRE À LIRE EN FRANÇAIS, ANGLAIS ET ALLEMAND 1 - LE LOGICIEL 1000 MOTS 1000 mots est un logiciel destiné aux classes du cycle II en France
COMMUNE DE GORGIER. Madame la Présidente, Mesdames et Messieurs, 1. Préambule
 COMMUNE DE GORGIER RAPPORT DU CONSEIL COMMUNAL AU CONSEIL GENERAL CONCERNANT LA DEMANDE DE CREDIT DE Fr. 32'700.- POUR LE REMPLACEMENT D'UN COLLECTEUR D'EAUX USEES AU CHEMIN DE LA PAYAZ Madame la Présidente,
COMMUNE DE GORGIER RAPPORT DU CONSEIL COMMUNAL AU CONSEIL GENERAL CONCERNANT LA DEMANDE DE CREDIT DE Fr. 32'700.- POUR LE REMPLACEMENT D'UN COLLECTEUR D'EAUX USEES AU CHEMIN DE LA PAYAZ Madame la Présidente,
GUIDE PRATIQUE ÉTOILE pei 2 ÉTOILE percoi 2
 GUIDE PRATIQUE ÉTOILE pei 2 ÉTOILE percoi 2 SOMMAIRE Composez votre dispositif sur mesure 4 Étoile PEI 2 - Étoile PERCOI 2 Principales caractéristiques 5 Conseils d optimisation pour le dirigeant et les
GUIDE PRATIQUE ÉTOILE pei 2 ÉTOILE percoi 2 SOMMAIRE Composez votre dispositif sur mesure 4 Étoile PEI 2 - Étoile PERCOI 2 Principales caractéristiques 5 Conseils d optimisation pour le dirigeant et les
CONSEIL. Memo page 2&3. La serrure à mortaiser page 4&5. La serrure en applique pages 6 POSER UNE SERRURE 10.02. Castorama
 10.02 POSER UNE SERRURE CONSEIL Castorama Memo page 2&3 La serrure à mortaiser page 4&5 La serrure en applique pages 6 page 1/6 MEMO Ce mémo vous permet de préparer votre chantier sans perdre de temps.
10.02 POSER UNE SERRURE CONSEIL Castorama Memo page 2&3 La serrure à mortaiser page 4&5 La serrure en applique pages 6 page 1/6 MEMO Ce mémo vous permet de préparer votre chantier sans perdre de temps.
DOSSIER DE CREATION D'ENTREPRISE
 DOSSIER DE CREATION D'ENTREPRISE BUSINESS PLAN Partie 1 : Présentation de votre projet 1 Vous êtes prêt à créer votre entreprise? Ce dossier va vous permettre de préciser et de mettre en forme votre projet
DOSSIER DE CREATION D'ENTREPRISE BUSINESS PLAN Partie 1 : Présentation de votre projet 1 Vous êtes prêt à créer votre entreprise? Ce dossier va vous permettre de préciser et de mettre en forme votre projet
David LUCAS 15/01/10 Ludovic HUET Sébastien LE NECHET Jason JAMOT. Projet BO
 David LUCAS 15/01/10 Ludovic HUET Sébastien LE NECHET Jason JAMOT Projet BO Table des matières I / Présentation de l équipe... 3 II/ Présentation générale du projet... 4 III/ Création des vues... 5 IV/Création
David LUCAS 15/01/10 Ludovic HUET Sébastien LE NECHET Jason JAMOT Projet BO Table des matières I / Présentation de l équipe... 3 II/ Présentation générale du projet... 4 III/ Création des vues... 5 IV/Création
a et b étant deux nombres relatifs donnés, une fonction affine est une fonction qui a un nombre x associe le nombre ax + b
 I Définition d une fonction affine Faire l activité 1 «une nouvelle fonction» 1. définition générale a et b étant deux nombres relatifs donnés, une fonction affine est une fonction qui a un nombre x associe
I Définition d une fonction affine Faire l activité 1 «une nouvelle fonction» 1. définition générale a et b étant deux nombres relatifs donnés, une fonction affine est une fonction qui a un nombre x associe
I. Ensemble de définition d'une fonction
 Chapitre 2 Généralités sur les fonctions Fonctions de références et fonctions associées Ce que dit le programme : Étude de fonctions Fonctions de référence x x et x x Connaître les variations de ces deux
Chapitre 2 Généralités sur les fonctions Fonctions de références et fonctions associées Ce que dit le programme : Étude de fonctions Fonctions de référence x x et x x Connaître les variations de ces deux
Innovation Centrosolar SOLARMIX, découvrez le solaire 2 en 1. Janvier 2015
 Innovation Centrosolar SOLARMIX, découvrez le solaire 2 en 1 Janvier 2015 SOMMAIRE Le solaire 2 en 1 SOLARMIX - Votre offre hybride clés en main Un module hybride unique au monde Le kit thermique Le kit
Innovation Centrosolar SOLARMIX, découvrez le solaire 2 en 1 Janvier 2015 SOMMAIRE Le solaire 2 en 1 SOLARMIX - Votre offre hybride clés en main Un module hybride unique au monde Le kit thermique Le kit
FORMULES DE CALCUL. Prix = PV TTC = PV HT x (1 + taux de TVA) TVA = PV HT x taux de TVA PV HT = PV TTC 1 + taux de TVA
 FORMULES DE CALCUL Le prix : Prix = PV TTC = PV HT x (1 + taux de TVA) TVA = PV HT x taux de TVA PV HT = PV TTC 1 + taux de TVA Ex : PV TTC = 250 x 1,196 = 299. TVA = 250 x 19,6 % = 49. PV HT = 299 = 250.
FORMULES DE CALCUL Le prix : Prix = PV TTC = PV HT x (1 + taux de TVA) TVA = PV HT x taux de TVA PV HT = PV TTC 1 + taux de TVA Ex : PV TTC = 250 x 1,196 = 299. TVA = 250 x 19,6 % = 49. PV HT = 299 = 250.
AVS INFOS. 6 Rappels service administratif 2-3 Rappels service qualité / comptabilité 7 4-5. Le Mot du Gérant SOMMAIRE
 AVS INFOS Groupe AVS : L emploi du 3ème millénaire Numéro 86 Juillet 2010 Le Mot du Gérant Bonjour à toutes et à tous, Le portage salarial, une lutte de tous les instants Un cap important a été franchi
AVS INFOS Groupe AVS : L emploi du 3ème millénaire Numéro 86 Juillet 2010 Le Mot du Gérant Bonjour à toutes et à tous, Le portage salarial, une lutte de tous les instants Un cap important a été franchi
LETTRE DE CONSULTATION
 LETTRE DE CONSULTATION Objet : Curage des fossés 2015 Réf. : 2015.06.04 Affaire suivie par : Julie DEGERY Madame, Monsieur, Lors de la programmation des travaux 2015, il a été décidé d engager une consultation
LETTRE DE CONSULTATION Objet : Curage des fossés 2015 Réf. : 2015.06.04 Affaire suivie par : Julie DEGERY Madame, Monsieur, Lors de la programmation des travaux 2015, il a été décidé d engager une consultation
Dossier d informations et de réservation
 Dossier d informations et de réservation Chère Madame, Chère Mademoiselle, Cher Monsieur, Vous avez manifesté votre intérêt pour la location d un studio meublé dans notre résidence «Les Lys du Pecq». Vous
Dossier d informations et de réservation Chère Madame, Chère Mademoiselle, Cher Monsieur, Vous avez manifesté votre intérêt pour la location d un studio meublé dans notre résidence «Les Lys du Pecq». Vous
Version V2.06. Points Forts. Module Achats (99.00 HT*)
 A2GI-COIFFURE Version V2.06 Microsoft Windows 2000, XP, XP-PRO, VISTA * Monoposte ou Réseau Points Forts. Caisse Tactile. Gestion des Rendez-vous. Gestion des Prestations par Employé(e). Gestion des Prestations
A2GI-COIFFURE Version V2.06 Microsoft Windows 2000, XP, XP-PRO, VISTA * Monoposte ou Réseau Points Forts. Caisse Tactile. Gestion des Rendez-vous. Gestion des Prestations par Employé(e). Gestion des Prestations
Bien concevoir son projet de SALLE DE BAINS
 Bien concevoir son projet de SALLE DE BAINS Une salle de bains bien pensée...... Lapeyre vous aide à la réaliser Un projet bien préparé, c est la clé de la réussite. Avant de rencontrer un conseiller LAPEYRE,
Bien concevoir son projet de SALLE DE BAINS Une salle de bains bien pensée...... Lapeyre vous aide à la réaliser Un projet bien préparé, c est la clé de la réussite. Avant de rencontrer un conseiller LAPEYRE,
315 et 495 sont dans la table de 5. 5 est un diviseur commun. Leur PGCD n est pas 1. Il ne sont pas premiers entre eux
 Exercice 1 : (3 points) Un sac contient 10 boules rouges, 6 boules noires et 4 boules jaunes. Chacune des boules a la même probabilité d'être tirée. On tire une boule au hasard. 1. Calculer la probabilité
Exercice 1 : (3 points) Un sac contient 10 boules rouges, 6 boules noires et 4 boules jaunes. Chacune des boules a la même probabilité d'être tirée. On tire une boule au hasard. 1. Calculer la probabilité
CONTRAT DE LOCATION LONGUE DUREE
 Association des Responsables de Services Généraux Facilities Managers Association CONTRAT DE LOCATION LONGUE DUREE DE VEHICULES Avertissement : ce document est un exemple de contrat de LLD de véhicules
Association des Responsables de Services Généraux Facilities Managers Association CONTRAT DE LOCATION LONGUE DUREE DE VEHICULES Avertissement : ce document est un exemple de contrat de LLD de véhicules
D i s p o s i t i f d i n t e r v e n t i o n EN MATIÈRE SPORTIVE. e n m a t i è r e s p o r t i v e. Les équipements sportifs
 D i s p o s i t i f d i n t e r v e n t i o n EN MATIÈRE SPORTIVE e n m a t i è r e s p o r t i v e Les équipements sportifs JANVIER 2010 Janvier 2010 2/10 LES EQUIPEMENTS SPORTIFS STRUCTURANTS Les équipements
D i s p o s i t i f d i n t e r v e n t i o n EN MATIÈRE SPORTIVE e n m a t i è r e s p o r t i v e Les équipements sportifs JANVIER 2010 Janvier 2010 2/10 LES EQUIPEMENTS SPORTIFS STRUCTURANTS Les équipements
Le portage salarial caractéristiques et avantages
 LE PORTAGE SALARIAL Le portage salarial caractéristiques et avantages Le portage salarial consiste à transformer des honoraires en salaires. Il permet: De bénéficier d un statut de salarié : continuité
LE PORTAGE SALARIAL Le portage salarial caractéristiques et avantages Le portage salarial consiste à transformer des honoraires en salaires. Il permet: De bénéficier d un statut de salarié : continuité
SITE INTERNET : Documents 2 ème année SOC. Taux. Déductions. Sous-total. Salaire versé. Décompte de salaire de Mme / Mlle / M
 SITE INTERNET : Documents 2 ème année SOC Calculez le décompte salaire suivant Décompte de salaire de Mme / Mlle / M Taux AVS/AI/APG 5.05% AC 1.00% AA non prof 1.44% Caisse de retraire 7.45 % Alloc. fam./enfants
SITE INTERNET : Documents 2 ème année SOC Calculez le décompte salaire suivant Décompte de salaire de Mme / Mlle / M Taux AVS/AI/APG 5.05% AC 1.00% AA non prof 1.44% Caisse de retraire 7.45 % Alloc. fam./enfants
Première société de portage salarial en Languedoc-Roussillon depuis 1999
 Première société de portage salarial en Languedoc-Roussillon depuis 1999 Qui est AXE ENTREPRISES? Qu est-ce que LE PORTAGE? Qu est-ce qu une SOCIÉTÉ DE PORTAGE? LE PORTAGE le principe qui est concerné?
Première société de portage salarial en Languedoc-Roussillon depuis 1999 Qui est AXE ENTREPRISES? Qu est-ce que LE PORTAGE? Qu est-ce qu une SOCIÉTÉ DE PORTAGE? LE PORTAGE le principe qui est concerné?
Quelle journée! Pêle-mêle. Qu est-ce que c est? DOSSIER 3. 65. Écoutez les phrases. Écrivez les mots de la page Pêle-mêle que vous entendez.
 DOSSIER 3 Quelle journée! Pêle-mêle 19 65. Écoutez les phrases. Écrivez les mots de la page Pêle-mêle que vous entendez. 1.... 2.... 3.... 4.... 5.... 6.... 66. Reconstituez les mots de la page Pêle-mêle.
DOSSIER 3 Quelle journée! Pêle-mêle 19 65. Écoutez les phrases. Écrivez les mots de la page Pêle-mêle que vous entendez. 1.... 2.... 3.... 4.... 5.... 6.... 66. Reconstituez les mots de la page Pêle-mêle.
Compréhension de l oral
 1 DOCUMENT RÉSERVÉ AUX CORRECTEURS CORRIGÉ ET BARÈME Compréhension de l oral 25 points Vous allez entendre trois documents sonores, correspondant à des situations différentes. Pour le premier et le deuxième
1 DOCUMENT RÉSERVÉ AUX CORRECTEURS CORRIGÉ ET BARÈME Compréhension de l oral 25 points Vous allez entendre trois documents sonores, correspondant à des situations différentes. Pour le premier et le deuxième
Baccalauréat ES/L Amérique du Sud 21 novembre 2013
 Baccalauréat ES/L Amérique du Sud 21 novembre 2013 A. P. M. E. P. EXERCICE 1 Commun à tous les candidats 5 points Une entreprise informatique produit et vend des clés USB. La vente de ces clés est réalisée
Baccalauréat ES/L Amérique du Sud 21 novembre 2013 A. P. M. E. P. EXERCICE 1 Commun à tous les candidats 5 points Une entreprise informatique produit et vend des clés USB. La vente de ces clés est réalisée
Construction de la bissectrice d un angle
 onstruction de la bissectrice d un angle 1. Trace un angle. 1. 2. Trace un angle cercle. de centre (le sommet de l angle) et de rayon quelconque. 1. 2. 3. Trace Le cercle un angle cercle coupe. de la demi-droite
onstruction de la bissectrice d un angle 1. Trace un angle. 1. 2. Trace un angle cercle. de centre (le sommet de l angle) et de rayon quelconque. 1. 2. 3. Trace Le cercle un angle cercle coupe. de la demi-droite
Clientèle des Particuliers
 Clientèle des Particuliers COMPTES ET SERVICES Compte particulier à vue Ouverture Salarié du privé et du public Ouverture Non salarié Frais de tenue de compte Frais de clôture Délivrance de chéquiers Gratuit
Clientèle des Particuliers COMPTES ET SERVICES Compte particulier à vue Ouverture Salarié du privé et du public Ouverture Non salarié Frais de tenue de compte Frais de clôture Délivrance de chéquiers Gratuit
Fonctions linéaires et affines. 1 Fonctions linéaires. 1.1 Vocabulaire. 1.2 Représentation graphique. 3eme
 Fonctions linéaires et affines 3eme 1 Fonctions linéaires 1.1 Vocabulaire Définition 1 Soit a un nombre quelconque «fixe». Une fonction linéaire associe à un nombre x quelconque le nombre a x. a s appelle
Fonctions linéaires et affines 3eme 1 Fonctions linéaires 1.1 Vocabulaire Définition 1 Soit a un nombre quelconque «fixe». Une fonction linéaire associe à un nombre x quelconque le nombre a x. a s appelle
