Table des matières. 1 Institut de Mathématiques de Luminy A propos de l'institut L'équipe Statistique et Applications...
|
|
|
- Yvonne St-Germain
- il y a 8 ans
- Total affichages :
Transcription
1
2 2
3 Remerciements Avant d'entamer ce rapport, je tiens à remercier mon maître de stage, Denys Pommeret, responsable de l'équipe Statistique et Applications de l'institut de Mathématiques de Luminy, ainsi que Pierre-Olivier Goard et Emilie Guyon, thésards dans cette même équipe, de m'avoir donné la chance d'eectuer ce stage au sein de l'université et d'avoir été disponibles pour le partage de leurs connaissances. 3
4 4
5 Table des matières 1 Institut de Mathématiques de Luminy A propos de l'institut L'équipe Statistique et Applications Le coecient Bonus-Malus dans l'automobile Description du système de tarication Fraude à l'assurance Description et analyse des données Régression de Poisson Régression Sélections des variables La surdispersion Détection Solutions Les modèles ZIP et ZINB Le modèle ZIP Une équidispersion des données Estimation des paramètres Interprétation des résultats Le modèle ZINB Comparaison des modèles de régression Le critère de Vuong La statistique du X 2 de Pearson et le critère AIC Choix d'un modèle Conclusion Conclusion 29 A ANNEXE - Démonstrations 30 B ANNEXE - Code et Programmation 35 5
6 6
7 Table des gures 1 Organigramme de l'iml Proportion du nombre d'accidents par personne en une année
8 8
9 Liste des tableaux 1 Liste des variables du modèle Sortie SAS après sélection backward à 5% pour le modèle de Poisson Statistique du X 2 de Pearson pour le modèle de Poisson Sortie SAS après sélection backward à 5% pour le modèle BN Statistique du X 2 de Pearson pour le modèle BN Test LR entre le modèle de Poisson et le modèle BN Sortie R via la fonction zeroin() après une sélection backward à 5% pour le modèle ZIP Interprétations des coecients pour le modèle ZIP Sortie R après une sélection backward à 5% pour le modèle ZINB Interprétations des coecients pour le modèle ZINB Test de Vuong Comparaison des modèles via les statistiques du X 2 de Pearson et le critère AIC Test LR entre le modèle ZIP et le modèle ZINB
10 10
11 1 Institut de Mathématiques de Luminy 1.1 A propos de l'institut L'institut de Mathématiques de Luminy (IML) a été créé le 1er janvier 1996 à partir de l'ancien Laboratoire de Mathématiques Discrètes. L'IML est une Formation de Recherche en Evolution (FRE) du CNRS qui dépend scientiquement de l'institut des Sciences Mathématiques et de leurs Interactions (INSMI). Elle accueille 32 d'enseignantschercheurs de la Faculté des Sciences de Luminy, cotutelle avec Aix-Marseille Université (AMU). 1.2 L'équipe Statistique et Applications L'IML est constitué de 9 équipes, elles-mêmes consituées d'enseignants-chercheurs. Le groupe Statistique et Applications (STA), ayant comme responsable Denys Pommeret, forme une équipe de 6 enseignants ayant pour thèmes principaux l'apprentissage statistique, les variables latentes, la construction de tests et les processus. L'environnement particulier de Luminy incite plus particulièrement les membres de cette équipe à développer des modèles et des outils pour des applications en biologie, en sciences humaines et sociales, en économie et en environnement. Figure 1 Organigramme de l'iml 2 Le coecient Bonus-Malus dans l'automobile La grande majorité de la population française possède aujourd'hui un véhicule, et souscrivent donc à un contrat d'assurance. Les assurances, à qui le client paye une cotisation annuelle, utilisent le système du Bonus-Malus. Ce coecient, appelé coecient de réduction-majoration (CRM), est une méthode de pondération de l'appréciation du risque par la sinistralité. Autrement dit, c'est un système d'assurance évaluant les clients sur leurs sinistres passés et leurs prols, et ainsi leur attribuer un tarif approprié. 11
12 2.1 Description du système de tarication En France, les règles de tarication sont les mêmes pour tous les assurés. La tarication se fait en deux étapes : la première, la "tarication à priori", consiste à se baser seulement sur les caractéristiques propre à l'assuré (âge, sexe, etc). La deuxième quant à elle, la "tarication à posteriori", prend en compte les sinistres passés déclarés par le client. C'est pour établir ce système de tarication que le coecient de bonus-malus a été créé, ce dernier étant mis à jour chaque année selon des règles xées par le code des assurance 1. En eet, les diérentes règles pour calculer ce coecient sont telles que : 1. Le coecient est égal à 1 pour toute première souscription à un contrat d'assurance. 2. Le fait de changer d'assurance ne remet en aucun cas les compteurs "à zéro", car chaque assureur connaît le prol d'un nouveau client et son antécédent. 3. Si aucun sinistre n'est déclaré pendant une année, alors le coecient est diminué de 5% pour l'année à venir. La réduction ne peut cependant pas être inférieure à 50% (correspondant donc à un coecient de 0.5, le "bonus maximal"). 4. Un sinistre à responsabilité totale majore le coecient de bonus-malus de 25%. La majoration est de 12,5% si le sinistre est considéré comme à torts partagés. Les sinistres sont bien entendus cumulables pendant l'année. La majoration est également plafonée, avec un coecient maximum de Si le client reste pendant trois ans au bonus maximal, soit à 50% du tarif standard, alors il ne verra pas son coecient de bonus-malus augmenter si un sinistre est déclaré. 6. Si le client passe deux années consécutives sans déclarer de sinistres, à coecients supérieurs à 1.06, alors il retrouve le coeent standard égal à 1. Ceci décrit la règle de la "descente rapide". 2.2 Fraude à l'assurance Les règles liées à un contrat d'assurance décrites ci-dessus permettent donc d'établir chaque année le CRM associé à chacun des clients. De nos jours, il arrive très souvent qu'un assuré choisisse de ne pas déclarer son sinistre et de se dédommager lui-même, car il cherchera soit à optimiser son propre coecient de bonus-malus, soit à ne pas payer plus cher qu'il sera indemnisé (cf. annexe page 30 pour l'explication de la franchise en assurance). Par exemple, si le client a un coecient CRM élevé, mais qu'il n'a pas eu d'accident l'année précédente, alors il préfèrera (si les dommages ne sont pas trop importants) ne pas déclarer l'accident de l'année en cours pour pouvoir retrouver l'année suivante un coecient initial (règle de la descente rapide). Ou encore, si le coût de la franchise est plus élevé que celui des réparations, alors il préfèrera également ne rien déclarer. Ces deux phénomènes représentent ainsi la "fraude" à l'assurance Code des assurances d'après les articles A à A Le terme de fraude est ici un abus de langage. En eet, pour le cas où la franchise est plus élevée que le coût du sinistre, le client préfèrera naturellement s'auto-nancer plutôt que de déclarer son sinistre. 12
13 2.3 Description et analyse des données Les données fournies pour l'étude proviennent d'un jeu de données issu du site Freakonometrics [1], contenant observations. L'unité statistique est le numéro du contrat d'assurance, apparenté donc à un et un seul client. Nous avons, pour chaque individu, > son âge, > les caractéristiques de son véhicule (l'âge et la puissance), > la densité de population de la ville, > l'exposition de son contrat (en années), > son coecient Bonus-Malus de l'année passée, > son nombre d'accidents durant l'année passée. On cherchera alors à expliquer ce dernier (le nombre d'accidents par personne) à l'aide des autres caractéristiques de l'individu. A noter qu'il n'y a pas de fortes corrélations entre ces variables explicatives, ce qui permet de considérer l'ensemble des variables disponibles (cf. tableau B page 35). Cette étude sera eectuée dans la continuité d'une étude sur les régressions Zero-Inated Poisson[2] et Zero-Inated Negative Binomial 3, en s'appuyant également sur l'étude statistique des ZIP de Lambert[3], considérée comme la base de ces modèles. Synthétisons et familiarisons-nous dès à présent avec les notations des variables qui suivront : Modalité âge du conducteur âge du véhicule puissance du véhicule densité exposition coecient CRM nombre d'accidents Nom de la variable AGEC AGEV PUISS DENS EXPO BONUS S Table 1 Liste des variables du modèle Ces variables seront donc les variables explicatives du nombre de sinistres déclarés, la variable à expliquer, S. 3. Le modèle ZIP (resp. ZINB), dit modèle Zero-Inated Poisson (resp. Zero-Inated Negative Binomial) est un modèle à variable réponse suivant une loi de Poisson (resp. binomiale négative) avec possibilité que zéro soit une valeur plus probable qu'avec la loi de Poisson (resp. binomiale négative) standard. 13
14 3 Régression de Poisson Comme dit dans la section 2 page 12, le coecient de bonus-malus est estimé en fonction de la tarication à priori, autrement dit en fonction des caractéristiques propres au client. Intuitivement et statistiquement, nous supposerons dans un premier temps que la variable à expliquer, à savoir le nombre d'accidents déclarés, suit une loi de Poisson de paramètre λ : S X P (λ) 4. La vecteur X correspond aux covariables citées dans le tableau 1. Le graphique 2 reète le comportement poissonien du nombre d'accidents par personne. Figure 2 Proportion du nombre d'accidents par personne en une année. 3.1 Régression Sélections des variables Le but ici est donc d'expliquer le nombre de sinistres S par personne en fonction des caractéristiques propres à cette dernière. En utilisant la procédure GENMOD sous le logiciel SAS (ou la fonction glm sous R), nous obtenons les paramètres estimés par l'analyse du maximum de vraisemblance (avec fonction de lien LOG, cf. annexes page 36). A noter que la variable exposition intervient en dehors de toutes les autres variables explicatives. En eet, si S P (λ) pour une année, alors pour une durée d'exposition t, S P (λt). Ainsi, E(S i x i, t) = t.e (β x i) = e (β x i+log(t)). λ λk 4. On rappelle que si S X P (λ), alors P (S = k) = e k! 14
15 La variable log(exposition) sera donc la variable oset du modèle. Après avoir testé l'apport de chaque variable indépendamment (test de Type 3 5, cf. annexe page 35), il se trouve que toutes les variables ont un eet signicatif sur S, excepté la variable AGEC. Par ailleurs, la p-valeur 6 associée au paramètre estimé de la variable AGEC n'est pas signicative au niveau 5%. Cette p-valeur vaut en eet ; on ne rejette donc pas l'hypothèse de nullité du coecient. Avec une sélection backward au niveau 5% (cf. tableau 2), le modèle de Poisson retenu est : log(λ i ) = P UISS i CARBi =D BONUS i + log(e i ). Paramètre Code Estimateur Écart-type Khi-2 P > Khi-2 Intercept <.0001 PUISS CARB D <.0001 CARB E AGEV DENS BONUS <.0001 Scale Table 2 Sortie SAS après sélection backward à 5% pour le modèle de Poisson. D'après les estimations du tableau 2, nous pouvons tirer quelques résultats : plus on aura un coecient faible, moins on sera amené à déclarer un sinistre, le fait de rouler en carburant diesel augmente les chances d'en déclarer, plus la densité de population est forte, plus le conducteur déclare d'accidents, plus la voiture dispose d'un moteur puissant, plus l'assuré déclare d'accidents, et enn, plus le véhicule sera ancien, moins le conducteur sera amené à déclarer un sinistre. Bien sûr, il faut nuancer ces résultats. En eet, on peut deviner en réalité que le fait d'avoir un coecient CRM très bon (égal à 50) pousse l'assuré à vouloir le conserver, et donc à ne pas déclarer un possible sinistre (surtout si les coûts d'indemnisation sont faibles). De même, plus le véhicule est vieux, moins l'assuré sera amené à déclarer un accident : d'une part, il accorde moins d'importance à un véhicule âgé, et d'autre part, il améliorera son bonus-malus. 5. Les tests de type 3 indiquent si la variable considérée apporte de l'information sur la variable à expliquer en présence de toutes les autres variables explicatives. 6. La p-valeur (p-value en anglais) est la probabilité d'obtenir la même valeur ou une valeur plus extrème du test si l'hypothèse nulle est vraie. 15
16 3.2 La surdispersion Nous avons supposé (en page 14) que nos individus suivaient une loi de Poisson de paramètre λ. Il est intuitif de penser que les individus, à une variable xée (par l'exemple l'âge), ne vont pas réagir de la même façon, et donc ne suivent pas la même loi de Poisson. Le paramètre λ va certes dépendre de l'âge, mais aussi de variables ne rentrant pas dans le modèle (comme l'envie, le "talent", etc), qui ne sont pour la plupart pas "mesurables". Ceci peut alors entraîner un phénomène de surdispersion, c'est-à-dire que la variance empirique observée de S dépasse signicativement la variance attendue théorique. Autrement dit, cela signie que l'on n'a pas égalité entre espérance et variance thériques de S Détection Pour poursuivre l'étude sur le nombre de sinistres, il est nécessaire de savoir si les variables S i sont surdispersées. Si l'on considère, pour x xé, que la moyenne m est aléatoire, alors V(S) = V(E(S m)) + E(V(S m)) = V(m) + E(m) > E(m), où E(m) est la variance attendue. Pour vérier si les données sont bien équidispersées, il faut que la statistique X 2 de Pearson, égale à la somme des carrés des résidus de Pearson, soit de la même grandeur que son degré de liberté (n-p) (cf. annexe page 32). X Le tableau 3 révèle ainsi une légère surdispersion des données. En eet, la valeur 2 (n p) pour chaque statistique devrait, si les données étaient parfaitement équidispersées, être proches de 1. Ici, elle est de On a donc des individus surdispersés (mais cela reste faible). Critère DL X 2 X 2 /DL Pearson Chi-Square 5E Scaled Pearson X2 5E Table 3 Statistique du X 2 de Pearson pour le modèle de Poisson. sera pour la suite un des critères de comparaison des mo- La statistique du XP 2 earson dèles Solutions (i) La première solution pour corriger la surdispersion des variables serait de considérer le fait que les individus ne suivraient pas la même loi de Poisson. En d'autres termes, il faudrait considérer que le paramètre λ suit une distribution Gamma. 7. Si S P (λ), alors E(S) = λ = V(S) 16
17 Cette première approche conduit à supposer que le nombre de sinistres déclarés suivrait une loi binomiale négative. En eet, si l'on considère que le paramètre λ suit une loi Gamma, alors l'occurence du phénomène suit une loi de mélange Gamma-Poisson (cf annexe page 30). On sait alors que ce mélange suit une loi binomiale négative ("BN"). Pour éviter la surdispersion, il faudrait donc supposer que notre variable S X suive une loi BN. La densité de la distribution BN est :, avec f i = P (S i = k) = Γ(k + 1 α ) 1 α Γ(k + 1)Γ( 1 α )( 1 α + λ i ) 1 λ i α ( 1 α + λ ) k (1) i E(S i X i ) = λ i et V(S i X i ) = λ i (1 + αλ i ). On peut ainsi prendre en compte une éventuelle surdispersion des données avec α > 0 en cas de surdispersion et α = 0 en l'absence de surdispersion. Ainsi, le modèle de Poisson est un cas particulier du modèle BN, puisque équivalent lorsque α = 0. Avec les tests de type 3, toutes les variables ont un eet signicatif sur le nombre de sinistres (cf. annexe page 37). On ne rejette pas, une nouvelle fois, l'hypothèse de nullité de la variable AGEC au seuil 5% (avec une p-valeur égale à 0.34). Après une sélection backward de seuil 5%, le modèle BN retenu est d'après le tableau 4 : log(λ i ) = P UISS i CARBi =D BONUS i + log(e i ). Paramètre Code Estimateur Écart-type Khi-2 P > Khi-2 Intercept < 2e-16 PUISS CARB D AGEV DENS BONUS < 2e-16 Table 4 Sortie SAS après sélection backward à 5% pour le modèle BN. Criterion DF Value Value/DF Pearson Chi-Square 5E Table 5 Statistique du X 2 de Pearson pour le modèle BN. A noter que les inuences des variables du modèle BN sont les mêmes que celles du modèle de Poisson : le fait de rouler en diesel augmente le nombre de déclarations d'accidents, le nombre de sinistres déclarés décroît avec l'âge du véhicule,... 17
18 Bien que les données soient moins dispersées ( X 2 (n p) = < 1.41, cf. tableau 5), les estimations des paramètres du modèle BN ont des variances plus forte que pour le modèle de Poisson, avec les amplitudes des intervalles de conance plus importantes. La spécication du modèle de Poisson peut cependant être testée par l'hypothèse nulle : H 0 : α = 0 vs H 1 : α 0 (2) Pour tester (2), on calcule la statistique de test du rapport des vraisemblance 8 (test LR) du modèle BN (non contraint) et du modèle de Poisson (contraint à α = 0). La sortie R du tableau 6 indique ainsi que l'hypothèse nulle est rejetée au niveau 5%, avec une p-valeur inférieure à 2.2e-16. On a donc un α 0, et le modèle BN est préféré au modèle de Poisson. DF LogLik X 2 Pr(> X 2 ) < 2.2e-16 Table 6 Test LR entre le modèle de Poisson et le modèle BN. (ii)la deuxième solution, qui correspond à la continuité de l'étude sur les ZIP et ZINB, serait de prendre en compte les fraudes à l'assurance citées dans la section 2.2 page 12. C'est le but de la prochaine section. 8. La statistique de test LR ("Likelihood Ratio Test") est égale à 2(log(L R) log(l U )) et suit un X 2 à 1 degré de liberté, avec L R la vraisemblance du modèle contraint et L U celle du modèle non contraint. 18
19 4 Les modèles ZIP et ZINB 4.1 Le modèle ZIP Pour prendre en compte la dispersion, le modèle ZIP va ainsi stipuler que le nombre de sinistres suivra un loi de Poisson-Bernouilli, soit P (λ).b(p) : les évènements P (S = k) pour k 1 vont tous suivre une loi de Poisson. On va en eet supposer que si une personne déclare au moins un sinistre, alors elle n'en cachera aucun. En revanche, il est possible que la population des assurés pour lesquels S = 0 soit composée de deux sous populations : une population ne déclarant rien à raison (les assurés n'ont eectivement pas eu d'accident) -l'évènement rentre donc dans la loi de Poisson-, et une population qui ne déclarera pas ses sinistres responsables (fraude à l'assurance). Plus précisément, si l'on note p i la probabilité que S i ne provienne pas d'une loi de Poisson, alors :, où, { P(S i = k) = { pi + (1 p i )e λ i si S i = 0 (1 p i )e λ i λk i k! sinon log(λ i ) = B i β i λ i = e B iβ i logit(p i ) = G i γ p i = 1 1+e G i γ où B = {B 1,..., B n } et G = {G 1,..., G n } sont les covariables associées respectivement à λ et p Une équidispersion des données L'approche des données par un modèle ZIP permet de prendre en compte l'excès de zéros des sinistres déclarés. Ainsi, cela rend l'estimation bien moins dispersive, avec un rapport V alue DF égal à (cf. annexe page 37 pour le code R). L'étude peut donc se poursuivre avec la sélection des covariables Estimation des paramètres Pour l'estimation du modèle, il est nécessaire d'estimer les paramètres du modèle, soient β et γ. Pour cela, la méthode du maximum de vraisemblance est utilisée. La vraisemblance du modèle s'écrit alors : n L(β, γ, y) = (f(β i, γ i, y i )) log(l(β, γ, y)) = i=1 f(β, γ, y i ) i=1 19
20 Ainsi, log(l(β, γ, y)) = = + = + i,y i =0 i,y i =0 i,y i >0 i,y i =0 i,y i >0 ( ) log p i + (1 p i )e λ i + [ e G i γ log 1 + e G iγ ( log (1 p i )e λ λ ) i i y i! ] i,y i >0 + (1 egiγ 1 + e G iγ )e ebiβ log [(1 eg iγ e Biβyi 1 + e G iγ )e ebiβ y i! [ log e Giγ + e β] eb i [ y i B i β e B iβ ] i,y i >0 i,y i =0 ] log(1 + e G iγ ) log y i! i,y i >0 log(1 + e G iγ ) (3) L'étape suivante consisterait à dériver cette log-vraisemblance en β et γ pour la maximiser. Mais l'expression de celle-ci amène à un calcul trop complexe (cf. annexe page 31). Pour pallier ce problème, l'algorithme Espérance-Maximisation ("EM") permet de trouver le maximum de vraisemblance, en considérant l'existence d'une ou de plusieurs variable latentes non observée(s). Cet algorithme comporte les deux étapes suivantes : on évalue l'espérance (E) de la variable cachée, on maximise (M) la vraisemblance des paramètres λ et γ en maximisant la vraisemblance de l'étape E. Pour appliquer cet algorithme, considérons tout d'abord la variable latente cachée Z, telle que : Z = { 1 si les zéros observés ne proviennent pas d'une loi de Poisson 0 sinon Puis, procédons aux étapes E et M : 1. initialisation : on initialise au hasard γ (0) et β (0). 2. tant que l'algorithme n'a pas convergé, on procède aux deux étapes E et M : (a) étape E : estimation de Z (k+1) à γ (k) et β (k) xés : Z (k+1) = E(Z i Y i, γ (k), β (k) ) = k=0 kp (Z i = k) = P (Z i = 1) 20
21 = { 1 1+e G i γ(k) +e B i β(k) si y i = 0 0 si y i > 0 (b) etape M : maximisation de β et γ La log-vraisemblance complétée est donnée par : ( n ) L c (γ, β, y) = log f(z i γ)f(y i z i, β) = = + = + = + i=1 log f(z i γ) + i=1 log f(y i z i, β) i=1 ( log e z i G i γ log(1 + e z ig i γ ) ) i=1 ( [ e B i βy i e( e Biβ ]) ) (1 z i ) log y i! ( zi G i γ log(1 + e z ig i γ ) ) i=1 i=1 [ ] (1 z i ) B i βy i e Biβ log(y i!) i=1 ( zi G i γ log(1 + e z ig i γ ) ) i=1 [ ] (1 z i ) B i βy i e B iβ i=1 = L c (γ; y, z) + L c (β; y, z) (1 z i ) log(y i!) i=1 (1 z i ) log(y i!) L'étape M consiste à remplacer z i par l'expression z (k) i estimée à l'étape précédente, puis à résoudre les équations suivantes an de déterminer de nouvelles valeurs β (k+1) et γ (k+1) : i=1 L c(γ;y,z) γ = 0 donne une estimation de γ : ˆγ (k+1) L c(β;y,z) β = 0 donne une estimation de β : ˆβ (k+1) C'est ainsi avec cet algorithme EM que les paramètres vont être estimés, sous R, via la fonction zeroin (cf. annexe page 38). A noter que la variable log(exposition) est de nouveau la variable oset du zéro-modèle. En 21
22 eet, de manière analogue à la loi de Poisson, pour une durée d'exposition t, S i B(p i t). Ainsi, E(S i x i, t) = 1 t. 1 + e G iγ = e (G iγ+log(t)). D'après le tableau en annexe page 38, certaines covariables ne sont pas signicatives pour les deux modèles (Poisson et Probit). Nous pouvons remarquer par exemple que la p-valeur associée au coecient de la variable PUISS dans le modèle Probit est égale à On ne rejette donc pas l'hypothèse de nullité du coecient au seuil de 5%. Avec une sélection backward au même seuil, nous obtenons d'après le tableau 7 le modèle suivant :. log(λ i ) = BONUS i CARBi =D AGEV i + log(e i ) logit(p i ) = BONUS i AGEV i + log(e i ) Paramètre Estimateur Écart-type Khi-2 P > Khi-2 (Intercept) < 2e-16 BONUS e-11 CARBD AGEV (Intercept) BONUS e-05 AGEV e-06 (4) Table 7 Sortie R via la fonction zeroin() après une sélection backward à 5% pour le modèle ZIP. Le modèle ZIP admet ainsi une dispersion faible : XP 2 earson = < (modèle complet) Interprétation des résultats Le modèle ZIP retenu nous permet de tirer quelques informations concernant les déclarations d'accidents. Le tableau 8 récapitule les interprétations du modèle, classant dégressivement les facteurs favorisant d'une part le nombre de sinistres réels, et d'autre part la fraude à l'assurance. Tous ces résultats ont une interprétation assez logique : en eet, concernant le ou les sinistre(s) : 1. Si l'assuré a un bon CRM, cela signie qu'il est bon conducteur, et donc qu'il a peu d'accidents. 22
23 Facteurs favorisant les accidents Un CRM élevé Un véhicule ancien Le carburant diesel Facteurs favorisant la fraude Un CRM faible Un véhicule ancien Table 8 Interprétations des coecients pour le modèle ZIP. 2. Plus le véhicule sera âgé, plus il aura de dysfonctionnements et donc provoquera en moyenne plus d'accidents. 3. Circuler en diesel implique peut-être plus de kilomètres parcourus, et donc, plus de chances d'avoir un accident. concernant la fraude : 1. Plus le coecient de bonus-malus est faible (proche ou égal à 50), moins l'assuré sera amené à déclarer un accident, pour pouvoir garder ou améliorer son CRM. 2. Plus le véhicule du client sera vieux, moins il aura de la valeur, et donc moins l'assuré sera susceptible de déclarer un sinistre. 4.2 Le modèle ZINB Comme pour le modèle ZIP, le modèle ZINB va considérer de la même manière la gestion des zéros. En notant à nouveau p i la probabilité que le client fraude, alors : P (S i = k) = { pi + (1 p i )P (S = 0) si S i = 0 (1 p i )P (S = k) sinon,, P (S i = k) = { p i + (1 p i )( 1 α 1 α +λ i ) 1 α si k=0 (1 p i )f i pour k 1 où f i est la densité de la loi BN vue en équation (1) page 17, et { log(λ i ) = B i β i λ i = e B iβ i logit(p i ) = G i γ p i = 1 1+e G i γ où B = {B 1,..., B n } et G = {G 1,..., G n } sont les covariables associées respectivement à λ et p. En utilisant la même méthode que pour le modèle ZIP, on construit un algorithme EM, via la variable latente cachée Z : 23
24 Z = { 1 si les zéros observés ne proviennent pas d'une loi binomiale négative 0 sinon. Avec cet algorithme utilisé par la fonction zeroin, nous obtenons, après une sélection backward de seuil 5%, le modèle suivant (cf tableau 9) : log(λ i ) = BONUS i CARBi =D AGEV i + log(e i ) logit(p i ) = BONUS i P UISS i + log(e i ) (5). Paramètre Estimateur Écart-type Khi-2 P > Khi-2 BONUS e-14 CARBD AGEV Log(theta) (Intercept) e-05 BONUS e-06 AGEV e-07 AGEC DENS PUISS Table 9 Sortie R après une sélection backward à 5% pour le modèle ZINB. Concernant le modèle de Poisson, le modèle ZINB retenu contient les mêmes variables explicatives que celles du modèle ZIP, avec les mêmes interprétations des coecients. Le modèle ZINB considère par contre plus de variables explicatives signicatives pour le modèle des zéros. L'âge du conducteur par exemple joue ici un rôle dans la décision de frauder : plus l'assuré est jeune, plus il aura tendance à ne pas déclarer un possible accident. Comme pour le modèle ZIP, le tableau 10 récapitule les interprétations. Facteurs favorisant les accidents Un CRM élevé Un véhicule ancien Le carburant diesel Facteurs favorisant la fraude Un CRM faible Un véhicule ancien Un assuré jeune Une faible densité de population Une puissance de moteur faible Table 10 Interprétations des coecients pour le modèle ZINB. Nous pouvons également constater dans le modèle que le paramètre de dispersion log(θ) est signicativement diérent de zéro (la p-valeur associée au test de nullité étant 24
25 égale à 0.003, l'hypothèse de nullité est rejetée). Cela suggère que θ est signicativement diérent de 1, et donc que nos données sont bien surdispersées 9 La statistique du X 2 de Pearson vaut pour ce modèle Comparaison des modèles de régression 5.1 Le critère de Vuong Pour comparer des modèles non-emboîtés, Vuong a proposé une statistique de test qui permet de comparer le modèle ZIP (resp. ZINB) avec le modèle de Poisson (resp. binomial négatif) correspondant. En notant ( ) P1 (S i X i = s i ) m i = log, P 2 (S i X i = s i ), les hypothèses du test sont : { H0 : E(m i ) = 0 H 1 : E(m i ) 0. La statistique de Vuong pour tester l'hypothèse du modèle 1 (ZIP ou ZINB) contre le modèle 2 (Poisson ou BN) est : V = [ n 1 m n i=1 m i] 1 = n n i=1 (mi m)2 n m S m (6). V suit ainsi une loi de Student à n degré de liberté, et peut être approchée ici (car n est grand) par une loi normale. Il en résulte, pour un seuil de conance de niveau xé à 5%, que :, où 2 F 1 (0.95). si V <2, aucun modèle n'est privilégié, si V>2, le modèle 1 est favorisé, si V<-2, le modèle 2 est favorisé, Modèles Statistique V P-valeur > V Poisson vs ZIP e-7 BN vs ZINB e-43 Table 11 Test de Vuong. 9. Le test de nullité sur le θ correspond à la modélisation : V (Y X) = θ.e(y X). Si θ = 1, alors il y a équidispersion des données. Sinon, il y a une surdispersion. 25
26 Résultats : le test de Vuong, d'après le tableau 11, amène à deux résultats : le modèle ZIP est préférable au modèle de Poisson (on rejète l'hypothèse H 0 au niveau 5%), le modèle ZINB est préférable au modèle BN (on rejète l'hypothèse H 0 au niveau 5%). 5.2 La statistique du X 2 de Pearson et le critère AIC Comme expliqué précedemment, la statistique du XP 2 earson d'un modèle va reéter sa qualité. De plus, le critère AIC (cf. annexe page 32) renseigne sur la qualité d'ajustement d'un modèle : plus il est faible, meilleur est le modèle. Le tableau suivant renseigne donc sur ces deux critères pour les modèles étudiés : Critères Modèles Poisson BN ZIP ZINB X 2 (n p) AIC Table 12 Comparaison des modèles via les statistiques du X 2 de Pearson et le critère AIC. 5.3 Choix d'un modèle Le test de Vuong permet donc de privilégier les modèles prenant en compte les excès de zéros, i.e. les modèles ZIP et ZINB. Pour pouvoir comparer ces 2 modèles, on peut utiliser le test LR entre le modèle ZINB (modèle non contraint) et le modèle ZIP (modèle contraint) (cf. tableau 13), le critère AIC ou la statistique de Pearson (cf. tableau 12). DF LogLik X 2 Pr(> X 2 ) < 2.2e-16 Table 13 Test LR entre le modèle ZIP et le modèle ZINB. > le test LR amène à privilégier le modèle ZINB (L ZIP < L ZINB ), > le critère AIC amène également à privilégier le modèle ZINB (AIC ZINB < AIC ZIP ), > la statistique de Pearson conduit elle à préférer le modèle ZIP (X 2 plus proche de 1). On ne peut donc pas directement privilégier un modèle zero-inated. 26
27 5.4 Conclusion La fraude en assurance semble être bien reétée par le nombre important de nondéclarations de sinistres, autrement dit les excès de zéros dans une loi de Poisson. Le fait de considérer ces excès de zéros dans la modélisation semble amener à de meilleurs modèles, qui correspondront mieux aux comportements des assurés. Les modèles ZINB et ZIP conduisent à des résultats assez semblables, et le choix d'un modèle par rapport à l'autre ne peut pas réellement être justié. Cependant, dans la pratique, c'est le modèle ZIP qui est le plus utilisé. Les modèles zero-inated ont cependant des limites. En eet, on a supposé au début de l'étude que les individus ne pouvaient frauder que lorsqu'ils ne déclaraient aucun sinistre. En réalité, rien n'est dit que l'assuré peut déclarer un ou plusieurs sinistre(s), tout en fraudant un autre dans la même année. Pour modéliser cette approche, une étude généralisée sur les modèles de Poisson a été eectuée au sein de l'université, les modèle GIP (cf. en annexe page 33). Une autre approche possible pour le système de fraude dans l'assurance aurait été d'utiliser la modélisation du système de bonus-malus par les chaînes de Makov[4]. 27
28 28
29 6 Conclusion Ainsi, j'ai eectué mon stage de deuxième année au sein de l'institut de Mathématiques de Luminy, à Marseille. Lors de ce stage, jai pu mettre en pratique mes connaissances théoriques acquises durant ma formation, et me confronter, non pas à la vie professionnelle future, mais au travail théorique et autonome de tout enseignant-chercheur. Bien que ce ne soit pas le domaine que je recherche pour mon avenir, ce stage m'a permis de découvrir un univers que je connaissais nalement que très peu, mais qui m'apportera plus tard de solides connaissances et compétences statistiques. En eet, les tâches qui m'ont été conées dans ma mission relevaient de connaissances aussi bien théoriques que pratiques. Je pense que l'aspect théorique des cours de l'en- SAI ont énormément apporté dans l'approche du problème, notamment dans la rigueur statistique (hypothèses, justication d'un modèle,...). Le stage m'a également permis de travailler sur le côté pratique du domaine statistique, en appliquant les modèles construits sur des données. Mes connaissances pratiques, comme l'utilisation des logiciels SAS et R par exemple, ont aussi été indispensables et approfondies tout au long de ce stage. En eet, les tâches qui m'ont été conées dans ma mission relevaient de connaissances aussi bien théoriques que pratiques. Je pense que l'aspect théorique des cours de l'en- SAI ont énormément apporté dans l'approche du problème, notamment dans la rigueur statistique (hypothèses, justication d'un modèle,...). Le stage m'a également permis de travailler sur le côté pratique du domaine statistique, en appliquant les modèles construits sur des données. Mes connaissances pratiques, comme l'utilisation des logiciels SAS et R par exemple, ont aussi été indispensables et approfondies tout au long de ce stage. La mission qui m'a été conée a permis aux chercheurs, et plus particulièrement à une doctorante, de conrmer et justier ou non la qualité des modèles construits et des méthodes d'estimation utilisées. Je pense que cette expérience m'a oert une bonne préparation à mon insertion professionnelle, autant pour les compétences statistiques apportées, mais également pour le caractère autonome que requiert le métier de chercheur. 29
30 A ANNEXE - Démonstrations A.1 - Explications du système d'assurance En version simpliée, si l'on considère x le montant associé aux dommages du sinistre, I le montant des dédommagements, F le montant de la franchise associée au contrat d'assurance et C la cotisation mensuelle du client, alors, avec P le prix que le client doit payer, on a : si le client déclare le sinistre si le client ne déclare pas le sinistre. Ainsi, l'assuré déclarera son accident si P (x) = C + x I = C + x x + F = C + F P (x) = C + x C + F < C + x F < x, c'est-à-dire si la franchise est moins élevée que le coût du sinistre. L'étude faite ici est très largement simpliée, car on ne prend pas en compte certains facteurs comme celui du coecient de bonus-malus. Le seuil à partir duquel le client ne fraudera pas est donc plus élevé en réalité. Mais nous pouvons tout de même armer que le client ne déclarera pas son accident si x est inférieur à F (car il est alors "doublement" gagnant, des points de vue de la franchise et du coecient CRM). A.2 - Démonstration de la loi binomiale négative La loi de probabilité d'une variable aléatoire distribuée selon une loi binomiale négative de paramètres n et p prend la forme suivante : P (X = k) = f(k; n, p) = C k k+n 1.pn.q k. La loi binomiale négative est ainsi la loi de probabilité de la variable aléatoire X qui comptabilise le nombre d'échecs nécessaires avant obtention de n succès. Si le phénomène du nombre d'accidents par personne suit une loi de Poisson de paramètre λ variant d'un individu à l'autre, alors en considérant que λ suit une distribution Gamma de paramètres r et θ, l'occurence du phénomène suit une loi de mélange Gamma-Poisson. La probabilité devient : 30
31 P (X = k) = = 0 0 P (X λ = k).f(λ; r, θ)dλ λ k e λ k! λ r 1 e λ θ Γ(r)θ r avec le changement de variable t = λ. θ + 1 θ ( ) θ r+k 1 = θ + 1 Γ(r)k!θ r t k+r 1 e t dt 0 ( ) Γ(k + r) 1 r ( ) θ k = Γ(r)k! θ + 1 θ + 1 en posant p = 1 θ + 1 et q = θ θ + 1 Γ(k + r) = p r q k Γ(r)k! = C k k+n 1 pr (1 p) k. Le mélange Gamma-Poisson est donc une loi binomiale négative de paramètres r et p = 1 θ+1. Maximum de vraisemblance Pour estimer les paramètres du modèle, on procède par dérivation de la log-vraisemblance : Pour le paramètre γ log(l(β, γ, y) = log(l(β, γ, y)) γ log(l(β, γ, y)) γ + = = 0 i,y i =0 i,y i >0 i,y i =0 [ log e Giγ + e β] eb i [ y i B i β e B iβ ] G i e G iγ e G iγ + e eb i β i,y i >0 i,y i =0 i,y i =0 log(1 + e G iγ ) log y i! i,y i > e G iγ log(1 + e G iγ ) i,y i > e G iγ 31
32 i=1 Pour le paramètre β i= e G iγ = 0 si y i = 0 1 e eb iβ (1 + e G iγ )(e G iγ + e eb i β ) G ie G iγ si y i > 0 log(l(β, γ, y)) β log(l(β, γ, y)) γ = = 0 B i e Biβ e eb iβ + y i,y i e =0 Giγ e eb i β i B i B i e B iβ i,y i >0 B i e Biβ e eb iβ si y e i=1 Giγ e eb i β i = 0 y i B i = B i e Biβ si y i > 0 i=1 i Ces calculs amènent ainsi à des équations complexes de maximisation de la vraisemblance, d'où l'utilisation d'algorithme EM. A.3 - L'AIC L'AIC ("Akaike Information Criterion") est une mesure de la qualité d'ajustement d'un modèle statistique, tel que : AIC = 2k 2 log(l), où k est le nombre de paramètres dans le modèle, et L est la valeur du maximum de vraisemblance du modèle estimé. A.4 - La statistique de Pearson La statistique de Pearson est dénie par : XP 2 earson = ri 2 = ( S i Ŝi ) 2 = (S i Ŝi) 2 V (S ˆ ˆ i ) V (S i ), où les r i correspondent aux résidus de Pearson. On a alors, si les données sont équidispersées, X 2 P earson n p 1. 32
33 A.5 - Une autre approche : le modèle GIP Une autre approche a été eectuée au sein de l'université pour simuler les accidents automobiles : le modèle General-inated Poisson. En eet, si l'on considère d'une part les "vraies" déclarations de sinistres, ceux-ci suivent alors une loi de Poisson de paramètre λ. En revanche, les réponses des fraudes à l'assurance vont "fausser" le nombre d'accidents déclarés, mais aussi la loi qu'elles suivent. On peut en eet constater sur le graphique 2 page 14 que le nombre de sinistres déclarés par personne est très faible, ne suivant sans doute pas une loi de Poisson, ceci étant du au probable grand nombre de fraudes à l'assurance. Pour modéliser ces situations, on considère la variable S observée, correspondant aux réelles déclarations des assurés, et les variables Y et Z, suivant des lois de Poisson de paramètres diérents : Y correspond à la variable de loi connue P (λ 1 ), représentant la distribution théorique des sinistres (la réalité "sous-jacente"), et Z la variable de loi P (λ 2 ) de paramètre λ 2 inconnu, représentant la perturbation liée aux fraudes. En clair, i [0, n], S i = Y i Z i, avec. S i : les variables observées des sinistres déclarés Y i P (λ 1 ) : variable théorique sous-jacente, de paramètre λ 1 connu Z i P (λ 2 ) : variable perturbatrice de paramètre λ 2 inconnu Par dénition d'un modèle de Poisson, on a : { log(λ1 ) = Bβ log(λ 2 ) = Aα,où A et B sont les covariables associées respectivement aux variables Y et Z. On a alors : P (S = s) = P (Y Z = s) = P (Y = s ) s z Z = z z N = s z N P = s z N = s z N ( Y = s ) P (Z = z) z λ s z 1 s z! exp λ 1 λz 2 z! exp λ 2 exp Bβ s z s z! exp λ 1 expaαz z! exp λ 2 Ainsi, de la même manière que pour les modèles ZIP et ZINB, on pourra estimer les paramètres par un algorithme EM : 33
34 1. initialisation : on initialise au hasard α (0) et β (0). 2. tant que l'algorithme n'a pas convergé, on procède aux deux étapes E et M : (a) étape E : estimation de Z (k+1) à α (k) et β (k) xés Z (k+1) = E(Z i S i, α (k), β (k) ) = z = z = z Div(s) zp (Z i = z S i, α (k), β (k) ) z P (Z i, S i α (k), β (k) ) P (S i α (k), β (k) ) exp Aαz exp Bβs/z (z 1)!( s z )! s exp Aαz exp Bβs/z z!( s z )! (b) etape M : maximisation de α et β ( n ) L c (s, z, α, β) = log f(z i α)f(s i z i, β) = i=1 log f(z i α) + i=1 =... log f(s i z i, β) i=1 = Aα (k) z e Aα(k) log(z!) + Bβ (k) s z ebβ(k) log(( s z )!) On remplace alors z i par z (k) i estimé, puis on résout les équations suivantes an de déterminer de nouvelles valeurs β (k+1) et α (k+1) : L c(α;s,z) α = 0 donne une estimation de α : ˆα (k+1) L c(β;s,z) β = 0 donne une estimation de β : ˆβ (k+1) Les estimateurs ne convergeaient cependant pas, ce qui ne permettait pas de valider le modèle (ni de tirer d'informations pertinentes). Le code sous R se trouve dans la partie suivante. 34
35 B ANNEXE - Code et Programmation EXPO PUISS AGEV AGEC BONUS DENS EXPO PUISS AGEV AGEC BONUS DENS Corrélations entre les variables explicatives du modèle. B.1 - Le modèle de Poisson. Proc genmod data=stage.exzip2 ; class carb ; model s = puiss carb bonus agev dens agec / type3 dist=pois link=log oset=logexpo ; output out=sortie1 pred=nombre reschi=res1 resdev=res2 ; run ; Code SAS - Le modèle de Poisson. Paramètre Khi-2 P-valeur > Khi-2 BONUS <.0001 PUISS CARB <.0001 DENS AGEV AGEC Sortie SAS des tests de type 3 de la Proc Genmod - Le modèle de Poisson. Paramètre Code Estimateur Khi-2 de Wald P-valeur > Khi-2 Intercept <.0001 PUISS CARB D <.0001 CARB E BONUS <.0001 AGEV DENS AGEC Scale
36 Sortie SAS de la Proc Genmod - Le modèle de Poisson. Proc genmod data=stage.exzip2 ; class carb ; model s = puiss carb bonus agev dens / dist=pois link=log oset=logexpo pscale ; output out=sortie1 pred=nombre reschi=res1 resdev=res2 ; run ;. Code SAS - Estimation du paramètre de surdispersion φ avec l'option pscale Paramètre Code Estimateur Écart-type Khi-2 P > Khi-2 Intercept <.0001 PUISS CARB D CARB E AGEV DENS BONUS <.0001 Scale Sortie SAS de la Proc Genmod après sélection backward à 5% avec l'option pscale - Le modèle de Poisson. B.2 - Le modèle Binomial Négatif. Proc genmod data=stage.exzip2 ; class carb ; model s = puiss carb bonus agev dens / dist=negbin link=log oset=logexpo intercept=-2 ; output out=sortie2 pred=nombre reschi=res1 resdev=res2 ; run ; Code SAS - Le modèle BN. 36
37 Variables Khi-2 P-valeur > Khi-2 BONUS <.0001 PUISS <.0001 CARB <.0001 AGEC <.0001 DENS <.0001 AGEV <.0001 Sortie SAS des tests de type 3 de la Proc Genmod - Le modèle BN. Paramètre Code Estimateur Khi-2 de Wald P-valeur > Khi-2 Intercept <.0001 BONUS <.0001 PUISS CARB D <.0001 CARB E AGEC DENS AGEV Sortie SAS de la Proc Genmod - Le modèle BN. B.3 - Le modèle ZIP. f<-function(model){ p<-modelrank phi.p.zip <- sum(residuals(model,"pearson") 2 ) khi.p.zip<-phi.p.zip/(n-p) Code R - Calcul du X 2 de Pearson. library(pscl) zip <- zeroin (S BONUS+CARB+AGEV+AGEC+DENS+PUISS+oset(logexpo) BONUS+CARB+AGEV+AGEC+DENS+PUISS+oset(logexpo), data = donnees, dist ="poisson", link="logit"). Code R - Le modèle ZIP. 37
38 Explications du code : le premier modèle [s BONUS+...] correspond au modèle de Poisson estimé (avec la fonction de lien log), le deuxième modèle (le "zeromodel") correspond au modèle probit associé aux zéros. Paramètre Estimateur Écart-type P-valeur > Khi-2 Modèle de Poisson (Intercept) e e-01 < 2e-16 BONUS 1.190e e e-11 CARBD 2.599e e AGEV 3.220e e e-06 DENS e e AGEC e e PUISS e e Modèle de zéros (Intercept) BONUS e-06 AGEV e-08 DENS CARBD AGEC PUISS B.4 - Le modèle ZINB Sortie R de la régression ZIP via la fonction zeroin().. library(pscl) zinb <- zeroin(s BONUS + CARB + AGEV + AGEC + DENS + P UISS BONUS+CARB+AGEV+AGEC+DENS+PUISS, data = donnees, dist ="negbin", link="logit", oset=logexpo) Code R - Le modèle ZINB. 38
39 Algorithme EM. while (critere>d){ E = c(rep(0,50000)) beta0=beta1 alpha0=alpha1 for(i in 1 :50000){ esp = 0 denom2 = 0 denom1=0 if (X[i]!=0){ for(z in 1 :X[i]){ denom2 = denom2 + sum(exp(a[i,]%*%alpha0*z)*exp(b[i,]%*%beta0*x[i]/z) /(fact(z)*fact(x[i]/z))) } for (x in 0 :4){ denom1 = denom1+x*denom2 } for (z in 1 :X[i]){ esp = esp + (sum(z*exp(a[i,]%*%alpha0*z)*exp(b[i,]%*%beta0*x[i]/z) /(fact(z)*fact(x[i]/z))))/denom1 }} E[i] = esp Z = E ## Algorithme de Newton-Raphson pour estimer les paramètres alpha et beta if (X[i]!=0){ # log vraisemblance de alpha loglikalpha = function(alpha1) sum(z[i]*a[,i]*alpha1 - exp(a[,i]*alpha1)) # Newton-Raphson a = maxnr(loglikalpha, start=c(rep(0,p)), print.level=2) # log vraisemblance de beta loglikbeta = function(beta1) sum(x[i]*b[,i]*beta1/z - exp(b[i]*beta1)) # Newton-Raphson b = maxnr(loglikbeta, start=c(rep(0,j)), print.level=2) # valeurs des estimateurs alpha1 = a$estimate beta1 = b$estimate loglik1 = sum(-exp(a%*%alpha1) - exp(b%*%beta1)) + sum(z*a*alpha1) + sum(x*b*beta1/z) - log(fact(z)) - log(fact(x/z)) } else{ beta=c(rep(0,j)) loglikalpha = function(alpha1) sum(z[i]*a[,i]*alpha1 - exp(a[,i]*alpha1)) a = maxnr(loglikalpha, start=c(rep(0,p)), print.level=2) } critere=loglik1-loglik0} Code R - L'algorithme EM pour le modèle GIP. 39
40 Références [1] Alain Charpentier. "freakonometrics". http ://freakonometrics.blog.free.fr, mis en ligne le 28 novembre [2] K. PRESENT. Utilisation des régressions Zero-Inated Poisson pour modéliser des données de sinistres. PhD thesis, Ingénieurie Statistiques et Mathématiques Actuarielles (ISMA), Marseille, France, mars [3] Diane LAMBERT. "zero-inated poisson regression, with an application to defects in manufacturing". http :// mis en ligne en [4] M.KELLE. Modélisation du système de bonus malus. PhD thesis, Ingénieur en mathématiques, INSA Rouen, France, janvier
TD 3 : suites réelles : application économique et nancière
 Mathématiques Appliquées Cours-TD : K. Abdi, M. Huaulmé, B. de Loynes et S. Pommier Université de Rennes 1 - L1 AES - 009-010 TD 3 : suites réelles : application économique et nancière Exercice 1 Calculer
Mathématiques Appliquées Cours-TD : K. Abdi, M. Huaulmé, B. de Loynes et S. Pommier Université de Rennes 1 - L1 AES - 009-010 TD 3 : suites réelles : application économique et nancière Exercice 1 Calculer
Contents. 1 Introduction Objectifs des systèmes bonus-malus Système bonus-malus à classes Système bonus-malus : Principes
 Université Claude Bernard Lyon 1 Institut de Science Financière et d Assurances Système Bonus-Malus Introduction & Applications SCILAB Julien Tomas Institut de Science Financière et d Assurances Laboratoire
Université Claude Bernard Lyon 1 Institut de Science Financière et d Assurances Système Bonus-Malus Introduction & Applications SCILAB Julien Tomas Institut de Science Financière et d Assurances Laboratoire
CONCOURS D ENTREE A L ECOLE DE 2007 CONCOURS EXTERNE. Cinquième épreuve d admissibilité STATISTIQUE. (durée : cinq heures)
 CONCOURS D ENTREE A L ECOLE DE 2007 CONCOURS EXTERNE Cinquième épreuve d admissibilité STATISTIQUE (durée : cinq heures) Une composition portant sur la statistique. SUJET Cette épreuve est composée d un
CONCOURS D ENTREE A L ECOLE DE 2007 CONCOURS EXTERNE Cinquième épreuve d admissibilité STATISTIQUE (durée : cinq heures) Une composition portant sur la statistique. SUJET Cette épreuve est composée d un
Gestion du niveau de la franchise d'un contrat avec bonus-malus
 Gestion du niveau de la franchise d'un contrat avec bonus-malus Pierre Thérond Stéphane Bonche Résumé Réduire la franchise d'un contrat d'assurance permet d'améliorer la qualité du contrat du point de
Gestion du niveau de la franchise d'un contrat avec bonus-malus Pierre Thérond Stéphane Bonche Résumé Réduire la franchise d'un contrat d'assurance permet d'améliorer la qualité du contrat du point de
2. RAPPEL DES TECHNIQUES DE CALCUL DANS R
 2. RAPPEL DES TECHNIQUES DE CALCUL DANS R Dans la mesure où les résultats de ce chapitre devraient normalement être bien connus, il n'est rappelé que les formules les plus intéressantes; les justications
2. RAPPEL DES TECHNIQUES DE CALCUL DANS R Dans la mesure où les résultats de ce chapitre devraient normalement être bien connus, il n'est rappelé que les formules les plus intéressantes; les justications
ANTISELECTION ET CHOIX D'ASSURANCE : LE CAS DU VOL EN HABITATION UNE APPROCHE DE LA MESURE DU PHENOMENE
 ANTISELECTION ET CHOIX D'ASSURANCE : LE CAS DU VOL EN HABITATION UNE APPROCHE DE LA MESURE DU PHENOMENE Yannick MACÉ Statisticien-Economiste Responsable du Secteur Analyses Techniques, Groupama (C.C.A.M.A.)
ANTISELECTION ET CHOIX D'ASSURANCE : LE CAS DU VOL EN HABITATION UNE APPROCHE DE LA MESURE DU PHENOMENE Yannick MACÉ Statisticien-Economiste Responsable du Secteur Analyses Techniques, Groupama (C.C.A.M.A.)
CNAM 2002-2003 2léments de cours Bonus-malus et Crédibilité
 1 CNAM 2002-2003 2léments de cours Bonus-malus et Crédibilité Une situation fréquente en pratique est de disposer non pas d un résultat mais de plusieurs. Le cas se présente en assurance, par exemple :
1 CNAM 2002-2003 2léments de cours Bonus-malus et Crédibilité Une situation fréquente en pratique est de disposer non pas d un résultat mais de plusieurs. Le cas se présente en assurance, par exemple :
Les conducteurs automobiles évaluent-ils correctement leur risque de commettre un accident?
 Les conducteurs automobiles évaluent-ils correctement leur risque de commettre un accident? Nathalie LEPINE GREMAQ, Université de Toulouse1, 31042 Toulouse, France GRAPE, Université Montesquieu-Bordeaux
Les conducteurs automobiles évaluent-ils correctement leur risque de commettre un accident? Nathalie LEPINE GREMAQ, Université de Toulouse1, 31042 Toulouse, France GRAPE, Université Montesquieu-Bordeaux
Couples de variables aléatoires discrètes
 Couples de variables aléatoires discrètes ECE Lycée Carnot mai Dans ce dernier chapitre de probabilités de l'année, nous allons introduire l'étude de couples de variables aléatoires, c'est-à-dire l'étude
Couples de variables aléatoires discrètes ECE Lycée Carnot mai Dans ce dernier chapitre de probabilités de l'année, nous allons introduire l'étude de couples de variables aléatoires, c'est-à-dire l'étude
Introduction à la Statistique Inférentielle
 UNIVERSITE MOHAMMED V-AGDAL SCIENCES FACULTE DES DEPARTEMENT DE MATHEMATIQUES SMI semestre 4 : Probabilités - Statistique Introduction à la Statistique Inférentielle Prinemps 2013 0 INTRODUCTION La statistique
UNIVERSITE MOHAMMED V-AGDAL SCIENCES FACULTE DES DEPARTEMENT DE MATHEMATIQUES SMI semestre 4 : Probabilités - Statistique Introduction à la Statistique Inférentielle Prinemps 2013 0 INTRODUCTION La statistique
La problématique des tests. Cours V. 7 mars 2008. Comment quantifier la performance d un test? Hypothèses simples et composites
 La problématique des tests Cours V 7 mars 8 Test d hypothèses [Section 6.1] Soit un modèle statistique P θ ; θ Θ} et des hypothèses H : θ Θ H 1 : θ Θ 1 = Θ \ Θ Un test (pur) est une statistique à valeur
La problématique des tests Cours V 7 mars 8 Test d hypothèses [Section 6.1] Soit un modèle statistique P θ ; θ Θ} et des hypothèses H : θ Θ H 1 : θ Θ 1 = Θ \ Θ Un test (pur) est une statistique à valeur
ACTUARIAT 1, ACT 2121, AUTOMNE 2013 #12
 ACTUARIAT 1, ACT 2121, AUTOMNE 2013 #12 ARTHUR CHARPENTIER 1 Une compagnie d assurance modélise le montant de la perte lors d un accident par la variable aléatoire continue X uniforme sur l intervalle
ACTUARIAT 1, ACT 2121, AUTOMNE 2013 #12 ARTHUR CHARPENTIER 1 Une compagnie d assurance modélise le montant de la perte lors d un accident par la variable aléatoire continue X uniforme sur l intervalle
Série TD 3. Exercice 4.1. Exercice 4.2 Cet algorithme est destiné à prédire l'avenir, et il doit être infaillible! Exercice 4.3. Exercice 4.
 Série TD 3 Exercice 4.1 Formulez un algorithme équivalent à l algorithme suivant : Si Tutu > Toto + 4 OU Tata = OK Alors Tutu Tutu + 1 Tutu Tutu 1 ; Exercice 4.2 Cet algorithme est destiné à prédire l'avenir,
Série TD 3 Exercice 4.1 Formulez un algorithme équivalent à l algorithme suivant : Si Tutu > Toto + 4 OU Tata = OK Alors Tutu Tutu + 1 Tutu Tutu 1 ; Exercice 4.2 Cet algorithme est destiné à prédire l'avenir,
Algorithmes d'apprentissage
 Algorithmes d'apprentissage 1 Agents qui apprennent à partir d'exemples La problématique : prise de décision automatisée à partir d'un ensemble d'exemples Diagnostic médical Réponse à une demande de prêt
Algorithmes d'apprentissage 1 Agents qui apprennent à partir d'exemples La problématique : prise de décision automatisée à partir d'un ensemble d'exemples Diagnostic médical Réponse à une demande de prêt
Introduction à l'actuariat
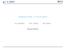 Introduction à l'actuariat 3A MMEFI M2 AMSE M2 IMSA Renaud Bourlès Introduction (1) Spécicité de l'assurance : cycle de production inversé Contrat d'assurance = promesse Importance de la prévision Importance
Introduction à l'actuariat 3A MMEFI M2 AMSE M2 IMSA Renaud Bourlès Introduction (1) Spécicité de l'assurance : cycle de production inversé Contrat d'assurance = promesse Importance de la prévision Importance
Actuariat I ACT2121. septième séance. Arthur Charpentier. Automne 2012. charpentier.arthur@uqam.ca. http ://freakonometrics.blog.free.
 Actuariat I ACT2121 septième séance Arthur Charpentier charpentier.arthur@uqam.ca http ://freakonometrics.blog.free.fr/ Automne 2012 1 Exercice 1 En analysant le temps d attente X avant un certain événement
Actuariat I ACT2121 septième séance Arthur Charpentier charpentier.arthur@uqam.ca http ://freakonometrics.blog.free.fr/ Automne 2012 1 Exercice 1 En analysant le temps d attente X avant un certain événement
Principe d un test statistique
 Biostatistiques Principe d un test statistique Professeur Jean-Luc BOSSON PCEM2 - Année universitaire 2012/2013 Faculté de Médecine de Grenoble (UJF) - Tous droits réservés. Objectifs pédagogiques Comprendre
Biostatistiques Principe d un test statistique Professeur Jean-Luc BOSSON PCEM2 - Année universitaire 2012/2013 Faculté de Médecine de Grenoble (UJF) - Tous droits réservés. Objectifs pédagogiques Comprendre
Estimation et tests statistiques, TD 5. Solutions
 ISTIL, Tronc commun de première année Introduction aux méthodes probabilistes et statistiques, 2008 2009 Estimation et tests statistiques, TD 5. Solutions Exercice 1 Dans un centre avicole, des études
ISTIL, Tronc commun de première année Introduction aux méthodes probabilistes et statistiques, 2008 2009 Estimation et tests statistiques, TD 5. Solutions Exercice 1 Dans un centre avicole, des études
Problème : Calcul d'échéanciers de prêt bancaire (15 pt)
 Problème : Calcul d'échéanciers de prêt bancaire (15 pt) 1 Principe d'un prêt bancaire et dénitions Lorsque vous empruntez de l'argent dans une banque, cet argent (appelé capital) vous est loué. Chaque
Problème : Calcul d'échéanciers de prêt bancaire (15 pt) 1 Principe d'un prêt bancaire et dénitions Lorsque vous empruntez de l'argent dans une banque, cet argent (appelé capital) vous est loué. Chaque
Calcul élémentaire des probabilités
 Myriam Maumy-Bertrand 1 et Thomas Delzant 1 1 IRMA, Université Louis Pasteur Strasbourg, France Licence 1ère Année 16-02-2006 Sommaire La loi de Poisson. Définition. Exemple. 1 La loi de Poisson. 2 3 4
Myriam Maumy-Bertrand 1 et Thomas Delzant 1 1 IRMA, Université Louis Pasteur Strasbourg, France Licence 1ère Année 16-02-2006 Sommaire La loi de Poisson. Définition. Exemple. 1 La loi de Poisson. 2 3 4
Chapitre 3 : Principe des tests statistiques d hypothèse. José LABARERE
 UE4 : Biostatistiques Chapitre 3 : Principe des tests statistiques d hypothèse José LABARERE Année universitaire 2010/2011 Université Joseph Fourier de Grenoble - Tous droits réservés. Plan I. Introduction
UE4 : Biostatistiques Chapitre 3 : Principe des tests statistiques d hypothèse José LABARERE Année universitaire 2010/2011 Université Joseph Fourier de Grenoble - Tous droits réservés. Plan I. Introduction
LE PROBLEME DU PLUS COURT CHEMIN
 LE PROBLEME DU PLUS COURT CHEMIN Dans cette leçon nous définissons le modèle de plus court chemin, présentons des exemples d'application et proposons un algorithme de résolution dans le cas où les longueurs
LE PROBLEME DU PLUS COURT CHEMIN Dans cette leçon nous définissons le modèle de plus court chemin, présentons des exemples d'application et proposons un algorithme de résolution dans le cas où les longueurs
I3, Probabilités 2014 Travaux Dirigés F BM F BM F BM F BM F B M F B M F B M F B M 20 20 80 80 100 100 300 300
 I3, Probabilités 2014 Travaux Dirigés TD 1 : rappels. Exercice 1 Poker simplié On tire 3 cartes d'un jeu de 52 cartes. Quelles sont les probabilités d'obtenir un brelan, une couleur, une paire, une suite,
I3, Probabilités 2014 Travaux Dirigés TD 1 : rappels. Exercice 1 Poker simplié On tire 3 cartes d'un jeu de 52 cartes. Quelles sont les probabilités d'obtenir un brelan, une couleur, une paire, une suite,
1.5 0.5 -0.5 -1.5 0 20 40 60 80 100 120. (VM(t i ),Q(t i+j ),VM(t i+j ))
 La logique oue dans les PME/PMI Application au dosage de l'eau dans les bétons P.Y. Glorennec INSA de Rennes/IRISA glorenne@irisa.fr C. Hérault Hydrostop christophe@hydrostop.fr V. Hulin Hydrostop vincent@hydrostop.fr
La logique oue dans les PME/PMI Application au dosage de l'eau dans les bétons P.Y. Glorennec INSA de Rennes/IRISA glorenne@irisa.fr C. Hérault Hydrostop christophe@hydrostop.fr V. Hulin Hydrostop vincent@hydrostop.fr
Baccalauréat ES/L Amérique du Sud 21 novembre 2013
 Baccalauréat ES/L Amérique du Sud 21 novembre 2013 A. P. M. E. P. EXERCICE 1 Commun à tous les candidats 5 points Une entreprise informatique produit et vend des clés USB. La vente de ces clés est réalisée
Baccalauréat ES/L Amérique du Sud 21 novembre 2013 A. P. M. E. P. EXERCICE 1 Commun à tous les candidats 5 points Une entreprise informatique produit et vend des clés USB. La vente de ces clés est réalisée
Analyse de la variance Comparaison de plusieurs moyennes
 Analyse de la variance Comparaison de plusieurs moyennes Biostatistique Pr. Nicolas MEYER Laboratoire de Biostatistique et Informatique Médicale Fac. de Médecine de Strasbourg Mars 2011 Plan 1 Introduction
Analyse de la variance Comparaison de plusieurs moyennes Biostatistique Pr. Nicolas MEYER Laboratoire de Biostatistique et Informatique Médicale Fac. de Médecine de Strasbourg Mars 2011 Plan 1 Introduction
LA NOTATION STATISTIQUE DES EMPRUNTEURS OU «SCORING»
 LA NOTATION STATISTIQUE DES EMPRUNTEURS OU «SCORING» Gilbert Saporta Professeur de Statistique Appliquée Conservatoire National des Arts et Métiers Dans leur quasi totalité, les banques et organismes financiers
LA NOTATION STATISTIQUE DES EMPRUNTEURS OU «SCORING» Gilbert Saporta Professeur de Statistique Appliquée Conservatoire National des Arts et Métiers Dans leur quasi totalité, les banques et organismes financiers
TESTS D'HYPOTHESES Etude d'un exemple
 TESTS D'HYPOTHESES Etude d'un exemple Un examinateur doit faire passer une épreuve type QCM à des étudiants. Ce QCM est constitué de 20 questions indépendantes. Pour chaque question, il y a trois réponses
TESTS D'HYPOTHESES Etude d'un exemple Un examinateur doit faire passer une épreuve type QCM à des étudiants. Ce QCM est constitué de 20 questions indépendantes. Pour chaque question, il y a trois réponses
LE ROLE DES INCITATIONS MONETAIRES DANS LA DEMANDE DE SOINS : UNE EVALUATION EMPIRIQUE.
 LE ROLE DES INCITATIONS MONETAIRES DANS LA DEMANDE DE SOINS : UNE EVALUATION EMPIRIQUE. Synthèse des travaux réalisés 1. Problématique La question D7 du plan d exécution du Programme National de Recherches
LE ROLE DES INCITATIONS MONETAIRES DANS LA DEMANDE DE SOINS : UNE EVALUATION EMPIRIQUE. Synthèse des travaux réalisés 1. Problématique La question D7 du plan d exécution du Programme National de Recherches
PROBLEMES D'ORDONNANCEMENT AVEC RESSOURCES
 Leçon 11 PROBLEMES D'ORDONNANCEMENT AVEC RESSOURCES Dans cette leçon, nous retrouvons le problème d ordonnancement déjà vu mais en ajoutant la prise en compte de contraintes portant sur les ressources.
Leçon 11 PROBLEMES D'ORDONNANCEMENT AVEC RESSOURCES Dans cette leçon, nous retrouvons le problème d ordonnancement déjà vu mais en ajoutant la prise en compte de contraintes portant sur les ressources.
Processus aléatoires avec application en finance
 Genève, le 16 juin 2007. Processus aléatoires avec application en finance La durée de l examen est de deux heures. N oubliez pas d indiquer votre nom et prénom sur chaque feuille. Toute documentation et
Genève, le 16 juin 2007. Processus aléatoires avec application en finance La durée de l examen est de deux heures. N oubliez pas d indiquer votre nom et prénom sur chaque feuille. Toute documentation et
Baccalauréat S Antilles-Guyane 11 septembre 2014 Corrigé
 Baccalauréat S ntilles-guyane 11 septembre 14 Corrigé EXERCICE 1 6 points Commun à tous les candidats Une entreprise de jouets en peluche souhaite commercialiser un nouveau produit et à cette fin, effectue
Baccalauréat S ntilles-guyane 11 septembre 14 Corrigé EXERCICE 1 6 points Commun à tous les candidats Une entreprise de jouets en peluche souhaite commercialiser un nouveau produit et à cette fin, effectue
Biostatistiques Biologie- Vétérinaire FUNDP Eric Depiereux, Benoît DeHertogh, Grégoire Vincke
 www.fundp.ac.be/biostats Module 140 140 ANOVA A UN CRITERE DE CLASSIFICATION FIXE...2 140.1 UTILITE...2 140.2 COMPARAISON DE VARIANCES...2 140.2.1 Calcul de la variance...2 140.2.2 Distributions de référence...3
www.fundp.ac.be/biostats Module 140 140 ANOVA A UN CRITERE DE CLASSIFICATION FIXE...2 140.1 UTILITE...2 140.2 COMPARAISON DE VARIANCES...2 140.2.1 Calcul de la variance...2 140.2.2 Distributions de référence...3
La survie nette actuelle à long terme Qualités de sept méthodes d estimation
 La survie nette actuelle à long terme Qualités de sept méthodes d estimation PAR Alireza MOGHADDAM TUTEUR : Guy HÉDELIN Laboratoire d Épidémiologie et de Santé publique, EA 80 Faculté de Médecine de Strasbourg
La survie nette actuelle à long terme Qualités de sept méthodes d estimation PAR Alireza MOGHADDAM TUTEUR : Guy HÉDELIN Laboratoire d Épidémiologie et de Santé publique, EA 80 Faculté de Médecine de Strasbourg
Gestion du niveau de la franchise d un contrat avec bonus-malus. Pierre THEROND & Stéphane BONCHE
 Gestion du niveau de la franchise d un contrat avec bonus-malus Pierre THEROND & Stéphane BONCHE SOMMAIRE 1. Réduction de franchise en l absence de système bonus-malus A - Bonnes propriétés du modèle collectif
Gestion du niveau de la franchise d un contrat avec bonus-malus Pierre THEROND & Stéphane BONCHE SOMMAIRE 1. Réduction de franchise en l absence de système bonus-malus A - Bonnes propriétés du modèle collectif
TABLE DES MATIERES. C Exercices complémentaires 42
 TABLE DES MATIERES Chapitre I : Echantillonnage A - Rappels de cours 1. Lois de probabilités de base rencontrées en statistique 1 1.1 Définitions et caractérisations 1 1.2 Les propriétés de convergence
TABLE DES MATIERES Chapitre I : Echantillonnage A - Rappels de cours 1. Lois de probabilités de base rencontrées en statistique 1 1.1 Définitions et caractérisations 1 1.2 Les propriétés de convergence
BONUS MALUS. Voici, la façon de calculer la prime : Le montant de la prime à acquitter est égale à : P = PB. C où : P
 BONUS MALUS Le propriétaire d un véhicule automobile est tenu d assurer sa voiture auprès d une compagnie d assurances. Pour un véhicule donné, le propriétaire versera annuellement une «prime» à sa compagnie.
BONUS MALUS Le propriétaire d un véhicule automobile est tenu d assurer sa voiture auprès d une compagnie d assurances. Pour un véhicule donné, le propriétaire versera annuellement une «prime» à sa compagnie.
«Cours Statistique et logiciel R»
 «Cours Statistique et logiciel R» Rémy Drouilhet (1), Adeline Leclercq-Samson (1), Frédérique Letué (1), Laurence Viry (2) (1) Laboratoire Jean Kuntzmann, Dép. Probabilites et Statistique, (2) Laboratoire
«Cours Statistique et logiciel R» Rémy Drouilhet (1), Adeline Leclercq-Samson (1), Frédérique Letué (1), Laurence Viry (2) (1) Laboratoire Jean Kuntzmann, Dép. Probabilites et Statistique, (2) Laboratoire
Modélisation aléatoire en fiabilité des logiciels
 collection Méthodes stochastiques appliquées dirigée par Nikolaos Limnios et Jacques Janssen La sûreté de fonctionnement des systèmes informatiques est aujourd hui un enjeu économique et sociétal majeur.
collection Méthodes stochastiques appliquées dirigée par Nikolaos Limnios et Jacques Janssen La sûreté de fonctionnement des systèmes informatiques est aujourd hui un enjeu économique et sociétal majeur.
1 Imputation par la moyenne
 Introduction au data mining L3 MIS - STA 1616-2010 V. Monbet Données manquantes L'objectif de ce TD est de manipuler et de comparer plusieurs méthodes d'imputation de données manquantes. La première partie
Introduction au data mining L3 MIS - STA 1616-2010 V. Monbet Données manquantes L'objectif de ce TD est de manipuler et de comparer plusieurs méthodes d'imputation de données manquantes. La première partie
UFR de Sciences Economiques Année 2008-2009 TESTS PARAMÉTRIQUES
 Université Paris 13 Cours de Statistiques et Econométrie I UFR de Sciences Economiques Année 2008-2009 Licence de Sciences Economiques L3 Premier semestre TESTS PARAMÉTRIQUES Remarque: les exercices 2,
Université Paris 13 Cours de Statistiques et Econométrie I UFR de Sciences Economiques Année 2008-2009 Licence de Sciences Economiques L3 Premier semestre TESTS PARAMÉTRIQUES Remarque: les exercices 2,
Méthodes de Simulation
 Méthodes de Simulation JEAN-YVES TOURNERET Institut de recherche en informatique de Toulouse (IRIT) ENSEEIHT, Toulouse, France Peyresq06 p. 1/41 Remerciements Christian Robert : pour ses excellents transparents
Méthodes de Simulation JEAN-YVES TOURNERET Institut de recherche en informatique de Toulouse (IRIT) ENSEEIHT, Toulouse, France Peyresq06 p. 1/41 Remerciements Christian Robert : pour ses excellents transparents
TSTI 2D CH X : Exemples de lois à densité 1
 TSTI 2D CH X : Exemples de lois à densité I Loi uniforme sur ab ; ) Introduction Dans cette activité, on s intéresse à la modélisation du tirage au hasard d un nombre réel de l intervalle [0 ;], chacun
TSTI 2D CH X : Exemples de lois à densité I Loi uniforme sur ab ; ) Introduction Dans cette activité, on s intéresse à la modélisation du tirage au hasard d un nombre réel de l intervalle [0 ;], chacun
Feuille 6 : Tests. Peut-on dire que l usine a respecté ses engagements? Faire un test d hypothèses pour y répondre.
 Université de Nantes Année 2013-2014 L3 Maths-Eco Feuille 6 : Tests Exercice 1 On cherche à connaître la température d ébullition µ, en degrés Celsius, d un certain liquide. On effectue 16 expériences
Université de Nantes Année 2013-2014 L3 Maths-Eco Feuille 6 : Tests Exercice 1 On cherche à connaître la température d ébullition µ, en degrés Celsius, d un certain liquide. On effectue 16 expériences
Evolution de la fréquence des sinistres 2002-2011 en assurance RC automobile
 Evolution de la fréquence des sinistres 2002-2011 en assurance RC automobile Contenu 1. Nombre de sinistres en RC tourisme et affaires... 2 Fréquence des sinistres en RC tourisme et affaires... 2 Fréquence
Evolution de la fréquence des sinistres 2002-2011 en assurance RC automobile Contenu 1. Nombre de sinistres en RC tourisme et affaires... 2 Fréquence des sinistres en RC tourisme et affaires... 2 Fréquence
ASSURANCE AUTOMOBILE ÉTUDES ACTUARIELLES ET POLITIQUE TARIFAIRE EN 2001 (x)
 ÉTUDES ACTUARIELLES ET POLITIQUE TARIFAIRE EN 2001 (x) Gilbert THIRY Membre d'honneur de l'iaf E.S.R.A. - Paris Dans toutes les sociétés d'assurances, le rôle de l'actuaire est incontournable pour optimiser
ÉTUDES ACTUARIELLES ET POLITIQUE TARIFAIRE EN 2001 (x) Gilbert THIRY Membre d'honneur de l'iaf E.S.R.A. - Paris Dans toutes les sociétés d'assurances, le rôle de l'actuaire est incontournable pour optimiser
Analyses de Variance à un ou plusieurs facteurs Régressions Analyse de Covariance Modèles Linéaires Généralisés
 Analyses de Variance à un ou plusieurs facteurs Régressions Analyse de Covariance Modèles Linéaires Généralisés Professeur Patrice Francour francour@unice.fr Une grande partie des illustrations viennent
Analyses de Variance à un ou plusieurs facteurs Régressions Analyse de Covariance Modèles Linéaires Généralisés Professeur Patrice Francour francour@unice.fr Une grande partie des illustrations viennent
Probabilités III Introduction à l évaluation d options
 Probabilités III Introduction à l évaluation d options Jacques Printems Promotion 2012 2013 1 Modèle à temps discret 2 Introduction aux modèles en temps continu Limite du modèle binomial lorsque N + Un
Probabilités III Introduction à l évaluation d options Jacques Printems Promotion 2012 2013 1 Modèle à temps discret 2 Introduction aux modèles en temps continu Limite du modèle binomial lorsque N + Un
Loi binomiale Lois normales
 Loi binomiale Lois normales Christophe ROSSIGNOL Année scolaire 204/205 Table des matières Rappels sur la loi binomiale 2. Loi de Bernoulli............................................ 2.2 Schéma de Bernoulli
Loi binomiale Lois normales Christophe ROSSIGNOL Année scolaire 204/205 Table des matières Rappels sur la loi binomiale 2. Loi de Bernoulli............................................ 2.2 Schéma de Bernoulli
Chaînes de Markov au lycée
 Journées APMEP Metz Atelier P1-32 du dimanche 28 octobre 2012 Louis-Marie BONNEVAL Chaînes de Markov au lycée Andreï Markov (1856-1922) , série S Problème 1 Bonus et malus en assurance automobile Un contrat
Journées APMEP Metz Atelier P1-32 du dimanche 28 octobre 2012 Louis-Marie BONNEVAL Chaînes de Markov au lycée Andreï Markov (1856-1922) , série S Problème 1 Bonus et malus en assurance automobile Un contrat
TESTS PORTMANTEAU D ADÉQUATION DE MODÈLES ARMA FAIBLES : UNE APPROCHE BASÉE SUR L AUTO-NORMALISATION
 TESTS PORTMANTEAU D ADÉQUATION DE MODÈLES ARMA FAIBLES : UNE APPROCHE BASÉE SUR L AUTO-NORMALISATION Bruno Saussereau Laboratoire de Mathématiques de Besançon Université de Franche-Comté Travail en commun
TESTS PORTMANTEAU D ADÉQUATION DE MODÈLES ARMA FAIBLES : UNE APPROCHE BASÉE SUR L AUTO-NORMALISATION Bruno Saussereau Laboratoire de Mathématiques de Besançon Université de Franche-Comté Travail en commun
RapidMiner. Data Mining. 1 Introduction. 2 Prise en main. Master Maths Finances 2010/2011. 1.1 Présentation. 1.2 Ressources
 Master Maths Finances 2010/2011 Data Mining janvier 2011 RapidMiner 1 Introduction 1.1 Présentation RapidMiner est un logiciel open source et gratuit dédié au data mining. Il contient de nombreux outils
Master Maths Finances 2010/2011 Data Mining janvier 2011 RapidMiner 1 Introduction 1.1 Présentation RapidMiner est un logiciel open source et gratuit dédié au data mining. Il contient de nombreux outils
Lois de probabilité. Anita Burgun
 Lois de probabilité Anita Burgun Problème posé Le problème posé en statistique: On s intéresse à une population On extrait un échantillon On se demande quelle sera la composition de l échantillon (pourcentage
Lois de probabilité Anita Burgun Problème posé Le problème posé en statistique: On s intéresse à une population On extrait un échantillon On se demande quelle sera la composition de l échantillon (pourcentage
NOTATIONS PRÉLIMINAIRES
 Pour le Jeudi 14 Octobre 2010 NOTATIONS Soit V un espace vectoriel réel ; l'espace vectoriel des endomorphismes de l'espace vectoriel V est désigné par L(V ). Soit f un endomorphisme de l'espace vectoriel
Pour le Jeudi 14 Octobre 2010 NOTATIONS Soit V un espace vectoriel réel ; l'espace vectoriel des endomorphismes de l'espace vectoriel V est désigné par L(V ). Soit f un endomorphisme de l'espace vectoriel
1 TD1 : rappels sur les ensembles et notion de probabilité
 1 TD1 : rappels sur les ensembles et notion de probabilité 1.1 Ensembles et dénombrement Exercice 1 Soit Ω = {1, 2, 3, 4}. Décrire toutes les parties de Ω, puis vérier que card(p(ω)) = 2 4. Soit k n (
1 TD1 : rappels sur les ensembles et notion de probabilité 1.1 Ensembles et dénombrement Exercice 1 Soit Ω = {1, 2, 3, 4}. Décrire toutes les parties de Ω, puis vérier que card(p(ω)) = 2 4. Soit k n (
Analyse de corrélation Étude des dépendances - Variables quantitatives
 Ricco Rakotomalala Analyse de corrélation Étude des dépendances - Variables quantitatives Version 1.1 Université Lumière Lyon 2 Page: 1 job: Analyse_de_Correlation macro: svmono.cls date/time: 8-Mar-2015/7:21
Ricco Rakotomalala Analyse de corrélation Étude des dépendances - Variables quantitatives Version 1.1 Université Lumière Lyon 2 Page: 1 job: Analyse_de_Correlation macro: svmono.cls date/time: 8-Mar-2015/7:21
Télécom Nancy Année 2013-2014
 Télécom Nancy Année 2013-2014 Rapport 1A Ajout du langage C dans la Programmer's Learning Machine GIANNINI Valentin Loria 615, rue du Jardin Botanique 54600, Villers-Lès-Nancy Maître de stage : QUINSON
Télécom Nancy Année 2013-2014 Rapport 1A Ajout du langage C dans la Programmer's Learning Machine GIANNINI Valentin Loria 615, rue du Jardin Botanique 54600, Villers-Lès-Nancy Maître de stage : QUINSON
Poursuivre ses études à l'université de Rouen Masters professionnels en Informatique et en Mathématiques. UFR Sciences et Techniques 20-03-2014 1/18
 Poursuivre ses études à l'université de Rouen Masters professionnels en Informatique et en Mathématiques UFR Sciences et Techniques 20-03-2014 1/18 Masters pro GIL, SSI et AIMAF Taux d'insertion : 100
Poursuivre ses études à l'université de Rouen Masters professionnels en Informatique et en Mathématiques UFR Sciences et Techniques 20-03-2014 1/18 Masters pro GIL, SSI et AIMAF Taux d'insertion : 100
Nombres, mesures et incertitudes en sciences physiques et chimiques. Groupe des Sciences physiques et chimiques de l IGEN
 Nombres, mesures et incertitudes en sciences physiques et chimiques. Groupe des Sciences physiques et chimiques de l IGEN Table des matières. Introduction....3 Mesures et incertitudes en sciences physiques
Nombres, mesures et incertitudes en sciences physiques et chimiques. Groupe des Sciences physiques et chimiques de l IGEN Table des matières. Introduction....3 Mesures et incertitudes en sciences physiques
Programmes des classes préparatoires aux Grandes Ecoles
 Programmes des classes préparatoires aux Grandes Ecoles Filière : scientifique Voie : Biologie, chimie, physique et sciences de la Terre (BCPST) Discipline : Mathématiques Seconde année Préambule Programme
Programmes des classes préparatoires aux Grandes Ecoles Filière : scientifique Voie : Biologie, chimie, physique et sciences de la Terre (BCPST) Discipline : Mathématiques Seconde année Préambule Programme
Voyager en voiture : louer un véhicule
 Les fiches pratiques de la concurrence et de la consommation Voyager en voiture : louer un véhicule Avant la location Comparer les offres des loueurs (en agence ou sur sites Internet) : s informer sur
Les fiches pratiques de la concurrence et de la consommation Voyager en voiture : louer un véhicule Avant la location Comparer les offres des loueurs (en agence ou sur sites Internet) : s informer sur
Evolution de la fréquence des sinistres 2003-2012 en assurance RC automobile
 Evolution de la fréquence des sinistres 2003-2012 en assurance RC automobile Contenu 1. Nombre de sinistres en RC tourisme et affaires... 2 Fréquence des sinistres en RC tourisme et affaires... 2 Fréquence
Evolution de la fréquence des sinistres 2003-2012 en assurance RC automobile Contenu 1. Nombre de sinistres en RC tourisme et affaires... 2 Fréquence des sinistres en RC tourisme et affaires... 2 Fréquence
Probabilités Loi binomiale Exercices corrigés
 Probabilités Loi binomiale Exercices corrigés Sont abordés dans cette fiche : (cliquez sur l exercice pour un accès direct) Exercice 1 : épreuve de Bernoulli Exercice 2 : loi de Bernoulli de paramètre
Probabilités Loi binomiale Exercices corrigés Sont abordés dans cette fiche : (cliquez sur l exercice pour un accès direct) Exercice 1 : épreuve de Bernoulli Exercice 2 : loi de Bernoulli de paramètre
SAS ENTERPRISE MINER POUR L'ACTUAIRE
 SAS ENTERPRISE MINER POUR L'ACTUAIRE Conférence de l Association des Actuaires I.A.R.D. 07 JUIN 2013 Sylvain Tremblay Spécialiste en formation statistique SAS Canada AGENDA Survol d Enterprise Miner de
SAS ENTERPRISE MINER POUR L'ACTUAIRE Conférence de l Association des Actuaires I.A.R.D. 07 JUIN 2013 Sylvain Tremblay Spécialiste en formation statistique SAS Canada AGENDA Survol d Enterprise Miner de
Processus de comptage, Poisson mélange, fonction de perte exponentielle, système bonus-malus.
 JF WALHIN* J PARIS* * Université Catholique de Louvain, Belgique Le Mans Assurances, Belgique RÉSUMÉ Nous proposons une méthodologie générale pour construire un système bonus-malus équilibré basé sur une
JF WALHIN* J PARIS* * Université Catholique de Louvain, Belgique Le Mans Assurances, Belgique RÉSUMÉ Nous proposons une méthodologie générale pour construire un système bonus-malus équilibré basé sur une
Retournement Temporel
 Retournement Temporel Rédigé par: HENG Sokly Encadrés par: Bernard ROUSSELET & Stéphane JUNCA 2 juin 28 Remerciements Je tiens tout d'abord à remercier mes responsables de mémoire, M.Bernard ROUSSELET
Retournement Temporel Rédigé par: HENG Sokly Encadrés par: Bernard ROUSSELET & Stéphane JUNCA 2 juin 28 Remerciements Je tiens tout d'abord à remercier mes responsables de mémoire, M.Bernard ROUSSELET
GEA II Introduction aux probabilités Poly. de révision. Lionel Darondeau
 GEA II Introduction aux probabilités Poly. de révision Lionel Darondeau Table des matières Énoncés 4 Corrigés 10 TD 1. Analyse combinatoire 11 TD 2. Probabilités élémentaires 16 TD 3. Probabilités conditionnelles
GEA II Introduction aux probabilités Poly. de révision Lionel Darondeau Table des matières Énoncés 4 Corrigés 10 TD 1. Analyse combinatoire 11 TD 2. Probabilités élémentaires 16 TD 3. Probabilités conditionnelles
PROBABILITES ET STATISTIQUE I&II
 PROBABILITES ET STATISTIQUE I&II TABLE DES MATIERES CHAPITRE I - COMBINATOIRE ELEMENTAIRE I.1. Rappel des notations de la théorie des ensemble I.1.a. Ensembles et sous-ensembles I.1.b. Diagrammes (dits
PROBABILITES ET STATISTIQUE I&II TABLE DES MATIERES CHAPITRE I - COMBINATOIRE ELEMENTAIRE I.1. Rappel des notations de la théorie des ensemble I.1.a. Ensembles et sous-ensembles I.1.b. Diagrammes (dits
Modélisation des risques
 2 Modélisation des risques 2. Introduction L objectif de ce chapitre est de présenter les modèles de base utilisés pour décrire le comportement aléatoire d un risque en actuariat pour une période xe. Les
2 Modélisation des risques 2. Introduction L objectif de ce chapitre est de présenter les modèles de base utilisés pour décrire le comportement aléatoire d un risque en actuariat pour une période xe. Les
Accident de voiture : six bons réflexes pour remplir le constat amiable
 Accident de voiture : six bons réflexes pour remplir le constat amiable La qualité et la précision des informations sur le constat amiable permettront une meilleure indemnisation. Pour définir clairement
Accident de voiture : six bons réflexes pour remplir le constat amiable La qualité et la précision des informations sur le constat amiable permettront une meilleure indemnisation. Pour définir clairement
Journées d études IARD
 Journées d études IARD Gestion des risques liés à la refonte tarifaire d un portefeuille automobile Niort, le 20 mars 2014 Marie Foucher mfoucher@galea-associes.eu Pierre Thérond ptherond@galea-associes.eu
Journées d études IARD Gestion des risques liés à la refonte tarifaire d un portefeuille automobile Niort, le 20 mars 2014 Marie Foucher mfoucher@galea-associes.eu Pierre Thérond ptherond@galea-associes.eu
RÉSOLUTION DE SYSTÈMES À DEUX INCONNUES
 RÉSOLUTION DE SYSTÈMES À DEUX INCONNUES Sommaire 1 Méthodes de résolution... 3 1.1. Méthode de Substitution... 3 1.2. Méthode des combinaisons linéaires... 6 La rubrique d'aide qui suit s'attardera aux
RÉSOLUTION DE SYSTÈMES À DEUX INCONNUES Sommaire 1 Méthodes de résolution... 3 1.1. Méthode de Substitution... 3 1.2. Méthode des combinaisons linéaires... 6 La rubrique d'aide qui suit s'attardera aux
Moments des variables aléatoires réelles
 Chapter 6 Moments des variables aléatoires réelles Sommaire 6.1 Espérance des variables aléatoires réelles................................ 46 6.1.1 Définition et calcul........................................
Chapter 6 Moments des variables aléatoires réelles Sommaire 6.1 Espérance des variables aléatoires réelles................................ 46 6.1.1 Définition et calcul........................................
Propagation sur réseau statique et dynamique
 Université de la Méditerranée UFR Sciences de Luminy Rapport de stage informatique pour le Master 2 de Physique, Parcours Physique Théorique et Mathématique, Physique des Particules et Astroparticules.
Université de la Méditerranée UFR Sciences de Luminy Rapport de stage informatique pour le Master 2 de Physique, Parcours Physique Théorique et Mathématique, Physique des Particules et Astroparticules.
CONTRAT AUTO VAM Avril 2007 UN CONTRAT DÉCLINÉ EN 5 FORMULES VAM :
 UN CONTRAT DÉCLINÉ EN 5 FORMULES VAM : UN CONTRAT D'ASSURANCE AUTOMOBILE ADAPTÉ AUX BESOINS DES SOCIÉTAIRES VAM est un contrat d'assurance automobile qui couvre les dommages corporels et matériels et qui
UN CONTRAT DÉCLINÉ EN 5 FORMULES VAM : UN CONTRAT D'ASSURANCE AUTOMOBILE ADAPTÉ AUX BESOINS DES SOCIÉTAIRES VAM est un contrat d'assurance automobile qui couvre les dommages corporels et matériels et qui
FORMULAIRE DE STATISTIQUES
 FORMULAIRE DE STATISTIQUES I. STATISTIQUES DESCRIPTIVES Moyenne arithmétique Remarque: population: m xμ; échantillon: Mx 1 Somme des carrés des écarts "# FR MOYENNE(série) MOYENNE(série) NL GEMIDDELDE(série)
FORMULAIRE DE STATISTIQUES I. STATISTIQUES DESCRIPTIVES Moyenne arithmétique Remarque: population: m xμ; échantillon: Mx 1 Somme des carrés des écarts "# FR MOYENNE(série) MOYENNE(série) NL GEMIDDELDE(série)
choisir H 1 quand H 0 est vraie - fausse alarme
 étection et Estimation GEL-64943 Hiver 5 Tests Neyman-Pearson Règles de Bayes: coûts connus min π R ( ) + ( π ) R ( ) { } Règles Minimax: coûts connus min max R ( ), R ( ) Règles Neyman Pearson: coûts
étection et Estimation GEL-64943 Hiver 5 Tests Neyman-Pearson Règles de Bayes: coûts connus min π R ( ) + ( π ) R ( ) { } Règles Minimax: coûts connus min max R ( ), R ( ) Règles Neyman Pearson: coûts
NOTIONS DE PROBABILITÉS
 NOTIONS DE PROBABILITÉS Sommaire 1. Expérience aléatoire... 1 2. Espace échantillonnal... 2 3. Événement... 2 4. Calcul des probabilités... 3 4.1. Ensemble fondamental... 3 4.2. Calcul de la probabilité...
NOTIONS DE PROBABILITÉS Sommaire 1. Expérience aléatoire... 1 2. Espace échantillonnal... 2 3. Événement... 2 4. Calcul des probabilités... 3 4.1. Ensemble fondamental... 3 4.2. Calcul de la probabilité...
Recherche dans un tableau
 Chapitre 3 Recherche dans un tableau 3.1 Introduction 3.1.1 Tranche On appelle tranche de tableau, la donnée d'un tableau t et de deux indices a et b. On note cette tranche t.(a..b). Exemple 3.1 : 3 6
Chapitre 3 Recherche dans un tableau 3.1 Introduction 3.1.1 Tranche On appelle tranche de tableau, la donnée d'un tableau t et de deux indices a et b. On note cette tranche t.(a..b). Exemple 3.1 : 3 6
Chapitre 3 : INFERENCE
 Chapitre 3 : INFERENCE 3.1 L ÉCHANTILLONNAGE 3.1.1 Introduction 3.1.2 L échantillonnage aléatoire 3.1.3 Estimation ponctuelle 3.1.4 Distributions d échantillonnage 3.1.5 Intervalles de probabilité L échantillonnage
Chapitre 3 : INFERENCE 3.1 L ÉCHANTILLONNAGE 3.1.1 Introduction 3.1.2 L échantillonnage aléatoire 3.1.3 Estimation ponctuelle 3.1.4 Distributions d échantillonnage 3.1.5 Intervalles de probabilité L échantillonnage
Exercice autour de densité, fonction de répatition, espérance et variance de variables quelconques.
 14-3- 214 J.F.C. p. 1 I Exercice autour de densité, fonction de répatition, espérance et variance de variables quelconques. Exercice 1 Densité de probabilité. F { ln x si x ], 1] UN OVNI... On pose x R,
14-3- 214 J.F.C. p. 1 I Exercice autour de densité, fonction de répatition, espérance et variance de variables quelconques. Exercice 1 Densité de probabilité. F { ln x si x ], 1] UN OVNI... On pose x R,
Chapitre 7. Statistique des échantillons gaussiens. 7.1 Projection de vecteurs gaussiens
 Chapitre 7 Statistique des échantillons gaussiens Le théorème central limite met en évidence le rôle majeur tenu par la loi gaussienne en modélisation stochastique. De ce fait, les modèles statistiques
Chapitre 7 Statistique des échantillons gaussiens Le théorème central limite met en évidence le rôle majeur tenu par la loi gaussienne en modélisation stochastique. De ce fait, les modèles statistiques
Auto Standard ASSURANCES DE BIENS. Conducteurs ayant du bonus et au moins 3 ans d assurance. Automobile. Notice. Garantie du conducteur incluse
 ASSURANCES DE BIENS Automobile ( Auto ) Standard Conducteurs ayant du bonus et au moins 3 ans d assurance Notice Garantie du conducteur incluse Excellents principes indemnitaires Bris de glace sans franchise
ASSURANCES DE BIENS Automobile ( Auto ) Standard Conducteurs ayant du bonus et au moins 3 ans d assurance Notice Garantie du conducteur incluse Excellents principes indemnitaires Bris de glace sans franchise
 Mémoire d Actuariat Tarification de la branche d assurance des accidents du travail Aymeric Souleau aymeric.souleau@axa.com 3 Septembre 2010 Plan 1 Introduction Les accidents du travail L assurance des
Mémoire d Actuariat Tarification de la branche d assurance des accidents du travail Aymeric Souleau aymeric.souleau@axa.com 3 Septembre 2010 Plan 1 Introduction Les accidents du travail L assurance des
STATISTIQUES. UE Modélisation pour la biologie
 STATISTIQUES UE Modélisation pour la biologie 2011 Cadre Général n individus: 1, 2,..., n Y variable à expliquer : Y = (y 1, y 2,..., y n ), y i R Modèle: Y = Xθ + ε X matrice du plan d expériences θ paramètres
STATISTIQUES UE Modélisation pour la biologie 2011 Cadre Général n individus: 1, 2,..., n Y variable à expliquer : Y = (y 1, y 2,..., y n ), y i R Modèle: Y = Xθ + ε X matrice du plan d expériences θ paramètres
Précision d un résultat et calculs d incertitudes
 Précision d un résultat et calculs d incertitudes PSI* 2012-2013 Lycée Chaptal 3 Table des matières Table des matières 1. Présentation d un résultat numérique................................ 4 1.1 Notations.........................................................
Précision d un résultat et calculs d incertitudes PSI* 2012-2013 Lycée Chaptal 3 Table des matières Table des matières 1. Présentation d un résultat numérique................................ 4 1.1 Notations.........................................................
Probabilités sur un univers fini
 [http://mp.cpgedupuydelome.fr] édité le 7 août 204 Enoncés Probabilités sur un univers fini Evènements et langage ensembliste A quelle condition sur (a, b, c, d) ]0, [ 4 existe-t-il une probabilité P sur
[http://mp.cpgedupuydelome.fr] édité le 7 août 204 Enoncés Probabilités sur un univers fini Evènements et langage ensembliste A quelle condition sur (a, b, c, d) ]0, [ 4 existe-t-il une probabilité P sur
Production des Services d Assurance non-vie selon le SCN 2008
 REPUBLIQUE DU CAMEROUN Paix - Travail Patrie ---------- INSTITUT NATIONAL DE LA STATISTIQUE ---------- REPUBLIC OF CAMEROON Peace - Work Fatherland ---------- NATIONAL INSTITUTE OF STATISTICS ----------
REPUBLIQUE DU CAMEROUN Paix - Travail Patrie ---------- INSTITUT NATIONAL DE LA STATISTIQUE ---------- REPUBLIC OF CAMEROON Peace - Work Fatherland ---------- NATIONAL INSTITUTE OF STATISTICS ----------
Direction des Études et Synthèses Économiques Département des Comptes Nationaux Division des Comptes Trimestriels
 Etab=MK3, Timbre=G430, TimbreDansAdresse=Vrai, Version=W2000/Charte7, VersionTravail=W2000/Charte7 Direction des Études et Synthèses Économiques Département des Comptes Nationaux Division des Comptes Trimestriels
Etab=MK3, Timbre=G430, TimbreDansAdresse=Vrai, Version=W2000/Charte7, VersionTravail=W2000/Charte7 Direction des Études et Synthèses Économiques Département des Comptes Nationaux Division des Comptes Trimestriels
Les indices à surplus constant
 Les indices à surplus constant Une tentative de généralisation des indices à utilité constante On cherche ici en s inspirant des indices à utilité constante à définir un indice de prix de référence adapté
Les indices à surplus constant Une tentative de généralisation des indices à utilité constante On cherche ici en s inspirant des indices à utilité constante à définir un indice de prix de référence adapté
données en connaissance et en actions?
 1 Partie 2 : Présentation de la plateforme SPSS Modeler : Comment transformer vos données en connaissance et en actions? SPSS Modeler : l atelier de data mining Large gamme de techniques d analyse (algorithmes)
1 Partie 2 : Présentation de la plateforme SPSS Modeler : Comment transformer vos données en connaissance et en actions? SPSS Modeler : l atelier de data mining Large gamme de techniques d analyse (algorithmes)
CHAPITRE VIII : Les circuits avec résistances ohmiques
 CHAPITRE VIII : Les circuits avec résistances ohmiques VIII. 1 Ce chapitre porte sur les courants et les différences de potentiel dans les circuits. VIII.1 : Les résistances en série et en parallèle On
CHAPITRE VIII : Les circuits avec résistances ohmiques VIII. 1 Ce chapitre porte sur les courants et les différences de potentiel dans les circuits. VIII.1 : Les résistances en série et en parallèle On
VI. Tests non paramétriques sur un échantillon
 VI. Tests non paramétriques sur un échantillon Le modèle n est pas un modèle paramétrique «TESTS du CHI-DEUX» : VI.1. Test d ajustement à une loi donnée VI.. Test d indépendance de deux facteurs 96 Différentes
VI. Tests non paramétriques sur un échantillon Le modèle n est pas un modèle paramétrique «TESTS du CHI-DEUX» : VI.1. Test d ajustement à une loi donnée VI.. Test d indépendance de deux facteurs 96 Différentes
APPLICATION DU SCN A L'EVALUATION DES REVENUS NON DECLARES DES MENAGES
 4 mars 1996 FRANCAIS Original : RUSSE COMMISSION DE STATISTIQUE et COMMISSION ECONOMIQUE POUR L'EUROPE CONFERENCE DES STATISTICIENS EUROPEENS OFFICE STATISTIQUE DES COMMUNAUTES EUROPEENNES (EUROSTAT) ORGANISATION
4 mars 1996 FRANCAIS Original : RUSSE COMMISSION DE STATISTIQUE et COMMISSION ECONOMIQUE POUR L'EUROPE CONFERENCE DES STATISTICIENS EUROPEENS OFFICE STATISTIQUE DES COMMUNAUTES EUROPEENNES (EUROSTAT) ORGANISATION
Régression linéaire. Nicolas Turenne INRA nicolas.turenne@jouy.inra.fr
 Régression linéaire Nicolas Turenne INRA nicolas.turenne@jouy.inra.fr 2005 Plan Régression linéaire simple Régression multiple Compréhension de la sortie de la régression Coefficient de détermination R
Régression linéaire Nicolas Turenne INRA nicolas.turenne@jouy.inra.fr 2005 Plan Régression linéaire simple Régression multiple Compréhension de la sortie de la régression Coefficient de détermination R
Baccalauréat ES/L Métropole La Réunion 13 septembre 2013 Corrigé
 Baccalauréat S/L Métropole La Réunion 13 septembre 2013 Corrigé A. P. M.. P. XRCIC 1 Commun à tous les candidats Partie A 1. L arbre de probabilité correspondant aux données du problème est : 0,3 0,6 H
Baccalauréat S/L Métropole La Réunion 13 septembre 2013 Corrigé A. P. M.. P. XRCIC 1 Commun à tous les candidats Partie A 1. L arbre de probabilité correspondant aux données du problème est : 0,3 0,6 H
Raisonnement par récurrence Suites numériques
 Chapitre 1 Raisonnement par récurrence Suites numériques Terminale S Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES Raisonnement par récurrence. Limite finie ou infinie d une suite.
Chapitre 1 Raisonnement par récurrence Suites numériques Terminale S Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES Raisonnement par récurrence. Limite finie ou infinie d une suite.
4. L assurance maladie
 L ASSURANCE MALADIE 73 4. L assurance maladie Comme l assurance maladie est obligatoire, toute personne domiciliée en Suisse doit être convenablement couverte. C est actuellement le cas, avec un très large
L ASSURANCE MALADIE 73 4. L assurance maladie Comme l assurance maladie est obligatoire, toute personne domiciliée en Suisse doit être convenablement couverte. C est actuellement le cas, avec un très large
Pourquoi l apprentissage?
 Pourquoi l apprentissage? Les SE sont basés sur la possibilité d extraire la connaissance d un expert sous forme de règles. Dépend fortement de la capacité à extraire et formaliser ces connaissances. Apprentissage
Pourquoi l apprentissage? Les SE sont basés sur la possibilité d extraire la connaissance d un expert sous forme de règles. Dépend fortement de la capacité à extraire et formaliser ces connaissances. Apprentissage
