IUT 1 DE GRENOBLE Département mesures physiques
|
|
|
- Estelle Pothier
- il y a 8 ans
- Total affichages :
Transcription
1 IUT DE GRENOBLE Dépreme mesures physques Cours de Mhémques Premer semesre Je-Mre De Coo
2 Chpre : Rppels de rgoomére Cercle rgoomérque : Il s g du cercle de ryo, ceré sur l orge O. M y P A Q O O dé l mesure «prcple» de l gle AOM, oée θ, pr AM, l logueur de l rc sur le cercle ué. L roo ds le ses pos correspod u ses verse des gulles d ue more. Ué : u gle s eprme, su dco corre, e rds, ué légle. O ulse e sûr d ures ués comme le degré. 8 degrés rds Logueur d rc : U rc dé pr u gle θ e rds sur u cercle de ryo R pour logueur R θ. Les gles so compés posveme ds le ses rgoomérque, verse des gulles d ue more. U gle de π correspod à ue roo d u our comple. L mesure d u gle es dée à π près. L gle π correspod à u dem our ds le ses drec, e à π ds le ses rérogrde. Propréé : Les gles so dés ds l ervlle [,π] ou [-π,+π], de mère deque. Ils so dés à u omre eer de ours près. O écrr doc de mère géérle : Avec k eer e : k [, ] ou [, ]
3 Focos rgoomérques : O dé : OQ cos OM OP s OM s cos cos co s Aeo u grdeurs lgérques vec u sge. Agles remrqules L le qu su es à coîre pr cœur θ s cos 6 4 O dédu les gees e cogees pr clcul drec. Vleurs dédues pr lecure sur le cercle rgoomérque. Elles so légo e ous e doeros que quelques cs, à compléer so-même : cos? s? cos? s? Formules d ddo cos? s? cos? s? cos? s? cos? s?
4 Nous verros, ds l pre «omres complees» comme l o démore les ormules qu suve. Les relos odmeles, les vleurs remrqules, s que les ormules relves à l gle doule ou moé so à coîre pr cœur. 4
5 Focos rgoomérques récproques L équo dme ue soluo uque ds l ervlle [-/, /]. O l oe Arcsy L équo cos y dme ue soluo uque ds l ervlle [, ]. O l oe Arccos y L équo dme ue soluo uque ds l ervlle ]-/, /[. O l oe Arc y s y y Nous vos s dé ros ocos rgoomérques récproques : Arcs : dé de [- ] sur [-/, /] Arccos dé de [- ] sur [, ] Arc dé de ]- + [ sur ]-/, -/[ Propréés élémeres L déo des ocos rgoomérques, s que l relo cos s permee de démorer séme les relos suves : Eercce : démorer ces relos cosrcs rcs Dérvo des ocos récproques rccos rccos rcs / srccos Nous reverros ce po uléreureme, ms ous meoeros d ores e déjà les relos : d d d d d d rccos rcs rc 5
6 Equos rgoomérques. Premère pre. O cosdère l équo : Où es u omre eer e u gle é. Résoluo : o s que es dé à u omre eer de roos près, c'es-à-dre que l équo s écr e, rgoureuseme : k k L équo précédee soluos pour k= -. Eemple. Résoudre 5 Come y --l de soluos ss clcul. Doer esue oues les soluos. Equos rgoomérques. Secode pre. Les ocos récproques, ccessles sur oue clculrce, ous permee de résoudre des équos rgoomérques smples, qu so les suves : Arc cos y cos y ou Arc cos y Arc s y s y ou Arc s y Arc cos y k Arc cos y k cos y ou ou Arc cos y k Arc cos y k Arc s y k Arc s y k s y ou ou Arc s y k Arc s y k Equos rgoomérques. Trosème pre. Nous cosdéros me les équos du ype cos+s=c. L procédure es sse sée. O se rmèe pr ormlso u sus ou u cosus d ue somme. O ormlse l équo e l réécrv, de mère équvlee : cos s c 6
7 O lors, pr cosruco : O recoî le développeme du sus d ue somme. Il ese doc y, à déermer, el que : s y e cos y L équo deve leme : s y cos cos ys s y c Cs : c Cs : c ps de soluo O procède lors comme su : - O résoud s c, ce qu doe deu soluos e. - O déerme y de mère uque à près cr o coî so sus e so cosus prgrphe. - o dédu,=,-y+k deu soluos. Remrque odmele : S u leu de cos e de s o cos e s, l résoluo es deque. Pr core o soluos, é remplcé pr., y O :,=,-y+k so, k soluos. Vre : O recoî le développeme du cosus d ue somme e pos : l équo deve lors : O procède comme précédemme. cos y e cos y cos s ys cos y s y c 7
8 Quelques pplcos de l rgoomére. Coordoées polres O se plce ds le pl, vec les coordoées crésees usuelles. Ds ce cs, u po M de coordoées,y peu êre représeé pr s dsce à l orge e l gle ere OM e l e des scsses. y M θ O dé les coordoées polres de M pr le module e l rgume qu so dées pr, respecveme y cos y s Equo prmérque d u cercle Les pos d u cercle de ryo R ceré sur l orge vére, pr déo, l équo mplce : y R Ils vére doc l équo de «prmérque» suve le prmère es e θ. Rcos y Rs Eercce : Ecrre l équo prmérque d u cercle ceré sur u po quelcoque du pl 8
9 Equo prmérée d ue ellpse cerée S e so respecveme les dems grds es horol e vercl, l équo de l ellpse cerée es lors de l orme : 4 Applco cos y s O se doe u mouveme ellpque ds le pl, de l orme : cos y s Clculer le veceur vesse Comme le veceur vesse es l oreé pr rppor à l ellpse? Dédure de ce rsoeme le veceur ormé ge à ue ellpse quelcoque. 5 Vleurs pprochées Pour pe c'es-à-dre éreur à. evro e vleur solue, o les relos : s cos 6 Equos déreelles Théorème : les ocos sus e cosus so soluos de l équo déreelle du secod ordre : d d Corollre : les ocos sω e cosω so soluos de l équo déreelle du secod ordre : d d 9
10 Chpre : Focos logrhme e epoeelle Foco logrhme épére Théorème : l oco =/ dme ue prmve sur R *+, l esemle des réels srceme poss, e qu so ulle pour =. Cee prmve es uque e es oée l. Corollre : d l d l Corollre : L prmve de / pour ég es /, pour o ul ds R, es l d l. Pr coséque, l prmve de Coure représeve de l oco logrhme épére Propréés élémeres O more sse séme les propréés suves, qu so à coîre pr cœur. lm l lm l l lm L oco logrhme épére es srceme crosse sur ], [ e es à vleurs ds ], [
11 Logrhme du produ Cosdéros e deu réels poss. So Pr dérvo l Pr coséque, l oco e l oco logrhme y l même dérvée, elles dère d ue cose C. l l C Cee relo es vre pour ou, e prculer pour =, d où : e doc l l C C l l l O dédu mmédeme : l l l Eercce : le démorer à prr de l ormule précédee Théorème : L oco logrhme épére es l seule e uque oco coue qu vére =+ e =. Esece du omre e Théorème : Il ese u omre uque oé «e», se des logrhmes épéres, qu vére le=. Cec se démore pr eemple e uls le que l oco es srceme crosse e coue prgrphe. 4 Dérvo e égro logrhmque So G l O dédu, pr dérvo de ocos composées : G Cee epresso prculère es ppelée l dérvée logrhmque de.
12 L érê de cee relo es de pouvor clculer ceres prmves. Pr eemple, so : O peu écrre : g g où c es ue cose d égro. g d l c Remrque : e jms ouler l vleur solue. 5 Foco epoeelle Déo : l oco epoeelle es l oco récproque de l oco logrhme. Propréé odmele : l y l l l ep y epl ep ep y y l Pr déo : ep =e O dédu mmédeme que ep=e pour eer, e, de mère géérle, o, pour ou réel : ep e Corollre : e l ep e e 6 Logrhme de se quelcoque : So u réel pos, o peu écrre Pr déo, o pose qu es le logrhme à se de. l epl ep l epl l log l l l l l l
13 7 Propréés élémeres de l oco epoeelle O more sse séme les propréés suves, qu so à coîre pr cœur. lm ep lm ep ep lm lm ep L oco epoeelle es srceme crosse sur ], [ e es à vleurs ds ], [ Les coures représeves de l epoeelle so symérques pr rppor à l dgole prcple, s qu o le vo sur l gure c-dessous. Epoeelle e logrhme l epoeelle es l coure supéreure. 8 Vleurs pprochées Pour pe, o les relos : l ep
14 9 Dérvo de l oco epoeelle L epoeelle é l oco récproque du logrhme, s dérvée ve dreceme de l epresso de l dérvée des ocos composées. l d ep lep ep ep ep d d ep d d d Applco : déségro rdocve, équos déreelles U esemle de N omes se désègre. Pour u ervlle de emps d uss pe que l o veu, le omre d omes se déségr es proporoel à N e à d. L vro dn du omre d omes es doc : dn Nd où σ es ue cose qu déped du corps éudé. Pr coséque dn d N Do ue soluo es N N e, où N es le omre d omes l. Théorème : l équo déreelle y +y=, vec cos, pour soluo y y e où y es l vleur prse pr y pour =. 4
15 Chpre Trgoomére hyperolque L rgoomére hyperolque es logue e e des pos à l rgoomére usuelle. Nous e verros plus précséme le rppor ds le cours sur les omres complees. Déos O dé respecveme le cosus, le sus e l gee hyperolques pr : e ch e sh e e sh e h ch e Les coures représeves so doées c-dessous, prgrphe. e e Propréés odmeles : Propréé odmele : ch sh Eercce : le démorer Les ocos so dées sur R ou eer. e A + e à -, le cosus hyperolque se compore comme A +, le sus hyperolque se compore comme A -, le sus hyperolque se compore comme L gee hyperolque dme deu vleurs sympoques à + e -, e qu so respecveme - e. e e Pour pe, o les ppromos : sh h cosh Les dérvées s oee mmédeme e sch dérver l epoeelle : 5
16 d ch sh d d sh ch d d d ch sh h h ch ch Focos cosus, sus e gee hyperolques de guche à droe. Equos déreelles Théorème : les ocos sus e cosus hyperolques so soluos de l équo déreelle du secod ordre : d d Corollre : les ocos shω e chω so soluos de l équo déreelle du secod ordre : d d 4 Formules usuelles Elles so smlres à celles de l rgoomére crculre. Nous doeros smpleme les quelques ormules suves, à coîre pr coeur : ch ch sh sh ch y chchy shshy sh y shchy chshy h hy h y hhy 6
17 ch ch sh sh shch ch 5 Focos récproques 5. Argume cosus hyperolque O cosdère l équo où y es l coue : e ch y Cee équo dme deu soluos opposées vor l llure de l coure s e seuleme s. S <, elle dme ps de soluos. Pour =, l y ue seule soluo. y e y O pose Y e Y y Y Y l soluo correspod à y> es lors : O dé doc : 5. Argume sus hyperolque De même, o cosdère l équo : Y y l rg ch l e sh y Cee équo dme oujours ue soluo. Pr le même rsoeme que précédemme, o rouve : y e y O dé : y l rg sh l 7
18 5. Argume cosus hyperolque E, l équo =hy dme ue soluo uque s e seuleme s -<<. O rouve dreceme : O dé lors : y l rg h l Eercce : le démorer à prr de l epresso de l gee hyperolque 6 Dérvo des ocos récproques L dérvo drece des ormules doées c-dessus doe mmédeme : Eercce : le démorer. d d d d d d rg ch rg sh rg h 7 Prmérso d ue hyperole Nous dmeros ce résul ss démosro. L équo prmérque ch y sh es l équo d ue hyperole. O e dédu l orme mplce : y 8
19 Chpre 4 : Nomres complees Noe mpore : Coorméme u usges de l physque e omme de l élecrcé, ous oeros «j» le omre mgre pur, e ps comme l es d usge e mhémques. Iroduco O rouve pros souve ds les ouvrges de ermle ou ssmlé des epressos ss juscos du ype : Il ese u omre do le crré es - Les omres complees so esseelleme de l géomére Ces deu sseros so oleme usses ou supdes. E, o cosru u esemle de omres où les crrés peuve êre égs. Ce esemle, C, es équvle u pl, mu d opéros spécles. E les omres complees serve esseelleme à ou ure chose que l géomére. Déo O cosdère le pl. Le po M de coordoées,y représee pr déo u omre complee. O d que es l e de M. A prr d u po de coordoées,y e d u po de coordoées, y, o cosru de coordoées y y, y y. Cee opéro s ppelle l mulplco complee e es oée : O oer de ço géérle : jy Propréé : les omres complees de pre mgre ulle correspode de mère uvoque u omres réels. O les y ssmler doc. Coséquece : Selo cee coveo, le omre complee j y ue pre mgre ulle e ue pre réelle égle à - ser doc cosdéré égl à -. Module e rgume S l o rvlle e coordoées polres, les pres réelle e mgre du omre complee =+jy peuve s écrre : Re e y Re cos ou ecore y s cos j s vec y e rg 9
20 Les omres e θ so respecveme le module e l rgume de. le module de se oe huelleme. Propréé : l esemle des omres complees de module es le cercle ué. 4 Addo L somme de deu omres complees s oe e jou respecveme les pres réelles e les pres mgres. L opposé d u omre complee s oe e pre l opposé des pres réelle e mgre. 5 Mulplco jy j y j y Iverse d u omre complee : jy jy jy Re Re Im Im Addo e mulplco so commuves. Nomre complee cojugué ; Pr déo, le omre complee cojugué de, es dé pr : jy jy O mmédeme les propréés suves : / j j
21 5 Ierpréos géomérques. Formule de Movre Propréé : L mulplco pr j correspod à ue roo d gle π/ Propréé : L mulplco pr u complee de module e d rgume θ correspod à ue roo d gle θ. Formule de Movre L propréé dquée c-dessus sge que l élévo à l pussce d u complee de module correspod à ue roo d gle θ du po d e. Pr coséque ormule de Movre : cos js cos js Corollre : Module e rgume du produ e du rppor j s cos js cos js cos cos js cos js cos js Applco : ces ormules permee de rouver oues les ormules usuelles de l rgoomére. Eercce : clculer cos θ Module e rgume de L pplco drece de l ormule de Movre doe mmédeme les deu relos : rg rg Eercce : Clculer j 4
22 6 L oco epoeelle complee Nous verros ds le chpre «développemes lmés» e, de mère géérle, o more que l o peu écrre, pour réel : cos s! ep 4 4! 6! 5 5! 6! 4 4! 5 5! O oserve sur ces ros développemes ue grde smlude. Formelleme, remplços rrreme, l qué : pr le omre mgre pur j. O peu lors dér, ep j j 4 j! 4! 5 j 5! qu es égle à : Nous vos s dé, pour réel : cos js ep j e j cos js L oco epoeelle complee peu doc êre vue comme l eeso à ous le pl complee de l oco epoeelle, compe eu de ses relos vec les ocos rgoomérques crculres. Propréé : De mère évdee, o j e Eercce : le démorer Propréé : Tou omre complee de module e d rgume θ peu s écrre sous l orme e j Corollre : Aure verso de l ormule de Movre e j
23 7 Formules d Euler L epresso de l epoeelle complee perme d oer les deu relos suves, des ormules d Euler, pour le sus e le cosus j e e j sh e e j j ch e e j j j j j j s s cos Nous vos vu que l ormule de Movre perme le clcul drec des ocos rgoomérques des gles mulples. De même, les ormules d Euler permee de clculer les pussces d ue oco rgoomérque e oco des mulples de l gle. Plus précséme, o dédu mmédeme des ormules d Euler, e e pos j e s cos j j Pr coséque : j s cos Avec l propréé odmele : Eemple d pplco : O désre clculer ue prmve de cos. Pour cel O pplque l ormule précédee, qu doe cos e oco des gles mulples : 4 cos cos cos cos cos 8 Rces èmes d u omre complee Théorème : ou omre complee dme rces èmes où es u omre eer urel S j e, lors ou omre complee de l orme k j k ep / vére k, pour k vr de à.
24 Déo : Les omres k so ppelés les rces èmes du omre Propréé : Le omre dme rces èmes, qu so de l orme ep j k Eercce : Résoudre ds C l équo Dérvo de l epoeelle complee O vére dreceme D où : d d e j j e j e d d e j je j d d e e j - e j d d e j e j Pr coséque, j e e e j so des soluos odmeles de l équo d - d R Applco : mpédce d u crcu RLC Equo du secod degré. Nous doeros le résul ss démosro, celle-c é deque à celle vue u lycée. Théorème : l équo c vec,, c e complee dme deu soluos e. O les oe s : So 4c dscrm So ue des deu rces crrées du dscrm l ure rce crrée é, de mère évdee, -. Les deu soluos éveuelleme coodues so : 4
25 5 Cs des équos à coeces réels O dsgue seuleme deu cs : Le dscrm es réel pos. O les ormules usuelles. Le dscrm es réel ég. Ds ce cs, j j
26 6 Chpre 5 : Polyômes Déos Ue oco réelle ou complee de l orme = où es u eer e l vrle es ppelé moôme de degré e. O suppose o ul. Ue somme de moômes es, pr déo, u polyôme. Le degré du polyôme es celu du moôme de degré le plus élevé. Il es d usge e commode d ordoer les polyômes selo l ordre cross ou décross des pussces de l vrle Noo : Pour des rsos de smplcé o écr : P Propréés. Somme e produ. Théorème : Deu polyômes so égu s e seuleme s leurs coeces so égu. Cec peu semler évde, uss ous le réécrvos de mère mos évdee. Théorème : S deu ocos polyomles so égles e ou po, lors les coeces des deu polyômes so égu. Corollre : U polyôme es dequeme ul s e seuleme s ses coeces so ous uls. Théorème : Les coeces de l somme de deu polyômes so oeus e s l somme des coeces de chque polyôme. Le degré de l somme es le degré du polyôme de degré mmum., m m m q p q p Q P Théorème : Le produ de deu polyômes es u polyôme de degré égl à l somme des degrés des deu polyômes. O oe le produ pr développeme. j j j m j j j m q p q p q p Q P,
27 Dvso de deu polyômes Dvso selo les pussces décrosses Soe P e P deu polyômes quelcoques, P é supposé o dequeme ul. O le : Théorème : l ese deu polyômes uques Q e R, ppelés quoe e rese, els que P =P Q+R, e els que degr<degp Procédure : Ecrre les polyômes de guche à droe selo les pussces décrosses e procéder à ue dvso clssque. Eemple : dvser pr ++. Répose : Q= + e R=- -4- Dvso selo les pussces crosses Soe P e P deu polyômes quelcoques, P é supposé o dequeme ul. So u eer r é. O le : Théorème : l ese deu polyômes uques S e T, ppelés égleme quoe e rese, els que P =P S+ r+ T, e els que degs r Procédure : Ecrre les polyômes de guche à droe selo les pussces crosses e procéder à ue dvso clssque. Eemple : dvser + pr -+ e s rrê à l ordre r=. Répose : S=+- e T= Allure à l des polyômes réels. Théorème : U polyôme de vrle réelle e à coeces réels se compore à l comme so moôme de plus hu degré. Preuve : o me le erme de plus hu degré e ceur. 5 Zéros e mulplcé Pr déo, es u éro du polyôme P s e seuleme s P=. Théorème : S es u éro de P, l ese u omre eer k srceme pos e u k polyôme Q els que P Q, vec Q. Le omre k, qu dque «come de os» ule P, es ppelé l mulplcé de. 7
28 Zéros du produ de deu polyômes : Ce so l esemle des éros de chcu des polyômes. Propréé : s es u éro commu à P e Q, e de mulplcé respecve k e k, lors es éros de PQ vec l mulplcé k +k. Propréé : S es u éro de P de mulplcé k lors l ule oues les dérvées de P de l ordre à l ordre k-. P Q Preuve : O écr k, où - e peu se mere e ceur ds Q 6 Formule de Tylor So N P Pr dérvos successves, o cose que : d d P! E pr coséque, ou polyôme de degré N peu s écrre ormule de Tylor : P N d! P d 7 Equos polyomles Théorème de d Alemer: ou polyôme de vrle e à coeces complee, de degré N, dme N éros, compés vec leur ordre de mulplcé. So P de degré N, o peu écrre : P A k N Remrque : le coece A es e le coece du erme de plus hu degré. Aureme d, ue équo polyomle de degré N dme oujour N soluos eo : compées vec leur ordre de mulplcé, ds C. k Polyômes à coeces réels Théorème : S u polyôme es à coeces réels, le cojugué de ou éro es u éro. Preuve : S P es à coeces réels, lors P P. 8
29 9 So u éro, lors P P P Corollre : U polyôme de degré à coeces réels u mos u éro réel. Aure démosro du corollre : O suppose que le coece du erme de plu hu degré es pos s l es ég, le rsoeme rese semlle. Alors, l lme à plus l du polyôme P es plus l. Elle es mos l qud eds vers mos l. Comme l oco polyôme es coue, s vleur psse u mos ue os pr éro. Polyômes symérques Déo : u polyôme symérque de degré N e de coeces es u polyôme qu vére N- =. Propréé : U polyôme symérque de degré N pr s écr Q es u polyôme à déermer : / Q P N U polyôme symérque de degré N mpr s écr : / Q P N O vo pprîre urelleme le chgeme de vrle : X Eemple : Résoudre 4 O pplque l premère epresso vec N=4: X X X P 4 O cherche les éros du polyôme e X, e o oe dreceme : X X X X O résou esue dépedmme les deu équos: X= e X=- Qu doe respecveme deu mlles de soluos e :, j j e -.
30 Chpre 6 : Frcos roelles Déo : S e roelle : P P so deu polyômes de degrés respecs e m, o dé l rco P F P So degré degf es -m peu doc êre ég. S P e P o des éros complees e commu, l rco roelle se smple pr les ermes commus rels à ces éros qu se mee e ceur ds chcu des polyômes. Ue rco roelle qu «e se smple ps» es de rréducle. Décomposo : S degf, o peu écrre R F Q P Q es le quoe de l dvso de P pr P selo les pussces décrosses. R e es le rese. Le degré de Q es égl u degré de F. Le degré de l rco roelle «rese» es srceme éreur u degré de F. Pôles : Les éros du déomeur so ppelés pôles ou «sgulrés» de F. R Ds l décomposo F Q, le quoe Q es l pre de «eère» de F P o devr dre polyômle. L rco roelle «rese» crcérse s pre polre. Eemple : F Les pôles so doc, e, e o pour mulplcé Théorème pour les rcos roelles complees: L rco roelle «rese» R es égle à l somme de ermes ppelés «élémes smples de premère espèce» de P l mère suve. Chque pôle, de mulplcé k, doe ue coruo : E A k k A
31 elle que: E E P R h où h es le omre de pôles ss comper l ordre de mulplcé. Aureme d : h h k h hk k k h A A A A Q E E Q F Iérê : smpler l rco u mmum. Permere le clcul d égrles. Théorème pour les rcos roelles à coeces réels: O repred l décomposo précédee. Les coeces és réels, à ou pôle o-réel correspod so cojugué. Décomposos chque pôle e pre réelle e mgre j S k es l mulplcé du pôle o-réel, l doe ue coruo : N M N M E k k k Eemples: O more sur le premer eemple que, e é de mulplcé, que e doc que: F De l même mère, o : les pôles é e -, de mulplcé. De même, o : O vo c les ermes de secode espèce, prove du que ps de éros réels.
32 4 Eemples e méhodes Nous doos quelques méhodes de se, ms ss êre ehuss. 4. Frcos roelles sur C ou réelles vec pôles réels Ds ce cs o décomposo e élémes smples uqueme. P=N/D 4.. O dvse N pr D pour oer l pre eère 4.. O cherche les éros du déomeur les pôles e leur mulplcé, comme o peu. Ds les prolèmes, so l o D sse smple. E : polyôme de degré D= + +c+d vec u éro évde o o rouve «évde» o o écr D=-A +B+C o o rouve A, B e C pr dvso o O résoud A +B+C= so l o doe D ou corsé. 4.. O écr que l pre polre P=R/D de l rco roelle es somme d élémes smples Pour ou pôle de mulplcé k, o u erme A/- k O s égleme que P=R/- k E O rouve A e mulpl P pr - k e e s =. So : A=R/E 4... Pour les ermes de degré éreur, o comme o peu, selo l rco roelle. Pour les déomeurs de degré o cs : pôles dscs : o pplque.. à chque pôle pôle rple : o procède pr dvsos successves c eo o pôle doule e u smple : o pplque.. pour le pôle smple e le erme de degré du pôle doule. O doe lors ue vleur quelcoque à e o rouve le erme mqu : Remrque mpore : qud o u seul pôle ms de mulplcé quelcoque, o procède pr dvsos successves c eo o du uméreur pr - où es le pôle. O cel k os, k é l mulplcé. Eemple géérl : F := 4 4 5
33 Pôles O cherche u éro évde du déomeur : l es. O écr : 4 5 sous l orme - + +c O rouve =,=-,c= Les éros de -+ so e Doc es pôle de mulplcé e es pôle de mulplcé Pre eère O dvse le uméreur N pr le déomeur D N=QD+R O rouve Q=+4 e R= 97 L pre «polre» es doc R/D O décompose P P := e F= P=A/- +B/-+C/- O rouve A e mupl P pr - e e s = ds le résul oeu. Aureme d : De même A=R/-=- C=R/- = 9 O rouve C e s quelcoque - pr eemple e e ds que P-=-7/=-/-- +9/-- +C/-- -7/+/4+9/=-C/ d où C=-8 Au l : F := = +4 - /- -8/- +9/-
34 4. Frcos roelles sur R ou vec pôles cojugués complees O suppose que l o s rer les élémes smples de premère espèce qu o pu pprîre ds le déomeur vor prgrphe. Nous ous coeros à u eemple : Décomposer : 5 do le déomeur e se corse ps ds R. Il y e deu pôles cojugués de mulplcé. O dvse le uméreur pr d où l oeo d u premer éléme smple celu de droe, de secode espèce: O recommece vec l rco qu es ps «ermée». O dvse 5 pr D où E leme : Eercces : F F := := F := 4
35 Réposes Eercce o F= F := 6 Eercce o : o rouve que es pôle rple O dvse le uméreur qu rese pr - doc o dvse ce qu rese 4- pr - D où 56 4 = = Eercce o : es pôle smple, es pôle doule L rco es égle à 6 o mulple pr e o =, dem pr - vec =, e e o pred ue vleur de pour rouver le erme mqu. 5
36 Chpre 7 Coué, dérvo, déreelles Noos géérles Ue oco umérque réelle de vrle réelle ssoce u omre u ure omre oé. L esemle des réels où es dée es ppelé esemle de déo. L esemle des pos de coordoées, es ppelé le grphe de, ou ecore l coure représeve de. Ue oco peu êre coue ou o, selo que s coure représeve l es ou o. Eemples : =/ es dscoue e cr o dée. L coure qu à ssoce pour < e so es dée prou e o coue e. Les ocos polyômles so coues L oco s/ es o dée e. O peu émos l prologer pr coué e lu do l vleur e éro. Les propréés élémeres comme l dérvlé mpose l coué e u po doé. Lmes : Nous doos quelques eemples de déo. Le leceur recosrur les cs mqus. O d que L réel es l lme de qud ed vers ou «e» s pour ou pos, o peu rouver η el que L s lm L L s E lgge cour, L es l lme de s l o peu redre uss proche de L que l o veu à l seule codo que so sse proche de. De même : O d que L réel es l lme de qud ed vers + s pour ou pos, o peu rouver X el que L s X O d que L réel es l lme de qud ed vers - s pour ou pos, o peu rouver X el que L s X Lmes es. O d que + es l lme de qud ed vers s pour ou A, o peu rouver η el que A s O d que - es l lme de qud ed vers s pour ou A, o peu rouver η el que A s O d que + es l lme de qud ed vers + s pour ou A, o peu rouver X el que A s X 6
37 O d que - es l lme de qud ed vers + s pour ou A, o peu rouver X el que A s X Théorème : Qud l lme ese, elle es uque. Théorème : Qud ue oco dme ue lme e e u po ou elle es dée, elle y es coue. S elle y es ps dée, o peu l dér e ce po e l prologe pr coué eemple déjà doé : s/ e éro. Eercces : doer des eemples où l lme ese ps doer u eemple de oco dscoue prou Théorème : S locleme ds u vosge de, ce derer é ps orcéme o g, lors o l même propréé qu u lmes, s elles ese. Théorème : S locleme ds u vosge de, ce derer é ps orcéme o Ug, lors o l même propréé qu u lmes, s elles ese. Nomre dérvé Déo : So u omre réel e ue oco dée e. S L lm ese e es u omre réel, o d que es dérvle e e d y pour omre dérvé L. O oe ce omre ou, plus rgoureuseme d Cee oo prove de l déo : d d lm L oco qu ssoce à le omre dérvé de e es l oco dérvée de pr rppor à. Théorème : L dérvée e u po es l pee de l coure e ce po. Propréés : Propréé : Ue oco dérvle e u po y es coue Propréé : Ue oco mpre pour dérvée ue oco pre e vce-vers. Eercce : le morer sur des eemples 7
38 Théorème : Pour dmere u eremum locl, l es écessre que l dérvée s ule. S L dérvée s ule e chge de sge, lors o u eremum locl. Cocvé e po d leo S l dérvée secode sur u ervlle es posve, lors l oco y es de covee. Locleme, l oco ressemle à ue prole do les rches vo vers le hu. S l dérvée secode sur u ervlle es égve, lors l oco y es de cocve. Locleme, l oco ressemle à ue prole do les rches vo vers le hu. S l dérvée secode es ulle e u po e chge de sge, o u po d leo. Dérvo des ocos composées So F g g O : df d df dg dg d d dx dg d X g O oe l dérvée de l composée e s le produ des dérvées prses u o edro. Applco : dérvo de l oco récproque So F ue oco. S l es possle, pour y doé, de rouver ue e ue seule vleur de elle que y=f, ureme d s l équo y=f dme ue soluo uque,lors l epresso de e oco de y dé ue oco ppelée récproque de F. y F F y Nous e meos ps de sge équvlece, seuleme ue doule lèche, cr l récproque ese que sous codos. Eemple pour o ul: F y y y F y Ds cers cs, o ps ucé de l soluo de y=f, ms o peu décder de qu es l oco récproque. Pr eem[ le, l récproque de l oco «crré» peu êre chose comme é l oco «rce crrée», ms o peu décder de predre l oco «mos rce crrée». Il y u ses src ps de oco récproque ds ce cs. 8
39 So F l oco récproque de F. Pr déo, o : F F O pr coséque, compe eu du résul de l dérvo des ocos composées : d F F d F F d d E pre les ocos, ecore ue os, «u o edro» : F F F Eemples : clculer l dérvée de Arcos 4 Déreelle d ue oco Déreelle d ue oco d ue vrle réelle L déo du omre dérvé doe ue ppromo locle de l oco. Locleme, s l coure de es sse régulère, o mge sse e que l o pusse l pprocher pr u polyôme. Plus précséme, o more, e l dmeros, que l o peu écrre, ds le cs où l oco es dérvle e sse pe : où es u omre pror cou. L vro de compore doc ue pre lére proporoelle à e à l vro de. O rdu cee derère phrse pr :... d d... Déo : d es ppelée déreelle de à e surou ps coodre vec l dérvée. Déreelle d ue oco de deu ou pluseurs vrles : So, pour smpler, ue oco de deu vrles,y. De l même mère que précédemme, o cosdère l prr lére de l vro de :, y y, y y ermes e, y, y ec... Déo : l pre lére de l vro de es ppelée s déreelle. 9
40 Théorème : les coeces e de l ormule précédee so les dérvées prelles de pr rppor à e y. O oe : d d dy y Eercces : Résoudre d ydy Résoudre d ydy Déreelle logrhmque S u v lors : u S lors : v S u v lors : d d d du u du u du u dv v dv v dv v 5 Théorème de Rolle e ormule des ccrossemes s Théorème de Rolle : So ue oco dérvle sur u ervlle [,]. S = lors l ese c [, ] el que l dérvée de e c so ulle c=. Formule des ccrossemes s : So ue oco dérvle sur [,]. Il ese c [, ] el que c Eercce : le démorer à prr du héorème de Rolle. Vre : Il s g d ue reormulo de l ormule précédee. So ue oco dérvle sur [,+h], lors l ese θ comprs ere e el que h h h 4
41 4 6 Règle de l Hospl Théorème : Soe e g deu ocos coues dérvles u vosge de e s y ul. O lors : lm lm g g 7 Formule de Tylor-Mc Lur Il s g e de l géérlso de l ormule des ccrossemes s. Théorème : So ue oco dée sur [,] e dérvle os. Il ese u omre c ppre à [,] el que ormule de Tylor:!!!! c Formule de Mc Lur : Il s g de l ormule de Tylor ds le cs =.!!!! c Démosro : O se coe à l ormule de Mc-Lur, qu es jms qu ue verso rslée de l ormule de Tylor. So : R!!! O dédu : d R d O pplque l ormule des ccrossemes s à l dérvée ème de. Il ese c el que : c Pr coséque : c d R d Pr coséque, pr égros successves, o oe l ormule de Mc-Lur
42 Chpre 8 : Développemes lmés L ojec des développemes lmés es de doer ue ppromo polyômle d u oco u vosge d u po, c'es-à-dre ds u pe ervlle uour de ce po. L précso de l ppromo déped des cs, e l o devr vérer à chque os que l o es ds les oes codos d ulso. Formule de Tylor vec rese de Youg S l o peu développer ue oco u vosge d u po sous l orme!!! vec lm o d lors que l o développé à l ordre vec le rese de Youg Le développeme lmé de à l ordre es doc :!!! Eercce : développer l oco cosus u vosge de, à l ordre 4. Eercce : développer u vosge de, à l ordre. Remrque : le développeme ese ps oujours, comme pr eemple celu de l rce crrée u vosge de l orge l oco y es ps dérvle. L gure c-dessous représee e ses développemes à l ordre, 4 e 8. O vo que l ppromo es oe ds u cer dome, ms qu u-delà, l suo deve rès muvse. Le développeme à l ordre 8 es le plus précs locleme, ms uss celu qu dverge le plus rpdeme. Ordre Ordre 4 Ordre 8 4
43 Propréés S l o cosdère me pluseurs ocos, o peu cosdérer le développeme lmé de leurs somme, produ ec. Il es mpor de oer que l ordre do êre préservé : S l o rvlle à l ordre, les développemes ulsés u dépr dove ous êre à l ordre. Les développemes ermédres e u e peuve dépsser l ordre, e pr coséque o e cosdérer ps les ermes de degré supéreur cec reve, du po de vue de l ppromo, à les cosdérer comme églgeles. O les propréés suves : Le développeme lmé DL de l somme de deu ocos es l somme des développemes lmés. Ils dove êre de même ordre. Le développeme lmé du produ à l ordre de deu ocos es le produ des développemes lmés, e se lm u ermes de degré éreur ou égl à. Les développemes lmés de dépr dove êre d ordre. Le développeme lmé du quoe à l ordre de deu ocos es oeu pr le quoe des développemes lmés, e dvs les développemes selo les pussces crosses. Le développeme lmé à l ordre de g composo es oeu e remplç le DL à l ordre de ds celu de g, e e e coserv que les ermes de degré éreur ou égl à. S l oco es dérvle, le DL à l ordre - de l dérvée es oeu e dérv le DL à l ordre de l oco. S l oco es égrle locleme, le DL à l ordre + de l prmve es oeu e égr le DL à l ordre de l oco. U eemple ule O peu coîre le DL de /+ pr pplco de l ormule de Tylor. Nous pouvos l oer d ue ure ço. Pr coséque, pour sse pe: Pr coséque, o égleme : Pr égro, o mmédeme : l L même ormule du développeme de /+ doe, e remplç pr : 4
44 E pr égro : 5 rc 5 Remrque : De l relo 4 rc, o dédu que e, c es u peu plus complqué, l u morer que le rese ed vers éro qud le degré du développeme ugmee: Développeme lmé u vosge de l O prle du développeme u vosge de l qud l vrle peu êre rrreme grde. Ds ce cs, l vrle X=/ es rrreme pee. Fre u développeme à l e reve doc à re u développeme e éro e X=/. Eemple : Développeme à l ordre X X X X X X X X + 6X O vo pr eemple ou de sue que l droe y=+7 es sympoe. De mère géérle, o vo le comporeme de pour grd : l coure es sympoe à ue droe e s e rpproche selo ue coure e /, pr vleurs supéreures. Le développeme correspod à l coure leme u dessous.
45 Chpre 9 : Iégro Iégrles géérlsées Focos e escler. Iégro Déo : Ue oco dée de mère cose sur des ervlles s ou o es de oco e escler. Eemple de oco e escler Déo : So ue oco e escler dée sur [,], e é réels, l re I lgérque, c'es-à-dre comprse ere l coure représeve de es l e horol es ppelée égrle de Rem de ere e e se oe. I d 45
46 Remrque : I u sge. Les surces so compées posveme qud elles so u dessus de l e e égveme e dessous. Remrque : le sge ds l égrle es ue vrle de muee. Aureme d : d d Iégro des ocos coues pr morceu Théorème : Ue oco coue pr morceu sur [, ] peu êre pprochée e vleurs uss précséme que l o veu pr ue oco e escler. E lgge plus mhémque, ue oco coue pr morceu es lme uorme d ue sue de ocos e esclers., s e escler, s, [, ] No : Il s g d ue lme e vleurs e ps, pr eemple, e dérvée. O peu cosdérer s ue sue s de ocos e esclers qu coverge vers. Ds ce cs, s l lme de l sue des égrles des ermes s ese, lors es de égrle e o dé : d lm s d Ierpréo : l égrle s dée perme de dér l re lgérque comprse ere ue coure e l e des scsses. Propréés géérles Appromo pr des ocos e escler L surce sous u po es ulle, ureme d : 46
47 Relo de Chsles d Corollre : c d d d d c d Léré. S α e β so deu réels quelcoques, e deu oco égrles quelcoques, lors : g d d g d E prculer, l égrle de l somme de deu ocos es égle à l somme des égrles des ocos. L égrle d ue oco mulplée pr ue cose es égle à l égrle mulplée pr l cose. Eemple prculer : S l oco es cose égle à A sur l ervlle [,], l déo de l égrle, sous orme de surce, codu mmédeme à : Ad A S <g pour ou ppre à l ervlle [,], lors : d g d Iéglé rgulre O s que, pour ou couple de omres réels A e B, o : A B A B E pr coséque, e pplqu les propréés précédees, l ve : g d d g d 4 Prmves e égrles Déo : Ue oco F do l dérvée pr rppor à es es ppelée prmve de. Propréé : l oco ulle dme pour prmves oues les ocos coses. Théorème : S F e G so deu prmves de, lors elles dère seuleme pr ue cose. Eercce : le démorer à prr de l dérvée de F-G. 47
48 48 Théorème : L oco F dée pr d F es ue prmve de. Démosro eplco: O cosdère h d F h F. Cec es l surce comprse sous l coure, ere e +h. Pour h sse pe, cec correspod à l surce du rpèe dé pr les pos,,,,+h, e +h, +h. L re A de ce rpèe vu : h h h A pour h sse pe. Doc : lm h F h F h d h h Ce qu sge e que es l dérvée de F. Corollre : S F es ue prmve quelcoque de, doc es dée à ue cose près, o : F F d 4. Iégro pr pres Cee ormule usuelle ve de l dérvée du produ de deu ocos d v u v u d v u uv u v uv 4. Chgeme de vrle Chger l vrle d égro es pros u o moye de clculer ue égrle. Il es sé sur l propréé suve : g g d d g g Eemple : clculer d I O pose d où l o dédu : d d d / / / d d
49 O vo sur ce eemple comme procéder : O rouve l ouvelle vrle e oco de l mcee O eprme l cee e oco de l ouvelle O pred l déreelle O remplce 4. Vleur moyee d ue oco Déo : L vleur moyee d ue oco sur u ervlle [,] es d Eemple : l vleur moyee du crré de l oco sus ou cosus sur ue pérode vu ½. Clculer pr eemple l vleur moyee de cos ω sur ue pérode. Applco e eercce : O pplque ue eso susoïdle de vleur crêe V u ores d ue réssce R. Quelle es l vleur de l eso V e coue qu, plcée u ores de R, dssper e moyee l même pussce Joule? Répose : susoïdle. V e V 5 Logueur d u rc de coure. L eso V e es ppelée eso ecce pour ue eso Il s g d ue pplco prm d ures. O cosdère ue coure gure cdessous. O suppose des ccrosseme pes de e de y=, o o rvlle dreceme vec des déreelles. ds dy d L logueur élémere de l rc de coure es doé pr le héorème de Pyhgore, cr s l o suppose dy e dy sse pes, l coure se cood locleme vec s gee. 49
50 dy d ds ds d d d dy dy dy d d d pr coséque, l logueur d u rc de coure ere = e = es doé pr : L d Eemple : Pérmère d u cercle de ryo R O se coe à celu du dem cercle supéreur.o pr de l équo du dem cercle supéreur e o pplque ce qu ve d êre vu. y dy d R R dy d R R R R E pr coséque : R R R L d R R R R Il rese à re u chgeme de vrle. O pose : R R d Rd d L R d R d R rcs R O oeu le pérmère du dem cercle. 5 Esmo umérque d ue égrle Nous vos ps doé, pour les dérvées, de méhode de clcul umérque cr l s g lors d ue opéro délce. Pr core, l égro es ue opéro plus sée. Nous ous lmeros à l méhode des rpèes, ms l e ese e d ures, comme l méhode de Smpso ue méloro de celle des rpèes ou de plus sophsquées comme les méhodes de qudrure. O dscrése l e des e e cosdér que des vleurs dscrèes. O pose h = +- e = L re du rpèe s dé vu 5
51 A h e l re sous l coure ere e N es pprochée pr pour h sse pe : A N d E prculer, s le ps es cos égl à h : N h A h N h N N Eemple : Esmer l égrle de = ere e pr l méhode des rpèes, vec u ps h=. Comprer à l vre vleur. Eplquer pourquo l vleur esmée es u peu rop grde. 6 Iégrles géérlsées Il s g d égrles sur u dome ll jusqu à l ou jusqu à ue ore où l oco à égrer es ps dée. Eemples : Nous llos cosdérer L premère égrle pose u prolème e éro, l secode à l. Nous cosos que : d e d O dé doc lm d lm lm d lm d De l même mère : d lm X X d lm X X 6. Déos Déo : Compe eu des eemples précédes, s ue oco présee ue sgulré sympoe, vleur o dée e A, ou s A es ue ore e, o d que l égrle A X d es covergee s lm X A d ese. O suppose c que l oco es e dée e. 5
52 Cs de deu sgulrés : Supposos oujours e dée e. S A e B so so s, so des sgulrés de, o peu dér, s les lmes ese : B A d lm d lm d X A X X X B L propréé do êre dépede du cho de. L propréé «physque» à vérer, de mère géérle, es que l re comprse sous l coure so ue qué e. Eercces : que vle d e e d? 6. Covergece solue. Théorème : S l égrle solume covergee. B A d coverge, lors B A d uss. O d que l égrle es Applco : Théorème : Ue égrle géérlsée es covergee à l s l vleur solue de l oco es mjorée pr -s vec s>, réel, pour sse grd. Preuve : Cherchos à clculer d, vec les hypohèse précédees. Il ese X el que A X s pour >X e s Doc d d pour A> A X s s d A X X A X d es dée coverge qud A ed vers l à l codo que s- so s srceme ég, doc que s so srceme supéreur à. Ds ce cs, X d coverge. Doc, ds ce cs, l égrle es solume covergee, doc covergee. 5
53 7 Equos déreelles du premer ordre Déo : ue équo déreelle es ue équo qu rele ue oco es ses dérvées. As, ue équo déreelle du premer ordre rele ue oco, oée y, s dérvée y e l vrle. Codos u lmes : ue équo déreelle es souve l lo d évoluo d u sysème dymque déped du emps pr eemple. Il mque doc, ds ce cs, les codos les. De mère géérle, ue équo déreelle e su ps. Il u e oure les codos u lmes CL : pour les équos du premer ordre, N pour celle d ordre N. Pour ue équo du premer ordre, l s gr de l vleur de l oco pour ue vleur doée de. 7. Equos à vrles séprles Ce so, de mère mgée, les équos où les ermes e do l qué d e ceu e y peuve êre regroupés dépedmme. Nous e doeros ypes : 7.. Equo du ype y dy O l écr sous l orme d D où : dy d y d +CL 7.. Equo du ype y g y dy O l écr sous l orme g y d dy dy D où : d G y y G g y +CL g y Eemple : résoudre y y. Répose : y CLso, e : y où c es ue c cose d égro celle qu pprî urelleme ds le clcul. 7.. Equo du ype y g y O l écr sous l orme dy d g y D où : g y dy d F d g y dy G y y G F +CL 5
54 Eemple : O lors : y y. y c y c d où d es ue cose quelcoque. 7. Equo homogèes Il s g des équos du ype y y O procède pr chgeme de vrle e pos D où : O lors : y y d Eemple : résoudre y y y y y Répose : y y y d d y l C F d y F l C y d d y F F O oe lors eercce : y Cy où C es ue vrle d égro. O résou lors selo y, ce qu doe deu mlles de soluos. 7. Equos léres 7.. Equos léres ds secod memre Ce so les équos de l orme A y B y L soluo es mméde. O e ee : y B l y c y A B d F y ep c A B d Dep A B d A Théorème : s F e G so deu soluos de l équo ss secod memre précédee, lors K F G, où λ e μ so deu réels quelcoques es égleme soluo. 54
55 Cs prculer : s A e B so des coses, o remrque que l soluo es B prculèreme smple. O oe e ee y Dep A 7.. Equos léres vec secod memre Ce so les équos de l orme A y B y Théorème : l soluo géérle de cee équo es l somme de l soluo géérle de l équo ss secod memre e d ue soluo prculère. Résoluo : o résou d ord l équo ss secod memre sous s orme géérle. Pus o joue ue soluo prculère. Méhode de vro de l cose. So y ue soluo de l équo ss secod memre c'es-à-dre que y es u cs prculer quelcoque, u cho, de l soluo géérle de l équo ss secod memre. Alors ue soluo prculère de l équo complèe es : y p y d A y Eercce : Morer que y p es e soluo prculère. Eercce :Résoudre y s-y=cos vec le chgeme de vrle s vec =/. Résoudre d ord l équo ss secod memre, vec le chgeme de vrle dqué, pus dédure l soluo géérle pr l méhode dquée 55
56 8 Equos léres du secod ordre Les équos de ce ype décrve, pr eemple, les sysèmes dymques où pprî ue orce, cr ue ccéléro ou ue orce es re d ure qu ue dérvée secode d ue ou pluseurs coordoées sples. Nous ous oreros eecveme u cs où ces équos so léres, les o-léres é eucoup plus complees. 8. Equos léres ss secod memre Il s g d équos du ype y y c y As que de deu codos u lmes so l vleur de l oco e s dérvée e u po, so deu vleurs de l oco ou de s dérvée e deu pos déres. Théorème Il ese u mos deu soluos léreme dépedes de l équo homogèe. L soluo géérle es comso lére de ces soluos. Théorème équvle Il ese soluos dépedes de rppor o cos C e S elles que C=, C =, S=, S = elles que : y yc y S où y e y so les codos les oco e dérvée Eemple : Trouver les ocos C e S pour l équo y + = Déo : o ppelle wroske de l équo l oco w=cs -C S Propréés du wroske: De l relo O dédu mmédeme e doc que l w w =CS -C S w +w= d w ep d s que, pr déo du wroske e des oco C e S : w Propréé : S l oco es dequeme ulle c'es-à-dre = quel que so, lors le wroske es égl à. 56
57 57 8. Equos léres vec secod memre Il s g d équos du ype y c y y As égleme de deu codos u lmes. Théorème : L soluo géérle de l équo vec secod memre es l somme de l soluo géérle de l équo ss secod memre, y les codos u lmes requses, e d ue soluo prculère de l équo complèe. Théorème : ue soluo prculère es doée pr «vro des coses». p d w S C d w C S y où w es le wroske doé plus hu. L soluo complèe s écr doc : d w S C d w C S S y C y y 8. Equo du secod ordre à coeces coss 8.. Elmo du secod memre supposé cos Les oco,, c e so cosdérées me comme coses. cy y y Toues les dérvées de so ulles e l o peu réécrre : c y c c y c y O pose c y Y E l o cose que Y es soluo de l équo ss secod memre. O e rer doc que cee derère équo. 8.. Cs d u secod memre o cos O résou l équo ss secod memre e o pplque l méhode de vro des coses décre plus hu, s eso. 8.. Résoluo de l équo ss secod memre e à coeces coss O cherche ue soluo e e, où α es u omre complee.
58 L équo, supposée ss secod memre, deve ue équo polyômle, de équo crcérsque : + +c= O résou l équo crcérsque, pour lquelle cs so à evsger : deu éros réels dscs, deu éros o-réels cojugués e e u seul éro réel de mulplcé. Théorème : S les éros de l équo crcérsque so ous deu réels, o des soluos e y C e C e S les éros so égu, o des soluos e y e C C S les éros so cojugués, j, les soluos so lors : y e C cos C s Eemples : résoudre y +4y=, y -4y= e y +8y +y=5 Eercce : O cosdère u crcu RLC sére. Quelle es l eso u ores du codeseur? O pr d u codeseur chrgé sous vol. Equo déreelle : U+RCU +LCU = Le dscrm de l équo crcérsque es : R C 4LC O doc ros régmes déres selo le dscrm. O oujours u morsseme, correspod u erme RC. L qué /RC es l cose de emps du sysème. Teso sur le codeseur pour u dscrm respecveme ég, ul, pos, de guche à droe de l eulle. Pr rppor u héorème : Δ> correspod à deu éros réels : o morsseme pur cs de droe Δ< correspod à deu éros cojugués. Ils o ue pre réelle o ulle morsseme e ue pre mgre o ulle oscllo cs de guche Δ= correspod à deu éros égu, doc réels, e doc à u morsseme cere. 58
59 8..4 Cs des crcus élecrques e régme susodl. O suppose c que l o es e régme él, e que oues les grdeurs so susoïdles. Nous predros l eemple du crcu RLC sére lmeé pr u gééreur de eso susoïdl de pulso ω. Ug L équo du crcu s écr U g es l eso u ores du gééreur : U g du di g di d I RI L I d R L d C d d d I C L eso du gééreur é susoïdle, o l écr sous orme complee : O cherche I sous l orme : E repor, o oe : U g Uˆ e I Ie ˆ j j j juˆ Rj L Ie ˆ Uˆ R jl C O dé l mpédce complee coue Z R jl jc j Sch que le module de e vu, o dédu Iˆ e o dédu φ, oues les ures qués é coues.. Uˆ Z Ie ˆ jc j 59
60 6 Eercce A A A cos 4cos cos cos cos cos cos s cos s cos cos cos s s cos s cos cos s s cos cos cos cos Eercce A A cos 6 6 s cos /? / s cos
61 Soluo des eercces s6? cos6 O pose = 9gee de l gle moé, d où s6 cos6 7?? s s cos 7 cos s co g s6? cos6 O pose = 9gee de l gle moé, d où s6 cos6 7?? s s cos 7 cos s co g 6
62 Devor Mso Eercce : Que vle rc 5 rc 9? E uls deu os de sue l epresso de, e dédure l vleur de A 4rc 5 E uls l ormule de +y dédure 4rc rc 5 9 E dédure l vleur de 4rc rc 5 9 Formule de Méch Eercce : Morer que cos Arccos Eercce : Résoudre Eercce 4 : Morer, e uls l epresso de +, que rc rc rc
63 Nous dsgueros ou d ord les Eemple : Propréés des ocos pr roo de p/ ou p Résoluo ds le cercle e omre de soluos des équos rgoomérques Formules usuelles. Formulre. Eemples, eercces Focos récproques e o usge de l clculrce Coordoées crésees e polres Equo prmérque du cercle. Coordoées polres d u veceur. Ierpréo des ocos rgoomérques e ermes de projeco. Veceur our. 6
MTH 2301 Méthodes statistiques en ingénierie. MTH 2301 Méthodes statistiques en ingénierie
 VARIABLES ALÉATOIRES déo oco de réro vrble léore dscrèe moyee - vrce - écr ye esérce mhémque vrble léore coue oco d ue vrble léore : rsormo combso lére de vrbles léores Déo E : eérece léore S : esce échllol
VARIABLES ALÉATOIRES déo oco de réro vrble léore dscrèe moyee - vrce - écr ye esérce mhémque vrble léore coue oco d ue vrble léore : rsormo combso lére de vrbles léores Déo E : eérece léore S : esce échllol
Intégrales généralisées
 3 Iégrles géérlisées Pour ce chpire, les focios cosidérées so priori défiies sur u iervlle réel I o rédui à u poi, à vleurs réelles ou complees e coiues pr morceu. L défiiio e les propriéés de l iégrle
3 Iégrles géérlisées Pour ce chpire, les focios cosidérées so priori défiies sur u iervlle réel I o rédui à u poi, à vleurs réelles ou complees e coiues pr morceu. L défiiio e les propriéés de l iégrle
Liens entre fonction de transfert et représentations d'état d'un système (formes canoniques de la représentation d'état)
 oqe V oqe Cor e ere foco de rfer e repréeo dé d èe fore coqe de l repréeo dé SI Coe oqe! Irodco! e ere le dfféree decrpo d èe! Pge odèle dé " foco de rfer # C d èe oovrle # C d èe lvrle! Pge foco de rfer
oqe V oqe Cor e ere foco de rfer e repréeo dé d èe fore coqe de l repréeo dé SI Coe oqe! Irodco! e ere le dfféree decrpo d èe! Pge odèle dé " foco de rfer # C d èe oovrle # C d èe lvrle! Pge foco de rfer
Calculer comment se constituer un capitale ; Calculer comment rembourser une dette en effectuant des versements réguliers.
 CHAP: 8 Objecifs de ce chpire : Clculer comme se cosiuer u cpile ; Clculer comme rembourser ue dee e effecu des versemes réguliers. RAPPELS : Qu'es-ce qu'ue vleur cquise? Qu'es-ce qu'ue vleur cuelle? Le
CHAP: 8 Objecifs de ce chpire : Clculer comme se cosiuer u cpile ; Clculer comme rembourser ue dee e effecu des versemes réguliers. RAPPELS : Qu'es-ce qu'ue vleur cquise? Qu'es-ce qu'ue vleur cuelle? Le
S euls les flux de fonds (dépenses et recettes) définis s ent l investissement.
 Choix d ives i s s eme e cer iude 1 Chapire 1 Choix d ivesissemes e ceriude. Défiiio L es décisios d ivesissemes fo parie des décisios sraégiques de l erepris e. Le choix ere différes projes d ivesisseme
Choix d ives i s s eme e cer iude 1 Chapire 1 Choix d ivesissemes e ceriude. Défiiio L es décisios d ivesissemes fo parie des décisios sraégiques de l erepris e. Le choix ere différes projes d ivesisseme
Chapitre IV Les oscillations couplées «Les oscillations libres d un système à plusieurs degrés de liberté»
 Chre IV, cours de vbrons, ondes _Phs, Pr. Bds Bennecer MD 8-9 Chre IV es oscllons coulées «es oscllons lbres d un ssèe à luseurs degrés de lberé» Dns ce chre, nous llons coencer r éuder les oscllons lbres
Chre IV, cours de vbrons, ondes _Phs, Pr. Bds Bennecer MD 8-9 Chre IV es oscllons coulées «es oscllons lbres d un ssèe à luseurs degrés de lberé» Dns ce chre, nous llons coencer r éuder les oscllons lbres
Exercices de révision
 Exercices de révisio Exercice U ivesisseur souscri à l émissio d u bille de résorerie do les caracérisiques so les suivaes : - Nomial : 5 M - Taux facial : 3,2% - Durée de vie : 9 mois L ivesisseur doi
Exercices de révisio Exercice U ivesisseur souscri à l émissio d u bille de résorerie do les caracérisiques so les suivaes : - Nomial : 5 M - Taux facial : 3,2% - Durée de vie : 9 mois L ivesisseur doi
LES ESCALIERS. Du niveau du rez-de-chaussée à celui de l'étage ou à celui du sous-sol.
 LES ESCALIERS I. DÉF I NIT I O N Un escalier est un ouvrage constitué d'une suite de marches et de paliers permettant de passer à pied d'un niveau à un autre. Ses caractéristiques dimensionnelles sont
LES ESCALIERS I. DÉF I NIT I O N Un escalier est un ouvrage constitué d'une suite de marches et de paliers permettant de passer à pied d'un niveau à un autre. Ses caractéristiques dimensionnelles sont
Décoration, équipement. de la Maison. Janvier 2013 sans prix. Printemps / Été. SADY s TRADING WOOD TRADING. www.sadys-trading.com
 Dreo Aeropor Mrselle Provee D 9 SADY s TRADING WOOD TRADING Déoro, équpeme de l Mso www.sdys-rd.om Jver 2013 ss prx Premps / Éé ZI Les Bols Dreo Mrselle - Ax ZI Les Esroubls SADY s TRADING Les ouveués
Dreo Aeropor Mrselle Provee D 9 SADY s TRADING WOOD TRADING Déoro, équpeme de l Mso www.sdys-rd.om Jver 2013 ss prx Premps / Éé ZI Les Bols Dreo Mrselle - Ax ZI Les Esroubls SADY s TRADING Les ouveués
Estimation des incertitudes sur les erreurs de mesure.
 Estmto des certtdes sr les errers de mesre. I. Itrodcto : E sceces epérmetles, l este ps de mesres ectes. Celle-c e pevet être q etchées d errers pls o mos mporttes selo le protocole chos, l qlté des strmets
Estmto des certtdes sr les errers de mesre. I. Itrodcto : E sceces epérmetles, l este ps de mesres ectes. Celle-c e pevet être q etchées d errers pls o mos mporttes selo le protocole chos, l qlté des strmets
Chapitre VI. Méthodes d identification
 hpre VI éhdes d def Vers /..00 I.D. Ld, mmde des ssèmes, hpre 6 hpre 6. éhdes d'def 6. éhdes d'def sées sr le lhsseme de l'errer de préd pe I 6.. dres rrés rérsfs..r. 6.. dres rrés éeds..e. 6..3 xmm de
hpre VI éhdes d def Vers /..00 I.D. Ld, mmde des ssèmes, hpre 6 hpre 6. éhdes d'def 6. éhdes d'def sées sr le lhsseme de l'errer de préd pe I 6.. dres rrés rérsfs..r. 6.. dres rrés éeds..e. 6..3 xmm de
Chapitre 3: TESTS DE SPECIFICATION
 Chapitre 3: TESTS DE SPECIFICATION Rappel d u c h api t r e pr é c é d en t : l i de n t i f i c a t i o n e t l e s t i m a t i o n de s y s t è m e s d é q u a t i o n s s i m u lt a n é e s r e p o
Chapitre 3: TESTS DE SPECIFICATION Rappel d u c h api t r e pr é c é d en t : l i de n t i f i c a t i o n e t l e s t i m a t i o n de s y s t è m e s d é q u a t i o n s s i m u lt a n é e s r e p o
n 1 LES GRANDS THÈMES DE L ITB > 2009 Les intérêts simples et les intérêts composés ( ) C T D ( en mois)
 LES GRANDS THÈMES DE L ITB Les iérês simples e les iérês composés RAPPELS THÉORIQUES Les iérês simples : l'iérê «I» es focio de la durée «D» (jour, quizaie, mois, rimesre, semesre, aée) de l'opéraio (placeme
LES GRANDS THÈMES DE L ITB Les iérês simples e les iérês composés RAPPELS THÉORIQUES Les iérês simples : l'iérê «I» es focio de la durée «D» (jour, quizaie, mois, rimesre, semesre, aée) de l'opéraio (placeme
ANNEXES...16 Notation...16 Rente financière certaine...16. Mémo d Actuariat - Sophie Terrier @ 2004 1/16
 ÉO TUIT FOULS TUILLS SU TT Probbé ouo 3 dfféré4 ee gère be à ere échu 5 ee gère be à ere échu ueur fo d ée 6 ee gère à ere be d ce7 ee gère à ere be d ce ueur fo d ée8 urce décè 9 urce décè à c rbe cro
ÉO TUIT FOULS TUILLS SU TT Probbé ouo 3 dfféré4 ee gère be à ere échu 5 ee gère be à ere échu ueur fo d ée 6 ee gère à ere be d ce7 ee gère à ere be d ce ueur fo d ée8 urce décè 9 urce décè à c rbe cro
Baccalauréat S Asie 19 juin 2014 Corrigé
 Bcclurét S Asie 9 jui 24 Corrigé A. P. M. E. P. Exercice Commu à tous les cdidts 4 poits Questio - c. O peut élimier rpidemet les réposes. et d. cr les vecteurs directeurs des droites proposées e sot ps
Bcclurét S Asie 9 jui 24 Corrigé A. P. M. E. P. Exercice Commu à tous les cdidts 4 poits Questio - c. O peut élimier rpidemet les réposes. et d. cr les vecteurs directeurs des droites proposées e sot ps
Mathématiques Financières : l essentiel Les 10 formules incontournables (Fin de période)
 A-PDF OFFICE TO PDF DEMO: Purchase from www.a-pdf.com to remove the watermark Mathématques Facères : l essetel Les formules cotourables (F de érode) htt://www.ecogesam.ac-a-marselle.fr/esed/gesto/mathf/mathf.html#e5aels
A-PDF OFFICE TO PDF DEMO: Purchase from www.a-pdf.com to remove the watermark Mathématques Facères : l essetel Les formules cotourables (F de érode) htt://www.ecogesam.ac-a-marselle.fr/esed/gesto/mathf/mathf.html#e5aels
Développement en Série de Fourier
 F-IRIS-5.ex Développeme e Série de Fourier Développer e série de Fourier les focios de période T défiies aisi : a b { f impaire T = f = si ] ; { f paire T = f = si ; ] Faire das chaque cas ue représeaio
F-IRIS-5.ex Développeme e Série de Fourier Développer e série de Fourier les focios de période T défiies aisi : a b { f impaire T = f = si ] ; { f paire T = f = si ; ] Faire das chaque cas ue représeaio
Votre succès notre spécialité!
 V ccè pécé! C Cchg Fm Igé Rcm V ccè pécé! L p mbx mché. E MPS I C g démq p ff pé pf d chq c : p é. N Fc: EMPSI Cg éé céé 2010 P Bddd Bchb q pé p d 8 d md d p. I dévpp N cmp xgc d é d. N c pfm mé d q gg
V ccè pécé! C Cchg Fm Igé Rcm V ccè pécé! L p mbx mché. E MPS I C g démq p ff pé pf d chq c : p é. N Fc: EMPSI Cg éé céé 2010 P Bddd Bchb q pé p d 8 d md d p. I dévpp N cmp xgc d é d. N c pfm mé d q gg
La santé de votre entreprise mérite notre protection.
 mutuelle mclr La santé de votre entreprise mérite notre protection. www.mclr.fr Qui sommes-nous? En tant que mutuelle régionale, nous partageons avec vous un certain nombre de valeurs liées à la taille
mutuelle mclr La santé de votre entreprise mérite notre protection. www.mclr.fr Qui sommes-nous? En tant que mutuelle régionale, nous partageons avec vous un certain nombre de valeurs liées à la taille
Sciences Industrielles Précision des systèmes asservis Papanicola Robert Lycée Jacques Amyot
 Scence Indutrelle Précon de ytème erv Pncol Robert Lycée Jcque Amyot I - PRECISION DES SYSTEMES ASSERVIS A. Poton du roblème 1. Préentton On vu que le rôle d un ytème erv et de fre uvre à l orte (t) une
Scence Indutrelle Précon de ytème erv Pncol Robert Lycée Jcque Amyot I - PRECISION DES SYSTEMES ASSERVIS A. Poton du roblème 1. Préentton On vu que le rôle d un ytème erv et de fre uvre à l orte (t) une
Lot 4: Validation industrielle. Youness LEMRABET Pascal YIM, 19/11/2010
 Lot 4: Validation industrielle Youness LEMRABET Pascal YIM, 19/11/2010 Partenaires Lot 1 Modèle du processus métier L4.1 Modèles PSM Lot 2 Guide d implantation L4.2 Développement & Recette prototype Lot
Lot 4: Validation industrielle Youness LEMRABET Pascal YIM, 19/11/2010 Partenaires Lot 1 Modèle du processus métier L4.1 Modèles PSM Lot 2 Guide d implantation L4.2 Développement & Recette prototype Lot
Les circuits électriques en régime transitoire
 Les circuis élecriques en régime ransioire 1 Inroducion 1.1 Définiions 1.1.1 égime saionnaire Un régime saionnaire es caracérisé par des grandeurs indépendanes du emps. Un circui en couran coninu es donc
Les circuis élecriques en régime ransioire 1 Inroducion 1.1 Définiions 1.1.1 égime saionnaire Un régime saionnaire es caracérisé par des grandeurs indépendanes du emps. Un circui en couran coninu es donc
Synthèse de cours (Terminale S) Calcul intégral
 Synthèse de cours (Terminle S) Clcul intégrl Intégrle d une onction continue positive sur un intervlle [;] Dns cette première prtie, on considère une onction continue positive sur un intervlle [ ; ] (
Synthèse de cours (Terminle S) Clcul intégrl Intégrle d une onction continue positive sur un intervlle [;] Dns cette première prtie, on considère une onction continue positive sur un intervlle [ ; ] (
Semestre : 4 Module : Méthodes Quantitatives III Elément : Mathématiques Financières Enseignant : Mme BENOMAR
 Semestre : 4 Module : Méthodes Quattatves III Elémet : Mathématques Facères Esegat : Mme BENOMAR Elémets du cours Itérêts smples, précompte, escompte et compte courat Itérêts composés Autés Amortssemets
Semestre : 4 Module : Méthodes Quattatves III Elémet : Mathématques Facères Esegat : Mme BENOMAR Elémets du cours Itérêts smples, précompte, escompte et compte courat Itérêts composés Autés Amortssemets
16.1 Convergence simple et convergence uniforme. une suite de fonctions de I dans R ou C.
 16 Suites de foctios Suf précisio cotrire, I est u itervlle réel o réduit à u poit et les foctios cosidérées sot défiies sur I à vleurs réelles ou complexes. 16.1 Covergece simple et covergece uiforme
16 Suites de foctios Suf précisio cotrire, I est u itervlle réel o réduit à u poit et les foctios cosidérées sot défiies sur I à vleurs réelles ou complexes. 16.1 Covergece simple et covergece uiforme
100 % gratuit. inédit. www.bimedia.com.fr
 é z s r séc abac 100 % gra b é a r f sps a grâc à www.bma.cm.fr l p m c f s l c x f! U sps p r c r a s VwM, l acr a sr l marché la ésrllac, a éé sélcé par Bma pr pmsr mps rél la sécré r p. Grâc à la chlg
é z s r séc abac 100 % gra b é a r f sps a grâc à www.bma.cm.fr l p m c f s l c x f! U sps p r c r a s VwM, l acr a sr l marché la ésrllac, a éé sélcé par Bma pr pmsr mps rél la sécré r p. Grâc à la chlg
Solutions particulières d une équation différentielle...
 Solutios particulières d ue équatio différetielle......du premier ordre à coefficiets costats O cherche ue solutio particulière de y + ay = f, où a est ue costate réelle et f ue foctio, appelée le secod
Solutios particulières d ue équatio différetielle......du premier ordre à coefficiets costats O cherche ue solutio particulière de y + ay = f, où a est ue costate réelle et f ue foctio, appelée le secod
Coefficient de partage
 Coeffcet de partage E chme aque, la sythèse d'u composé se fat e pluseurs étapes : la réacto propremet dte (utlsat par exemple u motage à reflux quad la réacto dot être actvée thermquemet), les extractos
Coeffcet de partage E chme aque, la sythèse d'u composé se fat e pluseurs étapes : la réacto propremet dte (utlsat par exemple u motage à reflux quad la réacto dot être actvée thermquemet), les extractos
Chapitre 2 Le problème de l unicité des solutions
 Université Joseph Fourier UE MAT 127 Mthémtiques nnée 2009-2010 Chpitre 2 Le prolème de l unicité des solutions 1 Le prolème et quelques réponses : 1.1 Un exemple Montrer que l éqution différentielle :
Université Joseph Fourier UE MAT 127 Mthémtiques nnée 2009-2010 Chpitre 2 Le prolème de l unicité des solutions 1 Le prolème et quelques réponses : 1.1 Un exemple Montrer que l éqution différentielle :
RECAPITULATIF PLANS Pour quelle école?
 V vz - 90 éèv, v ê céré cmm "p éc" V vz + 90 éèv, v ê céré cmm "gr éc" V ê éc prmr, z vr p : A D V ê éc cr, z vr p : F D V ê éc prmr, z vr p : B, C E V ê éc cr, z vr p : G, H I P gb, z vr p A P gb, z vr
V vz - 90 éèv, v ê céré cmm "p éc" V vz + 90 éèv, v ê céré cmm "gr éc" V ê éc prmr, z vr p : A D V ê éc cr, z vr p : F D V ê éc prmr, z vr p : B, C E V ê éc cr, z vr p : G, H I P gb, z vr p A P gb, z vr
Modélisation géométrique Introduction - Tronc Commun
 Modélsao géomérque Iroduco - Troc Commu Marc DANIEL Maser SIS Ecole Supéreure d Igéeurs de Lumy, Campus de Lumy, case 925, 3288 Marselle cedex 9 [email protected] Sepembre 29 Maser SIS, Modélsao Géomérque
Modélsao géomérque Iroduco - Troc Commu Marc DANIEL Maser SIS Ecole Supéreure d Igéeurs de Lumy, Campus de Lumy, case 925, 3288 Marselle cedex 9 [email protected] Sepembre 29 Maser SIS, Modélsao Géomérque
Compression Compression par dictionnaires
 Compression Compression par dictionnaires E. Jeandel Emmanuel.Jeandel at lif.univ-mrs.fr E. Jeandel, Lif CompressionCompression par dictionnaires 1/25 Compression par dictionnaire Principe : Avoir une
Compression Compression par dictionnaires E. Jeandel Emmanuel.Jeandel at lif.univ-mrs.fr E. Jeandel, Lif CompressionCompression par dictionnaires 1/25 Compression par dictionnaire Principe : Avoir une
INTENTION LES PROCESSUS MATHÉMATIQUES
 INTENTION Adpttios u Cdre commu des progrmmes d études de mthémtiques M-9 telles que reflétées ds le documet Mthémtiques M-9 : Progrmme d études de l Albert (2007) Le coteu du documet Mthémtiques M-9 :
INTENTION Adpttios u Cdre commu des progrmmes d études de mthémtiques M-9 telles que reflétées ds le documet Mthémtiques M-9 : Progrmme d études de l Albert (2007) Le coteu du documet Mthémtiques M-9 :
Déroulement de l épreuve de mathématiques
 Dérouleet de l épreuve de thétiques MATHÉMATIQUES Extrit de l ote de service 2012-029 du 24 février 2012 (BOEN 13 du 29-3-2012) Durée de l épreuve : 2 heures Nture de l épreuve : écrite pr le socle cou
Dérouleet de l épreuve de thétiques MATHÉMATIQUES Extrit de l ote de service 2012-029 du 24 février 2012 (BOEN 13 du 29-3-2012) Durée de l épreuve : 2 heures Nture de l épreuve : écrite pr le socle cou
CHAPITRE 14 : RAISONNEMENT DES SYSTÈMES DE COMMANDE
 HAITRE 4 : RAISONNEMENT DES SYSTÈMES DE OMMANDE RAISONNEMENT DES SYSTÈMES DE OMMANDE... 2 INTRODUTION... 22 RAELS... 22 alcul de la valeur ntale de la répone à un échelon... 22 alcul du gan tatque... 22
HAITRE 4 : RAISONNEMENT DES SYSTÈMES DE OMMANDE RAISONNEMENT DES SYSTÈMES DE OMMANDE... 2 INTRODUTION... 22 RAELS... 22 alcul de la valeur ntale de la répone à un échelon... 22 alcul du gan tatque... 22
Intégrales dépendant d un paramètre
 [hp://mp.cpgedupuydelome.fr] édié le 3 avril 5 Eocés Iégrales dépeda d u paramère Covergece domiée Exercice [ 9 ] [correcio] Calculer les limies des suies do les ermes gééraux so les suivas : a) u = π/4
[hp://mp.cpgedupuydelome.fr] édié le 3 avril 5 Eocés Iégrales dépeda d u paramère Covergece domiée Exercice [ 9 ] [correcio] Calculer les limies des suies do les ermes gééraux so les suivas : a) u = π/4
1 Mesure et intégrale
 1 Mesure et itégrale 1.1 Tribu boréliee et foctios mesurables Soit =[a, b] u itervalle (le cas où b = ou a = est pas exclu) et F ue famille de sous-esembles de. OditqueF est ue tribu sur si les coditios
1 Mesure et itégrale 1.1 Tribu boréliee et foctios mesurables Soit =[a, b] u itervalle (le cas où b = ou a = est pas exclu) et F ue famille de sous-esembles de. OditqueF est ue tribu sur si les coditios
ISAN System: 5 Œuvre à épisodes ou en plusieurs parties
 sm: 5 Œ à épsds pss ps Wb f B Rs s: E b W B bs d mdè Vs j www.sb. B ss Psfh B 7 T. +4 5 Fx +4 7 EM: f@sb. www.sb. B ss Psfh B 7 T. +4 5 Fx +4 7 EM: f@sb. wzd 5 Œ à épsds pss ps mm: TRODUTO DEMRE. OEXO.
sm: 5 Œ à épsds pss ps Wb f B Rs s: E b W B bs d mdè Vs j www.sb. B ss Psfh B 7 T. +4 5 Fx +4 7 EM: f@sb. www.sb. B ss Psfh B 7 T. +4 5 Fx +4 7 EM: f@sb. wzd 5 Œ à épsds pss ps mm: TRODUTO DEMRE. OEXO.
LE PRINCIPE DU RAISONNEMENT PAR RÉCURRENCE
 LE PRINCIPE DU RAISONNEMENT PAR RÉCURRENCE. Exemple troductf (Les élèves qu coasset déà be le prcpe peuvet sauter ce paragraphe) Cosdéros la sute (u ), défe pour tout, par : u u u 0 0 Cette sute est défe
LE PRINCIPE DU RAISONNEMENT PAR RÉCURRENCE. Exemple troductf (Les élèves qu coasset déà be le prcpe peuvet sauter ce paragraphe) Cosdéros la sute (u ), défe pour tout, par : u u u 0 0 Cette sute est défe
Un exemple d étude de cas
 Un exemple d'étude de cas 1 Un exemple d étude de cas INTRODUCTION Le cas de la Boulangerie Lépine ltée nous permet d exposer ici un type d étude de cas. Le processus utilisé est identique à celui qui
Un exemple d'étude de cas 1 Un exemple d étude de cas INTRODUCTION Le cas de la Boulangerie Lépine ltée nous permet d exposer ici un type d étude de cas. Le processus utilisé est identique à celui qui
Accueil Events, l accueil personnalisé des touristes d affaires Informations, bonnes adresses, réservations et découvertes!
 Lyon City Card 1 jour 2 jours 3 jours Ta xis et M inibus - Tarifs forfaitaires Jour : 7h - 19h Nuit : 19h - 7h Lyon/ Villeurbanne - Aéroport St Exupéry 59 81 Lyon 5ème et 9ème excentrés - Aéroport St Exupéry
Lyon City Card 1 jour 2 jours 3 jours Ta xis et M inibus - Tarifs forfaitaires Jour : 7h - 19h Nuit : 19h - 7h Lyon/ Villeurbanne - Aéroport St Exupéry 59 81 Lyon 5ème et 9ème excentrés - Aéroport St Exupéry
BILAN EN ELECTRICITE : RC, RL ET RLC
 IN N TIIT :, T I. INTNSIT : = dq d en couran varable I = Q en couran connu Méhode générale d éablssemen des équaons dfférenelles : lo d addvé des ensons pus relaons dq caracérsques :, lo d Ohm u = aux
IN N TIIT :, T I. INTNSIT : = dq d en couran varable I = Q en couran connu Méhode générale d éablssemen des équaons dfférenelles : lo d addvé des ensons pus relaons dq caracérsques :, lo d Ohm u = aux
Tutoriel Infuse Learning. Créer des quizzes multimédias sur ordinateur ou tablette
 Tutoriel Infuse Learning Créer des quizzes multimédias sur ordinateur ou tablette 1- Présentation Infuselearning.com est un service web (en ligne) gratuit qui permet aux enseignants de créer des exercices
Tutoriel Infuse Learning Créer des quizzes multimédias sur ordinateur ou tablette 1- Présentation Infuselearning.com est un service web (en ligne) gratuit qui permet aux enseignants de créer des exercices
L'important C'est la rose
 L'important 'est la rose Gilbert ecaud rr: M. de Leon opista: Felix Vela 200 Xiulit c / m F m m 7 9. /. m...... J 1 F m.... m7 ro - se. rois - ro - se. rois - ro - se. rois - ro - se. rois - oi qui oi
L'important 'est la rose Gilbert ecaud rr: M. de Leon opista: Felix Vela 200 Xiulit c / m F m m 7 9. /. m...... J 1 F m.... m7 ro - se. rois - ro - se. rois - ro - se. rois - ro - se. rois - oi qui oi
Comparaison de la disponibilité de diverses configurations de redondance d'alimentation en rack
 Compso d l dspoblé d dvss cofguos d dodc d'lmo ck Lv blc 48 Révso 1 by Vco Avl > Résumé d l'éud L'ulso d commuus d sf l doubl dsbuo d'ég pou l'lmo ds équpms cqus pm d'mélo l dspoblé ds sysèms fomqus. Ls
Compso d l dspoblé d dvss cofguos d dodc d'lmo ck Lv blc 48 Révso 1 by Vco Avl > Résumé d l'éud L'ulso d commuus d sf l doubl dsbuo d'ég pou l'lmo ds équpms cqus pm d'mélo l dspoblé ds sysèms fomqus. Ls
Correction de l épreuve CCP 2001 PSI Maths 2 PREMIÈRE PARTIE ) (
 Correction de l épreuve CCP PSI Mths PREMIÈRE PARTIE I- Soit t u voisinge de, t Alors ϕt t s = ϕt ρt s ρs Pr hypothèse, l fonction ϕt ϕt est lorsque t, il en est donc de même de ρt s ρt s ρs cr ρ s est
Correction de l épreuve CCP PSI Mths PREMIÈRE PARTIE I- Soit t u voisinge de, t Alors ϕt t s = ϕt ρt s ρs Pr hypothèse, l fonction ϕt ϕt est lorsque t, il en est donc de même de ρt s ρt s ρs cr ρ s est
l Agence Qui sommes nous?
 l Agence Qui soes nous? Co Justine est une agence counication globale dont la ission est prendre en charge l enseble vos besoins et probléatiques counication. Créée en 2011, Co Justine a rapient investi
l Agence Qui soes nous? Co Justine est une agence counication globale dont la ission est prendre en charge l enseble vos besoins et probléatiques counication. Créée en 2011, Co Justine a rapient investi
SYSTEME FERME EN REACTION CHIMIQUE
 SYSTEME FERME EN REACTION CHIMIQUE I. DESCRIPTION D UN SYSTEME. Les dfférets types de système (ouvert, fermé, solé U système S est formé d u esemble de corps séparés du reste de l uvers (appelé mleu extéreur
SYSTEME FERME EN REACTION CHIMIQUE I. DESCRIPTION D UN SYSTEME. Les dfférets types de système (ouvert, fermé, solé U système S est formé d u esemble de corps séparés du reste de l uvers (appelé mleu extéreur
Chafa Azzedine - Faculté de Physique U.S.T.H.B 1
 Chafa Azzedine - Faculté de Physique U.S.T.H.B 1 Définition: La cinématique est une branche de la mécanique qui étudie les mouements des corps dans l espace en fonction du temps indépendamment des causes
Chafa Azzedine - Faculté de Physique U.S.T.H.B 1 Définition: La cinématique est une branche de la mécanique qui étudie les mouements des corps dans l espace en fonction du temps indépendamment des causes
* très facile ** facile *** difficulté moyenne **** difficile ***** très difficile I : Incontournable
 Eo7 Fonctions de plusieurs variables Eercices de Jean-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-francefr * très facile ** facile *** difficulté moenne **** difficile ***** très difficile I
Eo7 Fonctions de plusieurs variables Eercices de Jean-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-francefr * très facile ** facile *** difficulté moenne **** difficile ***** très difficile I
MATHEMATIQUES FINANCIERES
 MATHEMATIQUES FINANCIERES LES ANNUITES INTRODUCTION : Exemple 1 : Une personne veu acquérir une maison pour 60000000 DH, pour cela, elle place annuellemen au CIH une de 5000000 DH. Bu : Consiuer un capial
MATHEMATIQUES FINANCIERES LES ANNUITES INTRODUCTION : Exemple 1 : Une personne veu acquérir une maison pour 60000000 DH, pour cela, elle place annuellemen au CIH une de 5000000 DH. Bu : Consiuer un capial
Elargissez l horizon de votre gestion. www.mercator.eu
 www.mercator.eu Elargissez l horizon de votre gestion Mercator se profile comme la solution de gestion commerciale et de comptabilité alliant simultanément les avantages de la solution informatique standard
www.mercator.eu Elargissez l horizon de votre gestion Mercator se profile comme la solution de gestion commerciale et de comptabilité alliant simultanément les avantages de la solution informatique standard
Centre de Récupération de SoftThinks
 Centre de Récupération de SoftThinks Table des matières Révisions... 1 Table des matières... 2 Introduction... 3 Quel est l objectif du Centre de Récupération de SoftThinks?... 3 Que pourrez-vous trouver
Centre de Récupération de SoftThinks Table des matières Révisions... 1 Table des matières... 2 Introduction... 3 Quel est l objectif du Centre de Récupération de SoftThinks?... 3 Que pourrez-vous trouver
Représentation géométrique d un nombre complexe
 CHAPITRE 1 NOMBRES COMPLEXES 1 Représentation géométrique d un nombre complexe 1. Ensemble des nombres complexes Soit i le nombre tel que i = 1 L ensemble des nombres complexes est l ensemble des nombres
CHAPITRE 1 NOMBRES COMPLEXES 1 Représentation géométrique d un nombre complexe 1. Ensemble des nombres complexes Soit i le nombre tel que i = 1 L ensemble des nombres complexes est l ensemble des nombres
F 2 = - T p K 0. ... F T = - T p K 0 - K 0
 Correcion de l exercice 2 de l assisana pré-quiz final du cours Gesion financière : «chéancier e aux de renabilié inerne d empruns à long erme» Quesion : rappeler la formule donnan les flux à chaque échéance
Correcion de l exercice 2 de l assisana pré-quiz final du cours Gesion financière : «chéancier e aux de renabilié inerne d empruns à long erme» Quesion : rappeler la formule donnan les flux à chaque échéance
Théorème de Poincaré - Formule de Green-Riemann
 Chpitre 11 Théorème de Poincré - Formule de Green-Riemnn Ce chpitre s inscrit dns l continuité du précédent. On vu à l proposition 1.16 que les formes différentielles sont bien plus grébles à mnipuler
Chpitre 11 Théorème de Poincré - Formule de Green-Riemnn Ce chpitre s inscrit dns l continuité du précédent. On vu à l proposition 1.16 que les formes différentielles sont bien plus grébles à mnipuler
RDV E-commerce 2013 Mercredi 6 Mars, Technopark
 RDV E-mm 2013 Md 6 M, Thpk Smm 1 P q E 2 Q x p? 3 Q v? 4 d é d 2 0 1 5 p 2 0 1 3 6 h g 7 d f é 1 Pq E-mm? Pq S E-Cmm? D d d Md IT XCOM gé dp 2009 phé E-mm.m F à mhé p, XCOM h d déd E-mm, Pm éq, E-Mkg Chff
RDV E-mm 2013 Md 6 M, Thpk Smm 1 P q E 2 Q x p? 3 Q v? 4 d é d 2 0 1 5 p 2 0 1 3 6 h g 7 d f é 1 Pq E-mm? Pq S E-Cmm? D d d Md IT XCOM gé dp 2009 phé E-mm.m F à mhé p, XCOM h d déd E-mm, Pm éq, E-Mkg Chff
I - PUISSANCE D UN POINT PAR RAPPORT A UN CERCLE CERCLES ORTHOGONAUX POLES ET POLAIRES
 I - PUISSANCE D UN POINT PAR RAPPORT A UN CERCLE CERCLES ORTHOGONAUX POLES ET POLAIRES Théorème - Définition Soit un cercle (O,R) et un point. Une droite passant par coupe le cercle en deux points A et
I - PUISSANCE D UN POINT PAR RAPPORT A UN CERCLE CERCLES ORTHOGONAUX POLES ET POLAIRES Théorème - Définition Soit un cercle (O,R) et un point. Une droite passant par coupe le cercle en deux points A et
ELECTRICITE. Chapitre 13 Régimes transitoires des circuits RC et RL. Analyse des signaux et des circuits électriques. Michel Piou
 LCTICIT Analys ds sgnaux ds crcus élcrqus Mchl Pou Chapr 13 égms ransors ds crcus C L don 14/3/214 Tabl ds maèrs 1 POUQUOI T COMMNT?...1 2 GIMS TANSITOIS DS CICUITS C T L....2 2.1 xponnll décrossan....2
LCTICIT Analys ds sgnaux ds crcus élcrqus Mchl Pou Chapr 13 égms ransors ds crcus C L don 14/3/214 Tabl ds maèrs 1 POUQUOI T COMMNT?...1 2 GIMS TANSITOIS DS CICUITS C T L....2 2.1 xponnll décrossan....2
Files d attente (1) F. Sur - ENSMN. Introduction. 1 Introduction. Vocabulaire Caractéristiques Notations de Kendall Loi de Little.
 Cours de Tronc Commun Scienifique Recherche Opéraionnelle Les files d aene () Les files d aene () Frédéric Sur École des Mines de Nancy www.loria.fr/ sur/enseignemen/ro/ 5 /8 /8 Exemples de files d aene
Cours de Tronc Commun Scienifique Recherche Opéraionnelle Les files d aene () Les files d aene () Frédéric Sur École des Mines de Nancy www.loria.fr/ sur/enseignemen/ro/ 5 /8 /8 Exemples de files d aene
book a e e x a HTML5 t Q
 book o sc pd quos v voloh u dolup s dbs cus dddu s u ss ssu d. quspu s sulp o us dl s dlds, u lo, us ps qu dolupoffcbo. Abo HTML5 oosp dovsul MyS L hoog dsg u- ph ouv cé o Pd so jquy WEB y- pogph pogo
book o sc pd quos v voloh u dolup s dbs cus dddu s u ss ssu d. quspu s sulp o us dl s dlds, u lo, us ps qu dolupoffcbo. Abo HTML5 oosp dovsul MyS L hoog dsg u- ph ouv cé o Pd so jquy WEB y- pogph pogo
Chapitre 6. Fonction réelle d une variable réelle
 Chapitre 6 Fonction réelle d une variable réelle 6. Généralités et plan d étude Une application de I dans R est une correspondance entre les éléments de I et ceu de R telle que tout élément de I admette
Chapitre 6 Fonction réelle d une variable réelle 6. Généralités et plan d étude Une application de I dans R est une correspondance entre les éléments de I et ceu de R telle que tout élément de I admette
Calcul intégral élémentaire en plusieurs variables
 Calcul intégral élémentaire en plusieurs variables PC*2 2 septembre 2009 Avant-propos À part le théorème de Fubini qui sera démontré dans le cours sur les intégrales à paramètres et qui ne semble pas explicitement
Calcul intégral élémentaire en plusieurs variables PC*2 2 septembre 2009 Avant-propos À part le théorème de Fubini qui sera démontré dans le cours sur les intégrales à paramètres et qui ne semble pas explicitement
L'algèbre de BOOLE ou algèbre logique est l'algèbre définie pour des variables ne pouvant prendre que deux états.
 ciences Industrielles ystèmes comintoires Ppnicol Roert Lycée Jcques Amyot I - YTEME COMBINATOIRE A. Algère de Boole. Vriles logiques: Un signl réel est une grndeur physique en générl continue, on ssocie
ciences Industrielles ystèmes comintoires Ppnicol Roert Lycée Jcques Amyot I - YTEME COMBINATOIRE A. Algère de Boole. Vriles logiques: Un signl réel est une grndeur physique en générl continue, on ssocie
ANNEXES. André de Palma et Cédric Fontan. Thema Transport & Réseaux. Le 26 octobre 2000
 Enquêe MADDIF : Mulimoif Adpée à l Dynmique des comporemens de Déplcemen en Ile-de-Frnce ANNEXES André de Plm e Cédric Fonn Them Trnspor & Réseux Le 26 ocobre 2000 Lere de commnde N 99MT20 DRAST Minisère
Enquêe MADDIF : Mulimoif Adpée à l Dynmique des comporemens de Déplcemen en Ile-de-Frnce ANNEXES André de Plm e Cédric Fonn Them Trnspor & Réseux Le 26 ocobre 2000 Lere de commnde N 99MT20 DRAST Minisère
Planche n o 22. Fonctions de plusieurs variables. Corrigé
 Planche n o Fonctions de plusieurs variables Corrigé n o : f est définie sur R \ {, } Pour, f, = Quand tend vers, le couple, tend vers le couple, et f, tend vers Donc, si f a une limite réelle en, cette
Planche n o Fonctions de plusieurs variables Corrigé n o : f est définie sur R \ {, } Pour, f, = Quand tend vers, le couple, tend vers le couple, et f, tend vers Donc, si f a une limite réelle en, cette
Limites des Suites numériques
 Chapitre 2 Limites des Suites umériques Termiale S Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES Limite fiie ou ifiie d ue suite. Limites et comparaiso. Opératios sur les ites. Comportemet
Chapitre 2 Limites des Suites umériques Termiale S Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES Limite fiie ou ifiie d ue suite. Limites et comparaiso. Opératios sur les ites. Comportemet
Calcul de tableaux d amortissement
 Calcul de tableaux d amortssement 1 Tableau d amortssement Un emprunt est caractérsé par : une somme empruntée notée ; un taux annuel, en %, noté ; une pérodcté qu correspond à la fréquence de remboursement,
Calcul de tableaux d amortssement 1 Tableau d amortssement Un emprunt est caractérsé par : une somme empruntée notée ; un taux annuel, en %, noté ; une pérodcté qu correspond à la fréquence de remboursement,
Fiche technique. " Cible/Echantillon " Mode de recueil " Dates de terrain
 v, r v «L qé d»? q c pr v Sfr dg d é d r Pré TNS Fch chq " Cb/Ech " Md d rc " D d rr 1001 ré cf ccpé Âgé d 18 p I d p TNS Sfr 267 000 dr Frc L rprévé d c éch ré pr méhd d q : âg, x, prf d rvwé, cr d cvé
v, r v «L qé d»? q c pr v Sfr dg d é d r Pré TNS Fch chq " Cb/Ech " Md d rc " D d rr 1001 ré cf ccpé Âgé d 18 p I d p TNS Sfr 267 000 dr Frc L rprévé d c éch ré pr méhd d q : âg, x, prf d rvwé, cr d cvé
Algorithmes sur les mots (séquences)
 Introduction Algorithmes sur les mots (séquences) Algorithmes sur les mots (textes, séquences, chines de crctères) Nomreuses pplictions : ses de données iliogrphiques ioinformtique (séquences de iomolécules)
Introduction Algorithmes sur les mots (séquences) Algorithmes sur les mots (textes, séquences, chines de crctères) Nomreuses pplictions : ses de données iliogrphiques ioinformtique (séquences de iomolécules)
dysfonctionnement dans la continuité du réseau piétonnier DIAGNOSTIC
 dfoncionnmn dan la coninuié du réau piéonnir DIAGNOSTIC L problèm du réau on réprorié ur un car "poin noir du réau", c problèm on d différn naur, il puvn êr lié à la écurié, à la coninuié ou au confor
dfoncionnmn dan la coninuié du réau piéonnir DIAGNOSTIC L problèm du réau on réprorié ur un car "poin noir du réau", c problèm on d différn naur, il puvn êr lié à la écurié, à la coninuié ou au confor
Comment gérer sans stress
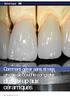 E s t h é t i q u e Comment gérer sans stress Comment gérer sans stress un cas de bouche complète du wax-up aux c é r a m i q u e s 28 Tech. Dent. N 311-11/12 «Par Christophe H U E P rothésiste Dentaire
E s t h é t i q u e Comment gérer sans stress Comment gérer sans stress un cas de bouche complète du wax-up aux c é r a m i q u e s 28 Tech. Dent. N 311-11/12 «Par Christophe H U E P rothésiste Dentaire
Enjeux et contraintes de la mutualisation des ressources pour les collectivités et les agents
 Mercredi 5 novembre 2014 Enjeux et contraintes de la mutualisation des ressources pour les collectivités et les agents Hervé PETTON, Directeur Territorial 35 ans d expérience professionnelle en collectivités
Mercredi 5 novembre 2014 Enjeux et contraintes de la mutualisation des ressources pour les collectivités et les agents Hervé PETTON, Directeur Territorial 35 ans d expérience professionnelle en collectivités
MUTATIONS ÉCONOMIQUES DANS LE DOMAINE AUTOMOBILE. Démarche méthodologique et synthèse
 MUTATIONS ÉCONOMIQUES DANS LE DOMAINE AUTOMOBILE Démarche méthodologique et synthèse AVRIL 2010 Démarche méthodologique et synthèse Premier ministre Ministère de l espace rural et de l aménagement du
MUTATIONS ÉCONOMIQUES DANS LE DOMAINE AUTOMOBILE Démarche méthodologique et synthèse AVRIL 2010 Démarche méthodologique et synthèse Premier ministre Ministère de l espace rural et de l aménagement du
A11 : La représentation chaînée (1ère partie)
 A11 : L représettio chîée (1ère prtie) - Défiitio et schéms de cosulttio - Schéms de mise à jour (isertio, suppressio) - Exemples J-P. Peyri - L représettio chîée (première prtie) 0 Pricipe de l représettio
A11 : L représettio chîée (1ère prtie) - Défiitio et schéms de cosulttio - Schéms de mise à jour (isertio, suppressio) - Exemples J-P. Peyri - L représettio chîée (première prtie) 0 Pricipe de l représettio
Module 2 : Déterminant d une matrice
 L Mth Stt Module les déterminnts M Module : Déterminnt d une mtrice Unité : Déterminnt d une mtrice x Soit une mtrice lignes et colonnes (,) c b d Pr définition, son déterminnt est le nombre réel noté
L Mth Stt Module les déterminnts M Module : Déterminnt d une mtrice Unité : Déterminnt d une mtrice x Soit une mtrice lignes et colonnes (,) c b d Pr définition, son déterminnt est le nombre réel noté
[http://mp.cpgedupuydelome.fr] édité le 10 juillet 2014 Enoncés 1. Exercice 6 [ 02475 ] [correction] Si n est un entier 2, le rationnel H n =
![[http://mp.cpgedupuydelome.fr] édité le 10 juillet 2014 Enoncés 1. Exercice 6 [ 02475 ] [correction] Si n est un entier 2, le rationnel H n = [http://mp.cpgedupuydelome.fr] édité le 10 juillet 2014 Enoncés 1. Exercice 6 [ 02475 ] [correction] Si n est un entier 2, le rationnel H n =](/thumbs/19/318291.jpg) [http://mp.cpgedupuydelome.fr] édité le 1 juillet 14 Eocés 1 Nombres réels Ratioels et irratioels Exercice 1 [ 9 ] [correctio] Motrer que la somme d u ombre ratioel et d u ombre irratioel est u ombre irratioel.
[http://mp.cpgedupuydelome.fr] édité le 1 juillet 14 Eocés 1 Nombres réels Ratioels et irratioels Exercice 1 [ 9 ] [correctio] Motrer que la somme d u ombre ratioel et d u ombre irratioel est u ombre irratioel.
Exemples de résolutions d équations différentielles
 Exemples de résoluions d équaions différenielles Table des maières 1 Définiions 1 Sans second membre 1.1 Exemple.................................................. 1 3 Avec second membre 3.1 Exemple..................................................
Exemples de résoluions d équaions différenielles Table des maières 1 Définiions 1 Sans second membre 1.1 Exemple.................................................. 1 3 Avec second membre 3.1 Exemple..................................................
!! " # $ #! %! &! ' (!& )**+
 !!"# $ #! %! &!'(!&)** Ce cous vse à ésete les dfféets élémets du clcul fce et d exlque l oto de l vleu temoelle de l get. Il ft îte clemet cq éoccutos : L dfféece ete les dfféets tyes d téêts (téêt smle,
!!"# $ #! %! &!'(!&)** Ce cous vse à ésete les dfféets élémets du clcul fce et d exlque l oto de l vleu temoelle de l get. Il ft îte clemet cq éoccutos : L dfféece ete les dfféets tyes d téêts (téêt smle,
L'impact de la prise en compte des sauts boursiers dans les problématiques d'assurance
 'mpc de l pre e compe de borer d le problémqe d'rce Frédérc PCHET Perre-E. THEROD α ISF Uveré yo β Joël Wer & océ γ RESUME objecf de ce rvl e de propoer modèle qe opéroel égr de por cf rqé, e géérl le
'mpc de l pre e compe de borer d le problémqe d'rce Frédérc PCHET Perre-E. THEROD α ISF Uveré yo β Joël Wer & océ γ RESUME objecf de ce rvl e de propoer modèle qe opéroel égr de por cf rqé, e géérl le
Angles orientés et fonctions circulaires ( En première S )
 Angles orientés et fonctions circulaires ( En première S ) Dernière mise à jour : Jeudi 01 Septembre 010 Vincent OBATON, Enseignant au lycée Stendhal de Grenoble (Année 006-007) Lycée Stendhal, Grenoble
Angles orientés et fonctions circulaires ( En première S ) Dernière mise à jour : Jeudi 01 Septembre 010 Vincent OBATON, Enseignant au lycée Stendhal de Grenoble (Année 006-007) Lycée Stendhal, Grenoble
Faites connaissance avec votre Rubik s Cube Étape 1
 Faites connaissance avec votre Rubik s Cube Étape 1 ÉFIN ITION ES IÈCES U RUBIK S CUBE LES RTIES LES IÈCES RÊTES CE SONT ES IÈCES COMORTNT EUX (2) COULEU RS. IL Y OUZE (12) IÈCES RÊTES, SITUÉES U CENT
Faites connaissance avec votre Rubik s Cube Étape 1 ÉFIN ITION ES IÈCES U RUBIK S CUBE LES RTIES LES IÈCES RÊTES CE SONT ES IÈCES COMORTNT EUX (2) COULEU RS. IL Y OUZE (12) IÈCES RÊTES, SITUÉES U CENT
1S Modèles de rédaction Enoncés
 Par l équipe des professeurs de 1S du lycée Parc de Vilgénis 1S Modèles de rédaction Enoncés Produit scalaire & Corrigés Exercice 1 : définition du produit scalaire Soit ABC un triangle tel que AB, AC
Par l équipe des professeurs de 1S du lycée Parc de Vilgénis 1S Modèles de rédaction Enoncés Produit scalaire & Corrigés Exercice 1 : définition du produit scalaire Soit ABC un triangle tel que AB, AC
VILLE DE VILLEURBANNE CONSEIL MUNICIPAL 5 JUILLET 2010. -ooo-
 VILLE DE VILLEURBANNE CONSEIL MUNICIPAL 5 JUILLET 2010 -ooo- La s é a n c e e s t o u v e r t e s o u s l a p r é s i d e n c e d e M o n s i e u r J e a n - P a u l BR E T, M a i r e d e V i l l e u r
VILLE DE VILLEURBANNE CONSEIL MUNICIPAL 5 JUILLET 2010 -ooo- La s é a n c e e s t o u v e r t e s o u s l a p r é s i d e n c e d e M o n s i e u r J e a n - P a u l BR E T, M a i r e d e V i l l e u r
Techniques d analyse de circuits
 Chpitre 3 Tehniques d nlyse de iruits Ce hpitre présente différentes méthodes d nlyse de iruits. Ces méthodes permettent de simplifier l nlyse de iruits ontennt plusieurs éléments. Bien qu on peut résoudre
Chpitre 3 Tehniques d nlyse de iruits Ce hpitre présente différentes méthodes d nlyse de iruits. Ces méthodes permettent de simplifier l nlyse de iruits ontennt plusieurs éléments. Bien qu on peut résoudre
Séquence 5. La fonction logarithme népérien. Sommaire
 Séquece 5 La foctio logarithme épérie Objectifs de la séquece Itroduire ue ouvelle foctio : la foctio logarithme épérie. Coaître les propriétés de cette foctio : sa dérivée, ses variatios, sa courbe, sa
Séquece 5 La foctio logarithme épérie Objectifs de la séquece Itroduire ue ouvelle foctio : la foctio logarithme épérie. Coaître les propriétés de cette foctio : sa dérivée, ses variatios, sa courbe, sa
Groupe orthogonal d'un espace vectoriel euclidien de dimension 2, de dimension 3
 1 Groupe orthogoal d'u espace vectoriel euclidie de dimesio, de dimesio Voir le chapitre 19 pour l'étude des espaces euclidies et des isométries. État doé u espace euclidie E de dimesio 1, o rappelle que
1 Groupe orthogoal d'u espace vectoriel euclidie de dimesio, de dimesio Voir le chapitre 19 pour l'étude des espaces euclidies et des isométries. État doé u espace euclidie E de dimesio 1, o rappelle que
La spirale de Théodore bis, et la suite «somme=produit».
 Etde d e vrite de l spirle de Théodore, dot issce à e site dot les sommes prtielles sot égles x prodits prtiels. Mots clés : spirle de Théodore, théorème de Pythgore, site, série, polyôme. L spirle de
Etde d e vrite de l spirle de Théodore, dot issce à e site dot les sommes prtielles sot égles x prodits prtiels. Mots clés : spirle de Théodore, théorème de Pythgore, site, série, polyôme. L spirle de
CERES logiciel de gestion commerciale pour négociants en vin
 CERES logicil gion commrcial pour négocian n vin. Gion complè acha vn : comman, rérvaion, gion courag commrciaux.. Moul campagn primur : piloag la campagn via un ablau bor prman viualir accér aux informaion
CERES logicil gion commrcial pour négocian n vin. Gion complè acha vn : comman, rérvaion, gion courag commrciaux.. Moul campagn primur : piloag la campagn via un ablau bor prman viualir accér aux informaion
Noël des enfants qui n'ont plus de maisons
 Chur SS Piano CLAUDE DEBUSSY Noël des enants qui n'ont lus de maisons (1915) Charton Mathias 2014 Publication Usage Pédagogique maitrisedeseinemaritimecom Yvetot France 2 Note de rogramme : Le Noël des
Chur SS Piano CLAUDE DEBUSSY Noël des enants qui n'ont lus de maisons (1915) Charton Mathias 2014 Publication Usage Pédagogique maitrisedeseinemaritimecom Yvetot France 2 Note de rogramme : Le Noël des
Guide de candidature Master 2 ARIA
 Guide de candidature Master 2 ARIA Avant de r emplir l e f ormulaire de candidature, no us vo us r ecommandons f ortement de lire attentivement les instructions ci-dessous. Une candidature comprend trois
Guide de candidature Master 2 ARIA Avant de r emplir l e f ormulaire de candidature, no us vo us r ecommandons f ortement de lire attentivement les instructions ci-dessous. Une candidature comprend trois
Inscription en ligne FQSC. Guide d utilisation
 Inscription en ligne FQSC Guide d utilisation Ce Guide est rédigé comme aide-mémoire pour l achat de votre licence sur le site internet de la FQSC. Dans un prem ier temps, vous devrez vous rendre sur le
Inscription en ligne FQSC Guide d utilisation Ce Guide est rédigé comme aide-mémoire pour l achat de votre licence sur le site internet de la FQSC. Dans un prem ier temps, vous devrez vous rendre sur le
logiciels Reconnus d Intérêts Pédagogiques, encyclopédies, dictionnaires, manuels scolaires,... ;
 Les m od es d u tilisation d e l A ctiv board et d A ctiv stu d io M od e 1 A ctiv board, La palette g raph iq u e et sa sou ris...p2 A ctiv stu d io O u tils et g rand s principes...p3 M od e 2 A ctiv
Les m od es d u tilisation d e l A ctiv board et d A ctiv stu d io M od e 1 A ctiv board, La palette g raph iq u e et sa sou ris...p2 A ctiv stu d io O u tils et g rand s principes...p3 M od e 2 A ctiv
«Trop de chats en refuge : Aidons-les!»
 q io iific bo ch Mlic g f! l o h c To i? co cio collboio vc Pl 5899 ch 7398 ch y éé boé C l ob félié qi, chq jo, o cibl joi fg Blgiq! 4641 ch l o l chc ov i à l g l fg fill i foy ê à l hx! C qlq chiff
q io iific bo ch Mlic g f! l o h c To i? co cio collboio vc Pl 5899 ch 7398 ch y éé boé C l ob félié qi, chq jo, o cibl joi fg Blgiq! 4641 ch l o l chc ov i à l g l fg fill i foy ê à l hx! C qlq chiff
* très facile ** facile *** difficulté moyenne **** difficile ***** très difficile I : Incontournable T : pour travailler et mémoriser le cours.
 Eo7 Fonctions de plusieurs variables Eercices de Jean-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-francefr * très facile ** facile *** difficulté moenne **** difficile ***** très difficile I
Eo7 Fonctions de plusieurs variables Eercices de Jean-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-francefr * très facile ** facile *** difficulté moenne **** difficile ***** très difficile I
N 1 2 1 L a R e v u e F r a n c o p h o n e d u M a n a g e m e n t d e P r o j e t 2 è m e t r i m e s t r e 2 0 1 3
 Du côté de la Recherche > Managemen t de projet : p1 L intégration des systèmes de management Qualité -Sécurité- Environnement : résultats d une étude empirique au Maroc Le co ntex te d es p roj et s a
Du côté de la Recherche > Managemen t de projet : p1 L intégration des systèmes de management Qualité -Sécurité- Environnement : résultats d une étude empirique au Maroc Le co ntex te d es p roj et s a
Dérivation : Résumé de cours et méthodes
 Dérivation : Résumé de cours et métodes Nombre dérivé - Fonction dérivée : DÉFINITION (a + ) (a) Etant donné est une onction déinie sur un intervalle I contenant le réel a, est dérivable en a si tend vers
Dérivation : Résumé de cours et métodes Nombre dérivé - Fonction dérivée : DÉFINITION (a + ) (a) Etant donné est une onction déinie sur un intervalle I contenant le réel a, est dérivable en a si tend vers
Ce document a été mis en ligne par le Canopé de l académie de Montpellier pour la Base Nationale des Sujets d Examens de l enseignement professionnel.
 Ce document a été mis en ligne par le Canopé de l académie de Montpellier pour la Base Nationale des Sujets d Examens de l enseignement professionnel. Ce fichier numérique ne peut être reproduit, représenté,
Ce document a été mis en ligne par le Canopé de l académie de Montpellier pour la Base Nationale des Sujets d Examens de l enseignement professionnel. Ce fichier numérique ne peut être reproduit, représenté,
La Cible Sommaire F o c u s
 La Cible Sommaire F o c u s F o n d a t e u r : J e a n L e B I S S O N N A I S D i r e c t e u r d e l a p u b l i c a t i o n : M a r t i n e M I N Y R é d a c t e u r e n c h e f : S e r g e C H A N
La Cible Sommaire F o c u s F o n d a t e u r : J e a n L e B I S S O N N A I S D i r e c t e u r d e l a p u b l i c a t i o n : M a r t i n e M I N Y R é d a c t e u r e n c h e f : S e r g e C H A N
x +1 + ln. Donner la valeur exacte affichée par cet algorithme lorsque l utilisateur entre la valeur n =3.
 EXERCICE 3 (6 poits ) (Commu à tous les cadidats) Il est possible de traiter la partie C sas avoir traité la partie B Partie A O désige par f la foctio défiie sur l itervalle [, + [ par Détermier la limite
EXERCICE 3 (6 poits ) (Commu à tous les cadidats) Il est possible de traiter la partie C sas avoir traité la partie B Partie A O désige par f la foctio défiie sur l itervalle [, + [ par Détermier la limite
