Introduction : Mesures et espaces de probabilités
|
|
|
- Henri Lebel
- il y a 8 ans
- Total affichages :
Transcription
1 Itroductio : Mesures et espaces de probabilités Référeces : Poly cédric Berardi et Jea Michel Morel. J.-F. Le Gall, Itégratio, Probabilités et Processus Aléatoire J.-Y. Ouvrard, Probabilités 2, maîtrise-agrégatio, Cassii, (2) D. Williams, Probability with martigales, Cambridge Uiversity Press, (1991) Durrett R., Probability : Theory ad examples, Duxburry, (1995). Grimmett G., Stirzaker D., Probability ad Radom Processes, Oxford Uiversity Press, Third Editio, (21) Lecos : Loi des grads ombres. Théorème de la limite cetrale. Applicatios. Idépedace d évéemets et de variables aléatoires. Exemples. Suite de va de beroulli idepedates Utilisatio e probas de la trasformatio de Fourier ou de Laplace et du produit de covolutio. Nous sommes habitués à muir u espace Ω d ue topologie pour regarder des covergeces. Nous allos ici le muir d ue tribu pour mesurer des esembles et itégrer. Nous avos surtout e tête de regarder des tribus egedrées par ue topologie pour faire les deux et cosidèrer des mesures de masse 1, c.a.d. des probabilités. 1 Algèbres, tribus, π-systèmes, λ-systèmes et espaces mesurables Soit Ω u esemble quelcoque. O commece par défiir toute ue typologie de collectios d esembles que l o utilisera tout au log du cours. Défiitio 1.1. (π,λ-systèmes, algèbres et tribus) 1. Ue classe P de sous-esembles de Ω est appelée u π-système ssi : A, B P A B P 2. Ue classe F de sous-esembles de Ω est appelée ue algèbre ssi : i) Ω F. ii) F F F c F. iii) F, G F = F G F. 3. Ue classe F de sous-esembles de Ω est ue tribu (ou σ-algèbre) ssi : i) F est ue algèbre. 1
2 ii) Si F F pour tout N alors N F F. Défiitio 1.2. (λ-systèmes) Ue classe L de sous-esembles de Ω est appelée u λ-système ssi : i) Ω L. ii) Si A, B L et A B alors B\A L. iii) Si (A ) N est ue suite croissate d élémets de L alors N A L. Remarque 1.1. (i) U tribu est ue algèbre (qui est u π système) et u λ système. U λ système est pas forcemet u π système (et doc ue tribu), à cause de l itersectio. Predre par exemple {, A, B, Ω A, Ω B, Ω} qui est u λ système mais e cotiet pas A B. Ue algèbre est u π système, mais pas forcémet vrai u λ système. Les parties de N fiies ou de complémetaires fiies formet ue algèbre mais pas u λ système à cause des etiers pairs, tout commes les uios fies d itervalles semi-ouverts. (ii) La différece etre topologie et tribu? Le passage par complemetaire marche pour les tribus (pas pour les topologies) mais pour les tribus l uio doit etre déombrable. La topologie est doée par l uio quelcoque d itersectio fiie d élémets des esembles qui l egedret (ces itersectios sot des bases de voisiage), la tribu c est plus compliqué... (iii) O peut remplacer les stabilités par itersectio par des stabilités par uio pour l algèbre (et doc la tribu, mais pas le λ système) qui possèdet le passage au complémetaire et à l uio, et l uio par ue uio disjoite ou croissate pour la tribu. (iv) Ue itersectio quelcoque (déombrable ou pas) de π-systèmes, λ-systèmes, d algèbres ou de tribus est (respectivemet) u π-système, u λ-système, ue algèbre ou ue tribu. (v) Le π-système, le λ-système, l algèbre ou la tribu egedrée par ue partie χ est l itersectio de tous ceux coteat χ. (vi) Vous savez egedrer ue topologie par ue base de voisage e preat l uio quelcoque d itersectio fiie d élémet de cette base. Le coi du curieux (cf le cours d Amaury Lambert à Jussieu e L3, TD 4). O pourrait peser (au vue aussi de certais cas particuliers) que trouver la tribu egedrée par ue classe C se fait e ajoutat à C les uios déombrables et les complémetaires des parties de C. Maque de chace, cela e marche pas toujours, otammet pour le cas de la tribu boréliee sur R. Et ce même si c est u π système (ou que l o ajoute les itersectios déombrables). Si l o obtiet aisi ue tribu, o a bie trouvé la tribu egedrée par (C). Si l o procède de la sorte e partat des itervalles réels, o e tombe e effet pas sur ue tribu. Il faut e fait itérer ce processus par récurrece trasfiie pour obteir la tribu des borélies. Cela explique pourquoi il est impossible de fourir ue descriptio explicite complète des borélies de R. O peut motrer que la tribu boréliee sur R a la puissace du cotiu, ce qui motre l existece de o-borélies (car P(R) a ue puissace strictemet supérieure à celle du cotiu). Propositio 1.1. Ue collectio de sous-esembles de Ω est ue tribu ssi c est à la fois u λ-système et u π-système. Le théorème suivat est fodametal das tout ce qui suit et otammet das la démostratio du théorème de Carathéodory dot ous parleros plus loi. Théorème 1.1. (Dyki) Si P est u π-système coteu das u λ-système alors ce λ-système cotiet la tribu egedrée par ce π-système. 2
3 Démostratio. Voir TD. Itérêt : Motrer que les esembles vérifiat ue propriété P formet u λ système qui cotiet u π système pour obteir que la tribu egedrée par le π système vérifie P. Défiitio 1.3. Espace mesurable Ue paire (Ω, F), où Ω est u esemble et F est ue tribu sur Ω, est appelée u espace mesurable. U élémet de F est appelé u esemble F-mesurable. Passos maiteat à u exemple fodametal d espace mesurable. Soit S u espace topologique mui de sa famille S d ouverts. O appelle tribu boréliee sur S la tribu egedrée par S. O la ote B(S) et ses élémets sot appelés les borélies de S. Cette tribu est egedrée (par exemple) par l ue des classes suivates (qui sot des π système), voir TD : { d } { d } { d } i=1 [a i ; b i ]; a i, b i R, i=1 ( ; b i ]; b i R, i=1 [a i ; + ); a i R Les élémets de B(R d ) peuvet être très compliqués mais il est possible de costruire des esembles o borélies (voir TD) 2 Mesure Défiitio 2.1. Soit µ ue applicatio de F das [, + ]. 1. µ est dite additivemet déombrable si pour toute suite d élémets disjoits F F tels que F F, µ( F ) = µ(f ). 2. µ est appelée mesure sur u espace (Ω, F) mesurable ssi µ( ) = et µ est additivemet déombrable. Remarque 2.1. L addititive déombrabilité de la mesure etraîe sa mootoie : si A A avec A F, alors µ(a ) A. Bie sur préciser µ( ) = est iutile par 2) si µ est pas idetique à l ifii car µ( ) = µ( ). Tout comme préciser F F est iutile das 2) ici mais utile das Carathéodory. O dira que la mesure µ est fiie (ou de masse fiie) ssi µ(ω) < +. O dira qu elle est σ-fiie ssi il existe ue suite (Ω ) d esembles mesurables tels que µ(ω ) < + et Ω = Ω. O appelera probabilité toute mesure µ de masse µ(ω) égale à 1. (Ω, F, µ) est alors appelé u espace probabilisé ou espace de probabilité. O peut compléter u espace mesuré (Ω, F, µ) e ajoutat les esembles égligeables, i.e. les esembles X tels qu il existe Z F coteat X de mesure ulle. Pour les Borelies, o obtiet la tribu des Lebesguies. O e peut espérer avoir µ( x I F x ) = x I µ(f x) e gééral comme o peut le voir avec l esemble o déombrable I = [, 1], F x = {x} et la mesure de Lebesgue (o obtiet 1 = ). 2.1 Prologemet de mesures Le problème posé est le suivat et est bie illustré par le cas de la mesure de Lebesgue λ. O cherche à défiir ue mesure λ sur (R, B(R)) telle que pour tous réels a < b, λ(]a, b[) = b a. Première questio : existe-t-il ue telle mesure? Si oui, est-elle uique? Théorème 2.1. (Carathéodory) Soit Ω u esemble mui d ue algèbre F et soit F la tribu egedrée par cette algèbre. Si µ est ue applicatio déombrablemet additive µ : F [; + ] alors il existe ue mesure µ sur (Ω, F) telle que Si µ (Ω) < + alors cette extesio est uique. µ = µ sur F 3
4 Pour obteir la mesure de Lebesgue sur ((, 1], B((, 1])), o peut predre comme algèbre avec r N et a 1... a r b r 1. F = (a 1, b 1 ]... (a r, b r ] Pour la preuve, o commece par établir que deux mesures qui coïcidet sur u π-système (ou doc ue algèbre) coïcidet aussi sur la tribu qu egedre ce π-système (ou cette algèbre). Propositio 2.1. (d uicité des prologemets de mesures) Soit Ω u esemble mui d u π-système P et soit F = σ(p). Supposos que l o ait deux mesures µ 1 et µ 2 sur F de même masse fiie, µ 1 (Ω) = µ 2 (Ω), qui coïcidet sur P. Alors µ 1 = µ 2 Ce résultat (comme d autres plus loi) se gééralise aux mesure σ fiie par limite croissate. Pour le prouver, o défiit la classe D = {F F; µ 1 (F ) = µ 2 (F )}. Il est facile de voir que c est u λ-système puisque puisque le fait que les deux mesures aiet même masse motre que Ω D et les masses fiies assuret que D est stable par différece propre. Doc par le théorème de Dyki, D cotiet F. Passos maiteat à la preuve du théorème de Carathéodory. Démostratio. (Théorème de Carathéodory). Nous idiqueros que les pricipales étapes, les détails état parfaitemet expliqués das [Williams, Probability with martigales]. Etape 1 : Soit P(Ω) la tribu composée de toutes les parties de Ω. Pour u G P(Ω), o défiit { } λ(g) = if µ (F ) où l ifimum est pris sur toutes les suites (F ) d élémets de F qui recouvret G, i.e. G F. λ est pas ue mesure mais est ce que l o appelle (impropremet) ue mesure exterieure, c est-à-dire qu elle jouit des propriétés suivates : a) λ( ) =. b) λ est croissate : G 1 G 2 λ(g 1 ) λ(g 2 ). c) λ est déombrablemet sous-additive : si (G k ) k est ue suite d élémets de P(Ω) alors λ ( k G k ) k λ(g k ) Seule c) mérite d être expliquée. Soit (G ) ue suite supposée telle que pour chaque, λ(g ) < + (sio c est trivial). O se doe ε > et pour chaque, o se doe ue suite d élémets (F,k ) k de F pour lesquels G k F,k, µ (F,k ) λ(g ) + ε2. Alors G,k F,k et o a : λ(g),k k µ (F,k ) Puisque ε est arbitraire, e le faisat tedre vers, o obtiet c). λ(g ) + ε. Etape 2 : O itroduit alors la otio de λ-esembles. U élémet L de P(Ω) est appelé u λ-esemble ssi il décompose tout élémet de P(Ω) propremet, c est-à-dire : λ(l G) + λ(l c G) = λ(g), G P(Ω) 4
5 Lemme 2.1. Les λ-esembles formet ue tribu L sur laquelle λ est déombrablemet additive si bie que (Ω, L, λ) est u espace mesuré. Démostratio. Motros ce lemme. L est ue algèbre qui jouit de la propriété suivate : Si L 1, L 2,..., L sot des élémets de L disjoits et G P(Ω) ue partie quelcoque de Ω alors λ ( k=1(l k G)) = λ(l k G) k=1 Nous avos doc à démotrer que si (L k ) k est ue suite d élémets disjoits de L alors L = k L k L (cf. la remarque après la défiitio de la otio de tribu) et ( ) λ(l) = k λ(l k ) Par sous-additivité de λ, o a pour tout G P(Ω) : λ(g) λ(l G) + λ(l c G) Passos maiteat à l iégalité iverse. Soit M = k L k. Puisque L est ue algèbre (cf ce qui précède), M L doc Or L c M c si bie que et par ( ), λ(g) = λ(m G) + λ(m c G) λ(g) λ(m G) + λ(l c G) λ(g) λ(l k G) + λ(l c G) k=1 Par passage à la limite quad +, o obtiet λ(g) λ(l k G) + λ(l c G) λ(l G) + λ(l c G) k=1 la deuxième iégalité état ue coséquece de la sous-additivité de λ. O e déduit que L L. D autre part, puisque la derière iégalité est e fait ue égalité, o voit qu il e est de même des autres et que fialemet λ(l G) = k λ(l k G) Il suffit maiteat de predre G = Ω pour coclure. Il ous reste à voir que F L et λ = µ sur F pour achever la preuve du théorème. Etape 3 : Preuve que λ = µ sur F. Soit F F. O a bie etedu λ(f ) µ (F ). Supposos maiteat que F F où F F. O défiit ue suite (E ) d élémets disjoits de F par : E 1 = F 1, E = F ( k< F k ) c 5
6 si bie que E F et F F = E. E utilisat la σ-additivité de µ sur F, o a µ (F ) = µ ( (F E )) = µ (F E ) Doc µ (F ) µ (E ) µ (F ) si bie que λ(f ) µ (F ) ce qui coclut la troisième étape. Etape 4 : Preuve de F L. Il ous faut voir que si E est u élémet de F alors E décompose propremet les élémets de P(Ω). Soit doc G P(Ω) et soit pour ε > quelcoque ue suite (F ) d élémets de F tels que G F avec µ (F ) λ(g) + ε Par défiitio de λ, µ (F ) = µ (E F ) + µ (E c F ) λ(e G) + λ(e c G) car E G (E F ) et E c G (E c F ). Puisque ε est aussi petit que l o veut, Puisque λ est sous-additive, Doc E est u λ-esemble. λ(g) λ(e G) + λ(e c G) λ(g) λ(e G) + λ(e c G) 2.2 Foctios mesurables Défiitio 2.2. Ue foctio f : (Ω, F) (R d, B(R d )) sera dite mesurable si A B(R d ), f 1 (A) F. O dit qu elle est boréliee quad (Ω, F) (R, B(R )). O doe maiteat ue versio foctioelle du Théorème de Dyki, souvet utile et appliquée sous ue forme das la costructio de l itégrale esuite. Exercice 2.1. (Théorème de la classe mootoe, D. Williams, Probability with martigales, p. 25 ) Soit H ue classe de foctios borées de Ω das R vérifiat (i) H est u espace vectoriel sur R (ii) la foctio costate 1 est u élémet de H (iii) si f est ue suite croissate de foctios positives de H, tedat vers ue foctio f borée sur Ω, alors f H. Alors, si H cotiet les foctios idicatrices de tous les esembles d u π-système I, H cotiet aussi toutes les foctios σ(i)-mesurables et borées sur Ω. 6
7 1) Soit D la classe des esembles F tels que 1 F H. Motrer que D est u λ-système et e déduire que D cotiet σ(i). 2) Soit f ue foctio σ(i)-mesurable telle qu il existe K N, f(s) K, s Ω. Pour N, o cosidère les foctios e escalier approximat f, où f (s) = i2 1 A(,i) (s), K2 i= A(, i) = {s, i2 f(s) (i + 1)2 }. Motrer que f H, puis que f H. E déduire le théorème. 3 Exercices : Algèbres, tribus et compagie Exercice 3.1. Motrer que la tribu des borélies de R est egedrée par : 1. la classe des itervalles ouverts borés 2. la classe des itervalles borés [a; b) 3. la classse des demi-droites ouvertes ( ; a) 4. la classse des demi-droites fermées ( ; a] Idicatio : Obteir la première e utilisat que tout ouvert est l uio déombrable disjoite d itervalles ouverts (o motre cela e cosidérat la relatio d équivalece xry ssi [x, y] O) et e écrivat u itervalle o boré comme l uio de ses restrictios à [, ] pour N. Exercice 3.2. Exercice (Lemme de Dyki) (Williams, p 193) U π-système est u esemble de parties de Ω stable par itersectio fiie. U λ-système est u esemble L de parties de Ω qui est stable par différece propre et uio déombrable croissate et tel que Ω L. 1) Démotrer qu ue collectio Σ de sous-esembles de Ω est ue tribu si et seulemet si Σ est à la fois u π-système et u λ-système. 2) O va motrer que si I est u π-système, alors la tribu σ(i) egedrée par I et le λ-système egedré par I sot égaux : λ(i) = σ(i). La démostratio est détaillée das les deux questios qui suivet. 2a) Soit D 1 = {B λ(i) : C I, B C λ(i)}. Motrer que D 1 hérite de la structure de λ-système de λ(i). E déduire que D 1 = λ(i). 2b) Posos D 2 = {A λ(i) : B λ(i), B A λ(i)}. Motrer que D 2 cotiet I et hérite de la structure de λ-système de λ(i). E déduire que D 2 = λ(i) est u π-système. 3) Déduire le théorème de Dyki : Soit P u π-système et L u λ-système tel que P L. Alors la tribu egedrée par P est coteue das L. Idicatios 2.a) D 1 est u λ système qui cotiet I et qui est iclus das λ(i) doc D 1 = λ(i). 2.b)Le fait que D 2 cotiet I se déduit de 2a). Puis e substituat λ(i) à I das 2a) et e remarquat que λ(λ(i)) = λ(i), o obtiet D 2 = λ(i) Exercice 3.3. (Il y a pas de tribu déombrable. Cet exercice est extrait de Le Calcul Itegral, H. Buchwalter (e doe pas la correctio).) Soit F ue tribu sur Ω supposée au plus déombrable. 7
8 a) Démotrer que tout ω Ω est coteu das u plus petit élémet de F. b) E déduire que F est exactemet la tribu egedrée par ue partitio au plus déombrable. c) Motrer alors que F est écessairemet fiie de cardial ue puissace de 2 et que doc il existe pas de tribu déombrable au ses strict. d) Trouver toutes les tribus de N. Réposes : a) Predre l itersectio des élémets de F coteat w. b) O ote F (w) l esemble miimal précédet. La famille {F (w) : w Ω} forme ue partitio pour w Ω. E effet supposos F (w 1 ) F (w 2 ). Alors w 1 F (w 2 ) puisque w 1 / F (w 1 ) F (w 2 ) et doc F (w 1 ) F (w 2 ) puis par symétrie F (w 1 ) = F (w 2 ). Cette famille est au plus déombrable car F l est. Elle egedre la tribu car si F F alors F = w F F (w) puisque w F implique F (w) F. c) La tribu egedrée par ue partitio fiie A 1,, A k fii est doée par k i=1 (A i ou A c i )et a u cardial égal à ue puissace de deux. La tribu egedrée par ue partitio ifiie est o déombrable car elle cotiet (au mois) {, 1} N. d) Toutes les tribus egedrées par ue partitio de N. E effet, o peut ecore motrer la propriété a) : soit et preos pour tout ue partie A coteat telle que / A (si u tel A existe : sio predre A = N). O pose F ( ) = A. Esuite o motre comme pour b) que ces esembles formet ue partitio qui egedre la tribu. Exercice 3.4. (Exemple d esemble o borélie) (Williams, p 192) Soit (R, B(R), λ) l espace des réels mui de la tribu boréliee et de la mesure de Lebesgue. 1) O défiit la relatio biaire suivate sur R xry ssi x y Q Motrer que R est ue relatio d équivalece. 2) O désige par C l esemble des classes d équivalece. Motrer que pour toute classe C C il existe x C [, 1). O choisit alors pour chaque classe C u x C vérifiat la propriété précédete et o ote A = {x C /C C}. 3) Motrer que [, 1] q + A [ 1, 2) q [ 1,1] Q et que les q + A sot deux à deux disjoits. 4) E supposat A borélie, aboutir à ue cotradictio. Exercice 3.5. Ouvert dese de mesure petite : Hauchecore, Les cotre-exemples e mathématiques, pp Motrer qu il existe u ouvert de R coteat Q et de mesure iférieure à ε. Remarquer que cela prouve qu il y a des ouverts deses de mesure aussi petite qu o veut. Idicatio : éumérer les ratioels q, N et cosidérer les itervalles ] q, q [. Exercice 3.6. (Esembles de Cator) (Hauchecore, Les cotre-exemples e mathématiques, pp ) O cosidère pour < α < 1 l opératio suivate S α : elever à u itervalle [a, b] so itervalle cetral ] a + b 2 α b a 2, a + b + α b a 2 2 [. Soit E R ue uio fiie d itervalles disjoits. O ote s α (E) le résultat de l applicatio de s α à tous les itervalles de E. Quad α = 1 3, l esemble K 1 = 3 1 s 1 ([, 1]) est appelé esemble triadique de Cator. 3 Plus gééralemet, si α = (α 1,..., α,...) est ue suite de coefficiets < α < 1, o pose ecore K α = s α s α 1...s α1 ([, 1]), K α = 1 K α. 1) Motrer que pour toute suite α, l esemble K α est u compact d itérieur vide, équipotet à l esemble des suites biaires (gauche, droite) N. 8
9 Idicatio : tout élémet de K α est défii de maière uique par le fait qu il appartiet à l itervalle de droite ou de gauche de K 1 α, puis au sous itervalle de cet itervalle de gauche ou de droite das K 2 α, etc. E déduire que K α est équipotet à [, 1]. 2) Motrer que K α est de mesure strictemet positive si et seulemet si α < +. E déduire qu il y a des esembles borélies équipotets à R et de mesure ulle et des fermés de mesure positive et d itérieur vide. Idicatio : La mesure de K α est Π i 1 (1 α i ). Exercice 3.7. (Il existe u esemble égligeable et o borélie) 1) Soit K l esemble triadique de Cator. Motrer que c est u compact o vide (doc borélie) égligeable de R. 2) Motrer par récurrece que l o peut défiir ue suite d applicatios ɛ : [, 1) {, 1}, 1 telle que O défiit alors pour x das [, 1) x [, 1), 1, i=1 f(x) = ɛ i (x) 2 i x < i=1 2ɛ i (x) 3 i Motrer que f est strictemet croissate, ijective et boréliee. 3) Soit A l esemble o borélie de léxercice Motrer que f([, 1)) K 2. Motrer que f(a) est égligeable pour λ. 3. E utilisat l ijectivité de f, établir que f(a) est pas borélie. i=1 ɛ i (x) 2 i Exercice 3.8. Les seules mesures sur R fiies sur les borés et ivariates par traslatio sot des multiples de la mesure de Lebesgue. (Problème 12.1 p. 18 du Billigsley). Solutio : appeler a la mesure d u itervalle de logueur 1, motrer d abord que les itervalles de logueur 1 ot mesure a, puis que les itervalles de logueur ratioelle q ot mesure aq, fialemet que les itervalles de logueur quelcoque b ot mesure ab. Déduire que la mesure cosidérée coïcide sur u π-système qui egedre les borélies avec la mesure de Lebesgue et coclure. Exercice 3.9. La formule du crible. Soit µ ue mesure sur u espace mesurable (Ω, F) et A 1,..., A F. 1) Motrer que par récurrece que P ( i=1a i ) = ( 1) p+1 p=1 1 i 1<...<i p P (A i1... A ip ). 2) Motrer par récurrece sur que pour 1 m, m ( 1) p+1 p=1 1 i 1<...<i p P (A i1...a ip ) est ue majoratio (resp. mioratio) de P ( i=1 A i) lorsque m est impair (resp. pair). Exercice 3.1. (Théorème de Sard) Soit f ue foctio C 1 d u ouvert de R das lui-même. O appelle poit sigulier de f u poit x R tel que Df(x) est o iversible. O ote Df(x) le jacobie de f. 9
10 L esemble des poits siguliers est doc S(f) = ( Df ) 1 (). Le théorème de Sard dit simplemet que l esemble f(s(f)) est de mesure ulle. 1) Se covaicre que l o peut se coteter de motrer le théorème de Sard quad f est défiie sur u compact. Alors S(f) est compact. 2) O ote B(x, r) la boule de cetre x et de rayo r. Soit x S(f). E écrivat la formule de Taylor, f(x) = f(x ) + Df(x )(x x ) + o( x x ), motrer qu il existe u sous-espace propre V de R N et ue costate C tels pour tout ε > il existe r > tel que où B V (, r) désige la boule de rayo r das V. f(b(x, r)) f(x ) + B V (, Cr) + B(, εr), 3) Soit K u compact de R. Motrer qu il existe C > tel que pour tout r >, K soit recouvert par des cubes (C i,r ) i I de diamètre r et i mesure(c i,r) C. 4) E recouvrat S(f) comme idiqué das la questio précédete, motrer le résultat aocé. Solutio : O écrit R N = KerDf(x ) (KerDf(x )) et, sur cette somme orthogoale d espaces, o décompose x x = y+z, de sorte que y r, z r si x x B(, r). O ote V = Df(x )(KerDf(x ) ). Doc si x x < r assez petit, f(x) = f(x ) + Df(x )(z) + o(x x ) f(x ) + B V (, Cr) + B(, εr), avec C = Df(x ) et où B V (, Cr) est la boule de cetre et de rayo Cr das V. O vérifie aisémet que la mesure de f(b(x, r)) est alors plus petite que C 1 r N ε d où d est la dimesio de KerDf(x ) et C 1 ue costate adéquate. O coclut esuite avec le recouvremet fii par des cubes, e sommat les mesures des cubes de diamètres (qui sot iclues das les boules de diamètres) r, ce qui majore la mesure globale par ɛr.#i r ɛc. 4 Itégrale cotre ue mesure O doe ici les grades liges pour la costructio de l itégrale cotre ue mesure fiie et l objectif sera d itégrer cotre ue probabilité P et d itroduire l espérace d ue variable aléatoire X comme f(x)µ(dx), E(X) := X(ω)P(dω) O peut e fait étedre cette costructio à des mesures σ fiie par limite croissate. Ω 4.1 Costructio : la machie stadard Etape 1. Soit f ue foctio simple (ou étagée) positive, c est-à-dire de la forme N f = a k 1 Ak k=1 où les a k sot des réels positifs et A k des élémets de F. O défiit l itégrale de f relativemet à µ par N fµ = a k µ(a k ) k=1 1
11 O vérifie aisémet que cette défiitio est cohérete, c est-à-dire qu elle e déped pas de l écriture de f choisie. D autre part, des propriétés simples comme la liéarité, la positivité se démotret aisémet. O peut costruire des modes d approximatio simples pour ue foctio mesurable positive. Par exemple si f est positive mesurable, f k := k2 k 1 l= l 2 k 1 [ l l+1 2k f< 2 k ] + k 1 [f k] coverge simplemet vers f et uiformémet si f est e plus borée. Ceci motive la défiitio suivate et préfigure les résultats de passage à la limite mootoe (Beppo-Lévy) Etape 2. Soit maiteat f ue foctio positive mesurable. O défiit so itégrale par fµ = sup{ hµ : h foctio simple positive, h f} Cette quatité peut être ifiie et o dira que f est itégrable si elle est fiie. O vérifie que si h est ue foctio simple positive, alors cette ouvelle défiitio reste cohérete avec l aciee. O vérifie sas mal la liéarité de l itégrale. Viet alors le théorème de covergece mootoe pour les foctios mesurables positives : Si (f ) est ue suite de foctios mesurables positives covergeat e croissat µ p.p. vers ue foctio f (mesurable positive) alors f µ f (4.1) Cette démostratio est pas difficile car ce théorème viet essetiellemet du fait que si A A, alors µ(a ) µ(a). Voici la marche de la démostratio. O va la faire das le cas fµ < + ; le cas fµ = + suit exactemet la même démarche. O commece par remarquer qu il existe ue suite croissate de foctios simples g telle que g µ fµ et g f p.s. Pour cela o pred ue suite croissate g de foctios simples telles que g µ fµ. O peut toujours remplacer g par sup i=1,..., g i, qui est bie ue suite croissate. O motre alors que g f p.s., par l absurde E effet, si µ(sup g < f) >, par la propriété de cotiuité de la mesure pour les suites croissates pour quelque η >, l esemble A := {g f η} est de mesure strictemet positive. Alors e remplaçat g par h := g + η 1 A, o arrive à ue cotradictio car h g et gµ h µ g µ + ηµ(a) gµ + ηµ(a). Fixos maiteat g telle que g f et gµ fµ ε. Par l étape précédete des foctios simples g telles que P(g f ε) < 1 2. O remarque que par l étape précédete g g ted vers g p.p. et qu il ous suffit de motrer que gµ ted vers gµ. Comme P(g g ) > ε, o peut predre assez grad pour que cette probabilité soit plus petite que ε. Comme g et g sot simples, e ommat A k la famille fiie des itersectios d esembles où elles sot chacue costates, o peut écrire g = k a k 1 Ak et g = k b k 1 Ak et o a alors P( k bk a k >εa k ) ε. Il suffit d exprimer les espéraces de ces deux foctios simples pour coclure que gµ g µ < ε + ε sup g. Le lemme de Fatou se déduit aisémet du théorème de covergece mootoe. O démotre aussi à ce stade la liéarité et la positivité de l espérace. Etape 3. Soit f ue foctio mesurable de sige quelcoque. O décompose f e sa partie positive f + = sup(f, ) et sa partie égative f = sup( f, ) si bie que f = f + f et f = f + + f. O dira 11
12 que f est itégrable ssi f l est (ce qui implique que f + et f le sot). Si f est itégrable, o défiit so espérace par fµ = f + µ f µ L esemble des foctios itégrables forme u espace vectoriel sur lequel l espérace aisi défiie est ue forme liéaire positive. C est à ce stade que le théorème de covergece domiée s établit modulo le lemme de Sheffé (voir TD). O remarquera que la costructio de l itégrale se fait selo trois grades étapes : o commece par défiir l espérace sur les foctios simples, puis sur les foctios mesurables positives grâce à ue propriété de mootoie et efi o passe au cas d ue foctio de sige quelcoque grâce à la décompositio de f e sa partie positive et sa partie égative. Cette structure e trois étapes est costammet utilisée das diverses preuves. O peut aussi souvet s appuyer das ce gere de démarche sur le Théorème de la classe mootoe doé précedemmet. 4.2 Rappel : Itégrale de Lebesgue Nous rappelos ici les résultats pricipaux et doos u certai ombre d exercices plus ou mois stadards. Théorème 4.1. (Beppo Levi, ou covergece mootoe) Si f est ue suite croissate de foctios défiies sur R N et à valeurs das R + {+ }, o a lim f (x)dx = lim f (x)dx +. Corollaire 4.1. Soit u (x) ue suite de foctios défiies sur R N et à valeurs das R + {+ }. O peut alors l itégrer terme à terme, c est-à -dire que Σ =1u (x)dx = Σ =1 u (x)dx +. Théorème 4.2. (Théorème de Lebesgue) Soit f (x) ue suite de foctios qui coverge presque partout vers ue foctio f. O suppose qu il existe ue foctio positive sommable fixe h telle que pour tout, f (x) h(x) pour presque tout x. Alors f (x) f(x) dx, f (x)dx f(x)dx. Théorème 4.3. (Réciproque du théorème de Lebesgue). Si f f das L 1, alors il existe ue sous-suite f k de la suite f qui coverge presque partout vers f et u chapeau itégrable h tel que k, f k (x) h(x) p.p.. Théorème 4.4. (Théorème de dérivatio sous le sige somme) Soiet I u itervalle de R et A u sousesemble de R. O se doe ue foctio f défiie sur A I vérifiat les trois hypothèses suivates. (a) Pour tout λ I, la foctio x f(x, λ) est sommable sur A. (b) La dérivée partielle f λ (x, λ) existe e tout poit de A I. (c) Il existe ue foctio h positive et sommable sur A telle que l o ait f λ (x, λ) h(x) pour tous x et λ. Alors la foctio F défiie par F (λ) = f(x, λ)dx est dérivable das I et o a F (λ) = A A f (x, λ)dx. λ 12
13 Théorème 4.5. (de chagemet de variable, Buchwalter H., Le Calcul irégral) Soiet Ω 1 et Ω 2 deux ouverts de R et ϕ u difféomorphisme etre Ω 1 et Ω 2. O otera J ϕ (x) le détermiat de la matrice jacobiee de ϕ au poit x. Soit f ue foctio défiie sur Ω 2. (a) Si la foctio f est à valeurs das R + {+ }, o a l égalité suivate, où les deux membres ot u ses das R + {+ }, f(y)dy = Ω 2 f(ϕ(x)) J ϕ (x) dx. Ω 1 (b) Si f est à valeurs complexes, elle est sommable das Ω 2 si et seulemet si f(ϕ(x))j ϕ (x) est sommable das Ω 1, et les deux membres de l égalité précédete sot alors égaux. Théorème 4.6. (Fubii) Soit f(x, y) ue foctio défiie das R p R q. (a) Si f est à valeurs das R + {+ }, o a l égalité suivate, où les trois membres défiisset u élémet de R + {+ }, ( f(x, y)dxdx = f(x, y)dy ) ( dx = f(x, y)dx ) dy. R p+q R p R q R q R p Si f est sommable das R p+q, les trois membres de l égalité précédete ot u ses et sot égaux. Plus précisémet, dire que le troisième membre a u ses sigifie : pour presque tout y, la foctio x f(x, y) est sommable das R p, la foctio ϕ(y) = f(x, y)dx qui est aisi défiie presque partout est sommable das R q. 4.3 Exercices Exercice 4.1. Tout graphe est de mesure ulle. 1) Démotrer que le graphe d ue applicatio cotiue f de R das R est u sous-esemble de mesure ulle das R 2. (O motrera que la portio du graphe comprise etre les abcisses k et k peut être recouverte par des rectagles dot la somme des mesures est arbitrairemet petite). 2) Même questio si f L 1 loc (R), puis si f est boréliee. Solutio Comme [ k, k] est u compact, la foctio f cosidérée est uiformémet cotiue sur [ k, k]. Il existe doc N tel que x y 1 ε, x, y [ k, k] f(x) f(y) 4k. O recouvre [ k, k] par itervalles cosécutifs de logueur 2k. O vérifie aisémet que les 2 rectagles [l 1, (l+1) 1 ] [f((l+ 1 2 ) k ) ε 4k, f((l ) k ) + ε 4k )], l =, ( 1),..., 1 recouvret le graphe de f sur [ k, k]. Doc la mesure de ce graphe est plus petite que 2 2k ε 4k = ε. Solutio plus élégate : Soit ϕ : R 2 R défiie par ϕ(x, y) = y f(x). Alors ϕ 1 () = {(x, f(x)), x R} et par le théorème de Fubii-Toelli, λ({(x, f(x)), x R}) = ( 1 y=f(x) (x, y)dy)dx = car les sigletos sot de mesure de Lebesgue ulle. R Exercice 4.2. Soit A u borélie de R N et soit h égale à + das A et à das so complémetaire. Démotrer que l o a h(x)dx = si λ(a) =, h(x)dx = + si λ(a) >. R N R N R 13
14 Supposos que λ(a) =. O pose h k (x) = mi(h(x), k). Comme A est de mesure ulle, o a par défiitio de λ(a), 1 A dx = λ(a) =. Doc h k (x)dx = k 1 A dx =. Par le théorème de la covergece mootoe, h(x)dx = lim k h k (x)dx =. Si maiteat λ(a) >, o a, ecore par le théorème de la covergece mootoe, h(x)dx = lim h k (x)dx = lim kλ(a) = +. k k O déduit immédiatemet que si f vérifie f <, alors l esemble A = {x, f(x) = + } est de mesure ulle. Exercice 4.3. Soit f et g deux foctios cotiues telles que f(x) = g(x) p.p.. Motrer que f et g sot égales partout. Solutio : Comme les boules sot de mesure strictemet positive, o déduit que f(x) = g(x) sur u esemble dese de R N, et, par cotiuité, partout. Exercice 4.4. Soit f ue foctio itégrable sur R. Démotrer que b a f(x)dx R f(x)dx quad a, b +. Gééralisatio : soit A ue suite croissate d esembles tels que A = R N. Démotrer que R N f(x)dx = lim A f(x)dx. Solutio : Appliquer le théorème de covergece domiée de Lebesgue à la suite (f 1 A ). Exercice 4.5. Soit h ue foctio positive itégrable sur R N et A des borélies de R N tels que λ(a ). Démotrer que A h(x)dx quad. Solutio Notos [h M] l esemble {x, h(x) M}. O écrit h(x) h(x)dx + h(x)dx Mλ(A ) + A A [h(x) M] A [h(x)>m] [h(x)>m] h(x)dx. (4.2) Par le théorème de la covergece domiée, o a [h(x)>m] h(x)dx. E effet, h(x) 1 [h(x)>m] ted vers zéro presque partout car λ([h = + ]) = et h(x) est chapeau itégrable. O peut doc fixer pour tout ε >, M tel que [h(x)>m] h(x)dx < ε. O choisit esuite suffisammet grad pour que Mλ(A ) < ε et o déduit alors de (4.2), A h(x)dx < 2ε. Exercice 4.6. Calculer ( 1) +1 =1 à l aide de l itégrale 1 dx 1+x. Idicatio : o posera f (x) = Σ ( 1) k x k pour x [, 1]. O trouvera u chapeau itégrable pour les f et o appliquera le théorème de Lebesgue. Solutio O sait que f (x) Σ ( 1) k x k = 1 1+x pour tout x < 1. Par ailleurs, la série état alterée, f (x) = 1 est chapeau itégrable pour f (x) sur [,1]. Par le théorème de Lebesgue, o déduit que f (x) 1 1+x das L1 (, 1), ce qui implique que 1 f (x)dx xdx = Log2. E itégrat terme à terme, o obtiet Σ 1 = Log2. ( 1) +1 Exercice 4.7. Soit f L 1 (R). Calculer la limite de 1 f(x)dx quad +. 14
15 Solutio : E posat y = x, o a f(x)dx = 1 f(y)dy = R 1 [,+ [ (y)f(y)dy. La foctio f(y) 1 [, [ (y) ted poctuellemet vers zéro quad et f e est chapeau itégrable. Doc par le théorème de Lebesgue, l itégrale cosidérée ted vers zéro. Exercice 4.8. (Déduire le Lemme de Fatou du théorème de covergece mootoe) O rappelle la défiitio de la limite iférieure d ue suite a de réels : lim if a = lim N if N a Cette limite est ue limite croissate et doc elle existe toujours das R {+ } { }. i) Remarquer que si g est ue suite de foctios sommables positives, alors if g if g. ii) Soit f ue suite de foctios à valeurs das R + {+ }. O pose g N = if N f. Motrer que lim N gn = lim N g N. iii) Déduire des questios précédetes le lemme de Fatou : lim if f lim if f. Solutio : i) Si g est ue suite de foctios sommables positives, o a pour tout if g g. E preat l ifimum des deux cotés, o obtiet if g if g. ii) La suite (g N ) N est ue suitecroissate de foctios positives ou ulles. Par le théorème de la covergece mootoe, o a doc lim N gn = lim N g N. iii) E combiat l égalité du ii) et l iégalité du i), o obtiet directemet le lemme de Fatou : lim if f lim if f. Exercice 4.9. cotrexemples Doer des exemples de suites de foctios f L 1 (, 1) telles que f f das L 1 et f (x) e ted pas presque partout vers f(x). f e ted pas vers f das L 1 et f (x) ted vers f(x) presque partout. Solutio : O cosidère la suite de foctios f défiies sur [, 1] par f 1 = 1 sur [,1] f 2 = 1 sur [, 1 2 ], ailleurs f 3 = 1 sur [ 1 2, 1], ailleurs f 4 = 1 sur [, 1 4 ], ailleurs f 5 = 1 sur [ 1 4, 1 2 ], ailleurs f 6 = 1 sur [ 1 2, 3 4 ], ailleurs... La formule géérale est : Si 2 k 1 < 2 k, alors f = 1 sur [ 2k 1, +1 2k 1 ] = [ 1, +1 1]. 2 k 1 2 k 1 2 k 1 2 k 1 Cette suite de foctios est ue bosse roulate dot la largeur ted vers zéro, mais qui balaye costammet l itervalle [, 1]. Elle est positive et so itégrale ted vers zéro. Doc f das L 1. Par cotre, f (x) e ted jamais vers. E effet, si x est u poit de [,1], o peut poser par divisio euclidiee x = N + r, 2 k 1 avec N < 2 k 1 et r < 1. Posos = N + 2 k 1, ce qui permet d écrire x sous la forme x = 2k 1 + r. 2 k 1 2 k 1 O voit que f (x) = 1, alors que f +2 (x) = par exemple. Doc f (x) e coverge ulle part! O pose f (x) = si x 1 et f (x) = sio. Alors f (x) ted vers pour tout x ], 1]. Par cotre, f = 1 et doc f e ted pas vers das L 1. Exercice 4.1. Coupes d u esemble mesurable Soit E u sous-esemble de mesure borée de R N. Démotrer que pour tout α 1, E cotiet u sous-esemble de mesure α.λ(e). 15
16 Solutio : O pose x = (x 1,..., x N ) et m(r) = λ({x E, x 1 r}) = 1 {x, x1 r}dx. R N Ue applicatio immédiate du théorème de Lebesgue motre que m est ue foctio cotiue. Toujours par le même théorème, o motre que m(r) quad r et m(r) λ(e) quad r +. (Das tous les cas, o utilise tout boemet la foctio 1 E comme chapeau itégrable). Par le théorème des valeurs itermédiaires appliqué à la foctio m(r), il existe doc pour tout < a < λ(e) u réel r tel que m(r) = a. Exercice Covergece L 1 quad il y a coservatio de la masse (Lemme de Scheffé) Motrer que si ue suite de foctios (w ) L 1 vérifie w, w (x) w(x) presque partout, w L 1 et w w, alors w w das L 1. Idicatio : écrire w w = (w w ) + (w w ) et w w = (w w ) + + (w w ) et appliquer le théorème de Lebesgue. Solutio Comme w, o a (w w ) + w L 1 et doc par le théorème de Lebesgue (w w ) +. O déduit de la relatio (w w ) + (w w ) = w w que (w w ) ted aussi vers zéro et fialemet que la somme des deux mêmes itégrales w w = (w w ) + + (w w ) ted vers zéro. Exercice Critère d itégrabilité sur u boré B de R N O va motrer das cet exercice que f L 1 (B) si et seulemet si ε η, λ(k) η f ε. K i) Motrer que si le critère d itégratio est vérifié, alors f est itégrable. ii) Pour la réciproque, o raisoe par cotradictio et o suppose qu il existe f L 1 (B) telle que le critère d itégratio e soit pas vérifié. Motrer qu il existe alors ε > et ue suite K de sous-esembles de B tels que K f ε et λ(k ) 1 2. O pose J = +1K k. Motrer que J f et coclure. Autre méthode : appliquer directemet le résultat de l exercice 4.5! iii) (facultatif) Adapter le critère d itégrabilité à R N. Solutio O applique le critère d itégratio avec par exemple ε = 1. Il existe doc η tel que λ(k) η f 1. Comme B est boré, il peut être recouvert par u ombre fii de boules de mesure iférieure K à η, B 1,..., B k. O a doc B f Σk i=1 B i f k, ce qui prouve que f L 1 (B). Réciproquemet, soit f L 1 (B) et supposos par cotradictio qu il existe ε et ue suite K de sousesembles de B tels que K f ε et λ(k ). Quitte à extraire ue sous-suite, o peut supposer que λ(k ) 1 2. O pose J = k=+1 K k. Doc mes(j ) Σ k= k 2. La suite g des foctios caractéristiques des J est ue suite décroissate de foctios positives dot l itégrale ted vers zéro. Elle coverge doc presque partout vers zéro. Reveat à f, o a J f = B g (x) f(x) dx. Comme g (x) f(x) ted presque partout vers zéro et que f est chapeau itégrable, o coclut que J f, ce qui cotredit le fait que J f ε. Exercice Réciproque du Théorème de Lebesgue O va motrer que si f est ue suite covergete das L 1, alors il existe ue sous-suite qui coverge presque partout et qui a u chapeau itégrable. i) Motrer que si la suite f coverge vers f das L 1, o peut e extraire ue sous-suite telle que f i+1 f i 1 < 2. ii) O pose g = f i+1 f i ; motrer e appliquat le théorème de covergece mootoe que la série Σ g (x) appartiet à L 1 et coverge doc pour presque tout x. E déduire que f i coverge presque partout. iii) Déduire aussi que f i a u chapeau itégrable. iv) Adapter le raisoemet précédet à ue suite f qui est de Cauchy das L 1 pour motrer que L 1 est u espace complet. Solutio : i)si f f das L 1, alors i, f i f 1 < 2 1. Doc f i+1 f i 1 < < 2. 16
17 ii) O a Σ g 1 Σ2 = 1. O pose h(x) = Σ g (x). Cette série est positive et coverge partout (évetuellemet vers l ifii). Par le théorème de covergece mootoe, h(x)dx = Σ g (x) dx = Σ g 1 1. Doc h(x) L 1 et o déduit que la série de réels Σ g (x) est covergete pour presque tout x. Il est doc de même pour la série Σ g (x). Cette derière série a h(x) pour chapeau itégrable. Par le théorème de Lebesgue, elle est doc covergete das L 1. Comme f i+1 = f i1 + Σ 1 g, o e déduit que (f i ) coverge das L 1. iii) f i1 + h(x) est u chapeau itégrable pour la suite (f i ). iv) Adaptatio à la démostratio de complétude de L 1 : Si f est ue suite de Cauchy das L 1, o peut défiir g comme précédemmet et appliquer exactemet le même raisoemet pour prouver que la série Σ g (x) coverge pour presque tout x et a doc ue limite poctuelle f(x). O déduit alors du théorème de Lebesgue que (f i ) coverge vers f das L 1. Il est alors immédiat (iégalité triagulaire) que toute la suite (f ) coverge vers f. Exercice Calculer la dérivée à droite e zéro de la foctio t 1 (g(x) + t 2 ) 1 2 dx = ϕ(t), où g vérifie g 1. Idicatio : pour évaluer la limite du rapport ϕ(t) ϕ() t, peser à utiliser le théorème de Lebesgue. Solutio O a ϕ(t) ϕ() t = 1 t t f(x)2 + t 2 + f 2 (x) dx = k t (x)dx. O voit que k t (x) = 1 si f(x) = et k t (x) quad t si f(x). Doc k t (x) 1 {f(x)=}, la foctio caractéristique de l esemble des poits où f(x) s aule. Ceci ous doe la limite poctuelle. Cherchos u chapeau itégrable. O voit immédiatemet que k t (x) 1. Doc, par le théorème de Lebesgue, k t 1 {f(x)=} quad t das L 1 (, 1). D où ϕ ( + ) = 1 {f(x)=} = λ({x, f(x) = }). Exercice Calculer lim + Γ, où Γ = (1 x ) e x 2 dx. Solutio Notos 1 [,] la foctio caractéristique de [, ], qui vaut 1 si x [, ] et ailleurs. Alors Γ = + (1 x ) e x 2 1[,] (x)dx. O calcule la limite poctuelle de l itégrad : Comme (1 x ) = e log(1 x ) e x quad +, o voit que l itégrad ted vers e x 2. Reste à trouver u chapeau itégrable. Si x, log(1 x ) x 2. Doc (1 x ) e x 2 1 [,] (x) e x 2 pour tout x. O coclut par le théorème de Lebesgue que Γ + e x 2 dx = 2. Exercice O pose, pour x >, Γ(x) = e t t x 1 dt. Démotrer que Γ est de classe C sur ], + [. Démotrer que Γ(x) + quad x. Pour la deuxième questio, peser à utiliser le lemme de covergece mootoe! Solutio O pose f(t, x) = e t t x 1 = e t+(x 1)Logt. Fixos < α < M. O a, pour (t, x) ], + ] ]α, M], f x (t, x) = e t (log t) t x 1 h (t), où h (t) = e t (log t) t α 1 si < t 1 et h (t) = e t (log t) t M 1 si t > 1. Les foctios h (t) état sommables sur ], ], o voit (pour = ) que Γ est bie défiie, puis qu o peut appliquer successivemet à tous ordres le théorème de dérivatio sous le sige somme à l itégrale défiissat Γ(x). O obtiet, pour tout α < x < M, Γ (t, x) = x e t (log t) t x 1 dt. 17
18 Comme α est arbitrairemet petit et M arbitrairemet grad, o coclut que Γ(x) est C sur ], + [. Quad x, le théorème de covergece mootoe ous dit que Γ(x) 1 e t t x 1 dt 1 e t t dt = +. Remarque : o peut aussi motrer que Γ(z) est holomorphe sur le demi-pla Re(z) >, c est plus rapide. Exercice Soit f ue foctio sommable. Démotrer que lim α + αλ({x, f(x) α}) =. O a Solutio α dx f(x) dx = { f(x) α} { f(x) α} χ { f(x) α} (x) f(x) dx. O remarque que 1 { f(x) α} f(x) quad α +, presque partout, et que 1 { f(x) α} f(x) f(x) qui est doc chapeau itégrable. Par le théorème de Lebesgue, o a doc f(x) dx { f(x) α} Exercice Si f L 1 (R), motrer que f(x) = Σ Q f(x+) L 1 ([, 1]) et que [,1] f(x)dx = R f(x)dx. Solutio Par le théorème de la covergece mootoe, o a Σ Z f(x + ) = Σ Z f(x + ) dx = Σ Z f(x) dx = R f(x) dx. La série Σ Z f(x + ) coverge doc pour presque tout x et il e de même pour la série Σ Z f(x + ). Celle-ci a Σ Z f(x + ) comme chapeau itégrable. Par le théorème de Lebesgue, elle est doc covergete das L 1 et obtiet la formule demadée. Exercice U cotre-exemple à méditer au théorème de dérivatio sous le sige somme. Soit φ ue foctio cotiue sur [, 1]. O cosidère, das [, 1] [, 1] la foctio f défiie par f(x, λ) = φ(x) si x λ et f(x, λ) = sio. O pose F (λ) = 1 f(x, λ)dx. Pour chaque λ, la dérivée partielle existe sauf e u poit, et elle est majorée par ue foctio sommable fixe : la foctio. Détermier la dérivée de F. Solutio O a F (λ) = 1 f(x, λ)dx = λ φ(x)dx. Doc F (λ) = φ(λ). O voit que la coclusio du théorème de dérivatio sous le sige somme est fausse. E effet, l hypothèse b) est ivalidée : f λ (x, λ) existe pas e tout poit de A I = [, 1] [, 1], mais seulemet e presque tout poit. Exercice 4.2. (Iégalité de Hardy, Chambert-Loir A., Exercices d aalyse pour l agrégatio) Soit p u réel strictemet supérieur à 1. 1) Soit f L p (R + ). O pose F (x) = 1 x f(t)dt. Le but de la questio est de motrer que F est das x L p (R + ) et que : ( ) p F (x) p dx p f p (x) dx p 1 18
19 a) Etablir le résultat lorsque f est cotiue positive. b) E déduire le résultat lorsque f est cotiue et de sige quelcoque. c) Traiter le cas gééral. 2) Motrer que cette costate est optimale (id. : o pourra utiliser des foctios puissaces). Solutio 1) a) f état cotiue, F est cotiue (y compris e, le vérifier) et dérivable sur (, + ) avec (xf ) = F + xf = f. E écrivat que F p (x) = F p 1 (x)f(x) xf p 1 (x)f (x) et e effectuat ue itégratio par parties, o obtiet T F p (x)dx = T p 1 F p (T ) + ( p ) T p 1 F p 1 (x)f(x)dx (o vérifiera qu il y a pas de problème e e preat l itégrale etre ε et T et e faisat tedre ε vers ). Or T p 1 F p (T ) car f est supposée positive. E appliquat l iégalité de Hölder das la deuxième itégrale, o a ( ) p T p T F p (x)dx f p (x)dx p 1 b) O gééralise l iégalité précédete au cas où f est de sige quelcoque e remarquat qu alors x F (x) G(x) = x 1 f(t) dt et l iégalité précédete est valable avec le couple ( f, G). O e déduit facilemet l iégalité pour (f, F ). c) O viet de motrer que l applicatio T : f C F L p était liéaire cotiue avec ue orme iferieure à p/(p 1). Puisque C est dese das L p, o a que pour tout f L p, il existe ue suite (f ) de foctios cotiues tedat e orme L p vers f. Soit F = T (f ) : (F ) est ue suite de Cauchy das L p doc elle coverge vers ue certaie foctio G. Par la réciproque du théorème de Lebesgue, de la suite f o peut extraire ue sous-suite qui coverge simplemet (et das L p ) vers f. O e déduit facilemet que F (x) = x 1 x f(t)dt = G(x) p.p. Doc F est das Lp et vérifie l iégalité de Hardy. 2) Facile. Exercice (Chambert-Loir A., Exercices d aalyse pour l agrégatio) Soit a >. Calculer ( ) 1/a lim 1 xa dx (id. : o pourra utiliser le théorème de covergece mootoe) Solutio Soit u >. O cosidère la foctio g u (t) = t log(1 u/t) pour t > u. o a g u(t) = log(1 u/t) + u/(t u) et g u(t) = u 2 /[t(t u) 2 ] et doc g u positive car g u(+ ) =. Doc g u (t) est ue foctio croissate de t > u et t (u, + ) (1 u/t) t aussi. Il e reste alors plus qu à appliquer le théorème de covergece mootoe et la limite cherchée est exp( x a )dx = a 1 Γ(a 1 ). 19
20 Exercice (Chambert-Loir A., Exercices d aalyse pour l agrégatio) 1) Soit γ la costate d Euler. Motrer que γ = 1 ( 1 x 1 ) dx E(x) où E(x) désige la partie etière de x. E déduire que γ >. 2) Motrer que γ = e s log(s)ds. Solutio 1) Trivial. 2) O a k (1 s/k) k log(s)ds = 1 (1 s/k) k log(s)ds + k 1 (1 s/k) k log(s)ds Quad k ted vers +, la première itégrale ted grâce au théorème de covergece domiée vers 1 e s log(s)ds et la deuxième, grâce au théorème de covergece mootoe (voir exercice précédet), vers e s log(s)ds. 1 O est doc rameé à l étude de k (1 s/k)k log(s)ds qui après u chagemet de variables doe k 1 (1 u) k log(u)du k k + 1 log k = 1 kv k log(1 v)dv Or log(1 v) = v j j=1 d où par le théorème de covergece mootoe j 1 v k log(1 v)dv = k ( k ) k + 1 O e déduit le résultat. k k + 1 log k Exercice (J. Dieudoé, Calcul ifiitésimal) Pour z >, p, q >, o défiit les foctios Γ(z) = Motrer que B(p, q) = Γ(p)Γ(q) Γ(p + q) t z 1 e t dt, B(p, q) = 1 t p 1 (1 t) q 1 dt Exercice Rappels : u esemble égligeable de R N est u esemble coteu das u borélie de R N de mesure ulle. O ajoute à la tribu des borélies les esembles égligeables. O obtiet aisi la tribu de Lebesgue, otée L. 1) U esemble est Lebesgue mesurable s il diffère d u borélie par u esemble de mesure ulle. 2) O dira qu ue foctio est Lebesgue-mesurable si elle est mesurable de (R N, L) das R, B où B est la tribu de Borel. Ue foctio est Lebesgue-mesurable si et seulemet si elle est presque partout égale à ue foctio boréliee. 2
1 Mesure et intégrale
 1 Mesure et itégrale 1.1 Tribu boréliee et foctios mesurables Soit =[a, b] u itervalle (le cas où b = ou a = est pas exclu) et F ue famille de sous-esembles de. OditqueF est ue tribu sur si les coditios
1 Mesure et itégrale 1.1 Tribu boréliee et foctios mesurables Soit =[a, b] u itervalle (le cas où b = ou a = est pas exclu) et F ue famille de sous-esembles de. OditqueF est ue tribu sur si les coditios
Chapitre 3 : Fonctions d une variable réelle (1)
 Uiversités Paris 6 et Paris 7 M1 MEEF Aalyse (UE 3) 2013-2014 Chapitre 3 : Foctios d ue variable réelle (1) 1 Lagage topologique das R Défiitio 1 Soit a u poit de R. U esemble V R est u voisiage de a s
Uiversités Paris 6 et Paris 7 M1 MEEF Aalyse (UE 3) 2013-2014 Chapitre 3 : Foctios d ue variable réelle (1) 1 Lagage topologique das R Défiitio 1 Soit a u poit de R. U esemble V R est u voisiage de a s
. (b) Si (u n ) est une suite géométrique de raison q, q 1, on obtient : N N, S N = 1 qn+1. n+1 1 S N = 1 1
 Premières propriétés des ombres réels 2 Suites umériques 3 Suites mootoes : à faire 4 Séries umériques 4. Notio de série. Défiitio 4.. Soit (u ) ue suite de ombres réels ou complexes. Pour N N, o ote S
Premières propriétés des ombres réels 2 Suites umériques 3 Suites mootoes : à faire 4 Séries umériques 4. Notio de série. Défiitio 4.. Soit (u ) ue suite de ombres réels ou complexes. Pour N N, o ote S
[http://mp.cpgedupuydelome.fr] édité le 10 juillet 2014 Enoncés 1. Exercice 6 [ 02475 ] [correction] Si n est un entier 2, le rationnel H n =
![[http://mp.cpgedupuydelome.fr] édité le 10 juillet 2014 Enoncés 1. Exercice 6 [ 02475 ] [correction] Si n est un entier 2, le rationnel H n = [http://mp.cpgedupuydelome.fr] édité le 10 juillet 2014 Enoncés 1. Exercice 6 [ 02475 ] [correction] Si n est un entier 2, le rationnel H n =](/thumbs/19/318291.jpg) [http://mp.cpgedupuydelome.fr] édité le 1 juillet 14 Eocés 1 Nombres réels Ratioels et irratioels Exercice 1 [ 9 ] [correctio] Motrer que la somme d u ombre ratioel et d u ombre irratioel est u ombre irratioel.
[http://mp.cpgedupuydelome.fr] édité le 1 juillet 14 Eocés 1 Nombres réels Ratioels et irratioels Exercice 1 [ 9 ] [correctio] Motrer que la somme d u ombre ratioel et d u ombre irratioel est u ombre irratioel.
* très facile ** facile *** difficulté moyenne **** difficile ***** très difficile I : Incontournable
 Exo7 Topologie Exercices de Jea-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-fracefr * très facile ** facile *** difficulté moyee **** difficile ***** très difficile I : Icotourable Exercice **
Exo7 Topologie Exercices de Jea-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-fracefr * très facile ** facile *** difficulté moyee **** difficile ***** très difficile I : Icotourable Exercice **
CHAPITRE 2 SÉRIES ENTIÈRES
 CHAPITRE 2 SÉRIES ENTIÈRES 2. Séries etières Défiitio 2.. O appelle série etière toute série de foctios ( ) f dot le terme gééral est de la forme f ()=a, où (a ) désige ue suite réelle ou complee et R.
CHAPITRE 2 SÉRIES ENTIÈRES 2. Séries etières Défiitio 2.. O appelle série etière toute série de foctios ( ) f dot le terme gééral est de la forme f ()=a, où (a ) désige ue suite réelle ou complee et R.
Etude de la fonction ζ de Riemann
 Etude de la foctio ζ de Riema ) Défiitio Pour x réel doé, la série de terme gééral,, coverge si et seulemet si x >. x La foctio zeta de Riema est la foctio défiie sur ], [ par : ( x > ), = x. Remarque.
Etude de la foctio ζ de Riema ) Défiitio Pour x réel doé, la série de terme gééral,, coverge si et seulemet si x >. x La foctio zeta de Riema est la foctio défiie sur ], [ par : ( x > ), = x. Remarque.
Processus et martingales en temps continu
 Chapitre 3 Processus et martigales e temps cotiu 1 Quelques rappels sur les martigales e temps discret (voir [4]) O cosidère u espace filtré (Ω, F, (F ) 0, IP). O ote F = 0 F. Défiitio 1.1 Ue suite de
Chapitre 3 Processus et martigales e temps cotiu 1 Quelques rappels sur les martigales e temps discret (voir [4]) O cosidère u espace filtré (Ω, F, (F ) 0, IP). O ote F = 0 F. Défiitio 1.1 Ue suite de
Séries réelles ou complexes
 6 Séries réelles ou complexes Comme pour le chapitre 3, les suites cosidérées sot a priori complexes et les résultats classiques sur les foctios cotiues ou dérivables d ue variable réelle sot supposés
6 Séries réelles ou complexes Comme pour le chapitre 3, les suites cosidérées sot a priori complexes et les résultats classiques sur les foctios cotiues ou dérivables d ue variable réelle sot supposés
Intégration et probabilités ENS Paris, 2012-2013. TD (20)13 Lois des grands nombres, théorème central limite. Corrigé :
 Itégratio et probabilités EN Paris, 202-203 TD 203 Lois des grads ombres, théorème cetral limite. Corrigé Lois des grads ombres Exercice. Calculer e cet leços Détermier les limites suivates : x +... +
Itégratio et probabilités EN Paris, 202-203 TD 203 Lois des grads ombres, théorème cetral limite. Corrigé Lois des grads ombres Exercice. Calculer e cet leços Détermier les limites suivates : x +... +
Limites des Suites numériques
 Chapitre 2 Limites des Suites umériques Termiale S Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES Limite fiie ou ifiie d ue suite. Limites et comparaiso. Opératios sur les ites. Comportemet
Chapitre 2 Limites des Suites umériques Termiale S Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES Limite fiie ou ifiie d ue suite. Limites et comparaiso. Opératios sur les ites. Comportemet
Suites et séries de fonctions
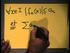 [http://mp.cpgedupuydelome.fr] édité le 3 avril 5 Eocés Suites et séries de foctios Propriétés de la limite d ue suite de foctios Eercice [ 868 ] [correctio] Etablir que la limite simple d ue suite de
[http://mp.cpgedupuydelome.fr] édité le 3 avril 5 Eocés Suites et séries de foctios Propriétés de la limite d ue suite de foctios Eercice [ 868 ] [correctio] Etablir que la limite simple d ue suite de
Exo7. Déterminants. = 4(b + c)(c + a)(a + b). c + a c + b 2c Correction. b + a 2b b + c. Exercice 2 ** X a b c a X c b b c X a c b a X
 Exo7 Détermiats Exercices de Jea-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-fracefr * très facile ** facile *** difficulté moyee **** difficile ***** très difficile I : Icotourable T : pour
Exo7 Détermiats Exercices de Jea-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-fracefr * très facile ** facile *** difficulté moyee **** difficile ***** très difficile I : Icotourable T : pour
Exercice I ( non spé ) 1/ u 1 = 3 4. 2 3 u 2 4 + 3 9. 19 4 2/ Soit P la propriété : u n + 4. > 0 pour n 1. P est vraie au rang 1 car u 1
 Bac blac TS Correctio Exercice I ( Spé ) / émotros par récurrece que 5x y = pour tout etier aturel 5x y = 5 8 = La propriété est doc vraie au rag = Supposos que la propriété est vraie jusqu au rag, o a
Bac blac TS Correctio Exercice I ( Spé ) / émotros par récurrece que 5x y = pour tout etier aturel 5x y = 5 8 = La propriété est doc vraie au rag = Supposos que la propriété est vraie jusqu au rag, o a
Séquence 5. La fonction logarithme népérien. Sommaire
 Séquece 5 La foctio logarithme épérie Objectifs de la séquece Itroduire ue ouvelle foctio : la foctio logarithme épérie. Coaître les propriétés de cette foctio : sa dérivée, ses variatios, sa courbe, sa
Séquece 5 La foctio logarithme épérie Objectifs de la séquece Itroduire ue ouvelle foctio : la foctio logarithme épérie. Coaître les propriétés de cette foctio : sa dérivée, ses variatios, sa courbe, sa
x +1 + ln. Donner la valeur exacte affichée par cet algorithme lorsque l utilisateur entre la valeur n =3.
 EXERCICE 3 (6 poits ) (Commu à tous les cadidats) Il est possible de traiter la partie C sas avoir traité la partie B Partie A O désige par f la foctio défiie sur l itervalle [, + [ par Détermier la limite
EXERCICE 3 (6 poits ) (Commu à tous les cadidats) Il est possible de traiter la partie C sas avoir traité la partie B Partie A O désige par f la foctio défiie sur l itervalle [, + [ par Détermier la limite
* très facile ** facile *** difficulté moyenne **** difficile ***** très difficile I : Incontournable
 Eo7 Séries etières Eercices de Jea-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-fracefr * très facile ** facile *** difficulté moyee **** difficile ***** très difficile I : Icotourable Eercice
Eo7 Séries etières Eercices de Jea-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-fracefr * très facile ** facile *** difficulté moyee **** difficile ***** très difficile I : Icotourable Eercice
14 Chapitre 14. Théorème du point fixe
 Chapitre 14 Chapitre 14. Théorème du poit fixe Si l o examie de plus près les méthodes de Lagrage et de Newto, étudiées au chapitre précédet, elles revieet das leur pricipe à remplacer la résolutio de
Chapitre 14 Chapitre 14. Théorème du poit fixe Si l o examie de plus près les méthodes de Lagrage et de Newto, étudiées au chapitre précédet, elles revieet das leur pricipe à remplacer la résolutio de
4 Approximation des fonctions
 4 Approximatio des foctios Ue foctio f arbitraire défiie sur u itervalle I et à valeur das IR peut être représetée par so graphe, ou de maière équivalete par la doée de l esemble de ses valeurs f(t) pour
4 Approximatio des foctios Ue foctio f arbitraire défiie sur u itervalle I et à valeur das IR peut être représetée par so graphe, ou de maière équivalete par la doée de l esemble de ses valeurs f(t) pour
Les Nombres Parfaits.
 Les Nombres Parfaits. Agathe CAGE, Matthieu CABAUSSEL, David LABROUSSE (2 de Lycée MONTAIGNE BORDEAUX) et Alexadre DEVERT, Pierre Damie DESSARPS (TS Lycée SUD MEDOC LETAILLAN MEDOC) La première partie
Les Nombres Parfaits. Agathe CAGE, Matthieu CABAUSSEL, David LABROUSSE (2 de Lycée MONTAIGNE BORDEAUX) et Alexadre DEVERT, Pierre Damie DESSARPS (TS Lycée SUD MEDOC LETAILLAN MEDOC) La première partie
Groupe orthogonal d'un espace vectoriel euclidien de dimension 2, de dimension 3
 1 Groupe orthogoal d'u espace vectoriel euclidie de dimesio, de dimesio Voir le chapitre 19 pour l'étude des espaces euclidies et des isométries. État doé u espace euclidie E de dimesio 1, o rappelle que
1 Groupe orthogoal d'u espace vectoriel euclidie de dimesio, de dimesio Voir le chapitre 19 pour l'étude des espaces euclidies et des isométries. État doé u espace euclidie E de dimesio 1, o rappelle que
Comportement d'une suite
 Comportemet d'ue suite I) Approche de "ses de variatio et de ite d'ue suite" : 7 Soit la suite ( ) telle que = 5 ( + ) 2 Représetos graphiquemet la suite das u pla mui d' u repère. Il suffit de placer
Comportemet d'ue suite I) Approche de "ses de variatio et de ite d'ue suite" : 7 Soit la suite ( ) telle que = 5 ( + ) 2 Représetos graphiquemet la suite das u pla mui d' u repère. Il suffit de placer
STATISTIQUE : TESTS D HYPOTHESES
 STATISTIQUE : TESTS D HYPOTHESES Préparatio à l Agrégatio Bordeaux Aée 203-204 Jea-Jacques Ruch Table des Matières Chapitre I. Gééralités sur les tests 5. Itroductio 5 2. Pricipe des tests 6 2.a. Méthodologie
STATISTIQUE : TESTS D HYPOTHESES Préparatio à l Agrégatio Bordeaux Aée 203-204 Jea-Jacques Ruch Table des Matières Chapitre I. Gééralités sur les tests 5. Itroductio 5 2. Pricipe des tests 6 2.a. Méthodologie
EXERCICES : DÉNOMBREMENT
 Chapitre 7 ECE 1 - Grad Nouméa - 015 EXERCICES : DÉNOMBREMENT LISTES / ARRANGEMENTS Exercice 1 : Le code ativol Pour so vélo, Toto possède u ativol a code. Le code est ue successio de trois chiffres compris
Chapitre 7 ECE 1 - Grad Nouméa - 015 EXERCICES : DÉNOMBREMENT LISTES / ARRANGEMENTS Exercice 1 : Le code ativol Pour so vélo, Toto possède u ativol a code. Le code est ue successio de trois chiffres compris
Convergences 2/2 - le théorème du point fixe - Page 1 sur 9
 Au sommaire : Suites extraites Le théorème de Bolzao-Weierstrass La preuve du théorème de Bolzao-Weierstrass3 Foctio K-cotractate4 Le théorème du poit fixe5 La preuve du théorème du poit fixe6 Utilisatios
Au sommaire : Suites extraites Le théorème de Bolzao-Weierstrass La preuve du théorème de Bolzao-Weierstrass3 Foctio K-cotractate4 Le théorème du poit fixe5 La preuve du théorème du poit fixe6 Utilisatios
Dénombrement. Introduction. 1 Cardinaux d'ensembles nis. ECE3 Lycée Carnot. 12 novembre 2010. 1.1 Quelques dénitions
 Déombremet ECE3 Lycée Carot 12 ovembre 2010 Itroductio La combiatoire, sciece du déombremet, sert comme so om l'idique à compter. Il e s'agit bie etedu pas de reveir au stade du CP et d'appredre à compter
Déombremet ECE3 Lycée Carot 12 ovembre 2010 Itroductio La combiatoire, sciece du déombremet, sert comme so om l'idique à compter. Il e s'agit bie etedu pas de reveir au stade du CP et d'appredre à compter
FEUILLE D EXERCICES 17 - PROBABILITÉS SUR UN UNIVERS FINI
 FEUILLE D EXERCICES 7 - PROBABILITÉS SUR UN UNIVERS FINI Exercice - Lacer de dés O lace deux dés à 6 faces équilibrés. Calculer la probabilité d obteir : u double ; ue somme des deux dés égale à 8 ; ue
FEUILLE D EXERCICES 7 - PROBABILITÉS SUR UN UNIVERS FINI Exercice - Lacer de dés O lace deux dés à 6 faces équilibrés. Calculer la probabilité d obteir : u double ; ue somme des deux dés égale à 8 ; ue
Dénombrement. Chapitre 1. 1.1 Enoncés des exercices
 Chapitre 1 Déombremet 1.1 Eocés des exercices Exercice 1 L acie système d immatriculatio fraçais était le suivat : chaque plaque avait 4 chiffres, suivis de 2 lettres, puis des 2 uméros du départemet.
Chapitre 1 Déombremet 1.1 Eocés des exercices Exercice 1 L acie système d immatriculatio fraçais était le suivat : chaque plaque avait 4 chiffres, suivis de 2 lettres, puis des 2 uméros du départemet.
Des résultats d irrationalité pour deux fonctions particulières
 Collect. Math. 5, 00, 0 c 00 Uiversitat de Barceloa Des résultats d irratioalité pour deux foctios particulières Richard Choulet 7, Rue du 4 Août, 40 Aveay, Frace E-mail: richardchoulet@waadoo.fr Received
Collect. Math. 5, 00, 0 c 00 Uiversitat de Barceloa Des résultats d irratioalité pour deux foctios particulières Richard Choulet 7, Rue du 4 Août, 40 Aveay, Frace E-mail: richardchoulet@waadoo.fr Received
Cours de Statistiques inférentielles
 Licece 2-S4 SI-MASS Aée 2015 Cours de Statistiques iféretielles Pierre DUSART 2 Chapitre 1 Lois statistiques 1.1 Itroductio Nous allos voir que si ue variable aléatoire suit ue certaie loi, alors ses réalisatios
Licece 2-S4 SI-MASS Aée 2015 Cours de Statistiques iféretielles Pierre DUSART 2 Chapitre 1 Lois statistiques 1.1 Itroductio Nous allos voir que si ue variable aléatoire suit ue certaie loi, alors ses réalisatios
Exercices de mathématiques
 MP MP* Thierry DugarDi Marc rezzouk Exercices de mathématiques Cetrale-Supélec, Mies-Pots, École Polytechique et ENS Coceptio et créatio de couverture : Atelier 3+ Duod, 205 5 rue Laromiguière, 75005 Paris
MP MP* Thierry DugarDi Marc rezzouk Exercices de mathématiques Cetrale-Supélec, Mies-Pots, École Polytechique et ENS Coceptio et créatio de couverture : Atelier 3+ Duod, 205 5 rue Laromiguière, 75005 Paris
Deuxième partie : LES CONTRATS D ASSURANCE VIE CLASSIQUES
 DEUXIEME PARTIE Deuième partie : LES CONTRATS D ASSURANCE VIE CLASSIQUES Chapitre. L assurace de capital différé Chapitre 2. Les opératios de retes Chapitre 3. Les assuraces décès Chapitre 4. Les assuraces
DEUXIEME PARTIE Deuième partie : LES CONTRATS D ASSURANCE VIE CLASSIQUES Chapitre. L assurace de capital différé Chapitre 2. Les opératios de retes Chapitre 3. Les assuraces décès Chapitre 4. Les assuraces
20. Algorithmique & Mathématiques
 L'éditeur L'éditeur permet à l'utilisateur de saisir les liges de codes d'u programme ou de défiir des foctios. Remarque : O peut saisir directemet des istructios das la cosole Scilab, mais il est plus
L'éditeur L'éditeur permet à l'utilisateur de saisir les liges de codes d'u programme ou de défiir des foctios. Remarque : O peut saisir directemet des istructios das la cosole Scilab, mais il est plus
II LES PROPRIETES DES ESTIMATEURS MCO 1. Rappel : M1 LA REGRESSION : HYPOTHESES ET TESTS Avril 2009
 M LA REGRESSION : HYPOTHESES ET TESTS Avril 009 I LES HYPOTHESES DE LA MCO. Hypothèses sur la variable explicative a. est o stochastique. b. a des valeurs xes das les différets échatillos. c. Quad ted
M LA REGRESSION : HYPOTHESES ET TESTS Avril 009 I LES HYPOTHESES DE LA MCO. Hypothèses sur la variable explicative a. est o stochastique. b. a des valeurs xes das les différets échatillos. c. Quad ted
Statistique descriptive bidimensionnelle
 1 Statistique descriptive bidimesioelle Statistique descriptive bidimesioelle Résumé Liaisos etre variables quatitatives (corrélatio et uages de poits), qualitatives (cotigece, mosaïque) et de types différets
1 Statistique descriptive bidimesioelle Statistique descriptive bidimesioelle Résumé Liaisos etre variables quatitatives (corrélatio et uages de poits), qualitatives (cotigece, mosaïque) et de types différets
Baccalauréat S Asie 19 juin 2014 Corrigé
 Bcclurét S Asie 9 jui 24 Corrigé A. P. M. E. P. Exercice Commu à tous les cdidts 4 poits Questio - c. O peut élimier rpidemet les réposes. et d. cr les vecteurs directeurs des droites proposées e sot ps
Bcclurét S Asie 9 jui 24 Corrigé A. P. M. E. P. Exercice Commu à tous les cdidts 4 poits Questio - c. O peut élimier rpidemet les réposes. et d. cr les vecteurs directeurs des droites proposées e sot ps
LES ÉCLIPSES. Éclipser signifie «cacher». Vus depuis la Terre, deux corps célestes peuvent être éclipsés : la Lune et le Soleil.
 Qu appelle-t-o éclipse? Éclipser sigifie «cacher». Vus depuis la Terre, deu corps célestes peuvet être éclipsés : la Lue et le Soleil. LES ÉCLIPSES Pour qu il ait éclipse, les cetres de la Terre, de la
Qu appelle-t-o éclipse? Éclipser sigifie «cacher». Vus depuis la Terre, deu corps célestes peuvet être éclipsés : la Lue et le Soleil. LES ÉCLIPSES Pour qu il ait éclipse, les cetres de la Terre, de la
PROMENADE ALÉATOIRE : Chaînes de Markov et martingales
 PROMENADE ALÉATOIRE : Chaîes de Markov et martigales Thierry Bodieau École Polytechique Paris Départemet de Mathématiques Appliquées thierry.bodieau@polytechique.edu Novembre 2013 2 Table des matières
PROMENADE ALÉATOIRE : Chaîes de Markov et martigales Thierry Bodieau École Polytechique Paris Départemet de Mathématiques Appliquées thierry.bodieau@polytechique.edu Novembre 2013 2 Table des matières
Polynésie Septembre 2002 - Exercice On peut traiter la question 4 sans avoir traité les questions précédentes.
 Polyésie Septembre 2 - Exercice O peut traiter la questio 4 sas avoir traité les questios précédetes Pour u achat immobilier, lorsqu ue persoe emprute ue somme de 50 000 euros, remboursable par mesualités
Polyésie Septembre 2 - Exercice O peut traiter la questio 4 sas avoir traité les questios précédetes Pour u achat immobilier, lorsqu ue persoe emprute ue somme de 50 000 euros, remboursable par mesualités
STATISTIQUE AVANCÉE : MÉTHODES
 STATISTIQUE AVANCÉE : MÉTHODES NON-PAAMÉTIQUES Ecole Cetrale de Paris Arak S. DALALYAN Table des matières 1 Itroductio 5 2 Modèle de desité 7 2.1 Estimatio par istogrammes............................
STATISTIQUE AVANCÉE : MÉTHODES NON-PAAMÉTIQUES Ecole Cetrale de Paris Arak S. DALALYAN Table des matières 1 Itroductio 5 2 Modèle de desité 7 2.1 Estimatio par istogrammes............................
SÉRIES STATISTIQUES À DEUX VARIABLES
 1 ) POSITION DU PROBLÈME - VOCABULAIRE A ) DÉFINITION SÉRIES STATISTIQUES À DEUX VARIABLES O cosidère deux variables statistiques umériques x et y observées sur ue même populatio de idividus. O ote x 1
1 ) POSITION DU PROBLÈME - VOCABULAIRE A ) DÉFINITION SÉRIES STATISTIQUES À DEUX VARIABLES O cosidère deux variables statistiques umériques x et y observées sur ue même populatio de idividus. O ote x 1
Probabilités et statistique pour le CAPES
 Probabilités et statistique pour le CAPES Béatrice de Tilière Frédérique Petit 2 3 jui 205. Uiversité Pierre et Marie Curie 2. Uiversité Pierre et Marie Curie 2 Table des matières Modélisatio de phéomèes
Probabilités et statistique pour le CAPES Béatrice de Tilière Frédérique Petit 2 3 jui 205. Uiversité Pierre et Marie Curie 2. Uiversité Pierre et Marie Curie 2 Table des matières Modélisatio de phéomèes
Processus géométrique généralisé et applications en fiabilité
 Processus géométrique gééralisé et applicatios e fiabilité Lauret Bordes 1 & Sophie Mercier 2 1,2 Uiversité de Pau et des Pays de l Adour Laboratoire de Mathématiques et de leurs Applicatios - Pau UMR
Processus géométrique gééralisé et applicatios e fiabilité Lauret Bordes 1 & Sophie Mercier 2 1,2 Uiversité de Pau et des Pays de l Adour Laboratoire de Mathématiques et de leurs Applicatios - Pau UMR
UV SQ 20. Automne 2006. Responsable d Rémy Garandel ( m.-el. remy.garandel@utbm.fr ) page 1
 UV SQ 0 Probabilités Statistiques UV SQ 0 Autome 006 Resposable d Rémy Garadel ( m.-el. remy.garadel@utbm.fr ) page SQ-0 Probabilités - Statistiques Bibliographie: Titre Auteur(s) Editios Localisatio Niveau
UV SQ 0 Probabilités Statistiques UV SQ 0 Autome 006 Resposable d Rémy Garadel ( m.-el. remy.garadel@utbm.fr ) page SQ-0 Probabilités - Statistiques Bibliographie: Titre Auteur(s) Editios Localisatio Niveau
Chaînes de Markov. Arthur Charpentier
 Chaîes de Markov Arthur Charpetier École Natioale de la Statistique et d Aalyse de l Iformatio - otes de cours à usage exclusif des étudiats de l ENSAI - - e pas diffuser, e pas citer - Quelques motivatios.
Chaîes de Markov Arthur Charpetier École Natioale de la Statistique et d Aalyse de l Iformatio - otes de cours à usage exclusif des étudiats de l ENSAI - - e pas diffuser, e pas citer - Quelques motivatios.
55 - EXEMPLES D UTILISATION DU TABLEUR.
 55 - EXEMPLES D UTILISATION DU TABLEUR. CHANTAL MENINI 1. U pla possible Les exemples qui vot suivre sot des pistes possibles et e aucu cas ue présetatio exhaustive. De même je ai pas fait ue étude systématique
55 - EXEMPLES D UTILISATION DU TABLEUR. CHANTAL MENINI 1. U pla possible Les exemples qui vot suivre sot des pistes possibles et e aucu cas ue présetatio exhaustive. De même je ai pas fait ue étude systématique
DETERMINANTS. a b et a'
 2003 - Gérard Lavau - http://perso.waadoo.fr/lavau/idex.htm Vous avez toute liberté pour télécharger, imprimer, photocopier ce cours et le diffuser gratuitemet. Toute diffusio à titre oéreux ou utilisatio
2003 - Gérard Lavau - http://perso.waadoo.fr/lavau/idex.htm Vous avez toute liberté pour télécharger, imprimer, photocopier ce cours et le diffuser gratuitemet. Toute diffusio à titre oéreux ou utilisatio
Théorie de la Mesure et Intégration
 Ecole Nationale de la Statistique et de l Administration Economique Théorie de la Mesure et Intégration Xavier MARY 2 Table des matières I Théorie de la mesure 11 1 Algèbres et tribus de parties d un ensemble
Ecole Nationale de la Statistique et de l Administration Economique Théorie de la Mesure et Intégration Xavier MARY 2 Table des matières I Théorie de la mesure 11 1 Algèbres et tribus de parties d un ensemble
Cours 5 : ESTIMATION PONCTUELLE
 Cours 5 : ESTIMATION PONCTUELLE A- Gééralités B- Précisio d u estimateur C- Exhaustivité D- iformatio E-estimateur sas biais de variace miimale, estimateur efficace F- Quelques méthode s d estimatio A-
Cours 5 : ESTIMATION PONCTUELLE A- Gééralités B- Précisio d u estimateur C- Exhaustivité D- iformatio E-estimateur sas biais de variace miimale, estimateur efficace F- Quelques méthode s d estimatio A-
UNIVERSITÉ DE SFAX École Supérieure de Commerce
 UNIVERSITÉ DE SFAX École Supérieure de Commerce Aée Uiversitaire 2003 / 2004 Auditoire : Troisième Aée Études Supérieures Commerciales & Scieces Comptables DÉCISIONS FINANCIÈRES Note de cours N 3 Première
UNIVERSITÉ DE SFAX École Supérieure de Commerce Aée Uiversitaire 2003 / 2004 Auditoire : Troisième Aée Études Supérieures Commerciales & Scieces Comptables DÉCISIONS FINANCIÈRES Note de cours N 3 Première
16.1 Convergence simple et convergence uniforme. une suite de fonctions de I dans R ou C.
 16 Suites de foctios Suf précisio cotrire, I est u itervlle réel o réduit à u poit et les foctios cosidérées sot défiies sur I à vleurs réelles ou complexes. 16.1 Covergece simple et covergece uiforme
16 Suites de foctios Suf précisio cotrire, I est u itervlle réel o réduit à u poit et les foctios cosidérées sot défiies sur I à vleurs réelles ou complexes. 16.1 Covergece simple et covergece uiforme
Chapitre 3 : Transistor bipolaire à jonction
 Chapitre 3 : Trasistor bipolaire à joctio ELEN075 : Electroique Aalogique ELEN075 : Electroique Aalogique / Trasistor bipolaire U aperçu du chapitre 1. Itroductio 2. Trasistor p e mode actif ormal 3. Courats
Chapitre 3 : Trasistor bipolaire à joctio ELEN075 : Electroique Aalogique ELEN075 : Electroique Aalogique / Trasistor bipolaire U aperçu du chapitre 1. Itroductio 2. Trasistor p e mode actif ormal 3. Courats
Intégration et probabilités TD1 Espaces mesurés Corrigé
 Intégration et probabilités TD1 Espaces mesurés Corrigé 2012-2013 1 Petites questions 1 Est-ce que l ensemble des ouverts de R est une tribu? Réponse : Non, car le complémentaire de ], 0[ n est pas ouvert.
Intégration et probabilités TD1 Espaces mesurés Corrigé 2012-2013 1 Petites questions 1 Est-ce que l ensemble des ouverts de R est une tribu? Réponse : Non, car le complémentaire de ], 0[ n est pas ouvert.
Université de Bordeaux - Master MIMSE - 2ème année. Scoring. Marie Chavent http://www.math.u-bordeaux.fr/ machaven/ 2014-2015
 Uiversité de Bordeaux - Master MIMSE - 2ème aée Scorig Marie Chavet http://www.math.u-bordeaux.fr/ machave/ 2014-2015 1 Itroductio L idée géérale est d affecter ue ote (u score) global à u idividu à partir
Uiversité de Bordeaux - Master MIMSE - 2ème aée Scorig Marie Chavet http://www.math.u-bordeaux.fr/ machave/ 2014-2015 1 Itroductio L idée géérale est d affecter ue ote (u score) global à u idividu à partir
Statistique Numérique et Analyse des Données
 Statistique Numérique et Aalyse des Doées Arak DALALYAN Septembre 2011 Table des matières 1 Élémets de statistique descriptive 9 1.1 Répartitio d ue série umérique uidimesioelle.............. 9 1.2 Statistiques
Statistique Numérique et Aalyse des Doées Arak DALALYAN Septembre 2011 Table des matières 1 Élémets de statistique descriptive 9 1.1 Répartitio d ue série umérique uidimesioelle.............. 9 1.2 Statistiques
Consolidation. C r é e r un nouveau classeur. Créer un groupe de travail. Saisir des données dans un groupe
 Cosolidatio La société THEOS, qui commercialise des vis, exerce so activité das trois villes : Paris, Nacy et Nice. Le directeur de la société souhaite cosolider les résultats de ses vetes par ville das
Cosolidatio La société THEOS, qui commercialise des vis, exerce so activité das trois villes : Paris, Nacy et Nice. Le directeur de la société souhaite cosolider les résultats de ses vetes par ville das
UNIVERSITE MONTESQUIEU BORDEAUX IV. Année universitaire 2006-2007. Semestre 2. Prévisions Financières. Travaux Dirigés - Séances n 4
 UNVERSTE MONTESQUEU BORDEAUX V Licece 3 ère aée Ecoomie - Gestio Aée uiversitaire 2006-2007 Semestre 2 Prévisios Fiacières Travaux Dirigés - Séaces 4 «Les Critères Complémetaires des Choix d vestissemet»
UNVERSTE MONTESQUEU BORDEAUX V Licece 3 ère aée Ecoomie - Gestio Aée uiversitaire 2006-2007 Semestre 2 Prévisios Fiacières Travaux Dirigés - Séaces 4 «Les Critères Complémetaires des Choix d vestissemet»
Module 3 : Inversion de matrices
 Math Stat Module : Iversio de matrices M Module : Iversio de matrices Uité. Défiitio O e défiira l iverse d ue matrice que si est carrée. O appelle iverse de la matrice carrée toute matrice B telle que
Math Stat Module : Iversio de matrices M Module : Iversio de matrices Uité. Défiitio O e défiira l iverse d ue matrice que si est carrée. O appelle iverse de la matrice carrée toute matrice B telle que
Gérer les applications
 Gérer les applicatios E parcourat les rayos du Widows Phoe Store, vous serez e mesure de compléter les services de base de votre smartphoe à travers plus de 10 000 applicatios. Gratuites ou payates, ces
Gérer les applicatios E parcourat les rayos du Widows Phoe Store, vous serez e mesure de compléter les services de base de votre smartphoe à travers plus de 10 000 applicatios. Gratuites ou payates, ces
c. Calcul pour une évolution d une proportion entre deux années non consécutives
 Calcul des itervalles de cofiace our les EPCV 996-004 - Cas d u ourcetage ou d ue évolutio e oit das la oulatio totale des méages - Cas d u ourcetage ou d ue évolutio das ue sous oulatio das les méages
Calcul des itervalles de cofiace our les EPCV 996-004 - Cas d u ourcetage ou d ue évolutio e oit das la oulatio totale des méages - Cas d u ourcetage ou d ue évolutio das ue sous oulatio das les méages
Statistiques appliquées à la gestion Cours d analyse de donnés Master 1
 Aalyse des doées Statistiques appliquées à la gestio Cours d aalyse de doés Master F. SEYTE : Maître de coféreces HDR e scieces écoomiques Uiversité de Motpellier I M. TERRAZA : Professeur de scieces écoomiques
Aalyse des doées Statistiques appliquées à la gestio Cours d aalyse de doés Master F. SEYTE : Maître de coféreces HDR e scieces écoomiques Uiversité de Motpellier I M. TERRAZA : Professeur de scieces écoomiques
Contribution à la théorie des entiers friables
 UFR STMIA École Doctorale IAE + M Uiversité Heri Poicaré - Nacy I DFD Mathématiques THÈSE présetée pour l obtetio du titre de Docteur de l Uiversité Heri Poicaré, Nacy-I e Mathématiques par Bruo MARTIN
UFR STMIA École Doctorale IAE + M Uiversité Heri Poicaré - Nacy I DFD Mathématiques THÈSE présetée pour l obtetio du titre de Docteur de l Uiversité Heri Poicaré, Nacy-I e Mathématiques par Bruo MARTIN
THÉORIE DE LA MESURE ET DE L INTÉGRATION.
 THÉORIE DE LA MESURE ET DE L INTÉGRATION. THIERRY GALLAY Transcrit par Tancrède LEPOINT 29 UNIVERSITÉ JOSEPH FOURIER, GRENOBLE TABLE DES MATIÈRES Avant-propos Biographie sommaire...........................................
THÉORIE DE LA MESURE ET DE L INTÉGRATION. THIERRY GALLAY Transcrit par Tancrède LEPOINT 29 UNIVERSITÉ JOSEPH FOURIER, GRENOBLE TABLE DES MATIÈRES Avant-propos Biographie sommaire...........................................
Fonctions de plusieurs variables, intégrales multiples, et intégrales dépendant d un paramètre
 IUFM du Limousin 2009-10 PLC1 Mathématiques S. Vinatier Rappels de cours Fonctions de plusieurs variables, intégrales multiples, et intégrales dépendant d un paramètre 1 Fonctions de plusieurs variables
IUFM du Limousin 2009-10 PLC1 Mathématiques S. Vinatier Rappels de cours Fonctions de plusieurs variables, intégrales multiples, et intégrales dépendant d un paramètre 1 Fonctions de plusieurs variables
Chap. 5 : Les intérêts (Les calculs financiers)
 Chap. 5 : Les itérêts (Les calculs fiaciers) Das u cotrat de prêt, le prêteur met à la dispositio de l empruteur, à u taux d itérêt doé, ue somme d arget (le capital) qu il devra rembourser à ue certaie
Chap. 5 : Les itérêts (Les calculs fiaciers) Das u cotrat de prêt, le prêteur met à la dispositio de l empruteur, à u taux d itérêt doé, ue somme d arget (le capital) qu il devra rembourser à ue certaie
2 ième partie : MATHÉMATIQUES FINANCIÈRES
 2 ième partie : MATHÉMATIQUES FINANCIÈRES 1. Défiitios L'itérêt est l'idemité que doe au propriétaire d'ue somme d'arget celui qui e a joui pedat u certai temps. Divers élémets itervieet das le calcul
2 ième partie : MATHÉMATIQUES FINANCIÈRES 1. Défiitios L'itérêt est l'idemité que doe au propriétaire d'ue somme d'arget celui qui e a joui pedat u certai temps. Divers élémets itervieet das le calcul
Intégration et probabilités TD1 Espaces mesurés
 Intégration et probabilités TD1 Espaces mesurés 2012-2013 1 Petites questions 1) Est-ce que l ensemble des ouverts de R est une tribu? 2) Si F et G sont deux tribus, est-ce que F G est toujours une tribu?
Intégration et probabilités TD1 Espaces mesurés 2012-2013 1 Petites questions 1) Est-ce que l ensemble des ouverts de R est une tribu? 2) Si F et G sont deux tribus, est-ce que F G est toujours une tribu?
Intégrale de Lebesgue
 Intégrale de Lebesgue L3 Mathématiques Jean-Christophe Breton Université de Rennes 1 Septembre Décembre 2014 version du 2/12/14 Table des matières 1 Tribus (σ-algèbres) et mesures 1 1.1 Rappels ensemblistes..............................
Intégrale de Lebesgue L3 Mathématiques Jean-Christophe Breton Université de Rennes 1 Septembre Décembre 2014 version du 2/12/14 Table des matières 1 Tribus (σ-algèbres) et mesures 1 1.1 Rappels ensemblistes..............................
capital en fin d'année 1 C 0 + T C 0 = C 0 (1 + T) = C 0 r en posant r = 1 + T 2 C 0 r + C 0 r T = C 0 r (1 + T) = C 0 r 2 3 C 0 r 3...
 Applicatios des maths Algèbre fiacière 1. Itérêts composés O place u capital C 0 à u taux auel T a pedat aées. Quelle est la valeur fiale C de ce capital? aée capital e fi d'aée 1 C 0 + T C 0 = C 0 (1
Applicatios des maths Algèbre fiacière 1. Itérêts composés O place u capital C 0 à u taux auel T a pedat aées. Quelle est la valeur fiale C de ce capital? aée capital e fi d'aée 1 C 0 + T C 0 = C 0 (1
Théorie de la Mesure et Intégration
 Université Pierre & Marie Curie (Paris 6) Licence de Mathématiques L3 UE LM364 Intégration 1 & UE LM365 Intégration 2 Année 2010 11 Théorie de la Mesure et Intégration Responsable des cours : Amaury LAMBERT
Université Pierre & Marie Curie (Paris 6) Licence de Mathématiques L3 UE LM364 Intégration 1 & UE LM365 Intégration 2 Année 2010 11 Théorie de la Mesure et Intégration Responsable des cours : Amaury LAMBERT
Université Pierre et Marie Curie. Biostatistique PACES - UE4 2013-2014
 Uiversité Pierre et Marie Curie Biostatistique PACES - UE4 2013-2014 Resposables : F. Carrat et A. Mallet Auteurs : F. Carrat, A. Mallet, V. Morice Mise à jour : 21 octobre 2013 Relecture : V. Morice,
Uiversité Pierre et Marie Curie Biostatistique PACES - UE4 2013-2014 Resposables : F. Carrat et A. Mallet Auteurs : F. Carrat, A. Mallet, V. Morice Mise à jour : 21 octobre 2013 Relecture : V. Morice,
MESURE DE L'INFORMATION
 MESURE DE L'INFORMATION Marc URO TABLE DES MATIÈRES INTRODUCTION... 3 INCERTITUDE D'UN ÉVÉNEMENT (OU SELF-INFORMATION)... 7 INFORMATION MUTUELLE DE DEUX ÉVÉNEMENTS... 9 ENTROPIE D'UNE VARIABLE ALÉATOIRE
MESURE DE L'INFORMATION Marc URO TABLE DES MATIÈRES INTRODUCTION... 3 INCERTITUDE D'UN ÉVÉNEMENT (OU SELF-INFORMATION)... 7 INFORMATION MUTUELLE DE DEUX ÉVÉNEMENTS... 9 ENTROPIE D'UNE VARIABLE ALÉATOIRE
Mesure et Intégration (Notes de cours de L3)
 Mesure et Intégration (Notes de cours de L3) Ahmed Zeriahi Version préliminaire-octobre 2011 Avertissement : Ceci est une version préliminaire des notes du cours que l auteur a dispensé en troisème année
Mesure et Intégration (Notes de cours de L3) Ahmed Zeriahi Version préliminaire-octobre 2011 Avertissement : Ceci est une version préliminaire des notes du cours que l auteur a dispensé en troisème année
Chapitre 2 SONDAGE ALEATOIRE SIMPLE OU A PROBABILITES EGALES. 2.1 DEFINITIONS 2.2 SONDAGE ALEATOIRE SIMPLE SANS REMISE (PESR) 2.2.
 Chapitre 2 SONDAGE ALEATOIRE SIMPLE OU A PROBABILITES EGALES PLAN DU CHAPITRE 2 2.1 DEFINITIONS 2.2 SONDAGE ALEATOIRE SIMPLE SANS REMISE (PESR) 2.2.1 Pla de sodage 2.2.2 Probabilités d iclusio 2.3 SONDAGE
Chapitre 2 SONDAGE ALEATOIRE SIMPLE OU A PROBABILITES EGALES PLAN DU CHAPITRE 2 2.1 DEFINITIONS 2.2 SONDAGE ALEATOIRE SIMPLE SANS REMISE (PESR) 2.2.1 Pla de sodage 2.2.2 Probabilités d iclusio 2.3 SONDAGE
Chap. 6 : Les principaux crédits de trésorerie et leur comptabilisation
 1 / 9 Chap. 6 : Les pricipaux crédits de trésorerie et leur comptabilisatio Le cycle d exploitatio des etreprises (achats stockage productio stockage vetes) peut etraîer des décalages de trésorerie plus
1 / 9 Chap. 6 : Les pricipaux crédits de trésorerie et leur comptabilisatio Le cycle d exploitatio des etreprises (achats stockage productio stockage vetes) peut etraîer des décalages de trésorerie plus
3.1 Différences entre ESX 3.5 et ESXi 3.5 au niveau du réseau. Solution Cette section récapitule les différences entre les deux versions.
 3 Réseau Le réseau costitue u aspect essetiel d u eviroemet virtuel ESX. Il est doc importat de compredre la techologie, y compris ses différets composats et leur coopératio. Das ce chapitre, ous étudios
3 Réseau Le réseau costitue u aspect essetiel d u eviroemet virtuel ESX. Il est doc importat de compredre la techologie, y compris ses différets composats et leur coopératio. Das ce chapitre, ous étudios
Image d un intervalle par une fonction continue
 DOCUMENT 27 Image d un intervalle par une fonction continue La continuité d une fonction en un point est une propriété locale : une fonction est continue en un point x 0 si et seulement si sa restriction
DOCUMENT 27 Image d un intervalle par une fonction continue La continuité d une fonction en un point est une propriété locale : une fonction est continue en un point x 0 si et seulement si sa restriction
Mesures et Intégration
 Mesures et Intégration Marc Troyanov - EPFL - Octobre 2005 30 avril 2008 Ce document contient les notes du cours de Mesure et Intégration enseigné à l EPFL par Marc Troyanov, version 2005-2006. Table des
Mesures et Intégration Marc Troyanov - EPFL - Octobre 2005 30 avril 2008 Ce document contient les notes du cours de Mesure et Intégration enseigné à l EPFL par Marc Troyanov, version 2005-2006. Table des
La mesure de Lebesgue sur la droite réelle
 Chapitre 1 La mesure de Lebesgue sur la droite réelle 1.1 Ensemble mesurable au sens de Lebesgue 1.1.1 Mesure extérieure Définition 1.1.1. Un intervalle est une partie convexe de R. L ensemble vide et
Chapitre 1 La mesure de Lebesgue sur la droite réelle 1.1 Ensemble mesurable au sens de Lebesgue 1.1.1 Mesure extérieure Définition 1.1.1. Un intervalle est une partie convexe de R. L ensemble vide et
PROBLEMES DIOPTIMISATION EN NOMBRES ENTIERS J. L. NICOLAS
 PROBLEMES DIOPTIMISATION EN NOMBRES ENTIERS ET APPROXIMATIONS DIOPHANTIENNES J. L. NICOLAS Cet article expose sup 3 e quelques iter'f~reces etre les pr'obl~res dloptimisatio e hombres etiers et la th~or-ie
PROBLEMES DIOPTIMISATION EN NOMBRES ENTIERS ET APPROXIMATIONS DIOPHANTIENNES J. L. NICOLAS Cet article expose sup 3 e quelques iter'f~reces etre les pr'obl~res dloptimisatio e hombres etiers et la th~or-ie
Les algorithmes de tri
 CONSERVATOIRE NATIONAL DES ARTS ET METIERS PARIS MEMOIRE POUR L'EXAMEN PROBATOIRE e INFORMATIQUE par Nicolas HERVE Les algorithmes de tri Souteu le mai JURY PRESIDENTE : Mme COSTA Sommaire Itroductio....
CONSERVATOIRE NATIONAL DES ARTS ET METIERS PARIS MEMOIRE POUR L'EXAMEN PROBATOIRE e INFORMATIQUE par Nicolas HERVE Les algorithmes de tri Souteu le mai JURY PRESIDENTE : Mme COSTA Sommaire Itroductio....
TRANSFERT DE CHARGE DANS UN RÉSEAU DE PROCESSEURS TOTALEMENT CONNECTÉS (*) par Maryse BÉGUIN ( 1 )
 RAIRO Operatios Research RAIRO Oper. Res. 34 (2000) 99-129 TRANSFERT DE CHARGE DANS UN RÉSEAU DE PROCESSEURS TOTALEMENT CONNECTÉS (*) par Maryse BÉGUIN ( 1 ) Commuiqué par Berard LEMAIRE Résumé. L étude
RAIRO Operatios Research RAIRO Oper. Res. 34 (2000) 99-129 TRANSFERT DE CHARGE DANS UN RÉSEAU DE PROCESSEURS TOTALEMENT CONNECTÉS (*) par Maryse BÉGUIN ( 1 ) Commuiqué par Berard LEMAIRE Résumé. L étude
Formation d un ester à partir d un acide et d un alcool
 CHAPITRE 10 RÉACTINS D ESTÉRIFICATIN ET D HYDRLYSE 1 Formatio d u ester à partir d u acide et d u alcool 1. Nomeclature Acide : R C H Alcool : R H Groupe caractéristique ester : C Formule géérale d u ester
CHAPITRE 10 RÉACTINS D ESTÉRIFICATIN ET D HYDRLYSE 1 Formatio d u ester à partir d u acide et d u alcool 1. Nomeclature Acide : R C H Alcool : R H Groupe caractéristique ester : C Formule géérale d u ester
Chap. 6 : Les principaux crédits de trésorerie et leur comptabilisation
 Chap. 6 : Les pricipaux crédits de trésorerie et leur comptabilisatio Les etreprises ot souvet besoi de moyes de fiacemet à court terme : elles ot alors recours aux crédits bacaires (découverts bacaires
Chap. 6 : Les pricipaux crédits de trésorerie et leur comptabilisatio Les etreprises ot souvet besoi de moyes de fiacemet à court terme : elles ot alors recours aux crédits bacaires (découverts bacaires
Théorie de la mesure. S. Nicolay
 Théorie de la mesure S. Nicolay Année académique 2011 2012 ii Table des matières Introduction v 1 Mesures 1 1.1 Sigma-algèbres................................. 1 1.2 Mesures.....................................
Théorie de la mesure S. Nicolay Année académique 2011 2012 ii Table des matières Introduction v 1 Mesures 1 1.1 Sigma-algèbres................................. 1 1.2 Mesures.....................................
Régulation analogique industrielle ESTF- G.Thermique
 Chapitre 5 Stabilité, Rapidité, Précisio et Réglage Stabilité. Défiitio Coditio de stabilité. Critères de stabilité.. Critères algébriques.. Critère graphique ou de revers das le pla de Nyquist Rapidité
Chapitre 5 Stabilité, Rapidité, Précisio et Réglage Stabilité. Défiitio Coditio de stabilité. Critères de stabilité.. Critères algébriques.. Critère graphique ou de revers das le pla de Nyquist Rapidité
Produits d espaces mesurés
 Chapitre 7 Produits d espaces mesurés 7.1 Motivation Au chapitre 2, on a introduit la mesure de Lebesgue sur la tribu des boréliens de R (notée B(R)), ce qui nous a permis d exprimer la notion de longueur
Chapitre 7 Produits d espaces mesurés 7.1 Motivation Au chapitre 2, on a introduit la mesure de Lebesgue sur la tribu des boréliens de R (notée B(R)), ce qui nous a permis d exprimer la notion de longueur
INTRODUCTION AUX MATRICES ALÉATOIRES. par. Djalil Chafaï
 INTRODUCTION AUX MATRICES ALÉATOIRES par Djalil Chafaï Résumé. E cocevat les mathématiques comme u graphe, où chaque sommet est u domaie, la théorie des probabilités et l algèbre liéaire figuret parmi
INTRODUCTION AUX MATRICES ALÉATOIRES par Djalil Chafaï Résumé. E cocevat les mathématiques comme u graphe, où chaque sommet est u domaie, la théorie des probabilités et l algèbre liéaire figuret parmi
Un nouvel opérateur de fusion adaptatif. A new adaptive operator of fusion. 1. introduction
 A ew adaptive operator of fusio par Fraçois DELMOTTE LAMIH, Uiversité de Valeciees et du Haiaut-Cambrésis, Le Mot Houy, BP 3, 5933 Valeciees CEDEX 9 fdelmott@flore.uiv-valeciees.fr résumé et mots clés
A ew adaptive operator of fusio par Fraçois DELMOTTE LAMIH, Uiversité de Valeciees et du Haiaut-Cambrésis, Le Mot Houy, BP 3, 5933 Valeciees CEDEX 9 fdelmott@flore.uiv-valeciees.fr résumé et mots clés
MESURE ET INTÉGRATION EN UNE DIMENSION. Notes de cours
 MSUR T INTÉGRATION N UN DIMNSION Notes de cours André Giroux Département de Mathématiques et Statistique Université de Montréal Mai 2004 Table des matières 1 INTRODUCTION 2 1.1 xercices.............................
MSUR T INTÉGRATION N UN DIMNSION Notes de cours André Giroux Département de Mathématiques et Statistique Université de Montréal Mai 2004 Table des matières 1 INTRODUCTION 2 1.1 xercices.............................
Échantillonnage et estimation
 Stage «Nouveaux programmes de Termiale S» - Ho Chi Mih-Ville Novembre 202 Échatilloage et estimatio Partie C - Frédéric Barôme page Échatilloage et estimatio Partie C : Capacités et exercices-types. Rappelos
Stage «Nouveaux programmes de Termiale S» - Ho Chi Mih-Ville Novembre 202 Échatilloage et estimatio Partie C - Frédéric Barôme page Échatilloage et estimatio Partie C : Capacités et exercices-types. Rappelos
Principes et Méthodes Statistiques
 Esimag - 2ème aée 0 1 2 3 4 5 6 7 0 5 10 15 x y Pricipes et Méthodes Statistiques Notes de cours Olivier Gaudoi 2 Table des matières 1 Itroductio 7 1.1 Défiitio et domaies d applicatio de la statistique............
Esimag - 2ème aée 0 1 2 3 4 5 6 7 0 5 10 15 x y Pricipes et Méthodes Statistiques Notes de cours Olivier Gaudoi 2 Table des matières 1 Itroductio 7 1.1 Défiitio et domaies d applicatio de la statistique............
Séries numériques. Chap. 02 : cours complet.
 Séris méris Cha : cors comlt Séris d réls t d comlxs Défiitio : séri d réls o d comlxs Défiitio : séri corgt o dirgt Rmar : iflc ds rmirs trms d séri sr la corgc Théorèm : coditio écssair d corgc Théorèm
Séris méris Cha : cors comlt Séris d réls t d comlxs Défiitio : séri d réls o d comlxs Défiitio : séri corgt o dirgt Rmar : iflc ds rmirs trms d séri sr la corgc Théorèm : coditio écssair d corgc Théorèm
Intégrales dépendant d un paramètre
 [hp://mp.cpgedupuydelome.fr] édié le 3 avril 5 Eocés Iégrales dépeda d u paramère Covergece domiée Exercice [ 9 ] [correcio] Calculer les limies des suies do les ermes gééraux so les suivas : a) u = π/4
[hp://mp.cpgedupuydelome.fr] édié le 3 avril 5 Eocés Iégrales dépeda d u paramère Covergece domiée Exercice [ 9 ] [correcio] Calculer les limies des suies do les ermes gééraux so les suivas : a) u = π/4
Calcul fonctionnel holomorphe dans les algèbres de Banach
 Chapitre 7 Calcul fonctionnel holomorphe dans les algèbres de Banach L objet de ce chapitre est de définir un calcul fonctionnel holomorphe qui prolonge le calcul fonctionnel polynômial et qui respecte
Chapitre 7 Calcul fonctionnel holomorphe dans les algèbres de Banach L objet de ce chapitre est de définir un calcul fonctionnel holomorphe qui prolonge le calcul fonctionnel polynômial et qui respecte
La fibre optique arrive chez vous Devenez acteur de la révolution numérique
 2 e éditio Edité par l Autorité de régulatio des commuicatios électroiques et des postes RÉPUBLIQUE FRANÇAISE DÉCEMBRE 2010 La fibre optique arrive chez vous Deveez acteur de la révolutio umérique Petit
2 e éditio Edité par l Autorité de régulatio des commuicatios électroiques et des postes RÉPUBLIQUE FRANÇAISE DÉCEMBRE 2010 La fibre optique arrive chez vous Deveez acteur de la révolutio umérique Petit
La tarification hospitalière : de l enveloppe globale à la concurrence par comparaison
 ANNALES D ÉCONOMIE ET DE STATISTIQUE. N 58 2000 La tarificatio hospitalière : de l eveloppe globale à la cocurrece par comparaiso Michel MOUGEOT * RÉSUMÉ. Cet article cosidère différetes politiques de
ANNALES D ÉCONOMIE ET DE STATISTIQUE. N 58 2000 La tarificatio hospitalière : de l eveloppe globale à la cocurrece par comparaiso Michel MOUGEOT * RÉSUMÉ. Cet article cosidère différetes politiques de
Compte Sélect Banque Manuvie Guide du débutant
 GUIDE DU DÉBUTANT Compte Sélect Baque Mauvie Guide du débutat Besoi d aide? Preez quelques miutes pour lire attetivemet votre Guide du cliet. Le préset Guide du débutat vous facilitera l utilisatio de
GUIDE DU DÉBUTANT Compte Sélect Baque Mauvie Guide du débutat Besoi d aide? Preez quelques miutes pour lire attetivemet votre Guide du cliet. Le préset Guide du débutat vous facilitera l utilisatio de
POLITIQUE ECONOMIQUE ET DEVELOPPEMENT
 POLTQU ONOMQU T DVLOPPMNT TRUTUR DU MAR NATONAL DU AF-AAO T PR AU PRODUTUR MALAN Beïla Beoit osultat PD N 06/008 ellule d Aalyse de Politiques coomiques du R Aée de pulicatio : Avril 009 Résumé e papier
POLTQU ONOMQU T DVLOPPMNT TRUTUR DU MAR NATONAL DU AF-AAO T PR AU PRODUTUR MALAN Beïla Beoit osultat PD N 06/008 ellule d Aalyse de Politiques coomiques du R Aée de pulicatio : Avril 009 Résumé e papier
Terminale S. Terminale S 1 F. Laroche
 Termiale S Exercices. Rappels et exercices de base 3.. QCM (P. Egel) 3.. QCM, Atilles 005 4. 3. QCM, Liba 009, 3 poits 4. 4. QCM, C. étragers 007. 5. QCM, Frace 007 5 6. 6. QCM, N. Calédoie 007 7. 7. QCM
Termiale S Exercices. Rappels et exercices de base 3.. QCM (P. Egel) 3.. QCM, Atilles 005 4. 3. QCM, Liba 009, 3 poits 4. 4. QCM, C. étragers 007. 5. QCM, Frace 007 5 6. 6. QCM, N. Calédoie 007 7. 7. QCM
