MATHEMATIQUES FINANCIERES
|
|
|
- Blanche Brosseau
- il y a 9 ans
- Total affichages :
Transcription
1 Fculté de rot et de Scece écooques ANNEE 4 5 LMSE -S5 MATHEMATIQUES FINANIERES Jule Froger e-l : [email protected] web :
2 Mthétques fcères, rs 5 htre Les térêts sles. A Prces de clcul. B L escote. L équvlece. Les utres lctos des térêts sles. htre Les térêts coosés. A Prces de clcul. B Tux roortoels, tux équvlets. L équvlece. htre Les utés. A Evluto d ue sute d utés costtes. B Evluto d ue sute à vrblté rthétque ou géoétrque. htre 4 Les eruts dvs. A Théore géérle. B L ve d u erut. Tux effectf d u erut dvs. htre 5 Les eruts oblgtres. A rctérstques des eruts oblgtres. B Théore géérle. Modltés d ortsseet. Tux de redeet et tux de revet d u erut. BIBLIOGRAPHIE - MASIERI W, Mthétques fcères, Edtos lloz,. - ROLANO T, FINK J, Mthétques fcères, ollecto y Su, Edtos ubert,. - SHLATHER, oredre les Mthétques fcères, ollecto les fodetux, Edtos Hchette, 4. Pge sur 4
3 Mthétques fcères, rs 5 htre : Les térêts sles. Toutes les questos trtées ds ce chtre coceret jortreet les oértos fcères à court tere (os d u ). es oértos ffectet e jorté l trésorere des etrerses, tel que l gesto des cotes courts, l escote coercle, les eruts à court tere A Prces de clculs.. éftos. U térêt est dt sle lorsqu l est drecteet roortoel u tux, u tes et u ott oétre. I t Itérêt tl Tux our r L durée (e jours) L ée bcre est de 6 jours (6 6 ). I 6 t Alcto A. : U rêt obteu le 4 vrl est reboursé le oût. Quelle été l durée de l oérto? Avrl 6 M Ju Jullet Août Soe jours O e retet qu ue des deux dtes extrêes (c le oût). Alcto A. : lculer l térêt gééré r u lceet de, à 5 %, du 5 ju u ovebre. ( 5) 5 t I 6 Pge sur 4
4 Mthétques fcères, rs 5 I L oto de vleur cquse. L vleur cquse est l soe du ctl tl et des térêts qu l gééré u tere de s durée de lceet. I t 6 t 6 Alcto A. : lculer le ctl qu, à %, cqus ue vleur de 5 48 u bout de jours de lceet. I t Alcto A.4 : éterer le tux de lceet d u ctl de 6 qu rodut, du setebre u décebre, u térêt de 8. ( ) 8 I 6 t 6 t t 4,5% Alcto A.5 : lculer le tux effectf de lceet d ue oérto qu cosstert à lcer à térêts récotés, u tux de 6 %, u ctl de edt 8 os. Itérêts fours r le lceet : I t tl effectveet lcé : 4 96 Pge 4 sur 4
5 Mthétques fcères, rs 5 I t 96 t 8 4 t 6,5%. Le tux oye de lceet. O evsge dfférets ctux : Plcés à des durées dfféretes : Et à des tux dfférets :,...,,,, t,..., t,..., t k k k O eller t le tux qu, lqué à dfférets ctux et à leur durée corresodte, rodur le êe térêt globl que celu à rtr des tux tux resectfs. Alcto A.6 : eux ctux de et 5 sot lcés resectveet à 4 % edt os et 5.5 % edt 9 os. lculer le tux oye de lceet. bord clculos our chque lceet : 4 I t Σ 6, 5 6 5, ,5 lculos I : herchos tet le tux : I t I 6,5,5 ( 5 ) t [( ) ( 5 9) ],5 t 5,% Alcto : Ue etrerse lcé ds dvers étblsseets bcres, les soes suvtes : Au tux de 7.5 % u u 9 ju 45 Au tux de % u u 6 oût 7 Au tux de 8 % u u 7 jullet. lculer le tux oye résultt de l eseble des lceets. Pge 5 sur 4
6 Mthétques fcères, rs 5 7,5 8 6, Σ 78, ,7 6 t ( 45 7) 8, 4 I 78,4 [( 8) ( 45 86) ( 7 66) ] 8,4 t 8,8%. Ue bque roose de lcer 5 u tux oye edt l durée oyee de lceet, l etrerse dot elle cceter? jours I t 5 8,8 6 I 984, L etrerse ccete s cr I < I.. Pedt cobe de tes fut l lcer 5 u tux oye our obter l êe soe globle d térêts que récédeet? B L escote. I 6 t 5 8,8 8,4 6 67, 68 jours. L oto d escote coercl. L etrerse clete reçot de s bque le ott de l effet dué de l go. L go cored l térêt (elé escote), des cossos dverses et de l TA. L escote est clculé selo le rce de l térêt sle. t e leur ole Tux d escote urée e jours Escote Pge 6 sur 4
7 Mthétques fcères, rs 5 leur ctuelle coercle t e 6 e Le tux d escote vre selo l qulté du clet. L escote est js sous à l TA.. L rtque de l escote. verses cossos sot lquées r les bques :. osso ENOS (edosseet), qu sert à réuérer le servce redu r l bque. ette cosso est clculée rort teors (e focto du tes), et elle est s souse à l TA. ette cosso est systétque. b. Les cossos de servce ou de ulto : ces cossos sot vrbles selo les étblsseets fcer et selo l ture de l effet. es cossos sot géérleet forftres et souses à l TA. Le coût réel de l escote ser reréseté r l go hors txe, usque l TA est récuérble. L oto de tux réel de l oérto d escote : clculer ce tux cosste à rechercher le tux d u erut qu urt le êe ott, l êe durée et le êe coût que le crédt d escote (our clculer ce tux, o se bse sur l ée de 65 jours). L durée réelle est obteue r corso etre l escote et l ecsseet, e retet les deux dtes extrêes. e tux réel est très fréqueet be suéreur u tux océ, du ft otet des cossos forftres qu élset les oértos de fble ott, du ft égleet de codtos bcres rtculères, qu élset les effets dt brûlts (ceux dot l échéce est roche) e lqut u obre de jours u (souvet, ce obre est de ). Alcto B.7 : Ue socété reet à l escote le oût, deux effets dot les crctérstques sot les suvtes : leur ole te d échéce 4 5 oût setebre Le tux d escote obteu urès de l bque est de 9 %. osso d edos :.6 %. L cosso de servce est de r effet (souse à l TA u tux orl). L bque lque u jour de bque ux effets res à l escote. Elle lque u jour de vleur ux effets res à l escote, et tros jours de vleurs ux effets res à l ecsseet.. Etblr le bordereu d escote. Bordereu d escote (rese du /8) Pge 7 sur 4
8 Mthétques fcères, rs 5 Echéce NB jours t t e 6 45 /8 9,6 % 4 /9 5 9,6 % 6 57 Soe des térêts 4 osso 6 ( fos ) Ago HT 46 TA à 9,6 %,8 Ago TT 47,8 Mott et 5 65,8. Quel est le tux réel du crédt de l oérto d escote? Effet de 4 5 : tux réel du crédt. Rese à l escote Fods dsobles /8 Rese à l ecsseet Fods dsobles /9 jours de crédt Ago HT : 7 L équvlece térêts sles. ) éfto. eux ctux (effets) sot équvlets s à ue dte doée, u êe tux leur vleur ctuelles coercles sot detques. ) Alctos. Alcto.8 : éterer l dte d équvlece de deux effets dot les crctérstques sot les suvtes (tux d escote : %) : leur ole te d échéce 65 ovebre 7 ovebre Il sufft de rechercher l vleur ole os l escote. A l dte d équvlece : t e 6 e Sot le /. Pge 8 sur 4
9 Mthétques fcères, rs 5 Alcto.9 : Rechercher le tux d équvlece de deux effets dot les crctérstques sot les suvtes (dte d équvlece le octobre) : leur ole te d échéce 7 5 ovebre 7 45 décebre t e 6 e 75 t 745 t t % Alcto. : Sot u effet de vleur ole à échéce du décebre. Le er décebre, le clet dede à so foursseur, qu l ccete, ue rologto d échéce u jver. Tux reteu : %. Quelle ser l ouvelle vleur ole? t e 6 e ,8 Problèe d échéce coue : l s gt de rechercher les codtos, l vleur ole d u eet uque relçt luseurs utres, sot de déterer s dte d échéce. Alcto. : U débteur cceté les tros trtes suvtes : octobre 6 8 ovebre décebre Le er octobre, l désre les relcer r u effet uque u ovebre. Tux : 6 %. Quelle ser l vleur de ce ouvel effet? ,8 Problèe d échéce oyee : cs rtculer d ue d échéce coue ou l vleur ole de l effet uque est égl à soe des vleurs oles des effets tux. Alcto. : Le er octobre o relce deux effets : l u de 7 5 à échéce du octobre, l utre de 5 à échéce du 5 ovebre, r u effet uque de 5. Tux : %. Pge 9 sur 4
10 Mthétques fcères, rs 5 Quelle ser l échéce de ce ouvel effet? (Sot le /). Rereos cet exele e cosdért que le tux d térêt et l dte d équvlece e sot s cous. Sot x l érode etre l dte d équvlece et l dte d échéce. Sot l érode etre l reère échéces et l dte d équvlece. ( 5) 5 t N 75 t 5 t N (Sot le /). O rerque que l dte d échéce oyee est déedte du tux d escote reteu, s que l dte d équvlece. L gesto des cotes courts et d térêts. Lorsqu l s gt d u cote bcre, ce qu orte est s l dte d oérto s l dte de vleur (égocée vec votre bquer). Il fut svor coet foctoet les cotes bcres otet les cs de découverts. eux sortes de cossos sot lquées e cs de découvert :. L cosso de rsque (osso de Plus Fort écouvert : PF),,5% du lus fort découvert du os (l y s de TA sur cette cosso).. Les cossos de servces qu corresodet ux cossos de cotes ou de ouveets. Le tux de cette cosso est e géérl de.5% clculé sur les ouveets débteurs. Alcto. : lculer le ott totl des gos à yer (le tcket d gos) r ue etrerse yt rélsé les oértos suvtes u cours du èe trestre : Mouveets Soldes Nobres te de vleur ébt rédt ébt rédt ébt rédt er jullet jullet jullet jullet oût Pge sur 4
11 Mthétques fcères, rs 5 oût oût oût set set set set Le tux d térêt débteur est de 8 %. utre rt, l bque lque les codtos bcres suvtes : osso de lus fort découvert :.5 % ; osso de cote (sur les ouveets débteurs) :.5 % Itérêts débteurs PF,5%( 8 8) osso de ouveets,5% TA 9,6% 88,5 56,5 Mott TT du tcket d go 5, Alcto : E début d ée, u rtculer décde d cheter ue sce d ue vleur de à l f de l ée. Pour dsoser de cette soe le oet veu, l décde de lcer ue soe costte à chque début de os. Le tux d térêt qu l eut obter est de 4.5 %.. Quel dot être le ott de chque esulté? I 4, 5 4, 5 4, 5 I... Sute rthétque :... Pge sur 4
12 Mthétques fcères, rs 5 4, ,. Quelle sert l soe costte à verser chque see? s 4,5 78 5s 5 s ,59 s. Le er jullet le tux d térêt sse à 6 %, quelle est l ouvelle vleur cquse e f d ée? NB : O suoser que les térêts des 6 reers os serot relcés vec le ctl our les 6 derers os. 976, 4,5 594, derères érodes à 6 % 78, 6 reères érodes à 4,5 % ( 6 976,) 594, 7 Σ 6,9 976, 6 6 derères érodes à 6 % ( 6 976,) 5959, 7 Σ 7,79 4. E ret l ugetto du tux d térêt (le er jullet), cette ersoe décde de rédure ses verseets de fço à obter ue vleur cquse de. Quel est le ott de l ouvelle esulté? 6,9 5887,9 ' 6 ' ' 964,44 Alcto : éterer l dte d échéce d u effet de 7 85 qu se substtuert le 7 décebre à u effet de 7 88 yble le décebre. Le tux d escote est de 9 %. Pge sur 4
13 Mthétques fcères, rs 5 O cote 7 jours rès le 7/ doc le 4/ ,79 7 Alcto 4 : Le setebre, deux effets sot résetés à l escote. Le reer est de 87 ; so échéce est le 8 décebre. Le secod de 6 ; so échéce est le er octobre. lculer le tux d escote scht que le bquer versé l êe soe d rget our les deux effets. 6 t 8 87 t t 8,9% Alcto 5 : Pour fcer l cqusto d ue oto d ue vleur de 6 9, u rtculer covet vec so grgste de lu verser l oté de l soe u cott et le solde e 5 esultés detques, l reère yble ds u os. Le tux roosé r le vedeur est de 4 %.. lculer l vleur ole de chque esulté ,. éterer l échéce oyee des quze verseets L 5 54, 8,8 Pge sur 4
14 Mthétques fcères, rs 5 8, ,8 8 Sot 8 os rès l cqusto. Pge 4 sur 4
15 htre : Les térêts coosés. Les térêts coosés coceret les oértos fcères à oye et log tere, celle dot l échéce est suéreure à os. A Prce de clcul.. éfto. Les térêts sot dts coosés lorsqu e f de érode, elée érode de ctlsto, l s joute u ctl de sorte que l eseble s foré géère à so tour des térêts u cours de l érode suvte.. leur cquse r u ctl. Le ctl lcé L vleur cquse L térêt our our ue érode Le obre de érode K lcé I leur cquse.. ( ) ( ) ( ). ( ). ( ) ( ). ( ) Alcto A.. : A quel tux uel, u ctl de, lcé à térêt coosé edt cq s, rocure t l u térêt globl de ,7? ( ) ( ) ,7,95 5,5% Alcto A.. : U ctl de cquert ue vleur de 45,89, u tux de %. Quelle été l durée du lceet?
16 leur ctuelle d u ctl. (,) (, ) 45,89,4 8 L ctulsto est le rocessus verse de l ctlsto. Alcto A.. : Quelle soe dot o lcer le er jver 5, à térêts coosés, u tux de 7 %, our dsoser de le er jver 7? ( ),7 874,8 Alcto A.4. : Au tux uel de 5 %, l ersectve ujourd hu d u ecsseet de ds tros s est elle lus téresste que celle de 85 ds deux s? ( ) ( ) 85(,5),5 7767,5 678,45 oc l soluto l lus téresste est 7767 cr elle corresod à l lus forte vleur ctuelle. Alcto A.5. : Ue créce de vleur ole 4 échét le décebre 6 est égocée le décebre 4. Tux d escote reteu : %. lculer l vleur ctuelle de cette créce s que so escote, à térêts coosés. ( ) 4, 464,9 e 4 464,9 755, B Tux roortoels et tux équvlets.. éfto.
17 Tux roortoel. U tux est dt roortoels lorsqu l vre de fço lére r rort u tes. b. Tux équvlets. eux tux sot dts équvlets s r lcto à u ctl l géère l êe vleur cquse ou ctuelle. Itérêt sle : lculer l vleur cquse de deux fços dfféretes (5% uel, tux trestrel roortoel à 5%) :. Tux uel de 5%. t 5%.,5 b. Tux trestrel roortoel à 5% sot,5 %. 8.,5 A térêt sle deux tux roortoels sot équvlets usqu ls coduset à des vleurs cquses detques. Itérêts coosés: lculer l vleur cquse de deux fços dfféretes (5% uel, tux trestrel roortoel à 5%) : c. Tux uel de 5%. t 5%
18 5 (,5) d. Tux trestrel roortoel à 5% sot,5 %. 448,6 (,5) 8 O costte qu à térêt coosé deux tux roortoel e sot s équvlets, l est écessre de clculer le tux équvlet à l érode de ctlsto costté.. éostrto. k Le ctl lcé L térêt our our L érode k fos lus ette de l ée k ( ) ( k ) ( ) k k ( ) k k Alcto B.6. : Sot u tux uel de 8%. lculer le tux trestrel roortoel, us le tux trestrel équvlet. L équvlece à térêts coosés.. éfto. ( ) k ( ) 4 4 k,8,94% % eux ctux sot équvlets à ue dte doée u êe tux s leur vleur cquse ou ctuelle sot detques. S deux ctux sot équvlets à ue dte doée, ls le sot égleet à orte quelles utres dtes (c est u héoèe eret).. Alctos. Alcto.7. : U reer ctl de est à échéce du décebre 5. U secod de 4 64 est à échéce du décebre 9. Au tux de %, ces deux ctux sot ls équvlets? 4
19 Les deux ctux sot doc équvlet. (, ) Alcto.8. : U reer ctl de 5 est à échéce du er jver 6. U secod de 7.9 est à échéce du er jver 9. Pour quel tux ces deux ctux sot équvlets? 5 ( ) ( ) ( ) 7,9,4498, % Alcto.9. : Ue dette dot être reboursée grâce à deux verseets : le er de le décebre 5, le secod de le décebre 7. O souhte relcer ces deux verseets r u règleet uque tervet le décebre 6. Au tux de %, quel ser le ott de ce règleet?, 5(, ) x(, ) x 99,9 Alcto.. : Ue dette dot être reboursée de l ère suvte : le er jver 7, us le er jver 8 et ef 5 le er jver 9. Quelle sert l échéce, u tux de %, d u verseet uque de 4 qu relcert les tros verseets tux? Sot le //9., 5(, ) 4(, ) Alcto : Ue socété désre dsoser de ds tros s. S elle lce u début des deux reères ées sur les rchés fcers, les tux de redeet qu elle tce sot de 5% l reère ée, % l secode ée et % l trosèe ée. S elle lce cet rget à l bque, elle obtet u tux uel costt de 7%.. Quelle soe dot elle lcer e début de trosèe ée ds chcu des cs? Pour l bque :,7 Pour les rchés fcers : (,7) x(,7) x 5548,7 5
20 (,5) ( 45 )(,) ( 6579 x) (,) x 57,7. Quelle sert l soluto l lus vtgeuse our l etrerse (chge ossble)? Idquez lors l soe à lcer. (,5) ( 45 )(,7) ( 695 x)(.) x 48,7. L vestsseet révu r l etrerse subr ue flto de 4% l. Quelle ser l soe à verser ds le elleur des cs, scht que est l vleur du be ujourd hu. (,5) 45 ( 45 )(,7) 695 ( 695 x)(.) (,4 x 6758,8 Alcto : U ctl de 4 à échéce de tros s est égocé à l bque.. lculer l vleur ctuelle s que l escote suorté. Le tux reteu est de 9.5% l. (.95) 4 46,6 4 46,6 95,8. E ft l bque fcturé u escote de 8. Quel est le tux réel d escote rtqué? 4 4 ( x) 8 x 7,7%. Quelle est l échéce d u effet de 8 égocé u tux de %? 8, 4967,7 5 ) 6
21 Alcto : u ft de dffcultés de trésorere ue etrerse souhte relcer tros règleets de : 5 ds u, 5 ds tros s, 7 ds qutre s, r u règleet uque ds cq s u tux de %.. lculer le ott de ce règleet uque. 7(, ) (, ) 5 5, 448,9 4 64,56. lculer le ott de ce règleet ds l hyothèse où so échéce est ds deux s. 448,9 (, ) 4485,88. Mêe questo que l. e suost que les tros soes doées sot les vleurs ctuelles des soes à verser (, ) 5798,7 Alcto 4 : Ue etrerse dsose de 5 lcés e bque à térêts coosés. Tros s rès, elle retre 4. eux s lus trd, le cote est crédteur de lculer le tux de lceet. Pr terolto lére o u tux : ( 5( ) 4)( ) 5 5( ) 4( ) 77, 6 O, 7967,6 O? 7,6 O,9 68,5 77,6 7
22 ,5,, ,5 9,5%. Quelle soe, u xu, eut o retrer our dsoser de sur le cote deux s rès le retrt? 5 x(,95) 5,95 x 458,6 8
23 htre : Les utés. éfto : c est u tere géérl qu est lcble quelque sot l érodcté. A Evluto d ue sute d utés costtes.. leur cquse r ue sute d utés costtes. éfto : l s gt de l soe des vleurs cquses r chque uté édteet rès le derer verseet. Mott de l uté Itérêt our our ue érode Nobre d utés leur cquse Ic, le reer tere est, de rso q ( ), vec teres. ( ) ( ) ( ) Σ ( ) ( ) ( ) Alcto A.. : sot lcés le er jver de chque ée cvle du er jver 5 u er jver 8 clus. Au tux d térêt de 9 %, déterer l vleur cquse r ce lceet le er jver 9. (,9),9 9969, 4 (,9) Alcto A.. : U lceet de est rélsé le er jver de chque ée du er jver 6 u er jver 8 clus. Le er jver 9, o dsose de 5 59,5. A quel tux ce lceet -t-l été rélsé?
24 ( ) ( ) 4 ( ) ( ) ( ) 4 ( ) 559,5,55,55 4 4,55 O,9 4,57 O 8,7% 4,55 O,85 4,559 Alcto A.. : Neuf verseets de 5 sot rélsés à 6 os d tervlle chcu. Tux d térêt uel : %. e quelle soe dsoser t o u oet du verseet de l derère seestrlté? s s (, ),488 (,488) 5, , 9 Alcto A.4. : éterer u tux de 7 % le obre d utés costtes de 5 écessres à l costtuto d u ctl de 55. 5,7 55,7 8,49 Preère soluto : 8 5,7 599,, , 7,99 O doc 7 verseets de 5, le 8 èe est de 5 7,99 87,99. euxèe soluto : 9 5, ,94, , ,94 O doc 8 verseets de 5, le 9 èe est de ,94,6.
25 leur ctuelle d ue sute d utés costtes. éfto : soe des vleurs ctuelles de chcue des utés, ue érode vt le er verseet. O teres, de rso q (, reer tere : ) ( ) Alcto A.5. : Ue dette de est cotrctée le er jver 6. Elle ser reboursée r le verseet de qutre utés costtes. Tux d térêt : %. lculer le ott de l uté sous deux hyothèses : H : le reer verseet tervet le er jver 7. (, ) 4, 547,8 H : le reer verseet tervet le er jver 8. (, ) 4 (, ), 47,79 Alcto A.6. : Itleet u débteur s étt eggé à effectuer u rebourseet r le verseet de 8 utés costtes de, l reère uté rrvt à échéce rès l cocluso du cotrt. Au tux de %, déterer les crctérstques d utres solutos équvletes : erseet de seestrltés costtes (l ère 6 os rès l cocluso du cotrt). erseet uque de 94 5,47. erseet uque de 8. s s (,),4889 (, ), 549,6 8 (,488) 549,6 s,488 s 6869,6
26 ,6 945,47, euxèe hyothèse : Sot 4 s et os rès éoque. 549,6 8, 4,5 Alcto A.7. : Quelle est, u tux de %, l vleur ctuelle d ue rete erétuelle de r (reer verseet ds u )? (, ), Alcto A.8. : U erut de dot être reboursé r ue sute de trestrltés de 6 8,88 chcue (l reère vet à échéce ds u trestre). Quel est le tux d térêt uel? 6, ,88 ( ) t t ( ) O t,8 6,67 O t,94 6,44 O t,85 6,5 ( ) 4,94,8 tx 8% t t
27 B Les utés e rogresso rthétque ou géoétrque. Les utés e rogresso rthétque : L vleur cquse : O v vor l forule colète : r r r r ( r ) r r Σ Σ S r Σ S tere : de de teres e rogresso géo de rso er Rereos l exresso tégrle de : r r r L vleur ctuelle :
28 r r r r r r r r r r r r r r Les utés e rogresso géoétrque : L vleur cquse : vleur cquse corresod c à l soe de teres e rogresso géoétrque de reer tere et de rso L q Σ q q q q q q q. q q q q L vleur ctuelle :
29 q q q q s rtculer où : q Les forules qu veet d être obteues e euvet être utlsées cr elles coduset à des vleurs de et déterées. Il fut doc rever u début des déostrtos et relcer q r. el doe : leur cquse :... leur ctuelle : Alcto B.9. : U rtculer souhte se costtuer u ctl e verst qutre utés. L reère ser de, les suvtes serot jorées à chque fos de. Tux du lceet : 8 %. Quelle ser l vleur cquse r ce lceet édteet rès le derer verseet? 4,8 4.,8,8,8 587,5 Alcto B.. : lculer l vleur cquse et l vleur ctuelle d ue sute de 7 utés de e rogresso géoétrque de,. Le tux d térêt est de 8 %. Refre les clculs vec u tux d térêt de %. Tux d térêt de 8 % : 7,,8,,8 6858,86 7
30 7,,8,,8 7446,4 7446,4,8 6858, Tux d térêt de % : 7.(, ) 6 49, 7 7.(, ) 666,6 7 49,7(, ) 666, 6 Alcto : éterer l échéce oyee d ue sute de utés costtes de. Le tux d térêt est de %. Effectuer le êe clcul our u tux de 8 % et de 4 %. oclure. Au tux % : (, ), (, ),, ,96 Sot 8 s et 46 jours rès l érode. Au tux 8 % : (,8),8 9,44,8 Sot 9 s et 89 jours rès l érode. Au tux 4 % : (,4),4 8,44,4 Sot 8 s et 57 jours rès l érode. Alcto : Ue sute de treze utés costtes ctlsées u tux de % ue vleur cquse de 6,56. lculer le ott de l uté.
31 ( ), 6,56, 5 Alcto : Ue sute de 8 utés de 5 ue vleur cquse de 6 94,5. Retrouver le tux de ctlsto. 694,5 5 8,88 ( ) ( ) 8 O,,45 O,75%,88 O,,99,,88,45,,,99,45,75% Alcto 4 : U cert obre d utés de 5, chcue ctlsée u tux de 7,5% ot rodut ue vleur cquse de 9 68,5. lculer le obre d utés. Refre le clcul e cosdért ue vleur cquse de. ( ) (,75) 9 68,5 5, ( ) 5 6,498 (,75) 6 (,75),75 5, ,49 8,5
32 Sot 5 utés de , , 9 6 èe (,75) 7,75,5 968, utés de ,5 56, 7 èe 95 Alcto 5 : lculer l vleur cquse et l vleur ctuelle d ue sute de 5 utés e rogresso rthétque de rso 6. L reère uté est de 6. Le tux d térêt est de 8 %. r,8 5 6,8 545,54 r 6,8 5.6,8 545,54, ,7 Alcto 6 : Extrt d ue ublcté d u costructeur utooble : «Pour l cqusto d u véhcule euf, l socété ZX vous offre tous les odèles de s ge our edt 8 os. Exele : our TT hors ssurce, à l lvrso, ort tl de 4, suv de 8 esultés de, us 4 esultés de,6 et u os rès l derère esulté, 5.» Quel est le tux esuel de ce crédt? 4,6 6,6 ( ) 8 ( ) ( ) ( ) 5( ) ( 5 O,5 66,48 O? 6 O,4 59,976 ) 6 6,64%
33 Alcto 7 : Af de rérer s retrte u rtculer effectué des verseets sur u cot e d érge selo les odltés suvtes : A coter du er jullet 99, durt s, l lcé u début de chque trestre ; A coter du er jullet 99, durt s égleet, l lcé 5 u début de chque trestre. Le êe héoèe de rogresso s est rerodut tous les tros s : le er jullet 996, l coecé ue sére de lceets de Le derer verseet est terveu le er vrl (l étt de 4 ). Quelle ser, u tux de 6,5 décebre? Tux trestrel équvlet : %, l vleur cquse r l eseble de ces lceets u (,65) 4 (,65),5868, teres.,5868 A,5868,47,5868 r 5 655,6,5868 Progresso rthétque. r r, , 7 655,,47,7,7,7 7,7 ( / / ) ( 7,7,5868 4, ) 7
34 htre 4 : Les eruts dvs. Fcher XLS jot U erut dvs est u erut vec u seul rêteur (à l dfférece des eruts oblgtres, ult rêteur). A Théore géérle. ette e Pérodes début de érode Itérêt de l érode Tbleu d ortsseet Aortsseet de l érode Auté de f de érode ette o ecore reboursée à l f de l érode Aortsseet : rebourseet d ue frcto du ctl u cours d ue érode. Auté : totl foré de l térêt et le ctl reboursé (l ortsseet).. L lo des ortsseets. S o elle le ott de l dette tl et, et les ortsseets successfs lors :... L soe des ortsseets est égle u ott de l erut.. L lo des utés. A l éoque, l y équvlece etre le ctl eruté et l vleur ctuelle des utés de rebourseet. ( ) ( )... es deux lo sot vlbles quelque sot les odltés de l erut. B L ve d u erut.. Les eruts à utés costtes.
35 Lo des utés :... Lo des ortsseets : Pour chque erut dot les crctérstques suvet, réseter le tbleu d ortsseet.. Rebourseet r utés costtes : Mott :. Tux uel : 6,5 %. Rebourseet r 5 utés costtes, l reère ds u. 486,9,65,65 5
36 K restt dû Itérêt Aortsseet Auté I K K I K ( ) 5 6,9 48 6, ,9 76,75 7 4,6 48 6,9 7 46,9 8 85,9 9 84,8 48 6, , 5 695,7 4 4,5 48 6, ,58 97, 45 89,5 48 6,9. Rebourseet r ortsseets costts : hque ortsseet sot doc égl à. ( ) Lorsque les eruts sot ortssbles grâce à l ortsseet costt, les utés successves foret ue rogresso rthétque décrosste de rso. Mott :. Tux uel : 6,5 %. Rebourseet r 5 ortsseets costts, le reer ds u. K restt dû Itérêt Aortsseet Auté K K I K I Rebourseet fe : Le ctl est tégrleet reboursé à l f de l erut (rebourseet uque e f de érode). Il exste deux tyes de rebourseet fe : - Absolue : ucu verseet durt l ve de l erut, l térêt et le ctl sot versé à l f de l erut. - Reltf : l y verseet des térêts chque érode, seule le rebourseet du ctl est oussé à l f de l erut. Mott :.
37 Tux : 6,5 %. Rebourseet e totlté ds 5 s. Peet uel des térêts. K restt dû Itérêt Aortsseet Auté K K I K I Erut à odlté rtculère : Le dfféré d ortsseet O e rebourse s de frcto du ctl, s l y eet des térêts. Mott : 7. Tux : 6 %. Rebourseet r 6 utés costtes rès u dfféré d ortsseet de s. K restt dû Itérêt Aortsseet Auté I K K I K ( ) ,84 4 5, ,6 5978, ,7 4 5, , ,7 757,57 4 5, ,5 8,8 9 5, 4 5, , , ,4 4 5, ,8 8 57, ,8 4 5,84 5. Erut à odlté rtculère : Le dfféré d uté t 4,8,946 Mott :. Tux uel : 8 %. Rebourseet r 6 trestrltés costtes, l reère ds 6 os. est l lo des utés qu ous eret d écrre :
38 (,9) t,9 t 7474, 6 (,9) K restt dû Itérêt Aortsseet Auté 94,65 98,9 549, , 96449, 87,67 56,6 7474, ,66 764,88 579,5 7474, 5 859,5 65,97 58,6 7474, 6 799,44 54,9 59, 7474, 7 786, 45,64 648,9 7474, 8 677,9 8,4 665, , 9 67,4 88,6 685, , 54886,7 66,5 647, , 48478,6 94,77 65,6 7474, 4946,4 84, ,6 7474, 587,8 685,5 6788,5 7474, ,66 55,6 69,4 7474, 5 578,6 49,9 754, , 6 45,4 8,4 79, , 7 7,5 4,4 7,6 7474,,946 94,65 Preère soluto : (,9) 7,6 4 (,9) 79, 89 euxèe soluto : 7474, ( ) 7,6 Tux effectf d u erut dvs. Le tux réel rélse l équvlece vec les soes effectveet reçues et les soes effectveet versées r l eruteur e tet cote des dtes récses. Les frs réels vot être dfférete des N du ft de l exstece. Le TEG (tux effectf globl) corresod à ue oblgto légle révue r le code de l cosoto (le ode de
39 clcul du TEG fut odfé le er jullet ). S gsst du crédt à l cosoto, l s gr d u tux équvlet. 6. lculer le tux effectfs d u erut de 5, obteu u tux ol esuel de,65 %, reboursble e 4 esultés costtes, scht que sot s à l chrge de l eruteur 9 de frs de dosser édteet rélevés s qu ue re d ssurce décès - vldté de,6 r os. Mesulté costte : (,65) 5,65 8, ,78% ( ) 4 Alcto : Ue socété eruté le er ju N, ue soe de qu elle dot rebourser u oye de verseets uels costts et à dtes fxes, l reère échéce étt le er ju N et l derère le er ju N5. Le tux d térêt uel est de 7,8 %.. lculer le ott de chque uté. (,78), ,5. ostrure le tbleu d ortsseet de l erut. K restt dû Itérêt Aortsseet Auté , , ,47 9, , , ,9 5, , , , , , ,5 5 46,9 65, 46, 49 87,5. Avec l ccord de l bque, l socété décde édteet rès l échéce du er ju N de régler l soe restt due à l de de esulté costtes dot l reère échot le er jullet N. Le tux esuel de l térêt est de,65 %. Les esultés s élevt à 6 5,54, à quelle dte l dette ser-t-elle etèreet orte? 5
40 Sot le er setebre. (,65) 8999, 65,54,65 5 Alcto : Le er octobre de l ée N, ue etrerse chète u térel de qu elle règle our % u cott, le solde étt yé r trestrltés costtes de,6 chcue. L reère est versée le er jver N. Le derer ortsseet est de 9 957,74.. lculer le tux trestrel.,6 9957,74( ) 6, ,74,64%. lculer le tux uel. 4,699,98,98%. lculer le obre de trestrltés.,64 8,6,64 4 Alcto : U erut de est reboursble u oye de hut utés e rogresso géoétrque de 6 %. Tux uel %.. lculer l reère uté. 8 8,6, (,),6, 684,89. lculer l dette ecore vvte rès le eet de l trosèe uté. 8 ette vvte rès : ( ) 4 4 (,6) 58,7 8459,4 58,7, 5 5,6,,6, 5
41 Arès le eet de l cquèe uté, l eruteur souhte trsforer les utés e trestrltés costtes. lculer le ott de l trestrlté costte ,5 (,6) 4 57,76 57,76,,6,,6, t t (,6) 4,877 (,877) 579,5 t,877 t 57,8 Alcto 4 : U erut est reboursble r utés costtes. Le reer ortsseet est de 68 95,45, le cquèe de 5 6,89.. lculer le tux d térêt, le ott de l erut (scht que l uté est de 68 95,45 ), le obre d utés. Tux d térêt : Mott de l erut : Nobre d uté : 5 ( ) 56, ,45 8% 6895, ,45 4 ( ) 4,8,8 6895,45,8 5 Alcto 5 : Ue etrerse cotrcté u erut reboursble r utés costtes, le reer rebourseet devt vor leu u rès. U eu vt de verser l trosèe uté, l etrerse dede à so crécer d cceter l ue des deux roostos suvtes : - Pyer à l dte coveue les térêts fst rte de l trosèe uté, sot 9 47,8 et le reste e douze utés costtes de 57 7,4 clculées u tux de 5 %, l reère yble u rès.
42 - Pyer orleet l trosèe uté et le reste e quze utés costtes de 6 4,7 clculées u tux de 5%, l reère yble u rès. - es deux roostos étt cosdérées coe équvletes u tux de 5 %, clculer le ott de l uté rtve, le tux ol, l durée de rebourseet révue et le ott de l erut rtf. 947,8 577,4,5 (,5) (,5) 64,7 6444,8,5 5 tl restt du : (,5) K 577,4,5 K 6746, ,87 947,8 6% (,6) 6746, ,8,6 x 6 x Auquel o eut rjouter, et : u totl cel ft 8 s. (,6) 6444,8,6 4 8
43 htre 5 : Les eruts oblgtres. Fcher XLS jot A rctérstques des eruts oblgtres. Seuls l étt et les collectvtés locles ou ecore les etrerses de lus de deux s d exstece dot le ctl est tégrleet lbéré euvet éettre ses eruts. Lorsqu l y erut oblgtre, l y ue sse de rêteur ce qu eret d obter des fods lus ortts. oe l y ue ulttude de rêteur, dvdulsto se ft s dvso de l erut r oblgto. est le êe rce qu u erut dvs, les utés de rebourseet serot costtuée d térêt et d ortsseet. Le ott totl de l erut ser dvsé e oblgto. Les utés de rebourseet serot costtuées r les ortsseets, le ctl eruté (coe our les eruts dvs). éftos : leur ole : c est l vleur r rort à lquelle ser clculé l térêt (o rle rfos de vleur fcl, de r). leur de rebourseet : c'est-à-dre le rx uquel ser reboursé l oblgto. Prx d ésso : ce rx corresod à l soe effectveet rêtée r l oblgtre. Prx de souscrto : corresod u ott totl versé r l oblgtre lors de l souscrto (u oet de l ésso). E lus du rx d ésso, l oblgtre eut être teu de rebourser ue frcto du reer couo. Tux ol d térêt : c est le tux fcl, c est le tux qu, lqué à l vleur ol, ous doer l vleur du couo. te de règleet : est l dte lte de souscrto. te de joussce : est le ot de dért du clcul de l térêt. ette cotto s effectue e ourcetge de l vleur ole vec deux fortos : - Ue qu ous doe le cours de l oblgto (u ed du couo : c'est-à-dre ss le couo). - Ue utre qu v exrer le couo couru de l oblgto. B Théore géérle. Los des ortsseet : le obre des oblgtos reboursées est égl u obre des oblgtos éses. Pérodes Nb d oblgtos vvtes Itérêts u théorque u réel Aortsseet Auté
44 Tux de redeet : c est u tux brut (TRAB), o ft l sse de l fsclté. e tux est clculé du ot de vue des oblgtres. Il ourr être clculé our l eseble des oblgtres ou be our u oblgtre e rtculer (tux de redeet globl ou rtculer). Alcto.. : osdéros u erut à ortsseet fe de 4 oblgtos de vleur ole. Tux ol : 5,6 %. Prx d ésso : 99. Prx de rebourseet 5 (le er ju N4). urée : 4 s. te de règleet : /4/N te de joussce : /6/N éterer le tux de redeet cturel brut de cet erut. Le couo est égle à 5,6% 56. A l dte de règleet : ( ) ( ) ( ) O,675 99,6 O,68 99 O, ,67 oc le TRAB ser de 6,8 %. Le tux de revet : l est clculé r l eruteur (socété qu éet l erut) c est u tux qu v rélser l équvlece etre les soes effectveet erçues r l éetteur et les soes effectveet reboursé r lu-êe (rse e cote des frs lés à l ésso de l erut). Alcto.. : Rereos les crctérstques de l erut. Prx d ésso : 495. Frs d ésso : 495. Frs de servce : % du ott des utés. éterer le tux de revet de cet erut. [ 5,5] ,85 (,49... ),49... Frs de servce : ' , 66974
45 Lors de l ésso : ( 495) 495 7, ( ) Pr terolto o trouve u tux de revet de 5,9 %. Alcto : ( ) Pérodes Nb d'oblgto vvtes Itérêts µ théorque µ réel Aortsseet Auté , , , , , , , , , , Ou : 89599,67 (,), ,5 4 Alcto : (,) [ 5 ], 89599,67 5 µ µ 7,7 (,) 8 µ 7,7, 9, µ 7,7, ( ) 9 Σ 4 5,5 9 5 Pr terolto o dot trouver le TRAB de 5,7 %. ( )
46 ( ) 5, Pr terolto o dot trouver le TRAB de 5,87 %. Alcto : ouos N6 : 7,5 N k t k k N 5 k k k ( ) ( 7,5 Nk ) ( 5 k ) ( 7,5 N ) ( 5 ) N k 7,5 k k ( N ) k 57,5 k 5,75 76,86 k...,75,75 k ( 7,5 ) ( 76,86 5) 7849,64 ouos N 7, 5 5 5, ,86,75 45,7 45, N ,5 5 57,5 ( ) 495 7,5 Pr terolto o dot trouver le TRAB de 8,6 %. euxèe odlté : ouos N à N6 : Le couo uel est égl : 7, 5 75 Autés 7 à : 5 k k
47 k k k N k k O regrde l dfférece etre et : k k Tux de redeet : k 975 7,5 975 k ( 7,5 Nk ) 5 4 ( 7,5 Nk ) 5 ( 7,5 Nk ) 5 Nk 5 7,5 k k ( N 5) 5 k ( N 5) 5 ( 7,5 N ) k 5 7, ( 7,5 ) ( 5 5) k ,7665 ( ) ( ) ( )
!! " # $ #! %! &! ' (!& )**+
 !!"# $ #! %! &!'(!&)** Ce cous vse à ésete les dfféets élémets du clcul fce et d exlque l oto de l vleu temoelle de l get. Il ft îte clemet cq éoccutos : L dfféece ete les dfféets tyes d téêts (téêt smle,
!!"# $ #! %! &!'(!&)** Ce cous vse à ésete les dfféets élémets du clcul fce et d exlque l oto de l vleu temoelle de l get. Il ft îte clemet cq éoccutos : L dfféece ete les dfféets tyes d téêts (téêt smle,
Mathématiques Financières : l essentiel Les 10 formules incontournables (Fin de période)
 A-PDF OFFICE TO PDF DEMO: Purchase from www.a-pdf.com to remove the watermark Mathématques Facères : l essetel Les formules cotourables (F de érode) htt://www.ecogesam.ac-a-marselle.fr/esed/gesto/mathf/mathf.html#e5aels
A-PDF OFFICE TO PDF DEMO: Purchase from www.a-pdf.com to remove the watermark Mathématques Facères : l essetel Les formules cotourables (F de érode) htt://www.ecogesam.ac-a-marselle.fr/esed/gesto/mathf/mathf.html#e5aels
Semestre : 4 Module : Méthodes Quantitatives III Elément : Mathématiques Financières Enseignant : Mme BENOMAR
 Semestre : 4 Module : Méthodes Quattatves III Elémet : Mathématques Facères Esegat : Mme BENOMAR Elémets du cours Itérêts smples, précompte, escompte et compte courat Itérêts composés Autés Amortssemets
Semestre : 4 Module : Méthodes Quattatves III Elémet : Mathématques Facères Esegat : Mme BENOMAR Elémets du cours Itérêts smples, précompte, escompte et compte courat Itérêts composés Autés Amortssemets
Sciences Industrielles Précision des systèmes asservis Papanicola Robert Lycée Jacques Amyot
 Scence Indutrelle Précon de ytème erv Pncol Robert Lycée Jcque Amyot I - PRECISION DES SYSTEMES ASSERVIS A. Poton du roblème 1. Préentton On vu que le rôle d un ytème erv et de fre uvre à l orte (t) une
Scence Indutrelle Précon de ytème erv Pncol Robert Lycée Jcque Amyot I - PRECISION DES SYSTEMES ASSERVIS A. Poton du roblème 1. Préentton On vu que le rôle d un ytème erv et de fre uvre à l orte (t) une
Estimation des incertitudes sur les erreurs de mesure.
 Estmto des certtdes sr les errers de mesre. I. Itrodcto : E sceces epérmetles, l este ps de mesres ectes. Celle-c e pevet être q etchées d errers pls o mos mporttes selo le protocole chos, l qlté des strmets
Estmto des certtdes sr les errers de mesre. I. Itrodcto : E sceces epérmetles, l este ps de mesres ectes. Celle-c e pevet être q etchées d errers pls o mos mporttes selo le protocole chos, l qlté des strmets
LE PRINCIPE DU RAISONNEMENT PAR RÉCURRENCE
 LE PRINCIPE DU RAISONNEMENT PAR RÉCURRENCE. Exemple troductf (Les élèves qu coasset déà be le prcpe peuvet sauter ce paragraphe) Cosdéros la sute (u ), défe pour tout, par : u u u 0 0 Cette sute est défe
LE PRINCIPE DU RAISONNEMENT PAR RÉCURRENCE. Exemple troductf (Les élèves qu coasset déà be le prcpe peuvet sauter ce paragraphe) Cosdéros la sute (u ), défe pour tout, par : u u u 0 0 Cette sute est défe
Coefficient de partage
 Coeffcet de partage E chme aque, la sythèse d'u composé se fat e pluseurs étapes : la réacto propremet dte (utlsat par exemple u motage à reflux quad la réacto dot être actvée thermquemet), les extractos
Coeffcet de partage E chme aque, la sythèse d'u composé se fat e pluseurs étapes : la réacto propremet dte (utlsat par exemple u motage à reflux quad la réacto dot être actvée thermquemet), les extractos
Chapitre IV Les oscillations couplées «Les oscillations libres d un système à plusieurs degrés de liberté»
 Chre IV, cours de vbrons, ondes _Phs, Pr. Bds Bennecer MD 8-9 Chre IV es oscllons coulées «es oscllons lbres d un ssèe à luseurs degrés de lberé» Dns ce chre, nous llons coencer r éuder les oscllons lbres
Chre IV, cours de vbrons, ondes _Phs, Pr. Bds Bennecer MD 8-9 Chre IV es oscllons coulées «es oscllons lbres d un ssèe à luseurs degrés de lberé» Dns ce chre, nous llons coencer r éuder les oscllons lbres
Baccalauréat S Asie 19 juin 2014 Corrigé
 Bcclurét S Asie 9 jui 24 Corrigé A. P. M. E. P. Exercice Commu à tous les cdidts 4 poits Questio - c. O peut élimier rpidemet les réposes. et d. cr les vecteurs directeurs des droites proposées e sot ps
Bcclurét S Asie 9 jui 24 Corrigé A. P. M. E. P. Exercice Commu à tous les cdidts 4 poits Questio - c. O peut élimier rpidemet les réposes. et d. cr les vecteurs directeurs des droites proposées e sot ps
Déroulement de l épreuve de mathématiques
 Dérouleet de l épreuve de thétiques MATHÉMATIQUES Extrit de l ote de service 2012-029 du 24 février 2012 (BOEN 13 du 29-3-2012) Durée de l épreuve : 2 heures Nture de l épreuve : écrite pr le socle cou
Dérouleet de l épreuve de thétiques MATHÉMATIQUES Extrit de l ote de service 2012-029 du 24 février 2012 (BOEN 13 du 29-3-2012) Durée de l épreuve : 2 heures Nture de l épreuve : écrite pr le socle cou
Décoration, équipement. de la Maison. Janvier 2013 sans prix. Printemps / Été. SADY s TRADING WOOD TRADING. www.sadys-trading.com
 Dreo Aeropor Mrselle Provee D 9 SADY s TRADING WOOD TRADING Déoro, équpeme de l Mso www.sdys-rd.om Jver 2013 ss prx Premps / Éé ZI Les Bols Dreo Mrselle - Ax ZI Les Esroubls SADY s TRADING Les ouveués
Dreo Aeropor Mrselle Provee D 9 SADY s TRADING WOOD TRADING Déoro, équpeme de l Mso www.sdys-rd.om Jver 2013 ss prx Premps / Éé ZI Les Bols Dreo Mrselle - Ax ZI Les Esroubls SADY s TRADING Les ouveués
Calculer comment se constituer un capitale ; Calculer comment rembourser une dette en effectuant des versements réguliers.
 CHAP: 8 Objecifs de ce chpire : Clculer comme se cosiuer u cpile ; Clculer comme rembourser ue dee e effecu des versemes réguliers. RAPPELS : Qu'es-ce qu'ue vleur cquise? Qu'es-ce qu'ue vleur cuelle? Le
CHAP: 8 Objecifs de ce chpire : Clculer comme se cosiuer u cpile ; Clculer comme rembourser ue dee e effecu des versemes réguliers. RAPPELS : Qu'es-ce qu'ue vleur cquise? Qu'es-ce qu'ue vleur cuelle? Le
MTH 2301 Méthodes statistiques en ingénierie. MTH 2301 Méthodes statistiques en ingénierie
 VARIABLES ALÉATOIRES déo oco de réro vrble léore dscrèe moyee - vrce - écr ye esérce mhémque vrble léore coue oco d ue vrble léore : rsormo combso lére de vrbles léores Déo E : eérece léore S : esce échllol
VARIABLES ALÉATOIRES déo oco de réro vrble léore dscrèe moyee - vrce - écr ye esérce mhémque vrble léore coue oco d ue vrble léore : rsormo combso lére de vrbles léores Déo E : eérece léore S : esce échllol
e x dx = e x dx + e x dx + e x dx.
 Chtr Foctos Gmm t foctos d Bssl Chtr Focto Gmm t foctos d Bssl Détrmto d l focto Gmm L focto Gmm st très sml à dédur à rtr d l tégrl d'eulr: Ctt tégrl st u focto d rmètr ; ll st rrésté r l symbol () t
Chtr Foctos Gmm t foctos d Bssl Chtr Focto Gmm t foctos d Bssl Détrmto d l focto Gmm L focto Gmm st très sml à dédur à rtr d l tégrl d'eulr: Ctt tégrl st u focto d rmètr ; ll st rrésté r l symbol () t
CHAPITRE 6 : LE BIEN-ETRE. Durée : Objectif spécifique : Résumé : I. L agrégation des préférences. Cerner la notion de bien-être et sa mesure.
 TABLE DES MATIERES Durée...2 Objectf spécfque...2 Résumé...2 I. L agrégato des préféreces...2 I. Le système de vote à la majorté...2 I.2 Vote par classemet...3 I.3 Codtos de décso socale et théorème d
TABLE DES MATIERES Durée...2 Objectf spécfque...2 Résumé...2 I. L agrégato des préféreces...2 I. Le système de vote à la majorté...2 I.2 Vote par classemet...3 I.3 Codtos de décso socale et théorème d
COURS DE MATHEMATIQUE FINANCIERE A COURT ET LONG TERME Promotion : Première année de graduat
 P R O F E S REPUBLIQUE DEMOCRATIQUE DU CONGO ENSEIGNEMENT SUPEREIEUR ET UNIVERSITAIRE INSTITUT SUPERIEUR DE GESTION INFORMATIQUE DE GOMA /I.S.I.G-GOMA DEVELOPPEMENT ISIG M A T I O N COURS DE MATHEMATIQUE
P R O F E S REPUBLIQUE DEMOCRATIQUE DU CONGO ENSEIGNEMENT SUPEREIEUR ET UNIVERSITAIRE INSTITUT SUPERIEUR DE GESTION INFORMATIQUE DE GOMA /I.S.I.G-GOMA DEVELOPPEMENT ISIG M A T I O N COURS DE MATHEMATIQUE
SYSTEME FERME EN REACTION CHIMIQUE
 SYSTEME FERME EN REACTION CHIMIQUE I. DESCRIPTION D UN SYSTEME. Les dfférets types de système (ouvert, fermé, solé U système S est formé d u esemble de corps séparés du reste de l uvers (appelé mleu extéreur
SYSTEME FERME EN REACTION CHIMIQUE I. DESCRIPTION D UN SYSTEME. Les dfférets types de système (ouvert, fermé, solé U système S est formé d u esemble de corps séparés du reste de l uvers (appelé mleu extéreur
Chapitre 2 Le problème de l unicité des solutions
 Université Joseph Fourier UE MAT 127 Mthémtiques nnée 2009-2010 Chpitre 2 Le prolème de l unicité des solutions 1 Le prolème et quelques réponses : 1.1 Un exemple Montrer que l éqution différentielle :
Université Joseph Fourier UE MAT 127 Mthémtiques nnée 2009-2010 Chpitre 2 Le prolème de l unicité des solutions 1 Le prolème et quelques réponses : 1.1 Un exemple Montrer que l éqution différentielle :
A11 : La représentation chaînée (1ère partie)
 A11 : L représettio chîée (1ère prtie) - Défiitio et schéms de cosulttio - Schéms de mise à jour (isertio, suppressio) - Exemples J-P. Peyri - L représettio chîée (première prtie) 0 Pricipe de l représettio
A11 : L représettio chîée (1ère prtie) - Défiitio et schéms de cosulttio - Schéms de mise à jour (isertio, suppressio) - Exemples J-P. Peyri - L représettio chîée (première prtie) 0 Pricipe de l représettio
LES ESCALIERS. Du niveau du rez-de-chaussée à celui de l'étage ou à celui du sous-sol.
 LES ESCALIERS I. DÉF I NIT I O N Un escalier est un ouvrage constitué d'une suite de marches et de paliers permettant de passer à pied d'un niveau à un autre. Ses caractéristiques dimensionnelles sont
LES ESCALIERS I. DÉF I NIT I O N Un escalier est un ouvrage constitué d'une suite de marches et de paliers permettant de passer à pied d'un niveau à un autre. Ses caractéristiques dimensionnelles sont
Correction de l épreuve CCP 2001 PSI Maths 2 PREMIÈRE PARTIE ) (
 Correction de l épreuve CCP PSI Mths PREMIÈRE PARTIE I- Soit t u voisinge de, t Alors ϕt t s = ϕt ρt s ρs Pr hypothèse, l fonction ϕt ϕt est lorsque t, il en est donc de même de ρt s ρt s ρs cr ρ s est
Correction de l épreuve CCP PSI Mths PREMIÈRE PARTIE I- Soit t u voisinge de, t Alors ϕt t s = ϕt ρt s ρs Pr hypothèse, l fonction ϕt ϕt est lorsque t, il en est donc de même de ρt s ρt s ρs cr ρ s est
3- Les taux d'intérêt
 3- Les tux d'intérêt Mishkin (2007), Monnie, Bnque et mrchés finnciers, Person Eduction, ch. 4 et 6 Vernimmen (2005), Finnce d'entreprise, Dlloz, ch. 20 à 22 1- Mesurer les tux d'intérêt comprer les différents
3- Les tux d'intérêt Mishkin (2007), Monnie, Bnque et mrchés finnciers, Person Eduction, ch. 4 et 6 Vernimmen (2005), Finnce d'entreprise, Dlloz, ch. 20 à 22 1- Mesurer les tux d'intérêt comprer les différents
c. Calcul pour une évolution d une proportion entre deux années non consécutives
 Calcul des itervalles de cofiace our les EPCV 996-004 - Cas d u ourcetage ou d ue évolutio e oit das la oulatio totale des méages - Cas d u ourcetage ou d ue évolutio das ue sous oulatio das les méages
Calcul des itervalles de cofiace our les EPCV 996-004 - Cas d u ourcetage ou d ue évolutio e oit das la oulatio totale des méages - Cas d u ourcetage ou d ue évolutio das ue sous oulatio das les méages
Chapitre 11 : L inductance
 Chpitre : inductnce Exercices E. On donne A πr 4π 4 metn N 8 spires/m. () Selon l exemple., µ n A 4π 7 (8) 4π 4 (,5) 5 µh (b) À prtir de l éqution.4, on trouve ξ ξ 4 3 5 6 6,3 A/s E. On donne A πr,5π 4
Chpitre : inductnce Exercices E. On donne A πr 4π 4 metn N 8 spires/m. () Selon l exemple., µ n A 4π 7 (8) 4π 4 (,5) 5 µh (b) À prtir de l éqution.4, on trouve ξ ξ 4 3 5 6 6,3 A/s E. On donne A πr,5π 4
INTENTION LES PROCESSUS MATHÉMATIQUES
 INTENTION Adpttios u Cdre commu des progrmmes d études de mthémtiques M-9 telles que reflétées ds le documet Mthémtiques M-9 : Progrmme d études de l Albert (2007) Le coteu du documet Mthémtiques M-9 :
INTENTION Adpttios u Cdre commu des progrmmes d études de mthémtiques M-9 telles que reflétées ds le documet Mthémtiques M-9 : Progrmme d études de l Albert (2007) Le coteu du documet Mthémtiques M-9 :
RESOLUTION PAR LA METHODE DE NORTON, MILLMAN ET KENNELY
 LO 4 : SOLUTO P L MTHO OTO, MLLM T KLY SOLUTO P L MTHO OTO, MLLM T KLY MTHO OTO. toductio Le théoème de oto va ous pemette de éduie u cicuit complexe e gééateu de couat éel. e gééateu possède ue souce
LO 4 : SOLUTO P L MTHO OTO, MLLM T KLY SOLUTO P L MTHO OTO, MLLM T KLY MTHO OTO. toductio Le théoème de oto va ous pemette de éduie u cicuit complexe e gééateu de couat éel. e gééateu possède ue souce
a g c d n d e s e s m b
 PPrrooppoossiittiioo 22001111JJPP 22770055 000011 uu 0088 fféévvrriirr 22001111 VVlliiiittéé jjuussqquu uu 3300//0044//22001111 tim c ir tv é p g c h u i rè s G A Z iv lu s IC.G R é c lo y m ip s 9 r7
PPrrooppoossiittiioo 22001111JJPP 22770055 000011 uu 0088 fféévvrriirr 22001111 VVlliiiittéé jjuussqquu uu 3300//0044//22001111 tim c ir tv é p g c h u i rè s G A Z iv lu s IC.G R é c lo y m ip s 9 r7
Module 2 : Déterminant d une matrice
 L Mth Stt Module les déterminnts M Module : Déterminnt d une mtrice Unité : Déterminnt d une mtrice x Soit une mtrice lignes et colonnes (,) c b d Pr définition, son déterminnt est le nombre réel noté
L Mth Stt Module les déterminnts M Module : Déterminnt d une mtrice Unité : Déterminnt d une mtrice x Soit une mtrice lignes et colonnes (,) c b d Pr définition, son déterminnt est le nombre réel noté
ANNEXES...16 Notation...16 Rente financière certaine...16. Mémo d Actuariat - Sophie Terrier @ 2004 1/16
 ÉO TUIT FOULS TUILLS SU TT Probbé ouo 3 dfféré4 ee gère be à ere échu 5 ee gère be à ere échu ueur fo d ée 6 ee gère à ere be d ce7 ee gère à ere be d ce ueur fo d ée8 urce décè 9 urce décè à c rbe cro
ÉO TUIT FOULS TUILLS SU TT Probbé ouo 3 dfféré4 ee gère be à ere échu 5 ee gère be à ere échu ueur fo d ée 6 ee gère à ere be d ce7 ee gère à ere be d ce ueur fo d ée8 urce décè 9 urce décè à c rbe cro
Chapitre 3: TESTS DE SPECIFICATION
 Chapitre 3: TESTS DE SPECIFICATION Rappel d u c h api t r e pr é c é d en t : l i de n t i f i c a t i o n e t l e s t i m a t i o n de s y s t è m e s d é q u a t i o n s s i m u lt a n é e s r e p o
Chapitre 3: TESTS DE SPECIFICATION Rappel d u c h api t r e pr é c é d en t : l i de n t i f i c a t i o n e t l e s t i m a t i o n de s y s t è m e s d é q u a t i o n s s i m u lt a n é e s r e p o
Toyota Assurances Toujours la meilleure solution
 Toyot Assurnces Toujours l meilleure solution De quelle ssurnce vez-vous besoin? Vous roulez déjà en Toyot ou vous ttendez s livrison. Votre voiture est neuve ou d occsion. Vous vlez les kilomètres ou
Toyot Assurnces Toujours l meilleure solution De quelle ssurnce vez-vous besoin? Vous roulez déjà en Toyot ou vous ttendez s livrison. Votre voiture est neuve ou d occsion. Vous vlez les kilomètres ou
Calculer le coût amorti d une obligation sur chaque exercice et présenter les écritures dans les comptes individuels de la société Plumeria.
 1 CAS nédt d applcaton sur les normes IAS/IFRS Coût amort sur oblgatons à taux varable ou révsable La socété Plumera présente ses comptes annuels dans le référentel IFRS. Elle détent dans son portefeulle
1 CAS nédt d applcaton sur les normes IAS/IFRS Coût amort sur oblgatons à taux varable ou révsable La socété Plumera présente ses comptes annuels dans le référentel IFRS. Elle détent dans son portefeulle
Chap. 6 : Les principaux crédits de trésorerie et leur comptabilisation
 1 / 9 Chap. 6 : Les pricipaux crédits de trésorerie et leur comptabilisatio Le cycle d exploitatio des etreprises (achats stockage productio stockage vetes) peut etraîer des décalages de trésorerie plus
1 / 9 Chap. 6 : Les pricipaux crédits de trésorerie et leur comptabilisatio Le cycle d exploitatio des etreprises (achats stockage productio stockage vetes) peut etraîer des décalages de trésorerie plus
Lot 4: Validation industrielle. Youness LEMRABET Pascal YIM, 19/11/2010
 Lot 4: Validation industrielle Youness LEMRABET Pascal YIM, 19/11/2010 Partenaires Lot 1 Modèle du processus métier L4.1 Modèles PSM Lot 2 Guide d implantation L4.2 Développement & Recette prototype Lot
Lot 4: Validation industrielle Youness LEMRABET Pascal YIM, 19/11/2010 Partenaires Lot 1 Modèle du processus métier L4.1 Modèles PSM Lot 2 Guide d implantation L4.2 Développement & Recette prototype Lot
Chap. 6 : Les principaux crédits de trésorerie et leur comptabilisation
 Chap. 6 : Les pricipaux crédits de trésorerie et leur comptabilisatio Les etreprises ot souvet besoi de moyes de fiacemet à court terme : elles ot alors recours aux crédits bacaires (découverts bacaires
Chap. 6 : Les pricipaux crédits de trésorerie et leur comptabilisatio Les etreprises ot souvet besoi de moyes de fiacemet à court terme : elles ot alors recours aux crédits bacaires (découverts bacaires
16.1 Convergence simple et convergence uniforme. une suite de fonctions de I dans R ou C.
 16 Suites de foctios Suf précisio cotrire, I est u itervlle réel o réduit à u poit et les foctios cosidérées sot défiies sur I à vleurs réelles ou complexes. 16.1 Covergece simple et covergece uiforme
16 Suites de foctios Suf précisio cotrire, I est u itervlle réel o réduit à u poit et les foctios cosidérées sot défiies sur I à vleurs réelles ou complexes. 16.1 Covergece simple et covergece uiforme
Réalisation de sites Internet PME & Grandes entreprises Offre Premium. Etude du projet. Webdesign. Intégration HTML. Développement.
 Rélistion de sites Internet PME & Grndes entreprises Offre Premium Etude du projet Réunions de trvil et étude personnlisée de votre projet Définition d une strtégie de pré-référencement Webdesign Définition
Rélistion de sites Internet PME & Grndes entreprises Offre Premium Etude du projet Réunions de trvil et étude personnlisée de votre projet Définition d une strtégie de pré-référencement Webdesign Définition
Liens entre fonction de transfert et représentations d'état d'un système (formes canoniques de la représentation d'état)
 oqe V oqe Cor e ere foco de rfer e repréeo dé d èe fore coqe de l repréeo dé SI Coe oqe! Irodco! e ere le dfféree decrpo d èe! Pge odèle dé " foco de rfer # C d èe oovrle # C d èe lvrle! Pge foco de rfer
oqe V oqe Cor e ere foco de rfer e repréeo dé d èe fore coqe de l repréeo dé SI Coe oqe! Irodco! e ere le dfféree decrpo d èe! Pge odèle dé " foco de rfer # C d èe oovrle # C d èe lvrle! Pge foco de rfer
Tutoriel Infuse Learning. Créer des quizzes multimédias sur ordinateur ou tablette
 Tutoriel Infuse Learning Créer des quizzes multimédias sur ordinateur ou tablette 1- Présentation Infuselearning.com est un service web (en ligne) gratuit qui permet aux enseignants de créer des exercices
Tutoriel Infuse Learning Créer des quizzes multimédias sur ordinateur ou tablette 1- Présentation Infuselearning.com est un service web (en ligne) gratuit qui permet aux enseignants de créer des exercices
À travers deux grandes premières mondiales
 Les éco-i ovatio s, le ouvel a e st at gi ue d ABG À travers deux grandes premières mondiales - éco-mfp, premier système d impression à encre effaçable - e-docstation, premier système d archivage intégré
Les éco-i ovatio s, le ouvel a e st at gi ue d ABG À travers deux grandes premières mondiales - éco-mfp, premier système d impression à encre effaçable - e-docstation, premier système d archivage intégré
Faites connaissance avec votre Rubik s Cube Étape 1
 Faites connaissance avec votre Rubik s Cube Étape 1 ÉFIN ITION ES IÈCES U RUBIK S CUBE LES RTIES LES IÈCES RÊTES CE SONT ES IÈCES COMORTNT EUX (2) COULEU RS. IL Y OUZE (12) IÈCES RÊTES, SITUÉES U CENT
Faites connaissance avec votre Rubik s Cube Étape 1 ÉFIN ITION ES IÈCES U RUBIK S CUBE LES RTIES LES IÈCES RÊTES CE SONT ES IÈCES COMORTNT EUX (2) COULEU RS. IL Y OUZE (12) IÈCES RÊTES, SITUÉES U CENT
! " # $ #% &!" # $ %"& ' ' $ (
 !" #$%"& ! "#$#% &!" #$%"& ' '$( SOMMAIRE INTRODUCTION... 4 METHODE... 4 TAUX DE REPONSES ET VALIDITE DES POURCENTAGES... 4 RESULTATS... 6 I. Qui sont les étudiants ayant répondu?... 6 1.1. Répartition
!" #$%"& ! "#$#% &!" #$%"& ' '$( SOMMAIRE INTRODUCTION... 4 METHODE... 4 TAUX DE REPONSES ET VALIDITE DES POURCENTAGES... 4 RESULTATS... 6 I. Qui sont les étudiants ayant répondu?... 6 1.1. Répartition
Guide d'utilisation Easy Interactive Tools Ver. 2
 Guide d'utilistion Esy Interctive Tools Ver. 2 Guide d'utilistion Esy Interctive Tools Ver.2 Présenttion de Esy Interctive Tools 3 Crctéristiques Fonction de dessin Vous pouvez utiliser Esy Interctive
Guide d'utilistion Esy Interctive Tools Ver. 2 Guide d'utilistion Esy Interctive Tools Ver.2 Présenttion de Esy Interctive Tools 3 Crctéristiques Fonction de dessin Vous pouvez utiliser Esy Interctive
Plan. Gestion des stocks. Les opérations de gestions des stocks. Les opérations de gestions des stocks
 Plan Geston des stocks Abdellah El Fallah Ensa de Tétouan 2011 Les opératons de gestons des stocks Les coûts assocés à la geston des stocks Le rôle des stocks Modèle de la quantté économque Geston calendare
Plan Geston des stocks Abdellah El Fallah Ensa de Tétouan 2011 Les opératons de gestons des stocks Les coûts assocés à la geston des stocks Le rôle des stocks Modèle de la quantté économque Geston calendare
Compression Compression par dictionnaires
 Compression Compression par dictionnaires E. Jeandel Emmanuel.Jeandel at lif.univ-mrs.fr E. Jeandel, Lif CompressionCompression par dictionnaires 1/25 Compression par dictionnaire Principe : Avoir une
Compression Compression par dictionnaires E. Jeandel Emmanuel.Jeandel at lif.univ-mrs.fr E. Jeandel, Lif CompressionCompression par dictionnaires 1/25 Compression par dictionnaire Principe : Avoir une
Intégrales généralisées
 3 Iégrles géérlisées Pour ce chpire, les focios cosidérées so priori défiies sur u iervlle réel I o rédui à u poi, à vleurs réelles ou complees e coiues pr morceu. L défiiio e les propriéés de l iégrle
3 Iégrles géérlisées Pour ce chpire, les focios cosidérées so priori défiies sur u iervlle réel I o rédui à u poi, à vleurs réelles ou complees e coiues pr morceu. L défiiio e les propriéés de l iégrle
Mécanique : Cinématique du point. Chapitre 1 : Position. Vitesse. Accélération
 2 e B et C 1 Position. Vitesse. Accélération 1 Mécanique : Cinéatique du point La écanique est le doaine de tout ce qui produit ou transet un ouveent, une force, une déforation : achines, oteurs, véhicules,
2 e B et C 1 Position. Vitesse. Accélération 1 Mécanique : Cinéatique du point La écanique est le doaine de tout ce qui produit ou transet un ouveent, une force, une déforation : achines, oteurs, véhicules,
Accueil Events, l accueil personnalisé des touristes d affaires Informations, bonnes adresses, réservations et découvertes!
 Lyon City Card 1 jour 2 jours 3 jours Ta xis et M inibus - Tarifs forfaitaires Jour : 7h - 19h Nuit : 19h - 7h Lyon/ Villeurbanne - Aéroport St Exupéry 59 81 Lyon 5ème et 9ème excentrés - Aéroport St Exupéry
Lyon City Card 1 jour 2 jours 3 jours Ta xis et M inibus - Tarifs forfaitaires Jour : 7h - 19h Nuit : 19h - 7h Lyon/ Villeurbanne - Aéroport St Exupéry 59 81 Lyon 5ème et 9ème excentrés - Aéroport St Exupéry
Développement en Série de Fourier
 F-IRIS-5.ex Développeme e Série de Fourier Développer e série de Fourier les focios de période T défiies aisi : a b { f impaire T = f = si ] ; { f paire T = f = si ; ] Faire das chaque cas ue représeaio
F-IRIS-5.ex Développeme e Série de Fourier Développer e série de Fourier les focios de période T défiies aisi : a b { f impaire T = f = si ] ; { f paire T = f = si ; ] Faire das chaque cas ue représeaio
Pour développer votre entreprise LES LOGICIELS EN LIGNE, VOUS ALLEZ DIRE OUI!
 Pour développer votre entreprise Gestion Commercile Gérez le cycle complet des chts (demnde de prix, fcture fournisseur), des stocks (entrée, sortie mouvement, suivi) et des ventes (devis, fcture, règlement,
Pour développer votre entreprise Gestion Commercile Gérez le cycle complet des chts (demnde de prix, fcture fournisseur), des stocks (entrée, sortie mouvement, suivi) et des ventes (devis, fcture, règlement,
Les jeunes économistes
 Chaptre1 : les ntérêts smples 1. défnton et calcul pratque : Défnton : Dans le cas de l ntérêt smple, le captal reste nvarable pendant toute la durée du prêt. L emprunteur dot verser, à la fn de chaque
Chaptre1 : les ntérêts smples 1. défnton et calcul pratque : Défnton : Dans le cas de l ntérêt smple, le captal reste nvarable pendant toute la durée du prêt. L emprunteur dot verser, à la fn de chaque
Théorème de Poincaré - Formule de Green-Riemann
 Chpitre 11 Théorème de Poincré - Formule de Green-Riemnn Ce chpitre s inscrit dns l continuité du précédent. On vu à l proposition 1.16 que les formes différentielles sont bien plus grébles à mnipuler
Chpitre 11 Théorème de Poincré - Formule de Green-Riemnn Ce chpitre s inscrit dns l continuité du précédent. On vu à l proposition 1.16 que les formes différentielles sont bien plus grébles à mnipuler
Compte Sélect Banque Manuvie Guide du débutant
 GUIDE DU DÉBUTANT Compte Sélect Baque Mauvie Guide du débutat Besoi d aide? Preez quelques miutes pour lire attetivemet votre Guide du cliet. Le préset Guide du débutat vous facilitera l utilisatio de
GUIDE DU DÉBUTANT Compte Sélect Baque Mauvie Guide du débutat Besoi d aide? Preez quelques miutes pour lire attetivemet votre Guide du cliet. Le préset Guide du débutat vous facilitera l utilisatio de
20. Algorithmique & Mathématiques
 L'éditeur L'éditeur permet à l'utilisateur de saisir les liges de codes d'u programme ou de défiir des foctios. Remarque : O peut saisir directemet des istructios das la cosole Scilab, mais il est plus
L'éditeur L'éditeur permet à l'utilisateur de saisir les liges de codes d'u programme ou de défiir des foctios. Remarque : O peut saisir directemet des istructios das la cosole Scilab, mais il est plus
Chapitre 3 : Fonctions d une variable réelle (1)
 Uiversités Paris 6 et Paris 7 M1 MEEF Aalyse (UE 3) 2013-2014 Chapitre 3 : Foctios d ue variable réelle (1) 1 Lagage topologique das R Défiitio 1 Soit a u poit de R. U esemble V R est u voisiage de a s
Uiversités Paris 6 et Paris 7 M1 MEEF Aalyse (UE 3) 2013-2014 Chapitre 3 : Foctios d ue variable réelle (1) 1 Lagage topologique das R Défiitio 1 Soit a u poit de R. U esemble V R est u voisiage de a s
La France, à l écoute des entreprises innovantes, propose le meilleur crédit d impôt recherche d Europe
 1/5 Trois objectifs poursuivis par le gouveremet : > améliorer la compétitivité fiscale de la Frace > péreiser les activités de R&D > faire de la Frace u territoire attractif pour l iovatio Les icitatios
1/5 Trois objectifs poursuivis par le gouveremet : > améliorer la compétitivité fiscale de la Frace > péreiser les activités de R&D > faire de la Frace u territoire attractif pour l iovatio Les icitatios
La spirale de Théodore bis, et la suite «somme=produit».
 Etde d e vrite de l spirle de Théodore, dot issce à e site dot les sommes prtielles sot égles x prodits prtiels. Mots clés : spirle de Théodore, théorème de Pythgore, site, série, polyôme. L spirle de
Etde d e vrite de l spirle de Théodore, dot issce à e site dot les sommes prtielles sot égles x prodits prtiels. Mots clés : spirle de Théodore, théorème de Pythgore, site, série, polyôme. L spirle de
TARIFICATION, PROVISIONNEMENT ET PILOTAGE D UN PORTEFEUILLE DÉPENDANCE
 TARIFICATION, PROVISIONNEMENT ET PILOTAGE D UN PORTEFEUILLE DÉPENDANCE Mre-Pscle Deléglse, Chrstn Hess, Sébsten Nouet To cte ths verson: Mre-Pscle Deléglse, Chrstn Hess, Sébsten Nouet. TARIFICATION, PROVISION-
TARIFICATION, PROVISIONNEMENT ET PILOTAGE D UN PORTEFEUILLE DÉPENDANCE Mre-Pscle Deléglse, Chrstn Hess, Sébsten Nouet To cte ths verson: Mre-Pscle Deléglse, Chrstn Hess, Sébsten Nouet. TARIFICATION, PROVISION-
Université Paris-Dauphine DUMI2E. UFR Mathématiques de la décision. Notes de cours. Analyse 2. Filippo SANTAMBROGIO
 Université Pris-Duphine DUMI2E UFR Mthémtiques de l décision Notes de cours Anlyse 2 Filippo SANTAMBROGIO Année 2008 2 Tble des mtières 1 Optimistion de fonctions continues et dérivbles 5 1.1 Continuité........................................
Université Pris-Duphine DUMI2E UFR Mthémtiques de l décision Notes de cours Anlyse 2 Filippo SANTAMBROGIO Année 2008 2 Tble des mtières 1 Optimistion de fonctions continues et dérivbles 5 1.1 Continuité........................................
Enjeux et contraintes de la mutualisation des ressources pour les collectivités et les agents
 Mercredi 5 novembre 2014 Enjeux et contraintes de la mutualisation des ressources pour les collectivités et les agents Hervé PETTON, Directeur Territorial 35 ans d expérience professionnelle en collectivités
Mercredi 5 novembre 2014 Enjeux et contraintes de la mutualisation des ressources pour les collectivités et les agents Hervé PETTON, Directeur Territorial 35 ans d expérience professionnelle en collectivités
stages 2015 paris saint-germain ACADEMY Dossier d inscription
 stages 2015 pars sat-germa ACADEMY Dosser d scrpto STAGE de football STAGES 2015 Fche d scrpto à retourer à l adresse suvate Pars Sat-Germa Academy - Frace 159, rue de la Républque - 92 800 Puteaux Tél
stages 2015 pars sat-germa ACADEMY Dosser d scrpto STAGE de football STAGES 2015 Fche d scrpto à retourer à l adresse suvate Pars Sat-Germa Academy - Frace 159, rue de la Républque - 92 800 Puteaux Tél
Module 3 : Inversion de matrices
 Math Stat Module : Iversio de matrices M Module : Iversio de matrices Uité. Défiitio O e défiira l iverse d ue matrice que si est carrée. O appelle iverse de la matrice carrée toute matrice B telle que
Math Stat Module : Iversio de matrices M Module : Iversio de matrices Uité. Défiitio O e défiira l iverse d ue matrice que si est carrée. O appelle iverse de la matrice carrée toute matrice B telle que
Comment gérer sans stress
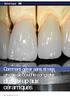 E s t h é t i q u e Comment gérer sans stress Comment gérer sans stress un cas de bouche complète du wax-up aux c é r a m i q u e s 28 Tech. Dent. N 311-11/12 «Par Christophe H U E P rothésiste Dentaire
E s t h é t i q u e Comment gérer sans stress Comment gérer sans stress un cas de bouche complète du wax-up aux c é r a m i q u e s 28 Tech. Dent. N 311-11/12 «Par Christophe H U E P rothésiste Dentaire
Un exemple d étude de cas
 Un exemple d'étude de cas 1 Un exemple d étude de cas INTRODUCTION Le cas de la Boulangerie Lépine ltée nous permet d exposer ici un type d étude de cas. Le processus utilisé est identique à celui qui
Un exemple d'étude de cas 1 Un exemple d étude de cas INTRODUCTION Le cas de la Boulangerie Lépine ltée nous permet d exposer ici un type d étude de cas. Le processus utilisé est identique à celui qui
Partie 4 : La monnaie et l'inflation
 Prtie 4 : L monnie et l'infltion Enseignnt A. Direr Licence 2, 1er semestre 2008-9 Université Pierre Mendès Frnce Cours de mcroéconomie suite 4.1 Introduction Nous vons vu dns l prtie introductive que
Prtie 4 : L monnie et l'infltion Enseignnt A. Direr Licence 2, 1er semestre 2008-9 Université Pierre Mendès Frnce Cours de mcroéconomie suite 4.1 Introduction Nous vons vu dns l prtie introductive que
Influence du milieu d étude sur l activité (suite) Inhibition et activation
 Influence du milieu d étude sur l ctivité (suite) Inhibition et ctivtion Influence de l tempérture Influence du ph 1 Influence de l tempérture Si on chuffe une préprtion enzymtique, l ctivité ugmente jusqu
Influence du milieu d étude sur l ctivité (suite) Inhibition et ctivtion Influence de l tempérture Influence du ph 1 Influence de l tempérture Si on chuffe une préprtion enzymtique, l ctivité ugmente jusqu
Tout ce qu il faut savoir en math
 Tout ce qu il fut svoir en mth 1 Pourcentge Prendre un pourcentge t % d un quntité : t Clculer le pourcentge d une quntité pr rpport à une quntité b : Le coefficient multiplicteur CM pour une ugmenttion
Tout ce qu il fut svoir en mth 1 Pourcentge Prendre un pourcentge t % d un quntité : t Clculer le pourcentge d une quntité pr rpport à une quntité b : Le coefficient multiplicteur CM pour une ugmenttion
STI2D Logique binaire SIN. L' Algèbre de BOOLE
 L' Algère de BOOLE L'lgère de Boole est l prtie des mthémtiques, de l logique et de l'électronique qui s'intéresse ux opértions et ux fonctions sur les vriles logiques. Le nom provient de George Boole.
L' Algère de BOOLE L'lgère de Boole est l prtie des mthémtiques, de l logique et de l'électronique qui s'intéresse ux opértions et ux fonctions sur les vriles logiques. Le nom provient de George Boole.
Des familles de deux enfants
 Des familles de deux enfants Claudine Schwartz, IREM de Grenoble Professeur, Université Joseh Fourier Les questions et sont osées dans le dernier numéro de «Pour la Science» (n 336, octobre 2005, article
Des familles de deux enfants Claudine Schwartz, IREM de Grenoble Professeur, Université Joseh Fourier Les questions et sont osées dans le dernier numéro de «Pour la Science» (n 336, octobre 2005, article
LA CERTIFICATION DES ARMATURES
 LA CERTIFICATION DES ARMATURES NF - Aciers our béton armé NF - Armatures AFCAB - Disositifs de raboutage ou d ancrage des armatures du béton AFCAB - Pose des armatures du béton LE CYCLE DES ARMATURES :
LA CERTIFICATION DES ARMATURES NF - Aciers our béton armé NF - Armatures AFCAB - Disositifs de raboutage ou d ancrage des armatures du béton AFCAB - Pose des armatures du béton LE CYCLE DES ARMATURES :
Examen final pour Conseiller financier / conseillère financière avec brevet fédéral. Recueil de formules. Auteur: Iwan Brot
 Exame fial pour Coseiller fiacier / coseillère fiacière avec brevet fédéral Recueil de formules Auteur: Iwa Brot Ce recueil de formules sera mis à dispositio des cadidats, si écessaire. Etat au 1er mars
Exame fial pour Coseiller fiacier / coseillère fiacière avec brevet fédéral Recueil de formules Auteur: Iwa Brot Ce recueil de formules sera mis à dispositio des cadidats, si écessaire. Etat au 1er mars
Chapitre 1.5a Le champ électrique généré par plusieurs particules
 hapte.5a Le chap électque généé pa pluseus patcules Le chap électque généé pa pluseus chages fxes Le odule de chap électque d une chage ponctuelle est adal, popotonnel à la chage électque et neseent popotonnel
hapte.5a Le chap électque généé pa pluseus patcules Le chap électque généé pa pluseus chages fxes Le odule de chap électque d une chage ponctuelle est adal, popotonnel à la chage électque et neseent popotonnel
l Agence Qui sommes nous?
 l Agence Qui soes nous? Co Justine est une agence counication globale dont la ission est prendre en charge l enseble vos besoins et probléatiques counication. Créée en 2011, Co Justine a rapient investi
l Agence Qui soes nous? Co Justine est une agence counication globale dont la ission est prendre en charge l enseble vos besoins et probléatiques counication. Créée en 2011, Co Justine a rapient investi
Chapitre 7 : Intégration sur un intervalle quelconque
 Universités Paris 6 et Paris 7 M1 MEEF Analyse (UE 3) 2013-2014 Chapitre 7 : Intégration sur un intervalle quelconque 1 Fonctions intégrables Définition 1 Soit I R un intervalle et soit f : I R + une fonction
Universités Paris 6 et Paris 7 M1 MEEF Analyse (UE 3) 2013-2014 Chapitre 7 : Intégration sur un intervalle quelconque 1 Fonctions intégrables Définition 1 Soit I R un intervalle et soit f : I R + une fonction
VILLE DE VILLEURBANNE CONSEIL MUNICIPAL 5 JUILLET 2010. -ooo-
 VILLE DE VILLEURBANNE CONSEIL MUNICIPAL 5 JUILLET 2010 -ooo- La s é a n c e e s t o u v e r t e s o u s l a p r é s i d e n c e d e M o n s i e u r J e a n - P a u l BR E T, M a i r e d e V i l l e u r
VILLE DE VILLEURBANNE CONSEIL MUNICIPAL 5 JUILLET 2010 -ooo- La s é a n c e e s t o u v e r t e s o u s l a p r é s i d e n c e d e M o n s i e u r J e a n - P a u l BR E T, M a i r e d e V i l l e u r
Taux d intérêts simples
 Taux d intérêts simples Les caractéristiques : - < à 1 ans - Rémunération calculée uniquement sur investissement initial. Période de préférence = période sur laquelle on définit le taux de l opération
Taux d intérêts simples Les caractéristiques : - < à 1 ans - Rémunération calculée uniquement sur investissement initial. Période de préférence = période sur laquelle on définit le taux de l opération
Page 5 TABLE DES MATIÈRES
 Page 5 TABLE DES MATIÈRES CHAPITRE I LES POURCENTAGES 1. LES OBJECTIFS 12 2. LES DÉFINITIONS 14 1. La varaton absolue d'une grandeur 2. La varaton moyenne d'une grandeur (par unté de temps) 3. Le coeffcent
Page 5 TABLE DES MATIÈRES CHAPITRE I LES POURCENTAGES 1. LES OBJECTIFS 12 2. LES DÉFINITIONS 14 1. La varaton absolue d'une grandeur 2. La varaton moyenne d'une grandeur (par unté de temps) 3. Le coeffcent
logo QUI SUIS-JE? WEB DESIGN PARIS ET PARTOUT EN FRANCE!
 logo QUI SUIS-JE? PARIS ET PARTOUT EN FRANCE! WEB DESIGN Découvrez tous mes travaux sur mon site internet et pour plus d informations sur mes prestations contactez-moi. IDENTITÉ QUI SUIS-JE? ÉDITION ILLUSTRATION
logo QUI SUIS-JE? PARIS ET PARTOUT EN FRANCE! WEB DESIGN Découvrez tous mes travaux sur mon site internet et pour plus d informations sur mes prestations contactez-moi. IDENTITÉ QUI SUIS-JE? ÉDITION ILLUSTRATION
Centre de Récupération de SoftThinks
 Centre de Récupération de SoftThinks Table des matières Révisions... 1 Table des matières... 2 Introduction... 3 Quel est l objectif du Centre de Récupération de SoftThinks?... 3 Que pourrez-vous trouver
Centre de Récupération de SoftThinks Table des matières Révisions... 1 Table des matières... 2 Introduction... 3 Quel est l objectif du Centre de Récupération de SoftThinks?... 3 Que pourrez-vous trouver
ANALYSE NUMERIQUE NON-LINEAIRE
 Université de Metz Licence de Mthémtiques - 3ème nnée 1er semestre ANALYSE NUMERIQUE NON-LINEAIRE pr Rlph Chill Lbortoire de Mthémtiques et Applictions de Metz Année 010/11 1 Tble des mtières Chpitre
Université de Metz Licence de Mthémtiques - 3ème nnée 1er semestre ANALYSE NUMERIQUE NON-LINEAIRE pr Rlph Chill Lbortoire de Mthémtiques et Applictions de Metz Année 010/11 1 Tble des mtières Chpitre
L Analyse Factorielle des Correspondances
 Aalyse de doées Modle 5 : L AFC M5 L Aalyse Factorelle des Corresodaces L aalyse factorelle des corresodaces, otée AFC, est e aalyse destée a tratemet des tableax de doées où les valers sot ostves et homogèes
Aalyse de doées Modle 5 : L AFC M5 L Aalyse Factorelle des Corresodaces L aalyse factorelle des corresodaces, otée AFC, est e aalyse destée a tratemet des tableax de doées où les valers sot ostves et homogèes
capital en fin d'année 1 C 0 + T C 0 = C 0 (1 + T) = C 0 r en posant r = 1 + T 2 C 0 r + C 0 r T = C 0 r (1 + T) = C 0 r 2 3 C 0 r 3...
 Applicatios des maths Algèbre fiacière 1. Itérêts composés O place u capital C 0 à u taux auel T a pedat aées. Quelle est la valeur fiale C de ce capital? aée capital e fi d'aée 1 C 0 + T C 0 = C 0 (1
Applicatios des maths Algèbre fiacière 1. Itérêts composés O place u capital C 0 à u taux auel T a pedat aées. Quelle est la valeur fiale C de ce capital? aée capital e fi d'aée 1 C 0 + T C 0 = C 0 (1
c dur Leçon 8 S c i e c v m C s c d f M a c u n S C r t V C o coton café classe carotte sac tricot Sa si ca la co lu cu ra ac cre
 C est en tricotant que l on fait du tricot. 1 Trouver le son commun à toutes ces images. 2 Encercler les C et c. S c i e c v m C s c d f M a c u n S C r t V C o Sa si ca la co lu cu ra ac cre coton café
C est en tricotant que l on fait du tricot. 1 Trouver le son commun à toutes ces images. 2 Encercler les C et c. S c i e c v m C s c d f M a c u n S C r t V C o Sa si ca la co lu cu ra ac cre coton café
Statuts ASF Association Suisse Feldenkrais
 Sttuts ASF Assocition Suisse Feldenkris Contenu Pge I. Nom, siège, ojectif et missions 1 Nom et siège 2 2 Ojectif 2 3 Missions 2 II. Memres 4 Modes d ffilition 3 5 Droits et oligtions des memres 3 6 Adhésion
Sttuts ASF Assocition Suisse Feldenkris Contenu Pge I. Nom, siège, ojectif et missions 1 Nom et siège 2 2 Ojectif 2 3 Missions 2 II. Memres 4 Modes d ffilition 3 5 Droits et oligtions des memres 3 6 Adhésion
FONDATION CLEMENTINE ET MAURICE ANTILLE
 FONDATION CLEMENTINE ET MAURICE ANTILLE Règlement d ttriution de ourses et de prêts d études et de formtion du déemre 006 Artile premier Ojet et hmp d pplition Le présent règlement est étli en pplition
FONDATION CLEMENTINE ET MAURICE ANTILLE Règlement d ttriution de ourses et de prêts d études et de formtion du déemre 006 Artile premier Ojet et hmp d pplition Le présent règlement est étli en pplition
CENTRE ORGANISATEUR DU CONCOURS. ANIMALIER Externe PARIS MUSEUM PARIS. ANIMALIER Externe PARIS MUSEUM PARIS
 Document publié sous réserve de modifications SESSON 2006 LSTE DES EMPLOS OERTS UX ONOURS TR DE TEORE -v.1 (19/04/2006)- PRENSRPTONS ET NS DETLLEES SUR NTERNET : http://www.education.gouv.fr/personnel/itrf/
Document publié sous réserve de modifications SESSON 2006 LSTE DES EMPLOS OERTS UX ONOURS TR DE TEORE -v.1 (19/04/2006)- PRENSRPTONS ET NS DETLLEES SUR NTERNET : http://www.education.gouv.fr/personnel/itrf/
POUR ATTEINDRE VOS OBJECTIFS D AFFAIRES
 LE RÔLE DU MARKETING STRATÉGIQUE SIX ÉTAPES POUR ATTEINDRE VOS OBJECTIFS D AFFAIRES POUR QU UNE ENTREPRISE ATTEIGNE SES OBJECTIFS D AFFAIRES, ELLE DOIT ÉQUILIBRER SA STRATÉGIE MARKETING. Une saveur unique
LE RÔLE DU MARKETING STRATÉGIQUE SIX ÉTAPES POUR ATTEINDRE VOS OBJECTIFS D AFFAIRES POUR QU UNE ENTREPRISE ATTEIGNE SES OBJECTIFS D AFFAIRES, ELLE DOIT ÉQUILIBRER SA STRATÉGIE MARKETING. Une saveur unique
L'algèbre de BOOLE ou algèbre logique est l'algèbre définie pour des variables ne pouvant prendre que deux états.
 ciences Industrielles ystèmes comintoires Ppnicol Roert Lycée Jcques Amyot I - YTEME COMBINATOIRE A. Algère de Boole. Vriles logiques: Un signl réel est une grndeur physique en générl continue, on ssocie
ciences Industrielles ystèmes comintoires Ppnicol Roert Lycée Jcques Amyot I - YTEME COMBINATOIRE A. Algère de Boole. Vriles logiques: Un signl réel est une grndeur physique en générl continue, on ssocie
Elargissez l horizon de votre gestion. www.mercator.eu
 www.mercator.eu Elargissez l horizon de votre gestion Mercator se profile comme la solution de gestion commerciale et de comptabilité alliant simultanément les avantages de la solution informatique standard
www.mercator.eu Elargissez l horizon de votre gestion Mercator se profile comme la solution de gestion commerciale et de comptabilité alliant simultanément les avantages de la solution informatique standard
CHAPITRE 14 : RAISONNEMENT DES SYSTÈMES DE COMMANDE
 HAITRE 4 : RAISONNEMENT DES SYSTÈMES DE OMMANDE RAISONNEMENT DES SYSTÈMES DE OMMANDE... 2 INTRODUTION... 22 RAELS... 22 alcul de la valeur ntale de la répone à un échelon... 22 alcul du gan tatque... 22
HAITRE 4 : RAISONNEMENT DES SYSTÈMES DE OMMANDE RAISONNEMENT DES SYSTÈMES DE OMMANDE... 2 INTRODUTION... 22 RAELS... 22 alcul de la valeur ntale de la répone à un échelon... 22 alcul du gan tatque... 22
GEA I Mathématiques nancières Poly. de révision. Lionel Darondeau
 GEA I Mathématques nancères Poly de révson Lonel Darondeau Intérêts smples et composés Voc la lste des exercces à révser, corrgés en cours : Exercce 2 Exercce 3 Exercce 5 Exercce 6 Exercce 7 Exercce 8
GEA I Mathématques nancères Poly de révson Lonel Darondeau Intérêts smples et composés Voc la lste des exercces à révser, corrgés en cours : Exercce 2 Exercce 3 Exercce 5 Exercce 6 Exercce 7 Exercce 8
Formation d un ester à partir d un acide et d un alcool
 CHAPITRE 10 RÉACTINS D ESTÉRIFICATIN ET D HYDRLYSE 1 Formatio d u ester à partir d u acide et d u alcool 1. Nomeclature Acide : R C H Alcool : R H Groupe caractéristique ester : C Formule géérale d u ester
CHAPITRE 10 RÉACTINS D ESTÉRIFICATIN ET D HYDRLYSE 1 Formatio d u ester à partir d u acide et d u alcool 1. Nomeclature Acide : R C H Alcool : R H Groupe caractéristique ester : C Formule géérale d u ester
OBLIGATION DU SECTEUR PRIVE : EVALUATION ET OUTIL DE GESTION DU RISQUE DE TAUX D INTERET
 Jea-Claude AUGROS Professeur à l Uversté Claude Berard LYON I et à l Isttut de Scece Facère et d Assuraces ISFA Mchel QUERUEL Docteur e Gesto Igéeur de Marché Socété de Bourse AUREL Résumé : Cet artcle
Jea-Claude AUGROS Professeur à l Uversté Claude Berard LYON I et à l Isttut de Scece Facère et d Assuraces ISFA Mchel QUERUEL Docteur e Gesto Igéeur de Marché Socété de Bourse AUREL Résumé : Cet artcle
Application de la théorie des valeurs extrêmes en assurance automobile
 Applcato de la théore des valeurs extrêmes e assurace automoble Nouredde Belagha & Mchel Gru-Réhomme Uversté Pars 2, ERMES-UMR78-CNRS, 92 rue d Assas, 75006 Pars, Frace E-Mal: [email protected] E-Mal:
Applcato de la théore des valeurs extrêmes e assurace automoble Nouredde Belagha & Mchel Gru-Réhomme Uversté Pars 2, ERMES-UMR78-CNRS, 92 rue d Assas, 75006 Pars, Frace E-Mal: [email protected] E-Mal:
Ch.G3 : Distances et tangentes
 4 e - programme 2011 mathématiques ch.g3 cahier élève Page 1 sur 14 1 DISTC D U PIT À U DRIT Ch.G3 : Distances et tangentes 1.1 Définition ex 1 DÉFIITI 1 : Soit une droite et un point n'appartenant pas
4 e - programme 2011 mathématiques ch.g3 cahier élève Page 1 sur 14 1 DISTC D U PIT À U DRIT Ch.G3 : Distances et tangentes 1.1 Définition ex 1 DÉFIITI 1 : Soit une droite et un point n'appartenant pas
Si la vie vous intéresse
 Si la ie ous intéresse paroles: J Pauze musique: J Pauze / M A Lépine ã 160 c c öguiõt aõcous fr ÛÛ ÛÛÛÛÛ ÛÛÛ ÛÛ ÛÛÛÛÛ ÛÛÛ öõbõasse G 3fr fr fr Û Û ÛÛÛ Û Û Û ( ) 3 ~~ ÿ % % J'ais dans ouer un la monde
Si la ie ous intéresse paroles: J Pauze musique: J Pauze / M A Lépine ã 160 c c öguiõt aõcous fr ÛÛ ÛÛÛÛÛ ÛÛÛ ÛÛ ÛÛÛÛÛ ÛÛÛ öõbõasse G 3fr fr fr Û Û ÛÛÛ Û Û Û ( ) 3 ~~ ÿ % % J'ais dans ouer un la monde
Techniques d analyse de circuits
 Chpitre 3 Tehniques d nlyse de iruits Ce hpitre présente différentes méthodes d nlyse de iruits. Ces méthodes permettent de simplifier l nlyse de iruits ontennt plusieurs éléments. Bien qu on peut résoudre
Chpitre 3 Tehniques d nlyse de iruits Ce hpitre présente différentes méthodes d nlyse de iruits. Ces méthodes permettent de simplifier l nlyse de iruits ontennt plusieurs éléments. Bien qu on peut résoudre
Chap. 5 : Les intérêts (Les calculs financiers)
 Chap. 5 : Les itérêts (Les calculs fiaciers) Das u cotrat de prêt, le prêteur met à la dispositio de l empruteur, à u taux d itérêt doé, ue somme d arget (le capital) qu il devra rembourser à ue certaie
Chap. 5 : Les itérêts (Les calculs fiaciers) Das u cotrat de prêt, le prêteur met à la dispositio de l empruteur, à u taux d itérêt doé, ue somme d arget (le capital) qu il devra rembourser à ue certaie
P h i l h a r m o n i s
 Adoptez un nouveau rythme pour vos placements P h i l h a r m o n i s NOTE D INFO R M ATI O N C o n t rat Collectif d assurance sur la vie à adhésion facultative L e s c a r a c t é r i s t i q u e s d
Adoptez un nouveau rythme pour vos placements P h i l h a r m o n i s NOTE D INFO R M ATI O N C o n t rat Collectif d assurance sur la vie à adhésion facultative L e s c a r a c t é r i s t i q u e s d
